- 1Department of Geosciences, University of Arkansas, Fayetteville, AR, United States
- 2Department of Systems and Control, Jožef Stefan Institute, Ljubljana, Slovenia
- 3Computer and Information Sciences, University of St. Thomas, St. Paul, MN, United States
Variability of CO2 concentrations within the Earth system occurs over a wide range of time and spatial scales. Resolving this variability and its drivers in terrestrial and aquatic environments ultimately requires high-resolution spatial and temporal monitoring; however, relatively high-cost gas analyzers and data loggers can present barriers in terms of cost and functionality. To overcome these barriers, we developed a low-cost Arduino monitoring platform (CO2-LAMP) for recording CO2 variability in electronically harsh conditions: humid air, soil, and aquatic environments. A relatively inexpensive CO2 gas analyzer was waterproofed using a semi-permeable, expanded polytetrafluoroethylene membrane. Using first principles, we derived a formulation of the theoretical operation and measurement of PCO2(aq) by infrared gas analyzers submerged in aquatic environments. This analysis revealed that an IRGA should be able to measure PCO2(aq) independent of corrections for hydrostatic pressure. CO2-LAMP theoretical operation and measurement were also verified by accompanying laboratory assessment measuring PCO2(aq) at multiple water depths. The monitoring platform was also deployed at two sites within the Springfield Plateau province in northwest Arkansas, USA: Blowing Springs Cave and the Savoy Experimental Watershed. At Blowing Springs Cave, the CO2-LAMP operated alongside a relatively greater-cost CO2 monitoring platform. Over the monitoring period, measured values between the two systems covaried linearly (r2 = 0.97 and 0.99 for cave air and cave stream dissolved CO2, respectively). At the Savoy Experimental Watershed, measured soil CO2 variability capturing sub-daily variation was consistent with previously documented studies in humid, temperate soils. Daily median values varied linearly with soil moisture content (r2 = 0.84). Overall, the CO2-LAMP captured sub-daily variability of CO2 in humid air, soil, and aquatic environments that, while out of the scope of the study, highlight both cyclical and complex CO2 behavior. At present, long-term assessment of platform design is ongoing. Considering cost-savings, CO2-LAMP presents a working base design for continuous, accurate, low-power, and low-cost CO2 monitoring for remote locations.
Introduction
Carbon exchange within the Earth system is facilitated, in part, by the production, transfer, and uptake of carbon dioxide (Schimel et al., 2001; Brantley et al., 2007). Unraveling biologic and biogeochemical (Broecker and Sanyal, 1998; Davidson et al., 2010; Demars et al., 2015; Florea, 2015), geologic (Lowenstern, 2001; Werner and Cardellini, 2006; Burton et al., 2013; Queiβer et al., 2016), and anthropogenic factors (Olah et al., 2011; Ward et al., 2015; Decina et al., 2016) that influence CO2 concentrations require not only accurate, high-frequency measurements of CO2 concentrations, but widely distributed, and if possible, spatially dense CO2 measurements (Schimel et al., 2001; Hari et al., 2008; McDowell et al., 2008; Richter and Mobley, 2009; Brantley et al., 2016).
Long-term, high-frequency measurements of CO2 concentrations are limited across Earth (McDowell et al., 2008; Andrews et al., 2014) compared to other continuous environmental monitoring in terrestrial and aquatic environments (e.g., air and stream temperature, air pressure, humidity, stream pH; Martin et al., 2017). In turn, the inter- and intra-seasonal variability of CO2 and environmental factors controlling variability across terrestrial ecosystems remains poorly constrained (Serrano-Ortiz et al., 2010; Lombardozzi et al., 2015). Reducing these uncertainties in carbon transfers hinges upon increasing the spatial and temporal coverage of CO2 measurements across the Earth system (Schimel et al., 2001, 2015; Lombardozzi et al., 2015; Bradford et al., 2016).
While the availability of commercial, field-deployable infrared gas analyzers (IRGA) have greatly enhanced measurement capacity, costs due to instrumentation acquisition, maintenance, and in some cases, limited storage capacity and control over measurement frequency using proprietary systems greatly limit the spatial and temporal extent of monitoring (Fisher and Gould, 2012; Martin et al., 2017). Furthermore, ancillary data, such as temperature (in air or water), are needed for environmental correction of CO2 values, but combined sensor, and data logger selection may be limited between proprietary systems stemming from incompatibilities between manufacturers (Fisher and Gould, 2012).
Over the last decade, the availability and use of relatively inexpensive microcontrollers and “microcomputers” for scientific research has increased significantly (Cressey, 2017). Use of these platforms to interface sensors has grown, in part, from the increasing availability of sensors, and the need for customized interfacing to measure, and monitor conditions both in increasingly complex laboratory experiments, and challenging environmental settings (e.g., caves; Pearce, 2012; Beddows and Mallon, 2018). Low-cost CO2 IRGAs (<$150 USD) and low-cost Arduino monitoring platforms (LAMPs) have been specifically used to measure and monitor dissolved CO2 using automated floating chambers (Bastviken et al., 2015) and ambient CO2 (Martin et al., 2017); however, adoption of a low-cost IRGA for electronically harsh conditions, such as high-humidity environments (e.g., caves) or within stream environments (i.e., submerged, direct dissolved CO2 measurement), have been limited. If similar methods for waterproofing CO2 sensors are used (Johnson et al., 2009), adoption of a low-cost IRGA to monitor CO2 in electronically harsh environments should be possible.
We present a low-cost ($250–300 USD), Arduino-based monitoring platform (CO2-LAMP) for measuring atmospheric, soil, and dissolved CO2 concentrations. Included in this study are methods for fabrication, reference measurement (i.e., zero and span reference gases), instrument value corrections and post-processing, and results from field-trial evaluations. As part of the reference measurement and post-processing, a novel presentation of theoretical sensor operation, sensor output, and accompanying empirical experiments were made to verify theoretical instrument output, and applicable environmental corrections. Consequently, the description and corrections are highly relevant to other direct, dissolved gas measurement systems by IRGAs (Johnson et al., 2009; Yoon et al., 2016). Field evaluation comprised: (1) A comparative field trial between the CO2-LAMP and a relatively greater-cost system for monitoring ambient CO2 and dissolved CO2, and (2) monitoring soil CO2 in a shallow soil pit. Lastly, recommendations, and future work with respect to fabrication, improving measurement accuracy, and deployment of the CO2-LAMP are discussed.
Measurement of CO2 in Earth's Near-Surface Environment
Measurements of CO2 within ambient air, soil, and aqueous environments encompass a range of sampling protocols and gas analyses. While not an exhaustive review, this section provides theoretical principles and practical aspects of measuring CO2 in Earth's near-surface environment used in this study. Moreover, this brief overview presents information on discrete and continuous CO2 measurement methods within air, soil, and aqueous environments with emphasis on the operating principles of direct dissolved CO2 measurements using IRGAs within aqueous environments specifically investigated.
Analysis of CO2 in Air and Soils
Analysis of ambient CO2 and soil CO2 are routinely conducted by discrete sampling and in situ gas analyzers (Jassal et al., 2005; Andrews et al., 2014; Sánchez-Cañete et al., 2017; Jochheim et al., 2018). Discrete sampling is conducted primarily through gas collection into evacuated air-tight or “inert gas flushed” (e.g., helium flushing) containers. Extracted gases are subsequently sampled, typically using an IRGA, gas chromatography (GC), or isotope ratio mass spectrometer (Breecker and Sharp, 2008; Joos et al., 2008). Common in situ gas analyzers for measuring CO2(soil) have included the Vaisala GMD20, GMM221, and GMM222, and the Eosense eosGP (Hirano et al., 2003; Jassal et al., 2005; Sánchez-Cañete et al., 2017). Unlike discrete measurements, in situ sensors allow greater measurement frequency directly located within air and soil environments. However, in situ sensors require continual reference measurements to ensure accountability of sensor drift and offsets during deployment (Moran et al., 2010; Andrews et al., 2014). To further ensure measurement accuracy through time, ancillary parameters, which include temperature, relative humidity, and atmospheric pressure, must also be measured to correct for differences between calibration, and field environmental conditions (e.g., pressure and temperature corrections; Fietzek et al., 2014). To protect against instrument damage in soil environments, protective membranes, such as silicone or polytetrafluoroethylene, are used to cover the sensor, but still allowing for gas exchange (Tang et al., 2003; Jassal et al., 2005).
Obtaining Dissolved CO2 Concentrations
Dissolved CO2 concentrations are most often obtained through three common methods: (1) Estimation of CO2 concentrations from alkalinity titration and carbonate species equilibria calculations (Stumm and Morgan, 1996; Abril et al., 2015; Jarvie et al., 2017); (2) Manual gas extraction from water sample collection in air-tight containers (e.g., copper tubing, manual headspace analysis; Sanford et al., 1996 and references therein); and (3) Directly measured through gas equilibration (Takahashi, 1961; Frankignoulle et al., 2001; Johnson et al., 2009; Yoon et al., 2016). The majority of dissolved CO2 values reported for natural waters have been, to date, through carbonate equilibria calculations from measured pH, and total alkalinity (Abril et al., 2015; Liu and Raymond, 2018). However, reported partial pressures of dissolved CO2, and corresponding dissolved CO2 concentrations in organic-rich, low pH inland freshwaters are likely overestimated due to a combination of: (1) Greater total alkalinity derived from organic acid anions (e.g., greater dissolved organic carbon) and (2) Greater sensitivity of calculated dissolved CO2 for low pH, low alkalinity waters vs. relatively higher pH, higher alkalinity waters (Abril et al., 2015). Importantly, Abril et al. (2015) highlight the critical need for direct measurements of CO2 given the large uncertainty that may arise from carbonate equilibria estimations.
Direct Measurement of Dissolved CO2 Principles
Direct dissolved CO2 measurement systems have been previously described by Yoon et al. (2016) and are separated into two categories of active-equilibration and passive-equilibration. The active-equilibration methods being: manual gas extraction; a spray-type equilibrator (Takahashi, 1961); and a marble-type equilibrator (Frankignoulle et al., 2001). In active-equilibration systems, an external power-source facilitates water-air equilibration by pumping external water through sprayers or marble media. Enclosed, internal air volumes are circulated through an IRGA. The passive method is referred to as a “membrane-enclosed sensor.” Passive membrane-enclosed sensors work via diffusion and equilibration of gases across a liquid impermeable, but gas permeable, membrane (Sanford et al., 1996; Johnson et al., 2009).
Compared to spray-, and marble-type equilibrators, membrane-enclosed sensors are practical in harsher environments such as soil, and surface waters, which can be variably saturated or highly turbid, and prone to tubing clogging or instrument fouling. This method is also more useful in situations where power delivery is limited (e.g., caves). However, membrane-enclosed sensors have the drawback of longer equilibration times (>10 min), and therefore they may not fully capture short-term, large magnitude variation in surface waters (e.g., rapid mixing during storm events; Yoon et al., 2016).
Hybrid systems also exist, which interface with surrounding water through membrane mediated gas exchange (i.e., a membrane-enclosed equilibrator) but also internally circulate air for heating and thermal equilibrium (De Gregorio et al., 2011; Fietzek et al., 2014). To decrease equilibration time in membrane-enclosed systems, external pumps near the membrane move adjacent water to the membrane interface which limit expansion of a static-boundary layer (Manning et al., 2003; Fietzek et al., 2014).
For all direct-measurement systems, CO2 measured by an IRGA or GC is the equivalent partial pressure of CO2, PCO2(aq), in equilibrium with the dissolved CO2 of the water in accordance with Henry's Law:
where KCO2 is the Henry's Law constant for CO2 at a given temperature, T, salinity, S, and pressure, P, and Ci is the concentration of dissolved CO2 in water (Colt, 2012). Dalton's Law states that the sum of partial pressures for all dissolved gas species are equal to the total dissolved gas pressure in the water, PTDG:
For most shallow surface waters and unconfined groundwater systems PTDG is approximately equal to ambient atmospheric pressures (Manning et al., 2003; Gardner and Solomon, 2009). However, some notable exceptions include: (1) dam tailwaters (D'Aoust and Clark, 1980; Urban et al., 2008) and similar surface water conditions that promote entrainment of bubbles at greater depths where PTDG may be upwards of 1.3 times atmospheric pressure; (2) deep, confined groundwater systems (Gardner and Solomon, 2009; Ryan et al., 2015); and (3) deep, crater lake systems containing submarine gas vents at depth, such as Lakes Monoun, and Nyos in Cameroon (Kling et al., 1987; Kusakabe and Sano, 1992). In both confined groundwater and deep, lake gas vent systems, increased hydrostatic pressure allows for greater gas saturation (i.e., increased concentration). As such, PTDG values may be several times that of atmospheric pressure if waters are gas saturated at these greater hydrostatic pressures. In practice, dual measurement of total dissolved gas pressure and dissolved CO2 are recommended in environments where PTDG is suspected to be higher than atmospheric pressure to account for greater dissolved concentrations (Ryan et al., 2015).
At abyssopelagic depths (> ~4,000 m) in marine systems, changes in Henry's constant due to hydrostatic pressure must also be taken in account when calculating expected PCO2 for a given dissolved CO2 concentration or vice versa (Enns et al., 1965; Hamme et al., 2015). Inland freshwater systems, however, do not encounter such depths. For example, Henry's Law constants for dissolved gas measurements at Lake Baikal (i.e., Earth's deepest lake at ~1600 m) would only be offset ~2.2% (Enns et al., 1965; Hamme et al., 2015). Therefore, changes in Henry's Law constants with respect to hydrostatic pressure are negligible for relatively shallow water bodies.
Membrane-Enclosed Equilibration Principles
Fluid movement across membranes occurs through convective mass transfer comprising diffusive and advective transport (Bergman et al., 2011; Kruczek, 2015). Diffusive gas exchange between an external environment (i.e., atmosphere, soil, or water) and a membrane-enclosed volume, or headspace containing an IRGA, has been previously described using a Solution-Diffusion model. In this Solution Diffusion model, gas exchange is driven by differences between the partial pressures of the external environment, Penv, and within the headspace, PIRGA (Bareer, 1939; Sanford et al., 1996; De Gregorio et al., 2005; Gardner and Solomon, 2009). From De Gregorio et al. (2005), assuming Penv to be constant, the partial pressure of CO2 in the headspace at some time, t, may be estimated by
where Pi is the initial partial pressure of CO2 in the headspace, Kp is equal to the effective diffusivity of the gas through the environment-membrane boundary and the membrane material (Gardner and Solomon, 2009), A is membrane surface area, and h is membrane thickness.
Empirically, the exponential term can be calculated from experimental data using a modified form of Equation (3) whereby generalizing the exponential term, KpA/Vh, as a constant q, and subsequently solving for q:
If Kp is unknown, but A, V, and h are well-constrained, Kp can be solved by rearranging the obtained q constant:
In the case of membrane submersion within water, diffusion of the gas within the water may have an important impact on transfer rates, rather than mass transfer being controlled by diffusion through the membrane alone. In this case, using a slight modification of Equation (4) to calculate the mass transfer coefficient, k, where k = Kp/h may be more meaningful.
For description of percent equilibration of CO2 to a reference gas, an exponential, or e-folding, timescale can be used to describe the amount of time over which changes in concentration or percent equilibration associated with an exponential process (i.e., gas equilibration in this case) occur by factors of e ~ 2.718. From measured PCO2 using a waterproofed IRGA, e-folding time units, Tf in seconds, can be expressed as
where t is equal to the time elapsed from the beginning of the observation period. To determine n e-folding time, where n is the folding time interval (e.g., three-folding times), n is divided by the q constant value, redefined here as τ, obtained from the exponential function term (see Equation 4): e-folding time = n/τ. For example, at three e-folding time (or 3/τ), equilibration of a mixture from the initial to final concentration is at ~95%, i.e., 1–(1/e3). In turn, solving for 3/τ determines the specific Tf equivalent to a measured value and actual time, t, where the partial pressure or concentration of CO2 is 95% equilibrated.
Materials and Methods
CO2-LAMP Fabrication for Humid and Aqueous Environments
Fabrication of CO2-LAMP consisted of waterproofing a relatively low-cost IRGA using a semi-permeable membrane (Figure 1) and interfacing the IRGA with an Arduino-based platform to read and record instrument values. The IRGAs used in this study were the K30 1 and 10% analyzers manufactured by Senseair AB (Delsbo, Sweden). Analyzer accuracies are reported by the manufacturer as ±30 parts per million by volume (ppmv) ± 3% for the K30 1% model and ±300 ppmv ±3% for the 10% model, respectively. The resolution of CO2 concentrations reported by the K30 1 and 10% are 1.0 and 10.0 ppmv, respectively.
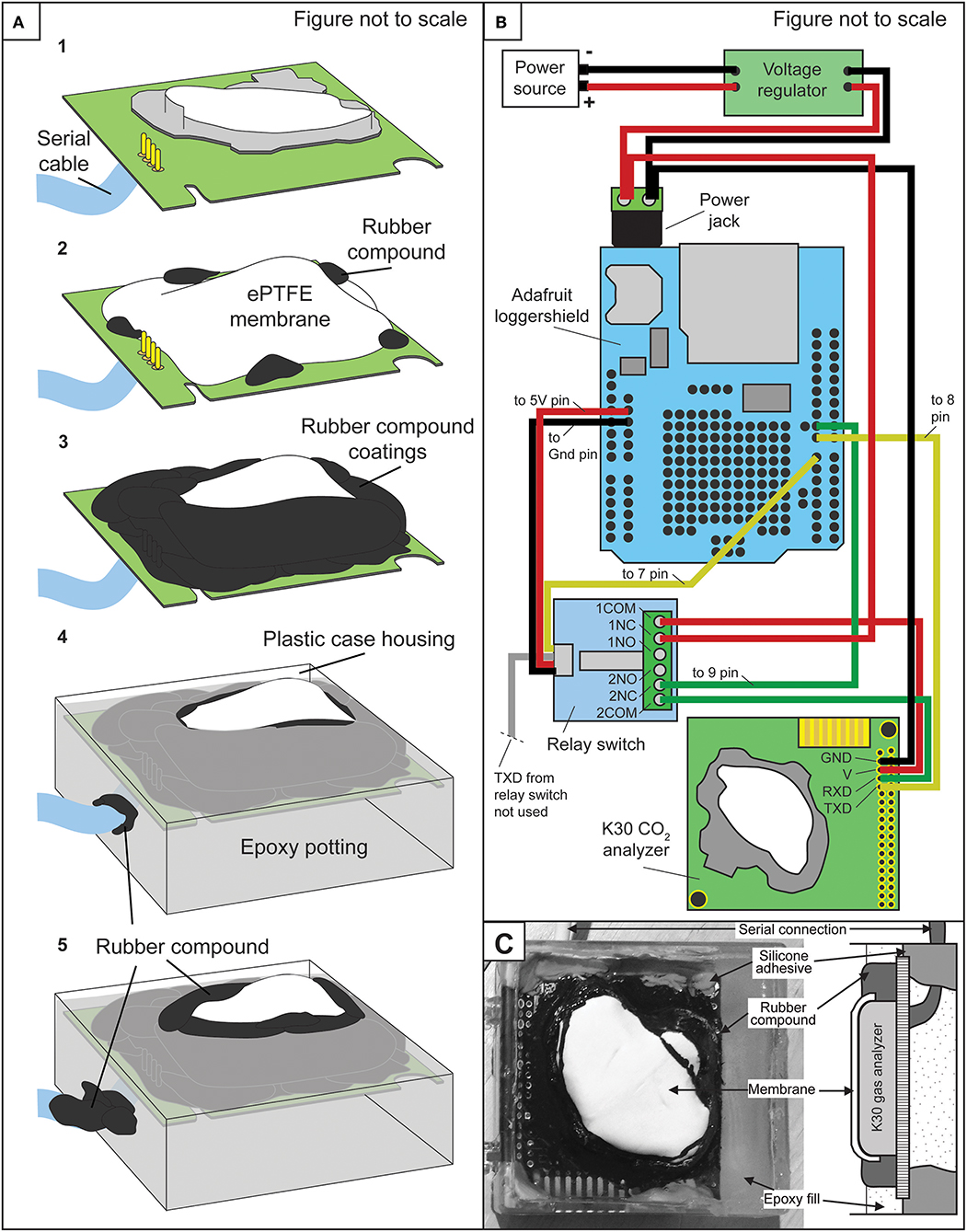
Figure 1. (A) Simplified schematic of step-wise waterproofing of K30 sensor. (B) Schematic wiring diagram among the power source, voltage regulator, Arduino Uno, and Adafruit loggershield, relay switch, and K30 IRGA. (C) Labeled photograph of waterproofed K30 and corresponding IRGA components in cross section.
The membranes used were an expanded polytetrafluoroethylene ePTFE sleeve (Product number 200-07; International Polymer Engineering, Tempe, AZ, USA) and ePTFE gasket disc (Product number 1084N86, McMaster-Carr, Douglasville, GA, USA). Before enclosing the sensor, a serial cable was soldered to the K30 printed circuit boards (PCB) for interfacing the sensor with either Arduino microcontroller or desktop-PC. Then, the ePTFE membrane was placed over the K30 hydrophobic filter and attached to the K30 PCB by applying a small amount of Plasti Dip rubber compound (Plasti Dip International, Blaine, MN, USA). Subsequent coats of Plasti Dip were applied to create an effective seal at the contact of the membrane and the printed circuit board.
During coating steps, small holes in the rubber compound can form from degassing of the curing agent requiring multiple rubber compound coats. Small openings on the underside of the K30 PCB were then also filled with Plasti Dip. Importantly, a 1 h curing period was allowed between applying coats of the rubber compound. After application, to ensure a complete seal, a 24 h wait period was allotted allowing for a full cure of the rubber compound. A hole large enough for the serial cable was then drilled into a small plastic case and the K30 was placed inside the plastic case with the serial cable extending through the hole in the plastic case.
A small amount of Sugru silicone adhesive (FormFormForm Ltd., London, United Kingdom) was also used to horizontally level the K30. Subsequently, the K30 was then “potted” in Hysol 9460 epoxy (Henkel Corporation, Rocky Hill, CT, USA) just up to the point of covering the membrane. Lastly, a final rubber coating was applied at the contact between the epoxy and membrane and at the serial cable-epoxy contact (Figure 1). Membrane thickness and estimated area were ~1 mm and 8 cm2.
For the majority of lab experiments, respectively, and all field trials, the K30 was interfaced to an Arduino Uno (https://www.arduino.cc) with a connected Adafruit (New York, NY, USA) Data Logging shield using a universal asynchronous receiver/transmitter (UART) serial connection. During some laboratory trials, the K30s were instead interfaced via USB to a desktop computer where readings were read and logged using CO2Meter GasLab software (CO2Meter.com, Ormond Beach, FL, USA). Two Arduino sketches (i.e., programs) were written to interface the Uno and a power relay switch (Seeed Studio, Shenzhen, China) to control power delivery to the K30 in two modes: (1) a semi-continuous mode, where values were logged every 10 s for 60 s and then the sensor was powered off for 1 min before another measurement period began; and (2) a lower-power mode where values were logged every 10 s for 20 min, followed by a 45 min sleep period. Between measurement cycles the Uno was in “sleep” mode to reduce power consumption. In general, the low-power mode is advantageous in environments where direct power and battery recharge (e.g., solar panels) are not possible (e.g., caves).
Power was delivered to the K30 and Arduino Uno using regulated power supplies in the laboratory and 12 V batteries in the field (Figure 2). Between the power source and CO2-LAMP components, a step-down regulator was used to ensure a 6.5 V delivery to the Arduino and K30. While the K30 required only 5.5 V for operation, the additional voltage was applied to supplement for transmission loss given the length of the cable to the K30 (~8 m). Measured K30 values were recorded on an SD Card using an Adafruit Assembled Data Logging shield for Arduino (Product 1141, Adafruit, New York, NY, USA).

Figure 2. Arrangement of 12 V battery power source, voltage regulator, Arduino-based data logger, relay switch, and terminal block connections that lead to a waterproofed K30. Terminal block was used to reduce physical strain and potential disruption to interior wired connections in the event the connecting cable to the waterproofed K30 is disturbed (e.g., external force pulling cable out of the box).
Zero and Span Reference Measurements
To initially verify K30 accuracy, span gas measurements were made using certified CO2-Nitrogen balanced gas mixtures of 2,000 and 10,000 ppmv CO2 (±2% analytical uncertainty) both in a dry, gas-filled chamber (Figure 3A) and partially water-filled chamber where the sensor was submerged (Figure 3B). For the dry reference measurements, a waterproofed K30 1 and 10% were placed in a dry, vented chamber while the reference gas mixture was continuously delivered to the chamber until equilibration with the reference gas was obtained. For submerged reference measurements, waterproofed K30 1 and 10% sensors were placed in a vented, partially water-filled chamber where reference gas mixtures were delivered to the chamber via a diffuser stone at the base of the chamber.
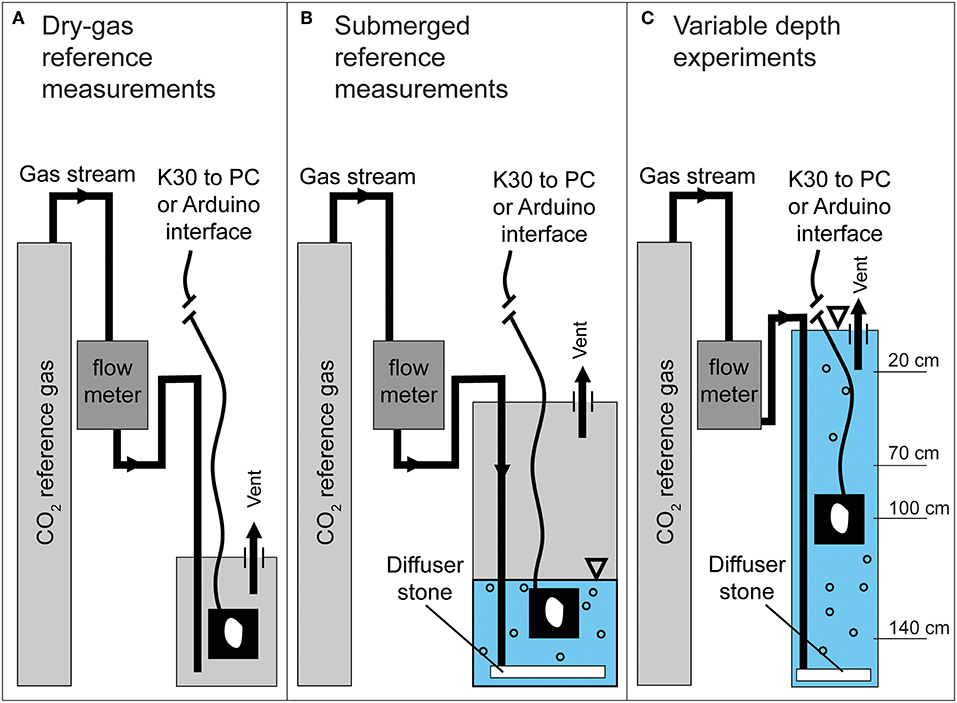
Figure 3. Schematic of reference measurement configurations for (A) dry-gas, (B) submerged, PCO2, and (C) variable depth experiments. Not to scale.
The water in the chamber was considered equilibrated to 95% once the CO2-LAMP readings reached the three e-folding time. The waterproofed K30 was then removed, allowed to re-equilibrate with the ambient laboratory air, and then re-submerged and allowed to reach the three e-folding time over three different submerged trials. Importantly, intervals for e-folding times were separately calculated for the individual submerged trials. Using Equations 4 and 5, values for Kp were then calculated using an estimated volume of 5.6 cm3. Hereafter, PCO2(aq) refers to laboratory measurement of the partial pressure of dissolved CO2.
Submerged IRGA Operation and Validation
Seminal work by Johnson et al. (2009) on the construction of a passive, permeable membrane equilibrator suggested a depth-correction for IRGA output to account for increased hydrostatic pressure acting on a submerged gas analyzer. However, gas exchange will occur across a membrane until such time that PCO2 is equal between the water and the membrane enclosed volume, irrespective of changes in the enclosed headspace volume brought on by increased hydrostatic pressure, suggesting that such a depth correction is not needed. To address this discrepancy related to potential effects of increasing hydrostatic pressure on membrane-enclosed IRGA operation, we explore the theory behind PCO2 calculation for a membrane-enclosed submerged IRGA and describe laboratory experiments that we use to test the derived principles.
Submerged IRGA Output: Theoretical Principles
In air, concentrations of CO2 are typically reported by IRGAs as volumetric fractions, xc, of CO2 in dimensionless units either as parts per million volume (ppmv) or percent values for greater concentrations (>10,000 ppm or 1%) where xc may be expressed as
where Vi equals the volume of CO2 per total volume of gas, Vtotal. Alternatively, CO2 in air may also be expressed as a partial pressure, PCO2, from the product of xi and total pressure (or sum of partial pressures, i.e., Dalton's Law), Ptotal:
While Ptotal can be directly measured, or assumed to be near standard pressure, IRGAs do not directly measure xc.
Principally, an IRGA measures the molecular density of CO2 using the Beer-Lambert Law through the measured absorbance of CO2 for a given wavelength (Fietzek et al., 2014). Molecular density, ρ, is expressed as ρ = NCO2/Vtotal where NCO2 is the number of CO2 molecules.
The xc value from an IRGA is obtained using the ideal gas law, with
where R is the universal gas constant, T is temperature in Kelvin, and NA is Avogadro's number. From Equation 11, xc values depend on ρ, T, and Ptotal. If T and Ptotal are not measured, factory calibrated values for temperature, T0, and pressure, P0, are used to calculate a “reported” volume fraction, xr, which is expressed as
For the majority of low-cost CO2 gas analyzers, where T and Ptotal are not measured simultaneously, IRGA output will generally follow Equation (12), where T0 and P0 are at or near 25°C and 1 atm, respectively. If T and Ptotal are measured a corrected volume fraction xc, can be calculated, with
While the correction in Equation (13) is routinely employed for measurements of CO2 concentrations in ambient air and soil, dissolved CO2 concentrations are most commonly calculated from PCO2, not a volumetric fraction. From Equation (10), PCO2 can be calculated directly from molecular density, ρ, temperature, and known constants. However, IRGA output using factory calibrated temperature, and pressure is xr. To determine PCO2 from xr, Equation (12) is solved for ρ, and substituted into Equation (13), giving
Note that calculation of PCO2 from the reported volumetric fraction only requires the calibration pressure (typically ~1 atm), not the pressure during measurement. On the other hand, a temperature correction is needed if temperature during measurement is substantially different calibration conditions.
Equation (14) demonstrates with introduction of sensor operating principles, total pressure factors out of the calculation of PCO2. Therefore, for a well-mixed, relatively shallow water body of equal temperature, salinity, and dissolved gas concentrations, the partial pressure of CO2 measured by an IRGA at equilibrium (i.e., no gas exchange across the membrane) should be equal at all depths irrespective of hydrostatic pressure. Combining Equations (1) and (14), the concentration of dissolved CO2 determined from direct, membrane equilibration methods using an IRGA can be expressed as
While the theoretical results suggest that no depth correction is needed for calculation of PCO2, if a sensor is suddenly lowered to greater depths, compression of the membrane or sensor housing may introduce increases in total gas pressure within the IRGA. This will produce a short-term spike in the pressures of all gases, including CO2. However, this produces disequilibrium between the gas pressures within the water, and the IRGA which will drive exchange across the membrane until dissolved gas pressure in the water, and gas pressure in the IRGA are back in equilibrium.
Variable Water Depth Experiments: Laboratory Simulation
An accompanying depth compensation experiment measuring CO2 at multiple depth intervals (Figure 3C) was conducted to observe if PCO2(aq) values varied with submerged depth. A 7.62 cm PVC pipe, 152.5 cm in length was filled with water (i.e., synthetic well) to accommodate varying depth interval measurements. The gas mixture was delivered via a porous stone at the bottom of the well. Initially, the submerged K30 10% recorded PCO2(aq) values as the reference gas was delivered to the water in to confirm the PCO2(aq) of the water in the PVC tube had equilibrated with the reference gas (same method described in section Zero and Span Reference Measurements). Once the water in the PVC tube had equilibrated to the reference gas, the K30 10% was removed from the well and allowed to re-equilibrate with laboratory atmospheric CO2 concentrations, which was assumed to be ~500–600 ppmv.
The K30 was then quickly submerged to an initial depth of 20 cm and allowed to re-equilibrate with the PCO2(aq) imposed with the reference gas. Once equilibrated, the K30 was then dropped quickly from the 20 to 70 cm depth and allowed to re-equilibrate. This process was further repeated for depth intervals of 100 and 140 cm. During the experiment, equilibration was assumed to be reached once values were both within the analytical uncertainty of the reference gas, and reading variability was equal to the K30 10% reading resolution of 10 ppm for at least 10 min. Values for three e-folding time were estimated, however, after the experiments.
Field Trials
Field trials were carried out at Blowing Springs Cave and the Savoy Experimental Watershed located in Northwest Arkansas, USA (Figure 4). The two sites represent karst environments within the Springfield Plateau physiographic province overlying the Springfield Plateau aquifer (Kresse et al., 2014). The Springfield Plateau province can be characterized as a mantled karst terrain consisting of a cherty regolith overlying the Boone Formation, a cave forming Paleozoic carbonate unit (Brahana et al., 1999; Knierim et al., 2013; Al-Qinna et al., 2014; Jarvie et al., 2014).
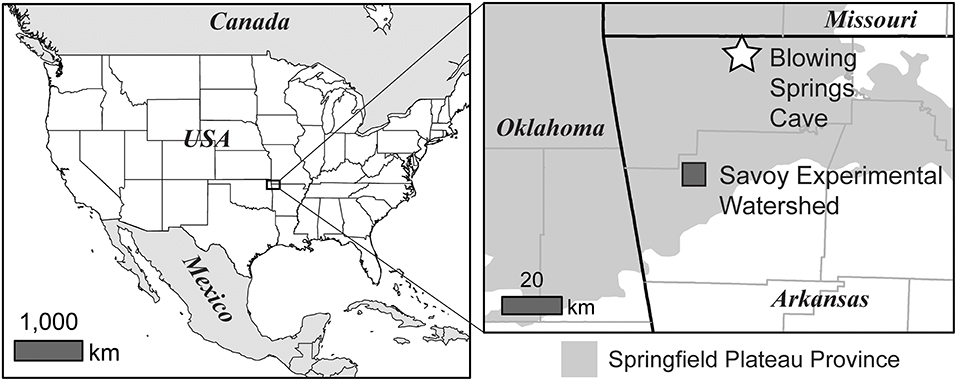
Figure 4. Location of Blowing Springs Cave and the Savoy Experimental Watershed located within the Springfield Plateau physiographic province in northwestern Arkansas, USA.
Blowing Springs Cave
At Blowing Springs Cave, both cave air, CO2(air), and dissolved CO2 within the cave stream, PCO2(stream) were measured independently by: (1) the CO2-LAMP, and (2) an enclosed membrane-equilibrator similar to Johnson et al. (2009), hereafter referred to as the “Vaisala system.” Sensors were located ~100 m within the cave. In the CO2-LAMP platform, concentrations of CO2 for CO2(air), and PCO2(stream) were measured by a waterproofed K30 1, and 10%, respectively. For the Vaisala system, CO2(air), and PCO2(stream) were measured using a waterproofed (see Johnson et al., 2009), Vaisala GMT220 (Helsinki, Finland), and logged using a Campbell Scientific (Logan, UT) CR850. Cave air temperature and cave air pressure were measured using a Campbell Scientific HC2S3 and CS106, respectively. Cave stream temperature was recorded using Cave air direction and speed were recorded using a Campbell Scientific WINDSONIC1-L sonic wind sensor. Cave stream temperature was measured using a Campbell Scientific CS547A-L. Cave air temperature, cave air pressure, cave air flow direction and speed, and cave stream temperature were logged using the Campbell Scientific CR850. For CO2(air) and PCO2(stream) monitoring locations, waterproofed Vaisala CO2 IRGAs, and K30 IRGA sensors were placed alongside each other. Monitoring using the CO2-LAMP lasted from 25 February to 9 March, 2017.
Percent differences between the Vaisala and CO2-LAMP were calculated for measurements of CO2(air) and PCO2(stream), respectively:
Savoy Experimental Watershed
The Savoy Experimental Watershed (SEW) is a long-term experimental research station owned by the University of Arkansas encompassing numerous karst features including sinking streams, caves, cave springs, and epikarst springs (Brahana et al., 1999; Al-Qinna et al., 2014; Covington and Vaughn, 2018). Soil series at SEW have been previously classified as Clarksville (Loamy-skeletal, siliceous, semiactive, mesic Typic Paleudults), Nixa (Loamy-skeletal, siliceous, active, mesic Glossic Fragiudults), Razort (Fine-loamy, mixed, active, mesic Mollic Hapludalfs), and Pickwick (Fine-silty, mixed, semiactive, thermic Typic Paleudults; Soil Survey Staff, 2019). Soils consist of very deep, moderately to excessively drained, slow to moderately permeable soils with clay contents ranging from 20 to 50% (Soil Survey Staff, 2019).
Soil CO2 concentrations at the SEW are reported for the period of 9–22 July, 2017 and were measured ~2 m from a centrally located weather station. Concentrations of CO2(soil) were measured using a waterproofed K30 10% at ~10 cm depth within a soil cavity with the dimensions of ~10 cm depth and 4 cm diameter. A small opening was dug into the wall of the soil cavity where the sensor was placed laterally in the base of the cavity wall. The soil cavity was back-filled as to minimize soil disturbance. Unlike at Blowing Springs, a greater accuracy CO2 gas analyzer system was not co-deployed while the CO2-LAMP was deployed. Considering the Vaisala system (or similar) as a field reference measurement, assessment of absolute accuracies were not possible. However, relative magnitudes of daily CO2 variability were compared to previous studies in a humid-temperate environment (Hirano et al., 2003). At the weather station, measurements of air temperature, soil moisture, and rainfall were recorded every 5 min.
Post-processing Field Data
During field deployments, the low-power mode Arduino sketch was used to record measurements. As mentioned previously, CO2 concentrations were logged every 10 s for 20 min, followed by a 40 min sleep period. Post-processing consisted of removing data during warm-up and stabilization periods and then extracting the final, stabilized values (Figures 5A–D). Final values measured during measurement cycles at Blowing Springs for cave air and dissolved CO2 and soil CO2 at SEW are reported here.

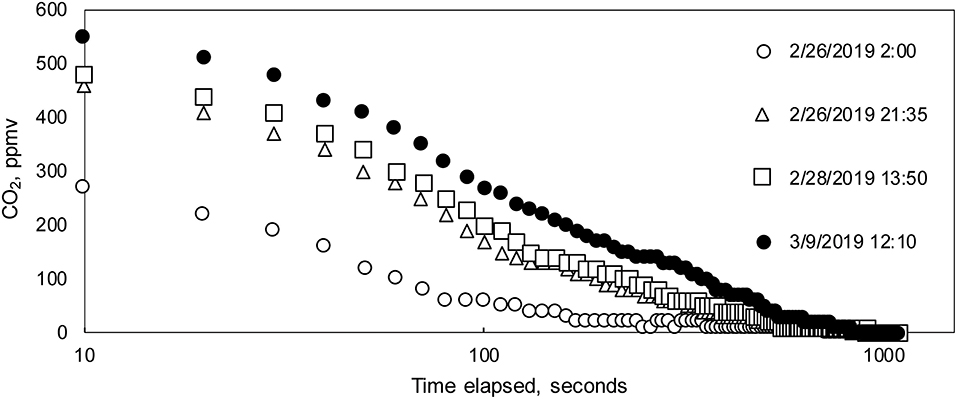
Figure 5. (A–D) Post-processing steps for PCO2(stream) data. (A) Example of full measurement cycle data, which includes initial peak in first 100 s. (B) Example of initial filtering removing first 100 s of measurement cycles for nine measurement cycles on 26 February. (C) The last measurement value during each measurement cycle was selected as the “stabilized” value for comparison with the interpolated Vaisala data. The measurement cycle data comprise the gray-shaded area in (B). (D) Example of filtered from data set in (B).
At Blowing Springs, stabilization periods for the sensor during warm-up changed through the monitoring period (Figure 6). Using a heuristic approach, the Hill-equation (Hill, 1910)—a non-linear, four-parameter equation—was fit to data collected during the monitoring after 100 s to evaluate changes in stabilization times over the monitoring period. Fitting to the data after 100 s minimized influence of the initial CO2 peak (Figure 5A). In general, the Hill equation is useful in describing experimental data that are sigmoid in shape where multiple non-linear processes may be present (Goutelle et al., 2008; Gadagkar and Call, 2015).
The formulation of the Hill equation used in this study was
where the coefficients calculated for this study were: d, the initial CO2 value; a is the final CO2 value; b is the time at which the PCO2 value has changed halfway between a and d; c, the “Hill Slope” or “steepness” value (Gadagkar and Call, 2015); and t is the time elapsed during the measurement period. Calculated coefficients for curve steepness, c, were analyzed.
At Blowing Springs, measurement timestamps between the CO2-LAMP, and Vaisala system (which included cave air temperature, cave air pressure, and cave stream temperature) were variably offset because of different logging intervals. For the CO2-LAMP, the sum duration of time spanning the two-cycle operation (i.e., the “sleep” mode and measurement period) was 65 min with the two-cycle operation beginning as soon as the platform is powered. The Vaisala system was programmed to also include a two-cycle operation, however, the total time duration was 60 min. To address the variable temporal offset, values of cave air temperature, cave air pressure, cave stream temperature, Vaisala CO2(air), and Vaisala PCO2(stream) were linearly interpolated to match CO2-LAMP time stamps to the nearest second. As the inter-hourly variability of CO2(air), PCO2(stream), cave air temperature, cave air pressure, and cave stream temperature were relatively low at Blowing Springs during the monitoring period, differences between true, and interpolated Vaisala values are likely small. In turn, CO2-LAMP data are directly compared to linearly interpolated Vaisala values of CO2(air), PCO2(stream), cave air temperature, cave air pressure, and cave stream temperature. For the following sections, reference to values of cave air temperature, cave air pressure, cave stream temperature, Vaisala CO2(air), and Vaisala PCO2(stream) refer to the linearly interpolated values. As cave air flow direction and speed were not directly compared to CO2-LAMP data, these values were not linearly interpolated. When cave air flow reversals were present, cave air flow was from the interior of the the cave toward the south entrance (or exiting the cave). Cave air flow reversals was defined when cave air flow direction >100° (Young, 2018; Covington et al., in prep.).
CO2-LAMP CO2(air) and Vaisala CO2(air) data were corrected using ancillary pressure and temperature measurements made of cave air temperature using Equation (13). Values for CO2-LAMP PCO2(stream) and Vaisala PCO2(stream) were corrected using only water temperature data (Equation 14).
Parameter Estimation and Regression Analysis
The constants q (see Equation 4) and c (see Equation 17) were estimated using EXCEL Solver (Microsoft, Redmond, WA, USA) applying a least-sum-square error procedure, which uses the Generalized Reduced Gradient method (Gadagkar and Call, 2015). Bivariate relationships were assessed by ordinary least squares linear regression using PAST version 3.25 (Hammer et al., 2001; Hammer, 2019).
Results
Reference Measurements to Known Gas Mixtures
Gas equilibrated reference measurements of CO2 and PCO2 using the CO2-LAMP were within the accuracy stated by the manufacturer for the K30 1 and 10% IRGAS, respectively, in both dry, and aqueous environments. To begin the aqueous (or submerged) reference gas mixture experiments, tap water from the laboratory was equilibrated with the reference by delivering the gas mixture to the water using the diffuser stone. Considering the initial starting time as when the gas flow from the cylinder to the water began, the time needed for the water to reach three e-folding intervals (or 95% equilibration) was ~86 min for a volume of ~2.5 L (Figure 7A). This duration of time encompasses both diffusion of CO2 into the water and the subsequent exchange of CO2 across the membrane of the submerged waterproofed K30. Once the measurements read by waterproofed K30 reached the three e-folding time for the given reference gas mixture, the waterproofed K30 was removed from the water and allowed to re-equilibrate with laboratory ambient air. At this stage, the dissolved PCO2(aq) of the water in the wet chamber was considered equilibrated with the reference gas mixture.
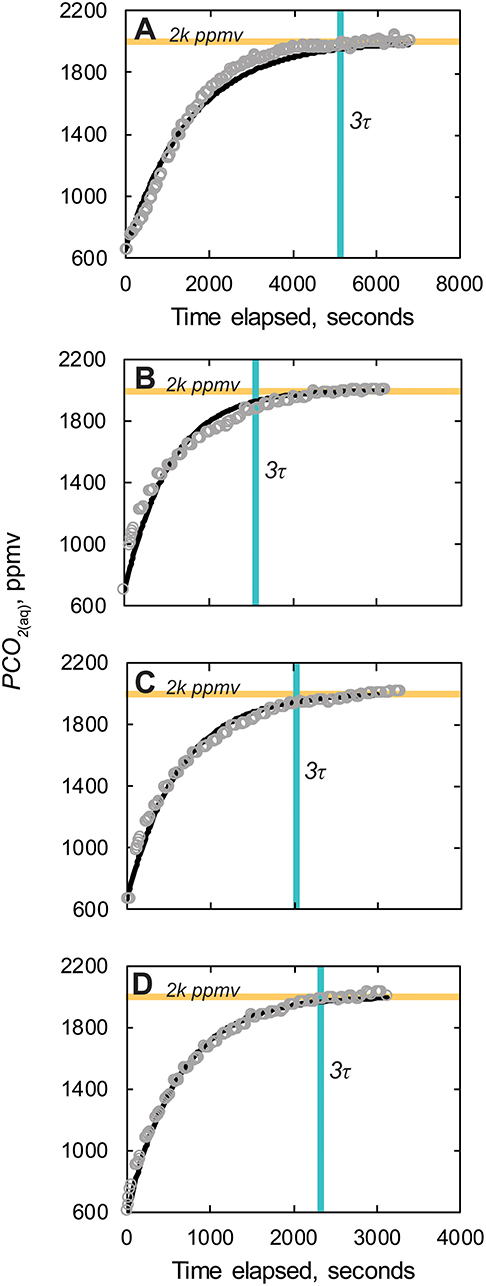
Figure 7. (A) PCO2(aq) measured during injection of 2,000 ppmv CO2 reference gas. (B–D) PCO2(aq) measured re-equilibration after equilibration of water to reference gas. Modeled exponential fits are solid black lines. Horizontal orange line, 2k ppmv, denotes 2,000 reference PCO2(aq) value. Vertical blue line indicated three e-folding time, 3τ, or ~95% equilibration. Measurements made using the K30 1% gas analyzer.
The K30s were then re-submerged three separate times for a minimum period to reach three e-folding times in the reference gas equilibrated water volume (Figures 7B–D). The times needed to reach 95% equilibration were 27, 33, and 38 min for three reference experiments, respectively. The average effective Kp value calculated was 1.2 × 10−4 cm2/s, which while nearly two orders of magnitude lower than CO2 diffusivity through ePTFE from air-to-air environments (0.01 cm2 s−1; Johnson et al., 2009), was nearly an order of magnitude greater than the diffusivity of CO2 in water (1.77 × 10−5 cm2 s−1 at 20°C; Scott, 2000). Final PCO2(aq) values were all within the analytical uncertainty of the reference gas composition 2,000 ppm ± 2% ppmv CO2 (or 2,000 ± 40 ppmv CO2).
Variable Depth Trials
At all depths intervals, PCO2(aq) values during the final 10 min of data logging were: (1) within the analytical uncertainty of the 2,000 ± 2% ppmv CO2 reference gas (or 2,000 ± 40 ppmv CO2); and (2) did not vary more than K30 10% resolution of 10 ppm (Figure 8). At depths 20, 70, 100, and 140 cm, final stabilized PCO2(aq) values and the percent difference (%) with respect to the reference gas value of 2,000 ppm CO2 were 2,020 (1%), 2,000 (0%), 2,010 (0.5%), and 2,030 (1.5%), respectively. As predicted, there were repeated patterns of an initial sharp increase in PCO2 followed by a decline to imposed PCO2 values upon rapid lowering of the K30 10% to greater depth. At depths 20, 70, 100, and 140, PCO2(aq) values were within analytical uncertainty of the reference gas after 36.7, 36.3, 16.8, and 12.8 min. Three e-folding times, 3τ, calculated after the experiments were 30, 72, 50, and 124 min for the respective 20, 70, 100, and 140 cm depths.
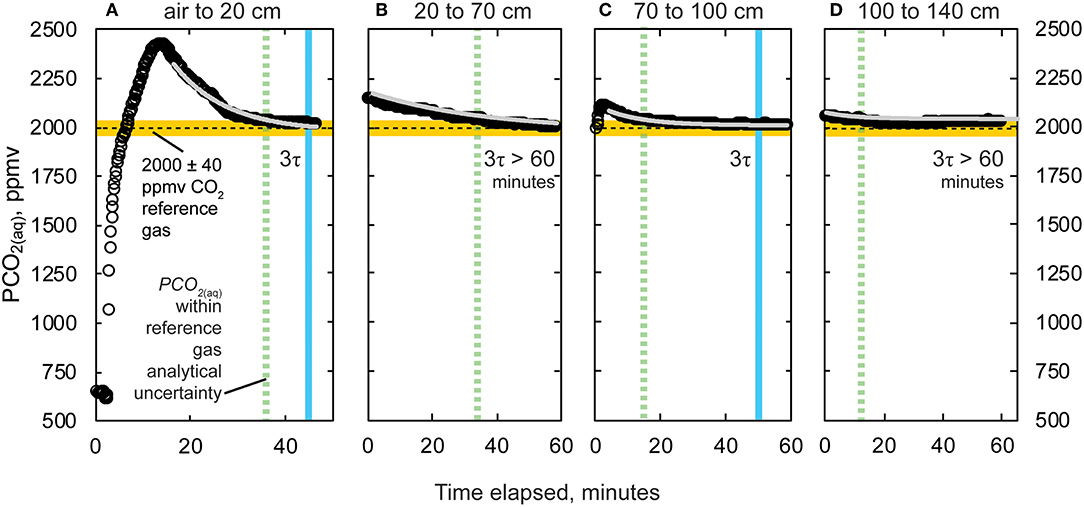
Figure 8. Change in PCO2(aq) and time elapsed lowering from (A) air to 20 cm, (B) 20 to 70 cm, (C) 70 to 100 cm, and (D) 100 to 140 cm depth intervals. Recorded values missed initial peaks when submerged for (B) (20 to 70 cm) and (D) (100 to 140 cm) due to lagged start time on data logger. Modeled equilibration and three e-folding times are shown for (A) (20 cm) and (C) (100 cm). Estimated three e-folding times were >60 min on (B) (70 cm) and (D) (140 cm). However, the time is denoted in all panels when values are within analytical uncertainty of the reference gas mixture (hatched green line). Measurements made using the K30 10% gas analyzer.
Blowing Springs Cave CO2(air) and CO2(stream)
During the field test, multiple periods occurred when cave air flow reversed whereby cave air exited through the southern entrance (Figure 9A). Increases in CO2(air) concentrations up to 749 ppm CO2 (as recorded by the Vaisala system) were observed when cave air flowed toward the southern entrance (Figure 9B). Increases in CO2(air) were generally followed by periods of increased PCO2(stream) values (Figure 9C). However, broader peaks of PCO2(stream) (i.e., 2–3 and 6–9 March) lagged behind peaks in CO2(air) associated with the cave air flow reversals. Excluding CO2(air) during cave air reversals, CO2(air) concentrations (n = 220 measurements) were relatively constant with a mean of 472 ± 2 ppm (mean ± standard error). However, PCO2(stream) increased, overall, during the monitoring period from an initial value of 1,276–1,318 ppm CO2 (as recorded by the Vaisala system for both CO2(air) and PCO2(stream)).
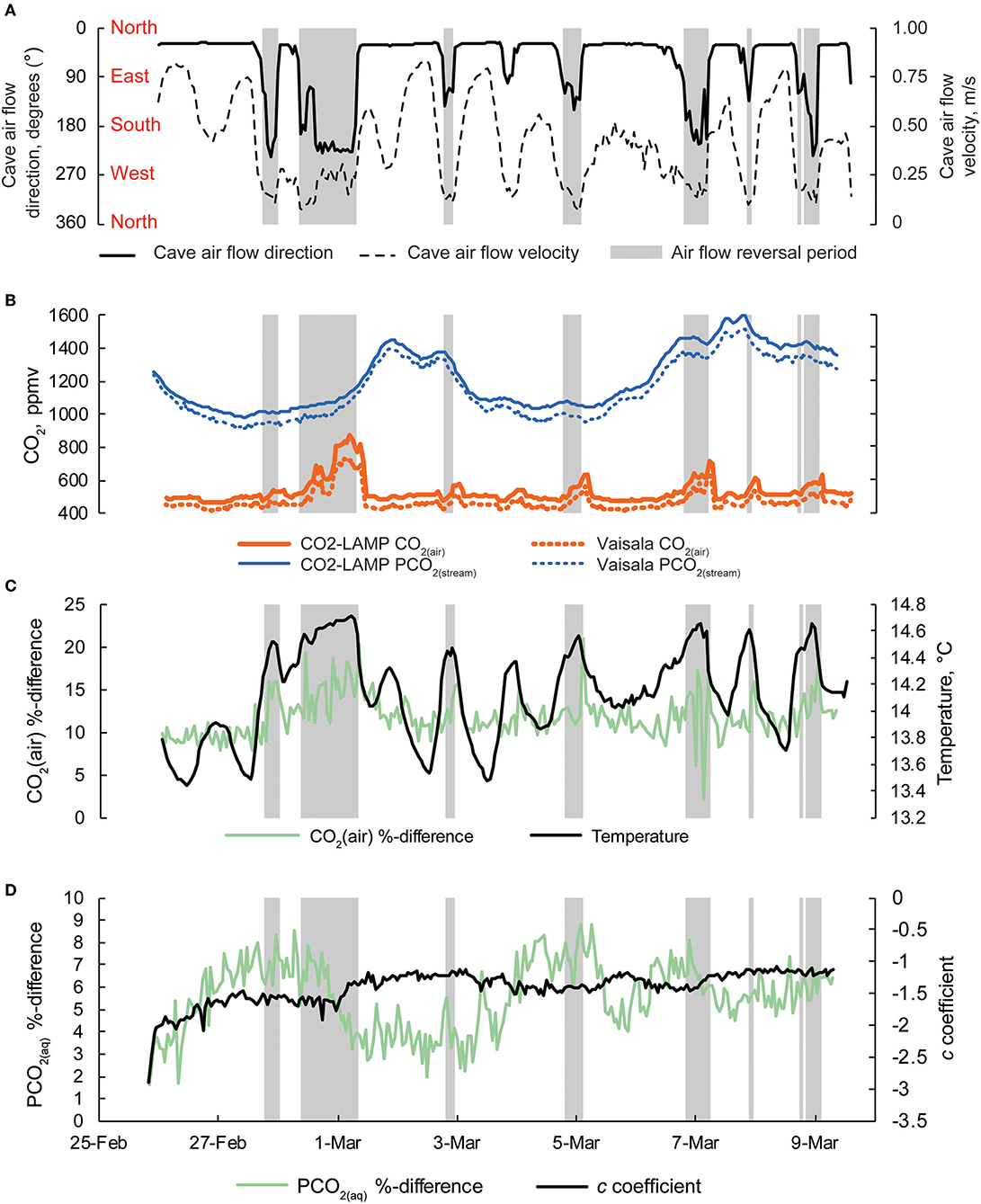
Figure 9. (A) Cave air flow direction and cave air flow velocity. Cardinal directions are shown. Periods when cave air flow direction are >100° are shaded gray in all panels. (B) Concurrent measurements of CO2(air) and PCO2(stream) collected by the CO2-LAMP and Vaisala platforms from 26 February to 9 March, 2017. (C) Percent difference for CO2(air) between the CO2-LAMP and Vaisala and changes in cave air temperature over the monitoring period. (D) Percent differences for PCO2(stream) between the CO2-LAMP and Vaisala and changes in curvature (i.e., c coefficient) derived from the Hill-equation.
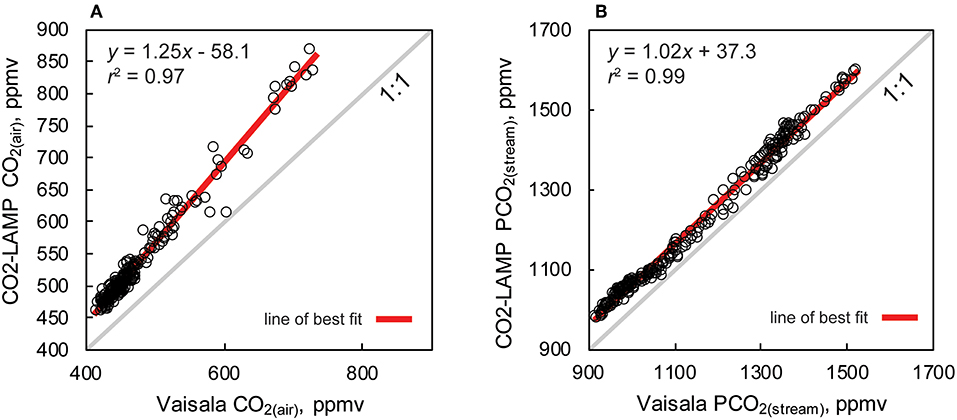
Percent and ppmv differences between the Vaisala and CO2-LAMP for CO2(air) ranged from 2.1 to 20.9% and 13 to 147 ppmv, respectively (Figure 9C). Percent and ppmv differences between the Vaisala and CO2-LAMP for PCO2(stream) ranged from 1.3 to 11.9% and 16 to 147 ppmv, respectively, and exhibited a slight overall increase in percent difference during deployment (Figure 9D). Median percent and ppmv differences between CO2(air) and PCO2(stream) were 11.6% and 56 ppmv and 8.1% and 92 ppmv, respectively. Values for CO2(air) measured using a K30 1% were often outside the manufacturer absolute accuracy ±30 ppmv ±3% stated for the K30. Values for PCO2(stream) measured using the K30 10%, however, were within the stated absolute accuracy of ±300 ppmv ±3%.
Measurements of CO2(air) and PCO2(stream) between the Vaisala and CO2-LAMP measurements did not appear to vary randomly during the monitoring period. The largest differences between CO2(air) values for the two instruments were observed during temperature peaks and coincided with cave air flow reversals. Differences in PCO2(stream) between the Vaisala and CO2-LAMP appeared to exhibit a quasi-oscillatory behavior and some covariation was observed between measurement differences and curvature (or c coefficient) values calculated from the Hill-equation fits to the equilibration curves for the CO2-LAMP. Overall, measurements of CO2(air) (r 2 = 0.97, p < 0.01) and PCO2(stream) (r 2 = 0.99, p < 0.01) between the Vaisala and CO2-LAMP platform were well-correlated during the monitoring period (Figure 10).
Savoy Experimental Watershed CO2(soil)
Measurements of CO2(soil) at SEW exhibited both diurnal variation and an overall decline during the monitoring period (Figure 11). The daily amplitude of CO2 variation ranged from 1,170 to 5,460 ppm with daily minimum and maximum values of CO2(soil) observed at approximately mid-night and mid-day (local time), respectively. Similar timing of minimum and maximum CO2(soil) values were also reported by Hirano et al. (2003). During the monitoring period, a light rain event occurred on 14 July evident from small rainfall totals and reduced daily temperatures, but no change in soil moisture was observed. However, CO2(soil) values decreased over 7,000 ppm from 14 to 15 July, increasing into 16 July, and subsequently decreasing over the remainder of the monitoring period. Overall, daily median CO2(soil) values were well-correlated with daily median soil moisture values (r2 = 0.84; p < 0.01).
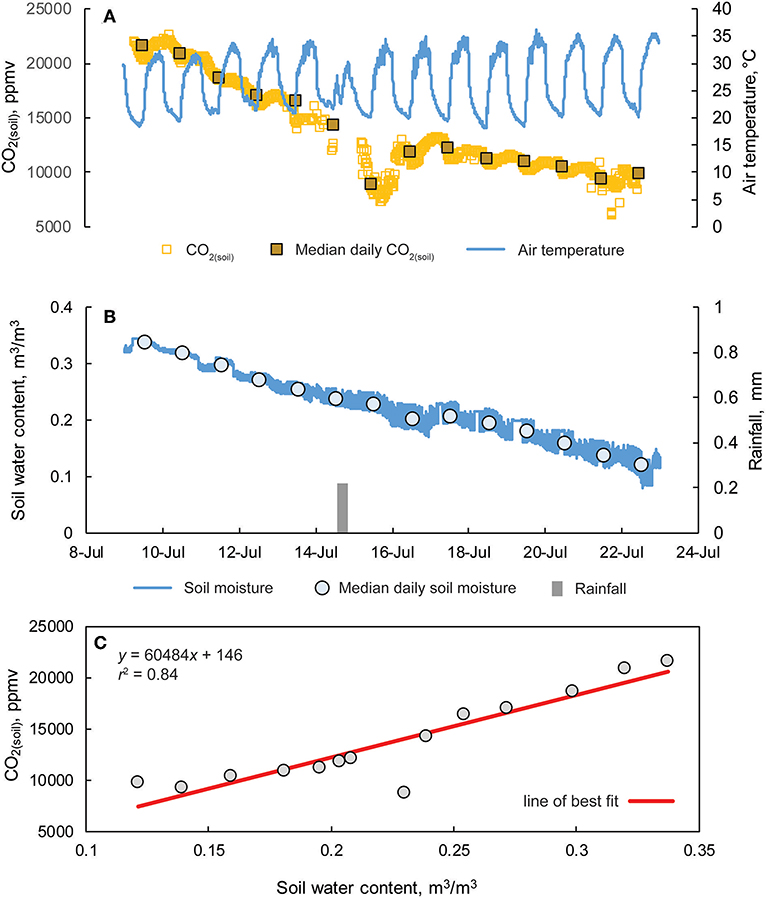
Figure 11. (A) Hourly CO2 (soil) concentrations and median daily values from a 10 cm soil cavity and overlying air temperature from 9 to 24 July at the Savoy Experimental Watershed. (B) Fifteen-minute interval measurement of soil moisture, median daily soil moisture values, and rainfall totals measured from a weather station located ~2 m from the soil cavity. (C) CO2(soil) vs. soil water content.
Discussion
Measurement Accuracy and Assessment
Laboratory reference experiments using known CO2 concentrations and imposing PCO2(aq) values in a volume of water demonstrated the viability of a K30 sensor for accurate, direct measurement of PCO2(aq) with equilibration times of 27–38 min. Compared to other commercial and non-commercial membrane-equilibration systems similar to Johnson et al. (2009) (<30 min), observed equilibration times in this study were slower most likely due to smaller membrane surface area to enclosed membrane volume ratios.
From both the submerged reference experiments (Figure 7) and variable depth trials (Figure 8), K30 1 and K30 10%, respective final measured values were all within the analytical error of the reference gas mixture. Initial offsets and drift that might have occurred during and post-laboratory measurements were not assessed; however, accounting for any drift over the laboratory experiment period would have had negligible difference for the reported PCO2(aq) values and the outcome of the reference experiments.
IRGA Principle Operation and PCO2 Depth Independence
Based on both theoretical principles and empirical evidence, the measurement of partial pressure of CO2 using a submerged IRGA in equilibrium with surrounding water is independent of hydrostatic pressure (Equation 17; Figure 8). However, CO2 concentration spikes occur with sudden increases in hydrostatic pressure (i.e., submerging to deeper depths) before the submerged IRGA returns to the reference CO2 value. This temporary increase in CO2 is interpreted to indicate compression of the enclosed membrane volume, which leads to a decrease in the gas volume, Vtotal, whereby: (1) there is an increased molecular density of CO2 without adding more CO2 molecules; which (2) yields a greater CO2 concentration measured by the IRGA; and (3) creates a situation where the total gas pressure inside the enclosed membrane volume was greater than the total dissolved gas pressure of the external water and drives re-equilibration by both diffusion (i.e., partial pressure differences) and advective (i.e., total pressure differences). As N2 was the predominant species present in the reference gas mixtures (i.e., 99.8% nitrogen balance for reference gas mixture of 2,000 ppm CO2), total pressure equilibration was likely driven by N2 exchange. As total pressure within the enclosed membrane re-equilibrates with the total dissolved gas pressure of the water, remaining gas exchange was driven by re-equilibration of partial pressures of the dissolved CO2.
Assuming an initial Vtotal of 5 cm3 and rearranging Equation (14), a volume change of 6.7% would produce the observed increase in PCO2 of ~150 ppmv during the 20–70 cm variable depth experiment from 0 to 20 min of elapsed time (Figure 8C). Given the K30 10% materials and waterproofing components being partially flexible, this percent change was within reason.
Accounting for increased hydrostatic pressure acting on the sensor (Johnson et al., 2009) with depth gives rise to overestimates of PCO2, and these overestimates are proportional to the submerged depth. Assuming a water density of 1,000 kg/m3, every 10 cm imparts an increase in hydrostatic pressure equivalent to 9.81 hPa, which would equal an ~8.77% overestimation per meter. Considering the comparative accuracy of dissolved CO2 measurement between various equilibration methods to be ~15% (Abril et al., 2015; Yoon et al., 2016), an equal value of overestimation because of the hydrostatic pressure correction is incurred at only 1.68 m depth.
Field Instrument Comparison
Measured CO2 relations between the Vaisala and CO2-LAMP for CO2(air) and PCO2(stream) covaried linearly and were statistically significant (r2 > 0.97, p < 0.01). As previously mentioned, inter-comparison assessments of manual, active, and passive equilibration methods for direct PCO2 measurement exhibited average differences of ~15% between measurement methods from field sampling (Abril et al., 2015; Yoon et al., 2016). At Blowing Springs, the observed median differences for PCO2(stream) between the Vaisala and CO2-LAMP in this study was only 8.6%. For both CO2(air) and PCO2(stream), differences between the Vaisala and CO2-LAMP likely arose from the varying ability to drive off moisture build up inside the IRGA.
At Blowing Springs, the Vaisala IR source generates more heat than the K30 IR source. In turn, the Vaisala heating element potentially allows for faster removal of any moisture within the IRGA given 100% humidity conditions in the enclosed membrane volume, which can interfere with measurement magnitude and stability. Greater initial PCO2(aq) concentrations for CO2-LAMP data during warm-up periods (Figures 5A–C) could be resultant from liquid water condensate decreasing light intensity at the infrared detector (i.e., resulting in artificially large CO2 values; Fietzek et al., 2014). This may explain greater differences among CO2(air) measurements vs. PCO2(aq) between the CO2-LAMP and Vaisala system. As greater temperature variations occurred in the cave air vs. the cave stream, the likelihood for condensation development and overestimation would have been greater for the K30 measuring cave air. Measurement stability over time was likely better sustained in the Vaisala given the ability to remove excess moisture over the deployment period.
Specific factors and correction coefficients for the aforementioned factors vary not only between manufacturers, but also among individual IRGAs of the same manufacturer (McDermitt et al., 1993; Martin et al., 2017). Fully explaining observed differences between CO2(air) and PCO2(stream) were outside of the scope of this study, but work toward accounting for humidity, temperature, and pressure within the membrane-enclosed headspace should, in theory, allow for increased measurement accuracy. Related effects from moisture interference, such as band broadening, effective pressure, and particularly, water dilution effects (McDermitt et al., 1993; Welles and McDermitt, 2005), will affect IRGA accuracy, but were also not fully assessed in this study.
Capturing CO2 Variability in Natural Settings
Carbon dioxide variability at both sites may be generally described as arising from complex carbon exchange pathways and biogeochemical cycling, which vary down to hourly time-scales. At Blowing Springs Cave, large changes in CO2(air), and PCO2(stream) are linked to cave ventilation, and air flow reversals in the cave system; when CO2(air) increases, the flux of CO2 from the stream decreases, subsequently increasing PCO2(stream). At SEW, CO2(soil) decreases over the monitoring period are likely related to changes in soil moisture (i.e., drying), and coupled reduced soil respiration (Hirano et al., 2003).
Ultimately, the IRGA selection for capturing CO2(air), PCO2(aq), or CO2(soil) variability within environmental systems should be determined based on needed accuracy, priori knowledge of CO2 variability (i.e., temporal and absolute magnitude), and site conditions. With respect to the K30 IRGAs, small variations in CO2(air), and PCO2(stream) <1% (or 10,000 ppm) CO2 like those at Blowing Springs are better suited for the K30 1%. While no reference measurement system was in place (e.g., Vaisala or similar accuracy IRGA) at SEW, CO2(soil) exhibited similar ranges, and environmental response observed in previous studies (Hirano et al., 2003; Jassal et al., 2005). As such, if CO2(soil) is known to be >1% at times when soil respiration is more active, monitoring large changes in CO2(soil) present in most soil systems is better suited for the K30 10%.
When not submerged in water or a fully saturated soil, equilibration of CO2 between the enclosed membrane volume and the environment will be relatively fast, and is likely to fully capture the temporal, and absolute magnitude of CO2 variability. In aquatic environments, such as surface waters, the temporal, and absolute magnitude of PCO2(aq), however, may not be fully captured due to slower equilibration time of the membrane-equilibration method (Yoon et al., 2016). Given site conditions, however, the membrane-equilibration method may still be the only viable method. As the CO2-LAMP equilibration time for PCO2(aq) was measured to be up to 37 min, collection of discrete, direct measurements using faster equilibration methods (see section Direct Measurement of Dissolved CO2 Principles) during varying flow regimes would, at the least, aid in elucidating the magnitude of CO2 variability not captured.
In all cases, field deployments should include: (1) accounting for environmental factors (i.e., humidity, pressure, temperature); (2) performing zero-gas (i.e., no CO2 gas present) measurements; and (3) span gas measurements before, during, and after deployment. Incorporation of these field checks should increase measurement accuracy for CO2 measurements (Fietzek et al., 2014; Martin et al., 2017) without use of an accompanying greater-cost system (e.g., Vaisala system) and yield assessment of both the K30 1% and 10% performance over longer deployment periods (>2 weeks).
Instrument Fouling, Fabrication Considerations, and Future Field Deployment
From initial deployments of the CO2-LAMP system, environmental factors have been noted which may have solely or in part caused temporary and permanent K30 instrument fouling. First, suspended sediments and other materials (e.g., branches, shells, etc.) can abrade the membrane surface causing microtears. Microtears, while not always visible, allow for liquid water to seep through and damage the K30 instrument's components. Second, upon epoxy application, and waterproofing of the K30, careful attention is needed to ensure the rubber compound seals the contact between the serial cable, epoxy, and plastic case to prevent water intrusion to the K30 from openings that, similar to microtears, are not always visually apparent. Moreover, application of the rubber compound greatly aids strain relief for the serial cable exiting the plastic case. Third, silt and smaller clay size particles can accumulate on the membrane surface particularly if oriented “face up” relative to the stream surface. If left unprotected, a mud layer or biofilm can accumulate. In both cases, dissolved CO2 concentrations would be more influenced by dissolved CO2 changes within the mud or algal mass rather than the surrounding water. For protection against sediment and biofilm buildup on the membrane surface, it is recommended to orient the sensor vertically in the water column or “face down” relative to the stream surface. For biofilms specifically, use of a bronze mesh has been found to be successful in preventing biofilm accumulation in other freshwater and marine environments (Steven et al., 2014).
Recommendations for future, long-term field deployments using a design similar presented here should consider three modifications. During fabrication, a conformal coating was not applied; however, previous studies employing the K30 for use in floating chambers noted the utility in application of a protective coating on the electronic components for both assembly and field operation (Bastviken et al., 2015). A conformal coating would serve as a protective layer with no disturbance to the K30 printed circuit board. The conformal coating would also provide additional structural support to the initial UART serial connection made to the circuit board before attaching the membrane and rubber compound coating and may help limit any effects from either contraction or expansion of the epoxy-resin during curing. Second, increasing the surface area of the membrane relative to the enclosed membrane volume will increase equilibration time. Lastly, inability to remove excess condensation that results from membrane saturation (Manning et al., 2003) or in-stream temperature changes will greatly diminish instrument accuracy and potentially cause permanent instrument fouling over time (Fietzek et al., 2014). While condensation buildup was not directly investigated, removal of excess moisture from condensation is warranted for long-term CO2-LAMP deployment and CO2 accuracy.
Conclusions
Expanding the variety of sites and frequency of CO2 measurements in ambient, soil, and aqueous environments are critical in constraining local carbon dynamics and addressing gaps in efforts to quantify the planetary-scale carbon cycle. Reduction of instrument costs provides a pathway to expand CO2 monitoring across Earth, particularly in research programs where relatively greater-cost platforms are cost-prohibitive.
As part of the CO2-LAMP development, a theoretical presentation of IRGA output, and accompanying experimentation demonstrate that, for PCO2 measurements, temperature is the only correcting variable; however, for measurements in ambient air, total pressure is needed for calculating xc (i.e., pressure- and temperature-corrected values). Importantly, these findings hold significant implications for past, current, and future implementation of IRGA analyzers for dissolved PCO2 measurement, and, where applicable, recalculation of reported values from previous studies should be considered, particularly for probes at deeper water depths.
Recorded observations in both the laboratory and field demonstrate the CO2-LAMP to be a viable, low-cost alternative to monitoring CO2 in field settings. In the case of PCO2(aq), reported values were within reported uncertainties between different methods. Future work will modify the gas analyzer-water interface to minimize potential fouling due to moisture intrusion and/or long-term condensation buildup.
Data Availability Statement
The datasets analyzed for this study can be found at the CO2-LAMP GitHub repository https://github.com/CovingtonResearchGroup/CO2-LAMP.
Author Contributions
JB fabricated, designed, carried out laboratory experiments, and conducted CO2-LAMP field trial in collaboration with MC. Initial formulation of theoretical principles were done by MP. Initial selection, interfacing, and coding was carried out by JM. JB prepared the manuscript with valuable contributions from all co-authors.
Funding
JB acknowledges support Van Brahana Hydrogeology from the University of Arkansas, Department of Geosciences Scholarship. MP acknowledges financial support from the Slovenian Research Agency (research core funding No. P2-0001, bilateral collaboration funding BI-US/17-18-062). JM acknowledges funding from NSF grant EAR-PF 1249895.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would especially like to thank Sarah Williams, Holly Young, Josue Rodriguez, Hannah Gnoza, and Max Cooper for their assistance during field work. We would also like to thank Max Cooper for troubleshooting Arduino connectivity and power related issues in the OZ27 office. An important set of thanks go to Jerry Fairley, Megan Aunan, and the Hydrologic Computational Group at the University of Idaho for hosting, organizing, and providing invaluable feedback through the wonderful workshop at the University of Idaho MILL which introduced students and faculty to building an earlier version of the CO2-LAMP. Lastly, we would very much like to thank the reviewers. Their valuable comments and suggestions have greatly improved this manuscript.
References
Abril, G., Bouillon, S., Darchambeau, F., Teodoru, C. R., Marwick, T. R., Tamooh, F., et al. (2015). Technical note: large overestimation of pCO2 calculated from pH and alkalinity in acidic, organic-rich freshwaters. Biogeosciences 12, 67–78. doi: 10.5194/bg-12-67-2015
Al-Qinna, M., Scott, H. D., Brye, K. R., Van Brahana, J., Sauer, T. J., and Sharpley, A. (2014). Coarse fragments affect soil properties in a mantled-karst landscape of the ozark highlands. Soil Sci. 179, 42–50. doi: 10.1097/SS.0000000000000034
Andrews, A. E., Kofler, J. D., Trudeau, M. E., Williams, J. C., Neff, D. H., Masarie, K. A., et al. (2014). CO2, CO, and CH4 measurements from tall towers in the NOAA Earth system research laboratory's global greenhouse gas reference network: instrumentation, uncertainty analysis, and recommendations for future high-accuracy greenhouse gas. Atmos. Meas. Tech. 7, 647–687. doi: 10.5194/amt-7-647-2014
Bareer, R. M. (1939). Permeation, diffusion and solution of gases. Trans. Faraday Soc. 35, 628–643. doi: 10.1039/tf9393500628
Bastviken, D., Sundgren, I., Natchimuthu, S., Reyier, H., and Gålfalk, M. (2015). Technical note: cost-efficient approaches to measure carbon dioxide (CO2) fluxes and concentrations in terrestrial and aquatic environments using mini loggers. Biogeosciences 12, 3849–3859. doi: 10.5194/bg-12-3849-2015
Beddows, P. A., and Mallon, E. K. (2018). Cave pearl data logger: a flexible arduino-based logging platform for long-term monitoring in harsh environments. Sensors 18:530. doi: 10.3390/s18020530
Bergman, T. L., Lavine, A. S., Incropera, F. P., and DeWitt, D. P. (2011). Fundamentals of Heat and Mass Transfer, 7th Edn. New York, NY: John Wiley and Sons.
Bradford, M. A., Wieder, W. R., Bonan, G. B., Fierer, N., Raymond, P. A., and Crowther, T. W. (2016). Managing uncertainty in soil carbon feedbacks to climate change. Nat. Clim. Chang. 6, 751–758. doi: 10.1038/nclimate3071
Brahana, J. V., Hays, P. D., Kresse, T. M., Sauer, T. J., and Stanton, G. P. (1999). “The Savoy Experimental Watershed–early lessons for hydrogeologic modeling from a well-characterized karst research site,” in Karst Waters Institute Special Publication 5, eds A. N. Palmer, M. V. Palmer, and I. D. Sasowsky (Charles Town, WV: Karst Waters Institute), 247–254.
Brantley, S. L., Dibiase, R. A., Russo, T. A., Shi, Y., Lin, H., Davis, K. J., et al. (2016). Designing a suite of measurements to understand the critical zone. Earth Surf. Dyn. 4, 211–235. doi: 10.5194/esurf-4-211-2016
Brantley, S. L., Goldhaber, M. B., and Vala Ragnarsdottir, K. (2007). Crossing disciplines and scales to understand the critical zone. Elements 3, 307–314. doi: 10.2113/gselements.3.5.307
Breecker, D., and Sharp, Z. D. (2008). A field and laboratory method for monitoring the concentration and isotopic composition of soil CO2. Rapid Commun. Mass Spectrom. 22, 449–454. doi: 10.1002/rcm.3382
Broecker, W. S., and Sanyal, A. (1998). Does atmospheric CO2 police the rate of chemical weathering? Global Biogeochem. Cycles 12, 403–408. doi: 10.1029/98GB01927
Burton, M. R., Sawyer, G. M., and Granieri, D. (2013). Deep carbon emissions from volcanoes. Rev. Mineral. Geochem. 75, 323–354. doi: 10.2138/rmg.2013.75.11
Colt, J. (2012). Computation of Dissolved Gas Concentration in Water as Functions of Temperature, Salinity and Pressure, 2nd Edn. Oxford: Elsevier.
Covington, M. D., and Vaughn, K. A. (2018). Carbon dioxide and dissolution rate dynamics within a karst underflow-overflow system, Savoy Experimental Watershed, Arkansas, USA. Chem. Geol. doi: 10.1016/j.chemgeo.2018.03.009. [Epub ahead of print].
D'Aoust, B. G., and Clark, M. J. R. (1980). Analysis of supersaturated air in natural waters and reservoirs. Trans. Am. Fish. Soc. 109, 708–724. doi: 10.1577/1548-8659(1980)109<708:AOSAIN>2.0.CO;2
Davidson, E. A., Figueiredo, R. O., Markewitz, D., and Aufdenkampe, A. K. (2010). Dissolved CO2 in small catchment streams of eastern Amazonia: a minor pathway of terrestrial carbon loss. J. Geophys. Res. Biogeosci. 115, 1–6. doi: 10.1029/2009JG001202
De Gregorio, S., Camarda, M., Longo, M., Cappuzzo, S., Giudice, G., and Gurrieri, S. (2011). Long-term continuous monitoring of the dissolved CO2 performed by using a new device in groundwater of the Mt. Etna (southern Italy). Water Res. 45, 3005–3011. doi: 10.1016/j.watres.2011.03.028
De Gregorio, S., Gurrieri, S., and Valenza, M. (2005). A PTFE membrane for the in situ extraction of dissolved gases in natural waters: theory and applications. Geochem. Geophys. Geosyst. 6, 1–13. doi: 10.1029/2005GC000947
Decina, S. M., Hutyra, L. R., Gately, C. K., Getson, J. M., Reinmann, A. B., Short Gianotti, A. G., et al. (2016). Soil respiration contributes substantially to urban carbon fluxes in the greater Boston area. Environ. Pollut. 212, 433–439. doi: 10.1016/j.envpol.2016.01.012
Demars, B. O. L., Thompson, J., and Manson, J. R. (2015). Stream metabolism and the open diel oxygen method: principles, practice, and perspectives. Limnol. Oceanogr. Methods 13, 356–374. doi: 10.1002/lom3.10030
Enns, T., Scholander, P. F., and Bradstreet, E. D. (1965). Effect of hydrostatic pressure on gases dissolved in water. J. Phys. Chem. 69, 389–391. doi: 10.1021/j100886a005
Fietzek, P., Fiedler, B., Steinhoff, T., and Körtzinger, A. (2014). In situ quality assessment of a novel underwater pCO2 sensor based on membrane equilibration and NDIR spectrometry. J. Atmos. Ocean. Technol. 31, 181–196. doi: 10.1175/JTECH-D-13-00083.1
Fisher, D. K., and Gould, P. J. (2012). Open-source hardware is a low-cost alternative for scientific instrumentation and research. Mod. Instrum. 1, 8–20. doi: 10.4236/mi.2012.12002
Florea, L. J. (2015). Carbon flux and landscape evolution in epigenic karst aquifers modeled from geochemical mass balance. Earth Surf. Process. Landforms 40, 1072–1087. doi: 10.1002/esp.3709
Frankignoulle, M., Borges, A., and Biondo, R. (2001). A new design of equilibrator to monitor carbon dioxide in highly dynamic and turbid environments. Water Res. 35, 1344–1347. doi: 10.1016/S0043-1354(00)00369-9
Gadagkar, S. R., and Call, G. B. (2015). Computational tools for fitting the Hill equation to dose–response curves. J. Pharmacol. Toxicol. Methods 71, 68–76. doi: 10.1016/j.vascn.2014.08.006
Gardner, P., and Solomon, D. K. (2009). An advanced passive diffusion sampler for the determination of dissolved gas concentrations. Water Resour. Res. 45, 1–12. doi: 10.1029/2008WR007399
Goutelle, S., Maurin, M., Rougier, F., Barbaut, X., Bourguignon, L., Ducher, M., et al. (2008). The Hill equation: a review of its capabilities in pharmacological modelling. Fundam. Clin. Pharmacol. 22, 633–648. doi: 10.1111/j.1472-8206.2008.00633.x
Hamme, R. C., Berry, J. E., Klymak, J. M., and Denman, K. L. (2015). In situ O2 and N2 measurements detect deep-water renewal dynamics in seasonally-anoxic Saanich inlet. Cont. Shelf Res. 106, 107–117. doi: 10.1016/j.csr.2015.06.012
Hammer, Ø. (2019). Reference Manual: PAST PAleontological STatistics. Version 3.25. System. Olso: Natural History Museum University of Oslo.
Hammer, Ø., Harper, D. A. T., Ryan, D. D., and Ryan, P. D. (2001). PAST : paleontological statistics software package for education and data analysis. Palaeontol. Electron. 4:9. doi: 10.1016/j.bcp.2008.05.025
Hari, P., Pumpanen, J., Huotari, J., Kolari, P., Grace, J., Vesala, T., et al. (2008). High-frequency measurements of productivity of planktonic algae using rugged nondispersive infrared carbon dioxide probes. Limnol. Oceanogr. Methods 6, 347–354. doi: 10.4319/lom.2008.6.347
Hill, A. V. (1910). The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. Proc. Physiol. Soc. 53, 1689–1699. doi: 10.1017/CBO9781107415324.004
Hirano, T., Kim, H., and Tanaka, Y. (2003). Long-term half-hourly measurement of soil CO2 concentration and soil respiration in a temperate deciduous forest. J. Geophys. Res. Atmos. 108, 1–13. doi: 10.1029/2003JD003766
Jarvie, H. P., King, S. M., and Neal, C. (2017). Inorganic carbon dominates total dissolved carbon concentrations and fluxes in British rivers: application of the THINCARB model – thermodynamic modelling of inorganic carbon in freshwaters. Sci. Total Environ. 575, 496–512. doi: 10.1016/j.scitotenv.2016.08.201
Jarvie, H. P., Sharpley, A. N., Brahana, V., Simmons, T., Price, A., Neal, C., et al. (2014). Phosphorus retention and remobilization along hydrological pathways in karst terrain. Environ. Sci. Technol. 48, 4860–4868. doi: 10.1021/es405585b
Jassal, R., Black, A., Novak, M., Morgenstern, K., Nesic, Z., and Gaumont-Guay, D. (2005). Relationship between soil CO2 concentrations and forest-floor CO2 effluxes. Agric. For. Meteorol. 130, 176–192. doi: 10.1016/j.agrformet.2005.03.005
Jochheim, H., Wirth, S., and von Unold, G. (2018). A multi-layer, closed-loop system for continuous measurement of soil CO2 concentration. J. Plant Nutr. Soil Sci. 181, 61–68. doi: 10.1002/jpln.201700259
Johnson, M. S., Billett, M. F., Dinsmore, K. J., Wallin, M., Dyson, K. E., and Jassal, R. S. (2009). Direct and continuous measurement of dissolved carbon dioxide in freshwater aquatic systems-method and applications. Ecohydrology 3, 68–78. doi: 10.1002/eco.95
Joos, O., Saurer, M., Heim, A., Hagedorn, F., Schmidt, M. W. I., and Siegwolf, R. T. W. (2008). Can we use the CO2 concentrations determined by continuous-flow isotope ratio mass spectrometry from small samples for the Keeling plot approach? Rapid Commun. Mass Spectrom. 22, 4029–4034. doi: 10.1002/rcm.3827
Kling, G. W., Clark, M. A., Compton, H. R., Devine, J. D., Evans, W. C., Humphrey, A. M., et al. (1987). The 1986 Lake Nyos gas disaster in Cameroon, West Africa. Science 236, 169–175. doi: 10.1126/science.236.4798.169
Knierim, K. J., Pollock, E., and Hays, P. D. (2013). Using isotopes of dissolved inorganic carbon species and water to separate sources of recharge in a cave spring, Northwestern Arkansas, USA. Acta Carsologica 42, 261–276. doi: 10.3986/ac.v42i2-3.667
Kresse, T. M., Hays, P. D., Merriman, K. R., Gillip, J. A., Fugitt, D. T., Spellman, J. L., et al. (2014). Aquifers of Arkansas-Protection, Management, and Hydrologic and Geochemical Characteristics of Groundwater Resources in Arkansas: U.S. Geological Survey Scientific Investigations Report, U.S. Geological Survey, 2014–5149. doi: 10.3133/sir20145149
Kruczek, B. (2015). “Convective transport,” in Encyclopedia of Membranes, eds E. Drioli and L. Giorno (Berlin; Heidelberg: Springer), 1–3. doi: 10.1007/978-3-642-40872-4_1994-1
Kusakabe, M., and Sano, Y. (1992). “The origin of gases in Lake Nyos, Cameroon,” in Natural Hazards in West and Central Africa eds S. J. Freeth, C. O. Ofoegbu, and K. M. Onuoha (Wiesbaden: Vieweg+Teubner Verlag), 83−95. doi: 10.1007/978-3-663-05239-5_9
Liu, S., and Raymond, P. A. (2018). Hydrologic controls on pCO2 and CO2 efflux in US streams and rivers. Limnol. Oceanogr. Lett. 3, 428–435. doi: 10.1002/lol2.10095
Lombardozzi, D. L., Bonan, G. B., Smith, N. G., Dukes, J. S., and Fisher, R. A. (2015). Temperature acclimation of photosynthesis and respiration: a key uncertainty in the carbon cycle-climate feedback. Geophys. Res. Lett. 42, 8624–8631. doi: 10.1002/2015GL065934
Lowenstern, J. B. (2001). Carbon dioxide in magmas and implications for hydrothermal systems. Miner. Depos. 36, 490–502. doi: 10.1007/s001260100185
Manning, A. H., Solomon, D., and Sheldon, A. L. (2003). Applications of a total dissolved gas pressure probe in ground water studies. Ground Water 41, 440–448. doi: 10.1111/j.1745-6584.2003.tb02378.x
Martin, C. R., Zeng, N., Karion, A., Dickerson, R. R., Ren, X., Turpie, B. N., et al. (2017). Evaluation and environmental correction of ambient CO2 measurements from a low-cost NDIR sensor. Atmos. Meas. Tech. 10, 2383–2395. doi: 10.5194/amt-10-2383-2017
McDermitt, D. K., Welles, J. M., and Eckles, R. D. (1993). Effects of Temperature, Pressure and Water Vapor on Gas Phase Infrared Absorption by CO2. Lincoln, NE: LI-COR Tech. Publ.
McDowell, N., Baldocchi, D., Barbour, M., Bickford, C., Cuntz, M., Hanson, D., et al. (2008). Understanding the stable isotope composition of biosphere-atmosphere CO2 exchange. Eos Trans. Am. Geophys. Union 89, 94–95. doi: 10.1029/2008EO100002
Moran, D., Tirsgård, B., and Steffensen, J. F. (2010). The accuracy and limitations of a new meter used to measure aqueous carbon dioxide. Aquac. Eng. 43, 101–107. doi: 10.1016/j.aquaeng.2010.07.003
Olah, G. A., Prakash, G. K. S., and Goeppert, A. (2011). Anthropogenic chemical carbon cycle for a sustainable future. J. Am. Chem. Soc. 133, 12881–12898. doi: 10.1021/ja202642y
Pearce, J. M. (2012). Building research equipment with free, open-source hardware. Science 337, 1303–1304. doi: 10.1126/science.1228183
Queiβer, M., Granieri, D., and Burton, M. (2016). A new frontier in CO2 flux measurements using a highly portable DIAL laser system. Sci. Rep. 6:33834. doi: 10.1038/srep33834
Richter, D. deB., and Mobley, M. L. (2009). Monitoring earth's critical zone. Science 326, 1067–1068. doi: 10.1126/science.1179117
Ryan, M. C., Roy, J. W., and Heagle, D. J. (2015). Dissolved gas “concentrations” or “concentration estimates” - a comment on ‘Origin, distribution and hydrogeochemical controls on methane occurrences in shallow aquifers, southwestern Ontario, Canada’ by Jennifer C. McIntosh, Stephen E. Grasby, Stewart M. Appl. Geochem. 63, 218–221. doi: 10.1016/j.apgeochem.2015.08.015
Sánchez-Cañete, E. P., Scott, R. L., van Haren, J., and Barron-Gafford, G. A. (2017). Improving the accuracy of the gradient method for determining soil carbon dioxide efflux. J. Geophys. Res. Biogeosci. 122, 50–64. doi: 10.1002/2016JG003530
Sanford, W. E., Shropshire, R. G., and Solomon, D. K. (1996). Dissolved gas tracers in groundwater: Simplified injection, sampling, and analysis. Water Resour. Res. 32, 1635–1642. doi: 10.1029/96WR00599
Schimel, D., Stephens, B. B., and Fisher, J. B. (2015). Effect of increasing CO2 on the terrestrial carbon cycle. Proc. Natl. Acad. Sci. U.S.A. 112, 436–441. doi: 10.1073/pnas.1407302112
Schimel, D. S., House, J. I., Hibbard, K. A., Bousquet, P., Ciais, P., Peylin, P., et al. (2001). Recent patterns and mechanisms of carbon exchange by terrestrial ecosystems. Nature 414, 169–172. doi: 10.1038/35102500
Scott, H. D. (2000). Soil Physics: Agricultural and Environmental Applications. Ames, IA: Iowa State University Press.
Serrano-Ortiz, P., Roland, M., Sanchez-Moral, S., Janssens, I. A., Domingo, F., Goddéris, Y., et al. (2010). Hidden, abiotic CO2 flows and gaseous reservoirs in the terrestrial carbon cycle: review and perspectives. Agric. For. Meteorol. 150, 321–329. doi: 10.1016/j.agrformet.2010.01.002
Soil Survey Staff (2019). National Cooperative Soil Characterization Database. Soil Series Classification Database. Natural Resources Conservation Service, United States Department of Agriculture.
Steven, A., Hodge, J., Cannard, T., Carlin, G., Franklin, H., McJannet, D., et al. (2014). ContinuousWater Quality Monitoring on the Great Barrier Reef. Brisbane, QLD: CSIRO. Available online at: https://publications.csiro.au/rpr/pub?pid=csiro:EP15170
Takahashi, T. (1961). Carbon dioxide in the atmosphere and in Atlantic Ocean water. J. Geophys. Res. 66:477. doi: 10.1029/JZ066i002p00477
Tang, J., Baldocchi, D. D., Qi, Y., and Xu, L. (2003). Assessing soil CO2 efflux using continuous measurements of CO2 profiles in soils with small solid-state sensors. Agric. For. Meteorol. 118, 207–220. doi: 10.1016/S0168-1923(03)00112-6
Urban, A. L., Gulliver, J. S., and Johnson, D. W. (2008). Modeling total dissolved gas concentration downstream of spillways. J. Hydraul. Eng. 134, 550–561. doi: 10.1061/(ASCE)0733-9429(2008)134:5(550)
Ward, H. C., Kotthaus, S., Grimmond, C. S. B., Bjorkegren, A., Wilkinson, M., Morrison, W. T. J., et al. (2015). Effects of urban density on carbon dioxide exchanges: observations of dense urban, suburban and woodland areas of southern England. Environ. Pollut. 198, 186–200. doi: 10.1016/j.envpol.2014.12.031
Welles, J. M., and McDermitt, D. K. (2005). “Measuring carbon dioxide in the atmosphere,” in Micrometerology in Agricultural Systems, eds M. K. Viney, J. L. Hatfield and J. M. Baker (Madison, WI: American Society of Agronomy, Inc.; Crop Science Society of America, Inc; Soil Science Society of America, Inc., 287–320. Available online at: https://dl.sciencesocieties.org/publications/books/tocs/agronomymonogra/micrometeorolog
Werner, C., and Cardellini, C. (2006). Comparison of carbon dioxide emissions with fluid upflow, chemistry, and geologic structures at the Rotorua geothermal system, New Zealand. Geothermics 35, 221–238. doi: 10.1016/j.geothermics.2006.02.006
Yoon, T. K., Jin, H., Oh, N. H., and Park, J. H. (2016). Technical note: assessing gas equilibration systems for continuous pCO2 measurements in inland waters. Biogeosciences 13, 3915–3930. doi: 10.5194/bg-13-3915-2016
Young, H. (2018). Quantifying carbon dioxide fluxes in the air and water in Blowing Springs Cave, Arkansas (Theses and Dissertations), 2844. Available online at: https://scholarworks.uark.edu/etd/2844
Keywords: Arduino®, carbon dioxide, hydrology, soil carbon, karst, low-cost, critical zone
Citation: Blackstock JM, Covington MD, Perne M and Myre JM (2019) Monitoring Atmospheric, Soil, and Dissolved CO2 Using a Low-Cost, Arduino Monitoring Platform (CO2-LAMP): Theory, Fabrication, and Operation. Front. Earth Sci. 7:313. doi: 10.3389/feart.2019.00313
Received: 23 March 2019; Accepted: 08 November 2019;
Published: 26 November 2019.
Edited by:
Rolf Hut, Delft University of Technology, NetherlandsReviewed by:
Ryan D. Stewart, Virginia Tech, United StatesSierra Young, North Carolina State University, United States
Copyright © 2019 Blackstock, Covington, Perne and Myre. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joshua M. Blackstock, am1ibGFja0B1YXJrLmVkdQ==
 Joshua M. Blackstock
Joshua M. Blackstock Matthew D. Covington
Matthew D. Covington Matija Perne
Matija Perne Joseph M. Myre
Joseph M. Myre