Dynamic Failure Properties of Sandstone Under Radial Gradient Stress and Cyclical Impact Loading

In order to analyze the dynamic fracture responses of surrounding rocks in underground space to cyclic impact loads, a series of dynamic compressive tests were conducted using hollow cylindrical and intact sandstone specimens under confining pressures corresponding to 5, 10, and 12 MPa, and the hollow cylindrical sandstone were subject to radial gradient stresses. In the study, the impact loads were applied via a large diameter split Hopkinson pressure bar (SHPB). The results indicated that the hollow cylindrical sandstone exhibited a lower dynamic strength and larger critical strain under radial gradient stress as compared to intact sandstone. The dynamic strength and critical strain of all rock specimens increased significantly with the increase of the number of impact loading, whereas the cumulative absorption energy decreased. Under impact loads with velocity of 11.89 m/s, the cumulative absorption energy increased with the increase of confining pressure. The impact load was a complex process of repeated tension and compression which easily affected the hollow cylindrical sandstone in the radial direction during cyclical impact loading, and the characteristics of zonal disintegration indicated dominant tensile failure and local shear failure. However, a compression-shear failure mode was observed under confining pressure for intact sandstone.

Introduction

After the excavation of an underground space (e.g., underground tunnels and mining roadways), the surrounding rocks near the surface of the underground space experience a radial gradient stress. The vertical and horizontal stress values increase from zero to the primary stress values along their effect directions and change from the maximum value to the primary stress value along the directions perpendicular to their effect directions (Brady and Brown, 1985), as shown in Figure 1. Hence, it is necessary to examine the mechanical properties of the rock under a radial gradient stress in detail. Thus, hollow cylindrical rock specimens (with a hole along the axial direction of the rock specimens) were used to investigate the failure properties of rocks under a radial gradient stress (Wang et al., 2018a). Based on previous studies (Yang, 2016; Zhao et al., 2016, 2019; Weng et al., 2017), the radial gradient stress can be realized by the effect of the holes that significantly affect the failure properties of rocks. A series of conversional triaxial compression tests using hollow cylindrical rock specimens were performed by Lee et al. (1999) to investigate the potential effect of stress paths on the mechanical behavior of sandstone were carried out, and the tests were successfully used to determine the effect of stress paths on the mechanical behavior and to construct its failure surface (Lee et al., 1999). A simple and practical solution to designing an apparatus for a hollow cylinder test through a novel conventional triaxial cell, was proposed by Alsayed (2002) and an internal pressure loading configuration was also designed. A simulation numerical mode predicting the mechanical responses of concrete hollow cylinders under multiaxial compression stresses was proposed by Fantilli and Vallini (2010). With increases in the diameter of the borehole, the ductility of rocks decreases, and the level of peak strength increment in thick-walled hollow cylinder specimens decreases with an increase in the confining pressure (Hashemi et al., 2015). The deformation, peak strength, and crack damage behavior of hollow sandstone specimens, with various hole diameters (d = 0, 11, 15, and 26 mm), under varying confining pressures were investigated (Yang, 2016).

FIGURE 1

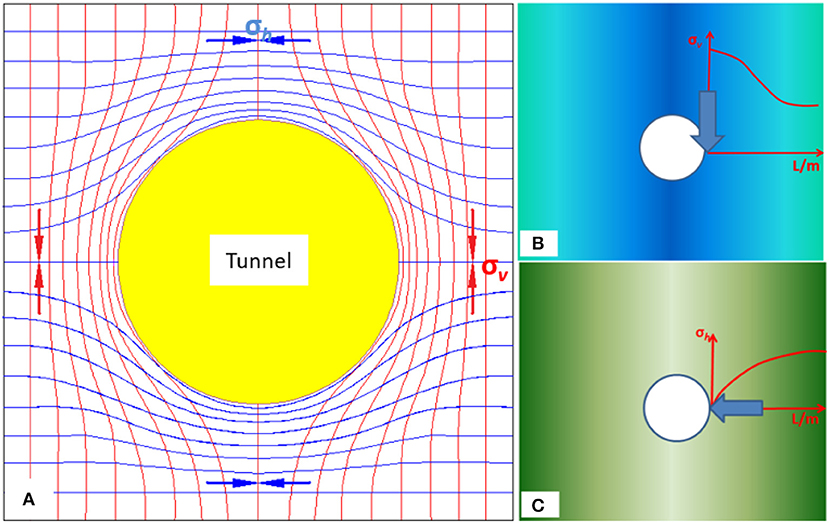
Figure 1. Radial stress gradient state of rocks: (A) overall perspective; (B) vertical stress; (C) horizontal stress.

However, the aforementioned experimental studies mainly focused on the static failure properties of the rocks. The surrounding rocks of the underground excavation are also affected by dynamic loadings such as repeated blasting, earthquakes, and rock bursts. It was reported that the dynamic loads significantly affected safety of underground tunnels (Wang et al., 2019b), and it is necessary to examine the dynamic failure properties of rocks under radial gradient stress. An ideal and reliable testing technique to measure the dynamic properties of rocks at a high strain rate (up to 10¹-10³ s⁻¹) corresponds to a split Hopkinson pressure bar (SHPB) test (Kolsky, 1949; Xia and Yao, 2015; Yin et al., 2019), which is commonly used to study mechanical properties of rock under uniaxial compression and tension loads (Li et al., 2009; Lu and Li, 2011; Gong and Zhao, 2014; Wu et al., 2019a,b). After a significant improvement in obtaining a complete triaxial loading test by many researchers, SHPB is a commonly used method to investigate dynamic mechanical properties under confining pressure (Li et al., 2008; Frew et al., 2010; Bailly et al., 2011; Peng et al., 2019). Many studies on the failure properties of intact cylindrical specimens under conversional confining pressure were performed using SHPB. However, there is a paucity of studies that use hollow cylindrical rock specimens.

Therefore, in the study, a novel SHPB testing system with a confining pressure vessel was used to investigate the failure properties of rocks under various confining pressures and cyclical impact loading. A series of tests using hollow cylindrical sandstone specimens were conducted under different levels of confining pressures subjected to multiple impacts. For the purpose of comparison, a series of confining pressure impact tests using intact specimens, under the same conditions as the hollow cylindrical specimens, were also performed systematically.

Experiential Procedures

Specimen Preparation

Based on the suggested methods for determining the basic mechanical parameters of rocks (Du et al., 2019; Wang et al., 2019a), the rocks are tested using specimens with a diameter corresponding to 50 mm and height corresponding to 100 mm. The mechanical parameters of the specimens are summarized in Table 1. With reference to studies related to SHPB tests (Zhou et al., 2012; Wu et al., 2019c), the size of specimens for impact loading test included specimens with a diameter corresponding to 50 mm and height corresponding to 25 mm. The top and bottom ends of the specimens were polished to ensure that the two surfaces were smooth and parallel to each other. Additionally, a circular hole with an aperture corresponding to 10 mm is drilled in the rock specimens used in the SHPB tests, as shown in Figure 2) (You and Su, 2010; Yang, 2016).

TABLE 1

Table 1. Physical and mechanical parameters of sandstone under static loading.

FIGURE 2

Figure 2. Specimen: (A) Intact specimen (Type A), (B) B Hollow specimen (Type B).

Testing Apparatus and Stress Path

An RMT-150C testing system was used to determine the basic mechanical indexes of the rock specimens with a diameter corresponding to 50 mm and height corresponding to 100 mm, while a novel SHPB testing system with a large diameter corresponding to 50 mm, was used to investigate the impact failure properties of hollow cylindrical rock specimens. The schematic of the SHPB experimental system used in the study is shown in Figure 3. A confining pressure vessel was located at the middle of the device, and the hydrostatic confinement stress was loaded by the vessel (Li et al., 2008; Xia and Yao, 2015). The SHPB testing system can apply impact loads with the medium at high strain rates ranging from 10¹-10³ s⁻¹. Additionally, the impact loads generated by a spindle-type structure punch in the SHPB testing system were shaped as a half-sine stress wave (Li et al., 2000). The experimental steps undertaken in the study was as follows:

FIGURE 3

Figure 3. Schematic of the SHPB experimental system.

Applied Confining Pressure

The rock specimen, packed in a barrel-shaped rubber sleeve, was placed in the confining pressure vessel, and fixed by the input and output bars. A small amount of butter was smeared into the contact face of the rock specimens and bars to minimize the friction effect. Additionally, confining pressures corresponding to 5, 10, and 12 MPa were applied on the curved surface of the cylindrical specimens. It was noted that the axial stress was equal to the value of the confining pressure.

Loaded Cyclic Impact Loads

Impact loads excited by a spindle-type structure punch were applied along the axial direction of the rock specimens. The information of stress wave was recorded and saved by a strain instrument. In the absence of macroscopic damage to the specimen, it is impacted again until the rock breaks. During SHPB testing of the sandstones under the three confining pressures, if the confining pressure corresponds to 5 MPa, then the impact velocity corresponds to 10.89 m/s, and the specimen should be impacted more than 10 times to undergo macroscopic crack damage. When the impact velocity corresponds to 13.90 m/s, the specimen is destroyed after two impacts. As the experiment should consider the cyclic impact and failure form analysis of the specimen, we comprehensively consider the test effect and operability of the test. Hence, the test mainly analyzes the mechanical characteristics of the specimen at the impact velocity corresponding to 11.89 m/s under the confining pressure corresponding to 5, 10, and 12 MPa. Furthermore, the test of the specimen under traditional confining pressure (radial uniform stress) under identical conditions is performed. A typical waveform is recorded during the test. As shown in Figure 4, the stress–strain curve, strain rate, and incident energy of the rock specimens are numbered as DH4-3, transmission energy, and absorption energy, respectively, and are calculated by Equations (1–7). The test data are shown in Table 2.

$\begin{array}{llll}\sigma & =& \frac{A_e}{2A_s}{E}_e\left[{\epsilon }_I(t)+{\epsilon }_R(t)+{\epsilon }_T(t)\right]& (1)\end{array}$

$\begin{array}{llll}\epsilon & =& \frac{C_e}{L_s}{\displaystyle {\int }_0^t}\left[{\epsilon }_I(t)-{\epsilon }_R(t)-{\epsilon }_T(t)\right]dt& (2)\end{array}$

$\begin{array}{llll}\stackrel{•}{\epsilon }& =& \frac{C_e}{L_s}\left[{\epsilon }_I(t)-{\epsilon }_R(t)-{\epsilon }_T(t)\right]& (3)\end{array}$

$\begin{array}{llll}{E}_I& =& \frac{A_e}{C_e}{\displaystyle {\int }_0^t}{\epsilon }_I^2(t)dt& (4)\end{array}$

$\begin{array}{llll}{E}_R& =& \frac{A_e}{C_e}{\displaystyle {\int }_0^t}{\epsilon }_R^2(t)dt& (5)\end{array}$

$\begin{array}{llll}{E}_T& =& \frac{A_e}{C_e}{\displaystyle {\int }_0^t}{\epsilon }_T^2(t)dt& (6)\end{array}$

$\begin{array}{llll}{E}_s& =& E_I-E_R-E_T& (7)\end{array}$

where A_e denotes the area of the input or output rods, A_s denotes the area of the rock specimens, ρ_e denotes the density of the input or output rods, C_e denotes the velocity of the input or output rods, L_s denotes the height of the rock specimens, t denotes the duration of the stress wave, E_s denotes the absorption energy of the rock specimens, and E_I, E_R, and E_T denote the incident, reflected, and transmitted energy, respectively.

FIGURE 4

Figure 4. Waveform of specimen under cyclic impact.

TABLE 2

Table 2. Mechanical properties of sandstone under cyclical impact loading.

Results and Discussion

Figure 4 shows the cyclic impact waveform of the specimen (DH4-3) under radial gradient stress. The impact velocities are well-controlled, and the incident wave is almost identical for each impact. With increases in the impact times, the waveform changes significantly, transmitted waves are increasingly smaller, and reflected waves are increasingly larger. With increases in the impact times, the waveform of the falling edge of the reflected wave changes from the initial gradual decline to a gentle, even rising. This is because increase in impact times continuously damages the specimen while the increased cracks decrease the wave impedance of the specimen. This is expressed as a decrease in the transmitted wave, increase in the reflected wave, and an early arrival of the peak value of the transmitted wave until macroscopic cracking occurs in the specimen, which prevents some of the stress wave from transmitting and directly reflects back to the input bar, thereby manifesting itself as a delay or even elevation of the reflected wave (for e.g., reflected waves 5 and 6 in Figure 4). It should be noted that the destructive form in Figure 4 corresponds to the destruction of different specimens.

Figure 5 shows the stress–strain curves of the specimen, which are obtained after the signal wave was processed by Equation (1). As shown in Figure 5, increases in the impact times changes the stress–strain curve in a similar pattern wherein strength decreases, the rebound becomes increasingly smaller, and the critical strain increases in different confining pressure conditions. Therefore, when combined with Figures 4, 5F, the variation in stress and strain with respect to impact times is analyzed. As shown in Figure 5F, the strength and deformability of the specimen exhibit a slight weakening in the first three impacts. With increases in the impact times, the amplitude of the stress–strain curve decreased. When compared with the previous impacts, the specimen does not show macroscopic cracks during the fourth impact and still exhibits good strength as shown in curve 4 in Figure 5. The strength of the specimen severely weakens, and the critical strain is high at the fifth impact, which displays macroscopic cracks as shown in Figure 4. It should be noted that the crack does not penetrate, and the specimen still exhibits a high strength of ~150 MPa. The critical strain of the specimen during the sixth impact evidently increases, and then the specimen crack leads to a certain misalignment as shown in Figure 4. The crack misalignment causes more stress waves to be reflected during the propagation when compared with the fifth impact, which was manifested because the reflection wave is significantly raised. However, given the existence of confining pressure, the specimen is still maintained as intact and exhibits a certain degree of strength. This is consistent with the two failure modes as shown in Figure 4. Additionally, under confining pressure conditions, even if macroscopic damage occurs in the specimen, the specimen still exhibits a certain compressive strength due to the presence of confining pressure as shown in curves 5 and 6 in Figure 4. It should be noted that although the stress–strain curves vary with impact times, they are similar in different confining pressures, and the strength and deformation of the specimen are more affected by the impact times under the radial gradient stress condition as shown in Figure 5. Therefore, we analyze the effects of radial gradient stress on the mechanical properties of sandstone in terms of several aspects such as strength, critical strain, and energy absorption.

FIGURE 5

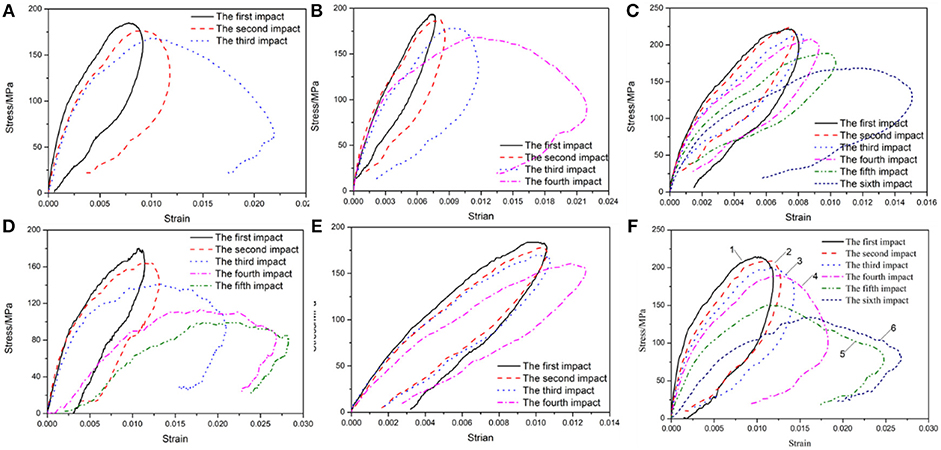
Figure 5. Stress–strain curves under cyclic impact: (A) DW3-7, (B) DW3-8, (C) DW3-9, (D) DH2-2, (E) DH3-3, (F) DH4-3.

Strength Characteristics

The relationship between the dynamic strength, strain rate, and impact times of the specimen under cyclic impact loading is shown in Figure 6. The representative strain rate in the study corresponds to the average strain rate, which is the average value of the strain rate between the specimen to reach a stress equilibrium state and peak stress (Zhou et al., 2012). As shown in Figure 6, an increase in the impact times decreases the strength and increases the strain rate under different confining pressure conditions. Additionally, the strain rate is more sensitive to the change in impact times under radial gradient stress conditions with the exception of Figure 5E because the specimen in DH3-3 only exhibits slight damage. For example, in Figure 6C, at identical impact level, the average strain rate and strength do not exhibit significant change during the first three impacts under radial uniform stress while it is change significantly after the second impact under the radial gradient stress. Furthermore, the average strain rate gradually increases. Specifically, during the last impact, the average strain rate is almost twice that at first time. This implies that when the impact progresses, the micro cracks of the specimen initiate and expand and result in a decrease in deformability of the specimen. This cannot be clearly observed from the strain–stress curves. Therefore, under cyclic shock conditions, the change in strain rate with impact times is used as a basis for determining the degree of damage of the specimen. This is also proven by the results of the DH3-3 specimen in Table 2, wherein it is observed that the change in the strain rate is small because only small local cracks appear after the impact.

FIGURE 6

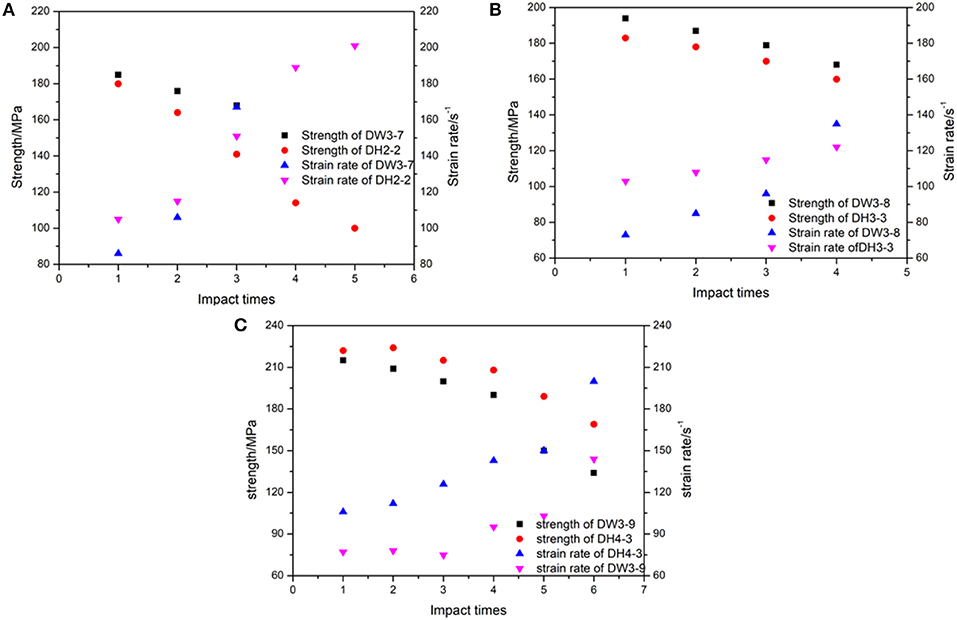
Figure 6. Variation in dynamic strength and strain rate with respect to impact time: (A) confining pressure at 5 MPa, (B) confining pressure at 10 MPa, (C) confining pressure at 12 MPa.

Figure 7 shows the variation in the dynamic strength of sandstone with impact times under different confining pressures at the impact velocity corresponding to 11.89 m/s. As shown in the Figure 8, the impact times and confining pressure affect the dynamic strength of sandstone (Guo et al., 2017; Ma et al., 2017; Zhao et al., 2018). Under identical impact level, the dynamic strength of sandstone under radial gradient stress is lower than that under uniform stress conditions. The dynamic strength varies significantly with the impact times under confining pressure at 5 MPa. With increases in the impact times, the strength of the specimen under gradient stress significantly decreases when compared with that under radial uniform stress, and the degree of decrease subsequently increases although the phenomenon is not evident with increases in the confining pressure.

FIGURE 7

Figure 7. Variation in dynamic strength with respect to impact times.

FIGURE 8

Figure 8. Variation in critical strain with respect to impact times.

Deformation Characteristics

Figure 8 shows the critical strain of sandstone with the impact times under different radial stresses at the impact velocity corresponding to 11.89 m/s. As shown in Figure 8, the critical strain of sandstone increases with increases in the impact times while it decreases with increases in the confining pressure under different radial stresses. At an identical impact level, the critical strain of sandstone under radial gradient stress exceeds that under radial uniform stress, and the rate of increase rises with increases in the impact times although the phenomenon is not evident with increases in confining pressure. The difference in strength and deformation with respect to the impact times under different types of confining pressures decrease with increases in the confining pressure. This is potentially due to the existence of a hole, and holes allow for greater deformation of the specimen in the radial direction. The confining pressure effect was also lower and resulted in a higher strain rate and a lower strength of the sandstone under radial gradient stress at an identical impact level (Wang et al., 2018b). Given the small size of the hole, the deformability provided by the free faces of the hole is limited. Hence, the aforementioned phenomena are also not evident with increases in the confining pressure. Additionally, the sandstone exhibits better deformation ability under the radial gradient stress although the deformation ability decreases with increases in impact times. In engineering practice, rock deformability can be increased by changing the model of rock stress or it can be accelerated by changing the model of rock stress.

Energy Absorption Characteristics

Figure 9 shows the change in cumulative energy absorbed by sandstone with respect to impact times under different radial stress modes. As shown in Figure 9, cumulative absorption energy of sandstone increases with the impact times under different conditions and decreases with increases in the confining pressure. The cumulative absorption energy varies with the impact times under different radial stress modes as shown in Figure 9. Generally, sandstone can absorb more energy under the condition of radial uniform stress while sandstone absorbs less energy in the first few impacts under radial gradient stress although this increases with increases in the confining pressure. Subsequently, the amount of absorbing energy can increase rapidly. This is different from the accumulative absorption energy of sandstone with increases in the impact times under uniform conditions. This is potentially related to the deformation characteristics of the specimen under radial gradient stress. Large deformations can better mitigate the dynamic load impact when the specimen is intact. Hence, when cracks appear, the amount of absorbing energy increases rapidly.

FIGURE 9

Figure 9. Variation in cumulative absorption energy with respect to impact times.

Failure Mode

Figure 10 shows the failure mode of the specimen after cyclic loading under different radial stress modes (damage was not observed after a single impact under different radial stresses). As shown in the figure, under the condition of a uniform radial stress, the failure mode of sandstone is dominated by compression and shear (Li et al., 2009; Lu and Li, 2011; Xia and Yao, 2015; Zhou et al., 2016; Wang et al., 2017). It is clearly seen that the evident shear cracks appear in the axial direction under confining pressures corresponding to 5 MPa and 12 MPa, as shown in Figure 10A. However, the failure mode of sandstone under radial gradient stress appears similar to the zonal disintegration phenomenon (Guo et al., 2017). As shown in Figure 10B, under the three levels of confining pressure, two evident zonings appear in the specimen as denoted by the red circle. The first area corresponds to a complete rock area. In the area, the whole area appears as a complete rock with few cracks. The second zone corresponds to the tensile failure zone and there is an evident loop line with the first zone. As shown in the lateral view of the specimen under confining pressure of 10 MPa, as shown in Figure 10B, the axial cracks of the specimen are essentially parallel to the loading stress and a shear failure exists locally, which is consistent with the characteristics of the zonal disintegration phenomenon as reported in extant studies (Li et al., 2017).

FIGURE 10

Figure 10. Failure modes of sandstone impact under cyclic loading under difference stress modes: (A) Type A, (B) Type B.

At the first few impacts, the specimen does not exhibit any damage (for e.g., macroscopic cracks). Additionally, a gradient stress exists in the radial direction of the specimen due to the existence of confining pressure and holes. The displacement is extended to the hole during the loading process and shrinks back during the unloading process. With increases in the impact times, the specimen is repeatedly compressed and stretched in the radial direction until the formation of zonal disintegration.

Hence, under cyclic impact, the specimen repeats the above process and is repeatedly subject to loading and unloading. Rock radial deformation occurs toward the hole in the loading section of the incident wave due to the existence of confining pressure and holes. The hole shrinks in the unloading section of the incident wave and subjects the specimen to repeated tension and compression in the radial direction until a detachment circle is formed. Chen and Weng noted that the transient unloading in surrounding rock can induce dynamic action on the rock near cavern periphery, thereby resulting in a tension crack zone (Chen et al., 2011; Weng et al., 2018). This is consistent with the cyclical impact failure mode of sandstone under gradient stress in the experiment. The rock outside the circle is dominated by tensile failure after the formation of the detachment circle.

With respect to the zonal disintegration phenomenon of deep rock subdivisions, several extant studies focused on numerical simulations, similar materials, and theoretical analysis, and many conclusions were obtained. However, the new findings discovered in the present study indicated that the zonal disintegration phenomenon can occur when using cyclic impact on sandstone under radial gradient stress, and this provides a new testing method to examine partition rupture although the feasibility requires further verification.

Conclusions

In the study, cyclic impact tests of sandstone under different confining pressures corresponding to 5, 10, and 12 MPa, were conducted using a SHPB. The mechanical properties of the specimens under radial gradient stress were compared with the mechanical properties of those under radial uniform stress. The conclusions obtained in the study are as follows:

Under an impact loads with velocity of 11.89 m/s, when compared with the impact under radial uniform stress, the sandstone under the radial gradient stress is repeatedly subjected to loading–unloading, and this indicates that the dynamic strength and critical strain increase with impact times. The rate of change in energy absorption characteristics with increases in impact times is slower, and the changes significantly weakened with an increase in the confining pressure. Additionally, the strain rate under radial gradient is more sensitive to the impact times.

Under the radial gradient stress, the failure mode of the sandstone reveals that the characteristics of the zonal disintegration phenomenon after cyclical impact is that the crushing zone is mainly subjected to tensile and partial shear failure. However, it corresponds to compression-shear under confining pressure.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

SW designed the tests, provided funds, and experimental apparatus. YL performed the tests and processed the data. KD performed the tests, wrote the paper, and also he was responsible for contacting the journal editor. JZ performed the lab tests.

Funding

The work described in this paper was supported by the National Natural Science Foundation of China (Grant Nos. 51604109, 51774326, 51704109, 41807259).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Alsayed, M. I. (2002). Utilising the hoek triaxial cell for multiaxial testing of hollow rock cylinders. Int. J. Rock Mech. Min. 39, 355–366. doi: 10.1016/S1365-1609(02)00030-8

CrossRef Full Text | Google Scholar

Bailly, P., Delvare, F., Vial, J., Hanus, J. L., Biessy, M., and Picart, D. (2011). Dynamic behavior of an aggregate material at simultaneous high pressure and strain rate: shpb triaxial tests. Int. J. Impact Eng. 38, 73–84. doi: 10.1016/j.ijimpeng.2010.10.005

CrossRef Full Text | Google Scholar

Brady, B. H. G., and Brown, E. T. (1985). Rock Mechanics for Underground Mining. London: Allen and Unwin.

Google Scholar

Chen, J. G. C., He, H., and Zhang, Y. X. (2011). Dynamic and static analysis of mechanism of loosen zone in surrounding rock of tunnels. Chin. J. Geotech. Eng. 33, 1964–1968.

Google Scholar

Du, K., Su, R., Tao, M., Yang, C., Momeni, A., and Wang, S. (2019). Specimen shape and cross-section effects on the mechanical properties of rocks under uniaxial compressive stress. B Eng. Geol. Environ. doi: 10.1007/s10064-019-01518-x

CrossRef Full Text | Google Scholar

Fantilli, A. P., and Vallini, P. (2010). Crushing failure in hollow cylinders made of quasi-brittle materials. Comput. Struct. 88, 426–436. doi: 10.1016/j.compstruc.2009.12.003

CrossRef Full Text | Google Scholar

Frew, D. J., Akers, S. A., Chen, W., and Green, M. L. (2010). Development of a dynamic triaxial kolsky bar. Meas. Sci. Technol. 21:105704. doi: 10.1088/0957-0233/21/10/105704

CrossRef Full Text | Google Scholar

Gong, F. Q., and Zhao, G. F. (2014). Dynamic indirect tensile strength of sandstone under different loading rates. Rock Mech. Rock Eng. 47, 2271–2278. doi: 10.1007/s00603-013-0503-7

CrossRef Full Text | Google Scholar

Guo, H., Guo, W., Zhai, Y., and Su, Y. (2017). Experimental and modeling investigation on the dynamic response of granite after high-temperature treatment under different pressures. Constr. Build. Mater. 155, 427–440. doi: 10.1016/j.conbuildmat.2017.08.090

CrossRef Full Text | Google Scholar

Hashemi, S. S., Melkoumian, N., and Taheri, A. (2015). A borehole stability study by newly designed laboratory tests on thick-walled hollow cylinders. J. Rock Mech. Geotech. Eng. 7, 519–531. doi: 10.1016/j.jrmge.2015.06.005

CrossRef Full Text | Google Scholar

Kolsky, H. (1949). An investigation of the mechanical properties of materials at very high rates of loading. Proc. Phys. Soc. Sect. B. 62, 676–700. doi: 10.1088/0370-1301/62/11/302

CrossRef Full Text | Google Scholar

Lee, D. H., Juang, C. H., Chen, J., Lin, H., and Shieh, W. (1999). Stress paths and mechanical behavior of a sandstone in hollow cylinder tests. Int. J. Rock Mech. Min. 36, 857–870. doi: 10.1016/S0148-9062(99)00063-7

CrossRef Full Text | Google Scholar

Li, Q. M., Lu, Y. B., and Meng, H. (2009). Further investigation on the dynamic compressive strength enhancement of concrete-like materials based on split Hopkinson pressure bar tests. Part II: numerical simulations. Int. J. Impact Eng. 36, 1335–1345. doi: 10.1016/j.ijimpeng.2009.04.010

CrossRef Full Text | Google Scholar

Li, X., Tao, M., Wu, C., Du, K., and Wu, Q. (2017). Spalling strength of rock under different static pre-confining pressures. Int. J. Impact Eng. 99, 69–74. doi: 10.1016/j.ijimpeng.2016.10.001

CrossRef Full Text | Google Scholar

Li, X., Zhou, Z., Lok, T. S., Hong, L., and Yin, T. (2008). Innovative testing technique of rock subjected to coupled static and dynamic loads. Int. J. Rock Mech. Min. 45, 739–748. doi: 10.1016/j.ijrmms.2007.08.013

CrossRef Full Text | Google Scholar

Li, X. B., Lok, T. S., Zhao, J., and Zhao, P. J. (2000). Oscillation elimination in the Hopkinson bar apparatus and resultant complete dynamic stress–strain curves for rocks. Int. J. Rock Mech. Min. 37, 1055–1060. doi: 10.1016/S1365-1609(00)00037-X

CrossRef Full Text | Google Scholar

Lu, Y. B., and Li, Q. M. (2011). About the dynamic uniaxial tensile strength of concrete-like materials. Int. J. Impact Eng. 38, 171–180. doi: 10.1016/j.ijimpeng.2010.10.028

CrossRef Full Text | Google Scholar

Ma, D., Ma, Q., and Yuan, P. (2017). SHPB tests and dynamic constitutive model of artificial frozen sandy clay under confining pressure and temperature state. Cold Reg. Sci. Technol. 136, 37–43. doi: 10.1016/j.coldregions.2017.01.004

CrossRef Full Text | Google Scholar

Peng, K., Liu, Z. P., Zou, Q. L., Zhang, Z. Y., and Zhou, J. Q. (2019). Static and dynamic mechanical properties of granite from various burial depths. Rock Mech. Rock Eng. doi: 10.1007/s00603-019-01810-y. [Epub ahead of print].

CrossRef Full Text | Google Scholar

Wang, S., Li, X., Yao, J., Gong, F., Li, X., Du, K., et al. (2019a). Experimental investigation of rock breakage by a conical pick and its application to non-explosive mechanized mining in deep hard rock. Int. J. Rock Mech. Min. Sci. 122:104063. doi: 10.1016/j.ijrmms.2019.104063

CrossRef Full Text | Google Scholar

Wang, S. F., Li, X. B., Du, K., Wang, S. Y., and Tao, M. (2018a). Experimental study of the triaxial strength properties of hollow cylindrical granite specimens under coupled external and internal confining stresses. Rock Mech. Rock Eng. 51, 2015–2031. doi: 10.1007/s00603-018-1452-y

CrossRef Full Text | Google Scholar

Wang, S. M., Liu, Y., Zhou, J., Wu, Q., Ma, S., and Zhou, Z. (2018b). Dynamic compressive characteristics of sandstone under confining pressure and radial gradient stress with the SHPB test. Adv. Civ. Eng. 2018, 1–8. doi: 10.1155/2018/1387390

CrossRef Full Text | Google Scholar

Wang, Y. X., Guo, P. P., Ren, W. X., Yuan, B. X., Yuan, H. P., Zhao, Y. L., et al. (2017). Laboratory investigation on strength characteristics of expansive soil treated with jute fiber reinforcement. Int. J. Geomech. 17:04017101. doi: 10.1061/(ASCE)GM.1943-5622.0000998

CrossRef Full Text | Google Scholar

Wang, Y. X., Shan, S. B., Zhang, C., and Guo, P. P. (2019b). Seismic response of tunnel lining structure in a thick expansive soil stratum. Tunn. Undergr. Space Technol. 88, 250–259. doi: 10.1016/j.tust.2019.03.016

CrossRef Full Text | Google Scholar

Weng, L., Huang, L., Taheri, A., and Li, X. (2017). Rockburst characteristics and numerical simulation based on a strain energy density index: a case study of a roadway in linglong gold mine, china. Tunn. Undergr. Space Technol. 69, 223–232. doi: 10.1016/j.tust.2017.05.011

CrossRef Full Text | Google Scholar

Weng, L., Li, X., Taheri, A., Wu, Q., and Xie, X. (2018). Fracture evolution around a cavity in brittle rock under uniaxial compression and coupled static–dynamic loads. Rock Mech Rock Eng. 51, 531–545. doi: 10.1007/s00603-017-1343-7

CrossRef Full Text | Google Scholar

Wu, Q., Chen, L., Shen, B., Dlamini, B., Li, S., and Zhu, Y. (2019a). Experimental investigation on rockbolt performance under the tension load. Rock Mech. Rock Eng. doi: 10.1007/s00603-019-01845-1. [Epub ahead of print].

CrossRef Full Text | Google Scholar

Wu, Q., Li, X., Weng, L., Li, Q., Zhu, Y., and Luo, R. (2019b). Experimental investigation of the dynamic response of prestressed rockbolt by using an SHPB-based rockbolt test system. Tunnel. Undergr. Space Technol. 93:103088. doi: 10.1016/j.tust.2019.103088

CrossRef Full Text | Google Scholar

Wu, Q. H., Weng, L., Zhao, Y. L., Guo, B. H., and Luo, T. (2019c). On the tensile mechanical characteristics of fine-grained granite after heating/cooling treatments with different cooling rates. Eng Geol. 253, 94–110. doi: 10.1016/j.enggeo.2019.03.014

CrossRef Full Text | Google Scholar

Xia, K. W., and Yao, W. (2015). Dynamic rock tests using split Hopkinson (kolsky) bar system—a review. J. Rock Mech. Geotech. Eng. 7, 27–59. doi: 10.1016/j.jrmge.2014.07.008

CrossRef Full Text | Google Scholar

Yang, S. Q. (2016). Experimental study on deformation, peak strength and crack damage behavior of hollow sandstone under conventional triaxial compression. Eng. Geol. 213, 11–24. doi: 10.1016/j.enggeo.2016.08.012

CrossRef Full Text | Google Scholar

Yin, Z. Q., Chen, W. S., Hao, H., Chang, J. C. C., Zhao, G. M., Chen, Z. Y., et al. (2019). Dynamic compressive test of gas-containing coal using a modified split Hopkinson pressure bar system. Rock Mech. Rock Eng. doi: 10.1007/s00603-019-01955-w. [Epub ahead of print].

CrossRef Full Text | Google Scholar

You, M. Q., and Su, C. D. (2010). Study of strength and failure of hollow cylinders and rings of sandstone under compression-tension stress. Chin. J. Rock Mech. Eng. 29, 1096–1105.

Google Scholar

Zhao, Y., Wang, Y., Wang, W., Tang, L., Liu, Q., and Cheng, G. (2019). Modeling of rheological fracture behavior of rock cracks subjected to hydraulic pressure and far field stresses. Theor. Appl. Fract. Mech. 101, 59–66. doi: 10.1016/j.tafmec.2019.01.026

CrossRef Full Text | Google Scholar

Zhao, Y. L., Zhang, L., Wang, W., Pu, C., Wan, W., and Tang, J. (2016). Cracking and stress–strain behavior of rock-like material containing two flaws under uniaxial compression. Rock Mech. Rock Eng. 49, 2665–2687. doi: 10.1007/s00603-016-0932-1

CrossRef Full Text | Google Scholar

Zhao, Y. L., Zhang, L. Y. Z., Wang, W. J., Wan, W., and Ma, W. H. (2018). Separation of elastoviscoplastic strains of rock and a nonlinear creep model. Int. J. Geomech. 2018:04017129. doi: 10.1061/(ASCE)GM.1943-5622.0001033

CrossRef Full Text | Google Scholar

Zhou, J., Li, X., and Mitri, H. S. (2016). Classification of rockburst in underground projects: comparison of ten supervised learning methods. J. Comput. Civ. Eng. 30:04016003. doi: 10.1061/(ASCE)CP.1943-5487.0000553

CrossRef Full Text | Google Scholar

Zhou, Y. X., Xia, K., Li, X. B., Li, H. B., Ma, G. W., Zhao, J., et al. (2012). Suggested methods for determining the dynamic strength parameters and mode-i fracture toughness of rock materials. Int. J. Rock Mech. Min. 49, 105–112. doi: 10.1016/j.ijrmms.2011.10.004

CrossRef Full Text | Google Scholar