CHNOSZ: Thermodynamic Calculations and Diagrams for Geochemistry

Dick, Jeffrey M.

doi:10.3389/feart.2019.00180

TECHNOLOGY AND CODE article

Front. Earth Sci., 16 July 2019

Sec. Geochemistry

Volume 7 - 2019 | https://doi.org/10.3389/feart.2019.00180

CHNOSZ: Thermodynamic Calculations and Diagrams for Geochemistry

$\nJeffrey M. Dick,$ Jeffrey M. Dick^1,2^*

¹Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring, Ministry of Education, Central South University, Changsha, China
²School of Geosciences and Info-Physics, Central South University, Changsha, China

Thermodynamic calculations are an essential tool for many areas of geochemistry. Thermodynamics provides a framework for the quantitative description and prediction of the solubilities and relative stabilities of different minerals, metal transport in hydrothermal fluids, and geobiochemical reactions that drive microbial metabolism and contribute to the compositional variation of proteins. Accessible and up-to-date software and databases are important for the development and reproducible application of thermodynamic models. CHNOSZ is a free package for R that has been frequently updated since its first release in 2008. The package provides an integrated set of functions to calculate the standard molal thermodynamic properties and chemical affinities of reactions. It uses the graphical capabilities of R to produce high-quality chemical activity diagrams for aqueous species and predominance diagrams including Eh-pH (Pourbaix) and logf _O₂ -T diagrams. The extensive database utilizes the well-known revised Helgeson-Kirkham-Flowers (HKF) equations for aqueous species. Recent additions to the database include the Berman equations for minerals, the Deep Earth Water model, which extends the applicability of the HKF equations to higher pressures, and the Akinfiev-Diamond model for aqueous nonelectrolytes. The package comes with many types of documentation, including technical help pages with short code examples, longer code demos, and in-depth vignettes combining code, text and graphics, giving users a wide array of starting points for their own research. This paper provides a concise overview of the package and illustrates the new features using examples selected from the literature. Although the package does not provide a complete chemical speciation model, numerous examples from the package demonstrate the ease of reproducing selected published calculations and sometimes identifying issues with existing datasets and models.

1. Introduction

Thermodynamics is an established tool for both low-temperature and hydrothermal geochemistry (Anderson, 1998), and is more recently being recognized for applications in organic geochemistry and geobiochemistry. Thermodynamic calculations can provide insight on the generation of petroleum (Helgeson et al., 2009), reactions involving more mature organic matter (Dick et al., 2013), and even organic reactions occurring deep in subduction zones (Sverjensky et al., 2014a,b). At the geobiological interface, thermodynamic calculations can be used to estimate the energy required for biomass synthesis (LaRowe and Amend, 2016) as well as the energy that is made available by inorganic and organic disequilibria in the environment (Shock et al., 2010; Rogers and Schulte, 2012; Osburn et al., 2014). Thermodynamic calculations have also been used to explore geochemical influences on the relative abundances of microbial taxa and the chemical compositions of DNA and proteins in diverse environments (Dick and Shock, 2013; Dick et al., 2019).

These and many other calculations are becoming more tractable through the expansion of thermodynamic databases to include more organic and biochemical species at greater ranges of temperature and pressure (Shock and Helgeson, 1990; Shock, 1995; Amend and Helgeson, 1997; Helgeson et al., 1998; Richard and Helgeson, 1998; Dick et al., 2006; LaRowe and Helgeson, 2006a,b; LaRowe and Dick, 2012; Kitadai, 2014; Canovas and Shock, 2016; Lowe et al., 2017; Azadi et al., 2019). However, there are limited choices of software packages for thermodynamic calculations and diagrams commonly used in hydrothermal geochemistry. Moreover, relatively few programs are available under open-source licenses, which are recognized for their benefit to reproducible research (Jiménez et al., 2017). For instance, the Wikipedia page for “Pourbaix diagram” has nine external links to software¹, of which three are open-source. None of the latter has a thermodynamic database that permits calculations for minerals and aqueous species above 100°C.

The CHNOSZ package was developed to promote and take advantage of the convergence of thermodynamic, biomolecular, and environmental data with a focus on visualization and a high degree of reproducibility. The initial development of the package provided functions for calculating the standard molal thermodynamic properties of species and reactions, similar to the functionality of SUPCRT92 (Johnson et al., 1992), which is widely used for thermodynamic calculations in aqueous geochemistry at temperatures and pressures up to 1,000°C and 5,000 bar. The R software environment (R Core Team, 2019) permits interactive use, graphical output and data-intensive calculations that are not feasible with SUPCRT92.

CHNOSZ is freely available on the Comprehensive R Archive Network (CRAN) for all major desktop operating systems. Because all the steps for any calculation can be saved and shared as R script files, reproducibility is greatly enhanced. Another major advantage of R is that it supports documentation in a variety of formats, which is used extensively in the package to reproduce many published calculations. Development over more than 10 years has yielded a package with a comprehensive database that is integrated with functions to specify a chemical system, calculate chemical affinities of reactions, and generate many types of chemical activity diagrams that are useful for characterizing inorganic, organic, and biochemical reactions in aqueous geochemistry.

A timeline summarizing the major developments of the package since its initial announcement (Dick, 2008) is presented in Figure 1. The text describes these developments in more detail and gives an updated overview of the package to inform both current and prospective users about features that may be applicable to their research problems. The overview is combined with examples selected from the literature to illustrate the actual usage of CHNOSZ and demonstrate how the package can be used to rapidly investigate the sensitivity of the calculations to choices of models and data and reveal possible issues related to assumptions about the reactions in geochemical systems.

FIGURE 1

Figure 1. Timeline of the development of CHNOSZ since 2008. Red boxes indicate major release versions, blue boxes indicate new features or other updates, and green boxes indicate the addition of vignettes to the package documentation.

2. Methods

This section summarizes the workflow in CHNOSZ and describes examples for the calculation of standard thermodynamic properties of reactions and generation of predominance and solubility diagrams.

2.1. Standard Thermodynamic Properties and Affinity

The data sources and major functions in CHNOSZ are connected by the main user workflow, which is indicated by the thick lines in Figure 2. The first function in the main workflow, named info, allows searching the thermodynamic database using chemical formulas or names and returns the numerical index of matching species in the database. Given one or more species indices, info returns the thermodynamic data for those species and also performs checks of the self-consistency of the thermodynamic properties and parameters. These include checking that the standard Gibbs energy, enthalpy and entropy of formation at 25°C and 1 bar (ΔG_f°, ΔH_f°, and ΔS_f°) satisfy ΔG_f° = ΔH_f° − TΔS_f°. (ΔS_f° in this equation is calculated by combining the standard entropy of the species in the database (S°) with the entropies of the elements.) Other checks are done to compare the 25°C values of the heat capacity and volume in the database with the heat capacity and volume equation-of-state parameters for that species. These checks are not performed if the data entered for a species has missing 25°C values for heat capacity, volume, or one of ΔG_f°, ΔH_f°, or S°, but instead the values of the missing properties are computed from the available parameters in order to supply a full set of thermodynamic properties.

FIGURE 2

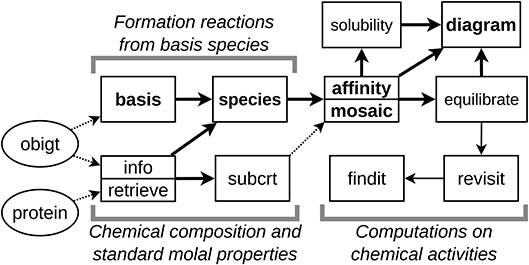
Figure 2. Databases (ellipses) and major functions (rectangles) in CHNOSZ. Thick lines represent the main workflow, thin lines the extended workflow, and dotted lines the transfer of data between functions. Bold text indicates functions used in the maximum affinity method for predominance diagrams. Split rectangles represent pairs of similar functions with more basic (top) and advanced (bottom) features.

For calculating the properties of chemical reactions, the function named subcrt uses info to get the thermodynamic properties from the database, performs calculations at higher temperature (T) and pressure (P), and combines the properties of the reactants and products. Note that subcrt checks the reaction balance using the chemical formulas of species in the database. Any user-entered reaction that is not balanced produces a warning. However, if the basis species are defined, then incomplete reactions can be automatically balanced.

To illustrate the actual usage of the program, a transcript is shown in Figure 3 of an R session using CHNOSZ to calculate the standard and overall Gibbs energy of aerobic oxidation of ammonia at conditions representative of the interface between seawater and hydrothermal vent fluid (Reed et al., 2015). A brief explanation of each command follows. Note that “>” is the R command prompt; the prompts are numbered here for easier reference. 01> Load the CHNOSZ package. 02> Load a predefined set of basis species that includes default values of logarithm of chemical activity (“logact”); this calculation uses different values that are specified below. 03> Change the state of the O₂ basis species from gas to aqueous. 04> Change the units of energy in the output to Joules (the default is calories). 05> Calculate the standard molal thermodynamic properties of a reaction at 2°C and 210 bar. As entered, the reaction is unbalanced (1 mole of NH₃ reacts to give 1 mole of NO₂^-); however, subcrt automatically balances it using the available basis species. The output of subcrt consists of two parts: the reaction definition and the calculated properties. The bold number shown in Figure 3 is the standard Gibbs energy of the reaction; it is equal to the value listed for this reaction in Table S1 of Reed et al. (2015).

FIGURE 3

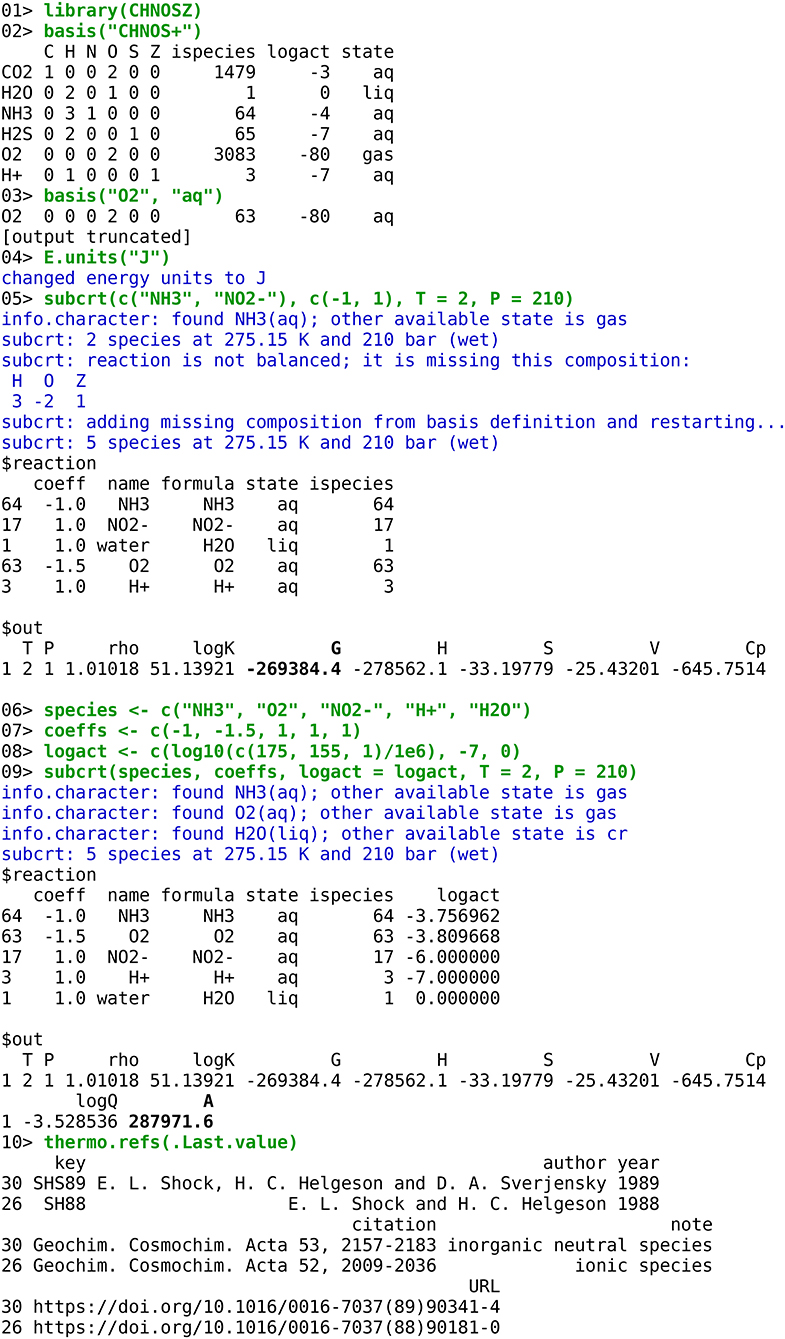
Figure 3. Transcript of a microbial bioenergetic calculation in CHNOSZ. User-entered commands are in green text, messages from functions are in blue text, and output (results) is in black text. The bold numbers are the calculated values, in J/mol, of standard Gibbs energy for ammonia oxidation, and chemical affinity (opposite of overall Gibbs energy of reaction) calculated using activities of species from Table S3 of Reed et al. (2015).

So that the code is easier to follow, the input for the calculation of chemical affinity is defined in separate lines: 06> the formulas of the species in the reaction, 07> their reaction coefficients, and 08> the logarithms of activity used to calculate the activity quotient for the reaction (Q). The values of activity, which are equal to molality assuming that activity coefficients are unity, were obtained from Table S3 of Reed et al. (2015), except for H₂O, which is assigned unit activity. 09> The second call to subcrt calculates the standard molal properties of the reaction as above, but also gives the values of Q and the chemical affinity (A), which is highlighted in bold. The opposite of this value, i.e., the overall Gibbs energy of reaction, is equal to that shown for aerobic oxidation of ammonia in Figure 6 of Reed et al. (2015). 10> Passing the output of subcrt to the function named thermo.refs retrieves the reference information for the species involved in the reaction, other than H₂O. This function can also be used to look up the references given the species index for any species in the database.

2.2. Basis Species and Formed Species

The type of calculation described above is useful for single combinations of reactions and conditions, but for making diagrams, it is convenient to be able to calculate the chemical affinities of reactions representing the formation of any number of “species of interest” on an n-dimensional grid of variable temperature (T), pressure (P), ionic strength, or chemical activities of basis species. This supports the creation of a wide range of diagrams, such as those showing chemical activities of species as a function of one variable or predominance diagrams as a function of two variables.

A chemical system is defined by first using basis to select the basis species. The number of basis species, like components, is the minimum needed to represent the compositional space of a chemical system. Operationally, in CHNOSZ there must be one basis species for each element in the system and charge, if present. A set of predefined basis species, or any stoichiometrically valid user-defined set, can be used. Following the setting of basis species, species is used to generate a stoichiometric matrix representing the reactions to form the species of interest from the basis species. The program does not automatically find these species; it is up to the user to identify the species. The info function can be used to help find the species by name or chemical formula, and another function, retrieve, is provided for finding species with a desired combination of chemical elements. In addition, a listing of the entire database can be produced using the function dumpdata and opened and searched using a spreadsheet program; this file (alldata.csv) is also available for download from the project website.

The function named affinity is used to calculate the chemical affinities of formation reactions by combining the standard Gibbs energies of reactions (taken from subcrt) with values of the chemical activities of basis species and reference values for the species of interest (most often equal activities). This can be done at a single set of conditions, or one or more variable T, P, ionic strength, and/or chemical activities of basis species, depending on the arguments passed to the function. It is also possible to set the activities of one or more basis species to those calculated from a mineral buffer assemblage; some common buffers such as hematite-magnetite (HM) and pyrite-pyrrhotite-magnetite (PPM) are built in, and others can be added using the mod.buffer command. The ability to make a grid for two variables permits the construction of Eh-pH, logf _O₂-T, and other types of chemical activity diagrams. Affinity calculations along a transect involving simultaneous changes of multiple variables are also possible.

After running a calculation in CHNOSZ that involves setting the basis species and formed species, or changing any other settings including the units and database, the reset command can be used to restore all settings to their default values.

2.3. Maximum Affinity Diagrams and Mosaic Calculations

By definition, the basis species have unambiguous stoichiometric coefficients in any reaction representing the formation of a particular species. However, the basis species themselves do not determine the stoichiometric constraints on possible chemical transformations between species. These constraints are present in descriptions of reactions that are, for example, “balanced on aluminum” or “conserve Al.” In CHNOSZ, these constraints are implemented as balancing coefficients that must be specified in order to make diagrams representing the relative stabilities of the species. By default, the balancing coefficients correspond to the reaction coefficient of the first basis species that is present in all of the formation reactions of the species; this is referred to as the “conserved basis species.” Defining the main metal in the system, or a corresponding metal-bearing species, as the first basis species, usually provides the desired balancing constraints. In organic systems where reactions are often balanced on carbon, it is convenient to use a species such as CO₃^-2 as the conserved basis species (see section 4.1). Less often, arguments in the diagram and equilibrate functions can be used to balance on a different basis species, unity (one mole of the formed species on either side of the reaction), volumes of species, or any user-supplied numerical value.

Equal-activity or predominance diagrams as a function Eh and pH, logf _O₂ and T, or any two other variables, can be made efficiently using the maximum affinity method (MAM), which does not involve an equilibration step. In a simple scenario, with balancing coefficients equal to unity, the affinities of reactions to form the species of interest are computed at grid points on the diagram; the species with the highest affinity is identified as the predominant one at that point. This is certainly not a novel approach to the construction of predominance diagrams; for example, Singh et al. (2017) describe a similar method to identify the range of highest relative stability of a particular solid or ionic species over others by finding the reaction with minimum Gibbs free energy. However, this method appears to have no commonly accepted name, and no published example could be found where the method is compared with the exact calculation of equal-activity boundaries from equilibrium constants, taking into account the possibility of balancing coefficients other than unity. Such a comparison is shown in Figure S1 and described in more detail in the Supplementary Materials.

An Eh-pH diagram for aqueous sulfur species made using the MAM is shown in Figure 4A. This requires only four calls to CHNOSZ functions, as follows. 01> Define the basis species. 02> Define the species of interest (formed species), which are species whose compositions can be formed from the basis species. 03> Calculate the chemical affinity of the formation reactions on an Eh-pH grid at 200°C. Because this is above the boiling point of water at 1 bar, the pressure is automatically taken from the liquid-vapor saturation curve (known as P_sat), which is about 15.5 bar at this temperature. 04> Make the diagram, using arguments to set the color of the stability field boundaries and species names. The diagram function applies axis labels based on the variables used in the affinity calculation, and also masks the areas outside of the water stability region; these are the gray areas in Figure 4. Optionally, the water stability limits can be drawn as lines, or excluded altogether.

FIGURE 4

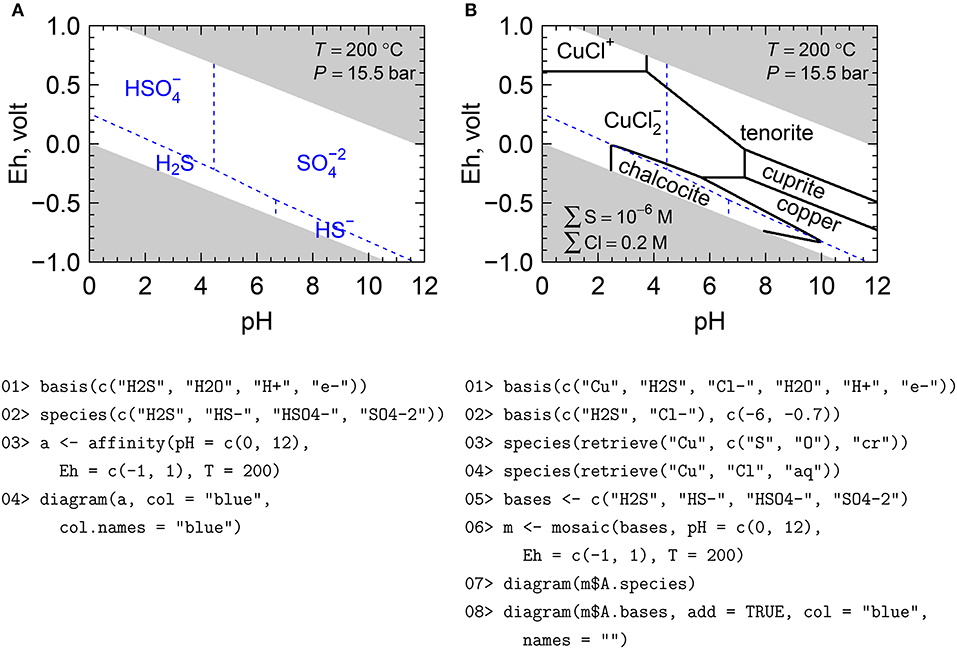
Figure 4. (A) Eh-pH predominance diagram for aqueous sulfur species, and (B) mosaic diagram for Cu–S–Cl species. Shaded areas of the diagrams are outside the stability region of liquid H₂O. Thermodynamic data for minerals are from Helgeson et al. (1978) and data for aqueous species are from Shock and Helgeson (1988), Shock et al. (1989), and Sverjensky et al. (1997), except Cu(I) species from Akinfiev and Zotov (2001). The R script shown here is simplified for clarity; the complete script, which includes code to increase the plot resolution and to adjust the colors and labels, is available (Dick, 2019).

It is often important to consider the speciation of the basis species that are themselves used to write the reactions. For example, reactions to form sulfide minerals can be written with HSO₄^-, SO₄^-2, H₂S, or HS^- depending on the values of Eh and pH. The mosaic function facilitates the construction of a combined diagram by joining the corresponding subsectors of diagrams for each candidate basis species. In this manner, Eh-pH diagrams having a pyrite or other sulfide mineral wedge (Garrels and Christ, 1965; Wood, 1998) can easily be created. In general, there are not sharp transitions between basis species, but they coexist near their equal-activity boundaries, and their variable concentrations consequently affect the affinities of formation of the species. Calculations of the speciation of basis species are activated using the “blend” argument of mosaic, which is TRUE by default. If this argument is changed to FALSE, then sharp boundaries between the basis species are assumed, which may be required to reproduce some published diagrams. Note added in revision: An error in the calculation of the speciation of basis species was found in version 1.3.2 of CHNOSZ, on which this paper is based. This bug is apparent as a slight negative curvature around the chalcocite field that is barely visible in Figure 4B but is more noticeable in Figure S2. A correction has been applied to the development version of the package, which is available on R-Forge (see section 4.3).

The diagram for the Cu–S–Cl–H₂O system in Figure 4B was made using the mosaic function together with the maximum affinity method, as follows. 01> Set the basis species. 02> Set the logarithms of activities of S and Cl in the system, which correspond to molalities assuming activity coefficients of unity. 03> Add all of the Cu-bearing minerals from the database whose formulas have any number of S and O atoms (including native copper). 04> Add all of the Cu-bearing aqueous species from the database whose formulas have any number of Cl atoms. 05> Define the basis species that will change across the diagram; these are the same as the species shown in Figure 4A. 06> Perform the mosaic calculation. This function runs affinity for all possible combinations of basis species, then combines the results according to the relative abundances of the basis species. 07> Make a diagram for the species defined in lines 3 and 4. 08> Overlay the equal-activity lines for the basis species, which are identical to those shown in Figure 4A.

Note that Figure 4B is qualitatively different from the diagram for the same chemical system calculated by Caporuscio et al. (2017) using CHNOSZ. Figure 5 in that paper can be reproduced in CHNOSZ by (1) activating the SLOP98 optional data file in order to load data for aqueous Cu(I) species that have since been superseded in CHNOSZ (see section 3.1), and (2) changing the balancing coefficients to unity, which can be done by adding the argument “balance = 1” to line 7 of the code in Figure 4B. The complete code is available (Dick, 2019) and the resulting diagram is in Figure S2. By setting the balancing coefficients to unity, the boundaries of the predominance fields represent reactions written for one mole of the species on each side of the reaction. With this balancing constraint, reactions involving chalcocite (Cu₂S) have native Cu in addition to another Cu-bearing species on the other side of the reaction. In contrast, the appearance of two Cu-bearing species on one side of the reaction is not possible if the reactions are balanced on Cu, which is the default method in CHNOSZ for this system. The geometry of the diagram for reactions balanced on Cu (Figure 4B) is consistent with earlier publications (e.g., Garrels and Christ, 1965, Figure 7.25; Brookins, 1988, Figure 28). Diagrams made using different balancing constraints require different interpretations. Figure 5 of Caporuscio et al. (2017), in which the chalcocite field extends to pH <0 and there is no stability field for tenorite, is valid only under the assumption that Cu participates in all reactions with chalcocite, as represented by equations 3a–3d in their paper.

FIGURE 5

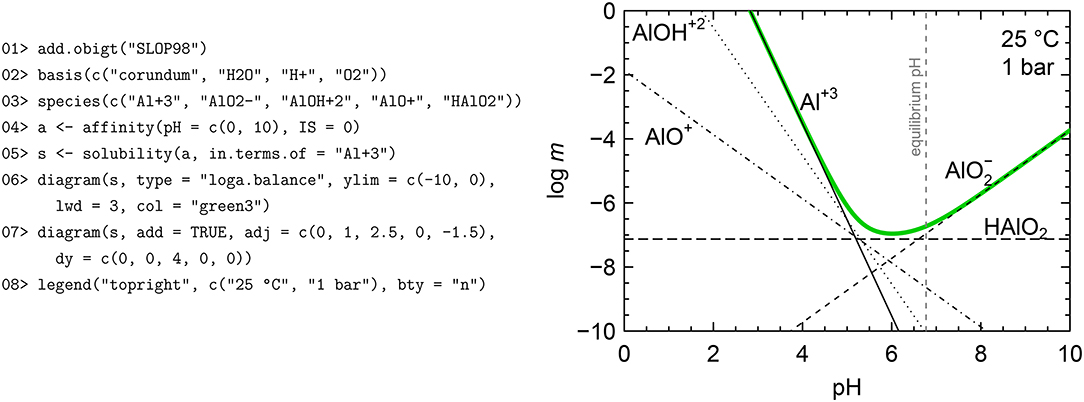
Figure 5. Solubility of corundum as a function of pH. Equilibrium molalities of aqueous Al species are identified (black lines) together with the their total molality, corresponding to the solubility of corundum (green line). The vertical line shows the pH of the solution in equilibrium with corundum (dashed gray line). Thermodynamic data for corundum is from Berman (1988) and data for aqueous species are from Shock et al. (1997). The R script shown here is simplified for clarity; the complete script, which includes code to calculate and plot the pH values, is available (Dick, 2019).

2.4. Speciation and Solubility Diagrams

In CHNOSZ, two functions can be used to calculate the chemical activities of species in equilibrium. The first of these, named equilibrate, computes the relative abundances of aqueous species for a given total concentration (activity or molality) of the conserved basis species. If the balancing coefficients are all equal to one, then equilibrium activities are calculated using the Boltzmann distribution with exponential terms derived from the affinities of formation reactions (see Equations 3–7 in Dick and Shock, 2013). Otherwise, equilibrium chemical activities are computed by solving a system of equations (see Equations 12–14 in Dick, 2008 for a specific example involving proteins). Unlike a free energy minimization for a system with minerals and an aqueous phase, specifying the total concentration of the conserved basis species corresponds in general to a metastable equilibrium. However, it is possible to use the concentration of the conserved basis species as a variable in the equilibrium calculation, which can be useful for calculations along mixing paths and temperature gradients where the concentration of a dissolved component is available from experiments or models (see section 4.1).

Equilibration calculations can also be used to make diagrams for two variables, but they are more computationally intensive than the maximum affinity method. Unlike the MAM, where predominance field boundaries are defined by a single reference value for equal activities of species without explicit provision for mass balance constraints, an equilibration calculation in CHNOSZ uses a single mass balance constraint, which is given by the total concentration of the conserved basis species. For systems where the balancing coefficients are other than unity, the activities of the predominant species vary across the diagram, which leads to the appearance of curved predominance field boundaries, particularly near points of equal activity of three or more species. Examples and further discussion are available in the vignette “Equilibrium in CHNOSZ.”

The second function for equilibrium calculations, named solubility, considers equilibrium between one solid phase and multiple dissolved species. Again, the mass balance is expressed in terms of a single conserved basis species, so the current functionality is applicable to systems involving only one metal but any number of possible ligands. An example calculation for corundum, based on a diagram in Manning (2013), is shown in Figure 5 and described here. 01> Load superseded data for aqueous Al species (Shock et al., 1997) from the optional SLOP98 data file (see section 3.1). 02> Set the basis species; because we are calculating the solubility of corundum, it must be listed first. 03> Define the aqueous species. All of these must be Al-bearing species in order to balance the reactions on the conserved basis species, which is Al⁺³. 04> Calculate the affinities of the reactions to form the species from the basis species as a function of pH. The temperature and pressure are left at their default values, but the ionic strength is explicitly set to 0 to express the concentrations as molality instead of activity (see section 3.3). 05> Calculate the molalities of all the aqueous species in equilibrium with corundum, and the total solubility. Because the formula of corundum (Al₂O₃) has 2 Al, it is necessary to specify that the solubility is calculated in terms of Al⁺³, or moles of Al in solution. 06> Start the diagram by plotting the solubility curve (green). Here, “loga.balance” refers to the total molality of the conserved basis species. 07> Add lines showing the molalities of the individual aqueous species. The “adj” (horizontal adjustment) and “dy” arguments are used to manually position the labels. 08> Add the legend. Additional code, omitted from Figure 5 for clarity, can be used to calculate neutral pH using the equilibrium constant of H₂O dissociation and the pH of the solution in equilibrium with corundum from the electroneutrality condition (Dick, 2019).

2.5. Extended Workflow and Considerations for Biomacromolecules

As described by Dick (2008), normalization of protein formulas by dividing them by protein length (number of amino acid residues) permits calculations of the relative abundances of proteins in metastable equilibrium that are comparable to natural ranges. The calculated chemical activities can be used in further calculations with the function named revisit. In particular, the Gibbs energy of transformation (ΔG_tr), which measures the energetic difference between two configurations of a system with different chemical activities of species (Dick and Shock, 2013), can be seen as a thermodynamic analog of the Kullback-Leibler divergence in information theory. ΔG_tr is calculated by integrating the affinities of formation reactions of individual species between reference and observed values of chemical activity, then taking the sum for all species in the system. If the reference values correspond to an equilibrium distribution, then ΔG_tr is always greater than zero, which makes it useful for quantifying the distance from equilibrium for a natural or experimentally observed distribution of species. Figure S3 demonstrates the always-positive values of ΔG_tr for a hypothetical system of n-alkanes with non-equilibrium abundances. As an example of its utility, the energetic difference between the calculated metastable equilibrium abundances of representative proteins and the observed phylum-level relative abundances of organisms was used by Dick and Shock (2013) as an objective function to optimize an equilibrium model. Values of hydrogen activity derived in this way were found to parallel changes of other redox proxies in a Yellowstone hot spring (Dick and Shock, 2013).

Another function, findit, is provided for iterative gridded optimization of T, P, and activities of basis species to minimize ΔG_tr or other possible objective functions. This is an experimental feature that could be used to explore the conditions for equilibrium assemblages of species in multiple dimensions. For example, it may be of interest in some systems to find conditions where the activities of many species are similar, that is, where their differences are minimized. Figure S4 shows a minimization of the standard deviation of the logarithms of activities of 11 aqueous sulfur species that were considered by Seewald (1996). This example progressively increases the number of optimized variables: first log f _O₂, then log f _O₂ and pH, and finally log f _O₂, pH, and temperature. The resulting minimum at log f _O₂ = -48.3, pH = 8.7, and T = 139°C, would be difficult to obtain by manual adjustment of the variables.

Finally, different considerations may affect the choice of basis species for thermodynamic descriptions of reactions in biochemical systems. For example, there is a strong negative correlation between the stoichiometric numbers of O₂ and H₂O in the compositions of different proteins when using CO₂, NH₃, H₂S, H₂O, and O₂ as basis species (Figure S1 of Dick, 2017). This correlation may be controlled more by the mathematical projection of chemical composition than by the compositional differences of the proteins themselves. Choosing a particular set of basis species that includes amino acids greatly reduces the correlation between O₂ and H₂O, making it possible to easily visualize distinct trends in the chemical composition of proteins in hypoxia and hyperosmotic stress experiments (Dick, 2017). That concept is further developed in a separate package, canprot², which uses CHNOSZ for compositional and thermodynamic analysis of proteomic datasets.

3. Results

This section summarizes the thermodynamic data and models used in CHNOSZ for calculating standard molal thermodynamic properties and activity coefficients.

3.1. Default and Optional Thermodynamic Data

Because it was derived from a database and computer program named “OrganoBioGeoTherm” (Helgeson et al., 2009) for calculating the standard molal thermodynamic properties of a wide range of organic and inorganic species, the default thermodynamic database in CHNOSZ was given the name OBIGT. All thermodynamic data, including names and chemical formulas of species, literature references, standard molal Gibbs energy, enthalpy, and entropy at 25°C and 1 bar, and parameters for calculating the standard thermodynamic properties at other temperatures and pressures, are stored in the “obigt” data object, which constitutes the active database in the R session (see Figure 2). The sources of data are comprehensively described in the vignette “Thermodynamic data in CHNOSZ,” and the specifications for the flat-file (CSV) format are also provided in the package documentation.

The default database in the current release version of CHNOSZ contains 3,360 species, and the optional data files (see below) have 641 species. The supplied database provides wide coverage of aqueous species with parameters in the revised Helgeson-Kirkham-Flowers (HKF) equations of state (Tanger and Helgeson, 1988). Unlike SUPCRT92, which is restricted to the 3-term Maier-Kelley equation for the heat capacity of crystalline, liquid, and gas species, parameters can be entered in OBIGT for the 5-term Haas-Fisher polynomial equation (Haas and Fisher, 1976; Robie and Hemingway, 1995, p. 2). The T² term in this equation is also used for organic gases and liquid alcohols (Helgeson et al., 1998). In addition, there is provision for a sixth term that can carry an arbitrary exponent, for instance T³ for the gases Si(OH)₄ and As(OH)₃ (Akinfiev and Plyasunov, 2014).

The “protein” data object (Figure 2) holds the amino acid compositions of selected proteins, which are used to calculate their thermodynamic properties using group additivity (Dick et al., 2006). Utility functions are available to obtain amino acid compositions from user-supplied FASTA sequence files or from the UniProt online database (The UniProt Consortium, 2019). Recent updates to OBIGT that affect the protein calculations include corrected values for aqueous methionine and the methionine side chain (LaRowe and Dick, 2012) and revised values for glycine and the glycine side chain as well as the protein backbone group (Kitadai, 2014). The updated group-additivity parameters for the protein backbone significantly decrease the computed energetic cost of amino acid polymerization to form peptides (Kitadai, 2014) compared to the superseded values (Dick et al., 2006). The database also contains recently reported data for monovalent and divalent metal-glycinate complexes (Azadi et al., 2019) that are linked to the properties for glycine reported by Kitadai (2014).

Although there is considerable overlap with the slop16.dat update for SUPCRT92 (Shock, 2016), OBIGT uses different data sources for aqueous Al species (Tagirov and Schott, 2001), As species (Nordstrom and Archer, 2003), Au, Ag, and Cu species (Akinfiev and Zotov, 2001, 2010), Pd species (Tagirov et al., 2013), Zn species (Akinfiev and Tagirov, 2014), and Pt species (Tagirov et al., 2015). Other notable differences are the inclusion of goethite, other Fe-oxyhydroxides, and evaporite minerals (Majzlan et al., 2003; Grevel and Majzlan, 2009), aqueous phenanthrene and methylphenanthrene isomers (Dick et al., 2013), experimentally derived HKF parameters for aqueous adenine (Lowe et al., 2017), and all of the organic compounds reported by Helgeson et al. (1998) and Richard and Helgeson (1998).

In addition to the default database, some optional data files are provided in the package to support newer models or to reproduce calculations from earlier publications. These data can be added to the active database using the function named add.obigt. A summary of these optional data files follows. The first three files are provided to support the reproduction of published calculations using older data; the last three files have data to support newer models.

3.1.1. SUPCRT92

This optional data file contains minerals, originally from the SUPCRT92 database, that were present in earlier versions of CHNOSZ but that have been superseded by the Berman (1988) dataset or other sources. The superseded minerals maintained in this file include all of the silicates and Al-bearing minerals from Helgeson et al. (1978), as well as calcite, dolomite, hematite, and magnetite. Additionally, this file contains the SUPCRT92 versions of boehmite, gibbsite, and dawsonite, which were updated following the recommendations of Zimmer et al. (2016), and the 25°C thermodynamic properties of celestite (Reardon and Armstrong, 1987), as recommended by Hörbrand et al. (2018). Other minerals from SUPCRT92, including native elements, sulfides, halides, sulfates, and carbonates and oxides that do not duplicate those in the Berman dataset, are still present in OBIGT.

3.1.2. SLOP98

This file includes data that were compiled in slop98.dat (Shock, 1998), or later versions of the slop files, that were present in earlier versions of CHNOSZ but have been replaced by or are incompatible with subsequent updates to the default database (see above). Data for metal complexes with arsenate and arsenite (Marini and Accornero, 2007, 2010), which are linked to the properties of arsenate and arsenite found in slop98.dat, are also present in this file. Similarly, data for Au(I)-acetate complexes (Shock and Koretsky, 1993) have been moved to this file, but Au⁺³ (Shock et al., 1997) has been kept in the default database because it is not affected by the updates applied to Au⁺.

3.1.3. OldAA

This has superseded data for amino acids and proteins (see above). The data are kept here to enable reproduction of previously published calculations (e.g., Dick, 2008; Dick and Shock, 2013).

3.1.4. AS04

This file has updates for aqueous SiO₂ (Apps and Spycher, 2004) reflecting a higher solubility of quartz in experiments compared to predictions of the SUPCRT92 dataset; see Wolery and Jové Colón (2017) for a review. The updates are not included in OBIGT because the standard Gibbs energy of SiO₂ used by Berman (1988) for comparisons with mineral solubilities is much closer to the previous value (Shock et al., 1989), which is also linked to the thermodynamic data of Helgeson et al. (1978).

3.1.5. DEW

This file includes data for species using revised correlations for the HKF a₁ parameter to support calculations up to 60 kbar using the Deep Earth Water model (Sverjensky et al., 2014a). The data in this file were taken from the DEW spreadsheet (Deep Earth Water Community, 2017), which is also the source of macros that were translated to R functions to implement the DEW model in CHNOSZ.

3.1.6. AkDi

This file has parameters in the Akinfiev-Diamond model that are available for selected aqueous nonelectrolytes (Akinfiev and Diamond, 2003; Akinfiev and Plyasunov, 2014). Compared to the revised HKF equations, this model can significantly improve the predictions of thermodynamic properties for neutral aqueous species (Akinfiev and Diamond, 2003).

Another use of the add.obigt function is to read data files supplied by the user. The easiest way to create such a file is to use one of the CSV data files in the package as a template; the package documentation describes the format of the data files in detail. As noted above, the info function can be used to check the self-consistency of values for a single species (e.g., that the value of heat capacity at 25°C is consistent with the entered HKF parameters). However, it is the user's responsibility to ensure that any data added are consistent with other species in the default database.

3.2. Thermodynamic Models

The dataset of Helgeson et al. (1978) was a landmark for the development internally-consistent thermodynamic data for minerals. Although it also has the advantage of representing the thermodynamic properties of polymorphic phase transitions, it adopts a constant-volume approximation for minerals, which can be a limitation for some high-pressure geological applications. More recent formulations, such as that of Berman (1988), account for the volume changes of minerals and have an integrated representation of phase transitions. CHNOSZ implements this model and includes Berman's dataset for 67 minerals with adjustments for alkalic minerals (Sverjensky et al., 1991) and newer data including F- and Cl-endmembers of biotite and apatite (Zhu and Sverjensky, 1992), chlorites (Vidal et al., 2005), minerals associated with skarn deposits (Delgado Martín and Soler i Gil, 2010), and aragonite (Facq et al., 2014). For compatibility with other data used in CHNOSZ, the berman function converts apparent Gibbs energies from the Berman-Brown convention to the Benson-Helgeson convention (Anderson, 2005, p. 60 and 144).

The default computational option for liquid and supercritical water in CHNOSZ uses the H2O92 Fortran subroutine from SUPCRT92 (Johnson et al., 1992) to calculate the thermodynamic and electrostatic properties using the models of Haar et al. (1984) and Johnson and Norton (1991). CHNOSZ provides an option to use the IAPWS-95 equations for thermodynamic properties (Wagner and Pruß, 2002) combined with equations for the dielectric constant from Archer and Wang (1990). This option is meant for testing and model development purposes and is not recommended for routine use, because it is slower, and differences in the derivatives of the dielectric constant can cause large deviations in the properties computed for charged species (Miron et al., 2019). A third option is available to calculate the thermodynamic and electrostatic properties using the Deep Earth Water (DEW) model (Sverjensky et al., 2014a), which should be used in conjunction with revised data for aqueous species (see above).

Fitting the HKF equations to calorimetric and volumetric data can be tedious, as it requires computation of the Born functions of water. The function named EOSregress facilitates this process by combining calculations of the properties of water with regressions using the linear model functionality of R. The vignette “Regressing Thermodynamic Data” demonstrates this capability and outlines an iterative method to account for the T and P dependence of the Born coefficient (ω) for charged species in the revised HKF equations. The regression functions were used in a recent study to regress HKF parameters for aqueous adenine from experimental data (Lowe et al., 2017).

Finally, CHNOSZ has an option named “varP” for calculating standard Gibbs energies of gases using a variable-pressure standard state (Anderson and Crerar, 1993, chapter 12). This permits the correct calculation of boiling curves on T-P diagrams. Leaving the option off defaults to a fixed-pressure (1 bar) standard state for gases, as used in SUPCRT92.

3.3. Nonideal Calculations

Calculations of activity coefficients can be invoked by setting the ionic strength in the “IS” argument of subcrt; the output then contains the adjusted Gibbs energies and equilibrium constants at specified ionic strength. The “IS” argument can also be supplied to affinity, which causes it to use adjusted Gibbs energies in its calculations.

Three forms of the extended Debye-Hückel equation for activity coefficients of charged aqueous species are available. The “Alberty” option uses the equation of Alberty (2003) with parameters suitable for relatively low temperatures and ionic strengths relevant for some biochemical calculations. The B-dot equation, which is the default in CHNOSZ, uses an extended term parameter that is a function only of temperature (Helgeson, 1969), and values of the distance of closest approach (or ion size parameter) taken from Garrels and Christ (1965, Table 2.7), which are consistent with those used in the HCh package (Shvarov and Bastrakov, 1999). The third option corresponds to the b_γ equation, with a constant value for the distance of closest approach, and values of the extended term parameter calculated as a function of temperature and pressure (Helgeson, 1969; Helgeson et al., 1981; Manning et al., 2013). For calculations at the high pressures that are possible with the DEW model, a geometric progression fit to the 10–30 kb values from Manning et al. (2013) was used to obtain provisional estimates to 60 kb (see Figure S5). These options, which are named “Bdot” and “bgamma” in CHNOSZ, both have sub-options to set the extended term parameter to zero, as used in some publications. The A and B Debye-Hückel parameters are calculated from the density and dielectric constant of H₂O using the selected water option (SUPCRT92, IAPWS95, or DEW).

For neutral species, the Setchénow equation is used, as described in Shvarov and Bastrakov (1999). It should be noted that activity coefficient calculations for both neutral and charged species involve a contribution associated with the conversion of units from mole fraction to molality. This conversion depends on the total molality of all dissolved species (Shvarov and Bastrakov, 1999), and a precise calculation of it together with activity coefficients would require a computationally difficult recursive loop. This term is included in the equations in CHNOSZ, but its value is simply estimated from the ionic strength, so activity coefficient calculations in CHNOSZ do not exactly reproduce those in HCh or other packages where the term is calculated more precisely. Specifically, the activity coefficient calculated in CHNOSZ for a singly charged ion in a 1 molal solution of a completely dissociated 1:1 electrolyte (ionic strength = 1 mol/kg) is about 1.8% higher than that calculated taking account of the total molality of solute species (2 mol/kg); in a 0.1 molal solution the difference decreases to 0.18%.

CHNOSZ is based on equations written for chemical activities as independent variables. With the default argument values for subcrt and affinity, no ionic strength is specified, activity coefficients are assumed to be unity, and activities of aqueous species are equal to their molalities. By specifying the ionic strength, the values of the standard Gibbs energies used in the equations are adjusted for the given ionic strength (Alberty, 1996). The use of adjusted Gibbs energies for given ionic strength means that all of the variables representing activity of aqueous species are transformed to molality. Although it is not possible to dynamically change the variable names used to write the code, the diagram function does change the axis label on chemical activity diagrams from “log a” to “log m” if the ionic strength is set.

4. Discussion

This section describes in detail an example calculation using the Deep Earth Water model and discusses the sensitivity of the calculation to sources of data and activity coefficient models. We also discuss other examples from the documentation that show the use of CHNOSZ to reproduce published calculations and summarize the dependencies, distribution, and testing of the package.

4.1. Calculation Using the Deep Earth Water Model

Here we describe a calculation of carbon speciation in subduction zone conditions, following Sverjensky et al. (2014b), particularly their Figure 3. The code used to construct this diagram (Figure 6) takes advantage of some of the newer and more advanced features of CHNOSZ, such as changing the water computational setting, loading optional aqueous species data, calculating log f _O₂ from a mineral buffer, calculating chemical affinity along a multivariable transect, and varying the concentration of the conserved basis species along the transect.

FIGURE 6

Figure 6. Speciation calculation for aqueous organic species whose thermodynamic properties are calculated using the Deep Earth Water model (Sverjensky et al., 2014a). The logarithm of oxygen fugacity (log f _O₂) is set to 2 units below the quartz-fayalite-magnetite (QFM) buffer. See text for more details about the calculation. The R script shown here is simplified for clarity; the complete script, which includes code to adjust the colors and labels, is available (Dick, 2019).

The numbered lines of code in Figure 6 execute a series of R functions that are described next. 01> Activate the computational option for water to use the Deep Earth Water (DEW) model. 02> Update the active thermodynamic database with parameters of species used for the DEW model and save the species indices for later. 03> Set the basis species; Fe and SiO₂ are included for constructing an oxygen fugacity (f _O₂) buffer from minerals. 04> Set the quartz-fayalite-magnetite (QFM) mineral buffer for f _O₂. 05> Define the temperature values used for the calculations: 600 to 1,000°C at 100°C increments. 06> Calculate the values of log f _O₂ in the QFM buffer as a function of temperature at P = 50,000 bar (5.0 GPa). 07> Select the species of interest; these are just some of the species that can be formed from the basis species. The commands in the next three lines are used to define the 08> ionic strength, 09> pH, and 10> the total moles of dissolved carbon, each at 100°C intervals. These values were taken from the Supplementary Information of Sverjensky et al. (2014b). 11> Use the B-dot option for calculating activity coefficients with the extended term parameter of the Debye-Hückel equation set to zero. 12> Calculate the chemical affinities of the formation reactions of the species along a transect with simultaneously varying temperature, log f _O₂ (2 units below the QFM buffer), ionic strength and pH, at P = 50,000 bar. 13> Calculate the equilibrium concentrations of the species. The molality of the conserved basis species (CO₃^-2) is set to the total amount of dissolved carbon in the solution, which is distributed among the species of interest. 14> Plot the mole fractions of carbon in each species, calculated by multiplying the molalities of species by their respective balancing coefficients (i.e., number of CO₃^-2 in the formation reactions). The lines are smoothed using spline interpolations of the points calculated at 100°C intervals. 15> Run the reset function so that any later calculations start with default values for the computational settings and thermodynamic database.

This example highlights a limitation of CHNOSZ: it is not a speciation program, so the pH, ionic strength, and total molality of dissolved carbon must be taken from the speciation calculations of Sverjensky et al. (2014b). Using these input values, the diagram produced here is very close to Figure 3 of Sverjensky et al. (2014b), demonstrating that consistent results can be obtained in CHNOSZ given the fluid composition predicted by speciation models.

Although CHNOSZ does not have code for a full equilibrium speciation calculation, it can be used as a tool to rapidly explore the proximate effects of differences in thermodynamic data, the addition or removal of species from the system, or the effects of different oxidation state buffers or activity coefficient models. To give an example, if acetate is omitted from the updated DEW parameters in line 4, the calculation then uses the values for acetate from the default database. In this case a small amount of acetate is formed, with a carbon fraction that is about half that of HCO₃^- at 600°C (see Figure S6A). Notably, the logK values in this calculation and the presence of a small amount of acetate are consistent with the EQ3NR output in the Supplementary Information of Sverjensky et al. (2014b), although acetate is not shown in their Figure 3. It follows that the default parameters for acetate in the CHNOSZ database, instead of the recently updated ones from the DEW spreadsheet (Deep Earth Water Community, 2017), should be used to more closely reproduce the calculations reported by Sverjensky et al. (2014b). As another example, by changing line 11 in the code in Figure 6, activity coefficients can be calculated using the “bgamma” method, which estimates the extended term parameter in the Debye-Hückel equation (b_γ) at high pressures by extrapolation from the values in Manning et al. (2013) (see Figure S5). With these settings, the calculated abundance of the organic species drop more quickly with temperature. The carbon fraction of propanoate becomes equal to that of methane at 870°C and drops below one percent by 1,000°C, where the predicted abundance of formate is negligible (see Figure S6B). Although there is considerable uncertainty in the extrapolation of b_γ, this calculation suggests that provision for non-zero (positive) values, which seem consistent with the estimates made by Manning et al. (2013), leads to somewhat lower predicted stabilities of organic compounds in subduction zones.

4.2. Package Examples, Demos and Vignettes

Besides the examples shown in this paper, the package documentation has many other examples of calculations derived from the literature. A partial listing is given in Table 1. In many cases, CHNOSZ provides additional data and functionality that can be used extend the original calculations. For instance, the “Introduction to CHNOSZ” vignette shows how a calculation of ATP speciation described by Alberty (2003) can be enhanced by inclusion of the temperature dependence of standard Gibbs energies (LaRowe and Helgeson, 2006b). CHNOSZ also facilitates the rapid visual comparison of different sources of thermodynamic data. In the “glycinate” demo, calculations of the association constant for divalent metal-glycinate complexes using data from Azadi et al. (2019) (in the default database) yield lower values than Shock and Koretsky (1995) (in the SLOP98 optional data file).

TABLE 1

Table 1. Selected reproductions of published calculations in the CHNOSZ package.

In other cases, rapid visualization of the results of calculations can be used to identify issues with the data or models. The “g function” is a component of the revised HKF model that allows calculations at temperatures and pressures up to 1,000°C and 5 kbar. In accord with the boundaries of region II of Figure 6 in Shock et al. (1992), SUPCRT92 and CHNOSZ set the upper temperature limit of the g function to 355°C at pressures between the saturation curve and 500 bar; at higher temperatures the function is assigned a value of zero in the code. Nevertheless, calculated values of logK for the NaCl dissociation reaction are plotted as lines that extend smoothly up to 366°C at P_sat and 467°C at 500 bar in Figure 1 of Shock et al. (1992). In contrast, owing to the 355°C limit of the g function, the “NaCl” demo shows discontinuous behavior at this temperature (see Figure S7). The values calculated in CHNOSZ for 500 bar, including the break in the curve, can be confirmed by calculations in SUPCRT92; the latter does not permit calculations above 350°C at P_sat. There is no obvious way to resolve the issue of non-continuous values of logK in the critical region, other than by further modifications to the HKF model itself, which are beyond the scope of this study.

Occasionally, development of the examples in CHNOSZ has revealed disparities between published calculations. The help page for the solubility function contains an example calculation of the solubility of atmospheric CO₂ and calcite in a closed system. The different stoichiometric constraints in these two systems lead to qualitatively different behavior of carbonate speciation; in the CO₂-water system, the logarithms of activities of aqueous carbonate species are represented by straight lines across the entire pH range (Stumm and Morgan, 1996, Figure 4.5), but in the calcite-water system, each carbonate species has linear segments with different slopes (Stumm and Morgan, 1996, Figure 7.9). This occurs because the equilibrium state for each reaction to form the various aqueous carbonate species from the dissolution of calcite is also sensitive to the total amount of dissolved metal in the system, which is not a feature of the CO₂-water system. However, the logarithms of activities of aqueous carbonate species are plotted in the calcite solubility diagram of Manning et al. (2013, Figure 4) as straight lines across the entire pH range, suggesting that each reaction was treated independently in their calculations, without accounting for the total concentration of the Ca⁺² ion. The solubility function in CHNOSZ does account for the dissociation of CaCO₃ to yield both dissolved carbonate species and a metal ion, and yields a diagram that is in agreement with that of Stumm and Morgan (1996) (Figure S8A), but an argument for the function is available to calculate the equilibrium state for each reaction independently, making it possible to reproduce the diagram of Manning et al. (2013) (Figure S8B).

Despite the wide range of possible calculations, it is important to be aware of the limitations of CHNOSZ. While calculations of gold solubility described by Williams-Jones et al. (2009) were likely performed using a Gibbs energy minimization program such as HCh (Shvarov and Bastrakov, 1999), CHNOSZ doesn't account for complete equilibrium speciation of the solution. Instead, the “gold” demo calculates the distribution of Au-bearing species using values of ionic strength that are computed for a simplified representation of a solution of NaCl in water using the function named NaCl, which was written to support this demo. Calculations of Au solubility using this simplified solution model compare favorably with speciation calculations carried out using HCh using the same thermodynamic data for aqueous Au complexes. In addition, CHNOSZ shows good agreement with the calculations by Pokrovski et al. (2014) of Au solubility at constant pH under either pyrite-pyrrhotite-magnetite (PPM) buffered conditions or hematite-magnetite with high sulfide (see Figures S9, S10). On the other hand, calculations of Au solubilities with both CHNOSZ and HCh are lower than those presented by Williams-Jones et al. (2009), particularly for solutions with the PPM buffer, probably owing to differences in thermodynamic data used in the calculations.

Another demo, “aluminum,” provides a set of comparisons between measured equilibrium data and different sources of thermodynamic data for Al-bearing minerals and reactions. The plot in Figure 7A, which is based on Figure A1 of Zhu and Lu (2009), shows that CHNOSZ (with the Berman minerals) gives a better fit to the data for the kaolinite—boehmite reaction from Hemley et al. (1980) than SUPCRT92 (with the Helgeson minerals). However, an even better fit can be obtained by using the data for SiO₂(aq) from Apps and Spycher (2004). Nevertheless, updated parameters for SiO₂(aq) are not currently included in the default database of CHNOSZ because changing it is likely to create inconsistencies with other minerals. The plot in Figure 7B shows that calculations with the default database in CHNOSZ are close to the experimental data for dawsonite solubility from Bénézeth et al. (2007). The data file of the current version of the SUPCRTBL³ program (Zimmer et al., 2016) has values of 0 for the heat capacity coefficients of dawsonite. Replacing these with values from Robie and Hemingway (1995) as listed in Tutolo et al. (2014) yields results that are more consistent with the experimental data (also see Figure 2 of Zimmer et al., 2016).

FIGURE 7

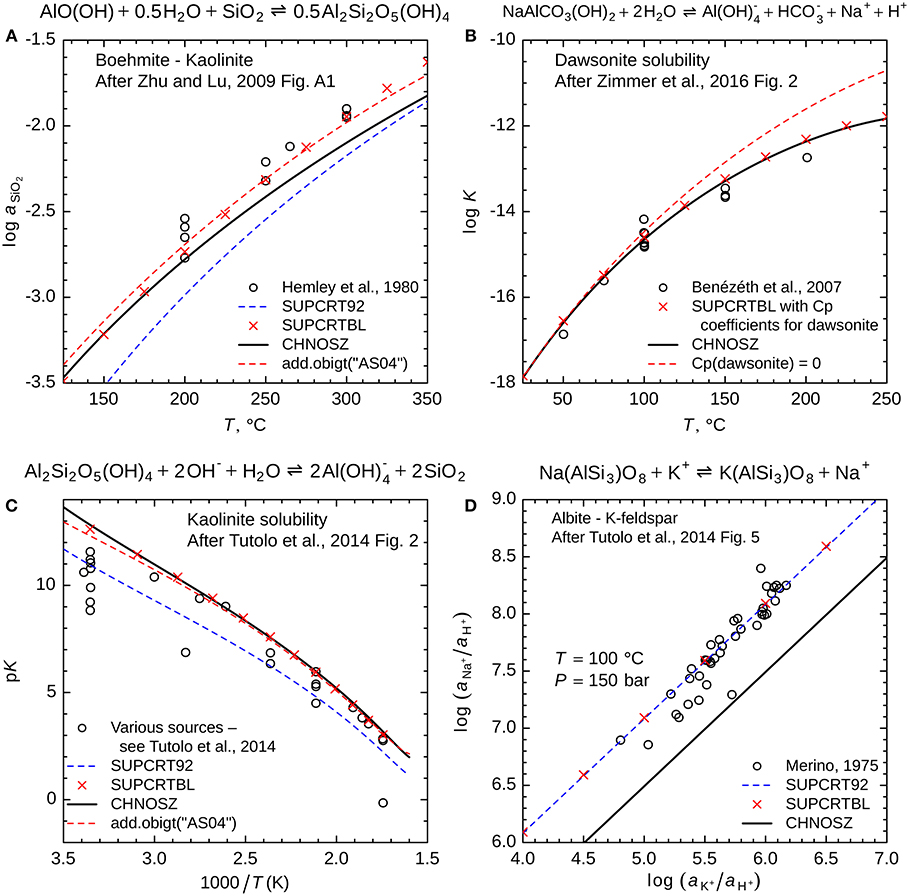
Figure 7. These plots, from the output of demo(~aluminum~), compare experimental and field data for Al-bearing minerals with different thermodynamic datasets. (A) Activity of SiO₂ in equilibrium with boehmite and kaolinite; (B) equilibrium constant for dawsonite stability, (C) equilibrium constant (negative logarithm: pK) for kaolinite solubility, and (D) equilibrium activities of Na⁺ and K⁺ in the reaction between albite and K-feldspar. The open circles represent experimental data from the sources identified in the legends. Red “x” symbols represent calculations performed in SUPCRTBL (Zimmer et al., 2016) with its data file modified to include heat capacity parameters of dawsonite (Robie and Hemingway, 1995; Tutolo et al., 2014). All lines are calculated using CHNOSZ; the solid black lines represent the default database, with properties of kaolinite, K-feldspar (microcline) and low albite from Berman (1988) and parameters for boehmite and dawsonite as described by Zimmer et al. (2016), except for the heat capacity parameters of dawsonite (Robie and Hemingway, 1995; Tutolo et al., 2014). The black lines also represent calculations using default data in CHNOSZ for Na⁺, K⁺, OH^-, and HCO₃^- (Shock and Helgeson, 1988), SiO₂(aq) (Shock et al., 1989), and Al(OH)₄^- (Tagirov and Schott, 2001). Dashed red lines indicate (A) the substitution of data for SiO₂(aq) from Apps and Spycher (2004) and (B) overriding the parameters in the default database to set the heat capacity of dawsonite to 0. Dashed blue lines (A–D) represent calculations using data for kaolinite, K-feldspar and albite from Helgeson et al. (1978), which are present in SUPCRT92 (Johnson et al., 1992).

In Figure 7C, the calculation with CHNOSZ follows the high range of solubility values for kaolinite, similar to the recommendation of Tutolo et al. (2014), which is markedly higher than SUPCRT92, especially at low temperatures. In their calculations, Tutolo et al. (2014) used the properties of H₄SiO₄ taken from Stefánsson (2001). In contrast, the reaction here is written in terms of SiO₂ with parameters taken from Shock et al. (1989). Substituting the parameters from Apps and Spycher (2004) improves the fit to experimental data at low temperatures, but has a smaller effect at the highest temperatures considered here.

The plot in Figure 7D reveals that field-based data (Kharaka and Berry, 1974; Merino, 1975) for the activities of K⁺ and Na⁺ set by the albite—K-feldspar exchange reaction are represented better by SUPCRT92 (i.e., Helgeson et al., 1978) than by the default database in CHNOSZ (Berman, 1988). These differences between databases have been noted before (Apps and Chang, 1992). Although internally consistent datasets for particular sets of minerals (e.g., Tutolo et al., 2014) could simultaneously improve all the comparisons in Figure 7, adopting them is problematic because they would likely break consistency with experimental phase equilibrium data for other reactions involving these minerals (Miron et al., 2016).

4.3. Package Availability and Tests

CHNOSZ is licensed under version 2 or greater of the GNU GPL. The current release version of CHNOSZ is 1.3.2, and requires R version 3.1.0 or later. Installation packages can be downloaded for major desktop operating systems from the Comprehensive R Archive Network (CRAN). Development versions of the package, including Windows binaries, are available on R-Forge (Theußl and Zeileis, 2009)⁴; building the package for other platforms requires a Fortran compiler.

The CRAN packages testthat, knitr, rmarkdown, and tufte are used for testing the package and generating the vignettes. An extensive set of tests, utilizing the testthat system (Wickham, 2011), is used to ensure the functions in the package operate as intended, including checks for argument and error handling and numerical results of particular calculations. Before updates of the package are submitted to CRAN, and many times before, all of the code in the vignettes, examples and tests is run, helping to protect against code regression during development. The vignettes, demos, and help pages are available on the user's computer after installing the package and are also posted on the project website⁵.

5. Conclusions

CHNOSZ provides the basic tools for thermodynamic calculations in aqueous geochemistry, namely calculations of standard thermodynamic properties of species and reactions using an integrated thermodynamic database. Given a user-specified set of basis species and ranges of temperature, pressure, and chemical activities, CHNOSZ also provides a flexible workflow for the calculation of chemical affinities and generation of chemical activity diagrams. The workflow is based on activities of species, rather than their amounts, and CHNOSZ can calculate the equilibrium distribution of species for only a single conserved basis species, so it is not a general-purpose code for equilibrium solubility and speciation modeling. Nevertheless, the interactive usage and powerful scripting capabilities available in R make CHNOSZ useful for rapid prototyping and experimenting with different assumptions for thermodynamic calculations. Continuing updates to thermodynamic models and data are combined with a system for reverting to previous datasets, and the sources of all data are thoroughly documented. These features together with many examples of calculations taken from the literature and an open-source license mean that CHNOSZ contributes substantially to the reproducibility of thermodynamic calculations in geochemistry.

Data Availability

CHNOSZ is available on the Comprehensive R Archive Network⁶. The code used to make the figures has been deposited on Zenodo (Dick, 2019). All other data supporting the conclusions of this article are within the article and Supplementary Files.

Author Contributions

JD developed the package and wrote the manuscript.

Funding

This work was supported in part by funding from NSF in 2009–2011 (EAR 0847616) and CSIRO in 2011–2014 (Organic Geochemistry of Mineral Systems flagship cluster).

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I thank Evgeniy Bastrakov, Grayson Boyer, Peter Canovas, Katy Evans, Doug LaRowe, Marc Neveu, Apar Prasad, Nic Spycher, and Miao Yu for helpful discussions about thermodynamic data and calculations, Alysia Cox, Kristin Johnson, and Everett Shock for discussions and opportunities to present the package to new users, the CRAN volunteers for their diagnostic checks and providing a wonderful resource for free software, and all users who have sent bug reports, feature requests, or other feedback.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00180/full#supplementary-material

Footnotes

1. ^https://en.wikipedia.org/wiki/Pourbaix_diagram, accessed on 2019-04-10

2. ^https://cran.r-project.org/package=canprot, accessed on 2019-04-06

3. ^https://www.indiana.edu/~hydrogeo/SUPCRTBL_linux.zip, accessed on 2019-04-16

4. ^https://r-forge.r-project.org/projects/chnosz/, accessed on 2019-04-06

5. ^http://chnosz.net, accessed on 2019-04-06

6. ^https://cran.r-project.org/package=CHNOSZ, accessed on 2019-04-16

References

Akinfiev, N. N., and Diamond, L. W. (2003). Thermodynamic description of aqueous nonelectrolytes at infinite dilution over a wide range of state parameters. Geochim. Cosmochim. Acta 67, 613–629. doi: 10.1016/S0016-7037(02)01141-9