Modeling the Re-appearance of a Crashed Airplane on Gauligletscher, Switzerland

In this study we used a modeling approach to reconstruct the space-time trajectory of the Dakota airplane which crashed on the Gauligletscher in 1946 and was subsequently buried by snow accumulation. Our aim was to localize its present position and predict when and where it would re-appear at the surface. As a first step we modeled the ice flow field and the evolution of Gauligletscher from 1946 using a combined Stokes ice flow and surface mass balance model, which was calibrated with surface elevation and velocity observations. In a second step the modeled ice velocity fields were integrated forward-in-time, starting from the crash location. Our results suggest that the main body of the damaged aircraft will be released approximately between 2027 and 2035, 1 km upstream of the parts that emerged between 2012 and 2018. Our modeling results indicate that the recently found pieces of the Dakota might have been removed from the original aircraft location and moved down-glacier before being abandoned in the late 40s.

1. Introduction

In the last century, more than 50 airplanes crashed on glaciers in Antarctica, Greenland, and in high mountain environments (Aviation Safety Network, 2018). Due to their remote locations, most of these aircraft have not been recovered. For crashes that occurred in the accumulation area, the wreckage was buried naturally under layers of snow and ice and transported along with the ice flow. In some cases, pieces of crashed airplanes re-appeared several years after the crash in the ablation area. This was the case on Glacier des Bossons (Massif du Mont Blanc, France), where pieces of two airplanes that crashed in 1950 and in 1966 were found in recent decades (Sesiano, 1982; Samuel, 2014). Two Boeing B-17 and six Lockheed P-38 that landed on Greenland's east coast (Wieland, 1997) were abandoned on the ice sheet in 1942, and located using Ground-Penetrating Radar (GPR) in 1992. The wreckages were found ~80 m beneath the ice surface (Annan, 2004). To our knowledge, a modeling approach has never been used to estimate the trajectory of a crashed airplane within the ice.

In 1946, when a Douglas C-53 Dakota airplane crashed in the upper accumulation area of the Gauligletscher (Berner Oberland, Switzerland). Once the Dakota was found and the passengers rescued, the airplane was left on the glacier at the request of the president of the Swiss glacier commission, Prof. P.L. Mercanton, who argued that the Dakota could be used to learn more about the internal motion of glaciers for future glaciological studies (Archiv-Gletscherkommision SANW, 1946-1947). In the following years, the Dakota aircraft was gradually buried under seasonal snow accumulation and was advected down-glacier as result of ice dynamics. The propellers, one engine and wing pieces were released in the ablation area of the glacier and found between 2012 and 2018 (Rothacher, 2014; Petroni, 2015, 2018), but the main body of the Dakota remains embedded in the ice. The question remains as to where and when the main body will re-appear on the surface.

To answer these questions we reconstruct the trajectory of the main body of the Dakota and other debris by closely following the approach proposed by Jouvet and Funk (2014). First, we model the ice dynamics and the time evolution of Gauligletscher starting from 1947. Second, we integrate the resulting ice flow field forward-in-time starting from the known crash location and backward-in-time from recently found pieces. Jouvet and Funk (2014) reconstructed the trajectory of the corpses of three ill-fated mountaineers missing since 1926, which re-appeared on the surface of the Grosser Aletschgletscher in 2012. Starting at the point where the corpses were found on the glacier surface in 2012, they integrated the time-dependent velocity field obtained with a three-dimensional ice flow model, and deduced the location where the brothers probably died in 1926.

Combined three-dimensional (3D) Stokes ice flow and surface mass balance models have been used to reproduce the complex ice flow field of mountain glaciers and their time-transient evolutions (Le Meur et al., 2004; Jouvet et al., 2008, 2009; Zwinger and Moore, 2009; Réveillet et al., 2015). For this reason, in the present study we use a 3D Stokes model to simulate the ice flow and the time evolution of the surface topography of the Gauligletscher since the crash of the Dakota. To compute the time evolution of the ice surface elevation since 1947, we apply the mass conservation equation (e.g., Greve and Blatter, 2009), which takes into account the ice dynamics and the surface mass balance. Mass balance is computed using a distributed temperature index melt model coupled to a snow accumulation model (Huss et al., 2008). Ice flow parameters are calibrated according to observed surface elevations and ice surface velocities. By integrating the modeled velocity fields from 1947 to the year of emergence, we can estimate the position of the main body of the Dakota at any point in time.

This paper is organized as follows. First we summarize historical facts related to the crash of the Dakota, and the data available. Then we describe the model and the method for reconstructing the trajectory of the Dakota aircraft within the ice. To conclude, we discuss our results in the historical context.

2. Background

On 19 November 1946, a US Dakota airplane took off from München (Germany) in the direction of Marseille (France). Because of bad weather conditions, the pilot became disoriented when flying over the Alps and crashed into the upper part of the Gauligletscher at 3,300 m a.s.l. As the crash site was fairly flat, the fuselage of the Dakota remained intact (Figure 1a), and none of the passengers or crew was seriously injured. Despite a major search and rescue operation, the Dakota was located only 3 days later, on November 22. Two days after that, two airplanes equipped for landing on glaciers (Figure 1b) rescued the passengers (Hug, 1990; Bürgi and Stierli, 2006).

FIGURE 1

Figure 1. Historical and recent photographs showing (a) the Dakota aircraft during the rescue operation in 1946 (Foto MHMLW, source: www.vtg.admin.ch), (b) the two airplanes used for the recovery of the most valuable pieces in 1947 (source: Swiss Alpine Museum), (c) the removal of one engine while the Dakota was already covered by snow in 1947 (source: Swiss Alpine Museum) (d) the engine released at the surface of the glacier and found in 2018 (Foto VBS, source: www.vtg.admin.ch).

About 6 months later, on 29 May 1947, the Swiss Army organized an expedition in order to recover the most valuable pieces of the Dakota (Swiss Archives, 1947–1949; Cornioley, 2006). Similar to the rescue operation in November 1946, the Army again built a landing strip on the ice at 2,850 m a.s.l.—about 1.6 km downstream of the crash location—where the glacier was sufficiently flat. Parts of the Dakota (about 2,100 kg) were transported by sled down to the landing strip, before being picked up by two airplanes (see Figure 1b; Hug, 1990). Other parts of the wrecked aircraft that were not considered worth bringing to the valley were thrown into nearby crevasses (Swiss Archives, 1947–1949). The main body of the Dakota was left at the crash site and gradually disappeared into the glacier under snow accumulation condition over the following years. The coordinates of the crash site have been estimated based on aerial photos from 1947 at (654 205, 163 848, 3 303), in line with the Swiss Coordinate system (CH1903–easting, northing, and elevation in m; see Figure 2).

FIGURE 2

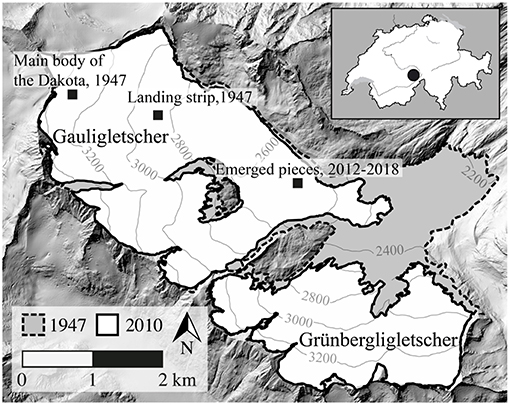
Figure 2. Overview of the topography of Gauligletscher and the former tributary Grünbergligletscher, in 1947 (dashed) and 2010 (continuous), showing the Dakota crash location, the landing strip for the rescue operation and recover expedition, and the location where the emerged pieces were found.

In recent years, some pieces of the Dakota have been released by the glacier, and found at the tongue of Gauligletscher at about 3.5 km downstream of the crash site (657 442, 162 587, 2 540): a propeller in June 2012 (Rothacher, 2014), a wing part in September 2015 (Petroni, 2015), and the second propeller, an engine and other wing parts in August 2018 (Petroni, 2018; see Figure 1d).

3. Data

To model the reappearance of the crashed airplane, we used a wide range of the data available for the Gauligletscher, including:

1) Two Digital Elevation Models (DEMs), derived from aerial photographs (1947 and 2010) (Bauder et al., 2007). The DEMs have a spatial resolution of 25 m and an accuracy of ±0.3–1 m.

2) Helicopter-borne Ground Penetrating Radar (GPR) profiles acquired in 2012 to determine the ice thickness along these profiles (Rutishauser et al., 2016). An ice thickness distribution approach was used (Farinotti et al., 2009) to spatially extrapolate the data.

3) Measurements of the position of glacier snout in 1969, 1980, 1993, 2002-2010, and 2013-2015 obtained by photogrammetrical analysis (GLAMOS, 2018).

4) Horizontal ice flow velocity at the surface of the glacier between March 2011 and December 2016 (not temporally continuous) with a repeat pass of 11 days inferred from Synthetic Aperture Radar (SAR) data of TanDEM-X.

5) Averaged horizontal ice flow velocities at the surface of the ablation area between August 2015 and August 2017 inferred by feature tracking from Sentinel-2 satellite images. The Matlab toolbox ImGRAFT was used here (http://imgraft.glaciology.net), which relies on template matching techniques (Messerli and Grinsted, 2015).

6) Meteorological time series of different MeteoSwiss weather stations located nearby to force the surface mass balance model (Huss et al., 2008).

4. Methods

The approach of Jouvet and Funk (2014) was followed closely in order to compute the 3D trajectory of the main body of the Dakota within the ice. Starting from the known crash location in 1947, we integrated forward-in-time modeled ice velocity fields until the damaged aircraft emerged on the glacier surface. For that purpose, a 3D glacier model capable of simulating the time-transient evolution of the ice thickness and velocity of the Gauligletscher was required for the time period when the Dakota aircraft was in the ice. Therefore, our modeled domain includes the former tributary Grünbergligletscher, which was connected with the Gauligletscher until 2002 and influenced its dynamics (Figure 2). In the following paragraphs we describe the ice flow model, the surface mass balance model and how the two interact.

Ice is commonly assumed to be an incompressible and non-Newtonian viscous fluid, so that the dynamics of ice can be computed by solving non-linear Stokes equations (Greve and Blatter, 2009). In this study we further assume ice to be isothermal and temperate. This assumption is supported by the analysis of the elevation range and the exposure of the Gauligletscher (Suter et al., 2001). Additionally, we allow basal sliding of the ice over the bedrock applying a Weertman sliding law (Weertman, 1957). We used the finite-element Elmer/Ice software (Gagliardini et al., 2013) to solve the Stokes and mass conservation equations, which computes the time evolution of Gauligletscher, providing a time series of annual surface mass balance. We initialized the model with the glacier geometry according to the surface DEM of 1947 and the bedrock DEM, which was reconstructed using GPR profiles (Rutishauser et al., 2016) and an ice thickness distribution approach (Farinotti et al., 2009; see Figure S1). With a horizontal grid resolution of 40 m vertically extruded with 16 equidistant layers, and a time resolution of 1 year, we ultimately obtained the 3D ice velocity fields of the glacier between 1947 and 2040, which were used to reconstruct the trajectory of the Dakota aircraft.

The two least known parameters of the model are the rate factor A, which controls the ice viscosity, and the Weertman friction coefficient c, which controls the amount of sliding (Jouvet et al., 2011). To minimize the discrepancy between modeled results and observations, several combination of parameters A and c were tested. For each combination, the Root Mean Square Error (RMSE) between modeled and measured ice surface elevations and surface velocities was computed (see Table S1). To compute the RMSE of surface elevation and surface velocities, the DEM of 2010, the TanDEM-X SAR and Sentinel-2 velocity measurements were used as a reference. As a result, the combination of parameters that minimized the discrepancy in elevation and surface velocity was found to be (A, c) = (60 MPa⁻³ a⁻¹, 12, 500 MPa⁻³ m a⁻¹) with an RMSE of 13.7 m, 11.2 and 9.8 m a⁻¹, respectively (see Figure S2). The rate factor is close to literature value for temperate ice (76 MPa⁻³ a⁻¹) (Cuffey and Paterson, 2010), while the Weertman friction coefficient is lower when compared with the optimal sliding value (23,300 MPa⁻³ m a⁻¹) used by Jouvet and Funk (2014).

Glacier mass balance was determined by computing solid precipitation (accumulation) and melt (ablation; Huss et al., 2010). We coupled a temperature index melt model with an accumulation model. The mass balance model was calibrated using observed volume changes (see Huss et al., 2008) for more details. To run the model for future time periods, two contrasting climate scenarios were considered. In this case, the modeled surface mass balances of 2011 and 2013—2 extreme years —were used as a warm-dry scenario and a cold-wet scenario, respectively, and held them constant-in-time to simulate the response of Gauligletscher in the future according to each scenario (see Figure S3). The aim of these two contrasting scenarios was to provide a lower and an upper boundary for the emergence position of the Dakota aircraft, to account for uncertainties in climate projections.

5. Results

5.1. Modeling Ice Flow and Surface Elevation of Gauligletscher

Calculations were initialized using the DEM of Gauligletscher from 1947 and its evolution was modeled until 2014 (the last year with available surface mass balance data, Figure 3). During this time period, the model shows a glacier retreat of ~2 km and a volume decrease of 43 % (Figure 4). Modeled surface velocities changed significantly between 1947 and 2014. Between about 1960 and 1980, the glacier moved at velocities up to 75 m a⁻¹, which decreased to 40 m a⁻¹ in the same region in 2014 (Figure 3). This evolution was most likely the consequence of positive surface mass balances before the 1980s, which increased the ice thickness and velocities. By contrast, the surface mass balances after the 1980s were much more negative. This trend is similar to the one observed at Rhonegletscher (Huss et al., 2008), which is located only 15 km east of Gauligletscher and is of comparable size.

FIGURE 3

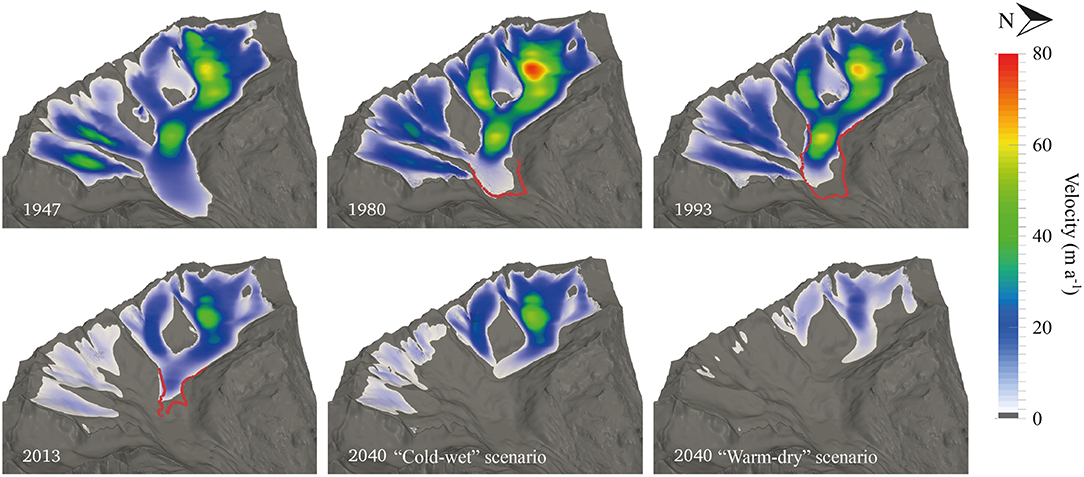
Figure 3. Modeled velocity and ice extent of Gauligletscher between 1947 and 2040. The results of both climatic scenarios in 2040 are shown. The red lines indicate the observed glacier extent.

FIGURE 4

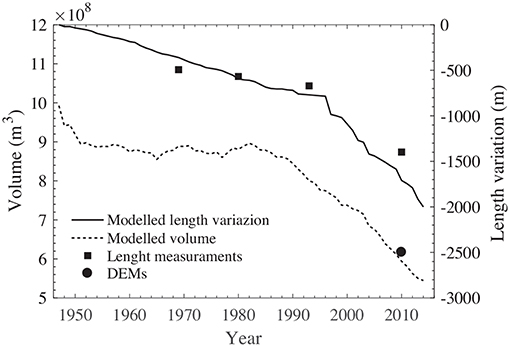
Figure 4. Modeled glacier length and volume change of Gauligletscher between 1947 and 2014 (black lines) compared with observed length (black squares) and volume inferred from the DEM of 2010 (black dots). The glacier length is relative to the extent in 1947.

To validate our model, we used the DEM from 2010, as well as observed glacier lengths. As a result, both observed and modeled glacier volumes in 2010 agree well (Figure 4) validating our coupled mass balance and dynamical model. However, the rate of retreat of the glacier was slightly underestimated before 1980, and slightly overestimated afterwards (Figure 4).

Using the two future climate scenarios defined previously, the glacier time evolution was modeled until 2040 (Figure 3). The results show an additional glacier retreat of 780 and 1,230 m and an additional decrease in volume of 21 and 49 % by 2040 when using the cold-wet and warm-dry scenarios, respectively. The ice surface velocities remained generally unchanged between 2014 and 2040 with the cold-wet scenario, while they were halved in the same time period with the warm-dry scenario.

5.2. Trajectory of the Main Body of the Dakota and the Emerged Pieces

We computed the trajectory of the main body of the Dakota aircraft starting from the crash to its emergence locations. Figure 5 shows the horizontal trajectory between 1947 and the year of re-appearance on the surface. Additionally, Figure 6 displays the elevation of the Dakota aircraft, the ice surface with respect to time, and the bedrock along the flowline as a function of the horizontal distance to its position in 1947. The Dakota aircraft reached a maximum ice depth of 68 m in 2000, before rising slowly to reach an ice depth of 35 m in 2014. Using the two extreme climate scenarios defined previously, we found that the Dakota aircraft will most likely emerge between 2027 and 2035 at a location between 200 and 340 m downstream of its presumed position in 2014, which is ~1.4 km upstream of the location where the emerged pieces were found (Table 1).

FIGURE 5

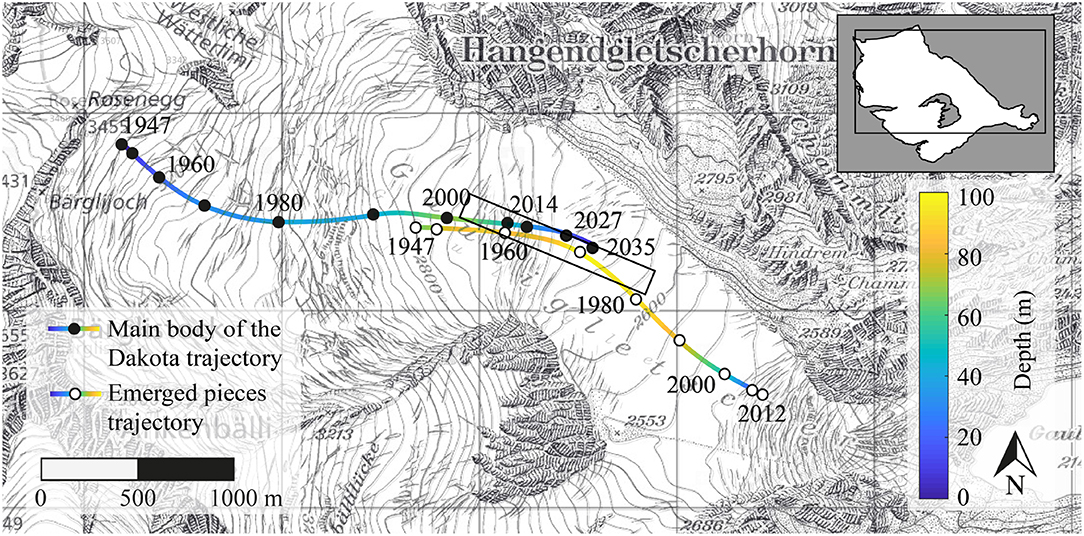
Figure 5. Modeled horizontal trajectories of the main body of the Dakota (line with solid marker) and emerged pieces (line with open marker). The rectangle indicates the confidence area of the main body of the Dakota emergence location, taking into account the uncertainness listed in the text.

FIGURE 6

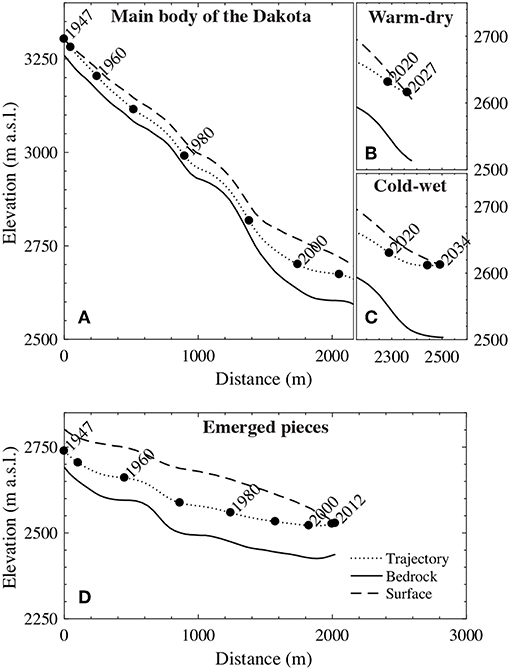
Figure 6. Vertical section of the main body of the Dakota, of the surface with respect to time, and of the glacier and the bedrock (A) from 1947 to 2014, (B) using the warm-dry scenario from 2014 to 2027, and (C) using the cold-wet scenario from 2014 to 2034, where the x-axis shows the distance from the crash site. Image (D) shows the same for the emerged pieces from 1947 to 2012, where the x-axis indicates the distance from their initial position.

TABLE 1

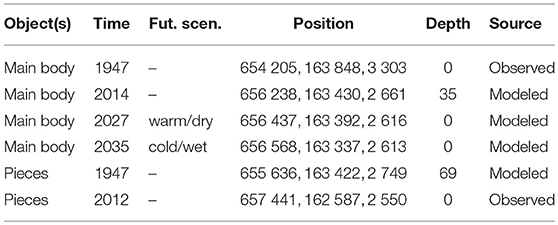
Table 1. Position and depth of the main body of the Dakota and emerged pieces (Swiss coordinate system, CH1903) at different times and under both future climate scenarios.

Due to a significant bias between the modeled emerging position of the Dakota aircraft and the position of the emerged pieces, we also computed the trajectory of the emerged pieces starting from the location where they were found backward-in-time until 1947 (see Figures 5, 6). Since the emerged pieces were discovered very close to each other, we considered them as one single piece, and computed only one trajectory. The modeled trajectory of the emerged pieces starts in 1947 at a location ~1.6 km downstream of the crash location and 69 m depth (see Table 1). This discrepancy is addressed in the discussion.

5.3. Sensitivity of the Results With Respect to Model Errors

The modeled trajectory of the main body of the Dakota and other pieces is subject to various sources of error that we quantify in this section.

Despite calibrations, significant model errors might occur due to uncertainties in the rate factor A, and the Weertman friction coefficient c (Jouvet and Funk, 2014). For this reason, we then computed the trajectory of the Dakota aircraft with other pairs of parameters, which have shown higher RMSE with respect to observed surface velocities and surface elevations, but still at a reasonable extent (see Table S1). The first setting—which accounts for more sliding (c = 23, 000 MPa⁻³ m a⁻¹) and the same viscosity (A = 60 MPa⁻³ a⁻¹) – shows a longitudinal deviation of the estimated Dakota position in 2014 of 390 m downstream and the distance to the surface increased by 11 m. The second setting – which takes into account zero sliding (c = 0 MPa⁻³ m a⁻¹) but a lower viscosity (A = 150 MPa⁻³ a⁻¹)—shows a longitudinal deviation of 670 m upstream and the distance to the surface decreased by 12 m.

In addition to these factors our results are likely influenced by errors in:

1. the modeled surface mass balance from 1947 to 2014,

2. future projections of surface mass balance,

3. the initial position of the Dakota aircraft,

4. the DEM of the bedrock inferred from GPR profiles, and

5. surface DEMs from 1947 and 2010.

Among the previously mentioned presumed causes of the errors, (1) is expected to have a limited effect, as errors in surface mass balance mostly affect the surface of the glacier and have only a minor effect on the trajectories of deep ice particles (Jouvet and Funk, 2014). To test the influence of the source of error (2), we used two extreme surface mass balance scenarios so that the re-appearance year and position will likely lie somewhere between the two, which are located 140 m apart. Computing the trajectory of four additional points (each 30 m from the initial position of the Dakota in the direction of the four cardinal points, which is the estimated georeferencing error of photogrammetrical analysis), we found that the source of error (3) can cause the modeled position of the Dakota in 2014 to deviate by 20 m laterally, 105 m longitudinally, and 10 m vertically. To assess the impact of the source of error (4), we used a second DEM of the bedrock obtained from a different parameter set of the ice thickness distribution method (Farinotti et al., 2009). As a result, the longitudinal deviation of the modeled Dakota aircraft position in 2014 with the alternative bedrock never exceeded 14 m (and 5 m vertically), see Compagno (2018) for more details. Error source (5) has a negligible effect, as the DEMs of 1947 and 2010 have a high accuracy (±0.3–1 m) (Bauder et al., 2007).

Taking into account all the sources of uncertainty listed above as in Jouvet and Funk (2014), the confidence area of the Dakota location in 2014 (resp. its future emergence location) corresponds to a 1,012 m (or 954 m) long and 67 m (or 119 m) wide band along its main trajectory (see Figure 5; Figure S4). The same analysis was performed for the trajectory of the emerged pieces, with comparable results (949 m long and 74 m wide area). As expected, the size of our confidence area is similar to the one proposed by Jouvet and Funk (2014) (1,622 m long and 307 m wide), which defines the estimated area of the place where the corpses of the three ill-fated mountaineers were probably buried in 1926 on Aletschgletscher.

6. Discussion

The recent emergence of one engine, wing parts, and propellers suggests that the Dakota aircraft might re-appear in the coming years near the same location, assuming that these pieces were not spread over the glacier in 1947. However, this hypothesis is challenged by our modeling results, which indicate the emergence point of the Dakota aircraft as being more than 1 km upstream of the recently found pieces (Figure 5). This theory is supported by additional numerical results (not shown), which show unrealistically high ice flow velocities and inconsistent ice thickness distribution—i.e., high RMSE (see Table S1)—if the model was tuned by assuming that the emerged pieces originated as close as possible to the crash location of the Dakota in 1947. Furthermore, even using the ice flow parameter that led to the fastest glacial motion, in 2012 the model position of the Dakota aircraft would still lie 404 m upstream of the position where the emerged pieces where found. As is known from old photographs (Figure 1c) that engines (one of them found in 2018) were removed from the Dakota in 1947, we hypothesize that these pieces were moved from the original site of the crash, which explains why one of the motors was released from the glacier in 2018 (it took a shorter trajectory).

Indeed, it has been documented that some pieces of the Dakota were transported further down on the glacier during the 1947 expedition in order to retrieve them with two airplanes equipped to land on the snow (see Figure 1b). For that purpose, a landing strip was built on the glacier at an elevation of about 2,850 m (Hug, 1990; Cornioley, 2006), which is the closest place to the crash site suitable for landing (see Figure 2). However, it is not known whether all the pieces were retrieved or if some were left there. Interestingly, the 1947 modeled position of the pieces that emerged after 2012 coincides with the location of the landing strip. Thus, we assume that these pieces were part of the material transported downstream to the landing strip, but were left there, because the two airplanes were too small to transport a heavy engine weighing nearly half a ton.

Backwards trajectories calculated for pieces found on the surface in 2012 wind up 69 m beneath the 1947 glacier surface. This mismatch is possibly caused by numerical and physical model errors and/or errors in the modeled surface elevation at the position where the emerged pieces were found. However, small changes in sliding and/or viscosity parameters only result in minor changes in trajectory (Table S1) and can reduce the deposition depth of the aircraft pieces to ~40 m. As the historical record suggests that unrecoverable aircraft pieces were thrown into crevasses (Swiss Archives, 1947–1949), our backwards calculated trajectory of the pieces being deposited within the glacier in 1947 is highly realistic.

As the emerged pieces and the Dakota aircraft might have taken different trajectories, the question is raised as to the current location of the Dakota aircraft. According to our model, in 2014 was within the central part of the glacier at an elevation of ≈2,660 m a.s.l., 35 m deep within the ice (Figures 5, 6), and about 1.7 km upstream of the location where the Dakota pieces emerged. Unfortunately, we could not locate the Dakota aircraft using the surface-based GPR (see Figure S5), as was achieved on the east coast of Greenland (Annan, 2004).

Our modeling results for the 2014-2040 period indicate that the Dakota aircraft might emerge between 2027 and 2035, between 200 and 350 m downstream of its 2014 position, respectively (Figures 5, 6). It is likely that it will re-appear highly deformed and broken apart at the surface, since the Dakota aircraft was subjected to strong pressure and shearing (up to 6 bar as it moved along within the glacier, according to our model). In support of this, the B-17 airplane—which has approximately the dimensions of the Dakota and which was localized by GPR at a depth 80 m beneath the surface (similar to the Dakota) in the Greenland ice sheet (Wieland, 1997)—was found in several pieces after being excavated.

7. Conclusions

In this paper we modeled the 3D flow field of the Gauligletscher in order to reconstruct the trajectory within the ice of an airplane which crashed on Gauligletscher in 1946. By reconstructing the initial geometry of the glacier from old aerial photographs as well as the bedrock topography from ice thickness measurements, we modeled the evolution of the glacier from 1947 onwards by combining a Stokes model and a surface mass balance model until 2014, and using two climate scenarios after 2014. The model was calibrated with digital elevation model of 2010 and observed ice flow velocities. Once the model calibrated, the result showed a good fit between modeled and observed terminus position and volume changes.

Starting from the known location where the Dakota crashed, we computed its trajectory by integrating the modeled velocity field from 1947 to 2014, and found an estimate of its actual location—about 1.7 km upstream of the location where pieces were found between 2012 and 2018—with a confidence area of ± 500 m and ± 35 m in the longitudinal and lateral directions of ice flow, respectively. Our results show that the main body of the Dakota might have followed a trajectory different from that of the pieces that had already been released and found. The only plausible explanation for this is that the recently emerged Dakota pieces were transported ≈1.6 km downstream to a flatter area to be retrieved by air (as reported by historical records), but were finally abandoned in a crevasse. The main body of the Dakota was likely advected along a longer trajectory in time, and is expected to re-appear between 2027 and 2035, at a distance between 200 and 350 m downstream from the 2014 estimated position.

Our method can be used to predict the timing and location of the re-appearance of other airplanes similar to the Dakota that have crashed into glaciers worldwide (Aviation Safety Network, 2018), as long as the crash location is known and accurate data on glacier bed topography and surface mass balance are available. Beyond this specific application, this method can serve to track any other objects within the ice for which the emerging time and location is desired to be known.

Author Contributions

LC did the numerical modeling with Elmer/Ice and analyzed the data with support from GJ and AB. LC, GJ, and AB wrote the manuscript. GJ, AB, and MF conceived the original idea. GC, AB, and LC conducted the GPR measurements and GC analyzed the data. SL performed the velocity analysis using his offset tracking algorithms from TanDEM-X radar images. GJ processed the Sentinel-2A satellite images to extract the velocity field with ImGRAFT. GJ, AB, MF, and ML contributed to the discussion of the results.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are grateful to the Swiss Federal Archive and to the Library Am Guisanplatz BiG for their help providing us with documentation on the Dakota accident and the Swiss Army expedition in spring 1947. The Sentinel-2 satellite images were processed by J. Seguinot using SentinelFlow. They contain modified Copernicus Sentinel data (2015, 2016, and 2017). We thank the Elmer/Ice team for their support during the Elmer/Ice course held at Stockholm University the 23rd and 24th of October 2017. We thank the Swiss Alpine Museum for give us the historical pictures of the Swiss Army expedition in 1947 on Gauligletscher (Ernst Reiss: Fotoalbum Gauligletscher-Flugzeugabsturz 1946. Alpines Museum der Schweiz, Bern). A supplementary with codes and all relevant data sets is available from doi: 10.3929/ethz-b-000339583. We also thank S. Braun-Clarke for proofreading the English.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00170/full#supplementary-material

References

Annan, A. (2004). Applications of ground penetrating radar in archaeological and forensic contexts. First Break 22, 41–44.

Google Scholar

Archiv-Gletscherkommision SANW (1946-1947). Korrispondezdossier betreffend Absturz einer Dakota der US-Army auf dem Gauligletscher.

Aviation Safety Network (2018). ASN Aviation Safety Database. Available online at: http://aviation-safety.net/database/.

Bauder, A., Funk, M., and Huss, M. (2007). Ice-volume changes of selected glaciers in the Swiss Alps since the end of the 19th century. Ann. Glaciol. 46, 145–149. doi: 10.3189/172756407782871701

CrossRef Full Text | Google Scholar

Bürgi, H., and Stierli, B. (2006). Der Start zur Luftrettung. SkyNews. Available online at: http://www.history-comix.ch/up/pdf/dieerstehochalpinefluttungskynewsweblw.pdf.

Compagno, L. (2018). Modelling the reappearance of a crashed airplane on Gauligletscher (Master's thesis). ETH, Zürich.

Cornioley, R. (2006). Der Flugzeugabsturz einer amerikanischen Dakota auf dem Gauligletscher im November 1946 Vor 60 Jahren war das Haslital Schauplatz der grössten alpinen Rettungsaktion. Berner Z. Geschichte 68, 115–155.

Cuffey, K. M., and Paterson, W. S. B. (2010). The Physics of Glaciers. Burlington, NJ: Elsevier Science.

Google Scholar

Farinotti, D., Huss, M., Bauder, A., Funk, M., and Truffer, M. (2009). A method to estimate the ice volume and ice-thickness distribution of alpine glaciers. J. Glaciol. 55, 422–430. doi: 10.3189/002214309788816759

CrossRef Full Text | Google Scholar

Gagliardini, O., Zwinger, T., Gillet-Chaulet, F., Durand, G., Favier, L., de Fleurian, B., et al. (2013). Capabilities and performance of Elmer/Ice, a new-generation ice sheet model. Geosci. Model Dev. 6, 1299–1318. doi: 10.5194/gmd-6-1299-2013

CrossRef Full Text | Google Scholar

GLAMOS (1881–2018). The Swiss Glaciers, 1880–2016/17. Glaciological reports 1-138, Cryospheric Commission of the Swiss Academy of Sciences (SCNAT). published since 1964 by Laboratory of Hydraulics, Hydrology and Glaciology (VAW) of ETH Zürich. Available online at: http://glaciology.ethz.ch/swiss-glaciers/.

Greve, R., and Blatter, H. (2009). Dynamics of Ice Sheets and Glaciers. Advances in Geophysical and Environmental Mechanics and Mathematics. Dordrecht; New York, NY: Springer.

Google Scholar

Hug, V. (1990). Rettungsaktion der Besatzung einer Dakota C-53 der US-Army auf dem Gauligletscher am 23/24.11.1946. Bibliothek am Guisanplatz, ILV-BiG: KOP 42610 (d51771).

Huss, M., Bauder, A., Funk, M., and Hock, R. (2008). Determination of the seasonal mass balance of four Alpine glaciers since 1865. J. Geophys. Res. 113:F01015. doi: 10.1029/2007JF000803

CrossRef Full Text | Google Scholar

Huss, M., Hock, R., Bauder, A., and Funk, M. (2010). 100-year mass changes in the Swiss Alps linked to the Atlantic Multidecadal Oscillation. Geophys. Res. Lett. 37:L10501. doi: 10.1029/2010GL042616

CrossRef Full Text | Google Scholar

Jouvet, G., and Funk, M. (2014). Modelling the trajectory of the corpses of mountaineers who disappeared in 1926 on Aletschgletscher, Switzerland. J. Glaciol. 60, 255–261. doi: 10.3189/2014JoG13J156

CrossRef Full Text | Google Scholar

Jouvet, G., Huss, M., Blatter, H., Picasso, M., and Rappaz, J. (2009). Numerical simulation of Rhonegletscher from 1874 to 2100. J. Comput. Phys. 228, 6426–6439. doi: 10.1016/j.jcp.2009.05.033

CrossRef Full Text | Google Scholar

Jouvet, G., Huss, M., Funk, M., and Blatter, H. (2011). Modelling the retreat of Grosser Aletschgletscher, Switzerland, in a changing climate. J. Glaciol. 57, 1033–1045. doi: 10.3189/002214311798843359

CrossRef Full Text | Google Scholar

Jouvet, G., Picasso, M., Rappaz, J., and Blatter, H. (2008). A new algorithm to simulate the dynamics of a glacier: theory and applications. J. Glaciol. 54, 801–811. doi: 10.3189/002214308787780049

CrossRef Full Text | Google Scholar

Le Meur, E., Gagliardini, O., Zwinger, T., and Ruokolainen, J. (2004). Glacier flow modelling: a comparison of the Shallow Ice Approximation and the full-Stokes solution. Comptes Rendus Phys. 5, 709–722. doi: 10.1016/j.crhy.2004.10.001

CrossRef Full Text | Google Scholar

Messerli, A., and Grinsted, A. (2015). Image georectification and feature tracking toolbox: ImGRAFT. Geosci. Instrum. Methods Data Syst. 4, 23–34. doi: 10.5194/gi-4-23-2015

CrossRef Full Text | Google Scholar

Petroni, B. (2015, September 19). Sensation auf dem Gauligletscher-Wrackteile der Dakota entdeckt. Berner Zeitung.

Petroni, B. (2018, August 10). Der Gauligletscher gibt weitere Flugzeugteile frei. Berner Zeitung.

Réveillet, M., Rabatel, A., Gillet-Chaulet, F., and Soruco, A. (2015). Simulations of changes to Glaciar Zongo, Bolivia (16 S), over the 21st century using a 3-D full-Stokes model and CMIP5 climate projections. Ann. Glaciol. 56, 89–97. doi: 10.3189/2015AoG70A113

CrossRef Full Text | Google Scholar

Rothacher, P. (2014, April 25). Der Dakota-Propeller bleibt in Innertkirchen. Berner Zeitung.

Rutishauser, A., Maurer, H., and Bauder, A. (2016). Helicopter-borne ground-penetrating radar investigations on temperate alpine glaciers: a comparison of different systems and their abilities for bedrock mapping. Geophysics 81, WA119–WA129. doi: 10.1190/geo2015-0144.1

CrossRef Full Text | Google Scholar

Samuel, H. (2014, August 17). French treasure hunter finds 50 pieces of jewellery on Mont Blanc from Air India crash 48 years ago. The Telegraph.

Sesiano, J. (1982). Le glacier des Bossons : la forte crue de 1981-1982 et une estimation de sa vitesse sur 30 ans. Revue Géogr. Alpine 70, 431–438.

Google Scholar

Suter, S., Laternser, M., Haeberli, W., Frauenfelder, R., and Hoelzle, M. (2001). Cold firn and ice of high-altitude glaciers in the alps: measurements and distribution modelling. J. Glaciol. 47, 85–96. doi: 10.3189/172756501781832566

CrossRef Full Text | Google Scholar

Swiss Archives (1947–1949). (E5464#19381/178#739) az. 2152.136, faden nr. 22: Bergung einer amerik. dakota auf dem gauligletscher 23./24.11.1946.

Weertman, J. (1957). On the sliding of glaciers. J. Glaciol. 3, 33–38.

Google Scholar

Wieland, C. (1997). The lost squadron. Creat. Mag. 19, 10–14.

Google Scholar

Zwinger, T., and Moore, J. C. (2009). Diagnostic and prognostic simulations with a full Stokes model accounting for superimposed ice of Midtre Lovénbreen, Svalbard. Cryosphere 3, 217–229. doi: 10.5194/tc-3-217-2009

CrossRef Full Text | Google Scholar