
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Earth Sci., 26 February 2019
Sec. Earth and Planetary Materials
Volume 7 - 2019 | https://doi.org/10.3389/feart.2019.00023
Dynamic-compression experiments on geological materials are important for understanding the composition and physical state of the deep interior of the Earth and other planets. These experiments also provide insights into impact processes relevant to planetary formation and evolution. Recently, new techniques for dynamic compression using high-powered lasers and pulsed-power systems have been developed. These methods allow for compression on timescales ranging from nanoseconds to microseconds and can often achieve substantially higher pressure than earlier gas-gun-based loading techniques. The capability to produce shockless (i.e., ramp) compression provides access to new regimes of pressure–temperature space and new diagnostics allow for a more detailed understanding of the structure and physical properties of materials under dynamic loading. This review summarizes these recent advances, focusing on results for geological materials at ultra-high pressures above 200 GPa. Implications for the structure and dynamics of planetary interiors are discussed.
There is a growing interest in application of experimental studies of geological materials at ultra-high pressure–temperature conditions to both new and long-standing problems in Earth and planetary science (Duffy et al., 2014). Such experiments can address fundamental questions about the structure, dynamics, and evolution of the deep Earth. In addition, the discovery of thousands of extra-solar planets around other stars in our galaxy raises new questions about the diversity of planetary architectures and how such planets might form and evolve. The size range between Earth and Neptune represents the most abundant population of exoplanets detected to date (Borucki, 2016). These planets have no direct analogs in our own solar system and potentially represent novel planetary types. The measured densities of some of these planets are indicative of bulk compositions comparable to those of terrestrial planets in our solar system (Howe et al., 2014). There has been a considerable interest in the interior structure and dynamics of these so-called “super-Earths” (Driscoll, 2018). Fundamentally different types of planets may also exist including mini-Neptunes and water- or carbon-enriched planets (Seager, 2013). Knowledge of the composition and mineralogy of a planet is necessary for determining its evolution, inner structure, and thermal behavior (Unterborn et al., 2014). Currently, a lack of constraints on the physical and chemical properties of materials at extreme conditions severely limits progress on these questions.
The pressure and temperature range encompassed in planetary interiors are vast (Figure 1). The Earth’s silicate mantle extends to 2,900-km depth and reaches a pressure of 135 GPa (1.35 Mbar) at its base. The core, which contains one-third of the Earth’s mass, extends to 6,371-km depth and reaches a pressure of 363 GPa. Temperatures in the Earth’s interior are less well constrained but are expected to range from ∼1,500 to 2,500 K through the mantle and may reach as high as 6,500 K at the center of the Earth. Ice-giant planets such as Uranus and Neptune are estimated to achieve pressures up to 700 GPa at their centers whereas Jupiter’s central conditions is estimated at ∼7 TPa and 10,000 K. A rocky super-Earth planet of ten Earth masses in size is expected to reach more than 1 TPa at the base of its silicate mantle and close to 4 TPa at the center of the iron-alloy core (Wagner et al., 2012) (Figure 1A). The plausible temperatures in these bodies span a wide range depending on assumptions about their formation and interior evolution (Wagner et al., 2012; Stixrude, 2014) (Figure 1B).
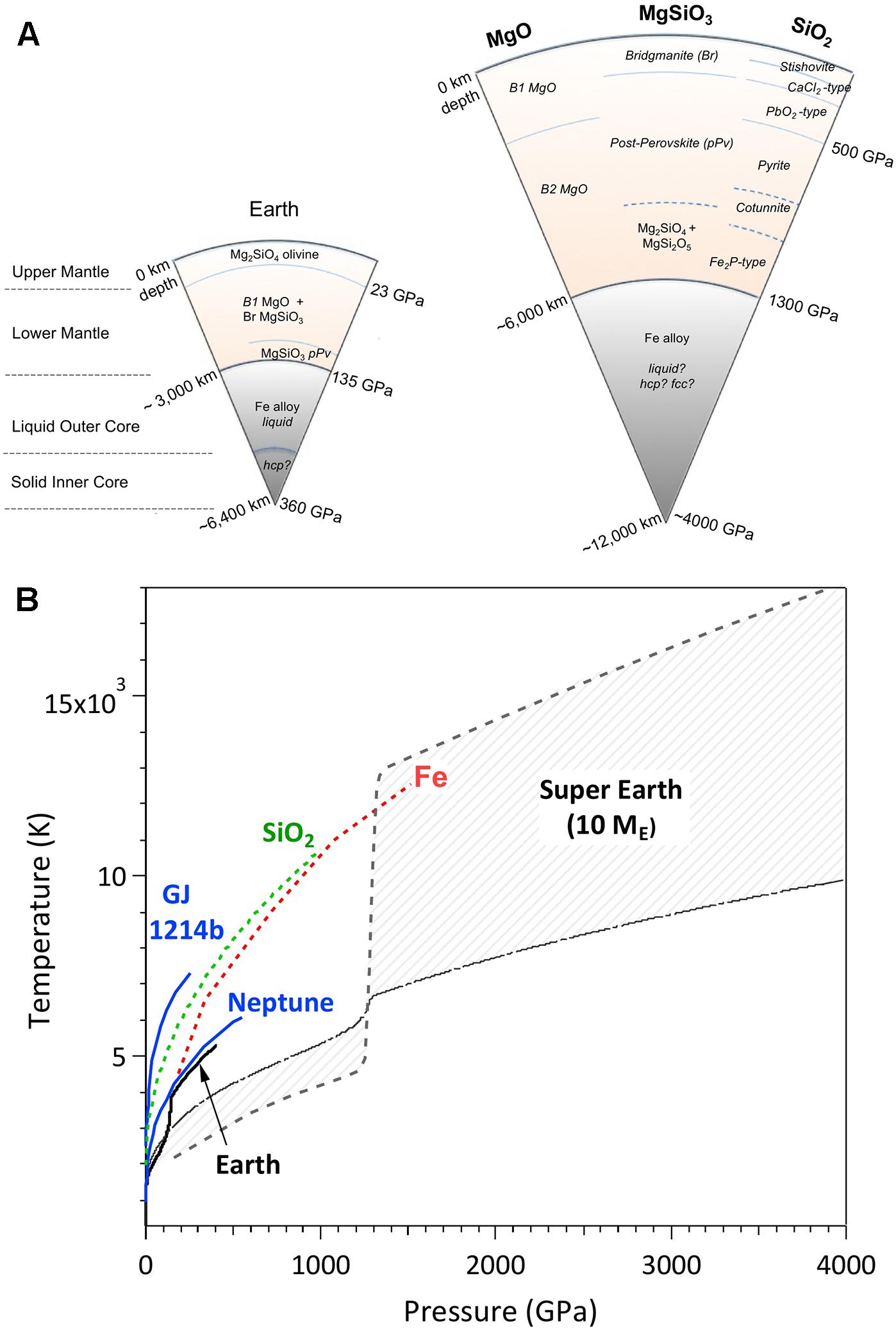
Figure 1. (A) Schematic representation of interior structure of Earth and a ten-Earth-mass planet showing selected expected phases in the MgO-SiO2 system. (B) Range of pressure–temperature conditions in representative planetary interiors. Pressure–temperature range for Earth and plausible range for a ten-Earth-mass rocky planet are shown as black curves and gray shaded regions (Wagner et al., 2012; Stixrude, 2014). Ice giants (blue) are represented by Neptune and exoplanet GJ1214b (Nettelmann et al., 2011). Melting curves for SiO2 (Millot et al., 2015) and Fe (Bouchet et al., 2013) are shown as dashed green and red lines.
Experimental studies of materials at deep planetary-interior conditions have historically been performed mainly via static compression using the diamond anvil cell (Duffy, 2005; Shen and Mao, 2017). Such studies are usually restricted to less than 200 GPa although recent advances are extending this limit to higher pressure. To experimentally reach pressures into the terapascal range and temperatures up to 10,000 K or more, dynamic-loading techniques – shock and ramp compression – are the only experimental methods available. Dynamic compression techniques, which involve loading durations from nano- to microseconds, have undergone rapid development in the last decade, greatly extending the accessible conditions and types of measurements that can be performed. While the extended pressure–temperature range is a significant advantage of dynamic compression, the short timescales involved may result in non-equilibrium material behavior (Duvall and Graham, 1977; Smith et al., 2013). For example, phase transitions may need to be overdriven in pressure or result in transformation to a metastable phase. Careful comparisons between static, dynamic, and theoretical results are necessary to evaluate these effects.
There is strong interest in material behavior under extreme conditions of pressure and temperature across many disciplines including materials science, chemistry, and condensed matter physics (Remington et al., 2015; Falk, 2018). The large reduction in volume of solids at multi-megabar pressure and beyond produces substantial changes in coordination, packing, and bond distances. When pressure exceeds 100 GPa, the energy changes associated with compression reach electron-volt levels and begin to equal or exceed chemical bonding energies (Jeanloz, 1989). This can lead to delocalization of electrons or participation of filled valence or core shells in chemical reactions. Existing bonds may be greatly modified and new bonds created. Our conventional understanding of structure, electronic, and magnetic properties based on periodic trends among the elements at low pressures may no longer be valid (Grochala et al., 2007). Theoretical studies predict that many materials will exhibit unusual structural or chemical behavior at these pressures (Zurek and Grochala, 2015).
In this review, recent advances in dynamic compression focusing on geological materials at ultra-high pressure of 200 GPa and above will be summarized and applications to geophysics and planetary science will be discussed.
Investigations of material properties at high pressure and temperature are conducted using a wide array of experimental techniques. Static compression studies are most commonly based on the use of multi-anvil or diamond anvil cell devices to achieve sustained high-pressure states. Dynamic compression was historically conducted primarily through the use of gas-gun technology, but more recently high-powered lasers and pulsed-power drivers have increasingly been adopted. Traditionally dynamic compression was restricted to the generation of shock-compressed states only, but ramp (shockless) dynamic compression has developed rapidly in recent years. Dynamic-loading techniques and the major diagnostics used to probe material properties are described in detail below.
Figure 2 depicts the historical progression of pressures achieved in laboratory experiments using static, ramp, and shock compression techniques. Increases in experimental pressures achievable under static compression have been marked during the last century by a number of technical advances: the use by Bridgman of tungsten carbide cells in the mid-1930s (Bridgman, 1935) and the first diamond anvil cell in the late 1950s (Weir et al., 1959; Van Valkenburg, 1962; Bassett, 2009). Diamond cell technology together with the development of the optical ruby fluorescence method of pressure measurement in 1972 (Forman et al., 1972) stimulated profound advances in high-pressure research. In recent years, the application of microfabrication techniques to improve conventional anvils had led to the development of toroidal (Dewaele et al., 2018; Jenei et al., 2018) and double-stage anvils (Dubrovinskaia et al., 2016) allowing for static pressure approaching a terapascal (TPa) to be reached, although restricted to room-temperature compression thus far.
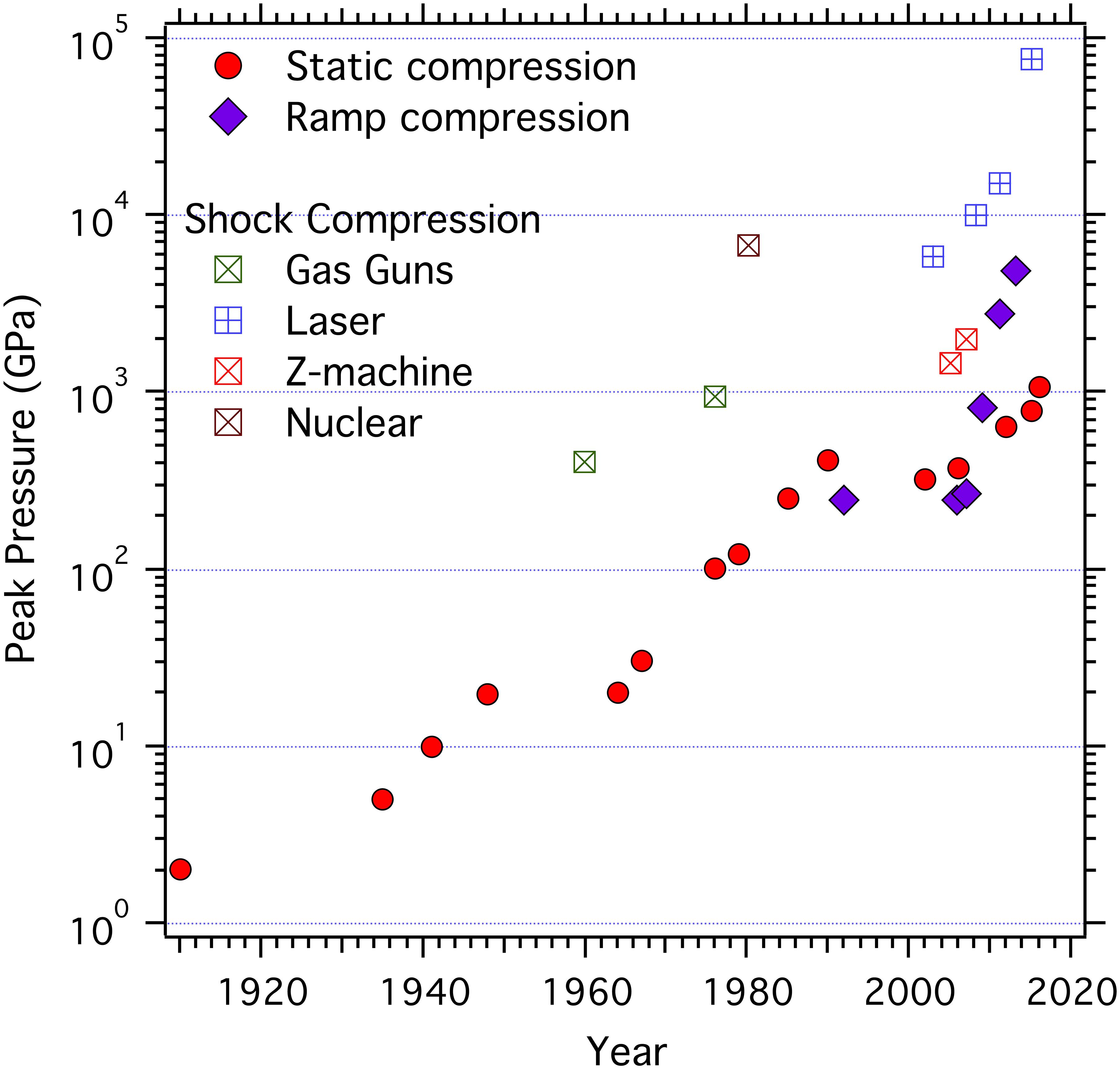
Figure 2. Progression of pressures achieved in the laboratory as a function of year for shock (open squares), static (red circles), and ramp-compression techniques (purple diamonds). Nuclear refers to experiments conducted in association with the testing of nuclear weapons.
Large laser facilities emerged in the 1970s with the first demonstration of generating strong shock waves with lasers occurring in 1979 (Trainor et al., 1979). The first high-accuracy shock wave-profile measurements under laser compression resulted from advances in laser interferometry diagnostics (see discussion below) (Celliers et al., 1998). Ramp-wave loading techniques, which access a cooler compression path compared with shocks (Figure 3), have been demonstrated using several drivers such as magnetic-pulse loading (Hawke et al., 1972; Asay, 2000), graded-density-impactors on gas-gun facilities (Chhabildas and Barker, 1986), chemical energy of high explosives (Barnes et al., 1974), and high-powered lasers (Edwards et al., 2004; Swift and Johnson, 2005). The characteristic loading time for graded-density-impactor loading is ∼1 μs, for magnetic ramp loading it is ∼100 ns, and for laser-ramp-loading it is ∼10 ns. The ability to vary the ramp-compression time scales enables the study of time-dependent material behavior associated with structural changes and deformation in solids subjected to extreme compressions (Smith et al., 2013). Recent advances in laser-pulse shaping and power have enabled measurements of material properties along a ramp compression path to as high as 5 TPa on the National Ignition Facility (Smith et al., 2014).
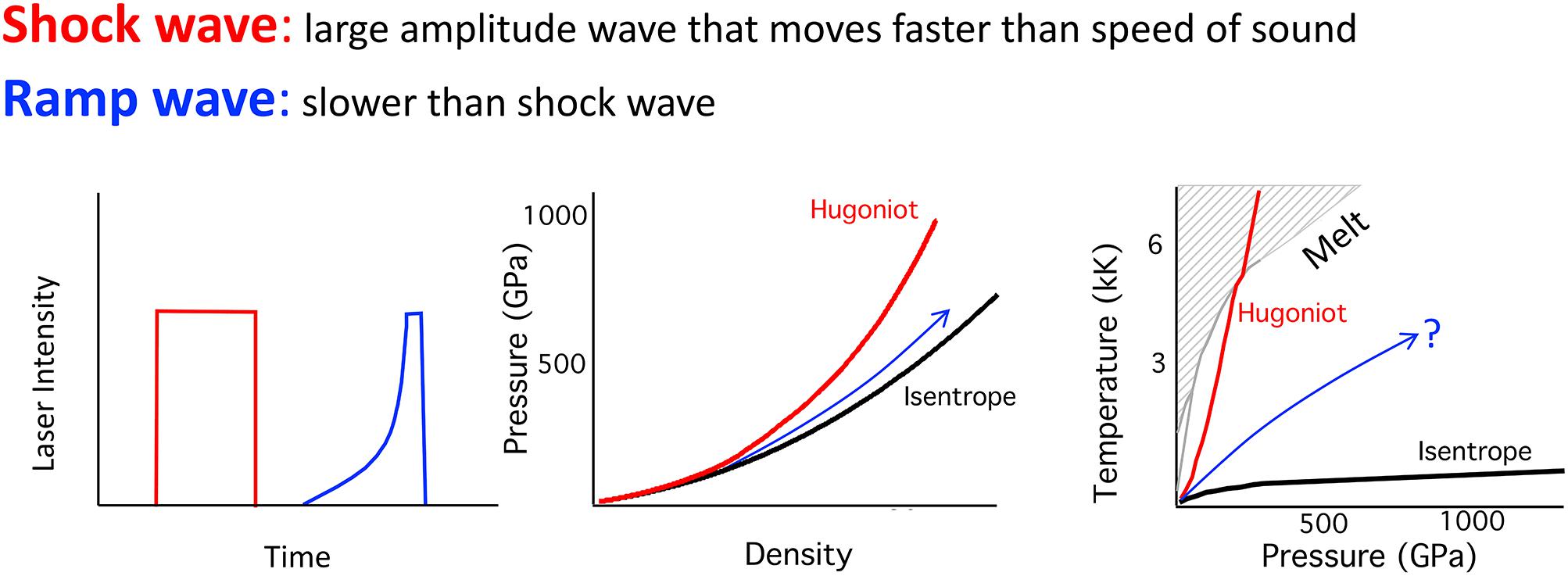
Figure 3. For laser-based compression, the temporal profile of laser intensity determines the pressure, temperature, and density states within a sample. Shock experiments produce a single state along the Hugoniot, which at high pressure, is characterized by strong sample heating. A significantly cooler compression path is generated in ramp compression experiments which access pressure–density close to the material’s isentrope. In ramp experiments the solid state can be maintained to high pressure (Wicks et al., 2018) although the exact pressure–temperature path is not directly constrained in these experiments.
A shock wave is a large-amplitude mechanical wave across which pressure, density, particle velocity, temperature, and other material properties change nearly discontinuously (Asimow, 2015). Shock waves propagate with supersonic velocity relative to unperturbed material ahead of the shock front, and the shock velocity, US, is amplitude dependent. A particle velocity, up, is imparted to material behind the shock front. The Rankine-Hugoniot equations express conservation of mass, momentum, and energy across the shock discontinuity:
where P is pressure, ρ is density, E is specific internal energy, and the subscript 0 refers to the initial unshocked state. These equations assume fluid-like behavior. For a solid, owing to the one-dimensional loading and intertial confinement, a uniaxial strain state is generated. A correction is then needed to account for deviatoric stresses to relate the measured longitudinal stress to a corresponding hydrostatic pressure.
Shock compression is thermodynamically irreversible and a substantial portion of the energy in a shock wave goes into raising the entropy and temperature of the material (Figure 3). At low pressures, the temperature rise is modest, but temperature increases strongly at higher compression. Shock heating ultimately leads to the melting of solids. This typically occurs at pressures of ∼100–300 GPa for silicates, oxides, and metals of geological interest, so shock-wave experiments at ultra-high pressures are usually probing high-temperature liquid states (Figure 3). There is also a limiting value to the compression achievable by shock compression as the energy becomes increasingly partitioned into additional heating of the sample rather than compression (Johnson, 1999).
Historically most shock-compression experiments have been based on the use of two-stage gas guns to accelerate a disk-shaped flyer plate to several kilometers per second. The flyer plate impacts a target generating a shock wave that propagates through the sample (Ahrens, 1987) (Figure 4). Measurement of the shock and particle velocities in the sample enable the thermodynamic state (P, ρ, E) to be constrained through application of the Rankine-Hugoniot equations (Eqs. 1–3). In addition, a linear relationship between the shock wave velocity and corresponding particle velocity is observed empirically over a range of compression for many materials. This is known as the shock wave equation of state. Deviations from a linear US - up relationship may be indicative of dynamic yielding or phase transitions.
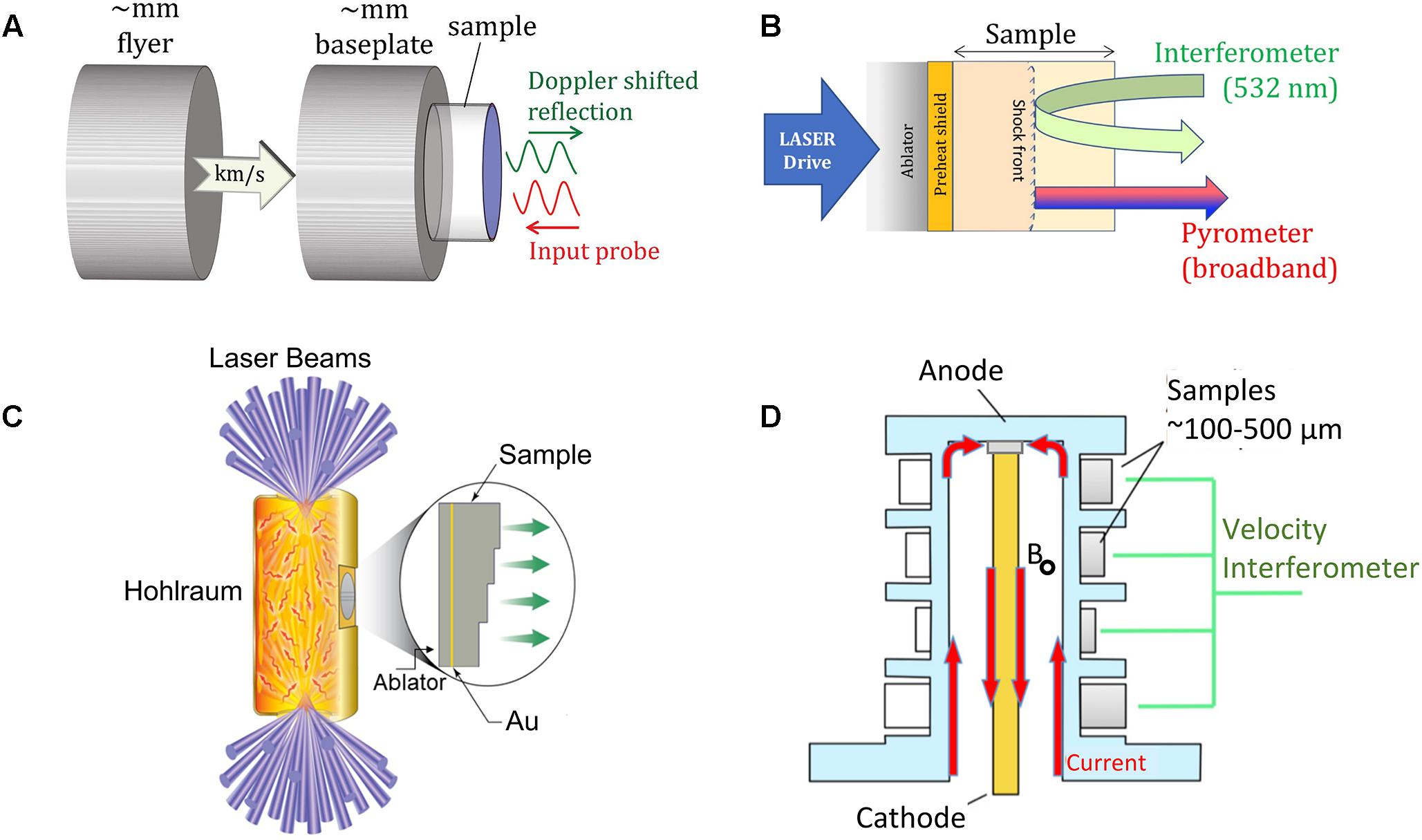
Figure 4. Dynamic-compression platforms for generating high-pressure states: (A) flyer-plate impact using gas guns, (B) direct-drive ablation using a high-powered laser (C) indirect-drive ablation using a high-powered laser and (D) pulsed power machine. In all cases, sample velocity is determined through laser interferometry (see text for details).
The Hugoniot curve is the locus of final states achieved with a single shock from a given set of initial conditions (note that it is not the thermodynamic path followed during shock compression). Each shock experiment thus determines a single datum on the Hugoniot curve (Figure 5A). An important consequence of Eqs. (1–3) is that an independent pressure calibrant is not necessarily required for shock experiments as pressure can in many cases be determined from the measured flow variables (US and up) and conservation of momentum. For this reason shock-wave data corrected for the effects of temperature are commonly used for the calibration of pressure standards in static diamond anvil cell experiments (Nellis, 2007). Note also that the Hugoniot equations do not constrain temperature directly, but temperatures can be calculated using thermodynamic relationships or by measurement of the thermal radiation emitted by the shocked sample (Svendsen and Ahrens, 1987; Luo et al., 2004; Eggert et al., 2009).
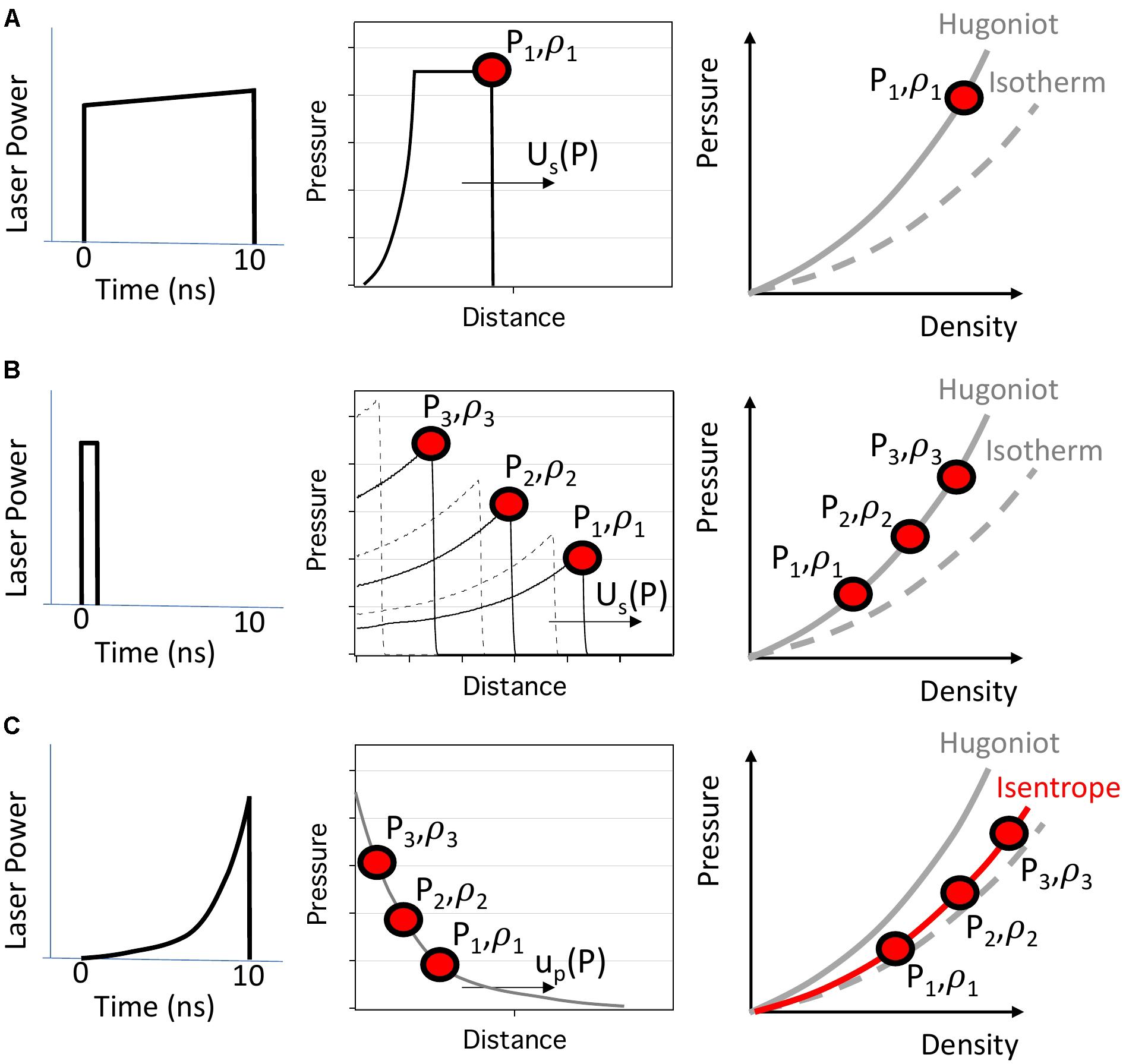
Figure 5. The thermodynamic compression path within the sample under study can be controlled in dynamic compression experiments as illustrated here for the case of laser-based compression. (A) A near flat-top laser pulse shape generates a temporally steady shock wave which propagates with a pressure-dependent shock speed, Us(P), and generates a single compression state along the material’s Hugoniot. (B) A ∼1 ns pulse shape generates a temporally decaying shock which samples a continuum of shock states along the Hugoniot (broken and solid curves) as it propagates through a sample. (C) A ramp-compression profile generates a continuum of states close to a material’s isentrope.
Thermodynamic paths of interest for compressed states of matter are compared in Figure 5. The isotherm is the pressure-volume response of a material at constant temperature. The 300-K isotherm can be measured in a diamond anvil cell experiment, whereas the 0-K isotherm or cold curve can be obtained from ground-state theoretical calculations such as those using density functional theory (DFT). The isentrope is the thermodynamic path that corresponds to continuous compression that is both adiabatic and reversible. In this case, there is no heat flow out of the system and as a result a modest temperature rise results from compression. The isentrope thus lies above the isotherm in pressure–density and pressure–temperature space (Figures 3, 5). The Hugoniot is the result of adiabatic, irreversible shock compression, resulting in a high-temperature state and a pressure offset from the isotherm and isentrope that increases with compression. At lower pressures where shock heating is small, the Hugoniot lies close to the isentrope (neglecting strength effects), but the curves diverge increasingly at higher pressure (Figure 3). Shock experiments produce extremely high rates of loading (strain rates of ∼108–109 s-1) and thus kinetics and time-dependent material behavior may be important. These factors, together with the different pressure–temperature states achievable, make shock experiments distinct from, but complementary to, static compression using diamond anvil cells. Detailed reviews of the fundamentals of dynamic compression with an emphasis on shock-wave studies of geological materials are available in the literature (Ahrens, 1987; Asimow, 2015).
An alternative dynamic-loading technique attracting increasing interest for the study of materials under ultra-high pressures is ramp loading (Hall et al., 2001; Reisman et al., 2001; Edwards et al., 2004). Ramp compression is achieved through a continuous increase in dynamic pressure rather than a discrete jump associated with a shock wave. It can viewed as the limit of a series of weak shocks that compress a sample in small steps up to the final pressure. Ramp compression rise times are typically 10–100 ns, compared with ∼1 ps for shock compression (Figure 5C). As a result the sample is compressed sufficiently rapidly that heat flow remains negligible but slowly enough to avoid forming a shock. In the ideal case, ramp compression thus follows an isentropic thermodynamic path. However, due to the presence of shear or viscous stresses, irreversible processes such as plastic work heating result in an entropy increase and a rise in temperature (Figure 3).
Ramp loading has a number of advantages for studying materials at ultra-high pressures. The reduced heating means that solids can be compressed to very high pressure without melting. Furthermore, there is no upper limit on compression achievable by ramp methods, in contrast to shock compression. The technique enables access to the wide range of pressure–temperature states that lie between the isotherm and the Hugoniot (Figure 3). Moreover, ramp loading produces measurements of a continuum of pressure–density states along the load curve, unlike traditional steady shock compression which yields only one data point on the Hugoniot per experiment (Figure 5). However, ramp loading can be challenging to maintain experimentally during propagation through a sample because the increase in sound velocity with pressure tends to cause large-amplitude pressure waves to steepen into shocks.
In a laser-compression experiment, a large pulse of laser energy (∼1013 - 1014 W/cm2) is deposited on the surface of an absorbing medium (Figure 4B). This rapidly heats and ablates the material which expands outward at high velocity as a result. Conservation of momentum results in a corresponding compression wave being driven into the sample as the heated material expands backward. The temperature of the ablated material reaches to above 1 keV (1 eV = 11,600 K) resulting in ionization and plasma formation. The following expression can be used to estimate the ablation pressure, Pab (Drake, 2006):
where λ is the laser wavelength. Here the laser irradiance, I = E/(At), where E is the laser energy, A is the laser focal spot area, and t is the pulse duration. Based on this expression, the use of a 351-nm laser focused to a 0.8-mm-diameter spot and a 4-ns pulse can generate pressures from 200 GPa to 1 TPa with laser energies ranging from 100 J to 1 kJ. A detailed description of the laser-matter interactions involved in generating ultra-high pressures can be found in the literature (Drake, 2006; Falk, 2018).
Laser facilities in use for dynamic-compression experiments on geological materials include the Omega Laser Facility at the University of Rochester (Boehly et al., 1997), the GEKKO XII laser at the University of Osaka (Ozaki et al., 2004), the LULI2000 laser at the École Polytechnique in Palaiseau, France (Ozaki et al., 2006), and the National Ignition Facility (NIF) at Lawrence Livermore National Laboratory (LLNL) (Hurricane and Herrmann, 2017). Table 1 lists these and selected other major laser facilities and some basic characteristics.
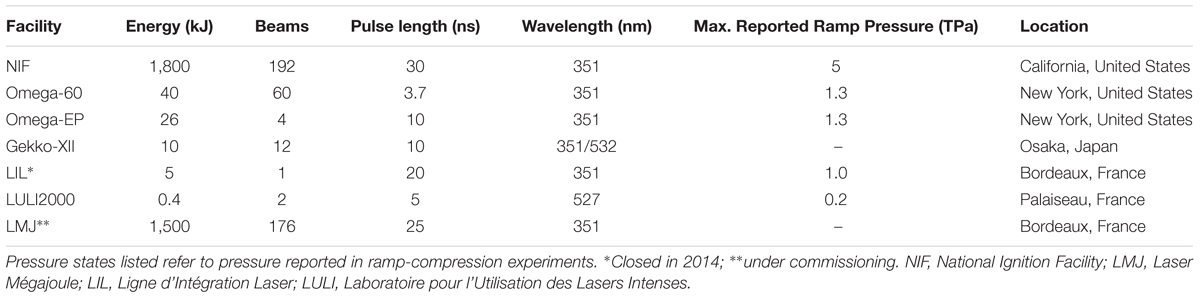
Table 1. Characteristics of representative high-powered laser facilities for dynamic-compression experiments.
The Omega facility consists of two neodymium:glass laser systems (Omega-60 and Omega-EP) operating at 351 nm. Omega-60 has 60 beams, each of which can provide up to 500 J of energy. Omega-EP has four beams that can deliver as much as 6,500 J/beam over 10-ns pulse lengths. The lasers can be focused onto mm-sized targets at the center of a spherical chamber with each beam capable of being individually positioned with a pointing accuracy of 15 μm and a timing accuracy of 5 ps. Optical components known as phase plates are used to smooth intensity variations in the beam. A key feature of laser facilities is their flexible pulse shaping, which allow users to design and apply a range of pulse shapes to produce controlled loading states (Figure 5). Individual pulses at Omega-60 can be up to 3.7 ns in duration but longer composite pulses using multiple beams can also be designed. The independent spatial and temporal targeting capability at multi-beam laser facilities allows for complex experimental designs such as driving a compression wave into the sample with some of the beams while using others to generate an X-ray source to probe the compressed sample after a time delay.
The National Ignition Facility at LLNL, the world’s largest laser system, was designed primarily for studies of inertial confinement fusion but a portion of shot days are allocated to basic science. NIF has 192 beams capable of delivering up to 1.8 MJ of total laser energy at 351 nm. In addition to unprecedented high power, NIF has the ability to deliver shaped pulses up to 30 ns in duration, with an accuracy within 1% in power. These capabilities provide the energy and control necessary to ramp compress matter to several terapascals (Smith et al., 2014).
Ultra-high pressure dynamic experiments can also be conducted using the Z machine at Sandia National Laboratory. Z is a pulsed-power facility that can produce currents as high as 20 MA and magnetic fields to 10 MG (Matzen et al., 2005). Discharge of a large capacitor bank through a closely positioned anode and cathode pair with currents flowing in opposite directions generates a magnetic force that can rapidly accelerate materials at high strain rates with different possible loading profiles including both shock and ramp compression (Figure 4D). Additionally, Z can be used to accelerate flyer plates and thus drive shock waves through plate-impact techniques. Experiments on Z have reached 450 GPa along a ramp compression path (Kraus, 2016) and nearly 1.7 TPa along the shock Hugoniot (Knudson and Desjarlais, 2013; Ozaki et al., 2016).
There are three major dynamic compression techniques being used to achieve ultra-high pressure: steady shock compression, decaying shock compression, and ramp compression. Figure 5 provides an example of how laser pulse shaping (left column) can achieve each of these and produce different thermodynamic compression paths within a sample under study. In Figure 5A, a 10-ns near-flat-top laser pulse shape generates a temporally steady-shock traveling through the sample at a pressure-dependent shock speed, US(P). Here, a single peak compression state on Hugoniot (P1, ρ1) is generated. Alternatively, if the laser pulse is short (∼1 ns), a release wave from the drive surface overtakes the shock front and the shock decays as it propagates, generating a continuum of Hugoniot states (Figure 5B). Measurements of shock velocity and temperature as the decaying shock traverses the sample can be used to make a series of continuous measurements along the Hugoniot (Figure 5B) (Millot et al., 2015). If the applied laser pulse has a ramp-like shape (Figure 5C), the compression wave that propagates through the sample has a pressure-dependent particle velocity, up(P). Here the compression states generated are close to the material’s isentrope. Other types of drivers, gas guns and pulsed power, can also be used to access different types of compression pathways (Chhabildas and Barker, 1986; Knudson, 2012).
Both laser and pulsed-power facilities can be used to generate steady shock waves in samples (Figure 5A). For laser experiments, a typical target package consists of a foil sample sandwiched between a polyimide ablator material and a LiF or quartz window (Figure 4B). For typical experiments at the Omega-60 laser, a ∼4-ns flat-topped laser pulse is focused using phase plates to a diameter of ∼1 mm on the surface of the polyimide. Ablation of the polyimide produces a steady shock wave in the target package resulting in sample compression to 100s of GPa (Wang et al., 2015).
Alternatively, the laser pulse may be used to accelerate a flyer plate across a gap to strike a target (Swift et al., 2005). A similar approach can be used to generate very high impact velocities at pulsed-power facilities. The large current pulses generated by the Z machine create a strong magnetic field and the combination of the current and magnetic field create a Lorentz force, F = J × B that can be used to accelerate flyer plates to as fast as 40 km/s (Lemke et al., 2005; Knudson et al., 2008; Root et al., 2015). This is much higher than the projectile velocities that can be achieved with two-stage light-gas guns (<8 km/s). The current pulse is designed so that the flyer plates are shocklessly accelerated such that the impact side of the flyer plate remains at solid density upon impact.
In a decaying shock wave experiment, the laser pulse is designed to produce a strong shock that decays as it propagates through the sample (Figure 5B). That is, each successive layer in the material is compressed from its initial condition to a different final Hugoniot state with pressure and temperature decreasing with shock propagation distance (Bradley et al., 2004; Eggert et al., 2009). An advantage of this technique is that it allows for measurements along a continuous series of Hugoniot states in a single experiment rather than obtaining only a single datum as in a traditional plate-impact or laser-shock experiment. The samples used in these experiments must be initially transparent but become ionized and partially reflecting upon shock loading of sufficiently high amplitude (typically a few hundred GPa). The sample reflectivity allows for continuous measurements of the shock velocity and shock-front temperature as the shock decays during its transit across the sample (see Diagnostics section below). To convert the measured shock velocity to pressure and density requires either knowledge of the Hugoniot relationship of the sample or use of a calibrated standard. Phase transitions such as melting can be identified in these experiments by observation of temperature anomalies associated with energy changes resulting from the transition (Bradley et al., 2004; Millot et al., 2015). Relative to more traditional supported shock experiments, the main disadvantage of decaying shocks, in addition to restrictions on sample properties, is that the technique may be less likely to achieve equilibrium or a phase transition to a well-defined shock state.
The effort to develop dynamic ramp-loading techniques began in the 1970s (Barnes et al., 1974) but made only modest progress for many years. The advent of high-powered laser and pulsed-power facilities reinvigorated this effort (Remington et al., 2015). Ramp loading to ultra-high pressures typically uses temporally shaped compression pulses of ∼10–100 ns in duration (Bradley et al., 2009; Knudson, 2012). In direct-drive experiments, a laser directly impinges on an ablator in the target assembly (Figure 4B). Alternatively, in indirect-drive experiments the laser beams are directed into a small hollow gold cylinder called a hohlraum (Figure 4C). The laser heats the hohlraum which emits X-rays that impinge on and ablate the sample (Smith et al., 2014). Indirect drive produces a more spatially uniform compression wave, although some energy loss occurs during the conversion to X-rays.
In a ramp-compression experiment, the in situ particle velocity is measured at two or more positions within the sample under uniaxial strain. This is accomplished using velocimetry measurements (described below) on a stepped target containing multiple thicknesses (Smith et al., 2018) (Figure 4C). Data analysis is performed using a Lagrangian approach and the method of characteristics and involves solution of the differential form of the Rankine-Hugoniot equations (Rothman and Maw, 2006). Measurements of the sample’s free-surface velocity are used as initial conditions for spatial integration backward into the interior of the sample. Wave interactions arising at the free surface or material interfaces can strongly perturb the analysis, and corrections for these effects must be applied. The method is strictly applicable in the case of simple wave propagation, where deformation is not affected by changes in compression rate, and the presence of phase transitions and elastic-plastic behavior may lead to non-uniqueness in the solutions.
The target design is a key element of a successful dynamic-compression experiment (Prencipe et al., 2017). A schematic illustration of representative designs for different types of dynamic-compression experiments is shown in Figure 4. For laser experiments (Figure 4B), the target package typically includes a low-Z ablator (∼50–100 μm thick), the sample (∼10–50 μm thick), and a window (100–500 μm thick). While in some cases, the sample can be directly irradiated by the incident laser, the use of separate ablator material is generally advantageous for smoothing spatial variations in the load arising from the intensity variations in the laser. Depending on experimental requirements, a wide range of materials may be suitable ablators including plastics, beryllium, and diamond. Diamond is particularly useful in ramp-compression experiments as its low compressibility makes it resistant to forming a shock wave.
Samples may be either single crystals or polycrystalline. Typical dimensions range from 10 to 50 μm in thickness and up to several mm in lateral dimensions. The thickness of the sample should be optimized to maintain inertially confined loading conditions over the duration of the experiment. In some cases a thin film of a metal such as gold will be deposited in front of the sample as a shield to prevent pre-heating by the laser drive (Figure 4B). A window mounted on the back surface of the sample maintains the pressure and avoids rapid release into the surrounding vacuum. Commonly used window materials include single-crystal diamond, LiF, quartz, and Al2O3. In most cases, a transparent window is desired although materials may lose transparency under dynamic compression. For example, diamonds becomes opaque above its elastic limit near 100 GPa. The different layers of the target package are bonded using glue layers that must be made as thin as possible, ideally submicron. Additional metallic or anti-reflection coatings may need to be applied to target layers as well. Strict tolerances on thickness, parallelism, roughness, and optical quality are often required.
Advances in ultra-high pressure experiments stem not only from development of facilities and but also from advances in diagnostic capabilities (Remington et al., 2015; Falk, 2018). Laser velocimetry and pyrometry are established techniques that provide fundamental continuum-level constraints on the behavior of dynamically compressed materials. More recently, development of X-ray diffraction and absorption spectroscopy capabilities have allowed for examination of atomic-level structural behavior with the potential to greatly enhance our understanding of material response to extreme loading.
Measurement of the time history of the velocity at a sample-window interface or free surface by laser interferometry is a primary diagnostic in dynamic-compression experiments. In this technique, a moving target is illuminated with laser light causing the reflected beam to return with a Doppler shift in frequency. There are a variety of types of laser-interferometer designs suitable for dynamic compression but for ultra-high pressure experiments the VISAR (velocity interferometer system for any reflector) is the most generally useful (Barker and Hollenbach, 1972; Celliers et al., 2004). In the VISAR approach, the reflected light from the sample at a given time is combined in an interferometer with light reflected at a slightly earlier time and the phase difference between the two beams produces interference fringes which are proportional to the surface or interface velocity (Figure 6). The VISAR is typically focused along a line across the target (∼1 mm in length) and a streak camera is used to record the interference fringes as a function of time (Celliers et al., 2004). An additional role of laser velocimetry is to provide a measure of optical reflectivity of the sample at the VISAR laser wavelength (typically at 532 nm). This is done by comparing the intensity of the reflected VISAR beam with the intensity of the beam prior to compression. Reflectivity measurements can provide information on ionization and electrical conductivity under compression (Hicks et al., 2003; Millot et al., 2018).
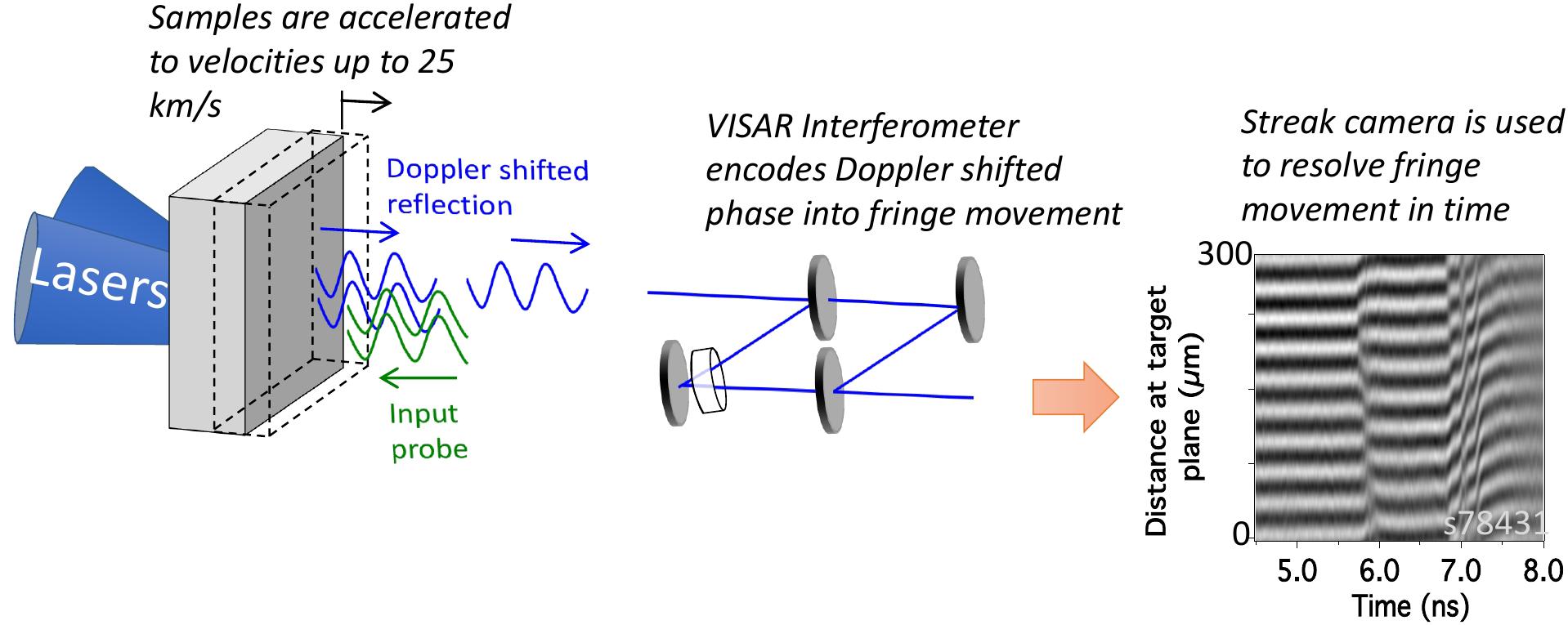
Figure 6. A velocity interferometer (VISAR) is used to determine shock or particle velocity in a sample.
Pyrometry involves time-resolved measurements of thermal radiation emitted from a shocked solid and can be used to constrain temperatures during shock compression or release (Asimow, 2015). Temperature measurements provide a means to determine the isochoric heat capacity (Hicks et al., 2006). In addition, phase transformations may be revealed by thermal changes associated with latent heat of transition in either steady or decaying-shock experiments (Eggert et al., 2009; Millot et al., 2015). Pyrometry techniques have long been used in gas-gun experiments on a variety of materials with temperatures usually determined using spectroradiometry (Asimow, 2015). In ultra-high pressure laser-compression experiments, the total thermal self-emission from the shock front is recorded as a function of time using a streak camera (Miller et al., 2007). Temperatures are extracted by comparison to a calibrated standard (α-quartz) or against a tungsten ribbon filament lamp of known radiance (Gregor et al., 2016). Ramp-compression experiments do not lend themselves to temperature measurements by pyrometry but alternative methods for obtaining temperature constraints such as X-ray absorption spectroscopy (described below) are under development.
The development of X-ray diffraction techniques under in situ dynamic loading began as early as 1970 with the first demonstration of Bragg diffraction from pulsed X-rays on a shocked crystal (Johnson et al., 1970). Due to the limitations of available X-ray sources, such studies were primarily restricted to examination of single crystals at relatively low pressure. The application of brighter X-rays sources including laser-plasma sources (i.e., X-ray emission by highly ionized atoms produced by laser-matter interactions) (Wark et al., 1987, 1989), synchrotrons (Gupta et al., 2012), and free-electron lasers (Milathianaki et al., 2013) to dynamically compressed materials has now made it possible to extend such studies to terapascal pressures (Wang et al., 2016; Polsin et al., 2018; Wicks et al., 2018).
X-ray diffraction can be carried out with a multi-beam laser source in which lasers are used to generate both the dynamically compressed state and the X-ray pulse that probes it. The development of such a system at the Omega laser (Rygg et al., 2012) has enabled a number of studies of geological materials and their analogs at ultra-high pressure (Coppari et al., 2013; Wang et al., 2015, 2016; Wicks et al., 2018). A quasi-monochromatic X-ray source is produced by irradiation of a metallic foil (e.g., Fe, Cu, or Ge) with a short-duration (∼1 ns), high-intensity (∼1014–1016 W/cm2) laser pulse. This creates an ablation plasma in which the atoms are ionized to a He-like state with two bound electrons and produce K-shell emission. The experimental set-up is shown in Figure 7. The sample is dynamically compressed with either shock or ramp loading using a subset of the beams from the laser. At the expected time of peak compression the laser-plasma X-rays are generated and impinge on the sample. A metallic foil with a pinhole positioned in the sample assembly is used to collimate the incident X-ray beam. X-rays passing through the sample will be diffracted if they satisfy Bragg’s Law: λ = 2dsinθ, where λ is the X-ray wavelength, d is the interplanar lattice spacing and θ is the angle between the incident beam and the lattice plane. Diffracted X-rays are recorded on image plates behind the sample (Figure 7). The He-α X-rays have a bandwidth of ∼60–90 eV and diffraction lines can be typically recorded to ∼0.1 degree (0.01 Å in d-spacing). Diffraction from the edges of the pinhole produces peaks that provide a reference to calibrate the diffraction geometry. At pressures above a few hundred GPa, the rapid increase of X-ray noise from the drive plasma makes detection of diffracted photons from the sample more challenging. Although laser-plasma sources are very bright, the source is uncollimated and only a small fraction of the generated X-rays pass through the sample. To date, this technique has mostly been applied to high-symmetry and/or high-atomic-number samples such as MgO, Fe–Si alloys, or other materials that produce a few intense diffraction lines (Coppari et al., 2013; Wang et al., 2016; Polsin et al., 2018; Wicks et al., 2018).
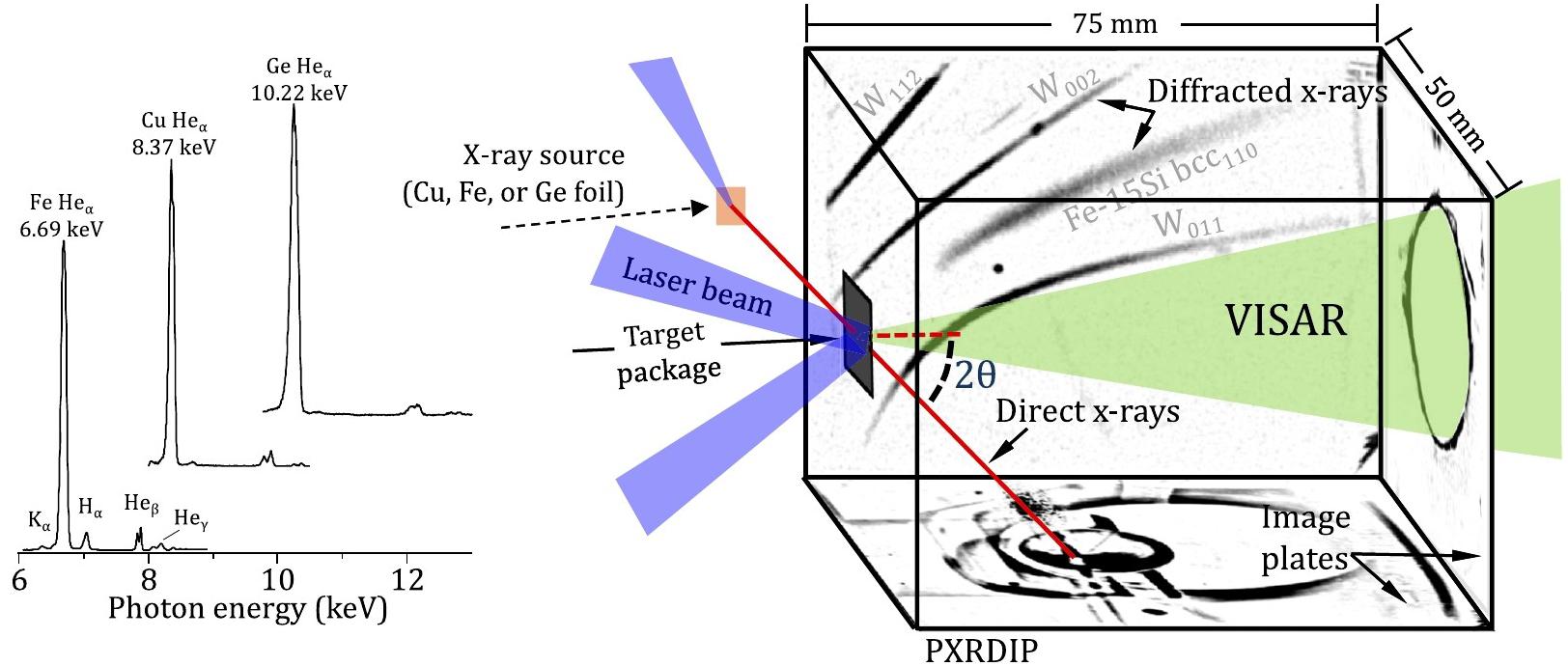
Figure 7. Experimental set-up for laser ramp-compression experiments with X-ray diffraction. The target package is affixed to one side of a box and illuminated by laser-plasma X-rays from a Cu, Fe, or Ge foil. Measured X-ray emission spectra (left) demonstrate the quasi-monochromatic nature of the radiation. X-rays scattered by the sample are recorded on image plates that line the box interior, while a VISAR laser is focused onto the rear surface of the target package through an aperture in the back panel. Adapted from Wicks et al. (2018).
X-ray absorption fine-structure (XAFS) spectroscopy probes the local atomic environment around an absorption edge of a specific element. The method includes XANES (X-ray absorption near edge structure) which examines fine structure near an absorption edge and EXAFS (extended X-ray absorption fine structure) which examines the structure over a larger energy range above the edge. Both methods arise from interference effects that occur when a photoelectron ejected from an atom by incoming X-rays is scattered by its neighbors. XAFS methods are sensitive to a variety of atomic-level properties including electronic structure, bond lengths, and coordination The decay of interference-produced modulations is controlled by the Debye-Waller factor from which constraints on temperature can be obtained.
XAFS is a widely established tool for materials under static high pressures using synchrotron X-ray sources (Shen and Mao, 2017) and is being adapted for use in ultra-high pressure dynamic compression. At the Omega laser, EXAFS capabilities have been applied to iron and other materials (Ping et al., 2013b; Ping and Coppari, 2016). Experiments are performed using a thin sample foil embedded between two diamond layers that serve to confine the sample. Compression is achieved using a series of 1-ns long square laser pulses stacked in time to drive multiple shocks into the sample. A key requirement for XAFS is a bright and smooth X-ray source of sufficient energy range and resolution to capture the absorption fine structure. At Omega-60, the X-ray source is created by imploding a plastic sphere to produce short (∼120 ps), bright, and smoothly decaying X-rays from about 6.5–10 keV with an energy resolution sufficient for EXAFS (Ping and Coppari, 2016). The X-ray source pulses are delayed in time relative to the loading pulses to probe the sample at peak pressure. X-rays transmitted through the target are dispersed by a spectrometer and recorded on image plates. A reference spectrum of the X-ray source is recorded in a separate experiment under identical conditions. For iron, the measured spectra showed oscillations above the iron K edge that provided information on density and temperature with a precision of ∼10% and ∼20%, respectively, up to 560 GPa (Ping et al., 2013a). Development of similar capabilities for EXAFS measurements are being carried out at NIF (Coppari et al., 2017). XAFS measurements have also been reported on laser-driven samples at pressure extending to the multimegabar range using other X-ray sources including laser-driven backlighter foils (Denoeud et al., 2014, 2016a), synchrotrons (Torchio et al., 2016), and free electron lasers (Harmand et al., 2015).
Diamond is an important material for planetary science, high-pressure physics, and inertial confinement fusion. In ice-giant planets such as Uranus and Neptune, decomposition of hydrocarbons at high pressure and temperature may lead to the formation of diamond-containing layers in the interior (Benedetti et al., 1999). Exoplanets that form around C-rich host stars or by local carbon enrichment of a protoplanetary disk may also have diamond and silicon carbide bearing interior layers (Bond et al., 2010).
Carbon is stable in the diamond structure over a wide range of pressures and temperatures. A phase transformation to a BC8–type structure near 1 TPa followed by a further transition to a simple cubic structure near 3 TPa have been predicted theoretically (Yin and Cohen, 1983; Correa et al., 2008). The BC8 structure remains tetrahedrally coordinated but is 10% denser than diamond. The coordination increases from fourfold to sixfold in the simple cubic structure. Theoretical studies have explored the melting behavior of diamond, predicting a maximum in the melting curve around 500 GPa and 8,000–9,000 K (Grumbach and Martin, 1996; Correa et al., 2006; Benedict et al., 2014) and the triple point between diamond, the BC8 phase, and liquid at ∼850 GPa and ∼7,400 K (Correa et al., 2006).
A number of ultra-high pressure shock-compression experiments on diamond have been carried out extending to as high as 4 TPa (Bradley et al., 2004; Nagao et al., 2006; Brygoo et al., 2007; Hicks et al., 2008; Knudson et al., 2008; Eggert et al., 2010; Gregor et al., 2017). In decaying shock experiments, it has been found that diamond melts to a dense metallic fluid with a negative melting slope at 600–1,050 GPa (Brygoo et al., 2007; Eggert et al., 2010), broadly consistent with the theoretical predictions (Figure 8). Evidence for the existence of a new solid phase, possibly BC8, has also been reported in shock-compression experiments at 90–950 GPa (Knudson et al., 2008).
Figure 8. Ultra-high pressure phase diagram of carbon. Shock temperatures from decaying-shock experiments in diamond samples are shown as black lines. Blue and orange symbols are from theoretical calculations. See Eggert et al. (2010) for details.
A comparison of the Hugoniot behavior of single-crystal and nanocrystalline diamond has been reported up to 2.6 TPa in laser-shock experiments (Hicks et al., 2008; Gregor et al., 2017). From the measured shock and release data of these two forms of diamond, the Grüneisen parameter of dense liquid carbon was constrained to be 1.0 ± 0.1 at 1.1–2.5 TPa (Gregor et al., 2017). Diamond has also been explored under ramp compression. The pressure–density relationship and strength of diamond has been characterized up to 800 GPa using the Omega laser (Bradley et al., 2009). In experiments at the National Ignition Facility, measurement of the stress-density relationship of diamond was extended to 5 TPa, achieving 3.7-fold compression at the peak pressure (Smith et al., 2014). These are the highest pressure equation-of-state data recorded under ramp compression and represent the first experimental data in the high-pressure, modest-temperature regime for constraining condensed-matter theory and planetary evolution models at terapascal conditions.
MgO (periclase) is an endmember of the (Mg,Fe)O solid solution which is expected to be a major component of the deep mantles of terrestrial planets and exoplanets (Figure 1). Its high-pressure behavior has long attracted widespread attention due to its simple rocksalt (B1-type) structure, wide stability field, and geophysical importance (Duffy et al., 1995; Wang et al., 2014). Recent interest in the behavior of MgO at ultra-high pressure and temperature has focused on its phase transformation to the B2 (CsCl-type) structure, its melting behavior, and possible metallization (Boates and Bonev, 2013; Cebulla and Redmer, 2014; Taniuchi and Tsuchiya, 2018).
Experimental studies have been conducted using both steady and decaying shocks but have reached conflicting conclusions about the solid-solid phase transition and melting. The first laser-based decaying-shock measurements identified two temperature discontinuities interpreted as the B1–B2 transition at ∼440 GPa and 9,000 K and melting at ∼650 GPa and 14,000 K (McWilliams et al., 2012). In contrast, plate-impact experiments performed using the Z machine (Figure 9) coupled with theoretical calculations indicate that the B1–B2 transition occurs at lower pressure (363 GPa) and melting initiates near 460 GPa and is completed by 620 GPa (Root et al., 2015). More recent results using laser-driven steady (Miyanishi et al., 2015) and decaying-shock techniques (Bolis et al., 2016) are generally consistent with the Z machine results.

Figure 9. Comparison of ultra-high-pressure shock-compression data for SiO2 (gray) (Knudson and Desjarlais, 2013), Mg2SiO4 (red) (Root et al., 2018), and MgO (blue) (Miyanishi et al., 2015; Root et al., 2015).
Optical reflectivity measurements have also been used to place constraints on the electrical conductivity of shocked liquid MgO. The initial decaying-shock measurements suggested metallization occurred upon melting (McWilliams et al., 2012), but later measurements indicate that MgO is a poorly conducting liquid close to the Hugoniot melting point and an increase in reflectivity consistent with metallization occurs around 550 GPa and 13,000 K (Root et al., 2015; Bolis et al., 2016). Gas-gun shock experiments on MgO preheated to 1,800 K report no evidence of melting up to 250 GPa and 9,100 K, placing a lower limit on the melting curve of the B1 phase (Fat’yanov et al., 2018).
The transformation of periclase to the B2 phase in shock-compression experiments is inferred only indirectly through temperature or density changes. The first direct identification of the B2 phase was made using laser-driven ramp compression combined with X-ray diffraction (Coppari et al., 2013). In these experiments, diffraction peaks were recorded for MgO compressed up to 900 GPa. Measured d-spacings were consistent with the B1 phase up to 560 GPa whereas diffraction from the B2 phase was observed from 570 to 900 GPa (Figure 10). Temperature is not measured in these ramp-compression experiments, but is expected to be significantly lower than achieved under shock compression. The observation of a B2 peak at higher pressure in the ramp data compared with inferences from shock measurements is consistent with a negative Clapeyron slope for the transition, consistent with theoretical predications. However, the experimentally measured pressure of the transition (570 GPa) is substantially higher than predicted along an isentrope (450 GPa) by theory (Cebulla and Redmer, 2014). This may reflect over-pressurization of the equilibrium phase boundary under the short timescales of dynamic compression. In the case of aluminum, however, phase transitions from a face-centered-cubic structure to hexagonal-close packed (hcp) and body-centered-cubic (bcc) phases at ∼200–300 GPa under laser-based ramp loading are in good agreement with transition pressures from static compression data and theoretical calculations (Akahama et al., 2006; Fiquet et al., 2018; Polsin et al., 2018). Understanding possible kinetics factors associated with phase transformations under ultra-high pressure–temperature conditions is an important goal for future experiments.
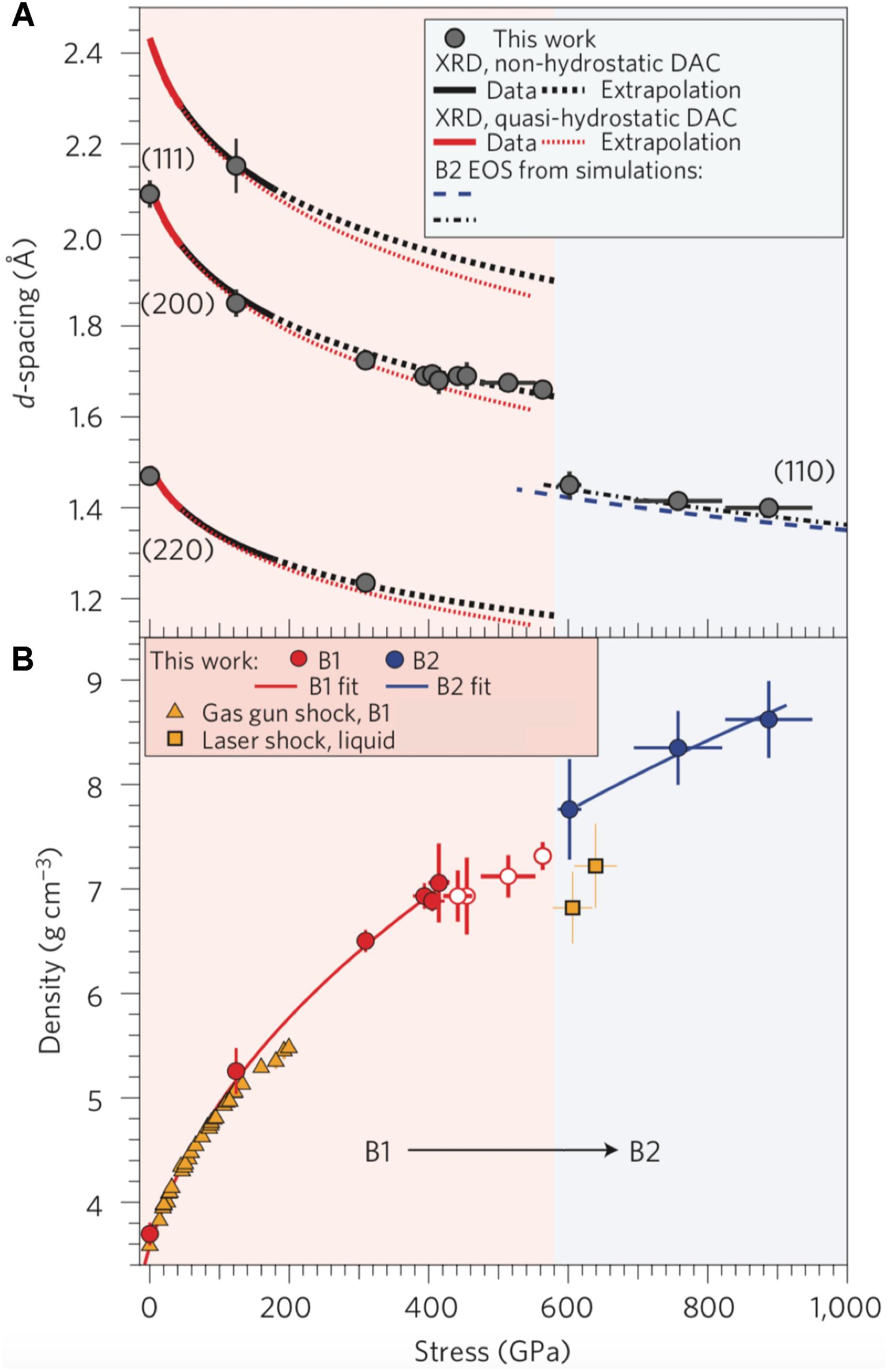
Figure 10. (A) Interplanar d-spacing vs. stress for MgO under ramp compression (gray symbols) compared with extrapolated diamond cell data and theoretical calculations. A discontinuity in d-spacing above 570 GPa is due to the B1–B2 phase transition in MgO. (B) Density of MgO in the B1 (open and filled red) and B2 (blue) structures determined from ramp X-ray diffraction compared with shock data (yellow). See Coppari et al. (2013) for details.
The transformation to the B2 phase is expected to occur in large rocky exoplanets (Wagner et al., 2012). Empirical systematics and theoretical studies have suggested that the MgO phase transformation may be accompanied by a strong change in rheological properties with the high-pressure B2 phase exhibiting a reduction in viscosity (Karato, 2011; Ritterbex et al., 2018). The viscosity of the constituent minerals strongly influences dynamic flow in the mantle and hence is important for understanding the heat flow and the style of mantle convection (Driscoll, 2018). The negative Clapeyron slope of the phase transition combined with the viscosity reduction may produce mantle layering in super Earths with strong differences in convective flow above and below the transition which may affect the long-term thermal evolution of these planets (Shahnas et al., 2018).
Silica is the most abundant oxide component of terrestrial mantles and serves as an archetype for the dense highly coordinated silicates of planetary interiors. Based on theoretical calculations, it is expected that silicates such as post-perovskite will eventually dissociate at conditions of the deep interior of super-Earths (Umemoto et al., 2017). Consequently, SiO2 phases are expected to be potentially important constituents of these exoplanets (Figure 1).
The Hugoniot behavior of quartz at ultra-high pressure has been extensively studied due to its role as an impedance-matching standard for shock experiments (Hicks et al., 2005; Knudson and Desjarlais, 2009). Quartz is a useful standard because above its Hugoniot melting point (∼90–100 GPa), it becomes a conductive fluid with sufficient reflectivity that shock velocities at ultra-high pressure can be measured with high precision using standard laser velocimetry (Knudson and Desjarlais, 2009). A large number plate impact experiments were performed on the Z machine to tightly constrain the Hugoniot equation of state of α-quartz from 0.1 to 1.6 TPa (Knudson and Desjarlais, 2009) (Figure 9). A significant degree of non-linearity was found in the shock velocity-particle velocity relationship and attributed to disorder and dissociation in the SiO2 fluid. In subsequent work, an analytical Mie-Grüneisen model for characterizing the release isentropes of SiO2 was developed by combining theoretical calculations with experimental measurements (Knudson and Desjarlais, 2013). The release isentropes provide a more accurate description of the unloading path of shocked α-quartz and thus provide improved impedance matching compared with the standard reflected Hugoniot techniques (Knudson and Desjarlais, 2013). Recently, the α-SiO2 standard has been further extended to 3 TPa based on first-principles molecular dynamics calculations and extension of the release isentropes to as low as 200 GPa, based on additional Hugoniot experiments and theoretical calculations (Desjarlais et al., 2017).
Temperatures, shock velocities, and reflectivities were reported using pyrometry and velocimetry measurements on fused silica and quartz starting materials in decaying-shock experiments up to 1 TPa (Hicks et al., 2006). The specific heat derived from the temperature measurements was found to be substantially above the classical Dulong-Petit limit and attributed to complex polymerization and bond breaking in a melt that evolves from a regime dominated by chemical bonding of Si-O units (bonded liquid) to an atomic fluid consisting of separated Si and O atoms. Electrical conductivity values derived from measured reflectivities assuming Drude behavior indicate the atomic fluid is highly conductive.
More recent decaying-shock measurements on quartz, fused silica, and stishovite starting materials extend constraints on the melting curve of SiO2 to 500 GPa and 8,300 K (Millot et al., 2015). The melting curve of SiO2 (and other silicates) was found to be higher than that of iron at these extreme conditions. Comparison of these results to planetary adiabats suggests that silica (and MgO) are likely to be in a solid state in the cores of giant planets such as Neptune and Jupiter. However, the deep mantles of large rocky exoplanets may contain long-lived silicate magma oceans. Electrical conductivities inferred from measured reflectivities and a Drude model suggest the conductivity of liquid silica approaches that of liquid iron at TPa pressure and thus liquid silicates in a deep magma ocean could contribute to dynamo generation of magnetic fields in large exoplanets (Millot et al., 2015; Soubiran and Militzer, 2018).
Hugoniot equation-of-state measurements have also be reported for fused silica samples to 1.6 TPa (McCoy et al., 2016b). Additional thermodynamic constraints can be obtained from measurements of bulk sound velocities that have been recorded for fused silica and quartz samples compressed into the liquid state to as high as 1.1 TPa in fused silica (McCoy et al., 2016a) and 1.45 TPa in quartz (Li et al., 2018). Both studies find that the Grüneisen parameter decreases with compression reaching a value of 0.66 at TPa pressure. The structural properties of laser-shocked fused silica were examined using X-ray absorption spectroscopy (XANES), which shows evidence for increasing coordination of silicon by oxygen atoms from 4 at low pressure to 9 at a pressure of ∼1.4 TPa (Denoeud et al., 2016a). The XANES measurements were also used to explore the electronic structure at densities up to 5 g/cm3 and temperatures up to 5 eV (Denoeud et al., 2014) suggesting that liquid silica has a significant metallic character at these conditions.
Magnesium silicates dominate the Earth’s mantle and are expected to be major phases in rocky exoplanets. Enstatite (MgSiO3) and forsterite (Mg2SiO4) are silicates representing different Mg/Si ratios, an important compositional parameter for terrestrial-planet mantles. Traditional studies of these compositions using gas-gun shock compression are summarized in Mosenfelder et al. (2007, 2009). In recent laser-shock work on MgSiO3 glasses and crystals, the Hugoniot pressure–density equation of state has been measured to 950 GPa (Spaulding et al., 2012; Fratanduono et al., 2018) and decaying shock measurements have reached 500 GPa (Spaulding et al., 2012; Bolis et al., 2016; Fratanduono et al., 2018). The latter measurements on enstatite crystals indicate that melting is completed on the Hugoniot at 227 GPa and ∼5,745 K (Fratanduono et al., 2018). Sound velocity measurements from 240 to 380 GPa using an acoustic perturbation technique (Figure 11) place constraints on the Grüneisen parameter, yielding a value of = 0.88 to 0.97 over this range (Fratanduono et al., 2018). Shock temperatures in MgSiO3 glass have also been measured reaching as high as 22,000 K at 500 GPa (Bolis et al., 2016). Initial reports of a liquid-liquid phase transition above 300 GPa and 10,000 K (Spaulding et al., 2012) have not been confirmed in subsequent experimental or theoretical studies (Boates and Bonev, 2013; Militzer, 2013; Bolis et al., 2016; Fratanduono et al., 2018).
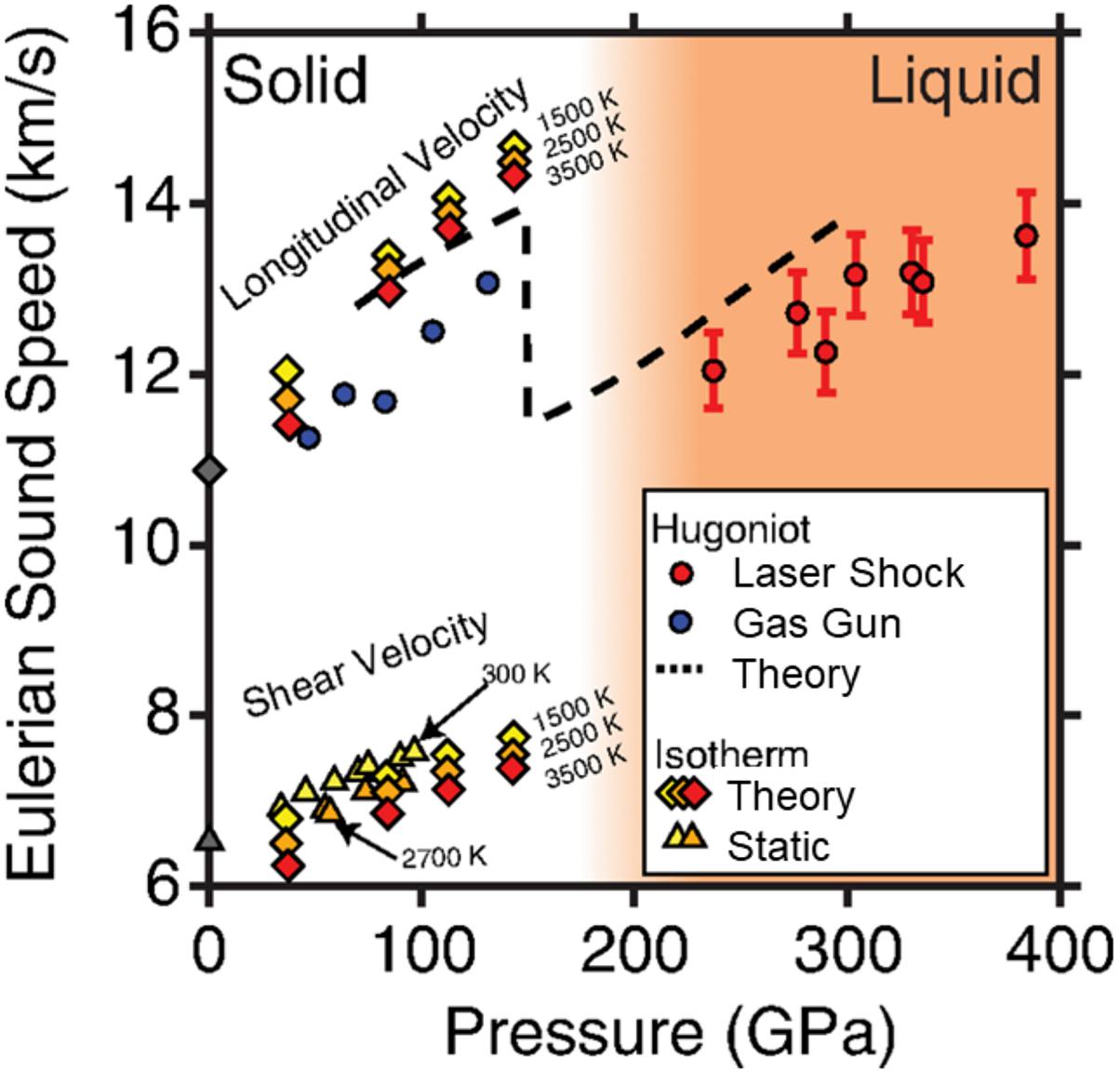
Figure 11. Sound velocities along the principal Hugoniot for MgSiO3 compared with theoretical calculations and diamond anvil cell measurements. Adapted from Fratanduono et al. (2018).
The behavior of forsterite, Mg2SiO4, shocked beyond 200 GPa has been the subject of studies using laser-driven shocks and magnetic compression (Bolis et al., 2016; Sekine et al., 2016; Root et al., 2018). Two studies using laser-shock techniques reached different conclusions regarding the behavior of this material. From measurements of Hugoniot states and shock temperatures, Sekine et al. (2016) inferred a series of transitions from 270 to 500 GPa including incongruent crystallization of MgO from melt, a solid-solid phase transition in MgO, and finally remelting at higher pressure. However, later experiments using similar loading techniques did not observe discontinuities in this range (Bolis et al., 2016). The shock Hugoniot of forsterite was explored from 200 to 950 GPa using both plate-impact experiments and laser-driven decaying shocks, complemented by theoretical calculations (Root et al., 2018) (Figure 9). The shock velocity – particle velocity data in these experiments show a monotonic increase, and no evidence for any phase transformations was detectable.
Iron is one of the most cosmochemically abundant elements and the major constituent of planetary cores. The Earth’s core which is divided into a larger liquid outer core and a smaller solid inner core makes up about one-third of the planet’s total mass. In addition to iron, the core contains Ni as well as lighter elements accounting for ∼10% of its mass (Birch, 1964). Because the pressure–temperature conditions of Earth’s core are difficult to achieve with static high-pressure experiments (Tateno et al., 2010), there remain fundamental uncertainties regarding the crystal structure, density, and other properties of iron and iron alloys that are crucial for interpreting seismic and other geophysical data for this region of the Earth (Hirose et al., 2013).
At even higher pressures, the nature of the expected iron-rich cores in terrestrial-type exoplanets is important for understanding their interior structure and evolution. Due to the high density of iron compared with silicates, the core can strongly influence a planet’s mass-radius relationship (Swift et al., 2012). The size of the iron core can also affect the production of partial melt in the mantle (due to the steepness of the internal pressure gradient) which in turn influences atmospheric formation and evolution through outgassing of the interior (Noack et al., 2014). Knowledge of the nature of the core is also essential for understanding possible dynamo-generated magnetic fields. Heat flux from the core is important for a planet’s thermal evolution. The relative size of core and mantle may affect the ability of the planet to initiate plate tectonics (Noack et al., 2014).
In laser-shock experiments using the GEKKO-XII laser, X-ray diffraction on iron was recorded up to 170 GPa, demonstrating the stability of the hexagonal-close-packed (hcp) ε-phase under shock loading (Denoeud et al., 2016b). Another study using the LULI laser showed that Hugoniot equation-of-state measurements could be made on iron laser-shocked to as high as 800 GPa by measurements of shock and particle velocities on stepped targets (Benuzzi-Mounaix et al., 2002).
The behavior of iron under ramp compression was explored with the Omega laser. Using wave-profile measurements on mutliple-thickness iron foils compressed over serveral nanoseconds, the sound speed and stress-density relationship of iron was measured to 273 GPa (Wang et al., 2013). Time-dependent effects in these experiments due to the low-pressure iron phase transition were overdriven by an initial shock demonstrating the feasibility of a two-stage compression path involving shock followed by ramp compression. Initial shocks of different amplitudes would futher allow different thermodynamic compression paths to be explored. This method was also used in experiments on the LIL laser in which shock pre-compression to ∼200 GPa was followed by ramp compression to achieve off-Hugoniot conditions inferred to be ∼700 GPa and 8,500 K (Amadou et al., 2015).
Higher pressure experiments were performed at the National Ignition Facility where the combination of higher laser power and longer, more complex pulse shapes allowed ramp compression of iron to be extended to 1.4 TPa (Smith et al., 2018) (Figure 12). In addition to stress-density and sound speed, the Grüneisen parameter was constrained by comparison with shock data. The peak pressure in these experiments approaches that predicted at the center of a terrestrial-type exoplanet of three to four Earth masses, representing the first absolute equation-of-state measurements for iron at such conditions. These results provide an experiment-based mass–radius relationship for a hypothetical pure iron planet that can be used to evaluate plausible compositional space for large, rocky exoplanets.
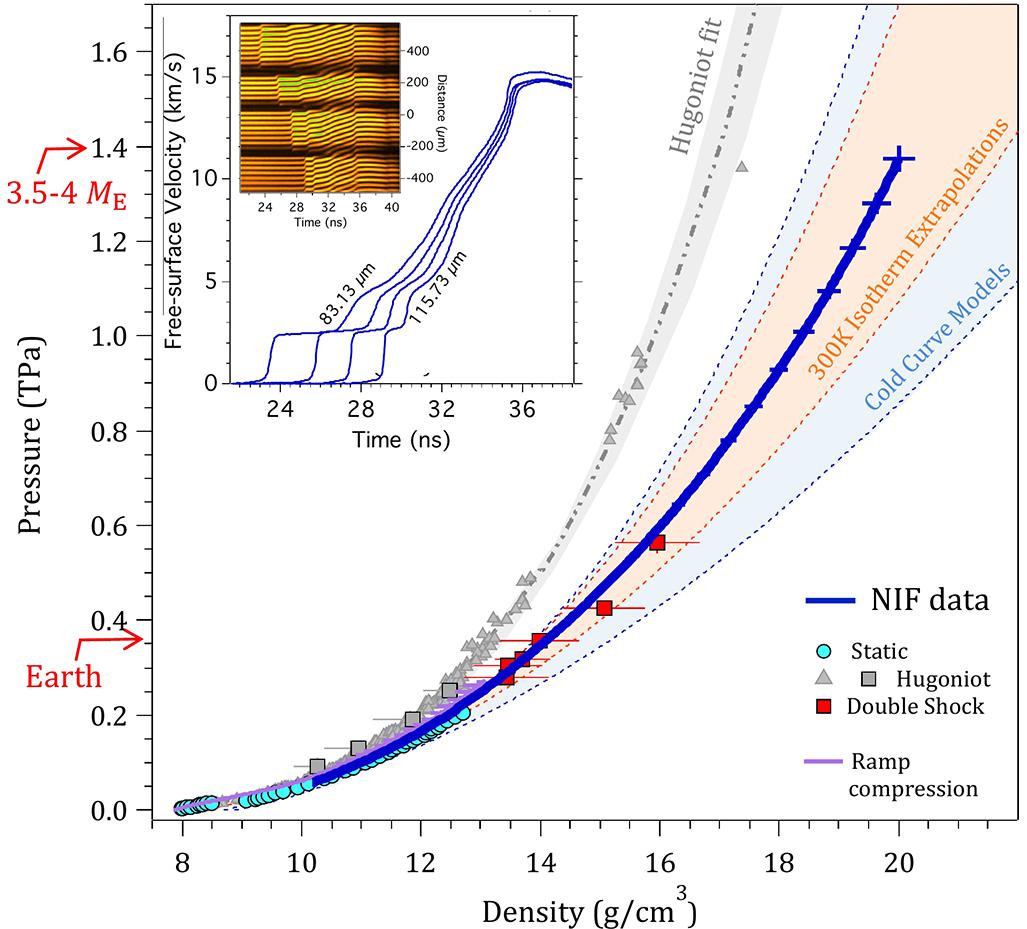
Figure 12. Isentropic P–ρ path of Fe to 3.7 Earth-mass planet core conditions (Smith et al., 2018). Weighted average of pressure versus density with experimental uncertainties (bold blue curve). Hugoniot data are shown as gray triangles and squares. Double-shock data are shown as red squares. A fit to the Hugoniot data (gray dashed–dotted line) with uncertainties (gray shaded region). Also plotted are previous ramp compression data (purple curve) and static diamond anvil cell data (light blue circles). The ranges of EOS extrapolations of low-pressure static data (orange shaded region) and first-principles cold curve calculations (light blue shaded region) represent the uncertainty in the EOS of Fe at TPa pressures. Central pressures for Earth and a 3.5–4.0 Earth-mass (ME) planet are shown for reference. Inset: Raw velocity interferogram with extracted free-surface velocity profiles for each of four sample thicknesses. Modifided after Smith et al. (2018).
In experiments conducted using the Omega laser, the density, temperature, and local structure of iron were explored using multiple-shock compression combined with EXAFS measurements (Ping et al., 2013a). The results showed that iron remains in a close-packed structure (i.e., hcp) up to the peak pressure of 560 GPa. A surprising result was that the temperatures inferred from the Debye-Waller factor were higher than expected and may indicate that the dynamic strength of Fe is larger than predicted based on extrapolation of lower pressure data.
XANES was performed on laser-shocked iron (Harmand et al., 2015) in experiments using a free electron laser X-ray source (Linac Coherent Light Source). Shock waves were generated in the sample using 3-ns pulses from a 532-nm laser with irradiances of 1012–1013 W/cm2. Iron samples were sandwiched between plastic and copper to maintain steady pressure conditions during the experiment. The sample was probed with 80 fs, 7.1 keV X-rays from the free electron laser (FEL) X-ray source. The FEL source has a spectral bandwidth of a few percent, sufficient to allow XANES spectra to be recorded near the Fe absorption edge. The short timescale and high brightness of the FEL source were advantageous for these experiments but the narrow energy range (∼25 eV) and intrinsic intensity variations of the incident FEL beam were limiting factors. Through a series of pump-probe experiments in which the sample was compressed and the XANES spectrum recorded after different time delays, the Hugoniot of iron was explored to as high as 420 GPa and during isentropic release dowm to 12 GPa. The signature of molten iron was observed above 260 GPa and 5,680 K, consistent with observations of shock melting in gas-gun experiments.
Iron has also been used in a proof-of-principle experiment to demonstrate EXAFS capabilities on laser-shocked iron using a synchrotron X-ray source. In experiments performed at the European Synchrotron Radiation Facility, iron was shock compressed to as high as 500 GPa using a 35-J laser focused down to a 90-μm spot size (Torchio et al., 2016). Synchrotron X-rays were dispersed and focused on the sample using a curved crystal. The transmitted X-rays were recorded by a position sensitive detector enabling simultaneous collection of a spectrum extending up to 300 eV above the iron K-edge (7.112 keV). The use of a synchrotron source for dynamic-compression experiments has advantages of high energy resolution, large spectral range, and small X-ray spot size, all of which can lead to better recovery of the detailed behavior of the sample. With improved laser drives, further advances in XAFS capability at synchrotron and FEL facilities are likely.
The identity of the core’s light element(s) is crucial for constraining the bulk chemistry of the Earth and core formation and dynamics (McDonough, 2014). It is also needed for understanding phase relationships in the core, melting point depression relative to pure iron, and potential reactions between the core and mantle (Hirose et al., 2013; Morard et al., 2014). Cosmochemical considerations and planetary formation models suggest that terrestrial-type exoplanets are also likely to incorporate significant quantities of light elements into their cores. However, existing models for exoplanet interiors have generally assumed a pure iron composition (Valencia et al., 2006; Wagner et al., 2012; Dorn et al., 2015).
Silicon is one of the most promising candidates for a core light element as it is abundant cosmochemically but not highly volatile. Si alloys with iron over a wide range of conditions. In the Earth, the presence of silicon in the core can provide an explanation for the otherwise puzzling difference in silicon content between the Earth’s mantle and the primitive chondritic meteorites which are thought to be representative of the materials from which the Earth accreted (Drake and Righter, 2002).
Laser-based ramp compression experiments combined with nanosecond X-ray diffraction were recently reported up to ∼1.3 TPa on two compositions of Fe–Si alloys (Fe-7wt%Si and Fe-15wt%Si) (Wicks et al., 2018). It was found that Fe-7wt%Si adopts the hexagonal-close-packed structure over the measured pressure range, whereas Fe-15wt%Si was observed in a body-centered-cubic structure. The pressure conditions achieved in these experiments correspond to those expected near the center of ∼3 Earth-mass terrestrial planet. Current static-compression experiments on Fe–Si alloys extend to about 400 GPa (Tateno et al., 2015) so the laser-compression experiments extend this range by over threefold. The measured density of Fe–Si alloys is in the range of 17–18 g/cm3 at peak pressure, yielding a compression of 2.5 relative to ambient values.
The effect of silicon incorporation in a rocky exoplanet core was modeled using the above results for the planet Kepler-10b as a representative example (Wicks et al., 2018). This planet has a radius of 1.47 (0.03) RE and a mass of 3.72 (0.42) ME where RE and ME are the radius and mass of the Earth (Wagner et al., 2012). A model for the planet was constructed assuming a silicate mantle and an iron-rich core. The mantle was assumed to have a Mg-rich composition and was divided into layers as a result of structural phase transitions. Two cases were considered for the core: a pure iron core and an Fe-15wt%Si core. The interior structure was calculated by solving the coupled differential equations for hydrostatic equilibrium, mass within a sphere, and the equation of state of each component with solutions constrained to reproduce the observed mass and radius of the planet (Figure 13). The addition of 15wt%Si to the core increases the core radius of Kepler-10b by 16% while decreasing the central density and pressure by 20% and 14%, respectively (Wicks et al., 2018). This illustrates that the incorporation of light elements into exoplanetary cores should be considered in construction of interior structure models.
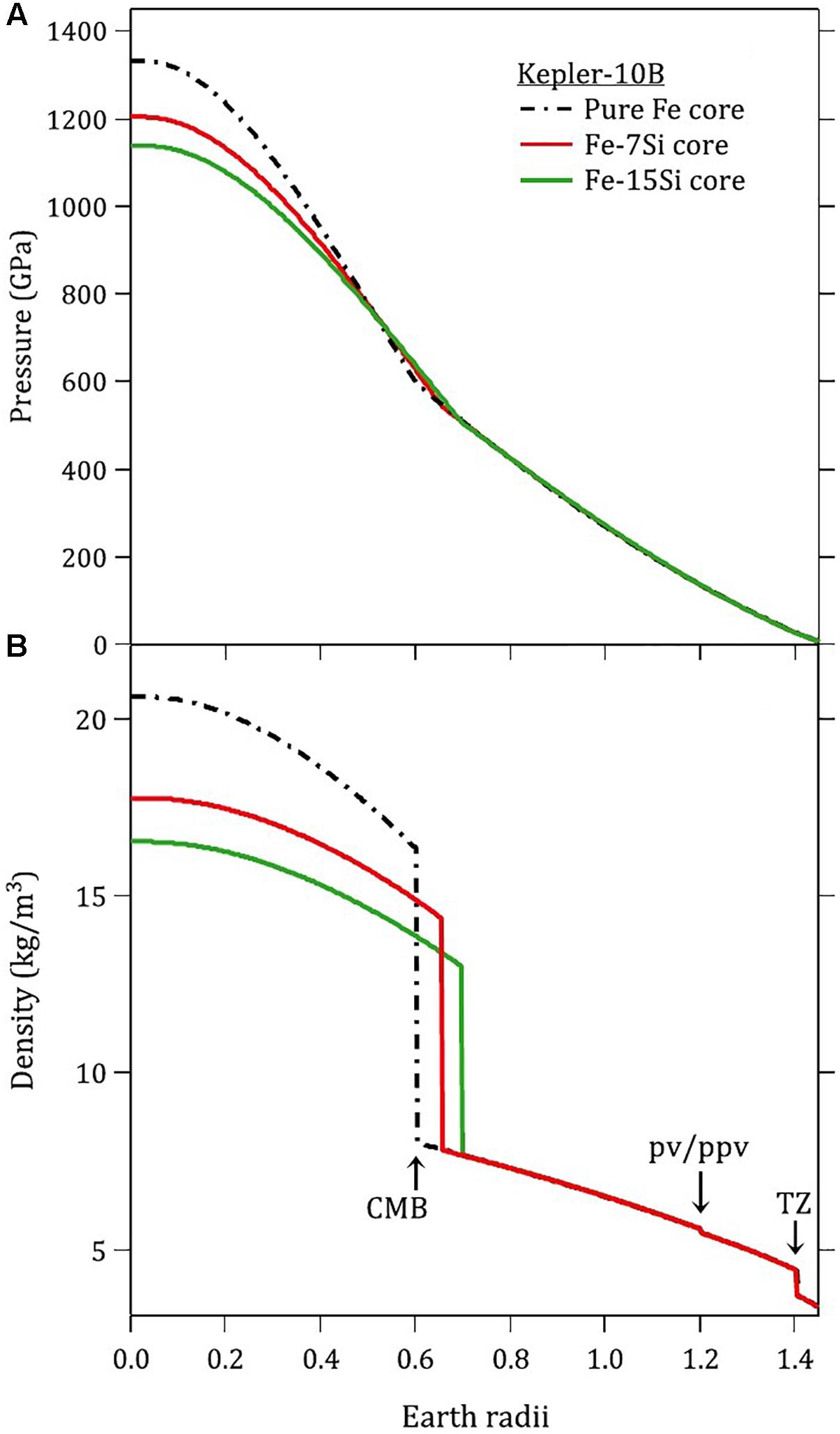
Figure 13. (A,B) Interior pressure and density of exoplanet Kepler-10b assuming silicate mantle and comparing pure Fe and Fe-15wt%Si cores (Wicks et al., 2018). Relative to a pure iron core, the addition of Si produces a larger core radius and lower densities and pressures in the core. Adapted from Wicks et al. (2018).
According to models for early solar-system evolution, the planets grew by successive accumulation of materials from impacting bodies (Stevenson, 1989). As planetary bodies grow in size, larger and more energetic collisions occur. At late stages of accretion, it is expected that Earth would be impacted multiple times by Moon- and Mars-sized objects. Such giant impacts may play a major role in determining certain characteristics of planets such as their rotation rates and existence of satellites. The effects of large impacts also set the initial conditions for a planet’s subsequent thermal and chemical evolution (Stevenson, 1989). Knowledge of the shock and unloading properties of geological materials is an important component of modeling the effects of large, late-stage collisions.
Accurate predictions of material behavior throughout the shock and release process require knowledge of equations of state over a wide range of conditions from the very high pressures and temperatures of the shocked state to the low densities but high temperatures of shock-released material. During isentropic release from a shocked state, a material may melt or even vaporize due to the entropy gained during shock loading. For many geological materials, traditional shock-compression experiments using gas guns are unable to reach sufficient shock pressure to produce vaporization upon release. The higher pressure achievable with lasers and pulsed power now allow such experiments to be performed (Kraus et al., 2015).
Kraus et al. (2012) carried out a series of shock entropy experiments on quartz using the Janus laser at LLNL. SiO2 samples were laser shocked and then allowed to release as a liquid–vapor mixture across a vacuum gap and stagnate against a window. This enabled measurements of both the temperature and density in the shocked and released SiO2. The results were used to constrain the entropy of the shocked state and to make an improved determination of the liquid–vapor boundary for SiO2. It was found that the energy required for vaporization of silicates is much lower than assumed in standard equation-of-state models.
Silicate vaporization was also studied using the GEKKO XII laser (Kurosawa et al., 2010, 2012a,b). Shock-induced irradiance from quartz, diopside, and forsterite was recorded in decaying shocks that reached as high as 760 GPa. Measurements performed as the samples released from the shocked state and become vaporized revealed the presence of ionic and atomic emission lines in the gas phase. This was due to shock-induced ionization followed by atomic recombination later in time in the expanding vapor. The ionization and recombination processes affect temperatures, energy partitioning and vapor production. These phenomena need to be accounted for to understand the thermal and chemical evolution of silicate vapor clouds. This has applications to understanding such processes as the impact origin of the Moon and atmospheric blow-off from the early Earth (Kurosawa et al., 2012b).
Using the Sandia Z machine, the entropy of iron along the Hugoniot was measured using shock-and-release experiments (Kraus et al., 2015). The shock pressure required to vaporize iron was found to be ∼500 GPa, considerably lower than previously thought. This means that high-velocity impacts at the latter stages of planetary accretion would be able to vaporize the iron cores of impacting planetesimals. This has implications for the geochemical state of the early Earth as the dispersal of vaporized iron over the surface of the Earth would enhance metal-silicate mixing and chemical equilibration. This process would be less effective on the Moon due to its smaller size and may help to explain differences in mantle siderophile element abundances between the two bodies.
Ultra-high pressure experimental data on crystal structure, equations of state, and other properties of geological materials are essential for constraining models for the internal structure, dynamics, and evolution of planets within and outside our solar system. Dynamic compression experiments play a central role in this effort as ramp and shock compression techniques can reach to as high as several terapascal pressure, directly achieving conditions of large impacts and the deep interior of rocky and giant planets. Ramp and shock-compression equations of state provide accurate constraints on density at ultra-high pressures and provide sensitive tests of theoretical calculations at extreme conditions. Additional properties such as sound velocities, heat capacity, and the Grüneisen parameter are important components of thermodynamic models of deep planetary interiors. Determination of melting curves at ultrahigh pressure is important for evaluating the physical state of exoplanetary cores and the possible presence of long-lived magma oceans. Transport properties such as thermal and electrical conductivity are also key parameters, with the measurements of the latter providing evidence for possible contributions of the deep magma oceans to planetary magnetic field generation.
Lack of constraints on the lattice-level crystal structure under in situ dynamic loading has long been a major limitation of the technique. This is especially problematic at very high pressures where structural phase transitions often involve very small volume changes making them difficult to detect with continuum-level measurements. The development of pulsed X-ray diffraction techniques for ramp and shock compression is thus a major advance, allowing for unambiguous structure determination and identification of phase transitions at ultrahigh pressures. This allows for experimentally based models of interior mineralogy of rocky exoplanets.
Shock compression and subsequent unloading behavior are also relevant to understanding the formation and early evolution of planets, especially the role of large-scale impacts and the evolution of magma oceans. Shock and unloading processes have applications to such phenomena as the impact origin of satellites, formation of atmospheres and the initial thermal and chemical state of planets and their satellites.
Despite the many advances outlined in this review, there remain fundamental limitations and unanswered questions. Better constraints on the temperatures achieved are needed from both ramp and shock experiments. The short timescales and high strain rates in dynamic compression may preclude the achievement of thermodynamic equilibrium. Phase transitions may need to be significantly overdriven in pressure or may produce metastable phases. It is thus important to carefully compare the results of dynamic experiments, static experiments, and theoretical calculations to fully understand the effects of time scale and strain rate on material behavior at extreme conditions.
Dynamic compression of geological materials at multi-megabar pressure is still in its infancy, but the work reviewed here highlights the considerable progress that has been made in recent years. The development of new large-scale user facilities promises to greatly expand the opportunities for probing Earth materials over a range of pressure, temperature, and strain-rate conditions. New laser-compression capabilities are under development at synchrotron beamlines (Dynamic Compression Sector, Advanced Photon Source), free electron lasers (European XFEL, Hamburg, Germany), and high-powered laser facilities (Laser Megajoule, Bordeaux, France; SG-III, Shanghai, China). The ability to constrain lattice-level structures and physical properties of geological materials at extreme pressure and temperature will provide the fundamental data which in combination with new astronomical observations, theoretical calculations, and geodynamical models will enable fundamental advances in our understanding of planetary systems.
Both authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Support for this work was provided by the National Nuclear Security Agency (National Laser Users’ Facility Program) and the National Science Foundation.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Sally June Tracy and Eleanor J. Berryman provided helpful comments on the manuscript.
Ahrens, T. J. (1987). “Shock wave techniques for geophysics and planetary physics,” in Methods of Experimental Physics, eds C. G. Sammis and T. L. Henyey (New York, NY: Academic Press), 185–235.
Akahama, Y., Nishimura, M., Kinoshita, K., Kawamura, H., and Ohishi, Y. (2006). Evidence of a fcc-hcp transition in aluminum at multimegabar pressure. Phys. Rev. Lett. 96:045505. doi: 10.1103/PhysRevLett.96.045505
Amadou, N., Brambrink, E., Vinci, T., Benuzzi-Mounaix, A., Huser, G., Brygoo, S., et al. (2015). Probing iron at Super-Earth core conditions. Phys. Plasmas 22:022705. doi: 10.1063/1.4907244
Asay, J. R. (2000). “Isentropic compression experiments on the Z accelerator,” in Shock Compression of Condensed Matter - 1999, eds M. D. Furnish, L. C. Chhabildas, and R. S. Hixson (Snowbird: AIP), 261–266.
Asimow, P. D. (2015). “Dynamic compression,” in Treatise on Geophysics (Second Edition), ed. G. Schubert (Oxford: Elsevier), 393–416. doi: 10.1016/B978-0-444-53802-4.00050-6
Barker, L. M., and Hollenbach, R. E. (1972). Laser interferometer for measuring high velocities of any reflecting surface. J. Appl. Phys. 43, 4669–4675. doi: 10.1063/1.1660986
Barnes, J. F., Blewett, P. J., McQueen, R. G., Meyer, K. A., and Venable, D. (1974). Taylor instability in solids. J. Appl. Phys. 45, 727–732. doi: 10.1063/1.1663310
Bassett, W. A. (2009). Diamond anvil cell, 50th birthday. High Press. Res. 29, 163–186. doi: 10.1080/08957950802597239
Benedetti, L. R., Nguyen, J., Caldwell, W. A., Liu, H. J., Kruger, M., and Jeanloz, R. (1999). Dissociation of CH4 at high pressures and temperatures: diamond formation in giant planet interiors? Science 286, 100–102. doi: 10.1126/science.286.5437.100
Benedict, L. X., Driver, K. P., Hamel, S., Militzer, B., Qi, T., Correa, A. A., et al. (2014). Multiphase equation of state for carbon addressing high pressures and temperatures. Phys. Rev. B 89:224109. doi: 10.1103/PhysRevB.89.224109
Benuzzi-Mounaix, A., Koenig, M., Huser, G., Faral, B., Batani, D., Henry, E., et al. (2002). Absolute equation of state measurements of iron using laser driven shocks. Phys. Plasmas 9, 2466–2469. doi: 10.1063/1.1478557
Birch, F. (1964). Density and composition of mantle and core. J. Geophys. Res. 69, 4377–4388. doi: 10.1029/JZ069i020p04377
Boates, B., and Bonev, S. A. (2013). Demixing instability in dense molten MgSiO3 and the phase diagram of MgO. Phys. Rev. Lett. 110:135504. doi: 10.1103/PhysRevLett.110.135504
Boehly, T. R., Brown, D. L., Craxton, R. S., Keck, R. L., Knauer, J. P., Kelly, J. H., et al. (1997). Initial performance results of the OMEGA laser system. Opt. Commun. 133, 495–506. doi: 10.1063/1.3478680
Bolis, R. M., Morard, G., Vinci, T., Ravasio, A., Bambrink, E., Guarguaglini, M., et al. (2016). Decaying shock studies of phase transitions in MgO-SiO2 systems: implications for the super-Earths’ interiors. Geophys. Res. Lett. 43, 9475–9483. doi: 10.1002/2016GL070466
Bond, J. C., O’Brien, D. P., and Lauretta, D. S. (2010). The compositional diversity of extrasolar terrestrial planets. I. In situ simulations. Astrophys. J. 715, 1050–1070. doi: 10.1088/0004-637X/715/2/1050
Borucki, W. J. (2016). Kepler mission: development and overview. Rep. Prog. Phys. 79:036901. doi: 10.1088/0034-4885/79/3/036901
Bouchet, J., Mazevet, S., Morard, G., Guyot, F., and Musella, R. (2013). Ab initio equation of state of iron up to 1500 GPa. Phys. Rev. B 87:094102. doi: 10.1103/PhysRevB.87.094102
Bradley, D. K., Eggert, J. H., Hicks, D. G., Celliers, P. M., Moon, S. J., Cauble, R. C., et al. (2004). Shock compressing diamond to a conducting fluid. Phys. Rev. Lett. 93:195506. doi: 10.1103/PhysRevLett.93.195506
Bradley, D. K., Eggert, J. H., Smith, R. F., Prisbrey, S. T., Hicks, D. G., Braun, D. G., et al. (2009). Diamond at 800 GPa. Phys. Rev. Lett. 102:075503. doi: 10.1103/PhysRevLett.102.075503
Bridgman, P. W. (1935). Polymorphism, principally of the elements, up to 50,000 kg/cm(2). Phys. Rev. 48, 893–906. doi: 10.1103/PhysRev.48.893
Brygoo, S., Henry, E., Loubeyre, P., Eggert, J., Koenig, M., Loupias, B., et al. (2007). Laser-shock compression of diamond and evidence of a negative-slope melting curve. Nat. Mater. 6, 274–277. doi: 10.1038/nmat1863
Cebulla, D., and Redmer, R. (2014). Ab initio simulations of MgO under extreme conditions. Phys. Rev. B 89:134107. doi: 10.1103/PhysRevB.89.134107
Celliers, P. M., Bradley, D. K., Collins, G. W., Hicks, D. G., Boehly, T. R., and Armstrong, W. J. (2004). Line-imaging velocimeter for shock diagnostics at the OMEGA laser facility. Rev. Sci. Instrum. 75, 4916–4929. doi: 10.1063/1.1807008
Celliers, P. M., Collins, G. W., Da Silva, L. B., Gold, D. M., and Cauble, R. (1998). Accurate measurement of laser-driven shock trajectories with velocity interferometry. Appl. Phys. Lett. 73, 1320–1322. doi: 10.1063/1.121882
Chhabildas, L. C., and Barker, L. M. (1986). Dynamic Quasi-Isentropic Compression Techniques: Applications to Aluminum and Tungsten. Albuquerque, NM: Sandia National Laboratories.
Coppari, F., Smith, R. F., Eggert, J. H., Wang, J., Rygg, J. R., Lazicki, A. E., et al. (2013). X-ray diffraction study of a new phase of MgO at exo-planet interior pressures. Nat. Geosci. 6, 926–929. doi: 10.1038/ngeo1948
Coppari, F., Thorn, D. B., Kemp, G. E., Craxton, R. S., Garcia, E. M., Ping, Y., et al. (2017). X-ray source development for EXAFS measurements on the National Ignition Facility. Rev. Sci. Instrum. 88:083907. doi: 10.1063/1.4999649
Correa, A. A., Benedict, L. X., Young, D. A., Schwegler, E., and Bonev, S. A. (2008). First-principles multiphase equation of state of carbon under extreme conditions. Phys. Rev. B 78:024101. doi: 10.1103/PhysRevB.78.024101
Correa, A. A., Bonev, S. A., and Galli, G. (2006). Carbon under extreme conditions: phase boundaries and electronic properties from first-principles theory. Proc. Natl. Acad. Sci. U.S.A. 103, 1204–1208. doi: 10.1073/pnas.0510489103
Denoeud, A., Benuzzi-Mounaix, A., Ravasio, A., Dorchies, F., Leguay, P. M., Gaudin, J., et al. (2014). Metallization of warm dense SiO2 studied by xanes spectroscopy. Phys. Rev. Lett. 113:116404. doi: 10.1103/PhysRevLett.113.116404
Denoeud, A., Mazevet, S., Guyot, F., Dorchies, F., Gaudin, J., Ravasio, A., et al. (2016a). High-pressure structural changes in liquid silica. Phys. Rev. E 94:031201. doi: 10.1103/PhysRevE.94.031201
Denoeud, A., Ozaki, N., Benuzzi-Mounaix, A., Uranishi, H., Kondo, Y., Kodama, R., et al. (2016b). Dynamic X-ray diffraction observation of shocked solid iron up to 170 GPa. PNAS 113, 7745–7749. doi: 10.1073/pnas.1512127113
Desjarlais, M. P., Knudson, M. D., and Cochrane, K. R. (2017). Extension of the Hugoniot and analytical release model of alpha-quartz to 0.2-3 TPa. J. Appl. Phys. 122:035903. doi: 10.1063/1.4991814
Dewaele, A., Loubeyre, P., Occelli, F., Marie, O., and Mezouar, M. (2018). Toroidal diamond anvil cell for detailed measurements under extreme static pressures. Nat. Commun. 9:2913. doi: 10.1038/s41467-018-05294-2
Dorn, C., Khan, A., Heng, K., Connolly, J. A. D., Alibert, Y., Benz, W., et al. (2015). Can we constrain the interior structure of rocky exoplanets from mass and radius measurements? Astron. Astrophys. 577:A83. doi: 10.1051/0004-6361/201424915
Drake, M. J., and Righter, K. (2002). Determining the composition of the Earth. Nature 416, 39–44. doi: 10.1038/416039a
Drake, R. P. (2006). High-Energy-Density Physics: Fundamentals, Inertial Fusion, and Experimental Astrophysics. Berlin: Springer-Verlag. doi: 10.1007/3-540-29315-9_1
Driscoll, P. E. (2018). “Planetary interiors, magnetic fields, and habitability,” in Handbook of Exoplanets, eds H. J. Deeg and J. A. Belmonte (Cham: Springer International Publishing), 1–18.
Dubrovinskaia, N., Dubrovinsky, L., Solopova, N. A., Abakumov, A., Turner, S., Hanfland, M., et al. (2016). Terapascal static pressure generation with ultrahigh yield strength nanodiamond. Sci. Adv. 2:e1600341. doi: 10.1126/sciadv.1600341
Duffy, T. S. (2005). Synchrotron facilities and the study of the Earth’s deep interior. Rep. Prog. Phys. 68, 1811–1859. doi: 10.1088/0034-4885/68/8/R03
Duffy, T. S., Hemley, R. J., and Mao, H.-K. (1995). Equation of state and shear strength at multimegabar pressures: magnesium oxide to 227 GPa. Phys. Rev. Lett. 74, 1371–1374. doi: 10.1103/PhysRevLett.74.1371
Duffy, T. S., Madhusudhan, N., and Lee, K. K. M. (2014). “Mineralogy of super-Earth planets,” in Treatise on Geophysics, ed. G. Schubert (Amsterdam: Elsevier), 149–178.
Duvall, G., and Graham, R. (1977). Phase transitions under shock-wave loading. Rev. Mod. Phys. 49, 523–579. doi: 10.1103/RevModPhys.49.523
Edwards, J., Lorenz, K. T., Remington, B. A., Pollaine, S., Colvin, J., Braun, D., et al. (2004). Laser-driven plasma loader for shockless compression and acceleration of samples in the solid state. Phys. Rev. Lett. 92:075002. doi: 10.1103/PhysRevLett.92.075002
Eggert, J. H., Hicks, D. G., Celliers, P. M., Bradley, D. K., McWilliams, R. S., Jeanloz, R., et al. (2009). Melting temperature of diamond at ultrahigh pressure. Nat. Phys. 6, 40–43. doi: 10.1038/nphys1438
Eggert, J. H., Hicks, D. G., Celliers, P. M., Bradley, D. K., McWilliams, R. S., Jeanloz, R., et al. (2010). Melting temperature of diamond at ultrahigh pressure. Nat. Phys. 6, 40–43. doi: 10.1038/NPHYS1438
Falk, K. (2018). Experimental methods for warm dense matter research. High Power Laser Sci. Eng. 6:e59. doi: 10.1017/hpl.2018.53
Fat’yanov, O. V., Asimow, P. D., and Ahrens, T. J. (2018). Thermodynamically complete equation of state of MgO from true radiative shock temperature measurements on samples preheated to 1850 K. Phys. Rev. B 97:024106. doi: 10.1103/PhysRevB.97.024106
Fiquet, G., Narayana, C., Bellin, C., Shukla, A., Estève, I., Ruoff, A. L., et al. (2018). Structural phase transitions in aluminium above 320 GPa. Comptes Rendus Geosci. (in press). doi: 10.1016/j.crte.2018.08.006
Forman, R. A., Piermarini, G. J., Barnett, J. D., and Block, S. (1972). Pressure measurement made by the utilization of ruby sharp-line luminescence. Science 176, 284–285. doi: 10.1126/science.176.4032.284
Fratanduono, D. E., Millot, M., Kraus, R. G., Spaulding, D. K., Collins, G. W., Celliers, P. M., et al. (2018). Thermodynamic properties of MgSiO3 at super-Earth mantle conditions. Phys. Rev. B 97:214105. doi: 10.1103/PhysRevB.97.214105
Gregor, M. C., Boni, R., Sorce, A., Kendrick, J., McCoy, C. A., Polsin, D. N., et al. (2016). Absolute calibration of the OMEGA streaked optical pyrometer for temperature measurements of compressed materials. Rev. Sci. Instrum. 87:114903. doi: 10.1063/1.4968023
Gregor, M. C., Fratanduono, D. E., McCoy, C. A., Polsin, D. N., Sorce, A., Rygg, J. R., et al. (2017). Hugoniot and release measurements in diamond shocked up to 26 Mbar. Phys. Rev. B 95:144114. doi: 10.1103/PhysRevB.95.144114
Grochala, W., Hoffmann, R., Feng, J., and Ashcroft, N. W. (2007). The chemical imagination at work in very tight places. Angew. Chem. Int. Ed. Engl. 46, 3620–3642. doi: 10.1002/anie.200602485
Grumbach, M. P., and Martin, R. M. (1996). Phase diagram of carbon at high pressures and temperatures. Phys. Rev. B 54, 15730–15741. doi: 10.1103/PhysRevB.54.15730
Gupta, Y. M., Turneaure, S. J., Perkins, K., Zimmerman, K., Arganbright, N., Shen, G., et al. (2012). Real-time, high-resolution x-ray diffraction measurements on shocked crystals at a synchrotron facility. Rev. Sci. Instrum. 83:123905. doi: 10.1063/1.4772577
Hall, C. A., Asay, J., Knudson, M. D., Stygar, W., Spielman, R., Pointon, T., et al. (2001). Experimental configuration for isentropic compression of solids using pulsed magnetic loading. Rev. Sci. Instrum. 72, 3587–3595. doi: 10.1063/1.1394178
Harmand, M., Ravasio, A., Mazevet, S., Bouchet, J., Denoeud, A., Dorchies, F., et al. (2015). X-ray absorption spectroscopy of iron at multimegabar pressures in laser shock experiments. Phys. Rev. B 92:024108. doi: 10.1103/PhysRevB.92.024108
Hawke, R. S., Duerre, D. E., Huebel, J. G., Klapper, H., Steinberg, D. J., and Keeler, R. N. (1972). Method of isentropically compressing materials to several megabars. J. Appl. Phys. 43, 2734–2741. doi: 10.1063/1.1661586
Hicks, D., Boehly, T., Celliers, P., Eggert, J., Vianello, E., Meyerhofer, D., et al. (2005). Shock compression of quartz in the high-pressure fluid regime. Phys. Plasmas 12:082702. doi: 10.1063/1.2009528
Hicks, D. G., Boehly, T. R., Celliers, P. M., Bradley, D. K., Eggert, J. H., McWilliams, R. S., et al. (2008). High-precision measurements of the diamond Hugoniot in and above the melt region. Phys. Rev. B 78:174102. doi: 10.1103/PhysRevB.78.174102
Hicks, D. G., Boehly, T. R., Eggert, J. H., Miller, J. E., Celliers, P. M., and Collins, G. W. (2006). Dissociation of liquid silica at high pressures and temperatures. Phys. Rev. Lett. 97:025502. doi: 10.1103/PhysRevLett.97.025502
Hicks, D. G., Celliers, P. M., Collins, G. W., Eggert, J. H., and Moon, S. J. (2003). Shock-induced transformation of Al2O3 and LiF into semiconducting liquids. Phys. Rev. Lett. 91:035502. doi: 10.1103/PhysRevLett.91.035502
Hirose, K., Labrosse, S., and Hernlund, J. (2013). Composition and state of the core. Annu. Rev. Earth Planet. Sci. 41, 657–691. doi: 10.1146/annurev-earth-050212-124007
Howe, A. R., Burrows, A., and Verne, W. (2014). Mass-radius relations and core-envelope decompositions of super-Earths and sub-Neptunes. Astrophys. J. 787:173. doi: 10.1088/0004-637X/787/2/173
Hurricane, O. A., and Herrmann, M. C. (2017). High-energy-density physics at the national ignition facility. Annu. Rev. Nucl. Sci. 67, 213–230. doi: 10.1146/annurev-nucl-101916-123227
Jeanloz, R. (1989). “High pressure chemistry of the Earth’s mantle and core,” in Mantle Convection: Plate Tectonics and Global Dynamics, ed. W. R. Peltier (New York: Gordon and Breach), 203–257.
Jenei, Z., O’Bannon, E. F., Weir, S. T., Cynn, H., Lipp, M. J., and Evans, W. J. (2018). Single crystal toroidal diamond anvils for high pressure experiments beyond 5 megabar. Nat. Commun. 9:3563. doi: 10.1038/s41467-018-06071-x
Johnson, J. D. (1999). A bound and estimate for the maximum compression of single shocks. Phys. Rev. E 59, 3727–3728. doi: 10.1103/PhysRevE.59.3727
Johnson, Q., Mitchell, A., Keeler, R., and Evans, L. (1970). X-ray diffraction during shock-wave compression. Phys. Rev. Lett. 25:1099. doi: 10.1103/PhysRevLett.25.1099
Karato, S. (2011). Rheological structure of the mantle of a super-Earth: some insights from mineral physics. Icarus 212, 14–23. doi: 10.1016/j.icarus.2010.12.005
Knudson, M. D. (2012). Megaamps, megagauss, and megabars: using the Sandia Z Machine to perform extreme material dynamics experiments. AIP Conf. Proc. 1426, 35–42. doi: 10.1063/1.3686216
Knudson, M. D., and Desjarlais, M. (2009). Shock compression of quartz to 1.6 TPa: redefining a pressure standard. Phys. Rev. Lett. 103:225501. doi: 10.1103/PhysRevLett.103.225501
Knudson, M. D., and Desjarlais, M. P. (2013). Adiabatic release measurements in alpha-quartz between 300 and 1200 GPa: characterization of alpha-quartz as a shock standard in the multimegabar regime. Phys. Rev. B 88:184107. doi: 10.1103/PhysRevB.88.184107
Knudson, M. D., Desjarlais, M. P., and Dolan, D. H. (2008). Shock-wave exploration of the high-pressure phases of carbon. Science 322, 1822–1825. doi: 10.1126/science.1165278
Kraus, R. G. (2016). Dynamic compression of copper to over 450 GPa: a high-pressure standard. Phys. Rev. B 93:134105. doi: 10.1103/PhysRevB.93.134105
Kraus, R. G., Root, S., Lemke, R. W., Stewart, S. T., Jacobsen, S. B., and Mattsson, T. R. (2015). Impact vaporization of planetesimal cores in the late stages of planet formation. Nat. Geosci. 8, 269–272. doi: 10.1038/NGEO2369
Kraus, R. G., Stewart, S. T., Swift, D. C., Bolme, C. A., Smith, R. F., Hamel, S., et al. (2012). Shock vaporization of silica and the thermodynamics of planetary impact events. J. Geophys. Res. 117:E09009. doi: 10.1029/2012JE004082
Kurosawa, K., Kadono, T., Sugita, S., Shigemori, K., Hironaka, Y., Sano, T., et al. (2012a). “Time-resolved spectroscopic observations of shock-induced silicate ionization,” in Shock Compression of Condensed Matter - 2011, Pts 1 and 2, eds M. L. Elert, W. T. Buttler, J. P. Borg, J. L. Jordan, and T. J. Vogler (Melville: Amer Inst Physics), 855–858.
Kurosawa, K., Kadono, T., Sugita, S., Shigemori, K., Sakaiya, T., Hironaka, Y., et al. (2012b). Shock-induced silicate vaporization: the role of electrons. J. Geophys. Res. 117:E04007. doi: 10.1029/2011JE004031
Kurosawa, K., Sugita, S., Kadono, T., Shigemori, K., Hironaka, Y., Otani, K., et al. (2010). In-situ spectroscopic observations of silicate vaporization due to > 10 km/s impacts using laser driven projectiles. Geophys. Res. Lett. 37:L23203. doi: 10.1029/2010GL045330
Lemke, R. W., Knudson, M. D., Bliss, D. E., Cochrane, K., Davis, J.-P., Giunta, A. A., et al. (2005). Magnetically accelerated, ultrahigh velocity flyer plates for shock wave experiments. J. Appl. Phys. 98:073530. doi: 10.1063/1.2084316
Li, M., Zhang, S., Zhang, H., Zhang, G., Wang, F., Zhao, J., et al. (2018). Continuous sound velocity measurements along the shock hugoniot curve of quartz. Phys. Rev. Lett. 120:215703. doi: 10.1103/PhysRevLett.120.215703
Luo, S.-N., Akins, J. A., Ahrens, T. J., and Asimow, P. D. (2004). Shock-compressed MgSiO3 glass, enstatite, olivine, and quartz: optical emission, temperatures, and melting. J. Geophys. Res. 10:B05205.
Matzen, M. K., Sweeney, M. A., Adams, R. G., Asay, J., Bailey, J. E., Bennett, G. R., et al. (2005). Pulsed-power-driven high energy density physics and inertial confinement fusion research. Phys. Plasmas 12:055503. doi: 10.1063/1.1891746
McCoy, C. A., Gregor, M. C., Polsin, D. N., Fratanduono, D. E., Celliers, P. M., Boehly, T. R., et al. (2016a). Measurements of the sound velocity of shock-compressed liquid silica to 1100 GPa. J. Appl. Phys. 120:235901. doi: 10.1063/1.4972338
McCoy, C. A., Gregor, M. C., Polsin, D. N., Fratanduono, D. E., Celliers, P. M., Boehly, T. R., et al. (2016b). Shock-wave equation-of-state measurements in fused silica up to 1600 GPa. J. Appl. Phys. 119:215901. doi: 10.1063/1.4952975
McDonough, W. F. (2014). “Compositional model for the Earth’s core,” in Treatise on Geochemistry (Second Edition), eds H. D. Holland and K. K. Turekian (Oxford: Elsevier), 559–577. doi: 10.1016/B978-0-08-095975-7.00215-1
McWilliams, R. S., Spaulding, D. K., Eggert, J. H., Celliers, P. M., Hicks, D. G., Smith, R. F., et al. (2012). Phase transformations and metallization of magnesium oxide at high pressure and temperature. Science 338, 1330–1333. doi: 10.1126/science.1229450
Milathianaki, D., Boutet, S., Williams, G. J., Higginbotham, A., Ratner, D., Gleason, A. E., et al. (2013). Femtosecond visualization of lattice dynamics in shock-compressed matter. Science 342, 220–223. doi: 10.1126/science.1239566
Militzer, B. (2013). Ab initio investigation of a possible liquid liquid phase transition in MgSiO3 at megabar pressures. High Energy Density Phys. 9, 152–157. doi: 10.1016/j.hedp.2012.11.006
Miller, J., Boehly, T. R., Melchior, A., Meyerhofer, D., Celliers, P. M., Eggert, J. H., et al. (2007). Streaked optical pyrometer system for laser-driven shock-wave experiments on OMEGA. Rev. Sci. Instrum. 78:034903. doi: 10.1063/1.2712189
Millot, M., Dubrovinskaia, N., Černok, A., Blaha, S., Dubrovinsky, L., Braun, D. G., et al. (2015). Shock compression of stishovite and melting of silica at planetary interior conditions. Science 347, 418–420. doi: 10.1126/science.1261507
Millot, M., Hamel, S., Rygg, J. R., Celliers, P. M., Collins, G. W., Coppari, F., et al. (2018). Experimental evidence for superionic water ice using shock compression. Nat. Phys. 14, 297–302. doi: 10.1038/s41567-017-0017-4
Miyanishi, K., Tange, Y., Ozaki, N., Kimura, T., Sano, T., Sakawa, Y., et al. (2015). Laser-shock compression of magnesium oxide in the warm-dense-matter regime. Phys. Rev. E 92:023103. doi: 10.1103/PhysRevE.92.023103
Morard, G., Andrault, D., Antonangeli, D., and Bouchet, J. (2014). Properties of iron alloys under the Earth’s core conditions. Comptes Rendus Geosci. 346, 130–139. doi: 10.1016/j.crte.2014.04.007
Mosenfelder, J. L., Asimow, P. D., and Ahrens, T. J. (2007). Thermodynamic properties of Mg2SiO4 liquid at ultra-high pressures from shock measurements to 200 GPa on forsterite and wadsleyite. J. Geophys. Res. 112:B06208. doi: 10.1029/2006JB004364
Mosenfelder, J. L., Asimow, P. D., Frost, D. J., Rubie, D. C., and Ahrens, T. J. (2009). The MgSiO3 system at high pressure: thermodynamic properties of perovskite, postperovskite, and melt from global inversion of shock and static compression data. J. Geophys. Res. 114:B01203. doi: 10.1029/2008JB005900
Nagao, H., Nakamura, K. G., Kondo, K., Ozaki, N., Takamatsu, K., Ono, T., et al. (2006). Hugoniot measurement of diamond under laser shock compression up to 2 TPa. Phys. Plasmas 13, 052705–052705-5. doi: 10.1063/1.2205194
Nellis, W. J. (2007). Adiabat-reduced isotherms at 100 GPa pressures. High Pressure Res. 27, 393–407. doi: 10.1080/08957950701659734
Nettelmann, N., Fortney, J. J., Kramm, U., and Redmer, R. (2011). Thermal evolution and structure models of the transiting super-earth GJ 1214b. Astrophys. J. 733:2. doi: 10.1088/0004-637X/733/1/2
Noack, L., Godolt, M., von Paris, P., Plesa, A.-C., Stracke, B., Breuer, D., et al. (2014). Can the interior structure influence the habitability of a rocky planet? Planet Space Sci. 98, 14–29. doi: 10.1016/j.pss.2014.01.003
Ozaki, N., Koenig, M., Benuzzi-Mounaix, A., Vinci, T., Ravasio, A., Esposito, M., et al. (2006). Laser-driven flyer impact experiments at the LULI 2000 laser facility. J. Phys. IV France 133, 1101–1105. doi: 10.1051/jp4:2006133224
Ozaki, N., Nellis, W. J., Mashimo, T., Ramzan, M., Ahuja, R., Kaewmaraya, T., et al. (2016). Dynamic compression of dense oxide (Gd3Ga5O12) from 0.4 to 2.6 TPa: Universal Hugoniot of fluid metals. Sci. Rep. 6:26000. doi: 10.1038/srep26000
Ozaki, N., Tanaka, K. A., Ono, T., Shigemori, K., Nakai, M., Azechi, H., et al. (2004). GEKKO/HIPER-driven shock waves and equation-of-state measurements at ultrahigh pressures. Phys. Plasmas 11, 1600–1608. doi: 10.1063/1.1650845
Ping, Y., and Coppari, F. (2016). Laser shock XAFS studies at OMEGA facility. High Pressure Res. 36, 303–314. doi: 10.1080/08957959.2016.1196203
Ping, Y., Coppari, F., Hicks, D. G., Yaakobi, B., Fratanduono, D. E., Hamel, S., et al. (2013a). Solid iron compressed up to 560 GPa. Phys. Rev. Lett. 111:065501. doi: 10.1103/PhysRevLett.111.065501
Ping, Y., Hicks, D. G., Yaakobi, B., Coppari, F., Eggert, J., and Collins, G. W. (2013b). A platform for x-ray absorption fine structure study of dynamically compressed materials above 1 Mbar. Rev. Sci. Instrum. 84:123105. doi: 10.1063/1.4841935
Polsin, D. N., Fratanduono, D. E., Rygg, J. R., Lazicki, A., Smith, R. F., Eggert, J. H., et al. (2018). X-ray diffraction of ramp-compressed aluminum to 475 GPa. Phys. Plasmas 25:082709. doi: 10.1063/1.5032095
Prencipe, I., Fuchs, J., Pascarelli, S., Schumacher, D. W., Stephens, R. B., Alexander, N. B., et al. (2017). Targets for high repetition rate laser facilities: needs, challenges and perspectives. High Power Laser Sci. Eng. 5:e17. doi: 10.1017/hpl.2017.18
Reisman, D., Toor, A., Cauble, R., Hall, C., Asay, J., Knudson, M., et al. (2001). Magnetically driven isentropic compression experiments on the Z accelerator. J. Appl. Phys. 89, 1625–1633. doi: 10.1063/1.1337082
Remington, B. A., Rudd, R. E., and Wark, J. S. (2015). From microjoules to megajoules and kilobars to gigabars: probing matter at extreme states of deformation. Phys. Plasmas 22:090501. doi: 10.1063/1.4930134
Ritterbex, S., Harada, T., and Tsuchiya, T. (2018). Vacancies in MgO at ultrahigh pressure: about mantle rheology of super-Earths. Icarus 305, 350–357. doi: 10.1016/j.icarus.2017.12.020
Root, S., Shulenburger, L., Lemke, R. W., Dolan, D. H., Mattsson, T. R., and Desjarlais, M. P. (2015). Shock response and phase transitions of MgO at planetary impact conditions. Phys. Rev. Lett. 115:198501. doi: 10.1103/PhysRevLett.115.198501
Root, S., Townsend, J. P., Davies, E., Lemke, R. W., Bliss, D. E., Fratanduono, D. E., et al. (2018). The principal Hugoniot of forsterite to 950 GPa. Geophys. Res. Lett. 45, 3865–3872. doi: 10.1029/2017GL076931
Rothman, S. D., and Maw, J. (2006). Characteristics analysis of isentropic compression experiments (ICE). Journal de Physique IV (Proceedings) 134, 745–750. doi: 10.1051/jp4:2006134115
Rygg, J. R., Eggert, J. H., Lazicki, A. E., Coppari, F., Hawreliak, J. A., Hicks, D. G., et al. (2012). Powder diffraction from solids in the terapascal regime. Rev. Sci. Instrum. 83:113904. doi: 10.1063/1.4766464
Sekine, T., Ozaki, N., Miyanishi, K., Asaumi, Y., Kimura, T., Albertazzi, B., et al. (2016). Shock compression response of forsterite above 250 GPa. Sci. Adv. 2:e1600157. doi: 10.1126/sciadv.1600157
Shahnas, M. H., Pysklywec, R. N., and Yuen, D. A. (2018). Penetrative convection in super-Earth planets: consequences of MgSiO3 postperovskite dissociation transition and implications for super-earth GJ876d. J. Geophys. Res. 123, 2162–2177. doi: 10.1029/2018JE005633
Shen, G., and Mao, H. K. (2017). High-pressure studies with x-rays using diamond anvil cells. Rep. Prog. Phys. 80, 1–53. doi: 10.1088/1361-6633/80/1/016101
Smith, R. F., Eggert, J. H., Jeanloz, R., Duffy, T. S., Braun, D. G., Patterson, J. R., et al. (2014). Ramp compression of diamond to five terapascals. Nature 511, 330–333. doi: 10.1038/nature13526
Smith, R. F., Eggert, J. H., Swift, D. C., Wang, J., Duffy, T. S., Braun, D. G., et al. (2013). Time-dependence of the alpha to epsilon phase transformation in iron. J. Appl. Phys. 114:223507. doi: 10.1063/1.4839655
Smith, R. F., Fratanduono, D. E., Braun, D. G., Duffy, T. S., Wicks, J. K., Celliers, P. M., et al. (2018). Equation of state of iron under core conditions of large rocky exoplanets. Nat. Astron. 2, 452–458. doi: 10.1038/s41550-018-0437-9
Soubiran, F., and Militzer, B. (2018). Electrical conductivity and magnetic dynamos in magma oceans of super-Earths. Nat. Commun. 9:3883. doi: 10.1038/s41467-018-06432-6
Spaulding, D. K., McWilliams, R. S., Jeanloz, R., Eggert, J. H., Celliers, P. M., Hicks, D. G., et al. (2012). Evidence for a phase transition in silicate melt at extreme pressure and temperature conditions. Phys. Rev. Lett. 108:065701. doi: 10.1103/PhysRevLett.108.065701
Stevenson, D. J. (1989). “Formation and early evolution of the earth,” in Mantle Convection: Plate Tectonics and Global Dynamics, ed. W. R. Peltier (New York: Gordon and Breach Science Publishers), 817–873.
Stixrude, L. (2014). Melting in super-Earths. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 372:20130076. doi: 10.1098/rsta.2013.0076
Svendsen, B., and Ahrens, T. (1987). Shock-induced temperatures of MgO. Geophys. J. Int. 91, 667–691. doi: 10.1111/j.1365-246X.1987.tb01664.x
Swift, D. C., Eggert, J. H., Hicks, D. G., Hamel, S., Caspersen, K., Schwegler, E., et al. (2012). Mass-radius relationships for exoplanets. Astrophys. J. 744:59. doi: 10.1088/0004-637X/744/1/59
Swift, D. C., and Johnson, R. P. (2005). Quasi-isentropic compression by ablative laser loading: response of materials to dynamic loading on nanosecond time scales. Phys. Rev. E 71:066401. doi: 10.1103/PhysRevE.71.066401
Swift, D. C., Niemczura, J. G., Paisley, D. L., Johnson, R. P., Luo, S.-N., and Tierney, T. E. (2005). Laser-launched flyer plates for shock physics experiments. Rev. Sci. Instrum. 76:093907. doi: 10.1063/1.2052593
Taniuchi, T., and Tsuchiya, T. (2018). The melting points of MgO up to 4 TPa predicted based on ab initio thermodynamic integration molecular dynamics. J. Phys. Condens. Matter 30:114003. doi: 10.1088/1361-648X/aaac96
Tateno, S., Hirose, K., Ohishi, Y., and Tatsumi, Y. (2010). The structure of iron in Earth’s inner core. Science 330, 359–361. doi: 10.1126/science.1194662
Tateno, S., Kuwayama, Y., Hirose, K., and Ohishi, Y. (2015). The structure of Fe-Si alloy in Earth’s inner core. Earth Planet. Sci. Lett. 418, 11–19. doi: 10.1016/j.epsl.2015.02.008
Torchio, R., Occelli, F., Mathon, O., Sollier, A., Lescoute, E., Videau, L., et al. (2016). Probing local and electronic structure in warm dense matter: single pulse synchrotron x-ray absorption spectroscopy on shocked Fe. Sci. Rep. 6:26402. doi: 10.1038/srep26402
Trainor, R. J., Shaner, J. W., Auerbach, J. M., and Holmes, N. C. (1979). Ultrahigh-pressure laser-driven shock-wave experiments in aluminum. Phys. Rev. Lett. 42, 1154–1157. doi: 10.1103/PhysRevLett.42.1154
Umemoto, K., Wentzcovitch, R. M., Wu, S., Ji, M., Wang, C.-Z., and Ho, K.-M. (2017). Phase transitions in MgSiO3 post-perovskite in super-Earth mantles. Earth Planet. Sci. Lett. 478, 40–45. doi: 10.1016/j.epsl.2017.08.032
Unterborn, C. T., Kabbes, J. E., Pigott, J. S., Reaman, D. M., and Panero, W. R. (2014). The role of carbon in extrasolar planetary geodynamics and habitability. Astrophys. J. 793:2. doi: 10.1088/0004-637X/793/2/124
Valencia, D., O’Connell, R. J., and Sasselov, D. (2006). Internal structure of massive terrestrial planets. Icarus 181, 545–554. doi: 10.1016/j.icarus.2005.11.021
Van Valkenburg, A. (1962). Visual observations of high pressure transitions. Rev. Sci. Instrum. 33, 1462–1462. doi: 10.1063/1.1717803
Wagner, F. W., Tosi, N., Sohl, F., Rauer, H., and Spohn, T. (2012). Rocky super-Earth interiors structure and internal dynamics of CoRoT-7b and Kepler-10b. Astron. Astrophys. 541:A103. doi: 10.1051/0004-6361/201118441
Wang, J., Coppari, F., Smith, R. F., Eggert, J. H., Lazicki, A. E., Fratanduono, D. E., et al. (2015). X-ray diffraction of molybdenum under shock compression to 450 GPa. Phys. Rev. B 92:174114. doi: 10.1103/PhysRevB.92.174114
Wang, J., Coppari, F., Smith, R. F., Eggert, J. H., Lazicki, A. E., Fratanduono, D. E., et al. (2016). X-ray diffraction of molybdenum under ramp compression to 1 TPa. Phys. Rev. B 94:104102. doi: 10.1103/PhysRevB.94.104102
Wang, J., Smith, R. F., Coppari, F., Eggert, J. H., Boehly, T. R., Collins, G. W., et al. (2014). Ramp compression of magnesium oxide to 234 GPa. J. Phys. Conf. Ser. 500:062002. doi: 10.1088/1742-6596/500/6/062002
Wang, J., Smith, R. F., Eggert, J. H., Braun, D. G., Boehly, T. R., Patterson, J. R., et al. (2013). Ramp compression of iron to 273 GPa. J. Appl. Phys. 114:023513. doi: 10.1063/1.4813091
Wark, J., Whitlock, R., Hauer, A., Swain, J., and Solone, P. (1987). Shock launching in silicon studied with use of pulsed x-ray-diffraction. Phys. Rev. B 35, 9391–9394. doi: 10.1103/PhysRevB.35.9391
Wark, J., Whitlock, R., Hauer, A., Swain, J., and Solone, P. (1989). Subnanosecond x-ray diffraction from laser-shocked crystals. Phys. Rev. B 40, 5705–5714. doi: 10.1103/PhysRevB.40.5705
Weir, C. E., Lippincott, E. R., Van Valkenburg, A., and Bunting, E. N. (1959). Infrared studies in the 1-to 15-micron region to 30,000 atmospheres. J. Res. Natl. Bur. Stand. A 63, 55–62. doi: 10.6028/jres.063A.003
Wicks, J. K., Smith, R. F., Fratanduono, D. E., Coppari, F., Kraus, R. G., Newman, M. G., et al. (2018). Crystal structure and equation of state of Fe-Si alloys at super-Earth core conditions. Sci. Adv. 4:eaao5864. doi: 10.1126/sciadv.aao5864
Yin, M. T., and Cohen, M. L. (1983). Will diamond transform under megabar pressures? Phys. Rev. Lett. 50, 2006–2009. doi: 10.1103/PhysRevLett.50.2006
Keywords: shock compression, Hugoniot, iron, quartz, olivine, exoplanet, mantle, core
Citation: Duffy TS and Smith RF (2019) Ultra-High Pressure Dynamic Compression of Geological Materials. Front. Earth Sci. 7:23. doi: 10.3389/feart.2019.00023
Received: 23 November 2018; Accepted: 04 February 2019;
Published: 26 February 2019.
Edited by:
Sébastien Merkel, Lille University of Science and Technology, FranceReviewed by:
Guillaume Morard, UMR7590 Institut de Minéralogie, de Physique des Matériaux et de Cosmochimie (IMPMC), FranceCopyright © 2019 Duffy and Smith. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Thomas S. Duffy, ZHVmZnlAcHJpbmNldG9uLmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.