- Department of Earth Sciences, University of Firenze, Firenze, Italy
We propose a methodology to couple rainfall thresholds and susceptibility maps for dynamic landslide hazard assessment at regional scale. Both inputs are combined in a purposely-built hazard matrix to get a spatially and temporally variable definition of landslide hazard: while statistical rainfall thresholds are used to accomplish a temporal forecasting with very coarse spatial resolution, landslide susceptibility maps provide static spatial information about the probability of landslide occurrence at fine spatial resolution. The test site is the Northern part of Tuscany (Italy), where a recent landslide susceptibility map and a set of recently updated rainfall thresholds are available. These products were modified and updated to meet the requirements of the proposed procedure: the susceptibility map was reclassified and the threshold set was expanded defining additional thresholds. The hazard matrix combines three susceptibility classes (S1, low susceptibility; S2 medium susceptibility; S3 high susceptibility) and three rainfall rate classes (R1, R2, R3), defining five hazard classes, from H0 (null hazard) to H4 (high hazard). A key passage of the procedure is the appropriate calibration and validation of the matrix, letting the hazard classes have a precise meaning in terms of expected consequences and hazard management. The employ of the proposed procedure in a regional warning system brings two main advantages: (i) it is possible to better hypothesize when and where landslide are expected and with which hazard degree, thus fostering a more effective hazard and risk management (e.g., setting priorities of intervention); (ii) the spatial resolution of the regional scale warning system is markedly refined because from time to time the areas where landslides are expected represent only a fraction of the alert zone.
Introduction
Since landslides are continuously responsible of damages and casualties worldwide, landslide hazard assessment is a cogent research topic, aiming to determine the spatial and temporal probability of occurrence of landslides (Fell et al., 2008; Corominas et al., 2013).
Spatial occurrence is called susceptibility. A landslide susceptibility map subdivides the terrain into zones with differing likelihoods that landslides of a certain type may occur (Fell et al., 2008). A large part of the quantitative methods to produce landslide susceptibility maps relies on regression or classification approaches (Aleotti and Chowdhury, 1999; Fell et al., 2008). The techniques most widely used are discriminant analysis (Carrara, 1983; Chung and Fabbri, 1995; Baeza and Corominas, 1996), logistic regression (Hosmer and Lemeshow, 2000; Lee, 2005; Manzo et al., 2013), artificial neural networks (ANN) (Bianchi and Catani, 2002; Lee et al., 2003, 2004; Ermini et al., 2005; Yilmaz, 2009; Lu et al., 2012), linear regression (Atkinson and Massari, 1998), fuzzy membership (Kanungo et al., 2006), conditional probability or Bayesian methods (Yilmaz, 2010; Catani et al., 2013).
The temporal occurrence of landslides is normally expressed in terms of frequency, return period, or exceedance probability (Corominas et al., 2013). Usually the approaches followed to determine the temporal occurrence of landslides are: heuristic methods (judgmental approaches) (Lee et al., 2000; Wong, 2005), physically based methods (Montgomery and Dietrich, 1994; Pack et al., 1998; Iverson, 2000; Crosta and Frattini, 2003; Baum et al., 2005; Godt et al., 2008; Mercogliano et al., 2013; Rossi et al., 2013; Tofani et al., 2017) and empirical/statistical rainfall thresholds (Guzzetti et al., 2008; Segoni et al., 2018; and references therein).
Hazard assessment can be quantitative or qualitative. It is generally preferable to determine the actual frequency of landsliding in a quantitative way but in some situations it may not be practical to assess frequencies sufficiently accurately and a qualitative system based on hazard classes may be adopted (Catani et al., 2005; Fell et al., 2008). Landslide susceptibility maps and hazards assessments are static products that provide a detailed quantitative or qualitative scenario with a good spatial resolution. In this regard, they have complementary characteristics respect to rainfall thresholds, which are widely employed in regional scale landslide warning systems with good temporal resolution but with very coarse spatial resolutions, since warnings are usually issued over large alert zones (Segoni et al., 2018). Indeed, the joint use of rainfall thresholds and landslide susceptibility maps has already proven to be a promising tool in advanced landslide hazard assessment. Hong and Adler (2008) hypothesized a real-time detection system at global scale where a prototype global landslide susceptibility map was overlaid with satellite-based observations of rainfall intensity-duration, to identify the location and time of landslide hazards when areas with significant landslide susceptibility are receiving heavy rainfall. Segoni et al. (2015b) integrated a landslide susceptibility map into a regional scale landslide waning system based on rainfall thresholds to increase the spatial resolution of a warning system used in Emilia Romagna (Italy). Jemec Auflič et al. (2016) described a prototype prediction system for rainfall-induced landslides in Slovenia based on a landslide susceptibility map and a rainfall threshold.
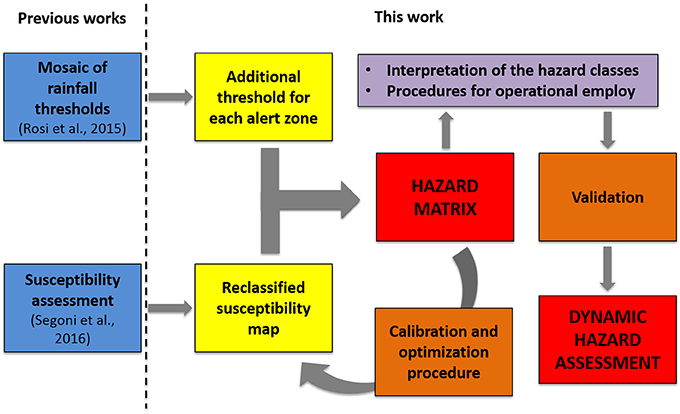
In this work we propose a methodology to couple rainfall thresholds and susceptibility maps for dynamic landslide hazard assessment at regional scale, according to the workflow shown in Figure 1. While statistical rainfall thresholds are used to accomplish a dynamic temporal forecasting with good temporal resolution but very coarse spatial resolution, landslide susceptibility maps provide static spatial information about the probability of landslide occurrence with a finer resolution. The test site is the Northern part of Tuscany (Italy), where a recent landslide susceptibility map (Segoni et al., 2016) and a set of recently updated rainfall thresholds (Rosi et al., 2015) are available. This work provides an added value to these two products because for the first time two very different techniques are coupled together to establish a landslide hazard management tool. The proposed approach is based on the definition of a purposely-built hazard matrix that provides different qualitative level of landslide hazard based on different intensity-duration rainfall thresholds and susceptibility classes. In the discussion section, the potential application to real time hazard management is outlined.
Materials and Methods
Test Site
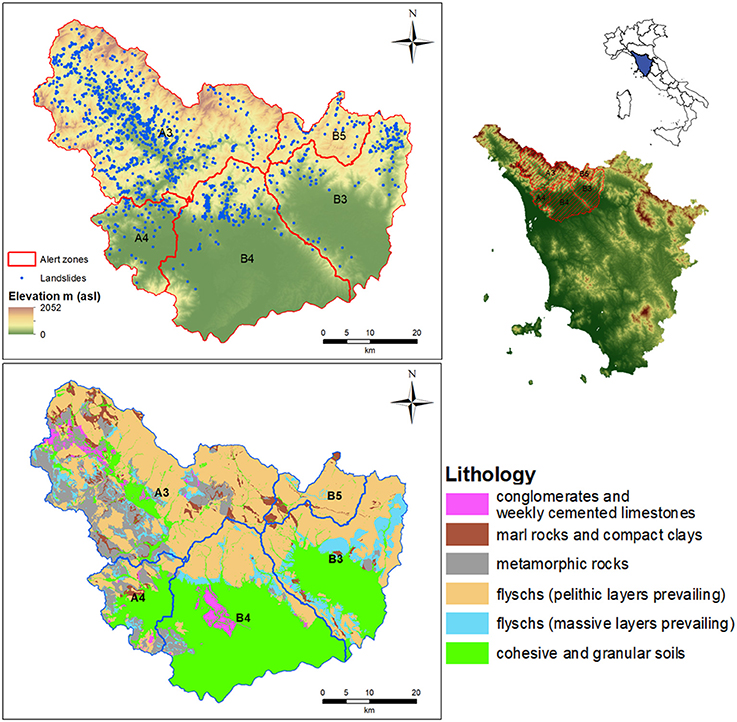
The test area is located in Northern Tuscany (Italy), including part of the northern Apennines with an extension of 3,103 Km2 (Figure 2). We selected this area as a test site since we have at disposal the results of a recent landslide susceptibility study (Segoni et al., 2016) and a set of recently updated rainfall thresholds (Rosi et al., 2015), regarding five alert zones (namely A3, A4, B3, B4, and B5) of the Tuscany regional warning system (Segoni et al., 2015a) (Figure 2).
The Northern Apennines is a complex thrust-belt system made up by the juxtaposition of several tectonic units, piled during the Tertiary under a compressive regime that was followed by extensional tectonics from the Upper Tortonian. The latter phase produced a sequence of horst-graben structures with an alignment NW-SE that resulted in the emplacement of Neogene sedimentary basins, mainly of marine (to the West) and fluvio-lacustrine (to the East) origin (Vai and Martini, 2001). Today, the morphology is dictated by the presence of NW-SE trending ridges where Mesozoic and Tertiary flysch and calcareous units outcrop, separated by Pliocene-Quaternary basins.
These geological settings clearly affect the typology and occurrence of surface processes, primarily through the differences in the mechanical properties linked to the various prevalent lithologies while the rainfall is the main triggering factor. In particular, the study area shows two different geological settings in the east and west sectors respectively (Tofani et al., 2017). In the west sector carbonaceous rocks and metamorphic sandstone and phyllitic–schist mainly outcrop. The slopes are largely characterized by soils that are rather thin (0.5–2 m thick). On the contrary, the calcareous and dolomitic slopes are usually rocky or with very thin soil cover. The east sector shows a more uniform geological condition with the prevalence of flysch formation rock-type (Macigno) which is composed of quartz and feldspar sandstone alternated with layers of siltstone. The slope gradient varies from 0° in the plain to 55°. In the mid and upper sections of the valley, where most landslides usually occur, the stratigraphy consists of a 1.5–5 m thick layer of colluvial soil overlying the bedrock (Tofani et al., 2006, 2017).
In the study area, mean annual precipitation varies from about 800 mm/y in the southern valleys to about 1,800 mm/y on the north-western mountain ridges. During the year, rainfalls concentrate in autumn and spring, with November and March being the rainiest months, while summer is typically dry, except for occasional short and intense storms (Rosi et al., 2012).
Northern Tuscany is affected by serious geological hazards as landslides and subsidence (Rosi et al., 2014, 2018). According to the Inventario dei Fenomeni Franosi Italiani (IFFI) (Trigila et al., 2010, 2013) database, more than 5,000 landslides are present. Their dimensions range from 102 to 106 m2 (Rosi et al., 2018) and they are almost entirely categorized as rotational/translational slides (37% of the entire database) of or as complex movements (63%), i.e., shallow landslides or soil slips evolving into flows. It is worth to notice that the hazard assessment procedure that we propose in this work is related only to these types of landslides involving mainly soil material, while we do not take into account rock falls and topples (less than 1% of the database).
Data and Previous Works
Rainfall Thresholds
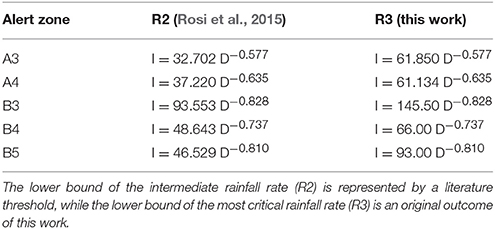
Tuscany is covered by a prototype regional warning system based on a set of rainfall thresholds differentiated for 25 alert zones (Segoni et al., 2014b, 2015a). Rainfall thresholds are based on intensity and duration and were defined with a highly automated procedure using a purposely developed software called MaCumBA (Segoni et al., 2014a). The subdivision into 25 alert zones following the main regional divides allows relating each threshold to a hydrographic basin with homogeneous meteorological and geomorphological settings, thus strengthening the forecasting effectiveness of the system (Segoni et al., 2014b). In the alert zones extending over the study area, the thresholds have been recently updated using an extended landslide dataset (Rosi et al., 2015).
The source of landslide data is mainly constituted by event reports performed by the regional Civil Protection offices and by a catalog of geotagged internet news (Battistini et al., 2017), which was automatically obtained using a purposely-developed web-based semantic search engine called SECAGN (Battistini et al., 2013). These landslide data were also used to calibrate the hazard matrix, which is the main objective of this work (section Hazard Assessment).
To date, each alert zone of the regional warning systems is monitored by a rainfall threshold, calibrated at the 95% confidence level, that discriminates between “warning” and “no warning.” The high confidence level is a conservative choice that allows having a high “hits” rate at the cost of a not negligible number of false positives (Rosi et al., 2015).
Susceptibility Model
In the study area, a susceptibility assessment has been recently carried out (Segoni et al., 2016) using “Random forest,” a machine-learning algorithm for non-parametric multivariate classification (Breiman, 2001). Although this methodology can be considered relatively new, it has already been consolidated in landslide studies through different applications (Brenning, 2005; Vorpahl et al., 2012; Catani et al., 2013; Trigila et al., 2013; Segoni et al., 2015b; Pourghasemi and Kerle, 2016; Youssef et al., 2016). Random Forest has the advantage of handling both numerical and categorical variables without requiring assumptions about the distribution of the input data. Moreover, it can use a large number of input parameters, then a procedure of forward selection, which accounts also for interactions and nonlinearities among variables, discards the ones that do not bring a positive contribution and selects the optimal configuration. The landslide susceptibility analysis was performed using the software ClaReT (Lagomarsino et al., 2017), which uses a random forest implementation based on Matlab [Matworks, version 7.11, treebagger object (RFtb) and methods].
Two kinds of input parameters were considered as explanatory variables for the susceptibility map: morphometric attributes and attributes derived from thematic maps. In particular, the morphometric attributes are: curvature, flow accumulation, topographic wetness index, elevation, profile curvature, planar curvature, slope gradient, aspect. The thematic attributes are: land use and lithology. Topographic attributes were derived from the official and most recent 10 m resolution DEM (Digital Elevation Model) produced by Tuscany Region. Land use was derived from CORINE Land Cover Map (1:50,000), updated in 2006 (https://www.eea.europa.eu/publications/COR0-landcover) which in the study area was reclassified into 9 classes: urban areas, crops, grasslands, heterogenic rural areas, forests (broad-leaved); forests (conifers); shrubs; bare rocks; humid areas. Lithology was derived from Regional Geological Maps at the 1:10,000 scale, by reclassifying each geological formation into six lithological classes (Segoni et al., 2016): conglomerates and weekly cemented limestones; marl rocks and compact clays; metamorphic rocks; flyschs (pelithic layers prevailing); flyschs (massive layers prevailing); cohesive and granular soils (Figure 2).
The IFFI database (Trigila et al., 2010), the Italian national inventory of landslides at 1:10,000 scale, was used to train and validate the susceptibility model.
As described in Segoni et al. (2016) the grid for each morphometric or thematic attribute was resampled to a 100 m pixel size and split into two variables: the average value encountered in the 100 × 100 m cell (mean value for numerical attributes and prevailing class for categorical values), and the variability inside the 100 × 100 m cell (standard deviation for numerical attributes and number of classes for categorical values). For the slope gradient and all kinds of curvature we have considered also the maximum value. The total number of input parameters used is 23 (Segoni et al., 2016).
To calibrate the “Random forest” classification algorithm, the study area was randomly sampled to select 10% of the pixels for training and 10% for testing. Such percentages have been proved to be a good compromise between quality of the results and speed of the calculations (Catani et al., 2013); indeed, a validation of the susceptibility map provided satisfactory results, with an AUC (area under ROC curve) value of 0.84 (Segoni et al., 2016), highlighting a good agreement with the observed truth and the potentiality of new landslide activations in the future (Segoni et al., 2016).
The raw output data of the susceptibility assessment is a raster map with a 100 m cell size, where each pixel has a percentage value expressing the probability of being affected by a landslide. The map has a range of susceptibility values from 0% to 91.
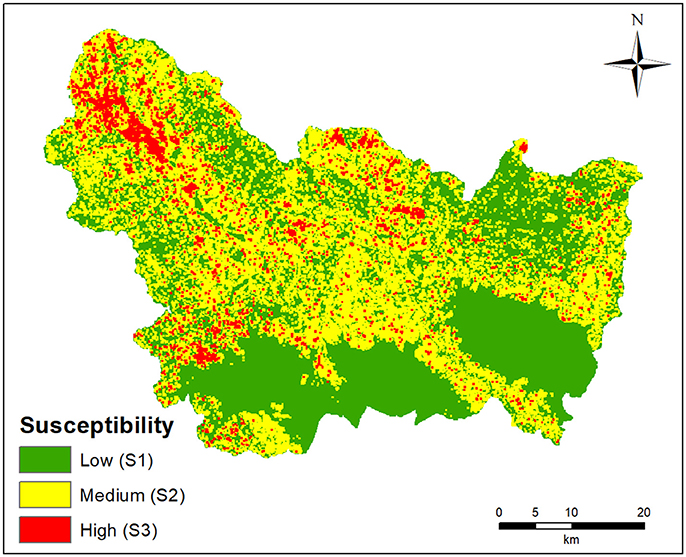
In this work, these raw data will be reclassified in three classes: low susceptibility (S1), medium susceptibility (S2), and high susceptibility (S3). The definition of the thresholds values between the susceptibility classes is part of the calibration of our hazard model; therefore, it is explained in the following section.
Hazard Assessment
To assess the landslide hazard, the rainfall levels defined from the rainfall thresholds have been integrated with the susceptibility classes. The basic assumption of this work is that if the susceptibility map is classified in a number of classes that equals the number of possible alert levels featured in the threshold system, a square matrix can be built and it is possible to establish a straightforward correspondence between hazard, rainfall rates and susceptibility classes.
The general classification scheme is reported in Figure 3, where the hazard matrix, based on susceptibility classes (S1, low susceptibility; S2, medium susceptibility; S3, high susceptibility) and rainfall classes (R1, low rainfall; R2, medium rainfall; R3, high rainfall), defines five hazard classes from H0 (null hazard) to H4 (very high hazard). The hazard matrix is based on the assumption that the higher the susceptibility, the lower the rainfall level that could trigger landslides.
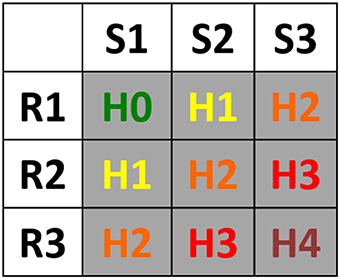
Figure 3. Combination of susceptibility classes and rainfall rates into the hazard matrix: H0, null hazard; H1, low hazard; H2, medium hazard; H3, high hazard; H4, very high hazard.
To obtain the needed number of rainfall classes to build a square matrix, in each alert zone an additional threshold has been defined to discriminate between low and high criticality. To define this threshold, we simply translated upward the original threshold until a consistent reduction of false alarms (i.e., rainfall events above the thresholds without triggering landslides) is obtained. The downward or upward translation of a previously defined threshold to defining different alert levels is a quite consolidated approach in the international literature (Guzzetti et al., 2008; Segoni et al., 2018). In this work, three warning levels have been defined for each alert zone: R1 (low rainfall rate), R2 (medium rainfall rate), and R3 (high rainfall rate) (Table 1).
For each alert zone, the three susceptibility classes have been defined separately using, in order to define the class breaks, a simple trial and error optimization procedure. All 1,761 landslides used in the rainfall threshold analysis were taken into account and they were associated to: (i) a landslide susceptibility value (by means of a simple elaboration in GIS environment); (ii) a rainfall class as defined above (querying the database of past events of the regional warning systems). Then, optimal susceptibility class breaks have been defined after this procedure:
• First, the class breaks from Segoni et al. (2016) have been taken into account and the hazard matrix (Figure 3) has been defined.
• The S1/S2 limit has been progressively lowered until no occurrence was found in the S1/R1 cell of the hazard matrix.
• In case the S1/R1 cell was already at zero, the S1/S2 limit was progressively raised to the highest susceptibility value that allows maintaining a count of zero landslides in the S1/R1 cell.
• The S2/S3 limit has been lowered or raised until the count of landslides in the H2, H3, and H4 classes was 90% of the total.
This procedure has been applied separately to every Alert Zone. Therefore, every AZ is expected to have a characteristic set of susceptibility values defining the susceptibility classes.
Results
Hazard Matrix Implementation
According to the methodology described in the previous section, susceptibility classes have been defined with class break values very different from ZA to ZA (Table 2). Figure 4 displays the reclassified susceptibility map for the whole test site.
An original feature the proposed reclassification is that the classes are conceived to be used in conjunction to rainfall thresholds and to become hazard classes of different severity according to the dynamic outputs of the regional warning system based on rainfall thresholds. In other words, based on the rainfall rate (R1, R2, or R3) of each alert zone, the landslide susceptibility classes are transformed into hazard classes according to the scheme reported in Figure 3.
To test this approach, we performed a back-analysis on the whole landslides dataset: each landslide was associated to a hazard class according to the susceptibility class of its location and to the rainfall rate provided by the thresholds of the warning system for the day in which the landslide was triggered. Table 3 shows the results of this test counting the hazard level associated to each landslide. In Table 3, the count is provided separately for each alert zone and it is also aggregated over the whole test site. It can be easily verified that only about 10% of the landslides is in the H1 class and no landslide is in the H0 class.
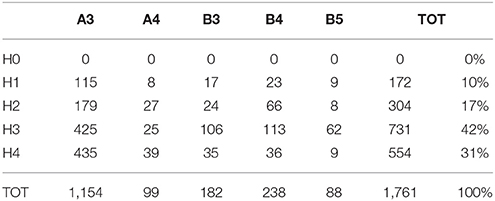
Table 3. Back-analysis of the landslides dataset: each landslide is associated to a hazard class according to the susceptibility class of its location and to the rainfall rate provided by the thresholds of the warning system.
Validation
The proposed approach was validated using an independent dataset, pertaining to the period from 01-01-2017 to 30-4-2108. The validation consists in simulating an operational employ of the dynamic hazard matrix through the whole validation period and to check what is the hazard class associated to each landslide occurred in the study area during that period.
SECAGN search engine (Battistini et al., 2013, 2017) was applied to retrieve online news of landslides occurred in the study area during the validation period. The result was a catalog of 39 landslides for which triggering time is known with hourly or daily approximation. For each landslide, the rainfall level (R) provided by the warning system during the day of occurrence and the landslide susceptibility class characterizing the landslide location were combined to get the corresponding hazard level (according to Figure 3).
It was possible to ascertain that in a hypothetic operational employ of the proposed dynamic hazard assessment, 9 landslides would have occurred in H4 class, 14 in H3, 15 in H2, 1 in H1 and none in H0. These numbers are in accordance with the criteria used for the hazard assessment calibration: no landslides would have occurred in the “no hazard class,” less than 10% (namely, a single landslide) in the H1 class and 38 out of 39 would have been associated to one of the hazard levels interpreted as very likely to be associated with landslides.
Although the validation results are encouraging, we are aware that the dataset used for validation is limited; therefore, further tests should be performed before deeming the proposed procedure ready for the operational employ in the risk management.
Discussion
Hazard Interpretation
Given the physical meaning of the input susceptibility and rainfall classes and the outcomes of the back-analysis, the qualitative hazard classes obtained with the proposed approach could be interpreted as follows:
• H0 - null hazard. No landslides are expected. This hazard class can originate only from the intersection of R1 and S1 classes: it represents a condition for which both the susceptibility map and the threshold model calculated the minimum level of hazard. A landslide occurrence in this box would represent an error of the proposed methodology, as it would occur in a pixel deemed as stable by the susceptibility assessment and during a time when no alarm in terms of rainfall duration and intensity (neither moderate nor high) is issued. Therefore, the hazard matrix was calibrated to have no landslides in this cell, in an effort to account also for the errors and the uncertainties in the data and in the two input models (susceptibility and rainfall thresholds) originating the hazard matrix.
• H1 - low hazard. Theoretically, no landslides should be expected. However, this class encompasses a residual possibility of landslide occurrence because of errors in one of the input models (susceptibility model or rainfall thresholds model), uncertainties in the data, or triggers other than rainfall (e.g., snow melting). The hazard matrix has been calibrated to encompass only 10% of the known landslides dataset in this hazard class. This hazard class can be generated in two different cases:
◦ R1/S2. Landslides occurred here represent an error of the proposed hazard model, because harmless rainfalls (no alarms issued by the rainfall thresholds) actually triggered some landslides in a medium susceptibility area.
◦ R2/S1. Landslides occurred here represent an error of the proposed hazard model, because mild rainfalls (medium criticality level provided by the rainfall thresholds) triggered some landslides in an area where landslides should not be expected (low susceptibility).
• H2 - medium hazard. In this hazard class, landslides are expected, since one of the inputs is high and the other is low, or they both are medium:
◦ R1/S3. Landslides are located in the highest susceptibility class but in the low rainfall rate class. These situations represent errors of the rainfall thresholds model, for example situations related to snow melting, which is not taken into account in the rainfall thresholds definition. Therefore, with this class the proposed dynamic hazard approach is capable of accounting also for occurrences that would be missed by the original warning system.
◦ R3/S1. Conversely, this class could be associated to an intrinsic error of the susceptibility model, since landslides occur in an area with low susceptibility, but according to our hazard approach this could be possible only in rainfall conditions belong to the highest rainfall class.
◦ R2/S2. In this class, both input models provide the intermediate level of criticality, thus resulting in an intermediate hazard level.
• H3 - high hazard. In this hazard class, one of the input models provides the maximum level of criticality while the other provides the intermediate one:
◦ R3/S2. The interpretation of this class is that when the rainfall rate is at the maximum level, landslides can be expected also in areas with medium landslide susceptibility.
◦ R2/S3. Where the susceptibility to landslides is at the highest level, landslides can be triggered also when the rainfall rate is at a medium level of criticality.
• H4 - very high hazard. This hazard class originates only from the intersection of R3 and S3 classes, thus representing a condition for which both the susceptibility assessment and the threshold model calculated the highest possible level of spatial and temporal (respectively) hazard.
Possible Use
The methodology presented could be easily integrated into the regional landslide warning system and used to obtain real time dynamic hazard maps. Since the warning system combines rainfall forecasts and real time rainfall data recorded at hourly time step by a network of automated rain gauges, the hazard scenarios could be displayed both for the real-time condition and for the future.
In addition, the dynamic hazard scenario may change as soon as new outputs of the warning systems are provided. If the system is running in now-casting mode, every hour the dynamic hazard map can be refreshed and a new scenario can be built using the new rainfall data coming from the regional network of rain gauges providing hourly rainfall measures. If the system is run in forecast mode, whenever a new forecast of distributed rainfall field is available (normally, twice a day), the dynamic hazard map can be refreshed and updated.
Traditionally, regional warning systems provide a spatially constant alert level for the whole area of application or for large subdivisions called alert zones. The actual consequence of the application of our methodology is that when a rainfall rate (R1, R2, and R3) is recorded/forecasted in a given alert zone, its territory is automatically partitioned in three hazard classes, thanks to the availability of the susceptibility map (Figure 5). Therefore, a double advantage is obtained:
1. It is possible to better hypothesize where landslides are expected and with which hazard degree, thus fostering a more effective hazard and risk management (e.g., setting priorities of intervention);
2. The spatial resolution of the warning system is markedly refined because from time to time the areas where landslides should be expected are only a fraction of the alert zone.
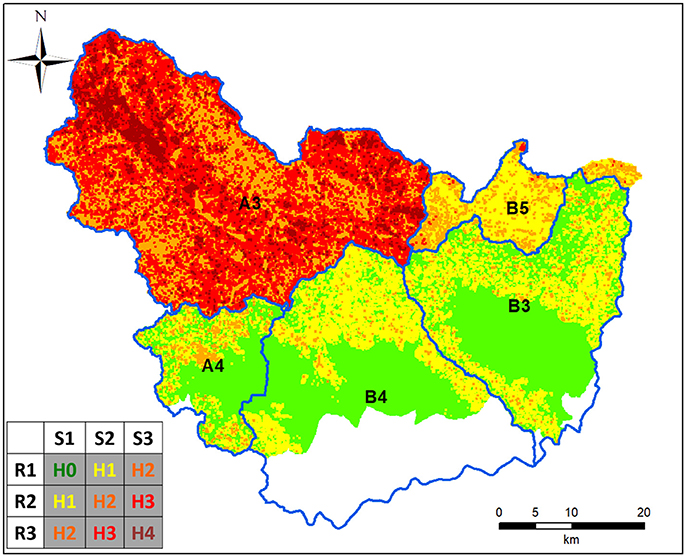
Figure 5. Example of dynamic hazard map for a complex rainfall scenario, with different rainfall rates (R3, R1, R1, R1, R2) in the alert zones (A3, A4, B2, B3, B5, respectively).
Table 4 quantifies to which extent the spatial resolution of the warning system can be refined by the proposed approach: at every time, the territory of each alert zone is partitioned into three out of the five proposed hazard classes, depending on the current rainfall rate. As instance, when the maximum rainfall rate is encompassed (R3: rainfall above the highest threshold), in 26% of the territory of the A3 alert zone the landslide hazard is medium, in 52% is high and in 21% is very high. Taking into account the rainfall threshold warning system alone, the whole alert zone territory would be considered at the maximum hazard level. Therefore, the proposed methodology can be used to obtain a consistent refinement of the spatial resolution of the hazard assessment providing a dynamic hazard classification, which can be used in hazard and risk management.
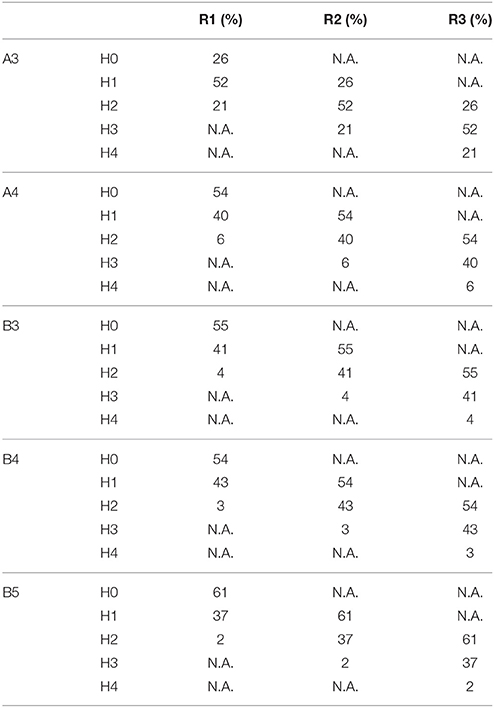
Table 4. Spatial extension of the hazard classes determined in each alert zone in case of rainfall rates R1, R2, or R3.
Comments on the Physical Settings
Rainfall thresholds and susceptibility maps are products that are traditionally created independently for different needs (namely: temporal forecasting for warning purposes and spatial assessment for land management). The objective of this work is finding a dependence between the two approaches to couple the temporal and the spatial forecasting. Form this point of view, rainfall thresholds and susceptibility maps can be considered as complimentary products that can be conveniently coupled to have a dynamic hazard assessment. These two methodologies can be considered complimentary also from another point of view: while rainfall thresholds relate landslide initiation with the main triggering factor (rainfall), susceptibility maps relate landslide occurrence to the predisposing factors (e.g., morphometry, lithology, and land use). It is important to note that both approaches neglect an explicit analysis of the physic behind the landslide initiation: both rainfall thresholds and susceptibility maps used a statistical approach and not a physically based one. As a consequence, the same can be said for the resulting hazard matrix and hazard assessment proposed in this work. However, some characteristics of the hazard assessment can be put into close correlation with some physical features of the test site.
The study area is wide and presents heterogeneous physical features; therefore the approach of subdividing the site into alert zones calibrated independently allowed strengthening the statistical correlation between landslide initiation and triggering/predisposing factors. The very different threshold equations (Table 1) and the difference in susceptibility values used to separate susceptibility classes (Table 2) corroborates further the effectiveness of the approach consisting in partitioning the study area into independent physiographic units. Among these, A3 is the most prone to landslides: here landslide density is higher than in the other alert zones (Segoni et al., 2014b; Battistini et al., 2017), due to the higher slope gradients, the highest altitudes and the presence of lithologies very susceptible to landslides (pelitic flyschs and shistose metamorphic rocks). This is also reflected by the outcomes of the calibration procedure: A3 has the lowest rainfall thresholds combined with the lowest susceptibility, while B3 shows the highest ones. The subdivision of the study area into alert zones to be monitored independently allow also the better encompass the spatial and temporal variability of the rainfall variable: a check on the validation period revealed that in 39% of the days, the rainfall amounts were so different from an alert zone to another that the systems returned different rainfall rate classes (R1, R2, R3), and this occurred mainly during storms: during the validation period it never happened that all the alert zones were at the R2 or R3 level during the same day.
According to the validation procedure, the dynamic hazard assessment proposed in this work underestimated landslide hazard only in one circumstance out of 39. A thorough investigation of this error revealed that it is related to a single landslide event occurred in a S2 spot of the alert zone A3, in a day when the warning system state was in R1 mode, thus providing a H1 (low hazard) matrix output. In this case, both the rainfall threshold system and the susceptibility map underestimated the hazard: the former because no threshold was overcome, the latter because probably some anthropic predisposing factor were not take into account properly (indeed, the landslides occurred close to a mountain road and to a drainage system, which both could have favored the triggering mechanism). This was the only circumstance for which the proposed hazard assessment could not encompass properly the inherent uncertainty of the two original models that were combined into the matrix, but it is a flaw within the error limits imposed by the calibration and optimization procedure explained in section Hazard Assessment.
Conclusion
We propose a dynamic landslide hazard assessment procedure based on the combination of rainfall thresholds and susceptibility maps. Inside each alert zone, the dynamic but spatially constant input provided by a warning system based on rainfall thresholds is combined with the spatially variable but static input provided by a susceptibility map into a matrix defining five possible hazard levels.
The proposed hazard classification scheme underwent a calibration procedure against a large landslide dataset, counting 1,761 landslides, to ensure a good constraint between hazard classification and experimental data. This allowed minimizing the number of landslide occurrences in the lowest hazard classes and to provide an interpretation of the hazard classes. A validation procedure was performed against an independent dataset simulating an operational employ of the dynamic hazard assessment through a 16 months period. The validation provided encouraging results, as 38 landslides out of 39 would have been associated to a consistent hazard level.
The proposed procedure could be easily applied to early warning systems based on rainfall thresholds bringing two main advantages: a consistent refinement of the spatial resolution of the forecasts and a robust tool to assist hazard and risk management and spatial-temporal forecasting of rainfall induced landslides at regional scale.
Author Contributions
SS has written the manuscript, conceived the work and assisted the data interpretation. VT has conceived the work and she has provided a specific contribution to the methodological part with special reference to the susceptibility assessment. AR has contributed to the rainfall thresholds assessment and to the data elaboration. FC and NC have supervised the work.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research has been performed in the framework of the project SARnet, funded by the Italian Department of Civil Protection, Presidency of the Council of Ministers.
References
Aleotti, P., and Chowdhury, R. (1999). Landslide hazard assessment: summary, review and new perspectives. Bull. Eng. Geol. Environ. 58, 21–44. doi: 10.1007/s100640050066
Atkinson, P. M., and Massari, R. (1998). Generalized linear modeling of susceptibility to landsliding in the central Apennines, Italy, Comput. Geosci. 24, 373–385. doi: 10.1016/S0098-3004(97)00117-9
Baeza, C., and Corominas, J. (1996). “Assessment of shallow landslide susceptibility by means of statistical techniques,” in Proceedings of the Seventh International Symposium on Landslides, ed K. Senneset (A.A. Balkema: Trondheim), 147–152.
Battistini, A., Rosi, A., Segoni, S., Lagomarsino, D., Catani, F., and Casagli, N. (2017). Validation of landslide hazard models using a semantic engine on online news. Appl. Geogr. 82, 59–65. doi: 10.1016/j.apgeog.2017.03.003
Battistini, A., Segoni, S., Manzo, G., Catani, F., and Casagli, N. (2013). Web data mining for automatic inventory of geohazards at national scale. Appl. Geogr. 43, 147–158. doi: 10.1016/j.apgeog.2013.06.012
Baum, R., Coe, J., Godt, J., Harp, E., Reid, M., Savage, W., et al. (2005). Regional landslide-hazard assessment for Seattle, Washington, USA. Landslides 2, 266–279. doi: 10.1007/s10346-005-0023-y
Bianchi, F., and Catani, F. (2002). “Landscape dynamics risk management in Northern Apennines (ITALY),” in Development and Application of Computer Techniques to Environmental Studies, Development and Application of Computer Techniques to Environmental Studies, eds F. Bianchi, F. Catani, C. A. Brebbia, and P. Zannetti (Southampton: WIT Press), 319–328.
Brenning, A. (2005). Spatial prediction models for landslide hazards: review, comparison and evaluation. Nat. Haz. Earth Syst. Sci. 5, 853–862. doi: 10.5194/nhess-5-853-2005
Carrara, A. (1983). Multivariate methods for landslide hazard evaluation. Math. Geol. 15, 403–426. doi: 10.1007/BF01031290
Catani, F., Casagli, N., Ermini, L., Righini, G., and Menduni, G. (2005). Landslide hazard and risk mapping at catchment scale in the Arno river basin. Landslides 2, 329–342. doi: 10.1007/s10346-005-0021-0
Catani, F., Lagomarsino, D., Segoni, S., and Tofani, V. (2013). Landslide susceptibility estimation by random forests technique: sensitivity and scaling issues. Natl. Haz. Earth Syst. Sci. 13, 2815–2831. doi: 10.5194/nhess-13-2815-2013
Chung, C. F., and Fabbri, A. G. (1995). “Multivariate regression analysis for landslide hazard zonation,” in Geographical Information Systems in Assessing Natural Hazards, eds A. Carrara and F. Guzzetti (Dordrecht: Kluwer Academic), 107–142.
Corominas, J., van Westen, C., Frattini, P., Cascini, L., Malet, J., Fotopoulou, S., et al. (2013). Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 73, 209–263. doi: 10.1007/s10064-013-0538-8
Crosta, G. B., and Frattini, P. (2003). Distributed modelling of shallow landslides triggered by intense rainfall. Nat. Hazards Earth Syst. Sci. 3, 81–93. doi: 10.5194/nhess-3-81-2003
Ermini, L., Catani, F., and Casagli, N. (2005). Artificial neural networks applied to landslide susceptibility Assessment. Geomorphology 66, 327–343. doi: 10.1016/j.geomorph.2004.09.025
Fell, R., Corominas, J., Bonnard, C., Cascini, L., Leroi, E., and Savage, W. Z. (2008). Guidelines for landslide susceptibility, hazard and risk zoning for land use planning. Eng. Geol. 102, 85–98. doi: 10.1016/j.enggeo.2008.03.022
Godt, J. W., Baum, R. L., Savage, W. Z., Salciarini, D., Schulz, W. H., and Harp, E. L. (2008). Transient deterministic shallow landside modelling: requirements for susceptibility and hazard assessment in a GIS framework. Eng. Geol. 102, 214–226. doi: 10.1016/j.enggeo.2008.03.019
Guzzetti, F., Peruccacci, S., Rossi, M., and Stark, C. P. (2008). The rainfall intensity–duration control of shallow landslides and debris flows: an update. Landslides 5, 3–17. doi: 10.1007/s10346-007-0112-1
Hong, Y., and Adler, R. F. (2008). Predicting global landslide spatiotemporal distribution: integrating landslide susceptibility zoning techniques and real-time satellite rainfall estimates. Int. J. Sediment Res. 23, 249–257. doi: 10.1016/S1001-6279(08)60022-0
Hosmer, D. W., and Lemeshow, S. (2000). Applied Logistic Regression. New York, NY: John Wiley and Sons.
Iverson, R. (2000). Landslide triggering by rain infiltration. Water Resour. Res. 36, 1897–1910. doi: 10.1029/2000WR900090
Jemec Auflič, M., Šinigoj, J., Krivic, M., Podboj, M., Peternel, T., and Komac, M. (2016). Landslide prediction system for rainfall induced landslides in Slovenia (Masprem). Geologija 59, 259–271. doi: 10.5474/geologija.2016.016
Kanungo, D. P., Arora, M. K., Sarkar, S., and Gupta, R. P. (2006). A comparative study of conventional, ANN black box, fuzzy and combined neural and fuzzy weighting procedures for landslide susceptibility zonation in Darjeeling Himalayas. Eng. Geol. 85, 347–366. doi: 10.1016/j.enggeo.2006.03.004
Lagomarsino, D., Tofani, V., Segoni, S., Catani, F., and Casagli, N. (2017). A tool for classification and regression using random forest methodology: applications to landslide susceptibility mapping and soil thickness modeling. Environ. Model. Assess. 22, 201–214. doi: 10.1007/s10666-016-9538-y
Lee, E. M., Brunsden, D., and Sellwood, M. (2000). “Quantitative risk assess- ment of coastal landslide problems,” in Landslides in Research Theory and Practice: Eighth International Symposium on Landslides, eds E. Bromhead, N. Dixon, and M-L. Ibsen (London: Thomas Telford), 2, 899–904.
Lee, S. (2005). Application of logistic regression model and its validation for landslide susceptibility mapping using GIS and remote sensing data. Int. J. Remote Sens. 26, 1477–1491. doi: 10.1080/01431160412331331012
Lee, S., Choi, J., and Min, K. (2004). Probabilistic landslide hazard mapping using GIS and remote sensing data at Boun, Korea. Int. J. Remote Sens. 25, 2037–2052. doi: 10.1080/01431160310001618734
Lee, S., Ryu, J. H., Lee, M. J., and Won, J. S. (2003). Use of an artificial neural network for analysis of the susceptibility to landslides at Boun, Korea. Environ. Geol. 44, 820–833. doi: 10.1007/s00254-003-0825-y
Lu, P., Casagli, N., Catani, F., and Tofani, V. (2012). Persistent scatterers interferometry hotspot and cluster analysis (PSI-HCA) for detection of extremely slow-moving landslides. Int. J. Remote Sens. 33, 466–489. doi: 10.1080/01431161.2010.536185
Manzo, G., Tofani, V., Segoni, S., Battistini, A., and Catani, F. (2013). GIS techniques for regional-scale landslide susceptibility assessment: the Sicily (Italy) case study. Int. J. Geogr. Inform. Sci. 27, 1433–1452. doi: 10.1080/13658816.2012.693614
Mercogliano, P., Segoni, S., Rossi, G., Sikorsky, B., Tofani, V., Schiano, P., et al. (2013). Brief communication: a prototype forecasting chain for rainfall induced shallow landslides. Nat. Hazards Earth Syst. Sci. 13, 771–777. doi: 10.5194/nhess-13-771-2013
Montgomery, D. R., and Dietrich, W. E. (1994). A physically based model for the topographic control on shallow landsliding. Water Resour. Res. 30, 1153–1171. doi: 10.1029/93WR02979
Pack, R., Tarboton, D., and Goodwin, C. (1998). “The sinmap approach to terrain stability mapping,” in 8th Congress of the International Association of Engineering Geology, eds D. Moore and O. Hungr (Vancouver, BC).
Pourghasemi, H. R., and Kerle, N. (2016). Random forests and evidential belief function-based landslide susceptibility assessment in western Mazandaran province, Iran. Environ. Earth Sci. 75:185. doi: 10.1007/s12665-015-4950-1
Rosi, A., Agostini, A., Tofani, V., and Casagli, N. (2014). A procedure to map subsidence at the regional scale using the persistent scatterer interferometry (PSI) technique. Remote Sens. 6, 10510–10522. doi: 10.3390/rs61110510
Rosi, A., Lagomarsino, D., Rossi, G., Segoni, S., Battistini, A., and Casagli, N. (2015). Updating EWS rainfall thresholds for the triggering of landslides. Nat. Hazards 78, 297–308. doi: 10.1007/s11069-015-1717-7
Rosi, A., Segoni, S., Catani, F., and Casagli, N. (2012). Statistical and environmental analyses for the definition of a regional rainfall thresholds system for landslide triggering in Tuscany (Italy). J. Geogr. Sci. 22, 617–629. doi: 10.1007/s11442-012-0951-0
Rosi, A., Tofani, V., Tanteri, L., Stefanelli, C. T., Agostini, A., Catani, F., et al. (2018). The new landslide inventory of Tuscany (Italy) updated with PS-InSAR: geomorphological features and landslide distribution. Landslides 15, 5–19. doi: 10.1007/s10346-017-0861-4
Rossi, G., Catani, F., Leoni, L., Segoni, S., and Tofani, V. (2013). HIRESSS: a physically based slope stability simulator for HPC applications. Nat. Hazards Earth Syst. Sci. 13, 151–166. doi: 10.5194/nhess-13-151-2013
Segoni, S., Battistini, A., Rossi, G., Rosi, A., Lagomarsino, D., Catani, F., et al. (2015a). Technical note: an operational landslide early warning system at regional scale based on space–time-variable rainfall thresholds. Natl. Hazards Earth Syst. Sci. 15, 853–861. doi: 10.5194/nhess-15-853-2015
Segoni, S., Lagomarsino, D., Fanti, R., Moretti, S., and Casagli, N. (2015b). Integration of rainfall thresholds and susceptibility maps in the Emilia Romagna (Italy) regional-scale landslide warning system. Landslides 12, 773–785. doi: 10.1007/s10346-014-0502-0
Segoni, S., Piciullo, L., and Gariano, S. L. (2018). A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 1–19. doi: 10.1007/s10346-018-0966-4
Segoni, S., Rossi, G., Rosi, A., and Catani, F. (2014a). Landslides triggered by rainfall: a semiautomated procedure to define consistent intensity-duration thresholds. Comput. Geosci. 3063, 123–131. doi: 10.1016/j.cageo.2013.10.009
Segoni, S., Rosi, A., Rossi, G., Catani, F., and Casagli, N. (2014b). Analysing the relationship between rainfalls and landslides to define a mosaic of triggering thresholds for regional-scale warning systems. Nat. Hazards Earth Syst. Sci. 14, 2637–2648. doi: 10.5194/nhess-14-2637-2014
Segoni, S., Tofani, V., Lagomarsino, D., and Moretti, S. (2016). Landslide susceptibility of the Prato–Pistoia–Lucca provinces, Tuscany, Italy. J. Maps 12, 401–406. doi: 10.1080/17445647.2016.1233463
Tofani, V., Bicocchi, G., Rossi, G., Segoni, S., D'Ambrosio, M., Casagli, N., et al. (2017). Soil characterization for shallow landslides 390 modeling: a case study in the Northern Apennines (Central Italy). Landslides 14, 755–770. doi: 10.1007/s10346-017-0809-8
Tofani, V., Dapporto, S., Vannocci, P., and Casagli, N. (2006). Infiltration, seepage and slope instability mechanisms during the 20–21 November 2000 rainstorm in Tuscany, central Italy. Nat. Hazards Earth Syst. Sci. 6, 1025–1033. doi: 10.5194/nhess-6-1025-2006
Trigila, A., Casagli, N., Catani, F., Crosta, G., Esposito, C., Frattini, P., et al. (2013). “Landslide susceptibility mapping at national scale: the Italian case study,” in Landslide Science and Practice, Vol. 1: Landslide Inventory and Susceptibility and Hazard Zoning, eds C. Margottini, P. Canuti and K. Sassa (Rome: Springer), 287–295.
Trigila, A., Iadanza, C., and Spizzichino, D. (2010). Quality assessment of the Italian landslide inventory using GIS processing. Landslides 7, 455–470. doi: 10.1007/s10346-010-0213-0
Vai, G. B., and Martini, I. P. (2001). Anatomy of an Orogen (2001). The Appennines and adjacent Mediterranean Basins. Dortdrecht; Boston; London: Kluver Academic Publishers.
Vorpahl, P., Elsenbeer, H., Märker, M., and Schröder, B. (2012). How can statistical models help to determine driving factors of landslides? Ecol. Model. 239, 27–39. doi: 10.1016/j.ecolmodel.2011.12.007
Wong, H. N. (2005). “Landslide risk assessment for individual facilities— state of the art report,” in Proceedings of the International Conference on Land- slide Risk Management, eds O. Hungr, R. Fell, R. Couture, and E. Eberhardt (London: Taylor & Francis), 237–296.
Yilmaz, I. (2009). Landslide susceptibility mapping using frequency ratio, logistic regression, artificial neural networks and their comparison: a case study from Kat landslides (Tokat-Turkey). Comput. Geosci. 35, 1125–1138. doi: 10.1016/j.cageo.2008.08.007
Yilmaz, I. (2010). Comparison of landslide susceptibility mapping methodologies for Koyulhisar, Turkey: conditional probability, logistic regression, artificial neural networks, and support vector machine. Environ. Earth Sci. 61, 821–836. doi: 10.1007/s12665-009-0394-9
Youssef, A. M., Pourghasemi, H. R., Pourtaghi, Z. S., and Al-Katheeri, M. M. (2016). Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at wadi tayyah basin. Asir Region, Saudi Arabia. Landslides. 13, 839–856. doi: 10.1007/s10346-015-0614-1
Keywords: landslide, hazard, rainfall thresholds, susceptibility maps, northern Apennines
Citation: Segoni S, Tofani V, Rosi A, Catani F and Casagli N (2018) Combination of Rainfall Thresholds and Susceptibility Maps for Dynamic Landslide Hazard Assessment at Regional Scale. Front. Earth Sci. 6:85. doi: 10.3389/feart.2018.00085
Received: 16 March 2018; Accepted: 04 June 2018;
Published: 20 June 2018.
Edited by:
Davide Tiranti, Agenzia Regionale per la Protezione Ambientale (ARPA), ItalyReviewed by:
Matthieu Kervyn, Vrije Universiteit Brussel, BelgiumMilad Janalipour, K.N.Toosi University of Technology, Iran
Copyright © 2018 Segoni, Tofani, Rosi, Catani and Casagli. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Veronica Tofani, dmVyb25pY2EudG9mYW5pQHVuaWZpLml0
 Samuele Segoni
Samuele Segoni Veronica Tofani
Veronica Tofani Ascanio Rosi
Ascanio Rosi