Retrograde Accretion of a Caribbean Fringing Reef Controlled by Hurricanes and Sea-level Rise

Predicting the impact of sea-level (SL) rise on coral reefs requires reliable models of reef accretion. Most assume that accretion results from vertical growth of coralgal framework, but recent studies show that reefs exposed to hurricanes consist of layers of coral gravel rather than in-place corals. New models are therefore needed to account for hurricane impact on reef accretion over geological timescales. To investigate this geological impact, we report the configuration and development of a 4-km-long fringing reef at Punta Maroma along the northeast Yucatan Peninsula. Satellite-derived bathymetry (SDB) shows the crest is set-back a uniform distance of 315 ±15 m from a mid-shelf slope break, and the reef-front decreases 50% in width and depth along its length. A 12-core drill transect constrained by multiple ²³⁰Th ages shows the reef is composed of an ~2-m thick layer of coral clasts that has retrograded 100 m over its back-reef during the last 5.5 ka. These findings are consistent with a hurricane-control model of reef development where large waves trip and break over the mid-shelf slope break, triggering rapid energy dissipation and thus limiting how far upslope individual waves can fragment corals and transport clasts. As SL rises and water depth increases, energy dissipation during wave-breaking is reduced, extending the clast-transport limit, thus leading to reef retrogradation. This hurricane model may be applicable to a large sub-set of fringing reefs in the tropical Western-Atlantic necessitating a reappraisal of their accretion rates and response to future SL rise.

Introduction

Swimming over the surface of a coral reef, it's not difficult to imagine that successive generations of coral would produce an interlocking framework and, over time, lead to simple vertical reef accretion. This assumption of what you see on the surface is what you get in the interior, underlies all major explanations of how reefs develop: Darwin (1842) proposed that vertical-accretion kept reefs at sea level (SL) during progressive subsidence of volcanic islands, producing a genetic sequence of reef types; Daly (1915) thought reefs accreted vertically from lowstand erosion terraces during postglacial SL rise; Purdy (1974) claimed they did so from residual karst topography; Adey (1978) suggested that vertical accretion was a multidimensional response to wave energy, substrate depth and SL rise; and Neumann and Macintyre (1985) proposed that vertical accretion was controlled by the rate of SL rise, leading to three reef types: those that drowned, those that caught up, and those that kept up.

There is good evidence in some areas that this assumption is correct, and reefs do consist of vertically-building coralgal framework, especially barrier reefs and atolls in the Indo-Pacific (e.g., Cabioch et al., 1999; Blanchon et al., 2014). But in an increasing number of areas, coring has shown that not all reefs develop this way (Blanchon et al., 1997; Braithwaite et al., 2000; Meyer et al., 2003; Blanchon and Perry, 2004; Palmer et al., 2010; Ryan et al., 2016). Studies of fringing reefs in the tropical Western-Atlantic in particular, are beginning to show that hurricanes play a prominent role in controlling both the configuration and composition of these structures (Blanchon et al., 1997; Macintyre et al., 2001; Perry, 2001; Blanchon and Perry, 2004). For example, a study of short cores and excavations through a fringing reef encircling Grand Cayman revealed it to be composed of layers of coral gravel (Blanchon et al., 1997). Although the study did not fully reconstruct the reef structure, it did establish that the crest lay a uniform distance of ~350 m behind a mid-shelf slope break seaward of the reef structure. To explain the gravel composition and uniform position of the Cayman reef, Blanchon et al. (1997) speculated that hurricane waves were tripped by the slope break and plunged over the entire reef front, fragmenting corals, and depositing clasts at a uniform distance from the trip point, producing a linear breakwater composed of coral gravel. They argued that although reefs destroyed by hurricanes would recover to their pre-storm state, the frequency of intense hurricanes over geological time ensured that the shallow-reef structures would be dominated by storm-generated detritus.

Such studies imply that simple vertical accretion of coralgal framework has been overemphasized in models of reef accretion. If hurricanes do indeed influence fringing-reef development as claimed, then additional models of reef accretion are needed. Here, we test the hypothesis that hurricanes control reef configuration and development by investigating the geomorphology, composition, and internal structure of a typical hurricane-impacted fringing reef at Punta Maroma along the north-east coast of the Yucatan Peninsula (Figure 1). We show that, like Grand Cayman, the reef at Punta Maroma is composed of coral clasts, rather than in-place framework, and its location is a uniform distance behind a mid-shelf slope break. We further show that the reef has retrograded over its backreef during the last 5.5 ka. To explain its detrital composition and retrograde development, we propose a hurricane-control model that links the cycle of reef destruction and recovery with the gradual rise in SL since the mid Holocene (e.g., Khan et al., 2017). By identifying similar set-back distances on other reefs in the region we argue that this new model is representative of a large subset of fringing reefs in the hurricane belt of the tropical Western-Atlantic.

FIGURE 1

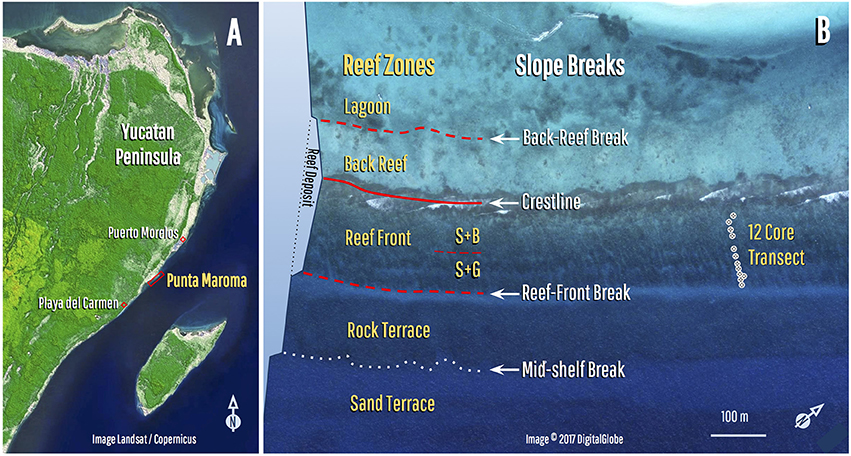
Figure 1. Location and zonation of the Punta Maroma fringing reef. (A) Reef is located between Playa del Carmen and Puerto Morelos along the coast of the northeast Yucatan Peninsula (20.724921–86.963876°). (B) Reef shows a typical Caribbean zonation with zones delineated by slope breaks: the crestline separates the back-reef and reef-front zones. Reef front is subdivided into a stump-and-boulder (S+B) and spur-and-groove (S+G) zone (position of core transect also shown). Reef deposit is flanked by a lagoon on the landward side, and a rock-terrace and deeper sand-terrace on seaward side. Schematic depth profile illustrates slope breaks that define the main zones.

Methods

Satellite Derived Bathymetry

Bathymetric data was derived by Ohlendorf et al. (2011) from WV2 high-resolution multispectral satellite images, and reported in Cerdeira-Estrada et al. (2012). Water depth was calculated using the EOMAP Modular Inversion and Processing System which is based on physical modeling and does not require calibration with ground data (EOMAP, 2014). Satellite derived bathymetry (SDB) used in this study was part of a mosaicked dataset extending over ~400 km of coastline derived from multiple satellite images, with data for our study area covered by a single satellite image within this. Bathymetry was supplied as gridded data at 4 m spacing, and interpolated values for sonar comparisons, profile generation, and rendering of plan views were generated from this using a linear filter which responds from 10 to 90% of a step change in input over a distance of ~13 m without overshoot. Using an Ecosound SyQwest Bathy 500 DF Hydrographic Survey Echosounder synchronized ex post with a dual frequency Leica 1,200 Differential Global Positioning System, we collected 1,478 sonar points (one point every 5 s at a spacing of ~10 m) within the image area in 10 coast-normal transects to validate and adjust the SDB using a least-squares fit quadratic estimator of sonar depth (see Supplementary Material). Adjusted results were compared with sonar transects and indicate a progressively declining SDB accuracy with depth resulting from heterogeneity in the data, consistent with progressive confounding of depth estimates by variations in bottom reflectance (see Figure S1, Table S1 in Supplementary Material). Although there is an overall reduction in root-mean-square error from adjusting the SDB to sonar data, whether or not the adjustment results in an improvement on a given transect varies, presumably due to variations in bottom reflectance (Ohlendorf et al., 2011).

Core Drilling and Logging

To characterize reef composition, 12 cores were taken with a 3-speed rotary diamond drill (Spitznas^®) powered from a hydraulic pump (JCB-Trojan^® 700-cm3/18-hp) mounted on a shallow-draft boat (core-transect location was triangulated from coastal landmarks). Cores with a 9.2 cm-diameter were recovered using a 1.1 m-long core barrel to which 30 cm-long extension rods were attached as required, up to a maximum of 3 m. Cores were cut lengthwise and scanned. Scans were integrated with the recovery and composition logs to provide an accurate visual record of each core. Detailed logging of the cores involved a standard sedimentological characterization of framework/sediment size and composition to species level following Blanchon and Perry (2004). We used several distinguishing criteria to differentiate large clasts from in-place coral colonies, including (i) the presence of lateral or basal attachment surfaces, formed when a growing coral encrusts its substrate, (ii) distinctive asymmetrical thicknesses of corallite growth in branches and fronds of Acropora palmata (Lighty et al., 1982), and (iii) Orientation of the growth axis of A. palmata branches, assuming angles >20° from the horizontal represent in-situ colonies (Blanchon and Eisenhauer, 2000).

Geochronology

The samples were U-series dated by isotope-dilution MC-ICPMS using a Thermo-Finnigan Neptune Plus at Centro de Geociencias, UNAM, using a high-purity ²²⁹Th spike obtained from Oakridge National Laboratory, and ²³³U from IRMM 051a reference material (Hernández-Mendiola et al., 2011). All sample preparations were carried out in a class-100 clean-lab, with blanks typically lower than 3 pg of ²³⁸U and 1 pg of ²³²Th. Uranium and Thorium were measured independently. ²³⁴U was measured with an ion-counter (SEM) behind a retardant potential quadrupole (RPQ) filter, providing an abundance sensitivity of 0.5 ppm at m-1, but was unable to fully remove the tailing contributions from ²³⁸U to ²³⁵U upon ²³⁴U. Consequently, we added a fast magnet jump in the measurement routine to monitor at m/Z+ = 233.5 and 234.5 on the SEM and remove any contribution by linear interpolation. ²³⁰Th was measured with the SEM behind the RPQ filter. Because all samples measured here produced low ²³²Th signals (>0. 1 V), no tailing corrections on ²³⁰Th were necessary. All ages were calculated with Isoplot v. 3.75 (Ludwig, 2012) using half-lives for ²³⁸U from Jaffey et al. (1971) and for ²³⁴U and ²³⁰Th from Cheng et al. (2013).

Hurricane Wave Breaking

To develop the hurricane-control model we estimated the breaking depth and breaking mode of hurricane waves. The depth at which breaking occurs is commonly described in terms of the breaker ratio γ_b, sometimes also known as the breaker depth index (e.g., Blenkinsopp and Chaplin, 2008), which is the ratio of the wave height at breaking (H_b) to the water depth at which breaking occurs (h_b).

$\begin{array}{l}\text{Breaker ratio }(\text{breaker depth index}){\text{γ}}_{\text{b}}\equiv {\text{H}}_{\text{b}}/{\text{h}}_{\text{b}}\\ \text{i}.\text{e}.,{\text{h}}_{\text{b}}/{\text{H}}_{\text{b}}=1/{\text{γ}}_{\text{b}}\end{array}$

To estimate the breaking depth for hurricane waves of known deep-water characteristics (height and period/wavelength), we used the breaker index Ω_b, also known as the breaker height index (e.g., Blenkinsopp and Chaplin, 2008), which is the ratio of the significant wave height at breaking (H_b) to the deep-water wave height (H_∞), recognizing that this is underparameterised and cannot reflect specific conditions in our bathymetric setting.

$\begin{array}{l}\text{Breaker index }(\text{breaker height index}){\text{Ω}}_{\text{b}}\equiv {\text{H}}_{\text{b}}/{\text{H}}_{\text{∞}}=\text{a}{({\text{H}}_{\text{∞}}/{\text{L}}_{\text{∞}})}^{\text{b}}\\ \text{i}.\text{e}.,{\text{h}}_{\text{b}}/{\text{H}}_{\text{b}}={\text{h}}_{\text{b}}/({\Omega }_{\text{b}}{\text{H}}_{\text{∞}})\end{array}$

We considered five formulas for breaker ratio (McCowan, 1894; Weggel, 1972; Madsen, 1976; Hanson and Kraus, 1989; Larson and Kraus, 1989) and seven for breaker index (Munk, 1949; Le Méhauté and Koh, 1967; Komar and Gaughan, 1972; Singamsetti and Wind, 1980; Sunamura, 1982; Smith and Kraus, 1990; Gourlay, 1992). Formulas for breaker ratio variously include dependencies on floor slope, period, and deep-water wave length (L_∞) and deep-water height. The Hanson and Kraus (1989) formula is for barred beaches, and the others for planar beaches. Parameters a and b for breaker index vary between models and are in some cases dependent on bottom slope (m or tan β). We re-expressed Weggel's Equation (9) as γ_b = b/[1+ah_b/(gT²)]. Applicability of the breaker index formulas is restricted to explicit ranges of gradient and deep-water wave steepness (H_∞/L_∞). The two formulas for breaker index based on field data (Smith and Kraus, 1990; Gourlay, 1992) are claimed to be applicable to gradients up to 0.1; Singamsetti and Wind (1980) is claimed to be applicable to gradients up to 0.2.

In evaluating these formulas we use a constant gradient of 0.025 (the lowest gradient for which all of the formulas are valid) to represent the slope of the shelf lead-in to the mid-shelf slope break. Although we could have used a gradient derived from one of our bathymetry profiles and dependent on h_b to better reflect gradient-dependence of breaking, the gradients on the slope break exceed the applicability range of some of the formulas. Hence our results are not valid indicators of where on the slope break a wave might break according to the formulas used, merely whether the waves are indicated as breaking on the lead-in, at an unknown point on the slope break, or on the rock terrace (see Supplementary Material).

The breaking mode of hurricane waves can be predicted using a surf similarity parameter such as the deep water Iribarren number ξ_∞ (Battjes, 1974):

$\begin{array}{l}{\xi }_{\text{∞}}=m/\surd (H_{\text{∞}}/L_{\text{∞}})\end{array}$

where H_∞ and L_∞ are the wave height and length in deep water, and m is the gradient of the bottom. For a given deep-water wave height, the Iribarren number is larger for breaking on steep slopes (m) and for longer waves (L_∞), and smaller for higher waves (H_∞). Transition values for breaking wave types are, according to Battjes (1974) for planar beaches, spilling for ξ_∞ < 0.5, plunging for 0.5 < ξ_∞ < 3.3, and surging for ξ_∞ > 3.3, and according to Smith and Kraus (1990) for barred beaches, spilling for ξ_∞ < 0.4 plunging for 0.4 < ξ_∞ < 1.2, and surging for ξ_∞ > 1.2. Low and high Iribarren numbers are associated with saturated and unsaturated surf conditions respectively, with unsaturated conditions within the surf zone (i.e., on the terrace) due to high Iribarren numbers favoring continued propagation of wave bores at the incident wave frequency (Baldock et al., 1998).

Results

Reef Morphology and Zonation

Using satellite-derived bathymetry (SDB), we delineated the morphological zonation and configuration of the fringing-reef at Punta Maroma. The image, bathymetry and slope data in Figure 2 show that the reef deposit consists of two shore-parallel zones: a back-reef sand flat, and a more steeply sloping reef-front zone, with the slope break between them marking the position of the crestline (see also Figure 1). The sand flat is delimited by an irregular 1 m slope-break along its lagoonal edge (the back-reef break), and the crestline along its seaward edge. The reef-front extends from the crestline to a 1–3 m slope-break (the reef-front break) that marks the seaward edge of the reef deposit (Figures 1, 2). In its northern section, the reef front can be subdivided into a shallow (<3 m) stump-and-boulder zone, characterized by sparsely distributed colonies of A. palmata, and a deeper (3–8 m) spur-and-groove zone more densely covered by A. palmata and other corals (Figures 1–3). In the southern section, however, the spur-and-groove diminishes and eventually disappears (Figure 2).

FIGURE 2

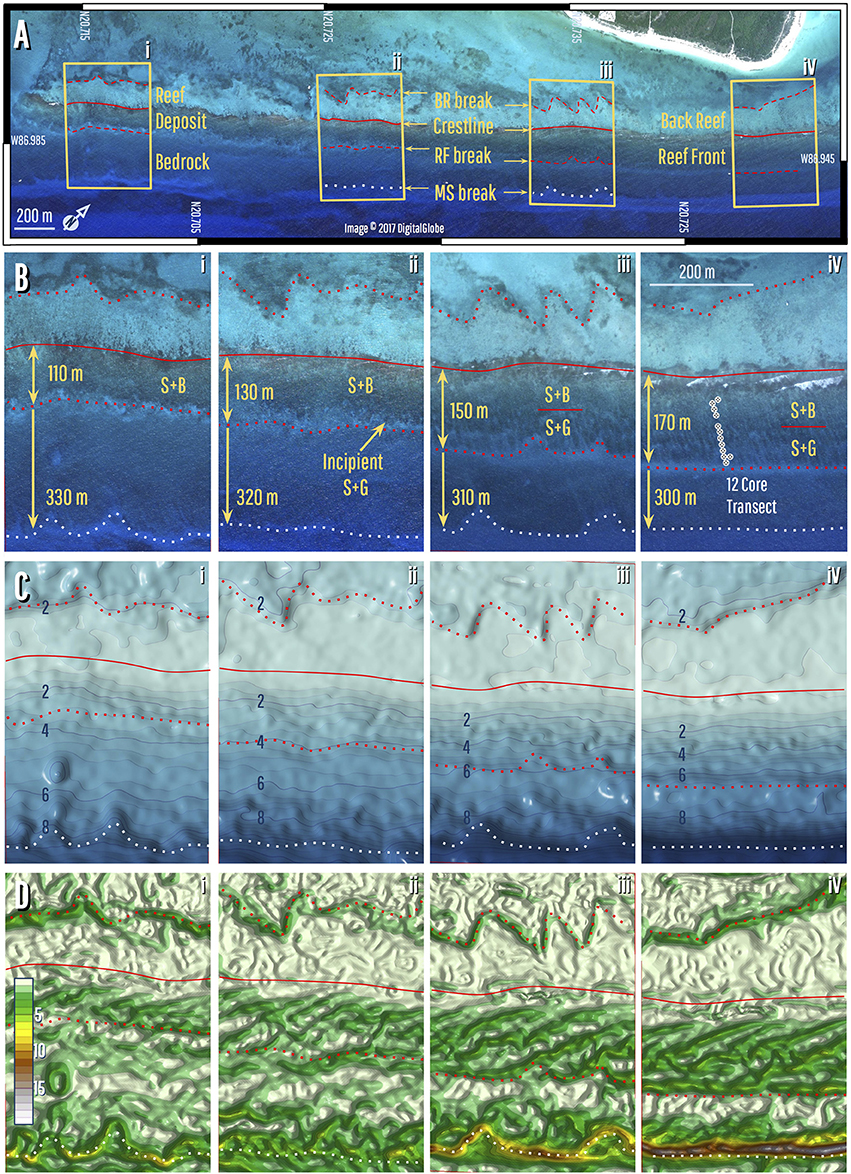
Figure 2. Morphological zonation of the fringing reef. (A) Satellite image showing the reef deposit and its visible zonation; note zone boundaries are marked by slope-breaks. (B) Close-up image of inset areas in (A), showing location of the core transect, as well as the individual morphological zones and how they change down reef. The reef front is divided into a stump-and-boulder zone (S+B) and a spur-and-groove zone (S+G). The width of the S+G zone diminishes to the south until it disappears completely, causing the reef-front zone to thin to the south (bidirectional arrows). Also note how the distance between crestline and the mid-shelf break increases slightly in the same direction (unidirectional arrows). (C) Satellite-derived bathymetry within inset areas in (A), showing the depths of slope breaks that mark zone boundaries. Note how the reef-front break shallows from 7 to 3 m along the reef. Data resolution is insufficient to resolve the S+G morphology (see methods). (D) Slope reconstruction, showing gradient changes over the shelf and highlighting slope breaks. Although the main zones are clear, boundaries and morphology of sub-zones, such as the S+G, are not. Slope changes within the S+G zone, for example, look to be artifacts of wave shoaling.

FIGURE 3

Figure 3. Photographs of the fringing reef and adjacent zones. (A) Back-reef coral-gravel forming a talus slope generated during Hurricane Ivan in 2004. Note how talus slope is encroaching on a head coral. (B) Coral-gravel completely entombing head coral, providing evidence of talus-slope retreat into lagoon (retrogradation). (C) Stump-and-boulder zone, showing dead A. palmata stump. (D) Proximal spur-and-groove zone where substrate is heavily encrusted with crustose coralline algae. (E) Distal spur-and-groove showing highest spur relief (tubes show locations of core holes F2 and F3). (F) Mid-shelf slope break at edge of rock terrace and transition into sand-covered terrace.

These parallel reef zones are flanked by a shallow (<3 m) lagoon on the landward side, and a deeper (4–10 m) bedrock terrace on the seaward side (Figures 1, 2). The edge of the bedrock terrace is marked by a mid-shelf slope break, which passes seawards into a low-gradient sand terrace of the outer shelf (Figures 1–3). To the north, the mid-shelf break is ~6 m high and lies between the 10 and 16 m isobaths and, although its relief diminishes toward the south, possibly as a result of sand burial, it can be identified on satellite imagery due to contrast between the bedrock and sand substrates (Figures 2, 3).

The SDB and image data show a systematic variation in the depth, width and position of these zones along the reef. First, the crestline is located a near-uniform distance behind the mid-shelf break at the edge of the rock terrace, suggesting that its position is somehow influenced by this feature (Figure 2). This distance increases from ~300 m in the north to ~330 m in the south giving a variation of ~315 ± 15 m (Figure 2). Second, the reef-front zone narrows and becomes shallower along its length, varying from 170 m wide to 7 m deep in the north, to only 110 m wide and 3 m deep in the south (Figure 2).

Reef Composition

To determine the internal structure and composition of the reef, we drilled a 12-hole core transect over the northern section of the reef-front zone (location shown in Figures 1, 2). In order to recover the basal section of the reef deposit, some cores were taken from grooves in the spur-and-groove zone. In total, seven cores were taken from the spur-and-groove zone (F1–6, F9), and five cores from the stump-and-boulder zone (F7–8, F10–12) (Figure 4).

FIGURE 4

Figure 4. Core Transect over the reef front. Cores F1-2 recovered fully consolidated late Pleistocene (MIS-5e) substrate with rhizoliths (only the first meter of the cores is shown; scale in cm). This substrate also found at base of core F6 with an age of ~114 ka (ages in ka shown in red circles). Cores F3-7 and 9 recovered a semi-consolidated to unconsolidated A. palmata cobble-gravel (~90% clasts) with abundant evidence of cementation of internal sediment (Cs). These cores contained rare colonies of A. palmata interpreted to be in-place (green lines), and either bottomed in bedrock or thin sand-gravel sections close to bedrock. Core 3 was drilled on a spur, and clasts show an intergrowth of crustose coralline algae and encrusting foraminifera Homotrema rubrum (cCA-Hr). The drill jammed in this hole and it was abandoned. Cores 8, 10–12 recovered a similar A. palmata gravel with some in-place colonies of Diploria (Ds) and Montastrea (Ma). These cores bottomed in sand and gravel sections ~1 m deep that could not be penetrated further by drilling due to hole collapse. For each hole, water depth at top of hole (WD) and total depth (TD) are shown.

The Pleistocene bedrock of the adjacent rock terrace was recovered in cores F1 and F2, taken from a groove at the distal end of the spur-and-groove zone, and at the base of core F6. It consists of a fully-consolidated carbonate gravelly-sand unit with dispersed coral fragments overprinted by terrestrial rhizoliths (Figure 4). The other cores, F3–12, show that the overlying reef deposit is an ~2 m thick layer of poorly to unconsolidated A. palmata cobble gravel (90%) with rare in-place colonies of large A. palmata or head corals (10%). Closer to the crest in cores F8, F10–12, the cobble-gravel layer is underlain by an unconsolidated carbonate sand that was partly penetrated (up to 1 m) during drilling, but unrecovered in the cores (Figure 4). Differences in encrusters and the in-place corals allow two subfacies to be differentiated in the cobble-gravel layer: Cores F3–7 and F9 consist of an A. palmata cobble-gravel with dispersed in-place colonies with upper surfaces encrusted by cm-thick intergrowths of crustose coralline algae and Homotrema rubrum. Interstices are filled with fully- to poorly-cemented internal sediment. Cores F8, F10–12 similarly consist of an A. palmata cobble-gravel but have dispersed in-place colonies of M. annularis, and D. strigosa, and generally lack intergrown encrusters and cemented internal sediment.

We interpret these two sub-facies as having formed in distinct morphological zones. The A. palmata gravel with cemented sand and cm-thick encrusters was likely the result of hurricane deposition in a surf-zone environment typical of the shallow reef-front. This is based on reports of active cementation and intergrowth of encrusters in shallow Caribbean reef fronts (e.g., Blanchon and Perry, 2004). The absence of thick encrusters and cementation in the other sub-facies, together with the presence of upright head corals, suggests clast deposition in a calmer, shallow, environment such as the proximal back-reef. Entombment of head corals by hurricane talus is common in the back-reef zone close to the crestline, as shown in Figure 3.

Reef Age and Development

To determine the reef's chronological structure and reconstruct its development, we measured U-series radiogenic isotopes of 14 corals from 10 of the cores using Multi-Collector Inductively Coupled Mass Spectrometry. The results in Table 1 show that ²³⁰Th ages range from 5.46 to 1.81 ka, with nine corals between 4 and 5.5 ka and only four with ages <4 ka. A sample from the underlying Pleistocene bedrock returned an age of 114 ka confirming development sometime during MIS-5e.

TABLE 1

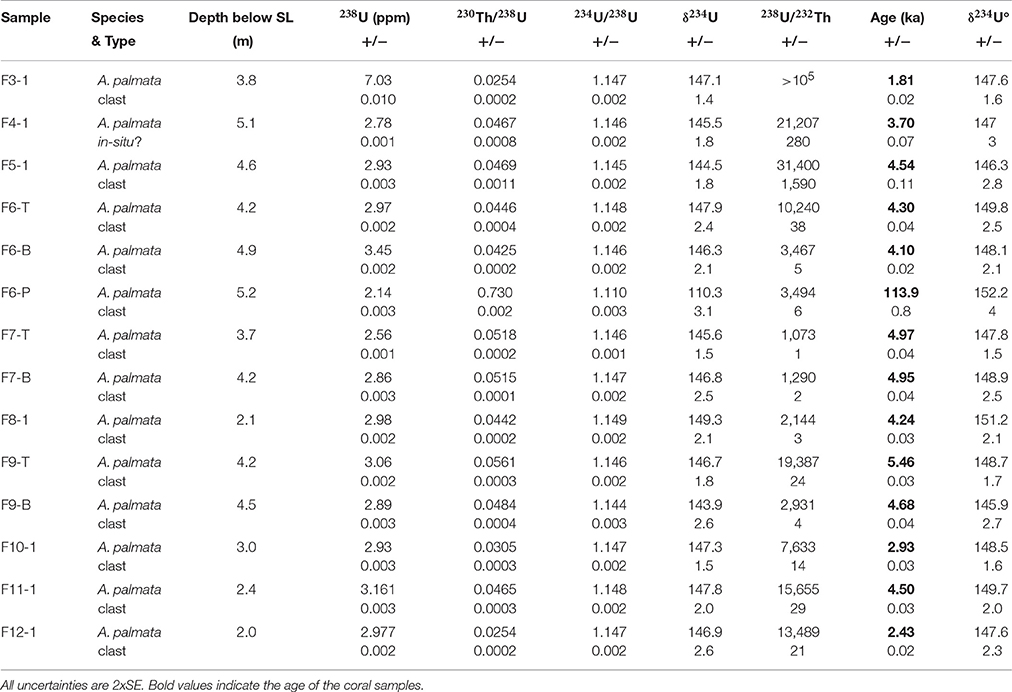
Table 1. U and Th activity ratios and ²³⁰Th-ages (ka) for corals samples of cores from Punta Maroma.

Within the reef deposit itself, all cores with two dates show age inversions of between 2 and 780 years. This is consistent with the interpretation that the composition of the cores is clast dominated. The reconstruction of reef development in Figure 5 reveals that the oldest part of the reef developed 5.5 ka ago at ~3 m below present SL, between sites F7 and 9 located below the present spur-and-groove zone (Figure 5). From this point, the reef deposit generally gets younger in both a landward and seaward direction. Although it progrades downslope for ~50 m over the Pleistocene bedrock terrace, the main accretion axis retrogrades ~100 m upslope over the unconsolidated back-reef sand and gravel (Figure 5). Interpretation of the isochron sequence showing retrograde development is complicated by lateral age inversions, consistent with re-mobilization of previously deposited clasts.

FIGURE 5

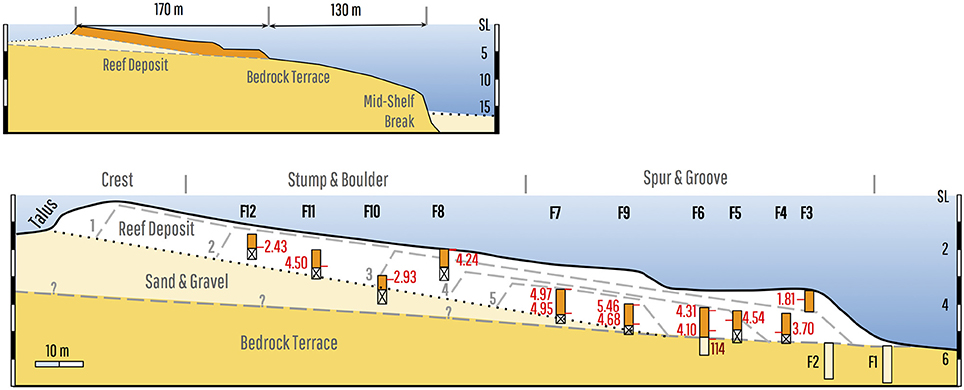
Figure 5. Reconstruction of fringing reef development. Upper panel shows the general architecture of the reef deposit over the rock terrace and back-reef sediment. Lower panel illustrates the detailed reconstruction of the internal structure of the reef deposit. Isochrons show the reef initiated below the Spur and Groove zone and retrograded ~100 m over it's back reef in the last 5.5ka. Note bedrock position under the crest is uncertain, but is likely constrained by maximum lagoon depths of 3–4 m.

Discussion

One of our main findings from the reef at Punta Maroma is that the surface community of in-place corals is not reflected in the reef interior, which is composed almost entirely of clasts (90%). This is consistent with the hypothesis that reef development has been controlled by hurricane-induced processes over geological timescales. To explain how hurricanes control development and account for the reef's 315 m set-back distance, its retrograde architecture, and longshore changes in geomorphology, we propose a semi-quantitative model that considers how hurricane waves interact with the bathymetry to control reef composition and configuration, and then how repeated hurricane impact coupled with SL rise controls reef architecture.

Hurricane Wave Impact

Measurement of wave fields generated by intense Hurricanes are uncommon but wave heights depend on maximum wind, translation speed, and position relative to the hurricane path (e.g., Wright et al., 2001). Sensors directly under the path of category 4 Hurricane Ivan (2004), for example, recorded significant wave heights of 16–18 m, maximum heights of 20–28 m, and a spectral peak period close to 15 s (Teague et al., 2007). The 8 h sampling interval, however, implies that these measurements likely missed the largest waves near the storm's eyewall and hence underrepresent the wave field.

Field data recording how large steep hurricane waves shoal and break upon reaching the shelf is also limited, but a number of formulas have been derived to estimate breaking depth of smaller less-steep waves (see Supplementary Material). Application of a selection of these formulas, shown in Figure 6, broadly indicates that waves with deep-water heights of 6–12 m will break between 10 and 16 m on the mid-shelf break, and waves >12 m will initiate breaking on the shelf prior to the break (see Supplementary Material). Figure 6 also illustrates that Iribarren numbers (Battjes, 1974) indicate plunging breakers for waves breaking on the slope-break itself, and spilling breakers for larger and/or steeper waves breaking on the shelf prior to the break. Plunging waves break over a relatively short distance and ultimately develop into a high-amplitude bore-like wave front (Galvin, 1968; Gaughan and Komar, 1975), but spilling is gentle and gradual, and spilling waves may go on largely unchanged to break on the mid-shelf break in a plunging manner as well (Battjes, 1974; Gaughan and Komar, 1975; Janssen and Battjes, 2007). Hence a mid-shelf slope break should act to produce plunging breakers and high-amplitude turbulent bores from a wide range of incident wave heights from as low as 6 m (Figure 6).

FIGURE 6

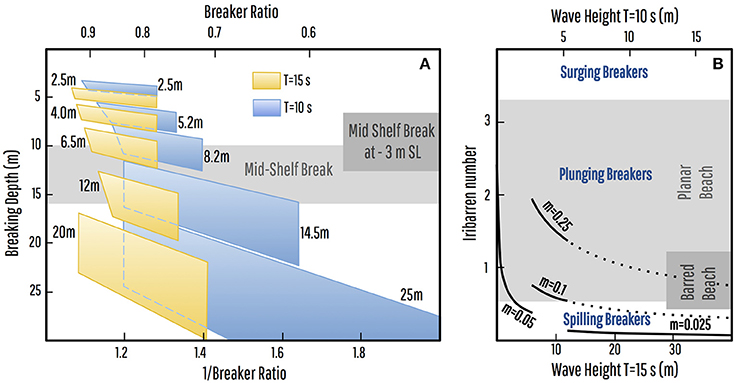
Figure 6. Estimation of breaking depths and breaker types for large waves. (A) Breaking depth polygons for deep-water wave heights of 2.5–25 m and wave periods of 10–15 s derived from a selection of formulas for breaker ratio and breaker index and assuming a gradient of 0.025. These indicate that waves with heights of 6–12 m will break at depths between 10 and 16 m, on the mid-shelf break, and waves >12 m will initiate breaking on the shelf prior to the break, with a commensurate reduction in wave heights at SL-3 m (4–9 m for T = 15 s). (B) Graph of deep-water Iribarren numbers (ξ_∞) for waves breaking on the outer shelf (represented by gradient m = 0.025), the mid-shelf break (0.1 < m < 0.25), or on the rock terrace (m = 0.05) with wave-height scales for periods of 15 and 10 s. Breaker type is correlated with Iribarren number, with plunging waves reported as occurring on planar beaches at 0.5 < ξ_∞ < 3.3 (Battjes, 1974) and on barred beaches at 0.4 < ξ_∞ < 1.2 (Smith and Kraus, 1990). In broad terms and allowing for breaker type being a continuum (Galvin, 1968), the graph is consistent with plunging breakers for waves breaking on the mid-shelf break and rock terrace, and spilling breakers for larger waves breaking on the outer shelf (see Supplementary Materials).

Turbulent bores generated by such large plunging hurricane waves are capable of fragmenting coral thickets (Madin and Connolly, 2006), and would transport the fragments upslope until water velocity/energy fell below some threshold. Our proposed explanation of the 315 ± 15 m distance between the crestline and the mid-shelf break at Punta Maroma is therefore that the slope break fixes the breaking point of a large subset of hurricane waves and thus controls the upslope distance of clast deposition, generating a linear gravel breakwater set-back a uniform distance from the edge of the rock terrace.

Destruction-Recovery Cycle

Between storms this linear gravel breakwater would become progressively colonized and stabilized by reef benthos. The degree to which reef benthos can recover to pre-storm levels is determined by the recurrence interval between intense storms capable of destroying shallow reef communities. If we assume that this level of destruction is generated by large waves from close passage of Category 4–5 hurricanes, then identifying the frequency of such a close passage at a given location will provide an estimate of time available for recovery.

The recurrence interval of large waves generated by Category 4–5 hurricanes has been documented at several locations in the Caribbean from over-wash deposits in coastal lagoons protected by beach/dune barriers. Although varying due to climatic forcing, recurrence intervals at these sites have been reported as being between 150 and 300 years (Liu and Fearn, 1993, 2000; Woodruff et al., 2008; Wallace and Anderson, 2010; Brandon et al., 2013). This time interval is significantly longer than is generally considered for a reef to recover to its pre-storm state, estimated to be as much as 50–70 years for healthy reefs (Stoddart, 1974; Pearson, 1981; Dollar and Tribble, 1993). Hence the disparity between recurrence of intense hurricanes and reef recovery means that reefs would undergo a continuous cycle of destruction and recovery on geological timescales (Woodley, 1992; Blanchon et al., 1997). In the case of Punta Maroma, the fringing reef is near the center of the hurricane belt and so likely has a similar 150–300 year recurrence interval of Category 4–5 hurricanes (Lugo et al., 2000). If this assumption is valid then the 5.5 ka-old reef would have experienced between 20 and 40 cycles of destruction and recovery, explaining why it's structure is dominated by hurricane detritus rather than in-place corals.

Rising SL and Retrogradation

Superimposed on this millennial-scale cycle of destruction and recovery is the effect of SL rise (Figure 7). On a shelf with a low uniform gradient, the effect of rising SL would be to cause a retreat of the breaking point equal to the amount of the SL rise divided by the gradient. But if breaking always occurs at the mid-shelf break, with a slope of about 0.25, then retreat of the breaking point could only account for <20 m of reef retrogradation rather than the 100 m observed at Punta Maroma. In this context, a gradual SL rise would progressively increase wave transmission over the mid-shelf break and reduce wave-energy dissipation rates shoreward of it, thus allowing bores from wave breaking to transport hurricane-generated detritus further shoreward. This gradual reduction in energy dissipation over time would therefore cause reef retrogradation (Figure 7).

FIGURE 7

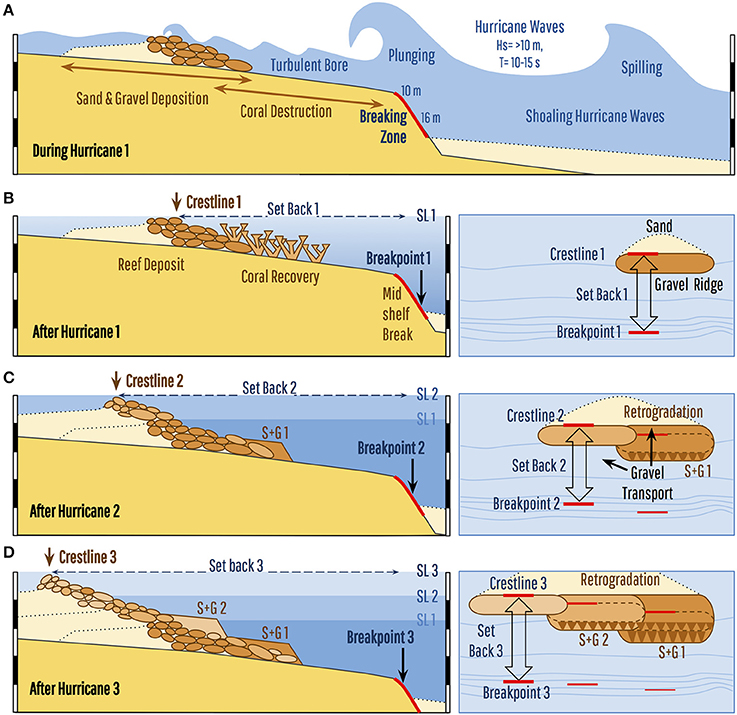
Figure 7. Fringing-reef development controlled by hurricane waves and sea-level rise. (A) The presence of a mid-shelf slope break trips large hurricane waves, causing them to plunge and break onto the rock terrace and produce a turbulent bore that fragments the standing crop of coral and transports the clasts upslope, eventually depositing them in a linear gravel ridge. (B) Given that all waves break from the same position, the gravel ridge is deposited at a near-uniform (set-back) distance from the mid-shelf break. After the hurricane, the linear gravel ridge is colonized by new corals as the reef recovers to its pre-storm state and develops spur-and groove (S+G 1). (C) As SL rises and water depth increases over the mid-shelf break, wave-energy dissipation during the next hurricane is reduced thereby extending the distance that clasts can be transported upslope, causing retrogradation of the reef-crest position (crestline). Lateral clast transport by oblique hurricane waves also leads to gradual extension of the reef alongshore and upslope. (D) The combination of cyclic destruction and recovery, coupled with rising sea level, allows hurricanes to produce a linear fringing reef that retrogrades over its back-reef through time. It also leads to the development of multiple spur and groove zones (S+G 1 and S+G 2).

The 315 m set-back distance of the modern crestline thus represents the distance that present hurricane waves can transport coral detritus upslope and, assuming constant wave heights, is controlled by water depth at the mid-shelf break. At lower SL this set-back distance was reduced and when coral clasts began accumulating ~5 ka ago the crestline was only ~200 m from the mid-shelf break (Figure 5). Assuming a constant SL rise over the last 5 ka therefore gives a retrogradation rate of 33 m per meter of SL rise or ~20 m/ka. Isochrons on the reconstruction in Figure 5 however show an accelerating rate of retrogradation which perhaps suggests that clasts production is proportional to reef-front area and thus increases over time.

In addition to retrogradation, the approach of storm waves with oblique vectors would create longshore currents and transport debris along the reef, resulting in the lateral extension of the gravel breakwater (Figure 7). Swell with a northeast vector is commonly generated by hurricanes that cross the Yucatan coast at high angles, due to the higher wind-speed and trapped-fetch effect in the right-forward (NE) quadrant (Wright et al., 2001). Furthermore, Punta Maroma is shielded to the southeast by the island of Cozumel, reducing the fetch of waves from that direction. Through time, therefore, recurring hurricanes and rising SL would not only cause retrogradation but also the extension of the reef southward along the coast (Figure 7). This may explain why the reef at Punta Maroma has a well-developed spur-and-groove zone in the north, but lacks it in the south: the northern section is older and has had more time to develop spur-and-grooves, whereas the southern section is younger due to a southward extension through time.

Our hurricane-control model is therefore consistent with all findings at Punta Maroma: the near-uniform reef-crest position results from hurricane waves breaking at the mid-shelf break, thereby producing a uniform distance limit to upslope clast transport; reef retrogradation results from the upslope translation of that transport limit caused by SL rise; and reduced reef development to the south is a result of southern clast transport and reef extension forced by hurricane waves from the northeast.

Hurricane-Control on Other Reefs?

The fringing-reef at Punta Maroma is typical of those along the hurricane-prone east coast of the Yucatan Peninsula, and so the hurricane-control model is likely applicable to other reefs in the tropical Western Atlantic. Coring studies in other hurricane-prone regions have reported thin A. palmata units underlain by sediment or back-reef corals (Adey and Burke, 1976; Shinn et al., 1982; Macintyre et al., 1985; Hubbard et al., 1997, 2005), or with A. palmata units composed of layers of hurricane generated detritus (Blanchon et al., 1997, 2002; Blanchon and Perry, 2004). But few have employed transects of closely-spaced cores to determine reef structure. A notable exception is a study at Looe Key, Florida, where Shinn et al. (1982) reported that closely-spaced A. palmata spurs formed a layer that had retrograded 200 m over a sandy back-reef in the last 6.5 ka—very similar to our findings from Punta Maroma. Conversely in Panama, which lies outside the main hurricane belt, a 12 core transect over a fringing reef at Galeta Point documented the aggrading/prograding development of an A. palmata reef over the last 7 ka. In this case, the absence of hurricanes allowed ‘normal’ vertical reef accretion.

With such limited data from core transects, application of the hurricane-control model to other Caribbean fringing reefs is uncertain. Nevertheless, we argue that the reef at Punta Maroma is representative of a large subset of reefs in this region for two reasons. First, its retrogressive architecture and clast-dominated composition are consistent with well-studied hurricane-prone reefs in Florida and Grand Cayman (Shinn et al., 1982; Blanchon et al., 1997). And second, its fixed configuration with the mid-shelf break provides a conspicuous indicator of hurricane control on reef development. In addition to Punta Maroma, this indicator has been identified on Grand Cayman, where the crestline is set-back 350 ± 50 m from a mid-shelf slope break (Blanchon et al., 1997). Furthermore, as shown in Figure 8, similar set-back distances can be tentatively identified in satellite imagery on many linear fringing reefs throughout the region.

FIGURE 8

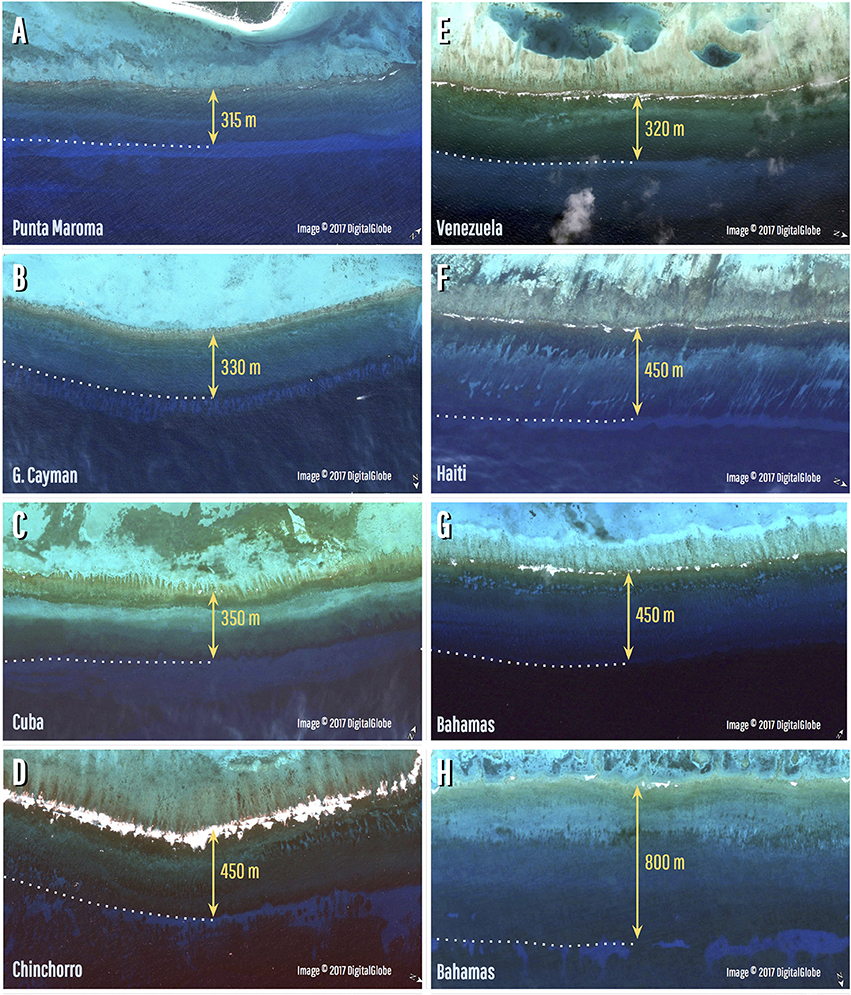
Figure 8. Caribbean Reefs where uniform crestline positions indicate hurricane-control on reef development. (A) Punta Maroma, NE Yucatan (20.724921–86.963876°): set-back distance 315 m. (B) Grand Cayman, north side (Lat. 19.380904° Long–81.313585°): set-back distance 330 m. (C) Cuba, south side Isla de la Juventud (21.470546–82.724107°): set-back distance 350 m. (D) Banco Chinchorro, northeast side (18.713563–87.244869°): set-back distance 450 m. (E) Los Roques archipelago, Venezuela (11.864242–66.562904°): set-back distance 320 m. (F) Haiti, southwest side (18.107978–73.574587°): set-back distance 450 m. (G) Mayaguana, Bahamas, south side (22.325027–73.021463°): set-back distance 450 m. (H) Mayaguana, Bahamas, north side (22.431774–72.996461°): set-back distance 800 m.

If further core transects over fringing reefs with similar configurations support our hurricane-control model, it will have implications for predicting the accretion response of reefs to scenarios of future SL rise. Hurricane control, for example, would mean that rather than being characterized by a census-based budget of coral growth and bioerosion over the shallow-reef zones (e.g., Perry et al., 2015), accretion would be determined by the total mean volumetric growth rate over the storm-wave impacted reef area, averaged over the long term, and allowing for regeneration time between storms. Moreover, accretion rates determined from drill cores on other fringing reefs have implicitly assumed a vertical accretion axis (e.g., Hubbard, 2012), and so underestimate accretion potential of reefs with a retrograde geometry and inclined axis (Blanchon and Blakeway, 2003). The volume of material required to produce reef retrogradation depends on the rate of retrogradation per unit SL rise and exceeds that required for simple vertical accretion. As a consequence the hurricane-control model would require a re-evaluation of the accretion potential of modern and Holocene Caribbean fringing reefs under projections of future SL rise.

Author Contributions

PB conceived the study and collected and analyzed the core data with MSI; JB and LC collected and analyzed the chronological data, SC and RM collected, and SR analyzed and rendered, the bathymetry data. PB and SR analyzed the data and wrote the manuscript. All authors contributed in editing the manuscript.

Funding

This study was funded by CONACyT Project 23749 to PB.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are grateful to support staff and students at UASA (ICML) and thank Amauri Mendoza-López, A. Guillermo Jordán Garza, and P. Karen Becerril Tinoco for field assistance, and Francisco G. Ruiz Rentería, and J. Edgar Escalante Mancera (Meteorological and Oceanographic Monitoring Service) for providing sonar data. We found materials on Researchgate published by Willem P. de Lange, including his oceanography spreadsheet and manual, a useful source of understanding and references on wave breaking. We thank the editor and referees for their comments.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2017.00078/full#supplementary-material

A YouTube presentation can be found online at: https://www.youtube.com/watch?v=Au_79Y3xsK0

References

Adey, W. H. (1978). Coral reef morphogenesis: a multidimensional model. Science 202, 831–837. doi: 10.1126/science.202.4370.831

PubMed Abstract | CrossRef Full Text | Google Scholar

Adey, W. H., and Burke, R. (1976). Holocene bioherms (algal ridges and bank-barrier reefs) of the eastern Caribbean. Geol. Soc. Am. Bull. 87, 95–109. doi: 10.1130/0016-7606(1976)87<95:HBARAB>2.0.CO;2

CrossRef Full Text | Google Scholar

Baldock, T. E., Holmes, P., Bunker, S., and Van Weert, P. (1998). Cross-shore hydrodynamics within an unsaturated surf zone. Coast. Eng. 34, 173–196. doi: 10.1016/S0378-3839(98)00017-9

CrossRef Full Text | Google Scholar

Battjes, J. A. (1974). “Surf similarity,” in Proceeding 14th Coastal Engineering Conference (New York, NY), 466–479.

Google Scholar

Blanchon, P., and Blakeway, D. (2003). Are catch-up reefs an artefact of coring? Sedimentology 50, 1271–1282. doi: 10.1111/j.1365-3091.2003.00603.x

CrossRef Full Text | Google Scholar

Blanchon, P., and Eisenhauer, A. (2000). Multi-stage reef development on Barbados during the Last Interglaciation. Quat. Sci. Rev. 20, 1093–1112. doi: 10.1016/S0277-3791(00)00173-6

CrossRef Full Text | Google Scholar

Blanchon, P., and Perry, C. T. (2004). Taphonomic differentiation of Acropora palmata facies in cores from Campeche Bank Reefs, Gulf of Mexico. Sedimentology 51, 53–76. doi: 10.1046/j.1365-3091.2003.00610.x

CrossRef Full Text | Google Scholar

Blanchon, P., Granados-Corea, M., Abbey, E., Braga, J. C., Braithwaite, C., Kennedy, D. M., et al. (2014). Postglacial Fringing-Reef to Barrier-Reef conversion on Tahiti links Darwin's reef types. Sci. Rep. 4:4997. doi: 10.1038/srep04997

PubMed Abstract | CrossRef Full Text | Google Scholar

Blanchon, P., Jones, B., and Ford, D. C. (2002). Discovery of a submerged relic reef and shoreline off Grand Cayman: further support for an early Holocene jump in sea level. Sediment. Geol. 147, 253–270. doi: 10.1016/S0037-0738(01)00143-9

CrossRef Full Text | Google Scholar

Blanchon, P., Jones, B., and Kalbfleisch, W. (1997). Anatomy of a fringing reef around Grand Cayman; storm rubble, not coral framework. J. Sediment. Res. 67, 1–16.

Google Scholar

Blenkinsopp, C. E., and Chaplin, J. R. (2008). The effect of relative crest submergence on wave breaking over submerged slopes. Coast. Eng. 55, 967–974. doi: 10.1016/j.coastaleng.2008.03.004

CrossRef Full Text | Google Scholar

Braithwaite, C. J. R., Montaggioni, L. F., Camoin, G. F., Dalmasso, H., Dullo, W. C., and Mangini, A. (2000). Origins and development of Holocene coral reefs: a revisited model based on reef boreholes in the Seychelles, Indian Ocean. Int. J. Earth Sci. 89, 431–445. doi: 10.1007/s005310000078

CrossRef Full Text | Google Scholar

Brandon, C. M., Woodruff, J. D., Lane, D., and Donnelly, J. P. (2013). Tropical cyclone wind speed constraints from resultant storm surge deposition: a 2500 year reconstruction of hurricane activity from St. Marks, F. L. Geochem. Geophys. Geosyst. 14, 2993–3008. doi: 10.1002/ggge.20217

CrossRef Full Text | Google Scholar

Cabioch, G., Camoin, G. F., and Montaggioni, L. F. (1999). Postglacial growth history of a French Polynesian barrier reef tract, Tahiti, central Pacific. Sedimentology 46, 985–1000. doi: 10.1046/j.1365-3091.1999.00254.x

CrossRef Full Text | Google Scholar

Cerdeira-Estrada, S., Heege, T., Kolb, M., Ohlendorf, S., Uribe, A., Müller, A., et al. (2012). “Benthic habitat and bathymetry mapping of shallow waters in Puerto Morelos reefs using remote sensing with a physics based data processing,” in 2012 IEEE International Geoscience and Remote Sensing Symposium (Munich), 4383–4386. doi: 10.1109/IGARSS.2012.6350402

CrossRef Full Text | Google Scholar

Cheng, H., Edwards, R. L., Shen, C. C., Polyak, V. J., Asmerom, Y., Woodhead, J., et al. (2013). Improvements in 230Th dating, 230Th and 234U half-life values, and U–Th isotopic measurements by multi-collector inductively coupled plasma mass spectrometry. Earth Planet. Sci. Lett. 371, 82–91. doi: 10.1016/j.epsl.2013.04.006

CrossRef Full Text | Google Scholar

Daly, R. A. (1915). The glacial-control theory of coral reefs. Proc. Am. Acad. Arts Sci. 51, 157–251. doi: 10.2307/20025572

CrossRef Full Text | Google Scholar

Darwin, C. R. (1842). The Structure and Distribution of Coral Reefs. Being the First Part of the Geology of the Voyage of the Beagle, Under the Command of Capt. Fitzroy, RN, During the Years 1832 to 1836. (Smith Elder, London).

Dollar, S. J., and Tribble, G. W. (1993). Recurrent storm disturbance and recovery: a long-term study of coral communities in Hawaii. Coral Reefs 12, 223–233. doi: 10.1007/BF00334481

CrossRef Full Text | Google Scholar

EOMAP, C. (2014). Satellite Derived Bathymetry White Paper. Available online at: http://www.eomap.com/exchange/pdf/EOMAP_Bathy_20140410.pdf

Galvin, C. J. (1968). Breaker type classification on three laboratory beaches. J. Geophys. Res. 73, 3651–3659. doi: 10.1029/JB073i012p03651

CrossRef Full Text | Google Scholar

Gaughan, M. K., and Komar, P. D. (1975). The theory of wave propagation in water of gradually varying depth and the prediction of breaker type and height. J. Geophys. Res. 80, 2991–2996. doi: 10.1029/JC080i021p02991

CrossRef Full Text | Google Scholar

Gourlay, M. R. (1992). Wave set-up, wave run-up and beach water table: interaction between surf zone hydraulics and groundwater hydraulics. Coast. Eng. 17, 93–144. doi: 10.1016/0378-3839(92)90015-M

CrossRef Full Text | Google Scholar

Hanson, H., and Kraus, N. C. (1989). Genesis: Generalized Model for Simulating Shoreline Change, Report 1, Technical reference. US Army Engineer Waterways Experiment Station, Coastal Engineering Research Center, Vicksburg, MS Technical Report CERC-89–C-19.

Google Scholar

Hernández-Mendiola, E., Bernal, J. P., Lounejeva, E., Mortimer, G. E., and McCulloch, M. T. (2011). U-series dating of carbonates using inductively coupled plasma-quadrupole mass spectrometry. Quat. Geochronol. 6, 564–573. doi: 10.1016/j.quageo.2011.09.001

CrossRef Full Text | Google Scholar

Hubbard, D. K. (2012). Depth-Related and Species-Related Patterns of Holocene Reef Accretion in the Caribbean and Western Atlantic: A Critical Assessment of Existing Models. Perspectives in Carbonate Geology: A Tribute to the Career of Robert Nathan Ginsburg (Salt Lake City, UT: Special Publication 41 of the IAS), 98, 1–18.

Google Scholar

Hubbard, D. K., Gill, I. P., Burke, R. B., and Morelock, J. (1997). “Holocene reef backstepping, southwestern Puerto Rico shelf,” in Proceedings of the Eighth International Coral Reef Symposium 2, 1779–1784.

Hubbard, D. K., Zankl, H., Van Heerden, I., and Gill, I. P. (2005). Holocene reef development along the northeastern St. Croix shelf, Buck Island, US Virgin Islands. J. Sedim. Res. 75, 97–113. doi: 10.2110/jsr.2005.009

CrossRef Full Text | Google Scholar

Jaffey, A. H., Flynn, K. F., Glendenin, L. E., Bentley, W. C., and Essling, A. M. (1971). Precision measurement of half-lives and specific activities of 235U and 238U. Phys. Rev. 4, 1889–1906. doi: 10.1103/PhysRevC.4.1889

CrossRef Full Text | Google Scholar

Janssen, T. T., and Battjes, J. A. (2007). A note on wave energy dissipation over steep beaches. Coast. Eng. 54, 711–716. doi: 10.1016/j.coastaleng.2007.05.006

CrossRef Full Text | Google Scholar

Khan, N. S., Ashe, E., Horton, B. P., Dutton, A., Kopp, R. E., Brocard, G., et al. (2017). Drivers of Holocene sea-level change in the Caribbean. Quat. Sci. Rev. 155, 13–36. doi: 10.1016/j.quascirev.2016.08.032

CrossRef Full Text | Google Scholar

Komar, P. D., and Gaughan, M. K. (1972). “Airy wave theory and breaker height prediction,” in Proceedings of 13th Coastal Engineering Conference (Vancouver, BC: American Society of Civil Engineers), 419–432.

Google Scholar

Larson, M., and Kraus, N. C. (1989). SBEACH: Numerical Model for Simulating Storm-Induced Beach Change, Report 1, Empirical foundation and model development. US Army Engineer Waterways Experiment Station, Coastal Engineering Research Center, Technical Report CERC-89-9.

Le Méhauté, B., and Koh, R. C. Y. (1967). On the breaking of waves arriving at an angle to the shore. J. Hydr. Res. 5, 67–88. doi: 10.1080/00221686709500189

CrossRef Full Text | Google Scholar

Lighty, R. G., Macintyre, I. G., and Stuckenrath, R. (1982). Acropora palmata reef framework: a reliable indicator of sea level in the western Atlantic for the past 10,000 years. Coral Reefs 1, 125–130. doi: 10.1007/BF00301694

CrossRef Full Text | Google Scholar

Liu, K. B., and Fearn, M. L. (1993). Lake-sediment record of late Holocene hurricane activities from coastal Alabama. Geology 21, 793–796. doi: 10.1130/0091-7613(1993)021<0793:LSROLH>2.3.CO;2

CrossRef Full Text | Google Scholar

Liu, K. B., and Fearn, M. L. (2000). Reconstruction of prehistoric landfall frequencies of catastrophic hurricanes in northwestern Florida from lake sediment records. Quat. Res. 54, 238–245. doi: 10.1006/qres.2000.2166

CrossRef Full Text | Google Scholar

Ludwig, K. R. (2012). Users Manual for Isoplot/Ex. Ver 3.75. Berkeley, CA: Berkeley Geochronology Center Special publication No. 1a.

Lugo, A. E., Rogers, C. S., and Nixon, S. W. (2000). Hurricanes, coral reefs and rainforests: resistance, ruin and recovery in the Caribbean. Ambio 29, 106–114. doi: 10.1579/0044-7447-29.2.106

CrossRef Full Text | Google Scholar

Macintyre, I. G., Glynn, P. W., and Steneck, R. S. (2001). A classic Caribbean algal ridge, Holandes Cays, Panama: an algal coated storm deposit. Coral Reefs 20, 95–105. doi: 10.1007/s003380000135

CrossRef Full Text | Google Scholar

Macintyre, I. G., Multer, H. G., Zankl, H. L., Hubbard, D. K., Weiss, M. P., and Stuckenrath, R. (1985). “Growth and depositional facies of a windward reef complex,” in Proceedings 5th Integrated Coral Reef Symposium (Antigua, WI), 605–610.

Madin, J. S., and Connolly, S. R. (2006). Ecological consequences of major hydrodynamic disturbances on coral reefs. Nature 444, 477–480. doi: 10.1038/nature05328

PubMed Abstract | CrossRef Full Text | Google Scholar

Madsen, O. S. (1976). “Wave climate of the continental margin: elements of its mathematical description,” in Marine Sediment Transport and Environmental Management, eds D. J. Stanley and D. J. P. Swift (New York, NY: Wiley and Sons), 65–87.

Google Scholar

McCowan, J. (1894). On the highest wave of permanent type. Philos. Mag. 5, 351–357. doi: 10.1080/14786449408620643

CrossRef Full Text | Google Scholar

Meyer, D., Bries, J., Greenstein, B., and Debrot, A. (2003). Preservation of in situ reef framework in regions of low hurricane frequency: pleistocene of Curaçao and Bonaire, southern Caribbean. Lethaia 36, 273–285. doi: 10.1080/00241160310004675

CrossRef Full Text | Google Scholar

Munk, W. H. (1949). The solitary wave theory and its application to surf problems. Ann. N. Y. Acad. Sci. 51, 376–424. doi: 10.1111/j.1749-6632.1949.tb27281.x

CrossRef Full Text | Google Scholar

Neumann, A. C., and Macintyre, I. (1985). “Reef response to sea level rise: keep–up, catch–up or give–up,” in Proceedings of the 5th International Coral Reef Congress International Society for Reef Studies, Antenne Museum-Ephe, Moorea, French Polynesia (Tahiti), 105–110.

Google Scholar

Ohlendorf, S., Müller, A., Heege, T., Cerdeira-Estrada, S., and Kobryn, H. T. (2011). Bathymetry mapping and sea floor classification using multispectral satellite data and standardized physics-based data processing. Int. Soc. Opt. Phot. 2011:817503. doi: 10.1117/12.898652

CrossRef Full Text | Google Scholar

Palmer, S. E., Perry, C. T., Smithers, S. G., and Gulliver, P. (2010). Internal structure and accretionary history of a nearshore, turbid-zone coral reef: Paluma Shoals, central Great Barrier Reef, Australia. Mar. Geol. 276, 14–29. doi: 10.1016/j.margeo.2010.07.002

CrossRef Full Text | Google Scholar

Pearson, R. G. (1981). Recovery and recolonization of coral reefs. Mar. Ecol. Prog. Ser. 4, 105–122. doi: 10.3354/meps004105

CrossRef Full Text | Google Scholar

Perry, C. (2001). Storm-induced coral rubble deposition: pleistocene records of natural reef disturbance and community response. Coral Reefs 20, 171–183. doi: 10.1007/s003380100158

CrossRef Full Text | Google Scholar

Perry, C. T., Murphy, G. N., Graham, N. A., Wilson, S. K., Januchowski-Hartley, F. A., and East, H. K. (2015). Remote coral reefs can sustain high growth potential and may match future sea-level trends. Sci. Rep. 5:18289. doi: 10.1038/srep18289

PubMed Abstract | CrossRef Full Text | Google Scholar

Purdy, E. G. (1974). “Reef configurations: cause and effect,” in Reefs in Time and Space, eds L. F. Laporle (Tulsa, OK: The Society of Economic Paleontologists and Mineralogists (SEPM)), 9–76.

Google Scholar

Ryan, E. J., Smithers, S. G., Lewis, S. E., Clark, T. R., and Zhao, J. X. (2016). The influence of sea level and cyclones on Holocene reef flat development: middle Island, central Great Barrier Reef. Coral Reefs 35, 805–818. doi: 10.1007/s00338-016-1453-9

CrossRef Full Text | Google Scholar

Shinn, E. A., Hudson, J. H., Robbin, D. M., and Lidz, B. (1982). “Spurs and grooves revisited: construction versus erosion,” in Proceeding of the 4th Integrated Coral Reef Symposium (Florida, FL), 475–483.

Google Scholar

Singamsetti, S. R., and Wind, H. G. (1980). Breaking Waves; Characteristics of Shoaling and breaking Periodic Waves Normally Incident to Plane Beaches of Constant Slope. Delft Hydraulics Laboratory, Delft, The Netherlands, Report M1371, 80.

Google Scholar

Smith, E., and Kraus, N. (1990). Laboratory Study on Macro-Features of Wave Breaking Over Bars and Artificial Reefs. Technical Report. CERC-90-12, U.S. Army Corps of Eng., Waterways Exp. Stn., Vicksburg, VA.

Google Scholar

Stoddart, D. R. (1974). “Post-hurricane changes on the British Honduras reefs: re-survey of 1972,” in Proceedings of the Second International Coral Reef Symposium (Brisbane, QLD), 473–483.

Google Scholar

Sunamura, T. (1982). “Laboratory study of on-offshore sediment transport rate in shallow water region,” in Proceedings of 29th Japanese Conference on Coastal Engineering, Japanese Society of Civil Engineers (Tokyo), 239–243.

Google Scholar

Teague, W. J., Jarosz, E., Wang, D. W., and Mitchell, D. A. (2007). Observed oceanic response over the upper continental slope and outer shelf during Hurricane Ivan. J. Phys. Oceanogr. 37, 2181–2206. doi: 10.1175/JPO3115.1

CrossRef Full Text | Google Scholar

Wallace, D. J., and Anderson, J. B. (2010). Evidence of similar probability of intense hurricane strikes for the Gulf of Mexico over the late Holocene. Geology 38, 511–514. doi: 10.1130/G30729.1

CrossRef Full Text | Google Scholar

Weggel, J. R. (1972). “Maximum breaker height for design,” in Proceedings of 13th Coastal Engineering Conference (Vancouver, BC: American Society of Civil Engineers), 419–432.

Google Scholar

Woodley, J. D. (1992). The incidence of hurricanes on the north coast of Jamaica since 1870: are the classic reef descriptions atypical? Hydrobiologia 247, 133–138.

Google Scholar

Woodruff, J. D., Donnelly, J. P., Mohrig, D., and Geyer, W. R. (2008). Reconstructing relative flooding intensities responsible for hurricane-induced deposits from Laguna Playa Grande, Vieques, Puerto Rico. Geology 36, 391–394. doi: 10.1130/G24731A.1

CrossRef Full Text | Google Scholar

Wright, C. W., Walsh, E. J., Vandemark, D., Krabill, W. B., Garcia, A. W., Houston, S. H., et al. (2001). Hurricane directional wave spectrum spatial variation in the open ocean. J. Phys. Oceanogr. 31, 2472–2488. doi: 10.1175/1520-0485(2001)031<2472:HDWSSV>2.0.CO;2

CrossRef Full Text | Google Scholar