Stress Field Control during Large Caldera-Forming Eruptions

Crustal stress field can have a significant influence on the way magma is channeled through the crust and erupted explosively at the surface. Large Caldera Forming Eruptions (LCFEs) can erupt hundreds to thousands of cubic kilometers of magma in a relatively short time along fissures under the control of a far-field extensional stress. The associated eruption intensities are estimated in the range 10⁹–10¹¹ kg/s. We analyse syn-eruptive dynamics of LCFEs, by simulating numerically explosive flow of magma through a shallow dyke conduit connected to a shallow magma (3–5 km deep) chamber that in turn is fed by a deeper magma reservoir (>~10 km deep), both under the action of an extensional far-field stress. Results indicate that huge amounts of high viscosity silicic magma (>10⁷ Pa s) can be erupted over timescales of a few to several hours. Our study provides answers to outstanding questions relating to the intensity and duration of catastrophic volcanic eruptions in the past. In addition, it presents far-reaching implications for the understanding of dynamics and intensity of large-magnitude volcanic eruptions on Earth and to highlight the necessity of a future research to advance our knowledge of these rare catastrophic events.

Introduction

There is compelling evidence that Large Caldera-Forming Eruptions (LCFEs) are characterized by extremely large intensities. Estimations of Mass Eruption Rates (MERs) obtained with different independent methods (Wilson and Walker, 1981; Hildreth and Mahood, 1986; Wilson and Hildreth, 1997; Baines and Sparks, 2005; Costa et al., 2014; Martí et al., 2016; Roche et al., 2016) indicate MERs of the orders 10⁹–10¹¹ kg/s (e.g., Bishop Tuff, Campanian Ignimbrite, Oruanui eruption, Taupo eruption, Peach Spring Tuff, Young Toba Tuff), implying durations of few to several hours only to evacuate even thousands of km³ of magma.

Most LCFEs occur in both subduction zone and extensional environments characterized by relatively low rates of magma production (see Jellinek and De Paolo, 2003 and references therein) implying that the thousand km³ volume magma chambers feeding those events have to accumulate over long periods (>10⁵ years; Jellinek and De Paolo, 2003).

In order to erupt, magmas stored in relatively shallow chambers (3–8 km; e.g., Smith et al., 2005, 2006; Matthews et al., 2011; Chesner, 2012) normally have to overcome critical overpressures up to ~50 MPa for nucleating new fractures and up to ~10 MPa for propagating magma up to the surface (Rubin, 1995; Jellinek and De Paolo, 2003). Whereas for small magma chambers such overpressures can be easily achieved, for very large chamber volumes it is more problematic to reach such overpressures, and dyke formation and propagation are, as a consequence, inhibited (Jellinek and De Paolo, 2003). In some cases there is clear evidence of new injection of magma (and associated oversaturation of volatiles) as main cause to achieve the required overpressure to open the magma chamber (e.g., Sparks et al., 1977; Pallister et al., 1992; Self, 1992; Folch and Martí, 1998). However, in most large calderas this is not so clear. In contrast, tectonic triggers (i.e., decrease of ambient pressure due to tectonic—earthquake—activity) would be a plausible mechanism (see Aguirre-Díaz and Labarthe-Hernañdez, 2003; Martí et al., 2009), despite they have not been sufficiently explored yet. In the case of tectonic triggers, the magma chamber would evacuate the magma through the pre-existing faults or newly formed fractures without needing any over-pressurization of the magma chamber (Martí et al., 2009).

Irrespectively of the mechanism that leads to the rupture of the magma chamber during caldera eruptions, syn-eruptive dynamics of magma ascent in high intensity eruptions are not clear and there have not been many attempts to quantitatively describe them (Costa et al., 2011). Dykes feeding these eruptions have to be long enough and remain open over much of their length throughout the entire explosive activity. The mechanics of feeding explosive silicic ignimbrite eruptions through a linear fissure (Korringa, 1973; Aguirre-Díaz and Labarthe-Hernañdez, 2003) or from multiple vents along a fissure (Suzuki-Kamata et al., 1993; Wilson, 2001; Smith et al., 2005, 2006; Folch and Martí, 2009) are largely unexplored.

Magma emplacement through dykes and the capability of magma to reach the surface strongly depend on the local stresses across the different layers that constitute the volcano (Gudmundsson, 2006). As explained for instance by Gudmundsson (2006), a dyke propagated upward from a magma chamber can reach the surface only if the stress field along all its path is favorable to magma-fracture propagation. This implies that the stress field has to promote extension-fracture formation as well as keep the stress field homogenized along the entire path of the dyke to the surface.

Moreover, once that a critical magma chamber pressure is reached (e.g., by intrusion of new magma or by evolution of volatiles or both or by external triggering because a fracture can reach the chamber roof) and a dyke can propagate in the surrounding rocks, in order to produce an explosive eruption, magma has to fragment. Because of the typical silicic compositions (e.g., Chesner, 1998, 2012; Matthews et al., 2012) and high crystal contents (e.g., Gottsmann et al., 2009; Costa et al., 2011) effective viscosity of those magmas is very high (>10⁷ Pa s; e.g., Costa et al., 2011). Since the fragmentation depth is controlled by effective magma viscosity, in order to be able to keep dykes open at deep fragmentation levels it is necessary that local magma overpressure counterbalances the lithostatic load at that depth (Costa et al., 2009, 2011). Hence extremely larger overpressures should be attained.

Concerning this point, Costa et al. (2011) showed that coupling of magma overpressure with the effects of a far-field extensional stress can play a pivotal role. As we mentioned above, most LCFEs have been recorded in extensional environments (e.g., Jellinek and De Paolo, 2003; Sobradelo et al., 2010), but even where LCFEs occur in convergent regions they appear to be associated with local extension (Miller et al., 2008; Acocella and Funiciello, 2010).

Besides tectonic stress, local extension can be produced by the growth of magma chambers and reservoirs exceeding several hundreds of cubic kilometers in volume due to a “magmatic” stress field on local and regional scales. Either counteracts or adds to dominant tectonic stresses depending on the sign and intensity of the far-field stress and on the magma chamber shape and orientation (Gudmundsson, 1988, 1998; Gudmundsson et al., 1997).

In this contribution, we start briefly reviewing the general tectonic settings of LCFEs and other evidence of stress field control during LCFE. Then we summarize the model of Costa et al. (2011) for LCFEs adapted in order to account for the effects of a pressurized magma reservoir (Figure 1). Finally, we apply the Costa et al. (2011) model to show how, for magma chamber and reservoir depths and magma properties typical of a LCFE similar to the Young Toba Tuff (YTT), the local stress field, due to the combined effects of relatively low pressurizations of magma chamber and reservoir, and far-field stress, can promote large MERs.

FIGURE 1

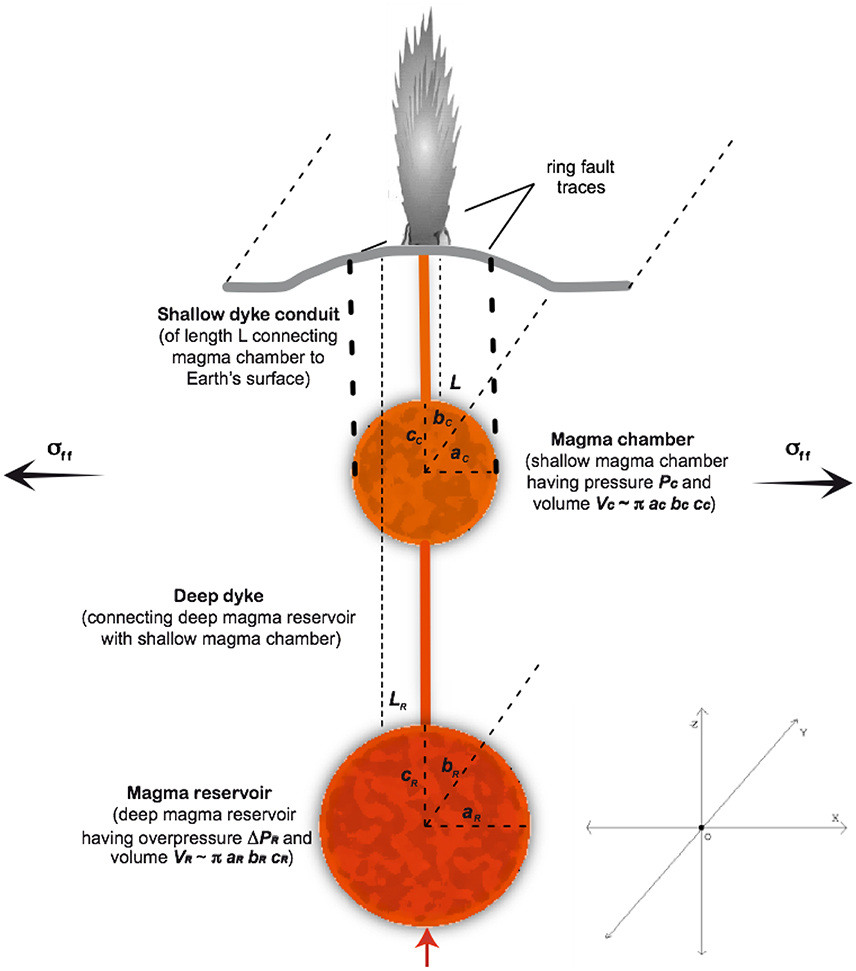
Figure 1. Schematic view of the investigated system. The magma chamber having a roof placed at a depth L, is assumed to be an ellipsoid with semi-axes a_C, b_C, and c_C with b_C ≫ a_C, c_C (Costa et al., 2011). The magma reservoir having a roof placed at a depth L_R, is also assumed to be an ellipsoid with semi-axes a_R, b_R, and c_R with b_R ≫ a_R, c_R. The cross-section of the shallow dyke conduit is assumed to be elliptical with a finite length 2a_d (along the y-direction) and width 2b_d (along the x-direction).

Tectonic Settings of LCFEs and Eruption Conditions

Collapse calderas are volcanic subsidence structures that can be recognized in many volcanic systems and may form in any geodynamic environment (Gudmundsson, 1988). However, the largest caldera eruptions, those that erupt hundreds to thousands of cubic kilometers of magma, are invariably associated with silicic magmas and extensional structures occurring mostly in subduction zones, continental rifts or extensional environments of Basin and Range type, always related to a thick continental crust (Geyer and Martí, 2008; Cole et al., 2010; Reyners, 2010; Rowland et al., 2010). This fact suggests that this type of extensional stress is a requisite (or a favorable factor) for the formation of large magma chambers responsible for calderas (see also e.g., Gudmundsson, 1998, 2006; Hughes and Mahood, 2008).

It is generally accepted that there is a positive linear relationship between the area of the caldera and the volume of material extruded during the eruption (Smith, 1979; Spera and Crisp, 1981; Geyer and Martí, 2008). So, large calderas are related to the eruption of large volumes of magma. The tendency of large collapse calderas to form in areas with extensional tectonics and in relatively thick (≥30 km) continental crusts suggests that these conditions are the most favorable to accumulate large volumes of silicic magmas at shallow depths (Sobradelo et al., 2010). Another feature that characterizes large collapse calderas is their association with shallow (3–5 km deep) magma chambers, thus suggesting that mechanical conditions to form such calderas are only achieved under stress configurations related to small aspect ratios, i.e., depth vs. extent of the chamber (Martí et al., 2009; Geyer and Martí, 2014).

The mechanisms by which a magma chamber opens to the surface and then evolves into a caldera-forming event are still not fully understood. In any case, there is general consensus that collapse calderas require very specific stress conditions to form, which will be defined by the stress field, size, shape, and depth of the magma chamber, magma rheology and gas content, and state of deformation (e.g., presence of local and regional faults) of the host rock (see Acocella, 2007; Martí et al., 2009; Acocella et al., 2015). Under these circumstances, the rupture of a magma chamber may be an intrinsic cause by an increase of magma pressure due to injection of new magma into the chamber and/or oversaturation of volatiles due to crystallization, or may be favored by outside by reducing stresses through a tectonic event (e.g., earthquake). The mechanisms by which the eruption will progress and caldera will collapse may be different depending on each scenario (see Martí et al., 2009), but it is not the aim of this study to discuss in detail such differences. On the contrary, we will concentrate on common aspects related to magma flow through fractures and on the conditions needed for having large MERs characteristics of LCFEs, regardless on how these fractures have opened.

According to the stratigraphic features shown by caldera forming deposits we can differentiate two main caldera types or end members. One comprises the caldera forming episode preceded by a Plinian eruption that may erupt a considerable volume of magma. This type of calderas, named underpressure calderas by Martí et al. (2009), are characterized in the field by the presence of relatively thick Plinian deposits underlying the caldera-forming ignimbrites, and would correspond to those calderas in which the initiation of caldera collapse requires a substantial decompression of the magma chamber (Druitt and Sparks, 1984). Examples of such calderas are Crater Lake (e.g., Bacon, 1983), Katmai (e.g., Hildreth, 1991), Santorini (e.g., Druitt and Francaviglia, 1992). The other end-member corresponds to those calderas in which caldera collapse starts at the beginning of the eruption, without any Plinian phase preceding it. The succession of deposits that characterize these calderas, called overpressure calderas by Martí et al. (2009), is composed only of the caldera forming ignimbrites, with occasional some minor pyroclastic surge deposits at the base of the caldera-forming succession. In this case, it is interpreted that these calderas start forming since the beginning of the eruption without needing (significant) decompression of the magma chamber (Gudmundsson et al., 1997; Martí et al., 2009). Examples of this type of caldera are La Pacana (e.g., Gardeweg and Ramirez, 1987), Cerro Galán (Folkes et al., 2011), Aguas Calientes (Petrinovic et al., 2010); El Abrigo (Pittari et al., 2008), Bolaños graben caldera (Aguirre-Díaz et al., 2008).

Basic Model of Magma Ascent During LCFEs

Previous numerical models of LCFE were used to study syn-eruptive dynamics of magma ascent of these eruptions. In particular, Folch and Martí (2009) presented simulations of LCFE based on Macedonio et al. (2005) conduit model, considering an initial eruption phase from a central-vent conduit, a transition to peripheral fissure-vent conduits, and a final phase controlled by piston-like subsidence. In line with their results, during the eruption phase from peripheral ring fissures, MERs would increase by almost an order of magnitude. During the piston-like subsidence, pressure increases back to lithostatic and the MER tends to stabilize near these larger values and does not change significantly after the subsidence starts. Because of the limitations of the model and the assumed rigid conduit geometry, the simulations by Folch and Martí (2009) were limited to relatively small MERs, < 10⁹ kg/s. Such low MERs would imply long eruption durations, in the range of few tens to hundreds hours, or longer, even for erupting relatively small volumes of magma.

Contrarily to the simplifying assumptions of most volcanic conduit models, rock mechanics imply the most efficient way of moving magma through cold lithosphere is via dykes (Rubin, 1995), and this is supported from field evidence (e.g., Gudmundsson, 2002) and geophysical analysis (e.g., Hautmann et al., 2009; Sigmundsson et al., 2010). Because the complexity in describing coupled magma-rock dynamics, explosive volcanic eruptions have been commonly modeled in terms of multiphase flows through rigid conduits of a fixed cross-section. Costa et al. (2009) and Costa et al. (2011) generalized Macedonio et al. (2005) model considering magma flow from an elastic dyke with elliptical cross-section emanating from magma chamber reaching the surface as a linear dyke or as dyke evolving to a cylinder at shallower depths. Costa et al. (2011) showed that MERs of the order of 10⁹–10¹¹ kg/s can be obtained for realistic input parameters if the effect of an extensional stress field on the dynamics of magma ascent is accounted for.

Here we summarize the model proposed by Costa et al. (2011) that is based on the following mass and momentum equations:

$\begin{array}{cc}\frac{\partial }{\partial z}\left(\rho AU\right)=0& \left(1\right)\end{array}$

and

$\begin{array}{cc}U\frac{\partial U}{\partial z}=-\frac{1}{\rho }\frac{\partial P}{\partial z}-g-f_{ft}& \left(2\right)\end{array}$

where z denotes the vertical coordinate along the dyke axis, A = πa_db_d, is the cross-section area of an elliptical dyke having semi-axes a_d and b_d, U is the vertical mixture velocity, g is the gravity acceleration, and f_ft is the friction term calculated for an elliptical cross-section (Costa et al., 2009). The model assumes steady-state conditions. This is justified because eruption durations and time-scales of pressure variations at base of the conduit are of the order of hours, much longer than magma travel times in the conduit that are of the order of minutes (e.g., Wilson et al., 1980; Folch et al., 1998).

The model considers that fragmentation occurs when the gas volume fraction, α, reaches a critical value of 0.75 (Sparks, 1978). Despite this simplification, the results are in line with other fragmentation criteria proposed by e.g., Melnik (1999), or Papale (1999).

The dyke semi-axes a_d and b_d depend on the difference between magmatic pressure and normal stress in host rocks ΔP in accord to the following relationships (e.g., Muskhelishvili, 1963; Sneddon and Lowengrub, 1969; Costa et al., 2009):

$\begin{array}{cc}{a}_d(z)=a_{d0}\left(z\right)+\frac{\Delta P}{2G}\left[2\left(1-\upsilon \right)b_{d0}\left(z\right)-(1-2\upsilon )a_{d0}\left(z\right)\right]& \left(3\text{a}\right)\end{array}$

$\begin{array}{cc}{b}_d(z)=b_{d0}\left(z\right)+\frac{\Delta P}{\text{2}G}\left[2\left(1-\upsilon \right)a_{d0}\left(z\right)-(1-2\upsilon )b_{d0}\left(z\right)\right]& \left(3\text{b}\right)\end{array}$

$\begin{array}{cc}\Delta P=P-({\rho }_{r}gz-{\sigma }_t)& \left(4\right)\end{array}$

where, G is the rigidity of wallrock, ν is Poisson's ratio, a_d0 and b_d0 are the unpressurized values of the semi-axes, σ_t is the tensile stress along the axis of the dyke conduit due to the presence of magma chamber under the effect of an extensional far-field stress σ_ff acting on the plane y–z (see Figure 1).

As in Costa et al. (2011), as first-order approximation, the tensile stress along the dyke conduit due the effects of magma chamber and reservoir under the effect of an extensional far-field stress is calculated using the general analytical solutions by Gao (1996) obtained in the limit of a plane 2D geometry. Such a first-order approximation can capture general large-scale features (Costa et al., 2011). We would like to remark that, in this way, we account for the effects of magma chamber and reservoir on the tensile stress during magma transport in the shallow dyke conduit but we do not investigate their internal dynamics (out of the scope of this study). Magma chamber pressure is used as boundary condition at the base of the shallow dyke conduit and assumed chamber volumes to estimate durations once we calculated MERs.

The main limitations of the magma transport model presented above and the solving methodology are discussed in Costa et al. (2009) and Costa et al. (2011).

Control of Local Stress Field on Eruption Dynamics and Intensities

In the framework of the model described in Section Basic Model of Magma Ascent during LCFE, we consider a relatively shallow magma chamber connected to the surface through a shallow dyke conduit. Internal pressures of the shallow chamber range from over- to under-pressure conditions. In terms of stress distribution we also consider the effect of a deeper reservoir that can be in neutral conditions or over-pressurized with respect to the lithostatic loading (Figure 1, terminology as in Gudmundsson, 2012). Irrespectively of the process that formed the fracture (magma chamber overpressure or tectonic events), we assume that dyke is already opened and we study syn-eruptive magma transport.

In the approximation of elastic deformation, valid because the short time scales (from few to several hours) characterizing LCFEs, the dyke will tend to open or close as function of the local magmatic pressure with respect the local loading. Besides the lithostatic loading we need to account for the contribution σ_t to the tensile stress along the axis of the shallow dyke conduit, due to the presence of a more or less pressurized magma chamber and reservoir under the effect of an extensional far-field stress. The contribution of an extensional stress on keeping open the base of the dyke was discussed by Costa et al. (2011) who, however, have not considered the effect due to the presence of a deep pressurized reservoir. They described a critical extensional stress that produces a tensile stress at the base of the dyke able to counterbalance the lithostatic loading. Nevertheless, because fragmentation levels during LCFEs are very deep due to the typical large magma viscosities (Costa et al., 2011), the critical extensional stress was very high (σ_ff ≈ 50–60 MPa) and close to rifting regime (Turcotte and Schubert, 2002).

Here, our results show that even the contribution of a deep magma reservoir with an over-pressure of about 10 MPa is able to halve critical extensional stresses allowing the dyke to remain open until the magma pressure goes back to sub-neutral conditions. Once formed, a long dyke can remain open even for magma chamber pressures from ~10 MPa above the lithostatic loading (considered a typical value to propagate a dyke; e.g., Gudmundsson, 2006, 2012) to ~10 MPa below the lithostatic loading. Once the pressure at the base of the dyke decreases below a critical value, the eruption stops and the system has to recover again large magmatic pressure before it can erupt, i.e. the dyke can act as a valve.

Although, Jellinek and De Paolo (2003) show the difficulty to overpressurize a large magma chamber with typical magma rate production in subduction zone and extensional environments, overpressures of ~10 MPa could be easily achieved because of magma crystallization (and as we discussed above, magma associated to LCFEs are typically characterized by high crystallinity; Costa et al., 2011). Such overpressures can be sufficient to trigger an eruption, as the roof of the shallow magma chamber can undergo to intensive heating that can significantly weaken the strength of the overlying rocks (Gregg et al., 2012, 2015). Another end-member for triggering the eruption could be when a fracture opens from surface or all through the host rock above the magma chamber if there is a pre-existing fault.

Concerning deep magma reservoirs, overpressures of ~10 MPa may be generated by the contribution of CO₂ exsolution (e.g., Folch and Martí, 1998; Gudmundsson, 2015).

However, we would like to remark that here we focus on the syn-eruptive dynamics of magma ascent inside the shallow dyke conduit during LCFEs and not on magma chamber dynamics and mechanics able to trigger such eruptions that are likely related to magma chamber roof failure and have been explored by other authors (e.g., Burov and Guillou-Frottier, 1999; Folch and Martí, 2004; Gray and Monaghan, 2004; Gregg et al., 2012, 2015; Geyer and Martí, 2014). For the purposes of this study, aimed at describing the first-order features only, chamber and reservoir shapes are not crucial and for simplicity, as in Costa et al. (2011), we assume them as elongated bodies with circular cross-sections. This choice is consistent with the observation that common geometries are general oblate-ellipsoidal chambers (Gudmundsson, 2012 and references therein). Moreover, as discussed in (Gudmundsson, 2012) long-lived magma chambers cannot have very irregular shapes as their surfaces can be assumed smooth (Jaeger, 1961, 1964; Gudmundsson, 2012). On this basis, under isotropic conditions, on very long time-scales, chamber geometries should tend to become sub-circular.

We also need to consider that the aspect ratio of the caldera produced during those eruptions may not be indicative of the chamber shape because as magma overpressure decreases below a critical value, the shallow dyke cannot anymore be kept opened around the fragmentation depth and tends to collapse forming a local restriction that would stop the eruption (Costa et al., 2009, 2011) even if a large fraction of the stored magma is still in the chamber. Caldera shapes can reflect only chamber cross-sections and the fraction of magma volumes evacuated. However, caldera eruptions tend to erupt all eruptible magma (all magma that may vesiculate and have a density lower than the host rock while the crustal block in collapsing) likely because the control of the piston-like subsidence able to maintain the necessary excess pressure (Martí et al., 2000; Folch and Martí, 2009; Gudmundsson, 2015; Geshi and Miyabuchi, 2016). Also it is common to see in large silicic calderas the emplacement of degassed magma in the form of extrusive dome along the ring faults immediately after caldera formation (e.g., Williams, 1941; Lipman, 1984). This implies that we should not expect a large volume of magma remaining in the chamber. In fact many calderas (see Geyer and Martí, 2008) exhibit post-caldera volcanism of mafic composition, thus indicating that nothing or very little was remaining in the magma chamber after caldera collapse, so deeper mafic magmas can cross it without being trapped (mixed) by the resident magma.

In our model the solution for the stress field is calculated using the general analytical solutions by Gao (1996) valid for a pressurized elliptical hole obtained in the limit of a plane 2D geometry (approximation valid for c_C ≫ a_C, b_C, and c_R ≫ a_R, b_R, Figure 1). Such solutions also assume that the medium is homogeneous and purely elastic. The elastic rheology is however a reasonable approximation because the time scales of the eruption, that are of the order of few to several hours, are much shorter than the viscous time of the magmatic system, of the order of hundreds of years or longer (Jellinek and De Paolo, 2003). However, concerning assumption of medium homogeneity we need keep in mind that rock stress distribution can be affected by presence of pore fluids, temperature, and alteration of the different layers (Gudmundsson, 2006). Moreover, active faults, block boundaries are neglected. In addition the solution is valid for an unbounded domain, neglects the effect of topography, and the far field stress is assumed to be homogeneous. However, the analytical solution is able to capture first-order, general large- scale features even with all these limitations (Costa et al., 2011).

We applied the model described above to a LCFE similar to YTT for which magma physical parameters, erupted volumes, tectonic settings are known and independent estimations of MERs are available (Costa et al., 2014). In particular, we studied a magma chamber located at 3–5 km depth under extensional far-field stresses, σ_ff, ranging from 0 to −50 MPa (Figure 1). The upper limit of this spectrum (comparable with stresses needed for nucleating new fractures) can be considered representative of the transition toward an active extensional setting (Turcotte and Schubert, 2002). The stress field perturbation due to a magma reservoir having a top at 10 km depth was also considered.

Concerning magma chamber and reservoir volumes, we assumed a chamber volume, $V_C=\frac{4}{3}\pi a_C{b}_C{c}_C$, of ~5000 km³ (considering a chamber extension c_C of 100 km, consistent with Toba caldera geometry) and a similar reservoir volume, $V_R=\frac{4}{3}\pi a_R{b}_R{c}_R$, of ~5000 km³.

Before to proceed, it is useful to summarize some basic effects due to the combination of different magma chamber geometries under the action of a far-field extensional stress. For an elongated magma chamber with a circular cross-section (i.e., with an aspect ratio a_C/c_C ≈ 1) near neutral pressure conditions, the maximum tensile stress is at the base of the dyke (x = 0, z = c_C; Figure 1) and in this case is σ_t ≈ 3σ_ff (e.g., Gudmundsson, 1988). For a prolate cross-section σ_t ≈ (1 + 2a_C/c_C)σ_ff with a_C ≥ c_C and b_C ≫ a_C (e.g., Gudmundsson, 1988). For an oblate cross-section the maximum stress is at the two lateral tips of the ellipse. The stress along the dyke, connecting the magma chamber to the surface, depends on the intensity of extensional stress, magma chamber pressure, and magma chamber aspect ratio a_C/c_C, magma reservoir depth, magma reservoir aspect ratio a_R/c_R, and magma reservoir overpressure ΔP_R.

Considering the above estimation for the magma chamber volume, and the geometry of the Toba caldera (~100 × 30 km), the chamber would be roughly approximated by an oblate ellipsoid having an elongation of ~100 km, a width of ~30 km, and a height of ~3 km. However, for the sake of simplicity, consistently with our basic magma conduit flow model and the analytical solution for the stress field, we assumed a chamber (and reservoir) with a circular cross section, _{bC ≫ aC} = c_C with 2a_C = D_C being D_C the equivalent diameter (in our case D_C ~ 10 km). In our approximation the maximum effect on the tensile stress is along the dyke conduit at the center of the circular cross section of the chamber, whereas, considering the more realistic case of an oblate ellipsoid, it would be around the lateral tips of the ellipse with an intensity factor an order of magnitude larger due to the different geometry aspect ratio (~10). We would like to remark that we aim to estimate the order of magnitude control of the stress along the dyke conduit due to magma chamber and reservoir and not investigate their detailed magma-rock mechanics. Our approximation represents a minimum bound for the actual effects on the tensile stress that can be even an order of magnitude larger in case of elongated geometries.

Concerning chemical and physical magma properties of the shallow chamber, we considered a magma composition like that of YTT (e.g., Chesner, 2012; Matthews et al., 2012) characterized by a high SiO₂ content (~70–75%), a water content of about 5–6%, temperatures of 700–780⋅C and high crystallinity (up to 40%). These properties are very similar to those characterizing magmas of other LCFEs such as, for example, those associated to the Aira Caldera which erupted more than 300 km³ of magma (Aramaki, 1984) and to the fissure eruptions of ignimbrite from Southern Sierra Madre Occidental, Mexico (Aguirre-Díaz and Labarthe-Hernañdez, 2003; Gottsmann et al., 2009).

Since our model uses cross-section averaged variables only, magma properties are treated in an approximate way. This includes equilibrium water exsolution, absence of gas overpressure with respect to magma pressure, and constant viscosity assumptions. A more realistic description of the effective viscosity (out of the scope of this paper) should account for the coupling with dissolved water, heat loss, viscous dissipation, crystal resorption, and the associated local effects (Costa and Macedonio, 2005; Costa et al., 2007).

Considering those properties and approximations, using the models of Giordano et al. (2008) for melt viscosity and Costa et al. (2009) and Cimarelli et al. (2011) for accounting for the effects of crystals, we estimated a reference effective magma viscosity of ₁₀₈ Pa s. In our simplified model, the main effect of magma viscosity is on magma fragmentation depth as high viscosities tend to move fragmentation level at greater depths, because the critical volume fraction of bubbles is attained earlier upon magma ascent. Initial dyke thickness is assumed to be ~100 m, consistent with typical values estimated for such magma viscosity (Wada, 1994).

Other simplifications are related to rock properties that, for the sake of simplicity, are assumed constant with depth. Although, the variations with depth of some properties such as the Young modulus are evident (e.g., Paulatto, 2010; Costa et al., 2013), the dependence of others, such as the variation of fracture toughness with confining pressure, is not very clear (Rubin, 1993). For example Abou-Sayed (1977) found a 50% increase for limestone toughness at confining pressure of 7 MPa, whereas Schmidt and Huddle (1977) found almost no increase at a confining pressure of 7 MPa but an increase up to a factor 4 at 60 MPa.

All the model input parameters are reported in Table 1.

TABLE 1

Table 1. Parameters used in the simulations (estimated from Costa et al., 2011, 2014; Chesner, 2012).

The effect of the far-field extensional stresses is shown in Figure 2 where we reported the profiles of the tensile stress, σ_t, along the vertical axis of the shallower dyke conduit for both an unpressurized magma reservoir and for a magma reservoir with 10 MPa overpressure (for each condition three different magma chamber pressures are considered). Figure 2 shows that, for an unpressurized magma reservoir, σ_t can counterbalance the lithostatic loading at the dyke base only if the far-field stress is about −40 MPa or larger. Whereas when the reservoir has an overpressure of 10 MPa such condition is reached for a far-field stress around −30 MPa or lower.

FIGURE 2

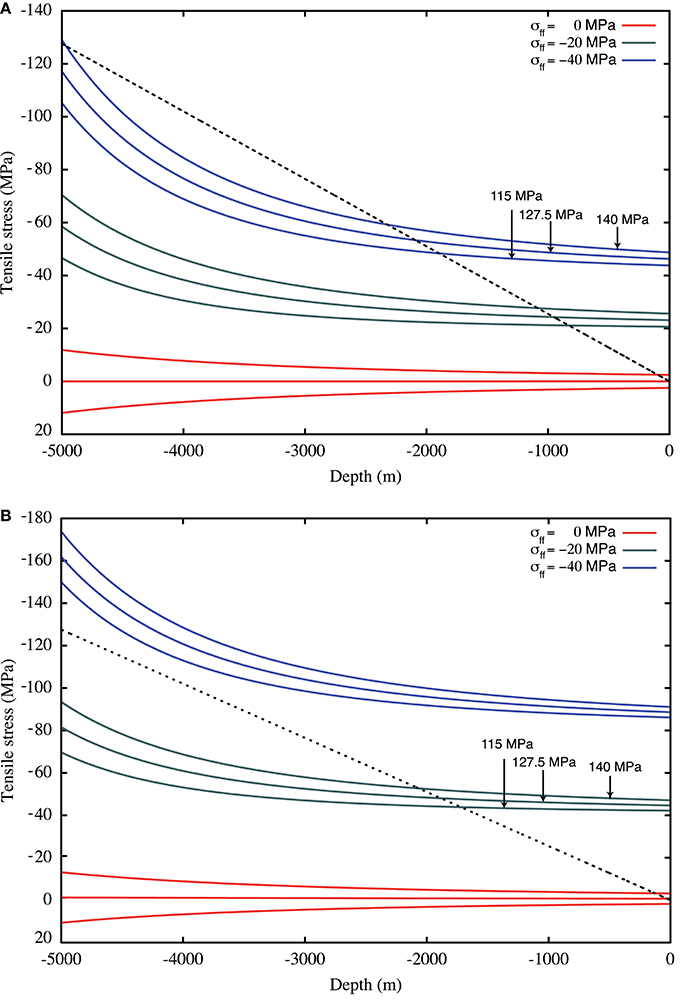
Figure 2. Dyke tensile stress σ_t profile along the vertical axis of the shallower dyke conduit obtained using the analytical solution presented by Gao (1996) for a pressurized magma chamber at 5 km depth (at lithostatic pressure and ±12.5 MPa, as indicated) under the effect of different far-field extensional stresses (from 0 to −40 MPa, as indicated in the figures), for an unpressurized magma reservoir (A) and a pressurized (+10 MPa) reservoir at 10 km depth (B). Dashed line represents the lithostatic pressure. Note that the critical extensional stress that will produce a tensile stress at the dyke base able to counterbalance the lithostatic pressure is different in the two cases: in (A) for σ_ff of −40 MPa or stronger the dyke remains open, whereas in (B), due to the presence of a pressurized magma reservoir, this critical stress is decreased at 20–30 MPa (for more realistic geometries these effects will be much larger, see Section Discussion and Open Problems).

As shown in Figure 3, the increased tensile stress affects the local pressure difference (given as the magma pressure minus the effects of lithostatic loading and tensile stress). In order to get almost neutral conditions at the base of the dyke, in absence of a pressurized reservoir, a far-field stress of about −40 MPa or larger is needed. Whereas, considering a pressurized reservoir a far-field stress of about −30 MPa or lower is enough.

FIGURE 3

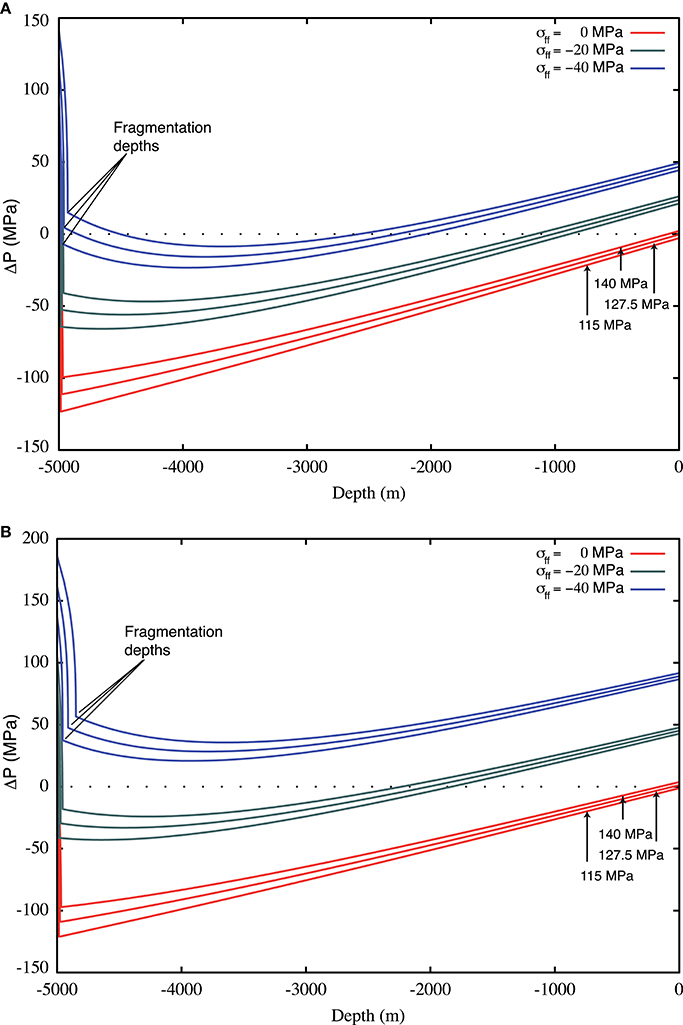
Figure 3. Pressure difference (magma pressure—lithostatic loading—tensile stress) profile along the vertical axis of the shallow dyke conduit obtained using the analytical solution presented by Gao (1996) for a pressurized magma chamber at 5 km depth (at lithostatic pressures and ±12.5 MPa, as indicated) under the effect of different far-field extensional stresses (from 0 to −40 MPa, as indicated in the figures), for a unpressurized magma reservoir (A) and a pressurized (+10 MPa) reservoir at 10 km depth (B). On the top (A), for an unpressurized magma reservoir σ_ff moduli larger then 40 MPa are needed to reach neutral conditions along the dyke. On the bottom (B), the presence of a pressurized magma reservoir reduces the critical extensional stress needed to reach neutral conditions at 20–30 MPa.

The maximum sustainable length of the shallow dyke conduit (Costa et al., 2009, 2011) and the MER as function of the extensional far-field stress are reported in Figure 4. We can see that maximum sustainable lengths of the dyke can range from a few to a few tens kms depending on the extensional far-field stress and magma reservoir overpressure. Similarly the maximum MER can span from 10⁹ to about 10¹¹ kg/s as function of the extensional stress, magma chamber depth, and magma reservoir overpressure. As it is shown for comparison in Figure 4 and discussed by Costa et al. (2011), a much shallower magma chamber (e.g., 3 km depth) would be able to erupt higher MER for the same far-field stress.

FIGURE 4

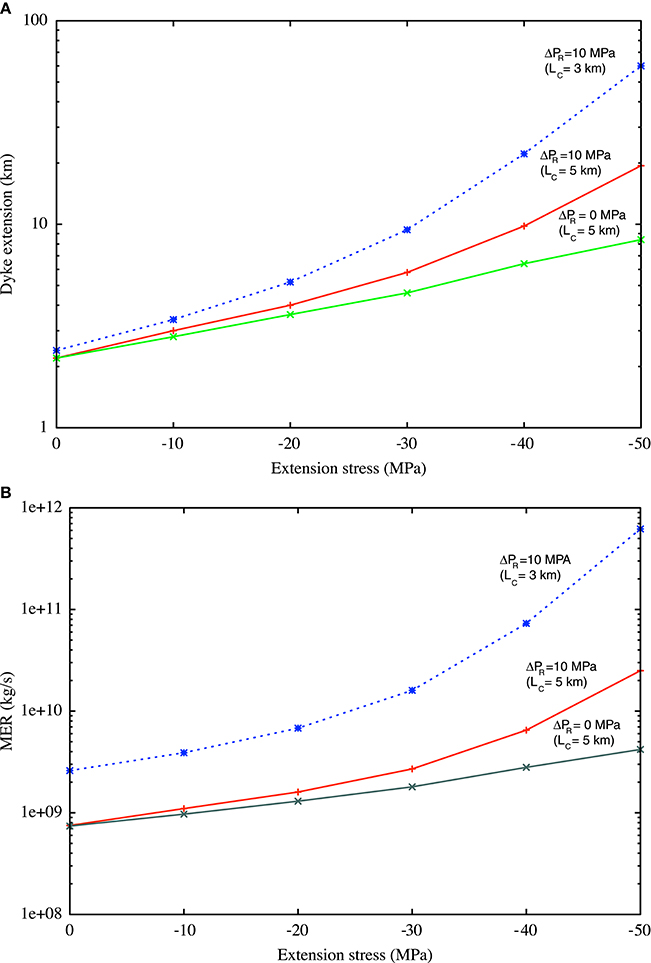
Figure 4. Effects of extensional far-field stress on (A) maximum sustainable length of the shallow dyke conduit and (B) MER. (A) Maximum sustainable lengths of the shallow dyke conduit depend on the extensional far-field stress and magma reservoir overpressure, ranging from a few to a few tens kms. (B) Similarly maximum MERs are a function of the extensional stress and magma reservoir overpressure, ranging from 10⁹ to 10¹¹ kg/s.

Discussion and Open Problems

We have shown that in order to produce extremely large eruption intensities of highly silicic magmas, such as those characterizing LCFEs, it is necessary to consider the effects of the local stress field resulting from the combination of an extensional far-field stress and a pressurized magma reservoir. Our simulations indicate that MERs of 10¹⁰ − 10¹¹ kg/s are promoted during moderate to high extensional far field stress (20–40 MPa), a pressurized magma reservoir (~10 MPa), and relatively shallow magma chambers (3–5 km).

We need to remark that these calculations represent a first-order description aimed at capturing some general features and the proper order of magnitude of the estimated quantities. For a more accurate description other factors should be considered besides the approximations described above. A more correct description of a dual magma chamber system (Melnik and Costa, 2014) should consider not only the effect of a pressurized magma reservoir on the tensile stress within the shallow dyke conduit, but even the control of the magma reservoir on the dynamics of the shallow magma chamber. This is important to characterize how the response of the deeper dyke to local pressure variation can alter magma feeding into the chamber on time-scales comparable to the eruption duration. Dealing with such complex dynamics is out the scope of this work and is the subject of ongoing research.

Our study analyses the conditions required to keep magma conduits open during caldera formation and these will be the same irrespectively on how these eruption pathways have been opened. Because the high magma viscosity, fragmentation level is typically very deep (basically at the roof of the chamber). The effect of a far-field extensional stress is needed in order to permit magma pressure can counterbalance lithostatic loading. However, the current model does not consider rock failure occurring in over- and under-pressure conditions (Costa et al., 2009). In our case significant rock failure should occur below and across fragmentation depth (Figure 3), implying the partial destruction of the roof of the magma chamber likely moving the fragmentation inside the chamber producing a stable system more suitable to maintain the dyke opened. This implies that, in caldera eruptions that are preceded by a Plinian phase (i.e., MER ≲ 10⁹ kg/s; Koyaguchi et al., 2010) for getting a transition to larger MER, the caldera collapse phase must be accompanied by a change in the mechanical conditions of the system that allow magma to fragment much deeper when flowing up through the ring fault. This agrees with previous models (e.g., Williams, 1941; Druitt and Sparks, 1984; Martí et al., 2000) that assume a considerable decompression on the magma chamber as a necessary requisite to permit caldera collapse. In the case where a part of the ring fault was open by a tectonic event, the conditions for magma fragmentation to occur very deep in the conduit would be achieved early in the eruption. In such situations it would not be necessary to have a significant decompression of the chamber to allow caldera collapse, as it is suggested by the lack of pre-caldera deposits in many LCFE (Martí et al., 2009).

Conclusions

Our study indicates that in order to erupt large volumes of silicic magmas during LCFE in relatively short times (e.g., large MER estimated in the range 10⁹ − 10¹¹ kg/s), it is necessary to account for the combined effect of extensional far-field stress and pressurization conditions of magma chambers and reservoirs. In presence of a pressurized deep reservoir even intermediate extensional crustal stresses (20–30 MPa) facilitate an efficient evacuation of large magmatic chambers through a shallow dyke conduit. Largest MERs are promoted in system having a shallow magma chamber (3–5 km). Large MERs are maintained even for under-pressurized magma chamber. Simulation results are consistent with geological observations of LCFE. However, the model assumes that the dyke is already formed and does not account for rock failure that could change drastically the geometry of the system (e.g., chamber roof collapse) as the eruption proceeds. Our results help to address future research aimed to advance our knowledge on the dynamics of these rare catastrophic events.

Author Contributions

AC developed the new code version and ran the simulations. AC, JM analyzed the results and wrote the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Two reviewers and the editor Agust Gudmundsson are warmly thanked for their constructive feedback. AC is grateful to T. Koyaguchi and P. Gregg for fruitful discussion during his stay at the Earthquake Research Institute, the University of Tokyo.

References

Abou-Sayed, A. S. (1977). “Fracture toughness KIC of triaxially loaded Indiana limestone,” in Proc. 17th U.S. Symposium Rock Mechanics (Keystone).

Acocella, V. (2007). Understanding caldera structure and development: An overview of analogue models compared to natural calderas. Earth Sci. Rev. 85, 125–160. doi: 10.1016/j.earscirev.2007.08.004.

CrossRef Full Text | Google Scholar

Acocella, V., Di Lorenzo, R., Newhall, C., and Scandone, R. (2015). An overview of recent (1988 to 2014) caldera unrest: knowledge and perspectives. Rev. Geophys. 53, 896–955. doi: 10.1002/2015RG000492

CrossRef Full Text | Google Scholar

Acocella, V., and Funiciello, F. (2010). Kinematic setting and structural control of arc volcanism, Earth Planet. Sci. Lett. 289, 43–53. doi: 10.1016/j.epsl.2009.10.027

CrossRef Full Text | Google Scholar

Aguirre-Díaz, G. J., Labarthe-Hernández, G., Tristán-González, M., Nieto-Obregón, J., and Gutiérrez-Palomares, I. (2008). “Ignimbrite Flare-up and graben-calderas of the Sierra Madre Occidental, Mexico,” in Caldera Volcanism: Analysis, Modelling and Response, Developments in Volcanology, Vol. 10., eds J. Martí and J. Gottsmann (Amsterdam: Elsevier), 492.

Aguirre-Díaz, G., and Labarthe-Hernañdez, G. (2003). Fissure ignimbrites: fissure-source origin for voluminous ignimbrites of the Sierra Madre Occidental and its relationship with Basin and Range faulting. Geology 31, 773–776. doi: 10.1130/G19665.1

CrossRef Full Text | Google Scholar

Aramaki, S. (1984). Formation of the Aira Caldera, Southern Kyushu, 22,000 Years Ago. J. Geophys. Res. 89, 8485–8501.

Google Scholar

Bacon, C. R. (1983). Eruptive history of Mount Mazama and Crater Lake Caldera, Cascade Range, U.S.A. J. Volcanol. Geother. Res. 18, 57–115.

Google Scholar

Baines, P. G., and Sparks, R. S. J. (2005). Dynamics of giant volcanic ash clouds from supervolcanic eruptions. Geophys. Res. Lett. 32, L24808. doi: 10.1029/2005GL024597

CrossRef Full Text | Google Scholar

Burov, E. B., and Guillou-Frottier, L. (1999). Thermomechanical behaviour of large ash flow calderas. J. Geophys. Res. 104, 23081–23109. doi: 10.1029/1999JB900227

CrossRef Full Text | Google Scholar

Chesner, C. A. (1998). Petrogenesis of the Toba Tuffs, Sumatra, Indonesia. J. Petrol. 39, 397–438.

Google Scholar

Chesner, C. A. (2012). The toba caldera complex. Quat. Int. 258, 5–18. doi: 10.1016/j.quaint.2011.09.025

CrossRef Full Text | Google Scholar

Cimarelli, C., Costa, A., Mueller, S., and Mader, H. (2011). Rheology of magmas with bimodal crystal size and shape distributions: insights from analogue experiments. Geochem. Geophys. Geosyst. 12, Q07024. doi: 10.1029/2011GC003606

CrossRef Full Text | Google Scholar

Cole, J. W., Spinks, K. D., Deering, C. D., Nairn, I. A., and Leonard, G. S. (2010). Volcanic and structural evolution of the Okataina Volcanic Centre; dominantly silicic volcanism associated with the Taupo Rift, New Zealand. J. Volcanol. Geother. Res. 190, 123–135. doi: 10.1016/j.jvolgeores.2009.08.011

CrossRef Full Text | Google Scholar

Costa, A., Gottsmann, J., Melnik, O., and Sparks, R. S. J. (2011). A stress-controlled mechanism for the intensity of very large magnitude explosive eruptions. Earth Planet. Sci. Lett. 310, 161–166. doi: 10.1016/j.epsl.2011.07.024

CrossRef Full Text | Google Scholar

Costa, A., and Macedonio, G. (2005). Viscous heating effects in fluids with temperature-dependent viscosity: triggering of secondary flows. J. Fluid Mech. 540, 21–38. doi: 10.1017/S0022112005006075

CrossRef Full Text | Google Scholar

Costa, A., Melnik, O., and Vedeneeva, E. (2007). Thermal effects during magma ascent in conduits. J. Geophys. Res. 112:B12205. doi: 10.1029/2007JB004985

CrossRef Full Text | Google Scholar

Costa, A., Smith, V., Macedonio, G., and Matthews, N. (2014). The magnitude and impact of the Youngest Toba Tuff super-eruption. Front. Earth Sci. 2:16. doi: 10.3389/feart.2014.00016

CrossRef Full Text | Google Scholar

Costa, A., Sparks, R. S. J., Macedonio, G., and Melnik, O. (2009). Effects of wall-rock elasticity on magma flow in dykes during explosive eruptions. Earth Planet. Sci. Lett. 288, 455–462. doi: 10.1016/j.epsl.2007.05.024

CrossRef Full Text | Google Scholar

Costa, A., Wadge, G., Stewart, R., and Odbert, H. (2013). Coupled sub-daily and multi-week cycles during the lava dome eruption of Soufriere Hills Volcano, Montserrat. J. Geophys. Res. 118, 1895–1903. doi: 10.1002/jgrb.50095

CrossRef Full Text | Google Scholar

Druitt, T. H., and Francaviglia, V. (1992). Caldera formation on Santorini and the physiography of the islands in the late Bronze Age. Bull. Volcanol. 54, 484–493.

Google Scholar

Druitt, T. H., and Sparks, R. S. J. (1984). On the formation of calderas during ignimbrite eruptions. Nature 310, 679–681.

Google Scholar

Folch, A., and Martí, J. (1998). The generation of overpressure in felsic magma chambers by replenishment. Earth Planet. Sci. Lett. 163, 301–314.

Google Scholar

Folch, A., and Martí, J. (2004). Geometrical and mechanical constraints on the formation of ring-fault calderas. Earth Planet. Sci. Lett. 221, 215–225. doi: 10.1016/S0012-821X(04)00101-3

CrossRef Full Text | Google Scholar

Folch, A., and Martí, J. (2009). Time-dependent chamber and vent conditions during explosive caldera-forming eruptions. Earth Planet. Sci. Lett. 280, 246–253. doi: 10.1016/j.epsl.2009.01.035

CrossRef Full Text | Google Scholar

Folch, A., Martí, J., Codina, R., and Vazquez, M. (1998). A numerical model for temporal variations durino explosive central vent eruptions. J. Geophys. Res. 103, 20883–20899.

Google Scholar

Folkes, C. B., Wright, H. M., Cas, R. A. F., de Silva, S. L., Lesti, C., and Viramonte, J. G. (2011). A re-appraisal of the stratigraphy volcanology of the Cerro Galan volcanic system, NW Argentina. Bull. Volcanol. 73:1427–1454. doi: 10.1007/s00445-011-0459-y

CrossRef Full Text | Google Scholar

Gao, X.-L. (1996). A general solution of an infinite elastic plate with an elliptic hole under biaxial loading. Int. J. Pres. Ves. Piping 67, 95–104.

Google Scholar

Gardeweg, M., and Ramirez, C. F. (1987). La Pacana caldera and the Atana Ignimbrite - A major ash-flow and resurgent caldera complex in the Andes of northern Chile. Bull. Volcanol. 49, 547–566.

Google Scholar

Geshi, N., and Miyabuchi, Y. (2016). Conduit enlargement during the precursory Plinian eruption of Aira Caldera, Japan. Bull. Volcanol. 78, 63. doi: 10.1007/s00445-016-1057-9

CrossRef Full Text | Google Scholar

Geyer, A., and Martí, J. (2008). The new worldwide Collapse Caldera Database (CCDB): a tool for studying and understanding caldera processes. J. Volcanol. Geotherm. Res. 175, 334–354. doi: 10.1016/j.jvolgeores.2008.03.017

CrossRef Full Text | Google Scholar

Geyer, A., and Martí, J. (2014). A short review of our current understanding of the development of ring faults during collapse caldera formation. Front. Earth Sci. 2:22, doi: 10.3389/feart.2014.00022

CrossRef Full Text | Google Scholar

Giordano, D., Russel, J. K., and Dingwell, D. B. (2008). Viscosity of magmatic liquids: a model, Earth Planet. Sci. Lett. 271, 123–134, doi: 10.1016/j.epsl.2008.03.038

CrossRef Full Text

Gottsmann, J., Lavallée, Y., Martí, J., and Aguirre-Díaz, G. (2009). Magma–tectonic interaction and the eruption of silicic batholiths. Earth Planet. Sci. Lett. 284, 426–434. doi: 10.1016/j.epsl.2009.05.008

CrossRef Full Text | Google Scholar

Gray, J. P., and Monaghan, J. J. (2004). Numerical modelling of stress fields and fracture around magma chambers. J. Volcanol. Geotherm. Res. 135, 259–283. doi: 10.1016/j.jvolgeores.2004.03.005

CrossRef Full Text | Google Scholar

Gregg, P. M., de Silva, S. L., Grosfils, E. B., and Parmigiani, J. P. (2012). Catastrophic caldera-forming eruptions: thermomechanics and implications for eruption triggering and maximum caldera dimensions on Earth. J. Volcanol. Geotherm. Res. 241–242, 1–12. doi: 10.1016/j.jvolgeores.2012.06.009

CrossRef Full Text | Google Scholar

Gregg, P. M., Grosfils, E. B., and de Silva, S. L. (2015). Catastrophic caldera-forming eruptions II: the subordinate role of magma buoyancy as an eruption trigger. J. Volcanol. Geotherm. Res. 305, 100–113. doi: 10.1016/j.jvolgeores.2015.09.022

CrossRef Full Text | Google Scholar

Gudmundsson, A. (1988). Effect of tensile stress concentration around magma chambers on intrusion and extrusion frequencies. J. Volcanol. Geotherm. Res. 35, 179–194.

Google Scholar

Gudmundsson, A. (1998). Formation and development of normal-fault calderas and the initiation of large explosive eruptions. Bull. Volcanol. 60, 160–170.

Google Scholar

Gudmundsson, A. (2002). Emplacement and arrest of sheets and dykes in central volcanoes. J. Volcanol. Geotherm. Res. 116, 279–298. doi: 10.1016/S0377-0273(02)00226-3

CrossRef Full Text | Google Scholar

Gudmundsson, A. (2006). How local stresses control magma-chamber ruptures, dyke injections, and eruptions in composite volcanoes. Earth Sci. Rev. 79, 1–31. doi: 10.1016/j.earscirev.2006.06.006

CrossRef Full Text | Google Scholar

Gudmundsson, A. (2012). Magma chambers: Formation, local stresses, excess pressures, and compartments. J. Volcanol. Geotherm. Res. 237–238, 19–42. doi: 10.1016/j.jvolgeores.2012.05.015

CrossRef Full Text | Google Scholar

Gudmundsson, A. (2015). Collapse-driven eruptions. J. Volcanol. Geotherm. Res. 304, 1–10. doi: 10.1016/j.jvolgeores.2015.07.033

CrossRef Full Text | Google Scholar

Gudmundsson, A., Martí, J., and Turon, E. (1997). Stress fields generating ring faults in volcanoes. Geophys. Res. Lett. 24, 1559–1562. doi: 10.1029/97GL01494

CrossRef Full Text | Google Scholar

Hautmann, S., Gottsmann, J., Sparks, R. S. J., Costa, A., Melnik, O., and Voight, B. (2009). Modelling ground deformation caused by oscillating overpressure in a dyke conduit at Soufriere Hills Volcano, Montserrat. Tectonophysics 471, 87–95. doi: 10.1016/j.tecto.2008.10.021

CrossRef Full Text | Google Scholar

Hildreth, W. (1991). The timing of caldera collapse at Mount Katmai in response to magma withdrawal toward Novarupta. Geophys. Res. Lett. 18, 1541–1544.

Google Scholar

Hildreth, W., and Mahood, G. A. (1986). Ring-fracture eruption of the Bishop Tuff. Geol. Soc. Am. Bull. 97, 396–403.

Google Scholar

Hughes, G. H., and Mahood, G. A. (2008). Tectonic controls on the nature of large silicic calderas in volcanic arcs. Geology 36, 627–630. doi: 10.1130/G24796A.1

CrossRef Full Text | Google Scholar

Jaeger, J. C. (1961). The cooling of irregularly shaped igneous bodies. Am. J. Sci. 259, 721–734.

Google Scholar

Jaeger, J. C. (1964). Thermal effects of intrusions. Rev. Geophys. 2, 443–466.

Google Scholar

Jellinek, A. M., and De Paolo, D. J. (2003). A model for the origin of large silicic magma chambers: precursors of caldera-forming eruptions. Bull. Volcanol. 65, 363–381. doi: 10.1007/s00445-003-0277-y

CrossRef Full Text | Google Scholar

Korringa, M. K. (1973). Linear vent area of the Soldier Meadow Tuff, an ash-flow sheet in northwestern Nevada. Geol. Soc. Am. Bull. 84, 3849–3866.

Google Scholar

Koyaguchi, T., Suzuki, Y. J., and Kozono, T. (2010). Effects of the crater on eruption column dynamics. J. Geophys. Res. 115, B07205. doi: 10.1029/2009JB007146

CrossRef Full Text | Google Scholar

Lipman, P. W. (1984). The roots of ash-flow calderas in North America: windows into the tops of granitic batholiths. J. Geophys. Res. 89, 8801–8841.

Google Scholar

Macedonio, G., Neri, A., Martí, J., and Folch, A. (2005). Temporal evolution of flow conditions in sustained magmatic explosive eruptions. J. Volcanol. Geotherm. Res. 143, 153–172. doi: 10.1016/j.jvolgeores.2004.09.015

CrossRef Full Text | Google Scholar

Martí, J., Folch, A., Macedonio, G., and Neri, A. (2000). Pressure evolution during caldera forming eruptions. Earth Planet. Sci. Lett. 175, 275–287. doi: 10.1016/S0012-821X(99)00296-4

CrossRef Full Text | Google Scholar

Martí, A., Folch, A., Costa, A., and Engwell, A. (2016). Reconstructing the plinian and co-ignimbrite sources of large volcanic eruptions: a novel approach for the Campanian Ignimbrite. Nat. Sci. Rep. 6:21220. doi: 10.1038/srep21220

PubMed Abstract | CrossRef Full Text | Google Scholar

Martí, J., Geyer, A., and Folch, A. (2009). “A genetic classification of collapse calderas based on field studies, analogue and theoretical modelling,” in Volcanology: the Legacy of GPL Walker, eds T. Thordarson and S. Self (London: IAVCEI-Geological Socety of London), 249–266.

Matthews, N. E., Pyle, D. M., Smith, V. C., Wilson, C. J. N., Huber, C., and van Hinsberg, V. (2011). Quartz zoning and the pre-eruptive evolution of the ~340 ka Whakamaru magma systems, New Zealand. Contr. Mineral. Petrol. 163, 87–107. doi: 10.1007/s00410-011-0660-1

CrossRef Full Text | Google Scholar

Matthews, N. E., Smith, V. C., Costa, A., Pyle, D. M., Durant, A. J., and Pearce, N. J. G. (2012). Ultra-distal tephra deposits from super-eruptions: examples from Toba, Indonesia and Taupo Volcanic Zone, New Zealand. Toba Super Erupt. Impact Ecosys. Hominin 258, 34–79. doi: 10.1016/j.quaint.2011.07.010

CrossRef Full Text | Google Scholar

Melnik, O. (1999). Fragmenting magma. Nature 397, 394–395.

Google Scholar

Melnik, O., and Costa, A. (2014). “Dual chamber-conduit models of non-linear dynamics behaviour at Soufriere Hills volcano,” in The Eruption of Soufriere Hills Volcano, Montserrat from 2000 to 2010, eds G. Wadge, R. E. A. Robertson and B. Voight (London: Memoir of the Geological Society of London, The Geological Society of London), 501. doi: 10.1144/M39.3

CrossRef Full Text

Miller, C., Wark, D., Self, S., Blake, S., and John, D. (2008). (Potentially) Frequently asked questions about supervolcanoes and supereruptions. Elements 4, 16.

Google Scholar

Muskhelishvili, N. (1963). Some Basic Problems in the Mathematical Theory of Elasticity. Leiden: Noordhof.

Google Scholar

Pallister, J. S., Hoblitt, R. P., and Reyes, A. G. (1992). A basalt trigger for the 1991 eruptions of Pinatubo volcano. Nature 356, 426–428.

Google Scholar

Papale, P. (1999). Strain-induced magma fragmentation in explosive eruptions. Nature 397, 425–428.

Google Scholar

Paulatto, M., Minshull, T. A., Baptie, B., Dean, S., Hammond, J. O. S., Henstock, T., et al. (2010). Upper crustal structure of an active volcano from refraction/reflection tomography, Montserrat, Lesser Antilles. Geophys. J. Int. 180, 685–696. doi: 10.1111/j.1365-246X.2009.04445.x

CrossRef Full Text | Google Scholar

Petrinovic, I., Martí, J., Aguirre-Díaz, G., Guzmán, S., Geyer, A., and Salado Paz, N. (2010). The Cerro Aguas Calientes caldera, NW Argentina: an example of a tectonically controlled, polygenetic collapse caldera, and its regional significance. J. Volcanol. Geotherm. Res. 194, 15–26. doi: 10.1016/j.jvolgeores.2010.04.012

CrossRef Full Text | Google Scholar

Pittari, A., Cas, R. A. F., Wolff, J. A., Nichols, H. J., and Martí, J. (2008). The use of lithic clast distributions in pyroclastic deposits to understand pre- and syn-caldera collapse processes: a case study of the Abrigo Ignimbrite, Tenerife, Canary Islands,” in Caldera Volcanism: Analysis, Modelling and Response: Developments in Volcanology, eds J. Gottsmann, and J. Martí (Amsterdam: Elsevier), 97–142.

Reyners, M. E. (2010). Stress and strain from earthquakes at the southern termination of the Taupo Volcanic Zone, New Zealand. J. Volcanol. Geotherm. Res. 190, 82–88. doi: 10.1016/j.jvolgeores.2009.02.016

CrossRef Full Text | Google Scholar

Roche, O., Buesch, D. C., and Valentine, G. A. (2016). Slow-moving and far-travelled dense pyroclastic flows during the Peach Spring super-eruption. Nat. Communic. 7:10890. doi: 10.1038/ncomms10890

PubMed Abstract | CrossRef Full Text | Google Scholar

Rowland, J. V., Wilson, C. J. N., and Gravley, D. M. (2010). Spatial and temporal variations in magma-assisted rifting, Taupo Volcanic Zone, New Zealand. J. Volcanol. Geotherm. Res. 190, 89–108. doi: 10.1016/j.jvolgeores.2009.05.004

CrossRef Full Text | Google Scholar

Rubin, A. M. (1993). Tensile fracture of rock at high confining pressure: implications for dike propagation. J. Geophys. Res. 98, 15919–15935.

Google Scholar

Rubin, A. M. (1995). Propagation of magma-filled cracks. Annu. Rev. Earth Planet. Sci. 23, 287–336.

Google Scholar

Schmidt, R. A., and Huddle, C. W. (1977). Effect of confining pressure on fracture toughness of Indiana limestone. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 14, 289–293.

Google Scholar

Self, S. (1992). Krakatau revisited: the course of events and interpretation of the 1883 eruption. Geol. J. 28, 109–121.

Google Scholar

Sigmundsson, F., Hreinsdóttir, S., Hooper, A., Arnadottir, T., Pedersen, R., Roberts, M. J., et al. (2010). Intrusion triggering of the 2010 Eyjafjallajokull explosive eruption. Nature 468, 426–430. doi: 10.1038/nature09558

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, R. L. (1979). Ash flow magmatism. Geol. Soc. Am. Spec. Papers 180, 5–27.

Google Scholar

Smith, V. C., Shane, P. A., Nairn, I. A., and Williams, C. M. (2006). Geochemistry and magmatic properties of eruption episodes from Haroharo Linear Vent Zone, Okataina Volcanic Centre, Taupo Volcanic Zone, New Zealand during the last 10 kyr. Bull. Volcanol. 69, 57–88. doi: 10.1007/s00445-006-0056-7

CrossRef Full Text | Google Scholar

Smith, V. C., Shane, P., and Nairn, I. A. (2005). Trends in rhyolite geochemistry, mineralogy, and magma storage during the last 50 kyr at Okataina and Taupo volcanic centres, Taupo Volcanic Zone, New Zealand. J. Volcanol. Geotherm. Res. 148, 372–406. doi: 10.1016/j.jvolgeores.2005.05.005

CrossRef Full Text | Google Scholar

Sneddon, I. N., and Lowengrub, M. (1969). Crack Problems in the Classical Theory of Elasticity. New York, NY: Wiley & Sons.

Sobradelo, R., Geyer, A., and Martí, J. (2010). Statistical data analysis of the CCDB (Collapse Caldera Database): Insights on the formation of caldera systems. J. Volcanol. Geother. Res. 198, 241–252. doi: 10.1016/j.jvolgeores.2010.09.003

CrossRef Full Text | Google Scholar

Sparks, R. S. J. (1978). The dynamics of bubble formation and growth in magmas: a review and analysis. J. Volcanol. Geotherm. Res. 3, 1–37.

Google Scholar

Sparks, R. S. J., Sigurdsson, H., and Wilson, L. (1977). Magma mixing: a mechanism for triggering acid explosive eruptions. Nature 267, 315–318.

Google Scholar

Spera, F., and Crisp, J. A. (1981). Eruption volume, periodicity, and caldera area: relationships and inferences on development of compositional zonation in silicic magma chambers. J. Volcanol. Geother. Res. 11, 169–187.

Google Scholar

Suzuki-Kamata, K., Kamata, H., and Bacon, C. R. (1993). Evolution of the caldera-forming eruption at Crater Lake, Oregon, indicated by component analysis of lithic fragments. J. Geophys. Res. 98, 14059–14074.

Google Scholar

Turcotte, D. L., and Schubert, G. (2002). Geodynamics, 2nd Edn. Cambridge: Cambridge University Press.

Google Scholar

Wada, Y. (1994). On the relationship between dike width and magma viscosity. J. Geophys. Res. 99, 17743–17755. doi: 10.1029/94JB00929

CrossRef Full Text | Google Scholar

Williams, H. (1941). “Calderas and their origin”, in Bulletin of the Department of Geological Sciences, Vol. 25, eds University of California Press (Berkeley, CA: University of California Press), 239–346.

Wilson, C. J. N. (2001). The 26.5 ka Oruanui eruption, New Zealand: an introduction and overview. J. Volcanol. Geotherm. Res. 112, 133–174. doi: 10.1016/S0377-0273(01)00239-6

CrossRef Full Text | Google Scholar

Wilson, C. J. N., and Hildreth, W. (1997). The Bishop Tuff: new insights from eruptive stratigraphy. J. Geol. 105, 407–439.

Google Scholar

Wilson, C. J. N., and Walker, G. P. L. (1981). “Violence in pyroclastic flow eruptions,” in Tephra Studies, eds S. Self and R. S. J. Sparks (Dordrecht: D. Reidel), 441–448.

Wilson, L., Sparks, R. S. J., and Walker, G. P. L. (1980). Explosive volcanic eruptions: IV. The control of magma properties and conduit geometry on eruptive column behaviours. Geophys. J. R. Astron. Soc. 63, 117–148.

Google Scholar