The Current Energetics of Earth's Interior: A Gravitational Energy Perspective

The Earth's mantle convects to lose heat (Holmes, 1931); doing so drives plate tectonics (Turcotte and Oxburgh, 1967). Significant gravitational energy is created by the cooling of oceanic lithosphere atop hotter, less dense mantle. When slabs subduct, this gravitational energy is mostly (~86% for whole mantle flow in a PREM-like mantle) transformed into heat by viscous dissipation. Using this perspective, we reassess the energetics of Earth's mantle. We also reconsider the terrestrial abundances of heat producing elements U, Th, and K, and argue they are lower than previously considered and that consequently the heat produced by radioactive decay within the mantle is comparable to the present-day potential gravitational energy release by subducting slabs—both are roughly ~10–12 TW. We reassess possible core heat flow into the base of the mantle, and determine that the core may be still losing a significant amount of heat from its original formation, potentially more than the radioactive heat generation within the mantle. These factors are all likely to be important for Earth's current energetics, and argue that strong plume-driven upwelling is likely to exist within the convecting mantle.

Introduction

Roles of Gravitational Energy Transformations in Mantle Convection

A wonderful realization of the Plate Tectonics revolution was that the surface oceanic plates form the upper thermal boundary layer of a convecting mantle (Turcotte and Oxburgh, 1967). When oceanic plates cool near the Earth's surface, they become denser than underlying mantle. This density contrast provides the gravitational pull that causes plates to sink when they subduct. It is perhaps most familiar to think of convection in terms of cooling- or heating-linked buoyancy forces that cause hot regions to rise and cold regions to sink within a convecting fluid. While less familiar, an equivalent way to think about these phenomena is in terms of gravitational potential energy. Both rising low-density and sinking high-density regions release gravitational potential energy. In a highly viscous fluid like the Earth's mantle where inertial forces are negligible, the gravitational energy released from a sinking thermal density anomaly is completely transformed into viscous dissipation energy within the deforming fluid. For example, the Stokes problem of a sinking heavy ball in a highly viscous medium can be treated either as a force balance between the net buoyancy force on the ball and the viscous resisting force from the surrounding fluid's deformation, or as an energy balance between the gravitational energy released by the ball's sinking and the viscous dissipation within the surrounding fluid. (In fluid dynamics, it is well-known that all slow viscous flow involves viscous friction—or viscous dissipation—that generates heat as the material strains. In this perspective, the gravitational potential energy release from a rigid sinking ball is transformed into heat, via viscous dissipation, in the surrounding viscous fluid. In Earth's mantle and core this effect is slightly more complicated in that local heating from viscous dissipation will always be associated with adiabatic thermal expansion that simultaneously transforms a fraction of the dissipation-heat back into gravitational potential energy. This effect is small but non-negligible, with an average ~19% adiabatic heat-transformation for Earth's mantle and core. It will be quantified and discussed later in Section Adiabatic Effects Transform ~14% of the Mantle's Heat Production into Gravitational Energy).

The gravitational energy perspective is a useful way to elucidate several aspects of mantle convection, and also lets us determine the energetics associated with present-day mantle flow. The intuition gained from this perspective is independent of whether we think about an incompressible or compressible mantle. However, in compressible mantle convection it has been obscured historically by a formulation and terminology that focuses on “adiabatic heating” instead of gravitational power release. Thinking about gravitational energy release and gravitational to thermal energy transformations in a high-viscosity compressible fluid is likely to be unfamiliar to the reader, as is the idea that viscous dissipation-heating can be concentrated in low-viscosity circuits within mantle flow. To justify the soundness of this perspective, we will first demonstrate that gravitational power—the rate of transformation of gravitational potential energy in the system—is simply a more intuitive way to visualize the “adiabatic heating” or “work done against the adiabatic gradient” term in compressible convection. The following analysis applies to the convecting mantle.

Energy Balance for Incompressible Convection

We start by demonstrating this equivalence for incompressible slow viscous flow. The equations describing this flow describe conservation of momentum (Equation 1), conservation of mass (Equation 2), and conservation of energy, which is not needed for the following analysis. Here, τ_ij, denotes deviatoric stress components, p pressure, and u_i velocity components. The notation uses a comma to represent partial differentiation in a given direction, the Einstein summation convention is used for repeated indices (e.g., there is an implicit summation whenever a particular set of indices is repeated), and 1, 2, 3 refer to the x, y, z directions.

$\begin{array}{ll}-p_{,i}+{\tau }_{ij,j}+\Delta \rho g{\delta }_{i3}=0& (1)\end{array}$

where δ_ι3 is the Kroneker delta, i.e, it is defined to have a value of 1 when i = 3 and 0 otherwise. For incompressible flow, mass conservation implies volume conservation, so that the divergence of velocity

$\begin{array}{ll}{u}_{i,i}=0& (2)\end{array}$

If we multiply Equation (1) by the velocity field u_i and integrate over volume, we find that

$\begin{array}{ll}-{\displaystyle \int }{p}_{,i}{u}_{i}dV+{\displaystyle \int }{\tau }_{ij,j}{u}_{i}dV+{\displaystyle \int }\Delta \rho g{u}_{3}dV=0& (3)\end{array}$

Gauss's Theorem states that

$\begin{array}{ll}{\displaystyle \int }{\tau }_{ij,j}{u}_{i}dV={\displaystyle \oint }{\tau }_{ij}{u}_{i}d{\widehat{n}}_j-{\displaystyle \int }{\tau }_{ij}{u}_{i,j}dV& (4)\end{array}$

where ∮ is the surface integral around the volume, and ${\widehat{n}}_j$ is the unit normal to the surface. Likewise

$\begin{array}{ll}{\displaystyle \int }{p}_{,i}{u}_{i}dV={\displaystyle \oint }p{u}_{i}d{\widehat{n}}_j-{\displaystyle \int }p{u}_{i,i}dV& (5)\end{array}$

Using Equations (4) and (5) we can rewrite Equation (3) as

$\begin{array}{ll}{\displaystyle \oint }\left(-p+{\tau }_{ij}\right)u_{i}d{\widehat{n}}_j-{\displaystyle \int }{\tau }_{ij}{u}_{i,j}dV+{\displaystyle \int }p{u}_{i,i}dV+{\displaystyle \int }\Delta \rho g{u}_{3}dV=0& (6)\end{array}$

The first term in Equation (6) is the rate of work done to material along the surface of the volume. For an isolated, closed system this term is zero, which is easy to visualize for the zero shear stress boundary conditions appropriate for the top free surface and bottom core-mantle boundary (CMB) interface of the mantle. The third term in Equation (6) is also zero because of the incompressibility condition (2), so we are left with the familiar interpretation that

$\begin{array}{ll}{\displaystyle \int }{\tau }_{ij}{u}_{i,j}dV={\displaystyle \int }\Delta \rho g{u}_{3}dV& (7)\end{array}$

In words, the integral of the viscous dissipation (1st term) associated with incompressible Stokes flow is equal to the rate of gravitational energy release or gravitational power associated with rising or sinking density anomalies. Gravitational potential energy is being transformed into viscous dissipation energy within the deforming viscous fluid.

Energy Balance in Compressible Convection

The same type of balance between gravitational power release and viscous dissipation takes place in compressible slow viscous flow. To show this we follow a similar approach to that of (Leng and Zhong, 2008), but without using any non-dimensionalizations. For this type of slow viscous flow where inertial effects are completely negligible, we can idealize the fluid to be an infinite Prandtl number anelastic liquid that is in mechanical equilibrium throughout (The Prandtl number μC_P/k is the non-dimensional ratio of the kinematic viscosity μ/ρ[m²/s] to thermal diffusivity $\kappa \equiv k/\rho C_P\left[m^2/s\right]$, and the anelastic approximation means that pressure/stress variations are assumed to be in mechanical equilibrium over the entire deforming fluid, e.g., transient effects on the timescale of seismic wave-propagation are neglected). The fluid is assumed to have a compressible reference density ρ_r(z) and a reference adiabatic temperature T_r(z), where ρ_r(z) is given by the Adams-Williamson equation-of-state for a compressible homogeneous fluid with an adiabatic compressibility β:

$\begin{array}{ll}\frac{1}{{\rho }_r}\frac{d{\rho }_r}{dz}=-\beta {\rho }_r\left(z\right)g& (8)\end{array}$

and dT_r/dz = αgT_r/C_P. Density is assumed to vary linearly with the difference in deviatoric pressure p from the Adams-Williamson state and with differences in temperature from the reference state:

$\begin{array}{ll}\rho \left(p,T\right)={\rho }_r\left(1-\alpha \left(T-T_r\right)+\beta p\right)& (9)\end{array}$

In this case, the equations describing momentum and mass conservation for this anelastic fluid are:

$\begin{array}{rcll}-p_{,i}+{\tau }_{ij,j}-{\rho }_{r}g\left(\beta p-\alpha \left(T-T_r\right)\right){\delta }_{i3}& =& 0& (10)\end{array}$

$\begin{array}{rcll}{({\rho }_r{u}_i)}_{,i}& =& 0& (11)\end{array}$

As in the incompressible case, if we multiply Equation (10) by the velocity field and integrate over the region, we find:

$\begin{array}{ll}-{\displaystyle \int }{p}_{,i}{u}_{i}dV+{\displaystyle \int }{\tau }_{ij,j}{u}_{i}dV+{\displaystyle \int }{\rho }_{r}g\left(\alpha \left(T-T_r\right)-\beta p\right)u_{3}dV=0& (12)\end{array}$

Again as in the incompressible analog, we use Gauss's Theorem (Equations 4 and 5) and the fact that we have a closed isolated system to transform Equation (12) into:

$\begin{array}{r}{\displaystyle \int }p{u}_{i,i}dV-{\displaystyle \int }{\tau }_{ij}{u}_{i,j}dV+{\displaystyle \int }{\rho }_{r}g\alpha \left(T-T_r\right)u_{3}dV\\ -{\displaystyle \int }{\rho }_{r}g\beta p{u}_{3}dV=0\hfill & (13)\end{array}$

where we have split the gravitational force-integral into separate p− and T−dependent parts. Now Equation (11) describing mass conservation can be written in expanded form as:

$\begin{array}{ll}{u}_{i,i}=\left[-\frac{{({\rho }_r)}_{,i}}{{\rho }_r}\right]u_i=\left[{\rho }_{r}g\beta \right]u_3& (14)\end{array}$

where the Adams-Williamson Equation (8) has been used to simplify the term in brackets in (17). If we now substitute u_{i, i} = ρ_rgβu₃ into the first term in Equation(13), we see that the first and last terms in Equation (13) exactly cancel each other, so that:

$\begin{array}{ll}-{\displaystyle \int }{\tau }_{ij}{u}_{i,j}dV+{\displaystyle \int }{\rho }_{r}g\alpha \left(T-T_r\right)u_{3}dV=0& (15)\end{array}$

In words, Equation (15) states that the viscous dissipation in a compressible fluid is equal to the gravitation power released by rising or sinking thermal density anomalies. In contrast, the advection of compression (pressure)-linked density variations is linked to reversible p − Vpower. The second term in Equation (15) is commonly referred to as “adiabatic heating.” It is a historical accident that the relationship between adiabatic heating and viscous dissipation was derived by a steady-state analysis of the equation for energy conservation (Turcotte et al., 1974; Backus, 1975; Hewitt et al., 1975) instead of from statements of momentum and mass-conservation, so it was not realized at that time how closely gravitational power-release and viscous dissipation are linked in compressible as well as incompressible flow. (Another reason this was not realized by many early workers is because they usually decided to ignore the fourth term (− ∫ρ_rgβpu₃dV) of Equation (13) in their numerical experiments—this is called the “Truncated Anelastic Approximation,” so that their numerical experiments never demonstrated an exact balance between viscous dissipation and gravitational power release (Jarvis and McKenzie, 1980; Leng and Zhong, 2008).

Note that the above derivation does not depend on the assumption of a 1-D adiabatic reference state. For a perfectly adiabatic reference state, viscous dissipation is directly linked to gravitational power release of rising and sinking thermal density anomalies. For a non-adiabatic state, gravitational energy release from rising or sinking density anomalies with respect to a non-adiabatic 1-D background density profile is still directly linked to viscous dissipation, but it is also possible to release or store gravitational energy by changing the horizontally-averaged density vs. depth profile. If the 1-D reference state is subadiabatic, then changing the reference state toward an adiabatic one will consume thermal energy as discussed below in the second thought experiment, while if it is superadiabatic then extra stored gravitational energy will be transformed into viscous dissipation as the 1-D average reference state changes toward a more adiabatic state.

Thought Experiments on the Energetics of Mantle Convection

Motivation and Objectives

After this long theoretical introduction, we will now explore several thought experiments followed by numerical experiments to build intuition on the energetics of mantle-like convection. In particular, we will see how the gravitational power released by rising or falling thermal density anomalies is transformed into viscous dissipation within this convective flow. After discussing these experiments, we will use the gravitational energy perspective to show that surface plates are presently cooling and subducting much faster than is sustainable by internal heating of the mantle, a conclusion that has been previously reached using other approaches (e.g., Hart and Zindler, 1989). From this perspective, we can also see how the adiabatic expansion associated with internal heating continuously transforms a fraction of internal energy production into new gravitational energy. In steady-state, this fraction of heat-production-energy to gravitational energy transformation plus the gravitational energy generated by cooling at the top of the mantle is exactly balanced by an equivalent net amount of gravitational energy transformation into viscous dissipation-heat. This is why it is possible to ignore the roles of the creation and destruction of gravitational energy when considering the energetics of steady-state convection. However, when we estimate the observed rates of these energy transformations within the present-day Earth, we find that present gravitational energy-release by slab-sinking alone is occurring at a much higher rate than the creation of new gravitational energy by the adiabatic expansion associated with internal heating plus the top-cooling of heat sustained by radioactive energy production in the mantle.

Relationships between Surface Heat Loss, Internal/Basal Heating, and Viscous Dissipation within Steady-State Convection

The first thought experiment determines the relationship between viscous dissipation and surface heat loss during steady-state convection within a very idealized basally and internally heated region that loses heat through its upper surface. It reproduces and then builds upon a result first obtained as Equation 36 of Hewitt et al. (1975). (Note that there is a typo in Hewitt et al.'s equation in that both terms in the right-hand side of that equation should be multiplied by the surface area). Like Hewitt et al. (1975), we will assume that all heat transfer occurs by convective flow except in conductive top and bottom thermal boundary layers, and that the fluid is highly viscous so that inertial forces and the fluid's kinetic energy are completely negligible (e.g., we consider “slow viscous flow”). Again like Hewitt et al. we assume for simplicity that the gravitational accelerationg, thermal expansivity α, and specific heat C_p are constant with depth, and the fluid's density ρ depends only on temperature. We first look at the component of viscous dissipation associated with the transport of the basal heat input through the convecting region. Consider a parcel of fluid that loses heat within the top boundary layer and then sinks to the bottom of the box to transfer its “cold” to the bottom boundary layer. The heat-flux Q_B lost through the top boundary layer and gained through the bottom boundary layer is equal to the rate of volume-flux of material through these boundary layers R times the material's heat capacity ρC_p times the mean temperature drop ΔT between the boundary layers, i.e.,

$\begin{array}{ll}{Q}_B=R·\left(\rho C_p\Delta T\right)& (16)\end{array}$

Note that heat transport can be viewed to occur by the convective “switch” of equal mass parcels between the top and bottom boundary layers. The gravitational work released by parcels of cold upper and hot lower boundary layer switching places is equal to the product of their difference in buoyancy force Δρg = ρgαΔT times the distance h between the top and bottom; for a convective volume-flux R, the gravitational energy release Φ (= viscous dissipation) associated with this convective heat transport is

$\begin{array}{ll}{\Phi }_B=R·\left(\rho g\alpha \Delta Th\right)& (17)\end{array}$

Thus, we find that for bottom-heated, top-cooled convection the ratio of viscous dissipation to basal heat input (or equivalently, the ratio of viscous dissipation to surface heat loss) is

$\begin{array}{ll}{\Phi }_B∕Q_B=\left[R·\left(\rho g\alpha \Delta Th\right)\right]∕\left[R·\left(\rho C_p\Delta T\right)\right]=\alpha gh∕C_p=D& (18)\end{array}$

where D = αgh/C_p is the dissipation number of the system.

We can use the same approach to estimate the viscous dissipation associated with the convective transport that removes internally generated heat. Assuming that internal heat production is uniformly distributed within the box, then the average height a parcel will ascend to transport heat between the interior and top surface is half the depth of the box, so that using exactly the same logic but with ΔT now referring to the mean temperature drop between the interior and top boundary layer, and the average parcel only sinking half the depth of the box to release its gravitational energy, the ratio of viscous dissipation to surface heat loss (or equivalently, the ratio of viscous dissipation to internal heat production) for internally heated convection is

$\begin{array}{ll}{\Phi }_I/Q_I=\left[R·\left(\rho g\alpha \Delta Th/2\right)\right]/\left[R·\left(\rho C_p\Delta T\right)\right]=D/2& (19)\end{array}$

Now combine these two results. Define the surface heat loss Q_S(= Q_B + Q_I), where Q_B denotes energy gained by the convecting region through the bottom boundary layer and Q_I energy generated within the convecting region. Then, since Φ = Φ_B + Φ_I, Φ/Q_S = (Φ_B/Q_B)(Q_B/Q_S) + (Φ_I/Q_I)(Q_I/Q_S) = (Φ_B/Q_B)(1 − Q_I/Q_S) + (Φ_I/Q_I)(Q_I/Q_S) = D(1 − Q_I/Q_S) + (D/2)(Q_I/Q_S). If we further define μ≡(Q_I/Q_S)to be the ratio of internal energy production Q_I to surface heat loss Q_S, then, for steady-state convection, the ratio of viscous dissipation to surface heat loss is

$\begin{array}{ll}\Phi ∕Q_S=D\left(1-0.5\mu \right)& (20)\end{array}$

This gravitational-energy-based derivation reproduced—but with much simpler math—Hewitt et al.'s result (Equation 36 of Hewitt et al., 1975).

Let's explore this thought experiment a little further. For a steady-state system, neither its internal temperature nor its net gravitational energy changes with time. This implies that gravitational energy must be created within the system at the same rate that it is released by convective flow. Adiabatic thermal expansion work is what replenishes the gravitational energy of the system. Anticipating the results of the next thought-experiment, when a region of the system absorbs internal heat q (from either internal radioactive decay or viscous dissipation), it expands. If this thermal expansion occurs under a confining pressure, not all of the absorbed heat will go into making a local temperature rise; instead a fraction of the absorbed thermal energy is adiabatically converted into pressure-volume work that lifts overlying material, thereby increasing the gravitational potential energy of the system. The increase in gravitational energy exactly equals the thermal energy decrease from adiabatic expansion, which for material at the bottom of the region is equal to q · (D/(1 + D)). A simple way to determine this effect is to imagine that a layer of mantle of thickness Δz above the CMB at depth h undergoes heating of an amount Q(= ρC_PΔT). The overburden pressure at this depth is P(= ρgh). The thermal expansion δz associated with a temperature increase (ΔT − δT) within a layer of thickness Δz is δz = Δzα(ΔT − δT). This expansion leads to pressure-volume work that induces local cooling of an amount δT = (Δzα(ΔT − δT)P)/(ΔzρC_P) = (α(ΔT − δT)ρgh)/(ρC_P) = D(ΔT − δT), or equivalently, δT = ΔT(D/(1 + D)). Thus, pressure-volume work associated with adiabatic expansion transforms this fraction of the energy input into the base of the region into a corresponding increase in Earth's gravitational energy due to the expansion in Earth's radius by the amount δz.

Now let's consider the effects of this gravitational energy replenishment within a bottom-heated fluid (Figure 1A). As just seen, when heat flows into the bottom, not all of this heat causes a rise in the boundary layer temperature, instead a fraction D/(1 + D) is directly transformed into gravitational energy. This replenishes the gravitational energy of the system at a rate

$\begin{array}{ll}{\dot{G}}^{+}=Q_B\left(D∕\left(1+D\right)\right)=R·\left(\rho C_p\Delta T\right)\left(D∕1+D\right)& (21)\end{array}$

If we substitute C_p = αgh/D obtained by rearranging the definition of the dissipation number D = αgh/C_p, this can be rewritten as

$\begin{array}{ll}{Q}_B(D∕(1+D))=\left[R·(\rho g\alpha \Delta Th)\right]∕(1+D)& (22)\end{array}$

Furthermore, of the viscous dissipation/gravitational energy released by the convective “switching” of the top and bottom boundary layers, only a fraction 1 − (D/(1 + D)) of this dissipation energy becomes thermal heat, while the rest is immediately transformed back into new gravitational energy via adiabatic expansion. Thus, the net rate of gravitational power loss Ġ⁻ by viscous dissipation is

$\begin{array}{l}{\dot{G}}^{-}={\Phi }_B(1-(D∕(1+D)))\\ =-[R·(\rho g\alpha \Delta Th)](1-(D∕(1+D)))\\ =-[R·(\rho g\alpha \Delta Th)]∕(1+D)& (23)\end{array}$

which exactly counterbalances the rate Ġ⁺ at which adiabatic expansion due to bottom heating replenishes the gravitational energy of the system. The same line of reasoning can be applied to steady-state internally-heated convection, with the same conclusion. Thus, if a system is at steady state, then the measured gravitational power-release associated with upwelling and downwellings will be equal to the gravitational power generation by top-cooling plus the adiabatic expansion associated with its internal energy generation. The point that makes this of practical importance, is that, unlike viscous dissipation, these quantities can be directly estimated for the present-day mantle. We will see in a later section that it is likely that much more gravitational power is currently being released than is being replenished by internal heating within the mantle and top-cooling at a rate sustainable by its internal heating—one of the most significant results of this study.

FIGURE 1

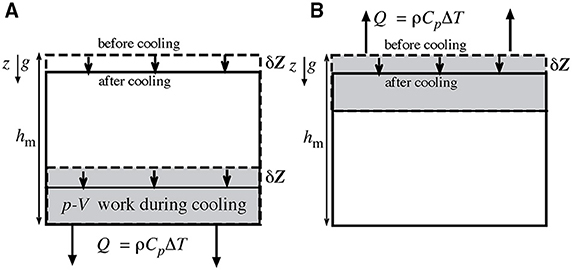
Figure 1. Cartoon illustrating the first thought experiment in Section Thought Experiment on Top vs. Bottom Cooling in the Presence of Gravity comparing the gravitational effects associated with top- and bottom-cooling of the mantle. (A) During bottom cooling, gravitational energy is instantaneously transformed into 'additional' boundary layer heat. (B) During top cooling, similar gravitational energy is created by the heat loss from the cooler, denser boundary layer that forms at the top of the mantle. However, this gravitational energy can only be released if the boundary layer subducts. Note that neither of these cooling scenarios is in thermal and gravitational equilibrium, for this to occur, the heat-loss must be distributed uniformly through the mantle, i.e., at an average mid-mantle depth. See text for further discussion.

Thought Experiment on Top vs. Bottom Cooling in the Presence of Gravity

The next thought experiment lets us better visualize the energy transformations inherent in mantle convection. This thought-experiment focuses on the similarities and differences between how gravitational energy is released when a fluid cools from its top or bottom and also illustrates the important role of adiabatic expansion. The physical origin and necessity of viscous-dissipation heating from sinking slabs is highlighted by comparing cooling from the bottom and top of a fluid in the presence of gravity. Again for simplicity we will assume that the gravitational acceleration g, thermal expansivity α, and heat capacity C_p are constant with depth, while the fluid's density ρ depends only upon temperature.

First, imagine that a fluid-filled box of height h with insulating side walls is cooled from the bottom by an amount Q = Δz(ρC_pΔT) until a cold thermal boundary layer of thickness Δz forms as sketched in Figure 1A. The boundary layer contracts by δz = −Δzα(ΔT − δT) as it cools, which induces pressure-volume work of an amount ρgzδz = Δzρghα(ΔT − δT). This pressure-volume work is adiabatically transformed into additional boundary layer heat of an amount ΔzρC_pδT = Δzρghα(ΔT − δT). Thus, cooling of the bottom boundary by the amount Q = Δz(ρC_pΔT) has indeed led to a net energy loss equal to Q, but the bottom boundary layer temperature has cooled by only ΔT − δT = ΔT/(1 + D), with the same definition as above of the dissipation number D = αgh/C_p. The bottom boundary layer has not cooled by as much as the extracted thermal energy because adiabatic pressure-volume work on the cooling boundary layer has transformed ΔzρC_pΔT(D/(1 + D)) of the box's gravitational energy into heat.

Now imagine that the same fluid-filled box is cooled from the top (Figure 1B) until a cold, unstable thermal boundary layer of thickness Δz and temperature anomaly ΔT develops (but does not yet sink). This boundary layer contracts by δz = ΔzαΔT as it cools, but since the top surface is stress-free, no work is initially done on the fluid and only heat is lost. Now if we insulate the top boundary and let the fluid sink to the bottom of the box to reach the same configuration as in the previous bottom cooling case, then a fraction of the top boundary layer's gravitational energy ρghΔzα(ΔT − δT) will be transformed into viscous dissipation heat. [As seen above in Equation (21), a fraction D/(1 + D) of the boundary layer's gravitational energy will be adiabatically transformed back into gravitational energy instead of heat; this is the origin of the δT term in the previous expression]. The net cooling and total internal energy change are the same as in the bottom-cooled example. The difference is that gravitational work is immediately released during the cooling event for bottom-cooling, while this work is delayed in the top-cooling scenario until the unstable top boundary layer actually sinks and releases its stored gravitational potential energy.

The scenarios in Figures 1A,B are both still in thermal disequilibrium; for this to exist the entire box must re-equilibrate both thermally and gravitationally. This thermal change can occur without convection since a cold bottom boundary layer is gravitationally stable. The net effect is to slowly conduct heat downward so that the average temperature drop in the box occurs at the mid-box pressure instead of the pressure at the base of the box. This heat transfer is associated with heating and expansion of the lower region as the upper region cools and contracts. It reduces the final gravitational energy release associated with top- or bottom-cooling by a factor of two—the average heat-loss occurs at the ambient mid-box pressure ρgh/2 instead of the bottom-box pressure ρgh. During the initial bottom boundary layer cooling “transient,” more gravitational energy was transformed into heat than is compatible with the thermal equilibrium of the box, so that eventual equilibration occurs by the further transformation of internal heat into gravitational energy.

Adiabatic Effects Transform ~14% of the Mantle's Heat Production into Gravitational Energy

We have already seen in Section Relationships between Surface Heat Loss, Internal/Basal Heating, and Viscous Dissipation within Steady-State Convection that because the mantle expands adiabatically when heated, a fraction of any interior heat production is transformed into increased terrestrial gravitational energy instead of heat, with the stored gravitational energy reversibly transformable back into heat should the interior ever cool. The same approach also works to determine the depth-dependent fraction that will be transformed in a more Earth-like mantle and core. Again assume the mantle has energy equivalent to Q = Δz(ρC_pΔT) emplaced into a layer of thickness Δz that is at an ambient pressure P. This energy input will induce thermal expansion that is associated with adiabatic pressure-volume work Pα(ΔT − δT)Δz, where the energy transformed into an increase in gravitational energy is also seen as a local “adiabatic cooling” δT associated with this work Δz(ρC_pΔT). We can rewrite this equivalence as:

$\begin{array}{r}\rho C_P\delta T=\rho C_{P}P\alpha \left(\Delta T-\delta T\right)∕\left(\rho C_P\right)or\rho C_P\delta T\left(1+\left(\alpha P∕\rho C_P\right)\right)\\ =\rho C_P\Delta T\left(\alpha P∕\rho C_P\right).\hfill & (24)\end{array}$

The fraction of energy transformed into gravitational energy by pressure-volume work as the mantle (or core) heats is

$\begin{array}{ll}\left(\rho C_P\delta T\right)∕\left(\rho C_P\Delta T\right)=\left(\alpha P∕\rho C_P\right)∕\left(1+\left(\alpha P∕\rho C_P\right)\right).& (25)\end{array}$

We assume the heat capacity of the mantle to be 1187 J/kg-K [the Dulong-Petit value for a mantle with the composition of PRIM (Hart and Zindler, 1989)] and for the core to be 840 J/kg-K (Nimmo, 2007), If we further assume the mantle's (Birch, 1968) and core's (Labrosse, 2003) thermal expansivities decrease linearly with depth as shown in Figure 2A and Table 1, while the depth-dependent mantle and core density and gravity are given by PREM (Dziewonski and Anderson, 1981), then the resulting fraction of internal heating transformed into gravitational energy is shown in Figure 2B. Adiabatic effects will transform almost no low-pressure uppermost mantle heating into gravitational energy, a maximum of ~19% of heating near the base of the mantle into gravitational energy, and a (per-unit-mass) average amount of ~14% of uniform mantle heating and 29% of uniform core heating into gravitational energy (see Figure 2B). This estimate agrees quite well with an estimate based on a different approach by Stacey (1981), who evaluated the extra gravitational energy released during secular cooling of the Earth's mantle and core. Stacey found that uniform secular cooling of mantle and core releases 17% “extra” heat by the adiabatic transformation of gravitational to thermal energy during cooling (Stacey, 1981). We find 19% average adiabatic transformation per unit mass for Earth's mantle and core, with the depth-dependent adiabatic transformation distribution shown in Figure 2B.

FIGURE 2

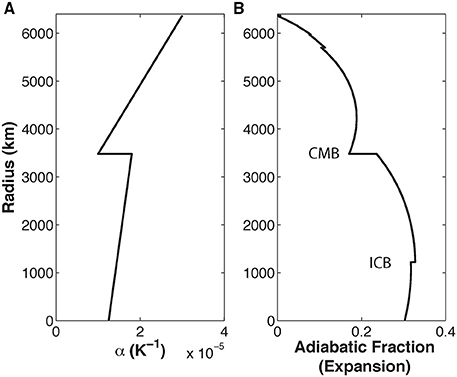
Figure 2. The fraction of heat release (or consumption) associated with adiabatic contraction (or expansion) in a PREM-like Earth. Section Adiabatic Effects Transform ~14% of the Mantle's Heat Production into Gravitational Energy describes how this result is obtained. (A) Depth-dependent thermal expansivity of the mantle (Birch, 1968) and core (Labrosse, 2003) that was assumed for this calculation (equations given in line 7 in Table 1). (B) Resulting adiabatic fraction of transformed heat for a PREM-like mantle and core pressure and density and the thermal expansion profile shown in panel (A). On average, this calculation shows the mantle would transform 14% of internal heating into gravitational potential energy, the core 29% of its internal heating, and the mantle plus core together 19% of their internal heating into gravitational potential energy. This gravitational energy would be reversibly transformed back into heat if they cooled and contracted under pressure.

TABLE 1

Table 1. Variables and definitions used to estimate present-day mantle energetics.

Transformations between Gravitational and Thermal Energy in Steady-State and Transient Mantle Convection

With this additional background, let's revisit the first thought experiment as it applies to an Earthlike mantle. Consider the energy transformations that occur in steady-state convection in a mantle layer heated from below without any internal radioactive energy production. In this case (see Figure 3A), the heat Q_B supplied to the base of the mantle is equal to the heat Q_S lost through the top-surface and neither the mean mantle temperature nor its gravitational energy changes with time. Yet, for an Earthlike mantle the incoming heat-flux at the base of the mantle leads to ~18% transformation of the thermal energy input into adiabatic pressure-volume expansion (Figures 2B, 3B), adiabatic work that raises the gravitational energy of overlying mantle instead of increasing the local temperature/thermal energy at the base of the mantle. Since a steady-state system's gravitational and thermal energy remain constant, another convection-related process—namely viscous dissipation—must be continually transforming the same net amount of gravitational potential energy back into internal heat. Thus, even steady-state convection of a compressible Earthlike mantle heated at its base must induce internal viscous heating that is a significant fraction of the heat-flux across its bottom and top thermal boundary layers. Next, consider a final thought-experiment that illustrates how most of the gravitational energy released by a sinking slab or rising plume is transformed into viscous dissipation instead the gravitational potential energy gain associated with advectively deflecting an internal density interface away from its equilibrium rest state.

FIGURE 3

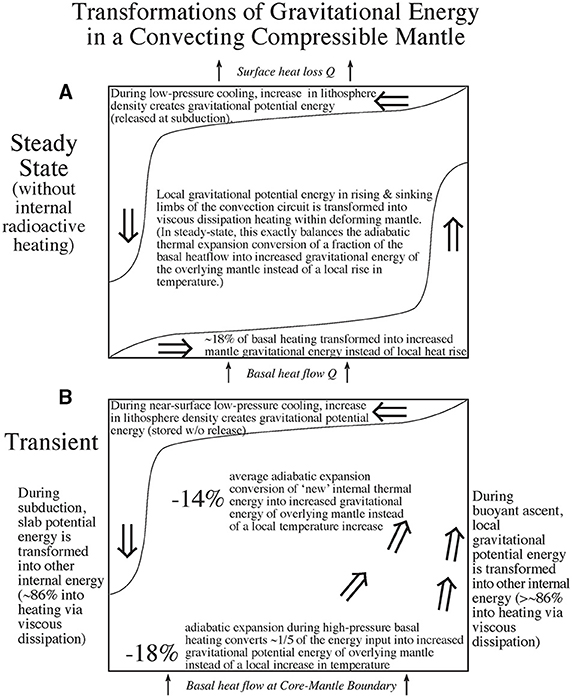
Figure 3. Transformations between gravitational and thermal energy in a convecting mantle. (A) Steady-state convection driven by bottom-heating. For a PREM-like compressible mantle, roughly one-fifth of the heatflow into the base of the layer is transformed through adiabatic expansion into increasing the gravitational energy of the overlying mantle instead of the local thermal energy of the base. To maintain steady-state, an equal amount of gravitational energy must be continually transformed by viscous-dissipation back into thermal energy. This implies that internal viscous-dissipation heating must be larger than a fifth of the basal heatflow—because ~14% of the energy released by viscous dissipation, if uniformly distributed through the mantle, would be transformed by adiabatic expansion into gravitational instead of thermal energy. (B) Sites of possible energy transformation in transient convection of a PREM-like mantle that is heated both within and below.

Gravitational Energy Stored by Non-Hydrostatic Deflections of Internal Density Interfaces and the Earth's Surface is Negligible in Comparison to Viscous Dissipation

In the thought-experiment illustrated in Figure 4, a small dense point-mass sinks through two viscous layers of differing density. When the mass begins to sink (between time-step 0 and 1), it creates flow-induced stresses that deflect the internal density interface, thereby transforming gravitational energy released by the sinker's descent into internally stored gravitational potential energy associated with the non-hydrostatic deflection of the internal density interface. During this transient time-interval, most of the gravitational energy release from the sinker is being transformed directly into another form of stored internal gravitational energy. But this phase is short-lived, having a timescale similar to that of post-glacial mass readjustments (Figure 5E shows a numerical demonstration of this effect). It lasts only until the interface has been deflected so that its internal relief has a net “mass anomaly” comparable to that of the sinker. As the sinker continues to descend (time-steps 2 to N), only a small fraction of the sinker's released gravitational energy is transformed into additional interface gravitational energy. While approaching the interface, most of the sinker's gravitational energy release goes into viscous dissipation associated with the flow-induced stress-field resisting the sinker's descent. Once the sinker descends beneath the interface, the interface itself begins to return some of its internal “stored” gravitational energy as it returns toward its neutral state. Eventually, at time-step N when the sinker has reached the bottom of the region, all of its gravitational potential energy has been transformed into viscous dissipation. The internal density horizon delayed this transformation during the start-up transient when it generated an internal surface-deflection of density anomaly comparable to that of the sinker, but only to return this energy when it deformed back into its neutral hydrostatic state. This thought-experiment suggests that for typical slab-subduction speeds of ~100 km/Ma, the onset of plate subduction in a given region will be associated with a brief period where the gravitational energy release from slab subduction goes into deflecting the 410 and 660 km internal density horizons. After this brief onset phase [these interfaces at present have less than ±15 km of long-wavelength internal relief (Shearer, 2000)], almost all subsequent gravitational energy released by slab descent will be transformed into viscous dissipation. This means that when estimating the current energetics of the mantle we can safely neglect the gravitational energy storage at internal density interfaces.

FIGURE 4

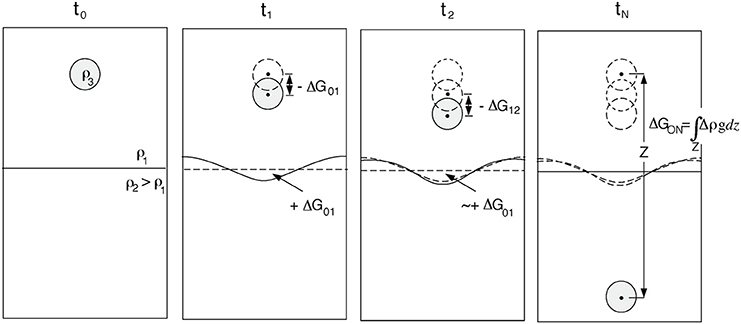
Figure 4. Cartoon illustrating a thought experiment that illustrates the gravitational energy changes and viscous dissipation work associated with a sinking density anomaly in an internally density-stratified viscous fluid. (t₀) A density anomaly ρ₃ − ρ₁ is introduced into a density-stratified viscous fluid. (t₁) The initial flow-response to this density anomaly is for internal flow to create dynamic flow-stress-supported relief on the internal density interface that creates non-hydrostatic stresses opposing the sinker's descent. During this interval, some of the gravitational energy release by the sinker's descent is transformed into gravitational potential energy associated with the non-hydrostatic interface deflection, and some goes into viscous dissipation within the deforming fluid region. (t₂) Subsequent descent of the sinker is associated with much smaller changes to the interface relief as the net “mass anomaly” of the displaced interface barely changes, it mainly becomes more localized as the sinker nears the interface. During this descent, almost all of the sinker's gravitational energy release is transformed into viscous dissipation within the fluid while the strored gravitational energy at the interface stays roughly the same. After the sinker passes through the interface, the interface relief decreases as its stored gravitational energy is transformed back into viscous dissipation within the fluid and the interface returns toward its neutral hydrostatic state. (The sinker also loses less gravitational energy as it descends because its local density constrast is now reduced to ρ₃ − ρ₂.) (t_N) When the sinker has reached the base of the layer, all of its gravitational energy release has been converted into viscous dissipation within the layer.

FIGURE 5

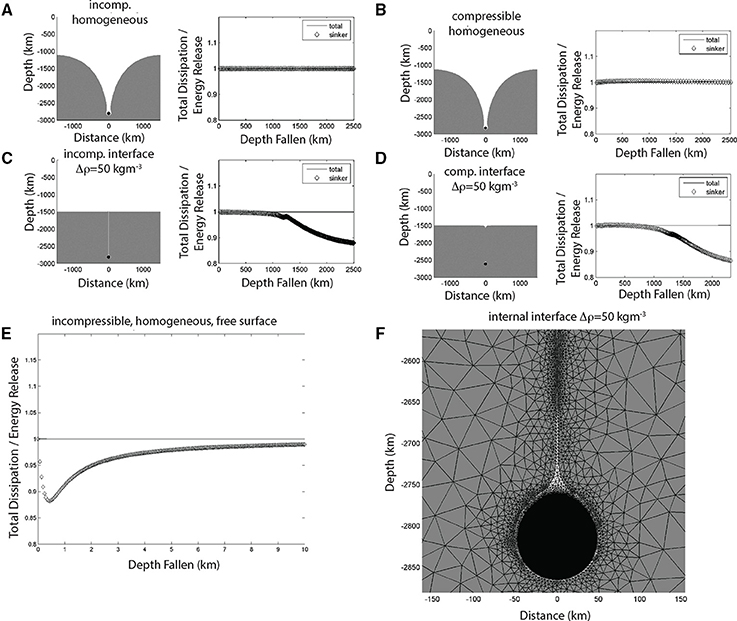
Figure 5. Numerical experiments that further explore the thought experiment detailed in Figure 4. (A) A dense sinker falling in an incompressible fluid of uniform density (l hs) Final configuration for a sinker initially released at a depth of 300 km below the surface. Here the black ball shows the cylindrical sinker, while the white region is material that was shallower than 1500 km depth when the sinker began to fall. (rhs) Ratio of viscous dissipation to net gravitational energy release shown by solid line, while the diamonds show this ratio estimated by only considering the gravitational energy release of the sinker. (B) A dense sinker falling in a compressible fluid otherwise similar to (A) (l hs) Final configuration for a sinker initially released at a depth of 300 km below the surface. Here the black ball shows the cylindrical sinker, while the white region is material that was shallower than 1500 km depth when the sinker began to fall. (rhs) Ratio of viscous dissipation to net gravitational energy release. (Labels defined in A). Note the almost exact similarity between the incompressible (A) and compressible (B) numerical experiments. (C) A dense sinker falling in an incompressible fluid with an internal density interface at 1500 km depth. (l hs) Final configuration for a sinker initially released at a depth of 300 km below the surface. Here the black ball shows the cylindrical sinker, while the white region is material that was shallower than 1500 km depth when the sinker began to fall. (rhs) Ratio of viscous dissipation to net gravitational energy release. (Labels defined in A). In this case, because of entrainment effects (shown as a blow-up in F), the net gravitational energy release is only ~85% of that estimated by considering only the mass-density anomaly of the sinker. (D) A dense sinker falling in a density-stratified compressible fluid otherwise similar to (B). (l hs) Final configuration for a sinker initially released at a depth of 300 km below the surface. Here the black ball shows the cylindrical sinker, while the white region is material that was shallower than 1500 km depth when the sinker began to fall. (rhs) Ratio of viscous dissipation to net gravitational energy release. (Labels defined in A). Note again the almost exact similarity between the incompressible (C) and compressible (D) numerical experiments. (E) Startup transient for a dense sinker falling in an isodensity incompressible fluid like (A) but with a free top surface. For the first few km of descent, there is a small startup transient where ~10% of the gravitational energy release from the sinker is stored as gravitational potential energy in the deflected free surface. After this short transient, the experiment becomes identical to (A), illustrating that there is negligible gravitational energy stored in dynamic deflections of the top and bottom surfaces to the mantle. [Panels (C,D) demonstrate the same conclusion for gravitational energy storage at a internal density interface]. (F) Blowup of the upper layer material (white) entrained by the dense sinker (black) into the 50 kg/m³ denser layer in (C). The finite element mesh is also shown by black lines. Because of this entrainment-induced mixing between the upper and lower layers, the net gravitational energy release is slightly lower than that of the ball alone.

Estimates based on observational constraints of observed dynamic relief indicates that we can also safely neglect gravitational energy storage at the top and bottom of the mantle. For example, imagine that we have 1 km of dynamic stress-supported relief on Earth's surface, an amount greater than the upper end of values consistent with the observed distribution of seafloor depths that are predominantly influenced by the near-surface cooling of the ocean lithosphere as it ages. A km of dynamic relief over Earth's surface of area A is associated with stored gravitational energy $A\underset{0}{\overset{h}{\int }}\Delta \rho gzdz$ = AΔρgh²/2 or 5.75 × 10²⁴ of stored potential energy for A = 5.1 × 10¹⁴ m², the surface density contrast Δρ = 2300 kg/m³, gravity g = 9.8 m/s², and h = 1000 m. This amount of stored gravitational energy is only equivalent to storing the gravitational energy released by ~20,000 years of global subduction at a present-day-like rate of ~10 TW. Even 10 km of global dynamic surface relief would only store gravitational energy equivalent to that released during the last ~2 Ma of recent subduction. Since AΔρ for the CMB is only 1/3 as large as at Earth's surface, the CMB also contains negligible stored gravitational energy for current seismic estimates of relief that range from ±1.5 (Sze and van der Hilst, 2003) to ±6 km (Morelli and Dziewonski, 1987; Obayashi and Fukao, 1997; Boschi and Dziewonski, 2000). Likewise, the maximum stored gravitational potential energy at the 410 and 660 km mantle density interfaces can be estimated from seismic observations that they contain less that ~15 km of associated dynamic relief (Shearer, 2000). PREM estimates for the density jumps across these interfaces are 180 kg/m³ across the 410 km discontinuity and 389 kg/m³ across the 660 km discontinuity [note only half this amount is inferred from seismic estimates based on the observed velocity and impedance contrast across the 660 km discontinuity (Shearer and Flanaghan, 1999; Kato and Kawakatsu, 2001)]. Using PREM values for density jumps and gravitational acceleration, AΔρ for the 410-km discontinuity is 8.7% as large as at Earth's surface, and AΔρ for the 660-km discontinuity is 14% as large as at Earth's surface. If ~15 km of dynamic relief were stored at each surface, their stored gravitational energy would be equivalent to the gravitational energy released by ~0.3 Ma (410-km discontinuity) and 0.6 Ma (660-km discontinuity) of recent subduction. These are also negligible amounts of stored gravitational potential energy within the convecting mantle.

Numerical Experiments

Because the above thought experiment is critical to our following discussion, we have verified it with 2D numerical experiments of incompressible and compressible slow viscous flow. The incompressible experiments were done using the MILAMIN code (Dabrowski et al., 2008), and the compressible experiments were done with our modified version of the MILAMIN code, with changes made to implement the anelastic compressible liquid (ALA) approximation (Jarvis and McKenzie, 1980; Leng and Zhong, 2008). These code modifications are described in Appendix A (Supplementary Material). In the compressible experiments, the depth-dependent density, pressure, and gravity all follow an Adams-Williamson equation of state (see Appendix A in Supplementary Material).

The first numerical experiments show the reference case of incompressible and compressible flow of an isoviscous fluid that has a single cylinder-shaped density anomaly sinking within it. In this case, the net gravitational energy release is simply the potential energy change of the sinking cylinder; this energy is completely transformed into viscous dissipation in both the incompressible (Figure 5A) and compressible (Figure 5B) experiments.

In the second set of experiments shown in Figures 5C,D, the cylinder sinks within a fluid containing a single internal density interface. After the short start-up phase described in the above thought experiment (Figure 4), the gravitational energy release of the sinking cylinder transforms into viscous dissipation within the fluid. There is an additional complexity when the cylinder sinks beneath the internal density horizon, but the complication is linked to entrainment effects, not the presence of significant stored gravitational energy within the deflected interface. Because the sinking cylinder entrains a small but discernable amount of lower-density upper layer fluid into the denser lower layer, this reduces the net gravitational energy release as the cylinder sinks. The entrainment occurs both around the cylinder, and as a small “tail” of fluid connecting the sinker to the upper layer. Figure 5E shows a zoom of this entrained fluid. Entrainment is a entropy-like effect for the gravitational energy of a stratified viscous fluid that tends to homogenize the upper and lower layers and so slightly reduce the net gravitational energy release associated with the sinking cylinder. The viscous dissipation remains equal to the net gravitational energy release, as shown in the black lines in the rhs of Figures 5C,D. This effect is linked to the viscosity of the fluid, not its compressibility, since both the compressible and incompressible experiments have nearly identical dissipation patterns (compare rhs panels of Figures 5C,D).

For completeness, we also performed a similar numerical experiment to illustrate the gravitational energy stored by dynamic topography at the top free surface of a viscous fluid. This free surface calculation is more computationally intensive since we resolve the surface evolution at a much shorter time-scale characteristic of post-glacial rebound. In this experiment (see Figure 5E) we see that there is a short-lived start-up phase where the free-surface deforms so that its buoyancy-linked stresses balance those induced by flow driven by the sinking cylinder. After this short transient start-up phase, subsequent gravitational energy release is transformed into viscous dissipation within the fluid. As the cylinder moves away from the top surface, its small amount of stored gravitational energy also transforms into dissipation as the surface returns to a flat geometry. This behavior verifies another pattern anticipated from the above thought experiment.

These numerical experiments show that, for an unstratified fluid, the gravitational energy release estimated by considering only the sinking of the density anomaly that drives the viscous flow is equal to the dissipation within the fluid. For a fluid containing an internal density stratification, the dissipation is >85% of the dissipation estimated from the sinking of the density anomaly, and is exactly equal to the net gravitational energy release. There is a second-order complication in that viscous entrainment somewhat reduces the net gravitational energy release associated with the sinking density anomaly in the lower mantle, because the sinker drags a small amount of upper mantle along with it as it falls into the lower mantle. Here we will choose to neglect the potential effect of viscous entrainment when estimating the mantle dissipation induced by sinking slabs since observational uncertainties are larger than ~15%, and also since we also usually choose to neglect the up to ~50% additional contribution of gravitational energy release due to buoyant ascending plume material.

Observational Constraints on Mantle and Core Energetics

Observational Constraints on Gravitational Energy Release from Present-Day Slabs and Plumes

Now let's assess the present-day gravitational energy release and generation in Earth's mantle. The gravitational energy release from sinking slabs is easy to estimate, and we will see that it is ~11-14 TW. An upper bound on the gravitational energy release from rising plume mantle is also easy to determine—if deep mantle plumes begin their ascent with same magnitude temperature contrast as sinking slabs, then the maximum amount would be about half the energy release from an equivalent downward flux of sinking slabs, because adiabatic effects enhance the temperature contrasts between cold downwellings and surrounding mantle while they diminish the temperature contrasts between hot upwellings and their surroundings as will be discussed in the next section. We will see that present-day gravitational energy release is much higher than would be predicted for steady-state internally-heated mantle convection.

The gravitational power release by sinking slabs is obviously a lower bound on the mantle's gravitational energy release because it neglects the gravitational power release from plume upwelling that may be the return flow to sinking slabs. However, we will see below that sinking slabs are quite likely to be ~2/3 of the gravitational energy release within the mantle. The rate of gravitational energy release is the product of the slabs' weight anomaly Δρg, the mean speed of slab sinking, and the mean depth h to which cold slabs sink within the mantle, i.e., the gravitational energy release from subducting slabs is ~Δρgh multiplied by the current volume flux of subducting slabs (See Figure 6). Details of the estimates summarized in Figure 6 will be considered in later sections. Table 1 summarizes these notational definitions and values. The slab's density anomaly is directly proportional to the heat that the oceanic lithosphere has lost while cooling near the Earth's surface. Recent seismic studies suggest that many slabs subduct deeper than 1000 km in the mantle, and, based on the good correlation between the low-harmonic shear-wavespeed structure of D″ compared and the surface locations of recent plate subduction, that at least some slabs reach the core–mantle boundary at depth h_m (Masters et al., 1996). Here, the depth to which slab material sinks within the mantle is parameterized by a function ϕ(z), which is the fraction of slab material that reaches a depth z. (i.e., if ϕ equals 1 at a given depth, then all slab material reaches at least this depth). Note that the slab mass anomaly depends on the depth-dependence of its coefficient of thermal expansion. Thermal expansivity is believed to linearly decrease with increasing pressure (Birch's Law, Birch, 1938), so that, at the base of the mantle, the thermal expansivity is ~1/3 its near-surface value (Birch, 1968).

FIGURE 6

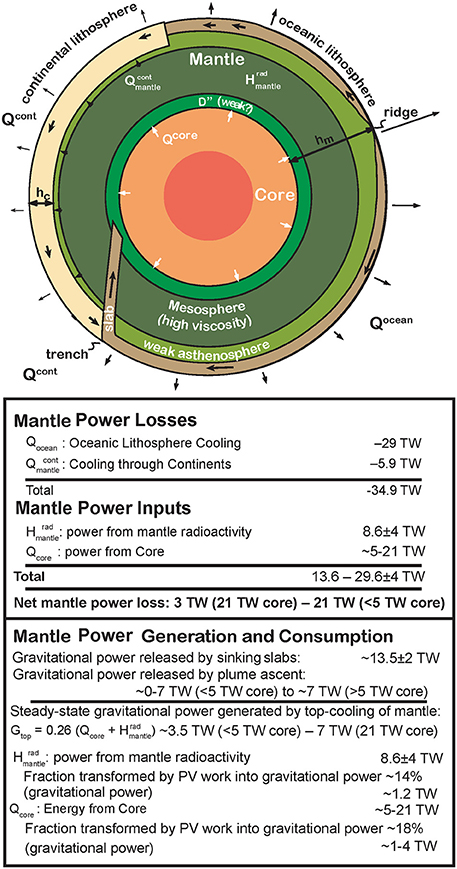
Figure 6. A sketch showing the current modes and amounts of heat loss and energy supply for Earth's mantle. All heatfluxes and energy production/loss rates are in units of TW (10¹² W). Dense subducting oceanic slabs contain significant gravitational energy. This energy is released into the mantle as viscous dissipation, at a present-day rate comparable to the energy released by radioactive decay of U, Th, and K within the mantle. See Tables 1–3 for further summarized details of mantle and core energetics.

As we see in Table 1, the slab's stored gravitational energy is large. Roughly 1/3-1/2 of the heat loss from the cooling of oceanic plates—11 to 14 TW—is being transformed into gravitational potential energy. Adiabatic effects on the downgoing slab will augment both the slab's temperature contrast relative to an “average mantle adiabat” and its gravitational work, leading to an increase in mantle viscous dissipation but no net change in the mantle's heat. These effects will be further explored in the next section. Since, the Earth's surface is a free surface, gravitational slab energy cannot be transformed into work that loses energy outside the earth. Similarly, only a negligible amount of this work can be lost in affecting the moon's orbit (Oxburgh and Turcotte, 1978), or in heating near-surface faults through surface plate deformation. Therefore, upon slab subduction, this energy will heat Earth's interior. Ultimately, the Earth will also contract as it cools, and pressure-volume work will adiabatically transform some gravitational potential energy into heat within the contracting mantle and core. Since there is no obvious mechanism for the mantle to do other work on the shear-stress-free surface of the outer core, most of the slab's potential energy appears likely to be transformed into viscous dissipation and gravitational energy within the Earth's mantle. At present, the average rate of gravitational slab work is large in comparison to the mantle's internal radioactive energy production (see Table 1). This suggests that local heating from viscous dissipation has the potential to have a significant effect upon the structure of present-day mantle convection if this heating preferentially occurred within already hotter and weaker flow circuits within the mantle as explored in Section The Structure of Viscous Dissipation within the Mantle.

Adiabatic Effects Increase the Local Slab-Mantle Temperature Contrast and Slab Power

Adiabatic effects will increase the temperature and density contrast between a cold subducting slab and its surrounding hotter ambient mantle. Hotter ambient mantle heats up more during descent along its adiabat than cooler slab mantle does along its, because the local adiabatic gradient

$\begin{array}{ll}d{T}_{ad}∕dz=\alpha gT∕C_p& (26)\end{array}$

is a linear function of the local temperature. For the same reason, hot upwelling plumes will have larger adiabatic cooling than their surrounding cooler mantle that will tend to decrease their temperature contrast with surrounding ambient mantle. Note that while this effect increases the amount of gravitational power that is released by a slab as it sinks, it leads to no net change in total mantle energy—the ~30% depth-averaged decrease in thermal energy from the slab's extra cooling with respect to ambient warmer mantle is exactly balanced by an equivalent increase in the gravitational energy release associated with slab-sinking. However, it does increase the viscous dissipation within the mantle that is induced by subducting slabs by a further ~30% (see Table 1). To estimate the impact of adiabatic effects on the slab temperature, compare the adiabatic temperature gradient dT_s/dz within the subducting slab, dT_s/dz = α(z)gT_s(z)/C_p, with that of the average ambient mantle, dT_m/dz = α(z)gT_m(z)/C_p. Subtracting these two relations, we find that the temperature difference ΔT_sm = T_s − T_m between the slab and ambient mantle increases with depth, i.e., dΔT_sm/dz = α(z)gΔT_sm(z)/C_p. If $\Delta T_{{}_{sm}}^0$ is the temperature difference between the incoming slab and adjacent ambient uppermost mantle, then the gravitational work per kg due to subduction by Δz will be $\Delta z\alpha g\left(\Delta T_{sm}^0+\Delta T_{sm}^a\right)$. The additional adiabatic cooling of the slab relative to ambient mantle is $\Delta z\left(c_{p}d\Delta T_{sm}^a/dz\right)=\Delta z\alpha g\Delta T_{sm}^a$, equal and opposite to the adiabatic increase in the rate of gravitational work. Furthermore, the extra adiabatic slab-cooling with depth is $\Delta T_{ms}^a(z)=\Delta T_{ms}^0\left(exp(\bar{\alpha }gz/c_p)-1\right)$, where $\bar{\alpha }$ is the thermal expansivity averaged over the depth interval z. Thus adiabatic effects act to further cool the subducting slab, while creating an equivalent amount of extra energy through enhanced viscous dissipation.

Observational Constraints on the Mantle's Heat Loss through the Surface and Internal Radioactive Heating

The geologic record of the basaltic products of mantle melting indicates that the mantle has cooled by < 25–50 K/Ga through the past ~3.5 Ga (see Figure 7) (Jarvis and Campbell, 1983; Campbell and Griffiths, 1992; Abbott et al., 1994; Herzberg et al., 2010). This implies that the mantle's energy loss through Earth's surface has been balanced, to within ~25–50 K/Ga, by internally generated energy—radioactive mantle heating and heating from core heatflow (Gubbins et al., 1979) that will be examined in Section An Outline of Core Energetics with Implications for Heatflow into the Base of the Mantle. Mantle secular cooling will release both thermal and gravitational energy at the rate

$\begin{array}{l}1.14M_{mantle}{C}_P=1.14\times \left(4.04\times 10^{24}kg\right)\times \left(1167J∕kg-K\right)\\ =5.37\times 10^{27}J∕K& (27)\end{array}$

where M_mantle is the mass of the mantle, C_P the mantle heat capacity (Dulong-Petit limit for a PRIM composition), and the 1.14 factor accounts for the mean mantle gravitational energy release during secular cooling of a PREM-like mantle (Figure 2B). Mantle secular cooling would release 2 × 10²⁹ J/Ga of energy for a secular cooling rate of 37.5 K/Ga.

FIGURE 7

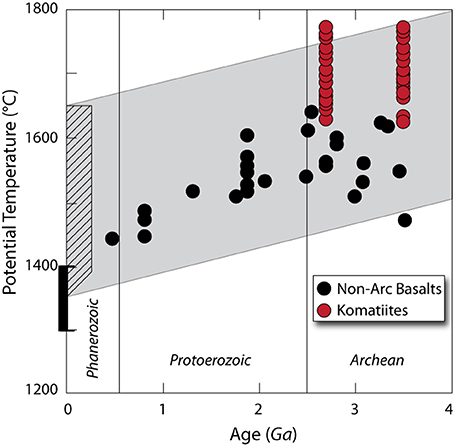
Figure 7. Petrological estimates of mantle potential temperature (T_P) for non-arc lavas and komatiites from Herzberg et al. (2010). The black rectangule at zero age marks their estimate for the range of the present-day potential temperatures of MORB-source mantle. The diagonal crossed area is their range of estimated T_P of Phanerozoic mantle plumes. Gray band corresponds to secular cooling of the mantle at an average rate of 37.5 K/Ga. Modified from Herzberg et al. (2010).

Note that actual heat transport in the upper 100 km by the ascent of basaltic magmas is about the same as that by a comparable volume of ascending peridotite. Basalts have a latent heat of crystallization per unit volume equivalent to the heat associated with a temperature that is enhanced by 300 K, i.e., ρC_P(300K). This enhances their ability to transport heat by ~1/5 relative to solid material, but peridotites are ~1/6 denser than basaltic magmas which almost counterbalances this effect. If plates moved much faster in the Archean so that the subducting thermal boundary layer was thinner than the depth of basalt generation and heat removal via the latent heat of melting, then heat transport by rising magmas would enhance heatloss from the regions below the thermal boundary layer, but as only a second-order effect.

Historically, geochemical estimates of the radioactive element budget of the Earth (Jagoutz et al., 1979; Hart and Zindler, 1989; McDonough and Sun, 1995; Palme and O'Neill, 2003; Lyubetskaya and Korenaga, 2007a,b) have been based on the assumption that refractory lithophile elements (i.e., elements, such as U and Th, that condense at high temperature from the solar nebula and concentrate in the silicate parts of planets) are present in chondritic relative proportions in the Earth and all these models yield similar estimates of total terrestrial heat production of around 20 ± 0.5 TW. Hart and Zindler (1989) inferred that the mantle is currently losing 2.7 times as much heat as is produced by radioactive decay. A more recent estimate of the Earth's composition that somewhat relaxes the constraint of chondritic relative abundances of refractory lithophile abundances (RLE) by Lyubetskaya and Korenaga (2007a,b) yields a 20% lower radioactive heat production of about 16 TW, implying an even greater ratio of present-day heat loss to radiogenic heat production. In the following discussion, we argue that actual heat production may be even lower than estimated by Lyubetskaya and Korenaga and that the Urey ratio, the ratio of current heat production to current heat loss in the Earth, may be as low as 0.3. Since much of the heat production is in the crust, this ratio is even lower in the mantle.

We begin by assessing the current surface heat loss of the mantle. (As discussed above, surface heat loss and associated lithospheric cooling is also linked to the creation of gravitational potential energy, which we will estimate below.) Mantle heat loss through the cooling and growth of ocean lithosphere is easy to estimate (Parsons and Sclater, 1977; Stein and Stein, 1992), since the total heat removal from the oceanic lithosphere is directly measurable through its effect on the cooling and deepening of the ocean seafloor through time, which is associated with an age-dependent conductive heat flux $q\left[mW/m^2\right]=473/\sqrt{age\left[Ma\right]}$ (Parsons, 1982). This approach yields a value of 29 TW (Sclater et al., 1981; Parsons, 1982; Mareschal and Jaupart, 2011) (cf. Figure 6 and Table 1). This estimate of heat flow is larger than measurements with conductive heat probes on young ocean seafloor, but the discrepancy is thought to be caused by a component of hydrothermal heatflow from the ocean crust that conductive heat probes do not measure (Stein and Stein, 1992) except when young seafloor is heavily sedimented (Davis and Chapman, 1996).

Mantle heat loss through the base of the continents is more difficult to quantify. The average continental heat flow is 63 mW/m², corresponding to 13.1 TW lost through the entire continental area) (Mareschal and Jaupart, 2011). However, most of the heat lost through the continents is produced by radioactive decay within the continental crust, so that the mantle heatflow through continents is significantly less. Two independent approaches give similar answers for mantle heat loss through the continents. The simpler, but less accurate, approach is to assume that continents are in steady-state equilibrium, and that the thickness of the continental lithosphere, determined from seismic measurements (cf. Larson and Ekström, 2001) averages roughly 175 km. In this case, for a continental lithosphere conductivity of 3 W/m-K, and surface and mantle temperatures of 0 and 1400°C, respectively, and an assumed linear continental geotherm, the mantle heat flux is on the order of 25 mW/m² [5.2 TW for the entire continental area of 2.073 × 10¹⁴m² (Davies and Davies, 2010)].

A better way to estimate mantle heatflow through the continents is to determine and subtract the contribution from crustal radioactivity to continental heatflow (the continental crust is much more enriched in radioactive elements than its oceanic counterpart). While surface concentrations are fairly straightforward to measure, it is more difficult to estimate radioactive element concentrations within the mostly inaccessible lower continental crust. Perhaps the current ‘best’ estimate (see Table 1) is that 34.5 mW/m² (or 7.2 TW) of continental heat loss comes from radioactive heat production within the continental crust (Rudnick and Gao, 2003), which implies that the mantle heatflux through the continents is 28.5 mW/m² (5.9 TW). This value agrees well with that of Weaver and Tarney (1984) and lies between the estimate of 5.63 TW of Taylor and McClennan (1985) and those of (Shaw et al., 1986; Wedepohl, 1994) of around 10.3 TW. The latter estimates appear too large—they would imply that steady-state conductive continental lithospheric roots should extend deeper than 500 km beneath the continents, which seems difficult to reconcile with seismic measurements.

Note that our estimates of present-day surface heat loss of 42.1 TW are conservative, and slightly below the lower-end of recent estimates of 46 ± 3 (Mareschal and Jaupart, 2011) and-47 ± 2 TW (Davies and Davies, 2010). The primary reason for our lower estimate is that we disagree that it is valid to assume that hotspots are associated with an additional ~3 TW of surface heat loss, as we disagree with their assumed hotspot swell argument for the surface heat flow associated with mantle plumes. (See Morgan et al., 1995 for our perspective on this issue). However, using these slightly higher estimates for present-day heat loss would only slightly increase the difference between current heat loss and heat production that we further explore below and would strengthen the conclusions we draw.

We now turn to the question of heat production. Geochemical estimates of the abundance of radioactive heat-producing elements in the Earth (e.g., Hofmann, 1988; Hart and Zindler, 1989; McDonough and Sun, 1995; Palme and O'Neill, 2003), have historically been based on the assumption that the relative abundances of refractory lithophile elements (i.e., their concentration ratios) in the Earth and other planets are the same as in chondrites, the most primitive class of meteorites, whose composition is thought to represent that of the nebula of gas and dust from which the solar system formed. This assumption is based on the observation that ratios of the concentrations of the elements to each other do not vary between classes of chondrites, even though other aspects of composition, such as volatile element content and oxidation state, vary dramatically. Two of the radioactive heat producing elements, U and Th, are such refractory lithophile elements (RLE), while the third, K, is not. Once U is estimated, however, K can be estimated from the K/U ratio, which shows only limited variation in the mantle and crust. Being based on the same fundamental assumption, these estimates of present-day (i.e., after 4.56 Ga of radioactive decay) heat production are similar (5.08–5.17 pW/kg of crust+mantle), and imply between 19.7 and 20.3 TW of radioactive energy production within the Earth's present-day crust and mantle [since the heat producing elements, U, Th, and K, are highly lithophile, all terrestrial radiogenic heat production should be in the crust and mantle; as we explain below, little heat production is expected from the core (McDonough, 2005)].

These estimates of heat production are substantially below the estimates of heat loss discussed above. For example, Hart and Zindler (1989) concluded that the mantle is currently losing 2.7 times as much heat as is being produced by radioactive decay. A more recent estimate of the Earth's composition that somewhat relaxes the constraint of chondritic relative abundances of refractory lithophile element (RLE) abundances (Lyubetskaya and Korenaga, 2007a,b) yields a 20% lower radioactive heat production of about 16 TW, implying an even greater ratio of present-day heat loss to radiogenic heat production. In the following discussion, we argue that actual heat production may be even lower than estimated by Lyubetskaya and Korenaga and that the ratio of current heat production to current heat loss in the Earth, the Urey ratio, may be as low as 0.3. Since much of the heat production is in the crust, this ratio is even lower in the mantle.

There is now, however, reason to question the assumption of the constancy of refractory lithophile element ratios. ¹⁴²Nd was produced in the early solar system by alpha decay of ¹⁴⁶Sm (half-life: 68 million years). As rare earth elements, Nd and Sm are refractory and lithophile, hence the Sm/Nd ratio of the Earth should be chondritic. If it were, the ¹⁴²Nd/¹⁴⁴Nd ratio in the Earth should be the same as in chondrites. This is not the case; ¹⁴²Nd/¹⁴⁴Nd ratios in all modern terrestrial materials differ from those in chondrites The terrestrial ¹⁴²Nd/¹⁴⁴Nd ratio is 18 × 10⁻⁶ higher than in ordinary chondrites. The difference between the modern terrestrial value and enstatite chondrites is smaller: only 10 × 10⁻⁶ (Gannoun et al., 2011).

One possible explanation for this variation in ¹⁴²Nd/¹⁴⁴Nd is isotopic heterogeneity in the solar nebula from which the Earth and meteorites formed. This would occur if nuclides synthesized in different stellar environments, specifically red giant stars and supernovae, were not completely mixed in the solar nebula before planetary bodies formed. Indeed, the ¹⁴²Nd/¹⁴⁴Nd varies between various classes of chondrites in ways unrelated to the Sm/Nd ratio. However, a new study by Qin et al. (2011) concludes that while nucleosynthetic-related isotopic heterogeneity was present in the early solar system (as evidenced by, for example, correlated variations in the ¹⁴²Nd and ¹⁴⁸Nd abundances in chondrites), this cannot fully explain the difference between terrestrial and chondritic ¹⁴²Nd/¹⁴⁴Nd ratios. This difference must therefore be due to a difference in Sm/Nd between chondrites and the observable Earth. Though the difference is small, it implies that the Sm/Nd ratio of the Earth is 3 to 6% higher than in chondrites.

This difference in Sm/Nd is well outside the observed variation of this ratio in equilibrated chondrites. Consequently, it seems unlikely that such a difference could have arisen in the solar nebula. On the other hand, the Moon and Earth share the same ¹⁴²Nd/¹⁴⁴Nd ratio (Boyet and Carlson, 2007; Caro et al., 2008), implying the terrestrial value was fixed before the Moon-forming impact. There are two possible explanations; both involve very early differentiation of the Earth and formation of a basaltic protocrust enriched in incompatible elements such as Nd and, importantly, K, U, and Th. In the first case, suggested by Boyet and Carlson (2006), this protocrust, or “early enriched reservoir” (EER) became unstable and sank into the deep mantle where it has remained ever since (e.g., as the D″ layer). As Boyet and Carlson envisioned this occurring as a consequence of the Moon-forming impact, it is difficult to see why the Moon and the Earth should share the same Sm/Nd ratio. In the second case, the crust, or a significant part of it was abraded and lost from the Earth as a consequence of “collisional erosion” during its growth (Caro et al., 2008; O'Neill and Palme, 2008). The final stages of planetary growth are thought to involve infrequent, very energetic collisions between large bodies. Sufficient energy is released in these collisions that the growing planet extensively melts. Between collisions, one might reasonably expect a primitive basaltic proto-crust to form through crystallization at the surface. Caro et al. (2008), O'Neill and Palme (2008), and Caro and Bourdon (2010) propose that a substantial fraction of this proto-crust was blasted away in these collisions, leaving the Earth depleted in elements that were concentrated in that crust: incompatible elements.

O'Neill and Palme (2008) suggest a way to modify the chondritic assumption to account for erosional loss of a primitive crust and we will follow their approach here. O'Neill and Palme (2008) begin by assuming that the growing proto-earth partially melted to produce a proto-crust of mass fraction $f_{p-c}^1$. The concentration $c_i^{pc}$ of an element, i, in the proto-crust with respect to its initial concentration $c_i^0$ in the proto-earth is given by the batch melting equation:

$\begin{array}{ll}\frac{c_i^{pc}}{c_i^o}=\frac{1}{D_i+f_{p-c}^1(1-D_i)}& (28)\end{array}$

where D_i is the bulk partition coefficient of i. They assume that some of this crust corresponding to a mass fraction $f_{p-c}^2$ is removed by erosion, along with a fraction of the residue of crust formation, $f_{res}^2$. The depletion of element i in the bulk silicate Earth is then:

$\begin{array}{ll}\frac{c_i^{BSE}}{c_i^o}=\frac{f_{p-c}^1(1-D_i)+D_i(1-f_{res}^2)-f_{p-c}^2}{(D_i+f_{p-c}^1(1-D_i))(1-f_{res}^2-f_{p-c}^2)}& (29)\end{array}$

The unknowns in this equation are the three mass fraction terms and the partition coefficients. Using various geochemical constraints, O'Neil and Palme estimate the mass fraction lost, $f_{p-c}^2+f_{res}^2$, to be 10% and $f_{p-c}^1=0.026$ and $f_{p-c}^2=0.014$. In other words, the early differentiated proto-crust which formed during accretion contained about 2.6% of the mass of the Earth. About 0.014/0.026 = 54% of this crust was lost along with about seven times as large a fraction of the depleted silicate residues to this early proto-crustal melting and differentiation.

Using O'Neill and Palme's (2008) equations and values that assume a Sm/Nd ratio 6% greater than chondritic, the calculated bulk silicate Earth concentrations of U and Th are 12 and 46 ppb, respectively, values that are 40% lower than those based on the assumption of chondritic relative abundances of refractory lithophile elements. Arevalo et al. (2009) recently revaluated the K/U ratio of the Earth and obtained a value of 13800, somewhat higher than the earlier “canonical” value of 12000. Using this value, we calculate a K concentration of 166 ppm and a terrestrial heat production of only 11.9 TW.

The terrestrial ¹⁴²Nd/¹⁴⁴Nd ratio is only about 10 ppm greater than that of enstatite chondrites (Gannoun et al., 2011). Enstatite chondrites uniquely share several geochemical features with the Earth, such as oxygen isotopic composition. This has led some to suggest that they are a better compositional model for the Earth than ordinary or carbonaceous chondrites (e.g., Javoy et al., 2010). The 10 ppm ¹⁴²Nd/¹⁴⁴Nd isotopic difference implies a 3% Sm/Nd difference. Using the O'Neill and Palme approach to match this composition, and the Arevalo et al. (2009) K/U ratio we calculate a total terrestrial heat production of 15.8 TW (U = 16 ± 4 ppb, Th = 61 ± 20 ppb, K = 219 ± 40 ppm). This estimate agrees remarkably well with independently derived 16.0 TW value of Lyubetskaya and Korenaga (2007a,b). We adopt the value of 16 ± 4 TW for terrestrial heat production, noting that this range encompasses all estimates made over the last 30 years. After correcting for radiogenic energy production in the continental crust, the best current estimates imply that radioactive decay within the mantle is currently producing 2.1 ± 1 × 10⁻⁶μW/kg, corresponding to 8.6 ± ~4 TW of power. Of this, about 86% or ~7.4 TW is heat, and the rest is gravitational power due to the adiabatic expansion of the regions undergoing radioactive heating. The above “best” estimate for suboceanic plus subcontinental mantle heat loss is 34.9 TW. This heat loss is associated with the current accumulation of gravitational potential energy ġ_top at the top of the cooling mantle at a rate ~9–10.5 TW through the mechanism described in Section Thought Experiment on Top vs. Bottom Cooling in the Presence of Gravity. (The above estimates are summarized in Table 1).

An Outline of Core Energetics with Implications for Heatflow into the Base of the Mantle

Heat loss from the convecting core also contributes to mantle energetics. Several energy sources have been proposed to drive the core dynamo, and their approximate sizes quantified. These sources are:

(1) Radioactive decay of ⁴⁰K in the core. This possibility will be further discussed below, but we favor current geochemical arguments that it is a negligible energy source within the core.

(2) Freezing and growth of a compositionally denser inner core. This process involves both a latent heat of freezing and a gravitational energy release as the core segregates into a compositionally denser inner core and less dense outer core. The mass of the inner core is 1.23 × 10²³ kg and its latent heat of freezing is estimated to be ~7.5 × 10⁵ J/kg (Nimmo, 2007), for a net latent heat release of 9.2 × 10²⁸ J associated with the growth of the inner core. One can estimate the gravitational energy release for a PREM-like core by determining the difference in gravitational binding energy between an outer core and inner core with a PREM-inferred density-depth profile, and a hypothetical unsegregated core with the same net mass, and a PREM-like density-depth gradient that has no density jump at the inner core/outer core boundary. This initial density model implies a net gravitational energy release of 1.15 × 10²⁹ J associated with the formation of the denser inner core, and a net release of (1.15 + 0.92) × 10²⁹ J = 2.07 × 10²⁹ J released with the growth of the inner core. If inner core growth occurred during the last 1 Ga ≃3.15 × 10¹⁶s, it would release core energy at a rate of 6.6 TW across the CMB. If growth occurred over the past 3 Ga, it would release core energy at an average rate of 2.2 TW over the past 3 Ga.

(3) Secular cooling of the core, augmented by its associated gravitational energy release. The heat capacity of the core is estimated to be 840 J/kg-K, and its mass 1.95 × 10²⁴ kg (Nimmo, 2007). For a compressible PREM-like Earth, the core also releases stored gravitational energy as it cools and contracts. This effect (see Figure 2B and Section Adiabatic Effects Transform ~14% of the Mantle's Heat Production into Gravitational Energy) augments the formal heat capacity of the core by (1/(1–0.71)) = 41%, so that the core energy release due to secular cooling is estimated to be 1.41 × 840Jkg⁻¹K⁻¹×1.95 × 10²⁴kg = 2.31 × 10²⁷ J/K of secular cooling. A uniform core cooling rate of 50 K/Ga would release 2.31 × 10²⁷ J/K × 50 K/3.15 × 10¹⁶s = 3.7 TW across the CMB.

Constraints on the Secular Cooling Rate from the Size, Solidus-Pressure Slope, and Longevity of the Inner Core

Historically, researchers have extrapolated experimental determinations of the solidus for liquid Fe to temperature-pressure conditions at the inner core-outer-core boundary (ICB). Previous preferred estimates for the solidus dT_m/dP)_cmb at the core-mantle boundary (cmb), have been of order ~8.7–17 K/GPa (these estimates are reviewed by Nimmo, 2007). The outer core's temperature is assumed to increase along an adiabatic gradient

$\begin{array}{ll}d{T}_{ad}∕=\alpha T∕\rho C_P.& (30)\end{array}$

It is the difference between the core freezing solidus-pressure gradient and outer core adiabat that lets us determine the additional temperature needed for the inner core to have started to freeze at the center of the Earth. Nimmo (2007) summarizes the results of several workers that, working with similar assumptions, reached similar conclusions that the outer core adiabat at the CMB is of order 5.1–8.3 K/GPa, and the difference between the solidus-pressure gradient and outer-core adiabat at the current ICB is of order ~1.3–6.1 K/GPa (However, below we will estimate a much larger value for the Clapeyron slope at the ICB). PREM estimates for the pressure at the center of the Earth (364 GPa) are ~35 GPa higher than at the current ICB (329 GPa). With these numbers, core secular cooling of

$\begin{array}{ll}~(1.3-6.1)\mathit{\text{K/GPa}}\times 35\mathit{\text{GPa }}or~45-213\mathit{\text{K}}& (31)\end{array}$

has occurred since the initial freezing of the inner core at an earlier, hotter, Earth's center. Nimmo (2007) favors the lower end of this estimated range, which would imply ~15 K/Ga of secular core cooling over ~3 Ga of growth of the inner core. Note ~3Ga is based on paleomagnetic observations that the Earth has had a significant magnetic field for at least 3.5 Gyr (= 1.1 × 10¹⁷s). Secular core cooling at 15 K/Ga would be associated with ~1 TW average energy release from this cooling core, roughly half the energy released by the latent heat and gravitational energy release associated with inner core growth. A secular cooling rate of ~213 K/3Ga would release an average ~5 TW of energy over 3 Ga, roughly 2.5 times the energy release by the freezing of a denser inner core. These estimates—all much too low if the analysis in the next section is correct—would imply that secular core cooling and freezing has been supplying an average of ~3.2–7.2 TW to the base of the mantle over the past 3 Ga, during which time the core has been cooling at an average rate of ~15–70 K/Ga.

Clapeyron-Slope Estimate for the Solidus-Pressure Gradient at the Inner Core Implies Core Secular Cooling of Order 250 K/Ga

As an alternative to extrapolating lower pressure measurements to inner-core conditions, we can directly estimate the Clapeyron Slope of the inner core freezing reaction from its PREM-inferred density change, estimates for the current temperature at the inner core-outer core boundary and the latent heat release of the core-freezing reaction (Morgan and Vannucchi, 2014). The inverse Clapeyron slope

$\begin{array}{ll}\frac{d{T}_{Clapeyron}}{dP}=\frac{T_{ICB}\Delta v_{ICB}}{L_{ICB}}=\frac{T_{ICB}\left(1∕{\rho }_{OC}-1∕{\rho }_{IC}\right)}{L_{ICB}},& (32)\end{array}$

where T_ICB is the present-day temperature at the inner core-outer core boundary, Δv_ICB = (1/ρ_OC−1/ρ_IC) is the change in specific volume at this boundary, and L_ICB = is the latent heat of the inner core freezing reaction. Using PREM values for inner core ${\rho }_{IC}=12,763kg/m^3$and outer core ${\rho }_{OC}=12,166kg/m^3$densities at the inner core-outer core boundary, $\Delta v_{ICB}=3.67\times 10^{-6}{m}^3/kg$. Using Nimmo's (2007) estimate that the latent heat of the freezing reaction L_ICB = 7.5 × 10⁵ J/kg, and a recent experimental determination (Anzellini et al., 2013) of ~6200 K for the temperature at the inner core-outer core boundary, this method estimates

$\begin{array}{ll}d{T}_{Clapeyron}∕dP=\left(6200\right)\left(3.67\times 10^{-6}\right)∕\left(7.5\times 10^5\right)=~30.3K∕GPa& (33)\end{array}$

The ratio of the outer core adiabat to the Clapeyron slope for the inner core freezing reaction appears to be more robustly determined than either alone. This ratio is given by the expression

$\begin{array}{ll}\frac{d{T}_{ad}∕dP}{d{T}_{Clapeyron}∕dP}=\frac{{\alpha }_{ICB}{T}_{ICB}∕{\rho }_{OC}{C}_p}{T_{ICB}\Delta v_{ICB}∕L_{ICB}}& (34)\end{array}$

that is independent of the temperature at this boundary. The ratio can be expressed in a simpler form:

$\begin{array}{ll}\frac{d{T}_{ad}∕dP}{d{T}_{Clapeyron}∕dP}=\frac{{\alpha }_{ICB}{L}_{ICB}}{C_p\left(1-{\rho }_{OC}∕{\rho }_{IC}\right)}.& (35)\end{array}$

Taking $L_{ICB}=7.5\times 10^5$ J/kg (Nimmo, 2007), ${\alpha }_{ICB}=1.44\times 10^{-5}{K}^{-1}$ (Labrosse, 2003), C_p = 840J/kg−K (Nimmo, 2007), and a PREM-model outer core density ${\rho }_{OC}=12,166kg/m^3$ and inner core density ${\rho }_{IC}=12,763kg/m^3$ at the IC-OC boundary, we infer that (dT_ad/dP)/(dT_Clapeyron/dP)≃0.23, which means that the “effective” Clapeyron slope minus adiabatic slope

$\begin{array}{ll}d{T}_{Clapeyron}∕dP-d{T}_{ad}∕dP=0.77\times 30.3\mathit{\text{K/GPa}}=~23.3\mathit{\text{K/GPa}}.& (36)\end{array}$

This estimate predicts there has been of order 23.3 K/GPa × 35 GPa or ~815 K of secular cooling during the growth of the inner core, e.g., a ~272 K/Ga mean secular cooling rate over a ~3 Ga lifetime of the inner core. We can slightly improve this estimate by integrating Equation (32) under the assumption that Δv_ICB and L_ICB remain constant throughout the ~10% increase in pressure from the present-day ICB to Earth's center. This integration yields

$\begin{array}{ll}T\left(P\right)=T_{ICB}{e}^{\Delta v_{ICB}\left(P-P_{ICB}\right)∕L_{ICB}}& (37)\end{array}$

If we also take account of the anticipated (minor) differences in adiabatic gradients between today's outer core and the hotter conditions at the time of initial inner-core freezing at Earth's center, as shown in Figure 8, then our preferred estimate for the mean temperature difference between the ~3 Ga and present-day core adiabats corresponds to an mass-averaged 774 K (~258 K/Ga over 3 Ga) of secular cooling during the growth of the inner core. This better observationally-constrained estimate is much higher than previous estimates based on extrapolation of experimentally-determined values under core-mantle-boundary-like pressure-temperature conditions. If accurate, it would imply ~258 K/Ga of core secular cooling that would be releasing ~10 times more energy than the freezing reaction that grows the inner core, and would release an average of 2.31 × 10²⁷ J/K × 258 K/3.15 × 10¹⁶s = 18.9 TW of energy across the CMB, ~21.1 TW when also including the additional energy release from the freezing reaction itself. In this case, basal heating from the core would be the largest energy source driving mantle convection, and the mantle would gain ~21 TW of energy from heat flowing across the present-day CMB. After accounting for adiabatic-expansion effects that transform ~18% of heatflow across the base of the mantle into gravitational energy (Figure 2B), the base of the mantle would gain ~3.8 TW of gravitational energy and ~17.3 TW of thermal energy as a consequence of secular cooling of the core at a time-averaged rate of ~258 K/Ga. The net energy release at this rate of core-cooling would be ~2 times larger than the rate of current radioactive energy production within the mantle.

FIGURE 8

Figure 8. (A) Inner core solidus determined from the inverse Clapeyron slope determination dT_Clapeyron/dP = T_ICBΔv_ICB/L_ICB in Equation (37) of the text. The predicted solidus of the inner core's freezing reaction is shown by the solid red line, with its extension to future growth of the inner core by the dashed extension to this red line. It is based on the assumption of a PREM-like density jump at the inner core boundary which results in a specific volume change Δv_ICB = (1/ρ_OC−1/ρ_IC) = 3.67 × 10⁻⁶m³/kg, a current inner core freezing temperature T_ICB = 6200K T_ICB = 6200 K (Anzellini et al., 2013), and a latent heat of freezing $L_{ICB}=7.5\times 10^{5}J/K$ (Nimmo, 2007). Also shown by the black solid line is a PREM-like adiabat for the current outer core assuming the linear thermal expansivity distribution in Figure 2A (Labrosse, 2003), and in a black-dashed line the predicted hotter adiabat for the core at the time that the core had cooled enough for the inner core to start to freeze at Earth's center. This adiabat was determined with the approximation that there was the same net core mass as at present, PREM-like density gradients except for no density jump at the depth of the current inner core boundary, and the thermal expansivity profile shown in Figure 2A. (B) The net average core temperature drop associated with secular cooling between the time of initial inner core freezing and the present is the shaded region between the initial and present core temperature profiles. The resulting mean mass-averaged core temperature drop is 774 K, or a secular cooling rate of ~258 K/Ga over a ~3 Ga duration for the growth of the inner core.

Preferential Segregation of Potassium into the Core is Chemically Implausible

Recently, revised estimates for the conductivity of the outer core [cf. (Lay et al., 2008; Buffett, 2012; Pozzo et al., 2012)] have led to the assessment that ~10–15 TW is likely be conducted along the outer core adiabat expected to form in a vigorously convecting and unstratified outer core. Pozzo et al.'s recent determination of a ~100 W/m-K outer core conductivity near the CMB implies that 15.7 TW would be conducted up a PREM-like outer-core adiabat for Labrosse's (2003) preferred value for the thermal expansivity of the outer core near the CMB of 1.7 × 10⁻⁵ K⁻¹. This has led people to search for other energy sources to power the geodynamo, since core secular cooling has been usually assessed to be a relatively small energy source, as discussed above. Several recent studies [cf. (Buffett, 2012; Lay et al., 2008; Pozzo et al., 2012)] have revisited their preferred “least bad” hypothesis that there is a large amount (~10–15TW) of radioactive power generation within the core due to the radioactive decay of ⁴⁰K. However, the amount of potassium required to generate this amount of radiogenic power production in the core is extremely large. To generate ~15 TW of radiogenic energy by decay of ⁴⁰K, the core, with a mass of 1.9 × 10²⁴ kg and potassium's radiogenic energy production of 3.48 × 10⁻⁹ W/kg, would need to contain 4.31 × 10²¹ kg of potassium or 0.22% (2200 ppm) potassium by weight. For context, this is 10 times higher than the concentration estimated within the silicate mantle and crust, and thousands of times higher than the concentrations measured in iron meteorites. From a geochemical perspective, this seems highly unlikely because potassium is not a siderophile element as discussed in depth in McDonough's recent review of core composition (McDonough, 2005).

Instead, observational, theoretical, and experimental chemical arguments all point to potassium being depleted in the core relative to the silicate mantle. First, the iron meteorites, thought to be pieces of asteroidal cores, are extremely depleted in potassium and typically contain < 1 ppm K, e.g., (Kaiser and Zaehringer, 1968). In fact, the intrinsic abundance of potassium is so low in iron-meteorites that in some cases a significant fraction of their potassium has been produced by cosmic-ray spallation, and its build-up can been used to determine cosmic-ray exposure ages of these meteorite samples. The little data that do exist on K concentrations came from K-Ar dating of iron meteorites, which has subsequently been supplanted by more modern techniques like Re-Os dating. Second, while asteroidal cores formed at low pressure and there has been speculation that more potassium might have partitioned into the Earth's core under higher pressures (Bukowinski, 1976; Parker et al., 1996), other theoretical considerations suggest it will never have a strong affinity for a high pressure iron-alloy liquid (Sherman, 1990). Third, laboratory experiments have confirmed theoretical expectations and shown that while there is some increase in the metal/silicate partition coefficient of potassium with pressure, it never partitions preferentially into the metal phase (these experiments are well-summarized in McDonough, 2005 review and by Corgne et al., 2007). These experiments place a maximum possible abundance of potassium in the core at ~250 ppm (Gessmann and Wood, 2002). Finally, potassium sulfide minerals have been found in enstatite chondrites, which formed under extremely reducing conditions. This has led to the suggestion in an enstatite-chondrite model of the Earth with a sulfur-rich core, the potassium content might be as high as 290–810 ppm (Lodders, 1995). However, recently published silicon isotope data virtually exclude the enstatite-chondrite model and furthermore indicate that silicon, not sulfur, is more likely to be the predominant light element in the core, e.g., (Fitoussi and Bourdon, 2012).

Laboratory experiments show that U is even more unlikely to partition into the core as it remains highly lithophile at all relevant temperatures and pressures. However, like K, it will partition somewhat into a sulfide liquid or sulfide-rich metallic liquid under highly reducing conditions. Nevertheless, even under these assumptions, Malavergne et al. (2007) estimate the U concentration in the core to be 0.63 ppb (compared to a silicate Earth concentration of 12 to 22 ppb).

Geochemical constraints based on laboratory experiments at high pressure and temperature thus limit radioactive heat production to a maximum of 1.79 TW (250 ppm K generating 1.67 TW and 0.67 ppm U generating 0.12 TW), with the most probable number being far lower.

Summary of Core Energetics

If >10–15 TW of heat loss from the core is truly needed to sustain a convective outer core geodynamo, we favor the interpretation that this is further evidence supporting our above “in-situ ICB” Clapeyron-slope estimate which suggests that the core has been cooling at a rapid rate of ~258 K/Ga over the past 3 Ga. This mean cooling rate during the formation of the inner core would be associated with a mean heatflow of ~24 TW across the CMB. The initial heat for a core that has always been much hotter than overlying mantle would need to be linked to core-formation itself, either from an abundant short-lived radionuclide, or from the gravitational energy release from core segregation being preferentially concentrated into heating the growing core. For example, (Flasar and Birch, 1973) estimated that the gravitational energy of initial core segregation, if concentrated into the core, would have been enough to raise its temperature by 8000 K, and is enough, if distributed uniformly within mantle and core, to have increased their temperatures by 1800 K. The currently understood chemistry of element partitioning during segregation of iron core from silicate mantle appears to be strongly inconsistent with ~2200 ppm potassium in the core. However, it could also be possible to power a core dynamo with much lower levels of energy release from the core—this too remains uncertain.

Geodynamo Constraints do not Demand Large Energy Losses from the Core

Measurements of the present-day magnetic field at the CMB, when combined with exploration of numerical dynamo experiments, can be used to assess the present-day rate of power loss associated with geodynamo (Jackson and Livermore, 2009; Jackson et al., 2011). However, this approach actually leads to the estimate that less than 2 TW of heat loss is needed to generate Earth's current magnetic field (Jackson and Livermore, 2009; Jackson et al., 2011). Current numerical models for the geodynamo predict a roughly one to one ratio between dissipation and magnetic energy flux, suggesting that the geodynamo could work with an efficiency of 0.27–0.52 (Christensen and Tilgner, 2004; Christensen, 2010). While Christensen and coworkers used higher core heat fluxes in their numerical experiments of order 30–100 mW/m² (or 4.6–15TW), the scaling relationships they determined, coupled to the magnetic energy density inferred by Jackson et al. (2011) actually requires up to an order of magnitude less than 1 TW of CMB heat loss to sustain. Thus, the existence of a geodynamo, while requiring there be active convection within the core, does not directly place a large minimum bound on core heat loss across the CMB.

Potential Effects of Higher Radioactivity in the Continental Crust or a Higher Mantle Secular Cooling Rate

The above analysis of the energy sources in mantle energetics is not very sensitive to the exact value for continental heat production, since higher continental heat production would both reduce the implied mantle heat flow through the continents, and would reduce the estimated budget of radioactive elements within the mantle.

We also note that if the missing heat in the “cold-core” scenario were to be supplied by heat from the secular cooling of the mantle, a 21.3 TW shortfall would imply a secular mantle cooling rate of ~130 K/Ga =

$\begin{array}{ll}\frac{\left(21.3TW\right)\times \left(3.15\times 10^{16}s∕Ga\right)}{1.14\times \left(4.04\times 10^{24}kg\right)\times \left(1167J∕kg-K\right)}& (38)\end{array}$

where the 1.14 factor accounts for the mean gravitational energy release during secular cooling of a PREM-like mantle (Figure 2B). This is a significantly higher cooling rate than the longterm average shortfall of ~4–8 TW that appears to be consistent with the crudely observed secular mantle cooling rate of ~25–50 K/Ga over the past ~3.5 Ga (Figure 7) (Jarvis and Campbell, 1983; Campbell and Griffiths, 1992; Abbott et al., 1994; Herzberg et al., 2010).

Current Net Gravitational Power Release within the Mantle

Above we have estimated that roughly 11–14 TW of gravitational power is currently being released by sinking slabs. The gravitational power being created by adiabatic expansion from internal energy generation is much less (the following estimates are summarized in Table 1 and Figure 6). For example, if we assume that the mantle's 8.6 ± 4 TW of radiogenic energy production is uniformly distributed through the mantle, then this energy generation would be currently generating 0.14 × (8.6 ± 4 TW) = 0.7–1.8 TW of new gravitational power. The 5–21 TW of heat flowing across the CMB can generate up to an additional 0.19 × (5–21) TW = 1–4 TW of new gravitational energy, for a total production rate of 1.7–5.8 TW of new gravitational power. Gravitational energy replenishment by adiabatic expansion linked to slab-induced viscous dissipation is of order 0.14 × (11–14 TW) = ~1.5–2 TW.

Finally, we can estimate the gravitational energy replenishment associated with top-surface cooling if it cooled at a rate—8.6 TW—compatible with steady-state release of the mantle energy being generated by internal radioactivity and heating across the CMB. This heat loss leads to accumulation of gravitational potential energy ġ_top at the top of the cooling mantle at a rate Q_top(ġ_top/Q_top) =

$\begin{array}{r}{Q}_{top}\left(0.5\rho \bar{\alpha }gh\Delta T\delta z∕\Delta T\delta z\rho C_P\right)=\left(8.6\pm 4TW\right)\left(\bar{\alpha }gh∕2C_P\right)\\ =~2.5\mathit{\text{TW}}.\hfill & (39)\end{array}$

See Section Thought Experiment on Top vs. Bottom Cooling in the Presence of Gravity for a discussion of the ġ_top and Q_top expressions in this estimate. If we want to add the effects of core heat-loss to estimate “quasi-sustainable” gravitational energy generation within the mantle, we use the same expression with the core heat-flux added to the 8.6 TW of radiogenic heat-production within the mantle as is done in line 28 of Table 1. This expression is analogous to the one for the gravitational energy release associated with slab sinking with the additional assumption that the heat released by mantle cooling at its top surface is ultimately extracted uniformly from within the mantle.

These estimates suggest that, for the cold-core scenario, replenishment of gravitational potential energy is presently occurring at the rate ~6 TW, so that at present there would be a net gravitational power consumption rate in the mantle of ~5–10 TW. If core heatloss is a significant energy source at the base of the mantle as it is in the warm-core and hot-core scenarios (see also Tables 2, 3), then strong mantle plumes with associated gravitational energy release would seem to be an inescapable structure of mantle flow. In this case as discussed in Section Observational Constraints on Gravitational Energy Release from Present-day Slabs and Plumes above, the potential gravitational energy release in ascending plumes would be of order ~6 TW if the return plume flux had the same initial temperature contrast and mass-flux as that of present-day sinking slabs. Including this additional gravitational energy release, the warm-core scenario would also be in a current state of net gravitational power consumption. Only the hot-core scenario could be in a “quasi-steady-state” for the mantle, although the mantle+core as a whole would still be losing at least ~10 TW of gravitational power. This assessment implies that slab subduction is at present not at a sustainable, steady-state level for “cold-core” and “warm-core” scenarios; instead, the mantle would be in a phase of faster-than-normal slab subduction and plate spreading. Even the median-estimates for “hot-core” scenarios are associated with faster-than-normal speeds of mantle flow.

TABLE 2

Table 2. Evolution of mantle energy supply.

TABLE 3

Table 3. Evolution of mantle energetics.

The Mantle is Possibly in a Geologically Recent Phase of Faster-Than-Normal Heat Loss

The seafloor magnetic record suggests that mean subduction rates could have been as much as twice as large ~80–100 Ma ago than at present (Larson, 1991), which implies that the “characteristic” plate motion speeds from the present through the past ~140 Ma may be as much as 2–4 times faster than the typical average speed during the last 0.5–1 Ga. Perhaps speeds are higher now because the Earth is in an active ocean-opening phase of a Wilson cycle where it happens to have subduction zones simultaneously active on both the Eastern and Western margins of the Pacific (only one such subduction zone margin is “necessary” for active spreading and subduction).

Prior Episodes of Faster-Than-Normal Mantle Heat Loss are also Likely

Faster-than-normal slab subduction and plate spreading is also implied by the age-dependence of preserved continental crust (Figure 9) (Hawkesworth et al., 2010). Geochronologists have long noted that there are “preferred age” spikes in the age-distribution of the continental crust, and suggested that these crustal age-peaks are linked to peaks of crustal generation or crustal preservation likely to be associated with the presence of supercontinents (Taylor and McClennan, 1985; Condie, 1998; Hawkesworth et al., 2010). This interpretation is compatible with the strong time-variation in oceanic plate subduction implied by Earth's preserved seafloor record, and suggests this type of variable-rate overturn has persisted through almost all of Earth history, with mean speeds slowing over time due to slowing radioactive mantle energy release.

FIGURE 9

Figure 9. Volume percent of the continental crust as a function of its age of creation based on radiometric dating, mostly of zircons. This is evidence for non-steady-state cycles in mantle rates. Names of corresponding hypothesized “supercontinents” are shown. Modified from Condie and Aster (2010).

The Structure of Viscous Dissipation within the Mantle

Heat production from viscous dissipation is not expected to be uniformly distributed throughout the mantle (Balachandar et al., 1995). In general, viscous dissipation tends to be concentrated in the regions where the mantle's viscosity is lowest (Balachandar et al., 1995), since the heat production by viscous dissipation depends on the ratio of the square of the stress divided by viscosity, and stress-squared typically varies less rapidly than inverse-viscosity within a deforming medium. This continuity in stress is the reason why large-scale geoid anomalies are similar in shape to the large-scale apparent density structure of the lower mantle (Hager and Clayton, 1989; Forte et al., 1991; Ricard and Wuming, 1991). If mantle stresses were not reasonably continuous from top to bottom of the mantle, then the density anomalies in the lower mantle would be unable to produce spatially correlated but opposite sense anomalies in the low-order Geoid (Hager and Clayton, 1989).

Geoid studies have been used to infer the Earth's radial viscosity structure. They commonly suggest that two mantle regions are likely to be of lower viscosity than the main central region of the mantle (Hager and Clayton, 1989; Forte et al., 1991; Ricard and Wuming, 1991). These regions, the ~200–300 km thick asthenosphere that underlies the oceanic and continental lithosphere (Anderson, 1989, p. 51–53), and the ~100–300 km thick D″ thermal boundary layer between the mantle and the outer core (Kendall and Shearer, 1994) (see Figure 6), are prime candidates for regions where the mantle's viscous dissipation is likely to be concentrated. Other regions of enhanced dissipation are likely to be near the base of slabs, where slabs preferentially buckle within the mantle, and in mantle plumes. Seismic studies have shown that the Earth's asthenosphere is significantly slower in seismic velocity than underlying mantle, and that shear velocities are so low (Dziewonski and Anderson, 1981) and shear-attenuation is so high (Widmer et al., 1991) that this is likely to be a region of incipient partial melting. Viscous dissipation may be the heat source that is keeping the asthenosphere in this critical near-melting state. Anomalously low shear velocities within the D″ region have also been proposed to be caused by incipient mantle melting due to viscous heating (Steinbach and Yuen, 1999), and high-pressure experiments (Zerr et al., 1998) (Boehler, 1996) suggest that the D″ region may locally partially melt (Steinbach and Yuen, 1999). Possibly the strong seismic signal from the D″ thermal boundary layer is due to the combination of a hotter temperature and strong flow-induced anisotropy within it.

The hypothesis that the ~5 cm thick pyroxenite veins found in exhumed mantle peridotites at Ronda, Spain and Beni-Bousera, Morocco are produced by the stirring and thinning of recycled oceanic crust during mantle convection (Allegre and Turcotte, 1986) leads to an interesting, but very-model-dependent argument that most mantle strain occurs within low-viscosity boundary layers. If produced by convective thinning, this strain is an indirect record of the dissipation history experienced by these peridotites. A strain of 10⁵ (from ~5 to ~5 cm) within ~2 Ga (Allegre and Turcotte, 1986) implies an average strain-rate $\overline{\stackrel{°}{\epsilon }}=1.6\times 10^{-12}{s}^{-1}$. If the average gravitational slab-work during the past ~2 Ga was comparable to the inferred present-day rate of ~10¹³W$\left(\stackrel{°}{\phi }=2.5\times 10^{-12}W/k{g}_{mantle}\right)$, and this work was mainly dissipated within a low-viscosity fraction f of the mantle, then, for this strain to occur at this rate of work, the strain-averaged viscosity during the deformation of this parcel of mantle is given by equating $\stackrel{°}{\phi }/f=\left({\mu }_{\text{low}\mathrm{\text{-}}viscosity}/{\rho }_{\text{mantle}}\right){\overline{\stackrel{°}{\epsilon }}}^2$. This estimate, for f = 0.03 (flow concentrated within ~100-km-thick low-viscosity boundary layers) implies a strain-averaged boundary-layer viscosity μ_{low-viscosity} of only ~2 × 10¹⁷ Pa-s—an extremely low value that is 5–50 times lower than other estimates of the viscosity of the asthenosphere or D″. It is conceivable that this could be representative of the viscosity in upwelling plumes where extremely high strain rates and a power-law rheology might be able to generate viscosities this low. However, we think the above estimate more likely indicates that this magnitude of strain-thinning must in fact not be typical of the convecting mantle, but instead is either typical of strain-thinning during plume ascent, a local feature of the strain during the emplacement of these mantle peridotite massifs, or simply indirect evidence that these layers in exhumed mantle peridotites are not produced by simple mantle convection-related thinning of recycled oceanic crust but are instead made by some other process like magma-wallrock reactions. In any case, the above estimate does show that if the low-viscosity mantle boundary layers that deform in response to gravitational slab work have a strain-averaged viscosity of ~2 × 10¹⁹ Pa-s, then they would be able to stretch and thin subducted oceanic crust from ~5 km to ~50 cm.

Conrad and Hager (1999) proposed that a very large fraction of a sinking slab's gravitational energy release could be dissipated by the bending and unbending of the lithosphere as it “turns the corner” at a trench. If true, their scenario would greatly reduce the above estimates of slab gravitational power available for mantle dissipation; they estimate that >70% of the gravitational work released from a sinking slab will go into bending and unbending of the lithosphere during subduction. We think that their analysis is likely to be incorrect because it neglects the effects of serpentinization and deserpentinization on the subducting slab (Ranero et al., 2003; Rüpke et al., 2004), effects which are likely to greatly reduce the amount of work needed to bend and unbend it. In part, serpentinization can reduce the work needed to bend and unbend a slab by weakening the deep lithospheric faults along which much near-trench slab deformation occurs (Ranero et al., 2003). While this effect alone could be enough to allow low-power-consumption bending of subducting oceanic lithosphere, if there is a significant volume of plate-bending-linked serpentinization, then the volume expansion associated with near-trench serpentinization of the uppermost, coldest portions of the slab lithosphere, and the volume reduction associated with deserpentinization and basalt-eclogite reactions at >70 km depths, could also provide a large chemical force to actively bend the slab during trench-faulting-related serpentinization, and unbend the slab once it reaches depths >70 km (Morgan, 2001). Note that serpentinization-related bending and unbending forces do not provide a net energy source to drive plate motions—they only help it to bend and unbend. Furthermore, these reactions result in the top ~70–150 km of the slab being less dense than assumed during the previous analysis because a significant fraction of the slab cooler than ~650°C is partially serpentinized. We neglect this gravitational effect just as we have neglected the gravitational effect of the basalt-eclogite transformation of the crustal portion of the subducting slab that will tend to make the slab denser than assumed in the previous analysis. Both are second order complications to the above energy estimations. Recent high-resolution numerical experiments incorporating a non-Newtonian creep rheology also find that slab-bending involves less than ~20% of the mantle's viscous dissipation (Stadler et al., 2010). However, if Conrad and Hager are right and slab-bending and unbending itself consumes a large fraction of the subducting slab's gravitational energy release, then the conclusions reached in the next section would need to be revised.

The actual pattern of viscous dissipation will depend strongly on whether a low-viscosity flow ‘circuit’ forms within the convecting mantle. The numerical experiments shown in Figure 10 illustrate this effect. This effect is insensitive to whether the mantle is compressible or not—we show results for compressible experiments, but the corresponding incompressible experiments are visually identical to the compressible ones shown here. Figure 10A shows details of the experimental configuration. To highlight that viscous dissipation need not occur where the gravitational work occurs, in each experiment the sinking slab is modeled as the sole density contrast /source of gravitational work. First, if a dense and more viscous slab sinks within an isoviscous mantle, then most of the viscous dissipation will take place in a wide region adjacent to the slab (Figure 10B). If, however, a low-viscosity D″ + plume + asthenosphere circuit exists for potential return flow, than practically all of the viscous dissipation is concentrated within these low viscosity regions of the mantle, even though they are far from the subducting slab (Figures 10C,D). The actual distribution of viscous dissipation within the low viscosity path will depend on which part of the circuit (D″, plume, or asthenosphere) has the most resistance to return flow—both pressure gradients and viscous heating will be largest within the most “resistive” part of the low-viscosity circuit (compare Figure 10C and Figure 10D). Over time, the increased heating in the places of greatest resistance may tend to equipartition viscous dissipation between regions of return flow. Proper study of this effect will require well-resolved three-dimensional, variable viscosity, compressible mantle flow simulations. For an introduction to the effects of viscous dissipation on “lubricating” different regions of the mantle flow circuit see (Schubert et al., 1976; Larsen and Yuen, 1997; Van den Berg and Yuen, 1997).

FIGURE 10

Figure 10. Compressible numerical experiments showing that the presence of low-viscosity mantle regions is not sufficient for these regions to generate significant viscous dissipation to gravitational slab work. Instead, what is needed is a connected low-viscosity network supplying the return flow to sinking slabs. Panel (A) shows the experimental configuration. Gravitational power is generated by a dense subducting slab on the right side of each box. This power is viscously dissipated within each box. In each experiment, the mantle has a 100-fold linear increase in viscosity from its top to bottom. Low viscosity regions approximating weak bottom D″, plume (right hand side), and upper asthenosphere regions of the mantle are each 1% of the strength of the uppermost mantle. Panel (B) shows a calculation that does not contain a low viscosity plume region connecting the D″ and asthenosphere regions. All calculations were done using the 2D code for compressible convection described in Appendix A (Supplementary Material). In each calculation, the only density anomaly is associated with the sinking slab. For clarity, velocity vectors are shown on a much coarser interpolated grid. The independently calculated rates of net gravitational work and total viscous dissipation provide a check on the internal accuracy of each solution. For all calculations the two quantities are equal to 0.5% or better. Panels (B–D) show the distribution of viscous dissipation generated by the sinking of the denser slab (the slab is highlighted in A). Annotated viscosity contours are shown, these also serve to outline the sinking slab and the regions where low-viscosity channels are present. The dissipation is normalized to the gravitational energy release divided by the area of the region, e.g., a value of 1 would be releasing dissipation at the average rate if dissipation were uniform throughout the entire volume. In panel (B) the unconnected low viscosity D″ and asthenosphere layers are regions of little viscous dissipation to balance the gravitational power released by slab sinking. Only 4% of the mantle 's viscous dissipation is occurring within these regions. In panel (C), a connected network for return flow leads to higher flow rates. In this case, 75% of the viscous dissipation concentrated within the low-viscosity return flow circuit. In panel (D), the “asthenosphere” channel is widened and the plume channel narrowed in comparison to panel (C). In this case 69% of the viscous dissipation occurs within the low-viscosity region of return flow. In comparison to panel (C), the narrower plume channel is a region of higher viscous dissipation. These experiments demonstrate that, if an interconnected low-viscosity network contains the primary return flow to subducting slabs, then the gravitational energy release from subducting slabs can be concentrated within the highest viscosity sections of this low-viscosity network, so that viscous dissipation from slab sinking could preferentially heat regions within the hotter low-viscosity material that forms the return plume upwelling to slab downwelling.

As noted in Section Observational Constraints on Gravitational Energy Release from Present-day Slabs and Plumes, if upwelling plumes had the same mass flux and initial temperature contrast as downwelling slabs, they would perform only about half as much work as slabs during their ascent through the mantle. Unlike slab-work, the plume's mechanical work tends to be locally dissipated within the low-viscosity plume conduit where it contributes to heating the plume material and adjacent mantle. For example, in the Poiseuille-flow idealization of buoyant upwelling within a narrow low-viscosity plume pipe, all viscous dissipation would take place within the plume conduit. This may be the reason why regions of concentrated plume activity (plume “provinces”) appear to be associated with large-scale thermal anomalies within the lower mantle (Su et al., 1994; Masters et al., 1996). Perhaps the lower mid-mantle “between” the plumes within the South-Pacific and African “mega-plume” provinces has been heated by viscous dissipation within the numerous plume conduits that traverse these regions. For example, if 10% of the mantle's viscous dissipation (i.e., ~1/4 of Earth's plume dissipation) is concentrated within a mantle high cylindrical region that is 1500 km in radius, then the average temperature rise from plume viscous dissipation within this region (corrected for adiabatic expansion work) would be ~1100 K/Ga, i.e., 220 K after 200 Ma of continuous plume activity. Note that Burke et al. (2008) have a completely different interpretation of these plume provinces as being a byproduct of dense Fe-rich compositional piles in the lower mantle.

The Effect of Viscous Dissipation upon the Structure of Mantle Convection

If the hot D″ boundary layer at the base of the mantle, rising low viscosity plumes, and the asthenosphere layer underlying the lithosphere are regions of significant viscous heat dissipation, then viscous dissipation may play an important role in shaping the structure of mantle convection. In particular, this may be a factor contributing to why strong mantle plumes originate from the D″ boundary layer. Even if core heat loss were only 10–20% of that from the mantle, if a significant fraction of mantle dissipation occurs within in the D″ region, then the total heat flux out of D″ could be as much as half the total mantle heat flow. Of course, if secular cooling of the core provides ~23 TW of present-day power at the base of the mantle, enhanced viscous dissipation within the D″–Plume–Asthenosphere circuit would only further amplify the plume-like character of the upwelling component of mantle flow.

Possible Effects of Time-Varying Viscous Dissipation

As was earlier noted, the subduction of oceanic slabs is not uniform through time, and the present-day mantle appears to be in a phase of faster-than-average slab subduction. During a Wilson cycle, ocean basins open until a point is reached where previous passive margins, such as the east coasts of North and South America, are transformed into subduction zones like the west coasts of North and South America. During the initiation of new trench systems, the viscous dissipation within the mantle will have a large transient increase, since twice the usual amount of old seafloor may subduct for several tens of Ma. This increase may lead to increased heating near the CMB, which in turn could affect the core's heat loss, and thus the pattern of magnetic anomaly reversals within the convecting core. Eventually, this phase must end. The complementary slower-than-average phase may occur at the ‘end’ of a Wilson cycle. A pulse of slab heating may also lead to transient heating of the Earth's mantle and episodes of more active than usual surface volcanism. The proposed Cretaceous “super-plume” period of activity (Larson, 1991) may thus have originated as a response to a previous transient increase in plate subduction associated with the development of new trench systems in the western Pacific and the rifting of the Gondwana supercontinent. This may also have been the cause for the nearly simultaneous occurrence (Larson, 1991) of the Cretaceous “Quiet Zone” when the Earth's magnetic field did not reverse for over 35 million years.

Time-varying viscous dissipation may also affect volcanism on other terrestrial planets. For example, Venus has been postulated to have had a global resurfacing event about 600 Ma ago (Turcotte, 1995). If this event was due to massive lithosphere “foundering” (i.e., episodic subduction), then the resulting viscous heating may have led to a pulse of heating of the weakest, nearest-to-solidus portions of Venusian mantle that caused a subsequent period of prolonged surface volcanism.

Mantle Secular Cooling and Plate Spreading Rates in the Early Earth

Observed Archaean rocks clearly hint that Earth's mantle was once hotter than it is at present. Some Archaean rocks are an eruptive basalt type formed by ultra-large-degrees-of-melting—komatiites—for which there is only one clear Phanerozoic occurrence at Gorgona (Arndt et al., 1997). If komatiites record peak melting temperatures in a variable temperature mantle, they suggest that peak temperatures have cooled by ~100–150°C over the past 4 Ga (see Figure 7). This cooling implies convective heat loss in addition to that needed to lose heat being generated by in-situ radioactive decay. With our downward estimate of radiogenic isotope concentrations in the mantle to produce internal energy at the rate 2.2 ± 1 × 10⁻¹² W/kg, the present-day mantle would create the equivalent of ~63 ± 29 K of in-situ energy production over 1 Ga (ΔT(1Ga) = (3.15 × 10¹⁶(s/Ga))(2.2±1 × 10⁻¹²(W/kg)/1100(J/kg−K))), and at ~4.5 Ga would have heated roughly 5 times faster than the present rate, for an average in-situ energy generation equivalent to roughly twice the present-day rate over the past 4.5 Ga—or ~120 × 4.5 = 540 K-equivalent of heat production over the past 4.5 Ga. If we add this heat loss to that from secular cooling, the mantle has lost more than ~700 K worth of heat-energy from the Hadean to present-day.

Tables 2, 3 summarize the resulting long-term and post-Archean energetics of Earth's mantle and core. Earth's mantle has convected with an average of ~15% of its energy coming into the base of the mantle in the cold-core scenario (~30% over the last Ga), ~35% basal-heating in the warm-core scenario (50% over the last Ga), and 47% heating in the hot-core scenario, ~61% basal-heating within the last Ga. All of these estimates have a significantly higher fraction of basal heating than the ~10% basal heating fraction favored in the 1990s. All these estimates of basal energy supply to mantle convection would be further augmented if a significant fraction of the mantle's viscous dissipation occurs within the D″ part of a D″-plume-asthenosphere circuit as discussed in Sections The Structure of Viscous Dissipation Within the Mantle and The Effect of Viscous Dissipation upon the Structure of Mantle Convection. This line of reasoning strengthens the argument that deep mantle plumes are not only likely to exist within the convecting mantle, but also are likely to transport a significant component of the upward return flow to subducting slabs.

Since, plate tectonics, e.g., the near-surface boundary-layer cooling of lithosphere and subsequent slab- injection into the mantle, is the most efficient way to cool the mantle, and heat loss by lithosphere formation and slab-injection is only proportional to the square-root of the mean-speed of surface plate motions (Morgan, 1997), this analysis also implies that the Earth is likely to have had more rapid mean plate motions in the Archaean than the Phanerozoic. A steady-state assumption, while appealing because of its simplicity, is simply not consistent with secular cooling of the mantle and the strong time-dependent decay in the internal radioactive energy production within the Earth. The non-arc basalt eruption temperature record compiled by Herzberg et al. (2010) suggests that the Earth has had widely varying basalt source temperatures throughout its history, with intraplate basalts having significantly hotter source temperatures than MORB. The difference between “hot” and “cold” basaltic source temperatures may have slightly decreased since the era of frequent komatiite preservation, but only by ~75 K or even less. While the erupted basaltic record by itself does not contain strong hints of the episodicity implied by the present-day ratio of gravitational energy release to in-situ radiogenic mantle heat production, the age-distribution of preserved continental crust does contain strong evidence for episodic processes on the timescale of ~200–500 Ma (Figure 9). As Condie and Aster (2010) and Hawkesworth et al. (2010) emphasize, Figure 9 is a record of the preservation of continental crust and hence reflects the balance between continental crustal creation and destruction. Nevertheless, both these processes occur principally in subduction zones, and Condie and Aster (2010) interpret this record as one of “subduction system episodicity.” We interpret this imperfect record as implying that plate motions have been quite variable through time, but the Wilson cycle (and associated plate motions) has generally been slowing in frequency as Earth's internal energy production slows with time.

Summary

The energetics of Earth's mantle and core are reassessed. A gravitational energy perspective provides new insights on the current energetics of the mantle. Most of the Earth's surface heat loss occurs through the growth of cold oceanic lithosphere. When this lithosphere subducts, the cold slabs cool the Earth's mantle in the region about the subducting slabs. However, they also heat the Earth's mantle by viscous dissipation of the gravitational potential energy that they have gained during their cooling near the Earth's surface. We find that the gravitational power being released by presently subducting slabs is of similar magnitude (~10–12 TW) to the mantle's current internal radioactive heat production. Viscous dissipation of gravitational slab energy is expected to be asymmetrical. In fact it is likely to be lower within the cooled, more viscous regions around the subducting slabs and higher away from slabs within the low-viscosity boundary layers of mantle convection. Viscous dissipation from slab work may be responsible for the formation of a stratified hot, light, and weak asthenosphere fed from below by mantle plumes rising from D″, and removed upwards by incorporation into the cooling, growing, and subducting oceanic lithosphere. Variations through time in the rates of plate subduction are likely to occur as a natural consequence of plate tectonic evolution. During the birth of a major subduction zone, heat production within the mantle is likely to rise. This could lead to a pulse of D″ heating, an increase in plume activity, a change in core-heat loss and magnetic reversal frequency, and a period of enhanced asthenospheric melting.

We also reevaluated current estimates of energy supply into the base of the mantle. Current estimates of the heatflux conducted down an adiabatic temperature gradient in the outer core imply that core heatflow through the CMB could be more than ~15 TW. We examine a simple seismic observation-based estimate for the Clapeyron-slope of the freezing reaction associated with the growth of the inner core that suggests that there has been a per-mass average of ~774 K of secular cooling since the initial formation of the inner core at Earth's center. Secular cooling of the core at an average rate of ~774 K/3 Ga or ~258 K/Ga would lead to an average core energy flow into the base of the mantle of order ~24 TW. Based on the currently uncertain current state of the heat flowing through the CMB, cold-core (~5 TW), warm-core (~15 TW), and hot-core (~24 TW) scenarios for mantle energetics were examined. All scenarios imply that the energy flux from the core through the CMB has been significant, with ~31% (cold-core) to ~62% (hot-core) of the mantle's energy being supplied through the CMB during the last 1 Ga. Both general estimates of mantle and core energetics and specific viscous dissipation estimates based on the gravitational energy released by current slab subduction favor a mode of current mantle convection in which mantle plumes are a major component of the mantle upwelling that is the return flow to subducting slabs.

Author Contributions

JM conceived of this project, did the analytical analysis, and wrote the manuscript with input from all authors. All authors made substantial contributions to the overall science case and manuscript, and approved it for publication.

Funding

JM was supported by a Wolfson Research Merit Award.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

JM thanks W. Jason Morgan for extensive discussions during the initial development of these ideas between 1998 and 2002, and for also providing critical feedback on the 2000, 2003, and 2010 submitted versions of this paper. The long gap between the 2003 and 2010 revisions was due to our need to develop a compressible code in response to a 2003 critical review that flatly, and erroneously, stated that “compressible mantle flow experiments refute the idea that one can understand mantle convection from the perspective of gravitational energy release.” (Probably this critical reviewer's insights had been sharpened by analysis of numerical experiments based on the incorrect “Truncated Anelastic Approximation”). Thanks also to Matthias Hort for helpful discussions, Arlene Jacobs for finding several very hard-to-get references, and Uli Christensen for his stimulating feedback on a preprint version that motivated the estimates of the impact of adiabatic effects upon slab and mantle cooling and heating. Dan McKenzie provided helpful comments on the 2000 manuscript, and Dave Yuen gave many useful suggestions to improve the 2003 version. Kevin Burke also provided an energetic review of the 2013 version. Two anonymous reviewers gave much useful feedback on this (2015) version.

Supplementary Material

The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/feart.2016.00046

References

Abbott, D., Burgess, L., Longhi, J., and Smith, W. H. F. (1994). An empirical thermal history of the Earth's upper mantle. J. Geophys. Res. 99, 13835–13850. doi: 10.1029/94jb00112

CrossRef Full Text | Google Scholar

Allegre, C. J., and Turcotte, D. L. (1986). Implications of a two-component marble-cake mantle. Nature 323, 123–127. doi: 10.1038/323123a0

CrossRef Full Text | Google Scholar

Anderson, D. L. (1989). Theory of the Earth. Boston, MA: Blackwell Scientific Publications.

Google Scholar

Anzellini, S., Dewaele, A., Mezouar, M., Loubeyre, P., and Morard, G. (2013). Melting of iron at earth's inner core boundary based on fast x-ray diffraction. Science 340, 464–466. doi: 10.1126/science.1233514

PubMed Abstract | CrossRef Full Text | Google Scholar

Arevalo, R. Jr., McDonough, W. F., and Luong, M. (2009). The K/U ratio of the silicate Earth: insights into mantle composition, structure and thermal evolution. Earth Planet. Sci. Lett. 278, 361–369. doi: 10.1016/j.epsl.2008.12.023

CrossRef Full Text | Google Scholar

Arndt, N., Kerr, A. C., and Tarney, J. (1997). Dynamic melting in plume heads: the formation of the Gorgona komatiites and basalts. Earth Planet. Sci. Lett. 146, 289–301. doi: 10.1016/S0012-821X(96)00219-1

CrossRef Full Text | Google Scholar

Backus, G. E. (1975). Gross thermodynamics of heat engines in deep interior of Earth. Proc. Natl. Acad. Sci. U.S.A. 72, 1555–1558. doi: 10.1073/pnas.72.4.1555

PubMed Abstract | CrossRef Full Text | Google Scholar

Balachandar, S., Yuen, D. A., Ruetler, D. M., and Lauer, G. (1995). Viscous dissipation in three-dimensional convection with temperature-dependent viscosity. Science 267, 1150–1153. doi: 10.1126/science.267.5201.1150

PubMed Abstract | CrossRef Full Text | Google Scholar

Birch, F. (1938). The effect of pressure upon the elastic properties of isotropic solids according to Murnaghan's theory of finite strain. J. Appl. Phys. 9, 279–288. doi: 10.1063/1.1710417

CrossRef Full Text | Google Scholar

Birch, F. (1968). Thermal expansion at high pressures. J. Geophys. Res. 73, 817–819. doi: 10.1029/JB073i002p00817

CrossRef Full Text | Google Scholar

Boehler, R. (1996). Melting temperature of the Earth's mantle and core: earth's thermal structure. Annu. Rev. Earth Planet. Sci. 24, 15–40. doi: 10.1146/annurev.earth.24.1.15

CrossRef Full Text | Google Scholar

Boschi, L., and Dziewonski, A. M. (2000). Whole Earth tomography from delay times of P, PcP, PKP phases: lateral heterogeneties in the outer core, or radial anisotropy in the mantle? J. Geophys. Res. 105, 13675–13696. doi: 10.1029/2000JB900059

PubMed Abstract | CrossRef Full Text | Google Scholar

Boyet, M., and Carlson, R. L. (2006). A new geochemical model for the Earth's mantle inferred from 146Sm–142Nd systematics. Earth Planet. Sci. Lett. 250, 254–268. doi: 10.1016/j.epsl.2006.07.046

CrossRef Full Text | Google Scholar

Boyet, M., and Carlson, R. W. (2007). A highly depleted moon or a non-magma ocean origin for the lunar crust? Earth Planet. Sci. Lett. 262, 505–516. doi: 10.1016/j.epsl.2007.08.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Buffett, B. (2012). Geomagnetism under scrutiny. Nature 485, 319–320. doi: 10.1038/485319a

PubMed Abstract | CrossRef Full Text | Google Scholar

Bukowinski, M. S. T. (1976). The effect of pressure on the physics and chemistry of potassium. Geophys. Res. Lett. 3, 491–503. doi: 10.1029/GL003i008p00491

CrossRef Full Text | Google Scholar

Burke, K., Steinberger, B., Torsvik, T. H., and Smethurst, M. A. (2008). Plume generation zone at the margins of large low shear velocity provinces on the core-mantle boundary. Earth Planet. Sci. Lett. 265, 49–60. doi: 10.1016/j.epsl.2007.09.042

CrossRef Full Text | Google Scholar

Campbell, I. H., and Griffiths, R. W. (1992). The changing nature of mantle hotspots through time: implications for the chemical evolution of the mantle. J. Geol. 92, 497–523. doi: 10.1086/629605

CrossRef Full Text | Google Scholar

Caro, G., and Bourdon, B. (2010). Non-chondritic Sm/Nd ratio in the terrestrial planets: consequences for the geochemical evolution of the mantle crust system. Geochim. Cosmochim. Acta 74, 3333–3349. doi: 10.1016/j.gca.2010.02.025

CrossRef Full Text | Google Scholar

Caro, G., Bourdon, B., Halliday, A. N., and Quitté, G. (2008). Super-chondritic Sm/Nd ratios in Mars, the Earth, and the Moon. Nature 452, 336–339. doi: 10.1038/nature06760

PubMed Abstract | CrossRef Full Text | Google Scholar

Christensen, U. R. (2010). Dynamo scaling laws and applications to planets. Space Sci. Rev. 152, 565–590. doi: 10.1007/s11214-009-9553-2

CrossRef Full Text | Google Scholar

Christensen, U. R., and Tilgner, A. (2004). Power reqirement of the geodynamo from ohmic losses in numerical and laboratory dynamos. Nature 429, 169–171. doi: 10.1038/nature02508

PubMed Abstract | CrossRef Full Text | Google Scholar

Condie, K. C. (1998). Episodic continental growth: afterthoughts and extensions. Tectonophysics 322, 153–162. doi: 10.1016/S0040-1951(00)00061-5

CrossRef Full Text | Google Scholar

Condie, K. C., and Aster, R. C. (2010). Episodic zircon age spectra of orogenic granitoids: the super-continent connection and continental growth. Precamb. Res. 180, 227–236. doi: 10.1016/j.precamres.2010.03.008

CrossRef Full Text | Google Scholar

Conrad, C. P., and Hager, B. H. (1999). Effects of plate bending and fault strength at subduction zones on plate dynamics. J. Geophys. Res. 104, 17551–17571. doi: 10.1029/1999jb900149

CrossRef Full Text | Google Scholar

Corgne, A., Keshav, S., Fei, Y., and McDonough, W. F. (2007). How much potassium in the core? New insights from partitioning experiments. Earth Planet. Sci. Lett. 256, 567–576. doi: 10.1016/j.epsl.2007.02.012

CrossRef Full Text | Google Scholar

Dabrowski, M., Krotkiewski, M., and Schmid, D. W. (2008). MILAMIN: MATLAB-based finite element method solver for large problems. Geochem. Geophys. Geosyst. 9:Q04030. doi: 10.1029/2007gc001719

CrossRef Full Text | Google Scholar

Davies, J. H., and Davies, D. R. (2010). Earth's surface heat flux. Solid Earth 1, 5–24. doi: 10.5194/se-1-5-2010

CrossRef Full Text | Google Scholar

Davis, E. E., and Chapman, D. S. (1996). Problems with imaging cellular hydrothermal convection in oceanic crust. Geophys. Res. Lett. 23, 3551–3554. doi: 10.1029/96GL03074

CrossRef Full Text | Google Scholar

Demets, C., Gordon, R. G., Argus, D. F., and Stein, S. (1994). Effect of recent revisions to the geomagnetic reversal timescale on estimates of current plate motions. Geophys. Res. Lett. 21, 2191–2194.

Google Scholar

Dziewonski, A., and Anderson, D. L. (1981). Preliminary Earth reference model. Phys. Earth Planet. Inter. 25, 297–356. doi: 10.1016/0031-9201(81)90046-7

CrossRef Full Text

Fitoussi, C., and Bourdon, B. (2012). Silicon isotope evidence against an enstatite chondrite Earth. Science 335, 1477–1480. doi: 10.1126/science.1219509

PubMed Abstract | CrossRef Full Text | Google Scholar

Flasar, F. M., and Birch, F. (1973). Energetics of core formation: a correction. J. Geophys. Res. 78, 6101–6103.

Google Scholar

Forte, A. M., Peltier, W. R., and Dziewonski, A. M. (1991). Inferences of mantle viscosity from tectonic plate velocities. Geophys. Res. Lett. 18, 1747–1750. doi: 10.1029/91GL01726

CrossRef Full Text | Google Scholar

Gannoun, A., Boyet, M., Rizo, H., and El Goresy, A. (2011). 146Sm/142Nd systematics measured in enstatite chondrites reveals a heterogeneous distribution of 142Nd in the solar Nebula. Proc. Natl. Acad. Sci. U.S.A. 108, 7693–7697. doi: 10.1073/pnas.1017332108

CrossRef Full Text | Google Scholar

Gessmann, C. K., and Wood, B. J. (2002). Potassium in the Earth's core? Earth Planet. Sci. Lett. 200, 63–78. doi: 10.1016/S0012-821X(02)00593-9

CrossRef Full Text | Google Scholar

Gubbins, D., Masters, T. G., and Jacobs, J. A. (1979). Thermal evolution of the Earth's core. Geophys. J. 59, 57–100. doi: 10.1111/j.1365-246X.1979.tb02553.x

CrossRef Full Text | Google Scholar

Hager, B. H., and Clayton, R. W. (1989). “Constraints on the structure of mantle convection using seismic observations, flow models, and the geoid,” in Mantle Convection, ed W. R. Peltier (New York, NY: Gordon and Breach Science Publishers), 657–763.

Google Scholar

Hart, S., and Zindler, A. (1989). “Constraints on the nature and development of chemical heterogeneities in the mantle,” in Mantle Convection, ed W. R. Peltier (New York, NY: Gordon and Breach Science Publishers), 261–387.

Hawkesworth, C. J., Dhume, B., Pietranik, A. B., Cawood, P. A., Kemp, A. I. S., and Storey, C. D. (2010). The generation and evolution of the continental crust. J. Geol. Soc. Lond. 167, 229–248. doi: 10.1144/0016-76492009-072

CrossRef Full Text | Google Scholar

Herzberg, C., Condie, K., and Korenaga, J. (2010). Thermal history of the Earth and its petrological expression. Earth Planet. Sci. Lett. 292, 79–88. doi: 10.1016/j.epsl.2010.01.022

CrossRef Full Text | Google Scholar

Hewitt, J. M., McKenzie, D. P., and Weiss, N. O. (1975). Dissipative heating in convective flows. J. Fluid Mech. 68, 721–738. doi: 10.1017/S002211207500119X

CrossRef Full Text | Google Scholar

Hofmann, A. W. (1988). Chemical differentiation of the Earth: the relationship between mantle, continental crust and oceanic crust. Earth Planet. Sci. Lett. 90, 297–314. doi: 10.1016/0012-821X(88)90132-X

CrossRef Full Text | Google Scholar

Holmes, A. (1931). Radioactivity and Earth Movements. Geol. Soc. Glasgow 18, 559–606. doi: 10.1144/transglas.18.3.559

CrossRef Full Text | Google Scholar

Jackson, A., and Livermore, P. (2009). On Ohmic heating in the Earth's core I: nutation constraints. Geophys. J. Int. 177, 367–382. doi: 10.1111/j.1365-246X.2008.04008.x

CrossRef Full Text | Google Scholar

Jackson, A., Livermore, P., and Ierley, G. (2011). On ohmic heating in the Earth's core II: poloidal magnetic fields obeying Taylor's constraint. Phys. Earth Planet. Int. 187, 322–327. doi: 10.1016/j.pepi.2011.06.003

CrossRef Full Text | Google Scholar

Jagoutz, E., Palme, H., Baddenhausen, H., Blum, K., Cendales, M., Dreibus, G., et al. (1979). The abundance of major, minor and trace elements in the Earth's mantle as derived from primitive ultramafic nodules. Proc. Lunar. Sci. Conf. 10th, 2031–2050.

Jarvis, G. T., and McKenzie, D. P. (1980). Convection in a compressible fluid with infinite Prandtl number. J. Fluid Mech. 96, 515–583. doi: 10.1017/S002211208000225X

CrossRef Full Text | Google Scholar

Jarvis, G., and Campbell, I. H. (1983). Archean Komattites and geotherms: solution to an apparent contradiction. Geophys. Res. Lett. 10, 1133–1136. doi: 10.1029/GL010i012p01133

CrossRef Full Text | Google Scholar

Javoy, M., Kaminski, E., Guyot, F., Andrault, D., Sanloup, C., Moreira, M., et al. (2010). The chemical composition of the Earth: enstatite chondrite models. Earth Planet. Sci. Lett. 293, 259–268. doi: 10.1016/j.epsl.2010.02.033

CrossRef Full Text | Google Scholar

Kaiser, W., and Zaehringer, J. (1968). K/Ar Age determinations of iron meteorites IV: new results with refined experimental procedures. Earth Planet. Sci. Lett. 4, 84–88. doi: 10.1016/0012-821X(68)90059-9

CrossRef Full Text | Google Scholar

Kato, M., and Kawakatsu, H. (2001). Seismological in situ Estimation of Density Jumps across the Transition Zone Discontinuities beneath Japan. Geophys. Res. Lett. 28, 2541–2544. doi: 10.1029/2000GL012747

CrossRef Full Text | Google Scholar

Kendall, J.-M., and Shearer, P. M. (1994). Lateral variations in D″ thickness from long-period shear wave data. J. Geophys. Res. 99, 11575–11590. doi: 10.1029/94jb00236

CrossRef Full Text | Google Scholar

Labrosse, S. (2003). Thermal and magnetic evolution of the Earth's core. Phys. Earth Planet. Int. 140, 127–143. doi: 10.1016/j.pepi.2003.07.006

CrossRef Full Text | Google Scholar

Larsen, T. B., and Yuen, D. A. (1997). Ultrafast upwelling bursting through the upper mantle. Earth Planet. Sci. Lett. 146, 393–400. doi: 10.1016/S0012-821X(96)00247-6

CrossRef Full Text | Google Scholar

Larson, E. W. F., and Ekström, G. (2001). Global models of surface-wave group velocity. Pure Appl. Geophys. 158, 1377–1400.

Google Scholar

Larson, R. L. (1991). Latest pulse of the Earth: evidence for a mid-Cretaceous superplume. Geology 19, 547–550.

Google Scholar

Lay, T., Hernlund, J., and Buffett, B. A. (2008). Core-mantle boundary heat flow. Nat. Geosci. 1, 25–32. doi: 10.1038/ngeo.2007.44

CrossRef Full Text | Google Scholar

Leng, W., and Zhong, S. (2008). Viscous heating, adiabatic heating and energetic consistency in compressible mantle convection. Geophys. J. Int. 173, 693–702. doi: 10.1111/j.1365-246X.2008.03745.x

CrossRef Full Text | Google Scholar

Lodders, K. (1995). Alkali elements in the Earth's core: evidence from enstatite meteorites. Meteoritics 30, 93–101. doi: 10.1111/j.1945-5100.1995.tb01215.x

CrossRef Full Text | Google Scholar

Lyubetskaya, T., and Korenaga, J. (2007a). Chemical composition of Earth's primitive mantle and its variance: 1. Method and results. J. Geophys. Res. 112, B03211. doi: 10.1029/2005jb004223

CrossRef Full Text | Google Scholar

Lyubetskaya, T., and Korenaga, J. (2007b). Chemical composition of Earth's primitive mantle and its variance: 2. Implications for global geodynamics. J. Geophys. Res. 112, B03212. doi: 10.1029/2005jb004224

CrossRef Full Text | Google Scholar

Malavergne, V., Tarrida, M., Combes, R., Bureau, H., Jones, J., and Schwandt, C. (2007). New high-pressure and high-temperature metal/silicate partitioning of U and Pb: implications for the cores of the Earth and Mars. Geochem. Cosmo. Acta 71, 2637–2655. doi: 10.1016/j.gca.2007.03.011

CrossRef Full Text | Google Scholar

Mareschal, J.-C., and Jaupart, C. (2011). “Energy Budget of the Earth,” in Encyclopedia of Solid Earth Geophysics, ed H. Gupta (Dordrecht: Springer), 285–291.

Masters, G., Johnson, S., Laske, G., and Bolton, H. (1996). A shear-velocity model of the mantle. Philos. Trans. R. Soc. Lond. Ser. A 354, 1385–1411. doi: 10.1098/rsta.1996.0054

CrossRef Full Text | Google Scholar

McDonough, W. F. (2005). “Compositional model for the Earth's core,” in The Mantle and Core Vol. 2, ed R. W. Carlson (Oxford: Elsevier-Pergamon), 547–568.

McDonough, W. F., and Sun, S.-S. (1995). The composition of the Earth. Chem. Geol. 120, 223–253. doi: 10.1016/0009-2541(94)00140-4

CrossRef Full Text | Google Scholar

Morelli, A., and Dziewonski, A. M. (1987). Topography of the core-mantle boundary and lateral homogeneity of the liquid core. Nature 325, 678–683. doi: 10.1038/325678a0

CrossRef Full Text | Google Scholar

Morgan, J. P. (1997). Thermal and rare gas evolution of the mantle. Chem. Geol. 145, 431–445. doi: 10.1016/S0009-2541(97)00153-8

CrossRef Full Text | Google Scholar

Morgan, J. P. (2001). The Role of Serpentination and Deserpentinization in Bending and Unbending the Subducting Slab. San Francisco, CA: EOS Trans. AGU; Fall Meeting Supplement. Abstract # T22D-03 82.

Morgan, J. P., and Vannucchi, P. (2014). Earth's Fiercely Cooling Core—24 TW. Vienna: EGU General Assembly 2014.

Morgan, J. P., Morgan, W. J., and Price, E. (1995). Hotspot melting generates both hotspot volcanism and a hotspot swell? J. Geophys. Res. 100, 8045–8062. doi: 10.1029/94JB02887

CrossRef Full Text

Nimmo, F. (2007). “Energetics of the Core,” in Treatise on Geophysics, ed G. Schubert (Amsterdam: Elsevier), 31–65.

Obayashi, M., and Fukao, Y. (1997). P and PcP travel time tomography for the core-mantle boundary. J. Geophys. Res. 102, 17825–17841. doi: 10.1029/97JB00397

CrossRef Full Text | Google Scholar

O'Neill, H. S. C., and Palme, H. (2008). Collisional erosion and the non-chondritic composition of the terrestrial planets. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 366, 4205–4238. doi: 10.1098/rsta.2008.0111

PubMed Abstract | CrossRef Full Text | Google Scholar

Oxburgh, E. R., and Turcotte, D. L. (1978). Mechanisms of continental drift. Rep. Prog. Phys. 41, 1249–1312. doi: 10.1088/0034-4885/41/8/003

CrossRef Full Text | Google Scholar

Palme, H., and O'Neill, H. S. C. (2003). “Cosmochemical estimates of mantle composition,” in The Mantle and Core, eds D. H. Heinrich and K. T. Karl (Amsterdam: Elsevier), 1–38.

Parker, L. J., Atou, T., and Badding, J. V. (1996). Transition element-like chemistry for potassium under pressure. Science 273, 95–97. doi: 10.1126/science.273.5271.95

PubMed Abstract | CrossRef Full Text | Google Scholar

Parsons, B. A. (1982). Causes and consequences of the relation between area and age of the ocean floor. J. Geophys. Res. 87, 289–302. doi: 10.1029/JB087iB01p00289

CrossRef Full Text | Google Scholar

Parsons, B., and Sclater, J. G. (1977). An analysis of the variation of ocean floor bathymetry and heat flow with age. J. Geophys. Res. 82, 803–827. doi: 10.1029/JB082i005p00803

CrossRef Full Text | Google Scholar

Pozzo, M., Davies, C., Gubbins, D., and Alfè, D. (2012). Thermal and electrical conductivity of iron at Earth's core conditions. Nature 485, 355–358. doi: 10.1038/nature11031

PubMed Abstract | CrossRef Full Text | Google Scholar

Qin, L., Carlson, R. W., and Alexander, C. M. O. Ä. (2011). Correlated nucleosynthetic isotopic variability in Cr, Sr, Ba, Sm, Nd and Hf in Murchison and QUE 97008. Geochem. Cosmo. Acta 75, 7806–7828. doi: 10.1016/j.gca.2011.10.009

CrossRef Full Text | Google Scholar

Ranero, C. R., Phipps Morgan, J., McIntosh, K. D., and Reichert, C. (2003). Bending, faulting, and mantle serpentinization at the Middle America trench. Nature 425, 367–373. doi: 10.1038/nature01961

PubMed Abstract | CrossRef Full Text | Google Scholar

Ricard, Y., and Wuming, B. (1991). Inferring the viscosity and the 3-D density structure of the mantle from geoid, topography, and plate velocities. Geophys. J. Int. 105, 561–571. doi: 10.1111/j.1365-246X.1991.tb00796.x

CrossRef Full Text | Google Scholar

Rudnick, R. L., and Fountain, D. M. (1995). Nature and composition of the continental crust: a lower crustal perspective. Rev. Geophys. 33, 267–309.

Google Scholar

Rudnick, R. L., and Gao, S. (2003). “Composition of the Continental crust,” in The Crust Vol. 3 Treatise on Geochemistry, ed R. L. Rudnick (Pergamon: Oxford), 1–64.

Rüpke, L., Morgan, J. P., Hort, M. A., and Connolly, J. A. D. (2004). Serpentine and the subduction zone water cycle. Earth Planet. Sci. Lett. 223, 17–34. doi: 10.1016/j.epsl.2004.04.018

CrossRef Full Text | Google Scholar

Schubert, G., Froidevaux, C., and Yuen, D. A. (1976). Oceanic lithosphere and asthenosphere: thermal and mechanical structure. J. Geophys. Res. 81, 3525–3541. doi: 10.1029/JB081i020p03525

CrossRef Full Text | Google Scholar

Sclater, J. G., Parsons, B., and Jaupart, C. J. (1981). Oceans and continents: similarities and differences in the mechanism of heat transport. J. Geophys. Res. 86, 11535–11552.

Google Scholar

Shaw, D. M., Cramer, J. J., Higgins, M. D., and Truscott, M. G. (1986). “Composition of the Canadian Precambrian shield and the continental crust of the earth,” in The Nature of the Lower Continental Crust, Vol. 24, eds J. B. Dawson, D. A. Carswell, J. Hall, and K. H. Wedepohl (London: Geological Society), 257–282.

Shearer, P. M. (2000). Upper mantle seismic discontinuities. Geophys. Monogr. 117, 115–131. doi: 10.1029/gm117p0115

CrossRef Full Text | Google Scholar

Shearer, P. M., and Flanaghan, M. P. (1999). Seismic velocity and density jumps across the 410- and 660-km discontinuities. Science 285, 1545–1548. doi: 10.1126/science.285.5433.1545

PubMed Abstract | CrossRef Full Text | Google Scholar

Sherman, D. M. (1990). Chemical bonding and the incorporation of potassium into the Earth's core. Geophys. Res. Lett. 17, 693–696. doi: 10.1029/GL017i006p00693

CrossRef Full Text | Google Scholar

Stacey, F. D. (1981). “Cooling of the Earth - A constraint on paleotectonic hypotheses,” in Evolution of the Earth, eds R. J. O'Connell and W. S. Fyfe (Washington, DC: AGU), 272–276.

Stadler, G., Gurnis, M., Burstedde, C., Wilcox, L. C., Alisic, L., and Ghattas, O. (2010). The dynamics of Plate Tectonics and mantle flow: from local to global scales, Science 329, 1033–1038. doi: 10.1126/science.1191223

PubMed Abstract | CrossRef Full Text | Google Scholar

Stein, C. A., and Stein, S. (1992). A model for the global variation in oceanic depth and heat flow with lithospheric age. Nature 359, 123–129. doi: 10.1038/359123a0

CrossRef Full Text

Steinbach, V., and Yuen, D. A. (1999). Viscous heating: a potential mechanism for the formation of the ultralow velocity zone. Earth Planet. Sci. Lett. 172, 213–220. doi: 10.1016/S0012-821X(99)00205-8

CrossRef Full Text | Google Scholar

Su, W.-J., Woodward, R. L., and Dziewonski, A. M. (1994). Degree 12 model of shear velocity heterogeneity in the mantle. J. Geophys. Res. 99, 6945–6980. doi: 10.1029/93JB03408

CrossRef Full Text | Google Scholar

Sze, E. K. M., and van der Hilst, R. D. (2003). Core mantle boundary topography from short period PcP, PKP, and PKKP data. Phys. Earth Planet. Int. 135, 27–46. doi: 10.1016/S0031-9201(02)00204-2

CrossRef Full Text | Google Scholar

Taylor, S. R., and McClennan, S. M. (1985). The Continental Crust: Its Composition and Evolution. Oxford: Blackwell Scientific Publishing.

Google Scholar

Turcotte, D. L. (1995). How does Venus lose heat? J. Geophys. Res. 100, 16931–16940.

Google Scholar

Turcotte, D. L., and Oxburgh, E. R. (1967). Finite amplitude convective cells and continental drift. J. Fluid Mech. 28, 29–42. doi: 10.1017/S0022112067001880

CrossRef Full Text | Google Scholar

Turcotte, D. L., Hsui, A. T., Torrance, K. E., and Schubert, G. (1974). Influence of viscous dissipation on Benard convection. J. Fluid Mech. 64, 369–374. doi: 10.1017/S0022112074002448

CrossRef Full Text | Google Scholar

Van den Berg, A. P., and Yuen, D. A. (1997). The role of shear heating in lubricating mantle flow. Earth Planet. Sci. Lett. 151, 33–42. doi: 10.1016/S0012-821X(97)00110-6

CrossRef Full Text | Google Scholar

Weaver, B. L., and Tarney, J. (1984). Major and trace element composition of the continental lithosphere. Phys. Chem. Earth 15, 39–68.

Google Scholar

Wedepohl, K. H. (1994). The composition of the continental crust (abstract). Minerak. Mag. 58, 959–960. doi: 10.1180/minmag.1994.58A.2.234

CrossRef Full Text

Widmer, R., Masters, G., and Gilbert, F. (1991). Spherically symmetric attenuation within the Earth from normal mode data. Geophys. J. Int. 104, 541–553. doi: 10.1111/j.1365-246x.1991.tb05700.x

CrossRef Full Text | Google Scholar

Zerr, A., Diegler, R., and Boehler, R. (1998). Solidus of the Earth's deep mantle. Science 281, 243–246. doi: 10.1126/science.281.5374.243

PubMed Abstract | CrossRef Full Text | Google Scholar