Comparative analysis of the differences between using LiDAR and contour-based DEMs for hydrological modeling of runoff generating debris flows in the Dolomites

Present work aims to explore the differences in hydrological modeling when using digital elevation models (DEMs) generated by points from LiDAR surveys and those digitized on the contour lines of the regional technical map (RTM) and their relevance for the simulation of debris flow triggering. Hydrological models for mountainous areas are usually based on DEMs. DEMs are used to determine the flow path from each pixel, by which the basin is discretized, to the outlet. Hydrological simulations of runoff that triggered debris flows occurred in two rocky headwater basins of Dolomites, Fiames Dimai (area approximately 0.03 km²), and Cancia (area approximately 0.7 km²) are carried out using a DEM-based model designed for simulating runoff that descends from headwater areas. For each basin, the runoff is simulated using DEMs that are generated using points from LiDAR, and those digitized on the contour lines of the regional technical map, respectively. The results show that the peak discharge values corresponding to the simulations carried out using the LiDAR-based DEMs are higher than those corresponding to the simulations carried out using the RTM-based DEMs. Larger differences are observed for the Dimai basin, where the area corresponding to the RTM-based DEM is markedly smaller than the area corresponding to LiDAR-based DEM, whereas for the Cancia basin, the two areas are similar. Both the differences in the peak discharge and the basin area are due to the poor accuracy of the contour-based DEM (i.e., elevation accuracy), that is, a poor representation of the morphological features that leads to errors on the watershed divide and simplifications of the flow paths from each cell to the outlet. This result is highly relevant for estimating the triggering conditions of runoff generated debris flows. An incorrect simulated value of peak discharge can lead to errors both in planning countermeasures against debris flows and in predicting their occurrence.

Introduction

Digital elevation models (DEMs) are fundamental for determining flow paths in mountainous areas (Jenson, 1991; Moore et al., 1991; Tarboton et al., 1991). Flow paths are used by GIS-base distributed hydrological models for the transfer of excess precipitation from each pixel of the basin to the outlet for computing the runoff hydrograph. Then, the accuracy of spatial information (i.e., DEM accuracy or elevation accuracy) becomes crucial for simulating the hydrological responses (Quinn et al., 1991; Hornberger and Boyer, 1995; Garbrecht et al., 2001; Clarke and Burnett, 2003). Conventional DEMs are usually obtained by digitizing the contours on existing topographical maps (Moore et al., 1991; Robinson, 1994). These contour-based DEMs, also known as cartometric DEMs (Walker and Willgoose, 1999), are not sufficiently accurate if the density of the original topographical points by which they were generated is low or if the points are nonexistent (Robinson, 1994). Therefore, conventional DEMs of mountainous areas, where rocky walls and very steep slopes zones are not always captured in sufficient detail via usual topographical surveys, often exhibit low accuracy. Such insufficiencies can be resolved by DEMs obtained using high-resolution photogrammetrics, terrestrial laser scanners (TLS), and laser imaging detection and ranging (LiDAR) surveys. The more frequent use of unmanned aerial vehicles (UAV) and helicopters or aircraft flights has exploited the topographical surveys via stereoscopic imagery and laser, although their costs remain quite high. The use of photogrammetric or LiDAR points should increase the accuracy of DEMs over that of conventional DEMs due to the higher density of points (at least one order of magnitude higher). In the present work, we aim to understand the effect of DEM accuracy on the runoff hydrographs of headwater basins. In recent years, the frequency of high intensity and short duration precipitations in mountainous areas of Europe and North-America has increased due to climate change (Haberli et al., 1990; Evans and Claugue, 1994; Jomelli et al., 2007; Pelfini and Santilli, 2008; Flores et al., 2010) and, consequently, the occurrence of debris flows has increased. These local, intense, convective rainfalls (Underwood et al., submitted) produce abundant runoffs at the feet of rocky headwater walls that are able to entrain large quantities of sediments and debris flows. Runoff-generated debris flows, initially observed in laboratory facilities (Gregoretti, 2000a,b; Tognacca et al., 2000), are common both in the Alpine region (Berti and Simoni, 2005; Gregoretti and Dalla Fontana, 2008; Theule et al., 2012; Tiranti and Deangeli, 2015) and in other mountainous regions such as the Pyrenees (Hurlimann et al., 2014), Japan Alps (Imaizumi et al., 2006; Okano et al., 2012), Colorado and California (Cannon et al., 2008; Coe et al., 2008; Kean et al., 2012). The routing of debris flow in settled areas can cause damage and casualties. Accordingly, the computation of runoff triggering debris flows is important for risk analyses. Consequently, understanding the effect of DEM accuracy on runoff hydrographs is very useful for scientists and technicians involved in debris flow risk assessment and countermeasures planning.

For this purpose we compare the results of the hydrological simulations of runoff that triggered occurred debris flows in two headwater basins of Dolomites using both LiDAR and conventional (contour-based) DEMs.

The paper is organized as follows. Section Results from Previous Authors summarizes the works of previous authors. Section Materials and Methods is divided in four subsections. The first and second subsections shows the topographical dataset and two headwater basins with their morphological characteristics respectively. The third and fourth subsections introduces the DEM-based hydrological model and the occurred debris flow events. Section Results presents and discusses the results of the simulations. Finally, Section Conclusions reports some conclusions.

Results from Previous Authors

As recognized by Walker and Willgoose (1999), few studies have evaluated the effects of DEM accuracy on hydrologic modeling. A brief description of the contributions of previous authors on this topic is outlined below.

Lagacherie et al. (1996) carried out hydrological simulations of a French basin (0.91 km²; mean slope 10%) using a parametric non-linear model that converts rainfall runoff at a sub-catchment scale (approximately 0.01 km²) based on the Green and Ampt equations and routes the runoff to the outlet according to an Hayami response function. The simulations were carried out using six different DEMs of the same grid size (2 m). One of the DEMs was a conventional DEM obtained by digitizing the topographical map of France. The remaining DEMs were obtained via photogrammetric points derived from low altitude aerial photographs (five different DEMs were generated considering all parts of the photogrammetric points). Results of the simulations show small differences among the hydrographs simulated using the different DEMs at the basin scale but noticeable differences up to 50% at the sub-catchment scale. Walker and Willgoose (1999) carried out a detailed analysis of the effect of DEM accuracy on hydrological responses without hydrological simulations due to the difficulty of drawing general conclusions but instead focused on the comparison of the hydromorphic features and the functions that were computed using DEMs obtained from different data sources. The data sources included a 1:250000 topographic map (10 m contour interval), aerial photographs and ground points taken by a total station (electronic distance measurement) with a catchment of approximately 0.42 km² for which cartometric, photogrammetric and ground DEMs were obtained, respectively. The ground DEM was characterized by a higher level of accuracy compared to the elevation of the original data. An assessment of the DEM accuracy on hydrological response was performed both qualitatively and quantitatively. First, the stream network and the catchment boundaries of the cartometric and photogrammetric DEMs were compared to those obtained via the ground DEM, which was considered to be the “true DEM” due to its higher level of accuracy. Second, the plots of the width functions directly related to the unit hydrograph and the runoff routing were compared (Surkan, 1969). The qualitative investigations performed at different grid sizes show that, in some cases, the catchment area of the cartometric and photogrammetric DEMs range between half and unity of the true ground DEM area. The stream networks identified from the cartometric and photogrammetric DEMs exhibit differences compared to those derived by the true ground DEM, which vary from low to high degrees. Walker and Willgoose (1999) explained the significant differences through localized effects of elevations that are not captured by cartometric and photogrammetric DEMs. Quantitative assessments show that the width functions for the cartometric and photogrammetric DEMs are markedly different from the true ground DEM in all cases, even when the difference in the stream networks is not large or significant. Walker and Willgoose (1999) attributed this behavior to the elevation errors due to the source of the elevation data. Kenward et al. (2000) evaluated the effects of the vertical accuracy of three different DEMs on hydrological modeling by simulating runoff in a 7.2 km² catchment. The three DEMs were obtained by low altitude aerial photographs, digitized contour maps and space imaging radar, respectively. The first DEM was assumed as the reference DEM. The remaining DEMs were denoted as cartometric and SIR-C DEMs. Catchment areas corresponding to cartometric and reference DEMs are the same, whereas the SIR-C DEM provides an area 3.6% larger than that of the reference DEM. However, both the catchment divides and the stream networks boundaries of stream networks differ considerably. Hydrological simulations performed using distributed models that route subsurface flow from one cell to neighboring cells according to the elevation differences and direct runoff to the outlet by using a unit hydrograph exhibit larger differences in the peak discharge values. Peak discharge values computed by using the cartometric DEM are smaller (1–10%) than those computed the reference DEM, whereas those computed by SIR-C DEM are approximately 30–50 % smaller than those corresponding to the reference DEM. The peak times are anticipated (approximately 3 h) or postponed (approximately 4 h) by cartometric or SIR-C DEMs, respectively, in relation to the peak times of the reference DEM. Kenward et al. (2000) attributed these results to the smoothness of cartometric and SIR-C DEMs, which are not able to capture all of the topographical features of the catchment. Murphy et al. (2008) analyzed the differences among stream networks identified using a LiDAR-based DEM (LiDAR elevation points at 0.5 m intervals and a stated vertical accuracy of 0.04 m) and a photogrammetric DEM (elevation points captured at 100 m intervals and a stated vertical accuracy of 3 m) in a catchment of Alberta (Canada). The catchment area corresponding to the LiDAR-based DEM is 1.93 km², whereas that corresponding to the photogrammetric DEM is 1.68 km². The stream network, obtained using the LiDAR-based DEM, has a length twice as long as that of the photogrammetric DEM. Stream networks identified using both DEMs are broadly similar for the lower streams orders but differ for the higher stream orders where flow lines tend to accumulate as several lines of convergence running parallel or sub-parallel to one another. According to the authors, this phenomenon results from the failure to capture topographic details and slopes due to the lower original density of the elevation points (two orders of magnitude lower), used for the construction of the photogrammetric DEM. Vaze et al. (2010) obtained analogous results for comparing a LiDAR-based DEM with a cartometric DEM. In the present work, we investigate the differences between the results of runoff modeling obtained using DEMs developed from different data sources (digitized and LiDAR points) based on the stream network, the catchment area and the hydrogeomorphic functions. Our aim is to explain the differences in the simulation of the hydrological response in headwater basins when using DEMs from different data sources. Moreover, because many mountainous areas in the world are not yet covered by LiDAR surveys, this work could also provide some quantitative estimation of the hydrological response simulation if carried out only by using cartometric DEMs.

Materials and Methods

In the first and the second parts of this section, the topographical dataset and the two basins with their morphometric characteristics are introduced. The third part presents the hydrological model. The fourth part documents the debris flow events that occurred in the two basins and the rainfalls that triggered them.

Topographical Dataset

The topographical data used in the present work are the contour lines of the Regional Technical Map (RTM) of the Veneto Region and LiDAR points acquired in 2010 (Dimai basin) and 2011 (Dimai and Rovina di Cancia basins). The 2010 and 2011 LiDAR surveys have a density of approximately 1 and 3 points/m², respectively, and were provided by the association “Regole d'Ampezzo” and the Department Land Defence and Civil Protection of the Province of Belluno, respectively. The points of the LiDAR surveys and those digitized at 0.25 m spacing on the contour lines of the RTM are used for extracting the DEMs. The DEMs are obtained by building a triangular irregular network (TIN) mesh whose nodes are the grounds points (LiDAR or contour digitized points) and performing a 3D interpolation using the natural neighbor method. Natural neighbor interpolation finds the closest subset of input samples to a query point and applies weights to them based on the proportion of the area to interpolate a value. Therefore, this method guarantees an interpolation height within the range of the samples and prevents the representation of non-existing peaks, pits, ridges, or valleys. Herein, the DEMs are denoted RTM DEM, LiDAR10DEM, and LiDAR11DEM. The grid size of the DEM is 1 m and corresponds very well with the density of points of the 2010 LiDAR. As the distance of the digitized points along the contour line is 0.25 m, and the distance between neighboring contour lines is 1–20 m, the choice of 1 m grid size is a reasonable compromise between the various point densities and distributions. Regarding the LiDAR-based DEMs accuracy, the elevation error is approximately 0.1–0.2 m on the plane areas and increases with the slope reaching 1.5 m at 60° (Scheidl et al., 2008), whereas the horizontal error is approximately 0.5–1 m according to Cavalli and Tarolli (2011). The RTM-based DEM accuracy is uncertain and difficult to assess. The RTM used here is a topographical map on a scale of 1:5000 meters that is derived from a stereoscopic restitution (photogrammetric spatial triangulation) of land from an aerial image survey corresponding to an average ground sampling distance of 0.2 m (i.e., the pixel size). The elevation points acquired via stereoscopy are used to build 5-m spaced contour lines with a relative distance of 1–20 m on the horizontal plane in the present basins. The points of contour lines of the RTM that was used here have a horizontal error tolerance of 1 m and a vertical error tolerance of 1.5 m with respect to the “stereoscopical” points by which the contour lines were built in approximately planar areas. For rock walls, these tolerance values can increase up to one order of magnitude. Then, the accuracy of the digitized points is the ensemble of the errors of the “stereoscopical” points, which are not provided by the Veneto Region, with the tolerance associated with the contour lines. The accuracy of the RTM-based DEM is assessed according to the ensemble of the errors of the digitized points with those derived from the interpolation process during DEM construction, as explained above. The error from the interpolation process of the digitized points depends both on the spacing of points along the contour line and the spacing between neighboring contour lines. The 0.25 m spacing minimizes the error due to the distances of points along the contour line and is negligible with respect to the error due to the distances between neighboring contour lines, which vary from 1 to 20 m on the horizontal plane in the present study. The distances between neighboring contour lines noticeably increases the errors due to the interpolation of points because the morphological features, such as peaks or hollows between two contour lines, cannot be reproduced when the distances between neighboring contour lines become very large. In this case, the interpolation process provides unrealistic planar slopes, and DEM appears as an ensemble of sloping surfaces. Therefore, the errors due to the interpolation process for the RTM-based DEM are mainly given by the digitized point distribution rather than by the point density, and the errors cannot be quantified exactly due to the local terrain morphology. Finally, the accuracies of the RTM-based or conventional DEM are much lower than the accuracy of LiDAR-based DEMs because the ensemble of errors of the global positions of the digitized points, with those due to their distribution could be one or more orders of magnitude larger compared to LiDAR (Hodgson et al., 2003).

The Two Basins

The two head water basins of the Fiames-Dimai and the Rovina di Cancia (Figure 1) are located on the right side of the Boite Valley in the Dolomites, North-Eastern Italy, and their outlets correspond to the triggering areas of debris flow. The morphometric characteristics and divides of the two basins depend on the DEMs. Figure 1 shows the divides of the two basins, and Table 1 shows their morphological characteristics that were obtained using the five different DEMs. There are large differences for the Dimai basin area among the values derived from the RTM DEM and the values derived from the two LiDAR-based DEMs. The relative differences between the RTM and the 2010 LiDAR areas and between the RTM and the 2011 LiDAR areas are 20 and 25%, respectively. The relative difference between the LiDAR2010 and the LiDAR2011 areas is 6%. Figure 2 shows the outlets positions for the different DEMs and the coordinates obtained via the field surveys using a differential GPS with real time correction (GRS-1 of TOPCON). The outlet positions derived from the LiDAR surveys nearly coincide with the points of the GPS, whereas those derived from the RTM are far (approximately 10 pixels) for both of the watersheds. The elevation of the GPS point at the Dimai basin is 1–0.4 m lower than LiDAR2010 and LiDAR2011 outlet elevations, respectively, and 7 m higher than the RTM DEM outlet elevation. For the Cancia basin, the GPS point elevation coincides with that of the outlet of the LiDAR2011 and is 1.44 m higher than that of the RTM DEM outlet. The horizontal errors of the GPS points are 0.022 and 0.018 for the outlets of Dimai and Cancia basin, respectively, whereas the vertical errors are 0.043 and 0.032 m, respectively. The exact planimetrical coincidence at the outlets corresponding to the GPS and the LiDAR DEMs points, with an elevation error less than 1 m, show higher accuracies of the LiDAR-based DEMs with respect to the RTM DEM, which exhibited both vertical and horizontal errors of approximately 10 m. The smaller elevation error of the LiDAR2011 than that of LiDAR2010 at the outlet is expected, because a larger LiDAR point density produces a more accurate DEM (Gong et al., 2000; James et al., 2007; Cavalli et al., 2008). Therefore, the difference between the Dimai basin areas computed by the two LiDAR DEMs is due to the different point densities. The large difference (20–25%) in the areas of the Dimai basin between the RTM DEM and the LiDAR-based DEMs is primarily due to the lower accuracy of the RTM-based DEM, which can be one order less than that of the LiDAR-based DEM, as shown in the previous section. For this reason, large border parts of the basin can be ignored, or external parts can be added. For small basins such as Dimai, the ignored or the added external parts are not negligible fractions of the entire basin, and the RTM DEM basin may be significantly smaller or larger than the real basin. For Rovina di Cancia, the effects of the ignored/added parts are negligible because the basin is much larger with respect to the ignored or added parts. In addition, these parts serve to balance one another, as per the observation of the divides of the Cancia basin, shown in Figure 1: the difference in area values computed using the RTM and LiDAR11 DEMs is approximately 1%.

FIGURE 1

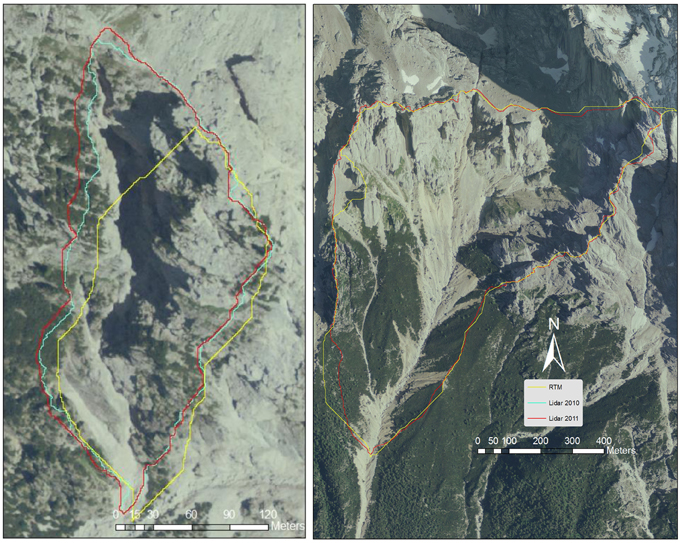
Figure 1. The divides of the two basins of Dimai (left) and Rovina di Cancia (right), obtained by using DEMs derived from different data source (yellow RTM, blue LiDAR 2010, red LiDAR 2011).

TABLE 1

Table 1. Morphometric characteristics obtained by the five different DEMs.

FIGURE 2

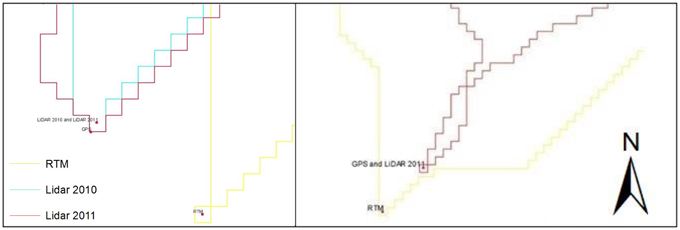
Figure 2. The outlet position of basins of Dimai (left) and Rovina di Cancia (right), according to the different DEMs and the GPS topographical survey.

The DEM based Hydrological Model

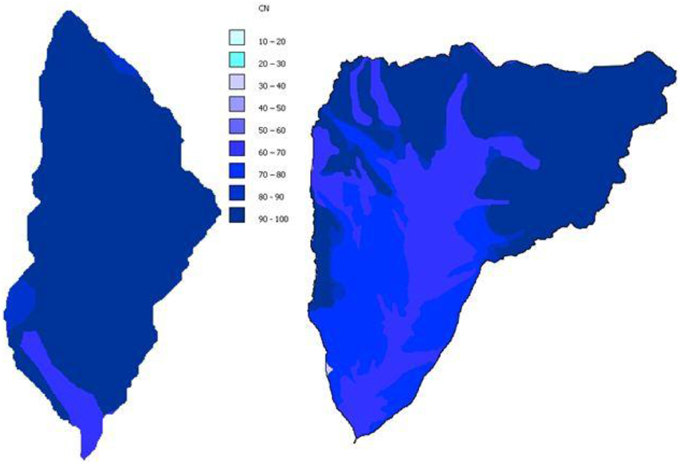
The hydrological model is that of Gregoretti and Dalla Fontana (2008) and is designed for simulating runoff triggering debris flow in headwater basins. The model computes the excess rainfall using the soil conservation service curve number method (SCS-CN) for each pixel by which the basin is discretized and transfers it to the outlet along the maximum slope direction. The sum of the excess rainfall pulses that reach the outlet in the same time step is the hydrograph value. The flow path from each pixel of the basin to the outlet is the sum of the pixel lengths (pixel size in the straight direction, diagonal pixel length in the oblique direction) along the direction with the highest slope. The highest slope is computed via the D8 method (Da Ros and Borga, 1997; Tarboton, 1997), and it is the largest of the slopes between the center of a cell and those of the eight neighboring cells. The flow paths are divided into slope and channel paths. The slope paths are divided based on the terrain typology (i.e., rock, scree, wood) because each terrain is assigned a slope velocity. In such a high mountainous environment, the terrain typology also corresponds to the slope (i.e., rocky terrain has slope much larger slope than scree). The slope velocities used by Gregoretti and Dalla Fontana are 0.3 m/s for rocky surfaces, 0.1 m/s for scree, and 0.04 m/s for woody terrain. These values are within the same range as the values proposed by Sangati et al. (2009) and Grimaldi et al. (2010), except that the higher value used for rocky terrain. The channel path is extracted using the threshold area concept (Montgomery and Foufoula-Georgiou, 1993). The threshold area value for determining the channel is assumed equal to 0.005 km², according to McGlynn and Seibert (2003) and McGuire et al. (2005). The computed channels coincide with that incised on the rock wall of Dimai Peak and with those visible at Rovina di Cancia (Figure 3). The channel velocity is the mean cross-sectional velocity corresponding to the peak discharge and is computed using an iterative method with a very fast convergence. The simulation is carried out using an initial value of the channel velocity and is compared with the mean cross-sectional velocity corresponding to the simulated peak discharge. If these two values are within 2%, the simulation ends; otherwise, another simulation is carried out until the two values are within 2%. The channel velocities are usually larger than 1 m/s. This model, as illustrated in Figure 4, is analogous to the models proposed by Botter and Rinaldo (2003), Sangati et al. (2009) and Grimaldi et al. (2012). The SCS-CN method computes the excess rainfall P_e according to the following equations:

$\begin{array}{cc}{P}_e\left(t\right)=0\left(t\le t_{IA}\right);P_e\left(t\right)=\frac{P\left(t\right)-Ia}{P\left(t\right)-Ia+S\left(t>t_{IA}\right)}& (1)\end{array}$

where, P(t) is the rainfall height at time t, Ia is the initial abstraction, t_IA is the time corresponding to Ia, and S is the potential maximum retention. The parameter Ia is assumed by Gregoretti and Dalla Fontana (2008) equal to 0.1 S, where S = 1000/CN–10. The parameter curve number, CN, is tabulated according to the terrain hydrologic characteristics and the land use. The values of CN for mountainous terrain are provided by Gregoretti and Dalla Fontana (2008) and are shown in Figure 5. The tabulated values of CN correspond to the intermediate antecedent moisture condition, denoted as AMCII. Algebraic equations (Chow et al., 1988) allow for the computation of CN for the AMC corresponding to dry (AMCI) and wet states (AMCIII). The AMC condition is assigned after computing the previous 5 days rainfall. In a mountainous environment, the limit between AMCI and AMCII is 13.6 mm, and the limit between AMCII and AMCIII is 28 mm. The comparison of simulations carried out using the model of Gregoretti and Dalla Fontana (2008) with the measured hydrographs at the outlets of a rocky channel in the Dolomites (Gregoretti et al., submitted) shows that the model is not able to capture both the peak and the shape of the hydrographs due to a partially incorrect representation of the temporal pattern of infiltration predicted by the SCS-CN method. The computation of the excess rainfall is therefore modified following the approach of Grimaldi et al. (2013), by combining the SCS-CN method with an Hortonian simplified law (Gregoretti et al., submitted). The expression for computing the excess rainfall, P_e (t + Δt) − P_e(t), during the time step Δt for t > t_IA, is given by Equation (2) if fc ≥ I and by the following equation if fc < I:

$\begin{array}{cc}{P}_e\left(t+\Delta t\right)-P_e\left(t\right)=\frac{P\left(t\right)+\Delta t-Ia}{P\left(t+\Delta t\right)-Ia+S}-\frac{P\left(t\right)-Ia}{P\left(t\right)-Ia+S}& (2)\end{array}$

$\begin{array}{cc}{P}_e\left(t+\Delta t\right)-P_e\left(t\right)=P\left(t+\Delta t\right)-P\left(t\right)-\text{fc}\Delta \text{t}& (3)\end{array}$

where fc is the infiltration rate, I is the rainfall intensity, and Δt is the time step. The use of Equations (2) and (3) allows for a good simulation of the peaks of the measured hydrograph after increasing the slope velocity on rocky terrain up to 0.7 m/s. This last value approaches the channel velocity values, which are approximately 1 m/s for the Dimai basin and approximately 2 m/s for the Cancia basin, due the impervious nature of the basins. The parameter fc is computed through the expression, fc = 0.309 − 0.13*h₅ (Gregoretti et al., submitted), which is obtained empirically by fc values that allow the equality of the measured and simulated peak discharges (h₅ is the rainfall precipitated in the previous 5 days).

FIGURE 3

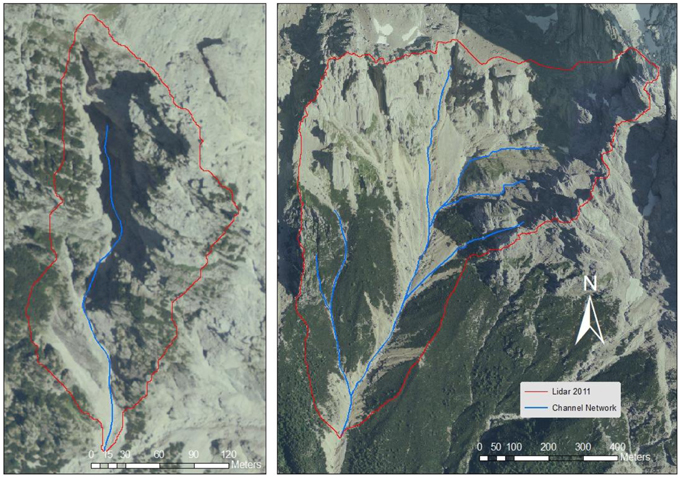
Figure 3. Channel network (blue line) of the two basins of Dimai (left) and Rovina di Cancia (right) obtained through LiDAR2011 DEMs.

FIGURE 4

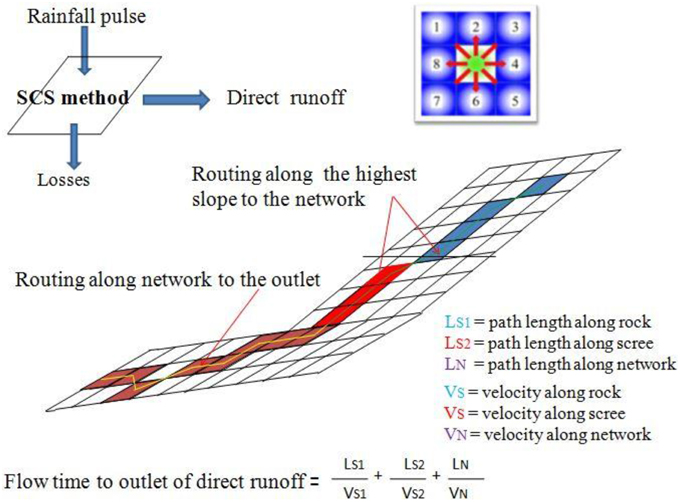
Figure 4. Conceptual sketch of the model of Gregoretti and Dalla Fontana (2008).

FIGURE 5

Figure 5. Map of the CN values of the two basins of Dimai (left) and Rovina di Cancia (right).

Precipitation Events that Triggered Debris Flows in the Two Basins

The rainfalls that trigger runoff generated debris flows exhibit the larger precipitated height in a time interval between 5 and 30 min. Only short duration, high intensity precipitations are able to deliver the high discharge required for moving a sediment bed for the generation of a debris flow (Berti and Simoni, 2005; Gregoretti and Dalla Fontana, 2007, 2008; Cannon et al., 2008; Kean et al., 2011; Staley et al., 2013). The rainfall events responsible for debris flows in the two basins are listed in Table 2 (h, precipitation height; D, precipitation duration). These data refer both to documented events provided by Gregoretti and Dalla Fontana (2008) and direct surveys of the authors. The rain gauges of Podestagno, Rovina Bassa, Rovina Alta, and Villanova are managed by the regional hydro-meteorological service. The rain gauges of Dimai and Pomagagnon were installed in July of 2010 close to the outlet and upstream extremity of the Dimai basin, respectively, by the authors in collaboration with professors Berti and Simoni of the University of Bologna (Italy). The rainfall data given by the rain gauges of Dimai and Pomagagnon are also used by (Underwood et al., submitted).

TABLE 2

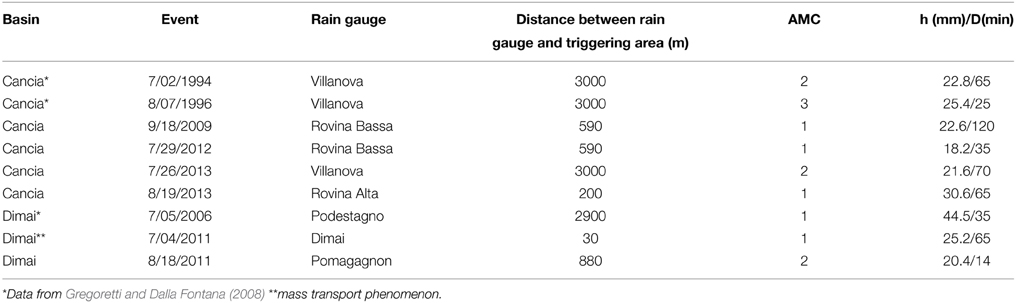
Table 2. Documented events of occurred debris flows in the two basins and the corresponding rainfall data.

Results

Results from Hydrological Simulations

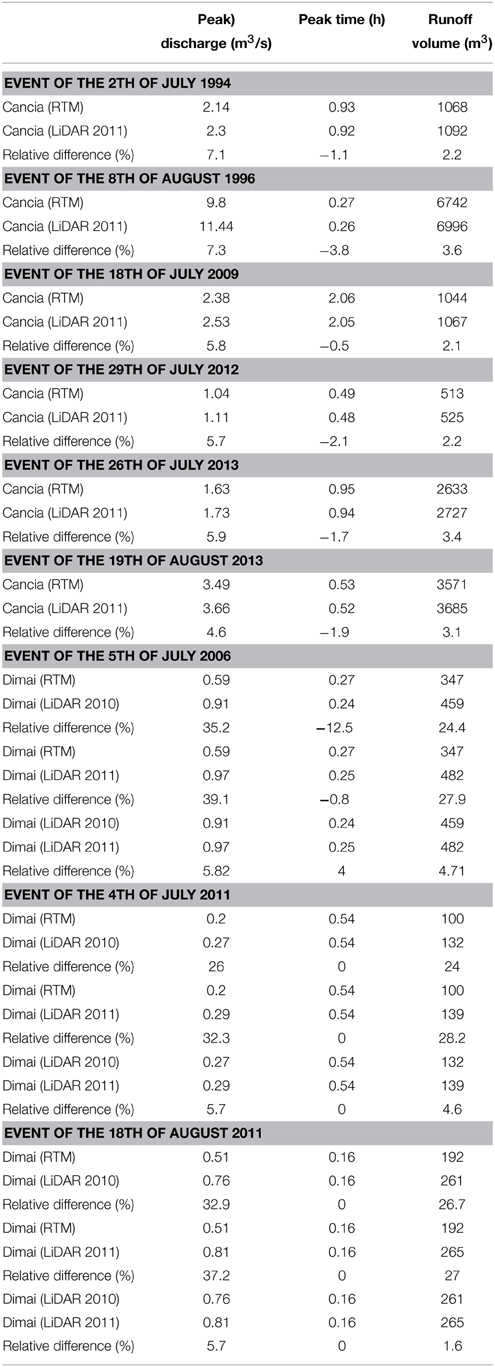
For each basin, we carry out the simulations of the runoff that triggered the debris flows or the mass transport phenomena, listed in Table 2, using the hydrological model described in the previous section. For clarity and simplicity, only the simulations of two events for each basin are shown in Figures 6, 7. Figure 6 shows the results of simulations corresponding to the events of July 5, 2006 and of August 18, 2011 for the Dimai basin, and Figure 7 shows the simulations corresponding to the events of July 2, 1994 and of August 7, 1996. The simulations are carried out using both the RTM and LiDAR-based DEMs. For both basins, simulations corresponding to the LiDAR-based DEMs provide a larger peak flow than the RTM DEMs, whereas the corresponding peak times are smaller for Cancia and equal for Dimai. The hydrograph shapes are roughly comparable for Cancia, whereas for Dimai, the hydrograph shape corresponding to the RTM DEM is less peaked than that of the LiDAR-based DEMs. Table 3 summarizes the quantitative results of the simulations and the relative differences among the corresponding simulations. The simulations of the runoff events of the Cancia basin carried out using LiDAR11DEM and the RTM DEM exhibit a relative difference between the peak discharge values in the range of 5–7%. The relative differences between the peak times and the runoff volumes values are nearly half of the relative difference between the peak discharges. The simulations of the runoff events of the Dimai basin carried out using LiDAR11DEM, LiDAR10DEM and the RTM DEM exhibited relative differences among the peak discharge values in the range of 26–39.1% (all values but one are over 32%) for the LiDAR-based DEM results compared to the RTM DEM results and a relative difference of 5.7–5.8% between the results of the LiDAR DEMs. The relative differences among the peak times are negligible, whereas the relative differences among the runoff volumes ranges from 24 to 28% for the LiDAR-based DEM results compared to the RTM DEM results and from 1.4 to 4.7% between the results of the LiDAR DEMs.

FIGURE 6

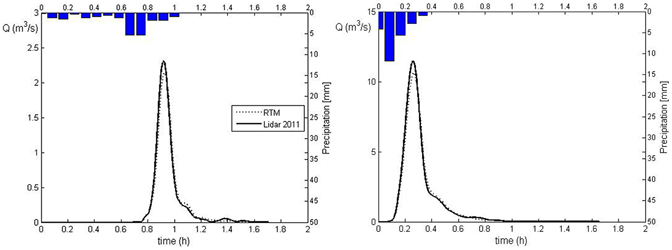
Figure 6. Runoff simulations corresponding to the precipitations that triggered the debris flows occurred July 2, 1994 (left) and August 7, 1996 (right) at Rovina di Cancia basin.

FIGURE 7

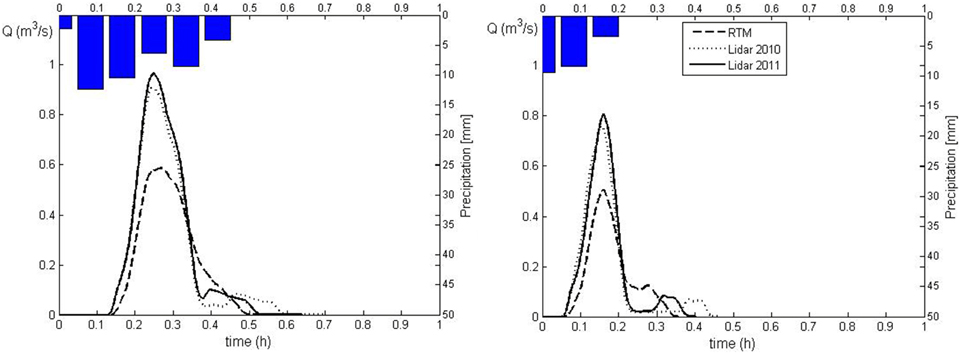
Figure 7. Runoff simulations corresponding to the precipitations that triggered the debris flows occurred July 5, 2006 (left) and August 18, 2011 (right) in Dimai basin.

TABLE 3

Table 3. Quantitative results from hydrological simulations.

Discussion of Results

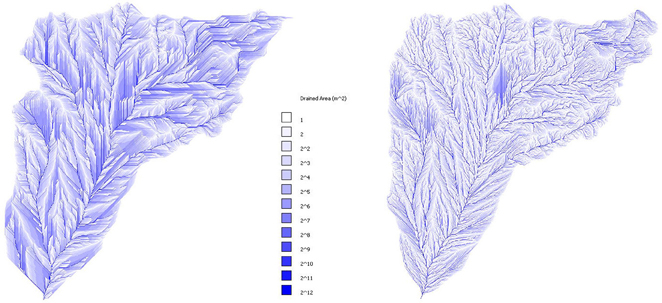
The differences in the peak discharge when using the LiDAR-based and the RTM DEMs for the Dimai basin could be due to the differences in the DEMs area of 20–25% (see subsection The Two Basins) at a first sight. This explanation is not valid for the Cancia basin, for which the difference in the area between the LiDAR2011 and RTM DEMs is approximately 1% (see subsection The Two Basins). The main cause of the differences in the peak discharge values for the Cancia basin and the Dimai basin is the difference in the flow path lengths and their ramifications provided by the different DEMs. Figures 8, 9 show the drained areas corresponding to each DEM of the Cancia and Dimai basins, respectively. The flow lines corresponding to the LiDAR-based DEMs appear more branched than those of the RTM DEMs, which tend to run parallel and sub-parallel to one another. This behavior is due to the failure to capture the topographic details of the slope and the channel location, as noted by Murphy et al. (2008). The main reason is the errors during the interpolation process caused by the digitized point distributions. As explained in subsection Topographical dataset, the distance between the neighboring contour lines could cause the morphological features to be neglected, for which the flow lines (i.e., the flow paths) tend to be straight when intersecting progressive contour lines, indicating shorter flow paths and their parallel or sub-parallel disposition. Table 4 provides the lengths of the channel networks that were extracted using the threshold area concept (Montgomery and Foufoula-Georgiou, 1993) with a threshold value of 0.005 km² (see subsection The DEM based Hydrological Model) and the drainage density. For Cancia, where the two DEMs areas are equal, the length of LiDAR-based channel network is 10% longer than that extracted by RTM, suggesting its higher ramification and further extending upslope. A greater length and ramification of the channel network indicates a faster transfer of excess rainfall to the outlet because the channel velocity is larger than the slope velocity, leading to a higher peak flow and a smaller peak time. In fact, regarding Cancia, when the two basins areas are equal, the peak flow corresponding to the LiDAR-based DEM is 5–7% higher than that corresponding to the RTM DEM, and the peak time is smaller. The difference in the drainage density values (i.e., the basin area percentage corresponding to the unit length of the channel network), which is slightly larger than those of the channel network length, further indicates the faster transfer of excess rainfall to the outlet and consequently higher peak discharge values. For the Dimai basin, the channel networks computed using the two LiDAR-based DEMs are nearly the double the network computed using the RTM DEM because the LiDAR-based areas are 20–25% larger than the area of the RTM DEM and has a greater ramification. The drainage density computed using the LiDAR-based DEMs is approximately 80% larger than the drainage density computed using the RTM DEM. Therefore, the larger values of the peak discharge corresponding to the LiDAR-based DEMs are both due to the greater length and ramification of the channel networks and to the larger areas. Therefore, the influence of the channel network length on the peak discharge is more remarkable with respect to Cancia because the drainage density is much larger (approximately 80%). For Cancia, the difference in the network length and the drainage density is slightly larger than 10%, and the peak flow difference is 5–7%, whereas for Dimai, the relative differences between the area, the channel network and the drainage density are 20–25, 100, and 80%, respectively, and the peak flow is on average larger than 32%, approaching 40%. The differences between the runoff volume values appear to be strictly linked to the differences in the basin area. The similar values of the peak time for the Dimai depend on the drainage density. The LiDAR-based DEM areas are larger than those corresponding to the RTM DEM, with the portion neglected by the RTM DEM much far from the outlet. The relative long distance of neglected part from the outlet should lead to a larger peak time due to the longer flow path, but the larger drainage density reduces the flow times and peak times corresponding to each simulation carried out by the LiDAR-based DEMs, such that they become nearly equal to those simulated using the RTM DEM. The relative differences in the peak discharges between the simulations carried out using the LiDAR10DEM and LiDAR11DEM are 5.7–5.8%, which is the relative difference value between the two DEM areas. This result may indicate that the relative difference in the peak discharge could only be due to the difference between areas given by the different point densities of the two surveys.

FIGURE 8

Figure 8. Drained area of Cancia basin provided by RTM (left) and Lidar-based (right) DEMs.

FIGURE 9

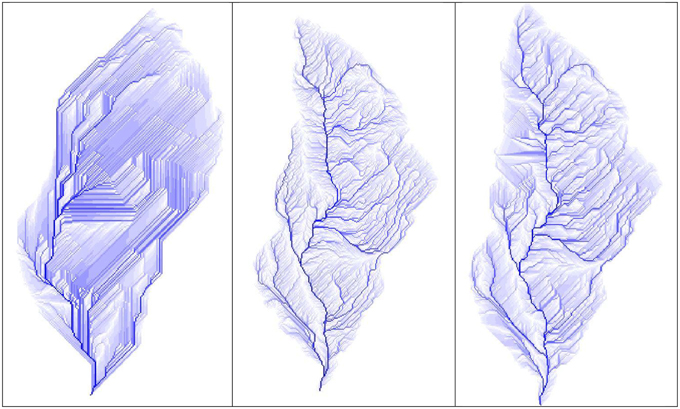
Figure 9. Drained area of Dimai basin provided by RTM (left), Lidar2010 (middle) and Lidar2011 (right) based DEMs.

TABLE 4

Table 4. Morphometric characteristics obtained by the five different DEMs.

The findings presented above are also evaluated based on a more general approach that does not depend on the peculiarities of the simulations (i.e., the rainfall distribution). The width function, according to Walker and Willgoose (1999), and also the rescaled width function are computed for each DEM for both of the basins. The width function is a frequency curve corresponding to the number of drainage links at a given distance from the outlet. It is also denoted as a geomorphological width function representing the pdf of the links and is normalized by the maximum path distance from the outlet (Rinaldo and Rodriguez-Iturbe, 1996). If the components of the path length are rescaled based on their own velocities (slope and channel velocity), the rescaled width functions are obtained (Rinaldo and Rodriguez-Iturbe, 1996), representing the effective pdf of the residence times (Di Lazzaro and Volpi, 2011). The rescaled width function is a frequency curve of the area with the same residence time (routing time to the outlet) and is normalized by the maximum value of the residence time. The maximum length of the path distance and the maximum residence time value corresponding to each DEM are shown in Table 4. Figures 10, 11 show the normalized width function and the normalized rescaled width function for both of the basins, respectively. The normalized figures are obtained using the maximum value of the flow path length or the residence time among those in Table 4. The shape of width functions of the RTM and the LiDAR-based DEMs are nearly equal for both of the basins. For Dimai, the flow path distribution of the RTM DEM compared to the LiDAR-based DEMs exhibits higher values for the normalized distance smaller than 0.65 and lower o zero values for a larger normalized distance, whereas the flow path distribution of the DEMs of Cancia are nearly equivalent. These results provide no outcome, and regarding the hypothesis of a constant velocity, they indicate the opposite of previously obtained results: a larger peak discharge value obtained by the RTM DEM for the Dimai basin and approximately the same peak discharge for the Cancia basin, where the distributions of flow paths obtained by the two DEMs is nearly equal. This stalemate is broken by considering the rescaled width function, which shows a different behavior, as depicted in Figure 11. The higher values of the normalized rescaled width function close to the outlet correspond to the LiDAR-based DEMs for both of the basins. Only for the Dimai basin there is a secondary small peak observed far from the outlet for both of the frequency distributions derived by the LiDAR-based DEMs. These secondary peaks are due to the portion of the upper part of the basin area that is neglected by the RTM DEM. These results show that the higher peak discharge values corresponding to the LiDAR-based DEMs are due to the higher degree of ramification of the channel network. Moreover, the analysis above shows that the width function is not useful for explaining the difference in the peak discharge and time, for which the rescaled width function should be considered because the difference in the velocities corresponding to each component of the flow path causes different dispersions for basin areas smaller than 10 km² (Robinson et al., 1995). The rescaled width function quantifies the routing times of the flow paths and can be considered as the quantitative assessment of the DEM error of the hydrological response that corresponds to the qualitative assessment given by the channel network. For a larger basin where a small percent of rocky terrain is present or for a basin without rocky terrain, the difference between the peak discharges simulated using the LiDAR-based DEM and the RTM DEM should increase. The lower values of the slope velocities on non-rocky terrains should increase the difference between the channel velocity and the slope velocity, and therefore, the effects of the channel network ramification on the peak discharge increase. Thus, conventional DEMs directly increase the geomorphologic dispersion due to the different lengths of flow paths and indirectly increase the kinematic dispersion due to the difference between the slope and channel velocities.

FIGURE 10

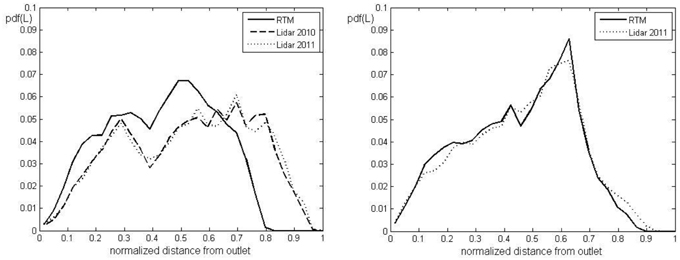
Figure 10. Frequency distributions of the width function for the Dimai (left) and Cancia (right) basins (L = flow path length).

FIGURE 11

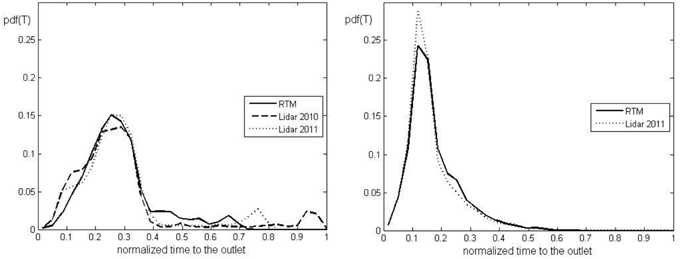
Figure 11. Frequency distributions of the rescaled width function for the Dimai (left) and Cancia (right) basins (T = flow time).

Conclusions

In present work, the influence of the DEM data source and the corresponding elevation accuracy on simulating the peak discharges in two rocky head-water basins is investigated. The runoff events that triggered debris flows in the two basins of Dimai and Cancia are simulated using the model proposed by Gregoretti and Dalla Fontana (2008), incorporating a correction to the rainfall excess computation according to (Gregoretti et al., submitted). The present study shows that both the point density and the point distribution influence DEM accuracy. Conventional DEMs (i.e., RTM DEM) obtained by digitizing points along the contour lines of topographical maps with smaller spacing fail to represent the terrain features due to the possible large distances between neighboring contour lines. This situation leads to the smoothing of impervious surfaces during the interpolation process of the DEM construction and the following creation of artificial, uncorrected and no-existing flow paths. The failure to represent terrain surfaces can lead to errors in determining the divides of a basin, and therefore, bordering parts of the basin could be ignored or external parts added. If the basin is very small, the ignored/added parts can be very large or comparable in size to the basin area, as in the case of the Dimai where the relative differences between the RTM DEM and the LiDAR-based DEMs increase up to 20–25%. For larger basins, the relative differences are not relevant because the ignored/added parts are generally smaller than the basin area and may compensate one another, as exhibited by the Cancia (the relative difference between the RTM DEM and the LiDAR-based DEMs is approximately 1%). The failure to represent terrain surface also leads to a simplification of the flow paths, and the computed channel network appears to be less branched and smaller in length than the actual channel network. The simulations of the considered runoff events show that, for both of the basins, the peak discharge values obtained using the LiDAR-based DEMs are larger than those obtained using the RTM DEMs. For the Cancia basin, this phenomenon is due to the longer channel network length and its higher ramification for which the transfer times of excess rainfall to the outlet diminish because the channel velocity is larger than the slope velocity. The smaller values of the peak times of the simulations corresponding to the LiDAR11DEM confirm this finding. For Dimai, the effect of the longer channel network length and its higher ramification is combined with the larger extension of the LiDAR-based DEM for which the relative differences in the peak discharge values (32% on average) are higher than those of the Cancia basin (5–7%). This explanation is opposite to what can be gathered from the width function computations. In fact, the sum of all of the basin flow path lengths (channel network and slope) is lower for the RTM DEM, which is due to the smoothness of the terrain surface and the lower degree of ramification. However, the routing times depend not only on the length but also on the velocity values. The flow paths computed using the LiDAR-based DEMs have, on average, a smaller length along the slope and a longer length along the channel network for which the routing time from a pixel to the outlet decreases compared to that derived using conventional or RTM DEMs. The rescaled width function (i.e., the routing time distribution in the basin) quantifies the effects of the network lengths and its ramification on the runoff routed to the outlet. Therefore, the rescaled width function, rather than the width function, quantifies the effect of the vertical accuracy of a DEM. In addition, the use of conventional DEMs increases both the geomorphologic and kinematic dispersions. For watersheds with small percentage of or without rocky terrain, the difference between the peak discharges obtained using the LiDAR-based and conventional DEMs should increase due to the smaller values of the slope velocity, and correspondingly the geomorphologic and kinematic dispersion. Finally, the difference between the peak discharges values obtained from both LiDAR-based DEMs, which are built using different point densities, may be due to the difference in the areas of the two DEMs. The points density correlates well with the grid size for which the channel network and the flow path are equal in the overlapping part of their areas.

The use of DEMs based on different data sources can lead to noticeable differences in hydrological responses if the DEM accuracies are markedly different. Poor accuracy due to an insufficient topographical measurement of the point density and distribution as well to elevation error, may lead to a poor representation of the morphological features, which can largely influence runoff simulations. The present study shows that use of DEMs with poor accuracy can lead to a large underestimation of the peak discharge values and an overestimation of the peak time due to the poor representation of flow paths. This fact emphasized in basins with small areas because errors in the boundary determination can lead to a large underestimation of the basin area and when difference between slope and channel velocity is large. The use of reliable data sources, such as LiDAR points, plays a significant role in the determination of the divides and terrain features of rocky headwater basins and allows for a more reliable simulation of the runoff-generated debris flows.

Conflict of Interest Statement

The Reviewer Borga declares that, despite being affiliated to the same institution as the authors Massimo Degetto, Carlo Gregoretti and Martino Bernard, the review process was handled objectively and no conflict of interest exists.

Acknowledgments

This work was supported by the following projects: “GIS-based integrated platform for Debris Flow Monitoring, Modeling, and Hazard Mitigation” funded by the CARIPARO foundation and “Study of new early warning systems against hydrogeological risk and their social perception in a high valuable area for tourism and environment” funded by the University of Padova. The authors thank the association “Regole d'Ampezzo” and the Department Land Defence and Civil Protection of the Province of Belluno for providing the 2010 and 2011 LiDAR data, respectively. The Environment Protection Agency of Veneto Region is also acknowledged for providing the rainfall data.

References

Berti, M., and Simoni, A. (2005). Experimental evidences and numerical modelling of debris flow initiated by channel runoff. Landslides 2, 171–182. doi: 10.1007/s10346-005-0062-4

CrossRef Full Text | Google Scholar

Botter, G., and Rinaldo, A. (2003). Scale effect on geomorphological and kinematic dispersion. Water Resour. Res. 39, 1286. doi: 10.1029/2003WR002154

CrossRef Full Text | Google Scholar

Cannon, S., Gartner, J. E., Wilson, R. C., Bowers, J. C., and Laber, J. L. (2008). Storm rainfall conditions for floods and debris flows from recently burned areas in Southwestern Colorado and Southern California. Geomorphology 96, 250–269. doi: 10.1016/j.geomorph.2007.03.019

CrossRef Full Text | Google Scholar

Cavalli, M., and Tarolli, P. (2011). Application of LiDAR Technology for river analysis. Ital. J. Eng. Geol. Environ. 33–44. doi: 10.4408/IJEGE.2011-01-s-03

CrossRef Full Text

Cavalli, M., Tarolli, P., Marchi, L., and Dalla Fontana, G. (2008). The effectiveness of airborne LiDAR data in the recognition of channel-bed morphology. Catena 73, 249–260. doi: 10.1016/j.catena.2007.11.001

CrossRef Full Text | Google Scholar

Chow, V. T., Maidment, D. R., and Mays, L. W. (1988). Applied Hydrology. McGraw-Hill International Editions.

Clarke, S., and Burnett, K. (2003). Comparison of digital elevation models for acquatic data development. Photogrammetric Eng. Remote Sens. 69, 1367–1375.

Coe, J. A., Kinner, D. A., and Godt, J. W. (2008). Initiation conditions for debris flows generated by runoff at Chalk Cliffs, central Colorado. Geomorphology 96, 270–297. doi: 10.1016/j.geomorph.2007.03.017

CrossRef Full Text | Google Scholar

Da Ros, D., and Borga, M. (1997). On the use of digital elevation model data for the derivation of the geomorphologic instantaneous unit hydrograph. Hydrol. Process. 11, 13–33.

Google Scholar

Di Lazzaro, M., and Volpi, E. (2011). Effect of hillslope dynamics and network geometry on the scaling properties of the hydrologic response. Adv. Water Resour. 34, 1496–1507. doi: 10.1016/j.advwatres.2011.07.012

CrossRef Full Text | Google Scholar

Evans, S. G., and Claugue, J. J. (1994). Recent climate change and catastrophic geomorphic processes in mountain environments. Geomorphology 10, 107–128.

Google Scholar

Flores, J., D'Alpaos, A., Squarzoni, C., Genevois, R., and Marani, M. (2010). Recent changes in rainfall characteristics and GIS and their influence on threshold for debris flow triggering on Dolomitc area of Cortina d'Ampezzo, North-eastern Italian Alps. Nat. Hazard Earth Syst. Sci. 10, 571–580. doi: 10.5194/nhess-10-571-2010

CrossRef Full Text | Google Scholar

Garbrecht, J., Ogden, F. L., De Barry, P. A., and Maidment, D. R. G. (2001). GIS and distributed watershed models. I: data coverages and sources. J. Hydrol. Eng. 6, 506–514. doi: 10.1061/(ASCE)1084-0699(2001)6:6(506)

CrossRef Full Text | Google Scholar

Gong, J., Zhilin, L., Zhu, H., Sui, H., and Zhou, Y. (2000). Effects of various factors on the accuracy of DEMs: an intensive experimental investigation. Photogramm. Eng. Remote Sens. 66, 1113–1117.

Google Scholar

Gregoretti, C. (2000a). Experimental evidence from the triggering of debris flow along a granular slope. J. Phys. Chem. Earth B 25, 387–390.

Google Scholar

Gregoretti, C. (2000b). The initiation of debris flow at high slopes: experimental results. J. Hydraulic Res. 38, 83–88. doi: 10.1080/00221680009498343

CrossRef Full Text | Google Scholar

Gregoretti, C., and Dalla Fontana, G. (2007). “Rainfall threshold for the initiation of debris flows by channel bed failure of Dolomites,” in Fourth International Conference On Debris Flow Hazard Mitigations: Mechanics, Prediction and Assessment (Chengdu).

Gregoretti, C., and Dalla Fontana, G. (2008). The triggering of debris flow due to channel-bed failure in some alpine headwater basins of the Dolomites: analyses of critical runoff. Hydrol. Process. 22, 2248–2263. doi: 10.1002/2007hyp.6821

CrossRef Full Text | Google Scholar

Grimaldi, S. A., Petroselli, G., Alonso, G., and Nardi, F. (2010). Flow time estimation with spatially variable hillslope velocity in ungauged basins. Adv. Water Resour. 33, 1216–1223. doi: 10.1016/j.advwatres.2010.06.003

CrossRef Full Text | Google Scholar

Grimaldi, S., Petroselli, A., and Nardi, F. (2012). A parsimonious geomorphological unit hydrograph for rainfall-runoff modelling in small ungauged basins. Hydrol. Sci. J. 57, 73–83. doi: 10.1080/02626667.2011.636045

CrossRef Full Text | Google Scholar

Grimaldi, S., Petroselli, A., and Romano, R. (2013). Green-Ampt Curve-Number procedure as an empirical tool for rainfall-runoff modelling in small and ungauged basins. Hydrol. Process. 27, 1253–1264. doi: 10.1002/hyp.9303

CrossRef Full Text | Google Scholar

Haberli, W., Rickenmann, D., and Zimmerman, M. (1990). “Investigation of 1987 debris flows in Swiss Alps: general concept and geophysical soundings,” in Hydrology of Mountainous Regions, Vol. 194, eds R. O. Sinniger and M. Monbaron (Lousanne: IAHS), 303–310.

Hodgson, M. E., Jensen, J. R., Schmidt, L., Schill, S., and David, B. (2003). An evaluation of LiDAR- and IFSAR-derived digital elevation models in leaf-on conditions with USGS Level 1 and Level 2 DEMs. Remote Sens. Environ. 84, 295–308. doi: 10.1016/S0034-4257(02)00114-1

CrossRef Full Text | Google Scholar

Hornberger, G. M., and Boyer, E. G. W. (1995). Recent advances in watershed modelling. Rev. Geophys. 33, 949–957

Google Scholar

Hurlimann, M., Abanco, C., Moya, J., and Vilajosana, I. (2014). Results and experiences gathered at the Rebaixader debris-flow monitoring site, Central Pyrenees, Spain. Landslides 11, 939–953. doi: 10.1007/s10346-013-0452-y

CrossRef Full Text | Google Scholar

Imaizumi, F., Sidle, R. C., Tsuchiya, S., and Ohsaka, O. (2006). Hydrogeomorphic processes in a steep debris flow initiation zone. Geophys. Res. Lett. 33:L10404. doi: 10.1029/2006GL026250

CrossRef Full Text | Google Scholar

James, L. A., Watson, D. G., and Hansen, W. F. (2007). Using LiDAR data to map gullies and headwater streams under forest canopy: South Carolina, USA. Catena 71, 132–144. doi: 10.1016/j.catena.2006.10.010

CrossRef Full Text | Google Scholar

Jenson, S. K. (1991). Application of hydrologic information automatically extracted from digital elevation models. Hydrol. Process. 5, 31–44.

Google Scholar

Jomelli, V., Brunstein, D., Grancher, D., and Pech, P. (2007). Is the response of hill slope debris flows to recent climate change univocal? A case study in the massif des Ecrins (French Alps). Clim. Change 85, 119–137. doi: 10.1007/s10584-006-9209-0

CrossRef Full Text | Google Scholar

Kean, J. W., Staley, D. M., and Cannon, S. E. (2011). In situ measurements of post-fire debris flows in Southern California: comparison of the timing and magnitude of 24 debris flows events with rainfall and soil moisture conditions. J. Geophys. Res. 116:F04019. doi: 10.1029/2011JF002005

CrossRef Full Text | Google Scholar

Kean, J. W., Staley, D. M., Leeper, R. J., Schmidt, K. M., and Gartner, J. E. (2012). A low-cost method to measure the timing of postfire flash floods and debris flows relative to rainfall. Water Resour. Res. 48:W05516. doi: 10.1029/2011WR011460

CrossRef Full Text | Google Scholar

Kenward, T., Lettenmaier, D. P., Wood, E. F., and Fielding, E. (2000). Effect of digital elevation model accuracy on hydrology predictions. Remote Sens. Environ. 74, 432–444. doi: 10.1016/S0034-4257(00)00136-X

CrossRef Full Text | Google Scholar

Lagacherie, P., Moussa, R., Cormary, D., and Molenat, J. (1996). Effects of DEM Data Source and Sampling Pattern on Topographical Parameter and on a Topography-Based Hydrological Model. (Vienna: IAHS), 191–199.

Google Scholar

McGlynn, J. J., and Seibert, J. (2003). Distributed assessment of contributing area and riparian buffering along stream networks. Water Resour. Res. 39, 1082. doi: 10.1029/2002WR001521

CrossRef Full Text | Google Scholar

McGuire, K. J., McDonnel, J. J., Weiler, M., McGlynn, B. L., Welker, J. M., and Seibert, J. (2005). The role of topography on catchment-scale water residence time. Water Resour. Res. 41, W05002. doi: 10.1029/2004WR003657

CrossRef Full Text | Google Scholar

Montgomery, D. R., and Foufoula-Georgiou, E. (1993). Channel network source representation using digital elevation models. Water Resour. Res. 29, 3925–3934.

Google Scholar

Moore, I. D., Grayson, R. B., and Ladson, A. R. (1991). Digital terrain modelling: a review of hydrological, geomorphological, and biological applications. Hydrol. Process. 5, 3–30

Google Scholar

Murphy, P. N. C., Ogilvie, J., Meng, F. R., and Arp, P. (2008). Stream network modelling usingn LiDAR and photogrammetric digital elevation models: a comparison and field verification. Hydrol. Process. 22, 1747–1754. doi: 10.1002/hyp.6770

CrossRef Full Text | Google Scholar

Okano, K., Suwa, H., and Kanno, T. (2012). Characterization of debris flows by rainstorm condition at a torrent on the Mount Yakedake volcano, Japan. Geomorphology 136, 88–94. doi: 10.1016/j.geomorph.2011.04.006

CrossRef Full Text | Google Scholar

Pelfini, M., and Santilli, M. (2008). Frequency of debris flows and their relation with precipitation: a case study in Central Alps, Italy. Geomorphology 101, 721–730. doi: 10.1016/j.geomorph.2008.04.002

CrossRef Full Text | Google Scholar

Quinn, P., Beven, K., Chevallier, P., and Planchon, O. (1991). The prediction of hillslope flow paths for distributed hydrological modelling using digital terrain models. Hydrol. Process. 5, 59–79. doi: 10.1002/hyp.3360050106

CrossRef Full Text | Google Scholar

Rinaldo, A., and Rodriguez-Iturbe, I. (1996). Geomorphological theory of the hydrological response. Hydrol. Process. 10, 803–829.

Google Scholar

Robinson, G. J. (1994). The accuracy of digital elevation models derived by contour data. Photogrammetic Rec. 14, 805–814.

Google Scholar

Robinson, J. S., Sivapalan, M., and Snell, J. D. (1995). On the relatives roles of hillslope processes, channel routing, and network morphology in the hydrologic response of natural catchments. Water Resour. Res. 30, 3089–3101.

Google Scholar

Sangati, M., Borga, M., Rabuffetti, D., and Bechini, R. (2009). Influence of rainfall and soil properties spatial aggregation on extreme flash flood response modelling: an evaluation based on the Sesia river basin, North Western Italy. Adv. Water Resour. 32, 1090–1106. doi: 10.1016/j.advwatres.2008.12.007

CrossRef Full Text | Google Scholar

Scheidl, C., Rickenmann, D., and Chiari, M. (2008). The use of airborne LiDAR data for the analysis of debris flow events in Switzerland. Nat. Hazards Earth Syst. Sci. 8, 1113–1127. doi: 10.5194/nhess-8-1113-2008

CrossRef Full Text | Google Scholar

Staley, D. M., Kean, W. J., Cannon, S. H., Schmidt, K., and Laber, J. L. (2013). Objective definition of rainfall intensity-duration thresholds for the initiation of post-fire debris flows in southern California. Landslide 10, 547–562. doi: 10.1007/s10346-012-0341-9

CrossRef Full Text | Google Scholar

Surkan, A. J. (1969). Syntethic hydrographs: effects of network geometry. Water Resour. Res. 5, 112–128.

Google Scholar

Tarboton, D. G. (1997). A new method for the determination of flow directions and upslope areas in grid digital elevation models. Water Resour. Res. 33, 309–319.

Google Scholar

Tarboton, D. G., Bras, R. L., and Rodriguez Iturbe, I. (1991). On the extraction of channel networks from digital elevation data. Hydrol. Process. 5, 81–100.

Google Scholar

Theule, J. I., Liebault, F., Loye, A., Laigle, D., and Jabedoff, M. (2012). Sediment budget monitoring of debris flow and bedload transport in the Manival Torrent, SE France. Hydrol. Process. 5, 81–100. doi: 10.5194/nhess-12-731-2012

CrossRef Full Text | Google Scholar

Tiranti, D., and Deangeli, C. (2015). Modeling of debris flow depositional patterns according to the catchment and sediment source area characteristics. Front. Earth Sci. 3:8. doi: 10.3389/feart.2015.00008

CrossRef Full Text | Google Scholar

Tognacca, C., Bezzola, G. R., and Minor, H. E. (2000). “Threshold criterion fo debrisflow initiation due to channel bed failure,” in Proceedings of the Second International Conference on Debris Flow Hazards Mitigation (Taipei), 89–97.

Vaze, J., Teng, J., and Spencer, G. (2010). Impact of DEM accuracy and resolution on topographic indices. Environ. Model. Softw. 25, 1086–1098. doi: 10.1016/j.envsoft.2010.03.014

CrossRef Full Text | Google Scholar

Walker, J. P., and Willgoose, G. P. (1999). On the effect of digital elevation model accuracy on hydrology and geomorphology. Water Resour. Res. 35, 2259–2268.

Google Scholar