Sixty years of anisotropy of magnetic susceptibility in deformed sedimentary rocks

Parés, Josep M.

doi:10.3389/feart.2015.00004

REVIEW article

Front. Earth Sci., 17 February 2015

Sec. Geomagnetism and Paleomagnetism

Volume 3 - 2015 | https://doi.org/10.3389/feart.2015.00004

Sixty years of anisotropy of magnetic susceptibility in deformed sedimentary rocks

$\r\nJosep M. Pars*$ Josep M. Parés^*

Geochronology, Research Center for Human Evolution (CENIEH), Burgos, Spain

The use of the Anisotropy of Magnetic Susceptibility (AMS) has become a rather common practice in Earth Sciences since the pioneer note by Graham (1954). The versatility of the technique, and the rapidness in obtaining and processing AMS data largely improved in the past thirty years, and has generated a wealth of literature, notably on mudrock fabrics. The assessment of the current trends in magnetic fabric studies reveals that AMS has one of its largest potential in sedimentary rocks from structural settings where the ductile component of deformation is cryptic or hindered by the brittle component. Abundant evidence provided by AMS data reveal that deformation extents beyond the deformation or cleavage front in contractional settings, including fold-and-thrust belts and active accretionary prisms, configuring magnetic fabrics as a standard method for fabric quantification in deformed sedimentary rocks.

Introduction

After John W. Graham proposed 60 years ago, the use of the anisotropy of magnetic susceptibility (AMS) in rocky materials, the subject, with no doubt, has gained an enormous popularity. What Graham referred to as an “unexploited petrofabric element” in 1954, is nowadays an indispensable tool in a wide range of disciplines in Earth Sciences. The study of what we know as AMS in sedimentary rocks begins well before Graham's time nevertheless. Gustav Ising (at the Geophysical Laboratory at Djursholm, Sweden) was interested in varved clays for geomagnetic purposes, i.e., secular variation (Ising, 1942). He had been investigating clay rich sediments since 1926, using first the facility at the Physical Laboratory of the Stockholm University and then the Geophysical Laboratory at Djursholm. Although the aim of Ising's studies was the record of secular variation in varved sediments, he noticed that “the two principal axes (of susceptibility) lying in the horizontal plane posses considerably higher susceptibility values (10–20%), … over the vertical susceptibility.” From the performed susceptibility measurements obtained, he concluded that the axis of maximum susceptibility is decisive for the “problem of determining the secular variation of the declination from clay measurements.”

Graham's seminal paper, 25 years after Ising's work, focused on the application of AMS to deformed sedimentary rocks, where considerable research has shown to have its maximum potential. Indeed he noticed that flat-lying sediments have an oblate magnetic susceptibility ellipsoid, whereas folded sandstones from the Valley and Ridge (Appalachians), have principal axes of maximum susceptibility that are normal to bedding and minimum axes normal to the fold axis of the structures. In the current paper we will further explore the main concept outlined in Graham (1966), namely that magnetic anisotropy in deformed sedimentary rocks is appreciable and that it is related to plastic deformation of sediments very often semiconsolidated.

Shortly after Graham's work, it was well-established that sedimentary rocks acquire a magnetic fabric during deposition (Granar, 1958; Rees, 1961, 1965; Hamilton and Rees, 1971; Kent and Lowrie, 1975) and also that cleaved rocks, slates, have a magnetic fabric that is consistent with the macroscopic foliation (Fuller, 1960, 1963). Although beyond the scope of this paper, the application of AMS to the study of igneous rocks also started soon after to emerge as a powerful fabric tool (Girdler, 1961; Khan, 1962; King, 1966; Heller, 1973; see Bouchez, 1997 and references therein). The AMS studies have been since then employed for purposes as uncommon as characterizing tsunami deposits (Wassmer et al., 2010; Schneider et al., 2014) or for understanding preferred orientation in speleothems (e.g., Zhu et al., 2012).

A remarkable development after Graham's paper is the concept of magnetic carriers that contribute to the magnetic anisotropy. Although what he referred as to “dimensional orientations of ferromagnetic grains” holds true for many rock types, over the years it became apparent that both ferromagnetism and paramagnetism contribute to the total magnetic anisotropy (e.g., Daly, 1967; Parry, 1971), and soon after many scholars emphasized specifically the role of phyllosilicates to the total fabric (Owens and Bamford, 1976; Henry, 1983; Henry and Daly, 1983; Rochette and Vialon, 1984; Borradaile et al., 1986; Lamarche and Rochette, 1987; Borradaile, 1988). Because phyllosilicates (most abundant paramagnetic minerals in sedimentary rocks) occur as platy grains whereas magnetite typically as euhedral, they will behave differently upon stress and therefore is critical to separately characterize their preferred orientation and degree of alignment. Also, in sedimentary rocks, phyllosilicate minerals often represent a larger volume fraction than ferromagnetic (accessory) minerals and therefore are likely to yield more accurate and representative fabric information. After the pioneering studies by Daly (1967) and Parry (1971), a number of scholars became interested and developed methods aimed at fabric separation (Owens and Bamford, 1976; Henry, 1983; Rochette and Fillion, 1988, and more recent Bilardello and Jackson, 2014). The rationale for such separation of magnetic anisotropies is based on the variation of susceptibility with either temperature or applied field. Basically there are two different approaches, namely tensor subtraction and instrumental isolation of the paramagnetic anisotropy (see Martín-Fernández and Ferré, 2007 for a comprehensive review). Here follows a summary of the methods.

Scriba and Heller (1978) and Schmidt et al. (1988) used a 100 μT radial field in a SQUID magnetometer and rotated the sample about each of three mutually perpendicular axes in steps of 45°, for a total of 24 positions, to determine the anisotropy tensor. Rochette and Fillion (1988) used a vertical-access SQUID magnetometer and trapped a DC field. By rotating the sample about a horizontal axis at a frequency of 0.01 Hz and analyzing the generated signal, they determined the susceptibility anisotropy of both ferromagnetic and paramagnetic fractions.

The principle of a vibrating sample magnetometer (VSM) is based on the flux change in the pick-up coil system produced by a sample that is vibrating (rather than by rotation, as in spinner magnetometers). There have been several studies using a VSM to obtain directional hysteresis curves for different positions of the specimen, and hence enabling to the calculation of a High Field AMS (Thill et al., 2000; Kelso et al., 2002; Ferré et al., 2004).

The torque magnetometer is possibly the most popular instrument to measure high field magnetic susceptibility (Banerjee and Stacey, 1967; Owens and Bamford, 1976; Ellwood, 1978; Parma, 1988; Borradaile and Werner, 1994). The basic principle is the measurement of torque exerted on a sample by an applied magnetic field due to the anisotropy of the sample as it is rotated to different azimuths about an axis perpendicular to the field. The torque T is given by T = dE/dθ, where E is the energy of magnetization of the sample and θ is the direction of the applied field. It is thus possible to estimate the anisotropy present in the rock from a Fourier analysis of the torque curve. Hrouda and Jeliınek (1990) presented a mathematical method for separating the components by measuring a sample in two different fields above the saturation magnetization of the ferromagnetic contribution. More recently, Martín-Hernández and Hirt (2001) presented a mathematical method that utilizes measurements in several high fields toward separating the ferromagnetic and paramagnetic components of the magnetic fabric. By using a larger number of fields, instead of two as described by Lowrie (1989), a more accurate definition of the paramagnetic susceptibility tensor can be obtained.

Source of Magnetic Susceptibility

Most studies that followed Graham's (1954) work focused on sedimentary rocks, including sandstones and mudstones. Although in Graham's view, the magnetic fabric obeys “dimensional orientations of the ferromagnetic grains” we now know that the paramagnetic contribution is usually more significant that the former in these rocks (see Tarling and Hrouda, 1993 and references therein). To illustrate this issue of ferromagnetism vs. paramagnetism in sedimentary rocks, we need to look at the rock composition and constituents. Sandstones are sedimentary rocks consisting of detrital sand-sized grains, that form the framework of the sediment, fine-grained matrix between the grains, and authigenic minerals. The most common detrital mineral in sandstone is quartz, on average 65% although some sandstones are made of practically 100% quartz. Feldspar content averages between 10 and 15%, except in arkoses where it reaches 50%. The remaining minerals typically include phyllosilicate minerals (biotite, muscovite, chlorite, kaolinite, smectite, illite), and heavy minerals (zircon, rutile, amphiboles, hematite, magnetite, etc.). Mudstones—a mixture of clay and silt sized particles- constitute some 45–55% of sedimentary rock sequences. Shale is a laminated and fissile mudrock, as opposed to the blocky, non-fissile mudstones. By definition the main constituents of mudrocks are clay minerals (42% on average) and silt-grade quartz (38%). Other minerals (less than 5%) include feldspar, calcite, plagioclase pyrite, etc. Whereas ferromagnetic (sensu lato), moderate to high susceptibility minerals (e.g. magnetite, hematite) are minor components, the dominant mineralogy corresponds to paramagnetic, lower magnetic susceptibility phases. Indeed, the average value of bulk magnetic susceptibility of mudrocks (10⁻⁴ to 10⁻⁵ SI) suggests that the concentration of iron oxides such as magnetite is typically less than 0.01 wt% (Figure 1) which is consistent with the dominance of paramagnetic susceptibility in mudrocks. Numerous rock-magnetic studies where paramagnetic and ferromagnetic susceptibilities have been quantified revealed that typically the former dominates in mudstones (e.g., Martín-Hernández and Hirt, 2001 and references therein), therefore the AMS is dominated by the paramagnetic component, and most specifically by the shape anisotropy of clay minerals although very fine magnetic particles attached to the clay fabric might also contribute (Kodama and Sun, 1992).

FIGURE 1

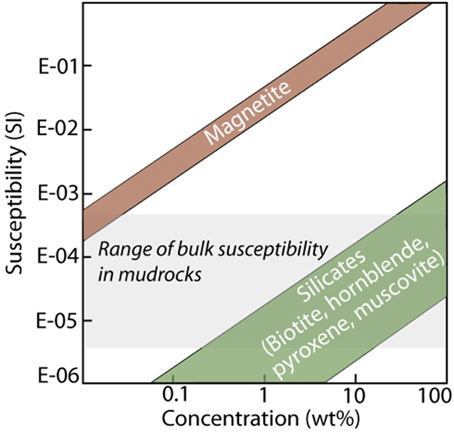
Figure 1. Bulk susceptibility and mineral contribution. The total susceptibility in a given rock will depend on both the intrinsic susceptibility and the concentration of the individual minerals. Magnetite (ferromagnetic) and some common rock-forming silicates have been shown as a reference. The gray, horizontal bar shows the susceptibility range for most mudrocks, revealing that the contribution by paramagnetic grains (in particular phyllosilicate) is larger than magnetite.

Although there is agreement in that AMS in pelitic rocks is typically controlled by paramagnetic phyllosilicate minerals, errors might arise when such very fine magnetic particles, specifically single domain (SD) magnetite, are present in large quantities. The magnetic anisotropy of magnetite is determined by its magnetic grain size (Stephenson et al., 1986). For multidomain (MD) particles, the maximum/minimum susceptibility coincides with the long/short axes of the grains, and therefore the bulk magnetic fabric mimics grain orientation. However, in SD particles the minimum axis of susceptibility is parallel to the long axes of the grain, producing an “inverse magnetic anisotropy” (Jackson, 1991). The term “inverse magnetic fabrics” was originally coined by Rochette and Fillion (1988), who actually sought two causative models: (1) c-axis preferred orientation of ferroan calcite grains whose maximum susceptibility is parallel to the c-axis, and (2) single-domain elongated magnetite grains. In mudrocks, the former is rather uncommon due to the very low concentration of calcite. Several authors have observed “inverse fabrics” in Fe-calcite rich rocks (Ihmlé et al., 1989; Hirt and Gehring, 1991; de Wall et al., 2000; Hounslow, 2001). However, because unusually high proportions of SD magnetite would be required, few rocks show a net inverse magnetic fabric due to magnetite (Borradaile and Jackson, 2004). The inverse fabric, i.e., SD-related inverse fabric, is otherwise rather common in igneous rocks (e.g., Borradaile and Gauthier, 2001; Zhang et al., 2011).

The topic of inverse fabric related to SD magnetite is explored in Jackson (1991), and as of today it is still a poorly resolved topic (e.g., Tarling and Hrouda, 1993). Determining whether SD-magnetite is producing inverse fabric requires methods that can isolate different magnetic grain size of magnetite, which include measurements such as the anisotropy of anhysteretic remanent magnetization (AARM) (Jackson, 1991). Some theoretical models for inverse magnetic fabrics have also been developed (e.g., Ferré, 2002).

Anisotropy of Magnetic Susceptibility (AMS)

The low field magnetic susceptibility of a rock (the ratio of magnetization to the applied field or K = M/H) is given by the total contribution of its bulk mineralogy, including paramagnetic (e.g., phyllosilicates, iron-bearing feldspars), diamagnetic (e.g., quartz, calcite) and ferromagnetic (sensu lato; e.g., magnetite, goethite, hematite) grains. An intrinsic property of most of these rock-forming minerals is that their magnetic susceptibility is anisotropic (Nye, 1957) and thus K_ij = M_i/H_j. For example, it has been demonstrated that magnetic axes in biotite crystals conform to the density distributions of mineral lattice planes obtained by x-ray goniometry (Richter et al., 1993; Schmidt et al., 2009) (Figure 2). These results reveal that densities from x-ray for chlorite and mica are perfectly reflected by the distribution of the minimum susceptibility axes. The study by Richter et al. (1993) was possibly the first demonstration that the normalized magnetic parameters (M_i = ln (k_i/[kmax * kint * Kmin]^1/3) correlate directly with March strains as obtained from x-ray texture goniometry. The study was an important step forward showing the AMS as a sensitive and rapid gage for bulk crystallographic preferred orientation in rocks, with the advantage of using large sample volumes (typically about 1 l cm³), as opposed to the essentially two-dimensional slice used in optical and X-ray methods (Figure 2). Later studies by Borradaile and Werner (1994), Martín-Hernández and Hirt (2003), and Biedermann et al. (2014) have provided more details on the magnetic anisotropy of single silicate crystals.

FIGURE 2

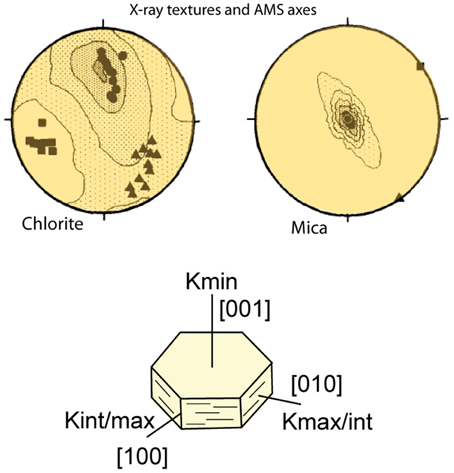
Figure 2. Stereoplots for chlorite and mica dominated specimens, comparing the x-ray texture data (shaded regions) and the orientation of the principal axes of magnetic susceptibility (squares = K_max, triangles = K_int, dots = K_min) (modified from Richter et al., 1993). The minimum susceptibility axes show perfect agreement with the maximum density of the chlorite and mica basal plane.

AMS defines a symmetric, second-rank tensor that has six independent matrix elements. When the coordinate system is referred to the eigenvectors, these trace an ellipsoid that is known as the magnitude ellipsoid (Nye, 1957) whose semi-axes are the three principal susceptibilities (K_max > K_int > K_min). In sedimentary rocks, AMS depends mostly on the crystallographic preferred orientation of the individual components, compositional layering, distribution and size of microfractures, and the shape fabric of grains. The AMS tensor tracks preferred orientation and consequently its applications embrace a wide range of disciplines in Geosciences, and notably in structural geology (e.g., Housen et al., 1993; Borradaile and Henry, 1997; Martín-Hernández et al., 2004; Borradaile and Jackson, 2010 and references therein).

Sedimentary Magnetic Fabric

Sediments acquire and develop a magnetic fabric throughout a long and complex process. The term fabric for sedimentary rocks involves the grains orientation and packing, and the nature of the boundaries between grains. Clay particles in muds tend to have positively charged edges and negatively charged faces (Langston and Pask, 1958), which will cause small flocs of edge to face (EF) particles in the earliest stages of deposition (Bennett et al., 1991). The peds are often electrostatically connected by long-chained clay platelets interconnected by high angle EF contacts (e.g., Kawamura and Ogawa, 2002, 2004). The porosity between these peds is relatively large (10 μm). During progressive consolidation as overburden pressure increases, the clay platelets collapse developing face to face (FF) contacts and the porosity is reduced (Figure 3). The collapse of the clay structure during burial results in a volume decrease by diminishing macropores. Hence, the normal progressive consolidation and burial of clay-rich sediments results in a downsection decrease in porosity. This progressive clay fabric change during burial determines to large extent the magnetic properties, which many scholars have studied throughout AMS (Housen et al., 1996; Kopf and Berhman, 1997; Kawamura and Ogawa, 2002, 2004; Schwehr et al., 2006) (Figure 3C).

FIGURE 3

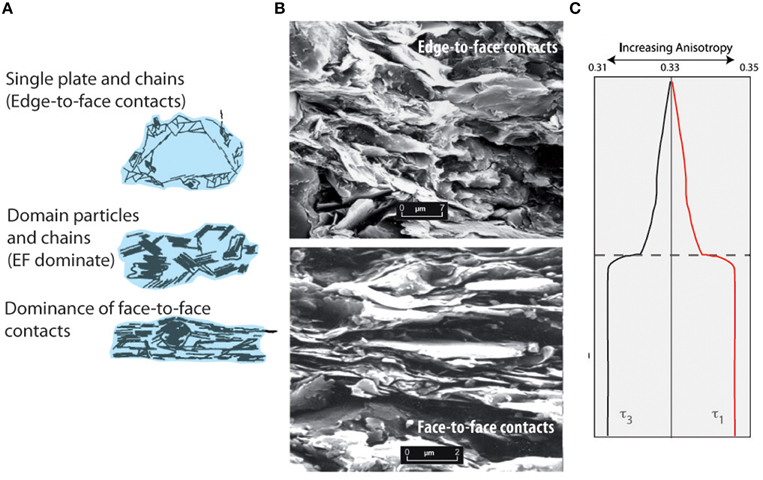
Figure 3. Progressive change of clay microstructure during burial process. (A) The contact between particles changes from high-angle EF (edge-to-face) to low-angle EF and FF contact compaction. Particles slide and rotate normal to the maximum stress direction (modified from Bennett et al., 1991). (B) Example of mudstone compaction fabrics. Photo on top shows a weakly oriented clay assemblage, with open pore structure dominated by EF contacts. The example below shows a more oriented clay population, with as classic FF contact distribution (modified from Wilson and Wilson, 2014). (C) Conceptual model of degree of anisotropy evolution with burial. As compaction progresses, the overall anisotropy of susceptibility increases shown as the minimum and maximum eigenvalues of the susceptibility tensor (modified from Schwehr et al., 2006).

From the abundant AMS data, it is apparent that the pattern evolution of sediments depositing has a strong imprint on the AMS. For burial depths of several centimeters, EF contacts and long chains of clay flakes dominate the clay fabric, which results in a certain degree of magnetic lineation. The underlying reason is the “magnetic zone axis” (Henry, 1997), which is expressed as a magnetic lineation and thus ellipsoids are typically prolate. At depths of several meters clay flakes rotate from EF to FF contacts, shortening the connectors (Kawamura and Ogawa, 2004), and hence there is an increase in both the magnetic foliation and the anisotropy degree (Figure 3C). Although several studies suggested that several hundred meters are required to develop a horizontally preferred orientation in muds (e.g., Moon and Hurst, 1984; Bennett et al., 1991; Kawamura and Ogawa, 2004), recent magnetic studies show that a horizontal anisotropy develops much earlier on in the sedimentary column (Taira and Niitsuma, 1986; Kanamatsu and Matsuo, 2003; Ujiie et al., 2003a; Kanamatsu et al., 2012; Novak et al., 2014).

Upon progressive increase in overburden, and as clay fabric changes from EF to FF, magnetic ellipsoids will tend to become oblate and the anisotropy degree (P) will increase with depth as porosity decreases and packing increases (Figure 4). An exception would be when sediments are in a state of overconsolidation. Overpressured sediments form under many circumstances, such as under high sediment accumulation rates, mineral dehydration, gas liberation, and low permeability. As a result, pore fluid escape is inhibited and it has to temporarily sustain the entire stress acting on the sediment. Sediments become overpressurized in such high water content zones. Among other effects, such zones of high water content prevent the EF contacts from changing to FF contacts (Schwehr et al., 2006). More importantly, as will be discussed below, overpressure weakens the sediments (e.g., Maltman, 1994), which facilitates grain sliding. The fluid between pores sustains part of the burial stress, which reduces friction and hence sediment strength. Overpressured zones are potential sites for shear and therefore are critical for sediment deformation.

FIGURE 4

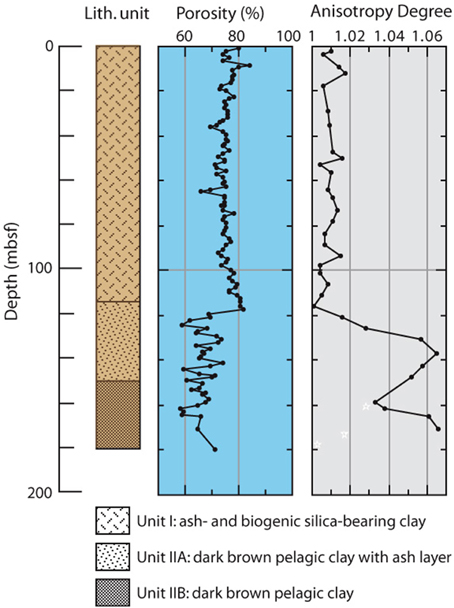
Figure 4. Changes of porosity and anisotropy degree (P) with depth (IODP Hole 1149A) (modified from Kawamura and Ogawa, 2002).

Underconsolidated layers have been detected via AMS (e.g., Schwehr et al., 2006) revealing a new approach to detect compaction disequilibrium in marine environments. Such layers are characterized by a reduced magnetic anisotropy, as compared to what would be expected in a standard consolidation profile.

Magnetic Anisotropy and Weak Deformation

Since the seminal paper by Graham (1966) where he pointed out that AMS in sediments indicate “the final shape distortions,” many scholars have exploited the property in order to retrieve the strain imprint in sedimentary rocks, particularly in the weak deformation realm. In the late seventies and through the eighties, and possibly due to the development of improved measuring techniques (Molyneux, 1971; Jelinek, 1973; Rathore, 1975) rock magnetic anisotropy studies intensified, and specifically in shales and slates (Hrouda and Janak, 1976; Kligfield et al., 1977, 1981; Rathore, 1980; Turner and Gough, 1983; Rochette and Vialon, 1984; Hirt et al., 1988 among others). In anchimetamorphic grade rocks, AMS has been shown to have a great potential to track early deformation stages (Hirt et al., 1995, 2000, 2004; Robion et al., 1995, 1997, 1999; Lüneburg et al., 1999; Gil-Imaz et al., 2000; Parés and van der Pluijm, 2003; Debacker et al., 2004). Although Borradaile and Tarling (1981) reported results from “weakly deformed slates,” the study by Kissel et al. (1986) is possibly the first to demonstrate the great potential of AMS, as these authors showed that by using this technique it is possible to detect very subtle deformation in rocks otherwise considered to be undeformed. More recent contributions by Aubourg et al. (1991), Averbuch et al. (1992), Owens (1993), Parés and Dinarès (1993), Sagnotti and Speranza (1993), Collombat et al. (1995), Parés et al. (1999), Sagnotti et al. (1999) (also see Borradaile and Jackson, 2004 for a review) take advantage of the sensitivity of AMS to identify and define the orientation of weak tectonic magnetic fabrics arising from phyllosilicate minerals. In most of these examples, the studied mudrocks are uncleaved, typically flat-lying, and macroscopically undeformed. Despite the field appearance of these mudrocks, a subtle, weak tectonic fabric is observed due to the AMS features. In an effort to merge all these models for fabric development arising from tectonic deformation with magnetic fabrics, Parés et al. (1999) proposed a model for progressive stages in AMS evolution in strained mudrocks. The model includes four type of magnetic fabrics that develop in weakly deformed mudrocks undergoing progressive deformation and has subsequently been observed and adopted in later studies of similar rock types (Figure 5) (Frizon de Lamotte et al., 2002; Saint-Bezar et al., 2002; Souqué et al., 2002; Sans et al., 2003; Larrasoaña et al., 2004; Parés, 2004; Robion et al., 2007; Cifelli et al., 2009; Debacker et al., 2009; Oliva et al., 2009; Soto et al., 2009; Weil and Yonkee, 2009; Mochales et al., 2010; Pueyo-Anchuela et al., 2010). A common feature in most of these studies is the realization that AMS records preferred grain orientation in sedimentary rocks with no macroscopic strain indicators, even before the appearance of embryonic cleavage (Ramsay and Huber, 1983). The deformation pathway represented in Figure 5 summarizes the magnetic fabric path of mudrocks under progressive deformation (layer parallel shortening).

FIGURE 5

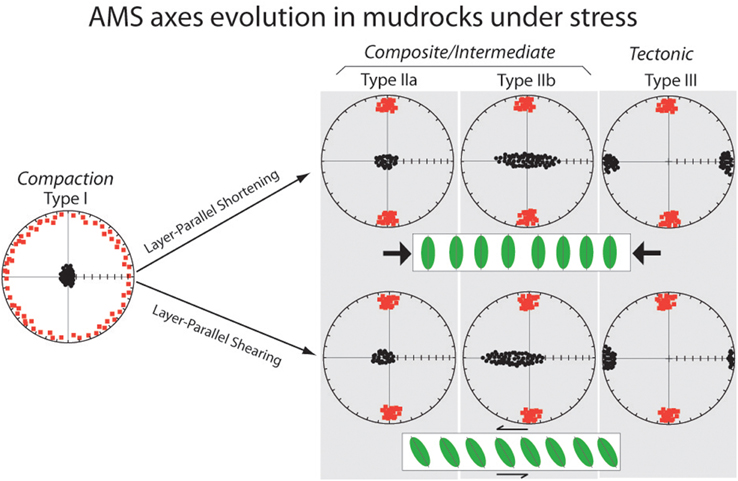
Figure 5. Conceptual model of AMS development in mudrocks undergoing progressive deformation. Type I fabric is essentially a compaction, sedimentary fabric with K_min axes normal to the deposition plane and K_max axes scatter along it. Type II (a and b) fabric reveals the imprint of the first lateral shortening on the initial sedimentary fabric where both LPS (layer parallel shortening) (or shearing) plane and depositional plane compete to define the total magnetic fabric. K_max axes parallel the intersection direction between these two planes. K_min axes eventually show a girdle that is parallel to the maximum shortening direction. Ultimately K_min axes become parallel to the shortening direction and K_max axes remain parallel to the intersection direction and not necessarily to the maximum extension direction. Rocks deformed by layer-parallel shearing, Types IIa and IIb ellipsoids show a girdle of K_min axes that are plunging away from the tectonic extension direction.

A summary of the AMS studies developed in deformed mudrocks is as follows:

(1) Principal axes of maximum susceptibility (K_max) are particularly sensitive to tectonic shortening, as they develop a magnetic lineation that mimics the intersection of bedding and tectonic flattening plane (the strain XY plane).

(2) Layer parallel shortening extends well-beyond the “deformation front” in orogenic settings.

(3) An intermediate fabric (Types IIa and IIb) is very common where bedding and flattening planes compete to identify the finite magnetic anisotropy ellipsoid.

AMS Data from Active Accretionary Prisms Sediments

Accretionary prims closely resemble fold-and-thrusts belts exposed onshore, and therefore constitute a natural laboratory to better understand the mechanical behavior of shortening in the crust. The process of accretion is a preliminary process in mountain building and hence in continental growth. With the advent of ocean deep drilling since the mid 1960's (DSSP, ODP, and IODP), thousands of meters of sediment from many accretionary prisms were made available for studying several geologic and geophysic properties, including AMS, after several decades of drilling in Barbados, Costa Rica, and Nankai accretionary prisms. Because large volume of sediments in accretionary prims have never been exhumed, and they are under active shortening, we can measure physical properties that are otherwise unavailable in uplifted and exhumed fold-and-thrust belts.

We will discuss results from the Nankai accretionary prism (Figure 6), although more data are available by Hounslow (1990), Housen et al. (1996); Housen (1997) as far as the Barbados accretionary prism, and by Housen and Sato (1995) and Owens (1995) for the Cascadia. The Nankai trough marks the boundary between Eurasia and the Philippine Sea Plate along southwest Japan, and has been the site of deep drilling since DSDP Leg 31 in 1991. Although Legs 56 and 57 were drilled in the forearc of the Japan Trench, no magnetic anisotropy data are available for the recovered cores. During Leg 31, Site 298 was drilled into the toe of the accretionary prism, but unfortunately core recovery was too poor for any meaningful study.

FIGURE 6

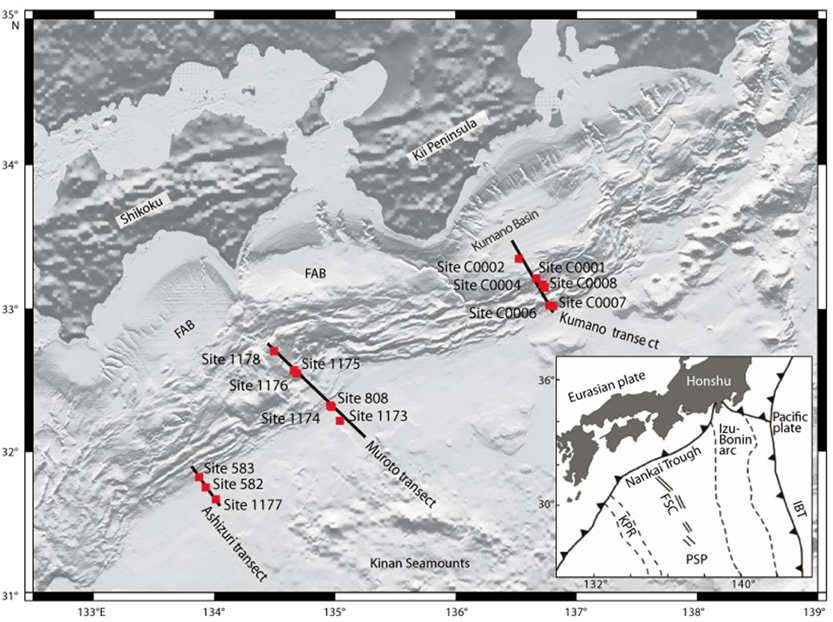
Figure 6. Regional setting o northern Shikoku Basin and Nankai Trough region showing existing DSDP, ODP and IODP drilling transects. FAB, forearc basin; Inset, tectonic map showing plate tectonic setting of the region; IBT, Izu-Bonin Trench; KPR, Kyushu-Palau Ridge; FSC, fossil spreading center; PSP, Philippine Sea plate (Moore et al., 2009).

Taira and Niitsuma (1986) reported the first rock-magnetic data including AMS in sediments from the active accretionary prism in SW Japan, along the Ashizuri transect. Two sites from Leg 87 were studied, 583 and 582, which come from near the frontal thrust and ahead of the deformation front, respectively (Figure 7). Site 582, at about 7 km ahead (seawards) of the frontal thrust, was sampled for AMS between depths 66 to about 750 mbsf (meters below sea floor), including Quaternary turbidites and Pliocene hemipelagic muds. Site 583, behind the frontal thrust, was sampled to a depth of 442 m. Because the ages of the sediments are known and hence the reference paleomagnetic direction, samples for AMS analysis were re-oriented using remanence data and therefore the principal axes of susceptibility for these two sites could be referred to geographic coordinates. In this earliest study in the Ashizuri transect, the AMS data already show a pattern that later on is observed not only in acretionary prisms but also in their onshore analogs, foreland basins ahead of fold-and-thrust belts. Site 582, farther away from the frontal thrust, reveals a predominance of sub-vertical K_min axes and a scatter, in the horizontal plane, of K_max axes (Figure 7). In contrast, Site 583, just NW of the frontal thrust, reveals a slightly NW-SE elongated dispersion of K_min axes while K_max have dominantly a NE-SW direction. In their study, Taira and Niitsuma (1986) interpret the K_max grouping to be related to a NE-SW paleocurrent, so axial to the main trend of the trough. A possible alternative explanation for the distribution of K_min axes at Site 583 is a NW-SE tectonic shortening (as already pointed out by Taira and Niitsuma, 1986). The fact that ellipsoids at Site 583 are dominantly prolate would support that interpretation.

FIGURE 7

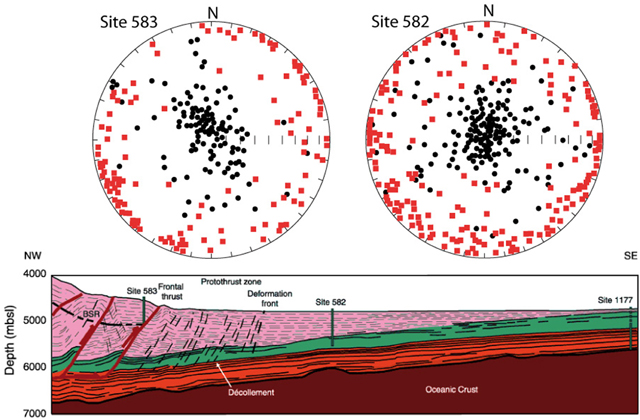
Figure 7. AMS axes for two DSDP sites in the Ashizuri transect (Nankai Trough). Lower-hemisphere, equal-area projection of the K_max (red squares) and K_min (black dots) principal axes of susceptibility for Sites 583 and 582 (re-drawn from Taira and Niitsuma, 1986). Cross section shows the structural position of the two drill sites along the transect.

Along the second large transect targeted by the ODP and IODP programs is the so-called “Muroto transect” (Figure 6), which runs from the Shikoku Basin, in the NE and ahead of the frontal thrust zone, to the accreted sediments, landward-dipping zone (Moore et al., 2001), encompassing over 80 km from the SW to the NE. Unfortunately, only a few sites have been analyzed for AMS (including Site 808, next to the protothrust zone, and Site 1178, well in to the overthrusting plate). ODP Leg 131 (Site 808) was a milestone in the study of active accretionary prisms, as it recovered more than 1000 m of hemipelagic silt and clay, across the basal décollement of the Nankai Trough subduction zone. The AMS study by Owens (1993) possibly allows for the first time to observe the changes in magnetic fabrics above and below a décollement in an accretionary prism. The samples from below the décollement, covering a depth range of 950-1050 mbsf, once oriented (using paleomagnetic directions), reveal a typical depositional fabric, including vertical K_min axes and scattered K_max axes within the depositional plane (Figure 8). The magnetic ellipsoid is strongly oblate, consistent with a sedimentary fabric. Above the décollement, between 400 and 935 mbsf, the magnetic ellipsoid moves toward the prolate field and the axes distribution resembles that of a tectonically deformed flatlying sedimentary rock, i.e., subvertical K_min axes and a SW-NE clustered K_max axes, so normal to the local shortening direction (NW-SE). Later AMS studies of Site 1174 (Ujiie et al., 2003b), just farther SE, produce very similar patterns to Site 808C.

FIGURE 8

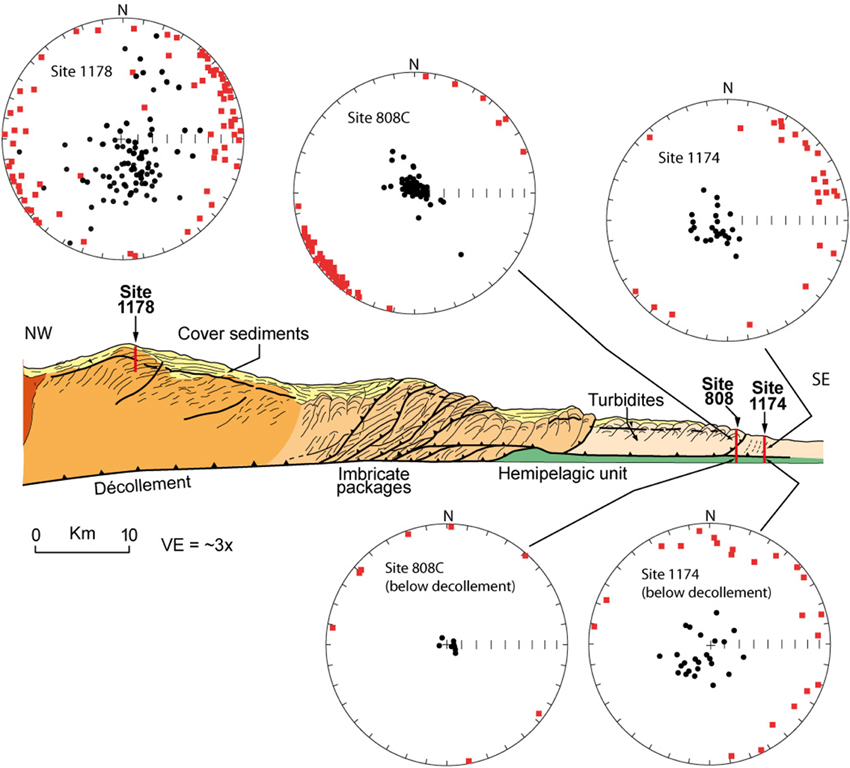
Figure 8. AMS from selected ODP and IODP sites along the Muroto transect (Nankai Trough) (cross section modified from Moore et al., 2001). Lower-hemisphere, equal-area projection of the K_max (red squares) and K_min (black dots) principal axes of susceptibility for Sites 1178, 808C, and 1174 (re-drawn from (Ujiie et al., 2003a,b), and (Owens, 1993), respectively). For sites 808C and 1174, we have represented the AMS axes from above and below de décollement.

The NW part of the Muroto transect includes a locality on the accreted sediments, which makes possible contrasting the fabrics of sediments from the overthrusting plate away from the subduction zone. Site 1178, Leg 190/196, is a good example (Ujiie et al., 2003a,b). The magnetic fabrics obtained in Site 1178, which encompass a thickness of around 450 m, reveal features that the previous transect does not show. A total of 147 oriented samples show that the K_min axes are dominantly SE dipping, whereas K_max axes yield a slight NE-SW magnetic lineation trend (Figure 8). Because bedding can be determined using paleomagnetic data, Site 1178 offers a unique view of the internal fabric in accreted sediments within the prism. The SE plunging K_min axes are consistent with a top to the SE shearing, as expected in the subduction zone. Ujiie et al. (2003a) interpreted the AMS data as S-C fabrics, related to the initial strain development at the frontal part of the prism.

A corollary of the AMS studies in accretionary prisms is that layer parallel shortening is recorded in unlithified mudrocks at very shallow depths, a question that probably has not been yet studied in detail.

Mechanisms of Preferred Orientation Development

AMS data from mudrocks open the question of the origin of tectonic magnetic fabric in such rocks, including whether is domainal or penetrative, and ultimately the mechanism for grain preferred orientation. In rocks with discrete cleavage surfaces (by pressure-solution), Borradaile and Tarling (1981) showed that the AMS axes orientation results from the interference between such planes and the original sedimentary fabric. Anisotropy in such rocks is characterized by ellipsoids with K_max axes that follow the cleavage-bedding intersection, essentially Type IIa or IIb magnetic ellipsoids (Parés et al., 1999), and so not parallel to the X-direction (maximum extension) of the strain ellipsoid (Parés and van der Pluijm, 2002).

Many tectonic microstructures including kink bands, cleavage steps, and biotite fish, which would have a profound impact on the magnetic fabric, are known to form in shales and slates. Folding and intragranular kinking in mica grains is a rather common process in very low grade rocks (e.g., Van der Pluijm and Kaars-Sijpesteijn, 1984). Kanaori et al. (1991) reported mica kink bands and cleavage steps in granites, and Goswami and Sarmah (2013) also observed kinking in the sandstones from the Siwalik belt in the western and Central Himalayas. In both cases, rocks are found in cataclasites, formed under higher P-T conditions. In an AMS study of the Sevier fold and thrust belt, Weil and Yonkee (2009) reported kinked mica grains in Triassic redbeds, which would explain the magnetic fabric in the redbeds. However, biotite typically requires temperatures above 250°C to behave ductilely and develop microstructures such as kinking (e.g., Stesky, 1978). Such temperatures are seemingly too high for the deformation realm that we are discussing in this paper. It seems, therefore, that the process of kinking cannot account for the tectonic fabric observed in mudrocks due to the lower temperatures where deformation takes place.

Studies of mudrocks obtained in DSDP Sites 583 (Lundberg and Karig, 1986), ODP Site 808 (Maltman et al., 1993), and IODP Site C0008 (Milliken and Reed, 2010), offer an alternative explanation for the AMS fabric that is widespread in weakly deformed rocks. Milliken and Reed (2010) studied a number of samples of semi-consolidated mud from Nankai (IODP Expedition 316) to determine preferred alignment of platy particles. Using field-emission SEM imaging they observed a number of planar deformation bands, having parallel alignment of both silt and clay-size particles, and the loss of intergranular porosity. Most deformation bands intersect at a high angle to bedding and have a thickness of few to about 200 microns. Such deformation bands do not necessarily involve grain comminution, but they certainly impart a significant small-scale anisotropy that is widespread in the mudrocks.

The AMS properties widely observed in mudrocks from the Nankai accretionary prism are certainly compatible with deformation bands. It is very likely that such planar deformation structures play a crucial role in determining the AMS in weakly consolidated mud, an aspect that needs to be further explored.

We propose four possible deformation mechanisms that individually or in combination can explain AMS patterns observed in mudrocks from many different tectonic settings (Figure 9). The study of weakly deformed mudrocks using both magnetic and imaging techniques can provide critical validation of these models and advance our understanding of the rock fabric development.

FIGURE 9

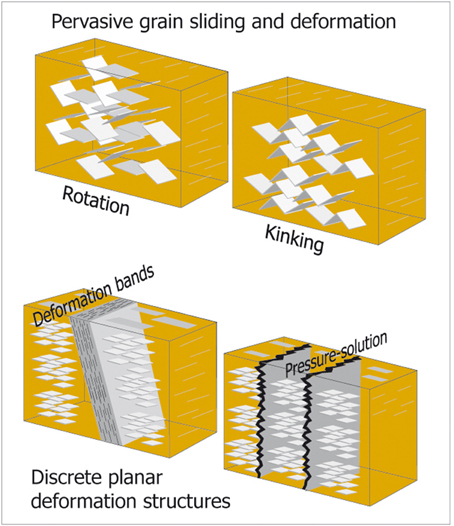
Figure 9. Summary of possible deformation mechanisms that can produce tectonic magnetic fabrics in mudrocks.

Final Remarks

Over the past 60 years, AMS data have been shown to be a very sensitive petrofabric tool in mudrocks, with the possibility of becoming a standard method for the quantification of mudrocks fabrics. The main achievements can be summarized as follows:

(1) AMS senses the ductile component of deformation in mudrocks.

(2) Because AMS sense preferred grain orientation (mostly from phyllosilicate grains), grain slippage and rotation must have occurred to develop such tectonic fabric. Both mechanisms sliding and rotation require a reduction in shear strength in order to facilitate the grains to slide past each other. It is thus very likely that sediments were overpressured by an increased fluid pressure. In this regard, because sediments in accretionary prims approach a visco-elastic body, the duration of the applied force (strain rate) has a profound effect on the deformation.

(3) AMS tectonic fabric development predates incipient (“embryonic”) cleavage formation, so thus far is possibly the most sensitive proxy for elucidating extremely weak deformation.

(4) Whether AMS tectonic fabric is sensing pervasive deformation, localized deformation (e.g., deformation bands) or a combination of mechanisms (Figure 9) is an issue that needs to be further explored.

Overall, there is no doubt that investigations of magnetic fabrics have largely evolved in sixty years, since the seminal study by J. Graham. This review illustrates that AMS is not an “unexploited tool” anymore (Graham, 1954), but certainly an underexploited discipline that is becoming a standard method for the quantification of rock fabrics in deformed mudrocks.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Most of the ideas summarized in this paper were developed during a sabbatical stay at the Lehigh University. I am very grateful to my colleagues at the Department of Earth and Environmental Sciences for making that stay possible, and for discussions and insights, in particular Dave Anastasio, Ken Kodama, and Frank Pazzaglia. My time was supported by the MECD through the “Salvador de Madariaga Program” (PRX12/00722). I also like to thank the Editor John Geissman, Eric Font, and Dario Bilardello for their comments which helped improving the manuscript.

References

Aubourg, C., Rochette, P., and Vialon, P. (1991). Subtle stretching lineation revealed by magnetic fabric of Callovian-Oxfordian black shales (French Alpes). Tectonophysics 185, 211–223. doi: 10.1016/0040-1951(91)90445-X