- 1Department of Physics, University at Albany, State University of New York, Albany, NY, United States
- 2Department of Physics, University of California Davis, Davis, CA, United States
- 3Sandia National Laboratories, Livermore, CA, United States
- 4Department of Physics, Applied Physics and Astronomy, Rensselaer Polytechnic Institute, Troy, NY, United States
- 5Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM, United States
- 6Lawrence Livermore National Laboratory, Livermore, CA, United States
- 7Deepgram, Mountain View, CA, United States
- 8Department of Physics and Astronomy, Rice University, Houston, TX, United States
- 9Department of Physics, University of California San Diego, La Jolla, CA, United States
- 10Department of Physics and Astronomy, University of California Los Angeles, Los Angeles, CA, United States
- 11Institute for Theoretical and Experimental Physics Named by A.I. Alikhanov of National Research Centre “Kurchatov Institute”, Moscow, Russia
- 12Moscow Engineering Physics Institute (MEPhI), National Research Nuclear University, Moscow, Russia
- 13Lawrence Berkeley National Laboratory, Berkeley, CA, United States
- 14Department of Physics, University of California Berkeley, Berkeley, CA, United States
- 15Department of Physics, Colorado State University, Fort Collins, CO, United States
- 16Department of Physics, University of Michigan, Ann Arbor, MI, United States
- 17Physik-Institut, University of Zürich, Zürich, Switzerland
- 18Department of Physics and Astronomy, University of California Riverside, Riverside, CA, United States
This paper discusses the microphysical simulation of interactions in liquid xenon, the active detector medium in many leading rare-event searches for new physics, and describes experimental observables useful for understanding detector performance. The scintillation and ionization yield distributions for signal and background are presented using the Noble Element Simulation Technique (NEST), a toolkit based on experimental data and simple empirical formulas, which mimic previous microphysics modeling but are guided by data. The NEST models for light and charge production as a function of the particle type, energy, and electric field are reviewed, along with models for energy resolution and final pulse areas. NEST is compared with other models or sets of models and validated against real data, with several specific examples drawn from XENON, ZEPLIN, LUX, LZ, PandaX, and table-top experiments used for calibrations.
1 Introduction
For the past 15+ years, leading results in dark matter direct detection searches have been obtained from detectors based on the principle of the dual-phase Time Projection Chamber (TPC) using a liquefied noble element as the detection medium (Baudis, 2018). Liquid xenon (LXe) TPCs, in particular, have produced the most stringent cross-section constraints for Spin-Independent (SI) and neutron Spin-Dependent (SD) interactions between Weakly Interacting Massive Particles (WIMPs) and xenon nuclei. More recently, the use of LXe has also led to WIMP limits using different Effective Field Theory (EFT) operators for mass-energies above
To interpret results from past, present, and future experiments, a reliable Monte Carlo (MC) simulation is required. Recent works have demonstrated the utility of NEST, the cross-disciplinary, detector-agnostic MC software reviewed in this study (Akerib et al., 2021b; Yan et al., 2021; Aprile et al., 2021), for a variety of active detector materials: LAr (Caratelli, 2022; Abud et al., 2023; Westerdale, 2024) and GXe, especially LXe. As the multi-tonne-scale TPCs have commenced data collection (Aalbers et al., 2023; Yan et al., 2021; Aprile et al., 2021), improved MC techniques will not only assist in limit setting but also be essential for determining the mass and cross section of dark matter particles in the event of a WIMP discovery. In either scenario or for the design of a new TPC, predictions of performance are needed on key metrics like the fundamental scintillation light and ionization charge yields for LXe, which is the focus of this work. NEST v2.4 is its default model; different versions are specified as needed. This manuscript is a technical overview of updates to NEST, including new models and comparisons. More pedagogical reviews of the models and related physics are available in the studies of Szydagis et al. (2011) and Szydagis et al. (2021a).
Section 2.1 presents the mean scintillation and ionization yields of electronic recoil (ER) backgrounds, along with comparisons to experimental data. These serve as the basis for the ER background (BG) models in Xe-based dark matter detectors. Section 2.2 summarizes the methods for varying these mean yields to model realistic fluctuations, with variations in the total number of quanta (light and charge) produced. Section 2.3 focuses on the yields of nuclear recoils (NRs) and their fluctuations. These form the foundation for the signal model in an LXe-based dark matter search, as well as for NR backgrounds (such as those from fast neutron scattering and coherent elastic neutrino-nucleus scattering, CE
2 Microphysics modeling evaluation
The NEST model choices were justified earlier by Szydagis et al. (2021a) and in the references therein, but they are re-evaluated in this study more comprehensively with newer and more extensive datasets. NEST is openly shared, allowing for regular re-evaluation using the latest calibrations (Szydagis, 2020). Although such data often provide relative light and charge yields, these can be converted to absolute yields if the detector gains are calculable, known as
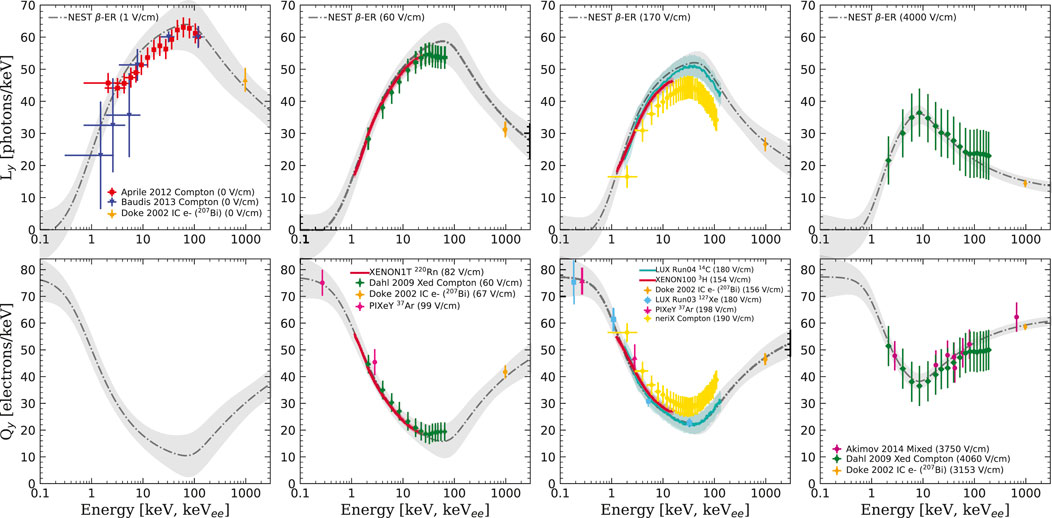
Figure 1.
2.1 Electronic recoils (beta, gamma, and X rays)
NEST begins with a model of the total yield, summing the vacuum ultraviolet (VUV) scintillation photons and ionization electrons produced. IR photons are not included as their yield in LXe is lower by a factor of
Here, ρ is the mass density in units of g/cm3. LXe TPCs typically operate at temperatures of 165–180 K and pressures of 1.5–2 bar(a), leading to
where
where
where
with
A Thomas–Imel approach historically uses
The recombination fraction or probability,
Figure 1 summarizes both
The absorption of any high-energy photon, a
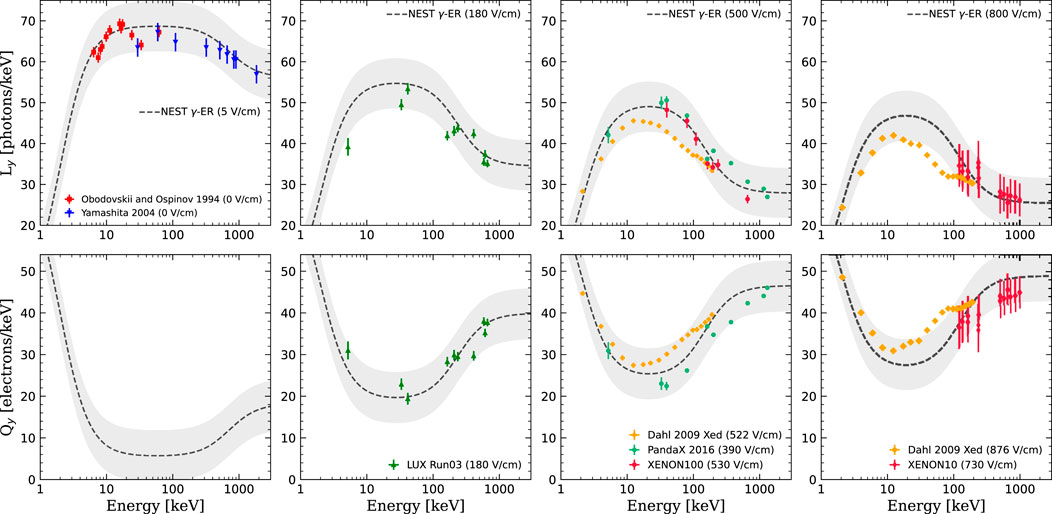
Figure 2.
2.2 Yield fluctuations
Energy resolution typically refers to Gaussian spreads (
2.2.1 Total quanta: correlated fluctuations
Realistic smearing of mean yields begins with a Fano-like factor,
where
The first part of Equation 7 is a spline of data (Aprile et al., 2008) from gas, liquid, and solid. The constant 0.13 represents the theoretical value of the Xe Fano factor, following the traditional definition
There are many possible explanations for
2.2.2 Anti-correlated excitation and recombination fluctuations
While it remains unclear which explanation is correct, NEST proceeds with a fully empirical approach to simply model what is observed in data; following the works by Akerib et al. (2017b) and Akerib et al. (2020a) closely, NEST defines recombination variance as follows:
A skew centroid
Longer, less technical descriptions of all the steps in Section 2.2.2 can be found in the studies by Akerib et al. (2020a) and Rischbieter (2022).
2.2.3 Recombination skewness
We note that the skewed Gaussian
A positive
2.2.4 Uncorrelated fluctuations: detector effects (known and unknown)
Lastly, while the simulated
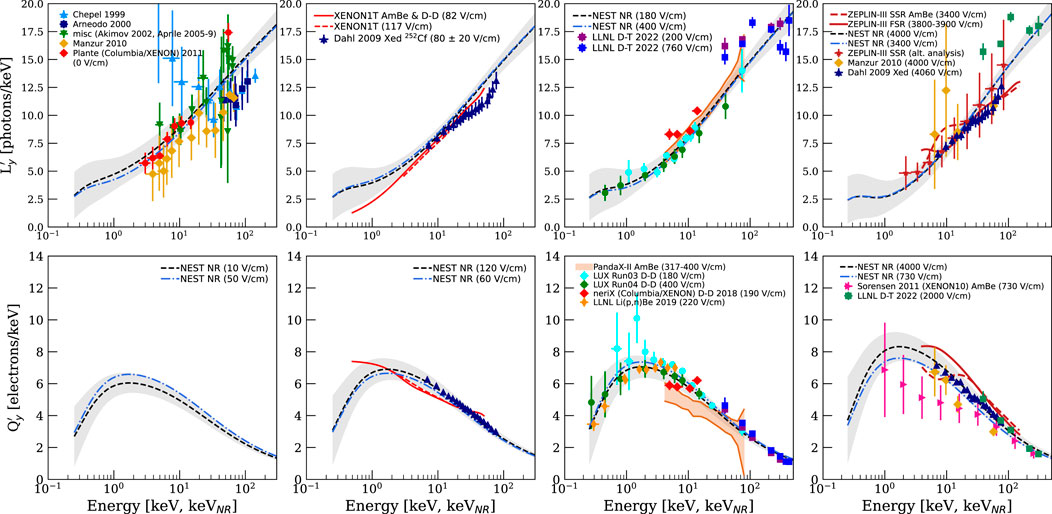
Figure 3. NR
2.2.5 Computational implementation
NEST is publicly available as a GitHub repository, which includes the source code, interface scripts, and examples. It is C++-based but can be run with dedicated scripts using either C++ or Python, both of which are available in the repository. These can be used to generate expectation values of yields and their fluctuations for different detectors using Xe or Ar. The step-by-step procedure that NEST follows to perform these tasks is summarized below:
•
• ER quanta are differentiated (
• A normal or skew-normal [Eq 8–12 (Akerib et al., 2020b)] in
Two more lists cover detector specifics for S1 and S2, closely following Supplementary Appendix SC of Aprile (2024b). First, S1 comprises the following:
• S1.1 A binomial distribution with probability
• S1.2 Single photo-electrons in sensors are modeled by zero-truncated Gaussians of sensor-specific width. Spike counting is emulated using artificially reduced width but non-zero for matching real data.
• S1.3 An if-else structure determines whether a second photoelectron is produced due to the secondary PE effect. This step and S1.2 are Gaussian-approximated at high
• S1.4 Geant4 (G4), Chroma, OptiX, or some other ray-tracer, or NEST’s built-in analytic-approximation ability simulates photon arrival times at S1 sensors and dictates whether a sufficient number of photons were detected in MC with above-threshold (experiment DAQ-specific) pulse areas, based upon stages S1.2 and S1.3 above.
The procedure to model the charge signal or S2 is more intricate, especially in a two-phase experiment:
• S2.1 Electrons (numbered
• S2.2 An electron survival fraction is set by an exponential function depending on the originating depth in a detector and a characteristic electron MFP. It is used as the probability in a binomial distribution.
• S2.3 Another binomial distribution is utilized to find how many electrons survive extraction from the liquid to the gas. The efficiency is a function of the gas field
• S2.4 Each extracted electron produces
• S2.5 A binomial of probability
More precise S2 simulation is possible in the optional integration of Garfield with NEST, which also possesses an optional G4 integration for simulating
2.3 Nuclear recoils (neutrons and WIMPs and Boron-8)
NR
The uncertainties here are
Equation 9 can be used to define “quenching,”
which is interpreted as the fraction of total NR energy shared with the electron cloud to produce ions and excitons.
While the previous equation sets the total quanta, the next equation determines the field- and density-dependent division into individual yields (charge or light) in an anti-correlated fashion, reducing
The reference density is
We use Equation 11 to produce a
Energy deposited is again
Similar to ER,
The top row of Figure 3, especially when read from right to left, shows the same
The two sigmoids reduce the predictive power of NEST for extrapolation into newer, lower-
Decreasing
In contrast to ER, for which the data suggest strict anti-correlation, simulated
Using the same functional form as in Equation 8 from ER, NEST models fluctuations in recombination for the redistribution of photons and electrons prior to measurable NR S1 and S2. The new parameters are distinguished using a prime symbol superscript again for NR
Parameter values are similar but not identical to those from ER:
3 Comparisons to first-principles approaches
By smoothly interpolating datasets taken at individual energies and/or electric fields, NEST is now fully empirical, built upon sigmoids and power laws as needed for a continuous model. However, inherent uncertainty is introduced by extrapolating into new energy and/or field regimes. To assess that and further validate an empirical approach, we show agreement with the models closer to “first principles.” Within NEST’s earliest versions, the Thomas–Imel (T-I) box model (Thomas and Imel, 1987) was used for low energy, while Birks’ law of scintillation was adapted for high energy. Both were qualitatively explained in Section 2.1 but are quantified in this section. The latter approach inside NEST was similar to Doke’s modification (Szydagis et al., 2011) for scintillation alone but applied directly to recombination, allowing it to model both
This is Birks’ law for other scintillators (Birks, 1964) but with an additional constant
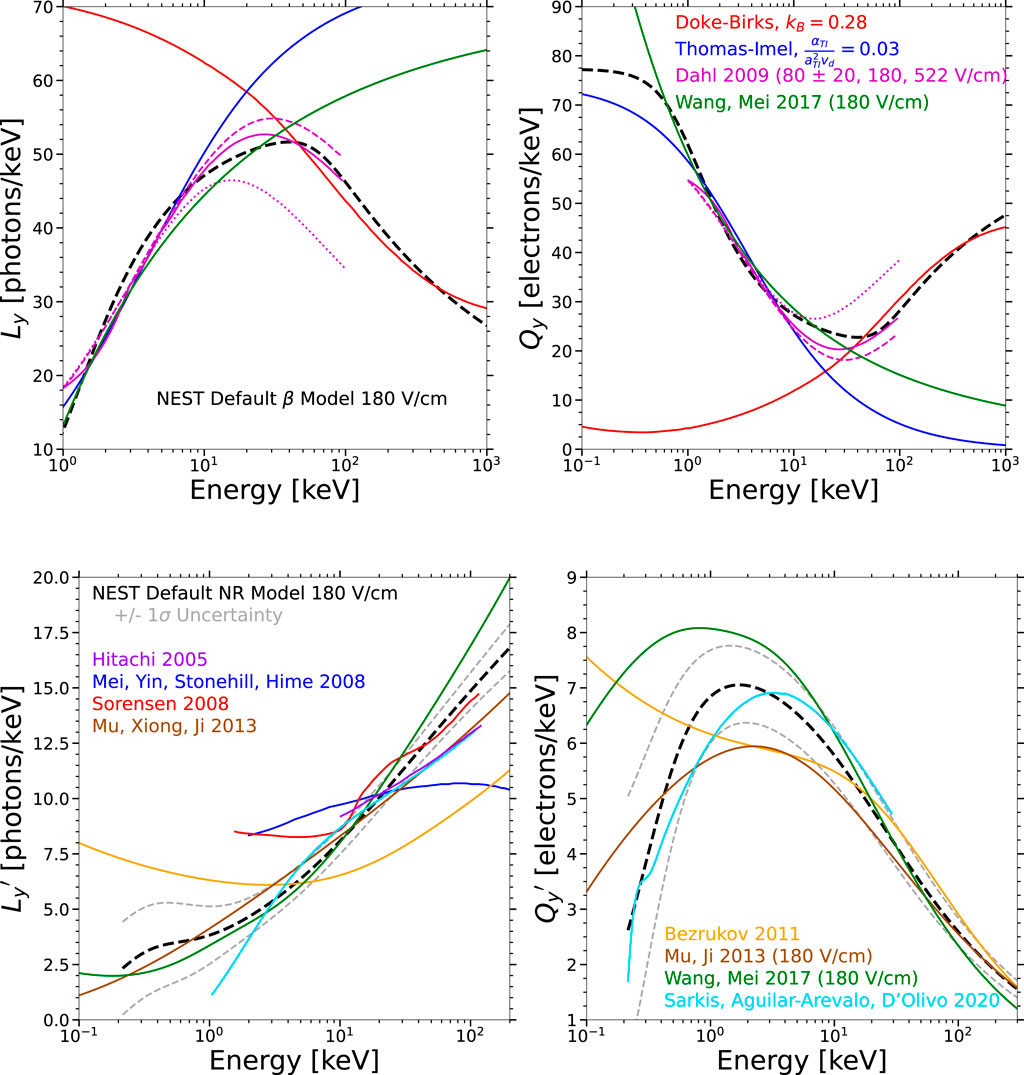
Figure 4. Comparing NEST with other approaches:
Despite Birks’ great success in explaining data at high
We interpret
Dahl found best-fit values of TIB ranging from 0.03 to 0.04 for both ER and NR data at 60–522 V/cm (Dahl, 2009). Our contemporary fits (for NEST and data), the blue lines at low energies in the first two panels at top in Figure 4, used 0.0300. If
For NR, Figure 4 (bottom row) presents many different past models, mainly for
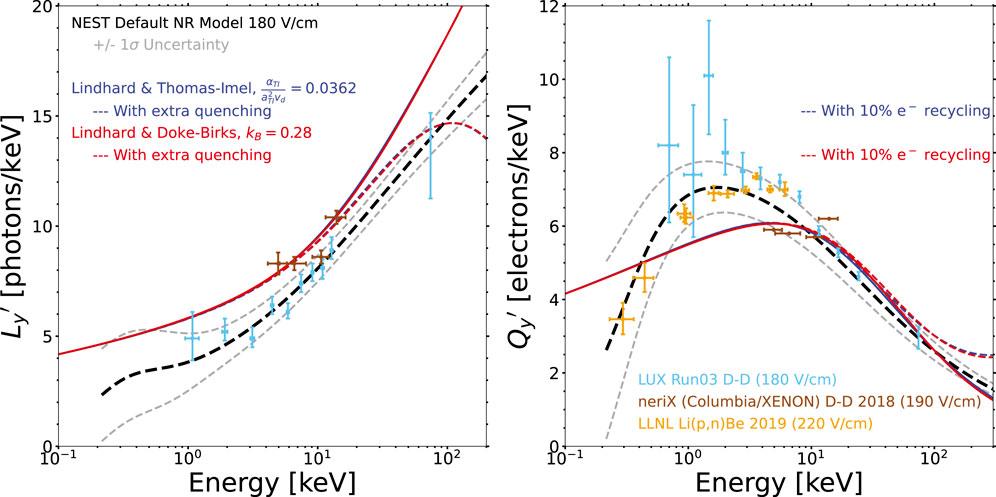
Figure 5. Comparisons of NEST and selected NR data to only the Thomas–Imel box (blue) and Birks (red) models of recombination, always using Lindhard to define
We identify
An additional quenching is applied to just
where
Unlike with ER, Birks’ law models NR over the entire
Looking back at alternatives to Lindhard, Figure 4 shows that NEST’s power law models for
The good agreement between the fully empirical NEST model and the first-principle models of both NR and ER shown in this study demonstrates that NEST can accurately simulate potential dark matter signals and backgrounds, respectively. This should hold true even for the regimes where data are still lacking, or they exist but have large uncertainties. In the case of NR, the fully empirical approach reproduces all data more accurately while using a comparable number of free parameters, offering much greater flexibility than semi-empirical approaches. For fluctuations, the number of NEST free parameters increased to two Fano factors (excitation and ionization) and four numbers for recombination width and skew to fully model the
4 Discussion and future work
Beginning with our models of beta ER, gamma-ray ER, and the NR light and charge yields, along with resolution modeling, a coherent picture was built up inside the NEST framework, which enables a good agreement with data. NEST was also shown to have features from multiple first-principles approaches, such as the box and Birks models. NEST already works for LAr (Szydagis et al., 2021a) using the same formulas as LXe but with unique parameter values. However, it still only works best for point-like interactions, like those in dark matter experiments like DarkSide, not tracks, as will be observed by DUNE. The list of NEST collaborators includes TESSERACT (Biekert et al., 2022) members, so the addition of liquid helium (LHe) to NEST is planned.
Looking beyond LHe, short-term future work includes NEST re-writing to account for the lower
The modified box model of LArTPC-based high-
where
where we employ, in order, the approximations
which is valid in the range of 0–100 keV. However, near 50 keV, a square root function with an offset also fits SRIM:
recovering the high-
Improved modeling of the MeV (ERs) scale is important for searches for neutrinoless double-beta
Long-term future work on NEST will involve an ab initio MC approach incorporating cross sections for recombination and the other relevant processes (Piazza et al., 2025), and molecular dynamics modeling of Xe atoms with the 12-6 Lennard-Jones potential for van der Waals forces will be explored (Equation 21). The LXe values for the L-J parameters as well as for other, more advanced versions of the model are well-established (Rutkai et al., 2017):
While these approaches are challenging at high (MeV) energies, they become more feasible at sub-keV scales, where yields are more uncertain; e.g., for 8B, fewer interactions are involved, leading to a more computationally tractable problem.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: https://github.com/NESTCollaboration/nest.
Author contributions
MS: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. JB: formal analysis, software, and writing–review and editing. GB: formal analysis, software, and writing–review and editing. JB: software and writing–review and editing. EB: investigation, supervision, validation, and writing–review and editing. JC: formal analysis, software, visualization, and writing–review and editing. SF: formal analysis, software, visualization, and writing–original draft. JH: formal analysis, software, and writing–review and editing. AK: resources, software, supervision, and writing–review and editing. EK: formal analysis, investigation, software, validation, visualization, writing–original draft, and writing–review and editing. CL: formal analysis, software, and writing–original draft. DM: investigation, resources, software, supervision, validation, and writing–review and editing. KM: formal analysis, software, and writing–review and editing. RM: software, validation, and writing–review and editing. MM: methodology, resources, software, supervision, validation, and writing–review and editing. JM: formal analysis, software, and writing–review and editing. KN: conceptualization, funding acquisition, investigation, methodology, resources, software, supervision, writing–original draft, and writing–review and editing. GR: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. KT: formal analysis, software, and writing–review and editing. MT: conceptualization, data curation, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, and writing–original draft. CT: conceptualization, data curation, funding acquisition, investigation, methodology, project administration, resources, software, supervision, writing–original draft, and writing–review and editing. VV: conceptualization, data curation, formal analysis, investigation, methodology, project administration, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. SW: supervision, validation, and writing–review and editing. MW: formal analysis and writing–review and editing. ZZ: formal analysis, software, and writing–review and editing. MZ: data curation, formal analysis, investigation, software, validation, visualization, writing–original draft, and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the U.S. Department of Energy (DOE) under Awards DE-SC0015535, DE-SC0024225, DE-SC0021388, DE-SC0018982 and DE-AC02-05CH11231, and by the National Science Foundation (NSF) under Awards 2046549 and 2112802.
Acknowledgments
The authors thank the LZ/LUX plus XENON1T/nT/DARWIN collaborations for useful recent discussion and continued support for NEST work. They especially thank LUX for providing key detector parameters and LUX collaborator Prof. Rick Gaitskell (of Brown University), Xin Xiang (formerly of Brown, now at Brookhaven National Laboratory), and Quentin Riffard (Lawrence Berkeley National Laboratory) for critical discussions regarding the detector performance of a potential Generation-3 liquid Xe TPC detector.
Conflict of interest
Author JC was employed by company Deepgram.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fdest.2024.1480975/full#supplementary-material
References
Aalbers, J., AbdusSalam, S. S., Abe, K., Aerne, V., Agostini, F., Ahmed Maouloud, S., et al. (2022). A next-generation liquid xenon observatory for dark matter and neutrino physics. J. Phys. G Nucl. Part. Phys. 50, 013001. doi:10.1088/1361-6471/ac841a
Aalbers, J., Akerib, D., Akerlof, C., Al Musalhi, A., Alder, F., Alqahtani, A., et al. (2023). First dark matter search results from the LUX-ZEPLIN (LZ) experiment. Phys. Rev. Lett. 131, 041002. doi:10.1103/physrevlett.131.041002
Aalbers, J., Akerib, D., Al Musalhi, A., Alder, F., Amarasinghe, C., Ames, A., et al. (2024). First constraints on WIMP-nucleon effective field theory couplings in an extended energy region from LUX-ZEPLIN. Phys. Rev. D. 109, 092003. doi:10.1103/physrevd.109.092003
Abe, S., Asami, S., Eizuka, M., Futagi, S., Gando, A., Gando, Y., et al. (2023). Search for the majorana nature of neutrinos in the inverted mass ordering region with KamLAND-zen. Phys. Rev. Lett. 130, 051801. doi:10.1103/PhysRevLett.130.051801
Abud, A. A., Abi, B., Acciarri, R., Acero, M., Adames, M., Adamov, G., et al. (2023). Identification and reconstruction of low-energy electrons in the ProtoDUNE-SP detector. Phys. Rev. D. 107, 092012. doi:10.1103/PhysRevD.107.092012
Acciarri, R., Adams, C., Asaadi, J., Baller, B., Bolton, T., Bromberg, C., et al. (2013). A study of electron recombination using highly ionizing particles in the ArgoNeuT Liquid Argon TPC. JINST 8, P08005. doi:10.1088/1748-0221/8/08/p08005
Akerib, D., Alsum, S., Araújo, H., Bai, X., Balajthy, J., Baxter, A., et al. (2019a). Improved measurements of the β-decay response of liquid xenon with the LUX detector. Phys. Rev. D. 100 022002. doi:10.1103/PhysRevD.100.022002
Akerib, D. S. (2016). Low-energy (0.7-74 keV) nuclear recoil calibration of the LUX dark matter experiment using D-D neutron scattering kinematics. arXiv:1608.05381. doi:10.48550/arXiv.1608.05381
Akerib, D. S. (2022). Improved dark matter search sensitivity resulting from LUX low-energy nuclear recoil calibration. arXiv:2210.05859. doi:10.48550/ARXIV.2210.05859
Akerib, D. S., Akerlof, C., Alqahtani, A., Alsum, S., Anderson, T., Angelides, N., et al. (2021b). Simulations of events for the LUX-ZEPLIN (LZ) dark matter experiment. Astropart. Phys. 125, 102480. doi:10.1016/j.astropartphys.2020.102480
Akerib, D. S., Akerlof, C. W., Alqahtani, A., Alsum, S. K., Anderson, T. J., Angelides, N., et al. (2020c). Projected sensitivity of the LUX-ZEPLIN experiment to the 0vββ decay of 136Xe. Phys. Rev. C 102 014602. doi:10.1103/PhysRevC.102.014602
Akerib, D. S., Alsum, S., Araújo, H., Bai, X., Bailey, A., Balajthy, J., et al. (2017c). Results from a search for dark matter in the complete LUX exposure. Phys. Rev. Lett. 118, 021303. doi:10.1103/PhysRevLett.118.021303
Akerib, D. S., Alsum, S., Araújo, H., Bai, X., Bailey, A., Balajthy, J., et al. (2017b). Signal yields, energy resolution, and recombination fluctuations in liquid xenon. Phys. Rev. D. 95, 012008. doi:10.1103/PhysRevD.95.012008
Akerib, D. S., Alsum, S., Araújo, H., Bai, X., Bailey, A., Balajthy, J., et al. (2017a). Ultra-low energy calibration of LUX detector using 127Xe electron capture. Phys. Rev. D. 96, 112011. doi:10.1103/PhysRevD.96.112011
Akerib, D. S., Alsum, S., Araújo, H., Bai, X., Balajthy, J., Baxter, A., et al. (2021a). Effective field theory analysis of the first LUX dark matter search. Phys. Rev. D. 103, 122005. doi:10.1103/PhysRevD.103.122005
Akerib, D. S., Alsum, S., Araújo, H., Bai, X., Balajthy, J., Baxter, A., et al. (2020a). Improved modeling of β electronic recoils in liquid xenon using LUX calibration data. J. Instrum. 15, T02007. doi:10.1088/1748-0221/15/02/t02007
Akerib, D. S., Alsum, S., Araújo, H., Bai, X., Balajthy, J., Baxter, A., et al. (2020b). Discrimination of electronic recoils from nuclear recoils in two-phase xenon time projection chambers. Phys. Rev. D. 102, 112002. doi:10.1103/PhysRevD.102.112002
Akerib, D. S., Alsum, S., Araújo, H., Bai, X., Balajthy, J., Beltrame, P., et al. (2019b). Results of a search for sub-GeV dark matter using 2013 LUX data. Phys. Rev. Lett. 122, 131301. doi:10.1103/PhysRevLett.122.131301
Akerib, D. S., Araújo, H., Bai, X., Bailey, A., Balajthy, J., Bedikian, S., et al. (2014). First results from the LUX dark matter experiment at the Sanford Underground Research Facility. Phys. Rev. Lett. 112, 091303. doi:10.1103/PhysRevLett.112.091303
Akerib, D. S., Araújo, H., Bai, X., Bailey, A., Balajthy, J., Beltrame, P., et al. (2016b). Improved limits on scattering of weakly interacting massive particles from reanalysis of 2013 LUX data. Phys. Rev. Lett. 116, 161301. doi:10.1103/PhysRevLett.116.161301
Akerib, D. S., Araújo, H., Bai, X., Bailey, A., Balajthy, J., Beltrame, P., et al. (2016a). Tritium calibration of the LUX dark matter experiment. Phys. Rev. D. 93, 072009. doi:10.1103/physrevd.93.072009
Akimov, D., Afanasyev, V., Alexandrov, I., Belov, V., Bolozdynya, A., Burenkov, A., et al. (2014). Experimental study of ionization yield of liquid xenon for electron recoils in the energy range 2.8–80 keV. JINST 9, P11014. doi:10.1088/1748-0221/9/11/p11014
Akimov, D., Bewick, A., Davidge, D., Dawson, J., Howard, A., Ivaniouchenkov, I., et al. (2002). Measurements of scintillation efficiency and pulse shape for low energy recoils in liquid xenon. Phys. Lett. B 524, 245–251. doi:10.1016/s0370-2693(01)01411-3
Albert, J., Barbeau, P. S., Beck, D., Belov, V., Breidenbach, M., Brunner, T., et al. (2017). Measurement of the drift velocity and transverse diffusion of electrons in liquid xenon with the EXO-200 detector. Phys. Rev. C 95, 025502. doi:10.1103/PhysRevC.95.025502
Albert, J. B., Anton, G., Arnquist, I. J., Badhrees, I., Barbeau, P., Beck, D., et al. (2018). Sensitivity and discovery potential of the proposed nEXO experiment to neutrinoless double-β decay. Phys. Rev. C 97 065503. doi:10.1103/PhysRevC.97.065503
Alvarez, V., Borges, F., Cárcel, S., Castel, J., Cebrián, S., Cervera, A., et al. (2013). Near-intrinsic energy resolution for 30–662 keV gamma rays in a high pressure xenon electroluminescent TPC. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 708, 101–114. doi:10.1016/j.nima.2012.12.123
Amoruso, S., Antonello, M., Aprili, P., Arneodo, F., Badertscher, A., Baiboussinov, B., et al. (2004). Study of electron recombination in liquid argon with the ICARUS TPC. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 523, 275–286. doi:10.1016/j.nima.2003.11.423
Anton, G., Badhrees, I., Barbeau, P., Beck, D., Belov, V., Bhatta, T., et al. (2019). Search for neutrinoless double-β decay with the complete EXO-200 dataset. Phys. Rev. Lett. 123 161802. doi:10.1103/PhysRevLett.123.161802
Anton, G., Badhrees, I., Barbeau, P. S., Beck, D., Belov, V., Bhatta, T., et al. (2020). Measurement of the scintillation and ionization response of liquid xenon at MeV energies in the EXO-200 experiment. Phys. Rev. C 101, 065501. doi:10.1103/PhysRevC.101.065501
Aprile, E. (2024a). First measurement of solar 8B neutrinos via coherent elastic neutrino-nucleus scattering with XENONnT. arXiv:2408.02877.
Aprile, E., Aalbers, J., Agostini, F., Ahmed Maouloud, S., Alfonsi, M., Althueser, L., et al. (2021). Search for coherent elastic scattering of solar 8B neutrinos in the XENON1T dark matter experiment. Phys. Rev. Lett. 126, 091301. doi:10.1103/PhysRevLett.126.091301
Aprile, E., Aalbers, J., Agostini, F., Alfonsi, M., Althueser, L., Amaro, F., et al. (2020b). Excess electronic recoil events in XENON1T. Phys. Rev. D. 102, 072004. doi:10.1103/PhysRevD.102.072004
Aprile, E., Aalbers, J., Agostini, F., Alfonsi, M., Althueser, L., Amaro, F., et al. (2019c). Search for light dark matter interactions enhanced by the Migdal effect or bremsstrahlung in XENON1T. Phys. Rev. Lett. 123, 241803. doi:10.1103/physrevlett.123.241803
Aprile, E., Aalbers, J., Agostini, F., Alfonsi, M., Althueser, L., Amaro, F., et al. (2019b). XENON1T dark matter data analysis: signal and background models and statistical inference. Phys. Rev. D. 99, 112009. doi:10.1103/PhysRevD.99.112009
Aprile, E., Aalbers, J., Agostini, F., Alfonsi, M., Althueser, L., Amaro, F. D., et al. (2019a). Observation of two-neutrino double electron capture in 124Xe with XENON1T. Nature 568, 532–535. doi:10.1038/s41586-019-1124-4
Aprile, E., Aalbers, J., Agostini, F., Alfonsi, M., Althueser, L., Amaro, F. D., et al. (2020a). Energy resolution and linearity of XENON1T in the MeV energy range. Eur. Phys. J. C 80, 785. doi:10.1140/epjc/s10052-020-8284-0
Aprile, E., Aalbers, J., Agostini, F., Alfonsi, M., Amaro, F., Anthony, M., et al. (2017). First dark matter search results from the XENON1T experiment. Phys. Rev. Lett. 119, 181301. doi:10.1103/PhysRevLett.119.181301
Aprile, E., Aalbers, J., Agostini, F., Alfonsi, M., Amaro, F., Anthony, M., et al. (2018a). Signal yields of keV electronic recoils and their discrimination from nuclear recoils in liquid xenon. Phys. Rev. D. 97, 092007. doi:10.1103/PhysRevD.97.092007
Aprile, E., Abe, K., Agostini, F., Ahmed Maouloud, S., Alfonsi, M., Althueser, L., et al. (2022). Double-weak decays of 124Xe and 136Xe in the XENON1T and XENONnT experiments. Phys. Rev. C 106, 024328. doi:10.1103/PhysRevC.106.024328
Aprile, E., Angle, J., Arneodo, F., Baudis, L., Bernstein, A., Bolozdynya, A., et al. (2011). Design and performance of the XENON10 dark matter experiment. Astropart. Phys. 34, 679–698. doi:10.1016/j.astropartphys.2011.01.006
Aprile, E., Anthony, M., Lin, Q., Greene, Z., de Perio, P., Gao, F., et al. (2018b). Simultaneous measurement of the light and charge response of liquid xenon to low-energy nuclear recoils at multiple electric fields. Phys. Rev. D. 98, 112003. doi:10.1103/PhysRevD.98.112003
Aprile, E., Arisaka, K., Arneodo, F., Askin, A., Baudis, L., Behrens, A., et al. (2010). First dark matter results from the XENON100 experiment. Phys. Rev. Lett. 105, 131302. doi:10.1103/PhysRevLett.105.131302
Aprile, E., Baudis, L., Choi, B., Giboni, K. L., Lim, K., Manalaysay, A., et al. (2009). New measurement of the relative scintillation efficiency of xenon nuclear recoils below 10 keV. Phys. Rev. C 79, 045807. doi:10.1103/PhysRevC.79.045807
Aprile, E., Bolotnikov, A. E., Bolozdynya, A. L., and Doke, T. (2008). Noble gas detectors. Wiley. doi:10.1002/9783527610020
Aprile, E., Budnik, R., Choi, B., Contreras, H. A., Giboni, K. L., Goetzke, L. W., et al. (2012). Measurement of the scintillation yield of low-energy electrons in liquid xenon. Phys. Rev. D. 86, 112004. doi:10.1103/PhysRevD.86.112004
Aprile, E., Dahl, C. E., de Viveiros, L., Gaitskell, R. J., Giboni, K. L., Kwong, J., et al. (2006). Simultaneous measurement of ionization and scintillation from nuclear recoils in liquid xenon for a dark matter experiment. Phys. Rev. Lett. 97, 081302. doi:10.1103/PhysRevLett.97.081302
Aprile, E., Giboni, K. , Majewski, P., Ni, K., Yamashita, M., Hasty, R., et al. (2005). Scintillation response of liquid xenon to low energy nuclear recoils. Phys. Rev. D. 72, 072006. doi:10.1103/physrevd.72.072006
Aprile, E., Giboni, K. L., Majewski, P., Ni, K., and Yamashita, M. (2007). Observation of anticorrelation between scintillation and ionization for MeV gamma rays in liquid xenon. Phys. Rev. B 76, 014115. doi:10.1103/PhysRevB.76.014115
Aprile, E., Mukherjee, R., and Suzuki, M. (1991). Performance of a liquid xenon ionization chamber irradiated with electrons and gamma-rays. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 302, 177–185. doi:10.1016/0168-9002(91)90507-M
Arneodo, F., Baiboussinov, B., Badertscher, A., Benetti, P., Bernardini, E., Bettini, A., et al. (2000). Scintillation efficiency of nuclear recoil in liquid xenon. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 449, 147–157. doi:10.1016/s0168-9002(99)01300-5
Baudis, L., Dujmovic, H., Geis, C., James, A., Kish, A., Manalaysay, A., et al. (2013). Response of liquid xenon to Compton electrons down to 1.5 keV. Phys. Rev. D. 87, 115015. doi:10.1103/physrevd.87.115015
Baudis, L., Sanchez-Lucas, P., and Thieme, K. (2021). A measurement of the mean electronic excitation energy of liquid xenon. Eur. Phys. J. C 81, 1060. doi:10.1140/epjc/s10052-021-09834-x
Berger, M., Coursey, J., Zucker, M., and Chang, J. (2005). “ESTAR, PSTAR, and ASTAR: computer programs for calculating stopping-power and range tables for electrons,” in Protons, and helium ions. Gaithersburg, MD: National Institute of Standards and Technology.
Bezrukov, F., Kahlhoefer, F., and Lindner, M. (2011). Interplay between scintillation and ionization in liquid xenon dark matter searches. Astropart. Phys. 35, 119–127. doi:10.1016/j.astropartphys.2011.06.008
Biekert, A., Chang, C., Fink, C., Garcia-Sciveres, M., Glazer, E., Guo, W., et al. (2022). Scintillation yield from electronic and nuclear recoils in superfluid He-4. Phys. Rev. D. 105, 092005. doi:10.1103/physrevd.105.092005
Birks, J. (1964). “The theory and practice of scintillation counting (chapter 8 - organic liquid scintillators),” in International series of monographs in electronics and instrumentation. Pergamon. doi:10.1016/B978-0-08-010472-0.50001-X
Bo, Z. (2024). First indication of solar 8B neutrino flux through coherent elastic neutrino-nucleus scattering in PandaX-4T. arXiv:2407.10892.
Boulton, E. M., Bernard, E., Destefano, N., Edwards, B., Gai, M., Hertel, S., et al. (2017). Calibration of a two-phase xenon time projection chamber with a 37Ar source. JINST 12, P08004. doi:10.1088/1748-0221/12/08/P08004
Bressi, G., Carugno, G., Conti, E., Noce, C., and Iannuzzi, D. (2001). Infrared scintillation: a comparison between gaseous and liquid xenon. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 461, 378–380. 8th Pisa Meeting on Advanced Detectors. doi:10.1016/S0168-9002(00)01249-3
Chepel, V., and Araújo, H. (2013). Liquid noble gas detectors for low energy particle physics. J. Instrum. 8, R04001. doi:10.1088/1748-0221/8/04/r04001
Chepel, V. Y. (1999). “Primary scintillation yield and alpha/beta ratio in liquid xenon,” in Proceedings of the 1999 IEEE 13th international conference on dielectric liquids, 52.
Conti, E., DeVoe, R., Gratta, G., Koffas, T., Waldman, S., Wodin, J., et al. (2003). Correlated fluctuations between luminescence and ionization in liquid xenon. Phys. Rev. B 68, 054201. doi:10.1103/PhysRevB.68.054201
Dahl, C. E. (2009). The physics of background discrimination in liquid xenon, and first results from XENON10 in the hunt for WIMP dark matter. Princeton University. Ph.D. thesis.
Davis, C., Hall, C., Albert, J., Barbeau, P., Beck, D., Belov, V., et al. (2016). An optimal energy estimator to reduce correlated noise for the EXO-200 light readout. JINST 11, P07015. doi:10.1088/1748-0221/11/07/P07015
Delaquis, S., Jewell, M., Ostrovskiy, I., Weber, M., Ziegler, T., Dalmasson, J., et al. (2018). Deep neural networks for energy and position reconstruction in EXO-200. J. Instrum. 13, P08023. doi:10.1088/1748-0221/13/08/p08023
Dobi, A. (2014). Measurement of the electron recoil band of the LUX dark matter detector with a tritium calibration source. Maryland U. College Park: Ph.D. thesis. doi:10.13016/M24P5P
Doke, T., Crawford, H. J., Hitachi, A., Kikuchi, J., Lindstrom, P. J., Masuda, K., et al. (1988). LET dependence of scintillation yields in liquid argon. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 269, 291–296. doi:10.1016/0168-9002(88)90892-3
Doke, T., Hitachi, A., Kikuchi, J., Masuda, K., Okada, H., and Shibamura, E. (2002). Absolute scintillation yields in liquid argon and xenon for various particles. Jpn. J. Appl. Phys. 41, 1538–1545. doi:10.1143/jjap.41.1538
Doke, T., Hitachi, A., Kubota, S., Nakamoto, A., and Takahashi, T. (1976). Estimation of Fano factors in liquid argon, krypton, xenon and xenon-doped liquid argon. Nucl. Instrum. Methods 134, 353–357. doi:10.1016/0029-554X(76)90292-5
Edwards, B., Bernard, E., Boulton, E., Destefano, N., Gai, M., Horn, M., et al. (2018). Extraction efficiency of drifting electrons in a two-phase xenon time projection chamber. JINST 13, P01005. doi:10.1088/1748-0221/13/01/P01005
Faham, C., Gehman, V., Currie, A., Dobi, A., Sorensen, P., and Gaitskell, R. (2015). Measurements of wavelength-dependent double photoelectron emission from single photons in VUV-sensitive photomultiplier tubes. J. Instrum. 10, P09010. doi:10.1088/1748-0221/10/09/p09010
Fano, U. (1947). Ionization yield of radiations. II. The fluctuations of the number of ions. Phys. Rev. 72, 26–29. doi:10.1103/PhysRev.72.26
Goetzke, L., Aprile, E., Anthony, M., Plante, G., and Weber, M. (2017). Measurement of light and charge yield of low-energy electronic recoils in liquid xenon. Phys. Rev. D. 96, 103007. doi:10.1103/physrevd.96.103007
Hitachi, A. (2005). Properties of liquid xenon scintillation for dark matter searches. Astropart. Phys. 24, 247–256. doi:10.1016/j.astropartphys.2005.07.002
Horn, M., Belov, V., Akimov, D., Araújo, H., Barnes, E., Burenkov, A., et al. (2011). Nuclear recoil scintillation and ionisation yields in liquid xenon from ZEPLIN-III data. Phys. Lett. B 705, 471–476. doi:10.1016/j.physletb.2011.10.038
Huang, D. (2020). Ultra-low energy calibration of the LUX and LZ dark matter detectors. Brown U: Ph.D. thesis. doi:10.26300/zvs6-fx07
James, R., Palmer, J., Kaboth, A., Ghag, C., and Aalbers, J. (2022). FlameNEST: explicit profile likelihoods with the Noble Element Simulation Technique. J. Instrum. 17, P08012. doi:10.1088/1748-0221/17/08/p08012
Lenardo, B., Kazkaz, K., Manalaysay, A., Mock, J., Szydagis, M., and Tripathi, M. (2015). A global analysis of light and charge yields in liquid xenon. IEEE Trans. Nucl. Sci. 62, 3387–3396. doi:10.1109/TNS.2015.2481322
Lenardo, B., Xu, J., Pereverzev, S., Akindele, O. A., Naim, D., Kingston, J., et al. (2019). Measurement of the ionization yield from nuclear recoils in liquid xenon between 0.3 – 6 keV with single-ionization-electron sensitivity. arXiv:1908.00518. doi:10.48550/arXiv.1908.00518
Lin, Q., Fei, J., Gao, F., Hu, J., Wei, Y., Xiao, X., et al. (2015). Scintillation and ionization responses of liquid xenon to low energy electronic and nuclear recoils at drift fields from 236 V/cm to 3.93 kV/cm. Phys. Rev. D. 92, 032005. doi:10.1103/PhysRevD.92.032005
Lindhard, J. (1963). Range concepts and heavy ion ranges. Mat. Fys. Medd. K. Dan. Vidensk. Selsk. 33, 10.
Manzur, A., Curioni, A., Kastens, L., McKinsey, D., Ni, K., and Wongjirad, T. (2010). Scintillation efficiency and ionization yield of liquid xenon for mono-energetic nuclear recoils down to 4 keV. Phys. Rev. C 81, 025808. doi:10.1103/PhysRevC.81.025808
McMonigle, R. (2024). Updating nuclear recoil models in the Noble Element Simulation Technique for the LUX-ZEPLIN experiment. Ph.D. thesis, UAlbany SUNY.
Mei, D. M., Yin, Z. B., Stonehill, L., and Hime, A. (2008). A model of nuclear recoil scintillation efficiency in noble liquids. Astropart. Phys. 30, 12–17. doi:10.1016/j.astropartphys.2008.06.001
Mozumder, A. (1995). Free-ion yield in liquid argon at low-LET. Chem. Phys. Lett. 238, 143–148. doi:10.1016/0009-2614(95)00384-3
Mu, W., and Ji, X. (2015). Ionization yield from nuclear recoils in liquid-xenon dark matter detection. Astropart. Phys. 62, 108–114. doi:10.1016/j.astropartphys.2014.07.013
Mu, W., Xiong, X., and Ji, X. (2015). Scintillation efficiency for low energy nuclear recoils in liquid xenon dark matter detectors. Astropart. Phys. 61, 56–61. doi:10.1016/j.astropartphys.2014.06.010
Nygren, D. R. (2013). Columnar recombination: a tool for nuclear recoil directional sensitivity in a xenon-based direct detection WIMP search. J. Phys. Conf. Ser. 460, 012006. doi:10.1088/1742-6596/460/1/012006
Obodovskii, I., and Ospanov, K. (1994). Scintillation output of liquid xenon for low-energy gamma-quanta. Instrum. Exp. Tech. 37, 42–45.
Piazza, O., Velan, V., and McKinsey, D. (2025). A first principles approach to e-ion recombination in liquid Xe. To be published .
Plante, G. (2012). The XENON100 dark matter experiment: design, construction, calibration and 2010 search results with improved measurement of the scintillation response of liquid xenon to low-energy nuclear recoils. Ph.D. thesis, Columbia U. (main).
Plante, G., Aprile, E., Budnik, R., Choi, B., Giboni, K. L., Goetzke, L. W., et al. (2011). New measurement of the scintillation efficiency of low-energy nuclear recoils in liquid xenon. Phys. Rev. C 84, 045805. doi:10.1103/physrevc.84.045805
Platzman, R. L. (1961). Total ionization in gases by high-energy particles: an appraisal of our understanding. Int. J. Appl. Radiat. Isotopes 10, 116–127. doi:10.1016/0020-708x(61)90108-9
Rischbieter, G. R. C. (2022). Signal yields and detector modeling in xenon time projection chambers, and results of an effective field theory dark matter search using LUX data. Ph.D. thesis, UAlbany SUNY.
Rutkai, G., Thol, M., Span, R., and Vrabec, J. (2017). How well does the Lennard-Jones potential represent the thermodynamic properties of noble gases? Mol. Phys. 115, 1104–1121. doi:10.1080/00268976.2016.1246760
Sarkis, Y., Aguilar-Arevalo, A., and D’Olivo, J. C. (2020). Study of the ionization efficiency for nuclear recoils in pure crystals. Phys. Rev. D. 101, 102001. doi:10.1103/PhysRevD.101.102001
Sorensen, P. (2011a). Lowering the low-energy threshold of xenon-based detectors. Proc. Identif. Dark Matter 2010 — PoS(IDM2010), 017. doi:10.22323/1.110.0017
Sorensen, P. (2011b). Anisotropic diffusion of electrons in liquid xenon with application to improving the sensitivity of direct dark matter searches. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 635, 41–43. doi:10.1016/j.nima.2011.01.089
Sorensen, P. (2015). Atomic limits in the search for galactic dark matter. Phys. Rev. D. 91, 083509. doi:10.1103/PhysRevD.91.083509
Sorensen, P., and Dahl, C. E. (2011). Nuclear recoil energy scale in liquid xenon with application to the direct detection of dark matter. Phys. Rev. D. 83, 063501. doi:10.1103/PhysRevD.83.063501
Sorensen, P., Manzur, A., Dahl, C., Angle, J., Aprile, E., Arneodo, F., et al. (2009). The scintillation and ionization yield of liquid xenon for nuclear recoils. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 601, 339–346. doi:10.1016/j.nima.2008.12.197
Szydagis, M. (2020). NEST: Noble Element Simulation Technique, A symphony of scintillation. Available at: http://nest.physics.ucdavis.edu.
Szydagis, M., Barry, N., Kazkaz, K., Mock, J., Stolp, D., Sweany, M., et al. (2011). NEST: a comprehensive model for scintillation yield in liquid xenon. JINST 6, P10002. doi:10.1088/1748-0221/6/10/p10002
Szydagis, M., Block, G. A., Farquhar, C., Flesher, A. J., Kozlova, E. S., Levy, C., et al. (2021a). A review of basic energy reconstruction techniques in liquid xenon and argon detectors for dark matter and neutrino physics using NEST. Instruments 5, 13. doi:10.3390/instruments5010013
Szydagis, M., Balajthy, J., Block, G. A., Brodsky, J. P., Cutter, J. E., Farrell, S. J., et al. Noble Element Simulation Technique (2022). doi:10.5281/zenodo.6989015
Szydagis, M., Fyhrie, A., Thorngren, D., and Tripathi, M. (2013). Enhancement of NEST capabilities for simulating low-energy recoils in liquid xenon. JINST 8, C10003. doi:10.1088/1748-0221/8/10/C10003
Szydagis, M., Levy, C., Blockinger, G., Kamaha, A., Parveen, N., and Rischbieter, G. (2021b). Investigating the XENON1T low-energy electronic recoil excess using NEST. Phys. Rev. D. 103, 012002. doi:10.1103/PhysRevD.103.012002
Tan, A., Xiao, M., Cui, X., Chen, X., Chen, Y., Fang, D., et al. (2016). Dark matter results from first 98.7 Days of data from the PandaX-II experiment. Phys. Rev. Lett. 117, 121303. doi:10.1103/PhysRevLett.117.121303
Thomas, J., and Imel, D. A. (1987). Recombination of electron-ion pairs in liquid argon and liquid xenon. Phys. Rev. A 36, 614–616. doi:10.1103/PhysRevA.36.614
Thomas, J., Imel, D. A., and Biller, S. (1988). Statistics of charge collection in liquid argon and liquid xenon. Phys. Rev. A 38, 5793–5800. doi:10.1103/PhysRevA.38.5793
Wang, L., and Mei, D. M. (2017). A comprehensive study of low-energy response for xenon-based dark matter experiments. J. Phys. G Nucl. Part. Phys. 44, 055001. doi:10.1088/1361-6471/aa6403
Westerdale, S. (2024). The DEAP-3600 liquid argon optical model and NEST updates. JINST 19, C02008. doi:10.1088/1748-0221/19/02/C02008
Xu, J., Pereverzev, S., Lenardo, B., Kingston, J., Naim, D., Bernstein, A., et al. (2019). Electron extraction efficiency study for dual-phase xenon dark matter experiments. Phys. Rev. D. 99, 103024. doi:10.1103/PhysRevD.99.103024
Yamashita, M., Doke, T., Kawasaki, K., Kikuchi, J., and Suzuki, S. (2004). Scintillation response of liquid Xe surrounded by PTFE reflector for gamma rays. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 535, 692–698. doi:10.1016/j.nima.2004.06.168
Keywords: WIMPs, dark matter, direct detection, liquid Xenon, simulations / models
Citation: Szydagis M, Balajthy J, Block GA, Brodsky JP, Brown E, Cutter JE, Farrell SJ, Huang J, Kamaha AC, Kozlova ES, Liebenthal CS, McKinsey DN, McMichael K, McMonigle R, Mooney M, Mueller J, Ni K, Rischbieter GRC, Trengove K, Tripathi M, Tunnell CD, Velan V, Westerdale S, Wyman MD, Zhao Z and Zhong M (2025) A review of NEST models for liquid xenon and an exhaustive comparison with other approaches. Front. Detect. Sci. Technol 2:1480975. doi: 10.3389/fdest.2024.1480975
Received: 14 August 2024; Accepted: 04 December 2024;
Published: 07 January 2025.
Edited by:
Diego Gonzalez-Diaz, University of Santiago de Compostela, SpainReviewed by:
Aleksey Bolotnikov, Brookhaven National Laboratory (DOE), United StatesCarlos Ourivio Escobar, Fermi National Accelerator Laboratory (DOE), United States
Copyright © 2025 Szydagis, Balajthy, Block, Brodsky, Brown, Cutter, Farrell, Huang, Kamaha, Kozlova, Liebenthal, McKinsey, McMichael, McMonigle, Mooney, Mueller, Ni, Rischbieter, Trengove, Tripathi, Tunnell, Velan, Westerdale, Wyman, Zhao and Zhong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: M. Szydagis, bXN6eWRhZ2lzQGFsYmFueS5lZHU=; G. R. C. Rischbieter, cmlzY2hiaWVAdW1pY2guZWR1
 M. Szydagis
M. Szydagis J. Balajthy2,3
J. Balajthy2,3 C. D. Tunnell
C. D. Tunnell V. Velan
V. Velan M. Zhong
M. Zhong