Workpiece temperature control in friction stir welding of Inconel 718 through integrated numerical analysis and process control

Friction stir welding (FSW) offers significant advantages over fusion welding, particularly for high-strength alloys like Inconel 718. However, achieving optimal surface quality in Inconel 718 FSW remains challenging due to its sensitivity to temperature fluctuations during welding. This study integrates finite element simulations, statistical analysis, and advanced control methodologies to enhance weld surface quality through adequate thermal management. High-fidelity simulations of the FSW process were conducted using a validated 3D transient COMSOL Multiphysics model, producing a comprehensive dataset correlating process parameters (rotational speed, axial force, and welding speed) with workpiece temperature. This dataset facilitated statistical analysis and parameter optimization through Analysis of variance (ANOVA) method, leading to a deeper understanding of process variables. A nonlinear state-space system model was subsequently developed using experimental data and the system identification toolbox in Matlab, incorporating domain-specific insights. This model was rigorously validated with an independent dataset to ensure predictive accuracy. Utilizing the validated model, tailored control strategies, including proportional-integral-derivative (PID) and model predictive control (MPC) in both single and multivariable configurations, were designed and evaluated. These control strategies excelled in maintaining welding temperatures within optimal ranges, demonstrating robustness in response times and disturbance handling. This precision in thermal management is poised to significantly refine the FSW process, enhancing both surface integrity and microstructural uniformity. The strategic implementation of these controls is anticipated to substantially improve the quality and consistency of welding outcomes.

1 Introduction

FSW, a solid-state welding technique, involves using a non-consumable tool to join metal or thermoplastic pieces together. The tool rotates at high speeds, creating frictional heat that softens the metal without melting it. As the tool moves along the joint, it blends the softened metal, resulting in a solid-state weld. Compared to traditional welding methods like gas tungsten arc welding (GTAW) or gas metal arc welding (GMAW), FSW offers benefits such as reduced distortion and improved mechanical properties. It can weld dissimilar materials and thin sections, making it versatile. The process comprises three stages: penetration, probing, and withdrawal. Different FSW tools, like shouldered, pin, or flat tools, are used based on material and application requirements (Lakshminarayanan et al., 2009; Mahoney et al., 1998).

FSW stands as a solid-state hot-deformation method employed to fuse two metal pieces together. This technique involves rotating a tool and pushing it into the junction between two workpieces, generating heat and softening the metal (the plunge phase). Subsequently, as the metal reaches the desired softness, the tool gradually accelerates along the seam (the traverse ramp phase), ultimately reaching full speed. Throughout this process, the tool stirs the softened metal, effectively joining the two pieces. Notably, significant thermal fluctuations occur during both the plunge and traverse ramp phases, often persisting even after achieving a constant traverse speed. Since FSW does not induce melting in the weld zone, post-weld properties such as strength, ductility, and fracture toughness tend to be superior compared to conventional welding methods (Mahoney et al., 1998).

Inconel 718, a nickel-based superalloy, is essential for applications demanding high strength, ductility, and corrosion resistance under normal and elevated temperatures. The viability of components made from such alloys relies on their ability to join with similar and dissimilar materials. Traditional methods like arc welding, electron beam welding, and laser welding have been used for manufacturing, refurbishing, and repairing Inconel 718 and other nickel superalloys. Recently, there’s been a focus on developing precise models to predict the microstructure and mechanical properties of friction stir welded Inconel 718. These models target areas like the heat-affected zone (HAZ) and thermo-mechanically affected zone (TMAZ), aiding in optimizing the welding process and ensuring joint quality. Researchers also investigate the impact of welding parameters like speed and force on the weld’s microstructure and mechanical properties. Furthermore, efforts are made to develop models predicting residual stress and distortion, critical for structural stability (Loria, 1992; Debarbadillo and Mannan, 2012; Song et al., 2011).

Limited research exists in the literature concerning friction stir welding and processing of Inconel 718 alloy. Successful outcomes have been reported only under specific conditions, namely low tool rotations (100–500 rpm), slow welding speeds (30–150 mm/min), and high axial loads (≈35 kN) (Lemos et al., 2017; Ahmed et al., 2013; Rule and Lippold, 2013; Alexopoulos et al., 2014; Song and Nakata, 2010; Song et al., 2009). These parameters, while yielding promising results like refined grain structures and increased microhardness, pose limitations on the industrial application of FSW for Inconel 718, raising concerns about its economic feasibility (Song and Nakata, 2010; Song et al., 2009). Despite these challenges, studies (Song and Nakata, 2010) have shown improved mechanical properties in welds, including microhardness and tensile strength, attributed to grain refinement. However, achieving successful FSW welds under a broader range of process parameters remains a key technical hurdle. While some research has explored the application of FSW to other Ni-based alloys like Inconel 625 and 718, the majority has focused on Inconel 600 due to its lower yield strength (Ye et al., 2006), making it more weldable. Conversely, research on high-yield-strength alloys like Inconel 718 in the context of FSW is limited.

On the other hand, effective control methodologies have been employed in real-world problems to make significant advancements. For instance, adaptive model predictive control (MPC) has been shown to effectively regulate NSCLC cell signaling dynamics in simulations, optimizing drug combinations to reduce toxicity and resistance, offering a novel control strategy for cancer treatment (Smart et al., 2022). Similarly, a process-model-free MPC method using a DDE-PID controller has been proposed to enhance control in thermal power plants. This approach addresses challenges such as process constraints and disturbances without relying on accurate plant models. Simulations and field tests in coal-fired units demonstrate superior disturbance rejection and reference tracking, highlighting its strong potential for practical application in power plants (Shi et al., 2023).

In another study, a stochastic model predictive control method combined with time-series forecasting was introduced to manage microgrid energy under uncertainty. By utilizing data-driven chance constraints, this approach optimizes energy management with minimal computational power, reducing costs and enhancing reliability in a grid-connected microgrid with PV generation and battery storage (Babić et al., 2023). Furthermore, in industrial processes, a predictor-based phase-lead active disturbance rejection control (PLADRC) method has been proposed to improve disturbance rejection in systems with input delays. The integration of a phase-lead module and extended state observer (ESO) reduces phase lag, enhances disturbance estimation, and improves overall performance. Practical digital implementation and robust stability analysis further demonstrate its effectiveness, as shown in illustrative examples (Li et al., 2022).

Moreover, tuning control parameters is crucial for real-world applications. A recent study addresses performance issues in PID controllers caused by proportional and derivative kick, proposing resilient PID tuning to minimize performance loss when switching between controller structures like PI-D and I-PD. By employing robust tuning based on more accurate process models (FOPDT and SOPDT), this approach ensures improved control performance and robustness, even when changing controller equations (Alfaro and Vilanova, 2022).

FSW relies on temperature control to ensure optimal weld properties within a specific thermal process range. Initially, FSW was conducted on adapted milling machines where temperature monitoring was sporadic, leading to temperature fluctuations during welding (Mayfield and Sorensen, 2010). Early attempts at temperature regulation often involved adjusting spindle speed (Fehrenbacher et al., 2011). Various techniques have been employed to measure stir zone temperature. Placing a thermocouple closer to the tool-plate interface significantly reduces system response time, enhancing control effectiveness. By regulating temperature and other welding parameters, weld quality can be preserved even in the face of external disruptions to the system (Fehrenbacher et al., 2014a; Fehrenbacher et al., 2014b).

FSW was initially performed by setting specific parameters for depth, travel speed, and spindle rotation speed, techniques that have proven effective over time (Ross, 2012; Chimbli et al., 2007). However, maintaining constant input parameters during welding may result in temperature fluctuations within the weld due to transients and external disturbances. Given that FSW heavily relies on temperature control, deviations in weld temperature can adversely impact the strength and integrity of the weld. Poor temperature regulation can even render the welded piece unusable in certain instances (Cederqvist et al., 2011).

An advancement in temperature regulation was achieved through the implementation of power control systems and enhanced system identification and tuning for controllers. Temperature regulation adopted a “cascade” method (Cederqvist et al., 2012): power was utilized to regulate temperature within a slower outer loop, while a faster inner loop was employed to regulate power itself. Ross (Ross et al., 2016) employed spindle power and a PID controller to maintain weld temperature within a 2°C range. Both Ross (Ross et al., 2016) and Marshall (Marshall et al., 2016) recognized FSW as primarily a first order plus dead-time (FOPDT) system. Marshall utilized a relay feedback test to ascertain FOPDT system parameters and determined PID gains using tuning rules (Marshall et al., 2016). This approach shown to be able to uphold temperature stability within a 2°C range, achieving superior settling characteristics compared to Ross’s initial efforts and demonstrating commendable disturbance rejection capabilities (Ross, 2012; Ross et al., 2016). On the other hand, Model Predictive Control (MPC) is an effective technique for multivariate control of intricate and extensive systems (Qin et al., 2015). It relies on a system model to forecast how alterations in inputs affect output parameters and utilizes an optimizer to adjust input parameters accordingly for optimal control of outputs. MPC has a long history of successful application across various industries (García et al., 1989; Cortinovis et al., 2015; Ma et al., 2014). Furthermore, Cederqvist and Nielsen (Nielsen et al., 2013; Cederqvist et al., 2016) created nonlinear models to address welding issues with non-circular copper canisters, emphasizing depth and force regulation. Employing these models, they conducted simulations to explore nonlinear multiple-input multiple-output (MIMO) MPC control of depth and temperature. While their research holds substantial theoretical potential, it has mainly concentrated on process simulation to assess controllers. Other FSW models have emerged: a FOPDT model and a more intricate Hybrid Heat Source model (Summary for Policymakers, 2014; Taysom et al., 2016). These models demonstrate satisfactory temperature forecasts, relying on spindle power and traverse speed post the initial transient phase of a weld. Given the accuracy of these temperature predictions, an MPC controller utilizing these models is anticipated to deliver effective performance, provided the gains and time constants align closely with those of the actual process (Hedengren and Eaton, 2017).

Furthermore, the study conducted by Taysom et el. (2016), have investigated the temperature control of FSW in Al 7075-T7 using model predictive control and compares it with well-tuned PID controllers. The research compares two MPC controllers, one based on a first order plus dead-time (FOPDT) model and the other on a Hybrid Heat Source model, against PID controllers in various welding conditions. The results show that both MPC and PID controllers can maintain temperature within 2°C of the setpoint during steady-state welding, with MPC showing advantages in handling specific process disturbances. However, during the initial traverse, the Hybrid Heat Source MPC and PID with regulatory tuning provided better temperature control within 5°C of the setpoint, while FOPDT and PID with servo gains struggled. The study recommends using PID controllers for steady-state conditions and unmodeled disturbances due to their ease of implementation and reliability. Conversely, MPC is suggested for scenarios where process changes or disturbances are anticipated, with specific recommendations for using the FOPDT model for traverse speed changes and the Hybrid Heat Source model for managing thermal transients during initial traverses or complex welding paths.

Another study (Marliana et al., 2024) focuses on enhancing the motion control accuracy of FSW robots, specifically those based on the 3-PUU parallel manipulator mechanism, by developing a fuzzy-PID controller optimized using genetic algorithms (GA) and particle swarm optimization (PSO). The fuzzy-PID controller’s performance, tuned with these optimization methods, was compared against a conventional PID controller in simulations. The results revealed that the fuzzy-PID-PSO controller, which optimized both rules and output, provided the most accurate and robust control, outperforming other configurations, especially in minimizing overshoot and integral absolute error (IAE) during disturbances. The study recommends implementing this controller design in real-world applications and suggests further research involving advanced algorithms like artificial neural networks (ANN) for tuning, as well as integrating FSW robots with image processing for enhanced visual sensing.

On the other hand, several researchers have utilized numerical analysis techniques to optimize the FSW parameters to achieve certain mechanical properties and improve the welding quality. Elathasaran and Kumar (2013) investigated the impact of three parameters - rotational speed, traverse speed, and axial force - on ultimate tensile strength, yield strength, and elongation. Their study utilized ANOVA analysis to demonstrate the effectiveness of the model at a 95% confidence level. Meanwhile, Zhang and Liu (2013) proposed examining the welding of aluminum to high-strength steel by considering three parameters: rotational speed, tool offset, and traverse speed. Venkateshkannam et al. (2014) explored the characterization of FSW welds, determining that defect-free joints were achievable using a stepped pin profile tool at 1,000 rpm and 40 mm/min. Although a cylindrical threaded pin yielded smooth welds without defects, the resulting tensile strength and microhardness were inferior to those achieved with the stepped pin tool. Hasan et al. (Shojaeefard et al., 2013a) optimized tool rotational speed, traverse speed, and shoulder diameter for grain size, ultimate tensile strength, and hardness using Taguchi L9 orthogonal DoE. Silva et al. (2014) focused on optimizing Friction Stir Welding AA6063-T6 T-joints using Taguchi L27 orthogonal Array, with tool rotation speed, welding speed, and tool geometry as the selected parameters. They reported a joint efficiency of 56% for the tensile test, highlighting the significant role of tool rotational speed in joint mechanical properties. Sadeesh et al. (2014) analyzed the FSW process concerning microstructure and tensile properties, utilizing five different tools to assess the influence of welding and traverse speed on microstructure. They found that the shoulder-to-pin diameter ratio played a significant role in determining better mechanical properties and microstructure. Lastly, Shojaeefard et al. (2013b) employed an Artificial Neural Network model to establish the relationship between process parameters and mechanical properties, predicting the ultimate tensile strength and hardness of butt joints based on the ANN model.

This study introduces a comprehensive approach that combines numerical analysis and process control to effectively manage workpiece temperature, thus enhancing weld quality and component performance in aerospace and automotive sectors. The approach involves creating a comprehensive dataset from numerical FSW trials to determine optimal process parameters for achieving desired surface quality, particularly focusing on reducing defects such as surface roughness and voids. Dynamic process control systems allow for adaptive adjustments based on feedback from embedded temperature sensors, ensuring precise regulation of workpiece temperature and reducing metallurgical defects. The investigation primarily focuses on three input parameters—rotational speed, transverse speed, and axial force—which influence workpiece temperature, as determined through numerical analysis. Regression models are utilized to establish equations that correlate workpiece temperature with input parameters, offering insights into the thermal effects on material characteristics during FSW.

This research distinguishes itself from existing work in the literature by being the first to implement an effective thermal management system for the FSW of nickel-based alloys using appropriate process control on the three main variables that affect the welding process (rotational speed, welding speed, and axial force). While there have been attempts on other materials like aluminum and magnesium alloys, high-strength alloys present additional challenges due to their nonlinearity and strain hardening effects at elevated temperatures. Therefore, this work is highly relevant for implementation in most high-strength alloys and other highly nonlinear systems.

2 Methodology

In order to conduct a proper process control in FSW technology, the methodology followed (See Figure 1) starts with conducting finite element simulations using COMSOL Multiphysics v5.3 to understand the interaction between process parameters and workpiece temperature (see Figure 2). These simulations are validated against experimental data, facilitating the generation of a comprehensive dataset detailing relationship and interdependencies among main process parameters (rotational speed, welding speed, shoulder diameter, pin diameter and axial force) and outcomes like temperature and grain size. Statistical analysis by using ANOVA method is conducted to identify the most significant parameters, which are then subjected to non-linear regression analysis to understand their influence on workpiece temperature. Insights from this analysis guided the development of a non-linear state-space system model, which is validated with an independent dataset. Upon successful validation, advanced control strategies, namely, PID and MPC, are designed and fine-tuned to manage the welding process effectively. Implementing these control strategies ensures effective thermal management, maintaining optimal temperatures and mitigating thermal fluctuations. This approach ought to lead to enhanced surface quality and improved microstructural uniformity in the welds.

Figure 1

Figure 1. Flow chart for the developed model system.

Figure 2

Figure 2. (A) FSW model domain, (B) System mesh.

The main governing equations used to construct the finite element model are summarized in the Electronic Supplementary Material (ESI). The model integrates heat fluxes arising from friction between the rotating tool and contact surfaces (See Figure 2A), contingent upon the normal force and rotational speed. Should the temperature surpass the melting point, heat fluxes from friction are disregarded. Heat transfer within the plate is enabled through surface-to-ambient radiation and convection, under the assumption of maintaining an ambient temperature on the supply side. Ensuring precise definition of workpiece properties is imperative for accurate simulation in FSW. Temperature fluctuations during welding induce alterations in workpiece properties, which are managed by specifying temperature-dependent properties derived from literature (Weld Integrity and Performance, 1997; Raj and Biswas, 2023). Furthermore, intricate strains and strain rates occurring during welding are replicated through the utilization of the Johnson-Cook model, effectively capturing work hardening and thermal softening phenomena.

Figure 2A depicts the model domain and system geometry, showcasing a setup comprising two plates of Inconel 718. Each plate measures 250 by 75 by 3 mm and is flanked by two infinite domains in the x-direction. The tool, made of tungsten carbide with 10% cobalt, is sturdy, featuring a flat circular bottom with a 25-mm diameter for the shoulder and a cylindrical pin with a diameter of 5 mm and a depth of 2.7 mm. By incorporating temperature-dependent material properties for both the tool and workpiece plates, the simulation enables concurrent calculation of thermal and mechanical effects. Utilizing the Arbitrary Lagrangian-Eulerian (ALE) technique alongside adaptive meshing ensures the maintenance of mesh quality during welding, thus preventing excessive distortion, albeit at the expense of computational time. Mesh convergence studies are essential in numerical simulations to ensure result accuracy and reliability without incurring high computational costs. The aim is to find the smallest mesh size that produces consistent results. This involves adjusting the mesh size and comparing outcomes until they show minimal change with further refinement. In this study, a mesh with 108,000 elements (see Figure 2B) and an average element quality of 0.81 was used. The simulation was executed on a system equipped with a 16 GB Intel(R) Core(TM) i7-8565U CPU @ 1.80 GHz 1.99 GHz, with a total completion time of approximately 6.2 h, the transient nature of the process necessitated longer durations to capture the full dynamic behavior of the FSW process.

The thermomechanical and thermophysical properties of the workpiece were obtained from literature sources (Weld Integrity and Performance, 1997; Raj and Biswas, 2023). Temperature-sensitive attributes such as sensible heat, density, and thermal conductivity were incorporated, alongside parameters like expansion coefficient, Young’s modulus, and Poisson’s ratio. To simulate the material’s plastic behavior during FSW, the Johnson-Cook plasticity model was utilized, accounting for variables such as strain hardening, strain rate, and thermal softening.

The finite element model underwent verification against previously documented experimental results conducted on Inconel 718 plates (See Supplementary Figure S1). These experiments recorded a plate temperature of 577°C at a distance of 5 mm from the welding nugget zone. Conversely, the temperature projected by the developed COMSOL Multiphysics model in this study was 600°C, indicating a 4% disparity. indicating close alignment between the FE model and published experimental outcomes for friction stir welding.

Datasets were generated using the developed finite element model to investigate the effects of various process parameters (see Supplementary Table S1). These parameters included axial force ranging from 5 to 50 kN, rotational speed from 100 to 600 RPM, welding speed from 50 to 150 mm/min, shoulder diameter from 15 to 25 mm, and pin diameter from 4 to 8 mm on the workpiece thermal profile.

On the other hand, one-way ANOVA was employed to identify the most significant parameters affecting the FSW process. This statistical technique allowed for the comparison of multiple process parameters, including axial force, rotational speed, welding speed, shoulder diameter, and pin diameter, to determine their impact on the workpiece’s thermal profile. By analyzing the variance among different parameter levels, the one-way ANOVA helped pinpoint which factors had the most substantial effect on the process. Following this, non-linear regression analysis was utilized to establish a relationship between these significant parameters and the workpiece temperature. This approach enabled the development of a predictive model that accurately connects the identified influential parameters with the resulting thermal profile, providing deeper insights into optimizing the FSW process.

Furthermore, the methodology followed in this study to perform the adequate process control involves importing and preprocessing input-output data from experiments or simulations to enhance relevance and accuracy. A suitable model structure is then selected based on the system’s characteristics, with options including transfer functions, state-space models, and ARX (AutoRegressive with eXogenous inputs) models available in MATLAB’s toolbox. Specific data subsets are defined for model estimation, and advanced algorithms are applied to optimize the model parameters for the best fit. The model’s accuracy is rigorously evaluated against a separate validation dataset to ensure it replicates the system’s behavior effectively. Adjustments and refinements are made as necessary to enhance performance.

In industrial control systems, Proportional Integral Derivative (PID) control and Model Predictive Control (MPC) are widely employed due to their ability to be finely tuned to meet specific performance criteria. These control strategies have been extensively utilized within the context of the FSW process as explained above. PID controllers, known for their simplicity and effectiveness in a wide range of operating conditions, adjust the process based on the error between a setpoint and the process variable. On the other hand, MPC provides a more sophisticated approach by predicting future system behavior and optimizing control moves accordingly. This predictive capability makes MPC particularly valuable for managing the intricate dynamics of FSW, allowing for precise adjustments in response to the thermal and mechanical variables affecting the welding quality.

Two operational modes are considered for each control strategy to adapt to different process requirements. The first mode simplifies the control structure by using only the Rotational Speed (RtS) as the control variable, treating Axial Force (AF) and Welding Speed (WS) as disturbances. This mode focuses on controlling the rotational speed to stabilize the welding process temperature while monitoring the effects of AF and WS. The second mode expands the control framework to include RtS, AF, and WS as control variables, aiming for more robust control. This comprehensive approach ensures that all influencing factors are actively regulated, enhancing the process’s adaptability and performance under varying operational conditions. Both control techniques were implemented to enhance the process stability and optimize the welding parameters, ensuring the robustness and accuracy of the FSW process.

3 Results and discussion

3.1 Numerical analysis, system identification, statistical analysis and process optimization

The FSW process parameters used in this study are a rotational speed of 600 RPM, a welding speed of 90 mm/min, an axial force of 40 kN, a shoulder diameter of 25 mm, and a pin diameter of 5 mm, without any cooling effect or preheating. Figure 3A illustrates the 3D temperature profile of the Inconel plates, where the peak temperature was recorded to be around 1,000°C, localized to the welding regions only. This figure shows the temperature distribution across the plates, with the maximum temperature focused on the welding regions and an almost uniform distribution in the x-direction. These results demonstrate that the temperature distribution of Inconel 718 is more concentrated around the welding regions, resulting in better heat dissipation across the plates. This suggests that Inconel 718 may have better resistance to thermal degradation and a longer lifespan at high temperatures. Figure 3B shows a 1D temperature profile of the workpiece across the welding centerline, with the highest temperatures concentrated around the welding nugget at 1,000°C. Figure 3C shows the 1D average grain size across the welding centerline, emphasizing grain refinement in the weld zone with a grain size of 50 μm, while Figure 3D displays the 1D hardness profile across the welding centerline, where hardness peaks in the weld zone at 410 HV and tapers off with increasing distance from the weld, showing a flat performance close to the nugget zone.

Figure 3

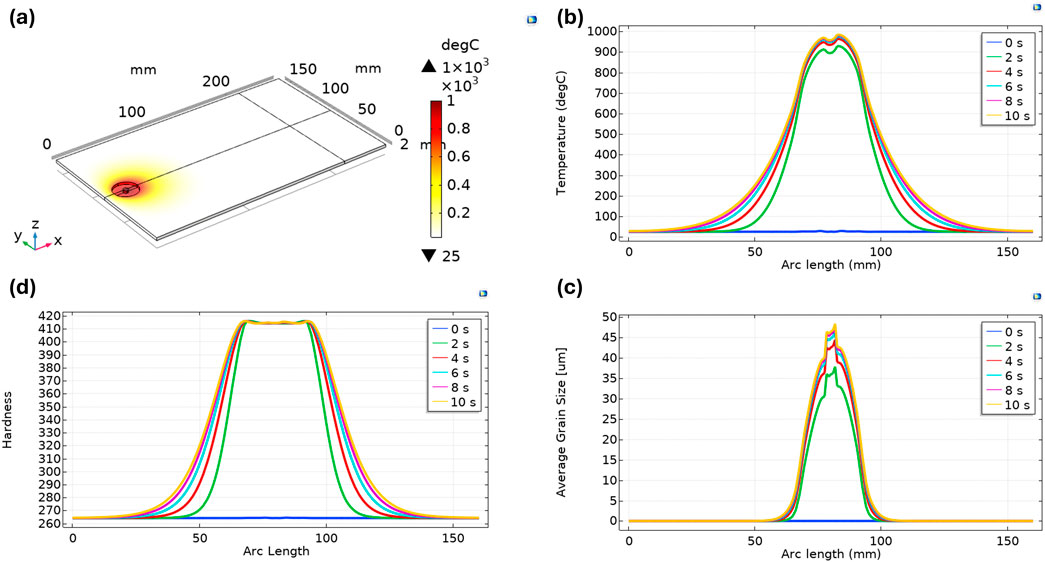
Figure 3. (A) 3D Temperature profile, (B) 1D Temperature profile, (C) 1D Hardness profile, and (D) 1D Average grain size.

Based on the developed finite element model, a dataset was generated by parameterizing the process parameters (rotational speed, axial force, welding speed, shoulder diameter and pin diameter) and capturing the dynamic behavior of the FSW process. One-way ANOVA was used to understand the effect of these parameters on the workpiece temperature, where the Tukey Simultaneous 95% Confidence Intervals (CIs) graph from the ANOVA results provides insightful comparisons across various parameters of the FSW process (See Supplementary Figure S2; Table 1; Supplementary Table S2). The obtained results reveal significant differences where the CIs do not cross the zero line, highlighting influential relationships between parameters such as welding speed, axial force, and rotational speed. Notably, the significant deviation in axial force across different settings suggests its critical role in influencing material deformation and joint quality during welding. Conversely, the temperature comparisons across multiple parameters (shoulder diameter, pin diameter, welding speed) mostly cross the zero line, indicating no significant differences. This suggests that temperature remains relatively stable across these variables, possibly due to effective thermal management within the tested range. Such findings are crucial for optimizing FSW parameters, where understanding the impact of axial force and rotational speeds could guide adjustments to achieve optimal weld conditions. Meanwhile, the stable temperature response across various settings supports the robustness of the process under the tested conditions.

Table 1

Table 1. Analysis of variance.

Supplementary Figure S3–S6 present the outcomes of the nonlinear regression analysis for predicting workpiece temperature based on process parameters (rotational speed, axial force, and welding speed) using non-linear regression conducted with Minitab software. Equations 1–10 summarize the main equations used to develop the process control methodology. The final model equation shows temperature as a function of time (X1), rotational speed (X2), welding speed (X3), and axial force (X4), including quadratic terms and interactions:

$\text{Temperature\hspace{0.17em}}\left(°\mathrm{C}\right)=25.33+0.7829\mathrm{X}1+1.1894\mathrm{X}2-0.1388\mathrm{X}3+18.123\mathrm{X}4-0.005194\mathrm{X}{1}^2-0.00761\mathrm{X}{2}^2-0.17246\mathrm{X}{4}^2-0.000938\mathrm{X}2*\mathrm{X}4(1)$

The model building sequence chart indicates the incremental addition of terms, starting with the most significant variable, axial force (X4), followed by rotational speed (X2), their quadratic terms, and interactions, culminating in an adjusted R-squared value near 100%, reflecting a high model fit. The right-hand graphs show the incremental impact of each variable on R-squared, highlighting that axial force contributes the most significant increase (approximately 45%) in explaining temperature variance. Furthermore, the “Each X Regressed on All Other Terms” graph reveals that axial force and rotational speed are the most influential variables, contributing substantially to the model’s explanatory power.

In addition, Supplementary Figure S7 illustrates the Multiple Regression for Temperature Prediction and Optimization report, which was generated using Minitab software to establish a relationship between workpiece temperature and the process parameters: rotational speed, axial force, and welding speed. The goal was to achieve a target temperature of 700°C. The predicted optimal settings to reach this temperature are presented, with the equation yielding a predicted Y value of 700°C within a 95% prediction interval of 675.16°C–724.84°C. Additionally, the top five alternative solutions with predicted T values closest to the optimal solution are provided, demonstrating slightly varied combinations of process parameters that still achieve a temperature near 700°C, ensuring the reliability and robustness of the model.

On the other hand, FSW is characterized by significant nonlinearities. An initial system identification was conducted using MATLAB’s System Identification Toolbox, leveraging the FSW dataset generated from the COMSOL finite element model. After importing the numerical experimental data into the toolbox, a curve fitting procedure was utilized to approximate the FSW process model. Among the various tested models, it is found that the ARXQS (Fourth-order autoregressive ARX model) and TF (Transfer Function) generate the best estimates. This is shown in Supplementary Figure S8. It was concluded that the match of the ARXQS model output with that of numerical experimental data is 99.21% whereas that of continuous time TF has a match of 99.63% and discrete time TF has a match of 99.95. These three have good matches but do not actually capture the real system behavior due to the inherent nonlinearities. Thus, the system identification toolbox could not give a realistic system model of the FSW. Among all the tested models, the closest fit found was the discrete time model using transfer function which is given below:

$\left[\begin{array}{ccc}\frac{0.38248z^{-1}}{\left(1-0.6078z^{-1}\right)\left(1+0.2544z^{-1}\right)}& \frac{2.095\times {10}^{-5}{z}^{-1}}{\left(1-z^{-1}\right)\left(1-0.1662z^{-1}\right)}& \frac{3.7657z^{-1}}{\left(1-0.8189z^{-1}\right)\left(1+0.1232z^{-1}\right)}\end{array}\right](2)$

Accordingly, here the Nonlinear Model Identification and refinement is proposed, where the initial application of the system identification toolbox captured main features of the process but failed to accurately capture the whole system dynamics, necessitating a refinement of the model identification process. This was achieved by integrating expert knowledge and insights about the physical system to address accuracy issues and obtain a valid nonlinear model. Adopting this strategy, an initial nonlinear model was established, and various parameters and nonlinear elements were fine-tuned to optimize the correlation with experimental data. Multiple iterations enhanced the model’s fit significantly. This refined process led to the accurate identification of a nonlinear state-space model as described below:

State equations:

${\dot{x}}_1=-10.43x_1-12.86x_2+12.86u_1$

${\dot{x}}_2=x_1$

${\dot{x}}_3=\left(0.0011u_2-0.056\right)x_4$

${\dot{x}}_4=\frac{-12.5}{0.0011u_2-0.0555}{x}_3-11.25x_4+12.5u_2$

${\dot{x}}_5=x_6$

${\dot{x}}_6=-8.75x_5-8.25x_6+8.75u_3$

Output equation:

$y=\left(-0.00075u_1+1.21\right)x_2-x_3+\left(-0.2396u_3+21.3\right)x_5$

Where

$u_1=\text{Rotational\hspace{0.17em}Speed}$

$u_2=\text{Welding\hspace{0.17em}Speed}$

$u_3=\text{Axial\hspace{0.17em}Force}$

$y=\text{Temperature}$

$x_1,x_2,x_3,x_4,and{x}_5\text{\hspace{0.17em}are\hspace{0.17em}state\hspace{0.17em}variables\hspace{0.17em}of\hspace{0.17em}the\hspace{0.17em}space}-\text{space\hspace{0.17em}model}$

x₁ - x₆ are state variables of the space-space model with x₁ being the instantaneous weld temperature at the primary welding zone. x₂ (given that ${\dot{x}}_2$ = x₁) represents accumulated thermal energy at the weld area. As for x₃ and x₄, these variables interact with u2 (axial force) representing the mechanical aspects of the weld process which indirectly influence heat generation process. Variable x₅ and x₆ (with ${\dot{x}}_5$ being = x₆) represent additional dynamic variables of displacement and displacement rate related to the welding tool’s travel along the weld line influencing the spread and dissipation of heat.

The state-space model in matrix form is as follows:

System matrix (A)

$\mathrm{A}=\left[\begin{array}{cccccc}-10.43& -12.86& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0\\ 0& 0& 0& -0.056& 0& 0\\ 0& 0& -0.0555& -11.25& 0& 0\\ 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& -8.75& -8.25\end{array}\right]$

Input matrix (B)

$\mathrm{B}=\left[\begin{array}{ccc}12.86& 0& 0\\ 0& 0& 0\\ 0& 0.0011& 0\\ 0& 12.5& 0\\ 0& 0& 0\\ 0& 0& 8.75\end{array}\right]$

Output matrix (C)

$\mathrm{C}=\left[\begin{array}{ccc}0& 1.21& \begin{array}{ccc}-1& 0& \begin{array}{cc}21.3& 0\end{array}\end{array}\end{array}\right]$

Feedthrough matrix (D)

$\mathrm{D}=\left[\begin{array}{ccc}-0.00075& 0& -0.2396\end{array}\right]$

3.2 Model construction and validation

The developed nonlinear model was implemented in Simulink, as depicted in Figures 4A, B. Figure 4A presents the subsystem block diagram, and Figure 4B details the internal configuration of the Simulink model. The model achieved an excellent match with the numerical experimental data, a conclusion supported by numerous simulations using varied control input values. Supplementary Figure S9 illustrates the system’s response from simulations of the nonlinear model alongside plots of experimental data for selected cases. The model was also exposed to input disturbance in the form of step change of axial force as shown in Supplementary Figure S10. This confirms the model’s ability to satisfactorily capture the underlying physical system dynamics. Having developed a satisfactory mathematical model, it is feasible to design adequate control systems that accurately track the desired reference welding temperature across different operating conditions.

Figure 4

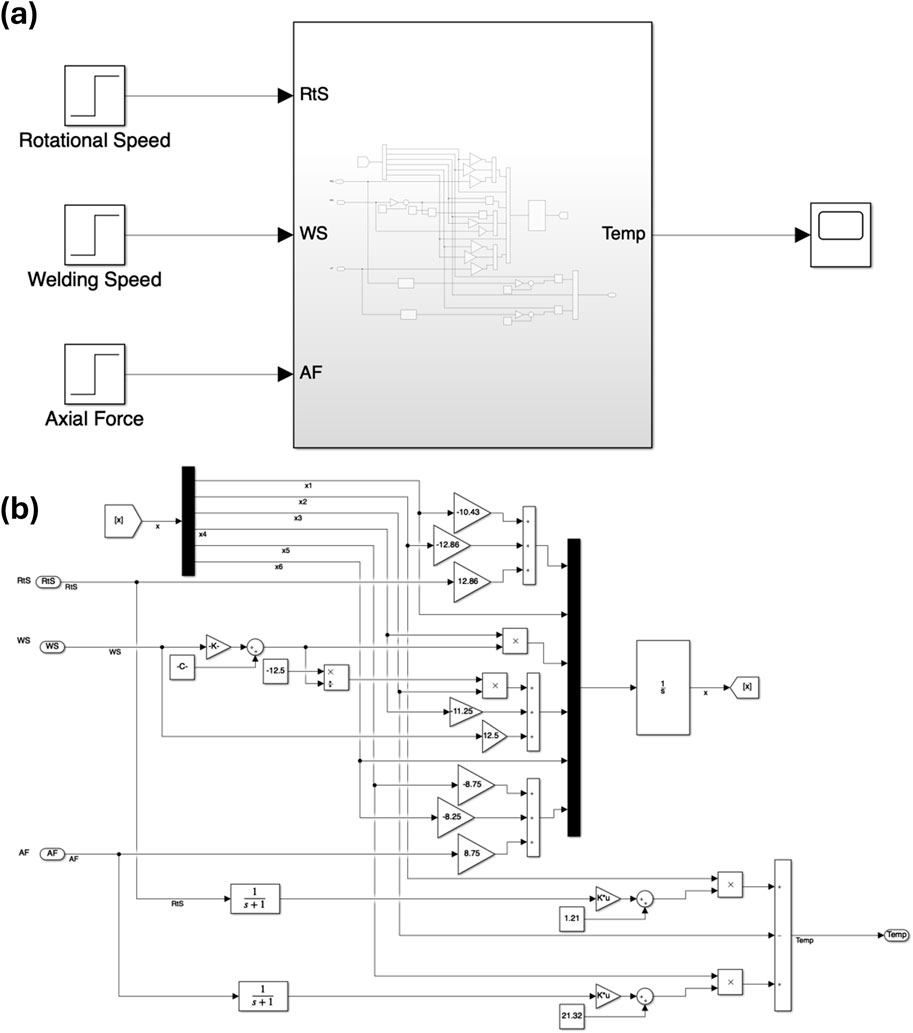
Figure 4. Simulink implementation of nonlinear model (A) Block diagram (B) Detailed description of the Simulink implementation.

3.3 Process control

For the purpose of FSW process control, two primary control strategies are explored: Proportional-Integral-Derivative (PID) and Model Predictive Control (MPC). Each strategy is implemented in two distinct configurations: single-variable and multi-variable control modes. In the single-variable mode, rotational speed serves as the primary control variable for adjusting the welding temperature, with axial force and welding speed treated as external disturbances. This approach focuses on straightforward control by manipulating one key variable to achieve desired temperature outcomes. The reason for selecting rotational speed is due to its significant effect on the workpiece temperature, and it is practically easier to control compared to axial force. Conversely, the multi-variable mode leverages a more comprehensive approach by simultaneously controlling multiple variables—rotational speed, axial force, and welding speed. This mode aims to optimize the control performance by adjusting several inputs in concert, allowing for a more refined and responsive control system. These configurations highlight the versatility and adaptability of PID and MPC strategies in addressing different complexities within the FSW process.

3.3.1 PID control

PID control is one of the most widely used controllers for industrial processes. The PID controller utilizes three terms to compute the control signal sent to an actuator, these are the Proportional (P) Term, Integral (I) Term, and the Derivative (D) Term. Proportional Term responds immediately to the current error value - a larger error results in a higher output correction. Integral Term addresses long-term errors by accumulating the error over time. It helps eliminate any steady-state error, where the output settles at a value different from the setpoint. Derivative Term anticipates future errors by considering the rate of change of the error signal. It helps reduce oscillation and speeds up the system’s response to setpoint changes.

The control law for PID controller can be expressed in the Laplace domain as follows:

$C\left(s\right)=K_p+\frac{K_i}{s}+K_{d}s(3)$

where K_p,K_i and K_d are the P, I, and D parameters. In time-domain, the controller output u(t) is formulated as follows:

$u\left(t\right)=K_{p}e\left(t\right)+K_i\int e\left(t\right)dt+K_d\frac{d}{dt}e\left(t\right)(4)$

Where e(t) is the error signal, defined as the difference between the setpoint and the process variable.

3.3.1.1 Controller design and tuning methodology

For the design of PID controllers, Ziegler-Nichols method was used initially to estimate appropriate controller adequate controller parameters. This method is based on the system’s response to open-loop testing. The Ziegler-Nichols method starts by pushing the system to its limits to identify two critical parameters, namely Ku (Ultimate gain) and Tu (Ultimate period). Based on the system’s model Ku and Tu values are found to be ≈3.741 and 1.516 s respectively. Having determined the ultimate gain and period, Ziegler-Nichols formula was applied as follows:

$K_p=0.6\times 3.741=2.2446$

$K_i=\frac{2\times 2.2446}{1.516}=2.9640\left(\frac{1}{\text{second}}\right)$

$K_d=\frac{2.2446\times 1.5168}{8}=0.4233\left(\text{seconds}\right)$

With these initial estimates, further fine-tuning was conducted using Matlab’s advanced PID tuning App. For the FSW process, two different control modes are considered to design and implement the PID controller, single variable, and multi-variable modes.

3.3.1.1.1 Single variable PID control

In the first configuration of PID control strategy, a single PID controller is designed, as indicated in the Simulink block diagram of Figure 5. The Rotational Speed (RtS) is taken as the control input, whereas Axial Force (AF) and Welding Speed (WS) are treated as disturbances. The initial design of the PID controller is fine-tuned using the Simulink Response Optimization Toolbox. The tuned PID controller parameters are given in Supplementary Table S3. It is worth mentioning that the controller parameters are tuned to tackle the actuator saturation problem as well. That is, the controller ensures the performance while keeping all the variables within their defined limits.

Figure 5

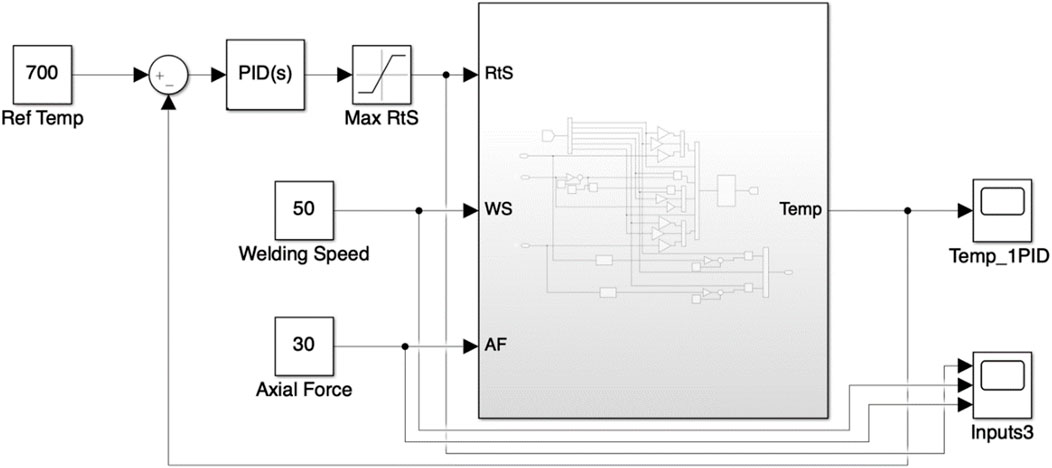
Figure 5. PID control for FSW process. Rotational Speed is taken as control input, Welding Speed and Axial force are treated as disturbances.

The simulation results corresponding to the designed controller with the welding speed equal to 35 mm/min and Axial Force equal to 25 kN are shown in Figure 6. The controller successfully stabilized the temperature at the desired value (in simulations at 700°C). The simulations are repeated for several different values of welding speed and axial force, and it is seen that the controller successfully tracks the reference signal despite variations in AF and WS, which facilitate the setting of the AF and WS at any level and the controller will automatically adjust the RtS to achieve desired temperature. The response of the system to a step change in Axial Force at time T = 10 s is shown in Supplementary Figure S11, which again shows the proficiency of the controller. One advantage of single PID controller is the freedom to choose any suitable, convenient and cost-effective values of WS and AF.

Figure 6

Figure 6. Closed-loop response of the FSW system with single PID controller.

3.3.1.1.2 Multi-variable PID control

In the second case, three distinct PID controllers are tuned, each controller to control each of the three control inputs, that is the RtS, WS, and AF. The Simulink block diagram corresponding to this scenario is shown in Figure 7. The parameters of the PID controllers are optimally tuned using the Simulink Response Optimization Toolbox, the parameters of the tuned PID controllers are given in Supplementary Table S4. Like the previous case of single PID controller, the problem of actuator saturation is taken care of for the three PID controllers. The simulation results corresponding to the case of three PID controllers are shown in Figure 8. It can be clearly seen that this design can also successfully track the reference temperature with good performance.

Figure 7

Figure 7. Three PID controllers with adjustable weights are designed for FSW.

Figure 8

Figure 8. Response of FSW with three PID controllers.

Compared with the case of one PID controller, the three PID controller automatically adjusts all the three control inputs (RtS, WS, and AF) to track the desired temperature, thereby, putting proportional load to all the control inputs. However, with this arrangement, we lose the freedom of manual adjustments on the AF and WS. An additional advantage in the three PID controller case is that tunable weights associated with three control inputs are also provided. These tunable weights can provide additional freedom which can be utilized to achieve some other optimization. For example, if any of the three control inputs is associated with some additional cost/energy consumption, that variable can be given more weight to achieve the desired temperature with less consumption of energy.

3.3.2 Model predictive control

MPC is an advanced technique used to control dynamic systems while adhering to constraints. Unlike PID controllers which focus on the present error, MPC takes a future-oriented approach. MPC relies on a mathematical model that predicts the future behavior of the system based on current state and control inputs. MPC considers a finite window of time steps into the future, called the prediction horizon. It predicts the system’s response for various control actions over this horizon. MPC solves an optimization problem to determine the control sequence that minimizes a cost function while keeping the predicted system behavior within specified constraints.

3.3.2.1 MPC controller design

Given the aforementioned actual system state-space model, the model configuration baseline can be established through the matrices that describe the system’s dynamics, where:

$\dot{x}=Ax+Bu,y=Cx+Du(5)$

Where, x represents the state vector, u is the input vector, and y is the output vector.

The next step in configuring the MPC controller is to choose an appropriate Prediction and control horizon (N_p and N_c) values. For the FSW process, where the response characteristics might change rapidly, an initial moderate horizon of N_p = 10 was selected to balance foresight with computational tractability. N_c Defines the number of future control moves the controller optimizes at each step of the time horizon. A value of N_c = 3 was selected as part of the initial controller configuration.

Being a predictive control strategy, MPC optimizes control action using a system model by employing a solver to minimize the error between model predictions and actual value through a cost function as given below:

$J=\underset{0}{\overset{T}{\int }}{\left(x_D\left(t\right)-x\left(t\right)\right)}^{T}Q\left(t\right)\left(x_D\left(t\right)-x\left(t\right)\right)dt(6)$

Where, Q(t) is the time-varying weight matrix that emphasizes different state deviations at various times. The discrete-time version of such cost function is as follows:

$J={\displaystyle \sum _{k=0}^{N_p}}{‖y\left(\left.k\right|t\right)-r\left(k\right)‖}_Q^2+{\displaystyle \sum _{k=0}^{N_c}}{‖u\left(k\right)‖}_R^2(7)$

Q and R, are constant or time-invariant weighting matrices that penalize the deviation from the reference trajectory and the use of control inputs, respectively. The minimization of cost function is subject to the system dynamics and constraints that limit control actions within operational limits as described by:

$u_{\mathit{min}}\le u\left(t\right)\le u_{\mathit{max}},0\le t\le T(8)$

Implemented within MATLAB/Simulink for both simulation and real-time control, the MPC’s performance is validated through various tests, including step response and disturbance rejection. Adjustments to the weight matrices Q and R and the horizons N_p and N_c are made based on the observed performance.

For the FSW process, two different strategies, like the situations in the design of PID controller, are proposed to design and implement MPC. That is, in the first strategy, a single MPC is there to control RtS and treat AF and WS as disturbances. In the second strategy, three different MPC to adjust each of the three control inputs (RtS, WS and AF) to track the temperature.

3.3.2.1.1 Single mode predictive control

The block diagram of a single MPC for the FSW is shown in Figure 9. Like the case of single PID controller, there is a freedom to choose any value of the AF and WS and the MPC will adjust the RtS to track the reference temperature. The simulation results for the case of single MPC are shown in Figure 10.

Figure 9

Figure 9. Single MPC for FSW with WS and AF considered as disturbances.

Figure 10

Figure 10. Response of FSW with single MPC.

3.3.2.1.2 Multi-variable model predictive controllers

In the second case of MPC, where three MPC are designed to control each of the three control inputs, that is the Rotational Speed, Axial Speed and the Welding Speed. The block diagram of three MPC is shown in Figure 11. The MPC are designed using Simulink Model Predictive Control Toolbox. Each of the three control inputs have some saturation limits, therefore, saturation blocks are also added in the design procedure. Furthermore, two gain blocks are added to the controller against welding speed and axial force. These gain blocks are adjustable and can be utilized for some additional optimization, for example, energy/cost optimization. For the design of the MPC, the following parameters are set.

• Sampling time: 0.5 (seconds)

• Prediction Horizon: 5

• Control Horizon: 1

Figure 11

Figure 11. Simulink diagram of three MPC for FSW.

The simulation results for the case of three MPC is shown Figure 12. It can be seen from the figure that the three MPC case can also be utilized to maintain the temperature at the desired level. Furthermore, the effect of sudden disturbance in Axial Force introduced at a time of T = 10 s is shown in Supplementary Figure S12. It is observed that the controller can maintain the temperature despite some bias or variation in some of the actuators.

Figure 12

Figure 12. Response of closed loop system with three MPC.

3.3.3 Comparison of designed control systems

After exploring various control system designs, it is beneficial to compare and evaluate them to gain a comprehensive understanding of their performance, along with the advantages and disadvantages of each model. It is worth mentioning that all controllers have been tuned to give the best possible performance. Figure 13 below presents a comparison of the PID and MPC controllers in both their single and multi-variable control modes through a hypothetical scenario of temperature set point alteration and disturbances in axial force and welding speed.

Figure 13

Figure 13. Comparison of designed control systems.

Initially, during the transient state, all controllers exhibit similar responses, with the PID controllers (3PID followed by 1PID) responding slightly faster than their MPC counterparts, a trend that persists after the second temperature setpoint change. At the 70-s mark, when the temperature setpoint dropped by 400°C, the PID controllers maintained their faster response, but the multi-variable controllers (3PID and 3MPC) experienced noticeable undershoots with approximately 30°C, while the single-variable controllers (1PID and 1MPC) approached the new setpoint more steadily. During the axial force disturbance introduced at 85 s, the single-variable controllers (1PID and 1MPC) managed the disturbance more effectively, showing minimal overshot. In contrast, both multi-variable controllers (3PID and 3MPC) struggled with significant overshoots up to 150°C. Surprisingly, when it came to handling disturbances from welding speed at 100 s, the multi-variable controllers (3PID and 3MPC) performed better, exhibiting minimal undershoot, while the single-variable controllers displayed more significant undershoot up to 20°C. Throughout the remainder of the test, PID controllers consistently demonstrated a faster response to changes in desired temperature, indicating their potential superiority in scenarios where speed of response is critical. Figure 14 illustrates the response of the four designed control systems to changes in the temperature setpoint and disturbances caused by variations in axial force and welding speed.

Figure 14

Figure 14. Controller output.

As observed in Figure 14, there are slight variations in the response of each controller to changes during steady-state conditions, which can be attributed to differences in their level of complexity and operating principles. Nonetheless, all proposed control systems demonstrate satisfactory performance in maintaining the temperature within acceptable operating limits. These observations and analysis underscore that while no single controller excels in every aspect, the choice between them can be optimized based on specific operational priorities such as response speed, stability, or disturbance handling.

3.4 Effect of workpiece temperature on weld quality

In FSW technology, the workpiece temperature plays a crucial role in determining both the surface quality and the mechanical properties of the welded material. Elevated temperatures during FSW facilitate the plastic deformation and material flow necessary for forming a solid-state bond, directly influencing the surface finish by reducing defects and ensuring a smoother weld seam. Additionally, the temperature affects grain size and distribution, which in turn impacts the mechanical properties such as hardness, strength, and ductility of the welded joint. Optimal temperature control ensures a balance between sufficient material mixing and minimizing thermal degradation, resulting in superior surface quality and enhanced mechanical performance of the welded material.

Supplementary Figure S13 illustrates the results of a multiple regression analysis performed using Minitab software to explore the relationship between the average grain size (Y) in µm of a friction stir welded workpiece and its temperature (X) in °C. The analysis aimed to establish a quadratic model, yielding the equation:

$\mathrm{Y}=16.39-0.09086\mathrm{X}+0.000117{\mathrm{X}}^2(9)$

The fitted line plot shows the quadratic model’s curve, indicating how average grain size varies with temperature. The p-value (<0.001) confirms that the relationship between grain size and temperature is statistically significant. The R-squared value (99.09%) demonstrates that the model explains 99.09% of the variation in average grain size, signifying a high degree of reliability. This regression model can be used to predict average grain size from temperature data, thereby aiding in the estimation of workpiece surface quality by monitoring the workpiece temperature.

Moreover, Supplementary Figure S14 presents the results of a multiple regression analysis conducted using Minitab software to determine the relationship between the microhardness (Y) of a friction stir welded workpiece and its temperature (X) in °C. A quadratic model was fitted, resulting in the equation:

$\mathrm{Y}=246.5+0.4079\mathrm{X}-0.000243{\mathrm{X}}^2(10)$

The fitted line plot illustrates the model’s curve, showing how microhardness varies with temperature. The p-value (<0.001) indicates a statistically significant relationship between microhardness and temperature. The R-squared value (98.70%) reveals that the model explains 98.70% of the variation in microhardness, indicating a high level of accuracy. This regression model can be utilized to predict microhardness based on temperature data, thereby assisting in the estimation of the workpiece’s mechanical properties by monitoring its temperature.

4 Conclusion

This research outlines a comprehensive methodology for controlling the workpiece temperature of friction stir welds in Inconel 718 through the integration of finite element simulations, statistical analysis, and system control. Initial high-accuracy numerical modeling provided a robust dataset that informed the statistical optimization of process parameters. The insights gained from ANOVA guided the selection of best process parameters then the development of a nonlinear state-space model, which was validated for accuracy against a secondary dataset. The confirmed model underpinned the formulation of precise PID and MPC control strategies, optimizing thermal dynamics during welding. Both PID and MPC strategies in their single variable and multi-variable modes proved to be successful in controlling the FSW workpiece temperature with minor differences in terms of response time and disturbance handling. The application of these strategies effectively addresses temperature control issues commonly known for causing defects associated with FSW. This approach not only advances the FSW process for Inconel 718 but also sets a precedent for applying similar methodologies to other high-performance alloys, with implications for enhancing manufacturing processes and operational scalability.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AA: Conceptualization, Data curation, Formal Analysis, Investigation, Software, Writing–original draft, Writing–review and editing, Methodology. MA-A: Software, Validation, Writing–original draft, Writing–review and editing, Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Resources. MK: Supervision, Writing–review and editing, Resources, Validation. YR: Supervision, Writing–review and editing, Project administration, Validation. SA: Supervision, Writing–review and editing, Conceptualization, Investigation, Methodology, Project administration, Validation, Visualization.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcteg.2024.1459399/full#supplementary-material

References

Ahmed, M. M. Z., Wynne, B. P., and Martin, J. P. (2013). Effect of friction stir welding speed on mechanical properties and microstructure of nickel based super alloy Inconel 718. Sci. Technol. Weld. Join. 18 (8), 680–687. doi:10.1179/1362171813y.0000000156

CrossRef Full Text | Google Scholar

Alexopoulos, N. D., Argyriou, N., Stergiou, V., and Kourkoulis, S. K. (2014). Fatigue behavior of Inconel 718 TIG welds. J. Mater. Eng. Perform. 23 (8), 2973–2983. doi:10.1007/s11665-014-1028-2

CrossRef Full Text | Google Scholar

Alfaro, V. M., and Vilanova, R. (2022). PID control: resilience with respect to controller implementation. Front. Control Eng. 3. doi:10.3389/fcteg.2022.1061830

CrossRef Full Text | Google Scholar

Babić, L., Lauricella, M., Ceusters, G., and Biskoping, M. (2023). Data-driven non-parametric chance-constrained model predictive control for microgrids energy management using small data batches. Front. Control Eng. 4. doi:10.3389/fcteg.2023.1237759

CrossRef Full Text | Google Scholar

Cederqvist, L., Garpinger, O., Cervin, A., and Nielsen, I. (2016). “Improved temperature and depth control during FSW of copper canisters using feedforward compensation,” in Friction stir welding and. Editors VIII Processing, R. S. Mishra, M. W. Mahoney, Y. Sato, and Y. Hovanski (Cham: Springer International Publishing), 69–76.

Google Scholar

Cederqvist, L., Garpinger, O., Hagglund, T., and Robertsson, A. (2011). Reliable sealing of copper canisters through cascaded control of power input and tool temperature. Frict. Stir Weld. Process. VI, 49–58. doi:10.1002/9781118062302.ch7

CrossRef Full Text | Google Scholar

Cederqvist, L., Garpinger, O., Hägglund, T., and Robertsson, A. (2012). Cascade control of the friction stir welding process to seal canisters for spent nuclear fuel. Control Eng. Pract. 20 (1), 35–48. doi:10.1016/j.conengprac.2011.08.009

CrossRef Full Text | Google Scholar

Chimbli, S., Medlin, D., and Arbegast, W. (2007). Minimizing lack of consolidation defects in friction stir welds. Frict. Stir Weld. IV, 135–142.

Google Scholar

Cortinovis, A., Ferreau, H. J., Lewandowski, D., and Mercangöz, M. (2015). Experimental evaluation of MPC-based anti-surge and process control for electric driven centrifugal gas compressors. J. Process Control 34, 13–25. doi:10.1016/j.jprocont.2015.07.001

CrossRef Full Text | Google Scholar

Debarbadillo, J. J., and Mannan, S. K. (2012). Alloy 718 for oilfield applications. JOM 64 (2), 265–270. doi:10.1007/s11837-012-0238-z

CrossRef Full Text | Google Scholar

Elatharasan, G., and Kumar, V. S. S. (2013). An experimental analysis and optimization of process parameter on friction stir welding of AA 6061-T6 aluminum alloy using RSM. Procedia Eng. 64, 1227–1234. doi:10.1016/j.proeng.2013.09.202

CrossRef Full Text | Google Scholar

Fehrenbacher, A., Duffie, N. A., Ferrier, N. J., Pfefferkorn, F. E., and Zinn, M. R. (2011). Toward automation of friction stir welding through temperature measurement and closed-loop control. J. Manuf. Sci. Eng. 133 (5). doi:10.1115/1.4005034

CrossRef Full Text | Google Scholar

Fehrenbacher, A., Duffie, N. A., Ferrier, N. J., Pfefferkorn, F. E., and Zinn, M. R. (2014a). Effects of tool–workpiece interface temperature on weld quality and quality improvements through temperature control in friction stir welding. Int. J. Adv. Manuf. Technol. 71 (1), 165–179. doi:10.1007/s00170-013-5364-4

CrossRef Full Text | Google Scholar

Fehrenbacher, A., Smith, C. B., Duffie, N. A., Ferrier, N. J., Pfefferkorn, F. E., and Zinn, M. R. (2014b). Combined temperature and force control for robotic friction stir welding. J. Manuf. Sci. Eng. 136 (2). doi:10.1115/1.4025912

CrossRef Full Text | Google Scholar

García, C. E., Prett, D. M., and Morari, M. (1989). Model predictive control: theory and practice—a survey. Automatica 25 (3), 335–348. doi:10.1016/0005-1098(89)90002-2

CrossRef Full Text | Google Scholar

Hedengren, J. D., and Eaton, A. N. (2017). Overview of estimation methods for industrial dynamic systems. Optim. Eng. 18 (1), 155–178. doi:10.1007/s11081-015-9295-9

CrossRef Full Text | Google Scholar

Lakshminarayanan, A. K., Balasubramanian, V., and Elangovan, K. (2009). Effect of welding processes on tensile properties of AA6061 aluminium alloy joints. Int. J. Adv. Manuf. Technol. 40 (3), 286–296. doi:10.1007/s00170-007-1325-0

CrossRef Full Text | Google Scholar

Lemos, G. V. B., Hanke, S., Dos Santos, J. F., Bergmann, L., Reguly, A., and Strohaecker, T. R. (2017). Progress in friction stir welding of Ni alloys. Sci. Technol. Weld. Join. 22 (8), 643–657. doi:10.1080/13621718.2017.1288953

CrossRef Full Text | Google Scholar

Li, X., Hao, S., Liu, T., Yan, B., and Zhou, Y. (2022). Predictor-based phase-lead active disturbance rejection control design for industrial processes with input delay. Front. Control Eng. 3. doi:10.3389/fcteg.2022.954164

CrossRef Full Text | Google Scholar

Loria, E. A. (1992). Recent developments in the progress of superalloy 718. JOM 44 (6), 33–36. doi:10.1007/bf03222252

CrossRef Full Text | Google Scholar

Ma, J., Qin, S. J., and Salsbury, T. (2014). Application of economic MPC to the energy and demand minimization of a commercial building. J. Process Control 24 (8), 1282–1291. doi:10.1016/j.jprocont.2014.06.011

CrossRef Full Text | Google Scholar

Mahoney, M. W., Rhodes, C. G., Flintoff, J. G., Bingel, W. H., and Spurling, R. A. (1998). Properties of friction-stir-welded 7075 T651 aluminum. Metallurgical Mater. Trans. A 29 (7), 1955–1964. doi:10.1007/s11661-998-0021-5

CrossRef Full Text | Google Scholar

Marliana, E., Wahjudi, A., Nurahmi, L., Batan, I. M. L., and Wei, G. (2024). Optimizing the tuning of fuzzy-PID controllers for motion control of friction stir welding robots. J. Robotics Control (JRC) 5 (No 4). doi:10.18196/jrc.v5i4.216972024

CrossRef Full Text | Google Scholar

Marshall, D., and Sorensen, C. (2016). “System parameter identification for friction stir processing,” in Friction stir welding and processing VII. Editors R. Mishra, M. W. Mahoney, Y. Sato, Y. Hovanski, and R. Verma (Cham: Springer International Publishing), 289–299.

Google Scholar

Mayfield, D. W., and Sorensen, C. D. (2010) “An improved temperature control algorithm for friction stir processing,” in 8th international friction stir welding symposium. Germany: Timmendorfer Strand.

Google Scholar

Nielsen, I., Garpinger, O., and Cederqvist, L. (2013) “Simulation based evaluation of a nonlinear model predictive controller for friction stir welding of nuclear waste canisters,” in 2013 European control conference (ECC), 2074–2079.

CrossRef Full Text | Google Scholar

Qin, W., Gong, M., Chen, X., Shastry, T. A., Sakidja, R., Yuan, G., et al. (2015). Charge-transfer magnets: multiferroicity of carbon-based charge-transfer magnets (adv. Mater. 4/2015). Adv. Mater. 27 (4), 733. doi:10.1002/adma.201570024

PubMed Abstract | CrossRef Full Text | Google Scholar

Raj, S., and Biswas, P. (2023). Effect of induction preheating on microstructure and mechanical properties of friction stir welded dissimilar material joints of Inconel 718 and SS316L. CIRP J. Manuf. Sci. Technol. 41, 160–179. doi:10.1016/j.cirpj.2022.12.014

CrossRef Full Text | Google Scholar

Ross, K., and Sorensen, C. (2016). “Advances in temperature control for FSP,” in Friction stir welding and processing VII. Editors R. Mishra, M. W. Mahoney, Y. Sato, Y. Hovanski, and R. Verma (Cham: Springer International Publishing), 301–310.

Google Scholar

Ross, K. A. (2012). Investigation and implementation of a robust temperature control algorithm for friction stir welding. Theses and Dissertations. Available at: https://scholarsarchive.byu.edu/etd/3919.

Google Scholar

Rule, J. R., and Lippold, J. C. (2013). Physical simulation of friction stir welding and processing of nickel-base alloys using hot torsion. Metallurgical Mater. Trans. A 44 (8), 3649–3663. doi:10.1007/s11661-013-1742-7

CrossRef Full Text | Google Scholar

Sadeesh, P., Venkatesh Kannan, M., Rajkumar, V., Avinash, P., Arivazhagan, N., Devendranath Ramkumar, K., et al. (2014). Studies on friction stir welding of AA 2024 and AA 6061 dissimilar metals. Procedia Eng. 75, 145–149. doi:10.1016/j.proeng.2013.11.031

CrossRef Full Text | Google Scholar

Shi, G., Ma, M., Li, D., Ding, Y., and Lee, K. Y. (2023). A process-model-free method for model predictive control via a reference model-based proportional-integral-derivative controller with application to a thermal power plant. Front. Control Eng. 4. doi:10.3389/fcteg.2023.1185502

CrossRef Full Text | Google Scholar

Shojaeefard, M. H., Behnagh, R. A., Akbari, M., Givi, M. K. B., and Farhani, F. (2013b). Modelling and Pareto optimization of mechanical properties of friction stir welded AA7075/AA5083 butt joints using neural network and particle swarm algorithm. Mater. and Des. 44, 190–198. doi:10.1016/j.matdes.2012.07.025

CrossRef Full Text | Google Scholar

Shojaeefard, M. H., Khalkhali, A., Akbari, M., and Tahani, M. (2013a). Application of Taguchi optimization technique in determining aluminum to brass friction stir welding parameters. Mater. and Des. 52, 587–592. 1980-2015. doi:10.1016/j.matdes.2013.06.003

CrossRef Full Text | Google Scholar

Silva, A. C. F., Braga, D. F. O., Figueiredo, M. A. V. d., and Moreira, P. M. G. P. (2014). Friction stir welded T-joints optimization. Mater. and Des. 55, 120–127. doi:10.1016/j.matdes.2013.09.016

CrossRef Full Text | Google Scholar

Smart, B., de Cesare, I., Renson, L., and Marucci, L. (2022). Model predictive control of cancer cellular dynamics: a new strategy for therapy design. Front. Control Eng. 3. doi:10.3389/fcteg.2022.935018

CrossRef Full Text | Google Scholar

Song, K. H., Fujii, H., and Nakata, K. (2009). Effect of welding speed on microstructural and mechanical properties of friction stir welded Inconel 600. Mater. and Des. 30 (10), 3972–3978. doi:10.1016/j.matdes.2009.05.033

CrossRef Full Text | Google Scholar

Song, K. H., Kim, H. S., and Kim, W. Y. (2011). Precipitates formation and its impact in friction stir welded and post-heat-treated Inconel 718 alloy. MRS Online Proc. Libr. 1363 (1), 517. doi:10.1557/opl.2011.1335

CrossRef Full Text | Google Scholar

Song, K. H., and Nakata, K. (2010). Microstructural and mechanical properties of friction-stir-welded and post-heat-treated Inconel 718 alloy. J. Alloys Compd. 505 (1), 144–150. doi:10.1016/j.jallcom.2010.06.016

CrossRef Full Text | Google Scholar

Summary for Policymakers. In Climate change 2013 – the physical science basis: working group I Contribution to the fifth assessment Report of the intergovernmental Panel on climate change, intergovernmental panel on climate, C., Ed. Cambridge University Press: Cambridge, 2014; pp 1–30.

Google Scholar

Taysom, B. S., Sorensen, C. D., and Hedengren, J. D. (2016). Dynamic modeling of friction stir welding for model predictive control. J. Manuf. Process. 23, 165–174. doi:10.1016/j.jmapro.2016.06.004

CrossRef Full Text | Google Scholar

Venkateshkannan, M., Rajkumar, V., Sadeesh, P., Arivazhagan, N., Narayanan, S., and Ramkumar, K. D. (2014). Influences of tool geometry on metallurgical and mechanical properties of friction stir welded dissimilar AA 2024 and AA 5052. Procedia Eng. 75, 154–158. doi:10.1016/j.proeng.2013.11.033

CrossRef Full Text | Google Scholar

Weld integrity and performance. ASM International: 1997.

Google Scholar

Ye, F., Fujii, H., Tsumura, T., and Nakata, K. (2006). Friction stir welding of Inconel alloy 600. J. Mater. Sci. 41 (16), 5376–5379. doi:10.1007/s10853-006-0169-6

CrossRef Full Text | Google Scholar

Zhang, H., and Liu, H. (2013). Mathematical model and optimization for underwater friction stir welding of a heat-treatable aluminum alloy. Mater. and Des. 45, 206–211. doi:10.1016/j.matdes.2012.09.022

CrossRef Full Text | Google Scholar