Optimization design of crude oil distillation unit using bi-level surrogate model

Crude Oil Distillation Unit (CDU) is one of the most important separation installations in the petroleum refinery industries. In this work, a Bi-level Surrogate column model Aided Constrained Optimization Design (Bi-SACOD) is proposed for time-consuming objectives and constraints in the evolutionary optimization design of CDUs. The main components of Bi-SACOD include bi-level surrogate model construction (Bi-SMC), bi-level model management (Bi-MM), and particle swarm optimization (PSO) mixed-integer constrained evolutionary (PSO-MICE) search. Bi-SMC implements surrogate column model construction and feasible domain identification. Bi-MM combines surrogate column models with rigorous CDU simulations to perform model management, and PSO-MICE implements optimum search works. The optimization results of the CDUs indicate that Bi-SACOD outperforms the single-level surrogate column model approaches, and are more consistent with the rigorous CDU model optimization approach, whereas the evaluation numbers of the time-consuming rigorous models are significantly reduced.

Introduction

Crude oil distillation is the most widely used separation process in the petroleum refinery industry. Recently, the optimal design of crude oil distillation units (CDUs) has attracted considerable research interest, while the component structural units, such as the pump-around flow system, side strippers, and a large number of equilibrium stages, incorporate the overhead reflux drums make the design of CDUs a complex task (Ibrahim et al.,2021). Combining CDU models and optimization-based design can determine the best configuration of CDUs (Xin et al., 2020), moreover, evolutionary optimization approaches provide probable ways for simultaneous optimization of structural and operating parameters for CDUs, and can achieve better optimization results (Ibrahim et al., 2021; Ibrahim et al., 2018). While optimizing the structural and operating parameters of CDUs will face the problems of a large number of constraints, time-consuming objectives and constraints, continuous and discrete decision variables, and limited samples, these will make great challenges for traditional optimization methodologies.

Generally, three main categories of CDU models have been used to simulate the complex distillation columns, namely, rigorous, simplified, and statistical models, and have recently been incorporated in approaches considering structural and operational optimization designs. Rigorous models provide more accurate predictions than simplified and statistical models. However, implementing them in an optimization algorithm is more challenging because of the large number of non-linear equations and the need to start the calculations from a perfect initial guess in order to avoid convergence problems (Kunru et al., 2020). Besides, simplified models have also been applied to the optimization of CDUs (Alattas et al., 2011). Simplified models have the advantage of being more robust and converging faster than rigorous models. However, they may have large errors and often cannot predict the behaviors of complex CDUs accurately, also, they are highly sensitive to initial guesses. Further, some statistical models, such as polynomial regression, support vector regression (SVM), and artificial neural networks (ANNs), have become popular in the optimization of CDUs (Lopez et al., 2013; Ibrahim et al., 2018; Xin et al., 2021). In (Xin et al., 2021) and (Lopez et al., 2013), the authors constructed SVM and polynomial regression models, respectively, to search for the optimal conditions for economic profit. Ibrahim et al. designed a distillation column configuration and its operating conditions using a mixed-integer non-linear program approach to maximize heat recovery (Ibrahim et al., 2018). Statistical models are more robust and more straightforward than rigorous and simplified distillation models, however, one of the main problems of this modeling is sampling, since the quality of the model depends on the quality of the data used, poor-quality sampling models will cause large model errors and affect the optimization results.

Recently, the studies on the surrogate models have shown that local surrogate models cannot assist the algorithm escaping from the local optimum, while bi-level models, i.e., global-local models are expected to take advantages of the global and local surrogate models, generally outperform most individual surrogates in terms of accuracy and efficiency in complex optimization problems (Zhou et al., 2007; Wang et al., 2017; Zhong et al., 2019). Zhou et al. presented a global-local surrogate-assisted evolutionary algorithm for expensive constrained optimization problems (Zhou et al., 2007). Wang et al. introduced the global-local model management to improve the approximation quality of the surrogate model without increasing the size of the training dataset (Wang et al., 2017). And Zhong et al. proposed an adaptive step-size global and local search strategy (GLSS) for operation optimization of hydrocracking process (Zhong et al., 2019). Therefore, in this work, an approach, termed as Bi-level Surrogate column model Aided Constrained Optimization Design (Bi-SACOD), is proposed by combining global-local surrogate column models and rigorous CDU models for fitness evaluations. Since Gaussian process (also known as the Kriging) has better global statistical characteristics (Wang et al., 2017), in the global surrogate-aided phase, we construct Kriging model to smooth out the local optima to speed up the search, while in the local phase, RBF model is often used to further approximate the fitness landscape (Zhou et al., 2007). The global-local surrogate column model management incorporated with the SVM feasibility learning approach is implemented to search for the column structural variables and operating conditions to maximize the total economic profit in this work.

The remainder of this article is organized as follows. Section 2 is the preliminary, which describes global and local surrogate models and distillation MESH equations. In Section 3, a detailed optimization formulation is presented including bi-level surrogate column model construction, bi-level model management, and PSO mixed-integer constraint evolutionary search methodology. Section 4 is the results and discussion. The conclusions of the future work are finally presented in Section 5.

Preliminary

Kriging surrogate global model

The Kriging models based on the optimal linear unbiased estimation method, which is composed of two parts: a polynomial expression and a deviation from that polynomial:

$F\left(\mathbf{x}\right)=\beta +z\left(\mathbf{x}\right)(1)$

Where $\beta$ is a polynomial expression which is to approximate to the real function, $z\left(\mathbf{x}\right)$ is a stochastic process obeying normal distribution $N\left(0,{\delta }^2\right)$. The characteristics of $z\left(\mathbf{x}\right)$ are as follows:

$E\left(z\left(\mathbf{x}\right)\right)=0(2)$

$cov\left[z\left(\mathbf{x}\right),z\left({\mathbf{x}}^{\prime }\right)\right]={\delta }^{2}R\left(\mathbf{\theta },\mathbf{x},{\mathbf{x}}^{\prime }\right)(3)$

$R\left(\mathbf{\theta },\mathbf{x},{\mathbf{x}}^{\prime }\right)={\prod }_{j=1}^n{R}_j\left({\mathbf{\theta }}_j,{\mathbf{x}}_j-{\mathbf{x}}_j^{\prime }\right)(4)$

Where σ2 is the variance of the response process; $\mathbf{\theta }=\left\{{\mathbf{\theta }}_1,{\mathbf{\theta }}_2,\cdots ,{\mathbf{\theta }}_n\right\}$ is a set of parameters that determine the gradient of $R=\left\{\mathbf{\theta },\mathbf{x},{\mathbf{x}}^{\prime }\right\}$; and σ is the dimension of variable $\mathbf{x}$, and the Gaussian correlation function is employed in this work. It is defined as follows:

$R({\mathbf{\theta }}_j,{\mathbf{x}}_j,{\mathbf{x}}_j^{\prime })=\exp (-{\mathbf{\theta }}_j{\left|{\mathbf{x}}_j-{\mathbf{x}}_j^{\prime }\right|}^2)(5)$

RBF surrogate local model

Let $\mathbf{D}=\left\{{\mathbf{x}}_i,y_i\right\},i=1,\cdots n$ , ${\mathbf{x}}_i\in R^d$ and $y_i\in R$ are the input and output, respectively, which denotes the training dataset. Then the local surrogate models are interpolating radial basis function networks (RBFNs) of the form:

$F\left(\mathbf{x}\right)={\sum }_1^n{\alpha }_{i}K\left(‖\mathbf{x}-{\mathbf{x}}_i‖\right)(6)$

Where $K\left(‖\mathbf{x}-{\mathbf{x}}_i‖\right):R^d\to R$ is a RBF and $\mathbf{\alpha }=\left\{{\alpha }_1,{\alpha }_2,\cdots {\alpha }_n\right\}\in R^n$ denotes the vector of weights. Typical choices the kernel for RBFNs include linear splines, cubic splines, thin plate splines, and Gaussian functions (Zhou et al., 2007). We use linear splines, i.e., $‖\mathbf{x}-{\mathbf{c}}_i‖$ in our work since this kernel can provide models with good generalization capability at a low computational cost.

Distillation MESH equations

As we know, distillation columns are chief devices for the CDU processes. In the construction of rigorous distillation models, a series of equations, such as the mass balance equations, enthalpy balance equations, equilibrium, and the summation equations collectively termed as MESH equations are applied by stage-by-stage modeling considerations (Chen, 2008).The MESH equations which are comprised of a large number of equations are applied on each stage in a column. For example, if a column has $C$ components (if $C=10$) and $N$ stages (if $N=60$), the total number of equations will be $2\times C\times N+N$ (=1,260) (Chen, 2008). Therefore, figuring out the distillation production performance from these equations is a time-consuming task.

BI-SACOD approach

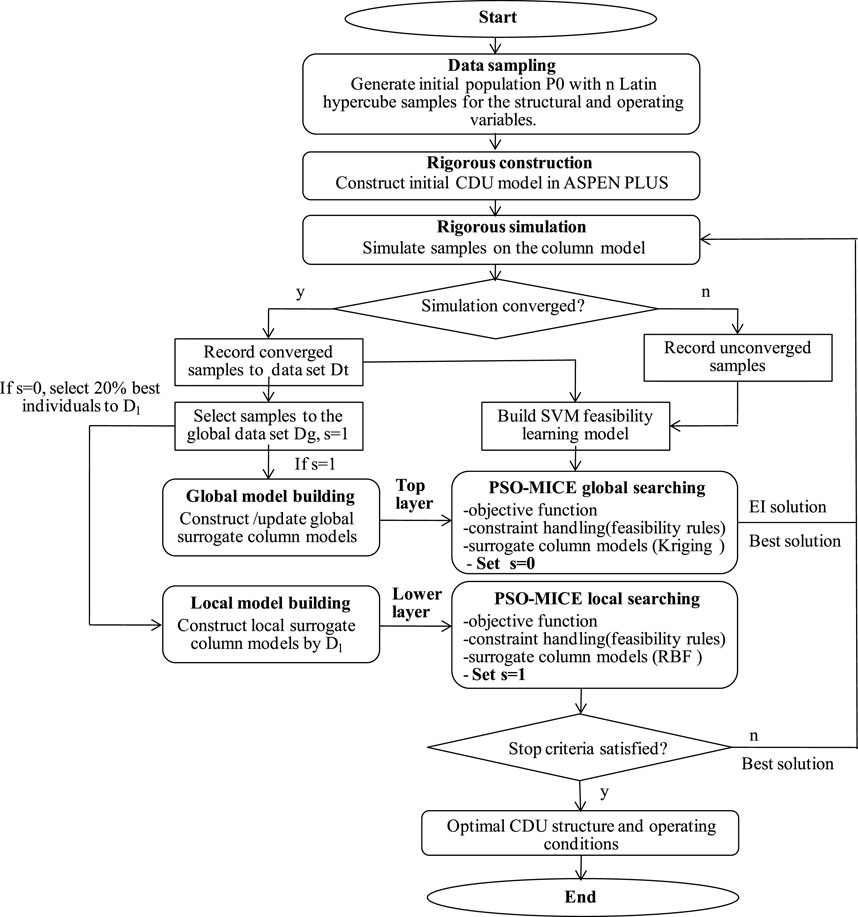
Bi-SACOD which is proposed in this paper integrates surrogates and support vector machines to handle time-consuming objectives and constraints, it consists of three parts: Bi-level Surrogate column Model Construction (Bi-SMC), Bi-level Model Management (Bi-MM), and PSO Mixed-Integer Constraint Evolutionary (PSO-MICE) search. Bi-SMC mainly implements the constructing or updating of the global-local surrogate model. Bi-MM combines global and local surrogates with rigorous CDU simulations for the model management, and global and local optimal samples searching is performed using PSO-MICE strategy.

Bi-SMC and Bi-MM

Data generation and sampling are critical points for online Bi-SMC (Wang et al., 2017). For data generation, we use time-consuming rigorous CDU simulations via a commercial simulation platform Aspen Plus in this paper, three following aspects are considered: selecting industrial input and output variables, generating initial random samples, and infilling input variables in the evolution process (Ibrahim et al., 2017). For each input variable set, the corresponding outputs can be obtained by simulating the rigorous CDU models. In this work, both structural and operational input variables are selected and adjusted to improve the performance of the crude distillation column, meanwhile, the chosen output variables are related to the optimization objectives and constraints.

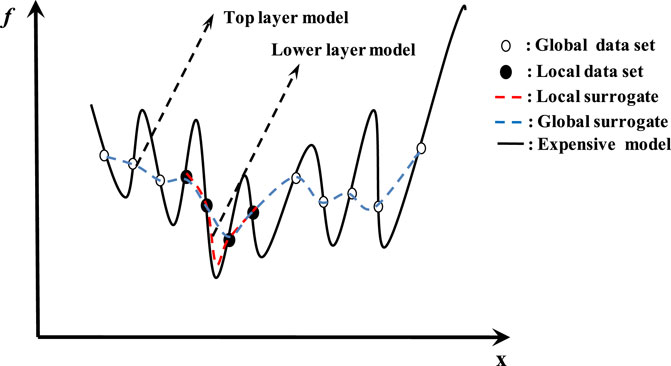
Model management involves how to manipulate the surrogate models to ensure that the designers acquire a reasonable solution during the search process. Figure 1 illustrates the bi-level surrogate model search diagram, where the solid line indicates the expensive model to be optimized, in the top-level, global surrogate column models are used to smooth out the local optima to speed up the search, the hollow circles represent the potential samples from the global dataset, whereas in the lower-level, the local surrogate column models which are constructed from the best m% of the global dataset are utilized to approximate the fitness landscape accurately, the solid circles denote the potential samples from the local dataset. Therefore, the search for the optimal expensive model can be conducted by finding the optimal solution of the local surrogate model.

FIGURE 1

FIGURE 1. Bi-level surrogate model search diagram.

PSO-MICE search

Here, we apply a PSO Mixed-Integer Constraint Evolutionary (PSO-MICE) strategy to search for the CDU’s global and local potential samples. The velocity and position updating for the particles is described in Eqs 7–9. For all the continuous and discrete decision variables, two ways are employed to deal with the updating. If all the individuals satisfy the constrained feasible domain, for discrete variables, the updating is shown in Eqs 7, 9 respectively, where $\lfloor \rfloor$ is a rounding operator; and for continuous variables, the updating refer to Eqs 8, 9, separately.

${\mathbf{v}}^{\mathrm{g}+1}=\lfloor {\omega }_g{\mathbf{v}}^g\rfloor +\lfloor c_1{r}_1\left({\mathbf{x}}_{pbest}-{\mathbf{x}}^g\right)\rfloor +\lfloor c_2{r}_2\left({\mathbf{x}}_{gbest}-{\mathbf{x}}^g\right)\rfloor (7)$

${\mathbf{v}}^{g+1}={\omega }_g{\mathbf{v}}^g+c_1{r}_1\left({\mathbf{x}}_{pbest}-{\mathbf{x}}^g\right)+c_2{r}_2\left({\mathbf{x}}_{gbest}-{\mathbf{x}}^g\right)(8)$

${\mathbf{x}}^{g+1}={\mathbf{x}}^g+{\mathbf{v}}^{g+1}(9)$

where ${\omega }_g$ is the inertia weight described as Eq. 10 (Chatterjee and Siarry, 2006) and $g_{\mathit{max}}$ is the maximal number of generations. Further, $c_1$ and $c_2$ are two positive constants, $r_1$ and $r_2$ are random numbers in the range of [0, 1], and ${\mathbf{x}}_{pbest}$ and ${\mathbf{x}}_{\mathrm{g}best}$ represent the personal best and the global best solutions individually.

$w_g=0.9-0.5\frac{g}{g_{\mathit{max}}}(10)$

Confronted with the distillation time-consuming MESH equations, here, we adopt the SVM-feasibility approach to solve constraint handling for both the global and the local searching processes. New individuals generated by PSO-MICE are separated into two families, i.e., feasible and infeasible solutions by SVM classifier (Ibrahim et al., 2018). Only a winner individual is eligible to update its velocity and position shown in Eqs 7–9.

Implementational description

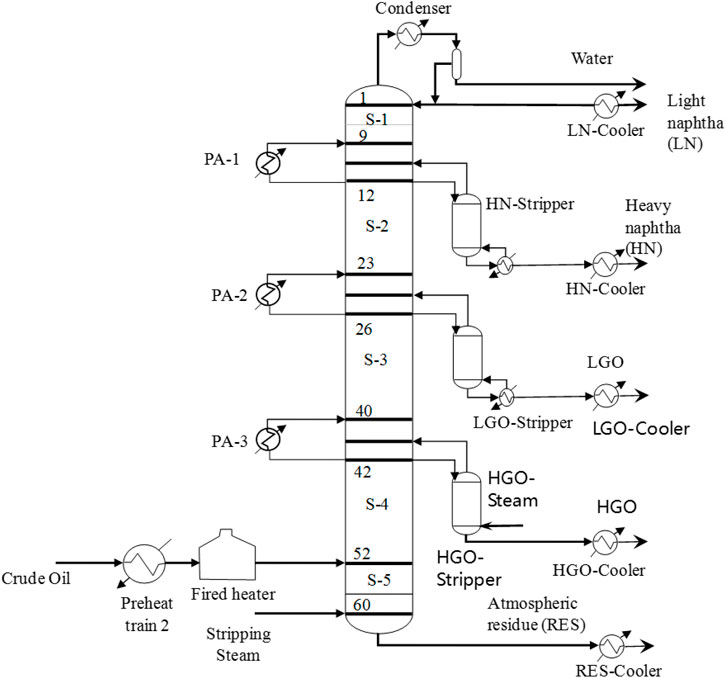
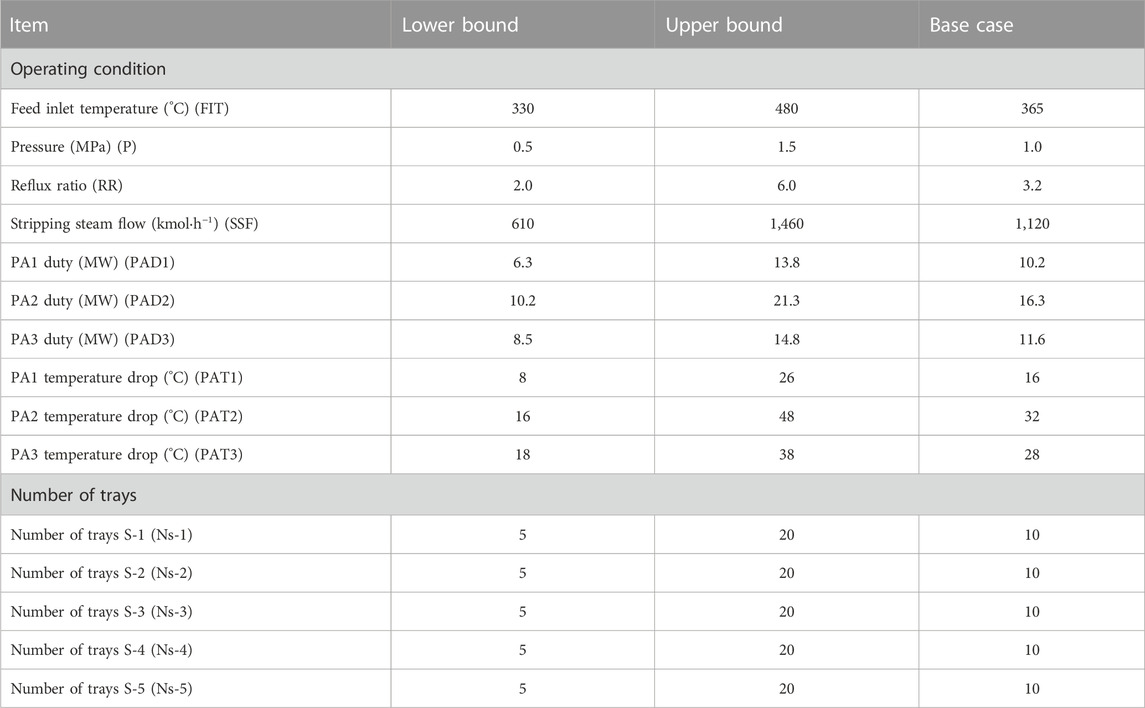
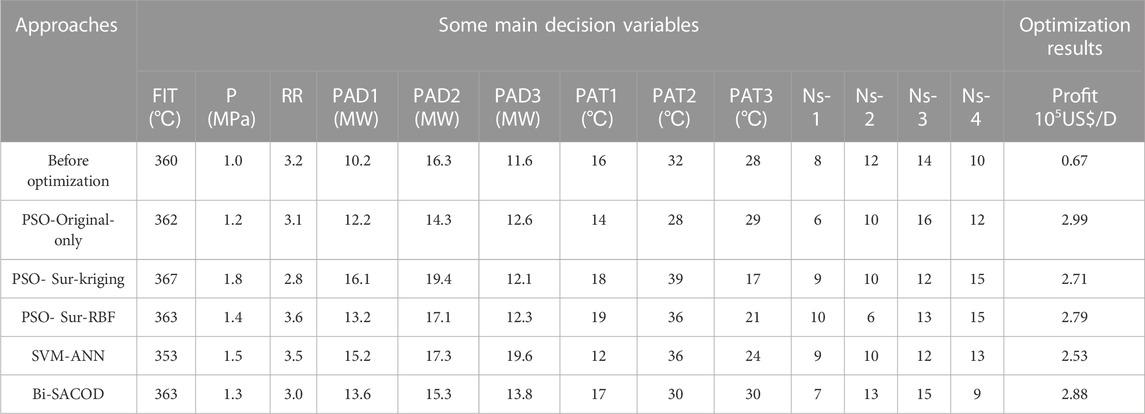
The initial industrial CDU used in this study consists of a main column with 60 stages, one condenser, three side strippers, and three pump arounds (i.e., the top circulation reflux and two middle circulation refluxes), as illustrated in Figure 2. The preheated crude oil enters the column at the 52nd stage, numbered from the top downwards, with the condenser as the first stage. In addition to the two conventional products from the top and bottom of the column, i.e., from unstabilized naphtha (UN) and long residue (LR), the distillation unit processes 0.16 m³/s of crude into four products, including light naphtha (LN), heavy naphtha (HN), light gas oil (LGO), and heavy gas oil (HGO), and the residue. The main column has five sections with 8, 12, 14, 10, and 8 sieve trays, respectively. The HN, LGO, and HGO side strippers have 8, 7, and 8 trays in order. The distillation uses steam at 250°C as the stripping agent. The column’s steam flow rate is approximately 220 kmol/h, the reflux ratio is 3.2, and the operating pressure is 1.0 Mpa, respectively. The optimization objective, in this case, is to maximize the profit. Additionally, the constraints considered in the process include the lower and upper bounds of the optimization variables, and the T5% and T95% True Boiling Point (TBP) temperatures. The problem of how to maximize the profit can be expressed as follows:

$\begin{array}{l}P{r}_{\max }=\max \hspace{0.17em}f\left(\mathbf{x}\right),\hspace{1em}\mathbf{x}=\left\{\mathbf{x}d,\mathbf{x}s,\mathbf{x}o\right\},\mathbf{x}d,\mathbf{x}o\in \mathbf{R},\mathbf{x}s\in \mathbf{N}\\ f\left(\mathbf{x}\right)={\displaystyle \sum _{s\in \mathbf{S}}}Cs{F}_l^{vol}-Cc{F}_{\mathbf{c}}^{vol},\hspace{0.17em}l=\mathrm{1,2},\cdots ,N_{product}\\ s.t.\\ \left\{\begin{array}{l}{F}_l^{vol}=MESH\left(\mathbf{x}\right),\hspace{0.17em}l=\mathrm{1,2},\cdots ,N_{product}\\ \mathbf{m}\le {\mathbf{x}}_s\le \mathbf{n},\hspace{0.17em}\mathbf{m},\hspace{0.17em}\mathbf{n}\in N\\ {\mathbf{x}}_l\le \mathbf{x}o\le {\mathbf{x}}_h\\ l{a}_l\le T{5}_l\le u{a}_l,\hspace{0.17em}l=\mathrm{1,2},\cdots ,N_{product}\\ l{b}_l\le T{95}_l\le u{b}_l,\hspace{0.17em}\hspace{0.17em}l=\mathrm{1,2},\cdots ,N_{product}\end{array}\right.\end{array}(11)$

where $Cs$ and $Cc$ represent the prices in United States dollars per kilogram (USD/kg) for the products and the crude oil feed stock individually, $N_{product}$ denotes the number of CDU products; $F_l^{vol}$ and $F_c^{vol}$ stand for the volumetric flow rates in cubic meters per second of the final product and the crude oil, and $T{5}_l$ and $T{95}_l$ define the boiling point temperatures of product $l$ at 5% and 95% separately. The volumetric flow rate of each product needs to satisfy the MESH equations. Considering the problem of maximum economic benefits, we select 15 decision variables, including the CDU’s operating and structural variables. The operating variables comprise the feed inlet temperature $T_{in}$, the pressure $P_T$ on the top of the CDU, the CDU’s reflux ratio $R_T$, the main stripping steam flow $F_s$, three pump-around duties (PA1–PA3) $D{p}_i,i=\mathrm{1,2,3}$, three pump-around temperature drops $\Delta T{p}_i,i=\mathrm{1,2,3}$. Meanwhile, the structural variables contain the tray numbers in each section of the column $S_i,i=\mathrm{1,2},\cdots ,5$. These variables must satisfy the bound constraints, which are subject to the operational and structural conditions’ upper and lower limits and the distillation product quality expressed in terms of T5% and T95%.The 10%–90% TBP curve, according to the ASTM-D86 standard of the crude oil, is distributed at 245.0°C–797.2°C. Table 1 shows the base case values of the selected decision variables.

FIGURE 2

FIGURE 2. Crude oil distillation column.

TABLE 1

TABLE 1. Base case values of the selected decision variables.

For each product, three kinds of models are considered, the definitions are as follows:

①$Su{r}_1^i$:Global: $F_i^{vol}=S_{kri\left(\mathbf{X}s,\mathbf{X}o\right)}^{Fi}$ ; Local: $F_i^{vol}=S_{rbf\left(\mathbf{x}s,\mathbf{x}o\right)}^{Fi},$$i=\mathrm{1,2,3,4};$

② $Su{r}_2^i:T{5}_i=S_{rbf\left(\mathbf{x}s,\mathbf{x}o\right)}^{T5i},i=\mathrm{1,2,3,4};$

③ $Su{r}_3^i:T{95}_i=S_{rbf\left(\mathbf{x}s,\mathbf{x}o\right)}^{T95i},i=\mathrm{1,2,3,4};$

where $F_i^{vol}$ is the flow rate of product $i$, and $T{5}_i$ and $T{95}_i$ represent the boiling temperature of product $i$ at 5% and 95% vaporization, respectively. $S_{kri\left(\mathbf{x}s,\mathbf{x}o\right)}^{Fi}$ and $S_{rbf\left(\mathbf{x}s,\mathbf{x}o\right)}^{Fi}$ represent the kriging (global) and RBF flow rate model (local model) respectively. Thus, four initial Kriging global models for the products’ flow rate and eight RBF networks for the products’ boiling temperatures at 5% and 95% are established for bi-SACOD.

Figure 3 illustrates the framework of the proposed approach. First, the initial population ${\mathbf{P}}_{\mathbf{0}}$ is generated by the Latin hypercube design in the upper and lower bounds of the decision variables. Subsequently, the functions of the objective and constraints are evaluated by running the simulator of the CDU Aspen Plus at ${\mathbf{P}}_{\mathbf{0}}$ to create the initial samples, which are stored in the database ${\mathbf{D}}_t$. And then, the SVM classifier is constructed using all the samples in ${\mathbf{D}}_t$ to identify the convergent and non-convergent individuals. In the top level phase, because it is not necessary to use all the data in ${\mathbf{D}}_t$ to construct the global surrogate model, the samples size is adapted by the current feasibility individuals in ${\mathbf{D}}_t$, which size is:

$\max \left\{latindesign\left(feasibility\left(D_t\right),\alpha Num\left(D_t\right)\right),N_{g-\min }\right\}$

FIGURE 3

FIGURE 3. The framework of the Bi-SACOD.

The individuals of the global database ${\mathbf{D}}_g$ are generated by the Latin hypercube design of the feasibility individuals of ${\mathbf{D}}_t$ with $\mathit{max}\left(\alpha Num\left({\mathbf{D}}_t\right),N_{g-\min }\right)$ individuals, where, $\alpha Num\left({\mathbf{D}}_t\right)$ represents the design numbers for ${\mathbf{D}}_g$, $\alpha$ is a factor, and $N_{g-\mathit{min}}$ is the least number of ${\mathbf{D}}_g$. At each generation, both the global and local surrogate-aided searching phases should be performed. In the global surrogate-aided phase, the kriging models functioning as the global surrogates ${\mathbf{S}}_{kri}$ are constructed from the global dataset ${\mathbf{D}}_g$ to approximate the CDU original objective function, and two offspring: ${\mathbf{P}}_g$ and ${{\mathbf{P}}_g}^{\prime }$ termed as the expectation improvement (EI) solution and the best solution respectively are generated successively by searching the ${\mathbf{S}}_{kri}$ using PSO-MICE. Subsequently ${\mathbf{P}}_g$ and ${{\mathbf{P}}_g}^{\prime }$ are reevaluated with the original CDU objective function and constraints. If convergence is met, ${\mathbf{P}}_g$ and ${{\mathbf{P}}_g}^{\prime }$ are stored in the dataset ${\mathbf{D}}_t$, otherwise, it should be deleted. When in the lower level, the local RBF surrogate column model ${\mathbf{S}}_{rbf}$ is constructed by selecting the best 20% individuals from the dataset ${\mathbf{D}}_g$, and ${\mathbf{P}}_l$ is generated by searching the best individual of ${\mathbf{S}}_{rbf}$ using PSO-MICE. ${\mathbf{P}}_l$ is then reevaluated with the original CDU objective function and constraints. If convergence is met, ${\mathbf{P}}_l$ is stored in ${\mathbf{D}}_t$, otherwise, it should be deleted. It should be noted that all the constraint surrogates are constructed using the dataset ${\mathbf{D}}_t$. The above procedure is repeated until the termination criteria is met.

Results and discussion

To evaluate the effectiveness of the combination search strategy of global and local surrogate column models in bi-SACOD, we compare the proposed approach with the PSO-Original-Only, PSO-Sur-Kriging, PSO-Sur-RBF, and SVM-ANN (Ibrahim et al., 2018) algorithms. PSO-Original-Only is a common CDU optimization approach with the rigorous CDU model evaluation only, searching by the traditional PSO algorithm. PSO-Sur-Kriging and PSO-Sur-RBF are approaches only employing the Kriging and RBF surrogate column models respectively. It should be noted that the Kriging and RBF surrogate models used in this work are implemented using the SURROGATES toolbox (Viana and Goel, 2010). SVM-ANN is an ANN surrogate combined with the SVM feasibility penalty constraint-handling method that is recently proposed (Ibrahim et al., 2018). Besides, the parameters of bi-SACOD are set as follows: NP = 80, c1 = c2 = 0.5, $\alpha =0.2$, and $N_{g-\min }=100$. SVM-ANN parameters are from the paper (Ibrahim et al., 2018). The maximum generation number of all comparative algorithms is defined to 1,000. The PSO utilized in all comparative algorithms shares the same parameter settings. It should be noted that the constructing and updating of the global-local bi-level surrogate CDU models utilize the rigorous distillation column simulations, which are facilitated via an interface between the commercial simulation platform Aspen Plus and MatLab R2012.

To further compare the proposed algorithm with other methods, the following three performance metrics are implemented:

1) Success rate (SR): This represents the percentage of successful runs that can find feasible solutions within the given maximum number of generations.

2) Number of rigorous model evaluations (REs): This is an important performance metric for the time-consuming optimization system. It denotes the number of CDU rigorous model evaluations to reach successful conditions.

3) Convergence speed (CS): This can be described as follows:

$CS=1-\left|\frac{f_g-f_{g-1}}{f_g-f_0}\right|(12)$

where $f_g$ and $f_{g-1}$ define the objective values at $g$ and $g-1$ generations, respectively, and $f_0$ stands for the initial time of the objective value. If “CS” approaches “1” with deviations of ${10}^{-3}$ during ten consecutive generations, we consider that the search is in the convergence state, termed as $“CS\approx 1”$ . Therefore, smaller REs at $“CS\approx 1”$ implies a better convergence speed. Table 2 summarizes the average statistics of SR and REs at $“CS\approx 1”$ based on five comparative approaches for 20 runs.

TABLE 2

TABLE 2. Comparative performance metrics of the algorithms for average of 20 runs.

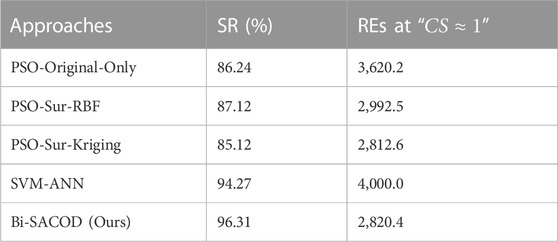
It is clear that only Bi-SACOD and SVM-ANN could obtain their optimal solutions with a high success rate (SR); Bi-SACOD saves the number of REs up to 2,820, considerably smaller than that of SVM-ANN. Although the REs at $“CS\approx 1”$ for PSO-Sur-Kriging are nearly similar to those of Bi-SACOD, the SR metrics for PSO-Sur-Kriging are remarkably lower. In general, both SR and REs metrics at $“CS\approx 1”$ for PSO-Original-Only and PSO-Sur-RBF are slightly inferior to those of the other approaches. From the above, we infer that Bi-SACOD has a better success rate and convergence speed than the other methods.

Figure 4A plots the CDU average economic profit profiles in the 20 runs of the comparative algorithms. It indicates that PSO-Original-Only achieved the highest profit, while Bi-SACOD is the second. PSO-Sur-RBF reached a slightly higher profit than PSO-Sur-Kriging, while the convergence speed of PSO-Sur-Kriging is marginally higher than that of PSO-Sur-RBF, this is probably because the local optimum is trapped with the search of PSO-Sur-Kriging. As far as the number of original CDU evaluations is concerned, as shown in Table 2. The rigorous model evaluations number of the PSO-Original-Only is 3,620.2, while the evaluation number of Bi-SACOD, PSO-Sur-Kriging, and PSO-Sur-RBF is 2,820.4, 2,812.6, and 2,992.5 in order. Therefore, the original model evaluation number of Bi-SACOD is considerably smaller than that of the PSO-Original-Only method.

FIGURE 4

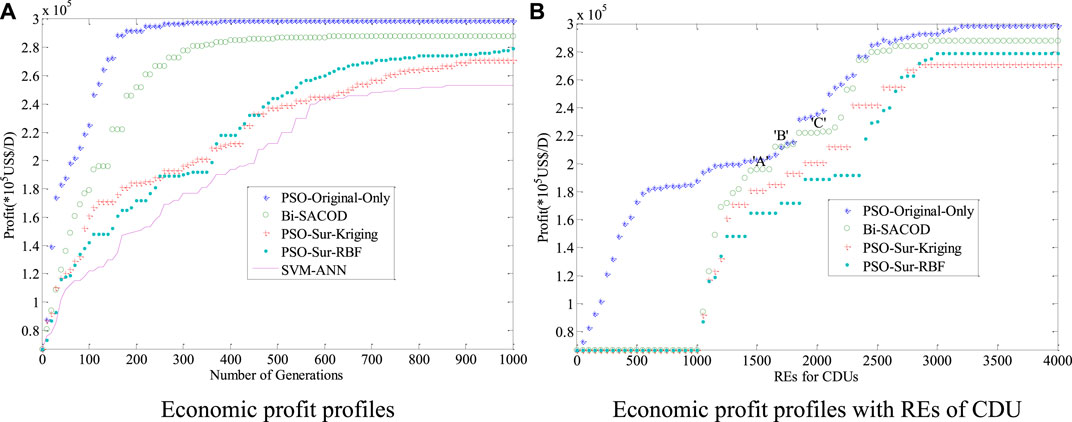
FIGURE 4. Optimization results for the comparative approaches. (A) Economic profit profiles (B) Economic profit profiles with REs of CDU.

Figure 4B illustrates the CDU column comparative economic profit profiles with the REs of the original model simulation. As shown in Figure 4B, REs from 0 to 1,000 formed the data-sampling period, and the profit of the CDU is maintained in the initial state before optimization. The slow change in the profit of Bi-SACOD labeled as “A”, “B”, and “C” attributed to the fact that it is in the local searching state. Figure 4B indicates that the plot of Bi-SACOD is remarkably more consistent with that of the PSO-Original-Only method.

Table 3 reflects the contributions of the proposed algorithm. We can see from Table 3 that in the case of the Bi-SACOD approach, the economic profit could reach USD 2.88 × 10⁵/day, which is closer to the profit of the PSO-Original-Only method (USD 2.99 × 10⁵/day), while the number of rigorous model evaluations of Bi-SACOD is considerably reduced.

TABLE 3

TABLE 3. Comparison of the optimization results.

Conclusion

The evolutionary optimization design of CDUs is challenging due to its mixed-integer variables with time-consuming objectives and constraints. The presented work focuses on Bi-SACOD approach for time-consuming objectives and constraints of CDUs’ design. The main contributions of this work include:1) For time consuming optimization design, we construct a two-level global-local surrogate column model for CDU optimization, in which global Kriging models are adopted to smooth out the local optima to speed up the search, and RBF local models are used to further approximate the fitness landscape. 2) Confronted with the distillation time-consuming MESH equations, we apply a PSO mixed-Integer constraint evolutionary strategy and simultaneously adopt SVM-feasibility approach to solve constraint handling for both the global and local searching processes. The optimization results of the CDUs show that Bi-SACOD outperforms the single-level surrogate column model approaches, and are more consistent with the rigorous CDU model optimization approach, whereas the number of evaluations for time-consuming rigorous models is significantly reduced. In our follow-up research, we will further improve the proposed method and extend it to other types of distillation units.

Data availability statement

The original contributions presented in the study are included inthe article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

YX: Methodology, Software, Data curation, Verification, and Writing—original draft and revising. XS: Conceptualization, Project administration, and Writing—reviewing and editing. YM: Verification. YC: Resources. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China under Grant Nos. 61773225 and 61803214; the K. C. Wong Magna Fund in Ningbo University, China.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alattas, A., Grossmann, I., and Palou-Rivera, I. (2011). Integration of nonlinear crude distillation unit models in refinery planning optimizationfinery planning optimization. Industrial Eng. Chem. Res. 50 (11), 6860–6870. doi:10.1021/ie200151e

CrossRef Full Text | Google Scholar

Chatterjee, A., and Siarry, P. (2006). Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization. Comput. &Operations Res. 33 (3), 859–871. doi:10.1016/j.cor.2004.08.012

CrossRef Full Text | Google Scholar

Chen, L. (2008). Heat-integrated crude oil distillation design. Ph.D. Thesis. Manchester, UK. The University of Manchester, 35–39.

Google Scholar

Ibrahim, D., Jobson, M., and Gonzalo, G. (2017). Optimization-based design of crude oil distillation units using rigorous simulation models. Industrial Eng. Chem. Res. 56 (23), 6728–6740. doi:10.1021/acs.iecr.7b01014

CrossRef Full Text | Google Scholar

Ibrahim, D., Jobson, M., Li, J., and Guillen-Gosalbez, G. (2018). Optimization-based design of crude oil distillation units using surrogate column models and a support vector machine. Chem. Eng. Res. Des. 134, 212–225. doi:10.1016/j.cherd.2018.03.006

CrossRef Full Text | Google Scholar

Ibrahim, D., Jobson, M., Jie, L., and Gonzalo, G. (2021). Optimal design of flexible heat-integrated crude oil distillation units using surrogate models. Chem. Eng. Res. Des. 165, 280–297. doi:10.1016/j.cherd.2020.09.014

CrossRef Full Text | Google Scholar

Kunru, Y., Shirun, L., Chang, H., Bingjian, Z., Qinglin, C., and Ming, P. (2020). Improving energy saving of crude oil distillation units with optimal operations. J. Clean. Prod. 263, 121340–121349. doi:10.1016/j.jclepro.2020.121340

CrossRef Full Text | Google Scholar

Lopez, D. C., Hoyos, L. J., Mahecha, C. A., Arellano-Garcia, H., and Wozny, G. (2013). Optimization model of crude oil distillation units for optimal crude oil blending and operating conditions. Industrial Eng. Chem. Res. 52, 12993–13005. doi:10.1021/ie4000344

CrossRef Full Text | Google Scholar

Viana, F., and Goel, T. (2010). Surrogates toolbox user’s guide. Available at: http://fchegury.googlepages.com, Tech. Rep.

Google Scholar

Wang, H., Jin, Y., and Doherty, J. (2017). Committee-based active learning for surrogate-assisted particle swarm optimization of expensive problems. IEEE Trans. Cybern. 47 (9), 2664–2677. doi:10.1109/tcyb.2017.2710978

PubMed Abstract | CrossRef Full Text | Google Scholar

Xin, D., Xiaoqiang, W., Renchu, H., Wenli, D., Weimin, Z., Liang, Z., et al. (2020). Data-driven robust optimization for crude oil blending under uncertainty. Comput. Chem. Eng. 136 (8), 106595-1–106595-7. doi:10.1016/j.compchemeng.2019.106595

CrossRef Full Text | Google Scholar

Xin, D., Liang, Z., Zhi, L., Wenli, D., Weimin, Z., Renchu, H., et al. (2021). A data-driven approach for crude oil scheduling optimization under product yield uncertainty. Chem. Eng. Sci. 246, 116971–116979. doi:10.1016/j.ces.2021.116971

CrossRef Full Text | Google Scholar

Zhong, W., Qiao, C., Peng, X., Li, Z., Fan, C., and Qian, F. (2019). Operation optimization of hydrocracking process based on Kriging surrogate model. Control Eng. Pract. 85, 34–40. doi:10.1016/j.conengprac.2019.01.001

CrossRef Full Text | Google Scholar

Zhou, Z., Ong, Y. S., Nair, P. B., Keane, A. J., and Lum, K. Y. (2007). Combining global and local surrogate models to accelerate evolutionary optimization. IEEE Trans. Syst. Man, Cybern. Part C: Appl. Rev. 37 (1), 66–76. doi:10.1109/tsmcc.2005.855506

CrossRef Full Text | Google Scholar