- 1Key Laboratory of Intelligent Control and Optimization for Industrial Equipment of Ministry of Education, Dalian University of Technology, Dalian, China
- 2Institute of Advanced Control Technology, Dalian University of Technology, Dalian, China
For industrial processes subject to input delay, a predictor-based phase-lead active disturbance rejection control (ADRC) scheme is proposed in this article for improving disturbance rejection performance by introducing a phase-lead module for feedback control. First, an extended state observer (ESO) in combination with a generalized delay-free output predictor is presented to estimate the delay-free system state together with load disturbance lumped with process uncertainties. To reduce the phase lag caused by not only ESO but also the delay-free output predictor, a phase-lead module is then added into the disturbance observation channel so as to expedite disturbance estimation and thus improve the disturbance rejection performance. Consequently, the ESO gain vector and feedback controller are analytically designed by specifying the desired poles for the observer and the closed-loop system, respectively. Moreover, a digital implementation of the proposed scheme is presented to facilitate the practical applications, followed by a robust stability analysis of the closed-loop system based on the small gain theorem. Illustrative examples from the literature are used to demonstrate the effectiveness and merits of the proposed method over the existing methods.
1 Introduction
Time delay, in particular for input/output delay, is pervasive in various industrial processes owing to mass transportation, energy exchange, and signal processing. (Liu and Gao, 2012). Control design without considering time delay usually degrades the system performance and sometimes even destabilizes the controlled system. Over the past few decades, a lot of effort has been devoted to developing advanced control methods for industrial processes with time delay (Normey-Rico and Camacho, 2007; Zhou, 2014; Fridman, 2014; Richard, 2003; Zhu et al., 2017; Cacase and Germani, 2017). It is well known that the proportional-integral-derivative (PID) controller which is most widely adopted in practice could only be capable of controlling systems without delay or with a small time delay (Ang et al., 2005). The pioneering work of dealing with long-time delays could be dated back to the well-known Smith predictor (SP) (Smith, 1957). However, the original SP could only be applied to open-loop stable processes owing to the internal stability issue (Normey-Rico and Camacho, 2007). In the past decades, various modified SPs have been developed for application to stable, integrating, or unstable processes, such as filtered SP (FSP) (Normey-Rico and Camacho, 2009), generalized predictor (GP) (Garcia and Albertos, 2013), simplified generalized predictor (SGP) (Liu et al., 2018), and generalized Smith predictor (Sanz et al., 2018).
Apart from time delay, disturbance rejection is another core issue to be tackled in process control. The existing anti-disturbance control methods can be roughly classified into two categories: one is passive-type disturbance rejection based on the classical unity feedback control loop, for example, PID control and H infinity control, etc., and the other is active-type disturbance rejection, for example, disturbance observer based control (Li et al., 2016), equivalent-input-disturbance-based control (Wang et al., 2021), active disturbance rejection control (ADRC) (Han, 2009), etc. The former could accommodate bounded disturbance to some extent or eliminate constant-type disturbance by leveraging the integral action. In contrast, the latter first estimates process disturbance and then compensates it timely, such that the disturbance rejection performance could be apparently improved in comparison with the former. Therefore, active-type disturbance rejection methods have received increasing attention over the past 2 decades; see the survey paper (Chen et al., 2016) and the references therein. Among the developed active-type disturbance rejection methods, ADRC has received adhoc attention in recent years (Huang and Xue, 2014; Chen et al., 2020; Tan and Fu, 2016). The essence of ADRC is to treat internal uncertainties (e.g., unmodeled dynamics and model uncertainties) and external disturbances as a total disturbance and then estimate it timely by an extended state observer (ESO) for counteraction in the control law. However, most of the existing ADRC methods were devoted to delay-free systems.
For the presence of time delay, Zhao et al. (Zhao and Gao, 2014) proposed a modified ADRC to tackle the time delay by synchronizing the input signal in the controlled plant and ESO. In Su et al. (2021), a standard robust tuning rule was developed for a time-delayed ADRC structure based on a second-order plus time delay process model, followed by a quantitative tuning rule for a typical first-order plus time delay process model in (Sun et al., 2022). In Fu and Tan (2017), a two-degree-of-freedom (2DOF) control structure was studied for unstable time-delayed systems. Recently, the analytical design of ADRC for nonlinear uncertain systems with time delay was presented in Chen et al. (2019). It should be noted that the abovementioned methods may not maintain the closed-loop stability in the presence of a large time delay. To cope with this issue, a predictive ADRC scheme in the combination of a standard Smith predictor with ESO was proposed in Zheng and Gao (2014) for stable processes, such that large time delays could be properly compensated. Based on the internal model control principle, Zhang et al. (2020) investigated the parameter tuning of SP-based generalized ADRC for time-delayed processes. Recently, Liu et al. (2019) developed a predictive disturbance rejection control (PDRC) method for sampled systems by combining FSP with model-based ESO, which could be applied for stable, integrating, or unstable processes. For non-minimum phase systems with input delay, a generalized PDRC method was proposed in Geng et al. (2019) to improve system performance in aspects of set-point tracking and disturbance rejection. Nevertheless, the existing predictor-based ESOs (Zheng and Gao, 2014; Zhang et al., 2020; Liu et al., 2019; Geng et al., 2019) inevitably suffer a phase lag in estimating the total disturbance, which could affect the disturbance rejection performance. To alleviate this deficiency, a phase-leading ESO has been recently proposed in Wei et al. (2021) for a delay-free nanopositioning stage, such that the accuracy of disturbance estimation and disturbance rejection performance could be evidently improved. However, it remains open as yet to combine phase-lead compensation with a predictor-based ADRC scheme to further improve disturbance rejection performance for industrial processes with a large time delay. In fact, the use of a delay-free output predictor for dealing with input delay to design ESO for disturbance rejection, as studied in recent articles (Geng et al., 2019; Liu et al., 2019), may provoke a larger phase lag for disturbance estimation in comparison with the developed ADRC methods (Zheng & Gao, 2014; Zhang, Tan, & Li, 2020; Wei, Zhang, & Zuo, 2021), where the phase lag is merely caused by ESO. This motivates our study in this article.
In this article, a modified predictor-based phase-lead ADRC scheme is proposed for industrial stable, integrating, and unstable processes with input delay by plugging in a phase-lead module for expediting disturbance estimation, such that the disturbance rejection performance of the controlled processes could be significantly enhanced in comparison with the existing predictor-based ADRC methods (Zheng and Gao, 2014; Zhang et al., 2020; Geng et al. 2019). In contrast to the recently developed phase-lead ADRC method (Wei et al. 2021) for delay-free systems, the proposed design is capable of dealing with industrial processes with large input delays. A novel predictor-based phase-lead ESO (PLESO) is constructed to improve the estimation accuracy of system state and disturbance based on a generalized predictor for delay-free output prediction. Accordingly, the observer and the feedback controller gains are analytically designed by specifying the desired poles for the observer and the closed-loop system, respectively. Meanwhile, the robust stability condition of the proposed closed-loop control structure is established in terms of nonlinear inequality constraints based on the small gain theorem.
For clarity, the remainder of this article is structured as follows: in Section 2, a problem statement and some preliminaries are presented. The proposed predictor-based phase-lead ADRC scheme along with its digital implementation is detailed in Section 3. The control constraints for holding the closed-loop robust stability are analyzed in Section 4. In Section 5, three illustrative examples from the existing literature studies are given to validate the proposed method. Finally, some conclusions are drawn in Section 6.
2 Problem statement and some preliminaries
Consider the following second-order process with input delay widely adopted to describe the industrial processes:
where
For the convenience of control design in this study, the nominal model of the process in Eq. 1 is expressed by the following transfer function:
where
By regarding
where
Note that the existing ESO for delay-free systems cannot be directly applied to the augmented system in (Eq. 3) due to the time-wise misalignment of control input, especially in the presence of a large time delay. To circumvent this issue, an artificially delayed input was introduced in the conventional ESO (Tan and Fu, 2016) to make the control input synchronous. However, only real-time system state and total disturbance could be estimated for control design, which is also not applicable to system with large time delays. To tackle the abovementioned issues, a predictor-based ESO has recently been developed in recent work (Liu et al., 2019), which will be briefly introduced below for designing the proposed predictor-based PLESO,
where
To obtain a delay-free output prediction
where
where
Denote another transfer function by
Then, the delay-free output prediction can be constructed by
where
3 Predictor-based phase-lead ADRC
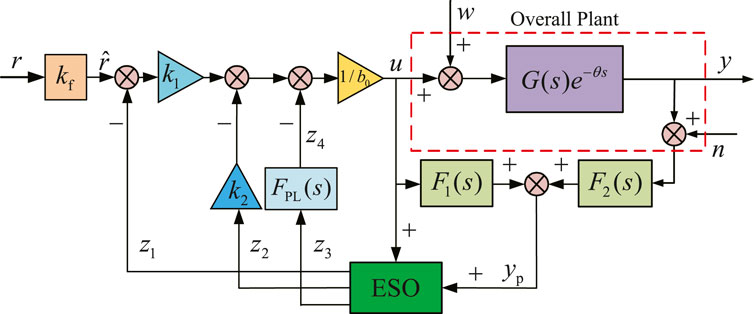
The proposed predictor-based phase-lead ADRC (PLADRC) scheme is shown in Figure 1, where
For better understanding, the proposed control scheme, together with its digital implementation, will be detailed in the following subsections, respectively.
3.1 Proposed predictor-based PLADRC scheme
Motivated by the fact that fast disturbance estimation could facilitate control counteraction and therefore improve disturbance rejection performance, enhanced disturbance estimation denoted by
where
It follows from the transfer function in (Eq. 14) that
Combining Eq. 4 and Eq. 15 yields
By regarding
where
Based on the improved estimation of the
where
and
Remark 1. Note that the PLESO gain
Remark 2. In the ideal case, that is,
which implies that the input delay is fully compensated for control implementation.By taking the Laplace transforms of the state-space realization in Eq. 17 and the feedback controller in Eq. 18, it follows that
where
where
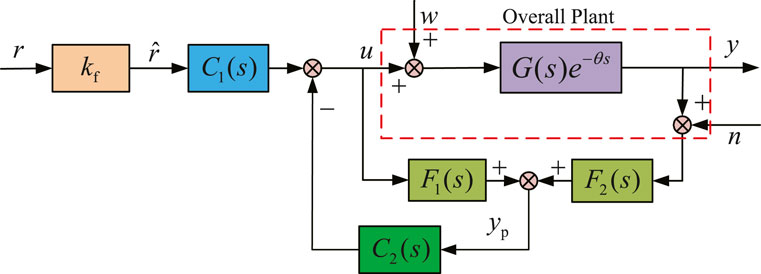
Therefore, the proposed predictor-based PLADRC scheme can be implemented by
Suppose that the delay-free output prediction denoted by
where
To be specific, if the disturbance is of step-type with amplitude of A, that is,
Correspondingly, the steady-state estimation error on the delay-free disturbance is derived as follows:
which indicates that zero prediction error on a step-type disturbance is guaranteed by the proposed control scheme.If the disturbance is of ramp-type with an amplitude of A, that is,
Correspondingly, the steady-state estimation error on the delay-free disturbance can be derived as follows:
It is seen from Eq. 30 that there exists an evident steady-state estimation error
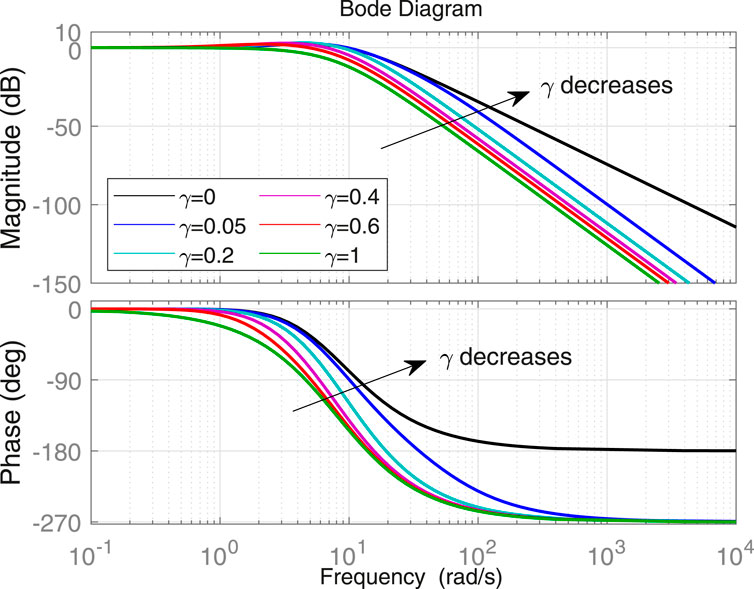
This indicates that a more accurate disturbance estimation could be acquired by the proposed PLESO. In practice, it is suggested to take the phase-lead parameter
The frequency response of the abovementioned transfer function in Eq. 32 with respect to the tuning of
Remark 3. Note that the robust stability of the closed-loop system may be degraded if a smaller
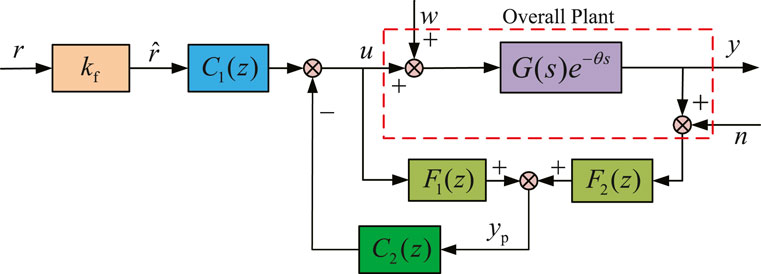
3.2 Digital implementation
For the convenience of practical applications, a digital implementation of the proposed control scheme is shown in Figure 4, where
To alleviate the sensitivity of the prediction scheme when the process has non-minimum phase zeros and unstable poles as studied in Sanz et al. (2018), the continuous-time predictor filters
Assume that the time delay is a multiple of the sampling period, that is,
where
where
All the unstable poles and non-minimum phase zeros of
Moreover, denote another transfer function by
Then, the discrete-time realization of the delay-free output prediction is given as follows:
with the stable filters
Note that there is one tuning parameter
4 Robust stability analysis
Due to the fact that the filters
Given the process uncertainties of the discrete-time process with time delay in Eq. 33 described in a multiplicative form
where
where
According to the small gain theorem (Morari and Zafiriou, 1989), the closed-loop structure in Figure 4 holds robust stability if and only if
Substituting Eq. 23, Eq. 33, and Eq. 39 into Eq. 42 gives the following closed-loop robust stability constraint:
which can be further reformulated as follows:
where
Consider the following descriptions of the process uncertainty that are often adopted for assessment in engineering practice,
Based on the fact that a rational Z-transform (i.e.,
where
Note that the abovementioned robust stability constraints in Eq. 48–Eq. 50 are typical nonlinear inequalities in terms of adjustable parameters
5 Illustrative examples
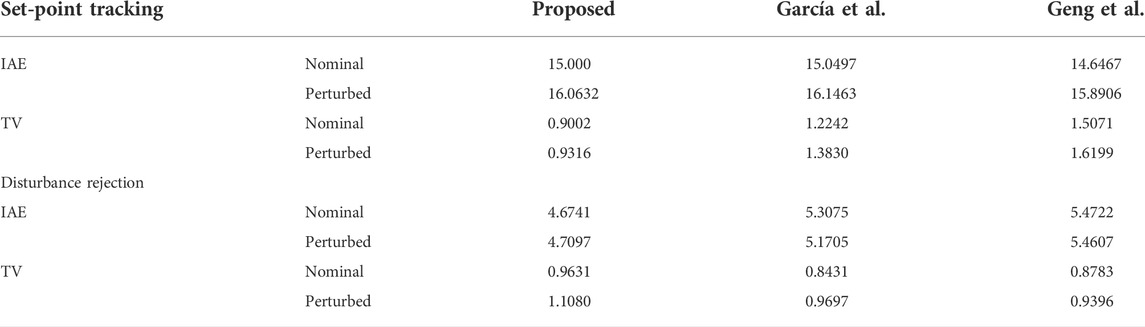
In this section, two commonly used performance indices, that is, integral-of-absolute-error (IAE) and total variation (TV), are adopted to assess the control performance of the proposed method.
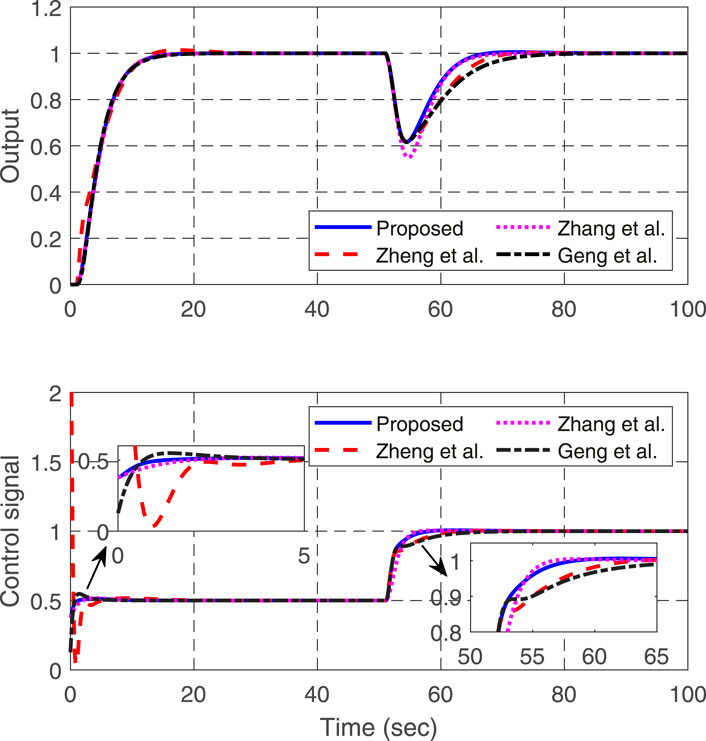
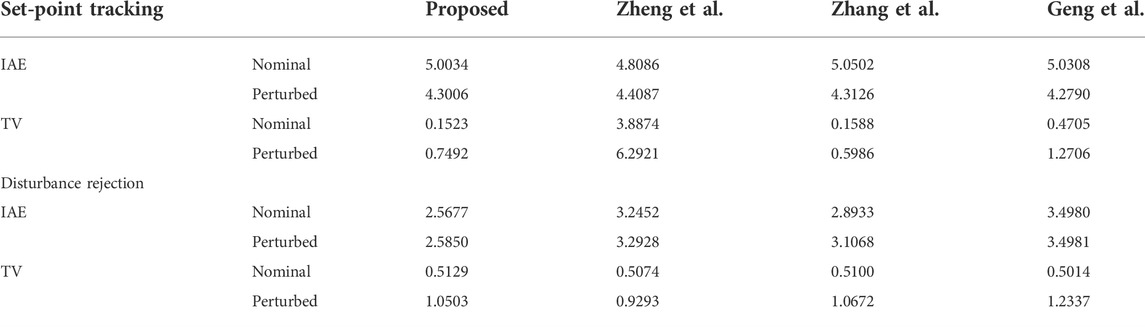
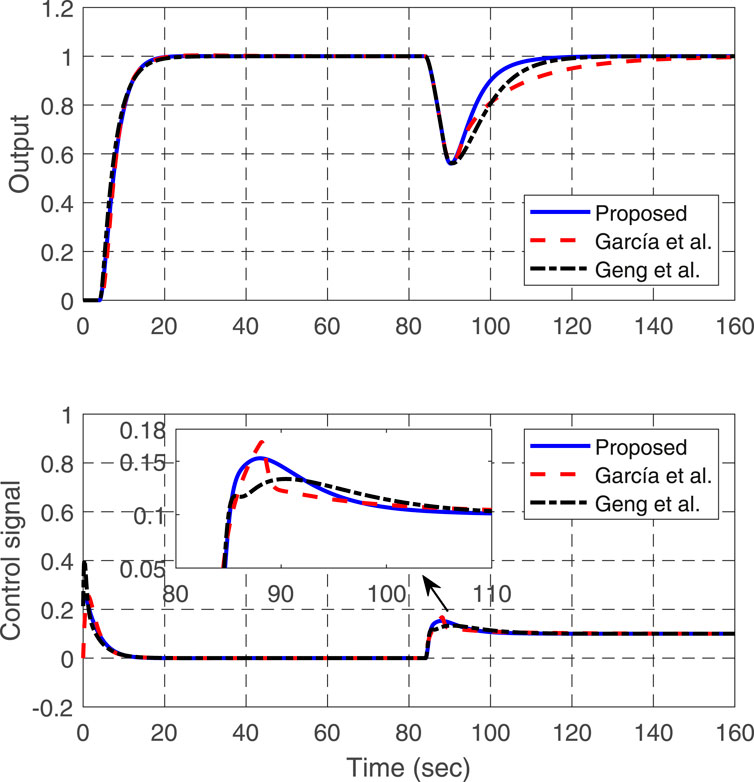
Example 1. Consider a stable process with time delay studied in Tan and Fu (2016)
With a sampling period of
In the proposed scheme,
where
For the purpose of illustration, a unit step change is added to the system input at
whose discrete-time counterparts for digital implementation are given as follows:
Correspondingly, the set-point gain
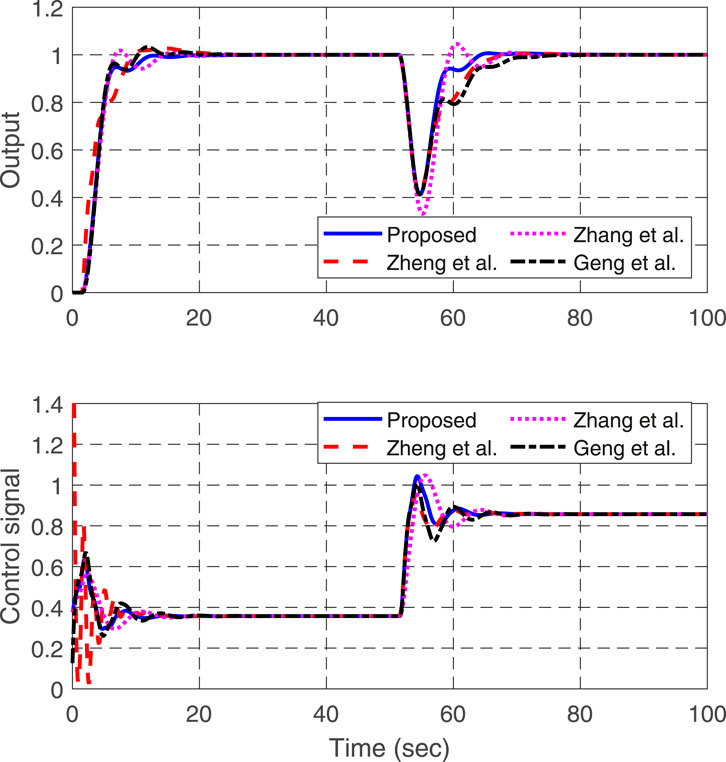
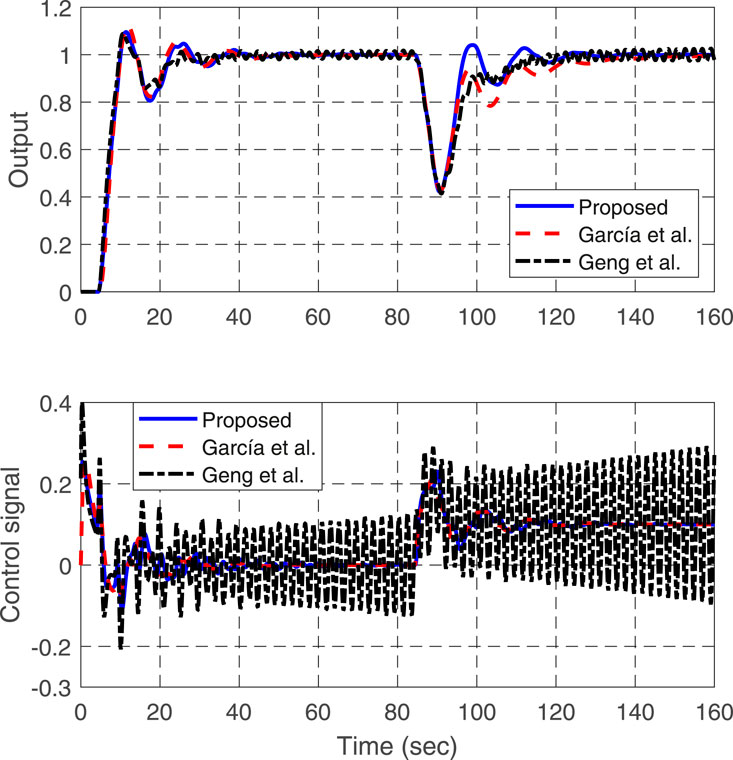
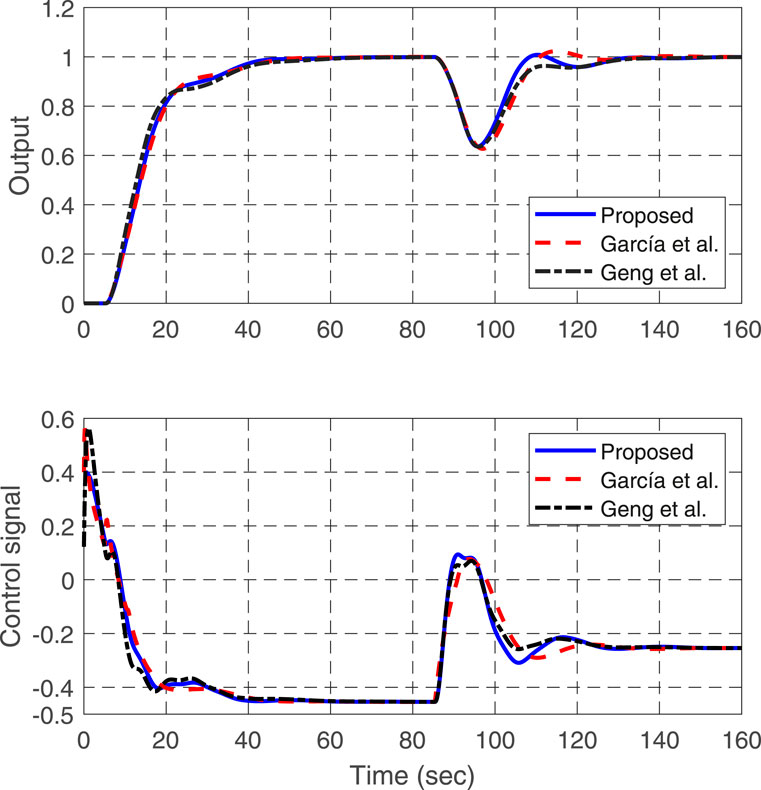
Example 2. Consider an integrating process with time delay studied in García and Albertos (2013):
With a sampling period of
Based on the formulae in Eq. 38 and Eq. 39, together with the choice of
where
For illustration, a unit step change is added to the system input at
whose discrete-time counterparts are given by
Based on the selected parameters, the set-point gain
and
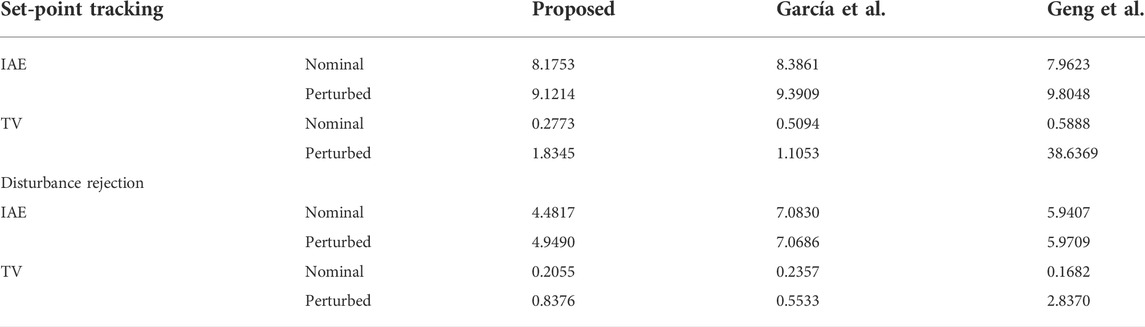
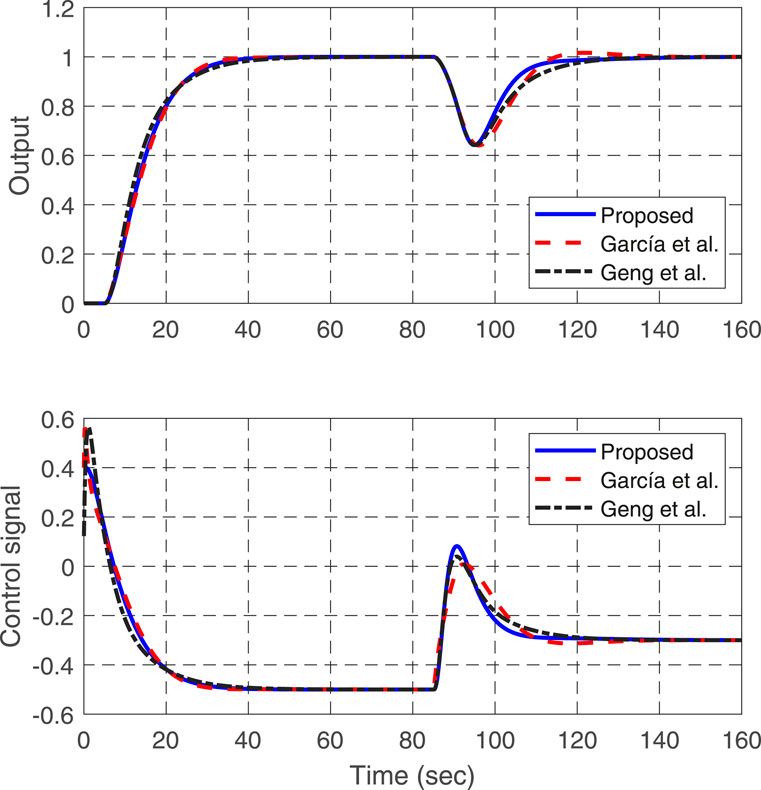
Example 3. Consider an unstable process with time delay studied in García and Albertos (2013):
Given a sampling period of
By taking
where
For the simulation purpose, a unit step change is added to the system input at
along with their discrete-time counterparts
The corresponding set-point gain can be solved as
and
6 Conclusion
In this article, a predictor-based PLADRC scheme has been proposed for open-loop stable, integrating, and unstable industrial processes with input delay. It further extends the recently developed PLADRC in Wei et al. (2021) that could only be applied to delay-free systems. By introducing a phase-lead module in the proposed ADRC scheme, the phase lag for disturbance estimation caused by not only ESO but also delay-free output predictor could be apparently reduced, such that the disturbance rejection performance could be evidently improved in comparison with the existing ADRC methods. To facilitate practical application, a digital implementation of the proposed scheme is presented. It is a merit that each controller or filter in the proposed control scheme has a single parameter that could be tuned in a monotonic way to procure a trade-off between its performance and robustness against process uncertainties. Meanwhile, the tuning constraints on the PLESO and the feedback controller are analyzed for holding robust stability of the closed-loop system in the presence of process uncertainties. Illustrative examples from recent references have well demonstrated the effectiveness and advantages of the proposed control scheme in comparison with the existing predictor-based ADRC methods (Zheng and Gao, 2014, Zhang et al., 2020, Geng et al. 2019) that have already demonstrated superiority over other methods.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
Author contributions
XL, SH, and TL contributed to conceptualization and methodology. XL wrote the first draft of the manuscript. BY and YZ contributed to the edition of formulae and figures. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This work is supported in part by the National Thousand Talents Program of China, NSF China Grants 62173058, 61903060, the Talent Project of Revitalizing Liaoning (XLYC1902030), and the Fundamental Research Funds for the Central Universities of China (DUT22RC (3)020).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ang, K. H., Chong, G., and Yun, L. (2005). PID control system analysis, design, and technology. IEEE Trans. Control Syst. Technol. 13 (4), 559–576. doi:10.1109/TCST.2005.847331
Cacase, F., and Germani, A. (2017). Output feedback control of linear systems with input, state and output delays by chains of predictors. Automatica 85, 455–461. doi:10.1016/j.automatica.2017.08.013
Chen, S., Bai, W., Hu, Y., Huang, Y., and Gao, Z. (2020). On the conceptualization of total disturbance and its profound implications. Sci. China Inf. Sci. 63 (2), 129201–129223. doi:10.1007/s11432-018-9644-3
Chen, S., Xue, W., and Huang, Y. (2019). Analytical design of active disturbance rejection control for nonlinear uncertain systems with delay. Control Eng. Pract. 84, 323–336. doi:10.1016/j.conengprac.2018.12.007
Chen, W., Yang, J., Guo, L., and Li, S. (2016). Disturbance-observer-based control and related methods-an overview. IEEE Trans. Ind. Electron. 63 (2), 1083–1095. doi:10.1109/TIE.2015.2478397
Fridman, E. (2014). Introduction to time-delay systems: Analysis and control. Berlin, Germany: Springer International Publishing.
Fu, C., and Tan, W. (2017). Tuning of linear ADRC with known plant information. ISA Trans. 65, 384–393. doi:10.1016/j.isatra.2016.06.016
García, P., and Albertos, P. (2013). Robust tuning of a generalized predictor-based controller for integrating and unstable systems with long time-delay. J. Process Control 23 (8), 1205–1216. doi:10.1016/j.jprocont.2013.07.008
Geng, X., Hao, S., Liu, T., and Zhong, C. (2019). Generalized predictor based active disturbance rejection control for non-minimum phase systems. ISA Trans. 87, 34–45. doi:10.1016/j.isatra.2018.11.002
Han, J. (2009). From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 56 (3), 900–906. doi:10.1109/TIE.2008.2011621
Huang, Y., and Xue, W. (2014). Active disturbance rejection control: Methodology and theoretical analysis. ISA Trans. 53 (4), 963–976. doi:10.1016/j.isatra.2014.03.003
Li, S., Yang, J., Chen, W., and Chen, X. (2016). Disturbance observer based control: Methods and applications. Boca Raton, FL, USA: CRC Press.
Liu, T., and Gao, F. (2012). Industrial process identification and control design. Berlin, Germany: Springer London.
Liu, T., Gil, G., Chen, Y., Ren, X., Albertos, P., Sanz, R., et al. (2018). New predictor and 2DOF control scheme for industrial processes with long time delay. IEEE Trans. Ind. Electron. 865 (5), 4247–4256. doi:10.1109/TIE.2017.2760839
Liu, T., Hao, S., Li, D., Chen, W., and Wang, Q. (2019). Predictor-based disturbance rejection control for sampled systems with input delay. IEEE Trans. Control Syst. Technol. 27 (2), 772–780. doi:10.1109/TCST.2017.2781651
Morari, M., and Zafiriou, E. (1989). Robust process control. New Jersey, United States: Prentice-Hall.
Normey-Rico, J., and Camacho, E. (2007). Control of dead-time processes. Berlin, Germany: Springer London.
Normey-Rico, J., and Camacho, E. (2009). Unified approach for robust dead-time compensator design. J. Process Control 19 (1), 38–47. doi:10.1016/j.jprocont.2008.02.003
Richard, J. (2003). Time-delay systems: An overview of some recent advances and open problems. Automatica 39 (10), 1667–1694. doi:10.1016/S0005-1098(03)00167-5
Sanz, R., García, P., and Albertos, P. (2018). A generalized smith predictor for unstable time-delay SISO systems. ISA Trans. 72, 197–204. doi:10.1016/j.isatra.2017.09.020
Su, Z., Sun, Y., Zhu, X., Chen, Z., and Sun, L. (2021). Robust tuning of active disturbance rejection controller for time-delay systems with application to a factual electrostatic precipitator. IEEE Trans. Control Syst. Technol. 30, 2204–2211. [in press]. doi:10.1109/TCST.2021.3127794
Sun, L., Xue, W., Li, D., Zhu, H., and Su, Z. (2022). Quantitative tuning of active disturbance rejection controller for FOPTD model with application to power plant control. IEEE Trans. Ind. Electron. 69 (1), 805–815. doi:10.1109/TIE.2021.3050372
Tan, W., and Fu, C. (2016). Linear active disturbance-rejection control: Analysis and tuning via IMC. IEEE Trans. Ind. Electron. 63 (4), 1–2359. doi:10.1109/TIE.2015.2505668
Wang, Z., She, J., Liu, Z., and Wu, M. (2021). Modified equivalent-input-disturbance approach to improving disturbance-rejection performance. IEEE Trans. Ind. Electron. 69 (1), 673–683. doi:10.1109/TIE.2021.3053889
Wei, W., Zhang, Z., and Zuo, M. (2021). Phase leading active disturbance rejection control for a nanopositioning stage. ISA Trans. 116, 218–231. doi:10.1016/j.isatra.2021.01.004
Zhang, B., Tan, W., and Li, J. (2020). Tuning of smith predictor based generalized ADRC for time-delayed processes via IMC. ISA Trans. 99, 159–166. doi:10.1016/j.isatra.2019.11.002
Zhao, S., and Gao, Z. (2014). Modified active disturbance rejection control for time-delay systems. ISA Trans. 53 (4), 882–888. doi:10.1016/j.isatra.2013.09.013
Zheng, Q., and Gao, Z. (2014). Predictive active disturbance rejection control for processes with time delay. ISA Trans. 53 (4), 873–881. doi:10.1016/j.isatra.2013.09.021
Zhou, B. (2014). Truncated predictor feedback for time-delay systems. Berlin Heidelberg: Springer. doi:10.1007/978-3-642-54206-0
Keywords: input delay, generalized Smith predictor, extended state observer, active disturbance rejection control, phase-lead compensation
Citation: Li X, Hao S, Liu T, Yan B and Zhou Y (2022) Predictor-based phase-lead active disturbance rejection control design for industrial processes with input delay. Front. Control. Eng. 3:954164. doi: 10.3389/fcteg.2022.954164
Received: 27 May 2022; Accepted: 26 August 2022;
Published: 27 September 2022.
Edited by:
Rames Panda, Central Leather Research Institute (CSIR), IndiaReviewed by:
Patrick Lanusse, Institut Polytechnique de Bordeaux, FranceRajagopalan Devanathan, Hindustan University, India
Copyright © 2022 Li, Hao, Liu, Yan and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shoulin Hao, c2xoYW9AZGx1dC5lZHUuY24=; Tao Liu, bGl1cm91dGVyQGllZWUub3Jn
 Xiaomeng Li1,2
Xiaomeng Li1,2 Shoulin Hao
Shoulin Hao