Model predictive control of cancer cellular dynamics: a new strategy for therapy design

Recent advancements in cybergenetics have led to the development of new computational and experimental platforms that enable us to robustly steer cellular dynamics by applying external feedback control. Such technologies have never been applied to regulate intracellular dynamics of cancer cells. Here, we show in silico that adaptive model predictive control (MPC) can effectively be used to steer the simulated signalling dynamics of Non-Small Cell Lung Cancer (NSCLC) cells to resemble those of wild type cells. Our optimisation-based control algorithm enables tailoring the cost function to force the controller to alternate different drugs and/or reduce drug exposure, minimising both drug-induced toxicity and resistance to treatment. Our results pave the way for new cybergenetics experiments in cancer cells, and, longer term, can support the design of improved drug combination therapies in biomedical applications.

1 Introduction

Cybergenetics is a recent field of synthetic biology, which refers to the forward engineering of complex phenotypes in living cells applying principles and techniques from control engineering (Del Vecchio et al., 2016; Khammash et al., 2019).

Three main approaches have been proven to be effective for the control of different processes (such as gene expression and cell proliferation), namely: i) open- or closed-loop controllers embedded into cells by means of synthetic gene networks (Bloom et al., 2015; Hsiao et al., 2015; Briat et al., 2016; Ciar et al., 2018; Aoki et al., 2019; Pedone et al., 2019; Ye et al., 2016; Andrews et al., 2018; Gao et al., 2018; Siu et al., 2018; Bashor et al., 2019; Cuba Samaniego and Franco, 2021; Shakiba et al., 2021); ii) external controllers, where the controlled processes are within cells, while the controller (either at single cell or cell-population level) and the actuation functions are implemented externally via microfluidics-optogenetics/microscopy-flow cytometry platforms and adequate algorithms for online cell output quantification and control (Milias-Argeitis et al., 2011; Toettcher et al., 2011; Uhlendorf et al., 2012; Menolascina et al., 2014; Lugagne et al., 2017; Postiglione et al., 2018; Khazim et al., 2019; Shannon et al., 2020; de Cesare et al., 2021; Khazim et al., 2021; Pedone et al., 2021; de Cesare et al., 2022); iii) multicellular strategies, where both the control and actuation functions are embedded into cellular consortia (Matyjaszkiewicz et al., 2017; Fiore et al., 2016; Fiore et al., 2017; Kylilis et al., 2018; Postiglione et al., 2019; Ren et al., 2021). Plenty of examples of embedded controllers have been engineered across different cellular chassis; instead, applications of external and multicellular controllers in mammalian cells are scarce and either just theoretical or limited to proofs of concept.

Here, we propose to apply cybergenetics, in particular external feedback control, to predict combinations of drugs (i.e., control inputs) which can bring deregulated cellular variables (i.e., gene expression, control output of the system) within tightly controlled ranges in cancer cells. We take Non-Small Cell Lung Cancer (NSCLC) as an example; using a previously proposed differential equations mathematical model which describes the dynamics of the EGFR and IGF1R pathways, we show in silico that external feedback controllers can effectively steer intracellular gene expression dynamics in cancer cells to resemble those of wild type cells.

The use of feedback control is advantageous as it enables coping with changes in both steady-state levels and temporal dynamics of genes involved in deregulated signalling cascades. The control action is implemented by means of adaptive model predictive control (MPC), using either a full-order and physics-based non-linear model (linearised at each time step to be, at best, locally accurate), or a simpler, data-based reduced order model. In the latter case, our controller does not require an exact model of the system; this is particularly advantageous in biological applications, where the derivation of detailed models can be time-consuming and troublesome (Marucci et al., 2011; Marucci, 2017; Browning et al., 2020). Experimentally, the controller would not have access to measurements of all the internal states of the model, as just a few variables would be measured (for example, by means of fluorescent proteins in time-lapses); therefore, we included a Kalman filter to estimate the internal states.

If the results proposed here were applied experimentally (e.g., to steer signalling and/or proliferation dynamics in living cells, or in patient-cell derived organoids), they could predict combination therapies which target different nodes in signalling cascades. In this regard, our optimisation-based control algorithm also enables tailoring the cost function to force the controller to alternate different drugs and/or reduce drug exposure. The controller should also be able to cope with the crosstalk of signalling pathways, which might be one of the mechanisms causing drug resistance (Vasan et al., 2019).

In what follows, we demonstrate via simulations that adaptive MPC can be used to effectively steer the concentration of proteins involved in cancer, whilst reducing the dose of each drug provided as an input. Our results pave the way for extending the scope of synthetic biology cybergenetic applications for the direct and automatic control of cancer cell intracellular dynamics.

2 Methods

2.1 Control scheme used in external feedback

We applied a feedback controller to regulate the concentrations of two downstream genes (ERK and Akt) of the mTOR and MAPK pathways, as modelled in (Bianconi et al., 2012), and as shown in Figure 1.

FIGURE 1

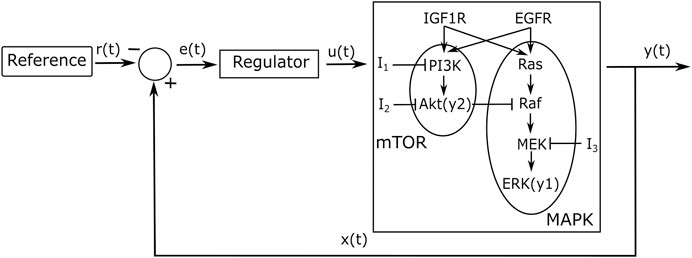
FIGURE 1. A control scheme including three inputs $(\mathbf{u}(t)={[I_1,I_2,I_3]}^T)$ that interact with the mTOR and MAPK pathways. Two observable protein concentrations, ERK and Akt, are used as control outputs for the two pathways (y(t) = [ERK,Akt]^T). The regulator used throughout this project is an adaptive MPC program which attempts to steer the concentrations of the outputs to the transient response of the wild type cell, set as the control reference, as shown in Figure 2.

Figure 2 shows the response of y1 (ERK) and y2 (Akt) in a wild type (−) and in a NSCLC (−) cell to a phosphorylation of EGFR and IGF1R as modelled by varying the system’s initial conditions as in (Bianconi et al., 2012), referred to as an activation. A wild type cell’s activation is modelled using an active concentration of 8,000 μM for EGFR and 800 μM for IGF1R, while an activation in NSCLC cells is triggered by an active concentration of 800,000 and 400,000 μM for EGFR and IGF1R, respectively. The term ‘free’ refers to an open loop response (i.e. if no feedback control is applied) in NSCLC cells. It can be seen that y1 (ERK) and y2 (Akt) activation dynamics are different in cancer vs. wild type cells in Figure 2; of note, the activation of y1 (ERK) occurs over a timescale of an order of magnitude faster than the activation of y2 (Akt). The notation (−) shows the colour of the plot in the related figure that is being discussed.

FIGURE 2

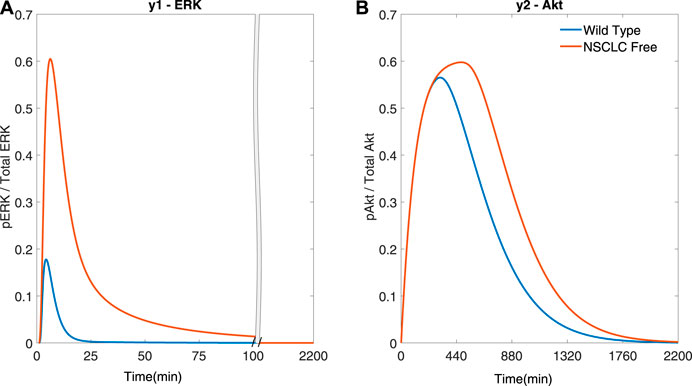
FIGURE 2. Simulations of the NSCLC model (Bianconi et al., 2012): free NSCLC cell response (−) compared to a wild type cell (−) (Bianconi et al., 2012) (A) The response of y1 (ERK) (B) The response of y2 (Akt).

The two pathways are both kinase activated cascades, meaning that an activation at the receptors at the cell membrane causes a cascade of phosphorylation in downstream genes. Therefore it is difficult to robustly control the system as, once an error is measured in the outputs, it can be too late to have a significant effect by acting on the internal states higher up the cascade.

Embedding a model of the system in the controller helps predict the difference between a small change in the output due to an oncoming activation and a small change which is just due to a disturbance in the states, because the controller has knowledge of other states within the cascade. On the other hand, model-free feedback strategies with large gains can have undesirable consequences, such as poor dynamic performance. A Proportional controller can be tuned to decrease the control error, but gains have to be carefully chosen, and the user cannot impose desired constraints on the input (Supplementary Section S8).

Adaptive MPC is used as the model-based control scheme here (Figure 1). The success of MPC relies on the quality of the model used to predict the future behaviour of the system, and on the cost function the controller uses to calculate the optimal inputs to be fed to the process. The novelty of the controller used here lies in the choice of adaptive model and in the cost function used. The MPC implementation is presented in Supplementary Section S4.

2.2 MPC’s linearised model

The NSCLC model (Bianconi et al., 2012) contains significant non-linear terms and a large number of internal states. An adaptive MPC controller computes a linear approximation of the NSCLC model at each time step, predicts the future of the internal states and calculates the optimal input profile. The controller then applies the first input of its calculated optimal input profile to the actual system. At the next time step, the controller calculates a new linear model by linearising the NSCLC model. The use of a linear system results in a convex optimisation problem which can be solved quickly. Adaptive MPC is used in all simulations unless stated otherwise.

Alternatively, non-linear MPC could be used; however, it would introduce additional complexity in the search for the optimal input as local minima will likely be introduced in the cost function. Non-linear MPC is also computationally expensive, and the time needed to compute the next input could be longer than the sampling/actuation temporal intervals (see Supplementary Section S7).

2.3 Improving the traditional MPC cost function

The cost function used by the adaptive MPC algorithm to find the optimal input depends on the current internal state error, e₀, and on the inputs, u(t). The error, e(t), is the difference between the reference, r(t), and the internal states of the NSCLC system, x(t), as shown in Figure 1. The standard cost function used for linear MPC controllers (Rawlings et al., 2020) focuses on how readily the inputs, u(t), are used and on reducing the proportion error in the states, e(t).

In order to include both the magnitude and duration of the error, the integral of the state error, ∫e(t) dt, is added to the standard cost function. It has been shown that it is beneficial to integrate the state error (Hornberg et al., 2005), meaning that the controller acts due to these longer, smaller errors in the outputs caused by states higher in the cascade. Moreover, to avoid rapid fluctuations in the control input, u(t), a differential cost of the inputs is also added to cost function. The derivation of the cost function and a description of the weights of its terms (α, β, γ, η, θ) can be found in Supplementary Section S4.

2.4 MPC simulation parameters

The MPC simulations are reproducible thanks to the deterministic nature of the model and controller, as long as the cost function coefficient weights and other MPC related parameters are kept constant. Table 1 gives a summary of these parameters. Several key parameters are added to the figures’ captions.

TABLE 1

TABLE 1. Parameters used for MPC simulations.

2.5 Indexes used to quantify control performance

To assess quantitatively the performance of our controller, we define an Error Index, EI. It is the sum of the squared error between the output and the reference for the outputs, as used in (Fiore et al., 2015).

$\begin{array}{c}\hfill EI={\int }_0^T{\mathbf{e}}^T\mathbf{C}\mathbf{e}dt\hfill \end{array}(1)$

C is the output matrix of the linearised NSCLC model. A small EI indicates a good performance of the controller.

To quantify the controller effort needed to achieve a certain output, we assess the dose of input drug(s) using a Dose Index, DI_i. It is the integral of the input signal, where u(t) = [I₁(t), I₂(t), I₃(t)].

$\begin{array}{c}\hfill D{I}_i={\int }_0^T{I}_i\left(t\right)dt\hfill \end{array}(2)$

The inputs can never be negative as they are physical concentrations, therefore there is no need to square the input signal.

2.6 Reduced-order models

For a given control scheme (as shown in Figure 1) it is possible to measure various input(u)/output(y) data sets, which can then be used to identify a model of the system. We derived two simplified models (a three state linear and non-linear grey box model); this identification process is discussed in Supplementary Section S9 and will be referred to as the ‘reduced order model’, used in Section 3.5. A Kalman filter was used at each step of the controller to estimate the internal states, using the linearised model of the previous step and the measured outputs.

3 Results

Non-Small Cell Lung Cancer (NSCLC) accounts for 80% of lung cancer cases and is characterised by various mutations which usually lead to an overexpression of the EGF and IGF1R receptors. These receptors trigger several cascades including the mTOR and MAPK pathways; their downstream genes FOXO1 and C-FOS regulate cell apoptosis and proliferation. The differential equations-based mathematical model for NSCLC signalling developed in (Bianconi et al., 2012) includes the mTOR and MAPK pathways along with some of the reactions between the two pathways, as shown in Figure 1; the model enables comparing gene expression dynamics in wild type vs. cancer cells. The model we used and its parameters are based on two previous mathematical models of these signalling pathways, which were fitted and validated on existing and new experimental data (Brown et al., 2004; Orton et al., 2009). We chose the downstream genes ERK and Akt (noted as y1 and y2, respectively) as the control outputs for the external feedback loop (Figure 1); if experiments were performed, it should be possible to measure the dynamics of those proteins using fluorescent reporters. The two outputs can be tuned by varying three inputs (I₁, I₂, I₃), which inhibit three specific proteins within the mTOR and MAPK pathways. The pathways can influence each others’ reactions, creating internal feedback loops (crosstalk).

The code used to implement an adaptive MPC program on this NSCLC model used in these simulations is available on GitHub: https://github.com/Ben-Smart/Adaptive_MPC_on_NSCLC.git.

3.1 Assessing the cost function

Firstly, Single-Input Single-Output (SISO) simulations were performed. The controller tries to steer the dynamics of either y1 (ERK) or y2 (Akt) by varying the concentrations of a drug that acts directly on one of the two signalling cascades (I₃ for y1 (ERK) and either I₁ or I₂ for y2 (Akt)). Figure 3 uses I₂ to regulate y2 (Akt), and shows the effect of different cost function terms on the performance of the controller.

FIGURE 3

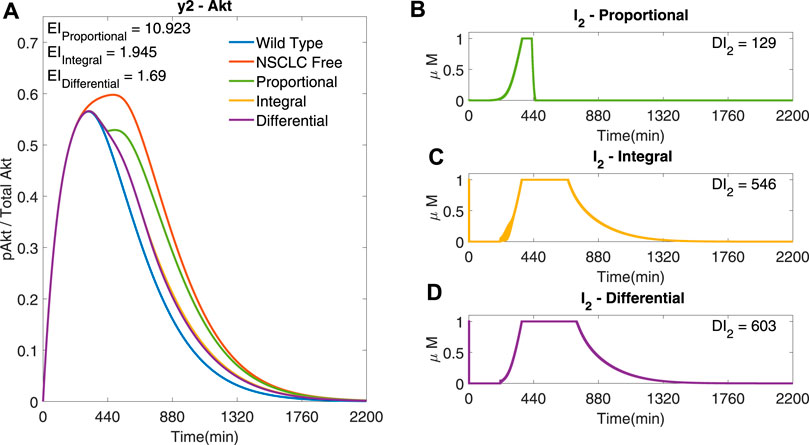
FIGURE 3. SISO adaptive MPC simulation using I₂ to control y2 (Akt), and comparing different cost functions (A) The response of y2 to different cost functions. (B) The input profile (I₂) using the proportional error (−) within the cost function. β = 1, γ = [ − ,10⁵, − ], θ = 0 and η = 0 (C) The input profile (I₂) using the integral error (−). β = 0, γ = [ − ,10⁵, − ], θ = 0 and η = 1 (D) The input profile (I₂) using the integral error and differential terms (−) in the cost function. β = 0, γ = [ − ,10⁵, − ], θ = 10⁵ and η = 1. T_s = 1 min and N = 10 for all plots.

Figure 3A shows that using integral terms within the cost function reduces the error in y2 (Akt), as compared to the proportional terms (EI → 1.945 (−)$<10.923$(−)). However, it can be seen in Figure 3C that the controller using integral terms (−) can cause fluctuations in the input. Such fluctuations are reduced when using a differential cost, which also has a lower Error Index, but higher Dose Index (EI → 1.690 (−)$<1.945$(−)$<10.923$(−), DI₂ → 603 (−)$>546$(−)$>129$(−)).

The cost functions used in the following simulations include β = 0 (i.e. no output error cost), θ = 0 (i.e. no differential input cost) and η = 1 (i.e. a non-zero integral output error cost), as in Figure 3C, apart from the weight associated with each input, γ, that is varied (as indicated in figures’ captions).

3.1.1 Single-input single-output control

Figure 4 shows SISO adaptive MPC simulations for I₁, I₂ and I₃; each drug is used to control the downstream molecule in the cascade it acts on. It can be seen that plots C) and D) of Figure 4 are identical to (−) in plot A) and plot C) of Figure 3 as these are both SISO responses of I₂ using the chosen cost function (costing the integral and input terms). The SISO controller moves the NSCLC response towards the wild type one (−) using a lower dose than just a step of each input at the maximum allowed dose (1 μM), thus decreasing the Dose Index. The step input response can be found in Supplementary Section S3. This demonstrates the benefits of using an external feedback loop compared to an open loop response with a static step input.

FIGURE 4

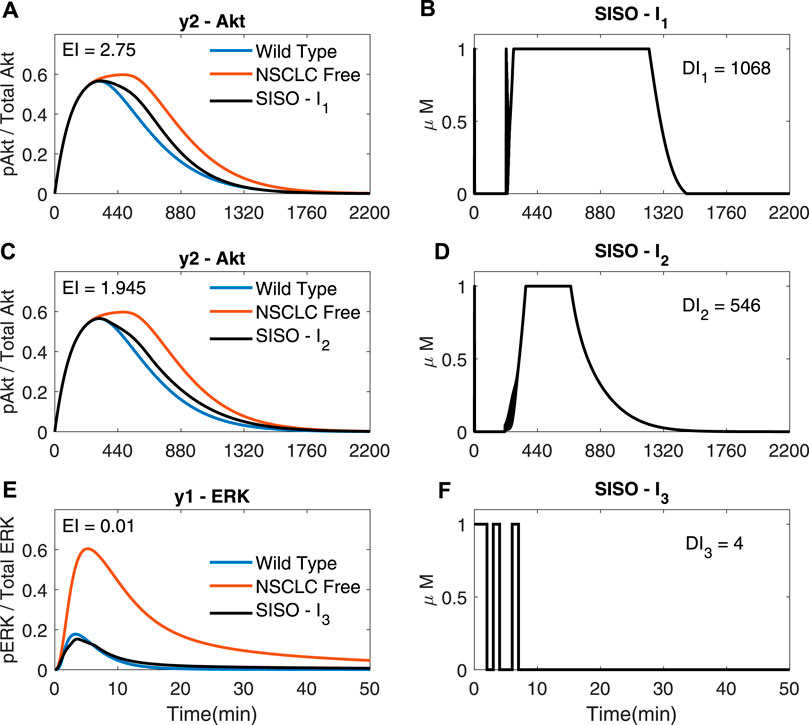
FIGURE 4. SISO adaptive MPC simulations (A,B) The response of y2 (Akt, in (A) to the input of I₁ (shown in (B)); γ = [1, −, − ] (C,D) The response of y2 (Akt, in (C) to the input of I₂ (shown in D); γ = [ − ,10⁵, − ] (E,F) The response of y1 (ERK, in (E) to the input of I₃ (shown in (F)); γ = [ − , − ,10⁹]. (A–F): T_s = 1, N = 10, α = 0, β = 0, θ = 0 and η = 1.

3.2 Multi-input multi-output control

Adaptive MPC can also be used to steer both outputs using all three inputs in Multi-Input Multi-Output (MIMO) simulations, as shown in Figure 5.

FIGURE 5

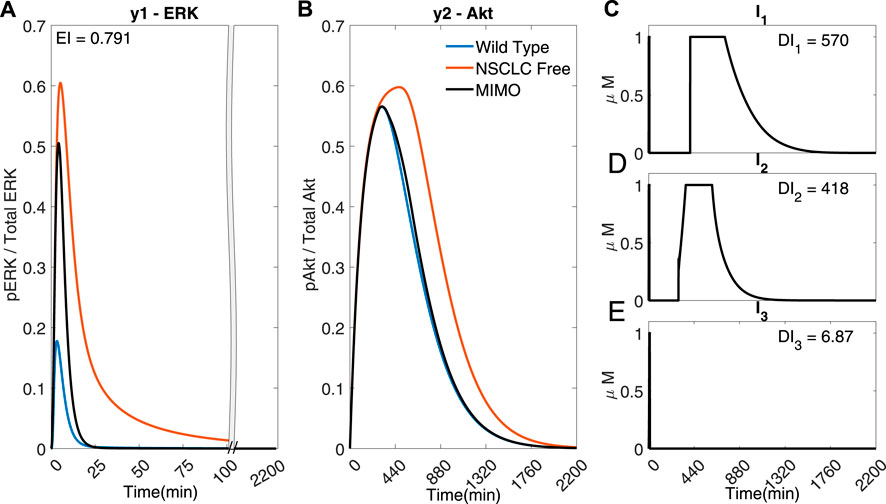
FIGURE 5. A MIMO adaptive MPC simulation using I₁, I₂ and I₃ to control the concentrations of y1 (ERK) and y2 (Akt) (A) The response of ERK. (B) The response of Akt (C–E) The inputs used in the simulations. Parameters: T_s = 1 min, N = 10, α = 0, β = 0, γ = [1, 10⁵, 10⁹], θ = 0 and η = 1.

The error of y2 (Akt) (Figure 5)) is significantly smaller in comparison to Figures 4A,C (EI → 0.791 < 1.954 < 2.75), whilst using significantly less I₁ (DI₁ → 570 <1068) and I₂ (DI₂ → 418 < 546), suggesting that it might be advantageous to use adaptive MPC to predict and apply combination drug profiles.

However, due to the fast dynamics of the MAPK pathway, the output y1 (ERK) fails to adequately follow the reference activation curve. Figure 6 shows that if the time step is adequately reduced (for instance, to T_s = 0.02 min), the controller can handle the faster dynamics of the pathway and effectively control both outputs (EI → 0.001 < 0.791) whilst using a lower dosage of all the inputs (DI₁ → 545 < 570, DI₂ → 297 < 418, DI₃ → 4.35 < 6.87). Figure 6 shows that the controller can overcome the effect of crosstalk, balancing the error in y1 (ERk) and the use of I₁ and I₂.

FIGURE 6

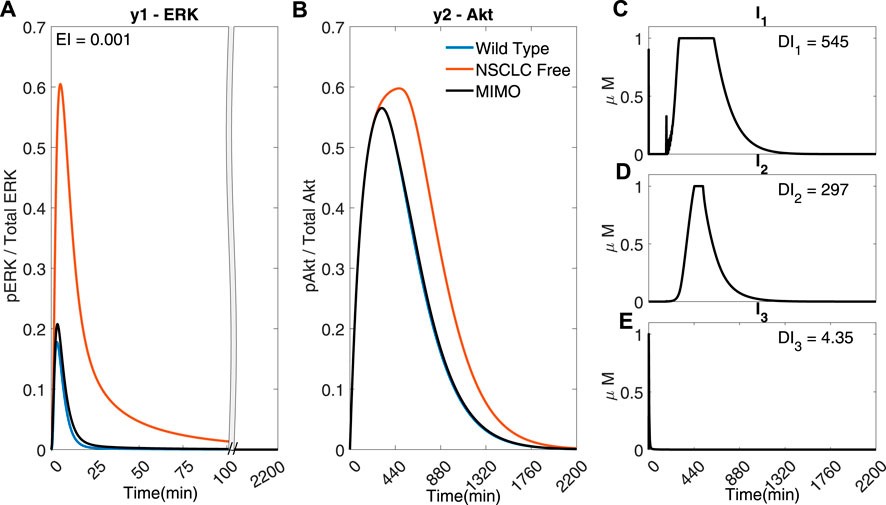
FIGURE 6. A MIMO adaptive MPC simulation using I₁, I₂ and I₃ to control the concentrations of y1 (ERK) and y2 (Akt) (A) The response of ERK. (B) The response of Akt (C–E) The inputs used in the simulation. Parameters: T_s = 0.02 min, N = 10, α = 0, β = 0, γ = [1, 10⁵, 10⁹], θ = 0 and η = 1.

To emulate capabilities of current microfluidics devices, the time step will be kept at T_s = 1 min. Therefore, in what follows, we investigate only Multi-Input Single-Output (MISO) simulations where y2 (Akt) is controlled only with I₁ and I₂. In this way, we remove the effect of the crosstalk (through the inherent negative feedback loops shown in Figure 1), which would restrict the MPC’s use of I₁ and I₂ caused by the high error in y1 (ERK) due to the faster timescale of this output at the controller’s current time step (T_s = 1 min).

3.3 Combination therapies using I₁ and I₂

If cells are exposed to drugs for an extended period of time, side effects and resistance might become an issue (Salgia and Kulkarni, 2018). The controller could be used to find potential drug combinations that can achieve a low Error Index (EI) whilst reducing the dose of the inputs (DI_i). The weight associated with using each input, γ, within the cost function can be varied for this aim, as shown in Figure 7. The Bliss Independence (BI) formula (Demidenkoid and Miller, 2019; Vakil and Trappe, 2019) has been used here as a normalised Dose Index to summarise the combined effect of multiple drugs (see Supplementary Section S5).

FIGURE 7

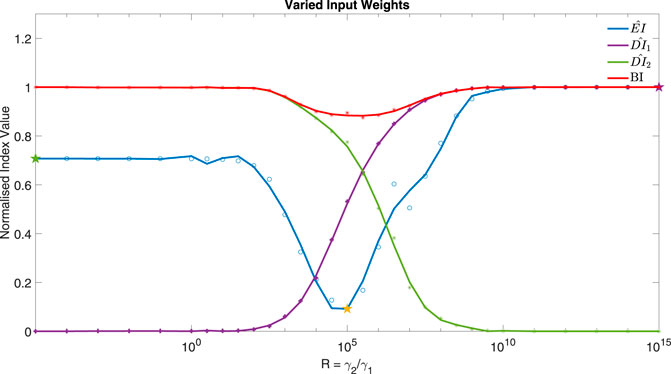
FIGURE 7. The normalised Error Index of y2 (Akt) (−), Dose Indexes of I₁ (−) and I₂ (−) and Bliss Independence (−), from 31 MISO adaptive MPC simulations using varied ratio of input weights, R = γ₂/γ₁, for example, when R = 100, γ = [1, 100, − ]. Parameters: T_s = 1 min, N = 10, α = 0, β = 0, θ = 0 and η = 1. The three star markers show the ratio used in the plots of Figure 8.

Figure 7 focuses on the control of y2 (Akt) using I₁ and I₂ as control inputs (MISO control). The weights in the cost function associated with each input can be varied as a ratio of $R=\frac{{\gamma }_2}{{\gamma }_1}$, ranging from low R values (where a high weight is associated with I₁ (γ₁), thus producing a SISO-like simulation only using I₂), all the way through to a high R value (where γ₂ is relatively large and the controller will only use I₁). Figure 7 compares the normalised Error Index, $\widehat{EI}$ (−), and the Bliss Independence BI (−) to the weight ratio (R). It shows that there is a range of R which can significantly reduce both EI (−) and BI (−). Therefore, the control performance of the MISO controller is better than any SISO simulation while keeping drug concentrations low. For the purpose of designing combination therapies, here the optimal input is associated to the minimum value of the EI (−).

It can be seen from Figure 7 that the minimum occurs when R = 10⁵, corresponding to γ₁ = 1 and γ₂ = 10⁵. Figure 8 compares the responses obtained using a very low or high R value to the MISO simulation at the optimum of EI. This optimum achieves a significantly lower Error Index (EI → 0.25 (−) $<1.95$ (−) $<2.75$ (−)), and a lower Dose Index (DI₁ → 568 (−)$<1068$(−) and DI₂ → 423 (−) $<546$(−)).

FIGURE 8

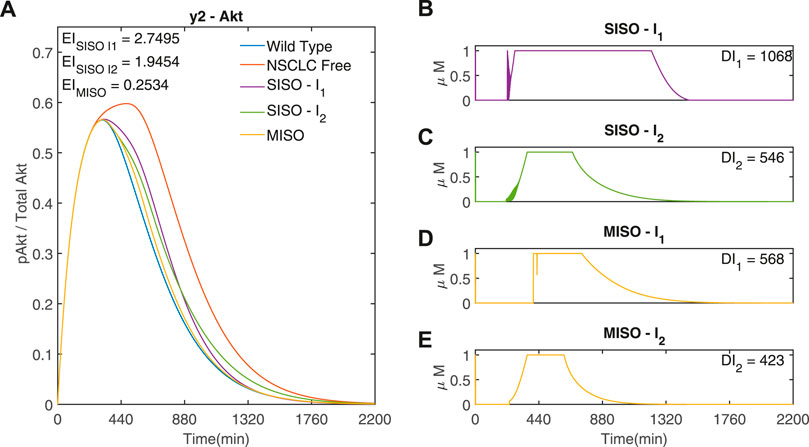
FIGURE 8. Three adaptive MPC simulations using I₁ and I₂ to control y2 (Akt) (A) The response of y2 (Akt) to three different input weightings, SISO - I₁ (−) (γ = [1, 10¹⁵, − ]), SISO - I₂ (−) (γ = [10⁵, 1, − ]) and MISO (−) (γ = [1, 10⁵, − ]). γ was selected from the minimum point of the EI and the limits of R in Figure 7 (B,C) Inputs I₁ and I₂ used in the two SISO simulations. (D,E) Inputs I₁ and I₂, respectively, used in the MISO simulation. Parameters: T_s = 1min, N = 10, α = 0, β = 0, θ = 0 and η = 1

3.4 Drug holidays

If using an adaptive MPC, the user can set specific time intervals in which the controller does not give specific drugs (for example, to avoid toxicity induced by long exposure). These drug holidays can be achieved by the controller by varying the weights associated with each input, online, during a single simulation.

As an example, Supplementary Figure S3 shows that the controller can retain a low Error Index whilst swapping inputs after 600 min (EI → 1.989 ≈ 1.950 <2.75, the SISO EI of Figure 4). Therefore, a programmed change of cost function weights during the simulation can decide which input to stop using.

Alternatively, the controller can be set to only choose one input at each time step. The inputs shown in Supplementary Figure S5 have an ON or OFF state, 1 μM or 0 μM (discrete inputs). The step size T_s used makes a significant difference to the response. When T_s = 1min the drugs can switch ON or OFF every minute, leading to rapidly fluctuating inputs (shown in Supplementary Figure S4). Supplementary Figure S5 shows the discrete simulation with a larger time step (T_s = 30min). It can be seen that there is a better performance when compared to the SISO simulations (Figure 4) as EI → 1.6878 < 1.95 < 2.75, whilst still using less of each input (DI₁ → 630 < 1068, DI₂ → 450 < 546). However, when compared to the optimal MISO response (Figure 8), these added constraints result in a higher Error Index (EI → 1.6878 > 0.2534) and a higher dose (DI₁ → 630 > 568, DI₂ → 450 > 423).

3.5 MPC based on a reduced order model and an estimator

If adaptive MPC was to be used experimentally, then the controller would not have access to all of the internal states. We tested the effectiveness of two reduced order models (three states) within the MPC program, run alongside a Kalman filter to estimate the other two internal states from the measurements of Akt only.

The performance of a standard MPC using a linear reduced order model (−) is compared to an adaptive MPC based on a non-linear reduced order model (−), labelled ‘Fixed’ and ‘Adaptive’ respectively in Figure 9. The adaptive MPC simulation has a lower EI than the fixed MPC simulation (EI → 0.319 (−) < 0.477 (−)), showing that, at least with this identified models, updating the linear model at each iteration improves the performance of the controller.

FIGURE 9

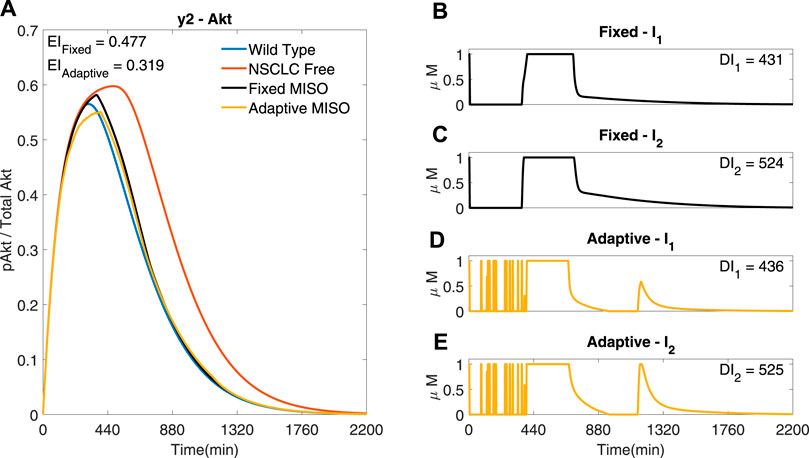
FIGURE 9. Two MISO adaptive MPC simulation based of a three state model identified from input/output data including a Kalman filter to estimate the internal states from the measured output, comparing the adaptive and the fixed models. I₁ and I₂ are used to control y2 (Akt) (A) The response of Akt to the inputs in (B) and (C) for the fixed response and (D,E) for the adaptive response. Parameters: T_s = 1min, N = 10, α = 0, β = 0, γ = [1, 1e5, − ], θ = 10⁸ and η = 1.

The reduced order model simulations with the same cost function used in Figure 8 shows rapid fluctuations of the inputs (Supplementary Figure S9), therefore we set the simulation in Figure 9 with the same cost function as in Figure 8 except for the increase of the differential cost term, θ. It can be seen that the MISO response of the reduced order model in Figure 9 can achieve a similar EI to that of the optimal full order model shown in Figure 8, whilst using a similar combined input dose. Therefore the reduced order model manages to achieve a similar performance to the full order model, whilst not representing all the dynamics of the full order NSCLC model and only using the measured data of one output.

4 Discussion

Computational approaches have been extensively proposed in the search for effective cancer treatments. Initially, mathematical models were used to investigate the pathways within the system, design the inputs themselves, and observe how the system reacts (Konstorum et al., 2017; Cova et al., 2019). Optimisation algorithms have supported the identification of open loop optimal input profiles for target phenotypes (Castiglione and Piccoli, 2006; Kassara, 2006; Piccoli and Castiglione, 2006; Castiglione and Piccoli, 2007; Ledzewicz and Schattler, 2007; Itik et al., 2009; Ghaffari and Naserifar, 2010; Oke et al., 2018). Open loop schemes cannot compensate for model inaccuracies or adapt to observations. Therefore, negative feedback controllers were developed, for example to control cancer tissues with model free controllers (Chareyron and Alamir, 2009; Bratus et al., 2013; Goharrizi et al., 2013; Tang et al., 2016; Ledzewicz et al., 2019) and model based controllers (Sápi et al., 2012; Alamir, 2014; Teles and Lemos, 2019).

This is, to the best of our knowledge, the first attempt of simulating feedback controllers to regulate intracellular dynamics of cancer cells by using an adaptive control scheme.

We showed that an adaptive MPC program can be used to inform treatments for NSCLC cells, steering the dynamics of several key signalling pathways, whilst offering a tunable cost function that allows the user to adjust the characteristics of an optimal input. Indeed, the controller can be tuned to choose different drug profiles that will achieve a similar control performance whilst reducing exposure to one or more drugs. We also mimicked future in vitro experiments through the use of a simple model (identified through input/output data) alongside a Kalman filter within the adaptive MPC program.

Other control strategies, like PID controllers, cannot be directly tuned to affect the desired input and only act on the observed output. The use of a linear model within the MPC makes the control algorithm running time short enough for it to be used, in the future, in external feedback control experiments. The implementation of those would require some practical aspects to be considered, which we did not account for. Firstly, there might be delays in cell responses to drugs/actuation, which the model used by the controller should consider. Also, the sampling/actuation time might need to be fast enough, if aiming at controlling genes with fast dynamics. This issue might be overcome using experimental optogenetics-based platforms instead of microfluidics-based ones, as they can reduce delays in the actuation.

We foresee a growing interest in applying cybergenetics approaches, and in particular feedback controllers, to steer mammalian cells dynamics. If we realise our ambition to implement the experiments proposed here on living cells and, longer term, on patient-derived organoids, feedback control might be a valuable tool for the design of personalised optimal treatments for a range of conditions.

5 Conclusion

It has been demonstrated, through simulations, that adaptive MPC can be used to inform drug combinations which can steer signalling dynamics in NSCLC cells, offering a tunable cost function to modify ad hoc both the rapidity of inputs’ changes and the ways inputs are chosen. The weights can also be changed to choose different drug profiles that will achieve a similar control performance whilst giving the cell a break from individual drugs. In the future, we hope to test the controller in living cells using microfluidics/microscopy platforms.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/Ben-Smart/Adaptive_MPC_on_NSCLC.

Author contributions

BS designed and carried out the simulations in Matlab2021b and wrote the manuscript with inputs from all the authors. IC supported the project. LR and LM conceived the project, contributed to manuscript writing and supervised the entire work.

Funding

BS and IdC are supported by an EPSRC DTP Scholarship. LR is funded by a Research Fellowship from the Royal Academy of Engineering (RF1516/15/11). LM is supported by the Engineering and Physical Sciences Research Council (EPSRC) grant EP/S01876X/1, and by the European Union’s Horizon 2020 under Grant Agreement No. 766840.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcteg.2022.935018/full#supplementary-material

References

Alamir, M. (2014). Robust feedback design for combined therapy of cancer. Optim. Control Appl. Methods 35, 77–88. doi:10.1002/oca.2057

CrossRef Full Text | Google Scholar

Andrews, L., Nielsen, A. A. K., and Voigt, C. A. (2018). Cellular checkpoint control using programmable sequential logic. Science 361 (6408), 9. doi:10.1126/SCIENCE.AAP8987

PubMed Abstract | CrossRef Full Text | Google Scholar

Aoki, S., Lillacci, G., Gupta, A., Baumschlager, A., Schweingruber, D., and Khammash, M. (2019). A universal biomolecular integral feedback controller for robust perfect adaptation. Nature 570, 533–537. doi:10.1038/s41586-019-1321-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Bashor, C., Patel, N., Choubey, S., Beyzavi, A., Kondev, J., Collins, J. J., et al. (2019). Complex signal processing in synthetic gene circuits using cooperative regulatory assemblies. Science 364 (6440), 593–597. doi:10.1126/science.aau8287

PubMed Abstract | CrossRef Full Text | Google Scholar

Bianconi, F., Baldelli, E., Ludovini, V., Crino, L., Flacco, A., and Valigi, P. (2012). Computational model of EGFR and IGF1R pathways in lung cancer: A systems biology approach for translational oncology. Biotechnol. Adv. 30 (1), 1421–2153. doi:10.1016/J.BIOTECHADV.2011.05.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Bloom, R., Winkler, S. M., and Smolke, C. D. (2015). Synthetic feedback control using an RNAi-based gene-regulatory device. J. Biol. Eng. 9 (1), 5. doi:10.1186/S13036-015-0002-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Bratus, A., Todorov, Y., Yegorov, I., and Yurchenko, D. (2013). Solution of the feedback control problem in the mathematical model of leukaemia therapy. J. Optim. Theory Appl. 159, 590–605. doi:10.1007/s10957-013-0324-6

CrossRef Full Text | Google Scholar

Briat, C., Gupta, A., and Khammash, M. (2016). Antithetic integral feedback ensures robust perfect adaptation in noisy bimolecular networks. Cell Syst. 2 (1), 15–26. doi:10.1016/J.CELS.2016.01.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, K., Hill, C. C., Calero, G. A., Myers, C. R., Lee, K. H., Sethna, J. P., et al. (2004). The statistical mechanics of complex signaling networks: Nerve growth factor signaling. Phys. Biol. 1 (3), 184–195. doi:10.1088/1478-3967/1/3/006

PubMed Abstract | CrossRef Full Text | Google Scholar

Browning, A., Warne, D. J., Burrage, K., Baker, R. E., and Simpson, M. J. (2020). Identifiability analysis for stochastic differential equation models in systems biology. J. R. Soc. Interface 17 (173), 20200652. doi:10.1098/RSIF.2020.0652

PubMed Abstract | CrossRef Full Text | Google Scholar

Castiglione, F., and Piccoli, B. (2007). Cancer immunotherapy, mathematical modeling and optimal control. J. Theor. Biol. 247, 723–732. doi:10.1016/j.jtbi.2007.04.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Castiglione, F., and Piccoli, B. (2006). Optimal control in a model of dendritic cell transfection cancer immunotherapy. Bull. Math. Biol. 68, 255–274. doi:10.1007/s11538-005-9014-3

PubMed Abstract | CrossRef Full Text | Google Scholar

de Cesare, I., Salzano, D., di Bernardo, M., Renson, L., and Marucci, L. (2022). Control-based continuation: A new approach to prototype synthetic gene networks. ACS Synth. Biol. 6. doi:10.1021/ACSSYNBIO.1C00632

CrossRef Full Text | Google Scholar

Chareyron, S., and Alamir, M. (2009). Model-free feedback design for a mixed cancer therapy. Biotechnol. Prog. 25 (3), 690–700. doi:10.1002/BTPR.114

PubMed Abstract | CrossRef Full Text | Google Scholar

Ciar, C., Harris, A. W., Steel, H., Hancock, E. J., Heap, J. T., and Papachristodoulou, A. (2018). Synthetic negative feedback circuits using engineered small RNAs. Nucleic Acids Res. 46 (18), 9875–9889. doi:10.1093/nar/gky828

PubMed Abstract | CrossRef Full Text | Google Scholar

Cova, T., Bento, D. J., and Nunes, S. C. C. (2019). Computational approaches in theranostics: Mining and predicting cancer data. Pharmaceutics 11, 119. doi:10.3390/PHARMACEUTICS11030119

PubMed Abstract | CrossRef Full Text | Google Scholar

Cuba Samaniego, C., and Franco, E. (2021). Ultrasensitive molecular controllers for quasi-integral feedback. Cell Syst. 12 (3), 272–288. doi:10.1016/J.CELS.2021.01.001

PubMed Abstract | CrossRef Full Text | Google Scholar

de Cesare, I., Zamora-Chimal, C. G., Postiglione, L., Khazim, M., Pedone, E., Shannon, B., et al. (2021). ChipSeg: An automatic tool to segment bacterial and mammalian cells cultured in microfluidic devices. ACS Omega 6 (4), 2473–2476. doi:10.1021/ACSOMEGA.0C03906

PubMed Abstract | CrossRef Full Text | Google Scholar

Del Vecchio, D., Dy, A. J., and Qian, Y. (2016). Control theory meets synthetic biology. J. R. Soc. Interface 13 (120), 20160380. doi:10.1098/RSIF.2016.0380

PubMed Abstract | CrossRef Full Text | Google Scholar

Demidenkoid, E., and Miller, T. W. (2019). Statistical determination of synergy based on Bliss definition of drugs independence. PLOS ONE 14, e0224137. doi:10.1371/journal.pone.0224137

PubMed Abstract | CrossRef Full Text | Google Scholar

Fiore, G., Matyjaszkiewicz, A., Annunziata, F., Grierson, C., Savery, N. J., Marucci, L., et al. (2016). “Design of a multicellular feedback control strategy in a synthetic bacterial consortium,” in 2016 IEEE 55th Conference on Decision and Control CDC, Las Vegas, NV, USA, 12-14 Dec. 2016, 3338–3343. doi:10.1109/CDC.2016.7798771

CrossRef Full Text | Google Scholar

Fiore, G., Matyjaszkiewicz, A., Annunziata, F., Grierson, C., Savery, N. J., Marucci, L., et al. (2017). In-silico analysis and implementation of a multicellular feedback control strategy in a synthetic bacterial consortium. ACS Synth. Biol. 6 (3), 5073–5517. doi:10.1021/ACSSYNBIO.6B00220

CrossRef Full Text | Google Scholar

Fiore, G., Perrino, G., di Bernardo, M., and di Bernardo, D. (2015). In vivo real-time control of gene expression: A comparative analysis of feedback control strategies in yeast. ACS Synth. Biol. 5 (2), 154–162. doi:10.1021/ACSSYNBIO.5B00135

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, X., Chong, L. S., Kim, M. S., and Elowitz, M. B. (2018). Programmable protein circuits in living cells. Science 361 (6408), 1252–1258. doi:10.1126/SCIENCE.AAT5062

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghaffari, A., and Naserifar, N. (2010). Optimal therapeutic protocols in cancer immunotherapy. Comput. Biol. Med. 40 (3), 261–270. doi:10.1016/J.COMPBIOMED.2009.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Goharrizi, A., N'Djin, W. A., Kwong, R., and Chopra, R. (2013). Development of a new control strategy for 3D MRI-controlled interstitial ultrasound cancer therapy. Med. Phys. 40 (3), 033301. doi:10.1118/1.4793261

PubMed Abstract | CrossRef Full Text | Google Scholar

Hornberg, J., Binder, B., Bruggeman, F. J., Schoeberl, B., Heinrich, R., and Westerhoff, H. V. (2005). Control of MAPK signalling: From complexity to what really matters. Oncogene 24 (36), 55338–55542. doi:10.1038/SJ.ONC.1208817

PubMed Abstract | CrossRef Full Text | Google Scholar

Hsiao, V., de los Santos, E. L. C., Whitaker, W. R., Dueber, J. E., and Murray, R. M. (2015). Design and implementation of a biomolecular concentration tracker. ACS Synth. Biol. 4 (2), 150–161. doi:10.1021/SB500024B

PubMed Abstract | CrossRef Full Text | Google Scholar

Itik, M., Salamci, M. U., and Banks, S. P. (2009). Optimal control of drug therapy in cancer treatment. Nonlinear Analysis Theory Methods & Appl. 71, 1473–1486. doi:10.1016/j.na.2009.01.214

CrossRef Full Text | Google Scholar

Kassara, Khalid (2006). A set-valued approach to control immunotherapy. Math. Comput. Model. 44 (11-12), 1114–1125. doi:10.1016/J.MCM.2006.03.016

CrossRef Full Text | Google Scholar

Khammash, M., Di Bernardo, M., and Di Bernardo, D. (2019). “Cybergenetics: Theory and methods for genetic control system,” in Proceedings of the IEEE Conference on Decision and Control, Nice, France, 11-13 December 2019, 916–926. doi:10.1109/CDC40024.2019.9030209

CrossRef Full Text | Google Scholar

Khazim, M., Pedone, E., Postiglione, L., di Bernardo, D., and Marucci, L. (2021). A microfluidic/microscopy-based platform for on-chip controlled gene expression in mammalian cells. Methods Mol. Biol. 2229, 205–219. doi:10.1007/978-1-0716-1032-9_10

PubMed Abstract | CrossRef Full Text | Google Scholar

Khazim, M., Postiglione, L., Pedone, E., Rocca, D. L., Zahra, C., and Marucci, L. (2019). Towards automated control of embryonic stem cell pluripotency. IFAC-PapersOnLine 52 (26), 82–87. doi:10.1016/J.IFACOL.2019.12.240

CrossRef Full Text | Google Scholar

Konstorum, A., Vella, A. T., Adler, A. J., and Laubenbacher, R. C. (2017). Addressing current challenges in cancer immunotherapy with mathematical and computational modelling. J. R. Soc. Interface 14, 20170150. doi:10.1098/rsif.2017.0150

PubMed Abstract | CrossRef Full Text | Google Scholar

Kylilis, N., Tuza, Z. A., Stan, G. B., and Polizzi, K. M. (2018). Tools for engineering coordinated system behaviour in synthetic microbial consortia. Nat. Commun. 9 (1), 2677. doi:10.1038/s41467-018-05046-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Ledzewicz, U., Maurer, H., and Schattler, H. (2019). Optimal combined radio- and anti-angiogenic cancer therapy. J. Optim. Theory Appl. 180, 321–340. doi:10.1007/s10957-018-1426-y

CrossRef Full Text | Google Scholar

Ledzewicz, U., and Schattler, H. (2007). Antiangiogenic therapy in cancer treatment as an optimal control problem. SIAM J. Control Optim. 46 (3), 1052–1079. doi:10.1137/060665294

CrossRef Full Text | Google Scholar

Lugagne, J., Sosa Carrillo, S., Kirch, M., Kohler, A., Batt, G., and Hersen, P. (2017). Balancing a genetic toggle switch by real-time feedback control and periodic forcing. Nat. Commun. 8, 1671. doi:10.1038/s41467-017-01498-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Marucci, L. (2017). Nanog dynamics in mouse embryonic stem cells: Results from systems biology approaches. Stem cells Int. 2017, 1–14. doi:10.1155/2017/7160419

CrossRef Full Text | Google Scholar

Marucci, L., Santini, S., di Bernardo, M., and di Bernardo, D. (2011). Derivation, identification and validation of a computational model of a novel synthetic regulatory network in yeast. J. Math. Biol. 62 (5), 685–706. doi:10.1007/S00285-010-0350-Z

PubMed Abstract | CrossRef Full Text | Google Scholar

Matyjaszkiewicz, A., Fiore, G., Annunziata, F., Grierson, C. S., Savery, N. J., Marucci, L., et al. (2017). BSim 2.0: An advanced agent-based cell simulator. ACS Synth. Biol. 6 (10), 1969. doi:10.1021/ACSSYNBIO.7B00121

PubMed Abstract | CrossRef Full Text | Google Scholar

Menolascina, F., Fiore, G., Orabona, E., De Stefano, L., Ferry, M., Hasty, J., et al. (2014). In-vivo real-time control of protein expression from endogenous and synthetic gene networks. PLoS Comput. Biol. 10 (5), 1003625. doi:10.1371/journal.pcbi.1003625

PubMed Abstract | CrossRef Full Text | Google Scholar

Milias-Argeitis, A., Summers, S., Stewart-Ornstein, J., Zuleta, I., Pincus, D., El-Samad, H., et al. (2011). In silico feedback for in vivo regulation of a gene expression circuit. Nat. Biotechnol. 29 (12), 1114–1116. doi:10.1038/nbt.2018

PubMed Abstract | CrossRef Full Text | Google Scholar

Oke, S., Matadi, M., and Xulu, S. (2018). Optimal control analysis of a mathematical model for breast cancer. Math. Comput. Appl. 23, 21. doi:10.3390/MCA23020021

CrossRef Full Text | Google Scholar

Orton, R., Adriaens, M. E., Gormand, A., Sturm, O. E., Kolch, W., and Gilbert, D. R. (2009). Computational modelling of cancerous mutations in the EGFR/ERK signalling pathway. BMC Syst. Biol. 3 (1), 100. doi:10.1186/1752-0509-3-100

PubMed Abstract | CrossRef Full Text | Google Scholar

Pedone, E., de Cesare, I., Zamora-Chimal, C. G., Haener, D., Postiglione, L., La Regina, A., et al. (2021). Cheetah: A computational toolkit for cybergenetic control. ACS Synth. Biol. 10 (5), 979–989. doi:10.1021/ACSSYNBIO.0C00463

PubMed Abstract | CrossRef Full Text | Google Scholar

Pedone, E., Postiglione, L., Aulicino, F., Rocca, D. L., Montes-Olivas, S., Khazim, M., et al. (2019). A tunable dual-input system for on-demand dynamic gene expression regulation. Nat. Commun. 10, 4481. doi:10.1038/s41467-019-12329-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Piccoli, B., and Castiglione, F. (2006). Optimal vaccine scheduling in cancer immunotherapy. Phys. A Stat. Mech. its Appl. 370, 672–680. doi:10.1016/j.physa.2006.03.011

CrossRef Full Text | Google Scholar

Postiglione, L., Napolitano, S., Pedone, E., Rocca, D. L., Aulicino, F., Santorelli, M., et al. (2018). Regulation of gene expression and signaling pathway activity in mammalian cells by automated microfluidics feedback control. ACS Synth. Biol. 7 (11), 2558–2565. doi:10.1021/ACSSYNBIO.8B00235

PubMed Abstract | CrossRef Full Text | Google Scholar

Postiglione, L., Wan, J., di Bernardo, M., and Marucci, L. (2019). “A strategy for multicellular feedback control in mammalian cells,” in 2019 18th European Control Conference, ECC, Naples, Italy, 25-28 June 2019, 2669–2674. doi:10.23919/ECC.2019.8796200

CrossRef Full Text | Google Scholar

Rawlings, J. B., Mayne, D. Q., and Diehl, M. M. (2020). Model predictive control : Theory, computation, and design. 2nd edition. Wisconsin, US: Nob Hill Publishing.

Google Scholar

Ren, X., Samaniego, C. C., Murray, R. M., and Franco, E. (2021). “Bistable state switch enables ultrasensitive feedback control in heterogeneous microbial populations,” in 2021 American Control Conference (ACC), New Orleans, LA, USA, 25-28 May 2021, 652–659. doi:10.23919/ACC50511.2021.9482836

CrossRef Full Text | Google Scholar

Salgia, R., and Kulkarni, P. (2018). The genetic/non-genetic duality of drug ‘resistance’ in cancer. Trends cancer 4 (2), 1102–1118. doi:10.1016/J.TRECAN.2018.01.001

CrossRef Full Text | Google Scholar

Sápi, J., Drexler, D. A., Harmati, I., Sapi, Z., and Kovacs, L. (2012). “Linear state-feedback control synthesis of tumor growth control in antiangiogenic therapy,” in IEEE 10th Jubilee International Symposium on Applied Machine Intelligence and Informatics, SAMI 2012 - Proceedings, Herl'any, Slovakia, 26-28 January 2012, 143–148. doi:10.1109/SAMI.2012.6208945

CrossRef Full Text | Google Scholar

Shakiba, N., Jones, R. D., Weiss, R., and Del Vecchio, D. (2021). Context-aware synthetic biology by controller design: Engineering the mammalian cell. Cell Syst. 12 (6), 5616–6592. doi:10.1016/J.CELS.2021.05.011

CrossRef Full Text | Google Scholar

Shannon, B., Zamora-Chimal, C. G., Postiglione, L., Salzano, D., Grierson, C. S., Marucci, L., et al. (2020). In vivo feedback control of an antithetic molecular-titration motif in Escherichia coli using microfluidics. ACS Synth. Biol. 9 (10), 2617–2624. doi:10.1021/ACSSYNBIO.0C00105

PubMed Abstract | CrossRef Full Text | Google Scholar

Siu, Y., Fenno, J., Lindle, J. M., and Dunlop, M. J. (2018). Design and selection of a synthetic feedback loop for optimizing biofuel tolerance. ACS Synth. Biol. 7 (1), 16–23. doi:10.1021/ACSSYNBIO.7B00260

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, B., Xiao, Y., Tang, S., and Cheke, R. A. (2016). A feedback control model of comprehensive therapy for treating immunogenic tumours. Int. J. Bifurc. Chaos 26 (3), 1650039. doi:10.1142/S0218127416500395

CrossRef Full Text | Google Scholar

Teles, F., and Lemos, J. M. (2019). Cancer therapy optimization based on multiple model adaptive control. Biomed. Signal Process. Control 48, 255–264. doi:10.1016/j.bspc.2018.09.016

CrossRef Full Text | Google Scholar

Toettcher, J., Gong, D., Lim, W. A., and Weiner, O. D. (2011). Light-based feedback for controlling intracellular signaling dynamics. Nat. Methods 8 (10), 837–839. doi:10.1038/NMETH.1700

PubMed Abstract | CrossRef Full Text | Google Scholar

Uhlendorf, J., Miermont, A., Delaveau, T., Charvin, G., Fages, F., Bottani, S., et al. (2012). Long-term model predictive control of gene expression at the population and single-cell levels. Proc. Natl. Acad. Sci. U. S. A. 109 (35), 14271–14276. doi:10.1073/pnas.1206810109

PubMed Abstract | CrossRef Full Text | Google Scholar

Vakil, V., and Trappe, W. (2019). Drug combinations: Mathematical modeling and networking methods. Pharmaceutics 11 (5), 208. doi:10.3390/PHARMACEUTICS11050208

CrossRef Full Text | Google Scholar

Vasan, N., Baselga, J., and Hyman, D. M. (2019). A view on drug resistance in cancer. Nature 575, 29957529911–29957530309. doi:10.1038/s41586-019-1730-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Ye, H., Xie, M., Xue, S., Hamri, G. C. E., Yin, J., Zulewski, H., et al. (2016). Self-adjusting synthetic gene circuit for correcting insulin resistance. Nat. Biomed. Eng. 1 (1), 0005. doi:10.1038/S41551-016-0005

PubMed Abstract | CrossRef Full Text | Google Scholar