Self-Triggered Control of Multi-Agent Systems With External Disturbances

This paper investigates the consensus of multi-agent systems (MASs) by virtue of event-triggered mechanism. Considering the existence of external disturbances, we use a disturbance observer to estimate the disturbance signals and eliminate the corresponding effects by using estimators to compensate the input control terms. The self-triggered condition is designed and proved that there is no Zeno behavior. We show that the proposed disturbance observer can estimate the external disturbance signals well under the self-triggered condition. Finally, simulation examples are presented to verify the theoretical results.

1 Introduction

Inspired by the behavior of cluster organisms in nature, people find that the ability of a distributed network system is far better than the sum of individual abilities when encountering large-scale complex tasks. In recent years, more attention has been paid to the study of multi-agent systems (MASs), especially to the formation control problem (Beard et al. (2001), Dai et al. (2018), and He et al. (2019)), the consensus problem (Yuan et al. (2008) and Li et al. (2015)), and the flocking problem (Olfati-Saber (2006) and Chen et al. (2019)) in MASs.

In practice, most control systems are subjected to uncertainties caused by time delay, inaccurate modeling, or external disturbance, which may largely degrade the system performance somehow. Therefore, it is of significant practical importance to investigate the control system with uncertainties, giving rise to numerous available developments in the literature. Chen W. H. et al. (2016) carry out detailed and comprehensive analysis on many anti-interference/uncertainty methods, including disturbance-observer-based-control (DOBC), active disturbance rejection control (ADRC), and other methods, and discuss and compare the design process of each disturbance rejection method. Kempf and Kobayashi (1999) design the discrete-time tracking controller by using the disturbance observer and proportional derivative (PD) compensation for precision positioning table actuated by direct-drive motors. For the containment control problem of the multi-agent system, Xiao et al. (2017) use the disturbance observer to estimate the exogenous disturbances, and propose the distributed containment control protocol, and obtain sufficient conditions by using Lyapunov theories. Chen C. L. P. et al. (2016) studied the tracking control problem of second-order MASs with nonlinear dynamics, immeasurable states, and disturbances, and used the fuzzy system and adaptive high-gain observer to estimate the unknown nonlinear dynamics and unmeasured states, respectively. Ding (2015) uses the relative state information to reject part of the disturbances that impact the common trajectories and obtain the consensus conditions. As for three-phase two-level grid-connected power converters, Liu et al. (2017) put forward the extended state observer (ESO) by virtue of second-order sliding-mode control such that the currents can track the desired values for a high performance.

Despite the considerable advances on the consensus of MASs subjected to external disturbances, the communications resource consumption poses a more difficult problem. Note that the communication and computing resources in MASs are usually limited. Frequent communications between agents do not always enhance the control performance. It may result in a waste of resources, poor performance, and even system crash. Motivated by this, this paper proposes a self-triggered control strategy by improving the centralized event-triggered mechanism raised in Wu et al. (2018), Cheng and Li (2019), He et al. (2020), Hu et al. (2020), and Li et al. (2017) with the use of a disturbance observer. The contribution of this paper is that 1) we design a distributed disturbance observer to estimate the external disturbance of each agent in real time and reduce the influence of disturbances, and 2) we design a self-triggered control strategy, which can effectively reduce the updating times of agent control law and reduce the network burden on the premise of ensuring the consensus of MASs. At the same time, we show that there is no Zeno behavior in the proposed self-triggered control strategy. Compared with the traditional event-triggered control strategy (Li et al. (2017), Cheng and Li (2019), and He et al. (2020)), the self-triggered control strategy proposed in this paper not only has a simple structure and does not occupy a large amount of computing resources of every agent, but also does not require external devices to monitor error signals in real time, which saves costs to some extent.

The rest of this paper is organized as follows. Section 2 introduces the basic ides of graph theory and gives some useful definitions and lemmas. Section 3 includes the design process of our methods; that is, the design of the disturbance observer, and the event-triggered mechanism. We show that the proposed disturbance observer can estimate the external disturbance signal exponentially, and the self-triggered control mechanism can make the system consensus without Zeno behavior. The simulation experiment is presented in Section 4 to verify the effectiveness of our theorems, and conclusions are given in Section 5.

2 Materials and Methods

2.1 Graph Theory

Let us begin the section with notations in this paper. A^T represents the transpose of matrix A. $‖\cdot ‖$ represents the Euclidean norm of a matrix or vector. For a complex number x, the real part is denoted by Re(x). The eigenvalue of matrix A is denoted by λ(A). For a matrix A, we say that A is Hurwitz if and only if all eigenvalues of A have negative real parts.

Then we shall introduce some background on graph theory. Let $G=\left(V,E,A\right)$ be a graph of order $n\left(n\ge 2\right)$, where $V=\left\{v_1,v_2,\dots ,v_n\right\}$, E ⊆ V × V, and $A=\left[a_{ij}\right]$ are called the set of nodes, the set of edges, and the adjacency matrix, respectively. Each edge is denoted by $e_{ij}=\left(v_i,v_j\right)\in E,i,j\in I$.The adjacency elements associated with the edges of the graph are positive, i.e.,e_ij ∈ E if and only if a_ij > 0. If all agents do not have self-loops, i.e., a_ii = 0 for all i ∈ I. The set of neighbors of node v_i is denoted by $N_i=\left\{v_j\in V:\left(v_j,v_i\right)\in E\right\}$. The Laplacian matrix $L=\left[l_{ij}\right]$ can be written as follows:

$l_{ij}=\left\{\begin{array}{c}\sum _{j=1,j\ne i}^n{a}_{ij},j=i,\hfill \\ -a_{ij},j\ne i.\hfill \end{array}\right.$

2.2 Problem Formulation

In this paper, we consider the following systems:

$\dot{x_i}\left(t\right)=u_i\left(t\right)+w_i\left(t\right)(1)$

where x_i(t), u_i(t), and w_i(t) are the system state, system input, and external disturbance of the i-th agent, respectively. The following are the essential assumption and definition used in this paper.

Assumption 1 The disturbance in the MAS control channel is harmonic or periodic noise, which can be described by the external system,

$\left\{\begin{array}{c}{\dot{\xi }}_i\left(t\right)=W{\xi }_i\left(t\right),\hfill \\ w_i\left(t\right)=Y{\xi }_i\left(t\right),\hfill \end{array}\right.$

where Y is a known constant matrix and (W, Y) is observable. The matrices W and Y determine the upper bound of the disturbances w_i(t).

Definition 1 Consider the linear continuous-time MAS with n agents. For any initial state x_i(0), there exists some distributed control protocol such that

$\underset{t\to \infty }{\lim }‖x_i\left(t\right)-x_j\left(t\right)‖=0(2)$

for all i, j = 1, 2, … , n, i ≠ j, then Equation 1 achieves consensus.To achieve consensus in the multi-agent network, we consider the following distributed linear control:

$u_i\left(t\right)=\sum _{v_j\in N_i}{a}_{ij}\left[x_j\left(t\right)-x_i\left(t\right)\right]-\widehat{w_i}\left(t\right),(3)$

Under protocol Equation 3, system Equation 1 is equivalent to

$\dot{x_i}\left(t\right)=\sum _{v_j\in N_i}{a}_{ij}\left[x_j\left(t\right)-x_i\left(t\right)\right]-\widehat{w_i}\left(t\right)+w_i\left(t\right),(4)$

The following lemma is essential in our subsequent results.

Lemma 1| Assume matrix $A\in {\mathbb{R}}^{n\times m}$, $B\in {\mathbb{R}}^{m\times p}$ and vector $x\in {\mathbb{R}}^m$. The following inequalities hold

(1) ‖AB‖ ≤ ‖A‖‖B‖,

(2) ‖Ax‖ ≤ ‖A‖‖x‖.

3 Main Results

In this section, we shall elaborate our main results on the consensus of MASs subjected to external disturbances. As depicted by Figure 1, the system (1) is partitioned into two parts, one is the design of the disturbance observer, the other is the event-triggered mechanism. More specifically, the disturbance observer performs continuous real-time estimation of an external disturbance and compensates the estimation to the plant to eliminate the influence of the disturbance. The switch is used in the event-triggered control, while the change of control input is segmented.

FIGURE 1

FIGURE 1. Control structure of the system (1).

3.1 Disturbance Observer Design

The first part is the design of the disturbance observer. Since the system Equation 1 is affected by the external disturbance w_i(t), we use the disturbance-observer-based control to estimate the existing disturbance. To reduce the adverse impact of the disturbance, we compensate the control input u_i(t) according to the disturbance estimate obtained by the disturbance observer. Here we put forward the theorem:

Theorem 1 Consider the MAS (Equation 1) subjected to the external disturbance w_i(t). The disturbance observer is as follows:

$\left\{\begin{array}{cc}\dot{z_i}\left(t\right)\hfill & =\left(W-KY\right)\left(z_i\left(t\right)-K{x}_i\left(t\right)\right)-K{u}_i\left(t\right),\hfill \\ \widehat{{\xi }_i}\left(t\right)\hfill & =z_i\left(t\right)+K{x}_i\left(t\right),\hfill \\ \widehat{w_i}\left(t\right)\hfill & =Y\widehat{{\xi }_i}\left(t\right),\hfill \end{array}\right.(5)$

where i = 1, 2, … , n, z_i(t) is an intermediate vector, K is some constant matrix, $\widehat{{\xi }_i}(t)$ and $\widehat{w_i}(t)$ are the estimates of ξ_i(t) and w_i(t), respectively. Then, the observed value of the external disturbance converges to w_i(t) asymptotically.

Proof 1| Denote the estimation error by

$e_{\xi }^i\left(t\right)={\xi }_i\left(t\right)-\widehat{{\xi }_i}\left(t\right).(6)$

The following equation is readily derived:

$\begin{array}{cc}\hfill {\dot{e}}_{\xi }^i\left(t\right)& =W{\xi }_i\left(t\right)-\left(\dot{z_i}\left(t\right)+K\dot{x_i}\left(t\right)\right)\hfill \\ \hfill & =W{\xi }_i\left(t\right)-\left[\left(W-KY\right)\left(\widehat{{\xi }_i}\left(t\right)-K{x}_i\right)\left.\right)+WK{x}_i\left(t\right)+K\left(u_i\left(t\right)+KY{x}_i\right)+K\left(u_i\right)+Y{\xi }_i\left(t\right)\left.\right)\right]\hfill \\ \hfill & =W{\xi }_i\left(t\right)-\left[\left(W-KY\right){\widehat{\xi }}_i\left(t\right)+KY{\xi }_i\left(t\right)\right]\hfill \\ \hfill & =W{\xi }_i\left(t\right)-KY{\xi }_i\left(t\right)-\left(W-KY\right)\widehat{{\xi }_i}\left(t\right)\hfill \\ \hfill & =\left(W-KY\right)e_{\xi }^i\left(t\right).\hfill \end{array}(7)$

Noting that (W, Y) is observable, there exists a matrix K such that the matrix (W − KY) is Hurwitz. Hence, the system Equation 6 is asymptotically stable. Therefore, the disturbance estimate ${\widehat{w}}_i(t)$ can asymptotically estimate the actual external disturbance signal w_i(t).The proof is thus completed.Under the premise that (W − KY) is Hurwitz, if we choose K such that Re (λ(W − KY)) is smaller, according to Equation 7, the estimate error e_ξ(t) will converge to zero slower, at the same time, the multi-agent system Equation 1 will be more affected by the disturbance observer, which shows that there is a big difference between the final convergence of the system Equation 1 and that of the system without disturbance. Therefore, in the process of application, if we do not want to make a big change in the convergence state of the system, we can choose K to make Re (λ(W − KY)) close to 0. When the agent is affected by the external disturbance signal w_i(t), its state shows an obvious periodic fluctuation, and at the same time, the estimate error $e_{\xi }^i(t)$ of the disturbance observer is very close to 0, so the convergence state of the system will not be very different from the convergence state of the system without the disturbance.

3.2 Event-Triggered Control Mechanism Design

In the MAS Equation 1 subjected to external disturbance w_i(t), we denote the state measurement error by

$e_i\left(t\right)=x_i\left(t_i\right)-x_i\left(t\right),t\in \left[t_i,t_{i+1}\right)(8)$

where t_i represents the i-th triggering instant of the multi-agent system Equation 1.

For the sake of convenience, we write e_i(t), w_i(t), and ${\widehat{w}}_i(t)$ in vector form

$\begin{array}{c}\hfill e\left(t\right)={\left[e_1\left(t\right)e_2\left(t\right)\dots ,e_n\left(t\right)\right]}^T\hfill \\ \hfill w\left(t\right)={\left[w_1\left(t\right)w_2\left(t\right)\dots ,w_n\left(t\right)\right]}^T\hfill \\ \hfill \widehat{w}\left(t\right)={\left[{\widehat{w}}_1\left(t\right){\widehat{w}}_2\left(t\right)\dots ,{\widehat{w}}_n\left(t\right)\right]}^T\hfill \end{array}$

Then the proposed control law in the centralized case is defined as

$u\left(t\right)=-Lx\left(t_i\right)-\widehat{w}\left(t\right)(9)$

Given Equation 8, the closed loop system is set up as

$\dot{x}\left(t\right)=-Lx\left(t_i\right)+w\left(t\right)-\widehat{w}\left(t\right)=-L\left(x\left(t\right)+e\left(t\right)\right)+w\left(t\right)-\widehat{w}\left(t\right)(10)$

Construct the Lyapunov function as follows:

$V=\frac{1}{2}{x}^{T}Lx(11)$

Then

$\begin{array}{cc}\dot{V}\hfill & \hfill =x^{T}L\dot{x}\hfill \\ \hfill \hfill & =x^{T}L\left(-L\left(x\left(t\right)+e\left(t\right)\right)+w\left(t\right)-\widehat{w}\left(t\right)\right)\hfill \\ \hfill \hfill & =-x^{T}LLe-x^{T}LLx+x^{T}L{e}_w\hfill \\ \hfill \hfill & \le -\Vert Lx{\Vert }^2+\Vert Lx\Vert \Vert L\Vert \Vert e\Vert +\Vert Lx\Vert \Vert e_w\Vert \hfill \end{array}$

where $e_w(t)=w(t)-\widehat{w}(t)$.

Through the design of the disturbance observer, lim_t→∞e_w(t) = 0, the following inequality holds:

$\begin{array}{c}\hfill \underset{t\to \infty }{\lim }\dot{V}=-x^{T}LLe-x^{T}LLx\hfill \\ \hfill \le -\Vert Lx{\Vert }^2+\Vert Lx\Vert \Vert L\Vert \Vert e\Vert \hfill \end{array}$

Let e satisfy

$\Vert e\Vert \le \sigma \frac{\Vert Lx\Vert }{\Vert L\Vert }$

with σ > 0, we have

$\dot{V}\le \left(\sigma -1\right)\Vert Lx{\Vert }^2(12)$

Therefore, $\dot{V}<0$ if σ ∈ (0, 1).

Consequently, we design the following event-triggered condition:

$event\left\{\begin{array}{cc}occurs,when\hfill & \Vert e\Vert \ge \sigma \frac{\Vert Lx\Vert }{\Vert L\Vert },\hfill \\ does{n}^{\prime }toccur,when\hfill & \Vert e\Vert <\sigma \frac{\Vert Lx\Vert }{\Vert L\Vert },\hfill \end{array}\right.(13)$

In the centralized event-triggered condition Equation 13, external devices are required to continuously monitor the measurement error ‖e(t)‖ of the system, which undoubtedly increases the cost of the system. Here, we improve the event-triggered condition proposed above and propose a novel self-triggering control method.

Theorem 2 Consider the MAS Equation 1 subjected to the external disturbance w(t), where the communication topology is undirected graph. The system can achieve consensus if the control input (Equation 3) and self-triggered condition (Equation 14) are adopted, where (i + 1)-th triggering instant is determined by i-th triggering instant and the system state x(t) with

$t_{i+1}=t_i+\frac{\sigma \Vert Lx\left(t\right)\Vert }{\Vert L\Vert \left(\Vert Lx\left(t_i\right)\Vert +\Vert e_w\left(t_i\right)\Vert \right)}(14)$

where σ is some constant within the range [0, 1]. Furthermore, the Zeno behavior can be ruled out.

Proof 2 Consider the time interval t ∈ (t_i, t_i+1). The system Equation 10 is equivalent to

$\dot{x}\left(t\right)=-Lx\left(t_i\right)+e_w\left(t\right)(15)$

Take the integral of Equation 15 from both sides. We are led to

$x\left(t\right)-x\left(t_i\right)=-Lx\left(t_i\right)\left(t-t_i\right)+{\int }_{t_i}^t{e}_w\left(s\right)ds(16)$

Note that e_w(t) exponentially converges to zero, and $|e_w^i(t_i)|\ge |e_w^i(t)|$ for t ∈ [t_i, ∞).Equation 16 can be rewritten as

$\begin{array}{cc}\hfill \Vert x\left(t\right)-x\left(t_i\right)\Vert \hfill & \hfill =\Vert -Lx\left(t_i\right)\left(t-t_i\right)+{\int }_{t_i}^t{e}_w\left(s\right)ds\Vert \hfill \\ \hfill \hfill & \hfill \le \Vert -Lx\left(t_i\right)\left(t-t_i\right)\Vert +\Vert {\int }_{t_i}^t{e}_w\left(s\right)ds\Vert \hfill \\ \hfill \hfill & \hfill \le \Vert Lx\left(t_i\right)\Vert \left(t-t_i\right)+\Vert e_w\left(t_i\right)\Vert \left(t-t_i\right)\hfill \\ \hfill \hfill & \hfill =\left(t-t_i\right)\left(\Vert Lx\left(t_i\right)\Vert +\Vert e_w\left(t_i\right)\Vert \right)\hfill \end{array}$

Then with the definition of e(t), Equation 13 is rewritten as

$\sigma \frac{\Vert Lx\left(t\right)\Vert }{\Vert L\Vert }\le \left(t-t_i\right)\left(\Vert Lx\left(t_i\right)\Vert +\Vert e_w\left(t_i\right)\Vert \right)(17)$

or equivalently,

$t-t_i\ge \frac{\sigma \Vert Lx\left(t\right)\Vert }{\Vert L\Vert \left(\Vert Lx\left(t_i\right)\Vert +\Vert e_w\left(t_i\right)\Vert \right)}(18)$

Here, the upper bound on the next trigger time t_i+1 is given by

$t^{*}-t_i=\frac{\sigma \Vert Lx\left(t\right)\Vert }{\Vert L\Vert \left(\Vert Lx\left(t_i\right)\Vert +\Vert e_w\left(t_i\right)\Vert \right)}(19)$

We denote inter-execution time by T = t* − t_i, so

$T=\frac{\sigma \Vert Lx\left(t\right)\Vert }{\Vert L\Vert \left(\Vert Lx\left(t_i\right)\Vert +\Vert e_w\left(t_i\right)\Vert \right)}>0(20)$

Note that Lx and e_w are indicators used to represent the consensus problem of the multi-agent system and the estimation performance of the disturbance observer Equation 5, respectively. Lx = 0 means that the system achieves consensus. e_w = 0 shows that the observer estimates the external disturbance signals perfectly.The proof is thus completed.For the case that the communication topology of the agent system is a directed graph, the Lyapunov function Equation 11 can be modified, and the corresponding event-triggered mechanism can be designed according to a similar process.If the communication topology of the system changes due to some external factors, the event should get triggered in the moments of switching topology (see Li et al. (2015)).

4 Experimental Examples

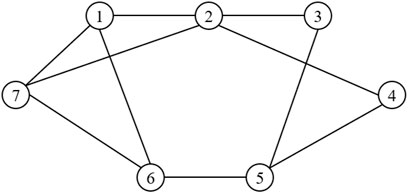
In this section, we will use several examples to verify the effectiveness of the above-mentioned control method. Here in this scenario, we consider a multi-agent network system consisting of seven agents. These agents’ initial states are x (0) = (40, 55, 75, 60, 80, 20, 15)^T, respectively. Select σ = 0.9. The communication network of the system is depicted in Figure 2.

FIGURE 2

FIGURE 2. Communication topology.

Then the Laplacian matrix is

$L=\left[\begin{array}{ccccccc}\hfill 3\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill -1\hfill \\ \hfill -1\hfill & \hfill 4\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill \\ \hfill 0\hfill & \hfill -1\hfill & \hfill 2\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 2\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill 3\hfill & \hfill -1\hfill & \hfill 0\hfill \\ \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 3\hfill & \hfill -1\hfill \\ \hfill -1\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 3\hfill \end{array}\right]$

Suppose that the external disturbance signal w_i(t) is generated by the following external system:

$\left\{\begin{array}{cc}\hfill & {\dot{\xi }}_i\left(t\right)=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 5\hfill \\ \hfill -5\hfill & \hfill 0\hfill \end{array}\right]{\xi }_i\left(t\right),\hfill \\ \hfill & w_i\left(t\right)=\left[63\right]{\xi }_i\left(t\right),\hfill \end{array}\right.$

Here, let$\begin{array}{c}\hfill {\xi }_1\left(0\right)={\left[1.15040.1196\right]}^T,{\xi }_2\left(0\right)={\left[0.46960.7063\right]}^T,{\xi }_3\left(0\right)={\left[1.64240.0308\right]}^T,{\xi }_4\left(0\right)={\left[0.08600.3380\right]}^T,{\xi }_5\left(0\right)={\left[1.29821.4634\right]}^T,{\xi }_6\left(0\right)={\left[1.29550.9018\right]}^T,{\xi }_7\left(0\right)={\left[1.09400.5926\right]}^T\hfill \end{array}$be the initial state of the external disturbance system.

To make the matrix (W − KY) mentioned in Equation 7 be Hurwitz, we choose the observer gain matrix $K={[\frac{1}{3}\frac{43}{3}]}^T$.

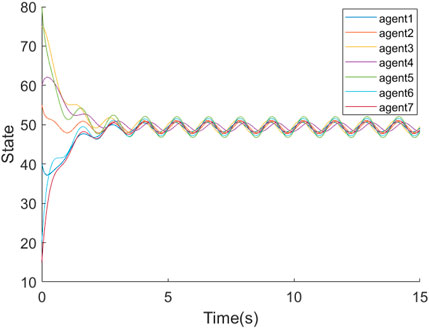
When the multi-agent system is exposed to external disturbances w_i(t), as shown in Figure 3, the state of each agent produces periodic fluctuations after a transition time of about 10 s, but the agents’ states do not converge over time, implying that the presence of external disturbances may prevent the system from achieving consensus.

FIGURE 3

FIGURE 3. The states of a multi-agent system without the disturbance observer.

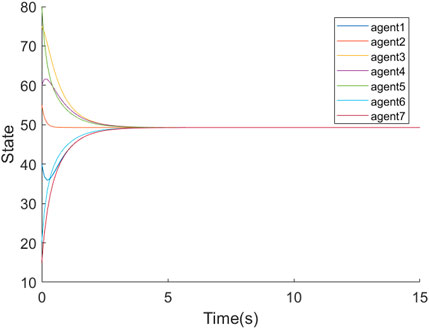
As shown in Figure 4, when a disturbance observer Equation 5 is added, the states of the five agents converge after about 20 s and the whole system eventually achieves consensus, despite the influence of external disturbance signals w_i(t) in the input channel of agents, due to the inclusion of a disturbance suppression term in the control input term.

FIGURE 4

FIGURE 4. The states of a multi-agent system with the disturbance observer.

Figure 5 shows the state of the multi-agent system unaffected by external disturbance w_i(t). Comparing Figures 4 and 5, it can be seen that although the system converges for each agent after the addition of the disturbance observer Equation 5, the convergence value of the system after the disturbance suppression term $\widehat{w_i}(t)$ is not the same as the convergence value of the system without external disturbance, which is mainly due to the influence of the disturbance observer gain matrix K.

FIGURE 5

FIGURE 5. The states of a multi-agent system without the external disturbance.

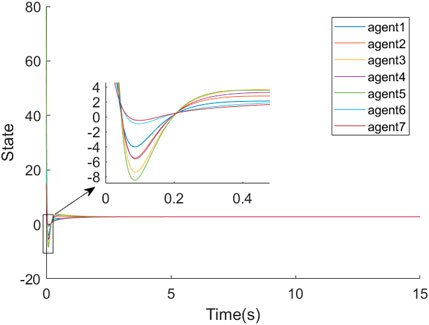
Figure 6 depicts the curve of the measurement error norm ‖e(t)‖ over time. At about 3 s, ‖e(t)‖ is very close to 0. It can be known from the above theoretical analysis.

FIGURE 6

FIGURE 6. The error norm ‖e(t)‖ of seven agents evolves under the self-triggered control method.

For the sake of simplicity, Figure 7 only shows the evolution of the estimate of the external disturbance w₁(t). Other disturbance estimates are similar to those shown in Figure 7. From the curves, we can see that the estimate $\widehat{w_1}(t)$ is very close to w₁(t) at about 0.5 s. Here if we take a bigger observer gain K such that Re (λ(W − KY)) is smaller, the estimated error e_w will converge to zero faster.

FIGURE 7

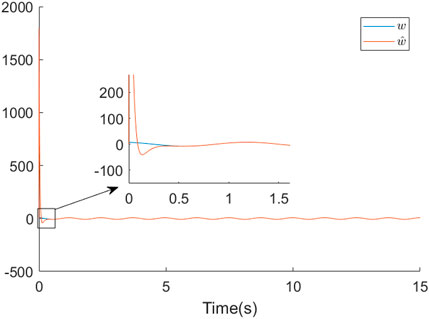
FIGURE 7. The comparison between the real external disturbance signal w(t) and the estimate signal $\widehat{w}(t)$.

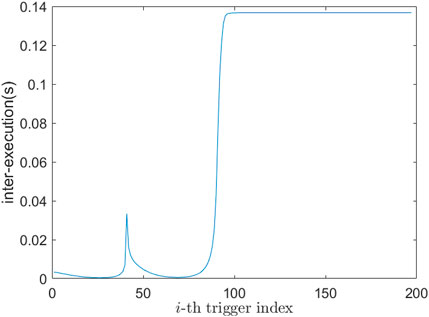
The evolution of inter-execution time is depicted in Figure 8. In the simulation time of 15 s, the simulation step size is 0.0001 s, and the event is triggered 198 times, that is, the triggering probability of the event is 0.132%. There are several key triggering instants in Figure 8, which are the 26th, 41st, 68th, and 100th triggered indexes, respectively. The corresponding time of these triggered indexes are 0.0 399 s, 0.0 635 s, 0.2 068 s, and 1.4 671 s, respectively. It can be seen from Figure 4, at 0.0 399 s and 0.2 068 s, the states of the seven agents are close, Lx(t) ≈ 0_7×1, according to Equation 20, which makes inter-execution time be close to 0 at this time. After 0.0 635 s, the reason for the larger inter-execution time is mainly caused by the larger ‖Lx(t)‖. Over time, because e_w(t) converges to 0, i.e., $T\approx \frac{\sigma \Vert Lx(t)\Vert }{\Vert L\Vert \Vert Lx(t_i)\Vert }$, the inter-execution time remains near 0.1367s, or equivalently, $\frac{\Vert Lx(t)\Vert }{\Vert Lx(t_i)\Vert }=0.74$, which means the event occurs when ‖Lx(t)‖ = 0.74‖Lx (t_i)‖. Specifically, if we increase the value of σ, the event will be harder to trigger, and the ratio $\frac{\Vert Lx(t)\Vert }{\Vert Lx(t_i)\Vert }$ will be smaller, and vice versa.

FIGURE 8

FIGURE 8. The inter-execution time between two contiguous triggering instants.

5 Conclusion

This paper studies the consensus problem of a multi-agent system with external disturbance based on self-triggered control. Through the designed disturbance observer, the estimate error can converge to 0 exponentially for periodic external disturbance signals. On this basis, we design a self-triggered control strategy, and the multi-agent system can achieve consensus under this control protocol. In addition, we obtain a strict positive lower bound of the inter-execution through theoretical analysis, which rules out the possibility of Zeno behavior. Finally, the simulation results show that the proposed control algorithm can suppress external disturbances and make the system achieve consensus.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This research was supported in part by the China Postdoctoral Science Foundation under Grant 2019T120427, in part by the Fundamental Research Funds for the Central Universities under Grant NS2020023, and in part by the Macao Young Scholars Program under Grant AM2020006.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Beard, R. W., Lawton, J., and Hadaegh, F. Y. (2001). A Coordination Architecture for Spacecraft Formation Control. IEEE Trans. Contr. Syst. Technol. 9, 777–790. doi:10.1109/87.960341

CrossRef Full Text | Google Scholar

Chen, C. L. P., Ren, C.-E., and Du, T. (2016). Fuzzy Observed-Based Adaptive Consensus Tracking Control for Second-Order Multiagent Systems with Heterogeneous Nonlinear Dynamics. IEEE Trans. Fuzzy Syst. 24, 906–915. doi:10.1109/tfuzz.2015.2486817

CrossRef Full Text | Google Scholar

Chen, W.-H., Yang, J., Guo, L., and Li, S. (2016). Disturbance-Observer-Based Control and Related Methods-An Overview. IEEE Trans. Ind. Electron. 63, 1083–1095. doi:10.1109/tie.2015.2478397

CrossRef Full Text | Google Scholar

Chen, S., Pei, H., Lai, Q., and Yan, H. (2019). Multitarget Tracking Control for Coupled Heterogeneous Inertial Agents Systems Based on Flocking Behavior. IEEE Trans. Syst. Man. Cybern, Syst. 49, 2605–2611. doi:10.1109/tsmc.2017.2789335

CrossRef Full Text | Google Scholar

Cheng, B., and Li, Z. (2019). Fully Distributed Event-Triggered Protocols for Linear Multiagent Networks. IEEE Trans. Automat. Contr. 64, 1655–1662. doi:10.1109/tac.2018.2857723

CrossRef Full Text | Google Scholar

Dai, S.-L., He, S., Lin, H., and Wang, C. (2018). Platoon Formation Control with Prescribed Performance Guarantees for Usvs. IEEE Trans. Ind. Electron. 65, 4237–4246. doi:10.1109/tie.2017.2758743

CrossRef Full Text | Google Scholar

Ding, Z. (2015). Consensus Disturbance Rejection with Disturbance Observers. IEEE Trans. Ind. Electron. 62, 5829–5837. doi:10.1109/tie.2015.2442218

CrossRef Full Text | Google Scholar

He, S., Wang, M., Dai, S.-L., and Luo, F. (2019). Leader-Follower Formation Control of USVs with Prescribed Performance and Collision Avoidance. IEEE Trans. Ind. Inf. 15, 572–581. doi:10.1109/tii.2018.2839739

CrossRef Full Text | Google Scholar

He, W., Xu, B., Han, Q.-L., and Qian, F. (2020). Adaptive Consensus Control of Linear Multiagent Systems with Dynamic Event-Triggered Strategies. IEEE Trans. Cybern. 50, 2996–3008. doi:10.1109/tcyb.2019.2920093

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, W., Yang, C., Huang, T., and Gui, W. (2020). A Distributed Dynamic Event-Triggered Control Approach to Consensus of Linear Multiagent Systems with Directed Networks. IEEE Trans. Cybern. 50, 869–874. doi:10.1109/tcyb.2018.2868778

PubMed Abstract | CrossRef Full Text | Google Scholar

Kempf, C. J., and Kobayashi, S. (1999). Disturbance Observer and Feedforward Design for a High-Speed Direct-Drive Positioning Table. IEEE Trans. Contr. Syst. Technol. 7, 513–526. doi:10.1109/87.784416

CrossRef Full Text | Google Scholar

Li, H., Chen, Z., Wu, L., Lam, H.-K., and Du, H. (2017). Event-triggered Fault Detection of Nonlinear Networked Systems. IEEE Trans. Cybern. 47, 1041–1052. doi:10.1109/tcyb.2016.2536750

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Z., Wen, G., Duan, Z., and Ren, W. (2015). Designing Fully Distributed Consensus Protocols for Linear Multi-Agent Systems with Directed Graphs. IEEE Trans. Automat. Contr. 60, 1152–1157. doi:10.1109/tac.2014.2350391

CrossRef Full Text | Google Scholar

Liu, J., Vazquez, S., Wu, L., Marquez, A., Gao, H., and Franquelo, L. G. (2017). Extended State Observer-Based Sliding-Mode Control for Three-phase Power Converters. IEEE Trans. Ind. Electron. 64, 22–31. doi:10.1109/tie.2016.2610400

CrossRef Full Text | Google Scholar

Olfati-Saber, R. (2006). Flocking for Multi-Agent Dynamic Systems: Algorithms and Theory. IEEE Trans. Automat. Contr. 51, 401–420. doi:10.1109/tac.2005.864190

CrossRef Full Text | Google Scholar

Wu, Z.-G., Xu, Y., Lu, R., Wu, Y., and Huang, T. (2018). Event-triggered Control for Consensus of Multiagent Systems with Fixed/switching Topologies. IEEE Trans. Syst. Man. Cybern, Syst. 48, 1736–1746. doi:10.1109/tsmc.2017.2744671

CrossRef Full Text | Google Scholar

Xiao, B., Han, T., Tang, Q., and Jin, T. (2017). “Containment Control of Multiagent Systems: A Dobc Approach,” in 2017 13th IEEE Conference on Automation Science and Engineering (CASE), 1577–1580. doi:10.1109/coase.2017.8256328

CrossRef Full Text | Google Scholar

Yuan, G. S., Long, W., and Xie, G. (2008). Average Consensus in Networks of Dynamic Agents with Switching Topologies and Multiple Time-Varying Delays. Syst. Control. Lett. 57, 175–183.

Google Scholar