Brain modeling for control: A review

Neurostimulation technologies have seen a recent surge in interest from the neuroscience and controls communities alike due to their proven potential to treat conditions such as epilepsy, Parkinson’s Disease, and depression. The provided stimulation can be of different types, such as electric, magnetic, and optogenetic, and is generally applied to a specific region of the brain in order to drive the local and/or global neural dynamics to a desired state of (in)activity. For most neurostimulation techniques, however, an underlying theoretical understanding of their efficacy is still lacking. From a control-theoretic perspective, it is important to understand how each stimulus modality interacts with the inherent complex network dynamics of the brain in order to assess the controllability of the system and develop neurophysiologically relevant computational models that can be used to design the stimulation profile systematically and in closed loop. In this paper, we review the computational modeling studies of 1) deep brain stimulation, 2) transcranial magnetic stimulation, 3) direct current stimulation, 4) transcranial electrical stimulation, and 5) optogenetics as five of the most popular and commonly used neurostimulation technologies in research and clinical settings. For each technology, we split the reviewed studies into 1) theory-driven biophysical models capturing the low-level physics of the interactions between the stimulation source and neuronal tissue, 2) data-driven stimulus-response models which capture the end-to-end effects of stimulation on various biomarkers of interest, and 3) data-driven dynamical system models that extract the precise dynamics of the brain’s response to neurostimulation from neural data. While our focus is particularly on the latter category due to their greater utility in control design, we review key works in the former two categories as the basis and context in which dynamical system models have been and will be developed. In all cases, we highlight the strength and weaknesses of the reviewed works and conclude the review with discussions on outstanding challenges and critical avenues for future work.

1 Introduction

Neurostimulation technologies have shown promising, initial success over the last 20 years in treating neurological disorders such as drug-resistant epilepsy (DRE), Parkinson’s disease (PD), and psychological conditions such as depression (Marangell et al., 2007; Ben-Menachem, 2012; Lin and Wang, 2017). Stimulation of the brain is also being increasingly used as a means to map the functional properties of various regions of the brain (Mandonnet et al., 2010) and is also seen as a mode to enhance sensory-motor activity (Jones et al., 2015; Toth et al., 2021). While the potency of external electromagnetic stimulation has been established in the literature and neuromodulation under varying input conditions has been studied, clinical delivery of stimulation has largely been applied in an open-loop expert-driven manner where constant stimulation is provided for large periods of time (sometimes months). Such open-loop stimulation has been associated with inconsistent responses and sub-optimal modulation which can be linked to the high sensitivity of the brain to stimulation parameters (Deeb et al., 2016). Although closed-loop control of stimulation can potentially help address these issues (e.g., the RNS^®system from NeuroPace, Inc. (Skarpaas et al., 2019)), a large majority of works have focused on ON-OFF control that relies on medically-derived biomarkers such as signal line length, signal power in certain frequency bands, or tremor onset as opposed to predictive evaluation of the brain’s response to stimulation. These factors, together with the low efficacy of state-of-the-art controllers (e.g., complete seizure abatement in the case of the RNS^®system was reported in only 20% of individuals) and the demand for more energy-efficient systems (Ramirez-Zamora et al., 2018) make stimulation tuning via fully closed loop control a necessity.

A major hurdle in the development of fully-closed-loop controllers is the mechanistic complexity of the brain and modeling its response to various forms of stimulation. Despite the rising relevance of neurostimulation and the rapid advancement in brain activity monitoring systems (e.g., fMRI, iEEG), the exact mechanism through which neurostimulation inputs interact with the brain connectome is still poorly understood. In this paper, we present a focused review of methods employed in the literature towards understanding the response of the brain to five of the most commonly used neurostimulation techniques, namely, deep brain stimulation (DBS), transcranial magnetic stimulation (TMS), direct electric stimulation (DES), transcranial electric stimulation (tES), and optogenetic stimulation.

Existing reviews on different neurostimulation methods have largely focused on the efficacy of each method towards treating conditions such as PD, depression, or epilepsy and have had little emphasis on the brain modeling approaches that have been employed for each method (Magis and Schoenen, 2012; De Raedt et al., 2015; Schoenen et al., 2016; Kassiri et al., 2017; Starnes et al., 2019). A few works have provided focused reviews of specific stimulation mechanisms (Chervyakov et al., 2015; Montagni et al., 2019) based on the underlying neuroscience and usage of different biomarkers towards adaptive stimulation (Bouthour et al., 2019). In Lozano et al. (2019) and Herrington et al. (2016), the authors have compiled various neural mechanisms (the inhibition of thalamic neurons, e.g.) explaining the DBS response to a range of disorders. To the best of our knowledge, existing reviews lack compiled collections of works on the modeling of the brain’s response to various neurostimulation techniques, hence motivating the present review.Broadly, the computational modeling studies of the aforementioned neurostimulation methods can be categorized into three types of approaches:

1) Works that use electric field equations and/or neuron models to build biophysically-derived models of the interaction between the stimulation input and the brain. These models are often parameterized by factors such as conductivity and geometry of brain tissues and are tuned to mimic observed data. As such, they are then commonly simulated to computationally optimize stimulation parameters such as input location and intensity.

2) Works that use statistical and machine learning tools such as correlation, hypothesis testing, and/or artificial neural networks to model the overall stimulus-response profile of stimulation. Unlike the theory-driven nature of the first category, these models are fundamentally data-driven. However, they often are not intended to capture the temporal dynamics of the brain’s response to neurostimulation, as done by the last category.

3) Lastly, we have works where the impact of neurostimulation on the brain’s network neural dynamics is learned using observed input-output time series data. In general, these methods do not make any assumptions regarding the underlying biophysics and rely mainly on data-driven algorithms. For simplicity of exposition, we will refer to this latter category as “Dynamical System Models” while acknowledging the presence of dynamical system components in several of the works in the biophysical category.

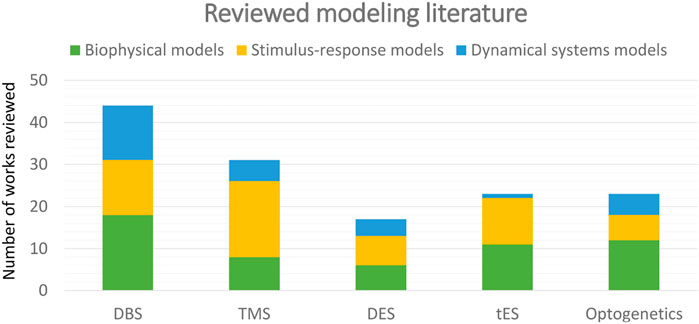
In the following section, we provide an itemized review of the existing literature for each of the aforementioned five neurostimulation technologies and three methodological categories, see Figure 1 for a pictorial summary. While the first two categories have longer histories and more studies uniformly across all the reviewed stimulation technologies as seen in Figures 1, 2, our particular focus in this review is on the dynamical systems models due to their applicability for therapeutic control design. A summary of models in this latter category is illustrated in Figure 3 with breakdowns over output variables, model structures, datasets, and model selection criteria. Nevertheless, we also review key studies and popular approaches in the biophysical and stimulus-response categories as they provide the historical context in which dynamical system models have been developed. Finally, we review modeling works in the context of some of the most commonly studied brain disorders in order to facilitate interested readers’ focused analyses of disease-specific literature.

FIGURE 1

FIGURE 1. Distribution of literature reviewed in this paper.

FIGURE 2

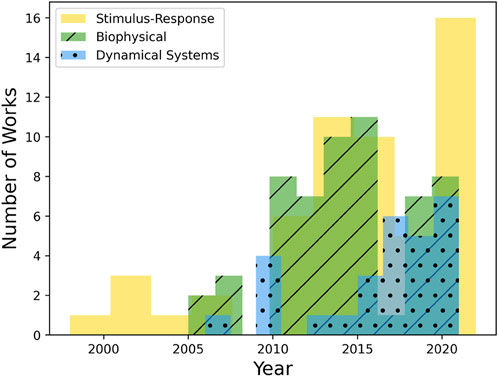
FIGURE 2. Year-wise spread of reviewed literature for the three types of approaches. The use of data-driven dynamical systems modeling has markedly increased in recent years while biophysical and stimulus-response models have been employed for significantly longer times. Important to note is the fact that this figure is only intended to inform comparisons between categories, not the absolute historical frequency of the use of each category. The latter would require a historically uniform synthesis of the literature, particularly for biophysical and stimulus-response categories, as opposed to the focus of the present review on more recent works.

FIGURE 3

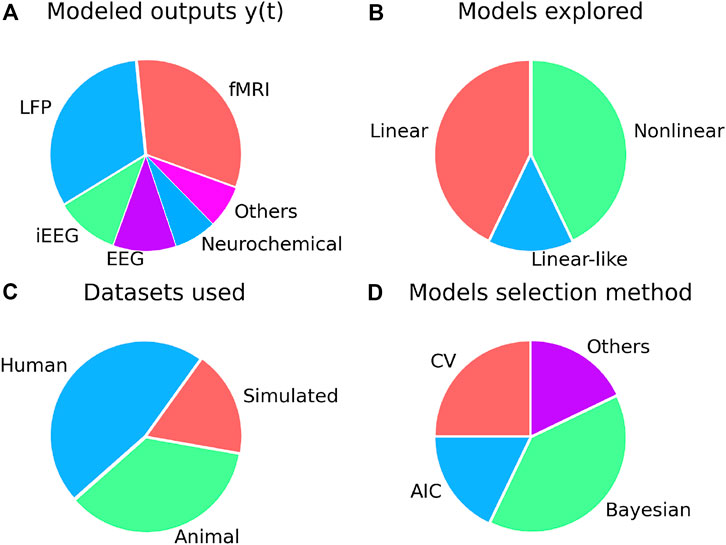
FIGURE 3. Summary of dynamical systems models reviewed in this survey. In (A), the distribution of modeled output y(t) is plotted as a pie chart. DCM-based works have for the most part used fMRI output, while LFP/EEG/iEEG is more commonly used in works that use linear models like ARX/LSSM. In (B), we plot the proportion of model classes used in the modeling of brain dynamics under stimulation. Non-linear models include DCM, and ANN, while hybrid linear and Volterra models are grouped as linear-like. (C) Distribution of type/source of datasets used across reviewed works. In panel (D), we present various model order selection methods used in the literature.

1.1 Review criteria

The works presented in this review were largely obtained using keyword search from the Google Scholar database. Searched keywords were generally of the form “{stimulation}+{approach}+{specific model}” where {stimulation} refers to one of the five neurostimulation techniques discussed in this paper, {approach} refers to one of three above-mentioned modeling approaches and {specific model} refers to commonly used modeling methods such as autoregressive models or neural networks. Our search provided us with a relatively larger number of literature for works concerning biophysical and stimulus-response models in comparison to dynamical system models. With the aim of keeping the review concise while investigating common modeling methods across literature, we have placed higher weight on more highly cited and recent works for inclusion in this review, while also carefully examining less cited and/or less recent works and including them if they provided sufficient methodological novelty or significance of findings compared to already-included references that would warrant an extended discussion. While the list of works reviewed here is not exhaustive, we hope to provide the reader with a broad and general understanding of prevailing methods that have been proposed for the modeling of the complex dynamics of the brain in response to neurostimulation. Finally, in the few cases where we refer to pre-prints which have not yet gone through peer-review, we indicate this with a ^† mark next to the publication year of the respective articles.

2 Modeling the Brain’s response to neurostimulation

Consider a standard state-space model

$\begin{array}{ll}\hfill \dot{\mathbf{x}}\left(t\right)\text{or}\mathbf{x}\left(t+1\right)& =f\left(\mathbf{x}\left(t\right),\mathbf{u}\left(t\right)\right)+\mathbf{w}\left(t\right),\hfill \\ \hfill \mathbf{y}\left(t\right)& =h\left(\mathbf{x}\left(t\right),\mathbf{u}\left(t\right)\right)+\mathbf{v}\left(t\right),\hfill \end{array}(1)$

where x(t), u(t), and y(t)¹ denote the system’s state, input, and output and w(t) and v(t) denote process and measurement noise. Network control models of this form have been used extensively, particularly over the past decade, to study various aspects of brain function and dynamics (see, e.g. (Chen and Sarma, 2017; Nozari et al., 2020^†; Gu et al., 2015; Kenett et al., 2018; Schiff, 2011; Becker et al., 2018; Yang et al., 2021; Singh et al., 2020; Pedoto et al., 2010; Nozari and Cortés, 2020)). Arguably, the most distinctive feature of these models compared to the classical dynamical systems models of the brain is the presence of the control input u(t).² However, the precise physiological meaning of the control term u(t) and its ties both to the brain’s intrinsic dynamics as well as to the measurable waveforms of neurostimulation are neither adequately understood nor a matter of consensus. In this section, we focus on neurostimulation and review recent research and progress in characterizing the meaning of the control input u(t) and its impact on the local and global dynamics of the brain in the context of the most widely studied neurostimulation technologies listed in Section 1.

2.1 Deep brain stimulation

Deep Brain Stimulation (DBS) is one of the oldest and most effective neurostimulation technologies with applications in various neuropsychiatric disorders (Ramirez-Zamora et al., 2018), particularly in treating movement disorders (Wichmann and DeLong, 2016) such as Parkinson’s disease (Ligaard et al., 2019). DBS involves the (invasive) placement of electrodes that penetrate to varying depths inside the brain and injection of electrical currents to the surrounding brain tissue using one or more contacts on the implanted electrode (Perlmutter and Mink, 2006). In this section, we first briefly review some of the key studies on the modeling of the low-level biophysics as well as the stimulus-response characteristics of DBS and then provide a more in-depth account of the data-driven dynamical system modeling studies thereof.

2.1.1 Biophysical models

The eye-catching success of DBS has led to significant computational research, both to understand its mechanisms of action and to optimize them (Herrington et al., 2016). A common approach has been a combination of finite element modeling to estimate the electrical field distribution in the tissue surrounding the DBS electrode and conductance-based neuron modeling simulated under the resulting electrical field to test whether the neurons in any given location will be sufficiently depolarized to generate an action potential (Teplitzky et al., 2016; Keane et al., 2012; Zitella et al., 2013; Birdno et al., 2012; Anderson et al., 2019; Anderson et al., 2020; van Dijk et al., 2018). In a (single-compartment) conductance-based model (CBM), each neuron is modeled as a capacitive element (Dayan and Abbott, 2001; Koch, 2004)

$C_i\frac{d}{dt}{v}_i\left(t\right)=I_i\left(t\right)+\sum _{j=1}^n{\bar{g}}_{ij}{p}_{ij}\left(t\right)\left[E_j-v_i\left(t\right)\right],i=1,\dots ,n,(2)$

where v_i is the membrane potential of neuron i, C_i is its membrane capacitance, I_i = I_i(v_i) denotes the total internal voltage-dependent currents of this neuron (responsible for creating nonlinear spiking activity), ${\bar{g}}_{ij}$ is the maximal conductance of the synapse from neuron j to neuron i (with ${\bar{g}}_{ij}>0$ for excitatory synapses, ${\bar{g}}_{ij}<0$ for inhibitory ones, and ${\bar{g}}_{ij}=0$ for disconnected neuron pairs), p_ij(t) is the time-dependent probability that the channels in this synapse are open (most strongly dependent on the time of neuron j’s action potentials), and the constant E_j is the reversal potential of the synapse.³ In the absence of DBS, each neuron will spike whenever its v_i(t) increases beyond a threshold. Depending on the geometric morphology of each neuron, the electrical field created by the DBS will then increase (de-polarize) or decrease (hyper-polarize) this autonomous potential, thus increasing or decreasing its likelihood of spiking.

The complexity of this approach has motivated a number of simplifications, including the elimination of the CBM (Buhlmann et al., 2011; Martens et al., 2011; Nguyen et al., 2019; Janson et al., 2020). These works still estimate the electrical field distribution, but use a simple and fixed threshold for neuron activation, either from prior experimental implementations of DBS or from a comparison with CBMs.

A further simplification, and a rather critical one, comes from works that assume a “naive model” of how DBS affects the input current of nearby neurons (Lysyansky et al., 2011; Popovych and Tass, 2012; Brocker et al., 2013; Gorzelic et al., 2013). We refer to a dynamical model of neurostimulation as naive when differential/difference equations describing autonomous neural dynamics are simply augmented by an extra additive term which directly equals (or is proportional to) the applied stimulation waveform. In the case of a CBM, e.g., Eq. 2 changes to

$C_i\frac{d}{dt}{v}_i\left(t\right)=I_i\left(t\right)+\sum _{j=1}^n{\bar{g}}_{ij}{p}_{ij}\left(t\right)\left[E_j-v_i\left(t\right)\right]+u\left(t\right)$

where u(t) is taken to be equal (or proportional) to the applied DBS waveform. Clearly, these idealized models are quite generic and almost equally applicable to any stimulation technique. In return, however, these works are able to examine beyond the activation of the tissue near the DBS electrode and study the local network effects of DBS, such as desynchronizing reset modulation (Lysyansky et al., 2011; Popovych and Tass, 2012), temporally non-regular stimulation (Brocker et al., 2013), and closed-loop feedback stimulation (Gorzelic et al., 2013), as well as the optimization of the waveform shape of the DBS stimulation using a genetic algorithm (Brocker et al., 2017).

Grant and Lowery (2012) take this one step further, combining electrical field calculations with CBMs of the subthalamic nucleus (the main stimulation region for the treatment of PD) and mean-field models of a handful of other subcortical and cortical regions. While a valuable extension, the considered network is still far from a complete connectome. The importance of the latter and global network effects have indeed been shown at least in the response of patients with treatment-resistant depression to DBS (Riva-Posse et al., 2018) and is perhaps relevant for most psychiatric disorders. To account for this, Riva-Posse et al. (2018) combine estimations of the activated tissue similar to the ones above together with region of interest (ROI) tractography to find the network of white matter connecting to the tissue activated by DBS and use that to plan surgical targeting of the DBS electrode.

Overall, the bottom-up approach of biophysical models inevitably sacrifices scalability in return for maximum biological interpretability. Indeed, large-scale interconnections of biophysical models are possible (Amunts et al., 2016), but they require randomly distributed synaptic weights (${\bar{g}}_{ij}$ in Eq. 2) which in turn take away from the model’s biological realism. These and other issues with bottom-up modeling has motivated works that directly use the observed DBS data to study the underlying stimulation dynamics in a top-down manner, as reviewed in Section 2.1.2 and Section 2.1.3.

2.1.2 Stimulus-response models

A commonly used approach to study the modulation achieved by DBS is via the statistical analysis of stimulation effects on collected brain measurements like local field potentials (LFPs) or intracranial EEG (iEEG) (Marceglia et al., 2007; Swann et al., 2011). Unlike biophysical models, these works use statistical methods to locate regions and periods where DBS has had an effect on the measurement data. In works like (Rosin et al., 2011), this is done by cross-correlating the DBS input waveform with LFPs to find channels where the effects are significant. However, the most widely used technique involves the computation of biomarkers (Bouthour et al., 2019) such as beta-band power (signal power in the 13–30 Hz range), high gamma oscillations (60–90 Hz), and tremor bursts (4–6 Hz) from the measured data and the comparison of biomarker values corresponding to periods with no DBS to those with stimulation (Swann et al., 2011; Saenger et al., 2017). The exact biomarker that needs to be used has been a matter of debate for decades (Little and Brown, 2012; Bouthour et al., 2019) and it varies based on the disease and the DBS application.

One of the main research objectives concerning neurostimulation is the development of Brain-Computer Interfaces (BCIs), where the goal is to process brain measurements in real-time in order to obtain stimulation-relevant biomarkers and decide about stimulation parameters in an adaptive manner. The majority of the existing works regarding adaptive DBS (aDBS) are based on the comparison of computed biomarkers with a clinically obtained threshold (Little et al., 2013; Priori et al., 2013; Beudel and Brown, 2016; Hoang et al., 2017). While these methods have been shown to perform better than open-loop continuous DBS, biomarkers are still only manually-selected low-dimensional representations of the brain activity that may not fully capture the DBS effects. Further, the adaptation achieved in these works is limited to controlling DBS durations in an on/off manner and requires expert intervention to adjust other parameters like frequency and amplitude. Motivated by these, data-driven machine learning methods have been employed in (Shukla et al., 2012; Khobragade et al., 2015) and have been shown to perform better than biomarker-based aDBS. In both these works, an artificial neural network (ANN) was used to predict tremors using surface-electromyogram (sEMG) data which was then used to decide the application of DBS input. However, these works are still oblivious to the rich temporal dynamics of DBS response, as reviewed next.

2.1.3 Dynamical system models

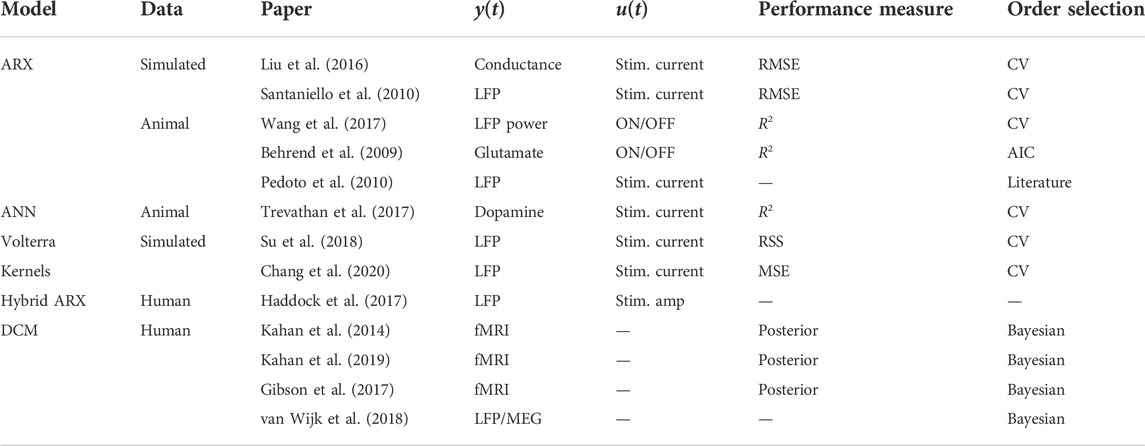
More recently, a number of works have approached the problem of DBS modeling from a completely different, system identification approach (Table 1). In (Liu et al., 2016), the authors carry out an input-output black-box system identification to fit an autoregressive with exogenous input (ARX) model of the form in Eq. 3 which takes the DBS signal as the input u(t) and produces the basal ganglia-to-thalamus synaptic conductance as the output y(t). The resulting model is then used to optimize the DBS input via the generalized predictive control framework. Similarly (Santaniello et al., 2010), also fits an ARX model that takes the DBS signal as the input, but they instead choose the DBS-generated LFP as the model output.

$y\left(t+1\right)=\sum _{j=0}^{p-1}{a}_{j}y\left(t-j\right)+\sum _{k=0}^{m-1}{b}_{k}u\left(t-k\right)+\mathbf{w}\left(t\right)(3)$

TABLE 1

TABLE 1. Summary of data-driven dynamical system models for DBS.

The authors generate the LFP data by applying a range of stimulation frequencies/amplitudes and the resulting model is then used together with minimum variance control to shape the power spectral density of the LFP. Even though both works train their ARX models on simulated rather than experimental data, their pragmatic and data-driven methodology can be valuable in mitigating the complexity of the DBS mechanism. The latter is in turn achieved by focusing only on the end-to-end, input-output mapping from tunable stimulation parameters to neural biomarkers of interest in any disorders, or even behavioral measurements similar to those studied in (Medvedev et al., 2019).As far as learning parametric input-output models from real-world data is concerned, most of the existing DBS literature focuses on non-human subjects, including rodents (Behrend et al., 2009; Wang et al., 2017), rhesus macaques (Pedoto et al., 2010), or swines (Trevathan et al., 2017). In (Pedoto et al., 2010), the authors extend the work in (Santaniello et al., 2010) to data collected from non-human primates (NHPs) via an experimental design that involved varying the stimulation frequency randomly while keeping the amplitude fixed. Although the model learned from this design could not generalize as well as the one in (Santaniello et al., 2010), it is interesting to note that a relatively low-order scalar model was able to explain a large portion of the variance seen in the real data.

In (Wang et al., 2017), the authors train an ARX model with the input being the application of DBS (binary on/off) and the output being an LFP-based psychological marker sampled on a daily basis. Unlike in (Santaniello et al., 2010) where the learned model was used to control the DBS current in real-time, the model obtained here was used to design a fuzzy logic-based controller to decide the application of DBS once every day based on the biomarker history. Application of ARX modeling has also been demonstrated in (Behrend et al., 2009) for the prediction of the extracellular glutamate (the brain’s main excitatory neurotransmitter) level in rat brains as the output response. The success of linear models such as ARX in modeling what is inherently a nonlinear process is a subject of research and has been attributed to the brain’s inherent spatio-temporal averaging processes, among other reasons (Nozari et al., 2020^†).

Nonlinear models such as AR-Volterra Kernels (Su et al., 2018) and ANNs (Trevathan et al., 2017) have also been used for the modeling of DBS response. In (Chang et al., 2020), the authors take this one step further by learning a nonlinear ARMA-Volterra model and providing a predictive control algorithm based thereon. While these nonlinear models and the linear models discussed earlier are demonstrated to achieve good accuracy in predicting DBS response (e.g., R² = 0.99 in (Behrend et al., 2009) and normalized MSE of 0.07 in (Chang et al., 2020)), they are still scalar models where the output of any brain region/channel is modeled independently of the measurements at other regions/channels. Hence, these models have limited utility in understanding how DBS affects the brain’s large-scale network dynamics and the connectivity between different regions. Furthermore, these models’ lack of network interactions has made it inevitable to give the model of all regions direct access to the DBS input history, as opposed to the more biologically realistic scenario where input enters into the dynamics only through the stimulation site.

Combining the power of data-driven modeling with the interpretative nature of biophysical models is an ongoing area of research (Rowe et al., 2004; Freestone et al., 2014; Dura-Bernal et al., 2019). Perhaps dynamic causal modeling (DCM) originally proposed in (Friston et al., 2003) has been the most leveraged modeling framework towards this objective. While the exact formulation of DCM can vary widely depending on the stimulation type and the measurement modality, it is ultimately a special case of the model in Eq. 1 where f (.) often has a bi-linear form for fMRI outputs and (sigmoidal) mean-field forms for EEG and MEG outputs and external inputs (neurostimulation in this case) “modulate” (increase or decrease in an affine form) the interaction weights between the states (corresponding to the activity of modeled brain regions). In the case of fMRI outputs, for instance, the dynamics take the form

$\begin{array}{cc}\hfill \dot{\mathbf{x}}\left(t\right)& =\left(\mathbf{A}+u\left(t\right)\mathbf{B}\right)\mathbf{x}\left(t\right)\hfill \\ \hfill \mathbf{y}& =h\left(\mathbf{x}\right)\hfill \end{array}(4)$

where u(t) is the neurostimulation input and h (⋅) models the hemodynamic (for fMRI) or electromagnetic (for EEG and MEG) processes by which the neuronal states x(t) give rise to the recorded neuroimaging time series. Note that h (⋅) is often a dynamic process, hence the used notation. We point interested readers to (Marreiros et al., 2010; Stephan et al., 2010) for more details on the DCM theory and learning. While DCM models are learned from data and can potentially be used for feedback control, it is largely seen as a tool to examine the changes in effective connectivity (i.e., (A+ u(t)B)) between brain regions when comparing the stimulus-on and stimulus-off conditions. In the majority of works involving DCM and neurostimulation (e.g., Kahan et al. (2014)), a set $\mathcal{M}=\{m_1,m_2,\dots ,m_M\}$ of biophysically plausible network models are initially proposed (corresponding to different sparsity patterns in A and B), all fit to data using the standard Bayesian paradigm of DCM, and the configuration with maximum model evidence (i.e., arg max_mp (y|m)) is selected. This model m is then used to identify the effect of stimulation on the connections between the selected regions of interest. Such analyses have been done for DBS with fMRI data in works such as Kahan et al. (2014, 2019); Gibson et al. (2017) and with LFP/MEG recordings in van Wijk et al. (2018). Note that, as described, these works learn separate models for stimulation-on and stimulation-off durations and do not consider stimulation as a driving input to network nodes.

A similar split-modeling approach has also been employed in the context of autoregressive models in (Haddock et al., 2017), where hybrid ARX modeling was used to model tremor power obtained from LFP recorded during the stimulation of human brain. The authors here trained an AR and ARX model by separating the data into DBS-off and DBS-on durations, respectively. The learned hybrid model was then used in a simulation to develop a predictive controller with the goal to optimize the DBS effects while minimizing power consumption. Despite its limitations, a valuable aspect of this work lies in its demonstration of model effectiveness for closed-loop DBS control which we believe is a critical factor to be considered in addition to cross-validated predictive accuracy when assessing the quality of learned dynamical models.

2.2 Transcranial magnetic stimulation

Transcranial Magnetic Stimulation (TMS) is a non-invasive technology whereby neuronal tissue is stimulated by the generation of a focal magnetic field using one or more electromagnetic coil(s) placed near the scalp (Hallett, 2007). In turn, the time-varying magnetic field creates an electric field that can de/hyper-polarize (excite/inhibit) neurons.

Throughout the decades-long history of TMS, various stimulation waveforms with distinct effects have been devised, the most notable of which are single-pulse, paired-pulse, and repetitive TMS (Galletta et al., 2011). Unlike DBS which is often believed to activate all neurons in the volume of tissue activated (VTA), TMS has long been recognized to have a potential for differentially activating excitatory or inhibitory interneurons in its VTA (Beynel et al., 2020). Such differential effects have been recognized both for paired-pulse TMS, with short inter-pulse internals ($<5$ms) giving rise to local inhibition and long inter-pulse intervals ($>5$ms) resulting in local excitation (Mishra et al., 2011), as well as for repetitive TMS (rTMS), where low-frequency and high-frequency rTMS are widely believed to give rise to local inhibitory and excitatory effects, respectively (Guse et al., 2010; Beynel et al., 2020). The threshold for switching from inhibitory to excitatory (ranging between 1 − 5 Hz) and the mechanisms responsible for such frequency dependence are nevertheless still a matter of debate (Luber and Deng, 2016; Beynel et al., 2020). Nevertheless, from a network controls perspective, the potential for having a differentially excitatory or inhibitory effect (both positive and negative u(t)) provides a remarkable advantage for TMS over DBS and many other stimulation technologies. Without such a direct means of inhibition, network control can still be possible but more sophisticated control algorithms would be required to indirectly create inhibition, e.g., using excitation of local inhibitory interneurons.

In the following and in parallel to Section 2.1, we review the literature on the biophysical, stimulus-response, and dynamical system modeling of TMS across these stimulation modalities.

2.2.1 Biophysical models

A major body of work has sought to model the effects of TMS on neural activity via calculations of the electric field that results from TMS. Electric field calculations are often performed via finite-element modeling (FEM) (Salinas et al., 2007; Thielscher et al., 2015) and can be performed at varying levels of accuracy or simplification. Once the electric field is obtained across space and time, a standard approach consists of simulating the response of CBMs such as those in Eq. 2 at various positions/orientations to the electric field (Salvador et al., 2011; Goodwin and Butson, 2015; De Geeter et al., 2016; Gomez-Tames et al., 2020; Shirinpour et al., 2021). Similar to the biophysical analyses for DBS, this is often achieved by first transforming electric field to electric potential (by integrating E = −∇V over space) and then adding the resulting potential to the neuron’s extracellular potential. This is often performed either directly using the cable equation (Salvador et al., 2011; De Geeter et al., 2016) or using multi-compartmental CBMs which essentially provide a spatial discretization of the cable equation to simplify the partial differential equation (PDE) thereof into multiple ordinary differential equations (ODEs) (Goodwin and Butson, 2015).

In comparison to naive models defined in Section 2.1.1, the effect of TMS using these field-based calculations also boils down to a simple, additive term in a CBM. Unlike a naive model, however, the waveform of this additive term is not simply the waveform of the TMS pulse, but rather the result of the detailed FEM and electromagnetic transformations. Nevertheless, naive models have also been used for the computational modeling of TMS (Alagapan et al., 2016), albeit less often than DBS due to the more indirect mechanisms of action of the TMS.

Also similar to, but distinct from, the naive models is the framework of (Esser et al., 2005) where the effect of TMS is modeled directly (without field calculations) by a change in the synaptic conductance of neurons within the TMS focus. A second-order synaptic dynamics of the form (cf. Eq. 2)

$p_{ij}\left(t\right)\propto -e^{t/{\tau }_1}+e^{t/{\tau }_2}(5)$

is also included, where τ₁, τ₂ are the synapse’s rise and decay time constants, further departing from the naive models and increasing biophysical realism.

2.2.2 Stimulus-response models

Most of the existing closed loop controllers of TMS are based on feedback from surface measurements like EEG, EMG (Kraus et al., 2016; Tervo et al., 2020, 2022) or imaging modes like functional magnetic resonance imaging (fMRI) (Hernández-Ribas et al., 2013; Jung et al., 2020). Some of the earliest studies of neural response to TMS are based on the changes in the motor evoked potentials (MEPs) (Pascual-Leone et al., 1998; Peterchev et al., 2013). MEPs refer to EMG signals recorded from muscle activity in response to stimulation of the respective area in the motor cortex and constitute one of the major paradigms for studying the neural effects of TMS. The aforementioned works typically attempt to characterize the TMS response via input-output plots under different stimulation parameters such as intensity and duration which could then be used for functional mapping or TMS control.

TMS-induced blood-oxygenation-level-dependent (BOLD) changes as observed by fMRI is another popular method of analysis due to its spatial resolution (millimeter range) (Jung et al., 2020). However, its use for real-time control of TMS is limited due to its low sampling rate (seconds range) and the fact that imaging techniques capture blood flow changes and not direct neuronal activity induced by stimulation. More recently EEG has gained great attention as a tool to study TMS-evoked transient changes (Iramina et al., 2002; Komssi et al., 2002; Kähkönen et al., 2005; Bonato et al., 2006). This is largely influenced by the high temporal resolution (millisecond range) associated with EEG and the consistency of the EEG responses to TMS (Bonato et al., 2006). Nonetheless, these works still often provide qualitative templates of the brain’s regional responses to TMS, leaving the generative mechanisms through which the input interacts with the connectome unexplored.

Finally, a rather large body of work has explored the power of deep neural networks for computing the electrical activity induced by TMS in the brain (Yarossi et al., 2019; Yokota et al., 2019; Akbar et al., 2020; Afuwape et al., 2021; Sathi et al., 2021). While these works can be differentiated based on the exact specification of input and output variables, most of these models can be better categorized based on the direct or indirect usage of magnetic resonance (MR) images along with the coil parameters. The indirect approach involves the processing of MR images to compute anatomic brain models, which are then used along with the TMS parameters to simulate the E-field distribution. This in turn is fed into to a deep neural network to estimate the MEP (Yarossi et al., 2019; Akbar et al., 2020) or activation thresholds (Aberra et al., 2022^†). While using processed MR images can help simplify the modeling (by requiring smaller network size and lesser data, for example), this step is often computationally expensive and relies on conduction models that are manually tuned. In contrast, MR images and coil parameters have been used directly as inputs to a convolution neural network to determine either the whole-brain electric field distribution (Yokota et al., 2019) or the electric field statistics such as maximum induced electric field (Afuwape et al., 2021). While the models in the direct approach were trained and tested using simulated TMS data, the predictability achieved with these models combined with the computational performance that comes with not having to pre-process MR images still provides a case for end-to-end data-driven modeling.

2.2.3 Dynamical system models

Recent works have employed a data-driven approach to dynamical system modeling for TMS (Chang et al., 2019; Kiakojouri et al., 2020), where linear state space models (LSSM) were used to fit EEG response to TMS. In essence, LSSMs of the form shown in Eq. 6 are learned using subspace identification methods. However, Chang et al. (2019) instead parameterize their state equation using a linear multivariable ARX (MVARX) style model, which is then trained using an expectation-maximization style algorithm. In this work, it was observed that fully-connected LSSMs perform better than disconnected models, thus validating the largely presumed importance of modeling recurrent interactions between different cortical regions. In Kiakojouri et al. (2020), the authors compare LSSM against trained multi-layer perceptrons (MLP) in their ability to predict TMS-evoked EEG response and it was found that the introduction of nonlinearity in modeling did not necessarily improve the fit accuracy.

$\begin{array}{ll}\hfill \mathbf{x}\left(t+1\right)& =\mathbf{A}\mathbf{x}\left(t\right)+\mathbf{B}\mathbf{u}\left(t\right)+\mathbf{w}\left(t\right)\hfill \\ \hfill \mathbf{y}\left(t\right)& =\mathbf{C}\mathbf{x}\left(t\right)+\mathbf{D}\mathbf{u}\left(t\right)+\mathbf{v}\left(t\right)\hfill \end{array}(6)$

Similar to DBS, DCM based on fMRI has also been used to investigate changes in connectivity in response to TMS (Pleger et al., 2006; Grefkes et al., 2010; Hodkinson et al., 2021). While in both (Grefkes et al., 2010) and (Pleger et al., 2006) the pre-stimulus and post-stimulus changes in the neural dynamics were analyzed, the work in Hodkinson et al. (2021) uses simultaneous TMS and fMRI data to determine changes induced during the application of stimulation. However, all these works are similar in their use of a fixed set of stimulation parameters (frequency and intensity) throughout the entire duration of data acquisition, thus limiting the persistence of excitation and richness of the used data for learning. A summary of TMS-related dynamical system models is presented in Table 2.

TABLE 2

TABLE 2. Summary of data-driven dynamical system models for TMS.

2.3 Direct electrical stimulation

Direct electric stimulation (DES) is an invasive neurostimulation method similar to DBS which involves direct application of electric current to the brain via surgically placed electrodes. However, unlike DBS where the stimulation is provided in deep subcortical regions (such as the subthalamic nucleus for the treatment of PD), DES is generally limited to either the cortex or the dura mater. Nevertheless, DES has found applications well beyond therapeutic neuromodulation. In particular, DES has been considered a gold standard for functional mapping of the brain for over a decade (Mandonnet et al., 2010; Opitz et al., 2014; Mahon et al., 2019) and has been used widely in identifying regions important for language, somatosensory and motor functions (Ojemann, 1983; Ostrowsky et al., 2002; Matsumoto et al., 2007; Orena et al., 2019). Moreover, cortico-cortical evoked potentials (CCEPs) induced in regions distant from the DES site has gained importance as a tool to map the spatio-temporal causal connectivity of the brain (Mandonnet et al., 2010; Keller et al., 2014). In brief, CCEP refers to a mapping of the brain’s “effective connectivity” (essentially, transfer function/impulse response) between pairs of cortical regions, where DES is applied to each cortical region and responses (electrocorticography, or ECoG) are recorded from electrodes placed over other cortical regions (Keller et al., 2014). Even though only available for patients with drug-resistant epilepsy undergoing pre-surgical evaluation, CCEPs (and DES in general) provide an invaluable window into the brain’s dynamics and have been studied through various approaches, as summarized next.

2.3.1 Biophysical models

A large amount of work describing computational modeling of DES focus on epidural and subdural cortical stimulation. Like DBS, the most common DES response modeling method involves computing the electric field around the stimulation site using FEM (Wongsarnpigoon and Grill, 2008; Seo et al., 2016). Commonly, the area around the stimulation including the cortex, grey matter, and dura mater is approximated using a three-dimensional extruded slab model (Wongsarnpigoon and Grill, 2008, 2012; Vrba et al., 2019). The distribution of the electric potential is then estimated using FEM based on tissue conductivity assumptions and used to determine the de/hyper-polarization of neurons on the cortical surface. Recent progress in computational techniques has allowed researchers to incorporate more realistic 3D brain models which have been shown to explain the electric field distribution more accurately (Kim et al., 2014; Seo et al., 2016).

In Manola et al. (2007), pyramidal neuron CBMs were used in conjunction with a 3D volume conductor model similar to the one in (Wongsarnpigoon and Grill, 2008) to estimate the electrical field corresponding to the stimulation of the motor cortex. A similar approach to combine neural dynamics with FEM was proposed by Mandonnet and Pantz (2011), where a homogenized axonal model was adopted to estimate the regions where action potentials are generated. However, the stimulation response modeled in all these works is limited to regions near the stimulus site and as such can only be used to understand local de/hyper-polarization activity. While these methods help elucidate functional relevance of specific sites, they have little utility for modeling network-level activities such as CCEPs. Also, FEM calculations often require precise knowledge of electro-geometric properties of cortical regions, even though normative (average) head models can also be assumed.

2.3.2 Stimulus-response models

As seen in Figure 1, stimulus-response modeling of DES has been pursued as frequently as biophysical modeling. The former can be roughly divided into two categories based on the repetitiveness of the applied stimulation. First, we have studies that use single-pulse electric stimulation (SPES) to understand the response of the brain under low-frequency DES (Valentin et al., 2002; Matsumoto et al., 2017; Crocker et al., 2021; Paulk et al., 2022). Such studies have used temporally well-spaced stimulation pulses (1–5 s between consecutive stimulations) and, as a result, evoked activity only in a limited population of localized neurons. In (Paulk et al., 2022), the authors conducted multiple SPES experiments to find the degree of dependency of the evoked responses on stimulation parameters such as input strength (current), distance of the region from the grey-white matter boundary, and the distance of stimulation site from white matter. The results indicated that the responses vary nonlinearly, particularly in regions close to the stimulus site.

In the second category are works that have analyzed the response to a range of low and high-frequency pulses. In studies conducted by Mohan et al. (2020) and Keller et al. (2018), the mapping between DES parameters and responses under repetitive stimulation was modeled using a linear regression models. While these works provide significant insights into the input-output correlation between DES and the expected response, they still have too little temporal resolution for being used in designing closed-loop controllers. Also, attempts to map the brain’s response to varying DES parameters without considering the underlying state of the brain at the time of stimulation have been shown to lack the capability to model the heterogeneity of responses evoked by DES (Borchers et al., 2012; Papasavvas et al., 2020).

2.3.3 Dynamical system models

Similar to DBS, several data-driven dynamical system modeling methods have been proposed to examine the brain’s spatio-temporal dynamics under DES as showcased in Table 3. In (Steinhardt et al., 2020), rectified linear (ReLU) finite impulse response (FIR) models were used to predict the CCEP dynamics at each electrode location. While such an approach does not make use of “network information” from electrode recordings from other sites, the reasonable level of predictability achieved using this model poses the question of under what circumstances is it important to consider network effects in the system design.

TABLE 3

TABLE 3. Summary of data-driven dynamical system models for DES.

In (Chang et al., 2012), MVARX was instead leveraged to model the DES-evoked activity as measured (invasively) by Stereo-EEG (sEEG) and iEEG. Here, the model input was selected to be the injected current. As in the work of Steinhardt et al. (2020), the MVARX modeling here does not restrict the direct flow of input information in the dynamics of non-stimulation channels (as opposed to the more biologically plausible structure where input can only flows through the network from the stimulation site). However unlike in the FIR model of the former, input information could also enter the model through network interactions. While the learned model is able to make predictions agreeable with the recorded data, it has to be noted that in this and the majority of similar studies, the input pattern used for the system identification experiment only involved repeatedly stimulating the brain at uniform intervals without varying the current amplitude or waveform shape in any ways, thus limiting the generalizability of the learned models in predicting dynamics under unseen input conditions. However, given that model was learned using real human data and can predict both pre-stimulus and evoked responses makes a promising case for learning more generalizable models. Also, it is worthwhile to mention that the results showcased here indicate that the learned MVARX performs better in comparison to a learned ARX model, thus verifying the often presumed benefits of including network interactions for model predictability.

In (Yang et al., 2018), the authors use binary noise (BN)-modulated stimulation patterns to learn the input-output brain response parameterized using a linear state-space model (LSSM) of the form in Eq. 6 and develop an LQR-based controller for curing neurological conditions, particularly depression, using the developed model. Similar to the DBS-related works of Santaniello et al. (2010) and Liu et al. (2016), the model here was trained using only synthetically generated data. However, instead of using physiologically-derived models (e.g., the basal ganglia network) to generate the simulated input-output data, the authors use a hardware in the loop (HIL)-based simulator to generate ECoG data that simulates real-world delays and noise statistics associated with DBS. Also, the modeling considers the input u(t) to be a vector of the form [amp(t), freq(t)] where amp(t) and freq(t) are the stimulation amplitude and frequency, respectively, and, hence, is generally more explainable from a clinical perspective. While the synthetic nature of the data used here may not accurately correspond to the activity observed in the brain, incorporating realistic delays in the data appears to be a crucial step in developing clinically transferable DES controllers. Additionally, the authors presented a way to transform abstract behavioral objectives (e.g., mitigating depression) to computable control cost functions by relating a mood-based marker with the internal brain state. Although such an approach is yet to be validated using human experiments, it provides a first step towards translations between control-theoretic cost functions and clinical objectives.

In (Yang et al., 2021), the authors extend the same BN-based system identification approach to model the dynamics of large-scale brain networks in non-human primates. The authors compared the predictability of general LSSM against a range of constrained linear models and nonlinear ARX models and it was observed that linear models perform better than the extensively parameterized nonlinear models. Further, among linear models, those which were forced to have non-oscillatory dynamics performed poorly in comparison to unconstrained LSSMs, indicating the importance of oscillatory dynamics in modeling the brain’s response to DES. Furthermore, to mitigate the often low signal to noise ratio in neural recordings, the same BN-stimulation pattern was applied multiple times to average out any noise associated with the internal brain functions.

Considering that data-driven models like MVARX or LSSM require the user to select a wide range of hyper-parameters such as model lags and order, it is important to highlight the tuning methodology followed in the aforementioned models. In (Yang et al., 2018) and (Yang et al., 2021), the authors use Akaike’s information criterion (AIC) to determine the subspace model order. AIC has been widely popular in the modeling literature due to its simple yet effective formulation for balancing model predictability and complexity without the need to use a separate validation dataset. While it has been used in tuning complex models such as ANNs, its application to nonlinear models where one may not clearly define a model order is still a matter of debate. In (Chang et al., 2012), the authors instead define and use a cross-validation (CV) cost function to tune the model lags. While cross-validation methods like k-fold CV are computationally expensive, it is a powerful tool in determining the optimal model order and is a good indicator of model generalizability. In general, various factors such as the model linearity and data stationarity can affect the hyper-parameter selection criteria (AIC, CV, etc.).

2.4 Transcranial electric stimulation

Transcranial electric stimulation (tES) is a non-invasive neuro-stimulation technology that involves the application of electric currents to the scalp via two or more electrodes. Unlike DBS or TMS, stimulation delivered via tES is weak and is not in general sufficient to evoke action potentials by itself. However, neuronal spiking has been shown to be altered by tES depending on the exact stimulation pattern applied and the timing of the applied stimulation relative to the ongoing brain oscillations (Liu et al., 2018; Krause et al., 2019; Johnson et al., 2020; Huang et al., 2021). While a large body of tES work focuses on the modulation due to direct current (tDCS), effects concerning the application of alternating current (tACS) and random noise stimulation (tRNS) have also been studied.

2.4.1 Biophysical models

Similar to other neurostimulation techniques, biophysical models have been proposed to understand the effects of tES on the brain. A large number of works approach this problem using a head model including the geometry of the scalp, skull, cortex, and their respective conductivity (Sadleir et al., 2010; Minhas et al., 2012; Indahlastari et al., 2016). Finite element analysis is then used to determine either the current density or the electric field distribution, which can then be used to optimize stimulation parameters. Recent progress in MRI-based anatomical head modeling has allowed for more realistic estimation of the effects in comparison to spherical head models such as the one used in Miranda et al. (2006). This is particularly relevant in tES due to its non-invasive nature where it is critical to model the current flow from the scalp through the skull to the cortex, sub-cortical regions, and the white matter.

Neuronal models like multi-compartment CBMs or neural mass models have been used in the literature to determine the excitatory-inhibitory effects of tDCS (Dutta and Nitsche, 2013; Molaee-Ardekani et al., 2013; Arora et al., 2021). In Arora et al. (2021), the authors propose the use of multiple pathways such as modeling tDCS perturbation to ionic gates and ion concentrations to simulate tDCS current density effects. A different approach involving oscillatory neural mass model was used in Kunze et al. (2016) to model the temporal evolution of large-scale brain networks under tES. The parameters of these models (connectivity between regions, for example) are determined through comparison of simulated data against experimental measurements such as EEG and provide interpretable insights into the underlying dynamics. However, these neuronal models still use a highly abstracted representation of the input and do not capture the exact nature of electric conduction from the scalp to individual neurons. More recent works have attempted to alleviate this gap by combining conduction head models with neuronal models, see, e.g., (Rahman et al., 2015; Seo and June 2017, 2019).

2.4.2 Stimulus-response models

Similar to TMS, stimulus-response analysis of the brain’s response to tES has been largely done using non-invasive recordings such as EEG, MEP, and fMRI. In Jamil et al. (2017), the authors monitor pre- and post-stimulation MEP to determine the dependency of cortical excitation on the tDCS intensity. This process of establishing a pre-stimulation baseline and comparison to post-stimulation activity is a recurring mode of analysis in MEP-related literature (Gálvez et al., 2013; Wiethoff et al., 2014; Ammann et al., 2017). Similar post-hoc studies have been performed using fMRI in works such as (Keeser et al., 2011) where the network connectivity before and after tES are studied. With respect to the simultaneous analysis of response and stimulation, EEG-based monitoring has been leveraged in a large fraction of works (Schestatsky et al., 2013; Song et al., 2014). Also, a notable pattern in recent works is an increase in the studies of closed-loop tES control design via EEG-based feedback (Boyle and Fröhlich, 2013; Leite et al., 2017; Frohlich and Townsend, 2021). For the most part, these works perform on/off control determined by the thresholding of EEG-based bio-markers such as alpha band power (Boyle and Fröhlich, 2013) (signal power in the range 8–12 Hz). While the control design here is not based on state prediction and optimization, these works shed light on the prospective use of non-invasive signals such as EEG for real-time feedback control of tES.

2.4.3 Dynamical system models

The data-driven dynamical system modeling of brain dynamics under tES is still in its infancy as seen from Table 4. One attempted approach here pertains to the modeling of near-infrared spectroscopy (NIRS)-based hemodynamics taking the EEG recorded during tES (not the tES signal itself) as the input. In Sood et al. (2016), the authors combine ARX modeling with Kalman filters to learn such models online in order for the model to adjust to time-varying data. However, even though EEG can capture the effects of the applied input (stimulation current), such a model cannot directly be used for network control but instead would need to be combined with an inverse mapping from EEG to the actual input current. Nevertheless, the provided proof of concept on the predictability of blood flow activity altered by tDCS using an ARX model is promising.

TABLE 4

TABLE 4. Summary of data-driven dynamical system models for tES.

2.5 Optogenetics

Broadly, optogenetics refers to the combination of genetics and optics to control well-defined events within any specific cell type of living tissue, including neurons (Yizhar et al., 2011). Commonly, this is achieved via a viral insertion of genes into (neuronal) cells that endow them with light responsiveness and the (invasive) delivery of light to the affected neurons. Notably, this process can be finely controlled to generate both excitatory and inhibitory effects in the targeted neurons (even multiple interconnected populations of neurons within the same brain region) depending on the inserted genes, timing of gene insertion, and the used wavelength of light.

Even though not yet approved for use in humans, optogenetics plays a unique role in the applications of control theory in neuroscience. Indeed, one of the main goals of developing network control models of the form in Eq. 1 is control design, where it is often desirable to tap into the wealth of classical control methods and readily apply them to neural dynamics. However, doing so is challenging due to the great mismatch between the level of spatiotemporal specificity required by most control methods and that provided by existing neurotechnologies. This makes optogenetics a particularly attractive stimulation technology for control design, where cell-type specific spatial resolution and millisecond temporal resolution are combined (Deisseroth et al., 2006).

2.5.1 Biophysical models

A common approach to the modeling of neural responses to light stimuli involves detailed modeling of the physics underlying optogenetics. Briefly, optogenetics involves the opening of light-sensitive ion channels or pumps which leads to ionic currents similar to the natural currents on the right hand side of Eq. 2. In other words, each channel/pump has multiple, say ℓ internal states s₁, … , s_ℓ (at least two: open and close) whose dynamics change under the influence of light. Therefore, a popular family of models for optogenetic effect (Grossman et al., 2011; Foutz et al., 2012; Nikolic et al., 2013; Stefanescu et al., 2013; Selvaraj et al., 2014) start from a CBM of the form in Eq. 2 and augment it into.

$C_i\frac{d}{dt}{v}_i\left(t\right)=I_i\left(t\right)+\sum _{j=1}^n{\bar{g}}_{ij}{p}_{ij}\left(t\right)\left[E_j-v_i\left(t\right)\right]+g_{\text{opsin}}\left(t\right)\left[E_{\text{opsin}}-v_i\left(t\right)\right],(\mathrm{7a})$

$g_{\text{opsin}}\left(t\right)=\left(\sum _{k=1}^{\ell }{s}_k\left(t\right)g_k\right)\varphi \left(v_i\left(t\right)\right),(\mathrm{7b})$

$\frac{d}{dt}\mathbf{s}\left(t\right)=\mathbf{K}\left(u\left(t\right),t\right)\mathbf{s}\left(t\right).(\mathrm{7c})$

Here, g_opsin(t) is the light-dependent conductance of this channel/pump, E_opsin is the constant equilibrium potential of the optogenetically activated channel/pump (depending on the gene type and light wavelength used), s_k(t) is the fraction of channels/pumps on the surface of the neuron in state k (so s₁ + ⋯ + s_ℓ = 1), g_k is the conductance of the channels/pumps if they were all in state k, ϕ(⋅) is an optional nonlinear function that can model the voltage-dependence of g_opsin, u(t) is the light intensity, and K is a matrix of state transition rates which depends on various linear or nonlinear forms on u(t) and, possibly, time. Note that even though the light intensity signal is often a sequence of square pulses in implementation, u(t) is often taken as an impulse train

$u\left(t\right)=\sum _k\delta \left(t-t_k\right)(8)$

where the times t_k correspond to the onset times of the square pulses in light intensity. If the internal states s₁, … , s_ℓ are not important, Eq. 7 can be simplified by simply using a linear dynamical system to directly model the mapping from g_opsin(t) to u(t) (Vierling-Claassen et al., 2010; Witt et al., 2013; Shewcraft et al., 2020), often using a first-third order system with an impulse response similar to Eq. 5.

Such biophysical models have been used to build closed-loop feedback controllers of optogenetic input. One strategy that has been demonstrated is to let u(t) modulate certain parameters of the optogenetic input, such as the amplitude of a light intensity square-wave pulse while fixing other parameters such as frequency and duty cycle (Srinivasan et al., 2018). A more sophisticated version was used in (Newman et al., 2015), where a single control input u(t) in the model determines the parameters of two simultaneous sources of optogenetic stimulation, modulating the frequency, pulse width, and intensity envelope of one source (ChR2, excitatory) while directly mapping to the light intensity (as in a naive model) of the second source (eNpHR3.0, inhibitory).

Another class of methods involves using spiking network models. In Valverde et al. (2020), exponential integrate-and-fire neurons were used to build a simplified motor cortex network with around 1,000 neurons. While having access to all neuronal activities at a microscopic level provides great modeling flexibility and fidelity, it can be difficult to interpret such microscale models without resorting to aggregate statistics. As such, Mahrach et al. (2020) instead use population-level modeling, where connectivity between four neuronal populations was tuned to best explain experimental data.

2.5.2 Stimulus-response models

Analysis of response to optogenetic input has largely been done using fMRI-based monitoring of rodent brain activity (Kahn et al., 2013; Liang et al., 2015; Cover et al., 2021). For the most part, works using such opto-fMRI studies can be summarized as attempts to either profile BOLD signals in relation to the application of stimulation or map changes in functional connectivity. In Krawchuk et al. (2020), the authors go a step further and model the dependencies between cerebral blood flow and photo-stimulation parameters (pulse duration, frequency) using linear regression. Optogenetic response has also been studied in the context of non-human primates in works such as Yazdan-Shahmorad et al. (2018) and Bloch et al. (2022). While both the works study the changes in network connectivity induced by stimulation, the approach in Bloch et al. (2022) is particularly interesting as the authors explicitly model the connectivity between regions as a non-linear (polynomial) function of selected features including the anatomical location of the regions, their distance from the stimulus and the distance between considered regions.

2.5.3 Dynamical system models

System identification-based approaches for response modeling of optogenetic stimulation have been proposed as highlighted in Table 5. In Bolus et al. (2020), the authors demonstrated the ability of LSSM towards the prediction of neuronal firing rates in response to the intensity of input light. A distinguishing feature in this work is the addition of a “disturbance” term in the state model to account for drifts in the neural response, which was shown to significantly impact the estimation accuracy. Besides the prediction performance, the work here is particularly interesting as the model learned here was shown to be effective in modulating the firing activity of a single neuron in a live rat through an LQR-based controller.

TABLE 5

TABLE 5. Summary of data-driven dynamical system models for Optogenetics.

Consistent with the modeling literatures of DBS and TMS, dynamic causal modeling has also been employed in optogenetic modeling. In Pinotsis et al. (2017), a DCM based on real LFP data was used to study the effective connectivity changes between input on and off conditions. In a related work (Ryali et al., 2016), the authors propose the use of multivariate dynamical systems (MDS) modeling, a data-driven biophysical approach similar to DCM, to train separate models corresponding to stimulation on and off conditions. While this is one way to model the effects of the input, response can also be modeled by explicitly considering the stimulus as a driving input of the underlying brain network as seen in the DCM-related works of Bernal-Casas et al. (2017) and Grimm et al. (2021). In both works, DCM based on fMRI data was used to quantify the causal relationship between brain regions such as the subthalamic nucleus and motor cortex. While the response to optogenetic input is what is being modeled in these works, the analysis of effective connectivity in these regions can also potentially facilitate the understanding of the mechanism of other neurostimulation techniques such as subthalamic DBS in this case. Ultimately, the versatility of learned models can perhaps be regarded as an important factor in building a generalizable model of the brain.

3 Disease specific modeling approaches

In the above sections, we categorized the modeling literature based on the neurostimulation technique and the approach employed. While we discuss the use of these models briefly in areas such as control and functional mapping, the real appeal of these works lies in the treatment of neurological and psychiatric conditions. To that end, here we provide a complementary categorization of the literature based on the brain-related disorders considered and highlight important trends in building models geared towards treating specific diseases using stimulation.

Parkinson’s Disease (PD) marks one of the most widely studied disorders in the context of neurostimulation. It is a neurological disorder related to abnormalities in basal ganglia (BG) and associated reductions in dopamine production (Little and Bestmann, 2015). Naturally, a range of biophysical models of BG have been proposed to study the PD mechanism under free-response (i.e., no external input) and stimulation conditions (Popovych and Tass, 2012; Little and Bestmann, 2015). Several PD-focused review articles have synthesized this literature, see, e.g., Chia et al. (2020) and Shimohama et al. (2003). A majority of the neurostimulation models of PD use biologically-derived BG networks to evaluate the connectivity changes related to PD and stimulation. A wide range of modeling detail and network size has nevertheless been used, from model with a relatively small number of neurons (≈10) Terman et al. (2002) to denser network structures comprising of more neurons (≈500) aimed at accurately modeling the neuronal firing and oscillatory activity Hahn and McIntyre (2010). For the most part, these works focus on DBS as the mode of stimulation which comes as no surprise considering the proven effectiveness of DBS in treating PD.

A more control-theoretic description of the neuron population dynamics perhaps comes from the use of Kuramoto models (Kuramoto, 1975) in works such as (Lysyansky et al., 2011; Holt et al., 2016). While several variations of the Kuramoto model has been used, these works all seek to model the phase synchronization in the firing activity of neuron populations observed in patients with PD. Despite relying on assumptions such as homogeneity of neuron sub-systems and the type of coupling between then, the obtained models have proven useful in their ability to abstract the complex neural dynamics of PD into simple phase equations and hence allowing the user to define relatively simple objectives for control design. Furthermore, several dynamical system models discussed earlier were originally constructed with the precise intent of building closed loop controllers for the treatment of PD (Kahan et al., 2014, 2019; Liu et al., 2016; Haddock et al., 2017; Su et al., 2018). While a number of these works have used simulated datasets which use some of the aforementioned biophysical models as the ground truth in order to learn and validate linear models (Liu et al., 2016; Su et al., 2018), works such as (Kahan et al., 2014; Haddock et al., 2017) have used real human data to study the same.

Epilepsy refers to a group of chronic neurological diseases characterized by unprovoked seizures (Wang et al., 2015; Wendling et al., 2016) and marks another historical focus of neurostimulation. Unlike PD where the symptoms are rather persistent, the onset of epileptic seizures can be difficult to predict and hence modeling the dynamics under epilepsy requires investigating the mechanism that causes seizures and conditions that lead to their termination (Wendling et al., 2016). Similar to PD, biophysical neural mass models have been employed in the literature to mimic the activity seen during the seizure duration commonly known as the ictal phase (Goodfellow et al., 2012; Fisher, 2013; Mina et al., 2013). In Wilson and Moehlis (2014), the authors use a single-neuron CBM to build a minimum-time controller to guide the brain to a target set of desirable state in the smallest possible time. In Mina et al. (2013), the authors instead use a multi-compartment CBM of the cortex and the thalamus to model the LFP response during seizure and stimulation conditions using real human data. Besides biophysical modeling, data-driven large scale modeling of the brain seen in the works of Chang et al. (2012), Chang et al. (2020) and Steinhardt et al. (2020) is another approach in the pursuit of modeling the epileptic brain under stimulation.

In general biophysical models often need to precisely model the regions and biological interactions underlying the specific disorder of interest (Wang et al., 2015) which can in turn enhance their appeal for the treatment of that disorder while limiting their applicability to other conditions. Data-driven modeling, on the other hand, is often more universal in methodology and disorder-specific modeling often becomes a matter of using the correct input-output data u(t), y(t) and choosing the appropriate parametric model structure (Yang et al., 2018). This has allowed for the recent use of dynamical system models for modeling the effect of neurostimulation in a diverse class of disorders (Chang et al., 2012; Liu et al., 2016; Gibson et al., 2017; Yang et al., 2018). Besides the neurological disorders mentioned in the above paragraphs, this data-driven approach has also been extended to psychological conditions, such as the use of LSSM to model the activity of a DES-stimulated brain under depression in Yang et al. (2018) and the use of DCM-based connectivity models in the context of obsessive compulsive disorder (OCD) in Gibson et al. (2017).

4 Discussion

In this paper we reviewed a large body of work on the computational modeling of the brain’s response to five of the most commonly used neurostimulation technologies. For each technology, we categorized the surveyed works into three categories of biophysical, stimulus-response, and (data-driven) dynamical system modeling. Perhaps not surprisingly, similar biophysical models have been employed across neurostimulation techniques which, for the most part, use finite-element volume conduction models, conductance-based neuron models, or a combination thereof. In general, biophysical models are computationally intensive and may scale poorly to large-scale brain networks. This is due to their reliance on iterative finite element calculations which are well-known to be computationally expensive (Giudice et al., 2019) and/or detailed multi-neuron dynamics which would inevitably face a curse of dimensionality if combined to form large-scale brain networks. However, this complexity comes with the advantage of having a dynamical model that describes the neural activity at the fine and biologically transparent level of synaptic exchanges and neuron depolarization and hyper-polarization, leading to the popularity of these models in the literature (Lysyansky et al., 2011; Salvador et al., 2011; Popovych and Tass, 2012; Shirinpour et al., 2021).

The second category of reviewed works for each stimulation technology consisted of statistical stimulus-response models. While these models may not provide insights into the low-level neuronal response to neurostimulation, they instead allow for the abstraction of the complex network activity in terms of summary biomarkers of interest (connectivity, band power, tremor, etc.). The main limitation of this category of works lies in their need for large sample sizes and repeated experiments which may be costly to obtain, particularly in clinical settings (Yarossi et al., 2019; Akbar et al., 2020; Muñoz et al., 2020).

Lastly, we have dynamical system models as the main focus of the present review which take the data-driven aspect of the stimulus-response models one step further. By using time series data, these models learn temporal dependencies in input-output data via dynamical models. Here, a large body of works has used linear models such as ARX, MVARX, and LSSM and have indeed been shown to achieve good prediction accuracy despite the nonlinearity of the brain at the microscale (Yang et al., 2021; Nozari et al., 2020^†). In addition to lower computational complexity in model fitting and validation, the use of linear models has far-reaching implications for control design and the interpretability of network dynamics given the wealth of knowledge on the analysis and control of linear dynamical systems (Kailath, 1980; Anderson and Moore, 2007). We further reviewed several works that have approached nonlinear dynamical system modeling of neurostimulation and have shown the power of ANNs, nonlinear ARX, and DCMs based on one-step-ahead prediction objectives. Ultimately, data-driven dynamical system models, whether linear or nonlinear, are critical for control theoretic methods to find their potentially widespread application in neural engineering and therapeutics.

Data-driven modeling comes with its own pros and cons. The theory-driven nature of biophysical models and the many assumptions that underlie them often leaves a considerable amount of variance in real data unexplained (Nozari et al., 2020^†). On the other hand, data-driven models of an appropriate order and complexity can reduce the unexplained variance through model fitting. However, learning data-driven models, particularly at scale, requires the availability of extensive and distributionally rich input-output data. The latter, in particular, necessitates carefully designed data collection experiments with persistently exciting stimulation waveforms which are currently uncommon and costly. The problem of acquiring rich datasets is further exacerbated in clinical settings by the fact that events such as seizures are unpredictable and rare. This in turn contributes to the sparsity of samples corresponding to simultaneous occurrences of stimulation and medically relevant conditions and events.

The great potential of system identification and dynamical system models in neuroscience is paralleled with major limitations in the existing literature and challenges to be tackled in future works. These limitations and challenges stem in part from the many differences that exist between the brain and the engineering systems for which system identification and control theory have been classically developed (Ziegler and Nichols, 1942; Kirk, 1970; Qin and Badgwell, 2003). These include dimensionality and the number of constituent subsystems, stochasticity and maximum achievable predictive accuracy, the number of spatio-temporal scales relevant for system behavior, and technological limitations in sensing and actuation, to name a few. As such, different modeling and control techniques need to be developed for the brain. Moreover, and in part due to the mentioned challenges, the vast majority of the dynamical system models developed for the brain have used either simulated data or real data in a post-hoc manner, i.e., without demonstrating the utility of the learned models for control design. As such, we expect a combination of custom-designed modeling and control algorithms and iterative, system identification-informed experiments to be necessary (and perhaps sufficient) for unlocking the great potential of data-driven control design for neurostimulation.

Author contributions

Conceptualization: SR, EN. Literature synthesis: GA, EN. Writing: all.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer MS declared a shared affiliation, with no collaboration, with the author SR at the time of the review.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

AIC, akaike information criterion; ARX, auto-regressive with exogenous input; ANN, artificial neural network; BOLD, blood-oxygen-level-dependent; CBM, conductance-based model; CV, cross validation; DBS, deep brain stimulation; DCM, dynamic causal modeling; DES, direct electrical stimulation; EEG, electroencephalography; ECoG, electrocorticogram; EMG, electromyography; fMRI, functional magnetic resonance imaging; FEM, finite-element modeling; FIR, finite impulse response; iEEG, intercranial EEG; LFP, local field potential; LSSM, linear state-space model; MEG, magnetoencephalography; MEP, motor evoked potential; RMSE, root mean squared error; RSS, residual sum of squares; TMS, transcranial magnetic stimulation; tES, transcranial electrical stimulation.

Footnotes

¹y(t) refers to the raw or processed recordings of the brain activity (e.g., EEG or fMRI) observed during stimulation and its exact nature depends on factors such as stimulation mode (invasive vs. non-invasive), region (e.g., sub-cortical or cortical) and process of interest (e.g., electrical vs. chemical changes).

²Another distinctive feature, though not relevant here, is the presence of an output variable y(t) that can be in general different from the latent states x(t), see, e.g., (Chen and Sarma, 2017).

³Multi-compartment CBMs (more common in the biophysical modeling of DBS) are simple extensions of Eq. 2 where each neuron is instead modeled as a connection of multiple capacitive elements with different geometric orientations. Each compartment is then modeled as a capacitive element as in Eq. 2 but with additional terms representing the electrical flows between connected compartments.

References

Aberra, A. S., Lopez, A., Grill, W. M., and Peterchev, A. V. (2022). Rapid estimation of cortical neuron activation thresholds by transcranial magnetic stimulation using convolutional neural networks. bioRxiv.

Google Scholar

Afuwape, O. F., Olafasakin, O. O., and Jiles, D. C. (2021). Neural network model for estimation of the induced electric field during transcranial magnetic stimulation. IEEE Trans. Magnetics 58, 1–5.

Google Scholar

Akbar, M. N., Yarossi, M., Martinez-Gost, M., Sommer, M. A., Dannhauer, M., Rampersad, S., et al. (2020). “Mapping motor cortex stimulation to muscle responses: A deep neural network modeling approach,” in Proceedings of the 13th ACM international conference on PErvasive technologies related to assistive environments, 1. –6.

Google Scholar

Alagapan, S., Schmidt, S. L., Lefebvre, J., Hadar, E., Shin, H. W., and Frohlich, F. (2016). Modulation of cortical oscillations by low-frequency direct cortical stimulation is state-dependent. PLoS Biol. 14, e1002424. doi:10.1371/journal.pbio.1002424

PubMed Abstract | CrossRef Full Text | Google Scholar

Ammann, C., Lindquist, M. A., and Celnik, P. A. (2017). Response variability of different anodal transcranial direct current stimulation intensities across multiple sessions. Brain Stimul. 10, 757–763. doi:10.1016/j.brs.2017.04.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Amunts, K., Ebell, C., Muller, J., Telefont, M., Knoll, A., and Lippert, T. (2016). The human brain project: Creating a European research infrastructure to decode the human brain. Neuron 92, 574–581. doi:10.1016/j.neuron.2016.10.046

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, B. D., and Moore, J. B. (2007). Optimal control: Linear quadratic methods. Mineola, New York: Courier Corporation.

Google Scholar

Anderson, C. J., Anderson, D. N., Pulst, S. M., Butson, C. R., and Dorval, A. D. (2020). Neural selectivity, efficiency, and dose equivalence in deep brain stimulation through pulse width tuning and segmented electrodes. Brain Stimul. 13, 1040–1050. doi:10.1016/j.brs.2020.03.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, D. N., Duffley, G., Vorwerk, J., Dorval, A. D., and Butson, C. R. (2019). Anodic stimulation misunderstood: Preferential activation of fiber orientations with anodic waveforms in deep brain stimulation. J. Neural Eng. 16, 016026. doi:10.1088/1741-2552/aae590

PubMed Abstract | CrossRef Full Text | Google Scholar

Arora, Y., Walia, P., Hayashibe, M., Muthalib, M., Chowdhury, S. R., Perrey, S., et al. (2021). Grey-box modeling and hypothesis testing of functional near-infrared spectroscopy-based cerebrovascular reactivity to anodal high-definition tdcs in healthy humans. PLoS Comput. Biol. 17, e1009386. doi:10.1371/journal.pcbi.1009386

PubMed Abstract | CrossRef Full Text | Google Scholar

Becker, C. O., Bassett, D. S., and Preciado, V. M. (2018). Large-scale dynamic modeling of task-fmri signals via subspace system identification. J. Neural Eng. 15, 066016. doi:10.1088/1741-2552/aad8c7

PubMed Abstract | CrossRef Full Text | Google Scholar

Behrend, C. E., Cassim, S. M., Pallone, M. J., Daubenspeck, J. A., Hartov, A., Roberts, D. W., et al. (2009). Toward feedback controlled deep brain stimulation: Dynamics of glutamate release in the subthalamic nucleus in rats. J. Neurosci. methods 180, 278–289. doi:10.1016/j.jneumeth.2009.04.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Ben-Menachem, E. (2012). Neurostimulation—Past, present, and beyond: Neurostimulation—Past, present, and beyond. Epilepsy Curr. 12, 188–191. doi:10.5698/1535-7511-12.5.188

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernal-Casas, D., Lee, H. J., Weitz, A. J., and Lee, J. H. (2017). Studying brain circuit function with dynamic causal modeling for optogenetic fmri. Neuron 93, 522–532.e5. doi:10.1016/j.neuron.2016.12.035

PubMed Abstract | CrossRef Full Text | Google Scholar

Beudel, M., and Brown, P. (2016). Adaptive deep brain stimulation in Parkinson’s disease. Park. Relat. Disord. 22, S123–S126. doi:10.1016/j.parkreldis.2015.09.028

PubMed Abstract | CrossRef Full Text | Google Scholar

Beynel, L., Powers, J. P., and Appelbaum, L. G. (2020). Effects of repetitive transcranial magnetic stimulation on resting-state connectivity: A systematic review. Neuroimage 211, 116596. doi:10.1016/j.neuroimage.2020.116596

PubMed Abstract | CrossRef Full Text | Google Scholar

Birdno, M. J., Kuncel, A. M., Dorval, A. D., Turner, D. A., Gross, R. E., and Grill, W. M. (2012). Stimulus features underlying reduced tremor suppression with temporally patterned deep brain stimulation. J. neurophysiology 107, 364–383. doi:10.1152/jn.00906.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Bloch, J., Greaves-Tunnell, A., Shea-Brown, E., Harchaoui, Z., Shojaie, A., and Yazdan-Shahmorad, A. (2022). Cortical network structure mediates response to stimulation: An optogenetic study in non-human primates bioRxiv.

Bolus, M. F., Willats, A. A., Rozell, C. J., and Stanley, G. B. (2020). State-space optimal feedback control of optogenetically driven neural activity. J. Neural Eng. 18, 036006. doi:10.1088/1741-2552/abb89c

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonato, C., Miniussi, C., and Rossini, P. (2006). Transcranial magnetic stimulation and cortical evoked potentials: A tms/eeg co-registration study. Clin. Neurophysiol. 117, 1699–1707. doi:10.1016/j.clinph.2006.05.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Borchers, S., Himmelbach, M., Logothetis, N., and Karnath, H.-O. (2012). Direct electrical stimulation of human cortex—The gold standard for mapping brain functions? Nat. Rev. Neurosci. 13, 63–70. doi:10.1038/nrn3140

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouthour, W., Mégevand, P., Donoghue, J., Lüscher, C., Birbaumer, N., and Krack, P. (2019). Biomarkers for closed-loop deep brain stimulation in Parkinson disease and beyond. Nat. Rev. Neurol. 15, 343–352. doi:10.1038/s41582-019-0166-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Boyle, M. R., and Fröhlich, F. (2013). Eeg feedback-controlled transcranial alternating current stimulation. In 2013 6th international IEEE/EMBS conference on neural engineering. (IEEE), 140–143.

CrossRef Full Text | Google Scholar

Brocker, D. T., Swan, B. D., So, R. Q., Turner, D. A., Gross, R. E., and Grill, W. M. (2017). Optimized temporal pattern of brain stimulation designed by computational evolution. Sci. Transl. Med. 9, eaah3532. doi:10.1126/scitranslmed.aah3532

PubMed Abstract | CrossRef Full Text | Google Scholar

Brocker, D. T., Swan, B. D., Turner, D. A., Gross, R. E., Tatter, S. B., Koop, M. M., et al. (2013). Improved efficacy of temporally non-regular deep brain stimulation in Parkinson’s disease. Exp. Neurol. 239, 60–67. doi:10.1016/j.expneurol.2012.09.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Buhlmann, J., Hofmann, L., Tass, P. A., and Hauptmann, C. (2011). Modeling of a segmented electrode for desynchronizing deep brain stimulation. Front. Neuroeng. 4, 15. doi:10.3389/fneng.2011.00015

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, J.-Y., Fecchio, M., Pigorini, A., Massimini, M., Tononi, G., and Van Veen, B. D. (2019). Assessing recurrent interactions in cortical networks: Modeling eeg response to transcranial magnetic stimulation. J. Neurosci. methods 312, 93–104. doi:10.1016/j.jneumeth.2018.11.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, J.-Y., Pigorini, A., Massimini, M., Tononi, G., Nobili, L., and Van Veen, B. D. (2012). Multivariate autoregressive models with exogenous inputs for intracerebral responses to direct electrical stimulation of the human brain. Front. Hum. Neurosci. 6, 317. doi:10.3389/fnhum.2012.00317

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, S., Wei, X., Su, F., Liu, C., Yi, G., Wang, J., et al. (2020). Model predictive control for seizure suppression based on nonlinear auto-regressive moving-average volterra model. IEEE Trans. Neural Syst. Rehabil. Eng. 28, 2173–2183. doi:10.1109/tnsre.2020.3014927

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Z., and Sarma, S. V. (2017). Dynamic neuroscience. Springer.

PubMed Abstract | Google Scholar

Chervyakov, A. V., Chernyavsky, A. Y., Sinitsyn, D. O., and Piradov, M. A. (2015). Possible mechanisms underlying the therapeutic effects of transcranial magnetic stimulation. Front. Hum. Neurosci. 9, 303. doi:10.3389/fnhum.2015.00303

PubMed Abstract | CrossRef Full Text | Google Scholar

Chia, S. J., Tan, E.-K., and Chao, Y.-X. (2020). Historical perspective: Models of Parkinson’s disease. Int. J. Mol. Sci. 21, 2464. doi:10.3390/ijms21072464

PubMed Abstract | CrossRef Full Text | Google Scholar

Cover, C. G., Kesner, A. J., Ukani, S., Stein, E. A., Ikemoto, S., Yang, Y., et al. (2021). Whole brain dynamics during optogenetic self-stimulation of the medial prefrontal cortex in mice. Commun. Biol. 4, 66–68. doi:10.1038/s42003-020-01612-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Crocker, B., Ostrowski, L., Williams, Z. M., Dougherty, D. D., Eskandar, E. N., Widge, A. S., et al. (2021). Local and distant responses to single pulse electrical stimulation reflect different forms of connectivity. NeuroImage 237, 118094. doi:10.1016/j.neuroimage.2021.118094

PubMed Abstract | CrossRef Full Text | Google Scholar

Dayan, P., and Abbott, L. F. (2001). Theoretical neuroscience: Computational and mathematical Modeling of neural systems. Computational neuroscience. MIT Press.

Google Scholar

De Geeter, N., Dupré, L., and Crevecoeur, G. (2016). Modeling transcranial magnetic stimulation from the induced electric fields to the membrane potentials along tractography-based white matter fiber tracts. J. Neural Eng. 13, 026028. doi:10.1088/1741-2560/13/2/026028

PubMed Abstract | CrossRef Full Text | Google Scholar

De Raedt, R., Vanderhasselt, M.-A., and Baeken, C. (2015). Neurostimulation as an intervention for treatment resistant depression: From research on mechanisms towards targeted neurocognitive strategies. Clin. Psychol. Rev. 41, 61–69. doi:10.1016/j.cpr.2014.10.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Deeb, W., Giordano, J. J., Rossi, P. J., Mogilner, A. Y., Gunduz, A., Judy, J. W., et al. (2016). Proceedings of the fourth annual deep brain stimulation think tank: A review of emerging issues and technologies. Front. Integr. Neurosci. 10, 38. doi:10.3389/fnint.2016.00038

PubMed Abstract | CrossRef Full Text | Google Scholar

Deisseroth, K., Feng, G., Majewska, A. K., Miesenböck, G., Ting, A., and Schnitzer, M. J. (2006). Next-generation optical technologies for illuminating genetically targeted brain circuits. J. Neurosci. 26, 10380–10386. doi:10.1523/jneurosci.3863-06.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Dura-Bernal, S., Suter, B. A., Gleeson, P., Cantarelli, M., Quintana, A., Rodriguez, F., et al. (2019). Netpyne, a tool for data-driven multiscale modeling of brain circuits. Elife 8, e44494. doi:10.7554/elife.44494

PubMed Abstract | CrossRef Full Text | Google Scholar

Dutta, A., and Nitsche, M. A. (2013). “Neural mass model analysis of online modulation of electroencephalogram with transcranial direct current stimulation,” in 2013 6th international IEEE/EMBS conference on neural engineering (IEEE), 210.

CrossRef Full Text | Google Scholar

Esser, S. K., Hill, S. L., and Tononi, G. (2005). Modeling the effects of transcranial magnetic stimulation on cortical circuits. J. neurophysiology 94, 622–639. doi:10.1152/jn.01230.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Fisher, R. S. (2013). Deep brain stimulation for epilepsy. Handb. Clin. Neurol. 116, 217–234. doi:10.1016/b978-0-444-53497-2.00017-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Foutz, T. J., Arlow, R. L., and McIntyre, C. C. (2012). Theoretical principles underlying optical stimulation of a channelrhodopsin-2 positive pyramidal neuron. J. neurophysiology 107, 3235–3245. doi:10.1152/jn.00501.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

Freestone, D. R., Karoly, P. J., Nešić, D., Aram, P., Cook, M. J., and Grayden, D. B. (2014). Estimation of effective connectivity via data-driven neural modeling. Front. Neurosci. 383, 383. doi:10.3389/fnins.2014.00383

PubMed Abstract | CrossRef Full Text | Google Scholar

Friston, K. J., Harrison, L., and Penny, W. (2003). Dynamic causal modelling. Neuroimage 19, 1273–1302. doi:10.1016/s1053-8119(03)00202-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Frohlich, F., and Townsend, L. (2021). Closed-loop transcranial alternating current stimulation: Towards personalized non-invasive brain stimulation for the treatment of psychiatric illnesses. Curr. Behav. Neurosci. Rep. 8, 51–57. doi:10.1007/s40473-021-00227-8

CrossRef Full Text | Google Scholar

Galletta, E. E., Rao, P. R., and Barrett, A. M. (2011). Transcranial magnetic stimulation (tms): Potential progress for language improvement in aphasia. Top. stroke rehabilitation 18, 87–91. doi:10.1310/tsr1802-87

PubMed Abstract | CrossRef Full Text | Google Scholar

Gálvez, V., Alonzo, A., Martin, D., and Loo, C. K. (2013). Transcranial direct current stimulation treatment protocols: Should stimulus intensity be constant or incremental over multiple sessions? Int. J. Neuropsychopharmacol. 16, 13–21. doi:10.1017/s1461145712000041

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibson, W. S., Cho, S., Abulseoud, O. A., Gorny, K. R., Felmlee, J. P., Welker, K. M., et al. (2017). The impact of mirth-inducing ventral striatal deep brain stimulation on functional and effective connectivity. Cereb. Cortex 27, 2183–2194. doi:10.1093/cercor/bhw074

PubMed Abstract | CrossRef Full Text | Google Scholar

Giudice, J. S., Zeng, W., Wu, T., Alshareef, A., Shedd, D. F., and Panzer, M. B. (2019). An analytical review of the numerical methods used for finite element modeling of traumatic brain injury. Ann. Biomed. Eng. 47, 1855–1872. doi:10.1007/s10439-018-02161-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Gomez-Tames, J., Laakso, I., and Hirata, A. (2020). Review on biophysical modelling and simulation studies for transcranial magnetic stimulation. Phys. Med. Biol. 65, 24TR03. doi:10.1088/1361-6560/aba40d

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodfellow, M., Schindler, K., and Baier, G. (2012). Self-organised transients in a neural mass model of epileptogenic tissue dynamics. NeuroImage 59, 2644–2660. doi:10.1016/j.neuroimage.2011.08.060

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodwin, B. D., and Butson, C. R. (2015). Subject-specific multiscale modeling to investigate effects of transcranial magnetic stimulation. Neuromodulation Technol. A. T. Neural Interface 18, 694–704. doi:10.1111/ner.12296

PubMed Abstract | CrossRef Full Text | Google Scholar

Gorzelic, P., Schiff, S., and Sinha, A. (2013). Model-based rational feedback controller design for closed-loop deep brain stimulation of Parkinson’s disease. J. Neural Eng. 10, 026016. doi:10.1088/1741-2560/10/2/026016

PubMed Abstract | CrossRef Full Text | Google Scholar

Grant, P. F., and Lowery, M. M. (2012). Simulation of cortico-basal ganglia oscillations and their suppression by closed loop deep brain stimulation. IEEE Trans. Neural Syst. Rehabil. Eng. 21, 584–594. doi:10.1109/tnsre.2012.2202403

PubMed Abstract | CrossRef Full Text | Google Scholar

Grefkes, C., Nowak, D. A., Wang, L. E., Dafotakis, M., Eickhoff, S. B., and Fink, G. R. (2010). Modulating cortical connectivity in stroke patients by rtms assessed with fmri and dynamic causal modeling. Neuroimage 50, 233–242. doi:10.1016/j.neuroimage.2009.12.029

PubMed Abstract | CrossRef Full Text | Google Scholar

Grimm, C., Frässle, S., Steger, C., von Ziegler, L., Sturman, O., Shemesh, N., et al. (2021). Optogenetic activation of striatal d1/d2 medium spiny neurons differentially engages downstream connected areas beyond the basal ganglia. bioRxiv.

Google Scholar

Grossman, N., Nikolic, K., Toumazou, C., and Degenaar, P. (2011). Modeling study of the light stimulation of a neuron cell with channelrhodopsin-2 mutants. IEEE Trans. Biomed. Eng. 58, 1742–1751. doi:10.1109/tbme.2011.2114883

PubMed Abstract | CrossRef Full Text | Google Scholar

Gu, S., Pasqualetti, F., Cieslak, M., Telesford, Q. K., Alfred, B. Y., Kahn, A. E., et al. (2015). Controllability of structural brain networks. Nat. Commun. 6. doi:10.1038/ncomms9414

PubMed Abstract | CrossRef Full Text | Google Scholar

Guse, B., Falkai, P., and Wobrock, T. (2010). Cognitive effects of high-frequency repetitive transcranial magnetic stimulation: A systematic review. J. Neural Transm. (Vienna). 117, 105–122. doi:10.1007/s00702-009-0333-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Haddock, A., Velisar, A., Herron, J., Bronte-Stewart, H., and Chizeck, H. J. (2017). Model predictive control of deep brain stimulation for parkinsonian tremor. In 2017 8th international IEEE/EMBS conference on neural engineering. (IEEE), 358–362.

CrossRef Full Text | Google Scholar

Hahn, P. J., and McIntyre, C. C. (2010). Modeling shifts in the rate and pattern of subthalamopallidal network activity during deep brain stimulation. J. Comput. Neurosci. 28, 425–441. doi:10.1007/s10827-010-0225-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Hallett, M. (2007). Transcranial magnetic stimulation: A primer. Neuron 55, 187–199. doi:10.1016/j.neuron.2007.06.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Hernández-Ribas, R., Deus, J., Pujol, J., Segalàs, C., Vallejo, J., Menchón, J. M., et al. (2013). Identifying brain imaging correlates of clinical response to repetitive transcranial magnetic stimulation (rtms) in major depression. Brain Stimul. 6, 54–61. doi:10.1016/j.brs.2012.01.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Herrington, T. M., Cheng, J. J., and Eskandar, E. N. (2016). Mechanisms of deep brain stimulation. J. neurophysiology 115, 19–38. doi:10.1152/jn.00281.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoang, K. B., Cassar, I. R., Grill, W. M., and Turner, D. A. (2017). Biomarkers and stimulation algorithms for adaptive brain stimulation. Front. Neurosci. 11, 564. doi:10.3389/fnins.2017.00564

PubMed Abstract | CrossRef Full Text | Google Scholar

Hodkinson, D. J., Bungert, A., Bowtell, R., Jackson, S. R., and Jung, J. (2021). Operculo-insular and anterior cingulate plasticity induced by transcranial magnetic stimulation in the human motor cortex: A dynamic casual modeling study. J. Neurophysiology 125, 1180–1190. doi:10.1152/jn.00670.2020

PubMed Abstract | CrossRef Full Text | Google Scholar

Holt, A. B., Wilson, D., Shinn, M., Moehlis, J., and Netoff, T. I. (2016). Phasic burst stimulation: A closed-loop approach to tuning deep brain stimulation parameters for Parkinson’s disease. PLoS Comput. Biol. 12, e1005011. doi:10.1371/journal.pcbi.1005011

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, W. A., Stitt, I. M., Negahbani, E., Passey, D., Ahn, S., Davey, M., et al. (2021). Transcranial alternating current stimulation entrains alpha oscillations by preferential phase synchronization of fast-spiking cortical neurons to stimulation waveform. Nat. Commun. 12. doi:10.1038/s41467-021-23021-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Indahlastari, A., Chauhan, M., Schwartz, B., and Sadleir, R. J. (2016). Changing head model extent affects finite element predictions of transcranial direct current stimulation distributions. J. Neural Eng. 13, 066006. doi:10.1088/1741-2560/13/6/066006

PubMed Abstract | CrossRef Full Text | Google Scholar

Iramina, K., Maeno, T., Kowatari, Y., and Ueno, S. (2002). Effects of transcranial magnetic stimulation on eeg activity. IEEE Trans. Magn. 38, 3347–3349. doi:10.1109/tmag.2002.802309

CrossRef Full Text | Google Scholar

Jamil, A., Batsikadze, G., Kuo, H.-I., Labruna, L., Hasan, A., Paulus, W., et al. (2017). Systematic evaluation of the impact of stimulation intensity on neuroplastic after-effects induced by transcranial direct current stimulation. J. Physiol. 595, 1273–1288. doi:10.1113/jp272738

PubMed Abstract | CrossRef Full Text | Google Scholar

Janson, A. P., Anderson, D. N., and Butson, C. R. (2020). Activation robustness with directional leads and multi-lead configurations in deep brain stimulation. J. Neural Eng. 17, 026012. doi:10.1088/1741-2552/ab7b1d

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, L., Alekseichuk, I., Krieg, J., Doyle, A., Yu, Y., Vitek, J., et al. (2020). Dose-dependent effects of transcranial alternating current stimulation on spike timing in awake nonhuman primates. Sci. Adv. 6, eaaz2747. doi:10.1126/sciadv.aaz2747

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones, K. T., Stephens, J. A., Alam, M., Bikson, M., and Berryhill, M. E. (2015). Longitudinal neurostimulation in older adults improves working memory. PloS one 10, e0121904. doi:10.1371/journal.pone.0121904

PubMed Abstract | CrossRef Full Text | Google Scholar

Jung, J., Bungert, A., Bowtell, R., and Jackson, S. R. (2020). Modulating brain networks with transcranial magnetic stimulation over the primary motor cortex: A concurrent tms/fmri study. Front. Hum. Neurosci. 14, 31. doi:10.3389/fnhum.2020.00031

PubMed Abstract | CrossRef Full Text | Google Scholar

Kahan, J., Mancini, L., Flandin, G., White, M., Papadaki, A., Thornton, J., et al. (2019). Deep brain stimulation has state-dependent effects on motor connectivity in Parkinson’s disease. Brain 142, 2417–2431. doi:10.1093/brain/awz164

PubMed Abstract | CrossRef Full Text | Google Scholar

Kahan, J., Urner, M., Moran, R., Flandin, G., Marreiros, A., Mancini, L., et al. (2014). Resting state functional mri in Parkinson’s disease: The impact of deep brain stimulation on ‘effective’ connectivity. Brain 137, 1130–1144. doi:10.1093/brain/awu027

PubMed Abstract | CrossRef Full Text | Google Scholar

Kähkönen, S., Komssi, S., Wilenius, J., and Ilmoniemi, R. J. (2005). Prefrontal transcranial magnetic stimulation produces intensity-dependent eeg responses in humans. Neuroimage 24, 955–960. doi:10.1016/j.neuroimage.2004.09.048

PubMed Abstract | CrossRef Full Text | Google Scholar

Kahn, I., Knoblich, U., Desai, M., Bernstein, J., Graybiel, A., Boyden, E., et al. (2013). Optogenetic drive of neocortical pyramidal neurons generates fmri signals that are correlated with spiking activity. Brain Res. 1511, 33–45. doi:10.1016/j.brainres.2013.03.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Kailath, T. (1980). Linear systems. Information and system sciences series. Prentice-Hall.

Google Scholar

Kassiri, H., Tonekaboni, S., Salam, M. T., Soltani, N., Abdelhalim, K., Velazquez, J. L. P., et al. (2017). Closed-loop neurostimulators: A survey and a seizure-predicting design example for intractable epilepsy treatment. IEEE Trans. Biomed. Circuits Syst. 11, 1026–1040. doi:10.1109/tbcas.2017.2694638

PubMed Abstract | CrossRef Full Text | Google Scholar

Keane, M., Deyo, S., Abosch, A., Bajwa, J. A., and Johnson, M. D. (2012). Improved spatial targeting with directionally segmented deep brain stimulation leads for treating essential tremor. J. Neural Eng. 9, 046005. doi:10.1088/1741-2560/9/4/046005

PubMed Abstract | CrossRef Full Text | Google Scholar

Keeser, D., Meindl, T., Bor, J., Palm, U., Pogarell, O., Mulert, C., et al. (2011). Prefrontal transcranial direct current stimulation changes connectivity of resting-state networks during fmri. J. Neurosci. 31, 15284–15293. doi:10.1523/jneurosci.0542-11.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

Keller, C. J., Honey, C. J., Mégevand, P., Entz, L., Ulbert, I., and Mehta, A. D. (2014). Mapping human brain networks with cortico-cortical evoked potentials. Phil. Trans. R. Soc. B 369, 20130528. doi:10.1098/rstb.2013.0528

PubMed Abstract | CrossRef Full Text | Google Scholar

Keller, C. J., Huang, Y., Herrero, J. L., Fini, M. E., Du, V., Lado, F. A., et al. (2018). Induction and quantification of excitability changes in human cortical networks. J. Neurosci. 38, 5384–5398. doi:10.1523/jneurosci.1088-17.2018

PubMed Abstract | CrossRef Full Text | Google Scholar

Kenett, Y. N., Medaglia, J. D., Beaty, R. E., Chen, Q., Betzel, R. F., Thompson-Schill, S. L., et al. (2018). Driving the brain towards creativity and intelligence: A network control theory analysis. Neuropsychologia 118, 79–90. doi:10.1016/j.neuropsychologia.2018.01.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Khobragade, N., Graupe, D., and Tuninetti, D. (2015). “Towards fully automated closed-loop deep brain stimulation in Parkinson’s disease patients: A lamstar-based tremor predictor,” in 2015 37th annual international conference of the IEEE engineering in medicine and biology society (EMBC) (IEEE), 2616–2619.

Google Scholar

Kiakojouri, M., Momeni, H., and Ramezani, A. (2020).Brain state-space model parameters estimation during non-invasive stimulation. In 2020 27th Natl. 5th Int. Iran. Conf. Biomed. Eng. (ICBME). IEEE, 305–311.

CrossRef Full Text | Google Scholar

Kim, D., Seo, H., Kim, H.-I., and Jun, S. C. (2014). Computational study on subdural cortical stimulation-the influence of the head geometry, anisotropic conductivity, and electrode configuration. PLoS One 9, e108028. doi:10.1371/journal.pone.0108028

PubMed Abstract | CrossRef Full Text | Google Scholar

Kirk, D. E. (1970). Optimal control theory: An introduction. Mineola, New York: Prentice-Hall.

Google Scholar

Koch, C. (2004). Biophysics of computation: Information Processing in single neurons. Computational neuroscience series. USA: Oxford University Press.

Google Scholar

Komssi, S., Aronen, H. J., Huttunen, J., Kesäniemi, M., Soinne, L., Nikouline, V. V., et al. (2002). Ipsi-and contralateral eeg reactions to transcranial magnetic stimulation. Clin. Neurophysiol. 113, 175–184. doi:10.1016/s1388-2457(01)00721-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Kraus, D., Naros, G., Bauer, R., Khademi, F., Leão, M. T., Ziemann, U., et al. (2016). Brain state-dependent transcranial magnetic closed-loop stimulation controlled by sensorimotor desynchronization induces robust increase of corticospinal excitability. Brain Stimul. 9, 415–424. doi:10.1016/j.brs.2016.02.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Krause, M. R., Vieira, P. G., Csorba, B. A., Pilly, P. K., and Pack, C. C. (2019). Transcranial alternating current stimulation entrains single-neuron activity in the primate brain. Proc. Natl. Acad. Sci. U. S. A. 116, 5747–5755. doi:10.1073/pnas.1815958116

PubMed Abstract | CrossRef Full Text | Google Scholar

Krawchuk, M. B., Ruff, C. F., Yang, X., Ross, S. E., and Vazquez, A. L. (2020). Optogenetic assessment of vip, pv, som and nos inhibitory neuron activity and cerebral blood flow regulation in mouse somato-sensory cortex. J. Cereb. Blood Flow. Metab. 40, 1427–1440. doi:10.1177/0271678x19870105

PubMed Abstract | CrossRef Full Text | Google Scholar

Kunze, T., Hunold, A., Haueisen, J., Jirsa, V., and Spiegler, A. (2016). Transcranial direct current stimulation changes resting state functional connectivity: A large-scale brain network modeling study. Neuroimage 140, 174–187. doi:10.1016/j.neuroimage.2016.02.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuramoto, Y. (1975). “Self-entrainment of a population of coupled non-linear oscillators,” in International symposium on mathematical problems in theoretical physics (Springer), 420–422.

Google Scholar

Leite, J., Morales-Quezada, L., Carvalho, S., Thibaut, A., Doruk, D., Chen, C.-F., et al. (2017). Surface eeg-transcranial direct current stimulation (tdcs) closed-loop system. Int. J. Neural Syst. 27, 1750026. doi:10.1142/s0129065717500265

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, Z., Watson, G. D., Alloway, K. D., Lee, G., Neuberger, T., and Zhang, N. (2015). Mapping the functional network of medial prefrontal cortex by combining optogenetics and fmri in awake rats. Neuroimage 117, 114–123. doi:10.1016/j.neuroimage.2015.05.036

PubMed Abstract | CrossRef Full Text | Google Scholar

Ligaard, J., Sannæs, J., and Pihlstrøm, L. (2019). Deep brain stimulation and genetic variability in Parkinson’s disease: A review of the literature. npj Park. Dis. 5, 18–10. doi:10.1038/s41531-019-0091-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, Y., and Wang, Y. (2017). Neurostimulation as a promising epilepsy therapy. Epilepsia open 2, 371–387. doi:10.1002/epi4.12070

PubMed Abstract | CrossRef Full Text | Google Scholar

Little, S., and Bestmann, S. (2015). Computational neurostimulation for Parkinson’s disease. Prog. Brain Res. 222, 163–190. doi:10.1016/bs.pbr.2015.09.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Little, S., and Brown, P. (2012). What brain signals are suitable for feedback control of deep brain stimulation in Parkinson’s disease? Ann. N. Y. Acad. Sci. 1265, 9–24. doi:10.1111/j.1749-6632.2012.06650.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Little, S., Pogosyan, A., Neal, S., Zavala, B., Zrinzo, L., Hariz, M., et al. (2013). Adaptive deep brain stimulation in advanced Parkinson disease. Ann. Neurol. 74, 449–457. doi:10.1002/ana.23951

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, A., Vöröslakos, M., Kronberg, G., Henin, S., Krause, M. R., Huang, Y., et al. (2018). Immediate neurophysiological effects of transcranial electrical stimulation. Nat. Commun. 9. doi:10.1038/s41467-018-07233-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, C., Wang, J., Li, H., Lu, M., Deng, B., Yu, H., et al. (2016). Closed-loop modulation of the pathological disorders of the basal ganglia network. IEEE Trans. Neural Netw. Learn. Syst. 28, 371–382. doi:10.1109/tnnls.2015.2508599

PubMed Abstract | CrossRef Full Text | Google Scholar

Lozano, A. M., Lipsman, N., Bergman, H., Brown, P., Chabardes, S., Chang, J. W., et al. (2019). Deep brain stimulation: Current challenges and future directions. Nat. Rev. Neurol. 15, 148–160. doi:10.1038/s41582-018-0128-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Luber, B., and Deng, Z. D. (2016). Application of non-invasive brain stimulation in psychophysiology. Handb. Psychophysiol. 4, 116–150. doi:10.1017/9781107415782.007

CrossRef Full Text | Google Scholar

Lysyansky, B., Popovych, O. V., and Tass, P. A. (2011). Desynchronizing anti-resonance effect of m: n on–off coordinated reset stimulation. J. Neural Eng. 8, 036019. doi:10.1088/1741-2560/8/3/036019

PubMed Abstract | CrossRef Full Text | Google Scholar

Magis, D., and Schoenen, J. (2012). Advances and challenges in neurostimulation for headaches. Lancet Neurology 11, 708–719. doi:10.1016/s1474-4422(12)70139-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Mahon, B. Z., Miozzo, M., and Pilcher, W. H. (2019). Direct electrical stimulation mapping of cognitive functions in the human brain.

Google Scholar

Mahrach, A., Chen, G., Li, N., van Vreeswijk, C., and Hansel, D. (2020). Mechanisms underlying the response of mouse cortical networks to optogenetic manipulation. Elife 9, e49967. doi:10.7554/elife.49967

PubMed Abstract | CrossRef Full Text | Google Scholar

Mandonnet, E., and Pantz, O. (2011). The role of electrode direction during axonal bipolar electrical stimulation: A bidomain computational model study. Acta Neurochir. (Wien). 153, 2351–2355. doi:10.1007/s00701-011-1151-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Mandonnet, E., Winkler, P. A., and Duffau, H. (2010). Direct electrical stimulation as an input gate into brain functional networks: Principles, advantages and limitations. Acta Neurochir. (Wien). 152, 185–193. doi:10.1007/s00701-009-0469-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Manola, L., Holsheimer, J., Veltink, P., and Buitenweg, J. R. (2007). Anodal vs cathodal stimulation of motor cortex: A modeling study. Clin. Neurophysiol. 118, 464–474. doi:10.1016/j.clinph.2006.09.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Marangell, L., Martinez, M., Jurdi, R., and Zboyan, H. (2007). Neurostimulation therapies in depression: A review of new modalities. Acta Psychiatr. Scand. 116, 174–181. doi:10.1111/j.1600-0447.2007.01033.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Marceglia, S., Rossi, L., Foffani, G., Bianchi, A., Cerutti, S., and Priori, A. (2007). Basal ganglia local field potentials: Applications in the development of new deep brain stimulation devices for movement disorders. Expert Rev. Med. devices 4, 605–614. doi:10.1586/17434440.4.5.605

PubMed Abstract | CrossRef Full Text | Google Scholar

Marreiros, A. C., Stephan, K. E., and Friston, K. J. (2010). Dynamic causal modeling. Scholarpedia 5, 9568. doi:10.4249/scholarpedia.9568

CrossRef Full Text | Google Scholar

Martens, H., Toader, E., Decré, M., Anderson, D., Vetter, R., Kipke, D., et al. (2011). Spatial steering of deep brain stimulation volumes using a novel lead design. Clin. Neurophysiol. 122, 558–566. doi:10.1016/j.clinph.2010.07.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Matsumoto, R., Kunieda, T., and Nair, D. (2017). Single pulse electrical stimulation to probe functional and pathological connectivity in epilepsy. Seizure 44, 27–36. doi:10.1016/j.seizure.2016.11.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Matsumoto, R., Nair, D. R., LaPresto, E., Bingaman, W., Shibasaki, H., and Lüders, H. O. (2007). Functional connectivity in human cortical motor system: A cortico-cortical evoked potential study. Brain 130, 181–197. doi:10.1093/brain/awl257

PubMed Abstract | CrossRef Full Text | Google Scholar

Medvedev, A., Cubo, R., Olsson, F., Bro, V., and Andersson, H. (2019). “Control-engineering perspective on deep brain stimulation: Revisited,” in 2019 American control conference (IEEE), 860–865.

CrossRef Full Text | Google Scholar

Mina, F., Benquet, P., Pasnicu, A., Biraben, A., and Wendling, F. (2013). Modulation of epileptic activity by deep brain stimulation: A model-based study of frequency-dependent effects. Front. Comput. Neurosci. 7, 94. doi:10.3389/fncom.2013.00094

PubMed Abstract | CrossRef Full Text | Google Scholar

Minhas, P., Bikson, M., Woods, A. J., Rosen, A. R., and Kessler, S. K. (2012). “Transcranial direct current stimulation in pediatric brain: A computational modeling study,” in 2012 annual international conference of the IEEE engineering in medicine and biology society (IEEE), 859–862.

PubMed Abstract | CrossRef Full Text | Google Scholar

Miranda, P. C., Lomarev, M., and Hallett, M. (2006). Modeling the current distribution during transcranial direct current stimulation. Clin. Neurophysiol. 117, 1623–1629. doi:10.1016/j.clinph.2006.04.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Mishra, B. R., Sarkar, S., Praharaj, S. K., Mehta, V. S., Diwedi, S., and Nizamie, S. H. (2011). Repetitive transcranial magnetic stimulation in psychiatry. Ann. Indian Acad. Neurol. 14, 245. doi:10.4103/0972-2327.91935

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohan, U. R., Watrous, A. J., Miller, J. F., Lega, B. C., Sperling, M. R., Worrell, G. A., et al. (2020). The effects of direct brain stimulation in humans depend on frequency, amplitude, and white-matter proximity. Brain Stimul. 13, 1183–1195. doi:10.1016/j.brs.2020.05.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Molaee-Ardekani, B., Márquez-Ruiz, J., Merlet, I., Leal-Campanario, R., Gruart, A., Sánchez-Campusano, R., et al. (2013). Effects of transcranial direct current stimulation (tdcs) on cortical activity: A computational modeling study. Brain Stimul. 6, 25–39. doi:10.1016/j.brs.2011.12.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Montagni, E., Resta, F., Mascaro, A. L. A., and Pavone, F. S. (2019). Optogenetics in brain research: From a strategy to investigate physiological function to a therapeutic tool. Photonics (MDPI) 6, 92. doi:10.3390/photonics6030092

CrossRef Full Text | Google Scholar

Muñoz, K. A., Kostick, K., Sanchez, C., Kalwani, L., Torgerson, L., Hsu, R., et al. (2020). Researcher perspectives on ethical considerations in adaptive deep brain stimulation trials. Front. Hum. Neurosci. 14, 578695. doi:10.3389/fnhum.2020.578695

PubMed Abstract | CrossRef Full Text | Google Scholar

Newman, J. P., Fong, M.-f., Millard, D. C., Whitmire, C. J., Stanley, G. B., and Potter, S. M. (2015). Optogenetic feedback control of neural activity. Elife 4, e07192. doi:10.7554/elife.07192

PubMed Abstract | CrossRef Full Text | Google Scholar

Nguyen, T. K., Djilas, M., Nowacki, A., Mercanzini, A., Schüpbach, M., Renaud, P., et al. (2019). Analysis of patient-specific stimulation with segmented leads in the subthalamic nucleus. PloS one 14, e0217985. doi:10.1371/journal.pone.0217985

PubMed Abstract | CrossRef Full Text | Google Scholar

Nikolic, K., Jarvis, S., Grossman, N., and Schultz, S. (2013). “Computational models of optogenetic tools for controlling neural circuits with light,” in 2013 35th annual international conference of the IEEE engineering in medicine and biology society (IEEE), 5934–5937.

CrossRef Full Text | Google Scholar

Nozari, E., Bertolero, M. A., Stiso, J., Caciagli, L., Cornblath, E. J., He, X., et al. (2020). Is the brain macroscopically linear? A system identification of resting state dynamics. arXiv preprint arXiv:2012.12351.

Google Scholar

Nozari, E., and Cortés, J. (2020). Hierarchical selective recruitment in linear-threshold brain networks part ii: Multilayer dynamics and top-down recruitment. IEEE Trans. Autom. Contr. 66, 965–980. doi:10.1109/tac.2020.2997854

CrossRef Full Text | Google Scholar

Ojemann, G. A. (1983). Brain organization for language from the perspective of electrical stimulation mapping. Behav. Brain Sci. 6, 189–206. doi:10.1017/s0140525x00015491

CrossRef Full Text | Google Scholar

Opitz, A., Zafar, N., Bockermann, V., Rohde, V., and Paulus, W. (2014). Validating computationally predicted tms stimulation areas using direct electrical stimulation in patients with brain tumors near precentral regions. NeuroImage Clin. 4, 500–507. doi:10.1016/j.nicl.2014.03.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Orena, E., Caldiroli, D., Acerbi, F., Barazzetta, I., and Papagno, C. (2019). Investigating the functional neuroanatomy of concrete and abstract word processing through direct electric stimulation (des) during awake surgery. Cogn. Neuropsychol. 36, 167–177. doi:10.1080/02643294.2018.1477748

PubMed Abstract | CrossRef Full Text | Google Scholar

Ostrowsky, K., Magnin, M., Ryvlin, P., Isnard, J., Guenot, M., and Mauguiere, F. (2002). Representation of pain and somatic sensation in the human insula: A study of responses to direct electrical cortical stimulation. Cereb. cortex 12, 376–385. doi:10.1093/cercor/12.4.376

PubMed Abstract | CrossRef Full Text | Google Scholar

Papasavvas, C. A., Schroeder, G. M., Diehl, B., Baier, G., Taylor, P. N., and Wang, Y. (2020). Band power modulation through intracranial eeg stimulation and its cross-session consistency. J. Neural Eng. 17, 054001. doi:10.1088/1741-2552/abbecf

PubMed Abstract | CrossRef Full Text | Google Scholar

Pascual-Leone, A., Tormos, J. M., Keenan, J., Tarazona, F., Cañete, C., and Catalá, M. D. (1998). Study and modulation of human cortical excitability with transcranial magnetic stimulation. J. Clin. neurophysiology 15, 333–343. doi:10.1097/00004691-199807000-00005

PubMed Abstract | CrossRef Full Text | Google Scholar

Paulk, A. C., Zelmann, R., Crocker, B., Widge, A. S., Dougherty, D. D., Eskandar, E. N., et al. (2022). Local and distant cortical responses to single pulse intracranial stimulation in the human brain are differentially modulated by specific stimulation parameters. Brain Stimul. 15, 491–508. doi:10.1016/j.brs.2022.02.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Pedoto, G., Santaniello, S., Montgomery, E. B., Gale, J. T., Fiengo, G., Glielmo, L., et al. (2010). “System identification of local field potentials under deep brain stimulation in a healthy primate,” in 2010 annual international conference of the IEEE engineering in medicine and biology (IEEE), 4144–4147.

CrossRef Full Text | Google Scholar

Perlmutter, J. S., and Mink, J. W. (2006). Deep brain stimulation. Annu. Rev. Neurosci. 29, 229–257. doi:10.1146/annurev.neuro.29.051605.112824

PubMed Abstract | CrossRef Full Text | Google Scholar

Peterchev, A. V., Goetz, S. M., Westin, G. G., Luber, B., and Lisanby, S. H. (2013). Pulse width dependence of motor threshold and input–output curve characterized with controllable pulse parameter transcranial magnetic stimulation. Clin. Neurophysiol. 124, 1364–1372. doi:10.1016/j.clinph.2013.01.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinotsis, D. A., Geerts, J., Pinto, L., FitzGerald, T. H., Litvak, V., Auksztulewicz, R., et al. (2017). Linking canonical microcircuits and neuronal activity: Dynamic causal modelling of laminar recordings. Neuroimage 146, 355–366. doi:10.1016/j.neuroimage.2016.11.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Pleger, B., Blankenburg, F., Bestmann, S., Ruff, C. C., Wiech, K., Stephan, K. E., et al. (2006). Repetitive transcranial magnetic stimulation-induced changes in sensorimotor coupling parallel improvements of somatosensation in humans. J. Neurosci. 26, 1945–1952. doi:10.1523/jneurosci.4097-05.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Popovych, O. V., and Tass, P. A. (2012). Desynchronizing electrical and sensory coordinated reset neuromodulation. Front. Hum. Neurosci. 6, 58. doi:10.3389/fnhum.2012.00058

PubMed Abstract | CrossRef Full Text | Google Scholar

Priori, A., Foffani, G., Rossi, L., and Marceglia, S. (2013). Adaptive deep brain stimulation (adbs) controlled by local field potential oscillations. Exp. Neurol. 245, 77–86. doi:10.1016/j.expneurol.2012.09.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Qin, S. J., and Badgwell, T. A. (2003). A survey of industrial model predictive control technology. Control Eng. Pract. 11, 733–764. doi:10.1016/s0967-0661(02)00186-7

CrossRef Full Text | Google Scholar

Rahman, A., Lafon, B., and Bikson, M. (2015). Multilevel computational models for predicting the cellular effects of noninvasive brain stimulation. Prog. Brain Res. 222, 25–40. doi:10.1016/bs.pbr.2015.09.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramirez-Zamora, A., Giordano, J. J., Gunduz, A., Brown, P., Sanchez, J. C., Foote, K. D., et al. (2018). Evolving applications, technological challenges and future opportunities in neuromodulation: Proceedings of the fifth annual deep brain stimulation think tank. Front. Neurosci. 11, 734. doi:10.3389/fnins.2017.00734

PubMed Abstract | CrossRef Full Text | Google Scholar

Riva-Posse, P., Choi, K., Holtzheimer, P. E., Crowell, A. L., Garlow, S. J., Rajendra, J. K., et al. (2018). A connectomic approach for subcallosal cingulate deep brain stimulation surgery: Prospective targeting in treatment-resistant depression. Mol. Psychiatry 23, 843–849. doi:10.1038/mp.2017.59

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosin, B., Slovik, M., Mitelman, R., Rivlin-Etzion, M., Haber, S. N., Israel, Z., et al. (2011). Closed-loop deep brain stimulation is superior in ameliorating parkinsonism. Neuron 72, 370–384. doi:10.1016/j.neuron.2011.08.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Rowe, D. L., Robinson, P. A., and Rennie, C. J. (2004). Estimation of neurophysiological parameters from the waking eeg using a biophysical model of brain dynamics. J. Theor. Biol. 231, 413–433. doi:10.1016/j.jtbi.2004.07.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Ryali, S., Shih, Y.-Y. I., Chen, T., Kochalka, J., Albaugh, D., Fang, Z., et al. (2016). Combining optogenetic stimulation and fmri to validate a multivariate dynamical systems model for estimating causal brain interactions. Neuroimage 132, 398–405. doi:10.1016/j.neuroimage.2016.02.067

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadleir, R. J., Vannorsdall, T. D., Schretlen, D. J., and Gordon, B. (2010). Transcranial direct current stimulation (tdcs) in a realistic head model. Neuroimage 51, 1310–1318. doi:10.1016/j.neuroimage.2010.03.052

PubMed Abstract | CrossRef Full Text | Google Scholar

Saenger, V. M., Kahan, J., Foltynie, T., Friston, K., Aziz, T. Z., Green, A. L., et al. (2017). Uncovering the underlying mechanisms and whole-brain dynamics of deep brain stimulation for Parkinson’s disease. Sci. Rep. 7. doi:10.1038/s41598-017-10003-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Salinas, F., Lancaster, J., and Fox, P. (2007). Detailed 3d models of the induced electric field of transcranial magnetic stimulation coils. Phys. Med. Biol. 52, 2879–2892. doi:10.1088/0031-9155/52/10/016

PubMed Abstract | CrossRef Full Text | Google Scholar

Salvador, R., Silva, S., Basser, P., and Miranda, P. (2011). Determining which mechanisms lead to activation in the motor cortex: A modeling study of transcranial magnetic stimulation using realistic stimulus waveforms and sulcal geometry. Clin. Neurophysiol. 122, 748–758. doi:10.1016/j.clinph.2010.09.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Santaniello, S., Fiengo, G., Glielmo, L., and Grill, W. M. (2010). Closed-loop control of deep brain stimulation: A simulation study. IEEE Trans. Neural Syst. Rehabil. Eng. 19, 15–24. doi:10.1109/tnsre.2010.2081377

PubMed Abstract | CrossRef Full Text | Google Scholar

Sathi, K. A., Hossain, M. A., Hosain, M. K., Hai, N. H., and Hossain, M. A. (2021). A deep neural network model for predicting electric fields induced by transcranial magnetic stimulation coil. IEEE Access 9, 128381–128392. doi:10.1109/access.2021.3112612

CrossRef Full Text | Google Scholar

Schestatsky, P., Morales-Quezada, L., and Fregni, F. (2013). Simultaneous eeg monitoring during transcranial direct current stimulation. J. Vis. Exp., e50426. doi:10.3791/50426

PubMed Abstract | CrossRef Full Text | Google Scholar

Schiff, S. J. (2011). Neural control engineering: The emerging intersection between control theory and neuroscience. MIT Press.

Google Scholar

Schoenen, J., Roberta, B., Magis, D., and Coppola, G. (2016). Noninvasive neurostimulation methods for migraine therapy: The available evidence. Cephalalgia 36, 1170–1180. doi:10.1177/0333102416636022

PubMed Abstract | CrossRef Full Text | Google Scholar

Selvaraj, P., Sleigh, J. W., Freeman, W. J., Kirsch, H. E., and Szeri, A. J. (2014). Open loop optogenetic control of simulated cortical epileptiform activity. J. Comput. Neurosci. 36, 515–525. doi:10.1007/s10827-013-0484-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Seo, H., and Jun, S. C. (2017). Multi-scale computational models for electrical brain stimulation. Front. Hum. Neurosci. 11, 515. doi:10.3389/fnhum.2017.00515

PubMed Abstract | CrossRef Full Text | Google Scholar

Seo, H., and Jun, S. C. (2019). Relation between the electric field and activation of cortical neurons in transcranial electrical stimulation. Brain Stimul. 12, 275–289. doi:10.1016/j.brs.2018.11.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Seo, H., Kim, D., and Jun, S. C. (2016). Effect of anatomically realistic full-head model on activation of cortical neurons in subdural cortical stimulation—A computational study. Sci. Rep. 6. doi:10.1038/srep27353

PubMed Abstract | CrossRef Full Text | Google Scholar

Shewcraft, R. A., Dean, H. L., Fabiszak, M. M., Hagan, M. A., Wong, Y. T., and Pesaran, B. (2020). Excitatory/inhibitory responses shape coherent neuronal dynamics driven by optogenetic stimulation in the primate brain. J. Neurosci. 40, 2056–2068. doi:10.1523/jneurosci.1949-19.2020

PubMed Abstract | CrossRef Full Text | Google Scholar

Shimohama, S., Sawada, H., Kitamura, Y., and Taniguchi, T. (2003). Disease model: Parkinson’s disease. Trends Mol. Med. 9, 360–365. doi:10.1016/s1471-4914(03)00117-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Shirinpour, S., Hananeia, N., Rosado, J., Tran, H., Galanis, C., Vlachos, A., et al. (2021). Multi-scale modeling toolbox for single neuron and subcellular activity under transcranial magnetic stimulation. Brain Stimul. 14, 1470–1482. doi:10.1016/j.brs.2021.09.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Shukla, P., Basu, I., Graupe, D., Tuninetti, D., and Slavin, K. V. (2012). “A neural network-based design of an on-off adaptive control for deep brain stimulation in movement disorders,” in 2012 annual international conference of the IEEE engineering in medicine and biology society (IEEE), 4140–4143.

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, M. F., Braver, T. S., Cole, M. W., and Ching, S. (2020). Estimation and validation of individualized dynamic brain models with resting state fmri. NeuroImage 221, 117046. doi:10.1016/j.neuroimage.2020.117046

PubMed Abstract | CrossRef Full Text | Google Scholar

Skarpaas, T. L., Jarosiewicz, B., and Morrell, M. J. (2019). Brain-responsive neurostimulation for epilepsy (rns® system). Epilepsy Res. 153, 68–70. doi:10.1016/j.eplepsyres.2019.02.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, M., Shin, Y., and Yun, K. (2014). Beta-frequency eeg activity increased during transcranial direct current stimulation. Neuroreport 25, 1433–1436. doi:10.1097/wnr.0000000000000283

PubMed Abstract | CrossRef Full Text | Google Scholar

Sood, M., Besson, P., Muthalib, M., Jindal, U., Perrey, S., Dutta, A., et al. (2016). Nirs-eeg joint imaging during transcranial direct current stimulation: Online parameter estimation with an autoregressive model. J. Neurosci. methods 274, 71–80. doi:10.1016/j.jneumeth.2016.09.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Srinivasan, S. S., Maimon, B. E., Diaz, M., Song, H., and Herr, H. M. (2018). Closed-loop functional optogenetic stimulation. Nat. Commun. 9, 5303–5310. doi:10.1038/s41467-018-07721-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Starnes, K., Miller, K., Wong-Kisiel, L., and Lundstrom, B. N. (2019). A review of neurostimulation for epilepsy in pediatrics. Brain Sci. 9, 283. doi:10.3390/brainsci9100283

PubMed Abstract | CrossRef Full Text | Google Scholar

Stefanescu, R. A., Shivakeshavan, R., Khargonekar, P. P., and Talathi, S. S. (2013). Computational modeling of channelrhodopsin-2 photocurrent characteristics in relation to neural signaling. Bull. Math. Biol. 75, 2208–2240. doi:10.1007/s11538-013-9888-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Steinhardt, C. R., Sacré, P., Sheehan, T. C., Wittig, J. H., Inati, S. K., Sarma, S., et al. (2020). Characterizing and predicting cortical evoked responses to direct electrical stimulation of the human brain. Brain Stimul. 13, 1218–1225. doi:10.1016/j.brs.2020.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Stephan, K. E., Penny, W. D., Moran, R. J., den Ouden, H. E., Daunizeau, J., and Friston, K. J. (2010). Ten simple rules for dynamic causal modeling. Neuroimage 49, 3099–3109. doi:10.1016/j.neuroimage.2009.11.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Su, F., Wang, J., Niu, S., Li, H., Deng, B., Liu, C., et al. (2018). Nonlinear predictive control for adaptive adjustments of deep brain stimulation parameters in basal ganglia–thalamic network. Neural Netw. 98, 283–295. doi:10.1016/j.neunet.2017.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Swann, N., Poizner, H., Houser, M., Gould, S., Greenhouse, I., Cai, W., et al. (2011). Deep brain stimulation of the subthalamic nucleus alters the cortical profile of response inhibition in the beta frequency band: A scalp eeg study in Parkinson’s disease. J. Neurosci. 31, 5721–5729. doi:10.1523/jneurosci.6135-10.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

Teplitzky, B. A., Zitella, L. M., Xiao, Y., and Johnson, M. D. (2016). Model-based comparison of deep brain stimulation array functionality with varying number of radial electrodes and machine learning feature sets. Front. Comput. Neurosci. 10, 58. doi:10.3389/fncom.2016.00058

PubMed Abstract | CrossRef Full Text | Google Scholar

Terman, D., Rubin, J. E., Yew, A., and Wilson, C. (2002). Activity patterns in a model for the subthalamopallidal network of the basal ganglia. J. Neurosci. 22, 2963–2976. doi:10.1523/jneurosci.22-07-02963.2002

PubMed Abstract | CrossRef Full Text | Google Scholar

Tervo, A. E., Metsomaa, J., Nieminen, J. O., Sarvas, J., and Ilmoniemi, R. J. (2020). Automated search of stimulation targets with closed-loop transcranial magnetic stimulation. Neuroimage 220, 117082. doi:10.1016/j.neuroimage.2020.117082

PubMed Abstract | CrossRef Full Text | Google Scholar

Tervo, A. E., Nieminen, J. O., Lioumis, P., Metsomaa, J., Souza, V. H., Sinisalo, H., et al. (2022). Closed-loop optimization of transcranial magnetic stimulation with electroencephalography feedback. Brain Stimul. 15, 523–531. doi:10.1016/j.brs.2022.01.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Thielscher, A., Antunes, A., and Saturnino, G. B. (2015). “Field modeling for transcranial magnetic stimulation: A useful tool to understand the physiological effects of tms?,” in 2015 37th annual international conference of the IEEE engineering in medicine and biology society (IEEE), 222–225.

Google Scholar

Toth, A. J., Ramsbottom, N., Constantin, C., Milliet, A., and Campbell, M. J. (2021). The effect of expertise, training and neurostimulation on sensory-motor skill in esports. Comput. Hum. Behav. 121, 106782. doi:10.1016/j.chb.2021.106782

CrossRef Full Text | Google Scholar

Trevathan, J. K., Yousefi, A., Park, H. O., Bartoletta, J. J., Ludwig, K. A., Lee, K. H., et al. (2017). Computational modeling of neurotransmitter release evoked by electrical stimulation: Nonlinear approaches to predicting stimulation-evoked dopamine release. ACS Chem. Neurosci. 8, 394–410. doi:10.1021/acschemneuro.6b00319

PubMed Abstract | CrossRef Full Text | Google Scholar

Valentin, A., Anderson, M., Alarcon, G., Seoane, J. G., Selway, R., Binnie, C., et al. (2002). Responses to single pulse electrical stimulation identify epileptogenesis in the human brain in vivo. Brain 125, 1709–1718. doi:10.1093/brain/awf187

PubMed Abstract | CrossRef Full Text | Google Scholar

Valverde, S., Vandecasteele, M., Piette, C., Derousseaux, W., Gangarossa, G., Arbelaiz, A. A., et al. (2020). Deep brain stimulation-guided optogenetic rescue of parkinsonian symptoms. Nat. Commun. 11. doi:10.1038/s41467-020-16046-6

PubMed Abstract | CrossRef Full Text | Google Scholar

van Dijk, K. J., Verhagen, R., Bour, L. J., Heida, C., and Veltink, P. H. (2018). Avoiding internal capsule stimulation with a new eight-channel steering deep brain stimulation lead. Neuromodulation Technol. A. T. Neural Interface 21, 553–561. doi:10.1111/ner.12702

PubMed Abstract | CrossRef Full Text | Google Scholar

van Wijk, B. C., Cagnan, H., Litvak, V., Kühn, A. A., and Friston, K. J. (2018). Generic dynamic causal modelling: An illustrative application to Parkinson’s disease. NeuroImage 181, 818–830. doi:10.1016/j.neuroimage.2018.08.039

PubMed Abstract | CrossRef Full Text | Google Scholar

Vierling-Claassen, D., Cardin, J., Moore, C. I., and Jones, S. R. (2010). Computational modeling of distinct neocortical oscillations driven by cell-type selective optogenetic drive: Separable resonant circuits controlled by low-threshold spiking and fast-spiking interneurons. Front. Hum. Neurosci. 4, 198. doi:10.3389/fnhum.2010.00198

PubMed Abstract | CrossRef Full Text | Google Scholar

Vrba, J., Janca, R., Blaha, M., Jezdik, P., Belohlavkova, A., Krsek, P., et al. (2019). Modeling of brain tissue heating caused by direct cortical stimulation for assessing the risk of thermal damage. IEEE Trans. Neural Syst. Rehabil. Eng. 27, 440–449. doi:10.1109/tnsre.2019.2898253

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C.-F., Yang, S.-H., Lin, S.-H., Chen, P.-C., Lo, Y.-C., Pan, H.-C., et al. (2017). A proof-of-principle simulation for closed-loop control based on preexisting experimental thalamic dbs-enhanced instrumental learning. Brain Stimul. 10, 672–683. doi:10.1016/j.brs.2017.02.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Hutchings, F., and Kaiser, M. (2015). Computational modeling of neurostimulation in brain diseases. Prog. Brain Res. 222, 191–228. doi:10.1016/bs.pbr.2015.06.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Wendling, F., Benquet, P., Bartolomei, F., and Jirsa, V. (2016). Computational models of epileptiform activity. J. Neurosci. methods 260, 233–251. doi:10.1016/j.jneumeth.2015.03.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Wichmann, T., and DeLong, M. R. (2016). Deep brain stimulation for movement disorders of basal ganglia origin: Restoring function or functionality? Neurotherapeutics 13, 264–283. doi:10.1007/s13311-016-0426-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Wiethoff, S., Hamada, M., and Rothwell, J. C. (2014). Variability in response to transcranial direct current stimulation of the motor cortex. Brain Stimul. 7, 468–475. doi:10.1016/j.brs.2014.02.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, D., and Moehlis, J. (2014). A Hamilton-Jacobi-bellman approach for termination of seizure-like bursting. J. Comput. Neurosci. 37, 345–355. doi:10.1007/s10827-014-0507-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Witt, A., Palmigiano, A., Neef, A., El Hady, A., Wolf, F., and Battaglia, D. (2013). Controlling the oscillation phase through precisely timed closed-loop optogenetic stimulation: A computational study. Front. Neural Circuits 7, 49. doi:10.3389/fncir.2013.00049

PubMed Abstract | CrossRef Full Text | Google Scholar

Wongsarnpigoon, A., and Grill, W. M. (2008). Computational modeling of epidural cortical stimulation. J. Neural Eng. 5, 443–454. doi:10.1088/1741-2560/5/4/009

PubMed Abstract | CrossRef Full Text | Google Scholar

Wongsarnpigoon, A., and Grill, W. M. (2012). Computer-based model of epidural motor cortex stimulation: Effects of electrode position and geometry on activation of cortical neurons. Clin. Neurophysiol. 123, 160–172. doi:10.1016/j.clinph.2011.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Y., Connolly, A. T., and Shanechi, M. M. (2018). A control-theoretic system identification framework and a real-time closed-loop clinical simulation testbed for electrical brain stimulation. J. Neural Eng. 15, 066007. doi:10.1088/1741-2552/aad1a8

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Y., Qiao, S., Sani, O. G., Sedillo, J. I., Ferrentino, B., Pesaran, B., et al. (2021). Modelling and prediction of the dynamic responses of large-scale brain networks during direct electrical stimulation. Nat. Biomed. Eng. 5, 324–345. doi:10.1038/s41551-020-00666-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Yarossi, M., Quivira, F., Dannhauer, M., Sommer, M. A., Brooks, D. H., Erdoğmuş, D., et al. (2019). “An experimental and computational framework for modeling multi-muscle responses to transcranial magnetic stimulation of the human motor cortex,” in 2019 9th international IEEE/EMBS conference on neural engineering. (IEEE), 1122–1125.

CrossRef Full Text | Google Scholar

Yazdan-Shahmorad, A., Silversmith, D. B., Kharazia, V., and Sabes, P. N. (2018). Targeted cortical reorganization using optogenetics in non-human primates. Elife 7, e31034. doi:10.7554/elife.31034

PubMed Abstract | CrossRef Full Text | Google Scholar

Yizhar, O., Fenno, L. E., Davidson, T. J., Mogri, M., and Deisseroth, K. (2011). Optogenetics in neural systems. Neuron 71, 9–34. doi:10.1016/j.neuron.2011.06.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Yokota, T., Maki, T., Nagata, T., Murakami, T., Ugawa, Y., Laakso, I., et al. (2019). Real-time estimation of electric fields induced by transcranial magnetic stimulation with deep neural networks. Brain Stimul. 12, 1500–1507. doi:10.1016/j.brs.2019.06.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Ziegler, J. G., and Nichols, N. B. (1942). Optimum settings for automatic controllers. Trans. ASME 64.

Google Scholar

Zitella, L. M., Mohsenian, K., Pahwa, M., Gloeckner, C., and Johnson, M. D. (2013). Computational modeling of pedunculopontine nucleus deep brain stimulation. J. Neural Eng. 10, 045005. doi:10.1088/1741-2560/10/4/045005

PubMed Abstract | CrossRef Full Text | Google Scholar