Secure Dynamic State Estimation for Cyber Security of AC Microgrids

A timely, accurate, and secure dynamic state estimation is needed for reliable monitoring and efficient control of microgrids. The synchrophasor technology enables system operators to obtain synchronized measurements in real-time and to develop dynamic state estimators for monitoring and control of microgrids. However, in practice, sensor measurements can be corrupted or attacked. In this study, we consider an AC microgrid comprising several synchronous generators and inverter-interface power supplies, and focus on securely estimating the dynamic states of the microgrid from a set of corrupted data. We propose a secure dynamic state estimator which allows the microgrid operator to reconstruct the dynamic states of the microgrid from a set of attacked or corrupted data without any assumption on attacks or corruptions. Finally, we consider an AC microgrid with the same topology as the IEEE 33-bus distribution system, and show that the proposed secure estimation algorithm can accurately reconstruct the attack signals.

1 Introduction

Future distribution systems will include interconnected microgrids (Lasseter, 2002)- (Hatziagyriou et al., 2007). Such systems are designed to operate in a distributed fashion dealing with various dynamic phenomena with different time scales (Ilić and Liu, 1996)- (Kundur et al., 2004). The functionality of control systems in microgrids is highly dependent on state estimation schemes used to observe the system over time. Traditional energy management systems are using static state estimation schemes designed from steady-state models (Schweppe and Wildes, 1970) (Abur and Expósito, 2004). With the high penetration of distributed energy resources (DER) on the generation side, and flexible loads and new demand-response technologies on the demand side, static state estimation schemes will not be able to capture power systems’ dynamics accurately (Zhao et al., 2019). Dynamic state estimation schemes will be needed to accurately capture the system dynamics. Such state estimation schemes, designed based on dynamical models, will play a significant role in microgrid monitoring and control (Modir and Schlueter, 1981)- (Meliopoulos, 2017). In this paper, we focus on the design of dynamic state estimation schemes which are secure to cyber-physical attacks.

Large-scale integration of inverter-interfaced power supplies and distributed controls requires a widespread deployment of the synchrophasor technology and communication networks in future distribution systems. This will lead to high-volume data exchange between different controllers which will make microgrids vulnerable to cyber-physical attacks. Corrupted data in controllers can disrupt power generators’ synchrony and result in a network-wide instability. Several attack detection schemes have been proposed in recent years (Pasqualetti et al., 2012) (Liu et al., 2014a). With false-data injection attacks, disturbances are injected to sensors and actuators to disrupt the measurements and computed control inputs. While it is possible to identify misbehaving agents (Pasqualetti et al., 2012) (Pasqualetti et al., 2013), such solutions require full knowledge of the cyber layer and are hard to scale. In (Mo et al., 2014), the authors propose a computationally-efficient scheme to detect deception attacks on sensors. While such solutions enable us to detect cyber attacks efficiently, these solutions do not mitigate all possible adverse effects. Robust game-theoretic schemes can lead to conservative results (Alpcan and Basar, 2003) (Srikantha and Kundur, 2016).

Cyber attacks can be modeled as noise or disturbance to the system. Basseville et al. (Basseville and Nikiforov, 1993) use noise filtration techniques to detect and remove malicious attacks, and the authors in Jiao et al. (2016) develop disturbance attenuation methods for cyber attack detection. Notice that noise filtration or disturbance attenuation techniques operate under certain statistical properties, e.g., white Gaussian noise signal. However, in practice, cyber attacks can be deliberately designed by a malicious attacker. In Abhinav et al. (2018), the authors propose attack-resilient controls for synchronization of islanded microgrids. The authors study the effect of attacks on sensors and actuators, and numerically demonstrate the effectiveness of their distributed controls on a modified IEEE 34-bus system.

In recent years, several researchers have focused on state estimation with security guarantees for both linear and nonlinear dynamical systems (Fawzi et al., 2014) (Hu et al., 2018). The current literature on linear dynamical systems can be classified into two classes: noiseless measurements, and noisy measurements. For systems with noiseless measurements, the studies in (Fawzi et al., 2014) (Chang et al., 2018) show that the state of the system can be accurately reconstructed under certain conditions. For systems with noisy measurements, sparse attack vectors can be distinguished from the measurement noise under certain conditions (Shoukry et al., 2014) (Farahmand et al., 2011). In Hu et al. (2018), the authors focus on secure state estimation for two classes of nonlinear systems without any assumption on the sensor attacks. They assume that the set of attacked sensors or actuators can potentially change with time, and propose a secure state estimator for those nonlinear systems. Finally, they consider a power system comprising a set of synchronous generators and storage units connected to each other via a set of electrical lines. The authors assume that the storage units use feedback linearization controls, and then design a secure estimator that enables the system operator to securely estimate the dynamic states of the power grid, i.e., the states of the synchronous generators, under cyber-physical attacks and communication failures.

Several dynamic state estimators have been proposed in the literature. However, the existing dynamic state estimators have the following drawbacks:

1. Loads are considered to be quasi-static, i.e., load dynamics are neglected. Unlike large power systems, microgrids are small footprint power systems comprising distribution assets, DERs, and loads. DERs are typically of inverter-interfaced power supplies with no inertia. These resources respond to disturbances as fast as their controls, and hence dynamics of flexible loads and DERs are strongly coupled in microgrids. More precisely, load dynamics have significant transient impacts in microgrids (Zhang et al., 2016) (Haddadi et al., 2013).

2. Controllers are considered to have specific structure. For example, storage units are assumed to use feedback linearization controls in Hu et al. (2018). DERs can use several types of distributed and centralized control schemes (Yazdanian and Mehrizi-Sani, 2014) (Hooshyar and Iravani, 2017).

In summary, load dynamics cannot be neglected in securely estimating dynamic states, and controllers cannot be limited to any specific structure. To overcome these drawbacks, we addressed two drawbacks of existing dynamic state estimators; first we design a secure dynamic state estimator for AC microgrids without using any linearization techniques or reducing the microgrid into a network of oscillators. Second, we do not have any specific structure assumptions in controller.

In this study, we focus on secure dynamic state estimation in AC microgrids under cyber attacks or communication failures. We consider an AC microgrid comprising several synchronous generators, inverter-interfaced power supplies, and electric loads controlled via a central controller (i.e., the microgrid operator) and several local controllers. The controllers use phasor measurement units (PMU) to maintain the system’s reliability. Each bus is equipped with a controller, transceiver, and measurement unit so that the controller can exchange its information with other controllers. The transceivers send the feedback information to the microgrid operator via a communication network. We make the following assumptions:

A.1 The communication paths from the central controller to different buses are secured while other communication paths and PMUs are subject to cyber attacks.

A.2 The set of attacked PMUs or communication paths can change with time.

A.3 Attacks can follow any particular model.

Note that typically, central controllers are protected against cyber attacks strongly, and that local controllers are more vulnerable to cyber attacks (CIP Standards, 2020). Thus, assumption 1 is reasonable. Here we consider cyber attacks which corrupts the communication paths and affects measurement units.

A practical example of cyber attacks in which the set of attacked sensors can change with time is provided in Liu et al. (2014b).

The contributions of this study are summarized as follows:

1. We extend our previous work (Hu et al., 2018) to AC microgrids and propose a secure state estimator for reconstructing the dynamic states of an AC microgrid using a set of measurements that can be corrupted. The proposed estimators are computationally efficient and enable microgrid operators to reconstruct dynamic states without any assumptions on attacks or corruptions.

2. We then consider an AC microgrid with the same topology as the IEEE 33-bus distribution system, and demonstrate the effectiveness of our estimators in accurately reconstructing the attack or corruption signals with realistic attack scenarios.

The paper is organized as follows: In Section 2, we review the secure state estimation for linear dynamical systems and in Section 3, we introduce the microgrid model adopted in this work. In Section 4, we formulate the dynamic state estimation problem for AC microgrids, and propose a dynamic state estimator for recovering dynamic states. Finally, in Section 5, we demonstrate the effectiveness of the proposed estimator using the IEEE 33-bus distribution system.

2 Preliminaries

We first introduce the error correction problem and compressed sensing. We then describe secure state estimation for linear dynamical systems.

2.1 Compressed Sensing

Let $A\in {\mathbb{R}}^{m\times n}(m\ll n)$ and $b\in {\mathbb{R}}^m$ be a sensing matrix and measurement vector. Consider the following optimization problem:

${\min }_x{\left|\right|x\left|\right|}_0\text{subject\hspace{0.17em}to}b=Ax.(1)$

Notice that   ||x||₀ equals the number of non-zero entries of x. Lemma 1 provides a sufficient condition for obtaining a unique solution to Eq. 1.

Lemma 1. (Candes et al., 2006) If the sparsest solution to Eq. 1 has  ||x||₀ = q and m ≥ 2q and all subsets of 2q columns of A are full rank, then the solution is unique.

2.2 The Error Correction Problem

Consider a full rank coding matrix $C\in {\mathbb{R}}^{\ell \times n}(\ell >n)$ and a set of attacked measurements y = Cx + e where e is an arbitrary and unknown sparse error vector. The classical error correction problem aims at recovering the vector $x\in {\mathbb{R}}^n$ from the attacked measurements y. To achieve this goal, we need to compute the error vector e since given y = Cx + e and e, we can compute Cx. Then, x can be computed using the full rank matrix C (Candes et al., 2006). Candes et al. (Candes et al., 2006) construct a matrix F such that FCx = 0 for all x. Then, by applying F to y, they obtain

$\bar{Y}=F(Cx+e)=Fe.(2)$

Hence, the classical error correction techniques can be transformed into reconstructing a sparse error vector e from the measurement vector $\bar{Y}=Fe$. According to Lemma 1, any error vector e that satisfies ‖e‖₀ ≤ q, can be reconstructed if all the subsets of 2q columns of matrix F have full rank.

2.3 Secure State Estimation for Linear Dynamical Systems

Consider a discrete-time linear system as follows:

$\begin{array}{cc}\hfill & x[k+1]=Ax[k],\hfill \\ \hfill & y[k]=Cx[k]+e[k],\hfill \end{array}(3)$

where $x[k]\in {\mathbb{R}}^n$ and $y[k]\in {\mathbb{R}}^p$ denote the states and outputs of the system at time slot k, respectively. $e[k]\in {\mathbb{R}}^p$ denotes attack signals.

Let $Y\in {\mathbb{R}}^{p\cdot K}$ be the collection of the measurements over K time slots, and let E_q,K denote the set of error vectors $\left[\begin{array}{c}\hfill e[0];\dots ;e[K-1]\hfill \end{array}\right]\in {\mathbb{R}}^{p\cdot K}$ where each error vector e[k] satisfies ‖e[k]‖₀ ≤ q ≤ p. We have:

$\begin{array}{cc}\hfill Y& \triangleq \left[\begin{array}{c}\hfill y[0]\hfill \\ \hfill y[1]\hfill \\ \hfill ⋮\hfill \\ \hfill y[K-1]\hfill \end{array}\right]=\left[\begin{array}{c}\hfill Cx[0]+e[0]\hfill \\ \hfill CAx[0]+e[1]\hfill \\ \hfill ⋮\hfill \\ \hfill C{A}^{K-1}x[0]+e[K-1]\hfill \end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{c}\hfill C\hfill \\ \hfill CA\hfill \\ \hfill ⋮\hfill \\ \hfill C{A}^{K-1}\hfill \end{array}\right]x[0]+E_{q,K}\triangleq \mathrm{\Phi }x[0]+E_{q,K},\hfill \end{array}(4)$

where $\mathrm{\Phi }\in {\mathbb{R}}^{p\cdot K\times n}$ is the K-step observability matrix of the system at hand. Note that (A, C) represents the system dynamics matrix and if the system is observable, then this can be easily achievable. If the system is not observable, in order to guarantee full rank of Φ, we need to add/allocate measurement units to achieve full rank condition. We assume that rank(Φ) = n; otherwise, we cannot determine x [0] even if there was no attack E_q,K = 0. For instance, if the system is not observable, there is no way to infer any attack signal.

By following a two-step procedure Candes et al. (2006) and Hayden et al. (2016) we can now reconstruct the initial state x [0] from y [k]’s, where k = 0, … , K−1 First, we compute the error vector E_q,K, and then solve for x [0]. To compute E_q,K, we pre-multiply Eq. 4 by ${\left[\begin{array}{cc}\hfill Q_1\hfill & \hfill Q_2\hfill \end{array}\right]}^{\top }$, where $\left[\begin{array}{cc}\hfill Q_1\hfill & \hfill Q_2\hfill \end{array}\right]\in {\mathbb{R}}^{p\cdot K\times p\cdot K}$ is orthogonal, $Q_1\in {\mathbb{R}}^{p\cdot K\times n},Q_2\in {\mathbb{R}}^{p\cdot K\times (p\cdot K-n)}$, and $R_1\in {\mathbb{R}}^{n\times n}$ is a rank-n upper triangular matrix by using QR decomposition of F and then we obtain:

$\left[\begin{array}{c}\hfill Q_1^{\top }\hfill \\ \hfill Q_2^{\top }\hfill \end{array}\right]Y=\left[\begin{array}{c}\hfill R_1\hfill \\ \hfill 0\hfill \end{array}\right]x[0]+\left[\begin{array}{c}\hfill Q_1^{\top }\hfill \\ \hfill Q_2^{\top }\hfill \end{array}\right]E_{q,K}.(5)$

Using the second block row, we have:

$\bar{Y}\triangleq Q_2^{\top }Y=Q_2^{\top }{E}_{q,K},(6)$

where $Q_2^{\top }\in {\mathbb{R}}^{(p\cdot K-n)\times p\cdot K}$. Using Lemma 1, the above optimization has a unique, s-sparse solution (where s ≤ q ⋅ K) if all subsets of 2s columns (at most 2q ⋅ K columns) of $Q_2^{\top }$ are full rank. Using this observation, we consider solving the following l₁-minimization problem:

${\widehat{E}}_{q,K}=\arg {\min }_E\mathrm{norm}{E}_{l_1}\text{\hspace{0.17em}subject\hspace{0.17em}to\hspace{0.17em}}\bar{Y}=Q_2^{\top }E.(7)$

Here, we approximate the l₀-minimization problem with an l₁-minimization problem to obtain a convex decoder (Candes and Tao, 2005) (Tropp, 2004).

Using the first block row of Eq. 5, we can now compute x [0] as follows:

$x[0]=R_1^{-1}{Q}_1^{\top }(Y-{\widehat{E}}_{q,K}).(8)$

The following result provides the conditions under which exists a unique solution to Eq. 8. The proof follows by using Lemma 1 and the fact that the null space of $Q_2^{\top }$ is equal to the column space of Φ.

Lemma 2.Chang et al. (2018). There exists a unique solution x [0] if all subsets of 2s columns of $Q_2^{\top }$ are linearly independent and Φ is full column rank.

The role of Lemma 2 guarantees accurate decoding when the assumption holds.

3 System Model

We first introduce the physical layer model of an AC microgrid with generators and loads. We then describe the cyber layer over which the microgrid operator relies to control its DERs, and introduce the cyber attacks that we are considering in this study.

3.1 Physical Layer

Consider a microgrid with m + n + l buses. m of the m + n + l buses, indexed by ${\mathcal{N}}^{(S)}=\{1,\dots ,m\}$, have synchronous generators connected to them, and n of the microgrid buses, indexed by ${\mathcal{N}}^{(I)}=\{m+1,\dots ,m+n\}$, have inverter-interfaced power supplies attached to them. The remaining buses, indexed by ${\mathcal{N}}^{(L)}=\{m+n+1,\dots ,m+n+l\}$, have electric loads and no generation3. We further assume that the network interconnecting the buses is linear, i.e., the network can be represented by the nodal admittance matrix $Y=G+\sqrt{-1}B$ where G and B denote the conductance and susceptance matrices, respectively.

We use the standard structure-preserving model to describe the microgrid’s dynamics (Bergen and Hill, 1981). This model that incorporates the dynamics of generators’ rotor angle and response of load power output to frequency deviations, allows us to preserve the structure of the grid, i.e., no load bus elimination is made. We introduce fictitious buses representing the internal generation voltages for synchronous generators and inverter-interfaced power supplies. Each of these buses is connected to either a synchronous generator or inverter-interfaced power supply bus via reactances that account for transient reactances and connecting lines. These reactances can be considered as transmission lines (Sauer and Pai, 1998). Therefore, in the augmented network, the number of buses is 2(m + n) + l. We further denote the set of fictitious buses for synchronous generators and inverter-interfaced power supplies by ${\mathcal{N}}_f^{(S)}$ and ${\mathcal{N}}_f^{(I)}$, respectively. The augmented network can be modeled by graph, $\mathcal{G}(\mathcal{N},\mathcal{E})$, where $\mathcal{N}={\mathcal{N}}^{(S)}\cup {\mathcal{N}}^{(I)}\cup {\mathcal{N}}^{(L)}\cup {\mathcal{N}}_f^{(S)}\cup {\mathcal{N}}_f^{(I)}$; and where each element in the edge set $\mathcal{E}$ corresponds to an electrical line between a pair of buses in the augmented network. We assume that the network topology is fixed and known to the microgrid operator.

Let V_i and θ_i denote the voltage magnitude and phase angle of bus $i\in \mathcal{N}$, respectively. We use a structure-preserving model with constant complex voltage behind reactance [34, Sec. 7.9.2], to represent the dynamics of each synchronous generator. For a synchronous generator at fictitious bus $i\in {\mathcal{N}}_f^{(S)}$, let θ_i denote the angle of its voltage as measured with respect to a synchronous reference rotating at the nominal system electrical frequency ω₀. Further, let ω_i denote its rotor electrical angular speed, and let $P_i^m$ be the turbine’s mechanical power. For each synchronous generator $i\in {\mathcal{N}}_f^{(S)}$, we have

$\begin{array}{ll}\hfill {\dot{\theta }}_i& ={\omega }_i-{\omega }_0,\hfill \end{array}(9)$

$\begin{array}{ll}\hfill M_i{\dot{\omega }}_i& =P_i^m-D_i({\omega }_i-{\omega }_0)\hfill \\ \hfill & -\sum _{j\in {\mathcal{N}}_i}{V}_i{V}_j|y_{ij}|\sin ({\theta }_i-{\theta }_j+{\varphi }_{ij}),\hfill \end{array}(10)$

$\begin{array}{ll}\hfill {\tau }_i\dot{P_i^m}& =-P_i^m+P_i^s-R_i({\omega }_{i,\text{meas}}-{\omega }_0),\hfill \end{array}(11)$

where $y_{ij}=g_{ij}+\sqrt{-1}{b}_{ij}$ with g_ij and b_ij being the elements of the conductance and susceptance matrices, respectively, and ϕ_ij equals arctan (g_ij/b_ij). ${\mathcal{N}}_i$ is the set of neighbors of node i in graph $\mathcal{G}(\mathcal{N},\mathcal{E})$, D_i (in s/rad) is the generator damping coefficient, and M_i (in s²/rad) is the scaled inertia parameter. Further, R_i is the frequency-power speed-droop characteristic constant, τ_i is the generator governor time constant, and $P_i^s$ denotes the generator’s power set-point. Notice that ω_i,meas is the measured value of state ω_i for all $i\in {\mathcal{N}}_f^{(S)}$.

The dynamics of inverter-based power supplies can similarly be represented by a constant voltage behind reactance model, augmented to include a frequency-droop controller. For an inverter-based power supply at fictitious bus $i\in {\mathcal{N}}_f^{(I)}$, let θ_i denote the angle of the bus voltage measured with respect to the nominal system electrical frequency ω₀, and let $P_i^s$ denote the generation set-point. For each inverter-based power supply $i\in {\mathcal{N}}_f^{(I)}$, we have

$D_i{\dot{\theta }}_i=P_i^s-\sum _{j\in {\mathcal{N}}_i}{V}_i{V}_j|y_{ij}|\sin ({\theta }_i-{\theta }_j+{\varphi }_{ij}),(12)$

where D_i (in s/rad) is the speed-droop characteristic slope of the power supply.

In general, the relationship between the real power drawn at load bus $i\in {\mathcal{N}}^{(S)}\cup {\mathcal{N}}^{(I)}\cup {\mathcal{N}}^{(L)}$ and the bus voltage and frequency is nonlinear. However, for constant voltages and small frequency deviations around the nominal frequency ω₀, it is reasonable to assume that the real power drawn by the load equals $P_i^d+D_i\dot{{\theta }_i}$ where D_i > 0 and $P_i^d>0$ are the constant frequency coefficient of load and the nominal load at bus $i\in {\mathcal{N}}^{(S)}\cup {\mathcal{N}}^{(I)}\cup {\mathcal{N}}^{(L)}$, respectively. Therefore, for constant voltages and small frequency deviations, the dynamics of the phase angle at load bus $i\in {\mathcal{N}}^{(S)}\cup {\mathcal{N}}^{(I)}\cup {\mathcal{N}}^{(L)}$ can be modeled by

$D_i\dot{{\theta }_i}=-P_i^d-\sum _{j\in {\mathcal{N}}_i}{V}_i{V}_j|y_{ij}|\sin ({\theta }_i-{\theta }_j+{\varphi }_{ij}).(13)$

Here, we ignore reactive powers for generators and loads. Notice that reactive power analysis is unnecessary in this study.

3.2 Cyber Layer

Each bus i is equipped with a controller, transceiver, and measurement unit that allow bus i to communicate with the central controller (i.e., the microgrid operator) as well as other bus controllers. As mentioned earlier, fictitious buses represent the internal generation voltages for synchronous generators and inverter-interfaced power supplies. Each inverter-interfaced power supply is equipped with a controller, transceiver, and measurement unit so that the inverter-interfaced power supply at fictitious bus i can measure and communicate its internal voltage phase angle.

The rotor angle of synchronous generators has an electro-mechanic nature, and hence it cannot be measured via electric measurement units. However, we can estimate rotor angle by using other electric parameters of synchronous generators. In the literature, several studies are addressing the problem of estimating the rotor angle of synchronous generators (Tripathy et al., 2010) (Venkatasubramanian and Kavasseri, 2004). Each synchronous generator is equipped with a controller, transceiver, and measurement unit, and that the measurement unit at bus i is using a rotor angle estimator to compute the internal voltage phase angle for the synchronous generator at bus i.

A communication network connects the local controllers and the microgrid operator. This network allows the local controllers to send their feedback information, including rotors’ speeds and voltage phase angles, to the central controller. It also allows the microgrid operator to send different control commands to the local controllers. In this study, we assume that the communication paths from the microgrid operator to the local controllers are secure while other paths are not secure. Note that typically, central controllers are protected against cyber attacks strongly, and that local controllers are more vulnerable to cyber attacks (CIP Standards, 2020). In particular, we consider the following attack types:

• Attack 1: an attack that corrupts the communication paths from the transceivers to the central controller.

• Attack 2: an attack that affects measurement units.

We further assume that the set of attacked measurements can change with time. To illustrate different attack types, we refer the reader to Figure 1.

FIGURE 1

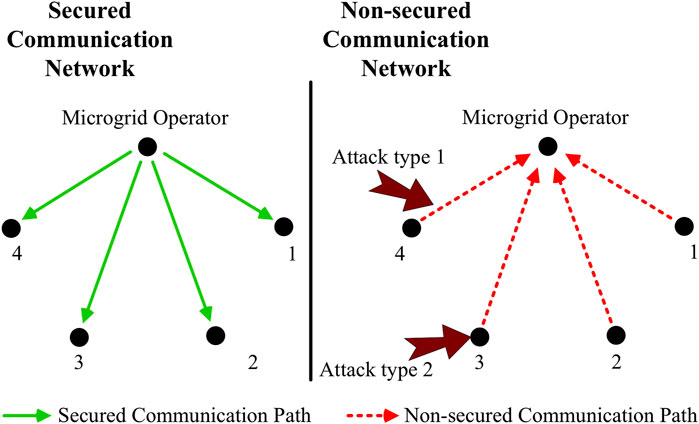
FIGURE 1. A graphical depiction of the cyber layer: consider a microgrid comprising four buses. The graph in left (sold lines) represents secured communication paths (i.e., communications path from the microgrid operator to bus controllers) while the graph in right (dotted lines) shows non-secured communication paths.

Next, we propose a secure dynamic state estimator for AC microgrids.

4 Secure State Estimation for AC Microgrids

Let us assume that the time is slotted in time slot of size δ. At each time slot k, the central controller receives the measured values of voltage phase angles, generators’ internal angles, and rotors’ speed. Let y_i [k] denote the measurement vector received from bus $i\in \mathcal{N}$. Each measurement y_i [k] is subject to cyber attacks and corruptions. Therefore, we have:

$\begin{array}{ll}\hfill y_i[k]& =\left[\begin{array}{c}\hfill {\theta }_i[k]\hfill \\ \hfill {\omega }_i[k]\hfill \end{array}\right]+e_i[k],\forall i\in {\mathcal{N}}_f^{(S)},\hfill \end{array}(14)$

$\begin{array}{ll}\hfill y_i[k]& ={\theta }_i[k]+e_i[k],\forall i\in \mathcal{N}\backslash \backslash {\mathcal{N}}_f^{(S)},\hfill \end{array}(15)$

where e_i [k] represents either a corruption or an attack signal injected by a malicious agent. In this study, the errors e_i [k]’s do not follow any particular model. Hence, $e_i[k]\in {\mathbb{R}}^2$ for all $i\in {\mathcal{N}}_f^{(S)}$, and $e_i[k]\in \mathbb{R}$ for all $i\in \mathcal{N}\backslash \backslash {\mathcal{N}}_f^{(S)}$. Our only limiting assumption is the number of attacked measurements, i.e., a corruption or an attack signal is sparse.

Our goal is to reconstruct θ_i [k] for all $i\in \mathcal{N}$ and ω_i [k] for all $i\in {\mathcal{N}}_f^{(S)}$ using the measurements. To achieve this goal, we first obtain a discrete-time approximation of the microgrid dynamics, and then propose a secure dynamic state estimator.

4.1 Discrete-Time System Model

We obtain a discrete-time approximation of the microgrid dynamics using the forward Euler discretization scheme. Let us begin with the synchronous generators, and use the same approach for inverter-interfaced power supplies and loads.

Synchronous Generators: For each synchronous generator at fictitious bus $i\in {\mathcal{N}}_f^{(S)}$, we have

$\begin{array}{cc}\hfill & {\theta }_i[k+1]={\theta }_i[k]+\delta ({\omega }_i[k]-{\omega }_0),\hfill \\ \hfill & {\omega }_i[k+1]={\alpha }_i{\omega }_i[k]+{\eta }_i{P}_i^m[k]+{\beta }_i\hfill \\ \hfill & +\sum _{j\in {\mathcal{N}}_i}{f}_{ij}({\theta }_i[k],{\theta }_j[k]),\hfill \\ \hfill & P_i^m[k+1]={\kappa }_i{P}_i^m[k]+{\zeta }_i[k]-{\nu }_i({\omega }_i[k]+\left[\begin{array}{c}\hfill \mathrm{0,1}\hfill \end{array}\right]e_i[k]),\hfill \end{array}$

where f_ij (θ_i[k], θ_j[k]) = γ_ij[k] sin (θ_i[k] −θ_j[k] + ϕ_ij),

$\begin{array}{cc}\hfill {\eta }_i& =\delta /M_i,\hfill \\ \hfill {\nu }_i& =R_i\delta /{\tau }_i,\hfill \\ \hfill {\kappa }_i& =(1-\delta /{\tau }_i),\hfill \\ \hfill {\alpha }_i& =(M_i-\delta D_i)/M_i,\hfill \end{array}\begin{array}{cc}\hfill {\beta }_i& =\delta D_i{\omega }_0/M_i,\hfill \\ \hfill {\zeta }_i[k]& =\delta (P_i^s[k]+R_i{\omega }_0)/{\tau }_i,\hfill \\ \hfill {\gamma }_{ij}[k]& =-\delta V_i[k]V_j[k]|y_{ij}|/M_i.\hfill \end{array}(16)$

Here we define some auxiliary variables for presentation purposes. There is no meaning to these parameters/variables. We defined the main variables and parameter in system model.

Notice that ω_i,meas [k] equals $\left[\begin{array}{c}\hfill \mathrm{0,1}\hfill \end{array}\right]y_i[k]$ which is equal to $({\omega }_i[k]+\left[\begin{array}{c}\hfill \mathrm{0,1}\hfill \end{array}\right]e_i[k])$. Using Eq. 14–15, we have

$\begin{array}{ll}\hfill f_{ij}({\theta }_i[k],{\theta }_j[k])& ={\gamma }_{ij}[k]\sin ({\theta }_i[k]-{\theta }_j[k]+{\varphi }_{ij})\hfill \\ \hfill =& {\gamma }_{ij}[k]\sin (y_i[k]-e_i[k]-y_j[k]+e_j[k]+{\varphi }_{ij})\hfill \\ \hfill =& {\gamma }_{ij}^s[k]-{\gamma }_{ij}^s[k]e_{ij}^c[k]-{\gamma }_{ij}^c[k]e_{ij}^s[k],\hfill \end{array}(17)$

where

$\begin{array}{cc}\hfill {\gamma }_{ij}^s[k]& ={\gamma }_{ij}[k]\sin (y_i[k]-y_j[k]+{\varphi }_{ij}),\hfill \\ \hfill {\gamma }_{ij}^c[k]& ={\gamma }_{ij}[k]\cos (y_i[k]-y_j[k]+{\varphi }_{ij}),\hfill \\ \hfill e_{ij}^c[k]& \triangleq 1-\cos (e_i[k]-e_j[k]),\hfill \\ \hfill e_{ij}^s[k]& \triangleq \sin (e_i[k]-e_j[k]).\hfill \end{array}(18)$

Notice that the coefficients of ${\gamma }_{ij}^c[k]$ and ${\gamma }_{ij}^s[k]$ can be calculated using the measurement received from the local controllers.

Now, the state space model of the synchronous generator at fictitious bus $i\in {\mathcal{N}}_f^{(S)}$ can be represented by

$\begin{array}{cc}\hfill & x_i[k+1]=A_i{x}_i[k]+u_i[k]-\left[\begin{array}{c}\hfill 0\hfill \\ \hfill H_i[k]{ϵ}_i[k]\hfill \\ \hfill 0\hfill \end{array}\right]-B_i{e}_i[k]\hfill \\ \hfill & y_i[k]=C_i{x}_i[k]+e_i[k]\hfill \end{array}(19)$

where the state vector $x_i[k]={\left[\begin{array}{c}\hfill {\theta }_i[k],{\omega }_i[k],P_i^m[k]\hfill \end{array}\right]}^{\top }$, and

$\begin{array}{cc}\hfill & A_i=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill \delta \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\alpha }_i\hfill & \hfill {\eta }_i\hfill \\ \hfill 0\hfill & \hfill -{\nu }_i\hfill & \hfill {\kappa }_i\hfill \end{array}\right],B_i=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\nu }_i\hfill \end{array}\right],C_i=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right],\hfill \\ \hfill & u_i[k]={\left[\begin{array}{c}\hfill -\delta {\omega }_0,{\beta }_i+\sum _{j\in {\mathcal{N}}_i}{\gamma }_{ij}^s[k],{\zeta }_i[k]\hfill \end{array}\right]}^{\top },\hfill \\ \hfill & {ϵ}_i[k]={\left[\begin{array}{c}\hfill e_{i{j}_1}^c[k],\dots ,e_{i{j}_{n(i)}}^c[k],e_{i{j}_1}^s[k],\dots ,e_{i{j}_{n(i)}}^s[k]\hfill \end{array}\right]}^{\top },\hfill \\ \hfill & H_i[k]=\left[\begin{array}{c}\hfill {\gamma }_{i{j}_1}^s[k],\dots ,{\gamma }_{i{j}_{n(i)}}^s[k],{\gamma }_{i{j}_1}^c[k],\dots ,{\gamma }_{i{j}_{n(i)}}^c[k]\hfill \end{array}\right].\hfill \end{array}$

Notice that n(i) denotes the number of neighbors of node i in graph $\mathcal{G}(\mathcal{N},\mathcal{E})$, i.e., $n(i)=|{\mathcal{N}}_i|$, and that nodes j₁, … , j_n(i) represent the neighbors of node i in $\mathcal{G}(\mathcal{N},\mathcal{E})$. More precisely, we have $H_i[k]\in {\mathbb{R}}^{1\times 2n(i)}$ and ${ϵ}_i[k]\in {\mathbb{R}}^{2n(i)}$. Next, by using the same approach, we obtain the state space model of inverter-interfaced power supplies and loads.

Inverter-interfaced Power Supplies: The state space model of the inverter-interfaced power supply at fictitious bus $i\in {\mathcal{N}}_f^{(I)}$ can be described by

$\begin{array}{cc}\hfill x_i[k+1]& =x_i[k]+u_i[k]-H_i[k]{ϵ}_i[k],\hfill \\ \hfill y_i[k]& =x_i[k]+e_i[k],\hfill \end{array}(20)$

where x_i [k] = θ_i [k] and $u_i[k]=\delta P_i^s[k]/D_i+{\sum }_{j\in {\mathcal{N}}_i}{\gamma }_{ij}^s[k]$. H_i [k] and ϵ_i [k] are defined above.

Loads: The state space model of the load at bus $i\in {\mathcal{N}}^{(S)}\cup {\mathcal{N}}^{(I)}\cup {\mathcal{N}}^{(L)}$ can be described by

$\begin{array}{cc}\hfill x_i[k+1]& =x_i[k]+u_i[k]-H_i[k]{ϵ}_i[k],\hfill \\ \hfill y_i[k]& =x_i[k]+e_i[k],\hfill \end{array}(21)$

where x_i [k] = θ_i [k] and $u_i[k]=-\delta P_i^d[k]/D_i+{\sum }_{j\in {\mathcal{N}}_i}{\gamma }_{ij}^s[k]$. H_i [k] and ϵ_i [k] are defined above.

4.2 Secure Dynamic State Estimator

Consider an enlarged system composed of all the system dynamics:

$\begin{array}{cc}\hfill X[k+1]& =AX[k]+U[k]-H[k]ϵ[k]-BE[k],\hfill \\ \hfill Y[k]& =\left[\begin{array}{c}\hfill y_1[k]\hfill \\ \hfill y_2[k]\hfill \\ \hfill ⋮\hfill \\ \hfill y_{|\mathcal{N}|}[k]\hfill \end{array}\right]=CX[k]+E[k],\hfill \end{array}(22)$

where

$\begin{array}{cc}\hfill & A\triangleq \text{blkdiag}\{A_1,\dots ,A_m,I_{m+2n+l}\}\in {\mathbb{R}}^{(|\mathcal{N}|+2m)\times (|\mathcal{N}|+2m)},\hfill \\ \hfill & B\triangleq \text{blkdiag}\{B_1,\dots ,B_m,0_{m+2n+l}\}\in {\mathbb{R}}^{(|\mathcal{N}|+2m)\times (|\mathcal{N}|+m)},\hfill \\ \hfill & C\triangleq \text{blkdiag}\{C_1,\dots ,C_m,I_{m+2n+l}\}\in {\mathbb{R}}^{(|\mathcal{N}|+m)\times (|\mathcal{N}|+2m)},\hfill \\ \hfill & X[k]\triangleq {\left[\begin{array}{c}\hfill x_1{[k]}^{\top },\dots ,x_{|\mathcal{N}|}{[k]}^{\top }\hfill \end{array}\right]}^{\top }\in {\mathbb{R}}^{(|\mathcal{N}|+2m)},\hfill \\ \hfill & U[k]\triangleq {\left[\begin{array}{c}\hfill u_1{[k]}^{\top },\dots ,u_{|\mathcal{N}|}{[k]}^{\top }\hfill \end{array}\right]}^{\top }\in {\mathbb{R}}^{(|\mathcal{N}|+2m)},\hfill \\ \hfill & ϵ[k]\triangleq {\left[\begin{array}{c}\hfill {ϵ}_1{[k]}^{\top },\dots ,{ϵ}_{|\mathcal{N}|}{[k]}^{\top }\hfill \end{array}\right]}^{\top }\in {\mathbb{R}}^{2\sum _{i\in \mathcal{N}}n(i)},\hfill \\ \hfill & E[k]\triangleq {\left[\begin{array}{c}\hfill e_1{[k]}^{\top },\dots ,e_{|\mathcal{N}|}{[k]}^{\top }\hfill \end{array}\right]}^{\top }\in {\mathbb{R}}^{|\mathcal{N}|+m},\hfill \\ \hfill & H[k]\triangleq \text{blkdiag}\left\{\left[\begin{array}{c}\hfill 0_{1\times 2n(1)}\hfill \\ \hfill H_1[k]\hfill \\ \hfill 0_{1\times 2n(1)}\hfill \end{array}\right],\dots ,\left[\begin{array}{c}\hfill 0_{1\times 2n(m)}\hfill \\ \hfill H_m[k]\hfill \\ \hfill 0_{1\times 2n(m)}\hfill \end{array}\right],\right.\hfill \\ \hfill & \left.,H_{m+1}[k],\dots ,H_{|\mathcal{N}|}[k]\right\}\in {\mathbb{R}}^{(|\mathcal{N}|+2m)\times 2\sum _{i\in \mathcal{N}}n(i)}.\hfill \end{array}$

Consider K time slots k = 0, … , K−1, and collect the measurements corresponding the K time slots in vector $\bar{Y}$ as follows:

$\bar{Y}=\left[\begin{array}{c}\hfill Y[0]\hfill \\ \hfill Y[1]-CU[0]\hfill \\ \hfill Y[2]-CAU[0]-CU[1]\hfill \\ \hfill ⋮\hfill \\ \hfill Y[K-1]-C\sum _{k=0}^{K-2}{A}^{K-2-k}U[k]\hfill \end{array}\right].(23)$

$\bar{Y}\in {\mathbb{R}}^{K(|\mathcal{N}|+m)}$ can be rewritten in the following form:

$\bar{Y}=\mathrm{\Phi }X[0]+\mathrm{\Psi }\bar{E},(24)$

where $\mathrm{\Psi }=\left[\begin{array}{cc}\hfill {\mathrm{\Psi }}_1\hfill & \hfill {\mathrm{\Psi }}_2\hfill \end{array}\right]$ with ${\mathrm{\Psi }}_1\in {\mathbb{R}}^{K(|\mathcal{N}|+m)\times K(|\mathcal{N}|+m)}$ and ${\mathrm{\Psi }}_2\in {\mathbb{R}}^{K(|\mathcal{N}|+m)\times 2K{\sum }_{i\in \mathcal{N}}n(i)}$, and

$\begin{array}{ll}\hfill {\mathrm{\Psi }}_1& =\left[\begin{array}{cccc}\hfill I_{|\mathcal{N}|+m}\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill -CB\hfill & \hfill I_{|\mathcal{N}|+m}\hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill -CAB\hfill & \hfill -CB\hfill & \hfill I_{|\mathcal{N}|+m}\hfill & \hfill \cdots \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill -C{A}^{K-2}B\hfill & \hfill \cdots \hfill & \hfill -CB\hfill & \hfill I_{|\mathcal{N}|+m}\hfill \end{array}\right],\hfill \\ \hfill {\mathrm{\Psi }}_2& =\left[\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill -CH[0]\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill -CAH[0]\hfill & \hfill -CH[1]\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill -C{A}^{K-2}H[0]\hfill & \hfill \cdots \hfill & \hfill -CH[K-2]\hfill & \hfill 0\hfill \end{array}\right],\hfill \\ \hfill \mathrm{\Phi }& =\left[\begin{array}{c}\hfill C;CA;C{A}^2;\cdots ;C{A}^{K-1}\hfill \end{array}\right],\hfill \\ \hfill \bar{E}& =\left[\begin{array}{c}\hfill E[0];\cdots ;E[K-1];ϵ[0];\cdots ;ϵ[K-1]\hfill \end{array}\right].\hfill \end{array}$

The number of columns of the matrix H [k] and the number of rows of the column vector ϵ [k] can be reduced from $2{\sum }_{i\in \mathcal{N}}n(i)$ to $2|\mathcal{E}|$ by using the following properties:

$\begin{array}{cc}\hfill e_{ij}^c[k]& =1-\cos (e_i[k]-e_j[k])=e_{ji}^c[k],\hfill \\ \hfill e_{ij}^s[k]& =\sin (e_i[k]-e_j[k])=-e_{ji}^s[k].\hfill \end{array}(25)$

Notice that we have γ_ij [k] = γ_ji [k] and ϕ_ij = ϕ_ji. Hence, the dimension of Ψ₂ and $\bar{E}$ can also be reduced as follows:

$\begin{array}{cc}\hfill \dim ({\mathrm{\Psi }}_2)& \to K(|\mathcal{N}|+m)\times 2K|\mathcal{E}|,\hfill \\ \hfill \dim (\bar{E})& \to K\left(|\mathcal{N}|+m+2|\mathcal{E}|\right).\hfill \end{array}(26)$

We now choose $\mathrm{\Omega }\in {\mathbb{R}}^{(K|\mathcal{N}|-2|\mathcal{N}|)\times K(|\mathcal{N}|+m)}$ which annihilates Φ, i.e., ΩΦ = 0. We then have:

$\bar{Y}=\mathrm{\Omega }\bar{Y}=\mathrm{\Omega }\tilde{\Psi }\tilde{E},(27)$

where $\tilde{\Psi }$ and $\tilde{E}$ are the reduced Ψ and $\bar{E}$.

In error correction, accurate decoding is guaranteed when the coding matrix (i.e., $\mathrm{\Omega }\tilde{\mathrm{\Phi }}$) satisfies the Restricted Isometric Properties (RIP). Notice that RIP can be obtained by randomly selecting a coding matrix a priori. In (Chang et al., 2018), Theorem 1 provides a sufficient condition for perfect reconstruction of the states against sensor attacks and describes estimator design by using a state feedback controller. However, in the current setting, since there is a limitation to manipulate the coding matrix, we combine our secure estimation scheme with a Kalman Filter (KF) to enhance its performance in practice.

5 Numerical Results

Consider an AC microgrid comprising m = 3 synchronous generators, n = 25 inverter-interfaced power supplies, and l = 5 load buses. The microgrid topology is shown in Figure 2. This microgrid topology is a modified IEEE 33-bus distribution system from Baran and Wu (1989). Notice that in the augmented network, the number of buses is 61. The synchronous generator buses are buses ${\mathcal{N}}^{(S)}=\{\mathrm{3,6,9}\}$, the load buses without generation are buses ${\mathcal{N}}^{(L)}=\{\mathrm{1,2,14,22,25}\}$, and the inverter-interfaced power supply buses are ${\mathcal{N}}^{(I)}=\{1,\dots ,33\}\backslash ({\mathcal{N}}^{(L)}\cup {\mathcal{S}}^{(L)})$. Further, we consider the fictitious buses for the synchronous generators to be buses 34, 35, and 36, and the fictitious buses for the inverter-interfaced power supplies to be buses 37–61. The microgrid is connected to the grid via the tie-line connected to bus one. We select the turbine time constants to be τ_i = 5 s, the generator damping coefficients to be D_i = 2, the inertia constants to be M_i = 10, and the droop coefficients to be R_i = 9.5 for all $i\in {\mathcal{N}}^{(S)}$. We further select the inverter-interfaced power supply droop coefficients to be D_i = 0.7 for all $i\in {\mathcal{N}}^{(I)}$, and the constant frequency coefficients of the loads to be D_i = 0.1 for all $i\in {\mathcal{N}}^{(L)}$.

FIGURE 2

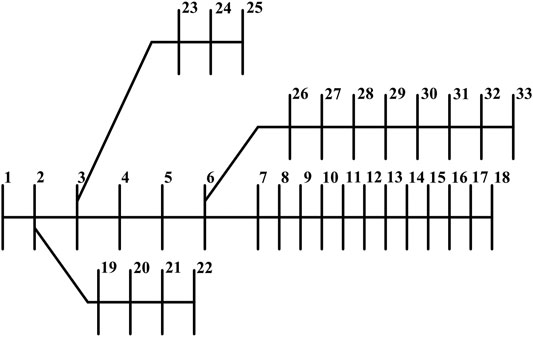
FIGURE 2. An AC microgrid comprising m = 3 synchronous generators, n = 25 inverter-interfaced power supplies, and l = 5 load buses.

The system is simulated for t = 20 s with a discretization step of δ = 1/60 seconds. We select the nominal loads $P_i^d$’s randomly from the interval [0, 0.5] pu, and select the generation set-points $P_i^s$’s such that the system is balanced. Notice that computing the active power set-points $P_i^s$’s is not the subject of this study. Therefore, we only need to select the values of $P_i^s$’s such that the demand and supply are balanced. Without loss of generality, we assume that voltage magnitudes V_i [k]’s are equal to 1 pu for all k and i = 1, … , 33.

We demonstrate the effectiveness of our secure state estimation method through simulations of the two types of attacks:

1. Type A: attacks targeted at synchronous generators, i.e., measurements y_i[k]’s, where $i\in {\mathcal{N}}^{(S)}\cup {\mathcal{N}}_f^{(S)}$, are corrupted.

2. Type B: attacks targeted at inverter-interfaced power supplies, i.e., measurements y_i [k]’s, where $i\in {\mathcal{N}}^{(I)}\cup {\mathcal{N}}_f^{(I)}$, are corrupted.

For each of these attack types, we simulate three scenarios:

1. Scenario 1: There is no cyber attack on the microgrid.

2. Scenario 2: Measurements are attacked, and they are not protected by any secure state estimator.

3. Scenario 3: Measurements are attacked, and they are protected by the proposed dynamic state estimator.

5.1 Attack Type A: Synchronous Generator Attacks

The microgrid operator measures rotor angle from the three synchronous generator buses, and rotor angle and speed from the three fictitious synchronous generator buses. Hence, the operator has access to nine measurements that are subject to cyber attacks. We assume that from t = 1.1 s onwards, the attacker randomly chooses a set of five measurements out of the nine measurements and corrupts them with random signals at each time step. Figure 3 shows the simulation results for the three scenarios: 1) there is no attack (No Attack), 2) the measurements are attacked and they are not protected with any secure estimator (SE), and 3) the measurements are attacked and the microgrid operator uses the proposed SE. Notice that in Figure 3, we only show phase angles and rotor speeds of the three fictitious synchronous generator buses.

FIGURE 3

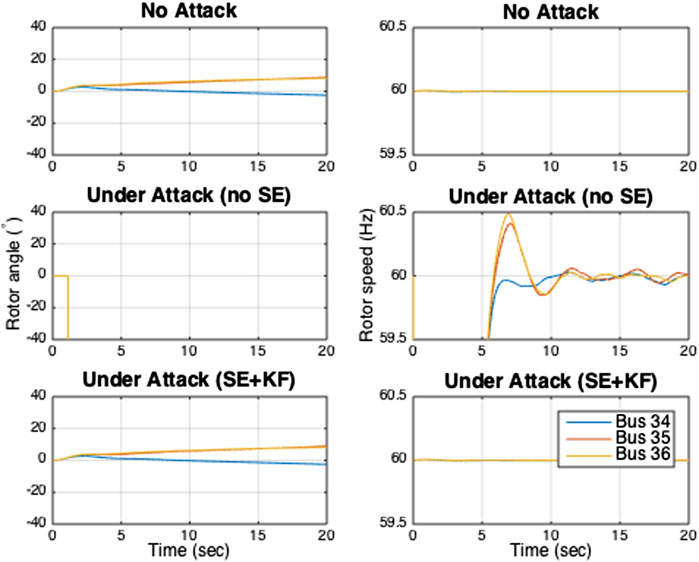
FIGURE 3. Phase angles and rotor speeds of the synchronous generators under attack Type A in the three scenarios.

In the microgrid without cyber attacks, the rotor speeds converge to 60 Hz after an initial transient period. As mentioned earlier, no secure estimation is used in Scenario 2 while the micorgrid operator uses the proposed secure state estimation to recover the system states in Scenario 3. Therefore, both rotor angles and speeds cannot be estimated correctly in Scenario 2, as shown in Figure 3. However, the operator can perfectly estimate both rotor angles and speeds in Scenario 3. Figure 4 shows the attack signal, secure estimator’s estimated attack signal, and the estimation error. The results show that the proposed dynamic state estimator accurately estimates the system state. Hence, the system’s dynamics are identical to the system without any attacks.

FIGURE 4

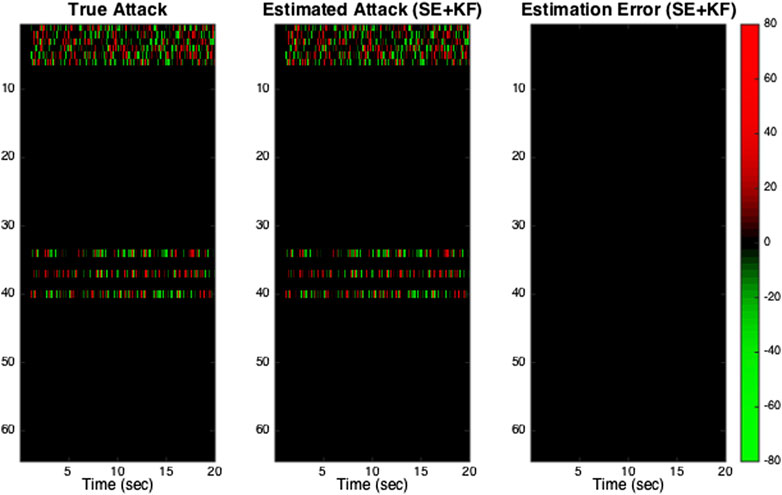
FIGURE 4. True and estimated attack signals: The rows and columns correspond to measurements and time steps, respectively. In the subfigures, the color indicates the attack signal: red is an attack with positive value, green is an attack with negative value, and black is no attack. Only measurements of the synchronous generators buses and their corresponding fictitious buses are corrupted by the attack. Notice that measurements 1–6 correspond to rotor angle and speed measurements from the fictitious synchronous generator buses, and measurements 34, 37 and 40 correspond to phase angle measurements from the synchronous generator buses. In subfigure “Estimation Error”, the black color indicates there is zero estimation error for all measurements at all times.

5.2 Attack Type B: Inverter-Interfaced Power Supply Attacks

The microgrid operator measures phase angles from the inverter-interfaced power supply buses. Hence, the operator has access to 50 measurements that are subject to cyber attack: 25 correspond to phase angle measurements of the inverter-interfaced power supply buses and 25 correspond to the phase angle measurements of the corresponding fictitious buses. We assume that from t = 1.1 s onwards, the attacker randomly chooses a set of five measurements out of the 50 measurements and corrupts them with random signals at each time step. The simulation results are shown in Figure 5 and Figure 6. The results show that both phase angles and rotor speeds are severely affected when the measurements are attacked and no secure estimator is used by the operator. However, the microgrid operator can perfectly recover the attack signals and restore the system’s normal dynamics as if there was no attack when secure state estimation is used.

FIGURE 5

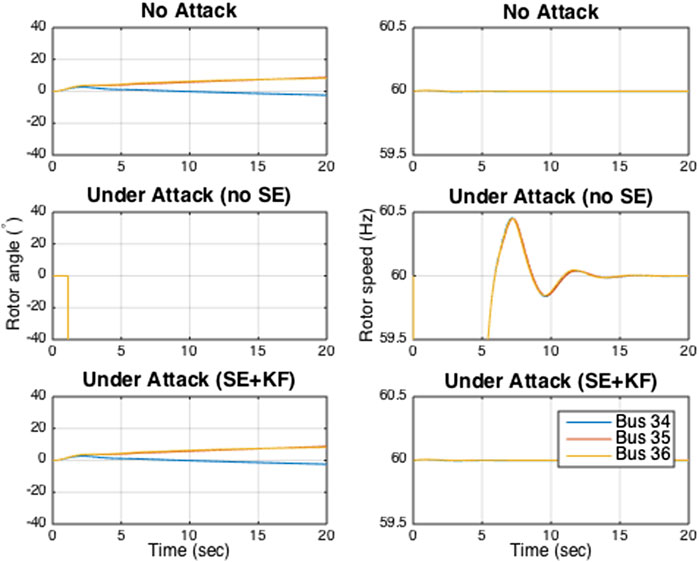
FIGURE 5. Phase angles and rotor speeds of the synchronous generators under attack Type B in the three scenarios.

FIGURE 6

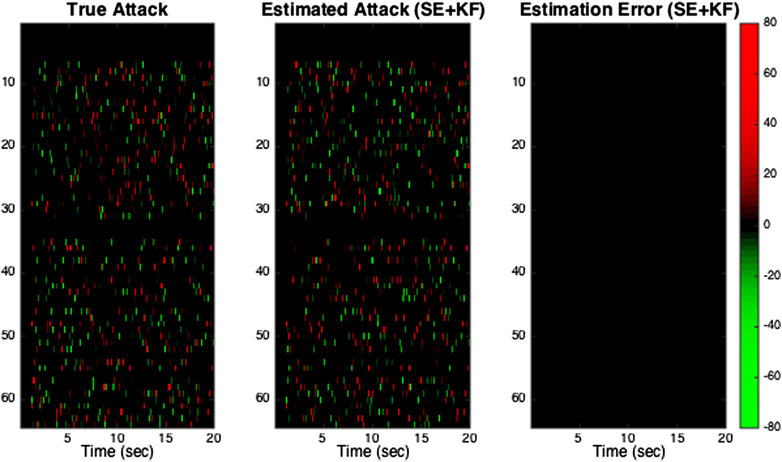
FIGURE 6. True and estimated attack signals: The rows and columns correspond to measurements and time steps, respectively. In the subfigures, the color indicates the attack signal: red is an attack with positive value, green is an attack with negative value, and black is no attack. Only measurements of the inverter-interfaced power supply buses and their corresponding fictitious buses are corrupted by the attack. In subfigure “Estimation Error”, the black color indicates there is zero estimation error for all measurements at all times.

6 Conclusion

We propose a secure state estimator for dynamic state estimation in AC microgrids under cyber physical attacks. We show that the microgrid operator can perfectly reconstruct the dynamic states in its AC microgrid using our estimator. We envision that the proposed approach ensures microgrid resilience and enables secure microgrid operations.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Without loss of generality, we consider tie-line buses that connect the microgrid to the grid, as load buses

References

Abhinav, S., Modares, H., Lewis, F. L., Ferrese, F., and Davoudi, A. (2018). “Synchrony in Networked Microgrids under Attacks,”. IEEE Trans. on Smart Grid. 9 (6), 6731–6741. doi:10.1109/tsg.2017.2721382

CrossRef Full Text | Google Scholar

Abur, A., and Expósito, A. G. (2004). Power System State Estimation: Theory and Application. Marcel Dekker.

Alpcan, T., and Basar, T. (2003). A Game Theoretic Approach to Decision and Analysis in Network Intrusion Detection. Proc. 42nd IEEE Conf. Decis. Control. 3, 2595–2600. doi:10.1109/cdc.2003.1273013

CrossRef Full Text | Google Scholar

Angel, A. D., Geurts, P., Ernst, D., Glavic, M. G., and Wehenkel, L. (2007). Estimation of Rotor Angles of Synchronous Machines Using Artificial Neural Networks and Local PMU-Based Quantities. Int. J. Neurocomput. 70 (16–18), 2668–2678. doi:10.1016/j.neucom.2006.12.017

CrossRef Full Text | Google Scholar

Baran, M. E., and Wu, F. F. (1989). Network Reconfiguration in Distribution Systems for Loss Reduction and Load Balancing. IEEE Trans. Power Deliv. 4 (2), 1401–1407. doi:10.1109/61.25627

CrossRef Full Text | Google Scholar

Basseville, M., and Nikiforov, I. V. (1993). Detection of Abrupt Changes: Theory and Application. Prentice Hall Englewood Cliffs. Vol. 104.

Google Scholar

Bergen, A. R., and Hill, D. J. (1981). “A Structure Preserving Model for Power System Stability Analysis,” Power Apparatus And Systems. IEEE Trans. 1, 25–35. doi:10.1109/tpas.1981.316883

CrossRef Full Text | Google Scholar

Bi, S., and Zhang, Y. J. (2014). Graphical Methods for Defense against False-Data Injection Attacks on Power System State Estimation. IEEE Trans. Smart Grid. 5 (3), 1216–1227. doi:10.1109/tsg.2013.2294966

CrossRef Full Text | Google Scholar

Candes, E. J., and Tao, T. (2005). Decoding by Linear Programming. IEEE Trans. Info. Theor. 51 (12), 4203–4215. doi:10.1109/tit.2005.858979

CrossRef Full Text | Google Scholar

Candes, E., Romberg, J., and Tao, T. (2006). Stable Signal Recovery From Incomplete and Inaccurate Measurements. Commun. Pure Appl. Math. 59 (8), 1207–1223. doi:10.1002/cpa.20124

CrossRef Full Text | Google Scholar

Chang, Y. H., Hu, Q., and Tomlin, C. J. (2018). Secure Estimation Based Kalman Filter for Cyber Physical Systems against Sensor Attacks. Automatica. 95, 399–412. doi:10.1016/j.automatica.2018.06.010

CrossRef Full Text | Google Scholar

CIP Standards (2020). Critical Infrastructure Protection. Available at: http://www.nerc.com/pa/Stand/Pages/CIPStandards.aspx.

Google Scholar

Donoho, D. L., and Elad, M. (2003). Optimally Sparse Representation in General (Nonorthogonal) Dictionaries via L₁ Minimization. Proc. Natl. Acad. Sci. 100 (5), 2197–2202. doi:10.1073/pnas.0437847100

PubMed Abstract | CrossRef Full Text | Google Scholar

Elad, M., and Bruckstein, A. M. (2002). A Generalized Uncertainty Principle and Sparse Representation in Pairs of Bases. IEEE Trans. Inf. Theor. 48 (9), 2558–2567. doi:10.1109/tit.2002.801410

CrossRef Full Text | Google Scholar

Farahmand, S., Giannakis, G. B., and Angelosante, D. (2011). Doubly Robust Smoothing of Dynamical Processes via Outlier Sparsity Constraints. IEEE Trans. Signal. Process. 59 (10), 4529–4543. doi:10.1109/tsp.2011.2161300

CrossRef Full Text | Google Scholar

Fawzi, H., Tabuada, P., and Diggavi, S. (2014). Secure Estimation and Control for Cyber-Physical Systems Under Adversarial Attacks. IEEE Trans. Automatic Control. 59 (6), 1454–1467. doi:10.1109/tac.2014.2303233

CrossRef Full Text | Google Scholar

Gribonval, R., and Nielsen, M. (2003). Sparse Representations in Unions of Bases. IEEE Trans. Inf. Theor. 49 (12), 3320–3325. doi:10.1109/tit.2003.820031

CrossRef Full Text | Google Scholar

Haddadi, A., Yazdani, A., Joos, G., and Boulet, B. (2013). A Generic Load Model for Simulation Studies of Microgrids. Proc. IEEE Power Energ. Soc. Gen. Meet., 1–5. doi:10.1109/pesmg.2013.6672962

CrossRef Full Text | Google Scholar

Hatziagyriou, N., Asano, H., Iravani, R., and Marnay, C. (2007). MicroGrids. IEEE Power Energ. Mag. 5 (4), 78–94. doi:10.1109/MPAE.2007.376583

CrossRef Full Text | Google Scholar

Hayden, D., Chang, Y. H., Goncalves, J., and Tomlin, C. (2016). Sparse Network Identifiability via Compressed Sensing. Automatica. 68, 9–17. doi:10.1016/j.automatica.2016.01.008

CrossRef Full Text | Google Scholar

Hooshyar, A., and Iravani, R. (2017). Microgrid Protection. Proc. IEEE. 105 (7), 1332–1353. doi:10.1109/jproc.2017.2669342

CrossRef Full Text | Google Scholar

Hu, Q., Fooladivanda, D., Chang, Y. H., and Tomlin, C. J. (2018). Secure State Estimation and Control for Cyber Security of the Nonlinear Power Systems. IEEE Trans. Control. Netw. Syst. 5 (3), 1310–1321. doi:10.1109/tcns.2017.2704434

CrossRef Full Text | Google Scholar

Ilić, M., and Liu, S. (1996). Hierarchical Power Systems Control: Its Value in a Changing Industry. Springer.

Jiao, Q., Modares, H., Lewis, F. L., Xu, S., and Xie, L. (2016). “Distributed ℓ₂-Gain Output-Feedback Control of Homogeneous and Heterogeneous Systems. Automatica. 71, 361–368. doi:10.1016/j.automatica.2016.04.025

CrossRef Full Text | Google Scholar

Kundur, P., Paserba, J., Ajjarapu, V., Andersson, G., Bose, A., Canizares, C., et al. (2004). Definition and Classification of Power System Stability IEEE/CIGRE Joint Task Force on Stability Terms and Definitions. IEEE Trans. Power Syst. 19 (3), 1387–1401. doi:10.1109/tpwrs.2004.825981

CrossRef Full Text | Google Scholar

Lasseter, R. (2002). MicroGrids. IEEE Power Eng. Soc. Winter Meet. 1, 305–308. doi:10.1109/PESW.2002.985003

Google Scholar

Liu, L., Esmalifalak, M., Ding, Q., Emesih, V. A., and Han, Z. (2014a). Detecting False Data Injection Attacks on Power Grid by Sparse Optimization. IEEE Trans. Smart Grid. 5 (2), 612–621. doi:10.1109/tsg.2013.2284438

CrossRef Full Text | Google Scholar

Liu, S., Chen, B., Zourntos, T., Kundur, D., and Butler-Purry, K. (2014b). A Coordinated Multi-Switch Attack for Cascading Failures in Smart Grid. IEEE Trans. Smart Grid. 5 (3), 1183–1195. doi:10.1109/tsg.2014.2302476

CrossRef Full Text | Google Scholar

Manandhar, K., Cao, X., Hu, F., and Liu, Y. (2014). Detection of Faults and Attacks Including False Data Injection Attack in Smart Grid Using Kalman Filter. IEEE Trans. Control. Netw. Syst. 1 (4), 370–379. doi:10.1109/tcns.2014.2357531

CrossRef Full Text | Google Scholar

Meliopoulos, A. P. S. (2017). Dynamic State Estimation-Based Protection: Status and Promise. IEEE Trans. Power Deliv. 32 (1), 320–330. doi:10.1109/tpwrd.2016.2613411

CrossRef Full Text | Google Scholar

Mo, Y., Chabukswar, R., and Sinopoli, B. (2014). Detecting Integrity Attacks on Scada Systems. IEEE Trans. Control. Syst. Technol. 22 (4), 1396–1407. doi:10.1109/tcst.2013.2280899

CrossRef Full Text | Google Scholar

Modir, H., and Schlueter, R. (1981). A Dynamic State Estimator for Dynamic Security Assessment. IEEE Trans. Power Apparatus Syst. PAS-100 (11), 4644–4652. doi:10.1109/tpas.1981.316806

CrossRef Full Text | Google Scholar

Pajic, M., Weimer, J., Bezzo, N., Tabuada, P., Sokolsky, O., Lee, I., et al. (2014). Robustness of Attack-Resilient State Estimators. In ACM/IEEE International Conference on Cyber-Physical Systems. ICCPS). doi:10.1109/iccps.2014.6843720

CrossRef Full Text | Google Scholar

Pasqualetti, F., Bicchi, A., and Bullo, F. (2012). Consensus Computation in Unreliable Networks: A System Theoretic Approach. IEEE Trans. Autom. Control. 57 (1), 90–104. doi:10.1109/tac.2011.2158130

CrossRef Full Text | Google Scholar

Pasqualetti, F., Dorfler, F., and Bullo, F. (2013). Attack Detection and Identification in Cyber-Physical Systems. IEEE Trans. Autom. Control. 58 (11), 2715–2729. doi:10.1109/tac.2013.2266831

CrossRef Full Text | Google Scholar

Sauer, P. W., and Pai, M. A. (1998). Power System Dynamics and Stability. Upper Saddle River, NJ, USA: Prentice-Hall.

Schweppe, F., and Wildes, J. (1970). Power System Static-State Estimation, Part I: Exact Model. IEEE Trans. Power Apparatus Syst. PAS-89 (1), 120–125. doi:10.1109/tpas.1970.292678

CrossRef Full Text | Google Scholar

Shoukry, Y., and Tabuada, P. (2015). Event-Triggered State Observers for Sparse Sensor Noise/Attacks. IEEE Trans. Automatic Control. 99, 1–13. doi:10.1109/TAC.2015.2492159

Google Scholar

Srikantha, P., and Kundur, D. (2016). A DER Attack-Mitigation Differential Game for Smart Grid Security Analysis. IEEE Trans. Smart Grid. 7 (3), 1476–1485. doi:10.1109/tsg.2015.2466611

CrossRef Full Text | Google Scholar

Shoukry, Y., Nuzzo, P., Puggelli, A., Sangiovanni-Vincentelli, A. L., Seshia, S. A., and Tabuada, P. (2014). “Secure State Estimation for Cyber Physical Systems under Sensor Attacks: a Satisfiability Modulo Theory Approach,” arXiv pre-print.

Google Scholar

Tripathy, P., Srivastava, S. C., and Singh, S. N. (2010). A Divide-by-Difference-Filter Based Algorithm for Estimation of Generator Rotor Angle Utilizing Synchrophasor Measurements. IEEE Trans. Instrumentation Meas. 59 (6), 1562–1570. doi:10.1109/tim.2009.2026617

CrossRef Full Text | Google Scholar

Tropp, J. A. (2004). Greed Is Good: Algorithmic Results for Sparse Approximation. IEEE Trans. Inf. Theor. 50 (10), 2231–2242. doi:10.1109/tit.2004.834793

CrossRef Full Text | Google Scholar

Venayagamoorthy, G. K., and Harley, R. G. (2005). MLP/RBF Neural-Networkbased Online Global Model Identification of Synchronous Generator. IEEE Trans. Ind. Electron. 52 (6), 1685–1695. doi:10.1109/tie.2005.858703

CrossRef Full Text | Google Scholar

Venkatasubramanian, V., and Kavasseri, R. G. (2004). Direct Computation of Generator Internal States from Terminal Measurements. Proc. 37th Annu. Hawaii Int. Conf. Syst. Sci., 6. doi:10.1109/hicss.2004.1265193

CrossRef Full Text | Google Scholar

Yazdanian, M., and Mehrizi-Sani, A. (2014). “Distributed Control Techniques in Microgrids,”. IEEE Trans. Smart Grid. 5 (6), 2901–2909. doi:10.1109/tsg.2014.2337838

CrossRef Full Text | Google Scholar

Zhang, X., Chen, J., and Wang, C. (2016). Stability Analysis of Islanded Microgrids With Dynamic Loads. Proc. IEEE 14th Int. Conf. Control Automation, Robotics, Vis. 1–6. doi:10.1109/icarcv.2016.7838765

CrossRef Full Text | Google Scholar

Zhao, J., Qi, J., Huang, Z., Sakis Meliopoulos, A. P., Gomez-Exposito, A., Netto, M., et al. (2019). Power System Dynamic State Estimation: Motivations, Definitions, Methodologies and Future Work. IEEE Trans. Power Syst. 34 (4), 3188–3198. doi:10.1109/tpwrs.2019.2894769

CrossRef Full Text | Google Scholar