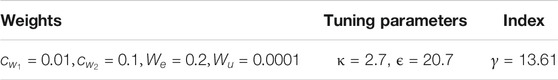- Department of Mechanical Engineering, University of Houston, Houston, TX, United States
This paper examines the control design for parameter-dependent input-delay linear parameter-varying (LPV) systems with saturation constraints and matched input disturbances. A gain-scheduled dynamic output feedback controller, coupled with a disturbance observer to cancel out input disturbance effects, was augmented with an anti-windup compensator to locally stabilize the input-delay LPV system under saturation, model uncertainty, and exogenous disturbances. Sufficient delay-dependent conditions to asymptotically stabilize the closed-loop system were derived using Lyapunov-Krasovskii functionals and a modified generalized sector condition to address the input saturation nonlinearity. The level of disturbance rejection was characterized via the closed-loop induced
1 Introduction
Controller saturation often leads to performance degradation and even instability in practical closed-loop feedback systems (Li and Lin, 2018). To avoid such problems, anti-windup strategies are typically introduced. Anti-windup control seeks to compensate for the discrepancy between the controller output signal and the actuation input to the controlled system. Methods for anti-windup control have been examined extensively in the control literature, e.g., see (Kapila and Grigoriadis, 2002; Benzaouia et al., 2018). The two-step method addresses the windup effects caused by actuator saturation following the initial design of a controller for the saturation-free closed-loop system. On the other hand, the single-step method simultaneously performs the controller and anti-windup compensator designs using, for example, differential inclusion or sector condition methods (Tarbouriech et al., 2011). The generalized sector condition method effectively facilitates linear parameter-varying (LPV) control system designs by introducing a new state representing a decentralized control input (Nguyen et al., 2015, 2018). In contrast, the differential inclusion method defines saturation-free polytopes, which may increase the computational complexity (Hu et al., 2018).
Practical systems are prone to input disturbances that can contribute to actuator saturation if not addressed. An observer can be designed to accommodate disturbance effects in control designs. In the literature, the input disturbance dynamics are typically assumed to be fully known (Wei et al., 2015; Fan et al., 2017; Gao et al., 2019; Shao et al., 2019). Other works assume that the disturbance dynamics were affected partially by unknown white noise signals that can better represent the varying and not fully predictable nature of disturbances (Wei et al., 2019, 2020). Controlling LPV systems under saturation and input disturbances becomes more challenging when a time delay exists in the control loop (Dou et al., 2014; de Souza et al., 2019). Delay frequently occurs in numerous engineering systems, such as power transmission, network and communication systems, biomedical systems, and economics. It leads to poor performance and in severe cases can induce oscillations and cause instability of the closed-loop system (Fridman, 2014). The stability and performance of time-delay LPV systems have been studied extensively in the literature (Briat, 2015; Salavati et al., 2019; Wang et al., 2019).
The present work examines the previously unexplored problem of control design for uncertain LPV systems with a parameter-dependent input delay and matched disturbances under control input constraints. In this work, disturbance dynamics are considered to be affected by unknown inputs. An output feedback LPV controller is coupled with a disturbance observer, and both are augmented with an anti-windup compensator to ensure the local stability of the uncertain closed-loop system. The design seeks to satisfy desired performance objectives along with disturbance estimation error minimization in terms of the induced
The control input is subject to disturbances and also drug injection limitations, and the MAP response is affected by exogenous disturbances, such as incisions, medicine interference, suturing, hemorrhage, and trauma. Precise automated drug delivery strategies are required to avoid over/under regulation, which could compromise the recovery of the patient. The proposed input-delay LPV MAP control along with the input disturbance observer favorably tracks a prescribed MAP profile under the model uncertainty and disturbances as closed-loop simulation results demonstrate.
The rest of this paper is structured as follows. Section 2 describes the mathematical formulation of the problem. Due to space limitations, the closed-loop stability and synthesis conditions of the disturbance observer with the anti-windup gain-scheduled controller in terms of LMIs are combined to form a single result and presented in Section 3. Section 4 briefly discusses the modeling of the MAP response dynamics to the vasoactive drug injection followed by the validation of the proposed controller design through simulations of the time-delay LPV MAP closed-loop system. Section 5 concludes the paper.
2 Problem Statement
Consider an uncertain input-delay LPV system as follows
where
where Ep and G’s are known constant matrices and the time-varying matrix F(t) satisfies the Euclidean matrix norm bound ‖F(t)‖ ≤ 1. The scheduling parameter vector belongs to a set
and
The input disturbance dynamics is
where
generates a harmonic disturbance signal with the frequency f.
The domain of attraction for 1) is defined as follows.
Definition 1. For
We use the notation t (t) hereafter and assume the system (1) is stabilizable and detectable. We seek to design a gain-scheduled dynamic output feedback LPV controller, (C), along with a disturbance observer, (IDO), to achieve a desired level of performance. To this end, consider a full-order non-rational gain-scheduled LPV controller
di(t) is an estimate of the input disturbance vector, di(t), and is generated by the following 103 disturbance observer
where the controller and observer matrix coefficients are to be designed in the single-step framework.
The design objective is to asymptotically stabilize the closed-loop system 11) and minimize the energy content of the mapping from the disturbance vector to the controlled output, that is
In this work, instead of the optimal problem (Eq. 13), we address the problem of the minimization of the bounded induced
where γ and c are positive scalars.
The assumption and lemmas used throughout this paper are as follows.
Assumption 1. The initial value of the scheduling parameter satisfies
Lemma 1. (Fridman, 2014). (Jensen’s Inequality) For a positive definite matrix
Lemma 2. (Fridman, 2014). For any positive scalar ɛ > 0, constant matrices Π and Ω and a time-varying matrix Δ(t) satisfying ‖Δ(t)‖ < 1 with appropriate dimensions, we have
Proof. The proof follows from the fact that
Lemma 3. (Park et al., 2011). If
with
where the scalar αi belongs to the unit simplex
Lemma 4. For a vector of positive scalars
is nonempty, then the following generalized sector condition holds
Similarly for the delay state, ξ(t − θ(ρt)), and a real matrix
Proof. The proof is similar to Lemma 2 in (Gomes da Silva Jr et al., 2013).
Lemma 5. (Tarbouriech et al., 2011). For a parameter-dependent positive definite matrix P (ρt), a positive scalar β, the variables in Lemma 4, and an ellipsoidal set
the ellipsoid is inside the polyhedron, i.e.,
and similarly for the delay state.
3 Main Results
The LPV controller and observer synthesis conditions are provided in the following result.
Theorem 1. For positive scalars ɛ, γ > 0, a real scalar κ, parameter and delay spaces
with the matrices
Then, the response of the closed-loop system 11) remains bounded under the initial conditions
with U1 given in (38), and satisfies the induced
and the observer is realized via
Proof. The following Lyapunov-Krasovskii functional (LKF) candidate is considered (Salavati et al., 2019)
where
with a differentiable positive definite matrix P (ρt) and positive definite matrices Q (ρt), S (ρt), and R. The time derivative of (Eq. 26) along the trajectories of (Eq. 11) is
with
Using Lemma 1, the last term can be upper bounded by
where
and
Through the descriptor method (Fridman, 2014), two slack variable matrices are introduced by adding the following term to (Eq. 27)
For satisfying the performance index
where
and
Next, using the inequalities of Lemma 4 and the
By applying the Schur complement formula (Fridman, 2014), for the dissipative part 32) and using Lemma 2 with Schur complement for the uncertainty part, 33) gives the following LMI
with
To restrict the closed-loop system trajectory ellipsoid inside the polyhedron (Eq. 16), using Lemma 5 for the delay free and delayed states and the Schur complement formula, the LMIs
are obtained.
In order to facilitate the derivation of the LPV controller and observer and avoid nonconvex synthesis conditions, we assume that the matrix variable P1 is full rank and satisfies
which decouples the observer and controller designs and the • and ⋄ block matrices do not contribute to the synthesis problem. Partitioning (37) also verifies (Eq. 24a). Then, we define
The subsequent congruent transformations are as follows. diag{U1, U1, U1, U1, T−1 (ρt), I, I, I, I} and its transpose pre- and post-multiplies (Eq. 34a), diag{U1, U1} multiplies (30), and finally, diag{I, U1} multiplies (35) and (36). We, then, substitute for closed-loop matrices (12) and redefine the resulting matrix multiplications using the notations
To verify the boundedness of all trajectories of (Eq. 11), integrating (32) yields
which implies that
since V (t = T)|T→∞ → 0 and satisfies (14). Moreover, (39) also yields
or ξT(T)P (ρT)ξ(T) ≤ V (t = T) ≤ β−1,
Based on (26) and Assumption 1, the basin of attraction is
which verifies
and thus
It is noted that conditions (20) are LMIs for constant values of the scalar parameters κ and ɛ. A 2D search can be exploited to solver the values of the parameters such that the LMIs (20) are feasible.
3.1 Saturation Control Objectives
Saturation control generally leads to three distinct optimization objectives.
• Worst-case disturbance amplification minimization: This is the induced
and is of main interest in this paper.
• Disturbance tolerance maximization: Since β ≤ δ and
• Initial condition set maximization: Seeks to minimize the eigenvalues of the positive definite matrices P (ρt), Q (ρt), S (ρt), and R that increases the initial values ‖ϕξ‖c and
Then, consider the following LMIs
from which, for instance (Eq. 45b), we can conclude that
With a similar approach for all LKF matrix variables, this objective can be formulated as follows
where αi, i = 1, … , 4 are weights to be selected based on the design requirements and
Remark 1. To solve the infinite-dimensional LMIs for LPV systems with any form of parameter dependence as in (1), we use the parameter space gridding technique (Apkarian and Adams, 1998) with a 2-D search for the scalars κ and ϵ, and then we check the obtained results on a denser grid to ensure the feasibility of the LMIs.
Moreover, the LKF matrix variables are assumed to be second-order polynomials facilitating the calculation of their derivative with respect to the parameter if needed, i.e.
where
4 MAP Response Input-Delay LPV Model and Control
The automated closed-loop drug delivery for blood pressure control in critical patients suffering from hypotension can be beneficial compared to traditional medical interventions. It is fast and precise and avoids medication administration errors which can result in over/under MAP regulation. To provide a closed-loop strategy for such patients modeling the associated dynamics is the first step. The MAP dynamics in response to the administration of vasopressor drugs can be represented via a first-order input-delay LPV system (Tasoujian et al., 2019)
where ΔP(t) is the output MAP deviation from the baseline value, namely Pb(t) (in mmHg), I(t) is the input or injected PNP rate (in mL/h), β(t) is the time-varying gain or sensitivity (in mmHg ⋅ h/mL), τ(t) is the time-varying lag time of the plant or the drug diffusion time constant in s, and θ(t) is the delay introduced during drug injection or the time it takes for the MAP dynamics to respond to PNP administration (in s). The vector of scheduling parameters is then
4.1 LPV Parameters and Delay Estimation via Cubature Kalman Filter
In order to provide the controller with instantaneous values of the scheduling parameters, a Bayesian estimator known as cubature Kalman filter (CKF) is used. CKF propagates the sample points via equally valued cubature points which are twice the system size. It uses a cubic rule to derive the covariance and approximates the moments integrals through a normal distribution using the third-degree spherical-radial cubature rule. Unlike EKF, CKF neither requires nonlinear model linearization nor as many sampling points as UKF. At the same computational cost of cubic order like EKF, CKF has better nonlinear performance, accuracy, and numerical stability. Random sampling filters like particle filters are likely to suffer from computational problems, particle degradation and curse of dimensionality in practical applications.
Consider the following general nonlinear discrete-time stochastic system
where
CKF estimates the state vector in a conditional PDF form, i.e. p (xk|yk) where
Moments integral in CKF are computed via the third-degree spherical-radial rule. Consequently, for a Gaussian white noise signal, the prediction and correction steps are carried out via integrating a nonlinear function with regards to a normal distribution, that is
Next, suppose an arbitrary function h(x) with Σ as the covariance of x. Then, the integral
can be expressed in the spherical coordinate system as
where x = Crz + μ with ‖z‖ = 1, μ is the mean and C is the Cholesky factor of the covariance matrix Σ, and
where ξi denotes the ith cubature point at the intersection of the unit sphere and its axes. The main advantage of this method is that the cubature points are obtained off-line using a third-degree cubature rule. For the detailed steps regarding the computation of states estimates through CKF, one can see (Tasoujian et al., 2020b). In order to avoid numerical problems, square-root CKF based on orthogonal triangular decomposition is adopted.
For the system given in (Eq. 48), assuming a small enough sampling time, Ts, we can rewrite the state equations as
The state vector is augmented with the parameters to be estimated assuming local random-walk dynamics, i.e.
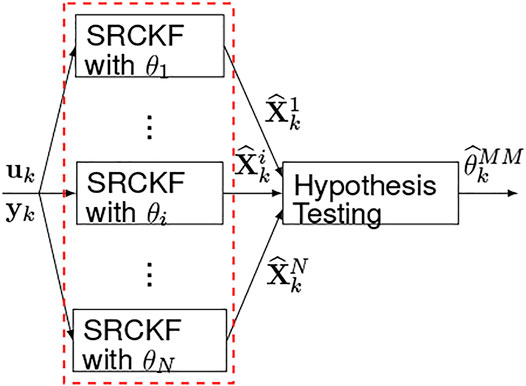
However, since the varying input delay cannot be described via a random-walk process, a multiple-model (MM) paradigm is used for delay estimation. It is noted the Padé rational approximation may introduce numerical errors specifically, for large delays and thus is not favorable. The MM approach uses N parallel SRCKFs (MMSRCKF) with dedicated delay values covering the whole delay space as θ1, θ2, … , θN. Then, a hypothesis testing is used to calculate the delay,
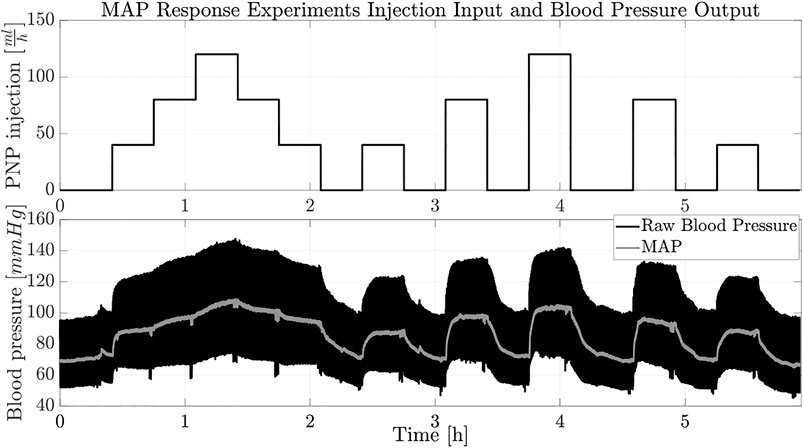
To avoid truncation and cumulative numerical errors, we use the square-root CKF (SRCKF) utilizing the square root decomposition of the covariance matrix (Tasoujian et al., 2020b). For validation purposes, we applied the proposed MMSRCKF estimation framework to animal experiment data collected at the Resuscitation Research Laboratory at the Department of Anesthesiology, the University of Texas Medical Branch (UTMB) in Galveston. The dataset contained the input PNP infusion rates and output MAP measurements for a 55 kg anesthetized swine. The swine was maintained under anesthetic conditions by the continuous infusion of propofol and an intramuscular injection of ketamine was used to sedate it. During a 6-h experiment, the PNP drug was infused through a bodyguard infusion pump. A Philips MP2 transport device with a sampling period of 0.05 s recorded the blood pressure response. Figure 2 depicts the piece-wise constant PNP drug infusion profile versus the corresponding measured blood pressure response and the MAP response over time.
4.2 Closed-Loop MAP Control Design and Validation
The main objective of the MAP control design is to track a target blood pressure while maintaining an acceptable level of disturbance rejection and avoid control input saturation. To this end and as per the internal model principle (Tasoujian et al., 2019) and in order to improve the tracking behavior, it is assumed that the integral of the error signal is fed to the controller. We define
where ς is a positive scalar added to avoid numerical singularities, We and Wu denote the weights introduced to penalize the tracking error and the control effort, respectively, and
To examine the LPV controller performance and the closed-loop stability over the MAP response envelope, a simulation model resembling realistic conditions is used.
4.2.1 Closed-Loop MAP Control Results
To conduct closed-loop patient’s model-in-the-loop simulations, we use a developed nonlinear patient MAP response simulator to generate the scheduling parameters (Luspay and Grigoriadis, 2015). Simulations are conducted via MATLAB and the LMIs are solved using YALMIP (Lofberg, 2004) and MOSEK with the numerical data provided in (Tasoujian et al., 2020a). The numerical results for the minimization of the performance index upper bound are shown in Table 1.
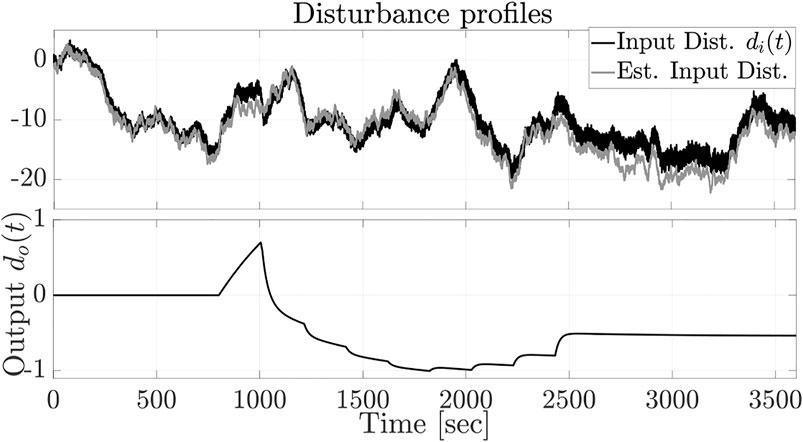
To better assess the design robustness, the input disturbance matrices are multiplied by a factor of 5. Figures 3, 4 show the disturbance profiles with the input disturbance estimation and reference MAP tracking results. Although the output disturbance and input saturation induce divergence in the disturbance observer output, the estimation is regarded in the admissible range as the tracking error remains close to zero and no significant over/under shoot occurs in the output MAP response. It can be concluded that the proposed disturbance rejection output-feedback LPV framework can properly regulate the patient’s MAP response to PNP injection to follow a target reference MAP profile while the system is subject to model mismatch, drug injection constraints, and disturbances.
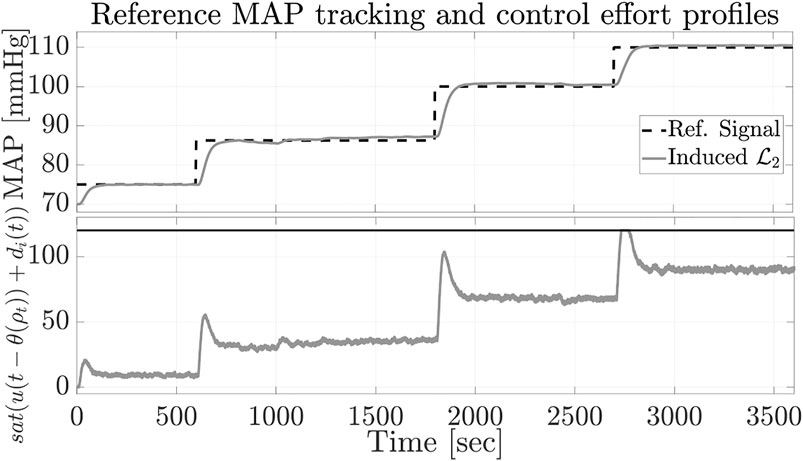
FIGURE 4. Tracking of reference MAP with anti-windup design and associated constrained control efforts.
5 Conclusion
The present work considers the design of an anti-windup linear parameter-varying (LPV) dynamic output feedback controller for input-delay LPV systems with input saturation constraints and matched disturbances under uncertainty. An anti-windup LPV controller and an LPV disturbance observer were introduced to characterize the disturbance attenuation level via the induced
To validate the control design method, we examined automated mean arterial blood pressure (MAP) regulation in response to vasopressor drug infusion for critical hypotensive patient resuscitation. To this end, a first-order input-delay LPV model described the MAP response dynamics. Based on data collected from animal experiments, a real-time Bayesian filtering estimator, known as cubature Kalman filter (CKF), confirmed the validity and sufficiency of the proposed model. To conduct the closed-loop simulations with a hypothetical patient-in-the-loop, the associated varying parameters of the MAP response dynamic model were generated in a patient simulation environment in accordance with clinical observations. Then, the LPV gain-scheduled saturation controller, as well as the CKF estimator were coupled with an input disturbance LPV observer and cascaded to the parameter generator to simulate the performance of the closed-loop system in tracking a target MAP signal under model uncertainty, medicine injection limitation, and matched input disturbances. Closed-loop simulations demonstrated desirable tracking performance in the presence of model uncertainty, parameter variations, disturbance, and input saturation constraints.
Data Availability Statement
The datasets presented in this article are not readily available because The dataset is collected at the University of Texas, Medical Branch at Galveston and not the University of Houston. Requests to access the datasets should be directed toa2Fyb2xvc0B1aC5lZHU=.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Apkarian, P., and Adams, R. J. (1998). Advanced Gain-Scheduling Techniques for Uncertain Systems. IEEE Trans. Contr. Syst. Technol. 6, 21–32. doi:10.1109/87.654874
Benzaouia, A., Mesquine, F., and Benhayoun, M. (2018). Saturated Control of Linear Systems. Springer.
Briat, C. (2015). Linear Parameter-Varying and Time-Delay Systems Analysis, Observation, Filtering & Control. Berlin Heidelberg: Springer-Verlag.
de Souza, C., Castelan, E. B., and Leite, V. J. S. (2019). Nice, France: IEEE, 3782–3787. doi:10.1109/cdc40024.2019.9029551Input-to-state Stabilization of Discrete-Time LPV Systems with Bounded Time-Varying State Delay and Saturating Actuators through a Dynamic Controller58th Conference on Decision and Control
Dou, X., Zhang, R., and Zhang, Y. (2014).Stabilization Control for LPV Systems with Time Delay and Actuator Saturation. In The 26th Chinese Control and Decision Conference. Changsha: CCDC, 453–458. doi:10.1109/ccdc.2014.6852191
Fan, X., Yi, Y., and Ye, Y. (2017). DOB Tracking Control for Systems with Input Saturation and Exogenous Disturbances via T-S Disturbance Modelling. Cham, Switzerland: Springer, 445–455. doi:10.1007/978-3-319-33581-0_35DOB Tracking Control for Systems with Input Saturation and Exogenous Disturbances via T-S Disturbance Modelling
Fridman, E. (2014). Introduction to Time-Selay Systems Analysis and Control. Switzerland: Birkhäuser.
Gao, X., Gao, Q., Qi, W., and Kao, Y. (2019). Disturbance-observer-based Control for Time-Delay Markovian Jump Systems Subject to Actuator Saturation. Trans. Inst. Meas. Control. 41, 605–614. doi:10.1177/0142331218756728
Gomes da Silva, J. M., Castelan, E. B., Corso, J., and Eckhard, D. (2013). Dynamic Output Feedback Stabilization for Systems with Sector-Bounded Nonlinearities and Saturating Actuators. J. Franklin Inst. 350, 464–484. doi:10.1016/j.jfranklin.2012.12.009
Hu, Y., Duan, G., and Tan, F. (2018). Control of LPV Systems Subject to State Constraints and Input Saturation. Trans. Inst. Meas. Control. 40, 3985–3993. doi:10.1177/0142331217742964
Li, Y., and Lin, Z. (2018). Stability and Performance of Control Systems with Actuator Saturation. Switzerland: Springer International Publishing AG.
Lofberg, J. (2004).YALMIP: A Toolbox for Modeling and Optimization in MATLAB. In IEEE International Conference on Robotics and Automation. New Orleans, LA, USA), 284–289.
Luspay, T., and Grigoriadis, K. (2015). Robust Linear Parameter-Varying Control of Blood Pressure Using Vasoactive Drugs. Int. J. Control. 88, 2013–2029. doi:10.1080/00207179.2015.1027953
Nguyen, A.-T., Chevrel, P., and Claveau, F. (2018). Gain-scheduled Static Output Feedback Control for Saturated LPV Systems with Bounded Parameter Variations. Automatica 89, 420–424. doi:10.1016/j.automatica.2017.12.027
Nguyen, M. Q., da Silva, J. M. G., Sename, O., and Dugard, L. (2015). A State Feedback Input Constrained Control Design for a 4-Semi-Active Damper Suspension System: a Quasi-LPV Approach. IFAC-PapersOnLine 48, 259–264. doi:10.1016/j.ifacol.2015.09.467
Park, P., Ko, J. W., and Jeong, C. (2011). Reciprocally Convex Approach to Stability of Systems with Time-Varying Delays. Automatica 47, 235–238. doi:10.1016/j.automatica.2010.10.014
Salavati, S., Grigoriadis, K., and Franchek, M. (2019). Reciprocal Convex Approach to Output‐feedback Control of Uncertain LPV Systems with Fast‐varying Input Delay. Int. J. Robust Nonlinear Control. 29, 5744–5764. doi:10.1002/rnc.4697
Shao, L. R., Yi, Y., Niu, C. B., and Liu, B. (20192019). T‐S Modelling‐based Anti‐disturbance Finite‐time Control with Input Saturation. J. Eng. 2019, 635–639. doi:10.1049/joe.2018.9396
Tarbouriech, S., Garcia, G., Gomes da Silva, J. M., and Queinnec, I. (2011). Stability and Stabilization of Linear Systems with Saturating Actuators. London: Springer Science & Business Media.
Tasoujian, S., Salavati, S., Franchek, M., and Grigoriadis, K. (2020a). Robust Delay-dependent LPV Synthesis for Blood Pressure Control with Real-Time Bayesian Parameter Estimation. IET Control. Theor. Appl. 14. doi:10.1049/iet-cta.2019.0651
Tasoujian, S., Salavati, S., Franchek, M., and Grigoriadis, K. (2019). Robust IMC-PID and Parameter-Varying Control Strategies for Automated Blood Pressure Regulation. Int. J. Control. Autom. Syst. 17, 1803–1813. doi:10.1007/s12555-018-0631-7
Tasoujian, S., Salavati, S., Grigoriadis, K., and Franchek, M. (2020b).Real-time Cubature Kalman Filter Parameter Estimation of Blood Pressure Response Characteristics under Vasoactive Drugs Administration. In American Control Conference. Denver, CO USA): ACC, 3355–3362. doi:10.23919/acc45564.2020.9147309
V. Kapila, and K. Grigoriadis (Editors) (2002). Actuator Saturation Control (Marcel Dekker, NY: CRC Press).
Wang, X., Zhang, X., and Yang, X. (2019). Delay-dependent Robust Dissipative Control for Singular LPV Systems with Multiple Input Delays. Int. J. Control. Autom. Syst. 17, 327–335. doi:10.1007/s12555-018-0237-0
Wassar, T., Luspay, T. s., Upendar, K. R., Moisi, M., Voigt, R. B., Marques, N. R., et al. (2014). Automatic Control of Arterial Pressure for Hypotensive Patients Using Phenylephrine. Int. J. Model. Simulation 34, 187–198. doi:10.2316/Journal.205.2014.4.205-6087
Wei, X., Dong, L., Zhang, H., Han, J., and Hu, X. (2020). Composite Anti-disturbance Control for Stochastic Systems with Multiple Heterogeneous Disturbances and Input Saturation. ISA Trans. 100, 436–445. doi:10.1016/j.isatra.2019.12.006
Wei, Y., Liu, G.-P., Hu, J., and Meng, F. (2019). Disturbance Attenuation and Rejection for Nonlinear Uncertain Switched Systems Subject to Input Saturation. IEEE Access 7, 58475–58483. doi:10.1109/access.2019.2914738
Keywords: linear parameter-varying systems, time-delay, actuator saturation, sector condition, linear matrix inequalities, mean arterial pressure control, Bayesian filtering and cubature Kalman filter
Citation: Salavati S, Grigoriadis K and Franchek M (2021) Observer-Based Control of LPV Systems with Input Delay and Saturation and Matched Disturbances via a Generalized Sector Condition. Front. Control. Eng. 2:710388. doi: 10.3389/fcteg.2021.710388
Received: 16 May 2021; Accepted: 04 October 2021;
Published: 10 December 2021.
Edited by:
Olivier Sename, Grenoble Institute of Technology, FranceReviewed by:
Alessandra Helena Kimura Palmeira, Federal University of Rio Grande do Sul, BrazilMickael Rodrigues, Université Claude Bernard Lyon 1, France
Copyright © 2021 Salavati, Grigoriadis and Franchek . This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Saeed Salavati, c2FlZWQuc2FsYXZhdGlAZ21haWwuY29t
 Saeed Salavati
Saeed Salavati Karolos Grigoriadis
Karolos Grigoriadis  Matthew Franchek
Matthew Franchek