An Improved Integral Inequality for Delay-Dependent Gain-Scheduled LPV Control

The present work examines the delay-dependent gain-scheduling feedback control with guaranteed closed-loop stability and induced ${\mathcal{L}}_2$ norm performance for continuous-time linear parameter-varying (LPV) systems with arbitrary time-varying delay. An extension of Lyapunov stability utilizing Krasovskii functionals is considered to derive stability analysis and synthesis conditions for delay-dependent dynamic output feedback LPV control design. The main challenges associated with this approach are selecting appropriate Lyapunov-Krasovskii functionals (LKFs) and finding efficient integral inequalities to bound the derivative of the LKF. Accordingly, a novel modified parameter-dependent LKF candidate along with an affine version of Jensen’s inequality bounding technique are employed leading to the derivation of less conservative sufficient conditions expressed in terms of convex linear matrix inequalities (LMIs). The proposed methodology is compared with past work in the literature in terms of conservatism reduction and performance improvement through a numerical example. Finally, the application of the proposed output-feedback LPV control design is evaluated on the automated mean arterial blood pressure (MAP) regulation in critical patient resuscitation via vasoactive drug infusion. Closed-loop simulation results are presented to illustrate the potential of the introduced LPV gain-scheduling design to provide MAP set-point tracking in the presence of disturbances and varying input delays.

1 Introduction

Linear parameter-varying (LPV) systems are linear dynamical systems whose dynamic characteristics depend on a time-varying measurable scheduling parameter vector. In this context of the LPV systems framework, the scheduling parameter vector captures the dynamics of nonlinear or time-varying systems in a systematic fashion (Briat, 2014) and has found applications in flight control (Lu et al., 2006), automotive systems (Tasoujian et al., 2016; Salavati et al., 2019), energy (Bianchi et al., 2005), and biomedical systems (Colmegna et al., 2015; Tasoujian et al., 2019b). Traditional gain-scheduling controllers are designed by interpolation of separately designed controllers for the system’s operation points. Such design methods suffer from implementation difficulties and lack of closed-loop stability and performance guarantees (Shamma and Athans, 1990; Bianchi et al., 2006). In order to tackle these challenges, the LPV gain-scheduling control approach was introduced to provide a direct, efficient, simple-to-implement, and systematic design process to meet closed-loop stability and performance of nonlinear and time-varying systems (Shamma, 1988).

Time-delay is ubiquitously encountered in numerous engineering systems, such as automotive systems (Tasoujian et al., 2016), biomedical systems (Tasoujian et al., 2019b), network control systems (Witrant et al., 2007), and manufacturing and chemical processes (Bozorg and Davison, 2006). In the context of feedback systems, time-delay or dead-time refers to the time that takes for the closed-loop system to receive the control input, to make the control decision, and to generate the control action (Fridman, 2014). In control systems, time-delay is a source of instability and performance degradation. Time-delay induces a phase lag which generates oscillatory behavior, diminishes the stability margin of a control system, and limits the achievable bandwidth (Albertos, 2006). Time delay systems cannot be treated properly using conventional control design methods, such as Laplace domain-based methods since the corresponding transfer function of the time-delay system is not rational. In this regard, stability analysis and control design of time-delay systems have been formulated into two main directions, namely, delay-independent and delay-dependent approaches (Fridman, 2014). Unlike the former direction, delay-dependent techniques take the size of the delay into consideration and result in less conservative results. Generally, in delay-dependent methods, Lyapunov theory is extended to either the Krasovskii method of Lyapunov functionals (Kharitonov, 2004) or Razumnikhin theory of Lyapunov functions (Jankovic, 2001). The former direction relies on using Lyapunov-Krasovskii functionals (LKFs) for accounting for the infinite-dimensionality of the system state in the time-delay systems and usually leads to less conservative results.

In time-delay systems analysis, frequency domain approaches are limited to systems with constant delays (Niculescu, 2001; Michiels and Niculescu, 2007). On the other hand, time-domain techniques utilizing LKFs have gained significant attention, primarily because of their potential in addressing the stability analysis and control synthesis of systems with varying time-delays. In the Lyapunov-Krasovskii method, the prominent sources of conservatism are rooted in choosing the LKF, the use of model transformations, such as Newton-Leibniz (Kolmanovskii and Richard, 1999) and Padé approximations (Knospe and Roozbehani, 2006), and the use of bounding techniques for constraining the quadratic integral terms of the form $-{\int }_{t-\tau (t)}^t{\dot{x}}^{\text{T}}(s)\mathcal{R}\dot{x}(s)ds$, obtained from the derivative of the LKF.

In many practical engineering systems the time-delay is varying and parameter dependent. In (Niculescu, 1999), the air fuel ratio control problem in internal combustion engines is examined using an LPV approach, where the measurement delay from the sensor downstream the catalyst is a function of the engine speed. A Padé approximation was used to obtain a rational approximation of the variable delay. The authors in (Niculescu, 1999) used an LKF with the parametrized Newton-Leibniz model transformation to obtain sufficient conditions for the stability of time-delay systems. In (Park, 1999), the same type of LKF, together with Park’s inequality, was employed for bounding the cross-terms. Although this bounding method has helped to better address the bounding of cross-terms and hence reducing the conservatism, it still suffers from the use of model transformations that has inherent conservatism. The authors in (Zhang et al., 2002) proposed a parameter-dependent LKF along with Jensen’s inequality for the integral term bounding, to derive delay-dependent ${\mathcal{H}}_{\infty }$ results for LPV time-delay systems. This approach has avoided any model transformations, and therefore, no conservatism has been introduced in this regard. In addition, the resulted conditions have been derived using a more accurate and tighter bounding technique compared to previous work in the literature. Nevertheless, the presented stability and performance conditions are not guaranteed for fast varying time delays with rates greater than one. In the same work, due to the use of a simpler version of Jensen’s inequality, intermediary values of the delay are all neglected, and only the worst-case delay value is considered, which leads to conservative results and poor performance, especially when the actual delay value is small.

In the present work, we consider an improved parameter-dependent LKF candidate and the affine Jensen’s inequality (Briat, 2011) is employed for bounding the integral terms that appears in the LKF derivative. The utilized affine Jensen’s inequality bounding technique considers intermediary values of delay instead of just assuming the worst-case delay value. These choices of LKF and bounding method, and avoiding model transformations enables the derivation of less conservative conditions for the synthesis of delay-dependent dynamic output-feedback controllers for the LPV time-delay systems with large and fast-varying time delays. The proposed control guarantees closed-loop stability and a specified performance level of induced ${\mathcal{L}}_2$-norm disturbance attenuation. The obtained synthesis conditions are formulated in terms of tractable parameter-dependent linear matrix inequ–alities (LMIs), representing convex optimization problems that are solved using efficient numerical algorithms. The conservatism and performance of the proposed approach have been assessed and compared with the results of previous work in the literature through a numerical example.

Mean arterial blood pressure (MAP) control and regulation via the administration of vasopressor drugs is essential in hypotensive critical emergency-care situations, such as, resuscitation of patients with severe hemorrhage, septic shock, maternal cesarean hypotension treatment, and traumatic brain injury, during which the human physiology fails to maintain homeostasis and to regulate the blood pressure to its normal limits (Kee et al., 2005). Vasopressor medications, such as phenylephrine (PHP), epinephrine, and norepinephrine, are administered to elevate blood pressure by stimulating the depressed cardiovascular system and causing vasoconstriction (Neves et al., 2010). The precise dosage of the administered vasopressor drug is essential to accomplish fast resuscitation and reliable MAP recovery, and therefore, sustain perfusions of vital organs without overdosing. Traditional drug administration methods are performed using a syringe or infusion pump with manual titration. Such MAP regulation approaches are time-consuming, labor-intensive and inaccurate, and can lead to under- or over-resuscitation with undesirable or potentially fatal consequences, such as cardiac arrest. Automated and computer-aided drug administration via feedback control strategies has been investigated to overcome the challenges of manual drug delivery and operator monitoring. Various feedback control paradigms have been used for the automated closed-loop blood pressure regulation in emergency care (Malagutti et al., 2013; Ahmed and Özbay, 2016; Sandu and Popescu, 2016; Tasoujian et al., 2019b; Urooj and Singh, 2019). In the present work we consider an LPV time-delay model to represent the MAP response to PHP drug infusion dynamics, as a benchmark example to evaluate the proposed delay-dependent LPV control design method for MAP regulation. Closed-loop simulations using a patient simulation model demonstrate the superiority and effectiveness of the proposed LPV control to achieve desired MAP reference tracking, transient response performance, disturbance rejection and noise attenuation.

The notation used in the paper is as follows. $\mathbb{R}$ denotes the set of real numbers, ${\mathbb{R}}_{+}$ is the set of non-negative real numbers, and ${\mathbb{R}}^n$ and ${\mathbb{R}}^{k\times m}$ are used to denote the set of real vectors of dimension n and the set of k × m real matrices, respectively. ${\mathbb{S}}^n$ and ${\mathbb{S}}_{++}^n$ represent the set of symmetric and symmetric positive definite n × n real matrices, respectively. M ≻0 and M ⪰0 (M ≺0 and M ⪯0) denote the positive (negative) definiteness and semidefiniteness of the matrix M. The transpose and inverse of a real matrix M are designated by M^T and M⁻¹, respectively. In a symmetric matrix, ⋆ in the (i, j) element denotes the transpose of the (j, i) element. $\mathcal{C}(J,K)$ stands for the set of continuous functions mapping a set J to a set K.

In the present work, we will take advantage of the following lemma, which plays a central role in deriving the proposed results for the delay-dependent LPV time-delay control design framework.

Lemma 1:(Affine Jensen’s inequality) (Briat, 2011): Given a matrix$\mathbf{J}\in {\mathbb{S}}_{++}^n$, a vector function$g:{\mathbb{R}}_{\ge 0}\to {\mathbb{R}}^n$integrable over [a, b], where 0 ≤ a < b, and a vector function$w:{\mathbb{R}}_{\ge 0}\times {\mathbb{R}}_{\ge 0}\to {\mathbb{R}}^{n+m}$satisfying${\int }_a^{b}g(s)ds=\mathbf{M}w(a,b)$for a constant matrix$\mathbf{M}\in {\mathbb{R}}^{n\times (n+m)}$, the following inequality

$-{\int }_a^{b}g{(s)}^T\mathbf{J}g(s)ds\le w{(a,b)}^T\mathcal{Q}w(a,b),(1)$

holds for all$\mathbf{N}\in {\mathbb{R}}^{n\times (n+m)}$with

$\mathcal{Q}={\mathbf{N}}^T\mathbf{M}+{\mathbf{M}}^T\mathbf{N}+(b-a){\mathbf{N}}^T{\mathbf{J}}^{-1}\mathbf{N}.(2)$

The rest of paper is organized as follows. Section 4 introduces the problem statement and the general LPV time-delay system representation. Design objectives, as well as the proposed delay-dependent LPV control synthesis is presented in Section 5. Section 6 provides a numerical example to assess the capability of the proposed method in reducing the conservatism compared to a prior work. In Section 7, an LPV formulation of the MAP response to a vasoactive drug infusion is introduced as a case study. Subsequently, the closed-loop validation study of the proposed control design method is demonstrated in a simulation environment and compared to prior control designs in the literature. Concluding remarks and future research directions are provided in Section 8.

2 LPV Time-Delay Systems

Consider a general time-delayed LPV system with the state-space representation

$\begin{array}{ccc}\hfill \dot{\mathbf{x}}(t)\hfill & \hfill =\hfill & \mathbf{A}(\mathit{\rho }(t))\mathbf{x}(t)+{\mathbf{A}}_{\tau }(\mathit{\rho }(t))\mathbf{x}\left(t-\tau (\mathit{\rho }(t))\right)+{\mathbf{B}}_1(\mathit{\rho }(t))\mathbf{w}(t)+{\mathbf{B}}_2(\mathit{\rho }(t))\mathbf{u}(t),\hfill \\ \hfill \mathbf{z}(t)\hfill & \hfill =\hfill & {\mathbf{C}}_1(\mathit{\rho }(t))\mathbf{x}(t)+{\mathbf{C}}_{1,\tau }(\mathit{\rho }(t))\mathbf{x}\left(t-\tau (\mathit{\rho }(t))\right)+{\mathbf{D}}_{11}(\mathit{\rho }(t))\mathbf{w}(t)+{\mathbf{D}}_{12}(\mathit{\rho }(t))\mathbf{u}(t),\hfill \\ \hfill \mathbf{y}(t)\hfill & \hfill =\hfill & {\mathbf{C}}_2(\mathit{\rho }(t))\mathbf{x}(t)+{\mathbf{C}}_{2,\tau }(\mathit{\rho }(t))\mathbf{x}\left(t-\tau (\mathit{\rho }(t))\right)+{\mathbf{D}}_{21}(\mathit{\rho }(t))\mathbf{w}(t),\hfill \\ \hfill \mathbf{x}(t_0+\theta )\hfill & \hfill =\hfill & \mathit{\varphi }(\theta ),\forall \theta \in [-\bar{\tau },0],\hfill \end{array}(3)$

where $\mathbf{x}(t)\in {\mathbb{R}}^{n_p=n}$ is the state vector, $\mathbf{w}(t)\in {\mathbb{R}}^{n_w}$ denotes the exogenous input vector with bounded ${\mathcal{L}}_2$-norm, $\mathbf{u}(t)\in {\mathbb{R}}^{n_u}$ is the control input vector, $\mathbf{z}(t)\in {\mathbb{R}}^{n_z}$ stands for the vector of controlled outputs, $\mathbf{y}(t)\in {\mathbb{R}}^{n_y}$ is the vector of measured outputs, and A(⋅), A_τ(⋅), B₁(⋅), B₂(⋅), C₁(⋅), C_1,τ(⋅), D₁₁(⋅), D₁₂(⋅), C₂(⋅), C_2,τ(⋅), and D₂₁ (⋅) are real-valued matrices that are continuous functions of the time-varying scheduling parameter vector $\mathit{\rho }(\cdot )\in {\mathcal{F}}_{\mathcal{P}}^{\nu }$. The scheduling parameter vector is assumed to be measurable or estimated in real-time and the set ${\mathcal{F}}_{\mathcal{P}}^{\nu }$ denotes the set of allowable trajectories defined as

${\mathcal{F}}_{\mathcal{P}}^{\nu }\triangleq \{\mathit{\rho }(t)\in \mathcal{C}({\mathbb{R}}_{+},{\mathbb{R}}^{n_s}):\mathit{\rho }(t)\in \mathcal{P},|{\dot{\rho }}_i(t)|\le {\nu }_i,i=\mathrm{1,2},\dots ,n_s\},(4)$

where n_s is the number of parameters and $\mathcal{P}$ is a compact subset of ${\mathbb{R}}^{n_s}$. Moreover, in (3), $\mathit{\varphi }(\theta )\in \mathcal{C}([-\bar{\tau }0],{\mathbb{R}}^n)$ is the functional initial condition, and τ(ρ(t)) is a differentiable scalar function representing the parameter-varying time delay which is considered to be dependent on the scheduling parameter vector and lies in the set ${\mathcal{F}}^{\mu }$ defined as

${\mathcal{F}}^{\mu }\triangleq \{\tau (\mathit{\rho }(t))\in \mathcal{C}(\mathcal{P},{\mathbb{R}}_{+}):0\le \tau (\cdot )\le \bar{\tau }<\infty ,\dot{\tau }(\cdot )\le \mu \}.(5)$

In the next section, we investigate the stability and ${\mathcal{H}}_{\infty }$ performance specification for the LPV time-delay system.

3 Output-Feedback LPV Control Design for Time-Delay Systems

A gain-scheduled dynamic LPV controller is considered to accomplish the following design objectives:

• Asymptotic stability of the LPV system (3) in the presence of parameter and delay variations,

• Minimization of the worst case amplification of the controlled output, z, to a disturbance signal, w, with bounded energy. That is, solution of the upper-bound minimization problem of induced ${\mathcal{L}}_2$-norm (energy-to-energy gain) of the closed-loop mapping T_zw: w → z given by

$\min \Vert {\mathbf{T}}_{\mathbf{z}\mathbf{w}}{\Vert }_{i,2}=\min \underset{\mathit{\rho }\in {\mathcal{F}}_{\mathcal{P}}^{\nu }}{\sup }\underset{\Vert \mathbf{w}{\Vert }_2\ne 0,\mathbf{w}\in {\mathcal{L}}_2}{\sup }\frac{\Vert \mathbf{z}{\Vert }_2}{\Vert \mathbf{w}{\Vert }_2}.(6)$

However, instead of the optimal objective (6) we are interested in the upper bound suboptimal problem

$\Vert \mathbf{z}{\Vert }_2<\gamma \Vert \mathbf{w}{\Vert }_2,(7)$

where γ is a positive scalar.

A full-order dynamic output-feedback LPV controller is considered in the following form

$\begin{array}{ccc}\hfill {\dot{\mathbf{x}}}_K(t)\hfill & \hfill =\hfill & \hfill {\mathbf{A}}_K(\mathit{\rho }(t)){\mathbf{x}}_K(t)+{\mathbf{A}}_{\tau ,K}(\mathit{\rho }(t)){\mathbf{x}}_K(t-\tau (\mathit{\rho }(t)))+{\mathbf{B}}_K(\mathit{\rho }(t))\mathbf{y}(t),\hfill \\ \hfill \mathbf{u}(t)\hfill & \hfill =\hfill & \hfill {\mathbf{C}}_K(\mathit{\rho }(t)){\mathbf{x}}_K(t)+{\mathbf{C}}_{\tau ,K}(\mathit{\rho }(t)){\mathbf{x}}_K(t-\tau (\mathit{\rho }(t)))+{\mathbf{D}}_K(\mathit{\rho }(t))\mathbf{y}(t),\hfill \end{array}(8)$

where ${\mathbf{x}}_K(t)\in {\mathbb{R}}^n$ is the controller state vector and ${\mathbf{x}}_K(t-\tau (\mathit{\rho }(t)))\in {\mathbb{R}}^n$ is the delayed state of the controller, which is included in the controller structure to improve the closed-loop results compared a the memoryless controller. It should be noted that, in order to obtain convex conditions, the controller is assumed to be full order, i.e. the order of the controller is equal to n. Considering Eq. 3, 8, and defining the closed-loop state vector as ${\mathbf{x}}_{cl}^{\text{T}}(t)\triangleq [\begin{array}{cc}\hfill {\mathbf{x}}^{\text{T}}(t)\hfill & \hfill {\mathbf{x}}_K^{\text{T}}(t)\hfill \end{array}]$, the final closed-loop dynamics results in following representation

$\begin{array}{ccc}\hfill {\dot{\mathbf{x}}}_{cl}(t)\hfill & \hfill =\hfill & \hfill {\mathbf{A}}_{cl}{\mathbf{x}}_{cl}(t)+{\mathbf{A}}_{\tau ,cl}{\mathbf{x}}_{cl}(t-\tau (\mathit{\rho }(t)))+{\mathbf{B}}_{cl}\mathbf{w}(t),\hfill \\ \hfill \mathbf{z}(t)\hfill & \hfill =\hfill & \hfill {\mathbf{C}}_{cl}{\mathbf{x}}_{cl}(t)+{\mathbf{C}}_{\tau ,cl}{\mathbf{x}}_{cl}(t-\tau (\mathit{\rho }(t)))+{\mathbf{D}}_{cl}\mathbf{w}(t),\hfill \end{array}(9)$

where

$\begin{array}{cc}\hfill {\mathbf{A}}_{cl}\hfill & \hfill =\left[\begin{array}{cc}\hfill \mathbf{A}+{\mathbf{B}}_2{\mathbf{D}}_K{\mathbf{C}}_2\hfill & \hfill {\mathbf{B}}_2{\mathbf{C}}_K\hfill \\ \hfill {\mathbf{B}}_K{\mathbf{C}}_2\hfill & \hfill {\mathbf{A}}_K\hfill \end{array}\right],{\mathbf{A}}_{\tau ,cl}=\left[\begin{array}{cc}\hfill {\mathbf{A}}_{\tau }+{\mathbf{B}}_2{\mathbf{D}}_K{\mathbf{C}}_{2,\tau }\hfill & \hfill {\mathbf{B}}_2{\mathbf{C}}_{\tau ,K}\hfill \\ \hfill {\mathbf{B}}_K{\mathbf{C}}_{2,\tau }\hfill & \hfill {\mathbf{A}}_{\tau ,K}\hfill \end{array}\right],\hfill \\ \hfill {\mathbf{B}}_{cl}\hfill & =\left[\begin{array}{c}\hfill {\mathbf{B}}_1+{\mathbf{B}}_2{\mathbf{D}}_K{\mathbf{D}}_{21}\hfill \\ \hfill {\mathbf{B}}_K{\mathbf{D}}_{21}\hfill \end{array}\right],{\mathbf{C}}_{cl}=\left[\begin{array}{cc}\hfill {\mathbf{C}}_1+{\mathbf{D}}_{12}{\mathbf{D}}_K{\mathbf{C}}_2\hfill & \hfill {\mathbf{D}}_{12}{\mathbf{C}}_K\hfill \end{array}\right],\hfill \\ \hfill {\mathbf{C}}_{\tau ,cl}\hfill & =\left[\begin{array}{cc}\hfill {\mathbf{C}}_{1,\tau }+{\mathbf{D}}_{12}{\mathbf{D}}_K{\mathbf{C}}_{2,\tau }\hfill & \hfill {\mathbf{D}}_{12}{\mathbf{C}}_{\tau ,K}\hfill \end{array}\right],{\mathbf{D}}_{cl}={\mathbf{D}}_{11}+{\mathbf{D}}_{12}{\mathbf{D}}_K{\mathbf{D}}_{21},\hfill \end{array}(10)$

and the dependence on the scheduling parameter has been dropped for brevity.

3.1 Closed-Loop Stability and Induced ${\mathcal{L}}_2$-Norm Performance Analysis

In order to achieve less conservative control synthesis results for time-delay LPV systems, we take advantage of the Lyapunov-Krasovskii approach by employing a new extended-state based quadratic LKF candidate with modified integral terms, which depend explicitly on the time delay. The utilized approach avoids a model transformation; hence, it leads to further conservatism reduction. Additionally, the affine Jensen’s inequality is used to bound the LKF derivative’s cross-terms. In order to derive tractable LMI-based results, other conservative bounding approaches, such as the rational Jensen’s inequality, consider the worst-case time-delay value to upper-bound the rational term. On the other hand, this paper’s utilized inequality is affine with respect to the time-delay (hence convex), so it provides a tighter bound of the integral terms of the LKF derivative by taking all the possible intermediate time-delay values into account. The following theorem provides sufficient conditions for the synthesis of a delayed dynamic output-feedback LPV controller to meet the control design objectives, namely, closed-loop asymptotic stability and a specified level of disturbance attenuation performance Eq. 7 for the closed-loop system Eq. 9.

Theorem 1. There exists an output-feedback LPV controller of the formEq. 8to asymptotically stabilize the LPV systemEq. 3and satisfy the induced${\mathcal{L}}_2$-norm bound performance specificationEq. 7with parameter trajectories$\mathit{\rho }\in {\mathcal{F}}_{\mathcal{P}}^{\nu }$and$\tau \in {\mathcal{F}}^{\mu }$, if we can find a continuously differentiable parameter dependent positive-definite matrix functions$\tilde{\mathbf{P}}(\mathit{\rho }(t)):{\mathcal{F}}_{\mathcal{P}}^{\nu }\to {\mathbb{S}}_{++}^{2n}$,$\mathbf{X}(\mathit{\rho }(t)),\mathbf{Y}(\mathit{\rho }(t)):{\mathcal{F}}_{\mathcal{P}}^{\nu }\to {\mathbb{S}}^n$, positive-definite matrices$\tilde{\mathbf{Q}}$,$\tilde{\mathbf{R}}\in {\mathbb{S}}_{++}^{2n}$, symmetric real matrices$\tilde{\mathbf{W}}$,$\tilde{\mathbf{T}}\in {\mathbb{S}}_{++}^{2n}$, real matrices${\tilde{\mathbf{N}}}_1$,${\tilde{\mathbf{N}}}_2$,${\tilde{\mathbf{N}}}_3\in {\mathbb{R}}^{2n\times 2n}$, parameter dependent real matrices$\widehat{A}(\mathit{\rho }(t))$,${\widehat{A}}_{\tau }(\mathit{\rho }(t)):{\mathcal{F}}_{\mathcal{P}}^{\nu }\to {\mathbb{R}}^{n\times n}$,$\widehat{B}(\mathit{\rho }(t)):{\mathcal{F}}_{\mathcal{P}}^{\nu }\to {\mathbb{R}}^{n\times n_y}$,$\widehat{C}(\mathit{\rho }(t))$,${\widehat{C}}_{\tau }(\mathit{\rho }(t)):{\mathcal{F}}_{\mathcal{P}}^{\nu }\to {\mathbb{R}}^{n_u\times n}$,${\mathbf{D}}_K(\mathit{\rho }(t)):{\mathcal{F}}_{\mathcal{P}}^{\nu }\to {\mathbb{R}}^{n_u\times n_y}$, a positive scalarγ, given scalars λ₂, λ₃, and λ₄such that the following LMI condition

$\left[\begin{array}{cccccccc}\hfill {\tilde{\Xi }}_{11}\hfill & \hfill \tilde{\mathbf{P}}-\tilde{\mathbf{V}}+{\lambda }_2{\mathcal{A}}^{\text{T}}\hfill & \hfill {\tilde{\Xi }}_{13}\hfill & \hfill (1-\dot{\tau })\tau \tilde{\mathbf{W}}+{\lambda }_4{\mathcal{A}}^{\text{T}}\hfill & \hfill \mathcal{B}\hfill & \hfill {\mathcal{C}}^{\text{T}}\hfill & \hfill \mathbf{0}\hfill & \hfill \tau {\tilde{\mathbf{N}}}_1^{\mathrm{T}}\hfill \\ \hfill \star \hfill & \hfill \tau \tilde{\mathbf{R}}+\frac{{\tau }^2{\tau }^{̄2}}{4}\tilde{\mathbf{W}}-2{\lambda }_2\tilde{\mathbf{V}}\hfill & \hfill {\lambda }_2{\mathcal{A}}_{\tau }-{\lambda }_3\tilde{\mathbf{V}}\hfill & \hfill -{\lambda }_4\tilde{\mathbf{V}}\hfill & \hfill {\lambda }_2\mathcal{B}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \star \hfill & \hfill \star \hfill & \hfill {\tilde{\Xi }}_{33}\hfill & \hfill {\lambda }_4{\mathcal{A}}_{\tau }^{\text{T}}\hfill & \hfill {\lambda }_3\mathcal{B}\hfill & \hfill {\mathcal{C}}_{\tau }^{\text{T}}\hfill & \hfill \mathbf{0}\hfill & \hfill \tau {\tilde{\mathbf{N}}}_2^{\mathrm{T}}\hfill \\ \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill (1-\dot{\tau })({\tilde{\mathbf{N}}}_3^{\text{T}}+{\tilde{\mathbf{N}}}_3-\tilde{\mathbf{W}})\hfill & \hfill {\lambda }_4\mathcal{B}\hfill & \hfill \mathbf{0}\hfill & \hfill \tau {\tilde{\mathbf{N}}}_3^{\text{T}}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill -{\gamma }^2\mathbf{I}\hfill & \hfill {\mathcal{D}}^{\text{T}}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill -\mathbf{I}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill -\tau \tilde{\mathbf{T}}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill -\tau \tilde{\mathbf{R}}\hfill \end{array}\right]\prec \mathbf{0},(11)$

Is feasible and in the given LMI Eq. 11

$\begin{array}{ccc}\hfill {\tilde{\Xi }}_{11}\hfill & \hfill =\hfill & \hfill \left[\sum _{i=1}^{n_s}\pm \left({\nu }_i\frac{\partial \tilde{\mathbf{P}}(\mathit{\rho })}{\partial {\rho }_i}\right)\right]+\tilde{\mathbf{Q}}+(\mathcal{A}+{\mathcal{A}}^{\text{T}})+\left[1-\sum _{i=1}^{n_s}\pm \left({\nu }_i\frac{\partial \tau }{\partial {\rho }_i}\right)\right]\left({\tilde{\mathbf{N}}}_1^{\text{T}}+{\tilde{\mathbf{N}}}_1-{\tau }^2\tilde{\mathbf{W}}\right)+\tau \tilde{\mathbf{T}},\hfill \\ \hfill {\tilde{\Xi }}_{13}\hfill & \hfill =\hfill & \left[1-\sum _{i=1}^{n_s}\pm \left({\nu }_i\frac{\partial \tau }{\partial {\rho }_i}\right)\right](-{\tilde{\mathbf{N}}}_1^{\text{T}}+{\tilde{\mathbf{N}}}_2)+{\mathcal{A}}_{\tau }+{\lambda }_3{\mathcal{A}}^{\text{T}},\hfill \\ \hfill {\tilde{\Xi }}_{33}\hfill & \hfill =\hfill & \left[1-\sum _{i=1}^{n_s}\pm \left({\nu }_i\frac{\partial \tau }{\partial {\rho }_i}\right)\right]\left(-{\tilde{\mathbf{N}}}_2^{\text{T}}-{\tilde{\mathbf{N}}}_2\right)-\tilde{\mathbf{Q}}+{\lambda }_3({\mathcal{A}}_{\tau }+{\mathcal{A}}_{\tau }^{\text{T}}),\hfill \\ \hfill \tilde{\mathbf{V}}\hfill & \hfill =\hfill & \left[\begin{array}{cc}\hfill \mathbf{Y}\hfill & \hfill \mathbf{I}\hfill \\ \hfill \mathbf{I}\hfill & \hfill \mathbf{X}\hfill \end{array}\right],\mathcal{A}=\left[\begin{array}{cc}\hfill \mathbf{A}\mathbf{Y}+{\mathbf{B}}_2\widehat{C}\hfill & \hfill \mathbf{A}+{\mathbf{B}}_2{\mathbf{D}}_K{\mathbf{C}}_2\hfill \\ \hfill \hat{\mathbf{A}}\hfill & \hfill \mathbf{X}\mathbf{A}+\hat{B}{\mathbf{C}}_2\hfill \end{array}\right],{\mathcal{A}}_{\tau }=\left[\begin{array}{cc}\hfill {\mathbf{A}}_{\tau }\mathbf{Y}+{\mathbf{B}}_2{\widehat{C}}_{\tau }\hfill & \hfill {\mathbf{A}}_{\tau }+{\mathbf{B}}_2{\mathbf{D}}_K{\mathbf{C}}_{2,\tau }\hfill \\ \hfill {\widehat{A}}_{\tau }\hfill & \hfill \mathbf{X}{\mathbf{A}}_{\tau }+\widehat{B}{\mathbf{C}}_{2,\tau }\hfill \end{array}\right],\hfill \\ \hfill \mathcal{B}\hfill & \hfill =\hfill & \left[\begin{array}{c}\hfill {\mathbf{B}}_1+{\mathbf{B}}_2{\mathbf{D}}_K{\mathbf{D}}_{21}\hfill \\ \hfill \mathbf{X}{\mathbf{B}}_1+\widehat{B}{\mathbf{D}}_{21}\hfill \end{array}\right],\mathcal{C}=\left[\begin{array}{cc}\hfill {\mathbf{C}}_1\mathbf{Y}+{\mathbf{D}}_{12}\widehat{C}\hfill & \hfill {\mathbf{C}}_1+{\mathbf{D}}_{12}{\mathbf{D}}_K{\mathbf{C}}_2\hfill \end{array}\right],\hfill \\ \hfill {\mathcal{C}}_{\tau }\hfill & \hfill =\hfill & \left[\begin{array}{cc}\hfill {\mathbf{C}}_{1,\tau }\mathbf{Y}+{\mathbf{D}}_{12}{\widehat{C}}_{\tau }\hfill & \hfill {\mathbf{C}}_{1,\tau }+{\mathbf{D}}_{12}{\mathbf{D}}_K{\mathbf{C}}_{2,\tau }\hfill \end{array}\right],\mathcal{D}=\left[\begin{array}{c}\hfill {\mathbf{D}}_{11}+{\mathbf{D}}_{12}{\mathbf{D}}_K{\mathbf{D}}_{21}\hfill \end{array}\right],\dot{\tau }=\sum _{i=1}^{n_s}\pm \left({\nu }_i\frac{\partial \tau }{\partial {\rho }_i}\right).\hfill \end{array}(12)$

Remark 1:Due to the affine presence of the derivative of the scheduling parameter, we may replace${\sum }_{i=1}^{n_s}{\dot{\rho }}_i(t)\frac{\partial \mathbf{P}(\mathit{\rho }(t))}{\partial {\rho }_i(t)}$and${\sum }_{i=1}^{n_s}{\dot{\rho }}_i(t)\frac{\partial \tau (t)}{\partial {\rho }_i(t)}$by${\sum }_{i=1}^{n_s}\pm \left({\nu }_i\frac{\partial \mathbf{P}(\mathit{\rho }(t))}{\partial {\rho }_i(t)}\right)$and${\sum }_{i=1}^{n_s}\pm \left({\nu }_i\frac{\partial \tau }{\partial {\rho }_i}\right)$, respectively, where the notation${\sum }_{i=1}^{n_s}\pm (\cdot )$indicates that every combination of + (⋅) and − (⋅) should be included in the LMI condition (e.i. all combinations of lower and upper bounds of${\dot{\rho }}_i$). Consequently, this leads to$2^{n_s}$LMIs that must be checked simultaneously.

Proof. The proof relies on employing an LKF candidate of the form

$V({\mathbf{x}}_{{cl}_t},{\dot{\mathbf{x}}}_{c{l}_t},\mathit{\rho },t)=V_1({\mathbf{x}}_{cl},\mathit{\rho },t)+V_2({\mathbf{x}}_{c{l}_t},\mathit{\rho },t)+V_3({\dot{\mathbf{x}}}_{c{l}_t},\mathit{\rho },t)+V_4({\mathbf{x}}_{c{l}_t},\mathit{\rho },t)+V_5({\dot{\mathbf{x}}}_{c{l}_t},\mathit{\rho },t)(13)$

with

$\begin{array}{ll}\hfill V_1({\mathbf{x}}_{cl},\mathit{\rho },t)& ={\mathbf{x}}_{cl}^{\text{T}}(t)\mathbf{P}(\mathit{\rho }(t)){\mathbf{x}}_{cl}(t),\hfill \\ \hfill V_2({\mathbf{x}}_{c{l}_t},\mathit{\rho },t)& ={\int }_{t-\tau (t)}^t{\mathbf{x}}_{cl}^{\text{T}}(\eta )\mathbf{Q}{\mathbf{x}}_{cl}(\eta )d\eta ,\hfill \\ \hfill V_3({\dot{\mathbf{x}}}_{c{l}_t},\mathit{\rho },t)& ={\int }_{-\tau (t)}^0{\int }_{t+\theta }^t{\dot{\mathbf{x}}}_{cl}^{\text{T}}(\eta )\mathbf{R}{\dot{\mathbf{x}}}_{cl}(\eta )d\eta d\theta ,\hfill \\ \hfill V_4({\mathbf{x}}_{c{l}_t},\mathit{\rho },t)& ={\int }_{-\tau (t)}^0{\int }_{t+\theta }^t{\mathbf{x}}_{cl}^{\text{T}}(\eta )\mathbf{T}{\mathbf{x}}_{cl}(\eta )d\eta d\theta ,\hfill \\ \hfill V_5({\dot{\mathbf{x}}}_{c{l}_t},\mathit{\rho },t)& ={\int }_{-\tau (t)}^0{\int }_{\alpha }^0{\int }_{t+\theta }^t{\dot{\mathbf{x}}}_{cl}^{\text{T}}(\eta )\frac{{\bar{\tau }}^2}{2}\mathbf{W}{\dot{\mathbf{x}}}_{cl}(\eta )d\eta d\theta d\alpha ,\hfill \end{array}$

The notation ${\mathbf{x}}_{c{l}_t}(\theta )$ refers to x_cl (t + θ) for $\theta \in [\begin{array}{cc}\hfill -\bar{\tau }\hfill & \hfill 0\hfill \end{array}]$ where ${\mathbf{x}}_{c{l}_t}\in \mathcal{C}([-\bar{\tau }0],{\mathbb{R}}^n)$ is the infinite-dimensional state vector of the system.Our next task is to establish the asymptotic stability and ${\mathcal{L}}_2$-gain performance of the LPV system, based on Lyapunov stability theory. Accordingly, our aim is to evaluate the time derivative of the LKF Eq. 13 along the trajectories of the closed-loop LPV system Eq. 9. After applications of Leibniz integral rule, the time derivative of LKF is obtained as follows

$\dot{\mathbf{V}}({\mathbf{x}}_{c{l}_t},{\dot{\mathbf{x}}}_{c{l}_t},\mathit{\rho },t)={\dot{\mathbf{V}}}_1({\mathbf{x}}_{cl},\mathit{\rho },t)+{\dot{\mathbf{V}}}_2({\mathbf{x}}_{c{l}_t},\mathit{\rho },t)+{\dot{\mathbf{V}}}_3({\dot{\mathbf{x}}}_{c{l}_t},\mathit{\rho },t)+{\dot{\mathbf{V}}}_4({\mathbf{x}}_{c{l}_t},\mathit{\rho },t)+{\dot{\mathbf{V}}}_5({\dot{\mathbf{x}}}_{c{l}_t},\mathit{\rho },t),(14)$

where

$\begin{array}{l}{\dot{\mathbf{V}}}_1({\mathbf{x}}_{cl},\mathit{\rho },t)=2{\dot{\mathbf{x}}}_{cl}^{\text{T}}(t)\mathbf{P}(\mathit{\rho }(t)){\mathbf{x}}_{cl}(t)+{\mathbf{x}}_{cl}^{\text{T}}(t)\left[\sum _{i=1}^{n_s}{\dot{\rho }}_i(t)\frac{\partial \mathbf{P}(\mathit{\rho }(t))}{\partial {\rho }_i(t)}\right]{\mathbf{x}}_{cl}(t),\hfill \\ {\dot{V}}_2({\mathbf{x}}_{c{l}_t},\mathit{\rho },t)={\mathbf{x}}_{cl}^{\text{T}}(t)\mathbf{Q}{\mathbf{x}}_{cl}(t)-\left(1-\sum _{i=1}^{n_s}{\dot{\rho }}_i(t)\frac{\partial \tau (t)}{\partial {\rho }_i(t)}\right){\mathbf{x}}_{cl}^{\text{T}}(t-\tau (t))\mathbf{Q}{\mathbf{x}}_{cl}(t-\tau (t)),\hfill \\ {\dot{V}}_3({\dot{\mathbf{x}}}_{c{l}_t},\mathit{\rho },t)=\tau (t){\dot{\mathbf{x}}}_{cl}^{\text{T}}(t)\mathbf{R}{\dot{\mathbf{x}}}_{cl}(t)-\left(1-\sum _{i=1}^{n_s}{\dot{\rho }}_i(t)\frac{\partial \tau (t)}{\partial {\rho }_i(t)}\right){\int }_{t-\tau (t)}^t{\dot{\mathbf{x}}}_{cl}^{\text{T}}(\eta )\mathbf{R}{\dot{\mathbf{x}}}_{cl}(\eta )d\eta ,\hfill \\ {\dot{\mathbf{V}}}_4({\mathbf{x}}_{c{l}_t},\mathit{\rho },t)=\tau (t){\mathbf{x}}_{cl}^{\text{T}}(t)\mathbf{T}{\mathbf{x}}_{cl}(t)-\left(1-\sum _{i=1}^{n_s}{\dot{\rho }}_i(t)\frac{\partial \tau (t)}{\partial {\rho }_i(t)}\right){\int }_{t-\tau (t)}^t{\mathbf{x}}_{cl}^{\text{T}}(\eta )\mathbf{T}{\mathbf{x}}_{cl}(\eta )d\eta ,\hfill \\ {\dot{\mathbf{V}}}_5({\dot{\mathbf{x}}}_{c{l}_t},\mathit{\rho },t)=\frac{{\tau }^2(t){\bar{\tau }}^2}{4}{\mathbf{x}}_{cl}^{\text{T}}(t)\mathbf{W}{\mathbf{x}}_{cl}(t)-\left(1-\sum _{i=1}^{n_s}{\dot{\rho }}_i(t)\frac{\partial \tau (t)}{\partial {\rho }_i(t)}\right)\times {\int }_{-\tau (t)}^0{\int }_{t+\theta }^t{\dot{\mathbf{x}}}_{cl}^{\text{T}}(\eta )\frac{{\bar{\tau }}^2}{2}\mathbf{W}{\dot{\mathbf{x}}}_{cl}(\eta )d\eta d\theta .\hfill \end{array}$

The affine Jensen’s inequality (introduced in Lemma 1) can now be used to bound the derivative terms with the negative integral cross term. This direct bounding technique enables us to provide a delayed-scheduled tight upper bound on the time derivative of the LKF and therefore obtain less conservative results. In this context, the third derivative term is bounded as follows

$\begin{array}{l}\hfill {\stackrel{\cdot }{\mathit{V}}}_3({\stackrel{\cdot }{\mathbf{x}}}_{c{l}_t},\mathit{\rho },t)\le \tau (t){\stackrel{\cdot }{\mathbf{x}}}_{cl}^{\text{T}}(t)\mathbf{R}{\stackrel{\cdot }{\mathbf{x}}}_{cl}(t)+\left(1-\sum _{i=1}^{n_s}{\stackrel{\cdot }{\rho }}_i(t)\frac{\partial \tau (t)}{\partial {\rho }_i(t)}\right)\underset{w{(t-\tau (t),t)}^{\text{T}}}{\underbrace{[\begin{array}{c}\hfill {\mathbf{x}}_{cl}^{\text{T}}(t){\mathbf{x}}_{cl}^{\text{T}}(t-\tau (t))\hfill \end{array}]}}\\ \hfill (\underset{{\mathbf{N}}^{\text{T}}\mathbf{M}+{\mathbf{M}}^{\text{T}}\mathbf{N}}{\underbrace{\left[\begin{array}{c}\hfill {\mathbf{N}}_1^{\text{T}}+{\mathbf{N}}_1-{\mathbf{N}}_1^{\text{T}}+{\mathbf{N}}_2\hfill \\ \hfill {\mathbf{N}}_2^{\text{T}}-{\mathbf{N}}_1-{\mathbf{N}}_2^{\text{T}}-{\mathbf{N}}_2\hfill \end{array}\right]}}+\tau (t)\underset{{\mathbf{N}}^{\text{T}}}{\underbrace{\left[\begin{array}{c}\hfill {\mathbf{N}}_1^{\text{T}}\hfill \\ \hfill {\mathbf{N}}_2^{\text{T}}\hfill \end{array}\right]}}\underset{{\mathbf{J}}^{-1}}{\underbrace{{\mathbf{R}}^{-1}}}\underset{\mathbf{N}}{\underbrace{[\begin{array}{c}\hfill {\mathbf{N}}_1{\mathbf{N}}_2\hfill \end{array}]}})\underset{w(t-\tau (t),t)}{\underbrace{\left[\begin{array}{c}\hfill {\mathbf{x}}_{cl}(t)\hfill \\ \hfill {\mathbf{x}}_{cl}(t-\tau (t)\hfill \end{array}\right]}}\end{array}(15)$

where by considering the affine Jensen’s inequality (1), we choose the function $g(t)\triangleq {\stackrel{\mathrm{\cdot }}{\mathbf{x}}}_{cl}(t)$, integrable over [t − τ(t), t] and verifying ${\int }_{t-\tau (t)}^t{\stackrel{\cdot }{\mathbf{x}}}_{cl}(t)dt=\mathbf{M}w(t-\tau (t),t)$, where $\mathbf{M}\triangleq [\mathbf{I},-\mathbf{I}]\in {\mathbb{R}}^{2n\times 4n}$ and $w(t-\tau (t),t)\triangleq \left[\begin{array}{c}\hfill {\mathbf{x}}_{cl}(t)\hfill \\ \hfill {\mathbf{x}}_{cl}(t-\tau (t))\hfill \end{array}\right]\in {\mathbb{R}}^{4n}$. Also, $\mathbf{J}=\mathbf{R}\in {\mathbb{S}}_{++}^{2n}$, and $\mathbf{N}=[{\mathbf{N}}_1,{\mathbf{N}}_2]\in {\mathbb{R}}^{2n\times 4n}$ where R, ${\mathbf{N}}_1\in {\mathbb{R}}^{2n\times 2n}$, and ${\mathbf{N}}_2\in {\mathbb{R}}^{2n\times 2n}$ are additional matrix variables to be determined to hold the inequality. By employing the same bounding technique on the next derivative terms we obtain

$\begin{array}{l}\hfill {\dot{\mathbf{V}}}_4({\mathbf{x}}_{c{l}_t},\mathit{\rho },t)\le \tau (t){\mathbf{x}}_{cl}^{\text{T}}(t)\mathbf{T}{\mathbf{x}}_{cl}(t)+\left(1-\sum _{i=1}^{n_s}{\dot{\rho }}_i(t)\frac{\partial \tau (t)}{\partial {\rho }_i(t)}\right)\underset{w{(t-\tau (t),t)}^{\mathrm{T}}}{\underbrace{{\int }_{t-\tau (t)}^t{\mathbf{x}}_{cl}^{\text{T}}(\eta )d\eta }}\\ \hfill \left(\underset{{\mathbf{N}}^{\text{T}}\mathbf{M}+{\mathbf{M}}^{\text{T}}\mathbf{N}}{\underbrace{{\mathbf{N}}_3^{\text{T}}+{\mathbf{N}}_3}}+\tau (t)\underset{{\mathbf{N}}^{\mathrm{T}}}{\underbrace{{\mathbf{N}}_3^{\mathrm{T}}}}\underset{{\mathbf{J}}^{-1}}{\underbrace{{\mathbf{T}}^{-1}}}\underset{\mathbf{N}}{\underbrace{{\mathbf{N}}_3}}\right)\underset{w(t-\tau (t),t)}{\underbrace{{\int }_{t-\tau (t)}^t{\mathbf{x}}_{cl}(\eta )d\eta }},\end{array}(16)$

and

$\begin{array}{l}\hfill {\dot{\mathbf{V}}}_5({\dot{\mathbf{x}}}_{c{l}_t},\mathit{\rho },t)\le \frac{{\tau }^2(t){\bar{\tau }}^2}{4}{\dot{\mathbf{x}}}_{cl}^{\text{T}}(t)\mathbf{W}{\dot{\mathbf{x}}}_{cl}(t)-\left(1-\sum _{i=1}^{n_s}{\dot{\rho }}_i(t)\frac{\partial \tau (t)}{\partial {\rho }_i(t)}\right)\frac{{\bar{\tau }}^2}{{\tau }^2(t)}\\ \hfill {\left[\tau (t){\mathbf{x}}_{cl}(t)-{\int }_{t-\tau (t)}^t{\mathbf{x}}_{cl}(\eta )d\eta \right]}^{\text{T}}\mathbf{W}\left[\tau (t){\mathbf{x}}_{cl}(t)-{\int }_{t-\tau (t)}^t{\mathbf{x}}_{cl}(\eta )d\eta \right],\end{array}(17)$

where we choose $\mathbf{M}\triangleq \mathbf{I}\in {\mathbb{R}}^{2n\times 2n}$ and $w(t-\tau (t),t)\triangleq {\int }_{t-\tau (t)}^t{\mathbf{x}}_{cl}(\eta )d\eta \in {\mathbb{R}}^{2n}$, $\mathbf{J}=\mathbf{T}\in {\mathbb{S}}_{++}^{2n}$, and $\mathbf{N}={\mathbf{N}}_3\in {\mathbb{R}}^{2n\times 2n}$ where T, $\mathbf{W}\in {\mathbb{S}}_{++}^{2n}$, and N₃ are matrix variables to be determined. The remaining task is to formulate the results in an LMI form. To this end, the descriptor technique (Fridman, 2014) is used, which introduces slack variables V₁, V₂, V₃, and V₄ as follows

$\begin{array}{l}\hfill \mathcal{I}\triangleq \left[{\mathbf{x}}_{cl}^{\text{T}}(t){\mathbf{V}}_1^{\text{T}}+{\dot{\mathbf{x}}}_{cl}^{\text{T}}(t){\mathbf{V}}_2^{\text{T}}+{\mathbf{x}}_{cl}^{\text{T}}(t-\tau (t)){\mathbf{V}}_3^{\text{T}}+{\int }_{t-\tau (t)}^t{\mathbf{x}}_{cl}^{\text{T}}(\eta )d\eta {\mathbf{V}}_4^{\text{T}}\right]\\ \hfill \left({\mathbf{A}}_{cl}{\mathbf{x}}_{cl}(t)+{\mathbf{A}}_{\tau ,cl}{\mathbf{x}}_{cl}(t-\tau (t))+{\mathbf{B}}_{cl}\mathbf{w}(t)-{\dot{\mathbf{x}}}_{cl}(t)\right)=0.\end{array}(18)$

By considering the derivative of the utilized LKF Eq. 14 and adding the terms $2\mathcal{I}$ and − γ²w^T(t)w(t) + z^T(t)z(t) to establish the prescribed closed-loop performance level γ given in Eq. 7, we obtain the following inequality

$\dot{\mathbf{V}}({\mathbf{x}}_{c{l}_t},{\dot{\mathbf{x}}}_{c{l}_t},\mathit{\rho },t)+2\mathcal{I}-{\gamma }^2{\mathbf{w}}^{\text{T}}(t)\mathbf{w}(t)+{\mathbf{z}}^{\text{T}}(t)\mathbf{z}(t)\le {\mathit{\zeta }}^{\text{T}}(t)\mathbf{\Omega }\mathit{\zeta }(t)<0,(19)$

where the augmented state vector ζ(t) is defined as:

${\mathit{\zeta }}^{\text{T}}(t)\triangleq \left[\begin{array}{ccccc}\hfill {\mathbf{x}}_{cl}^{\text{T}}(t)\hfill & \hfill {\dot{\mathbf{x}}}_{cl}^{\text{T}}(t)\hfill & \hfill {\mathbf{x}}_{cl}^{\text{T}}(t-\tau (t))\hfill & \hfill {\int }_{t-\tau (t)}^t{\mathbf{x}}_{cl}^{\text{T}}(\eta )d\eta \hfill & \hfill {\mathbf{w}}^{\text{T}}(t)\hfill \end{array}\right],(20)$

with

$\begin{array}{c}\hfill \mathbf{\Omega }=\left[\begin{array}{ccccc}\hfill {\Xi }_{11}\hfill & \hfill \mathbf{P}-{\mathbf{V}}_1^{\text{T}}+{\mathbf{A}}_{cl}^{\text{T}}{\mathbf{V}}_2\hfill & \hfill {\Xi }_{13}\hfill & \hfill (1-\dot{\tau })\tau \mathbf{W}+{\mathbf{A}}_{cl}^{\text{T}}{\mathbf{V}}_4\hfill & \hfill {\mathbf{V}}_1^{\text{T}}{\mathbf{B}}_{cl}\hfill \\ \hfill \star \hfill & \hfill \tau \mathbf{R}+\frac{{\tau }^2{\bar{\tau }}^2}{4}\mathbf{W}-{\mathbf{V}}_2-{\mathbf{V}}_2^{\text{T}}\hfill & \hfill {\mathbf{V}}_2^{\text{T}}{\mathbf{A}}_{\tau ,cl}-{\mathbf{V}}_{\mathbf{3}}\hfill & \hfill -{\mathbf{V}}_4\hfill & \hfill {\mathbf{V}}_2^{\text{T}}{\mathbf{B}}_{cl}\hfill \\ \hfill \star \hfill & \hfill \star \hfill & \hfill {\Xi }_{33}\hfill & \hfill {\mathbf{A}}_{\tau ,cl}^{\text{T}}{\mathbf{V}}_4\hfill & \hfill {\mathbf{V}}_3^{\text{T}}{\mathbf{B}}_{cl}\hfill \\ \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill (1-\dot{\tau })({\mathbf{N}}_3^{\text{T}}+{\mathbf{N}}_3-\mathbf{W})\hfill & \hfill {\mathbf{V}}_4^{\text{T}}{\mathbf{B}}_{cl}\hfill \\ \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill \star \hfill & \hfill -{\gamma }^2\hfill \end{array}\right]\hfill \\ \hfill +{\mathbf{\Gamma }}^{\text{T}}\mathbf{\Gamma }+\tau \left({\mathbf{\Pi }}^{\text{T}}{\mathbf{T}}^{-1}\mathbf{\Pi }+{\mathbf{\Phi }}^{\text{T}}{\mathbf{R}}^{-1}\mathbf{\Phi }\right),\hfill \end{array}(21)$

where

$\begin{array}{c}{\Xi }_{11}=\left[\sum _{i=1}^{n_s}\pm \left({\nu }_i\frac{\partial \mathbf{P}(\mathit{\rho })}{\partial {\rho }_i}\right)\right]+\mathbf{Q}+{\mathbf{V}}_1^{\text{T}}{\mathbf{A}}_{cl}+{\mathbf{A}}_{cl}^{\text{T}}{\mathbf{V}}_1\hfill \\ \hfill +\left[1-\sum _{i=1}^{n_s}\pm \left({\nu }_i\frac{\partial \tau }{\partial {\rho }_i}\right)\right]\left({\mathbf{N}}_1^{\text{T}}+{\mathbf{N}}_1-{\tau }^2\mathbf{W}\right)+\tau \mathbf{T},\hfill \\ \hfill {\Xi }_{13}=\left[1-\sum _{i=1}^{n_s}\pm \left({\nu }_i\frac{\partial \tau }{\partial {\rho }_i}\right)\right](-{\mathbf{N}}_1^{\text{T}}+{\mathbf{N}}_2)+{\mathbf{V}}_1^{\text{T}}{\mathbf{A}}_{\tau ,cl}+{\mathbf{A}}_{cl}^{\text{T}}{\mathbf{V}}_3,\hfill \\ \hfill {\Xi }_{33}=\left[1-\sum _{i=1}^{n_s}\pm \left({\nu }_i\frac{\partial \tau }{\partial {\rho }_i}\right)\right]\left(-{\mathbf{N}}_2^{\text{T}}-{\mathbf{N}}_2\right)-\mathbf{Q}+{\mathbf{V}}_3^{\text{T}}{\mathbf{A}}_{\tau ,cl}+{\mathbf{A}}_{\tau ,cl}^{\text{T}}{\mathbf{V}}_3,\hfill \\ \mathbf{\Gamma }=\left[\begin{array}{ccccc}\hfill {\mathbf{C}}_{cl}\hfill & \hfill \mathbf{0}\hfill & \hfill {\mathbf{C}}_{\tau ,cl}\hfill & \hfill 0\hfill & \hfill {\mathbf{D}}_{cl}\hfill \end{array}\right],\mathbf{\Pi }=\left[\begin{array}{ccccc}\hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill {\mathbf{N}}_3\hfill & \hfill \mathbf{0}\hfill \end{array}\right],\mathbf{\Phi }=\left[\begin{array}{ccccc}\hfill {\mathbf{N}}_1\hfill & \hfill \mathbf{0}\hfill & \hfill {\mathbf{N}}_2\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \end{array}\right].\hfill \end{array}(22)$

The slack variables in relation Eq. 18 are chosen as ${\lambda }_1{\mathbf{V}}_1\triangleq \mathbf{V}\in {\mathbb{S}}^{2n}$, V₂ ≜ λ₂V, V₃ ≜ λ₃V, and V₄ ≜ λ₄V, where λ₁ = 1, λ₂, λ₃, and λ₄ are real constants and V is a real-valued symmetric matrix which is partitioned as $\mathbf{V}\triangleq \left[\begin{array}{cc}\hfill \mathbf{X}\hfill & \hfill \mathcal{N}\hfill \\ \hfill {\mathcal{N}}^{\text{T}}\hfill & \hfill \star \hfill \end{array}\right]$, ${\mathbf{V}}^{-1}\triangleq \left[\begin{array}{cc}\hfill \mathbf{Y}\hfill & \hfill \mathcal{M}\hfill \\ \hfill {\mathcal{M}}^{\text{T}}\hfill & \hfill \star \hfill \end{array}\right]$, such that $\mathbf{X}\mathbf{Y}+\mathcal{N}{\mathcal{M}}^{\text{T}}=\mathbf{I}$. Next, substituting the closed-loop matrices Eq. 10 into Eq. 21 and then applying the Schur complement formula to Ω in Eq. 21, we obtain a 8 × 8 block matrix. Finally, by defining $\mathcal{Z}\triangleq \left[\begin{array}{cc}\hfill \mathbf{Y}\hfill & \hfill \mathbf{I}\hfill \\ \hfill {\mathcal{M}}^{\text{T}}\hfill & \hfill \mathbf{0}\hfill \end{array}\right]$, and performing a congruence transformation $diag\left({\mathcal{Z}}^{\text{T}},{\mathcal{Z}}^{\text{T}},{\mathcal{Z}}^{\text{T}},{\mathcal{Z}}^{\text{T}},\mathbf{I},\mathbf{I},{\mathcal{Z}}^{\text{T}},{\mathcal{Z}}^{\text{T}}\right)$ on the 8 × 8 block matrix and redefining the matrix multiplications as $\widetilde{⊡}\triangleq {\mathcal{Z}}^{\text{T}}⊡\mathcal{Z}$, the LMI Eq. 11 is obtained and the proof is complete.

3.2 Output-Feedback LPV Gain-Scheduled Controller Synthesis

Utilizing the LMI decision variables X, Y, $A$, $A_{\tau }$, $\widehat{B}$, $\widehat{C}$, ${\widehat{C}}_{\tau }$, and D_K, obtained by solving the LMI condition Eq. 11, the matrices of the delayed output-feedback controller Eq. 8 are computed with the following steps (Wu et al., 1996):

3.2.1 Determine $\mathcal{M}$ and $\mathcal{N}$ From the Factorization Problem

$\mathbf{I}-\mathbf{X}\mathbf{Y}=\mathcal{N}{\mathcal{M}}^{\text{T}},(23)$

where the obtained $\mathcal{M}$ and $\mathcal{N}$ matrices are square and invertible in the case of a full-order controller.

3.2.2 Compute the Following Parameter Matrices

$\begin{array}{ccc}\hfill A\hfill & \hfill =\hfill & \hfill \mathbf{X}\mathbf{A}\mathbf{Y}+\mathbf{X}{\mathbf{B}}_2{\mathbf{D}}_K{\mathbf{C}}_2\mathbf{Y}+\mathcal{N}{\mathbf{B}}_K{\mathbf{C}}_2\mathbf{Y}+\mathbf{X}{\mathbf{B}}_2{\mathbf{C}}_K{\mathcal{M}}^{\text{T}}+\mathcal{N}{\mathbf{A}}_K{\mathcal{M}}^{\text{T}},\hfill \\ \hfill A_{\tau }\hfill & \hfill =\hfill & \hfill \mathbf{X}{\mathbf{A}}_{\tau }\mathbf{Y}+\mathbf{X}{\mathbf{B}}_2{\mathbf{D}}_K{\mathbf{C}}_{2,\tau }\mathbf{Y}+\mathcal{N}{\mathbf{B}}_K{\mathbf{C}}_{2,\tau }\mathbf{Y}+\mathbf{X}{\mathbf{B}}_2{\mathbf{C}}_{\tau ,K}{\mathcal{M}}^{\text{T}}+\mathcal{N}{\mathbf{A}}_{\tau ,K}{\mathcal{M}}^{\text{T}},\hfill \\ \hfill B\hfill & \hfill =\hfill & \hfill \mathbf{X}{\mathbf{B}}_2{\mathbf{D}}_K+\mathcal{N}{\mathbf{B}}_K,\hfill \\ \hfill C\hfill & \hfill =\hfill & \hfill {\mathbf{D}}_K{\mathbf{C}}_2\mathbf{Y}+{\mathbf{C}}_K{\mathcal{M}}^{\text{T}},\hfill \\ \hfill C_{\tau }\hfill & \hfill =\hfill & \hfill {\mathbf{D}}_K{\mathbf{C}}_{2,\tau }\mathbf{Y}+{\mathbf{C}}_{\tau ,K}{\mathcal{M}}^{\text{T}}.\hfill \end{array}(24)$

3.2.3 Finally, the Controller Matrices Are Computed in the Following Order

$\begin{array}{c}{\mathbf{C}}_{\tau ,K}=(C_{\tau }-{\mathbf{D}}_K{\mathbf{C}}_{2,\tau }\mathbf{Y}){\mathcal{M}}^{-\text{T}},\hfill \\ {\mathbf{C}}_K=(C-{\mathbf{D}}_K{\mathbf{C}}_2\mathbf{Y}){\mathcal{M}}^{-\text{T}},\hfill \\ {\mathbf{B}}_K={\mathcal{N}}^{-1}(B-\mathbf{X}{\mathbf{B}}_2{\mathbf{D}}_K),\hfill \\ {\mathbf{A}}_{\tau ,K}=-{\mathcal{N}}^{-1}(\mathbf{X}{\mathbf{A}}_{\tau }\mathbf{Y}+\mathbf{X}{\mathbf{B}}_2{\mathbf{D}}_K{\mathbf{C}}_{2,\tau }\mathbf{Y}+\mathcal{N}{\mathbf{B}}_K{\mathbf{C}}_{2,\tau }\mathbf{Y}+\mathbf{X}{\mathbf{B}}_2{\mathbf{C}}_{\tau ,K}{\mathcal{M}}^{\text{T}}-A_{\tau }){\mathcal{M}}^{-\text{T}},\hfill \\ {\mathbf{A}}_K=-{\mathcal{N}}^{-1}(\mathbf{X}A\mathbf{Y}+\mathbf{X}{\mathbf{B}}_2{\mathbf{D}}_K{\mathbf{C}}_2\mathbf{Y}+\mathcal{N}{\mathbf{B}}_K{\mathbf{C}}_2\mathbf{Y}+\mathbf{X}{\mathbf{B}}_2{\mathbf{C}}_K{\mathcal{M}}^{\text{T}}-\hat{A}){\mathcal{M}}^{-\text{T}}.\hfill \end{array}(25)$

4 Numerical Example

A numerical example is examined to assess the performance and the conservatism reduction capability of the proposed control design methodology compared to previous work in the literature. We consider an LPV state-delayed system with the following state-space representation (Zope et al., 2012)

$\begin{array}{c}\hfill \dot{\mathbf{x}}(t)=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1+0.2\rho (t)\hfill \\ \hfill -2\hfill & \hfill -3+0.1\rho (t)\hfill \end{array}\right]\mathbf{x}(t)+\left[\begin{array}{cc}\hfill 0.2\rho (t)\hfill & \hfill 0.1\hfill \\ \hfill -0.2+0.1\rho (t)\hfill & \hfill -0.3\hfill \end{array}\right]\mathbf{x}\left(t-\tau (\rho (t))\right)\hfill \\ \hfill +\left[\begin{array}{c}\hfill 0.2\hfill \\ \hfill 0.2\hfill \end{array}\right]d(t)+\left[\begin{array}{c}\hfill 0.2\rho (t)\hfill \\ \hfill 0.1+0.1\rho (t)\hfill \end{array}\right]u(t),\hfill \\ \hfill \mathbf{z}(t)=\left[\begin{array}{cc}\hfill \varphi \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \xi \hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\mathbf{x}(t)+\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill \psi \hfill \end{array}\right]u(t),\hfill \\ \hfill y(t)=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \end{array}\right]\mathbf{x}(t),\hfill \end{array}(26)$

where ρ(t) = sin(t) is the LPV system scheduling parameter, $\tau (\rho (t))=\bar{\tau }|sin(\alpha t)|$ is the parameter-dependent time-varying delay with $0\le \tau (t)\le \bar{\tau }$ and $|\dot{\tau }|\le \nu =\bar{\tau }\alpha$. Weighting scalars ϕ, ξ, and ψ are selected to construct the desired controlled output vector, z(t), by penalizing the states of the system and the control input.

Based on the results of Theorem 1, an output-feedback controller of the form Eq. 8 is designed to minimize the induced ${\mathcal{L}}_2$-norm (or ${\mathcal{H}}_{\infty }$-norm) of the closed-loop LPV time-delay system Eq. 9. The design objective is to guarantee closed-loop stability and minimize the effect of the disturbance using the measurement information of state x₁, while maintaining the control input within reasonable limits over the entire range of the scheduling parameter and delay variations.

The condition in Theorem 1 leads to an infinite-dimensional convex optimization problem with an infinite number of LMI constraints. To tackle this issue, we take advantage of the gridding approach to convert the infinite-dimensional problem to a finite-dimensional convex optimization problem (Apkarian and Adams, 1998). In this regard, a quadratic parameter dependence is adopted for the parameter dependent matrices as follows: $\mathbf{G}(\mathit{\rho }(t))={\mathbf{G}}_0+\sum _{i=1}^{n_s}{\rho }_i(t){\mathbf{G}}_{i_1}+\frac{1}{2}\sum _{i=1}^{n_s}{\rho }_i^2(t){\mathbf{G}}_{i_2}$, where G(ρ(t)) represents any of the involved LMI decision variables. Finally, gridding the scheduling parameter space at appropriate intervals leads to a finite set of LMIs to be solved for the unknown LMI variables and γ. Also, in order to improve the results, a 3-dimensional search over the three scalar variables λ₂, λ₃, and λ₄ is performed to obtain the minimum value of γ. The MATLAB® toolbox YALMIP is used to solve the corresponding LMI optimization problems (Lofberg, 2004).

In the considered numerical example Eq. 26, the weighting scalars are chosen as ϕ = 1, ξ = 10, and ψ = 1. The time delay is considered to be τ(t) = 3|sin (0.3t)| (i.e.$\bar{\tau }=3$ and α = 0.3). The results of the proposed LPV control design approach are compared with prior results of an LPV time-delay control design with simpler LKF candidate with a conservative bounding technique (Tasoujian et al., 2019a). Figure 1 demonstrates the closed-loop responses of Eq. 26 for the proposed control and the one in (Tasoujian et al., 2019a). As illustrated, the proposed control scheme outperforms the one in (Tasoujian et al., 2019a) by regulating both system states to zero by minimizing the effect of the disturbance. We consider a simulation scenario where a pulse disturbance d(t) = 5 for t ∈ [5 8] sec and zero elsewhere, is assumed to affect the system. It should be noted that the same weighting scalars, parameter-dependence basis function, and the scheduling parameter grid points are considered for both approaches. The obtained optimal energy-to-energy performance levels γ are 1.1786 and 3.1546 for the proposed control and the one in (Tasoujian et al., 2019a), respectively. Accordingly, Theorem 1 provides better disturbance attenuation, faster regulation, and improved induced ${\mathcal{L}}_2$-norm performance levels compared with the prior results.

FIGURE 1

FIGURE 1. Closed-loop response of system states x₁, and x₂ subject to disturbance.

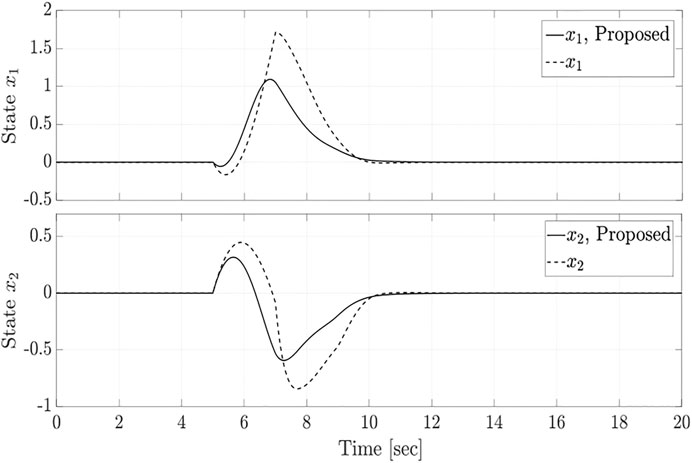
Table 1 compares the obtained performance level γ for both control design methods and for different maximum delay values, $\bar{\tau }$. It is noted that the control synthesis condition in (Tasoujian et al., 2019a) is not feasible for $\bar{\tau }\ge 3.5$. On the other hand, the proposed LPV delay-dependent control scheme, which utilizes the improved LKF candidate and the efficient use of the affine Jensen’s inequality bounding technique, can handle much larger allowable maximum delay values and provides considerably less conservative results for a larger delay range and delay variation rates ν > 1.

TABLE 1

TABLE 1. Performance levels γ of both methods for different time-delay maximum values $\bar{\tau }$

5 LPV Control Design for MAP Regulation in Hypotensive Patients

5.1 MAP Response Dynamics

To assess the capability of the proposed LPV control, we consider the problem of automated MAP regulation in critical hypotensive patients using vasoactive drug infusion. The following model is utilized to characterize the MAP response dynamics subject to PHP drug infusion (Luspay and Grigoriadis, 2015; Sandu and Popescu, 2016; Tasoujian et al., 2020a; Cao and Grigoriadis, 2020)

$T(t)\cdot \dot{\mathrm{\Delta }MAP}(t)+\mathrm{\Delta }MAP(t)=K(t)\cdot u(t-\tau (t)),(27)$

where ΔMAP(t) denotes the MAP variations in mmHg from its baseline value, i.e. ΔMAP(t) = MAP(t) − MAP_b(t), u(t) is the drug infusion rate in ml/h, K(t) is the patient’s sensitivity to the drug, T(t) is the lag time representing the uptake, distribution, and biotransformation of the drug (Isaka and Sebald, 1993), and τ(t) represents the time delay for the drug to reach the circulatory system from the infusion pump. Figure 2 shows an experimental MAP response to a step PHP infusion versus a matched simulated response of Eq. 27. The experimental data shown correspond to a swine experiment performed at the Resuscitation Research Laboratory at the University of Texas Medical Branch (UTMB), Galveston, Texas (Luspay and Grigoriadis, 2015). The figure also shows the interpretation of the model parameters K(t), T(t), τ(t), MAP_b(t) obtained using a least-squares optimization method to fit the actual MAP response.

FIGURE 2

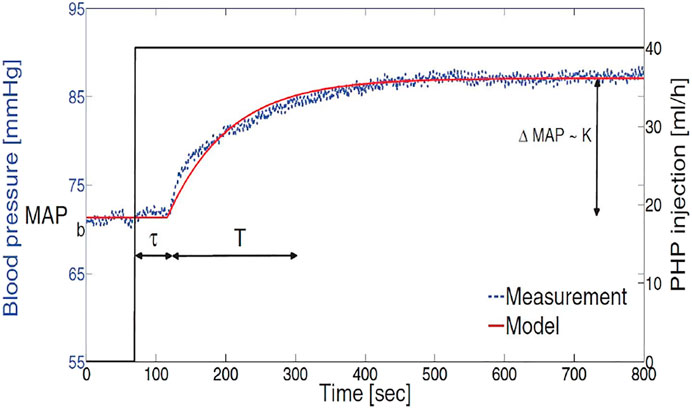
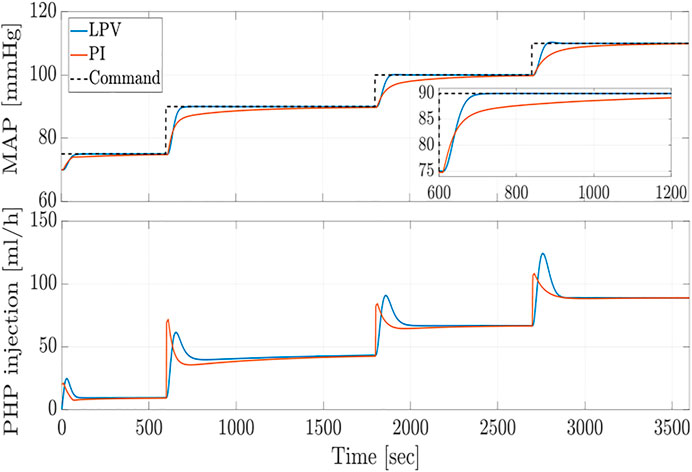
FIGURE 2. Closed-loop MAP response and control effort (PHP injection rate) of LPV controller against fixed structure PI controller for disturbance and noise free case.

It is noted that due to the patient’s physiological response variability, the model parameters and the delay could vary significantly from patient-to-patient (inter-patient variability), as well as, for a given patient over time (intra-patient variability) (Isaka and Sebald, 1993; Rao et al., 2003). Based on clinical observations (Tasoujian et al., 2019b), the model parameter variations can be approximated for simulation purposes as nonlinear functions of the drug injection rate as follows.

$\begin{array}{ll}\hfill & a_k\dot{K}(t)+K(t)=k_{0}exp\{-k_1\mathcal{U}(t)\},\hfill \end{array}(\mathrm{28a})$

$\begin{array}{ll}\hfill & T(t)=sa{t}_{[T_{\min },T_{\max }]}\left\{b_T{\int }_0^t\mathcal{U}(t)dt\right\},\hfill \end{array}(\mathrm{28b})$

$\begin{array}{ll}\hfill & \left\{\begin{array}{cc}{a}_{\tau ,2}\stackrel{\dots }{\tau }(t)+a_{\tau ,1}\stackrel{\mathrm{\cdot \cdot }}{\tau }(t)+\dot{\tau }(t)=b_{\tau ,1}\dot{\mathcal{U}}(t)+\mathcal{U}(t),\hfill & t\ge t_0,\hfill \\ \tau (t)=0,\hfill & otherwise,\hfill \end{array}\right.\hfill \end{array}(\mathrm{28c})$

where a_k, k₀, k₁, b_T, a_τ,2, a_τ,1, and b_τ,1 are uniformly distributed random coefficients given in Table 2 and $\mathcal{U}$ denotes the injection rate in mm/h (Craig and Stitzel, 2004). Consequently, the parameters variation ranges considered in our work are K(t) ∈ [0.2,0.8]mmHg ⋅ h/ml, T(t) ∈ [100,400]sec, and τ(t) ∈ [0,70]sec. Also, the MAP baseline value, MAP_b(t), is assumed to stay at a constant 70 mmHg value. For more details regarding the MAP response dynamics under drug infusion and the real-time model parameter estimation algorithm see (Tasoujian et al., 2020b) and the references therein.

TABLE 2

TABLE 2. Probabilistic distributions of the nonlinear patient coefficients in (28).

5.2 MAP Response LPV Modeling

To design the proposed delay-dependent LPV control synthesis for the MAP regulation problem, we first formulate the MAP response dynamics Eq. 27 into an LPV time-delay model representation. Considering the state variable as x(t) = ΔMAP(t), the state space representation of the MAP response model is rewritten as follows

$\begin{array}{ccc}\hfill \dot{x}(t)\hfill & \hfill =\hfill & \hfill -\frac{1}{T(t)}x(t)+\frac{K(t)}{T(t)}u(t-\tau (t)),\hfill \\ \hfill y(t)\hfill & \hfill =\hfill & \hfill x(t)+d_o(t),\hfill \end{array}(29)$

where y(t) is the patient’s measured MAP response and d_o(t) denotes output disturbances. In Eq. 29, the varying time delay, τ(t), is appearing in the input signal. In order to utilize the proposed time-delay LPV system control design framework, we transform the input delay system into a state-delay LPV representation. To this end, we introduce a low-pass input dynamics as follows

$u(s)=\frac{\mathrm{\Omega }}{s+\mathrm{\Lambda }}{u}_a(s),(30)$

where Ω and Λ are positive scalars that are selected based on the bandwidth of the actuators. Then, the state-space state-delay LPV representation of the MAP response dynamics takes the following form

$\begin{array}{c}\hfill {\dot{\mathbf{x}}}_a(t)=\mathbf{A}(\mathit{\rho }(t)){\mathbf{x}}_a(t)+{\mathbf{A}}_{\tau }(\mathit{\rho }(t)){\mathbf{x}}_a(t-\tau (t))+{\mathbf{B}}_1(\mathit{\rho }(t))\mathbf{w}(t)+{\mathbf{B}}_2(\mathit{\rho }(t))u_a(t),\hfill \\ \hfill \mathbf{z}(t)={\mathbf{C}}_1(\mathit{\rho }(t))\mathbf{x}(t)+{\mathbf{C}}_{1,\tau }(\mathit{\rho }(t))\mathbf{x}\left(t-\tau (t)\right)+{\mathbf{D}}_{11}(\mathit{\rho }(t))\mathbf{w}(t)+{\mathbf{D}}_{12}(\mathit{\rho }(t))u_a(t),\hfill \\ \hfill y_a(t)={\mathbf{C}}_2(\mathit{\rho }(t)){\mathbf{x}}_a(t)+{\mathbf{C}}_{2,\tau }(\mathit{\rho }(t)){\mathbf{x}}_a(t-\tau (t))+{\mathbf{D}}_{21}(\mathit{\rho }(t))\mathbf{w}(t),\hfill \end{array}(31)$

where ${\mathbf{x}}_a(t)={[\begin{array}{ccc}\hfill x(t)\hfill & \hfill u(t)\hfill & \hfill x_e(t)\hfill \end{array}]}^{\text{T}}$ is the augmented state vector and x_e(t) is defined for command tracking purposes, i.e.${\stackrel{\cdot }{x}}_e(t)\triangleq e(t)=r(t)-y(t)=r(t)-(x(t)+d_o(t))$, $\mathit{\rho }(t)={[\begin{array}{ccc}\hfill K(t)\hfill & \hfill T(t)\hfill & \hfill \tau (t)\hfill \end{array}]}^{\text{T}}$ denotes the scheduling parameter vector, $\mathbf{w}(t)={[\begin{array}{cc}\hfill r(t)\hfill & \hfill d_o(t)\hfill \end{array}]}^{\text{T}}$ stands for the exogenous disturbance vector including the reference command and output disturbance signal. Thus, the state space matrices of the augmented LPV system Eq. 31 are obtained as

$\begin{array}{l}\mathbf{A}(\mathit{\rho }(t))=\left[\begin{array}{ccc}\hfill -\frac{1}{T(t)}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\mathrm{\Lambda }\hfill & \hfill 0\hfill \\ \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],{\mathbf{A}}_{\tau }(\mathit{\rho }(t))=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill \frac{K(t)}{T(t)}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],\hfill \\ {\mathbf{B}}_1(\mathit{\rho }(t))=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill -1\hfill \end{array}\right],{\mathbf{B}}_2(\mathit{\rho }(t))=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill \mathrm{\Omega }\hfill \\ \hfill 0\hfill \end{array}\right],{\mathbf{C}}_1(\mathit{\rho }(t))=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill \varphi \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],\hfill \\ {\mathbf{C}}_{1,\tau }(\mathit{\rho }(t))={\mathbf{0}}_{2\times 3},{\mathbf{D}}_{11}(\mathit{\rho }(t))={\mathbf{0}}_{2\times 2},{\mathbf{D}}_{12}(\mathit{\rho }(t))=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill \psi \hfill \end{array}\right],\hfill \\ \hfill & {\mathbf{C}}_2(\mathit{\rho }(t))=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],{\mathbf{C}}_{2,\tau }(\mathit{\rho }(t))={\mathbf{0}}_{1\times 3},{\mathbf{D}}_{21}(\mathit{\rho }(t))=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \end{array}\right].\hfill \end{array}(32)$

The scheduling parameters K(t), T(t), and τ(t) are assumed to be estimated in real-time. In a practical scenario, a Bayesian-based square-root cubature Kalman filtering algorithm can be used to estimate the scheduling parameters (Tasoujian et al., 2020b).

5.3 Closed-Loop MAP Control Simulation Results

In the MAP dynamics LPV model Eq. 31, the performance controlled output vector is defined as $\mathbf{z}(t)={[\varphi \cdot x_e(t)\psi \cdot u(t)]}^{\text{T}}$ where the tracking error, x_e(t), and the control effort, u(t), are penalized by the weighting scalars ϕ and ψ, respectively. The choice of these scalars determines the relative weighting in the optimization scheme and depends on desired performance objectives. Following the controller synthesis steps in Section 5.2, the output-feedback delay-dependent LPV controller Eq. 8 is designed to provide asymptotic stability for the closed-loop LPV time-delay system Eq. 9 and to minimize the worst-case disturbance amplification over the entire range of the model parameter variations. Theorem 1 is employed to design a robust LPV output-feedback controller for the MAP regulation case study. We utilize the patient MAP response simulation model Eq. 27 with parameter and time-delay variabilities based on the relations in (28), to evaluate the proposed control design method.

For comparison purposes, we also evaluate the proposed controller performance against a fixed structure PI controller, see (Wassar et al., 2014), in an hour-long simulation scenario with a piecewise constant commanded reference MAP. Given the following nominal values of the model parameters and time-delay, $\bar{K}=0.55,\bar{T}=150$, and $\bar{\tau }=40$, the tuned PI controller transfer function is selected as follows

$G_c(s)=3+\frac{0.017}{s},(33)$

which is calculated based on the prescribed gain and phase margin control design constraints (Zhong, 2006). In the absence of disturbances and measurement noise, the MAP reference tracking profile and the control effort are shown in Figure 3, where the objective is to regulate the MAP response to track the commanded MAP with minimum overshoot, rise time, settling time, and zero steady-state error. According to these results, the closed-loop response overshoot remains within the acceptable range, and the delay-dependent LPV controller provides faster response with a smaller settling time compared to the conventional PI controller.

FIGURE 3

FIGURE 3. Typical MAP response due to step vasopressor drug infusion.

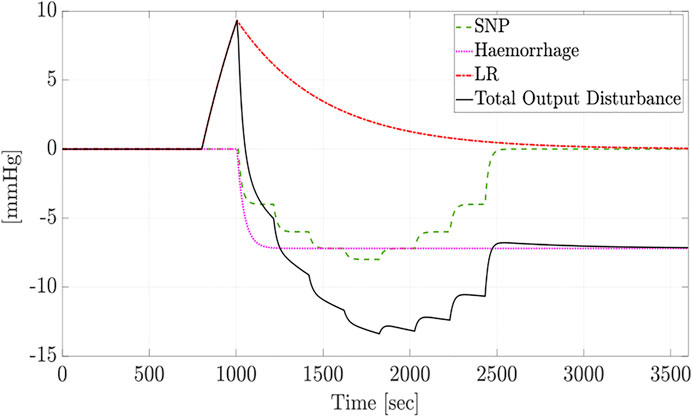
Subsequently, we assume that the closed-loop system is subject to measurement noise and output disturbances. These disturbances could result from medical interventions and physiological response variations due to hemorrhage or other administered medications like lactated ringers. Figure 4 shows a typical profile of such disturbances. Figure 5 depicts the performance of the LPV and PI controllers, where the measurement noise is a white noise signal with intensity of 10^–3. As expected, the proposed LPV controller outperforms the fixed structure PI controller with respect to the response’s rise time and speed due to its scheduling structure. The results demonstrate that the proposed time-delay LPV gain-scheduling control methodology provides desirable closed-loop performance in terms of commanded MAP tracking and disturbance rejection in the presence of model parameter variations, varying time-delay, and output disturbances.

FIGURE 4

FIGURE 4. Profile of output disturbances.

FIGURE 5

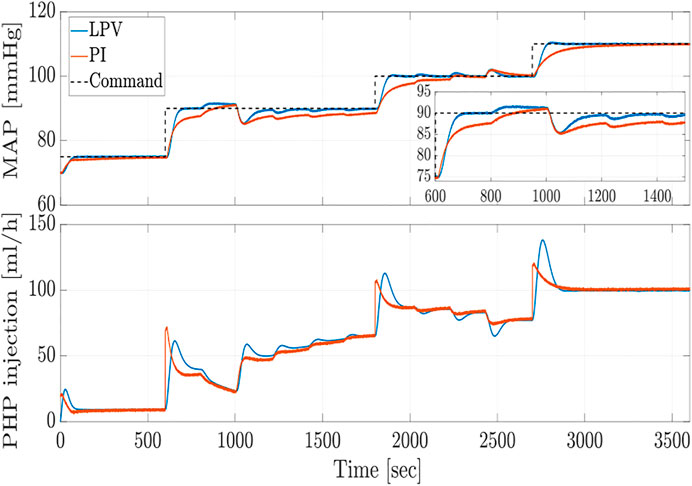
FIGURE 5. Closed-loop MAP response and control effort (PHP injection rate) of LPV controller against fixed structure PI controller subject to disturbance and measurement noise.

6 Conclusion

In the present study, a Lyapunov-Krasovskii based approach has been used to derive delay-dependent LPV control synthesis conditions for LPV time-delay systems. In this regard, an improved parameter-dependent Lyapunov Krasovskii functional (LKF) candidate was proposed, followed by an efficient bounding technique using the affine Jensen’s inequality, for the design of output-feedback LPV controllers. This choices of LKF and integral inequality constraints reduced the conservatism of the method by limiting the bounding gap in the integral cross-terms of the LKF derivative. By introducing appropriate slack variables, the final relaxed synthesis conditions have been formulated in terms of tractable convex linear matrix inequalities (LMIs). A numerical example compared the performance of the proposed scheme to past work in the literature. It is shown that the proposed delay-dependent LPV control that utilizes an improved LKF formulation and a more general Jensen’s inequality results in less conservative design and larger values of allowable delay. Finally, the mean arterial blood pressure (MAP) regulation in critical hypotensive patients was examined to evaluate the proposed control design in a challenging practical control problem. Closed-loop simulation results demonstrated the ability of the proposed time-delayed LPV control to regulate MAP in the presence of varying input delays and disturbances in comparison with past results in the literature. In the present work, the time-varying delay is considered to be a known quantity that can be estimated or evaluated in real time. Future work will investigate the stability analysis and robust control design for LPV systems with uncertain time-varying delays. Additionally, the effect of saturation constraints on the magnitude of the control input will be examined.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The animal study was reviewed and approved by the UTMB Galveston, TX, United States.

Author Contributions

The present research article is the result of ST’s work as a Ph.D. student under KG and MF. The detailed responsibilities are as follows: ST: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Writing-original draft, KG: Methodology, Writing-review, and editing, Supervision, Project administration, Funding acquisition MF: Methodology, Supervision, Project administration, Funding acquisition.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Financial support from the National Science Foundation under grant CMMI1437532 is gratefully acknowledged. The collaboration of the Resuscitation Research Laboratory at the University of Texas Medical Branch, Galveston, Texas, in providing experiment data is gratefully acknowledged.

References

Ahmed, S., and Özbay, H. (2016). Design of a Switched Robust Control Scheme for Drug Delivery in Blood Pressure Regulation. IFAC-PapersOnLine 49, 252–257. doi:10.1016/j.ifacol.2016.07.538

CrossRef Full Text | Google Scholar

Albertos, P. (2006). Phase-conditionally Stable Systems. Syst. Control Lett. 55, 803–808. doi:10.1016/j.sysconle.2006.03.011

CrossRef Full Text | Google Scholar

Apkarian, P., and Adams, R. J. (1998). Advanced Gain-Scheduling Techniques for Uncertain Systems. IEEE Trans. Contr. Syst. Technol. 6, 21–32. doi:10.1109/87.654874

CrossRef Full Text | Google Scholar

Bei Lu, B., Fen Wu, F., and SungWan Kim, S. (2006). Switching LPV Control of an F-16 Aircraft via Controller State Reset. IEEE Trans. Contr. Syst. Technol. 14, 267–277. doi:10.1109/tcst.2005.863656

CrossRef Full Text | Google Scholar

Bianchi, F. D., De Battista, H., and Mantz, R. J. (2006). Wind Turbine Control Systems: Principles, Modelling and Gain Scheduling Design. Springer Science & Business Media.

Bianchi, F. D., Mantz, R. J., and Christiansen, C. F. (2005). Gain Scheduling Control of Variable-Speed Wind Energy Conversion Systems Using Quasi-LPV Models. Control Eng. Pract. 13, 247–255. doi:10.1016/j.conengprac.2004.03.006

CrossRef Full Text | Google Scholar

Bozorg, M., and Davison, E. J. (2006). Control of Time Delay Processes with Uncertain Delays: Time Delay Stability Margins. J. Process Control 16, 403–408. doi:10.1016/j.jprocont.2005.06.012

CrossRef Full Text | Google Scholar

Briat, C. (2011). Convergence and Equivalence Results for the Jensen's Inequality-Application to Time-Delay and Sampled-Data Systems. IEEE Trans. Automat. Contr. 56, 1660–1665. doi:10.1109/tac.2011.2121410

CrossRef Full Text | Google Scholar

Briat, C. (2014). Linear Parameter-Varying and Time-Delay Systems. Berlin: Springer.

Cao, G., and Grigoriadis, K. M. (2020). Blood Pressure Response Simulator to Vasopressor Drug Infusion (Pressorsim). Int. J. Control 1–15. doi:10.1080/00207179.2020.1742385

CrossRef Full Text | Google Scholar

Colmegna, P. H., Sanchez-Pena, R. S., Gondhalekar, R., Dassau, E., and Doyle, F. J. (2015). Switched LPV Glucose Control in Type 1 Diabetes. IEEE Trans. Biomed. Eng. 63, 1192–1200. doi:10.1109/TBME.2015.2487043

PubMed Abstract | CrossRef Full Text | Google Scholar

Craig, C. R., and Stitzel, R. E. (2004). Modern Pharmacology with Clinical Applications. Baltimore, MD, USA: Lippincott Williams & Wilkins.

das Neves, J. F., Monteiro, G. A., de Almeida, J. R., Sant'Anna, R. S., Bonin, H. B., and Macedo, C. F. (2010). Phenylephrine for Blood Pressure Control in Elective Cesarean Section: Therapeutic versus Prophylactic Doses. Rev. Bras. Anestesiol. 60, 391–398. doi:10.1016/S0034-7094(10)70048-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Fridman, E. (2014). Introduction to Time-Delay Systems Analysis and Control. Basel: Springer.

Isaka, S., and Sebald, A. V. (1993). Control Strategies for Arterial Blood Pressure Regulation. IEEE Trans. Biomed. Eng. 40, 353–363. doi:10.1109/10.222328

PubMed Abstract | CrossRef Full Text | Google Scholar

Jankovic, M. (2001). Control Lyapunov-Razumikhin Functions and Robust Stabilization of Time Delay Systems. IEEE Trans. Automat. Contr. 46, 1048–1060. doi:10.1109/9.935057

CrossRef Full Text | Google Scholar

Kee, W. D. N., Khaw, K. S., and Ng, F. F. (2005). Prevention of Hypotension during Spinal Anesthesia for Cesarean Delivery. The J. Am. Soc. Anesthesiologists 103, 744–750. doi:10.1097/00000542-200510000-00012

CrossRef Full Text | Google Scholar

Kharitonov, V. L. (2004). Lyapunov-Krasovskii Functionals for Scalar Time Delay Equations. Syst. Control Lett. 51, 133–149. doi:10.1016/s0167-6911(03)00221-4

CrossRef Full Text | Google Scholar

Knospe, C. R., and Roozbehani, M. (2006). Stability of Linear Systems with Interval Time Delays Excluding Zero. IEEE Trans. Automat. Contr. 51, 1271–1288. doi:10.1109/tac.2006.878715

CrossRef Full Text | Google Scholar

Kolmanovskii, V. B., and Richard, J.-P. (1999). Stability of Some Linear Systems with Delays. IEEE Trans. Automat. Contr. 44, 984–989. doi:10.1109/9.763213

CrossRef Full Text | Google Scholar

Lofberg, J. (2004). “YALMIP: A Toolbox for Modeling and Optimization in MATLAB,” in IEEE International Conference on Robotics and Automation, 284–289.

Google Scholar

Luspay, T., and Grigoriadis, K. M. (2015). Adaptive Parameter Estimation of Blood Pressure Dynamics Subject to Vasoactive Drug Infusion. IEEE Trans. Control Syst. Techn. 24, 779–787. doi:10.1109/tcst.2015.2476775

CrossRef Full Text | Google Scholar

Malagutti, N., Dehghani, A., and Kennedy, R. A. (2013). Robust Control Design for Automatic Regulation of Blood Pressure. IET Control Theor. Appl. 7, 387–396. doi:10.1049/iet-cta.2012.0254

CrossRef Full Text | Google Scholar

Michiels, W., and Niculescu, S.-I. (2007). Stability and Stabilization of Time-Delay Systems: An Eigenvalue-Based Approach. Philadelphia: SIAM.

Niculescu, S.-I. (1999). “A Model Transformation Class for Delay-dependent Stability Analysis,” in American Control Conference, San Diego, CA, June 2—4, 1999 (ACC), 1, 314–318. doi:10.1109/acc.1999.782791

CrossRef Full Text | Google Scholar

Niculescu, S.-I. (2001). Delay Effects on Stability: A Robust Control Approach, Vol. 269. Springer Science & Business Media.

PooGyeon Park, P. (1999). A Delay-dependent Stability Criterion for Systems with Uncertain Time-Invariant Delays. IEEE Trans. Automat. Contr. 44, 876–877. doi:10.1109/9.754838

CrossRef Full Text | Google Scholar

Rao, R. R., Aufderheide, B., and Bequette, B. W. (2003). Experimental Studies on Multiple-Model Predictive Control for Automated Regulation of Hemodynamic Variables. IEEE Trans. Biomed. Eng. 50, 277–288. doi:10.1109/tbme.2003.808813

PubMed Abstract | CrossRef Full Text | Google Scholar

Salavati, S., Grigoriadis, K., and Franchek, M. (2019). Reciprocal Convex Approach to Output-Feedback Control of Uncertain LPV Systems with Fast-Varying Input Delay. Int. J. Robust Nonlinear Control 29 (16), 5744–5764. doi:10.1002/rnc.4697

CrossRef Full Text | Google Scholar

Sandu, C., and Popescu, D. (2016). Reinforcement Learning for the Control of Blood Pressure in post Cardiac Surgery Patients. U. P. B. Sci. Bull. Ser. C 78, 139–150.

Google Scholar

Shamma, J. S. (1988). Analysis and Design of Gain Scheduled Control Systems. Ph.D. thesis. Boston, MA: Massachusetts Institute of Technology.

Google Scholar

Shamma, J. S., and Athans, M. (1990). Analysis of Gain Scheduled Control for Nonlinear Plants. IEEE Trans. Automat. Contr. 35, 898–907. doi:10.1109/9.58498

CrossRef Full Text | Google Scholar

Tasoujian, S., Ebrahimi, B., Grigoriadis, K., and Franchek, M. (2016). “Parameter-varying Loop-Shaping for Delayed Air-Fuel Ratio Control in Lean-Burn SI Engines,” in ASME Dynamic Systems and Control Conference, Minneapolis, MN, October 12—14, 2016 (DSCC), 1–8. doi:10.1115/dscc2016-9813

CrossRef Full Text | Google Scholar

Tasoujian, S., Grigoriadis, K., and Franchek, M. (2019a). “Delay-dependent Output-Feedback Control for Blood Pressure Regulation Using LPV Techniques,” in ASME Dynamic Systems and Control Conference, Park City, UT, October 8—11, 2019 (DSCC). doi:10.1115/dscc2019-9098

CrossRef Full Text | Google Scholar

Tasoujian, S., Salavati, S., Franchek, M., and Grigoriadis, K. (2020a). “Robust Delay-dependent LPV Synthesis for Blood Pressure Control with Real-Time Bayesian Parameter Estimation,” in IET Control Theory & Applications.

Google Scholar

Tasoujian, S., Salavati, S., Franchek, M., and Grigoriadis, K. (2019b). Robust IMC-PID and Parameter-Varying Control Strategies for Automated Blood Pressure Regulation. Int. J. Control Autom. Syst. 17, 1803–1813. doi:10.1007/s12555-018-0631-7

CrossRef Full Text | Google Scholar

Tasoujian, S., Salavati, S., Grigoriadis, K., and Franchek, M. (2020b). “Real-time Cubature Kalman Filter Parameter Estimation of Blood Pressure Response Characteristics under Vasoactive Drugs Administration,” in American Control Conference, Denver, CO, July 1—3 (ACC), 1–8. doi:10.23919/acc45564.2020.9147309

CrossRef Full Text | Google Scholar

Urooj, S., and Singh, B. (2019). Fractional-Order PID Control for Postoperative Mean Arterial Blood Pressure Control Scheme. Proced. Comput. Sci. 152, 380–389. doi:10.1016/j.procs.2019.05.002

CrossRef Full Text | Google Scholar

Wassar, T., Luspay, T., Upendar, K. R., Moisi, M., Voigt, R. B., Marques, N. R., et al. (2014). Automatic Control of Arterial Pressure for Hypotensive Patients Using Phenylephrine. Int. J. Model. Simulation 34, 187–198. doi:10.2316/journal.205.2014.4.205-6087

CrossRef Full Text | Google Scholar

Witrant, E., Canudas-de-Wit, C., Georges, D., and Alamir, M. (2007). Remote Stabilization via Communication Networks with a Distributed Control Law. IEEE Trans. Automat. Contr. 52, 1480–1485. doi:10.1109/tac.2007.902757

CrossRef Full Text | Google Scholar

Wu, F., Yang, X. H., Packard, A., and Becker, G. (1996). Induced L2-Norm Control for Lpv Systems with Bounded Parameter Variation Rates. Int. J. Robust Nonlinear Control 6, 983–998. doi:10.1002/(sici)1099-1239(199611)6:9/10<983::aid-rnc263>3.0.co;2-c

CrossRef Full Text | Google Scholar

Zhang, X., Tsiotras, P., and Knospe, C. (2002). Stability Analysis of LPV Time-Delayed Systems. Int. J. Control 75, 538–558. doi:10.1080/00207170210123833

CrossRef Full Text | Google Scholar

Zhong, Q.-C. (2006). Robust Control of Time-Delay Systems. London: Springer-Verlag.

Zope, R., Mohammadpour, J., Grigoriadis, K., and Franchek, M. (2012). “Delay-dependent ${\mathcal{H}}_{\infty }$ Control for LPV Systems with Fast-Varying Time Delays,” in American Control Conference, Montréal, Canada, June 27—29 (ACC), 775–780.

Google Scholar