The Disconnect Between Short- and Long-Term Population Projections for Plant Reintroductions

The reintroduction of rare species in natural preserves is a commonly used restoration strategy to prevent species extinction. An essential first step in planning successful reintroductions is identifying which life stages (e.g., seeds or large adults) should be used to establish these new populations. Following this initial establishment phase, it is necessary to determine the level of survival, growth, and recruitment needed to maintain population persistence over time and identify management actions that will achieve these goals. In this 5-year study, we projected the short- and long-term population growth rates of a critically endangered long-lived shrub, Delissea waianaeensis. Using this model system, we show that reintroductions established with mature individuals have the lowest probability of quasi-population extinction (10 individuals) and the highest increase in population abundance. However, our results also demonstrate that short-term increases in population abundances are overly optimistic of long-term outcomes. Using long-term stochastic model simulations, we identified the level of natural seedling regeneration needed to maintain a positive population growth rate over time. These findings are relevant for planning future reintroduction efforts for long-lived species and illustrate the need to forecast short- and long-term population responses when evaluating restoration success.

Introduction

The reintroduction of rare plants is a commonly used restoration strategy to prevent species extinction (Maschinski and Haskins, 2012; Soorae, 2013). The end goal of this management strategy is to promote species recovery and establish new populations that will persist over time (Falk et al., 1996; Pavlik, 1996). With an increase in rare and at-risk species and continued anthropogenic change in environmental conditions (Wilcove et al., 1998; IUCN, 2013), the reintroduction of rare species has become an increasingly important component of many recovery efforts (Maunder, 1992). While many studies have evaluated initial signs of reintroduction success, including the survival of reintroduced individuals and rates of natural regeneration (Menges, 2008; Godefroid et al., 2011; Dalrymple et al., 2012; Guerrant Jr, 2013; Liu et al., 2015), our understanding of how likely and under what conditions the reintroduction of rare species will promote species recovery and long-term persistence is limited (but see, Bell et al., 2003, 2013; Liu et al., 2004, 2015; Maschinski and Duquesnel, 2007; Colas et al., 2008; Albrecht et al., 2018).

Previous assessments on the use of reintroductions as a successful restoration strategy have yielded mixed results (Menges, 2008; Godefroid et al., 2011; Dalrymple et al., 2012; Guerrant Jr, 2013; Liu et al., 2015). Contradictions among previous studies are driven, in part, by differences in the generation time of rare species, the criteria used to define success, and the timeframe that reintroductions were monitored for following initial establishment (Menges, 2008; Godefroid et al., 2011; Dalrymple et al., 2012; Guerrant Jr, 2013; Liu et al., 2015). While the abundance of short-lived species with fast generational turnover can decline rapidly following initial establishment, reintroduced individuals of long-lived species can survive for many years. Thus, to fully understand the usefulness of species reintroductions as a restoration tool, there is an increased need for analyses that can be used to make comparisons between short- vs. long-lived species and project the probability of short- and long-term population persistence.

Within the population ecology literature, there are a small but growing number of studies that have moved beyond evaluating initial benchmarks of reintroduction success, such as initial establishment, reproductive maturity, and recruitment (Bell et al., 2003; Maschinski and Duquesnel, 2007; Colas et al., 2008). Those studies used long-term population projection models to examine if the reintroduction of rare species will likely result in the desired outcome (i.e., establishing new populations that will persist over time). While useful for making comparisons among species, long-term projections rarely match short-term changes in population abundances. The mismatch in short- and long-term population dynamics has led to increased skepticism in the use of demographic models to evaluate restoration success.

The mismatch in short-term population dynamics (e.g., annual increases in population abundance) and long-term projections can be explained, in part, by the effect of the stage structure on the near-term population growth rate (Fox and Gurevitch, 2000; Koons et al., 2005; Haridas and Tuljapurkar, 2007). For populations with artificially skewed stage structures (e.g., only reproductively mature plants), the population growth rate can fluctuate in the near-term as outplanted individuals senesce and natural regeneration fill in early life stages (Haridas and Tuljapurkar, 2007). The skewed stage structure of newly established populations can also influence population inertia; wherein the population growth rate will eventually settle to long-term asymptotic dynamics but at a much higher or lower population abundance (Keyfitz, 1971; Stubben and Milligan, 2007; Ezard et al., 2010; Stott et al., 2011).

The use of short- and long-term population projections to characterize how skewed stage structures influence plant population dynamics over time has become increasingly important for understanding the effects of environmental change on fundamental patterns in ecology. For example, short- and long-term projections have been used to characterize plant population responses to herbivory pressure (Maron et al., 2010), harvesting (Gaoue, 2016), biological invasion (McMahon and Metcalf, 2008; Ezard et al., 2010), severe catastrophic events (Crain et al., 2019), and habitat disturbance (Ezard et al., 2010; Bialic-Murphy et al., 2017). While it is likely that the distinction between short- and long-term dynamics is particularly important for assessing the likely outcome of plant reintroductions with artificially skewed stage structures, there is a dearth of demographic studies on this topic (but see, Wong and Ticktin, 2015).

Here, we leverage a long-term demographic dataset of a multi-year reintroduction effort to characterize how the population dynamics of newly established reintroductions fluctuate over time. Specifically, we (i) compare the short- and long-term population growth rates of the newly established reintroduction effort, (ii) quantify the risk of quasi extinction in the short- and long-term, (iii) identify the management actions that would have the greatest positive effect on the short- and long-term population growth and, (iv) evaluate the level of seedling recruitment that would be needed to maintain positive population growth over time. We focused on setting biologically meaningful benchmark goals for seedling recruitment because it was the only life stage that could be improved by management.

METHODS

Study Species

Delissea waianaeensis (Campanulaceae) is a critically endangered long-lived shrub endemic to the island of O‘ahu (Wagner et al., 2012). Campanulaceae is the largest Hawaiian angiosperm family (Givnish et al., 2009) with 159 taxa (Soorae, 2018). This Campanulaceae family is also one of the most threatened Hawaiian groups, with over 60% of the endemic Hawaiian species extinct in the wild (Soorae, 2018). Delissea waianaeensis has a single or branched erect stem that produces fleshy purple, red, white, and pink berries, which is indicative of frugivorous bird dispersal (Lammers, 2005). The floral sugar composition suggest D. waianaeensis was historically pollinated by native birds in the honeycreeper (Drepanidinae) and Hawaiian Mohoideae (Mohoidae) groups (Lammers and Freeman, 1986; Pender, 2013). Following massive extinction of native birds in the Drepanidinae and Mohoidae groups, it is likely that D. waianaeensis is dispersal and pollen limited (Lammers and Freeman, 1986; Pender, 2013). Delissea waianaeensis is found between 245 and 760 m elevation, along the north facing slopes and gulch bottoms of the Waianae Mountain Range (Wagner et al., 1999). In 1996, D. waianaeensis was listed as federally endangered (USFWS, 1998) and by 2005 it was restricted to seven geographically isolated locations (USFWS, 2012).

Two of the main stressors implicated in the decline of D. waianaeensis are frugivory by Rattus rattus (black ship rat) and seedling herbivory by non-native molluscs (Mollusca: Gastropoda) (Joe and Daehler, 2007; Kawelo et al., 2012; Shiels et al., 2014; Bialic-Murphy et al., 2018). Frugivory by Rattus rattus and herbivory by non-native molluscs have pronounced negative effects on seedling recruitment of rare island endemics, including D. waianaeensis (Joe and Daehler, 2007; Shiels and Drake, 2011; Shiels et al., 2014; Bialic-Murphy et al., 2018). The density of R. rattus can be highly variable from year to year and is a primary driver of temporal variability in seedling recruitment (Innes et al., 2001; Meyer and Butaud, 2009; Franklin, 2014). At our field site, R. rattus consume, on average, 83% of the mature fruits (Bialic-Murphy et al., 2018). Similarly, non-native molluscs decrease seedling density of endemic plants in Hawai‘i by up to 33% (Kawelo et al., 2012). The suppression of these pests is among the most used management strategies to increase seedling regeneration for rare species across tropical islands, included D. waianaeensis. While the technologies used to suppress non-native pests continue to improve, the levels of pest control management and increases in seedling regeneration needed to reach the desired restoration outcome (e.g., population persistence) often remain unclear.

Study Site and Reintroduction Details

The study site is in the Central Kalua‘ā gulch of the Honouliuli Forest Reserve, which is located in the northern Wai‘anae Mountains, on the island of O‘ahu (HON; 21°28′^N, −158°6′^W). The mean monthly rainfall is 52–171 mm (Giambelluca et al., 2013). The site represents a tropical mesic forest, composed of mixed native and non-native flora and fauna (OANRP, 2011). Selection of the reintroduction site was based on similarities of associated species, proximity to naturally occurring D. waianaeensis (~4,000 m away), and relatively accessible location in the historic geographical distribution of naturally occurring D. waianaeensis (Dan Sailer, personal communication). In 2001, The Nature Conservancy constructed an ungulate exclusion fence at Central Kalua‘ā, eradicated feral pigs (Sus scrofa) from within the constructed fence, and implemented invasive vegetation control for the protection of D. waianaeensis and other managed taxa.

In 2002, The Nature Conservancy initiated reintroduction of D. waianaeensis into the Central Kalua‘ā Gulch, starting with the clearing of invasive species across the reintroduction location and the outplanting of 43 reproductively mature plants. The reintroduction site was ~1 acre. The founders used for the Kalua‘ā D. waianaeensis reintroduction were from a relictual geographically isolated population of five individuals, located 4,000 m from the outplanting site. Stock from the other six geographically isolated populations was not used for the Kalua‘ā reintroduction to avoid potential outbreeding depression and the loss of local adaptations (Kawelo et al., 2012). Prior to outplanting, seeds from the five Kalua‘ā founders were grown in a greenhouse for one growing season. In 2004, the management of the Kalua‘ā D. waianaeensis reintroduction was transferred to the U.S. Army's Natural Resources Program on O‘ahu. The program outplanted an additional 303 plants from 2004 to 2012. The mean height of all reintroduced plants at the time of outplanting was 56 cm in height to the apical meristem (OANRP, rare plant database). The 2012 outplanting included genetic representation from two additional individuals that were discovered in close proximity to the five original founders used for the Kalua‘ā reintroduction. At the start of the study, in 2010, the reintroduced population was composed of outplanted mature individuals and first filial plants in all life stages.

Data Collection

From 2010 to 2015, we collected annual demographic data for a total of 597 permanently tagged D. waianaeensis plants at the field site. Based on a combination of field observations and size measurement data over the 2010–2011 transition year, we divided the life cycle of D. waianaeensis into four life stages: reproductively mature (height >35 cm to the apical meristem and reproductive), large non-reproductive plants (height > 35 cm and vegetative), small non-reproductive plants (height 2–35 cm tall and no cotyledons), and seedlings (<2 cm tall with cotyledons). We determined the cut-off for the reproductively mature life stage by identifying the minimum size that plants flowered during the 2010–2011 transition year. Similarly, the cut-off for the seedling life stage was determined by evaluating the maximum size for true seedlings (new germinates with cotyledons that were <1-year old). The non-reproductive life stages are referred to hereafter as immature individuals. The stage structure of the population at the start of the study included 74 reproductively mature plants, 131 small and large immature plants, and 217 seedlings. The stage structure of the population in 2010 was based on census count data (i.e., plant size was not measured) so the total number of small and large immatures was unknown.

In the first year of the study, a minimum of 50 plants in the reproductively mature, large immature, and small immature life stages were haphazardly selected and permanently tagged. To maintain a sufficient sample size for each life stage in subsequent years, new individuals were tagged when needed. For each tagged plant, we recorded survival, height to the apical meristem, and reproductive status (i.e., evidence of flowers and/or fruits) annually in January or February. Each year, we also counted the total number of new seedlings (<1 year old) and reproductively mature plants in the population. The total number of new seedlings counted in the population ranged from 23 to 217 individuals. These annual count data were used to estimate the mean number of seedlings produced per mature plant (i.e., total number of seedlings/total number of mature plants the previous year), which is referred to hereafter as seedling recruitment. Surveys for new seedling recruitment were extended to ~5 m beyond the boundary of the reintroduction site. Since the focus of this study was local population viability, we did not examine long-distance seed dispersal outside of the population.

Projection Matrix Construction

We used the demographic data to construct a 4 x 4 Lefkovitch matrix A (Caswell, 2001) for five transition years (2010–2011, 2011–2012, 2012–2013, 2013–2014, and 2014–2015). Matrix A can be decomposed into two matrices: a survival-growth matrix U and fertility matrix F. Matrix A captured the yearly transition rate of stasis σ, survival and growth to the next stage class γ, shrinkage ρ, and seedling recruitment φ_m for the following discrete life stages: reproductively mature (m), large immature (li), small immature (si), and seedling (s). For φ_m, which represents the mean number of seedlings produced per mature plant, we were able to calculate an additional transition rate for year 2009–2010. Since the seed bank dynamics were not known for D. waianaeensis, we did not include this life stage transition in our matrix model.

$\begin{array}{l}\text{A}=\left(\begin{array}{c}000{\phi }_m\\ {\gamma }_{s-si}{\sigma }_{si}0{\rho }_{m_{si}}\\ 0{\gamma }_{si-li}{\sigma }_{li}{\rho }_{m_{li}}\\ 0{\gamma }_{si-m}{\gamma }_{li-m}{\sigma }_m\\ \end{array}\right)\end{array}$

The dominant eigenvalue of matrix A represents the long-term population growth rate λ, which has an associated stable stage distribution w and reproductive value v (Caswell, 2001). Specifically, the stable stage distribution represents the proportion of individuals in each stage class based on the matrix A transition probabilities and the reproductive value is the mean number of offspring that an individual contributed to the next generation. While the dimensions of a matrix can influence population projections, previous work suggests a 4 × 4 matrix is sufficient for comparative studies and species with relatively simple life cycles (Salguero-Gomez and Plotkin, 2010).

Matrix elements with 0 represent transition probabilities that were either not biologically feasible (e.g., seedlings remaining seedlings) or not observed during the study (e.g., large immatures shrinking to small immatures). The yearly transition rates used to construct the A and F matrices were derived from a subset of randomly selected individuals that were outplanted over multiple reintroduction efforts, starting in 2002, and a subset of first filial individuals. All analyses were done in R version 3.1.0.

Temporal Variability of Seedling Recruitment φ_m

Non-native pests influence the temporal variability of seedling recruitment (Innes et al., 2001; Meyer and Butaud, 2009) and can drive population decline (Bialic-Murphy et al., 2018). In Hawai‘i natural areas, the density of rats (Shiels, 2010) and slugs (Stephanie Joe, personal communication) fluctuate from year-to-year and the intensity of seasonal pest control management can be highly variable due to budget constraints.

To capture the effects of year-to-year fluctuations in seedling recruitment and variable intensities of pest control management, we modeled the frequency of high seedling recruitment years as a stochastic process. We did this by first created an array for seedling recruitment that consisted of φ_m values for transition years 2009–2010, 2010–2011, 2011–2012, 2012–2013, 2013–2014, and 2014–2015, which are referred to hereafter as years 1–6. We then classified seedling recruitment φ_m1−6 in years 1–6 as either high (h) and low (l), based on the across year average (φ_a=0.69). Seedling recruitment φ_m1 in year 1 was 3.09 seedlings per mature plant and seedling recruitment φ_m2−6 in years 2–6 ranged from 0.569 to 0.021 seedlings per mature plant respectively (see Appendix S1). Based on our classification, seedling recruitment φ_m1 in year 1 was high and seedling recruitment φ_m2−6 in years 2–6 as low. To evaluate the influence of temporal variability in seedling recruitment φ_m on population dynamics we created an array of F matrices for a total of six scenarios F1–F6, which are described below, by modifying the probability of high and low recruitment being selected following a temporally stochastic process (see below for the high and low recruitment probabilities used for each scenario). Independent of the fertility matrices F, we used our survival-growth data 2010–2011, 2011–2012, 2012–2013, 2013–2014, and 2014–2015 to create a stochastic array of U matrices (i.e., survival-growth matrix elements only) assuming an identically independent distribution (i.i.d). For modeling purposes, we assumed fertility and survival-growth were not linked through life history trade-offs and simulated each process independently.

Stochastic Long-Term Population Dynamics

To project the near-term transient and long-term asymptotic dynamics for D. waianaeensis, we used a stochastic stage-structured model (Caswell, 2001):

$\begin{array}{ll}n(t+1)=\text{X}(t)n(t)& (1)\end{array}$

where X(t) is a random transition matrix selected for at a given time t as the sum of two selected matrices U and F (see above), one from a pool of five U matrices (for transition years 2010–2011, 2011–2012, 2012–2013, 2013–2014, and 2014–2015) and the other from a pool of six F matrices (for transition years 2009–2010, 2010–2011, 2011–2012, 2012–2013, 2013–2014, and 2014–2015). The vector n(t) represents the number of individuals in each of the four life stages at a given time t, and n(t+1) represents the number of individuals at time t+1. For modeling proposes, we used the observed stage structure in 2015 as the initial condition. Since long-term asymptotic projections exclude transient dynamics, using 2015 as the initial condition had no effect on our long-population growth rate projections. We used this framework to project population dynamics for six scenarios F1– F6, differing in temporal variability of recruitment. For scenario F1, the probability that a high seedling recruitment year (h) is selected each time step t was 0.1666. Scenario F1 mimicked the probability of high seedling recruitment years based on observed field conditions (i.e., 1 in 6 years). For scenarios F2– F6, we increased the probability of a high seedling recruitment year (h) being selected each time step t. For each consecutive simulation (F2–F6) we increased the probability of a high seedling recruitment year (h) being selected each time step t, with the probability of a high seedling recruitment year ranging from 0.33 to 1 for scenarios F2 to F6 respectively. For all scenarios F1–F6, matrix U was selected with equal probability at each time step t from the pool of U matrices. We calculated the stochastic long-term growth rate λ_s by simulation, using 50,000 iterations following Tuljapurkar et al. (2003):

$\begin{array}{ll}{log\lambda }_s={\displaystyle \underset{t\to \infty }{lim}}\left(\frac{1}{t}\right)log\left[N(t)/N(0)\right],& (2)\end{array}$

where N(t) is the population size at time t, which is the sum of n(t) at a given time t. For each scenario, 95% bootstrap confidence intervals were estimated as the standard error of the mean, following methods outlined in Morris and Doak (2002). We used a density independent model, which is likely reasonable for a rare species, like D. waianaeensis, with low seedling recruitment.

In addition to projecting the asymptotic stochastic population growth rate for scenarios F1–F6, we conducted long-term stochastic elasticity analysis. These long-term elasticity projections allowed use to identify the relative importance of perturbations in vital rates on the stochastic population growth rate λ_s with respect to perturbation of the variance E^sδ (Tuljapurkar et al., 2003; Haridas and Gerber, 2010). Stochastic elasticity analysis captures the effects of an increase or decrease in the temporal variability in matrix elements (e.g., seedling recruitment) on the long-term population growth rate λ_s. It is important to note that long-term stochastic elasticity analysis is dependent on asymptotic dynamics and is not influenced by the initial population stage structure.

Stochastic Transient Population Dynamics

The D. waianaeensis reintroduction was established with only reproductively mature plants, and thus the population structure was expected to be initially far from its stable stage distribution. Thus, to characterize how the population would likely fluctuate in the near-term, we calculated the stochastic transient population growth rate r_s. For our simulations we used 10,000 independent sample paths of t = 5 years. For each scenario F1–F6, we altered the probability of a high (h) seedling recruitment year using the method described above. To mimic a plant reintroduction that was established using only reproductively mature individuals, we set the initial population structure n(0) to 100% reproductively mature individuals and 0 for the other life stages. Using a cohort of later life stages (e.g., reproductively mature individuals) is particularly relevant from an applied management perspective because many plant reintroductions, similarly to the case of D. waianaeensis, are established with later life stages because they have the highest initial establishment rate (Maschinski and Haskins, 2012).

For our short-term transient projections, we chose a timeframe of t = 5 years because prior studies suggest plant reintroductions are typically monitored for less than 5 years (Godefroid et al., 2011; Liu et al., 2015) and peer review assessments are typically reliant on ≤3 years of transition data (Dalrymple et al., 2012). Thus, our results provide insight to how short-term assessments will likely differ from long-term outcomes. The use of a 5 year timeframe to capture transient projections for D. waianaeensis was supported by the damping ratio ρ = |λ_subdom|/λ_dom of the mean matrix A, which is the ratio of the subdominant (λ_subdom) and dominant (λ_dom) eigenvalues (Haridas and Tuljapurkar, 2007). The damping ratio is a metric of convergence to the stable stage equilibrium: ρ close to 0 indicates that the population is far from equilibrium and a ρ close to 1 suggests a population that will converge to long-term dynamics relatively rapidly. The damping ratio for D. waianaeensis was ρ = 0.39, suggesting the population structure was relatively far from equilibrium.

In addition to the effects of the initial stage structure on the near-term population growth rate, plant populations dominated by mature life stage are expected to amplify beyond the long-term dynamics (Ezard et al., 2010; Stott et al., 2010, 2011). Thus, to characterize the effect of transient amplification on the D. waianaeensis population, we compared the projected population abundance for a reintroduction established with mature plants only to a population at a stable stage equilibrium (Stubben and Milligan, 2007). To further examine the viability of the D. waianaeensis population over time, we quantified the probability of quasi extinction in a stochastic environment at t = 5 years and t = 50 years (Caswell, 2001). For each scenario F1–F6, we simulated 1,000 independent sample paths of 5 and 50 time-steps respectively. For modeling purposes, we set the quasi-extinction threshold at 10 individuals.

To identify the relative importance of life stages on the stochastic transient population growth rate for scenarios F1–F6, we determined the stochastic transient elasticity with respect to perturbation of the variance e^sδ at t = 5 years. The transient elasticity captures the instantaneous influence of a single time step change in vital rates $e_{ij}^1$ and the long-term influence of perturbations in the stage structure $e_{ij}^2$ (Haridas and Tuljapurkar, 2007; Haridas and Gerber, 2010). Stochastic transient elasticity with respect to perturbations in the variance captures the effects of temporal variability in matrix elements (i.e., plant vital rates) and the effects of the initial stage structure (Ellis and Crone, 2013).

Results

The long-term stochastic population growth rate λ_s of D. waianaeensis for scenario F1 was 0.967 (95% CI of 0.963–0.972). These results indicate that the population will decline by 3.3% per year based on observed field conditions (Figure 1A). A two-fold increase in the probability of high recruitment years from 0.17 to 0.33 (scenario F2) resulted in a population growth rate close to 1 [λ_s = 0.996 (0.995, 1.00)]. A three-fold increase in the probability of high recruitment years from 0.17 (scenario F1) to 0.50 (scenario F3) shifted the long-term stochastic population growth rate from a 3.3% decline to a 2% increase in population size per year [λ_s =1.020, (1.015, 1.026); Figure 1A]. For scenarios F3–F6, the long-term stochastic population growth rates λ_s were > 1 indicating projected growing populations (Figure 1A). Consistent with our long-term population growth rate projects, we found that scenario F1 had the highest probability of quasi extinction within a 50-year timeframe (0.19 probability of dropping below 10 individuals), followed by scenario F2 (0.09 probability) and scenarios F3–F6 (0 probability) respectively (Figure 2).

FIGURE 1

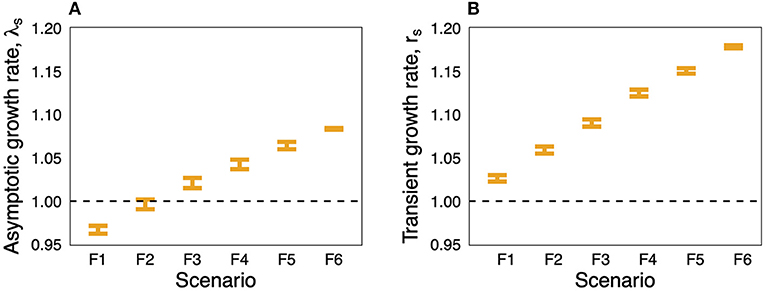
Figure 1. Stochastic (A) asymptotic and (B) transient growth rates with 95% confidence intervals, calculated from 1,000 bootstrap samples. For scenario F1 (i.e., field conditions), the probability of high recruitment years was 0.17 (i.e., once every 6 years). For scenarios F2–F6, the probability of high recruitment increased by 0.17 for each consecutive simulation.

FIGURE 2

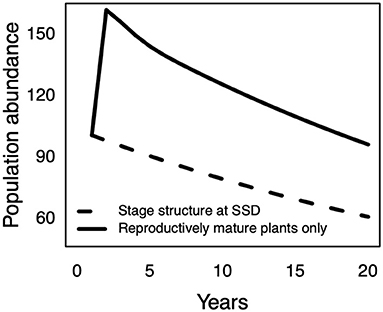
Figure 2. Change in population abundance over time for a plant reintroduction established with mature plants only compared to a population at a stable stage distribution from time t to time t+20 years. Differences in abundance illustrate the effect of population amplification on the density of plant reintroductions over time.

In contrast to the long-term projections, the near-term transient projections suggest the D. waianaeensis reintroduction will grow moderately for all scenarios (Figure 1B). We also found that establishing the D. waianaeensis reintroduction with mature individuals resulted in a higher population size than a population close to its stable stage equilibrium (Figure 2). These results show that a population established with later life stages will not only grow faster than a population started with early life stages, but it will also ultimately result in a greater population density over time. Additionally, the D. waianaeensis population had an extremely low probability of quasi extinction in the near-term for all scenarios F1–F6 (Supplementary Figure 1).

Long-term elasticity for all life stages varied between scenarios F1–F6. However, the survival of mature plants (stasis) was projected to have a substantially greater effect on the long-term population growth rate than all other life stage transitions (Figure 3A). An increase in the probability of high recruitment years increased the relative importance of the seedling to the small immature life stage transition. However, these changes in seedling survival and growth did not change the ranking of which life stage transitions would have the greatest effect on the long-term population growth rate (Figure 3A).

FIGURE 3

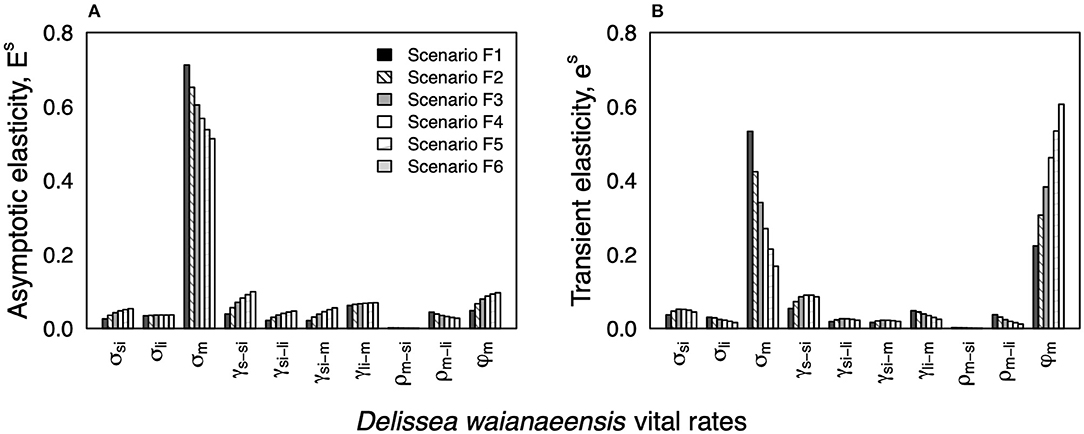
Figure 3. Stochastic (A) asymptotic elasticity E^sδ and (B) transient e^sδ to the mean and variance. Seedling (S); small immature > 40 cm (SI); large immature, >40 cm (LI); and mature signs of reproduction (M). For scenario F1 (i.e., field conditions), the probability of high recruitment years was 0.17 (i.e., once every 6 years). Elasticity values are grouped by demographic process (i.e., stasis σ, survival and growth to the next stage class γ, shrinkage ρ, and seedling recruitment φ_m). For scenarios F2–F6, the probability of high recruitment increased by 0.17 for each consecutive simulation.

Like our results for the long-term stochastic elasticity analysis, survival of mature plants (stasis) was projected to have the greatest effect on the transient near-term population growth rate for scenarios F1–F2 (Figure 3B). Interestingly, when the probability of high seedling recruitment years was ≥0.50 (i.e., scenarios F3–F6), seedling recruitment had a greater influence than mature plant survival on the near-term population growth rate (i.e., transient phase) (Figure 3B).

Discussion

The reintroduction of rare species is a commonly used restoration strategy to prevent rare species extinction worldwide (Maunder, 1992; Maschinski and Haskins, 2012). However, recent studies on the success of reintroduction yielded mixed results (Godefroid et al., 2011; Dalrymple et al., 2012; Guerrant Jr, 2013; Liu et al., 2015). Apparent contradictions of previous studies are due, in part, to the monitoring timeframe used following plant reintroduction efforts and the metric used to define success (e.g., initial survival, recruitment, etc) (Guerrant Jr, 2013; Liu et al., 2015). Here, we highlight the use of demographic data and short- and long-term population projections to evaluate the likely outcome of rare plant reintroduction efforts and set biologically meaningful benchmark goals. Our results are relevant for guiding reintroduction efforts for other long-lived species and evaluating restoration outcomes.

Population Growth Rate Projections

Wong and Ticktin (2015) found that restored populations of a long-lived woody vine that was composed of small individuals grew slower in the short-term than in the long-term. In contrast, our focal D. waianaeensis population that was composed of mature plants was projected to increase over the next 5 years for all six scenarios (Figure 1B). The short-term projections were also consistently higher than the long-term projections. Based on observed field conditions (scenario F1), the population was projected to slowly decline in the long-term (Figure 1A). The higher growth rate in the transient phase than in the asymptotic phase can be explained by the initial population structure dominated by life stages with high initial reproductive value, which can cause population amplification prior to reaching a stable stage distribution (Keyfitz, 1971; Stubben and Milligan, 2007; Ezard et al., 2010; Stott et al., 2011).

Since large individuals are more likely to survive and successfully establish a new population than seedlings, restoration ecologists often use this life stage to establish new plant populations (Maschinski and Haskins, 2012). Here, we demonstrate that establishing rare plant populations with reproductively mature individuals can lead to an increase in the short-term population growth rate. However, as demonstrated by higher growth rate for D. waianaeensis in the short-term (r_s) than in the long-term (λ_s), our results provide a mechanistic understanding for why intrinsic asymptotic growth rate projections commonly do not match realized population abundance (i.e., short-term change in population size) (Guerrant Jr, 1996). Our findings also suggest that stochastic transient projections are more appropriate than asymptotic projections to characterize the near-term population growth rate because it explicitly incorporates the effects of the initial stage structure and captures more realistic environmental variation based on current field conditions. We also illustrate that the near-term population projections of plant reintroductions established with mature individuals can be overly optimistic of long-term outcomes. These finds highlight the importance of decoupling short- and long-term responses when evaluating the use of reintroductions as a successful restoration tool.

For newly established populations that are projected to decline over time, it is essential to identify the level of management needed to achieve long-term goals. For D. waianaeensis, we found that seedling recruitment was temporally variable. We also found that a three-fold increase in the probability of years with high seedling recruitment would be required for the D. waianaeensis reintroduction to persist over time (Figure 1B). A potential restoration strategy to increase the frequency of years with high seedling recruitment (i.e., 3 seedlings per reproductively mature plant) would be to suppress non-native frugivores and seedling herbivores (Bialic-Murphy et al., 2018). While our simulations provide insight into the population-level responses of increased seedling recruitment via pest control, many other exogenous factors can influence temporal variability in seedling recruitment. For example, temporal variability in plant pollinator densities can influence year-to-year fluctuations in seed rain. In this context, hand-pollination could be an additional management strategy to bolster seed production for pollen limited species like D. waianaeensis. Regardless, our simulations emphasize the need to understand the mechanisms responsible for this variability in seedling recruitment, as this vital rate has a strong influence on the likely outcome of restoration efforts. It should be noted that we did not account for potential autocorrelation of stochastic processes (e.g., boom-and-bust cycles of seedling herbivores), which can strongly influence the dynamics of structured populations (Tuljapurkar and Haridas, 2006; Gaoue et al., 2011) and should be a focus of future research.

Elasticity Analysis

Previous studies have demonstrated that perturbations of earlier life stages are often more important in the transient phase than in the asymptotic phase (Fox and Gurevitch, 2000; McMahon and Metcalf, 2008; Haridas and Gerber, 2010; Miller and Tenhumberg, 2010; Bialic-Murphy et al., 2017). Furthermore, anthropogenic stressors can have a greater negative effect on the short-term population growth rate under more optimal abiotic conditions than less optimal abiotic conditions (Gaoue, 2016). Consistent with previous studies, we found that the short- and long-term elasticity patterns for D. waianaeensis diverged and varied based on the probability of years with high recruitment. Our results also illustrate that the key vital rates, including survival and fertility, that contribute to asymptotic population growth also have a strong influence on transient dynamics (Stott et al., 2010). Combined, our results and previous studies illustrate that the relative importance of vital rates on the near-term population growth rate is dependent, in part, on the level of habitat disturbance and variability of key life processes (e.g., seedling recruitment).

Implementing conservation recommendations stemming from stochastic perturbation analysis can be challenging (Ehrlén and Groenendael, 1998; Mills et al., 1999). Though perspective elasticity analysis is often used to indicate which demographic processes would have the greatest positive impact on native plant recovery (e.g., increasing mature plant survival), these recommendations are not always feasible in a naturally variable environment (Ehrlén and Groenendael, 1998; Mills et al., 1999). In this study, we found that maintaining high survival of mature plants in the transient phase would have the greatest influence on populations that were projected to decline over time (scenarios F1–F2) (Figure 3A). However, this management strategy would not lead to the desired outcome (population persistence). Interestingly, we also found that an increase in seedling recruitment would be the most beneficial management strategy for populations that were projected to persist over time (i.e., scenarios F3–F6). Globally, these findings illustrate the use of short- and long-term elasticity analyses to identify the life stages that, if improved by management, will have the greatest impact on population recovery over time.

As demonstrate by our short-term elasticity analysis with respect to perturbation of the variance E^sδ, we show that the population growth rate in the near-term transient phase is strongly influenced by temporal variability in seedling recruitment. Considering the density of non-native pests are often cyclical and dependent on resource availability (Chr, 1999; Korpimäki et al., 2005; Oksanen and Oksanen, 2005), our results suggest a potential management strategy to reduce variation in D. waianaeensis seedling recruitment would be to prioritize the control of biotic stressors in years with high pest outbreaks. However, further investigation is needed to accurately predict the boom-and-bust cycles of non-native pests and explicitly link these fluctuations to changes in D. waianaeensis seedling recruitment. While we did not conduct a manipulative experiment to explicitly test the effects of targeted management actions, our results are informative for setting biologically meaningful benchmark goals for this taxon and balancing the needs between multiple restoration efforts.

Conclusion

Our study has several important conservation implications. First, we demonstrate that the use of later life stages can maximize the establishment and initial short-term growth of plant reintroductions and lead to a larger population abundance than would be expected based on long-term projections (via transient amplification). These results support previous research and illustrate the benefits gained by using larger individuals to establish new populations (Guerrant Jr, 1996; Guerrant Jr and Kaye, 2007). Secondly, we show that long-term asymptotic projections do not capture the dynamics of newly established populations with skewed stage structures in the short-term. Thus, to fully evaluate the probability of population persistence in the short- and long-term requires the combined use of transient short-term and asymptotic long-term projects. Lastly, we demonstrate that the effect of restoration (e.g., increasing the survival of seedling or mature individuals) on the population growth rate is dependent on the timescale of interest and is context specific. Management actions that have the greatest positive effect early in the establishment process differ from management actions that have the greatest effect on the population dynamics once the structure of the population reaches a stable stage distribution. As demonstrated by a pronounced effect of temporal variability in D. waianaeensis seedling recruitment on the short-term population growth rate, our results illustrate the benefit gained by promoting high seedling recruitment early in the reintroduction process for long-lived species that were established with later life stages (reproductively mature plants). These results illustrate the use of short- and long-term elasticity analyses to pinpoint which management actions will have the greatest positive effect and at which time point these actions will be most beneficial. Globally, our results provide empirical support for the claim that caution should be taken when using isolated components of population fitness (e.g., seedling recruitment or mature plant survival) to evaluate the use of reintroductions to promote species recovery and long-term persistence of rare species. This is particularly true when making comparisons between reintroductions that were monitored at different time points and were established with different life stages (seedlings vs. mature plants).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

LB-M conducted the demographic modeling analyses and led the writing, with substantial input and revisions from all authors. LB-M, TK, KK, and OG contributed to the conceptual framework and development of the project. All authors contributed to the article and approved the submitted version.

Funding

This research as funded by the United States Army Corps of Engineers Cooperative Agreement grant ID W91269-11-2-0066. TK's participating in this research was funded by Washington University in St. Louis and by the Helmholtz Recruitment Initiative of the Helmholtz Association.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to thank the staff at the Army Natural Resources Program on O‘ahu for their help with data collection and logistical support.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcosc.2021.814863/full#supplementary-material

References

Albrecht, M. A., Osazuwa-Peters, O. L., Maschinski, J., Bell, T. J., Bowles, M. L., Brumback, W. E., et al. (2018). Effects of life history and reproduction on recruitment time lags in reintroductions of rare plants. Conserv. Biol. 33, 601–611. doi: 10.1111/cobi.13255

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, T., Bowles, M., and McEachern, A. (2003). Projecting the Success of Plant Population Restoration With Viability Analysis. Population Viability in Plants. Berlin: Springer, 313–348.

Google Scholar

Bell, T. J. P., Kristin, I., and Bowles, M. L. (2013). Viability model choice affects projection accuracy and reintroduction decisions. J. Wildl. Manage. 6, 1104–1113. doi: 10.1002/jwmg.525

PubMed Abstract | CrossRef Full Text | Google Scholar

Bialic-Murphy, L., Gaoue, O. G., and Kawelo, K. (2017). Microhabitat heterogeneity and a non-native avian frugivore drive the population dynamics of an island endemic shrub, Cyrtandra dentata. J. Appl. Ecol. 54, 1469–1477. doi: 10.1111/1365-2664.12868

CrossRef Full Text | Google Scholar

Bialic-Murphy, L., Gaoue, O. G., and Knight, T. (2018). Using transfer function analysis to develop biologically and economically efficient restoration strategies. Sci. Rep. 8:2094. doi: 10.1038/s41598-018-20178-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Caswell, H. (2001). Matrix Population Models. New York: Wiley Online Library.

Google Scholar

Chr, N. (1999). Population cycles in voles and lemmings: density dependence and phase dependence in a stochastic world. Oikos 1999, 427–461. doi: 10.2307/3546809

CrossRef Full Text | Google Scholar

Colas, B., Kirchner, F., Riba, M., Olivieri, I., Mignot, A., Imbert, E., et al. (2008). Restoration demography: a 10-year demographic comparison between introduced and natural populations of endemic Centaurea corymbosa (Asteraceae). J. Appl. Ecol. 45, 1468–1476. doi: 10.1111/j.1365-2664.2008.01536.x

CrossRef Full Text | Google Scholar

Crain, B. J., Raymond, L., and Tremblay Ferguson, J. M. (2019). Sheltered from the storm? Population viability analysis of a rare endemic under periodic catastrophe regimes. Popul. Ecol. 61, 74–92. doi: 10.1002/1438-390X.1002

PubMed Abstract | CrossRef Full Text | Google Scholar

Dalrymple, S. E., Banks, E., Stewart, G. B., and Pullin, A. S. (2012). A Meta-Analysis of Threatened Plant Reintroductions From Across the Globe. Plant Reintroduction in a Changing Climatepp. Berlin: Springer 31–50.

Google Scholar

Ehrlén, J., and Groenendael, J. V. (1998). Direct perturbation analysis for better conservation. Conserv. Biol. 12, 470–474. doi: 10.1046/j.1523-1739.1998.96420.x

CrossRef Full Text | Google Scholar

Ellis, M. M., and Crone, E. E. (2013). The role of transient dynamics in stochastic population growth for nine perennial plants. Ecology 94, 1681–1686. doi: 10.1890/13-0028.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Ezard, T. H., Bullock, J. M., Dalgleish, H. J., Millon, A., Pelletier, F., Ozgul, A., et al. (2010). Matrix models for a changeable world: the importance of transient dynamics in population management. J. Appl. Ecol. 47, 515–523. doi: 10.1111/j.1365-2664.2010.01801.x

CrossRef Full Text | Google Scholar

Falk, D. A., Millar, C. I., and Olwell, M. (1996). Restoring Diversity: Strategies for Reintroduction of Endangered Plants. Washington, DC: Island Press.

Google Scholar

Fox, G. A., and Gurevitch, J. (2000). Population numbers count: tools for near-term demographic analysis. Am. Nat. 156, 242–256. doi: 10.1086/303387

PubMed Abstract | CrossRef Full Text | Google Scholar

Franklin, K. R. (2014). “The Oahu Army natural resources program adaptive rat control strategy: protecting endangered Hawaiian species,” in Proceedings of the Vertebrate Pest Conference.

Google Scholar

Gaoue, O. G. (2016). Transient dynamics reveal the importance of early life survival to the response of a tropical tree to harvest. J. Appl. Ecol. 53, 112–119. doi: 10.1111/1365-2664.12553

CrossRef Full Text | Google Scholar

Gaoue, O. G., Horvitz, C. C., and Ticktin, T. (2011). Non-timber forest product harvest in variable environments: modeling the effect of harvesting as a stochastic sequence. Ecol. Appl. 21, 1604–1616. doi: 10.1890/10-0422.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Giambelluca, T. W., Chen, Q., Frazier, A. G., Price, J. P., Chen, Y.-L., Chu, P.-S., et al. (2013). Online rainfall atlas of Hawai‘i. Bull. Amer. Meteor. Soc. 94, 13–316. doi: 10.1175/BAMS-D-11-00228.1

CrossRef Full Text | Google Scholar

Givnish, T. J., Millam, K. C., Mast, A. R., Paterson, T. B., Theim, T. J., Hipp, A. L., et al. (2009). Origin, adaptive radiation and diversification of the Hawaiian lobeliads (Asterales: Campanulaceae). Proc. R. Soc. B Biol. Sci. 276, 407–416. doi: 10.1098/rspb.2008.1204

PubMed Abstract | CrossRef Full Text | Google Scholar

Godefroid, S., Piazza, C., Rossi, G., Buord, S., Stevens, A.-D., Aguraiuja, R., et al. (2011). How successful are plant species reintroductions? Biol. Conserv. 144, 672–682. doi: 10.1016/j.biocon.2010.10.003

CrossRef Full Text | Google Scholar

Guerrant, E. O. Jr (1996). Designing Populations: Demographic, Genetic, and Horticultural Dimensions. Restoring Diversity: Strategies for Reintroduction of Endangered Plants. Washington DC: Island Press, 171–207.

Google Scholar

Guerrant, E. O. Jr (2013). The value and propriety of reintroduction as a conservation tool for rare plants. Botany 91, v–x. doi: 10.1139/cjb-2012-0239

CrossRef Full Text | Google Scholar

Guerrant, E. O. Jr, and Kaye, T. N. (2007). Reintroduction of rare and endangered plants: common factors, questions and approaches. Aust. J. Bot. 55, 362–370. doi: 10.1071/BT06033

PubMed Abstract | CrossRef Full Text | Google Scholar

Haridas, C. V., and Gerber, L. R. (2010). Short-and long-term population response to changes in vital rates: implications for population viability analysis. Ecol. Appl. 20, 783–788. doi: 10.1890/09-0560.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Haridas, C. V., and Tuljapurkar, S. (2007). Time, transients and elasticity. Ecol. Lett. 10, 1143–1153. doi: 10.1111/j.1461-0248.2007.01108.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Innes, J., King, C., Flux, M., and Kimberley, M. (2001). Population biology of the ship rat and Norway rat in Pureora Forest Park, 1983–87. NZ. J. Zool. 28, 57–78. doi: 10.1080/03014223.2001.9518257

CrossRef Full Text | Google Scholar

IUCN (2013). The IUCN Red List of Threatened Species. Available online at: http://www.iucnredlist.org/about/summary-statistics.

Google Scholar

Joe, S. M., and Daehler, C. C. (2007). Invasive slugs as under-appreciated obstacles to rare plant restoration: evidence from the Hawaiian Islands. Biol. Invasions 10, 245–255. doi: 10.1007/s10530-007-9126-9

CrossRef Full Text | Google Scholar

Kawelo, H. K., Harbin, S. C., Joe, S. M., Keir, M. J., and Weisenberger, L. (2012). Unique reintroduction considerations in Hawaii: case studies from a decade of rare plant restoration at the Oahu Army Natural Resource Rare Plant Program. Plant Reintroduction in a Changing Climate. Berlin: Springer, 209–226

Google Scholar

Keyfitz, N. (1971). On the momentum of population growth. Demography 8, 71–80. doi: 10.2307/2060339

CrossRef Full Text | Google Scholar

Koons, D. N., Grand, J. B., Zinner, B., and Rockwell, R. F. (2005). Transient population dynamics: Relations to life history and initial population state. Ecol. Modell. 185, 283–297. doi: 10.1016/j.ecolmodel.2004.12.011

CrossRef Full Text | Google Scholar

Korpimäki, E., Lauri, O., ksanen, Tarja, O., ksanen, Tero Klemola, K. A. I., and Norrdahl Banks, P. B. (2005). Vole cycles and predation in temperate and boreal zones of Europe. J. Anim. Ecol. 1150–1159. doi: 10.1111/j.1365-2656.2005.01015.x

CrossRef Full Text | Google Scholar

Lammers, T. G. (2005). Revision of Delissea (Campanulaceae-Lobelioideae). Syst. Bot. Monogr. 2005, 1–75. doi: 10.2307/25027798

CrossRef Full Text | Google Scholar

Lammers, T. G., and Freeman, C. E. (1986). Ornithophily among the Hawaiian Lobelioideae (Campanulaceae): evidence from floral nectar sugar compositions. Am. J. Bot. 73, 1613–1619. doi: 10.1002/j.1537-2197.1986.tb10913.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, G. h. h, Zhou, J., Huang, D., and s. Li, W. (2004). Spatial and temporal dynamics of a restored population of Oryza rufipogon in Huli Marsh, South China. Restor. Ecol. 12, 456–463. doi: 10.1111/j.1061-2971.2004.00017.x

CrossRef Full Text | Google Scholar

Liu, H., Ren, H., Liu, Q., Wen, X., Maunder, M., and Gao, J. (2015). Translocation of threatened plants as a conservation measure in China. Conserv. Biol. 29, 1537–1551. doi: 10.1111/cobi.12585

PubMed Abstract | CrossRef Full Text | Google Scholar

Maron, J. L., Horvitz, C. C., and Williams, J. L. (2010). Using experiments, demography and population models to estimate interaction strength based on transient and asymptotic dynamics. J. Ecol. 98, 290–301. doi: 10.1111/j.1365-2745.2009.01617.x

CrossRef Full Text | Google Scholar

Maschinski, J., and Duquesnel, J. (2007). Successful reintroductions of the endangered long-lived Sargent's cherry palm, Pseudophoenix sargentii, in the Florida Keys. Biol. Conserv. 134, 122–129. doi: 10.1016/j.biocon.2006.07.012

CrossRef Full Text | Google Scholar

Maschinski, J., and Haskins, K. E. (2012). Plant reintroduction in a changing climate: promises and perils. Island Press. doi: 10.5822/978-1-61091-183-2

CrossRef Full Text | Google Scholar

Maunder, M. (1992). Plant reintroduction: an overview. Biodivers. Conserv. 1, 51–61. doi: 10.1007/BF00700250

CrossRef Full Text | Google Scholar

McMahon, S. M., and Metcalf, C. J. E. (2008). Transient sensitivities of non-indigenous shrub species indicate complicated invasion dynamics. Biol. Invasions 10, 833–846. doi: 10.1007/s10530-008-9242-1

CrossRef Full Text | Google Scholar

Menges, E. S. (2008). Restoration demography and genetics of plants- when is a translocation successful? Aust. J. Bot. 56, 187–196. doi: 10.1071/BT07173

PubMed Abstract | CrossRef Full Text | Google Scholar

Meyer, J.-Y., and Butaud, J.-F. (2009). The impacts of rats on the endangered native flora of French Polynesia (Pacific Islands): drivers of plant extinction or coup de grâce species? Biol. Invasions 11, 1569–1585. doi: 10.1007/s10530-008-9407-y

CrossRef Full Text | Google Scholar

Miller, T. E., and Tenhumberg, B. (2010). Contributions of demography and dispersal parameters to the spatial spread of a stage-structured insect invasion. Ecol. Appl. 20, 620–633. doi: 10.1890/09-0426.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Mills, L. S., Doak, D. F., and Wisdom, M. J. (1999). Reliability of conservation actions based on elasticity analysis of matrix models. Conserv. Biol. 13, 815–829. doi: 10.1046/j.1523-1739.1999.98232.x

CrossRef Full Text | Google Scholar

Morris, W. F., and Doak, D. F. (2002). Quantitative Conservation Biology. Massachusetts: Sinauer Associates Sunderland.

Google Scholar

OANRP (2011). Status reprot for the Makua and Oahu Implementation Plans. Honolulu, Hawaii: Pacific Cooperative Studies Unit.

Google Scholar

Oksanen, L., and Oksanen, T. (2005). The logic and realism of the hypothesis of exploitation ecosystems. Am. Nat. 155, 703–723. doi: 10.1086/303354

PubMed Abstract | CrossRef Full Text | Google Scholar

Pavlik, B. (1996). “Defining and measuring success,” in Restoring Diversity: Strategies for Reintroduction of Endangered Plants. Washington DC: Island Press, 127–155.

Google Scholar

Pender, R. (2013). Floral trait evolution and pollen ecology in the Hawaiian lobeliad genus, Clermontia (Campanulaceae) PhD, University of Hawaii at Manoa, ProQuest LLC (2013).

Google Scholar

Salguero-Gomez, R., and Plotkin, J. B. (2010). Matrix dimensions bias demographic inferences: implications for comparative plant demography. Am. Nat. 176, 710–722. doi: 10.1086/657044

PubMed Abstract | CrossRef Full Text | Google Scholar

Shiels, A. B. (2010). Ecology and impacts of introduced rodents (Rattus spp. and Mus musculus) in the Hawaiian islands. 72 PhD, Dissertations & Theses @ University of Hawai‘i at Manoa. (860957214), Available online at: http://eres.library.manoa.hawaii.edu/login?url=http://search.proquest.com/docview/860957214?accountid=27140

Google Scholar

Shiels, A. B., and Drake, D. R. (2011). Are introduced rats (Rattus rattus) both seed predators and dispersers in Hawaii? Biol. Invasions 13, 883–894. doi: 10.1007/s10530-010-9876-7

CrossRef Full Text | Google Scholar

Shiels, A. B., Pitt, W. C., Sugihara, R. T., and Witmer, G. W. (2014). Biology and impacts of pacific island invasive species. 11. Rattus rattus, the Black Rat (Rodentia: Muridae). Pac. Sci. 68, 145–184. doi: 10.2984/68.2.1

CrossRef Full Text | Google Scholar

Soorae, P. S. (2013). Global Re-introduction Perspectives: 2013. Further case studies from around the globe. IUCN/SSC Re-introduction Specialist Group and Abu Dhabi, UAE: Environment Agency-Abu Dhabi, Gland, Switzerland.

Google Scholar

Soorae, P. S. ed (2018). Global Reintroduction Perspectives, 2018: Case Studies From Around the Globe. IUCN-International Union for Conservation of Nature and Natural Ressources.

Google Scholar

Stott, I., Franco, M., Carslake, D., Townley, S., and Hodgson, D. (2010). Boom or bust? A comparative analysis of transient population dynamics in plants. J. Ecol. 98, 302–311. doi: 10.1111/j.1365-2745.2009.01632.x

CrossRef Full Text | Google Scholar

Stott, I., Townley, S., and Hodgson, D. J. (2011). A framework for studying transient dynamics of population projection matrix models. Ecol. Lett. 14, 959–970. doi: 10.1111/j.1461-0248.2011.01659.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Stubben, C., and Milligan, B. (2007). Estimating and analyzing demographic models using the popbio package in R. J. Stat. Softw. 22, 1–23. doi: 10.18637/jss.v022.i11

CrossRef Full Text | Google Scholar

Tuljapurkar, S., and Haridas, C. V. (2006). Temporal autocorrelation and stochastic population growth. Ecol. Lett. 9, 327–337. doi: 10.1111/j.1461-0248.2006.00881.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Tuljapurkar, S., Horvitz, C. C., and Pascarella, J. B. (2003). The many growth rates and elasticities of populations in random environments. Am. Nat. 162, 489–502. doi: 10.1086/378648

PubMed Abstract | CrossRef Full Text | Google Scholar

USFWS (1998). Recovery Plan for Oahu Plants. Portland, OR: USFWA.

Google Scholar

USFWS (2012). Endangered Species. Available online at: http://www.fws.gov/pacificislands/species.html (accessed December 1, 2014).

Google Scholar

Wagner, W. L., Herbst, D. R., Khan, N., and Flynn, T. (2012). Hawaiian vascular plant updates: a supplement to the Manual of the Flowering Plants of Hawai'i and Hawai'i's ferns and fern allies. Available online at: http://www.botany.si.edu/pacificislandbiodiversity/hawaiianflora/supplement.htm (accessed December 5, 2013).

Google Scholar

Wagner, W. L., Herbst, D. R., and Sohmer, S. H. (1999). Manual of the flowering plants of Hawai'i, Vols. 1 and 2. University of Hawai'i and Bishop Museum Press.

Google Scholar

Wilcove, D. S., Rothstein, D., Dubow, J., Phillips, A., and Losos, E. (1998). Quantifying threats to imperiled species in the United States. Bioscience 48, 607–615. doi: 10.2307/1313420

PubMed Abstract | CrossRef Full Text | Google Scholar

Wong, T. M., and Ticktin, T. (2015). Using population dynamics modelling to evaluate potential success of restoration: a case study of a Hawaiian vine in a changing climate. Environ. Conserv. 42, 20–30. doi: 10.1017/S0376892914000204

PubMed Abstract | CrossRef Full Text | Google Scholar