Simulating combined monoaminergic depletions in a PD animal model through a bio-constrained differential equations system

Introduction: Historically, Parkinson's Disease (PD) research has focused on the dysfunction of dopamine-producing cells in the substantia nigra pars compacta, which is linked to motor regulation in the basal ganglia. Therapies have mainly aimed at restoring dopamine (DA) levels, showing effectiveness but variable outcomes and side effects. Recent evidence indicates that PD complexity implicates disruptions in DA, noradrenaline (NA), and serotonin (5-HT) systems, which may underlie the variations in therapy effects.

Methods: We present a system-level bio-constrained computational model that comprehensively investigates the dynamic interactions between these neurotransmitter systems. The model was designed to replicate experimental data demonstrating the impact of NA and 5-HT depletion in a PD animal model, providing insights into the causal relationships between basal ganglia regions and neuromodulator release areas.

Results: The model successfully replicates experimental data and generates predictions regarding changes in unexplored brain regions, suggesting avenues for further investigation. It highlights the potential efficacy of alternative treatments targeting the locus coeruleus and dorsal raphe nucleus, though these preliminary findings require further validation. Sensitivity analysis identifies critical model parameters, offering insights into key factors influencing brain area activity. A stability analysis underscores the robustness of our mathematical formulation, bolstering the model validity.

Discussion: Our holistic approach emphasizes that PD is a multifactorial disorder and opens promising avenues for early diagnostic tools that harness the intricate interactions among monoaminergic systems. Investigating NA and 5-HT systems alongside the DA system may yield more effective, subtype-specific therapies. The exploration of multisystem dysregulation in PD is poised to revolutionize our understanding and management of this complex neurodegenerative disorder.

1 Introduction

Common theoretical and empirical approaches studying Parkinson's disease (PD) focus on dysfunctions in dopamine (DA)-producing cells in the substantia nigra pars compacta. This area projects to the striatum, the principal input gate of the basal ganglia, subcortical nuclei critical to managing motor behavior (Tozzi et al., 2021; Ledonne et al., 2023). Thus, a consistent reduction of striatal DA levels causes malfunctioning of the basal ganglia circuits that, in turn, contribute to the emergence of different PD symptoms (Pare et al., 1990; Dovzhenok and Rubchinsky, 2012; Caligiore et al., 2019). The main PD motor symptoms include resting tremor, bradykinesia, rigidity, and freezing of gait (Jankovic and Kapadia, 2001; Obeso et al., 2010; Caligiore et al., 2019). Cognitive impairments might be evident at diagnosis, even though they significantly manifest in the later stage of the disease progression (Williams-Gray et al., 2007; Aarsland et al., 2009). Moreover, several recent studies suggest that psychiatric disorders, such as depression or anxiety, often develop several years before typical motor symptoms (Faivre et al., 2019). In particular, motivational system dysfunctions manifest early in PD (Pagonabarraga et al., 2015; Cohen et al., 2022; Favier et al., 2022).

Based on this evidence, drug therapies for PD often aim at recovering DA levels (Antonini et al., 2023; Hansen et al., 2023; Pirker et al., 2023). However, while these approaches yield benefits for most PD motor dysfunctions, they generate variable responsiveness for others [e.g., resting tremor (Helmich et al., 2012; Wu and Hallett, 2013; Connolly and Lang, 2014)]. In addition, long-term use of DA may cause adverse effects such as dyskinesia and impulse control disorders (Voon and Fox, 2007; Espay et al., 2018; Castela et al., 2023). The dysfunctional mechanisms leading to PD involve a network of areas and circuits interacting dynamically and influencing each other rather than specific regions and molecular mechanisms working in isolation (Obeso et al., 2010; Caligiore et al., 2016, 2017, 2022; Helmich et al., 2018; Zach et al., 2020). This systemic view is critical for understanding the lack of DA-based therapy consistency. Several studies suggest that, aside from the dopaminergic system, PD could also involve dysfunctions of noradrenergic and serotonergic neuronal populations (Jellinger, 1991; Perez-Lloret and Barrantes, 2016; Wilson et al., 2019; Caligiore et al., 2022; Hezemans et al., 2022). In PD, impairments of locus coeruleus (LC), the dorsal pontine nucleus that synthesizes noradrenaline (NA), begin before nigral pathology and appear to be severe (German et al., 1992; Delaville et al., 2011, 2012). Similarly, the dorsal raphe nucleus (DRN), which is critical for serotonin (5-HT) release, could show impairments earlier than the dopaminergic system and is involved with the development of both non-motor and motor symptoms (Politis and Niccolini, 2015; Jankovic, 2018; Pasquini et al., 2018; Caligiore et al., 2021; Prange et al., 2022).

Starting from this system-level perspective, we propose a bio-constrained computational model that, for the first time, explicitly investigates the neural mechanisms underlying interactions between DA, NA, and 5-HT in a PD animal model. Data on basal ganglia and monoamine areas physiology (Kang and Kitai, 1993; Szabo and Blier, 2001; Liu et al., 2002; Damodaran et al., 2014), including evidence on the effects of NA and 5-HT depletions in a PD animal model (Delaville et al., 2012), constrain key model parameters, hinting at a potential causal dynamical interaction between basal ganglia regions and the areas responsible for neuromodulators release. The model produces predictions on expected activity changes in other brain areas which are not investigated in the target experiments of Delaville et al. (2012). It also highlights the potential efficacy of alternative treatments targeting LC and DRN, yet these are preliminary findings whose effectiveness needs further validation. A sensitivity analysis of the model parameters allows us to identify the critical features affecting the model activity. In this way, it could be possible to frame the most important features affecting the mechanisms underlying the activity of simulated brain areas. Finally, we made a stability analysis that confirms the soundness of the mathematical formulation used to design the model. This point could be critical to validate the effectiveness of the model (Fornari et al., 2020; Shi et al., 2020). It is a relevant aspect that is not readily apparent and seldom explored within computational neuroscience literature. While the soundness of the mathematical formulation is crucial, it becomes irrelevant if the model lacks robust theoretical foundations. Thus, both aspects, mathematical integrity and theoretical underpinnings, serve as indispensable pillars for developing a computational model.

The system-level computational model proposed in this article emphasizes that PD is a multifactorial disorder and opens promising avenues for early diagnosis and subtype-specific treatment tools, harnessing the intricate interactions among monoaminergic systems (Marras et al., 2020; Caligiore et al., 2021; Severson et al., 2021). The investigation into multisystem dysregulation in PD is poised to profoundly transform our comprehension and handling of this intricate neurodegenerative condition.

2 Methods

2.1 Dynamical model

We introduce a novel model designed to explore the dynamic interactions of three prominent brain monoamines: dopamine (DA), noradrenaline (NA), and serotonin (5-HT), within both typical and pathological contexts. Figure 1 provides an overview of the neural circuitry we assessed. We mimic monoamine efflux by simulating the activation of critical brain regions responsible for initiating such release. Regarding 5-HT/DRN, it is reported that DRN sends projection to striatum (Vertes, 1991; Miyanishi et al., 2023), and we model these projection as excitatory on both direct and indirect pathway. DRN to GP is modeled as excitatory due to serotonin increasing the firing rate of GP neurons as reported in the literature (Chen et al., 2008; Rav-Acha et al., 2008). The projections from DRN to SNcVTA were reported by Gervais and Rouillard (2000) to be dense, and the authors underline the possibility of this connection to be mainly inhibitory; there is a possibility for this projection to be both excitatory and inhibitory but future studies are required to investigate this matter further. Here, we assume this connection to be inhibitory as previously reported by several studies (Dray et al., 1976, 1978; Kelland et al., 1990, 1993). The projection from DRN to LC is also inhibitory (Segal, 1979). StrD1/D2 has inhibitory effects on GP (Nicholson and Brotchie, 2002), while SNcVTA has inhibitory effects on strD2 and excitatory effects on strD1 (Reed et al., 2013); moreover, SNcVTA has excitatory effects on LC as suggested in the literature (Deutch et al., 1986; Lin et al., 2008). The connection from SNcVTA to DRN is modeled as inhibitory because it is reported that after DA depletion, there is an increase of spontaneous activity in DRN (Wang et al., 2009).

Figure 1

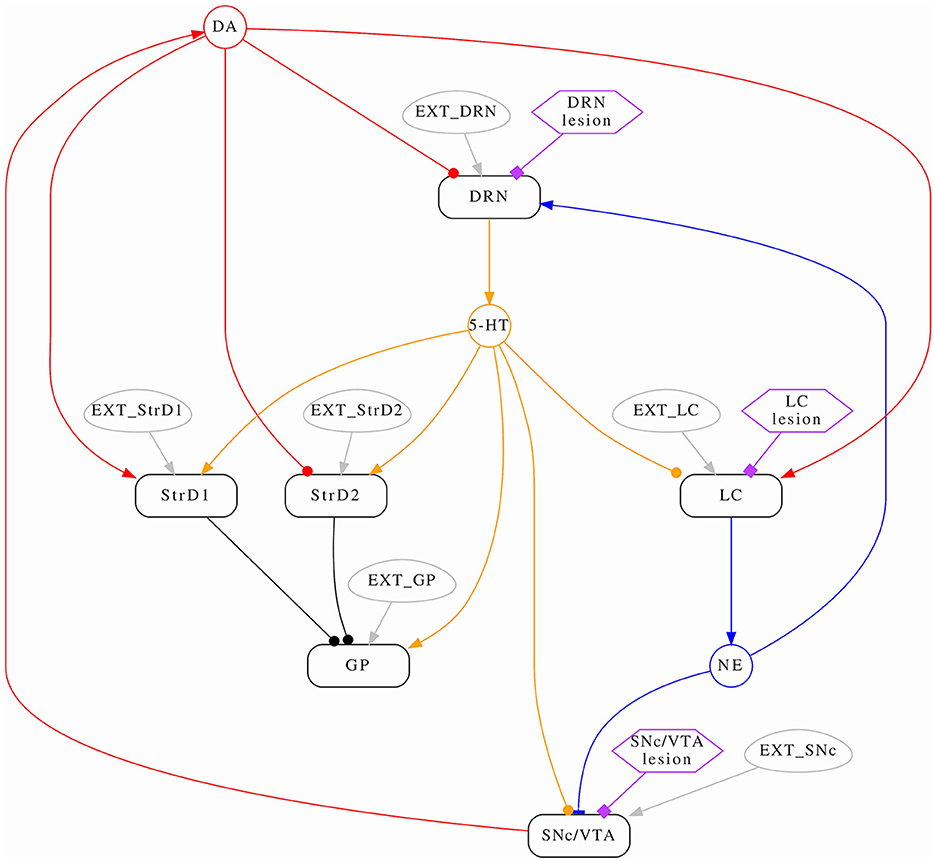
Figure 1. Conceptual model schema. The average activation frequencies of six brain areas are modeled (rounded rectangles); some interactions are modulated by monoamines (circles). Arrows represent positive (excitatory) effects, while circles represent negative (inhibitory) effects. Noradrenaline has a non-linear (both excitatory and inhibitory) effect on SNcVTA which is indicated by a bar. Each area has a corresponding stimulus (ovals) which represents self-activation as well all any other stimulus the area might receive from the rest of the brain which is not modeled. Lastly, hexagons serve as indicators for identifying the areas influenced by the administration of specific drugs.

The schema from Figure 1 implies the following system of equations:

$\begin{array}{l}\stackrel{.}{\text{GP}}=-\frac{1}{{\tau }_{\text{GP}}}\text{GP}-{\alpha }_{\text{GP}}^{\text{StrD}1}\text{StrD}1-{\alpha }_{\text{GP}}^{\text{StrD}2}\text{StrD}2+{\alpha }_{\text{GP}}^{\text{DRN}}\text{DRN}\\ +{\alpha }_{\text{GP}}^{\text{ext}}& (1)\end{array}$

$\begin{array}{l}\stackrel{.}{\text{StrD}1}=-\frac{1}{{\tau }_{\text{StrD}1}}\text{StrD}1+{\alpha }_{\text{StrD}1}^{\text{SNcVTA}}\text{SNcVTA}+{\alpha }_{\text{StrD}1}^{\text{DRN}}\text{DRN}\\ +{\alpha }_{\text{StrD}1}^{\text{ext}}& (2)\end{array}$

$\begin{array}{l}\stackrel{.}{\text{StrD}2}=-\frac{1}{{\tau }_{\text{StrD}2}}\text{StrD}2-{\alpha }_{\text{StrD}2}^{\text{SNcVTA}}\text{SNcVTA}+{\alpha }_{\text{StrD}2}^{\text{DRN}}\text{DRN}\\ +{\alpha }_{\text{StrD}2}^{\text{ext}}& (3)\end{array}$

$\begin{array}{l}\stackrel{.}{\text{SNcVTA}}=-\frac{1}{{\tau }_{\text{SNcVTA}}}\text{SNcVTA}-{\alpha }_{\text{SNcVTA}}^{\text{DRN}}\text{DRN}-{\alpha }_{\text{SNcVTA}}^{\text{LC}}\text{LC}\\ +{\beta }_{\text{SNcVTA}}^{\text{LC}}{\text{LC}}^2\\ +{\alpha }_{\text{SNcVTA}}^{\text{ext}}& (4)\end{array}$

$\begin{array}{l}\stackrel{.}{\text{DRN}}=-\frac{1}{{\tau }_{\text{DRN}}}\text{DRN}-{\alpha }_{\text{DRN}}^{\text{SNcVTA}}\text{SNcVTA}+{\alpha }_{\text{DRN}}^{\text{LC}}\text{LC}\\ +{\alpha }_{\text{DRN}}^{\text{ext}}& (5)\end{array}$

$\begin{array}{l}\stackrel{.}{\text{LC}}=-\frac{1}{{\tau }_{\text{LC}}}\text{LC}+{\alpha }_{\text{LC}}^{\text{SNcVTA}}\text{SNcVTA}-{\alpha }_{\text{LC}}^{\text{DRN}}\text{DRN}\\ +{\alpha }_{\text{LC}}^{\text{ext}}& (6)\end{array}$

where the abbreviated notation ẋ stands for $\frac{dx}{dt}$ and:

• the time constants τ_x are all positive and refer to a dampening term which brings back the activity of each area to its resting activation level in the absence of external stimulation (see Table 1);

• the parameters α represent the linear components of the system, are all positive, and follow the notation: ${\alpha }_{to}^{from}$; ${\alpha }_x^{\text{ext}}$ are synthetic terms that implicitly account for the rest activation of each area and other external stimuli which are not part of the modeled circuit; β is also positive and follows the same notation ${\beta }_{to}^{from}$ but accounts for non-linear effects;

• the ratios of monoaminic projections from an area to its targets are assumed to be constant.

Table 1

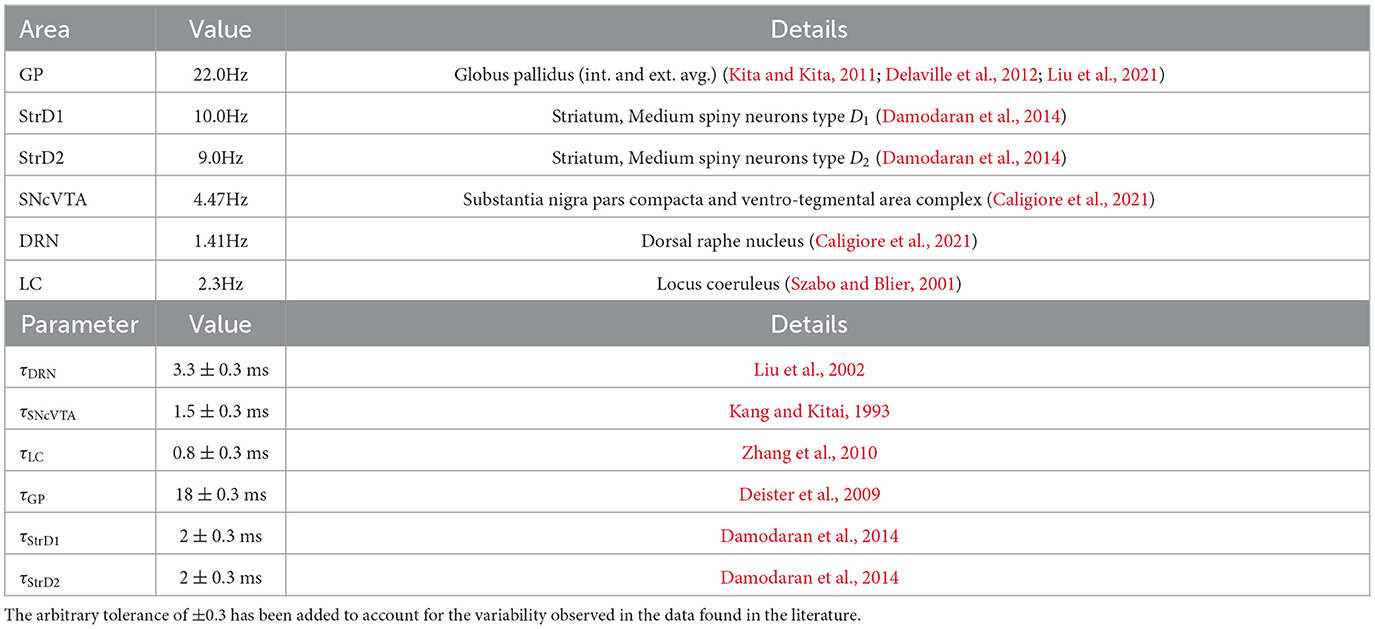
Table 1. Average activity target of the simulated healthy subjects, and time constants used in simulated healthy subjects.

2.2 Formalization

Let y be the status vector of the system of Equations 1–6; we also define s to be the size of y, hence the number of equations in the system. We therefore have

$\begin{array}{ll}\text{y}={(\text{GP},\text{StrD}1,\text{StrD}2,\text{SNcVTA},\text{DRN},\text{LC})}^T\in {ℝ}^s& (7)\end{array}$

The system is autonomous and can therefore be represented in the form:

$\begin{array}{ll}\stackrel{.}{\text{y}}(t)=\text{f}(\text{y}(t))& (8)\end{array}$

where each component of the function f:(ℝ × ℝ^s) → ℝ^s is defined by the corresponding equation in Equations 1–6, and where we assume the initial state y(t₀) = y₀ to be known.

Starting from Equation 8, Equations 1–6 can be represented in matrix form:

$\begin{array}{ll}\stackrel{.}{\text{y}}(t)=A\text{y}(t)+C(\text{y}(t).\text{y}(t))+\text{b},& (9)\end{array}$

where a_ij = 0 if the corresponding ${\alpha }_i^j$ is not defined and likewise b_i = 0 if ${\alpha }_i^{ext}$ is not defined, and also $c_{ij}={\beta }_i^j$ with c_ij = 0 if the corresponding ${\beta }_i^j$ coefficient is not defined; “°” indicates the element-wise vector product (or Hadamard).

2.3 Modeling lesions

Each element within the status vector (Equation 7) corresponds to the average activation frequency of the corresponding brain region. This, in turn, serves as an indirect indicator of the production and projection of monoamines to the affected areas. We posit that a depletion in monoamines results from the death or temporary incapacitation of a portion of neurons within a given area, which is directly manifested as a decrease in the average activation frequency of that area. Consequently, when the SNcVTA is lesioned, we observe a reduction in DA levels; lesioning the DRN results in a decrease in 5-HT, and lesioning the LC leads to a reduction in NA levels.

Each equation of the model is composed by three conceptual blocks: a damping term, a constant stimulus, and a reaction to projections from other areas. The constant stimulus represents external and internal activation sources that are not directly accounted for in this model. Together with the damping term, the constant stimulus accounts for the resting behavior of the area: The area will stabilize to its rest activation frequency. In absence of reaction terms, each equation has an equilibrium point:

$\begin{array}{ll}{y}^{\prime }(t)=-\frac{1}{\tau }y(t)+k,y^{\prime }(t)\equiv 0\Rightarrow y(t)=k\tau .& (10)\end{array}$

The time constants τ are derived from the literature (see Table 1), and we assume them to be typical values for the specific kind of neuron found in an area; we therefore assume that they are not altered by the lesion. It is, however, reasonable to expect that the sensitivity of lesioned area to internal and external stimuli will change in such a way that the average activation frequency changes to the levels which have been experimentally measured.

We can now define multiple versions of the same model, which differ from the healthy model only for the constant term and reaction coefficients of the lesioned area. For example, suppose a healthy subject is modeled using model (Equation 9) by the coefficients held in A, C, b. Having received a dopaminergic lesion (hence, SNcVTA neurons are malfunctioning), the subject will now be modeled by the same equations of model (Equation 9) but this time with coefficients A_LDA, C_LDA, b_LDA, which differ by A, C, b only by the values corresponding to the parameters of the equation for SNcVTA, namely, ${\alpha }_{\text{SNcVTA}}^{\text{DRN}}$, ${\alpha }_{\text{SNcVTA}}^{\text{LC}}$, ${\beta }_{\text{SNcVTA}}^{\text{LC}}$, ${\alpha }_{\text{SNcVTA}}^{\text{ext}}$. Likewise, when the subject also receives a serotonergic lesion, there will be a third set of parameters A_LDA+L5HT, C_LDA+L5HT, b_LDA+L5HT which again differ from A_LDA, C_LDA, b_LDA only by the parameters corresponding to the equation for DRN, and so on.

A single subject is therefore represented by multiple versions of the parameters matrices A, C, b, each set corresponding to one particular state: healthy (also called SHAM), LDA, L5HT, LNE when only one of the lesions is applied, LDA + L5HT, LDA + LNE when lesions are combined, and so on.

2.4 Stability conditions

The solution trajectories of a dynamical system are referred to as “stable” when small perturbations of the initial conditions lead to trajectories which have fundamentally the same behavior of the unperturbed ones and differ from the latter in a proportional way with respect to the the perturbation magnitude. An unstable system can otherwise have a high sensitivity to such perturbation, which originate wildly varying solution behavior. At the limit of instability, there are chaotic systems, for which very small perturbation of the initial conditions can lead to completely different dynamical behavior. Stability is a property of a particular solution (Kelley and Peterson, 2001; Lakshmikantham and Trigiante, 2002; Riley et al., 2006; Press, 2007; Butcher, 2016).

A system which has stable solution trajectories can have great predictive power since its low sensitivity to the initial conditions results in solutions which have comparable errors. Chaotic systems, on the other hand, are so sensitive to the errors on the initial conditions that it is effectively impossible to use them for obtaining useful predictions. For instance, weather is a chaotic system, and that is why it is so difficult to compute reliable long-term weather predictions. Fortunately enough, the aspects of brain chemistry that we are simulating in this study do not exhibit chaotic behavior; on the contrary, they exhibit self-regulation and great resilience to perturbations. It makes therefore sense to require them to be simulated using a system of equations having asymptotically stable equilibria.

Equation 9 has at least one equilibrium point $\bar{\text{y}}$ such that:

$\begin{array}{ll}\text{0}=A\bar{\text{y}}+C(\bar{\text{y}}.\bar{\text{y}})+\text{b}& (11)\end{array}$

The stability properties of the equilibrium point in Equation 11 are analyzed in details in Appendix 1; the resulting stability conditions are employed as one of the components of the fitness measure of the model, as described in Section 2.7. In this way, it is ensured that all the solution trajectories simulated by the model are asymptotically stable. Consequently, the numerical trajectories exhibit the expected behavior even for long-time simulations.

3 Simulation setup

3.1 Free parameters and constants

As hinted in Sections 2.3 and 3.3, we require a model to be able to reproduce its target data in four different states at the same time: healthy (SHAM), dopaminergic lesion (LDA), noradrenergic lesion (LNE), and serotonergic lesion (L5HT). The combinations LDA + LNE and LDA + L5HT are instead constrained only to a target range, to be able to also serve as a prediction (and hence as a measure of the agreement of the model with experimental data). Below, we briefly outline the mathematical formalism used to assess the model's stability properties and to establish the simulation setup (Equations 12–18).

Let S_i be the set of parameters that define the model representing test subject i. S_i contains the following:

• Six time constants: τ_GP, τ_StrD1, τ_StrD2, τ_SNcVTA, τ_DRN, τ_LC. As discussed in Section 2.3, the time constants are derived from the literature and are not optimized;

• SHAM: the healthy model has 20 free parameters, namely, all α and β parameters defined in Equations 1–6;

• LDA: the dopaminergic lesion instance has four free parameters, that is, ${\alpha }_{\text{SNcVTA}}^{\text{DRN}}$, ${\alpha }_{\text{SNcVTA}}^{\text{LC}}$, ${\beta }_{\text{SNcVTA}}^{\text{LC}}$, ${\alpha }_{\text{SNcVTA}}^{\text{ext}}$. Those are all the parameters of the SNcVTA equation. All the other parameters are kept constant and are the same as in SHAM;

• L5HT: the serotonergic lesion instance has three free parameters, that is, ${\alpha }_{\text{DRN}}^{\text{SNcVTA}}$, ${\alpha }_{\text{DRN}}^{\text{LC}}$, ${\alpha }_{\text{DRN}}^{\text{ext}}$. All the other parameters are kept constant and are the same as in SHAM;

• LNE: the Noradrenergic lesion has three free parameters, that is, ${\alpha }_{\text{LC}}^{\text{SNcVTA}}$, ${\alpha }_{\text{LC}}^{\text{DRN}}$, ${\alpha }_{\text{LC}}^{\text{ext}}$. All the other parameters are kept constant and are the same as in SHAM;

• LDA + L5HT, LDA + LNE: the combination of lesions do not have any free parameters but are constructed by applying to the SHAM values, in order, the relevant values from each lesion.

The set S_i therefore contains a total of 36 parameters, 30 of which must be optimized at the same time to fit the available data. Appropriate subsets of the parameters in S_i are then used to build the corresponding matrices A, C, b to completely define (Equation 9). and hence compute its solution and properties.

3.2 Model fitness definition

We will hereafter refer to S_i as the complete model for subject i, since it is the set of parameters that completely define it. The variations $S_i^{\text{kind}}$, such as $S_i^{\text{SHAM}}$ and $S_i^{\text{LDA}}$, will refer instead to the subset of parameters which are currently being applied to actually simulate the model.We will denote one solution as

$\begin{array}{ll}{S}_i^{\text{SHAM}}(y_0,t_0,T)=Y=\left(\begin{array}{ccc}{y}_1(t_0)& \cdots & y_1(t_N)\\ ⋮& & ⋮\\ y_s(t_0)& \cdots & y_s(t_N)\end{array}\right)& (12)\end{array}$

Y is therefore the solution obtained by integrating the model in the interval [t₀, T], with the starting vector y₀, and using the SHAM subset of parameters. The matrix Y comprises s rows, and the i-th row corresponds to the i-th equation in the system of differential equations.

The number N of integration steps, as well as their size, is usually variable and chosen by the integration method case-by-case; hence, it can potentially be different for each subset of parameters.

Likewise, we will denote with $T_i^{kind}$ the corresponding reference solutions that will be used to evaluate the fitness of the model:

$\begin{array}{ll}{T}_i^{SHAM}(J)=Y_T(J)=\left(\begin{array}{ccc}{y}_{T1}(t_0)& \cdots & y_{T1}(t_N)\\ ⋮& & ⋮\\ y_{Ts}(t_0)& \cdots & y_{Ts}(t_N)\end{array}\right)& (13)\end{array}$

where J = [t₀, ..., t_n] is a vector of times. The fitness of a model is finally obtained as a combination of many fitness figures f_i∈[0, 1], which measure a wide range of properties of the simulated solution with respect to the reference ones. In more detail:

$\begin{array}{ll}f=\sqrt{{\displaystyle \underset{i}{min}}(f_i)\frac{1}{n}{\displaystyle \sum _{i=1}^n}{f}_i},f_i\in F,n=\left|F\right|.& (14)\end{array}$

Details about the fitness computations are reported in Appendix 2.

3.3 Synthetic reference data

The average brain activation in healthy subjects, as well as the time constants, has been extracted from the literature and are reported in Table 1. Starting from these average values, we craft a synthetic activity profile for a population of subjects (240 simulated subjects). This is achieved by modeling a normal distribution centered around the average value, with a normalized maximum excursion of ±50%.

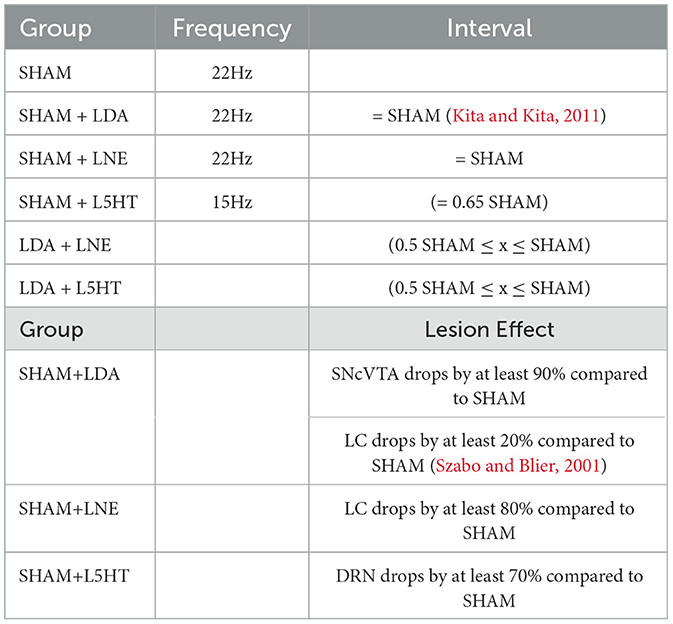
In the reference (or target) data that we aim to replicate using the computational model, a population of adult male rats is subdivided into six groups:

where:

• SHAM: indicates that subjects are treated with saline;

• LDA: dopamine depletion;

• LNE: noradrenaline depletion;

• L5HT: serotonin depletion.

Table 2 summarizes the reference changes in GP activity.

Table 2

Table 2. Reference data for area interaction and lesion effects.

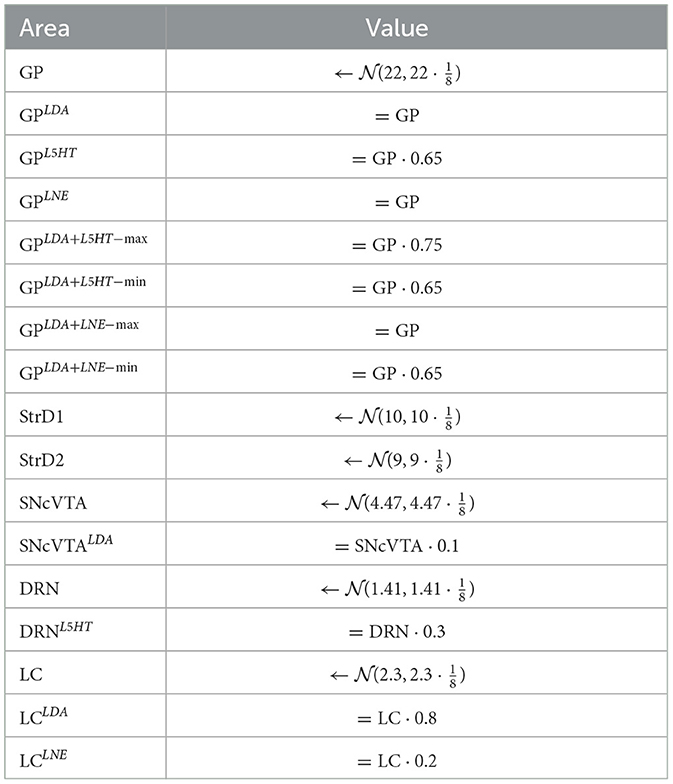
The experimental data we have collected, summarized in Tables 1, 2, ultimately consist of normal distributions around their respective center values which are to be considered constant; we do not have explicit information about the dynamic behavior of the system or about the transition from a state to the other. Of course, each subject must go through a dynamic transition from a healthy state to a lesioned state, but both states must be asymptotically stable solutions for the model. Since there is no single study that lists all the required brain area activation values for a particular subject at the same time, we have no choice but to generate a synthetic population of virtual subjects with area activation values which lie within the distributions identified across the literature. The generated target value distributions for all cases are summarized in Table 3 and Figure 2.

Table 3

Table 3. Target values.

Figure 2

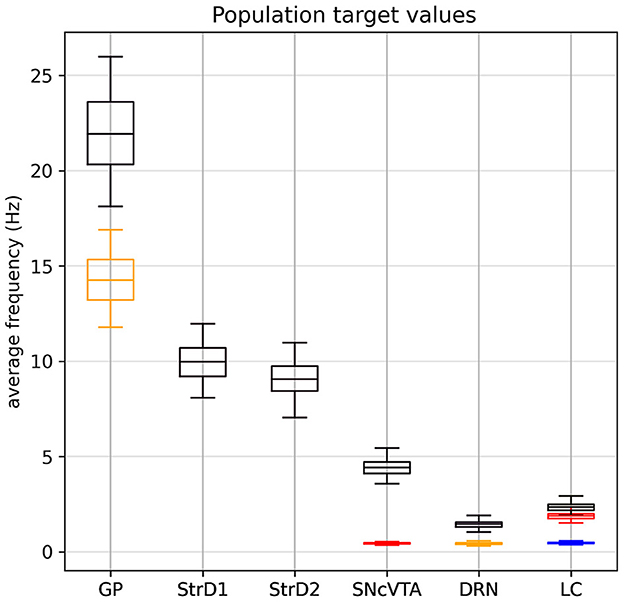
Figure 2. Generated target value distribution for all cases: in black, the SHAM case. The LDA dopaminergic lesion target (red) differs from SHAM only for SNcVTA and LC. The serotonergic L5HT lesion target (yellow) differs from SHAM only in for GP and DRN. Finally, the noradrenergic LNE lesion target (blue) differs from SHAM only for LC. Values for each individual are generated according to Section 3.3: Each area follows a normal distribution around a center value with a maximum spread of ±50% (4σ = 0.5μ). Lesioned activation values of an area, when defined, are scaled according to Table 2.

In particular, we generate a number of subjects S_i and each of them is associated with a set of target values T_i which are defined as described in Table 3, where $x\leftarrow \mathcal{N}(\mu ,\sigma )$ indicates that x is a random number drawn from a normal distribution using the provided parameters. Given the synthetic nature of this data, it is reasonable to assume activities of each area to have the same distribution. We impose every value to lie within ±50% of the center value by imposing $4\sigma =\frac{1}{2}\mu$. Since data from literature can be interpreted as an average percentage change in activity for lesioned areas, we decided to treat the generated healthy value for an area as the reference level of an individual and use that as a base to generate the lesioned values that where needed. In this way, a subject that has a higher than average value for an area in healthy conditions will also have an higher than average level in the same area when lesioned, although the value will change by the required proportional amount.

Reference solutions for subject i are therefore composed of constant values:

$\begin{array}{ll}{T}_i^d(J)=\left(\begin{array}{ccc}G{P}^d& \cdots & G{P}^d\\ ⋮& & ⋮\\ L{C}^d& \cdots & L{C}^d\end{array}\right)\in {ℝ}^{s\times n+1}& (15)\end{array}$

where d is one of SHAM, LDA, L5HT, LNE, LDA+L5HT, LDA+LNE; the appropriate value of each area for the respective lesion is chosen according to d when available, otherwise defaults to the SHAM (not labeled) value.

3.4 Choosing the simulation time

The simulation time is arbitrarily set to 0.5s under the assumption that the basic behavior of each equation in the system will resemble (Equation 10); hence, the transition time between any state to a stable solution will be dominated by the slowest time constant (which is derived from the literature). In fact, since the solution to:

$\begin{array}{ll}{y}^{\prime }(t)=-\frac{1}{\tau }y(t)+k& (16)\end{array}$

assuming y(0) = 0, is

$\begin{array}{ll}y(t)=-k\tau e^{-\frac{t}{\tau }}+k\tau & (17)\end{array}$

we can compute the time it takes for the solution to grow past 99% of its limit value:

$\begin{array}{ll}0.99k\tau =-k\tau e^{-\frac{t}{\tau }}+k\tau \Rightarrow t=log(0.01)\tau \approx 5\tau & (18)\end{array}$

(which in engineering contexts is broadly known as the “rule of the five taus”).

In this specific case, the slowest τ ≤ 20ms, therefore we can assume the transient phase to be finished after 5·0.02s = 0.1s, and a time 5 times longer, 0.5s, should be adequate to see a long stable steady state, and we would expect the dynamic behavior to have stabilized already around 0.1s.

3.5 Model parameters dimensionality analysis

Each component of the status vector y (Equation 9) directly represents the average activation frequency of a brain area and is therefore expressed in Hz. The derivative terms in each equation of Equations 1–6 are all derivatives with respect to time of a frequency; hence, they are all expressed in Hz/s (or 1/s²). Consequently, the external stimulus parameters α^ext must also be expressed in Hz/s, while the remaining α parameters must be 1/s, hence Hz. The second order term parameter β is instead a pure number, since Hz² =1/second² =Hz/s. Finally, all time constants τ are naturally expressed in seconds.

3.6 Simulation and optimization

All simulations are obtained using a variable order, variable step scheme backward-differentiation formulas (BDF) (Byrne and Hindmarsh, 1975) integrator provided by the Python scipy library. The optimization of parameters is then performed using differential evolution (DE), also as provided by the Python scipy package, with a population of 240 simulated subjects, DE/best/1/exp strategy with C_r = F = 0.95 initialized with a uniform Halton distribution.

An external optimization cycle which sets different random generator seeds has been used to retry the cases which did not find convergence. In so doing, all cases did eventually converge after a few attempts. The full codebase can be found at https://github.com/WohthaN/Simulating_noradrenaline_and_serotonin_depletions_in_parkinson.

4 Results

All models fit the corresponding target values as defined in Table 3 with a fitness f≥1 − 10⁻⁸. Since the measure is dominated by the smallest fitness value being combined by definition, also the mean square difference of each component of the solution from its reference value is bonded by the same order of magnitude, which is a suitable precision for the purposes of this study. Figure 3 shows an overview of the simulated behavior of all six areas in all conditions. The model reproduces the target data with animals presented in Delaville et al. (2012). In all cases, the simulated values for the SHAM case overlap the target values with the imposed tolerance. In the lesion groups, all areas which do not have a target defined are model predictions. All instances of the model meet the stability conditions defined in Section 2.4 as imposed by the fitness measure.

Figure 3

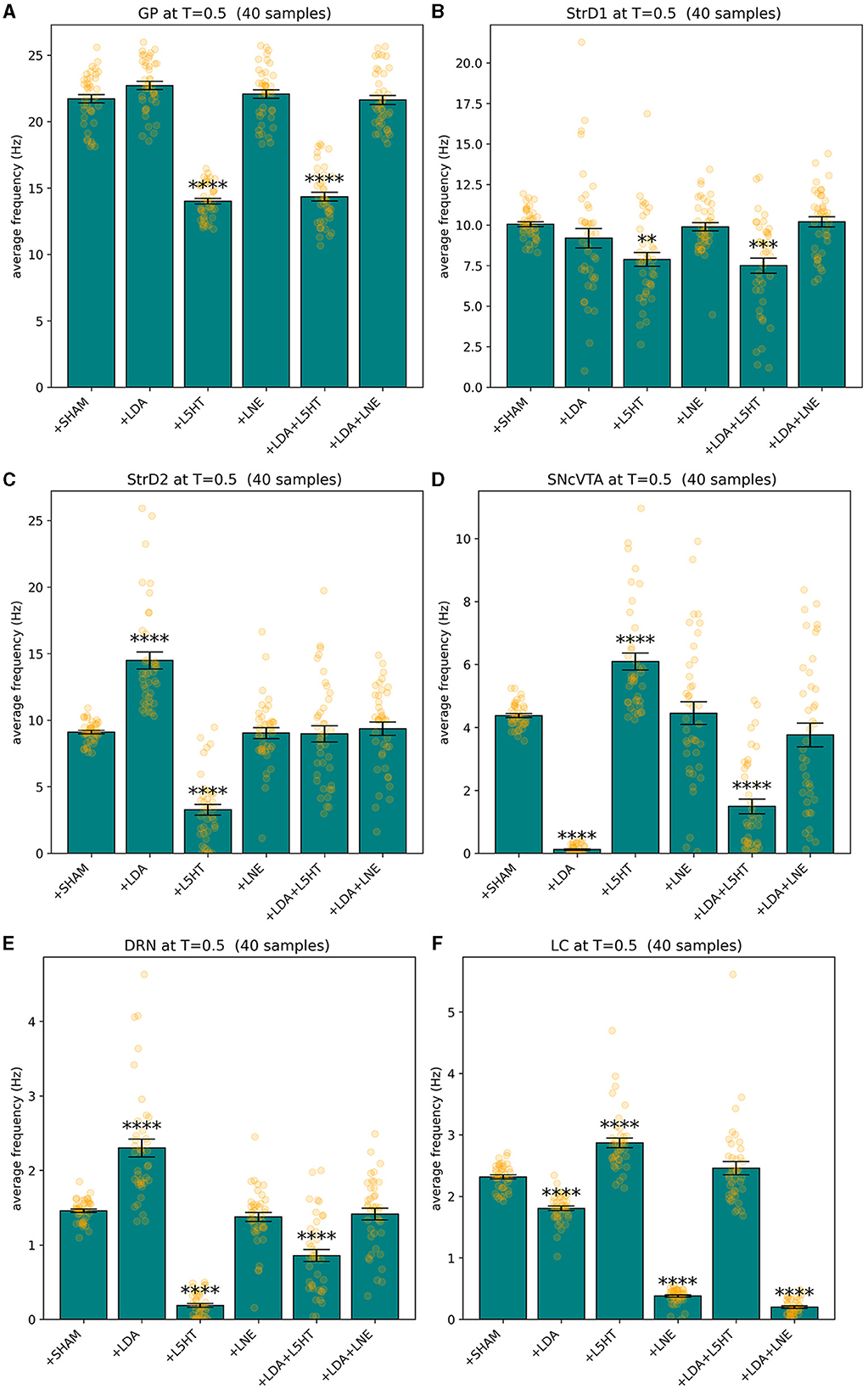
Figure 3. Summary of the behavior exhibited by GP (A), StrD1 (B), StrD2 (C), SNcVTA (D), DRN (E), and LC (F) across various groups including SHAM, LDA, L5HT, LNE, LDA + L5HT, and LDA+LNE, with each group consisting of 40 distinct subjects binned accordingly. ^**p ≤ 0.01, ^***p ≤ 0.001, and ^****p ≤ 0.0001.

Figures 4, 5 give more insight in the behavior of each modeled area, also offering a comparison between the distributions over the whole population (which unfortunately could never be measured in vivo) and the more realistic sampled population distributions. The left graphs show distributions over the whole population (synthetic result), while on the right populations are sliced to have each subject in only one group (as in Figure 3). This latter case reproduces real laboratory conditions where one subject can only be measured once and hence belongs to one group only. Values for SHAM, LDA, L5HT, and LNE are fitted exactly on the required value, while the respective combinations are instead predictions of the model, whose values are only range-constrained with the rules defined in F^COMB (see Equation 55 in Appendix 2.5).

Figure 4

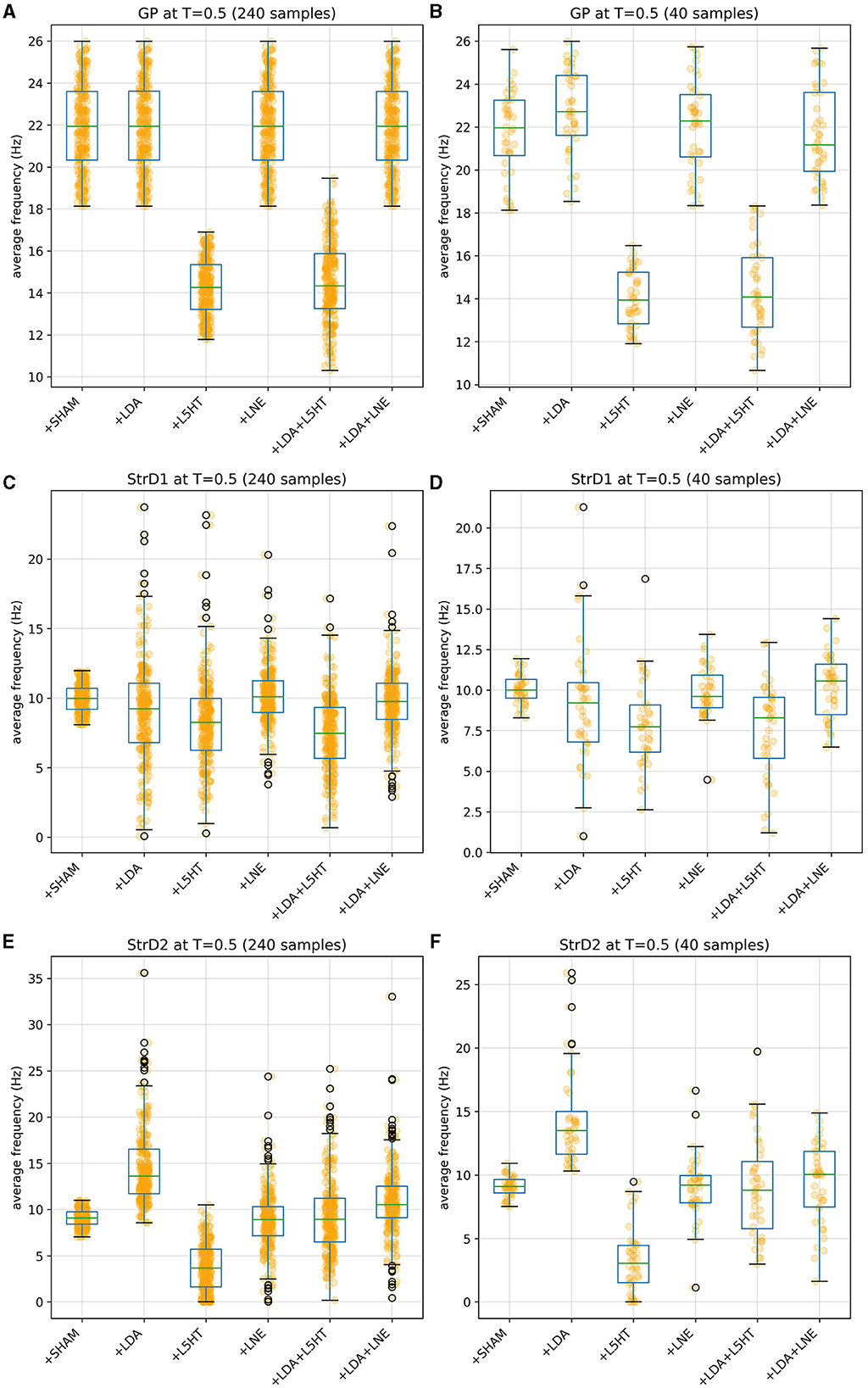
Figure 4. Distribution of simulated equilibrium points for the GP (A), StrD1 (C), and StrD2 (E) regions across the entire synthetic population. On the right, the simulated equilibrium points for GP (B), StrD1 (D), and StrD2 (F) are depicted within separate bins, each containing 40 samples.

Figure 5

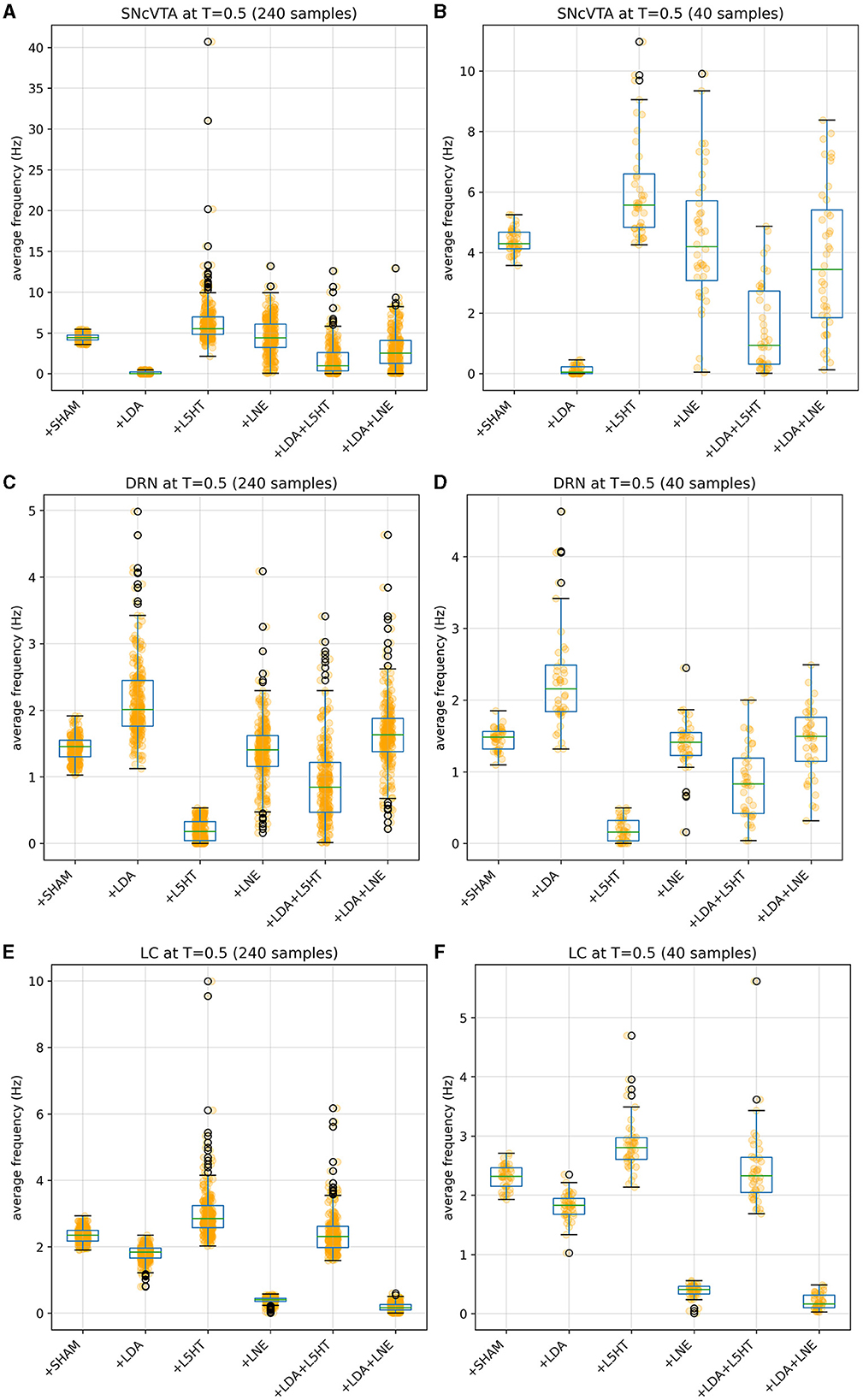
Figure 5. Distribution of simulated equilibrium points for the SNcVTA (A), DRN (C), and LC (E) regions across the entire synthetic population. On the right, the same simulated equilibrium points for SNcVTA (B), DRN (D), and LC (F) are displayed within separate bins, each containing 40 samples.

4.1 Sensitivity analysis

We used the computational model to gain insights into the critical parameters that govern the activity of simulated brain regions. Specifically, we conducted a sensitivity analysis for each simulated brain area in relation to the various model parameters. Each parameter can be varied independently (within some acceptable range) to record its effects on the simulated brain areas. Similar observations can be replicated for all individuals of the available population, and the average excursion of each area can then be compared with the average excursion of the parameter to infer a sort of “parameter importance”. Below, we briefly discuss the mathematical formalism used to conduct the sensitivity analysis (Equations 19, 20).

In particular, for each individual of the population and for each parameter, we:

• Vary the parameter around its original value ±50% in 100 uniform steps: if v is the parameter value for individual $S_i^{SHAM}$, we produce the set $V_{param,i}=\left\{(\frac{x}{99}+\frac{97}{198})v\right\}\subseteq \left[0.5v,1.5v\right]$, i = 1, ..., 100. We therefore have a V_{param, i} set for each parameter of each individual.

• Simulate the model using each value in V_{param, i} and save the final value for each brain area. If the simulation stops early (hence the simulation diverged or reached physically impossible states), the result is discarded and the parameter value removed from V_{param, i}. For each parameter and each individual, we therefore obtain six sets, one for each brain area, which we call $A_{param,i}^{area}$.

The sets are then joined across the population:

$\begin{array}{ll}{A}_{param}^{area}={\displaystyle \bigcup _i}{A}_{param,i}^{area},V_{param}={\displaystyle \bigcup _i}{V}_{param,i}& (19)\end{array}$

where param∈S^SHAM is one of the free parameters as defined in Section 3.1, area is one of the six brain areas {GP, StrD1, StrD2, SNcVTA, DRN, LC}, and i points to the i−th subject in the population.

A sensitivity index is then computed for each area by scaling both V and A by their respective median values and dividing the standard deviations:

$\begin{array}{ll}{I}_{param,area}=\frac{\text{std}(A_{param}^{area}/\text{median}(A_{param}^{area}))}{\text{std}(V_{param}/\text{median}(V_{param}))}& (20)\end{array}$

I_{param, area} can naturally be seen as a sensitivity matrix, with one column per area and one row per free parameter. As a last step, I_{param, area} is normalized with respect to its maximum value. Figure 6 shows the computed sensitivity matrix for the entire fitted population in the SHAM case; a value of 1 indicates the maximum measured sensibility, while a value of 0 would mean that a particular parameter has no effect on that area. It is evident from the matrix that all the areas are relatively sensitive to changes in noradrenalinergic balance (external activation of LC), and also, even if in a somewhat lesser extent, to changes in the serotonergic balance (external activation of DRN). It is therefore reasonable to expect the stimulation of LC and/or DRN to produce changes in the activation of all areas.

Figure 6

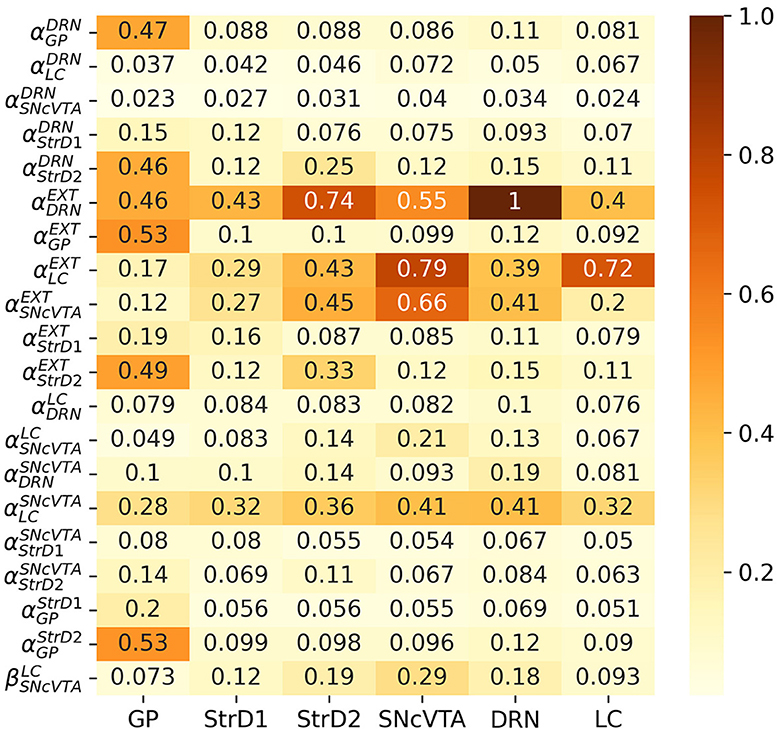
Figure 6. Comparative sensitivity of each area to individual parameters among healthy subjects. A higher value denotes a more pronounced impact (in absolute magnitude) of a parameter on the activation frequency of an area. Values are normalized to unity, highlighting the relative magnitude of effects obtained from each parameter.

4.2 Statistical analysis

Before performing the statistical analysis, all data were checked to verify normal distribution applying D'Agostino and Pearson's normality test, as provided by the scipy package. When appropriate, one-way ANOVA by post-hoc test using Tukey's honestly significant difference (HSD) (also as provided by the scipy package) was performed. Histograms are annotated according to the p-value of the HSD test as follows: ^**** ≤ 0.0001 < ^*** ≤ 0.001 < ^** ≤ 0.01 < ^* ≤ 0.05.

4.3 Possible roads to a treatment

We used the model that accurately replicates existing data to forecast potential outcomes in scenarios where experimental measurements have not yet been conducted. Our primary emphasis was on exploring alternative treatments centered around the manipulation of monoamines. The robustness of the model data reproduction, while rigorously adhering to stability criteria, bolstered the strength of our predictions.

Comparing the brain area activation level distributions in the SHAM to the LDA groups (Figures 7, 8), it is evident that the dopaminergic depletion also inhibits DRN and hence provokes a statistically significant serotonergic depletion. This behavior is compatible with the serotonin measurements reported in Delaville et al. (2012). The administration of LDA, however, does not alter significatively the behavior of LC (and hence noradrenaline production). In the context of dopaminergic depletion, particularly due to a lesion in the SNcVTA caused by LDA, we engage in simulations aimed at exploring strategies to alleviate activity dysfunctions by targeting alternative monoaminergic circuits.

Figure 7

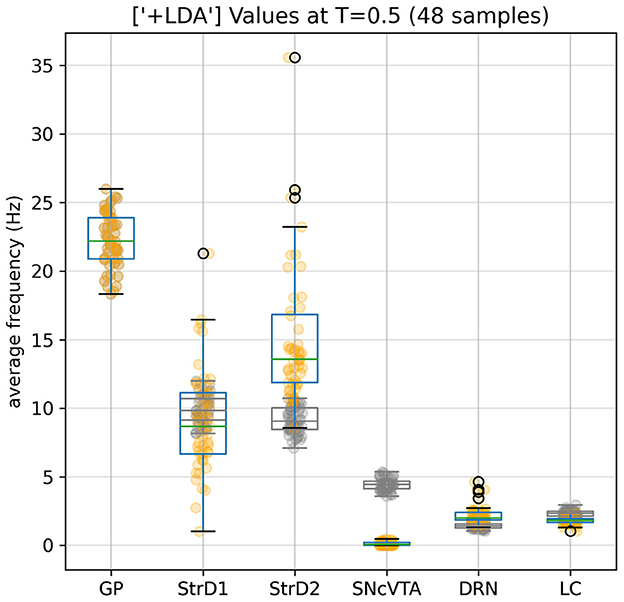
Figure 7. Effects of the dopaminergic (Parkinsonian) lesion to SNcVTA and LC induced by LDA. SNcVTA activation, and consequently the production of dopamine, is drastically lowered compared to the reference (gray) levels. LC activity is also lowered to 80% of its SHAM value. GP values remain unaltered as constrained by the fitness function; SNcVTA and LC are also subject to a softer constraint (see Appendix 2.3).

Figure 8

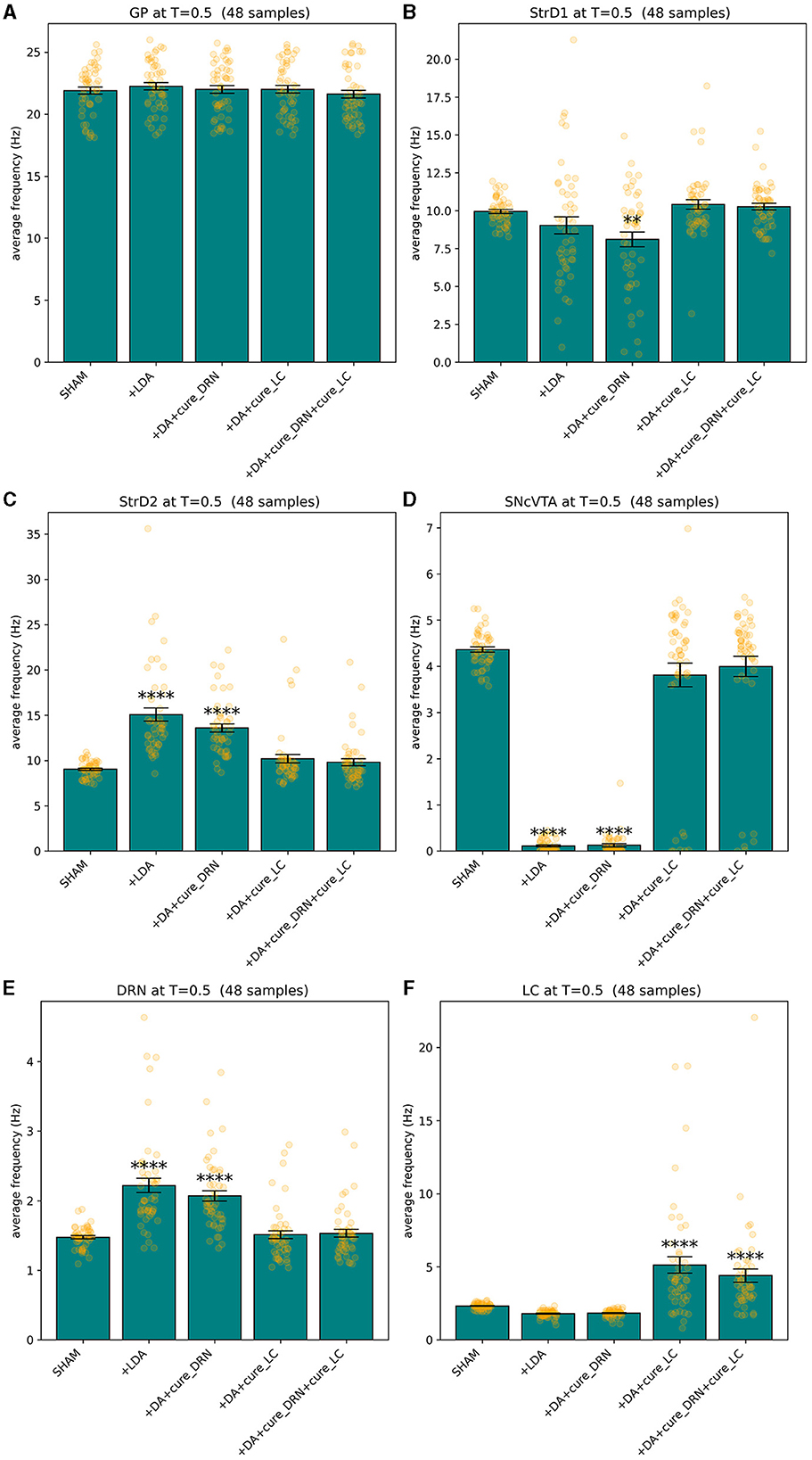
Figure 8. Lesion and treated values for GP (A), StrD1 (B), StrD2 (C), SNcVTA (D), DRN (E), and LC (F). A statistically significant boost of LC average activity (and hence of noradrenaline levels) can restore the activity (and hence monoamine production levels) of all the areas that were significatively impacted by LDA to SHAM levels. ^**p ≤ 0.01 and ^****p ≤ 0.0001.

According to the model schema in Figure 1, dopaminergic levels can potentially be altered in two ways:

1. Externally stimulate the LC to change its production of noradrenaline.

2. Externally stimulate the DRN change its production of serotonin.

The stimulation could either be chemical, by providing the area of the precursors needed to generate monoamines, or electrical, to artificially alter the average firing rate of the neurons from that area (and hence producing and projecting more monoamines to the areas which receive projections from the stimulated one). According to the sensitivity matrix in Figure 6, although, it is reasonable to expect LC stimulation to be strongly influential on dopamine levels, but DRN stimulation should have a smaller effect on the activation of the SNcVTA and strong side effects instead, which would not be compatible with a successful treatment.

4.3.1 Treatment optimization

Whether the stimulation of LC, DRN, or both could potentially restore healthy levels of brain areas in depleted subjects can be verified through the optimization of a subset of the parameters of our model. In particular, we can try to optimize the external stimulation parameter of LC, DRN, or both in the LDA version of our simulated subjects. First of all, we need to extend a subject set of parameters S_i, as previously defined in Section 3.1, with three new subsets of parameters, namely:

• LDA + cLC with free parameters ${\alpha }_{\text{LC}}^{\text{ext}}$ and corresponding fitness measure F^cLC

• LDA + cDRN: ${\alpha }_{\text{DRV}}^{\text{ext}}$ on F^cDRN

• LDA + cCOMB: ${\alpha }_{\text{LC}}^{\text{ext}}$,${\alpha }_{\text{DRV}}^{\text{ext}}$ on F^cCOMB

The corresponding model matrices A, C, b are constructed by using as base the LDA (hence, dopamine depleted) set of parameters for a subject and leaves as the only free parameters the external stimulation of the areas being tested. The three populations need to have different fitness measures because they each stimulate a different area to simulate the treatment. The stimulated area must of course be ignored by the respective fitness measure. Let us examine in detail the measure F^cLC. Similarly to the composed fitness measure described in Appendix 2.1 for the healthy model, this measure is defined as the composition of the following measures:

• The mean square error of the area activation value, one measure per area, as defined for the SHAM case in Equation 38 in Appendix 2.2, but excluding the area being stimulated (in this case, excluding LC).

• A parameter constraint similar to the one defined in Equation 56 in Appendix 2.6, but this time used to enforce the external stimulus parameter to be equal or greater than the original once (hence forcing the optimization to choose a stimulation rather than an inhibition). In particular, the component is defined as in Equation 21:

$\begin{array}{ll}{f}_{cLC}^{PAR}=\frac{1}{1+max(0,S^{SHAM}-S^{cLC})}.& (21)\end{array}$

• An asymptotic stability constraint as defined in Equation 58 in Appendix 2.7, where of course à is constructed using the current parameters subset S^LDA+cLC.

The fitness measures F^cDRN and F^cCOMB are of course constructed in an analogous way. In the latter case, mean square errors for both stimulated areas are ignored in the measure. The optimization is finally performed independently on all subjects of the three groups using the same algorithm described in Section 3.6, including the outer optimization cycles.

4.3.2 Treatment efficacy

The optimizer could successfully restore healthy levels of the measured areas in the vast majority of subjects by stimulating LC or both LC and DRN, but it never succeeded by only stimulating DRN. In particular, there was convergence in 197 subjects (which we refer here as responders) and did not find a satisfactory solution in the remaining 43 subjects (which we refer here as non-responders). Figure 9 shows that in the combined treatment, which obtained very similar results to the stimulation of LC alone, the relative increment to the external stimulation parameter of DRN is in fact several orders of magnitude smaller than the one applied to the corresponding parameter for LC. We can therefore assume that while the combined stimulation may have resulted in a slightly better fitness from the purely numerical perspective, DRN stimulation is indeed not useful as a treatment also in combination to LC stimulation.

Figure 9

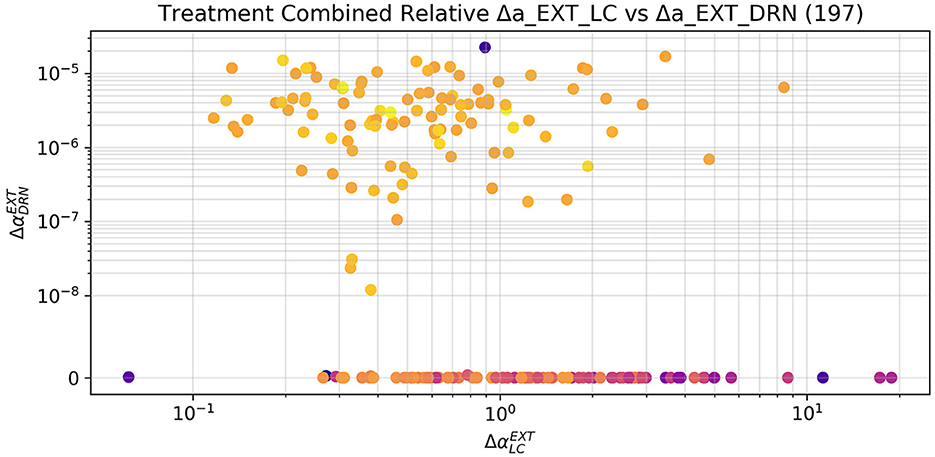
Figure 9. Relative increment applied by the optimizer to the external stimulation parameter of LC and DRN in the combined case, limited to the 197 subjects that were successfully treated. The increments to the DRN stimulation are several orders of magnitude smaller than the ones applied to LC. The sole stimulation of DRN is not a viable treatment. The small changes applied to the DRN stimulation by the optimizer may therefore have contributed to a numerically better solution, which is, however, not substantially different from the one obtain by the sole stimulation of LC. The subjects which did not reach a fitness of 5 (and hence are not to be considered successfully treated) have been excluded from this plot. The color scale gives an indication of the final fitness reached by the optimizer, blue is the lowest and yellow the highest.

Figure 8 provides compelling evidence of the profound impact of statistically significant LC stimulation in reinstating the equilibrium of serotonin and dopamine levels, as reflected in the activation levels of DRN and SNcVTA, respectively, within the population of LDA subjects.

Figures 10–12 illustrate the changes of distributions in the parameter space lesion and the subsequent treatment. The right side of Figure 12 highlights the differences in parameter distributions between the subjects that have been successfully treated (in green), and the ones whose levels could not be successfully restored (in red). None of the parameters of the responder subjects are significantly different from the one of the non-responder ones. The only parameter that shows a small significance difference is the sensitivity of SNcVTA toward noradrenaline from LC, as is shown in Figure 11. However, the spread of the distribution of that parameter is very large, and the value of that specific parameter alone is not useful for predicting if a subject is a responder or not. An accurate statistical study of the parameter space would be necessary to determine whether a particular combination of parameters could be used for predicting the curability of a subject, but this lies outside the scope of this study.

Figure 10

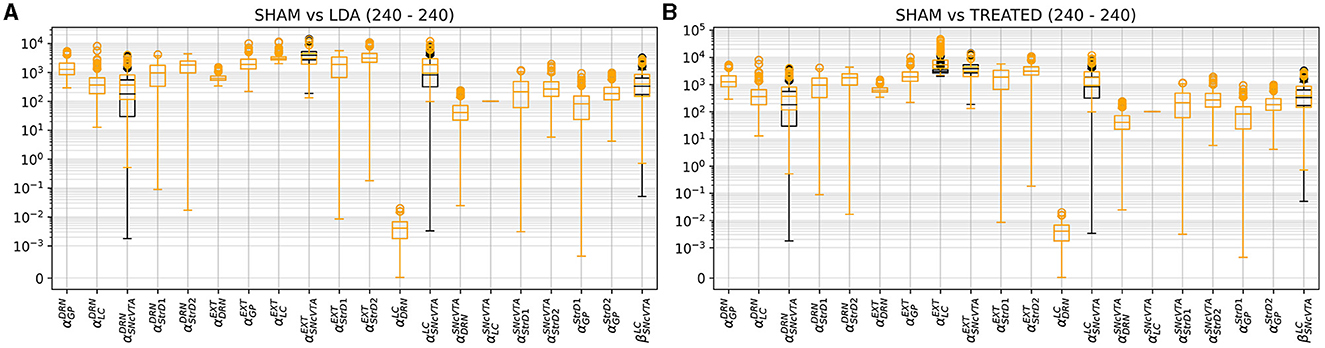
Figure 10. Comparison of parameter distribution among model subjects: SHAM subjects represented in black, while LDA subjects under two conditions, either LDA (A) or treated (B), depicted in orange. As outlined in Section 2.3, only four parameters, impacting the SNcVTA equation, undergo alteration in the LDA scenario compared to SHAM. In addition, the treatment induces changes in external stimulation to LC and DRN.

Figure 11

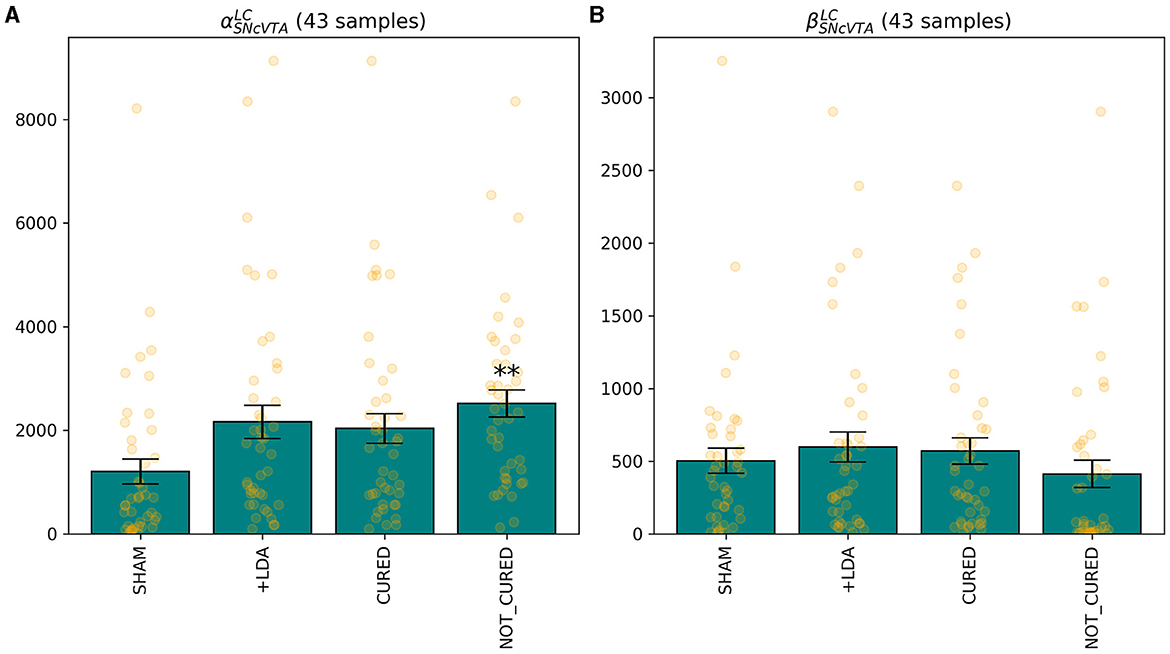
Figure 11. The only feature that differentiates, albeit with low significance, individuals for which it was possible to find a treatment stimulating either LC or DRN is the sensitivity of SNcVTA to noradrenaline from LC, for both the linear (A) and non-linear (B) terms. ^**p ≤ 0.01.

Figure 12

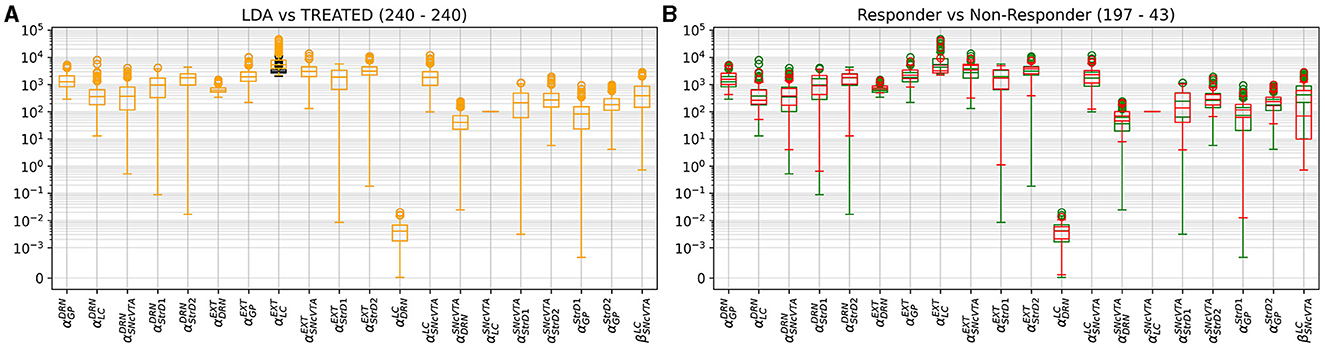
Figure 12. Distribution comparison of model parameters. In (A), a distribution comparison of model parameters in LDA subjects relative to treated subjects is presented. In (B), the parameter distribution of treated subjects is depicted, distinguishing between those successfully cured (green) and those who did not attain the desired fitness (red). Notably, among the non-responsive subjects, one exhibited reduced sensitivity of SNcVTA to noradrenaline.

Figure 12 also shows the parameter space comparison of responder (labeled “cured”) and non-responder (labeled “not cured”) individuals for all parameters. The treatment modifies the external stimulation to LC and DRN but is otherwise identical to the LDA case. This result agrees with Figure 9 demonstrating that there is a very small shift in the DRN stimulus distribution which is not appreciable in Figure 12.

5 Discussion

PD is a global health concern, impacting an estimated 10 million individuals worldwide (Balestrino and Schapira, 2020). Regrettably, a definitive treatment for PD remains elusive. However, there is optimism in the research community as numerous novel drugs are presently undergoing clinical trials. One of the pivotal facets of PD is its intricate association with various neural circuits, resulting in consequential alterations in the brain neurochemistry (Obeso et al., 2010; Caligiore et al., 2016, 2017; Helmich et al., 2018). Our research endeavor confronts the challenge of exploring the interplay among these distinct circuits and how the monoamine system adapts during the progression of this condition.

To tackle this challenge, we employed a bio-constrained differential equation model of PD. This model enabled us to investigate how different brain regions respond to the individual or combined depletion of dopamine (DA), serotonin (5-HT), and noradrenaline (NA). Initially, we harnessed the model to replicate data obtained from Delaville et al. (2012). The simulation results remarkably mirrored the observed alterations in the firing activity of the globus pallidus (GP) following 5-HT lesions in both control and dopamine-depleted rats. Notably, the model also yielded predictions of other deviations in firing activity within brain regions not examined in the original experimental setup involving rats. Ultimately, our model served as a valuable tool to simulate the effects of prospective therapies aimed at restoring the activity in the lesioned regions. To model the impairment of DA function associated with PD, we implemented a reduction in the activity of the SNcVTA (Berretta et al., 2005). As a result, we have a dysregulation of the baseline activity within the specific brain regions we examined. Notably, DRN exhibited a notable increase in firing activity (see Figures 3, 5) in line with the literature (Kaya et al., 2008; Zhang et al., 2018; Caligiore et al., 2021). The DRN intrinsic excitability (Prinz et al., 2013) projections back from the SNcVTA to the DRN (Kalen et al., 1988; Peyron et al., 1996; Kitahama et al., 2000) might support this effect. In addition, dopamine agonist increases excitation on DRN serotonergic neurons (Haj-Dahmane, 2001; Martın-Ruiz et al., 2001). However, there is also literature supporting that there is no change in the electrical activity of serotonergic-like neurons following L-Dopa injection (Miguelez et al., 2011, 2016), that lesion in VTA could lead to a reduction of serotonin in DRN, and that supports a DRN activity reduction after a dopaminergic lesion (Furlanetti et al., 2016). The different results showed in DRN firing activity showed in this literature might depend on several factors such as the type of lesion (unilateral or bilateral), the site of lesion, and time of recording after lesion. Moreover, we excluded from our model several brain regions that might affect DRN regulation, for example, the medial prefrontal cortex and subthalamic nucleus playing a critical role in the inhibition of DRN (Celada et al., 2001; Temel et al., 2007; Hartung et al., 2011). It could be possible that during the initial stages of the disease, the DRN activity increases, while it decreases with the disease progression. The inversed u-shape followed by the DRN activity with the PD progression could be similar to that followed by LC activity during PD and AD progression (Caligiore et al., 2020, 2022; O'Callaghan et al., 2021; Ye et al., 2023). Further research could confirm or refute this hypothesis.

The simulations run with the model show a reduction in striatal D1 activity and an increase in striatal D2 activity (see Figures 3, 4). This result agrees with the literature about hypokinetic Parkinsonian syndrome due to the activity dysregulation of the two populations of medium spiny neurons (MSNs). Dopamine D1 receptor-expressing MSNs (direct) become hypoactive, whereas dopamine D2 receptor-expressing MSNs (indirect) become hyperactive. The global effect is the excitation of the direct pathway and the inhibition of the indirect pathway, both conditions necessary for correctly managing motor output (Albin et al., 1989; Mallet et al., 2006; Parker et al., 2018; Caligiore et al., 2019).

The simulations also show a reduction of LC activity after dopaminergic depletion (Figures 3, 4). The DA excitatory effect on LC reproduced in our model could explain this result. However, the literature supports both decrease and increase in LC, depending on the PD animal models used for experiments (Ranjbar-Slamloo and Fazlali, 2020). Thus, future in vivo studies should confirm or refute the model result. The serotonin lesions allow reproduction of the GP firing activity decrease reported in the target experiment (Delaville et al., 2012). Moreover, the lesioned model shows an increase in SNcVTA activity (Figures 3, 5). The 5-HT inhibitory effect on dopaminergic neurons reproduced in our model could explain this result. However, future studies are required to confirm these data. Indeed, 5-HT could modulate SNpc and VTA DA neurons oppositely (Gervais and Rouillard, 2000).

5.1 Exploring potential monoamine-based therapies

Levodopa is the most common medication used in PD. However, this drug has a wide range of adverse effects, most notably motor fluctuations and dyskinesias (for a rev see Lang and Obeso, 2004). The discovery of alternative treatment that not only targets dopaminergic system but also noradrenergic or serotonergic system is a big challenge (Politis and Niccolini, 2015; Wilson et al., 2019; Caligiore et al., 2021, 2022). Figures 9–12 collectively indicate that the restoration of activity in the LC is sufficient to restore the regions under examination, while the DRN does not yield the same effect. This observation is consistent with current theories that underscore the central role of the LC in the progression of PD, particularly in relation to the early-stage emergence of non-motor symptoms (Bjerkén et al., 2019; Butkovich et al., 2020). Moreover, there is literature supporting the notion that the overexpression of specific transcription factors directly within the LC can effectively restore noradrenergic function and facilitate the recovery of the dopaminergic system (Cui et al., 2021). Notably, in the context of human studies, mounting evidence underscores the fact that LC degeneration can manifest at an earlier stage and with greater severity compared to the SNcVTA (German et al., 1992; Del Tredici et al., 2002; Rommelfanger and Weinshenker, 2007; Vermeiren and Deyn, 2017). Taken together, these findings strongly suggest that the LC may play a pivotal role in the emergence and progression of PD and present an intriguing avenue for therapeutic interventions targeting both the dopaminergic and noradrenergic systems.

The feasibility of this discovery is not straightforward. One plausible explanation for the lack of productivity of novel drugs targeting monoaminergic function could be the complexity of the brain neurotransmitter systems. While these systems play crucial roles in regulating mood and cognition, their functions are highly interconnected and often involve feedback loops and compensatory mechanisms. It is possible that the drugs developed to target these systems may inadvertently disrupt the delicate balance of neurotransmitter activity, leading to unintended side effects or diminishing efficacy over time. In addition, the existing drugs may primarily target specific receptor subtypes within the noradrenergic systems, leaving other potential therapeutic targets unexplored. This limited scope could hinder the development of more effective treatments (Tan et al., 2022; Pardo-Moreno et al., 2023). Finally, while the model suggests promising alternative treatments targeting the LC and DRN, it is crucial to consider the potential side effects associated with these approaches. Given the critical roles these regions play in regulating mood, arousal, and autonomic functions, interventions could lead to increased anxiety, sleep disturbances, and cardiovascular issues. These potential side effects highlight the need for comprehensive experimental validation and clinical studies to assess the safety and efficacy of these alternative treatments. Addressing these concerns will be essential for translating our model predictions into practical therapeutic strategies.

6 Conclusion

This article presents a novel system-level computational model that, for the first time, explores the roles of three important monoamines (dopamine, serotonin, and noradrenaline) in a PD animal model. The model assumes a direct relationship between reduced activity in specific brain areas (SNcVTA, DRN, and LC) and decreased neurotransmitter levels (DA, 5-HT, and NE) in target brain regions. In addition, it simulates VTA and SNc together and excludes some potentially relevant areas, such as the prefrontal and motor cortices, thalamus, and substantia nigra pars reticulata. Despite these simplifications, the model successfully reproduces some data on combined monoamine depletion, generates predictions regarding changes in other unexplored brain regions, suggesting avenues for further investigation, and highlights the potential efficacy of alternative treatments targeting the locus coeruleus and dorsal raphe nucleus. This suggests that the model captures crucial aspects of the interactions between the considered areas. Furthermore, it may also imply that the aspects not yet modeled might only play secondary roles in the system behaviors.

We do not subscribe to this belief. Our plan is to expand the model to incorporate more areas involved in PD (Dirkx et al., 2017; Helmich et al., 2018), to more accurately delineate macro-areas like SNc/VTA (Ledonne et al., 2023), and to include additional interaction paths. The upgraded versions of the model may be well-suited for delving into more mechanisms, such as those elucidating the effects of dopamine receptor activation (Mailman et al., 2021; Lewis et al., 2023) or exploring monoamine interactions within various brain regions (Oh et al., 2022). At this stage, the model represents an initial effort to employ a system-level computational approach to address the intricacies of PD as a systemic disease, with a focus on the interplay of monoamines. It serves as an initial attempt to demonstrate the feasibility of this approach, employing a rigorous mathematical framework specifically, the study of stability, a seldom-used approach in computational neuroscience. The results obtained through the model are preliminary, and their effectiveness requires further validation.

In this respect, a series of experimental approaches could validate the model predictions. In vivo, neurochemical assessments using microdialysis in PD animal models could measure extracellular levels of DA, NE, and 5-HT in the basal ganglia. Pharmacological manipulations could selectively alter NE and 5-HT levels, observing the effects on PD symptoms and neurochemical dynamics to validate the model predictions about these systems. Neuroimaging studies using functional magnetic resonance imaging (fMRI) and positron emission tomography (PET) can assess functional connectivity and receptor density changes in brain regions highlighted by the model. This analysis could help validate the predicted alterations in neuromodulator levels and activity patterns. In addition, analyzing functional connectivity using high-density electroencephalography (HD-EEG) could validate the model on a macroscale by measuring changes in band-specific cortico-cortical and subcortico-cortical connectivity before and after manipulations of the monoaminergic system (Conti et al., 2023). Moreover, electrophysiological recordings of neuronal activity in relevant brain regions before and after such manipulations could validate the model's predictions regarding neural circuitry alterations.

The model proposed here could enhance our comprehension of interactions between brain regions in both normal and pathological conditions, potentially aiding in the restoration of damaged brain regions to reestablish balance. The model could be adapted to study other neurodegenerative and neuropsychiatric disorders involving similar monoaminergic systems. For instance, there is increasing evidence of the critical role of monoamines in AD (Caligiore et al., 2022) and multiple sclerosis (Carandini et al., 2021). Adapting the model to these disorders would involve modifying the parameters to reflect the specific pathophysiological mechanisms and neurochemical dynamics unique to each condition. Future research could address these points.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: https://github.com/WohthaN/Simulating_noradrenaline_and_serotonin_depletions_in_parkinson.

Author contributions

SC: Conceptualization, Formal analysis, Methodology, Resources, Validation, Writing – original draft, Data curation, Investigation, Software, Visualization. LB: Formal analysis, Methodology, Validation, Writing – review & editing. DC: Conceptualization, Formal analysis, Funding acquisition, Methodology, Project administration, Resources, Supervision, Validation, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported by the “Advanced School in AI” (www.as-ai.org) and FISM - Fondazione Italiana Sclerosi Multipla - cod. 2022/R-Multi/040 and financed or co-financed with the “5 per mille” public funding. The authors declare that this study received funding from AI2Life s.r.l. (www.ai2life.com) and Entersys s.r.l. (www.entersys.it). The funders were not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

SC was employed by Entersys s.r.l. SC and DC were employed by AI2Life s.r.l.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fncom.2024.1386841/full#supplementary-material

References

Aarsland, D., Bronnick, K., Larsen, J. P., Tysnes, O. B., and Alves, G. (2009). Cognitive impairment in incident, untreated Parkinson disease: the Norwegian ParkWest Study. Neurology 72, 1121–1126. doi: 10.1212/01.wnl.0000338632.00552.cb

PubMed Abstract | Crossref Full Text | Google Scholar

Albin, R. L., Young, A. B., and Penney, J. B. (1989). The functional anatomy of basal ganglia disorders. Trends Neurosci. 12, 366–375. doi: 10.1016/0166-2236(89)90074-X

PubMed Abstract | Crossref Full Text | Google Scholar

Antonini, A., Emmi, A., and Campagnolo, M. (2023). Beyond the dopaminergic system: lessons learned from levodopa resistant symptoms in Parkinson's disease. Mov. Disord. Clin. Pract. 10:S50. doi: 10.1002/mdc3.13786

PubMed Abstract | Crossref Full Text | Google Scholar

Balestrino, R., and Schapira, A. H. (2020). Parkinson disease. Eur. J. Neurol. 27, 27–42. doi: 10.1111/ene.14108

PubMed Abstract | Crossref Full Text | Google Scholar

Berretta, N., Freestone, P. S., Guatteo, E., de Castro, D., Geracitano, R., and Bernardi, J. (2005). Acute effects of 6-hydroxydopamine on dopaminergic neurons of the rat substantia nigra pars compacta in vitro. Neurotoxicology 26, 869–881. doi: 10.1016/j.neuro.2005.01.014

PubMed Abstract | Crossref Full Text | Google Scholar

Bjerkén, S., Persson, R. S., Barkander, A., Karalija, N., Pelegrina-Hidalgo, N., Gerhardt, G. A., et al. (2019). Noradrenaline is crucial for the substantia nigra dopaminergic cell maintenance. Neurochem. Int. 131:104551. doi: 10.1016/j.neuint.2019.104551

PubMed Abstract | Crossref Full Text | Google Scholar

Butcher, J. C. (2016). Numerical Methods for Ordinary Differential Equations, 3rd Edn. Chichester: Wiley Blackwell. doi: 10.1002/9781119121534

Crossref Full Text | Google Scholar

Butkovich, L. M., Houser, M. C., Chalermpalanupap, T., Porter-Stransky, K. A., Iannitelli, A. F., Boles, J. S., et al. (2020). Transgenic mice expressing human α-synuclein in noradrenergic neurons develop locus coeruleus pathology and nonmotor features of Parkinson's disease. J. Neurosci. 40, 7559–7576. doi: 10.1523/JNEUROSCI.1468-19.2020

PubMed Abstract | Crossref Full Text | Google Scholar

Byrne, G. D., and Hindmarsh, A. C. (1975). A polyalgorithm for the numerical solution of ordinary differential equations. ACM Trans. Math. Softw. 1, 71–96. doi: 10.1145/355626.355636

Crossref Full Text | Google Scholar

Caligiore, D., Giocondo, F., and Silvetti, M. (2022). The Neurodegenerative Elderly Syndrome (NES) hypothesis: Alzheimer and Parkinson are two faces of the same disease. IBRO Neurosci. Rep. 13, 330–343. doi: 10.1016/j.ibneur.2022.09.007

PubMed Abstract | Crossref Full Text | Google Scholar

Caligiore, D., Helmich, R. C., Hallett, M., Moustafa, A. A., Timmermann, L., Toni, I., et al. (2016). Parkinson's disease as a system-level disorder. NPJ Parkinson's Dis. 2:16025. doi: 10.1038/npjparkd.2016.25

PubMed Abstract | Crossref Full Text | Google Scholar

Caligiore, D., Mannella, F., and Baldassarre, G. (2019). Different dopaminergic dysfunctions underlying parkinsonian akinesia and tremor. Front. Neurosci. 13:550. doi: 10.3389/fnins.2019.00550

PubMed Abstract | Crossref Full Text | Google Scholar

Caligiore, D., Montedori, F., Buscaglione, S., and Capirchio, A. (2021). Increasing serotonin to reduce parkinsonian tremor. Front. Syst. Neurosci. 15:682990. doi: 10.3389/fnsys.2021.682990

PubMed Abstract | Crossref Full Text | Google Scholar

Caligiore, D., Pezzulo, G., Baldassarre, G., Bostan, A. C., Strick, P. L., Doya, K., et al. (2017). Consensus paper: towards a systems-level view of cerebellar function: the interplay between cerebellum, Basal Ganglia, and Cortex. Cerebellum 16, 203–229. doi: 10.1007/s12311-016-0763-3

PubMed Abstract | Crossref Full Text | Google Scholar

Caligiore, D., Silvetti, M., D'Amelio, M., Puglisi-Allegra, S., and Baldassarre, G. (2020). Computational modeling of catecholamines dysfunction in Alzheimer's disease at pre-plaque stage. J. Alzheimers Dis. 77, 275–290. doi: 10.3233/JAD-200276

PubMed Abstract | Crossref Full Text | Google Scholar

Carandini, T., Cercignani, M., Galimberti, D., Scarpini, E., and Bozzali, M. (2021). The distinct roles of monoamines in multiple sclerosis: a bridge between the immune and nervous systems? Brain Behav. Immun. 94, 381–391. doi: 10.1016/j.bbi.2021.02.030

PubMed Abstract | Crossref Full Text | Google Scholar

Castela, I., Casado-Polanco, R., Rubio, Y. V.-W., da Silva, J. A., Marquez, R., Pro, J., et al. (2023). Selective activation of striatal indirect pathway suppresses levodopa induced-dyskinesias. Neurobiol. Dis. 176:105930. doi: 10.1016/j.nbd.2022.105930

PubMed Abstract | Crossref Full Text | Google Scholar

Celada, P., Puig, M. V., Casanovas, J. M., Guillazo, G., and Artigas, F. (2001). Control of dorsal raphe serotonergic neurons by the medial prefrontal cortex: involvement of serotonin-1a, gaba_a, and glutamate receptors. J. Neurosci. 21, 9917–9929. doi: 10.1523/JNEUROSCI.21-24-09917.2001

PubMed Abstract | Crossref Full Text | Google Scholar

Chen, L., Yung, K., Chan, Y., and Yung, W. (2008). 5-ht excites globus pallidus neurons by multiple receptor mechanisms. Neuroscience 151, 439–451. doi: 10.1016/j.neuroscience.2007.11.003

PubMed Abstract | Crossref Full Text | Google Scholar

Cohen, E., Bay, A. A., Ni, L., and Hackney, M. E. (2022). Apathy-related symptoms appear early in Parkinson's disease. Healthcare 10:91. doi: 10.3390/healthcare10010091

PubMed Abstract | Crossref Full Text | Google Scholar

Connolly, B. S., and Lang, A. E. (2014). Pharmacological treatment of Parkinson disease: a review. J. Am. Med. Assoc. 311, 1670–1683. doi: 10.1001/jama.2014.3654

PubMed Abstract | Crossref Full Text | Google Scholar

Conti, M., Guerra, A., Pierantozzi, M., Bovenzi, R., D'Onofrio, V., Simonetta, C., et al. (2023). Band-specific altered cortical connectivity in early Parkinson's disease and its clinical correlates. Mov. Disord. 38, 2197–2208. doi: 10.1002/mds.29615

PubMed Abstract | Crossref Full Text | Google Scholar

Cui, K., Yang, F., Tufan, T., Raza, M. U., Zhan, Y., Fan, Y., et al. (2021). Restoration of noradrenergic function in Parkinson's disease model mice. ASN Neuro 13:175909142110097. doi: 10.1177/17590914211009730

PubMed Abstract | Crossref Full Text | Google Scholar

Damodaran, S., Evans, R. C., and Blackwell, K. T. (2014). Synchronized firing of fast-spiking interneurons is critical to maintain balanced firing between direct and indirect pathway neurons of the striatum. J. Neurophysiol. 111, 836–848. doi: 10.1152/jn.00382.2013

PubMed Abstract | Crossref Full Text | Google Scholar

Deister, C. A., Chan, C. S., Surmeier, D. J., and Wilson, C. J. (2009). Calcium-activated sk channels influence voltage-gated ion channels to determine the precision of firing in globus pallidus neurons. J. Neurosci. 29, 8452–8461. doi: 10.1523/JNEUROSCI.0576-09.2009

PubMed Abstract | Crossref Full Text | Google Scholar

Del Tredici, K., Rüb, U., De Vos, R. A., Bohl, J. R., and Braak, H. (2002). Where does Parkinson disease pathology begin in the brain? J. Neuropathol. Exp. Neurol. 61, 413–426. doi: 10.1093/jnen/61.5.413

PubMed Abstract | Crossref Full Text | Google Scholar

Delaville, C., Chetrit, J., Abdallah, K., Morin, S., Cardoit, L., De Deurwaerdère, P., et al. (2012). Emerging dysfunctions consequent to combined monoaminergic depletions in Parkinsonism. Neurobiol. Dis. 45, 763–773. doi: 10.1016/j.nbd.2011.10.023

PubMed Abstract | Crossref Full Text | Google Scholar

Delaville, C., Deurwaerdere, P. D., and Benazzouz, A. (2011). Noradrenaline and Parkinson's disease. Front. Syst. Neurosci. 5:31. doi: 10.3389/fnsys.2011.00031

PubMed Abstract | Crossref Full Text | Google Scholar

Deutch, A. Y., Goldstein, M., and Roth, R. H. (1986). Activation of the locus coeruleus induced by selective stimulation of the ventral tegmental area. Brain Res. 363, 307–314. doi: 10.1016/0006-8993(86)91016-4

PubMed Abstract | Crossref Full Text | Google Scholar

Dirkx, M. F., den Ouden, H. E., Aarts, E., Timmer, M. H., Bloem, B. R., and Toni, R. C. (2017). Dopamine controls Parkinson's tremor by inhibiting the cerebellar thalamus. Brain 140, 721–734. doi: 10.1093/brain/aww331

PubMed Abstract | Crossref Full Text | Google Scholar

Dovzhenok, A., and Rubchinsky, L. L. (2012). On the origin of tremor in Parkinson's disease. PLoS ONE 7:e41598. doi: 10.1371/journal.pone.0041598

PubMed Abstract | Crossref Full Text | Google Scholar

Dray, A., Davies, J., Oakley, N., Tongroach, P., and Vellucci, S. (1978). The dorsal and medial raphe projections to the substantia nigra in the rat: electrophysiological, biochemical and behavioural observations. Brain Res. 151, 431–442. doi: 10.1016/0006-8993(78)91077-6

PubMed Abstract | Crossref Full Text | Google Scholar

Dray, A., Gonye, T., Oakley, N., and Tanner, T. (1976). Evidence for the existence of a raphe projection to the substantia nigra in rat. Brain Res. 113, 45–57. doi: 10.1016/0006-8993(76)90005-6

PubMed Abstract | Crossref Full Text | Google Scholar

Espay, A. J., Aybek, S., Carson, A., Edwards, M. J., Goldstein, L. H., Hallett, M., et al. (2018). Current concepts in diagnosis and treatment of functional neurological disorders. JAMA Neurol. 75:1132. doi: 10.1001/jamaneurol.2018.1264

PubMed Abstract | Crossref Full Text | Google Scholar

Faivre, F., Joshi, A., Bezard, E., and Barrot, M. (2019). The hidden side of Parkinson's disease: studying pain, anxiety and depression in animal models. Neurosci. Biobehav. Revi. 96, 335–352. doi: 10.1016/j.neubiorev.2018.10.004

PubMed Abstract | Crossref Full Text | Google Scholar

Favier, M., Carcenac, C., Savasta, M., and Carnicella, S. (2022). Dopamine D3 receptors: a potential target to treat motivational deficits in Parkinson's disease. Curr. Top. Behav. Neurosci. 60, 109–132. doi: 10.1007/7854_2022_316

PubMed Abstract | Crossref Full Text | Google Scholar

Fornari, C., Pin, C., Yates, J. W., Mettetal, J. T., and Collins, T. A. (2020). Importance of stability analysis when using nonlinear semimechanistic models to describe drug-induced hematotoxicity. CPT: Pharmacometrics Syst. Pharmacol. 9, 498–508. doi: 10.1002/psp4.12514

PubMed Abstract | Crossref Full Text | Google Scholar

Furlanetti, L., Coenen, V., and Dbrssy, M. (2016). Ventral tegmental area dopaminergic lesion-induced depressive phenotype in the rat is reversed by deep brain stimulation of the medial forebrain bundle. Behav. Brain Res. 299, 132–140. doi: 10.1016/j.bbr.2015.11.036

PubMed Abstract | Crossref Full Text | Google Scholar

German, D. C., Manaye, K. F., White, C. L., Woodward, D. J., McIntire, D. D., Smith, W. K., et al. (1992). Disease-specific patterns of locus coeruleus cell loss. Ann. Neurol. 32, 667–676. doi: 10.1002/ana.410320510

PubMed Abstract | Crossref Full Text | Google Scholar

Gervais, J., and Rouillard, C. (2000). Dorsal raphe stimulation differentially modulates dopaminergic neurons in the ventral tegmental area and substantia nigra. Synapse 35, 281–291. doi: 10.1002/(SICI)1098-2396(20000315)35:4<281::AID-SYN6>3.0.CO;2-A

Crossref Full Text | Google Scholar

Haj-Dahmane, S. (2001). D₂ -like dopamine receptor activation excites rat dorsal raphe 5-HT neurons in vitro. Eur. J. Neurosci. 14, 125–134. doi: 10.1046/j.0953-816x.2001.01616.x

PubMed Abstract | Crossref Full Text | Google Scholar

Hansen, L., Witzig, V., Schulz, J. B., and Holtbernd, F. (2023). Dopaminergic treatment strategies for people with Parkinson's disease in Europe: a retrospective analysis of prism trial data. Neurol. Sci. 44, 3905–3912. doi: 10.1007/s10072-023-06888-5

PubMed Abstract | Crossref Full Text | Google Scholar

Hartung, H., Tan, S., Steinbusch, H., Temel, Y., and Sharp, T. (2011). High-frequency stimulation of the subthalamic nucleus inhibits the firing of juxtacellular labelled 5-ht-containing neurones. Neuroscience 186, 135–145. doi: 10.1016/j.neuroscience.2011.04.004

PubMed Abstract | Crossref Full Text | Google Scholar

Helmich, R. C., Hallett, M., Deuschl, G., Toni, I., and Bloem, B. (2012). Cerebral causes and consequences of parkinsonian resting tremor: a tale of two circuits? Brain 135, 3206–3226. doi: 10.1093/brain/aws023

PubMed Abstract | Crossref Full Text | Google Scholar

Helmich, R. C., Vaillancourt, D. E., and Brooks, D. J. (2018). The future of brain imaging in Parkinson's disease. J. Parkinsons Dis. 8, S47–S51. doi: 10.3233/JPD-181482

PubMed Abstract | Crossref Full Text | Google Scholar

Hezemans, F. H., Wolpe, N., O'Callaghan, C., Ye, R., Rua, C., Jones, P. S., et al. (2022). Noradrenergic deficits contribute to apathy in Parkinson's disease through the precision of expected outcomes. PLoS Comput. Biol. 18:e1010079. doi: 10.1371/journal.pcbi.1010079

PubMed Abstract | Crossref Full Text | Google Scholar

Jankovic, J. (2018). Parkinson's disease tremors and serotonin. Brain 141, 624–626. doi: 10.1093/brain/awx361

PubMed Abstract | Crossref Full Text | Google Scholar

Jankovic, J., and Kapadia, A. S. (2001). Functional decline in Parkinson's disease. Arch. Neurol. 58:1611. doi: 10.1001/archneur.58.10.1611

PubMed Abstract | Crossref Full Text | Google Scholar

Jellinger, K. A. (1991). Pathology of Parkinson's disease. Mol. Chem. Neuropathol. 14, 153–197. doi: 10.1007/BF03159935

PubMed Abstract | Crossref Full Text | Google Scholar

Kalen, P., Skagerberg, G., and Lindvall, O. (1988). Projections from the ventral tegmental area and mesencephalic raphe to the dorsal raphe nucleus in the rat: evidence for a minor dopaminergic component. Exp. Brain Res. 73, 69–77. doi: 10.1007/BF00279662

PubMed Abstract | Crossref Full Text | Google Scholar

Kang, Y., and Kitai, S. (1993). A whole cell patch-clamp study on the pacemaker potential in dopaminergic neurons of rat substantia nigra compacta. Neurosci. Res. 18, 209–221. doi: 10.1016/0168-0102(93)90056-V

PubMed Abstract | Crossref Full Text | Google Scholar

Kaya, A. H., Vlamings, R., Tan, S., Lim, L. W., Magill, P. J., Steinbusch, H. W., et al. (2008). Increased electrical and metabolic activity in the dorsal raphe nucleus of parkinsonian rats. Brain Res. 1221, 93–97. doi: 10.1016/j.brainres.2008.05.019

PubMed Abstract | Crossref Full Text | Google Scholar

Kelland, M. D., Freeman, A. S., and Chiodo, L. A. (1990). Serotonergic afferent regulation of the basic physiology and pharmacological responsiveness of nigrostriatal dopamine neurons. J. Pharmacol. Exp. Ther. 253, 803–11.

PubMed Abstract | Google Scholar

Kelland, M. D., Freeman, A. S., Rubin, J., and Chiodo, L. A. (1993). Ascending afferent regulation of rat midbrain dopamine neurons. Brain Res. Bull. 31, 539–546. doi: 10.1016/0361-9230(93)90121-Q

PubMed Abstract | Crossref Full Text | Google Scholar

Kelley, W. G., and Peterson, A. C. (2001). Difference Equations: An Introduction with Applications, 2nd Edn. San Diego, CA: Harcourt/Academic Press.

Google Scholar

Kita, H., and Kita, T. (2011). Role of striatum in the pause and burst generation in the globus pallidus of 6-OHDA-treated rats. Front. Syst. Neurosci. 5:42. doi: 10.3389/fnsys.2011.00042

PubMed Abstract | Crossref Full Text | Google Scholar

Kitahama, K., Nagatsu, I., Geffard, M., and Maeda, T. (2000). Distribution of dopamine-immunoreactive fibers in the rat brainstem. J. Chem. Neuroanat. 18, 1–9. doi: 10.1016/S0891-0618(99)00047-2

PubMed Abstract | Crossref Full Text | Google Scholar

Lakshmikantham, V., and Trigiante, D. (2002). Theory of difference equations: numerical methods and applications. Number 251 in Monographs and textbooks in pure and applied mathematics, 2nd Edn. New York, NY: Marcel Dekker. doi: 10.1201/9780203910290

Crossref Full Text | Google Scholar

Lang, A. E., and Obeso, J. A. (2004). Challenges in Parkinson's disease: restoration of the nigrostriatal dopamine system is not enough. Lancet Neurol. 3, 309–316. doi: 10.1016/S1474-4422(04)00740-9

PubMed Abstract | Crossref Full Text | Google Scholar

Ledonne, A., Massaro Cenere, M., Paldino, E., D'Angelo, V., D'Addario, S. L., Casadei, N., et al. (2023). Morpho-functional changes of nigral dopamine neurons in an α-synuclein model of Parkinson's disease. Mov. Disord. 38, 256–266. doi: 10.1002/mds.29269

PubMed Abstract | Crossref Full Text | Google Scholar

Lewis, M. M., Van Scoy, L. J., De Jesus, S., Hakun, J. G., Eslinger, P. J., Fernandez-Mendoza, N., et al. (2023). Dopamine d1 agonists: first potential treatment for late-stage Parkinson's disease. Biomolecules 13:829. doi: 10.3390/biom13050829

PubMed Abstract | Crossref Full Text | Google Scholar

Lin, Y., Quartermain, D., Dunn, A. J., Weinshenker, D., and Stone, E. A. (2008). Possible dopaminergic stimulation of locus coeruleus alpha1-adrenoceptors involved in behavioral activation. Synapse 62, 516–523. doi: 10.1002/syn.20517

PubMed Abstract | Crossref Full Text | Google Scholar

Liu, J., Shelkar, G. P., Sarode, L. P., Gawande, D. Y., Zhao, F., Clausen, R. P., et al. (2021). Facilitation of glun2c-containing nmda receptors in the external globus pallidus increases firing of fast spiking neurons and improves motor function in a hemiparkinsonian mouse model. Neurobiol. Dis. 150:105254. doi: 10.1016/j.nbd.2021.105254

PubMed Abstract | Crossref Full Text | Google Scholar

Liu, R.-J., van den Pol, A. N., and Aghajanian, G. K. (2002). Hypocretins (orexins) regulate serotonin neurons in the dorsal raphe nucleus by excitatory direct and inhibitory indirect actions. J. Neurosci. 22, 9453–9464. doi: 10.1523/JNEUROSCI.22-21-09453.2002

PubMed Abstract | Crossref Full Text | Google Scholar

Mailman, R. B., Yang, Y., and Huang, X. (2021). D1, not d2, dopamine receptor activation dramatically improves mptp-induced parkinsonism unresponsive to levodopa. Eur. J. Pharmacol. 892:173760. doi: 10.1016/j.ejphar.2020.173760

PubMed Abstract | Crossref Full Text | Google Scholar

Mallet, N., Ballion, B., Le Moine, C., and Gonon, F. (2006). Cortical inputs and gaba interneurons imbalance projection neurons in the striatum of parkinsonian rats. J. Neurosci. 26, 3875–3884. doi: 10.1523/JNEUROSCI.4439-05.2006

PubMed Abstract | Crossref Full Text | Google Scholar

Marras, C., Chaudhuri, K. R., Titova, N., and Mestre, T. A. (2020). Therapy of Parkinson's disease subtypes. Neurotherapeutics 17, 1366–1377. doi: 10.1007/s13311-020-00894-7

PubMed Abstract | Crossref Full Text | Google Scholar

Martın-Ruiz, R., Puig, M. V., Celada, P., Shapiro, D. A., Roth, B. L., Mengod, G., et al. (2001). Control of serotonergic function in medial prefrontal cortex by serotonin-2a receptors through a glutamate-dependent mechanism. J. Neurosci. 21, 9856–9866. doi: 10.1523/JNEUROSCI.21-24-09856.2001

PubMed Abstract | Crossref Full Text | Google Scholar

Miguelez, C., Grandoso, L., and Ugedo, L. (2011). Locus coeruleus and dorsal raphe neuron activity and response to acute antidepressant administration in a rat model of Parkinson's disease. Int. J. Neuropsychopharmacol. 14, 187–200. doi: 10.1017/S146114571000043X

PubMed Abstract | Crossref Full Text | Google Scholar

Miguelez, C., Navailles, S., Deurwaerdère, P. D., and Ugedo, L. (2016). The acute and long-term l-dopa effects are independent from changes in the activity of dorsal raphe serotonergic neurons in 6-ohda lesioned rats. Br. J. Pharmacol. 173, 2135–2146. doi: 10.1111/bph.13447

PubMed Abstract | Crossref Full Text | Google Scholar

Miyanishi, H., Suga, S., Sumi, K., Takakuwa, M., Izuo, N., Asano, T., et al. (2023). The role of GABA in the dorsal striatum-raphe nucleus circuit regulating stress vulnerability in male mice with high levels of Shati/Nat8l. eNeuro 10, 1–14. doi: 10.1523/ENEURO.0162-23.2023

PubMed Abstract | Crossref Full Text | Google Scholar

Nicholson, S. L., and Brotchie, J. M. (2002). 5-hydroxytryptamine (5-ht, serotonin) and Parkinson's disease - opportunities for novel therapeutics to reduce the problems of levodopa therapy. Eur. J. Neurol. 9, 1–6. doi: 10.1046/j.1468-1331.9.s3.1.x

PubMed Abstract | Crossref Full Text | Google Scholar

Obeso, J. A., Rodriguez-Oroz, M. C., Goetz, C. G., Marin, C., Kordower, J. H., Rodriguez, M., et al. (2010). Missing pieces in the Parkinson's disease puzzle. Nat. Med. 16, 653–661. doi: 10.1038/nm.2165

PubMed Abstract | Crossref Full Text | Google Scholar

O'Callaghan, C., Hezemans, F. H., Ye, R., Rua, C., Jones, P. S., Murley, A. G., et al. (2021). Locus coeruleus integrity and the effect of atomoxetine on response inhibition in Parkinson's disease. Brain 144, 2513–2526. doi: 10.1093/brain/awab142

PubMed Abstract | Crossref Full Text | Google Scholar

Oh, Y.-S., Yoo, S.-W., Lyoo, C. H., and Kim, J.-S. (2022). Decreased thalamic monoamine availability in drug-induced parkinsonism. Sci. Rep. 12:3749. doi: 10.1038/s41598-022-07773-5

PubMed Abstract | Crossref Full Text | Google Scholar

Pagonabarraga, J., Kulisevsky, J., Strafella, A. P., and Krack, P. (2015). Apathy in Parkinson's disease: clinical features, neural substrates, diagnosis, and treatment. Lancet Neurol. 14, 518–531. doi: 10.1016/S1474-4422(15)00019-8

PubMed Abstract | Crossref Full Text | Google Scholar

Pardo-Moreno, T., García-Morales, V., Suleiman-Martos, S., Rivas-Domínguez, A., Mohamed-Mohamed, H., Ramos-Rodríguez, J. J., et al. (2023). Current treatments and new, tentative therapies for Parkinson's disease. Pharmaceutics 15:770. doi: 10.3390/pharmaceutics15030770

PubMed Abstract | Crossref Full Text | Google Scholar

Pare, D., Curro Dossi, R., and Steriade, M. (1990). Neuronal basis of the parkinsonian resting tremor: a hypothesis and its implications for treatment. Neuroscience 35, 217–226. doi: 10.1016/0306-4522(90)90077-H

PubMed Abstract | Crossref Full Text | Google Scholar

Parker, J. G., Marshall, J. D., Ahanonu, B., Wu, Y.-W., Kim, T. H., Grewe, B. F., et al. (2018). Diametric neural ensemble dynamics in parkinsonian and dyskinetic states. Nature 557, 177–182. doi: 10.1038/s41586-018-0090-6

PubMed Abstract | Crossref Full Text | Google Scholar

Pasquini, J., Ceravolo, R., Qamhawi, Z., Lee, J.-Y., Deuschl, G., Brooks, D. J., et al. (2018). Progression of tremor in early stages of Parkinson's disease: a clinical and neuroimaging study. Brain 141, 811–821. doi: 10.1093/brain/awx376

PubMed Abstract | Crossref Full Text | Google Scholar

Perez-Lloret, S., and Barrantes, F. J. (2016). Deficits in cholinergic neurotransmission and their clinical correlates in Parkinson's disease. NPJ Parkinsons Dis. 2:16001. doi: 10.1038/npjparkd.2016.1

PubMed Abstract | Crossref Full Text | Google Scholar

Peyron, C., Luppi, P.-H., Fort, P., Rampon, C., and Jouvet, M. (1996). Lower brainstem catecholamine afferents to the rat dorsal raphe nucleus. J. Comp. Neurol. 364, 402–413. doi: 10.1002/(SICI)1096-9861(19960115)364:3&lt;402::AID-CNE2&gt;3.0.CO;2-8

PubMed Abstract | Crossref Full Text | Google Scholar

Pirker, W., Katzenschlager, R., Hallett, M., and Poewe, W. (2023). Pharmacological treatment of tremor in Parkinson's disease revisited. J. Parkinsons Dis. 13:127. doi: 10.3233/JPD-225060

PubMed Abstract | Crossref Full Text | Google Scholar

Politis, M., and Niccolini, F. (2015). Serotonin in Parkinson's disease. Behav. Brain Res. 277, 136–145. doi: 10.1016/j.bbr.2014.07.037

PubMed Abstract | Crossref Full Text | Google Scholar

Prange, S., Klinger, H., Laurencin, C., Danaila, T., and Thobois, S. (2022). Depression in patients with Parkinson's disease: current understanding of its neurobiology and implications for treatment. Drugs Aging 39, 417–439. doi: 10.1007/s40266-022-00942-1

PubMed Abstract | Crossref Full Text | Google Scholar

Press W. H. (Ed.). (2007). Numerical Recipes: The Art of Scientific Computing, 3rd Edn. Cambridge: Cambridge University Press.

Google Scholar

Prinz, A., Selesnew, L.-M., Liss, B., Roeper, J., and Carlsson, T. (2013). Increased excitability in serotonin neurons in the dorsal raphe nucleus in the 6-ohda mouse model of Parkinson's disease. Exp. Neurol. 248, 236–245. doi: 10.1016/j.expneurol.2013.06.015

PubMed Abstract | Crossref Full Text | Google Scholar

Ranjbar-Slamloo, Y., and Fazlali, Z. (2020). Dopamine and noradrenaline in the brain; overlapping or dissociate functions? Front. Mol. Neurosci. 12:334. doi: 10.3389/fnmol.2019.00334

PubMed Abstract | Crossref Full Text | Google Scholar

Rav-Acha, M., Bergman, H., and Yarom, Y. (2008). Pre- and postsynaptic serotoninergic excitation of globus pallidus neurons. J. Neurophysiol. 100, 1053–1066. doi: 10.1152/jn.00845.2007

PubMed Abstract | Crossref Full Text | Google Scholar

Reed, M. C., Nijhout, H. F., and Best, J. (2013). Computational studies of the role of serotonin in the basal ganglia. Front. Integr. Neurosci. 7:41. doi: 10.3389/fnint.2013.00041

PubMed Abstract | Crossref Full Text | Google Scholar

Riley, K. F., Hobson, M. P., and Bence, S. J. (2006). Mathematical Methods for Physics and Engineering, 3rd Edn. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511810763

Crossref Full Text | Google Scholar

Rommelfanger, K., and Weinshenker, D. (2007). Norepinephrine: the redheaded stepchild of Parkinson's disease. Biochem. Pharmacol. 74, 177–190. doi: 10.1016/j.bcp.2007.01.036

PubMed Abstract | Crossref Full Text | Google Scholar

Segal, M. (1979). Serotonergic innervation of the locus coeruleus from the dorsal raphe and its action on responses to noxious stimuli. J. Physiol. 286, 401–415. doi: 10.1113/jphysiol.1979.sp012628

PubMed Abstract | Crossref Full Text | Google Scholar

Severson, K. A., Chahine, L. M., Smolensky, L. A., Dhuliawala, M., Frasier, M., Ng, K., et al. (2021). Discovery of Parkinson's disease states and disease progression modelling: a longitudinal data study using machine learning. Lancet Digit. Health 3, e555–e564. doi: 10.1016/S2589-7500(21)00101-1

PubMed Abstract | Crossref Full Text | Google Scholar

Shi, Z., Yao, W., Li, Z., Zeng, L., Zhao, Y., Zhang, R., et al. (2020). Artificial intelligence techniques for stability analysis and control in smart grids: methodologies, applications, challenges and future directions. Appl. Energy 278:115733. doi: 10.1016/j.apenergy.2020.115733

Crossref Full Text | Google Scholar

Szabo, S. T., and Blier, P. (2001). Functional and pharmacological characterization of the modulatory role of serotonin on the firing activity of locus coeruleus norepinephrine neurons. Brain Res. 922, 9–20. doi: 10.1016/S0006-8993(01)03121-3

PubMed Abstract | Crossref Full Text | Google Scholar

Tan, Y.-Y., Jenner, P., and Chen, S.-D. (2022). Monoamine oxidase-b inhibitors for the treatment of Parkinson's disease: past, present, and future. J. Parkinsons Dis. 12, 477–493. doi: 10.3233/JPD-212976

PubMed Abstract | Crossref Full Text | Google Scholar

Temel, Y., Boothman, L. J., Blokland, A., Magill, P. J., Steinbusch, H. W. M., Visser-Vandewalle, V., et al. (2007). Inhibition of 5-ht neuron activity and induction of depressive-like behavior by high-frequency stimulation of the subthalamic nucleus. Proc. Nat. Acad. Sci. 104, 17087–17092. doi: 10.1073/pnas.0704144104

PubMed Abstract | Crossref Full Text | Google Scholar

Tozzi, A., Sciaccaluga, M., Loffredo, V., Megaro, A., Ledonne, A., Cardinale, A., et al. (2021). Dopamine-dependent early synaptic and motor dysfunctions induced by α-synuclein in the nigrostriatal circuit. Brain 144, 3477–3491. doi: 10.1093/brain/awab242

PubMed Abstract | Crossref Full Text | Google Scholar

Vermeiren, Y., and Deyn, P. P. D. (2017). Targeting the norepinephrinergic system in Parkinson's disease and related disorders: the locus coeruleus story. Neurochem. Int. 102, 22–32. doi: 10.1016/j.neuint.2016.11.009

PubMed Abstract | Crossref Full Text | Google Scholar

Vertes, R. P. (1991). A pha-l analysis of ascending projections of the dorsal raphe nucleus in the rat. J. Comp. Neurol. 313, 643–668. doi: 10.1002/cne.903130409

PubMed Abstract | Crossref Full Text | Google Scholar

Voon, V., and Fox, S. H. (2007). Medication-related impulse control and repetitive behaviors in Parkinson's disease. Arch. Neurol. 64:1089. doi: 10.1001/archneur.64.8.1089

PubMed Abstract | Crossref Full Text | Google Scholar

Wang, S., Zhang, Q., Liu, J., Wu, Z., Wang, T., Gui, Z., et al. (2009). Unilateral lesion of the nigrostriatal pathway induces an increase of neuronal firing of the midbrain raphe nuclei 5-HT neurons and a decrease of their response to 5-HT1A receptor stimulation in the rat. Neuroscience 159, 850–861. doi: 10.1016/j.neuroscience.2008.12.051

PubMed Abstract | Crossref Full Text | Google Scholar

Williams-Gray, C. H., Foltynie, T., Brayne, C. E. G., Robbins, T. W., and Barker, R. A. (2007). Evolution of cognitive dysfunction in an incident Parkinson's disease cohort. Brain 130, 1787–1798. doi: 10.1093/brain/awm111

PubMed Abstract | Crossref Full Text | Google Scholar

Wilson, H., Dervenoulas, G., Pagano, G., Koros, C., Yousaf, T., Picillo, M., et al. (2019). Serotonergic pathology and disease burden in the premotor and motor phase of A53T α-synuclein parkinsonism: a cross-sectional study. Lancet Neurol. 18, 748–759. doi: 10.1016/S1474-4422(19)30140-1

PubMed Abstract | Crossref Full Text | Google Scholar

Wu, T., and Hallett, M. (2013). The cerebellum in Parkinson's disease. Brain 136, 696–709. doi: 10.1093/brain/aws360

PubMed Abstract | Crossref Full Text | Google Scholar

Ye, R., Hezemans, F. H., O'Callaghan, C., Tsvetanov, K. A., Rua, C., Jones, P. S., et al. (2023). Locus coeruleus integrity is linked to response inhibition deficits in Parkinson's disease and progressive supranuclear palsy. J. Neurosci. 43, 7028–7040. doi: 10.1523/JNEUROSCI.0289-22.2023

PubMed Abstract | Crossref Full Text | Google Scholar

Zach, H., Dirkx, M. F., Roth, D., Pasman, J. W., Bloem, B. R., Helmich, R. C., et al. (2020). Dopamine-responsive and dopamine-resistant resting tremor in Parkinson's disease. Neurology 95, e1461–e1470. doi: 10.1212/WNL.0000000000010316

PubMed Abstract | Crossref Full Text | Google Scholar

Zhang, H., Li, K., Chen, H.-S., Gao, S.-Q., Xia, Z.-X., Zhang, J.-T., et al. (2018). Dorsal raphe projection inhibits the excitatory inputs on lateral habenula and alleviates depressive behaviors in rats. Brain Struct. Funct. 223, 2243–2258. doi: 10.1007/s00429-018-1623-3

PubMed Abstract | Crossref Full Text | Google Scholar

Zhang, X., Cui, N., Wu, Z., Su, J., Tadepalli, J. S., Sekizar, S., et al. (2010). Intrinsic membrane properties of locus coeruleus neurons in mecp2-null mice. Am. J. Physiol.-Cell Physiol. 298, C635–C646. doi: 10.1152/ajpcell.00442.2009

PubMed Abstract | Crossref Full Text | Google Scholar