- 1School of Navigation, Dalian Maritime University, Dalian, China
- 2College of Marine Electrical Engineering, Dalian Maritime University, Dalian, China
This paper investigates the containment control of multiple unmanned surface vessels with nonlinear dynamics. To solve the leader-follower synchronization problem in a containment control system, a hierarchical control framework with a topology reconfiguration mechanism is proposed, and the process of containment control is converted into the tracking of a reference signal for each vessel on its respective target heading by means of the light-of-sight (LOS) guidance. In a control system, the neural networks (NNs) are adopted to consider the uncertainty. In the follower layer, a connectivity controller with a topology reconfiguration mechanism is embedded, to change the converging positions of followers so as to avoid collision within the system, and to maintain the system connectivity when the communication equality is poor. The effectiveness of the hierarchical control framework proposed in this paper is valid by simulation.
1. Introduction
Containment control (Cao and Ren, 2009; Meng et al., 2010) refers that, with the framework of multi-leader-multi-follower system, all the followers are driven by a control protocol so as to converge to the convex hull spanned by all the leaders. A significance of studying the containment control problem is that agents equipped with various advanced sensors can detect a variety of environmental information, including obstacles, etc., during the movement process, and complete the information fusion through distributed algorithms, whereby a dynamic security area is formed. Under the containment control protocol, the followers are able to converge to the safe zone and keep synchronized movement with the leader, achieving cooperation and guaranteeing system safety at the same time. In research aimed at multi-agent systems, containment control has yielded very rich research results (Li et al., 2013; Ma et al., 2015; Wen et al., 2016; Wang et al., 2020).
However, when the application background of the problem changes to marine, many theoretical results in multi-agent systems cannot be well applied. The reasons behind this phenomenon mainly result from the dynamics of the marine crafts, one is that the dynamic is complex, and it is difficult to deal with the strong nonlinearity and strong coupling, and the other is that the dynamic uncertainty is difficult to be known and describe. In motion control problems, there are two commonly used models for the dynamics of vessels: the model derived by Fossen (1994, 2002) and the Nomoto model (Banazadeh and Ghorbani, 2013). The three-degree-of-freedom model derived by Fossen is widely used in various types of problems because it includes kinematics-related state variables. However, the controller form is more complicated and often with higher-order derivative terms. The Nomoto model is usually applied to problems related to heading tracking because it establishes the transfer function relationship between rudder angle and heading. The controller form is simple and has fewer parameters to be determined, but the model accuracy is lower than that of the model derived by Fossen. When used in combination with guidance methods such as line-of-sight(LOS) guidance (Fossen et al., 2015), predictor-based line-of-sight(PLOS) guidance (Liu et al., 2016), adaptive line-of-sight(ALOS) guidance (Gu et al., 2017), etc., the controller form designed based on the Nomoto model is the simplest one. For the uncertainty, the neural networks(NNs) have been applied effectively due to their distinct advantages in recognizing unknown nonlinearity (Li et al., 2020, 2023; Ding and Wang, 2022; Ding et al., 2022; Shao et al., 2022; Teng et al., 2023; Zhou et al., 2023). In (Li et al., 2010), the radial basis function neural network (RBFNN) is used to consider the uncertainty of the system, which is combined with the dynamic surface control (DSC) technique to avoid the problem of complexity explosion, and its effectiveness is verified in the application of autopilot on marine crafts. In Peng et al. (2014), a distributed adaptive synchronization controller is proposed to provide good decoupling between the observer and controller design of a nonlinear multi-agent system, and to ensure that the state of each agent has bounded residuals. In Li et al. (2022), an RBFNN approximator was adopted to estimate the uncertainties, and by introducing the minimum learning parameter technique to minimize the computational burden associated with neural network weight updates. The NNs were combined with the described performance control when the dynamics were unmodeled (Shen et al., 2020), to guarantee all the followers asymptotically synchronized to the leader, and the synchronization errors within a prescribed level. In Chen et al. (2020), NNs were employed to approximate the unknown external disturbances and uncertain hydrodynamics of unmanned surface vessels, and an adaptive trajectory tracking controller with guaranteed transient performance was developed.
Besides the above model-related factors affecting the performance of the controller, safety is another important factor to be considered in practical application problems (Yang et al., 2022). In containment control problems, the topology of the system determines the convergence positions of followers (Wang et al., 2014). In practical problems, the follower is an entity with a certain volume rather than an idealized prime model, and the resulting collision problem within the system also constrains the translation of theory into practice. The collision avoidance and obstacle avoidance problem of a single vessel can be solved by the artificial potential field method (Liu et al., 2020; Mu and Peng, 2022) or other collision avoidance algorithm (Lu et al., 2022), but for the large-scale cooperative system, due to the network communication load and computational capacity constraints, this method is not very effective, and may even cause the system to be stuck due to repeatedly triggering the collision avoidance conditions. Therefore, considering system safety, it is necessary to seek a reasonable way to reconfigure the system topology from the perspective of the followers' convergence positions. That is to say, through some reasonable topology reconfiguration method, these topologies that may adversely affect the system are reconfigured to achieve specific control objectives such as collision avoidance, accelerating or decelerating the system convergence rate, and maintaining the system communication continuity (Mikulski et al., 2012; Haus et al., 2014; Griparic et al., 2022).
Inspired by the aforementioned studies, in this paper, based on the controller designed in Peng et al. (2014) which takes into account disturbances and model uncertainties with NNs, a synchronized control framework for a containment control system with topology reconfiguration mechanism is proposed, and the process of containment control is converted into the tracking of a reference signal for each vessel on its respective target heading by means of the LOS guidance method. With the proposed hierarchical control framework, the communication topology of the follower layer can be reconfigured to enable the transformation of follower formation and dispersion Securing the system throughout its operation.
2. Materials and methods
2.1. Graph theory
Consider a system composed by n agents, where represents the set of vertices, denotes the set of edges, representing the link between every two vertices. The link between every two vertices in the graph is defined by the adjacency matrix , where aij = 1 means that there is an edge directed to vi from vj, otherwise aij = 0. The degree matrix is a diagonal matrix where denotes the degree of vertex i. Another adjacency matrix is defined to describe the relationship between the virtual leader and the other agents, denoted , where ai0 = 1 indicates that there is an edge directed from the virtual leader to vi, otherwise ai0 = 0. In our study, a matrix denotes the whole system, which is given as .
The Laplacian matrix is defined
where
In ascendental order, the eigenvalues of the Laplace matrix are as follows
The second minimal eigenvalue of the Laplacian matrix, λ2, is also known as the algebraic connectivity. For undirected graph, when and only when λ2 > 0, the graph is connected (Fiedler, 1973).
2.2. Containment control
For a containment control system consisting m leaders as well as n − m followers, the Laplacian matrix can be expressed as
where , .
To analyze the containment control of a system, Lemma 1 is given:
Lemma 1. Assume that the communication digraph G has a directed spanning forest. The sum of each row of is 1 and the element of is positive if and only if the ith leader has a directed path to the jth follower (Shan et al., 2021).
Then, the position vectors of leaders as well as followers are denoted as
where denotes position vectors within XE − YE coordinate system.
2.3. System modeling
The kinematic model of the ith unmanned surface vessel is given as
where is the position vector within XE − YE coordinate system, ψi denotes the heading, denotes the linear velocity vector and the angular velocity vector of the ith unmanned surface vessel.
To make the controller design simpler, Assumption 1 is given.
Assumption 1. For each vessel in control system, the linear velocity u is a positive constant and the angular velocity v = 0.
For marine crafts, which usually have separate speed controllers for speed control, it is a reasonable assumption that u is a constant. During manipulation, the motion in the direction of the linear velocity is small relative to the motion in the other directions so it can be ignored (Li et al., 2009).
Considering a containment control system consisting of several unmanned surface vessels, the dynamics of each is stated as (Li et al., 2010)
where ψi, , and ωi representatively denote the heading, the rate of heading, and the heading moment of ith vessel, and are parameters that represent the maneuverability of marine crafts. is an unknown nonlinear function of , which is estimated by following equation
2.4. Control methods
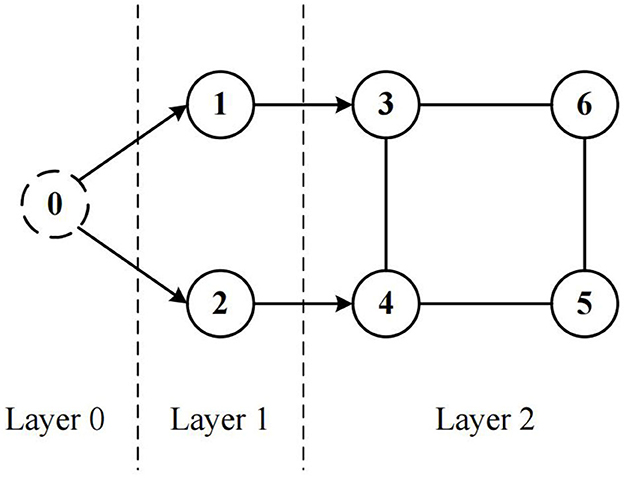
In the context of the cooperative containment control problem guided by a virtual leader, the system in terms of topology could be segmented into three layers, as shown in Figure 1. Layer 0 is the virtual leader layer, which gives the reference tracking signal. Layer 1 is the real leader layer, where all the real leaders track the reference signal through the virtual leader. Layer 2 is the follower layer, according to the real-time position of the real leaders, the respective reference trajectory point can be calculated for each follower, and the path-following process is converted as a heading tracking process through the LOS guidance, so as to achieve the cooperative containment control.
A topology reconfiguration strategy based on communication measurements is also incorporated in the second layer, to reconfigure the communication topology in time so as to maintain the performance level of the system.
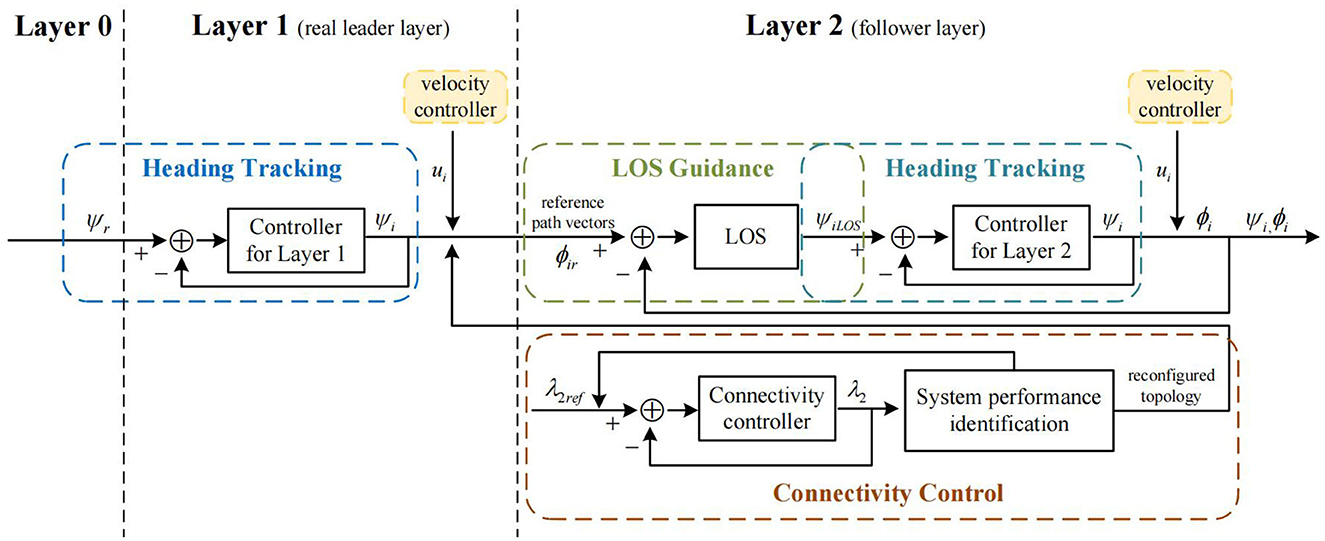
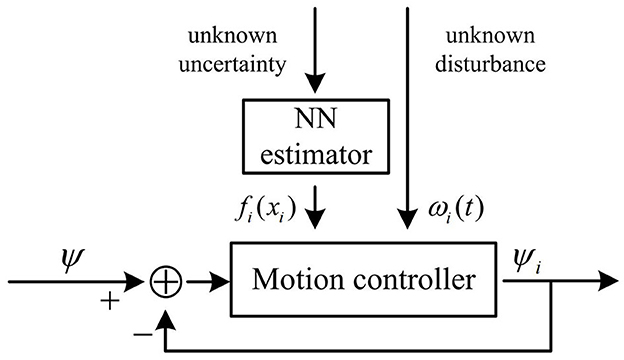
The control method of the system proposed in this paper is described in three steps: (i) the real leader's tracking of the reference heading, (ii) the follower's tracking of the respective reference trajectory under containment control, (iii) the follower's tracking of the new reference trajectory after a change of the system's communication topology. The hierarchical control framework proposed in this paper is shown in Figure 2. The controller for Layer1 and Layer 2 are the same in form, as shown in Figure 3, wherein the controller for Layer 1, ψ denotes ψr, and in the controller for Layer 2, ψ denotes ψiLOS.
2.4.1. Design of LOS guidance law based on containment control system
By the real leaders' tracking of the reference heading, combined with the kinematic equations given as Eq. (5), and with Eq. (4), the followers' desired positions could be calculated timely. For the goal of achieving containment control, the path-following process is converted as a time-varying heading tracking process by means of LOS guidance.
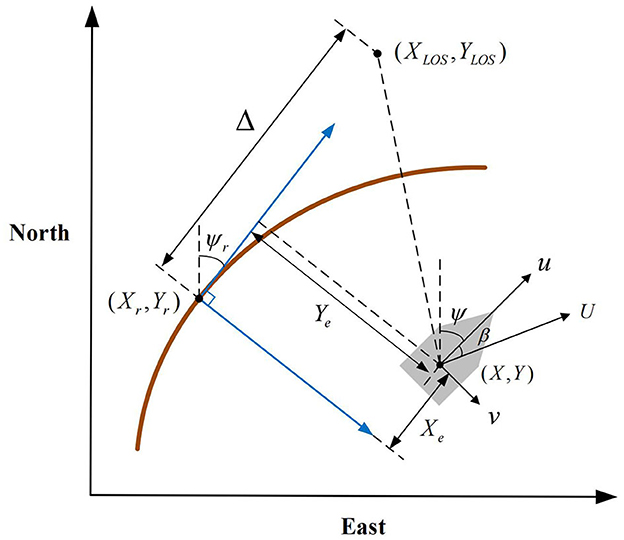
To design the tracking controller, the Serret-Frenet coordinate system is usually used, which is established by taking the current position of the marine craft (X, Y) projected on the reference path (Xd(ω), Yd(ω)) as the origin, where ω is the path parameter variable. The reference heading angle is
where p(ω) = dYp(ω)/dω, p(ω) = dXp(ω)/dω, the changing rate of the path parameter variable satisfying
where denotes the speed of navigation.
The schematic of LOS guidance is given in Figure 4, the LOS guidance law based on forward-looking distance is expressed as
where Δ is the forward-looking distance. Thus the reference heading angle of followers is
where reprensents the angle of drift.
From geometrical relations in Figure 1, the error of path tracking is obtained as follows
where Ye is the position tracking error, and the desired position can be calculated by Eq. (4).
For path-following problems where the path parameters are known, the LOS guidance law is stated as the above equation. In this paper, the reference heading is known while the global path is unknown, also, with Assumption 1, the effect of drift angle is not considered. Thus the guidance law for the ith follower marine craft in the system can be designed as
2.4.2. Controller design
Having , and selecting ωi = ui+Krxi, in which Kr is a feedback matrix, then the model can be written as
where
is Hurwitz, and
Lv, Lr and F denote the virtual leaders, the real leaders, and followers respectively, let Lv = {0}, Lr = {1, 2, ..., m}, F = {m + 1, m + 2, ..., n}. ψr(t) is the reference input, ui is the control input, fi(xi) is the unknown uncertainty and ωi(t) is disturbance which is unknown but bounded.
According to Stone (1948), fi(xi) is approximated with the neural networks, which is as follows
where denotes the ∈ ℝs×m satisfying ||Wi|| ≤ WM is a constant real matrix which denotes the ideal neural network (NN) weight matrix, φi(·) is a known basis function, εi is the neural network approximation error satisfying ||εi|| ≤ εM.
(1) Controller for vessels in Layer 1
As given in Zhang et al. (2011), the following control protocol is considered:
where c ∈ ℝ is a coupling gain, K = −BTP−1 is the feedback, of which P is a positive definite solution of linear matrix inequality (LMI)
where Q ∈ ℝn×n is positive definite.
Considering the uncertain nonlinear dynamical terms in the model, an adaptive control term uiad is given as
where is the estimation of Wi. Thus the control law can be written as
Combined with Figure 1 and the aforementioned, the object of the control law (13) implementation is a directed graph. According the results given in Peng et al. (2014), the update law of should be chosen as
where ΓWi, kW are constant to be designed, ei and τi is respectively given as follows
then, all signals in the closed-loop network can be uniformly ultimately bounded.
(2) Controller for vessels in Layer 2
From the former analysis, in the follower layer (i.e. Layer 2) the process of tracking the reference trajectory by each follower could be considered as the heading tracking process led by the virtual leader. Thus, in Layer 2, each follower can be also represented as follows, as shown in Figure 5, where x0i denotes the virtual leader for the ith follower. With this form, the follower receives control signals not directly from the leader, but from its corresponding virtual leader and its neighbors.
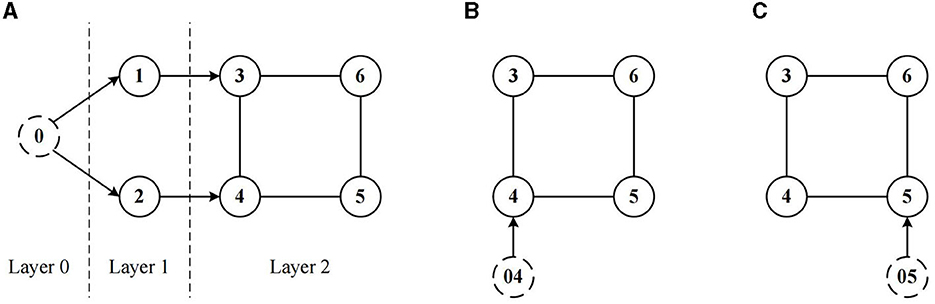
Figure 5. Communication topology of followers in Layer 2. (A) System topology, (B) communication topology of follower 4, and (C) communication topology of follower 5.
Thus, in Layer 2, the controller is designed as
where the update law of is
where ΓWFi, kFW are constant to be designed. According to the proof in Peng et al. (2014), it can be also obtained that all signals in the closed-loop network can be uniformly ultimately bounded.
(3) Connectivity control
The autopilot of the vessel, as an assistant tool in the process of navigation, if timely changes can be made based on the current or possible conditions when cooperating, the safety performance of the system and the efficiency of cooperation will be greatly improved. Several classical cases of topology reconfiguration are to change the converging positions of followers so as to avoid collision within the system, or to maintain the system connectivity when the communication equality is poor.
A topology reconfiguration algorithm was given by Griparic et al. (2022), which enabled the algebraic connectivity of the system to reach the desired value through its proposed method of adding/removing links. The inputs of the topology reconfiguration algorithm are the initial local adjacency matrix of each marine craft ( means that the marine craft is a follower and l = 1, 2, 3, ..., n − m represents the index of marine craft), desired level of system performance λ2ref, and user-defined value Kλ2. The connectivity controller can be stated as follows
the parameter Kλ2 > 0 is to be determined so as to have
Combined with the RNN-based system performance identification model proposed by Liu et al. (2023), the features of the containment control system can be extracted as the following matrix, which is considered as the input of the RNN-based performance identification model
where ΘInput represents the input to the NN where the first row composed of ones and zeros describes the connection relationship between the leader and follower agents in the system, θi = 1, i ∈ [1, n − m] indicates that the leader is connected to the ith follower while 0 denotes no connection. The remaining three rows are vectors transformed from the node degree relativity matrix, di denotes the degree of the ith follower, denotes the sum of degrees of the neighbor set of the ith follower, and denotes the sum of degrees of the neighbor set nodes of the ith follower's neighbors.
The output is the performance indicators of the containment control system, given as
where λ2 is the algebraic connectivity of the network in Layer 2, and is used to describe the dispersion of converging positions of followers in the convex hull spanned by all leader.
Through this RNN-based performance identification model, the system topology with good collision-avoiding performance can be selected. Thus the reconfiguration of topology is finished.
To integrate topology reconfiguration with system control, it is assumed that the communication between each marine craft is continuous. Thus, topology reconfiguration can be done within a very short period of time which is represented as a time-varying Laplacian matrix in the control system, expressed as
where Lc0 denotes the initial topology of Layer 2, and LcR denotes the reconfigured topology of Layer 2.
Based on the premise of the containment control problem, only the topology of Layer 2 is reconfigured in this paper. The framework of connectivity control is shown in Figure 6, where the denotes the algebraic connectivity after each processing, and the identification object of system performance is whether the dispersion of followers is large enough so as to keep a safe distance for each two followers. The system performance identification module is a determination of the reconfigured topology output by the connectivity controller. If the determination is ‘Yes”, the reconfigured topology satisfying the system performance requirements is obtained and output. If not, the control signal will be transmitted back to the first step which is to input λ2ref and start another round of topology reconfiguration.
3. Simulation results and discussions
The simulation is implemented to validate the effect of the control law (21) and (24), LOS guidance law (13), as well as the connectivity control algorithm designed in Section 3.2.3. Considering a multiple unmanned surface vessel system (6) with 1 virtual leader, 3 real leaders, and 9 followers, whose initial communication topology is shown in Figure 7A.
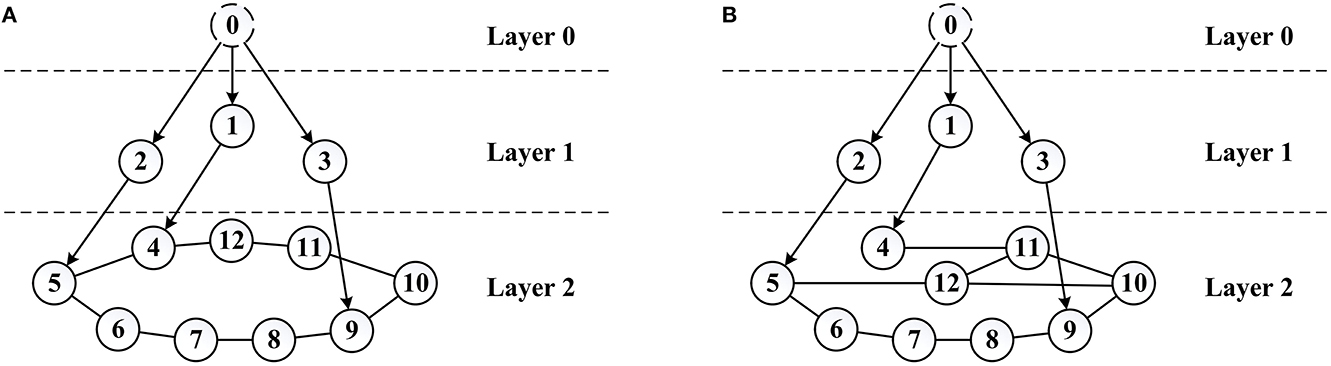
Figure 7. System communication topology. (A) Initial system topology and (B) reconfigured system topology.
The initial position vectors of real leaders are given as , and . The initial position vectors of followers are given as , , , , , , , and . The speed of each marine crat is u = 8m/s, v = 0. Forward-looking distance is Δ = 150m.
The parameters are given as bi1 = 0.1256, bi2 = 0.3576, bi3 = 0.0278. The coupling gain c = 30, the feedback matrix , and the ordered reference input ψr is given as
When using the neural network for estimation, to make the estimation better, the adaptive parameters of the NN should take larger values. Thus taking ΓWi = 100 and ΓWFi = 100. kW and kFW are taking as kW = kFW = 0.8. φi(xi) is given as .
Letting , through solving (19), one can obtain that
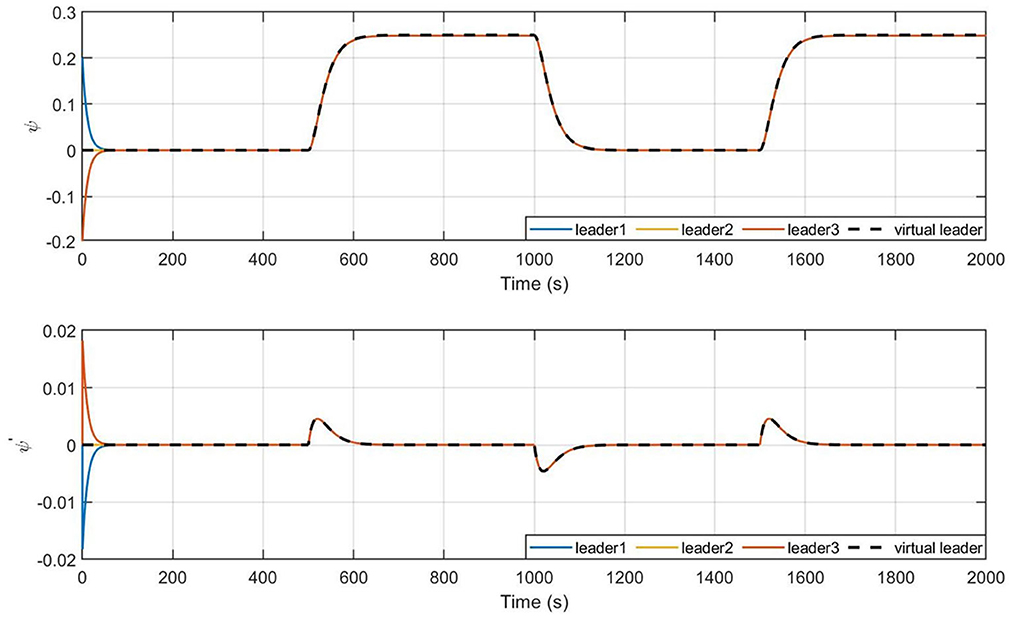
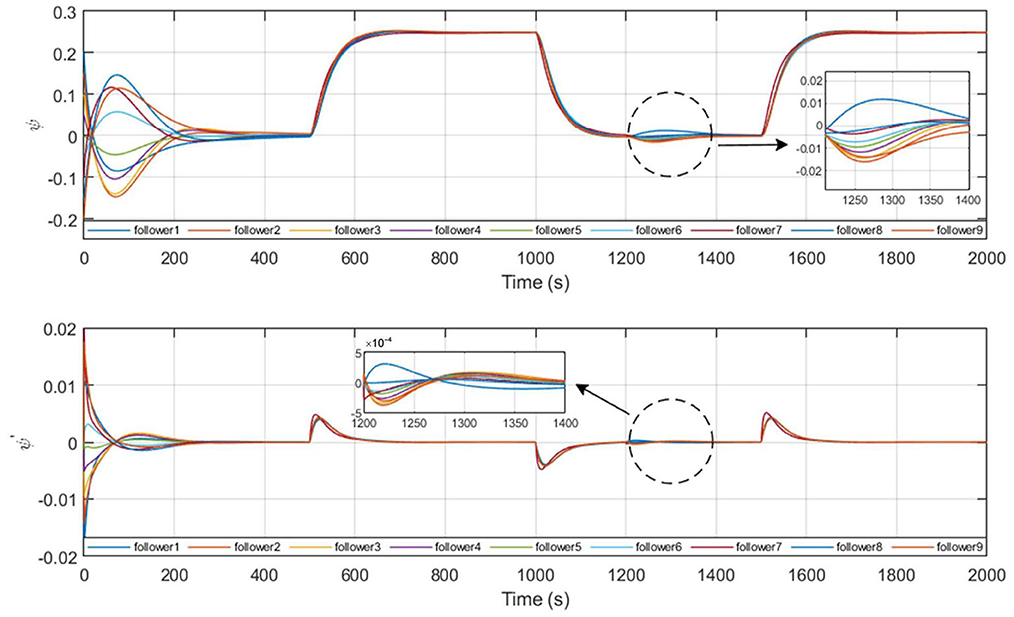
Figures 8, 9 give the state profile of real leaders and followers, in which the real leaders track well on the reference signal given by the virtual leader, and with the LOS guidance law, the followers also achieve tracking of the targeted heading, thus converging into the convex hull spanned by leaders.
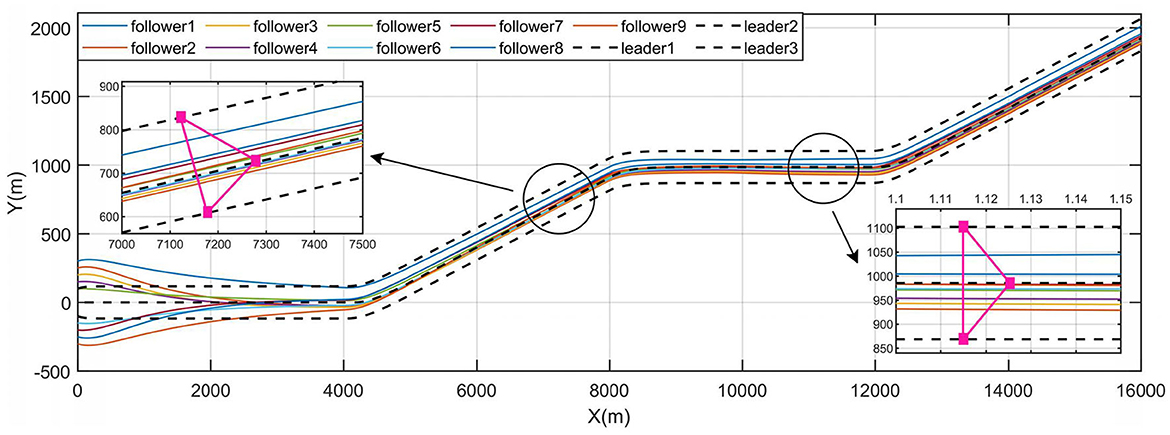
The path profile is given in Figure 10, in which can be observed that with the initial system communication topology, the converging positions of the followers are very tight. Most of the marine crafts are not distant enough from each other to meet the safety distance requirement, in which case the risk of collision within the system will be greatly increased. Thus, combined with the connectivity control method and the system performance identification model stated in Section 3.2.3, a reference value λ2ref = 0.4 is chosen as the desired performance index of Layer 2 and Kλ2 is taken as Kλ2 = 0.1, which is used to reconfigure the communication topology of Layer 2 so as to disperse the converging positions of followers. The reconfigured system topology is shown in Figure 7B, accordingly, λ2 = 0.4131.
The process of topology reconfiguration is performed as t = 1, 200s. It is presented in Figure 9 that the response of the control system when the reference path tracked by the followers is changed after the topology reconfiguration is completed.
4. Conclusion
This paper investigated the containment control of multiple unmanned surface vessels with NN control via reconfigurable hierarchical communication topology. A hierarchical control framework was proposed, so as to transform the containment control problem of followers to the synchronization of reference heading tracking, which is realized with the LOS guidance law. In the control system, the NNs are adopted to consider the uncertainty. In the follower layer, a connectivity controller with a topology reconfiguration mechanism was embedded to reconfigure the communication topology, which is used to improve the safety of the system when operating. It was shown in the simulation results that with this hierarchical control framework, the real leader and the virtual leader, and the follower and the real leader all achieved well-tracking, and the controller also achieved the tracking of the new reference signal without significant oscillations of control output when the communication topology of the follower layer was changed. In this case, the converging positions of the followers were dispersed throughout the system when tracking the reference heading during containment control of multiple marine crafts, which greatly reduced the risk of collisions within the system.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
WL: Conceptualization, Formal analysis, Methodology, Writing—original draft. FT: Conceptualization, Methodology, Validation, Writing—review and editing. HX: Software, Writing—original draft. CW: Writing—original draft.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Zhejiang Lab Open Research Project (No. K2022QA0AB03), National Natural Science Foundation of China (Nos. 52371360, 52201407, and 51939001), High Level Talents Innovation Support Plan of Dalian (Young Science and Technology Star Project) (No. 2021RQ058), Funds for the Central Universities (No. 3132023147), and Fundamental Research Funds for the Central Universities (No. 3132023103).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Banazadeh, A., and Ghorbani, M. (2013). Frequency domain identification of the nomoto model to facilitate kalman filter estimation and pid heading control of a patrol vessel. Ocean Eng. 72, 344–355. doi: 10.1016/j.oceaneng.2013.07.003
Cao, Y., and Ren, W. (2009). “Containment control with multiple stationary or dynamic leaders under a directed interaction graph,” in Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference (IEEE), 3014–3019. doi: 10.1109/CDC.2009.5399946
Chen, L., Cui, R., Yang, C., and Yan, W. (2020). Adaptive neural network control of underactuated surface vessels with guaranteed transient performance: Theory and experimental results. IEEE Trans. Ind. Electr. 67, 4024–4035. doi: 10.1109/TIE.2019.2914631
Ding, S., and Wang, Z. (2022). Synchronization of coupled neural networks via an event-dependent intermittent pinning control. IEEE Trans. Syst. Man Cybern. Syst. 52, 1928–1934. doi: 10.1109/TSMC.2020.3035173
Ding, S., Wang, Z., and Xie, X. (2022). Periodic event-triggered synchronization for discrete-time complex dynamical networks. IEEE Trans. Neural Netw. Learn. Syst. 33, 3622–3633. doi: 10.1109/TNNLS.2021.3053652
Fiedler, M. (1973). Algebraic connectivity of graphs. Czechosl. Mathem. J. 23, 298–305. doi: 10.21136/CMJ.1973.101168
Fossen, T. I. (2002). Marine Control Systems. Trondheim, Norway: Norwegian University of Science and Technology.
Fossen, T. I., Pettersen, K. Y., and Galeazzi, R. (2015). Line-of-sight path following for dubins paths with adaptive sideslip compensation of drift forces. IEEE Trans. Control Syst. Technol. 23, 820–827. doi: 10.1109/TCST.2014.2338354
Griparic, K., Polic, M., Krizmancic, M., and Bogdan, S. (2022). Consensus-based distributed connectivity control in multi-agent systems. IEEE Trans. Netw. Sci. Eng. 9, 1264–1281. doi: 10.1109/TNSE.2021.3139045
Gu, N., Wang, D., Liu, L., Zhang, B., and Peng, Z. (2017). “Adaptive line-of-sight guidance law for synchronized path-following of under-actuated unmanned surface vehicles based on low-frequency learning,” in 2017 36th Chinese Control Conference (CCC) (IEEE), 6632–6637. doi: 10.23919/ChiCC.2017.8028408
Haus, T., Palunko, I., Tolić, D., Bogdan, S., Lewis, F. L., and Mikulski, D. G. (2014). Trust-based self-organising network control. IET Control Theory Applic. 8, 2126–2135. doi: 10.1049/iet-cta.2014.0333
Li, J., Xiang, X., and Yang, S. (2022). Robust adaptive neural network control for dynamic positioning of marine vessels with prescribed performance under model uncertainties and input saturation. Neurocomputing 484, 1–12. doi: 10.1016/j.neucom.2021.03.136
Li, T., Bai, W., Liu, Q., Long, Y., and Chen, C. L. P. (2023). Distributed fault-tolerant containment control protocols for the discrete-time multiagent systems via reinforcement learning method. IEEE Trans. Neural Netw. Learn. Syst. 34, 3979–3991. doi: 10.1109/TNNLS.2021.3121403
Li, T.-S., Wang, D., Feng, G., and Tong, S.-C. (2010). A dsc approach to robust adaptive nn tracking control for strict-feedback nonlinear systems. IEEE Trans. Syst. Man Cyber. Part B 40, 915–927. doi: 10.1109/TSMCB.2009.2033563
Li, Z., Li, T., Feng, G., Zhao, R., and Shan, Q. (2020). Neural network-based adaptive control for pure-feedback stochastic nonlinear systems with time-varying delays and dead-zone input. IEEE Trans. Syst. Man Cybern. Syst. 50, 5317–5329. doi: 10.1109/TSMC.2018.2872421
Li, Z., Ren, W., Liu, X., and Fu, M. (2013). Distributed containment control of multi-agent systems with general linear dynamics in the presence of multiple leaders. Int. J. Robust Nonl. Control 23, 534–547. doi: 10.1002/rnc.1847
Li, Z., Sun, J., and Oh, S. (2009). Design, analysis and experimental validation of a robust nonlinear path following controller for marine surface vessels. Automatica 45, 1649–1658. doi: 10.1016/j.automatica.2009.03.010
Liu, L., Wang, D., Peng, Z., and Wang, H. (2016). Predictor-based los guidance law for path following of underactuated marine surface vehicles with sideslip compensation. Ocean Eng. 124, 340–348. doi: 10.1016/j.oceaneng.2016.07.057
Liu, W., Teng, F., Fang, X., Liang, Y., and Zhang, S. (2023). An rnn-based performance identification model for multi-agent containment control systems. Mathematics 11, 2760. doi: 10.3390/math11122760
Liu, Y., Huang, P., Zhang, F., and Zhao, Y. (2020). Distributed formation control using artificial potentials and neural network for constrained multiagent systems. IEEE Trans. Control Syst. Technol. 28, 697–704. doi: 10.1109/TCST.2018.2884226
Lu, N., Zhou, W., Yan, H., Fei, M., and Wang, Y. (2022). A two-stage dynamic collision avoidance algorithm for unmanned surface vehicles based on field theory and colregs. Ocean Eng. 259, 111836. doi: 10.1016/j.oceaneng.2022.111836
Ma, Q., Lewis, F. L., and Xu, S. (2015). Cooperative containment of discrete-time linear multi-agent systems. Int. J. Robust Nonl. Control 25, 1007–1018. doi: 10.1002/rnc.3124
Meng, Z., Ren, W., and You, Z. (2010). Distributed finite-time attitude containment control for multiple rigid bodies. Automatica 46, 2092–2099. doi: 10.1016/j.automatica.2010.09.005
Mikulski, D. G., Lewis, F. L., Gu, E. Y., and Hudas, G. R. (2012). “Trust method for multi-agent consensus,” in Unmanned Systems Technology XIV, eds. R. E. Karlsen, D. W. Gage, C. M. Shoemaker, and G. R. Gerhart (Bellingham, USA: SPIE), 83870E. doi: 10.1117/12.918927
Mu, C., and Peng, J. (2022). Learning-based cooperative multiagent formation control with collision avoidance. IEEE Trans. Syst. Man Cybern. Syst. 52, 7341–7352. doi: 10.1109/TSMC.2022.3153030
Peng, Z., Wang, D., Zhang, H., and Sun, G. (2014). Distributed neural network control for adaptive synchronization of uncertain dynamical multiagent systems. IEEE Trans. Neural Netw. Learn. Syst. 25, 1508–1519. doi: 10.1109/TNNLS.2013.2293499
Shan, Q., Teng, F., Li, T., and Chen, C. P. (2021). Containment control of multi-agent systems with nonvanishing disturbance via topology reconfiguration. Sci. China Inf. Sci. 64, 1–3. doi: 10.1007/s11432-018-9695-2
Shao, J., Shi, L., Cheng, Y., and Li, T. (2022). Asynchronous tracking control of leader–follower multiagent systems with input uncertainties over switching signed digraphs. IEEE Trans. Cybern. 52, 6379–6390. doi: 10.1109/TCYB.2020.3044627
Shen, Q., Shi, P., Zhu, J., Wang, S., and Shi, Y. (2020). Neural networks-based distributed adaptive control of nonlinear multiagent systems. IEEE Trans. Neural Netw. Learn. Syst. 31, 1010–1021. doi: 10.1109/TNNLS.2019.2915376
Stone, M. H. (1948). The generalized weierstrass approximation theorem. Mathem. Magaz. 21, 237–254. doi: 10.2307/3029337
Teng, F., Zhang, Y., Yang, T., Li, T., Xiao, Y., and Li, Y. (2023). “Distributed optimal energy management for we-energy considering operation security,” in IEEE Transactions on Network Science and Engineering 1–11. doi: 10.1109/TNSE.2023.3295079
Wang, F.-Y., Ni, Y.-H., Liu, Z.-X., and Chen, Z.-Q. (2020). Containment control for general second-order multiagent systems with switched dynamics. IEEE Trans. Cyber. 50, 550–560. doi: 10.1109/TCYB.2018.2869706
Wang, Y., Cheng, L., Hou, Z.-G., Tan, M., and Wang, M. (2014). Containment control of multi-agent systems in a noisy communication environment. Automatica 50, 1922–1928. doi: 10.1016/j.automatica.2014.05.018
Wen, G., Zhao, Y., Duan, Z., Yu, W., and Chen, G. (2016). Containment of higher-order multi-leader multi-agent systems: A dynamic output approach. IEEE Trans. Autom. Control 61, 1135–1140. doi: 10.1109/TAC.2015.2465071
Yang, Y., Xiao, Y., and Li, T. (2022). Attacks on formation control for multiagent systems. IEEE Trans. Cybern. 52, 12805–12817. doi: 10.1109/TCYB.2021.3089375
Zhang, H., Lewis, F. L., and Das, A. (2011). Optimal design for synchronization of cooperative systems: State feedback, observer and output feedback. IEEE Trans. Autom. Control 56, 1948–1952. doi: 10.1109/TAC.2011.2139510
Keywords: containment control, neural network control, topology reconfiguration, hierarchical communication topology, LOS guidance
Citation: Liu W, Teng F, Xiao H and Wang C (2023) Containment control of multiple unmanned surface vessels with NN control via reconfigurable hierarchical topology. Front. Comput. Neurosci. 17:1284966. doi: 10.3389/fncom.2023.1284966
Received: 29 August 2023; Accepted: 25 September 2023;
Published: 19 October 2023.
Edited by:
Yang Cui, University of Science and Technology Liaoning, ChinaReviewed by:
Yuliang Cai, Liaoning University, ChinaSanbo Ding, Hebei University of Technology, China
Copyright © 2023 Liu, Teng, Xiao and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fei Teng, dGVuZ2ZlaUBkbG11LmVkdS5jbg==
 Wei Liu
Wei Liu Fei Teng2*
Fei Teng2* Chen Wang
Chen Wang