- 1Department of Electrical and Computer Engineering, Michigan Technological University, Houghton, MI, United States
- 2Department of Biological Sciences, Michigan Technological University, Houghton, MI, United States
Introduction: Parkinson’s disease (PD) is a neurodegenerative disorder affecting millions of patients. Closed-Loop Deep Brain Stimulation (CL-DBS) is a therapy that can alleviate the symptoms of PD. The CL-DBS system consists of an electrode sending electrical stimulation signals to a specific region of the brain and a battery-powered stimulator implanted in the chest. The electrical stimuli in CL-DBS systems need to be adjusted in real-time in accordance with the state of PD symptoms. Therefore, fast and precise monitoring of PD symptoms is a critical function for CL-DBS systems. However, the current CL-DBS techniques suffer from high computational demands for real-time PD symptom monitoring, which are not feasible for implanted and wearable medical devices.
Methods: In this paper, we present an energy-efficient neuromorphic PD symptom detector using memristive three-dimensional integrated circuits (3D-ICs). The excessive oscillation at beta frequencies (13–35 Hz) at the subthalamic nucleus (STN) is used as a biomarker of PD symptoms.
Results: Simulation results demonstrate that our neuromorphic PD detector, implemented with an 8-layer spiking Long Short-Term Memory (S-LSTM), excels in recognizing PD symptoms, achieving a training accuracy of 99.74% and a validation accuracy of 99.52% for a 75%–25% data split. Furthermore, we evaluated the improvement of our neuromorphic CL-DBS detector using NeuroSIM. The chip area, latency, energy, and power consumption of our CL-DBS detector were reduced by 47.4%, 66.63%, 65.6%, and 67.5%, respectively, for monolithic 3D-ICs. Similarly, for heterogeneous 3D-ICs, employing memristive synapses to replace traditional Static Random Access Memory (SRAM) resulted in reductions of 44.8%, 64.75%, 65.28%, and 67.7% in chip area, latency, and power usage.
Discussion: This study introduces a novel approach for PD symptom evaluation by directly utilizing spiking signals from neural activities in the time domain. This method significantly reduces the time and energy required for signal conversion compared to traditional frequency domain approaches. The study pioneers the use of neuromorphic computing and memristors in designing CL-DBS systems, surpassing SRAM-based designs in chip design area, latency, and energy efficiency. Lastly, the proposed neuromorphic PD detector demonstrates high resilience to timing variations in brain neural signals, as confirmed by robustness analysis.
1 Introduction
Parkinson’s disease (PD) is a prevalent neurodegenerative condition affecting millions of patients worldwide (Ghasemi et al., 2018; Zhou et al., 2018). Although various medications are available to alleviate the symptoms, their effectiveness tends to diminish over time due to drug resistance. Consequently, later stages of PD patients require higher medication dosages, which can significantly impact cognitive abilities and mental health (Dostrovsky and Lozano, 2002; Arlotti et al., 2016). To address this challenge, deep brain stimulation (DBS) has emerged as a novel therapy for PD patients in advanced stages. In a DBS system, an electrode is implanted into a specific target in the brain for delivering electrical stimulation signals through a battery-powered programmable stimulator implanted in the chest of PD patients. The current DBS system continuously sends the stimulation signals to the brain with fixed parameters and frequency regardless of the clinical state of the patient, referred to as an open-loop DBS (OL-DBS) system (Ghasemi et al., 2018; Zhou et al., 2018; Lozano et al., 2019). The rigid fashion of the current OL-DBS technique poses two critical issues: (1) the high-frequency stimulation causes serious cognitive and psychiatric side effects, such as speech deficits and cognitive dysfunction (Dostrovsky and Lozano, 2002; Deuschl et al., 2006; Massano and Garrett, 2012; Arlotti et al., 2016; Cyron, 2016); (2) the continuous stimulation quickly drains the battery of energy-inefficient hardware platforms (Salam et al., 2015; Shukla, 2015; Ghasemi et al., 2018; Jovanov et al., 2018; Shah et al., 2018; Zhou et al., 2018). Therefore, a closed-loop DBS (CL-DBS) system (He et al., 2021) has been proposed to address the limitations of the OL-DBS system by incorporating a feedback loop. This feedback loop allows the detection of PD symptoms and the delivery of optimized stimulus impulses according to different severities of PD symptoms. The CL-DBS systems are widely identified as the future development direction of the DBS system (Allen et al., 2010; Rosin et al., 2011; Carron et al., 2013; Shukla, 2015; Arlotti et al., 2016; Little et al., 2016; Rossi et al., 2016; Ghasemi et al., 2018; Kuo et al., 2018; Zhou et al., 2018; Lozano et al., 2019; Velisar et al., 2019). In a CL-DBS system, stimulation parameters are automatically adjusted based on the clinical symptoms of the PD patients. The studies demonstrate that closed-loop paradigms with real-time adaptive stimulation yield fewer unpleasant side effects and greater clinical benefits compared to fixed paradigms (He et al., 2021; Su et al., 2021). CL-DBS systems that implement simple on-off control of stimulations have been developed and tested in human and animal studies (Marceglia et al., 2007; Little et al., 2013; Priori et al., 2013; Wu et al., 2015; He et al., 2021).
There are various challenges associated with CL-DBS systems. The continuous operation of implanted CL-DBS systems round-the-clock, 7 days a week, poses significant demands in terms of intelligence and energy efficiency. Accurately recognizing symptom-related signals and generating adaptive stimulation signals usually require computationally expensive algorithms, e.g., reinforcement learning (Shukla, 2015; Arlotti et al., 2016; Little et al., 2016; Kuo et al., 2018; Lozano et al., 2019; Velisar et al., 2019; Gao et al., 2020; Liu et al., 2020). Thus, a novel design of an intelligent CL-DBS device with low power consumption and high intelligence is in urgent demand. In this work, we apply a three-dimensional (3D) memristive neuromorphic system to the energy-efficient recognition and assessment of symptoms in a CL-DBS system. Specifically, we utilize the PD computational model (Kumaravelu et al., 2016), which includes a cortical-basal ganglion-thalamic circuit, to generate a substantial amount of data from the healthy and Parkinsonian rat brain. The Parkinson’s symptom is identified with the output of this PD computational model at the beta frequency range (13–30 Hz). The heightened power density of neural activities in the beta frequency range has been positively correlated with the severity of motor impairment (Perez-Alcazar et al., 2010; Connolly et al., 2015; de Hemptinne et al., 2015; Escobar et al., 2017). Therefore, the power density levels in the beta frequency range can serve as biomarkers for evaluating PD symptoms. The generated data with the PD computational models are used for training a novel neuromorphic PD detector that is implemented with a spiking long-short-term memory neural network (S-LSTM) (An et al., 2018a,b). The neuromorphic PD detector will be trained using the Whetstone method (Severa et al., 2019). The Whetstone method is a cutting-edge training algorithm for neuromorphic systems that gradually transforms conventional nonlinear functions, e.g., sigmoid function, into threshold functions during the training process. Furthermore, our neuromorphic PD detector can identify PD symptoms based on neural activities in time domain without converting them into the frequency domain, resulting in enhanced computational efficiency. The incorporation of memristive synapses in our neuromorphic PD detector significantly improves energy efficiency, a crucial factor for CL-DBS systems. The energy efficiency of our neuromorphic CL-DBS system is evaluated using a hardware simulator, named NeuroSIM (Chen et al., 2018; Peng et al., 2020; Lu et al., 2021; An et al., 2021a,b). Specifically, the weights and biases of the neuromorphic PD detector are saved and deployed into the NeuroSIM simulator as memristive synapses. After that, the hardware performance of our neuromorphic PD detector will be calculated under both monolithic and heterogeneous 3D chip architectures.
The contributions of this study are outlined as follows:
1. Utilizing spiking signals from the neural activities directly in time domain for PD symptom evaluation significantly reduces the time and energy required for converting signals from the time domain to the frequency domain.
2. To our best knowledge, we are the first to employ neuromorphic computing and memristors in the design of CL-DBS systems.
3. The neuromorphic PD detector with memristive synapse architectures outperforms traditional SRAM-based designs in CL-DBS systems regarding chip design area, latency, and energy efficiency.
4. Our study evaluates the enhancements gained by implementing three-dimensional technology in hardware for CL-DBS, considering chip design area, latency, and energy efficiency.
5. The robustness analysis of our neuromorphic PD detector demonstrates its high resilience to timing variations in brain neural signals.
2 Research background
2.1 Introduction to neuromorphic computing
The brains can perform remarkably intricate tasks with incredible energy efficiency. The adult human brain consumes approximately 20 W of power consumption (Jorgensen, 2021). In contrast, the average energy usage of modern digital computers is about 60–175 watts (Marković et al., 2020; Jorgensen, 2021) for comparable cognitive tasks. For instance, a typical computer requires approximately 250 watts of power to recognize just 1,000 unique items (Roy et al., 2019). Training a sophisticated natural language processing model on a modern supercomputer consumes 1,000 kWh of energy, equivalent to the energy needs of a human brain performing all its tasks for 6 years (Marković et al., 2020). The remarkable outperformance of the human brain can be attributed to several fundamental features, including the extensive high density of connectivity, spike-based information representation, and a structural and functional hierarchical organization (Felleman and Van Essen, 1991; Bullmore and Sporns, 2012). The human brain is estimated to have over 100 billion neurons connecting with trillions of synapses (Changeux, 1997). Synapses serve as the storage components for memory and learning, while neurons act as the computational units of the brain, exchanging information through discrete action potentials or spikes. Neuromorphic computing is a novel computational paradigm that seeks to replicate the functionality of biological neurons and synapses of the brains. The concept of neuromorphic computing was first envisioned by Mead in the 1980s (Mead and Ismail, 1989; An et al., 2018a,b).
The primary objective of neuromorphic computing is to create brain-inspired computations that overcome the challenges from the traditional von Neumann computer architecture (Davies et al., 2021). The von Neumann architecture consists of separate memory units and central processing units (CPU). Consequently, information must be repeatedly transferred between these units during computations, leading to speed bottlenecks and limitations in energy efficiency, widely known as the von Neumann bottleneck (Naylor and Runciman, 2007; Min and Corinto, 2021). Neuromorphic computing encompasses various technologies to overcome the von Neumann bottleneck (Mead, 1990). With co-located electronic neurons and synapses, neuromorphic chips, such as Intel Loihi, provide a much faster and energy-efficient computational paradigm (Wunderlich et al., 2019).
Additionally, the remarkable energy efficiency of neuromorphic systems can be attributed to the distinctive information coding schemes found in biological neural systems (Roy et al., 2019). In neural systems, the communication information among neurons is coded in a sequence of spiking signals at low frequency. Unlike the high-speed modern computer, the main frequency of the spiking signals in the nervous system is as low as ~kilohertz level (1–10 millisecond duration) with millivolt-level magnitudes (Kandel et al., 2000). The neuromorphic system is a software and hardware co-design approach to achieving a comparable power-efficient artificial intelligence system by taking inspiration from human brains and implementing low-fire-rate spiking communication, threshold activation functions, and spiking neural networks (Mead, 1990; Schemmel et al., 2008; Azevedo et al., 2009; Gerstner and Naud, 2009; De Garis et al., 2010; Goertzel et al., 2010; Smith, 2010; Versace and Chandler, 2010; Brüderle et al., 2011; Merolla et al., 2011; Seo et al., 2011; Joubert et al., 2012; Pfeil et al., 2012; Esser et al., 2013; Furber et al., 2013; Hasler and Marr, 2013; Painkras et al., 2013; Rajendran et al., 2013; Stromatias et al., 2013; Benjamin et al., 2014; Chen et al., 2014; Merolla et al., 2014; Putnam et al., 2014; Indiveri et al., 2015; Qiao et al., 2015; Schuman et al., 2015; Walter et al., 2015; Schuman, 2016; Ehsan et al., 2017; Ferreira de Lima et al., 2017; Lastras-Montaño et al., 2017; Osswald et al., 2017; Schuman et al., 2017; Bai and Bradley, 2018; Davies et al., 2018; An et al., 2018a,b; Severa et al., 2019). In contrast to conventional artificial neural networks, e.g., convolution neural networks (LeCun et al., 1989; Lecun et al., 2015; Bengio et al., 2017), recurrent neural networks (Zaremba et al., 2014; Bengio et al., 2017), etc., the information conveyed between layers in SNNs and neuromorphic systems is in a format of spiking pulses (Zenke and Ganguli, 2018; Neftci et al., 2019; Tavanaei et al., 2019; Taherkhani et al., 2020). Through this way, SNNs have the capability of emulating the functionalities and learning processes of biological neural networks (Maass, 1997). In an SNN, neurons interact through spikes transmitted via adjustable synapses (An et al., 2021a,b). While neurons in traditional ANNs exhibit fixed continuous-valued activity, biological neurons employ discrete spikes to compute and transmit information. The sparsity of low-frequency neuron spikes significantly increase the energy efficiency of the neuromorphic system (Yi et al., 2015). SNNs utilize biological neuron models for computation, bridging the gap between neuroscience and AI (Yamazaki et al., 2022). Furthermore, the activation functions, which are also referred to as neurons in deep learning, are threshold activation functions rather than traditional nonlinear activation functions in SNNs (Ramachandran et al., 2017; Lau and Lim, 2018; Nwankpa et al., 2018). Thus, the outputs of the threshold functions are either zero or one, which decreases the computational complexity of algorithms and hardware implementations.
The discrete spiking signals require particular training algorithms and encoding paradigms (Roy et al., 2019; Mead, 2020). In a digital system, the analog signals will be converted into binary numbers using analog-to-digital converters (ADCs) for further Boolean calculations (Indiveri et al., 2015; Liu et al., 2015; An, 2020). But in brains, the exterior analog signals, such as visual and auditory signals captured by sensory organs, are converted into a sequence of spikes (Kandel et al., 2000; Gerstner et al., 2012). Thus, the communication among neurons is the spiking signals. Several encoding methods are available, e.g., temporal encoding (Sakemi et al., 2020), rate encoding (Liu et al., 2009; Liu and Delbruck, 2010; Plank et al., 2018), and spatial-temporal encoding (Jin et al., 2018). Several training methods for SNNs have been proposed, including converting traditional ANNs into an SNN after the training process (O’Connor et al., 2013; Diehl et al., 2015; Esser et al., 2015, 2016; Rueckauer et al., 2017; Shrestha and Orchard, 2018; Severa et al., 2019), using biologically plausible algorithms, e.g., spike-timing-dependent plasticity (STDP), to directly train SNN from the beginning (Bohte et al., 2002; Shrestha and Song, 2017), or utilizing an approximation method for mimicking backpropagation training methods (Lee et al., 2016; Panda and Roy, 2016; Zenke and Ganguli, 2018), e.g., SpikeProp (Bohte et al., 2002; McKennoch et al., 2006; Shrestha and Song, 2017). These training methodologies particularly designed for SNNs and neuromorphic systems already have competitive training/inference accuracies (Wade et al., 2008; Lee et al., 2016; Severa et al., 2019) compared to conventional deep learning (O’Connor et al., 2013; Diehl et al., 2015; Esser et al., 2015, 2016; Guo et al., 2017; Rueckauer et al., 2017; Yan et al., 2018). Numerous neuromorphic chips are launched to further enhance the capability of neuromorphic computing, such as the Loihi chip (Davies et al., 2018), TrueNorth (Akopyan et al., 2015), etc. The Loihi chips are a digital-analog mix specially designed for adaptive self-modifying event-driven fine-grained parallel computations used to implement learning and inference with high power efficiency. The Loihi chip incorporates 128 neuromorphic cores fabricated on Intel’s 14 nm process and features a unique programmable microcode learning engine for on-chip SNN training. The power consumption of Loihi chips is significantly lower (109 X) than other state-of-the-art computing platforms, such as field-programmable gate array (FPGA), central processing unit (CPU), and graphics processing units (GPUs) (Lecun et al., 2015; Goodfellow et al., 2016; Schuman et al., 2017; Blouw et al., 2019; Roy et al., 2019). The distinctive capabilities and high energy efficiency of neuromorphic systems and SNNs offer invaluable advantages to CL-DBS systems and other implantable/wearable medical devices that demand low latency and energy efficiency.
2.2 Introduction to deep brain stimulation for Parkinson’s disease
The DBS technique is a neurosurgical procedure that implants special electrodes in specific regions of the brain for sending electrical stimulations. The DBS system consists of two essential components: the electrodes implanted in the brain and a stimulation generator placed in the chest. The patients would be carrying the entire DBS device all the time. The electrode is typically implanted into a specific region of the brain through a small hole in the skull. A thin wire connects the electrode to an implantable pulse generator. The pulse generator serves as the source of electrical stimulation. The DBS system is widely used for neurological diseases, such as Parkinson’s disease, dystonia, and Alzheimer’s Disease (Fang and Tolleson, 2017; Ghasemi et al., 2018; Zhou et al., 2018; Lozano et al., 2019).
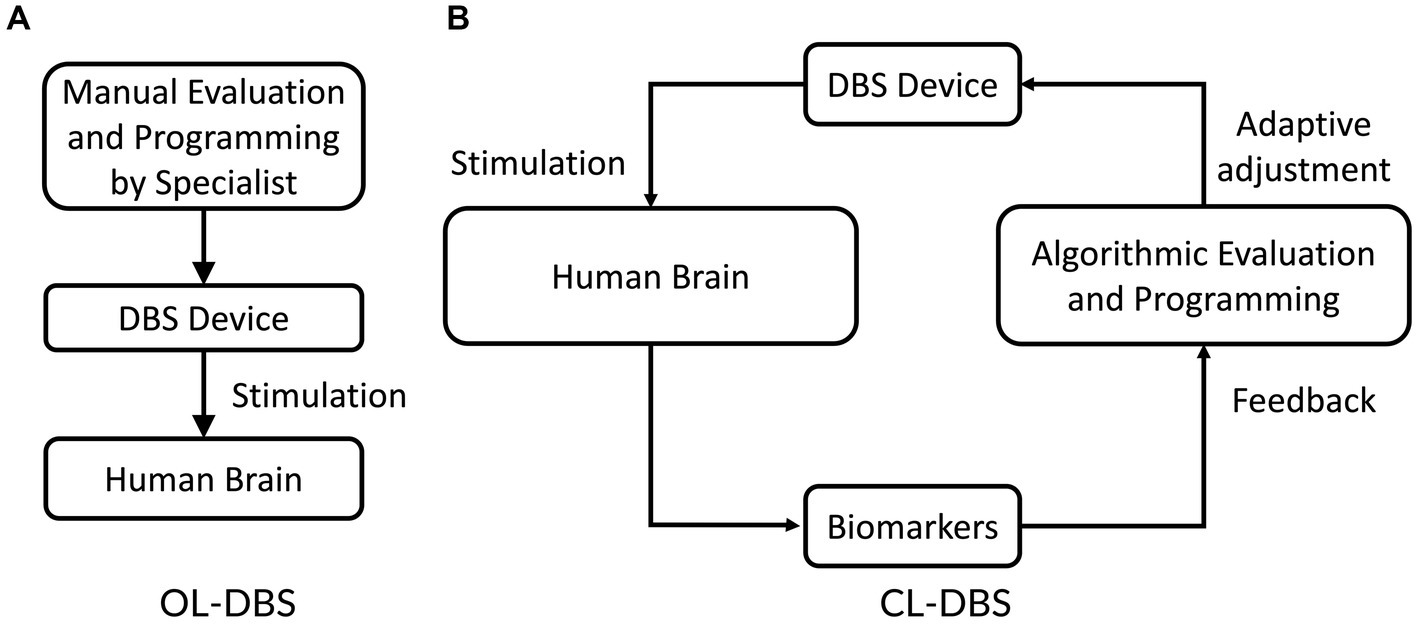
Parkinson’s disease is a multifaceted neurodegenerative disorder primarily characterized by the degeneration of dopamine-producing neurons in the brain, resulting in a wide array of motor symptoms. The symptoms of Parkinson’s disease include tremors, bradykinesia, stiffness, abnormal walking, etc. While medications are available to manage certain symptoms, they cannot halt or reverse the underlying neurodegenerative process. Thus, Parkinson’s disease is a complex condition, and treatment plans may involve a combination of medications, physical therapy, and lifestyle modifications. Researchers continue to investigate new therapeutic approaches and potential interventions to slow the progression of the disease and improve the quality of life for patients. Levodopa, a precursor to dopamine, is a frequently prescribed medication that aids in replenishing dopamine levels in the brain and can alleviate motor symptoms (Fahn et al., 2004). However, long-term use of levodopa often results in a condition known as “levodopa-induced dyskinesia,” which is characterized by uncontrollable and writhing movements (Fang and Tolleson, 2017). Moreover, as the disease progresses and the number of dopamine-producing neurons continues to decline, the effectiveness of these medications diminishes over time. In addition, the current medications also have side effects, such as cognitive decline, sleep disturbances, and mood disorders, which significantly impact the patient’s quality of life. When medications are no longer able to provide an adequate quality of life, DBS treatment is considered. Clinical trials have provided evidence for the efficacy of regular electrical stimulation of specific brain regions, such as the subthalamic nucleus (STN), in mitigating the symptoms of Parkinson’s disease. The stimulation frequency of a typical DBS system is commonly classified into two categories: high frequency (typically above 100 Hz, such as 130 or 150 Hz) and low frequency (typically below 100 Hz, such as 60 or 80 Hz) (Su et al., 2018). The therapeutic outcomes on motor function in individuals with Parkinson’s disease (PD) can differ substantially depending on the selected stimulation frequency. Low stimulation frequencies have demonstrated no significant impact on motor symptoms, whereas high stimulation frequencies have shown therapeutic benefits to the patients. Continuous electrical stimulation of brain targets such as STN and GPi has been shown to relieve the symptoms of movement disorders of Parkinson’s disease. This conventional DBS system is referred to as an open-loop DBS (OL-DBS) system (Figure 1A). However, high-frequency stimulation may induce unexpected cognitive and psychiatric side effects such as depression and speech disorders (Dostrovsky and Lozano, 2002; Hariz et al., 2008; Hwynn et al., 2011; Arlotti et al., 2016; Alomar et al., 2017). Additionally, it has the potential to exacerbate axial symptoms and manifestations that often arise during the long-term progression of the disease and treatment, including challenges with gait, speech, and swallowing (di Biase and Fasano, 2016). Another challenge related to OL-DBS system is the high energy consumption associated with continuous stimulation, leading to rapid depletion of the power in implanted devices. Consequently, patients often require additional surgical procedures to replace the neurostimulator battery. Another challenge of the OL-DBS system is the diversity and variability of individual patients. This variability necessitates personalized approaches to OL-DBS system and requires considering the unique characteristics of stimulation signals of each patient. To overcome these limitations, a novel closed-loop DBS (CL-DBS) system is proposed, which incorporates a feedback loop as illustrated in Figure 1B.
The essential distinction between CL-DBS and OL-DBS systems lies in their approach to monitoring PD symptoms and adjusting stimulation parameters accordingly. In an OL-DBS system, the stimulation parameters, e.g., frequency, pulse width, and magnitude, remain constant during operation (Deuschl et al., 2006; He et al., 2021). Thus, the OL-DBS lacks the capability of adjusting stimulations corresponding to the dynamic symptoms of Parkinsonians. CL-DBS devices, on the other hand, employ a feedback loop to monitor the brain’s clinical condition and adjust stimulation parameters accordingly (Rosin et al., 2011; Little et al., 2013; Wu et al., 2015; Parastarfeizabadi and Kouzani, 2017; He et al., 2021). These adaptive stimulation signals offer multiple significant advantages over OL-DBS system. Firstly, adaptive stimulation signals extend clinical efficacy while reducing side effects (Herron et al., 2016). Recent studies demonstrated that CL-DBS system, with its automatic modification of stimulation parameters, is more effective in reducing PD symptoms compared to OL-DBS system (Rosin et al., 2011). Secondly, the adjustment of stimulation parameters in DBS devices has been found to mitigate or eliminate side effects in a significant proportion of Parkinsonians. (Hamani et al., 2005). Secondly, CL-DBS system utilizes non-continuous stimulation signals, leading to reduced energy requirements of the DBS devices (Herron et al., 2016). Studies reported a 56% reduction in stimulation time and decreased energy demand with CL-DBS system compared to OL-DBS system (Little et al., 2013; Wu et al., 2021). This reduced power requirement may result in fewer neurostimulator battery replacement surgeries. Overall, CL-DBS system offers improved efficiency, fewer surgeries, reduced energy consumption, and extended battery life compared to OL-DBS system. Despite great advantages, several issues are still associated with CL-DBS system.
One challenge is the availability of detectable feedback signals that are stable and robust over time (Hosain et al., 2014). Several electrophysiological biomarkers linked to the symptoms of patients have been introduced for closing the feedback loop including local field potential (LFP), action potential, electroencephalogram potential, and electrocorticogram. The selection of biomarkers for the CL-DBS system in Parkinson’s disease faces several challenges. One of the challenges of selection biomarkers is to understand their evolution over time and their correlation with symptom severity. Studies are required to assess the stability and consistency of biomarkers. Localization specificity is another consideration, requiring biomarkers with good spatial specificity to accurately target specific brain regions. Precise localization and electrode placement are essential for optimal therapeutic outcomes. Robust clinical studies and consensus on selection criteria and assessment protocols are necessary. Addressing these challenges requires collaboration between clinicians, neuroscientists, and engineers to enhance the precision and effectiveness of CL-DBS system, ultimately improving outcomes for individuals with Parkinson’s disease (Rossi et al., 2007).
Another challenge of CL-DBS systems is the design of closed-loop control algorithms for the automatic adjustment of stimulation parameters (Parastarfeizabadi and Kouzani, 2017). A robust control mechanism is essential for CL-DBS systems to enable automatic updates of stimulus settings without the need for manual intervention. Current existing closed-loop controlling algorithms either control one pulse parameter such as amplitude or implement a simple on-off control of stimulations. However, to further optimize the efficiency of the system, it is ideal to set a threshold and continually monitor the biomarker and control stimulation on-off when the signal crosses the threshold. Thus, the development of an optimized controller for programming stimulation parameters is further needed. In addition, CL-DBS devices are expected to consume less power compared with the OL-DBS systems. Nevertheless, CL-DBS devices carry real-time recording and data processing circuits that cause high power consumption for the device. Therefore, there is an urgent need to develop an adaptive CL-DBS system with low power consumption, high intelligence, and minimal side effects to optimize patient outcomes.
Overall, designing CL-DBS algorithms with energy-efficient hardware implementation is essential. Due to the diverse variations in signs and symptoms among Parkinson’s patients, continuous monitoring of PD indicators and making appropriate adjustments to stimulus signals are crucial. Therefore, the development of an intelligent and energy-conscious PD symptom detector and controller is necessary to achieve optimal results for patients while minimizing negative side effects.
2.3 Overview of memristive synapse
A memristor is a non-volatile memory device that encodes information into its resistances. Therefore, memristors are also known as resistive random-access memory (ReRAM) or RRAM (Chua, 1971; Strukov et al., 2008; Williams, 2008; Eshraghian et al., 2012; Wong et al., 2012; An et al., 2021a,b; Chua et al., 2022; Zins et al., 2023). The memristor operates by modifying its resistances with a voltage stimuli (Strukov et al., 2008). This property allows memristive devices to exhibit their current–voltage (I–V) characteristic curves as shown in Figure 2A. Memristors have garnered attention as promising nanodevices for in-memory computing and electronic synapses due to their potential for high-density integration, fast writing and reading times, and high power efficiency (Upadhyay et al., 2019). Importantly, the conductance of a memristor is not solely influenced by the current control signals (applied voltage or current), but also by their history, such as the time integral of charge or flux (Chua, 1971; An et al., 2017). In addition, memristors offer the advantage of being compatible with CMOS (complementary metal-oxide-semiconductor) fabrication processes. This compatibility allows for the seamless vertical integration of memristors with CMOS-based integrated circuits (ICs), forming three-dimensional integrated circuits (3D-ICs).
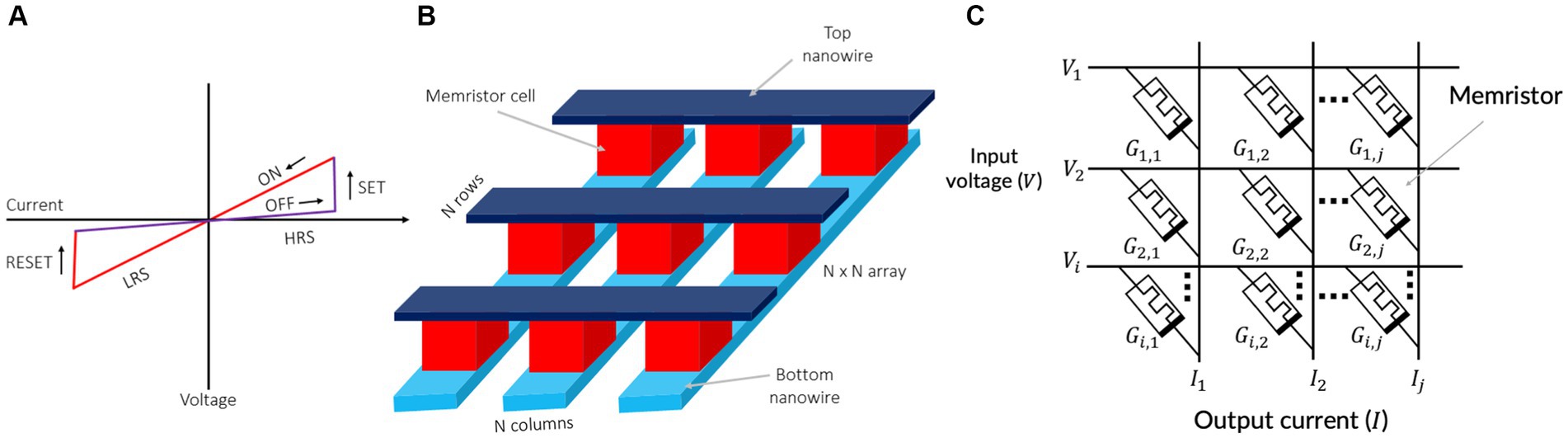
Figure 2. (A) Switching characteristics of memristive devices. (B) A crossbar array of memristors. (C) Vector matrix multiplication using a memristor crossbar.
The typical structure of a memristor is depicted in Figure 2. Memristive devices consist of insulating layers sandwiched between top and bottom nanowire electrodes (Figure 2B). Multiple memristors are commonly fabricated in a crossbar configuration, as illustrated in Figure 2B. This straightforward crossbar structure enables the scaling down of individual memristive devices into approximately 10 nm (Lu et al., 2011).
The crossbar configuration offers a high integration density and random-access capacity (Snider and Williams, 2007). As shown in Figure 2B, with the utilization of the n-rows and n-columns of the crossbar, all n × n cross points can be accessed. Memristive crossbars also have the capability for analog arithmetic calculations (Min and Corinto, 2021). The characteristics of in-memory computer architecture render it a highly promising approach for advancing neuromorphic systems. Vector-matrix multiplications, widely used in deep learning and in-memory computing, stand to gain significant benefits from this architecture. Figure 2C depicts a memristive vector-matrix multiplication (VMM) engine (Cui and Qiu, 2016), capable of performing analog computations of I = G · V using a conductance matrix G with dimensions i-by-j.
The VMM engine is composed of two layers of metal wires, denoted as i for the input voltage vector and j for the output current vector. Each memristor acts as a connection point between the overlapping top and bottom wires. By setting the conductance of the memristor at coordinates i on the bottom and j on the top to values Gi,j, the output current vector I can be generated on the bottom wires when an input voltage vector V is applied. The crossbar structure of the memristor allows for sampling the outputs by measuring the accumulated current on each bit line (BL). This facilitates the analog computation of VMM, where input tensors are mapped as voltages loaded in parallel on each word line (WL), and synaptic weights are represented by the conductance of memristor cells in a subarray as:
where Vi is the input voltage at i-th wordline (WL) and is the conductance of the memristor cell stacked between i-th WL and j-th bitline (BL). The crossbar cannot operate properly unless the bottom wires are held at ground potential. Another crossbar and subtraction circuit is required to support negative entries in the conductance (Pino et al., 2012). Memristor crossbars with a high density are able to conduct parallel vector-matrix multiplication while consuming an extremely minimal energy (Zhang et al., 2017). Furthermore, the parameters of the applied voltage pulses can be modulated in order to adapt the memristor’s conductance, offering tremendous potential for the development of adaptive systems with the capacity for online learning (Li and Ang, 2021). Thus, memristors are considered promising nanodevices for electronic synapses in a neuromorphic chips.
3 Design of neuromorphic CL-DBS detectors
Neuromorphic systems with memristive synapses are promising next-generation artificial intelligence platforms known for their remarkable energy efficiency. In this paper, we present the development of a novel neuromorphic PD symptom detector for the CL-DBS system. The detector utilizes spiking neural networks (SNNs) to detect and analyze PD symptoms based on spike patterns, particularly in the region of STN. Unlike previous approaches that involve converting spiking signals from the time domain to the frequency domain, our neuromorphic detector directly processes the spiking signals, eliminating the need for time-frequency conversion.
Specifically, the implementation of our neuromorphic PD detector involves the utilization of the long short-term memory (LSTM) architecture. The neural activities used for training are collected using a PD computational model (Kumaravelu et al., 2016). The dataset utilized for training encompasses spike timings spanning from 0 to 2,500 milliseconds per data sample.
To comprehensively evaluate the hardware performance of our detector, a strategic approach is employed. We systematically save the weights and biases during the training process and subsequently integrate them into NeuroSIM as memristive synapses. This integration enables a thorough evaluation, considering both monolithic and heterogeneous 3D chip designs.
Remarkably, our neuromorphic PD detector exhibits superior performance compared to the conventional 6 T SRAM memory architecture. This superiority is evident in various aspects, including chip design area, latency, and power consumption. The intricacies of the design and assessment methodology are visually depicted in Figure 3, offering a clear illustration of our neuromorphic PD detector’s functionality.
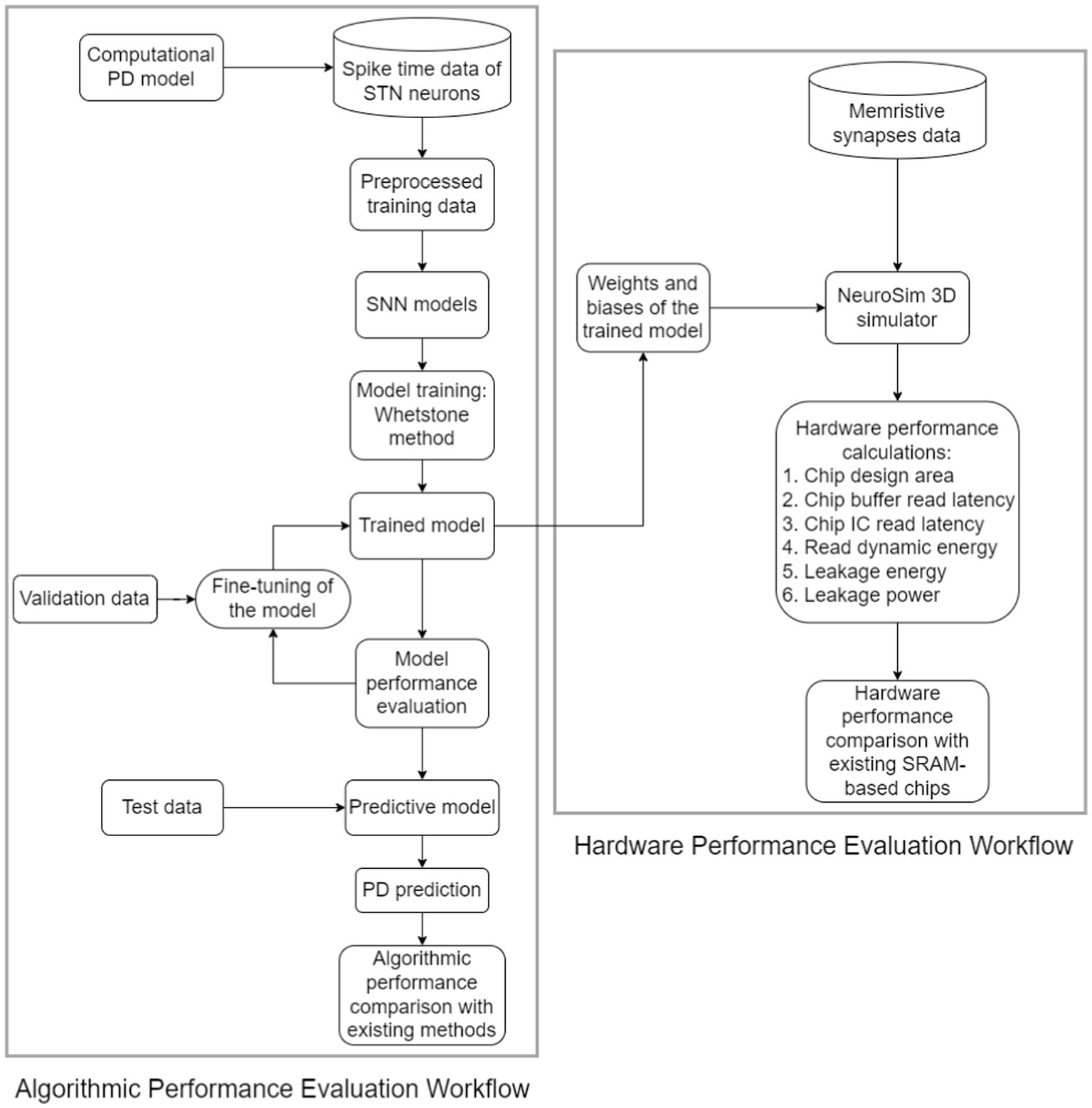
Figure 3. Workflow of the proposed hardware and algorithmic co-design methodology of neuromorphic CL-DBS detectors.
Moreover, a distinct validation dataset is employed as a crucial component of our evaluation process, ensuring a robust assessment of the detector’s performance. The weights and biases derived from the 8-layer detector are meticulously preserved throughout the training phase, and these parameters are seamlessly integrated into NeuroSIM as memristive synapses for a comprehensive analysis of hardware performance.
3.1 Acquisition of PD spiking data
The neural activity with typical PD symptoms for training our neuromorphic PD detector is obtained by a computational model, which includes the six brain regions as shown in Figure 4A (Kumaravelu et al., 2016). This model represents the cortical-basal ganglia-thalamus network, incorporating the brain regions of the cortex, striatum, subthalamic nucleus, globus pallidus externa, globus pallidus interna, and thalamus. Each of these regions is modeled using 10 single-compartment neurons. These neurons form a functional network by being interconnected through synapses. The cortex and striatum have stochastic connections, while other regions exhibit structured connections. During simulations, different time steps were tested, and the results remained stable regardless of the time step value.
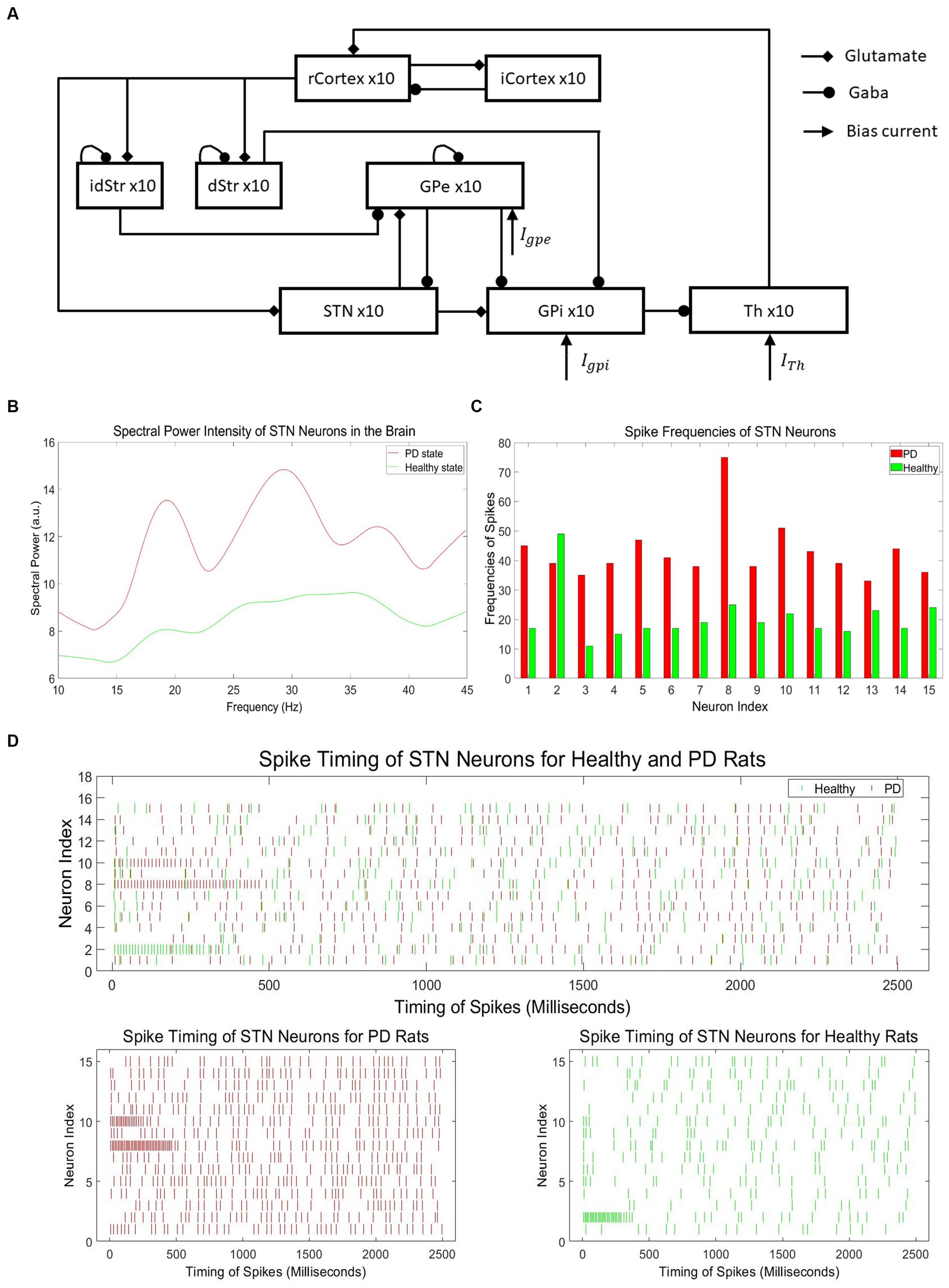
Figure 4. (A) Architecture of cortical-basal ganglia-thalamus network PD model (Kumaravelu et al., 2016). (B) Spectral power intensity of neurons in the STN region of the brain for PD and healthy states. (C) Spike frequencies of neurons in the STN region of the brain for PD and healthy states. (D) Neuronal spikes in the STN region for healthy and Parkinson’s disease rats.
The network model incorporates various types of connections among the neurons in the six regions. Regular cortex neurons receive excitatory input from thalamic neurons and inhibitory input from randomly selected inhibitory cortex neurons. Inhibitory cortex neurons, on the other hand, receive excitatory input from randomly chosen regular cortex neurons. Direct pathway striatum neurons receive excitatory input from regular cortex neurons and inhibitory input from randomly chosen direct pathway striatum neurons. Indirect pathway striatum neurons receive excitatory input from regular cortex neurons and inhibitory input from randomly selected indirect pathway striatum neurons. Subthalamic nucleus neurons receive inhibitory input from globus pallidus externa (GPe) neurons and excitatory input from regular cortex neurons. Globus pallidus externa neurons receive inhibitory input from any two other globus pallidus externa (GPe) neurons, as well as from all indirect pathway striatum neurons. Globus pallidus interna neurons receive inhibitory input from globus pallidus externa neurons and from all direct pathway striatum neurons. Additionally, some globus pallidus externa and globus pallidus interna neurons also receive excitatory input from subthalamic nucleus neurons. Finally, thalamic neurons receive inhibitory input from globus pallidus interna neurons.
To train our neuromorphic PD detector, we collected spike data from the neurons in the subthalamic nucleus (STN) region of the brain to construct the dataset. According to research on PD, there is an increased power spectrum in low-frequency oscillations in neurons of the basal ganglia (BG) in the Parkinsonian state compared to the healthy state. Hence, the spectral power at low frequencies, specifically beta oscillations (13–30 Hz), can be used as an indicator of PD and healthy states (McConnell et al., 2012). Figure 4B illustrates the intensity of spectral power in representative STN neurons for both PD and healthy states, clearly demonstrating the noticeable difference in beta oscillation levels between the two states. However, conducting spectral analysis on PD spike data to generate beta oscillations is a time-consuming and energy-intensive process. Hence, the utilization of spike timing directly offers notable advantages in terms of temporal and energy efficiency. Considering the difficulties involved in acquiring PD data from experimental studies, we employed a computational PD model (Kumaravelu et al., 2016) to generate a significant volume of spike timing data specifically tailored for PD.
Figure 4C depicts the spike frequencies of representative neurons in the STN region for PD and healthy states, clearly demonstrating the asymmetry between the two states, with significantly higher spike frequencies in the PD state. The PD spike data with no DBS stimuli consists of 1,000 independent samples, each representing the spiking signals of 15 neurons within the range of 0 to 2,500 ms. In total, the dataset contains 1,000 samples, encompassing spike timing information for a total of 15,000 neurons.
The spike timing intervals cover a range of 0 to 2,500 milliseconds, providing detailed temporal information of spikes. Similarly, the healthy spike data with no DBS stimuli comprises 1,000 distinct dataset samples, with each sample containing spike data of 15 neurons within the same 0 to 2,500 milliseconds range. The dataset includes 1,000 samples, capturing spike timing information for a total of 15,000 neurons. Figure 4D shows the spike timing data samples of 15 healthy and PD STN neurons. The spike timing data in the healthy state is much sparser compared to the PD state.
3.2 Design and training of spiking long short-term memory for neuromorphic detector
Our neuromorphic detectors can be successfully trained using spike data obtained from the PD biophysical computational model. While SNNs are known for their remarkable energy efficiency, training them using traditional gradient descent techniques becomes challenging due to the non-differentiability of threshold neurons. To address this challenge, a training method called Whetstone (Severa et al., 2019) are employed. The Whetstone approach simplifies hardware implementation by generating binary outputs of “1” or “0” instead of using other complex encoding schemes, such as temporal coding. In the Whetstone training method, the neural networks are initially trained using conventional backpropagation techniques and differentiable activation functions such as the rectified linear unit (ReLU) function. Subsequently, these differentiable activation functions are replaced with non-differentiable threshold functions during training. This transformation of the activation function during the training process is referred to as the sharpening process. Initially, the ReLU function is represented using conventional differentiable functions prior to the training procedure. However, during training, the ReLU function undergoes a transformation into a threshold function. Specifically, a bounded ReLU (bRELU) of an artificial neural network (ANN) gradually evolves into a traditional step function through the utilization of Eq. (2). This modification of the activation function occurs as part of the sharpening process, which enhances the efficiency of data processing and classification.
The assumption |β − 0.5| = |α − 0.5| in Eq. (2) illustrates the characteristics of the bounded ReLU (bRELU) activation function. The generic bRELU function, denoted as hα,β, undergoes a progressive transformation into a threshold function as α approaches 0.5 and h approaches 1. Importantly, throughout this modification, the activation function remains differentiable, allowing for effective training with gradient descent algorithms. By employing the sharpening procedure, the activation function hα,β (with α = 0 and h = 1) is converted into a threshold function. To mitigate potential accuracy loss during training, an adaptive sharpening process can be implemented. This approach periodically evaluates the training accuracy at the end of each epoch and, if the change in training loss is consistently smooth, suspends or terminates the sharpening process. By leveraging threshold neurons, the Whetstone method overcomes the non-differentiability challenge and enables the successful training of SNNs for spike PD symptom detection.
To detect abnormal neural activities associated with PD symptoms in STN neurons, we have developed three SNN-based neuromorphic PD detectors. These neuromorphic detectors are an 8-layer S-LSTM neuromorphic PD detector, a 7-layer neuromorphic S-LSTM PD detector, and a 7-layer neuromorphic SNN PD detector. The architectures of these detectors are depicted in Figure 5.
Figure 5. (A) The 8-layer neuromorphic PD detector with LSTM. (B) A 7-layer neuromorphic PD detector with LSTM. (C) the 7-layer neuromorphic PD detector with SNNs.
To assess their performance in recognizing PD symptoms, these detectors underwent training and validation using 30,000 spike data samples from STN neurons in our computational PD model. The train-test mechanism of SNN algorithms relies on data splitting, where a portion of the data is used for training and the remaining data for evaluation. Therefore, determining the appropriate percentage for training and validation is crucial. In this study, we employed the training-validation data-splitting technique. The data were divided into three groups using different training-validation splits: 60%–40%, 75%–25%, and 90%–10%. Each of the three PD detectors was tested on different data splits to evaluate the performance of the SNN algorithms. All the SNN-based PD detectors were trained for 100 epochs using the adadelta optimizer with a learning rate of 0.05. The classifiers were trained using the Whetstone training method, which incorporates an adaptive sharpening procedure. This procedure gradually transforms a bounded ReLU activation function into a threshold function based on the model’s accuracy and loss performance.
The neuromorphic PD detector was trained and evaluated for 100 epochs using a total of 30,000 spike data samples. The data were divided into three groups using the training (%)—validation (%) split technique. For the 60%–40% split, the training dataset consisted of 18,000 spike timing data samples, while the validation dataset contained 12,000 spike timing data samples. In the case of the 75%–25% split, the training dataset comprised 22,500 spike timing data samples, and the validation dataset had 7,500 spike timing data samples. Lastly, for the 90%–10% split, the training dataset included 27,000 spike timing data samples, and the validation dataset consisted of 3,000 spike timing data samples.
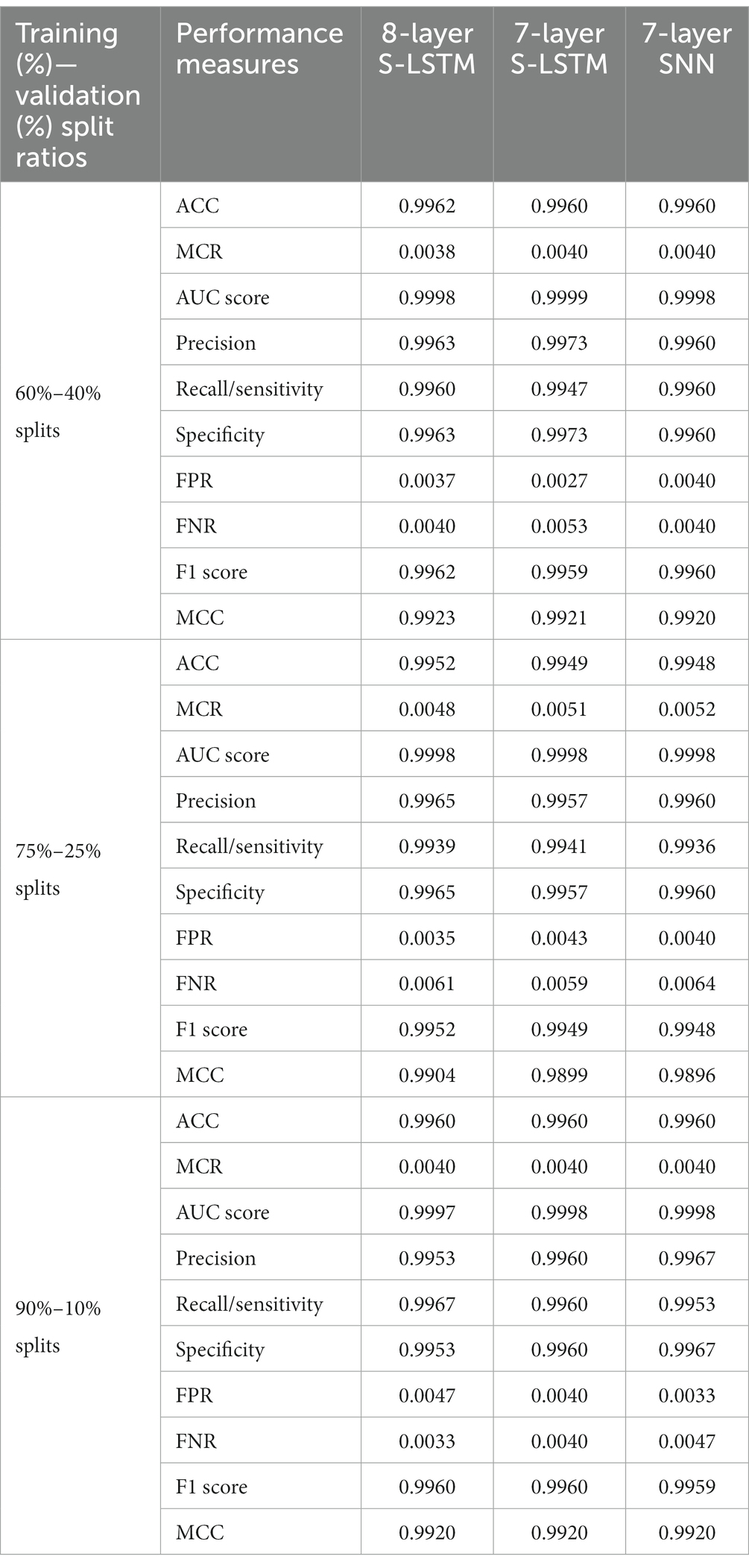
Table 1 presents a comparison of key performance measures for neuormorphic PD detection among the 8-layer S-LSTM, 7-layer S-LSTM, and 7-layer SNN detectors. The comparisons were made using different training-validation data split ratios of 60%–40%, 75%–25%, and 90%–10%.
For the 60%–40% data splits, the 8-layer S-LSTM outperforms the 7-layer SNN and the 7-layer S-LSTM in accuracy (ACC), misclassification rate (MCR), recall, false negative rate (FNR), F1 score, and Matthews correlation coefficient (MCC). The 7-layer S-LSTM outperforms the 7-layer SNN and the 8-layer S-LSTM in the area under the ROC curve (AUC score), precision, specificity, and false positive rate (FPR). The 7-layer SNN outperforms the 7-and 8-layer S-LSTM in recall and FNR. Therefore, the 8-layer S-LSTM classifier demonstrates the best performance, while the 7-layer SNN classifier exhibits inferior performance for the 60%–40% splits.
For the 75%–25% data splits, the 8-layer S-LSTM outperforms the 7-layer SNN and the 7-layer S-LSTM in ACC, MCR, precision, specificity, FPR, F1 score, and MCC. The 7-layer S-LSTM outperforms the 7-layer SNN and the 8-layer S-LSTM in recall and FNR. The 7-layer SNN outperforms the 7-and 8-layer S-LSTM in AUC score. Therefore, the 8-layer S-LSTM classifier demonstrates the best performance, while the 7-layer SNN classifier exhibits inferior performance for the 75%–25% splits.
For the 90%–10% data splits, the 8-layer S-LSTM outperforms the 7-layer SNN and the 7-layer S-LSTM in ACC, MCR, recall, FNR, F1 score, and MCC. The 7-layer S-LSTM outperforms the 7-layer SNN and the 8-layer S-LSTM in ACC and MCR. The 7-layer SNN outperforms the 7-and 8-layer S-LSTM in ACC, MCR, AUC score, precision, specificity, FPR, and MCC. Therefore, the 7-layer SNN classifier demonstrates the best performance, while the 7-layer S-LSTM classifier exhibits inferior performance for the 90%–10% splits. These observations indicate the varying performance of the classifiers based on different data split ratios.
Figure 6 illustrates six key performance measures for the three PD classifiers with training-validation data split ratios of 60%–40%, 75%–25%, and 90%–10%, respectively. In all three figures, the trend lines consistently demonstrate that the 8-layer S-LSTM classifier outperforms both the 7-layer SNN classifier and the 7-layer S-LSTM classifier. Additionally, the trend lines indicate that the performance of the 7-layer SNN classifier is the lowest among the three classifiers, as all trend lines point downward towards it (see Figure 6).
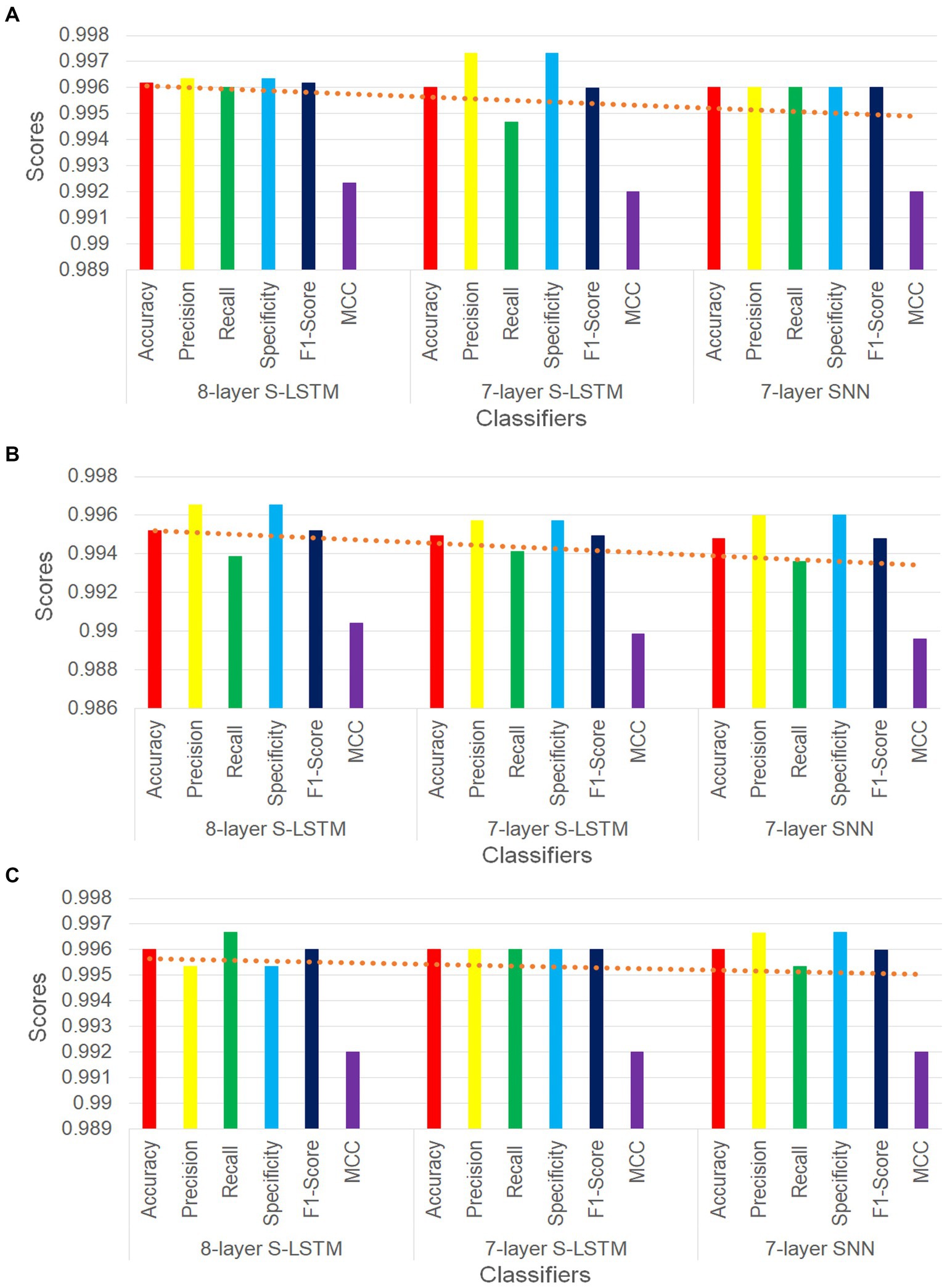
Figure 6. (A) Comparison of performance metrics of SNN classifiers for 60%–40% split. (B) Comparison of performance metrics of SNN classifiers for 75%–25% split. (C) Comparison of performance metrics of SNN classifiers for 90%–10% split.
Figure 7 displays the confusion matrices derived from evaluating the validation dataset using different training validation data splits. These matrices offer insights into the classification performance of the classifiers. For the 7-layer S-LSTM classifier, out of 6,000 healthy samples, 5,984 were correctly labeled as healthy, while 16 were mistakenly labeled as PD. Out of 6,000 PD samples, 5,968 were correctly identified as PD, but 32 were erroneously classified as healthy. For the 8-layer S-LSTM classifier, out of 6,000 healthy samples, 5,978 were accurately classified as healthy, while 22 were misclassified as PD. Regarding the PD samples, 5,976 were correctly labeled as PD, but 24 were incorrectly assigned as healthy. In the case of the 7-layer SNN classifier, out of 6,000 healthy samples, 5,976 were correctly identified as healthy, while 24 were erroneously labeled as PD. Similarly, out of 6,000 PD samples, 5,976 were correctly classified as PD, but 24 were mistakenly categorized as healthy. Based on these observations, it can be concluded that the 8-layer S-LSTM PD classifier exhibits superior performance compared to the other two classifiers, indicating its higher accuracy in classifying PD samples. However, the performance of the other two classifiers, the 7-layer S-LSTM and the 7-layer SNN, could be further improved to enhance their classification accuracy.
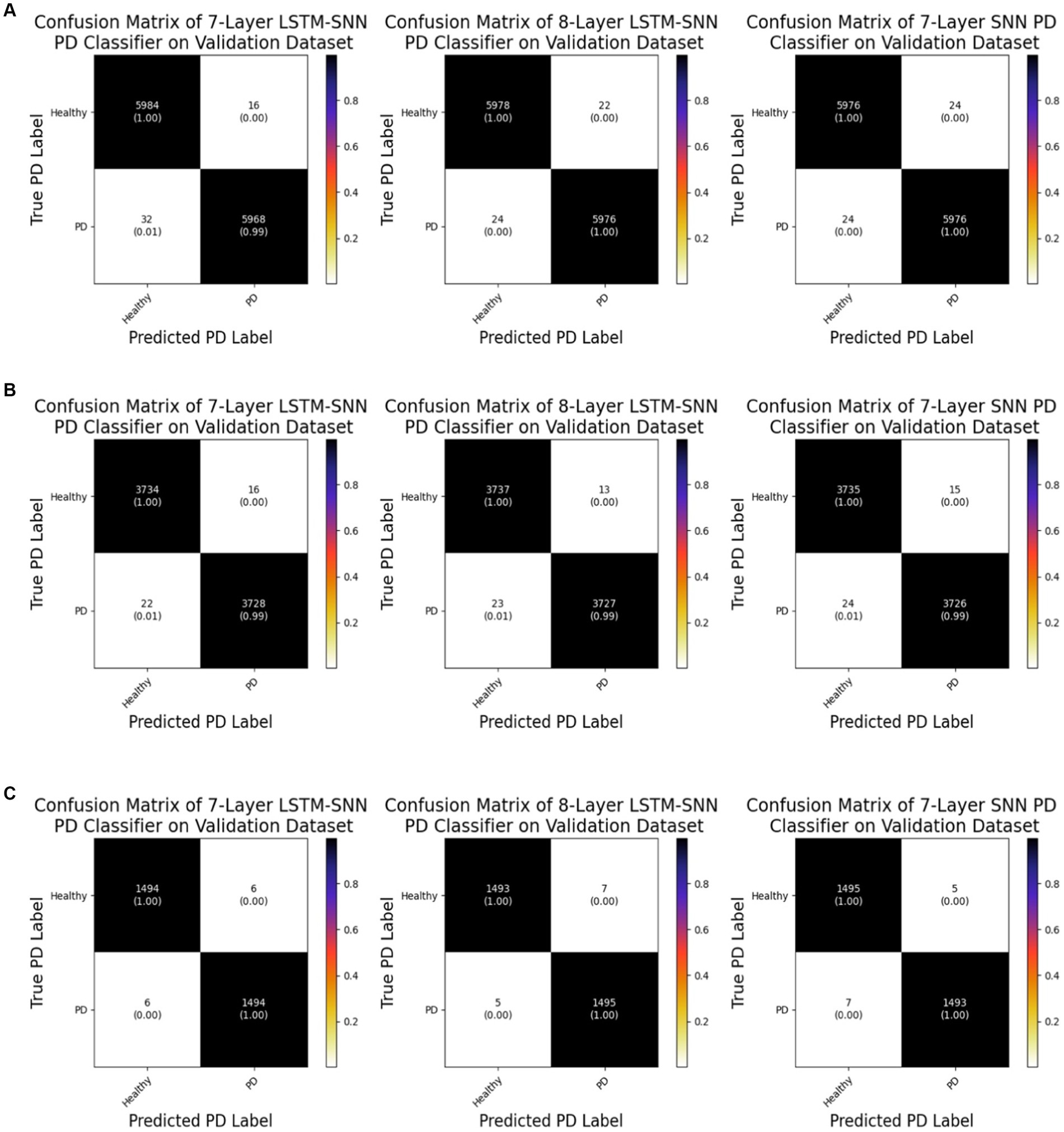
Figure 7. (A) Confusion matrices of neuromorphic PD detectors on the validation dataset for 60%–40% split. (B) Confusion matrices of neuromorphic PD detectors on the validation dataset for 75%–25% split. (C) Confusion matrices of neuromorphic PD detectors on the validation dataset for 90%–10% split.
Analysis of the confusion matrix reveals that all of the healthy data points were correctly identified, with only one out of the five PD data points being erroneously labeled as healthy. Consequently, we can conclude that our SNN classifier exhibits robustness in accurately identifying PD from new spike timing test data.
3.3 Noise robustness analysis of the proposed model
Noise robustness is a critical evolution metric in neuromorphic systems (Yang et al., 2021, 2022a,b; Yang and Chen, 2023; Yang, et al. 2023a,b). To validate the robustness of our model against timing noise in neural signaling, Gaussian noise is introduced to the timing of neural signal firings. Specifically, a series of random numbers drawn from a Gaussian distribution with a specified mean and standard deviation were added to the neural activity timings of the original data samples.
For each non-zero spike timing value in the dataset, we generate a random noise value using Gaussian distribution. This random noise value represents the amount of variability or perturbation that we are adding to the spike timing value. We then combine the original spike timing value with the Gaussian noise value to create a noisy spike timing value that replaces the original value in the dataset at the specified row and column as shown in Eqs. (3) and (4):
where is the noisy spike timing value, is the original spike timing value, and represents the Gaussian noise with mean ( ) and variance ( ). This simulates the effect of random noise on the spike timing data, making it more realistic and suitable for the robustness analysis. In specific, the Gaussian noise is added to the neural spike timing dataset using the Algorithm 1.
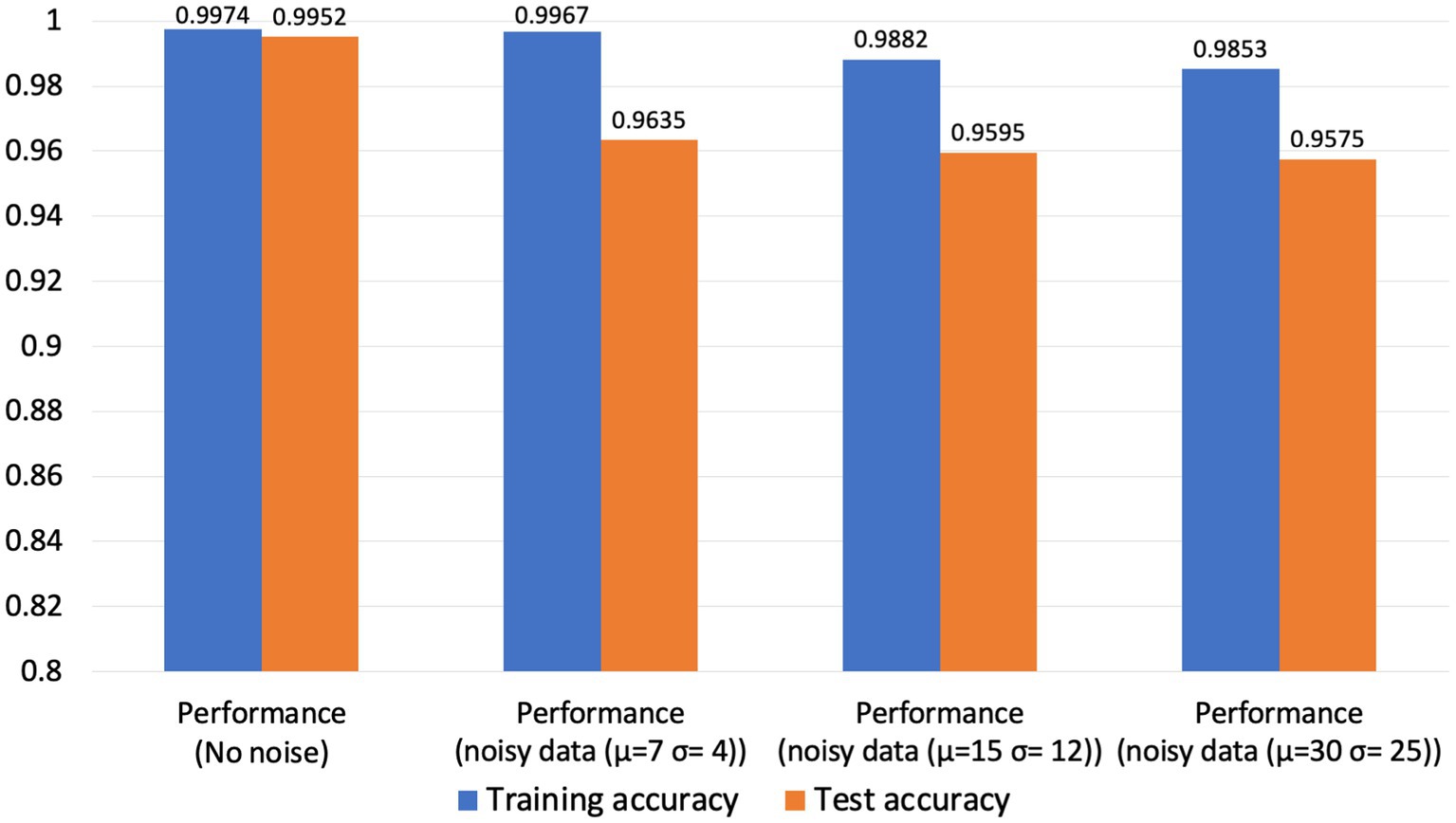
To evaluate the robustness of our neuromorphic PD model, we have tested it with three noise settings. In the first noise setting, we applied moderate Gaussian noise with a mean of 7 and a standard deviation of 4. In the second noise setting, we applied moderate to high Gaussian noise with a mean of 15 and a standard deviation of 12, and in the third noise setting, we applied very high Gaussian noise with a mean of 30 and a standard deviation of 25. The spike timing data before and after adding noise signals are illustrated in Figure 8.
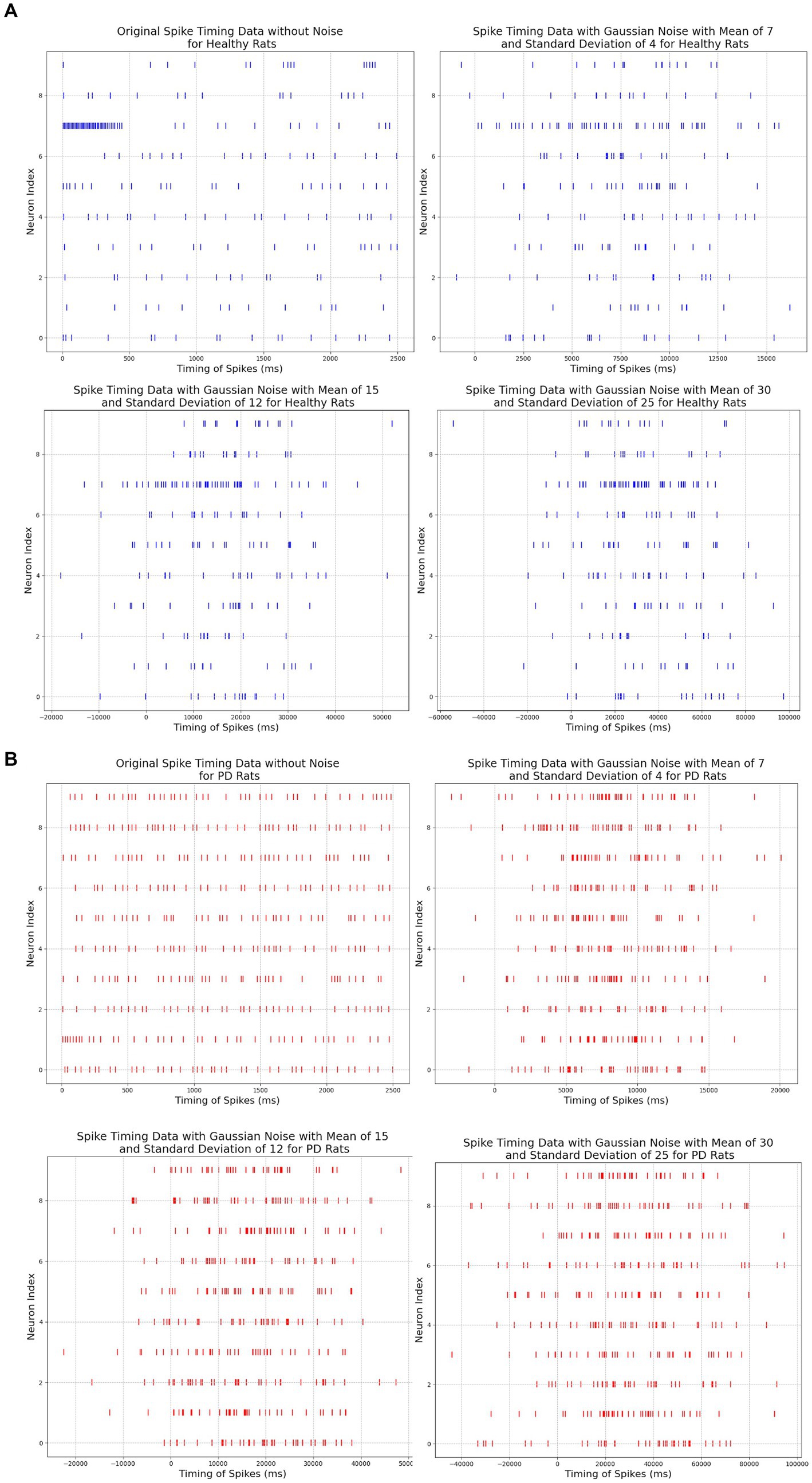
Figure 8. (A) Comparison among original and noisy spike timing of healthy rats on three parameter pairs: μ = 7 and σ = 4, μ = 15 and σ = 12, μ = 30 and σ = 25. (B) Comparison among original and noisy spike timing of PD rats on three parameter pairs: μ = 15 and σ = 12, μ = 30 and σ = 25, μ = 30 and σ = 25).
Our neuromorphic PD detector is trained over 100 epochs, employing a dataset partition of 75% for training and 25% for validation to assess the detector’s resilience to noisy data. The dataset comprises a total of 30,000 spike timing samples, with 22,500 samples allocated for the training set and 7,500 for validation. The tabulated results presented in the subsequent table demonstrate the model’s commendable accuracy in detecting Parkinson’s disease from noisy data. Furthermore, we have thoughtfully depicted the confusion matrix for all three cases. As illustrated in Figure 9, although the accuracy of our neuromorphic PD detector decreases with the addition of more intensive noise, the overall accuracy remains at a high level, demonstrating excellent noise immunity capability of our neuromorphic detector.
3.4 Hardware performance evaluation and comparison
To assess the hardware performance of our neuromorphic PD detector by using memristive synapses, the weights of the neuromorphic PD detector were recorded during training and encoded into the resistance of memristors using a simulator framework named NeuroSim3D (Chen et al., 2018) hardware simulator. Memristors are typically fabricated within a crossbar architecture. As depicted in Figure 10B, nanowires composed of inert cathodes and oxidizable active anodes are situated at the upper and lower regions of the crossbar, respectively. The metallic oxide layer is positioned at the crosspoints where the upper and lower nanowires intersect. This crossbar configuration closely parallels the architecture of a conventional memory array, such as SRAM shown in Figure 10B.
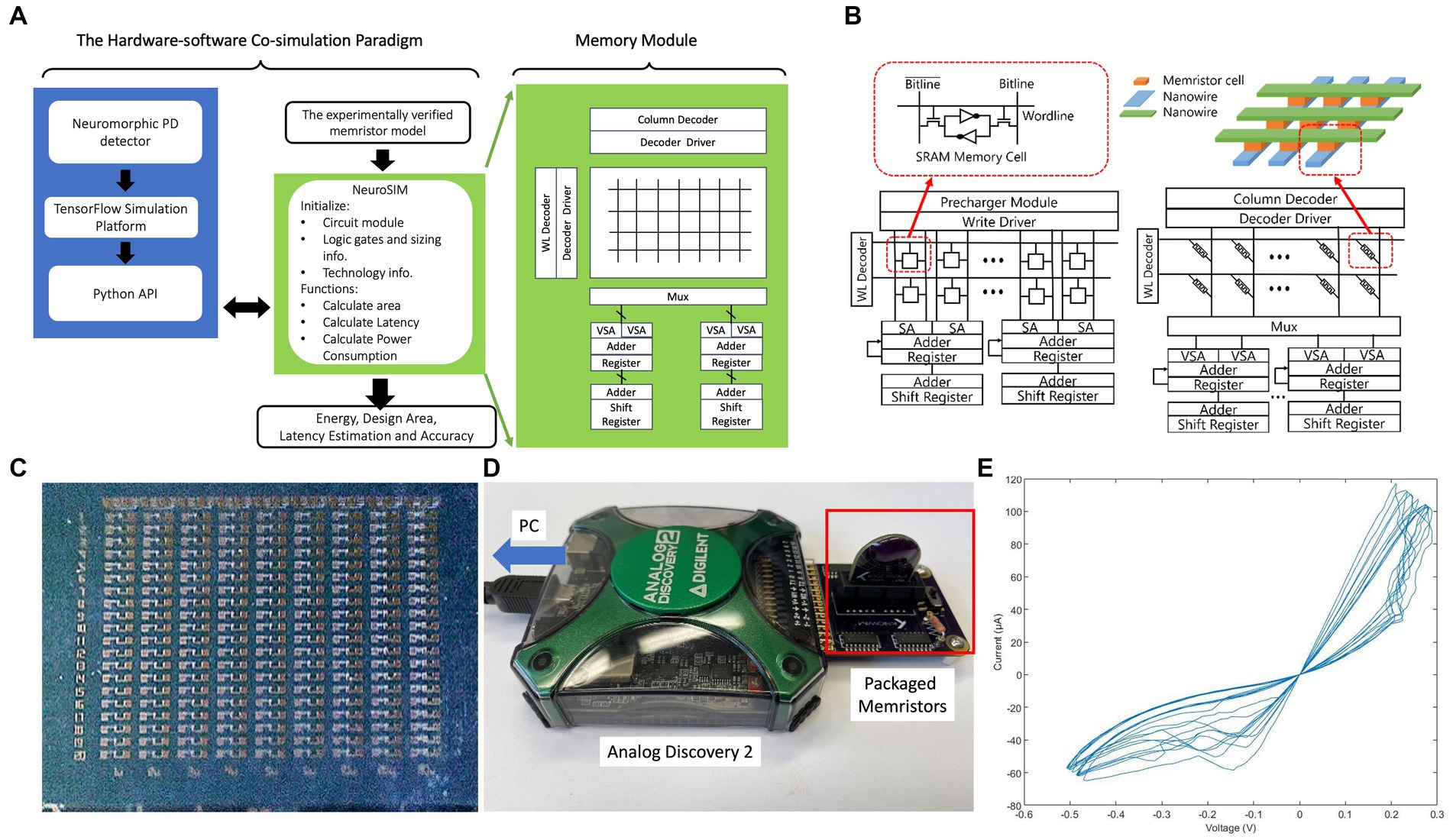
Figure 10. (A) Diagram of the hardware-software co-simulation paradigm of our neuormorphic PD detector with NeuroSIM and Whetstone. (B) Configuration comparison between the memristive crossbar and the conventional memory array with SRAM as memory cells in NeuroSIM (Chen et al., 2018). (C) Raw die of memristors; (D) Testing setup of memristors; (E) V–I curve of memristors.
The memristors are added to our neuromorphic PD detector as an electronic synapses (Likharev, 2011; Wang et al., 2012; Bichler et al., 2013; Kornijcuk et al., 2014; Park et al., 2015) storing the weights of neural networks. As the emerging electronic synapses, these memristors replace traditional memory devices, such as SRAM. The parameters of our memristor models are collected by measurement our memristor devices shown in Figures 10C,D. The V–I curves of the memristors are shown in Figure 10E.
As illustrated in Figure 10B, each memory cell within the memory array is linked to both a wordline and a bitline. The data stored in memristors is encoded in their resistances, and the nanowires serve as the bitline and wordline for accessing the memristive memory cells. Figure 10 illustrates the writing and reading phases of a memristive memory cell. In the writing phase, a voltage pulse, exceeding the set voltage, is applied to the nanowire within the crossbar structure, thus altering the resistance value of the memristor. During the reading stage, the applied voltage is significantly lower than the set voltage to preserve the resistance of the cell unaltered. The resistance value of the selected memristor is calculated as the applied voltage divided by the measured current at the end of the nanowire. The weight matrices are mapped onto the passive memristor crossbar using memory cell selection devices.
Figure 10B shows a traditional SRAM. NeuroSIM conducts weight sum and update operations in a row-by-row fashion (Chen et al., 2018). Row selection is activated through the WL decoder, and the BLs are precharged for each cell access. Memory data is captured by the sense amplifier (S/A). Subsequently, the adder and register are employed to sum the weight values in a row-by-row manner. By substituting SRAM core memory with memristors, the architecture remains largely unaltered shown in Figure 10B. The weighted sum operation in the memristor-based synaptic core also follows a row-by-row style, with the incorporation of multiplexers (MUX) (Chen et al., 2018).
To assess the performance of our neuromorphic PD detector, encompassing design area, latency, and energy efficiency, we have established a hardware-software co-simulation using NeuroSIM (Chen et al., 2018), as depicted in Figure 10A. The model is constructed through the following steps:
Firstly, our neuromorphic PD detector is built of multiple layers of S-LSTM for detecting power density at the beta bandwidth of the STN region. During the training progress, the weights and neural network configuration of the S-LSTM are monitored and stored.
Secondly, our experimentally verified memristor model is incorporated into the micro-architecture simulator NeuroSIM (Chen et al., 2018) incorporating parameters such as on-state resistance, off-state resistance, and others. The deployment method assesses the neural network’s performance within an offline training environment, which necessitates local computation. In contrast to online learning, offline learning training maintains the trained neural network on the client side, handling all prediction computations locally (Lane et al., 2015), due to the constraints imposed by limited power and space budgets energy.
Finally, the performance improvements of our memristor on energy efficiency, design area, and execution latency are estimated through the co-simulation paradigm. The pseudocode of our hardware-software co-simulation paradigm is introduced in Figure 10 and in Algorithm 2.
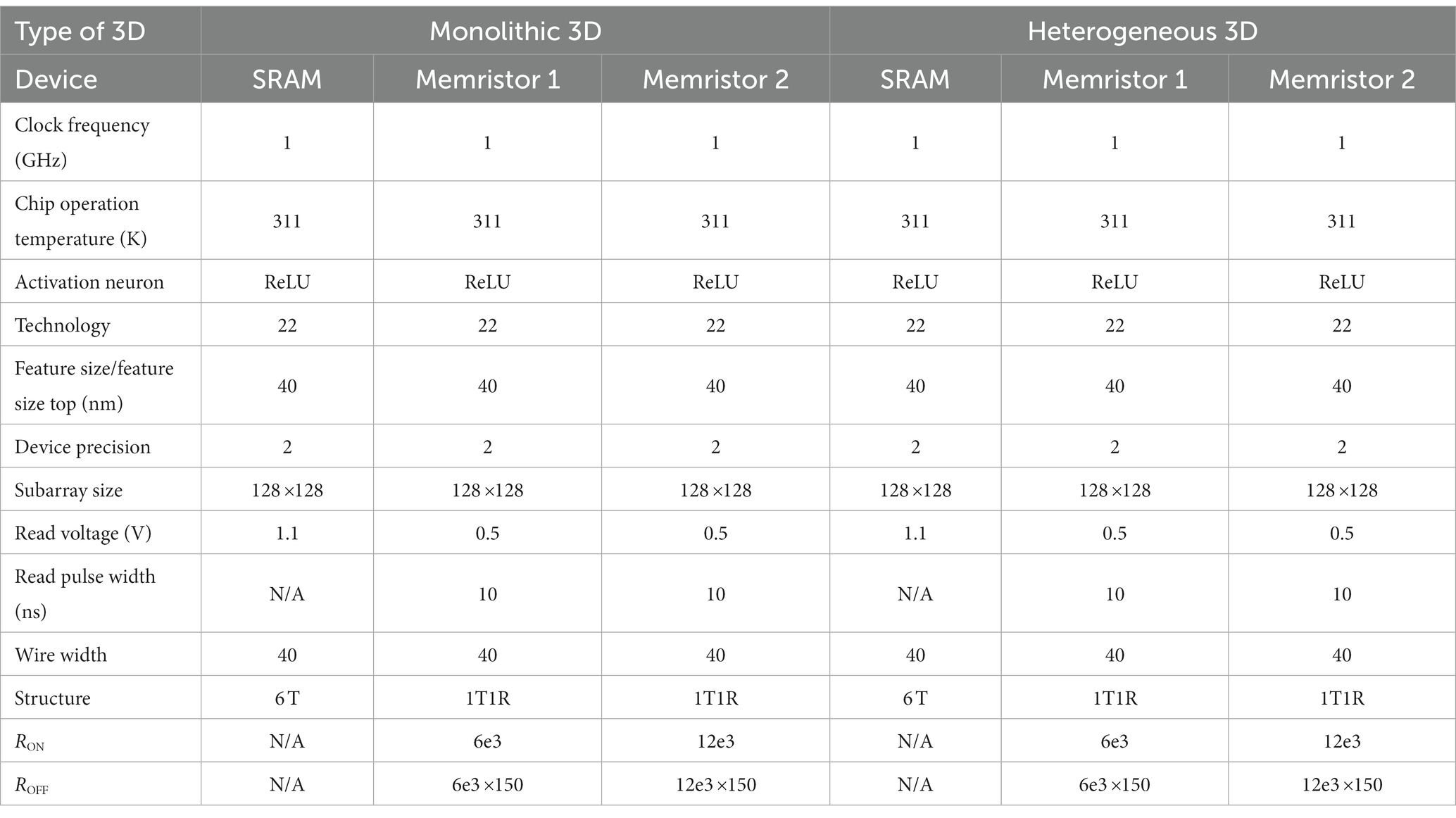
Table 2 shows the values used to set the simulation parameters of the 3D NeuroSim simulator for both monolithic and heterogeneous 3D memristor and SRAM chip designs.
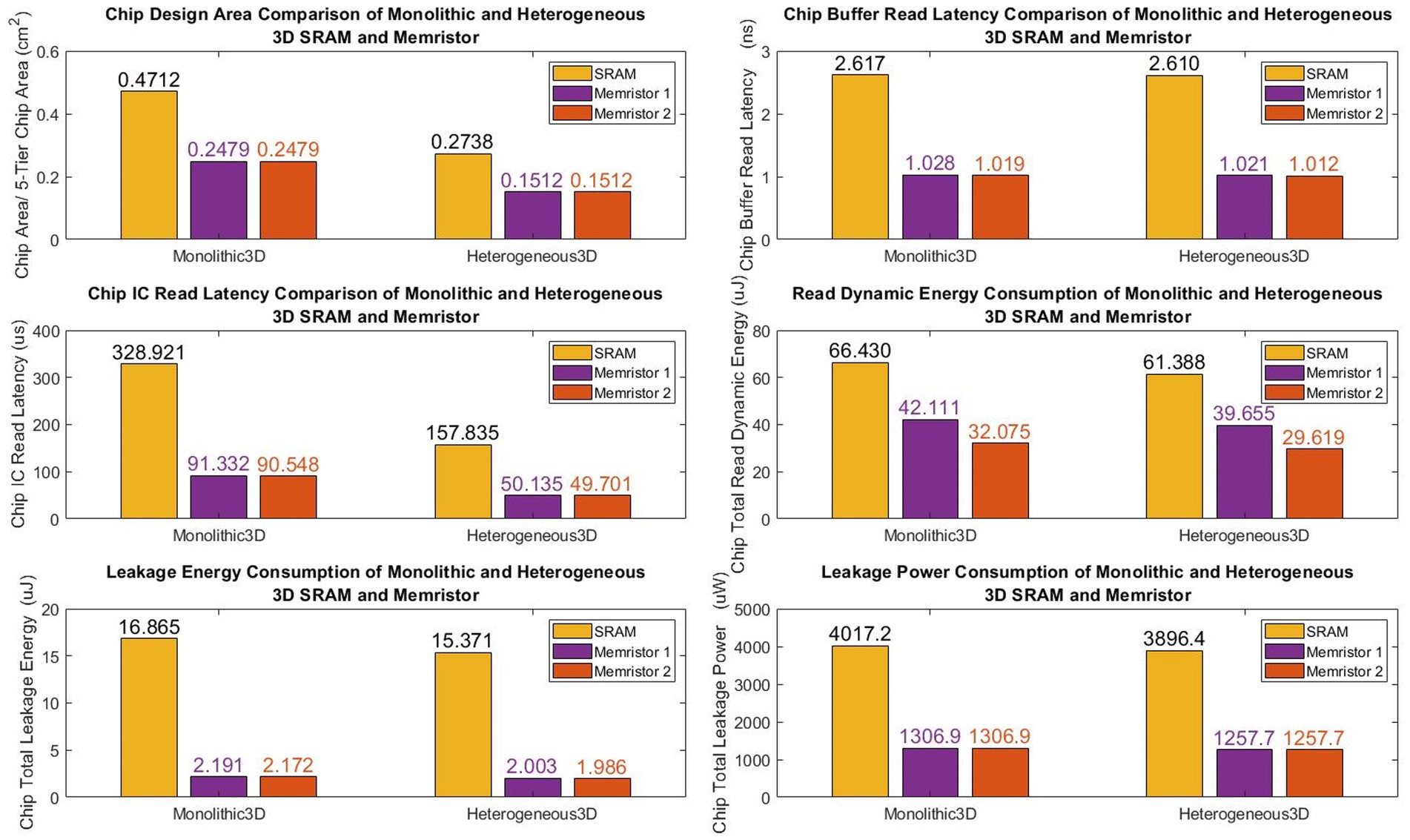
Figure 11 illustrates our designs offer a significant reduction in the chip design area, with a 47.5% decrease for monolithic 3D and 44.8% for heterogeneous 3D, when compared to conventional SRAM-based designs (see Table 3).
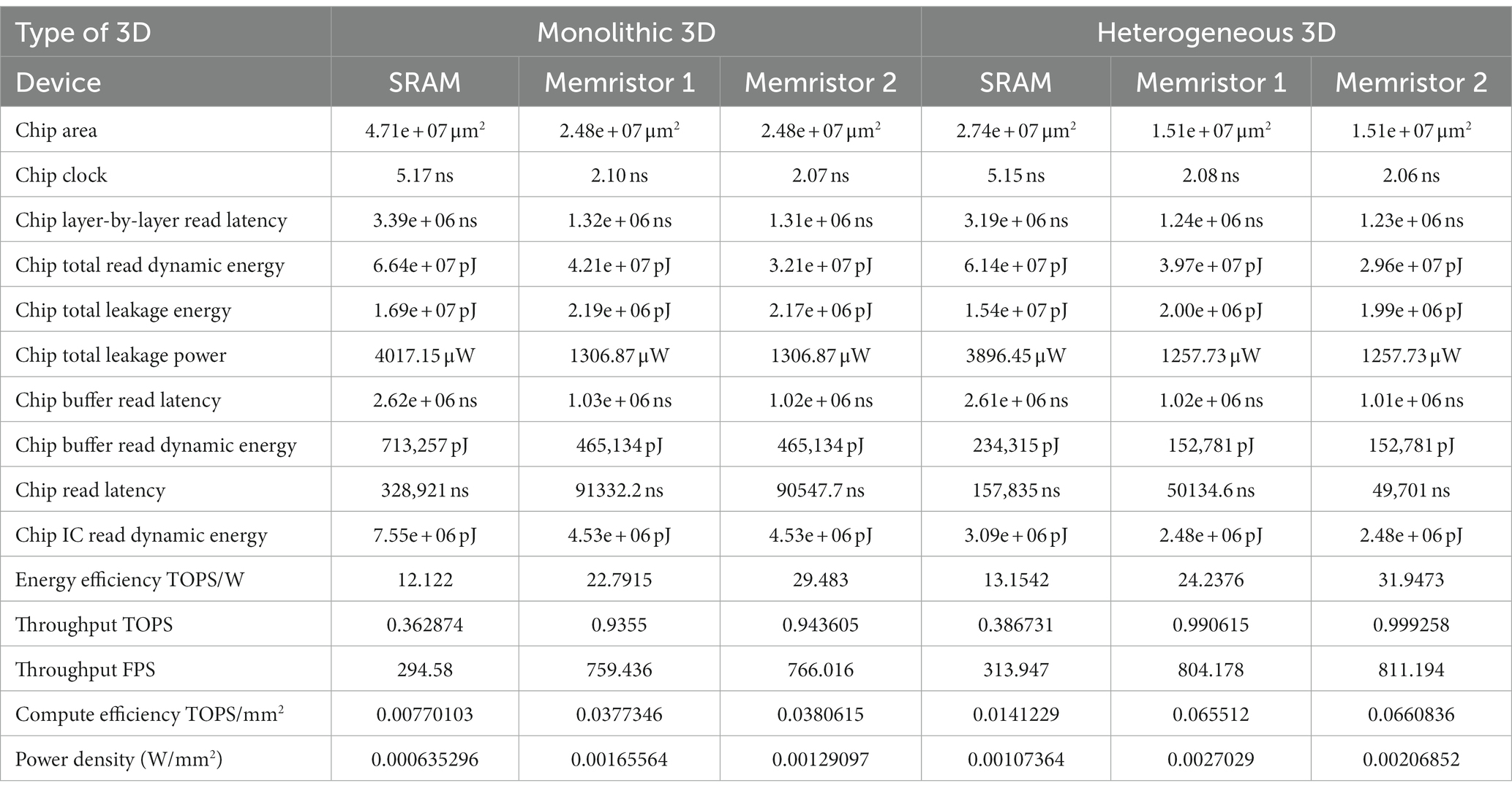
Table 3. Breakdown of hardware performance of monolithic and heterogeneous 3D SRAM and memristive chips.
Additionally, the first monolithic and heterogeneous 3D memristive designs demonstrate a substantial reduction in chip buffer read latency, with a decrease of 60.7% and 60.9% respectively, compared to SRAM architecture. Similarly, the second monolithic and heterogeneous 3D memristive designs achieve a reduction in chip buffer read latency of 61.06% and 61.2% respectively, compared to SRAM architecture. Furthermore, the first monolithic and heterogeneous 3D memristive designs significantly decrease chip read latency by 72.2% and 68.3% respectively, compared to SRAM architecture. Similarly, the second monolithic and heterogeneous 3D memristive designs result in a reduction of read latency by 72.5% and 68.5% respectively, compared to SRAM architecture. Furthermore, the first neuromorphic memristive circuit demonstrates a lower read dynamic energy consumption, with a reduction of 36.6% for monolithic 3D architectures and 35.3% for heterogeneous 3D systems compared to conventional 6 T SRAM. The second neuromorphic memristive circuit achieves an even greater reduction in read dynamic energy consumption, with decreases of 51.7% for monolithic 3D architectures and 51.8% for heterogeneous 3D systems compared to conventional 6 T SRAM.
Moreover, the first monolithic and heterogeneous 3D neuromorphic-based memristive architectures exhibit a substantial reduction in leakage energy consumption, with decreases of 86.180% and 87% respectively, compared to traditional 6 T SRAM. Similarly, the second monolithic and heterogeneous 3D neuromorphic-based memristive architectures demonstrate lower leakage energy consumption, with reductions of 87.1% and 87% respectively, compared to conventional 6 T SRAM.
Finally, when compared to SRAM-based chip designs, both monolithic and heterogeneous 3D memristive architectures show a significant decrease in leakage power consumption, with reductions of 67.5 and 67.7%, respectively.
Comparing the performance of these 7-layer SNN spike PD detectors with the beta oscillation detector by Kerman et al. (2022) is a valuable approach to evaluating the effectiveness of the detector. To conduct a fair comparison, we created a separate test dataset using spike timing data from 10 neurons in the STN region of the brain. This test dataset intentionally had a different spike timing data range, spanning from 0 to 2,000 milliseconds, compared to the training and validation datasets.
Table 4 summarizes the comparison of our work with other state-of-the-art CL-DBS systems. From Table 4, we can conclude that our 3D neuromorphic PD detector has outperformed in terms of recognition accuracy, showing an increase of 7.3% and 25%. Furthermore, it has significantly reduced the chip design area by 99.95% and 90.52%.
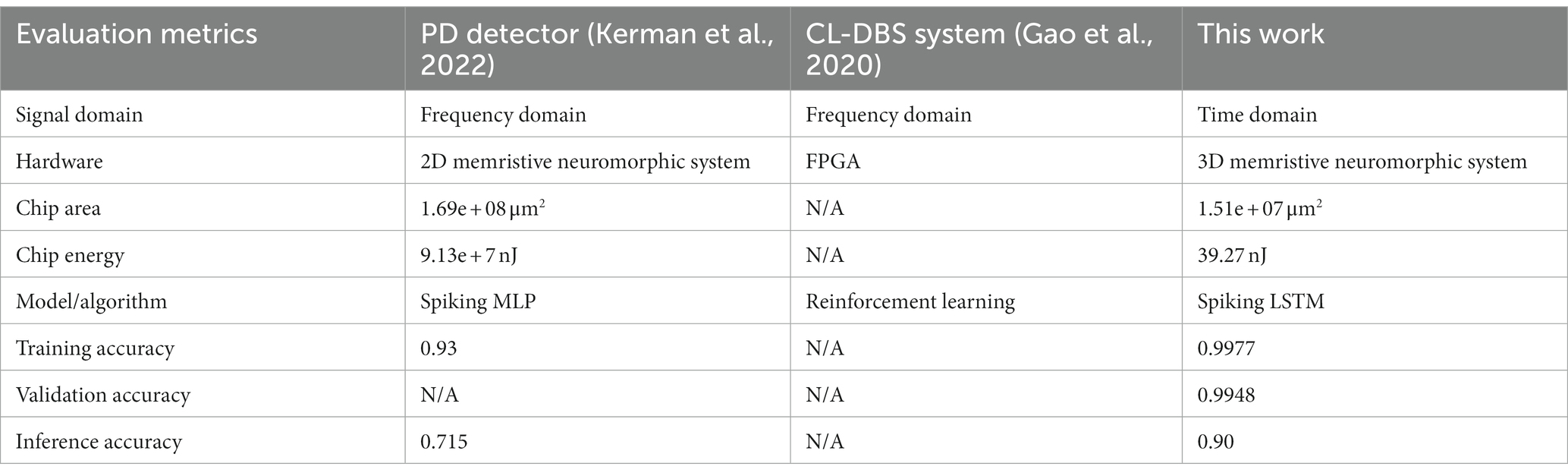
Table 4. Comparison of spike time PD classifier performance with beta oscillation detector performance.
4 Future research
This study presents a design of memristor-based neuromorphic PD detector for CL-DBS system. Nonetheless, the PD detector alone cannot constitute a comprehensive CL-DBS system. An intelligent control mechanism within the feedback loop, as illustrated in Figure 1B, stands as a critical component in a neuromorphic CL-DBS system. In the future, we intend to design and analyze a neuromorphic controller for the CL-DBS system. This neuromorphic controller will also be built upon memristor systems and spiking neural networks.
Another potential research direction involves the utilization of off-the-shelf neuromorphic chips, such as Intel Loihi chip (Davies et al., 2021), for the evaluation and validation of our neuromorphic PD detector and controller. Neuromorphic chips present an emerging and energy-efficient hardware for artificial intelligence (Severa et al., 2019). The Intel Loihi neuromorphic chips employ a digital-analog mixed design, enabling adaptive self-modifying event-driven fine-grained parallel computations. Impressively, these chips achieve exceptional energy efficiency, with less than 81 pJ per neuron update and less than 24 pJ per synaptic operation when operating at 0.75 V. This translates into a substantial reduction in energy usage, surpassing traditional GPUs (graphics processing units) by a factor of 109 and outperforming CPUs (central processing units) by a factor of 23 (Schuman et al., 2017; Blouw et al., 2019; Roy et al., 2019). Notably, one of the latest neuromorphic chips, DYNAPs, has been applied to processing EMG signals with remarkably low power consumption, as little as 614 μW (Sharifshazileh et al., 2021). In the future, the neuromorphic PD detector and controller, implemented with neuromorphic chips, will be incorporated into our PD animal models for real-time testing.
Lastly, we intend to design and fabricate our own neuromorphic chips to further enhance the energy efficiency and intelligence of the CL-DBS system. This project encompasses the design of electronic neurons and synapses using application-specific integrated circuits (ASICs) and memristors. Within this project, we will assess our design using a computational model of Parkinson’s disease (PD) (Davie, 2008; Jankovic, 2008; Ghasemi et al., 2018; Zhou et al., 2018; Lozano et al., 2019; Su et al., 2019). The PD model will provide brain neural activities as input for our circuit design.
Furthermore, our design is set to move forward to the tape-out stage. In this phase, we plan to develop a straightforward neuromorphic chip using electronic neurons and memristive synapses, specifically tailored for CL-DBS systems. Memristors will be integrated into our neuromorphic chip as electronic synapses to further enhance energy efficiency. If successful, this project’s outcome will yield more intelligent and energy-efficient implanted/wearable medical devices for CL-DBS systems. The resulting techniques will also have a broader impact on the future development of wearable and implanted medical devices by significantly reducing their size, weight, energy consumption, and, most importantly, making them more adaptive and intelligent.
5 Conclusion
In this paper, we have presented a novel neuromorphic PD detector for CL-DBS utilizing S-LSTMs and memristive synapses. To the best of our knowledge, this is the first technique that integrates memristors and S-LSTMs into the CL-DBS system for spike-time-based PD detection. The proposed neuromorphic-based memristive design chip outperforms conventional SRAM-based architecture, showing significant improvements in chip area, latency, energy usage, and power consumption. In the case of monolithic 3D architecture, the chip achieves a reduction of 47.4% in chip area, 66.63% in latency, 65.6% in energy usage, and 67.5% in power consumption. Similarly, for heterogeneous 3D architecture, the chip exhibits reductions of 44.8% in chip area, 64.75% in latency, 65.28% in energy usage, and 67.7% in power consumption. These advancements in chip design hold tremendous promise for the future development of implanted CL-DBS devices.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors upon request, without undue reservation.
Author contributions
MS: Data curation, Formal analysis, Software, Writing – original draft, Writing – review & editing. YZ: Formal analysis, Funding acquisition, Project administration, Writing – review & editing. HA: Conceptualization, Funding acquisition, Investigation, Project administration, Resources, Supervision, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the program: Disability and Rehabilitation Engineering (DARE) of National Science Foundation under Award Number 2301589.
Acknowledgments
The authors deeply appreciate Chunxiu Yu from Biomedical Engineering Department of Michigan Tech for generously sharing her knowledge on Parkinson’s disease. The authors also want to express our gratitude to Dr. William Severa from Sandia National Laboratories for his valuable insights and discussions on the Whetstone algorithm.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akopyan, F., Sawada, J., Cassidy, A., Alvarez-Icaza, R., Arthur, J., Merolla, P., et al. (2015). TrueNorth: design and tool flow of a 65 mW 1 million neuron programmable neurosynaptic chip. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 34, 1537–1557. doi: 10.1109/TCAD.2015.2474396
Allen, D. P., Stegemoller, E. L., Zadikoff, C., Rosenow, J. M., and Mackinnon, C. D. (2010). Suppression of deep brain stimulation artifacts from the electroencephalogram by frequency-domain Hampel filtering. Clin. Neurophysiol. 121, 1227–1232. doi: 10.1016/j.clinph.2010.02.156
Alomar, S., King, N. K., Tam, J., Bari, A. A., Hamani, C., and Lozano, A. M. (2017). Speech and language adverse effects after thalamotomy and deep brain stimulation in patients with movement disorders: a meta-analysis. Mov. Disord. 32, 53–63. doi: 10.1002/mds.26924
An, H. (2020). “Powering next-generation artificial intelligence by designing three-dimensional high-performance neuromorphic computing system with memristors” in Dissertation (Blacksburg, VA: Virginia Tech).
An, H., Al-Mamun, M. S., Orlowski, M. K., and Yi, Y. (2018a). Learning accuracy analysis of memristor-based nonlinear computing module on long short-term memory. Proceedings of the International Conference on Neuromorphic Systems.
An, H., Al-Mamun, M. S., Orlowski, M. K., and Yi, Y. (2021a). A three-dimensional (3D) memristive spiking neural network (M-SNN) system 22nd International Symposium on Quality Electronic Design (ISQED), IEEE.
An, H., Bai, K., and Yi, Y. (2018b). “The roadmap to realize memristive three-dimensional neuromorphic computing system” in Advances in memristor neural networks-modeling and applications (London, UK: IntechOpen).
An, H., Bai, K., and Yi, Y. (2021b). Three-dimensional memristive deep neural network with programmable attention mechanism International Symposium on Quality Electronic Design. IEEE
An, H., Li, J., Li, Y., Fu, X., and Yi, Y. (2017). Three dimensional memristor-based neuromorphic computing system and its application to cloud robotics. Comput. Electr. Eng. 63, 99–113. doi: 10.1016/j.compeleceng.2017.06.023
Arlotti, M., Rosa, M., Marceglia, S., Barbieri, S., and Priori, A. (2016). The adaptive deep brain stimulation challenge. Parkinsonism Relat. Disord. 28, 12–17. doi: 10.1016/j.parkreldis.2016.03.020
Azevedo, F. A., Carvalho, L. R., Grinberg, L. T., Farfel, J. M., Ferretti, R. E., Leite, R. E., et al. (2009). Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. J. Comp. Neurol. 513, 532–541. doi: 10.1002/cne.21974
Bai, K., and Bradley, Y. Y. (2018). A path to energy-efficient spiking delayed feedback reservoir computing system for brain-inspired neuromorphic processors. 19th International Symposium on Quality Electronic Design (ISQED). IEEE.
Benjamin, B., Gao, P., McQuinn, E., Choudhary, S., Chandrasekaran, A. R., Bussat, J. M., et al. (2014). Neurogrid: a mixed-analog-digital multichip system for large-scale neural simulations. Proc. IEEE 102, 699–716. doi: 10.1109/JPROC.2014.2313565
Bichler, O., Zhao, W., Alibart, F., Pleutin, S., Lenfant, S., Vuillaume, D., et al. (2013). Pavlov’s dog associative learning demonstrated on synaptic-like organic transistors. Neural Comput. 25, 549–566. doi: 10.1162/NECO_a_00377
Blouw, P., Choo, X., Hunsberger, E., and Eliasmith, C. (2019). Benchmarking keyword spotting efficiency on neuromorphic hardware. Proceedings of the 7th Annual Neuro-Inspired Computational Elements Workshop.
Bohte, S. M., Kok, J. N., and La Poutre, H. (2002). Error-backpropagation in temporally encoded networks of spiking neurons. Neurocomputing 48, 17–37. doi: 10.1016/S0925-2312(01)00658-0
Brüderle, D., Petrovici, M. A., Vogginger, B., Ehrlich, M., Pfeil, T., Millner, S., et al. (2011). A comprehensive workflow for general-purpose neural modeling with highly configurable neuromorphic hardware systems. Biol. Cybern. 104, 263–296. doi: 10.1007/s00422-011-0435-9
Bullmore, E., and Sporns, O. (2012). The economy of brain network organization. Nat. Rev. Neurosci. 13, 336–349. doi: 10.1038/nrn3214
Carron, R., Chaillet, A., Filipchuk, A., Pasillas-Lépine, W., and Hammond, C. (2013). Closing the loop of deep brain stimulation. Front. Syst. Neurosci. 7:112. doi: 10.3389/fnsys.2013.00112
Chen, Y., Luo, T., Liu, S., Zhang, S., He, L., Wang, J., et al. (2014). Dadiannao: a machine-learning supercomputer. Proceedings of the 47th Annual IEEE/ACM International Symposium on Microarchitecture. IEEE Computer Society.
Chen, P.-Y., Peng, X., and Yu, S. (2018). NeuroSim: a circuit-level macro model for benchmarking neuro-inspired architectures in online learning. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 37, 3067–3080. doi: 10.1109/TCAD.2018.2789723
Chua, L. (1971). Memristor-the missing circuit element. IEEE Trans. Circuits Theory 18, 507–519. doi: 10.1109/TCT.1971.1083337
Connolly, A. T., Jensen, A. L., Bello, E. M., Netoff, T. I., Baker, K. B., Johnson, M. D., et al. (2015). Modulations in oscillatory frequency and coupling in globus pallidus with increasing parkinsonian severity. J. Neurosci. 35, 6231–6240. doi: 10.1523/JNEUROSCI.4137-14.2015
Cui, J., and Qiu, Q. (2016) Towards memristor based accelerator for sparse matrix vector multiplication. 2016 IEEE International Symposium on Circuits and Systems (ISCAS) IEEE
Cyron, D. (2016). Mental side effects of deep brain stimulation (DBS) for movement disorders: the futility of denial. Front. Integr. Neurosci. 10:17. doi: 10.3389/fnint.2016.00017
Davie, C. A. (2008). A review of Parkinson’s disease. Br. Med. Bull. 86, 109–127. doi: 10.1093/bmb/ldn013
Davies, M., Srinivasa, N., Lin, T.-H., Chinya, G., Cao, Y., Choday, S. H., et al. (2018). Loihi: a neuromorphic manycore processor with on-chip learning. IEEE Micro 38, 82–99. doi: 10.1109/MM.2018.112130359
Davies, M., Wild, A., Orchard, G., Sandamirskaya, Y., Guerra, G. A. F., Joshi, P., et al. (2021). Advancing neuromorphic computing with Loihi: a survey of results and outlook. Proc. IEEE 109, 911–934. doi: 10.1109/JPROC.2021.3067593
De Garis, H., Shuo, C., Goertzel, B., and Ruiting, L. (2010). A world survey of artificial brain projects, part I: large-scale brain simulations. Neurocomputing 74, 3–29. doi: 10.1016/j.neucom.2010.08.004
de Hemptinne, C., Swann, N. C., Ostrem, J. L., Ryapolova-Webb, E. S., San Luciano, M., Galifianakis, N. B., et al. (2015). Therapeutic deep brain stimulation reduces cortical phase-amplitude coupling in Parkinson’s disease. Nat. Neurosci. 18, 779–786. doi: 10.1038/nn.3997
Deuschl, G., Herzog, J., Kleiner-Fisman, G., Kubu, C., Lozano, A. M., Lyons, K. E., et al. (2006). Deep brain stimulation: postoperative issues. Mov. Disord. 21, S219–S237. doi: 10.1002/mds.20957
di Biase, L., and Fasano, A. (2016). Low-frequency deep brain stimulation for Parkinson’s disease: great expectation or false hope? Mov. Disord. 31, 962–967. doi: 10.1002/mds.26658
Diehl, P. U., Neil, D., Binas, J., Cook, M., Liu, S.-C., and Pfeiffer, M. (2015). Fast-classifying, high-accuracy spiking deep networks through weight and threshold balancing. 2015 International Joint Conference on Neural Networks (IJCNN) IEEE
Dostrovsky, J. O., and Lozano, A. M. (2002). Mechanisms of deep brain stimulation. Mov. Disord. 17, S63–S68. doi: 10.1002/mds.10143
Ehsan, M. A., Zhou, Z., and Yi, Y. (2017). Neuromorphic 3D integrated circuit Proceedings of the Great Lakes Symposium on VLSI 2017 221–226.
Escobar, D., Johnson, L. A., Nebeck, S. D., Zhang, J., Johnson, M. D., Baker, K. B., et al. (2017). Parkinsonism and vigilance: alteration in neural oscillatory activity and phase-amplitude coupling in the basal ganglia and motor cortex. J. Neurophysiol. 118:2654. doi: 10.1152/jn.00388.2017
Eshraghian, K., Kavehei, O., Cho, K. R., Chappell, J. M., Iqbal, A., Al-Sarawi, S. F., et al. (2012). Memristive device fundamentals and modeling: applications to circuits and systems simulation. Proc. IEEE 100, 1991–2007. doi: 10.1109/JPROC.2012.2188770
Esser, S. K., Andreopoulos, A., Appuswamy, R., Datta, P., Barch, D., Amir, A., et al. (2013). Cognitive computing systems: algorithms and applications for networks of neurosynaptic cores Neural networks (IJCNN), The 2013 International Joint Conference on Neural Networks (IJCNN), IEEE
Esser, S. K., Appuswamy, R., Merolla, P., Arthur, J. V., and Modha, D. S. (2015). Backpropagation for energy-efficient neuromorphic computing Proceedings of the 28th International Conference on Neural Information Processing Systems: 1117–1125.
Esser, S. K., Merolla, P. A., Arthur, J. V., Cassidy, A. S., Appuswamy, R., Andreopoulos, A., et al. (2016). Convolutional networks for fast, energy-efficient neuromorphic computing. Proc. Natl. Acad. Sci. 113, 11441–11446. doi: 10.1073/pnas.1604850113
Fahn, S., Oakes, D., Shoulson, I., Kieburtz, K., Rudolph, A., Lang, A., et al. (2004). Levodopa and the progression of Parkinson’s disease. N. Engl. J. Med. 351, 2498–2508. doi: 10.1056/NEJMoa033447
Fang, J. Y., and Tolleson, C. (2017). The role of deep brain stimulation in Parkinson’s disease: an overview and update on new developments. Neuropsychiatr. Dis. Treat. 13, 723–732. doi: 10.2147/NDT.S113998
Felleman, D. J., and Van Essen, D. C. (1991). Distributed hierarchical processing in the primate cerebral cortex. Cerebral Cortex 1, 1–47. doi: 10.1093/cercor/1.1.1-a
Ferreira de Lima, T., Shastri, B. J., Tait, A. N., Nahmias, M. A., and Prucnal, P. R. (2017). Progress in neuromorphic photonics. Nano 6, 577–599. doi: 10.1515/nanoph-2016-0139
Furber, S. B., Lester, D. R., Plana, L. A., Garside, J. D., Painkras, E., Temple, S., et al. (2013). Overview of the SpiNNaker system architecture. IEEE Trans. Comput. 62, 2454–2467. doi: 10.1109/TC.2012.142
Gao, Q., Naumann, M., Jovanov, I., Lesi, V., Kamaravelu, K., Grill, W. M., et al. (2020). Model-based design of closed loop deep brain stimulation controller using reinforcement learning 2020 ACM/IEEE 11th International Conference on Cyber-Physical Systems (ICCPS)IEEE
Gerstner, W., and Naud, R. (2009). How good are neuron models? Science 326, 379–380. doi: 10.1126/science.1181936
Gerstner, W., Sprekeler, H., and Deco, G. (2012). Theory and simulation in neuroscience. Science 338, 60–65. doi: 10.1126/science.1227356
Ghasemi, P., Sahraee, T., and Mohammadi, A. (2018). Closed-and open-loop deep brain stimulation: methods, challenges, current and future aspects. J. Biomed. Phys. Eng. 8, 209–216. doi: 10.31661/jbpe.v8i2.898
Goertzel, B., Lian, R., Arel, I., de Garis, H., and Chen, S. (2010). A world survey of artificial brain projects, part II: biologically inspired cognitive architectures. Neurocomputing 74, 30–49. doi: 10.1016/j.neucom.2010.08.012
Guo, K., Han, S., Yao, S., Wang, Y., Xie, Y., and Yang, H. (2017). Software-hardware codesign for efficient neural network acceleration. IEEE Micro 37, 18–25. doi: 10.1109/MM.2017.39
Hamani, C., Richter, E., Schwalb, J. M., and Lozano, A. M. (2005). Bilateral subthalamic nucleus stimulation for Parkinson’s disease: a systematic review of the clinical literature. Neurosurgery 56, 1313–1324. doi: 10.1227/01.NEU.0000159714.28232.C4
Hariz, M. I., Rehncrona, S., Quinn, N. P., Speelman, J. D., and Wensing, C. (2008). Multicenter study on deep brain stimulation in Parkinson’s disease: an independent assessment of reported adverse events at 4 years. Mov. Disord. 23, 416–421. doi: 10.1002/mds.21888
Hasler, J., and Marr, B. (2013). Finding a roadmap to achieve large neuromorphic hardware systems. Front. Neurosci. 7:118. doi: 10.3389/fnins.2013.00118
He, S., Baig, F., Mostofi, A., Pogosyan, A., Debarros, J., Green, A. L., et al. (2021). Closed-loop deep brain stimulation for essential tremor based on thalamic local field potentials. Mov. Disord. 36, 863–873. doi: 10.1002/mds.28513
Herron, J. A., Thompson, M. C., Brown, T., Chizeck, H. J., Ojemann, J. G., and Ko, A. L. (2016). Chronic electrocorticography for sensing movement intention and closed-loop deep brain stimulation with wearable sensors in an essential tremor patient. J. Neurosurg. 127, 580–587. doi: 10.3171/2016.8.JNS16536
Hosain, M. K., Kouzani, A., and Tye, S. (2014). Closed loop deep brain stimulation: an evolving technology. Australas. Phys. Eng. Sci. Med. 37, 619–634. doi: 10.1007/s13246-014-0297-2
Hwynn, N., Hass, C. J., Zeilman, P., Romrell, J., Dai, Y., Wu, S. S., et al. (2011). Steady or not following thalamic deep brain stimulation for essential tremor. J. Neurol. 258, 1643–1648. doi: 10.1007/s00415-011-5986-0
Indiveri, G., Corradi, F., and Qiao, N. (2015). "Neuromorphic architectures for spiking deep neural networks." 2015 IEEE International Electron Devices Meeting (IEDM)
Jankovic, J. (2008). Parkinson’s disease: clinical features and diagnosis. J. Neurol. Neurosurg. Psychiatry 79, 368–376. doi: 10.1136/jnnp.2007.131045
Jin, M., Liu, S., Schiavon, S., and Spanos, C. (2018). Automated mobile sensing: towards high-granularity agile indoor environmental quality monitoring. Build. Environ. 127, 268–276. doi: 10.1016/j.buildenv.2017.11.003
Jorgensen, T. J. (2021). Spark: the life of electricity and the electricity of life. Princeton University Press, Princeton
Joubert, A., Belhadj, B., Temam, O., and Héliot, R. (2012). Hardware spiking neurons design: analog or digital? The 2012 International Joint Conference on Neural Networks (IJCNN)
Jovanov, I., Naumann, M., Kumaravelu, K., Grill, W. M., and Pajic, M. (2018). Platform for model-based design and testing for deep brain stimulation. 2018 ACM/IEEE 9th International Conference on Cyber-Physical Systems (ICCPS) IEEE
Kandel, E. R., Schwartz, J. H., Jessell, T. M., Siegelbaum, S. A., and Hudspeth, A. (2000). Principles of neural science, McGraw-Hill, New York.
Kerman, Z., Yu, C., and An, H. (2022). Beta oscillation detector design for closed-loop deep brain stimulation of Parkinson’s disease with memristive spiking neural networks. 23rd International Symposium on Quality Electronic Design (ISQED), IEEE.
Kornijcuk, V., Kavehei, O., Lim, H., Seok, J. Y., Kim, S. K., Kim, I., et al. (2014). Multiprotocol-induced plasticity in artificial synapses. Nanoscale 6, 15151–15160. doi: 10.1039/C4NR03405H
Kumaravelu, K., Brocker, D. T., and Grill, W. M. (2016). A biophysical model of the cortex-basal ganglia-thalamus network in the 6-OHDA lesioned rat model of Parkinson’s disease. J. Comput. Neurosci. 40, 207–229. doi: 10.1007/s10827-016-0593-9
Kuo, C.-H., White-Dzuro, G. A., and Ko, A. L. (2018). Approaches to closed-loop deep brain stimulation for movement disorders. Neurosurg. Focus. 45:E2. doi: 10.3171/2018.5.FOCUS18173
Lane, N. D., Georgiev, P., and Qendro, L. (2015). DeepEar: robust smartphone audio sensing in unconstrained acoustic environments using deep learning. Proceedings of the 2015 ACM International Joint Conference on Pervasive and Ubiquitous Computing
Lastras-Montaño, M. A., Chakrabarti, B., Strukov, D. B., and Cheng, K.-T. (2017). 3D-DPE: a 3D high-bandwidth dot-product engine for high-performance neuromorphic computing. Design, Automation & Test in Europe Conference & Exhibition (DATE) IEEE.
Lau, M. M., and Lim, K. H. (2018). Review of adaptive activation function in deep neural network. 2018 IEEE-EMBS Conference on Biomedical Engineering and Sciences (IECBES) IEEE
Lecun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. Nature 521, 436–444. doi: 10.1038/nature14539
LeCun, Y., Boser, B., Denker, J. S., Henderson, D., Howard, R. E., Hubbard, W., et al. (1989). Backpropagation applied to handwritten zip code recognition. Neural Comput. 1, 541–551. doi: 10.1162/neco.1989.1.4.541
Lee, J. H., Delbruck, T., and Pfeiffer, M. (2016). Training deep spiking neural networks using backpropagation. Front. Neurosci. 10:508. doi: 10.3389/fnins.2016.00508
Li, Y., and Ang, K.-W. (2021). Hardware implementation of neuromorphic computing using large-scale memristor crossbar arrays. Adv. Intell. Syst. 3:2000137. doi: 10.1002/aisy.202000137
Likharev, K. K. (2011). CrossNets: neuromorphic hybrid CMOS/nanoelectronic networks. Sci. Adv. Mater. 3, 322–331. doi: 10.1166/sam.2011.1177
Little, S., Pogosyan, A., Neal, S., Zavala, B., Zrinzo, L., Hariz, M., et al. (2013). Adaptive deep brain stimulation in advanced Parkinson disease. Ann. Neurol. 74, 449–457. doi: 10.1002/ana.23951
Little, S., Tripoliti, E., Beudel, M., Pogosyan, A., Cagnan, H., Herz, D., et al. (2016). Adaptive deep brain stimulation for Parkinson’s disease demonstrates reduced speech side effects compared to conventional stimulation in the acute setting. J. Neurol. Neurosurg. Psychiatry 87, 1388–1389. doi: 10.1136/jnnp-2016-313518
Liu, S.-C., and Delbruck, T. (2010). Neuromorphic sensory systems. Curr. Opin. Neurobiol. 20, 288–295. doi: 10.1016/j.conb.2010.03.007
Liu, X., Mao, M., Liu, B., Li, H., Chen, Y., Li, B., et al. (2015). RENO: a high-efficient reconfigurable neuromorphic computing accelerator design Proceedings of the 52nd Annual Design Automation Conference
Liu, J.-H., Wang, C.-Y., and An, Y.-Y. (2009) A survey of neuromorphic vision system: biological nervous systems realized on silicon. International Conference on Industrial Mechatronics and Automation. IEEE
Liu, C., Zhao, G., Wang, J., Wu, H., Li, H., Fietkiewicz, C., et al. (2020). Neural network-based closed-loop deep brain stimulation for modulation of pathological oscillation in Parkinson’s disease. IEEE Access 8, 161067–161079. doi: 10.1109/ACCESS.2020.3020429
Lozano, A. M., Lipsman, N., Bergman, H., Brown, P., Chabardes, S., Chang, J. W., et al. (2019). Deep brain stimulation: current challenges and future directions. Nat. Rev. Neurol. 15, 148–160. doi: 10.1038/s41582-018-0128-2
Lu, W., Kim, K.-H., Chang, T., and Gaba, S. (2011). Two-terminal resistive switches (memristors) for memory and logic applications. 16th Asia and South Pacific Design Automation Conference ASP-DAC 2011, IEEE
Lu, A., Peng, X., Li, W., Jiang, H., and Yu, S. (2021). NeuroSim simulator for compute-in-memory hardware accelerator: validation and benchmark. Front. Artif. Intell. 4:659060. doi: 10.3389/frai.2021.659060
Maass, W. (1997). Networks of spiking neurons: the third generation of neural network models. Neural Netw. 10, 1659–1671. doi: 10.1016/S0893-6080(97)00011-7
Marceglia, S., Rossi, L., Foffani, G., Bianchi, A., Cerutti, S., and Priori, A. (2007). Basal ganglia local field potentials: applications in the development of new deep brain stimulation devices for movement disorders. Expert Rev. Med. Devices 4, 605–614. doi: 10.1586/17434440.4.5.605
Marković, D., Mizrahi, A., Querlioz, D., and Grollier, J. (2020). Physics for neuromorphic computing. Nat. Rev. Phys. 2, 499–510. doi: 10.1038/s42254-020-0208-2
Massano, J., and Garrett, C. (2012). Deep brain stimulation and cognitive decline in Parkinson’s disease: a clinical review. Front. Neurol. 3:66. doi: 10.3389/fneur.2012.00066
McConnell, G. C., So, R. Q., Hilliard, J. D., Lopomo, P., and Grill, W. M. (2012). Effective deep brain stimulation suppresses low-frequency network oscillations in the basal ganglia by regularizing neural firing patterns. J. Neurosci. 32, 15657–15668. doi: 10.1523/JNEUROSCI.2824-12.2012
McKennoch, S., Liu, D., and Bushnell, L. G. (2006). Fast modifications of the spikeprop algorithm. 2006 IEEE International Joint Conference on Neural Network Proceedings, IEEE
Mead, C. (2020). How we created neuromorphic engineering. Nat. Electr. 3, 434–435. doi: 10.1038/s41928-020-0448-2
Mead, C., and Ismail, M. (1989). Analog VLSI implementation of neural systems, New York, NY Springer Science & Business Media
Merolla, P., Arthur, J., Akopyan, F., Imam, N., Manohar, R., and Modha, D. S. (2011). A digital neurosynaptic core using embedded crossbar memory with 45 pJ per spike in 45 nm. 2011 IEEE Custom Integrated Circuits Conference (CICC), IEEE
Merolla, P. A., Arthur, J. V., Alvarez-Icaza, R., Cassidy, A. S., Sawada, J., Akopyan, F., et al. (2014). A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 345, 668–673. doi: 10.1126/science.1254642
Min, K.-S., and Corinto, F. (2021). Memristor computing for neuromorphic systems. Front. Comput. Neurosci. 15:755405. doi: 10.3389/fncom.2021.755405
Naylor, M., and Runciman, C. (2007). The Reduceron: widening the von Neumann bottleneck for graph reduction using an FPGA. Symposium on Implementation and Application of Functional Languages, Springer.
Neftci, E. O., Mostafa, H., and Zenke, F. (2019). Surrogate gradient learning in spiking neural networks: bringing the power of gradient-based optimization to spiking neural networks. IEEE Signal Process. Mag. 36, 51–63. doi: 10.1109/MSP.2019.2931595
Nwankpa, C., Ijomah, W., Gachagan, A., and Marshall, S. (2018). Activation functions: comparison of trends in practice and research for deep learning. arXiv. Available at: https://doi.org/10.48550/arXiv.1811.03378. [Epub ahead of preprint]
O’Connor, P., Neil, D., Liu, S.-C., Delbruck, T., and Pfeiffer, M. (2013). Real-time classification and sensor fusion with a spiking deep belief network. Front. Neurosci. 7:178. doi: 10.3389/fnins.2013.00178
Osswald, M., Ieng, S. H., Benosman, R., and Indiveri, G. (2017). A spiking neural network model of 3D perception for event-based neuromorphic stereo vision systems. Sci. Rep. 7:40703. doi: 10.1038/srep40703
Painkras, E., Plana, L. A., Garside, J., Temple, S., Galluppi, F., Patterson, C., et al. (2013). SpiNNaker: a 1-W 18-core system-on-chip for massively-parallel neural network simulation. IEEE J. Solid State Circuits 48, 1943–1953. doi: 10.1109/JSSC.2013.2259038
Panda, P., and Roy, K. (2016). Unsupervised regenerative learning of hierarchical features in spiking deep networks for object recognition International Joint Conference on Neural Networks (IJCNN), IEEE
Parastarfeizabadi, M., and Kouzani, A. Z. (2017). Advances in closed-loop deep brain stimulation devices. J. Neuroeng. Rehabil. 14:79. doi: 10.1186/s12984-017-0295-1
Park, S., Chu, M., Kim, J., Noh, J., Jeon, M., Lee, B. H., et al. (2015). Electronic system with memristive synapses for pattern recognition. Sci. Rep. 5:10123. doi: 10.1038/srep10123
Peng, X., Huang, S., Jiang, H., Lu, A., and Yu, S. (2020). DNN+ NeuroSim V2. 0: an end-to-end benchmarking framework for compute-in-memory accelerators for on-chip training. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 40, 2306–2319. doi: 10.1109/TCAD.2020.3043731
Perez-Alcazar, M., Nicolas, M. J., Valencia, M., Alegre, M., Lopez-Azcarate, J., Iriarte, J., et al. (2010). Cortical oscillations scan using chirp-evoked potentials in 6-hydroxydopamine rat model of Parkinson’s disease. Brain Res. 1310, 58–67. doi: 10.1016/j.brainres.2009.11.031
Pfeil, T., Grübl, A., Jeltsch, S., Müller, E., Müller, P., Petrovici, M. A., et al. (2012). Six networks on a universal neuromorphic computing substrate. arXiv. Available at: https://doi.org/10.48550/arXiv.1210.7083. [Epub ahead of preprint]
Pino, R. E., Li, H., Chen, Y., Hu, M., and Liu, B. (2012). Statistical memristor modeling and case study in neuromorphic computing. DAC Design Automation Conference 2012 IEEE
Plank, J. S., Schuman, C. D., Bruer, G., Dean, M. E., and Rose, G. S. (2018). The TENNLab exploratory neuromorphic computing framework. IEEE Lett. Comput. Soc. 1, 17–20. doi: 10.1109/LOCS.2018.2885976
Priori, A., Foffani, G., Rossi, L., and Marceglia, S. (2013). Adaptive deep brain stimulation (aDBS) controlled by local field potential oscillations. Exp. Neurol. 245, 77–86. doi: 10.1016/j.expneurol.2012.09.013
Putnam, A., Caulfield, A. M., Chung, E. S., Chiou, D., Constantinides, K., Demme, J., et al. (2014). A reconfigurable fabric for accelerating large-scale datacenter services. IEEE Micro 35, 10–22. doi: 10.1109/MM.2015.42
Qiao, N., Mostafa, H., Corradi, F., Osswald, M., Stefanini, F., Sumislawska, D., et al. (2015). A re-configurable on-line learning spiking neuromorphic processor comprising 256 neurons and 128K synapses. Front. Neurosci. 9:141. doi: 10.3389/fnins.2015.00141
Rajendran, B., Liu, Y., Seo, J., Gopalakrishnan, K., Chang, L., Friedman, D. J., et al. (2013). Specifications of nanoscale devices and circuits for neuromorphic computational systems. IEEE Trans. Electron. Devices 60, 246–253. doi: 10.1109/TED.2012.2227969
Ramachandran, P., Zoph, B., and Le, Q. V. (2017). Searching for activation functions arXiv. Available at: https://doi.org/10.48550/arXiv.1710.05941. [Epub ahead of preprint]
Rosin, B., Slovik, M., Mitelman, R., Rivlin-Etzion, M., Haber, S. N., Israel, Z., et al. (2011). Closed-loop deep brain stimulation is superior in ameliorating parkinsonism. Neuron 72, 370–384. doi: 10.1016/j.neuron.2011.08.023
Rossi, L., Foffani, G., Marceglia, S., Bracchi, F., Barbieri, S., and Priori, A. (2007). An electronic device for artefact suppression in human local field potential recordings during deep brain stimulation. J. Neural Eng. 4, 96–106. doi: 10.1088/1741-2560/4/2/010
Rossi, P. J., Gunduz, A., Judy, J., Wilson, L., Machado, A., Giordano, J. J., et al. (2016). Proceedings of the third annual deep brain stimulation think tank: a review of emerging issues and technologies. Front. Neurosci. 10:119. doi: 10.3389/fnins.2016.00119
Roy, K., Jaiswal, A., and Panda, P. (2019). Towards spike-based machine intelligence with neuromorphic computing. Nature 575, 607–617. doi: 10.1038/s41586-019-1677-2
Rueckauer, B., Lungu, I.-A., Hu, Y., Pfeiffer, M., and Liu, S.-C. (2017). Conversion of continuous-valued deep networks to efficient event-driven networks for image classification. Front. Neurosci. 11:682. doi: 10.3389/fnins.2017.00682
Sakemi, Y., Morino, K., Morie, T., and Aihara, K. (2020). A supervised learning algorithm for multilayer spiking neural networks based on temporal coding toward energy-efficient VLSI processor design arXiv. Available at: https://doi.org/10.48550/arXiv.2001.05348. [Epub ahead of preprint].
Salam, M. T., Velazquez, J. L. P., and Genov, R. (2015). Seizure suppression efficacy of closed-loop versus open-loop deep brain stimulation in a rodent model of epilepsy. IEEE Trans. Neural Syst. Rehabil. Eng. 24, 710–719. doi: 10.1109/TNSRE.2015.2498973
Schemmel, J., Fieres, J., and Meier, K. (2008). Wafer-scale integration of analog neural networks. 2008 IEEE International Joint Conference on Neural Networks. IEEE
Schuman, C. D. (2016). Roadmap for neuromorphic computing: a computer science perspective arXiv. Available at: https://doi.org/10.48550/arXiv.2105.05956. [Epub ahead of preprint]
Schuman, C. D., Potok, T. E., Patton, R. M., Birdwell, J. D., Dean, M. E., Rose, G. S., et al. (2017). A survey of neuromorphic computing and neural networks in hardware. arXiv Available at: https://doi.org/10.48550/arXiv.1705.06963. [Epub ahead of preprint].
Schuman, C. D., Ridge, O., and Disney, A. (2015). "Dynamic adaptive neural network arrays: a neuromorphic architecture." Proceedings of the Workshop on Machine Learning in High-Performance Computing Environments—MLHPC. 1–4.
Seo, J.-s., Brezzo, B., Liu, Y., Parker, B. D., Esser, S. K., Montoye, R. K., et al. (2011). A 45nm CMOS neuromorphic chip with a scalable architecture for learning in networks of spiking neurons 2011 IEEE Custom Integrated Circuits Conference (CICC) IEEE
Severa, W., Vineyard, C. M., Dellana, R., Verzi, S. J., and Aimone, J. B. (2019). Training deep neural networks for binary communication with the whetstone method. Nat. Mach. Intell. 1, 86–94. doi: 10.1038/s42256-018-0015-y
Shah, S. A. A., Zhang, L., and Bais, A. (2018). Real time fixed point adaptive chaotic system generator for deep brain stimulation using FPGA. International Conference on Frontiers of Information Technology (FIT) IEEE
Sharifshazileh, M., Burelo, K., Sarnthein, J., and Indiveri, G. (2021). An electronic neuromorphic system for real-time detection of high frequency oscillations (HFO) in intracranial EEG. Nat. Commun. 12, 1–14. doi: 10.1038/s41467-021-23342-2
Shrestha, S. B., and Orchard, G. (2018). SLAYER: spike layer error reassignment in time arXiv Available at: https://doi.org/10.48550/arXiv.1810.08646. [Epub ahead of preprint]
Shrestha, S. B., and Song, Q. (2017). Robust spike-train learning in spike-event based weight update. Neural Netw. 96, 33–46. doi: 10.1016/j.neunet.2017.08.010
Shukla, P. (2015). Machine learning technique based closed-loop deep brain stimulation controller design. Chicago, Illinois, USA: University of Illinois at Chicago.
Smith, L. S. (2010). “Neuromorphic systems: past, present and future” in Brain inspired cognitive systems (New York, NY: Springer), 167–182.
Snider, G. S., and Williams, R. S. (2007). Nano/CMOS architectures using a field-programmable nanowire interconnect. Nanotechnology 18:035204. doi: 10.1088/0957-4484/18/3/035204
Stromatias, E., Galluppi, F., Patterson, C., and Furber, S. (2013). Power analysis of large-scale, real-time neural networks on SpiNNaker. International Joint Conference on Neural Networks (IJCNN), IEEE
Strukov, D. B., Snider, G. S., Stewart, D. R., and Williams, R. S. (2008). The missing memristor found. Nature 453, 80–83. doi: 10.1038/nature06932
Su, D., Chen, H., Hu, W., Liu, Y., Wang, Z., Wang, X., et al. (2018). Frequency-dependent effects of subthalamic deep brain stimulation on motor symptoms in Parkinson’s disease: a meta-analysis of controlled trials. Sci. Rep. 8, 1–9. doi: 10.1038/s41598-018-32161-3
Su, F., Chen, M., Zu, L., Li, S., and Li, H. (2021). Model-based closed-loop suppression of parkinsonian beta band oscillations through origin analysis. IEEE Trans. Neural Syst. Rehabil. Eng. 29, 450–457. doi: 10.1109/TNSRE.2021.3056544
Su, F., Kumaravelu, K., Wang, J., and Grill, W. M. (2019). Model-based evaluation of closed-loop deep brain stimulation controller to adapt to dynamic changes in reference signal. Front. Neurosci. 13:956. doi: 10.3389/fnins.2019.00956
Taherkhani, A., Belatreche, A., Li, Y., Cosma, G., Maguire, L. P., and McGinnity, T. M. (2020). A review of learning in biologically plausible spiking neural networks. Neural Netw. 122, 253–272. doi: 10.1016/j.neunet.2019.09.036
Tavanaei, A., Ghodrati, M., Kheradpisheh, S. R., Masquelier, T., and Maida, A. (2019). Deep learning in spiking neural networks. Neural Netw. 111, 47–63. doi: 10.1016/j.neunet.2018.12.002
Upadhyay, N. K., Jiang, H., Wang, Z., Asapu, S., Xia, Q., and Joshua Yang, J. (2019). Emerging memory devices for neuromorphic computing. Adv. Mater. Technol. 4:1800589. doi: 10.1002/admt.201800589
Velisar, A., Syrkin-Nikolau, J., Blumenfeld, Z., Trager, M., Afzal, M., Prabhakar, V., et al. (2019). Dual threshold neural closed loop deep brain stimulation in Parkinson disease patients. Brain Stimul. 12, 868–876. doi: 10.1016/j.brs.2019.02.020
Versace, M., and Chandler, B. (2010). The brain of a new machine. IEEE Spectr. 47, 30–37. doi: 10.1109/MSPEC.2010.5644776
Wade, J. J., McDaid, L. J., Santos, J. A., and Sayers, H. M. (2008). SWAT: an unsupervised SNN training algorithm for classification problems. IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence)
Walter, F., Röhrbein, F., and Knoll, A. (2015). Neuromorphic implementations of neurobiological learning algorithms for spiking neural networks. Neural Netw. 72, 152–167. doi: 10.1016/j.neunet.2015.07.004
Wang, F. Z., Helian, N., Wu, S., Yang, X., Guo, Y., Lim, G., et al. (2012). Delayed switching applied to memristor neural networks. J. Appl. Phys. 111, 1–4. doi: 10.1063/1.3672409
Williams, S. R. (2008). How we found the missing memristor. IEEE Spectr. 45, 28–35. doi: 10.1109/MSPEC.2008.4687366
Wong, H. S. P., Lee, H. Y., Yu, S., Chen, Y. S., Wu, Y., Chen, P. S., et al. (2012). Metal-oxide RRAM. Proc. IEEE 100, 1951–1970. doi: 10.1109/JPROC.2012.2190369
Wu, H., Ghekiere, H., Beeckmans, D., Tambuyzer, T., van Kuyck, K., Aerts, J. M., et al. (2015). Conceptualization and validation of an open-source closed-loop deep brain stimulation system in rat. Sci. Rep. 5:9921. doi: 10.1038/srep09921
Wu, Y., Mo, J., Sui, L., Zhang, J., Hu, W., Zhang, C., et al. (2021). Deep brain stimulation in treatment-resistant depression: a systematic review and meta-analysis on efficacy and safety. Front. Neurosci. 15:655412. doi: 10.3389/fnins.2021.655412
Wunderlich, T., Kungl, A. F., Müller, E., Hartel, A., Stradmann, Y., Aamir, S. A., et al. (2019). Demonstrating advantages of neuromorphic computation: a pilot study. Front. Neurosci. 13:260. doi: 10.3389/fnins.2019.00260
Yamazaki, K., Vo-Ho, V.-K., Bulsara, D., and Le, N. (2022). Spiking neural networks and their applications: a review. Brain Sci. 12:863. doi: 10.3390/brainsci12070863
Yan, X., He, F., Hou, N., and Ai, H. (2018). An efficient particle swarm optimization for large-scale hardware/software co-design system. Int. J. Coop. Inf. Syst. 27:1741001. doi: 10.1142/S0218843017410015
Yang, S., and Chen, B. (2023). SNIB: improving spike-based machine learning using nonlinear information bottleneck. IEEE Trans. Syst. Man Cybern.: Syst. 99, 1–12. doi: 10.1109/TSMC.2023.3300318
Yang, S., Linares-Barranco, B., and Chen, B. (2022a). Heterogeneous ensemble-based spike-driven few-shot online learning. Front. Neurosci. 16:850932. doi: 10.3389/fnins.2022.850932
Yang, S., Pang, Y., Wang, H., Lei, T., Pan, J., Wang, J., et al. (2023a). Spike-driven multi-scale learning with hybrid mechanisms of spiking dendrites. Neurocomputing 542:126240. doi: 10.1016/j.neucom.2023.126240
Yang, S., Tan, J., and Chen, B. (2022b). Robust spike-based continual meta-learning improved by restricted minimum error entropy criterion. Entropy 24:455. doi: 10.3390/e24040455
Yang, S., Tan, J., Lei, T., and Linares-Barranco, B. (2023b). Smart traffic navigation system for fault-tolerant edge computing of internet of vehicle in intelligent transportation gateway. IEEE Trans. Intell. Transp. Syst. 24, 13011–13022. doi: 10.1109/TITS.2022.3232231
Yang, S., Wang, J., Deng, B., Azghadi, M. R., and Linares-Barranco, B. (2021). Neuromorphic context-dependent learning framework with fault-tolerant spike routing. IEEE Trans. Neural Netw. Learn. Syst. 33, 7126–7140. doi: 10.1109/TNNLS.2021.3084250
Yi, G.-S., Wang, J., Tsang, K.-M., Wei, X.-L., and Deng, B. (2015). Input-output relation and energy efficiency in the neuron with different spike threshold dynamics. Front. Comput. Neurosci. 9:62. doi: 10.3389/fncom.2015.00062
Zaremba, W., Sutskever, I., and Vinyals, O. (2014). Recurrent neural network regularization arXiv Available at: https://doi.org/10.48550/arXiv.1409.2329. [Epub ahead of preprint]
Zenke, F., and Ganguli, S. (2018). Superspike: supervised learning in multilayer spiking neural networks. Neural Comput. 30, 1514–1541. doi: 10.1162/neco_a_01086
Zhang, T., Yin, M., Lu, X., Cai, Y., Yang, Y., and Huang, R. (2017). Tolerance of intrinsic device variation in fuzzy restricted Boltzmann machine network based on memristive nano-synapses. Nano Futures 1:015003. doi: 10.1088/2399-1984/aa678b
Zhou, J. J., Chen, T., Farber, S. H., Shetter, A. G., and Ponce, F. A. (2018). Open-loop deep brain stimulation for the treatment of epilepsy: a systematic review of clinical outcomes over the past decade (2008—present). Neurosurg. Focus. 45:E5. doi: 10.3171/2018.5.FOCUS18161
Keywords: memristors, neuromorphic computing, spiking neural networks, deep brain stimulation, Parkinson’s disease
Citation: Siddique MAB, Zhang Y and An H (2023) Monitoring time domain characteristics of Parkinson’s disease using 3D memristive neuromorphic system. Front. Comput. Neurosci. 17:1274575. doi: 10.3389/fncom.2023.1274575
Edited by:
Petia D. Koprinkova-Hristova, Institute of Information and Communication Technologies (BAS), BulgariaReviewed by:
Shuangming Yang, Tianjin University, ChinaAngela Slavova, Bulgarian Academy of Sciences (BAS), Bulgaria
Copyright © 2023 Siddique, Zhang and An. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yan Zhang, eXpoYW5nNDlAbXR1LmVkdQ==; Hongyu An, aG9uZ3l1YUBtdHUuZWR1
 Md Abu Bakr Siddique
Md Abu Bakr Siddique Yan Zhang2*
Yan Zhang2* Hongyu An
Hongyu An