Fault-tolerance in metric dimension of boron nanotubes lattices

The concept of resolving set and metric basis has been very successful because of multi-purpose applications both in computer and mathematical sciences. A system in which failure of any single unit, another chain of units not containing the faulty unit can replace the originally used chain is called a fault-tolerant self-stable system. Recent research studies reveal that the problem of finding metric dimension is NP-hard for general graphs and the problem of computing the exact values of fault-tolerant metric dimension seems to be even harder although some bounds can be computed rather easily. In this article, we compute closed formulas for the fault-tolerant metric dimension of lattices of two types of boron nanotubes, namely triangular and alpha boron. These lattices are formed by cutting the tubes vertically. We conclude that both tubes have constant fault tolerance metric dimension 4.

1. Introduction

Computer networks are graphs with vertices representing hosts, servers, or hubs, and edges as connecting mediums between them. Vertex is actually a possible location to find faults or some damaged devices in a computer network. This idea somehow created an urge in Slater and independently in Harary and Melter (1976) to uniquely recognize each vertex of a graph in a network so that fault could be controlled efficiently. Thus, the basis for the notion of locating sets and locating the number of graphs came into existence. Since then, the resolving sets have been extensively investigated (Buczkowski et al., 2003; Caceres et al., 2005; Javaid et al., 2008). The resolving set contributes to various areas such as network discovery (Khuller et al., 1994, 1996), connected joins in graphs, strategies for the mastermind games (Chvatal, 1983), applications of pattern recognition, combinatorial optimization, image processing (Melter and Tomescu, 1984), pharmaceutical chemistry, and game theory.

A moving point in a graph may be located by finding the distance from the point to the collection of sonar stations that have been properly positioned in the graph. Thus finding a minimal but sufficiently large set of labeled vertices such that a robot can find its position, is a well-established problem known as robot navigation. This sufficiently large set of labeled vertices is a resolving set of the graph space and the corresponding cardinality is the metric dimension. Similarly, on another node, a real-world problem is the study of networks whose structure has not been imposed by a central authority but has arisen from local and distributed processes. It is very difficult and expensive to obtain a map of all nodes and the links between them. A commonly used technique is to obtain a local view of the network from various locations and combine them to obtain a good approximation for the real network. Metric dimension also has some applications in this aspect as well.

Consider a simple, connected graph G, and metric d_G : V(G) × V(G) → ℕ ∪ {0}, where ℕ is the set of positive integers and d_G(x, y) is the minimum number of edges in any path between x and y. Let W = {w₁, w₂, ..., w_k} be an ordered set of vertices of G and let v be a vertex of G. The representation r(v|W) of v with respect to W is the k−tuple (d_G(v, w₁), d_G(v, w₂), ..., d_G(v, w_k)). If distinct vertices of G have a distinct representation with respect to W, then W is called a resolving set of G (see Khuller et al., 1994, 1996; Buczkowski et al., 2003; Javaid et al., 2008). Such a resolving set with minimum cardinality is a basis of G and the metric dimension of G, denoted by β(G) is its cardinality.

Buczkowski et al. (2003) established the metric dimension of wheel W_n to be $\lfloor \frac{2n+2}{5}\rfloor$ for n ≥ 7. Caceres et al. (2005) found that the metric dimension of fan to be $\lfloor \frac{2n+2}{5}\rfloor$ for n ≥ 7. Tomescu and Javaid (2007) determined the dimension of Jahangir graphs J_2n to be $\lfloor \frac{2n}{3}\rfloor$ for all n ≥ 4. A particular metric-feature of the family of graphs is independent of metric dimension on the particular element of the family. A connected graph has a constant metric dimension if β(G) = k, where k ∈ ℕ is fixed. This feature has been presented in Imran et al. (2012) study. Imran et al. (2013) computed metric dimension of flower graph and some families of convex polytopes. Chartrand et al. (2000) proved that a graph has a constant metric dimension of 1 if it is a path. Ali et al. (2012) computed partial results of the metric dimension of the Mobius ladder, whereas Munir et al. (2017) computed exact and complete results for the metric dimension of the Mobius Ladders. Hussain et al. (2010) computed upper bounds for the metric dimension and partition dimension of generalized Mobius ladders. Poisson and Zhang (2002) computed the metric dimension of uni-cyclic graphs. For detailed review of some variants of dimensions, please see Tomescu and Imran (2009), Manuel (2010), Afzal and Imran (2014), Raza et al. (2018).

Recent development in this context has paved way for a new related concept known as fault-tolerance in the metric dimension. Suppose that, in a network, n processing units are interlinked, and of these units, forming a chain of maximal length are used to solve some task. To have a fault-tolerant self-stable system, it is necessary that in the case of failure of any single unit, another chain of units not containing the faulty unit can replace the originally used chain. Thus, a fault-tolerant design enables a system to continue its intended operation, possibly at a reduced level, rather than failing completely. The units and the links are represented by graphs refer to Slater (1975, 1998, 2002) and Hayes (1985). A resolving set Ś is considered fault-tolerant if Ś\{v} is also a resolving set, for each v ∈ Ś, and the fault-tolerant metric dimension, β′(G), is the minimum cardinality of such Ś. A family ${G}$ of connected graphs is said to have a constant fault-tolerant metric dimension if it is independent of any choice of a member of that family. Fault-tolerant designs are widely used in engineering and computer sciences (Hayes, 1985). Slater (2002) introduced the study of fault-tolerant locating-dominating sets. Hernando et al. (2008) introduced the idea of a single fault-tolerant metric dimension. The authors discussed the single fault-tolerant metric dimension of trees. They also proved that fault-tolerant metric dimension is bounded by a function of the metric dimension irrespective of the choice of the graph given be $\acute{\beta (G)}\le \beta (G)(1+2.5^{\beta (G)-1})$. Javed et al. discussed fault tolerance in resolvability (Chaudhry et al., 2010) and computed fault tolerant metric dimension of some graphs (Javaid et al., 2009). It is easy to gather that $\acute{\beta (G)}\ge \beta (G)+1$ (Javaid et al., 2009). Shabbir and Zumfererscu (2016) discussed fault tolerance in triangular lattice networks.

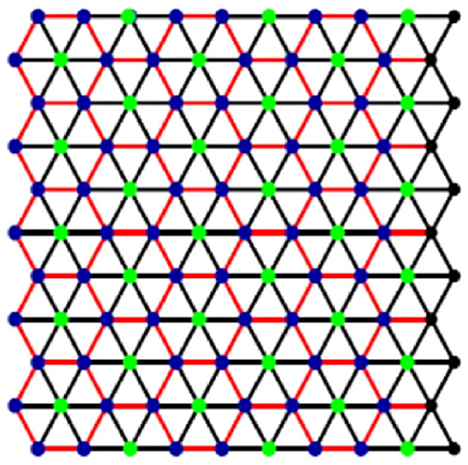
The subject matter of this article is fault tolerance in metric dimension of lattices of two types of boron nanotubes, alpha boron α_m×n and triangular boron nanotubes T_m×n. These lattices are formed by cutting both tubes vertically. Kwun et al. (2018) computed M-polynomials and related topological indices of these tubes and drew some nice comparative remarks about these tubes. Recently, Hussain et al. (2018) computed the metric dimension of α_m×n. Figure 1 presents a triangular boron tube lattice.

FIGURE 1

Figure 1. Triangular boron nanotube lattice, T_k×l.

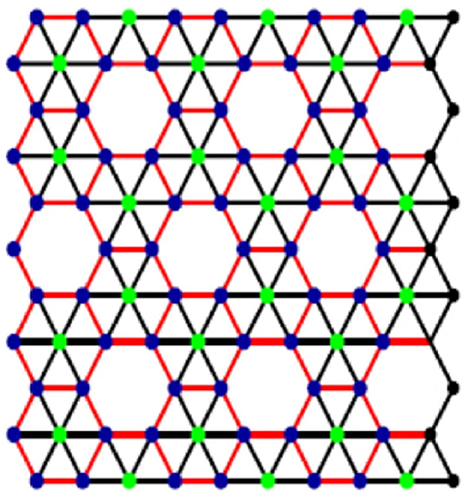
Figure 2 presents alpha boron tube lattice.

FIGURE 2

Figure 2. Alpha boron nanotube lattice, α_k×l.

2. Main results

This section discusses main results. At first, we compute the fault-tolerant metric dimension of triangular boron tubes and then we focus on alpha boron tubes.

Theorem 2.1. Let T_k,l denote the graph of k × l, 2D-lattice of triangular boron nano tubes. Then ${\beta }^{\prime }(T_{k,l})\le 4$.

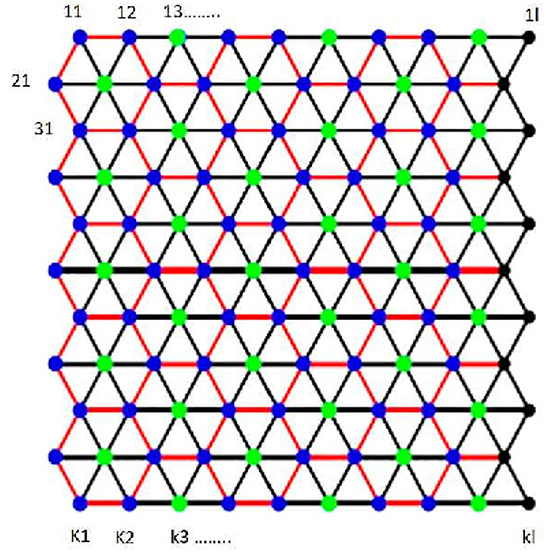
Proof. The vertex set of T_k,l is {v_1,1, v_1,2, v_1,3, ...., v_1,l, v_2,1, v_2,2, v_2,3, ...., v_2,l, v_3,1, v_3,2, v_3,3, ......, v_3,l, ......, v_k,1, v_k,2, v_k,3, ...., v_k,l}. Let F = {v_1,1, v_1,l, v_k,1, andv_k,l}. We prove that F is an FTRS for T_k,l. In general, the tube is “cut” vertically, and the upper left triangle is pointing up as shown in Figure 3. This figure presents labeling of vertices that becomes optimal for the basis of fault tolerance.

FIGURE 3

Figure 3. Labeling of vertices of T_k,l.

Case I: Let k ≤ 2l, k is odd.

We give the distance vectors of all vertices v_a,b of T_k,l relative to F.

For a = 1

$\begin{array}{l}r(v_{a,b}|F)\hfill \\ =\{\begin{array}{c}(b-1,l-b,k-1,\frac{k-1}{2}+l-b),\text{if }1\le b\le l-\frac{k+1}{2}\hfill \\ (b-1,l-b,k-1,k-1),\text{if }l-\frac{k-1}{2}\le b\le \frac{k+1}{2}\hfill \\ (b-1,l-b,\frac{k-3}{2}+b,k-1),\text{if }\frac{k+3}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

For a = 2

$\begin{array}{l}r(v_{a,b}|F)\hfill \\ =\{\begin{array}{c}(1,l,k-2,\frac{k-1}{2}+l-b),\text{if }b=1\hfill \\ (b-1,1+l-b,k-2,\frac{k-1}{2}+l-b),\text{if }2\le b\le l-\frac{k-1}{2}\hfill \\ (b-1,1+l-b,k-2,k-2),\text{if }l-\frac{k-3}{2}\le b\le \frac{k+1}{2}\hfill \\ (b-1,1+l-b,\frac{k-5}{2}+b,k-2),\text{if }\frac{k+3}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

In general, if k is odd, x = k − a, a is odd, and $3\le a\le \lceil \frac{k}{2}\rceil$ and then

$\begin{array}{l}r(v_{a,b}|F)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor +l-b,x,n+\frac{x}{2}-b),\text{if }1\le b\le \frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,x,\frac{x}{2}+l-b),\text{if }\frac{a+1}{2}\hfill \\ \le b\le \frac{x+2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,\frac{x-2}{2}+b,\frac{x}{2}+l-b),\hfill \\ \text{if }\frac{x+4}{2}\le b\le l-\frac{x+2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,\frac{x-2}{2}+b,x),\text{if }l-\frac{x}{2}\hfill \\ \le b\le l-\frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,x),\text{if }l-\frac{a-3}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If k is odd, a is odd, and $\lceil \frac{k}{2}\rceil +1\le a\le k$ then

$\begin{array}{l}r(v_{a,b}|F)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor +l-b,x,\frac{x}{2}+l-b),\text{if }1\le b\le \frac{x+2)}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor +l-b,\frac{x-2}{2}+b,\frac{x}{2}+l-b),\text{if }\frac{x+4}{2}\hfill \\ \le b\le \frac{a+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,\frac{x-2}{2}+b,\frac{x}{2}+l-b),\text{if }\frac{a+3}{2}\hfill \\ \le b\le l-\frac{a+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,\frac{x}{2}+l-b),\text{if }l-\frac{a-1}{2}\hfill \\ \le b\le l-\frac{x+2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,x),\text{if }l-\frac{x}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If k is odd, a is even, and $3<a\le \lceil \frac{k}{2}\rceil$ then

$\begin{array}{l}r(v_{a,b}|F)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor +l-b,x,\frac{x+1}{2}+l-b),\text{if }1\le b\le \frac{a}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,x,\frac{x+1}{2}+l-b),\text{if }\frac{a+2}{2}\hfill \\ \le b\le \frac{x+3}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,x,x),\text{if }\frac{x+5}{2}\hfill \\ \le b\le l-\frac{k-(a-1)}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,\frac{x-3}{2}+b,x),\text{if }l-\frac{x-1}{2}\hfill \\ \le b\le l-\frac{a-2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-3}{2}+b,x),\text{if }l-\frac{a-4}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If k is odd, a is even, and $\lceil \frac{k}{2}\rceil +1\le a\le k$ then

$\begin{array}{l}r(v_{a,b}|F)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,\frac{x+1}{2}+l-b),\text{if }1\le b\le \frac{x+1}{2}\hfill \\ (a-1,l+\lfloor \frac{a}{2}\rfloor -b,\frac{x-3}{2}+b,\frac{x+1}{2}+l-b),\text{if }\frac{x+3}{2}\hfill \\ \le b\le \frac{a}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,l+\lfloor \frac{a}{2}\rfloor -b,\frac{x-3}{2}+b,\frac{x+1}{2}+l-b),\text{if }\frac{a+2}{2}\hfill \\ \le b\le l-\frac{a}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-3}{2}+b,\frac{x+1}{2}+l-b),\text{if }l-\frac{a-2}{2}\hfill \\ \le b\le l-\frac{x+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-3}{2}+b,x),\text{if }l-\frac{x-1}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

For a = 2l − 1, r(V_a,b|S) = (2l − 2, 2l − 2, q − 1, l − q), if 1 ≤ q ≤ l

If k is even, a is odd, and $3\le a\le \lceil \frac{k}{2}\rceil$ then

$\begin{array}{l}r(v_{a,b}|F)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,\frac{x-1}{2}+l-b),\text{if }1\le b\le \frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,x,\frac{x-1}{2}+l-b),\text{if }\frac{a+1}{2}\hfill \\ \le b\le l-\frac{x+3}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,x,x),\text{if }l-\frac{x+1}{2}\hfill \\ \le b\le \frac{x+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,\frac{x-1}{2}+b,x),\text{if }\frac{x+3}{2}\hfill \\ \le b\le l-\frac{a+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-1}{2}+b,x),\text{if }l-\frac{a-1}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is odd, k is even, and $\lceil \frac{k}{2}\rceil +1\le a\le k$ then

$\begin{array}{l}r(v_{a,b}|F)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor +l-b,x,\frac{x-1}{2}+l-b),\text{if }1\le b\le \frac{x+1}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor +l-b,\frac{x-1}{2}+b,\frac{x-1}{2}+l-b),\text{if }\frac{x+3}{2}\hfill \\ \le b\le l-\frac{a+1}{2}\hfill \\ (a-1,a-1,b+\frac{x-1}{2},\frac{x-1}{2}+l-b),\text{if }l-\frac{a-1}{2}\hfill \\ \le b\le \frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-1}{2}+b,l+\frac{x-1}{2}-b),\text{if }\frac{a+1}{2}\hfill \\ \le b\le l-\frac{x+3}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-1}{2}+b,x),\text{if }l-\frac{x+1}{2}\hfill \\ \le b\le l\hfill \end{array}\hfill \end{array}$

If k is even, a is even, and $3<a\le \lceil \frac{k}{2}\rceil$ then

$\begin{array}{l}r(v_{a,b}|F)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor +l-b,x,\frac{k-a}{2}+l-b),\text{if }1\le b\le \frac{a}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,x,\frac{x}{2}+l-b),\text{if }\frac{a+2}{2}\hfill \\ \le b\le l-\frac{x+2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,\frac{x-2}{2}+b,\frac{x}{2}+l-b),\text{if }l-\frac{x}{2}\hfill \\ \le b\le \frac{k-(a-2)}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,\frac{x-2}{2}+b,k-a),\text{if }\frac{x+4}{2}\hfill \\ \le b\le l-\frac{a-2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,x),\text{if }l-\frac{a-4}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If k is even, a is even, and $\lceil \frac{k}{2}\rceil +1\le a\le k$ then

$\begin{array}{l}r(v_{a,b}|F)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor +l-b,x,\frac{x}{2}+l-b),\text{if }1\le b\le \frac{x+2}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor +l-b,\frac{x-2}{2}+b,\frac{x}{2}+l-b),\text{if }\frac{x+4}{2}\hfill \\ \le b\le l-\frac{a-2}{2}\hfill \\ (a-1,a-1,\frac{x-2}{2}+b,\frac{x}{2}+l-b),\text{if }l-\frac{a-4}{2}\le b\le \frac{a}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,\frac{x}{2}+l-b),\text{if }\frac{a+2}{2}\hfill \\ \le b\le l-\frac{x+2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,x),\text{if }l-\frac{x}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

For a = 2l, r(V_a,b|S) = (2l − 1, 2l − 1, b − 1, l − b), if 1 ≤ b ≤ l

For a = 2l − 1, r(V_a,b|S) = (2l − 2, 2l − 2, q − 1, l − q), if 1 ≤ q ≤ l

If k is even, a is odd, and $3\le a\le \lceil \frac{k}{2}\rceil$ then

$\begin{array}{l}r(V_{a,b}|F)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor +l-b,x,\frac{x-1}{2}+l-b),\text{if }1\le b\le \frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,x,\frac{x-1}{2}+l-b),\text{if }\frac{a+1}{2}\hfill \\ \le b\le l-\frac{x+3}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,x,x),\text{if }l-\frac{x+1}{2}\le b\le \frac{x+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,\frac{x-1)}{2}+b,k-a),\text{if }\frac{x+3}{2}\hfill \\ \le b\le l-\frac{a+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x+1}{2}+b,x),\text{if }l-\frac{a-1}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If k is even, a is odd, and $\lceil \frac{k}{2}\rceil +1\le a\le k$ then

$\begin{array}{l}r(V_{a,b}|F)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor +l-b,x,l+\frac{x-1}{2}-b),\text{if }1\le b\le \frac{x+1}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor +l-b,\frac{x-1}{2}+b,l+\frac{x-1}{2}-b),\text{if }\frac{x+3}{2}\hfill \\ \le b\le l-\frac{a+1}{2}\hfill \\ (a-1,a-1,\frac{x-1}{2}+b,l+\frac{x-1}{2}-b),\text{if }l-\frac{a-1}{2}\hfill \\ \le b\le \frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-1}{2}+b,l+\frac{x-1}{2}-b),\text{if }\frac{a+1}{2}\hfill \\ \le b\le l-\frac{x+3}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-1}{2}+b,x),\text{if }l-\frac{x+1}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If k is even, a is even, and $3<a\le \lceil \frac{k}{2}\rceil$ then

$\begin{array}{l}r(V_{a,b}|F)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor +l-b,x,\frac{x}{2}+l-b),\text{if }1\le b\le \frac{a}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,x,\frac{x}{2}+l-b),\text{if }\frac{a+2}{2}\hfill \\ \le b\le l-\frac{x+2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,\frac{x-2}{2}+b,\frac{x}{2}+l-b),\hfill \\ \text{if }l-\frac{x}{2}\le b\le \frac{x+2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor +l-b,\frac{x-2}{2}+b,x),\text{if }\frac{x+4}{2}\hfill \\ \le b\le l-\frac{b-2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,x),\text{if }l-\frac{a-4}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If k is even, a is even, and $\lceil \frac{k}{2}\rceil +1\le a\le k$ then

$\begin{array}{l}r(V_{a,b}|F)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor +l-b,x,\frac{x}{2}+l-b),\text{if }1\le b\le \frac{x+2}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor +l-b,\frac{x-2}{2}+b,\frac{x}{2}+l-b),\text{if }\frac{x+4}{2}\hfill \\ \le b\le l-\frac{a-2}{2}\hfill \\ (a-1,a-1,\frac{x-2}{2}+b,\frac{x}{2}+l-b),\text{if }l-\frac{a-4}{2}\le b\le \frac{a}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,\frac{x}{2}+l-b),\hfill \\ \text{if }\frac{a+2}{2}\le b\le l-\frac{x+2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,x),\text{if }l-\frac{x}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

For a = 2l, r(V_a,b|S) = (2l − 1, 2l − 1, b − 1, l − b), if 1 ≤ b ≤ l

Case II: Let k > 2l.

Let y = rl + p − 1. If r ≥ 2, rl < k ≤ (r + 1)l, and k is odd.

For a = rl + p, where 1 ≤ p ≤ l and a is odd

$\begin{array}{l}r(V_{a,b}|F)\hfill \\ =\{\begin{array}{c}(y,y,x,l+\frac{k-(rl+p)}{2}-b),\text{if }1\le b\le \frac{k-(rl+p-2)}{2}\hfill \\ (y,y,\frac{k-(rl+p+2)}{2}+b,l+\frac{k-(rl+p)}{2}-b),\hfill \\ \text{if }\frac{k-(rl+p-4)}{2}\le b\le l-\frac{k-(rl+p-2)}{2}\hfill \\ (y,y,\frac{k-(rl+p+2)}{2}+b,k-a),\text{if }l-\frac{k-(rl+p)}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is even

$\begin{array}{l}r(V_{a,b}|F)\hfill \\ =\{\begin{array}{c}(y,y,x,l+\frac{k-(y)}{2}-b),\text{if }1\le b\le \frac{k-(rl+p-3)}{2}\hfill \\ (y,y,\frac{k-(rl+p+3)}{2}+b,l+\frac{k-(rl+p-1)}{2}-b),\hfill \\ \text{if }\frac{k-(rl+p-5)}{2}\le b\le l-\frac{p-(rl+p-1)}{2}\hfill \\ (y,y,\frac{k-(rl+p+3)}{2}+b,k-a),\text{if }l-\frac{k-(rl+p+1)}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If k is even, r ≥ 2, and rl < k ≤ (r + 1)l then

Let y = rl + p − 1. For a = rl + p where 1 ≤ p ≤ l and a is odd

$\begin{array}{l}r(V_{a,b}|F)\hfill \\ =\{\begin{array}{c}(y,y,m-a,n+\frac{k-(rl+p+1)}{2}-b),\text{if }1\le b\le \frac{k-y}{2}\hfill \\ (y,y,\frac{k-(rl+p+1)}{2}+b,l+\frac{k-(rl+p+1)}{2}-b),\hfill \\ \text{if }\frac{k-(rl+p-3)}{2}\le b\le l-\frac{k-(rl+p-3)}{2}\hfill \\ (y,y,\frac{k-(rl+p+1)}{2}+b,k-a),\text{if }l-\frac{k-y}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is even

$\begin{array}{l}r(V_{a,b}|F)\hfill \\ =\{\begin{array}{c}(y,y,x,\frac{k-(rl+p)}{2}-b)+l,\text{if }1\le b\le \frac{k-(rl+p-2)}{2}\hfill \\ (y,y,\frac{m-(rl+p+2)}{2}+b,\frac{k-(rn+p)}{2}+l-b),\hfill \\ \text{if }\frac{k-(rl+p-4)}{2}\le q\le l-\frac{k-(rl+p-2)}{2}\hfill \\ (y,y,\frac{m-(rl+p+2)}{2}+b,k-a),\text{if }l-\frac{k-(rl+p)}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

These vectors are distinct in at least two coordinates. So F is an FTRS for T_k,l. Therefore, ${\beta }^{\prime }(T_{k,l})\le 4$.

Theorem 2.2. Let T_k,l denote the graph of k × l, 2D-lattice of triangular boron nano tubes. Then ${\beta }^{\prime }(T_{k,l})>3$.

Proof. For the lower bound on ${\beta }^{\prime }(T_{k,l})$, we discuss the following cases:

Case I: k ≤ l.

We claim that any set of cardinality 3 is not an FTRS for T_k,l. Let F = {v_i,j, v_a,b, v_r,s} where i < a < r and j < b < s be an FTRS for T_k,l. Then F₁ = F\{v} is a R.S. for each v ∈ F. We discuss the following possibilities:

Possibility 1: When all vertices in F lie on the same row.

(i) If all vertices in F lie in the first row, then i = a = r = 1. Let F₁ = {v_1,j, v_1,b} then r(v_1,b+1|F₁) = r(v_2,b+1|F₁), a contradiction.

(ii) If all vertices in F lie in p − th row and 1 < p. Let F₁ = {v_p,j, v_p,b} then either r(v_k,b+1|F₁) = r(v_k−1,b+1|F₁) or r(v_p,b+1|F₁) = r(v_p+1,b+1|F₁), a contradiction.

Possibility 2: When two vertices in F lie on the same row.

WLOG we may suppose that i = a = l and r ≠ l. Let F₁ = {v_l,j, v_l,q} then either r(v_l,q+1|F₁) = r(v_l−1,q+1|F₁) or r(v_l,q+1|F₁) = r(v_l+1,q+1|F₁), a contradiction.

Possibility 3: When the vertices in F lie on three different rows.

(i) Two vertices in F lie on same column, let j = b. If j = b = 1 and F₁ = {v_1,1, v_a,1} then r(v_2,1|F₁) = r(v_2,2|F₁), a contradiction.

(ii) If F₁ = {v_i,1, v_j,1}, 1 ≤ i < j < k then either r(v_j,3|F₁) = r(v_j+1,3|F₁) or r(v_j,3|F₁) = r(v_j+1,2|F₁), a contradiction.

(iii) If F₁ = {v_i,b, v_j,b}, 1 ≤ i < j < k, and 1 < q < l then either r(v_j+1,b|F₁) = r(v_j+1,b+1|F₁) or r(v_j+1,b|F₁) = r(v_j+1,b−1|F₁), a contradiction.

(iv) If all vertices in S lie on different columns. Let S₁ = {V_i,j, V_a,b}, i < a then

(a) If j < b then either r(v_a,b+1|F₁) = r(v_{a + 1, b+1}|F₁) or r(v_a,b+1|F₁) = r(v_{a + 1, b}|F₁), a contradiction.

(b) If j > b then either r(v_a−1,b|F₁) = r(v_a,b+1|F₁) or r(v_a−1,b+1|F₁) = r(v_a,b+1|F₁), a contradiction.

From the above discussion, we conclude that F is not an FTRS for T_m,n. So ${\beta }^{\prime }(T_{m,n})>3$ in this case. Hence ${\beta }^{\prime }(T_{k,l})=4$.

Case II: k > l

In order to prove that there is no FTRS for T_k,l having cardinality 3, it is enough to prove that any set of vertices having two elements is not an R.S. for T_k,l. Let F₁ = {v_i,j, v_a,b} be an R.S. for T_k,l. There are three possibilities

Possibility 1: If v_i,j, v_a,b are taken from same row, i.e., i = a then

(i) If F₁ = {v_1,1, v_1,l} then $r(v_{l+1,\frac{l}{2}}|F_1)=r(v_{l+1,\frac{l+2}{2}}|F_1)$ if l is even and $r(v_{l+1,\frac{l+1}{2}}|F_1)=r(v_{l+1,\frac{l+3}{2}}|F_1)$ if l is odd, a contradiction.

(ii) If F₁ = {v_i,j, v_i,b}, 1 ≤ i < k, and 1 ≤ j < b < l then r(v_i,b+1|F₁) = r(v_{i + 1, b+1}|F₁), a contradiction.

(iii) If F₁ = {v_i,j, v_i,b}, 1 ≤ i < k, and 1 < j < b = l then r(v_i,j−1|F₁) = r(v_{i + 1, j}|F₁), a contradiction.

(iv) If F₁ = {v_k,j, v_k,b} and 1 ≤ j < b < l then r(v_k,b+1|F₁) = r(v_k−1,b+1|F₁) or r(v_k,b+1|F₁) = r(v_k−1,b|F₁), a contradiction.

(v) If F₁ = {v_k,j, v_k,b} and 1 < j < b = l then r(v_k,j−1|F₁) = r(v_k−1,j|F₁), a contradiction.

(vi) If F₁ = {v_i,1, v_i,l} and 1 < i < k then r(v_i−1,1|F₁) = r(v_i+1,1|F₁), a contradiction.

(vii) If F₁ = {v_k,1, v_k,l} then r(v_{k − l, 3}|F₁) = r(v_{k − l, 4}|F₁), a contradiction.

Possibility 2: If v_i,j, v_a,b are taken from same column, i.e., j = b then

(i) If F₁ = {v_1,1, v_k,1} then r(v_2,1|F₁) = r(v_2,2|F₁), a contradiction.

(ii) If F₁ = {v_i,1, v_j,1} where 1 ≤ i < j < m then r(v_j,3|F₁) = r(v_j+1,3|F₁) or r(v_j,3|F₁) = r(v_j+1,2|F₁), a contradiction.

(iii) If F₁ = {v_i,1, v_j,1} and 1 < i < j = k then r(v_i,3|F₁) = r(v_i−1,2|F₁) or r(v_i,3|F₁) = r(v_i−1,3|F₁), a contradiction.

(iv) If F₁ = {v_i,b, v_j,b}, 1 ≤ i < j < k, and 1 < b < l then r(v_j+1,b|F₁) = r(v_j+1,b+1|F₁) or r(V_j+1,b|S₁) = r(V_j+1,b−1|S₁), a contradiction.

(v) If F₁ = {v_i,b, v_j,b}, 1 < i < j ≤ k, and 1 < b < l then r(v_i−1,j−1|F₁) = r(v_i−1,j|F₁) or r(v_i−1,j|F₁) = r(v_i−1,j+1|F₁), a contradiction.

(vi) If F₁ = {v_i,b, v_j,b}, i = 1, j = k, and 1 < q < l then r(v_2,j|F₁) = r(v_2,j+1|F₁), a contradiction.

(vii) If F₁ = {v_i,l−1, v_j,l−1} and i < j < k then r(v_j,l−2|F₁) = r(v_{j+1,l − 2}|F₁) or r(v_j,l−3|F₁) = r(v_{j+1,l − 2}|F₁), a contradiction.

(viii) If F₁ = {v_1,l, v_k,l} then r(v_k−1,l−1|F₁) = r(v_k−1,l|F₁) or r(v_k−2,l−1|F₁) = r(v_k−2,l|F₁), a contradiction.

Possibility 3: If v_i,j, v_a,b are taken from different rows and different columns, i.e., i ≠ p,j ≠ q. Let F₁ = {v_i,j, v_a,b} and i < a

(i) If j < b then r(v_a,b+1|F₁) = r(v_{a + 1, b+1}|F₁) or r(v_a,b+1|F₁) = r(v_{a + 1, b}|F₁), a contradiction.

(ii) If j > b then r(v_a−1,b|F₁) = r(v_a,b+1|F₁) or r(v_a−1,b+1|F₁) = r(v_a,b+1|F₁), a contradiction.

(iii) If a = k and i = 1 then r(v_2,j|F₁) = r(v_2,j+1|F₁) or r(v_1,j+1|F₁) = r(v_2,j+1|F₁) or r(v_k−1,b+1|F₁) = r(v_k,b−1|F₁), a contradiction.

Thus no set having two vertices is an R.S. for T_k,l. So ${\beta }^{\prime }(T_{k,l})>3$ in this case. Hence ${\beta }^{\prime }(T_{k,l})=4$.

The next theorem gives ${\beta }^{\prime }({\alpha }_{k,l})$.

Theorem 2.3. Let α_k,l denote the graph of k × l 2D-lattice of α boron nano tubes. Then ${\beta }^{\prime }({\alpha }_{k,l})=4$

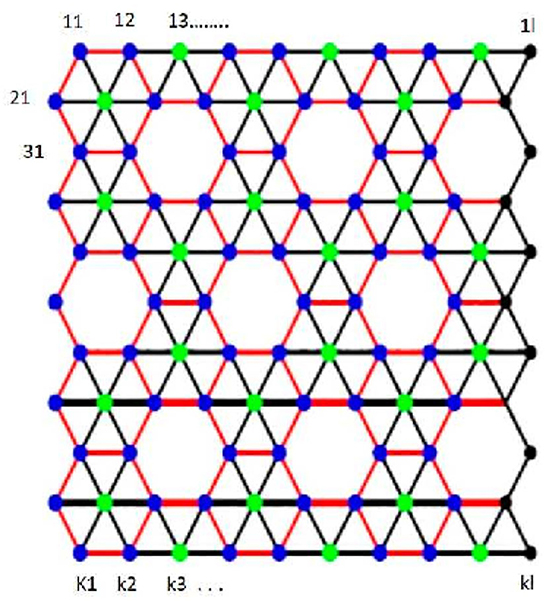
Proof. Consider k × l 2D-lattice of α-boron Nanotubes. We denote this graph by α_k,l. In general, the tube is “cut” vertically and the upper left triangle is pointing up as shown in Figure 4. This figure presents labeling of vertices that becomes optimal for the basis of fault tolerance. The vertex set of α_k,l is partitioned as {v_1,1, v_1,2, v_1,3, ...., v_1,l, v_2,1, v_2,2, ...., v_2,l, v_4,1, v_4,2, ......, v_4,l, v_5,1, v_5,2, ......, v_5,l, v_7,1, v_7,2, ......, v_7,l, ......, v_k,1, v_k,2, v_k,3, ...., v_k,l} ∪ {v_3,1, v_3,2, v_3,4, v_3,5, v_3,7, v_3,8, ...., v_3,l, v_6,1, v_6,3, v_6,4, v_6,6, v_6,7, v_6,9, ...., v_6,l, v_9,1, v_9,2, v₉₄,, v_9,5, v_9,7, v_9,8, ....,_9,l, ......}.

FIGURE 4

Figure 4. Labeling of vertices of α_k,l.

Case I: When k < l.

Let F = {v_1,1, v_1,l, v_k,1, v_k,l}. We show that F is an FTRS for α_k,l. We give the distance vectors of all vertices v_a,b of α_k,l relative to F.

Let k be odd and k ≠ 6q + 1, q ∈ Z⁺.

For a = 1

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(b-1,l-b,m-1,l+\frac{k-a}{2}-a),\text{if }1\le b\le \frac{k+1}{2}\hfill \\ (b-1,l-b,b+\frac{k-3}{2},l+\frac{k-a}{2}-b),\text{if }\frac{k+3}{2}\le b\le l-\frac{k+1}{2}\hfill \\ (b-1,l-b,b+\frac{k-3}{2},k-1),\text{if }l-\frac{k-1}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

For a = 2

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(1,l,k-2,l+\frac{x+1}{2}-b),\text{if }b=1\hfill \\ (b-1,1+l-b,k-2,l+\frac{x+1}{2}-b),\text{if }2\le b\le \frac{k+1}{2}\hfill \\ (b-1,1+l-b,b+\frac{k-5}{2},l+\frac{x+1}{2}-b),\text{if }\frac{k+3}{2}\hfill \\ \le b\le l-\frac{k-1}{2}\hfill \\ (b-1,1+l-b,b+\frac{k-5}{2},k-2),\text{if }l-\frac{k-3}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

In general, if a is odd, a ≠ 3p, p ∈ Z⁺, and $3\le a\le \lceil \frac{k}{2}\rceil$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,l+\frac{x}{2}-b),\text{if }1\le b\le \frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,l+\lfloor \frac{a}{2}\rfloor -b,x,l+\frac{x}{2}-b),\text{if }\frac{a+1}{2}\hfill \\ \le b\le l-\frac{x+2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,l+\lfloor \frac{a}{2}\rfloor -b,x,x),\text{if }l-\frac{x}{2}\hfill \\ \le b\le \frac{m-(a-2)}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,l+\lfloor \frac{a}{2}\rfloor -b,b+\frac{x-2}{2},k-a),\hfill \\ \text{if }\frac{x+4}{2}\le b\le l-\frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,b+\frac{x-2}{2},x),\text{if }l-\frac{a-3}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is odd, a ≠ 3p, p ∈ Z⁺, and $\lceil \frac{k}{2}\rceil +1\le a\le k$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,\frac{x}{2}+l-b),\text{if }1\le b\le \frac{x+2}{2}\hfill \\ (a-1,l+\lfloor \frac{a}{2}\rfloor -b,\frac{x-2}{2}+b,\frac{x}{2}+l-b),\text{if }\frac{x+4}{2}\hfill \\ \le b\le l-\frac{a-1}{2}\hfill \\ (a-1,a-1,b+\frac{x-2}{2},\frac{x}{2}+l-b),\text{if }l-\frac{a-3}{2}\le b\le \frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,b+\frac{x-2}{2},\frac{x}{2}-b+l),\text{if }\frac{a+1}{2}\hfill \\ \le b\le l-\frac{x+2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,b+\frac{x-2}{2},x),\text{if }l-\frac{x}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is even, a ≠ 3p, p ∈ Z⁺, and $3<a\le \lceil \frac{k}{2}\rceil$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,\frac{x+1}{2}+l-b),\text{if }1\le b\le \frac{a}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,l+\lfloor \frac{a}{2}\rfloor -b,x,\frac{x+1}{2}+l-b),\text{if }\frac{a+2}{2}\hfill \\ \le b\le \frac{x+3}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,l+\lfloor \frac{a}{2}\rfloor -b,x,x),\text{if }\frac{x+5}{2}\le b\le l-\frac{x+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,l+\lfloor \frac{a}{2}\rfloor -b,b+\frac{x-3}{2},k-a),\text{if }l-\frac{x-1}{2}\hfill \\ \le b\le l-\frac{a-2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-3}{2}+b,x),\text{if }l-\frac{a-4}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is even, a ≠ 3p, p ∈ Z⁺, and $\lceil \frac{k}{2}\rceil +1\le a\le k$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,k-a,\frac{x+1}{2}+l-b),\text{if }1\le b\le \frac{x+1}{2}\hfill \\ (a-1,l+\lfloor \frac{a}{2}\rfloor -b,q+\frac{x-3}{2},\frac{x+1}{2}+l-b),\text{if }\frac{x+3}{2}\hfill \\ \le b\le \frac{a}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,l+\lfloor \frac{a}{2}\rfloor -b,b+\frac{x-3}{2},\frac{x+1}{2}+l-b),\hfill \\ \text{if }\frac{a+2}{2}\le b\le l-\frac{a}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-3}{2}+b,\frac{x+1}{2}+l-b),\text{if }l-\frac{a-2}{2}\hfill \\ \le b\le l-\frac{x+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-3}{2}+b,x),\text{if }l-\frac{x-1}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

Let k = 6p + 1.

If a is odd, a ≠ 3p, k ∈ Z⁺, and $3<a\le \lceil \frac{k}{2}\rceil$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,\frac{x}{2}-b+l),\text{if }1\le b\le \frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,l+\lfloor \frac{a}{2}\rfloor -b,x,\frac{x}{2}-b+l),\text{if }\frac{a+1)}{2}\hfill \\ \le b\le l-\frac{x+2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,l+\lfloor \frac{a}{2}\rfloor -b,x,x),\text{if }l-\frac{x}{2}\le b\le \frac{x}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,l+\lfloor \frac{a}{2}\rfloor -b,x+1,x),\text{if }b=\frac{x+2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor -b+l,b+\frac{x-2}{2},x),\hfill \\ \text{if }\frac{x+4}{2}\le b\le l-\frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,x),\text{if }l-\frac{a-3}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is odd, a ≠ 3p, p ∈ Z⁺, and $\lceil \frac{k}{2}\rceil +1\le a\le k$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,\frac{x}{2}-b+l),\text{if }1\le b\le \frac{x}{2}\hfill \\ (a-1,l+\lfloor \frac{a}{2}\rfloor -b,x+1,\frac{x}{2}-b+l),\text{if }b=\frac{x+2}{2}\hfill \\ (a-1,l+\lfloor \frac{a}{2}\rfloor -b,b+\frac{x-2}{2},\frac{x}{2}-b+l),\text{if }\frac{x+4}{2}\hfill \\ \le b\le l-\frac{a-1}{2}\hfill \\ (a-1,a-1,b+\frac{x-2}{2},\frac{x}{2}-b+l),\text{if }l-\frac{a-3}{2}\le b\le \frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,\frac{x}{2}-b+l),\hfill \\ \text{if }\frac{a+1}{2}\le b\le l-\frac{x+2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,x),\text{if }l-\frac{x}{2}\le b\le k\hfill \end{array}\hfill \end{array}$

If a is even, a ≠ 3p, p ∈ Z⁺, and $3<a\le \lceil \frac{k}{2}\rceil$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor -b+l,x,\frac{x+1}{2}-b+l),\text{if }1\le b\le \frac{a}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor -b+l,x,\frac{x+1}{2}-b+l),\text{if }\frac{a+2}{2}\hfill \\ \le b\le \frac{x+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor -b+l,x+1,\frac{x+1}{2}-b+l),\text{if }b=\frac{x+3}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor -b+l,x,x),\text{if }\frac{x+5}{2}\hfill \\ \le b\le l-\frac{x+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor -b+l,b+\frac{x-3}{2},k-a),\text{if }l-\frac{x-1}{2}\hfill \\ \le b\le l-\frac{a-2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,b+\frac{x-3}{2},x),\text{if }l-\frac{a-4}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is even, a ≠ 3p, p ∈ Z⁺, and $\lceil \frac{k}{2}\rceil +1\le a\le k$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,\frac{x+1}{2}-b+l),\text{if }1\le b\le \frac{x+1)}{2}\hfill \\ (a-1,l+\lfloor \frac{a}{2}\rfloor -b,x+1,\frac{x+1}{2}-b+l),\text{if }b=\frac{x+3}{2}\hfill \\ (a-1,l+\lfloor \frac{a}{2}\rfloor -b,b+\frac{x-3}{2},\frac{x+1}{2}-b+l),\text{if }\frac{x+5)}{2}\hfill \\ \le b\le \frac{a}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,l+\lfloor \frac{a}{2}\rfloor -b,b+\frac{x-3}{2},\frac{x+1}{2}-b+l),\text{if }\frac{a+2}{2}\hfill \\ \le b\le l-\frac{a}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-3}{2}+b,\frac{x+1}{2}-b+l),\text{if }l-\frac{a-2}{2}\hfill \\ \le b\le l-\frac{x+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-3}{2}+b,x),\text{if }l-\frac{x-1}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is odd, a = 3p, p ∈ Z⁺, $3\le a\le \lceil \frac{k}{2}\rceil$, and b ≠ 3q then

$\begin{array}{l}r(va,b|S)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor -b+l,x,\frac{x}{2}-b+l),\text{if }1\le b\le \frac{a-1}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,\lfloor \frac{a}{2}\rfloor -b+l,x,\frac{x}{2}-b+l),\text{if }\frac{a+1}{2}\hfill \\ \le b\le l-\frac{x+2}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,l+\lfloor \frac{a}{2}\rfloor -b,x,x),\text{if }l-\frac{x}{2}\hfill \\ \le b\le \frac{x+2}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,l+\lfloor \frac{a}{2}\rfloor -b,\frac{x-2}{2}+b,x),\text{if }\frac{x+4}{2}\hfill \\ \le b\le l-\frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,b+\frac{x-2}{2},x),\text{if }l-\frac{a-3}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is odd, a = 3p, p ∈ Z⁺, $\lceil \frac{k}{2}\rceil +1\le a\le k$, and b ≠ 3q then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,l+\frac{x}{2}-b),\text{if }1\le b\le \frac{x+2}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor -b+l,\frac{x-2}{2}+b,\frac{x}{2}-b+l),\text{if }\frac{x+4}{2}\hfill \\ \le b\le l-\frac{a-1}{2}\hfill \\ (a-1,a-1,b+\frac{x-2}{2},l+\frac{k-a}{2}-b),\text{if }l-\frac{a-3}{2}\hfill \\ \le b\le \frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,\frac{x}{2}-b+l),\text{if }\frac{a+1}{2}\hfill \\ \le b\le l-\frac{x+2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,x),\text{if }l-\frac{x}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is even, a = 3p, p ∈ Z⁺, $3<a\le \lceil \frac{k}{2}\rceil$, and b ≠ 3q − 1 then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,\frac{x+1}{2}-b+l),\text{if }1\le b\le \frac{a}{2},\hfill \\ b\ne 3l-1\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,l+\lfloor \frac{a}{2}\rfloor -b,x,l+\frac{x+1}{2}-b),\text{if }\frac{a+2}{2}\hfill \\ \le b\le \frac{x+3}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,\lfloor \frac{a}{2}\rfloor -b+l,x,x),\text{if }\frac{x+5}{2}\le b\le l-\frac{x+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,l+\lfloor \frac{a}{2}\rfloor -b,b+\frac{x-3}{2},x),\text{if }l-\frac{x-1}{2}\hfill \\ \le b\le l-\frac{a-2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-3}{2}+b,x),\text{if }l-\frac{a-4}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is even, a = 3p, p ∈ Z⁺, $\lceil \frac{k}{2}\rceil +1\le a\le k$, and b ≠ 3q − 1 then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor -b+l,x,\frac{x+1}{2}-b+l),\text{if }1\le b\le \frac{x+1)}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor -b+l,\frac{x-3}{2}+b,\frac{x+1}{2}-b+l),\text{if }\frac{x+3}{2}\hfill \\ \le b\le \frac{a}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,l+\lfloor \frac{a}{2}\rfloor -b,b+\frac{x-3)}{2},\frac{x+1}{2}-b+l),\text{if }\frac{a+2}{2}\hfill \\ \le b\le l-\frac{a}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-3}{2}+b,\frac{x+1}{2}-b+l),\text{if }l-\frac{a-2}{2}\hfill \\ \le b\le l-\frac{x+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-3}{2}+b,x),\text{if }l-\frac{x-1}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

Let k be even and k ≠ 6p+2, p ∈ Z⁺.

If a is odd, a ≠ 3p, p ∈ Z⁺, and $3<a\le \lceil \frac{k}{2}\rceil$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor -b+l,x,\frac{x}{2}-b+l),\text{if }1\le b\le \frac{a-1}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,l+\lfloor \frac{a}{2}\rfloor -b,x,\frac{x-1}{2}-b+l),\text{if }\frac{a+1}{2}\hfill \\ \le b\le l-\frac{x-3}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,\lfloor \frac{a}{2}\rfloor -b+l,x,x),\text{if }n-\frac{x+1}{2}\le b\le \frac{x+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor -b+l,b+\frac{x-1)}{2},x),\text{if }\frac{x+3)}{2}\hfill \\ \le b\le l-\frac{a+1}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,a-1,b+\frac{x-1)}{2},x),\text{if }l-\frac{a-1}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is odd, a ≠ 3p, p ∈ Z⁺, and $\lceil \frac{k}{2}\rceil +1\le a\le k$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor -b+l,x,\frac{x-1}{2}-b+l),\text{if }1\le b\le \frac{x+1}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor -b+l,\frac{x-1}{2}+b,\frac{x-1}{2}-b+l),\text{if }\frac{x-3}{2}\hfill \\ \le b\le l-\frac{a+1}{2}\hfill \\ (a-1,a-1,b+\frac{k-(a+1)}{2},l+\frac{x-1}{2}-b),\text{if }l-\frac{b-1}{2}\hfill \\ \le b\le \frac{a-1}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,a-1,\frac{x-1)}{2}+b,\frac{x-1}{2}-b+l),\text{if }\frac{a+1}{2}\hfill \\ \le b\le l-\frac{x+3)}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,a-1,b+\frac{x-1)}{2},x),\text{if }l-\frac{x+1}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is even, a ≠ 3p, p ∈ Z⁺, and $3<a\le \lceil \frac{k}{2}\rceil$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor -b+l,x,\frac{x}{2}-b+l),\text{if }1\le b\le \frac{a}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,\lfloor \frac{a}{2}\rfloor -b+l,x,\frac{x}{2}-b+l),\text{if }\frac{a+2}{2}\hfill \\ \le b\le l-\frac{x+2}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,l+\lfloor \frac{a}{2}\rfloor -b,\frac{x-2)}{2}+b,\frac{x}{2}-b+l),\text{if }l-\frac{x}{2}\hfill \\ \le b\le \frac{x+2}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,l+\lfloor \frac{a}{2}\rfloor -b,\frac{x-2)}{2}+b,x),\text{if }\frac{x+4}{2}\hfill \\ \le b\le l-\frac{a-2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,b+\frac{x-2}{2},x),\text{if }l-\frac{a-4}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is even, a ≠ 3p, p ∈ Z⁺, and $\lceil \frac{k}{2}\rceil +1\le a\le k$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,l+\frac{x}{2}-b),\text{if }1\le b\le \frac{x+2}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor -b+l,\frac{x-2}{2}+b,\frac{x}{2}-b+l),\text{if }\frac{x+4}{2}\hfill \\ \le b\le l-\frac{a-2}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,\lfloor \frac{a}{2}\rfloor -b+l,\frac{x-3}{2}+b,l+\frac{x}{2}-b),\text{if }l-\frac{a-4}{2}\hfill \\ \le b\le \frac{a}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,\frac{x}{2}-b+l),\text{if }\frac{a+2}{2}\hfill \\ \le b\le l-\frac{x+2}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,a-1,b+\frac{x-2}{2},x),\text{if }l-\frac{x}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

Let m = 6k+2.

If a is odd, a ≠ 3p, p ∈ Z⁺, and $3\le a\le \lceil \frac{k}{2}\rceil$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor -b+l,x,\frac{x-1}{2}-b+l),\text{if }1\le b\le \frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor -b+l,x,\frac{x-1)}{2}-b+l),\text{if }\frac{a+1)}{2}\hfill \\ \le b\le l-\frac{x+3}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor -b+l,x,x),\text{if }l-\frac{x+1)}{2}\hfill \\ \le b\le \frac{x-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,l+\lfloor \frac{a}{2}\rfloor -b,x+1,x),\text{if }b=\frac{x+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor -b+l,\frac{x-1}{2}+b,x),\text{if }\frac{x+3}{2}\hfill \\ \le b\le l-\frac{a+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-1)}{2}+b,x),\text{if }l-\frac{a-1}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is odd, a ≠ 3p, p ∈ Z⁺, and $\lceil \frac{p}{2}\rceil +1\le a\le p$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,\frac{x-1}{2}-b+l),\text{if }1\le b\le \frac{a-1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor -b+l,x,\frac{x-1}{2}-b+l),\text{if }\frac{a+1}{2}\hfill \\ \le b\le l-\frac{x+3}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,l+\lfloor \frac{a}{2}\rfloor -b,x,x),\text{if }l-\frac{1+x}{2}\le b\le \frac{x-1}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,l+\lfloor \frac{a}{2}\rfloor -b,1+x,x),\text{if }b=\frac{1+x)}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor -b+l,\frac{x-1}{2}+b,x),\text{if }\frac{3+x}{2}\hfill \\ \le b\le l-\frac{a+1}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-1}{2}+b,x),\text{if }l-\frac{a-1}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is even, a ≠ 3p, p ∈ Z⁺, and $3<a\le \lceil \frac{k}{2}\rceil$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,\frac{1+x}{2}-b+l),\text{if }1\le b\le \frac{a}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,l+\lfloor \frac{a}{2}\rfloor -b,x,l+\frac{x+1}{2}-b),\text{if }\frac{2+a}{2}\hfill \\ \le b\le \frac{1+x}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,\lfloor \frac{a}{2}\rfloor -b+l,1+x,\frac{x+1)}{2}-b+l),\text{if }b=\frac{x+3)}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,\lfloor \frac{a}{2}\rfloor -b+l,x,x),\text{if }\frac{5+x}{2}\hfill \\ \le b\le l-\frac{1+x)}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,l+\lfloor \frac{a}{2}\rfloor -b,b+\frac{x-3}{2},x),\text{if }l-\frac{x-1}{2}\hfill \\ \le b\le l-\frac{a-2}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,b+\frac{x-3}{2},x),\text{if }l-\frac{a-4}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is even, a ≠ 3p, p ∈ Z⁺, and $\lceil \frac{k}{2}\rceil +1\le p\le k$ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,l+\frac{x}{2}-b),\text{if }1\le b\le \frac{x}{2}\hfill \\ (a-1,l+\lfloor \frac{a}{2}\rfloor -b,x+1,l+\frac{x}{2}-b),\text{if }b=\frac{x+2}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor -b+l,b+\frac{x-2}{2},\frac{x}{2}-b+l),\text{if }\frac{x+4}{2}\hfill \\ \le b\le l-\frac{a-2}{2}\hfill \\ (a-1,a-1,b+\frac{x-2}{2},l+\frac{x}{2}-b),\text{if }l-\frac{a-4}{2}\le b\le \frac{a}{2}\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,l+\frac{x}{2}-b),\text{if }l-\frac{a-2}{2}\hfill \\ \le b\le l-\frac{x+1}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,a-1,b+\frac{x-2)}{2},x),\text{if }l-\frac{x}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is odd, a = 3p, p ∈ Z⁺, $3\le a\le \lceil \frac{k}{2}\rceil$, b ≠ 3q, and q ∈ Z⁺ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor -b+l,x,\frac{x}{2}-b+l),\text{if }1\le b\le \frac{x}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor -b+l,1+x,\frac{x}{2}-b+l),\text{if }b=\frac{x+2}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor -b+l,\frac{x-2}{2}+b,\frac{x}{2}-b+l),\text{if }\frac{x+4}{2}\hfill \\ \le b\le l-\frac{a-2}{2}\hfill \\ (a-1,a-1,\frac{x-2)}{2}+b,\frac{x}{2}-b+l),\text{if }l-\frac{a-4}{2}\le b\le \frac{a}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,a-1,\frac{x-2)}{2}+b,\frac{x}{2}-b+l),\text{if }\frac{2+a}{2}\hfill \\ \le b\le l-\frac{m-(a-2)}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,a-1,\frac{x-2)}{2}+b,x),\text{if }l-\frac{x}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is odd, a = 3p, p ∈ Z⁺, $\lceil \frac{k}{2}\rceil +1\le a\le k$, b ≠ 3q, and q ∈ Z⁺ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,\frac{x-1}{2}-b+l),\text{if }1\le b\le \frac{x-1}{2}\hfill \\ (a-1,l+\lfloor \frac{a}{2}\rfloor -b,1+x,\frac{x-1}{2}-b+l),\text{if }b=\frac{1+x}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor -b+l,\frac{x-1}{2}+b,\frac{x-1}{2}-b+l),\text{if }\frac{3+x}{2}\hfill \\ \le b\le l-\frac{1+a}{2}\hfill \\ (a-1,a-1,\frac{x-1}{2}+b,\frac{x-1}{2}-b+l),\text{if }l-\frac{a-1}{2}\hfill \\ \le b\le \frac{a-1}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,a-1,b+\frac{x-1}{2},l+\frac{x-1}{2}-b),\text{if }\hfill \\ \frac{a+1}{2}\le b\le l-\frac{x+3}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,a-1,b+\frac{x-1}{2},x),\text{if }l-\frac{x+1}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is even, a = 3p, p ∈ Z⁺, $6\le a\le \lceil \frac{k}{2}\rceil$, b ≠ 3q − 1, and q ∈ Z⁺ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,\lfloor \frac{a}{2}\rfloor -b+l,x,\frac{x-1}{2}-b+l),\text{if }1\le b\le \frac{x-1}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor -b+l,1+x,l+\frac{x-1}{2}-b),\text{if }b=\frac{1+x}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor -b+l,b+\frac{x-1}{2},\frac{x-1}{2}-b+l),\text{if }\frac{3+x}{2}\hfill \\ \le b\le l-\frac{1+a}{2}\hfill \\ (a-1,a-1,\frac{x-1}{2}+b,\frac{x-1}{2}-b+l),\text{if }l-\frac{a-1}{2}\hfill \\ \le b\le \frac{a-1}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,a-1,\frac{x-1}{2}+b,\frac{x-1}{2}-b+l),\text{if }\frac{1+a}{2}\hfill \\ \le b\le l-\frac{3+x}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,a-1,\frac{x-1}{2}+b,x),\text{if }l-\frac{1+x}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is even, a = 3p, k ∈ Z⁺, $\lceil \frac{k}{2}\rceil +1\le a\le k$, b ≠ 3q − 1, and q ∈ Z⁺ then

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(a-1,l+\lfloor \frac{a}{2}\rfloor -b,x,l+\frac{x}{2}-b),\text{if }1\le b\le \frac{x}{2}\hfill \\ (a-1,l+\lfloor \frac{a}{2}\rfloor -b,1+x,\frac{x}{2}-q+l),\text{if }b=\frac{x+2}{2}\hfill \\ (a-1,\lfloor \frac{a}{2}\rfloor -b+l,\frac{x-2}{2}+b,\frac{x}{2}-b+l),\text{if }\frac{x+4}{2}\hfill \\ \le b\le l-\frac{a-2}{2}\hfill \\ (a-1,a-1,\frac{x-2)}{2}+b,\frac{x}{2}-b+l),\text{if }l-\frac{a-4}{2}\hfill \\ \le b\le \frac{a}{2},b\ne 3l\hfill \\ (\lfloor \frac{a-3}{2}\rfloor +b,a-1,\frac{x-2}{2}+b,\frac{x}{2}-b+l),\text{if }\frac{2+a}{2}\hfill \\ \le b\le l-\frac{x+2}{2}\hfill \\ (b+\lfloor \frac{a-3}{2}\rfloor ,a-1,b+\frac{x-2)}{2},x),\text{if }l-\frac{x}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

Case II: k ≥ 2l.

If r ≥ 2, rl ≤ k ≤ (r + 1)l, and k is odd then

For a = rn + p where 0 ≤ p ≤ l − 1, a ≠ 3p, and a is odd

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(y,y,k-a,n+\frac{k-(rn+p)}{2}-b),\text{if }1\le b\le \frac{k-(rl+p-2)}{2}\hfill \\ (y,y,\frac{k-(rl+p+2)}{2}+b,l+\frac{k-(rl+p)}{2}-b),\text{if }\frac{k-(rl+p-4)}{2}\hfill \\ \le b\le l-\frac{k-(rl+p-2)}{2}\hfill \\ (y,y,\frac{k-(rl+p+2)}{2}+b,k-a),\text{if }l-\frac{k-(rl+p)}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is even

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(y,y,x,\frac{k-y}{2}-b+l),\text{if }1\le b\le \frac{k-(rl+p-3)}{2}\hfill \\ (y,y,\frac{k-(rl+p+3)}{2}+b,\frac{k-y}{2}-b+l),\text{if }\frac{k-(rl+p-5)}{2}\hfill \\ \le b\le l-\frac{k-y}{2}\hfill \\ (y,y,b+\frac{k-(rl+p+3)}{2},x),\text{if }l-\frac{k-(rl+p+1)}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a = 3p, a is odd, b ≠ 3q, and q ∈ Z⁺

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(y,y,x,\frac{k-(rl+p)}{2}-b+l),\text{if }1\le b\le \frac{k-(rl+p-2)}{2}\hfill \\ (y,y,b+\frac{k-(rl+p+2)}{2},\frac{k-(rl+p)}{2}-b+l),\text{if }\frac{k-(rl+p-4)}{2}\hfill \\ \le b\le l-\frac{k-(rl+p-2)}{2}\hfill \\ (y,y,\frac{k-(rl+p+2)}{2}+b,x),\text{if }l-\frac{k-(rl+p)}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a = 3k, a is even, b ≠ 3q − 1, and q ∈ Z⁺

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(y,y,k-a,\frac{k-y}{2}+l-a),\text{if }1\le b\le \frac{k-(p+rl-3)}{2}\hfill \\ (y,y,b+\frac{k-(3+rl+p)}{2},l+\frac{k-y}{2}-b),\text{if }\frac{k-(rl+p-5)}{2}\hfill \\ \le b\le l-\frac{k-y}{2}\hfill \\ (y,y,\frac{k-(3+rl+p)}{2}+b,k-a),\text{if }l-\frac{k-(rl+p+1)}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If k is even, r ≥ 2, and rl ≤ k ≤ (r + 1)l then

For a = rl + p where 0 ≤ p ≤ l − 1

If a is odd, a ≠ 3p

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(y,x,l+\frac{k-1-rl-p)}{2}-b),\text{if }1\le b\le \frac{k-y}{2}\hfill \\ (y,b+\frac{k-rl-p-1)}{2},l+\frac{k-rl-p-1}{2}-b),\text{if }\frac{k-rl-p+3}{2}\hfill \\ \le b\le l-\frac{k-rl-p+3}{2}\hfill \\ (y,b+\frac{k-1-rl-p)}{2},x),\text{if }l-\frac{k-y}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a is even, a ≠ 3p

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(y,y,x,l+\frac{k-(rl+p)}{2}-b),\text{if }1\le b\le \frac{k-(rl+p-2)}{2}\hfill \\ (y,y,b+\frac{k-(rl+p+2)}{2},l+\frac{k-(rl+p)}{2}-b),\text{if }\frac{k-(rl+p-4)}{2}\hfill \\ \le b\le l-\frac{k-(rl+p-2)}{2}\hfill \\ (y,y,b+\frac{k-(rl+p+2)}{2},x),\text{if }l-\frac{k-(rl+p)}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a = 3p, a is odd, b ≠ 3q, and q ∈ Z⁺

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(y,y,x,l+\frac{k-(rl+p+1)}{2}-b),\text{if }1\le b\le \frac{k-(rl+p-1)}{2}\hfill \\ (y,y,b+\frac{k-1-rl-p}{2},\frac{k-1-rl-p}{2}-b+l),\text{if }\frac{k-(rl+p-3)}{2}\hfill \\ \le b\le l-\frac{k-(rl+p-3)}{2}\hfill \\ (y,y,\frac{k-1-rl-p}{2}+b,x),\text{if }l-\frac{k-(rl+k-1)}{2}\le b\le l\hfill \end{array}\hfill \end{array}$

If a = 3p, a is even, b ≠ 3q − 1, and q ∈ Z⁺

$\begin{array}{l}r(v_{a,b}|S)\hfill \\ =\{\begin{array}{c}(y,y,-b+k,\frac{k-(rl+p)}{2}-b+l),\text{if }1\le b\le \frac{k-(rl+p-2)}{2}\hfill \\ (y,y,\frac{k-2-rl-p}{2}+b,\frac{k-(rl+p)}{2}-b+l),\text{if }\frac{k-(rl+p-4)}{2}\hfill \\ \le b\le l-\frac{k-(rl+p-2)}{2}\hfill \\ (y,y,\frac{k-(rl+p+2)}{2}+b,x),\text{if }l-\frac{k-(rl+p)}{2}\le q\le l\hfill \end{array}\hfill \end{array}$

These representations are distinct in at least two coordinates. So F is an FTRS for α_k,l. Therefore ${\beta }^{\prime }({\alpha }_{k,l})\le 4$. For lower bound on ${\beta }^{\prime }({\alpha }_{k,l})$ we discuss the following cases:

Case I: k ≥ l.

Since β(α_k,l) = 3 [19], so ${\beta }^{\prime }({\alpha }_{k,l})>3$. Hence ${\beta }^{\prime }({\alpha }_{k,l})=4$ in this case.

Case II: k < l.

Since βα_k,l = 2 if k < l, so ${\beta }^{\prime }({\alpha }_{k,l})>2$ in this case. We claim that any set having three vertices is not an FTRS for α_k,l. Let F = {v_i,j, v_a,b, v_r,s} where i < a < r and j < b < s be an FTRS for α_k,l. Then F₁ = F\{v} is an R.S. for each v ∈ F. We discuss the following possibilities.

Possibility 1: When all vertices in S lie on the same row.

(i) If all vertices in F lie in the first row, then i = a = r = 1. Let F₁ = {v_1,j, v_1,b} then r(v_1,b+1|F₁) = r(v_2,b+1|F₁), a contradiction.

(ii) If all vertices in F lie in p − th row and 1 < p ≠ 3l, l ∈ Z⁺. Let F₁ = {v_p,j, v_p,b} then either r(v_p,b+1|F₁) = r(v_p−1,b+1|F₁) or r(v_p,b+1|F₁) = r(v_p+1,b+1|F₁), a contradiction.

(iii) If i = a = r = 3q, l ∈ Z⁺. Let F₁ = {v_{3q, j}, v_{3q, b}} then either r(v_{3q − 1, b+1}|F₁) = r(v_{3q + 1, b+1}|F₁) or r(v_{3q − 1, b+1}|F₁) = r(v_{3q, b+1}|F₁), a contradiction.

Possibility 2: When two of vertices in F lie on the same row.

WLOG let i = a = p and r ≠ l. Let F₁ = {v_p,j, v_p,b} then either r(v_p,b+1|F₁) = r(v_p−1,b+1|F₁) or r(v_p,b+1|F₁) = r(v_p+1,b+1|F₁), a contradiction.

Possibility 3: If all the three vertices in F lie on three different rows

(i) Two vertices in F lie on same column, let j = b. If j = b = 1 and F₁ = {v_1,1, v_a,1} then r(v_2,1|F₁) = r(v_2,2|F₁), a contradiction.

(ii) If F₁ = {v_i,1, v_j,1}, 1 ≤ i < j < k then either r(v_j,3|F₁) = r(v_j+1,3|F₁) or r(v_j,3|F₁) = r(v_j+1,2|F₁), a contradiction.

(iii) If F₁ = {v_i,b, v_j,b}, 1 ≤ i < j < k, and 1 < b < l then either r(v_j+1,b|F₁) = r(v_j+1,b+1|F₁) or r(v_j+1,b|F₁) = r(v_j+1,b−1|F₁), a contradiction.

(iv) If all vertices in F lie on different columns. Let F₁ = {v_i,j, v_a,b}, i < a then

(I) If j < b then either r(v_a,b+1|F₁) = r(v_{a + 1, b+1}|F₁) or r(v_a,b+1|F₁) = r(v_{a + 1, b}|F₁), a contradiction.

(II) If j > b then either r(v_a−1,b|F₁) = r(v_a,b+1|F₁) or r(v_a−1,b+1|F₁) = r(v_a,b+1|F₁), a contradiction.

Thus F is not an FTRS for α_k,l. So ${\beta }^{\prime }({\alpha }_{k,l})>3$ in this case. Hence ${\beta }^{\prime }({\alpha }_{k,l})=4$.

3. Conclusion

In this article, we computed the fault-tolerant metric dimension of triangular and alpha boron nanotubes. In both cases, we proved that this dimension is 4. Hence, these tubes are families of a constant fault-tolerant metric dimension. These facts can be used in the networking of nano-devices using these tubes and nano-engineering.

Author contributions

Formal analysis was done by MM. Investigation and draft are done by ZH. Both authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Afzal, H. M., and Imran, J. (2014). Computing the metric dimension of Wheel related graph. Appl. Math. Comput. 242, 624–632. doi: 10.1016/j.amc.2014.06.006

CrossRef Full Text | Google Scholar

Ali, M., Ali, G., Muhammad Imran, A., Baig, Q., and Kashif Shafiq, M. (2012). On the metric dimension of Möbius ladders. ARS Combinator. 105, 403–410.

Google Scholar

Buczkowski, P. S., Chartrand, G., Poisson, C., and Zhang, P. (2003). On k-dimensional graphs and their bases. Pariodica Math. Hung. 46, 9–15. doi: 10.1023/A:1025745406160

CrossRef Full Text | Google Scholar

Caceres, J., Hernando, C., Mora, M., Pelayo, I. M., Puertas, M. L., Seara, C., et al. (2005). On the metric dimension of some families of graphs. Electron. Notes Disc. Math. 22, 129–133. doi: 10.1016/j.endm.2005.06.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Chartrand, G., Eroh, L., Johnson, M. A., and Oellermann, O. R. (2000). Resolvibility in graphs and the metric dimension of a graph. Disc. Appl. Math. 105, 99–133. doi: 10.1016/S0166-218X(00)00198-0

CrossRef Full Text | Google Scholar

Chaudhry, M. A., Javaid, I., and Salman, M. (2010). Fault-tolerant metric and partition dimension of graphs. Util. Math. 83, 187–199.

Google Scholar

Chvatal, V. (1983). Mastermind. Combinatorica 3, 325–329. doi: 10.1007/BF02579188

CrossRef Full Text | Google Scholar

Harary, F., and Melter, R. A. (1976). On the metric dimension of a graph. ARS Combinator. 2, 191–195.

Hayes, J. P. (1985). A graph model for fault-tolerant computer systems. IEEE Trans. Comput. 34, 875–884.

Google Scholar

Hernando, C., Mora, M., Slater, P., and Wood, D. (2008). Fault-tolerant metric dimension of graphs. Convex. Discr. Struct. 5, 81–85.

Google Scholar

Hussain, Z., Khan, J. A., Munir, M., Saleem, M. S., and Iqbal, Z. (2010). Sharp bounds for partition dimension of Generalized Mobius Ladders. Open Math. 16, 1283–1290. doi: 10.1515/math-2018-0109

CrossRef Full Text | Google Scholar

Hussain, Z., Munir, M., Chaudhary, M., and Kang, S. M. (2018). Computing metric dimension and metric basis of 2D lattice of alpha-boron nanotubes. Symmetry 10:300. doi: 10.3390/sym10080300

CrossRef Full Text | Google Scholar

Imran, M., Baig, A. Q., and Ahmed, A. (2012). Families of plane graphs with constant metric dimension. Utilit. Math. 88, 43–57.

Google Scholar

Imran, M., Bashir, F., Baig, A. Q., Bokhary, S., and Riasat, A. (2013). On metric dimension of flower graphs f_n,m, and convex polytopes. Utilit. Math. 92, 389–409.

Google Scholar

Javaid, I., Rahim, M. T., and Ali, K. (2008). Families of regular graphs with constant metric dimension. Utilit. Math. 75, 21–33.

Google Scholar

Javaid, I., Salman, M., Chaudhry, M. A., and Shokat, S. (2009). Fault-tolerance in resolvability. Util. Math. 80, 263–275.

Google Scholar

Khuller, S., Raghavachari, B., and Rosenfeld, A. (1994). Location in Graphs. Technical Report CS-TR-3326, University of Maryland, Colleg Park, MD.

Google Scholar

Khuller, S., Raghavachari, B., and Rosenfeld, A. (1996). Landmarks in Graphs. Disc. Appl. Math. 70, 217–229. doi: 10.1016/0166-218X(95)00106-2

CrossRef Full Text | Google Scholar

Kwun, Y. C., Munir, M., Nazeer, W., Rafique, S., and Kang, S. M. (2018). Computational analysis of topological indices of two boron nanotubes. Sci. Rep. 8. doi: 10.1038/s41598-018-33081-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Manuel, P. (2010). Computational aspects of carbon and boron nanotubes. Molecules 15, 8709-8722. doi: 10.3390/molecules15128709

PubMed Abstract | CrossRef Full Text | Google Scholar

Melter, R. A., and Tomescu, I. (1984). Metric bases in digital geometry. Comput. Vis. Graph. Image Process. 25, 113–121. doi: 10.1016/0734-189X(84)90051-3

CrossRef Full Text | Google Scholar

Munir, M., Nizami, A. R., and Saeed, H. (2017). On the metric dimension of Möbius Ladder. ARS Combinator. 135, 249–256.

Poisson, C., and Zhang, P. (2002). The metric dimension of unicyclic graphs. J. Comb. Math Comb. Comput. 40, 17–32.

Google Scholar

Raza, H., Hayat, S., and Pan, X. (2018). On the fault-tolerant metric dimension of convex polytopes. Appl. Math. Comput. 339, 172–185. doi: 10.1016/j.amc.2018.07.010

CrossRef Full Text | Google Scholar

Shabbir, A., and Zumfererscu, T. (2016). Fault-tolerant designs in triangular lattice networks. Appl. Anal. Discr. Math. 10, 447-456. doi: 10.2298/AADM161013027S

CrossRef Full Text | Google Scholar

Slater, P. J. (1975). Leaves of trees. Congr. Number 14, 549–559.

Slater, P. J. (1998). Dominating and reference sets in graphs. J. Math. Phys. 22, 445–455.

Slater, P. J. (2002). Fault-tolerant locating-dominating sets. Discr. Math. 249, 179–189. doi: 10.1016/S0012-365X(01)00244-8

CrossRef Full Text | Google Scholar

Tomescu, I., and Imran, M. (2009). On metric and partition dimensions of some infinite regular graphs. Bull. Math. Soc. Math. Rouman. 52, 461–472.

Google Scholar

Tomescu, I., and Javaid, I. (2007). On the metric dimension of the Jahangir graph. Bull. Math. Soc. Math. Rouman. 50, 371–376.

Google Scholar