A Compartmental Model to Investigate Local and Global Ca2+ Dynamics in Astrocytes

Intracellular Ca²⁺ dynamics in astrocytes can be triggered by neuronal activity and in turn regulate a variety of downstream processes that modulate neuronal function. In this fashion, astrocytic Ca²⁺ signaling is regarded as a processor of neural network activity by means of complex spatial and temporal Ca²⁺ dynamics. Accordingly, a key step is to understand how different patterns of neural activity translate into spatiotemporal dynamics of intracellular Ca²⁺ in astrocytes. Here, we introduce a minimal compartmental model for astrocytes that can qualitatively reproduce essential hierarchical features of spatiotemporal Ca²⁺ dynamics in astrocytes. We find that the rate of neuronal firing determines the rate of Ca²⁺ spikes in single individual processes as well as in the soma of the cell, while correlations of incoming neuronal activity are important in determining the rate of “global” Ca²⁺ spikes that can engulf soma and the majority of processes. Significantly, our model predicts that whether the endoplasmic reticulum is shared between soma and processes or not determines the relationship between the firing rate of somatic Ca²⁺ events and the rate of neural network activity. Together these results provide intuition about how neural activity in combination with inherent cellular properties shapes spatiotemporal astrocytic Ca²⁺ dynamics, and provide experimentally testable predictions.

1. Introduction

In the last 25 years, the prevailing notion that astrocytes serve purely as structural and metabolic support has evolved to viewing them as units that interact with neuronal inputs and alter neuronal activity. This new paradigm of astrocyte function emerged after it was discovered that astrocytes possess Ca²⁺ excitability in the form of Ca²⁺ spikes and oscillations. These can be triggered by neuronal activity and the subsequent release of neurotransmitters and increase in extracellular K⁺. Following Ca²⁺ activity, astrocytes can release gliotransmitters that act at the synaptic or perisynaptic level to strengthen or weaken synapses, or to change neuronal activity. This fueled a number of modeling studies that investigated the mechanisms through which synaptic activity triggers Ca²⁺ spikes in astrocytes and how, in turn, the astrocyte response affects the synapses (Nadkarni and Jung, 2007; Postnov et al., 2007; De Pitta et al., 2009; Wade et al., 2011; Tewari and Majumdar, 2012; Khalid et al., 2017). These studies naturally focused on temporal Ca²⁺ dynamics.

Astrocyte-to-neuron signaling directly and indirectly impacts the dynamics of synapses and neurons (Halassa et al., 2009b; Henneberger et al., 2010; Kimelberg and Nedergaard, 2010; Perea and Araque, 2010). These effects can have a short or long duration, and they can affect single or multiple neurons (Halassa et al., 2009a). Paralleling this multiplicity of actions on different temporal and spatial scales, recent in vivo imaging of astrocyte Ca²⁺ activity in response to neuronal activity has revealed a spatiotemporal hierarchy of Ca²⁺ events. They range from fast Ca²⁺ fluctuations in the astrocyte periphery to Ca²⁺ spiking across the astrocyte branches and in the cell body (Di Castro et al., 2011; Araque et al., 2014; Kanemaru et al., 2014; Rusakov et al., 2014; Bindocci et al., 2017).

These spatiotemporal events interact in complex ways with governing rules that are important to clarify (Volterra et al., 2014; Bazargani and Attwell, 2016; Bindocci et al., 2017) since they may underlie different classes of astrocyte-to-neuron signaling. Recent work suggests that the most distal processes, which receive synaptic inputs, possess channels that allow fast, localized extracellular Ca²⁺ influx (Di Castro et al., 2011; Bindocci et al., 2017). However these peripheral perisynaptic processes lack the Ca²⁺ stores to trigger Ca²⁺-induced Ca²⁺ release (CICR) (Patrushev et al., 2013; Rusakov, 2015). Thus, wider Ca²⁺ events resulting from CICR are only observed in larger, more proximal processes, away from neuronal synapses (Rusakov, 2015). Bindocci et al. (2017) have used three-dimensional imaging and reconstructions of astrocytes to describe fast and local Ca²⁺ events scattered in the astrocyte gliapil (optically unresolved perisynaptic processes) and the larger events occuring in the astrocyte core (soma and major processes). Of those larger events, a much greater fraction occured in major processes than in the soma. Occasionally, global events that invaded most of the core were observed. These events were not sweeping waves, but were triggered by the simultaneous occurence of Ca²⁺ events in multiple loci, generally in the gliopil, and presumably due to synchronous neuronal activity.

This diversity and complexity of Ca²⁺ events calls for spatial models to understand astrocyte Ca²⁺ dynamics and how they affect neurons and synapses. To date, there are only a handful of spatial models designed to study the spatio-temporal Ca²⁺ dynamics in astrocytes. Kang and Othmer (2009) developed a 2D spatial model with realistic cellular morphology. Their goal, however, was not to study the dynamics of Ca²⁺ events within an astrocyte, but to study how network connectivity, IP₃ diffusion, and ATP transport affected the propagation of Ca²⁺ waves across astrocyte networks. Wu et al. (2014) modeled Ca²⁺ and IP₃ dynamics based on a temporal single point model (Ullah et al., 2006) extended to a homogeneous square domain. This model could reproduce the power-law distribution of Ca²⁺ event duration and intensity observed in hippocampal astrocytes, demonstrating that scale-free Ca²⁺ dynamics can arise from intracellular IP₃ diffusion. Gordleeva et al. (2018) developed a multi-compartmental model of an astrocyte with realistic morphology. They stimulated the most distal compartments on each of their astrocytic processes and considered how the resulting Ca²⁺ signal propagated toward the soma. Synchronous stimulation of multiple processes was necessary for activation of the astrocyte soma, suggesting that astrocytes can serve as detectors of spatial synchronization in a neural network. Finally, Savtchenko et al. (2018) developed a compartmental astrocyte-model builder to reproduce astrocyte morphology and function with high detail. They were able to fit parameters of such a model to physiological data, and demonstrated the use of the model to examine the role of fine details of astrocyte functional morphology, such as the distance between IP₃ receptor clusters, on Ca²⁺ dynamics.

Here, we develop an astrocyte compartmental model to study how stochastic Ca²⁺ influx due to neuronal activity triggers Ca²⁺ spikes in the main astrocyte processes and how this in turn triggers Ca²⁺ spikes in the soma and global events involving the soma and most major processes. This is similar to the work of Gordleeva et al. (2018), but here we distinguish between fast Ca²⁺ events due to synaptic activity and slower events involving CICR, inspired by the hierarchy of Ca²⁺ events described by Araque et al. (2014). We use a model of complexity intermediate between the single point model of Postnov et al. (2007) and the model of Gordleeva et al. (2018). Keeping the number of compartments and biophysical complexity to a minimum limits the number of variables and free parameters, providing better intuition and understanding of the model dynamics. We use this simple model architecture to ask the following questions:

1. How are neuronal inputs integrated to produce Ca²⁺ spikes in the astrocyte soma?

2. How do neuronal input properties, such as their correlations and distribution over the astrocyte, facilitate Ca²⁺ spikes in the soma and global events involving most processes?

3. How do diffusive properties of the cytosol and Ca²⁺ stores impact the production of soma Ca²⁺ spikes?

2. Methods and Model Description

2.1. Compartmental Model

We model the astrocyte as a soma with five major processes (see Figure 1). Each compartment defines its own single point model assuming homogeneization of Ca²⁺ concentration and interacts with the other compartments through diffusion. Compartmental Ca²⁺ in the cytosol and endoplasmic reticulum (ER) is expressed in terms of its concentrations $C_I^{(p_i)}$ and $C_E^{(p_i)}$ for process i, and $C_I^{(s)}$ and $C_E^{(s)}$ in the soma. Diffusion of Ca²⁺ between the soma and the process is proportional to the difference in Ca²⁺ concentration between the two compartments.

FIGURE 1

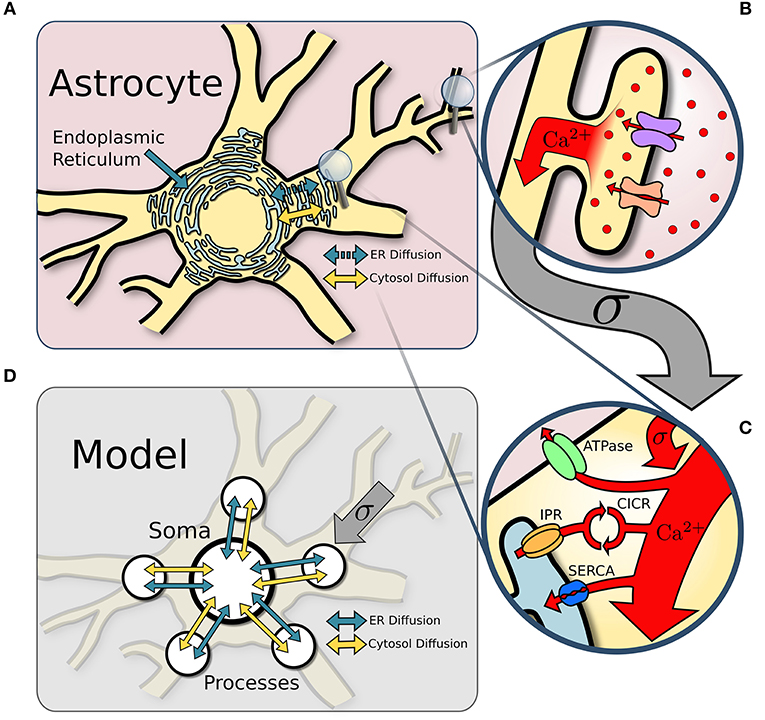
Figure 1. Model structure. (A) Overview of an astrocyte structure. The endoplasmic reticulum (ER) covers the astrocyte core (soma and major processes). (B) In response to neuronal activity, Ca²⁺ enters the perisynaptic astrocyte processes via the Na⁺/Ca²⁺ exchanger and other Ca²⁺ channels. (C) Ca²⁺ influx from perisynaptic processes sums at the larger ER-holding processes, which can activate Ca²⁺-induced-Ca²⁺-release (CICR). Removal of Ca²⁺ occurs via ATPase and SERCA pumps. (D) The astrocyte soma and five of its major processes are approximated with single point models connected via diffusion across both the ER and the cytosol.

The Ca²⁺ dynamics is governed by a system of ODEs based on the non-dimensional functional model of Postnov et al. (2007). The explicit influence of the neurons is described by a source term that models the input of extracellular Ca²⁺ into the process cytosol via a variety of channels. Model dynamics are governed by the fluxes between cytosol and ER due to IPR activation and reuptake of Ca²⁺ by the ER through SERCA pumps. Finally, Ca²⁺ ions diffuse through the cytosol between soma and processes; we also include in the model the possibility for Ca²⁺ ions to diffuse through the ER. The Ca²⁺ thus satisfies the following set of equations:

$\begin{array}{rcl}{\tau }_c\frac{d{C}_I^{(p_i)}}{dt}& =r+\sigma {\xi }_i+b_4(J_r-J_p)-C_I^{(p_i)}+J_{I,d}^{(p_i)}& (1)\end{array}$

$\begin{array}{rcl}{ϵ}_c{\tau }_c\frac{d{C}_E^{(p_i)}}{dt}& =-J_r+J_p+J_{E,d}^{(p_i)}& (2)\end{array}$

$\begin{array}{rcl}{\tau }_c\frac{d{C}_I^{(s)}}{dt}& =r+b_4(J_r-J_p)-C_I^{(s)}-{\displaystyle \sum _{i=1}^k}{J}_{I,d}^{(p_i)}& (3)\end{array}$

$\begin{array}{rcl}{ϵ}_c{\tau }_c\frac{d{C}_E^{(s)}}{dt}& =-J_r+J_p-{\displaystyle \sum _{i=1}^k}{J}_{E,d}^{(p_i)}& (4)\end{array}$

where Equations 1 and 3 represent process Ca²⁺ dynamics and Equations 4 and 5 represent Ca²⁺ dynamics in the soma. Diffusion of Ca²⁺ ions between process i and the soma in the cytosol and the ER are respectively denoted by $J_{I,d}^{(p_i)}=D_I(C_I^{(s)}-C_I^{(p_i)})$ and $J_{E,d}^{(p_i)}=D_E(C_E^{(s)}-C_E^{(p_i)})$. The small parameter ϵ_c in Equation 5 controls the separation of timescales of the calcium in the cytosol and the ER.

Table 1 lists the model parameters and their default values.

TABLE 1

Table 1. Default model parameters.

The parameter r controls the intrinsic Ca²⁺ excitability of each compartment, which may include a contribution from TRPA1 channels to basal Ca²⁺(Shigetomi et al., 2012). We set r = 0.31, which is just below the threshold for spontaneous Ca²⁺ spikes, as in Postnov et al. (2007). The effect of distal neuronal sources on the dynamics of Ca²⁺ in process i is captured by the source term σξ_i, where ξ_i is sampled from N(0, 1). This fluctuating Ca²⁺ term is due in part to the Na⁺/Ca²⁺ exchanger (NCX), which is co-localized with Na⁺-dependent glutamate transporters, as well as neurotransmitter-gated Ca²⁺-permeable ion channels such as AMPA, NMDA, or P2X receptors (Kirischuk et al., 1997, 2007; Bazargani and Attwell, 2016). These Ca²⁺ signals combine with many others upon reaching the primary branch (Araque et al., 2014; Bindocci et al., 2017).

The diffusion coefficient D_I is set to 0.05 unless otherwise noted. The role played by the distribution and the geometry of the ER in glial cells has been under debate with evidence supporting varying degrees of ER interaction between domains of the astrocyte (Blaustein and Golovina, 2001; Petersen et al., 2001; Levine and Rabouille, 2005). To be consistent with these recent findings, we start by setting D_E = 0, but later consider the influence of non-zero values.

In Equations 1 and 5, the Ca²⁺ flux from ER to cytosol through IPR is represented by J_r, while the flux from cytosol to ER due to SERCA pumps is represented by J_p. To simplify the notation, we express these fluxes below in terms of Hill functions, defined by:

$\begin{array}{rc}{\text{H}}_n(x,k)=\frac{x^n}{x^n+k^n}& (5)\end{array}$

Excitability of Ca²⁺ dynamics is the result of Ca²⁺ flow between the cytosol and IP₃-sensitive internal Ca²⁺ stores, which is initiated by the influx of either IP₃ or extracellular Ca²⁺. There is a large spectrum of IPR models that vary in their consideration of IP₃ and Ca²⁺. The primary characteristics that all IPR models share is that the steady-state open probability of the IPR channels are represented by a bell shaped function of Ca²⁺ (Dupont et al., 2016), which results in Ca²⁺-induced Ca²⁺ release (CICR) from internal stores. This work utilizes a representation of IPR flux taken from (Goldbeter et al., 1990) that assumes a sufficient level of IP₃ and models the release of Ca²⁺ from the ER by an interaction between the two Ca²⁺ pools,

$\begin{array}{rc}{J}_r(C_E,C_I)={\text{H}}_2(C_E,1){\text{H}}_4(C_I,b_2)& (6)\end{array}$

where C_I and C_E are the non-dimensional Ca²⁺ concentrations for the cytosol and ER respectively, and b₂ sets the half-activation value of C_I for the IP₃ channel. This model approximates IPR dynamics with a fast activation and slow inactivation of the channel by Ca²⁺ Dupont et al. (2016). We omit IP₃ dynamics and diffusion in order to present the simplest possible framework through which a hierarchy of Ca²⁺ activity can be represented and explored.

Cells continuously pump Ca²⁺ from the cytosol into the ER through SERCA pumps on the ER membrane, modeled as

$\begin{array}{rc}{J}_p(C_I)=b_1{\text{H}}_2(C_I,1)& (7)\end{array}$

where b₁ is the maximum velocity of the reaction Dupont et al. (2016). SERCA pumps are influential in sustaining non-linear dynamics because they replenish the ER which is the source of excitable behavior.

2.2. Numerical Method

The governing Equations (1-4) are solved numerically using a first order Euler-Maruyama method (Kloeden and Platen, 1992) to properly treat the stochastic neuronal input term σξ_i. To establish the appropriate time discretization, several simulations were run with σ = 0, with default model parameters found in Table 1, except for r, which was set to r = 0.32, just beyond the threshold for spontaneous spike generation. To establish the appropriate step size we ran a simulation of 10,000 time units with successively smaller Δt. We found that below Δt = 0.5, the change in all spike times in the processes and in the soma satisfied

$\begin{array}{rc}{t}_{spik{e}_{\Delta t}}-t_{spik{e}_{\frac{\Delta t}{2}}}\le \Delta t& (8)\end{array}$

where t_spikeΔt is a spike time for a step size Δt. Spike times are identified by C_I crossing a threshold of 1.2 while increasing Meyer and Stryer (1991). The numerical code is freely available and can be downloaded from https://github.com/FSUcilab/Compartmental_model_astrocytes.git

2.3. Correlated Neural Inputs

Astrocyte processes likely receive correlated input since the neuronal populations that contribute input to each process may overlap or have correlated activities (Averbeck et al., 2006; López-Hidalgo and Schummers, 2014). To allow flexible experimentation with correlated input, we construct a function that generates k input signals that have a fixed pairwise correlation coefficient ρ, where k is the number of active astrocyte processes. Starting with k uncorrelated signals ξ sampled from a normal distribution N(0, 1), we first compute the correlation matrix Σ such that Σ_ij = (1−δ_ij)ρ+δ_ij (where δ_ij is the Kronecker Delta) and perform a Cholesky factorization Σ = LL^T (Johnson, 1994). Multiplication of L by the vector of uncorrelated signals ξ produces k signals with the desired correlation ρ:

$\begin{array}{rc}\xi =L\tilde{\xi }& (9)\end{array}$

2.4. Spike-Triggered Average

To analyze the relationship between the activity in the different compartments, we use spike-triggered averaging (STA) (Schwartz et al., 2006). For each soma spike, the Ca²⁺ trace of a process is selected within a time window preceding the soma spike. This ensemble of Ca²⁺ traces are then averaged. For comparison, we compute a baseline for which Ca²⁺ traces of the same length are selected at random times and averaged.

3. Results

3.1. Response of a Compartmental Astrocyte Model to Neuronal Activity

Several studies have demonstrated that Ca²⁺ undergoes small, localized, oscillatory Ca²⁺ responses within the processes (Perea and Araque, 2002; Di Castro et al., 2011; Panatier et al., 2011; Araque et al., 2014; Bindocci et al., 2017). Integration of this activity may lead to local spiking in individual processes, which can recruit the soma and produce global spikes encompassing the soma and additional processes (Araque et al., 2014; Bindocci et al., 2017). In our model, each process i receives a neuronal input modeled as a Ca²⁺ source term ξ_i(t). We explore how this leads to CICR-driven spikes in processes and soma. In general, nearby neurons can be correlated (Averbeck et al., 2006), and thus, the Ca²⁺ dynamics in the different processes might be correlated as well. As mentioned in section 2.3, we assume a pairwise correlation between input sources of ρ and explore the effect of ρ on the spiking frequency in the processes and the soma. We begin our simulations with zero signal correlation.

A time course of cytosolic Ca²⁺ in each process and in the soma is shown in Figure 2A, which includes an insert that zooms in on the subthreshold Ca²⁺ activity in two processes in response to the noisy neural input. The neuronal input signal amplitude (defined as the standard deviation of the signal) is initially set to σ = 0.2 . One of the soma spikes is identified as a global event, defined when at least four of five processes spike within a period of 12.5 time units from the soma spike. Thus our model covers the three scales of Ca²⁺ activity observed experimentally (Araque et al., 2014): a small scale for subthreshold Ca²⁺ activity due to neuronal inputs (hundreds of ms, spatially restricted to < 5μm), an intermediate timescale set by the process spikes (seconds, spatially extending over the length of a process), and the large scale of global events (up to 10 s, extending to most of the astrocyte core). The interval between successive spikes in a given process follows a sharp, approximately log-normal distribution (Figure 2B). The soma spikes at a lower frequency than the processes, as observed experimentally (Nimmerjahn et al., 2009; Kanemaru et al., 2014; Bindocci et al., 2017) and the distribution of interspike intervals is much wider for the soma than for the processes (Figure 2B), that is, there is more randomness in spike timing in the soma than in the processes.

FIGURE 2

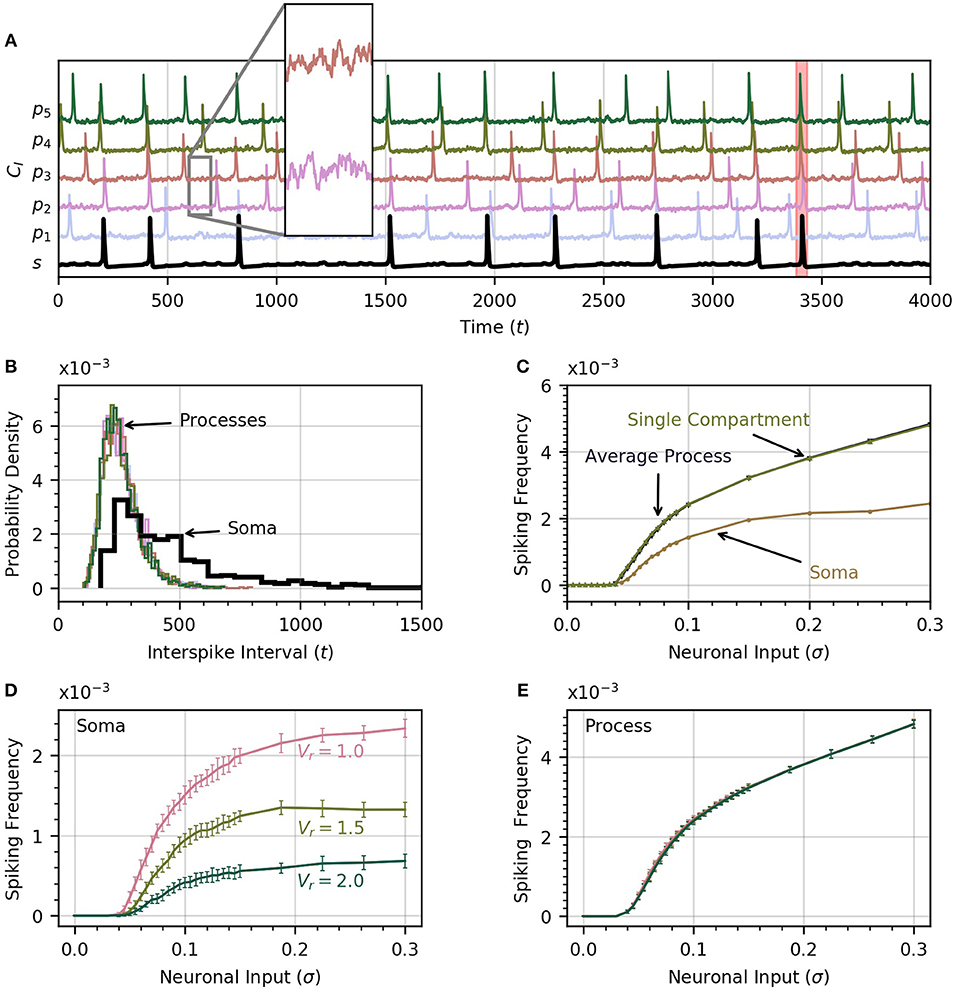
Figure 2. Astrocyte activity under random neuronal input. (A) Time course of cytosolic Ca²⁺ concentration in five processes (color) and the soma (black, bottom trace) over a 4000 time unit interval. All time traces have been normalized to their maximum value. Subthreshold oscillations are depicted in the inset. The shaded rectangle in the proximity of t = 3500 indicates a global event when at least four of five processes spike within 12.5 time units of the soma spike. (B) Histograms of interspike intervals for all processes and the soma are unimodal and follow an approximate log-normal distribution. (C) Both soma and average process spike frequency increase monotonically with neuronal input intensity. The variation of average process frequency with σ is identical to that for a single compartment model. (D) Spike frequency in the soma depends on the ratio V_r of soma to process volume. As V_r increases, the soma spikes less frequently. (E) On the other hand, spiking rates in the processes depend only very weakly on V_r. When process and soma have equal volume, the process spikes at about half the rate as the soma. In (D,E), error bars were obtained by breaking up a simulation over 10⁶ time units into 20 equal intervals and computing the standard deviation across each interval. The same approach is adoped in subsequent experiments. Note that in our functional model, all units in this and subsequent figures are arbitrary. Simulation parameters: ρ = 0.0, D_I = 0.05 and D_E = 0 (A–D), V_r = 1 (A–C).

As the intensity of the neuronal input σ is increased from 0 to 0.3, both the processes and the soma start to spike and the spiking rate increases monotonically with σ (Figure 2C). The soma spikes at a lower rate, and appears to saturate for σ>0.2. Below a threshold value of σ = 0.04, there are no process or soma spikes. The threshold is slightly higher for soma spikes that depend on one or more processes spiking before a sufficient amount of Ca²⁺ can diffuse into the soma. We examine the conditions that induce soma spikes in a later section. To determine how Ca²⁺ dynamics in the processes are affected by their connection to the soma, and via the soma by the other processes, we plot the spiking rate as a function of σ in a single compartment model. This curve is almost identical to the average spiking rate across processes for a low value of D_I. This suggests that in this diffusion regime, the processes of our astrocyte model behave similarly to single compartment models, with little effect from interactions between compartments.

3.1.1. Effect of Larger Soma Volume

For simplicity, we have assumed that all compartments have equal surface and equal volume. However, a recent investigation into the three-dimensional morphology of astrocytes implied that the volume of the soma is about 1.5 times the volume of a major process (Bindocci et al., 2017). To consider the effect of a larger soma volume on the spiking activity, we define the soma to process volume ratio

$\begin{array}{rc}{V}_r=\frac{V_{soma}}{V_{process}}& (10)\end{array}$

under the assumption that all the processes have identical geometry.

Taking this volume ratio into account, the equations for Ca²⁺ dynamics in the soma become

$\begin{array}{rcl}{\tau }_c{V}_r\frac{d{C}_I^{(s)}}{dt}& =V_{surf}(r+b_4(J_r-J_p-C_I^{(s)}))-{\displaystyle \sum _{i=1}^k}{J}_{I,d}^{(p_i)}& (11)\end{array}$

$\begin{array}{rcl}{ϵ}_c{\tau }_c{V}_r\frac{d{C}_E^{(s)}}{dt}& =V_{surf}(-J_r+J_p)-{\displaystyle \sum _{i=1}^n}{J}_{E,d}^{(p_i)}& (12)\end{array}$

where $V_{surf}=V_r^{2/3}$ accounts for the increase in membrane surface area through which Ca²⁺ flux occurs. Thus, the increased volume in the soma slows down its Ca²⁺ dynamics.

Through Figures 2D,E, we examine the effect of volume ratio on spiking rate in the soma and the processes for the three volume ratios 1, 1.5, and 2. Larger volume ratios decrease the average soma spiking frequency for all values of neuronal input. On the other hand, the spiking rate in the processes are independent of the volume ratio. A larger soma volume requires a larger amount of Ca²⁺ to diffuse to the soma before $C_I^{(s)}$ rises enough to trigger CICR. In the remainder of the paper we set V_r = 1 to reduce the computation time, and allow the collection of a large enough number of soma spikes to perform statistical analysis.

3.2. Effects of Input Distribution Onto the Astrocyte Model

3.2.1. Correlated Inputs Trigger Soma Spikes More Effectively and Produce Global Events

The amplitude of inputs is not the only factor that affects astrocyte Ca²⁺ dynamics. Since neurons in a given cortical area can have correlated activities, it is likely the case that the inputs to the different astrocyte processes also exhibit a (potentially variable) degree of correlation (Averbeck et al., 2006). To simulate this correlation, we generate input signals ξ_i(t) with pairwise correlation ρ. We then compute the activity in the processes and soma as a function of σ for different values of ρ. Frequency curves are shown in Figure 3A. As the correlation coefficient increases, soma spiking frequency increases, and plateaus at higher values.

FIGURE 3

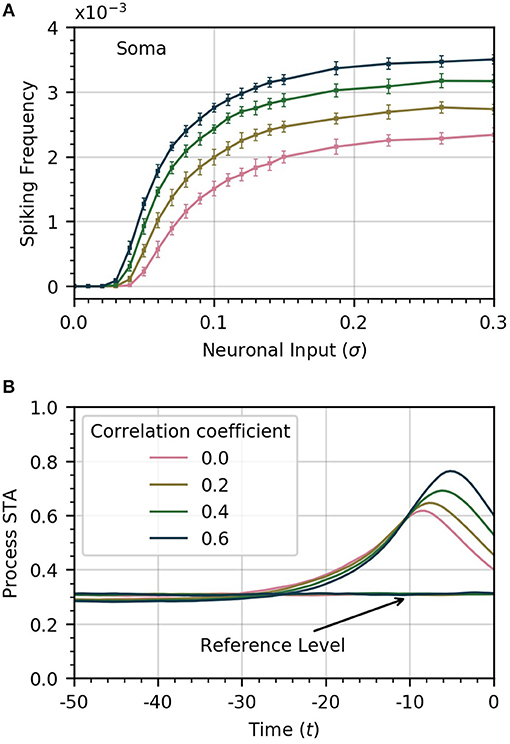
Figure 3. Increased correlation between neuronal inputs facilitates soma spike activity. (A) Variations of soma spike frequency with σ for different values of ρ. Higher input signal correlation raises the soma spiking frequency and decreases the threshold σ for soma spikes. (B) Spike-triggered average of C_I conditioned on the soma spikes within a window of 50 time units ahead of the soma spikes. At higher values of correlation, the process spikes are more concentrated and trigger closer to the soma spike. For reference, we show the average of C_I over random time windows. Simulation parameters: σ = 0.2, D_I = 0.05, D_E = 0.0, V_r = 1.0.

We also find that higher correlation between Ca²⁺ influx signals decreases the threshold σ necessary for the soma to spike. In Figure 3B, we plot the STA of process activity conditioned on soma spikes for various values of ρ. At higher levels of correlation, the STA is sharper and closer to the soma spike. This suggests that synchrony between process spikes facilitates soma spiking.

Finally, we show in Figure 4 that the occurrence of global events strongly increases with ρ. Thus, while finite correlation between input sources have a moderate effect on soma spiking, they greatly increase the number of global events. For the remainder of the paper, we set the pairwise correlation coefficient between neuronal signals to ρ = 0.2, unless explicitly stated otherwise.

FIGURE 4

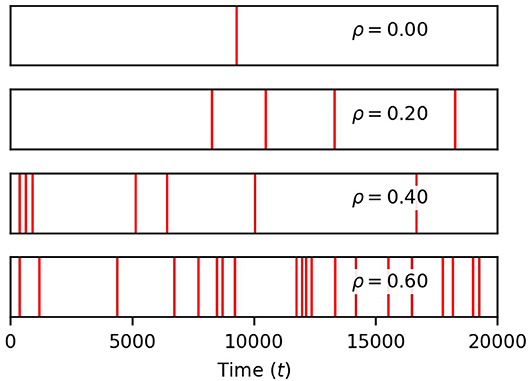
Figure 4. Correlation between neuronal inputs induce global events. Each red vertical bar marks the occurrence of a global event (four or more process spikes within a window of 12.5 time units of a soma spike). Their density rises with ρ. Simulation parameters: σ = 0.2, D_I = 0.05, D_E = 0.0, V_r = 1.0 .

3.2.2. Concentrating Neuronal Inputs Helps Trigger Soma Spikes

Up until this point, we have assumed a uniform distribution of Ca²⁺ due to neuronal activity. However, our model provides the ability to stagger the level of Ca²⁺ input between processes. We wish to better understand whether neuronal inputs should be distributed over many processes to effectively evoke somatic Ca²⁺ spikes.

To gain some insight into this question, we perform three experiments in which we vary the number of processes subject to neuronal input (Figure 5). In the base case, all five processes receive the same level of neuronal activity, denoted by σ. In the second case, each of three processes receives a level σ₃, and in the third case, a single process is active, with neuronal activity σ₁. We choose the levels σ₁ and σ₃ to ensure that in each case the sum of all active signals has identical variance.

FIGURE 5

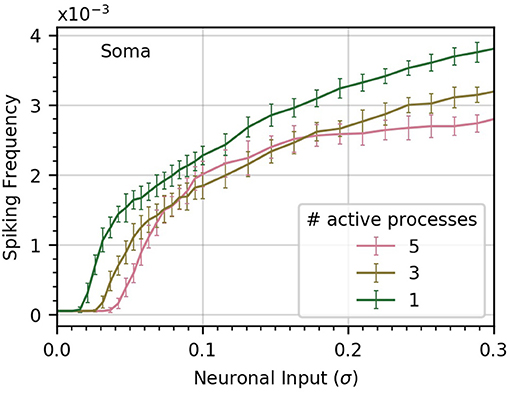
Figure 5. Concentrating inputs into fewer processes facilitates soma spiking. Curves (a-c) correspond respectively to 5, 3, and 1 processes receiving neuronal input; these are the active processes. By definition, σ is the standard deviation of the neuronal input signal into five processes, as in previous figures. As the number of active processes is decreased, σ is scaled up to maintain a constant standard deviation of the sum of the inputs. Concentrating the neuronal inputs into fewer processes increases soma spike rate across most of the σ range and decreases the threshold σ for soma spiking. Simulation parameters: ρ = 0.2, D_I = 0.05, D_E = 0.0 .

More generally, consider the sum S_m of m signals s_i with pairwise correlation ρ and variance σ². It can easily be shown that the standard deviation of S_m is given by

$\begin{array}{rc}\sigma (S_m)=\sigma \sqrt{m+m(m-1)\rho }.& (13)\end{array}$

With the help of Equation 14, we obtain relationships that ensure comparative total input between the standard deviations of the process neuronal input when one and three processes are active:

$\begin{array}{rcl}{\sigma }_1& =\sigma \sqrt{5+20\rho },& (14)\end{array}$

$\begin{array}{rcl}{\sigma }_3& =\sigma \frac{\sqrt{5+20\rho }}{\sqrt{3+6\rho }}.& (15)\end{array}$

We find that concentrating inputs onto fewer processes slightly increases spiking frequency in the soma, and decreases the threshold σ required to evoke soma spiking (Figure 5). At higher values of σ, concentrating inputs in fewer processes only has a small effect on somatic frequency. This suggests that neuronal inputs concentrated in only a few processes are more likely to trigger soma spikes than if they are distributed throughout the astrocyte processes.

3.3. Compartmental Diffusion Effects

Calcium gradients across neighboring cell regions are accounted for in our model by diffusion fluxes between adjacent processes, either through the cytosol (J_{I, d}) or through the ER (J_{E, d}). Accordingly, we set out to investigate how variations of diffusion coefficients D_I and D_E affect somatic spiking.

3.3.1. Diffusion Between Soma and Process Cytosol

The soma receives no input from neuronal activity, so it only becomes active because of the diffusion of cytosolic Ca²⁺ from spiking processes. Thus, the soma spiking rate should increase with D_I, as seen in Figure 6A. Curves (a) through (c) correspond to increasing levels of D_I (0.025, 0.050, 0.1). Increasing D_I also slightly decreases the threshold value of σ for soma spikes. To determine how the rate of diffusive Ca²⁺ transfer impacts the relationship between process and soma spiking, we plot the average spike-triggered average of processes Ca²⁺ conditioned on soma spikes for different values of D_I in Figure 6B. At higher values of D_I, the STA of process activity narrows and moves closer to the soma spike, suggesting that for higher values of D_I fewer process spikes occurring within a short time frame are needed to elicit a soma spike. To confirm this, we plot the likelihood of different process spike counts preceding a soma spike for several values of cytosolic diffusion. This information is summarized in Figure 6C. It shows that for D_I = 0.05 or less, most soma spikes are triggered only once two or three process spikes occur close to each other. Thus, soma spikes occur less frequently and less regularly than process spikes, explaining the wider distribution of ISI for soma spikes (Figure 2B).

FIGURE 6

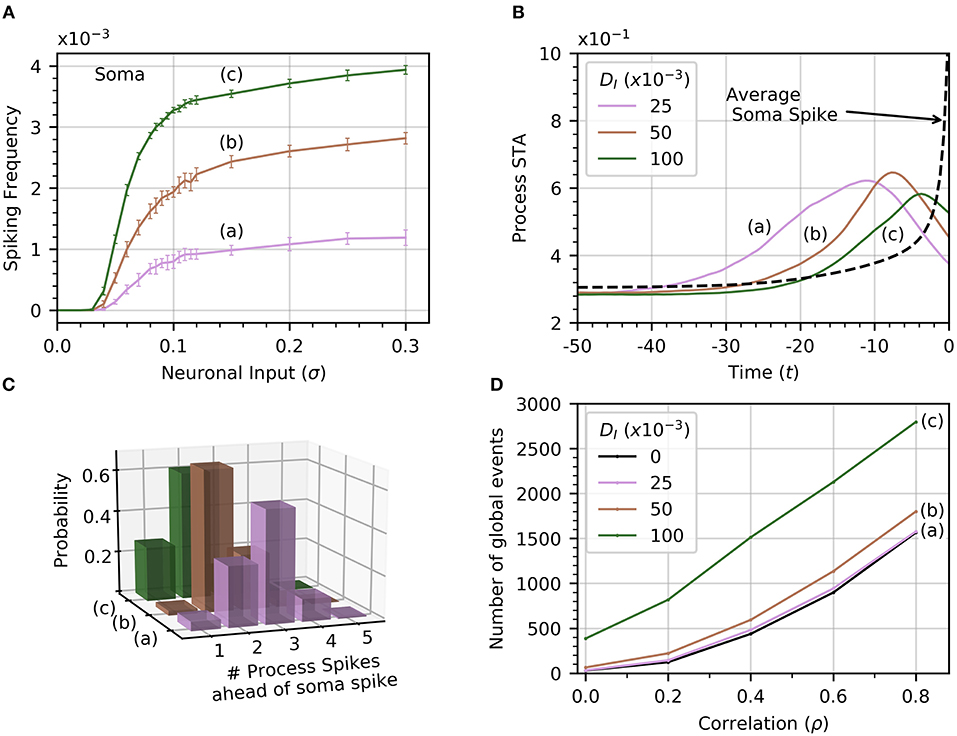
Figure 6. Effect of cytosolic diffusion on soma and global activity. (A) Soma spiking rate increases with cytosolic diffusion D_I for all levels of neuronal input. Higher D_I also decreases the threshold input for soma spikes. In (A,B,D), curves (a) through (c) correspond to D_I = 0.025, 0.05, 0.1, respectively. (B) Spike-triggered averages of $C_I^{(p)}$ in a single process (all processes produce a very similar curve) were computed in a window of 50 times units ahead of the soma spikes. Higher D_I shortens the average interval between soma spike and preceding process spikes. (C) The distribution of number of process spikes preceding a soma spike shifts toward lower values at higher D_I. The number of process spikes were only counted within a window of 30 time units ahead of the soma spikes. (D) Variations of the number of global events (defined by at least four processes spiking within a time window of 25, with or without a soma spike) with ρ. Cytosolic diffusion determines whether the soma directly influences the number of global events, or whether they are due to random process spike co-occurrences. As input correlation increases in the absence of soma activity (D_I = 0), so do the number of randomly occurring global events (dashed curve). Note that in the absence of cytosolic diffusion, the soma does not spike. When D_I increases to 0.025, the soma begins to spike [panel A, curve (a)], but the number of global events does not increase significantly. Further increases of D_I to 0.05 and 0.1 shows a substantial increase in the number of global events, which are almost certainly associated with soma spikes. That this is so is substantiated by noticing that process spiking frequency is unaffected by D_I, as seen in Figure 2C, which shows that the process spiking frequency at D_I = 0.05 is the same as in the single compartment (equivalent D_I = 0). Given a sufficiently strong cytosolic diffusion (D_I = 0.1), soma spikes help generate significantly more global events than those generated by input signal correlation alone. Simulation parameters: D_E = 0, σ = 0.2, V_r = 1 .

3.3.2. Are Global Events Random?

From Figure 4, we recall that increasing ρ increases the number of global events. Are these events the result of spike propagation from the soma to other processes, or are they simply random synchronizations between process spikes due to the correlation between neuronal inputs? To answer this question, we set D_I = 0 to ensure that events that involve four or more process spikes within 25 time units can only occur as random coincidence of process spikes. We plot the number of such global events for increasing signal correlation in Figure 6D. When D_I lies between 0.025 and 0.05, there is little difference with the number of global events found for D_I = 0. Thus, these global events are simply due to random occurrences. However, when D_I = 0.1, the number of global events rises markedly. This demonstrates that the soma is involved with the global event generation. Therefore, the strength of diffusion between compartments can change the nature of global events.

3.3.3. Diffusion Within the Endoplasmic Reticulum

Up until now, we have assumed that there was no connection between process and soma ER. We now relax this assumption and consider the impact of diffusion between the two. Since the extent of diffusion within the astrocyte ER is unknown, we consider a range of ER diffusivities. We set D_I = 0.05, which allows high frequency spiking in the soma when no diffusion occurs between ERs (see Figure 6A). Next, we compute the average soma frequency as a function of σ for three values of D_E in the range 0 to 0.002 . As soon as D_E > 0, the relationship between soma frequency and σ becomes non-monotonic (Figure 7A). As σ increases, the spike frequency in the soma initially increases toward a maximum value, and then decreases as σ continues to increase. This effect becomes stronger, limiting the maximum soma spike frequency, for larger values of D_E. Thus, diffusion between the soma and process ER impedes soma activity at high levels of neuronal inputs. Spiking activity in each process remains unchanged as shown in Figure 7B.

FIGURE 7

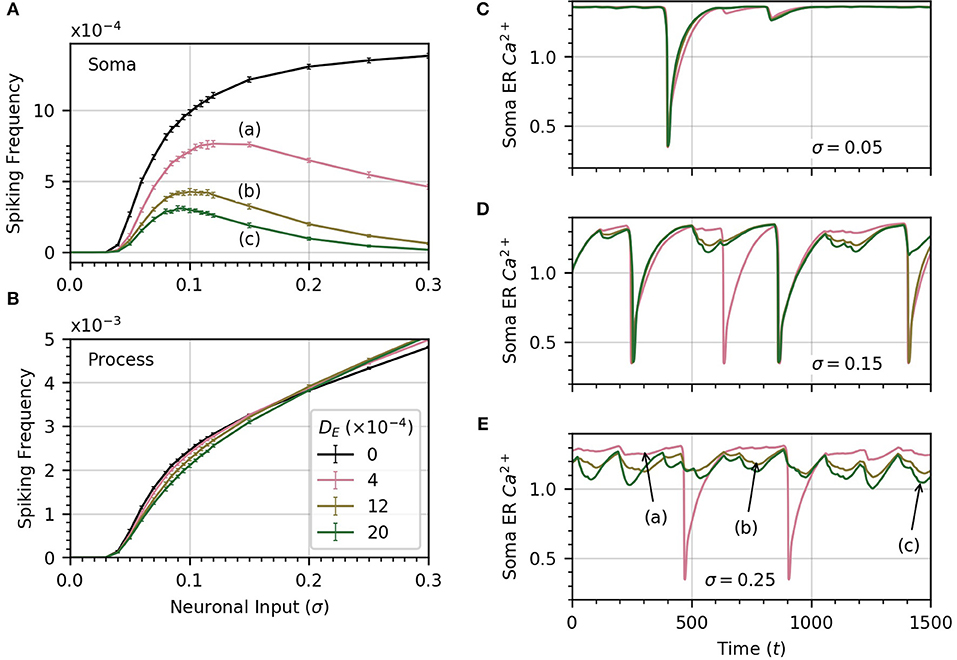
Figure 7. ER diffusion leads to non-monotonic variation of soma spike frequency with σ. (A) Non-monotonic variations of soma spike frequency with σ for non-zero D_E. The maximum soma spike frequency decreases and shifts toward lower σ for higher values of D_E (from a to c). The D_E = 0 curve is drawn in black. (B) The process spike frequency is mostly independent of D_E, except in the region near σ = 0.1 where the frequency is slightly elevated at lower D_E. Note that the error bars have similar magnitude to those in (A). Simulation parameters: ρ = 0.2, D_I = 0.05, V_r = 1 . (C–E) The bell-shaped curves in (A) are explained by examining the time course of soma ER Ca²⁺ for different levels of D_E at three levels of σ. At low σ (C), the level of the soma ER Ca²⁺ does not vary significantly with D_E. (D,E) At high σ, $C_E^{(s)}$ depletion increases with D_E, leading to missed soma spikes. Large downward deflections result from soma spikes while small downward deflections result from process spikes. All simulations were conducted with the same initial random seed to generate a consistent sequence of process spikes as D_E is varied. Simulation parameters: D_I = 0.05, ρ = 0.2 .

To explain why the soma spikes at a lower rate at high σ, we note that two opposite factors shape the relationship between the rate of spikes in the soma and the neuronal input intensity. As σ increases initially, the spike rate in the processes rises, which leads to more spikes in the soma. Accordingly, the first part of the curves in Figure 7A shows an increase in spiking frequency with σ. However, this picture changes at higher σ when D_E > 0. In that case, each process spike causes a flow of Ca²⁺ from the soma ER to the process ER, because process ER Ca²⁺ has rushed into the process cytosol. Thus, following a process spike, the soma ER becomes transiently depleted. The opposite is also true: a soma spike causes flow of Ca²⁺ from the process ER to the soma ER, but the soma spikes less frequently than the processes. Therefore, the net effect is that soma ER Ca²⁺ level will decrease, this effect becoming stronger with larger σ. This lowers soma excitability, lowering the soma spike frequency. (Below, we illustrate the ER Ca²⁺ depletion by process spikes.)

To summarize, at low σ, the spike rate increases as the slope of frequency vs σ is quite large. On the other hand, as σ increases, the higher spike rate due to higher excitation slows down, while the soma ER gets further depleted with increased process spike frequency. Around σ = 0.1, this depletion of soma ER Ca²⁺ lowers soma excitability so much that soma spike rate decreases with σ.

We confirm the above by displaying the time course of soma ER Ca²⁺ for $D_E=(4,12,20)\times 10^{-4}$, at three values of σ in panels C (σ = 0.05), D (σ = 0.15), E (σ = 0.25), of Figure 7. At low σ, the time course of the soma ER Ca²⁺ does not vary significantly over the range of D_E considered. At higher values of σ (Figures 7D,E), the differences between ER soma Ca²⁺ at different D_E levels grow, which leads to some missed soma spikes. Large downward deflections result from soma spikes while small downward deflections result from process spikes. At higher values of σ, the soma ER can be depleted for D_E > 0, causing the soma to miss some spikes.

4. Discussion

Astrocytes play a range of roles on neural circuits at different spatial and temporal scales. This range of astrocytic effects on neural circuits is mediated by a hierarchy of Ca²⁺ events in astrocytes. In turn, these events are a response to neuronal activity (Shigetomi et al., 2016; Bindocci et al., 2017). These events range from fast, localized transients, to slower global events that recruit the soma and major processes. To better understand the spatiotemporal propagation of Ca²⁺ signals in the cell and how these signals might be altered in neurodegenerative diseases, we need to investigate how neuronal inputs give rise to this hierarchy of Ca²⁺ events.

In this paper, we applied a compartmental model to investigate how the properties of neuronal inputs give rise to a variety of Ca²⁺ events in astrocytes. The model is adapted from the single compartment, functional model of Postnov et al. (2007) that describes astrocyte response to perisynaptic Ca²⁺ influx. We added compartments representing major astrocyte processes that couple to the soma through diffusion.

In this simple model, we demonstrated that the Ca²⁺ influx into each process in response to neuronal activity controls the occurrence of process Ca²⁺ spikes, and in turn soma Ca²⁺ spikes. The degree of correlation between the process neuronal inputs determines the frequency of global events involving the soma and at least four processes. These global events, in the model, are simply due to the random co-occurrence of process spikes in response to correlated neuronal inputs, unless cytosolic diffusion is large enough for soma spikes to trigger spikes in processes. Our simulations also indicate that the exchange of Ca²⁺ between the soma and process ER compartments severely curtails the number of somatic spikes in response to high levels of neural activity.

4.1. A First Model to Build Intuition

Our goal was to build an initial model that incorporates the spatial structure of astrocytes to explore their hierarchy of Ca²⁺ dynamics. This model investigates questions related to astrocyte geometry, Ca²⁺ diffusion across its compartments, the distribution of neuronal inputs received by its perisynaptic processes and the effect of these inputs on Ca²⁺ activity in both the soma and major processes. The adoption of a simple model as a starting point in our investigation helps build intuition about the origin of astrocytic Ca²⁺ events. Indeed, only a small number of variables interact to produce these events. A more complex model that incorporates details of astrocyte geometry and signaling pathways would be required to match experimental data. Such models, however, come at the expense of a large number of parameters and variables, which would make the analysis less intuitive and prone to fine tuning of parameters. Our model is built on reasonable assumptions, can be extended to ask more detailed questions, and may guide further model development and experiments since it provides a series of testable predictions.

One important assumption in our work is that all major processes possess Ca²⁺ excitability, and that neuronal activity only affects processes, not the soma. Experiments have shown that neuronal activity causes fast, local Ca²⁺ transients in distal, fine process branches that do not contain IP₃ receptors and therefore show no Ca²⁺ excitability. These Ca²⁺ events may be triggered by the opening of Ca²⁺-permeable channels in response to neuronal activity (Hamilton et al., 2008; Shigetomi et al., 2012; Lind et al., 2013; Srinivasan et al., 2015). Herein, we model the effects of the distant Ca²⁺ transients onto the major processes as a Gaussian distribution of Ca²⁺ input. We have implicitly assumed a constant level of IP₃, such that integration of the random Ca²⁺ influx events could trigger CICR. This is because Ca²⁺ entry through channels can happen without activation of G-protein coupled receptors that lead to the production of IP₃, and because IP₃ concentration within the astrocyte should equilibrate faster than the Ca²⁺ concentration. Since Ca²⁺ excitability in the processes may not require IP₃ receptors (Srinivasan et al., 2015), we did not use a model of Ca²⁺ excitability that explicitly depends on intracellular IP₃ levels. There is evidence, however, that the Ca²⁺ levels resulting from Ca²⁺ spikes may affect IP₃ levels, which may be important for the production of multiple modes of Ca²⁺ dynamics (De Pitta et al., 2009).

In addition, all processes have a basal rate of Ca²⁺ influx that brings them close to threshold for a Ca²⁺ spike in the absence of neuronal activity. We identify the level of astrocyte excitability with the spike frequency in the soma and in the processes. The implicit assumption is that spiking rate in response to sustained activity serves as a good measure of the effectiveness of the neuronal input patterns in evoking Ca²⁺ responses.

4.2. Control of Astrocyte Ca²⁺ Dynamics by Neuronal Activity

The framework underlying this work, and discussed further below, was built up from a series of experimental results summarized by Carmignoto (2000), Volterra and Meldolesi (2005), and Zorec et al. (2012), which in turn led to the presentation in Araque et al. (2014). According to this framework, neuronal activity causes fast, localized Ca²⁺ events that occur in distal branches, which can result in regenerative Ca²⁺ events in the main process through a process of integration not unlike integration of synaptic inputs by neurons. As neuronal activity increases, spikes in processes can in turn be integrated and trigger soma spikes and global events. To our knowledge, however, this has not been demonstrated experimentally and recent work, while not contradicting this simple framework, suggest that Ca²⁺ dynamics in astrocytes may exhibit a wide range of events (Wu et al., 2014; Bindocci et al., 2017), possibly with more complex rules than assumed here.

The model generates four types of Ca²⁺ events: (1) fast transients due to neuronal activity onto each process; (2) process spikes; (3) soma spikes; and (4) global events that involve spikes in soma and several processes within a short time window. Fast transients (1) are always produced as long as there is neuronal activity (σ > 0). Astrocyte processes integrate fast Ca²⁺ transients caused by neuronal inputs, leading to process spikes. The soma Ca²⁺ rises due to process spikes. We have not observed soma spikes (3) without process spikes (2) and rarely observed global events (4) without soma spikes (3). Thus the chain (1)-(4) of observable Ca²⁺ events defines a hierarchy, whereby an event high in the hierarchy only occurs when preceding events in the hierarchy have already been reached.

The particular Ca²⁺ events (1)-(4) observed in the hierarchy depend on the parameters σ and ρ, which respectively describe neuronal activity and input correlation. At very low σ, we do not observe spikes in either processes or soma: only fast Ca²⁺ transients (1) occur in the processes. At higher σ, processes begin to spike (2) and their spike rate increases with σ. The spiking frequency in the process reproduces the behavior of the spiking rate in a single compartment model with identical σ (Figure 2B). As σ is increased further, soma spikes appear and their spiking rate dependence on σ is similar to that of the processes. The soma spikes less frequently than the processes, as observed experimentally (Araque et al., 2014; Bindocci et al., 2017). Taking into account the fact that the soma volume is about 1.5 times the volume of a major process leads to an even lower soma spike rate than in the processes, since larger volume ratio slows down Ca²⁺ variations.

The role played by correlation between neuronal inputs on astrocyte Ca²⁺ dynamics differs from that played by σ. Increasing ρ has practically no effect on the average process spiking rate and only a modest effect on that of the soma (Figure 3A), except at low σ. In that case, increasing ρ facilitates soma spikes, and lowers the σ threshold for soma spikes. Beyond this effect of correlation on the soma spike rate, increasing ρ mainly increases the frequency of global events. That is, the proportion of soma spikes that are global events increases with ρ, but not with σ. Thus, the amount of neuronal input onto the processes controls the rate of spiking in the processes and in the soma, while the degree of correlation between neuronal inputs controls the frequency of global events.

4.3. Implications for the Role of Astrocytes in Neural Computations

In addition to many roles played by astrocytes as neuron support cells and regulators of blood flow, there is growing evidence that astrocytes also modulate the activity of neural circuits by acting on neuronal excitability and on synaptic activity and plasticity. It has been suggested that the spatiotemporal distribution of neuronal activity determines the profile of Ca²⁺ transients evoked in astrocytes. This in turn determines the extent of synaptic modifications by astrocytes (Araque et al., 2014). According to that hypothesis, localized and short-lived synaptic activity only evokes fast, local astrocyte transients–event (1) above–which in turn only affect synapses directly involved in triggering the fast Ca²⁺ events. Stronger, longer lasting, or slightly more widespread synaptic activity in the same area could trigger a spike in one major process (2). In turn, this affects synapses under its control, active or not. Finally, synaptic activity occurring in more than one process may evoke somatic spikes and global events, (3) and (4), depending on the degree of synchrony of synaptic activation. These events in turn may lead to synaptic plasticity in all synapses covered by the astrocyte. Araque's hypothesis only holds if a hierarchy of Ca²⁺ events results from a hierarchy of network synaptic activity. Our results support this hypothesis by demonstrating that the different types of astrocyte Ca²⁺ events follow such a hierarchy. The higher in the hierarchy, the more synapses over a larger area may be affected synchronously by astrocyte signaling.

Our results may also explain why astrocytes in the visual cortex maps have sharper tuning curves than do neurons. Schummers et al. (2008) measured global events in astrocytes in response to visual inputs with different orientation or spatial frequency. Astrocytes responded according to which orientation domain they belonged to, but their tuning curves were sharper than that of neurons within the same domain. These sharper tuning curves may result from the fact that the distributed activation of synapses over the whole astrocyte must exhibit a significant degree of temporal correlation to induce global events. However, by the same reasoning, astrocytes located around pinwheel centers, which do not receive tuned inputs, should therefore have an untuned response. This does not seem to be the case, as astrocytes located close to a pinwheel center still exhibit sharp tuning curves (López-Hidalgo and Schummers, 2014).

4.4. ER Geometry Affects the Soma Response to Inputs

CICR generates spikes while somatic and global events rely on diffusion between processes and the soma. Therefore the ER, which is the main store of astrocytic Ca²⁺, plays an important role in these Ca²⁺ events. Spiking in the soma occurs as a response to increased levels of neuronal activity when the ERs in the soma and processes connect through diffusion. Setting D_E to a non-zero value resulted in a qualitative change in the relationship between the amount of neural activity and the soma spike frequency. More specifically, the graph of average frequency vs. σ becomes non-monotonic, initially increasing at low values of σ, then decreasing back toward 0. During a process spike ER, Ca²⁺ in the process becomes depleted, which leads to diffusion of Ca²⁺ from the soma ER to the ER in the processes. Since the processes spike more frequently than the soma, the net result is a decrease of Ca²⁺ in the soma ER and lower soma excitability.

We note that in this model of Ca²⁺ excitability, Ca²⁺ in ER plays the role of the recovery variable. Thus, the loss of Ca²⁺ by the soma ER engenders a decrease in soma excitability as σ increases from the lower levels. With a different model with de-inactivation of IP₃R channels by Ca²⁺ as the recovery variable, we may not see the drop in soma spike frequency as some ER Ca²⁺ becomes depleted, but rather a drop in soma spike amplitude.

Our model does take into account the effect of store-operated Ca²⁺ channels. Store-operated Ca²⁺ entry would activate once the ER Ca²⁺ reaches a low level, potentially resulting in an influx of Ca²⁺ through the cytoplasm. This could prevent the decrease in soma excitability at high σ. Thus, a modification in the parametrization of Ca²⁺ excitability in the model might impact cause and effect between processes and soma ER.

4.5. Relevance to Neurodegenerative Diseases

Pathological changes in astrocytes alter Ca²⁺ activity in several forms of neurodegenerative disease (Nedergaard et al., 2010; Hamby et al., 2012; Sofroniew, 2014; Ben Haim et al., 2015; Rodŕıguez-Arellano et al., 2016; Verkhratsky et al., 2016). Neurological diseases can be viewed as a homeostatic failure and astrocytes are affected through alterations in multiple disease-specific homeostatic mechanisms generally known as reactive gliosis (Sofroniew, 2005; Nedergaard et al., 2010; Rodŕıguez-Arellano et al., 2016; Verkhratsky et al., 2016). Reactive gliosis is an evolutionarily conserved defense mechanism associated with neurodegenerative disease; the resultant remodeling undergone by astrocytes can contribute to pathological progression and alter Ca²⁺ dynamics (Verkhratsky et al., 2016).

In Alzheimer's disease (AD), β-amyloid buildup has been shown to initiate reactivity in astrocytes (Alberdi et al., 2013). For instance, exposure of astrocytes to β-amyloid in hippocampal slices resulted in Ca²⁺ release from the ER, which instigated astroglial reactivity (Alberdi et al., 2013). β-amyloid plaques also lead to aberrant physiology in the form of spontaneous Ca²⁺ oscillations as well as intercellular Ca²⁺ waves (Kuchibhotla et al., 2009; Lim et al., 2014).

Prior to the development of β-amyloid plaques, astrocytes undergo atrophy as a result of reactive gliosis (Verkhratsky et al., 2016). Atrophy in turn leads to decreased volume of the soma as well as a reduction in the number of primary processes (Olabarria et al., 2010; Yeh et al., 2011; Kulijewicz-Nawrot et al., 2012). A model like the one developed here may be used to predict the consequences of these morphological changes, together with functional changes in Ca²⁺ influx, on Ca²⁺ spiking and global events.

5. Conclusion

We have demonstrated that a functional compartmental model can answer questions about the rules that govern the generation of Ca²⁺ events observed in astrocytes. A parametric study conducted with respect to Ca²⁺ influx intensity and pairwise correlation, D_I, and D_E, suggests that the variability of neuronal activity seen by the astrocyte sets the spiking frequency in both the processes and in the soma. The correlation between the neuronal activity in the different processes controls the number of global events. Our calculations also suggest that diffusion between the ER of the soma and of the major processes has an important effect on the dynamics of Ca²⁺ events in astrocytes. A detailed look at the mechanics behind the global events and the conditions under which synchronization occurs remains a subject of future investigation.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Alberdi, E., Wyssenbach, A., Alberdi, M., Sánchez-Gómez, M. V., Cavaliere, F., Rodríguez, J. J., et al. (2013). Ca²⁺-dependent endoplasmic reticulum stress correlates with astrogliosis in oligomeric amyloid β-treated astrocytes and in a model of a lzheimer's disease. Aging Cell 12, 292–302. doi: 10.1111/acel.12054

CrossRef Full Text | Google Scholar

Araque, A., Carmignoto, G., Haydon, P. G., Oliet, S. H., Robitaille, R., and Volterra, A. (2014). Gliotransmitters travel in time and space. Neuron 81, 728–739. doi: 10.1016/j.neuron.2014.02.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Averbeck, B. B., Latham, P. E., and Pouget, A. (2006). Neural correlations, population coding and computation. Nat. Rev. Neurosci. 7, 358–366. doi: 10.1038/nrn1888

PubMed Abstract | CrossRef Full Text | Google Scholar

Bazargani, N., and Attwell, D. (2016). Astrocyte calcium signaling: the third wave. Nat. Neurosci. 19, 182–189. doi: 10.1038/nn.4201

PubMed Abstract | CrossRef Full Text | Google Scholar

Ben Haim, L., Carrillo-de Sauvage, M.-A., Ceyzériat, K., and Escartin, C. (2015). Elusive roles for reactive astrocytes in neurodegenerative diseases. Front. Cell. Neurosci. 9:278. doi: 10.3389/fncel.2015.00278

PubMed Abstract | CrossRef Full Text | Google Scholar

Bindocci, E., Savtchouk, I., Liaudet, N., Becker, D., Carriero, G., and Volterra, A. (2017). Three-dimensional Ca²⁺ imaging advances understanding of astrocyte biology. Science 356, 715–724. doi: 10.1126/science.aai8185

PubMed Abstract | CrossRef Full Text | Google Scholar

Blaustein, M. P., and Golovina, V. A. (2001). Structural complexity and functional diversity of endoplasmic reticulum Ca²⁺ stores. Trends Neurosci. 24, 602–608. doi: 10.1016/S0166-2236(00)01891-9

CrossRef Full Text | Google Scholar

Carmignoto, G. (2000). Reciprocal communication systems between astrocytes and neurones. Progr. Neurobiol. 62, 561–581. doi: 10.1016/S0301-0082(00)00029-0

PubMed Abstract | CrossRef Full Text | Google Scholar

De Pitta, M., Volman, V., Levine, H., and Ben-Jacob, E. (2009). Multimodal encoding in a simplified model of intracellular calcium signaling. Cogn. Process. 10, S55–S70. doi: 10.1007/s10339-008-0242-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Di Castro, M. A., Chuquet, J., Liaudet, N., Bhaukaurally, K., Santello, M., Bouvier, D., et al. (2011). Local Ca²⁺ detection and modulation of synaptic release by astrocytes. Natl. Neurosci. 14, 1276–1284. doi: 10.1038/nn.2929

PubMed Abstract | CrossRef Full Text | Google Scholar

Dupont, G., Falcke, M., Kirk, V., and Sneyd, J. (2016). “Nonlinear dynamics of calcium,” in Models of Calcium Signalling, eds S. S. Antman, L. Greengard, and P. J. Holmes (Springer), 207–242. Available online at: https://www.springer.com/series/1390

Google Scholar

Goldbeter, D. G., and Berridge, M. J. (1990). Minimal model for signal-induced Ca²⁺ oscillations and for their frequency encoding through protein phosphorylation. Proc. Natl. Acad. Sci. U.S.A. 87, 1461–1465. doi: 10.1073/pnas.87.4.1461

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordleeva, S. Y., Lebedev, S., Rumyantseva, M., and Kazantsev, V. (2018). Astrocyte as a detector of synchronous events of a neural network. JETP Lett. 107, 440–445. doi: 10.1134/S0021364018070032

CrossRef Full Text | Google Scholar

Halassa, M. M., Fellin, T., and Haydon, P. G. (2009a). Tripartite synapses: roles for astrocytic purines in the control of synaptic physiology and behavior. Neuropharmacology 57, 343–346. doi: 10.1016/j.neuropharm.2009.06.031

PubMed Abstract | CrossRef Full Text | Google Scholar

Halassa, M. M., Florian, C., Fellin, T., Munoz, J. R., Lee, S.-Y., Abel, T., et al. (2009b). Astrocytic modulation of sleep homeostasis and cognitive consequences of sleep loss. Neuron 61, 213–219. doi: 10.1016/j.neuron.2008.11.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamby, M. E., Coppola, G., Ao, Y., Geschwind, D. H., Khakh, B. S., and Sofroniew, M. V. (2012). Inflammatory mediators alter the astrocyte transcriptome and calcium signaling elicited by multiple g-protein-coupled receptors. J. Neurosci. 32, 14489–14510. doi: 10.1523/JNEUROSCI.1256-12.2012

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamilton, N., Vayro, S., Kirchhoff, F., Verkhratsky, A., Robbins, J., Gorecki, D. C., et al. (2008). Mechanisms of ATP-and glutamate-mediated calcium signaling in white matter astrocytes. Glia 56, 734–749. doi: 10.1002/glia.20649

PubMed Abstract | CrossRef Full Text | Google Scholar

Henneberger, C., Papouin, T., Oliet, S. H., and Rusakov, D. A. (2010). Long-term potentiation depends on release of d-serine from astrocytes. Nature 463:232. doi: 10.1038/nature08673

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, G. E. (1994). Constructions of particular random processes. Proc. IEEE 82, 270–285. doi: 10.1109/5.265353

CrossRef Full Text | Google Scholar

Kanemaru, K., Sekiya, H., Xu, M., Satoh, K., Kitajima, N., Yoshida, K., et al. (2014). In vivo visualization of subtle, transient, and local activity of astrocytes using an ultrasensitive Ca²⁺ indicator. Cell Reports 8, 311–318. doi: 10.1016/j.celrep.2014.05.056

CrossRef Full Text | Google Scholar

Kang, M., and Othmer, H. G. (2009). Spatiotemporal characteristics of calcium dynamics in astrocytes. Chaos 19:037116. doi: 10.1063/1.3206698

PubMed Abstract | CrossRef Full Text | Google Scholar

Khalid, M. U., Tervonen, A., Korkka, I., Hyttinen, J., and Lenk, K. (2017). “Geometry-based computational modeling of calcium signaling in an astrocyte,” in EMBEC & NBC 2017 (Singapore: Springer), 157–160. doi: 10.1007/978-981-10-5122-7_40

CrossRef Full Text | Google Scholar

Kimelberg, H. K., and Nedergaard, M. (2010). Functions of astrocytes and their potential as therapeutic targets. Neurotherapeutics 7, 338–353. doi: 10.1016/j.nurt.2010.07.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Kirischuk, S., Kettenmann, H., and Verkhratsky, A. (1997). Na⁺/Ca²⁺ exchanger modulates kainate-triggered Ca²⁺ signaling in Bergmann glial cells in situ. FASEB J. 11, 566–572. doi: 10.1096/fasebj.11.7.9212080

PubMed Abstract | CrossRef Full Text | Google Scholar

Kirischuk, S., Kettenmann, H., and Verkhratsky, A. (2007). Membrane currents and cytoplasmic sodium transients generated by glutamate transport in Bergmann glial cells. Pflügers Archiv. Eur. J. Physiol. 454, 245–252. doi: 10.1007/s00424-007-0207-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Kloeden, P. E., and Platen, E. (1992). Numerical Solution of Stochastic Differential Equations. Berlin; Heidelberg: Springer-Verlag Berlin Heidelberg, 636.

Google Scholar

Kuchibhotla, K. V., Lattarulo, C. R., Hyman, B. T., and Bacskai, B. J. (2009). Synchronous hyperactivity and intercellular calcium waves in astrocytes in alzheimer mice. Science 323, 1211–1215. doi: 10.1126/science.1169096

PubMed Abstract | CrossRef Full Text | Google Scholar

Kulijewicz-Nawrot, M., Verkhratsky, A., Chvátal, A., Syková, E., and Rodríguez, J. J. (2012). Astrocytic cytoskeletal atrophy in the medial prefrontal cortex of a triple transgenic mouse model of alzheimer's disease. J. Anat. 221, 252–262. doi: 10.1111/j.1469-7580.2012.01536.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Levine, T., and Rabouille, C. (2005). Endoplasmic reticulum: one continuous network compartmentalized by extrinsic cues. Curr. Opin. Cell Biol. 17, 362–368. doi: 10.1016/j.ceb.2005.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Lim, D., Ronco, V., Grolla, A. A., Verkhratsky, A., and Genazzani, A. A. (2014). Glial calcium signalling in alzheimer's disease. Rev. Physiol. Biochem. Pharmacol. 167, 45–65. doi: 10.1007/112_2014_19

PubMed Abstract | CrossRef Full Text | Google Scholar

Lind, B. L., Brazhe, A. R., Jessen, S. B., Tan, F. C., and Lauritzen, M. J. (2013). Rapid stimulus-evoked astrocyte Ca2+ elevations and hemodynamic responses in mouse somatosensory cortex in vivo. Proc. Natl. Acad. Sci. U.S.A. 110, E4678–E4687. doi: 10.1073/pnas.1310065110

PubMed Abstract | CrossRef Full Text | Google Scholar

López-Hidalgo, M., and Schummers, J. (2014). Cortical maps: a role for astrocytes? Curr. Opin. Neurobiol. 24, 176–189. doi: 10.1016/j.conb.2013.11.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Meyer, T., and Stryer, L. (1991). Calcium spiking. Ann. Rev. Biophys. Biophys. Chem. 20, 153–174.

PubMed Abstract | Google Scholar

Nadkarni, S., and Jung, P. (2007). Modeling synaptic transmission of the tripartite synapse. Phys. Biol. 4, 1–9. doi: 10.1088/1478-3975/4/1/001

PubMed Abstract | CrossRef Full Text | Google Scholar

Nedergaard, M., Rodríguez, J. J., and Verkhratsky, A. (2010). Glial calcium and diseases of the nervous system. Cell Calc. 47, 140–149. doi: 10.1016/j.ceca.2009.11.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Nimmerjahn, A., Mukamel, E. A., and Schnitzer, M. J. (2009). Motor behavior activates Bergmann glial networks. Neuron 62, 400–412. doi: 10.1016/j.neuron.2009.03.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Olabarria, M., Noristani, H. N., Verkhratsky, A., and Rodríguez, J. J. (2010). Concomitant astroglial atrophy and astrogliosis in a triple transgenic animal model of alzheimer's disease. Glia 58, 831–838. doi: 10.1002/glia.20967

PubMed Abstract | CrossRef Full Text | Google Scholar

Panatier, A., Vallée, J., Haber, M., Murai, K. K., Lacaille, J. C., and Robitaille, R. (2011). Astrocytes are endogenous regulators of basal transmission at central synapses. Cell 146, 785–798. doi: 10.1016/j.cell.2011.07.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Patrushev, I., Gavrilov, N., Turlapov, V., and Semyanov, A. (2013). Subcellular location of astrocytic calcium stores favors extrasynaptic neuron-astrocyte communication. Cell Calc. 54, 343–349. doi: 10.1016/j.ceca.2013.08.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Perea, G., and Araque, A. (2002). Communication between astrocytes and neurons: a complex language. J. Physiol. 96, 199–207. doi: 10.1016/S0928-4257(02)00007-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Perea, G., and Araque, A. (2010). Glia modulates synaptic transmission. Brain Res. Rev. 63, 93–102. doi: 10.1016/j.brainresrev.2009.10.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Petersen, O. H., Tepikin, A., and Park, M. K. (2001). The endoplasmic reticulum: one continuous or several separate Ca²⁺ stores? Trends Neurosci. 24, 271–276. doi: 10.1016/S0166-2236(00)01787-2

CrossRef Full Text | Google Scholar

Postnov, D. E., Ryazanova, L. S., and Sosnovtseva, O. V. (2007). Functional modeling of neural-glial interaction. Biosystems 89, 84–91. doi: 10.1016/j.biosystems.2006.04.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodríguez-Arellano, J., Parpura, V., Zorec, R., and Verkhratsky, A. (2016). Astrocytes in physiological aging and alzheimer's disease. Neuroscience 323, 170–182. doi: 10.1016/j.neuroscience.2015.01.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Rusakov, D. A. (2015). Disentangling calcium-driven astrocyte physiology. Nat. Rev. Neurosci. 16, 226–233. doi: 10.1038/nrn3878

PubMed Abstract | CrossRef Full Text | Google Scholar

Rusakov, D. A., Bard, L., Stewart, M. G., and Henneberger, C. (2014). Diversity of astroglial functions alludes to subcellular specialisation. Trends Neurosci. 37, 228–242. doi: 10.1016/j.tins.2014.02.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Savtchenko, L. P., Bard, L., Jansen, T. P., Reynolds, J. P., Kraev, I., Medvidov, M., et al. (2018). Biophysical underpinning of astroglial physiology probed with realistic cell models. bioRxiv, 1–25. doi: 10.1101/336974

CrossRef Full Text | Google Scholar

Schummers, J., Yu, H., and Sur, M. (2008). Tuned responses of astrocytes and their influence on hemodynamic signals in the visual cortex. Science 320, 1638–1643. doi: 10.1126/science.1156120

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwartz, O., Pillow, J., Rust, N., and Simoncelli, E. (2006). Spike-triggered neural characterization. J. Vis. 6, 484–507. doi: 10.1167/6.4.13

PubMed Abstract | CrossRef Full Text | Google Scholar

Shigetomi, E., Patel, S., and Khakh, B. S. (2016). Probing the complexities of astrocyte calcium signaling. Trends Cell Biol. 26, 300–312. doi: 10.1016/j.tcb.2016.01.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Shigetomi, E., Tong, X., Kwan, K. Y., Corey, D. P., and Khakh, B. S. (2012). TRPA1 channels regulate astrocyte resting calcium and inhibitory synapse efficacy through GAT-3. Nat. Neurosci. 15, 70–80. doi: 10.1038/nn.3000

PubMed Abstract | CrossRef Full Text | Google Scholar

Sofroniew, M. V. (2005). Reactive astrocytes in neural repair and protection. Neuroscientist 11, 400–407. doi: 10.1177/1073858405278321

PubMed Abstract | CrossRef Full Text | Google Scholar

Sofroniew, M. V. (2014). Astrogliosis. Cold Spring Harbor Perspect. Biol. 7:a020420. doi: 10.1101/cshperspect.a020420

PubMed Abstract | CrossRef Full Text | Google Scholar

Srinivasan, R., Huang, B. S., Venugopal, S., Johnston, A. D., Chai, H., Zeng, H., et al. (2015). Ca²⁺ signaling in astrocytes from IP3R2-/- mice in brain slices and during startle responses in vivo. Nature Neurosci. 18, 708–717. doi: 10.1038/nn.4001

CrossRef Full Text | Google Scholar

Tewari, S., and Majumdar, K. K. (2012). A mathematical model of the tripartite synapse: astrocyte-induced synaptic plasticity. J. Biol. Phys. 38, 465–496. doi: 10.1007/s10867-012-9267-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Ullah, G., Jung, P., and Cornell-Bell, A. H. (2006). Anti-phase calcium oscillations in astrocytes via inositol (1, 4, 5)-trisphosphate regeneration. Cell Calc. 39, 197–208. doi: 10.1016/j.ceca.2005.10.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Verkhratsky, A., Zorec, R., Rodriguez, J. J., and Parpura, V. (2016). Pathobiology of neurodegeneration: the role for astroglia. Opera Med. Physiol. 1, 13–22.

PubMed Abstract | Google Scholar

Volterra, A., Liaudet, N., and Savtchouk, I. (2014). Astrocyte Ca²⁺ signalling: an unexpected complexity. Nat. Rev. Neurosci. 15, 327–335. doi: 10.1038/nrn3725

CrossRef Full Text | Google Scholar

Volterra, A., and Meldolesi, J. (2005). Astrocytes, from brain glue to communication elements: the revolution continues. Nat. Rev. Neurosci. 6:626. doi: 10.1038/nrn1722

PubMed Abstract | CrossRef Full Text | Google Scholar

Wade, J. J., McDaid, L. J., Harkin, J., Crunelli, V., and Kelso, J. A. S. (2011). Bidirectional coupling between astrocytes and neurons mediates learning and dynamic coordination in the brain: a multiple modeling approach. PLoS ONE 6:e29445. doi: 10.1371/journal.pone.0029445

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y.-W., Tang, X., Arizono, M., Bannai, H., Shih, P.-Y., Dembitskaya, Y., et al. (2014). Spatiotemporal calcium dynamics in single astrocytes and its modulation by neuronal activity. Cell Calc. 55, 119–129. doi: 10.1016/j.ceca.2013.12.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeh, C.-Y., Vadhwana, B., Verkhratsky, A., and Rodríguez, J. J. (2011). Early astrocytic atrophy in the entorhinal cortex of a triple transgenic animal model of alzheimer's disease. ASN Neuro 3, 271–279. doi: 10.1042/AN20110025

PubMed Abstract | CrossRef Full Text | Google Scholar

Zorec, R., Araque, A., Carmignoto, G., Haydon, P. G., Verkhratsky, A., and Parpura, V. (2012). Astroglial excitability and gliotransmission: an appraisal of Ca²⁺ as a signalling route. ASN Neuro 4:AN20110061. doi: 10.1042/AN20110061

PubMed Abstract | CrossRef Full Text | Google Scholar