- 1Department of Neurobiology, School of Medicine, Yale University, New Haven, CT, USA
- 2Institute of Biophysics, National Research Council, Palermo, Italy
- 3Department of Computer Science, Yale University, New Haven, CT, USA
On their long lateral dendrites, mitral cells of the olfactory bulb form dendrodendritic synapses with large populations of granule cell interneurons. The mitral-granule cell microcircuit operating through these reciprocal synapses has been implicated in inducing synchrony between mitral cells. However, the specific mechanisms of mitral cell synchrony operating through this microcircuit are largely unknown and are complicated by the finding that distal inhibition on the lateral dendrites does not modulate mitral cell spikes. In order to gain insight into how this circuit synchronizes mitral cells within its spatial constraints, we built on a reduced circuit model of biophysically realistic multi-compartment mitral and granule cells to explore systematically the roles of dendrodendritic synapse location and mitral cell separation on synchrony. The simulations showed that mitral cells can synchronize when separated at arbitrary distances through a shared set of granule cells, but synchrony is optimally attained when shared granule cells form two balanced subsets, each subset clustered near to a soma of the mitral cell pairs. Another constraint for synchrony is that the input magnitude must be balanced. When adjusting the input magnitude driving a particular mitral cell relative to another, the mitral-granule cell circuit served to normalize spike rates of the mitral cells while inducing a phase shift or delay in the more weakly driven cell. This shift in phase is absent when the granule cells are removed from the circuit. Our results indicate that the specific distribution of dendrodendritic synaptic clusters is critical for optimal synchronization of mitral cell spikes in response to their odor input.
Introduction
Neural synchrony and oscillatory activity have been observed throughout the brain (Buzsáki and Draguhn, 2004; Wang, 2010). When downstream targets operate as coincident detectors of correlated input signals, as observed in cortical pyramidal neurons, neural synchrony has a prominent role in information processing (Mori et al., 1999; Engel et al., 2001; Linster and Cleland, 2001; Salinas and Sejnowski, 2001). Indeed, the mitral cells, the main projection neurons of the olfactory bulb, synchronize (Kashiwadani et al., 1999; Schoppa, 2006; Doucette et al., 2011) and the olfactory cortex appears tuned for such synchronous inputs (Luna and Schoppa, 2008; Davison and Ehlers, 2011). However, the specific mechanisms giving rise to mitral cell synchrony are poorly understood.
Mitral cells project a single apical dendrite to a glomerulus where they receive their only excitatory input. Along their long (∼1000 μm) lateral (basal) dendrites, they form dendrodendritic synapses with inhibitory granule cell interneurons. The mitral-granule circuit is activated when mitral cell backpropagating action potentials release glutamate at dendrodendritic synapses that activate granule cell α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid receptor (AMPA) and N-methyl D-aspartate (NMDA) receptors, depolarizing the granule cells. Such activation can induce the granule cell to release GABA to reciprocally inhibit the mitral cell through the same synapse (Shepherd et al., 2004).
Since neural synchrony can be orchestrated through inhibitory interneurons (Lytton and Sejnowski, 1991; Vreeswijk et al., 1994; Bartos et al., 2007), it has been proposed that granule cells may serve to synchronize mitral cells (Rall and Shepherd, 1968; Davison et al., 2003; Bathellier et al., 2006; Galán et al., 2006; Marella and Ermentrout, 2010; Giridhar et al., 2011; McTavish et al., submitted), which has also been supported experimentally (Kashiwadani et al., 1999; Schoppa, 2006). These reports demonstrate that synchrony is induced through correlated inhibitory inputs onto the mitral cells. However, models exploring synchrony in the mitral-granule cell circuit have not accounted for the fact that dendrodendritic synapses close to a mitral cell soma are much more effective at modulating somatic-generated mitral cell spikes than distal synapses (Lowe, 2002; Xiong and Chen, 2002). This is because inhibitory conductances decay passively along the dendrites so distal inputs have a reduced effect at the soma. Granule cells only have a lateral spread of about 100 μm in the external plexiform layer where they connect to mitral cells (Orona et al., 1983; Shepherd et al., 2004). Therefore, for mitral cells to synchronize through the correlated input from a shared granule cell implies that the dendrodendritic synapse is near both mitral cell bodies and ipso facto that the mitral cell bodies are also near to each other. Alternatively, widely separated mitral cells can synchronize through the dendrodendritic circuit when the granule cells connected close to one mitral cell body are synchronized with granule cells connected close to another mitral cell body (McTavish et al., submitted). In this scenario, the mitral cells receive correlated signals from the granule cell population so they can synchronize regardless of their spatial separation.
Through viral tracing studies, it has been shown that dendrodendritic synapses are clustered and not uniformly distributed along the mitral cell lateral dendrites (Willhite et al., 2006; Kim et al., 2011). This suggests that mitral cells operating through the granule cells form sparse, dedicated connections with specific subsets of other glomeruli. Since granule cells undergo adult neurogenesis, which is required for olfactory learning (Moreno et al., 2009), it has been hypothesized that dendrodendritic clusters naturally evolve through activity-dependent learning (Migliore et al., 2007, 2010). The clusters that emerge in these simulation studies are centered about the activated mitral cell somas.
In this paper, we continued utilizing the biophysical model in (Migliore and Shepherd, 2007; Migliore et al., 2007, 2010). While those reports focused on the emergence of dendrodendritic clusters and their functional relevance with respect to mitral cell spiking rates, here we evaluated the role of clusters on synchrony between mitral cell pairs while accounting for their spatial constraints. Our simulations reveal that mitral cells, even when widely separated, can synchronize when they share granule cells, but synchrony is optimally attained when the dendrodendritic synapses are clustered near the mitral cell bodies. Furthermore, while synchrony was enhanced with stronger inhibitory synapses and more connections, the effects were modest, indicating that synchrony can be attained with relatively few, optimally placed synapses. We also found that synchrony in this circuit, which auto-inhibits itself through the dendrodendritic synapse, is more sensitive to balanced inputs than if the circuit employed lateral-only inhibition. When odor input magnitudes are unbalanced, auto-inhibition serves to normalize the spike frequency while inducing a larger temporal shift than simulations that had lateral-only inhibition.
Methods
All simulations were carried out with the NEURON simulation program (Hines and Carnevale, 1997) version 7.2 on a parallel multi-processor IBM Linux cluster (CINECA, Bologna, Italy). The model and simulation files are available for public download under the ModelDB (Hines et al., 2004) section of the Senselab database (http://senselab.med.yale.edu).
Model Properties
To investigate the possible interactions between glomeruli operating through the dendrodendritic synapses, we used a network consisting of pairs of mitral cells with clusters of granule cells distributed along a 1 mm space (Figure 1B). Each mitral cell represents the synchronized activity from a single glomerulus (Schoppa and Westbrook, 2002; Christie et al., 2005; Gire and Schoppa, 2009). Simulations were 20 seconds in duration.
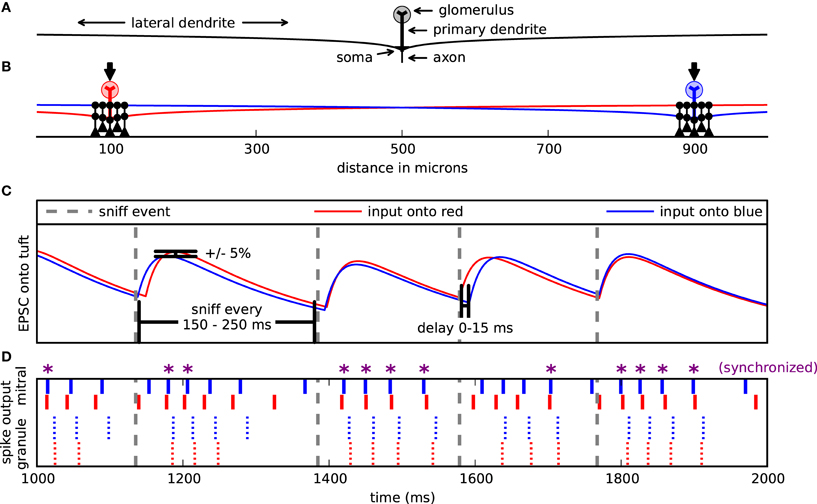
Figure 1. Model setup and design. (A) Cells were arranged spatially along one dimension. Mitral cell pairs (red and blue) were separated by 200, 400, or (as shown here) 800 μm. Mitral cells received excitatory input on their glomerular tuft dendrites (arrows). Each mitral cell extended a left and right dendrite 1000 μm and formed dendrodendritic synapses (black circles) with clusters of granule cells (black). For most simulations, the pair of granule cell clusters was respectively centered about the mitral pairs. (B) Example of 1 second input onto the mitral cells. Sniff events (dotted gray lines) occurred every 150–250 ms. With each sniff, the mitral cells were each activated by their own double exponential excitatory postsynaptic current (EPSC) (red or blue). The onset of each EPSC was delayed up to 15 ms after the sniff time and its magnitude fluctuated ±5%. (C) Corresponding spike raster from input in (B). Top, bold lines correspond to the mitral cell spikes. Smaller lines represent the granule cell spikes proximal to either the blue or red mitral cell. Purple asterisks (*) denote mitral cell spikes that co-occur within a 5 ms window.
Mitral cells were implemented largely as described in Migliore et al. (2005) and as used in (Migliore and Shepherd, 2007; Migliore et al., 2007, 2010) with a reduced model that includes an axon, soma, a primary dendrite, a glomerular tuft, and two 1000 μm long secondary dendrites (Figure 1A). We varied this mitral cell model from previous versions to have 10 tuft branches instead of 20 and for these branches to have a dendritic diameter of 1 μm instead of 0.4 μm. Granule cells were implemented as in Migliore et al. (2010) with a soma, a main radial dendrite (150 μm long) connected to a 100 μm long, second-order dendrite representing the medial and distal dendritic tree, which was used to make dendrodendritic synaptic contact with the mitral cells' lateral dendrites. Dendrodendritic synapses were modeled with two additional compartments on the granule cell, one for the spine and one for the neck. For all cells we used Ra = 70 Ω cm and τm = 30 ms, with Rm and Cm adjusted to obtain, under control conditions, an input resistance of about 70 MΩ and 1 GΩ, for mitral (Mori et al., 1981) and granule cells (Schoppa et al., 1998), respectively. Resting potential was set at −65 mV and temperature at 35°C. The same kinetics from Migliore et al. (2005) was used for Na, KA, and KDR conductances in all cells.
Each mitral cell was driven with virtual odor stimulation. An odor synchronously activated all 10 compartments of the mitral cell dendritic tuft with a double exponential conductance change with a 20 ms rise time and 200 ms decay time (Figure 1B). While glomerular responses to individual odors may vary, this double exponential represents generic odor excitation (Carey et al., 2009). Each excitatory input onto a dendritic tuft had an individual peak conductance of about 0.8 nS, corresponding to a total maximum input conductance of 8 nS inducing about 4–6 spikes per virtual sniff (Cang and Isaacson, 2003). Sniffs occurred randomly every 150–250 ms with a mean frequency of 5 Hz to simulate sniffing in awake animals (Wesson et al., 2009).
With each sniff, each mitral cell received its own excitatory input. Since we were interested in the role of the dendrodendritic synapse and not the effect of correlated excitation on synchrony between mitral cell pairs co-activated by an odor, it was necessary to decorrelate excitatory input signals. Therefore, with each sniff, the conductance amplitude of each input signal varied randomly by ±5%. Additionally, each input signal was activated randomly 0–15 ms after the sniff onset to further decorrelate them (Figure 1C). Granule cells were only driven by excitatory inputs from the mitral cells acting through the dendrodendritic synapse.
As previously described (Migliore and Shepherd, 2007), dendrodendritic coupling between each mitral lateral dendrite and a granule cell dendritic spine was modeled as a pair of independent reciprocal synapses with values from Schoppa et al. (1998), Schoppa and Westbrook (2002), and Schoppa (2006). The mitral-to-granule AMPA conductance was modeled as an alpha function with a time constant of 3 ms and a reversal of 0 mV. The mitral-to-granule NMDA channel conductance was based on a NEURON model (Destexhe et al., 1994) adjusted to obtain a time-to-peak and decay time constant of 10 and 50 ms, respectively. The peak excitatory conductance was 5 nS, about 10 times the values found experimentally, so a given mitral-to-granule synaptic event can be interpreted as 10 simultaneous events in the biological condition. There are 50–100 times more granule cells than mitral cells, each one with 50–100 dendrodendritic synapses (Shepherd et al., 2004). Therefore, multiplying our synaptic conductance by a factor of 10 represents 10 excitatory inputs from each of our mitral cells. With two active mitral cells, this represents 20–40% of the inputs onto the granule cells and was chosen to induce them to spike. The granule-to-mitral synapse was modeled as a GABAergic synapse double exponential with a rise time of 0.1 ms and 4.0 ms decay time and a −80 mV reversal potential. The base peak inhibitory conductance was 5 nS, about three times biological conditions. This was magnified in different instances as noted in the text. Synapses (excitatory or inhibitory) were activated whenever the corresponding presynaptic compartment reached the threshold of −40 mV (Chen et al., 2000).
Synchrony and Correlation Measure between Spike Trains
We measured synchrony by comparing the number of coincident spikes of two trains within a 5 ms interval to the number of coincident spikes expected by chance if a homogeneous Poisson process generated the spikes. This score is Ncoinc/2vΔ Nref where Ncoinc is the number of coincident spikes between the two trains within an interval of Δ and the number of expected coincident spikes is 2vΔ Nref, where v is the spike frequency of the comparing train, and Nref is the number of spikes in the reference train (Kistler et al., 1997). We refer to this value as the synchrony magnitude. In addition to comparing the two spike trains directly, we also time-shifted the comparing train against the reference train and applied this measure constructing correlograms to assess the sharpness of the synchrony and determine relative phase relationships. Figure 1D shows one second of spike output from a representative simulation. Those mitral cell spikes marked with an asterisk are synchronized.
Results
Synchrony between Mitral Cells/Glomeruli is Optimally Attained with Proximal Granule Cell Clusters
Given the presence of granule cell clusters (Willhite et al., 2006; Kim et al., 2011) that may self-assemble about the somas of active mitral cells (Migliore et al., 2007, 2010), we first evaluated the functional role of dendrodendritic synaptic clusters and their location along the mitral cell lateral dendrites on mitral cell synchrony. Figure 2A shows the configuration for four simulations where the mitral cells were separated by 800 μm. In three of the simulations, we applied two clusters of three granule cells to the mitral cells. In one condition (black granule cells), the granule cell clusters were centered about the mitral cells. In another simulation, we moved the clusters to the furthest extremes in our network (red granule cells). In the third simulation, we placed the two clusters in the middle of the lateral dendrites (blue granule cells). The results of the various configurations by their corresponding colors are shown in Figure 2B. As can be seen, synchrony between the mitral cell pairs was maximal when the clusters were centered near each mitral cell. As a control, we also measured synchrony in a network with no dendrodendritic synapses (gray). The control condition shows that there is some inherent correlation in our simulations simply due to the mitral cells receiving somewhat similar virtual odor inputs (Figure 1B).
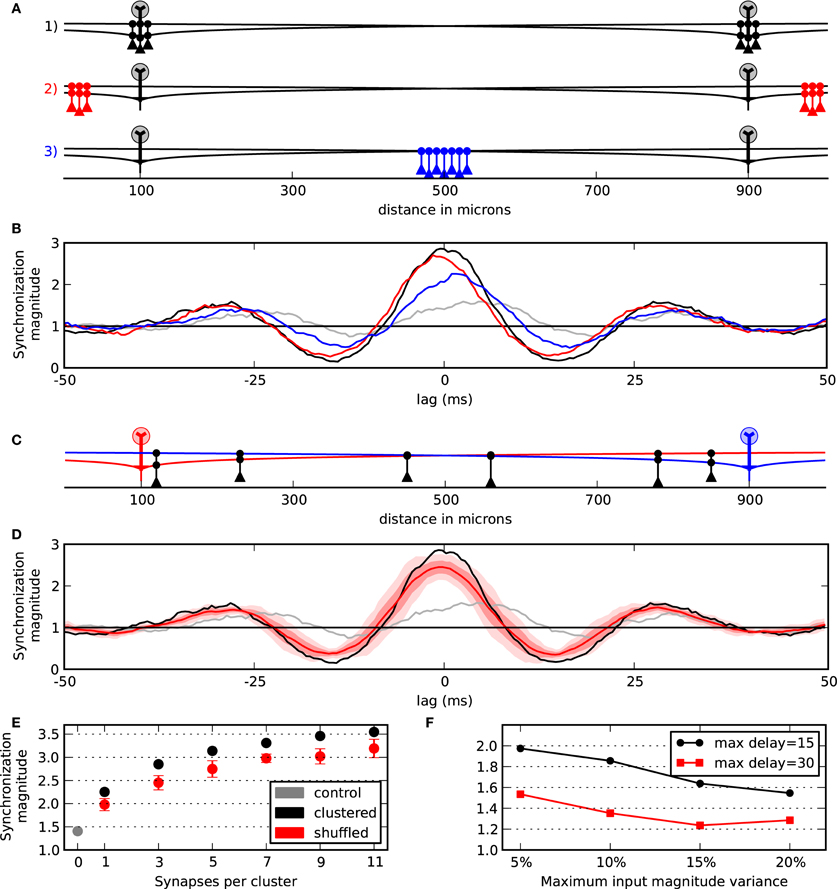
Figure 2. Synchrony between mitral cells/glomeruli is optimally attained with proximal granule cell clusters. (A) Model setup to evaluate the effect of cluster locations in three conditions. Two clusters each with three granule cells were applied. In one condition, the clusters were centered about the mitral cells (black). In another condition, the clusters were moved to the distal ends of the dendrites (red). In the final condition clusters were placed in the middle between the two mitral cells (blue). (B) Responses to the particular three conditions outlined in (A) and with a control condition with no granule cell connectivity (gray). (C) Example of shuffling two clusters with three granule cells each. (D) Response when the two clusters are centered about the mitral cells (black) compared with the mean of 10 shuffled simulations (bold red). One standard deviation (SD) of the 10 shuffled simulations is shown in light red and two SDs is shown in lightest red. (E) Synchronization magnitude at zero-lag while varying cluster width. Mean and SD at zero-lag for shuffled clusters (red) vs. clusters that are centered about the mitral cells (black). The synchronization magnitude with no dendrodendritic connectivity is shown in gray. (F) Network contribution to synchrony across variable conditions. Points show the synchrony magnitude with five granule cells per cluster divided by the control network with no granule cell activity. Conditions could vary by maximum input offset (15 or 30 ms) and by the maximum input magnitude (±5, 10, 15, or 20%).
To further test the effect of the proximal clusters centered near the mitral cell body, we compared simulations containing centered clusters to 10 simulations where the locations of the granule cells along the lateral dendrites were randomized. An example of such a shuffling of the granule cells is shown in Figure 2C. As can be seen in Figure 2D, when the synapses were arranged into proximal clusters, synchrony was optimally attained. The results from taking the synchronization magnitude value at zero-lag across several cluster widths is shown in Figure 2E. This shows, for example, that six granule cells optimally placed into two clusters yields nearly the same synchrony of 14 or 18 randomly placed granule cells (i.e., seven or nine granule cells per cluster shuffled). Collectively, our results indicate that synchrony between mitral cells is optimal with dendrodendritic synapses placed where they are most functionally relevant for the mitral cells to mutually inhibit each other—near each of their somas.
Increased Connectivity and Inhibitory Conductance Induce More Synchronization
As illustrated in Figure 2E, more connectivity through larger clusters increased the synchronization magnitude of the mitral cells. We, therefore, considered the general effect of the magnitude of inhibition and cluster width on synchrony. As shown in Figure 3, wider clusters and stronger inhibitory conductances increased the magnitude of synchronization. However, the rate of increase did not increase linearly for either parameter. This implies that a moderate level of synchrony can be obtained with just a few, moderately conducting synapses.
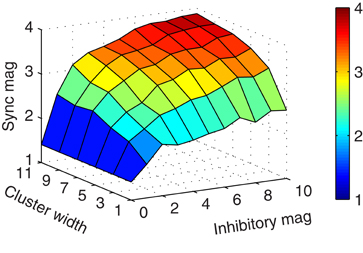
Figure 3. Increased connectivity and inhibitory conductance induce more synchronization. Surface plot showing the synchronization magnitude at zero-lag by cluster width and inhibitory magnitude of granule-to-mitral synapses from their base conductance of 5 nS.
Network Contribution to Synchrony
Our synchrony metric shows the cumulative effect of a semi-correlated driving input as well as the contributions of the network. To explicitly measure the network contribution to synchrony, we took the synchronization magnitude with the network intact (such as the black lines in Figures 2B,D) and divided it by the control case that does not incorporate the granule cells (gray lines). Additionally, to better understand the roles of our input parameters, we varied the maximum input delay to have 0–15 or 0–30 ms jitter and also varied the magnitude of the input—perturbations of up to 5%, 10%, 15%, and 20%. Figure 2F shows the results. As can be seen, with our typical case of 5% magnitude variability and 0–15 ms jitter, the network contributed two times over the control condition. Also, this shows that our results are more sensitive to the input jitter than the input magnitude for those values that we tested—a jitter of 0–30 ms and 5% magnitude variability was equal to the condition of up to 15 ms jitter and 20% magnitude variability. That is, a four-fold change in magnitude variability was equivalent to a two-fold change in jitter.
Granule Cell and Mitral Cell Synchrony
When the mitral cells are widely separated, the contribution of distal inhibitory synapses can be functionally negligible compared to the proximal synapses (Figure 4A). Because inhibitory conductances are passive, the maximal inhibitory current at the soma is proportional to the length constant of the dendritic cable (Koch, 2004). Functionally, this means that for the mitral cells to synchronize through correlated inhibitory inputs that the corresponding proximal granule-to-mitral synapses to each mitral cell must also act in concert. We, therefore, contrasted each spike train of nearby granule-to-mitral synaptic events from one cluster with each train of respective synaptic events from the other cluster. We found that the granule cells in the network strongly synchronized (Figure 4B, green). Therefore, correlated granule cell inputs acting on their proximal target mitral cells induced mitral cell synchrony.
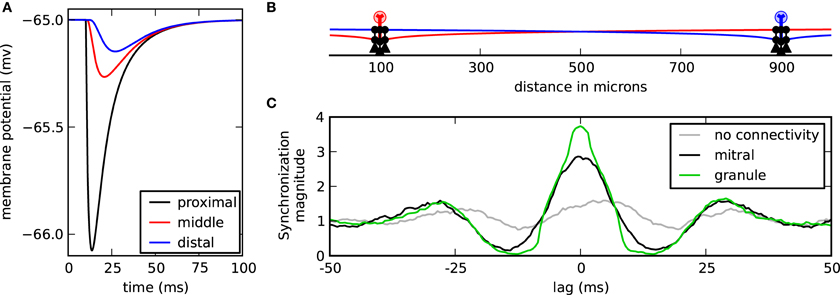
Granule cell and mitral cell synchrony. (A) Membrane response at the soma while the cell is at rest to one granule-to-mitral IPSC synaptic event applied along the lateral dendrite at 10 μ m (black), 500 μ m (red), or 1000 μ m (blue) from the mitral cell soma. (B) Model setup with two centered clusters, each with three granule cells. (C) Mean synchronization magnitude of IPSC synaptic events from each granule cell of one cluster compared with the events from the other granule cell cluster (green). The synchronization magnitude of the mitral cell spikes is shown in black and the synchronization magnitude of the mitral cells without any granule cell interaction is shown in gray.
Proximal Granule Cell Clusters Enable Mitral Cell Synchrony Regardless of Mitral Cell Spatial Separation
While the previous simulations showed that synchrony could occur when mitral cells were separated by 800 μm, we speculated that mitral cells closer in space would be even more likely to synchronize. After all, as the mitral cells neared each other, they would also carry their associative clusters with them, bringing those otherwise distal inhibitory synaptic inputs closer where they would have more impact at the soma. We found, however, that spatial separation did not impact the magnitude of synchronization (Figure 5). On reflection, there appear at least three reasons why spatial separation is irrelevant when the mitral cells have clusters of granule cells about them. First, our previous results showed that increasing inhibitory conductance did not scale linearly with increased synchrony. Therefore, the increase in synaptic conductance when bringing distal clusters nearer to the mitral cell somas would have, at best, minimal effect. Second, proximal conductances were still active. Because the passive decay is exponential, the IPSC magnitude measured at the mitral cell soma from proximal synapses is much greater than that provided by distal synapses, even when those distal synapses are brought nearer. This means that proximal synaptic currents will dominate somatic responses. Third, due to the effect of axial spread of current in the dendrites, the onset at the soma is sharper in proximal synapses than in distal synapses. As a result, the mitral cell somatic membrane response is also less dynamic (compare rise times in Figure 4A). The effect is that the more proximal the current is to the soma, the more abruptly and precisely it can modify the cell. Taken together, distal mitral-to-granule synapses do not effectively factor into the modulation of mitral cell spikes to influence synchrony. As long as the proximal granule cell clusters can synchronize, then the mitral cells will also synchronize.
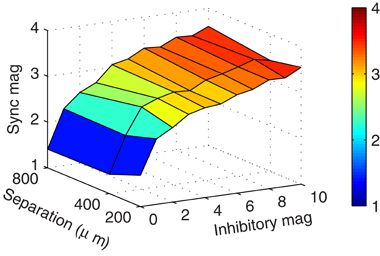
Figure 5. Clusters enable synchrony regardless of spatial separation. Surface plot showing the zero-lag mitral cell synchronization magnitudes with respect to mitral cell spatial separation and inhibitory magnitude of granule-to-mitral synapses from their base conductance of 5 nS. These results contain five granule cells per cluster.
Asymmetric Drive Normalizes Firing Rates and Induces Relative Temporal Delays
Each glomerulus is activated by olfactory sensory neurons that have a differential response to a variety of odors (Shepherd et al., 2004). Additionally, a glomerulus might respond differentially to concentrations of an odor. It is, therefore, reasonable to suspect that co-activated mitral cells of an odor might have different degrees of excitatory drive. We, therefore, tested the effect of relative drive on our model by varying the excitatory magnitude in the blue cell outlined in Figure 6A between −10% and +10% of the magnitude onto the red cell. In these simulations we found that the more weakly driven cell fired after the more strongly driven cell, which varied by the relative difference in drive (Figures 6B,C). Therefore, a change in excitatory drive was able to induce relative temporal delays. Such a shift in phase was absent when the granule cells were removed from the network (Figure 6B dotted brown).
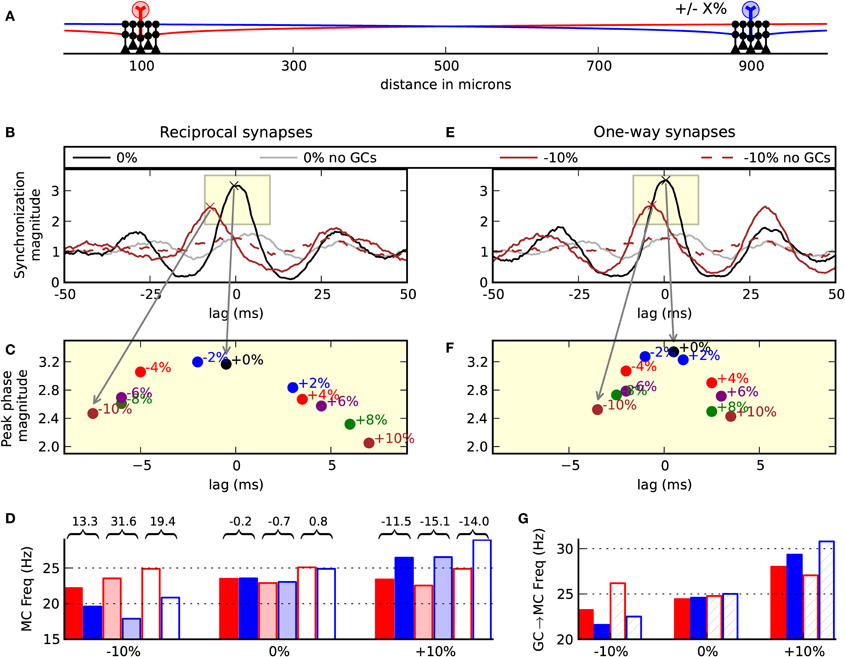
Figure 6. Asymmetric drive induces relative temporal delays. (A) Model setup. Two clusters of five granule cells each were centered about the mitral cells. The amplitude of the EPSC driving the blue cell was adjusted in the range −10% to +10% of the relative input driving the red mitral cell. Left column (B,C,D) shows the normal biological condition with reciprocal dendrodendritic synapses. (B) Correlogram of the synchronization magnitude of the mitral cells. When the inputs are balanced, there is a peak at zero-lag (black). When the blue cell receives 10% less input, there is a shift in the relative phase showing that the red cell tends to spike 7 ms before the blue mitral cell (brown line). This effect is absent when the granule cells are removed from the network (dotted brown line). The gray line is the balanced input condition with no granule cell connectivity. (C) Magnification of the subwindow shown in (B) displaying the peaks of various correlograms with input magnitudes across the range of −10% to 10%. (D) Output frequencies across a few conditions. Colors (red or blue) correspond to the spike outputs of the red or blue mitral cells. Solid bars denote the network with full reciprocal connectivity. Semi-transparent bars indicate unidirectional or one-way synapses of a classical lateral inhibitory network. Transparent bars indicate the network with no granule cell connectivity. Values over and between the red and blue bars indicate the relative percent of red spiking frequency compared to the blue spiking frequency. (E) The same inputs used in (B), but auto-inhibition was removed from the network utilizing one-way synapses. (F) Changing the relative drive shows that the mitral cells remain more correlated than when the cell auto-inhibits itself. (G) Mean number of granule-to-mitral inhibitory events by synapse type. Red bars denote granule-to-mitral synapses on the red mitral cell. Blue bars denote synapses onto the blue mitral cell. Solid bars denote synapses near to the mitral cell soma. Hashed bars denote distal synapses.
To further investigate the functionality of the reciprocal dendrodendritic synapse, we removed auto-inhibition from the network and performed the same simulations when changing the driving force on one of the cells. To remove self-inhibition, the synapses were made one-way. With the distal synapses, the mitral-to-granule synaptic conductance was magnified by 33% to drive the granule cell. The granule-to-mitral synaptic conductance of the distal synapses was set to 0. Conversely, in the proximal synapses, the mitral-to-granule weights were set to 0 while the granule-to-mitral weights remained the same as in the previous simulations. This gave each mitral cell the ability to laterally inhibit the other through granule cell clusters without direct feedback of self-inhibition.
We found in these lateral-only networks with one-way synapses a slight amplification in the magnitude of synchrony and less sensitivity of zero-phase synchrony to changes in drive (Figures 6E,F). For example, with −10% relative drive onto the blue cell, the blue cell tended to spike 3.5 ms after the red cell in the lateral-only synaptic network, but spiked 7 ms after the red cell in the normal condition with reciprocal synapses. We noticed that the way in which the firing rates can become more disparate while maintaining synchrony is that spikes in the more weakly driven cell tended to skip. For example, in a sniff, the stronger driven cell might make five spikes and the weaker driven cell would generate four spikes, of which three, say, would synchronize.
Interestingly, we noticed that the normal network operated to normalize the relative mitral cell spike frequencies (Figure 6D). For example, when the excitatory drive onto the blue mitral cell decreased by 10%, without the network intact, the red cell fired 19.4% more than the blue cell. With the network in place, the relative firing was 13.3% different. Contrastingly, in the case of lateral-only networks that employed more classical lateral inhibition, there was an increase in the dynamic range to 31.6%. Therefore, our results with the normal network intact are opposite of what is normally expected with lateral inhibition—that the more active cell squelches the more weakly driven cell. The reason that the spike frequencies became more similar with the normal network is because of the auto-inhibition that is part of the reciprocal dendrodendritic synapse, which served to inhibit the more strongly driven cell more than the weakly driven cell. That is, the synapses more likely to release GABA are the ones being more directly excited—those connected to the lateral dendrites of the more active mitral cell. This is highlighted in Figure 6G where the frequency of granule-to-mitral synaptic events is delineated by nearby (solid) or distal (hashed) synapses onto the red or blue cell.
The stimulus onto the red cell was the same across all conditions. Therefore, it was somewhat surprising to see that as the number of inhibitory granule-to-mitral synaptic events increased with more activity of the blue cell, that the firing of the red cell was largely unchanged. Closer examination revealed that as the blue cell's firing increased, the time of the inhibitory event became closer to the time of the red cell's spike (not shown). In these cases, the red cell was more likely to be in its refractory period rendering these inhibitory events ineffective.
To summarize, our results indicate that dendrodendritic clusters induce strong temporal delays in the spikes of mitral cells when they are given different magnitudes of drive. Additionally, auto-inhibition of the dendrodendritic synapse serves to normalize relative spiking frequencies. We found both of these effects across all cluster sizes tested (widths of 1, 3, 5, 7, 9, and 11).
Temporal Delays from Asymmetric Inputs Increase over the Duration of a Sniff
It has been shown that mitral cells activated by different odors can become more decorrelated with time (Niessing and Friedrich, 2010). We, therefore, subdivided the spike trains into two (roughly equal) amounts—spikes that occurred within 80 ms of the sniff and those that occurred between 80 ms and the next sniff. When the inputs driving the mitral cells were balanced, we found that zero-lag synchrony persisted throughout the sniff (Figure 7A). This shows that in the control condition without granule cells (thin lines) that due to the similar co-activation of the mitral cells that early spikes (black) are much more likely to be synchronized than those occurring later (red). Therefore, the network's contribution in keeping later spikes synchronized is quite pronounced. When the inputs were unbalanced, however, spikes within 80 ms of the sniff were closer to zero-lag synchrony than later spikes (Figures 7B,C,E,F). This phenomenon was seen in networks that included auto-inhibition (top row) as well as in lateral-only networks (bottom). However, the network with auto-inhibition induced a more dramatic temporal shift in both early and late phases of the sniff cycle.
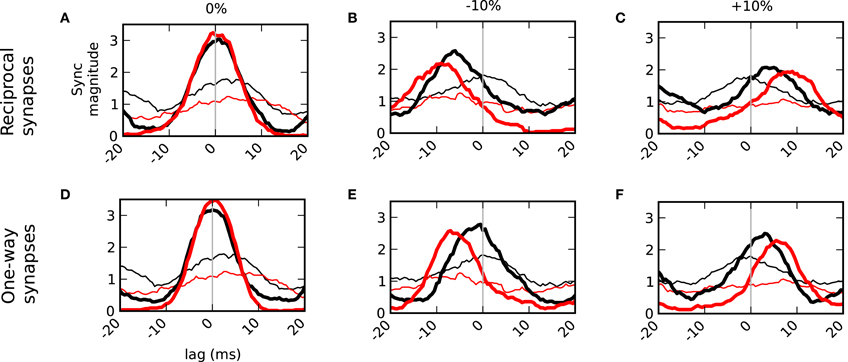
Figure 7. Temporal delays from asymmetric inputs increase over the duration of a sniff. Synchronization magnitudes for spikes within 80 ms of sniff onset (black) and spikes greater than 80 ms and less than the next sniff (red). Bold lines are results in the connected network. Thin lines do not have granule cell connectivity. Left column (A,D) balanced inputs onto the mitral cells. Middle column (B,E) one cell (blue cell in Figure 6A) received 10% less input drive. Right column (C,F) one cell received 10% more drive. Top row (A–C) shows the results with normal dendrodendritic synapses that have recurrent or auto inhibition. Bottom row (D–F) show the results of unilateral networks that do not employ auto inhibition.
Discussion
In this study we sought to address the role of sparsely distributed granule cell clusters (Willhite et al., 2006; Kim et al., 2011) on mitral cell spike synchrony. Since inhibition delivered distally onto mitral cell lateral dendrites decrements strongly in spreading to the soma (Lowe, 2002; Xiong and Chen, 2002), we were particularly interested in evaluating clusters in a spatial context. Our previous simulations (Migliore et al., 2007, 2010) using a variety of synaptic learning rules indicated that granule cell clusters self-organize along the lateral dendrites near to the somas of activated mitral cells. Since nearby dendrodendritic synapses are the most effective in modulating spikes, we hypothesized that clusters at these locations optimally synchronize mitral cells. Through simulations, we confirmed this hypothesis showing that mitral cell synchrony decreases when clusters are far from the somas of the mitral cells or when synapses were randomly distributed along the lateral dendrite (Figure 2).
Our other major finding was that the reciprocal property of the dendrodendritic synapse, which induces self- as well as lateral inhibition, makes the mitral-granule cell circuit operate differently from lateral-only inhibitory networks. In simulations with asymmetric inputs driving two mitral cells, the more active cell was the most inhibited. This normalized the spikes of the two neurons rather than following the classical case of lateral inhibition that further inhibits the weakly driven cell. Additionally, with these simulations using asymmetric input magnitudes, we found that the dendrodendritic synapse induced stronger temporal delays than when the networks provided lateral-only inhibition (Figure 6). Collectively, our results indicate that a function of the granule cells and the dendrodendritic synapses may be to coordinate the timing of mitral cell spikes for downstream targets.
Synchrony in the Olfactory Bulb
It has been observed that mitral cells synchronize (Kashiwadani et al., 1999; Schoppa, 2006; Doucette et al., 2011) and the olfactory cortex is sensitive to correlated inputs (Luna and Schoppa, 2008; Davison and Ehlers, 2011). Computational studies have described how the granule cell inhibitory network may be involved in mitral cell synchrony (Rall and Shepherd, 1968; Davison et al., 2003; Bathellier et al., 2006; Galán et al., 2006; Marella and Ermentrout, 2010; Giridhar et al., 2011). The underlying mechanism of mitral cell synchrony in these reports is the correlated signal from shared granule cells. Indeed, the reciprocal nature of the dendrodendritic synapse seems functionally poised to induce the positive feedback of mitral cell synchrony driving granule cell synchrony. At issue, however, are the spatial constraints and granule cell clusters that those reports did not consider. To illustrate the passive decay, a voltage clamp applied to our model's distal dendrite at 1000 μm and held at the GABAergic synaptic reversal of −80 mV causes the soma's membrane potential to go from its resting potential of −65 mV to only −66 mV. Therefore, the strongest synaptic scaling applied in the distal dendrite would still only hyperpolarize the soma 1 mV. The study of mitral-granule dynamics therefore, requires a spatial component.
With respect to space, however, our results demonstrate that given dedicated interactions between glomeruli operating through corresponding nearby clusters of granule cells, synchrony can ensue across any spatial separation as long as the lateral dendrites of each mitral cell can reach near the soma of the other cell. When two mitral cells share and operate on a few granule cells near each other mitral cell where they are most functionally relevant, then the positive feedback mechanisms of the dendrodendritic synapse can induce synchrony.
Because synchrony requires a correlated signal, our model is reliant on fully backpropagating spikes. This is because fully propagating spikes serve as a correlated signal onto the granule cell clusters that synchronizes them, which, in turn, serves as a correlated signal back onto the mitral cells. A propagating spike in one mitral cell, but not the other would result in a decorrelated signal onto the respective granule cell clusters. Likewise, if the output of one granule cell cluster was uncorrelated with the output of the other cluster, then the uncorrelated signals onto the mitral cells would operate to decorrelate them. While we have presented the optimal arrangements to induce synchrony between mitral cells, other mechanisms in the network could operate to dynamically prevent it. For example, mitral cell A and C may otherwise synchronize as we have outlined in our network model, but mitral cell B may operate on a cluster of granule cells between A and C. When mitral cell B is active, backpropagating spikes may be prevented from fully propagating between A and C thereby conditionally suppressing their ability to synchronize.
Temporal Decorrelation
With respect to temporal coding, odors may be encoded by specific synchronized subsets or by more complex temporal patterns. While synchrony may be important for signal propagation and information flow (Engel et al., 2001; Salinas and Sejnowski, 2001; Reyes, 2003), synchronized signals are also redundant. Not only does this duplication of effort cost more brain resources, but also by combining signals into one stream, it can limit the discriminability of those signals (Barlow, 1959; Zohary et al., 1994). Studies on insects, zebrafish, and mice report signals from olfactory projection neurons that become more decorrelated over time (Laurent et al., 2001; Laurent, 2002; Friedrich et al., 2004; Niessing and Friedrich, 2010; Giridhar et al., 2011). The general interpretation is that the early onset of synchronized spikes after an odor presentation gives rise to odor category perception, and as spikes become more decorrelated, this gives rise to more specific odor identity. When we varied the relative input drive onto the mitral cells, we saw a shift in the relative spiking of the two cells (Figure 6) that became more pronounced with time (Figure 7). This effect was greater in networks under the normal condition of incorporating auto-inhibition in the dendrodendritic synapse than from networks that did not. This demonstrates that the dendrodendritic synapse can set up particular temporal patterns with respect to concentration. It has been shown experimentally that varying mixture concentrations can lead to different temporal patterning (Niessing and Friedrich, 2010). This type of processing by the dendrodendritic synapses may be important for signal decorrelation (Cleland, 2010) especially when the firing rate of the cells is normalized (Wick et al., 2010) as we found in our simulations (discussed below).
Gating
Gating of backpropagating action potentials occurs when inhibition delivered on the mitral cell lateral dendrite is strong enough to prevent a spike from propagating more distally. Attenuation of backpropagating potentials has been observed when inducing inhibition on mitral cell lateral dendrites in olfactory bulb slices (Lowe, 2002; Xiong and Chen, 2002). Two reports (Migliore and Shepherd, 2007; Migliore et al., 2010), have described how granule cell clusters could be used to gate backpropagating potentials. The simulations performed here used only two clusters and the spikes backpropagated 100%. In a more complex network with more active clusters connected along a dendrite, spikes may be prevented from fully propagating. While the bulb network may indeed use granule cells in a variety of ways to modulate signals including gating and temporal modulation, as described above, our simulations indicate that long-range synchrony is optimal with fully propagating spikes. The implication is that strong mitral cell synchrony induced through lateral connections predicts an unimpeded communication channel over the relevant lateral dendrites and clusters near to each mitral cell. The corollary is that if gating is observed between two mitral cells then granule cell clusters are probably connected in the middle between them.
Lateral and Recurrent Inhibition
In addition to temporal modulation and gating, the mitral-granule cell circuit has been implicated in providing contrast enhancement through lateral inhibition (Rall et al., 1966; Yokoi et al., 1995; Isaacson and Strowbridge, 1998; Urban, 2002; Aungst et al., 2003; Davison et al., 2003; Shepherd et al., 2007; Arevian et al., 2008). As such, it provides a second and more far-reaching level of contrast enhancement from that delivered by the periglomerular interneurons (Cleland and Linster, 2005; Cleland and Sethupathy, 2006). We have also reported on how particular arrangements of granule cell clusters could be used to laterally inhibit specific targets (Migliore and Shepherd, 2007; Migliore et al., 2010). With this report, we describe how co-activated mitral cells mutually inhibit each other through their lateral interactions, but we found that recurrent- or auto-inhibition led to a normalizing effect on relative spike rates (Figure 6D). This was because while granule cell's spines had correlated membrane potentials, they were not identical and the spines receiving synaptic events from the most active mitral cells were, in turn, those synapses to most frequently generate granule cell inhibition.
Our model supports the finding by Arevian et al. (2008) that as one mitral cell is more and more activated, it will recruit more inhibition on another cell. Figures 6D,G show that as the blue cell is more strongly activated, there is more granule-to-mitral activation on the red mitral cell. However, our results differ from Arevian et al. (2008) showing that regardless of the amount of inhibition delivered onto the red cell, its spiking was largely unchanged. This was because as the blue mitral cell increased its firing, the timing of the inhibitory events onto the red cell shifted more to the red cell's refractory period rendering those events ineffective at modulating the next spike.
This normalizing effect has also been reported in vitro and in vivo (Margrie et al., 2001). Taken with the possible attenuation of backpropagating potentials (Lowe, 2002; Xiong and Chen, 2002), this implies that recurrent or auto inhibition may be quite strong and that the mitral-granule circuit may even operate against one of its predictive roles as a contrast enhancer toward more temporal modulation.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful for support by National Institutes of Health Grant DC 009977 from the National Institute of Deafness and Other Communication Disorders as well as National Institutes of Health Institutional Training Grant T15-LM007056 from the National Library of Medicine. We also thank the CINECA consortium (Bologna, Italy) for access to their 5120-processor IBM Linux cluster, and the DEISA Consortium (www.deisa.eu), co-funded through the EU FP6 project RI-031513 and the FP7 project RI-222919, for granting access to a 40960-processor IBM BlueGene/P within the DEISA Extreme Computing Initiative.
References
Arevian, A. C., Kapoor, V., and Urban, N. N. (2008). Activity-dependent gating of lateral inhibition in the mouse olfactory bulb. Nat. Neurosci. 11, 80–87.
Aungst, J. L., Heyward, P. M., Puche, A. C., Karnup, S. V., Hayar, A., Szabo, G., and Shipley, M. T. (2003). Centre-surround inhibition among olfactory bulb glomeruli. Nature 426, 623–629.
Barlow, H. B. (1959). “Sensory mechanisms, the reduction of redundancy, and intelligence,” in National Physical Laboratory Symposium No. 10, the Mechanisation of Thought Processes (London: Her Majesty's Stationery Office), pp. 535–539.
Bartos, M., Vida, I., and Jonas, P. (2007). Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nat. Rev. Neurosci. 8, 45–56.
Bathellier, B., Lagier, S., Faure, P., and Lledo, P. (2006). Circuit properties generating gamma oscillations in a network model of the olfactory bulb. J. Neurophysiol. 95, 2678–2691.
Buzsáki, G., and Draguhn, A. (2004). Neuronal oscillations in cortical networks. Science 304, 1926–1929.
Cang, J., and Isaacson, J. S. (2003). In vivo whole-cell recording of odor-evoked synaptic transmission in the rat olfactory bulb. J. Neurosci. 23, 4108–4116.
Carey, R. M., Verhagen, J. V., Wesson, D. W., Pirez, N., and Wachowiak, M. (2009). Temporal structure of receptor neuron input to the olfactory bulb imaged in behaving rats. J. Neurophysiol. 101, 1073–1088.
Chen, W. R., Xiong, W., and Shepherd, G. M. (2000). Analysis of relations between NMDA receptors and GABA release at olfactory bulb reciprocal synapses. Neuron 25, 625–633.
Christie, J. M., Bark, C., Hormuzdi, S. G., Helbig, I., Monyer, H., and Westbrook, G. L. (2005). Connexin36 mediates spike synchrony in olfactory bulb glomeruli. Neuron 46, 761–772.
Cleland, T., and Sethupathy, P. (2006). Non-topographical contrast enhancement in the olfactory bulb. BMC Neurosci. 7, 7.
Davison, A. P., Feng, J., and Brown, D. (2003). Dendrodendritic inhibition and simulated odor responses in a detailed olfactory bulb network model. J. Neurophysiol. 90, 1921–1935.
Davison, I. G., and Ehlers, M. D. (2011). Neural circuit mechanisms for pattern detection and feature combination in olfactory cortex. Neuron 70, 82–94.
Destexhe, A., Mainen, Z. F., and Sejnowski, T. J. (1994). An efficient method for computing synaptic conductances based on a kinetic model of receptor binding. Neural Comput. 6, 14–18.
Doucette, W., Gire, D., Whitesell, J., Carmean, V., Lucero, M., and Restrepo, D. (2011). Associative cortex features in the first olfactory brain relay station. Neuron 69, 1176–1187.
Engel, A. K., Fries, P., and Singer, W. (2001). Dynamic predictions: oscillations and synchrony in top-down processing. Nat. Rev. Neurosci. 2, 704–716.
Friedrich, R. W., Habermann, C. J., and Laurent, G. (2004). Multiplexing using synchrony in the zebrafish olfactory bulb. Nat. Neurosci. 7, 862–871.
Galán, R. F., Fourcaud-Trocmé, N., Ermentrout, G. B., and Urban, N. N. (2006). Correlation-induced synchronization of oscillations in olfactory bulb Neurons. J. Neurosci. 26, 3646–3655.
Gire, D. H., and Schoppa, N. E. (2009). Control of on/off glomerular signaling by a local GABAergic microcircuit in the olfactory bulb. J. Neurosci. 29, 13454–13464.
Giridhar, S., Doiron, B., and Urban, N. N. (2011). Timescale-dependent shaping of correlation by olfactory bulb lateral inhibition. Proc. Natl. Acad. Sci. U.S.A. 108, 5843–5848.
Hines, M. L., and Carnevale, N. T. (1997). The NEURON simulation environment. Neural Comput. 9, 1179–1209.
Hines, M. L., Morse, T., Migliore, M., Carnevale, N. T., and Shepherd, G. M. (2004). ModelDB: a database to support computational neuroscience. J. Comput. Neurosci. 17, 7–11.
Isaacson, J. S., and Strowbridge, B. W. (1998). Olfactory reciprocal synapses: dendritic signaling in the CNS. Neuron 20, 749–761.
Kashiwadani, H., Sasaki, Y. F., Uchida, N., and Mori, K. (1999). Synchronized oscillatory discharges of mitral/tufted cells with different molecular receptive ranges in the rabbit olfactory bulb. J. Neurophysiol. 82, 1786–1792.
Kim, D. H., Phillips, M. E., Chang, A. Y., and Willhite, D. C. (2011). Lateral connectivity in the olfactory bulb is sparse and segregated. Front. Neural Circuits 5, 5. doi: 10.3389/fncir.2011.00005
Kistler, W. M., Gerstner, W., and van Hemmen, J. L. (1997). Reduction of the hodgkin-huxley equations to a single-variable threshold model. Neural Comput. 9, 1015–1045.
Koch, C. (2004). Biophysics of Computation: Information Processing in Single Neurons (Computational Neuroscience Series). New York, NY: Oxford University Press.
Laurent, G. (2002). Olfactory network dynamics and the coding of multidimensional signals. Nat. Rev. Neurosci. 3, 884–895.
Laurent, G., Stopfer, M., Friedrich, R. W., Rabinovich, M. I., Volkovskii, A., and Abarbanel, H. D. (2001). Odor encoding as an active, dynamical process: experiments, computation, and theory. Annu. Rev. Neurosci. 24, 263–297.
Linster, C., and Cleland, T. A. (2001). How spike synchronization among olfactory neurons can contribute to sensory discrimination. J. Comput. Neurosci. 10, 187–193.
Lowe, G. (2002). Inhibition of backpropagating action potentials in mitral cell secondary dendrites. J. Neurophysiol. 88, 64–85.
Luna, V. M., and Schoppa, N. E. (2008). GABAergic circuits control input-spike coupling in the piriform cortex. J. Neurosci. 28, 8851–8859.
Lytton, W. W., and Sejnowski, T. J. (1991). Simulations of cortical pyramidal neurons synchronized by inhibitory interneurons. J. Neurophysiol. 66, 1059–1079.
Marella, S., and Ermentrout, B. (2010). Amplification of asynchronous inhibition-mediated synchronization by feedback in recurrent networks. PLoS Comput. Biol. 6, e1000679. doi: 10.1371/journal.pcbi.1000679
Margrie, T. W., Sakmann, B., and Urban, N. N. (2001). Action potential propagation in mitral cell lateral dendrites is decremental and controls recurrent and lateral inhibition in the mammalian olfactory bulb. Proc. Natl. Acad. Sci. U.S.A. 98, 319–324.
McTavish, T. S., Hunter, L. E., Restrepo, D., and Schoppa, N. E. (submitted). Contributions of gap junction coupling and granule cell connectivity to long-range synchrony in the olfactory bulb.
Migliore, M., Hines, M. L., McTavish, T. S., and Shepherd, G. M. (2010). Functional roles of distributed synaptic clusters in the mitral-granule cell network of the olfactory bulb. Front. Integr. Neurosci. 4, 122. doi: 10.3389/fnint.2010.00122
Migliore, M., Hines, M. L., and Shepherd, G. M. (2005). The role of distal dendritic gap junctions in synchronization of mitral cell axonal output. J. Comput. Neurosci. 18, 151–161.
Migliore, M., Inzirillo, C., and Shepherd, G. M. (2007). Learning mechanism for column formation in the olfactory bulb. Front. Integr. Neurosci. 1, 12. doi: 10.3389/neuro.07.012.2007
Migliore, M., and Shepherd, G. M. (2007). Dendritic action potentials connect distributed dendrodendritic microcircuits. J. Comput. Neurosci. 24, 207–221.
Moreno, M. M., Linster, C., Escanilla, O., Sacquet, J., Didier, A., and Mandairon, N. (2009). Olfactory perceptual learning requires adult neurogenesis. Proc. Natl. Acad. Sci. U.S.A. 106, 17980–17985.
Mori, K., Nagao, H., and Yoshihara, Y. (1999). The olfactory bulb: coding and processing of odor molecule information. Science 286, 711–715.
Mori, K., Nowycky, M. C., and Shepherd, G. M. (1981). Electrophysiological analysis of mitral cells in the isolated turtle olfactory bulb. J. Physiol. 314, 281–294.
Niessing, J., and Friedrich, R. W. (2010). Olfactory pattern classification by discrete neuronal network states. Nature 465, 47–52.
Orona, E., Scott, J. W., and Rainer, E. C. (1983). Different granule cell populations innervate superficial and deep regions of the external plexiform layer in rat olfactory bulb. J. Comp. Neurol. 217, 227–237.
Rall, W., and Shepherd, G. M. (1968). Theoretical reconstruction of field potentials and dendrodendritic synaptic interactions in olfactory bulb. J. Neurophysiol. 31, 884–915.
Rall, W., Shepherd, G. M., Reese, T. S., and Brightman, M. W. (1966). Dendrodendritic synaptic pathway for inhibition in the olfactory bulb. Exp. Neurol. 14, 44–56.
Reyes, A. D. (2003). Synchrony-dependent propagation of firing rate in iteratively constructed networks in vitro. Nat. Neurosci. 6, 593–599.
Salinas, E., and Sejnowski, T. J. (2001). Correlated neuronal activity and the flow of neural information. Nat. Rev. Neurosci. 2, 539–550.
Schoppa, N. E. (2006). Synchronization of olfactory bulb mitral cells by precisely timed inhibitory inputs. Neuron 49, 271–283.
Schoppa, N. E., Kinzie, J. M., Sahara, Y., Segerson, T. P., and Westbrook, G. L. (1998). Dendrodendritic inhibition in the olfactory bulb is driven by NMDA receptors. J. Neurosci. 18, 6790–6802.
Schoppa, N. E., and Westbrook, G. L. (2002). AMPA autoreceptors drive correlated spiking in olfactory bulb glomeruli. Nat. Neurosci. 5, 1194–1202.
Shepherd, G. M., Chen, W. R., and Greer, C. A. (2004). “Olfactory bulb,” in The Synaptic Organization of the Brain, ed Shepherd, G. M. (New York, NY: Oxford University Press), 165–216.
Shepherd, G. M., Chen, W. R., Willhite, D., Migliore, M., and Greer, C. A. (2007). The olfactory granule cell: from classical enigma to central role in olfactory processing. Brain Res. Rev. 55, 373–382.
Urban, N. N. (2002). Lateral inhibition in the olfactory bulb and in olfaction. Physiol. Behav. 77, 607–612.
Vreeswijk, C., Abbott, L. F., and Bard Ermentrout, G. (1994). When inhibition not excitation synchronizes neural firing. J. Comput. Neurosci. 1, 313–321.
Wang, X. J. (2010). Neurophysiological and computational principles of cortical rhythms in cognition. Physiol. Rev. 90, 1195.
Wesson, D. W., Verhagen, J. V., and Wachowiak, M. (2009). Why sniff fast? The relationship between sniff frequency, odor discrimination, and receptor neuron activation in the rat. J. Neurophysiol. 101, 1089–1102.
Wick, S., Wiechert, M., Friedrich, R., and Riecke, H. (2010). Pattern orthogonalization via channel decorrelation by adaptive networks. J. Comput. Neurosci. 28, 29–45.
Willhite, D. C., Nguyen, K. T., Masurkar, A. V., Greer, C. A., Shepherd, G. M., and Chen, W. R. (2006). Viral tracing identifies distributed columnar organization in the olfactory bulb. Proc. Natl. Acad. Sci. U.S.A. 103, 12592–12597.
Xiong, W., and Chen, W. (2002). Dynamic gating of spike propagation in the mitral cell lateral dendrites. Neuron 34, 115–126.
Yokoi, M., Mori, K., and Nakanishi, S. (1995). Refinement of odor molecule tuning by dendrodendritic synaptic inhibition in the olfactory bulb. Proc. Natl. Acad. Sci. U.S.A. 92, 3371–3375.
Keywords: olfaction, synchrony, mitral cells, dendritic processing, backpropagation
Citation: McTavish TS, Migliore M, Shepherd GM and Hines ML (2012) Mitral cell spike synchrony modulated by dendrodendritic synapse location. Front. Comput. Neurosci. 6:3. doi: 10.3389/fncom.2012.00003
Received: 20 September 2011; Accepted: 03 January 2012;
Published online: 30 January 2012.
Edited by:
Ken Miller, Columbia University, USAReviewed by:
Brent Doiron, University of Pittsburgh, USACarmen Canavier, LSU Health Sciences Center, USA
Copyright: © 2012 McTavish, Migliore, Shepherd and Hines. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Thomas S. McTavish, Department of Neurobiology, Yale School of Medicine, 333 Cedar Street, New Haven, CT, 06510-3206, USA. e-mail: thomas.mctavish@yale.edu



