
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Comput. Neurosci. , 08 February 2011
volume 5 - 2011 | https://doi.org/10.3389/fncom.2011.00005
This article is part of the Research Topic Structure, dynamics and function of brains: exploring relations and constraints View all 16 articles
Modern anatomical tracing and imaging techniques are beginning to reveal the structural anatomy of neural circuits at small and large scales in unprecedented detail. When examined with analytic tools from graph theory and network science, neural connectivity exhibits highly non-random features, including high clustering and short path length, as well as modules and highly central hub nodes. These characteristic topological features of neural connections shape non-random dynamic interactions that occur during spontaneous activity or in response to external stimulation. Disturbances of connectivity and thus of neural dynamics are thought to underlie a number of disease states of the brain, and some evidence suggests that degraded functional performance of brain networks may be the outcome of a process of randomization affecting their nodes and edges. This article provides a survey of the non-random structure of neural connectivity, primarily at the large scale of regions and pathways in the mammalian cerebral cortex. In addition, we will discuss how non-random connections can give rise to differentiated and complex patterns of dynamics and information flow. Finally, we will explore the idea that at least some disorders of the nervous system are associated with increased randomness of neural connections.
The development of advanced techniques for mapping connectivity in neural circuits and systems, in combination with new computational approaches to network analysis and modeling, is beginning to reveal the architecture and dynamics of brain networks in ever greater detail (Sporns, 2011). Significant progress in electron and light microscopy (Helmstaedter et al., 2008; Lichtman et al., 2008; Arenkiel and Ehlers, 2009), coupled with advanced reconstruction techniques (Anderson et al., 2009; Lu et al., 2009; Jain et al., 2010), will likely yield cellular connection maps of significant portions of a nervous system in the near future. In parallel, advances in classical histology and neuroanatomy (e.g., Palm et al., 2010), as well as the application of non-invasive neuroimaging as a new tool for mapping connections in the living human brain (Johansen-Berg and Behrens, 2009; Raichle, 2009; Hagmann et al., 2010), deliver increasingly detailed maps of neural connectivity at the large scale of brain regions and inter-regional pathways. Jointly, these developments in microscopy and imaging have revived the long-standing goal of charting detailed anatomical maps of neural circuits and systems, including those of the human brain (Sporns et al., 2005).
In parallel to these technological developments, a broad range of new methods for characterizing and modeling network data sets has become available (Brandes and Erlebach, 2005; Newman, 2010). Building on the well-established mathematical framework of graph theory, modern network analysis methods are beginning to be widely applied to structural and functional brain connectivity data sets (Sporns et al., 2004; Reijneveld et al., 2007; Bullmore and Sporns, 2009). For example, such methods allow the extraction of global metrics that capture various aspects of the network’s topological organization, as well as measures for the local contributions of individual nodes and edges to network function (Rubinov and Sporns, 2010). The power of network analysis derives from its applicability to brain connectivity data from different spatial scales, as well as networks derived from anatomical or physiological observations. At the time of writing, virtually all network studies carried out on neural data sets from a variety of species and neural systems have revealed characteristic non-random attributes. The ubiquity of non-random connectivity raises important questions about the origin and functional importance of non-random patterns.
This review focuses mainly on non-random aspects in the organization of mammalian cortex, mapped at the large scale of brain regions and pathways. While most examples are drawn from studies of anatomical connectivity, the relation of anatomical to functional networks will also be addressed. First, after a brief explanation of key terms in graph theory and network analysis, we will turn to a discussion of the meaning of randomness in networks and its manifestation in models and empirical studies of neural circuits. The next two sections are devoted to a survey of various non-random network attributes encountered at the large scale of brain regions and pathways, primarily within the mammalian cortex, and to the putative origin of non-random patterns in brain networks. After discussing the role of non-random connectivity in generating complex neural dynamics, we turn to a brief overview of disturbances of connectivity in brain disease and examine the hypothesis that several common brain disorders are associated with increased randomness in structural and functional brain networks.
Brain connectivity refers not only to a set of anatomical (axonal, synaptic) connections, but also to patterns of dynamic interactions that accompany spontaneous or evoked neural responses (Horwitz, 2003). Anatomical or structural connectivity describes the physical arrangement of connections between circuit elements, be they neurons or brain regions. Functional connectivity captures patterns of statistical dependence between neural elements, measured for example as cross-correlation, covariance, or mutual information. Clearly, structural and functional connectivity have very different spatiotemporal characteristics. Functional connectivity is inherently dynamic and variable, changing on time scales of milliseconds and in ways that reflect changing patterns of endogenous or stimulus-driven processing. Structural connectivity, on the other hand, changes on longer time scales as a result of growth processes, connectional maturation, or plasticity. Structural connections are generally sparse and form a network of directed relationships, while functional connections are often significantly denser and undirected.
Both structural and functional connectivity can be described as a graph or network, essentially a set of nodes and edges, with nodes representing neural elements and edges their structural or functional relations. The construction of such networks from empirical data generally proceeds along several steps (Bullmore and Sporns, 2009), beginning with the definition of nodes and the estimation of a (usually continuous) measure of their pair-wise relationships. At the microscale, nodes may be taken to correspond to individual neurons, while nodes in large-scale networks may be harder to define, requiring sophisticated parcellation strategies to extract functionally coherent brain regions from a continuous brain volume or surface (Cohen et al., 2008; Nelson et al., 2010).
Once a network description has been derived, analytic tools and measures can be used to quantify local and global aspects of the network’s topological organization (Figure 1). Three main classes of metrics are of particular importance in a neurobiological context, assessing the local segregation and global integration of the network, and the relative influence of individual network elements. Measures of segregation capture, for example, the degree to which network elements form distinct clusters or modules. Such modules may correspond to groups of elements that carry out common functions, share information, or engage in coherent neural processing. Measures of integration express the degree to which network nodes can cooperate or transmit information, for example by recording the lengths of the shortest paths that link each node pair. Finally, measures of influence quantify how individual elements are embedded in the network as a whole. Nodes and edges can participate in peripheral or more central roles, depending on their degree of connectedness, or their placement within or between modules. The number of edges attached to each node, the degree, is one of the simplest measures of its influence or centrality.
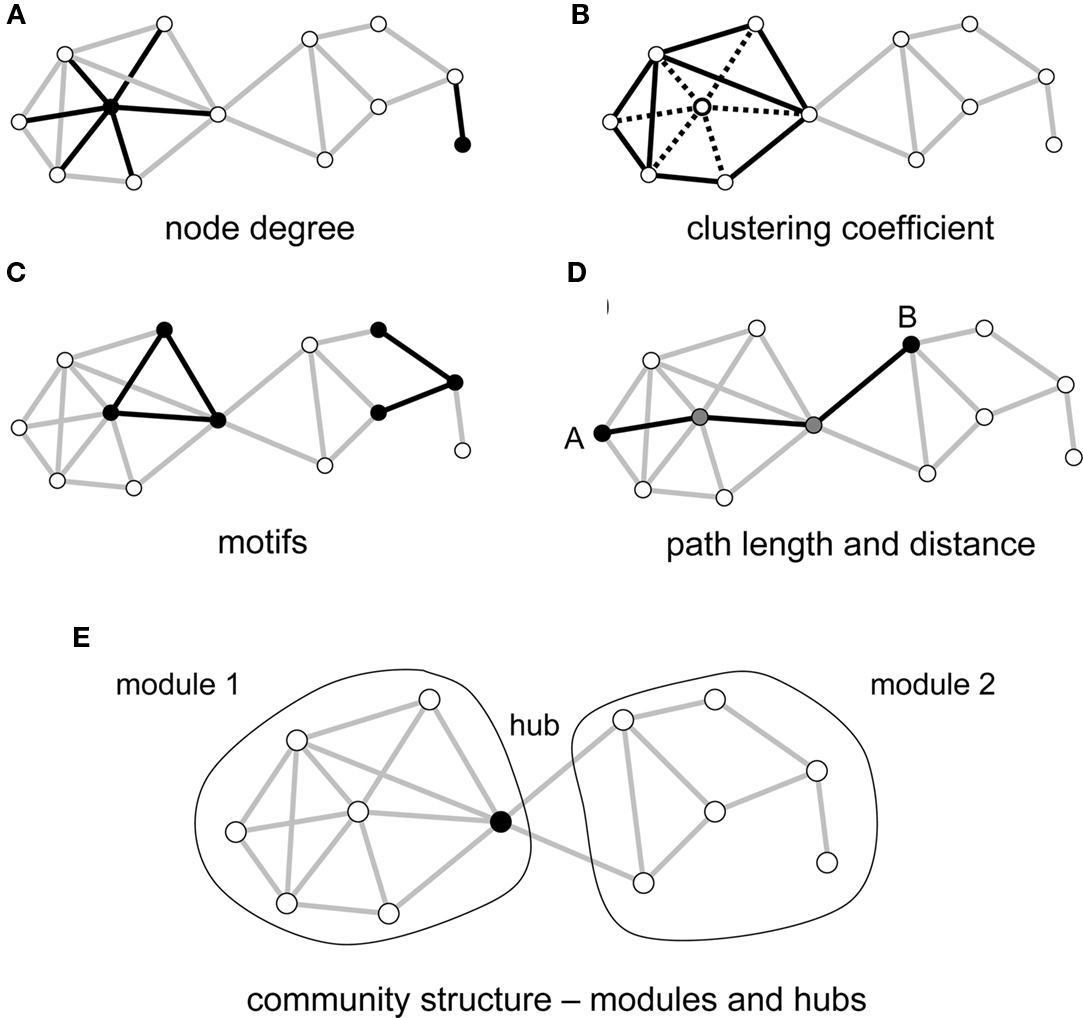
Figure 1. Key graph measures and their definitions. The measures are illustrated in a rendering of a simple undirected graph with 12 nodes and 23 edges. (A) Node degree corresponds to the number of edges attached to a given node, shown here for a highly connected node (left) and a peripheral node (right). (B) The clustering coefficient is shown here for a central node and its six neighbors. These neighbors maintain 8 out of 15 possible edges, for a clustering coefficient of 0.53. (C) Each network can be decomposed into subgraphs of motifs. The plot shows two examples of two different classes of three-node motifs. (D) The distance between two nodes is the length of the shortest path. Nodes A and B connect in three steps, through two intermediate nodes (shown in gray). The average of the finite distances for all node pairs is the graph’s path length. (E) The network forms two modules interconnected by a single hub node.
In most cases, empirically derived brain networks are naturally represented as weighted graphs, i.e., the associations between nodes are measured on a continuous scale. While older studies generally relied on graph methods that require binary edges, modern developments in network science now provide graph metrics that assess network topology in weighted networks (Rubinov and Sporns, 2010). Such weighted network metrics can eliminate the need to apply thresholds or binarize the original empirical data sets, which discards important information about graded interactions. If binary graph metrics are to be used, a range of thresholds should be applied in order to ensure that the resulting graph metrics are robust.
A further distinction, which was alluded to above, is that between directed and undirected graphs. In directed graphs, all edges express a directed relationship between a source and a target, and these types of edges are encountered in networks describing axonal or synaptic connections as well as in networks composed of linkages expressing causal relations between nodes. Undirected networks are found where the empirical measurement of the association between edges does not provide directional information – this is the case for structural networks derived from diffusion imaging or for functional networks derived from cross-correlations among time series. Mathematical definitions of graph metrics often vary for directed versus undirected networks, and some aspects of graph topology, for example hierarchical arrangements of network nodes, may only be accessible if the direction of edges is known.
A network architecture that has received an extraordinary amount of attention over the past decade and is particularly relevant for the brain is the so-called “small world” (Bassett and Bullmore, 2006; Figure 2). Originally investigated empirically in the social sciences, it refers to a type of network that combines high clustering of connections with a short overall path length (Watts and Strogatz, 1998). Clustering expresses the “cliquishness” of local neighborhoods, or the extent to which connected nodes share common neighbors. The path length of the network is computed as the average length of the shortest path between any two nodes. Small-world networks are found in many social, technological, and biological systems, and their non-random attributes are of central importance in neural systems as well. In the brain, small-world architectures arise because of characteristic non-random features of the connection topology, specifically the existence of modules and hubs. Before we turn to a more detailed discussion of these aspects of the small-world architecture of the brain, we need to clarify the terms “random” and “non-random” as they are commonly used in graph theory and neural models.
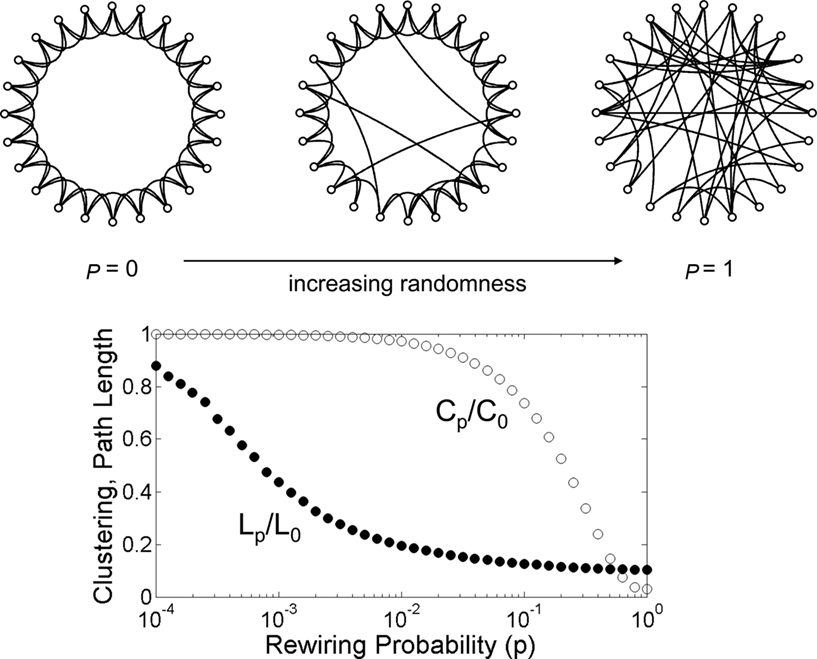
Figure 2. The Watts–Strogatz model of the small world. The network at the upper left hand corner represents a ring lattice with circular boundary conditions. Starting from this configuration connections are randomly rewired with a given rewiring probability p. For p = 0 (no rewiring), the network retains its regular lattice topology. For p = 1 the network is completely random and all lattice-like features have disappeared. Intermediate values of p result in networks that consist of a mixture of random and regular connections. The plot at the bottom shows the clustering coefficient Cp and the path length Lp, both normalized by their values for the regular network (P0, L0). Note that there is a broad range for the rewiring probability p where networks have clustering that is similar to that of the regular network, and a path length that is similar to that of the random network. Within this range, networks exhibit small-world attributes. Data computed following the procedure described in Watts and Strogatz (1998), with networks consisting of 1,000 nodes and 10,000 edges (data points represent averages of 400 rewiring steps).
Random networks are a central concept in classical graph theory. In one of the simplest random graph models, extensively studied by Erdös and Rényi (1960), the graph consists of a given number of nodes n and (undirected single) edges are assigned to node pairs with a fixed probability p. Clearly, for any given value of n and p a great number of different graphs can be constructed. These graphs form an ensemble of random graphs that contain, on average, p(n2 − n)/2 edges, with node degrees that follow a Poisson distribution and a mean degree given by (n − 1)p. The appeal of this simple model derives from the fact that many of the graph’s more complex structural parameters can be computed analytically. Importantly, the Erdös–Rényi random graph model is only one among many possible random models. Following the definition of Newman (2010), random graphs are graphs for which some specific sets of parameters take on fixed values, while other graph characteristics are unconstrained and, in this sense, “random”. For example, in the Erdös–Rényi model, only the number of nodes and the edge probability are fixed, while all other graph metrics can vary. Given the variety of random graph models there is no single network metric or attribute that identifies random graphs as “random.”
It has long been recognized that the Erdös–Rényi random graph model is not a very accurate model of real-world networks. Most real networks deviate in numerous ways from this rather simple random graph model. For example, their nodes often maintain highly clustered connections, and node degrees do not follow a Poisson distribution. Going beyond the particular example of the Erdös–Rényi random graph, it is possible to construct other random graph models that are characterized by non-Poissonian degree distributions or by desired levels of clustering. These types of random graphs form ensembles or populations that can be studied with statistical or computational approaches. Depending on which parameters are fixed, the resulting populations will show, on average, characteristic structural features that are specific for a particular class of random model.
Another important class of graph models is defined by a set of generative mechanisms for “growing” the network. These generative mechanisms often consist of a series of random or stochastic steps, and the growth process itself can have an impact on network properties (Callaway et al., 2001). For example, consider a network that is grown by the gradual addition of one node at a time. Let this node establish edges to already existing nodes with a probability that is proportional to their degree. Put differently, new nodes preferentially connect to already highly connected nodes in the network. This model of “preferential attachment” (Barabási and Albert, 1999) gives rise to power-law degree distributions, frequently encountered in real-world networks. Importantly in our context, generative graph models can incorporate stochastic growth rules and yet yield specific (aggregate) network properties.
Random graph models are of importance in most standard graph analyses, including those of brain networks, as they provide “null models” against which hypotheses about non-random structures can be tested. In real-world networks absolute values of most network metrics can vary widely, depending on the size and density of the graph. To determine their statistical significance, network metrics obtained from an empirical or real-world network should be compared to an appropriately constructed random graph (“null”) model. In one of the most widely used null models, the number of nodes and edges as well as the degrees of each node are preserved and all other graph characteristics, most importantly all aspects of global topology, are free to vary. One way to construct such a graph is by using a Markovian switching algorithm that randomizes edges while preserving node degrees (Maslov and Sneppen, 2002). This random graph model exactly preserves a given number of edges and thus differs from the previously discussed Erdös–Rényi model. In what follows we will refer to graph features as “non-random” if they deviate significantly from those of appropriately constructed populations of random or randomized graphs.
As even this very brief survey of random graph models shows, random graphs (in their most general formulation) do not constitute a single uniform population, nor are they featureless constructs that lack distinctive attributes. Rather, their attributes are specific for each random model, defined by fixing specific graph parameters and letting others vary freely, or by growing graphs in a stochastic process that follows specific generative rules. Thus, in the present context it might be more appropriate to define the term “random graphs” in relation to their mode of construction, since the term is associated less clearly with any particular structural attribute or lack of attribute. This realization is important as we consider the concept of “random graphs” in neurobiology.
The idea that at least some aspects of the synaptic connectivity of the brain result from random or stochastic processes has a long history in neuroscience (e.g., Tuckwell, 1989). A set of ideas that became influential around the middle of the twentieth century (e.g., Turing, 1948) placed great importance on learning processes to sculpt adaptive and efficient cognitive architectures from an essentially random substrate of neural connectivity. Neural connections were taken to form “random graphs,” with learning and experience carrying the burden of carving patterns corresponding to mental representations. Consequently, many models of neural circuits incorporated random or stochastic mechanisms. Various types of statistical neuroanatomical models were constructed from available experimental data on the number, density, and spatial distribution of neuronal cell types; the projections and arborizations of axons; the orientation and branching of dendrites; and from the probabilities and densities of synapses linking specific cell types.
Anatomical studies carried out in the 1950s suggested that neurons in the cerebral cortex and other parts of the brain, including the cerebellum, established synaptic connections following statistical rules that depended on spatial proximity and distance. Empirical work by Sholl (1953, 1955) and statistical analyses by Uttley (1955) provided important early insights into the important role of physical distance for determining connection probabilities. Building on this work, Beurle (1956) constructed mathematical models of population activity arising from “random masses” of neurons. Beurle contrasted the notion of specified wiring, as might be found for instance in a computer, with the apparently large role of randomness in establishing connections in neural tissue. Despite their microscopically random construction, Beurle’s models were capable of producing macroscopically organized spatiotemporal patterns such as traveling waves. In a similar vein, Grenander and Silverstein (1977) constructed large models of randomly connected neural networks and demonstrated that, as network size increased, global network structure followed a “law of large numbers.” According to the model, microscopic variations in a population of organisms due to random neural connectivity did not impact global network measures, for example the spectrum of eigenvalues characterizing the connectivity matrix. These models represent early example of how a set of stochastic generating mechanisms can yield networks and network dynamics with characteristic global attributes.
More recent studies of anatomical patterns and physiological interactions of different neuronal cell types in neocortex have helped to define statistical models of canonical microcircuits (Binzegger et al., 2004, 2009). The circuits are based on empirical data on cell type compositions and densities in cortical layers and their mutual connection probabilities. Thus, they describe characteristic patterns of “average connectivity” that can inform dynamic models of local (Kremkow et al., 2007) or large-scale cortical dynamics (e.g., Izhikevich and Edelman, 2008). Canonical microcircuit models combine non-random attributes related to cell layers and types with random connectivity governed by local connection probabilities. Their statistical description serves as a blueprint for a common computational “module” that is iterated over much of neocortex, possibly replacing the older notion of anatomically discrete cortical columns (Da Costa and Martin, 2010). Their linkage through long-range projections into large-scale systems gives rise to additional non-random topological features and more complex computational capacities.
Early analyses of comprehensive maps of mammalian cortical regions and their interconnections revealed a number of non- random attributes, including high proportions of reciprocal pathways and a propensity for neighboring cortical regions to be anatomically connected (Felleman and van Essen, 1991; Young, 1992). Thus, the spatial profile of large-scale inter-regional pathways is reminiscent of the distance-dependent distribution of synaptic contacts in neuronal microcircuits. But spatial distance alone does not account for the observed pattern of inter-regional pathways. Scannell et al. (1995) found that patterns of cat cortical connectivity generated on the basis of simple nearest-neighbor and next-door-but-one models could only account for a fraction of the existing pathways. These initial results suggested that network attributes other than spatial distance significantly contribute to the distinct topological features of large-scale structural networks. This point was reinforced by Costa et al. (2007) who confirmed that spatial distance alone was insufficient to reconstruct the connection pattern of the primate cerebral cortex and demonstrated that, instead, similarities in topological features provided more accurate prediction.
Mounting evidence points to modularity as one of the most consistent non-random attributes of large-scale structural and functional networks (for a recent review see Meunier et al., 2010). Modularity refers to the existence of clusters or “network communities” whose constituent brain regions are more densely connected to each other than to regions in other modules. It is important to underscore that modular networks constitute a subset of networks with spatially non-uniform connectivity profiles that reflect increased proportions of short connections. For example, lattice-like or “regular” networks contain short connections (and have high clustering) but are non-modular. The Watts–Strogatz small-world model (Watts and Strogatz, 1998) arises from an interpolation between fully random and fully regular networks but does not contain distinct modules or communities (see Figure 2).
Most extant studies of brain networks have employed a variant of a topological modularity metric developed by Mark Newman (Newman and Girvan, 2004; Newman, 2006). Given a partition of the network into non-overlapping modules, the metric expresses the difference between the density of within-module edges that is actually observed and the density expected by chance. The modularity of a network is defined by the partition that maximizes the modularity metric. Several efficient search algorithms for identifying an optimal module partition using the Newman metric have been described (e.g., Blondel et al., 2008). It is worth noting that the Newman metric can exhibit different degrees of sensitivity at different levels of edge density and module sizes (Fortunato and Barthelemy, 2007), and that numerous other modularity metrics and algorithms exist (Fortunato, 2010). A variant of the Newman metric that operates on fully connected and weighted networks, including negative edges, has recently been proposed.
The existence of modules is generally associated with numerous other non-random network features – high clustering and short path length (jointly representing the two main ingredients of the small-world architecture), high efficiency, an overabundance of specific classes of network motifs, and the appearance of specialized classes of nodes constituting network hubs. Graph analyses of the wiring diagram of the worm Caenorhabditis elegans revealed small-world features (Watts and Strogatz, 1998) as well as non-random distributions of three-node motifs (Milo et al., 2002). Similar analyses performed on connectivity matrices for macaque and cat cortex also showed high clustering and short path length (Hilgetag et al., 2000; Sporns et al., 2000; Figure 3), characteristic motif frequencies (Sporns and Kötter, 2004) and the existence of highly connected and highly central hub regions (Sporns et al., 2007). In several cases, these non-random structural features could be related to functional or physiological aspects. For example, structural modules in macaque visual cortex (Hilgetag et al., 2000) and cat cortex (Hilgetag and Kaiser, 2004) were found to correspond closely to known groupings of functionally related brain regions. Hub nodes identified on the basis of graph analysis (Sporns et al., 2007) were previously described as multimodal or transmodal association regions, a functional classification that is congruent with their topological centrality.
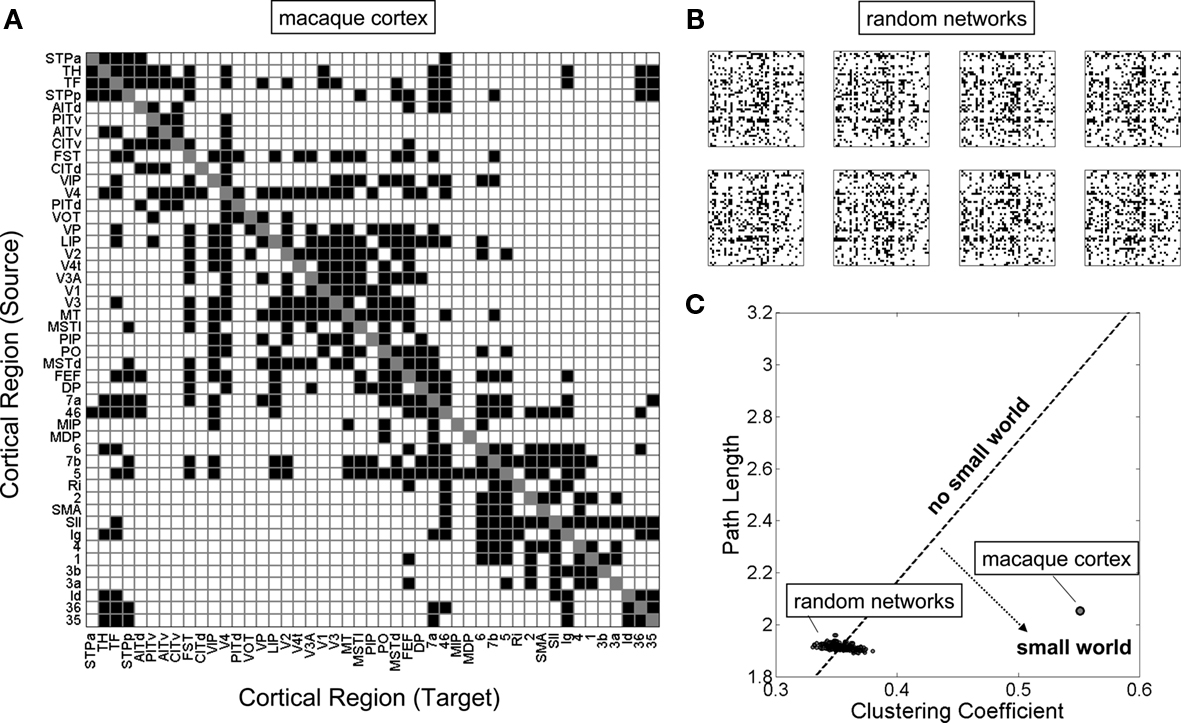
Figure 3. The small-world topology of the macaque neocortex. (A) A structural connectivity matrix of 47 regions of macaque visual and somatomotor cortex, described in detail elsewhere (Sporns et al., 2007). Connections that are present are shown as black squares, absent connections are shown as white squares. (B) A sample of eight random networks with equal number of nodes and edges, and preserved node degrees. These networks were constructed by thoroughly randomizing the network shown in (A) using a random switching algorithm (Maslov and Sneppen, 2002). (C) Clustering coefficient and path length for a population of 250 random networks as well as the real macaque cortex. Networks along the dotted line would have clustering and path length exactly proportional to the random population, and therefore a small-world index of 1 (“no small world”). Networks that fall into the region to the lower right have far greater clustering than path lengths, relative to the random population, and thus a small-world index that is much greater than 1 (“small world”).
The use of non-invasive magnetic resonance imaging now allows graph analysis to be carried out on structural brain networks recorded in the living human brain. Small-world attributes (He et al., 2007) and distinct structural modules (Chen et al., 2008) were demonstrated in a group-averaged regional connection matrix derived from gray matter thickness correlations. Structural modules largely corresponded to functionally specialized clusters of regions in distinct sensory and motor domains. The use of diffusion imaging and tractography has allowed more extensive studies of human brain networks at multiple spatial scales and in individual participants (Hagmann et al., 2010). Diffusion imaging reliably detects major white matter pathways (Schmahmann et al., 2007) but also suffers from limited sensitivity, particularly in regions with complex fiber architecture, and an inability to infer the direction of axonal projections. Iturria-Medina et al. (2007, 2008) reported numerous non-random features including robust small-world attributes, non-random motif distributions, and the existence of highly central hub regions in a cohort of healthy volunteers. Hub regions included the precuneus, the insula, as well as the superior parietal and superior frontal cortex, all of which represent multimodal association regions of the cerebral cortex. Several of these regions were also identified in other studies employing diffusion imaging and graph analysis (e.g., Gong et al., 2009).
Hagmann et al. (2008), in an analysis of fully weighted structural connectivity sampled at high spatial resolution, confirmed numerous non-random attributes of human cortical networks, including high clustering and short path length, and the existence of modules and hub regions. In addition, the study reported positive assortativity indicating that high-degree nodes had a tendency to cluster together. Consonant with this observation, further analysis revealed a core of highly central and mutually interconnected cortical nodes located in the posterior cingulate cortex and precuneus. These hub nodes linked to several distinct structural modules comprising frontal, temporoparietal, and medial cortical regions. The positive assortativity found in human cortical networks confers a degree of resilience as it is more difficult to disintegrate such a network by attacking individual highly connected hub nodes. The finding of positive assortativity in cortex contrasts with the negative assortativity reported earlier in C. elegans (Newman, 2002), a difference that may reflect differences in scale (areas versus neurons) or topological organization.
Highly interconnected hub nodes are also found in other large-scale data sets. Support for the idea of a highly central “association module” comes from analyses of macaque cortex where global connector hubs in parietal and prefrontal cortex were found to be more strongly interconnected than predicted by chance (Sporns et al., 2007). A detailed series of analyses carried out on the large-scale connection matrix of cat cortex originally collated by Scannell et al. (1999) provides additional evidence for the presence of a distributed but highly interconnected set of hub regions (Zamora-Lopez et al., 2010). These regions form an integrated central module whose topological position also plays an important role in cortical synchronization (Gomes-Gardenes et al., 2010). The authors suggest that this central module may perform important functions in the integration of multisensory information and higher-order processing.
Much additional insight into the modularity of the human brain is delivered by functional imaging, particularly of spontaneous resting-state neural activity, where at least some modules have been found to correspond to subnetworks that have differential involvement in different cognitive functions (e.g., Nelson et al., 2010). An in-depth review of functional modules and their spatial distribution is beyond the scope of the current article (see instead Meunier et al., 2010). We note that while structural and functional connectivity refer to two very different aspects of brain networks, they are related in that structural connections shape and constrain patterns of functional interactions and dynamic coupling (Honey et al., 2010). Because of this close relationship between structure and function in brain networks the distribution and integration of specialized information across the brain is crucially dependent on the non-random topology of anatomical connections, a point to which we will return shortly.
The existence of non-random structural attributes of brain networks raises the question of their origin and functional significance. This section attempts to address this question in the context of spatial embedding and wiring economy. The idea that the structure of neurons and neuronal circuitry is shaped by the conservation of resources such as space and material was already clearly articulated by Ramon y Cajal in 1891 (Cajal, 1995) and has since received much empirical support. A broad range of factors contribute to the cost of neuronal communication (Laughlin and Sejnowski, 2003), including wiring length and/or volume, axonal conduction delays and the timing of signal propagation, myelination, and the metabolic cost of neural activity and spike propagation. In general, communication cost increases with increasing spatial separation between neuronal elements. Another important aspect concerns the cost incurred by developmental mechanisms needed to build a nervous system, including the establishment of physical connectivity through growth mechanisms. Along any of these dimensions of neuronal economy, random networks of the Erdös–Rényi type discussed earlier carry extremely high cost, since their topology is completely unrelated to physical space. Hence, they are all but impossible to physically wire within the spatial and metabolic constraints of real nervous systems, and they cannot be generated during development given the way morphological processes unfold in space and time (and thus they cannot evolve). This realization suggests the hypothesis that at least some of the non-random attributes of brain connectivity currently realized in biological nervous systems trace their origins to insurmountable constraints of development or evolution.
Spatial embedding was recognized long ago as a major ingredient for determining neural wiring. Anatomical data on neurons in the mammalian neocortex show that connection densities generally fall off with distance or, put differently, the probability of two neurons to be synaptically connected decreases with their spatial separation (Braitenberg and Schüz, 1998; Hellwig, 2000). The important role of physical distance for non-random features of cortical synaptic connectivity has since been documented in a great number of anatomical and physiological studies. Network analysis was deployed in recent physiological recordings of cell pairs in mouse cortex (Song et al., 2005). These recordings confirmed the distance-dependence of connectivity and added important additional information about non-random distributions of synaptic weights. While these distance-dependent effects have strong experimental support, more recent physiological studies of microcircuits also suggest that distance alone is insufficient to explain the interactions of cortical neurons. Instead, it appears that cells are organized into spatially interleaved and functionally specialized subnetworks (Ohki et al., 2005; Yoshimura et al., 2005). First results from dense EM reconstructions of neural tissue also indicate that statistical descriptions based on cell types and distances do not fully account for observed patterns of synaptic connectivity (Mishchenko et al., 2010).
The neuronal layout and wiring of C. elegans has been closely examined in the context of neuronal economy. Even non- quantitative examination of the physical arrangement of neurons and connections suggested that spatial proximity is a major factor in determining synaptic connectivity (White, 1985), an idea that was pursued further in several studies aiming to relate physical placement of circuit elements and wiring minimization (Cherniak, 1995). A detailed analysis at the level of individual neurons and connections (Chen et al., 2006) revealed that the actual layout of the C. elegans nervous system indeed approximates an optimal layout that maintains connection topology while minimizing neuronal wiring. This supports the notion that wiring minimization can account for much (though not all) of the physical arrangement of neurons and connection in C. elegans. Interestingly, places in the connection matrix where wiring minimization is violated can be shown to relate to important functional demands, such as the presence of long-range connections that connect remote regions of the worm’s nervous system (Ahn et al., 2006; Chen et al., 2006).
This last point was examined in more detail by Kaiser and Hilgetag (2006) in a re-analysis of neuronal wiring data from C. elegans as well as large-scale connectivity of macaque cortex. Both networks could be spatially rearranged (while maintaining connection topology) such that the total cost of wiring decreased significantly below their actually observed values. Most of the excess wiring cost was due to the existence of long-range connections that are essential for maintaining functional integration, as measured by short path length or high efficiency. These results suggest that wiring appears to be conserved but that wiring economy alone is insufficient to explain observed patterns of brain connectivity. In addition to conserving neuronal communication cost, the topology of brain networks incorporates important non-random attributes such as small-world organization that ensure its computational efficiency and functional integration (Figure 4).
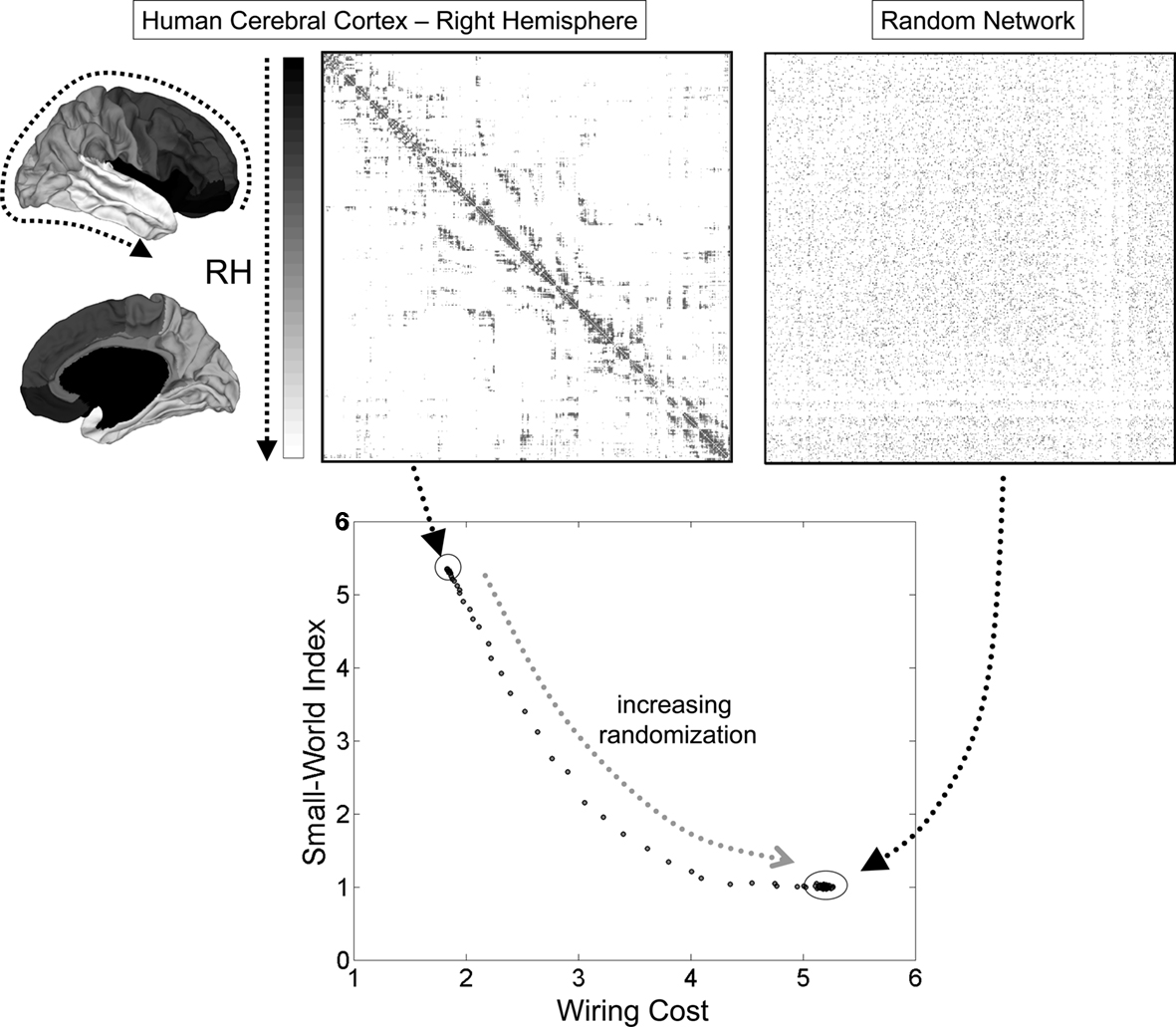
Figure 4. Small-world topology and wiring cost in the human cerebral cortex. Connection matrices at the top correspond to the empirically determined connection topology of the right hemisphere of the human cerebral cortex, as reported in Hagmann et al. (2008). The anatomical position of the nodes on the cortical surface is indicated by a gray scale at the left of the matrix. The plot at the right shows an example of a randomized network with equal number of nodes, edges, and equal node degrees. The plot at the bottom shows the small-world index and the wiring cost for the empirical network and a population of 100 randomized networks. Only the empirical network has a small-world index that is much greater than 1, due to high clustering and a path length that is approximately equal to the random case. Progressive randomization (curve) reduces the small-world index while at the same time incurring greater wiring cost. Wiring cost is approximated as the sum of all the Euclidean distances between connected brain nodes. The small-world index is the ratio of the normalized clustering coefficient and the normalized path length (both relative to randomized networks).
Modularity contributes to wiring economy. Topologically defined modules often comprise neural elements that are spatially close, e.g., brain regions that occupy adjacent territory on the cortical surface. Consequently, intra-module connections tend to be short, while connections linking modules to each other often extend over longer distances. Recent analyses of structural connectivity data sets from C. elegans and human cortex suggest that these networks are embedded in physical space in a manner that is “cost-efficient” (Bassett et al., 2010). Cost-efficiency refers to an organization characterized by economically arranged modules while preserving a highly efficient global connection topology. Bassett et al. (2010) also provided evidence that structural brain networks, including that of the human cerebral cortex (Hagmann et al., 2008), contain multiple levels of modules that are hierarchically arranged.
In addition to constraints on economy and efficiency, a host of other factors may have played an additional role in the appearance of non-random network attributes. As discussed earlier, the existence of modules in structural brain networks represents an important topological feature that has consequences for other aspects of topology, including clustering and motifs. More generally, the modular organization of many biological systems may also support their robustness and their capacity for evolutionary adaptation and innovation (Kirschner and Gerhart, 2005; Wagner et al., 2007). Furthermore, modularity of control architectures appears to be favored in the presence of a variable and partly unpredictable environment (Lipson et al., 2002; Kashtan and Alon, 2005). Finally, allometric scaling relations between components of an evolving nervous system, for example the relation between gray and white matter volume in brains of different sizes (Zhang and Sejnowski, 2000), place additional demands and constraints on patterns of connectivity that are likely associated with and, according to Bassett et al. (2010) may be explainable by, its non-random topology.
It is perhaps surprising to realize the extent to which the structure of brain connectivity is influenced by considerations of neuronal economy and cost, the spatial arrangement of neuronal elements, and the simple requirement that functioning nervous systems must be able to develop and evolve. Random networks whose topology does not make reference to physical space, incurs excessive cost, or precludes development or evolvability, simply cannot exist as part of biological organisms. While the non-random nature of brain networks is currently best documented at the large scale, the conservation of space, material, and energy likely plays a role across all scales of neuronal organization.
While economy is a central constraint for network topology, it must be reconciled with high functional performance, including high efficiency of information integration and the capacity for sustaining diverse and complex dynamic states. We already noted the importance of non-random network attributes such as modules and hubs for shaping the functional organization of the mammalian cortex. In this section, we expand upon this idea and argue that the non-random (small-world) architecture of anatomical brain networks plays a crucial role in constraining patterns of neuronal interactions, and in enabling diverse neural dynamics and high complexity. The term “complexity” is used here to indicate a type of neural dynamics that combines spontaneous variation with some degree of regularity – recurrent and diverse patterns that are shaped by the underlying neural architecture.
Numerous anatomical and physiological studies of the visual cortex have revealed the existence of functionally specialized domains, organized as distinct neuronal populations at the level of columns or minicolumns (Mountcastle, 1997; but see Da Costa and Martin, 2010). For example, patchy distributions of anatomical intra-regional connections extending over several millimeters correlate with populations of cells that exhibit similar physiological specificity (e.g., Bosking et al., 1997). These specific anatomical connections likely shape spontaneous and evoked activity, during which communities of neurons that share similar feature selectivity tend to become coherently active (Kenet et al., 2003). The dynamic efficacy of anatomical connections and their capacity to induce co-operativity among neurons can be modified on short time scales, for example by adjusting levels of inhibition and firing thresholds (Binzegger et al., 2009). This raises the interesting possibility that the non-random topology of canonical microcircuits can be dynamically adapted to different processing demands, for example by tuning the balance between strong and weak connections, which in turn affects small-world attributes such a local clustering.
Numerous empirical and computational studies have examined the role of anatomical connections in neuronal synchronization. Local and long-range synchrony depends critically on the patterning of corresponding axonal connections (Buzsáki et al., 2004), and the topology of neural circuits plays a major role in shaping emergent network dynamics (Wang, 2010). The central role of connection topology in determining synchronization has been extensively investigated in computational studies (e.g., Arenas et al., 2006; Zhou et al., 2007; Müller-Linow et al., 2008). Of particular interest is the role of non-random connectivity in creating “limited sustained activity” within and across modules (Kaiser and Hilgetag, 2010). Such activity consists of spontaneous or evoked network dynamics that neither dies out too quickly nor spreads explosively across the entire brain, and its generation is facilitated by connection topologies that incorporate hierarchical modularity.
Non-random features of local circuits such as clustering or motifs are likely to impact on the variety and diversity of neural dynamics. An attractive hypothesis suggests that dynamics in local circuits gives rise to a “computational reservoir” that can be molded by synaptic plasticity and support a variety of functional outcomes (Maass et al., 2002). Computational explorations of this idea suggest that the capacity of such a system to encode rich input–output relationships depends on the diversity of its intrinsic dynamics, and may become maximal in a dynamic regime that is poised between randomness and regularity (Bertschinger and Natschläger, 2004). In this regime, the network is able to respond uniquely to new inputs, while at the same time maintaining a degree of memory for recent stimulation history. Similar to the concept of limited sustained activity mentioned earlier, a diverse response repertoire is seen as an important ingredient of flexible and adaptive neural computation, possibly indicative of “critical” brain dynamics (Chialvo, 2010).
Highly structured non-random patterns of neural activity are encountered not only among individual neurons, but also at the level of the large-scale dynamics of the human brain. The covariance structure of spontaneous neuronal activity displays characteristic patterns, for example in the inter-regional cross-correlations of fluctuations in the blood-oxygenation-level-dependent (BOLD) response recorded during the brain’s “resting-state” (Raichle et al., 2001; Greicius et al., 2003; Fox et al., 2005). Several studies have shown that these patterns of resting-state functional connectivity are related to underlying patterns of structural connectivity (Koch et al., 2002; Vincent et al., 2007; Hagmann et al., 2008; Damoiseaux and Greicius, 2009; Honey et al., 2009). Recording structural and functional connections in the same cohort of participants allows direct comparison of their corresponding network representations (Honey et al., 2009). The presence and strength of a structural connection between two nodes was highly predictive of the presence and strength of functional connections at the same node pair. However, because functional connections are statistical constructs and can take on significant positive or negative values among nodes linked by indirect structural connections, the reverse prediction (of structural from functional connections) was found to be impractical.
Several computational studies of resting-state brain dynamics have demonstrated how large-scale non-random pattern of structural connections can generate functional connectivity (Honey et al., 2007; Ghosh et al., 2008; Deco et al., 2009). All studies point to the importance of structural connectivity for shaping functional relationships. While the distinctive community structure of the brain is reflected both in anatomy and dynamics, it is important to note that structural and functional modules do not always exactly correspond – functional connectivity is inherently statistical and time- as well as state-dependent in nature and therefore should not be expected to conform to the relatively stable “skeleton” of anatomical pathways. Dynamic modulations of the efficacy of anatomical pathways or exogenous perturbations of sensory inputs induce different functional networks to become active in different contexts. A comparison of task-evoked and resting-state regional co-activations suggests that both types of brain dynamics can be decomposed into a common repertoire of functional networks (Smith et al., 2009).
Recording and analysis of BOLD fluctuations at increasing time resolution is beginning to reveal the fine temporal structure of spontaneous brain dynamics. Resting-state functional connectivity, often represented as a single and static pattern of correlations, exhibits non-stationary fluctuations that reflect a temporal sequence of subpatterns (Chang and Glover, 2010). As a result functional correlations between brain regions exhibit rapid variations across time. Such variations are also observed in computational models (Honey et al., 2007) where they are partially driven by fluctuating metastable synchronization among regions due to cooperative dynamic interactions. How rapid fluctuations arise in the spontaneous dynamics of the human brain is as yet unknown.
These fluctuations in dynamic couplings greatly increase the dynamic repertoire of neuronal states. A large repertoire of diverse states may be beneficial to an organism as it contributes to its capacity to process signals from an environment that can only be partially predicted. The relationship between structural connectivity and rich and diverse neural dynamics continues to be relatively unexplored. Some computational studies suggest that non- random attributes of structural connectivity discussed earlier, such as modularity and small-world architecture, give rise to complex patterns of neural dynamics (Tononi et al., 1994). For example, the combination of high clustering and short path length encountered in small-world networks promotes the coexistence of segregation and integration of neural information, a key ingredient of neural complexity (Tononi et al., 1994; Sporns et al., 2000; Figure 5). Segregation and integration jointly capture different aspects of the way neural information is distributed and integrated in a network. High segregation involves the existence of many specialized communities that maintain coherence amongst their members, but relative independence between groups. High integration involves the flow if information between all elements of the network, both within and between communities. Viewed from a network perspective, the small-world attributes of clustering and efficiency, embodied in the brain’s module/hub architecture, jointly enable information specialization and integration. Non-random attributes of the structural connectivity of the human brain may thus have significant impact on the distribution and flow of information in neural circuits.
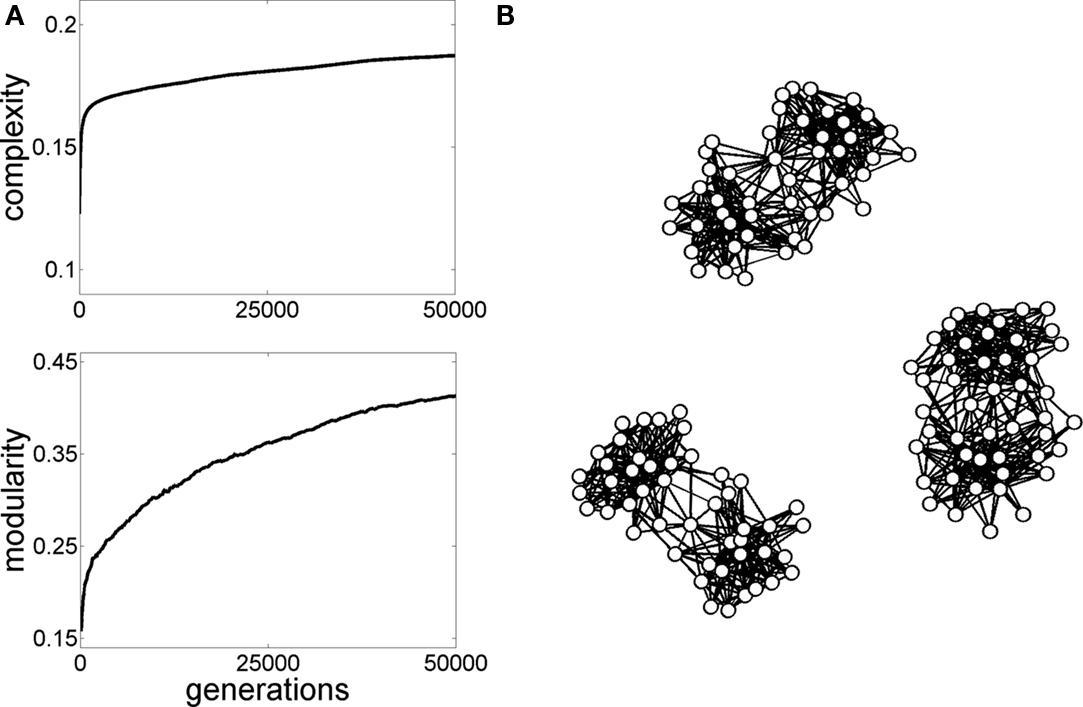
Figure 5. Graph evolution for neural complexity. The initial population of graphs in generation 1 consisted of 10 randomized graphs similar to the ones shown in Figure 3B, with 47 nodes and 505 edges. Simple linear dynamics (Galán, 2008) was run on these graphs and the graph generating the highest neural complexity (Tononi et al., 1994) was selected and copied forward to the next generation, as described in Sporns et al. (2000). Then, small random “mutations” were introduced in the graph’s “offspring” and the process of selecting for complex dynamics was continued for a total of 50,000 generations. (A) Plots show the increase in complexity and a parallel increase in modularity. (B) Examples of graphs obtained at the end of the simulations exhibit non-random topologies, including high modularity and hub nodes.
What happens if the balance between functional segregation and integration is perturbed? There is mounting evidence that brain disorders are associated with characteristic disturbances of large-scale structural and/or functional connections. In the past, these disturbances have been described as localized changes in the functioning of individual brain regions, or in the altered integrity, connection strength or efficacy of specific pathways. However, in an integrated network such as the brain, local disturbances do not remain isolated from the rest of the system. Increasingly, brain connectivity studies report distributed system-wide effects on the global topology of brain networks associated with specific disease states. Network approaches are beginning to reveal consistent patterns of abnormal network organization in patient populations (Bassett and Bullmore, 2009), for example in people with Alzheimer’s disease (AD), autism, or schizophrenia. Many of these studies use resting-state functional connectivity to chart patterns of dynamic correlations among brain regions (Fox and Greicius, 2010). While the nature of network disturbances varies between conditions, a number of reports indicate that brain disorders are associated with changes in the balance between randomness and regularity in large-scale topology.
A common neurodegenerative disorder, AD manifests itself in severe dementia and profound loss of memory. Several studies have reported disturbances of large-scale connection patterns associated with the condition. Magnetoencephalographic recordings of spontaneous brain activity in people with AD and in healthy controls revealed characteristic differences in local and global functional network topology (Stam et al., 2007, 2009). Resting-state fMRI recordings also showed that the small-world structure of functional brain networks was altered in people with AD. AD patients exhibited network attributes such as significantly reduced clustering (Supekar et al., 2008) that are consistent with an overall increase in randomness. The altered pattern of functional connectivity appeared to primarily result from specific disruptions of connectivity at highly connected hub nodes rather than random node failure (Stam et al., 2009). The latter point is consonant with the observation that the locations of cortical hubs and areas of high amyloid deposition in AD are highly correlated (Buckner et al., 2009).
Autism is a neurodevelopmental disorder characterized by abnormal social interactions and communication patterns, as well as a tendency toward stereotypic behavior. Several lines of evidence, including the application of diffusion imaging approaches (Keller et al., 2007) and functional connectivity studies (Just et al., 2007), suggest that autism is associated with disorganized white matter pathways. A recent study of resting-state functional connectivity suggested that autism was associated with a shift toward randomness in the temporal patterns of endogenous fluctuations in the BOLD signal (Lai et al., 2010). This shift was estimated by computing the Hurst exponent, a measure of the temporal ordering and randomness of time series data, and exhibited regionally specific patterns of disruption, with particularly strong differences in default mode and hub regions of the brain.
Resting-state fMRI studies in people with attention-deficit/hyperactivity disorder (ADHD) have demonstrated reduced functional connectivity among regions of the default mode network, particularly among regions along the cortical midline including the anterior and posterior cingulate cortex (Castellanos et al., 2008). More global network-wide effects of ADHD are beginning to be explored through network analyses of functional connectivity (Konrad and Eickhoff, 2010). One such study showed disruptions of the global organization of functional connectivity in children with ADHD (Wang et al., 2009), with some regions exhibiting significant alterations in their local and/or nodal efficiency. Interestingly, Wang et al. propose that the observed patterns suggest a shift, not toward increased randomness, but rather increased regularity in the global network.
It has long been hypothesized that schizophrenia is associated with a disconnection (or dysconnection) of long-range pathways and neurocognitive networks (e.g., Friston and Frith, 1995; Tononi and Edelman, 2000). Network analysis of resting-state functional connectivity revealed diminished levels of connectivity across many parts of the brain as well as specific alterations in small-world measures associated with the severity of the clinical condition (Zhou et al., 2007; Liu et al., 2008). These alterations result in a less integrated pattern of functional connectivity, bound together by hub regions that are less highly connected and less central than those of healthy participants (Lynall et al., 2010), a pattern also seen in structural brain networks (Van den Heuvel et al., 2010). Within the default mode network, functional connectivity was found to be increased, with the degree of hyperconnectivity in individual patients being highly predictive of the severity of their psychopathology (Whitfield-Gabrieli et al., 2009). Electrophysiological recordings support the view that schizophrenia is associated with disturbed small-world connectivity. Rubinov et al. (2009) suggested that schizophrenia is characterized by a randomization of connections, an alteration of the brain’s community structure that results in an imbalance of segregation and integration and reduced centrality of cortical hubs.
In summary, converging evidence suggests that several brain disorders are associated with specific changes to large-scale structural and functional connectivity that result in a disease-specific “mis-wiring diagram.” At least for some of these disorders mis-wiring of connections might result in an increased randomization of the overall network topology. If the emerging view of common brain disorders as “network diseases” turns out to be correct, it might offer new opportunities for the objective diagnosis of these disorders, and potentially even for future therapeutic intervention. Network metrics may represent candidate “biomarkers” that allow a new objective classification of disorders, and a basis for charting disease progression and prognosis.
Random networks have played an important role in the history of graph theory, and they have contributed deep conceptual insights across diverse scientific disciplines.
However, modern circuit mapping and neural recording studies unequivocally show that the brain is not a random network. Instead, at different levels of scale, network studies have identified a number of specific non-random structural attributes, particularly the existence of network communities interlinked by hub regions. The modular small world of brain networks simultaneously promotes their economy and efficiency, by enabling their physical realization at low cost of wiring volume and metabolic energy, while also allowing efficient information flow. Non-random structure leads to the emergence of complex dynamics, generating a diverse repertoire of brain states that are differentially engaged during ongoing neural activity as well as in response to stimulation and task demands. Future studies, informed by increasingly refined network mapping and analysis, will likely reveal additional non-random attributes of brain networks and thus further expand our understanding of how the non-randomness of the brain supports robust and flexible neural computation.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author gratefully acknowledges support from the JS McDonnell Foundation.
Ahn, Y. Y., Jeong, H., and Kim, B. J. (2006). Wiring cost in the organization of a biological neuronal network. Physica A 367, 531–537.
Anderson, J. R., Jones, B. W., Yang, J. H., Shaw, M. V., Watt, C. B., Koshevoy, P., Spaltenstein, J., Jurrus, E., Uv, K., Whitaker, R. T., Mastronarde, D., Tasdizen, T., and Marc, R. E. (2009). A computational framework for ultrastructural mapping of neural circuitry. PLoS Biol. 7, e1000074. doi: 10.1371/journal.pbio.1000074
Arenas, A., Díaz-Guilera, A., and Pérez-Vicente, C. (2006). Synchronization reveals topological scales in complex networks. Phys. Rev. Lett. 96, 114102.
Arenkiel, B. R., and Ehlers, M. D. (2009). Molecular genetics and imaging technologies for circuit-based neuroanatomy. Nature 461, 900–907.
Barabási, A. L., and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512.
Bassett, D. S., and Bullmore, E. T. (2006). Small world brain networks. Neuroscientist. 12, 512–523.
Bassett, D. S., and Bullmore, E. T. (2009). Human brain networks in health and disease. Curr. Opin. Neurol. 22, 340–347.
Bassett, D. S., Greenfield, D. L., Meyer-Lindenberg, A., Weinberger, D. R., Moore, S. W., and Bullmore, E. T. (2010). Efficient physical embedding of topologically complex information processing networks in brains and computer circuits. PLoS Comput. Biol. 6, e1000748. doi: 10.1371/journal.pcbi.1000748
Bertschinger, N., and Natschläger, T. (2004). Real-time computation at the edge of chaos in recurrent neural networks. Neural. Comput. 16, 1413–1436.
Beurle, R. L. (1956). Properties of a mass of cells capable of regenerating pulses. Philos. Trans. R. Soc. Lond., B, Biol. Sci. 240, 55–94.
Binzegger, T., Bouglas, R. J., and Martin, K. A. C. (2004). A quantitative map of the circuit of cat primary visual cortex. J. Neurosci. 24, 8441–8453.
Binzegger, T., Douglas, R. J., and Martin, K. A. (2009). Topology and dynamics of the canonical circuit of cat V1. Neural. Netw. 22, 1071–1078.
Blondel, V. D., Guillaume, J. L., Lambiotte, R., and Lefebvre, E. (2008). Fast unfolding of communities in large networks. J. Stat. Mech. 10, P10008.
Bosking, W. H., Zhang, Y., Schofield, B., and Fitzpatrick, D. (1997). Orientation selectivity and the arrangement of horizontal connections in tree shrew striate cortex. J. Neurosci. 17, 2112–2127.
Braitenberg, V., and Schüz, A. (1998). Statistics and Geometry of Neuronal Connectivity. Berlin: Springer.
Buckner, R. L., Sepulcre, J., Talukdar, T., Krienen, F. M., Liu, H., Hedden, T., Andrews-Hanna, J. R., Sperling, R. A., and Johnson, K. A. (2009). Cortical hubs revealed by intrinsic functional connectivity: mapping, assessment of stability, and relation to Alzheimer’s disease. J. Neurosci. 29, 1860–1873.
Bullmore, E., and Sporns, O. (2009). Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198.
Buzsáki, G., Geisler, C., Henze, D. A., and Wang, X. J. (2004). Interneuron diversity series: circuit complexity and axon wiring economy of cortical interneurons. Trends Neurosci. 27, 186–193.
Cajal, S. R. (1995). Histology of the Nervous System of Man and Vertebrates. New York: Oxford University Press.
Callaway, D. S., Hopcroft, J. F., Kleinber, J. M., Newman, M. E. J., and Strogatz, S. H. (2001). Are randomly grown graphs really random? Phys. Rev. E 64, 041902.
Castellanos, F. X., Margulies, D. S., Kelly, A. M. C., Uddin, L. Q., Ghaffari, M., Kirsch, A., Shaw, D., Shezad, Z., Di Martino, A., Biswal, B., Sonuga-Barke, E. J. S., Rotrosen, J., Adler, L. A., and Milham, M. P. (2008). Cingulate-precuneus interactions: a new locus of dysfunction in adult attention-deficit/hyperactivity disorder. Biol. Psychiatry 63, 332–337.
Chang, C., and Glover, G. H. (2010). Time-frequency dynamics of resting-state brain connectivity measured with fMRI. Neuroimage 50, 81–98.
Chen, B. L., Hall, D. H., and Chklovskii, D. B. (2006). Wiring optimization can relate neuronal structure and function. Proc. Natl. Acad. Sci. U.S.A. 103, 4723–4728.
Chen, Z. J., He, Y., Rosa-Neto, P., Germann, J., and Evans, A. C. (2008). Revealing modular architecture of human brain structural networks by using cortical thickness from MRI. Cereb. Cortex 18, 2374–2381.
Cohen, A. L., Fair, D. A., Dosenbach, N. U. F., Miezin, F. M., Dierker, D., Van Essen, D. C., Schlaggar, B. L., and Petersen, S. E. (2008). Defining functional areas in individual human brains using resting state functional connectivity MRI. Neuroimage 41, 45–57.
Costa, L. D. F., Kaiser, M., and Hilgetag, C. C. (2007). Predicting the connectivity of primate cortical networks from topological and spatial node properties. BMC Syst. Biol. 1, 16. doi: 10.1186/1752-0509-1-16
Da Costa, N. M., and Martin, K. A. C. (2010). Whose cortical column would that be? Front. Neuroanat. 4:16. doi: 10.3389/fnana.2010.00016
Damoiseaux, J. S., and Greicius, M. D. (2009). Greater than the sum of its parts: a review of studies combining structural connectivity and resting-state functional connectivity. Brain Struct. Funct. 213, 525–533.
Deco, G., Jirsa, V., McIntosh, A. R., Sporns, O., and Kötter, R. (2009). Key role of coupling, delay, and noise in resting brain fluctuations. Proc. Natl. Acad. Sci. U.S.A. 106, 10302–10307.
Erdös, P., and Rényi, A. (1960). On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 5, 17–61.
Felleman, D. J., and van Essen, D. C. (1991). Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1, 1–47.
Fortunato, S., and Barthelemy, M. (2007). Resolution limit in community detection. Proc. Natl. Acad. Sci. U.S.A. 104, 36–41.
Fox, M. D., and Greicius, M. (2010). Clinical applications of resting state functional connectivity. Front. Syst. Neurosci. 4:19. doi: 10.3389/fnsys.2010.00019
Fox, M. D., Snyder, A. Z., Vincent, J. L., Corbetta, M., Van Essen, D. C., and Raichle, M. E. (2005). The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc. Natl. Acad. Sci. U.S.A. 102, 9673–9678.
Friston, K. J., and Frith, C. D. (1995). Schizophrenia: a disconnection syndrome? Clin. Neurosci. 3, 89–97.
Galán, R. F. (2008). On how network architecture determines the dominant patterns of spontaneous neural activity. PLoS ONE 3, e2148. doi: 10.1371/journal.pone.0002148
Ghosh, A., Rho, Y., McIntosh, A. R., Kötter, R., and Jirsa, V. K. (2008). Noise during rest enables the exploration of the brain’s dynamic repertoire. PLoS Comput. Biol. 4, e1000196. doi: 10.1371/journal.pcbi.1000196
Gomes-Gardenes, J., Zamora-Lopez, G., Moreno, Y., and Arenas, A. (2010). From modular to centralized organization of synchronization in functional areas of the cat cerebral cortex. PLoS ONE 5, e12313. doi: 10.1371/journal.pone.0012313
Gong, G., He, Y., Concha, L., Lebel, C., Gross, D. W., Evans, A. C., and Beaulieu, C. (2009). Mapping anatomical connectivity patterns of human cerebral cortex using in vivo diffusion tensor imaging tractography. Cereb. Cortex 19, 524–536.
Greicius, M. D., Krasnow, B., Reiss, A. L., and Menon, V. (2003). Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc. Natl. Acad. Sci. U.S.A. 100, 253–258.
Grenander, U., and Silverstein, J. W. (1977). Spectral analysis of networks with random topologies. SIAM J. Appl. Math. 32, 499–519.
Hagmann, P., Cammoun, L., Gigandet, X., Gerhard, S., Grant, P. E., Wedeen, V., Meuli, R., Thiran, J. P., Honey, C. J., and Sporns, O. (2010). MR connectomics: principles and challenges. J. Neurosci. Meth. 194, 34–45.
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J., Wedeen, V. J., and Sporns, O. (2008). Mapping the structural core of human cerebral cortex. PLoS Biol. 6, e159. doi: 10.1371/journal.pbio.0060159
He, Y., Chen, Z. J., and Evans, A. C. (2007). Small-world anatomical networks in the human brain revealed by cortical thickness from MRI. Cereb. Cortex 17, 2407–2419.
Hellwig, B. (2000). A quantitative analysis of the local connectivity between pyramidal neurons in layers 2/3 of the rat visual cortex. Biol. Cybern. 82, 111–121.
Helmstaedter, M., Briggman, K. L., and Denk, W. (2008). 3D structural imaging of the brain with photons and electrons. Curr. Opin. Neurobiol. 18, 633–641.
Hilgetag, C. C., Burns, G. A., O’Neill, M. A., Scannell, J. W., and Young, M. P. (2000). Anatomical connectivity defines the organization of clusters of cortical areas in the macaque monkey and the cat. Philos. Trans. R. Soc. B 355, 91–110.
Hilgetag, C. C., and Kaiser, M. (2004). Clustered organization of cortical connectivity. Neuroinformatics 2, 353–360.
Honey, C. J., Kötter, R., Breakspear, M., and Sporns, O. (2007). Network structure of cerebral cortex shapes functional connectivity on multiple time scales. Proc. Natl. Acad. Sci. U.S.A. 104, 10240–10245.
Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J. P., Meuli, R., and Hagmann, P. (2009). Predicting human resting-state functional connectivity from structural connectivity. Proc. Natl. Acad. Sci. U.S.A. 106, 2035–2040.
Honey, C. J., Thivierge, J. P., and Sporns, O. (2010). Can structure predict function in the human brain? Neuroimage 52, 766–776.
Iturria-Medina, Y., Canales-Rodriguez, E. J., Melie-Garcia, L., Valdes-Hernandez, P. A., Martinez-Montes, E., Aleman-Gomez, Y., and Sanchez-Bornot, J. M. (2007). Characterizing brain anatomical connections using diffusion weighted MRI and graph theory. Neuroimage 36, 645–660.
Iturria-Medina, Y., Sotero, R. C., Canales-Rodriguez, E. J., Aleman-Gomez, Y., and Melie-Garcia, L. (2008). Studying the human brain anatomical network via diffusion-weighted MRI and graph theory. Neuroimage 40, 1064–1076.
Izhikevich, E. M., and Edelman, G. M. (2008). Large-scale model of mammalian thalamocortical systems. Proc. Natl. Acad. Sci. U.S.A. 105, 3593–3598.
Jain, V., Seung, H. S., and Turage, S. C. (2010). Machines that learn to segment images: a crucial technology for connectomics. Curr. Opin. Neurobiol. 20, 653–666.
Johansen-Berg, H., and Behrens, T. E. J. (eds). (2009). Diffusion MRI: From Quantitative Measurement to In Vivo Neuroanatomy. Amsterdam: Academic Press.
Just, M. A., Cherkassky, V. L., Keller, T. A., Kana, R. K., and Minshew, N. J. (2007). Functional and anatomical cortical underconnectivity in autism: evidence from an fMRI study of an executive function task and corpus callosum morphometry. Cereb. Cortex 17, 951–961.
Kaiser, M., and Hilgetag, C. C. (2006). Nonoptimal component placement, but short processing paths, due to long-distance projections in neural systems. PLoS Comput. Biol. 2, e95. doi: 10.1371/journal.pcbi.0020095
Kaiser, M., and Hilgetag, C. C. (2010). Optimal hierarchical modular topologies for producing limited sustained activation in neural networks. Front. Neuroinformatics 4:8. doi: 10.3389/fninf.2010.00008
Kashtan, N., and Alon, U. (2005). Spontaneous evolution of modularity and network motifs. Proc. Natl. Acad. Sci. U.S.A. 102, 13773–13778.
Keller, T. A., Kana, R. K., and Just, M. A. (2007). A developmental study of the structural integrity of white matter in autism. Neuroreport 18, 23–27.
Kenet, T., Bibitchkov, D., Tsodyks, M., Grinvald, A., and Arieli, A. (2003). Spontaneously emerging cortical representations of visual attributes. Nature 425, 954–956.
Kirschner, M., and Gerhart, J. (2005). The Plausibility of Life: Resolving Darwin’s Dilemma. New Haven: Yale University Press.
Koch, M. A., Norris, D. G., and Hund-Georgiadis, M. (2002). An investigation of functional and anatomical connectivity using magnetic resonance imaging. Neuroimage 16, 241–250.
Konrad, K., and Eickhoff, S. B. (2010). Is the ADHD brain wired differently? A review on structural and functional connectivity in attention deficit hyperactivity disorder. Hum. Brain Mapp. 31, 904–916.
Kremkow, J., Kumar, A., Rotter, S., and Aertsen, A. (2007). Emergence of population synchrony in a layered network of the cat visual cortex. Neurocomputing 70, 2069–2073.
Lai, M. C., Lombardo, M. V., Chakrabarti, B., Sadek, S. A., Pasco, G., Wheelwright, S. J., Bullmore, E. T., Baron-Cohen, S., MRC AIMS Consortium, Suckling, J. (2010). A shift to randomness of brain oscillations in people with autism. Biol. Psychiatry 68, 1092–1099.
Laughlin, S. B., and Sejnowski, T. J. (2003). Communication in neuronal networks. Science 301, 1870–1874.
Lichtman, J. W., Livet, J., and Sanes, J. R. (2008). A technicolour approach to the connectome. Nat. Rev. Neurosci. 9, 417–422.
Lipson, H., Pollack, J. B., and Suh, N. P. (2002). On the origin of modular variation. Evolution 56, 1549–1556.
Liu, Y., Liang, M., Zhou, Y., He, Y., Hao, Y., Song, M., Yu, C., Liu, H., Liu, Z., and Jiang, T. (2008). Disrupted small-world networks in schizophrenia. Brain 131, 945–961.
Lu, J., Fiala, J. C., and Lichtman, J. W. (2009). Semi-automated reconstruction of neural processes from large numbers of fluorescence images. PLoS ONE 4, e5655. doi: 10.1371/journal.pone.0005655
Lynall, M. E., Bassett, D. S., Kerwin, R., McKenna, P. J., Kitzbichler, M., Muller, U., and Bullmore, E. (2010). Functional connectivity and brain networks in schizophrenia. J. Neurosci. 30, 9477–9487.
Maass, W., Natschläger, T., and Markram, H. (2002). Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural. Comput. 14, 2531–2560.
Maslov, S., and Sneppen, K. (2002). Specificity and stability in topology of protein networks. Science 296, 910–913.
Meunier, D., Lambiotte, R., and Bullmore, E. (2010). Modular and hierarchically modular organization of brain networks. Front. Neurosci. 4:200. doi: 10.3389/fnins.2010.00200
Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N., Chklovskii, D., and Alon, U. (2002). Network motifs: simple building blocks of complex networks. Science 298, 824–827.
Mishchenko, Y., Hu, T., Spacek, J., Mendenhall, J., Harris, K. M., and Chklovsii, D. B. (2010). Ultrastructural analysis of hippocampal neuropil from the connectomics perspective. Neuron 67, 1009–1020.
Müller-Linow, M., Hilgetag, C. C., and Hütt, M. T. (2008). Organization of excitable dynamics in hierarchical biological networks. PLoS Comput. Biol. 4, e1000190. doi: 10.1371/journal.pcbi.1000190
Nelson, S. M., Cohen, A. L., Power, J. D., Wig, G. S., Miezin, F. M., Wheeler, M. E., Velanova, K., Donaldson, D. I., Phillips, J. S., Schlaggar, B. L., and Petersen, S. E. (2010). A parcellation scheme for human left lateral parietal cortex. Neuron 67, 156–170.
Newman, M. E. J. (2006). Modularity and community structure in networks. Proc. Natl. Acad. Sci. U.S.A. 103, 8577–8582.
Newman, M. E. J., and Girvan, M. (2004). Finding and evaluating community structure in networks. Phys. Rev. E 69, 026113.
Ohki, K., Chung, S., Ch’ng, Y. H., Kara, P., and Reid, R. C. (2005). Functional imaging with cellular resolution reveals precise micro-architecture in visual cortex. Nature 433, 597–603.
Palm, C., Axer, M., Grassel, D., Dammers, J., Lindemeyer, J., Zilles, K., Pietrzyk, U., and Amunts, K. (2010). Towards ultra-high resolution fibre tract mapping of the human brain – registration of polarized light images and reorientation of fibre vectors. Front. Hum. Neurosci. 4:9. doi: 10.3389/neuro.09.009.2010
Raichle, M. E., MacLeod, A. M., Snyder, A. Z., Powers, W. J., Gusnard, D. A., and Shulman, G. L. (2001). A default mode of brain function. Proc. Natl. Acad. Sci. U.S.A. 98, 676–682.
Reijneveld, J. C., Ponten, S. C., Berendse, H. W., and Stam, C. J. (2007). The application of graph theoretical analysis to complex networks in the brain. Clin. Neurophysiol. 118, 2317–2331.
Rubinov, M., Knock, S. A., Stam, C. J., Micheloyannis, S., Harris, A. W. F., Williams, L. M., and Breakspear, M. (2009). Small-world properties of nonlinear brain activity in schizophrenia. Hum. Brain Mapp. 30, 403–416.
Rubinov, M., and Sporns, O. (2010). Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52, 1059–1069.
Scannell, J. W., Blakemore, C., and Young, M. P. (1995). Analysis of connectivity in the cat cerebral cortex. J. Neurosci. 15, 1463–1483.
Scannell, J. W., Burns, G. A. P. C., Hilgetag, C. C., O’Neil, M. A., and Young, M. P. (1999). The connectional organization of the cortico-thalamic system of the cat. Cereb. Cortex 9, 277–299.
Schmahmann, J. D., Pandya, D. N., Wang, R., Dai, G., D’Arceuil, H. E., de Crespigny, A. J., and Wedeen, V. J. (2007). Association fibre pathways of the brain: parallel observations from diffusion spectrum imaging and autoradiography. Brain 130, 630–653.
Sholl, D. A. (1953). Dendritic organization in the neurons of the visual and motor cortices of the cat. J. Anat. 87, 387–406.
Smith, S. M., Fox, P. T., Miller, K. L., Glahn, D. C., Fox, P. M., Mackay, C. E., Filippini, N., Watkins, K. E., Toro, R., Laird, A., and Beckmann, C. F. (2009). Correspondence of the brain’s functional architecture during activation and rest. Proc. Natl. Acad. Sci. U.S.A. 106, 13040–13045.
Song, S., Sjöström, P. J., Reigl, M., Nelson, S., and Chklovskii, D. B. (2005). Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 3, e68. doi: 10.1371/journal.pbio.0030068
Sporns, O., Chialvo, D., Kaiser, M., and Hilgetag, C. C. (2004). Organization, development and function of complex brain networks. Trends Cogn. Sci. (Regul. Ed.) 8, 418–425.
Sporns, O., Honey, C. J., and Kötter, R. (2007). Identification and classification of hubs in brain networks. PLoS ONE 2, e1049. doi: 10.1371/journal.pone.0001049
Sporns, O., and Kötter, R. (2004). Motifs in brain networks. PLoS Biol. 2, 1910–1918. doi: 10.1371/journal.pbio.0020369
Sporns, O., Tononi, G., and Edelman, G. M. (2000). Theoretical neuroanatomy: relating anatomical and functional connectivity in graphs and cortical connection matrices. Cereb. Cortex 10, 127–141.
Sporns, O., Tononi, G., and Kötter, R. (2005). The human connectome: a structural description of the human brain. PLoS Comput. Biol. 1, 245–251. doi: 10.1371/journal.pcbi.0010042
Stam, C. J., de Haan, W., Daffertshofer, A., Jones, B. F., Manshanden, I., van Cappellen van Walsum, A. M., Montez, T., Verbunt, J. P. A., de Munck, J. C., van Dijk, B. W., Berendse, H. W., and Scheltens, P. (2009). Graph theoretical analysis of magnetoencephalographic functional connectivity in Alzheimer’s disease. Brain 132, 213–224.
Stam, C. J., Jones, B. F., Nolte, G., Breakspear, M., and Scheltens, P. (2007). Small-world networks and functional connectivity in Alzheimer’s disease. Cereb. Cortex 17, 92–99.
Supekar, K., Menon, V., Rubin, D., Musen, M., and Greicius, M. D. (2008). Network analysis of intrinsic functional brain connectivity in Alzheimer’s disease. PLoS Comput. Biol. 4, e1000100. doi: 10.1371/journal.pcbi.1000100
Tononi, G., and Edelman, G. M. (2000). Schizophrenia and the mechanisms of conscious integration. Brain Res. Rev. 31, 391–400.
Tononi, G., Sporns, O., and Edelman, G. M. (1994). A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. U.S.A. 91, 5033–5037.
Tuckwell, H. C. (1989). Stochastic Processes in the Neurosciences. Philadelphia: Society for Industrial and Applied Mathematics.
Turing, A. M. (1948). “Intelligent machinery, national physical laboratory report,” in Machine Intelligence, Vol. 5, eds B. Meltzer and D. Michie (Edinburgh: Edinburgh University Press), 3–23.
Van den Heuvel, M. P., Mandl, R. C. W., Stam, C. J., Kahn, R. S., and Hulshoff Pol, H. E. (2010). Aberrant frontal and temporal complex network structure in schizophrenia: a graph theoretical analysis. J. Neurosci. 30, 15915–15926.
Vincent, J. L., Patel, G. H., Fox, M. D., Snyder, A. Z., Baker, J. T., Van Essen, D. C., Zempel, J. M., Snyder, L. H., Corbetta, M., and Raichle, M. E. (2007). Intrinsic functional architecture in the anaesthetized monkey brain. Nature 447, 83–86.
Wagner, G. P., Pavlicev, M., and Cheverud, J. M. (2007). The road to modularity. Nat. Rev. Genet. 8, 921–931.
Wang, L., Zhu, C., Zang, Y., Cao, Q., Zhang, H., Zhong, Q., and Wang, Y. (2009). Altered small-world brain functional networks in children with attention-deficit/hyperactivity disorder. Hum. Brain Mapp. 30, 638–649.
Wang, X. J. (2010). Neurophysiological and computational principles of cortical rhythms in cognition. Physiol. Rev. 90, 1195–1268.
Watts, D. J., and Strogatz, S. H. (1998). Collective dynamics of “small-world” networks. Nature 393, 440–442.
Whitfield-Gabrieli, S., Thermenos, H. W., Milanovic, S., Tsuang, M. T., Faraone, S. V., McCarley, R. W., Shenton, M. E., Green, A. I., Nieto-Castanon, A., LaViolette, P., Wojcik, J., Gabrieli, J. D. E., and Seidman, L. J. (2009). Hyperactivity and hyperconnectivity of the default network in schizophrenia and in first-degree relatives of persons with schizophrenia. Proc. Natl. Acad. Sci. U.S.A. 106, 1279–1284.
Yoshimura, Y., Dantzker, J. L. M., and Callaway, E. M. (2005). Excitatory cortical neurons form fine-scale functional networks. Nature 433, 868–873.
Young, M. P. (1992). Objective analysis of the topological organization of the primate cortical visual system. Nature 358, 152–155.
Zamora-Lopez, G., Zhou, C., and Kurths, J. (2010). Cortical hubs form a module for multisensory integration on top of the hierarchy of cortical networks. Front. Neuroinformatics 4:1. doi: 10.3389/neuro.11.001.2010
Keywords: networks, neuroanatomy, connectome, neural dynamics, neuroimaging, complex systems
Citation: Sporns O (2011) The non- random brain: efficiency, economy, and complex dynamics. Front. Comput. Neurosci. 5:5. doi: 10.3389/fncom.2011.00005
Received: 31 October 2010;
Paper pending published: 06 December 2010;
Accepted: 25 January 2011;
Published online: 08 February 2011.
Edited by:
Arvind Kumar, Albert-Ludwig University Freiburg, GermanyReviewed by:
Xiao-Jing Wang, Yale University School of Medicine, USACopyright: © 2011 Sporns. This is an open-access article subject to an exclusive license agreement between the authors and Frontiers Media SA, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Olaf Sporns, Department of Psychological and Brain Sciences, Indiana University, Bloomington, IN 47405, USA. e-mail:b3Nwb3Juc0BpbmRpYW5hLmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.