Calcium messenger heterogeneity: a possible signal for spike-timing-dependent plasticity

Calcium concentrations as well as time courses have been used to model the signaling cascades leading to changes in the strength of synaptic connections. Previous models consider the dendritic spines as uniform compartments regarding calcium signaling. However, calcium concentrations can vary drastically on distances much smaller than typical spine sizes, and downstream targets of calcium signals are often found exactly in these calcium nanodomains. Even though most downstream targets are activated by calcium via calmodulin, which is a diffusive molecule, the capacity of calmodulin to bind to its targets even when it is not fully loaded with calcium allows its downstream cascade to be highly local. In this study, a model is proposed which uses the heterogeneity of calcium concentrations as a signal for spike-timing-dependent plasticity (STDP). The model is minimalistic and includes three sources of calcium in spines: NMDA receptors (NMDARs), voltage gated calcium channels (VGCCs) and IP3 receptors (IP3Rs). It is based on the biochemical cascades and assumption of spatial locations of four calcium-dependent enzymes: calcium/calmodulin-dependent protein kinase II located near NMDARs, calcineurin located near VGCCs, cyclic nucleotide phosphodiesterase (PDE) located near IP3Rs or NMDARs and adenylyl cyclase, located between VDCCs and NMDARs. To quantify the changes in synaptic weights the model also includes a simple description of AMPA receptor insertion in the membrane and docking to the postsynaptic density. Two parameters of the model are tuned such that weight changes produced by either pre or postsynaptic firing alone are minimal. The model reproduces the typical shape of STDP for spike doublets. If PDE is located near IP3Rs, the behavior for spike triplets is consistent with that observed in hippocampal cell culture; if near NMDAR, the behavior is similar to that observed in cortical L2/3 slices.

Introduction

In recent years several distinct classes of models have been proposed, which, in varying degrees of detail, map the rise in calcium concentration in a dendritic spine to the long-term potentiation (LTP) or depression (LTD) of the synaptic strength. One class of such models considers the calcium concentration resulting from a stimulation protocol as the main determinant of the future changes in plasticity: high calcium elevations lead to LTP, moderate calcium elevations lead to LTD and small calcium elevations produce no changes, which is generally referred as the “differential threshold hypothesis” (Lisman, 1989; Artola and Singer, 1993). This basic principle has both biochemical and physiological foundations. Calcium/calmodulin-dependent protein kinase II (CaMKII), which has been implicated in the expression of LTP (Glazewski et al., 1996; Frankland et al., 2001), can autophosphorylate, a process which maintains its kinase activity even in the absence of calcium (Bennett et al., 1983). Autophosphorylation is assumed to require one active CaMKII subunit neighboring a non-phosphorylated subunit with calmodulin bound to it. Thus, the most simplistic model of CaMKII activation assumes an initial step which is dependent on the square of the concentration of calcium-loaded calmodulin. At the same time, the activation of protein phosphatase 2B (calcineurin, CaN), besides some high affinity calcium binding sites, requires the binding of one calcium-loaded calmodulin. The most simplistic model for CaN activation is to consider its activity being proportional to the concentration of calcium-loaded calmodulin. Associating the kinase activity to LTP (making it quadratic in calmodulin activation) and phosphatase activity to LTD (making it linear in calmodulin activation), it is possible to build a very simple model of synaptic plasticity. While the core of the model is very simple, extensive modeling work has shown that it is possible for simulations of the biochemical signals within postsynaptic spines to reproduce these results (Bhalla, 2002; Hayer and Bhalla, 2005; Graupner and Brunel, 2007). In addition to the induction, these models have the property of including a bistable switch at the biochemical level. While experimental evidence of CaMKII autophosphorylation in the presence of protein phosphatase 1 (PP1) failed to observe bistability (Bradshaw et al., 2003), it can be included in the model at protein translation level (Aslam et al., 2009).

Traditional induction protocols: high and low frequency afferent stimulation, as well as more direct manipulations of calcium concentrations in postsynaptic spines (Yang et al., 1999; Cho et al., 2001; Cormier et al., 2001) support the “differential threshold hypothesis.” However, in typical spike-timing-dependent plasticity (STDP) induction (Markram et al., 1997; Bi and Poo, 1998), such a model would predict a second depression window at a long pre–post time interval. The model can be rescued by considering that pre stimulation alone does not produce calcium concentrations lower than those needed for LTD, but rather resides in the narrow band of calcium concentration between the induction of LTD and that of LTP, and that a post–pre at short time intervals produces smaller calcium input (Urakubo et al., 2008). This model can also qualitatively reproduce the spike triplet protocols measured in cortex (Froemke and Dan, 2002). A very high diversity of rules for synaptic plasticity can be observed in diverse systems (Nelson and Turrigiano, 2008). In hippocampal cell cultures a different triplet rule has been observed (Wang et al., 2005), in which symmetric pre–post–pre triplets at short time interval (5 and 10 ms) produce little synaptic change, while symmetric post–pre–post triplets at the same intervals produce robust LTP. This triplet structure was explained by considering the temporal structure of the calcium transient as the main signal for STDP (Rubin et al., 2005). Without being tuned for, this triplet structure is qualitatively reproduced in the model presented in this study. In addition, both theoretical (Karmarkar and Buonomano, 2002) and experimental (Sjostrom et al., 2003) work point toward an additional coincidence detector for the pre–post tLTD window. Experimental observations point toward a presynaptic mechanism, however in these experiments (Sjostrom et al., 2003) the presynaptic neuron fires multiple times in a short interval, which allows autocrine NMDA activation. In protocols in which this is absent, how can such a coincidence detector be implemented?

A minimalistic model is proposed which uses the assumption that different enzymes in the biochemical pathways localize to different calcium sources. This general principle is supported by multiple experiments which show problems in plasticity caused by interference with scaffold proteins and the general observation that the diversity of the forms of synaptic plasticity, while caused by a small number of second messengers, is surpassed by the diversity in scaffolds (Jordan et al., 2004). A potential problem with such a model is that, while calcium gradients are very sharp (Naraghi and Neher, 1997), most of the calcium-dependent enzymes are activated by calmodulin, which is soluble. Simulations of calcium dynamics in dendritic spines with simple geometries show the diffusion coefficient of calmodulin as having a strong influence on the local calmodulin signaling (Naoki et al., 2005). Using the calmodulin diffusion constant measured in vivo (Luby-Phelps et al., 1995), simulations show large differences between the nanodomain and spine-wide calmodulin activations. More detailed simulations also show a very different probability for a calmodulin to become fully calcium loaded if it is located in the postsynaptic density (PSD) or randomly in the spine (Keller et al., 2008). In addition, calmodulin with less than four calcium bound can bind to CaMKII (Shifman et al., 2006), and possibly, via a similar mechanism, to other targets. This influences the calcium transient dependence of CaMKII (Mihalas, 2009; Pepke et al., 2010), but also has drastic implication over the distance from a calcium source which produces activation of CaMKII (Mihalas, 2009). This distance is smaller than the typical size of a spine, such that it is reasonable to assume subspine size domains in signaling.

Model

Calcium Entry

Three calcium sources are considered in the model: NMDARs, VGCCs, and calcium release from internal stores via IP3-dependent channels (Figure 1). Since at the next step of the signaling cascade activation parameters are unknown, the relative timing of opening of the calcium channels and not their relative strength are important. Thus the magnitude of each current is normalized, and the parameters in future sections are relative to the magnitude of the calcium current. For a quantitative description of the model, see the Section “Appendix.”

FIGURE 1

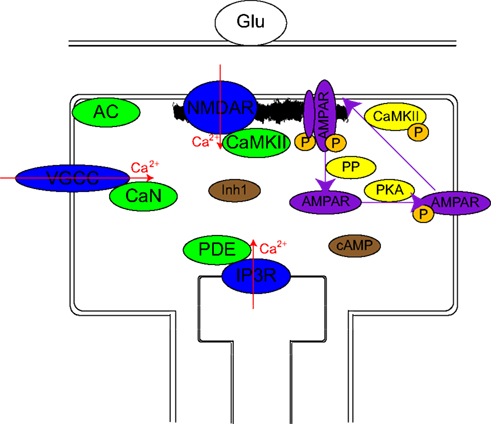
Figure 1. Schematic representation of the model. Calcium channels (blue ovals) are differentially activated by different stimulation protocols: The firing of the postsynaptic neuron activates mainly VGCCs, the firing of the presynaptic neuron via mGlus mainly activates IP3Rs, and to a lesser extent NMDARs and VGCCs while a pre–post activation results in large activation of all sources. The essential assumption of the model consists of localization of calcium-dependent enzymes (green ovals) near these calcium sources: CaMKII near NMDAR, CaN near VGCC, PDE near IP3R, and AC in between VGCC and NMDAR. Their transient (10 ms) calcium-dependent activation is assumed to remain localized. Either directly or via less localized intermediaries (Inh1 and cAMP: brown ovals), these produce changes over intermediate time scales in several enzyme activations (CaMKII, PKA, and several PPs: yellow ovals). These intermediate time scale changes produce long-term changes in the synaptic weight via phosphorylation or dephosphorylation of AMPAR and PSD targets which lead to insertion and stabilization of AMPAR in PSD or destabilization and endocytosis of AMPAR respectively.

Voltage gated calcium channels provide a short calcium current following depolarization. A model for L-type VGCC identical to previous simulation work was used (Urakubo et al., 2008). Both APs and EPSPs are assumed to be biexponential with a rise time of 0.5 ms, a decay time of 5 ms and maximum amplitudes of 60 and 10 mV respectively. APs and EPSPs are assumed to be linearly additive. The calcium current through VGCCs is mainly a result of backpropagating action potentials in the dendritic tree following postsynaptic neuron firing. To a smaller extent they respond to EPSPs caused by presynaptic neuron firings. The normalized calcium currents under different stimulation protocols are presented in Figure 2.

FIGURE 2

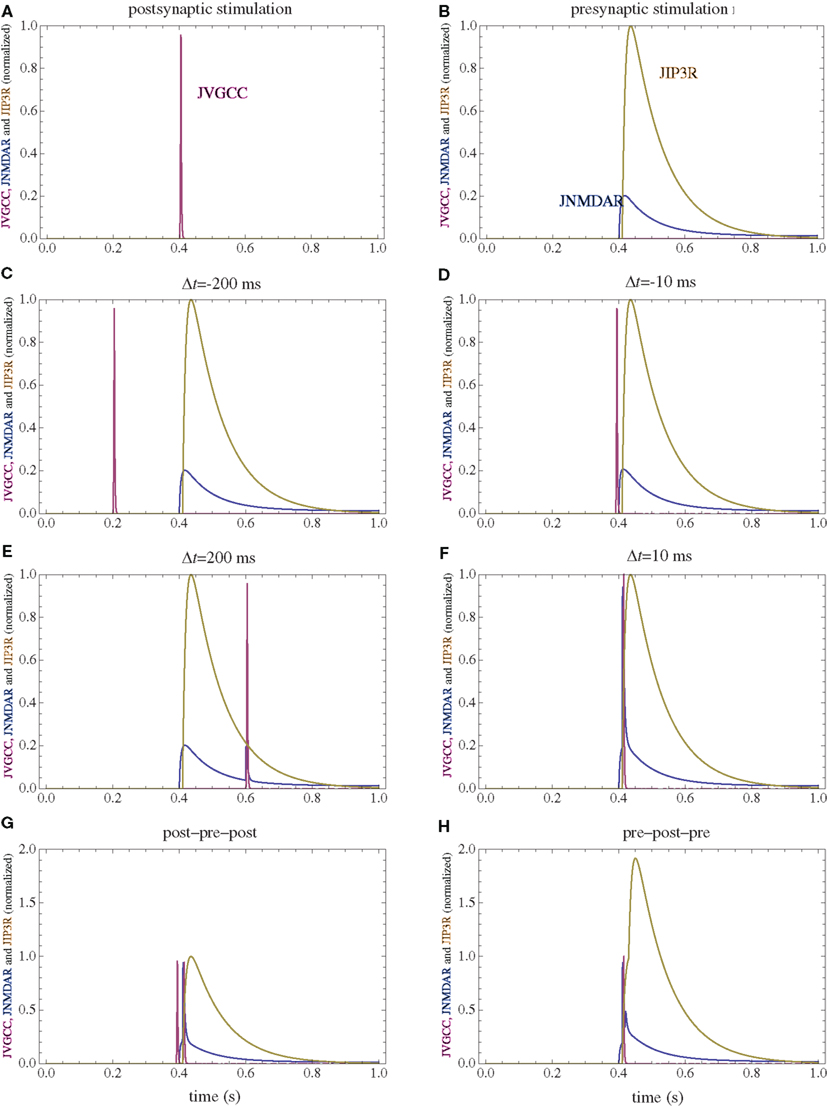
Figure 2. Calcium currents through NMDAR, VGCC, and IP3R following several stimulation paradigms. (A) Postsynaptic firing alone. (B) Presynaptic firing alone. (C,D) Post–pre at different time intervals. (E,F) Pre–post at different time intervals. (G) Post–pre–post symmetric triplet with 10 ms between each spike. (H) Pre–post–pre symmetric triplet with 10 ms between each spike. The currents for each channel type are normalized to the maximum current which can be observed for that channel type in the doublet simulations consisting of one spike for the pre and postsynaptic neuron.

Calcium release from internal stores via IP3-dependent channels (IP3R) is initiated by activation of mGluRs. Since there are many unknown parameters in the cascade resulting in calcium release, the calcium current is considered to be the convolution between glutamate concentration and a convolution kernel which is a biexponential delayed by 10 ms with a 10-ms rise time and a 100-ms decay time. For mGluR activation, glutamate diffusion is practically instantaneous and can be approximated by a delta function. To test the influence of the timing of the IP3R activation, all stimulations protocols were simulated in a model with a considerably slower (99 ms) rise time of the mGluR activation. The normalized calcium currents for the modified model are presented in Figure 8. With a corresponding change in the affinity for the calcium-dependent enzymes assumed to be in the vicinity of the IP3R, while keeping all the other parameters in the model to be identical, the simulated changes in synaptic weights are only modestly modified (Figure 9).

NMDARs provide a small and prolonged calcium current if the presynaptic neuron fires alone (pre), and a larger and shorter current in addition to the previous one if the postsynaptic neuron fires following presynaptic neuron activation (pre–post). Even though the model does not strongly depend on the minute details of the NMDAR current, since parameters are available a relatively detailed model of NMDAR is used. The parameters for the NMDAR activation are obtained from Lester and Jahr (1992), with magnesium block obtained from Jahr and Stevens (1990). Glutamate diffusion in the cleft is analytically solved using the approximations that the cleft is narrow compared to its length, glutamate has a point release and its reuptake mechanism is linear. Median values of previous, more detailed simulations were used (Franks et al., 2002).

Calcium-Dependent Enzyme Activation

After entering the postsynaptic spine, calcium ions are very quickly bound to buffers and are extruded. Calcium concentration differs vastly between the mouth of the channel and points hundreds of nanometers away (Naraghi and Neher, 1997). Calmodulin, as a diffusible calcium binding protein shows a less steep gradient. However, the fact that calmodulin with less than four calcium bound can bind to some target enzymes like CaMKII (Shifman et al., 2006), has a large influence on the spatial extent around the channel in which CaMKII can be activated. Calmodulin binding to its target before being fully calcium loaded is immobilized, forcing its subsequent activation to be dependent on the calcium concentration on that particular position rather than the average calcium concentration in its vicinity. For typical spine morphologies it can be estimated that the range of CaMKII half-activation is a few tens on nanometers surrounding an NMDAR (Mihalas, 2009). An enzyme bound near the mouth of a channel is also primarily activated by calcium coming though that type of channel. In order to focus exclusively on the effects caused calcium heterogeneity, the effects of global calcium concentration changes in the spine are neglected. The activation of calcium-dependent enzymes is considered to be dependent exclusively on the calcium current through the channel type near which they are located.

In this study, crosstalk between the different sources of calcium is neglected. This approximation allows a drastic reduction in the complexity of the model as the activation of each enzyme is considered dependent only on the calcium current from one source. While clustering of the same type of calcium channels certainly helps this approximation, it is not required. It is possible to consider a functional calcium domain near the mouth of VGCCs which consists of several spatially disjoined regions.

Calcium/calmodulin-dependent protein kinase II is enriched in the PSD (Kennedy, 2000), thus it is considered to be mainly activated by calcium influx though postsynaptic NMDARs.

Protein phosphatase 2B (CaN) is assumed to be, under physiological conditions, primarily activated by calcium coming through VGCCs. While proteomic studies have found small quantities of CaN in the PSD (Jordan et al., 2004), it is possible that small quantities of other protein aggregates are found in PSD fractions.

Adenylyl cyclase (AC) is assumed to have a mixed distribution and is partially activated by calcium coming either from NMDAR or VDCC. This assumption is consistent with a membrane-bound enzyme which can diffuse in the membrane and temporarily bind to other proteinaceous structures.

Cyclic AMP phosphodiesterase (PDE) is assumed to mainly be activated by signals related to the firing of the presynaptic neuron. This can be realized by localization of PDE near sources of calcium coming from internal stores as a result of mGluR activation. While a significant fraction of dendritic spines do not have endoplasmic reticulum protruding into the spine (Harris and Stevens, 1989), it is possible that either a dendritic calcium source is used, or that PDE localizes near NMDARs. Recent studies observed an enrichment of inactive protein kinase A in dendrites with an active removal from the spines (Zhong et al., 2009). A colocalization with PKA could help PDE in inhibiting cAMP downstream signaling. Three sets of simulations are performed: two sets assuming the PDE is localized in the vicinity of IP3Rs, and one set assuming PDE is localized in the vicinity of NMDARs.

The calcium unbinding rate from the low affinity sites of calmodulin is very fast (>1/ms). While calmodulin binding to target proteins slows down this unbinding (Olwin and Storm, 1985; Pepke et al., 2010), it is still faster than the NMDA and IP3 calcium transients, which will thus be determining the inactivation of the calcium-dependent enzymes.

Prolonged Enzyme Activation

Following calcium entry through either NMDARs or VGCCs, AC is transiently activated (Figure 3), which results in a rise in cAMP concentration (Figure 4). This rise is also transient, and the basal rate of consumption/diffusion is important in determining the length of the tLTD window and is chosen to be 0.1/s. The cAMP transient can be decreased or shortened by activation of PDE by IP3R. Long-term PKA activation is assumed to be proportional to the integral of cAMP concentration. The ratio of PDE and AC enzyme activities is a key parameter of the model. It was tuned such that the presynaptic activation alone produces little PKA activation.

FIGURE 3

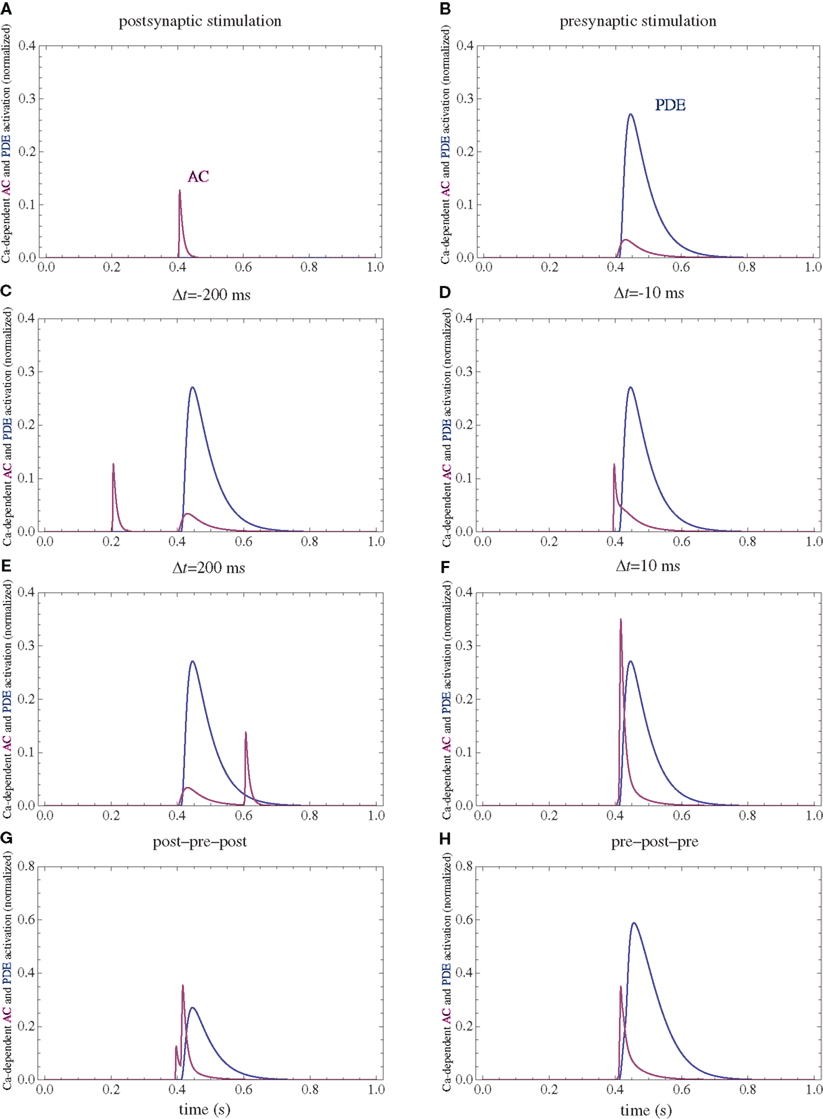
Figure 3. PDE and AC activations. (A) Postsynaptic firing alone. (B) Presynaptic firing alone. (C,D) Post–pre at different time intervals. (E,F) Pre–post at different time intervals. (G) Post–pre–post symmetric triplet with 10 ms between each spike. (H) Pre–post–pre symmetric triplet with 10 ms between each spike. The activation of each enzyme is normalized to their respective maximal activation under saturating calcium.

FIGURE 4

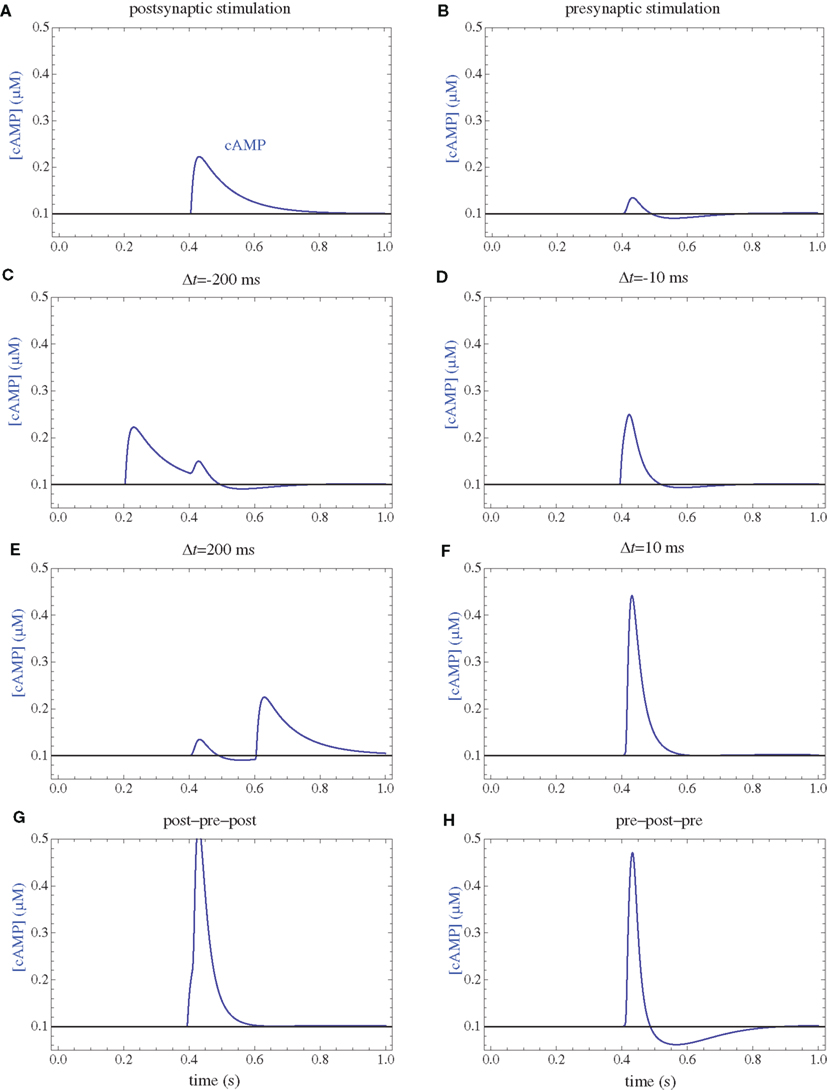
Figure 4. cAMP concentrations. (A) Postsynaptic firing alone. (B) Presynaptic firing alone. (C,D) Post–pre at different time intervals. (E,F) Pre–post at different time intervals. (G) Post–pre–post symmetric triplet with 10 ms between each spike. (H) Pre–post–pre symmetric triplet with 10 ms between each spike.

Following calcium entry through VGCCs, CaN is transiently activated (Figure 5). This leads to dephosphorylation of Inhibitor 1, and subsequent activation of PP1. Activation of PKA leads to phosphorylation of Inh1 and subsequent inactivation of PP1. The long-term PP1 activity is assumed to be proportional to the integral of CaN activity minus PKA activation, if this difference is positive and zero otherwise. The ratio between PKA and CaN activities is another crucial parameter in the model, and it was tuned such that the postsynaptic activation alone produces equal PKA and CaN activation (Figure 6).

FIGURE 5

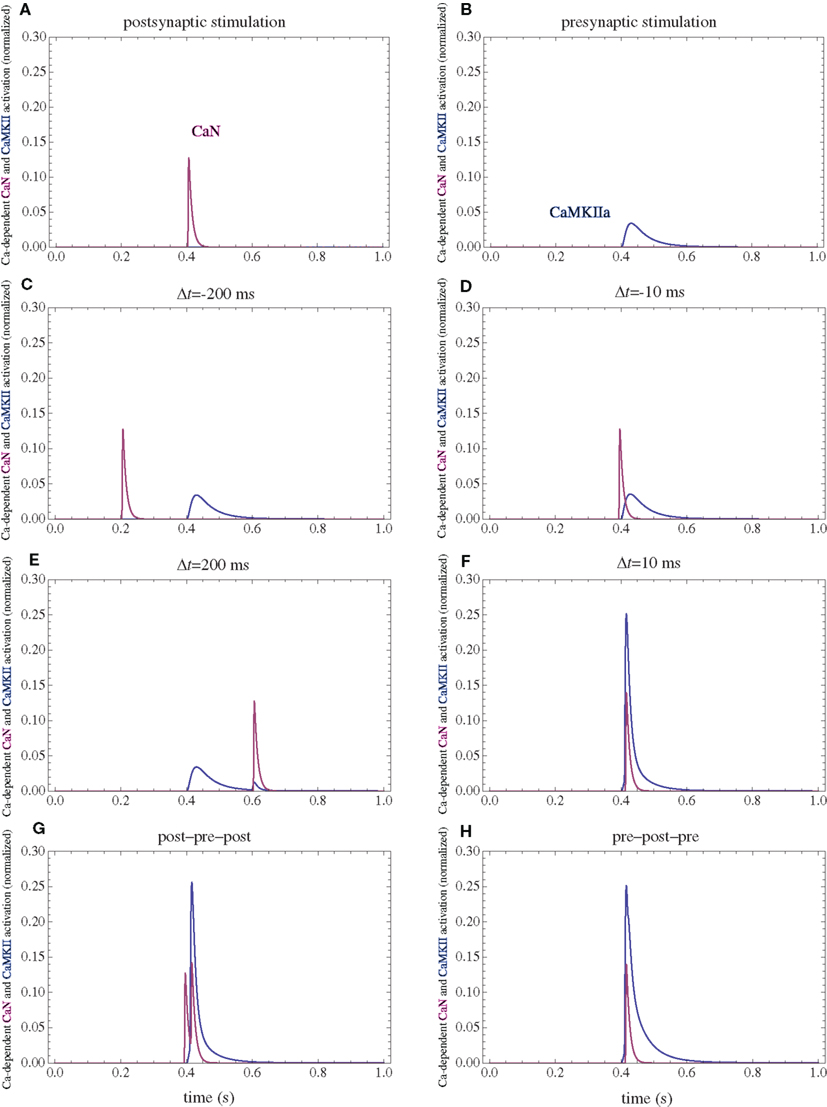
Figure 5. Calcium-dependent activation of CaMKII and CaN. (A) Postsynaptic firing alone. (B) Presynaptic firing alone. (C,D) Post–pre at different time intervals. (E,F) Pre–post at different time intervals. (G) Post–pre–post symmetric triplet with 10 ms between each spike. (H) Pre–post–pre symmetric triplet with 10 ms between each spike. The activation of each enzyme is normalized to their respective maximal activation under saturating calcium.

FIGURE 6

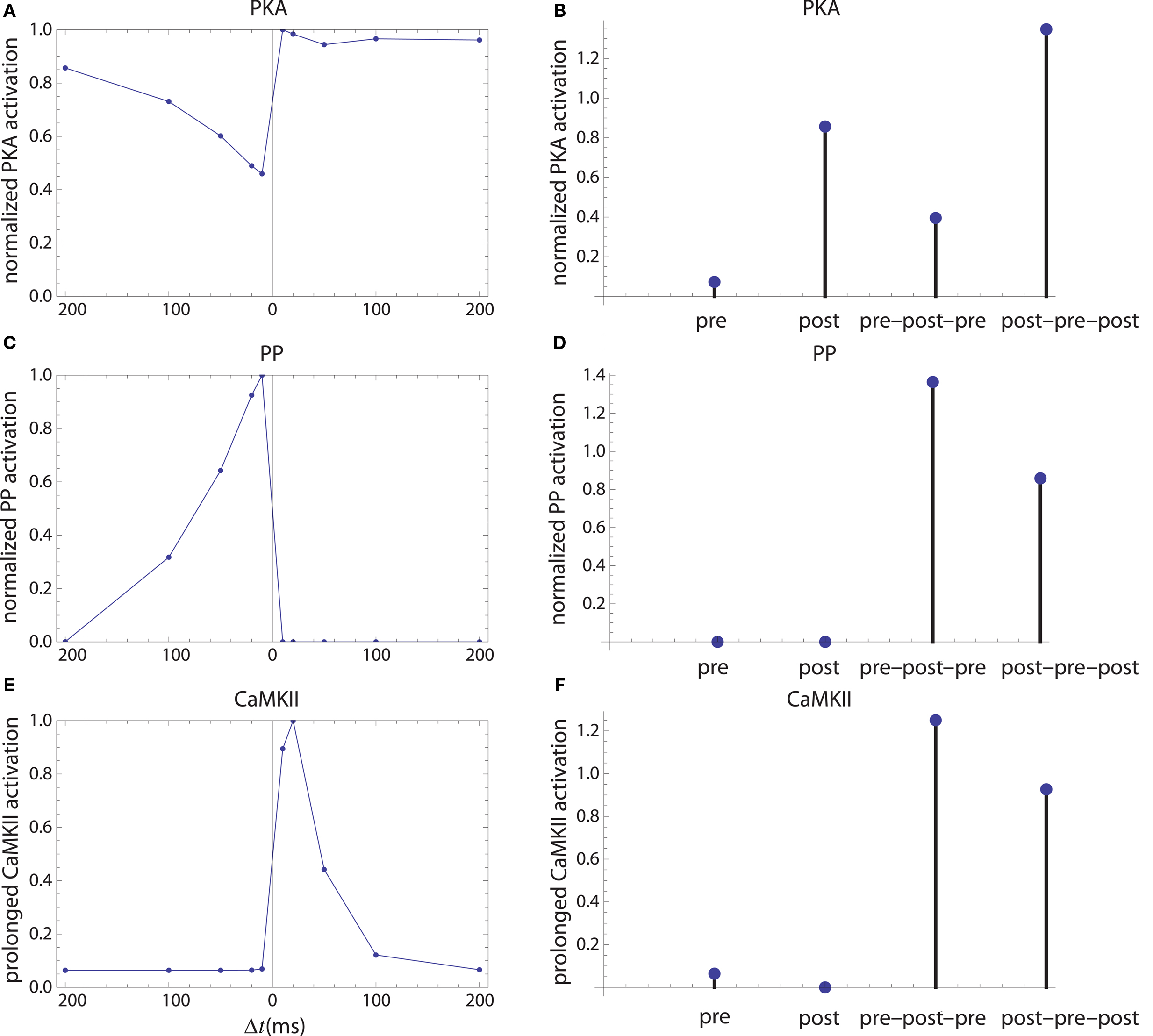
Figure 6. Long-term enzyme activations. Activation of PKA (A,B), PP1 [(C,D) which is considered as a proxy for average protein phosphatase activity in PSD] and calcium-independent activation of CaMKII (E,F). The first column corresponds to activation by pre–post doublets and the second column corresponds to activations caused by pre, post spiking alone, and by symmetric 10 ms time interval spike triplets.

Following calcium entry though NMDARs, CaMKII is transiently activated. A fraction of this activation can be transformed in long-term activity via autophosphorylation. The long-term CaMKII activity is assumed to be proportional to the integral of the square of the instantaneous calcium-dependent activity.

While the calcium-dependent enzyme activation which happens on time scales of tens of milliseconds is assumed to be localized, at least some of the downstream targets (Inh1, cAMP) are assumed to be present at similar concentrations in all the spine subcompartments.

Changes in Synaptic Weight

AMPAR trafficking, membrane insertion, binding to the PSD and extrusion are key elements in the expression of long-term changes in synaptic plasticity (Song and Huganir, 2002). Activation of PKA leads to GluR1 phosphorylation at Ser845 and its membrane insertion (Esteban et al., 2003). Subsequently (Yang et al., 2008), CaMKII phosphorylation of multiple postsynaptic targets as well as Ser831 stabilize AMPAR in the PSD. The concentration of the intermediate step: the perisynaptic AMPAR is assumed to be relatively small. Thus, the rate of AMPAR insertion and stabilization is proportional to the product of PKA and CaMKII activities.

Dephosphorylation of PSD proteins can interfere with AMPAR stability in the PSD, and dephosphorylation of Ser845 could prevent recently endocytosed AMPARs to be reinserted in the membrane. Multiple phosphatases can contribute to these dephosphorylation steps. Since some of the targets are in the PSD, PP1 activity is used as a proxy for this average protein phosphatase (PP) activity. Besides the role of CaMKII in LTP, it is assumed to have a divisive influence on LTD as well. This can be caused by its presence in large quantities in PSD providing competitive inhibition, or by rephosphorylating targets in the intermediate steps on endocytosis. Two models for AMPAR extrusion are used. In the first, the rate of AMPAR extrusion is assumed to be proportional to PP activity (Figures 7, 9, 10, E and F). In the second, it is proportional to PP activity and divided by a constant plus CaMKII long-term activity (Figures 7, 9, 10, G and H). The value of this constant was chosen to be the mean CaMKII long-term activity during a sampling of STDP protocols. The influence of CaMKII on LTD does not affect STDP for spike doublets, and plays a small role in the ability of the model to reproduce the STDP for spike triplets observed in cultured hippocampal neurons (Wang et al., 2005).

FIGURE 7

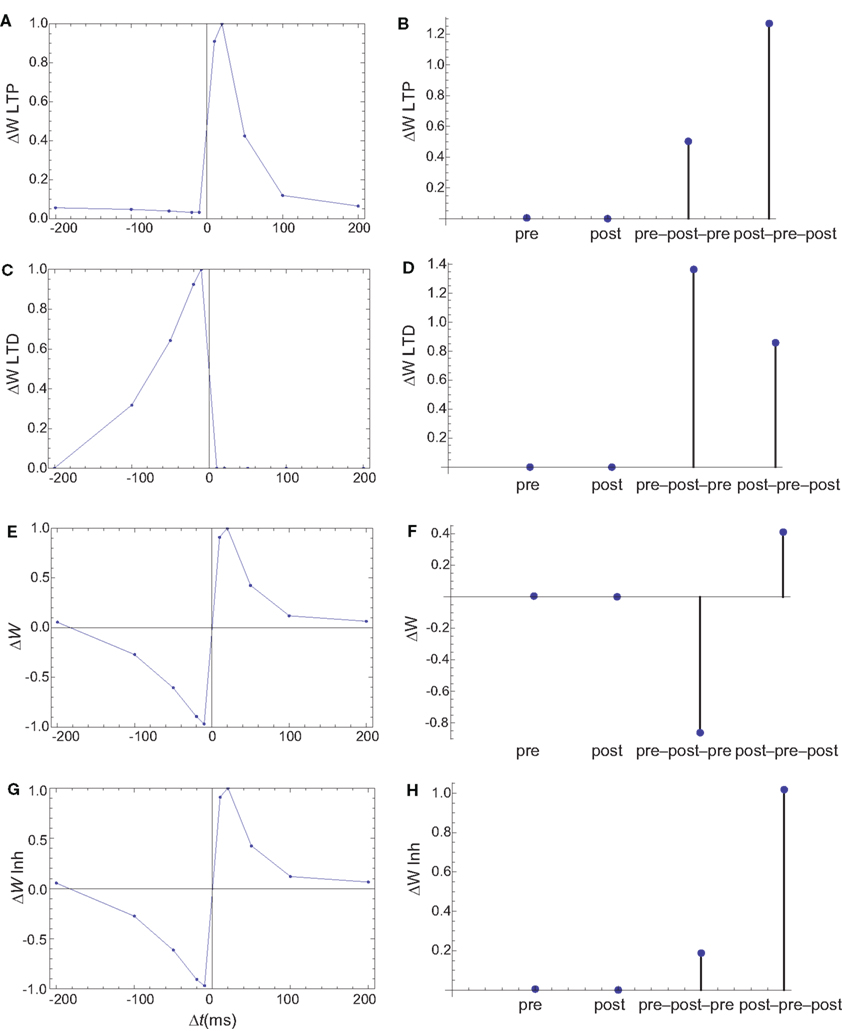
Figure 7. Changes in synaptic weights (E,F) caused by LTP (A,B) and LTD (C,D) pathways. (G,H) The changes in synaptic weights if the LTD pathway is inhibited by CaMKII. Columns as in Figure 6. The weight changes for single spike and spike doublets are qualitatively similar to those in cultured hippocampal neurons: antisymmetric STDP for spike doublets with a slightly longer window for depression and infinitesimal changes for pre and postsynaptic stimulation alone. If the LTD pathway is inhibited by CaMKII, the results for spike triplets are also similar to those observed in cultured hippocampal neurons: small changes for symmetric 10 ms pre–post–pre triplet, and strong potentiation for symmetric 10 ms post–pre–post triplet.

The final change in the synaptic weight is assumed to be the sum of LTP and LTD activities.

Results

Postsynaptic Firing

The firing of the postsynaptic neuron leads to calcium currents through VGCCs (Figure 2A) and activation of AC (Figure 3A) and CaN (Figure 5A). AC leads to activation of PKA (Figure 6B). The ratio between CaN and PKA activities was tuned such that postsynaptic firing alone produces equal CaN and PKA activation resulting in no PP1 activation (Figure 6D). This leads to no change in weight caused by the LTD mechanism (Figure 7D). Since CaMKII is not activated (Figure 6F), no change in synaptic weight is caused by the LTP mechanism (Figure 7B).

Presynaptic Firing

The firing of the presynaptic neuron alone activates to a low extent the NMDARs and IP3Rs. While the peak current through an NMDAR is small if the membrane is not depolarized, due to the slow dynamics of the channel the total current can not be neglected (Figure 2B). Given the assumption of enzyme localizations, presynaptic firing leads to transient AC, PDE (Figure 3B), and CaMKII (Figure 5B) activations, all to a small extent. The ratio of AC and PDE activity was tuned to cancel out (Figure 4B) and to lead to little PKA activation (Figure 6B). Without activation of PKA, the change in synaptic weight caused by LTP mechanisms is zero (Figure 7B). Presynaptic firing leads to little CaN (Figure 5B) activation, which, via PP1 leads to no change in synaptic weight caused by LTD mechanisms (Figure 7D).

Long delays

If pre and postsynaptic neurons fire at intervals longer than the transient enzyme activations (e.g., 200 ms, Figures 2–5 C,E), due to the linear characteristics of long-term enzyme activations, the total changes will be additive and zero in this case (Figure 7).

Post–Pre

The firing of the postsynaptic neuron leads to activation of CaN and AC. The transient activation of CaN is unaffected by the firing in quick succession of the presynaptic neuron (Figure 5D). The transient rise in cAMP is however truncated by the activation of PDE by the presynaptic neuron (Figure 4D). The closer the presynaptic neuron fires after the postsynaptic one, the shorter the cAMP transient is. This leads to a reduced PKA activation (Figure 6A) compared to the firing of the postsynaptic neuron alone (Figure 6B) and an imbalance between CaN and PKA which leads to activation of the LTD pathway (Figure 7C). Since little CaMKII activity is obtained, the LTP pathway is not activated in this case (Figure 7A). This mechanism is also consistent with experiments in which CaN was inhibited (Wang et al., 2005) producing no significant change in synaptic weight.

Pre–Post

The firing of the postsynaptic neuron quickly following the presynaptic one leads to opening of all calcium sources and massive currents through NMDAR (Figure 2F). These currents lead to high CaMKII (Figure 5F) and AC (Figure 3F) activation. At the same time, the superposition between the PDE activation and AC activation (Figure 3F) leads to efficient consumption of cAMP (Figure 4F). One free parameter in the model, the ratio of how well NMDAR and VGCC activate AC can shift the pre–post activation of PKA, but it has a small impact on the presynaptic firing only. The pre–post LTP window which results from this activation (Figure 7A) is roughly half the glutamate unbinding halftime from NMDAR due to the requirement that two CaMKII subunits to be active to produce an autophosphorylation event. In addition, adjusting the exact position of AC relative to NMDAR and VGCC can also influence this window. In this model, the rise in AC activation due to the large NMDARs current is larger than the PDE activation, leading to zero PP1 activation and zero weight change due to LTD mechanisms (Figure 7C). This result is consistent with biochemical manipulations in which CaMKII was inhibited (Wang et al., 2005), however no significant change in synaptic weigh is observed.

Post–Pre–Post

The post–pre–post symmetric triplet with 10 ms between each spike produces weight changes similar to the pre–post doublet (Wang et al., 2005). CaN (Figure 5G) and AC (Figure 3G) are increased, but they roughly cancel each other (though not perfectly). This results in a large LTP (similar to the best doublet) and a small LTD (Figures 7B,D). While the net effect is LTP (Figure 7H), both pathways are activated. This is qualitatively consistent with experimental results which show that inhibition of CaMKII produces LTD and inhibition of CaN produces LTP in this protocol (Wang et al., 2005).

Pre–Post–Pre

The symmetric pre–post–pre triplet with 10 ms between each spike produces an increased PDE activity (Figure 3H), which strongly reduces PKA activity (Figure 6B). The CaMKII activation is high, comparable to pre–post doublet (Figure 6H). The reduced PKA activity leads to a small activation of LTP (Figure 7B). If it is assumed to inhibit LTD, the high activation of CaMKII results in a small activation of the LTD pathway (Figure 7H). Their values are similar, and the net synaptic weight change is small (Figure 7H). This result is consistent with experimental observations in which CaMKII inactivation produces an LTD window and CaN inactivation produces LTP in this case (Wang et al., 2005).

Model Variations

Three sets of simulations were performed, which differ primarily in the quantitative aspects of PDE activation. In the first set of simulations, which was presented until now, the calcium current through IP3R has a fast rise time. This is possible considering the below micrometer distances second messengers need to travel in a spine.

In a second set of simulations the rise time for the calcium current through IP3R is increased by a factor of 10 (Figure 8), leading to a time scale similar to those observed in dendrites (Nakamura et al., 1999). The only other parameter which was changed in the second model is the on rate of the PDE for calcium which was decreased by a factor of square root of 10 (the square root was used since the hill coefficient for the calcium-dependent activation of enzymes was assumed to be 2). This change maintains the desired null change for the weight following a presynaptic stimulus only. Together, these modifications qualitatively reproduce the observed weight changes (Figure 9 E,F), but for a simpler LTD model.

FIGURE 8

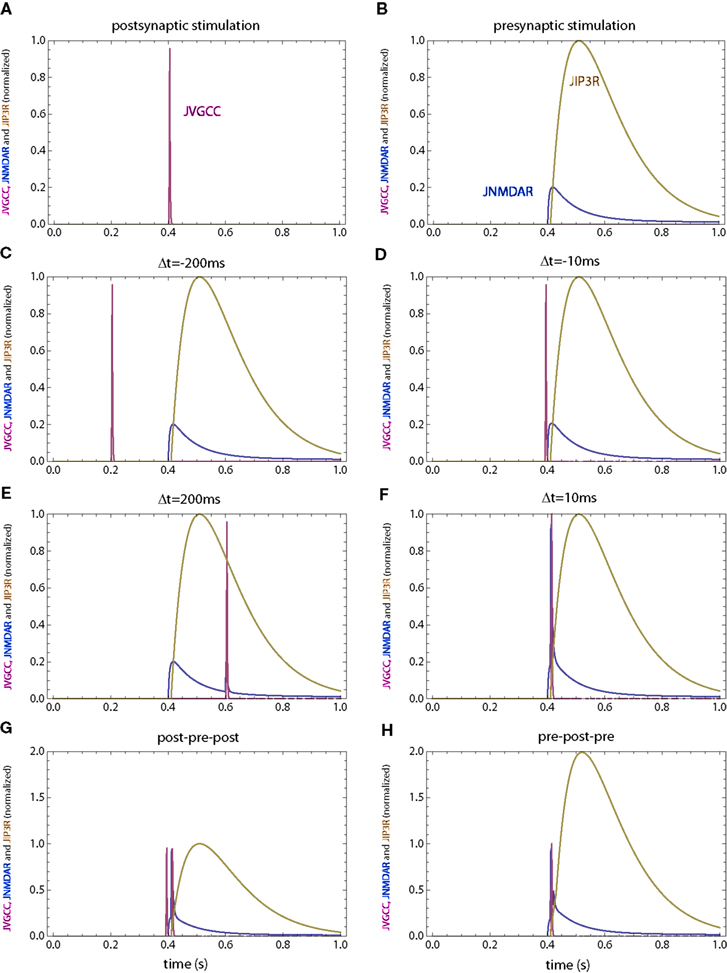
Figure 8. Calcium currents through NMDAR, VGCC and IP3R for the second set of simulations in which the IP3R has a slower rise time. (A) Postsynaptic firing alone. (B) Presynaptic firing alone. (C,D) Post–pre at different time intervals. (E,F) Pre–post at different time intervals. (G) Post–pre–post symmetric triplet with 10 ms between each spike. (H) Pre–post–pre symmetric triplet with 10 ms between each spike. The NMDAR and VGCC currents are the same as those in Figure 2.

FIGURE 9

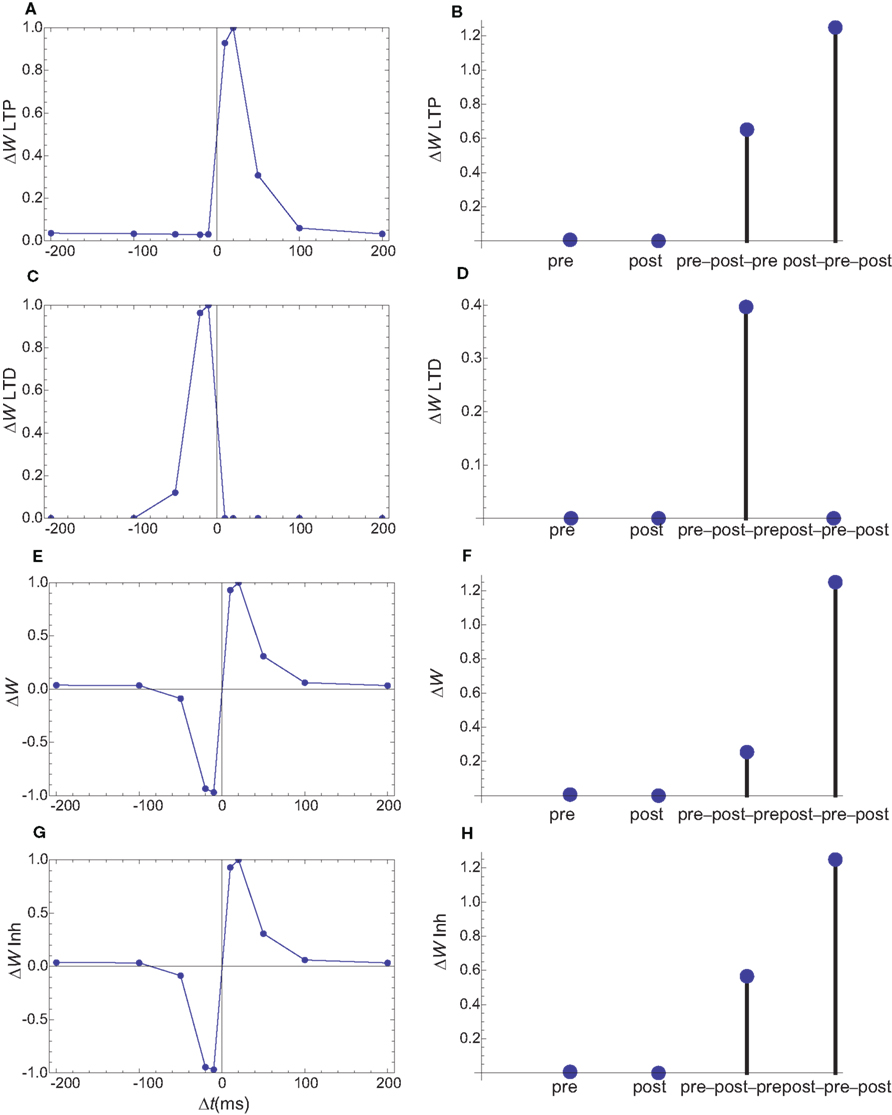
Figure 9. Changes in synaptic weights (E,F) caused by LTP (A,B) and LTD (C,D) pathways for the second set of simulations, in which the IP3R current has a slower rise time. Columns as in Figure 6. (G,H) The changes in synaptic weights if the LTD pathway is inhibited by CaMKII. As in the first simulation set, the weight changes for single spike and spike doublets are similar to those observed. However, for the slower IP3R current the observed triplet behavior is obtained without an inhibition of the LTD pathway by CaMKII.

A third set of simulations are performed for spines which lack internal calcium stores. In the model, PDE needs to be activated by a source mainly determined by presynaptic firing. This can theoretically be achieved by relying on a dendritic calcium source, however, under this condition, the shape of STDP for spike doublets could not be obtained by this simple model. An alternative is to consider that PDE is localized in the vicinity of NMDARs. While the NMDAR currents are very small in the absence of a backpropagating action potential, this trickle of calcium is sufficient to create a marker for the presynaptic firing (Figure 10). As in all the simulations, the on rate of PDE was tuned such that the presynaptic activation alone produces only minimal changes in synaptic weights. In these simulations, the shape of STDP produced by spike doublets is maintained, however qualitative changes are observed in the behavior of STDP caused by triplets (Figures 10E,F). Unlike the STDP caused by triplets observed in cultured hippocampal neurons (Wang et al., 2005), the symmetric pre–post–pre triplet is potent at inducing LTP, while the symmetric post–pre–post produces LTD. However, such a triplet behavior is consistent with those measured in L2/3 in visual cortical slices (Froemke and Dan, 2002).

FIGURE 10

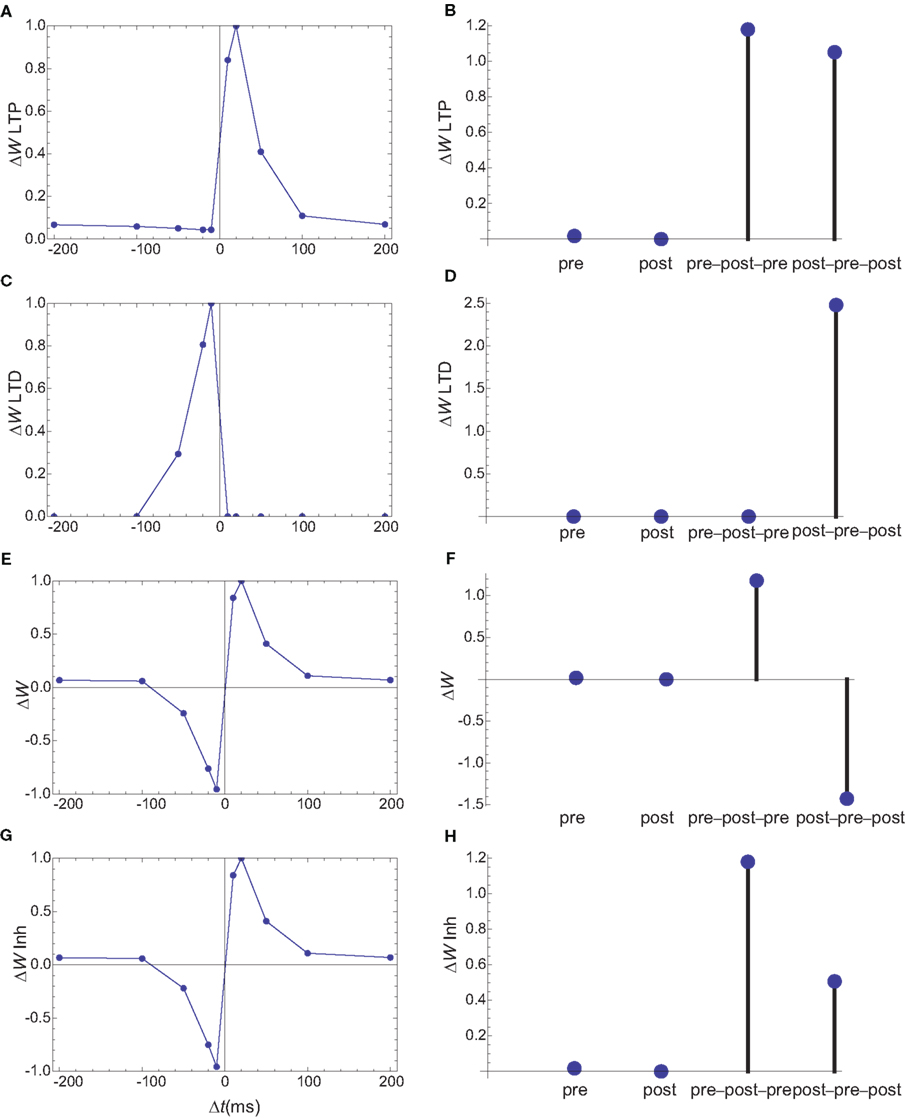
Figure 10. Changes in synaptic weights (E,F) caused by LTP (A,B) and LTD (C,D) pathways for a third set of simulations, in which PDE is assumed to localize in the vicinity of NMDARs. Columns as in Figure 6. (G,H) The changes in synaptic weights if the LTD pathway is inhibited by CaMKII. The results for spike doublets are qualitatively similar to those obtained if PDE is assumed to localize near IP3Rs, however the results for spike triplets are qualitatively different. In the absence of inhibition of LTD by CaMKII, the 10-ms symmetric pre–post–pre triplet lead to potentiation, while the post–pre–post triplet leads to inhibition.

Discussions

This study provides a very different paradigm of modeling biochemical networks, in which affinities and kinetics of different enzymes come secondary to their location. This can possibly allow robust and diverse signaling pathways based on a small number of second messengers. From an evolutionary perspective this type of signaling shifts the complexity from fine tuning the kinetics of different enzymes to produce diverse behaviors, to the production of novel scaffolds. The sheer diversity of existing scaffolds makes such a mechanism at least plausible.

The model can explain the apparently opposite behaviors observed for spike triplets in L2/3 visual cortical slices and hippocampal cell cultures by keeping all the parameters of the model the same and simply assuming a different localization for PDE: In the vicinity of IP3R for hippocampal cell cultures, and near the mouth of the NMDAR for cortical slices. It should be noted that, since the on rate for all calcium-dependent enzymes is described in term of calcium currents, it will be strongly affected by the exact position of the enzyme with respect to the mouth of the channel: A higher on rate for locations closer to the mouth. The localization of PDE which best reproduces the spike triplets for the two preparations seems reasonable, since cell cultures have typically stronger synapses than slices, which often correlates with larger spines, which are more likely to have a spine apparatus.

This study relies on the assumption that calcium concentrations and downstream cascades have strong spatial heterogeneities on scales smaller than the size of a spine. In previous simulations of calcium transients during STDP protocols, which involve strong calcium currents persisting only a few milliseconds, such a heterogeneity is observed (Keller et al., 2008; Mihalas, 2009). In earlier simulations (Holmes, 1990) a relatively uniform calcium concentration is observed at the end of the stimulation protocol simulating a 200-Hz tetanic stimulation. While these studies used different simulation methods, one key difference is in the stimulation protocol. In the former studies, simulating STDP, large calcium currents persist for 10 ms or less, while in the simulation of the tetanic stimulation large calcium currents persist for 40–100 ms. Even in the simulations of tetanic stimulation, calcium concentrations in a PSD-like compartment and near the base of the spine are very different for the first 30–50 ms, depending on the spine geometry.

Numerous additional gates can be added to the model. If activation of PKC by mGluR is included in the requirement for LTD, if PKC localized near either NMDARs or IP3Rs, the dynamic of the model is left practically unchanged. This is possibly supported by experimental observations showing that phosphorylation of Ser880 of GluR2 by PKC interferes with its anchoring in PSD. While qualitative aspects of the influence of neuromodulators (Seol et al., 2007) can be reproduced by the presented model, their exact effect on the STDP window might require additional gates or further tuning of the model’s parameters.

Some previous experimental results could be reinterpreted in the light of a spatial model. Introducing different levels of the calcium buffer EGTA reduces the average calcium concentration in spines (Cho et al., 2001). However it does so in a heterogeneous manner: the larger the distance to the calcium source, the bigger the effect. Increasing EGTA concentration results in smaller and smaller domains which are left unaffected. Thus their result: increasing EGTA concentrations first affects LTP and subsequently LTD can be interpreted that a key enzyme in the LTP pathway is located further away from the calcium sources than those in the LTD pathway. In the case of the model proposed this enzyme is AC, which is located between NMDARs and VGCCs.

The exact location of different enzymes proposed in this model is oversimplified and highly speculative. The space of possible spatial distributions of the entire biochemical network is very large, and other distributions could as well fit multiple experimental observations. Therefore this study should mainly be seen as an incentive for experimental studies of relative localizations for multiple steps of the biochemical networks. Considering that calcium/calmodulin-dependent enzymes are mainly activated by the calcium source in the vicinity of which they are anchored is also an oversimplification. A full description of the interactions between calcium sources at different distances with different dynamics is computationally complex. A simulation environment which performs these computations and has the spatial precision required to characterize calcium nanodomains near the mouth of calcium channels is MCell (Stiles et al., 2001). It has been used to describe calcium dynamics (Franks et al., 2002) and calmodulin activation (Keller et al., 2008) in dendritic spines. It is an excellent simulation environment for future detailed models of synaptic plasticity, but it is currently limited by the knowledge of the parameters describing the direct and scaffold-mediated interactions in the biochemical cascades as well as knowledge of typical spatial distributions of different molecules.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgment

NIH grant NEI R01EY016281 to E. Niebur.

References

Artola, A., and Singer, W. (1993). Long-term depression of excitatory synaptic transmission and its relationship to long-term potentiation. Trends Neurosci. 16, 480–487.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Aslam, N., Kubota, Y., Wells, D., and Shouval, H. Z. (2009). Translational switch for long-term maintenance of synaptic plasticity. Mol. Syst. Biol. 5, 284.

Pubmed Abstract | Pubmed Full Text

Bennett, M. K., Erondu, N. E., and Kennedy, M. B. (1983). Purification and characterization of a calmodulin-dependent protein kinase that is highly concentrated in brain. J. Biol. Chem. 258, 12735–12744.

Pubmed Abstract | Pubmed Full Text

Bhalla, U. S. (2002). Biochemical signaling networks decode temporal patterns of synaptic input. J. Comput. Neurosci. 13, 49–62.

Pubmed Abstract | Pubmed Full Text

Bi, G. Q., and Poo, M. M. (1998). Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472.

Pubmed Abstract | Pubmed Full Text

Bradshaw, J. M., Kubota, Y., Meyer, T., and Schulman, H. (2003). An ultrasensitive Ca²⁺/calmodulin-dependent protein kinase II-protein phosphatase 1 switch facilitates specificity in postsynaptic calcium signaling. Proc. Natl. Acad. Sci. U.S.A. 100, 10512–10517.

Pubmed Abstract | Pubmed Full Text

Cho, K., Aggleton, J. P., Brown, M. W., and Bashir, Z. I. (2001). An experimental test of the role of postsynaptic calcium levels in determining synaptic strength using perirhinal cortex of rat. J. Physiol. 532, 459–466.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cormier, R. J., Greenwood, A. C., and Connor, J. A. (2001). Bidirectional synaptic plasticity correlated with the magnitude of dendritic calcium transients above a threshold. J. Neurophysiol. 85, 399–406.

Pubmed Abstract | Pubmed Full Text

Esteban, J. A., Shi, S. H., Wilson, C., Nuriya, M., Huganir, R. L., and Malinow, R. (2003). PKA phosphorylation of AMPA receptor subunits controls synaptic trafficking underlying plasticity. Nat. Neurosci. 6, 136–143.

Pubmed Abstract | Pubmed Full Text

Frankland, P. W., O’Brien, C., Ohno, M., Kirkwood, A., and Silva, A. J. (2001). Alpha-CaMKII-dependent plasticity in the cortex is required for permanent memory. Nature 411, 309–313.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Franks, K. M., Bartol, T. M. Jr., and Sejnowski, T. J. (2002). A Monte Carlo model reveals independent signaling at central glutamatergic synapses. Biophys. J. 83, 2333–2348.

Pubmed Abstract | Pubmed Full Text

Froemke, R. C., and Dan, Y. (2002). Spike-timing-dependent synaptic modification induced by natural spike trains. Nature 416, 433–438.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Glazewski, S., Chen, C. M., Silva, A., and Fox, K. (1996). Requirement for alpha-CaMKII in experience-dependent plasticity of the barrel cortex. Science 272, 421–423.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Graupner, M., and Brunel, N. (2007). STDP in a bistable synapse model based on CaMKII and associated signaling pathways. PLoS Comput. Biol. 3, e221. doi: 10.1371/journal.pcbi.0030221

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Harris, K. M., and Stevens, J. K. (1989). Dendritic spines of CA 1 pyramidal cells in the rat hippocampus: serial electron microscopy with reference to their biophysical characteristics. J. Neurosci. 9, 2982–2997.

Pubmed Abstract | Pubmed Full Text

Hayer, A., and Bhalla, U. S. (2005). Molecular switches at the synapse emerge from receptor and kinase traffic. PLoS Comput. Biol. 1, 137–154. doi: 10.1371/journal.pcbi.0010020

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Holmes, W. R. (1990). Is the function of dendritic spines to concentrate calcium? Brain Res. 519, 338–342.

Pubmed Abstract | Pubmed Full Text

Jahr, C. E., and Stevens, C. F. (1990). Voltage dependence of NMDA-activated macroscopic conductances predicted by single-channel kinetics. J. Neurosci. 10, 3178–3182.

Pubmed Abstract | Pubmed Full Text

Jordan, B. A., Fernholz, B. D., Boussac, M., Xu, C., Grigorean, G., Ziff, E. B., and Neubert, T. A. (2004). Identification and verification of novel rodent postsynaptic density proteins. Mol. Cell Proteomics 3, 857–871.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Karmarkar, U. R., and Buonomano, D. V. (2002). A model of spike-timing dependent plasticity: one or two coincidence detectors? J. Neurophysiol. 88, 507–513.

Pubmed Abstract | Pubmed Full Text

Keller, D. X., Franks, K. M., Bartol, T. M. Jr., and Sejnowski, T. J. (2008). Calmodulin activation by calcium transients in the postsynaptic density of dendritic spines. PLoS ONE 3, e2045. doi: 10.1371/journal.pone.0002045

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kennedy, M. B. (2000). Signal-processing machines at the postsynaptic density. Science 290, 750–754.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lester, R. A., and Jahr, C. E. (1992). NMDA channel behavior depends on agonist affinity. J. Neurosci. 12, 635–643.

Pubmed Abstract | Pubmed Full Text

Lisman, J. (1989). A mechanism for the Hebb and the anti-Hebb processes underlying learning and memory. Proc. Natl. Acad. Sci. U.S.A. 86, 9574–9578.

Pubmed Abstract | Pubmed Full Text

Luby-Phelps, K., Hori, M., Phelps, J. M., and Won, D. (1995). Ca(2+)-regulated dynamic compartmentalization of calmodulin in living smooth muscle cells. J. Biol. Chem. 270, 21532–21538.

Pubmed Abstract | Pubmed Full Text

Markram, H., Lubke, J., Frotscher, M., and Sakmann, B. (1997). Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mihalas, S. (2009). How Local are Calcium Messenger Cascades in Postsynaptic Spines? SfN Program Number 135.12.

Nakamura, T., Barbara, J. G., Nakamura, K., and Ross, W. N. (1999). Synergistic release of Ca2+ from IP3-sensitive stores evoked by synaptic activation of mGluRs paired with backpropagating action potentials. Neuron 24, 727–737.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Naoki, H., Sakumura, Y., and Ishii, S. (2005). Local signaling with molecular diffusion as a decoder of Ca2+ signals in synaptic plasticity. Mol. Syst. Biol. 1, 2005.0027.

Pubmed Abstract | Pubmed Full Text

Naraghi, M., and Neher, E. (1997). Linearized buffered Ca2+ diffusion in microdomains and its implications for calculation of [Ca2+] at the mouth of a calcium channel. J. Neurosci. 17, 6961–6973.

Pubmed Abstract | Pubmed Full Text

Nelson, S. B., and Turrigiano, G. G. (2008). Strength through diversity. Neuron 60, 477–482.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Olwin, B. B., and Storm, D. R. (1985). Calcium binding to complexes of calmodulin and calmodulin binding proteins. Biochemistry 24, 8081–8086.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pepke, S., Kinzer-Ursem, T., Mihalas, S., and Kennedy, M. B. (2010). A dynamic model of interactions of Ca2+, calmodulin, and catalytic subunits of Ca2+/calmodulin-dependent protein kinase II. PLoS Comput. Biol. 6, e1000675. doi: 10.1371/journal.pcbi.1000675

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rubin, J. E., Gerkin, R. C., Bi, G. Q., and Chow, C. C. (2005). Calcium time course as a signal for spike-timing-dependent plasticity. J. Neurophysiol. 93, 2600–2613.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Seol, G. H., Ziburkus, J., Huang, S., Song, L., Kim, I. T., Takamiya, K., Huganir, R. L., Lee, H. K., and Kirkwood, A. (2007). Neuromodulators control the polarity of spike-timing- dependent synaptic plasticity. Neuron 55, 919–929.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shifman, J. M., Choi, M. H., Mihalas, S., Mayo, S. L., and Kennedy, M. B. (2006). Ca²⁺/calmodulin-dependent protein kinase II (CaMKII) is activated by calmodulin with two bound calciums. Proc. Natl. Acad. Sci. U.S.A. 103, 13968–13973.

Pubmed Abstract | Pubmed Full Text

Sjostrom, P. J., Turrigiano, G. G., and Nelson, S. B. (2003). Neocortical LTD via coincident activation of presynaptic NMDA and cannabinoid receptors. Neuron 39, 641–654.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Song, I., and Huganir, R. L. (2002). Regulation of AMPA receptors during synaptic plasticity. Trends Neurosci. 25, 578–588.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stiles, J. S., Bartol T. M. Jr., Salpeter, M. M., Salpeter, E. E., and Sejnowski, T. J. (2001). Synaptic Variability: New Insights from Reconstructions and Monte Carlo Simulations with MCell. Baltimore, MD: Johns Hopkins University Press.

Urakubo, H., Honda, M., Froemke, R. C., and Kuroda, S. (2008). Requirement of an allosteric kinetics of NMDA receptors for spike timing- dependent plasticity. J. Neurosci. 28, 3310–3323.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wang, H. X., Gerkin, R. C., Nauen, D. W., and Bi, G. Q. (2005). Coactivation and timing-dependent integration of synaptic potentiation and depression. Nat. Neurosci. 8, 187–193.

Pubmed Abstract | Pubmed Full Text

Yang, S. N., Tang, Y. G., and Zucker, R. S. (1999). Selective induction of LTP and LTD by postsynaptic [Ca2+]i elevation. J. Neurophysiol. 81, 781–787.

Pubmed Abstract | Pubmed Full Text

Yang, Y., Wang, X. B., Frerking, M., and Zhou, Q. (2008). Delivery of AMPA receptors to perisynaptic sites precedes the full expression of long-term potentiation. Proc. Natl. Acad. Sci. U.S.A. 105, 11388–11393.

Pubmed Abstract | Pubmed Full Text

Zhong, H., Sia, G. M., Sato, T. R., Gray, N. W., Mao, T., Khuchua, Z., Huganir, R. L., and Svoboda, K. (2009). Subcellular dynamics of type II PKA in neurons. Neuron 62, 363–374.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text