Insight into employees' perceptions on reform initiatives in public service organizations using fractional order derivatives with optimal control strategies

This study presents a compartmental model that classifies employees into three categories: “indifferent,” “resistant,” and “adaptive,” to explore their transitions based on adaptation to workplace reform initiatives. The researchers rigorously assessed the model for well-posedness and stability of its steady states. Utilizing Pontryagin’s maximum principle alongside numerical simulations, the researchers identified effective strategies aimed at reducing the number of resistant employees, thereby cultivating a more supportive atmosphere for reform efforts. The findings indicate that such an environment encourages employees to remain indifferent or adaptive, fostering a positive outlook toward change. The optimal strategies identified include providing training sessions to enhance employees' skills for adapting to new processes and technologies, as well as ensuring clear communication regarding the rationale, benefits, and impacts of the reforms. Furthermore, the study examined memory effects by transforming the integer order model into a fractional order model, with graphical representations highlighting the significance of fractional derivatives in illustrating the evolution of employees' perceptions over time. This research contributes valuable insights into managing employee adaptation during organizational change.

1 Introduction

In today’s fast-paced and ever-changing environment, public service organizations recognize the critical role employees play in adapting to and driving innovation within organizational dynamics (Jakobsen et al., 2023). A key aspect of this adaptation involves the implementation of reform initiatives aimed at enhancing efficiency, effectiveness, and overall service delivery (Lapuente and Van de Walle, 2020). However, the success of these reforms largely depends on employees' perceptions and their willingness to embrace change. Understanding how employees interpret and respond to reform initiatives is essential for organizations to design strategies that foster engagement and minimize resistance (Guest, 2002; Jones et al., 2008). This study aims to model and analyze employees’ perceptions of reform initiatives, providing insights that can help policymakers and organizational leaders develop targeted interventions to enhance reform adoption and effectiveness.

To improve the likelihood of successful reform adoption, public service organizations must foster a supportive environment that values employee input and acknowledges their contributions toward organizational objectives. By actively engaging employees in the reform process, organizations can cultivate a culture of collaboration and adaptability, ultimately enhancing service delivery to the community (Chang et al., 2021).

The concept of employees' perception regarding reform initiatives in public service organizations has garnered significant attention in recent years. Studies have shown that employee' attitudes, beliefs, and opinions play a critical role in shaping their behavior and reactions towards organizational change. By modeling and analyzing these perceptions, policymakers and organizational leaders can gain valuable insights into the factors influencing employee attitudes towards reform initiatives, thereby enabling them to design more targeted and effective strategies for implementation.

To capture the complexities of employee attitudes over time, the study employs a nonlinear mathematical modeling framework incorporating fractional order derivatives. Traditional integer-order models often fail to fully account for the intricate and evolving nature of human behavior in response to organizational change. Fractional calculus provides a novel approach to analyzing perception dynamics, providing for a more nuanced understanding of how employees respond to reform initiatives. Traditional integer-order models may fail to fully account for the intricate and evolving nature of human behavior in response to organizational change. The application of fractional order derivatives in real problems has been widely documented in various fields, as demonstrated by recent studies (Hailu and Teklu, 2024a; Hailu and Teklu, 2024b; Teklu et al., 2023; Naik et al., 2024; Junjua et al., 2024). The authors have utilized a nonlinear model across various contexts. In this study, individuals are categorized into stages of perception development, enabling the model to simulate and assess how various factors impact employees’ perceptions of reform initiatives over time. The application of fractional calculus to analyze employee perceptions of reform initiatives in public service organizations offers a novel perspective on understanding the underlying dynamics and relationships involved. By employing fractional order derivatives, researchers can capture the nuances and complexities of human behavior that traditional integer-order models may overlook. Utilizing nonlinear compartmental models enables the identification of crucial intervention points for more effective resource allocation.

In this study, the researchers explore the application of fractional order derivatives as a mathematical framework for modeling employees' perceptions of reform initiatives in public service organizations. This approach enables us to account for the complexities of employee attitudes, which traditional integer-order models may overlook. Additionally, by incorporating optimal control strategies, the researchers aim to identify effective interventions that can positively influence employee perceptions and foster a smoother transition during reform processes.

Furthermore, optimal control strategies are integrated to identify effective interventions that can positively influence perceptions and facilitate smoother transitions during reform processes. Numerical simulations using MATLAB’s ode45, based on the Runge-Kutta method, ensure accurate solutions for differential equations, enhancing the reliability of the study’s findings. The Runge-Kutta method is preferred due to its superior accuracy compared to the Euler method (E. I. et al., 1992).

This research contributes to the existing literature by offering a mathematical framework for assessing employee perceptions of reform initiatives in public service organizations. The insights gained can help in optimizing resource allocation and improving organizational outcomes. By examining relevant literature, employing modeling and analysis, and integrating theories of ordinary differential equations and optimal control theory, this study aims to provide meaningful insights into the factors influencing employee perceptions and their implications for future research and practical implementation.

The article is structured as follows: Section 2 introduces the fundamental terminologies of fractional calculus; Section 3 details the model formulation, covering assumptions, descriptions, and an assessment of the model’s well-posedness, along with qualitative analysis; Section 4 explores the optimal control problem, including numerical simulations and sensitivity analysis; finally, Section 5 concludes with a discussion and provides recommendations for future research.

2 Basic terminologies in fractional calculus

The concepts of fractional order calculus outlined below will serve as the foundation for creating the fractional order model in this study.

Definition 1. For a function $\mathrm{f}$ that belongs to the class of ${\mathbb{C}}^{\mathrm{n}}$,the Caputo derivative of fractional order κ is defined as follows: (Petrás, 2011; Vargas-De-León, 2015)

$D_t^{\kappa }f\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\mathrm{n}-\kappa \right)}{\int }_0^t{f}^n\left(\zeta \right)\frac{{\left(t-\zeta \right)}^{n-\kappa }}{t-\zeta }d\zeta ,n-1<\kappa \le n\mathbb{\in }\mathbb{N}(1)$

Note: When

$\kappa \to 1,D_t^{\kappa }f\left(t\right)\text{\hspace{0.17em}converges\hspace{0.17em}to\hspace{0.17em}}\dot{f}\left(t\right)(2)$

Definition 2. For a function $f$ that belongs to the class of ${\mathbb{C}}^{\mathrm{n}}$, the Caputo integral of fractional order κ is defined as follows: (Petrás, 2011; Vargas-De-León, 2015)

$I_t^{\kappa }f\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_0^{t}f\left(\zeta \right)\frac{{\left(t-\zeta \right)}^{\kappa }}{t-\zeta }d\zeta ,<\kappa <1,t>0(3)$

Definition 3. The two parameter Mittag–Leffler function is described as (Petrás, 2011; Vargas-De-León, 2015)

$E_{\alpha ,\beta }\left(t\right)={\displaystyle \sum _{k=1}^{\infty }}\frac{t^k}{\mathrm{\Gamma }\left(\alpha k+\beta \right)}\text{\hspace{0.17em}where\hspace{0.17em}}\alpha ,\beta >0(4)$

Definition 4. For $\beta =1$, the one-parameter Mittag–Leffler function is defined as

$E_{\alpha }\left(t\right)=E_{\alpha ,1}\left(t\right)={\displaystyle \sum _{k=1}^{\infty }}\frac{t^k}{\mathrm{\Gamma }\left(\alpha \mathrm{k}+1\right)}(5)$

Definition 5. A constant solution ${\theta }^{*}$ is referred to as a steady state of the Caputo-fractional order model if

$D_t^{\kappa }\theta \left(t\right)=f\left(t,\theta \left(t\right)\right),\kappa \in \left[0,1\right]\text{\hspace{0.17em}if\hspace{0.17em}and\hspace{0.17em}only\hspace{0.17em}if\hspace{0.17em}}f\left(t,{\theta }^{*}\right)=0(6)$

Proposition 1. The Laplace transform of the Caputo fractional order derivative of order $\kappa ,$ $m-1<\kappa \le m,m\in N$ is given by $\mathcal{L}\left(D_t^{\kappa }f\right)\left(s\right)=s^{\kappa }F\left(s\right)-{\displaystyle \sum _{i=0}^{m-1}}{s}^{\kappa -i-1}{f}^k\left(0\right)$ where $F\left(s\right)$ is $\mathcal{L}\left(f\left(t\right)\right)$ (Podlubny, 1999).

Over the past 40 years, the Mittag–Leffler function has become increasingly significant in fractional calculus because of its wide range of applications in different scientific and engineering fields (Haubold et al., 2011). In the sense of Caputo, the derivative and integral of a function $f$, which belongs to the class of ${\mathbb{C}}^{\mathrm{n}}$, are expressed in Equations 1, 3 respectively. The Laplace transform of the two-parameter Mittag–Leffler function is outlined in the following proposition.

Proposition 2. The Laplace transform of the two-parameter Mittag Leffler function, as defined in Equation 4, is described by Podlubny (1999)

$\mathcal{L}\left({\mathrm{t}}^{\beta -1}{E}_{\alpha ,\beta }\left(\pm \mathrm{\gamma }{\mathrm{t}}^{\mathrm{\alpha }}\right)\right)\left(\mathrm{s}\right)=\frac{{\mathrm{s}}^{\mathrm{\alpha }-\mathrm{\beta }}}{{\mathrm{s}}^{\mathrm{\alpha }}\mp \mathrm{\gamma }}$

Proposition 3. Suppose $h\left(t\right)\in \mathcal{L}\left[0,T_f\right]$ and $D_t^{\kappa }h\left(t\right)\in \mathcal{L}\left[0,T_f\right]$ for $\in$ (0,1]. The mean value theorem states that $h\left(t\right)=h\left(0\right)+\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}$ $D_t^{\kappa }h\left(\zeta \right)t^{\kappa }$ where $\zeta \in \left[0,t\right]$, for each $t$ such that $0<t\le T_f$ (Petrás, 2011).

Lemma 1: The following two statements have been derived from Proposition 3 (Denu and Kermausuor, 2022).

a) The function $h$ is non-decreasing for all $t\in \left[0,T_f\right]$ if ^C$D_t^{\kappa }h\left(t\right)\ge 0.$

b) The function $h$ is non-increasing for all $t\in \left[0,T_f\right]$ if ^C$D_t^{\kappa }h\left(t\right)\le 0.$

Proposition 4. Suppose $g\left(t\right)\in L^{\infty }\left(\mathbb{R}\right)\cap \mathcal{F}\left(\mathbb{R}\right)$ and $\mathbb{\in }\mathbb{R},$ $n-1<\kappa \le n,n\in N$. The following conditions are met (Denu and Kermausuor, 2022)

a) $\left(D_t^{\kappa }{I}^{\kappa }g\right)\left(t\right)=g\left(t\right),$

b) $\left(I^{\kappa }{D}_t^{\kappa }g\right)\left(t\right)=g\left(t\right)-{\displaystyle \sum _{i=0}^{n-1}}\frac{t^i}{i!}{g}^i\left(0\right),$

c) Specifically, if $0<\kappa <1$, then $\left(I^{\kappa }{D}_t^{\kappa }g\right)\left(t\right)=g\left(t\right)-g\left(0\right),$ and

d) For a constant function $g\left(t\right)=c$, $D_t^{\kappa }\left(c\right)=0.$

3 Model formulation

3.1 Assumptions and model descriptions

To evaluate how employees view the reform efforts of a specific public service organization, the researchers segmented the targeted population represented by K(t) at a certain time t into three distinct groups. Those in favor of the reform and with positive perceptions are classified as A(t). Those against the reform and displaying negative perceptions are categorized as R(t), while individuals with neutral views are labeled as I(t).

$\mathrm{M}\left(\mathrm{t}\right)=\mathrm{I}\left(\mathrm{t}\right)+\mathrm{A}\left(\mathrm{t}\right)+\mathrm{R}\left(\mathrm{t}\right)(7)$

Creating a Caputo fractional order model to analyze how employees perceive reform initiatives involves several key assumptions that serve as the foundation for the modeling process. Some of the possible underlying assumptions to consider include.

• The current perceptions are influenced not only by present factors but also by past experiences and interactions with reform initiatives. The fractional order derivative accounts for this memory effect by capturing the historical dynamics of perception changes over time.

• The Caputo fractional derivative assumes that the underlying dynamics of employees' perceptions change smoothly over time.

• The modeling process assumes that there are well-defined initial conditions governing employees' perceptions of reform initiatives at the beginning of the analysis period.

• A deterministic relationship between employees' perceptions and reform initiatives, where the impact of specific factors on perceptions can be quantified and predicted with a certain degree of certainty.

The rationale for these assumptions is mainly to develop a mathematical model that is manageable within a deterministic framework utilizing ordinary differential equations.

The population that the researchers are focusing on is separated into three specific compartments, each of which will be described in detail.

1. “Indifferent, I” employees refer to the number of individuals who are neither in favor nor against reform initiatives done by the public service organizations can be seen as neutral or indifferent. These employees are neutral or have no strong opinion about the reform initiatives. They are neither supportive nor opposed to the changes being implemented. Their attitude might suggest that they are unaffected by or disinterested in the reform, indicating a lack of engagement or enthusiasm for it. These employees are not actively working against the reforms, but they also are not actively promoting or advocating for them. They are simply neutral toward the change.

2. “Adaptable, A” employees refer to the number of individuals who support the reform initiatives implemented by the public service organizations. These employees are typically enthusiastic, forward-thinking, and dedicated individuals. They are open to change and innovation, understanding that these initiatives aim to improve the efficiency, effectiveness, and overall quality of services provided by their organization. They are willing to embrace new ideas, processes, and initiatives within the organization. These employees are typically proactive in seeking out opportunities for growth and improvement and are not afraid to step out of their comfort zones to try new approaches or methods.

3. “Resistant, R” employees refer to the number of individuals who are against the reform initiatives implemented by the public service organization. These individuals may exhibit a variety of characteristics and behaviors that hinder the progress of change. These employees may be resistant to change, feeling comfortable with the existing ways of working and skeptical of the need for reform.

If $M\left(t\right)$ represents the total number of employees at a specific time $t$, then:

$M\left(t\right)=I\left(t\right)+R\left(t\right)+A\left(t\right).$

Employees assess reform initiatives based on their own perspectives and may be influenced by the views of others. Accordingly, they are categorized as “Adaptive,” “Resistant,” or “Indifferent”. Through interactions with others, employees can shift from one category to another. When indifferent employees engage with adaptive ones, they may start to recognize the importance of the reforms and transition to the adaptive category at a rate of ${\alpha }_1$. Conversely, they can also be influenced by resistant employees at a rate of ${\alpha }_2.$ An optimistic employee may be swayed by a pessimistic perspective at a rate of ${\beta }_2$, while a pessimistic employee can be influenced by an optimistic viewpoint at a rate of ${\gamma }_2$.

Optimistic employees may encounter both positive and negative aspects of the reforms, which can lead them to become indifferent at a rate of ${\beta }_1$while pessimistic employees transition to indifference at a rate of ${\gamma }_1$. Other parameters are stated in Table 1.

Table 1

Table 1. Description of parameters.

Although other factors, such as transparency, job security concerns, resource availability, and leadership style can also affect opinions on reform initiatives, the researchers chose to focus on a simplified mathematical model that excludes these elements. A flowchart illustrating the interactions between the various categories is shown in Figure 1, where each circle denotes a compartment, and arrows indicate transitions among them.

Figure 1

Figure 1. Flow chart of AIR model.

3.2 Fractional order model

A widely used concept in mathematical modeling is the compartment. Essentially, a compartment is a collection, often of individuals, where different compartments can interact through exchanges or by influencing each other’s inputs and outputs.

The change in the number of employees within each compartment is determined by the difference between what enters and what leaves that compartment. This net rate of change, calculated as the difference between input and output, forms the basis for the governing differential equation.

The deterministic integer order model that reflects the dynamics of whether employees are adaptive, indifferent, or resistant to reform initiatives is represented by the following system of nonlinear differential equations:

$\begin{array}{l}\frac{dI\left(t\right)}{dt}=-{\mathrm{\alpha }}_1\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}-{\mathrm{\alpha }}_2\frac{R\left(t\right)I\left(t\right)}{M\left(t\right)}+{\gamma }_{1}R\left(t\right)+{\beta }_{1}A\left(t\right)\\ \frac{dR\left(t\right)}{dt}={\mathrm{\alpha }}_2\frac{R\left(t\right)I\left(t\right)}{M\left(t\right)}+{\beta }_2\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\gamma }_2\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\gamma }_{1}R\left(t\right)\\ \frac{dA\left(t\right)}{dt}={\mathrm{\alpha }}_1\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}+{\gamma }_2\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_2\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_{1}A\left(t\right)\end{array}(8)$

with the constraints $I\left(0\right)\ge 0$, $R\left(0\right)\ge 0,A\left(0\right)\ge 0$.

In the system dynamics, $I,R$ and $A$ are the state variables that characterize employees’ adaptation to reform initiatives.

In this section, the researchers reframe the traditional model that illustrates how employees' adaptation to reform initiatives evolves over time. This approach employs the Caputo fractional order derivative, allowing us to incorporate memory effects and deepen the understanding of the dynamics of employees’ adaptation. The fractional order model, with $\mathrm{\kappa }$ representing the Caputo fractional order in the range of [0, 1], is detailed in Equation 5.

$\begin{array}{l}{}^{C}D^{\kappa }\left(I\left(t\right)\right)=-{\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}-{\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)I\left(t\right)}{M\left(t\right)}+{\gamma }_1^{\kappa }R\left(t\right)+{\beta }_1^{\kappa }A\left(t\right)\\ {}^{C}D^{\kappa }\left(R\left(t\right)\right)={\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)I\left(t\right)}{M\left(t\right)}+{\beta }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\gamma }_1^{\kappa }R\left(t\right)\\ {}^{C}D^{\kappa }\left(A\left(t\right)\right)={\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}+{\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_1^{\kappa }A\left(t\right)\end{array}(9)$

where

$I\left(0\right)\ge 0,R\left(0\right)\ge 0,\text{and}A\left(0\right)\ge 0(10)$

The operator ${}^{\mathrm{C}}\mathrm{D}^{\mathrm{\kappa }}$ for the fractional derivative has a dimension of ${\left(\text{time}\right)}^{-\mathrm{\kappa }}$ instead of ${\left(\text{time}\right)}^{-1}$. Thus, according to dimensional analysis, all parameters on the right side of the fractional order model must be raised to the power of $\mathrm{\kappa }$. Because the fractional order model is nonlinear, analytical solutions cannot be obtained using traditional methods. Therefore, the solution is approached through numerical methods.

To further simplify the analysis, the researchers focus on the proportions of employees who are indifferent, resistant, and adaptive. The researchers can represent the fractions of I, R and A in the population as $i\left(t\right)=I\left(t\right)/M\left(t\right)$, $r\left(t\right)=\frac{R\left(t\right)}{M\left(t\right)}$ and $a\left(t\right)=\frac{A\left(t\right)}{M\left(t\right)}$, respectively. By substituting $I\left(t\right)$ with $i\left(t\right)$, $R\left(t\right)$ with $r\left(t\right)$ and $A\left(t\right)$ with $a\left(t\right)$, the researchers can express mode Equation 9 can be written as

$\begin{array}{l}{}^{C}D^{\kappa }\left(i\left(t\right)\right)=-{\alpha }_1^{\kappa }ai-{\alpha }_2^{\kappa }ri+{\gamma }_1^{\kappa }r+{\beta }_1^{\kappa }a\\ {}^{C}D^{\kappa }\left(r\left(t\right)\right)={\alpha }_2^{\kappa }ri-{\gamma }_1^{\kappa }r-{\gamma }_2^{\kappa }ar+{\beta }_2^{\kappa }ra\\ {}^{C}D^{\kappa }\left(a\left(t\right)\right)={\alpha }_1^{\kappa }ai+{\gamma }_2^{\kappa }ra-{\beta }_1^{\kappa }a-{\beta }_2^{\kappa }ra\end{array}(11)$

where

$i\left(0\right)\ge 0,r\left(0\right)\ge 0,\text{and\hspace{0.17em}}a\left(0\right)\ge 0.(12)$

Since $M\left(t\right)=I\left(t\right)+R\left(t\right)+A\left(t\right)$, $i\left(t\right)+r\left(t\right)+a\left(t\right)=1$.

The equations in model (7) can be reduced to the following differential equations.

$\begin{array}{c}{}^{C}D^{\kappa }\left(r\left(t\right)\right)={\alpha }_2^{\kappa }r\left(1-a-r\right)-{\gamma }_1^{\kappa }r-{\gamma }_2^{\kappa }ar+{\beta }_2^{\kappa }ra\\ {}^{C}D^{\kappa }\left(a\left(t\right)\right)={\alpha }_1^{\kappa }a\left(1-a-r\right)+{\gamma }_2^{\kappa }ra-{\beta }_1^{\kappa }a-{\beta }_2^{\kappa }ra\end{array}$

which can be simplified to

$\begin{array}{c}{}^{C}D^{\kappa }\left(r\left(t\right)\right)={\alpha }_2^{\kappa }r\left(1-a-r\right)-\chi ar-{\gamma }_1^{\kappa }r\\ {}^{C}D^{\kappa }\left(a\left(t\right)\right)={\alpha }_1^{\kappa }a\left(1-a-r\right)+\chi ar-{\beta }_1^{\kappa }a\end{array}$

where $\chi ={\gamma }_2^{\kappa }-{\beta }_2^{\kappa }$.

Given the importance of non-negative and bounded population values, the researchers identify certain qualitative properties, specifically the non-negativity and boundedness of the solutions in the fractional order model. Furthermore, the researchers examine the existence and uniqueness of the solutions for the Caputo fractional order model presented in Equation 11, along with the initial conditions specified in Equation 12.

3.3 Well posedness of the model

Theorem 1. The solutions of the system (as presented in Equation 11) remain non-negative when the initial conditions are non-negative (as indicated in Equation 8). This means that the solutions $\left(i\left(t\right),r\left(t\right),a\left(t\right)\right)$ for the model (Equation 7) are positively invariant in ${\mathbb{R}}_{+}^3$.

Proof:

The system of equations

$x^{\prime }=f\left(x_1,x_2,\dots ,x_n\right);x\left(0\right)=x_0\ge 0$

is considered a positive system if and only if

$x_i^{\prime }=f_i\left(x_1\ge 0,x_2\ge 0,\dots ,x_i=0,\dots ,x_k\ge 0\right)\ge 0.$

Thus, for the fractional order model (Equation 5), when $i=0,r=0\text{\hspace{0.17em}and\hspace{0.17em}}a=0,{}^{C}D^{\kappa }i\ge 0,{}^{C}D^{\kappa }r\ge 0\text{\hspace{0.17em}and\hspace{0.17em}}{}^{C}D^{\kappa }a\ge 0$ respectively.

Consequently, all solutions of the model are non-negative.

Theorem 2. The solutions of the system (as indicated in Equation 9) remain uniformly bounded at all times when the initial conditions are non-negative (as shown in Equation 10).

Proof: Observe that ${}^{C}D^{\kappa }\left(M\left(t\right)\right)={}^{C}D^{\kappa }\left(I\left(t\right)\right)+{}^{C}D^{\kappa }\left(R\left(t\right)\right)+{}^{C}D^{\kappa }\left(A\left(t\right)\right)=0$. This indicates that $M\left(t\right)=I\left(t\right)+R\left(t\right)+A\left(t\right)$ is a constant, leading to $I\le M,R\le M$, and $A\le M$.

Therefore, the total number of employees $M\left(t\right)$ is bounded.

Consequently, the solutions of the fractional order model (Equation 9) are bounded within the closed positively invariant feasible set defined by

$\mathfrak{H}=\left\{\left(I,R,A\right)\in {\mathbb{R}}_{+}^3:I+R+A=M\right\}$

To demonstrate the existence and uniqueness of the solution of the model, the researchers can rewrite the fractional order model (Equation 9) together with initial conditions (Equation 10) in the vector form

$\{\begin{array}{l}{}^{C}D^{\kappa }X\left(t\right)=C\left(t,X\left(t\right)\right),0<t<T<\infty \\ X=X_0\end{array}(13)$

where $X\left(t\right)={\left(I\left(t\right),R\left(t\right),A\left(t\right)\right)}^t$ and

$C\left(t,X\left(t\right)\right)=\left[\begin{array}{c}{C}_1\left(t,I\left(t\right)\right)\\ C_2\left(t,R\left(t\right)\right)\\ C_3\left(t,A\left(t\right)\right)\end{array}\right]=\left[\begin{array}{c}-{\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}-{\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)I\left(t\right)}{M\left(t\right)}+{\gamma }_1^{\kappa }R\left(t\right)+{\beta }_1^{\kappa }A\left(t\right)\\ {\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)I\left(t\right)}{M\left(t\right)}+{\beta }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\gamma }_1^{\kappa }R\left(t\right)\\ {\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}+{\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_1^{\kappa }A\left(t\right)\end{array}\right](14)$

By applying conditions (c) of proposition 4, the researchers have derived the following integral equations from Equations 13, 14.

$\begin{array}{l}{I\left(t\right)-I\left(0\right)=}^C{I}^{\kappa }\left(-{\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}-{\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)I\left(t\right)}{M\left(t\right)}+{\gamma }_1^{\kappa }R\left(t\right)+{\beta }_1^{\kappa }A\left(t\right)\right)\\ {R\left(t\right)-R\left(0\right)=}^C{I}^{\kappa }\left({\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)I\left(t\right)}{M\left(t\right)}+{\beta }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\gamma }_1^{\kappa }R\left(t\right)\right)\\ {A\left(t\right)-A\left(0\right)=}^C{I}^{\kappa }\left({\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}+{\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_1^{\kappa }A\left(t\right)\right)\end{array}(15)$

From Equation 15, the researchers concluded the following

$\begin{array}{l}I\left(t\right)=I\left(0\right)+\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_0^t{\left(t-\xi \right)}^{\kappa -1}{C}_1\left(\xi ,I\left(\xi \right)\right)d\xi \\ R\left(t\right)=R\left(0\right)+\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_0^t{\left(t-\xi \right)}^{\kappa -1}{C}_2\left(\xi ,R\left(\xi \right)\right)d\xi \\ A\left(t\right)=A\left(0\right)+\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_0^t{\left(t-\xi \right)}^{\kappa -1}{C}_3\left(\xi ,A\left(\xi \right)\right)d\xi \end{array}(16)$

Employing the Picard iterative method numerically, the researchers obtain the following

$\begin{array}{l}{I}_n\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_0^t{\left(t-\xi \right)}^{\kappa -1}{C}_1\left(\xi ,I_{n-1}\left(\xi \right)\right)d\xi \\ R_n\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_0^t{\left(t-\xi \right)}^{\kappa -1}{C}_2\left(s,R_{n-1}\left(\xi \right)\right)d\xi \\ A_n\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_0^t{\left(t-\xi \right)}^{\kappa -1}{C}_3\left(\xi ,A_{n-1}\left(\xi \right)\right)d\xi \end{array}(17)$

Ultimately, the initial value problem Equations 9, 10 is transformed to

$X\left(t\right)=X\left(0\right)+\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_0^t{C\left(\xi ,X\left(\xi \right)\right)\left(t-\xi \right)}^{\kappa -1}d\xi$

where the components of $C\left(\xi ,X\left(\xi \right)\right)$, namely $C_1$, $C_2$ and $C_3$, are given in Equation 17.

Then the researchers established the following Lemmas to prove existence uniqueness theorem.

Lemma 1. The vector function $C\left(t,X\right)$ is Lipschitz in the variable $X$ on a set $\left[0,T\right]\times {\mathbb{R}}_{+}^3$ with some Lipschitz constant $\mathfrak{K}$.

Proof:

One can observe that

$\begin{array}{c}‖C_1\left(t,I_1\left(t\right)\right)-C_1\left(t,I_2\left(t\right)\right)‖=‖\left(-{\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)I_1\left(t\right)}{M\left(t\right)}-{\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)I_1\left(t\right)}{M\left(t\right)}\right)-\left(-{\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)I_2\left(t\right)}{M\left(t\right)}-{\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)I_2\left(t\right)}{M\left(t\right)}\right)\Vert \\ =‖\left({\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)}{M\left(t\right)}+{\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)}{M\left(t\right)}\right)\left(I_1\left(t\right)-I_2\left(t\right)\right)‖\\ \le \mathit{Max}\left\{{\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)}{M\left(t\right)}+{\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)}{M\left(t\right)}\right\}‖\left(I_1\left(t\right)-I_2\left(t\right)\right)‖\end{array}$

$\begin{array}{c}‖C_2\left(t,R_1\left(t\right)\right)-C_2\left(t,R_2\left(t\right)\right)‖=‖\left({\mathrm{\alpha }}_2^{\kappa }\frac{R_1\left(t\right)I\left(t\right)}{M\left(t\right)}+{\beta }_2^{\kappa }\frac{A\left(t\right)R_1\left(t\right)}{M\left(t\right)}-{\gamma }_2^{\kappa }\frac{A\left(t\right)R_1\left(t\right)}{M\left(t\right)}-{\gamma }_1^{\kappa }{R}_1\left(t\right)\right)-\left({\mathrm{\alpha }}_2^{\kappa }\frac{R_2\left(t\right)I\left(t\right)}{M\left(t\right)}+{\beta }_2^{\kappa }\frac{A\left(t\right)R_2\left(t\right)}{M\left(t\right)}-{\gamma }_2^{\kappa }\frac{A\left(t\right)R_2\left(t\right)}{M\left(t\right)}-{\gamma }_1^{\kappa }{R}_2\left(t\right)\right)\Vert \\ =‖\left({\alpha }_2^{\kappa }\frac{I\left(t\right)}{M\left(t\right)}+{\beta }_2^{\kappa }\frac{A\left(t\right)}{M\left(t\right)}-{\gamma }_2^{\kappa }\frac{A\left(t\right)}{M\left(t\right)}-{\gamma }_1^{\kappa }\right)\left(R_1-R_2\right)‖\\ \le \mathit{Max}\left\{{\alpha }_2^{\kappa }\frac{I\left(t\right)}{M\left(t\right)}+{\eta }^{\kappa }+{\beta }_2^{\kappa }\frac{A\left(t\right)}{M\left(t\right)}-{\gamma }_2^{\kappa }\frac{A\left(t\right)}{M\left(t\right)}-{\gamma }_1^{\kappa }\right\}‖\left(R_1\left(t\right)-R_2\left(t\right)\right)‖\end{array}$

$\begin{array}{c}‖C_3\left(t,A_1\left(t\right)\right)-C_3\left(t,A_2\left(t\right)\right)‖=‖\left({\mathrm{\alpha }}_1^{\kappa }\frac{A_1\left(t\right)NI\left(t\right)}{M\left(t\right)}+{\gamma }_2^{\kappa }\frac{A_1\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_2^{\kappa }\frac{A_1\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_1^{\kappa }{A}_1\left(t\right)\right)-\left({\mathrm{\alpha }}_1^{\kappa }\frac{A_2\left(t\right)I\left(t\right)}{M\left(t\right)}+{\gamma }_2^{\kappa }\frac{A_2\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_2^{\kappa }\frac{A_2\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_1^{\kappa }{A}_2\left(t\right)\right)\Vert \\ =‖\left({\mathrm{\alpha }}_1^{\kappa }\frac{I\left(t\right)}{M\left(t\right)}+{\gamma }_2^{\kappa }\frac{R\left(t\right)}{M\left(t\right)}-{\beta }_2^{\kappa }\frac{R\left(t\right)}{M\left(t\right)}-{\beta }_1^{\kappa }\right)\left(A_1-A_2\right)‖\le \mathit{Max}\left\{\left({\mathrm{\alpha }}_1^{\kappa }\frac{I\left(t\right)}{M\left(t\right)}+{\gamma }_2^{\kappa }\frac{R\left(t\right)}{M\left(t\right)}-{\beta }_2^{\kappa }\frac{R\left(t\right)}{M\left(t\right)}-{\beta }_1^{\kappa }\right)\right\}‖\left(A_1\left(t\right)-A_2\left(t\right)\right)‖\end{array}$

Thus, the researchers conclude that

$‖C\left(t,X_1\left(t\right)\right)-C\left(t,X_2\left(t\right)\right)‖\le \mathfrak{K}‖X_1-X_2‖$

with

$\mathfrak{K}=\mathit{max}\left(\mathit{Max}\left\{{\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)}{M\left(t\right)}+{\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)}{M\left(t\right)}\right\},\right. \mathit{Max}\left\{{\alpha }_2^{\kappa }\frac{I\left(t\right)}{M\left(t\right)}+{\eta }^{\kappa }+{\beta }_2^{\kappa }\frac{A\left(t\right)}{M\left(t\right)}-{\gamma }_2^{\kappa }\frac{A\left(t\right)}{M\left(t\right)}-{\gamma }_1^{\kappa }\right\},\left. \mathit{Max}\left\{\left({\mathrm{\alpha }}_1^{\kappa }\frac{I\left(t\right)}{M\left(t\right)}+{\gamma }_2^{\kappa }\frac{R\left(t\right)}{M\left(t\right)}-{\beta }_2^{\kappa }\frac{R\left(t\right)}{M\left(t\right)}-{\beta }_1^{\kappa }\right)\right\}\right).$

Existence-Uniqueness theorem 3: The initial value problem (Equations 9-10) has a unique solution $X\left(t\right)\in \mathrm{\Omega }\left(J\right),$ the set of bounded continuous functions on $J$ with norm $‖X‖=\mathit{sup}\left\{\left|X\left(t\right)\right|:t\in J\right\}$.

Proof:

The IVP.

$X\left(t\right)=X\left(0\right)+\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_0^t{C\left(s,X\left(s\right)\right)\left(t-s\right)}^{\kappa -1}ds$ can be written as $X\left(t\right)=F\left(X\left(t\right)\right)$ where $F=\mathrm{\Omega }\left(\left[0,T\right],{\mathbb{R}}_{+}^3\right)\to \mathrm{\Omega }\left(\left[0,T\right],{\mathbb{R}}_{+}^3\right)$ defined by $F\left(X\left(t\right)\right)=$ $X\left(0\right)+\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_0^t{C\left(s,X\left(s\right)\right)\left(t-s\right)}^{\kappa -1}ds$.

Further, the researchers have $‖F\left(X_1\left(t\right)\right)-F\left(X_2\left(t\right)\right)‖=‖\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_0^t{\left(t-s\right)}^{\kappa -1}\times \left[C\left(s,X_1\left(s\right)\right)-C\left(s,X_2\left(s\right)\right)\right]‖$$ds\le \frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_0^t{\left(t-s\right)}^{\kappa -1}ds\times ‖C\left(s,X_1\left(s\right)\right)-C\left(s,X_2\left(s\right)\right)‖\le \frac{\mathfrak{K}}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_0^t{\left(t-s\right)}^{\kappa -1}ds\le \frac{\mathfrak{K}}{\kappa \mathrm{\Gamma }\left(\kappa \right)}T.$

This shows that $F$ is a contraction, and hence, the initial value problem has a unique solution.

Therefore, the fractional order model (Equations 9, 10) is well posed.

3.4 Qualitative analysis

The qualitative analysis of a compartmental model is essential for comprehending the behavior and dynamics of complex systems. By examining the steady states and their local stability, the researchers can obtain valuable insights into the system’s long behavior.

3.4.1 Steady states

This section aims to establish specific properties of the solutions to the AIR model. By quantitatively analyzing the steady states (or equilibria) of the model, the researchers can better understand the long-term behavior of employees adaptation to the reform initiatives and identify potential states of stability. The steady states are defined as the values ${\mathrm{x}}_{\mathrm{e}}$ of $\mathrm{x}$ which remain constant for all $t>t_0$ at a particular time ${\mathrm{t}}_0$. This implies that all model variables will stabilize, and eventually equal to zero, which can be used to identify the steady states.

It is important to note that the fractional order outlined in Equation 9 has two distinct steady state solutions: a resistant-free and resistant persistent steady states, represented by $E^0=\left(I^0,R^0,A^0\right)$ and $E^{*}=\left(I^{*},R^{*},A^{*}\right)$ respectively. The resistant-free steady state is the solution of ${}^{C}D^{\kappa }I\left(t\right)={}^{C}D^{\kappa }R\left(t\right)={}^{C}D^{\kappa }A\left(t\right)=0,$ for each $t\ge 0$.

This results in $R^0=0$, $I^0=\frac{{\beta }_1^{\kappa }}{{\alpha }_1^{\kappa }}M$ and $A^0=\frac{M\left({\alpha }_1^{\kappa }-{\beta }_1^{\kappa }\right)}{{\alpha }_1^{\kappa }}$ where $I^0$ and $A^0$ represent the number of indifferent and adaptive employees, respectively, in the absence of resistant employees.

Thus, for the evolutionary system governed by Equation 9, the resistant-free steady state is

$E^0=\left(\frac{{\beta }_1^{\kappa }}{{\alpha }_1^{\kappa }}M,0,\frac{M\left({\alpha }_1^{\kappa }-{\beta }_1^{\kappa }\right)}{{\alpha }_1^{\kappa }}\right)(18)$

In terms of $i=I/M$, $r=\frac{R}{M}$ and $a=\frac{A}{M},$ the resistant-free steady state given in Equation 18 simplifies to

$E^0=\left(\frac{{\beta }_1^{\kappa }}{{\alpha }_1^{\kappa }},0,1-\frac{{\beta }_1^{\kappa }}{{\alpha }_1^{\kappa }}\right)$, which exists provided that ${\alpha }_1^{\kappa }>{\beta }_1^{\kappa }$ holds.

To evaluate the resistant-persistent steady state denoted by $E^{*}=\left(r^{*},a^{*}\right)$, the researchers set ${}^{C}D^{\kappa }\left(i\left(t\right)\right)=0,$ ${}^{C}D^{\kappa }\left(r\left(t\right)\right)=0$ and ${}^{C}D^{\kappa }\left(a\left(t\right)\right)=0$ and simplify the resulting equations. Then, the researchers obtain the following $r^{*}=-\frac{\chi {\alpha }_1^{\kappa }-\chi {\beta }_1^{\kappa }+{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }-{\alpha }_2^{\kappa }{\beta }_1^{\kappa }}{\chi \left(\chi -{\alpha }_1^{\kappa }+{\alpha }_2^{\kappa }\right)}$ and $a^{*}=\frac{\chi {\alpha }_2^{\kappa }-\chi {\gamma }_1^{\kappa }+{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }-{\alpha }_2^{\kappa }{\beta }_1^{\kappa }}{\chi \left(\chi -{\alpha }_1^{\kappa }+{\alpha }_2^{\kappa }\right)}$.

Therefore, for the system governed by Equations 9, 10, the resistant-persistent equilibrium is $E^{*}=\left(i^{*},r^{*},a^{*}\right)$, where $i^{*}=1-r^{*}-a^{*}$.

3.4.2 Local stability of steady states

The stability of steady states plays a crucial role in understanding the long-term behavior of the system. In the context of employees' perceptions of reform initiatives in public service organizations, the resistant-free steady state represents a scenario where resistance to reforms is entirely absent, suggesting successful adaptation to change. On the other hand, the resistant-persistent steady state signifies a state where resistance remains within the system, influencing the effectiveness of reform strategies. By analyzing the stability of these steady states using fractional-order derivatives and optimal control strategies, we can determine the conditions under which reform initiatives are either fully embraced or continuously challenged. The local stability of the resistant-free steady state is analyzed through the effective reproduction number, ${\mathfrak{R}}_{\text{eff}}$, calculated using the next generation matrix (Van Den Driessche and Watmough, 2002). This number reflects the potential for resistance to reform initiatives within the workplace.

When ${\mathfrak{R}}_{\text{eff}}$ is less than unity, the number of resistant employees is unlikely to grow, meaning that any isolated instances of resistance are generally insufficient to influence the broader employee population. This environment fosters a more supportive atmosphere for reform initiatives. Employees are more likely to remain indifferent or adaptive, leading to a positive outlook toward change. The potential for successful implementation of reforms increases, as the collective sentiment is more favorable.

In contrast, if ${\mathfrak{R}}_{\text{eff}}$ is greater than one, the number of resistant employees can grow, leading to a collective negative outlook that may hinder reform efforts. This environment can create challenges in implementing changes and may require targeted strategies to address and mitigate resistance. The “resistant” compartment, which includes employees with a pessimistic view of the reforms, will be decoupled from the rest of the system. The equation governing this compartment is given by:

$\begin{array}{c}{}^{C}D^{\kappa }\left(r\left(t\right)\right)={}^{C}D^{\kappa }\left(r\left(t\right)\right)={\alpha }_2^{\kappa }ri-{\gamma }_1^{\kappa }r-{\gamma }_2^{\kappa }ar+{\beta }_2^{\kappa }ar\\ =\left({\alpha }_2^{\kappa }i+{\beta }_2^{\kappa }a\right)r-\left({\gamma }_1^{\kappa }+{\gamma }_2^{\kappa }a\right)r.\end{array}$

This takes the form ${}^{C}D^{\kappa }\left(r\left(t\right)\right)=\left(F-V\right)r\left(t\right)$, where $F\left(\mathit{x},\mathit{y}\right)={\alpha }_2^{\kappa }i+{\beta }_2^{\kappa }a$ and $V\left(\mathit{x},\mathit{y}\right)={\gamma }_1^{\kappa }+{\gamma }_2^{\kappa }a$.

Calculating $F$ and $\mathrm{V}$ at the resistant free steady state $E^0=\left(\frac{{\beta }_1^{\kappa }}{{\alpha }_1^{\kappa }},0,1-\frac{{\beta }_1^{\kappa }}{{\alpha }_1^{\kappa }}\right)$, the researchers get $F=\frac{{\alpha }_2^{\kappa }{\beta }_1^{\kappa }{+\beta }_2^{\kappa }{\alpha }_1^{\kappa }{-\beta }_1^{\kappa }{\beta }_2^{\kappa }}{{\alpha }_1^{\kappa }}$ and $V=\frac{{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }+{\gamma }_2^{\kappa }{\alpha }_1^{\kappa }-{\gamma }_2^{\kappa }{\beta }_1^{\kappa }}{{\alpha }_1^{\kappa }}$.

The next generation matrix, $F{V}^{-1}=\frac{{\alpha }_2^{\kappa }{\beta }_1^{\kappa }{+\beta }_2^{\kappa }{\alpha }_1^{\kappa }{-\beta }_1^{\kappa }{\beta }_2^{\kappa }}{{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }+{\gamma }_2^{\kappa }{\alpha }_1^{\kappa }-{\gamma }_2^{\kappa }{\beta }_1^{\kappa }}$, and the effective reproduction number, ${\mathfrak{R}}_{eff}=\frac{{\alpha }_2^{\kappa }{\beta }_1^{\kappa }{+\beta }_2^{\kappa }{\alpha }_1^{\kappa }{-\beta }_1^{\kappa }{\beta }_2^{\kappa }}{{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }+{\gamma }_2^{\kappa }{\alpha }_1^{\kappa }-{\gamma }_2^{\kappa }{\beta }_1^{\kappa }}$.

Theorem 4. The resistant-free steady state of the model (Equation 5) is locally asymptotically stable if ${\mathfrak{R}}_{eff}$ is lower than unity; otherwise, it is unstable.

Proof:

The researchers observe that the Jacobian matrix of the system calculated at the steady state where there is no resistant perception described in Equation 11 is expressed as:

$J=\left(\begin{array}{cc}{\beta }_1^{\kappa }-{\alpha }_1^{\kappa }& \left(\chi -{\alpha }_1^{\kappa }\right)\left({\alpha }_1^{\kappa }-{\beta }_1^{\kappa }\right)\\ 0& \chi \left(\frac{{\beta }_1^{\kappa }}{{\alpha }_1^{\kappa }}-1\right)-{\gamma }_1^{\kappa }+\frac{{\alpha }_2^{\kappa }{\beta }_1^{\kappa }}{{\alpha }_1^{\kappa }}\end{array}\right)$

Since the matrix is lower triangular, the eigenvalues are simply the values on the diagonal.

Hence,

${\lambda }_1={\beta }_1^{\kappa }-{\alpha }_1^{\kappa }$

and

${\lambda }_2=\chi \left(\frac{{\beta }_1^{\kappa }}{{\alpha }_1^{\kappa }}-1\right)-{\gamma }_1^{\kappa }+\frac{{\alpha }_2^{\kappa }{\beta }_1^{\kappa }}{{\alpha }_1^{\kappa }}=-\frac{\chi {\alpha }_1^{\kappa }-\chi {\beta }_1^{\kappa }+{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }-{\alpha }_2^{\kappa }{\beta }_1^{\kappa }}{{\alpha }_1^{\kappa }}.$

It is evident that ${\beta }_1^{\kappa }-{\alpha }_1^{\kappa }<0$. Otherwise, the steady state would not be viable. Consequently, the stability of the steady state relies on the eigenvalue ${\lambda }_2$. A straightforward calculation reveals that ${\lambda }_2=-\frac{\chi {\alpha }_1^{\kappa }-\chi {\beta }_1^{\kappa }+{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }-{\alpha }_2^{\kappa }{\beta }_1^{\kappa }}{{\alpha }_1^{\kappa }}<0$ if and only if ${\mathfrak{R}}_{eff}<1$. This indicates that if ${\mathfrak{R}}_{eff}$ is less than one, the resistant-free steady state is stable.

Theorem 5. The resistant-persistent steady state of the model (Equation 9, Equation 10) is locally asymptotically stable when ${\mathfrak{R}}_{eff}$ is greater than one; otherwise, it is unstable.

Proof:

The researchers adopt a similar approach as in the previous theorem. First, the researchers calculate the Jacobian matrix as done earlier, and then evaluate it at the resistant-persistent steady state. The eigenvalues of this matrix fulfill the characteristic equation.

$J\left(E^{*}\right)=J\left(-\frac{\chi {\alpha }_1^{\kappa }-\chi {\beta }_1^{\kappa }+{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }-{\alpha }_2^{\kappa }{\beta }_1^{\kappa }}{\chi \left(\chi -{\alpha }_1^{\kappa }+{\alpha }_2^{\kappa }\right)},\frac{\chi {\alpha }_2^{\kappa }-\chi {\gamma }_1^{\kappa }+{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }-{\alpha }_2^{\kappa }{\beta }_1^{\kappa }}{\chi \left(\chi -{\alpha }_1^{\kappa }+{\alpha }_2^{\kappa }\right)}\right)=\left(\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right)$ where

$\begin{array}{c}\hfill a_{11}=-\frac{{\alpha }_1^{\kappa }\left(\chi {\alpha }_2^{\kappa }-\chi {\gamma }_1^{\kappa }+{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }-{\alpha }_2^{\kappa }{\beta }_1^{\kappa }\right)}{\chi \left(\chi -{\alpha }_1^{\kappa }+{\alpha }_2^{\kappa }\right)},\hfill \\ \hfill a_{12}=\frac{\left(\chi -{\alpha }_1^{\kappa }\right)\left(\chi {\alpha }_2^{\kappa }-\chi {\gamma }_1^{\kappa }+{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }-{\alpha }_2^{\kappa }{\beta }_1^{\kappa }\right)}{\chi \left(\chi -{\alpha }_1^{\kappa }+{\alpha }_2^{\kappa }\right)},\hfill \\ \hfill a_{21}=\frac{\left(\chi +{\alpha }_2^{\kappa }\right)\left(\chi {\alpha }_1^{\kappa }-\chi {\beta }_1^{\kappa }+{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }-{\alpha }_2^{\kappa }{\beta }_1^{\kappa }\right)}{\chi \left(\chi -{\alpha }_1^{\kappa }+{\alpha }_2^{\kappa }\right)},\text{and\hspace{0.17em}}\hfill \\ \hfill a_{22}=\frac{{\alpha }_2^{\kappa }\left(\chi {\alpha }_1^{\kappa }-\chi {\beta }_1^{\kappa }+{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }-{\alpha }_2^{\kappa }{\beta }_1^{\kappa }\right)}{\chi \left(\chi -{\alpha }_1^{\kappa }+{\alpha }_2^{\kappa }\right)}.\hfill \end{array}$

The characteristic polynomial of the Jacobian matrix is.

${\lambda }^2+f\lambda +g=0$ where

$f=-\frac{{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }-{\alpha }_2^{\kappa }{\beta }_1^{\kappa }}{\chi },\text{and\hspace{0.17em}}g=\frac{-1}{\chi \left(\chi -{\alpha }_1^{\kappa }+{\alpha }_2^{\kappa }\right)}\times \left(\chi {\alpha }_1^{\kappa }-\chi {\beta }_1^{\kappa }+{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }-{\alpha }_2^{\kappa }{\beta }_1^{\kappa }\right)\left(\chi {\alpha }_2^{\kappa }-\chi {\gamma }_1^{\kappa }+{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }-{\alpha }_2^{\kappa }{\beta }_1^{\kappa }\right)$

Establish the conditions ${\alpha }_1^{\kappa }<{\beta }_1^{\kappa },$ ${\gamma }_1^{\kappa }<{\alpha }_2^{\kappa }$, and $\chi >0$. Then, when ${\mathfrak{R}}_{eff}>1$, $\chi {\alpha }_1^{\kappa }-\chi {\beta }_1^{\kappa }+{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }-{\alpha }_2^{\kappa }{\beta }_1^{\kappa }<0$. Hence, the researchers have $x,y>0$. The Routh-Hurwitz Stability Criterion indicates that the resistant-persistent steady state is locally asymptotically stable.

4 Optimal control problem (OCP)

This research seeks to enhance employees’ perceptions of reform initiatives by utilizing optimal control techniques. The researchers develop an optimal control problem that addresses the dynamics of how employees perceive these workplace reforms.

• Formulation of the Optimal Control Problem:

The first step is to establish the optimal control problem related to the dynamics of employees’ perceptions of workplace reform initiatives. This process involves defining the state variables, control variables, constraints, and the objective function that needs to be optimized.

• Selection of Improvement Strategies:

The control strategies are designed to create a more supportive environment for reform initiatives by focusing on key performance indicators.

• Definition of Performance Criterion:

A performance criterion, expressed as a cost function, was established to quantitatively assess how each improvement strategy influences the reduction of resistant employees to change. This criterion forms the foundation for evaluating the effectiveness of the proposed strategies.

• Application of Pontryagin’s Maximum Principle:

Pontryagin’s maximum principle, a key optimization tool in optimal control theory, is used to identify the optimal control strategies that encourage a positive attitude toward changes while taking into account system dynamics and constraints. This approach allowed for the identification of the most effective control strategies.

4.1 Optimal control strategies

This section examines methods for fostering a positive attitude toward changes through reform initiatives that could be implemented to alter the system’s behavior, ultimately optimizing its performance.

The researchers analyze the most effective control strategies for the AIR model presented in Equation 5, using the initial conditions defined in Equation 6 to identify the optimal control strategies that decrease the number of resistant employees to change through reform initiatives.

The goal is to determine the optimal intervention strategies $u^{*}=\left(u_1^{*},u_2^{*}\right)$ based on the control strategies $u=\left(u_1,u_2\right)$, ensuring that the resulting state trajectories $I^{*},R^{*}$ and $A^{*}$ satisfy the model described in Equation 5.

Organizational change requires shifting from familiar circumstances to unfamiliar ones, and due to the uncertainty surrounding the future, employees often resist change unless they are provided with convincing reasons to embrace it (Cummings and Worley, 2001). Providing training sessions to enhance employees' skills for adapting to new processes and technologies, and ensuring clear communication regarding the rationale, benefits, and impacts of the reforms are key issues in planning for action (Cummings and Worley, 2001).

To address the issue of reducing the number of employees with a negative outlook, the proposed control strategies focus on two key interventions. The first strategy ${\mathrm{u}}_1\left(\mathrm{t}\right)$ involves implementing targeted training sessions to enhance employees' adaptability to new processes and technologies. These sessions aim to equip employees with the necessary skills to navigate changes effectively, reducing uncertainty and resistance. The second strategy, ${\mathrm{u}}_2\left(\mathrm{t}\right)$, emphasizes clear and consistent communication about the rationale, benefits, and expected outcomes of the reforms. By fostering transparency and addressing concerns, this approach helps build trust and acceptance among employees. It is presumed that the number of individuals with an indifferent perception, potentially stemming from neither an optimistic nor a pessimistic outlook, diminishes by a factor of $1-{\mathrm{u}}_1$ due to the provision of training sessions to enhance employees' skills for adapting to new processes and technologies.

Likewise, the number of employees with a pessimistic outlook decreases by a factor of $1-{\mathrm{u}}_2,$ through the implementation of effective communication regarding the rationale, benefits, and impacts of the reforms.

The optimal control problem related to the Caputo fractional order model presented in Equation 9 is formulated by incorporating the previously mentioned control variables.

$\begin{array}{l}{}^{C}D^{\kappa }\left(I\left(t\right)\right)=-\left(1-u_1\right){\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}-{\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)I\left(t\right)}{M\left(t\right)}+{\gamma }_1^{\kappa }R\left(t\right)+{\beta }_1^{\kappa }A\left(t\right)\\ {}^{C}D^{\kappa }\left(R\left(t\right)\right)={\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)I\left(t\right)}{M\left(t\right)}+{\beta }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-\left(1-u_2\right){\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\gamma }_1^{\kappa }R\left(t\right)\\ {}^{C}D^{\kappa }\left(A\left(t\right)\right)={\left(1-u_1\right)\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}+\left(1-u_2\right){\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_1^{\kappa }A\left(t\right)\end{array}(19)$

along with the initial conditions outlined in Equation 10, and $\mathrm{\Omega }=\left\{\left(u_1\left(t\right),u_2\left(t\right)\right):0\le u_1\left(t\right),u_2\left(t\right)\le 1,t\in \left[0,t_f\right]\right\}$.

The system presented in Equation 19 can be expressed in state-space form as

$x^{\prime }\left(t\right)=f\left(t,x\left(t\right),u\left(t\right)\right);x\left(t_0\right)=x_0(20)$

The vector $u\left(t\right)$ represents the control variables at a given time $t$, while the vector $x\left(t\right)$ indicates the state variables that describe how employees’ perceptions evolve in response to the control $u\left(t\right)$ with the initial condition $x\left(t_0\right)=x_0$. Equation 20 completely defines the evolution of the state variables over time.

The researchers assume that $f$ is a continuous function of the variables $t,x,u$ and is continuously differentiable with respect to $x$. This assumption ensures the (at least local) existence and uniqueness of a solution to the equation represented by Equation 20.

Setting $u_{1}and{u}_2$ equal to zero indicates that no strategies are in place to help employees remain indifferent or adaptable to change. In contrast, setting the controls to their maximum value of one suggests that the intervention has been fully implemented, even if this does not accurately reflect real situation.

The performance criterion $\mathfrak{J}:\mathfrak{U}\left[0,T\right]\to \mathbb{R}$ can be expressed in what it is referred to as the Lagrange form

$\mathfrak{J}\left(u_1,u_2\right)={\int }_0^{t_f}\left({\mathfrak{h}}_{1}I+{\mathfrak{h}}_{2}R+\frac{{\mathfrak{y}}_1}{2}{u}_1^2+\frac{{\mathfrak{y}}_2}{2}{u}_2^2\right)dt.$

The coefficients ${\mathfrak{h}}_1$ and ${\mathfrak{h}}_2$ are positive weighting factors, while $\frac{{\mathfrak{y}}_1}{2}$ and $\frac{{\mathfrak{y}}_2}{2}$ denote the relative costs associated with the intervention strategies $u_1$ and $u_2$​, respectively. These factors help balance the units of the integrand. In the cost functional, the term ${\mathfrak{h}}_{1}I$ refers to the running cost related to providing training sessions to enhance employees' skills for adapting to new processes and technologies, while the term ${\mathfrak{h}}_{2}R$ represents the running cost associated with ensuring clear communication regarding the rationale, benefits, and impacts of the reforms. The existence of an optimal control is crucial, as it would be pointless to search for a solution if no such solution exists.

Given the complexity of many real-world issues, analytical solutions are often impractical, necessitating the use of computational algorithms to address optimal control problems.

Pontryagin’s Maximum Principle.

Examine the optimal control problem

$\text{minimize}:\mathfrak{J}\left(u_1,u_2\right);x^{\prime }\left(t\right)=f\left(t,x\left(t\right),u\left(t\right)\right);x\left(t_0\right)=x_0(21)$

Assume there is a (local) minimizer $u^{*}=\left(u_1^{*},u_2^{*}\right)\in {\left(C\left[0,t_f\right]\right)}^2$ for the problem defined in Equation 21, along with the corresponding perception state vector $\left(I^{*},R^{*},A^{*}\right)\in {\left(C\left[0,t_f\right]\right)}^3$. Next, there exists a vector function ${\mathrm{\lambda }}^{*}\in {\left(\mathrm{C}\left[0,{\mathrm{t}}_{\mathrm{f}}\right]\right)}^3$ such that the ordered triple $\left(u^{*},x^{*},{\lambda }^{*}\right)$ fulfills the Euler Lagrange equations:

$x^{\prime }\left(t\right)={\mathcal{H}}_{\lambda };x\left(t_0\right)=x_0$

${\lambda }^{\prime }\left(t\right)=-{\mathcal{H}}_x;\lambda \left(t_f\right)=0$

${\mathcal{H}}_u=0$

where $\mathcal{H}:\mathbb{R}\times {\mathbb{R}}^3\times {\mathbb{R}}^2\times {\mathbb{R}}^3\mathbb{⟶}\mathbb{R}$ is the Hamiltonian function, defined as described in

$\mathcal{H}\left(t,x\left(t\right),u\left(t\right),\lambda \right)=l\left(t,x\left(t\right),u\left(t\right)\right)+{\lambda }^{T}f\left(t,x\left(t\right),u\left(t\right)\right)$

$\begin{array}{c}\mathcal{H}\left(t,x\left(t\right),u\left(t\right),\lambda \right)={\mathfrak{h}}_{1}I+{\mathfrak{h}}_{2}R+\frac{{\mathfrak{y}}_1}{2}{u}_1^2+\frac{{\mathfrak{y}}_2}{2}{u}_2^2+{\lambda }_1\left(-\left(1-u_1\right){\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}-{\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)I\left(t\right)}{M\left(t\right)}+{\gamma }_1^{\kappa }R\left(t\right)+{\beta }_1^{\kappa }A\left(t\right)\right)\\ +{\lambda }_2\left({\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)I\left(t\right)}{M\left(t\right)}+{\beta }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-\left(1-u_2\right){\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\gamma }_1^{\kappa }R\left(t\right)\right)+{\lambda }_3\left({\left(1-u_1\right)\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}+\left(1-u_2\right){\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}-{\beta }_1^{\kappa }A\left(t\right)\right)\end{array}$

where ${\lambda }_1$, ${\lambda }_2$ and ${\lambda }_3$ are the co-state variables.

For all $t$ such that $0\le t\le t_f$, and for all admissible controls $u$, it hold that $\mathcal{H}\left(t,x\left(t\right),u\left(t\right),\lambda \right)\le \mathcal{H}\left(t,u^{*},x^{*},{\lambda }^{*}\right)$. This indicates that optimal control $u^{*}$ maximizes the Hamiltonian function $\mathcal{H}\left(t,x\left(t\right),u\left(t\right),\lambda \right)$.

Using the same approach as in Hailu and Teklu (2024a)

$\begin{array}{c}-\frac{d{\lambda }_1}{dt}=\frac{\partial \mathcal{H}}{\partial I}={\mathfrak{h}}_{1}I+{\lambda }_1\left(-\left(1-u_1\right){\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)}{M\left(t\right)}-{\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)}{M\left(t\right)}\right)+{\lambda }_2{\mathrm{\alpha }}_2^{\kappa }\frac{R\left(t\right)}{M\left(t\right)}+{\lambda }_3{\left(1-u_1\right)\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)}{M\left(t\right)},-\frac{d{\lambda }_2}{dt}\\ =\frac{\partial \mathcal{H}}{\partial R}={\mathfrak{h}}_2+{\lambda }_1\left(-{\mathrm{\alpha }}_2^{\kappa }\frac{I\left(t\right)}{M\left(t\right)}+{\gamma }_1^{\kappa }\right)+{\lambda }_2\left({\mathrm{\alpha }}_2^{\kappa }\frac{I\left(t\right)}{M\left(t\right)}+{\beta }_2^{\kappa }\frac{A\left(t\right)}{M\left(t\right)}-\left(1-u_2\right){\gamma }_2^{\kappa }\frac{A\left(t\right)}{M\left(t\right)}-{\gamma }_1^{\kappa }\right)+{\lambda }_3\left(\left(1-u_2\right){\gamma }_2^{\kappa }\frac{A\left(t\right)}{M\left(t\right)}-{\beta }_2^{\kappa }\frac{A\left(t\right)}{M\left(t\right)}\right),-\frac{d{\lambda }_3}{dt}\\ =\frac{\partial \mathcal{H}}{\partial A}={\lambda }_1\left(-\left(1-u_1\right){\mathrm{\alpha }}_1^{\kappa }\frac{I\left(t\right)}{M\left(t\right)}+{\beta }_1^{\kappa }\right)+{\lambda }_2\left({\beta }_2^{\kappa }\frac{R\left(t\right)}{M\left(t\right)}-\left(1-u_2\right){\gamma }_2^{\kappa }\frac{R\left(t\right)}{M\left(t\right)}\right)+{\lambda }_3\left({\left(1-u_1\right)\mathrm{\alpha }}_1^{\kappa }\frac{I\left(t\right)}{M\left(t\right)}+\left(1-u_2\right){\gamma }_2^{\kappa }\frac{R\left(t\right)}{M\left(t\right)}-{\beta }_2^{\kappa }\frac{R\left(t\right)}{M\left(t\right)}-{\beta }_1^{\kappa }\right)\end{array}(22)$

The transversality conditions are

${\lambda }_i^{*}\left(t_f\right)=0,i=1,2,3(23)$

For $u_i$ where $0<u_i<1,i=1,2$, the following equation is valid:

$\frac{\partial \mathcal{H}}{\partial u_1}={\mathfrak{y}}_1{u}_1+{\lambda }_1{\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}-{\lambda }_3{\mathrm{\alpha }}_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}=0,\text{and\hspace{0.17em}}\frac{\partial \mathcal{H}}{\partial u_2}={\mathfrak{y}}_2{u}_2+{\lambda }_2{\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}+{\lambda }_3{\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}=0.$

Solving for $u_1$ and $u_2$, the researchers get

$u_1=\frac{{{\lambda }_3{\alpha }_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}-\lambda }_1{\alpha }_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}}{{\mathfrak{y}}_1},\text{and\hspace{0.17em}}{u}_2=-\frac{{\lambda }_2{\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{P\left(t\right)}+{\lambda }_3{\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}}{{\mathfrak{y}}_2}.$

Theorem: The optimal control strategies $\left(u_1^{*},u_2^{*}\right)$ that minimizes $J\left(u_1,u_2\right)$ over ${\mathrm{\Omega }}_c$ can be determined as follows:

$u_1^{*}\left(t\right)=\mathit{Max}\left\{0,\min \left(1,\frac{{{\lambda }_3{\alpha }_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}-\lambda }_1{\alpha }_1^{\kappa }\frac{A\left(t\right)I\left(t\right)}{M\left(t\right)}}{{\mathfrak{y}}_1}\right)\right\}\text{and\hspace{0.17em}}{u}_2^{*}\left(t\right)=\mathit{Max}\left\{0,\min \left(1,-\frac{{\lambda }_2{\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{P\left(t\right)}+{\lambda }_3{\gamma }_2^{\kappa }\frac{A\left(t\right)R\left(t\right)}{M\left(t\right)}}{{\mathfrak{y}}_2}\right)\right\},$

where ${\lambda }_1\left(t\right)$, λ₂ (t) and ${\lambda }_3\left(t\right)$ are the co-state variables that satisfy Equation 22 and the condition for transversality outlined in Equation 23.

The researchers then arrive at the conditions listed below:

Proof: By applying the Pontryagin’s maximal principle as outlined in (Baba and Bilgehan, 2021), the researchers derived the following results.

${}^{C}D_t^{\kappa }{\lambda }_1=\frac{\partial \mathcal{H}}{\partial N}$, ${}^{C}D_t^{\kappa }{\lambda }_2=\frac{\partial \mathcal{H}}{\partial D}$, and ${}^{C}D_t^{\kappa }{\lambda }_3=\frac{\partial \mathcal{H}}{\partial S}$, with transversality conditions ${\lambda }_i^{*}\left(T\right)=0,i=1,2,3$.

The optimality conditions are determined by computing the partial derivatives of the Hamiltonian $\mathcal{H}$ with respect to the control variables $u_1$ and $u_2$ , resulting in $\frac{\partial \mathcal{H}}{\partial u_1}=0$ and $\frac{\partial \mathcal{H}}{\partial u_2}=0$.

4.2 Sensitivity analysis

Sensitivity analysis employs sensitivity indices to evaluate how changes in parameters affect employee perceptions of reform initiatives. These indices allow us to understand how perceptions shift when one parameter is altered while keeping others constant. The normalized forward sensitivity index of a perception variable in relation to a parameter reflects the ratio of the perception’s relative change to the parameter’s relative change. For differentiable functions of the parameter, this sensitivity index can also be represented using partial derivatives.

In our analysis, the researchers calculate the local sensitivity indices of employee perceptions regarding reform initiatives in relation to various model parameters. A sensitivity index of unity shows that a 10% change in a parameter results in a 10% change in ${\mathfrak{R}}_{\text{eff}}$. Values below 0 suggest a negative effect on perceptions, while values above 0 indicate a positive impact. These insights help identify the key parameters that significantly influence employee attitudes toward reform initiatives.

Sensitivity analysis of ${\mathfrak{R}}_{eff}$. The threshold ${\mathfrak{R}}_{eff}$ is a function of the model parameters ${\alpha }_{1,2}$, ${\beta }_{1,2}$ and ${\gamma }_{1,2}$.

${\mathfrak{R}}_{eff}=\frac{{\alpha }_2^{\kappa }{\beta }_1^{\kappa }{+\beta }_2^{\kappa }{\alpha }_1^{\kappa }{-\beta }_1^{\kappa }{\beta }_2^{\kappa }}{{\alpha }_1^{\kappa }{\gamma }_1^{\kappa }+{\gamma }_2^{\kappa }{\alpha }_1^{\kappa }-{\gamma }_2^{\kappa }{\beta }_1^{\kappa }}$

A slight change ${\delta }_x$ in a parameter $x$ results in a corresponding change in ${\mathfrak{R}}_{eff}$ , represented as $\delta {\mathfrak{R}}_{eff}$ as follows

$\delta {\mathfrak{R}}_{eff}={\mathfrak{R}}_{eff}\left(x+{\delta }_x\right)-{\mathfrak{R}}_{eff}$

$=\frac{{\mathfrak{R}}_{eff}\left(x+{\delta }_x\right)-{\mathfrak{R}}_{eff}}{{\delta }_x}{\delta }_x\approx {\delta }_x\frac{\partial {\mathfrak{R}}_{eff}}{\partial x}.$

Therefore, the normalized sensitivity index is defined as

${\phi }_x=\frac{\partial {\mathfrak{R}}_{eff}/{\mathfrak{R}}_{eff}}{\partial x/x}=\frac{x}{{\mathfrak{R}}_{eff}}\frac{\partial {\mathfrak{R}}_{eff}}{\partial x}$

The sensitivity indices for the parameters are calculated as

${\phi }_{{\alpha }_1^{\kappa }}=\frac{{\alpha }_1^{\kappa }}{{\mathfrak{R}}_{eff}}\frac{D.{\beta }_2^k-N.\left({\gamma }_1^{\kappa }+{\gamma }_2^{\kappa }\right)}{D^2},$

${\phi }_{{\alpha }_2^{\kappa }}=\frac{{\alpha }_2^{\kappa }}{{\mathfrak{R}}_{eff}}\frac{{\beta }_1^k}{D},$

${\phi }_{{\beta }_1^{\kappa }}=\frac{{\beta }_1^{\kappa }}{{\mathfrak{R}}_{eff}}\frac{D.\left({\alpha }_2^k-{\beta }_2^k\right)+N.{\gamma }_2^{\kappa }}{D^2},$

${\phi }_{{\beta }_2^{\kappa }}=\frac{{\beta }_2^{\kappa }}{{\mathfrak{R}}_{eff}}\frac{{\alpha }_1^{\kappa }}{D},$

${\phi }_{{\gamma }_1^{\kappa }}=-\frac{{\gamma }_1^{\kappa }}{{\mathfrak{R}}_{eff}}\frac{N.{\alpha }_1^{\kappa }}{D^2},and$

${\phi }_{{\gamma }_2^{\kappa }}=-\frac{{\gamma }_2^{\kappa }}{{\mathfrak{R}}_{eff}}\frac{N\left({\alpha }_1^{\kappa }-{\beta }_1^{\kappa }\right)}{D^2}$

where $N={\alpha }_2^{\kappa }{\beta }_1^{\kappa }{+\beta }_2^{\kappa }{\alpha }_1^{\kappa }{-\beta }_1^{\kappa }{\beta }_2^{\kappa }$ and $D={\alpha }_1^{\kappa }{\gamma }_1^{\kappa }+{\gamma }_2^{\kappa }{\alpha }_1^{\kappa }-{\gamma }_2^{\kappa }{\beta }_1^{\kappa }$.

Due to the lack of empirical data specific to this context, the parameter values are assumed. While these values may not be universally applicable, these assumptions provide a necessary foundational starting point for modeling the dynamics of employees’ perception towards reform initiatives. Future research, with access to more context-specific data, can refine these parameters and validate the model’s accuracy. Accordingly, the researchers used initial values of $\mathrm{I}\left(0\right)=201,\mathrm{R}\left(0\right)=93,\mathrm{A}\left(0\right)=87$, and assumed parameter values ${\mathrm{\alpha }}_1=0.17,{\mathrm{\beta }}_1=0.28,{\mathrm{\gamma }}_1=0.3,{\mathrm{\alpha }}_2=0.45,{\mathrm{\beta }}_2=0.17$ and ${\mathrm{\gamma }}_2=0.28$.

These parameter values lead to the corresponding parameter indices. ${\phi }_{{\alpha }_1^{\kappa }}=-3.15379$, ${\phi }_{{\alpha }_2^{\kappa }}=1.160573$, ${\phi }_{{\beta }_1^{\kappa }}=3.154331$, ${\phi }_{{\beta }_2^{\kappa }}=1.00054$, ${\phi }_{{\gamma }_1^{\kappa }}=-\mathrm{0.1.43622}$, and ${\phi }_{{\gamma }_2^{\kappa }}=0.43622$.

Based on the sensitivity indices of parameters shown in Figure 2, the negative values of the sensitivity indices for parameters ${\phi }_{{\alpha }_1^{\kappa }}$ and ${\phi }_{{\gamma }_1^{\kappa }}$ indicate a strong inverse relationship between these parameters and employee attitudes. This suggests that as these parameters increase, employee attitudes tend to decline significantly. Among these, ${\phi }_{{\alpha }_1^{\kappa }}$​​ shows the most pronounced negative impact, implying it is a critical factor to address in reform initiatives.

Figure 2

Figure 2. Sensitivity indices of parameters.

Conversely, the positive value of ${\phi }_{{\beta }_1^{\kappa }}$ and the relatively small positive values of ${\phi }_{{\alpha }_2^{\kappa }},$ ${\phi }_{{\beta }_2^{\kappa }}\mathrm{a}\mathrm{n}\mathrm{d}{\phi }_{{\gamma }_2^{\kappa }}$ suggest that these parameters may have a favorable influence on employee attitudes. Specifically, the positive influence of ${\phi }_{{\beta }_1^{\kappa }}$ indicates opportunities for leveraging this parameter to foster more positive employee perceptions during the reform process.

Overall, the findings highlight that reform initiatives should focus on mitigating the negative impacts of the parameters with significant negative sensitivity indices while enhancing the positive aspects of those with favorable sensitivity indices. By prioritizing these key parameters, organizations can better align their reform strategies with employee attitudes, ultimately facilitating smoother transitions and greater acceptance of change initiatives.

4.3 Numerical results

In this section, the researchers present the numerical results for the optimal control problem using a fourth-order Runge-Kutta iterative method. By utilizing MATLAB and the ODE45 solver, the researchers illustrated key qualitative findings of the AIR model through numerical representations. These representations demonstrate the behavior of the evolution of employees’ perception, as dynamic process, over a 3-year period. In the optimal control model shown in Equation 15, the researchers examined the effects of implementing strategies focused on providing training sessions to enhance employees' skills for adapting to new processes and technologies (${\mathbf{u}}_{\mathbf{1}}$), ensuring clear communication regarding the rationale, benefits, and impacts of the reforms (${\mathbf{u}}_{\mathbf{2}}$), and a combination of both ${\mathit{u}}_{\mathbf{1}}$ and ${\mathit{u}}_{\mathbf{2}}$ .

Figure 8 displays the trajectories of the model outlined in Equation 5, illustrating the projected trends in employees’ perception over time. The researchers used initial values of $I\left(0\right)=201,R\left(0\right)=93,A\left(0\right)=87$, and assumed parameter values ${\alpha }_1=0.17,{\beta }_1=0.28,{\gamma }_1=0.3,{\alpha }_2=0.45,{\beta }_2=0.17$ and ${\gamma }_2=0.28$.

The graphical representation of the numerical results indicates the stability of resistant persistent steady state ($\left.{\mathfrak{R}}_{eff}=2.72>1\right)$. The trajectories of the state variables are depicted in Figure 3, illustrating the solutions stabilize at the resistant persistent steady state. The consistency between numerical simulations and qualitative results confirms that the chosen parameter values are sufficient to provide insights into strategies for curbing the rising resistance to reform initiatives when, ${\mathfrak{R}}_{\text{eff}}=2.72$, exceeds unity. By acknowledging the limitations of existing research and providing a rational basis for the chosen parameter values, this study offers a foundation for future empirical validation, encouraging further research to refine these assumptions with real-world data. This contribution not only strengthens the theoretical framework but also paves the way for practical applications in understanding and managing similar dynamic systems.

Figure 3

Figure 3. Stability of resistant-persistent steady state.

Figure 4 presents the practical benefits of training programs designed to enhance employees' adaptability to organizational reforms (a). By equipping employees with the necessary skills to adapt new processes and technologies, these training sessions contribute to a more confident and capable workforce. Additionally, clear communication about the rationale, benefits, and expected outcomes of reform initiatives (b) plays a crucial role in shaping employees' perceptions. When employees understand the purpose and potential advantages of changes, they are more likely to view them positively and engage with the transition process more willingly.

Figure 4

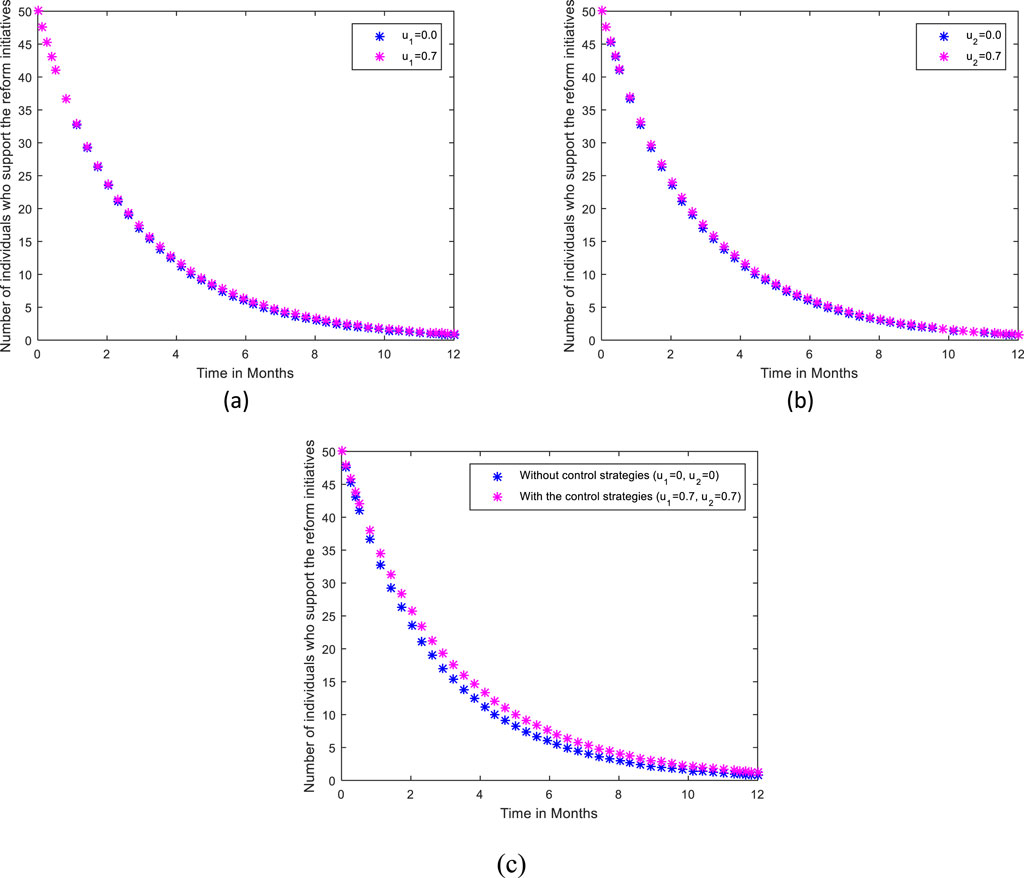
Figure 4. The impact of providing training sessions aimed at enhancing employees' skills for adapting to reform initiatives as illustrated in (A), the impact of clear communication about the rationale, benefits, and effects of reform initiatives as illustrated in (B), and the combined effect of (A) and (B) on variable A as illustrated in (C).

This finding implies that providing targeted training to boost employees' adaptability to new processes and technologies, alongside effective communication about the reasons, advantages, and consequences of reforms (c), may foster a more positive outlook among employees. Such an approach could lead to improved engagement and support for organizational changes, ultimately facilitating a smoother transition and greater success in implementing reform initiatives.

This suggests that a dual approach focusing both on skill development and effective communication can enhance employees' willingness to support and adapt to reforms. Organizations that prioritize these strategies may experience smoother transitions, reduced resistance, and a higher likelihood of successful reform implementation. By fostering a culture of learning and transparency, companies can create an environment where employees feel more secure and motivated to embrace change.

Figure 5 demonstrates the outcomes of numerical simulations that highlight the effects of various strategies on reducing employee resistance to reform initiatives. Specifically, it shows how training sessions aimed at enhancing employees' skills for adapting to reforms (a) and clear communication regarding the rationale, benefits, and expected outcomes of these initiatives (b). The combined impact of both approaches (a) and (b) is shown in (c), illustrating a significant reduction in the number of individuals resistant to reform. The simulation results suggest that an integrated strategy, combining skill development through training proactively and transparent communication, plays a critical role in minimizing opposition among employees. These findings imply that organizations can effectively reduce resistance by investing in such training programs and prioritizing clear, open communication. These approach not only address employee concerns but also creates a more supportive environment for change. As a result, organizations adopting these strategies may experience smoother transitions and increased success in their reform efforts.

Figure 5

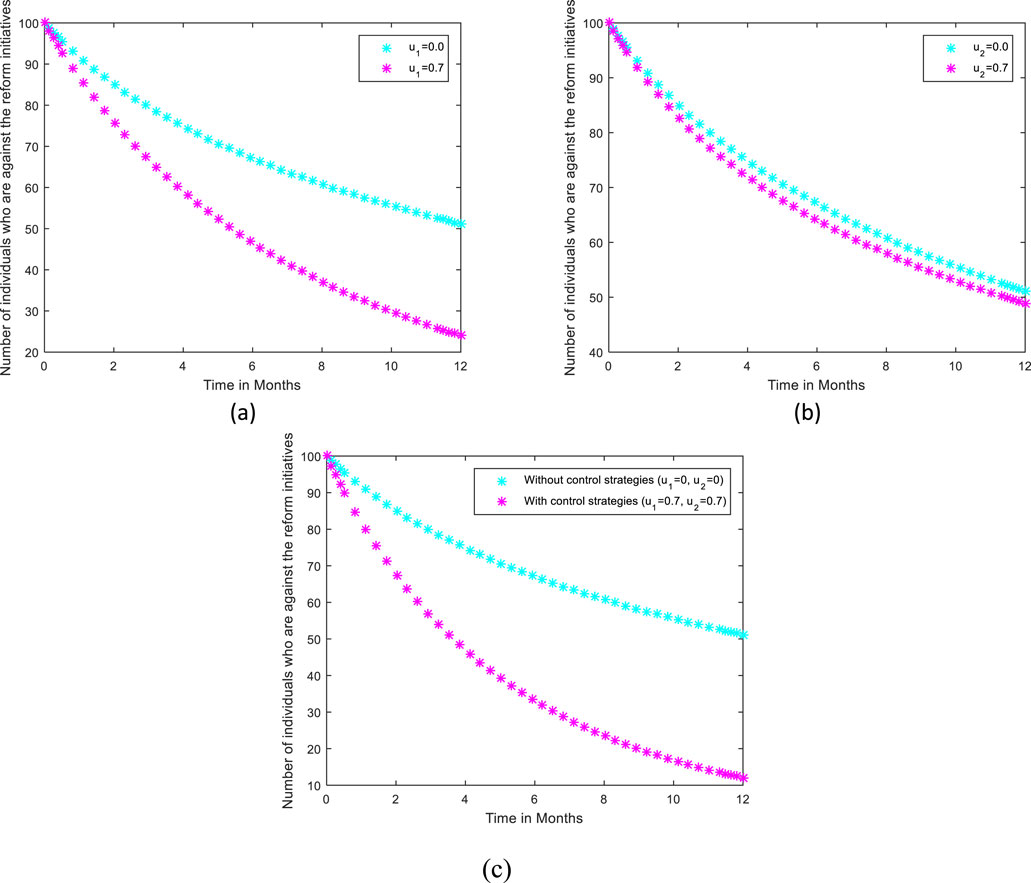
Figure 5. The impact of providing training sessions aimed at enhancing employees' skills for adapting to reform initiatives as shown in (A), the impact of clear communication about the rationale, benefits, and effects of reform initiatives as shown in (B), and the combined effect of (A) and (B) on variable R as shown in (C).

Figure 6 illustrates the impact of training sessions designed to enhance employees' skills for adapting to reform initiatives (a), the significance of clear communication regarding the rationale, benefits, and outcomes of these initiatives (b), and the combined effect of both (a) and (b) on the number of individuals who remain neutral toward reform initiatives. The results indicate that this integrated approach is essential for significantly increasing the number of employees with a neutral stance on reform initiatives.

Figure 6

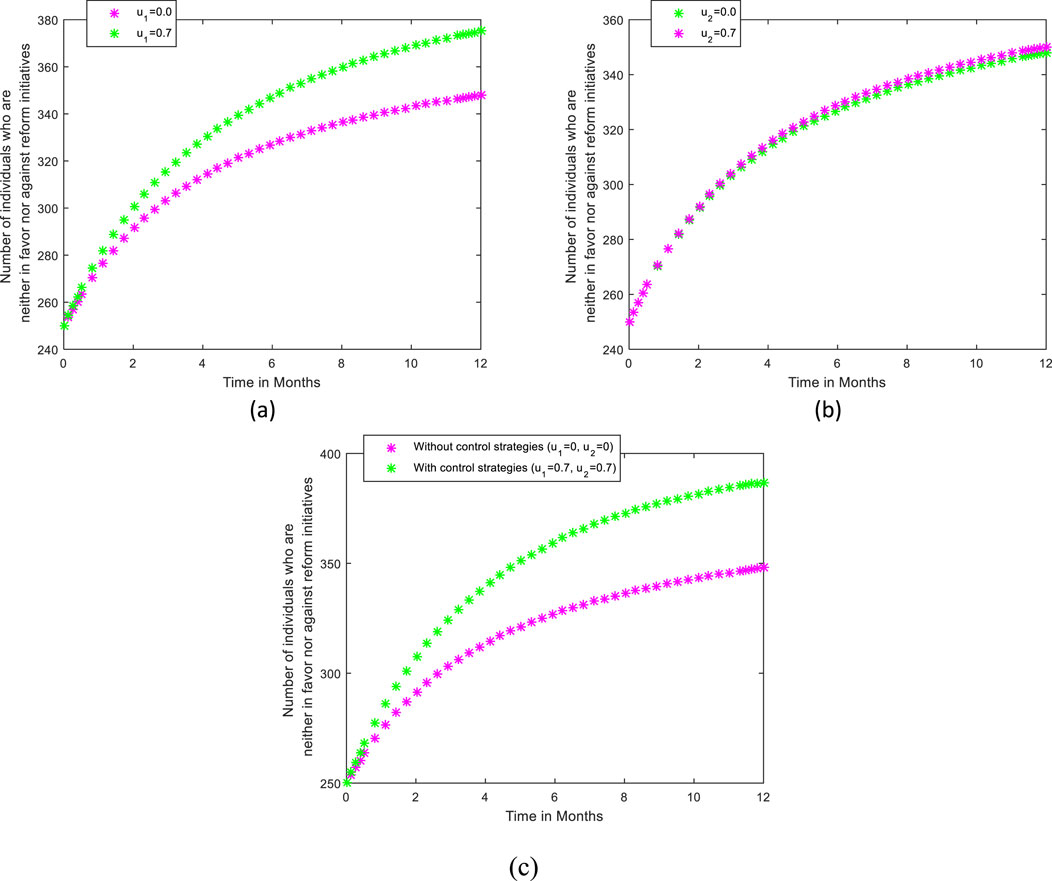
Figure 6. The impact of providing training sessions aimed at enhancing employees' skills for adapting to reform initiatives as depicted in (A), the impact of clear communication about the rationale, benefits, and effects of reform initiatives as depicted in (B), and the combined effect of (A) and (B) on variable I as depicted in (C).

These findings imply that providing targeted training and fostering transparent communication can effectively shift employee perspectives, encouraging a more balanced view toward reform initiatives. A neutral stance can be beneficial, as it often reflects an openness to change without active resistance or overwhelming enthusiasm. This equilibrium can facilitate constructive dialogue and engagement, allowing organizations to gather valuable feedback and insights from employees. By cultivating an environment where neutrality prevails, organizations may be better positioned to implement reforms successfully while minimizing potential conflicts and misunderstandings.

The numerical results presented in Figures 7–9 reveal that the memory effect significantly influences employees' perceptions of adaptability or resistance, shaped by their evaluations of past experiences. This influence ultimately affects their overall views on reform initiatives. Notably, The researchers observe that a decrease in the fractional order correlates with a reduction in the number of resistant employees as the memory effect intensifies. Conversely, this decrease also leads to an increase in indifferent employees.

Figure 7

Figure 7. Effect of memory on individuals who are against the reform initiatives.

Figure 8

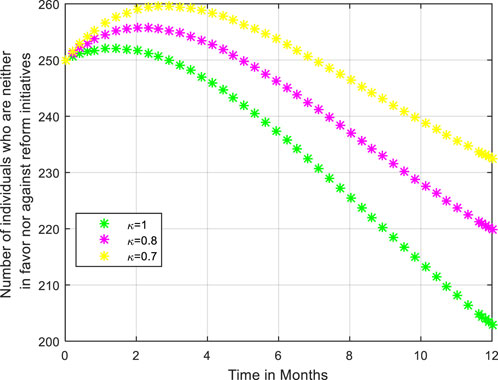
Figure 8. Effect of memory on number of individuals who are neither in favor nor against reform initiatives.

Figure 9

Figure 9. Effect of memory on number of individuals who support reform initiatives.

This phenomenon can be understood in light of the tendency for employees to become desensitized to certain challenges or shortcomings, leading to diminished perceptions of the reform initiatives. This suggests that if employees have previously encountered issues without resolution, they may develop a sense of resignation, resulting in a neutral or indifferent stance toward future changes. Furthermore, the decrease in the fractional order is linked to a slight increase in the number of employees who are adaptable to reform initiatives.

These insights imply that organizations must recognize the critical role of past experiences in shaping employee attitudes toward change. To mitigate resistance and indifference, it is essential for leaders to address previous shortcomings and foster a culture of continuous improvement. By actively engaging employees in discussions about their experiences and perceptions, organizations can leverage the memory effect positively, encouraging a more adaptable workforce that is open to embracing reform initiatives.

5 Conclusion and recommendation

In this study, the researchers developed a compartmental model categorizing employees as “indifferent,” “resistant,” and “adaptive” providing insights into how employees shift between these categories based on their adaptation to workplace reform initiatives. The researchers evaluated the model for well-posedness and examined the stability of its steady states. Through the application of Pontryagin’s maximum principle and numerical simulations, the researchers identified optimal strategies to decrease the number of resistant employees, fostering a more supportive environment for reform initiatives. This encourages employees to remain indifferent or adaptive, promoting a positive attitude toward change.

The optimal strategies focus on offering training sessions to equip employees with the skills necessary to adapt to new processes or technologies, as well as clearly communicating the reasons for the reforms, the anticipated benefits, and their impact on employees. Additionally, the study investigated memory effects by converting the integer order model into a fractional order model. Graphical representations of the numerical results emphasize the importance of the fractional derivatives' order in illustrating how employees' perceptions evolve over time. Our recommendation for stakeholders is to prioritize efforts that maximize both protection and treatment rates to effectively reduce social media addiction within communities. For future research, the researchers recommend expanding the model to incorporate additional parameters that could affect employees’ perceptions of reform initiatives, including job security, organizational culture, and leadership style, in order to develop more effective intervention strategies.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

GH: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. ST: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. YA: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. DM: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The author appreciates the reviewers for their insightful comments, which contributed to enhancing the paper’s current version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Baba, B. A., and Bilgehan, B. (2021). Optimal control of a fractional order model for the COVID – 19 pandemic. Chaos, Solit. and Fractals 144, 110678. doi:10.1016/j.chaos.2021.110678

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, C., Ling, L., Chen, S., Zhai, W., Wang, K., and Wang, G. (2021). Dynamic performance evaluation of an inspection wagon for urban railway tracks. Measurement 170, 108704. doi:10.1016/j.measurement.2020.108704

CrossRef Full Text | Google Scholar

Cummings, T, and Worley, C. (2001). Organization development and change.

Google Scholar

Denu, D., and Kermausuor, S. (2022). Analysis of a fractional-order COVID-19 epidemic model with lockdown. Vaccines 10 (11), 1773. doi:10.3390/vaccines10111773

PubMed Abstract | CrossRef Full Text | Google Scholar

E. I. Kincaid, D., and Cheney, W. (1992). Numerical analysis--mathematics of scientific computing. Math. Comput. 59 (199), 297. doi:10.2307/2152998

CrossRef Full Text | Google Scholar

Guest, D. (2002). Human resource management, corporate performance and employee wellbeing: building the worker into HRM. J. Industrial Relat. 44 (3), 335–358. doi:10.1111/1472-9296.00053

CrossRef Full Text | Google Scholar

Hailu, G. K., and Teklu, S. W. (2024a). Investigation into hate speech dissemination dynamics in a community using fractional order modeling approach. Res. Math. 11 (1). doi:10.1080/27684830.2024.2386748

CrossRef Full Text | Google Scholar

Hailu, G. K., and Teklu, S. W. (2024b). Improving passengers’ attitudes toward safety and unreliable train operations: analysis of a mathematical model of fractional order. Front. Appl. Math. Stat. 10. doi:10.3389/fams.2024.1290494

CrossRef Full Text | Google Scholar

Haubold, H. J., Mathai, A. M., and Saxena, R. K. (2011). Mittag-leffler functions and their applications. J. Appl. Math. 2011. doi:10.1155/2011/298628

CrossRef Full Text | Google Scholar

Jakobsen, M. L., Kjeldsen, A. M., and Pallesen, T. (2023). Distributed leadership and performance-related employee outcomes in public sector organizations. Public Adm. 101 (2), 500–521. doi:10.1111/padm.12801

CrossRef Full Text | Google Scholar

Jones, L., Watson, B., Hobman, E., Bordia, P., Gallois, C., and Callan, V. J. (2008). Employee perceptions of organizational change: impact of hierarchical level. Leadersh. and Organ. Dev. J. 29 (4), 294–316. doi:10.1108/01437730810876122

CrossRef Full Text | Google Scholar

Junjua, M. U. D., Ahmad, A., Kulachi, M. O., Hincal, E., Jan, A. Z., and Kedzia, K. (2024). Mathematical analysis and chaos control of HBV causing hepatocellular carcinoma by taking asymptomatic and early detection measures. doi:10.21203/RS.3.RS-4552916/V1

CrossRef Full Text | Google Scholar

Lapuente, V., and Van de Walle, S. (2020). The effects of new public management on the quality of public services. Governance 33, 461–475. doi:10.1111/gove.12502

CrossRef Full Text | Google Scholar

Naik, P. A., Farman, M., Zehra, A., Nisar, K. S., and Hincal, E. (2024). Analysis and modeling with fractal-fractional operator for an epidemic model with reference to COVID-19 modeling. Partial Differ. Equations Appl. Math. 10, 100663. doi:10.1016/j.padiff.2024.100663

CrossRef Full Text | Google Scholar

Petrás, I. (2011). “Fractional-order nonlinear systems. Modeling,” in Analysis and simulation.

Google Scholar

Podlubny, I. (1999). Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. 198.

Google Scholar

Teklu, S. W., Meshesha, A. A., and Ullah, S. (2023). Analysis of tinea capitis epidemic fractional order model with optimal control theory. Inf. Med. Unlocked 42, 101379. doi:10.1016/j.imu.2023.101379

CrossRef Full Text | Google Scholar

Van Den Driessche, P., and Watmough, J. (2002). Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180 (1–2). doi:10.1016/S0025-5564(02)00108-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Vargas-De-León, C. (2015). Volterra-type Lyapunov functions for fractional-order epidemic systems. Commun. Nonlinear Sci. Numer. Simul. 24 (1–3), 75–85. doi:10.1016/j.cnsns.2014.12.013

CrossRef Full Text | Google Scholar