Coevolutionary dynamics of group interactions: coevolving nonlinear voter models

We survey the coevolutionary dynamics of network topology and group interactions in opinion formation, grounded on a coevolving nonlinear voter model. The coevolving nonlinear voter model incorporates two mechanisms: group interactions implemented through nonlinearity in the voter model and network plasticity demonstrated as the rewiring of links to remove connections between nodes in different opinions. We show that the role of group interactions, implemented by the nonlinearity can significantly impact both the dynamical outcomes of nodes’ state and the network topology. Additionally, we review several variants of the coevolving nonlinear voter model considering different rewiring mechanisms, noise of flipping nodes’ state, and multilayer structures. We portray the various aspects of the coevolving nonlinear voter model as an example of network coevolution driven by group interactions, and finally, present the implications and potential directions for future research.

1 Introduction

The structures of complex networks that govern interactions between individuals have an essential impact on the dynamics of those agents (Boccaletti et al., 2006; Newman, 2018). The network structures not only affect the dynamical processes taking place within the system, but they themselves also evolve under the influence of individual states (Dorogovtsev and Mendes, 2002; Holme and Saramäki, 2012). In this regards, the integration of the dynamics of individual states and network structures has received much attention from physics, social science, and network science communities (Zimmermann et al., 2001; Zimmermann et al., 2004; Gross et al., 2006; Holme and Newman, 2006; Gross and Blasius, 2008; Vazquez et al., 2008; Gross and Sayama, 2009). Researchers have explored the coevolutionary dynamics of complex networks in various contexts by integrating the evolution of networks’ topology and the dynamics of nodes (Gross and Sayama, 2009). There have been many studies on coevolving or adaptive networks, such as coevolving voter models (Holme and Newman, 2006; Nardini et al., 2008; Vazquez et al., 2008; Durrett et al., 2012; Carro et al., 2014; Diakonova et al., 2014; Diakonova et al., 2015; Saeedian et al., 2019), coevolving spin systems (Biely et al., 2009; Mandrá et al., 2009; Raducha et al., 2018a; Korbel et al., 2023), coevolutionary opinion dynamics (Kimura and Hayakawa, 2008; Yi et al., 2013; Liu et al., 2023), language evolution and competition (carro et al., 2016), adaptive epidemic models (Gross et al., 2006; Shaw and Schwartz, 2008; Marceau et al., 2010; Demirel et al., 2014; Scarpino et al., 2016; Saeedian et al., 2017; Achterberg et al., 2020; Choi and Min, 2023), cultural evolution models (Centola et al., 2007; Vazquez et al., 2007), game theoretical models (Ebel and Bornholdt, 2002; Eguíluz et al., 2005; Perc et al., 2013; González Casado et al., 2023), and biological evolutions (Drossel et al., 2001; Liu and Bassler, 2006; Fialkowski et al., 2023). Owing to the feedback inherent in adaptive systems where the network structure influences the node dynamics and vice versa, these studies have revealed intriguing properties such as the dynamical organization of network structures and diverse phase transitions (Vazquez et al., 2007; Vazquez et al., 2008; Yi et al., 2013; Liu et al., 2023).

The majority of existing research on coevolving networks has largely focused on systems that change dynamically according to pair-wise interactions (Gross et al., 2006; Holme and Newman, 2006; Gross and Blasius, 2008; Vazquez et al., 2008; Gross and Sayama, 2009). However, in various social, neural, biological, and ecological systems, however, group or collective interactions are commonly observed (Schelling, 1973; Granovetter, 1978; Centola and Macy, 2007; Centola, 2010; Levine et al., 2017; Monsted et al., 2017; Min and San Miguel, 2018a; Min and San Miguel, 2018b; Centola, 2018; Hébert-Dufresne et al., 2020; Battiston et al., 2021) Group interaction refers to a process where more than two nodes participate simultaneously, rather than interactions occurring solely between pairs (Battiston et al., 2020). Such group interactions can either be composed of collections of pair-wise interactions or have the form of many-body interactions that cannot be reduced to mere pair-wise interactions (Battiston et al., 2020; Battiston et al., 2021). Understanding the group interactions is vital to predict and to control the behavior of complex systems (Watts, 2002; Hébert-Dufresne et al., 2020; Battiston et al., 2021).

While these group interactions are common in reality, there is a gap addressing the coevolutionary dynamics driven by group interactions, pointing to the need for further examination in this area. Despite the initial research on the coevolutionary dynamics on networks based on group interactions for evolutionary games (Perc et al., 2013; Alvarez-Rodriguez et al., 2021), spin models (Mandrá et al., 2009), contagion dynamics (Lambiotte and González-Avella, 2011; Min and San Miguel, 2023), and voter models (Min and Miguel, 2017), there remain several issues for more extensive and thorough studies to grasp its full implications. An interesting example of coevolutionary dynamics with group interactions would be a coevolving nonlinear voter model (CNVM) (Min and Miguel, 2017; Kureh and Porter, 2020). This model is an extension of a voter model which is a well established model based on pair-wise interactions (Holme and Newman, 2006; Vazquez et al., 2008), to include group interactions (Castellano et al., 2009; Schweitzer and Behera, 2009; Jędrzejewski, 2017; Peralta et al., 2018).

In this review article, we explore the dynamical consequences of the CNVM as a case study of combining group interactions and coevolutionary dynamics. We begin with the background of the CNVM, review its fundamental results, and also explore several variants of the model (Raducha et al., 2018b; Min and Miguel, 2019; Jędrzejewski et al., 2020; Raducha and San Miguel, 2020). This paper aims to provide an example for analyzing the effect of group interactions in coevolving networks and deepens our understanding within the broader landscape of coevolutionary dynamics.

The paper is organized as follows. First, as a benchmark for comparison, we introduce the coevolving voter model with pair-wise interactions in Sec. II. Next, we present the coevolving “nonlinear” voter model encoded with group interactions, outlining its fundamental results in Sec. III. We then sequentially introduce several variants of this model with incorporating triadic closure, rewire-to-random mechanism, noise, and multilayer coevolution in Sec. IV. Finally, summary and outlook are presented in Sec. V.

2 Coevolutionary dynamics of the voter model

The coevolving voter model is a compelling framework for understanding the coevolution of node states and network topology. This simple yet insightful model describes the evolution of node states under voter dynamics and the concurrent reorganization of the network through link rewiring (Vazquez et al., 2008). That is, unlike the classical voter model that assumes static connections among individuals, the coevolving voter model takes into account the change of social ties under the influence of the state of nodes.

The coevolving voter model consists of two dynamical processes: copying and rewiring (Holme and Newman, 2006; Vazquez et al., 2008; Durrett et al., 2012). A node can adopt the opinion of one of its neighbors chosen randomly. Concurrently, the connections between voters can be rewired, depending on the agreement or disagreement of states between two connected voters. The specific rule of the coevolving voter model is as follows: Initially, each node can be one of two states, called up or down, on a network. In this paper, we denote the state of node i as σ_i, and thus σ_i ∈ {−1, 1} where −1 and 1, respectively corresponds to down and up state. At each update step, we choose one node, say i, at random. Then with a complementary probability 1 − p, node i copies the state of one of its neighbors, for instance j, that is selected at random. With a probability p, if the states of node i and j are different, node i cuts its connection to node j and establishes a new connection to a node that has the “same” state with node i. The procedures continue until the system reaches a steady state.

The parameter p, called as network plasticity, represents the ratio between the link rewiring and copying processes, thereby determining the time scale between them. Depending on the value of p, there are two distinct phases, an active to a frozen phases, in the steady state. At a critical point p_c, the generic absorbing phase transition occurs from the active to the frozen phase (Vazquez et al., 2008). The active phase corresponds to a connected network at a steady state in the thermodynamic limit, and is characterized by a non-zero density of active links. On the other hand, the frozen phase corresponds to a fragmented network where each component is in a consensus state. The fragmentation transition between active and fragmented phases is a peculiar characteristic of the coevolving voter model.

3 Coevolving nonlinear voter model

The coevolving voter model provides an important insight into many interesting phenomena, such as polarization or consensus in society (Vazquez et al., 2008) and language competition (carro et al., 2016). In addition, there have been many variants of the coevolving voter model for more realistic modeling, i.e., incorporating noise in the flipping of opinions (Diakonova et al., 2015), multilayer coevolution (Diakonova et al., 2014; Klimek et al., 2016), and signed interactions (Saeedian et al., 2019). Along the studies on the coevolving voter models, it is steadily assumed that the dynamical processes are governed by dyadic interactions where the state of a node or network topology change based on the influence of pairs (Carro et al., 2014; Diakonova et al., 2014; Diakonova et al., 2015; Saeedian et al., 2019). However, this simple approach fails to capture the complexity of real-world social dynamics where multiple agents collectively influence an individual (Schelling, 1973; Granovetter, 1978; Centola, 2010; Levine et al., 2017; Monsted et al., 2017; Battiston et al., 2021). This suggests that an agent engages in “nonlinear” interactions with its neighbors, to implement group interactions in the voter model (Castellano et al., 2009; Schweitzer and Behera, 2009; Peralta et al., 2018).

To address the limitations of pairwise interactions in coevolving voter models, a coevolving nonlinear voter model that combines evolutionary dynamics of networks with nonlinear interactions between agents was proposed (Min and Miguel, 2017). The CNVM is an extension on coevolving networks of a nonlinear voter model (Castellano et al., 2009; Nyczka et al., 2012; Mobilia, 2015; Peralta et al., 2018). The dynamical rules of the CNVM are as follows (Figure 1). At each time step, we choose a node, say i, at random. Next, we measure the fraction π_i of active links of node i to its degree as

${\pi }_i=\frac{a_i}{k_i},(1)$

where a_i represents the number of active links of node i. Here, active links means links that connect a pair of two nodes with different opinions. We then choose at random an active link to a neighbor, say j with a probability, ${\pi }_i^q$, where q is the degree of nonlinearity. And, with the complementary probability $1-{\pi }_i^q$, nothing happens. Upon selecting nodes i and j, we proceed coevolutionary dynamics with network plasticity p. Specifically, with a probability p, node i disconnects its link to j and establishes a new link with another node that shares the same opinion as node i. Conversely, with a probability of 1 − p, node i changes its state to imitate the state of node j. This process continues until the system reaches an active steady state or an absorbing state. Note that the network structure changes over time while maintaining a constant link density of network, that is a constant average degree ⟨k⟩.

FIGURE 1

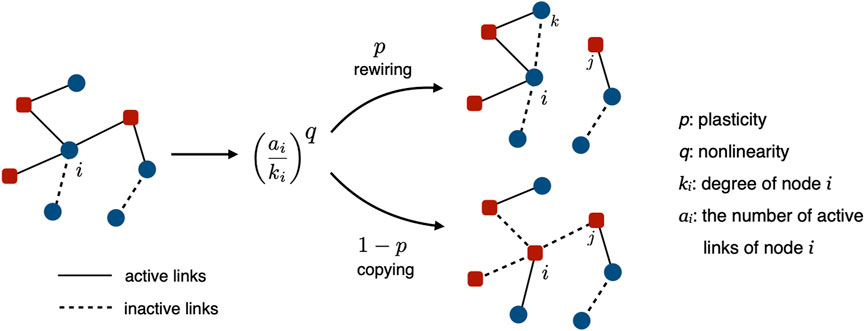
FIGURE 1. Schematic illustration of dynamical rules of the coevolving nonlinear voter model. Nodes are either up (red circle) or down (blue square). Dashed lines are active links while solid ones represent inactive links. At each step, we randomly select node i, then a neighbor j connected through an active link with probability ${(\frac{a_i}{k_i})}^q$, where a_i is the number of active links. With probability p, node i removes its connection with j and forms a new link with a node that has the same opinion as i. On the other hand, with probability 1− p node i changes its state to imitate that of node j.

In the CNVM, there are two important parameters: network plasticity p and nonlinearity q. The network plasticity p represents the rate of link rewiring. The degree of nonlinearity q is a parameter newly introduced in the CNVM to represent group interactions. To understand the role of this parameter, consider the following scenario. Suppose a voter, rather than asking a single neighbor, inquires about the opinions of multiple neighbors, specifically q neighbors. And, if all these q neighbors have the same opinion, then the voter does change its opinion. To be more precise, our model corresponds to the scenario when a voter randomly chooses one out of the neighbors q times, allowing repetition. If we mathematically describe it, we arrive at the introduced term ${\pi }_i^q$. Unlike the ordinary voter model, it reflects group interactions because it requires convergence of the opinions of multiple neighbors.

Let us examine the effect of q qualitatively. For the linear case, when q = 1, it corresponds to selecting an active link randomly, which is exactly the same as the ordinary coevolving voter model. If q > 1, the ratio between the probability of following the majority opinion and minority opinion among neighbors is higher compared to the linear voter model. Conversely, when q < 1, the probability of following with the minority opinion becomes relatively higher. The empirical evidences of the nonlinear interactions can be found in social impact theory (Nowak et al., 1990), language competition, and extinction (Nettle, 1999; Abrams and Strogatz, 2003). While it is observed that q < 1 in social impact theory (Nowak et al., 1990) and language evolution (Nettle, 1999), it was found to q = 1.3 in language extinction processes (Abrams and Strogatz, 2003).

Introducing the nonlinearity q as an additional dimension, the CNVM exhibits a rich variety of phenomena. As shown in Figure 2A, depending on the values of network plasticity p and nonlinearity q, there are three possible phases that can reach in the steady state: consensus, fragmentation, and coexistence. In the consensus phase, all nodes arrive at the same state, either up or down. This is an absorbing state, meaning that once reached the system remains in this phase permanently. The fragmentation phase, on the other hand, represents a situation where a network breaks into multiple components of localized consensus. In this phase, agents within a particular component share the same opinion, but this opinion may differ from component to component. Finally, the coexistence phase is characterized by the persistent presence of both opinions throughout the system without the formation of disconnected components. This phase is a dynamically active state where two different opinions exist in the same component and continuously interact each other.

FIGURE 2

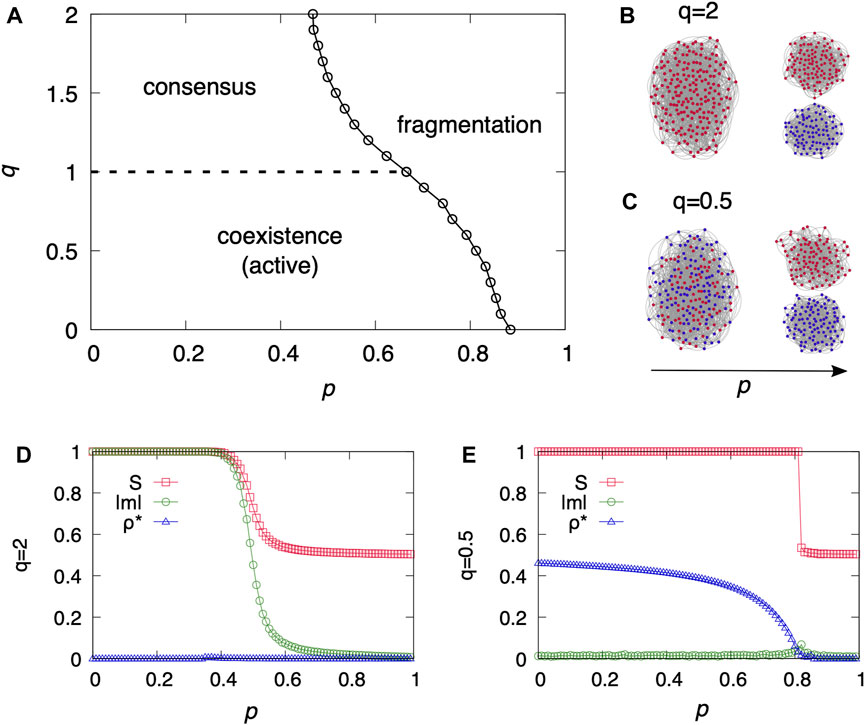
FIGURE 2. (A) Phase diagram of the CNVM with respect to p and q contains consensus, coexistence, and fragmentation phases. The diagram was obtained numerically from degree regular networks with ⟨k⟩ = 8, N = 10⁴, and initially neural magnetization m = 0. (B,C) Schematic illustrations of phase transitions: (B) transitions from consensus to fragmentation phases for q = 2 and (C) transitions from coexistence to fragmentation phases for q = 0.5. (D,E) Numerical results of the size of the largest component S, the absolute value of magnetization |m|, and the density of active links ρ as a function of p are shown together: (D) q = 2 and (E) q = 0.5, on degree regular networks with ⟨k⟩ = 8, N = 10⁴, and initially neural magnetization m = 0.

The three phases can be characterized by the quantities: the size of the largest component S, the absolute value of magnetization |m|, and the density of active links ρ. The magnetization m refers to the average value of the state of nodes, defined by

$m=\frac{1}{N}\sum _i{\sigma }_i,(2)$

where N is the total number of nodes and σ_i ∈ {−1, 1}. The consensus phase corresponds to (S, |m|, ρ) ≈ (1, 1, 0) since there is a single component with the same state of nodes. The fragmentation phases corresponds to (1/2, 0, 0), meaning that there are two separated components where agents within a component share the same opinion. Finally, the dynamically active coexistence phase is characterized by (1, 0, ρ*) where ρ* is a finite value of density of active links. In the coexistence phase, nodes with opposite opinions exist in the same component. Here we assume that the dynamics starts from neutral magnetization, m = 0.

The CNVM shows a fragmentation transition between connected and disconnected networks but with different mechanisms depending on the nonlinearity q. The transitions to fragmentation with increasing p are qualitatively illustrated in Figure 2B, which shows the transitions from consensus to fragmentation phases for q = 2, and in Figure 2C, which shows the transition from coexistence to fragmentation phases for q = 0.5. Figures 2 (D, E) shows the numerical results for the characteristics of phase transitions for (a) q = 2 and (b) q = 0.5. The size of the largest component S, absolute value of magnetization |m|, and the density of active links ρ* at the steady state are shown together. For q > 1 there is a transition between consensus and fragmentation phases as shown in Figure 2D for q = 2. Since the transition occurs between two absorbing states, it is different from the continuous absorbing transition observed in the coevolving linear voter model. However, for q < 1 the system undergoes a continuous transition between a dynamically active phase and a fragmentation phase [Figure 2E], similar to the linear case.

The behaviors of the CNVM can be understood by the coupled differential equations of the magnetization m and density of active links ρ. Based on the pair approximation, the coupled equations on a random network with average degree ⟨k⟩ can be derived as (Min and Miguel, 2017).

$\frac{dm}{dt}=2\left(1-p\right)\left[-n_{+}{\left(\frac{\rho }{2n_{+}}\right)}^q+n_{-}{\left(\frac{\rho }{2n_{-}}\right)}^q\right],(3)$

$\frac{d\rho }{dt}=\frac{2}{⟨k⟩}\left\{-p\left[n_{+}{\left(\frac{\rho }{2n_{+}}\right)}^q+n_{-}{\left(\frac{\rho }{2n_{-}}\right)}^q\right]\right.$

$\left.+\left(1-p\right)\left[n_{+}{\left(\frac{\rho }{2n_{+}}\right)}^q\left(⟨k⟩-2q-2\left(⟨k⟩-q\right)\frac{\rho }{2n_{+}}\right)+n_{-}{\left(\frac{\rho }{2n_{-}}\right)}^q\left(⟨k⟩-2q-2\left(⟨k⟩-q\right)\frac{\rho }{2n_{-}}\right)]\right]\right\},(4)$

where n₊ = (1 + m)/2 and n₋ = (1 − m)/2. In this approximation, a homogeneous structure of networks is assumed. The rationale of each term in the equations is following. If we select node i with state s where s ∈ { + 1, − 1}, the probability that its connected neighbor has a different state can be estimated by ρ/(2n_s), where n_s stands for the fraction of nodes in state s and s can be either +1 or −1. In addition, if node i in state s is selected for an update to be a different state with a probability of ${[\rho /(2n_s)]}^q$, then it is estimated that q of its neighbors are in a different state. Thus, the remaining neighbors, denoted as ⟨k⟩ − q, will have a different state with a probability of ρ/(2n_s) (Min and Miguel, 2017).

The coupled equations based on the pair approximation provide a phenomenological explanation for the phases and phase transitions observed in the CNVM model (Min and Miguel, 2017). Based on the approximation, the transition point p_c is predicted as

$p_c=\frac{\langle k\rangle -2q}{1+\langle k\rangle -2q}.(5)$

For p > p_c, the fragmented phase (m, ρ) = (0, 0) is a stable solution across all q values. On the other hand, for p < p_c, the system shows a dynamic active phase or an absorbing phase with a connected network structure, depending on the value of q. When q < 1, the solution (0, ρ*) becomes stable, suggesting a dynamically active phase. Conversely, when q > 1 the solutions (−1, 0) and (1,0) become stable, indicating an absorbing consensus phase.

4 Variants of coevolving nonlinear voter model

The “nonlinearity” in the CNVM model offers the group interactions that governs the change of state and network structure, beyond pair-wise interactions. For more realistic approaches, there have been several extensions in the CNVM. Among the generalized models, we focus on the effect of the triadic closure, rewire-to-random mechanism, noise, and multilayer coevolution. Triadic closure stands for the mechanism forming new connections with the neighbors of one’s neighbors, a departure from the standard random rewiring approach. Next, we discuss the difference between the rewire-to-same and rewire-to-random mechanism when we find a new neighbor during link rewiring. Noise in the CNVM means that individuals can randomly flip their opinions, irrespective of their neighbors’ states, introducing an unpredictable element to the dynamics. Finally, multilayer coevolution represents the coevolutionary dynamics within networks composed of multiple layers, examining how interactions between layers affect the dynamical consequences. In the following sections, we discuss the variations of the CNVM focusing on the difference to the ordinary CNVM.

4.1 Coevolving nonlinear voter model with triadic closures

It is common in social systems to form ties locally when seeking new connections (Newman and Park, 2003; Lee et al., 2010; Klimek and Thurner, 2013). Triadic closure is aptly captured by the local evolution of network structures. In other words, when individuals are on the look for new connections, they tend to connect with the neighbors of their current neighbors, to form a triangle. A natural and straightforward extension of the CNVM is to implement this triadic closure mechanism in link rewiring (Raducha et al., 2018b). Specifically, a node attempts to find a new neighbor among the neighbors of their current neighbors during link rewiring (Malik et al., 2016; Raducha et al., 2018b). This rewiring pattern reflects many real-world networks, especially social networks where acquaintances of acquaintances often become directly connected (Newman and Park, 2003; Lee et al., 2010).

A peculiar phenomenon with triadic closures compared to the CNVM is a shattered phase, which appears when q < 1 and p < p_c (Raducha et al., 2018b). In this phase, the system remains an active phase with zero magnetization, |m| = 0, like the coexistence phase in the CNVM. However, the structure of networks consists of a large active component alongside numerous isolated nodes, so called shattered phase. It implies for q < 1 with triadic closure that as p decreases a network, initially characterized by two separated components with opposite opinions, evolves into many isolated nodes and an active component, so called a shattering transition. In addition, the clustering coefficient shows values that are not close to zero, while it consistently approaches zero for all parameter sets for random link rewiring in the ordinary CNVM.

4.2 Coevolving nonlinear voter model with rewire-to-random mechanism

In the CNVM, when searching for new neighbors through rewiring, a new link is established with a neighbor in the same state. However, in real-world social systems, one may not precisely identify the opinions or states of other agents. Therefore, it may be natural to rewire with any random node from the entire network, regardless of its state (Durrett et al., 2012; Jędrzejewski et al., 2020). The specific model is as follows: A node i is randomly selected, and its state or link is changed depending on the nonlinearity q, similar to the previous model. However, when rewiring, a new neighbor is randomly chosen from the entire network, irrespective of its current state. Therefore with the modification a newly connected neighbor can have a different opinion.

The effect of the rewire-to-random mechanism was examined using the pair approximation and numerical simulations (Jędrzejewski et al., 2020). The modified model produces two dynamically active phases, symmetric and asymmetric, in addition to consensus and fragmentation. The active symmetric phase exhibits the same number of nodes in two states, indicating no preferred state in the network. Conversely, the active asymmetric phase shows a dominance of nodes in one state, meaning that a majority opinion appears via spontaneous symmetry breaking. While the symmetric active phase appears also in the CNVM with the rewire-to-same mechanism (Min and Miguel, 2017), the asymmetric active phase happens exclusively with the rewire-to-random mechanism. It implies that the nonlinearity along with the variation can produce a new phase and phase transition, with the slight modification in the details of the model.

4.3 Coevolving nonlinear voter model with noise

In social systems, noise is an inescapable factor. It arises from various aspects, such as the unpredictable nature of human interactions and the inherent randomness in individual choices. This stochasticity implies the possibilities to change the individual’s state irrespective of their neighbors’ states (Diakonova et al., 2015). In this respect, the coevolutionary dynamics combining both nonlinearity and inherent noise was studied (Raducha and San Miguel, 2020). In this model, each node can change its state autonomously with a probability ϵ, in addition to the dynamical rules of the CNVM. This probability produces a noise in coevolutionary dynamics.

In the CNVM with noise, there are three distinct phases similar to the original CNVM: consensus, coexistence, and fragmentation. However, noise prevents an absorbing or frozen state, turning the fragmentation and consensus states into dynamical states. That is, the consensus and fragmentation states are no longer absorbing states but become dynamically steady states. The similar patterns are observed in the coevolving linear voter model with noise (Diakonova et al., 2015).

In addition, the coexistence phases can be further divided into two distinct subclasses. In the coexistence phase for q < 1, there is a clear divide between a fully-mixing phase and a structured coexistence phase. The fully-mixing phase is the same phase as a coexistence phase observed in the ordinary CNVM However, the structured coexistence phase shows significantly lower the density of active link due to the existence of two large communities that shows highly homogeneous opinions internally.

In the consensus phase for q > 1, there are also two distinct subclasses: a strong consensus where most nodes in the system remain in the same state and an alternating consensus where the majority opinion switches in time. When the CNVM is integrated with noise, the resulting network structure and node states can be highly diverse. It implies that the noise can be a source of the diverse patterns in the structure and opinion evolution of social networks.

4.4 Coevolving nonlinear voter models on multilayer networks

Many real-world complex systems, from living organisms and human societies to transportation networks and critical infrastructures, function through multiple layers of interacting networks (Kivelä et al., 2014; Lee et al., 2015). Additionally, the synergy between these layers is vital to understand and control the function of networked systems (Min et al., 2014; Min and Goh, 2014). Networks with multiple layers can also influence the opinion dynamics, leading to emergent phenomena that can better reflect real-world systems. Therefore, some studies have been presented that extends the coevolutionary dynamics of opinion dynamics from a single layer to multilayer networks (Diakonova et al., 2014; Klimek et al., 2016; Min and Miguel, 2019).

Among these, there is a model of multilayer coevolution of the nonlinear voter model with synchronization of nodes’ state between different layers (Min and Miguel, 2019). In this model, at each step a layer and a node in the chosen layer are selected at random. Let us call it node i. Then, the coevolutionary rule is the same as the CNVM on a single layer (Min and Miguel, 2017). In addition, if the copying process has occurred, a node in the other layer that is interconnected to node i via an inter-link between layers also changes its state to become the same state as node i. This synchronization step ensures the same state for nodes connected across different layers. In this model, in addition to the network’s plasticity p and nonlinearity q that already exist in the CNVM, another parameter K has been introduced to represent the density of interlinks.

When the two layers have the same plasticity p, the fragmentation transition occurs with a larger value of p compared to that on a single layer. As the density of interlink K increases, the location p_c at which the fragment transition occurs becomes delayed. It means that multiple layer structures delay and suppress the fragmentation of networks. In addition, an asymmetric fragmented phase for q > 1 and an active shattered phase for q < 1 appear when two layers of networks have different values of plasticity, which does not exist in the CNVM in a single layer. The asymmetric fragmented phase represents the both layers undergo fragmentation but the sizes of largest components for different layers are different each other. And, the active shattered phase represents a state where the network becomes shattered into many isolated nodes, but the value of magnetization remains at zero. Such non-trivial results demonstrate that the introduction of multiple layers can give rise to new types of complex structures and dynamics, enriching our understanding of coevolutionary dynamics.

5 Summary and outlook

In this paper, we have explored the coevolving nonlinear voter models from various perspectives as a representative of coevolutionary dynamics with group interactions. The “nonlinearity” in the model represents an interaction where a node engages as a group with all of its neighbors, rather than pair-wise interactions. We have examined several variants of the CNVM incorporating the rewiring with the triadic closure, rewire-to-random mechanism, noise of flipping nodes’ state, and multilayer structures in coevolutionary dynamics. Integrating the group interactions and the various factors, we have found a rich variety of phases and phase transitions for both network structure and nodes’ state.

In addition to the approach discussed in this paper, group interactions have been studied from various contexts in network science, such as complex contagions in social and biological systems (Watts, 2002; Kook et al., 2021; Lee et al., 2023), cooperative epidemics (Chen et al., 2013; Cai et al., 2015; Min and Castellano, 2020), or higher-order representations of networked systems (Battiston et al., 2020; Battiston et al., 2021; Majhi et al., 2022). Despite the advances in understanding group interactions, there is a still gap in exploring group interactions within the framework of coevolving dynamics. Therefore, it underlines an imperative need for further research in this area, given coevolutionary dynamics is one of the key factors in complex systems (Bianconi et al., 2023). As a representative, the series of research related to the CNVM can provide a guide for further studies on coevolutionary dynamics considering diverse forms of group interactions.

Finally, we discuss a few recent advancements and future outlook on issues that are related to coevolutionary dynamics of group interactions. One active line of research related to group interaction is higher-order networks (Battiston et al., 2020; Battiston et al., 2021; Majhi et al., 2022). Therefore, a straightforward extension of a coevolving model incorporating group interactions is adaptive dynamics on higher-order networks such as simplicial complexes (Horstmeyer and Kuehn, 2020) and hypergraphs (Papanikolaou et al., 2022; Golovin et al., 2023). There are still more topics that need further research with the CNVM including multi-opinion versions (Shi et al., 2013), dynamics in directed links (Zschaler et al., 2012), and aging effects (Peralta et al., 2020), to name a few. From a broader perspective, the CNVM is a specific realization of coevolutionary dynamics with group interactions. The general effects of group interactions on coevolutionary dynamics, if any, still remain an open question. The CNVM offers a valuable framework for understanding coevolutionary dynamics, the research of group interactions combining coevolutionary dynamics presents vast opportunities for further exploration and refinement.

Author contributions

BM: Conceptualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2020R1I1A3068803).

Acknowledgments

We thank J. Choi and M. San Miguel for helpful discussion.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abrams, D. M., and Strogatz, S. H. (2003). Linguistics: modelling the dynamics of language death. Nature 424, 900. doi:10.1038/424900a

PubMed Abstract | CrossRef Full Text | Google Scholar

Achterberg, M. A., Dubbeldam, J. L. A., Stam, C. J., and Van Mieghem, P. (2020). Classification of link-breaking and link-creation updating rules in susceptible-infected-susceptible epidemics on adaptive networks. Phys. Rev. E 101, 052302. doi:10.1103/physreve.101.052302

PubMed Abstract | CrossRef Full Text | Google Scholar

Alvarez-Rodriguez, U., Battiston, F., de Arruda, G. F., Moreno, Y., Perc, M., and Latora, V. (2021). Evolutionary dynamics of higher-order interactions in social networks. Nat. Hum. Behav. 5, 586–595. doi:10.1038/s41562-020-01024-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Battiston, F., Amico, E., Barrat, A., Bianconi, G., Ferraz de Arruda, G., Franceschiello, B., et al. (2021). The physics of higher-order interactions in complex systems. Nat. Phys. 17 (10), 1093–1098. doi:10.1038/s41567-021-01371-4

CrossRef Full Text | Google Scholar

Battiston, F., Cencetti, G., Iacopini, I., Latora, V., Lucas, M., Patania, A., et al. (2020). Networks beyond pairwise interactions: structure and dynamics. Phys. Rep. 874, 1–92. doi:10.1016/j.physrep.2020.05.004

CrossRef Full Text | Google Scholar

Bianconi, G., Arenas, A., Biamonte, J., Carr, L. D., Kahng, B., Kertesz, J., et al. (2023). Complex systems in the spotlight: next steps after the 2021 Nobel Prize in Physics. J. Phys. Complex. 4, 010201. doi:10.1088/2632-072x/ac7f75

CrossRef Full Text | Google Scholar

Biely, C., Hanel, R., and Thurner, S. (2009). Socio-economical dynamics as a solvable spin system on co-evolving networks. Eur. Phys. J. B 67, 285–289. doi:10.1140/epjb/e2008-00390-7

CrossRef Full Text | Google Scholar

Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., and Hwang, D.-U. (2006). Complex networks: structure and dynamics. Phys. Rep. 424, 175–308. doi:10.1016/j.physrep.2005.10.009

CrossRef Full Text | Google Scholar

Cai, W., Chen, L., Ghanbarnejad, F., and Grassberger, P. (2015). Avalanche outbreaks emerging in cooperative contagions. Nat. Phys. 11, 936–940. doi:10.1038/nphys3457

CrossRef Full Text | Google Scholar

carro, A., Toral, R., and Miguel, M. S. (2016). Coupled dynamics of node and link states in complex networks: a model for language competition. New J. Phys. 18, 113056. doi:10.1088/1367-2630/18/11/113056

CrossRef Full Text | Google Scholar

Carro, A., Vazquez, F., Toral, R., and San Miguel, M. (2014). Fragmentation transition in a coevolving network with link-state dynamics. Phys. Rev. E 89, 062802. doi:10.1103/physreve.89.062802

PubMed Abstract | CrossRef Full Text | Google Scholar

Castellano, C., Muñoz, M. A., and Pastor-Satorras, R. (2009). Nonlinear q-voter model. Phys. Rev. E 80, 041129. doi:10.1103/physreve.80.041129

CrossRef Full Text | Google Scholar

Centola, D. (2010). The spread of behavior in an online social network experiment. Science 329, 1194–1197. doi:10.1126/science.1185231

PubMed Abstract | CrossRef Full Text | Google Scholar

Centola, D. (2018). How behavior spreads: the science of complex contagions how behavior spreads: the science of complex contagions. Princeton, New Jersey: Princeton University Press.

Google Scholar

Centola, D., Gonzalez-Avella, J. C., Eguíluz, V. M., and San Miguel, M. (2007). Homophily, cultural drift and the co-evolution of cultural groups. J. Confl. Resolut. 51, 905–929. doi:10.1177/0022002707307632

CrossRef Full Text | Google Scholar

Centola, D., and Macy, M. (2007). Complex contagions and the weakness of long ties. Am. J. Sociol. 113, 702–734. doi:10.1086/521848

CrossRef Full Text | Google Scholar

Chen, L., Ghanbarnejad, F., Cai, W., and Grassberger, P. (2013). Outbreaks of coinfections: the critical role of cooperativity. EPL Europhys. Lett.) 104 (5), 50001. doi:10.1209/0295-5075/104/50001

CrossRef Full Text | Google Scholar

Choi, J., and Min, B. (2023). Coevolutionary dynamics of information spreading and link rewiring. New Phys. Sae Mulli. doi:10.3938/npsm.73.886

CrossRef Full Text | Google Scholar

Demirel, G., Vazquez, F., Böhme, G., and Gross, T. (2014). Moment-closure approximations for discrete adaptive networks. Phys. D. Nonlinear Phenom. 267, 68–80. doi:10.1016/j.physd.2013.07.003

CrossRef Full Text | Google Scholar

Diakonova, M., Eguíluz, V. M., and San Miguel, M. (2015). Noise in coevolving networks. Phys. Rev. E 92, 032803. doi:10.1103/physreve.92.032803

PubMed Abstract | CrossRef Full Text | Google Scholar

Diakonova, M., San Miguel, M., and Eguíluz, V. M. (2014). Absorbing and shattered fragmentation transitions in multilayer coevolution. Phys. Rev. E 89, 062818. doi:10.1103/physreve.89.062818

PubMed Abstract | CrossRef Full Text | Google Scholar

Dorogovtsev, S. N., and Mendes, J. F. F. (2002). Evolution of networks. Adv. Phys. 51, 1079–1187. doi:10.1080/00018730110112519

CrossRef Full Text | Google Scholar

Drossel, B., Higgs, P. G., and McKane, A. J. (2001). The influence of predator–prey population dynamics on the long-term evolution of food web structure. J. Theor. Biol. 208, 91–107. doi:10.1006/jtbi.2000.2203

PubMed Abstract | CrossRef Full Text | Google Scholar

Durrett, R., Gleeson, J. P., Lloyd, A. L., Mucha, P. J., Shi, F., Sivakoff, D., et al. (2012). Graph fission in an evolving voter model. Proc. Natl. Acad. Sci. U. S. A. 109, 3682–3687. doi:10.1073/pnas.1200709109

PubMed Abstract | CrossRef Full Text | Google Scholar

Ebel, H., and Bornholdt, S. (2002). Coevolutionary games on networks. Phys. Rev. E 66, 056118. doi:10.1103/physreve.66.056118

PubMed Abstract | CrossRef Full Text | Google Scholar

Eguíluz, V. M., Zimmermann, M. G., Cela-Conde, C. J., and Miguel, M. (2005). Cooperation and the emergence of role differentiation in the dynamics of social networks. Am. J. Sociol. 110 (4), 977–1008. doi:10.1086/428716

CrossRef Full Text | Google Scholar

Fialkowski, J., Yanchuk, S., Sokolov, I. M., Schöll, E., Gottwald, G. A., and Berner, R. (2023). Heterogeneous nucleation in finite-size adaptive dynamical networks. Phys. Rev. Lett. 130, 067402. doi:10.1103/physrevlett.130.067402

PubMed Abstract | CrossRef Full Text | Google Scholar

Golovin, A., Mölter, J., and Kuehn, C. (2023). Polyadic opinion formation: the adaptive voter model on a hypergraph. Available at: https://arxiv.org/pdf/2308.03640.pdf.

Google Scholar

González Casado, M. A., Sánchez, A., and San Miguel, M. (2023). Network coevolution drives segregation and enhances Pareto optimal equilibrium selection in coordination games. Sci. Rep. 13 (1), 2866. doi:10.1038/s41598-023-30011-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Granovetter, M. (1978). Threshold models of collective behavior. Am. J. Sociol. 83, 1420–1443. doi:10.1086/226707

CrossRef Full Text | Google Scholar

Gross, T., and Blasius, B. (2008). Adaptive coevolutionary networks: a review. J. R. Soc. Interface 5 (20), 259–271. doi:10.1098/rsif.2007.1229

PubMed Abstract | CrossRef Full Text | Google Scholar

Gross, T., D’Lima, C. J. D., and Blasius, B. (2006). Epidemic dynamics on an adaptive network. Phys. Rev. Lett. 96 (20), 208701. doi:10.1103/physrevlett.96.208701

PubMed Abstract | CrossRef Full Text | Google Scholar

Gross, T., and Sayama, H. (2009). Adaptive networks: theory, models and applications. Berlin, Germany: Springer.

Google Scholar

Hébert-Dufresne, L., Scarpino, S. V., and Young, J.-G. (2020). Macroscopic patterns of interacting contagions are indistinguishable from social reinforcement. Nat. Phys. 16, 426–431. doi:10.1038/s41567-020-0791-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Holme, P., and Newman, M. E. J. (2006). Nonequilibrium phase transition in the coevolution of networks and opinions. Phys. Rev. E 74, 056108. doi:10.1103/physreve.74.056108

PubMed Abstract | CrossRef Full Text | Google Scholar

Holme, P., and Saramäki, J. (2012). Temporal networks. Phys. Rep. 519, 97–125. doi:10.1016/j.physrep.2012.03.001

CrossRef Full Text | Google Scholar

Horstmeyer, L., and Kuehn, C. (2020). Adaptive voter model on simplicial complexes. Phys. Rev. E 101, 022305. doi:10.1103/physreve.101.022305

PubMed Abstract | CrossRef Full Text | Google Scholar

Jędrzejewski, A. (2017). Pair approximation for the q-voter model with independence on complex networks. Phys. Rev. E 95, 012307. doi:10.1103/physreve.95.012307

PubMed Abstract | CrossRef Full Text | Google Scholar

Jędrzejewski, A., Toruniewska, J., Suchecki, K., Zaikin, O., and Hołyst, J. A. (2020). Spontaneous symmetry breaking of active phase in coevolving nonlinear voter model. Phys. Rev. E 102, 042313. doi:10.1103/physreve.102.042313

PubMed Abstract | CrossRef Full Text | Google Scholar

Kimura, D., and Hayakawa, Y. (2008). Coevolutionary networks with homophily and heterophily. Phys. Rev. E 78, 016103. doi:10.1103/physreve.78.016103

PubMed Abstract | CrossRef Full Text | Google Scholar

Kivelä, M., Arenas, A., Barthelemy, M., Gleeson, J. P., Moreno, Y., and Porter, M. A. (2014). Multilayer networks. J. Complex Netw. 2 (3), 203–271. doi:10.1093/comnet/cnu016

CrossRef Full Text | Google Scholar

Klimek, P., Diakonova, M., Eguíluz, V. M., San Miguel, M., and Thurner, S. (2016). Dynamical origins of the community structure of an online multi-layer society. New J. Phys. 18, 083045. doi:10.1088/1367-2630/18/8/083045

CrossRef Full Text | Google Scholar

Klimek, P., and Thurner, S. (2013). Triadic closure dynamics drives scaling laws in social multiplex networks. New J. Phys. 15, 063008. doi:10.1088/1367-2630/15/6/063008

CrossRef Full Text | Google Scholar

Kook, J., Choi, J., and Min, B. (2021). Double transitions and hysteresis in heterogeneous contagion processes. Phys. Rev. E 104, 044306. doi:10.1103/physreve.104.044306

PubMed Abstract | CrossRef Full Text | Google Scholar

Korbel, J., Lindner, S. D., Pham, T. M., Hanel, R., and Thurner, S. (2023). Homophily-based social group formation in a spin glass self-assembly framework. Phys. Rev. Lett. 130, 057401. doi:10.1103/physrevlett.130.057401

PubMed Abstract | CrossRef Full Text | Google Scholar

Kureh, Y. H., and Porter, M. A. (2020). Fitting in and breaking up: a nonlinear version of coevolving voter models. Phys. Rev. E 101, 062303. doi:10.1103/physreve.101.062303

PubMed Abstract | CrossRef Full Text | Google Scholar

Lambiotte, R., and González-Avella, J. C. (2011). On co-evolution and the importance of initial conditions. Phys. A Stat. Mech. its Appl. 390 (2), 392–397. doi:10.1016/j.physa.2010.09.024

CrossRef Full Text | Google Scholar

Lee, D., Goh, K.-I., Kahng, B., and Kim, D. (2010). Complete trails of coauthorship network evolution. Phys. Rev. E 82, 026112. doi:10.1103/physreve.82.026112

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, K.-M., Lee, S., Min, B., and Goh, K.-I. (2023). Threshold cascade dynamics on signed random networks. Chaos, Solit. Fractals 168, 113118. doi:10.1016/j.chaos.2023.113118

CrossRef Full Text | Google Scholar

Lee, K.-M., Min, B., and Goh, K.-I. (2015). Towards real-world complexity: an introduction to multiplex networks. Eur. Phys. J. B 88, 48. doi:10.1140/epjb/e2015-50742-1

CrossRef Full Text | Google Scholar

Levine, J. M., Bascompte, J., Adler, P. B., and Allesina, S. (2017). Beyond pairwise mechanisms of species coexistence in complex communities. Nature 546, 56–64. doi:10.1038/nature22898

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, J., Huang, S., Aden, N. M., Johnson, N. F., and Song, C. (2023). Emergence of polarization in coevolving networks. Phys. Rev. Lett. 130, 037401. doi:10.1103/physrevlett.130.037401

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, M., and Bassler, K. E. (2006). Emergent criticality from co-evolution in random Boolean networks. Phys. Rev. E 74, 041910. doi:10.1103/physreve.74.041910

PubMed Abstract | CrossRef Full Text | Google Scholar

Majhi, S., Perc, M., and Ghosh, D. (2022). Dynamics on higher-order networks: a review. J. R. Soc. Interface 19 (188), 20220043. doi:10.1098/rsif.2022.0043

PubMed Abstract | CrossRef Full Text | Google Scholar

Malik, N., Shi, F., Lee, H.-W., and Mucha, P. J. (2016). Transitivity reinforcement in the coevolving voter model. Chaos (Woodbury, N.Y.) 26, 123112. doi:10.1063/1.4972116

PubMed Abstract | CrossRef Full Text | Google Scholar

Mandrá, S., Fortunato, S., and Castellano, C. (2009). Coevolution of glauber-like ising dynamics and topology. Phys. Rev. E 80, 056105. doi:10.1103/physreve.80.056105

CrossRef Full Text | Google Scholar

Marceau, V., Noël, P.-A., Hébert-Dufresne, L., Allard, A., and Dubé, L. J. (2010). Adaptive networks: coevolution of disease and topology. Phys. Rev. E 82, 036116. doi:10.1103/physreve.82.036116

PubMed Abstract | CrossRef Full Text | Google Scholar

Min, B., and Castellano, C. (2020). Message-passing theory for cooperative epidemics. Chaos (Woodbury, N.Y.) 30, 023131. doi:10.1063/1.5140813

PubMed Abstract | CrossRef Full Text | Google Scholar

Min, B., and Goh, K.-I. (2014). Multiple resource demands and viability in multiplex networks. Phys. Rev. E 89, 040802. doi:10.1103/physreve.89.040802

PubMed Abstract | CrossRef Full Text | Google Scholar

Min, B., and Miguel, M. S. (2017). Fragmentation transitions in a coevolving nonlinear voter model. Sci. Rep. 7, 12864. doi:10.1038/s41598-017-13047-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Min, B., and Miguel, M. S. (2019). Multilayer coevolution dynamics of the nonlinear voter model. New J. Phys. 21, 035004. doi:10.1088/1367-2630/ab0985

CrossRef Full Text | Google Scholar

Min, B., and San Miguel, M. (2018a). Competing contagion processes: complex contagion triggered by simple contagion. Sci. Rep. 8 (1), 10422. doi:10.1038/s41598-018-28615-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Min, B., and San Miguel, M. (2018b). Competition and dual users in complex contagion processes. Sci. Rep. 8 (1), 14580. doi:10.1038/s41598-018-32643-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Min, B., and San Miguel, M. (2023). Threshold cascade dynamics in coevolving networks. Entropy 25, 929. doi:10.3390/e25060929

PubMed Abstract | CrossRef Full Text | Google Scholar

Min, B., Yi, S.-D., Lee, K.-M., and Goh, K.-I. (2014). Network robustness of multiplex networks with interlayer degree correlations. Phys. Rev. E 89, 042811. doi:10.1103/physreve.89.042811

PubMed Abstract | CrossRef Full Text | Google Scholar

Mobilia, M. (2015). Nonlinear q-voter model with inflexible zealots. Phys. Rev. E 92, 012803. doi:10.1103/physreve.92.012803

PubMed Abstract | CrossRef Full Text | Google Scholar

Monsted, B., Sapieżyński, P., Ferrara, E., and Lehmann, S. (2017). Evidence of complex contagion of information in social media: an experiment using Twitter bots. PLos ONE 12, e0184148. doi:10.1371/journal.pone.0184148

PubMed Abstract | CrossRef Full Text | Google Scholar

Nardini, C., Kozma, B., and Barrat, A. (2008). Who’s taking first? consensus or lack thereof in coevolving opinion formation models. Phys. Rev. Lett. 100, 158701. doi:10.1103/physrevlett.100.158701

PubMed Abstract | CrossRef Full Text | Google Scholar

Nettle, D. (1999). Using social impact theory to simulate language change. Lingua 108, 95–117. doi:10.1016/s0024-3841(98)00046-1

CrossRef Full Text | Google Scholar

Newman, M. E. J. (2018). Networks. Oxford, England: Oxford University Press.

Google Scholar

Newman, M. E. J., and Park, J. (2003). Why social networks are different from other types of networks. Phys. Rev. E 68, 036122. doi:10.1103/physreve.68.036122

PubMed Abstract | CrossRef Full Text | Google Scholar

Nowak, A., Szamrej, J., and Latané, B. (1990). From private attitude to public opinion: a dynamic theory of social impact. Psychol. Rev. 97, 362–376. doi:10.1037/0033-295x.97.3.362

CrossRef Full Text | Google Scholar

Nyczka, P., Sznajd-Weron, K., and Cisło, J. (2012). Phase transitions in the q-voter model with two types of stochastic driving. Phys. Rev. E 86, 011105. doi:10.1103/physreve.86.011105

PubMed Abstract | CrossRef Full Text | Google Scholar

Papanikolaou, N., Vaccario, G., Hormann, E., Lambiotte, R., and Schweitzer, F. (2022). Consensus from group interactions: an adaptive voter model on hypergraphs. Phys. Rev. E 105, 054307. doi:10.1103/physreve.105.054307

PubMed Abstract | CrossRef Full Text | Google Scholar

Peralta, A. F., Carro, A., San Miguel, M., and Toral, R. (2018). Analytical and numerical study of the non-linear noisy voter model on complex networks. Chaos (Woodbury, N.Y.) 28, 075516. doi:10.1063/1.5030112

PubMed Abstract | CrossRef Full Text | Google Scholar

Peralta, A. F., Khalil, N., and Toral, R. (2020). Ordering dynamics in the voter model with aging. Phys. A Stat. Mech. its Appl. 552, 122475. doi:10.1016/j.physa.2019.122475

CrossRef Full Text | Google Scholar

Perc, M., Gómez-Gardeñes, J., Szolnoki, A., Floría, L. M., and Moreno, Y. (2013). Evolutionary dynamics of group interactions on structured populations: a review. J. R. Soc. Interface 10 (80), 20120997. doi:10.1098/rsif.2012.0997

PubMed Abstract | CrossRef Full Text | Google Scholar

Raducha, T., Min, B., and San Miguel, M. (2018b). Coevolving nonlinear voter model with triadic closure. EPL Europhys. Lett.) 124, 30001. doi:10.1209/0295-5075/124/30001

CrossRef Full Text | Google Scholar

Raducha, T., and San Miguel, M. (2020). Emergence of complex structures from nonlinear interactions and noise in coevolving networks. Sci. Rep. 10, 15660. doi:10.1038/s41598-020-72662-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Raducha, T., Wilinski, M., Gubiec, T., and Stanley, H. E. (2018a). Statistical mechanics of a coevolving spin system. Phys. Rev. E 98, 030301. doi:10.1103/physreve.98.030301

CrossRef Full Text | Google Scholar

Saeedian, M., Azimi-Tafreshi, N., Jafari, G., and Kertesz, J. (2017). Epidemic spreading on evolving signed networks. Phys. Rev. E 95, 022314. doi:10.1103/physreve.95.022314

PubMed Abstract | CrossRef Full Text | Google Scholar

Saeedian, M., San Miguel, M., and Toral, R. (2019). Absorbing phase transition in the coupled dynamics of node and link states in random networks. Sci. Rep. 9, 9726. doi:10.1038/s41598-019-45937-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Scarpino, S. V., Allard, A., and Hébert-Dufresne, L. (2016). The effect of a prudent adaptive behaviour on disease transmission. Nat. Phys. 12, 1042–1046. doi:10.1038/nphys3832

CrossRef Full Text | Google Scholar

Schelling, T. (1973). Hockey helmets, concealed weapons, and daylight saving: a study of binary choices with externalities. J. Confl. Resolut. 17, 381–428. doi:10.1177/002200277301700302

CrossRef Full Text | Google Scholar

Schweitzer, F., and Behera, L. (2009). Nonlinear voter models: the transition from invasion to coexistence. Eur. Phys. J. B 67, 301–318. doi:10.1140/epjb/e2009-00001-3

CrossRef Full Text | Google Scholar

Shaw, L. B., and Schwartz, I. B. (2008). Fluctuating epidemics on adaptive networks. Phys. Rev. E 77, 066101. doi:10.1103/physreve.77.066101

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, F., Mucha, P. J., and Durrett, R. (2013). Multiopinion coevolving voter model with infinitely many phase transitions. Phys. Rev. E 88, 062818. doi:10.1103/physreve.88.062818

PubMed Abstract | CrossRef Full Text | Google Scholar

Vazquez, F., Eguíluz, V. M., and Miguel, M. S. (2008). Generic absorbing transition in coevolution dynamics. Phys. Rev. Lett. 100, 108702. doi:10.1103/physrevlett.100.108702

PubMed Abstract | CrossRef Full Text | Google Scholar

Vazquez, F., Gonzalez-Avella, J. C., Eguíluz, V. M., and San Miguel, M. (2007). Time scale competition leading to fragmentation and recombination transitions in the co-evolution of network and states. Phys. Rev. E 76, 046120. doi:10.1103/physreve.76.046120

PubMed Abstract | CrossRef Full Text | Google Scholar

Watts, D. J. (2002). A simple model of global cascades on random networks. Proc. Natl. Acad. Sci. U. S. A. 99, 5766–5771. doi:10.1073/pnas.082090499

PubMed Abstract | CrossRef Full Text | Google Scholar

Yi, S. D., Baek, S. K., Zhu, C.-P., and Kim, B. J. (2013). Phase transition in a coevolving network of conformist and contrarian voters. Phys. Rev. E 87, 012806. doi:10.1103/physreve.87.012806

PubMed Abstract | CrossRef Full Text | Google Scholar

Zimmermann, M. G., Eguíluz, V. M., and San Miguel, M. (2001). “Lecture notes in economics and mathematical systems,” in Economics with heterogeneous interacting agents. Editors A. Kirman, and J. B. Zimmerman (Berlin, Germany: Springer Verlag).

Google Scholar

Zimmermann, M. G., Eguíluz, V. M., and San Miguel, M. (2004). Coevolution of dynamical states and interactions in dynamic networks. Phys. Rev. E 69, 065102. doi:10.1103/physreve.69.065102

PubMed Abstract | CrossRef Full Text | Google Scholar

Zschaler, G., Böhme, G., Seißinger, M., Huepe, C., and Gross, T. (2012). Early fragmentation in the adaptive voter model on directed networks. Phys. Rev. E 85 (4), 046107. doi:10.1103/physreve.85.046107

PubMed Abstract | CrossRef Full Text | Google Scholar