When may a system be referred to as complex?—an entropic perspective

Defining complexity is hard and far from unique—like defining beauty, intelligence, creativity, and many other such abstract concepts. In contrast, describing concrete complex systems is a sensibly simpler task. We focus here on such an issue from the perspective of entropic functionals, either additive or nonadditive. Indeed, for the systems currently referred to as simple, the statistical mechanics and associated (additive) entropy is that of Boltzmann–Gibbs, formulated 150 years ago. This formalism constitutes a pillar of contemporary theoretical physics and is typically grounded on strong chaos, mixing, ergodicity, and similar hypotheses, which typically emerge for systems with short-range space–time generic correlations. It fails, however, for the so-called complex systems, where generic long-range space–time correlations prevail, typically grounded on weak chaos. Many such nontrivial systems are satisfactorily handled within a generalization of the Boltzmann–Gibbs theory, namely, nonextensive statistical mechanics, introduced in 1988 and grounded on nonadditive entropies. Illustrations are presented in terms of D-dimensional simplexes such as nodes (D = 0), bonds (D = 1), plaquettes (D = 2), polyhedra (D = 3, …), and higher-order ones. A regularly updated bibliography is available at http://tsallis.cat.cbpf.br/biblio.htm.

1 Introduction

Complexity has to do with systems whose constitutive elements are probabilistically intricate at different space–time scales. These elements are typically—but not necessarily—in great numbers and are correlated in many ways, for example, neural or metabolic networks in living matter, the smoke of a cigarette, the evolution of a galaxy or other astrophysical objects, solar wind, high-energy particle collisions, the connections within and between stock exchanges, ecosystems, psycho-social phenomena, evolutionary linguistics, high-level artificial intelligence and language model algorithms, conservative and dissipative nonlinear dynamical systems, quantum entanglement, Earth’s climate system, granular matter, seismic and rock fracture phenomena, anomalous chemical reactions, urban epidemiological spreads, and medical and non-medical image and signal processing; the list is endless. The perspectives along which such strongly intertwined systems can be analyzed and classified can by no means be unique (Thurner, 2017). Still, the physical formalism of statistical mechanics emerges as a privileged one for such a task. The main pillars of contemporary theoretical physics are Newtonian (also referred to as classical) mechanics, Einstein’s theory of special and general relativity, quantum mechanics, Maxwell electromagnetism, and Boltzmann–Gibbs (BG) statistical mechanics. The latter is essentially based on the former ones and on the mathematical theory of probabilities. Each of these theories has, as all human intellectual constructions, a restricted domain of validity. For instance, Newtonian mechanics is valid for masses that are neither too small (like that of an electron) nor too large (like that of a typical galaxy) and are moving with velocities that are negligible with regard to c, the speed of light in vacuum. The basic principle of special relativity is applicable for arbitrary velocities, but not for arbitrarily small or large masses. The basic principle of quantum mechanics (specifically, the Schrodinger equation) is valid for masses as small as that of an electron, but for velocities that are negligible with respect to that of light. These various issues, in particular the domains of validity of these first-principle theories, are intimately related to the values of the four contemporary universal constants: speed of light c, Planck’s constant h, Newton’s gravitation constant G, and Boltzmann’s constant k_B (Duff, 2014; Section 3.8 of Tsallis, 2023a); we remind that the electron charge e is determined by the previous ones through a pure number (hyperfine coupling constant).

The BG statistical mechanics is based, as already mentioned, on the theories intimately related to (c, h, G). In addition to that, it assumes hypotheses such as positive maximal Lyapunov exponent, and hence mixing and ergodicity, for the dynamics involving the elements of the system. More generically speaking, it assumes that the space–time correlations that are present in the system are basically local¹. This strong requirement is hidden in the choice of the entropic functional S_BG upon which BG statistical mechanics is grounded:

$S_{BG}=-k{\displaystyle \sum _{i=1}^W}{p}_i\ln p_i\left({\displaystyle \sum _{i=1}^W}{p}_i=1\right),(1)$

where k is a positive constant (in physics, k = k_B; in computational sciences, k = 1) and W is the total number of accessible microscopic possibilities of the system. The BG entropy is currently referred to as von Neumann entropy for quantum systems and Shannon entropy in computational sciences. This entropic functional satisfies a very important property, namely, additivity. More precisely, if A and B are two probabilistically independent systems², i.e., if $p_{i,j}^{A+B}=p_i^A{p}_j^B$, we straightforwardly verify

$S_{BG}\left(A+B\right)=S_{BG}\left(A\right)+S_{BG}\left(B\right).(2)$

The fact that this entropic additivity requirement is inadequate for those systems where space and/or time correlations are nonlocal is by no means obvious, but it gradually becomes obvious when generic classes of complex systems are successively focused on, and the need for violating Eq. 2 softly, though undoubtedly, emerges.

For nonlocally correlated systems, nonadditive entropic functionals (differing therefore from S_BG) must be used in order to have an entropy which is extensive (i.e., proportional to the number of particles N when N ≫ 1), as mandated by the Legendre transform structure of thermodynamics (see Tsallis and Cirto, 2013, and references therein). The appropriate nonadditive entropic functional depends on the specific class of nonlocal correlations of the system. For a vast class of nonlocally correlated systems, we have the following nonadditive entropic functional (Tsallis and Cirto, 2013):

$S_{q,\delta }=k{\displaystyle \sum _{i=1}^W}{p}_i{\ln }_{q,\delta }\frac{1}{p_i},(3)$

where

${\ln }_{q,\delta }z\equiv {\left(\frac{z^{1-q}-1}{1-q}\right)}^{\delta }\left(z>0;{\ln }_{1,\delta }z={\left(\ln z\right)}^{\delta };q\in \mathbb{R};\delta >0\right),(4)$

its inverse function being given by the q-stretched exponential

$e_{q,\delta }^z\equiv {\left[1+\left(1-q\right)z^{1/\delta }\right]}_{+}^{\frac{1}{1-q}},(5)$

with [(…)]₊ = (…) if (…) > 0 and zero otherwise.

The entropy (3) recovers as in particular cases such as the following ones:

$S_q\equiv S_{q,1}=k{\displaystyle \sum _{i=1}^W}{p}_i{\ln }_q\frac{1}{p_i},(6)$

$S_{\delta }\equiv S_{1,\delta }=k{\displaystyle \sum _{i=1}^W}{p}_i{\left[\ln \frac{1}{p_i}\right]}^{\delta },(7)$

and S_BG = S_1,1. Moreover, for equal probabilities, definition (3) yields $S_{q,\delta }=k{\ln }_{q,\delta }W=k{({\ln }_{q}W)}^{\delta }=k{\left[\frac{W{(N)}^{1-q}-1}{1-q}\right]}^{\delta }$, which is the inverse function of Eq. 5. The nonadditive entropic functionals (6) and (7) have been respectively proposed in Tsallis, (1988); Tsallis, (2009) to ground generalizations of BG statistical mechanics.

We illustrate, through a few simple cases of equal probabilities, how nonadditivity enables the entropy to be thermodynamically extensive. Let us start with the standard case, i.e., W(N) ∝ μ^N (μ > 1). This implies that S_BG(N) = k ln W(N) ∝ N, as required by the Legendre structure of thermodynamics. It happens, however, that due to nonlocal correlations, vast classes of complex systems exhibit the power-law behavior W(N) ∝ N^ρ (ρ > 0). In such a case, we straightforwardly verify that for q = 1 − 1/ρ, S_q(N) = k ln_qW(N) ∝ N, once again as required by the Legendre structure of thermodynamics. Another class of physical correlations corresponds to the stretched exponential function behavior $W(N)\propto {\nu }^{N^{\gamma }}(\nu >1;\gamma <1)$. In this case, we straightforwardly verify that for δ = 1/γ, S_δ(N) = k[ln W(N)]^δ ∝ N, once again as required by the Legendre structure of thermodynamics. Many other examples exist in the literature (Hanel and Thurner, 2011a) that prove that entropic indices such as (q, δ) make nonadditive entropies such as S_q,δ to be extensive for systems having specific classes of correlations, therefore, satisfying the basic requirement mandated by the Legendre structure of thermodynamics.

We see, therefore, that a discussion focusing on space–time correlations is a must within statistical mechanics generalizing the BG one. We now focus on this crucial issue which, from the entropic perspective, essentially defines when a system may be referred to as complex.

2 Correlations in many-body systems

$C_{\theta }\left(\vec{r},{\vec{r}}^{\prime };t,t^{\prime }\right)\equiv ⟨\theta \left(\vec{r},t\right)\theta (\overrightarrow{r^{\prime }},t^{\prime })⟩-⟨\theta \left(\vec{r},t\right)⟩⟨\theta (\overrightarrow{r^{\prime }},t^{\prime })⟩,(8)$

where $\theta (\vec{r},t)$ is a classical observable, such as an angle, linear momentum, angular momentum, or energy, at d-dimensional position $\vec{r}$ and time t. Quite frequently, but not always, such correlation functions satisfy $C_{\theta }(\vec{r},{\vec{r}}^{\prime };t,t^{\prime })=C_{\theta }(\vec{r}-{\vec{r}}^{\prime };t-t^{\prime })$ for all $(\vec{r},{\vec{r}}^{\prime },t,t^{\prime })$. We refer to local space–time correlations when dependencies of C_θ on both $(\vec{r}-{\vec{r}}^{\prime })$ and (t − t′) vanish quickly enough, i.e., exponentially quick or through cutoffs; generally speaking, by “quickly enough,” we mean that momenta of all orders are finite. We refer to nonlocal space–time correlations when dependencies of C_θ either on $(\vec{r}-{\vec{r}}^{\prime })$ or on (t − t′) vanish slowly and subexponentially, e.g., as a power law; generally speaking, by “slowly,” we mean that an infinity of momenta above some given order diverges.

The edge of chaos possibly emerging in ubiquitous nonlinear dynamical systems is a notorious particular instance of such definition. Indeed, the inverse sensitivity to the initial conditions ξ⁻¹ vanishes exponentially with time t (e.g., $\xi (t)\equiv {\lim }_{\mathrm{\Delta }x(0)\to 0}\frac{\mathrm{\Delta }x(t)}{\mathrm{\Delta }x(0)}\sim e^{\lambda t}$) when the Lyapunov exponent λ is positive (strong chaos), and subexponentially (typically as a power law, e.g., $\xi (t)\sim t^{1/(1-q_{\mathit{sensitivity}})}$ with q_sensitivity < 1) when the Lyapunov exponent vanishes (weak chaos). In fact, it is in the close vicinity of an edge of chaos (frontier between regular orbits and strong chaos) that life, languages, cities, economics, earthquakes, fractures, and neural and computational networks (to cite but a few) currently grow.

In summary, the present entropic perspective on complexity and its association to statistical mechanics are as follows:

$\begin{array}{ccc}\hfill simplesystems& \leftrightarrow \hfill & localspace-timecorrelations\hfill \\ \hfill & \leftrightarrow \hfill & Boltzmann-Gibbsadditiveentropicfunctional{S}_{BG}\hfill \\ \hfill & \leftrightarrow \hfill & Boltzmann-Gibbsstatisticalmechanics\hfill \\ \hfill & \hfill & \hfill \\ \hfill complexsystems& \leftrightarrow \hfill & nonlocalspace-timecorrelations\hfill \\ \hfill & \leftrightarrow \hfill & nonadditiveentropicfunctionals\left(e.g.,S_q,S_{\delta }\right)\hfill \\ \hfill & \leftrightarrow \hfill & generalizedstatisticalmechanics.\hfill \end{array}(9)$

Space correlations might exist between nodes (D = 0 simplexes), edges (D = 1 simplexes), nodes–edges, and higher-order simplexes; see Figure 1. An illustrative Ising-like Hamiltonian could be

$\mathbb{H}=-{\displaystyle \sum _{i=1}^N}{H}_i{S}_i-{\displaystyle \sum _{i\ne j}}{J}_{ij}{S}_i{S}_j-{\displaystyle \sum _{i,j,k}}{J}_{\mathit{ijk}}{S}_i{S}_j{S}_k-\dots ,(10)$

where {H_i} are local external fields, {J_ij} are two-body coupling constants, {J_ijk} are three-body coupling constants, and so on.

FIGURE 1

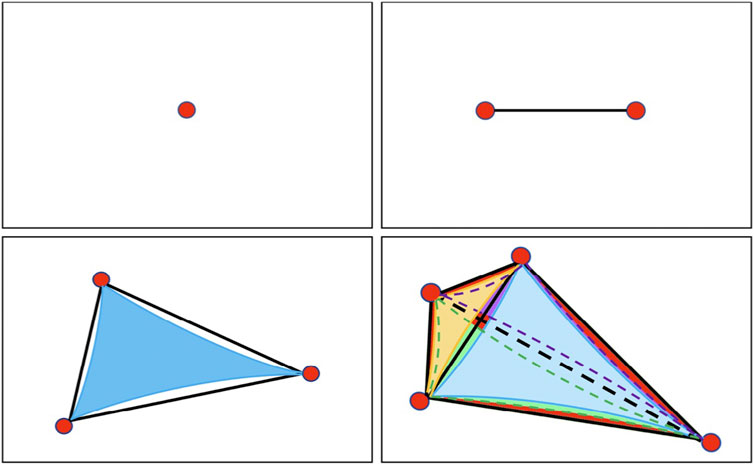
FIGURE 1. Top left: single node (site). Top right: two nodes linked by one bond (edge). Bottom left: three nodes linked by three two-body edges as well as by one three-body plaquette (blue), i.e., maximally linked. Bottom right: four nodes linked by six two-body edges as well as by four three-body plaquettes (blue, yellow, violet, and green) and by one four-body simplex (red), i.e., maximally linked.

In social systems, the relation between three people might be through two or three two-by-two links or through one (qualitatively very different) triangular simplex.

Time correlations might exist between edges, nodes, nodes–edges, and higher-order simplexes; see Figure 2.

FIGURE 2

FIGURE 2. Time correlations: t₋₁ → t₀, t₋₂ → t₋₁, and t₋₂ → t₋₁ are d = 1 simplexes; the shadowed area t₋₄, t₋₃, t₀ is a continuous version of a d = 2 simplex.

3 Illustrations

We review here some selected illustrations of the aforementioned concepts that have been analytically, experimentally, or computationally validated.

3.1 Quantum tunneling in chemical reactions

A very slow ion-molecule chemical reaction, namely, D⁻ + H₂ → H⁻ + HD, was recently shown (Wild et al., 2023) to occur based on quantum tunneling through the activation barrier. Due to quantum nonlocality, the distribution of velocities is shown to violate the Maxwellian distribution; it exhibits a q-Gaussian shape where the index q > 1 depends on the hydrogen density n, as shown in Figure 3.

FIGURE 3

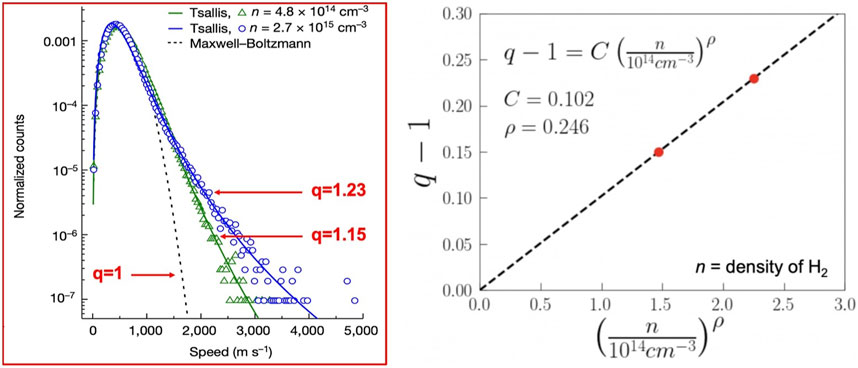
FIGURE 3. Left: distribution of velocities of the hydrogen molecules; from Wild et al. (2023). The values of q corresponding to the indicated values of the density n have been kindly communicated by Roland Wester. It should be noted that the slow-speed asymptotic behavior appears to be, as expected, one and the same for all values of q. Right: conjecture q − 1 ≃ n^1/4 from Tsallis, (2023b), which includes the value q = 1 for the ideal gas (n → 0). Further experimental data possibly validating this conjecture are welcome.

3.2 High-energy collisions of elementary particles

We focus here on the distributions of probabilities of the transverse momenta of the hadronic jets produced in proton–proton collisions at high energies in LHC/CERN experiments. The q-exponential distributions with q ≃ 1.14 satisfactorily fit the data along (experimentally impressive) fourteen ordinate decades; see Figure 4.

FIGURE 4

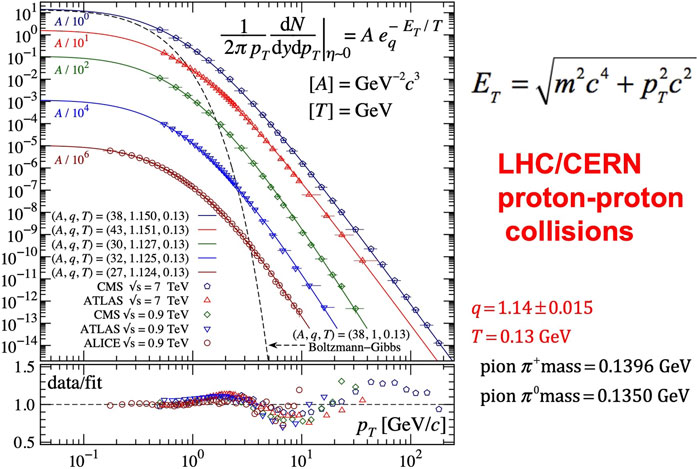
FIGURE 4. Distribution of transverse momenta in LHC/CERN experiments. It should be noted that the low-momenta distributions do not depend on q, which validates the use of Boltzmann–Gibbs statistics in this asymptotic limit. The presence of small log-periodic corrections should also be noted (see the bottom inset). From Wong et al. (2015a).

A slightly different value of q, namely, q ≃ 1.11, was advanced in Walton and Rafelski, (2000) for the motion of charm quarks within a quark–gluon plasma. Are these two slightly discrepant values for q understandable? Yes, as shown in Figure 5 from Megias et al., 2023). To understand the observation in the figure, we first need to recall an analytical result recently obtained in Deppman et al. (2020) through a QCD calculation within a Yang–Mills framework, namely,

$\frac{1}{q-1}=\frac{11}{3}{N}_c-\frac{4}{3}\frac{N_f}{2},(11)$

where N_c and N_f are, respectively, the numbers of colors and of flavors. Considering N_c = 3 and N_f = 6 (SU(6) symmetry), we get q = 8/7 ≃ 1.14, and while considering N_c = N_f = 3 (SU(3) symmetry), we get q = 10/9 ≃ 1.11.

FIGURE 5

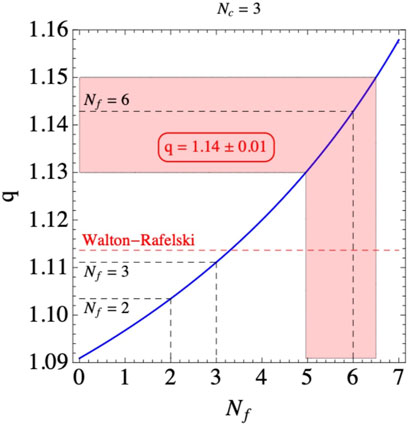
FIGURE 5. Plot of the entropic index q as a function of N_f (solid blue line), as given by Eq. 11 with N_c = 3; for N_f = 2, 3, 6, we, respectively, obtain q = 32/29 ≃ 1.10, q = 10/9 ≃ 1.11, and q = 8/7 ≃ 1.14 . The experimental LHC/CERN value (Wong et al., 2015b) is q = 1.14 ± 0.01, while the Walton–Rafelski value (Walton and Rafelski, 2000) is q = 1 + 1/8.8 ≃ 1.114 (red dashed line). We display as a shaded (red) area the region corresponding to q = 1.14 ± 0.01 and, as horizontal lines, the values of q for N_f = 2, 3, and 6.

3.3 Granular matter

A vertical, nearly two-dimensional system of inhomogeneous granular matter was filmed and measured under slow shear motion (Combe et al., 2015). The camera allowed the measuring of the positions of all particles, which in turn enabled the determination of the distribution of their horizontal fluctuations with regard to the average motion (see Figure 6), as well as the observation of the diffusive motion of the particles (⟨x²⟩∝ t^α; see Figure 7).

FIGURE 6

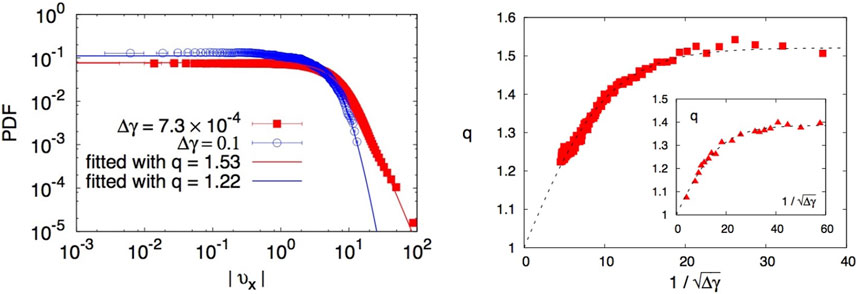
FIGURE 6. Left: q-Gaussian velocity distributions for two typical values of the experimental control parameter Δγ (shear angle increment). Right: The index q as a function of $1/\sqrt{\mathrm{\Delta }\gamma }$. The $1/\sqrt{\mathrm{\Delta }\gamma }\to 0$ extrapolation yields a Maxwellian distribution From Combe et al., (2015).

FIGURE 7

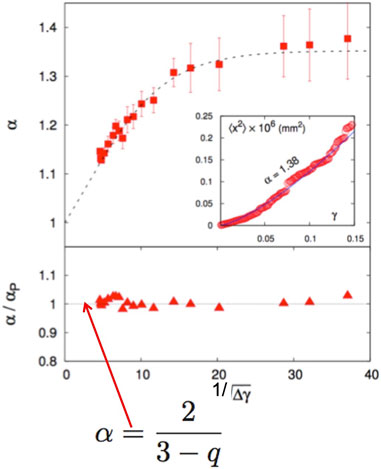
FIGURE 7. Top: The exponent α as a function of $1/\sqrt{\mathrm{\Delta }\gamma }$. The $1/\sqrt{\mathrm{\Delta }\gamma }\to 0$ extrapolation yields normal diffusion (⟨x²⟩∝ t). Bottom: validation within a 2% error of the scaling law α = 2/(3 − q) predicted in Tsallis and Bukman, (1996). From Combe et al. (2015).

3.4 Cold atoms

Lutz predicted (Lutz, 2003) that in systems such as cold atoms in dissipative optical lattices, the distribution of velocities would be q-Gaussians instead of Gaussians and that the index q would be given by

$q=1+\frac{44E_R}{U_0}>1,(12)$

where E_R and U₀ are, respectively, the recoil energy and the potential depth. The prediction was successfully verified, both experimentally and computationally, 3 years later in Douglas et al. (2006), as shown in Figure 8. This experimental validation was further confirmed in Lutz and Renzoni (2013).

FIGURE 8

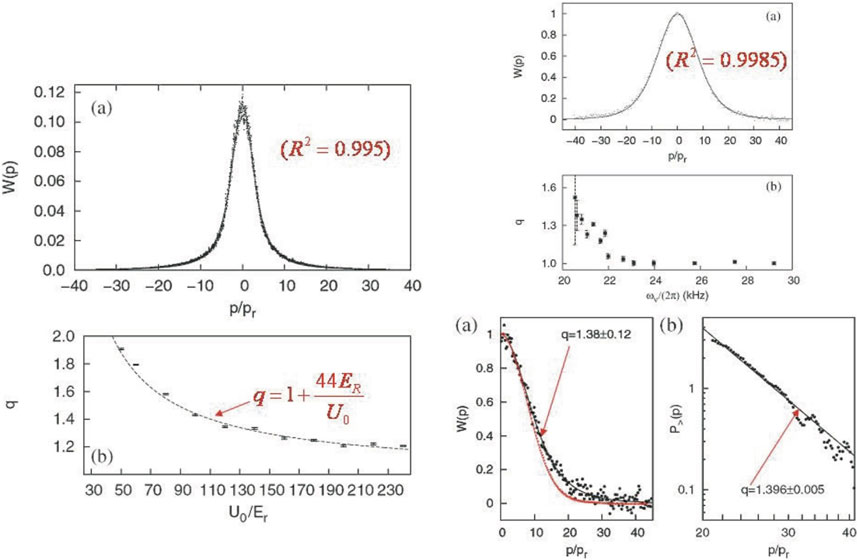
FIGURE 8. Computational validation with quantum Monte Carlo (left panels) and laboratory validation with C_s atoms (right panels) of Lutz 2003 theory. Left: Momenta distribution and dependence of q on the scaled energy. Right: Momenta distribution, frequency-dependence of q, C_s momenta distribution (linearlinear and log-log). From Douglas et al. (2006).

3.5 Second-order phase transitions

We now address an interesting connection. It is well-established in the standard theory of critical phenomena that relevant thermostatistical quantities of both classical and quantum many-body short-range-interacting systems exhibit power-law behaviors which are known to be related with long-range correlations. How are they correctly described within BG statistical mechanics? Most of such quantities exhibit zeros (e.g., the order parameter) or divergences (e.g., specific heat, susceptibility, and correlation length) when the critical point is approached (for the illustrative percolation problems, see Tsallis and Magalhaes (1996)). It is relevant to remark at this stage that, while approaching the critical point, but not at the critical point itself, the hypotheses legitimating the use of the BG theory are satisfied. For example, above T_c of the d = 3 Heisenberg ferromagnet, the collective dynamics is ergodic within the entire phase space. Analogously, below T_c, when the relevant symmetry is broken, the system is once again ergodic, this time within a nonvanishing Lebesgue measure part of the entire phase space. However, it is not so at T_c! If we want to specifically study what happens at T_c, for example, the dependence of the order parameter on the thermodynamically conjugate external field (e.g., uniform external magnetic field for the ferromagnetic–paramagnetic critical phenomenon), the BG formalism is at its limit of validity. This theory is unable to distinguish the different infinities associated with the magnetic susceptibility of the Ising, XY, and Heisenberg ferromagnets. However, the q ≠ 1 statistical mechanics (currently referred to as nonextensive statistical mechanics) can do it. An example of this point is provided in Robledo (2005) [see also Robledo, 1999; Robledo, 2007] for the exponent $\bar{\delta }$ characterizing the emergence of the ferromagnetic order parameter in the presence of a small magnetic field at precisely T_c. The analytical relation which has been proven for the associated q-exponential is as follows:

$q=\frac{1+\bar{\delta }}{2}\left(\bar{\delta }\ge 1\right),(13)$

where we used $\bar{\delta }$ instead of the traditional δ to avoid confusion with the index δ introduced in Eq. 3.

Let us now focus on the quantum critical points of (1+1)-dimensional quantum many-body systems with short-range interactions (i.e., at T_c = 0). One such example is the Ising ferromagnetic chain in the presence of an external transverse magnetic field (Caruso and Tsallis, 2008). Precisely at the T_c = 0 point, the block nonadditive entropy is extensive only for

$q=\frac{\sqrt{9+c^2}-3}{c},(14)$

where c is the quantum-field-theory central charge (the Ising and XY ferromagnetic chains in the presence of transverse magnetic field correspond to c = 1/2 and c = 1, respectively). When c increases from 0 to infinity, q increases from 0 to unity: see Figure 9. Similar results are available for the index q for other quantum systems (Saguia and Sarandy, 2010; Carrasco et al., 2016).

FIGURE 9

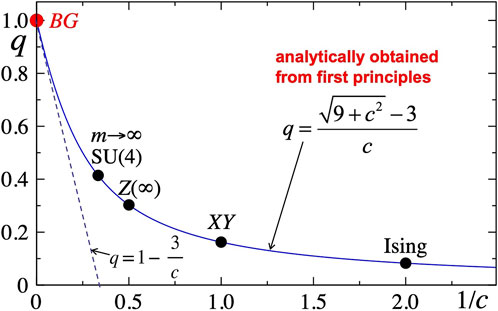
FIGURE 9. Dependence on the central charge c of the index q, which causes the block entropy S_q to be extensive (Caruso and Tsallis, 2008). The c → ∞ asymptotic behavior q ∼ 1 − 3/c is indicated as good (straight dashed line) From Caruso and Tsallis, 2008).

3.6 Asymptotically scale-free networks

The growth of the ubiquitous asymptotically scale-free networks is typically governed by q-statistics, as illustrated in several studies (Brito et al., 2016; Cinardi et al., 2020; de Oliveira et al., 2021; de Oliveira et al., 2022; Tsallis and de Oliveira, 2022; Sampaio Filho et al., 2023) and references therein. See Figure 10.

FIGURE 10

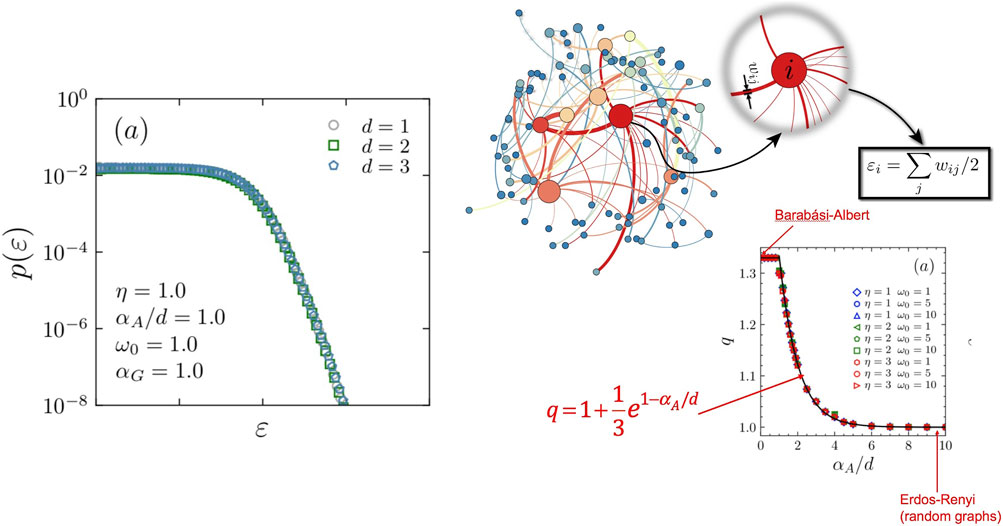
FIGURE 10. Left: the distribution of energies is given by a q-exponential. Right: Illustrative sub-graph and the corresponding index q is indicated as a function of α_A/d, where α_A characterizes the long-range interactions between the nodes of the growing d-dimensional network. The Barabasi-Albert and Erdos–Renyi models are recovered as the α_A/d → 0 and α_A/d → ∞ limits, respectively. See details in de Oliveira et al. (2021).

3.7 Long-range interactions in condensed matter classical systems

Here, we focus on classical long-range-interacting many-body Hamiltonian systems. Their total energy is nonextensive (superextensive in fact), hence the currently used name nonextensive statistical mechanics for the present generalized statistical mechanics.

The Hamiltonians of this kind that have been most studied from first principles (Newton’s law) are the α-XY, α-Heisenberg, and α-Fermi–Pasta–Ulam d-dimensional ones; see Rodriguez et al. (2023) and references therein. In all three models, we consider two-body coupling constants decaying with distance r as 1/r^α (α ≥ 0). In the first two systems, two quasi-stationary states are observed, for fixed number N of particles, as time t increases; in the third system, only one quasi-stationary state is observed. The distributions for momenta and energies are definitively non-Gibbsian, as illustrated in Figure 11 for α/d = 0.9 (d = 1, 2, 3) in the α-XY model at its second stationary state; see Cirto et al. (2018). In Figure 12, we exhibit the present numerical support for the conjecture

$\frac{q_p\left(\alpha /d\right)-1}{q_E\left(\alpha /d\right)-1}=2.(15)$

FIGURE 11

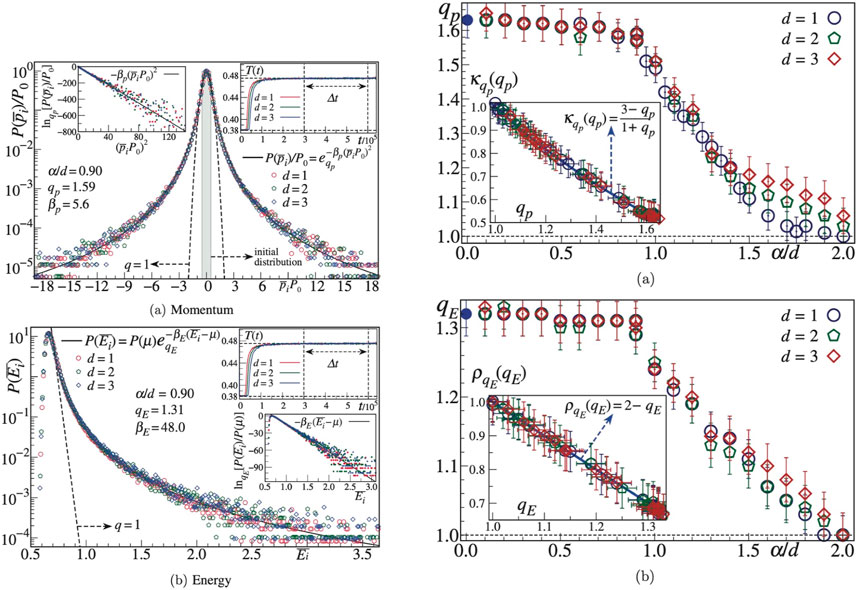
FIGURE 11. Second quasi-stationary state of the d-dimensional α-XY model. Left: distributions of one-particle momenta (top) and energies (bottom) for α/d = 0.9. Right: values of q_p (top) and q_E (bottom) as functions of α/d. See details in Cirto et al. (2018).

FIGURE 12

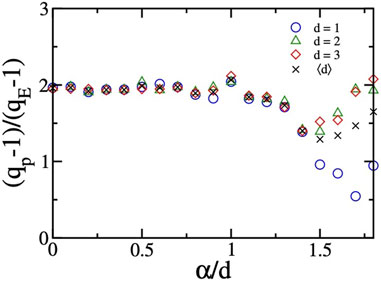
FIGURE 12. Present numerical support for the conjecture (15). From Rodriguez et al. (2023).

Moreover, some numerical indications exist for various models that [q(α/d) − 1)/(q(0) − 1] equals unity for 0 ≤ α/d ≤ 1 and decays exponentially to 0 in the α/d → ∞ limit.

Finally, we indicate in Figure 13 the role played by the limits N → ∞ and t → ∞ for the d = 1 α-Fermi–Pasta–Ulam model (Christodoulidi et al., 2014); similar nonuniform convergences are expected for other models as well.

FIGURE 13

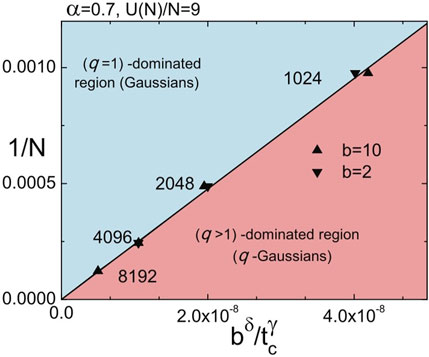
FIGURE 13. Roles played by the limits N → ∞ and t → ∞; b is the quartic coupling constant; δ > 0 and γ > 0. From Christodoulidi et al. (2014).

3.8 Astrophysics and gravitational systems

Until now, we focused on systems governed by S_q. Let us now consider some systems possibly governed by S_δ (Tsallis and Cirto, 2013; Zamora and Tsallis, 2022a; Zamora and Tsallis, 2022b).

To start with, what is the appropriate entropic functional for d = 3 black holes, and what is the corresponding temperature? The criterion that is to be used is that the requirement of the Legendre structure of thermodynamics must be met. This mandates that the entropic functional for a d = 3 black hole must be extensive. It is argued in Tsallis and Cirto (2013) that S_δ given by Eq. 7 is admissible (in contrast with S_BG), and that the appropriate index value is given by

${\delta }^{-1}=\frac{d-1}{d}=1-1/d,(16)$

and hence, δ = 3/2 for d = 3 black holes. However, Eq. 16 has been obtained under the (most probably wrong) assumption that all states are equally probable, which is but a first approximation. Such (wrong) assumption for S_q yields the asymptotic behavior q = 1 − 3/c indicated in Figure 9 instead of the correct value given in Eq. 14. Analogously, Eq. 16 might well not be the (presently unknown) exact δ(d) but only its d → ∞ asymptotic behavior. Consistently, the correct δ might not be exactly 3/2, but only close to it. Data from the IceCube Neutrino Observatory (South Pole) suggest δ = 1.565 (Jizba and Lambiase, 2022) instead of δ = 1.5. Consistently, data from the Planck Observatory/ESA suggest (Salehi et al., 2023) either δ ≡ 1 + Δ/2 = 1.87 or δ = 1.26 (whose mean value is precisely 1.565 ), depending on the approach that has been adopted to process the data (Δ denotes the index of the Barrow entropy). In summary, δ ≃ 1.5 could well be an admissible value, whereas δ = 1 (Bekenstein–Hawking entropy) is neatly out of the error bars.

4 Final remarks

Many other applications than those presented previously (e.g., conservative and dissipative low-dimensional nonlinear dynamical systems, overdamped evolution for many-body systems involving two-body repulsive interactions, engineering and computational algorithmic processes, economics, and signal and image optimizations) are available in the literature, but, for brevity, we have skipped them here. They can be seen in the study by Tsallis (2023a) and the references therein; in addition, a regularly updated bibliography is available at https://tsallis.cbpf.br/biblio.htm.

Here, we clarify some confusion that appears in the literature concerning entropic functionals and entropies. An entropic functional S is a function of a set of probabilities ({p_i} in the discrete case, and $p(\vec{x})$ in the continuous case) which satisfies some simple information-theoretical requirements. The verification of whether it is additive or not is mathematically trivial since it concerns probabilistically independent subsystems. The most general additive entropic functional known today is the Renyi one (which contains S_BG as a particular instance); all the (many) others accessible in the literature are nonadditive. Entropy is a specific entropic functional calculated for a specific class of systems, either simple or complex. The mathematical verification on whether an entropy of a system is thermodynamically extensive or not frequently turns out to be an intractable problem. For example, the so-called Barrow entropy $S_{\mathrm{\Delta }}^B$ is defined through $S_{\mathrm{\Delta }}^B\propto A^{1+\mathrm{\Delta }/2}$, where A is the standard horizon area of a black hole. It was obtained in Tsallis and Cirto (2013) that S_δ ∝ A^δ, from where comes the current connection δ ≡ 1 + Δ/2. It should, nevertheless, be clear that this connection emerges from comparison between entropies, not from comparison between entropic functionals. No Barrow entropic functional exists, whereas the entropic functional S_δ is defined in Eq. 7.

In conclusion, let us focus on an epistemologically important question, namely, that a wrong theory is not necessarily non-computable from the mathematical standpoint. A wrong theory can be mathematically calculable or not (yielding, for instance, intractable divergences). For example, collisions of high-speed particles are mathematically computable within Newtonian mechanics, but they are definitively wrong due to the well-known relativistic effects. Similarly, the (mean field-like) Landau theory for critical phenomena is mathematically elegant and perfectly computable, but it is undoubtedly wrong unless the many-body Hamiltonian system has a high enough dimension d.

Taking this into account, the multiple mean field-like calculations existing in the literature for long-range-interacting Hamiltonian systems [see, for instance, Dauxois et al. 2002; Campa et al., 2014, and references therein] by no means guarantee the applicability of BG statistical mechanics. We have illustrated in Section 3.7 that such systems, when plainly calculated from mechanical first principles, undoubtedly violate the BG distributions for energies and velocities in quasi-stationary states for thermodynamically large classical systems.

Similarly, uncountable analytical BG calculations can be found in the literature based on spin-glasses, in spite of the well-established fact that spin-glasses at realistic dimensions (say d = 2, 3) are strongly nonergodic, thus violating the basic assumption upon which BG statistical mechanics is constructed. In strong contrast, q-statistical indications emerge in experiments with real spin-glasses: see (Pickup et al., 2009). These facts do not exclude that an index such as q may approach unity (i.e., the BG theory) when a relevant dimensionality approaches infinity (see, for instance, the c → ∞ limit in Figure 9). Finally, another phenomenon which deserves deeper understanding is aging (Montemurro et al., 2003; Tamarit and Anteneodo, 2005). Its relations with ergodicity breakdown, possible violation of the fluctuation–dissipation theorem, and q-statistics remain to be further elucidated.

Scientists have made abundant mistakes of every kind; their knowledge has improved only because of their gradual abandonment of ancient errors, poor approximations, and premature conclusions. [George Sarton, 1884–1956].

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

CT: writing–original draft.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The author(s) acknowledge A. Rapisarda for inviting them to participate in the present issue, A. Pluchino for kindly helping them construct Figures 1, 2, and also CNPq and Faperj (Brazilian agencies) for partial financial support. The authors are also grateful to all authors who have kindly authorized them to use their figures.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor AR declared a past co-authorship with the author CT.

The author CT declared that they were an editorial board member of Frontiers at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹The standard theory of classical or quantum critical phenomena deserves a special analysis.

²This independence is not to be confused with the hypothesis of an ideal gas, which states that the total energy of the system equals its kinetic energy. Such an ideal system corresponds to probabilistic independence if the particles are distinguishable, and therefore follow the Maxwell–Boltzmann statistics. If they are, instead, indistinguishable, they must be either fermions or bosons, and therefore follow the Fermi–Dirac or the Bose–Einstein statistics, respectively, thus violating probabilistic independence.

References

Brito, S. G. A., da Silva, L. R., and Tsallis, C. (2016). Role of dimensionality in complex networks. Sci. Rep. 6, 27992. doi:10.1038/srep27992

PubMed Abstract | CrossRef Full Text | Google Scholar

Campa, A., Dauxois, T., Fanelli, D., and Ruffo, S. (2014). Physics of long-range interacting systems. Oxford, United Kingdom: Oxford University Press.

Google Scholar

Carrasco, J. A., Finkel, F., Gonzalez-Lopez, A., Rodriguez, M. A., and Tempesta, P. (2016). Generalized isotropic Lipkin-Meshkov-Glick models: ground state entanglement and quantum entropies. J. Stat. Mech. 2016, 033114. doi:10.1088/1742-5468/2016/03/033114

CrossRef Full Text | Google Scholar

Caruso, F., and Tsallis, C. (2008). Nonadditive entropy reconciles the area law in quantum systems with classical thermodynamics. Phys. Rev. E 78, 021102. doi:10.1103/physreve.78.021102

PubMed Abstract | CrossRef Full Text | Google Scholar

Christodoulidi, H., Tsallis, C., and Bountis, T. (2014). Fermi-Pasta-Ulam model with long-range interactions: dynamics and thermostatistics. EPL 108, 40006. doi:10.1209/0295-5075/108/40006

CrossRef Full Text | Google Scholar

Cinardi, N., Rapisarda, A., and Tsallis, C. (2020). A generalised model for asymptotically-scale-free geographical networks. J. Stat. Mech. 2020, 043404. doi:10.1088/1742-5468/ab75e6

CrossRef Full Text | Google Scholar

Cirto, L. J. L., Rodriguez, A., Nobre, F. D., and Tsallis, C. (2018). Validity and failure of the Boltzmann weight. EPL 123, 30003. doi:10.1209/0295-5075/123/30003

CrossRef Full Text | Google Scholar

Combe, G., Richefeu, V., Stasiak, M., and Atman, A. P. F. (2015). Experimental validation of a nonextensive scaling law in confined granular media. Phys. Rev. Lett. 115, 238301. doi:10.1103/physrevlett.115.238301

PubMed Abstract | CrossRef Full Text | Google Scholar

Dauxois, T., Ruffo, S., Arimondo, E., and Wilkens, M. (2002). Long range interactions. Berlin, Germany: Springer, 602.

Google Scholar

de Oliveira, R. M., Brito, S., da Silva, L. R., and Tsallis, C. (2021). Connecting complex networks to nonadditive entropies. Sci. Rep. 11, 1130. doi:10.1038/s41598-020-80939-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Deppman, A., Megias, E., and Menezes, D. P. (2020). Fractals, non-extensive statistics, and QCD. Phys. Rev. D. 101, 034019. doi:10.1103/physrevd.101.034019

CrossRef Full Text | Google Scholar

Douglas, P., Bergamini, S., and Renzoni, F. (2006). Tunable Tsallis distributions in dissipative optical lattices. Phys. Rev. Lett. 96, 110601. doi:10.1103/physrevlett.96.110601

PubMed Abstract | CrossRef Full Text | Google Scholar

Duff, M. J. (2014). How fundamental are fundamental constants? Contemp. Phys. 56, 35–47. doi:10.1080/00107514.2014.980093

CrossRef Full Text | Google Scholar

Hanel, R., and Thurner, S. (2011a). A comprehensive classification of complex statistical systems and an axiomatic derivation of their entropy and distribution functions. EPL Europhys. Lett. 93, 20006. doi:10.1209/0295-5075/93/20006

CrossRef Full Text | Google Scholar

Hanel, R., and Thurner, S. (2011b). When do generalised entropies apply? How phase space volume determines entropy. EPL Europhys. Lett. 96, 50003. doi:10.1209/0295-5075/96/50003

CrossRef Full Text | Google Scholar

Jizba, P., and Lambiase, G. (2022). Tsallis cosmology and its applications in dark matter physics with focus on IceCube high-energy neutrino data. Eur. Phys. J. C 82, 1123. doi:10.1140/epjc/s10052-022-11113-2

CrossRef Full Text | Google Scholar

Lutz, E. (2003). Anomalous diffusion and Tsallis statistics in an optical lattice. Phys. Rev. A 67, 051402. doi:10.1103/physreva.67.051402

CrossRef Full Text | Google Scholar

Lutz, E., and Renzoni, F. (2013). Beyond Boltzmann-Gibbs statistical mechanics in optical lattices. Nat. Phys. 9, 615–619. doi:10.1038/nphys2751

CrossRef Full Text | Google Scholar

Megias, E., Deppman, A., Pasechnik, R., and Tsallis, C. (2023). Comparative study of the heavy-quark dynamics with the Fokker-Planck equation and the Plastino-Plastino equation. Phys. Lett. B 845, 138136. doi:10.1016/j.physletb.2023.138136

CrossRef Full Text | Google Scholar

Montemurro, M. A., Tamarit, F., and Anteneodo, C. (2003). Aging in an infinite-range Hamiltonian system of coupled rotators. Phys. Rev. E 67, 031106. doi:10.1103/physreve.67.031106

PubMed Abstract | CrossRef Full Text | Google Scholar

Oliveira, R., Brito, S., da Silva, L. R., and Tsallis, C. (2022). Statistical mechanical approach of complex networks with weighted links. J. Stat. Mech. 2022, 063402. doi:10.1088/1742-5468/ac6f51

CrossRef Full Text | Google Scholar

Pickup, R. M., Cywinski, R., Pappas, C., Farago, B., and Fouquet, P. (2009). Generalized spin glass relaxation. Phys. Rev. Lett. 102, 097202. doi:10.1103/physrevlett.102.097202

PubMed Abstract | CrossRef Full Text | Google Scholar

Robledo *, A. (2005). Unorthodox properties of critical clusters. Mol. Phys. 103, 3025–3030. doi:10.1080/00268970500185989

CrossRef Full Text | Google Scholar

Robledo, A. (1999). Renormalization group, entropy optimization, and nonextensivity at criticality. Phys. Rev. Lett. 83, 2289–2292. doi:10.1103/physrevlett.83.2289

CrossRef Full Text | Google Scholar

Robledo, A. (2007). q-statistical properties of large critical clusters. Int. J. Mod. Phys. B 21, 3947–3953. doi:10.1142/s0217979207045001

CrossRef Full Text | Google Scholar

Rodriguez, A., Pluchino, A., Tirnakli, U., Rapisarda, A., and Tsallis, C. (2023). Nonextensive footprints in dissipative and conservative dynamical systems. Symmetry 15, 444. doi:10.3390/sym15020444

CrossRef Full Text | Google Scholar

Saguia, A., and Sarandy, M. S. (2010). Nonadditive entropy for random quantum spin-S chains. Phys. Lett. A 374, 3384–3388. doi:10.1016/j.physleta.2010.06.038

CrossRef Full Text | Google Scholar

Salehi, A., Pourali, M., and Abedini, Y. (2023). Search for neutrino masses in the Barrow holographic dark energy cosmology with Hubble horizon as IR cutoff. General Relativ. Gravit. 55, 57. doi:10.1007/s10714-023-03104-9

CrossRef Full Text | Google Scholar

Sampaio Filho, C. I. N., Bastos, M. M., Herrmann, H. J., Moreira, A. A., and Andrade, J. S. (2023). Random networks with q-exponential degree distribution. Phys. Rev. Res. 5, 033088. doi:10.1103/physrevresearch.5.033088

CrossRef Full Text | Google Scholar

Tamarit, F. A., and Anteneodo, C. (2005). Relaxation and aging in a long-range interacting system. Europhys. News 36, 194–197. doi:10.1051/epn:2005605

CrossRef Full Text | Google Scholar

Thurner, S. (2017). 43 visions for complexity. Singapore: World Scientific.

Google Scholar

Tsallis, C., and Bukman, D. J. (1996). Anomalous diffusion in the presence of external forces: exact time-dependent solutions and their thermostatistical basis. Phys. Rev. E 54, R2197–R2200. doi:10.1103/physreve.54.r2197

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsallis, C., and Cirto, L. J. L. (2013). Black hole thermodynamical entropy. Eur. Phys. J. C 73, 2487. doi:10.1140/epjc/s10052-013-2487-6

CrossRef Full Text | Google Scholar

Tsallis, C., and de Magalhaes, A. C. N. (1996). Pure and random Potts-like models: real-space renormalization-group approach. Phys. Rep. 268, 305–430. doi:10.1016/0370-1573(95)00064-x

CrossRef Full Text | Google Scholar

Tsallis, C. (2009). Introduction to nonextensive statistical mechanics - approaching a complex world. Berlin, Germany: Springer.

Google Scholar

Tsallis, C. (2023a). Introduction to nonextensive statistical mechanics - approaching a complex world. Berlin, Germany: Springer.

Google Scholar

Tsallis, C., and Oliveira, R. (2022). Complex network growth model: possible isomorphism between nonextensive statistical mechanics and random geometry. Chaos (Woodbury, N.Y.) 32, 053126. doi:10.1063/5.0090864

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsallis, C. (2023b). Online Comment on “Tunnelling measured in a very slow ion-molecule reaction”. Nature. doi:10.1038/s41586-023-05727-z

CrossRef Full Text | Google Scholar

Tsallis, C. (1988). Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 52, 479–487. doi:10.1007/bf01016429

CrossRef Full Text | Google Scholar

Walton, D. B., and Rafelski, J. (2000). Equilibrium distribution of heavy quarks in Fokker-Planck dynamics. Phys. Rev. Lett. 84, 31–34. doi:10.1103/physrevlett.84.31

PubMed Abstract | CrossRef Full Text | Google Scholar

Wild, R., Notzold, M., Simpson, M., Tran, T. D., and Wester, R. (2023). Tunnelling measured in a very slow ion-molecule reaction. Nature 615, 425–429. doi:10.1038/s41586-023-05727-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Wong, C. Y., Wilk, G., Cirto, L. J. L., and Tsallis, C. (2015b). From QCD-based hard-scattering to nonextensive statistical mechanical descriptions of transverse momentum spectra in high-energy pp and p\bar{p} collisions. Phys. Rev. D. 91, 114027. doi:10.1103/physrevd.91.114027

CrossRef Full Text | Google Scholar

Wong, C. Y., Wilk, G., Cirto, L. J. L., and Tsallis, C.: Possible implication of a single nonextensive pT distribution for hadron production in high-energy pp collisions, Proceedings of the EPJ Web of Conferences, Bologna, Italy (September 2015a): 04002

Google Scholar

Zamora, D. J., and Tsallis, C. (2022b). Thermodynamically consistent entropic late-time cosmological acceleration. Eur. Phys. J. C 82, 689. doi:10.1140/epjc/s10052-022-10645-x

CrossRef Full Text | Google Scholar

Zamora, D. J., and Tsallis, C. (2022a). Thermodynamically consistent entropic-force cosmology. Phys. Lett. B 827, 136967. doi:10.1016/j.physletb.2022.136967

CrossRef Full Text | Google Scholar