Crisis spreading in multinational firms’ network: the dual influence of local interactions

This study investigates the characteristics of multinational firm’s interactions within and across activity sectors and the impact of intra-urban connections, during crisis propagation. By employing data that reflect ownership relations aggregated on the city level, we constructed the partial-multiplex, directed network of cities, divided into five layers by activity sector. The network was examined in two states: one excluding intra-urban interactions and one including them. The difference between these two states highlight the significant role of intra-urban networking processes in the global economy. The five layers differ both structurally and in terms of vulnerability during crisis propagation. The Knowledge Intensive Services (KIS) layer is the densest and most populous layer of all and its firms are more likely to be owners than subsidiaries. Using a simple stochastic Susceptible-Infected-Recovered (SIR) model, we simulated a crisis diffusion on the network of cities. Our results revealed that in the absence of intra-urban connections, KIS was both the most vulnerable and most influential layer in crisis propagation. The inclusion of intra-urban links sets off a complex interplay of factors that affect diffusion outcomes in nuanced ways: while it generally enhances the impact of the crisis and the influence across layers becomes rather homogeneous it can also have a protective effect, in cases of very dense and well-connected layers, such as KIS.

1 Introduction

Transnational (“global”) firms entail ownership relations that form a complex worldwide network. Vitali et al. (2011) studied this network and found it to have a dense, intertwined, small-sized core that controls a large part of the whole network. Given the assumption that ownership relations are likely to reveal the financial connections between the firms (Santos and Rumble, 2006; Vitali et al., 2011), these conclusions further imply that the worldwide financial network is in turn very complex and heavily interconnected and thus susceptible to the spreading of a crisis (Stiglitz, 2010; Battiston et al., 2012). Furthermore, strong spatial concentrations of firms induce emerging local agglomeration economies (Camagni and Capello, 2004; Rozenblat, 2010) by fostering mutual reinforcement of global firms’ networks.

In that context, what is the role of cities–and regional interactions in general - in these networks, from this local/global perspective? As Sassen (1991) stated, cities play a vital role in the evolution of these networks and vice versa. Specifically, the cities attract firms because they contain and sustain what they need, i.e., experts in possession of special skills and, in turn, the firms contribute to the cities’ global character and significance in the world economy. Sassen notices a shift in activity precedence from manufacturing, commercial banking, etc. to the knowledge business, being at the heart of the reciprocal relationship that moulds both cities and firms into a worldwide network of complex interactions. Similar conclusions have been reached in a precursory empirical study of the European urban system by Rozenblat and Pumain (1993), who found evidence of skill and economic networks accumulation in its largest centres. Lastly, Taylor (2010) reviews Sassen’s and other similar ideas on the cities’ role and, drawing from them, he introduces a proper network perspective into the city/firms/world-economy interplay. The nodes of this network are the cities, but they are not the actors themselves. In practice, they are territorial active nodes, merely acting as “nests” that incorporate the firms’ interactions, both within and across cities. In other words, a city-node is a “catalyst” that reflects the collective emerging interactions between its firms to the outside world. These firms are the Advanced Producer Services¹ (APS)–also known as Knowledge Intensive Services (KIS) - which are considered the prime actors in the cities’ network formation, by seeking out and utilising the expertise accumulated in large cities. Thus, according to Taylor’s 3-level network model, the KIS firms’ interactions comprise the sub-nodal (basic-level) network that supports their industrial, management and financial strategies in different locations, while the cities’ interactions shape the geographical structure of the firms’ world-economy network that makes up the supra-nodal network level, sitting on top of the city level network.

Global cities often harbour many local ownership linkages between their firms, the most significant example being London, with the percentage of links among firms located within its urban region exceeding 70% in 2010, but decreasing to 50% in 2019 (Rozenblat, 2021). In an average city, more than 35% of the firms’ linkages are local (Lennert et al., 2010). A city with a dense network of local links is found to attract more external investments (Rozenblat, 2015). Additionally, these local linkages can potentially augment the effect of a crisis on the city’s firms, as witnessed in London, in 2008, when cascading failures put thousands of people out of job. The 2014–2016 first crisis of Russian cities due to the boycotts that followed the Crimea invasion showed an adaptive resilience of their multinational companies (Rogov et al., 2022) that asserts that the shock changed both intra-cities networks and the ones with their global environment (Laboy and Fannon, 2016). Locally–inside cities–the “relatedness” between specialised activity sectors (their inter-connections) quickly changed to adapt to new conditions of the global specialisation of other cities. However, as demonstrated by Pan et al. (2020) for Beijing, the global insertion of cities in globalisation largely depends on the capabilities of mobilisation of private and state investments and planning inside the cities.

The question of the impact of internal dynamics of cities on their global influence is critical, as cities are on the forefront of geopolitics, pandemic, and disaster turbulence. However, as suggested in economic geography, firms’ relations represent much more than pipelines of epidemic or innovation diffusion. For the whole economic health of cities, they create a tissue of diverse activities supporting the city’s system economy. This permits the emergence and the renewal of local powerful groups of interest directly or indirectly linked to global dynamics in top-down and bottom-up processes for activity sectors that continuously evolve in their production processes and their relations with other activity sectors. While the balance between intra-urban and inter-urban connections has been explored for over 20 years under the concept of “local buzz and global pipelines” (Bathelt et al., 2004), there are limited comparative studies that methodically assess the role of various activity sectors’ local networks within a broader global context across a vast network of cities. Therefore, it is essential to leverage the available databases and methodologies to address this issue in the present context.

In view of the above we asked the following questions:

• To what extent do the various activity sectors interact with and influence each other?

• Is there a sector that is more dominant in their interplay? What is the role of Knowledge Intensive Services (KIS) in the activities’ network?

• How vulnerable is the global multi-sectorial network of cities to the spreading of a crisis?

• Do local interactions between different types of sectors enhance the spreading of a crisis in the network and, if so, to what extent?

To explore these questions, we studied the worldwide network of cities, in a way that would presumably reveal the effect of both local and global interactions between the different sectors on the spreading of a financial crisis that can manifest either nationally, as observed in scenarios like wars and associated restrictions (akin to the challenges faced by Russian cities), or internationally, in which case the crises often have their roots in preceding national upheavals, particularly in the backdrop of strong inter-city linkages on a global platform. Specifically, we derived the directed network of cities from the aggregated interactions (ownership relations) between the firms harboured in them, and divided it into a 5-layer (corresponding to the 5 activity sectors) partial-multiplex, directed and weighted network. Subsequently, we distinguished between two distinct cases, the partial-multiplex in which the local interactions within cities have been excluded and the one in which they were included.

We performed a thorough structural analysis and an SIR simulation of crisis spreading on both these networks and compared the results. A previous attempt (Battiston et al., 2018) to model the sectorial interplay and the local interactions’ effect on crisis spreading, using the same data sets, failed to capture the intrinsic structural features and the dynamics of the system. In the present analysis, the stochastic SIR model employed was adjusted according to the inferences drawn from the rigorous structural analysis to make it more intuitive and fitting, and yield more robust results. Our findings are indicative of the unique role of KIS firms in the network of cities and also reveal that while the intra-urban connections intensify the spreading of a crisis, they can also have a protective effect in certain cases.

2 Materials and methods

2.1 Data description

The construction of the networks for this study was based on two databases, namely, the ORBIS databases (Bureau van Dijk, 2010 and Bureau van Dijk, 2013)^{2, 3}.

To obtain a robust account of the economic ties between cities worldwide, we started off by determining the financial links–reflected in ownership networks - between the firms harboured in these cities (Alderson and Beckfield, 2004; Wall, 2009; Taylor, 2010). To this end, we began by building a large database of all direct and indirect linkages formed by financial ownership of the top 3,000 multinational corporations worldwide, according to their turnover in 2012 (linkages observed in 2013) from the ORBIS database (Bureau van Dijk, 2013). It comprises 800,000 enterprises and 1.2 million ownership links in 2013. Subsequently, we worked to restore and fill out inaccurate or missing information by focusing mainly on the locations and activities of the firms. The team developed an original method of geographical aggregation of firms within comparable Large Urban Regions (LURs) at a world scale (Rozenblat, 2020), which include cities and their surrounding functional urban regions. Thus, the locational spatial units for each city are the extended functional urban areas defined as the accessibility zones around major worldwide metropolises. The LURs are coded by their IATA main airport’s 3 DIGIT codes, to avoid the ambiguity of the way cities’ names are written (Rozenblat et al., 2017). This LUR unit provides a consistent and universal frame of reference within which we can compare “cities”⁴ around the world in a meaningful way. It also allows us to approach “local linkages” using a unified concept of expanded areas for cities globally through a replicable method, a perspective not found in existing literature on comparative studies of cities’ global networks.

We then constructed the individual network of each of the 3,000 multinational corporations’ networks in this processed database. A firm’s individual network comprises the headquarters, its subsidiaries (nodes) and the subsidiaries of subsidiaries (which can extend up to more than 30 levels, in some cases) and the directed financial linkages between them (links), as derived from ownership relations. A threshold was enforced on the strength of the linkages, below which the link between two firms was omitted. Specifically, a link between two nodes is drawn only if the total percentage of a subsidiary’s capital owned by the headquarters, either directly or indirectly - through other subsidiaries - is at least 10%. This percentage corresponds to the generally admitted limit of ensured long term investment, and not only volatile portfolio of capital (Joisce and Patterson, 2006). Indeed, when the stake is below this threshold, it is typically perceived that there is neither decision-making influence nor technological transfer. In practice, holding more than 10% in equity is commonly viewed as the benchmark for asserting control over an asset (Bertrand, 2005; Corporations, 2007). The collection of all these individual networks resulted in a quasi-tree (20% of the linkages create cycles), weighted and directed network of 800,000 firms and their 1.2 million ownership relations that reflect the financial linkages between them, as captured in 2013. Additionally, the firms of this network were classified into five categories, according to their main field of activity, i.e., high-tech (HT), low-tech (LT), knowledge-intensive-services (KIS), less-knowledge-intensive-services (LKIS) and other (OTH) (Manual, 2005).

The next step was to move from the firm network to the geographically aggregated, overlaying network of cities. The exact proportion of owned capital is not always available with desired precision. Therefore, we used the total number of financial linkages between all firms located in a pair of cities as a measure of the intensity of their interaction. Specifically, a directed link from node i (corresponding to city i) to node j (corresponding to city j) is drawn if at least one firm located in city i owns part of another firm located in city j. The strength (weight) of this directed link is the total number of all such ownership relations⁵ (Eq. 1), where the summation is over all pairs of firms k of which the first is located in city i and owns a percentage of the second which is located in city j. When i = j the ownership relation is between a pair of firms in the same city, therefore these links represent intra-urban interactions.

$w_{ij}={\displaystyle \sum _k}{l}_k(1)$

Lastly, we divided the network of cities into five-layers, according to the five activity sectors specified in the OECD activity classification. Each of these five layers is a network of cities that harbour firms active in one specific sector, i.e., the HT cities’ network, the LT cities’ network, etc. Naturally, a city can be present in multiple layers at the same time. The five layers are also connected to each other, through the linkages between the levels’ cities, as the cities harbour firms of all activity types.

We considered two distinct cases: in the first case we only take into account the links between different cities, l_ij, i ≠ j and in the second, we also include intra-urban links, i.e., links that result from relations between firms located in the same city, l_ij, i = j. The resulting networks are shown in Figure 1. Each of these networks is a weighted, directed, multi-layered, partial-multiplex network of cities, featuring 36,952 (inter-urban) and 37,362 (inter + intra urban) pairs of cities, connected through 389,749 and 632,550 firms’ links, respectively (Figures 1A, B). The total of 242,801 intra-urban links present in just 410 cities constitute very dense sub-graphs in the underlying network of firms.

FIGURE 1

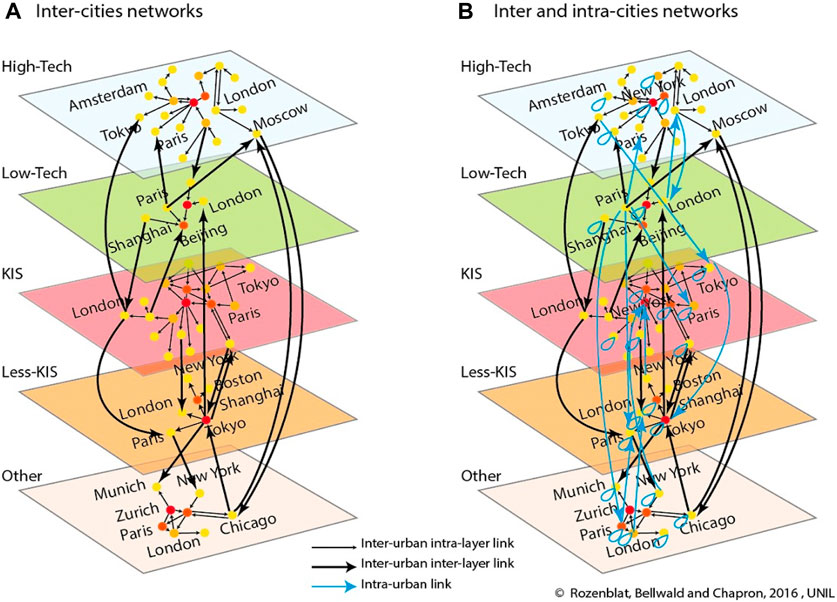
FIGURE 1. The partial-multiplex network of cities of multinational firms by activity sector. [1. (A): intra-urban connections excluded, 1. (B): intra-urban connections included].

2.2 Method of simulation

We use a simple stochastic SIR model (see Section 2.3) to simulate the spreading of a crisis on the two derived partial-multiplex networks of cities, one without any intra-urban links and one with the intra-urban links taken into consideration. The SIR model is frequently used in infection spreading simulations on networks (Kermack and McKendrick, 1927; Newman, 2002; Keeling and Rohani, 2008; Eames et al., 2009; Dickison et al., 2012; Kamp et al., 2013; Newman, 2018). There are many variations of this model, including the SI, SIS, SIR, SIRS, etc. models (Kermack and McKendrick, 1927; Newman, 2018). SIR stands for Susceptible (S), Infected (I) and Recovered (R), comprising the three states each node of a network is allowed to be in, at any given time. Susceptible nodes are the ones that are currently “healthy” and can potentially become infected through their first neighbours in the network, infected nodes are all nodes affected by the disease (here, the crisis) and the recovered/removed nodes are the nodes the have recovered from the infection, which cannot get re-infected and can no longer spread the infection to their first neighbours.

Another plausible choice for the stochastic model would be SIS or SIRS, however, given the temporal scope of the investigation, it is reasonable to assume that once a firm is affected by a crisis and subsequently recovers, it would not be immediately susceptible again within the short-term horizon. This is further bolstered by the adaptive nature of businesses. Typically, firms that emerge from economic downturns undertake corrective and preventive measures, enhancing their resistance against similar future shocks. These measures can range from financial restructuring and diversifying revenue streams, to building contingency reserves, all of which contribute to a form of “immunity” in the aftermath of a crisis. Thus, within a short-term perspective, the SIR model aptly captures this transient phase of susceptibility, impact, and subsequent “immunity”, making it a suitable choice for our analysis.

In each of the two partial-multiplex networks there are two different types of links between the nodes, regarding the activity types: the intra-layer type, which connect nodes of the same activity (e.g., HT-HT) and the inter-layer links, which connect nodes of different activities (e.g., HT-KIS). Both types of connections represent sets of interactions between the nodes of the partial-multiplex. Thus, each of the two partial-multiplex networks essentially represents 25 sets of interactions between its nodes, of which the five are within the bounds of each layer (intra-layer) and the rest are the sets of interactions of each layer with all the other layers. The SIR model in this study is parameterized to incorporate the network topology shaped by all 25 sets of interactions.

Initially (at time-step = 0 of the Monte Carlo simulation) all nodes (cities) are in the S state. A node, chosen at random, is considered to be infected. This node is considered the seed (or origin) of the infection/crisis. In all subsequent time-steps, the crisis can propagate from an infected node to any of its susceptible nearest neighbours, by following the network’s directed links. The probabilistic rate q at which a susceptible node can become infected is largely determined by the network topology.

In previous studies regarding epidemics on weighted networks q is intuitively presumed to be proportional to the weight of the directed link from the source to the target node (Eames et al., 2009; Kamp et al., 2013). In Garas et al. (2010), which includes a simulation of the spreading of an economic crisis in the worldwide network of countries, a protective factor represented by the node’s total weighted degree was added, introducing a measure of the country’s “immunity”, i.e., its resistance against being “infected” by the crisis.

This approach yielded very good results in Garas et al. (2010), therefore we followed it in Battiston et al. (2018)–our first attempt to model a crisis diffusion in the worldwide network of cities derived from our ownership relations data. However, the results indicated that this model was not an equally good fit to our network’s topology. That analysis comprised a basic structural analysis of the five network layers and the comparison of the time evolution of the spreading of the crisis with and without intra-urban connections. The main problems were that the comparison of the spreading effect within and across sectors, with and without intra-urban connections, revealed only minimal differences that were within the statistical error, and most importantly the intensity of the crisis diffusion was very low in all simulations, and therefore our results were incompatible with real-world catastrophic incidents such as the one witnessed in London, in 2008, when a single crisis brought on cascading failures.

The culprit was the use of the total weighted degree of the cities as the denominator of the model used in the simulation process. This denominator acts as a protective factor against the “infection”. As many connections in our network - and especially the intra-urban ones - represent strong relations they can have very high weights through which they can spread the crisis, however they often also add up to high total weighted degrees, overemphasising the stamina of the city, thus contributing to conditions that are highly unfavourable for spreading. Another repercussion of this complication is that the crisis diffusion is particularly hindered on a layer that is very dense and contains many highly intense connections, an indication that is mostly counterintuitive.

In this standpoint, we have chosen the total node degree, instead of the total weighted degree to serve as the protective factor in the model of the present analysis. By using the total degree we are focusing on the sheer number of connections a city has, rather than the strength of those connections. This can provide a clearer and more generalizable insight into how crises spread. In this context, cities with a higher number of connections, even if some of them are minor, might have a buffering or dilution effect on the transmission of a crisis. Each connection, regardless of its weight, represents a potential channel for economic interactions, resources, information flow, and support. A city with many connections might be able to distribute or buffer the impact of a crisis across its numerous ties, thereby reducing the probability of a concentrated shock from any single source. This buffering effect can hinder the transmission of the crisis, making the city more resistant to shocks from individual connections. Also, cities with a higher number of connections might be more diversified in their economic ties. Even if some of these connections are weak (low weight), they still represent different economic relationships and dependencies. A city with a diverse range of connections might be more resilient to shocks from any single source, similar to the concept of portfolio diversification in finance. Moreover, weighted connections can introduce noise, as they are determined by factors that can vary over time or are subject to measurement errors. By focusing on the total degree, the potential noise is reduced which enables capturing more stable and consistent patterns in the data and the simulation processes. Lastly, the range of the set of values of the link weights is very wide and therefore the total weighted degrees are highly non-uniform, whereas the total degrees’ values are considerably more uniform.

Therefore, in the subsequent analysis, q is intuitively presumed to be proportional to the intensity of the ownership relation between two cities, represented by the weight of the directed link from the source to the target node, and reversely proportional to the susceptible city’s economic resistance to the “infection”, represented by the total-degree of the target node. The weight of the directed link is determined by the number of subsidiary/headquarters relationships between firms located in the source and target cities, the total-degree of the target node is the sum of its in and out degrees, and k is a multiplicative factor that was set to 1 for all intra-layer and all intra-urban interactions. Moreover, a variety of (constant) values in the range 0 ≤ k ≤ 1 were considered for the (non-intra-urban) inter-layer links. The upper and lower bounds of this set are the limit values of k in our model. Specifically, setting k to 0 for all inter-layer interactions (including intra-urban ones) is the special case for which all layers are detached, and there are no inter-layer links between them. Accordingly, setting k to 1 for all inter-layer interactions is the special case for which all connections (intra and inter-layer and intra-urban) are treated the same and q is determined solely by the topology of the network, i.e., the weights of the links and the total degrees of the nodes. In conclusion, the probabilistic rate q at which a susceptible node can become infected is determined by the following formula (Eq. 2):

$q=k\frac{weightofthedirectedlink}{totaldegreeoftargetnode},(2)$

where k = 1 for all intra-layer and intra-urban interactions and 0 < k ≤ 1 for all inter-layer connections that are not intra-urban. In the special case for which the layers are examined as completely detached (single-layer cases), k = is set to 0 for all inter-layer interactions (including intra-urban ones).

Setting k equal to 1 for all intra-layer and intra-urban interactions aims to capture the intensity of these relations, as links between firms of the same activity or located in the same city are presumed to be stronger and more influential in the spread of the crisis compared to links between different types of activities and across different cities. This choice, in combination with exploring a range of k values for the inter-layer links, allows us to investigate the impact of inter-layer links on the spread of crises of varying intensities, while also controlling for the effect of the intra-layer and intra-urban links. Moreover, by comparing the spreading on the two partial-multiplex networks, one with intra-urban links and one without, we can isolate the contribution of inter-layer links to the overall spread of the crisis. Finally, at each time-step infected nodes recover at a constant average Recovery Rate (RR). Several values of RR were examined in our simulations, in the range 1/100 ≤ RR ≤ 1. RR = 1 is the upper limit for this parameter as it resolves to the special case for which an infected node recovers immediately, at the next time-step. By exploring various combinations of RR and k, we have determined that all qualitative diversity of the system unravels in the range 0 ≤ k ≤ 0.1 for k, and 1/30 ≤ RR ≤ 1 for RR. The simulation stops when no new nodes can be infected.

2.3 SIR model overview

The Susceptible-Infected-Recovered (SIR) model, traditionally used to describe the dynamics of infectious diseases, has been adapted in our study to represent the spread of an economic crisis through a network. At any given time t, the model identifies entities as either susceptible, infected, or recovered. Susceptible entities, denoted as S(t), have not yet been impacted by the crisis but remain at risk. Infected entities, represented by I(t), are currently affected by the crisis and can transmit it to those susceptible. Meanwhile, recovered entities, R(t), have been affected by the crisis and have since recovered, gaining immunity.

The dynamics of the SIR model can be described by the following set of differential equations:

$\text{dS}\left(\mathrm{t}\right)/\text{dt}=-\mathrm{\beta }\times \mathrm{S}\left(\mathrm{t}\right)\times \mathrm{I}\left(\mathrm{t}\right)$

$\text{dI}\left(\mathrm{t}\right)/\text{dt}=\mathrm{\beta }\times \mathrm{S}\left(\mathrm{t}\right)\times \mathrm{I}\left(\mathrm{t}\right)-\mathrm{\gamma }\times \mathrm{I}\left(\mathrm{t}\right)$

$\text{dR}\left(\mathrm{t}\right)/\text{dt}=\mathrm{\gamma }\times \mathrm{I}\left(\mathrm{t}\right)$

where β is the transmission rate, representing the probability of transmitting the crisis from an infected entity to a susceptible entity. In our model, β is influenced by the weight of the directed link between entities and the total degree of the target entity. γ is the recovery rate (RR), indicating the rate at which infected entities recover and become immune.

The term β × S(t) × I(t) represents the new infections that arise from interactions between susceptible and infected entities. The interaction between susceptible and infected entities is crucial here. As more entities become infected, the rate of new infections can increase, especially if there’s a large pool of susceptible entities. Conversely, as the number of susceptible entities decreases, the rate of new infections will slow down, even if there are many infected entities. The term γ × I(t) in the equations signifies entities that recover from the crisis.

The SIR model provides insights into how an initial economic shock can propagate through a network, affecting a subset of entities and leading to varying dynamics of susceptibility, impact, and recovery.

3 Results

3.1 Structural analysis

We started by performing a thorough structural analysis on the partial-multiplex and directed network. Initially, we examined the five layers (HT, LT, KIS, LKIS, and OTHER) of the partial-multiplex as five separate, directed networks. Each of these five networks represents the interactions between firms within the same activity sector.

The derived total, in and out-degree distributions of the five layers are right-skewed and heavy-tailed. None of the probability distribution functions [power-law, truncated power-law, exponential, lognormal, modified lognormal power-law (MLP)] most likely followed by such data was found to be a good fit to the derived distributions. The basic structural features, shown in Table 1, are a first indication that KIS is the most dominant of all layers, as expected [see Section 1 and (Sassen, 1991; Rozenblat and Pumain, 1993; Taylor, 2010)]. Specifically, it appears that of all five layers, layer KIS is the most numerous and densest network, with the intensity of its links - reflected in their corresponding weights - being spectacularly high. It also exhibits the most tightly connected communities and has the highest percentage of mutually connected pairs of nodes.

TABLE 1

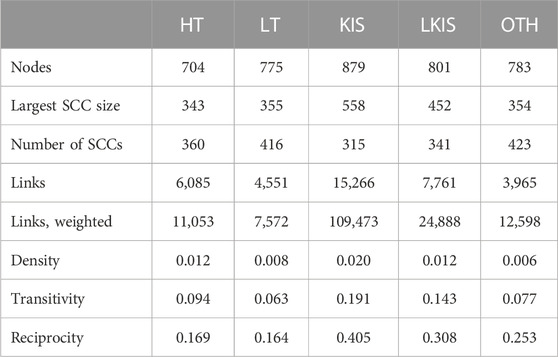
TABLE 1. Basic structural properties of the five layers, High-Tech (HT), Low-Tech (LT), Knowledge Intensive Services (KIS), Less Knowledge Intensive Services (LKIS) and Other (OTH), of the partial-multiplex, directed network. (SCC stands for Strongest Connected Component).

Furthermore, we ranked the nodes on the five layers according to their in/out-degree, in/out-weighted-degree, in/out-closeness, betweenness and weighted-betweenness centralities, to explore whether there are any nodes (cities) that rank high in all (or some) of these centralities, on all layers. Our results indicate that eight nodes (cities) of the five layers of the network stand out with respect to these eight centralities. Firstly, Paris and London were found to be major hubs, as they rank in the top-7 in all centralities, on all five layers. On LKIS in particular, the two cities rank in the top-2 in all centralities, except for London ranking third in out-weighted degree. Out of the two, London ranks higher in in-centralities, while Paris ranks higher in out ones, except for in-degree on LKIS and out-weighted degree on KIS. This finding could suggest that Paris hosts relatively more owner firms and less subsidiaries than London does.

Moreover, six more cities, namely, Tokyo, Milan, Madrid, Moscow, New York and Amsterdam were found to be significant in terms of high centrality rankings on all layers. Specifically, with respect to the criterion of ranking in the top-20 in any of the eight centralities considered, on all five layers, we found the following: First of all, all six cities satisfy this criterion with respect to the betweenness and weighted-betweenness centralities. This implies that all six cities are significant in terms of maintaining the network’s coherence. On top of that, Tokyo also ranks in the top 20 cities in all three out-centralities and none of the in ones, whereas the opposite holds for Milan; Madrid and Moscow meet the criterion only for in-degree centrality, and New York meets it for four out of the six centralities, namely, in, out and out-weighted degree and in-closeness centralities. These results could indicate that Tokyo is favoured by owner firms, Milan, Madrid and Moscow by subsidiaries, while New York is more of a mix.

Finally, we analysed the connections between the five layers, i.e., the inter-layer connections, for the partial-multiplex, directed network, for both cases: with and without the intra-urban links considered. The study of the inter-layer connections reveals information about the interactions between firms of different activity sectors. For each pair of layers, we determined three quantities, the source/target nodes, the links and the weighted links, for both the “without intra-urban links” and the “with intra-urban links” cases⁶. The results are shown in Tables 2, 3, respectively. Each of these tables can be thought as a matrix whose elements i, j depict the results for the pair of layers (L_i, L_j). For example, for i = 2 and j = 5, element (2, 5) (line 2/column 5) of Table 2, depicts the ownership relations from cities on layer 2, i.e., LT, to cities on layer 5, i.e., OTH.

TABLE 2

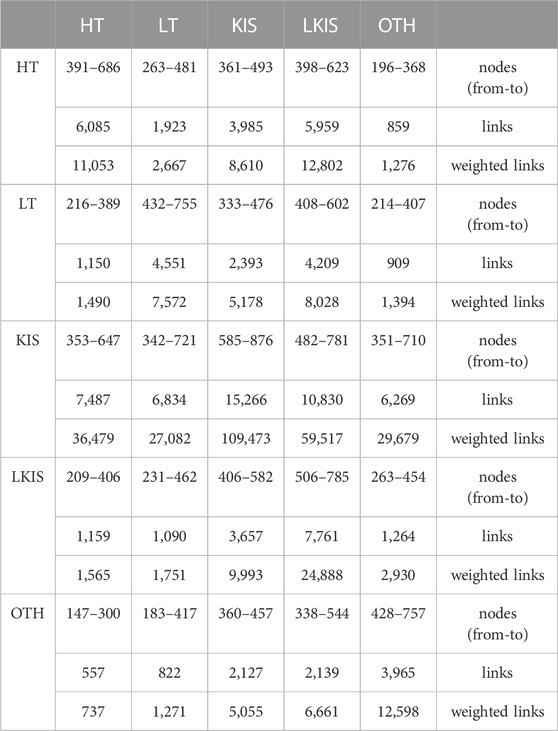
TABLE 2. Basic features of the connections between the five layers, High-Tech (HT), Low-Tech (LT), Knowledge Intensive Services (KIS), Less Knowledge Intensive Services (LKIS) and Other (OTH), of the partial-multiplex, directed network of cities, intra-urban connections excluded.

TABLE 3

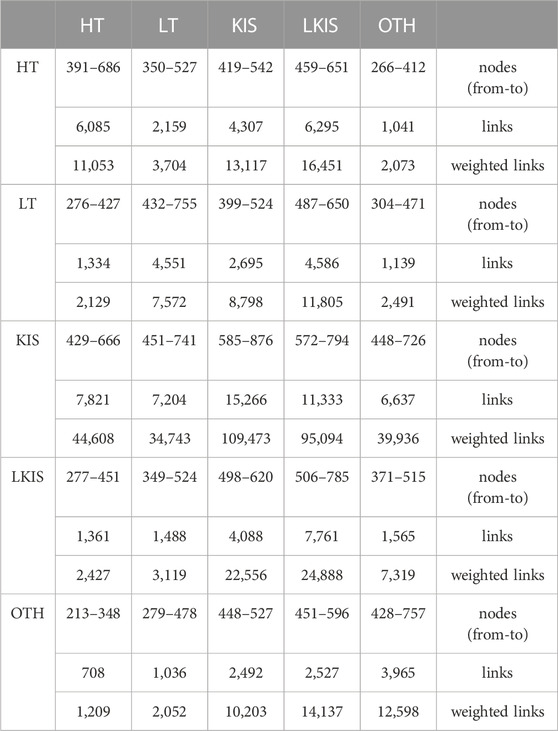
TABLE 3. Basic features of the connections between the five layers, High-Tech (HT), Low-Tech (LT), Knowledge Intensive Services (KIS), Less Knowledge Intensive Services (LKIS) and Other (OTH), of the partial-multiplex, directed network of cities, intra-urban connections included.

Specifically, there are 909 links (and 1,394 weighted links, i.e., the sum of the weights of the 909 links) directed from 214 source nodes (cities that harbour owner firms) on layer LT to 407 target nodes (cities that harbour subsidiaries) on layer OTH, in the partial-multiplex network without intra-urban links. Likewise, element (4, 2) of Table 3, reveals the ownership relations from cities on layer LKIS to cities on layer LT, represented as 1,488 links (and 3,119 weighted links, i.e., the sum of the weights of the 1,488 links) directed from 349 source nodes (cities that harbour owner firms) on layer LKIS to 524 target nodes (cities that harbour subsidiaries) on layer LT, in the partial-multiplex network with intra-urban links.

In that context, the non-diagonal elements of Tables 2, 3 show the extent and intensity of the inter-layer interactions, i.e., the interactions between firms of different activities. There are no intra-urban links in the diagonal elements of Table 3, as they would only yield self-loops on each layer. Both Tables indicate that layer LKIS is the layer that is impacted the most by other layers, as it is on the receiving end of inter-layer interactions more often than any other layer is. Likewise, KIS is the layer that impacts all other layers the most, as links to any other layer originate from KIS more often than on any other layer. In other words, LKIS firms tend to be subsidiaries to HT, LT, KIS and OTH owner firms, whereas KIS firms tend to be owners of HT, LT, LKIS and OTH firms. Thus, KIS and LKIS layers stand out in the partial-multiplex, directed network, as “source” and “sink” layers, respectively, of the directed links. This result also corroborates the crucial role that KIS firms play in shaping the global network of cities (see Section 1 and (Sassen, 1991; Camagni and Capello, 2004; Rozenblat, 2010)).

Lastly, the layers that influence KIS the most (other than itself) are LKIS and HT. Interestingly, although out of these two layers, LKIS is the one having the most firms that are owners to KIS firms, nonetheless, the layer that has the most links directed to KIS firms is HT and not LKIS. This implies a tendency for HT firms to be owners of more than one KIS firm, revealing the role of finance in the innovative processes of HT firms.

3.2 Spreading process simulations with SIR model

Subsequently, we simulated the spreading process on the two partial-multiplex networks, by employing the SIR model described in Section 2.2. We first performed a set⁷ of simulations on each of the five layers separately, for comparison purposes. Treating the layers as separate networks corresponds to the case of no inter-layer connections, i.e., k = 0. Then, we carried out six sets of simulations on each of the two partial-multiplex networks, while monitoring the spreading of the crisis on each of the five layers. Each set of simulations corresponds to one of the following cases of “seed” layer (the layer in which the crisis originates), namely, HT, LT, KIS, LKIS, OTH, and random. In the “random” case, the seed layer is chosen at random in each simulation.

Starting with the partial-multiplex network without intra-urban interactions, we initially calculated the average infected mass <M> and its distribution. For each simulation, the infected mass, M, also known as epidemic size, is measured by the percentage of the recovered nodes at the end of the spreading process.

Figure 2A depicts the evolution of the fractions of susceptible (S), infected (I) and recovered (R) nodes on layer LKIS, for k = 0.1 and RR = 1/30, for a crisis originating in the same layer. At the beginning of each simulation all nodes are susceptible (fraction of susceptible nodes = 1.0) and there are no infected nodes (fraction of infected nodes = 0). Note that S + I + R = 1 at all times. As can be seen, the percentage of recovered nodes starts is initially 0 and eventually reaches a constant value of 0.4, therefore, in this case <M> is approximately 40%. The corresponding frequency distribution of the infected mass distinct values (of each simulation) is shown in Figure 2B. The distribution comprises two strong peaks, one at M ≈ 0% and a second at around M ≈ 95%, with no intermediate values. Distributions of this type are called bimodal. The first peak arises from cases in which only one or a few nodes are affected, whereas the second one from cases in which the majority of the networks’ nodes are affected. Thus, in this case, the observed bimodality implies that in most cases the crisis dies out fast, however if it manages to survive through the initial simulation steps, it spreads over a large portion of the network nodes. Thus, the prediction on the course of the infection largely depends on the neighbourhood it originates from, i.e., the connectivity of the initially infected node, as also seen in (Gallos and Argyrakis, 2003).

FIGURE 2

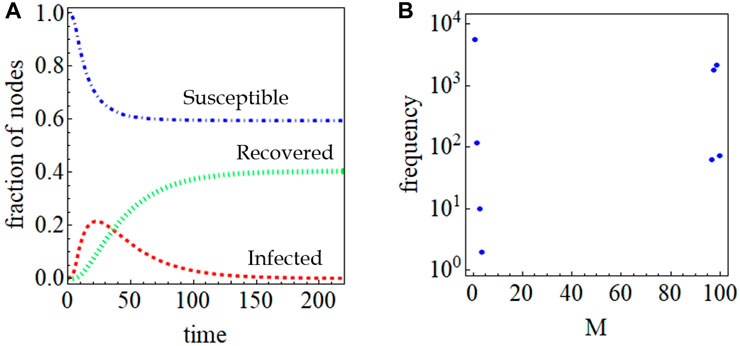
FIGURE 2. (A) Fraction of Susceptible (S), Infected (I) and Recovered (R) nodes on layer LKIS (k=0.1, RR=1/30), with the crisis originating on the same layer and (B) distribution of infected mass (M).

To examine the effect of k and RR on bimodality, the distribution of the infected mass M was calculated for a collection of values for the two parameters. The results for k = 0.01 and RR ranging from 1/6 to 1 (images not shown) show that for layer KIS the distribution of M is always bimodal, for every value of RR and in all cases of seed-layer, even in the single-layer case. For any other layer, i.e., HT, LT, LKIS, and OTH, one can readily observe the emergence of bimodality as RR increases. Specifically, as RR increases, a peak appears at relatively large M values, which becomes progressively more prominent and eventually breaks off as the distribution gets into its bimodal state. The rate at which this transition unravels varies for each layer and is also affected by the seed-layer to some extent.

Furthermore, by repeating the process of varying RR for k = 0.05 and k = 0.1, it was found that the value of RR at which the bimodality state is reached increases with k. Overall, our results suggest that for large values of RR the crisis is hampered early on and therefore it is highly improbable that it will affect large portions of the network. The lower the RR, the more likely it is that the crisis will afflict large parts of the network.

Subsequently, the same sets of simulations were performed on the partial-multiplex network with the intra-urban links included, to compare the spreading features on the two networks. We first calculated the distribution of infected mass M, to assess the effect of intra-urban connections on the probability that the crisis will survive and affect a large portion of the network. Figure 3 shows the distribution of infected mass, M, for varying values of k and RR, for both partial-multiplex networks.

FIGURE 3

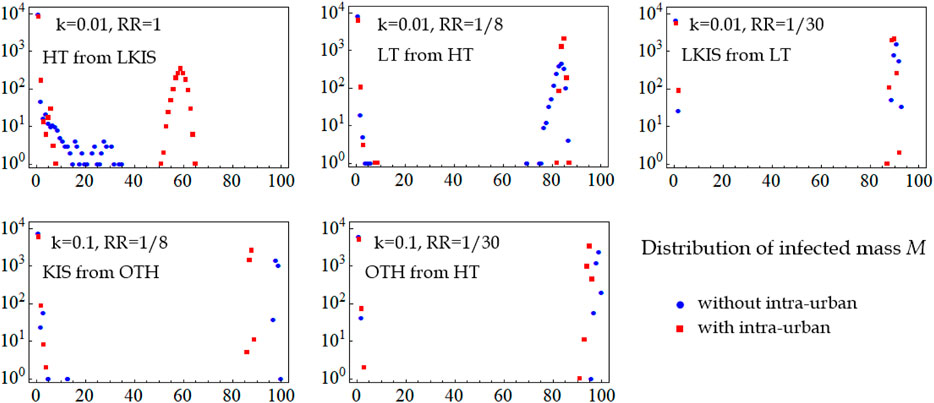
FIGURE 3. Distribution of infected mass M for varying values of k and RR for the two partial-multiplex networks, without (blue disks) and with (red squares) intra-urban connections.

It is evident that the presence of intra-urban links significantly increases the number of cases in which the crisis spreads to the majority of the cities in the network. This effect appears to be considerably more dramatic when the spreading is hindered, i.e., in cases of high RR and/or low k.

These findings were quantified by calculating the relative increment of large-M occurrence percentage in the intra-urban partial-multiplex, with respect to the percentage in the partial-multiplex without intra-urban connections (Eq. 3). The results are shown in Table 4.

$100\frac{\left({large-M-occurrences}_{with}\right)-\left({large-M-occurrences}_{without}\right)}{{large-M-occurrences}_{without}}(3)$

TABLE 4

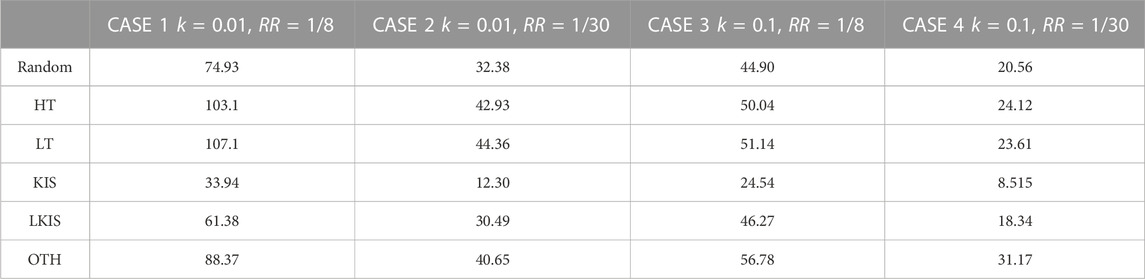
TABLE 4. Percentages of large-M-occurrences relative increment in the partial-multiplex network with intra-urban connections, with respect to the partial-multiplex network without intra-urban connections.

Our results suggest that for a fixed RR, smaller values of k result in higher occurrence of large-M (e.g., case 1–case 3 or case 2–case 4). Likewise, for a fixed k, larger values of RR lead to higher occurrence of large-M (e.g., case 1–case 2 or case 3–case 4). Finally, the greatest difference is observed between the two extremes (case 1–case 4).

Apart from the distribution of infected mass M, its average, <M>, was also calculated, for varying values of k and RR, in order to compare the extent of the crisis spreading on the layers of the two partial-multiplex networks. Figure 4 depicts the calculated average M, for all layers in the two networks, for five combinations of k and RR values.

FIGURE 4

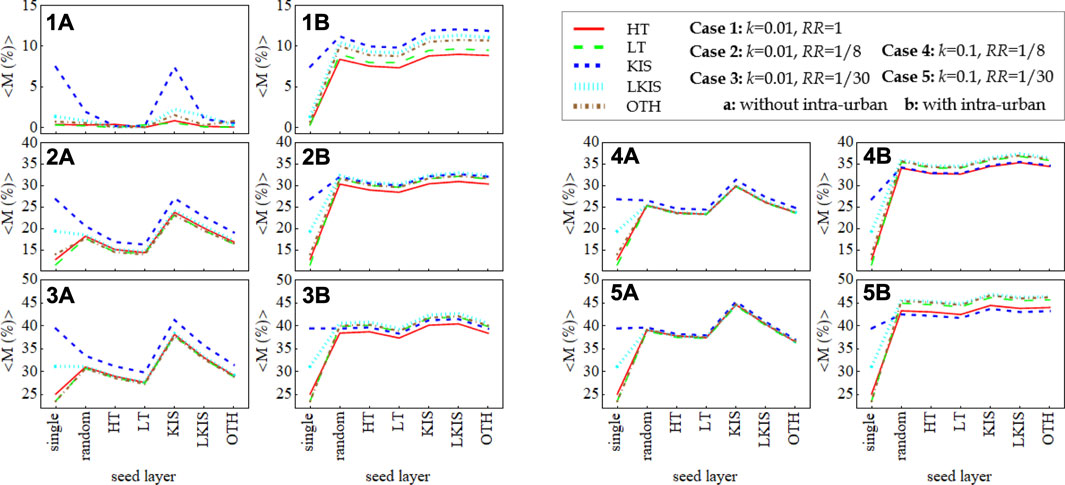
FIGURE 4. Average infected mass M on the five layers of the two partial-multiplex networks [without (cases (A)) and with (cases (B)) intra-urban connections], for varying values of k and RR, from all seed-layers. (The graph points are joined for visualisation purposes.)

Regarding the cases of the partial-multiplex network without the intra-urban connections [cases 1(a)-5(a)], our results indicate the following: In terms of the seed layer effect, <M> is clearly the highest on all layers when the crisis originates on layer KIS. The impact of the other layers as seed-layers varies, depending on the spreading conditions, i.e., the values of k and RR. For the most part, LKIS is the seed-layer that induces the second-highest <M> values. In terms of <M> levels in general, layer KIS is consistently affected the most, while the remaining four layers are rather indistinguishable. The difference in <M> levels between layer KIS and the other layers is progressively reduced as k increases and RR decreases, with all five layers being practically identical in the upper extreme state [case 5(a)].

Moreover, regarding the cases of the partial-multiplex network with the intra-urban connections included [cases 1(b)-5(b)], we notice the following: In terms of the seed-layer effect, LKIS is now the seed-layer that affects all layers the most, with KIS following close behind, except in case 5(b) where this situation is reversed. Furthermore, <M> levels are lowest when the crisis originates from LT. However, these differences are rather insignificant and, for the most part, the inclusion of the intra-urban links renders the seed-layer effect on the levels of <M> notably less prominent. In terms of <M> levels in general, the impact of crisis spreading on all layers has broadly increased with the inclusion of intra-urban links, as reflected in higher <M> levels, with the exception of KIS in cases 3b and 5b, when KIS is the seed-layer, where no significant difference or even a decrease in <M> levels is observed, respectively. A minor decrease is also observed for HT in case 5b with KIS as seed-layer. Overall, the differences between the layers are rather small, except for case 1b. However, despite the small differences between the layers, it is worth noting that for the most part HT is the layer that is affected the least by the crisis spreading, while KIS gradually shifts from being the most impacted layer in case 1b, to the least affected, ranking even lower than HT in case 5b. Therefore, we conclude that the intra-urban links do not enhance the spreading of a crisis on KIS as much as on the other four layers, as also implied by the results of Table 4.

Furthermore, by considering the extreme case (case 6) of RR = 1/100 and k = 1 (i.e., all connections are treated as equal and q is solely determined by the topology of the network, see Methods), we conclude that the system has already reached a qualitatively stable state by case 5. Specifically, as Figure 5 shows, cases 5 and 6 are qualitatively identical, and they only differ quantitatively, in that in case 6 <M> is considerably higher. Also, given that the standard deviation of the mean for <M> in all six cases, for all layers never exceeds the value of 0.5, we conclude that our basic findings regarding the overall behaviour of the system as we shift towards higher k and lower RR values are valid, i.e., in the cases with no intra-urban links, while in terms of <M> levels KIS is the most affected layer initially, the five layers gradually become indistinguishable. Also, the seed-layer effect is always significant for KIS, as all layers invariably exhibit the highest <M> values when the crisis starts on KIS than on any of the rest of the layers, for which the variation of the seed-layer effect becomes rather unremarkable. In the cases with the intra-urban connections included, the seed-layer effect tends to vanish, while KIS gradually becomes the least affected layer, ending up being the lowest layer in terms of <M>, even lower than HT, which has been persistently low from the start. Lastly, the tendency for KIS and HT to be less impacted when the intra-urban links are added, becomes progressively more apparent.

FIGURE 5

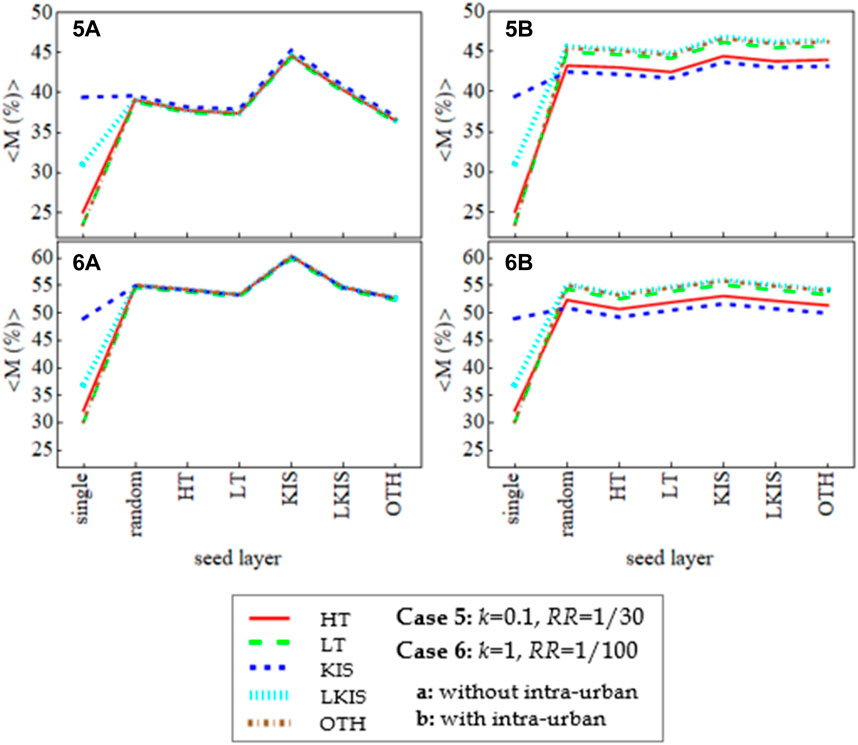
FIGURE 5. Comparison of case 5 of Figure 4 (RR = 1/30 and k = 0.1) and extreme case 6 (RR = 1/100 and k = 1). There are no qualitative differences between the two cases; the system has reached a qualitatively stable state by case 5. In cases (A) (left column) the intra-urban linkages are excluded, while in cases (B) (right column) the intra-urban linkages are included.

Additionally, the relative increment of <M> in the intra-urban partial-multiplex with respect to the partial-multiplex without intra-urban connections (Eq. 4) reveals that the spreading of the crisis is clearly amplified by the addition of the intra-urban connections in all cases, albeit the degree of the intensification varies with k and RR.

$100\frac{M_{with}-M_{without}}{M_{without}}(4)$

Specifically, for the five k-RR combinations featured in Figure 4, the overall difference in <M> levels (a-cases vs. b-cases), for the two partial-multiplex networks, averaged over the five layers and all seed-layer options, is 1187.2% (1a vs. 1b), 68.6% (2a vs. 2b), 26.7% (3a vs. 3b), 36.7% (4a vs. 4b), and 13.2% (5a vs. 5b). These results imply that the degree of <M> enhancement with the addition of the intra-urban links grows with increasing RR and with decreasing k, which is also in agreement with the results shown in Table 4.

Finally, the number of infected nodes was monitored on all five layers, for all seed-layers, in each of the five cases. Layers HT, LT, LKIS, and OTH were found to be very much alike, quantitatively. The results for layers HT and KIS are depicted in Figure 6.

FIGURE 6

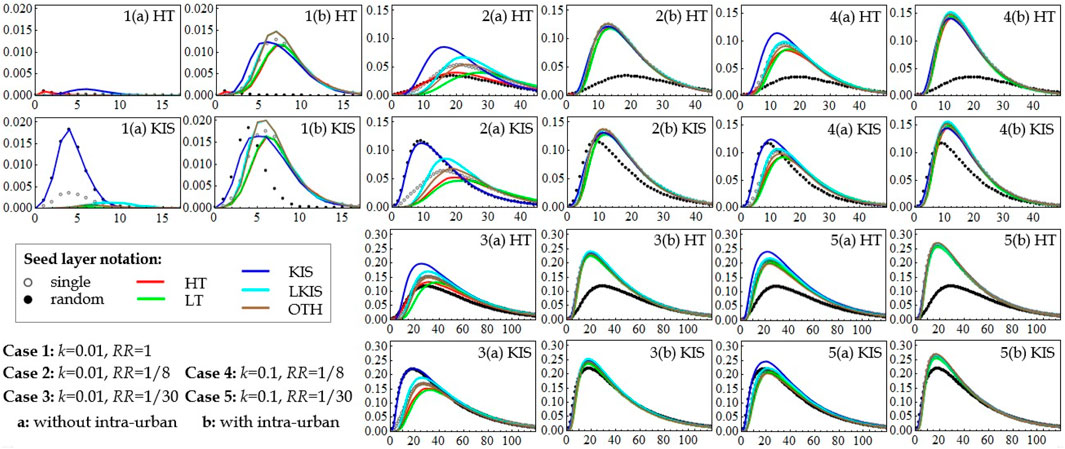
FIGURE 6. Average (from 10,000 simulations) fraction of infected nodes (cities) over time on the five layers of the two partial-multiplex networks, i.e., without [cases (A)] and with [cases (B)] intra-urban linkages, for varying values of k and RR, from all seed-layers. The curves shown in this Figure correspond to the dotted (red) curve of Figure 2A. The peak and the width of each curve relate to the intensity and duration of the infection (crisis).

In the cases without the intra-urban connections, there is a variation in the peak and the speed of the crisis diffusion on each layer with respect to the seed-layer, an effect that is more prominent when KIS is the seed-layer. Once the intra-urban connections are included, the seed-layer effect is significantly diminished, and the crisis propagation is roughly the same for all seed-layers. Moreover, both the average number of affected cities and duration of the crisis diffusion appear to be markedly enhanced with the inclusion of intra-urban connections, an effect that is greater in cases of large RR and small k values. These results complement those of Table 4; Figures 3, 4 as the intensity and the duration of the diffusion are closely connected to the average infected mass <M>.

4 Discussion

Our findings indicate that the Knowledge Intensive Services (KIS) layer is the most prominent layer in this network, structurally, as it was found to be the most populous and densest of all five, with strongly connected, mutually interacting nodes, arranged in intertwined communities. Additionally, our results imply that KIS firms are more likely to be owners while LKIS firms are more likely to be subsidiaries. Moreover, our analysis on the highest ranking cities, according to eight centrality indices (in/out-degree, in/out-weighted-degree, in/out-closeness, betweenness and weighted-betweenness), suggests that Paris is rather more likely to attract owner firms than London. Additionally, it was found that Tokyo tends to harbour more owner firms than subsidiaries, while for Milan, Madrid and Moscow the opposite is more likely. New York appears to be equally balanced between the two types of firms, while all these cities along with Amsterdam play a crucial role in maintaining connections between many other cities in the network. As we previously suggested (Rozenblat, 2021), cities around the world have varying roles and positions in the global networks. Rather than a clear division between global and non-global cities, there exist different levels and types of involvement that cities have in these global networks.

Furthermore, by employing a simple stochastic SIR model, we simulated the propagation of a crisis in both networks to compare the vulnerability of each layer, with respect to the layer on which the crisis originates and to assess the influence of the intra-urban connections on the magnitude of the “infection”. This is a major concern as, if an economic crisis arises in a city or a country, this crisis will have a widespread impact on other cities as well (and likewise in the case of economic growth or knowledge spillovers).

Our results reveal that in the absence of intra-urban connections and under conditions that hinder the spreading (small inter-layer connectivity and large recovery rate), the crisis is most assuredly suppressed very fast, affecting only a small portion of the network. This behaviour can largely be attributed to the structure of the network’s layers, and most notably their corresponding degree distributions. Specifically, the vast majority of the nodes have very low degree, and therefore most nodes have only one (or very few) neighbours to which they can spread the crisis. Additionally, the network is directed, which means that nodes cannot always transmit the crisis to their neighbouring nodes. This directional constraint can result in occasional “trapping” of the infection within specific areas of the network. Moreover, if the crisis does not originate from a node in the Largest Connected Component (LCC), it will remain confined within a smaller network component. As the conditions become more favourable to the spreading of the crisis (higher inter-layer connectivity and lower recovery rate), it affects larger portions of the network and eventually only two outcomes are possible: either - and most likely - the spreading dies out very fast, or, it covers a very large portion of the network. Furthermore, the crisis impact on each layer partly depends on the layer on which the crisis originates. Specifically, the effect of the crisis is highest on all layers when it originates from layer KIS and lowest when it starts from layer LT. Also, layer KIS is typically the most affected layer, although when the conditions particularly favour crisis propagation, differences in impact levels across layers become insignificant.

With the addition of the intra-urban connections, the effect of the crisis diffusion is substantially enhanced, resulting in a greater likelihood that a large portion of the network will be impacted (Figure 3; Table 4). The enhancement becomes greater as the conditions for crisis spreading become more adverse. Furthermore, the disparities in impact levels attributed to the layer of origin are markedly reduced (Figure 4). In terms of overall damage, for the most part the differences across layers are rather minimal, except in case of adverse diffusion conditions.

Moreover, while HT is generally the layer with the lowest overall impact, KIS gradually appears to shift from being the most affected layer to eventually falling below HT in terms of impact and becoming the least affected layer, as conditions become more favourable for crisis propagation. The comparison of the average infected mass <M> between cases 5a and 5b in Figure 4 reveals a small but noticeable decrease (∼1.6%) in the average impact levels on KIS and a marginal one (∼0.2%) on HT, with the addition of the intra-urban links. Also, the levels of <M> on KIS between cases 3a and 3b are roughly the same, with a minor decrease of ∼0.1%. At first glance, these findings appear to be counterintuitive and to contradict the results shown in Table 4.

This reduction occurs because the inclusion of the intra-urban links has two opposing effects on the diffusion. On one hand, it increases the likelihood that the crisis will survive through the initial steps of the simulation and infect a large portion of the network, resulting in a higher incidence of large-M cases (as shown in Table 4). On the other hand, in large-M cases the levels of M are relatively lower than that in the absence of intra-urban links. In other words, the addition of the intra-urban links increases the height of the second peak in the bimodal distribution of M, but it also slightly shifts it to the left.

To gain a deeper understanding of this result we need to examine the stochastic SIR model used and specifically how it maps the integration of the intra-urban links onto the process of crisis diffusion. According to the model, the addition of these links has both positive and negative effects on the process. On one hand, the added links create new pathways for the crisis to spread. Furthermore, the intra-urban connections often stem from very dense sub-graphs of intra-urban firms’ connections. In these cases, the resulting inter-urban links become inter-layer links of exceptionally high weights with very high probability of propagating the crisis to the layer of the opposite side, thus acting as “diffusion-highways” which greatly enhance the spreading across layers. On the other hand, each added link increases the total degree of both adjacent nodes by one, making them more resilient and hindering the spreading of the crisis. These opposing forces act to amplify or impede the diffusion, by respectively increasing either the numerator or the denominator of the stochastic model. The combined effect of these clashing forces leads to the increase in the count of large-M cases and the decrease of the overall average infected mass <M>, across all layers and cases examined. Therefore, the inclusion of intra-urban links results in a complex interplay, which ultimately affects the diffusion outcomes in nuanced ways.

This context offers some insight on previous findings regarding the impact of the intra-urban-links on <M> levels and the seed-layer effect. First, it was found that HT exhibits a significantly lower increase in the number of incoming links compared to other layers, with an enhancement that is 50% lower than the layer with the highest growth rate. This suggests that HT gains much fewer pathways through which the crisis can reach it. Consequently, the combined impact of the aforementioned factors affecting diffusion appears to be less positive for HT than for all other layers, resulting in generally lower <M> levels on HT.

As previously noted, KIS exhibits the lowest increase in both large-M incidence and <M> levels among all layers. Additionally, when KIS is the seed-layer, the increment in <M> levels is the lowest across all layers. In fact, under favourable conditions for crisis spreading, there is even a slight decrease in <M> levels for KIS, with HT experiencing a marginal decrease as well (Figure 4, cases 3b and 5b). However, KIS stands out as the densest layer with the most intra and inter-layer connections, which tend to have very high weights. This leads to a very high large-M incidence for KIS, making it the only layer for which the distribution of M is always bimodal, even in the absence of intra-urban links, for every value of RR and in all cases of seed-layer. Therefore, while the increment for KIS in both incoming and outgoing links is quite high in absolute numbers, the percentage increase is by far the lowest for the outgoing links and the second lowest for the incoming links. Moreover, the distribution of weights of the intra-urban links shows that the relative enhancement of “diffusion-highways'' for KIS is exceptionally low compared to those of the other layers.

Furthermore, the addition of the new links results in an upsurge of the total degrees in the other layers, while the difference in the degrees of KIS nodes is not very high. This means that, on one hand, there is no significant increase in pathways through which KIS can propagate the infection to other layers and, conversely, get infected by other layers. On the other hand, the upsurge in the total degree of the other nodes makes them more resilient, impeding the transmission of the infection from KIS to the other layers that would in turn feed the infection back to KIS. Consequently, it appears that the complex interplay of all these factors results in KIS exhibiting progressively lower <M> levels than the other layers and in exerting lower influence than one might expect on the other layers.

Nonetheless, KIS still is highly influential, having minimal differences from the most influential layer LKIS, and even being the most influential in very favourable conditions for spreading (Figure 4, 5b). However, the seed-layer effect is considerably reduced, resulting in layers having a rather uniform effect on propagation. It is possible to argue that on the basis of the particular diffusion model used, the partial-multiplex, directed network of economic relations between cities has a finite “crisis capacity”. Thus, KIS, which exhibits binomial <M> distribution, even before the addition of the intra-urban links, has reached a state of “saturation”, where further addition of links has little effect on propagation. In fact, under favourable conditions for diffusion, the addition of links can have a negative impact. It is important to note that the results are strongly related to the specific model that was used to simulate the spreading of an economic crisis, which includes a resistance factor that protects from the infection. A different model would likely produce different results, as in (Battiston et al., 2018), in which the denominator of the model used for the simulation process was taken to be the total weighted degree of the node instead of the total degree. In that case, the more intense a connection is, the stronger the protection against infection becomes. This led to an overestimation of the protective factor, especially in the case of intra-urban connections which typically have high weights, as they represent very strong interactions. Thus, this model resulted in findings that were inconsistent with real-world events such as the one witnessed in London, in 2008, when a single crisis brought on cascading failures that put thousands of people out of job. On the contrary, the model employed in the present study yields more intuitive results, which support real-world context such as the snowball effect seen in London.

In general, the addition of the intra-urban links for the most part enhances the overall crisis impact, particularly when the event originates in a layer that is not very dense or connected, or when the conditions hinder the diffusion. However, when the crisis starts from a dense and well-connected layer like KIS, the impact of the intra-urban links is less prominent, and could even have a protective effect when the conditions are highly favourable for spreading. In essence, the layers become significantly more uniform regarding the crisis impact with respect to the layer it originates from, i.e., the intra-urban connections level-out the seed-layer effect considerably.

This effect of the intra-urban linkages provides a valuable insight into the “agglomeration economies” that stem from the impact of local networks on the global one (Rozenblat, 2010; Rozenblat, 2021). The resulting spreading equalization across activity sectors highlights the role of cities in the connections between activities that share numerous services and cities’ properties, through which they engage in mutual learning and efficiency reinforcement activities (Duranton and Puga, 2004).

Future work could extend this empirical study to include recent data and also to investigate the networks of cities on the lower level of the micro-networks of firms that will enable us to incorporate intra-urban interactions of the same activity sector type (the intra-urban/intra-layer networks of cities), which are inevitably left out on the higher level of cities. Also, the inclusion of more recent data would enable us to explore the repercussions that we are inclined to believe that the recent COVID-19 pandemic and the sanctions on the Russian economy have had on the system. The pandemic’s economic strain has affected various industries, potentially altering their vulnerability to subsequent crises. While the ownership structures of many large, diversified firms may have remained stable during the pandemic’s initial phases, the long-term economic repercussions could lead to mergers, acquisitions, or even bankruptcies. Such shifts, over an extended period, have the potential to reconfigure the network, even if these changes are not immediately evident. Moreover, the sanctions on the Russian economy have directly influenced ownership structures, with Moscow-based firms adjusting their foreign stakes due to financial and regulatory pressures. Simultaneously, foreign entities have exhibited a tendency to pull back from Russian investments. This has likely reduced Moscow’s global network centrality. However, as foreign investments decline, Moscow might see strengthened internal linkages and a shift in economic partners, e.g., in Asia, further modifying the network dynamics. In the context of the contemporary rapid change in this international geopolitical reconciliations and boycotts, the pandemic aftermath and also perhaps considering the possible urban economic transformations due to climate warming, the gained insights of such analyses could help cities to better monitor and plan their future sustainable development.

5 Conclusion

The goal of this study was to investigate the characteristics of firms’ interactions within and across the activity sectors and the role of the intra-urban connections in case of crisis propagation. The partial-multiplex, directed network of cities of multinational firms, constructed through ownership relations and divided in layers by activity sector was examined in two states: one with the intra-urban links excluded and another with these link included. The difference between the two states outlined the strong role of intra-cities’ processes of networking in the global economy.

Through the use of a simple stochastic model that accounts for both positive and negative factors, i.e., influential ownership relations and stamina of the city, respectively, we simulated a crisis diffusion on a network of cities, and provided insight into the inner workings of urban economic networks. These networks that operate within cities but have far-reaching effects on inter-city dynamics, have remained a “black box” for many scholars. Our analysis sheds light on these complex processes, contributing to a better understanding of urban economic systems.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: The data is not publishable at the individual level of companies. Requests to access these datasets should be directed to CR, Celine.rozenblat@unil.ch.

Author contributions

MT: Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft, Writing–review and editing, Conceptualization. MK: Data curation, Formal Analysis, Methodology, Software, Visualization, Writing–original draft, Writing–review and editing, Conceptualization. PA: Conceptualization, Project administration, Resources, Supervision, Writing–review and editing. CR: Conceptualization, Investigation, Methodology, Project administration, Resources, Supervision, Writing–original draft, Writing–review and editing, Data curation.

Funding

The authors declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

This article is based on Chapter 4 of the first author’s PhD thesis (Tsouchnika, 2020).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author PA declared that they were an editorial board member of Frontiers at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹A producer service firm is one that serves businesses, as opposed to consumer service firm that serve individuals and households (Taylor et al., 2012).

²Bureau van Dijk Electronic Publishing http://www.bvdep.com/

³ORBIS 2010, 2013: BvD–University of Lausanne (CitaDyne group) and University of Paris (ERC GeoDiverCity group) http://geodivercity.parisgeo.cnrs.fr/blog/

⁴For the sake of simplicity, we will refer to this spatial unit as “city”.

⁵Each such ownership relation counts for 1.

⁶There are no intra-urban links in the diagonal elements of Table 3, as they would yield self-loops on each layer.

⁷Each set comprises 10,000 simulations; all results are the average of one set of simulations.

References

Alderson, A. S., and Beckfield, J. (2004). Power and position in the world city system. Am. J. Sociol. 109, 811–851. doi:10.1086/378930

CrossRef Full Text | Google Scholar

Bathelt, H., Malmberg, A., and Maskell, P. (2004). Clusters and knowledge: local buzz, global pipelines and the process of knowledge creation. Prog. Hum. Geogr. 28, 31–56. doi:10.1191/0309132504ph469oa

CrossRef Full Text | Google Scholar

Battiston, S., Caldarelli, G., and Garas, A. (2018). Multiplex and multilevel networks. Oxford University Press.

Google Scholar

Battiston, S., Delli Gatti, D., Gallegati, M., Greenwald, B., and Stiglitz, J. E. (2012). Liaisons dangereuses: increasing connectivity, risk sharing, and systemic risk. J. Econ. Dyn. control 36, 1121–1141. doi:10.1016/j.jedc.2012.04.001

CrossRef Full Text | Google Scholar

Bertrand, A. (2005). Measuring foreign direct investment,” statistics, Knowledge and policy: key Indicators to inform decision making, 597–618.

Google Scholar

Camagni, R., and Capello, R. (2004). The city network paradigm: theory and empirical evidence. Contributions Econ. Analysis 266, 495–529. doi:10.1016/S0573-8555(04)66016-0

CrossRef Full Text | Google Scholar

Corporations, T. (2007). World investment report.

Google Scholar

Dickison, M., Havlin, S., and Stanley, H. E. (2012). Epidemics on interconnected networks. Phys. Rev. E 85, 066109. doi:10.1103/physreve.85.066109

PubMed Abstract | CrossRef Full Text | Google Scholar

Duranton, G., and Puga, D. (2004)., 4. Elsevier, 2063–2117. Micro-foundations of urban agglomeration economies. Handb. regional urban Econ. doi:10.1016/S1574-0080(04)80005-1

CrossRef Full Text | Google Scholar

Eames, K. T. D., Read, J. M., and Edmunds, W. J. (2009). Epidemic prediction and control in weighted networks. Epidemics 1, 70–76. doi:10.1016/j.epidem.2008.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Gallos, L. K., and Argyrakis, P. (2003). Distribution of infected mass in disease spreading in scale-free networks. Phys. A Stat. Mech. its Appl. 330, 117–123. doi:10.1016/j.physa.2003.08.002

CrossRef Full Text | Google Scholar

Garas, A., Argyrakis, P., Rozenblat, C., Tomassini, M., and Havlin, S. (2010). Worldwide spreading of economic crisis. New J. Phys. 12, 113043. doi:10.1088/1367-2630/12/11/113043

CrossRef Full Text | Google Scholar

Joisce, J., and Patterson, N. (2006). “Direct investment,” in Fourth meeting of the advisory expert group on national accounts.

Google Scholar

Kamp, C., Moslonka-Lefebvre, M., and Alizon, S. (2013). Epidemic spread on weighted networks. PLoS Comput. Biol. 9, e1003352. doi:10.1371/journal.pcbi.1003352

PubMed Abstract | CrossRef Full Text | Google Scholar

Keeling, M. J., and Rohani, P. (2008). Modeling infectious diseases in humans and animals. Princeton, NJ: princeton univ.

Google Scholar

Kermack, W. O., and McKendrick, A. G. (1927). A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A, Contain. Pap. a Math. Phys. character 115, 700–721. doi:10.1098/rspa.1927.0118

CrossRef Full Text | Google Scholar

Laboy, M., and Fannon, D. (2016). Resilience theory and praxis: a critical framework for architecture. Enq. ARCC J. Archit. Res. 13. doi:10.17831/enq:arcc.v13i2.405

CrossRef Full Text | Google Scholar

Lennert, M., Van Hamme, G., Patris, C., Smȩtkowski, M., Płoszaj, A., Gorzelak, G., et al. (2010). J. Hryniewicz and others. FOCI Future Orientation for Cities.

Google Scholar

Manual, O. (2005). “Guidelines for collecting and interpreting innovation data,” in A joint publication of OECD and eurostat, organization for economic Co-operation and development. Statistical office of the European communities.

Google Scholar

Newman, M. (2018). Networks: an introduction. New York, USA: Oxford University Press.

Google Scholar

Newman, M. E. J. (2002). Spread of epidemic disease on networks. Phys. Rev. E 66, 016128. doi:10.1103/physreve.66.016128

PubMed Abstract | CrossRef Full Text | Google Scholar

Pan, F., Hall, S., and Zhang, H. (2020). The spatial dynamics of financial activities in Beijing: Agglomeration economies and urban planning. Urban Geogr. 41, 849–864. doi:10.1080/02723638.2019.1700071

CrossRef Full Text | Google Scholar

Rogov, M., Rozenblat, C., Bida, M., and Shutters, S. T. (2022). Evaluating multilevel resilience of Russian urban economies 2010–2019. Ecol. Soc. 27, art37. doi:10.5751/es-13691-270437

CrossRef Full Text | Google Scholar

Rozenblat, C. (2010). Opening the black box of agglomeration economies for measuring cities’ competitiveness through international firm networks. Urban Stud. 47, 2841–2865. doi:10.1177/0042098010377369

CrossRef Full Text | Google Scholar

Rozenblat, C. (2015). Inter-cities' multinational firm networks and gravitation model (international forum). Ann. Assoc. Econ. Geogr. 61, 219–237.

Google Scholar

Rozenblat, C. (2020). Extending the concept of city for delineating large urban regions (LUR) for the cities of the world. Cybergeo: European Journal of Geography.

Google Scholar

Rozenblat, C. (2021). “Intracity and intercity networks of multinational firms,” in Handbook of cities and networks. Cheltenham, UK: (Edward Elgar Publishing). 2010-2019.

Google Scholar

Rozenblat, C., and Pumain, D. (1993). The location of multinational firms in the European urban system. Urban Stud. 30, 1691–1709. doi:10.1080/00420989320081671

CrossRef Full Text | Google Scholar

Rozenblat, C., Zaidi, F., and Bellwald, A. (2017). The multipolar regionalization of cities in multinational firms' networks. Glob. Netw. 17, 171–194. doi:10.1111/glob.12130

CrossRef Full Text | Google Scholar

Santos, J. A. C., and Rumble, A. S. (2006). The American keiretsu and universal banks: investing, voting and sitting on nonfinancials’ corporate boards. J. Financial Econ. 80, 419–454. doi:10.1016/j.jfineco.2005.03.011

CrossRef Full Text | Google Scholar

Sassen, S. (1991). The global city. New York.

Google Scholar

Stiglitz, J. E. (2010). Risk and global economic architecture: why full financial integration may be undesirable. Am. Econ. Rev. 100, 388–392. doi:10.1257/aer.100.2.388

CrossRef Full Text | Google Scholar

Taylor, P. J. (2010). Specification of the world city network. Geogr. Anal. 33, 181–194. doi:10.1111/j.1538-4632.2001.tb00443.x

CrossRef Full Text | Google Scholar

Taylor, P. J., Ni, P., Derudder, B., Hoyler, M., Huang, J., and Witlox, F. (2012). Global urban analysis: a survey of cities in globalization. London, UK: Routledge.

Google Scholar

Tsouchnika, M., “Uncovering structural, evolutionary and spreading-phenomena characteristics of complex networks and systems using statistical mechanics methods on real-world data,” 2020 [dissertation/PhD thesis], Faculty of Sciences, School of Physics, Department of Condensed Matter and Materials Physics, Aristotle University of Thessaloniki (AUTh). doi:10.12681/eadd/48463

CrossRef Full Text | Google Scholar

Vitali, S., Glattfelder, J. B., and Battiston, S. (2011). The network of global corporate control. PloS one 6, e25995. doi:10.1371/journal.pone.0025995

PubMed Abstract | CrossRef Full Text | Google Scholar

Wall, R. (2009). Netscape: cities and global corporate networks.

Google Scholar