Abstract
The non-orthogonal multiple access (NOMA) scheme has been recognized as a promising candidate for future generation wireless communication networks that require a high data rate and spectral efficiency. In order to achieve a superior spectral efficiency, the orthogonal frequency division multiplexing (OFDM) technique with the robust channel estimation algorithm can be combined with the NOMA scheme. However, due to the inherent problem of inter-carrier interference in the OFDM-based systems, channel estimation using training symbols are not usually perfect. Furthermore, the successive interference cancellation (SIC) process commonly carried out in NOMA systems to address the interference among users is also imperfect under practical scenarios. Thus, a theoretical framework of the OFDM-based NOMA system to analyze the effect of both the imperfect SIC and channel estimation errors is presented in this paper. In particular, the effect of both the channel estimation errors and imperfect SIC, introduced at the receiver, on the bit error rate (BER) performance metric is analyzed under Rayleigh fading channel conditions. Our analytical results are compared to the corresponding simulation results for different design parameters. It is shown that the analytical and simulation results are in good agreement. Moreover, while revealing the importance of CSI and SIC, the results equally show that the assumption of perfect CSI and SIC is not practical, hence the need for accurate schemes for improved BER performance.
1 Introduction
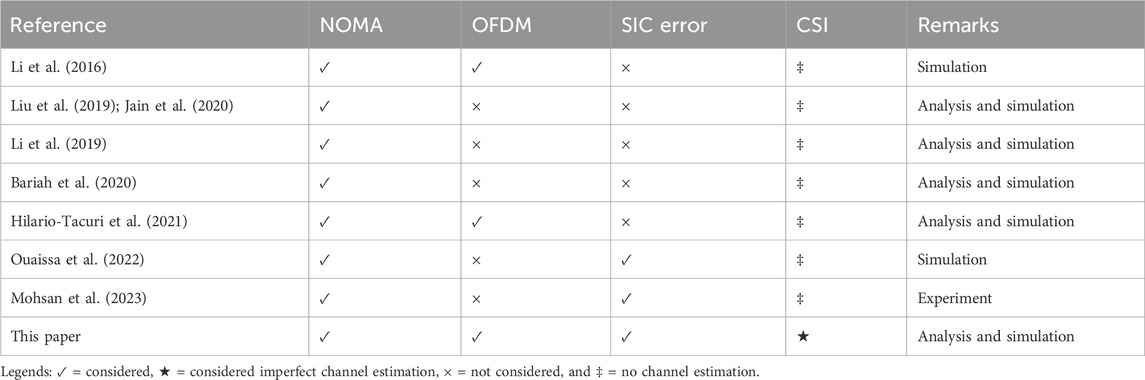
Future wireless networks are expected to support higher data rates, very large network capacity, high spectral efficiency, and more mobility. The non-orthogonal multiple access (NOMA) scheme is seen as a very viable and attractive scheme that can effectively meet the demands of future radio access networks and applications. Earlier multiple access schemes have focused on the orthogonal techniques (Gilhousen et al., 1991; Brannstrom et al., 2002; Liu et al., 2006; Wang et al., 2006; Liu et al., 2017). Although orthogonal techniques ensure the avoidance of intra-cell interference, the techniques usually involve stringent requirements. Orthogonal techniques also require a sufficient distance between re-used channels, which results in a reduced cellular spectral efficiency. On the other hand, the NOMA scheme ensures a high spectral efficiency and mass connectivity. The NOMA scheme is able to accommodate concurrent users through non-orthogonal resource allocation (Liu et al., 2019; Jain et al., 2020; Li et al., 2019; Bariah et al., 2020). Although this comes with an increased inter-cell interference (ICI), the successive interference cancellation (SIC) technique (Liu et al., 2017; Liu et al., 2019) is exploited to mitigate the ICI at the receiver.
In order to achieve a higher spectral efficiency and a better throughput, the NOMA scheme can be combined with the orthogonal frequency division-multiplexing (OFDM) scheme (Li et al., 2016; Moose, 1994; Chen, 2002; Morelli and Mengali, 2000; Hilario-Tacuri et al., 2021). The combination of the NOMA and the OFDM scheme, however, comes with challenges such as the peak-to-average power ratio (PAPR) and channel estimation problems (Mohsan et al., 2023; Kay, 1995). In Liu et al. (2019); Jain et al. (2020), the BER analysis of NOMA-enabled visible light communication systems was studied. Furthermore, the study in Li et al. (2019) provided a comprehensive performance analysis for spatial modulation-aided cooperative NOMA, while Bariah et al. (2020) carried out a study on error performance of NOMA-based systems with power constraints. In Hilario-Tacuri et al. (2021), authors focused on deriving the analytical expression of BER for the downlink NOMA-OFDM system in the presence of a high-power amplifier (HPA) with memory. Nevertheless, it is commonly assumed in the literature (Liu et al., 2019; Jain et al., 2020; Bariah et al., 2020; Hilario-Tacuri et al., 2021) that the successive interference cancellation method commonly carried out in the NOMA system to address the interference among users is perfect. However, this is not always true in practice, and the inaccurate interference assessment of the multiple users using SIC detection can lead to more prominent errors and affect the bit error rate (BER) performance of the system. So far in the literature, not so much has been done to mitigate the effect of the inaccurate interference assessment and to achieve some improvement in providing more accurate reconstruction in using SIC detection. In Ouaissa et al. (2022), the authors considered mitigating the effect of imperfection in NOMA by introducing a cancellation error in the receiver, while Mohsan et al. (2023) proposed a recurrent neural network-based guided frequency interference coefficient estimation algorithm in a NOMA visible light communication (VLC) system.
This work focuses on the theoretical BER analysis by derivations of closed-form analytical expressions to analyze the performance of the OFDM-based NOMA system. Unlike Li et al. (2016); Hilario-Tacuri et al. (2021) who investigated a downlink NOMA-OFDM system, our paper considers an uplink system. The consideration for the uplink introduces more challenges which include the need for accurate CSI for both users and potential error propagation on the weaker signal due to imperfect SIC. Consequent upon this, we studied a system that is plagued with channel estimation or channel state information (CSI) errors and successive interference cancellation (SIC) errors. To date, the BER derivation and analysis for an OFDM-based NOMA system with both channel estimation and SIC errors have not been comprehensively addressed in the literature. This gap is filled by deriving and analyzing the closed-form BER expressions using binary phase-shift keying (BPSK), quadrature phase-shift keying (QPSK), and 16-QAM modulation schemes in a multipath-fading channel. Notably, the approach employed for the BER derivations and analysis in this work can be easily extended to other modulation sizes. The derived BER expressions are in a simple form that requires no numerical integration, thus providing a practical and efficient tool for performance evaluation. Table 1 outlines the main differences between our work and the previous studies on the BER of the NOMA system.
TABLE 1
| Reference | NOMA | OFDM | SIC error | CSI | Remarks |
|---|---|---|---|---|---|
| Li et al. (2016) | Simulation | ||||
| Liu et al. (2019); Jain et al. (2020) | Analysis and simulation | ||||
| Li et al. (2019) | Analysis and simulation | ||||
| Bariah et al. (2020) | Analysis and simulation | ||||
| Hilario-Tacuri et al. (2021) | Analysis and simulation | ||||
| Ouaissa et al. (2022) | Simulation | ||||
| Mohsan et al. (2023) | Experiment | ||||
| This paper | Analysis and simulation |
Summary of the NOMA-based system in the literature.
Legends: = considered, = considered imperfect channel estimation, = not considered, and = no channel estimation.
Moreover, the results obtained in this study can significantly benefit research involving machine learning (ML) techniques. The closed-form BER expressions and insights into the impact of channel estimation and SIC errors can serve as a valuable benchmark for training and validating ML models. These models can be designed to optimize power allocation, improve the channel estimation accuracy, and mitigate the effects of SIC errors in OFDM-based NOMA systems. By integrating the analytical results from this work, future research direction can enhance the robustness and efficiency of ML-driven solutions, fostering advancements in adaptive and intelligent communication systems. By bridging the gap between theoretical analysis and practical implementation, this work not only advances the understanding of OFDM-based NOMA systems but also lays the groundwork for future ML-driven optimization in fifth generation (5G) and beyond wireless communications.
The main contributions in this paper, therefore, include the following:
1. The closed-form bit error expressions for OFDM-based NOMA systems are derived using BPSK, QPSK, and 16-QAM modulation schemes. This is different from the works in Li et al. (2016); Hilario-Tacuri et al. (2021). While Li et al. (2016) merely present the BER results obtained using computation and simulation with the assumption of perfect SIC and without consideration for channel estimation, the authors in Hilario-Tacuri et al. (2021),, although analytically investigated the BER performance of the OFDM-based NOMA system, did not consider channel estimation, and the work equally assumes a perfect SIC at the receiver in the analysis.
2. The impact of channel estimation errors on the BER performance of OFDM-based NOMA systems is investigated. In addition, this work theoretically shows the importance of power allocation and channel estimation in OFDM-based NOMA systems.
3. The effect of SIC error on the BER performance of OFDM-based NOMA systems is investigated. The effect of the SIC error is practically considered during the modeling and derivation of the closed-form BER expressions for the various modulation schemes considered.
The rest of this paper is organized as follows: Section 2 presents the NOMA-OFDM system model. Section 3 presents the closed-form BER derivations and analysis. Section 4 presents the simulation results, while Section 5 presents the conclusion.
2 The NOMA-OFDM system model
An uplink OFDM-based NOMA system with users is considered, where the users transmit signals , on the subcarrier . The SIC technique, which is a vital part of the OFDM-NOMA system, is utilized to separate the superimposed signals of various users. Moreover, transmit power is assigned to a particular user , based on its relative distance from the base station (BS). Thus, the signal for the th user on the subcarrier after power allocation can be mathematically represented as in Equation 1 (Wang et al., 2021; Chen, 2016)
For ease of notation, the superscript represents the type of data symbol. Although denotes the training symbol, represents the data symbol. Therefore, the received frequency domain signal, after the fast Fourier transform (FFT) has been performed, in the presence of carrier frequency offset (CFO) can be expressed aswhere in Equation 2, the parameter and . The parameter denotes the additive white Gaussian noise (AWGN) with covariance , while is an identity matrix. The covariance matrices of the channel can be also expressed as . In addition, the parameter H can be represented as in Equation 3 (Lopez-Martinez et al., 2010; Yih, 2007; Kara and Kaya, 2018; Savaux et al., 2016),where is the impulse response of the channel in the time domain, is the effective OFDM symbol period, and is the number of multipath, while the path gains are independently circularly symmetric complex Gaussian random variables. Two users (i.e., ) are assumed to minimize the multiuser interference (MUI) on each subcarrier and reduce complexity. Thus, the received signal can be expressed as in Equation 4awhich can be, otherwise, rewritten as Equation 4bwhere and . The parameters and represent the transmit signals from user 1 and user 2, respectively, while and represent the path losses of the first user and second user, respectively, from the base station. The path loss of a particular user from the base station is related to the distance, by the expression (Björnson et al., 2013), while is the total power.
3 The BER analysis for NOMA-OFDM
In this section, the OFDM-based NOMA system is analyzed to consider the effect of both the imperfect SIC and channel estimation errors on the bit error performance metric.
3.1 BPSK derivation
The BER expressions for an uplink OFDM-based NOMA system is derived and analyzed in this section. The BER expression is derived using BPSK signaling in a multipath fading channel. It is assumed that BS has the knowledge of the relative distance of the users in the OFDM-based NOMA system. Thus, the user with a shorter relative distance to the BS is taken as the stronger user, while the farther user is taken as the weaker user. For the purpose of this work, is taken as the stronger user, while is taken as the weaker user. Thus, for the channel estimation of the first user (user 1), the received training symbol can be expressed as in Equation 5and the covariance of can be obtained as (Hilario-Tacuri et al., 2021). A simple channel estimation method, based on training symbols, is given by Kay (1995); Savaux et al. (2016) as written in Equation 6.Thus, from Equation 6, a more compact expression can be obtained as in Equation 7where
Therefore, the received data symbol after FFT can be expressed as in Equation 8where and the parameters and denote the data symbols of user 1 and user 2, respectively.
3.1.1 Impact of SIC and channel estimation errors
For BPSK modulation, the impact of SIC imperfection and channel estimation errors on the error probability can be expressed in Equation 9 as (Savaux et al., 2016)
In Kara and Kaya (2018), to obtain the error probability, a joint distribution for the sum of the independent non-identical Rayleigh channel distributions is obtained. Furthermore, the probability density function for the difference of two independent non-identical Rayleigh distributions is derived. These joint distributions are then used to obtain the bit error probability of the NOMA system. However, a much simpler method is to obtain the error probability using the approach in Proakis (2001), which can be derived in such a way that numerical integration is not required. Hence, the derivation of follows Proakis (2001) and the Appendix, in order to characterize the effects of SIC and channel estimation errors on the bit error of the NOMA-OFDM system. Therefore, is obtained aswhere and are computed for the user 1 as follows:
The average bit error can be expressed in Equation 17 as
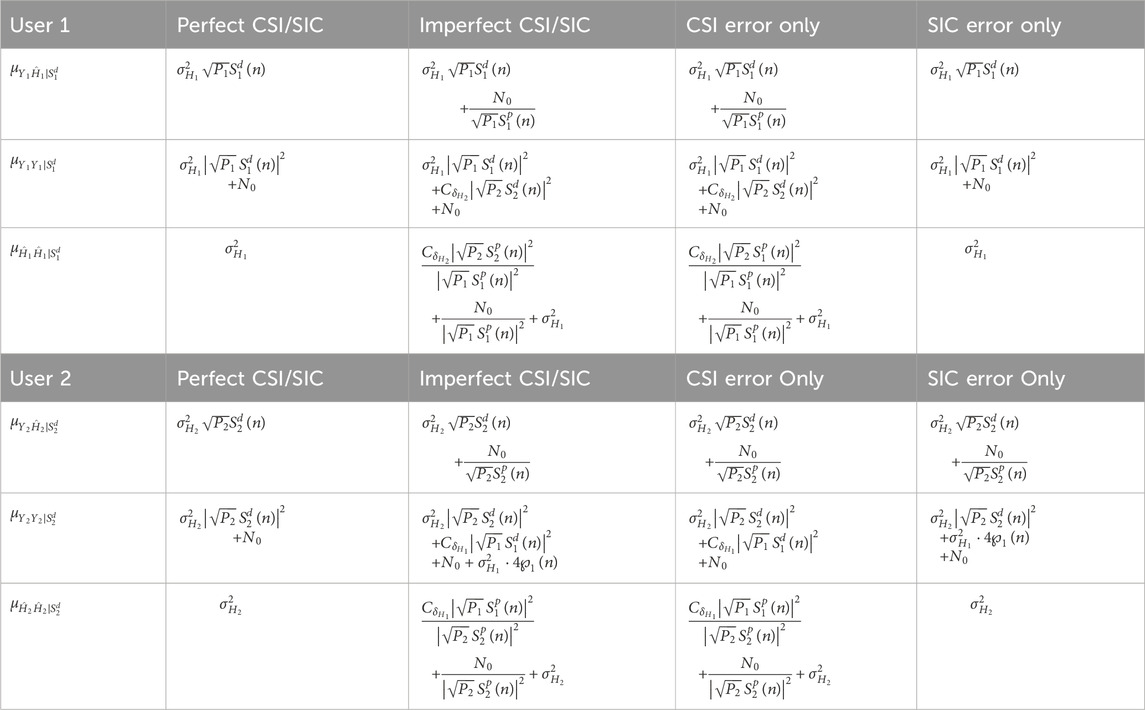
Since the SIC is only performed on user 2, it is assumed that there is no SIC error on user 1. Therefore, the impact of CSI errors only on the BER performance of user 1 can be considered by rewriting , , and in Equations 12, 14, 16 as , , and in Equations 18, 19, 20 assuch that Equation 10 can be written as Equation 21:where, , and . The expression in Equation 21 indicates that error probability increases with increasing CSI components in the denominator. However, for a system with perfect channel estimation and no SIC error at the receiver, Equation 21 reduces to Equation 22 as
If we assume results in a value greater than zero, then the error probability increases with increasing noise power only.
Now for the second user, the received data symbol before cancellation can be expressed in Equation 23 asAfter cancellation, we can obtain Equation 24 and, subsequently Equation 25 as follows:where and the covariance of can be expressed as (Kay, 1995). The parameter denotes the SIC error with its covariance since it assumes three values with probabilities and , respectively. Therefore, the covariance can be written as . In the literature, the SIC term is typically modeled as a Gaussian random variable (Im and Lee, 2019), and performance results are given for various values of . However, this does not model the SIC error correctly since depends on the SNR experienced by user 1. Thus, the SIC error, which is denoted as , should be . Furthermore, is the covariance matrix for , while the identity matrix is denoted by (Kay, 1995).
The expression for channel estimation is obtained in Equation 26 aswhere and . Thus, for BPSK modulation for the second user, the bit error is expressed in Equation 27 as
To obtain , and are computed for user 2 as follows:Therefore,
where Equations 29, 31, and 34 are obtained from Equations 28, 30, and 33 respectively. In a similar fashion to Equation 10, the probability of bit error on user 2 can be written as in Equation 35:
The average bit error can be expressed in Equation 36 as
The impact of SIC errors and the CSI errors on the BER performance can be considered under the following two scenarios as
imperfect CSI, perfect SIC and
imperfect SIC, perfect CSI.
Imperfect CSI, perfect SIC:
Under the scenario of imperfect CSI but a perfect interference assessment at the receiver, , , and in Equations 29, 32, 34 can be written as , , and in Equations 37–39 as
such that
Equation 35can be written as
Equation 40:where
,
, and
. The expression in
Equation 40indicates that error probability increases with increasing CSI components in the denominator.
Imperfect SIC, perfect CSI:
Analogous to Equations 37–39, the effect of the imperfection on SIC only (while it is assumed that there is perfect channel estimation) on the parameters , , and can be expressed as in Equations 41–43 respectivelywhere the expression in Equation 35 can now be written as in Equation 44:
The expression in Equation 44 shows that error probability increases with increasing imperfection in the interference assessment by the SIC at the receiver. As the component of the SIC, i.e., increases, the parameter increases.
However, for a system with perfect channel estimation and a perfect interference assessment at the receiver, the expressions in Equations 40, 44 reduce to Equation 45 as
If we assume results in a value greater than zero, then the error probability increases with increasing noise power only. Table 2 shows the summary for the derived BPSK scheme.
TABLE 2
| User 1 | Perfect CSI/SIC | Imperfect CSI/SIC | CSI error only | SIC error only |
|---|---|---|---|---|
| User 2 | Perfect CSI/SIC | Imperfect CSI/SIC | CSI error Only | SIC error Only |
|---|---|---|---|---|
Summary of the BPSK scheme.
3.2 QPSK derivation
The closed-form BER expressions for the BPSK-modulated OFDM-based NOMA have been derived in Section 3.1. Here, the BER expression for an OFDM-based NOMA, using QPSK signaling, is considered. Generally, the constellation of QPSK can be expressed mathematically as in Equation 46
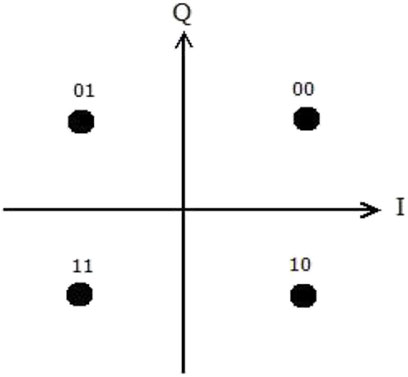
As shown in Figure 1, using Gray encoding, two information bits are mapped into a QPSK constellation symbol. In a scenario where perfect channel estimation is assumed, one constellation symbol can be sent as a result of the symmetry of the constellations and decision boundary. However, when considering an OFDM-based NOMA system with channel estimation errors, the constellations of the demodulated signals are scaled and rotated. Therefore, in this case, two constellation symbols are sent and the BER of the most significant bit (MSB) and the BER of the least significant bit (LSB) are then computed. Now, for the first user, considering two constellation symbols and , it can be seen from Figure 1 that the decision boundary for the MSB is the real axis. Thus, the BER of the MSB can be computed for the first user as
FIGURE 1
QPSK constellation.
For the BER of the LSB for the first user, the decision boundary is the imaginary axis. Thus, considering two constellation symbols and , the BER of the LSB can be computed as
The average bit error can then be expressed in Equation 49 as
The expressions in Equations 47, 48 are computed using Lemma 1 (See Supplementary Appendix S1), while and are computed as derived in Equations 11, 13, 15. Furthermore, for user 2, the same approach can be followed, with the bit error for the MSB and LSB given as in Equations 50 and 51respectively, while and are obtained as expressed in Equations 29, 32, 34.
3.3 16-QAM derivation
Here, the 16-QAM constellation, which is generally denoted by , is considered (Chen, 2016). The normalization coefficient is represented as , while and can take the values 1 or 3. The 16-QAM constellation with Gray coding is as shown in Figure 2. Moreover, the 16-QAM analyses can be divided into two parts, namely, the MSB and the LSB. As seen in the figure, the first and the third bits correspond to the in-phase (I) components, while the second and fourth bits correspond to the quadrature bits (Q). The Gray encoder assigns the bits 01, 00, 10, and 11 to the levels , respectively, where . The arrangement and the decision boundaries for the MSB and the LSB of the I/Q components are shown in the second and third lines of Figure 2, respectively (Chen, 2016). For this analysis, the BER calculation for only the I components is considered since the and components are symmetrical. Now, let the constellation of 16-QAM be denoted as . Let be the set of the four 16-QAM constellation symbols with as their I-component, which can be expressed as . Likewise, let the set of the four 16-QAM constellation symbols having as their I-component be denoted by , which can be expressed as . As the decision boundary for the MSB bit is the imaginary axis, the error probability of the MSB bit of the I-component can be expressed in Equation 52 as
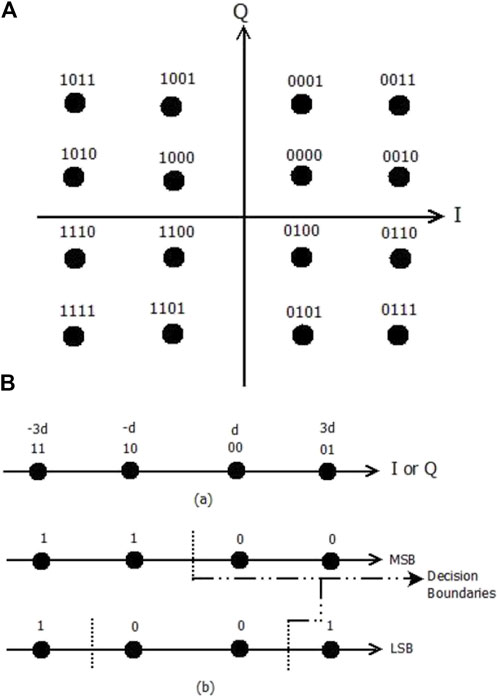
FIGURE 2
16-QAM constellation with Gray encoding: (A) 16-QAM constellation. (B) 16-QAM constellation (bit-by-bit demapping).
Next is to obtain the decision boundary for the LSB bit, which are and on the plane. Calculating the error probability of the LSB bit is not as straightforward as that of the MSB bit, which directly follows Lemma 1. In order to obtain the error probability of the LSB bit, in such a way that it is in the exact form as Lemma 1, the variable needs to be transformed into a new variable . Therefore, considering the probability in Equation 53,where denotes the decision variable at the detector of the communication system (please refer to Supplementary Appendix S1). A new variable can be defined in Equation 54 asHence,
Now, based on Equation 55, the LSB can be obtained using Lemma I. Therefore, , , and are computed as follows in Equations 56 and 57:while is given in Equation 15.
Therefore, can be computed as in Equation 58
Then, the average BER for the 16-QAM constellation can be expressed in Equation 59 as
Now, to obtain the BER for the second user, the error probability of the MSB bit of the I-components can be expressed in Equation 60 as
In order to obtain the error probability of the LSB for the second user, a new variable is obtained as in the case of the first user. Therefore, considering the probability as expressed in Equation 61,
Let , which can be written as Equation 62Thus,
Based on Equation 63,, , and are computed as follows in Equations 64–66:while is given in Equation 34.
4 Numerical results
In this section, the BER performances of the different modulation schemes considered are evaluated using the expressions derived in Section 3. The results are validated using simulations. The NOMA-OFDM system, in the presence of SIC and channel estimation errors, is implemented with 64 subcarriers and the cyclic prefix of length 16. The OFDM subcarrier spacing is , while the carrier center frequency is . The power delay profile of the multipath Rayleigh channel decays exponentially (Lopez-Martinez et al., 2010; Yih, 2007). Furthermore, the root mean square delay spread is , and the number of training symbols used for channel estimation is 2. The transmit power dBm and SNR = dBm, where . The BPSK, QPSK, and 16-QAM modulation schemes are considered. For the purpose of this work, the least-squares method is used for analytical purposes. Very importantly, because an uplink NOMA-based system is considered, the analysis of the SIC imperfections would be limited to the weaker signal (i.e., user 2) only since user 1 can be decoded without interference cancellation.
4.1 Impact of the modulation order on BER performance
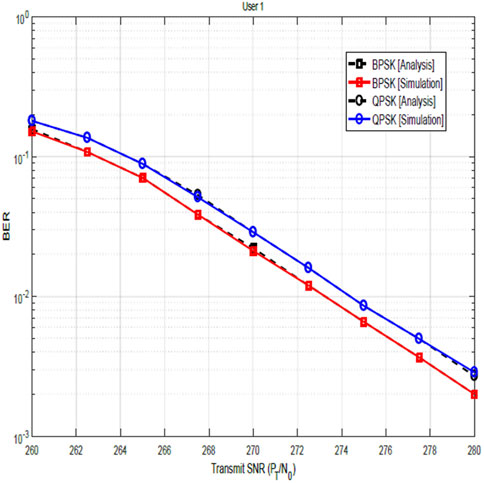
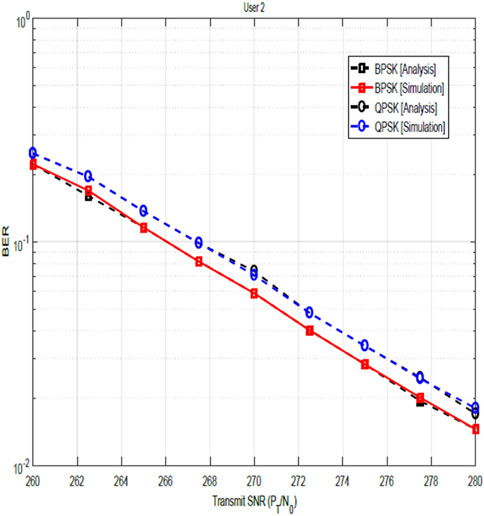
Figures 3, 4 illustrate the BER performances of the NOMA-OFDM system for user 1 and user 2, respectively, for BPSK and QPSK modulation schemes after channel estimation and SIC. The solid lines are obtained from simulations, while the dotted lines represent the plots from the theoretical computation. From these results, the following can be observed: ) user 1 has lower BER than user 2 and ) the BER is lower at a lower modulation order than at the higher modulation order. Although the former could be a result of the combined effects of the impact of SIC error and the reduced SNR for user 2 since it is the user with a weaker signal, the latter is essentially because lower modulation schemes have fewer possible symbol states, making them more robust against noise and signal degradation. It can be seen that the theoretical analysis closely matches the simulation results.
FIGURE 3
BER vs. transmit SNR for user 1.
FIGURE 4
BER vs. transmit SNR for user 2.
4.2 Impact of channel estimation errors on BER performance
In Figures 5, 6, the BER versus transmit SNR plots for the QPSK and the 16-QAM modulation schemes are shown respectively. For these plots, the BER performance of user 1 and user 2 is compared. It is assumed that the channel estimation and SIC are perfect. As modeled in Section 2, the user with the stronger signal and the user with the weaker signal are determined based on their relative distance from the base station. The path loss of a particular user is related to its distance from the base station and can be evaluated as dB (Lopez-Martinez et al., 2010). It is assumed that the distances of user 1 and user 2 from the base station are and , respectively. The total power dBm. Using these values, it can be seen from the plot that the average difference between the performance of the two users evaluated as is approximately due to path loss. This difference can increase even further in an imperfect CSI scenario. This reveals, theoretically, the importance of optimum power allocation in NOMA-OFDM systems. Employing an optimized power allocation method would ensure that the difference in performance loss among users is reduced.
FIGURE 5
BER of QPSK-modulated NOMA-OFDM signals under perfect conditions.
FIGURE 6
BER of 16-QAM-modulated NOMA-OFDM signals under perfect conditions.
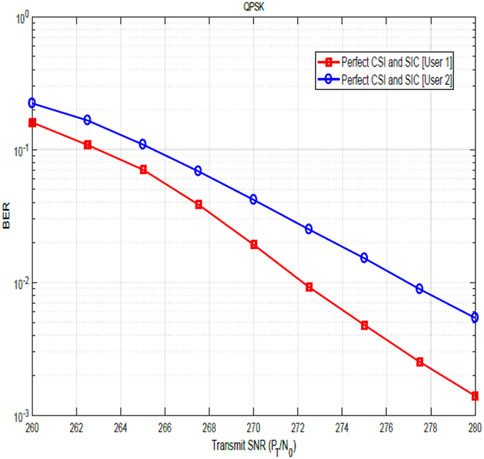
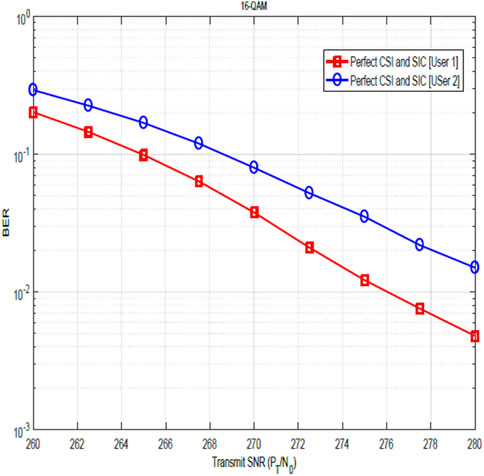
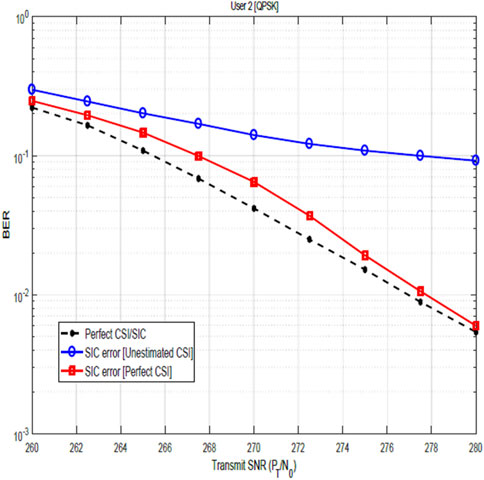
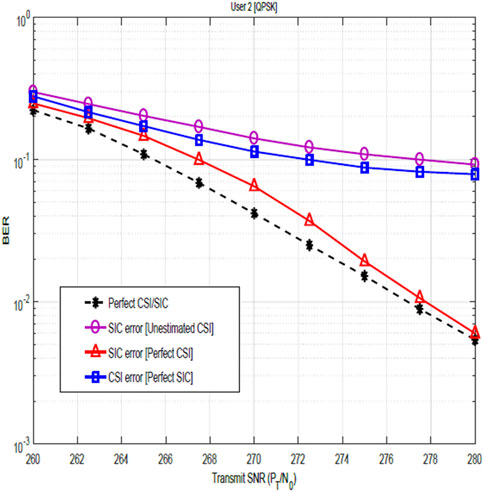
Figures 7, 8 show the relevance of CSI and the impact of CSI errors on the BER performance of user 1 for QPSK and 16-QAM constellations. The plots show the performance when the channel is not estimated and the performance after channel estimation. These figures, therefore, illustrate the significance of channel estimation and equally reveal the need for accurate CSI for improved BER performance. Although performance shows marked improvement after channel estimation, nevertheless, these results show that the assumption of perfect CSI is not practical as it can easily be seen that the plot for the estimated channel does not agree with the plot for perfect CSI. In Figure 12, the BER performance of user 2 is shown. The result compares the system performance under three scenarios: perfect CSI with SIC errors, perfect SIC but with the CSI error, and perfect CSI with perfect SIC. Focusing on the relevance of CSI and the impact of the CSI error, the obtained results reveal that with CSI errors only (i.e., with perfect SIC), performance improves marginally with increasing transmit SNR until a constant value of BER is reached. The reason for this is that at a low SNR regime, the received signal is highly corrupted by noise, leading to large estimation errors, and therefore, performance degrades significantly. As the SNR increases, the noise component reduces, making it easier to estimate the channel with better accuracy and thereby achieve some improvement in the BER performance. Nevertheless, the channel estimation errors cause a floor effect in the BER performance. Therefore, while increasing SNR reduces the noise, the system remains limited by the inaccuracies in the channel estimates, preventing further improvement in BER, regardless of the SNR level.
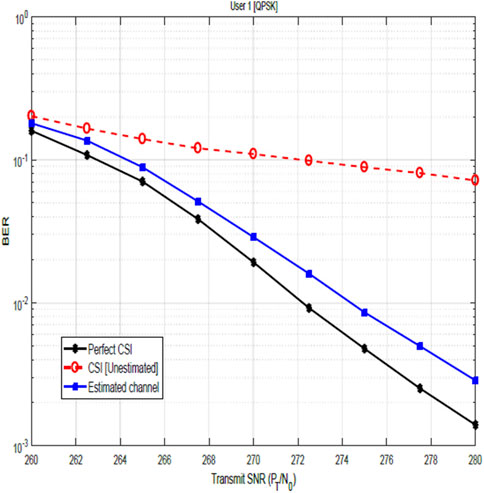
FIGURE 7
Impact of the channel estimation error on the BER of QPSK-modulated NOMA-OFDM signals for user 1.
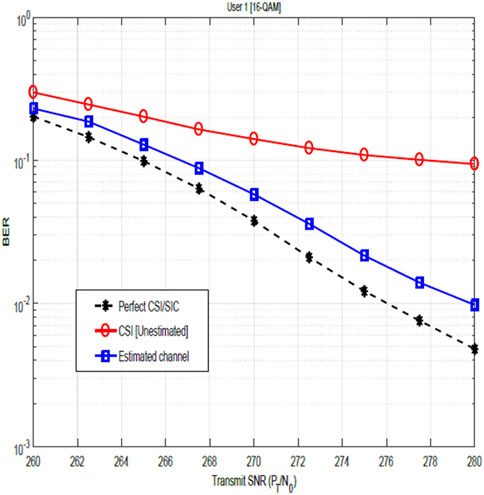
FIGURE 8
Impact of the channel estimation error on the BER of 16-QAM-modulated NOMA-OFDM signals for user 1.
4.3 Impact of SIC imperfection on BER performance
Figures 9, 10 show the impact of SIC imperfections together with CSI errors on the BER performance of user 2 for QPSK and 16-QAM constellations. These figures illustrate the degrading impact of SIC imperfection on the BER performance. In particular, when compared with the plots in Figures 7, 8, the impact of the SIC error becomes more obvious. In Figures 11, 12, the BER performance of user 2 is as shown. As earlier stated, the result compares the system performance under three scenarios: perfect CSI with SIC errors, perfect SIC with CSI errors, and perfect CSI, perfect SIC. However, focusing on the impact of the SIC, the obtained results reveal that with SIC errors only (i.e., with perfect CSI), performance improves significantly with increasing transmit SNR, and at sufficiently high SNR, degradation on the BER becomes negligible. This is because at low SNR, performance is dominated by noise, and even if there is some SIC imperfections, the system is already suffering from a lot of noise and the relative impact of SIC imperfections is less significant. However, as SNR increases, the noise level reduces and the system becomes more sensitive to the imperfection in SIC. Nevertheless, at sufficiently high SNR, the effect of noise is very minimal, and in addition, the receiver is able to detect the data more distinctly, thereby reducing the impact of SIC imperfection to achieving a very low BER.
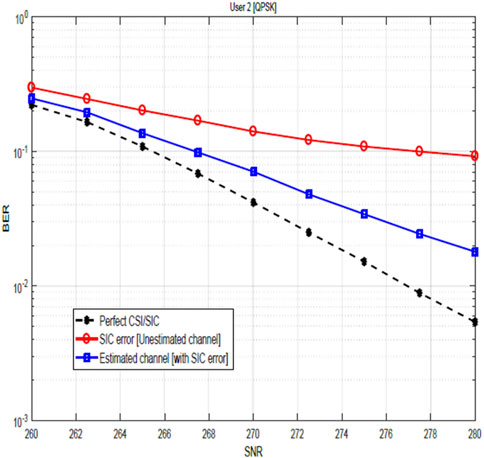
FIGURE 9
BER sensitivity of QPSK-modulated NOMA-OFDM signals in the presence of SIC and channel estimation errors for user 2.
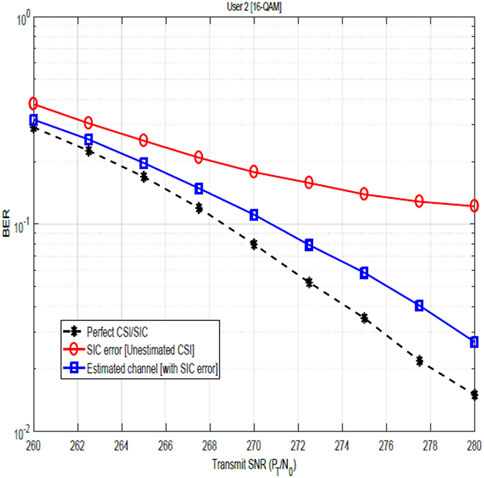
FIGURE 10
BER sensitivity of 16-QAM-modulated NOMA-OFDM signals in the presence of SIC and channel estimation errors for user 2.
FIGURE 11
Impact of SIC errors on the BER of QPSK-modulated NOMA-OFDM signals for user 2.
FIGURE 12
Impact of SIC errors on the BER of QPSK-modulated NOMA-OFDM signals.
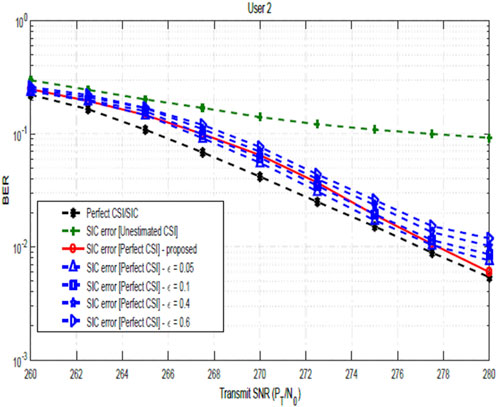
Figure 13 compares the SIC scheme in Im and Lee (2019), where the interference term is modeled as a Gaussian random variable and the proposed scheme in Section 3.1. The plot in the obtained result shows that based on the Im and Lee (2019) scheme, performance generally improves as the value of increases. Nevertheless, the proposed scheme in Section 3.1 outperforms the scheme in Im and Lee (2019), as shown in the figure.
FIGURE 13
Impact of SIC errors on the BER of QPSK-modulated NOMA-OFDM signals with varying .
4.4 Comparative analysis of the impact of CSI errors and SIC errors on BER performance
Revisiting Figure 12, the result further compares the impact of channel estimation, channel estimation errors, and SIC errors on the BER performance. The plot reveals that the impact of channel estimation errors is seen to be more significant that the impact of the SIC errors. This is due to the fundamental performance limit introduced by the CSI error, regardless of the SNR level stated as discussed. On the other hand, SIC errors decrease with increasing SNR. It is noteworthy to know that the worse-case scenario occurs when there is SIC imperfection and channel estimation is not carried out, while the best-case scenario happens with perfect channel estimation and perfect SIC, highlighting the critical role of channel estimation and successive interference cancellation in the NOMA-OFDM system.
5 Conclusion
In this paper, closed-form BER expressions for an uplink OFDM-based NOMA have been derived and analyzed. The BER expressions are derived while considering the degrading effects of imperfect SIC and channel estimation errors. The closed-form expressions are initially derived using BPSK signaling. Then, BER expressions for QPSK and 16-QAM constellations are derived and analyzed. Obtained results show agreement between the analytical and simulated results. It is also noteworthy to know that the impact of the SIC error on the overall performance wanes in higher SNR regions, while the influence of the SIC error is better characterized by the proposed model, as against the existing model in the literature. Moreover, it is equally important to note that CSI errors cause more degradation on the BER performance than the SIC imperfections particularly, at a high SNR level due to the fundamental performance limit introduced by the channel estimation errors. The obtained results while revealing the importance of CSI and SIC equally show that the assumption of perfect CSI and SIC is not practical, hence the need for accurate schemes for improved BER performance. Therefore, this work can provide insights into a general behavior of NOMA-OFDM systems in the presence of SIC imperfection and the channel estimation error with a view to understanding the system’s performance boundaries and limitations. The BER derivation approach utilized in this work can be extended easily for other high-order modulation schemes. Furthermore, the BER expressions obtained, which are dependent on the training symbols, are in simple forms that require no numerical integration.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
AO: writing–review and editing, writing–original draft, and conceptualization. MB: writing–review and editing, writing–original draft, software, and conceptualization. FO: writing–review and editing and writing–original draft. EO: writing–review and editing and writing–original draft. AF: writing–review and editing and writing–original draft.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
The authors would like to thank the editor and the reviewers for their constructive comments and suggestions, which improve the quality of this paper.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frcmn.2024.1472624/full#supplementary-material
References
1
Bariah L. Muhaidat S. Al-Dweik A. (2020). Error performance of noma-based cognitive radio networks with partial relay selection and interference power constraints. IEEE Trans. Commun.68, 765–777. 10.1109/TCOMM.2019.2921360
2
Björnson E. Kountouris M. Debbah m. (2013). Massive mimo and small cells: improving energy efficiency by optimal soft-cell coordination. Int. Conf. Telecommun. 10.1109/ICTEL.2013.6632074
3
Brannstrom F. Aulin T. Rasmussen L. (2002). Iterative detectors for trellis-code multiple-access. IEEE Trans. Commun.50, 1478–1485. 10.1109/TCOMM.2002.802563
4
Chen B. (2002). Maximum likelihood estimation of ofdm carrier frequency offset. IEEE Signal Process. Lett.9, 123–126. 10.1109/97.1001648
5
Chen Y. (2016). “Two-dimensional pilot design for non-orthogonal multiple access in multicarrier system,” in 2016 IEEE Globecom Workshops (GC Wkshps), Washington, DC, December 04–08, 2016, 1–6. 10.1109/GLOCOMW.2016.7849070
6
Gilhousen K. Jacobs I. Padovani R. Viterbi A. Weaver L. Wheatley C. (1991). On the capacity of a cellular cdma system. IEEE Trans. Veh. Technol.40, 303–312. 10.1109/25.289411
7
Hilario-Tacuri A. Maldonado J. Revollo M. Chambi H. (2021). Bit error rate analysis of noma-ofdm in 5g systems with non-linear hpa with memory. IEEE Access9, 83709–83717. 10.1109/ACCESS.2021.3087536
8
Im G. Lee J. H. (2019). Outage probability for cooperative noma systems with imperfect sic in cognitive radio networks. IEEE Commun. Lett.23, 692–695. 10.1109/LCOMM.2019.2903040
9
Jain M. Sharma N. Gupta A. Rawal D. Garg P. (2020). Performance analysis of noma assisted underwater visible light communication system. IEEE Wirel. Commun. Lett.9, 1291–1294. 10.1109/LWC.2020.2988887
10
Kara F. Kaya H. (2018). Ber performances of downlink and uplink noma in the presence of sic errors over fading channels. Institution of Engineering and Technology, 12, 1834–1844. 10.1049/iet-com.2018.5278
11
Kay S. (1995). Fundamentals of statistical signal processing: estimation theory. Upper Saddle River, NJ: Prentice Hall.
12
Li Q. Wen M. Basar E. Poor H. V. Chen F. (2019). Spatial modulation-aided cooperative noma: performance analysis and comparative study. IEEE J. Sel. Top. Signal Process.13, 715–728. 10.1109/JSTSP.2019.2898099
13
Li X. Li C. Jin Y. (2016). Dynamic resource allocation for transmit power minimization in ofdm-based noma systems. IEEE Commun. Lett.20, 2558–2561. 10.1109/LCOMM.2016.2612688
14
Liu L. Tong J. Ping L. (2006). Analysis and optimization of cdma systems with chip-level interleavers. IEEE J. Sel. Areas Commun.24, 141–150. 10.1109/JSAC.2005.858896
15
Liu X. Chen Z. Wang Y. Zhou F. Luo Y. Hu R. Q. (2019). Ber analysis of noma-enabled visible light communication systems with different modulations. IEEE Trans. Veh. Technol.68, 10807–10821. 10.1109/TVT.2019.2938909
16
Liu X. Liu Y. Wang X. Lin H. (2017). Highly efficient 3-d resource allocation techniques in 5g for noma-enabled massive mimo and relaying systems. IEEE J. Sel. Areas Commun.35, 2785–2797. 10.1109/JSAC.2017.2726378
17
Lopez-Martinez F. J. Martos-Naya E. Paris J. F. Entrambasaguas J. T. (2010). Ber analysis of direct conversion ofdm systems with mrc under channel estimation errors. IEEE Commun. Lett.14, 423–425. 10.1109/LCOMM.2010.05.092257
18
Mohsan S. A. H. Li Y. Zhang Z. Ali A. Xu J. (2023). Uplink and downlink noma based on a novel interference coefficient estimation strategy for next-generation optical wireless networks. Photonics10, 569. 10.3390/photonics10050569
19
Moose P. (1994). A technique for orthogonal frequency division multiplexing frequency offset correction. IEEE Trans. Commun.42, 2908–2914. 10.1109/26.328961
20
Morelli M. Mengali U. (2000). Carrier-frequency estimation for transmissions over selective channels. IEEE Trans. Commun.48, 1580–1589. 10.1109/26.870025
21
Ouaissa M. Ouaissa M. Boulouard Z. El Himer S. (2022). Deep learning-based non-orthogonal multiple access for 5G and beyond networks. Cham: Springer International Publishing.
22
Proakis J. G. (2001). Digital communications. New York: McGraw-Hill.
23
Savaux V. Skrzypczak A. Louët Y. (2016). Theoretical bit error floor analysis of 16-qam ofdm signal with channel estimation using polynomial interpolation. IET signal Process.10, 254–265. 10.1049/iet-spr.2015.0099
24
Wang P. Xiao J. Ping L. (2006). Comparison of orthogonal and non-orthogonal approaches to future wireless cellular systems. IEEE Veh. Technol. Mag.1, 4–11. 10.1109/MVT.2006.307294
25
Wang Q. Xu S. Yan X. Wu H.-C. Wu Y. (2021). Novel efficient multiwavelet-based modulation for downlink noma systems. IEEE Wirel. Commun. Lett.10, 1242–1246. 10.1109/LWC.2021.3063122
26
Yih C.-H. (2007). “Effects of channel estimation error on the ber performance of ofdm systems in multipath rayleigh fading channels,” in 2007 IEEE 66th Vehicular Technology Conference, Baltimore, MD, September 30–October 03, 2007, 1097–1101. 10.1109/VETECF.2007.237
Summary
Keywords
OFDM-based NOMA, orthogonal frequency division multiplexing, non-orthogonal multi-access, bit error rate, successive interference cancelation, channel estimation
Citation
Olawole AA, Balogun MB, Offiong FB, Obayiuwana E and Fisusi A (2024) Average BER evaluation of the uplink OFDM-based NOMA system under SIC and channel estimation error. Front. Comms. Net 5:1472624. doi: 10.3389/frcmn.2024.1472624
Received
29 July 2024
Accepted
23 October 2024
Published
07 November 2024
Volume
5 - 2024
Edited by
Qingchun Chen, Guangzhou University, China
Reviewed by
Hongjiang Lei, Chongqing University of Posts and Telecommunications, China
Milica Pejanovic-Djurisic, University of Montenegro, Montenegro
Updates
Copyright
© 2024 Olawole, Balogun, Offiong, Obayiuwana and Fisusi.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Akinbode A. Olawole, alex_olawole@oauife.edu.ng
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.