On the age of information for non-preemptive queues in tandem

A monitoring system operates over a network of first-come, first-served queues in tandem, in which a source is transmitting its status to a monitor at the end of the tandem. To characterize the freshness performance of this monitoring system, we analyze the average Age of Information for this system, in which the status update arrivals are Poisson distributed and each queue is served by a non-preemptive, memoryless server. We first study the case of single-capacity queues that are modeled as a stochastic hybrid system, and we derive the average age for two queues with different service rates and three queues with equal service rate. We then study the infinite capacity queue case and use the graphical approach to derive the average age for two queues in tandem with equal service rates. Finally, we simulate the average age for intermediate cases of k capacity queues, which fall in between the two extreme cases of k = 1 and k = ∞.

1 Introduction

In applications for the Internet of Things (IoT) or military applications, it is often important for a device or entity at one point in the network to have information (e.g., sensor data) from another point in the network that is as fresh as possible. The concept of Age of Information (AoI) applies to communication systems where the receiver has an interest in fresh (i.e., most recently generated) information. However, traditional metrics such as packet delay are insufficient for characterizing the performance of systems that rely on real-time monitoring applications. AoI is a widely-explored metric to measure the performance of real-time status updating applications, such as position tracking, environmental/health monitoring, or networked control systems (Kaul et al., 2011; 2012a). In most works studying AoI, the goal is to derive the age averaged over time for various single queue models (Kaul et al., 2012b; Yates and Kaul, 2012; Kam et al., 2013). However, in IoT systems or ad hoc military networks, real-time information is often needed over multiple hops, which can include wireless and wired links. In this work, we focus on analyzing the average AoI for queues in tandem to obtain insight into the performance of real-time status updating systems that operate over a multi-hop network.

Research on AoI has focused on understanding the performance of systems that are modeled by different types of queues, with various arrival/departure processes, number of servers, and queue capacities (Kam et al., 2016a; Bedewy et al., 2016; Costa et al., 2016; Kosta et al., 2017; Sun et al., 2017). While most studies have focused on analyzing single queues, tandem queues have recently been recognized as an important area of study for understanding the AoI for networks beyond a single hop. Chiariotti et al. (2020) studied a system of two connected satellite links for another age-related metric, called the Peak AoI (PAoI), by modeling the system as a series of M/M/1 queues. In contrast to the average AoI studied in this work, PAoI tracks the maximum instantaneous value of AoI for each update. Similarly, tandem satellite links were also studied by Soret et al. (2020), who derived a bound on the average AoI for satellites modeled as queues that received updates directly from ground stations and relayed updates from previous satellites in the tandem. Vikhrova et al. (2020) studied tandem queues with updates that are randomly sent to one of two queues and priority is given to the second queue. In Xu et al. (2020), the average PAoI was analyzed for an IoT network (multiple sources) feeding into tandem queues. In Kuang et al. (2019), a mobile edge computing system was modeled as a tandem queue and the average AoI was analyzed for a zero-wait message generation policy.

There has also been some earlier work on AoI in more general multi-hop networks. For example, wireless scheduling for AoI was studied in Talak et al. (2017), who derived the average and peak average AoI-optimal stationary scheduling policies for line networks, where links are activated according to a stationary probability distribution. However, the authors did not derive the average and peak average AoI in closed form. Bedewy et al. (2017) studied the preemptive Last Generated First Served (LGFS) policy, and show that this policy results in a smaller age at all nodes in the network than any other causal policy. The caveats are that the packets are generated at an external source and are dispersed throughout the network via a gateway node, packet transmission times over a network are exponentially distributed, and the age optimization is done in a stochastic ordering sense.

The work that most closely relates to this article is that of Yates (2018); Yates (2020), which studies a line network of preemptive servers. These works analyzed the AoI for this system using a stochastic hybrid system (SHS) modeling approach, as in Yates and Kaul (2019). It was shown in Yates (2020) that for this line network, the age at the destination (or any node in between) is identical in distribution to the sum of independent exponential service times up to the node. Although preemption has been shown to be optimal for exponential servers (Bedewy et al., 2017), the same is not true for general service time distributions. In addition, many practical communication systems do not allow for this type of control for packets in transmission. Furthermore, in most works on queues in tandem, closed form expressions are often given as bounds or for the more tractable PAoI metric. Therefore, it is still important to characterize the average AoI of non-preemptive servers in closed form, which is the focus of this article. The analysis here is more challenging than that in the preemption case because it does not allow for the reduction of states in the SHS model, which greatly simplifies the analysis.

More recently, the SHS approach has been extended to not only derive the average AoI but to actually derive the complete distribution of the AoI. The SHS approach for deriving the moment generating function (MGF) for the AoI was first presented in Yates (2020), where it was also applied to a line network of preemptive queues. However, few works have since applied that approach to different systems, such as an energy-harvesting node with varying types of preemptive and non-preemptive policies by Abd-Elmagid and Dhillon (2022a); Abd-Elmagid and Dhillon (2022b), and a two-source single-server system with packet management by Moltafet et al. (2021). In this work, we have derived the first moment (average) of the AoI for non-preemptive queues in tandem. However, deriving the MGF is a more complex derivation that is being considered for a follow-up work.

Koukoutsidis (2020) developed an approach to calculate the average AoI for an overtake-free network of quasi-reversible queues, including M/M/1/∞ queues in tandem (which we also consider), as well as networks with different classes of update packets. In contrast to the SHS approach, they used the queueing theoretical result that the end-to-end sojourn time for an overtake-free path is distributed as a sum of independent exponential sojourns at each node. However, in their AoI calculation, they make the assumption that, because the interarrival and interdeparture times are identically distributed, their correlation with the sojourn time is equal¹. This is not true in general and thus they derive a different result for the M/M/1/∞ queues in tandem².

In this work, we start by deriving the average age for two non-preemptive queues in tandem, in which each of the queues have a capacity equal to 1. This is done using the SHS approach. Limiting the queue capacity is based on the intuition that allowing updates to age in a queue may not be efficient when the objective is to maximize information freshness at the destination because the queues will not store obsolete packets unnecessarily. This has the additional advantage of making the analysis of the average age more tractable. Furthermore, this should approximate the performance of a non-preemptive LGFS and is likely to outperform it. To verify our theoretical result, we simulate the single-capacity non-preemptive queues in tandem. We extend the analysis by considering three non-preemptive queues in tandem. We then compare our result with an approximation for arbitrary number of non-preemptive single-capacity queues in tandem.

Next, we consider the case of infinite capacity queues in tandem, with a Poisson arrival process and exponential servers. Unfortunately, applying the SHS approach in this case makes the problem intractable because this results in an explosion of states in the SHS model. Therefore, we resort to the traditional method of deriving the average age using a graphical argument, whereby we evaluate the correlations between system times and interarrival or interdeparture times. Again, to verify the theoretical result, we simulate the infinite capacity non-preemptive queues in tandem. Finally, to develop a holistic understanding of this problem space, we study the case of capacity-k non-preemptive queues in tandem. We generate simulation results for capacity-k queues in tandem because we lack theoretical expressions of average age for arbitrary values of k.

The remainder of this article is organized as follows. The system model is described in Section 2. The average age for capacity-1 queues in tandem is derived in Section 3 using the SHS approach. The average age for infinite capacity queues in tandem is derived in Section 4 using the traditional graphical approach. Various simulation results, including those for capacity-k queues, are provided in Section 5. Finally, we summarize our results in Section 6.

2 System model

We study the AoI over a network of queues in tandem, as shown in Figure 1. A source generates arrivals as a rate λ Poisson process and then sends them to the first queue. The packets flow through a series of queues serving packets at rate μ_i until they reach the monitor (as depicted in the figure). There is no preemption in this system, such that a packet in service completes service before the server becomes available for another packet and a packet that arrives to a full queue is dropped. Aside from this queue overflow, there are no other packet losses under this model.

FIGURE 1

FIGURE 1. Queues in tandem.

The AoI at the monitor at time t is defined as Δ(t) = t − u(t), where u(t) is the time at which the freshest packet at the monitor was generated at the source. A sample path of the age for a single-capacity queue is given in Figure 2, where t_i and τ_i are the time of generation and time of arrival at the monitor of the ith update, respectively. In this figure, packet 2 is dropped due to the server being occupied. We are interested in deriving the average AoI,

$\mathrm{\Delta }={\lim }_{\mathcal{T}\to \infty }\frac{1}{\mathcal{T}}{\int }_0^{\mathcal{T}}\mathrm{\Delta }\left(t\right)\mathrm{d}t.(1)$

FIGURE 2

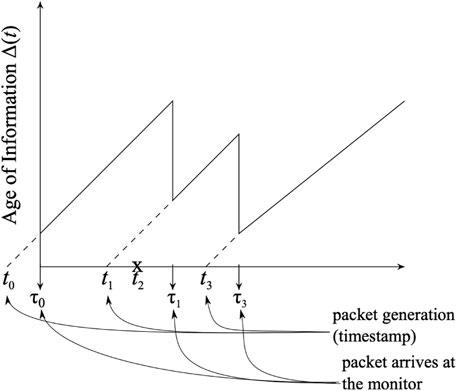
FIGURE 2. Age of information vs. time, single-capacity queue: t_i and τ_i are the time of generation and time of arrival at the monitor of the ith update, respectively.

3 Average age of single-capacity queues in tandem

3.1 Two ⋅/M/1/1 queues in tandem

For our theoretical analysis, we start by looking at two queues with a capacity of one, such that any packet that arrives to a queue with a packet already in service is dropped. We focus on a Poisson arrival process from the source into the first queue and the packets are served at each queue with an exponential service time. The traditional method of deriving the average AoI involves a graphical argument and the need to evaluate correlations between system times and interarrival or interdeparture times (Kaul et al. 2012a). With queues in tandem, this approach is non-trivial—not only in calculating the correlations between the waiting times and the interarrival times but it also requires the correlation between waiting times at the different queues to be calculated, among other correlations. In a capacity-limited system, we would also need to account for packet losses at both queues. In this section, we use the notation ⋅/M/1/1, where the initial “⋅” indicates that there are no exogenous arrivals to the queues further down the tandem.

An alternative method of calculating the average age was recently proposed that models the system as a SHS (Yates and Kaul, 2019), which avoids the complexity of computing the correlation quantities in the graphical approach. The SHS is modeled with a hybrid state (q(t), x(t)), where $q(t)\in \mathcal{Q}$ is the discrete Markov state of the queueing system and $\mathbf{x}(t)\in {\mathbb{R}}^n$ is the continuous state that captures the evolution of the ages at different points in the system. Following the approach in Yates (2018), we model the two ⋅/M/1/1 queues in tandem (as described in Section 2), with the discrete state set $\mathcal{Q}=\{\mathrm{00,10,01,11}\}$, where $q_1{q}_2\in \mathcal{Q}$, q_i = 1 indicates that queue i has a packet in service, and q_i = 0 when the queue is empty³. The continuous state for this system is x(t) = [x₁(t), x₂(t), x₃(t)], where x₃(t) is the age at the monitor and x_i(t) is the age of the packet being served at queue i when there is a packet in service, and otherwise x_i(t) is irrelevant and set to 0.

For the Markov chain q(t), the transitions between states $l\in \mathcal{L}$ are directed edges $(q_l,q_l^{\prime })$ with transition rate ${\lambda }^l{\delta }_{q_l,q{(t)}^{\prime }}$, where the Kronecker delta ensures that the transition l only occurs in state q_l. In SHS, these transitions correspond to changes in the discrete state q(t), as well as jumps in the continuous state x(t), according to x′ = xA_l, where A_l is a binary matrix that defines the jumps in x(t) for the discrete state transition l. These transitions may be self-transitions, in which the discrete state stays the same but the continuous state jumps. In addition, there may be multiple transitions between the same pair of states depending on the different impact on the continuous state, which is unlike typical continuous-time Markov chains. In this work, there are no self-transitions or multiple transitions that need to be modeled.

For all $\widehat{q}\in \mathcal{Q}$, we define ${\pi }_{\widehat{q}}(t)$ to be the discrete Markov state probabilities. We define $v_{\widehat{q}j}(t)$ as the correlation between the continuous age state x(t) and the occupancy of the discrete state at time t; that is, q(t). These definitions are given as follows:

${\pi }_{\widehat{q}}\left(t\right)=\mathbb{E}\left[{\delta }_{\widehat{q},q\left(t\right)}\right](2)$

$v_{\widehat{q}j}\left(t\right)=\mathbb{E}\left[x_j\left(t\right){\delta }_{\widehat{q},q\left(t\right)}\right],j\in \left\{1,\dots ,n\right\}.(3)$

From this, we also have the vector functions

${\mathbf{v}}_{\widehat{q}}\left(t\right)=\left[v_{\widehat{q}1}\left(t\right),\dots ,v_{\widehat{q}n}\left(t\right)\right]=\mathbb{E}\left[\mathbf{x}\left(t\right){\delta }_{\widehat{q},q\left(t\right)}\right],(4)$

where n is the number of dimensions in the continuous state x(t). For an ergodic queueing system, the average age is given by $\mathrm{\Delta }=\mathbb{E}[x_n]={\sum }_{\bar{q}\in \mathcal{Q}}{\bar{v}}_{\bar{q}n}$, where ${\bar{v}}_{\bar{q}j}={\lim }_{t\to \infty }{\bar{v}}_{\bar{q}j}(t)$ is the steady-state correlation between the discrete and age states. To derive the steady state ${\mathbf{v}}_{\bar{q}}(t)$, we need the following first order differential equation for all $\bar{q}\in \mathcal{Q}$ as derived in Yates and Kaul (2019):

${\dot{\mathbf{v}}}_{\bar{q}}\left(t\right)=\mathbf{1}{\bar{\pi }}_{\bar{q}}+\sum _{l\in {\mathcal{L}}_{\bar{q}}^{\prime }}{\lambda }^{\left(l\right)}{\mathbf{v}}_{q_l}\left(t\right){\mathbf{A}}_l-{\mathbf{v}}_{\bar{q}}\left(t\right)\sum _{l\in {\mathcal{L}}_{\bar{q}}}{\lambda }^{\left(l\right)}(5)$

where ${\mathcal{L}}_{\bar{q}}^{\prime }$ is the set of transitions entering $\bar{q}$ and ${\mathcal{L}}_{\bar{q}}$ is the set of transitions leaving $\bar{q}$. The rate at which the continuous state changes is the 1 vector because the age increases linearly with a slope of 1. To solve for the steady state ${\mathbf{v}}_{\bar{q}}(t)$, we let ${\dot{\mathbf{v}}}_{\bar{q}}(t)=0$, yielding

${\bar{\mathbf{v}}}_{\bar{q}}\sum _{l\in {\mathcal{L}}_{\bar{q}}}{\lambda }^{\left(l\right)}=\mathbf{1}{\bar{\pi }}_{\bar{q}}+\sum _{l\in {\mathcal{L}}_{\bar{q}}^{\prime }}{\lambda }^{\left(l\right)}{\bar{\mathbf{v}}}_{q_l}{\mathbf{A}}_l,\bar{q}\in \mathcal{Q}.(6)$

According to Yates and Kaul (2019, Theorem 4), if we can find a non-negative solution $\bar{\mathbf{v}}=[{\bar{\mathbf{v}}}_{00}\cdots {\bar{\mathbf{v}}}_{11}]$ to (6), then the then differential Eq. 5 is stable and the average age is given by $\mathrm{\Delta }={\sum }_{\bar{q}\in \mathcal{Q}}{\bar{v}}_{\bar{q}3}$.

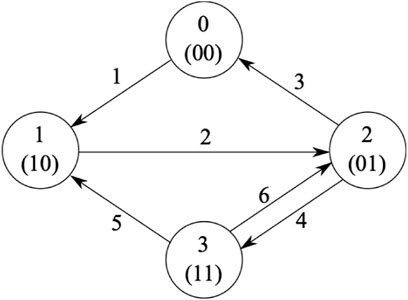
For the two single-capacity queue system in this section, the discrete Markov chain is given in Figure 3, where the states are $q\in \mathcal{Q}$ and the transition labels are $l\in \mathcal{L}$, which correspond to $q_l\to q_l^{\prime }$. Following Yates and Kaul (2019), we list the transitions, the transition rates, and the quantities in (6) associated with the mapping of jumps in the continuous state at transitions A_l in Table 1.

FIGURE 3

FIGURE 3. SHS Markov chain for two ⋅/M/1/1 queues in tandem.

TABLE 1

TABLE 1. Table of transitions for the Markov chain in Figure 3.

Two examples of how we determined the table entries follow. Transition l = 1 corresponds to a packet arrival to a completely empty system, which occurs at rate λ, and the jump in the continuous state (xA_l) is such that the age at the monitor remains the same (x₃), the packet in service at queue 1 starts at 0, and the age at the empty server does not matter, so it is set to 0. A transition that is specific to non-preemptive queues in tandem is l = 6, which corresponds to the packet in the first server completing service (at a rate of μ₁) in a full system, such that it gets dropped at the second queue. For xA_l, the age at the monitor remains the same (x₃), the age at the second queue remains the same because there is no preemption (x₂), and the age at the first monitor goes to zero because it was served and dropped at the second queue.

We use the balance equations to derive the discrete Markov state stationary probabilities ${\bar{\pi }}_{\bar{q}}$:

$\begin{array}{ll}\hfill {\bar{\pi }}_{\bar{q}}\sum _{l\in {\mathcal{L}}_{\bar{q}}}{\lambda }^{\left(l\right)}& =\sum _{l\in {\mathcal{L}}_{\bar{q}}^{\prime }}{\lambda }^{\left(l\right)}{\bar{\pi }}_{q_l},\bar{q}\in \mathcal{Q}\hfill \\ \hfill \sum _{\bar{q}\in \mathcal{Q}}{\bar{\pi }}_{\bar{q}}& =1.\hfill \end{array}$

Filling these equations with the quantities from Table 1 and by solving for the stationary probabilities, we obtain.

${\bar{\pi }}_{00}=\frac{{\mu }_1{\mu }_2}{\left(\lambda +{\mu }_1\right)\left(\lambda +{\mu }_2\right)}(\mathrm{7a})$

${\bar{\pi }}_{01}=\frac{\lambda {\mu }_1}{\left(\lambda +{\mu }_1\right)\left(\lambda +{\mu }_2\right)}(\mathrm{7b})$

${\bar{\pi }}_{10}=\frac{\lambda {\mu }_2\left(\lambda +{\mu }_1+{\mu }_2\right)}{\left(\lambda +{\mu }_1\right)\left(\lambda +{\mu }_2\right)\left({\mu }_1+{\mu }_2\right)}(\mathrm{7c})$

${\bar{\pi }}_{11}=\frac{{\lambda }^2{\mu }_1}{\left(\lambda +{\mu }_1\right)\left(\lambda +{\mu }_2\right)\left({\mu }_1+{\mu }_2\right)}.(\mathrm{7d})$

We can substitute these stationary probabilities and the quantities in Table 1 into (6) to obtain the following system of equations:

$\lambda {\bar{v}}_{003}={\pi }_{00}+{\mu }_2{\bar{v}}_{012}(\mathrm{8a})$

$\left(\lambda +{\mu }_2\right){\bar{v}}_{013}={\pi }_{01}+{\mu }_1\left({\bar{v}}_{103}+{\bar{v}}_{113}\right)(\mathrm{8b})$

${\mu }_1{\bar{v}}_{103}={\pi }_{10}+\lambda {\bar{v}}_{003}+{\mu }_2{\bar{v}}_{112}(\mathrm{8c})$

$\left({\mu }_1+{\mu }_2\right){\bar{v}}_{113}={\pi }_{11}+\lambda {\bar{v}}_{013}(\mathrm{8d})$

$\left(\lambda +{\mu }_2\right){\bar{v}}_{012}={\pi }_{01}+{\mu }_1\left({\bar{v}}_{101}+{\bar{v}}_{112}\right)(8e)$

$\left({\mu }_1+{\mu }_2\right){\bar{v}}_{112}={\pi }_{11}+\lambda {\bar{v}}_{012}(\mathrm{8f})$

${\mu }_1{\bar{v}}_{101}={\pi }_{10}+{\mu }_2{\bar{v}}_{111}(\mathrm{8g})$

$\left({\mu }_1+{\mu }_2\right){\bar{v}}_{111}={\pi }_{01}(\mathrm{8h})$

To derive the average age, it is not necessary to solve for all of the ${\bar{v}}_{\bar{q}j}$ but only ${\sum }_{\bar{q}\in \mathcal{Q}}{\bar{v}}_{\bar{q}3}$. We start by finding the linear combination of Eqs 8a–8d using coefficients a, b, c, and d, respectively, which yields

$\begin{array}{ll}\hfill a\lambda {\bar{v}}_{003}+b\left(\lambda +{\mu }_2\right){\bar{v}}_{013}+c{\mu }_1{\bar{v}}_{103}+d\left({\mu }_1+{\mu }_2\right){\bar{v}}_{113}& =a\left({\pi }_{00}+{\mu }_2{\bar{v}}_{012}\right)+b\left({\pi }_{01}+{\mu }_1\left({\bar{v}}_{103}+{\bar{v}}_{113}\right)\right)\hfill \\ \hfill & +c\left({\pi }_{10}+\lambda {\bar{v}}_{003}+{\mu }_2{\bar{v}}_{112}\right)+d\left({\pi }_{11}+\lambda {\bar{v}}_{013}\right)\hfill \end{array}$

We want to set the coefficients such that moving all ${\bar{v}}_{\bar{q}3}$ terms to the left-hand side yields ${\sum }_{\bar{q}\in \mathcal{Q}}{\bar{v}}_{\bar{q}3}$; that is, find a, b, c, and d that satisfies

$\begin{array}{l}\hfill \lambda a-\lambda c=1\\ \hfill \left(\lambda +{\mu }_2\right)b-\lambda d=1\\ \hfill {\mu }_{1}c-{\mu }_{1}b=1\\ \hfill \left({\mu }_1+{\mu }_2\right)d-{\mu }_{1}b=1\end{array}$

which has solution

$a=\frac{1}{\lambda }+\frac{1}{{\mu }_1}+\frac{1}{{\mu }_2},b=\frac{1}{{\mu }_2},c=\frac{1}{{\mu }_1}+\frac{1}{{\mu }_2},d=\frac{1}{{\mu }_2}.$

Combining Eqs 8a–8d with respective coefficients a, b, c, and d yields

$\sum _{\bar{q}\in \mathcal{Q}}{\bar{v}}_{\bar{q}3}=a{\pi }_{00}+b{\pi }_{01}+c{\pi }_{10}+d{\pi }_{11}+a{\mu }_2{\bar{v}}_{012}+c{\mu }_2{\bar{v}}_{112}.$

To find $a{\mu }_2{\bar{v}}_{012}+c{\mu }_2{\bar{v}}_{112}$, we again take linear combinations of Eqs 8e,8f, and we need to find the coefficients a′ and b′ that satisfy

$\left(\lambda +{\mu }_2\right)a^{\prime }-\lambda b^{\prime }=a{\mu }_2\left({\mu }_1+{\mu }_2\right)b^{\prime }-{\mu }_1{a}^{\prime }=c{\mu }_2$

which has solution

$a^{\prime }=\frac{{\mu }_1+{\mu }_2}{\lambda \left(\lambda +{\mu }_1+{\mu }_2\right)}+\frac{1}{{\mu }_1}+\frac{1}{{\mu }_2},b^{\prime }=\frac{1}{{\mu }_1}+\frac{{\mu }_1}{{\mu }_1+{\mu }_2}{a}^{\prime }.$

The last linear combination of equations is for (Eq. 8g) and (Eq. 8h) to find ${\mu }_1{a}^{\prime }{\bar{v}}_{101}$, and the coefficients satisfy

${\mu }_1{a}^{″}={\mu }_1{a}^{\prime }\left({\mu }_1+{\mu }_2\right)b^{″}-{\mu }_2{a}^{″}=0$

with solution

$a^{″}=a^{\prime },b^{″}=\frac{{\mu }_2}{{\mu }_1+{\mu }_2}{a}^{\prime }.$

Finally, we have

$\mathrm{\Delta }=a{\pi }_{00}+\left(b+a^{\prime }\right){\pi }_{01}+\left(c+a^{″}\right){\pi }_{10}+\left(d+b^{\prime }+b^{″}\right){\pi }_{11}$

After much simplification, we have our first result:

3.2 Three (equal rate) ⋅/M/1/1 queues in tandem

In this section, we build on the previous case and now consider three queues in tandem, for the case where the servers have equal service rate. Again we use the stochastic hybrid systems approach and the discrete state set is $\mathcal{Q}=\{\mathrm{000,001,010,011,100,101,110,111}\}$, where $q_1{q}_2{q}_3\in \mathcal{Q}$, q_i = 1 indicates that queue i has a packet in service, and q_i = 0 indicates when the queue is empty. Using the same approach for the two-queue case, we derive the following expression for the average age:

3.3 Numerical/simulation results

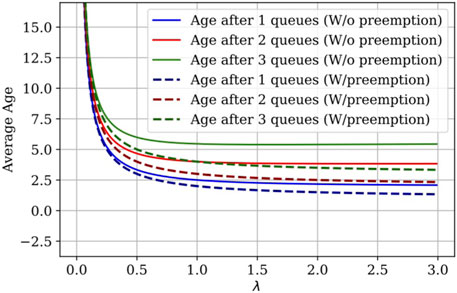
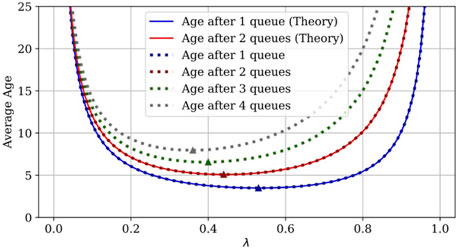
To verify our theoretical results, we look at the ⋅/M/1/1 queues with Poisson arrivals for up to four queues in tandem. The results for the average age as a function of λ are given in Figure 4. For comparison, we plot the numerically evaluated theoretical expressions for the average age up to three queues in tandem, and we observe that the plot lines for the theoretical and simulated results lie on top of one another. We also plot the minima from simulation and compare with (Eq. 11), which evaluates to 2.414 for m = 2. This matches with the simulation. We observe that the minimum λ is decreasing as the number of queues increases. For comparison, the case with preemption in Yates (2022) is shown alongside the non-preemptive case in Figure 5. The age for the preemptive case is lower than that of the non-preemptive case by about 40% at each point in the tandem network. We also consider the expression in (Eq. 10), which is exact for m = 1, 2 but is an approximation for m = 3, 4. Figure 6 shows the simulated, theoretical, and approximate results for m = 3, 4. The approximation overestimates the average age with a gap that increases with λ. For large λ, the approximation is only off by about 5% in the three-queue case. However, it is closer to 7% in the four-queue case, which suggests that the approximation may not scale well.

FIGURE 4

FIGURE 4. Average age vs. λ, μ = 1, queue capacity of one, without preemption. Simulation results are indicated by the points, theoretical results are indicated by the solid line, and simulation minima are indicated by △.

FIGURE 5

FIGURE 5. Average age vs. λ, μ = 1, queue capacity of one, preemption vs. non-preemption.

FIGURE 6

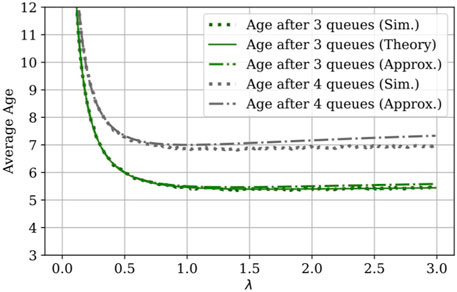
FIGURE 6. Average age vs. λ, μ = 1, queue capacity of one after three and four queues (vs. approximation).

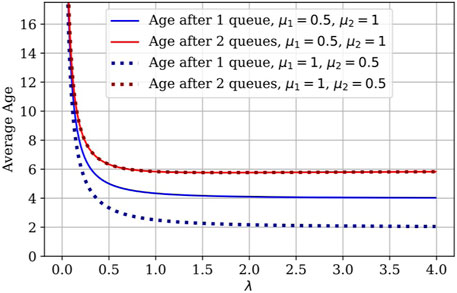
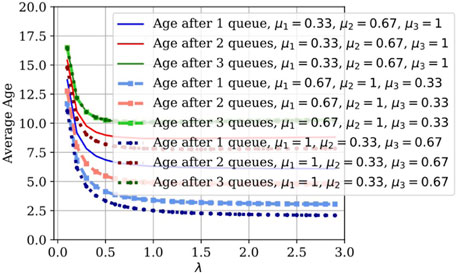
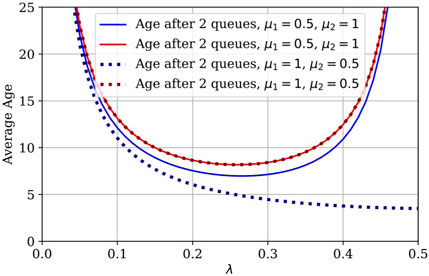
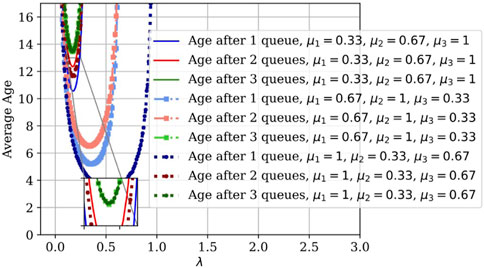
We also numerically evaluate (13) for a two-queue system with different service rates, 0.5 and 1, and the average age is plotted in Figure 7. It can be seen that the plot lines for the average age after two queues are right on top of each other, which demonstrates that the average age after the second queue is indeed insensitive to the ordering of the servers (as previously stated). To further validate this claim, we simulate a three-queue system with different service rates; that is, 0.33, 0.67, and 1. We plot the average age for different permutations of service rates in Figure 8. The average age after three queues is the same for all three permutations, which is further proof that the order of servers in the tandem does not impact the average age after the last queue.

FIGURE 7

FIGURE 7. Average age vs. λ, different μ₁, μ₂ queue capacity of one, non-preemption.

FIGURE 8

FIGURE 8. Average age vs. λ, different μ₁, μ₂, μ₃, queue capacity of one, non-preemption.

4 Average age of two ⋅/M/1/∞ queues in tandem

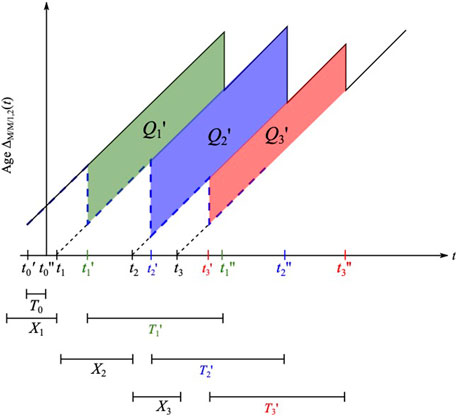
We next consider the case of infinite capacity first-come, first-served queues in tandem with Poisson arrival process and exponential servers. To derive the age after two queues, we use a graphical approach as in Kaul et al. (2012a) to derive the average age going after the second queue based on the average age after the first queue. We will show that for each packet i, the additional area under the age function beyond the age after the first queue is XT ′, where X is the interarrival time at the first queue and T′ is the system time in the second queue.

Theorem 3. The average age after two infinity capacity queues in tandem (M/M/1/∞ → ⋅/M/1/∞) is given by

$\begin{array}{ll}\hfill {\mathrm{\Delta }}_{M/M/\mathrm{1,2}}={\mathrm{\Delta }}_{M/M/\mathrm{1,1}}+\lambda \left(E\left[X{T}^{\prime }\right]\right)& =\frac{1}{\lambda }+\frac{1}{{\mu }_1}+\frac{{\lambda }^2}{{\mu }_1^2\left({\mu }_1-\lambda \right)}+\frac{1}{{\mu }_2}+\frac{{\lambda }^2}{2{\mu }_2-\lambda }+\frac{{\lambda }^2}{{\mu }_1{\mu }_2\left({\mu }_1+{\mu }_2-\lambda \right)}.\hfill \end{array}(13)$

Proof. An example of the evolution of the age function after queue 2 is shown in Figure 9. To derive the average age (1) using the graphical method, we calculate the total area under the age function by breaking it up into geometric shapes and then calculate their areas separately. The age function after queue 1, Δ_M/M/1,1(t), is shown in the figure by a dotted line, which is bounded above by the age after queue 2, Δ_M/M/1,2(t). We seek to calculate the remaining area under the age function after accounting for the average age Δ_M/M/1,1.

FIGURE 9

FIGURE 9. Age computation at (M/M/1) queue n based on age at queue n − 1.

At time $t_0^{\prime }$, the packet is served at queue 1 and arrives at queue 2. At the origin of the plot $(t_0^{″})$, the packet is served at queue 2 and the age after queue 2 (Δ_M/M/1,2) is defined. From $t_0^{″}$ until another packet arrives and is served at queue 1 $(t_1^{\prime })$, the ages after both queues are the same. At the service time $t_1^{\prime }$ at queue 1, the age Δ_M/M/1,1(t) resets to the lower age but the age Δ_M/M/1,2(t) does not yet reset to the age of the packet until it is served at $t_1^{″}$. The amount that the age is reduced by is equal to the difference between the ages of consecutive packets, which is equal to the interarrival time X₁ into queue 1. The area of the parallelogram is given by the X₁ times the system time in queue 2, $T_1^{\prime }=t_1^{″}-t_1^{\prime }$.

The average age at queue 2 is given by

$\begin{array}{ll}\hfill {\mathrm{\Delta }}_{M/M/\mathrm{1,2}}& ={\lim }_{\mathcal{T}\to \infty }\frac{1}{\mathcal{T}}{\int }_0^{\mathcal{T}}{\mathrm{\Delta }}_{M/M/\mathrm{1,2}}\left(t\right)\mathrm{d}t\hfill \\ \hfill & ={\lim }_{\mathcal{T}\to \infty }\left[\frac{1}{\mathcal{T}}{\int }_0^{\mathcal{T}}{\mathrm{\Delta }}_{M/M/\mathrm{1,1}}\left(t\right)\mathrm{d}t+\frac{R\left(\mathcal{T}\right)}{\mathcal{T}}+\frac{N\left(\mathcal{T}\right)}{\mathcal{T}}\sum _{i=1}^{N\left(\mathcal{T}\right)}\frac{T_i^{\prime }{X}_i}{N\left(\mathcal{T}\right)}\right]\hfill \\ \hfill & ={\mathrm{\Delta }}_{M/M/\mathrm{1,1}}+\lambda E\left[T^{\prime }X\right]\hfill \end{array}(14)$

where $N(\mathcal{T})$ is the number of update packets served before time $\mathcal{T}$ and $R(\mathcal{T})$ is the residual area under the curve less the area under Δ_M/M/1,1(t). The arrival rate into queue 2 is λ and $R(\mathcal{T})/\mathcal{T}$ disappears in the limit, provided λ < μ₂. The age after the first queue Δ_M/M/1,1 can be found in Kaul et al. (2012a).

To derive E[T′X], we have $E[T_i^{\prime }{X}_i]=E[X_i(W_i^{\prime }+S_i^{\prime })]=E[W_i^{\prime }{X}_i]+E[X]E[S]$. The waiting time can be written as $W_i^{\prime }={(T_{i-1}^{\prime }-Y_i)}^{+}$, where (x)⁺ = max(0, x) and Y_i is the interdeparture time of the first queue. We consider two cases for the interdeparture time. If the interarrival time for packet i is less than the system time for packet i − 1 (X_i ≤ T_i−1), then packet i immediately begins service and the interdeparture time is Y_i = S_i. Otherwise, Y_i = X_i − T_i−1 + S_i. By combining these two cases, we can write $Y_i={(X_i-T_{i-1})}^{+}+S_i$. The conditional expected waiting time at the second queue $W_i^{\prime }$ given the interarrival time at the first queue X_i = x is given by

$\begin{array}{ll}\hfill E\left[W_i^{\prime }|X_i=x\right]& =E\left[{\left(T_{i-1}^{\prime }-Y_i\right)}^{+}|X_i=x\right]\hfill \\ \hfill & =E\left[{\left(T_{i-1}^{\prime }-{\left(x-T_{i-1}\right)}^{+}-S_i\right)}^{+}\right].\hfill \end{array}$

Note that $T_{i-1}^{\prime }$ and T_i−1 are independent of the service time and interarrival time of future packets, including S_i and X_i. In addition, for the pair of M/M/1/∞ → ⋅/M/1/∞ queues in tandem, the system times T_i and $T_i^{\prime }$ are independent of one another (Karpelevitch and Kreinin (1992)). By Burke’s Theorem (Burke (1956)), the departure process from the first queue is Poisson with rate λ, so the second queue can also be viewed as an independent M/M/1 queue and the service time distribution for each queue is given by $f_T(t)=({\mu }_2-\lambda )e^{-({\mu }_2-\lambda )t}$. Therefore, we have

$\begin{array}{ll}\hfill E\left[W_i^{\prime }|X_i=x\right]=& {\int }_0^{\infty }{\int }_0^x{\int }_{x+s-t}^{\infty }\left(t^{\prime }-x+t-s\right)f_T\left(t^{\prime }\right)f_T\left(t\right)f_S\left(s\right)\mathrm{d}{t}^{\prime }\mathrm{d}t\mathrm{d}s+{\int }_0^{\infty }{\int }_x^{\infty }{\int }_s^{\infty }\left(t^{\prime }-s\right)f_T\left(t^{\prime }\right)f_T\left(t\right)f_S\left(s\right)\mathrm{d}{t}^{\prime }\mathrm{d}t\mathrm{d}s\hfill \\ \hfill =& \frac{{\mu }_1}{\left({\mu }_2-\lambda \right)\left({\mu }_1-{\mu }_2\right)\left({\mu }_1+{\mu }_2-\lambda \right)}\left(\left({\mu }_1-\lambda \right)e^{-\left({\mu }_2-\lambda \right)x}-\left({\mu }_2-\lambda \right)e^{-\left({\mu }_1-\lambda \right)x}\right).\hfill \end{array}(15)$

Using (Eq. 15), we can solve for E[W′X]:

$\begin{array}{ll}\hfill E\left[W^{\prime }X\right]& ={\int }_0^{\infty }xE\left[W_i^{\prime }|X_i=x\right]f_X\left(x\right)\mathrm{d}x\hfill \\ \hfill & ={\int }_0^{\infty }\left[\frac{{\mu }_1}{\left({\mu }_2-\lambda \right)\left({\mu }_1-{\mu }_2\right)\left({\mu }_1+{\mu }_2-\lambda \right)}\left(\left({\mu }_1-\lambda \right)x{e}^{-{\mu }_{2}x}-\left({\mu }_2-\lambda \right)x{e}^{-{\mu }_{1}x}\right)\right]\mathrm{d}x\hfill \\ \hfill & =\frac{\lambda }{{\mu }_2^2\left({\mu }_2-\lambda \right)}+\frac{\lambda }{{\mu }_1{\mu }_2\left({\mu }_1+{\mu }_2-\lambda \right)}.\hfill \end{array}$

Finally, we can substitute this into λE[T′X] = λ(E[W′X] + EXES) = λE[W′X] + 1/μ₂, which can be substituted into (Eq. 14) to complete the proof.

From Eq. 14, we can see that even when the service rates are different, the average age does not depend on the order of the servers. Also recall that the order of servers did not affect the average age for single-capacity queues.

This proof for two infinite capacity queues can be extended beyond two queues. However, this would be cumbersome because of the calculation of the conditional waiting time at the last queue given the interarrival time at the first queue and would require the cases where the interarrival/interdeparture times are longer or shorter than the system times to be tracked.

We evaluated the theoretical result for 1 M/M/1/∞ and the M/M/1/∞ → ⋅/M/1/∞ (Eq. 13), and then simulated for up to four queues in tandem; the results are shown in Figure 10. The plot lines for the simulations and numerically evaluated expressions after 1 and 2 queues lie on top of one another. We also include the minimum for each curve on the plot (indicated by △) and we see that the λ that minimizes the average age again decreases as the number of queues increases. Under these settings with Poisson arrival and exponential service times, the performance can be improved by backing off from the previously optimal packet generation rate λ as the number of queues increases. In Figure 11, we plot the age for two cases of heterogeneous queues in tandem: a) where μ₁ = 0.5 and μ₂ = 1 (solid line), and b) where μ₁ = 1 and μ₂ = 0.5 (dotted line). As we noted from the expression in Eq. 14, the order of the servers does not affect the average age after the second queue. We simulated this for three cases of three queues in Figure 12 and we observe that the average age after the third queue is the same in all three cases (and for all other permutations of queue orders not shown here).

FIGURE 10

FIGURE 10. Average age vs. λ, μ = 1, infinite queue capacity.

FIGURE 11

FIGURE 11. Average age vs. λ, different μ₁, μ₂, infinite queue capacity.

FIGURE 12

FIGURE 12. Average age vs. λ, different μ₁, μ₂, μ₃, infinite queue capacity.

5 Simulation results for k capacity queues

To study the regime between single-capacity and infinite capacity queues in tandem, we simulate the average AoI for k capacity queues in tandem $(k\in {\mathbb{Z}}^{+})$ with equal service rate μ. The results are shown in Figures 13A–D after 1–4 queues, with k = 1, 5, 10, ∞ in each plot. We observe that for finite capacity queues, the average age approaches some finite value as the arrival rate increases, and that the difference between this value and the minimum is increasingly greater for larger capacity queues. Thus, optimizing the arrival rate becomes critical very quickly, even for relatively small capacity queues.

FIGURE 13

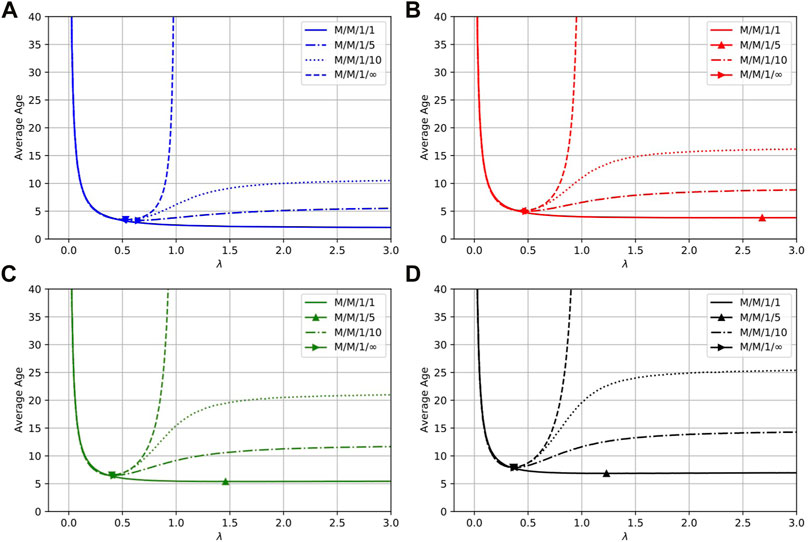
FIGURE 13. Average age vs. \λ, \μ = 1, k queue capacity. (A) 1 queue, (B) 2 queues in tandem, (C) 3 queues in tandem, (D) 4 queues in tandem.

The optimal arrival rate vs. queue capacity is shown in Figure 14 for queue capacity up to six. We observe that the optimal λ very quickly approaches the optimal for infinite capacity queues (dashed line). We have also plotted the optimal age in Figure 15 and again the optimal age for infinite capacity queues is quickly approached. These results suggest that the optimal age is very sensitive to queue capacity between the values of one and six. Meanwhile, for larger queue capacities, it suffices to optimize for infinite capacity queues. This can be easier to analyze theoretically, such as in the case for two queues in tandem. We have simulated this for different service rates μ = 0.1 and μ = 10, and have observed very similar behavior. Consequently, this result is insensitive to service rate.

FIGURE 14

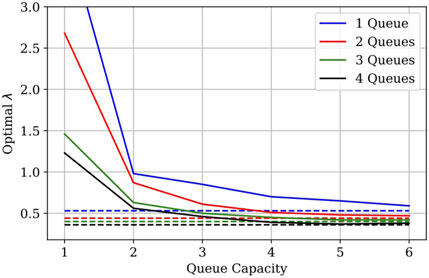
FIGURE 14. Optimal λ vs. queue capacity, μ = 1. The dotted line is the optimal λ for infinite capacity queues.

FIGURE 15

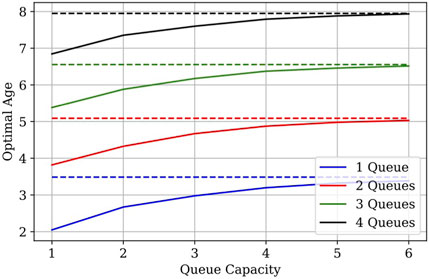
FIGURE 15. Optimal average age vs. queue capacity, μ = 1. The dotted line is the optimal age for infinite capacity queues.

6 Summary

In this work, we have analyzed the average AoI for non-preemptive queues in tandem, which is important for understanding how to control and optimize multi-hop networks for information freshness. For systems with Poisson arrivals and exponential service times, we applied the stochastic hybrid systems modeling approach to derive closed form expressions for the average age after two queues in tandem with capacity 1 and different service rates, as well as for the average age after three queues in tandem with equal service rates. Based on the average age expressions for one and two queues in tandem with equal service rates, we consider an approximation for m queues in tandem, which is shown to overestimate the age for the m = 3 and m = 4 cases with a gap that increases with λ. We have also derived the closed form expression for the average age after two infinite capacity queues with equal service rates. Finally, we studied other queue capacities k besides one and infinity. We observed that even for very small values of k, the optimal λ and age are close to that of the infinite capacity queue case.

Data availability statement

The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.

Author contributions

CK and SK contributed to conception and design of the study. CK conducted the analysis, simulations, and wrote the manuscript. Both authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was funded by the Office of Naval Research.

Acknowledgments

The content of this manuscript has been presented in part at MILCOM 2018 (Kam et al., 2018).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹In Koukoutsidis (2020), they incorrectly assume $E[S_i^{c,1\to n}{D}_i^c]=E[S_i^{c,1\to n}{A}_i^c]$, where for a packet class c, $S_i^{c,1\to n}$ is the sojourn time for the ith packet, $D_i^c$ is the interdeparture time between packet i and i + 1, and $A_i^c$ is the interarrival time between packet i − 1 and i.

²We have verified that simulation results do not match the numerical results from the expression in Koukoutsidis (2020) but the simulations validate our expression.

³In Yates (2018), the authors were able to simplify the derivation for any number of preemptive queues in tandem by using a “fake updates” trick to reduce the number of states to a single state. However, this trick does not work in the system here with non-preemptive queues. Consequently, we have the number of states being 2^m, where m is the number of queues.

References

Abd-Elmagid, M. A., and Dhillon, H. S. (2022a). Closed-form characterization of the mgf of aoi in energy harvesting status update systems. IEEE Transactions on Information Theory 68, 3896–3919. doi:10.1109/TIT.2022.3149450

CrossRef Full Text | Google Scholar

Abd-Elmagid, M. A., and Dhillon, H. S. (2022b). Distribution of aoi in eh-powered multi-source systems under non-preemptive and preemptive policies. in IEEE INFOCOM 2022 - IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), 1–8. doi:10.1109/INFOCOMWKSHPS54753.2022.9798131

CrossRef Full Text | Google Scholar

Bedewy, A. M., Sun, Y., and Shroff, N. B. (2017). “Age-optimal information updates in multihop networks,” in 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, June 25 to 30, 2017, 576–580. doi:10.1109/ISIT.2017.8006593

CrossRef Full Text | Google Scholar

Bedewy, A. M., Sun, Y., and Shroff, N. B. (2016). “Optimizing data freshness, throughput, and delay in multi-server information-update systems,” in 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10-15 July 2016, 2569–2573. doi:10.1109/ISIT.2016.7541763

CrossRef Full Text | Google Scholar

Burke, P. J. (1956). The output of a queuing system. Operations Res. 4, 699–704. doi:10.1287/opre.4.6.699

CrossRef Full Text | Google Scholar

Chiariotti, F., Vikhrova, O., Soret, B., and Popovski, P. (2020). Peak age of information distribution in tandem queue systems. arXiv e-prints , arXiv–2004. Available at: https://arxiv.org/pdf/2004.05088.pdf.

Google Scholar

Costa, M., Codreanu, M., and Ephremides, A. (2016). On the age of information in status update systems with packet management. IEEE Trans. Inf. Theory 62, 1897–1910. doi:10.1109/TIT.2016.2533395

CrossRef Full Text | Google Scholar

Kam, C., Kompella, S., and Ephremides, A. (2013). “Age of information under random updates,” in Proc. IEEE International Symposium on Information Theory (ISIT), Istanbul, Turkey, 7-12 July 2013, 66–70.

CrossRef Full Text | Google Scholar

Kam, C., Kompella, S., Nguyen, G. D., and Ephremides, A. (2016a). Effect of message transmission path diversity on status age. IEEE Trans. Inf. Theory 62, 1360–1374. doi:10.1109/TIT.2015.2511791

CrossRef Full Text | Google Scholar

Kam, C., Kompella, S., Nguyen, G. D., Wieselthier, J. E., and Ephremides, A. (2016b). “Controlling the age of information: Buffer size, deadline, and packet replacement,” in 2016 Military Communications Conference (MILCOM 2016), Baltimore, MD, USA, 1-3 Nov. 2016.

CrossRef Full Text | Google Scholar

Kam, C., Molnar, J. P., and Kompella, S. (2018). “Age of information for queues in tandem,” in MILCOM 2018 - 2018 IEEE Military Communications Conference (MILCOM), Angeles, CA, USA, 29-31 Oct. 2018. 1–6. doi:10.1109/MILCOM.2018.8599728

CrossRef Full Text | Google Scholar

Karpelevitch, F., and Kreinin, A. Y. (1992). Joint distributions in poissonian tandem queues. Queueing Syst. 12, 273–286. doi:10.1007/bf01158803

CrossRef Full Text | Google Scholar

Kaul, S., Gruteser, M., Rai, V., and Kenney, J. (2011). “Minimizing age of information in vehicular networks,” in IEEE Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON), Utah, USA, June 27-30,2011, 350–358.

CrossRef Full Text | Google Scholar

Kaul, S., Yates, R., and Gruteser, M. (2012a). “Real-time status: How often should one update?,” in Proc. IEEE INFOCOM, Orlando, FL, 25-30 March 2012, 2731–2735.

Google Scholar

Kaul, S., Yates, R., and Gruteser, M. (2012b). “Status updates through queues,” in Conference on Information Sciences and Systems (CISS), Princeton, NJ, 21-23 March 2012, 1–6.

CrossRef Full Text | Google Scholar

Kosta, A., Pappas, N., and Angelakis, V. (2017). Age of information: A new concept, metric, and tool. FNT. Netw. 12, 162–259. doi:10.1561/1300000060

CrossRef Full Text | Google Scholar

Koukoutsidis, I. (2020). “Age of information in an overtake- free network of quasi - reversible queues,” in 2020 28th International Symposium on Modeling, Analysis, and Simulation of Computer and Telecommunication Systems (MASCOTS), Nice, France, November 17–19, 2020. 1–6. doi:10.1109/MASCOTS50786.2020.9285958

CrossRef Full Text | Google Scholar

Kuang, Q., Gong, J., Chen, X., and Ma, X. (2019). “Age-of- information for computation- intensive messages in mobile edge computing,” in 2019 11th International Conference on Wireless Communications and Signal Processing (WCSP), Xi'an, China, October 23-25,2019. 1–6. doi:10.1109/WCSP.2019.8927944

CrossRef Full Text | Google Scholar

Moltafet, M., Leinonen, M., and Codreanu, M. (2021). Moment generating function of the aoi in a two-source system with packet management. IEEE Wireless Communications Letters 10, 882–886. doi:10.1109/LWC.2020.3048628

CrossRef Full Text | Google Scholar

Soret, B., Ravikanti, S., and Popovski, P. (2020). “Latency and timeliness in multi-hop satellite networks,” in ICC 2020 - 2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7-11 June 2020. 1–6. doi:10.1109/ICC40277.2020.9149009

CrossRef Full Text | Google Scholar

Sun, Y., Uysal-Biyikoglu, E., Yates, R. D., Koksal, C. E., and Shroff, N. B. (2017). Update or wait: How to keep your data fresh. IEEE Trans. Inf. Theory 63, 7492–7508. doi:10.1109/TIT.2017.2735804

CrossRef Full Text | Google Scholar

Talak, R., Karaman, S., and Modiano, E. (2017). “Minimizing age-of-information in multi-hop wireless networks,” in 2017 55th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 3-6 Oct. 2017, 486–493. doi:10.1109/ALLERTON.2017.8262777

CrossRef Full Text | Google Scholar

Vikhrova, O., Chiariotti, F., Soret, B., Araniti, G., Molinaro, A., and Popovski, P. (2020). “Age of information in multi-hop networks with priorities,” in GLOBECOM 2020 - 2020 IEEE Global Communications Conference, Taipei City Taiwan, 7 - 11 December 2020. 1–6. doi:10.1109/GLOBECOM42002.2020.9348175

CrossRef Full Text | Google Scholar

Xu, C., Yang, H. H., Wang, X., and Quek, T. Q. S. (2020). Optimizing information freshness in computing-enabled IoT networks. IEEE Internet Things J. 7, 971–985. doi:10.1109/JIOT.2019.2947419

CrossRef Full Text | Google Scholar

Yates, R. D. (2018). “Age of information in a network of preemptive servers,” in IEEE INFOCOM 2018 - IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Honolulu, HI, USA, 15-19 April 2018, 118–123. doi:10.1109/INFCOMW.2018.8406966

CrossRef Full Text | Google Scholar

Yates, R. D., and Kaul, S. (2012). “Real-time status updating: Multiple sources,” in Proc. IEEE International Symposium on Information Theory (ISIT), Cambridge, MA, 1-6 July 2012, 2666–2670.

CrossRef Full Text | Google Scholar

Yates, R. D., and Kaul, S. K. (2019). The age of information: Real-time status updating by multiple sources. IEEE Trans. Inf. Theory 65, 1807–1827. doi:10.1109/TIT.2018.2871079

CrossRef Full Text | Google Scholar

Yates, R. D. (2020). The age of information in networks: Moments, distributions, and sampling. IEEE Transactions on Information Theory 66, 5712–5728. doi:10.1109/TIT.2020.2998100

CrossRef Full Text | Google Scholar

Appendix: Proof of Theorem 2

Similar to the two-queue case, the states 0q₂q₃ all have outgoing transitions through arrivals into queue 1 of rate λ, and there is an outgoing transition of rate μ for each occupied queue. For incoming transitions, the states 1q₂q₃ have a transition of rate λ from 0q₂q₃ and there is a transition of rate μ from a state where q_i = 1 to a state where q_i = 0 and q_i+1 = 1 or if i = 3, so that the queue is followed by the monitor. The resulting global balance equations are given as follows:

$\begin{array}{ll}\hfill \lambda {\bar{\pi }}_{000}=& \mu {\bar{\pi }}_{001}\hfill \\ \hfill \left(\lambda +\mu \right){\bar{\pi }}_{001}=& \mu \left({\bar{\pi }}_{010}+{\bar{\pi }}_{011}\right)\hfill \\ \hfill \left(\lambda +\mu \right){\bar{\pi }}_{010}=& \mu \left({\bar{\pi }}_{011}+{\bar{\pi }}_{100}+{\bar{\pi }}_{110}\right)\hfill \\ \hfill \left(\lambda +2\mu \right){\bar{\pi }}_{011}=& \mu \left({\bar{\pi }}_{101}+{\bar{\pi }}_{111}\right)\hfill \\ \hfill \mu {\bar{\pi }}_{100}=& \lambda {\bar{\pi }}_{000}+\mu {\bar{\pi }}_{101}\hfill \\ \hfill 2\mu {\bar{\pi }}_{101}=& \lambda {\bar{\pi }}_{001}+\mu \left({\bar{\pi }}_{110}+{\bar{\pi }}_{111}\right)\hfill \\ \hfill 2\mu {\bar{\pi }}_{110}=& \lambda {\bar{\pi }}_{010}+\mu {\bar{\pi }}_{111}\hfill \\ \hfill 3\mu {\bar{\pi }}_{111}=& \lambda {\bar{\pi }}_{011}\hfill \end{array}$

with the solution

$\begin{array}{llll}\hfill {\bar{\pi }}_{000}=& \frac{{\mu }^3}{{\left(\lambda +\mu \right)}^3},\hfill & \hfill {\bar{\pi }}_{001}=& \frac{\lambda {\mu }^2}{{\left(\lambda +\mu \right)}^3},\hfill \\ \hfill {\bar{\pi }}_{010}=& \frac{\lambda \mu \left(5\lambda +8\mu \right)}{8{\left(\lambda +\mu \right)}^3},\hfill & \hfill {\bar{\pi }}_{011}=& \frac{3{\lambda }^2\mu }{8{\left(\lambda +\mu \right)}^3},\hfill \\ \hfill {\bar{\pi }}_{100}=& \frac{\lambda \left({\lambda }^2+3\lambda \mu +4{\mu }^2\right)}{4{\left(\lambda +\mu \right)}^3},\hfill & \hfill {\bar{\pi }}_{101}=& \frac{{\lambda }^2\left(\lambda +3\mu \right)}{4{\left(\lambda +\mu \right)}^3},\hfill \\ \hfill {\bar{\pi }}_{110}=& \frac{{\lambda }^2\left(3\lambda +4\mu \right)}{8{\left(\lambda +\mu \right)}^3},\hfill & \hfill {\bar{\pi }}_{111}=& \frac{{\lambda }^3}{8{\left(\lambda +\mu \right)}^3}.\hfill \end{array}$

Similar to the global balance equations, the steady-state correlation between discrete and age states satisfy (6), which for the age at the monitor ${\bar{v}}_{q4}$ gives us the following equations:

$\begin{array}{ll}\hfill \lambda {\bar{v}}_{0004}=& {\pi }_{000}+\mu {\bar{v}}_{0013}\hfill \\ \hfill \left(\lambda +\mu \right){\bar{v}}_{0014}=& {\pi }_{001}+\mu \left({\bar{v}}_{0104}+{\bar{v}}_{0114}\right)\hfill \\ \hfill \left(\lambda +\mu \right){\bar{v}}_{0104}=& {\pi }_{010}+\mu \left({\bar{v}}_{1004}+{\bar{v}}_{1104}+{\bar{v}}_{0113}\right)\hfill \\ \hfill \left(\lambda +2\mu \right){\bar{v}}_{0114}=& {\pi }_{011}+\mu \left({\bar{v}}_{1014}+{\bar{v}}_{1114}\right)\hfill \\ \hfill \mu {\bar{v}}_{1004}=& {\pi }_{100}+\lambda {\bar{v}}_{0004}+\mu {\bar{v}}_{1013}\hfill \\ \hfill 2\mu {\bar{v}}_{1014}=& {\pi }_{101}+\lambda {\bar{v}}_{0014}+\mu \left({\bar{v}}_{1104}+{\bar{v}}_{1114}\right)\hfill \\ \hfill 2\mu {\bar{v}}_{1104}=& {\pi }_{110}+\lambda {\bar{v}}_{0104}+\mu {\bar{v}}_{1113}\hfill \\ \hfill 3\mu {\bar{v}}_{1114}=& {\pi }_{111}+\lambda {\bar{v}}_{0114}.\hfill \end{array}$

Using a similar approach as in the two-queue case, we take linear combinations of these equations to yield ${\sum }_{\bar{q}\in \mathcal{Q}}{\bar{v}}_{\bar{q}4}$ when we move all ${\bar{v}}_{\bar{q}4}$ terms to the left-hand side, such that the coefficients must satisfy

$\begin{array}{ll}\hfill a\lambda -e\lambda =& 1\hfill \\ \hfill b\left(\lambda +\mu \right)-f\lambda =& 1\hfill \\ \hfill c\left(\lambda +\mu \right)-b\mu -g\lambda =& 1\hfill \\ \hfill d\left(\lambda +2\mu \right)-b\mu -h\lambda =& 1\hfill \\ \hfill e\mu -c\mu =& 1\hfill \\ \hfill 2f\mu -d\mu =& 1\hfill \\ \hfill 2g\mu -c\mu -f\mu =& 1\hfill \\ \hfill 3h\mu -d\mu -f\mu =& 1,\hfill \end{array}$

which is achieved with solution

$\begin{array}{llllllll}\hfill a=& \frac{1}{\lambda }+\frac{3}{\mu },\hfill & \hfill b=& \frac{1}{\mu },\hfill & \hfill c=& \frac{2}{\mu },\hfill & \hfill d=& \frac{1}{\mu }\hfill \\ \hfill e=& \frac{3}{\mu },\hfill & \hfill f=& \frac{1}{\mu },\hfill & \hfill g=& \frac{2}{\mu },\hfill & \hfill h=& \frac{1}{\mu }.\hfill \end{array}$

The linear combination of equations yields the following:

$\begin{array}{ll}\hfill \sum _{\bar{q}\in \mathcal{Q}}{\bar{v}}_{\bar{q}4}& =\left(\frac{1}{\lambda }+\frac{3}{\mu }\right){\pi }_{000}+\frac{1}{\mu }{\pi }_{001}+\frac{2}{\mu }{\pi }_{010}+\frac{1}{\mu }{\pi }_{011}+\frac{2}{\mu }{\pi }_{100}+\frac{1}{\mu }{\pi }_{101}+\frac{2}{\mu }{\pi }_{110}+\frac{1}{\mu }{\pi }_{111}\hfill \\ \hfill & +\left(\frac{\mu }{\lambda }+3\right){\bar{v}}_{0013}+2{\bar{v}}_{0113}+3{\bar{v}}_{1013}+2{\bar{v}}_{1113}\hfill \end{array}$

Next we need to find $(\frac{\mu }{\lambda }+3){\bar{v}}_{0013}+2{\bar{v}}_{0113}+3{\bar{v}}_{1013}+2{\bar{v}}_{1113}$, which is a function of the correlation functions for the age at the third queue ${\bar{v}}_{q3}$. To find this expression, we take linear combinations of the corresponding equations shown here:

$\begin{array}{ll}\hfill \left(\lambda +\mu \right)v_{0013}=& {\pi }_{001}+\mu \left(v_{0102}+v_{0113}\right)\hfill \\ \hfill \left(\lambda +2\mu \right)v_{0113}=& {\pi }_{011}+\mu \left(v_{1013}+v_{1113}\right)\hfill \\ \hfill 2\mu v_{1013}=& {\pi }_{101}+\lambda v_{0013}+\mu \left(v_{1102}+v_{1113}\right)\hfill \\ \hfill 3\mu v_{1113}=& {\pi }_{111}+\lambda v_{0113}\hfill \end{array}$

such that their coefficients satisfy

$\begin{array}{ll}\hfill a^{\prime }\left(\lambda +\mu \right)-c^{\prime }\lambda =& \left(\frac{\mu }{\lambda }+3\right)\hfill \\ \hfill b^{\prime }\left(\lambda +2\mu \right)-a^{\prime }\mu -d^{\prime }\lambda =& 2\hfill \\ \hfill c^{\prime }2\mu -b^{\prime }\mu =& 3\hfill \\ \hfill d^{\prime }3\mu -b^{\prime }\mu -c^{\prime }\mu =& 2.\hfill \end{array}$

The solution for the coefficients is given by

$\begin{array}{ll}\hfill a^{\prime }=& \frac{8{\lambda }^3+33{\lambda }^2\mu +39\lambda {\mu }^2+12{\mu }^3}{3\lambda \mu {\left(\lambda +2\mu \right)}^2}\hfill \\ \hfill b^{\prime }=& \frac{7\lambda +12\mu }{3\mu \left(\lambda +4\mu \right)}+\frac{2\mu }{\lambda +4\mu }{a}^{\prime }\hfill \\ \hfill c^{\prime }=& \frac{8\lambda +24\mu }{3\mu \left(\lambda +4\mu \right)}+\frac{\mu }{\lambda +4\mu }{a}^{\prime }\hfill \\ \hfill d^{\prime }=& \frac{7\lambda +20\mu }{3\mu \left(\lambda +4\mu \right)}+\frac{\mu }{\lambda +4\mu }{a}^{\prime }.\hfill \end{array}$

Next we find $a^{\prime }\mu {\bar{v}}_{0102}+c^{\prime }\mu {\bar{v}}_{1102}$ via linear combinations of

$\begin{array}{ll}\hfill \left(\lambda +\mu \right)v_{0102}=& {\pi }_{010}+\mu \left(v_{1001}+v_{1102}+v_{0112}\right)\hfill \\ \hfill \left(\lambda +2\mu \right)v_{0112}=& {\pi }_{011}+\mu \left(v_{1011}+v_{1112}\right)\hfill \\ \hfill 2\mu v_{1102}=& {\pi }_{110}+\lambda v_{0102}+\mu v_{1112}\hfill \\ \hfill 3\mu v_{1112}=& {\pi }_{111}+\lambda v_{0112}.\hfill \end{array}$

This is achieved with coefficients that satisfy

$\begin{array}{ll}\hfill a^{″}\left(\lambda +\mu \right)-c^{″}\lambda =& a^{\prime }\mu \hfill \\ \hfill b^{″}\left(\lambda +2\mu \right)-a^{″}\mu -d^{″}\lambda =& 0\hfill \\ \hfill c^{″}2\mu -a^{″}\mu =& c^{\prime }\mu \hfill \\ \hfill d^{″}3\mu -b^{″}\mu -c^{″}\mu =& 0,\hfill \end{array}$

which has solution

$\begin{array}{ll}\hfill a^{″}=& \frac{8{\lambda }^2+24\lambda \mu }{3\mu \left(\lambda +2\mu \right)\left(\lambda +4\mu \right)}+\frac{3\lambda \mu +8{\mu }^2}{\left(\lambda +2\mu \right)\left(\lambda +4\mu \right)}{a}^{\prime }\hfill \\ \hfill b^{″}=& \frac{4\lambda }{3\mu \left(\lambda +2\mu \right)}+\frac{\mu }{\lambda +2\mu }{a}^{\prime }\hfill \\ \hfill c^{″}=& \frac{8{\lambda }^2+32\lambda \mu +24{\mu }^2}{3\mu \left(\lambda +2\mu \right)\left(\lambda +4\mu \right)}+\frac{2\lambda \mu +5{\mu }^2}{\left(\lambda +2\mu \right)\left(\lambda +4\mu \right)}{a}^{\prime }\hfill \\ \hfill d^{″}=& \frac{4{\lambda }^2+16\lambda \mu +8{\mu }^2}{3\mu \left(\lambda +2\mu \right)\left(\lambda +4\mu \right)}+\frac{\lambda \mu +3{\mu }^2}{\left(\lambda +2\mu \right)\left(\lambda +4\mu \right)}{a}^{\prime }.\hfill \end{array}$

The last set of equations used to find $a^{″}\mu {\bar{v}}_{1001}+b^{″}\mu {\bar{v}}_{1011}$ is given by

$\begin{array}{ll}\hfill \mu v_{1001}=& {\pi }_{100}+\mu v_{1011}\hfill \\ \hfill 2\mu v_{1011}=& {\pi }_{101}+\mu \left(v_{1101}+v_{1111}\right)\hfill \\ \hfill 2\mu v_{1101}=& {\pi }_{110}+\mu v_{1111}\hfill \\ \hfill 3\mu v_{1111}=& {\pi }_{111},\hfill \end{array}$

and the coefficients must satisfy

$\begin{array}{ll}\hfill a‴\mu =& a^{″}\mu \hfill \\ \hfill b‴2\mu -a‴\mu =& b^{″}\mu \hfill \\ \hfill c‴2\mu -b‴\mu =& 0\hfill \\ \hfill d‴3\mu -b‴\mu -c‴\mu =& 0,\hfill \end{array}$

which has solution

$\begin{array}{ll}\hfill a‴=& a^{″}\hfill \\ \hfill =& \frac{8{\lambda }^2+24\lambda \mu }{3\mu \left(\lambda +2\mu \right)\left(\lambda +4\mu \right)}+\frac{3\lambda \mu +8{\mu }^2}{\left(\lambda +2\mu \right)\left(\lambda +4\mu \right)}{a}^{\prime }\hfill \\ \hfill b‴=& \frac{a^{″}+b^{″}}{2}\hfill \\ \hfill =& \frac{6{\lambda }^2+20\lambda \mu }{3\mu \left(\lambda +2\mu \right)\left(\lambda +4\mu \right)}+\frac{2\lambda \mu +6{\mu }^2}{\left(\lambda +2\mu \right)\left(\lambda +4\mu \right)}{a}^{\prime }\hfill \\ \hfill c‴=& \frac{a^{″}+b^{″}}{4}\hfill \\ \hfill =& \frac{3{\lambda }^2+10\lambda \mu }{3\mu \left(\lambda +2\mu \right)\left(\lambda +4\mu \right)}+\frac{\lambda \mu +3{\mu }^2}{\left(\lambda +2\mu \right)\left(\lambda +4\mu \right)}{a}^{\prime }\hfill \\ \hfill d‴=& \frac{a^{″}+b^{″}}{4}\hfill \\ \hfill =& \frac{3{\lambda }^2+10\lambda \mu }{3\mu \left(\lambda +2\mu \right)\left(\lambda +4\mu \right)}+\frac{\lambda \mu +3{\mu }^2}{\left(\lambda +2\mu \right)\left(\lambda +4\mu \right)}{a}^{\prime }.\hfill \end{array}$

We substitute the values into

$\begin{array}{ll}\hfill \sum _{\bar{q}\in \mathcal{Q}}{\bar{v}}_{\bar{q}4}& =\left(\frac{1}{\lambda }+\frac{3}{\mu }\right){\pi }_{000}+\left(\frac{1}{\mu }+a^{\prime }\right){\pi }_{001}+\left(\frac{2}{\mu }+a^{″}\right){\pi }_{010}+\left(\frac{1}{\mu }+b^{\prime }+b^{″}\right){\pi }_{011}+\left(\frac{3}{\mu }+a^{‴}\right){\pi }_{100}+\left(\frac{1}{\mu }+c^{\prime }+b^{‴}\right){\pi }_{101}\hfill \\ \hfill & +\left(\frac{2}{\mu }+c^{″}+c^{‴}\right){\pi }_{110}+\left(\frac{1}{\mu }+d^{\prime }+d^{″}+d^{‴}\right){\pi }_{111}\hfill \end{array}$

which, after much simplification, yields the final result.