Incentive-Based Delay Minimization for 6G-Enabled Wireless Federated Learning

Federated Learning (FL) is a promising decentralized machine learning technique, which can be efficiently used to reduce the latency and deal with the data privacy in the next 6th generation (6G) of wireless networks. However, the finite computation and communication resources of the wireless devices, is a limiting factor for their very low latency requirements, while users need incentives for spending their constrained resources. In this direction, we propose an incentive mechanism for Wireless FL (WFL), which motivates users to utilize their available radio and computation resources, in order to achieve a fast global convergence of the WFL process. More specifically, we model the interaction among users and the server as a Stackelberg game, where users (followers) aim to maximize their utility/pay-off, while the server (leader) focuses on minimizing the global convergence time of the FL task. We analytically solve the Stackelberg game and derive the optimal strategies for both the server and the user set, corresponding to the Stackelberg equilibrium. Following that, we consider the presence of malicious users, who may attempt to mislead the server with false information throughout the game, aiming to further increase their utility. To alleviate this burden, we propose a deep learning-aided secure mechanism at the servers’ side, which detects malicious users and prevents them from participating into the WFL process. Simulations verify the effectiveness of the proposed method, which result in increased users’ utility and reduced global convergence time, compared with various baseline schemes. Finally, the proposed mechanism for detecting the users’ behavior seems to be very promising in increasing the security of WFL-based networks.

1 Introduction

The 6th generation (6G) of wireless networks, is envisioned to support ubiquitous artificial intelligence services and be the evolution of wireless networks from “connected things” to “intelligent things” Letaief et al. (2019). Conventional machine learning approaches are usually conducted in a centralized manner, where a central entity collects the generated data, and performs the training. However, the increasing computing capabilities of wireless devices as well as the sensitive data-privacy concerns have paved the way for a promising decentralized solution, the Federated Learning (FL) Konečnỳ et al. (2016), McMahan et al. (2017). The salient feature of FL lies in the retention of the locally generated data at the device, thus, each learner individually trains the model locally without uploading any raw data to the server. Hence, the learners collaboratively build a shared model with the aid of a server, whose role is to update and redistribute the global training parameters to the learners. In this manner, the user data privacy is preserved, while the communication traffic is reduced leading to low latency, due to the absence of raw and big volume data transfer Li et al. (2020). In accordance with the key requirements of 6G networks, it is evident that 6G could be empowered by FL for ensuring low-latency and privacy preserving intelligent services Bouzinis et al. (2022a), Bouzinis et al. (2022b).

1.1 Motivation and State-of-the-Art

In the context of wireless networks, several studies have investigated the improvement of FL, in terms of model accuracy, energy efficiency, and reduced latency. For instance, the authors in Chen et al. (2020b), Shi et al. (2020b), minimized the training loss under latency and energy requirements, by jointly optimizing the computation and radio resources, as well as the user scheduling. Moreover, in another wireless FL (WFL) setup, the users’ total energy consumption and/or latency minimization, have been investigated in Tran et al. (2019), Chen et al. (2020a), Yang et al. (2021).

Although, the aforementioned research works have contributed for the efficient deployment of FL in wireless networks, there is still an open challenge regarding users’ willingness to participate into the WFL process. In particular, the users should be motivated, in order to contribute in this process with their limited energy resources. Thus, incentive designs are requisite, in order to attract the clients to be involved in this resource-consuming procedure. The considered incentives, could be expressed as a reward provided by the task publisher. For example, in Kang et al. (2019) an incentive mechanism for reliable FL was proposed, based on the contract theory, while a reputation metric was introduced, in order to measure the data-wise reliability and trustworthiness of the clients. In similar direction, authors in Lim et al. (2020) proposed an hierarchical incentive mechanism for FL. In the first level, a contract theory approach was proposed to incentivize workers to provide high quality and quantity data, while in the second level, a coalitional game approach was adopted among the model owners. In Zhan et al. (2020), a deep-reinforcement learning incentive mechanism for FL has been constructed. More specifically, a Stackelberg game was formulated, in order to obtain the optimal pricing strategy of the task publisher and the optimal training strategies of the edge nodes, which constituted the client set. Moreover, in Sarikaya and Ercetin (2019), authors formulated a Stackelberg game among workers and the task publisher, aiming to minimize the latency of a FL communication round, while in Khan et al. (2020), a Stackelberg game was formulated for FL in edge networks. Finally, in the context of a crowdsourcing framework, authors in Pandey et al. (2020) proposed a Stackelberg game for motivating the FL users to generate high accuracy models, while the server focused on providing high global model accuracy side. However, none of the above works designed an incentive mechanism, by taking into account the minimization of the FL global convergence time, which can finally result in achieving decreased delay. It should be also highlighted, that the number of scheduled devices affects the convergence speed of the global model, and its effects have not been investigated. More specifically, the trade-off between the duration of a global WFL round and the number of total rounds until convergence, has not been well-studied in the context of incentive criteria. Finally, it should be noted that when examining clients’ strategies, all previous works did not consider the joint optimization of the communication and computation resources, which can further enhance the performance and head towards meeting the strict latency requirements of 6G networks.

Also, the modeling of the interaction among the server and the users becomes more complicated when some of the users are not legitimate, degrading the overall quality of experience. However, this issue has not been considered by the existing literature, despite the progress in the development of techniques that have the potential to mitigate similar threats, such as deep learning. Recently, the application of deep learning into wireless communications has sparked widespread interest Zappone et al. (2019), while it is expected to realize the vision of 6G, which will heavily rely on AI services. For instance, deep learning has been used for simplifying the physical layer operations, such as data detection, decoding, channel estimation, as well as for resource allocation tasks and efficient optimization Sun et al. (2017). Owing to its encouraging results, deep learning may be appropriate for ensuring an unimpeachable interaction among the users and the server, as implied by the incentive mechanism during the WFL procedure, by detecting abnormal or malicious users’ behaviors.

1.2 Contribution

Driven by the aforementioned considerations, we propose a novel incentive mechanism for WFL, by modeling the interaction among users and the server/task publisher during an WFL task, by using tools from game theory. In particular, users’ objective goal is to maximize their utility, which is subject to their individual completion time of the WFL task and the energy consumption for local training and parameter transmission, given a reward for the timely task completion and an energy cost, respectively. On the other hand, the server aims to minimize the global convergence time of the WFL process. The aforementioned interaction between the server/task publisher and the users corresponds to a Stackelberg game, where the server acts as the leader of the game and announces the delay tolerance, and the users/clients constitute the set of followers and receive their decisions based on the reward given by the server and the announced delay tolerance. The convergence time is a metric of paramount importance for providing low-latency intelligent services in 6G networks, while its minimization has not been examined in the aforementioned works. Therefore, one of the main goals of the proposed incentive mechanism is to accelerate the convergence of the WFL procedure. Moreover, the convergence time is highly related with the number of communication rounds between the users and the task publisher, which is a function of the number of participating users. Hence, during the Stackelberg game, we show that the task publisher should urge a certain number of users for participation, in order to achieve the minimum convergence speed. This fact highlights the significance of user scheduling during the game, which aims to mitigate the straggler effect, i.e., excluding clients who are responsible for the occurrence of long delays. To this end, we consider the scenario where malicious users are involved into the game, which may strive to misinform the server regarding their consumed resources and possibly benefit from this action. In order to avert such behaviors, we propose the use of a Deep Neural Network (DNN), which aims to classify the users’ identity, as honest or malicious, based on resource-related observations. Through this approach, we aim to guarantee an irreproachable interaction among the users and the server, and exclude clients with malicious actions from the FL process.

The contributions of this work can be summarized as follows:

1) We construct an incentive mechanism, for motivating users to utilize their resources during a FL task, through the improvement of their utility, while the task publisher aims to minimize the global convergence time of the WFL process.

2) We formulate and solve a Stackelberg game for the considered user-server interaction. In particular, we obtain the optimal strategy of the users for maximizing their utility, i.e., the optimal adjustment of both computation and communication resources. Furthermore, we obtain the task publisher’s optimal strategies for minimizing the global convergence time. This translates to the selection of the optimal delay tolerance during a WFL communication round, based on the number of scheduled users.

3) During the user-server interaction via the Stackelberg game, we assume that malicious users may announce false information regarding their utilized resources, aiming to mislead the server and increase their pay-off. To tackle with this issue, we construct a security mechanism at the servers’ side, whose role is to recognize false announcements and subsequently identify malicious users. Specifically, we construct and train a DNN to accurately detect malicious users. The training of the DNN is supervised and it is based on observations regarding the users’ consumed resources.

4) Simulations were conducted to evaluate the performance of the proposed approaches. The results verify the effectiveness of the solutions to the game, in comparison with various baseline schemes. Moreover, insights for the Stackelberg game and its effects to the convergence time of the FL task are provided. Furthermore, the joint optimization of radio and computation resources is shown to result in increased user utility. Finally, the considered DNN for detecting malicious users, presents a quite satisfactory classification accuracy, corroborating the effectiveness of this security mechanism.

2 System Model

2.1 WFL Model

We consider a WFL system, consisting of K clients/users indexed as $k\in \mathcal{K}=\{\mathrm{1,2},\dots ,K\}$ and a task publisher/server. Each user k has a local dataset ${\mathcal{D}}_k={\{{\mathit{x}}_{n,k},y_{n,k}\}}_{n=1}^{D_k}$, where $D_k=|{\mathcal{D}}_k|$ are the data samples, x_n,k is the n-th input data vector of user k, while y_n,k is the corresponding labeled output on the respective input sample. The total size of all training data of the users is denoted as $D={\sum }_{k=1}^K{D}_k$.

The local loss function on the whole data set D_k is defined as

$f_k\left({\mathit{w}}_k\right)\triangleq \frac{1}{D_k}\sum _{n\in {\mathcal{D}}_n}f\left({\mathit{w}}_k,{\mathit{x}}_{n,k},y_{n,k}\right),\forall k\in \mathcal{K},(1)$

where f (w_k, x_n,k, y_n,k) is the loss function on the input-output pair {x_n,k, y_n,k} and captures the error of the model parameter w_k for the considered input-output pair. Therefore, each user is interested in obtaining the w_k which minimizes its loss function. For different FL tasks, the loss function also differs. For example, for a linear regression task the loss function is $f({\mathit{w}}_k,{\mathit{x}}_{n,k},y_{n,k})=\frac{1}{2}{({\mathit{x}}_{n,k}^T{\mathit{w}}_k-y_{n,k})}^2$. Following that, the aim of the FL training process is to find the global model parameter w, which minimizes the loss function on the whole data set across all users, which can be written as

$J\left(\mathit{w}\right)=\frac{1}{D}\sum _{k=1}^K{D}_k{f}_k\left(\mathit{w}\right),(2)$

i.e., to find ${\mathit{w}}^{*}=\underset{\mathit{w}}{\mathrm{arg\; min}}J(\mathit{w})$.

The training process consists of N rounds, denoted by i. Thus, the i-th round is described below

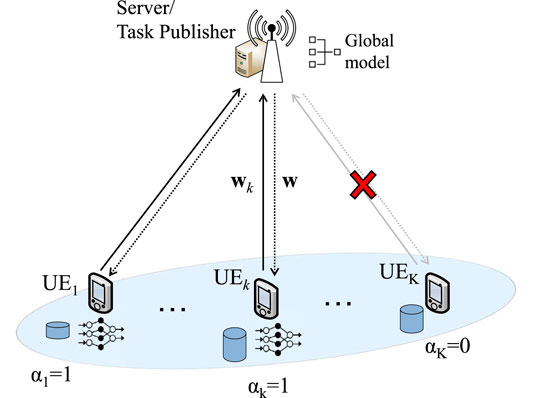
1) Firstly, the BS broadcasts the global parameter wⁱ to all participating users during the considered round. We highlight that it is not mandatory that all users are participating into the process. Let $a_k,\forall k\in \mathcal{K}$, be a binary variable which indicates whether user k is participating, i.e., a_k = 1. Furthermore, we define the set $\mathcal{S}\triangleq \{k\in \mathcal{K}|a_k=1\}\subseteq \mathcal{K}$, which consists of all the scheduled users. Moreover, the cardinality of $\mathcal{S}$ is given by $|\mathcal{S}|={\sum }_{k=1}^K{a}_k$.

2) After receiving the global model parameter, each user $k\in \mathcal{S}$, updates its local model by applying one step of the gradient descent method, towards minimizing its loss function on its whole dataset, i.e., ${\mathit{w}}_k^{i+1}={\mathit{w}}^i-\eta \nabla f_k({\mathit{w}}^i)$, where η is the learning rate, and then uploads the local parameter ${\mathit{w}}_k^{i+1}$ to the server.

3) After receiving all the local parameters, the server aggregates them, in order to update the global model parameter, by applying ${\mathit{w}}^{i+1}=\frac{1}{D^{\prime }}{\sum }_{k\in \mathcal{S}}{D}_k{\mathit{w}}_k^{i+1}$, where $D^{\prime }={\sum }_{k\in \mathcal{S}}{D}_k$ and represents the total size of all training data among the participating users.

The whole procedure is repeated for N rounds, until a required accuracy is achieved. During the first round, the global parameter w⁰ is initialized by the server. The WFL model is depicted in Figure 1. Also, Table 1 summarizes the list of notations used in this article.

FIGURE 1

FIGURE 1. WFL system model.

TABLE 1

TABLE 1. List of notations.

2.2 Computation Model

The computation resources for local model training, i.e., CPU cycle frequency, of the k-th user is denoted as f_k. The number of CPU cycles for a user k to perform one sample of data in local model training is denoted by c_k. Hence, the computation time dedicated for a local iteration, i.e., a step of the gradient descent method, is given as

$t_k^{\text{comp}}=\frac{c_k{D}_k}{f_k},\forall k\in \mathcal{K},(3)$

where D_k is the data size of the dataset ${\mathcal{D}}_k$. Accordingly, the energy consumption for a local iteration, can be expressed as follows

$E_k^{\text{comp}}=\zeta c_k{D}_k{f}_k^2,\forall k\in \mathcal{K},(4)$

where ζ is a constant parameter related to the hardware architecture of device k.

2.3 Communication Model

By using orthogonal frequency domain multiple access (OFDMA) to transmit a model update to the server/BS, the achievable transmission rate (bit/s) of user k can be written as

$r_k=B{\log }_2\left(1+\frac{p_k{g}_k}{B{N}_0}\right),\forall k\in \mathcal{K},(5)$

where B is the available bandwidth, N₀ is the spectral power density and p_k, g_k denote the transmit power, and channel gain of user k, respectively. The channel gain is modeled as $g_k=|h_k{|}^2{d}_k^{-2}$, where the complex random variable $h_k\sim \mathcal{C}\mathcal{N}(\mathrm{0,1})$ is the small scale fading and d_k is the distance between user k and the BS. Let t_k be the transmission time of k-th user, dedicated for transmitting the local training parameters to the server. To upload the training parameters w_k within the time duration t_k, the following condition should be satisfied

$t_k{r}_k\ge s_k,\forall k\in \mathcal{K}.(6)$

where s_k denotes the data size of the training parameters w_k. Moreover, the consumed energy for the considered transmission, is given by

$E_k=t_k{p}_k,\forall k\in \mathcal{K}.(7)$

Following that, the total time that a user should dedicate for both computation and communication purposes, is given as

${\tau }_k=t_k^{\text{comp}}+t_k=\frac{c_k{D}_k}{f_k}+t_k,\forall k\in \mathcal{K}.(8)$

Since the transmit power of the BS is much higher than that of the users’, we ignore the delay of the server for broadcasting the global parameter to the users. Finally, the total energy consumption of the k-th user during a communication round, for executing local computations, and uploading the local training parameters, can be written as

${\mathcal{E}}_k=E_k^{\text{comp}}+E_k=\zeta c_k{D}_k{f}_k^2+t_k{p}_k,\forall k\in \mathcal{K},(9)$

3 User Utility and Convergence Time of the Global Model

In the considered system, the server should wait for all users to terminate the local parameter transmission and afterwards update the global model. Thus, users who present large τ_k are considered as stragglers, since they will be responsible for the occurrence of large delay during a communication round. More specifically, the total delay of a round is given by $\underset{k\in \mathcal{K}}{\mathrm{m}\mathrm{a}\mathrm{x}}\{{\tau }_k\}$. Taking this into account, the case where all users are participating in the FL process may lead to increased delay, owing this to the poor wireless conditions that a user may suffer from. Moreover, it is of paramount importance that users have incentives for being involved into the considered procedure, since their participation comes at the expense of energy consumption, while devices are energy-constrained. In the continue, we proceed to the definition of users utility and the task publisher’s objective goal, i.e., global convergence time minimization.

3.1 User Utility Function

The utility function aims to quantify the incentive of a user for being involved into the FL process, in terms of a money-based reward, and it is a tool for facilitating the economic interaction among the users and the task publisher. In order to ensure low latency, we assume that the maximum delay tolerance that server requires during a communication round is $\tilde{T}$. As a result, only the users who are able to meet this delay demand should participate in the process. Driven by this consideration, we define the utility function of k-th user as

$U_k\triangleq \left(\left(\tilde{T}-{\tau }_k\right)q_1-{\mathcal{E}}_k{q}_2\right)a_k,\forall k\in \mathcal{K},(10)$

where q₁ > 0 is a constant reward given by the server to the user, for a timely task completion. Thus, q₁ is the price for a unit of time, received by the users. It is obvious that smaller task completion time τ_k, leads to higher earned reward. Moreover, q₂ > 0, denotes the cost of energy consumption and a_k is a binary variable, which indicates whether user k will participate in the process or not. We assume that user k will participate, i.e., a_k = 1, only if the condition U_k > 0 is satisfied, otherwise user k will decide not to be involved. In essence, the utility function consists of a term which reflects the reward for the timely task completion, i.e., $(\tilde{T}-{\tau }_k)q_1$, meeting the delay requirement imposed by the server, and an energy cost which is related with the resources consumption. Furthermore, it is obvious that when the condition ${\tau }_k\ge \tilde{T}$ holds, i.e., user k cannot satisfy the delay tolerance condition, the utility function will always be negative, while in this case the user will not indulge in participating and will set a_k = 0. Moreover, since smaller τ_k leads to higher earned reward, users are motivated to compute and send the local training parameters as fast as possible. However, this will lead to higher energy consumption. It should be highlighted, that the utility function can also be negative even if the case ${\tau }_k<\tilde{T}$ holds, owing this to an increased energy consumption. This fact implies that user k can satisfy the delay requirement of the server, but utilizes a great amount of resources for achieving low delay. As a result, an interesting tradeoff appears between task completion latency and energy consumption, since users are interested in maximizing their utility function.

3.2 Global Convergence Time

The objective goal of the task publisher is to minimize the convergence time of the FL process, in order to extract the global training model. The convergence time can be expressed as

$T^{\text{conv}}=T^{\text{max}}\times N,(11)$

where T^max is given by

$T^{\text{max}}=\underset{k\in \mathcal{K}}{\mathrm{m}\mathrm{a}\mathrm{x}}\left\{{\tau }_k{a}_k\right\},(12)$

and represents the total delay in a communication round, since it is determined by the slowest scheduled device, while N denotes the number of total communication rounds. As shown in Li et al. (2019), the total number of communication rounds to achieve a certain global accuracy, is on the order of $\mathcal{O}\left(G(1+\frac{1}{|\mathcal{S}|})+\mathrm{\Gamma }\right)$, where G, Γ are parameters related with data distribution and the FL settings. Hence, according to Shi et al. (2020a), the required number of total rounds in order to achieve the convergence of the global model, can be approximated as follows

$N=\beta \left(\theta +\frac{1}{|\mathcal{S}|}\right),(13)$

where the parameters θ and β can be determined through experiments to reflect data distribution characteristics. Moreover, this model can adopt both i.i.d. and non-i.i.d. data distributions among users Li et al. (2019). From (13) it is observed that by increasing the number of participating users, i.e., increasing $|\mathcal{S}|$, the number of total communication rounds decreases. However, increased number of scheduled users may lead to increased T^max, since it is more likely that users who present large τ_k will also participate. Therefore, the global convergence time in (11) is dependent on the number of scheduled users, in a non-trivial manner.

4 Stackelberg Game Formulation and Solution

4.1 Two-Stage Game Formulation

As discussed previously, each user is interested in maximizing its own utility function by optimally adjusting the available resources i.e., CPU clock speed f_k, transmission time t_k, transmit power p_k, and finally decide whether he will participate in the training process or not, by adjusting a_k. Moreover, the value of the utility function is being affected by the delay demand that the task publisher requires. On the other hand, the task publisher is willing to minimize the total convergence time of the FL process, by adjusting the maximum delay tolerance $\tilde{T}$ of a communication round, which influences users decision regarding participation into the procedure. Therefore, a two-stage Stackelberg game can be applied to model the interaction among users and the server, where the users are the followers while the server is the leader. Initially, an arbitrary value of $\tilde{T}$ is being set and users decide their optimal strategies. Given the response of the users, the server, i.e., the leader, announces the delay tolerance $\tilde{T}$, being aware of the users’ decisions. It is noted that correctly classifying a game is of paramount importance, since its classification specifies the solution concept and, thus, the best actions of the involved players. In the case of Stackelberg game, this set of actions is termed as Stackelberg Equilibrium (SE). From the practical point of view, an equilibrium is an optimal decision for a player, given that the strategy of the other player is also optimized. Thus, if the users optimize their utility functions ignoring the type and the structure of the game and deviate from the SE, then they will achieve worse pay-off. In the continue we proceed to the problem formulation regarding both the followers and the leader.

Clients’ goal is to maximize their utility function, given a value of $\tilde{T}$. The problem can be formally given as

$\begin{array}{cccc}\hfill & \hfill & \hfill & {\mathcal{P}}_{\mathit{1}}:\underset{t_k,p_k,f_k,a_k}{\mathrm{m}\mathrm{a}\mathrm{x}}{U}_k\hfill \\ \hfill & \hfill & \hfill & \mathit{s}.\mathit{t}.{\mathrm{C}}_1:t_{k}B{\log }_2\left(1+\frac{p_k{g}_k}{B{N}_0}\right)\ge a_k{s}_k,\hfill \\ \hfill & \hfill & \hfill & {\mathrm{C}}_2:0\le p_k\le p_k^{\text{max}},0\le f_k\le f_k^{\text{max}},t_k\ge 0,\hfill \\ \hfill & \hfill & \hfill & {\mathrm{C}}_3:a_k\in \left\{\mathrm{0,1}\right\},\hfill \end{array}(14)$

where

$U_k=\left[\left(\tilde{T}-t_k-\frac{c_k{D}_k}{f_k}\right)q_1-\left(t_k{p}_k+\zeta c_k{D}_k{f}_k^2\right)q_2\right]a_k.(15)$

C₁ represents the data transmission constraint, while $p_k^{\text{max}}$, $f_k^{\text{max}}$ are the maximum values of transmit power and CPU frequency of user k, respectively.

On the other hand, the optimization problem at the side of the task publisher for minimizing the global convergence time, can be formulated as

$\begin{array}{cccc}\hfill & \hfill & \hfill & {\mathcal{P}}_{\mathit{2}}:\underset{\tilde{T}}{\mathrm{m}\mathrm{i}\mathrm{n}}{T}^{\text{conv}}\hfill \\ \hfill & \hfill & \hfill & \mathit{s}.\mathit{t}.{\mathrm{C}}_1:\sum _{k=1}^K\left(\tilde{T}-{\tau }_k\right)a_k{q}_1\le Q,\hfill \end{array}(16)$

where

$T^{\text{conv}}=\underset{k\in \mathcal{K}}{\mathrm{m}\mathrm{a}\mathrm{x}}\left\{{\tau }_k{a}_k\right\}\beta \left(\theta +\frac{1}{{\sum }_{\mathcal{K}}{a}_k}\right),(17)$

while the left-hand-side of C₁ represents the overall fee that the task publisher is paying to all participating clients and Q denotes the total budget that the task publisher posses. The server is responsible for optimally adjusting $\tilde{T}$, in order to enforce a certain number of users to be scheduled for participation. It can be observed that problems ${\mathcal{P}}_{\mathit{1}}$ and ${\mathcal{P}}_{\mathit{2}}$ are coupled, since the delay tolerance $\tilde{T}$ influences the number of participating users and users’ decisions, which also impact the global convergence time in turn. The manner that $\tilde{T}$ affects the number of participating users, will be discussed in the subsequent subsection.

To what follows, the definitions regarding the users’ and server’s optimal actions, as well as the SE, are provided Başar and Olsder (1998), Pawlick et al. (2019). The Stackelberg games are solved backwards in time, since the followers move after observing the leader’s action. The optimal actions for each follower, i.e., the optimal values of f_k, p_k, t_k, a_k that are denoted by $f_k^{*},p_k^{*},t_k^{*},a_k^{*}$, respectively, to respond to the leader’s action, i.e., $\tilde{T}$, are the ones that satisfy the following inequality

$U_k\left(\tilde{T},f_k^{*},p_k^{*},t_k^{*},a_k^{*}\right)\ge U_k\left(\tilde{T},f_k,p_k,t_k,a_k\right),\forall k\in \mathcal{K}.(18)$

Based on the anticipated followers’ response, the leader chooses its optimal action T*, which satisfies

$T^{\text{conv}}\left({\tilde{T}}^{*},{\mathit{f}}^{*},{\mathit{p}}^{*},{\mathit{t}}^{*},{\mathit{a}}^{*}\right)\le T^{\text{conv}}\left(\tilde{T},{\mathit{f}}^{*},{\mathit{p}}^{*},{\mathit{t}}^{*},{\mathit{a}}^{*}\right).(19)$

Then, by using the aforementioned definitions of the optimal actions for each player, the point $({\tilde{T}}^{*},{\mathit{f}}^{*},{\mathit{p}}^{*},{\mathit{t}}^{*},{\mathit{a}}^{*})$ is the Stackelberg equilibrium, if the following set of inequalities are satisfied

$\begin{array}{cc}\hfill & T^{\text{conv}}\left({\tilde{T}}^{*},{\mathit{f}}^{*},{\mathit{p}}^{*},{\mathit{t}}^{*},{\mathit{a}}^{*}\right)\le T^{\text{conv}}\left(\tilde{T},{\mathit{f}}^{*},{\mathit{p}}^{*},{\mathit{t}}^{*},{\mathit{a}}^{*}\right)\hfill \\ \hfill & U_k\left({\tilde{T}}^{*},f_k^{*},p_k^{*},t_k^{*},a_k^{*}\right)\ge U_k\left({\tilde{T}}^{*},f_k,p_k,t_k,a_k\right),\forall k\in \mathcal{K}.\hfill \end{array}(20)$

4.2 Proposed Solution of the Stackelberg Game

4.2.1 Users’ Utility Function Maximization

As stated previously, users are eager to participate only if their utility function is positive, otherwise they set a_k = 0 and do not spend any of their available communication and computation resources. The optimization problem ${\mathcal{P}}_{\mathit{1}}$, for maximizing the utility function U_k of each user, given that a_k = 1, can be formulated as follows

$\begin{array}{cccc}\hfill & \hfill & \hfill & \underset{t_k,p_k,f_k}{\mathrm{m}\mathrm{a}\mathrm{x}}\left(\tilde{T}-t_k-\frac{c_k{D}_k}{f_k}\right)q_1-\left(t_k{p}_k+\zeta c_k{D}_k{f}_k^2\right)q_2\hfill \\ \hfill & \hfill & \hfill & \mathit{s}.\mathit{t}.{\mathrm{C}}_1:t_{k}B{\log }_2\left(1+\frac{p_k{g}_k}{B{N}_0}\right)\ge s_k,\hfill \\ \hfill & \hfill & \hfill & {\mathrm{C}}_2:0\le p_k\le p_k^{\text{max}},0\le f_k\le f_k^{\text{max}},t_k\ge 0,\hfill \end{array}(21)$

The optimization problem in (21) is non-convex due to the coupling of t_k and p_k. However it can be easily proved that $\frac{{\partial }^2{U}_k}{\partial f_k^2}<0$, which indicates that U_k is strictly concave with respect to f_k. Hence, by taking $\frac{\partial U_k}{\partial f}=0$, it is straightforward to show that the optimal f_k is given by

$f_k^{*}=\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\bar{f}}_k,f_k^{\text{max}}\right\},(22)$

where

${\bar{f}}_k=3\sqrt{\frac{q_1}{\zeta q_2}}.(23)$

It is obvious that $f_k^{*}$ does not depend on t_k and p_k. After obtaining the optimal $f_k^{*}$ the optimization problem can be transformed as follows

$\begin{array}{cccc}\hfill & \hfill & \hfill & \underset{t_k,p_k}{\mathrm{m}\mathrm{a}\mathrm{x}}-t_k{q}_1-t_k{p}_k{q}_2\hfill \\ \hfill & \hfill & \hfill & \mathit{s}.\mathit{t}.{\mathrm{C}}_1:t_{k}B{\log }_2\left(1+\frac{p_k{g}_k}{B{N}_0}\right)\ge s_k,\hfill \\ \hfill & \hfill & \hfill & {\mathrm{C}}_2:0\le p_k\le p_k^{\text{max}},t_k\ge 0.\hfill \end{array}(24)$

The problem is non-convex in its current formulation. However, it is easy to verify that the constraint C₁ always hold with equality, since the selection of larger t_k or p_k will lead to the decrease of the objective function. Following that, it holds

$t_k=\frac{s_k}{B{\log }_2\left(1+\frac{p_k{g}_k}{B{N}_0}\right)},(25)$

and by substituting t_k in (24), the optimization problem is equivalent to the following formulation

$\begin{array}{cccc}\hfill & \hfill & \hfill & \underset{p_k}{\mathrm{m}\mathrm{i}\mathrm{n}}\frac{s_k{q}_1+s_k{q}_2{p}_k}{B{\log }_2\left(1+\frac{p_k{g}_k}{B{N}_0}\right)}\hfill \\ \hfill & \hfill & \hfill & \mathit{s}.\mathit{t}.0<p_k\le p_k^{\text{max}}.\hfill \end{array}(26)$

Although problem (26) is non-convex, it can be transformed and solved efficiently with the aid of fractional programming. By observing the objective function in (26), it can be expressed as $G(p_k)=\frac{\mathrm{\Phi }(p_k)}{\mathrm{\Psi }(p_k)}$, where Φ(p_k) = s_kq₁ + s_kq₂p_k and $\mathrm{\Psi }(p_k)=B{\log }_2\left(1+\frac{p_k{g}_k}{B{N}_0}\right)$. Furthermore, Φ(p_k) is an affine function of p_k, while Ψ(p_k) is a concave function of p_k and it also holds that Ψ(p_k) > 0, ∀p_k. The case of p_k = 0 is trivial and is being excluded, since it would implied that user k is not willing to participate. Thus, the considered problem can be solved via the Dinkelbach’s algorithm Dinkelbach (1967). According to Dinkelbach (1967), solving (26) is equivalent to finding the unique root of

$F\left(\lambda \right)=\underset{p_k}{\mathrm{m}\mathrm{i}\mathrm{n}}\left\{\mathrm{\Phi }\left(p_k\right)-\lambda \mathrm{\Psi }\left(p_k\right)\right\}.(27)$

For a given λ, the function Z (p_k) ≜Φ(p_k) − λΨ(p_k) is convex with respect to p_k, since Φ(p_k) is affine and Ψ(p_k) is concave. Therefore, the optimal solution that minimizes Z (p_k), can be easily derived by taking $\frac{dZ(p_k)}{d{p}_k}=0$, yielding

${\bar{p}}_k=\mathrm{m}\mathrm{i}\mathrm{n}\left\{\frac{B\left(g_k\lambda -N_0{q}_2{s}_k\ln \left(2\right)\right)}{g_k{q}_2{s}_k\ln \left(2\right)},p_k^{\text{max}}\right\}.(28)$

Hence, the optimal $p_k^{*}$ of problem (26) can be found iteratively, by updating $p_k^{(n)}$ and λ⁽ⁿ⁾ in each step n, according to Algorithm 1.

Algorithm 1. Dinkelbach’s Algorithm for solving (26), ∀k

1: Initialize: $ϵ>0,n=0,p_k^{(0)}$

2: repeat

3:  n ← n + 1

4:  ${\lambda }^{(n)}\leftarrow \frac{\mathrm{\Phi }(p_k^{(n-1)})}{\mathrm{\Psi }(p_k^{(n-1)})}$

5:  $p_k^{(n)}\leftarrow \underset{p_k}{\mathrm{arg\; min}}\{\mathrm{\Phi }(p_k)-{\lambda }^{(n)}\mathrm{\Psi }(p_k)\}$, using (28)

6: until $\{\mathrm{\Phi }(p_k^{(n)})-{\lambda }^{(n)}\mathrm{\Psi }(p_k^{(n)})\}\le ϵ$

7: $p_k^{*}\leftarrow p_k^{(n)}$

After obtaining the optimal $p_k^{*}$, the optimal $t_k^{*}$ can also be calculated by using (25). Following that, the resolution of the optimization problem in (21) has been completed, since the optimal $f_k^{*},p_k^{*},t_k^{*}$, which maximize the utility function U_k, have been obtained. Also, we highlight that each user independently decides the optimal variables for maximizing its utility, since this decision is not subject to the residual users decisions. Moreover, the execution of Algorithm 1 is not computationally intensive for the devices, since the Dinkelbach’s algorithm is quite efficient, converging at a superlinear rate Schaible (1976). It is further observed that the optimal solutions $f_k^{*},p_k^{*},t_k^{*}$ are independent of the value $\tilde{T}$. However, $\tilde{T}$ can affect the sign of the utility function and subsequently the selection of $a_k^{*}$. It should be noted that the optimal solutions do not guarantee that $U_k(f_k^{*},p_k^{*},t_k^{*},)>0$. Thus, the maximization of the utility function, subject to f_k, p_k, t_k, does not ensures that the k-th user is eager to participate in the federating learning task. The condition that should be satisfied, to ensure that the k-th user has positive utility function, is given as follows by manipulating (10)

$\tilde{T}>\frac{{\tau }_k^{*}{q}_1+{\mathcal{E}}_k^{*}{q}_2}{q_1}\triangleq L_k^{*},\forall k\in \mathcal{K},(29)$

where ${\tau }_k^{*}=\frac{c_k{d}_k}{f_k^{*}}+t_k^{*}$ and ${\mathcal{E}}_k^{*}=p_k^{*}{t}_k^{*}+\zeta c_k{D}_k{f}_k^{*2}$. If the condition in (29) is satisfied, i.e., $U_k^{*}>0$, then user k sets $a_k^{*}=1$, otherwise sets $a_k^{*}=0$. As it can be observed, $L_k^{*}$ is the threshold value of $\tilde{T}$, which determines if user k is eager to participate into the FL process. In the continue, without loss of generality we assume that $L_1^{*}>L_2^{*}>\dots ,>L_l^{*}>\dots ,>L_K^{*}$. Following that, let $\tilde{T}=L_l^{*}$, which yields

$\begin{array}{cc}\hfill & a_1^{*}=a_2^{*}=\dots =a_l^{*}=0,\hfill \\ \hfill & a_{l+1}^{*}=\dots =a_{K-1}^{*}=a_K^{*}=1,\hfill \end{array}(30)$

since the condition $\tilde{T}>L_k^{*}$ will hold ∀ k ∈ {l + 1, … , K − 1, K}. As a matter of fact, $\tilde{T}$ acts as an adjusting factor that determines which users will be scheduled for participation.

4.2.2 Global Convergence Time Minimization

Next, we proceed to the minimization of the convergence time, which is executed by the task publisher. As discussed previously, the server is able to dynamically adjust the value of $\tilde{T}$ among the set of levels $\mathcal{L}=\{L_1^{*},L_2^{*},\dots ,L_K^{*}\}$, in order to determine the number of participating users. Given the optimal ${\tau }_k^{*}$ and ${\mathcal{E}}_k^{*}$ the server can derive $L_k^{*},\forall k\in \mathcal{K}$, from (29). Following that, the problem ${\mathcal{P}}_{\mathit{2}}$ can be written as

$\begin{array}{cccc}\hfill & \hfill & \hfill & \underset{\tilde{T}}{\mathrm{m}\mathrm{i}\mathrm{n}}\underset{k\in \mathcal{K}}{\mathrm{m}\mathrm{a}\mathrm{x}}\left\{{\tau }_k^{*}{a}_k^{*}\right\}\beta \left(\theta +\frac{1}{{\sum }_{\mathcal{K}}{a}_k^{*}}\right)\hfill \\ \hfill & \hfill & \hfill & \mathit{s}.\mathit{t}.{\mathrm{C}}_1:\tilde{T}\le \frac{\frac{Q}{q_1}+{\sum }_{\mathcal{K}}{\tau }_k^{*}{a}_k^{*}}{{\sum }_{\mathcal{K}}{a}_k^{*}},\tilde{T}\in \mathcal{L},\hfill \end{array}(31)$

where the constraint C₁ has occur by manipulating the C₁ in (16). In order to solve the problem in (31), the server will execute a search among the K possible values of $\tilde{T}$ from the set $\mathcal{L}$ and finally select the value that minimizes the objective function, while the selected value should also satisfy the constraint C₁. It should be again highlighted that ${\tau }_k^{*}$ is irrelevant of the $\tilde{T}$ selection, since $\tilde{T}$ only affects the number of scheduled users. Recall that during the selection of ${\tilde{T}}^{*}$, the server has knowledge of users’ upcoming decision, i.e., $a_k^{*}$ in (30), and can exploit this information to solve (31). For example, if the optimal $\tilde{T}$ equals to ${\tilde{T}}^{*}=L_l^{*}$, by using (30) we conclude to

$|\mathcal{S}|=K+1-\left(l+1\right)=K-l,(32)$

which implies that the number of scheduled users will be K − l, while the specific user participation is described by (30).

4.2.3 Stackeleberg Equilibrium

The whole procedure of the Stackelberg’s game is summarized in Algorithm 2. More specifically, in step 1, the server initializes the delay tolerance $\tilde{T}$ with an arbitrary value, which is announced to the users. Following that, the users solve ${\mathcal{P}}_{\mathit{1}}$ for the given $\tilde{T}$, derive the optimal $f_k^{*},p_k^{*},t_k^{*}$ and afterwards upload the values of ${\tau }_k^{*}$ and ${\mathcal{E}}_k^{*}$ to the server. In step 3 and 4, the server calculates ${\mathcal{L}}^{*}$, obtains the optimal ${\tilde{T}}^{*}\in \mathcal{L}$ which solves problem ${\mathcal{P}}_{\mathit{2}}$ and announces ${\tilde{T}}^{*}$ to the users. After the announcement of ${\tilde{T}}^{*}$, in step 5, users make a decision regarding participating or not in the training process, while the server is a-priori-aware of these impeding decisions, since ${\tilde{T}}^{*}$ is being selected with the knowledge of users’ incentive, which is the sign of their utility function. With the termination of the Stackelberg game, the server has managed to obtain the optimal delay tolerance of the FL round which minimizes the convergence time, while the users have adjusted their resources, so as to maximize their utility function.

Algorithm 2. Stackelberg equilibrium

1: Server initializes $\tilde{T}$ with an arbitrary value.

2: Each user derive $f_k^{*},p_k^{*},t_k^{*}$ by solving (21) and uploads the values of ${\tau }_k^{*},{\mathcal{E}}_k^{*}$ to the server.

3: Server calculates $L_k^{*},\forall k\in \mathcal{K}$, by using (29).

4: Server selects ${\tilde{T}}^{*}\in \mathcal{L}$ that minimizes the objective in (31) and announces ${\tilde{T}}^{*}$ to the users.

5: Users decide if they will participate, i.e., if $U_k^{*}>0$, set $a_k^{*}=1,\forall k\in \mathcal{K}$.

5 Detecting and Preventing Malicious Users From the FL Process

5.1 Malicious Users

During the considered interaction among users and the task publisher, a question that may arise is the following: What if users were malicious and announced false values of ${\tau }_k^{*}$ and ${\mathcal{E}}_k^{*}$ to the server, aiming to further improve their pay-off? Firstly, we assume that users could falsely announce their latency time, as ${\tau }_k^{\prime }$, instead of ${\tau }_k^{*}$. However, they are not really willing to deviate from the optimal strategy ${\tau }_k^{*}$, since this policy would reduce their utility function. Hence, in this case, the task publisher would notice this time divergence, since it is expected that user k finishes the transmission of the local parameters within ${\tau }_k^{\prime }$ duration, while he actually finishes within ${\tau }_k^{*}$. As a result, the task publisher can immediately detect an abnormal behavior and exclude those users from future participation. However, users could falsely announce ${\mathcal{E}}_k^{\prime }$ instead of ${\mathcal{E}}_k^{*}$, since the server has no knowledge of users’ computing capabilities and subsequently their consumed energy. As a result, users can influence L_k only by accordingly adjusting ${\mathcal{E}}_k$, in a effort to mislead the task publisher and benefit from this action. Next, any possible benefits of the aforementioned users’ action will be discussed.

Firstly, we assume that only one user is dishonest, e.g., the m-th user. In order to improve his utility, user m may select to announce $L_m^{\prime }>L_m^{*}$, aiming to influence the delay tolerance threshold that the server imposes, i.e., increasing the delay tolerance and subsequently increasing its pay-off. Following that, we consider the case where $L_1^{*}>L_2^{*}>\dots ,>L_m^{*}>\dots ,>L_l^{*}>\dots ,>L_K^{*}$ and ${\tilde{T}}^{*}=L_l^{*}$, meaning that the optimal strategy of the server is to enforce K − l users to participate. In this case, if the m-th user decides to announce $L_m^{\prime }$, will not have any impact in the outcome, since it holds ${\tilde{T}}^{\prime }={\tilde{T}}^{*}=L_l^{*}<L_m^{\prime }$, and user m will not be scheduled for participation. Next, we consider the case $L_1^{*}>L_2^{*}>\dots ,>L_l^{*}>\dots ,>L_m^{*}>\dots ,>L_K^{*}$ and ${\tilde{T}}^{*}=L_l^{*}$. Now, if user m selects to announce $L_m^{\prime }$ and it holds $L_l^{*}>L_m^{\prime }$, again user m can not benefit from such behavior since ${\tilde{T}}^{\prime }={\tilde{T}}^{*}=L_l^{*}<L_m^{\prime }$. This means that the m-th user will participate, as he would if he had announced the true value of $L_k^{*}$, while his utility function will stay unchanged. Only if the condition $L_m^{\prime }>L_l^{*}$ is satisfied, then it yields ${\tilde{T}}^{\prime }=\mathrm{m}\mathrm{i}\mathrm{n}\{L_{l-1}^{*},L_m^{\prime }\}>{\tilde{T}}^{*}$ and the selected delay tolerance of the server changes. However in this case, user m will not intend to participate, since his utility will be less than or equal to zero. As a result, in none of the aforementioned cases, could user m benefit from announcing a false value of L_m, or equivalently ${\mathcal{E}}_m$. However, in the later case it holds ${\tilde{T}}^{\prime }>{\tilde{T}}^{*}$, which implies that the server will select a larger value for the delay tolerance and subsequently all the participating users will benefit from this selection, since users’ utility function is monotonically increasing with respect to $\tilde{T}$. Therefore, the task publisher will end up paying additional rewards. Although, an independently acting user posses no motives for adopting the considered behavior, in a scenario where multiple dishonest users are present who probably act as a cooperating coalition, it is really hard to predict whether its secure for the task publisher to tolerate such behaviors. The reason for this is that the considered malicious users may exchange information regarding their available resources and also exchange pay-offs, e.g., splitting their pay-offs.

5.2 Deep Learning-Aided Malicious Users Detection

Driven by the aforementioned scenario, a secure mechanism which detects malicious/abnormal users’ behavior should be constructed, in order to ensure an irreproachable clients-task publisher interaction. Therefore, the servers’ aim is to recognize whether the users’ transmitted tuple $\{{\tau }_k,{\mathcal{E}}_k\},\forall k\in \mathcal{K}$, is reliable or not. Considering the underlying correlation between the task completion time τ_k and the consumed energy ${\mathcal{E}}_k$, we invoke the use of a deep neural network to identify if the declared $\{{\tau }_k,{\mathcal{E}}_k\}$, could be realistic. We foresee this process, as a supervised-learning task which trains the neural network, given that the labels of the training tuple $\{\tau ,\mathcal{E}\}$, belong to the set of classes {True, False}, specifying whether the considered tuple is reliable or not, respectively. Note that we slightly abuse the notation by dropping the subscript index k for simplicity. After the completion of the training process, the neural network is expected to successfully classify the forthcoming unknown $\{\tau ,\mathcal{E}\}$, that each user will announce to the server. Hopefully, the server will be capable of recognizing dishonest users and prevent them from future participation.

5.2.1 Deep Neural Network Structure

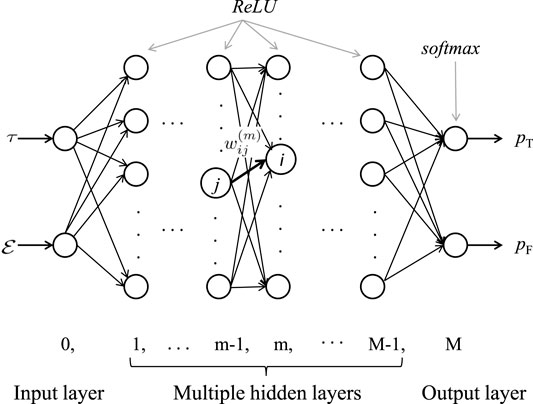
We consider a feed-forward DNN consisting of an input layer, an output layer and M − 1 fully connected hidden layers. All layers are indexed from 0 to M. We denote the number of nodes in the m-th layer as l_m. For the hidden layers, the output of the i-th node in the m-th layer, is calculated as follows

$a_i^{\left(m\right)}=\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}\left(\sum _{j=1}^{l_{m-1}}{w}_{ij}^{\left(m\right)}{a}_j^{\left(m-1\right)}+b_i^{\left(m\right)}\right),(33)$

where $w_{ij}^{(m)}$ represents the weight that connects the j-th node of the (m − 1)-th, with the i-th node of the m-th layer, $a_j^{(m-1)}$ is the output of the j-th node in the (m − 1)-th layer and $b_i^{(m)}$ is the bias term of the i-th node in the m-th layer. Furthermore, ReLU(⋅) = max (⋅, 0), denotes the Rectified Linear Unit function, which is a widely used activation function for neural networks. The output of $a_1^{(0)},a_2^{(0)}$ are by default the inputs of the neural network, i.e., $a_1^{(0)}=\tau$ and $a_2^{(0)}=\mathcal{E}$. Finally, for the output layer, we use the softmax activation function, which extracts the probabilities p_T, p_F of the input vector $\{\tau ,\mathcal{E}\}$, to belong to the class True or False, respectively, while p_T + p_F = 1. Therefore, it holds $a_1^{(M)}=p_{\mathrm{T}}$ and $a_2^{(M)}=p_{\mathrm{F}}$. The DNN’s structure is illustrated in Figure 2. In the continue, the data generation, training and testing stages are discussed.

FIGURE 2

FIGURE 2. Deep neural network structure.

5.2.1.1 Data Generation

The data are generated in the following manner. The τ* and ${\mathcal{E}}^{*}$ are derived according to the proposed method, for many channel realizations, in order to generate multiple samples. In the case where the user is honest, the label of $\{{\tau }^{*},{\mathcal{E}}^{*}\}$ is set as y = True. In the continue, the data set for the malicious users is generated. As mentioned previously, malicious users falsely declare the consumed energy as ${\mathcal{E}}^{\prime }>{\mathcal{E}}^{*}$. To model this behavior, we consider that their declared tuple is $\{{\tau }^{*},{\mathcal{E}}^{\prime }\}$, with ${\mathcal{E}}^{\prime }={\mathcal{E}}^{*}(1+\mathrm{\Delta })$, where Δ is a random variable, uniformly distributed in [δ₁, δ₂], with δ₂ > δ₁ > 0 being constants. In this case, the label is set as y = False. Thus, the entire data set, $\mathcal{T}$, consists of samples corresponding to both honest and dishonest users. More specifically, the whole data set is described by the tuple ${\left(\{{\tau }^{(t)},{\mathcal{E}}^{(t)}\},y^{(t)}\right)}_{t\in \mathcal{T}}$, where y^(t) ∈ {True, False} and the superscript (t) is used to denote the t-th sample. Similarly, a validation data set $\mathcal{V}$ is constructed.

5.2.1.2 Training Stage

The entire training data set ${\left(\{{\tau }^{(t)},{\mathcal{E}}^{(t)}\},y^{(t)}\right)}_{t\in \mathcal{T}}$ is used to optimize the weights and biases of the neural network. The loss function that we use in order to capture the error between the true label y^(t) and the predicted label ${\widehat{y}}^{(t)}$, is the categorical cross entropy. Moreover, the validation set is used for evaluating the neural network’s performance and accordingly adjusting the hyperparameters of the training process such as the learning rate (LR), total number of training epochs, batch size, etc.

5.2.1.3 Testing Stage

In the testing stage, a test set is generated, in a similar manner with the training stage. Following that, the test set is passed through the trained neural network and the predictions are collected. The predicted label of a test sample is given by

$\widehat{y}=\left\{\begin{array}{cc}True,\hfill & \text{if\hspace{0.17em}}{p}_T>p_F\hfill \\ False,\hfill & \text{if\hspace{0.17em}}{p}_T<p_F.\hfill \end{array}\right.(34)$

Finally, the classification accuracy is evaluated, i.e., the ability of the neural network to detect in which user category, honest or dishonest, do the testing samples correspond.

6 Numerical Results and Performance Evaluation

We consider K = 20 uniformly distributed users in a circular cell with radius R = 500 m, while the BS is located at the center of the cell. The wireless bandwidth is B = 150 KHz, the noise power spectral density is N₀ = −174 dBm/Hz, the maximum transmit power of the users is $p_k^{\text{max}}=20\mathrm{d}\mathrm{B}\mathrm{m}$, the maximum CPU clock speed is $f_k^{\text{max}}=1.5\mathrm{G}\mathrm{H}\mathrm{z},\forall k\in \mathcal{K}$ and the effective capacitance is ζ = 10⁻²⁷. Finally we set q₂ = 15. All variables retain their respective values, unless specified otherwise.

Next, we set β = 27.773 and θ = 0.941 2 Shi et al. (2020a). These values correspond to a specific data distribution when the MNIST data set is used, which is a well-known handwritten digit dataset. In particular, according to Shi et al. (2020a), the considered values of β, θ reflect an i.i.d. data distribution among users. Furthermore, we also adopt the classification of the handwritten digits as the FL task. Following that, the user training data has been set as D_k = 1.6 Mbit, the size of the training parameters is s_k = 1 Mbit and c_k is uniformly distributed in the interval [10, 40] cycles/bit. It is noted that in the following figures, all results are averaged over 10,000 trials, by means of Monte Carlo.

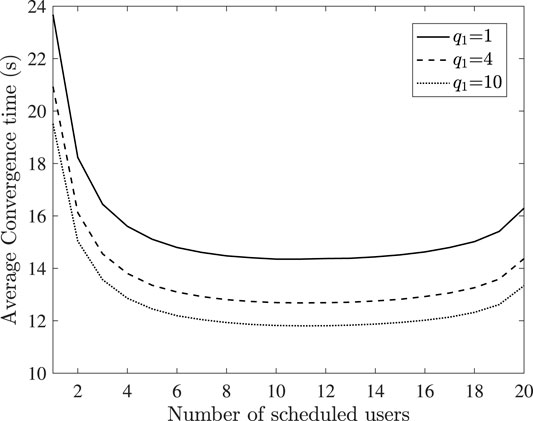
In Figure 3 the impact of the number of scheduled users on the average global convergence time is demonstrated, for various values of the task publisher’s reward q₁. Furthermore, we consider that users employ the optimal proposed strategy, in order to maximize their utility. As it can be observed, neither enforcing all users nor a small portion of them to participate, will lead to the average convergence time minimization. This phenomenon can be explained as follows. By scheduling a large amount of users to participate it is more likely that the latency during a communication round will be large, owing this to the straggler effect, while the convergence time will be negatively affected. On the contrary, by urging a small number of users to be involved, the required number of communication rounds to achieve global convergence will highly increase, deteriorating the convergence time. Moreover, it can be observed that higher reward q₁ leads to smaller convergence time. This is reasonable, since when the reward is higher, users are motivated to spend their available resources for a fast local training and parameter transmission to the server, leading to a decreased delay during each communication round.

FIGURE 3

FIGURE 3. Impact of number of scheduled users on the average convergence time of the FL task.

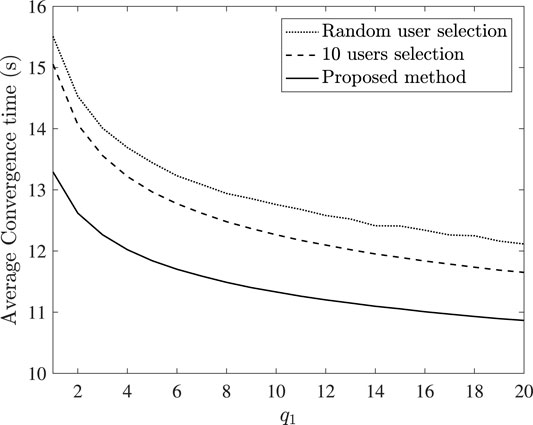
Following that, in Figure 4, the average convergence time versus the reward q₁ is depicted. We compare the proposed method with the following cases. Firstly, the server randomly selects the number of participating users and secondly, the server always schedules 10 users for participation. It can be seen that the proposed method outperforms the considered cases. Therefore, the importance of wisely selecting the delay tolerance $\tilde{T}$, in order to enforce a certain number of users to be involved in the training process, is corroborated. In addition to this, the significance of the user scheduling, which is performed by the server through the incentive design for minimizing the convergence time, is revealed. Thus, user scheduling should be a driving factor for the incentive design during the FL process.

FIGURE 4

FIGURE 4. Average convergence time versus q₁.

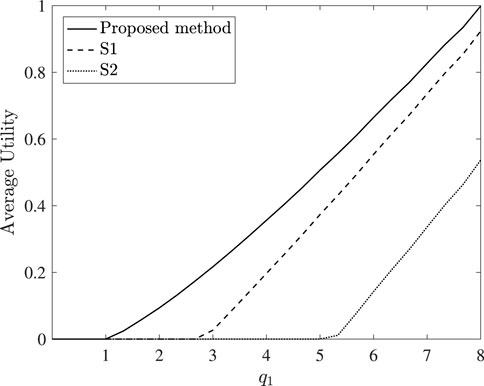
In the continue, Figure 5 exhibits the average utility of the users given that $\tilde{T}=0.6\mathrm{s}$. We compare our proposed solution for users’ utility function maximization with the following baseline schemes. Firstly, in Scheme 1 (S1), users select the optimal CPU frequency $f_k^{*}$ from (22), but they set p_k = p^max, i.e., select to transmit with the maximum available power. Secondly, in Scheme 2 (S2), users transmit with the optimal power $p_k^{*}$ as extracted by Algorithm 1, but use the whole CPU frequency for local training, i.e., $f_k=f^{\text{max}},\forall k\in \mathcal{K}$. It is clearly seen that our proposed method outperforms the baseline ones, which verifies the significance of the proposed optimization regarding users’ utility function maximization. Also, this example highlights the performance gains that the joint optimization of the wireless and computation resources could offer. In this manner, users are motivated to participate into the FL process, given that the resource allocation is tactfully conducted, which leads to increased utility. Furthermore, we highlight that when the utility is equal to zero, users do not intend to participate, while to do so, they would require higher reward q₁ for a timely task completion.

FIGURE 5

FIGURE 5. Average utility of users versus q₁.

6.1 DNN Setup and Performance

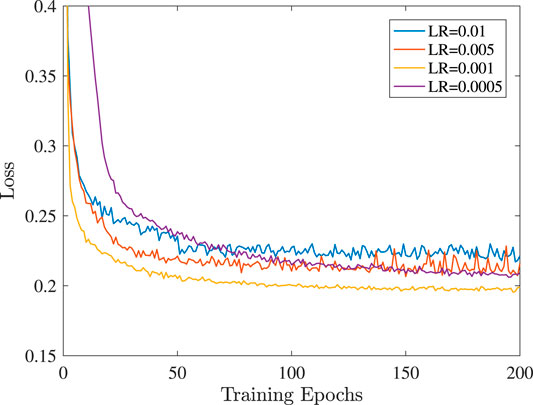
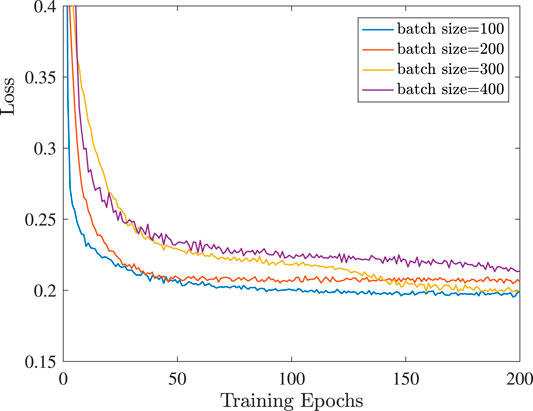
The neural network consists of three hidden layers. The first hidden layer contains 200 neurons, while the rest two layers contain 80 neurons. The optimization algorithm we use for minimizing the loss function of the neural network is the RMSprop, which is an efficient implementation of the mini-batch stochastic gradient descent method. The decay rate has been set as 0.9. In order to select suitable values for the learning rate and the batch size, the validation set was used for the evaluation of the loss function. More specifically, in Figure 6 and Figure 7, the evolution of the loss function throughout the training epochs is demonstrated. It can been observed that when the learning rate is equal to 0.001, the smallest loss is achieved. Moreover, the batch size which achieves the smallest loss is 100, which is finally adopted. In addition, the number of training epochs has been set as 200, since at this point the loss function is relatively close to a steady level. For the training of the neural network 36,000 samples were generated, while the validation set consists of 4,000 samples. Also, we used 5,000 testing samples, in order to evaluate the accuracy of the neural network. We highlight that throughout the generation of the training, validation and testing set, the ratio of honest to dishonest users was 1:1. Moreover, throughout the generation of the training and validation set, we fix δ₁ = 0.2 and δ₂ = 1, which means that $\mathrm{\Delta }\sim \mathcal{U}(0.2,1)$ and subsequently ${\mathcal{E}}^{\prime }\sim \mathcal{U}(1.2{\mathcal{E}}^{*},2{\mathcal{E}}^{*})$. Finally, the parameter selection of the neural network is summarized in Table 2.

FIGURE 6

FIGURE 6. Learning rate selection.

FIGURE 7

FIGURE 7. Batch size selection.

TABLE 2

TABLE 2. DNN’s parameters.

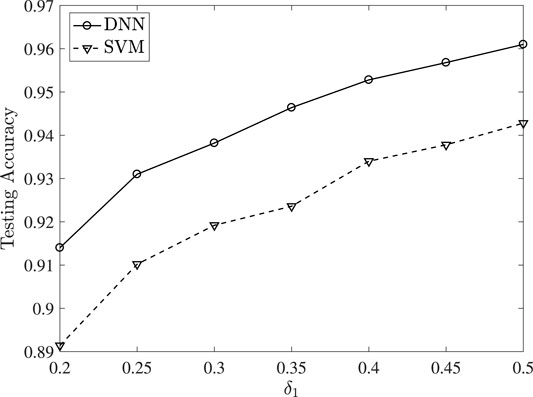
In Figure 8, the testing accuracy is evaluated, after passing the testing set through the DNN. Various values of δ₁ are considered, while we set δ₂ = 1. This implies that the malicious users’ false declared energy consumption ${\mathcal{E}}^{\prime }$, is uniformly distributed in $[{\mathcal{E}}^{*}(1+{\delta }_1),2{\mathcal{E}}^{*}]$. It can been seen that as δ₁ increases the accuracy also increases. An interpretation of this result comes as follow. For smaller δ₁, it is more likely that the honest users’ tuple $\{{\tau }^{*},{\mathcal{E}}^{*}\}$ and the malicious users’ tuple $\{{\tau }^{*},{\mathcal{E}}^{\prime }\}$ will be quite similar, which can be justified by observing the distribution of ${\mathcal{E}}^{\prime }$. Therefore, in such case, it is harder for the DNN to correctly classify the users’ identity. However, it is evident that the neural network’s ability to identify the label of the participating users, as honest or dishonest, is quite satisfactory. Therefore, through this mechanism the task publisher can exclude users who are likely to be malicious and subsequently increase the levels of security throughout the Stackelberg game. Moreover, we compare the performance of the DNN with a Support Vector Machine (SVM) classifier. It is obvious that the DNN outperforms the SVM, in terms of classification accuracy.

FIGURE 8

FIGURE 8. DNN’s testing accuracy.

7 Conclusion

In this paper, we propose a secure incentive mechanism for WFL in 6G networks. Specifically, we formulate a Stackelberg game between the clients and the server, where the clients aim to maximize their utility, while the server is focusing on minimizing the global convergence time of the FL task. The optimal solution to the game is obtained while the efficiency of the proposed solution is verified, leading to reduced latency, owing to the decreased global convergence time and increased user-utility. Moreover, we consider the presence of malicious users throughout the game, who may attempt to misinform the server regarding their utilized resources, aiming to further increase their profit. To prevent such behavior, we construct a deep neural network at the server’s side, which focuses on classifying the users’ identity, as malicious or honest. Simulation results validate the effectiveness of the proposed mechanism, as a promising solution for detecting malicious users. To this end, in order to further increase the incentive design efficiency, additional FL features may be taken into account. In this direction, an interesting future topic could be the consideration of the clients’ data quality and quantity throughout the construction of the incentive mechanism, as well as the investigation of their impact on the total convergence time of WFL.

Data Availability Statement

The datasets presented in this article are not readily available because they need to be converted in a presentable format. Requests to access the datasets should be directed to bXBvdXppbmlzQGF1dGguZ3I=.

Author Contributions

Conceptualization and Methodology, PB, PD, and GK. Formal Analysis, PB. Validations, PB and PD. Simulations and Visualization, PB. Writing-Review and Editing, PB, PD, and GK. Supervision, GK.

Funding

Part of the research leading to these results has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 957406. Also, part of this research has been co-financed by the European Regional Development Fund by the European Union and Greek national funds through the Operational Program Competitiveness, Entrepreneurship and Innovation, under the call: Special Actions: Aquaculture - Industrial Materials - Open Innovation in Culture (project code: T6YBP-00134).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Başar, T., and Olsder, G. J. (1998). Dynamic Noncooperative Game Theory. SIAM.

Google Scholar

Bouzinis, P. S., Diamantoulakis, P. D., and Karagiannidis, G. K. (2022a). Wireless Federated Learning (WFL) for 6G Networks⁴Part I: Research Challenges and Future Trends. IEEE Commun. Lett. 26, 3–7. doi:10.1109/lcomm.2021.3121071

CrossRef Full Text | Google Scholar

Bouzinis, P. S., Diamantoulakis, P. D., and Karagiannidis, G. K. (2022b). Wireless Federated Learning (WFL) for 6G Networks-Part II: The Compute-Then-Transmit NOMA Paradigm. IEEE Commun. Lett. 26, 8–12. doi:10.1109/lcomm.2021.3121067

CrossRef Full Text | Google Scholar

Chen, M., Poor, H. V., Saad, W., and Cui, S. (2020a). “Convergence Time Minimization of Federated Learning over Wireless Networks,” in ICC 2020-2020 IEEE International Conference on Communications (ICC), Dublin, June 2020 (IEEE), 1–6. doi:10.1109/icc40277.2020.9148815

CrossRef Full Text | Google Scholar

Chen, M., Yang, Z., Saad, W., Yin, C., Poor, H. V., and Cui, S. (2020b). A Joint Learning and Communications Framework for Federated Learning over Wireless Networks. IEEE Trans. Wireless Commun. 20 (1), 263–283. doi:10.1109/TWC.2020.3024629

CrossRef Full Text | Google Scholar

Dinkelbach, W. (1967). On Nonlinear Fractional Programming. Manage. Sci. 13, 492–498. doi:10.1287/mnsc.13.7.492

CrossRef Full Text | Google Scholar

Kang, J., Xiong, Z., Niyato, D., Xie, S., and Zhang, J. (2019). Incentive Mechanism for Reliable Federated Learning: A Joint Optimization Approach to Combining Reputation and Contract Theory. IEEE Internet Things J. 6, 10700–10714. doi:10.1109/jiot.2019.2940820

CrossRef Full Text | Google Scholar

Khan, L. U., Pandey, S. R., Tran, N. H., Saad, W., Han, Z., Nguyen, M. N. H., et al. (2020). Federated Learning for Edge Networks: Resource Optimization and Incentive Mechanism. IEEE Commun. Mag. 58, 88–93. doi:10.1109/mcom.001.1900649

CrossRef Full Text | Google Scholar

Konečnỳ, J., McMahan, H. B., Yu, F. X., Richtárik, P., Suresh, A. T., and Bacon, D. (2016). Federated Learning: Strategies for Improving Communication Efficiency. arXiv. [Preprint].

Google Scholar

Letaief, K. B., Chen, W., Shi, Y., Zhang, J., and Zhang, Y.-J. A. (2019). The Roadmap to 6g: Ai Empowered Wireless Networks. IEEE Commun. Mag. 57, 84–90. doi:10.1109/mcom.2019.1900271

CrossRef Full Text | Google Scholar

Li, X., Huang, K., Yang, W., Wang, S., and Zhang, Z. (2019). On the Convergence of Fedavg on Non-iid Data. arXiv. [Preprint].

Google Scholar

Li, T., Sahu, A. K., Talwalkar, A., and Smith, V. (2020). Federated Learning: Challenges, Methods, and Future Directions. IEEE Signal. Process. Mag. 37, 50–60. doi:10.1109/msp.2020.2975749

CrossRef Full Text | Google Scholar

Lim, W. Y. B., Xiong, Z., Miao, C., Niyato, D., Yang, Q., Leung, C., et al. (2020). Hierarchical Incentive Mechanism Design for Federated Machine Learning in mobile Networks. IEEE Internet Things J. 7, 9575–9588. doi:10.1109/jiot.2020.2985694

CrossRef Full Text | Google Scholar

McMahan, B., Moore, E., Ramage, D., Hampson, S., and y Arcas, B. A. (2017). “Communication-efficient Learning of Deep Networks from Decentralized Data,” in Artificial Intelligence and Statistics (PMLR), 1273–1282.

Google Scholar

Pandey, S. R., Tran, N. H., Bennis, M., Tun, Y. K., Manzoor, A., and Hong, C. S. (2020). A Crowdsourcing Framework for On-Device Federated Learning. IEEE Trans. Wireless Commun. 19, 3241–3256. doi:10.1109/twc.2020.2971981

CrossRef Full Text | Google Scholar

Pawlick, J., Colbert, E., and Zhu, Q. (2019). A Game-Theoretic Taxonomy and Survey of Defensive Deception for Cybersecurity and Privacy. ACM Comput. Surv. (Csur) 52, 1–28. doi:10.1145/3337772

CrossRef Full Text | Google Scholar

Sarikaya, Y., and Ercetin, O. (2019). Motivating Workers in Federated Learning: A Stackelberg Game Perspective. IEEE Networking Lett. 2, 23–27. doi:10.1109/lnet.2019.2947144

CrossRef Full Text | Google Scholar

Schaible, S. (1976). Fractional Programming. II, on Dinkelbach's Algorithm. Manage. Sci. 22, 868–873. doi:10.1287/mnsc.22.8.868

CrossRef Full Text | Google Scholar

Shi, W., Zhou, S., and Niu, Z. (2020a). “Device Scheduling with Fast Convergence for Wireless Federated Learning,” in ICC 2020-2020 IEEE International Conference on Communications (ICC), Dublin, June 2020 (IEEE), 1–6. doi:10.1109/icc40277.2020.9149138

CrossRef Full Text | Google Scholar

Shi, W., Zhou, S., Niu, Z., Jiang, M., and Geng, L. (2020b). Joint Device Scheduling and Resource Allocation for Latency Constrained Wireless Federated Learning. IEEE Trans. Wireless Commun. 20, 453–467. doi:10.1109/twc.2020.3025446

CrossRef Full Text | Google Scholar

Sun, H., Chen, X., Shi, Q., Hong, M., Fu, X., and Sidiropoulos, N. D. (2017). “Learning to Optimize: Training Deep Neural Networks for Wireless Resource Management,” in 2017 IEEE 18th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Sapporo, July 2017 (IEEE), 1–6. doi:10.1109/spawc.2017.8227766

CrossRef Full Text | Google Scholar

Tran, N. H., Bao, W., Zomaya, A., Nguyen, M. N., and Hong, C. S. (2019). “Federated Learning over Wireless Networks: Optimization Model Design and Analysis,” in IEEE INFOCOM 2019-IEEE Conference on Computer Communications, Paris, April–May 2019 (IEEE), 1387–1395. doi:10.1109/infocom.2019.8737464

CrossRef Full Text | Google Scholar

Yang, Z., Chen, M., Saad, W., Hong, C. S., and Shikh-Bahaei, M. (2021). Energy Efficient Federated Learning over Wireless Communication Networks. IEEE Trans. Wireless Commun. 20, 1935–1949. doi:10.1109/twc.2020.3037554

CrossRef Full Text | Google Scholar

Zappone, A., Di Renzo, M., and Debbah, M. (2019). Wireless Networks Design in the Era of Deep Learning: Model-Based, Ai-Based, or Both? IEEE Trans. Commun. 67, 7331–7376. doi:10.1109/tcomm.2019.2924010

CrossRef Full Text | Google Scholar

Zhan, Y., Li, P., Qu, Z., Zeng, D., and Guo, S. (2020). A Learning-Based Incentive Mechanism for Federated Learning. IEEE Internet Things J. 7, 6360–6368. doi:10.1109/jiot.2020.2967772

CrossRef Full Text | Google Scholar