- 1Key Laboratory for Information Science of Electromagnetic Waves (MoE), Fudan University, Shanghai, China
- 2Peng Cheng Laboratory, Shenzhen, China
- 3The School of Computer Science and Technology, Hangzhou Dianzi University, Hangzhou, China
As 6G research progresses, both visible light communication (VLC) and artificial intelligence (AI) become important components, which makes them appear to converge. Neural networks (NN) as equalizers are gradually occupying an increasingly important position in the research of the physical layer of VLC, especially in nonlinear compensation. In this paper, we will propose three categories of neural network equalizers, including input data reconfiguration NN, network reconfiguration NN and loss function reconfiguration NN. We give the definitions of these three neural networks and their applications in VLC systems. This work allows the reader to have a clearer understanding and future trends of neural networks in visible light communication, especially in terms of equalizers.
Introduction
As 6G research progresses, new spectrum resources will need to be continually expanded. Visible light communication (VLC) is receiving increasing attention as one of the potential spectrum resources for 6G (You et al., 2021). VLC utilizes the 400–800 THz spectrum, which has theoretical advantages, such as high capacity, high anti-electromagnetic interference, high confidentiality, and human safety (Chi et al., 2015). Furthermore, VLC enables simultaneous lighting and communication by multiplexing LEDs, which can greatly accelerate communication coverage and reduce construction costs. Based on these, it is foreseen that VLC is expected to become a powerful air interface technology in 6G.
However, one issue that needs to be addressed before it can be commercialized is the nonlinearity of VLC (Neokosmidis et al., 2009). Compared to conventional air interface technology, visible light communication has an additional electro-optical conversion, which can induce special nonlinearities. Due to the direct modulation of VLC, the voltage amplitude change of the signal will directly affect the recombination of carriers and holes (Windisch et al., 2000), which is the main nonlinear factor in VLC. Traditional nonlinear elimination algorithms are fitted using mathematical expansions, such as Volterra series (Wang et al., 2015). But, as nonlinearity increases, the computational complexity of such a compensation approach increases dramatically, making it difficult to apply in VLC systems. Fortunately, AI has become an integral part of 6G (Letaief et al., 2019), and, at the same time, a powerful tool for nonlinearity elimination, especially neural networks.
Machine learning (ML) has been used successfully for over a decade in prediction, classification, pattern recognition, data mining, feature extraction, and behavior recognition, among many other areas. In optical communication systems, many algorithms in the field of machine learning can be used to solve nonlinear problems (Khan et al., 2017). Among these methods, using neural networks as equalizers to compensate for signal impairment is one of the most important aspects of physical layer communication, especially for VLC (Haigh et al., 2014; Lin et al., 2021; Peng et al., 2022). In 5G, channel equalization is achieved through zero-forcing equalization based on pilot sequences. In 6G, considering VLC and other high-frequency communication, zero-forcing equalization will be difficult to perform superior performance, as it is only a linear equalizer. The neural network is a great choice for equalization, but it is a too powerful and heavy tool, which may bring large computation complexity, long computation time, and poor generalization. Therefore, it requires some modification to suit the actual communication system.
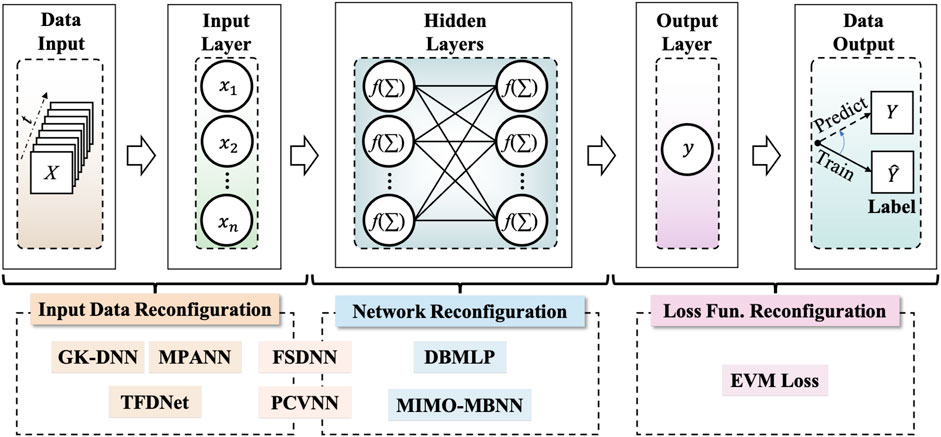
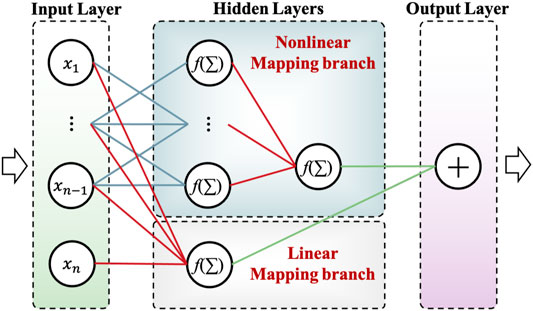
In this paper, we will introduce some structures of NN that have been utilized as an equalizer in a VLC system. Each neural network has a small change to better improve communication performance. Based on the three-layer architecture of neural networks, these NN efforts are all reconfigured at different layers to be more in line with the communication system. Here, we first propose three major categories of NN equalizers, including input data reconfiguration NN, network reconfiguration NN and loss function reconfiguration NN, as shown in Figure 1. GK-DNN (Chi et al., 2018), MPANN (Hu et al., 2020) and TFDNet (Chen et al., 2020) are typical input data reconfiguration NN, while DBMLP (Zhao and Chi, 2020) and MIMO-MBNN (Zou et al., 2020) are typical network reconfiguration NN. FSDNN (Chi et al., 2020) and PCVNN (Chen et al., 2021) have the characteristics of both input data and network reconfiguration. Error vector magnitude (EVM) based loss function (Stainton and Haigh, 2021) is a classic type-three network. Different reconfiguration methods imply mapping different communication concepts onto neural networks. We will present why these reconfiguration NNs work well in VLC and how to define these neural networks. Our goal is to give the reader a clear route to the subsequent work on neural network equalizers for VLC. It can be envisioned that high-speed VLC will become an integral part of 6G and cooperate with other communication approaches to build 6G space-air-ground-sea integrated networks.
Input Data Reconfiguration Neural Network
Input data reconfiguration neural network mainly originated from the idea of functional linked artificial neural network (FLANN) (Patra et al., 2008). In a visible light communication system, the received data is serial timing signal. The signal impairment is submerged in the data series, such as memory effect and nonlinearity. An untransformed signal will overload the neural network, bringing large computational complexity and long computation time. So, in input data reconfiguration NN, the main goal is to manually extract more communication features that will be used as input to the neural network, such as higher-order terms or frequency domain information. For the selection of the network output and the label, it is usually a simple corresponding time series data.
GK-DNN
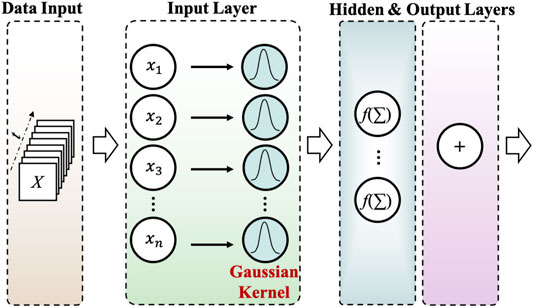
The non-linear effect of devices and the channel in the VLC system will seriously affect its performance. Traditional non-linear equalization algorithms based on the Volterra series suffer from the exponential increment of computational complexity as they deal with the third-order nonlinear responses or above. Recently, the DNN-based post-equalization methods with powerful nonlinear fitting ability have been developed by researchers to compensate for the nonlinearity in a VLC system. What’s more, the Gaussian kernel-aided DNN (GK-DNN) equalizer (Chi et al., 2018) has been reported to accelerate the training processing and greatly relieve the computational complexity of the equalizer.
The schematic diagram of the proposed GK-DNN is shown in Figure 2. As being one of the input data reconfiguration neural networks, here, we focus on the input layer of the GK-DNN. Firstly, the input data could be obtained by windowing the received signal sequence. The window length is n, considering the adjacent (n-1)/2 symbols’ influence towards the central one. Then these windowed samples (or input data) would go through a functional mapping based on Gaussian function, which helps map the input data to a non-linear space to reduce the number of iterations and duration of the fitting. This idea is enlightened by the assumption that the adjacent (n-1)/2 symbols’ influence towards the central one is in accordance with the Gaussian distribution. The Gaussian kernel could be expressed as follows:
Here, t is the expressions in the continuous domain and t' is the central time. ɑ is the parameter that controls the scope of the Gaussian kernel related to the 3dB bandwidth. As the ɑ increases, the variance of the Gaussian kernel mapping function decreases, which helps better emulate the nonlinear effect of the channel. Generally, the larger the ɑ is, the faster the training process would be. Subsequently, after the kernel function mapping, the mapped data would be input into the DNN. Here in the case of GK-DNN, two hidden layers where the ReLU activation function is utilized to emulate the nonlinearity of the system. The reason for choosing two hidden layers is a trade-off between consideration of the universal approximation theorem and the number of neurons. It should be noted that the number of nodes in the first hidden layer needs to be large enough to describe the relationship between features and labels. On the other hand, the number of nodes in the first hidden layer should not be too large in case of the massive computational complexity and long training time. Finally, the decision result is output through the softmax layer, where the number of nodes in the output layer is the same as the number of levels of the transmitted signal. With the kernel reducing the iteration epochs by nearly half (47.06%), the GK-DNN equalizer could efficiently realize the post equalization of the received signal in VLC system. And it could significantly improve the system’s anti-nonlinearity performance with the aid of DNN’s powerful nonlinear fitting ability.
MPANN
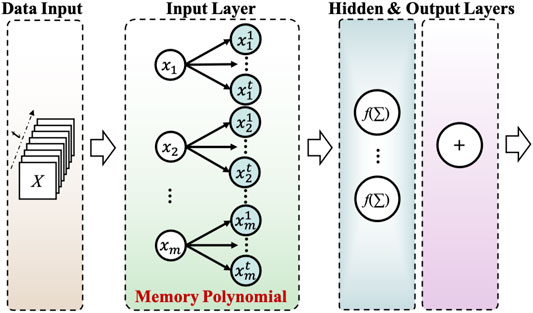
Utilizing neural networks as an equalizer for mitigating both the linear and nonlinear distortions in VLC systems has become common in recent years, while the great complexity still restrains the practical implementation. The optimal equalization performance usually comes at the cost of computational complexity. For example, digital pre-distortion (DPD) greatly relieves the equalizer’s complexity by moderately sacrificing partial performance. Therefore, a robust equalizer with relatively optimal equalization performance while still maintaining a low complexity is expected to be designed for the VLC system.
A novel memory-polynomial ANN (MPANN) equalizer is reported in (Hu et al., 2020) to simplify the network structure and still maintain similar equalization performance as DNNs. The structure of the applied MPANN is shown in Figure 3. Likewise, the input data could be obtained by windowing the received signal sequence. Here usually call the length of the window the memory length. The input layer of MPANN is a memory-polynomial layer (MP layer) where the input samples are expanded by one certain function which is memory polynomial expansion. This operation would map the input data to higher dimensional data space and provide prior knowledge of the nonlinear model, which helps significantly decrease the demanded nodes of the following NN structure.
Then the output pattern of functional mapping in the MP layer is multiplied by the corresponding weights and fed into the following hidden layer, which is fully connected with the output nodes of the MP layer. The outputs of the MP layer go through a regular activating process (ReLU) and weighting process in the hidden layer. Then finally the output layer is utilized to output the equalized symbol. The weights in MPANN are usually trained and updated according to the backpropagation (BP) algorithm on a large training set to minimize the mean square error (MSE) between the predicted received signals and transmitted signals. During the training process, the aim is to reduce the loss function by updating the weights. Then the validation set and test set are also used to prevent the overfitting problem and evaluate the MPANN’s performance. It should be noted that the order of all samples in every batch is randomized to avoid the memory effect of the PRBS sequence during the training or testing process. The experimental results also confirmed the fact that the MPANN could achieve the same equalization performance, or even better on some occasions, as the regular DNN while only requires less than a quarter of the complexity.
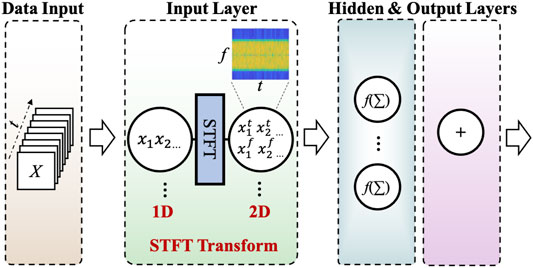
TFDNet
The commonly used NN equalizers in a VLC system usually process time-domain signals. However, this would sometimes result in the spectrum difference between the equalized signal and the original signal, which is not tally with the fact that the well-learned signal should have the same spectrum as the original one. This suggests that only considering the time-domain information is not good enough. Therefore, researchers begin to take both time and frequency-domain information into consideration to obtain a better performance in VLC systems.
Inspired by the time-frequency analysis for audio speech enhancement and image processing, a novel joint Time-Frequency post-equalizer based on Deep Neural Network (TFDNet) is reported in (Chen et al., 2020) to compensate the nonlinear distortions in a VLC system. The schematic diagram of the proposed TFDNet is shown in Figure 4. By considering both time and frequency domain information simultaneously, the TFDNet could reveal comprehensive information of non-stationary signals received in a VLC system. Short-time Fourier transformation (STFT) is utilized to transfer signal from one-dimension (1D, time domain) to two-dimensions (2D, time-frequency domain). If we assume the obtained STFT matrix as Y, and each row of Y, denoted as Y(f), represents a certain frequency component, then the mth element of Y(f) could be expressed as below:
where G(n) represents the window function whose length is P. Assuming the overlapping steps at the window edge is L, then the stride R between adjacent DFTs would be R = P–L. After the STFT operation, then matrix Y would be fed into the following network column by column. The labels that the NN needs could always be obtained by manipulating the original transmitting signal. Similarly, the NN is trained to minimize the MSE and the parameters of the net optimized by the Adam optimizer. The nonlinear activating function is ReLU. , the inverse STFT (ISTFT) is adopted to obtain the reconstructed transmitting signal x(n), which could be expressed as below:
It should be noted that the analysis window must satisfy the COLA constraint (Griffin and Lim, 1984) when using ISTFT to ensure successful reconstruction of the original signal. Experimental results also confirm that the proposed TFDNet could resist severe nonlinear distortions and provide better performance for a VLC system compared to other nonlinear compensators such as Volterra and DNN. This multi-domain analysis method provides us with new inspiration to introduce more interdisciplinary digital signal processing methods in a VLC system in the coming future.
Network Reconfiguration Neural Network
Network reconfiguration neural network mainly lies in making the same signal pass through different neural networks with different properties. For example, as for linear and nonlinear signal impairment, it is difficult to compensate for different impairments using the same neural network. What’s more, combining input data reconfiguration and network reconfiguration, the extracted signal characteristics can be passed through different networks to better recover the signal. So, in network reconfiguration NN, the input signal is not limited to the original signal, and different network structures are used as branches with different functions. A corresponding sequence of data is taken as the network output and the label.
DBMLP
In order to enhance the applicability of NN equalizer, the Dual-branch multi-layer perception post-equalization algorithm (DBMLP) is proposed to reduce energy and computing resource consumptions (Zhao et al., 2019; Zhao et al., 2020). It reconstructed the structure of the MLP post-equalization algorithm based on the structure of the Volterra series post-equalization algorithm as a template and proposed a dual-branch multi-layer perceptron post-equalization algorithm. DBMLP combined the advantages of linear adaptive filters and MLP, which could reduce the algorithm complexity by 74.1% and improve the algorithm’s BER performance. DBMLP’s core structure is the two tributaries, as shown in Figure 5. In the first tributary, a CNN with one convolution layer and one dense layer is utilized to emulate the linear distortion in the signal bandwidth. In the second tributary, hollow MLP with a hollow operator layer and two dense layers is applied to emulate the nonlinear distortion out of the signal bandwidth. The nonlinearity of the output of the first tributary is corrected by the output of the second tributary, and the hollow layer can ignore the effect of the middle signal on the signals on both sides. The expression of the hollow layer is followed, where L is the memory depth.
To further reduce power consumption and complexity and enhance the applicability in practical UVLC systems, a pruning algorithm is proposed based on the DBMLP (Zhao and Chi, 2020). During the training of the DBMLP, the partial pruning algorithm needs to be applied after the several epochs training to ensure that the DBMLP is trained to a relatively convergent state. The partial pruning algorithm first sorts the absolute values of the weights of the connections that need to be pruned. It then sets the weights with smaller absolute values to 0 according to the sparsity, thereby pruning the weights of DBMLP. The weights of red connections in Figure 5 are not prunable, whereas the weights of blue connections are prunable. Since the linear mapping branch of the DBMLP has very few weights, pruning these weights contributes little towards reducing the space complexity of the entire equalizer. In addition, the number of weights connected to the output nodes of the nonlinear branch is also small. Further, since the number of parameters of these two parts is low and over-parameterization is not severe, pruning them seriously affects the BER performance of the DBMLP. Hence, the green connections, which have no weight, do not participate in the training and pruning process. The experimental results confirm the superiority of this method.
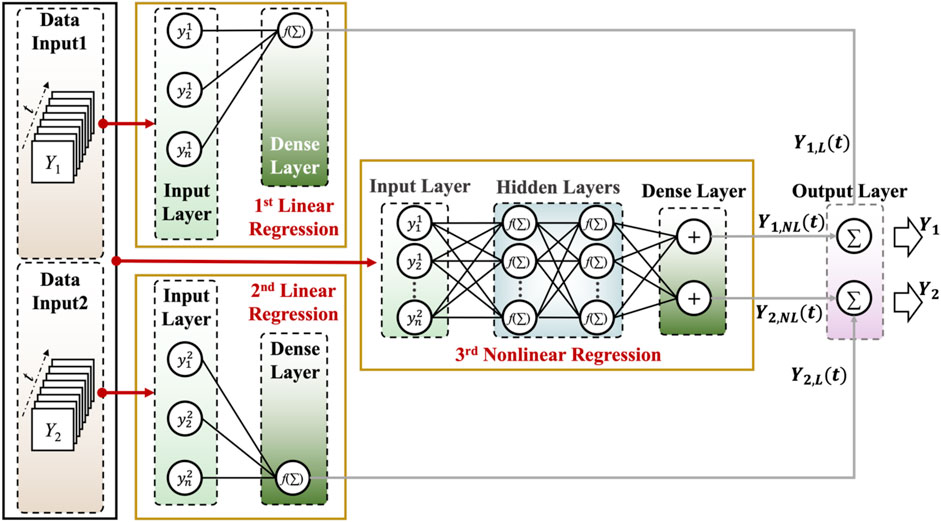
MIMO-MBNN
In a MIMO-VLC system, not only inter symbol interference (ISI) is severe but also inter-channel interference (ICI) is nonnegligible. MIMO-MBNN which has a multi-branch neural network is proposed for this issue. There are two linear branches and one nonlinear branch in this equalizer. It is a combination of both linear and nonlinear equalization that further removes the nonlinear loss beyond the capability of linear LMS/RLS or Volterra equalizer. When nonlinear loss becomes not negligible, especially when the operation in amplitude increases, the method would significantly outperform the three competitors mentioned. This advantage is brought by NN, which is powerful in fitting complex nonlinear functions. Another advantage is that signals from both channels are imported to the neural network. Therefore, the influence of ISI and ICI could be modeled and compensated in the meantime. It is shown that MIMO-MBNN has an advantage in operation rage 2.33 times larger than SISO-DNN and refreshed the record of communication rate in single receiver MIMO (SR-MIMO) VLC at that time (Zou et al., 2020).
In (Zou et al., 2020), it clearly states the reason of the three branches by deduction. Suppose that the receiver has an identical response to the two channels, and ignore the influence from the third-order term, its amplitude response in high Vpp is written as:
Where
Where
Figure 6 illustrates the principle of MIMO-MBNN. It is used to enhance the performance of single receiver MIMO, which receives signals from two independent channels by one receiver and must consider both the ICI and ISI. The input data are arranged in vectors in fixed length as the training data vector. For the linear regression branch, each of them only processes the signal from a single channel. But the nonlinear regression branch needs a signal from both channels. The linear branch acts like LMS/RLS equalizer looking for the linear ISI and outputs the result. In the meantime, the signals from the two channels are imported into the nonlinear regression branch to compute the cross terms related to nonlinear distortions and crosstalk. Afterward, MBNN sums the NN output with that from either the first or second linear branch as the equalized signal and feeds them into the optimizer to update parameters. Although the linear term might repeat in both linear and nonlinear branches, the optimizer would gradually remove it from the NN output.
FSDNN
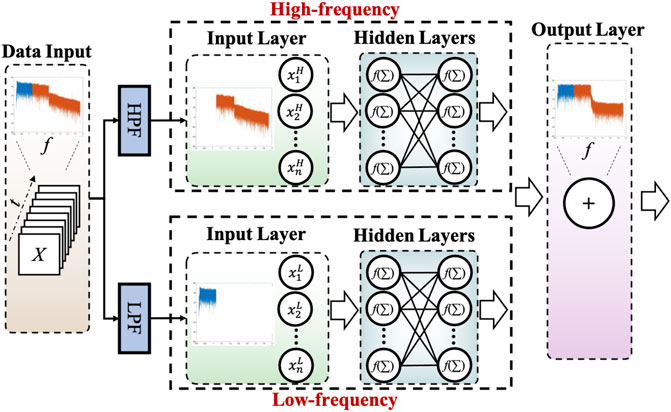
Frequency Slicing Deep Neural Network (FSDNN) is another variation of DNN that could be applied to carrierless amplitude and phase (CAP) modulation in a high-speed VLC system. Its ability has been proved to decrease the total computation complexity of traditional multi-layer perception (MLP) when it comes to the equalization performance in VLC system (Chi et al., 2020).
The frequency spectrum will suffer a nonlinear frequency fading issue after going through the VLC channel. DNN serves as an outstanding equalizer to equalize linear and nonlinear distortion due to its unique multi-layer structure, backpropagation algorithm, and advanced activation function. However, the neural network structure must be complex enough to handle complicated linear and nonlinear distortions, which means amounts of layers and nodes are needed if an MLP is used to equalize such a received signal and try to mitigate the frequency fading issue.
It is worth noticing that the high-frequency spectrum of a received signal in VLC suffers more serious amplitude attenuation while the low-frequency domain suffers less fading, which means a complex MLP structure is unnecessary for the low-frequency domain with low amplitude attenuation. Therefore, the damage to the high-frequency and low-frequency parts of the received signal is different, indicating that the complexity of DNN can be relieved if these two parts of signals are equalized separately, which are expected to relieve the equalization pressure of followed DNN.
In brief, FSDNN could be described as a process of reconstruction and combination of input data and neural network structure. The received wide-band signal after going through the VLC channel will be split into two parallel narrow-band parts of high-frequency and low-frequency, as shown in Figure 7. Its frequency spectrum will be split into two sub-bands using a digital low-pass filter (LPF) and a high-pass filter (HPF). In (Chi et al., 2020), two uniform root-raise-cosine (RRC) filters f1(t) and f2 (t) have been considered to filter the received signal R(t). Then two sub-bands signals, S1(t) and S2 (t), as two groups of input data are respectively fed into two MLPs that trained individually. To reach the best equalization performance in the system, the structure of the two equalizers should be tested artificially and fixed to optimal values, in which three main factors of DNN should be considered and adjusted, including the number of layers, nodes in every layer, taps, and epochs. Once the MLP is finished training and their weights are fixed, the sum of the output signal from two MLPs is the equalized and recovered signal.
The experiment result shows that the majority of the high-frequency fading from the channel is well compensated after the FSDNN and the complexity of the FSDNN to equalize two narrow-band signals separately is reduced to a lower value than the traditional DNN to equalize the whole-band signal (Chi et al., 2020). The method of frequency slicing successfully relieves the pressure on the training of NN. Moreover, the simple structure of FSDNN shows superior robustness in varying Vpp and bias current than traditional DNN when linear noise is the main limitation in a VLC system.
PCVNN
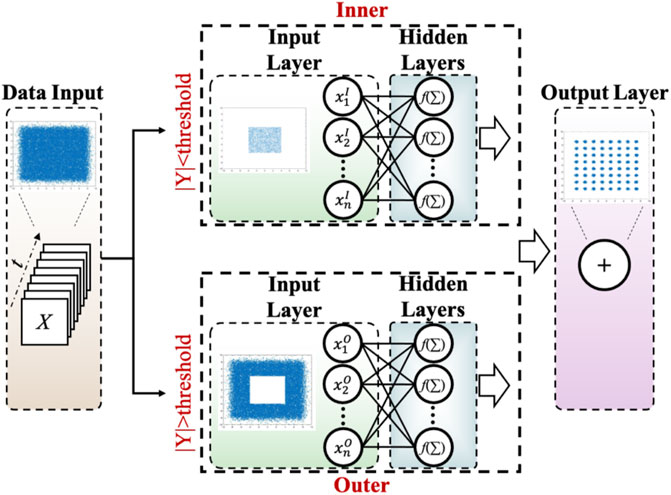
Due to the incoherent characteristics of LED and the serious attenuation of water medium, it is necessary to drive high power of LED to improve the signal-to-noise ratio (SNR) in an Underwater Visible Light Communication (UVLC) system. As the signal amplitude increases, the nonlinearity becomes more severe. So, the symbols located outside the constellation suffer more nonlinear distortion than inside ones. Therefore, an adaptive partition equalizer (PCVNN) is proposed (Chen et al., 2021) based on complex-valued neural network (CVNN) (Zhao et al., 2021), which has better performance and lower complexity than traditional CVNN and real-valued NN (RVNN) (Ahmad and Kumar, 2016).
The process of PCVNN is divided into several steps, as shown in Figure 8. Firstly, the position of the received signal
Where
The following mean square loss is used as the loss function of the complex-valued network (Hirose and Yoshida, 2012):
Where
Experiments demonstrate that PCVNN can achieve the bit error rate below the
Loss Function Reconfiguration Neural Network
In recent years, neural networks have been widely employed for signal processing such as equalization and classification. In the model training phase, the loss function is used to evaluate the difference between the predicted results and the true value, which plays an important role in the backpropagation process. When NN is used for classification, the cross-entropy loss function is widely used. While for equalization, MSE is the most used loss function. However, BER is the typical evaluation indicator in a communication system, so that the loss function of the model and the eventual metrics are not matched. Unfortunately, BER is not suitable to act as a loss function, because it is possible that there is no bit error but signal distortion exists, and it will lead to gradient disappearance. Therefore, a modified loss function that has a direct connection with BER is required.
In (Stainton and Haigh, 2021; Stainton et al., 2021), loss function based on EVM is first proposed in visible light communication. Supposing the predicted results
For a 1-dimensional signal, using MSE as a loss function performs similarly to using EVM as a loss function. While for 2-dimensional (complex-valued) signal, EVM has a closer relationship with BER (Schmogrow et al., 2011). This is because MSE focuses explicitly on sample amplitudes and does not consider any phase offset from the ideal constellation points. Experimental results indicate that the proposed EVM loss function performs better in equalization for complex-valued signals compared with using MSE as a loss function. In a spectrally efficient frequency division multiplexing (SEFDM) VLC system, up to 50% bandwidth compression can be supported. However, using EVM as a loss function the model tends to overfitting (Stainton and Haigh, 2021) when there is no compression. In addition to that, the above EVM enhancement is only applicable to real-valued neural networks. If a complex-valued network is used, the EVM and the complex-valued MSE are not fundamentally different.
Apart from the EVM loss function, several modified loss functions have also been proposed in wireless communication such as weighted sum-rate based loss function (Huang et al., 2018), which adds an extra penalty item and a hybrid loss function (Dörner et al., 2017), which adds the weighted MSE to the cross-entropy.
Discussion and Future Trends
The NN equalizer in the research of the physical layer of VLC is still in its early stage. Although previous works have shown promising results, the relationship between the visible light communication model and the neural network model is still not clear enough. Some work has made efforts on the nonlinear interpretation of VLC (Neokosmidis et al., 2009; Hu et al., 2021). However, due to the additional electro-optical conversion, it is difficult to represent using a mathematical formula. A sample example is that the recombination of carriers and holes (Windisch et al., 2000). The operating conditions of carrier recombination change as the signal amplitude changes, resulting in a dynamic electro-optical conversion formula rather than a static one. On the other hand, neural networks are indeed powerful equalization tools, but at the cost of huge computational complexity, extremely long computation time, and very poor generalization. These shortcomings will be amplified in the communication field, particularly in the real-time communication of 6G. Hence, there are numerous challenges and research directions of NN equalizers that should be pursued in the future.
Input Data Reconfiguration Neural Network
The major goal of this sort of neural network is to improve the neural network’s ability to extract communication features. In a communication system, the received signal is serial data that changes over time. In the ideal case, each signal is sampled exactly and without channel impairment. However, ISI will be introduced due to frequency selective fading. As the high-frequency response decays, the time domain pulses begin to broaden and spread into the adjacent time-series signal. This problem is greatly magnified in VLC due to the limited bandwidth. Another challenge is nonlinearity. In addition to the electro-optical conversion nonlinearity mentioned above, there are also nonlinearities in amplifiers, receivers, etc. that need attention.
To address ISI, traditional equalizers usually have a concept of taps to represent memory depth. This also applies in the neural network equalizer. Thus, we can see that in the input signal of the NN, it is usually the sliding window of the received signals. For nonlinearity, the easiest way is to use a nonlinear activation function and keep iterating through the neural network. This comes at a cost that is difficult to bear by the communication system. Therefore, memory polynomial expansion, Gaussian, Fourier basis functions, Volterra series, and other trigonometric polynomials (e.g., Chebyshev, etc.), which could consider both ISI and nonlinear, can be used as a way to reconstruct the input data. Frequency response is another important characteristic in a VLC system. It is difficult for the NN to identify the difference in frequency response by itself. So, it is a normal idea to use frequency-domain signals as input signals. Apart from that, Short-time Fourier transform or Wavelet transform is a smarter way to be able to consider the time dimension along with the frequency domain.
Network Reconfiguration Neural Network
In this neural network, the main objective is to give the network the ability to handle different impairments. Because of poor frequency response, high voltage nonlinearity, or different transmission channels, it is difficult to implement a universal neural network. The difficulty of this network design is based on what dimension to divide it. The designer has to identify the limitation of the communication system. If the system is bandwidth-constrained, as is often the case with a VLC system, the high-frequency and low-frequency signals will obviously experience different attenuation. This is the reason why FSDNN was proposed. If the system is nonlinearly constrained, high- and low-level signals will experience different electro-optical responses, such as the proposed PCVNN. As can be seen here, in order to get the signal into different networks, it is often also necessary to combine it with the input data reconstruction neural network. The former network can split the signal into different parts, which then logically go into different neural network models. A classical approach is to use the decision-feedback structure in the neural network (Yi et al., 2020).
Other kinds of network reconfiguration neural networks, such as convolutional neural network (CNN) (Chuang et al., 2018; Liu et al., 2019; Abu-romoh et al., 2021), recurrent neural network (RNN) (Peng et al., 2021), and cascade RNN(CRNN) (Xu et al., 2020a) change the structure of the network from another perspective. CNN is often used as a tool for image recognition. In TFDNet, the input signal has been transformed into a two-dimensional signal, which can be treated as an image. However, the computation using CNN has not been considered yet, and the common MLP is still used. RNNs are often used to process sequential data, such as speech, which seems to fit equally well with communication data. Further, bidirectional RNN (BRNN) is used in communication systems (Schaedler et al., 2021) that can consider both before and after timing data, just like the traditional equalizer concept of time windows. Furthermore, transformer (Amoiralis et al., 2009; Xu et al., 2020b) and multi-task NN(Xu et al., 2021), which have achieved great success in many AI fields such as natural language processing, computer vision, audio processing, etc. at this stage, are also expected to get better results in the field of communication.
Loss Function Reconfiguration Neural Network
In this kind of reconfiguration neural network, research progress is much slower than the other two networks. Because it is difficult to learn from neural network work in other fields. Using MSE in the majority of neural networks always gives great results, which also leads to a lack of motivation to explore. Another challenge is the reconstruction of the activation function, which requires both deep mathematical skills and communication knowledge.
BER is the typical and most important evaluation indicator in a communication system. But as mentioned above, it is not a good choice of a loss function. Typical metrics for communication systems include EVM (Stainton and Haigh, 2021), cross-entropy (Dörner et al., 2017; Yi et al., 2018), and so on. A tricky way to implement the reconfigured cost function is to combine several of these metrics. An effective direction is to target constellation points, such as the rotation angle between the constellation point of the recovered signal and the standard constellation point. Or it can use the maximum Euclidean distance to judge the equalization performance. Another direction is to use the signal as the input of the loss function after dimensionality increase or dimensionality reduction, such as Haar Transform (Stanković and Falkowski, 2003), principle component analysis (PCA) (Wold et al., 1987) and independent component analysis (ICA) (Comon, 1994).
Conclusion
In this paper, three categories of neural network equalizers, input data reconfiguration NN, network reconfiguration NN, and loss function reconfiguration NN are proposed for a VLC system. All of these reconfigurations allow neural networks to better explain the communication system and reflect the characteristics of the communication model. Almost all neural network equalizers in VLC can be classified into these three categories. The summary is shown in Table.1. Previous research work may not be aware of these, but it is clear from our analysis that they have something in common. Besides, we can see that there is still a lot of research space for loss function reconfigured neural networks. In addition, neural networks combining multiple categories should be expected to have better performance, as in the case of FSDNN combining both input data and network reconfiguration. As the research progresses, it is looking forward to the large-scale application of neural networks in 6G VLC, and achieving far beyond previous achievements.
Author Contributions
JS, OH, YH, WN, RJ, GQ, ZX and NC contributed to writing and conceptualization. JS designed the structure of the article and wrote the first draft of the manuscript. JS and OH drew the figures. JS, OH, YH, WN, RJ, GQ and ZX wrote sections of the manuscript. NC reviewed the article and format. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This work was partially supported by the Natural Science Foundation of China Project (No. 61925104, No. 62031011), the Major Key Project of PCL (PCL 2021A14), China Postdoctoral Science Foundation (2021M700025), and China National Postdoctoral Program for Innovative Talents (BX2021082).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abu-Romoh, M., Costa, N., Napoli, A., Pedro, J., Jaouën, Y., and Yousefi, M. (2021). “Low Complexity Convolutional Neural Networks for Equalization in Optical Fiber Transmission,” in Signal Processing in Photonic Communications, Washington, DC, 26–29 July 2021. (Washington, DC: Optical Society of America). doi:10.1364/SPPCOM.2021.SpM5C.5
Ahmad, S. T., and Kumar, K. P. (2016). Radial Basis Function Neural Network Nonlinear Equalizer for 16-QAM Coherent Optical OFDM. IEEE Photon. Technol. Lett. 28, 2507–2510. doi:10.1109/lpt.2016.2601901
Amoiralis, E. I., Tsili, M. A., and Kladas, A. G. (2009). Transformer Design and Optimization: a Literature Survey. IEEE Trans. Power Deliv. 24, 1999–2024. doi:10.1109/tpwrd.2009.2028763
Chen, H., Niu, W., Zhao, Y., Zhang, J., Chi, N., and Li, Z. (2021). Adaptive Deep-Learning Equalizer Based on Constellation Partitioning Scheme with Reduced Computational Complexity in UVLC System. Opt. Express 29, 21773–21782. doi:10.1364/oe.432351
Chen, H., Zhao, Y., Hu, F., and Chi, N. (2020). Nonlinear Resilient Learning Method Based on Joint Time-Frequency Image Analysis in Underwater Visible Light Communication. IEEE Photon. J. 12, 1–10. doi:10.1109/jphot.2020.2981516
Chi, N., Haas, H., Kavehrad, M., Little, T. D. C., and Huang, X.-L. (2015). Visible Light Communications: Demand Factors, Benefits and Opportunities [Guest Editorial]. IEEE Wireless Commun. 22, 5–7. doi:10.1109/mwc.2015.7096278
Chi, N., Hu, F., Li, G., Wang, C., and Niu, W. (2020). AI Based on Frequency Slicing Deep Neural Network for Underwater Visible Light Communication. Sci. China Inf. Sci. 63, 1–8. doi:10.1007/s11432-020-2851-0
Chi, N., Zhao, Y., Shi, M., Zou, P., and Lu, X. (2018). Gaussian Kernel-Aided Deep Neural Network Equalizer Utilized in Underwater PAM8 Visible Light Communication System. Opt. Express 26, 26700–26712. doi:10.1364/oe.26.026700
Chuang, C.-Y., Liu, L.-C., Wei, C.-C., Liu, J.-J., Henrickson, L., Huang, W.-J., et al. (2018). “Convolutional Neural Network Based Nonlinear Classifier for 112-Gbps High Speed Optical Link,” in Optical Fiber Communication Conference, San Diego, CA, 11–15 March 2018. (Washington, DC: Optical Society of America). doi:10.1364/ofc.2018.w2a.43
Comon, P. (1994). Independent Component Analysis, a New Concept? Signal. Processing 36, 287–314. doi:10.1016/0165-1684(94)90029-9
Dorner, S., Cammerer, S., Hoydis, J., and Brink, S. t. (2018). Deep Learning Based Communication over the Air. IEEE J. Sel. Top. Signal. Process. 12, 132–143. doi:10.1109/jstsp.2017.2784180
Griffin, D., and Jae Lim, J. (1984). Signal Estimation from Modified Short-Time Fourier Transform. IEEE Trans. Acoust. Speech, Signal. Process. 32, 236–243. doi:10.1109/tassp.1984.1164317
Haigh, P. A., Ghassemlooy, Z., Rajbhandari, S., Papakonstantinou, I., and Popoola, W. (2014). Visible Light Communications: 170 Mb/s Using an Artificial Neural Network Equalizer in a Low Bandwidth white Light Configuration. J. Lightwave Technol. 32, 1807–1813. doi:10.1109/jlt.2014.2314635
Hirose, A., and Yoshida, S. (2012). Generalization Characteristics of Complex-Valued Feedforward Neural Networks in Relation to Signal Coherence. IEEE Trans. Neural Netw. Learn. Syst. 23, 541–551. doi:10.1109/tnnls.2012.2183613
Hu, F., Chen, S., Zhang, Y., Li, G., Zou, P., Zhang, J., et al. (2021). High-speed Visible Light Communication Systems Based on Si-Substrate LEDs with Multiple Superlattice Interlayers. PhotoniX 2, 1–18. doi:10.1186/s43074-021-00039-9
Hu, F., Holguin-Lerma, J. A., A. Holguin-Lerma, J., Mao, Y., Zou, P., Shen, C., et al. (2020). Demonstration of a Low-Complexity Memory-Polynomial-Aided Neural Network Equalizer for CAP Visible-Light Communication with Superluminescent Diode. Opto-Electronic Adv. 3, 200009–200011. doi:10.29026/oea.2020.200009
Huang, H., Xia, W., Xiong, J., Yang, J., Zheng, G., and Zhu, X. (2019). Unsupervised Learning-Based Fast Beamforming Design for Downlink MIMO. IEEE Access 7, 7599–7605. doi:10.1109/access.2018.2887308
Khan, F. N., Lu, C., and Lau, A. P. T. (2017). “Machine Learning Methods for Optical Communication Systems,” in Signal Processing in Photonic Communications, New Orleans, 24–27 July 2017=San Diego, California. (Washington, DC: Optical Society of America). doi:10.1364/sppcom.2017.spw2f.3
Letaief, K. B., Chen, W., Shi, Y., Zhang, J., and Zhang, Y.-J. A. (2019). The Roadmap to 6G: AI Empowered Wireless Networks. IEEE Commun. Mag. 57, 84–90. doi:10.1109/mcom.2019.1900271
Lin, Y.-S., Chow, C.-W., Liu, Y., Chang, Y.-H., Lin, K.-H., Wang, Y.-C., et al. (2021). PAM4 Rolling-Shutter Demodulation Using a Pixel-Per-Symbol Labeling Neural Network for Optical Camera Communications. Opt. Express 29, 31680–31688. doi:10.1364/oe.430625
Liu, L., Deng, R., and Chen, L.-K. (2019). 47-kbit/s RGB-LED-Based Optical Camera Communication Based on 2D-CNN and XOR-Based Data Loss Compensation. Opt. Express 27, 33840–33846. doi:10.1364/oe.27.033840
Neokosmidis, I., Kamalakis, T., Walewski, J. W., Inan, B., and Sphicopoulos, T. (2009). Impact of Nonlinear LED Transfer Function on Discrete Multitone Modulation: Analytical Approach. J. Lightwave Technol. 27, 4970–4978. doi:10.1109/jlt.2009.2028903
Patra, J. C., Chin, W. C., Meher, P. K., and Chakraborty, G. (2008). “Legendre-FLANN-based Nonlinear Channel Equalization in Wireless Communication System,” in 2008 IEEE International Conference on Systems, Man and Cybernetics, Singapore, 12-15 Oct. 2008 (Manhattan, New York, U.S: IEEE), 1826–1831. doi:10.1109/icsmc.2008.4811554
Peng, C.-W., Chan, D. W. U., Tong, Y., Chow, C.-W., Liu, Y., Yeh, C.-H., et al. (2021). “Long Short-Term Memory Neural Network for Mitigating Transmission Impairments of 160 Gbit/s PAM4 Microring Modulation,” in 2021 Optical Fiber Communications Conference and Exhibition (OFC), San Francisco, CA, 6-10 June 2021 (Manhattan, New York, U.S: IEEE), 1–3. doi:10.1364/ofc.2021.tu5d.3
Peng, C.-W., Tsai, D.-C., Lin, Y.-S., Chow, C.-W., Liu, Y., and Yeh, C.-H. (2022). “Long Short-Term Memory Neural Network to Enhance the Data Rate and Performance for Rolling Shutter Camera Based Visible Light Communication (VLC),” in Optical Fiber Communication Conference, San Diego, CA, 05-09 March 2022.
Schadler, M., Bocherer, G., Pittala, F., Calabro, S., Stojanovic, N., Bluemm, C., et al. (2021). Recurrent Neural Network Soft-Demapping for Nonlinear Isi in 800gbit/s Dwdm Coherent Optical Transmissions. J. Lightwave Technol. 39, 5278–5286. doi:10.1109/jlt.2021.3102064
Schmogrow, R., Nebendahl, B., Winter, M., Josten, A., Hillerkuss, D., Koenig, S., et al. (2012). Error Vector Magnitude as a Performance Measure for Advanced Modulation Formats. IEEE Photon. Technol. Lett. 24, 61–63. doi:10.1109/lpt.2011.2172405
Stainton, S., and Haigh, P. A. (2021). “Doubling the Spectral Efficiency with EVM as the Objective Function for Training Neural Networks in Non-orthogonal Visible Light Communications Systems,” in Optical Fiber Communication Conference, Washington, DC 6–11 June 2021. (Washington, DC: Optical Society of America). doi:10.1364/ofc.2021.f1a.2
Stainton, S., Johnston, M., Dlay, S., and Haigh, P. A. (2021). EVM Loss: A Loss Function for Training Neural Networks in Communication Systems. Sensors 21, 1094. doi:10.3390/s21041094
Stanković, R. S., and Falkowski, B. J. (2003). The Haar Wavelet Transform: its Status and Achievements. Comput. Electr. Eng. 29, 25–44. doi:10.1016/s0045-7906(01)00011-8
Trabelsi, C., Bilaniuk, O., Zhang, Y., Serdyuk, D., Subramanian, S., Santos, J. F., et al. (2017). Deep Complex Networks. arXiv preprint arXiv:1705.09792.25 Feb 2018.
Windisch, R., Knobloch, A., Kuijk, M., Rooman, C., Dutta, B., Kiesel, P., et al. (2000). Large-signal-modulation of High-Efficiency Light-Emitting Diodes for Optical Communication. IEEE J. Quan. Electron. 36, 1445–1453. doi:10.1109/3.892565
Wold, S., Esbensen, K., and Geladi, P. (1987). Principal Component Analysis. Chemometrics Intell. Lab. Syst. 2, 37–52. doi:10.1016/0169-7439(87)80084-9
Xu, Z., Dong, S., Manton, J. H., and Shieh, W. (2021). Low-Complexity Multi-Task Learning Aided Neural Networks for Equalization in Short-Reach Optical Interconnects. J. Lightwave Tech. 40, 45–54.
Xu, Z., Sun, C., Ji, T., Dong, S., Zhou, X., and Shieh, W. (2020b). “Investigation on the Impact of Additional Connections to Feedforward Neural Networks for Equalization in PAM4 Short-Reach Direct Detection Links,” in 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, California, 08-12 March 2020. (Manhattan, New York: IEEE), 1–3. doi:10.1364/acpc.2020.s4i.1
Xu, Z., Sun, C., Ji, T., Ji, H., and Shieh, W. (2020a). “Cascade Recurrent Neural Network Enabled 100-Gb/s PAM4 Short-Reach Optical Link Based on DML,” in 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, California, 08-12 March 2020 (Manhattan, New York: IEEE), 1–3. doi:10.1364/ofc.2020.w2a.45
Yi, L., Liao, T., Huang, L., Xue, L., Li, P., and Hu, W. (2018). Machine Learning for 100 Gb/s/λ Passive Optical Network. J. Lightwave Tech. 37, 1621–1630.
Yi, L., Liao, T., Xue, L., and Hu, W. (2020). “Neural Network-Based Equalization in High-Speed PONs,” in 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8-12 March 2020 (Manhattan, New York, U.S: IEEE), 1–3. doi:10.1364/ofc.2020.t4d.3
Yiguang Wang, Y., Li Tao, L., Xingxing Huang, X., Jianyang Shi, J., and Nan Chi, N. (2015). 8-Gb/s RGBY LED-Based WDM VLC System Employing High-Order CAP Modulation and Hybrid post Equalizer. IEEE Photon. J. 7, 1–7. doi:10.1109/jphot.2015.2489927
You, X., Wang, C.-X., Huang, J., Gao, X., Zhang, Z., Wang, M., et al. (2021). Towards 6G Wireless Communication Networks: Vision, Enabling Technologies, and New Paradigm Shifts. Sci. China Inf. Sci. 64, 1–74. doi:10.1007/s11432-020-2955-6
Zhao, Y., and Chi, N. (2020). Partial Pruning Strategy for a Dual-branch Multilayer Perceptron-Based post-equalizer in Underwater Visible Light Communication Systems. Opt. Express 28, 15562–15572. doi:10.1364/oe.393443
Zhao, Y., Zou, P., and Chi, N. (2020). 3.2 Gbps Underwater Visible Light Communication System Utilizing Dual-branch Multi-Layer Perceptron Based post-equalizer. Opt. Commun. 460, 125197. doi:10.1016/j.optcom.2019.125197
Zhao, Y., Zou, P., Yu, W., and Chi, N. (2019). Two Tributaries Heterogeneous Neural Network Based Channel Emulator for Underwater Visible Light Communication Systems. Opt. Express 27, 22532–22541. doi:10.1364/OE.27.022532
Zhao, Z., Vuran, M. C., Guo, F., and Scott, S. D. (2021). Deep-waveform: A Learned OFDM Receiver Based on Deep Complex-Valued Convolutional Networks. IEEE J. Select. Areas Commun. 39, 2407–2420. doi:10.1109/jsac.2021.3087241
Keywords: visible light communication, neural networks, equalizer, machine learning, air interface
Citation: Shi J, Huang O, Ha Y, Niu W, Jin R, Qin G, Xu Z and Chi N (2022) Neural Network Equalizer in Visible Light Communication: State of the Art and Future Trends. Front. Comms. Net 3:824593. doi: 10.3389/frcmn.2022.824593
Received: 29 November 2021; Accepted: 14 March 2022;
Published: 28 April 2022.
Edited by:
Lilin Yi, Shanghai Jiao Tong University, ChinaReviewed by:
Zhaopeng Xu, The University of Melbourne, AustraliaChi-Wai Chow, National Chiao Tung University, Taiwan
Copyright © 2022 Shi, Huang, Ha, Niu, Jin, Qin, Xu and Chi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nan Chi, bmFuY2hpQGZ1ZGFuLmVkdS5jbg==
 Jianyang Shi
Jianyang Shi Ouhan Huang
Ouhan Huang Yinaer Ha
Yinaer Ha Wenqing Niu
Wenqing Niu Ruizhe Jin
Ruizhe Jin Guojin Qin
Guojin Qin Zengyi Xu
Zengyi Xu Nan Chi
Nan Chi