Non-Orthogonal Multiple Access: The Case of Improper Gaussian Signaling and Imperfect Successive Interference Cancellation

This paper studies a two-user downlink non-orthogonal multiple access (NOMA) system that adopts an improper Gaussian signaling (IGS) strategy to compensate for the performance loss due to imperfect successive interference cancellation (SIC). Joint optimization problems are formulated to maximize the overall spectral efficiency and energy efficiency of a two-user NOMA system under minimum user-rate requirements and total power constraints. Sub-optimal solutions of IGS circularity coefficients and power allocation are obtained for the formulated problems. Furthermore, improper constellation diagrams are designed using widely linear transformation with predefined optimized IGS coefficients to study the impact of IGS on throughput and error performance. Simulation results show that the performance of IGS-based NOMA systems, where the IGS strategy is adopted by both users, outperforms that of the proper Gaussian signal (PGS)-based NOMA system under imperfect SIC.

1 Introduction

Proper Gaussian Signaling (PGS) has been widely adopted in communication systems due to its attractive entropy-maximizing property, which is proved to achieve the maximum spectral efficiency in additive white Gaussian noise (AWGN) channels but not in the case of an interference channel (Zeng et al., 2013a; Zeng et al., 2013b; Lameiro et al., 2017). Moreover, the majority of the wireless products assume a proper signal model for the underlying circularly symmetric complex Gaussian (CSCG) signals, which is in contrast with many of the real-world applications. As a definition, a proper complex random variable has equal energy and uncorrelated real and imaginary components of a complex random entity, whereas any correlation between the two components results in an improper complex random variable. The improper characteristics with non-identical variance on the real and imaginary components are known to exist in some well-known constellation diagrams such as binary phase-shift keying and continuous phase modulation (CPM) (Javed et al., 2020).

The traditional complex-valued signal processing assumes a vanishing pseudo-covariance, i.e., equals zero, which is not accurate for many real-world scenarios where the concerned signals are frequently improper (Javed et al., 2020). Such simplified assumption not only results in misleading analysis and inaccurate results but also prohibits us from investigating the potential benefit of the additional degree of the freedom offered by improper signaling. By relaxing the constraints of PGS, i.e., equal power and uncorrelated real and imaginary components, we have what is called improper Gaussian signaling (IGS) (Schreier and Scharf, 2010; Javed et al., 2020). In practical systems, improper signaling techniques have already existed in linear receivers for Global System for Mobile communication and third Generation Partnership Project systems (Kurniawan and Sun, 2015). It has been shown that IGS attains higher degrees of freedom than PGS due to its ability to identify the interference signal dimension. In fact, it can be described as a kind of interference alignment technique since it mitigates interference by using its alignment in only one orthogonal signal space dimension, and by extracting the desired signal from the other orthogonal space (Cadambe et al., 2010). Due to these impropriety characteristics, IGS has been identified as a potential candidate for improving the spectral efficiency in interference-limited systems (Schreier and Scharf, 2010; Javed et al., 2020).

Non-orthogonal multiple access (NOMA) has been introduced as a potential candidate for enabling heavily-loaded systems using limited resources while improving the spectral efficiency (Islam et al., 2017). In that sense, in the downlink of NOMA systems, multiple users can be served simultaneously on one resource block by implementing superposition coding at the base-station side and successive interference cancellation (SIC) at the users’ side (Ding et al., 2014). This leads to spectrally-efficient systems provided that perfect SIC is performed, which is not a realistic assumption. In practice, detectors suffer from imperfect SIC, which leads to an interference-limited NOMA system (Yue et al., 2018). This encourages us to consider IGS as a promising solution to recompense for the SIC imperfections in such interference-limited scenarios.

In orthogonal multiple access (OMA) schemes, IGS has been investigated in interference Z-channel models (Zeng et al., 2013a; Zeng et al., 2013b; Lameiro et al., 2017), multiple-input multiple-output interference-limited systems (Nguyen et al., 2021), and broadcast channels (Shin et al., 2012; Nasir et al., 2019), where the achievable throughout regions and degrees of freedom were derived. IGS was also considered in Z-channel cognitive radio (CR) networks, where IGS was proven to be beneficial in reducing the interference to primary users in various unlicensed spectrum-sharing models (Lameiro et al., 2019). IGS was also evaluated in cooperative full-duplex relaying (CR) systems (Gaafar et al., 2017), where IGS was used to help the secondary user access the spectrum. Similar work in (Gaafar et al., 2018) was investigated in non-CR systems under Nakagami-m fading, where it was concluded that using IGS can eliminate the impact of residual self-interference by revising the signal impropriety.

Recent works considered IGS in NOMA interference-limited systems. The authors in (Hong and Bahk, 2020) investigated the performance of a two-user downlink NOMA system using IGS, by deriving the outage probability and the ergodic capacity expressions. In (Tuan et al., 2019), transmit precoding schemes were designed for a multi-cell network in order to maximize the users’ minimum rates under various power budget constraints. In (Yu et al., 2020), IGS scheme was generated for signal beamforming with the goal of improving the spectral efficiency of a multi-cell network and protecting the users’ secrecy. Our previous works in (Abu Mahady et al., 2019; Mahady et al., 2021) studied a two-user downlink point-to-point NOMA system with IGS under imperfect SIC, where sum-rate was maximized under user rate constraints in the cases of one user and two users employing IGS, respectively. Compared with these previous works, this work also considers the maximization of the system energy efficiency given the QoS and power budget requirements. In addition, this work designs IGS constellation diagrams using optimized IGS coefficients found through the spectral efficiency maximization problem. Moreover, error performance is simulated using the optimized constellation diagrams.

In particular, in this work, we investigate the potential merits of using IGS in a downlink two-user NOMA systems under SIC imperfection, where a BS serves two users in a near-far setup. In particular, the user closer to the BS (user 1) employs imperfect SIC to extract and forward user 2’s signal in addition to detecting its own signal. We first derive the exact expressions for each user’s rate when using IGS at both users. Due to the superiority of IGS over PGS in terms of spectral and energy efficiencies in interference-limited scenarios, we formulate two optimization problems for spectral efficiency and energy efficiency. In each formulated problem, we jointly optimize the BS transmit power and the transmit signal’s circularity coefficients. We propose iterative algorithms to find sub-optimal solutions to the developed non-convex optimization problems based on the Karush-Kuhn-Tucker (KKT) conditions. Additionally, we show the efficacy of the optimized circularity coefficient on the transmit constellations at the BS and the system error performance, where improper constellation diagrams are designed using widely linear transformation (WLT) based on the optimized IGS circularity coefficients. Simulation results demonstrate the vital impact of IGS over PGS in the context of NOMA systems under imperfect SIC.

Organization: The remainder of this paper is organized as follows: Preliminary IGS definition and generation are given in Section 2. The system and channel models are introduced in Section 3. The optimization problems are solved in Section 4. Simulation results are presented in Section 5. Finally, the conclusion is given in Section 6.

2 Preliminary: Improper Gaussian Signaling Definition and Generation

2.1 Improper Random Variables

Let Ω_x and ${\widehat{\mathrm{\Omega }}}_x$ be the variance and pseudo-variance of a zero-mean complex Gaussian random variable (RV) x, respectively. Then, they are defined as ${\mathrm{\Omega }}_x=\mathcal{E}[x{x}^{*}]$ and ${\widehat{\mathrm{\Omega }}}_x=\mathcal{E}[xx]$, respectively, where $\mathcal{E}[\cdot ]$ refers to the expectation of a random variable. Here, Ω_x is a real value and ${\widehat{\mathrm{\Omega }}}_x$ is typically a complex value.

Definition 1: A signal is called proper if it is uncorrelated with its complex conjugate and has a zero pseudo-variance, i.e., ${\widehat{\mathrm{\Omega }}}_x=0$; otherwise it is called an improper signal.

Definition 2. : The impropriety degree (or the IGS coefficient) of x is given as ${\mathcal{\backslash kappa}}_x=|{\widehat{\mathrm{\Omega }}}_x|/{\mathrm{\Omega }}_x$, where 0 ≤ κ_x ≤ 1. If κ_x = 0, then x is a proper signal, and if κ_x = 1, we have a maximally improper signal.

2.2 Improper Constellation Design

WLT is known as one of the most common ways of transforming proper signals into improper ones. In (Santamaria et al., 2018; Lopez-Fernandez et al., 2019; Javed et al., 2021), an easy design involving the generation of improper discrete constellations was considered, where a WLT of a standard unit energy proper M-quadrature amplitude modulation (QAM) constellation was used. In these works, the WLT was designed to maximize the minimum Euclidean distance between the improper constellation points, while keeping the signal energy the same.

Specifically, an improper constellation design, with a complex symbol x and predefined circularity coefficient κ_x, can be obtained from a proper constellation design with complex symbol s with a unit power $(\mathcal{E}|s{|}^2=1)$ with the following energy-preserving transformation.

$x=ϵs+\epsilon s^{*},(1)$

where the superscript (⋅)* refers to the complex conjugation operation, ϵ and ɛ are complex-valued quantities such that |ϵ|² + |ɛ|² = 1 (to maintain unit transmit power), $ϵ=\sqrt{0.5(1+\sqrt{1-{\kappa }_x^2})}$ and $\epsilon =\sqrt{0.5(1-\sqrt{1-{\kappa }_x^2})}{e}^{j\varphi }$, ϕ ∈ [0, π/2]. An optimal ϕ is selected to maximize the minimum distance between the constellation points. For 0 ≤ κ_x ≤ 0.5, the optimal ϕ for an arbitrary M is found to be ϕ = π/2. On the other hand, when $0.5\le {\kappa }_x\le 2/\sqrt{5}$, the optimal ϕ is found by solving the nonlinear equation sin(ϕ) − cos(ϕ) = 1/κ_x, which is equal to $\varphi =\arcsin \left(\frac{\sqrt{5}}{5{\kappa }_x}\right)+\arctan \frac{1}{2}$ (Lopez-Fernandez et al., 2019). Note that the optimal ϕ for the region of $2/\sqrt{5}\le {\kappa }_x\le 1$ is shown to be the same as the one in the solution for $0.5\le {\kappa }_x\le 2/\sqrt{5}$ at high signal-to-noise ratio (Lopez-Fernandez et al., 2019).

3 Channel and System Models

3.1 Channel Model

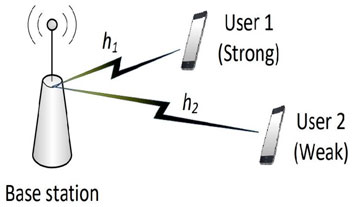
A downlink two-user NOMA system model with a base station (BS) is considered in this work as shown in Figure 1. The Rayleigh model is considered for the channels between the BS and users. We denote h_i, ∀i = 1, 2, as the channel variables with zero-mean and variance ${\sigma }_{h_i}^2$. Unlike the commonly used setups where users employ PGS, in this paper we consider IGS at both users, i.e., x_i, ∀i = 1, 2, are improper signals.

FIGURE 1

FIGURE 1. A NOMA system with IGS.

As per power-domain NOMA basics, users experience different channel conditions with the assumption of |h₁|² > |h₂|² and P₂ > P₁. Consequently, user 1, which has a better channel condition, can decode its own signal after removing the signal of user 2, which has worse channel condition, through SIC processing (Zeng et al., 2017). Meanwhile, user 2 can decode its own signal assuming the interference inflicted by user 1 is negligible and can thus be dealt with as noise. Since user 1’s receiver has imperfect SIC, there exists a residual interference as an outcome from this imperfection. Generally, the residual interference resulting from imperfect SIC is a complicated function of multiple factors, e.g., coding/modulation related parameters, channel related issues (fading and shadowing), device/hardware/battery related restrictions, etc. Furthermore, due to the characteristics of error propagation due to imperfect SIC, it is hard to model its impact. It is stated in (Sun et al., 2016a) and (Chen et al., 2018) that a linear model can effectively demonstrate the relationship between the residual interference and the received signal power. To introduce the impact of imperfect SIC, we adopt this linear model here. Under such a model of imperfect SIC, the received signal after SIC at user 1 is given in (Eq. 2), where η denotes the coefficient of imperfect SIC at user 1. Note that η = 0, corresponds to perfect SIC, and η = 1, corresponds to no interference cancellation.

3.2 Spectral Efficiency Analysis

Since IGS is considered at both users, i.e., x₁ and x₂ are improper, and imperfect SIC is assumed, we first need to find the new expressions for the users’ information rates. Hence, closed-form expressions are obtained for the spectral efficiency for each user in the considered system model. To do so, we characterize the received signals at each user as follows

$y_1=\sqrt{P_1}{h}_1{x}_1+\eta \sqrt{P_2}{h}_1{x}_2+n_1,(2)$

$y_2=\sqrt{P_2}{h}_2{x}_2+\sqrt{P_1}{h}_2{x}_1+n_2,(3)$

where x_i, ∀i = 1, 2, is the signal for the ith user and n_i is additive white Gaussian noise (AWGN) at the ith user’s receiver. The component $\eta \sqrt{P_2}{h}_1{x}_2$ in (Eq. 2) refers to the imperfect SIC at user 1.

To continue, based on (Zeng et al., 2013b), the user’s rate definition in the case of IGS is given as

${\mathcal{R}}_i=\frac{1}{2}{\log }_2\left(\frac{{\mathrm{\Omega }}_{y_i}^2-|{\widehat{\mathrm{\Omega }}}_{y_i}{|}^2}{{\mathrm{\Omega }}_{z_i}^2-|{\widehat{\mathrm{\Omega }}}_{z_i}{|}^2}\right),(4)$

where ${\mathrm{\Omega }}_{y_i}$ and ${\widehat{\mathrm{\Omega }}}_{y_i}$ refer respectively to the covariance and pseudo-covariance components of the received signal; while ${\mathrm{\Omega }}_{z_i}$ and ${\widehat{\mathrm{\Omega }}}_{z_i}$ refer to covariance and pseudo covariance components of interference plus noise signal, respectively.

After a few mathematical manipulations and assuming, for simplicity, that ${\sigma }_1^2={\sigma }_2^2={\sigma }^2$ and the powers P₁ = α₁P_T and P₂ = α₂P_T are assigned to user 1 and user 2, respectively, where 0 ≤ α_i ≤ 1, and α₁ + α₂ = 1, the rate of user 1, ${\mathcal{R}}_1$, is obtained as [see the details of the derivation in (Mahady et al., 2021)].

$\begin{array}{ll}\hfill & {\mathcal{R}}_1\left({\kappa }_{x_i},{\alpha }_i\right)=\underset{\text{Proper\hspace{0.17em}Signalling}}{\underbrace{{\text{log}}_2\left(1+\frac{{\alpha }_1{P}_T|h_1{|}^2}{{\eta }^2{\alpha }_2{P}_T|h_1{|}^2+{\sigma }^2}\right)}}\hfill \\ \hfill & +\underset{\text{Improper\hspace{0.17em}Signalling}}{\underbrace{\frac{1}{2}{\text{log}}_2\left(1-\frac{|{\alpha }_1{P}_T|h_1{|}^2{\kappa }_{x_1}{|}^2+|{\eta }^2{\alpha }_2{P}_T|h_1{|}^2{\kappa }_{x_2}{|}^2}{{\left({\alpha }_1{P}_T|h_1{|}^2+{\eta }^2{\alpha }_2{P}_T|h_1{|}^2+{\sigma }^2\right)}^2}\right)}}\hfill \\ \hfill & -\underset{\text{Improper\hspace{0.17em}Signalling}}{\underbrace{\frac{1}{2}{\text{log}}_2\left(1-\frac{|{\eta }^2{\alpha }_2{P}_T|h_1{|}^2{\kappa }_{x_2}{|}^2}{{\left({\eta }^2{\alpha }_2{P}_T|h_1{|}^2+{\sigma }^2\right)}^2}\right)}}.\hfill \end{array}(5)$

In the same way, the rate of user 2, ${\mathcal{R}}_2$, can be obtained as

$\begin{array}{ll}\hfill & {\mathcal{R}}_2\left({\kappa }_{x_i},{\alpha }_i\right)=\underset{\text{Proper\hspace{0.17em}Signalling}}{\underbrace{{\text{log}}_2\left(1+\frac{{\alpha }_2{P}_T|h_2{|}^2}{{\alpha }_1{P}_T|h_2{|}^2+{\sigma }^2}\right)}}\hfill \\ \hfill & +\underset{\text{Improper\hspace{0.17em}Signalling}}{\underbrace{\frac{1}{2}{\text{log}}_2\left(1-\frac{|{\alpha }_2{P}_T{h}_2^2{\kappa }_{x_2}{|}^2+|{\alpha }_1{P}_T{h}_2^2{\kappa }_{x_1}{|}^2}{{\left({\alpha }_2{P}_T|h_2{|}^2+{\alpha }_1{P}_T|h_2{|}^2+{\sigma }^2\right)}^2}\right)}}\hfill \\ \hfill & -\underset{\text{Improper\hspace{0.17em}Signalling}}{\underbrace{\frac{1}{2}{\text{log}}_2\left(1-\frac{|{\alpha }_1{P}_T{h}_2^2{\kappa }_{x_1}{|}^2}{{\left({\alpha }_1{P}_T|h_2{|}^2+{\sigma }^2\right)}^2}\right)}}.\hfill \end{array}(6)$

It is worth-note that each ${\mathcal{R}}_i,i=\mathrm{1,2}$, in (Eqs 5, 6) has three terms; the first term represents the proper signaling and the other two terms represent the improper signaling. If, for validation, we replace ${\kappa }_{x_i}=0,\forall i=\mathrm{1,2}$ and η = 0, the rates of PGS in the case of perfect SIC are obtained, which can be considered as a special case.

4 Optimization Problems

In this section, two optimization problems are formulated to maximize both the overall spectral efficiency and the energy efficiency under the constraints of each user’s minimum rate requirements and power budget.

4.1 Spectral Efficiency Maximization

Maximizing the overall spectral efficiency is a common objective in wireless systems. However, to avoid having all resources taken by one user, the quality of service (QoS) constraints are often enforced when formulating the overall spectral efficiency maximization. A joint optimization problem is developed to optimize both the IGS circularity coefficients $({\kappa }_{x_1},{\kappa }_{x_2})$ and power allocation at the BS. The objective is to maximize the system spectral efficiency given that the QoS of each user (minimum user rate) is met and the power budget is not exceeded.

In this optimization problem, we assume that the BS uses the total available power. For simplicity, we denote α₁ = α and α₂ = 1 − α. Based on the analysis of the rate expressions in Section 3.2., we can improve the overall sum rate in the case both users are employing IGS. That mentioned, the joint optimization problem can be developed as

$\mathcal{OP}1:\underset{{\kappa }_{x_1},{\kappa }_{x_2},\alpha }{\text{maximize}}{\mathcal{R}}_1\left({\kappa }_{x_1},{\kappa }_{x_2},\alpha \right)+{\mathcal{R}}_2\left({\kappa }_{x_1},{\kappa }_{x_2},\alpha \right)(\mathrm{7a})$

$\text{subject\hspace{0.17em}to}\mathcal{C}1:{\mathcal{R}}_1\left({\kappa }_{x_1},{\kappa }_{x_2},\alpha \right)\ge R_{m_1},(\mathrm{7b})$

$\mathcal{C}2:{\mathcal{R}}_2\left({\kappa }_{x_1},{\kappa }_{x_2},\alpha \right)\ge R_{m_2},(\mathrm{7c})$

$\mathcal{C}3:0\le {\kappa }_{x_1},{\kappa }_{x_2}\le 1,(\mathrm{7d})$

$\mathcal{C}4:0\le \alpha \le 1,(7e)$

where ${\mathcal{R}}_1({\kappa }_{x_1},{\kappa }_{x_2},\alpha )$ and ${\mathcal{R}}_2({\kappa }_{x_1},{\kappa }_{x_2},\alpha )$ are computed from (Eq. 5) and (Eq. 6), respectively. $R_{m_1}$ and $R_{m_2}$ are each user’s minimum rate requirement. The conditions $\mathcal{C}1$ and $\mathcal{C}2$ stress that the achieved rate of user 1 and user 2 are greater than $R_{m_1}$ and $R_{m_2}$, respectively, the condition $\mathcal{C}3$ enforced the range of IGS circularity coefficients between 0 and 1, and the condition $\mathcal{C}4$ represents the BS power budget.

The objective and rate constraints in the formulated optimization (Eqs 7a–7e) are non-convex which lead to a non-convex problem. To tackle this issue, the formulated problem can be optimized by using the necessary but not sufficient Karush-Kuhn-Tucker (KKT) conditions to find sub-optimal solutions for the circularity coefficient ${\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*}$, and power allocation parameter α* at less computational complexity.

The Lagrangian function corresponding to (Eqs 7a–7e) can be outlined as

$\begin{array}{ll}\hfill \mathcal{L}\left({\kappa }_{x_1},{\kappa }_{x_2},\alpha \right)=& -\left({\mathcal{R}}_1\left({\kappa }_{x_1},{\kappa }_{x_2},\alpha \right)+{\mathcal{R}}_2\left({\kappa }_{x_1},{\kappa }_{x_2},\alpha \right)\right)\hfill \\ \hfill & +{\lambda }_1\left(R_{m_1}-{\mathcal{R}}_1\left({\kappa }_{x_1},{\kappa }_{x_2},\alpha \right)\right)\hfill \\ \hfill & +{\lambda }_2\left(R_{m_2}-{\mathcal{R}}_2\left({\kappa }_{x_1},{\kappa }_{x_2},\alpha \right)\right),\hfill \end{array}(8)$

where λ₁ ≥ 0 and λ₂ ≥ 0 are the Lagrange multipliers associated with the minimum rates constraints of user 1 and user 2, respectively. Based on the above, the KKT conditions can be described as follows (Boyd et al., 2003).

$\frac{\partial \mathcal{L}\left({\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*},\alpha \right)}{\partial {\kappa }_{x_1}}=0,(\mathrm{9a})$

$\frac{\partial \mathcal{L}\left({\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*},\alpha \right)}{\partial {\kappa }_{x_2}}=0,(\mathrm{9b})$

$\frac{\partial \mathcal{L}\left({\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*},\alpha \right)}{\partial \alpha }=0,(\mathrm{9c})$

${\lambda }_1\left(R_{m_1}-{\mathcal{R}}_1\left({\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*},\alpha \right)\right)=0,(\mathrm{9d})$

${\lambda }_2\left(R_{m_2}-{\mathcal{R}}_2\left({\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*},\alpha \right)\right)=0,(9e)$

$R_{m_1}-{\mathcal{R}}_1\left({\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*},\alpha \right)\le 0,(\mathrm{9f})$

$R_{m_2}-{\mathcal{R}}_2\left({\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*},\alpha \right)\le 0,(\mathrm{9g})$

${\lambda }_1,{\lambda }_2\ge 0.(\mathrm{9h})$

The results of (Eqs 9a–9c) are found as in (Eq. 10), (Eq. 11), and (Eq. 12) at the top of the next page, where $\mathrm{\Phi }={\left(1+\frac{{\sigma }^2}{P_1|h_2{|}^2}\right)}^2$, $\mathrm{\Psi }={\left(1+\frac{P_2}{P_1}+\frac{{\sigma }^2}{P_1|h_2{|}^2}\right)}^2$, $\mathrm{\Omega }={\left(1+{\eta }^2\frac{P_2}{P_1}+\frac{{\sigma }^2}{P_1|h_1{|}^2}\right)}^2$, $\varphi ={\left({\eta }^2+\frac{{\sigma }^2}{P_2|h_1{|}^2}\right)}^2$, $\psi ={\left(1+\frac{P_1}{P_2}+\frac{{\sigma }^2}{P_2|h_1{|}^2}\right)}^2$, and $\omega ={\left({\eta }^2+\frac{P_1}{P_2}+\frac{{\sigma }^2}{P_2|h_1{|}^2}\right)}^2$. Then, (Eq. 10), (Eq. 11), and (Eq. 12) can be solved simultaneously to compute optimal ${\kappa }_{x_1}$, ${\kappa }_{x_2}$, and the allocation power parameter α, at λ₁ = λ₂ = 0.

Algorithm 1. : Spectral efficiency maximization algorithm.

From the KKT conditions mentioned earlier, we need to check all alternatives of λ_i, ∀i = 1, 2. As can be seen from (Eqs 9d, 9e), it is either we have λ₁ = 0 or ${\mathcal{R}}_1({\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*},{\alpha }^{*})=R_{m_1}$, or λ₂ = 0 or ${\mathcal{R}}_2({\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*},{\alpha }^{*})=R_{m_2}$. This leads to four potential cases as below:

Case 1. :Inactive QoS constraints, when both λ₁ = λ₂ = 0.

Case 2. : The sub-optimal solutions of ${\kappa }_{x_1},{\kappa }_{x_2}$, and α exist when λ₁ ≠ 0 and λ₂ = 0, and ${\mathcal{R}}_1({\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*},{\alpha }^{*})=R_{m_1}$.

Case 3. : The sub-optimal solutions of ${\kappa }_{x_1},{\kappa }_{x_2}$, and α exist when λ₁ = 0 and λ₂ ≠ 0, and ${\mathcal{R}}_2({\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*},{\alpha }^{*})=R_{m_2}$.

Case 4. : The sub-optimal solutions of ${\kappa }_{x_1},{\kappa }_{x_2}$, and α exist, if feasible, when λ₁ ≠ 0 and λ₂ ≠ 0 and both ${\mathcal{R}}_1({\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*},{\alpha }^{*})=R_{m_1}$ and ${\mathcal{R}}_2({\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*},{\alpha }^{*})=R_{m_2}$.The Lagrangian values will be computed using the Subgradient method as belowwhere ${\delta }_i^n$ is the a small increment at the nth iteration associated with the ith Lagrange multiplier.Based on the above-mentioned cases, we introduce Algorithm 1 to solve the optimization problem in $\mathcal{OP}1$. The optimal solution belongs to one of the following four cases: 1) both minimum user rate constraints are inactive, 2) user 1 minimum rate constraint is active and user 2 minimum rate constraint is inactive, 3) user 1 minimum rate constraint is inactive and user 2 minimum rate constraint is active, and 4) both minimum user rate constraints are active.

$\begin{array}{c}(1+{\lambda }_1)(\mathrm{\Phi }-{\kappa }_{x_1}^2)(\mathrm{\Psi }-({\kappa }_{x_1}^2+{(\frac{(1-\alpha )P_T}{\alpha P_T}{\kappa }_{x_2}^2)}^2))+(1+{\lambda }_2)\left[(\mathrm{\Omega }-({\kappa }_{x_1}^2+{\eta }^4{(\frac{(1-\alpha )P_T}{\alpha P_T}{\kappa }_{x_2}^2)}^2))\right.\hfill \\ \left.(\mathrm{\Psi }-({\kappa }_{x_1}^2+{(\frac{(1-\alpha )P_T}{\alpha P_T}{\kappa }_{x_2}^2)}^2))-(\mathrm{\Omega }-({\kappa }_{x_1}^2+{\eta }^4{(\frac{(1-\alpha )P_T}{\alpha P_T}{\kappa }_{x_2}^2)}^2))(\mathrm{\Phi }-{\kappa }_{x_1}^2)\right]=0,\hfill \end{array}(10)$

$\begin{array}{ccc}\hfill & {\eta }^4(1+{\lambda }_1)\left[(\varphi -{\eta }^4{\kappa }_{x_2}^2)(\psi -({\kappa }_{x_2}^2+{(\frac{(\alpha )P_T}{(1-\alpha )P_T}{\kappa }_{x_1}^2)}^2))-(\omega -({\eta }^4{\kappa }_{x_2}^2+{(\frac{(\alpha )P_T}{(1-\alpha )P_T}{\kappa }_{x_1}^2)}^2))\right.\hfill & \hfill \\ \hfill & \left.(\psi -({\kappa }_{x_2}^2+{(\frac{(\alpha )P_T}{(1-\alpha )P_T}{\kappa }_{x_1}^2)}^2))\right]+(1+{\lambda }_2)(\varphi -{\eta }^4{\kappa }_{x_2}^2)(\omega -({\eta }^4{\kappa }_{x_2}^2+{(\frac{(\alpha )P_T}{(1-\alpha )P_T}{\kappa }_{x_1}^2)}^2))=0,\hfill & \hfill \end{array}(11)$

$\begin{array}{ccc}\hfill & (1+{\lambda }_1)\left[\frac{-\frac{h_2^2{P}_T}{h_2^2{P}_T\alpha +{\sigma }^2}-\frac{h_2^4{P}_T^2\left(1-\alpha \right)}{{\left(h_2^2{P}_T\alpha +{\sigma }^2\right)}^2}}{\ln \left(2\right)\left(\frac{h_2^2{P}_T\left(1-\alpha \right)}{h_2^2{P}_T\alpha +{\sigma }^2}+1\right)}-\frac{\frac{2h_2^6{\kappa }_{x_1}^2{P}_T^3{\alpha }^2}{{\left(h_2^2{P}_T\alpha +{\sigma }^2\right)}^3}-\frac{2h_2^4{\kappa }_{x_1}^2{P}_T^2\alpha }{{\left(h_2^2{P}_T\alpha +{\sigma }^2\right)}^2}}{2\ln \left(2\right)\left(1-\frac{h_2^4{\kappa }_{x_1}^2{P}_T^2{\alpha }^2}{{\left(h_2^2{P}_T\alpha +{\sigma }^2\right)}^2}\right)}-\right.\hfill & \hfill \\ \hfill & \left.\frac{2h_2^4{\kappa }_{x_1}^2{P}_T^2\alpha -2h_2^4{\kappa }_{x_2}^2{P}_T^2\left(1-\alpha \right)}{2\ln \left(2\right){\left(h_2^2{P}_T\alpha +h_2^2{P}_T\left(1-\alpha \right)+{\sigma }^2\right)}^2\left(1-\frac{h_2^4{\kappa }_{x_1}^2{P}_T^2{\alpha }^2+h_2^4{\kappa }_{x_2}^2{P}_T^2{\left(1-\alpha \right)}^2}{{\left(h_2^2{P}_T\alpha +h_2^2{P}_T\left(1-\alpha \right)+{\sigma }^2\right)}^2}\right)}\right]+\hfill & \hfill \\ \hfill & (1+{\lambda }_2)\left[\frac{\frac{2\left(h_1^2{P}_T-{\eta }^2{h}_1^2{P}_T\right)\left(h_1^4{\kappa }_{x_1}^2{P}_T^2{\alpha }^2+{\eta }^4{h}_1^4{\kappa }_{x_2}^2{P}_T^2{\left(1-\alpha \right)}^2\right)}{{\left(h_1^2{P}_T\alpha +{\eta }^2{h}_1^2{P}_T\left(1-\alpha \right)+{\sigma }^2\right)}^3}-\frac{2h_1^4{\kappa }_{x_1}^2{P}_T^2\alpha -2{\eta }^4{h}_1^4{\kappa }_{x_2}^2{P}_T^2\left(1-\alpha \right)}{{\left(h_1^2{P}_T\alpha +{\eta }^2{h}_1^2{P}_T\left(1-\alpha \right)+{\sigma }^2\right)}^2}}{2\ln \left(2\right)\left(1-\frac{h_1^4{\kappa }_{x_1}^2{P}_T^2{\alpha }^2+{\eta }^4{h}_1^4{\kappa }_{x_2}^2{P}_T^2{\left(1-\alpha \right)}^2}{{\left(h_1^2{P}_T\alpha +{\eta }^2{h}_1^2{P}_T\left(1-\alpha \right)+{\sigma }^2\right)}^2}\right)}\right.+\hfill & \hfill \\ \hfill & \left.\frac{\frac{{\eta }^2{h}_1^4{P}_T^2\alpha }{{\left({\eta }^2{h}_1^2{P}_T\left(1-\alpha \right)+{\sigma }^2\right)}^2}+\frac{h_1^2{P}_T}{{\eta }^2{h}_1^2{P}_T\left(1-\alpha \right)+{\sigma }^2}}{\ln \left(2\right)\left(\frac{h_1^2{P}_T\alpha }{{\eta }^2{h}_1^2{P}_T\left(1-\alpha \right)+{\sigma }^2}+1\right)}-\frac{\frac{2{\eta }^4{h}_1^4{\kappa }_{x_2}^2{P}_T^2\left(1-\alpha \right)}{{\left({\eta }^2{h}_1^2{P}_T\left(1-\alpha \right)+{\sigma }^2\right)}^2}-\frac{2{\eta }^6{h}_1^6{\kappa }_{x_2}^2{P}_T^3{\left(1-\alpha \right)}^2}{{\left({\eta }^2{h}_1^2{P}_T\left(1-\alpha \right)+{\sigma }^2\right)}^3}}{2\ln \left(2\right)\left(1-\frac{{\eta }^4{h}_1^4{\kappa }_{x_2}^2{P}_T^2{\left(1-\alpha \right)}^2}{{\left({\eta }^2{h}_1^2{P}_T\left(1-\alpha \right)+{\sigma }^2\right)}^2}\right)}\right]=0.\hfill & \hfill \end{array}(12)$

${\lambda }_i^{n+1}={\left[{\lambda }_i^n-{\delta }_i^n\left({\mathcal{R}}_i-R_{m_i}\right)\right]}^{+},\forall i=\mathrm{1,2},(13)$

• Step 3: the proposed algorithm starts by assuming that both the minimum user rate constraints are inactive. Then, we find the optimal solution based on this assumption. If the inactive constraints are satisfied, then the optimal solution is reached.

• Step 4: based on the assumption that solution belongs to Case 1 (inactive constraints), the user 1 minimum rate constraint may be not inactive. This means that initial solution from step 3 is infeasible and the proposed algorithm finds the Lagrangian multipliers that enforce the solution to be in the feasible region. More specifically, the proposed algorithm finds the non-negative Lagrangian multiplier λ₁ that makes user 1 minimum rate constraint active (i.e., satisfied with equal sign)-Case 2.

• Step 5: based on the assumption that solution belongs to Case 1 (inactive constraints), the user 2 minimum rate constraint may be not inactive. This means that initial solution from step 3 is infeasible and the proposed algorithm finds the Lagrangian multipliers that enforce the solution to be in the feasible region. More specifically, the proposed algorithm finds the non-negative Lagrangian multiplier λ₂ that makes user 2 minimum rate constraint active (i.e., satisfied with equal sign)-Case 3.

• Step 6: based on the assumption that solution belongs to Case 1 (inactive constraints), both minimum rate constraints may be not inactive. This means that initial solution from step 3 is infeasible, and the proposed algorithm finds the Lagrangian multipliers that enforce the solution to be in the feasible region. More specifically, the proposed algorithm finds the non-negative Lagrangian multiplier λ₁, λ₂ that makes both minimum rate constraints active (i.e., satisfied with equal sign)-Case 4.

• At the end, the optimal IGS circularity coefficients and power allocation parameter are obtained and the corresponding maximum sum-rate can be computed.

4.2 Energy Efficiency Maximization

In this subsection, we maximize the energy efficiency of the two-user system considering both QoS and BS power constraints.

$\mathcal{OP}2:\underset{{\kappa }_{x_i},{\alpha }_i}{\text{maximize}}{\zeta }_{EE}=\frac{{\mathcal{R}}_1\left({\kappa }_{x_i},{\alpha }_i\right)+{\mathcal{R}}_2\left({\kappa }_{x_i},{\alpha }_i\right)}{P_c+\left({\alpha }_1+{\alpha }_2\right)P_T}(\mathrm{14a})$

$\text{subject\hspace{0.17em}to}\mathcal{C}1:{\mathcal{R}}_1\left({\kappa }_{x_i},{\alpha }_i\right)\ge R_{m_1},(\mathrm{14b})$

$\mathcal{C}2:{\mathcal{R}}_2\left({\kappa }_{x_i},{\alpha }_i\right)\ge R_{m_2},(\mathrm{14c})$

$\mathcal{C}3:{\alpha }_1+{\alpha }_2\le 1,(\mathrm{14d})$

$\mathcal{C}4:0\le {\alpha }_i\le 1,\forall i=\mathrm{1,2},(14e)$

$\mathcal{C}5:0\le {\kappa }_{x_i}\le 1,\forall i=\mathrm{1,2},(\mathrm{14f})$

where P_c is the BS’s circuitry power consumption. The optimization problem in (Eq. 14a) is equivalent to the following minimization problem $\mathcal{OP}3$:

$\begin{array}{ll}\hfill & \mathcal{OP}3:\underset{{\kappa }_{x_i},{\alpha }_i}{\text{minimize\hspace{0.17em}}}{\zeta }_{EE}^{-1}\hfill \\ \hfill & \text{subject\hspace{0.17em}to\hspace{0.17em}}\mathcal{C}1-\mathcal{C}5.\hfill \end{array}(15)$

The objective function of (Eq. 15) and rate constraints are non-convex; hence, the overall problem is non-convex, and the global optimal solution cannot be ensured.

The fractional non-convex optimization problem in (Eq. 15) can be converted to an equivalent parametric optimization problem using concepts from fractional programming, namely the Dinkelbach approach (Dinkelbach, 1967). Using this conversion, a new objective function can be found as

${\mathrm{\Phi }}_{EE}=\left(P_c+\left({\alpha }_1+{\alpha }_2\right)P_T\right)-\mathcal{K}\left({\mathcal{R}}_1\left({\kappa }_{x_i},{\alpha }_i\right)+{\mathcal{R}}_2\left({\kappa }_{x_i},{\alpha }_i\right)\right),(16)$

where $\mathcal{K}$ is a non-negative constant. Then, the new optimization problem $\mathcal{OP}4$ becomes

$\begin{array}{ll}\hfill & \mathcal{OP}4:\underset{{\kappa }_{x_i},{\alpha }_i}{\text{minimize}}{\mathrm{\Phi }}_{EE}\hfill \\ \hfill & \text{subject\hspace{0.17em}to}\mathcal{C}1-\mathcal{C}5.\hfill \end{array}(17)$

It was proved in (Dinkelbach, 1967) that at a certain value of $\mathcal{K}$, which is defined as ${\mathcal{K}}^{*}$, an optimal solution to $\mathcal{OP}4$ is also an optimal solution to $\mathcal{OP}3$. Hence, obtaining the optimal values of ${\kappa }_{x_i},{\alpha }_i$ for $\mathcal{OP}3$ can be reached by obtaining the optimal values of $({\kappa }_{x_i}(\mathcal{K}),{\alpha }_i(\mathcal{K}))$ for $\mathcal{OP}4$. We can then update the value of $\mathcal{K}$ until it reaches ${\mathcal{K}}^{*}$, where ${\mathcal{K}}^{*}$ is obtained when Φ_EE = 0 (Dinkelbach, 1967) at optimal ${\kappa }_{x_i}^{*}$ and ${\alpha }_i^{*}$.

To find the sub-optimal solutions, we solve $\mathcal{OP}4$ using the KKT conditions. The Lagrangian function ${\mathcal{L}}_{EE}({\kappa }_{x_i},{\alpha }_i)$ based on $\mathcal{OP}4$ can be expressed as

$\begin{array}{ll}\hfill {\mathcal{L}}_E& \left({E\kappa }_{x_i},{\alpha }_i\right)=\hfill \\ \hfill & \left(P_c+\left({\alpha }_1+{\alpha }_2\right)P_T\right)-\mathcal{K}\left({\mathcal{R}}_1\left({\kappa }_{x_i},{\alpha }_i\right)+{\mathcal{R}}_2\left({\kappa }_{x_i},{\alpha }_i\right)\right)\hfill \\ \hfill & +{\lambda }_1\left(R_{m_1}-{\mathcal{R}}_1\left({\kappa }_{x_i},{\alpha }_i\right)\right)+{\lambda }_2\left(R_{m_2}-{\mathcal{R}}_2\left({\kappa }_{x_i},{\alpha }_i\right)\right)\hfill \\ \hfill & +{\lambda }_3\left({\alpha }_1+{\alpha }_2-1\right),\hfill \end{array}(18)$

where λ₁, λ₂ and λ₃ are the Lagrange multipliers connected with the QoS conditions of user 1, user 2, and power allocation at the BS, respectively. The impact of the constraints $\mathcal{C}4$ and $\mathcal{C}5$ determine the valid ranges of ${\kappa }_{x_i},{\alpha }_i$. The KKT conditions can consequently be outlined as follows:

$\frac{\partial {\mathcal{L}}_{EE}\left({\kappa }_{x_i}^{*},{\alpha }_i^{*}\right)}{\partial {\kappa }_{x_i}}=0,\forall i=\mathrm{1,2},(\mathrm{19a})$

$\frac{\partial {\mathcal{L}}_{EE}\left({\kappa }_{x_i}^{*},{\alpha }_i^{*}\right)}{\partial {\alpha }_i}=0,\forall i=\mathrm{1,2},(\mathrm{19b})$

${\lambda }_1\left(R_{m_1}-{\mathcal{R}}_1\left({\kappa }_{x_i}^{*},{\alpha }_i^{*}\right)\right)=0,(\mathrm{19c})$

${\lambda }_2\left(R_{m_2}-{\mathcal{R}}_2\left({\kappa }_{x_i}^{*},{\alpha }_i^{*}\right)\right)=0,(\mathrm{19d})$

${\lambda }_3\left({\alpha }_1+{\alpha }_2-1\right)=0,(19e)$

$R_{m_1}-{\mathcal{R}}_1\left({\kappa }_{x_i}^{*},{\alpha }^{*}\right)\le 0,(\mathrm{19f})$

$R_{m_2}-{\mathcal{R}}_2\left({\kappa }_{x_i}^{*},{\alpha }_i^{*}\right)\le 0,(\mathrm{19g})$

${\alpha }_1+{\alpha }_2-1\le 0,(\mathrm{19h})$

${\lambda }_1,{\lambda }_2,{\lambda }_3\ge 0.(\mathrm{19i})$

From (Eq. 19a), we obtain

$\begin{array}{ll}\hfill & \frac{\partial {\mathcal{L}}_{EE}\left({\kappa }_{x_i}^{*},{\alpha }_i^{*}\right)}{\partial {\kappa }_{x_i}}=\hfill \\ \hfill & -\left({\lambda }_1+\mathcal{K}\right)\frac{\partial {\mathcal{R}}_1\left({\kappa }_{x_i},{\alpha }_i\right)}{\partial {\kappa }_{x_i}}-\left({\lambda }_2+\mathcal{K}\right)\frac{\partial {\mathcal{R}}_2\left({\kappa }_{x_i},{\alpha }_i\right)}{\partial {\kappa }_{x_i}}=0.\hfill \end{array}(20)$

and

$\begin{array}{ll}\hfill & \frac{\partial {\mathcal{L}}_{EE}\left({\kappa }_{x_i}^{*},{\alpha }_i^{*}\right)}{\partial {\alpha }_i}=\hfill \\ \hfill & P-\left({\lambda }_1+\mathcal{K}\right)\frac{\partial {\mathcal{R}}_1\left({\kappa }_{x_i},{\alpha }_i\right)}{\partial {\alpha }_i}-\left({\lambda }_2+\mathcal{K}\right)\frac{\partial {\mathcal{R}}_2\left({\kappa }_{x_i},{\alpha }_i\right)}{\partial {\alpha }_i}+{\lambda }_3=0.\hfill \end{array}(21)$

To find the sub-optimal solution in case of energy efficiency maximization, we follow similar steps to the previous analysis of KKT conditions in the spectral efficiency maximization algorithm. From (Eqs 19c–19e), we either have λ₁ = 0 or ${\mathcal{R}}_1({\kappa }_{x_i}^{*},{\alpha }_i^{*})=R_{m_1}$, λ₂ = 0 or ${\mathcal{R}}_2({\kappa }_{x_i}^{*},{\alpha }_i^{*})=R_{m_2}$, and λ₃ = 0 or α₁ + α₂ = 1. This leads to eight possible states through which we need to iterate to find the optimal solution.

Description of Step 3 in the Algorithm 2: We assume the optimal solution belongs to the case where the QoS and power allocation constraints are inactive. We initially find the sub-optimal solution when assuming all constraints are satisfied (inactive constraints), and then for those constraints that are not satisfied, we find their Lagrange multipliers to make them satisfied with equal sign. We initially set λ₁ = λ₂ = λ₃ = 0 and find initial ${\kappa }_{x_i}^{*},{\alpha }_i^{*}$ by simultaneously solving (Eqs 20, 21) using Newton’s method. If ${\mathcal{R}}_1\ge R_{m_1}$, ${\mathcal{R}}_2\ge R_{m_2}$, and if the power constraint is true, then, the sub-optimal solution can be reached.

If ${\mathcal{R}}_1<R_{m_1}$, ${\mathcal{R}}_2\ge R_{m_1}$, and the power constraint is true, i.e. this means that the initial solution of inactive constraints is infeasible, then we find non-negative λ₁ such that ${\mathcal{R}}_1({\kappa }_{x_i}^{*},{\alpha }_i^{*})=R_{m_1}$ (that enforces the solution to be in the feasible region) and re-calculate ${\kappa }_{x_i}^{*},{\alpha }_i^{*}$.

If ${\mathcal{R}}_1\ge R_{m_1}$, ${\mathcal{R}}_2<R_{m_1}$, and the power constraint is true, then, we find non-negative λ₂ such that ${\mathcal{R}}_2({\kappa }_{x_i}^{*},{\alpha }_i^{*})=R_{m_2}$ and re-calculate. ${\kappa }_{x_i}^{*},{\alpha }_i^{*}$

If ${\mathcal{R}}_1\ge R_{m_1}$, ${\mathcal{R}}_2\ge R_{m_1}$, and the power constraint is not true, then, we find non-negative λ₃ such that α₁ + α₂ = 1 and re-calculate. ${\kappa }_{x_i}^{*},{\alpha }_i^{*}$

If ${\mathcal{R}}_1<R_{m_1}$, ${\mathcal{R}}_2\ge R_{m_1}$, and the power constraint is not met, then, then we find non-negative λ₁, λ₃ such that ${\mathcal{R}}_1({\kappa }_{x_i}^{*},{\alpha }_i^{*})=R_{m_1}$ and α₁ + α₂ = 1 and re-calculate. ${\kappa }_{x_i}^{*},{\alpha }_i^{*}$

If ${\mathcal{R}}_1\ge R_{m_1}$, ${\mathcal{R}}_2<R_{m_1}$, and the power constraint is not met, then, we find non-negative λ₂, λ₃ such that ${\mathcal{R}}_2({\kappa }_{x_i}^{*},{\alpha }_i^{*})=R_{m_2}$ and α₁ + α₂ = 1 and re-calculate ${\xi }_i^{*},{\rho }_i^{*}$.

If ${\mathcal{R}}_1<R_{m_1}$, ${\mathcal{R}}_2<R_{m_1}$, and the power constraint is true, then, we find non-negative λ₁, λ₂ such that ${\mathcal{R}}_1({\kappa }_{x_i}^{*},{\alpha }_i^{*})=R_{m_1}$ and ${\mathcal{R}}_2({\kappa }_{x_i}^{*},{\alpha }_i^{*})=R_{m_2}$ and re-calculate ${\xi }_i^{*},{\rho }_i^{*}$.

If ${\mathcal{R}}_1<R_{m_1}$, ${\mathcal{R}}_2<R_{m_1}$, and the power constraint is not true, then, we find non-negative λ₁, λ₂ and λ₃ such that ${\mathcal{R}}_1({\kappa }_{x_i}^{*},{\alpha }_i^{*})=R_{m_1}$, ${\mathcal{R}}_2({\kappa }_{x_i}^{*},{\alpha }_i^{*})=R_{m_2}$, α₁ + α₂ = 1 are true, and re-calculate ${\kappa }_{x_i}^{*},{\alpha }_i^{*}$.

The energy efficiency solution is found at $\mathcal{K}$ = ${\mathcal{K}}^{*}$, where ${\mathcal{K}}^{*}=\frac{P_c+({\alpha }_1^{*}+{\alpha }_2^{*})P_T}{({\mathcal{R}}_1({\kappa }_i^{*},{\alpha }_i^{*})+{\mathcal{R}}_2({\kappa }_i^{*},{\alpha }_i^{*}))}$ and is computed by applying the Dinkelbach method (Dinkelbach, 1967). Here, we develop Algorithm 2, which follows an approach similar to Algorithm 1 with the aim of computing the optimal values of ${\kappa }_{x_i}^{*},{\alpha }_i^{*}$ that satisfy ${\mathrm{\Phi }}_{{EE}_{\min }}({\kappa }_i^{*},{\alpha }_i^{*})=0$, where ${\mathrm{\Phi }}_{{EE}_{\min }}$ is the minimum of Φ_EE. Algorithm 2 starts with an initial value of $\mathcal{K}$, denoted as ${\mathcal{K}}_{\text{initial}}$, and employs an error tolerance of δ. This energy efficiency Algorithm 2 is outlined at the top of this page.

The complexity analysis of Algorithm 2 can be described as follows.

• Step 3: the complexity order of this step is the complexity of Algorithm 1. Let us assume that the maximum number of iterations needed for the subgradient method to converge is T, then the number of operations is of a complexity order equal to $\mathcal{O}(T)$, which is the complexity of Step 2 in Algorithm 1. The computational requirement of Newton’s method to solve a system of M equations in M unknowns is $\mathcal{O}(ML)$, where L is the number of required iterations (Moré and Cosnard, 1979), which is the complexity of Steps 3 to 6 of Algorithm 1.

• Thus, the complexity order up to Step 4 (of Algorithm 2) is $\mathcal{O}(TML)$.

• Accordingly, the complexity order of the proposed Algorithm 2 is $\mathcal{O}(TML{N}_k)$, where N_k is the number of executions of the while loop to update $\mathcal{K}$ in the Dinkelbach approach.

Algorithm 2. : Energy efficiency maximization algorithm.

5 Simulation Results

In this section, we evaluate the proposed solutions of the formulated optimization problems. A comparison in terms of the overall spectral efficiency and energy efficiency of the system with its counterpart of a NOMA system employing traditional PGS at both users is performed. We also compare the proposed solution with (Abu Mahady et al., 2019) that considers IGS only at the strong user. We consider the distance-dependent path-loss model as a form of large-scale fading, and the Rayleigh fading model as small-scale multi-path fading. The channel from the BS to user i, ∀i = 1, 2, at a distance of d_i meters is generated as $\sqrt{10^{-\frac{{\sigma }_{PL}}{10}}}{h}_i$, where h_i is a Rayleigh fading channel coefficient and σ_PL = 38.46 + 10nlog₁₀(d_i) is the path-loss in dB. In the definition of σ_PL, the loss factor 38.46 is the free space path loss at a reference distance of 1 m and at carrier frequency of 2 GHz, and n = 3 is the path-loss exponent (Sun et al., 2016b). We set the noise power density N_o = −174 dBm/Hz with bandwidth B = 20 MHz. The distance d₁ between user 1 and the BS is set to 20 m and the distance d₂ between user 2 and the BS is set to 100 m. Unless otherwise stated, we assume that $\mathcal{E}[|h_1{|}^2]>\mathcal{E}[|h_2{|}^2]$, P_c = 20 dBm, and δ = 10^–4. $R_{m_1}=R_{m_2}=1.5$ bits/sec/Hz, and α = 0.4. Unless otherwise mentioned, we assume η = 0.1.

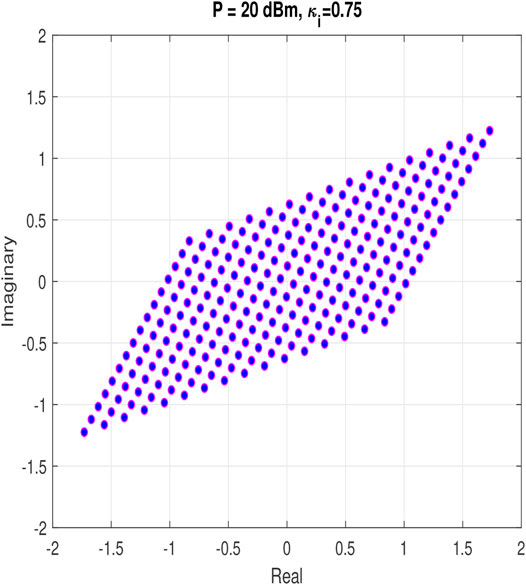
Figures 2, 3 show two examples of the improper constellation diagrams with 64-QAM and 256-QAM, respectively, which are designed based on WLT as described in Section 2. We generate unit average energy standard 64-QAM and 256-QAM constellations. Next, we find the optimized ${\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*}$ at certain channel realizations. At these optimized values, we then generate the improper constellations using WLT based on these prescribed ${\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*}$. Considering this optimized improper constellation diagram, the minimum Euclidean distance between the constellations points is maximized due to WLT compared to the PGS standard constellation diagrams, which yields lower error probability and hence better spectral efficiency.

FIGURE 2

FIGURE 2. Improper constellation diagram with 64-QAM.

FIGURE 3

FIGURE 3. Improper constellation diagram with 256-QAM.

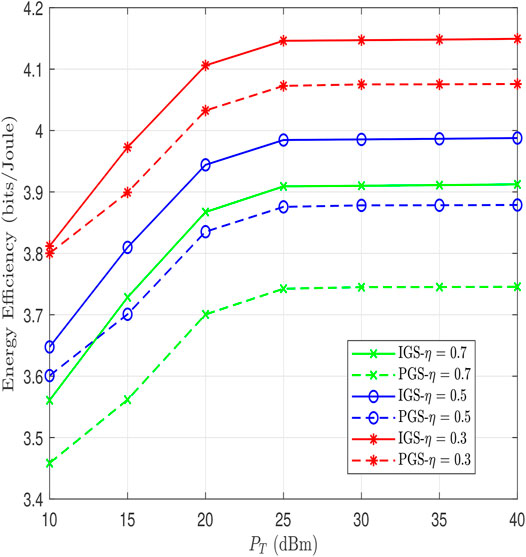
In Figure 4, the overall spectral efficiency of the system is depicted as a function of P_T, at different levels of the SIC imperfections η. The performance of the modified proposed Algorithm 1 (jointly optimizing IGS circularity coefficients ${\kappa }_{x_1}^{*},{\kappa }_{x_2}^{*}$ without power allocation, i.e., at fixed α = 0.4) is compared with the following two cases: 1) strong user only employs IGS [optimized ${\kappa }_{x_1}^{*}$ (Abu Mahady et al., 2019)], and 2) both users employ PGS (traditional case). As can be observed, the IGS-based scheme outperforms both one user only IGS-based and PGS-based schemes for all levels of η. Specifically, a considerable gain is attained at all power regimes compared with PGS-based. Moreover, the gain only appears at lower power regime in case of one-user only IGS-based scheme.

FIGURE 4

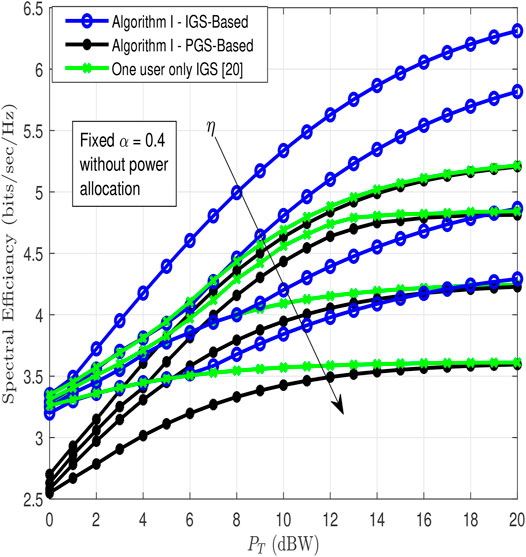
FIGURE 4. Spectral efficiency comparison between IGS-based and PGS-based (Abu Mahady et al., 2019) for various η = 0.1, 0.2, 0.3, 0.4, and fixed α = 0.4.

A spectral efficiency of about 4 bits/s/Hz can be attained by the modified proposed algorithm at 3 dBW power at η = 0.1 and α = 0.4. To achieve the same spectral efficiency of 4 bits/s/Hz using only one user IGS-based and PGS-based schemes, nearly 2 to 2.5 dBW power are needed, respectively. It is also observed that as the SIC becomes worse, i.e., from η = 0.1 to η = 0.4, the performance of all schemes gets worse. However, the PGS-based scheme is the most impacted scheme.

While Figure 4 assumes the fixed power allocation, i.e., (α = 0.4) scenario, Figure 5 presents the optimized power allocation scenario. In particular, Figure 5 shows the behaviour of the proposed spectral efficiency algorithm (IGS-based with optimized power allocation) and its counterpart PGS-based NOMA system. It is clear that there is a further gain improvement for IGS-based scheme over the PGS-based one at different values of η. In overall, the results reveal the positive influence of jointly optimizing both IGS coefficients and power allocation parameter to enhance the NOMA system’s spectral efficiency under imperfect SIC.

FIGURE 5

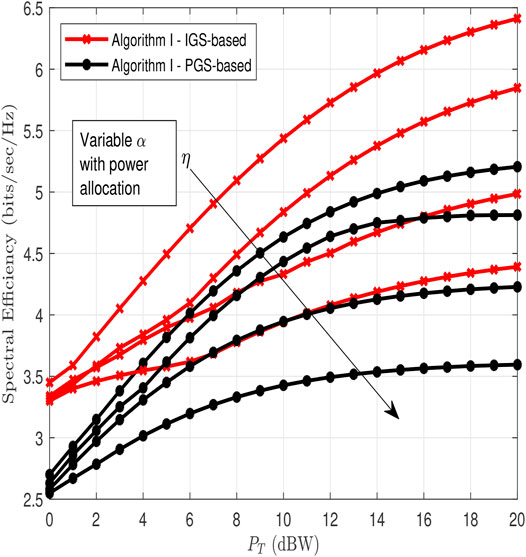
FIGURE 5. Spectral efficiency comparison between IGS-based and PGS-based for various values of η = 0.1, 0.2, 0.3, 0.4 and optimized α.

In Figure 6, the convergence of the proposed spectral efficiency algorithm is compared with the proposed algorithm for the one user only IGS-based scheme in (Abu Mahady et al., 2019) at η = 0.1. The number of iterations required for IGS in the proposed algorithm is approximately double the number of iterations required for the algorithm in (Abu Mahady et al., 2019) but it is still relatively low.

FIGURE 6

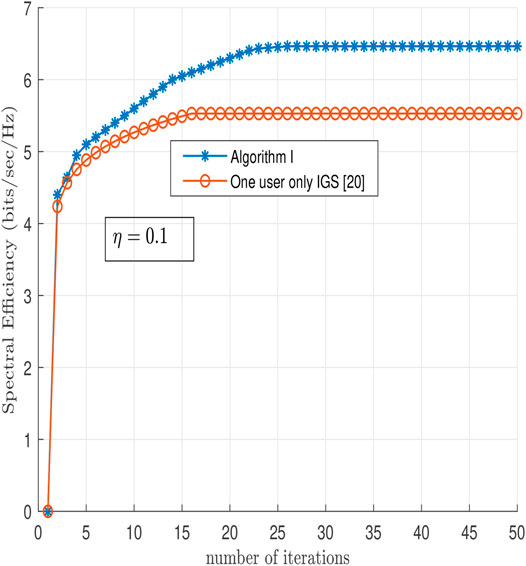
FIGURE 6. Comparison between the convergence of the Algorithm 1 and the Algorithm in (Abu Mahady et al., 2019) in terms of number of iterations at η = 0.1.

In Figure 7, the performance of the energy efficiency algorithm (in bits/joule) is plotted against P_T (dBm) at P_c = 20, 25 dBm. This figure shows that IGS enhances the energy efficiency performance in the proposed system by transmitting around 0.3 bits/joule more than PGS in all BS power regions. It is also observed that as the BS’s power increases from low to medium, the energy efficiency performance improves. However, the energy efficiency saturates when the BS’s transmit power increases which means that increasing the transmit power does not necessarily enhance the energy efficiency.

FIGURE 7

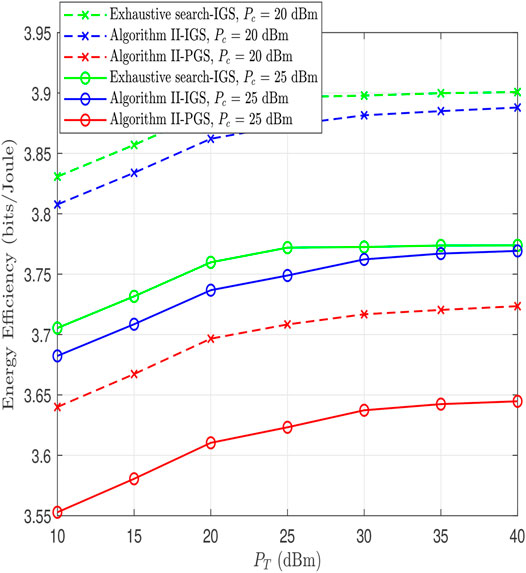
FIGURE 7. Energy efficiency vs. P (dBm) at different values of P_c for proposed Algorithm 2 and exhaustive search.

To demonstrate how closes it is to the optimal solution, we compared the proposed sub-optimal solution with optimal solution through an exhaustive search, where the latter is performed through three nested loops with a step size of 0.05 (the three optimization variables are all bounded between 0 and 1). The result is a gap of around of 0.1 dB, which is acceptable performance loss given the high computational complexity of the exhaustive search solution.

Figure 8 shows the energy efficiency performance against P_T dBm at different levels of SIC and at fixed P_c = 20 dBm. The figure shows the effectiveness of using IGS in the case of SIC imperfections when compared to the PGS case, especially at higher levels of η. As η increases, the gain due to using IGS becomes greater.

FIGURE 8

FIGURE 8. Energy efficiency vs. P (dBm) at different values of η and fixed P_c = 20 dBm.

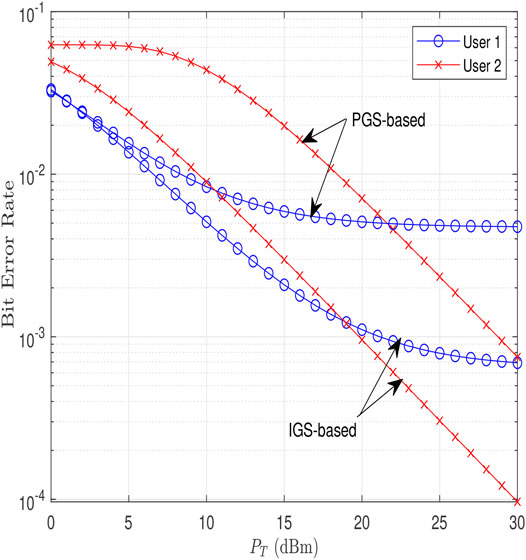
Figure 9 shows the bit error rate (BER) through simulations versus P_T for both users in case of IGS and PGS at 16-QAM at η = 0.1. For each channel realization, we find the optimal improper coefficients, then we find the corresponding improper constellation diagram, simulate the error rate, and repeat. For a given optimal IGS circularity coefficients, we study the BER performance of the new improper constellations, by means of 10⁴ simulations, where each simulation considering the decoding of 10⁴ symbols. The optimal maximum likelihood detector is applied at the receiver side for this problem, which aims to finding the closest constellation point to a given noisy received signal. It should be noted that this approach may not result in the optimal BER performance since the decision variables κ_i and α_i are optimized to maximize the transmission rates (to approach Shannon capacity).

FIGURE 9

FIGURE 9. BER with improper constellation 16-QAM at η = 0.1.

As can be seen in the figure, error performance in case of using improper constellation diagrams outperforms that of the proper constellation. The reason behind this is that since the improper constellation is designed based on WLT which relies on maximizing the minimum Euclidean distance, and hence achieves a better BER. Another observation is that as P_T increases, error performance improves as expected. However, error floor occurs at high P_T in case of user 1 due to residual interference resulting from the imperfect SIC.

6 Conclusion

In this work, the system spectral and energy efficiencies of a two-user NOMA system adopting IGS at both users are maximized such that the minimum rate requirements and power budget constraints are met under imperfect SIC. In addition, to study the system performance, improper constellations are designed using WLT based on predefined optimized IGS coefficients. Results showed that system spectral and energy efficiencies of the IGS-based NOMA systems are further improved by jointly optimizing the circularity coefficients at both users compared to the case of optimizing the circularity coefficient of the single user IGS-based systems and PGS-based NOMA systems. In contrast to PGS-based NOMA systems, results revealed that IGS can save around 0.2 dB of the transmit power, and hence, can be identified as an energy efficient signaling scheme. Furthermore, the results demonstrate that the error performance of the IGS-based system outperforms its counterpart PGS-based system due to impropriety characteristics of the constellation.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

IA: Sole author, idea, proposed algorithm, simulations, and writing up. EB: Technical supervision, contribute to the idea, discussion, and writing revision. SI: Technical supervision, contribute to the idea, discussion, and writing revision.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abu Mahady, I., Bedeer, E., Ikki, S., and Yanikomeroglu, H. (2019). Sum-rate Maximization of NOMA Systems under Imperfect Successive Interference Cancellation. IEEE Commun. Lett. 23 (3), 474–477. doi:10.1109/LCOMM.2019.2893195

CrossRef Full Text | Google Scholar

Boyd, S., Xiao, L., and Mutapcic, A. (2003). “Subgradient Methods,” in Lecture Notes of EE392o (Autumn Quarter: Stanford University).

Google Scholar

Cadambe, V. R., Jafar, S. A., and Wang, C. (2010). Interference Alignment with Asymmetric Complex Signaling-Settling the Høst-Madsen-Nosratinia Conjecture. IEEE Trans. Inform. Theor. 56 (9), 4552–4565. doi:10.1109/tit.2010.2053895

CrossRef Full Text | Google Scholar

Chen, X., Zhang, Z., Zhong, C., Jia, R., and Ng, D. W. K. (2018). Fully Non-orthogonal Communication for Massive Access. IEEE Trans. Commun. 66 (4), 1717–1731. doi:10.1109/tcomm.2017.2779150

CrossRef Full Text | Google Scholar

Ding, Z., Yang, Z., Fan, P., and Poor, H. V. (2014). On the Performance of Non-orthogonal Multiple Access in 5G Systems with Randomly Deployed Users. IEEE Signal. Process. Lett. 21 (12), 1501–1505. doi:10.1109/lsp.2014.2343971

CrossRef Full Text | Google Scholar

Dinkelbach, W. (1967). On Nonlinear Fractional Programming. Manage. Sci. 13 (7), 492–498. doi:10.1287/mnsc.13.7.492

CrossRef Full Text | Google Scholar

Gaafar, M., Amin, O., Abediseid, W., and Alouini, M.-S. (2017). Underlay Spectrum Sharing Techniques with In-Band Full-Duplex Systems Using Improper Gaussian Signaling. IEEE Trans. Wireless Commun. 16 (1), 235–249. doi:10.1109/twc.2016.2621767

CrossRef Full Text | Google Scholar

Gaafar, M., Khafagy, M. G., Amin, O., Schaefer, R. F., and Alouini, M.-S. (2018). Full-Duplex Relaying with Improper Gaussian Signaling over Nakagami- $m$ Fading Channels. IEEE Trans. Commun. 66 (1), 64–78. doi:10.1109/tcomm.2017.2759109

CrossRef Full Text | Google Scholar

Hong, S. G., and Bahk, S. (2020). Performance Analysis and Fairness Maximization in NOMA Systems with Improper Gaussian Signaling under Imperfect Successive Interference Cancellation. IEEE Access 8, 50439–50451. doi:10.1109/access.2020.2980167

CrossRef Full Text | Google Scholar

Islam, S. M. R., Avazov, N., Dobre, O. A., and Kwak, K.-s. (2017). Power-domain Non-orthogonal Multiple Access (NOMA) in 5G Systems: Potentials and Challenges. IEEE Commun. Surv. Tutorials 19 (2), 721–742. doi:10.1109/comst.2016.2621116

CrossRef Full Text | Google Scholar

Javed, S., Amin, O., Shihada, B., and Alouini, M.-S. (2020). A Journey from Improper Gaussian Signaling to Asymmetric Signaling. IEEE Commun. Surv. Tutorials 22 (3), 1539–1591. doi:10.1109/comst.2020.2989626

CrossRef Full Text | Google Scholar

Javed, S., Elzanaty, A., Amin, O., Shihada, B., and Alouini, M.-S. (2021). When Probabilistic Shaping Realizes Improper Signaling for Hardware Distortion Mitigation. IEEE Trans. Commun. 69 (8), 5028–5042. doi:10.1109/tcomm.2021.3074978

CrossRef Full Text | Google Scholar

Kurniawan, E., and Sun, S. (2015). Improper Gaussian Signaling Scheme for the Z-Interference Channel. IEEE Trans. Wireless Commun. 14 (7), 3912–3923. doi:10.1109/twc.2015.2414913

CrossRef Full Text | Google Scholar

Lameiro, C., Santamaria, I., and Schreier, P. J. (2019). Improper Gaussian Signaling for Multiple-Access Channels in Underlay Cognitive Radio. IEEE Trans. Commun. 67 (3), 1817–1830. doi:10.1109/TCOMM.2018.2880765

CrossRef Full Text | Google Scholar

Lameiro, C., Santamaría, I., and Schreier, P. J. (2017). Rate Region Boundary of the SISO Z-Interference Channel with Improper Signaling. IEEE Trans. Commun. 65 (3), 1022–1034. doi:10.1109/TCOMM.2016.2641948

CrossRef Full Text | Google Scholar

Lopez-Fernandez, J. A., Ayestaran, R. G., Santamaria, I., and Lameiro, C. (2019). Design of Asymptotically Optimal Improper Constellations with Hexagonal Packing. IEEE Trans. Commun. 67 (8), 5445–5457. doi:10.1109/tcomm.2019.2916857

CrossRef Full Text | Google Scholar

Mahady, I., Bedeer, E., Ikki, S., and Yanikomeroglu, H. (2021). “NOMA Spectral Efficiency Maximization with Improper Gaussian Signaling and SIC Imperfection,” in ICC 2021 - IEEE International Conference on Communications, Montreal, QC, 14-23 June 2021, 1–6. doi:10.1109/icc42927.2021.9500779

CrossRef Full Text | Google Scholar

Moré, J. J. M. Y., and Cosnard, M. (1979). Numerical Solution of Nonlinear Equations. ACM Trans. Math. Softw. 5 (1), 64–85. doi:10.1145/355815.355820

CrossRef Full Text | Google Scholar

Nasir, A. A., Tuan, H. D., Duong, T. Q., and Poor, H. V. (2019). Improper Gaussian Signaling for Broadcast Interference Networks. IEEE Signal. Process. Lett. 26 (6), 808–812. doi:10.1109/lsp.2019.2905959

CrossRef Full Text | Google Scholar

Nguyen, H. T., Tuan, H. D., Niyato, D., Kim, D. I., and Vincent Poor, H. (2021). Improper Gaussian Signaling for D2D Communication Coexisting MISO Cellular Networks. IEEE Trans. Wireless Commun. 20 (8), 5186–5198. doi:10.1109/twc.2021.3065961

CrossRef Full Text | Google Scholar

Santamaria, I., Crespo, P. M., Lameiro, C., and Schreier, P. J. (2018). Information-theoretic Analysis of a Family of Improper Discrete Constellations. Entropy (Basel) 20 (1), 1–22. doi:10.3390/e20010045

PubMed Abstract | CrossRef Full Text | Google Scholar

Schreier, P. J., and Scharf, L. L. (2010). Statistical Signal Processing of Complex-Valued Data: The Theory of Improper and Noncircular Signals. Cambridge, U.K.: Cambridge Univ. Press.

Google Scholar

Shin, H.-Y., Park, S.-H., Park, H., and Lee, I. (2012). A New Approach of Interference Alignment through Asymmetric Complex Signaling and Multiuser Diversity. IEEE Trans. Wireless Commun. 11 (3), 880–884. doi:10.1109/twc.2012.010312.102034

CrossRef Full Text | Google Scholar

Sun, H., Xie, B., Hu, R. Q., and Wu, G. (2016). “Non-orthogonal Multiple Access with SIC Error Propagation in Downlink Wireless MIMO Networks,” in 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, 18-21 Sept. 2016, 1–5. doi:10.1109/vtcfall.2016.7881111

CrossRef Full Text | Google Scholar

Sun, S., Rappaport, T. S., Rangan, S., Thomas, T. A., Ghosh, A., Kovacs, I. Z., et al. (2016). “Propagation Path Loss Models for 5G Urban Micro- and Macro-Cellular Scenarios,” in 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 15-18 May 2016, 1–6. doi:10.1109/vtcspring.2016.7504435

CrossRef Full Text | Google Scholar

Tuan, H. D., Nasir, A. A., Nguyen, H. H., Duong, T. Q., and Poor, H. V. (2019). Non-orthogonal Multiple Access with Improper Gaussian Signaling. IEEE J. Sel. Top. Signal. Process. 13 (3), 496–507. doi:10.1109/jstsp.2019.2901993

CrossRef Full Text | Google Scholar

Yu, H., Tuan, H. D., Duong, T. Q., Fang, Y., and Hanzo, L. (2020). Improper Gaussian Signaling for Integrated Data and Energy Networking. IEEE Trans. Commun. 68 (6), 3922–3934. doi:10.1109/tcomm.2020.2981332

CrossRef Full Text | Google Scholar

Yue, X., Qin, Z., Liu, Y., Kang, S., and Chen, Y. (2018). A Unified Framework for Non-orthogonal Multiple Access. IEEE Trans. Commun. 66 (11), 5346–5359. doi:10.1109/tcomm.2018.2842217

CrossRef Full Text | Google Scholar

Zeng, M., Yadav, A., Dobre, O. A., Tsiropoulos, G. I., and Poor, H. V. (2017). Capacity Comparison between MIMO-NOMA and MIMO-OMA with Multiple Users in a Cluster. IEEE J. Select. Areas Commun. 35 (10), 2413–2424. doi:10.1109/jsac.2017.2725879

CrossRef Full Text | Google Scholar

Zeng, Y., Yetis, C. M., Gunawan, E., Guan, Y. L., and Zhang, R. (2013). Transmit Optimization with Improper Gaussian Signaling for Interference Channels. IEEE Trans. Signal. Process. 61 (11), 2899–2913. doi:10.1109/tsp.2013.2254480

CrossRef Full Text | Google Scholar

Zeng, Y., Zhang, R., Gunawan, E., and Guan, Y. L. (2013). Optimized Transmission with Improper Gaussian Signaling in the K-User MISO Interference Channel. IEEE Trans. Wireless Commun. 12 (12), 6303–6313. doi:10.1109/twc.2013.103013.130439

CrossRef Full Text | Google Scholar