A Deep Neural Network-Based Interference Mitigation for MIMO-FBMC/OQAM Systems

Offset quadrature amplitude modulation-based filter bank multicarrier (FBMC/OQAM) is among the promising waveforms for future wireless communication systems. This is due to its flexible spectrum usage and high spectral efficiency compared with the conventional multicarrier schemes. However, with OQAM modulation, the FBMC/OQAM signals are not orthogonal in the imaginary field. This causes a significant intrinsic interference, which is an obstacle to apply multiple input multiple output (MIMO) technology with FBMC/OQAM. In this paper, we propose a deep neural network (DNN)-based approach to deal with the imaginary interference, and enable the application of MIMO technique with FBMC/OQAM. We show, by simulations, that the proposed approach provides good performance in terms of bit error rate (BER).

1 Introduction

Future wireless communication systems are expected to support a variety of use cases that are categorized into three categories: enhanced mobile broadband (eMBB), enhanced type communications (eHTC), and ultra-reliable low-latency communications (URLLC) (Renfors et al., 2017). Conventional orthogonal frequency-division multiplexing (OFDM) is not suitable to efficiently support these diverse use-cases with the same resources. In fact, OFDM exhibits poor spectral properties because it generates a high out-of-band (OOB) radiation. In addition, the use of a cyclic prefix (CP) between OFDM blocks lowers the spectral efficiency. To cope with these weak points, some processing improvements, such as windowing and filtering, were made on the CP-OFDM scheme. In spite of these improvements, offset quadrature amplitude modulation-based filter bank multicarrier (FBMC/OQAM) provides better spectral properties than CP-OFDM and its variants (Mattera and Tanda, 2019).

The idea of FBMC/OQAM is to transform a complex-valued symbol stream, chosen from QAM constellation, into a real valued stream before transmitting it over a set of subcarriers. Each subcarrier is individually shaped with a prototype filter that has a good localization in time and frequency so as to lower the OOB emission. Besides, compared to OFDM, data symbols are transmitted with an improved spectral efficiency since FBMC/OQAM doesn’t require any CP insertion.

In spite of its numerous advantages, FBMC/OQAM is an interference-limited system (RezazadehReyhani and Farhang-Boroujeny, 2017). In fact, due to OQAM constellation pattern, FBMC/OQAM signals are not orthogonal in the imaginary field. This causes intrinsic interference that makes it difficult to utilize multiple input multiple output (MIMO) technology for FBMC/OQAM transmissions. Many research studies have been recently carried out on the combination of MIMO techniques and FBMC/OQAM. In (Caus and Pérez-Neira, 2014), Caus et al. have dealt with the design of the precoding and decoding matrices for MIMO-FBMC/OQAM systems over highly frequency selective channels. Although the proposed solution performs closer to the optimal one, it exhibits a bit error rate (BER) floor with an increased complexity. A multistage parallel architecture of MIMO-FBMC/OQAM has been proposed in (Mestre and Gregoratti, 2016) exploiting the filterbank structure. The authors have shown that the system performance depends on the number of parallel stages used at the transmitter and the receiver. In addition, the system computational complexity increases with the number of implemented stages. An overview of signal processing challenges for MIMO-FBMC/OQAM has been presented in (Pérez-Neira et al., 2016).

In the last years, several approaches have been proposed to deal with the intrinsic interference in MIMO-FBMC/OQAM systems. In (Jintae et al., 2018), a linearly processed FBMC system has been suggested to support MIMO technologies. The authors employed a fast than Nyquist signaling with single value decomposition to remove the intrinsic interference. They also considered that data is only transmitted on even-numbered subcarriers to cancel the interference caused by odd-numbered subcarriers. Even if the proposed FBMC system can be combined with conventional MIMO technologies, it has a noticeable BER floor, especially for high order modulations. An interference-free method has been proposed in (Xu et al., 2021) to enable the combination of MIMO techniques and FBMC/OQAM.

Although the previously cited works provide better performance, they suffer from serious performance degradation along with an increased computational complexity, particularly in interference-limited environments. In this paper, we propose a deep neural network-based approach to interference mitigation to enable MIMO techniques for FBMC/OQAM systems. Our approach combines an adaptive neuro fuzzy inference system (ANFIS) and a deep neural network (DNN), which are mounted in cascade to detect the transmitted data symbols in the presence of the intrinsic interference. This latter is caused by the overlapping pattern of FBMC/OQAM signals. In addition, these signals are generally transmitted through a channel whose parameters are uncertain. Consequently, data detection, in this environment, is a challenging task for the receiver, especially when the channel state information is not available.

Our idea is to conceive a non linear receiver that takes benefit from the reasoning and learning capabilities of the ANFIS and the DNN to blindly and efficiently detect data symbols in an uncertain environment. In this receiver, the ANFIS observes the AFB output and mitigates the effects of intrinsic interference and noise. Afterwards, the DNN performs blind channel equalization while cancelling the eventual residual interference.

The remainder of this paper is structured as follows. MIMO-FBMC/OQAM System Model presents the FBMC/OQAM system model considering MIMO configuration. Adaptive Neuro Fuzzy Inference Systems and Deep Neural Networks gives a concise description of adaptive neuro fuzzy systems and deep neural networks. The proposed approach is presented in Proposed Deep Learning-Based Interference Cancellation Simulation results are given and analyzed in Simulation Results. Finally, the paper conclusion is provided in Conclusion.

2 MIMO-FBMC/OQAM System Model

To derive the MIMO-FBMC/OQAM system model, we use the vertical Bell labs layered space-time (V-BLAST) approach, where the transmitter and the receiver are equipped with N_T and N_R antennas respectively, as depicted in Figure 1. We consider that a set of data symbols is transmitted over M subcarriers using FBMC/OQAM waveform. These symbols, whose duration is denoted by T, are chosen from a QAM constellation, and are not directly mapped to the subcarriers as in the OFDM scheme (Fa-Long and Charlie, 2016; Renfors et al., 2017). In fact, the real and the imaginary parts of each modulation symbol x_m,n, where m and n denote the frequency and time index respectively, are time staggered by an offset of T/2. This results in offset QAM that generates real-valued symbols. Let $d_{m,n}^{(p)}$ designates the transmitted real symbol by the p^th antenna on the m^th subcarrier at $n\frac{T}{2}$ time instant. According to the filter bank theory, the discrete-time FBMC/OQAM signal transmitted from the p^th transmit antenna is written as

$s^{(p)}[k]=\sum _{m=0}^{M-1}\sum _{-\infty }^{+\infty }{d}_{m,n}^{(p)}{g}_{m,n}[k](1)$

Where g_m,n[k] is the synthesis filter corresponding to the m^th subcarrier at the n^th time instant. It is given by

$g_{m,n}[k]=g[k-nM/2]e^{j\frac{2\pi m}{M}\left(k-\frac{L_g-1}{2}\right)}{e}^{j{\varphi }_{m,n}}(2)$

Where g [k] is a well localized prototype filter of length L_g, and ϕ_m,n represents a phase term such that $e^{j{\varphi }_{m,n}}=e^{j\frac{\pi }{2}(m+n)}$ (Renfors et al., 2017).

FIGURE 1

FIGURE 1. Multiple input multiple output FBMC/OQAM system model.

If we denote by $H_m^{(p,q)}$ the frequency response of the channel linking the p^th transmit and the q^th receive antennas, the received signal at the q^th antenna is written as

$r^{(q)}[k]=\sum _{p=1}^{N_T}\left(\sum _{m=0}^{M-1}\sum _{n=-\infty }^{+\infty }{H}_m^{(p,q)}{d}_{m,n}^{(p)}{g}_{m,n}[k]\right)+{\eta }^{(q)}[k](3)$

Where η^(q)[k] is the Gaussian noise received at the q^th receive antenna. The demodulated real symbol corresponding to the m^th subcarrier and the n^th instance is obtained by evaluating the inner product of r^(q)[k] and g_m,n [k]. This is expressed as

$\begin{array}{ccc}\hfill y_{m,n}^{(q)}& =\hfill & <r^{(q)}[k],g_{m,n}[k]>\hfill \\ \hfill & =\hfill & \sum _{p=1}^{N_T}{H}_m^{(p,q)}\left(d_{m,n}^{(p)}+j{u}_{m,n}^{(p)}\right)+{\eta }_{m,n}^{(q)}\hfill \end{array}(4)$

Where $u_{m,n}^{(p)}$ represents the imaginary intrinsic interference coming from the p^th transmit antenna. If we denote the vector containing N_R demodulated real symbols by ${\mathbf{y}}_{m,n}={\left[y_{m,n}^{(1)},y_{m,n}^{(2)},\dots ,y_{m,n}^{(N_R)}\right]}^T$, and the vector composed of N_T transmitted real symbols by ${\mathbf{d}}_{m,n}={\left[d_{m,n}^{(1)},d_{m,n}^{(2)},\dots ,d_{m,n}^{(N_T)}\right]}^T$, the matrix form of the demodulation operation is expressed as

${\mathbf{y}}_{m,n}={\mathbf{H}}_m\left({\mathbf{d}}_{m,n}+j{\mathbf{u}}_{m,n}\right)+{\mathit{\eta }}_{m,n}(5)$

Where ${\mathbf{u}}_{m,n}={\left[u_{m,n}^{(1)},u_{m,n}^{(2)},\dots ,u_{m,n}^{(N_T)}\right]}^T$ is the interference vector, ${\mathit{\eta }}_{m,n}={\left[{\eta }_{m,n}^{(1)},{\eta }_{m,n}^{(2)},\dots ,{\eta }_{m,n}^{(N_R)}\right]}^T$ is the AWGN vector, and H_m is the channel frequency response matrix, which is given by

${\mathbf{H}}_m=\left[\begin{array}{cccc}\hfill H_m^{(\mathrm{1,1})}\hfill & \hfill H_m^{(\mathrm{1,2})}\hfill & \hfill \cdots \hfill & \hfill H_m^{(1,N_T)}\hfill \\ \hfill H_m^{(\mathrm{2,1})}\hfill & \hfill H_m^{(\mathrm{2,2})}\hfill & \hfill \cdots \hfill & \hfill H_m^{(2,N_T)}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill H_m^{(N_R,1)}\hfill & \hfill H_m^{(N_R,2)}\hfill & \hfill \cdots \hfill & \hfill H_m^{(N_R,N_T)}\hfill \end{array}\right](6)$

Clearly, in order to faithfully detect the transmitted data symbols, one has to deal with the uncertain channel behavior, the interference, and the noise. In this context, we are inspired by the idea of adaptive neuro-fuzzy inference systems (ANFIS), and propose a deep learning approach to cancel the intrinsic interference. Hereafter, we give an overview of adaptive neuro-fuzzy inference systems and deep neural networks. Then, we present the proposed approach for interference cancellation in MIMO-FBMC/OQAM systems.

3 Adaptive Neuro Fuzzy Inference Systems and Deep Neural Networks

An ANFIS combines neuro-fuzzy and neural networks to conceive a system that has the abilities of learning, thinking, and reasoning in uncertain environments (Raveendranathan, 2014). In other words, it is suitable for situations where quantitative analysis is difficult. For example, ANFIS can be used to make appropriate decisions in a noisy and interference-limited environment. To do so, ANFIS models the human knowledge using fuzzy If-Then rules with membership functions to provide the expected input-output mapping. A fuzzy inference system is composed of (Raveendranathan, 2014; Bedoui and Et-tolba, 2020):

• a rule base, which contains fuzzy If-Then rules

• a database that defines the membership functions used in the fuzzy rules

• an interface that performs the rules inference operations

• a fuzzification unit, which performs the transformation of the crisp input into the linguistic values

• a defuzzification unit, which transforms the fuzzy results of the inference into a crisp output

Consider that the system has two inputs denoted by x₁ and x₂, and one output y. In the case of two fuzzy conditional statements, the fuzzy If-Then rules are expressed as

$\begin{array}{ccc}\hfill \mathrm{R}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{1}& :\hfill & \mathrm{I}\mathrm{f}{x}_1\mathrm{i}\mathrm{s}{A}_1\mathrm{a}\mathrm{n}\mathrm{d}{x}_2\mathrm{i}\mathrm{s}{B}_1\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{n}{f}_1=p_1{x}_1+q_1{x}_2\hfill \\ \hfill \mathrm{R}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{2}& :\hfill & \mathrm{I}\mathrm{f}{x}_1\mathrm{i}\mathrm{s}{A}_2\mathrm{a}\mathrm{n}\mathrm{d}{x}_2\mathrm{i}\mathrm{s}{B}_2\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{n}{f}_1=p_2{x}_1+q_2{x}_2\hfill \end{array}(7)$

Where p₁, p₂, q₁, and q₂ are the consequent parameters. The quantities A₁, A₂, B₁, and B₂ represent the linguistic variables, which are individually characterized by a membership function. Note that these linguistic variables take values from the set {low, medium, high, …}.

In addition to a fuzzy inference system, an ANFIS incorporates an artificial neural network whose nodes are partly or entirely adaptive meaning that their involved parameters should be changed according to learning rules in order to generate the adequate output (Jang, 1993). When the neural network is composed of multiple hidden layers, it is considered as a deep learning network (DNN), which is suitable for blind detection in wireless communication systems. Indeed, a DNN is capable of providing accurate measurements since it employs deep learning algorithms and a large amount of data. Generally, a DNN consists of input, hidden, and output layers (Nikolaus and Tal, 2019). It is worth noting that all the computation and processing tasks, in a DNN, are performed by the hidden layers. In practical scenarios, which are non linear, a given node at the nth layer observes a vector ${\mathbf{v}}^{(n-1)}\in {\mathbb{R}}^D$, containing D outputs from the (n − 1)^th layer, to compute its output using an activation function. This is expressed as

$\begin{array}{ccc}\hfill y^{(n)}& =\hfill & f\left(\sum _{i=1}^D{w}_i{v}_i^{(n-1)}+b_n\right)\hfill \\ \hfill & =\hfill & f\left({\mathbf{w}}^T\mathbf{v}+b_n\right)\hfill \end{array}(8)$

Where f (.) represents the activation function, w is the vector of the weights connecting the nodes of the (n − 1)^th and those of the nth layer. The scalar quantity b_n in Eq. 8 is the bias at the nth layer. The activation function is selected depending on the range of the values it works with. The commonly used activation functions are sigmoid, hyperbolic tangent, and rectified linear unit (ReLU) functions. Note that ReLu function is widely adopted recently.

The weights of the DNN are first randomly initialized and then updated during the training phase using a considerable training data set composed of the inputs and the outputs (target values). In this manner, the system becomes autonomously adjustable to be adapted to the optimal status offline. During the training process, the relation between the input and the output can be established in a supervised way such that the error is smaller after every training iteration.

The error can be optimized by the use of several deep learning objective functions (loss functions). Mean square error (MSE) that represents the sum of the squared difference between the predicted values and the target variable is the most popular loss function used for regression. In addition, the Adam optimization algorithm has been recently adopted in deep learning applications, as an extension to stochastic gradient descent, for signal prediction (Diederik and Jimmy, 2017).

4 Proposed Deep Learning-Based Interference Cancellation

Due to uncertainties in the channel behavior together with strong interference, conventional channel equalization techniques are not suitable for MIMO-FBMC/OQAM in future wireless communication systems. As mentioned previously, several approaches to interference cancellation have been suggested to enable MIMO with FBMC/OQAM. For instance, the interference-free method, proposed for MIMO-FBMC/OQAM in (Xu et al., 2021), provides better performance. However, this is done at the expense of the computational complexity. The MIMO-FBMC/OQAM receiver we propose implements a nonlinear approach that combines an ANFIS and a DNN. Hereafter, we present and describe its structure.

4.1 Structure of the Proposed Approach

Figure 2 depicts the structure of the proposed approach, where an ANFIS and a DNN cooperate in cascade to perform a blind detection of FBMC/OQAM transmitted symbols in a MIMO configuration. The idea is to firstly offline train the ANFIS using the received OQAM symbols, without interference and noise [i,e. the first term on the right side of (5)], as a target, and the analysis filter bank outputs as input. Besides, the DNN is trained using the transmitted OQAM data symbols and the received OQAM symbols without interference as target and input values respectively. Afterwards, the ANFIS performs intrinsic interference mitigation, and outputs OQAM symbols with remaining channel effect and residual interference. The ANFIS output is delivered to the DNN that blindly detects the transmitted OQAM symbols. It is worth noting that the ANFIS and the DNN employ two neural networks that operate differently from each other. In the following, we describe the architecture of the two used neural networks including the training procedure and the development of the learning rules.

FIGURE 2

FIGURE 2. Structure of the proposed approach to interference cancellation for MIMO-FBMC/OQAM.

4.2 Data Set Building

The main part of the deep learning proposed approach is to learn the system using an associated data set, which is used to train the ANFIS and the DNN. It is a matrix containing the target and the input sequences. The ANFIS takes the AFB output, i.e. y_m,n, as the input sequence and z_m,n = d_m,nH_m,n as the target sequence. Accordingly, the ANFIS training set associated to the n^th FBMC/OQAM symbol on the m^th subcarrier is expressed as

$\left[{\mathbf{y}}_{m,n}^{(tr)},{\mathbf{z}}_{m,n}^{(tr)}\right](9)$

Where the subscript (tr) refers to training. The ANFIS output is delivered to the DNN module as the input sequence for training. In addition, the target sequence for the DNN training set is composed of the transmitted OQAM data symbols, i.e. d_m,n. Then, the DNN training set, corresponding to the m^th subcarrier and n^th symbol, is written as

$\left[{\mathbf{z}}_{m,n}^{(tr)},{\mathbf{d}}_{m,n}^{(tr)}\right](10)$

The sequences are concatenated until sufficient input and target arrays, for both ANFIS and DNN, are reached.

4.3 Neural Network 1: ANFIS

Due to the nonlinearity and the uncertainty of the channel impulse response, linear receivers can not be generally applied since the detection become a nonlinear problem. Providentially, an ANFIS, which combines an artificial neural network and a fuzzy logic system is capable of mapping the transmitter and the receiver signals in the presence of interference and noise. The structure of the ANFIS used in the proposed approach is presented in Figure 3. It uses a fuzzy modeling process to learn the training data set composed of the input and the output sequences. The aim is to provide the membership function parameters and build a suitable inference system to fit well the given data set. The ANFIS antecedent parameters are represented by the three vectors σ_z, σ_I, and σ_η corresponding to the standard deviations of the quantities z_m,n = H_m,nd_m,n, I_m,n = H_m,nd_m,n, and the noise η_n,m, respectively, and the consequent parameters are represented by the vector ρ_m,n. It is worth noting that the antecedent and the consequent parameters are identified during the learning process (Alizadeh e al., 2012). For ease of exposition, consider that the ANFIS observes the element $y_{m,n}^{(q)}$ corresponding to the q^th receive antenna in the observation vector y_m,n. The overall output of ANFIS ${\widehat{z}}_{m,n}^{(q)}$, at the q^th receive antenna, is expressed as,

${\widehat{z}}_{m,n}^{(q)}=\sum _i^R{w}_i^{(q)}{\widehat{z}}_{{m,n}_i}^{(q)}(11)$

Where $w_i^{(q)}$ is referred to as the firing strength calculated at the second layer of ANFIS (Rule layer), ${\widehat{z}}_{{m,n}_i}^{(q)}$ represents the outputs of the ANFIS fourth layer (deffuzification layer). Let ${\rho }_{{m,n}_i}^{(q)}$ with i = {1, 2, …R} be the ANFIS consequent parameters, and let the triplet $({\sigma }_z^{(q)},{\sigma }_I^{(q)},{\sigma }_{\eta }^{(q)})$ be its corresponding standard deviations. Then, the ANFIS rules, used to estimate the elements $z_{{m,n}_i}^{(q)}$, are expressed as

$\begin{array}{ccc}\hfill \mathrm{I}\mathrm{F}{\sigma }_z^{(q)}\mathrm{i}\mathrm{s}\mathrm{H}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{d}{\sigma }_I^{(q)}\mathrm{i}\mathrm{s}\mathrm{L}\mathrm{o}\mathrm{w}\mathrm{a}\mathrm{n}\mathrm{d}{\sigma }_{\eta }^{(q)}\mathrm{i}\mathrm{s}\mathrm{M}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{m};& \hfill & \hfill \\ \hfill \mathrm{T}\mathrm{H}\mathrm{E}\mathrm{N}{\widehat{z}}_{{m,n}_1}^{(q)}=\rho {{m,n}_1}^{(q)}{y}_{m,n}^{(q)}& \hfill & \hfill \\ \hfill \mathrm{I}\mathrm{F}{\sigma }_z^{(q)}\mathrm{L}\mathrm{o}\mathrm{w}and{\sigma }_I^{(q)}is\mathrm{L}\mathrm{o}\mathrm{w}and{\sigma }_{\eta }^{(q)}is\mathrm{H}\mathrm{i}\mathrm{g}\mathrm{h}\\ \hfill \mathrm{T}\mathrm{H}\mathrm{E}\mathrm{N}{\widehat{z}}_{{m,n}_2}^{(q)}=\rho {{m,n}_2}^{(q)}{y}_{m,n}^{(q)}& \hfill & \hfill \\ \hfill ⋮& \hfill & \hfill \end{array}(12)$

$\begin{array}{ccc}\hfill \mathrm{I}\mathrm{F}{\sigma }_z^{(q)}is\mathrm{L}\mathrm{o}\mathrm{w}and{\sigma }_I^{(q)}is\mathrm{H}\mathrm{i}\mathrm{g}\mathrm{h}and{\sigma }_{\eta }^{(q)}is\mathrm{M}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{m}& \hfill & \hfill \\ \hfill \mathrm{T}\mathrm{H}\mathrm{E}\mathrm{N}{\widehat{z}}_{{m,n}_R}^{(q)}={\rho }_{{m,n}_R}^{(q)}{y}_{m,n}^{(q)}& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}(13)$

As mentioned above, the antecedent and consequent parameters of the adaptive network depend mainly on the formulation of a learning rule. The typical learning rule for the ANFIS is performed using forward least square error and back-propagation gradient descent, which aims to recursively calculate the error signals (Raveendranathan, 2014). During the learning phase, ANFIS minimizes the least square error, between the actual output and the corresponding target value. At the qth receive antenna, this error is written as

$E_j^{(q)}=\sum _{i=1}^P{(z_{m,n_i}^{(q)}-{\widehat{z}}_{m,n_i}^{(q)})}^2(14)$

$z_{{m,n}_i}^{(q)}$ corresponds to the target value of the ith component of the jth data pair, ${\widehat{z}}_{{m,n}_i}^{(q)}$ is the estimated value at the output of the L^th (last) layer of ANFIS, where the number of layers is L, and P is the size of the training dataset.

FIGURE 3

FIGURE 3. Adaptive neuro fuzzy system structure.

4.4 Neural Network 2: Deep Neural Network

The ANFIS estimates the OQAM symbols with a remaining channel effect and an eventual residual interference. This is a nonlinear problem which can be dealt with using a deep learning regression. DNN represents a good choice to address this problem thanks to its high learning capabilities. In this work, we consider a multiple output DNN that is composed of three parts as shown in Figure 4:

• Long short-term memory (LSTM) input layer, whose input is the received OQAM symbols ${\widehat{z}}_{m,n}$ delivered by the ANFIS. This layer aims to extract the temporal features from these symbols.

• L fully-connected layers that use a ReLU objective function to extract high-level features of the received OQAM symbols.

• Regression output layer that provides the final estimation of the OQAM transmitted symbols.

FIGURE 4

FIGURE 4. Deep neural network structure.

In order to estimate the transmitted OQAM symbols in the most accurate way, the update of the weights W of the DNN is realized so as to minimize the difference between the predicted values and the corresponding targeted ones during the learning process. This can be done by the adaptive moment estimation known as Adam algorithm (Diederik and Jimmy, 2017). This method aims to compute individual adaptive learning rates from the estimates of the different parameters: The first moment (mean) and the second moment (uncentered variance) of the gradient. To obtain the final learning rule of the employed DNN, we first derive the gradient descent as the derivative of the loss, which can be expressed in terms of the objective functions of the different layers stated above. The loss associated to the data symbols coming from the pth transmit antenna is given by

$Los{s}^{(p)}=\sum _i\left({\widehat{d}}_{m,n_i}^{(p)}-d_{m,n_i}^{(p)}\right)(15)$

Where ${\widehat{d}}_{m,n_i}^{(p)}$ is the estimate, at the L^th layer, of the OQAM symbol transmitted by the p^th antenna. It is expressed as

${\widehat{d}}_{m,n_i}^{(p)}=f^{(L)}\left(\sum _s{W}_{l,s}^L\dots \left(f^{(2)}\left(\sum _j{W}_{k,j}^2\left(f^{(1)}\left(\sum _i{W}_{j,i}^1{\widehat{z}}_{m,n_i}^{(q)}+b_j^1\right)\right)+b_k^2\right)\dots \right)+b_s^L\right)(16)$

Where i, s, l, k, j, represent the DNN nodes indices, and ${\widehat{z}}_{m,n_i}^{(q)}$ is the ANFIS output corresponding to the q^th receive antenna.

Applying the derivative of the loss function, we obtain the gradient descent expression at the t^th iteration as,

$G_t={\mathrm{\Delta }}_W\left(Los{s}_t(W_{t-1})\right)(17)$

Where ${\mathrm{\Delta }}_W(.)=\frac{\delta }{\delta W}(.)$. Afterwards, we get the update formula of the first and second moments respectively,

$m_t={\theta }_1{m}_{t-1}+(1-{\theta }_1)G_t(18)$

$v_t={\theta }_2{v}_{t-1}+(1-{\theta }_2)G_t^2(19)$

Where θ₁ and θ₂ represent the decay rates. Finally, the learning rule of our DNN can be expressed as,

$W_{t+1}=W_t+\frac{\mu }{{\widehat{v}}_t}{\widehat{m}}_t(20)$

Where μ is the learning rate.

5 Simulation Results

To show the power of the proposed approach to interference mitigation in MIMO-FBMC/OQAM, we have evaluated its performance using computer simulations. In this section, we present and analyze the obtained results for 2 × 2 and 2 × 4 MIMO-FBMC/OQAM configurations. The simulation parameters are summarized in Table 1. We have implemented MIMO-FBMC/OQAM with the proposed method using deep learning and the fuzzy logic toolboxes of the MATLAB platform. Before its real-time execution, the receiver is trained with two predefined data set, composed of 2 × 10⁵ training samples, to ensure a good mapping between the received and the transmitted signals. The first data set is used to train the ANFIS. It comprises 131 nodes and up to 4 Gaussian membership functions. The second data set serves to train the DNN with N_R inputs and N_T targets. The initial learning rate is fixed at 3 × 10⁻³.

TABLE 1

TABLE 1. Simulation parameters.

In the real-time phase, the trained ANFIS is employed to mitigate the intrinsic interference for each receive antenna. Then, the ANFIS output is delivered to the trained DNN to blindly complete the detection while eliminating the eventual residual interference. We measured the BER and the root mean square error (RMSE), as functions of SNR, using the Monte Carlo simulation method.

5.1 RMSE and BER Performance Analysis

In order to determine how well the ANFIS regression algorithm fits the data samples, we evaluated the ANFIS performance in terms of RMSE versus SNR. Figure 5 shows the obtained results for different numbers of membership functions. We clearly notice that the RMSE decreases as the number of membership functions increases. This is due to the fact that the rise in this number improves the reasoning ability of the ANFIS.

FIGURE 5

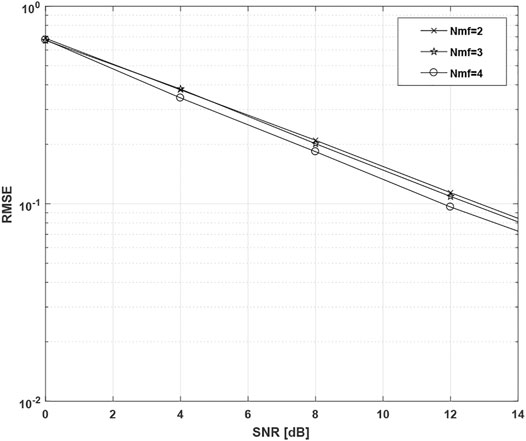
FIGURE 5. RMSE performance of the proposed method versus SNR for different numbers of membership functions.

To analyze the impact of the number of the membership functions on the BER results, we ran computer simulations for 2 × 2 and 2 × 4 MIMO-FBMC/OQAM configurations. We also compared the performance of the proposed method with respect to that provided by MIMO-FBMC/OQAM using conventional interference cancellation (CIC). Figure 6 depicts the obtained BER results for different numbers of the membership functions. Obviously, the proposed method outperforms the conventional one in terms of BER. In addition, the provided gain grows with the number of the membership functions. One can also observe that our method almost attains the same performance as MIMO-FBMC/OQAM using CIC and perfect channel knowledge.

FIGURE 6

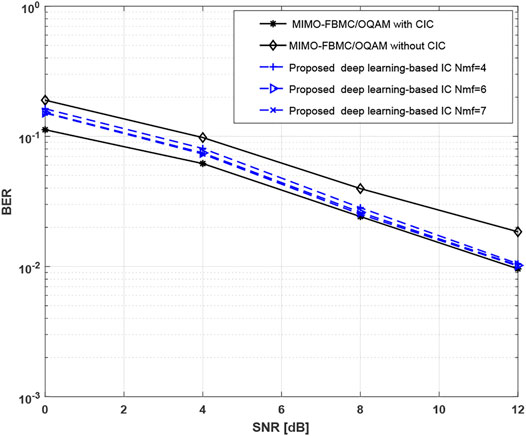
FIGURE 6. BER results of the proposed method in the case of 2 × 2 MIMO-FBMC/OQAM configuration using different numbers of membership functions. The performance is compared with that provided by 2 × 2 MIMO-FBMC/OQAM, with and without CIC.

Figure 7 presents the BER results, versus SNR, for 2 × 4 configuration using different numbers of the membership functions. Clearly, as the number of the membership functions increases, the performance of the proposed method approaches that obtained by MIMO-FBMC/OQAM with CIC assuming a perfect channel knowledge.

FIGURE 7

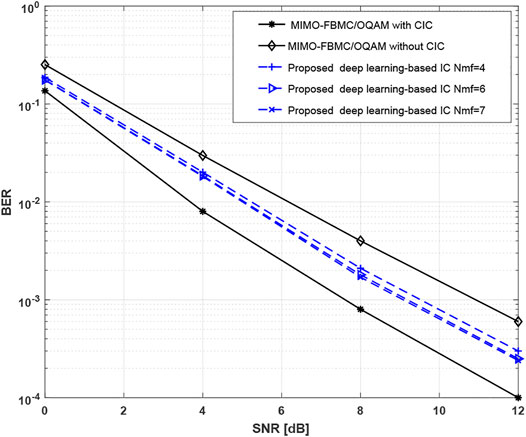
FIGURE 7. BER results of the proposed method in the case of 2 × 4 MIMO-FBMC/OQAM configuration using different numbers of membership functions. The performance is compared with that obtained with 2 × 4 MIMO-FBMC/OQAM, with and without CIC.

In order to improve the performance of the proposed approach, we increased the number of the convolutional layers in the DNN. Figure 8 depicts the BER evolution of the proposed approach versus SNR for 2 × 4 MIMO configuration with different numbers of convolutional layers. As we can see, the accuracy of the DNN increases as the value of L rises. Consequently, BER values decrease and get closer to those provided by MIMO-FBMC/OQAM with interference cancellation in the case of perfect channel knowledge. Note that the performance of the proposed deep learning-based interference cancellation method attains its maximum when L = 10. In addition, Figure 9 presents the BER results of the proposed method for different values of L in the case of 2 × 2 MIMO configuration. It is observed that the proposed method provides approximately the same BER values as those obtained in the case of MIMO-FBMC/OQAM with interference cancellation, considering perfect channel knowledge, when the SNR values are above 7dB.

FIGURE 8

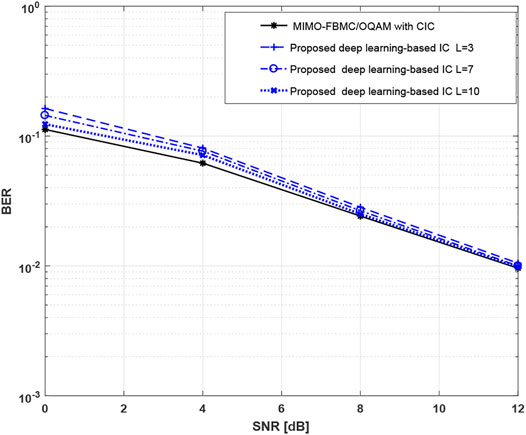
FIGURE 8. BER results of the proposed method in the case of 2 × 2 MIMO-FBMC/OQAM configuration using different numbers of hidden layers. Performance comparison is made with 2 × 2 MIMO-FBMC/OQAM configuration, with and without CIC.

FIGURE 9

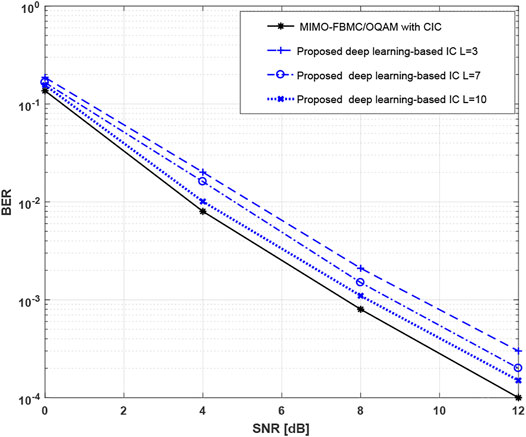
FIGURE 9. BER results of the proposed method in the case of 2 × 4 MIMO-FBMC/OQAM configuration using different numbers of hidden layers. Performance comparison is made with 2 × 4 MIMO-FBMC/OQAM, with and without CIC.

To analyze the performance of the proposed approach using higher order modulations, we conducted computer simulations considering 2 × 2 MIMO-FBMC/OQAM configuration. Figure 10 shows BER results for 16-QAM, 64-QAM, and 256-QAM constellations. It is seen that the proposed deep learning-based interference mitigation keeps its efficiency in terms of BER for higher order modulations. Indeed, the obtained performance is close to that provided by CIC, assuming perfect channel knowledge, for 16-QAM and 64-QAM. However, a considerable gap is observed between 256-QAM curves. This is due to the fact that higher order modulation schemes are sensitive to noise and interference.

FIGURE 10

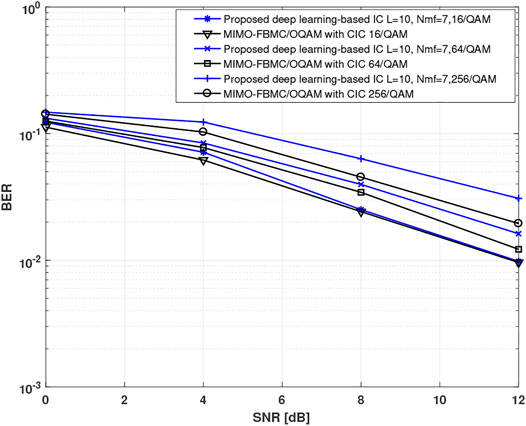
FIGURE 10. BER results of the proposed method in the case of 2 × 2 MIMO-FBMC/OQAM configuration using different QAM modulation orders.

5.2 Computational Complexity Analysis

In this paragraph, we analyze the computational complexity of the proposed method. For the ANFIS, the fact of increasing the number of rules produces better accuracy. At the same time, it also increases the computational cost since the rules contain most of the parameters. Hence, the reduction of the number of rules may lower the computational complexity. In this work, we have three input variables that can assume any one of the five possible membership functions from the set very low, low, medium, high, very high, leaving us with 125 possible combinations of rules. On the other hand, the DNN, used in this work, has few layers, and proves its effectiveness with only five layers, which means less computations and training time. However, fuzzy rule reduction techniques limit the total number of rules to 49. This decreases significantly the computational complexity of the ANFIS. Moreover, if we neglect the training computations since we are mainly interested in the real time implementation of the proposed approach, the trained ANFIS and the DNN require only few tens of multiplications as compared to the proposed scheme in Xu et al. (2021), which is higher due to the repeated blocks.

6 Conclusion

In this paper, we have proposed a nonlinear approach to interference mitigation for MIMO-FBMC/OQAM systems. Our technique exploits the reasoning and the learning capabilities of ANFIS and DNN to blindly detect the transmitted data symbols in an interference-limited environment. Simulation results show that the proposed method provides good performance in terms of the BER for several MIMO-FBMC/OQAM configurations. Moreover, the obtained SNR gain depends on the quality of the training, and the number of the hidden layers in the deep neural network.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary files, further inquiries can be directed to the corresponding author.

Author Contributions

All authors contributed to conception, the design of the study, manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alizadeh, M., Jolai, F., Aminnayeri, M., and Rada, R. (2012). Comparison of Different Input Selection Algorithms in Neuro-Fuzzy Modeling. Expert Syst. Appl. 39, 1536–1544. doi:10.1016/j.eswa.2011.08.049

CrossRef Full Text | Google Scholar

Bedoui, A., and Et-tolba, M. (2020). “A Neuro-Fuzzy Based Detection Approach for HARQ-CC in FBMC-OQAM Systems,” in 2020 9th IFIP International Conference on Performance Evaluation and Modeling in Wireless Networks (PEMWN) (IEEE), 1–7. doi:10.23919/PEMWN50727.2020.9293073

CrossRef Full Text | Google Scholar

Caus, M., and Pérez-Neira, A. I. (2014). Multi-Stream Transmission for Highly Frequency Selective Channels in MIMO-FBMC/OQAM Systems. IEEE Trans. Signal. Process. 62, 786–796. doi:10.1109/TSP.2013.2293973

CrossRef Full Text | Google Scholar

Diederik, P. K., and Jimmy, B. (2015). Adam: A Method for Stochastic Optimization. International Conference for Learning Representations. San Diego: IarXiv.

Fa-Long, L., and Charlie, Z. (2016). Signal Processing for 5G: Algorithms and Implementations. Chichester, United Kingdom: John Wiley and Sons.

Jang, J.-S. R. (1993). Anfis: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man. Cybern. 23, 665–685. doi:10.1109/21.256541

CrossRef Full Text | Google Scholar

Jintae, K., Yosub, P., Sungwoo, W., Jinkyo, J., Sooyong, C., and Daesik, H. (2018). A New Filter-Bank Multicarrier System: The Linearly Processed FBMC System. IEEE Trans. Wireless Commun. 17, 4888–4898. doi:10.1109/TWC.2018.2832646

CrossRef Full Text | Google Scholar

Mattera, D., and Tanda, M. (2019). “On the Uplink Spectral Efficiency of the FBMC-OQAM Transceiver,” in International Symposium on Wireless Communication Systems (ISWCS) (IEEE), 411–415. doi:10.1109/iswcs.2019.8877198

CrossRef Full Text | Google Scholar

Mestre, X., and Gregoratti, D. (2016). Parallelized Structures for MIMO FBMC under Strong Channel Frequency Selectivity. IEEE Trans. Signal. Process. 64, 1200–1215. doi:10.1109/TSP.2015.2493988

CrossRef Full Text | Google Scholar

Nikolaus, K., and Tal, G. (2019). Neural Network Models and Deep Learnings. Curr. Biol. 29, 231–236. doi:10.1109/TBC.2021.3051528

CrossRef Full Text | Google Scholar

Pérez-Neira, A. I., Caus, M., Zakaria, R., Le Ruyet, D., Kofidis, E., Haardt, M., et al. (2016). MIMO Signal Processing in Offset-QAM Based Filter Bank Multicarrier Systems. IEEE Trans. Signal. Process. 64, 5733–5762. doi:10.1109/tsp.2016.2580535

CrossRef Full Text | Google Scholar

Raveendranathan, K. C. (2014). Neuro-Fuzzy Equalizers for Mobile Cellular Channels. CRC Press Taylor & Francis Group.

Renfors, M., Mestre, X., Kofidis, E., and Bader, F. (2017). Orthogonal Waveforms and Filter Banks for Future Communication Systems. Elsevier Science.

RezazadehReyhani, A., and Farhang-Boroujeny, B. (2017). Capacity Analysis of FBMC-OQAM Systems. IEEE Commun. Lett. 21, 999–1002. doi:10.1109/lcomm.2017.2657496

CrossRef Full Text | Google Scholar

Xu, Y., Feng, Z., Zou, J., Kong, D., Xin, Y., and Jiang, T. (2021). “An Imaginary Interference-free Method for MIMO Precoding in FBMC/OQAM Systems,” in IEEE Transactions on Broadcasting (IEEE), 1–9. doi:10.1109/TBC.2021.3051528

CrossRef Full Text | Google Scholar