Rate-Splitting Multiple Access in Cache-Aided Cloud-Radio Access Networks

Rate-splitting multiple access (RSMA) has been recognized as a promising physical layer strategy for 6G. Motivated by the ever-increasing popularity of cache-enabled content delivery in wireless communications, this paper proposes an innovative multigroup multicast transmission scheme based on RSMA for cache-aided cloud-radio access networks (C-RAN). Our proposed scheme not only exploits the properties of content-centric communications and local caching at the base stations (BSs) but also incorporates RSMA to better manage interference in multigroup multicast transmission with statistical channel state information (CSI) known at the central processor (CP) and the BSs. At the RSMA-enabled cloud CP, the message of each multicast group is split into a private and a common part with the former private part being decoded by all users in the respective group and the latter common part being decoded by multiple users from other multicast groups. Common message decoding is done for the purpose of mitigating the interference. In this work, we jointly optimize the clustering of BSs and the precoding with the aim of maximizing the minimum rate among all multicast groups to guarantee fairness serving all groups. The problem is a mixed-integer nonlinear stochastic program (MINLSP), which is solved by a practical algorithm we propose including a heuristic clustering algorithm for assigning a set of BSs to serve each user followed by an efficient iterative algorithm that combines the sample average approximation (SAA) and weighted minimum mean square error (WMMSE) to solve the stochastic non-convex subproblem of precoder design. Numerical results show the explicit max-min rate gain of our proposed transmission scheme compared to the state-of-the-art trivial interference processing methods. Therefore, we conclude that RSMA is a promising technique for cache-aided C-RAN.

1 Introduction

1.1 Overview

The dramatically increasing popularity of smart communications devices has driven the current fifth generation (5G) and future beyond 5G (B5G) of wireless communication networks to handle a tremendous volume of mobile data traffics (Ericsson mobility report, 2020). Recently, wireless caching and physical layer multicast transmission have received considerable attention in the research community as two essential techniques to address the associated data-traffic challenges. Wireless caching brings the content closer to users and hence helps reducing latency of the requested content delivery and avoiding network congestion. Moreover, multicast transmission in which the same content is transmitted to multiple users offers an ideal transmit platform that fits the feature of content-oriented services. Hence, in video-on-demand applications such as YouTube and Netflix, the same content is requested by multiple users which leads to a content-reuse request type (Golrezaei et al., 2013; Yang et al., 2019; Saad et al., 2020). In its most general form, multigroup multicast transmission enables simultaneous transmission of multiple distinct messages to several multicast groups of users (Karipidis et al., 2008), which, however, introduces intergroup interference. Conventionally, the interference is addressed by transmitting beamforming design based on treating interference as noise (TIN) strategy at each user (Bandemer et al., 2008; Charafeddine et al., 2012; Tao et al., 2016; Alameer and Sezgin, 2017). However, in general, such a strategy is suboptimal, especially in moderate to strong interference scenarios.

Recently, rate-splitting multiple access- (RSMA-) based transmission strategy in which the transmitter splits the message of each user has been widely studied in the multiantenna broadcast channel (Mao and Clerckx, 2020) and applied in multigroup multicast transmission (Joudeh and Clerckx, 2017) and cloud-radio access network (C-RAN) (Ahmad et al., 2020a). Specifically, in multigroup multicast transmission, by splitting the group-specific messages into two parts and allowing one part (which is known as a common part) to be decoded by multiple users in different multicast groups, RSMA enables partially decoding the intergroup interference and partially treating the intergroup interference as noise. It therefore better manages the intergroup interference. The concept of RSMA dates back to the late 1970s when it was first suggested by (Carleial, 1978). The scheme is shown to attain the best achievable rate region for the two-users interference channel (IC) in (Te Han and Kobayashi, 1981), and later in (Etkin et al., 2008), the authors show that such strategy can achieve to within one bit of the capacity of two-user IC. Note that recent works mostly assume instantaneous (perfect or imperfect) channel state information (CSI) at the transmitter (CSIT). Contrary to that, in this paper motivated by the appealing performance of RSMA in statistical CSIT in (Ahmad et al., 2021; Yin et al., 2021), we focus on statistical CSIT which is more practical as it requires little communication overhead to acquire.

This paper considers the problem of optimizing RSMA-based transmission strategies in a C-RAN and makes use of multicast and caching techniques for efficient content delivery. C-RAN is a promising network architecture, which provides an ideal platform to enable the B5G wireless systems to handle the challenges of mobile communication service applications. Under such an architecture, a central processor (CP) located at the cloud employs most but not all baseband processing functions, e.g., encoding of the private and common messages of RSMA, which allows joint optimization of the resources and enables full cooperation among the set of base stations (BSs) controlled by the CP. The BSs that are distributed throughout the network are connected to the CP through high-speed digital fronthaul links with limited capacity. Through such an architecture, C-RAN allows for a flexible allocation of radio resources and facilitates coordinated and cooperative signal processing among all BSs (Patil et al., 2018). The former is especially practical due to the heterogeneous applications and requirements of B5G wireless systems.

A vital part of the system model is the location of different parts of baseband processing and the use of the fronthaul link; this is referred to as functional split. Functional splits in C-RAN can be divided into two major categories, referred to as compression and data-sharing strategies (Quek et al., 2017). Under each strategy, there are different usages of the fronthaul link and the baseband processing tasks are allocated in a different way. Utilizing the compression strategy, the CP performs every processing task leaving only the radio transmission to the respective BSs. To be more specific, the CP designs the beamforming vectors and performs compression and quantization of the signals to be transmitted. The fronthaul links are then used to forward the signals to the BSs, which thereafter only need to perform transmission. However, the quantization process, necessitated by the limited capacity of the fronthaul links, generates quantization noise diminishing the system performance (Park et al., 2013). As opposed to this, using data-sharing, the CP performs channel encoding and the BSs then continue with the remaining baseband processing tasks (Wei Yu and Yu, 2014). Therefore, under the data-sharing strategy, the BSs have more computational resources and responsibilities. The computational load is balanced between centralized computations at the CP and local computation at the BSs. Apart from that, other functional splits between the CP and the BSs can be employed thanks to the flexibility of the C-RAN system model. To this end, in this paper, we utilize the data-sharing strategy. The authors in (Liu and Yu, 2017) have shown that utilizing the data-sharing strategy results in better performance compared to using the compression strategy, especially when the fronthaul capacity is limited.

Recently, assisting C-RAN with RSMA-based transmission strategies has shown a considerable gain in performance compared to conventional TIN (Alameer Ahmad et al., 2019; Ahmad et al., 2021; Ahmad et al., 2020b; Ahmad et al., 2020c). Next, we discuss the related works and their relation to our setup.

1.2 Related Work

Wireless caching has been studied in many research works as an efficient content-based communication. Motivated by the extreme popularity of video streaming applications, the seminal work (Shanmugam et al., 2013) has shown that small cell dense networks can improve the spectral efficiency of the wireless system. The work (Kakar et al., 2019) studies a cache-enabled broadcast-relay wireless network from a latency-centric perspective. Furthermore, the authors in (Shanmugam et al., 2013) proposed to equip the BSs with local memory to cache the most popular content in order to alleviate the bottleneck of fronthaul/backhaul communications and efficiently provide the video content to users. Such a network architecture is best described by the C-RAN model. Cache-assisted wireless networks have been intensively explored recently. In (Ugur et al., 2016), the authors show that coded caching can significantly reduce the fronthaul and transmit power costs. The authors in (Alameer and Sezgin, 2017) proposed an efficient algorithm to solve the combinatorial optimization problem of content delivery in a cache-assisted C-RAN. In (Ye et al., 2018), the authors investigate a trade-off cache strategy to jointly minimize the outage probability and fronthaul costs in C-RAN. The work (Chen et al., 2017) considers the problem of minimizing the transmit power of cache-enabled unmanned aerial vehicles (UAVs) in C-RAN such that the quality of experience of each user is enhanced by finding an effective UAV deployment. The authors use echo-state networks (ESNs) to predict each user’s content request distribution for an efficient caching strategy. In the research work (Tao et al., 2016), the authors have shown the benefits of integrating multicast transmission with local caching in reducing the network-wide fronthaul and transmit power costs in C-RAN.

Multicast transmission is essential in content-based applications such as video streaming and video on demand (Maddah-Ali and Niesen, 2016), but also in other application areas such as satellite communications (Christopoulos et al., 2015; Joroughi et al., 2017). Yet, the seminal work (Sidiropoulos et al., 2006) has shown that the inherent beamforming vector optimization, even for a single multicast group, is an NP-hard problem. Thus, with multigroup multicast, we need to account for intergroup interference which represents the bottleneck in achieving a good performance in the system (Joudeh and Clerckx, 2017).

Interference is one major research challenge in wireless communication. Nevertheless, the authors in (Etkin et al., 2008) have shown that the RSMA strategy as proposed in (Carleial, 1978; Te Han and Kobayashi, 1981) can achieve within one bit of the capacity of two-users IC. Motivated by the theoretical works, the authors in (Dahrouj and Yu, 2011) show that the RSMA transmission scheme can significantly reduce the transmit power costs in multicell multiusers communication networks. Recently, several works illustrated the benefits of RSMA in flexibly managing the interference in downlink multiple input single output broadcast channels (MISO-BC) (Joudeh and Clerckx, 2016a) (Mao and Clerckx, 2020). In (Mao et al., 2018), it is shown that RSMA generalizes and outperforms other downlink transmission schemes such as TIN and nonorthogonal multiple access (NOMA). Moreover, information theoretical studies have shown that RSMA achieves the optimal degrees of freedom (DoF) in MISO-BC with imperfect CSIT (Joudeh and Clerckx, 2016b; Piovano and Clerckx, 2017; Mao and Clerckx, 2020), thus, making all other strategies achieve only the suboptimal DoF in the same setting. The works (Piovano et al., 2017; Piovano et al., 2019) investigated RSMA cache-aided MISO-BC. In (Piovano et al., 2017), the authors proposed an RSMA scheme combining coded caching and spatial multiplexing in an overloaded MISO-BC, which yields gains in terms of delivery time and CSIT requirements compared to the state-of-the-art schemes. The work (Piovano et al., 2019) characterized the generalized DoF of the symmetric cache-aided MISO-BC under partial CSIT up to a constant multiplicative factor. The setup of multigroup multicast with RSMA in downlink MISO-BC has been studied in (Joudeh and Clerckx, 2017; Tervo et al., 2018). The authors have investigated the problem of maximizing the minimum rate to guarantee fairness among all multicast groups. RSMA with imperfect CSIT and the goal to maximize the minimum achievable rate among all multicast groups was studied in (Yin and Clerckx, 2021) for multigroup multicast and multibeam satellite systems.

Interestingly, MISO-BC represents a special case of C-RAN where the capacity of fronthaul links tends to infinity (Quek et al., 2017). RSMA-assisted C-RAN has been recently studied in several works. In (Alameer Ahmad et al., 2019), the authors show significant gain in terms of spectral efficiency in a downlink C-RAN system where the CP has full knowledge of CSIT. In (Ahmad et al., 2021), RSMA has shown to be robust against imperfections of CSI. In (Yu et al., 2019), the authors apply the RSMA technique in a C-RAN where the CP uses a compression strategy to transfer information from the CP to the set of BSs. Other benefits of RSMA for enhancing the performance of downlink C-RAN have been shown in terms of minimizing the transmit power cost (Ahmad et al., 2020c) and maximizing the energy efficiency of the system (Ahmad et al., 2020b). Departing from all previous works, this paper studies an RSMA-assisted downlink C-RAN where the BSs are equipped with local cache memory. The CP assorts to a multigroup multicast transmission scheme for efficient content delivery and aims at maximizing the minimum rate (a.k.a. max-min fairness (MMF) rate) of all multicast groups. In the next subsection, we discuss the contributions made in this paper in more detail.

1.3 Contributions

In contrast to the recent related literature, to the best of the authors’ knowledge, this is the first work that considers an RSMA-assisted cache-enabled C-RAN. We focus on the multigroup multicast transmission and consider the maximization of the minimum rate of all multicast groups in the network. The major contributions in this work are summarized as follows:

1) Comprehensive System Model. This paper considers a novel C-RAN system model that integrates caching, RSMA, and multigroup multicast transmission. The functional split between CP and BSs is based on a data-sharing strategy. We enable caching at the BSs as they are equipped with local memories to store the popular content closer to the end users. This helps to alleviate the traffic on the fronthaul capacity, as BSs that cache a requested file are able to process the data locally. Multigroup multicasting is considered to account for the properties of content-based transmissions by grouping all users requesting the same content in the same multicast group. To mitigate the intergroup interference that limits the performance, we consider utilizing RSMA. In RSMA, each group-specific message is split and encoded into two streams, namely, a private stream that is decoded by all users in the multicast group and treated as noise by all users within other multicast groups and a common stream that is decoded by multiple users in different multicast groups. Hence, the users are able to not only decode their respective private messages but also decode a subset of common messages dedicated to other users so as to reduce interference throughout the network.

2) Problem Formulation. Herein, we formulate a resource allocation problem to maximize the minimum achievable rate guaranteeing fairness among all multicast groups in the cache-enabled RSMA-assisted C-RAN. Additionally, we consider that the CP only knows the channel statistics; i.e., we consider statistical CSIT, in contrast to the full CSIT assumption adopted by most works in C-RAN literature. The considered problem is a mixed-integer nonlinear stochastic program (MINLSP) which is known to be NP-hard.

3) Proposed Algorithms. To tackle such a challenging problem, we propose an optimization framework consisting of a novel multicast group-based clustering algorithm, the sample average approximation (SAA), and a weighted minimum mean square error- (WMMSE-) based algorithm.

4) Numerical Simulations. Through extensive numerical simulations, we evaluate the performance of our proposed scheme. To benchmark the performance, we compare our proposed RSMA scheme with classical TIN and a single common message RSMA (SCM-RSMA) scheme, which defines a single common message that is decoded by all users. Results imply that the performance gain of the proposed RSMA scheme over the benchmarks increases with fronthaul capacity and also with the number of BSs. The gain is most significant in low fronthaul regime with small cache sizes, as another result shows. Moreover, the MMF rate of the proposed RSMA scheme increases with the utilization of bigger caches and also more transmit antennas. With the increasing number of users, we observe a gain of the multigroup multicast transmission over using a simpler transmission scheme. At last, we highlight the numerical features of our proposed method.

1.4 Notations and Organization

As for the notations of this paper, we denote vectors, matrices, and sets as boldface lower-case, boldface-capital, and calligraphic letters, respectively (e.g., x, X, and $\mathcal{X}$). The cardinality of a set $\mathcal{X}$ is given by $|\mathcal{X}|$. A vectorization operator vec (⋅) is used throughout the paper. To be more specific, $\mathrm{v}\mathrm{e}\mathrm{c}(\mathcal{X})$ is a column vector holding all elements of the set $\mathcal{X}$. It is defined as $\mathrm{v}\mathrm{e}\mathrm{c}(\mathcal{X})\equiv {[x_1,\dots ,x_N]}^T$ or $\mathrm{v}\mathrm{e}\mathrm{c}(\mathcal{X})\equiv {[{\mathbf{x}}_1^T,\dots ,{\mathbf{x}}_N^T]}^T$ when the elements in $\mathcal{X}$ are scalars or vectors, respectively. Also, $\mathbb{R}$ and $\mathbb{C}$ denote the real and complex field and the expectation of random variable writes $\mathbb{E}\{\cdot \}$. The transpose and Hermitian transpose operators are denoted as ${\left(\cdot \right)}^T$ and ${\left(\cdot \right)}^H$, respectively. Finally, $\left|\cdot \right|$ is the absolute value and ‖⋅‖_p is the l_p-norm.

Please refer to Table 1 for a list of mathematical notations used throughout this work. We pursue the following structural organization in this paper. In Section 2 we present our system model consisting of signal, channel, cache, and receiver models. The considered optimization problem is formulated in Section 3 followed by the optimization algorithms we propose for solving the problem, including a clustering algorithm to determine the BS clustering, as well as an SAA and WMMSE-based algorithm to optimize the precoders. To evaluate the performance of the proposed algorithm, we conduct numerical simulations in Section 4. Finally, Section 5 concludes the paper.

TABLE 1

TABLE 1. List of mathematical notations.

2 System Model

We consider a C-RAN system operating in downlink mode with a transmission bandwidth B. The network consists of a set of multiple-antenna BSs, $\mathcal{N}=\left\{\mathrm{1,2},\dots ,N\right\}$, serving a group of single-antenna users indexed by $\mathcal{K}=\left\{\mathrm{1,2},\dots ,K\right\}$. Each BS $n\in \mathcal{N}$ is equipped with L > 1 antennas and a local cache memory of finite size. BS n is connected to a CP, located at the cloud, via a fronthaul link of capacity $C_n^{\text{max}}$. The CP has access to the library of files containing the set $\mathcal{F}=\left\{\mathrm{1,2},\dots ,F\right\}$, where the total number of files is F. At the beginning of each transmission block, each user in the network submits a request to receive a specific file from the library at the cloud. We assume that each requested content can be fetched and processed by the CP before sharing it with a cluster of BSs for the respective users. The users submit their demands according to a specific demand probability and we assume that the probability distribution of the users’ demands is available at the CP. All users requesting the same content are grouped together and served with a multicast transmission from a cluster of BSs as shown in Figure 1. Without loss of generality, we consider that the CP divides each requested file into several data chunks, so that the transmission of each file may take place on several consecutive transmission blocks and the number of required transmission blocks to transmit each file may be different from other files. Let the total number of multicast groups be G, such that 1 ≤ G ≤ min{F, K}. The set of all multicast groups is given by $\mathcal{G}=\left\{1,\dots ,G\right\}$ and the set of users in each group g is denoted as ${\mathcal{G}}_g$. We assume that each user in the network can submit a request to one content at a time, such that ${\mathcal{G}}_i\cap {\mathcal{G}}_j=\varnothing ,i\ne j$ and ${\sum }_{g=1}^G|{\mathcal{G}}_g|\le K$. Let v_g(t) be the data chunk of the file requested by group g at time slot t.

FIGURE 1

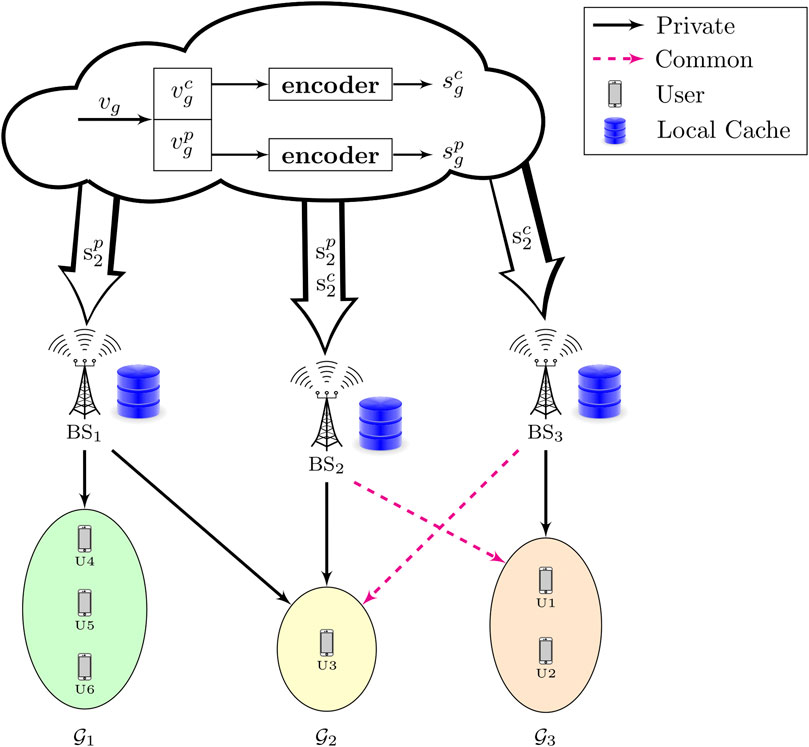
FIGURE 1. A C-RAN system with three BSs serving three groups of users with multicast messages. Private and common messages are encoded at the cloud. As a simple illustration, we show the shared private and common streams of group ${\mathcal{G}}_2$.

2.1 Received Signal Model

In downlink C-RAN, the data chunks in time slot t are encoded at the CP into streams s_g(t), $\forall g\in \mathcal{G}$. In data-sharing, due to limited capacity of the fronthaul links, the CP shares private and common parts of s_g(t) with a subset of BSs that are in the serving cluster of the multicast group g and that do not cache the content locally. However, the file is processed locally at the BS n if it caches the requested content and participates in transmitting it to the intended multicast group. Hence, by using local caches, the system can balance the traffic load on fronthaul links. Upon receiving these signals, the selected cluster of BSs cooperatively transmits the coded streams by cooperative beamforming. Hence, BS n constructs ${\mathbf{x}}_n\in {\mathbb{C}}^{L\times 1}$ and sends it according to the following transmit power constraint:

$\mathbb{E}\left\{{\mathbf{x}}_n^H(t){\mathbf{x}}_n(t)\right\}\le P_n^{\text{max}}\forall n\in \mathcal{N},(1)$

where $P_n^{\text{max}}$ is the maximum transmit power available at BS n. Let ${\mathbf{h}}_{n,k}(t)\in {\mathbb{C}}^{L\times 1}$ denote the channel vector between BS n and user k and ${\mathbf{h}}_k(t)=\mathrm{v}\mathrm{e}\mathrm{c}\left(\left\{{\mathbf{h}}_{n,k}(t)|\forall n\in \mathcal{N}\right\}\right)\in {\mathbb{C}}^{NL\times 1}$ be the aggregate channel vector of user k. We can write the received signal at user k as

$y_k(t)={\mathbf{h}}_k^H(t)\mathbf{x}(t)+n_k(t),(2)$

where $n_k(t)\sim \mathcal{CN}\left(0,{\sigma }_k^2\right)$ is the additive white Gaussian noise (AWGN), and we have $\mathbf{x}(t)=\mathrm{v}\mathrm{e}\mathrm{c}\left(\left\{{\mathbf{x}}_n(t)|\forall n\in \mathcal{N}\right\}\right)$. Without loss of generality, we assume the noise power to be the same for all users; i.e., ${\sigma }_k^2={\sigma }^2,\forall k\in \mathcal{K}$.

2.2 Channel Fading Model and CSI Uncertainty

Let us define the instantaneous channel state at time slot t as $\mathbf{h}(t)\triangleq \mathrm{v}\mathrm{e}\mathrm{c}\left(\left\{{\mathbf{h}}_k(t)|\forall k\in \mathcal{K}\right\}\right)\in {\mathbb{C}}^{NLK\times 1}$. This paper considers a block-fading model in which the channel state h(t) remains constant over multiple time slots and may vary independently in a random fashion from one block to another according to some stochastic process. Specifically, in block b with length t_b, the following relation in the block-fading model is satisfied:

$\mathbf{h}(t)=\mathbf{h}(b),\forall t\in \left\{(b-1)t_b+1,\dots ,b{t}_b\right\}.(3)$

Throughout the paper, we focus on optimizing the transmission scheme’s parameters, e.g., beamforming vectors, and the resource allocation strategy using the available CSI. Hence, we next drop the dependency on the time variable t for the brevity of notation and focus on the channel state in one transmission block.

To this end, we assume that the channel between BS n and user k follows the distribution ${\mathbf{h}}_{n,k}\sim \mathcal{CN}\left(0,{\mathbf{Q}}_{n,k}\right)$, where Q_n,k is a symmetric positive semidefinite matrix and depends mainly on the path loss between BS n and user k. Throughout the paper, we consider that the users (the receivers) can always estimate their channel vectors with high accuracy; i.e., we consider perfect CSI at the receiver (CSIR). This assumption is justified in practice, as CSIR can be estimated during the training phase with minimal communication overhead (Tse and Viswanath, 2005; Caire and Kumar, 2007). Concerning the CSIT, the CP obtains the channel estimations from the BSs in the network. The BSs acquire the CSI at the beginning of each transmission block, conventionally through uplink training in time division multiplex (TDD) systems (Hassibi and Hochwald, 2003) or via quantized feedback links in frequency division multiplex (FDD) systems (Love et al., 2008). In contrast to CSIR, obtaining high accuracy CSIT requires huge communication overhead, therefore, assuming full CSIT knowledge is somewhat optimistic, and in practice, it might not be possible, especially in dense networks. In this work, we investigate two cases concerning the CSIT assumption:

• Case 1: The CP estimates the channel state perfectly and the error due to quantized feedback or during the uplink training is negligible; i.e., we assume full CSIT. In this case, the CP has knowledge of all elements in the vector h. Obviously, the full CSIT case involves a large communication overhead between the users and the CP, which requires a considerable amount of communication resources, which may not be affordable in dense networks.

• Case 2: Alternatively, the CP can only access the matrices $\left\{{\mathbf{Q}}_{n,k}|\forall n\in \mathcal{N},\forall k\in \mathcal{K}\right\}$; i.e., the CP knows the channel statistics of all users. This case is referred to as statistical CSIT, as the CP does not know the channel coefficients $\left\{{\mathbf{h}}_{n,k}|\forall n\in \mathcal{N},\forall k\in \mathcal{K}\right\}$ exactly, but their covariance matrix is available to the CP. Note that the perfect estimate of the channel statistics can be easily obtained with minimal communication overhead, as it depends mainly on the user locations, which can be accurately estimated using off-the-shelf global positioning system (GPS) devices (Cui et al., 2019). Note that, in this paper, we focus on statistical CSIT. Integrating imperfect CSIT with modeling the channel estimation error is out of the scope of this work and will be considered in future works.

In the next subsection, we describe the transmission scheme which combines beamforming with RSMA and clustering.

2.3 Beamforming, Signal Construction, and Clustering

The proposed transmission scheme consists of RSMA, BS cluster design for data-sharing, and cooperative beamforming to transmit the private and common streams to the intended multicast groups. The data chunk of the file requested by group g, i.e., v_g, is split at the CP (or locally at the BS n) into a private part denoted by $v_g^p$ and a common part denoted by $v_g^c$. Afterwards, the CP encodes the private and common parts into $s_g^p$ and $s_g^c$, respectively, as illustrated in Figure 1. The encoded streams $s_g^p$ and $s_g^c$ are shared via fronthaul links with BSs that participate in transmitting to the multicast group g and do not cache the requested content. This RSMA strategy is referred to as RSMA and common message decoding (RS-CMD), throughout the paper. Let ${\mathbf{w}}_{n,g}^p$ and ${\mathbf{w}}_{n,g}^c$ be the beamforming vectors of BS n to serve the multicast group $g\in \mathcal{G}$. The aggregate beamforming vector from all BSs to a group g can thus be defined as ${\mathbf{w}}_g^o=\mathrm{v}\mathrm{e}\mathrm{c}\left(\left\{{\mathbf{w}}_{n,g}^o|\forall n\in \mathcal{N}\right\}\right)$, where o ∈ {p, c}. Note that the beamforming vectors of some BSs not participating in serving group g are vectors where all elements are zero, i.e., ${\mathbf{w}}_{n,g}^o={\mathbf{0}}_L$. Whether a BS n is selected to be serving group g or not is dependent on the proposed clustering algorithm. The respective rates of the private and common streams of multicast group $g\in \mathcal{G}$ are denoted by $R_g^p$ and $R_g^c$.

The BSs that already cached the requested content perform the required baseband processing tasks locally when participating in transmission to the intended multicast groups. However, we emphasize the fact that the beamforming vectors are jointly optimized at the CP to design the coordinated beamforming strategy. After that, the beamforming coefficients are shared directly with their respective cluster of BSs¹.

Let ${\mathcal{G}}_n^p,{\mathcal{G}}_n^c\subseteq \mathcal{G}$ be the subset of groups served by BS n with a private or common message, respectively; i.e.,

$\begin{array}{ll}\hfill {\mathcal{G}}_n^p& :=\left\{g\in \mathcal{G}|\text{BS}n\text{delivers}{s}_g^p\text{to\hspace{0.17em}multicast\hspace{0.17em}group}g\right\},\hfill \end{array}(4)$

$\begin{array}{ll}\hfill {\mathcal{G}}_n^c& :=\left\{g\in \mathcal{G}|\text{BS}n\text{delivers}{s}_g^c\text{to\hspace{0.17em}multicast\hspace{0.17em}group}g\right\}.\hfill \end{array}(5)$

2.4 Cache Model

In this paper, we consider storing content closer to the users in local cache memories at the BSs. Associated with this content delivery process, we distinguish between cache placement and cache delivery phases (Maddah-Ali and Niesen, 2014; Liu et al., 2017). While parts of recent related literature studied efficient designs of cache placement strategies to improve the overall content delivery, other works aimed at optimizing the cache delivery process for fixed cache placement. Generally, we can say that the cache placement phase spans over a wider time scale than the cache delivery phase, since the requested content’s popularity changes slowly with time. The particular execution of the cache placement phase is done in order to significantly improve the cache delivery phase, especially during peak traffic periods.

Herein, we aim to optimize the cache delivery phase and assume the cache placement to be known a priori at the CP (Ugur et al., 2016). Therefore, we let $\mathbf{C}\in {\left\{\mathrm{0,1}\right\}}^{F\times N}$ be the binary cache placement matrix where ${\left[\mathbf{C}\right]}_{f,n}=c_{f,n}=1$ means that the file f is cached at BS n and c_f,n = 0 means that it is not. All users in the multicast group g request the same file $f_g\in \mathcal{F}$. A cache hit means that a BS that caches f_g, i.e., $c_{f_g,n}=1$, processes the data locally and there is no need to burden the fronthaul link upon serving group g. Otherwise, $c_{f_g,n}=0$ means that, in order for n to serve group g, it has to receive data from the CP. Utilizing the binary cache placement matrix has an impact on the mathematical formulation of the fronthaul constraint. Based on the instantaneous rates $R_g^p$ and $R_g^c$ and the serving clusters defined in Eq. 4 and Eq. 5, the fronthaul capacity constraint of all BSs in the proposed C-RAN is

$\sum _{g\subseteq {\mathcal{G}}_n^p}(1-c_{f_g,n})R_g^p+\sum _{g\subseteq {\mathcal{G}}_n^c}(1-c_{f_g,n})R_g^c\le C_n^{\text{max}},\forall n\in \mathcal{N}.(6)$

Disregarding the caching ability, all common and private rates of messages served by BS n contribute to the sum and burden the fronthaul link of n. This leads to fronthaul congestion, especially when the serving clusters include many groups or the fronthaul capacity is limited. Therefore, in Eq. 6, if the file requested by group g, i.e., f_g, is cached by BS n, then $c_{f_g,n}=1$. Thus, the common and private rates of g do not contribute to the sum saving fronthaul capacity. Next, we elaborate on RSMA and define our receiver model, and also, we further specify the received signal formulation.

2.5 Receiver Model and Instantaneous Achievable Rates

In the context of this paper, common messages are employed for the sole purpose of mitigating interference in C-RAN to achieve better resource allocation. Hence, in a C-RAN system that deploys RSMA, each user in a multicast group is expected to decode multiple messages. Thus, the order in which user k decodes the intended messages plays an important role in assessing the efficiency of the relevant proposed interference mitigation techniques. Although joint decoding of all common and private messages at user k would result in optimized rates, its implementation is complicated in practice. Particularly when the network is large, the intended set of messages to be decoded by each user is large. However, the classical information theoretical results of a two-user IC already suggest that decoding a strong interferer’s common message can significantly improve a user’s achievable rate (Etkin et al., 2008). From this perspective, in this paper, we focus on a successive decoding strategy. User k decodes a subset of all common messages in a fixed decoding strategy, based on the descending order of the interferers’ channel gains, as described next.

Each user deploys successive interference cancelation (SIC) to remove parts of the interference in a successive order. A block diagram of the SIC at user 1 is given in Figure 2. From Figure 2, it becomes obvious that the set of common messages that user k is decoding and the order in which the messages are decoded play an essential role in characterizing the SIC at the users.

FIGURE 2

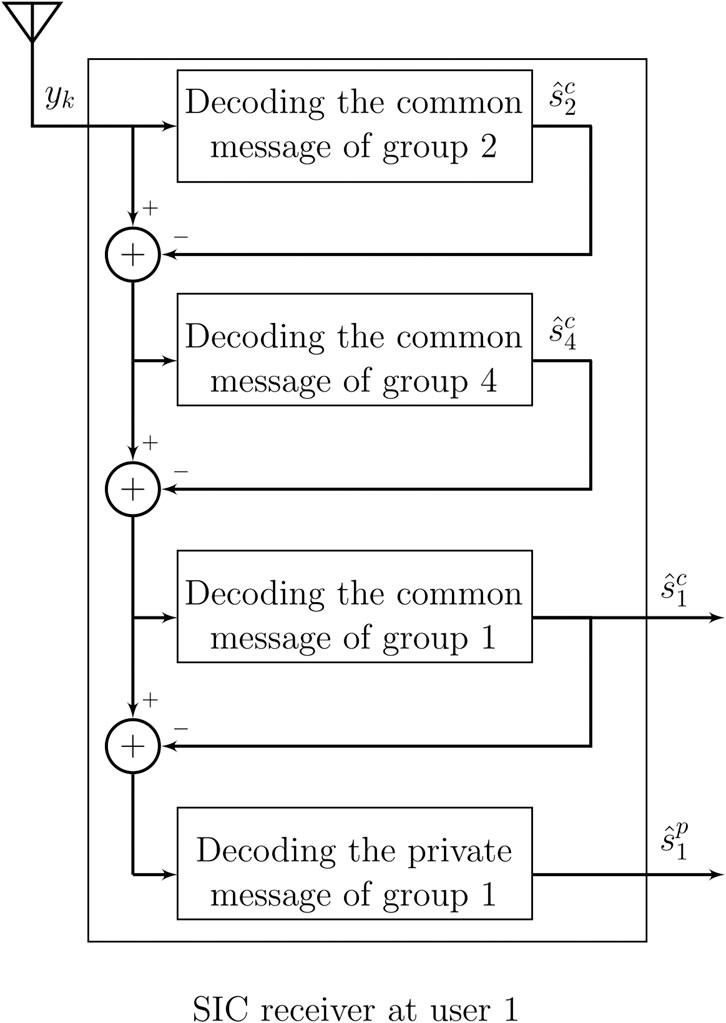
FIGURE 2. A block diagram for an SIC at user 1. In this example, the common messages decoded at user 1 are Φ₁ = {1, 2, 4}. The decoding order at user 1 is π₁ = {2, 4, 1}.

To this end, let ${\mathcal{M}}_g$ denote the set of users decoding $s_g^c$; i.e.,

${\mathcal{M}}_g\triangleq \left\{j\in \mathcal{K}|\text{user}j\text{decodes}{s}_g^c\right\}.(7)$

Indices of groups whose common messages are decoded by user k are given by

${\mathrm{\Phi }}_k\triangleq \left\{g\in \mathcal{G}|k\in {\mathcal{M}}_g\right\}.(8)$

The remaining groups whose common messages are not decoded by user k are included in set Ω_k. We note that once the set ${\mathcal{M}}_g$ is found, we can determine the set Φ_k, and vice versa. The choice of Φ_k (and consequently ${\mathcal{M}}_g$) has a crucial impact on the achievable rate of multicast group g. Consider the following decoding order at user k:

${\pi }_k:{\mathrm{\Phi }}_k\to \left\{\mathrm{1,2},\dots ,\left|{\mathrm{\Phi }}_k\right|\right\},(9)$

which represents a bijective function of the set Φ_k with cardinality $\left|{\mathrm{\Phi }}_k\right|$; i.e., π_k(g) is the successive decoding step in which the common message of multicast group g, i.e., $s_g^c\in {\mathrm{\Phi }}_k$, is decoded at user k. In other terms, π_k(g₁) > π_k(g₂) (where g₁ ≠ g₂) implies that user k decodes the common message of multicast group g₂ first and then the common message of multicast group g₁. Now, we can rewrite y_k, the received signal at user k in the multicast group g, as follows:

$y_k=\underset{\text{Signals\hspace{0.17em}to\hspace{0.17em}be\hspace{0.17em}decoded}}{\underbrace{\left({\mathbf{h}}_k^H{\mathbf{w}}_g^p{s}_g^p+\sum _{j\in {\mathrm{\Phi }}_k}{\mathbf{h}}_k^H{\mathbf{w}}_j^c{s}_j^c\right)}}+\underset{\text{Interference\hspace{0.17em}plus\hspace{0.17em}noise}}{\underbrace{\sum _{m\in \mathcal{G}\backslash \{g\}}{\mathbf{h}}_k^H{\mathbf{w}}_m^p{s}_m^p+\sum _{l\in {\mathrm{\Omega }}_k}{\mathbf{h}}_k^H{\mathbf{w}}_l^c{s}_l^c+n_k}}.(10)$

User k then uses SIC to remove the common messages in set Φ_k from the received signal y_k. The common messages are successively decoded according to the decoding order given by π_k. The common message decoding is solely performed to manage the interference and improve the detectability of the private message, which is decoded last. The average power of the messages received at user k when decoding the private stream $s_g^p$ and the common stream $s_i^c$ of multicast group i, respectively, are given as

$\begin{array}{ll}\hfill T_{g,k}^p& ={\left|{\mathbf{h}}_k^H{\mathbf{w}}_g^p\right|}^2+\underset{I_{g,k}^p}{\underbrace{\sum _{j\in \mathcal{G}\backslash \backslash \{g\}}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_j^p\right|}^2+\sum _{l\in {\mathrm{\Omega }}_k}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_l^c\right|}^2+{\sigma }^2}},\hfill \end{array}(11)$

$\begin{array}{ll}\hfill T_{i,k}^c& ={\left|{\mathbf{h}}_k^H{\mathbf{w}}_i^c\right|}^2+\underset{I_{i,k}^c}{\underbrace{\sum _{j\in \mathcal{G}}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_j^p\right|}^2+\sum _{l\in {\mathrm{\Omega }}_k}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_l^c\right|}^2+\sum _{m\in {\mathrm{\Psi }}_{i,k}}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_m^c\right|}^2+{\sigma }^2}},\hfill \end{array}(12)$

where ${\mathrm{\Psi }}_{i,k}\triangleq \left\{m\in {\mathrm{\Phi }}_k|{\pi }_k(m)>{\pi }_k(i)\right\}$. Ψ_i,k is a set including indices of all multicast groups m whose common messages are decoded after decoding the common message of group i, i.e., groups having common messages with higher decoding order π_k(m) > π_k(i). These multicast groups m contribute to the interference since they have yet to be decoded. Also, $I_{g,k}^p$ and $I_{i,k}^c$ denote the interference plus noise at user k decoding the private message of multicast group g and the common message of group i, respectively. Based on the expressions in Eq. 11 and Eq. 12, we define the SINR of user k from multicast group g, i.e., $k\in {\mathcal{G}}_g$, when decoding the private message of group g and the SINR of user k when decoding the common message of group i as

$\begin{array}{ll}\hfill {\gamma }_{g,k}^p& =\frac{{\left|{\mathbf{h}}_k^H{\mathbf{w}}_g^p\right|}^2}{{\sigma }^2+\sum _{j\in \mathcal{G}\backslash \backslash \{g\}}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_j^p\right|}^2+\sum _{l\in {\mathrm{\Omega }}_g}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_l^c\right|}^2},\hfill \end{array}(13)$

$\begin{array}{ll}\hfill {\gamma }_{i,k}^c& =\frac{{\left|{\mathbf{h}}_k^H{\mathbf{w}}_i^c\right|}^2}{{\sigma }^2+\sum _{j\in \mathcal{G}}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_j^p\right|}^2+\sum _{l\in {\mathrm{\Omega }}_i}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_l^c\right|}^2+\sum _{m\in {\mathrm{\Psi }}_{i,k}}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_m^c\right|}^2}.\hfill \end{array}(14)$

The instantaneous achievable rate of multicast group g is given as $R_g=R_g^p+R_g^c$, where the instantaneous private and common rates satisfy the following achievability conditions

$\begin{array}{ll}\hfill {\gamma }_{g,k}^p& \ge 2^{R_g^p/B}-1,\forall k\in {\mathcal{G}}_g,\forall g\in \mathcal{G},\hfill \end{array}(15)$

$\begin{array}{ll}\hfill {\gamma }_{g,k}^c& \ge 2^{R_g^c/B}-1,\forall k\in {\mathcal{M}}_g,\forall g\in \mathcal{G}.\hfill \end{array}(16)$

Note that the interference from sending the common message $s_g^c$ does not impact the users in ${\mathcal{M}}_g$ as they decode this message. This is the main motivation for employing RSMA in networks that suffer from interference. We emphasize that the instantaneous rate constraints are achievable under the assumption of full CSIT. However, when the CP knows only the channel’s statistical properties, i.e., statistical CSIT, the achievability constraints Eq. 15 and Eq. 16 are not valid, as the SINR expressions become functions of random variables. In this case, we assort instead to the ergodic achievable rate for sending private and common messages, as discussed next.

2.6 Achievable Ergodic Rates

In the statistical CSIT scenario, we consider that the CP has only information about the statistics of channel states. These assumptions are quite general and can model other inaccuracies in CSIT.

The assumption of statistical CSI knowledge, in particular, is reasonable because the path loss information varies slowly and needs to be updated when the users’ location changes only, which significantly reduces the communication overhead due to the CSIT acquisition process at the CP compared to the case in which the CP acquires full CSIT.

In this case, we consider sending the private and common streams of group g at the ergodic rate (Goldsmith, 2005). The total ergodic rate of group g is defined as ${\mathbb{E}}_{\mathbf{h}}\left\{R_g^p+R_g^c\right\}\triangleq {\bar{R}}_g^p+{\bar{R}}_g^c$, where ${\bar{R}}_g^p$ is the ergodic rate to send the private stream and ${\bar{R}}_g^c$ is the ergodic rate to send the common stream of multicast group g. The achievability relations of the ergodic private and common rates are

$\begin{array}{ll}\hfill {\bar{R}}_g^p\le B{\mathbb{E}}_{\mathbf{h}}\left\{{\log }_2\left(1+{\gamma }_{g,k}^p\right)\right\},& \forall k\in {\mathcal{G}}_g,\forall g\in \mathcal{G},\hfill \end{array}(17)$

$\begin{array}{ll}\hfill {\bar{R}}_g^c\le B{\mathbb{E}}_{\mathbf{h}}\left\{{\log }_2\left(1+{\gamma }_{g,k}^c\right)\right\},& \forall k\in {\mathcal{M}}_g,\forall g\in \mathcal{G}.\hfill \end{array}(18)$

In the next section, we formulate the optimization problem under consideration and propose our solution approach. To that end, we define the WMMSE-based algorithm for optimal resource allocation in the considered system model.

3 Problem Formulation and Proposed Algorithms

This paper considers the problem of system utility maximization in a cache-assisted C-RAN which adopts a multicast group-based transmission scheme combining RSMA and data-sharing. The constraints of the problem consist of per BS limited fronthaul capacity and transmit power constraints, as well as per-stream achievable rate constraints. The fronthaul link is needed to fetch data from the CP for multicast groups whose content is not locally cached at the BSs. The system utility under focus is the minimum achievable rate among all multicast groups. Thus, the resources in C-RAN are allocated to guarantee fairness among all multicast groups being served in C-RAN. The optimization problem to realize this target can be defined as follows:

$\begin{array}{ll}\hfill \underset{{\mathcal{V}}_0}{\text{max}}& \bar{R}\hfill \end{array}(\mathrm{19a})$

$\begin{array}{llll}\hfill \text{s.t.}& \bar{R}\le {\bar{R}}_g^p+{\bar{R}}_g^c,\hfill & \hfill & \forall g\in \mathcal{G},\hfill \end{array}(\mathrm{19b})$

$\begin{array}{llll}\hfill & \sum _{g\in {\mathcal{G}}_n^p}{\Vert {\mathbf{w}}_{n,g}^p\Vert }_2^2+\sum _{g\in {\mathcal{G}}_n^c}{\Vert {\mathbf{w}}_{n,g}^c\Vert }_2^2\le P_n^{\text{max}},\hfill & \hfill & \forall n\in \mathcal{N},\hfill \end{array}(\mathrm{19c})$

$\begin{array}{llll}\hfill & \sum _{g\subseteq {\mathcal{G}}_n^p}(1-c_{f_g,n}){\bar{R}}_g^p+\sum _{g\subseteq {\mathcal{G}}_n^c}(1-c_{f_g,n}){\bar{R}}_g^c\le C_n^{\text{max}},\hfill & \hfill & \forall n\in \mathcal{N},\hfill \end{array}(\mathrm{19d})$

$\begin{array}{llll}\hfill & {\bar{R}}_g^p\le {\mathbb{E}}_{\mathbf{h}}\left\{B{\log }_2(1+{\gamma }_{g,k}^p)\right\},\hfill & \hfill & \forall k\in {\mathcal{G}}_g,\forall g\in \mathcal{G},\hfill \end{array}(19e)$

$\begin{array}{llll}\hfill & {\bar{R}}_g^c\le {\mathbb{E}}_{\mathbf{h}}\left\{B{\log }_2(1+{\gamma }_{g,k}^c)\right\},\hfill & \hfill & \forall k\in {\mathcal{M}}_g,\forall g\in \mathcal{G},\hfill \end{array}(\mathrm{19f})$

${\mathcal{V}}_0\triangleq \left\{{\mathbf{w}}_g^p,{\mathbf{w}}_g^c,{\bar{R}}_g^p,{\bar{R}}_g^c,{\mathcal{G}}_n^p,{\mathcal{G}}_n^c|\forall g\in \mathcal{G},\forall n\in \mathcal{N}\right\}$ is the set of optimization variables. Here, we maximize the minimum achievable rate of all multicast groups $\bar{R}$ w.r.t. the private and common beamforming vectors, ergodic rates, and serving clusters. Constraint Eq. 19b represents the quality of service (QoS) ergodic minimum rate constraint, where ${\bar{R}}_g^p+{\bar{R}}_g^c$ is the ergodic achievable rate of multicast group g and $\bar{R}$ is the minimum ergodic rate. Eq. 19c is the maximum transmit power constraint per BS, where ${\mathbf{w}}_{n,g}^p$ and ${\mathbf{w}}_{n,g}^c$ are the beamforming vectors from BS n to serve the private and common message of multicast group g, respectively. ${\mathcal{G}}_n^p$ and ${\mathcal{G}}_n^c$ are the subsets of groups whose private and common messages are served by BS n, respectively. Eq. 19d is the available fronthaul capacity constraint per BS. The achievable ergodic rates of the private and common streams are given by constraints Eq. 19e and Eq. 19f, respectively.

With stochastic coordinated beamforming optimization, the same beamforming vectors, i.e., $\left\{{\mathbf{w}}_g^p,{\mathbf{w}}_g^c|\forall g\in \mathcal{G}\right\}$, are used for all transmit blocks in which the channel statistics remain constant. The same applies to the serving clusters and the allocated ergodic rates, which remain unchanged over several transmission blocks in which the channel statistics do not alter. Problem Eq. 19 is difficult and challenging to solve. In particular, the constraints Eq. 19e and Eq. 19f are functions of a stochastic quantity. Hence, the achievable rates depend on the current realization of channel fading which is unknown at the CP and the expectations in Eq. 19e and Eq. 19f have no closed form. Moreover, even when considering the deterministic version of this problem, i.e., when assuming full CSIT, the SINR expressions are non-convex functions of the design variables (i.e., the beamforming vectors), and the resulting problem is known to be NP-hard, as shown in (Sidiropoulos et al., 2006, Section 5). Therefore, to tackle problem Eq. 19, we require other optimization tools than those used for solving the counterpart deterministic problem. We use a three-step approach. First, we develop a group-based clustering algorithm to predetermine the serving clusters, i.e., ${\mathcal{G}}_n^p$ and ${\mathcal{G}}_n^c$, in order to simplify problem Eq. 19. Then, we use the SAA method to reformulate the expected value expressions. Afterward, we make use of a WMMSE-rate relationship, to construct a block coordinate ascent algorithm for solving the resulting continuous, deterministic NLP.

3.1 Group-Based Clustering

The authors in (Wei Yu and Yu, 2014) propose a clustering algorithm for assigning a set of BSs to serve each user in the network. It is based on the path loss, which depends on the user location and typically varies on a slow time scale. However, the algorithm is not directly applicable to our problem since it was developed for unicast streams. Specifically, the clustering algorithm originally proposed in (Wei Yu and Yu, 2014) is a user-centric clustering approach not suited for the group-based transmission in this work. The authors in (Ahmad et al., 2020a) extended this algorithm to a more general case, as they considered common messages to be decoded by a subset of users. However, the private messages in (Ahmad et al., 2020a) are also decoded at a single user only. To further extend the algorithm from (Ahmad et al., 2020a), in this subsection, we propose a group-based, rather than a user-based, clustering algorithm suited for the proposed multicast transmission scheme, which is more general since groups may consist of multiple users.

First, we define $A_n^{\text{max}}$ as the maximum number of streams a BS n can serve. Such a constant helps balancing the load, as it prevents BSs from being overloaded. Our group-based clustering approach starts by finding candidate clusters of BSs to serve each multicast group. These clusters are denoted as ${\mathcal{N}}_g^p$ and ${\mathcal{N}}_g^c$, containing all BSs that serve the private and common stream of multicast group g, respectively. We emphasize the multicast nature of our algorithm, as every BS in a serving cluster ${\mathcal{N}}_g^p$ or ${\mathcal{N}}_g^c$ has to have a good channel quality to all users in the group. Since the algorithm is based on path loss, we use a channel quality measure q_n,k from BS n to user k that is inversely proportional to the path loss. As aforementioned, we can not use this measure directly in our algorithm. Hence, we define the collective channel quality of all users decoding the private and common message of group g as ${\tilde{q}}_{n,g}^p$ and ${\tilde{q}}_{n,g}^c$, respectively. This collective quality is computed as

${\tilde{q}}_{n,g}^p=\frac{1}{|{\mathcal{G}}_g|}\sum _{j\in {\mathcal{G}}_g}{q}_{n,j},{\tilde{q}}_{n,g}^c=\frac{1}{|{\mathcal{M}}_g|}\sum _{j\in {\mathcal{M}}_g}{q}_{n,j}.(20)$

Thus, the candidate clusters of BSs serving a group g are given by

${\mathcal{N}}_g^p=\left\{n|\right)\underset{m\in \mathcal{N}}{\text{max}}({\tilde{q}}_{m,g}^p)-{\tilde{q}}_{n,g}^p\le \mu \},{\mathcal{N}}_g^c=\{n|\underset{m\in \mathcal{N}}{\text{max}}({\tilde{q}}_{m,g}^c)-{\tilde{q}}_{n,g}^c\le \mu \}.(21)$

The detailed steps of the group-based clustering procedure are listed in Algorithm 1. The first step is determining the candidate clusters of BSs for all multicast groups according to Eq. 21. This is done for each group’s private and common message, respectively. Further, sets $\mathcal{S}$ and $\mathcal{N}$ are initialized, where the former contains all private and common streams and the latter contains all BSs. The algorithm outputs the serving clusters ${\mathcal{G}}_n^p$ and ${\mathcal{G}}_n^c$, initialized as empty sets. The first for-loop assigns BS n from ${\mathcal{N}}_g^o$ with the best collective channel quality to serve the stream $s_g^o$. Thus, g is added to the serving cluster of BS n, while n is removed from the candidate cluster of stream $s_g^o$. If there is no candidate to serve $s_g^o$, the message is removed from $\mathcal{S}$. In the second for-loop, for each BS n, we check if n is overloaded; i.e., the number of assigned messages in n’s serving cluster exceeds $A_n^{\text{max}}$. If it is overloaded, $|{\mathcal{G}}_n^p|+|{\mathcal{G}}_n^c|-A_n^{\text{max}}$ groups with the weakest collective channel quality are removed from the serving cluster. BS n is then removed from $\mathcal{N}$ and from all candidate clusters. This procedure is repeated until all BSs reach their maximum capacity of messages, i.e., $A_n^{\text{max}}$, or all messages $s_g^o$ run out of BS candidates.

At this point, we utilize Algorithm 1 to precompute the serving clusters. Therefore, we can now fix ${\mathcal{G}}_n^p$ and ${\mathcal{G}}_n^c$, which makes problem Eq. 19 more traceable from an optimization perspective. The relaxed problem with serving clusters already precomputed can be stated as

$\begin{array}{ll}\hfill \underset{{\mathcal{V}}_1}{\text{max}}& \bar{R}\hfill \end{array}(\mathrm{22a})$

$\begin{array}{ll}\hfill \text{s.t.}& (19b),(19c),(19d),(19e),(19f).\hfill \end{array}(\mathrm{22b})$

Now, ${\mathcal{V}}_1\triangleq \left\{{\mathbf{w}}_g^p,{\mathbf{w}}_g^c,{\bar{R}}_g^p,{\bar{R}}_g^c|\forall g\in \mathcal{G}\right\}$ is the new set of optimization variables. Please note that the explicit formulations of problem Eq. 19 and problem Eq. 22 do not differ. These problems are different only in their optimization variables; i.e., problem Eq. 22 utilizes the fixed clustering determined by Algorithm 1, i.e., ${\mathcal{G}}_n^p$ and ${\mathcal{G}}_n^c$. Therefore, the quality of the solution to problem Eq. 22 depends on the quality of the heuristic Algorithm 1. However, Algorithm 1 provides a feasible solution to the integer part of problem Eq. 19. Considering different clustering algorithms and their impact on the gap between the optimal solutions of problem Eq. 19 and Eq. 22 is an interesting aspect for future works on this topic but left out here since it is out of the scope of this work. Next, we describe the SAA of problem Eq. 22.

. Algorithm 1 Group-based Clustering Algorithm

3.2 SAA Reformulation

A similar optimization framework which combines SAA and WMMSE-based optimization is first proposed in (Joudeh and Clerckx, 2016b), where it was developed to solve a sum-rate maximization problem for the MISO-BC. However, in this work, we generalize the algorithm to solve a problem of maximizing the minimum rate for multigroup multicast transmission in cache-assisted C-RAN with RSMA. First, we approximate the expected value in the achievable ergodic rate constraints Eq. 19e and Eq. 19f with the sample average (Shapiro and Ruszczyński, 2009). We use a Monte-Carlo sample size of M. With h as a random vector, we use h^m to denote the m-th independent realization of h. Consequently, we denote the SINR from Eq. 15 and Eq. 16 as ${\gamma }_{g,k}^p(m)$ and ${\gamma }_{g,k}^c(m)$, respectively. The corresponding SAA reformulation of problem Eq. 22 is defined as follows:

$\begin{array}{ll}\hfill \underset{{\mathcal{V}}_1}{\text{max}}& \bar{R}\hfill \end{array}(\mathrm{23a})$

$\begin{array}{ll}\hfill \text{s.t.}& (19b),(19c),(19d),\hfill \\ {\bar{R}}_g^p-\frac{B}{M}\sum _{m=1}^M{\log }_2(1+{\gamma }_{g,k}^p(m))\le 0,\hfill & \forall k\in {\mathcal{G}}_g,\forall g\in \mathcal{G},\hfill \end{array}(\mathrm{23b})$

$\begin{array}{lll}{\bar{R}}_g^c-\frac{B}{M}\sum _{m=1}^M{\log }_2(1+{\gamma }_{g,k}^c(m))\le 0,\hfill & \hfill & \forall k\in {\mathcal{M}}_g,\forall g\in \mathcal{G}.\hfill \end{array}(\mathrm{23c})$

At this point, problem Eq. 23 is still non-convex. An additional burden is the dependency on the sample size M. Nevertheless, problem Eq. 23 now comprises the deterministic constraints Eq. 23b and Eq. 23c, which denote the SAA of Eq. 19e and Eq. 19f, respectively. Note that, in the asymptotic regime, the globally optimal solutions of problem Eq. 22 and problem Eq. 23 converge.

Theorem 1. For M → ∞ and in the asymptotic regime, the global optimal solution of problem Eq. 23 converges to the global optimal solution of problem Eq. 22, which is of stochastic nature.

Proof. Please refer to Supplementary Appendix SA.

Problem Eq. 23 is still non-convex and the current formulation works for full CSIT only. In more details, constraints Eq. 23b and Eq. 23c are dependent on the explicit definition of the SINR variables ${\gamma }_{g,k}^p(m)$ and ${\gamma }_{i,k}^c(m)$, respectively. Since these definitions include the channel vector h_k for all users, full CSIT is required here. To cope with the statistical CSIT scenario, problem Eq. 23 has to be further reformulated. Therefore, in the next subsection, we will investigate the mean square error (MSE) and find receiver coefficients to minimize the MSE. To that end, we establish a WMMSE-rate relationship to alleviate the current achievable rate constraints.

3.3 WMMSE Rate Relationship

The MSE for user k decoding the private message of its respective multicast group g can be defined as

$e_{g,k}^p=\mathbb{E}\left\{{\left|u_{g,k}^p\left(y_k-\sum _{j\in {\mathrm{\Phi }}_k}{\mathbf{h}}_k^H{\mathbf{w}}_j^c{s}_j^c\right)-s_g^p\right|}^2\right\}.(24)$

Here, $u_{g,k}^p$ is the linear receiver coefficient at k decoding g’s private message. The middle term in the parenthesis represents the received signal after canceling all common messages j decoded by user k, i.e., j ∈ Φ_k. In a similar manner, we define the MSE for user k decoding the common message of multicast group i as

$e_{i,k}^c=\mathbb{E}\left\{{\left|u_{i,k}^c\left(y_k-\sum _{m\in {\tilde{\mathrm{\Psi }}}_{i,k}}{\mathbf{h}}_k^H{\mathbf{w}}_m^c{s}_m^c\right)-s_i^c\right|}^2\right\},(25)$

where ${\tilde{\mathrm{\Psi }}}_{i,k}=\{m\in {\mathrm{\Phi }}_k|{\pi }_k(i)>{\pi }_k(m)\}$. Please note the difference between ${\tilde{\mathrm{\Psi }}}_{i,k}$ and Ψ_i,k. The former ${\tilde{\mathrm{\Psi }}}_{i,k}$ contains all multicast groups (indexed by m) whose common messages are decoded before decoding group i’s common message, i.e., groups having messages with lesser decoding order π_k(i) > π_k(m). That is, the common messages of these groups are not included in the received signal since they are already decoded. In contrast, Ψ_i,k includes groups whose common messages are yet to be decoded. Also, $u_{i,k}^c$ is k’s receiver coefficient decoding the common message of multicast group i. Utilizing the definition of y_k from Eq. 10, we can transform Eq. 24 and Eq. 25 into

$\begin{array}{ll}\hfill e_{g,k}^p& =|u_{g,k}^p{|}^2{T}_{g,k}^p-2\text{Re}\{u_{g,k}^p{\mathbf{h}}_k^H{\mathbf{w}}_g^p\}+1,\hfill \end{array}(26)$

$\begin{array}{ll}\hfill e_{i,k}^c& =|u_{i,k}^c{|}^2{T}_{i,k}^c-2\text{Re}\{u_{i,k}^c{\mathbf{h}}_k^H{\mathbf{w}}_i^c\}+1.\hfill \end{array}(27)$

Receiver coefficients that minimize the MSE can be found computing $\frac{\partial e_{g,k}^p}{\partial u_{g,k}^p}=0$ and $\frac{\partial e_{i,k}^c}{\partial u_{i,k}^c}=0$. To this end, we obtain the minimum MSE (MMSE) receiver coefficients

$\begin{array}{ll}\hfill u_{g,k,\text{mmse}}^p& ={({\mathbf{w}}_g^p)}^H{\mathbf{h}}_k/T_{g,k}^p,\hfill \end{array}(28)$

$\begin{array}{ll}\hfill u_{i,k,\text{mmse}}^c& ={({\mathbf{w}}_i^c)}^H{\mathbf{h}}_k/T_{i,k}^c.\hfill \end{array}(29)$

Hence, to obtain the MMSE terms, Eq. 28 and Eq. 29 are inserted into Eq. 26 and Eq. 27, respectively. The MMSE at user k decoding the private message of group g is $e_{g,k,\text{mmse}}^p=I_{g,k}^p/T_{g,k}^p$. Equivalently, $e_{i,k,\text{mmse}}^c=I_{i,k}^c/T_{i,k}^c$ denotes the MMSE at k decoding i’s common message. Next, we observe a specific relation between the achievable rate and the MMSE in a form that is amenable for the WMMSE-based algorithm.

Lemma 1. The achievable rates from Eq. 15 and Eq. 16 can be expressed in another from including the receiver coefficients, the error terms, and error weight variables as follows:

$\begin{array}{ll}\hfill {\log }_2(1+{\gamma }_{g,k}^p)& =\underset{u_{g,k}^p,{\rho }_{g,k}^p}{\text{max}}\left(\frac{\log ({\rho }_{g,k}^p)-{\rho }_{g,k}^p{e}_{g,k}^p+1}{\log (2)}\right),\forall k\in {\mathcal{G}}_g,\forall g\in \mathcal{G},\hfill \end{array}(30)$

$\begin{array}{ll}\hfill {\log }_2(1+{\gamma }_{g,k}^c)& =\underset{u_{g,k}^c,{\rho }_{g,k}^c}{\text{max}}\left(\frac{\log ({\rho }_{g,k}^c)-{\rho }_{g,k}^c{e}_{g,k}^c+1}{\log (2)}\right),\forall k\in {\mathcal{M}}_g,\forall g\in \mathcal{G}.\hfill \end{array}(31)$

Hereby, we introduce ${\rho }_{g,k}^p$ and ${\rho }_{g,k}^c$ as weights for the MSE terms.

Proof. The partial derivative of the right hand side of Eq. 30 w.r.t. $u_{g,k}^p$ is set to zero. We obtain the optimal receiver coefficient at k decoding g’s common message as ${(u_{g,k}^p)}^{*}=u_{g,k,\text{mmse}}^p$, which is the optimal MSE receiver coefficient from Eq. 28. The same procedure for the weight coefficient ${\rho }_{g,k}^p$ results in ${({\rho }_{g,k}^p)}^{*}=1/e_{g,k,\text{mmse}}^p$. Inserting the optimal coefficients into Eq. 30 results in the equivalence of the right hand and left hand side. To prove the equivalence in Eq. 31, the same procedure can be repeated. This completes the proof.

At this point, we obtain a formulation for the achievable rate, which helps in formulating the WMMSE-based algorithm. Note that, for full CSIT, we could now have started discussing the final algorithm. However, as we consider statistical CSIT, the achievable rate relations in Eq. 15 and Eq. 16 become nondeterministic functions. Therefore, we next elaborate on the expressions Eq. 30 and Eq. 31 in the context of statistical CSIT.

Due to the lack of channel coefficient knowledge, we cannot use the rate expressions Eq. 15 and Eq. 16. Hence, we define the achievability relations of the ergodic private and common rates in Eq. 17 and Eq. 18, respectively. In a similar manner, we reformulate Eq. 30 and Eq. 31 as follows:

$\begin{array}{ll}\hfill {\mathbb{E}}_{\mathbf{h}}\{{\log }_2(1+{\gamma }_{g,k}^p)\}& =\frac{1}{\log (2)}{\mathbb{E}}_{\mathbf{h}}\left\{\underset{u_{g,k}^p,{\rho }_{g,k}^p}{\text{max}}\left(\log ({\rho }_{g,k}^p)-{\rho }_{g,k}^p{e}_{g,k}^p+1\right)\right\},\forall k\in {\mathcal{G}}_g,\forall g\in \mathcal{G},\hfill \end{array}(32)$

$\begin{array}{ll}\hfill {\mathbb{E}}_{\mathbf{h}}\{{\log }_2(1+{\gamma }_{g,k}^c)\}& =\frac{1}{\log (2)}{\mathbb{E}}_{\mathbf{h}}\left\{\underset{u_{g,k}^c,{\rho }_{g,k}^c}{\text{max}}\left(\log ({\rho }_{g,k}^c)-{\rho }_{g,k}^c{e}_{g,k}^c+1\right)\right\},\forall k\in {\mathcal{M}}_g,\forall g\in \mathcal{G}.\hfill \end{array}(33)$

In the next subsection, we will describe the following reformulation steps and, to that end, state the WMMSE-based algorithm.

3.4 WMMSE-Based Algorithm

To substitute the WMMSE-rate relationship into the constraints Eq. 23b and Eq. 23c, we apply SAA to the formulations from Eq. 32 and Eq. 33, respectively. Thus, we can define the reformulated optimization problem as

$\begin{array}{ll}\hfill \underset{{\mathcal{V}}_2}{\text{max}}& \bar{R}\hfill \end{array}(\mathrm{34a})$

$\begin{array}{ll}\hfill \text{s.t.}& (19b),(19c),(19d),\hfill \\ \hfill & {\bar{R}}_g^p-\frac{B}{M}\sum _{m=1}^M\underset{u_{g,k}^p(m),{\rho }_{g,k}^p(m)}{\text{max}}\left(\frac{\log ({\rho }_{g,k}^p(m))-{\rho }_{g,k}^p(m)e_{g,k}^p(m)+1}{\log (2)}\right)\le 0,\hfill \\ \hfill & \forall k\in {\mathcal{G}}_g,\forall g\in \mathcal{G},\hfill \end{array}(\mathrm{34b})$

$\begin{array}{ll}\hfill & {\bar{R}}_g^c-\frac{B}{M}\sum _{m=1}^M\underset{u_{g,k}^c(m),{\rho }_{g,k}^c(m)}{\text{max}}\left(\frac{\log ({\rho }_{g,k}^c(m))-{\rho }_{g,k}^c(m)e_{g,k}^c(m)+1}{\log (2)}\right)\le 0,\hfill \\ \hfill & \forall k\in {\mathcal{M}}_g,\forall g\in \mathcal{G}.\hfill \end{array}(\mathrm{34c})$

Here, ${\mathcal{V}}_2\triangleq \left\{{\mathbf{w}}_g^p,{\mathbf{w}}_g^c,{\bar{R}}_g^p,{\bar{R}}_g^c,{\mathit{\rho }}_g^p,{\mathit{\rho }}_g^c,{\mathbf{u}}_g^p,{\mathbf{u}}_g^c|\forall g\in \mathcal{G}\right\}$ is the set of optimization variables. We explicitly introduce the MSE weights ${\mathit{\rho }}_g^p=\mathrm{v}\mathrm{e}\mathrm{c}(\left\{{\rho }_{g,k}^p(m)|\forall k\in {\mathcal{G}}_g,\forall g\in \mathcal{G},\forall m:1\le m\le M\right\})$ and ${\mathit{\rho }}_g^c=\mathrm{v}\mathrm{e}\mathrm{c}(\left\{{\rho }_{g,k}^c(m)|\forall k\in {\mathcal{M}}_g,\forall g\in \mathcal{G},\forall m:1\le m\le M\right\})$. Additionally, we introduce the receiver coefficients ${\mathbf{u}}_g^p=\mathrm{v}\mathrm{e}\mathrm{c}(\left\{u_{g,k}^p(m)|\forall k\in {\mathcal{G}}_g,\forall g\in \mathcal{G},\forall m:1\le m\le M\right\})$ as well as ${\mathbf{u}}_g^c=\mathrm{v}\mathrm{e}\mathrm{c}(\left\{u_{g,k}^c(m)|\forall k\in {\mathcal{M}}_g,\forall g\in \mathcal{G},\forall m:1\le m\le M\right\})$. The constraints Eq. 34b and Eq. 34c explicitly show the channel realization dependence of these variables.

Please note that problem Eq. 34 is convex if we fix the newly introduced variables $\{{\mathit{\rho }}_g^p,{\mathit{\rho }}_g^c,{\mathbf{u}}_g^p,{\mathbf{u}}_g^c\}$. Also, these variables can be computed for fixed $\{{\mathbf{w}}_g^p,{\mathbf{w}}_g^c,{\bar{R}}_g^p,{\bar{R}}_g^c\}$ using Eq. 28 and Eq. 29, as well as ${\rho }_{g,k}^p=1/e_{g,k,\text{mmse}}^p$ and ${\rho }_{i,k}^c=1/e_{i,k,\text{mmse}}^c$. Another advantage of the WMMSE formulation is that we can find a formulation for the optimization problem, which does not depend on the respective channel realization. To achieve such a reformulation, we first define the following set of variables for the WMMSE-based algorithm:

$\begin{array}{llll}\hfill {\bar{t}}_{g,k}^o& =\frac{1}{M}\sum _{m=1}^M{\rho }_{g,k}^o(m){\left|u_{g,k}^o(m)\right|}^2,\hfill & \hfill & o\in \{p,c\},\hfill \end{array}(35)$

$\begin{array}{llll}\hfill {\bar{z}}_{g,k}^o& =\frac{1}{M}\sum _{m=1}^M\left(1-{\rho }_{g,k}^o(m)+\log ({\rho }_{g,k}^o(m))\right),\hfill & \hfill & o\in \{p,c\},\hfill \end{array}(36)$

$\begin{array}{llll}\hfill {\bar{\mathbf{f}}}_{g,k}^o& =\frac{1}{M}\sum _{m=1}^M{\rho }_{g,k}^o(m){\mathbf{h}}_k^m{(u_{g,k}^o(m))}^H,\hfill & \hfill & o\in \{p,c\},\hfill \end{array}(37)$

$\begin{array}{llll}\hfill {\bar{\mathbf{Y}}}_{g,k}^o& =\frac{1}{M}\sum _{m=1}^M\left({\rho }_{g,k}^o(m){\left|u_{g,k}^o(m)\right|}^2{\mathbf{h}}_k^m{({\mathbf{h}}_k^m)}^H\right),\hfill & \hfill & o\in \{p,c\}.\hfill \end{array}(38)$

These auxiliary variables are fixed during optimization, but they are updated after each iteration. The resulting optimization problem utilizing the variables from Eq. 35–Eq. 38 is then given by

$\begin{array}{ll}\hfill \underset{{\mathcal{V}}_1}{\text{max}}& \bar{R}\hfill \end{array}(\mathrm{39a})$

$\begin{array}{ll}\hfill \text{s.t.}& (19b),(19c),(19d),\hfill \\ \hfill & \sum _{j\in \mathcal{G}}{({\mathbf{w}}_j^p)}^H{\bar{\mathbf{Y}}}_{g,k}^p{\mathbf{w}}_j^p+\sum _{l\in {\mathrm{\Omega }}_k}{({\mathbf{w}}_l^c)}^H{\bar{\mathbf{Y}}}_{g,k}^p{\mathbf{w}}_l^c-2\text{Re}\{{({\bar{\mathbf{f}}}_{g,k}^p)}^H{\mathbf{w}}_g^p\}\hfill \\ \hfill & +\frac{\log (2)}{B}{\bar{R}}_g^p+{\sigma }^2{\bar{t}}_{g,k}^p-{\bar{z}}_{g,k}^p\le 0,\forall k\in {\mathcal{G}}_g,\forall g\in \mathcal{G},\hfill \end{array}(\mathrm{39b})$

$\begin{array}{ll}\hfill & \sum _{j\in \mathcal{G}}{({\mathbf{w}}_j^p)}^H{\bar{\mathbf{Y}}}_{g,k}^c{\mathbf{w}}_j^p+\sum _{l\in {\mathrm{\Omega }}_k}{({\mathbf{w}}_l^c)}^H{\bar{\mathbf{Y}}}_{g,k}^c{\mathbf{w}}_l^c+\sum _{m\in {\mathrm{\Psi }}_{g,k}}{({\mathbf{w}}_m^c)}^H{\bar{\mathbf{Y}}}_{g,k}^c{\mathbf{w}}_m^c\hfill \\ \hfill & +{({\mathbf{w}}_g^c)}^H{\bar{\mathbf{Y}}}_{g,k}^c{\mathbf{w}}_g^c-2\text{Re}\{{({\bar{\mathbf{f}}}_{g,k}^c)}^H{\mathbf{w}}_g^c\}+\frac{\log (2)}{B}{\bar{R}}_g^c\hfill \\ \hfill & +{\sigma }^2{\bar{t}}_{g,k}^c-{\bar{z}}_{g,k}^c\le 0,\forall k\in {\mathcal{M}}_g,\forall g\in \mathcal{G}.\hfill \end{array}(\mathrm{39c})$

Note that the set of optimization variables is now reduced to the set ${\mathcal{V}}_1$. Problem Eq. 39 is a convex optimization problem and thus amenable for solving using standard tools [e.g., CVX (Grant and Boyd, 2014)]. An advantage of problem Eq. 39 is the independence of the Monte-Carlo sample size M, which pronounces the computational complexity advantage of this solution compared to the state-of-the-art algorithms. Typically, M has to be very large in order for the SAA to be an accurate approximation. In order to find a stationary solution to Eq. 39, Algorithm 2 lists detailed steps for the WMMSE-based optimization to maximize the minimum achievable rate of all multicast groups.

Algorithm 2 starts by initializing each multicast group’s beamforming vectors, i.e., ${\mathbf{w}}_g^p$ and ${\mathbf{w}}_g^c$, to feasible values. Additionally, the algorithm generates M channel vector samples for the SAA. The following steps are repeated until convergence. First, the set of auxiliary variables $\{{\bar{t}}_{g,k}^o,{\bar{z}}_{g,k}^o,{\bar{\mathbf{f}}}_{g,k}^o,{\bar{\mathbf{Y}}}_{g,k}^o|o\in \{p,c\}\}$ is updated according to equations Eqs. 35–38. Then, the algorithm solves problem Eq. 39 using CVX (Grant and Boyd, 2014). The following theorem relates Algorithm 2, which iteratively solves problem Eq. 39 and problem Eq. 34.

Theorem 2. The solution${\mathrm{\Psi }}_{\nu }=\{{\mathbf{w}}_g^o,{\bar{R}}_g^o,{\mathit{\rho }}_g^o,{\mathbf{u}}_g^o,|\forall g\in \mathcal{G},\forall o\in \{p,c\}\}$is generated byAlgorithm 2in iterationν. The sequence${\{{\mathrm{\Psi }}_{\nu }\}}_{\nu =1}^{\infty }$converges to a KKT point of problem Eq. 34.Proof. Please refer to Supplementary Appendix SB.Note that our reformulated optimization problem Eq. 39 is independent of the sample size M. In every iteration of Algorithm 2, we first update parameters that depend on M using equations Eqs. 35–38, and then we solve problem Eq. 39 which is independent of M. Integrating different approaches such as stochastic successive convex approximation are left open for future works.

. Algorithm 2 WMMSE-based Minimum Achievable Rate Maximization

3.5 Complexity Analysis

In this subsection, we are interested in the overall computational complexity of Algorithm 2. This overall complexity mainly depends on two factors: 1) the complexity of problem Eq. 39; 2) the solution accuracy of the iterative procedure. Update step 3 of Algorithm 2, which essentially updates the beamforming vectors and the allocated rates and solves the quadratic constrained convex optimization problem (QCCP) Eq. 39. In order to state the worst-case computational complexity for Algorithm 2, we first need to determine the number of constraints and variables. There are $d_1=2N+G+{\sum }_{g\in \mathcal{G}}|{\mathcal{G}}_g|+{\sum }_{g\in \mathcal{G}}|{\mathcal{M}}_g|$ constraints, with $|{\mathcal{M}}_g|$ being the cardinality of ${\mathcal{M}}_g$, and d₂ = (2G (NL + 1)) variables. The complexity metric of problem Eq. 39 becomes $\mathcal{O}((d_1{d}_2^2+d_2^3)\sqrt{d_1}\log (1/ϵ))$, for given solution accuracy ϵ.

4 Numerical Simulations

In this section, numerical simulations illustrating the performance of our proposed scheme, compared to TIN and the SCM-RSMA scheme, are conducted. We consider a cache-enabled C-RAN over a square area of (−400 400) × (−400 400) m². Unless specified otherwise, we set the maximum transmit power to $P_n^{\text{max}}=28$ dBm and the total number of files in the library to F = 50. The noise spectral density is assumed to be −168 dBm/Hz. Also, we set the Monte-Carlo sample size to M = 1,000 and the parameter for Algorithm 1 to $A_n^{\text{max}}=8,\forall n\in \mathcal{N}$. The channel model used for our simulations is given as follows (Shi et al., 2014):

${\mathbf{h}}_{n,k}=D_{n,k}{\mathbf{e}}_{n,k},(40)$

with

$D_{n,k}=10^{-{\text{PL}}_{n,k}/20}\sqrt{g_{n,k}{s}_{n,k}}.(41)$

Here, g_n,k is the shadowing coefficient, s_n,k is the antenna gain, and PL_n,k defines the path loss between BS n and user k given by

${\text{PL}}_{n,k}=148.1+37.6{\log }_{10}(d_{n,k}),(42)$

where d_b,k is the distance in km between BS b and user k. The small-fading coefficients ${\mathbf{e}}_{n,k}\in {\mathbb{C}}^{L\times 1}$ are modeled as ${\mathbf{e}}_{n,k}\sim \mathcal{CN}\left(0,{\mathbf{I}}_L\right)$. This paper distinguishes between two cases: 1) full CSIT, where the CP has perfect channel knowledge, i.e., the vector h_n,k is known; 2) statistical CSIT, where the CP can only perfectly estimate the large-fading coefficient D_n,k, whereas the small-fading coefficient e_n,k is unknown.

As baseline schemes, we deploy two different approaches contrary to the proposed RS-CMD scheme. As the most basic scheme, TIN is used allowing only private streams to be transmitted. More specifically, the data for each multicast group are encoded into a private stream and then transmitted by the respective serving BSs. As every user in a multicast group only decodes their group’s private message, the rest of the streams are treated as noise. The second baseline scheme, referred to as SCM-RSMA, is based on the concept of (Joudeh and Clerckx, 2016b). In (Joudeh and Clerckx, 2016b), the authors propose an RSMA scheme using one common stream, which is then decoded by all users in the network. More specifically, there are G + 1 streams to be transmitted, one for every multicast group, i.e., the private streams, and one mutual stream to be decoded by all groups, i.e., the common stream.

4.1 MMF Rate vs. Fronthaul Capacity

In this setup, we consider a C-RAN consisting of 7 BSs and 15 users that are randomly placed throughout the network with uniform distribution. The BSs are equipped with L = 2 transmit antennas. The cache memory size is considered to be five files at each BS (10% of the total files).

Figure 3A shows the performance of all studied schemes as a function of the fronthaul capacity in Mbps for statistical CSIT. A general observation from Figure 3A is that our proposed RSMA scheme attains significant gain in terms of the achievable minimum rate, especially in the low fronthaul capacity regime. Specifically, in Figure 3A, the gain compared to conventional TIN is 63.85% when the fronthaul capacity per BS is equal to 20 Mbps and 29.69% when the fronthaul capacity is increased to 70 Mbps. By mitigating the interference more efficiently using RS-CMD, our proposed scheme achieves higher minimum rates compared to both reference schemes. Moreover, when the fronthaul capacity is 30 Mbps and higher, SCM-RSMA performs better than the conventional TIN scheme. These results clearly highlight the need for utilizing RSMA schemes in order to achieve a higher minimum rate. That is, RSMA assists the network to better ensure fairness among all users, especially using the proposed RS-CMD scheme.

FIGURE 3

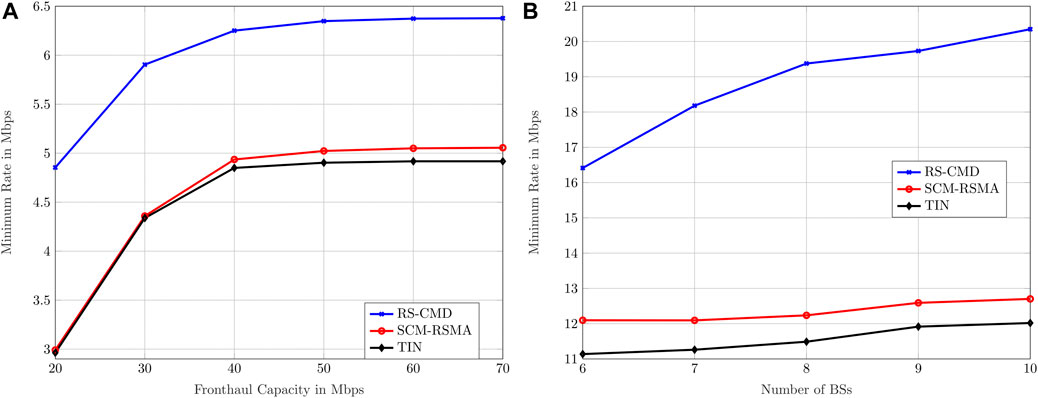
FIGURE 3. MMF rate as a function of different parameters. We consider the proposed RS-CMD scheme, the reference SCM-RSMA, and TIN. (A) shows the MMF rate vs. fronthaul capacity for statistical CSIT. (B) shows the MMF rate vs. number of BSs for full CSIT.

4.2 Minimum Achievable Rate Under Full CSIT

For the following set of simulations, we design a network with 15 users, a fronthaul capacity of 80 Mbps, 5-file cache size, and L = 2 antennas at each BS. The number of BSs controlled by the CP is the parameter under study; we vary the total BSs from 6 to 10.

The minimum achievable rate is plotted as a function of the number of users in Figure 3B. Consistent with the results from Subsection 4.1, our proposed scheme outperforms TIN and SCM-RSMA significantly. This gain is especially substantial when the number of BSs is high.

In contrast to the statistical CSIT case, in Figure 3B, we observe greater gains of SCM-RSMA over TIN, as well as greater gains of our proposed RS-CMD scheme over both baselines. Full knowledge of CSIT obviously results in better rates and thus better performance of all schemes.

4.3 Impact of Caching on the MMF Rate

In another set of simulations, we focus on the impact of different cache sizes on the achievable minimum rate using the RS-CMD scheme in the statistical CSIT scenario. Except for the different cache sizes, the network under consideration does not differ from Subsection 4.1.

In Figure 4A, we fix the cache size to different values, i.e., {0, 5, … , 25} files, and plot the achievable minimum rate for different fronthaul capacities. Matching with previous results, the minimum achievable rate increases with fronthaul capacity. First, in Figure 4A, we observe the gap between the graphs, i.e., the caching gain. Especially in low fronthaul regimes, the MMF rate is better when bigger caches are utilized since the fronthaul capacity is limited and thus transmitting data from the CP to the BSs is a sensible operation. A cache hit reduces the congestion on the fronthaul links.

FIGURE 4

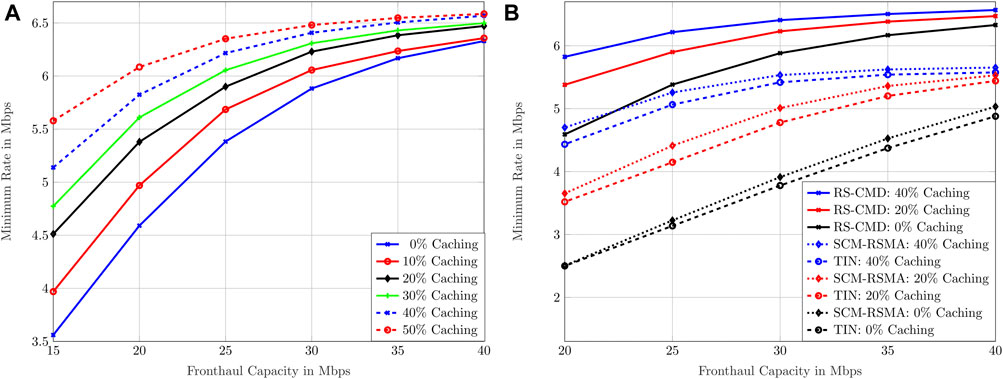
FIGURE 4. MMF rate as a function of the fronthaul capacity for the statistical CSIT case. We consider the impact of different cache sizes. (A) considers RS-CMD only. (B) depicts a comparison between the schemes.

Another major observation in Figure 4A is the decrease in caching gain with increasing fronthaul capacity; i.e., the gap between the graphs is decreasing. When a high quantity of fronthaul capacity is available, the importance of using caching lowers. As the fronthaul links are barely congested, there is no need to alleviate the congestion with cache hits. Since low fronthaul regimes are more common in practice, the results herein pronounce the role of caching in the proposed system model as a means to increase the MMF rate among the multicast groups.

In Figure 4B, we show the MMF rate of RS-CMD, SCM-RSMA, and TIN as a function of the fronthaul capacity. A comparison is conducted for three different cache sizes, i.e., {0, 20, 40} files per BS ({0, 10, 20}% of the total files). Generally, RS-CMD outperforms TIN and SCM-RSMA. Interestingly, the performance gain of RS-CMD over the benchmarks changes with different cache sizes. At 25 Mbps fronthaul capacity, RS-CMD gains 18.25, 33.79, and 67.08% over SCM-RSMA with 20, 10, and 0 files in the cache, respectively. In contrast, at 40 Mbps fronthaul capacity, RS-CMD gains 16.28, 16.99, and 25.84% over SCM-RSMA with 20, 10, and 0 files in the cache, respectively. RS-CMD significantly outperforms TIN and SCM-RSMA at low fronthaul regimes with small cache sizes.

4.4 Influence of Transmit Antennas on the MMF Rate

In order to investigate the influence of different amounts of transmit antennas at the BSs on the MMF rate among all multicast groups, we conduct the next set of simulations. We consider the same network as in Subsection 4.1.

The minimum achievable rate as a function of the fronthaul capacity for L ∈{1, … , 5} antennas is shown in Figure 5. As expected, we observe higher rates when utilizing more transmit antennas at the BSs. Interestingly, especially in high fronthaul capacity regimes, the minimum rate of the single-antenna system is considerably lower than the MMF rate in all other networks. This highlights the need for utilizing multiple antennas in the proposed cache-aided C-RAN with the multigroup multicast transmission scheme.

FIGURE 5

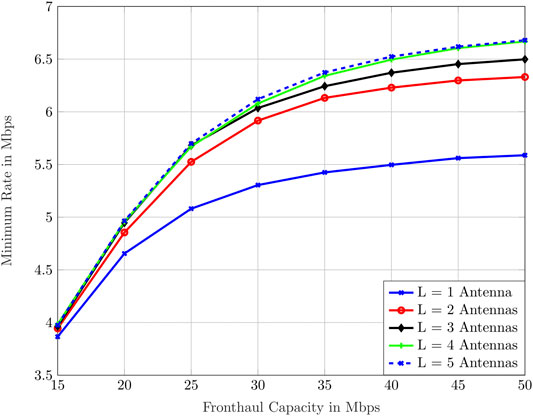
FIGURE 5. MMF rate as a function of the fronthaul capacity for the statistical CSIT case. We consider different numbers of transmit antennas at the BSs.

Another observation in Figure 5 is the similarity of the minimum achievable rate associated with 4- versus 5-antenna per BS system. Throughout all fronthaul capacities, the rate of the 5-antenna system achieves only minor gains over the 4-antenna system. Therefore, considering the herein defined network parameters, using more than four antennas to increase the minimum achievable rate is not a viable option. This is partially caused by power constraints at the BSs and partially by the fronthaul capacity constraints.

4.5 Comparison to a Simpler Transmission Scheme

Prior to introducing the next set of simulations, we present another state-of-the-art transmission scheme to be used as a performance reference. In this work, we group users into multicast groups based on their requested content; i.e., all users in a group receive the same private and common message. Many related works, e.g., (Ugur et al., 2016; Alameer and Sezgin, 2017), consider a special case of this scheme. More specifically, following the notations of this paper, each group comprises only one user. This is referred to as RS-CMD with G = K, while our proposed scheme is referred to as RS-CMD with G ≤ K.

Now, comparing our proposed multigroup multicast transmission scheme to the conventional scheme, in Figure 6A, we show the minimum achievable rate of all groups as a function of the number of users. The fronthaul capacity is fixed to 30 Mbps; we assume 7 BSs throughout the network and a cache memory size of 10 files (20% of the total files).

FIGURE 6

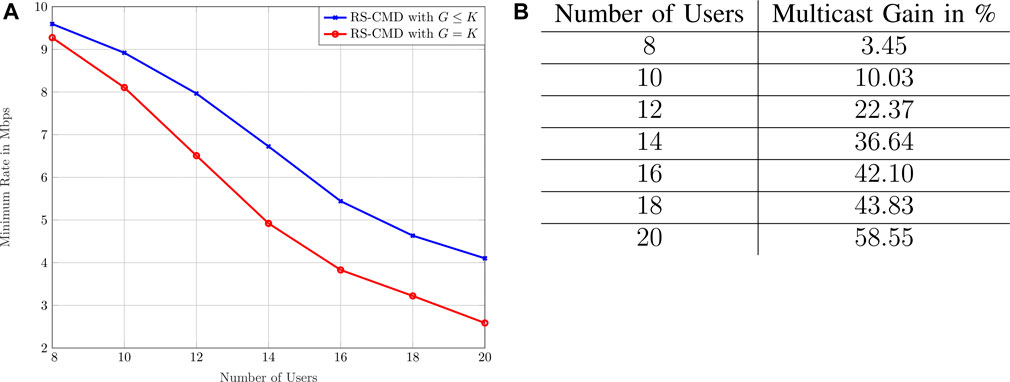
FIGURE 6. MMF rate versus the number of uses for the statistical CSIT case. We consider two different transmission schemes, i.e., RS-CMD with G ≤ K and G = K. (A) shows the MMF rate of RS-CMD with G ≤ K and G = K as a function of the number of users. (B) is the MMF rate gain of RS-CMD with G ≤ K and G = K in percent.

Generally, in Figure 6A, RS-CMD with G ≤ K outperforms RS-CMD with G = K. The performance gap is small when the number of users is low since multicast groups are more unlikely in this regime as the user requests are not coinciding with high probability. Note that RS-CMD with G ≤ K and with G = K are equal if no users request the same content.

As expected, the MMF rate among all groups decreases with the number of users for both schemes. Since the BSs serve additional users under the same power and fronthaul constraints, integrating more users into the same network reduces the MMF rate among the groups. Under RS-CMD with G ≤ K, these additional users may be included in an existing multicast group if they request the same content. Therefore, the proposed scheme suffers less MMF rate decrease as compared to RS-CMD with G = K; i.e., see Table 6b.

4.6 Convergence Behavior

To now illustrate the convergence behavior of our proposed Algorithm 2, we consider the same simulation parameters as in Section 4.5. Figure 7 shows the minimum achievable rate for RS-CMD with G ≤ K and G = K when the network consists of 12 and 14 users in every step of Algorithm 2 until convergence. Since the overall required iterations until convergence is relatively low, the results in Figure 7 exhibit the feature of the high execution speed of our proposed algorithm. Therefore, we observe good convergence behavior for the considered system model which further highlights another feature of the proposed algorithm.

FIGURE 7

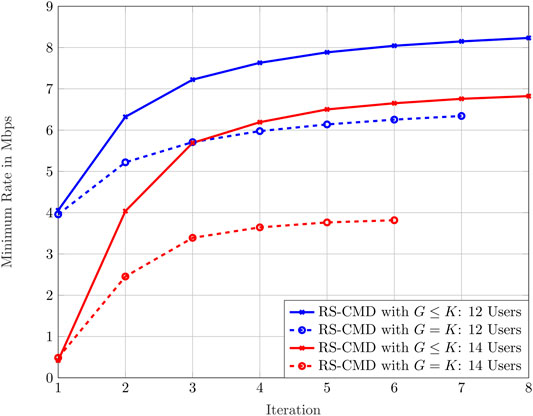
FIGURE 7. Convergence behavior of the proposed algorithm under statistical CSIT. Two different numbers of users are considered for RS-CMD with G ≤ K and G = K.

5 Conclusion

Handling the sophisticated requirements of B5G wireless communication networks is a difficult task. To tackle this task, this paper proposed a promising RSMA-assisted cache-enabled C-RAN under a multigroup multicast scenario. The proposed framework considers a more practical scenario where the CP and BSs operate under statistical CSIT. We aimed at designing the precoders and BS clustering with the aim of maximizing the minimum achievable rate among the multicast groups. The optimization problem is tackled by a novel multicast group-based clustering approach, as well as an effective algorithm based on SAA and WMMSE. Extensive numerical simulations showed the significant max-min rate gain of the proposed RSMA framework over the existing benchmarks in cache-aided C-RAN with various fronthaul capacities and cache sizes. Therefore, we conclude that RSMA has a great potential to enhance user fairness and spectral efficiency in cache-aided C-RAN.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

R-JR: substantial contributions to the conception or design of the work or the acquisition, analysis, or interpretation of data for the work; AA: substantial contributions to the conception or design of the work or the acquisition, analysis, or interpretation of data for the work; YM: substantial contributions to the conception or design of the work or the acquisition, analysis, or interpretation of data for the work; AS: revising it critically for important intellectual content; providing approval for publication of the content; BC: revising it critically for important intellectual content; providing approval for publication of the content.

Funding

This work has been partially funded by the Federal Ministry of Education and Research (BMBF) of the Federal Republic of Germany (Förderkennzeichen 01IS18063A, ReMiX) and by the U.K. Engineering and Physical Sciences Research Council (EPSRC) under grants EP/N015312/1 and EP/R511547/1.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frcmn.2021.716620/full#supplementary-material

Footnotes

¹We ignore the fronthaul bandwidth required to support the transmission of beamforming coefficients and we only consider the capacity required to deliver the encoded streams to the BSs in the serving cluster.

References

Ahmad, A. A., Mao, Y., Sezgin, A., and Clerckx, B. (2020a). “Rate Splitting Multiple Access in C-RAN,” in 2020 IEEE 31st Annual International Symposium on Personal, Dublin, Ireland, June 7–11, 2020, Indoor Mobile Radio Commun., 1–6.

CrossRef Full Text | Google Scholar

Ahmad, A. A., Dahrouj, H., Chaaban, A., Sezgin, A., Al-Naffouri, T. Y., and Alouini, M.-S. (2020b). “Power Minimization via Rate Splitting in Downlink Cloud-Radio Access Networks,” in 2020 IEEE International Conference on Communications Workshops, Dublin, Ireland, June 7–11, 2020 (New York: IEEE), 1–6. doi:10.1109/iccworkshops49005.2020.9145363

CrossRef Full Text | Google Scholar

Ahmad, A. A., Mao, Y., Sezgin, A., and Clerckx, B. (2020b). Rate Splitting Multiple Access in C-RAN: A Scalable and Robust Design. IEEE Trans. Commun. 1. doi:10.1109/TCOMM.2021.3085343

CrossRef Full Text | Google Scholar

Ahmad, A. A., Matthiesen, B., Sezgin, A., and Jorswieck, E. (2020c). “Energy Efficiency in C-RAN Using Rate Splitting and Common Message Decoding,” in 2020 IEEE International Conference on Communications Workshops, London, United Kingdom, August 31–September 3, 2020 (New York: ICC Workshops), 1–6.

CrossRef Full Text | Google Scholar

Alameer Ahmad, A., Dahrouj, H., Chaaban, A., Sezgin, A., and Alouini, M.-S. (2019). Interference Mitigation via Rate-Splitting and Common Message Decoding in Cloud Radio Access Networks. IEEE Access 7, 80350–80365. doi:10.1109/access.2019.2921626

CrossRef Full Text | Google Scholar

Alameer, A., and Sezgin, A. (2017). “Resource Cost Balancing with Caching in C-RAN,” in 2017 IEEE Wireless Communications and Networking Conference, San Francisco, CA, United States, March 19–22, 2017 (New York: WCNC), 1–6.

CrossRef Full Text | Google Scholar

Bandemer, B., Sezgin, A., and Paulraj, A. (2008). “On the Noisy Interference Regime of the MISO Gaussian Interference Channel,” in 2008 42nd Asilomar Conference on Signals, Pacific Grove, CA, United States, October 26–29, 2008, Syst. Comput., 1098–1102.

CrossRef Full Text | Google Scholar

Boyd, S., and Vandenberghe, L. (2004). Convex Optimization. Cambridge University Press.

Caire, G., and Kumar, K. R. (2007). Information Theoretic Foundations of Adaptive Coded Modulation. Proc. IEEE 95 (12), 2274–2298. doi:10.1109/jproc.2007.904444

CrossRef Full Text | Google Scholar

Carleial, A. (1978). Interference Channels. IEEE Trans. Inform. Theor. 24 (1), 60–70. doi:10.1109/tit.1978.1055812

CrossRef Full Text | Google Scholar

Charafeddine, M. A., Sezgin, A., Han, Z., and Paulraj, A. (2012). Achievable and Crystallized Rate Regions of the Interference Channel with Interference as Noise. IEEE Trans. Wireless Commun. 11 (3), 1100–1111. doi:10.1109/twc.2012.010312.110497

CrossRef Full Text | Google Scholar

Chen, M., Mozaffari, M., Saad, W., Yin, C., Debbah, M., and Hong, C. S. (2017). Caching in the Sky: Proactive Deployment of Cache-Enabled Unmanned Aerial Vehicles for Optimized Quality-Of-Experience. IEEE J. Select. Areas Commun. 35 (5), 1046–1061. doi:10.1109/jsac.2017.2680898

CrossRef Full Text | Google Scholar

Christopoulos, D., Chatzinotas, S., and Ottersten, B. (2015). Multicast Multigroup Precoding and User Scheduling for Frame-Based Satellite Communications. IEEE Trans. Wireless Commun. 14 (9), 4695–4707. doi:10.1109/twc.2015.2424961

CrossRef Full Text | Google Scholar

Clerckx, B., Joudeh, H., Hao, C., Dai, M., and Rassouli, B. (2016). Rate Splitting for MIMO Wireless Networks: a Promising PHY-Layer Strategy for LTE Evolution. IEEE Commun. Mag. 54 (5), 98–105. doi:10.1109/mcom.2016.7470942

CrossRef Full Text | Google Scholar

Clerckx, B., Mao, Y., Schober, R., and Poor, H. V. (2020). Rate-splitting Unifying SDMA, OMA, NOMA, and Multicasting in MISO Broadcast Channel: A Simple Two-User Rate Analysis. IEEE Wireless Commun. Lett. 9 (3), 349–353. doi:10.1109/lwc.2019.2954518

CrossRef Full Text | Google Scholar

Cui, W., Shen, K., and Yu, W. (2019). Spatial Deep Learning for Wireless Scheduling. IEEE J. Select. Areas Commun. 37 (6), 1248–1261. doi:10.1109/jsac.2019.2904352

CrossRef Full Text | Google Scholar

Dahrouj, H., and Yu, W. (2011). Multicell Interference Mitigation with Joint Beamforming and Common Message Decoding. IEEE Trans. Commun. 59 (8), 2264–2273. doi:10.1109/tcomm.2011.060911.100554

CrossRef Full Text | Google Scholar

Dai, M., Clerckx, B., Gesbert, D., and Caire, G. (2016). A Rate Splitting Strategy for Massive MIMO with Imperfect CSIT. IEEE Trans. Wireless Commun. 15 (7), 4611–4624. doi:10.1109/twc.2016.2543212

CrossRef Full Text | Google Scholar

Ericsson mobility report november (2020). Ericson, Tech. Rep. [Online]. Available: https://www.ericsson.com/en/mobility-report/reports/november-2020 Nov, 2020).

Google Scholar

Etkin, R. H., Tse, D. N. C., and Wang, H. (2008). Gaussian Interference Channel Capacity to within One Bit. IEEE Trans. Inform. Theor. 54 (12), 5534–5562. doi:10.1109/tit.2008.2006447

CrossRef Full Text | Google Scholar

Goldsmith, A. (2005). Wireless Communications. Cambridge, United Kingdom: Cambridge University Press.

Golrezaei, N., Molisch, A. F., Dimakis, A. G., and Caire, G. (2013). Femtocaching and Device-To-Device Collaboration: A New Architecture for Wireless Video Distribution. IEEE Commun. Mag. 51 (4), 142–149. doi:10.1109/mcom.2013.6495773

CrossRef Full Text | Google Scholar

Grant, M., and Boyd, S. (2014). CVX: Matlab Software for Disciplined Convex Programming. version 2.1. [Online]. Available: http://cvxr.com/cvx.

Hassibi, B., and Hochwald, B. M. (2003). How Much Training Is Needed in Multiple-Antenna Wireless Links? IEEE Trans. Inform. Theor. 49 (4), 951–963. doi:10.1109/tit.2003.809594

CrossRef Full Text | Google Scholar

Joroughi, V., Vázquez, M. A., and Pérez-Neira, A. I. (2017). Generalized Multicast Multibeam Precoding for Satellite Communications. IEEE Trans. Wireless Commun. 16 (2), 952–966. doi:10.1109/twc.2016.2635139

CrossRef Full Text | Google Scholar

Joudeh, H., and Clerckx, B. (2017). Rate-splitting for max-min Fair Multigroup Multicast Beamforming in Overloaded Systems. IEEE Trans. Wireless Commun. 16 (11), 7276–7289. doi:10.1109/twc.2017.2744629

CrossRef Full Text | Google Scholar

Joudeh, H., and Clerckx, B. (2016). Robust Transmission in Downlink Multiuser MISO Systems: A Rate-Splitting Approach. IEEE Trans. Signal. Process. 64 (23), 6227–6242. doi:10.1109/tsp.2016.2591501

CrossRef Full Text | Google Scholar

Joudeh, H., and Clerckx, B. (2016). Sum-rate Maximization for Linearly Precoded Downlink Multiuser MISO Systems with Partial CSIT: A Rate-Splitting Approach. IEEE Trans. Commun. 64 (11), 4847–4861. doi:10.1109/tcomm.2016.2603991

CrossRef Full Text | Google Scholar

Kakar, J., Alameer Ahmad, A., Chaaban, A., Sezgin, A., and Paulraj, A. (2019). Cache-assisted Broadcast-Relay Wireless Networks: A Delivery-Time Cache-Memory Tradeoff. IEEE Access 7, 76833–76858. doi:10.1109/access.2019.2921243

CrossRef Full Text | Google Scholar

Karipidis, E., Sidiropoulos, N. D., and Luo, Z.-Q. (2008). Quality of Service and max-min Fair Transmit Beamforming to Multiple Cochannel Multicast Groups. IEEE Trans. Signal. Process. 56 (3), 1268–1279. doi:10.1109/tsp.2007.909010

CrossRef Full Text | Google Scholar

Li, Z., Ye, C., Cui, Y., Yang, S., and Shamai, S. (2020). Rate Splitting for Multi-Antenna Downlink: Precoder Design and Practical Implementation. IEEE J. Select. Areas Commun. 38 (8), 1910–1924. doi:10.1109/jsac.2020.3000824

CrossRef Full Text | Google Scholar

Liu, J., Bai, B., Zhang, J., and Letaief, K. B. (2017). Cache Placement in Fog-RANs: From Centralized to Distributed Algorithms. IEEE Trans. Wireless Commun. 16 (11), 7039–7051. doi:10.1109/twc.2017.2737015

CrossRef Full Text | Google Scholar

Liu, L., and Yu, W. (2017). Cross-layer Design for Downlink Multihop Cloud Radio Access Networks with Network Coding. IEEE Trans. Signal. Process. 65 (7), 1728–1740. doi:10.1109/tsp.2017.2649486

CrossRef Full Text | Google Scholar

Love, D., Heath, R., N. Lau, V., Gesbert, D., Rao, B., and Andrews, M. (2008). An Overview of Limited Feedback in Wireless Communication Systems. IEEE J. Select. Areas Commun. 26 (8), 1341–1365. doi:10.1109/jsac.2008.081002

CrossRef Full Text | Google Scholar

Maddah-Ali, M. A., and Niesen, U. (2016). Coding for Caching: Fundamental Limits and Practical Challenges. IEEE Commun. Mag. 54 (8), 23–29. doi:10.1109/mcom.2016.7537173

CrossRef Full Text | Google Scholar

Maddah-Ali, M. A., and Niesen, U. (2014). Fundamental Limits of Caching. IEEE Trans. Inform. Theor. 60 (5), 2856–2867. doi:10.1109/tit.2014.2306938

CrossRef Full Text | Google Scholar

Mao, Y., and Clerckx, B. (2020). Beyond Dirty Paper Coding for Multi-Antenna Broadcast Channel with Partial CSIT: A Rate-Splitting Approach. IEEE Trans. Commun. 68 (11), 6775–6791. doi:10.1109/tcomm.2020.3014153

CrossRef Full Text | Google Scholar

Mao, Y., Clerckx, B., and Li, V. O. K. (2019). Rate-splitting for Multi-Antenna Non-orthogonal Unicast and Multicast Transmission: Spectral and Energy Efficiency Analysis. IEEE Trans. Commun. 67 (12), 8754–8770. doi:10.1109/tcomm.2019.2943168

CrossRef Full Text | Google Scholar

Mao, Y., Clerckx, B., and Li, V. O. K. (2018). Rate-splitting Multiple Access for Downlink Communication Systems: Bridging, Generalizing, and Outperforming SDMA and NOMA. J. Wireless Com Netw. 2018 (1), 133. doi:10.1186/s13638-018-1104-7 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Mei, W., Chen, Z., Li, L., Fang, J., and Li, S. (2017). On Artificial-Noise-Aided Transmit Design for Multiuser MISO Systems with Integrated Services. IEEE Trans. Veh. Technol. 66 (9), 8179–8195. doi:10.1109/tvt.2017.2676244

CrossRef Full Text | Google Scholar

Park, S.-H., Simeone, O., Sahin, O., and Shamai, S. (2013). Joint Precoding and Multivariate Backhaul Compression for the Downlink of Cloud Radio Access Networks. IEEE Trans. Signal. Process. 61 (22), 5646–5658. doi:10.1109/tsp.2013.2280111

CrossRef Full Text | Google Scholar

Patil, P., Dai, B., and Yu, W. (2018). Hybrid Data-Sharing and Compression Strategy for Downlink Cloud Radio Access Network. IEEE Trans. Commun. 66 (11), 5370–5384. doi:10.1109/tcomm.2018.2842758

CrossRef Full Text | Google Scholar

Piovano, E., and Clerckx, B. (2017). Optimal DoF Region of the $K$ -User MISO BC with Partial CSIT. IEEE Commun. Lett. 21 (11), 2368–2371. doi:10.1109/lcomm.2017.2724553

CrossRef Full Text | Google Scholar

Piovano, E., Joudeh, H., and Clerckx, B. (2019). Generalized Degrees of freedom of the Symmetric Cache-Aided MISO Broadcast Channel with Partial CSIT. IEEE Trans. Inf. Theor. 65 (9), 5799–5815. doi:10.1109/tit.2019.2914204

CrossRef Full Text | Google Scholar

Piovano, E., Joudeh, H., and Clerckx, B. (2017). “On Coded Caching in the Overloaded MISO Broadcast Channel,” in IEEE International Symposium on Information Theory, Aachen, Germany, June 25–30, 2017 (New York: ISIT), 2795–2799. doi:10.1109/isit.2017.8007039

CrossRef Full Text | Google Scholar

Quek, T. Q. S., Peng, M., Simeone, O., and Yu, W. (2017). Cloud Radio Access Networks: Principles, Technologies, and Applications. Cambridge, United Kingdom: Cambridge University Press.

Razaviyayn, M., Hong, M., and Luo, Z. (2011). “Linear Transceiver Design for a MIMO Interfering Broadcast Channel Achieving max-min Fairness,” in 2011 Conference Record of the Forty Fifth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, United States, November 6–9, 2011 (New York: ASILOMAR), 1309–1313.

CrossRef Full Text | Google Scholar

Saad, W., Bennis, M., and Chen, M. (2020). A Vision of 6G Wireless Systems: Applications, Trends, Technologies, and Open Research Problems. IEEE Netw. 34 (3), 134–142. doi:10.1109/mnet.001.1900287

CrossRef Full Text | Google Scholar

Shanmugam, K., Golrezaei, N., Dimakis, A. G., Molisch, A. F., and Caire, G. (2013). FemtoCaching: Wireless Content Delivery through Distributed Caching Helpers. IEEE Trans. Inform. Theor. 59 (12), 8402–8413. doi:10.1109/tit.2013.2281606

CrossRef Full Text | Google Scholar

Shapiro, D. D. A., and Ruszczyński, A. P. (2009). Lectures on Stochastic Programming: Modeling and Theory. PA, USA: SIAM.

Shi, Y., Zhang, J., and Letaief, K. B. (2014). Group Sparse Beamforming for green Cloud-RAN. IEEE Trans. Wireless Commun. 13 (5), 2809–2823. doi:10.1109/twc.2014.040214.131770

CrossRef Full Text | Google Scholar

Sidiropoulos, N. D., Davidson, T. N., and Zhi-Quan Luo, Z.-Q. (2006). Transmit Beamforming for Physical-Layer Multicasting. IEEE Trans. Signal. Process. 54 (6), 2239–2251. doi:10.1109/tsp.2006.872578

CrossRef Full Text | Google Scholar

Tao, M., Chen, E., Zhou, H., and Yu, W. (2016). Content-centric Sparse Multicast Beamforming for Cache-Enabled Cloud RAN. IEEE Trans. Wireless Commun. 15 (9), 6118–6131. doi:10.1109/twc.2016.2578922

CrossRef Full Text | Google Scholar

Te Han, T., and Kobayashi, K. (1981). A New Achievable Rate Region for the Interference Channel. IEEE Trans. Inform. Theor. 27 (1), 49–60. doi:10.1109/tit.1981.1056307

CrossRef Full Text | Google Scholar

Tervo, O., Trant, L.-N., Chatzinotas, S., Ottersten, B., and Juntti, M. (2018). “Multigroup Multicast Beamforming and Antenna Selection with Rate-Splitting in Multicell Systems,” in IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications, Kalamata, Greece, June 25–28, 2018 (New York: SPAWC), 1–5.

CrossRef Full Text | Google Scholar

Tse, D., and Viswanath, P. (2005). Fundamentals of Wireless Communication. Cambridge University Press.

Ugur, Y., Awan, Z. H., and Sezgin, A. (2016). “Cloud Radio Access Networks with Coded Caching,” in WSA 2016; 20th International ITG Workshop on Smart Antennas, Munich, Germany, March 9–11, 2016, 1–5.

Google Scholar

Wei Yu, B., and Yu, W. (2014). Sparse Beamforming and User-Centric Clustering for Downlink Cloud Radio Access Network. IEEE Access 2, 1326–1339. doi:10.1109/access.2014.2362860

CrossRef Full Text | Google Scholar

Yang, P., Xiao, Y., Xiao, M., and Li, S. (2019). 6G Wireless Communications: Vision and Potential Techniques. IEEE Netw. 33 (4), 70–75. doi:10.1109/mnet.2019.1800418

CrossRef Full Text | Google Scholar

Ye, Z., Pan, C., Zhu, H., and Wang, J. (2018). Tradeoff Caching Strategy of the Outage Probability and Fronthaul Usage in a Cloud-RAN. IEEE Trans. Veh. Technol. 67 (7), 6383–6397. doi:10.1109/tvt.2018.2797957

CrossRef Full Text | Google Scholar

Yin, L., Clerckx, B., and Mao, Y. (2021). Rate-splitting Multiple Access for Multi-Antenna Broadcast Channels with Statistical CSIT, in 2021 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), Nanjing, China, March 29, 2021, 1–6. doi:10.1109/WCNCW49093.2021.9420034

CrossRef Full Text | Google Scholar

Yin, L., and Clerckx, B. (2021). Rate-splitting Multiple Access for Multigroup Multicast and Multibeam Satellite Systems. IEEE Trans. Commun. 69 (2), 976–990. doi:10.1109/tcomm.2020.3037596

CrossRef Full Text | Google Scholar

Yu, D., Kim, J., and Park, S.-H. (2019). An Efficient Rate-Splitting Multiple Access Scheme for the Downlink of C-RAN Systems. IEEE Wireless Commun. Lett. 8 (6), 1555–1558. doi:10.1109/lwc.2019.2927206

CrossRef Full Text | Google Scholar