
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Commun. Netw., 04 June 2021
Sec. Optical Communications and Networks
Volume 2 - 2021 | https://doi.org/10.3389/frcmn.2021.658330
This article is part of the Research TopicMachine Learning Applications in Optical and Wireless Communication Systems and NetworksView all 4 articles
In this article, we demonstrate two transfer learning–based dual-branch multilayer perceptron post-equalizers (TL-DBMLPs) in carrierless amplitude and phase (CAP) modulation-based underwater visible light communication (UVLC) system. The transfer learning algorithm could reduce the dependence of artificial neural networks (ANN)–based post-equalizer on big data and extended training cycles. Compared with DBMLP, the TL-DBMLP is more robust to the jitter of the bias current (
The limited bandwidth of traditional communication systems has always been a major problem that hinders human exploration and marine resources development. With the in-depth research of scientific research organizations in visible light communication (VLC), many scientists have noticed the potential of VLC in underwater applications (Chi et al., 2018; Oubei, 2018; Zhao et al., 2020). VLC system has been widely proved to have GHz level system bandwidth (Wang et al., 2019; Zhao and Chi, 2020; Zhao et al., 2020). Because of the skin effect of wireless communication in the underwater environment, long-distance high-speed wireless communication cannot be realized. Fortunately, green and blue light is just located in the transmission window of seawater, which indicates the potential of VLC to realize long-distance and high speed UVLC. Therefore, to achieve Gbps-level wireless communication at a distance greater than 100 m underwater, it is necessary to introduce UVLC into the field of underwater wireless communication. To improve the efficiency of spectrum utilization and thus increase the system data rate, we have adopted high-order modulation, CAP64. High-order modulated signals have higher requirements for signal-to-noise ratio (SNR), which also poses challenges to the performance of post-equalization algorithms.
However, the nonlinear response of LED, electronic amplifier, and PIN introduces severe nonlinear distortion to the VLC system, which will reduce the SNR of VLC systems. Furthermore, the complex underwater environment composed of turbulence, marine life, and scattering will further aggravate the nonlinear distortion of the UVLC system, which challenged the digital signal processing algorithms related to signal recovery (Miramirkhani and Uysal, 2017; Oubei et al., 2017). Underwater optical turbulence is caused by refractive index fluctuations caused by changes in temperature, density, and salinity in the underwater environment. The change of the refractive index on the propagation path of the optical signal will cause the fluctuation of the intensity of the optical signal on the receiver, thereby causing nonlinear distortion of the received signal. It is necessary to perform post-equalization on such severely distorted received signals (Oubei et al., 2017). Conventional post-equalizer algorithms, such as least mean squares, recursive least squares, and Volterra series–based post-equalizer, could effectively recover the linear distorted received signal in UVLC systems. However, these post-equalization algorithms have a weak ability to recover high-order nonlinear distorted signal in the UVLC system. The conventional post-equalization algorithms essentially construct a mapping between the received signal and the transmitted signal. According to the universal approximation theorem, MLP can approximate the mapping between the received signal and the transmitted signal with arbitrary precision (Hornik et al., 1990; Barron, 1993). A lot of research work has confirmed that MLP post-equalizer has better BER performance than conventional post-equalizer algorithms in VLC systems (Ghassemlooy et al., 2013; Haigh et al., 2014; Chi et al., 2018). Our previous research demonstrated a DBMLP post-equalizer, which are experimentally proved to have dramatically better nonlinear distortion compensation capability than conventional post-equalizer algorithms (Zhao and Chi, 2020; Zhao and Chi, 2020). Just like ANN algorithms in other fields, such as natural language processing and computer vision, ANN post-equalization algorithms rely heavily on large-scale training sets and a large amount of training epochs. According to the previous research, the ANN post-equalizer training stage requires a training set with a size of more than
In this article, based on preliminary work, we propose two transfer learning–based ANN post-equalizers named as TL-DBMLPs (TL-DBMLP-I and TL-DBMLP-V) (Zhao et al., 2019a; Zhao et al., 2019b). As TL-DBMLP-I is robust to
The essence of transfer learning is to transfer the parameters and structure of a pretrained model to a new model to help the new model’s training process (Raghu and Schmidt, 2020; Panigrahi et al., 2021). Considering that the time-varying UVLC system still has some time-invariant characteristics, we can share the parameters of pretrained DBMLP (it can also be understood as the model learned the time-invariant characteristics of UVLC system) with the new model to optimize the learning efficiency and to reduce the requirements for the training data set. In the pretraining stage, the DBMLP is trained with a data set including
According to Figure 1, The DBMLP is pretrained in the pretraining stage. Two different training sets with varying
where
The mean square error (MSE) is then used as the loss function to evaluate the distance between the target distribution and the model distribution.
where
The pretrained DBMLP is then transferred to the practical UVLC system, which corresponds to the red arrow in Figure 1. Before the pretrained DBMLPs are used in a specific VLC system with constant
where
The function of TL-DBMLPs is to compensate the linear and nonlinear distortion of received signals to reduce the bit error rate (BER) of received signals. Since the initialization parameters of TL-DBMLPs are no longer random numbers but pretrained values, TL-DBMLP is only needed to be fine-tuned before the TL-DBMLPs are utilized in practical UVLC systems. Therefore, the fine-tuning process of TL-DBMLP only requires a small amount of training data and training cycles.
Figure 2A describes our experimental setup. At the transmitter end, we generated a set of QAM64 signal in MATLAB. Then we get the CAP64 signal through upsampling, I/Q separation, and pulse shaping. Then an arbitrary waveform generator (AWG) is used to convert the digital signal into the analog electrical signal. The amplified electrical signal is added to DC through Bias-Tee and used to drive the LED. The silicon-based blue LED is the transmitter to convert the electrical signal to the optical signal.
After propagating through the 1.2-m water tank, the optical signal is concentrated on the PIN via a convex lens at the receiver end. The receiver end is composed of a PIN photodetector, an electric amplifier, and an OSC. The PIN converts the optical signal to the electrical signal. The electrical signal is captured by OSC after it is amplified by the electric amplifier. After that, the captured signal will be processed offline through digital signal processing. The details of the components in Figure 2 are provided in Table 1.

TABLE 1. Details of components in Figure 2.
To show the nonlinearity in LED and UVLC system more intuitively, we measured the P–I curve of the silicon-based blue LED in Figure 3A, respectively. It can be clearly seen that the response between LED bias current and output power is nonlinear. Furthermore, we provided the AM/AM response of the UVLC system in Figure 3B. The units of x-axis and y-axis are the normalized amplitude of the transmitted signal and received signal, respectively. It can be seen that as the amplitude of the transmitted signal increases, the change of the received signal is not linear.
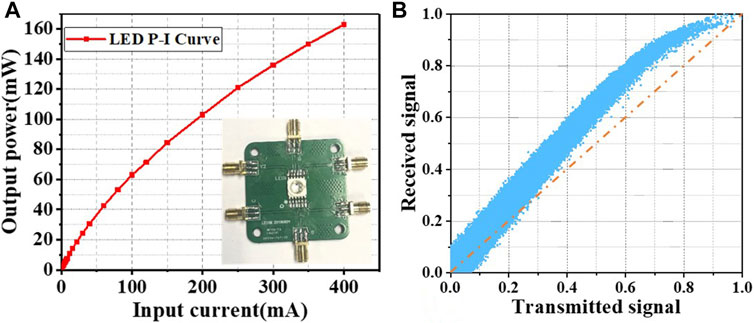
FIGURE 3. (A) P–I curve of the silicon-based blue LED. (B) Amplitude (AM/AM) response of the UVLC system.
In order to prove that the TL-DBMLPs training can converge faster under the new ULVC system, we experimentally compared the MSE of the two TL-DBMLPs (TL-DBMLP-I and TL-DBMLP-V) and the conventional DBMLP in the training process, which is described in Figure 4A. An ANN post-equalizer completes one training process on a whole set of training data, which is called one epoch. All the following experimental results are based on a training set containing
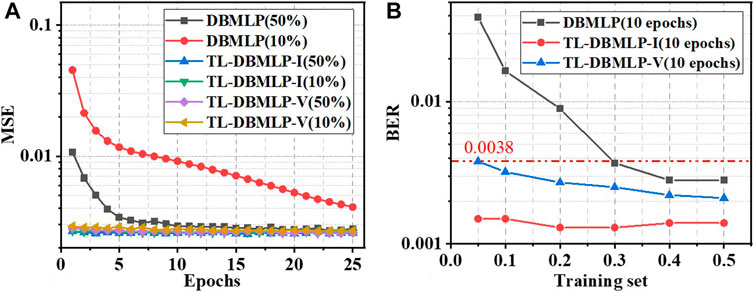
FIGURE 4. (A) Training process of DBMLP and two kinds of DBMLPs pretrained under
Furthermore, Figure 4A describes the dependence of three kinds of ANN post-equalizer algorithms on the training set’s size. We can find that TL-DBMLP-I and TL-DBMLP-V have minimal dependence on the size of the training set. Reducing the size of the training set from 50 to 10% of the total data set does not significantly increase the MSE of DBMLP-I and DBMLP-V. Take the state after 10 epochs of fine-tuning as examples, the MSE of DBMLP-I and DBMLP-V increase from 0.00260 and 0.00266 to 0.00263 and 0.00279, respectively. In terms of DBMLP, the loss increases from 0.00292 to 0.00916. Therefore, it can be concluded that the dependence of TL-DBMLPs on the size of the training set is much lower than that of conventional DBMLP.
Since MSE can only reflect the convergence state during the ANN training process, it cannot directly reflect the BER performance of the ANN post-equalization algorithms. Therefore, we tested the impact of the size of the training set on the error performance of DBMLP, TL-BMLP-I, and TL-DBMLP-V in Figure 4B. The gray curve verifies that DBMLP has a strong dependence on the size of the training set. When the training set is reduced from 50 to 10%, the BER of DBMLP equalized UVLC increase from 0.0028 to 0.0164. In terms of TL-DBMLP-V, the BER only increase from 0.0021 to 0.0032. This is because the rise in Vpp will significantly aggravate the nonlinear distortion of the UVLC system. This leads to a decrease in the commonality between channels in UVLC systems with different Vpp. Therefore, the commonalities that TL-DBMLP-V can learn during the pretraining phase will be reduced. In a specific Vpp UVLC system, a certain amount of training epochs is required to fine-tune TL-DBMLP-V. According to the experimental results, 10% of the total data set can reduce the BER of TL-DBMLP-V equalized UVLC below the 7% hard-decision forward error correction (HD-FEC) threshold (BER = 0.0038). The red curve shows that the BER performance of TL-BMLP-I has a very low dependence on the size of the training set. Since the change of
Figure 5 intuitively shows the impact of the training epochs on the BER performance of DBMLP and TL-DBMLPs. Since our target is to obtain a high BER performance ANN post-equalization algorithm trained on a small number of epochs and training data, we set the size of the training set to 10% of the length of the whole data set. When the size of training set is not large enough (10%), the BER performance of DBMLP after different epochs of training is very unstable. In fact, we found that even with training with the same epochs, the BER performance of the obtained DBMLP will be very different. Because, before each training process start, the trainable parameters of the DBMLP must be initialized. The initialization is based on uniform random numbers between −0.05 and 0.05. Therefore, the initialization state of the trainable parameters will be different in each training process. However, when the size of training set and the number of epochs is not large enough, the BER performance of DBMLP will be significantly affected by the initialization state. As a result, the BER performance of DBMLP is unstable. The instability of BER performance also hinders the application of DBMLP in practical UVLC systems. According to the green curve in Figure 5, the increase of the training epochs can slightly improve the BER performance of TL-DBMLP-V. The reason is consistent with the analysis in Figure 4B. Similarly, we could notice that the red curve hardly changes with the increase of epochs. So far, we have experimentally proved that TL-DBMLP-I has good generalization in the UVLC system with varying
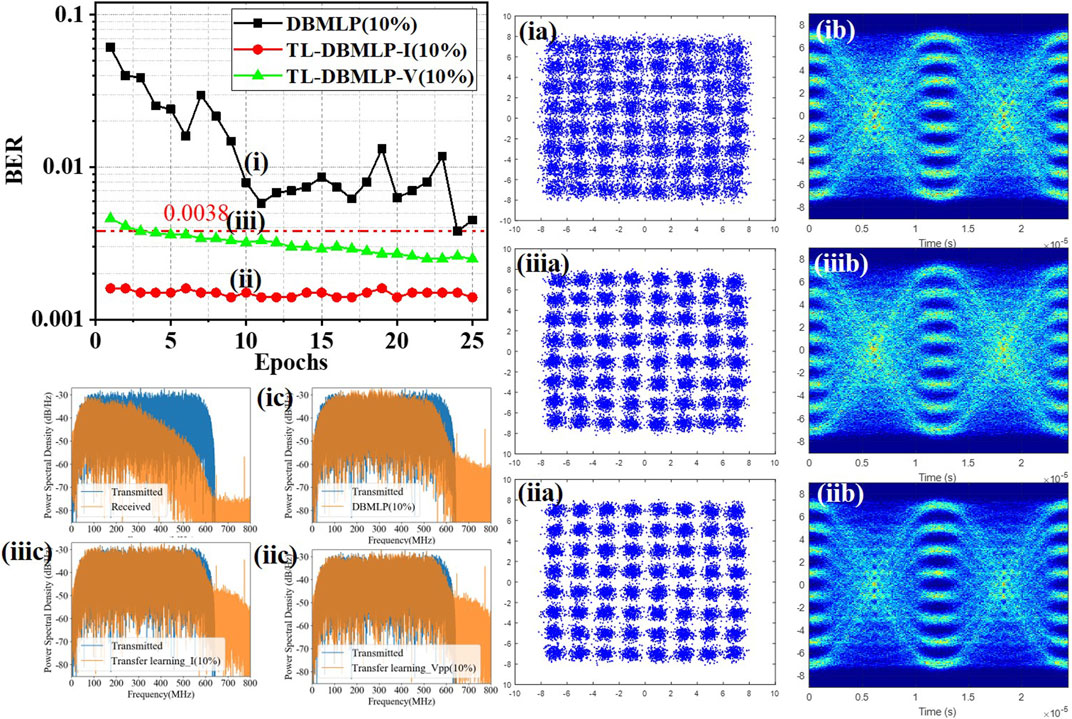
FIGURE 5. Relationship between DBMLP and TL-DBMLP training period and BER performance. Constellation diagram, eye diagram, and frequency spectrum of the equalized signal are provided in (i), (ii), (iii).
In order to compare the signals equalized by the three kinds of ANN equalizers intuitively, we visualized the equalized signals. According to Figure 5 (ia) (iia) and (iiia), the signals near the outer constellation points are not gathered together well. These show that there is a certain degree of nonlinear distortion in the UVLC system. Compared with DBMLP, the two fine-tuned TL-DBMLPs can recover the received signal better. Meanwhile, as the eye diagrams of signal equalized by two fine-tuned TL-DBMLPs (Figure 5 (iib) (iiib)) is clearer than DBMLP equalized signal in Figure 5 (ib), the SNR of TL-DBMLPs equalized signal is also better than DBMLP equalized signal. According to the frequency spectrum in Figure 5 (ic) (iic) and (iiic), all three kinds of ANN equalizers could effectively recover the distorted signal at receiver end. However, in the high-frequency range, the capability of TL-DBMLPs to compensate for high frequency fading is significantly better than DBMLP.
To test the generalization of TL-DBMLPs, we tested the BER performance of TL-DBMLP-I in UVLC systems with different
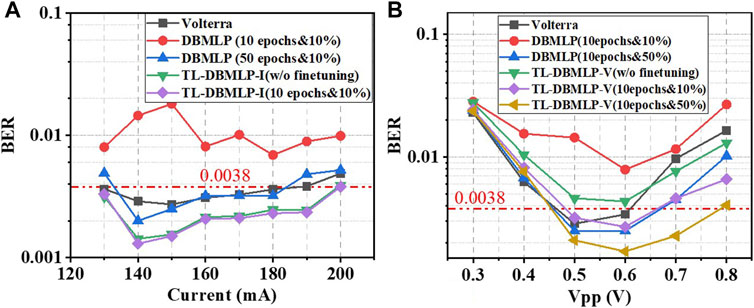
FIGURE 6. In 3.1 Gbps UVLC systems (A) with different
Correspondingly, we tested the BER performance of TL-DBMLP-V in UVLC systems with different Vpp. In order to make the BER performance of DBMLP comparable to TL-DBMLP-V, the training data need to be increased from 10 to 50%. In Figure 6B, the BER performance of the TL-DBMLP-V without fine-tuning is slightly inferior to Volterra-based post-equalizer. Compared with TL-DBMLP-V without fine-tuning, the performance of the fine-tuned TL-DBMLP-V has been significantly improved, which shows that TL-DBMLP-V needs to be fine-tuned. Simultaneously, when the training set is increased from 10 to 50%, the error performance of TL-DBMLP-V is improved. Figure 6B shows that TL-DBMLP-V still needs a certain amount of training data for fine-tuning. But the amount of data required is much smaller than that of DBMLP.
According to the results and analysis above, TL-DBMLP-I does not need to be fine-tuned when it is utilized in the actual UVLC system with varying
This study proposed two kinds of TL-DBMLPs, including TL-DBMLP-V and TL-DBMLP-I. For Vpp varying CAP64 UVLC system, the training process of TL-DBMLP-V required
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
YZ: conceptualization, methodology, software, validation, writing—original draft, review, and editing, and investigation. SY and NC: resources, formal analysis, project administration, supervision, and funding acquisition.
National Natural Science Foundation of China (No.61925104, No.62031011).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Barron, A. R. (1993). Universal Approximation Bounds for Superpositions of a Sigmoidal Function. IEEE Trans. Inform. Theor. 39 (3), 930–945. doi:10.1109/18.256500
Chi, N., Zhao, Y., Shi, M., Zou, P., and Lu, X. (2018). Gaussian Kernel-Aided Deep Neural Network Equalizer Utilized in Underwater PAM8 Visible Light Communication System. Opt. Express 26 (20), 26700–26712. doi:10.1364/OE.26.026700
Chuang, C-Y., Liu, L-C., Wei, C-C., Liu, J-J., Henrickson, L., Chen, Y-K., et al. (2018). “Study of Training Patterns for Employing Deep Neural Networks in Optical Communication Systems,” in In 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 1–3.
Ghassemlooy, Z., Haigh, P. A., Arca, F., Tedde, S. F., Hayden, O., Papakonstantinou, I., et al. (2013). Visible Light Communications: 375 Mbits/s Data Rate with a 160 KHz Bandwidth Organic Photodetector and Artificial Neural Network Equalization [Invited]. Photon. Res. 1 (2), 65–68. doi:10.1364/PRJ.1.000065
Haigh, P. A., Ghassemlooy, Z., Rajbhandari, S., Papakonstantinou, I., and Popoola, W. (2014). Visible Light Communications: 170 Mb/s Using an Artificial Neural Network Equalizer in a Low Bandwidth White Light Configuration. J. Lightwave Technol. 32 (9), 1807–1813. doi:10.1109/jlt.2014.2314635
Hornik, K., Stinchcombe, M., and White, H. (1990). Universal Approximation of an Unknown Mapping and its Derivatives Using Multilayer Feedforward Networks. Neural Networks 3 (5), 551–560. doi:10.1016/0893-6080(90)90005-6
Lohani, S., Knutson, E. M., O’Donnell, M., Huver, S. D., and Glasser, R. T. (2018). On the Use of Deep Neural Networks in Optical Communications. Appl. Opt. 57 (15), 4180. doi:10.1364/ao.57.004180
Matsumoto, M., and Nishimura, T. (1998). Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudo-Random Number Generator. ACM Trans. Model. Comput. Simul. 8 (1), 3–30. doi:10.1145/272991.272995
Miramirkhani, F., and Uysal, M. (2018). Visible Light Communication Channel Modeling for Underwater Environments with Blocking and Shadowing. IEEE Access 6, 1082–1090. doi:10.1109/ACCESS.2017.2777883
Oubei, H. M. (2018). Underwater Wireless Optical Communications Systems : From System- Level Demonstrations to Channel Modeling. Doctoral dissertation. doi:10.1109/ucomms.2018.8493227
Oubei, H. M., Zedini, E., ElAfandy, R. T., Kammoun, A., Abdallah, M., Ng, T. K., et al. (2017). Simple Statistical Channel Model for Weak Temperature-Induced Turbulence in Underwater Wireless Optical Communication Systems. Opt. Lett. 42 (13), 2455. doi:10.1364/ol.42.002455
Panigrahi, S., Nanda, A., and Swarnkar, T. (2021). A Survey on Transfer Learning. Smart Innovation, Syst. Tech. 194 (10), 781–789. doi:10.1007/978-981-15-5971-6_83
Raghu, M., and Schmidt, E. (2020). A Survey of Deep Learning for Scientific Discovery. New York America: ArXiv, 1–48.
Wang, F., Liu, Y., Shi, M., Chen, H., and Chi, N. (2019). 3.075 Gb/s Underwater Visible Light Communication Utilizing Hardware Pre-Equalizer with Multiple Feature Points. Opt. Eng. 58 (05), 1. doi:10.1117/1.oe.58.5.056117
Zhao, Y., and Chi, N. (2020). Partial Pruning Strategy for a Dual-Branch Multilayer Perceptron-Based Post-Equalizer in Underwater Visible Light Communication Systems. Opt. Express 28 (10), 15562. doi:10.1364/oe.393443
Zhao, Y., Zou, P., and Chi, N. (2020). 3.2 Gbps Underwater Visible Light Communication System Utilizing Dual-Branch Multi-Layer Perceptron Based Post-Equalizer. Opt. Commun. 460, 125197. doi:10.1016/j.optcom.2019.125197
Zhao, Y., Zou, P., Shi, M., and Chi, N. (2019a). Nonlinear Predistortion Scheme Based on Gaussian Kernel-Aided Deep Neural Networks Channel Estimator for Visible Light Communication System. Opt. Eng. 58 (11), 1. doi:10.1117/1.oe.58.11.116108
Keywords: visible light communication, artificial neural networks, underwater, post-equalizer, transfer learning
Citation: Zhao Y, Yu S and Chi N (2021) Transfer Learning–Based Artificial Neural Networks Post-Equalizers for Underwater Visible Light Communication. Front. Comms. Net 2:658330. doi: 10.3389/frcmn.2021.658330
Received: 25 January 2021; Accepted: 17 May 2021;
Published: 04 June 2021.
Edited by:
Junwen Zhang, CableLabs, United StatesReviewed by:
Zabih Ghassemlooy, Northumbria University, United KingdomCopyright © 2021 Zhao, Yu and Chi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nan Chi, bmFuY2hpQGZ1ZGFuLmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.