Prospect Theory for Human-Centric Communications

Entering the 5G/6G era, the core concept of human-centric communications has intensified the research effort into analytical frameworks for integrating technological and non-technological domains. Among non-technological domains, human behavioral, psychological, and socio-economic contexts are widely considered as indispensable elements for characterizing user experience (UE). In this study, we introduce the prospect theory as a promising methodology for modeling UE and perceptual measurements for human-centric communications. As the founding pillar of behavioral economics, the prospect theory proposes the non-linear quantity and probability perception of human psychology, which extends to five fundamental behavioral attributes that have profound implications for diverse disciplines. An example of applying the novel theoretic framework is also provided to illustrate how the prospect theory can be utilized to incorporate human factors and analyze human-centric communications. By expatiating on the prospect theoretic framework, we aim to provide a guideline for developing human-centric communications and articulate a novel interdisciplinary research area for further investigation.

1. Introduction

Telecommunication research so far has tended to become technology-centric and focused excessively on quality of service (QoS) metrics. On the other hand, due to the rapid emergence of end-user controllable and programmable devices in communication networks, quality of experience (QoE), and user experience (UE) have increasingly attracted researchers' attention in both academia and industry in recent years (Kilkki, 2008; Mitra et al., 2015; Finley et al., 2017; Yang et al., 2018; Boz et al., 2019)'. Furthermore, the development of human-centric communications in the 6G network requires not only technological factors but also UE to be considered when modeling, analyzing, and optimizing communication systems (Dang et al., 2020). This paradigm shift necessitates the interdisciplinary collaboration among telecommunications, economics, and psychology.

The first attempt to propose an ecosystem incorporating multiple stakeholders and end users is presented in Kilkki (2008), based on which several advanced versions of ecosystems are proposed in Reichl (2010), Rehman Laghari and Connelly (2012), Dong et al. (2014), and Seufert et al. (2019). However, due to the absence of a quantitative basis, existing ecosystems can hardly be utilized to carry out performance analysis for communication systems. To facilitate quantitative analysis, a standard approach is to measure UE via utility functions, such as logarithmic, sigmoid, and exponential functions (Fiedler et al., 2010; Reichl et al., 2013; Lee et al., 2014; Taleb Zadeh Kasgari et al., 2019). However, most QoE measurements are confined to simple quantitative relationships between QoS and QoE metrics. So far, no analytical framework has been proven to be generic and theoretically practicable for modeling UE in a human-centric manner.

Besides, recent studies on heterogeneous networks also recognize that user behaviors, including both individual and clustering user behaviors, can be leveraged to improve long-term network performance (Sun et al., 2018). In particular, the impacts of user behaviors on energy efficiency, hardware utility, and network throughput, and handover, are investigated (Cao et al., 2014; Guidolin et al., 2014; Zhang et al., 2014). Notwithstanding the ingenious craftsmanship of modeling user behaviors, these studies are still technology-centric, which aim to boost the QoS, instead of QoE.

In the area of economics, researchers resort to the prospect theory for accurately predicting decision-making behaviors of human beings (Kahneman and Tversky, 1979; Tversky and Kahneman, 1992). The prospect theory is a Nobel prize winning theory and the founding pillar of behavioral economics. It is widely perceived as the most satisfactory descriptive theory of quantity perception currently available. Since its proposal in 1979, this theory has been extensively applied in pricing strategy, labor supply, tax policy making, and finance related topics.

Due to its generality and versatility, the prospect theory is also introduced as a nexus to connect the disciplines of telecommunications, economics, and psychology. In Li and Mandayam (2014), the user behavior interference in networking protocols is modeled and analyzed according to the prospect theory. Specific resource allocation strategies using the prospect theory are investigated in Yu et al. (2016). Data pricing problems relying on the prospect theory for licensed and unlicensed communications are investigated in Yang et al. (2015), Yu et al. (2017), and Chen et al. (2019), respectively. The prospect theory has also been applied to provide secure protection mechanisms for communication systems by formulating dynamic defense games (Xu et al., 2016; Xiao et al., 2017). Incorporating game theory, the prospect theory can also help communication systems equip with better anti-jamming and random access functions (Li and Mandayam, 2012; Xiao et al., 2014). A generic but simplistic prospect theoretic analytical framework of UE is proposed in Lee (2015). Even though instructive and creative, the inappropriate and oversimplified modeling and assumptions in Lee (2015) result in a huge mismatch between the quantitative UE and resource utilization. In these interdisciplinary applications, however, the prospect theory serves only as a replacement for the utility or probability functions formulated in specific problems (e.g., game theoretic communications). This, to some extent, undervalues the prospect theory's implications and application aspects for human-centric communications. Meanwhile, it should also be emphasized that the prospect theory dedicated to studying the subjective perception of objective measurements is different from game theory developed to understand and predict user behaviors under the hypothesis of perfect rationality. In other words, perception might not necessarily be rational when applying the prospect theory, but, rather, can be distorted by a series of real-world factors.

In light of the review of existing literature given above, we summarize the contributions of this paper as follows:

• We outline five essential attributes of the prospect theory considering user psychology that should be taken into consideration for wireless system modeling.

• We construct a comprehensive analytical framework for modeling UE and perceptual measurements for human-centric communications. The proposed analytical framework can be directly applied to carry out performance analysis for most communication systems when non-technological factors are taken into consideration and can be easily tailored to fit a broader range of communication applications.

• We provide a simplified example of applying the novel theoretic framework to illustrate how the prospect theory can be utilized to incorporate human factors and analyze human-centric communications.

By the contributions given in this paper, we aim to provide a guideline for improving communication services and articulate a new interdisciplinary research area for further investigation.

The remainder of this paper is as follows. In section 2, we present the fundamentals of the prospect theory, including its economic background, concepts, intuitions, and five key attributes of human psychology. Based on the five key attributes, we formulate the prospect theoretic analytical framework in section 3. Case studies are provided as an example of applying the novel theoretic framework in section 4. We outline the challenges and promising research directions for further investigations in section 5 and conclude the paper in section 6.

2. Fundamentals of the Prospect Theory

As we are entering the 5G/6G era, the development of human-centric communications is becoming increasingly important but faces tremendous challenges. The paradigm shift from technology-centric to human-centric applications necessitates the interdisciplinary collaboration among telecommunications, economics, and psychology. In the following subsections, we explain step by step how this interdisciplinary collaboration is enabled by the prospect theory.

2.1. Existing Problems With Classic Telecommunication Research

Researchers employ different approaches to establish linkages between QoS (e.g., bandwidth and loss rate) and QoE. Perceptual measurements, such as the mean opinion score (MOS) and the pseudo-subjective quality assessment (PSQA) have been developed to quantify user experience (Piamrat et al., 2009; Streijl et al., 2016). There are also multi-dimensional evaluation systems designed to assess network performance from end-user perspectives (Rehman Laghari and Connelly, 2012). Although the QoE research is gaining strong momentum in recent years, the literature remains scattered, inconsistent, and excessively technology-centric (Kilkki, 2008; De Moor et al., 2010; Reichl, 2010). So far, no analytical framework has been proven sufficiently generic and theoretically practicable for modeling UE in a user-oriented manner.

Classic communication research focuses on technology-centric network optimization and bypasses the model of UE. In such settings, researchers have actually made an implicit assumption: the optimization process maximizes both network capacity and user's subjective utility simultaneously (Baraković and Skorin-Kapov, 2013). Conventionally, for n mutually exclusive outcomes y_i with occurrence probability p_i, the subjective utility can be considered as a linear function of probabilistic outcomes: $U=\sum _{i=1}^n{p}_i{y}_i$, given $\sum _{i=1}^n{p}_i=1$. However, the linear utility function is difficult to reconcile with human psychology due to its unrealistic attributes:

• Subjective utility is solely determined by the state of the final outcome (Utilitarianism).

• Marginal utility is constant (static viewing).

• Quantity perception over gains and losses is symmetric.

• There is no difference between objective and perceived probabilities.

Under the above erroneous characterization of human psychology, the optimization process does not necessarily guarantee optimal UE, and the derived theories would be of limited practical usefulness. As an applied discipline, communications become human-centric only if UE can be properly introduced and optimized in the modeling process, which should be the very foundation of communications science. Overall, there is an urgent need to incorporate UE into the modeling of telecommunication theories.

2.2. Prospect Theory

In the past decades, the rapid development of behavioral economics has greatly enriched our understanding of human psychology and proposed promising analytical frameworks for modeling UE. As the founding pillar of behavioral economics, the prospect theory is widely perceived as the most satisfactory descriptive theory of quantity perception and decision making currently available (Kahneman and Tversky, 1979; Tversky and Kahneman, 1992). The prospect theory is also a Nobel Prize winning theory, and the research article (Kahneman and Tversky, 1979) is the second most cited paper in economics. The prospect theory provides a well-established theoretical framework and mathematical tools for modeling real-life UE, and its gist is that the human perception of objective measurements, including quantity and probability, are non-linear.

In the current literature, most QoE measurements for telecommunication studies are confined to quantity perception of discrete states, i.e., quantitative relationships between UE and QoS (Fiedler et al., 2010; Reichl et al., 2013). As a major advantage, the prospect theory characterizes two indispensable dimensions of UE, i.e., quantity and probability, and can help to model and analyze UE in the continuous state. Under the prospect theory, the perception of quantity and probability perception can be expressed in Figure 1. This figure is believed to be the most important pictorial illustration of the prospect theory and can help with the mapping from QoS to QoE for telecommunication studies. A value function and a probability weighting function are employed to model the human perception, which can be characterized by the two-part value function given in Tversky and Kahneman (1992) and the Prelec function given in Prelec (1998), respectively.

FIGURE 1

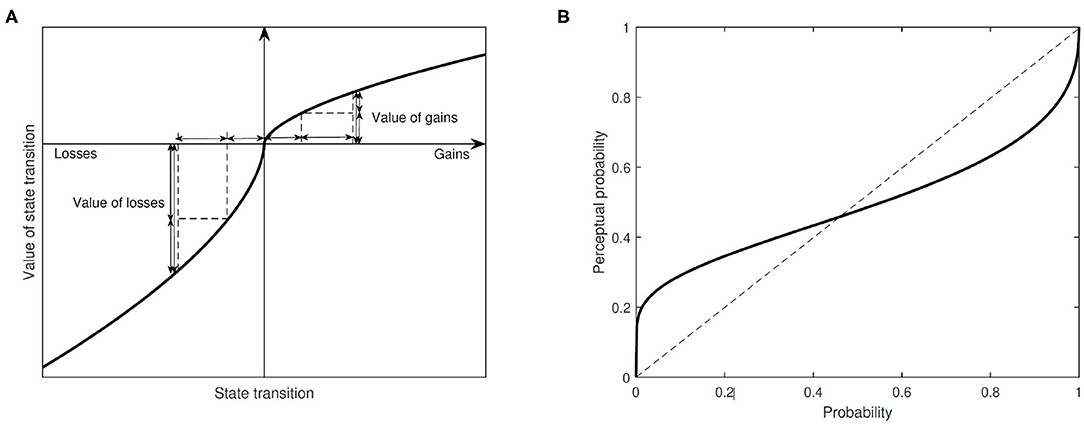
Figure 1. (A) Perceptual quantity under the prospect theory; (B) Perceptual probability under the prospect theory (Dhami, 2016).

2.3. Five Key Attributes

In this subsection, we introduce the features of the prospect theory in shaping human psychological foundations and discuss the insights into modeling UE. According to Figure 1, we can observe five important features of human psychology, captured by the prospect theory as follows.

2.3.1. Reference Dependence

The prospect theory states that individuals perceive quantity through changes (i.e., quantity deviations from a reference point) instead of states. There is always a reference point in each dimension of quantity perception. This can be explained by the following thought experiment. Communication network operators upgrade Jack's mobile network from 3G to 4G but downgrade Jim's from 5G to 4G. Jack and James now have the same network capacity but markedly different quantity perception (gains vs. losses), due to reference dependence. This characterization is consistent with the advanced notion of QoE: users' perceived value can be either positive (delight) or negative (annoyance) (Le Callet et al., 2012). As a fundamental trait in human psychology, reference dependence casts doubts on optimization approaches that focus merely on the level of final outcomes, which has also attracted research attention in recent QoE literature (Fiedler et al., 2010).

2.3.2. Diminishing Marginal Utility

Individuals have diminishing sensitivity toward the scale of changes. This means that the subjective difference between the data packages of 50 and 100 Mb is more salient than that between the data packages of 950 and 1,000 Mb. Diminishing marginal utility, also known as diminishing sensitivity and utility curvature, is a widely recognized psychological feature shared by living creatures. Under proper assumptions [e.g., exponential or logarithmic utility functions (Fiedler et al., 2010; Reichl et al., 2013)], the concept of diminishing sensitivity can be readily incorporated into the modeling process to improve the practical significance of telecommunication theories.

2.3.3. Loss Aversion

Individuals are more sensitive to losses than equivalent gains. Ample experimental evidence suggests that the magnitude of loss aversion is context-dependent, but losses are generally twice as significant as equivalent gains in quantity perception (Dhami, 2016). The phenomenon of loss aversion is captured by the value function in Figure 1A, where quantity perception is steeper in the domain of losses. This asymmetry calls for a reconsideration of conventional approaches that weight gains and losses equally.

2.3.4. Asymmetric Risk Attitudes

Under diminishing marginal utility and loss aversion, individuals are risk-seeking in the domain of losses but risk-averse in the domain of gains. A prime example is the behavior of compulsive gambling: money-winning gamblers tend to play safely and prefer low-risk-low-return options, whereas money-losing gamblers prefer high-risk-high-return options and expect a “grand slam home run.” Asymmetric risk attitudes indicate that users have different risk preferences for improvement and deterioration in communication services, which calls for revisions of risk modeling in the existing QoE research.

2.3.5. Probability Distortion

Individuals tend to overweight small probabilities and underweight moderate and high probabilities. Consider the thought experiment as follows:

• Problem 1: How much would you pay to reduce the dropping probability from 5 to 0%?

• Problem 2: How much would you pay to reduce the dropping probability from 55 to 50%?

The two problems seem identical because they are about 5% risk of dropping call in objective measurement. However, the great majority of people in real life are willing to pay much higher in Problem 1 than in Problem 2. This phenomenon suggests a non-linear subjective probability weighting, in contrast to the linear probability weighting that equates objective probability with perceptual probability¹. In probability perception, probability changes, such as 0–5 and 95–100% are subjectively more salient than other changes of the same magnitude, since they are qualitative changes between non-existence, a probabilistic outcome, and certainty. Extensive experimental evidence indicates that people are rather sensitive to the edges of probability interval [0,1], as documented by the inverse S-shaped probability weighting function in Figure 1.

2.4. Summary

Under the prospect theory, the five psychological features are transformed into a 4-fold pattern of risk attitudes in quantity perception: for low probabilities, individuals are risk-seeking in the domain of gains but risk-averse in the domain of losses; for moderate and high probabilities, individuals are risk-averse in the domain of gains but risk-seeking in the domain of losses. In summary, the prospect theory formulates the non-linear quantity and probability perception of human psychology, which has profound implications for developing human-centric communications in both academia and industry.

3. Prospect Theoretic Analytical Framework

The basic mathematical formulation based on the prospect theory enables the mapping from objective QoS to subjective QoE, capturing the behavioral, psychological, and contextual factors. In the process of quantity and probability perception, the QoE or UE is dependent on two metrics: the quantity metric and the probability metric.

3.1. Quantity Metric and Value Function

The quantity metric denotes conventional QoS parameters, such as bandwidth and latency. According to the prospect theory, individuals perceive quantity through state transition (i.e., quantity deviations from a reference point) instead of the state per se. In various disciplines, utility/value functions serve as the standard approach for modeling UE. Following the two-part form of value function given in Tversky and Kahneman (1992), the value function for telecommunications taking the reference dependence, diminishing marginal utility, and loss aversion into consideration can be modeled as^2,3

$\begin{array}{ll}v(x,x_0)=\{\begin{array}{c}{\lambda }_1{(x-x_0)}^{{\alpha }_1},x\ge x_0\\ -{\lambda }_2{(x_0-x)}^{{\alpha }_2},x<x_0,\\ \end{array}& (1)\end{array}$

where α₁, α₂, λ₁, and λ₂ are positive and user specific parameters; x₀ ≥ 0 is the reference point with respect to x, which captures the reference dependence. The reference point x₀ can be a previous quantity, an expected quantity, or a contractual quantity for different application scenarios. For generality, we model the process of quantity perception as a function of both x and x₀ so as to emphasize the equal importance of the actual quantity x and the reference point x₀. Both dimensions are indispensable in determining user perception of quantity metrics. It is worth noting that all the parameters, including the reference point x₀ are specific in terms of user preferences and socio-economic contexts and could change over time (Prashanth et al., 2016). Obviously, if α₁ = α₂ = 1, λ₁ = λ₂ = 1, and x₀ = 0, we have v(x, x₀) = x, ∀ x ≥ 0, and the formulated analytical framework reduces to the classic QoS analytical framework.

Without loss of generality, the value model given in (1) is called the four-parameter value model, which is different from the classic two-parameter value model widely used in behavioral economics that assumes α₁ = α₂ and fixes λ₁ = 1. For the four-parameter value model, it is worth inspecting and discussing the constraints on parameters that should jointly ensure the key attributes retrieved from the prospect theory. It has been summarized in Dhami (2016) that any value function v(x, x₀) complying with the prospect theory must satisfy the following fundamental properties:

• v(x, x₀) is continuous and strictly increasing with respect to x (the desirable metric assumption);

• v(x₀, x₀) = 0 (reference dependence);

• With respect to x, v(x, x₀) is concave when x ≥ x₀ and is convex when x < x₀ (diminishing marginal utility);

• v(x₀ + δ, x₀) < −v(x₀ − δ, x₀), ∀ δ > 0 (loss aversion).

The first two fundamental properties of v(x, x₀) are axiomatic for the four-parameter value model. To investigate the concavity and convexity, it is straightforward to derive the second-order piecewise partial derivative of v(x, x₀) with respect to x ≥ x₀ as $\frac{{\partial }^{2}v(x,x_0)}{\partial x^2}{|}_{x\ge x_0}={\alpha }_1({\alpha }_1-1){\lambda }_1{(x-x_0)}^{{\alpha }_1-2}$ and x < x₀ as $\frac{{\partial }^{2}v(x,x_0)}{\partial x^2}{|}_{x<x_0}=-{\alpha }_2({\alpha }_2-1){\lambda }_2{(x_0-x)}^{{\alpha }_2-2}$. Therefore, solving $\frac{{\partial }^{2}v(x,x_0)}{\partial x^2}{|}_{x\ge x_0}<0$ and $\frac{{\partial }^{2}v(x,x_0)}{\partial x^2}{|}_{x<x_0}>0$ yields 0 < α₁ < 1 and 0 < α₂ < 1, respectively. For the last property stipulating v(x₀ + δ, x₀) < −v(x₀ − δ, x₀), ∀ δ > 0, we can simplify the inequality to $\frac{{\lambda }_2}{{\lambda }_1}{\delta }^{{\alpha }_2-{\alpha }_1}>1$, ∀ δ > 0. By rigorous analysis, it can be proven that the only approach to ensure the validity of the inequality regardless of the value of δ is to let α₁ = α₂ and λ₁ < λ₂, which reduce the four-parameter model constructed in (1) to a three-parameter model regulating α = α₁ = α₂ ∈ (0, 1) and λ₁ < λ₂. Rigorous and comprehensive discussions and proofs regarding the parameters of value model in the prospect theory can be found in Al-Nowaihi et al. (2008).

For illustration purposes, we plot v(x, x₀) with different sets of parameters in Figure 2 by referring to the suggested parameter ranges yielded by empirical evidence given in Dhami (2016). We also plot Figure 3 to illustrate the effects of reference point on the value function. In these figures, we can confirm that the key attributes related to the value function from the prospect theory hold and inspect how these key attributes and the relevant parameters jointly affect the user perception of quantity metrics.

FIGURE 2

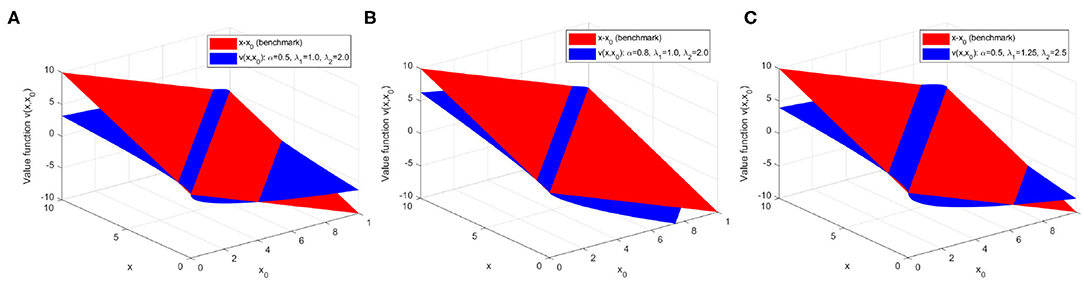
Figure 2. Perceived values of state transitions with different sets of parameters. (A) Parameter set I; (B) Parameter set II; (C) Parameter set III.

FIGURE 3

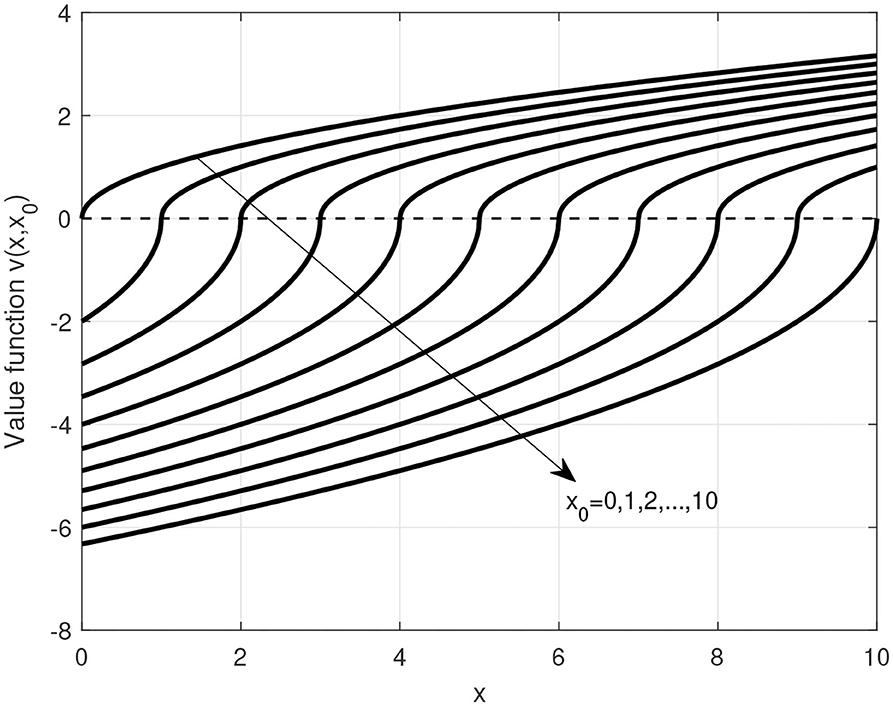
Figure 3. Perceived value vs. quantity metric with different reference points, given α = 0.5, λ₁ = 1.0, and λ₂ = 2.0.

3.2. Probability Metric and Probability Weighting Function

The probability metric in the context of telecommunications denotes the measurement of opportunistic performance, which encompasses outage probability, error probability, collision probability, handover probability, and etc. An objective probability will be distorted when being perceived by end users, corresponding to the last key attribute of the prospect theory: non-linear probability perception. Introducing the Prelec probability weighting function (Prelec, 1998), we model the perception of a probability metric 0 ≤ p ≤ 1 under psychological distortion as

$\begin{array}{ll}w(p)=\text{exp}(-\gamma {(-log(p))}^{\theta }),& (2)\end{array}$

where γ > 0 and 0 < θ < 1 are user specific parameters used to characterize the subjective perception of probability metric. The ranges γ and θ are derived by the necessary conditions for maintaining the basic properties of probability weighting function, especially its inverse S-shape. Detailed discussions on the functionality and property of γ and θ can be found in Dhami (2016). If γ = 1 and θ = 1, we have w(p) = p, ∀ p ∈ [0, 1], and thus the formulated analytical framework for probability perception reduces to the classic QoS analytical framework.

In a general case with a continuous random variable X, the probability argument in (2) could be any cumulative distribution function (CDF) F_X(s) = ℙ{X ≤ s}, where ℙ{·} denotes the objective probability of the random event enclosed. Following the definition of CDF and the attribute of probability distortion, we gives the perceptual CDF (PCDF) by

$\begin{array}{ll}{\tilde{F}}_X(s)=w(F_X(s)).& (3)\end{array}$

Such PCDF is elegant in mathematical terms and inherits all basic conditions of a legal CDF defined in the field of real numbers. First, we can prove that ${\tilde{F}}_X(s)$ is a monotone non-decreasing function of s by showing that the first derivative of ${\tilde{F}}_X(s)$ with respect to s is always non-negative when γ > 0 and 0 < θ < 1:

$\begin{array}{ll}\frac{\text{d}{\tilde{F}}_X(s)}{\text{d}s}=\gamma \theta w(F_X(s)){(-log(F_X(s)))}^{\theta -1}{f}_X(s)/F_X(s)>0.& (4)\end{array}$

Also, we can easily derive

$\begin{array}{ll}{\tilde{F}}_X(\infty )={\displaystyle \underset{s\to \infty }{lim}}\{{\tilde{F}}_X(s)\}={\displaystyle \underset{F_X(s)\to 1}{lim}}\{\text{exp}(-\gamma {(-log(F_X(s)))}^{\theta })\}=1& (5)\end{array}$

and

$\begin{array}{r}{\tilde{F}}_X(-\infty )={\displaystyle \underset{s\to -\infty }{lim}}\{{\tilde{F}}_X(s)\}\\ ={\displaystyle \underset{F_X(s)\to 0}{lim}}\{\text{exp}(-\gamma {(-log(F_X(s)))}^{\theta })\}=0& (6)\end{array}$

Denoting $f_X(s)=\frac{\text{d}F(s)}{\text{d}s}$ as the probability density function (PDF) of X, we can define the perceptual PDF (PPDF) as

$\begin{array}{l}{\tilde{f}}_X(s)=\frac{\text{d}{\tilde{F}}_X(s)}{\text{d}s}=\frac{\text{d}w(F_X(s))}{\text{d}s}\\ =\gamma \theta w(F_X(s)){(-log(F_X(s)))}^{\theta -1}{f}_X(s)/F_X(s).& (7)\end{array}$

For illustration purposes, we plot w(p), ${\tilde{F}}_X(s)$, and ${\tilde{f}}_X(s)$ in Figure 4 by referring to the suggested parameter ranges yielded by empirical evidence given in Dhami (2016), ditto. In this figure, we can testify that the attribute of probability distortion from the prospect theory hold and inspect how this attribute and the parameters γ and θ jointly affect the user perception of probability metrics.

FIGURE 4

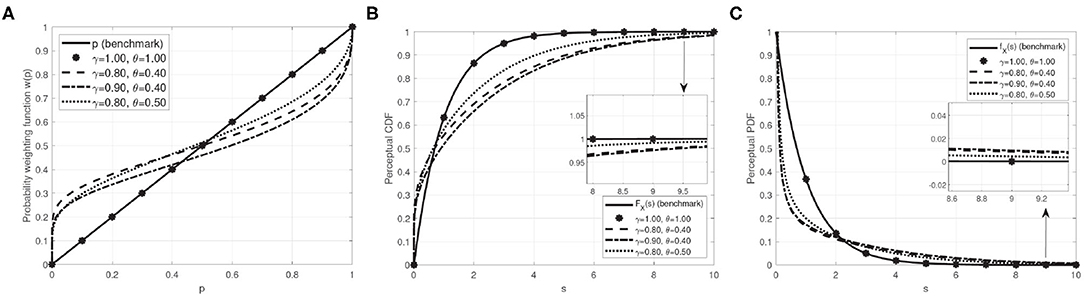
Figure 4. Perceived probability, PCDF, and PPDF with different sets of parameters. Here, we take the normalized exponential distribution as an example to illustrate PCDF and PPDF, i.e., F_X(s) = 1 − exp(−s) and f_X(s) = exp(−s) for s ≥ 0. (A) Perceived probability; (B) PCDF; (C) PPDF.

Similarly for the case with a discrete random variable X, the probability argument in (2) becomes the probability mass function (PMF) p_X(s) = ℙ{X = s_i}, $s_i\in {S}$, where ${S}$ is the support of discrete random variable X, and there exists an axiomatic property of PMF: $\sum _{s_i\in {S}}{p}_X(s_i)=1$. Likewise, we can have the perceptual PMF (PPMF) given by

$\begin{array}{ll}{\tilde{p}}_X(s_i)=w(p_X(s_i)).& (8)\end{array}$

It is evident that $0\le {\tilde{p}}_X(s_i)\le 1$. However, the sum of PPMFs over support ${S}$ might not necessarily be unity, which is term the aberration of probability space, which can be shrinkage or expansion depending on whether $\sum _{s_i\in {S}}{\tilde{p}}_X(s_i)<1$ or $\sum _{s_i\in {S}}{\tilde{p}}_X(s_i)>1$. When $\sum _{s_i\in {S}}{\tilde{p}}_X(s_i)=1$, it is said to be canonical. The aberration of probability space is dominated by parameters γ and θ.

3.3. Summary of the Proposed Analytical Framework

Having obtained v(x, x₀), w(p), ${\tilde{F}}_X(s)$, ${\tilde{f}}_X(s)$, and ${\tilde{p}}_X(s_i)$, we can reevaluate a set of advanced and composite performance metrics for communication systems incorporating non-technological factors. For example, given a composite metric Ω(g) that is a function of a continuous random variable g, and the PDF of g is denoted as f_G(g), we can define the perceptual utility (PU) of the composite metric by

$\begin{array}{ll}\tilde{\Omega }={\displaystyle {\int }_0^{\infty }}v(\Omega (g),{\Omega }_0){\tilde{f}}_G(g)\text{d}g,& (9)\end{array}$

where Ω₀ is the reference point of the composite metric. Similarly for a discrete random variable g, we can define the PU of the composite metric in a similar way:

$\begin{array}{ll}\tilde{\Omega }={\displaystyle \sum _{g_i\in {S}}}v(\Omega (g),{\Omega }_0){\tilde{p}}_G(g_i).& (10)\end{array}$

$\tilde{\Omega }$ can be employed to appraise the subjective performance pertaining to the composite variable. Different from objective performance evaluation metrics, the PU based on the prospect theory is allowed to be negative, which implies a negative user impression/perception of the objective performance provided. Figure 5 depicts the complete implementation process of the prospect theoretic analytical framework for perceptual performance analysis. Overall, the novel communication system model is constructed by adding a observer for analyzing QoS and a perceptor for analyzing QoE after the classic receiving module, as shown in⁴ Figure 6.

FIGURE 5

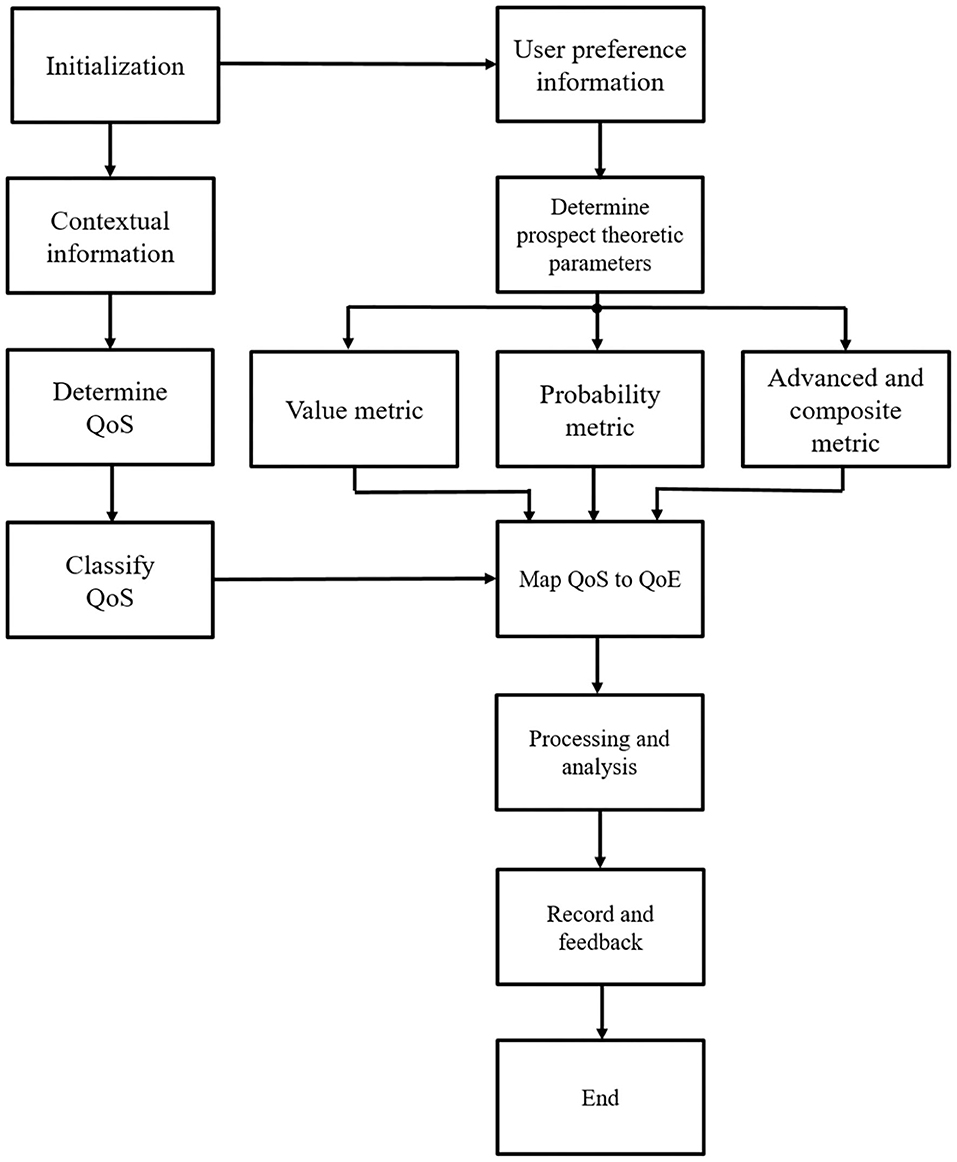
Figure 5. Implementation process of the prospect theoretic analytical framework for perceptual performance analysis.

FIGURE 6

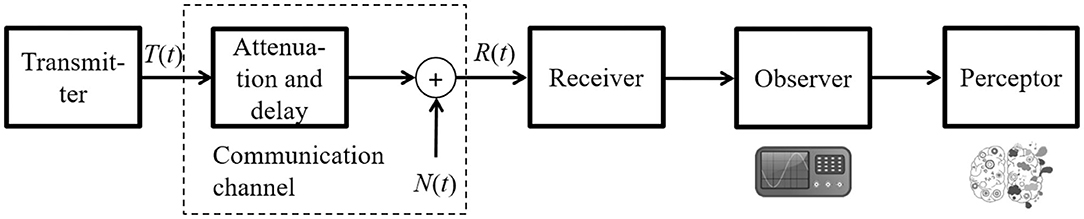
Figure 6. Novel communication system model constructed by adding a observer and a perceptor after the receiving module.

From the summary above, we can also easily find the advantages and disadvantages of the proposed analytical framework. Compared with classical analytical frameworks for communication systems, one of the obvious advantages is the capability of incorporating non-technological factors, especially the psychological effects of users, while much more complicated computations are involved which might be of poor mathematical tractability. In addition, the psychological effects of users are region-specific and time-varying, which indicates that the stochastic processes involved in the proposed analytical framework are non-stationary. Therefore, frequent estimations of model parameters by empirical studies are necessary to maintain the effectiveness of the proposed analytical framework.

4. Case Studies

In information and communications science, the essential foundation is the formulation of information, which has been well-studied since the original paper “A Mathematical Theory of Communication” by Claude E. Shannon. By the elegant definition of information given in Shannon's paper, information becomes objective, and the amount of information can be precisely measured. Specifically, the definition of information is constructed based on the consequence of uncertainty, which is thereby probabilistic. As a result, because of the five key attributes of human psychology given in section 2.3, the perception of uncertainty can be distorted, so as the perception of information. Due to the importance of uncertainty, we take the information entropy that is the measure of uncertainty in information science as an example to carry out preliminary case studies to show how the prospect theory can be utilized to incorporate human factors and the perception of uncertainty is interpreted in the context of human-centric communications.

Suppose that we have a random variable X, which can be either continuous or discrete. For the continuous case, the distribution of X can be fully characterized by its CDF F_X(s) or PDF f_X(s), while for the discrete case, the distribution of X can be fully described once PMF ${\{p_X(s_i)\}}_{s_i\in {S}}$ is known over support ${S}$. Because of the attribute of probability distortion, the corresponding probability perceived by users is supposed to be ${\tilde{F}}_X(s)=w(F_X(s))$ and ${\tilde{p}}_X(s_i)=w(p_X(s_i))$ for continuous and discrete X, respectively. Therefore, we can incorporate the effect of probability distortion in the perception of information by defining the perceptual entropy for continuous and discrete random variable X to be⁵

$\begin{array}{ll}\tilde{H}(X)=-{\displaystyle {\int }_{-\infty }^{\infty }}{\tilde{f}}_X(s)log({\tilde{f}}_X(s))\text{d}s,& (11)\end{array}$

and

$\begin{array}{ll}\tilde{H}(X)=-{\displaystyle \sum _{s_i\in {S}}}{\tilde{p}}_X(s)log({\tilde{p}}_X(s)).& (12)\end{array}$

For simplicity, again, we take the continuous case with the normalized exponential distribution f_X(s) = exp(−s) for s ≥ 0 to study the effect of probability distortion on the perceptual entropy. We plot the curves of perceptual entropy with different setups in Figure 7. As shown in this figure we can see that $\tilde{H}(X)<H(X)=-{\int }_{-\infty }^{\infty }{f}_X(s)log(f_X(s))\text{d}s=1$, indicating that the effect of probability distortion makes a perceptor feel less uncertain, while the authentic uncertainty characterized by H(X) = 1 is unchanged.

FIGURE 7

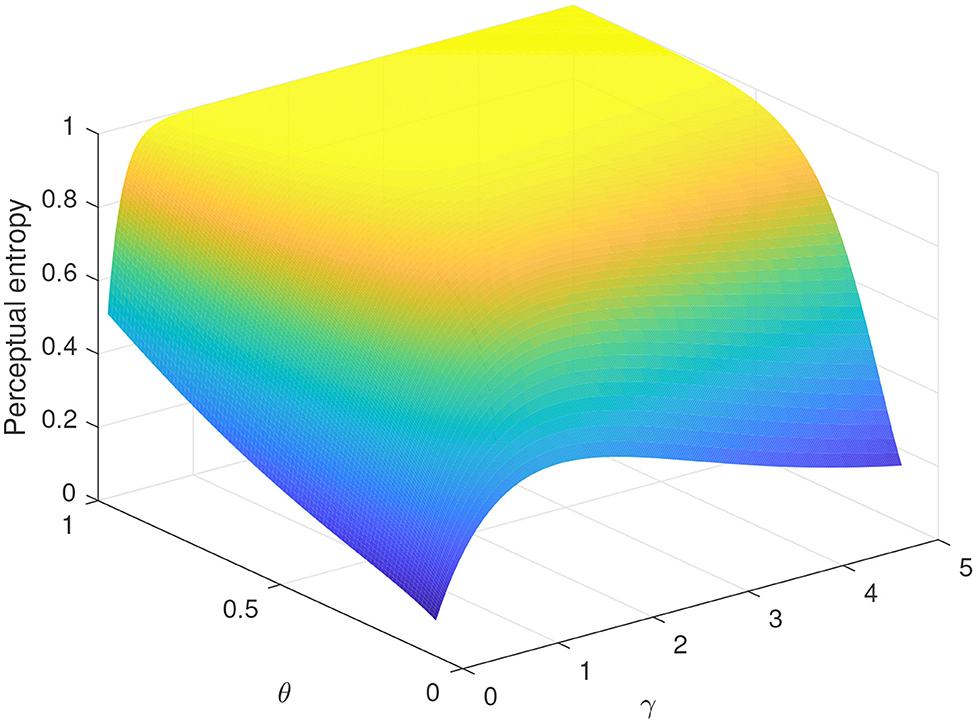
Figure 7. Perceptual entropy vs. γ and θ for continuous random variable, given f_X(s) = exp(−s) for s ≥ 0.

We also take a simplistic case of binary symmetric transmission of bit 0 and 1 as an example to test the effect of probability distortion on the perceptual entropy of a discrete random variable, given p_X(0) = 1/2, p_X(1) = 1/2, and ${S}=\left\{0,1\right\}$. By (12), the perceptual entropy is plotted in Figure 8, from which we can also find that $\tilde{H}(X)<H(X)=-\sum _{s_i\in \{0,1\}}{\tilde{p}}_X(s)log({\tilde{p}}_X(s))=1$. These results also indicate that a perceptor tends to underrate uncertainty brought by a discrete variable once abandoning the hypothesis of perfect rationality.

FIGURE 8

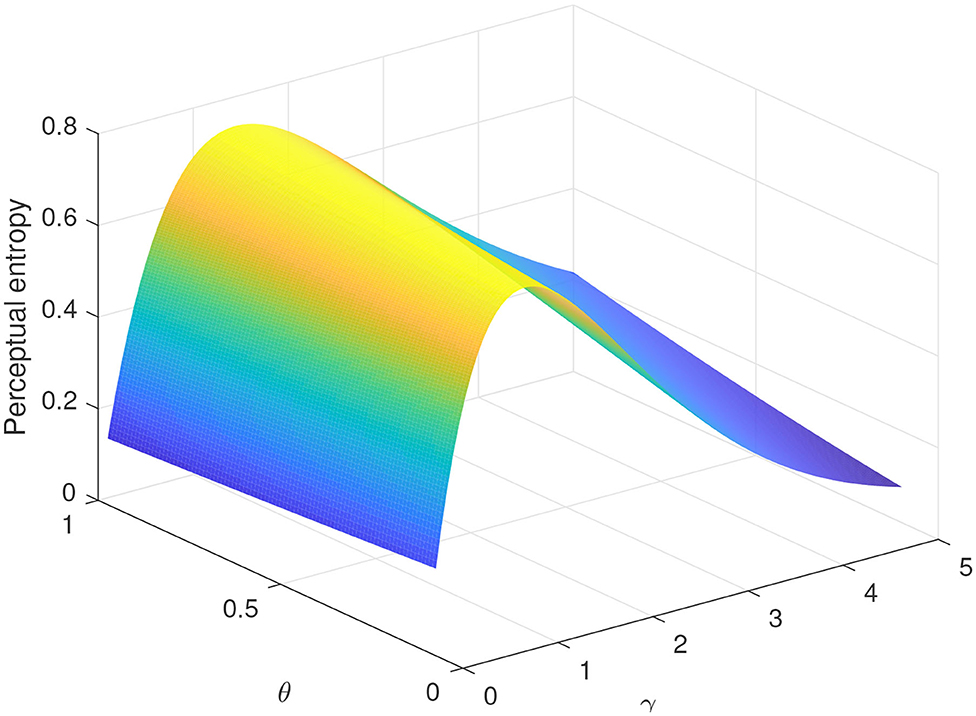
Figure 8. Perceptual entropy vs. γ and θ for discrete random variable, given p_X(0) = 1/2, p_X(1) = 1/2, and ${S}=\left\{0,1\right\}$.

5. Challenges and Promising Research Directions

In this study, we introduce the prospect theoretic analytical framework for modeling UE in communication systems. Although preliminary and immature, the proposed framework serves as a promising architecture for developing interdisciplinary applications of human-centric communications. In this section, we outline the challenges, potentials, and application aspects for future research on the prospect theoretic framework.

5.1. Extend Experimental Evidence to Non-monetary Contexts

Historically, the prospect theory has been developed based on monetary experiments (e.g., lottery-choice experiments). On the other hand, interdisciplinary applications of the prospect theory are becoming increasingly popular and have hitherto resulted in over a thousand research articles. In these applications, the analytical framework is based on the parameter estimates elicited by monetary experiments, for which an implicit assumption is that users must exhibit similar psychological features, such as loss aversion in non-monetary contexts (e.g., the choice of communication services). However, this critical assumption may not hold. For instance, it is widely recognized that individuals have different quantity and probability preferences for monetary and non-monetary stimuli. As suggested by Kilkki (2008), individuals seem less sensitive to QoS parameters (bit rates and delays) than monetary incentives, which indicates a higher degree of utility curvature. In the current stage, the practical significance of the QoE measurements remains unclear due to the lack of concrete empirical support (Saad et al., 2016). There is an urgent need to extend the experimental evidence to non-monetary contexts, which can provide a solid foundation and an explicit guideline for future interdisciplinary applications of the prospect theory.

5.2. Upgrade the Proposed Framework Using Advanced Behavioral Theory

In the past decade, the prospect theory has been successfully applied in diverse research topics that involve quantity and probability perception, which verifies the theory's potential in interdisciplinary applications. The prospect theory is now evolving at a rapid pace; the advances, such as the third- and fourth-generation prospect theory are readily applicable and begin to attract researchers' attention. Beyond the prospect theory, there is a bigger picture for interdisciplinary applications of behavioral economics. For instance, behavioral game theory has the potential to reshape the research landscape for game theoretic communications (e.g., radio resource management). Behavioral time discounting has enriched our understanding of time preferences and has profound implications for the intertemporal allocation of network resources. Psychological foundations, such as endowment effect, other-regarding preference, and judgment heuristics have promising application prospects in pricing strategy and product design in telecommunication industries. Overall, the paradigm shift from technology-centric to human-centric communications still faces tremendous challenges because communications science has long been preoccupied with classic QoS benchmarks. Human-centric communications remains a prospective uncultivated research area in the 5G era and the forthcoming 6G era.

5.3. Develop Mathematical Tools

Under the prospect theoretic framework, quantitative analysis of perpetual performance involves sophisticated mathematical manipulations (differentiation, integration, and power series expansion) on the value function v(x, x₀) and the probability weighting function w(p). However, the probability weighting function is generally employed within socioeconomics and lacks the application foundation in telecommunications. Due to the limited understanding of the mathematical properties of probability weighting function (especially the Prelec function), researchers always encounter challenges in solving the integral forms and find it difficult to further process the quantitative analysis (Rieger and Wang, 2006). A complete application of the prospect theory in communications science requires further exploration of the mathematical properties and analytical tools for the proposed functional forms.

5.4. Analyze the Information Theoretic Properties

The information theory constructed by Claude E. Shannon in “A Mathematical Theory of Communication” has been widely acknowledged as a landmark in telecommunications and the mathematical foundation of modern communication systems (Shannon, 1948). Developed from the information theoretic model, most communication system models consist of transmitter, channel, and receiver, in which objective noise, interference, impairments, and imperfection are taken into consideration (Wang et al., 2019). For developing human-centric communications, communication system models should incorporate the fundamental mechanism of human perception after the receiving module. We tentatively term this embodiment the perceptor under the prospect theoretic framework. The introduction of perceptor into communication systems can alter the formulation of information entropy and generate intriguing information theoretic properties.

5.5. Analyze the Perceptual Performance of Advanced Applications

In this paper, the prospect theoretic analytical framework was employed in several simplistic application scenarios for demonstration purposes. However, due to its generality and versatility, the proposed framework can be readily extended to advanced communication applications in beyond 5G networks. Promising application aspects include massive multiple-input and multiple-output (MIMO) systems, terahertz (THz) communication systems, visible light communication (VLC) systems, multi-user communication systems, cooperative relay aided communication systems, hybrid licensed/unlicensed communication systems, and etc. Overall, interdisciplinary collaborations between telecommunications, economics, and psychology is indispensable for the development of human-centric communications. In particular, communications researchers and engineers dedicate to the physical and technological characterizations in the analytical framework, while economists and psychologists focus on the non-technological characterizations. For newly identified non-technological issues and characteristics, economists also take the responsibility to design effective empirical approaches to test hypotheses and acquire the relevant model parameters.

6. Conclusion

In this paper, we proposed the prospect theoretic analytical framework for human-centric communications. This analytical framework takes non-technological factors and user psychology into consideration when modeling and analyzing communication systems, which enables quantitative analysis of perceptual performance. Case studies of perceptual entropy were introduced to illustrate how the prospect theory can be utilized to incorporate human factors and analyze human-centric communications. We also outlined the unresolved problems and promising directions for future research. Overall, this paper provides a guideline for improving communication services and introduces a common platform that unifies the nomenclature and endeavor from different disciplines, including telecommunications, economics, and psychology. Meanwhile, we also aim to use this paper as a fuze to trigger a new interdisciplinary research area for further investigation.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

BS and M-SA conceived the work and suggested the outline of the paper. KL and SD carried out investigations and wrote the paper. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^Similarly, one can consider the acceptable amount of compensation if the dropping probability increases by 5%. In most cases, people would not allow an increase of dropping probability from 0 to 5% but might be willing to negotiate over the compensation if the dropping probability increases from 50 to 55%. Again, the contrast between the increase and decrease of dropping probability is due to loss aversion, i.e., a loss is subjectively more significant than an equal gain.

2. ^Note that, there is a prerequisite for using this value model, the quantity metric of interest must be a desirable metric. A desirable metric is a metric that will be preferable with a larger value, e.g., transmission rate and network coverage. In this paper, we only consider desirable metrics without special notes, because of the limitation of the prospect theory originally dealing with the monetary benefit that is also a desirable metric.

3. ^For simplicity, we mainly analyze the single-metric scenario, in which only a single quantity metric x with its reference point x₀ is taken into consideration.

4. ^Note that, the proposed communication system model with the perceptor is different from the user-in-the-loop (UIL) model given in Schoenen and Yanikomeroglu (2014), which relies on incentives (e.g., dynamic pricing) to change user behaviors and responses.

5. ^There is not quantity metric involved in the definition of information entropy, and therefore the value function is not applicable in this case.

References

Al-Nowaihi, A., Bradley, I., and Dhami, S. (2008). A note on the utility function under prospect theory. Econ. Lett. 99, 337–339. doi: 10.1016/j.econlet.2007.08.004

CrossRef Full Text | Google Scholar

Baraković, S., and Skorin-Kapov, L. (2013). Survey and challenges of QoE management issues in wireless networks. J. Comput. Netw. Commun. 2013:165146. doi: 10.1155/2013/165146

CrossRef Full Text | Google Scholar

Boz, E., Finley, B., Oulasvirta, A., Kilkki, K., and Manner, J. (2019). Mobile QoE prediction in the field. Pervas. Mobile Comput. 59:101039. doi: 10.1016/j.pmcj.2019.101039

CrossRef Full Text | Google Scholar

Cao, Y., Duan, D., Cheng, X., Yang, L., and Wei, J. (2014). “Dynamic network selection in HetNets: a social-behavioral (SoBe) approach,” in 2014 IEEE Global Communications Conference (Austin, TX), 4653–4658. doi: 10.1109/GLOCOM.2014.7037542

CrossRef Full Text | Google Scholar

Chen, Y., He, S., and Hou, F. (2019). “A pricing strategy for D2D communication from a prospect theory perspective,” in Proceedings of IEEE VTC Spring (Kuala Lumpur), 1–5. doi: 10.1109/VTCSpring.2019.8746552

CrossRef Full Text | Google Scholar

Dang, S., Amin, O., Shihada, B., and Alouini, M. S. (2020). What should 6G be? Nat. Electron. 3, 20–29. doi: 10.1038/s41928-019-0355-6

CrossRef Full Text | Google Scholar

De Moor, K., Ketyko, I., Joseph, W., Deryckere, T., De Marez, L., Martens, L., et al. (2010). Proposed framework for evaluating quality of experience in a mobile, testbed-oriented living lab setting. Mobile Netw. Appl. 15, 378–391. doi: 10.1007/s11036-010-0223-0

CrossRef Full Text | Google Scholar

Dhami, S. (2016). The Foundations of Behavioral Economic Analysis. Oxford: Oxford University Press.

Google Scholar

Dong, M., Kimata, T., Sugiura, K., and Zettsu, K. (2014). Quality-of-experience (QoE) in emerging mobile social networks. IEICE Trans. Inform. Syst. 97, 2606–2612. doi: 10.1587/transinf.2013THP0011

CrossRef Full Text | Google Scholar

Fiedler, M., Hossfeld, T., and Tran-Gia, P. (2010). A generic quantitative relationship between quality of experience and quality of service. IEEE Netw. 24, 36–41. doi: 10.1109/MNET.2010.5430142

CrossRef Full Text | Google Scholar

Finley, B., Boz, E., Kilkki, K., Manner, J., Oulasvirta, A., and Hämmäinen, H. (2017). Does network quality matter? A field study of mobile user satisfaction. Pervas. Mobile Comput. 39, 80–99. doi: 10.1016/j.pmcj.2016.08.014

CrossRef Full Text | Google Scholar

Guidolin, F., Pappalardo, I., Zanella, A., and Zorzi, M. (2014). “A Markov-based framework for handover optimization in hetnets,” in 2014 13th Annual Mediterranean Ad Hoc Networking Workshop (MED-HOC-NET) (Piran), 134–139. doi: 10.1109/MedHocNet.2014.6849115

CrossRef Full Text | Google Scholar

Kahneman, D., and Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica 47, 263–292. doi: 10.2307/1914185

CrossRef Full Text | Google Scholar

Kilkki, K. (2008). Quality of experience in communications ecosystem. J. Univ. Comput. Sci. 14, 615–624.

Google Scholar

Le Callet, P., Möller, S., and Perkis, A. (2012). “Qualinet white paper on definitions of quality of experience,” in European Network on Quality of Experience in Multimedia Systems and Services (COST Action IC 1003), 3.

Google Scholar

Lee, C. (2015). “Prospect theoretic user satisfaction in wireless communications networks,” in Proceedings of IEEE WOCC (Taipei), 195–200. doi: 10.1109/WOCC.2015.7346204

CrossRef Full Text | Google Scholar

Lee, G., Kim, H., Cho, Y., and Lee, S. (2014). QoE-aware scheduling for sigmoid optimization in wireless networks. IEEE Commun. Lett. 18, 1995–1998. doi: 10.1109/LCOMM.2014.2354409

CrossRef Full Text | Google Scholar

Li, T., and Mandayam, N. B. (2012). “Prospects in a wireless random access game”, in Proceedings of IEEE CISS (Princeton, NJ), 1–6. doi: 10.1109/CISS.2012.6310922

CrossRef Full Text | Google Scholar

Li, T., and Mandayam, N. B. (2014). When users interfere with protocols: prospect theory in wireless networks using random access and data pricing as an example. IEEE Trans. Wireless Commun. 13, 1888–1907. doi: 10.1109/TWC.2013.021214.130472

CrossRef Full Text | Google Scholar

Mitra, K., Zaslavsky, A., and hlund, C. (2015). Context-aware QoE modelling, measurement, and prediction in mobile computing systems. IEEE Trans. Mobile Comput. 14, 920–936. doi: 10.1109/TMC.2013.155

CrossRef Full Text | Google Scholar

Piamrat, K., Viho, C., Bonnin, J., and Ksentini, A. (2009). “Quality of experience measurements for video streaming over wireless networks,” in Proceedings of IEEE ITNG (Las Vegas, NV), 1184–1189. doi: 10.1109/ITNG.2009.121

CrossRef Full Text | Google Scholar

Prashanth, L., Jie, C., Fu, M., Marcus, S., and Szepesvári, C. (2016). “Cumulative prospect theory meets reinforcement learning: prediction and control,” in International Conference on Machine Learning (New York City, NY), 1406–1415.

Google Scholar

Prelec, D. (1998). The probability weighting function. Econometrica 66, 497–527. doi: 10.2307/2998573

CrossRef Full Text | Google Scholar

Rehman Laghari, K. U., and Connelly, K. (2012). Toward total quality of experience: a QoE model in a communication ecosystem. IEEE Commun. Mag. 50, 58–65. doi: 10.1109/MCOM.2012.6178834

CrossRef Full Text | Google Scholar

Reichl, P. (2010). From charging for quality of service to charging for quality of experience. Ann. Telecommun. 65, 189–199. doi: 10.1007/s12243-009-0144-8

CrossRef Full Text | Google Scholar

Reichl, P., Tuffin, B., and Schatz, R. (2013). Logarithmic laws in service quality perception: where microeconomics meets psychophysics and quality of experience. Telecommun. Syst. 52, 587–600. doi: 10.1007/s11235-011-9503-7

CrossRef Full Text | Google Scholar

Rieger, M. O., and Wang, M. (2006). Cumulative prospect theory and the St. Petersburg paradox. Econ. Theory 28, 665–679. doi: 10.1007/s00199-005-0641-6

CrossRef Full Text | Google Scholar

Saad, W., Glass, A. L., Mandayam, N. B., and Poor, H. V. (2016). Toward a consumer-centric grid: a behavioral perspective. Proc. IEEE 104, 865–882. doi: 10.1109/JPROC.2016.2520760

CrossRef Full Text | Google Scholar

Schoenen, R., and Yanikomeroglu, H. (2014). User-in-the-loop: Spatial and temporal demand shaping for sustainable wireless networks. IEEE Commun. Mag. 52, 196–203. doi: 10.1109/MCOM.2014.6736762

CrossRef Full Text | Google Scholar

Seufert, M., Wassermann, S., and Casas, P. (2019). Considering user behavior in the quality of experience cycle: towards proactive QoE-aware traffic management. IEEE Commun. Lett. 23, 1145–1148. doi: 10.1109/LCOMM.2019.2914038

CrossRef Full Text | Google Scholar

Shannon, C. E. (1948). A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x

CrossRef Full Text | Google Scholar

Streijl, R. C., Winkler, S., and Hands, D. S. (2016). Mean opinion score (MOS) revisited: methods and applications, limitations and alternatives. Multimed. Syst. 22, 213–227. doi: 10.1007/s00530-014-0446-1

CrossRef Full Text | Google Scholar

Sun, Y., Feng, G., Qin, S., and Sun, S. (2018). Cell association with user behavior awareness in heterogeneous cellular networks. IEEE Trans. Vehicul. Technol. 67, 4589–4601. doi: 10.1109/TVT.2018.2796135

CrossRef Full Text | Google Scholar

Taleb Zadeh Kasgari, A., Saad, W., and Debbah, M. (2019). Human-in-the-loop wireless communications: machine learning and brain-aware resource management. IEEE Trans. Commun. 67, 7727–7743. doi: 10.1109/TCOMM.2019.2930275

CrossRef Full Text | Google Scholar

Tversky, A., and Kahneman, D. (1992). Advances in prospect theory: cumulative representation of uncertainty. J. Risk Uncertain. 5, 297–323. doi: 10.1007/BF00122574

CrossRef Full Text | Google Scholar

Wang, Z., Dang, S., Shaham, S., Zhang, Z., and Lv, Z. (2019). Basic research methodology in wireless communications: the first course for research-based graduate students. IEEE Access 7, 86678–86696. doi: 10.1109/ACCESS.2019.2925708

CrossRef Full Text | Google Scholar

Xiao, L., Liu, J., Li, Y., Mandayam, N. B., and Poor, H. V. (2014). “Prospect theoretic analysis of anti-jamming communications in cognitive radio networks,” in Proceedings of IEEE GLOBECOM (Austin, TX), 746–751. doi: 10.1109/GLOCOM.2014.7036897

CrossRef Full Text | Google Scholar

Xiao, L., Xu, D., Xie, C., Mandayam, N. B., and Poor, H. V. (2017). Cloud storage defense against advanced persistent threats: a prospect theoretic study. IEEE J. Select. Areas Commun. 35, 534–544. doi: 10.1109/JSAC.2017.2659418

CrossRef Full Text | Google Scholar

Xu, D., Li, Y., Xiao, L., Mandayam, N. B., and Poor, H. V. (2016). “Prospect theoretic study of cloud storage defense against advanced persistent threats,” in Proceedings of IEEE GLOBECOM (Washington, DC), 1–6. doi: 10.1109/GLOCOM.2016.7842178

CrossRef Full Text | Google Scholar

Yang, M., Wang, S., Calheiros, R. N., and Yang, F. (2018). Survey on QoE assessment approach for network service. IEEE Access 6, 48374–48390. doi: 10.1109/ACCESS.2018.2867253

CrossRef Full Text | Google Scholar

Yang, Y., Park, L. T., Mandayam, N. B., Seskar, I., Glass, A. L., and Sinha, N. (2015). Prospect pricing in cognitive radio networks. IEEE Trans. Cogn. Commun. Netw. 1, 56–70. doi: 10.1109/TCCN.2015.2488636

CrossRef Full Text | Google Scholar

Yu, J., Cheung, M. H., and Huang, J. (2016). Spectrum investment under uncertainty: a behavioral economics perspective. IEEE J. Select. Areas Commun. 34, 2667–2677. doi: 10.1109/JSAC.2016.2605279

CrossRef Full Text | Google Scholar

Yu, J., Cheung, M. H., Huang, J., and Poor, H. V. (2017). Mobile data trading: Behavioral economics analysis and algorithm design. IEEE J. Select. Areas Commun. 35, 994–1005. doi: 10.1109/JSAC.2017.2676958

CrossRef Full Text | Google Scholar

Zhang, X., Zhang, Y., Yu, R., Wang, W., and Guizani, M. (2014). Enhancing spectral-energy efficiency for LTE-advanced heterogeneous networks: a users social pattern perspective. IEEE Wireless Commun. 21, 10–17. doi: 10.1109/MWC.2014.6812286

CrossRef Full Text | Google Scholar