Quantifying the economic value of customers' social networks: does Metcalfe's law apply?

A recent article tries to improve upon the extant Customer Lifetime Value models by incorporating more of the information that companies have on their customers, including the size of their social networks. The present note argues that, in doing so, the authors mistakenly invoke Metcalfe's law and should rather have opted for Sarnoff's law.

1 Introduction

In a recent article, Lamela-Orcasitas and García-Madariaga (2023)—hereafter LOGM—propose a new model to quantify the value of the data that companies have on their customers. They also apply their model to a Spanish insurance company.

This conceptual note argues that, for the Customer Social Value (CSV) component of their model, the authors mistakenly invoke the well-known Metcalfe's law. Correcting this theoretical mismatch lowers LOGM's CSV estimates by 56%.

2 The V_ICRM model

LOGM start by pointing out that the traditional Customer Lifetime Value (CLV) concept “considers [only] the expected potential economic value of strictly transactional relationships” (o.c., p. 2). LOGM argue that customers can create value for companies in other ways. They therefore propose a new “customer relationship management information value model” (V_ICRM) that extends CLV as in Equation (1):

$\begin{array}{ll}f(CLV)\supset \left[+CEV\pm CKV\pm CSV\right],& (1)\end{array}$

where f (CLV) “includes the expected economic value […] of the customer's transactional operations together with the mediating effect of […] three factors” (o.c., p. 3). The latter are, respectively, customer engagement value, customer knowledge value, and customer social value. This note focuses on CSV because this is where the conceptual problem is situated.

LOGM define CSV as “the potential value that a customer contributes or detracts thanks to the influence they exert on the[ir] environment” (o.c., p. 4). In other words, the customer's network of contacts matters. LOGM therefore estimate CSV as:

$\begin{array}{ll}CSV=Q_{\text{m}}*N^2,& (2)\end{array}$

with Q_m ∈ [−1;1] = a measure of the quality of the contacts, and N = the “number of contacts […] whom the customer can influence sensitively” (o.c., p. 4). Specifically, Q_m is measured as the product of a customer's Influence and Authority. In this, Influence should be read as the Net Promoter Score—a metric for the customer's willingness to recommend the company to others. Authority is calculated as the average number of LinkedIn followers and the number of social networks the customer is active in, both normalized.

Finally, and crucially, LOGM justify the squaring of N in Equation (2) by referring to Metcalfe's law, which states that the value of a communications network is proportional to the number of members. Unfortunately, Metcalfe's law is not relevant to LOGM's setting.

3 Metcalfe's law does not apply

The intuition behind Metcalfe's law is straightforward: as a communications network adds members, the number of potential connections increases; hence, the utility of the network for individual members increases—there is a “network effect”—and so does its aggregate value. Formally, in a network of size N, any member can interact with N-1 other members. Hence, the utility of belonging to the network is proportional to N-1. The aggregate value of the network—individual utility times the number of members—is thus proportional to (N-1) ^* N—which, for large N, can be simplified to N² (Van Hove, 2016). Important to stress is that Metcalfe's law revolves around utility for users.

While Metcalfe's law might seem relevant for LOGM's setting—after all, the N in Equation (2) refers to the number of contacts in a customer's network—in fact, it is not. Consider a customer A, who has three contacts: B, C, and D. LOGM's premise is that the latter might be influenced—hopefully in a positive way—by A.

The left-hand panel of Figure 1 illustrates how the authors consider A's social network when computing her CSV. As LOGM rely on Metcalfe's law, all N ^* (N-1) = 6 connections between B, C, and D matter in their calculations. Hence, A's CSV is proportional to 6. (As is visible in the Figure 1, in LOGM's set-up, N excludes customer A herself.)

Figure 1

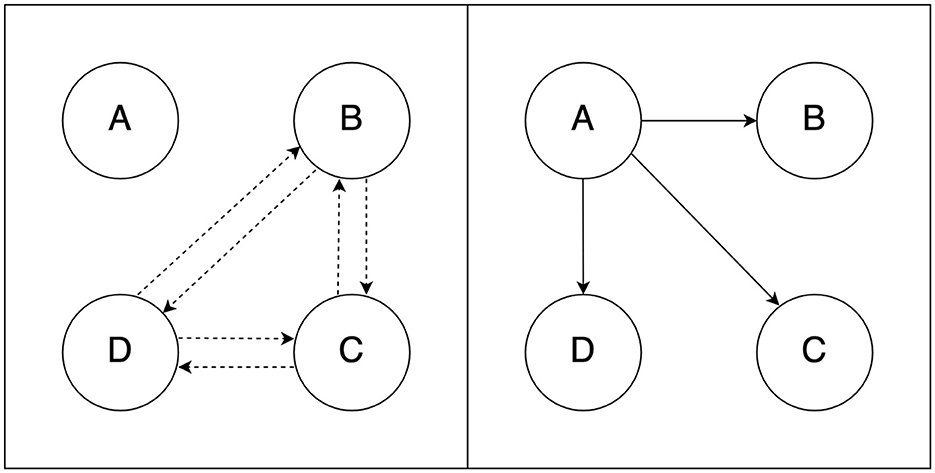
Figure 1. Relationships that bring value. The left-hand panel shows the six links that, according to Metcalfe's law (as invoked by LOGM), would bring value to the company; the right-hand panel shows the three relationships that matter according to the present note.

The key point in this note is that Metcalfe's law simply does not apply in LOGM's setting and that invoking it results in a mismeasurement of the relevant connections. To repeat, Metcalfe's law is about the utility of the network for its members. Connection B-C, for example, is included in the calculation of the aggregate utility because it is useful for customer B.

Conversely, LOGM are not concerned about the utility of the connections in A's social network for B, C, or D. Rather, they try to gauge the value of A's network for the company, and, crucially, this value comes from the number of contacts whom A “can influence sensitively.” As the metric is not a utility for users, there is no theoretical justification to invoke Metcalfe's law. In addition, as will become clear below, it is not as if utility for customers and value for the company somehow coincide.

Invoking Metcalfe's law is also problematic from a pragmatic angle. The reason is that it comes with non-neutral assumptions; namely, all connections matter, and they matter equally. The result is non-linear growth in network value: the value of a network with two contacts is proportional to 2 ^* 1 = 2; the value of a network with twice as many contacts is proportional to 4 ^* 3 = 12—a factor of 6 higher. This is hard to justify in LOGM's setting. As is illustrated with real data in Section 4, squaring N amounts to overweighting the social value of customers with a high number of contacts.

So, how should one measure A's CSV then? If the value of A's network for the company comes from possible recommendations to others, then a better metric would seem to be the simple number (pun intended) of contacts that A has. Put differently, if there is a “network law” that applies, it would appear to be Sarnoff's rather than Metcalfe's. Indeed, Sarnoff's law holds that the value of a one-to-many broadcasting network (such as radio or TV) increases proportionally to the number of users (Scala and Delmastro, 2023, p. 2).

From this perspective, as can be seen in the right-hand panel of Figure 1, the CSV of A is proportional to 3 rather than 6. That is, the three direct connections, A-B, A-C, and A-D, are what matters. (As can be seen in the left-hand panel of Figure 1, these links are not taken into account in LOGM's calculation of A's CSV—which is another sign that Metcalfe's law is not fit for purpose in their setting.)

More generally, the correct expression for the CSV of customer i is thus not Equation (2), but rather:

$\begin{array}{ll}CS{V}_{\text{i}}=Q_{\text{m}}^{\text{i}}*N_{\text{i}}.& (3)\end{array}$

One could counter—even though LOGM do not elaborate on this—that indirect connections such as A-B-D (or even A-B-C-D) might also matter because, in this way, if customer A does not talk about the company to D, D might still be influenced. However, it is not a given that B and D know each other; in other words, it is not a given that they are part of a network proper (this is why the lines in the left-hand panel are dashed, unlike those in the right-hand panel—as the latter connections are known to exist). If B and D do know each other, it is not a given that B transmits A's message, and if it is transmitted, the impact is likely lower. In any case, whatever the paths taken, in the example of Figure 1, the message would ultimately reach only three people—the N_i in Equation (3).

Note also that the Q_m in LOGM's Equation (2) incorporates A's Net Promoter Score. In other words, LOGM assume that A reaches out to B, C, and D—with equal probability. Any indirect influence would thus not seem to bring much additional value to the company, as it is trumped by the direct influence (which is measured). In addition, the use of a single Q_m in Equation (2)—that of the customer herself—indicates that LOGM assume that direct contacts between the customer and individuals in her network are what matter. This corresponds to the right-hand panel of Figure 1 rather than the left-hand panel. Still, to the extent that indirect links reinforce the transmission of influence across the graph, Sarnoff's law provides a lower bound for customers' CSV.

4 Implications

The examples above already indicate that the ramifications of the proposed correction are substantial. To gauge the precise impact, this section redoes LOGM's CSV calculations. As mentioned, LOGM apply their model to the case of a Spanish insurance company. From the entire client portfolio, the authors choose 60 randomly, 10 for each previously defined segment (Lamela-Orcasitas and García-Madariaga, 2023, p. 6).

Inspection of the data revealed that, surprisingly, the correction affects only a small subset of the 60 customers, 9 to be precise. The explanation lies in “the fact that very few relationships were reported in the [CRM] system” of the company (o.c., p. 8). For half of the observations (30), the number of active relationships is even 0. A further 21 observations have a reported value of 1 or 2. None of these are affected. For N = 2, the outcomes of Equations (2, 3) are the same because LOGM, in practice, calculate Equation (2) as Q_m ^* N ^* (N-1)—presumably in view of the low values for N. For N = 1, Q_m ^* N equals Q_m whereas Q_m ^* N ^* (N-1) equals 0, but, as LOGM find it unlikely that a customer has zero social value, they nevertheless give these customers a value of Q_m. They do the same for customers with zero reported relationships.

For the observations that are affected, the impact is substantial. As can be gleaned from a comparison of Equations (2, 3), all corrected “raw” CSV values are a factor N-1 lower than the original. For a customer with eight contacts in the CRM database, the factor is thus no less than 7. The correction obviously also impacts the CSV values in euro that LOGM compute. These are calculated as CLV ^* CSV ^* rCEV, with r = retention rate; see LOGM's Equation (7). Both the original and corrected values are shown in Table 1. Note that whereas customer I was supposedly 16.0 times more valuable for the company than customer A, after the correction, this was reduced to 4.6.

Table 1

Table 1. CSV of selected customers (in euro): original vs. corrected.

Finally, because the correction affects the customers with the bigger social networks, the total social value of LOGM's full sample (of 60 customers) is also dramatically reduced by no less than 56%. The standard deviation is also substantially lower. This is because LOGM's squaring of N in Equation (2) blows up the social value of customers with more than two contacts.

5 Discussion

This note has argued that, for the Customer Social Value component of their model, LOGM mistakenly invoke Metcalfe's law. The intuition is that the point of view is completely different: Metcalfe's law reasons in terms of the utility of a company's network for users; LOGM try to measure the value of customers' networks for the company. Imbedded in Metcalfe's law is a network effect that results in stronger-than-linear growth in network value; in LOGM's setting, there is no basis for such a pattern. Sarnoff's law would seem to be a more realistic option in that it only measures direct links and does not take into account a possible reinforcement of a customer's influence via indirect links.

Despite this critique, LOGM are to be commended for trying to overcome an important limitation of the extant CLV literature: “Almost all studies are limited to proposing exclusively theoretical models or models that, due to their technical complexity, can hardly be put into practice in a real work environment” (o.c., p. 2). It is thus to be hoped that their model will be put to the test, with a corrected CSV component, and with higher-quality CRM data.

Author contributions

LV: Conceptualization, Formal analysis, Visualization, Writing—original draft, Writing—review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The author is indebted to Carlos Lamela-Orcasitas for making available part of their dataset, as well as for all the clarifications and the interesting discussions that have allowed the author to hone their argument. The author also thanks one of the reviewers, as well as the Editor.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Lamela-Orcasitas, C., and García-Madariaga, J. (2023). How to really quantify the economic value of customer information in corporate databases. Humanit. Soc. Sci. Commun. 10:166. doi: 10.1057/s41599-023-01654-6

Crossref Full Text | Google Scholar

Scala, A., and Delmastro, M. (2023). The explosive value of the networks. Sci. Rep. 13:1037. doi: 10.1038/s41598-022-26961-x

Crossref Full Text | Google Scholar

Van Hove, L. (2016). Testing Metcalfe's law: pitfalls and possibilities. Inf. Econ. Policy 37, 67–76. doi: 10.1016/j.infoecopol.2016.09.001

Crossref Full Text | Google Scholar