Causal inference of diachronic semantic maps from cross-linguistic synchronic polysemy data

Semantic maps are used in lexical typology to summarize cross-linguistic implicational universals of co-expression between meanings in a domain. They are defined as networks which, using as few links as possible, connect the meanings so that every isolectic set (i.e., set of meanings that can be expressed by the same word in some language) forms a connected component. Due to the close connection between synchronic polysemies and semantic change, semantic maps are often interpreted diachronically as encoding potential pathways of semantic extension. While semantic maps are traditionally generated by hand, there have been attempts to automate this complex and non-deterministic process. I explore the problem from a new algorithmic angle by casting it in the framework of causal discovery, a field which explores the possibility of automatically inferring causal structures from observational data. I show that a standard causal inference algorithm can be used to reduce cross-linguistic polysemy data into minimal network structures which explain the observed polysemies. If the algorithm makes its link deletion decisions on the basis of the connected component criterion, the skeleton of the resulting causal structure is a synchronic semantic map. The arrows which are added to some links in the second stage can be interpreted as expressing the main tendencies of semantic extension. Much of the existing literature on semantic maps implicitly assumes that the data from the languages under analysis is correct and complete, whereas in reality, semantic map research is riddled by data quality and sparseness problems. To quantify the uncertainty inherent in the inferred diachronic semantic maps, I rely on bootstrapping on the language level to model the uncertainty caused by the given language sample, as well as on random link processing orders to explore the space of possible semantic maps for a given input. The maps inferred from the samples are then summarized into a consensus network where every link and arrow receives a confidence value. In experiments on cross-linguistic polysemy data of varying shapes, the resulting confidence values are found to mostly agree with previously published results, though challenges in directionality inference remain.

1 Introduction

Much of lexical typology, the discipline which tries to derive generalizations about the ways in which languages carve up semantic space into lexemes, rests on the notion of colexification (François, 2008). A polysemous word is said to colexify its meanings, providing evidence that its meanings can be co-expressed by the same form. The set of meanings of a polysemous word is called an isolectic set, or an isolectic area if we want the emphasize the assumption that each word picks out a contiguous subregion of an underlying semantic space. Isolectic sets provide us with evidence of the structure of this underlying space, which we assume to be constituted by a set of cross-linguistic meanings.

A semantic map, as first explored by Anderson (1982) and systematized by Haspelmath (2003) for the analysis of grammatical meanings, summarizes evidence of the structure of this space in the shape of a graph structure which consists of undirected links between pairs of meanings. Informed by the connectivity hypothesis (Croft, 2002, p. 134), meanings are connected in such a way that each isolectic set corresponds to a connected region in the graph, i.e., each pair of colexified concepts is connected by a path which consists only of additional meanings of the same word. This criterion implies that semantic maps express cross-linguistic universals of colexification. If the only connection between two meanings A and C in a semantic map is a path A — B — C, the map predicts that any word which has the meanings A and C will also have the meaning B. A semantic map additionally follows the economy principle (Georgakopoulos and Polis, 2018), i.e., it must be minimal in the sense that no link in it can be deleted without violating the criterion.

Semantic maps are far from unique for any given dataset, as many different sequences of link deletions or additions can lead to different locally minimal graph structures which meet the criterion. When linguists manually infer a semantic map from a dataset, the linking decisions are typically guided by intuition or additional knowledge, yet the result will not necessarily be globally optimal because the number of possible maps will often be intractably large. An automated inference algorithm for synchronic semantic maps was developed by Regier et al. (2013), which tries to make near-optimal decisions through a heuristic which always gives priority to the link which leads toward connecting the meanings for the highest number of isolectic sets for which the criterion is not yet met.

A recent trend in semantic map research tries to enrich the structures by diachronic information, detecting tendencies in changes of lexification patterns to derive a theory of “lexical tectonics” (François, 2022). The basic idea of a diachronic semantic map is that some of the edges in a semantic map receive a directionality, with the intention to represent common pathways or universal tendencies of semantic extension and change within the domain. This addition of directed links has so far very much been a manual process based on philological insight, as exemplified by Georgakopoulos and Polis (2021). The potential of determining cross-linguistically valid directionalities is severely limited by the very small number of language families for which historical texts are available in sufficient quantities, which is why no inference algorithm for diachronic semantic maps has been suggested so far.

This article presents a new approach to synchronic and diachronic semantic map inference which is based on techniques of causal discovery (Glymour et al., 2019), a class of statistical methods in which sets of variables are analyzed in order to assign a minimal model of the underlying causal structure. This causal structure is expressed as a directed acyclic graph connecting the variables. The application of causal inference to discrete data has not been explored very widely, but it turns out that existing work on causal inference of phylogenetic networks from cognacy data (Dellert, 2019) can be applied rather directly to the task of inferring semantic maps from a collection of overlapping isolectic sets. The algorithm starts with a fully connected graph over a set of meanings, and progressively deletes links based on a connecting path criterion which ensures that no isolectic set is split into several components. Eventually, the algorithm arrives at a graph where every link is necessary according to the criterion that each isolectic set needs to be a connected component. I present example results of my implementation of the new algorithm, discussing some of its properties, and show that inferring what is called the causal skeleton corresponds to the inference of a synchronic semantic map.

I then present some options for using my efficient implementation to run the algorithm many times on variations of the input data, and exploring the space of possible semantic maps, in order to quantify our uncertainty about each inferred link. Finally, I build on previous research on determining the directionality of semantic change (Dellert, 2016) in order to recover the directional signal, allowing the algorithm to automatically infer diachronic semantic maps from synchronic data alone, without requiring the presence and analysis of historically attested changes. To explore the potential of the method on currently available data, I attempt to reproduce classical findings on pathways of semantic change among body parts and verbs of perception.

2 Materials and methods

2.1 Semantic map inference as causal discovery

Causal discovery is a comparatively young field which develops approaches to the inference of causal structures from observational data. In the most popular model laid out by Pearl (2009), causal structures are expressed as directed acyclic graphs over the observed variables, and the observations are taken to be samples of the joint distribution of these variables. Beyond the purpose of other types of graphical models, where the focus is on modeling the joint distribution of variables, the directionality of causal structures additionally enables predictions of what would happen if one of the variables were manipulated. There is a mathematical procedure (the do-calculus) which enables the calculation of probabilities for counterfactuals (how would the outcome have been different given different actions and/or circumstances?), which is necessary to consistently identify primary and secondary causes of an event, as will often need to be done in the context of assessing legal responsibility, or finding the root cause of a system failure.

More crucially for our application, causal discovery algorithms are able to assign a directionality to at least some links in the structure, reflecting a monodirectional causal relationship. This provides causal discovery with the unique ability to infer causality from observational data alone, against the traditional scientific view that causality can only be established by experiment, i.e., by manipulating some variable while observing the behavior of others. As in many sciences, direct experimentation is potentially unethical (medicine, psychology) or infeasible (politics, economics), techniques which allow to infer causality from available observational data are very promising.

To cite a famous example for context, Spirtes et al. (2000) show how causal inference can be used to refute an argument proposed by lawyers representing the tobacco industry in order to explain away the link between smoking and lung cancer. The argument was that the apparent correlation (which was taken to suggest a direct causal link S→C from smoking to cancer) was due to a hidden common cause, such as a genetic predisposition G which causes both a tendency to develop lung cancer and a taste for cigarettes (S←G→C). Without being able to measure G, classical statistical methods are unable to resolve the question, and running a medical experiment to test the causality hypothesis directly is obviously unethical. By performing conditional independence tests involving additional variables (such as income and the parents' smoking habits), causal inference can, under certain conditions, prove the direction of causality must be S→C, independently of whether the claimed genetic predisposition exists or not.

For linguistic typology, causal discovery holds some promise because we obviously cannot (and would not want to) manipulate the grammar or the lexicon of an entire community of speakers. In lexical typology, we can try to use causal inference in order to infer pathways of semantic change from observational data in the shape of synchronic polysemies.

Causal discovery from linguistic data was previously explored by Dellert (2019) as a framework for phylogenetic network inference. Here, the variables are attested or reconstructed languages, and the presence or absence of cognate sets in these languages forms the observations which give rise to constraints that correspond to connected components. The underlying idea is that the lexicon of a language can be framed as being caused by the lexicon inherited from previous stages and by possible contributions from the lexicon of donor languages, with lexical replacement and semantic shift being treated as noise in this causal structure over languages. Results by Dellert (2019) have shown that in many situations, the application of causal inference results in plausible minimal contact networks between the languages, and that directionality inference (i.e., determining the directionality of borrowing between languages that were inferred to have been in contact) works reasonably well in a range of cases, but is generally much more difficult.

In order to apply causal discovery algorithms to polysemy data, we will instead treat the meanings of the relevant domain (the nodes of the semantic map) as variables, and take the ways in which different languages carve up the semantic space as joint observations of these variables. A link between two senses will imply that the associated variables are in a direct causal relationship, i.e., the forms for one sense can be seen as “causing” the forms for the other. This directly reflects our understanding of how lexifications tend to arise. To take a classical example, if the forms assigned to the meaning MONTH are often originally the forms for MOON, and the additional lexification of forms for MOON arises through semantic extension, we can quite literally frame this as the forms for MOON having a causal influence on the words for MONTH. Under the diachronic interpretation, a directed link between two meanings would imply that semantic extension across the link will typically only happen in the direction of the arrow, e.g., MOON → MONTH.

Under the do-calculus, if we have a directed link MOON → MONTH, and otherwise no indirect connection between the two meanings, this would imply that if a new word for MOON gets introduced into the language, there is a change in the expectation of what the word for MONTH could be, whereas a new word for MONTH will not allow any prediction about a possible change to the word for MOON.

The algorithm proposed here builds on the central insight that the semantic map inference problem can be seen as the transpose of the lexical flow network inference problem. Both problems can be addressed by the same algorithm on data of the same shape: a meaning-language matrix with a list of synonymous forms in each entry, which is often simply called a coexpression matrix. The only relevant difference between the two applications lies in exchanged roles for variables and observations. Where the previous application treated languages as being connected by cognate sets (denoting different meanings), we are now interested in meanings connected by isolectic sets (as observed in different languages). The meanings are the variables among which we want to infer a causal structure, and the isolectic sets are the (joint) observations of these variables.

2.2 Conditional mutual information and the connected component criterion

Causal inference has grown into a large field where a wide range of algorithmic approaches are being explored, but only the framework of constraint-based causal discovery provides a direct match to the lexical flow network and semantic map inference problems on discrete coexpression data. The PC* (read: “PC star”) algorithm (Spirtes et al., 2000), which we are going to apply to our polysemy data, is an improved version of the original PC (Peter-Clark) algorithm introduced by Spirtes and Glymour (1991) as the very first constraint-based causal inference algorithm. Most of the later improvements of the original PC algorithm carry over to the PC* algorithm, and my implementation will make use of some of these improvements. The core building block of constraint-based causal inference algorithms is a consistent conditional independence test. Instances of such a test need to decide whether the correlation between two (sets of) variables can be fully explained by mediation through a third set of variables, and each test result allows the discovery algorithm to narrow down the set of possible causal graph structures.

The PC* algorithm is usually applied to continuous variables, and most common conditional independence tests are based on testing for vanishing partial correlation. However, Steudel et al. (2010) show that consistent conditional independence tests for non-Gaussian variables can be based on tests for vanishing conditional mutual information on any information measure h which fulfills a small set of core properties. The requirement for this is a submodular information measure for sets of variables, which needs to behave to a sufficient degree like entropy H, allowing to understand the nature of such a measure in the multitude of ways in which entropy can be understood: as a measure of unpredictability, of chaos, or of joint descriptive complexity.

Dellert (2019) builds on these theoretical results, and shows that there is a straightfoward way of defining such a measure h for cognate sets. As the joint information for a set of languages, we can take the number of etyma which have reflexes in any of the languages. This means that for completely unrelated languages, the joint information will be equal to the sum of the information for the individual languages, whereas for closely related languages with a large etymological overlap, the joint information will barely exceed the information measure for each individual language. Under this definition, the derived mutual information i(L₁; L₂) is the number of etyma shared between languages L₁ and L₂, and conditional mutual information i(L₁; L₂|L) measures the number of shared etyma for which no reflex exists in any of the languages we are conditioning on.

It turns out that this definition can be applied in a completely analogous fashion to the transposed problem of semantic map inference, by simply defining the joint information measure h for a set of meanings as the number of isolectic sets which contain one or more of the relevant meanings. Mutual information i(C₁; C₂) between two meanings C₁ and C₂ is then based on the number of isolectic sets which include both meanings in relation to the number of isolectic sets including either meaning, and conditional mutual information i(C₁; C₂|C) measures the number of isolectic sets which include both meanings, but none of the additional meanings from the set C we are conditioning on. This definition of mutual information makes intuitive sense: given the frequency of the colexification between MOON and MONTH, if we know the words for MOON in a set of languages, we are likely to already have seen the words for MONTH in some of them. In the information-theoretic reading, a list of words for MOON is bound to contain some information about words for MONTH, as we have better chances of correctly guessing some of the words for MONTH if the words for MOON are available to us.

To illustrate the behavior of the information measure h and the measures derived from it, we take our example data from CLICS³ (Rzymski et al., 2020), a large database of cross-linguistic polysemies which is automatically extracted from the polysemy data contained in a large number of lexical databases covering many language families from all continents, and has already been put to use quite successfully in semantic map research (Georgakopoulos and Polis, 2022).

Staying with our example around MOON and MONTH, we find that CLICS³ contains a total of 2,878 isolectic sets which contain the meaning MOON, but only 715 isolectic sets containing MONTH, i.e., h(MOON) = 2, 878 and h(MONTH) = 715, quantifying the amounts of information we have about the two meanings. The joint information h(MONTH, MOON) = 3, 266 is defined as the number of isolectic sets containing at least one of the two meanings. Based on these three numbers, we can use the standard definition I(X; Y): = H(X)+H(Y)−H(X, Y) to compute the mutual information as i(MONTH;MOON) = 715+2, 878 − 3, 266 = 327, which is exactly the number of colexifications between MOON and MONTH in the database.

In order to explain the derived measure of conditional mutual information, we need to add a third meaning to the example. SUN turns out to work well for purposes of illustration. There is a total of 3,209 isolectic sets involving SUN, hence h(SUN) = 3, 209. The values of joint information with the two existing meanings are h(MONTH, SUN) = 3, 922 and h(MOON, SUN) = 6, 049, and all three meanings together are involved in h(MONTH, MOON, SUN) = 6, 437 isolectic sets. The two new mutual information values are i(MONTH;SUN) = 715+3, 209 − 3, 922 = 2 and i(MOON;SUN) = 2, 878+3, 209 − 6, 049 = 38, showing us that the two celestial bodies are colexified much more often than MONTH and SUN are, though of course, we are ignoring the fact that we have far less data about MONTH available, exemplifying a major problem of lexical typology on the basis of aggregated lexical databases with their uneven coverage.

Crucially, the numbers we computed so far allow us to apply the definition of conditional mutual information as I(X; Y|Z): = H(X, Z)+H(Y, Z)−H(X, Y, Z)−H(Z) in order to compute i(SUN;MONTH|MOON) = 6, 049+3, 266 − 6, 437 − 2, 878 = 0. This vanishing conditional mutual information directly reflects the fact that in the CLICS³ database, every isolectic set involving SUN and MONTH also involves MOON. In contrast, i(SUN;MOON|MONTH) = 3, 922+3, 266 − 6, 437 − 715 = 36 remains larger than zero, reflecting that there are isolectic sets which contain both SUN and MOON, but not MONTH. This implies that in a semantic map built for these three meanings, SUN and MOON would have to be linked in order to satisfy the connected component condition. In this small example, we find illustrated the close connection between vanishing conditional mutual information and the ability to delete a link from a semantic map under construction.

The core mechanism of the PC* algorithm consists in applying this logic systematically to all links in an initially fully connected graph, using certain heuristics to efficiently find separating sets which lead to successful conditional independence tests, progressively removing more links until it can be safely determined that no further separating set exists in the current reduced graph, implying that one cannot remove any additional link, which makes inference complete.

A major challenge in applying this logic to semantic map inference is that the choices of conditional independence tests rely on a faithfulness assumption, which states that true correlation will always remain identifiable and cannot be blocked by chance overlaps as we condition on additional variables. In a long chain between continuous variables, there will typically be some signal which cannot be blocked by spurious conditioning, so that it is not actually necessary to enforce the condition that each component of the shared signal can actually have traveled between the variable sets we are trying to separate, but it is sufficient to test for vanishing conditional mutual information at the variable level. Among continuous variables, a complete masking of correlations along some path will almost never occur by chance.

We can take a cycle A — B — C — D — E — A as an example of a configuration where this becomes apparent. Assume that in this configuration, A — E is made necessary by a single isolectic set containing the meanings A, B, D, E, but not C. Unfortunately, this single isolectic set will cancel itself out during the test, as the component of i(A; E|B, D) = h(A, B, D)+h(B, D, E)−h(A, B, D, E)−h(B, D) which is supposed to measure the need to keep the isolect sets connected, will evaluate to 1+1 − 1−1 = 0. This causes the conditional independence test to succeed, and the link to be erroneously deleted, violating the connected component criterion.

The lack of faithfulness on discrete data which becomes visible in such examples makes it necessary to ensure that the discrete pieces of information (in both linguistic applications discussed so far, these would be individual forms) can actually have traveled along the network formed by the variables we are conditioning on. In Dellert (2019), this intuition was formalized as the flow separation criterion. In the application to cognate sets, this amounts to reasoning about pathways of transmission of lexical material by inheritance or borrowing. On the dual problem of semantic map inference, the reasoning is about pathways of semantic extension within the conceptual space of which we are trying to infer the geometry.

In our example, the flow separation criterion would determine, based on the word not having the meaning C, that the isolectic set cannot be held together by assuming a path of semantic extension through C, which blocks the indirect path via A — B — C — D — E, and causes the separation test to fail, which means that A — E will not be deleted.

It could be argued that on many datasets, such a decision on whether a link is necessary should not hinge on a single missing entry in the list of meanings of a single polysemous word, because there can always be issues with missing or erroneous data. What is more, homonymy is often hard to distinguish from true polysemy, causing spurious connections which have no actual semantic justification. In order to reduce the risk of spurious links resulting from such data problems, a reasonable strategy is to relax the connectivity criterion in some limited and controlled way, at the risk of ignoring some less common colexifications so that the level of detail in the inferred map will be somewhat diminished. In the algorithm by Regier et al. (2013), this can be implemented by putting a threshold on the minimal improvement of isolectic set coverage which needs to motivate the addition of a link, and terminating semantic map construction as soon as there is no additional link whose utility exceeds this threshold. My implementation of this idea supports two different threshold values which can be used to configure the degree of robustness against noisy input data.

The first is a link strength threshold θ_l which can be applied on the level of the conditional independence tests, considering a conditional mutual information to vanish if i(C₁; C₂|C) ≤ θ_l, i.e., the test is treated as successful even if there is a certain small number θ_l of otherwise unexplained colexifications. With the default threshold (θ_l = 0), the connected component criterion is applied strictly, and the result will be a semantic map as one would produce it by hand under the assumption that the data are carefully curated and complete. During inference from noisier datasets such as CLICS³, where there is a certain percentage of spurious colexifications due to homophony or coding errors, it makes sense to set θ_l to a higher value. In one of my experiments with semantic map inference from CLICS³ (see Section 3.2.1), a setting of θ_l = 3 caused a number of obviously spurious colexifications to disappear, which is very similar to the edge weight threshold which Georgakopoulos and Polis (2022) found necessary in order to derive clearly interpretable patterns from the CLICS³ data about the domain of emotions.

The second threshold is the gap threshold θ_g, which filters data from the input for languages where data for some of the meanings is missing. In our example, it could just be the case that the word for C in the relevant language is simply not known, and that the meaning would actually have been present in the isolectic set given perfect information about the language. To limit the risks of such gaps leading to wrong conclusions, it makes sense to automatically restrict the input data to only those languages where information about the realizations of each meaning in the map is known (θ_g = 0). However, this criterion can be too restrictive in larger maps, or on databases which include less well-documented languages. In the second experiment with semantic map inference from CLICS³ (see Section 3.2.2), a setting of θ_g = 2 (allowing data for two of the meanings to be missing) made it possible to use the data from more than three times as many languages as at θ_g = 0, which leads to a much more detailed, albeit less reliable result.

2.3 Causal skeletons as synchronic semantic maps

We now turn to the question how the connectivity-based conditional independence tests are plugged into the first phase of the PC* algorithm, which infers the topology of the causal graph, in order to arrive at a new inference algorithm for synchronic semantic maps.

Unlike the semantic map inference algorithm by Regier et al. (2013), where links are progressively added until the connected component criterion is met for each isolectic set, the PC* algorithm starts out with a fully connected graph over the nodes, and proceeds by deleting links until no further link can be deleted without predicting spurious independences. Each link deletion is justified by a successful conditional independence test, allowing us to plug in the conditional independence test from the previous section, which fails exactly when the connected component criterion would be violated if the link were removed.

Because the PC* algorithm and its theoretical justification has been described in much detail in the aforementioned literature (Spirtes et al., 2000; Pearl, 2009), I can limit its presentation here to a very informal explanation, accompanied by relevant examples that keep the discussion close to the task of semantic map inference. A much broader discussion of the underlying assumptions and necessary adaptations of the original algorithm is provided in Dellert (2019).

The PC* algorithm goes through potential separating set candidates (which the independence tests will be conditioned on) in stages organized by the size of the separating set candidates. In the initial stage (size 0), every independence test will be conditioned on the empty set, which turns it into an unconditional independence test. In semantic map inference, this means that at this first stage, links will be deleted whenever the meanings are not colexified by any isolectic set in the first place. For instance, if we run the algorithm on a subset of the CLICS³ meanings which includes DAY and MOON (which are never colexified), the link between these two meanings will be removed at this initial stage, and the algorithm will store the information that the only minimal separating set between the two meanings is the empty set.

At each new stage, the size of separating set candidates is incremented by one. For instance, at stage 3, separating sets consisting of pairs of other variables are used for the tests. An exhaustive test of larger separating sets can easily lead to a combinatorial explosion (and exponential runtimes) in very difficult cases, but the crucial innovation of the PC* algorithm over the original PC algorithm is that it only needs to consider separating set candidates which are formed by neighbors of the nodes to be separated, and only those neighbors which lie on connecting paths between the nodes. While this criterion is costly to compute, it often reduces the number of variables which can be members of separating sets considerably, and makes causal discovery feasible in practice even for hundreds of variables.

In a small benchmark experiment, my open-source Java implementation (running on an Intel Core i7-8700 at 3.3 GHz) needed 24 min (92 min of processor time) to infer a semantic map with 1,321 links connecting 775 meanings from a dataset composed of 564 isolectic sets from 356 languages (a subset of all CLICS³ isolectic sets of size three or larger), whereas on the same machine, the implementation by Regier et al. (2013) had only managed to add 26 links after running for 90 min on this dataset, and had reached 108 links when the experiment had to be terminated after 12 h. Using my implementation, inference of a single semantic map for the experiments that will be detailed in Section 3 only takes 1 or 2 s, and it was possible to perform a thousand runs in less than half an hour. The limiting factor for the feasible size of the input seems to be memory consumption rather than execution time (an experiment on all of CLICS³ exceeded the 10 GB of memory that was available after just over 3 h, with about 6,000 links left). Memory efficiency will be a focus of further development, which will occur in the accompanying publicly accessible repository, allowing other researchers who would like to run the new algorithm on their own data to always benefit from the most recent optimisations.

Among the many refinements and optimization to PC* and similar algorithms which have been suggested in the literature, we adopt the stable PC strategy by Colombo and Maathuis (2012), which means that the graph does not get updated immediately after each successful conditional independence test, but all link deletions are only applied at the end of each stage. This makes the result less dependent on the order in which the links are processed.

2.4 Estimation of uncertainty through resampling

A previously underemphasized advantage of automated semantic map inference procedures is that they provide us with a systematic way to model uncertainty and the possible consequences of missing data. For tractability reasons, the existing literature on semantic maps has implicitly assumed that the data from the languages under analysis are correct and complete. In reality, semantic map research is riddled with problems of missing and imperfect data. The two main approaches to compiling coexpression matrices both come with their specific types of errors. In the onomasiological approach, we always risk that a consultant fails to remember a less common word for a meaning, or the fact that some word can actually be used for the desired meaning in some contexts. This applies even more to the work with dictionaries, where the number of usage examples is typically very limited, and focused on the more prototypical uses of the lexeme. In the semasiological approach, it puts a very high demand on language consultants if we expect them to be able to list all potential uses of some word in their language. Similarly, even a very good dictionary will never be able to fully cover the extent of an isolectic set for a given domain.

The advantage of having a fast implementation of semantic map inference is that it becomes possible to execute it many times on slight variations of the input data. This is the standard mechanism by which confidence values are associated with each element of complex output structures in probabilistic algorithms, such as in phylogenetic tree inference. To be more precise, we will use the bootstrapping technique, which consists in producing resamples by sampling from the original data with replacements. If the original dataset was small, these resamples will differ more than for larger datasets, reflecting the intuition that more data will give us more certainty. This process effectively allows us to get an impression of how different the results could have looked on a different sample from the same assumed underlying distribution, as long as we can assume that the processes generating the lexification patterns for each language are independent and identically distributed (which is not a major restriction, as it can be taken as an assumption which underlies the very idea of inferring a semantic map in the first place).

There are multiple ways in which resampling can be applied to our lexification data to account for different sources of uncertainty. The most obvious strategy, which I will therefore discuss first, is to perform bootstrapping at the language level, i.e., to generate a resample, we take our original dataset and randomly draw languages (with replacement) as many times as we had languages in the original dataset. In the resulting modified datasets, the data for some of the original languages will not be present, while for some other languages, multiple copies of the associated data will exist. Running the algorithm on these samples models the uncertainty that results from picking a subset of the given size among all the independent language samples that would theoretically have been available.

Independently from modeling the uncertainty for a given map extraction by resampling on the language level, we can also use resampling to model the uncertainty in the space of possible semantic maps given a fixed dataset. Here, the samples differ by processing the links in different orders, and the resampling is performed by drawing random permutations of this link processing order. The resulting confidence value for a given link will approximate the percentage of possible semantic maps over the same input which feature the link in question.

2.5 Directionality inference based on unshielded triples

In this section, we finally turn to the main advantage of applying a causal discovery algorithm to the inference of semantic maps, which is the possibility to infer a directionality for some of the links in a causal skeleton, turning a synchronic semantic map into a diachronic one.

Directionality inference in the PC* algorithm and its variants ultimately depends on the presence of unshielded triples, i.e., configurations of shape A — B — C where A and C are not directly connected in the causal skeleton. The crucial insight is that under the assumption of causal sufficiency (all potential causes are part of the input), each triple can be classified as having one of exactly four different causal patterns: the chain A ← B ← C, the chain A → B → C, the fork A ← B → C, or the collider A → B ← C. If we find that there is a dependence between A and C which only vanishes when conditioning on B (i.e., B is in the separating set which allowed us to delete the link A — C), the triple must have been either a chain or a fork, and if we find that conditioning on B was not necessary to delete the link between A and C, we must be dealing with a collider. Because chains can be oriented in either direction, only the latter result allows us to add arrows to the links A — B and C — B. Such an unshielded collider configuration is also called a v-structure.

To illustrate this logic on the basis of our running example, let us assume that successful independence tests have left us with an unshielded triple MONTH — MOON — SUN. If conditioning on MOON was necessary to separate MONTH from SUN, this means there are isolectic sets which contain all three meanings. Within such a set, there must have been semantic extensions from one of the three meanings to the others, and the three possibilites for this are the chains MONTH → MOON → SUN and MONTH ← MOON ← SUN as well as the fork MONTH ← MOON → SUN. The pattern we can reject is the collider MONTH → MOON ← SUN, because that would make it impossible for a form which starts out with one of the three meanings to be extended to the other two. Conversely, if we find in a very large database that the three meanings are never colexified, only a collider pattern will offer a good explanation of this observation. This simple reasoning pattern ultimately underlies the entire directional signal which the PC* algorithm can extract from synchronic polysemy data, and the only part that is left to describe is how this possibility to classify unshielded colliders as v-structures is used for maximum effect during the second phase of the algorithm.

Different variants of the algorithm vary in the conditions they apply when several separating sets lead to successful conditional independence tests during the same stage. In all examples discussed in this article, the algorithm was run with the conservative strategy (Ramsey et al., 2006), where a v-structure is only considered as safely established if B was not contained in a single one of the successful separating sets. This strategy provides some robustness against spurious successful conditional independence tests, which can easily occur on unbalanced data, and even more with an independence test based on discrete units, where the faithfulness assumption is problematic.

Once we have classified all unshielded triples in a causal skeleton as being either v-structures or not, the PC* algorithm propagates the directionality information from these v-structures through further unshielded triples of shape A → B — C (i.e., where only a single inward link was detected so far), based on the knowledge that they were found not to be v-structures, and must therefore be chains A → B → C. This propagation rule is applied recursively until there is no context for applying it any longer.

In the default PC* algorithm, further directionality propagation can be achieved based on an acyclicity condition (i.e., exclusion of any circular directed path A → … → A), which makes sense under the standard assumption that a cause needs to temporally precede its effect. However, this assumption is not natural for the concept of causality which we have taken to underlie diachronic semantic maps, so I chose to deactivate it for the purposes of semantic map inference in my implementation of the PC* algorithm.

Under the acyclicity assumption, it has be shown that the causal signal which can be determined based on conditional independence tests allows us to determine the causal structure up to its Markov equivalence class, where each such class is defined by the causal skeleton and the set of v-structures on that skeleton. For many semantic maps, especially densely connected ones, the Markov equivalence class can contain many possible directed graphs, because there will be many links for which the directionality cannot be determined in principle. In the extreme case, the fully connected graph, it is never possible to add any arrows to the skeleton, because there are no unshielded colliders which could serve as seed evidence of directionality. However, in sparser structures with many unshielded colliders, which characterizes many of the semantic maps derived in previous research, the number of directed links in the output of the PC* algorithm output will tend to be larger, as we will see when running the algorithm on real examples in Section 3.2.

3 Results

3.1 Synchronic semantic map inference

To demonstrate that the algorithm successfully infers near-optimal synchronic maps, we apply it to the loose colexification data from François (2008), the seminal study which pioneered the application of the semantic map methodology to a purely lexical domain, building on semasiological data about nouns denoting an act of breathing.

A recreation of the original map is given in Figure 1A, with somewhat shortened meaning names in order to facilitate rendering and mental processing. For more information about the data, the reader is referred to the original publication. My digitalized version of the original isolectic sets uses the meaning names as they appear on my version of the map, but is otherwise completely true to the original coexpression matrix. Figure 1B shows a causal skeleton which results from a run of the PC* algorithm. Figure 1C shows the output of Regier et al. (2013) on the same dataset. The layout of both outputs has been optimized for easier readability, and to make it obvious that the inferred map is not more chaotic in structure than the original map, though the differences are substantial.

Figure 1

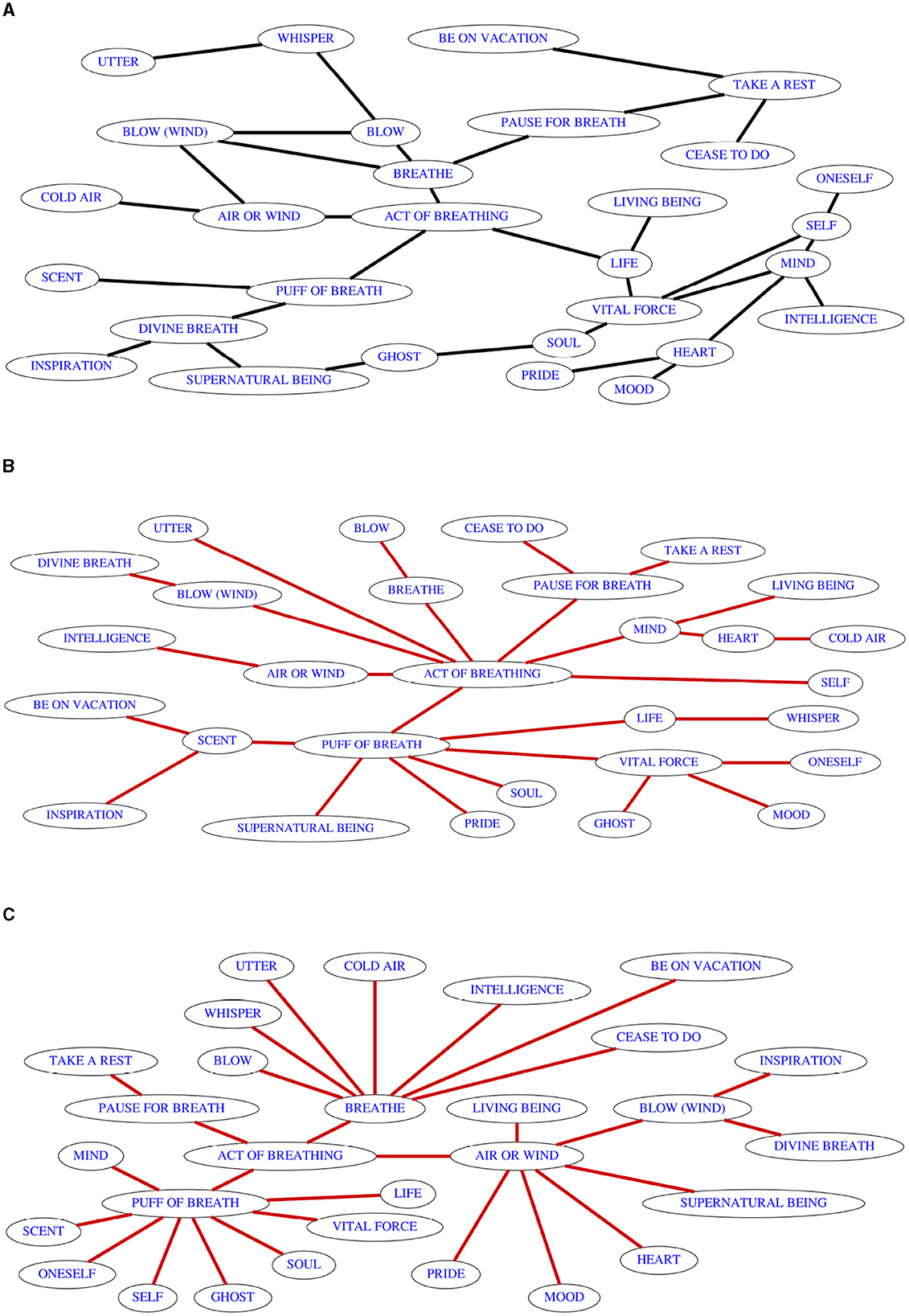
Figure 1. Result of synchronic semantic inference using the PC* algorithm on the data provided by François (2008). (A) Reproduction of the semantic map inferred by François (2008), approximating the original layout. (B) A result of applying the PC* algorithm with default link ordering. (C) Result of applying the inference algorithm by Regier et al. (2013).

As the reader will be able to verify by checking the connected component criterion for each of the 15 isolectic sets (the input data are provided as examples in the accompanying GitHub repository), the causal skeletons resulting from these example runs are indeed semantic maps, and at 28 links, they both require fewer edges than the original map by François (2008) with its 32 edges. Still, while the algorithms provide us with more parsimonious representations of the available colexification data, one would probably not want to claim that either of these maps is a better representation of universals than the original, because as a result of the purely data-driven algorithms which are not constrained in their choices by anything except for the connected component criterion, they assume some links that do not seem very plausible on semantic grounds. In order to correct for this, it would be possible to add some artificial isolectic sets which express the constraints under which the original map was drawn, e.g., one isolectic set each subsuming all verbal and all nominal meanings, or additional sets joining together all nouns which involve air, or the two meanings BLOW and BLOW (WIND) which were separated by both algorithm in the absence of English colexification data.

Summarizing the outputs of the PC* algorithm in a map which contains only those links which occur in the majority of outputs, we receive information about which lexification patterns are actually robust enough that we would expect them to be inferred from any sample of languages, not only the original one. For purposes of visualization, I represent the confidence value (the percentage of resamples for which the link survived in the resulting semantic map) by the thickness of the lines representing each link. For clarity, links which occurred in < 25% of samples are not shown, an arbitrary threshold reflecting the intuition that links which exist in less than a quarter of the sampled maps are much more likely to be unstable artifacts rather than actual patterns which we should infer from such as small dataset. To actually determine the links which can be considered safely established, a much higher threshold would be chosen.

Figure 2A shows the consensus map which results as the output of the bootstrapping procedure. While the colexifications at the center of the map are well-attested enough that we could expect them to be present on most maps derived from a different language sample of the same size, it becomes clear that almost nothing can be said about the outer reaches of the original map. Much larger amounts of cross-linguistic polysemy data would be needed to elucidate the structure of a domain of this size.

Figure 2

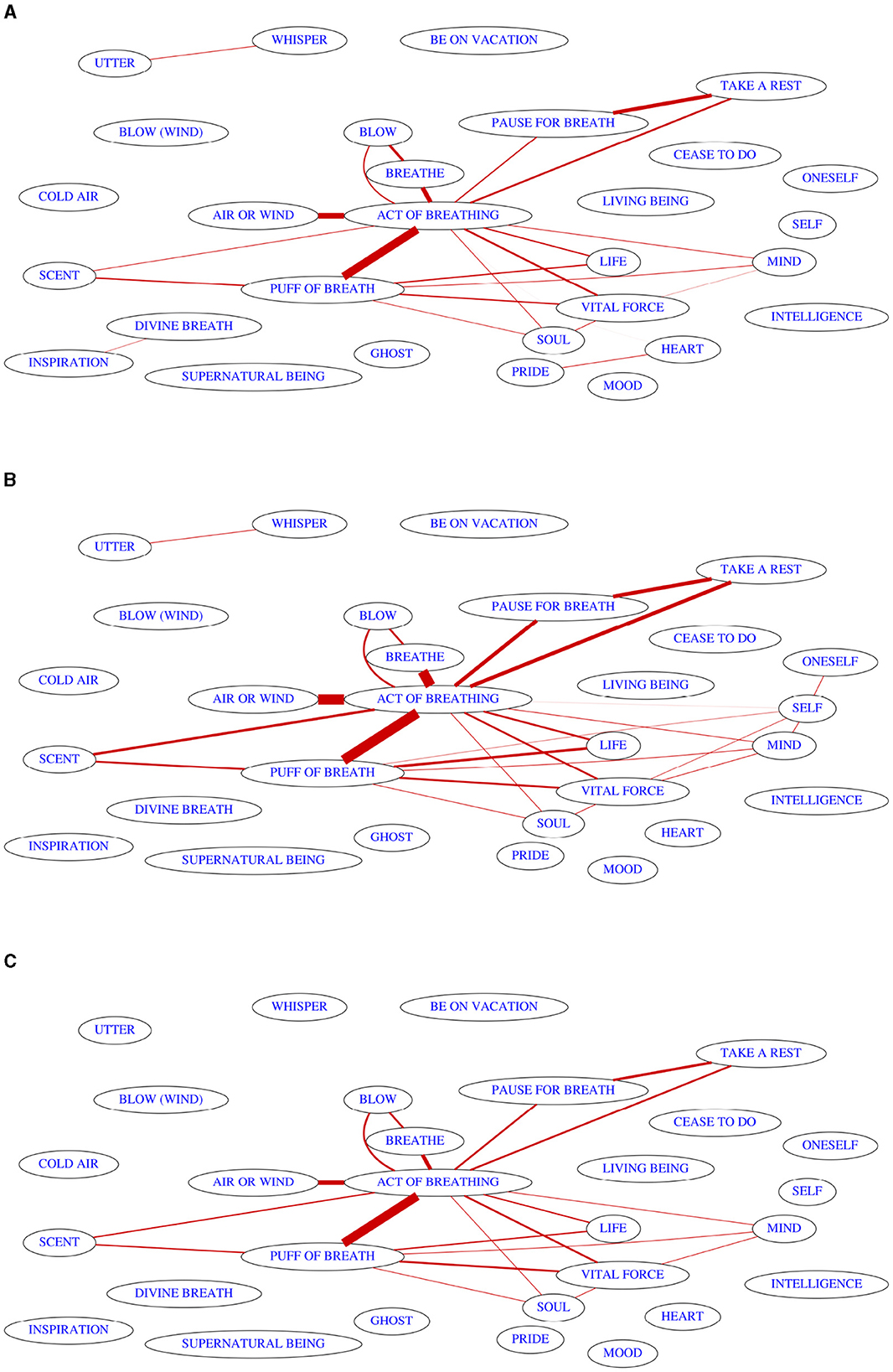
Figure 2. Consensus maps resulting from running the PC* algorithm on the data provided by François (2008) using resampling strategies for quantifying uncertainty. (A) Result of language-level bootstrapping under the default link prioritization strategy. (B) Consensus map resulting from 1,000 random variations in link processing order. (C) Result of bootrapping combined with randomized link processing order.

To illustrate the consequences of the non-determinism involved in map drawing, Figure 2B shows the summary map for 1,000 random permutations of link processing order when the algorithm is run on my digitalization of the colexification data. The minimum number of links in any of the outputs was 30, and the maximum was 49. If we attempt to delete links by their default order (by the number of isolectic sets showing the colexification, using some random noise to resolve ties), we get the output with 28 links in Figure 1B that we already discussed.

If we add the language-level bootstrapping to model the uncertainty caused by the small size of the language sample combined with the non-determinism in map drawing, we arrive at the consensus map in Figure 2C. As usual, every link which occurs in more than 25% of the maps is shown, but only six of these links are actually present in more than 50% of the outputs: ACT OF BREATHING has five connections (to AIR OR WIND, BREATHE, PAUSE FOR BREATH, PUFF OF BREATH, and TAKE A REST), and there is one additional connection between PAUSE FOR BREATH and TAKE A REST. In my view, this output is a good representation of what we can actually safely say about colexifications between meanings from the domain of breathing based on the dataset published by François (2008), if we do not use additional knowledge and intuition to structure the domain, as was done in the original paper.

3.2 Diachronic semantic map inference

In this section, we will revisit two classic papers in lexical typology which yielded semantic maps along with generally accepted directionality judgments, and check in how far the patterns established by these contributions can be reproduced by running the PC* algorithm on the CLICS³ data. But before we embark on testing the capabilities of the PC* algorithm in inferring diachronic semantic maps, some general remarks are in order about the quality of results we can expect even in the best case.

A major weakness of this approach to directionality inference is that triples with the target of semantic change in the middle are necessary to get any directionality signal, making it very difficult to get arrows which point into nodes of degree 1, i.e., nodes which are connected to the rest of the map only through one link, for which we would like to infer an outward-facing arrow. In many cases, maps with arrows facing either way across such a bridge will belong to the same Markov equivalence class, making it impossible in principle to infer the directionality.

A second major problem, which is however not due to inherent properties of the method, is that the size of non-trivial isolectic sets extracted even from major lexical databases is actually quite small. For instance, among the 16,746 non-singleton isolectic sets extracted from the CLICS³ database, only 4,036 cover three or more meanings. But for a v-structure test on an unshielded triple to fail, we need at least one isolectic set covering the three meanings, which we will not necessarily be able to observe, especially when less common colexifications are involved.

This sparsity of data means that we should not expect the method to perform very well on currently available cross-linguistic data. To give a concrete example, Georgakopoulos and Polis (2021) find diachronic evidence which leads them to posit an arrow TIME → AGE in their diachronic semantic map of the temporal domain. In CLICS³, there is not a single polysemy which covers all three relevant meanings (AGE, TIME, and HOUR) at the same time, which leads to the unshielded triple AGE — TIME — HOUR being detected as a v-structure (conditioning on TIME is not needed to break the connection between AGE and HOUR), and an arrow AGE → TIME.

In general, the sparsity of large isolectic sets will lead to a severe overgeneration of v-structures, which lead to a bidirectional signal being inferred for most links. Still, in the somewhat rare case where all v-structure tests which would predict some arrow to fail, the inference can be expected to detect the correct (inverse) directionality.

3.2.1 Example 1: body part terms

The study by Wilkins (1996) on pathways of semantic change within the domain of body parts is a classical example of a diachronic typology in a domain that is covered very well by large-scale lexical databases. Based on diachronic evidence from five large language families, Wilkins concludes that across different parts of the body, we can observe unidirectional synechdochic change, i.e., from parts to wholes, as in SOLE → FOOT, but never FOOT → SOLE.

For our analysis, we revisit the parts of the leg and the parts of the head, reducing Wilkin's original four-part maps of attested changes to subsets for which CLICS³ provides substantial cross-linguistic coverage. Among the parts of the leg covered by Wilkins, the toenail needs to be removed due to its ambiguous encoding, whereas among the parts of the head, we are lacking sufficient data for EYEBROW and CROWN OF HEAD. Once some obviously spurious connections are removed via a link strength threshold (θ_l = 3), EAR turns out to not be synchronically colexified with any other part of the head, which is why it was removed as well. The resulting reduced versions of the expected maps for these subdomains are visualized in Figure 3A.

Figure 3

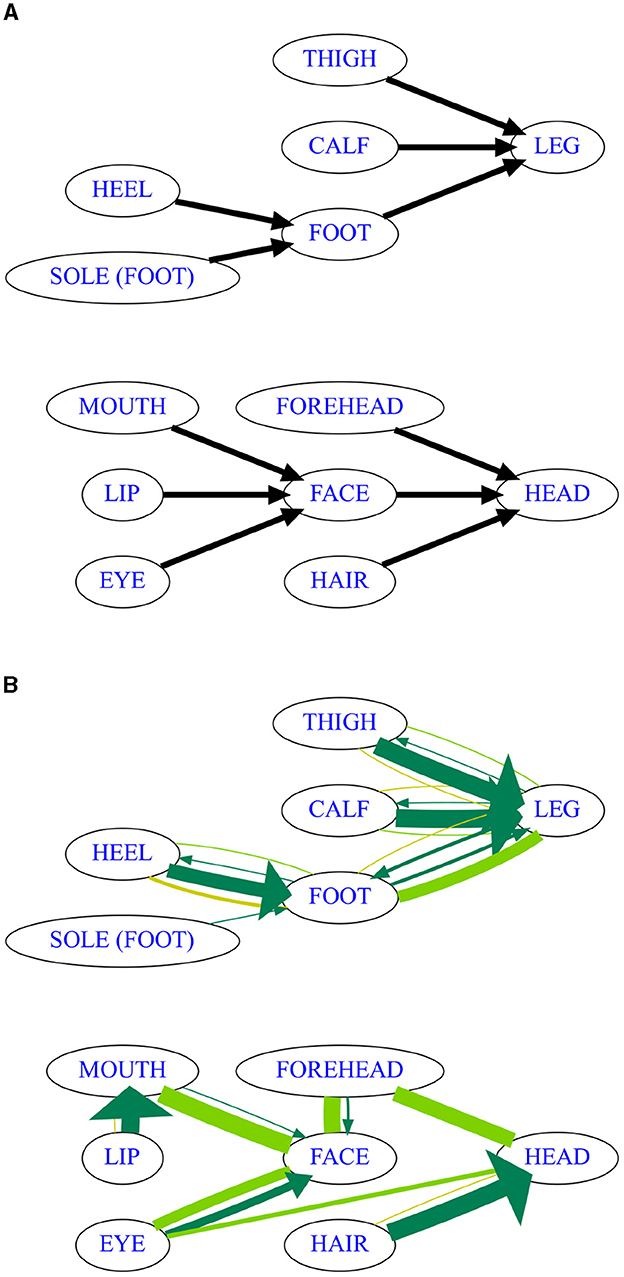
Figure 3. Results of diachronic map inference (bootstrap with random link processing order) on CLICS³ data about body parts. (A) CLICS approximation of the relevant parts of the original map by Wilkins (1996). (B) Consensus map based on inference results on 1,000 bootstrap samples with randomized link processing order, executed on CLICS³ data at θ_l = 3 (every link necessary for more than two isolectic sets). Thickness of links represents number of samples (at least 250) on which the respective link was inferred. Monodirectional arrows in dark green, bidirectional links in light green, links where the PC* algorithm could not assign a directionality in yellow.

In order to summarize the results of randomization in diachronic map inference, we again rely on a consensus map with a somewhat more complex format. Every link is represented by several arrows and lines, where the thickness of each line or arrow indicates the percentage of the samples in which the link had the respective shape. Dark green arrows represent the samples where a directionality was successfully inferred for the link (A → B or B → A), light green lines represent the samples where v-structures were found in both directions (A ↔ B, which we can interpret to mean that there is no strong unidirectional tendency in semantic change or expansion), and yellow lines represent samples where no directional evidence at all was found for that link in either direction (A — B, the Markov equivalence class includes graphs with arrows in both directions). As described previously, we can only expect to infer the directionality for some of the links, so the focus in an evaluation of the result will be on the arrows which were actually inferred (dark green).

Inspecting the consensus map under language bootstrapping and link order resampling for this dataset (Figure 3B), we see that the causal skeleton for the parts of the leg looks exactly as predicted by Wilkins, indicating that the algorithm is able to extract good semantic maps even from somewhat inconsistent datasets. In contrast, the causal skeleton for the parts of the head deviates in some interesting ways from the structure posited by Wilkins, though it still follows the suggested universal of synechdochic change. The two main differences are that cross-linguistically, the lips appear to be conceptualized chiefly as a part of the mouth (rather than directly a part of the face, as in Wilkins's link based on Dravidian evidence), and that the forehead can be conceptualized as either belonging to or not belonging to the face. The additional link between EYE and HEAD indicates that there are colexifications between the concepts which do not include FACE, which might be a data problem, but could also reflect cultures where the concept FACE only refers to the lower part of the denotation of its English equivalent, including e.g., the nose and the mouth, but not the eyes. The automatically inferred skeleton thus indicates that the exact region of the head conceptualized as “the face” in English is not in fact universal, making it rather problematic to treat it as a universal meaning FACE that can be compared easily across languages.

For the causal discovery algorithm, directionality is ambiguous in some cases, but if a clear directional signal (dark green arrow) appears on a link, the directionality always comes out as expected by Wilkins (1996), which can be taken as an encouraging sign. The unexpected situation of the LEG — FOOT link, where arrows in both directions are each inferred in about half of the samples, can be traced back to the problem that the concept which unambiguously includes the entire leg from waist to toe (Wilkin's “leg”) is actually mapped to an additional meaning FOOT OR LEG in CLICS³ in some of the languages which colexify FOOT and LEG, leading to some missing data in our subselection. In order to achieve a better result for these two meanings, it seems like the relevant parts of CLICS³ would have to be recoded very carefully.

3.2.2 Example 2: verbs of perception

As another classic example of a diachronic semantic map, we revisit the modality hierarchy first proposed by Viberg (1983), which was found to be generally consistent with observations on a very different language sample by Evans and Wilkins (2000). From the perspective of directionality inference, the problem with the original map by Viberg (1983) (visualized in Figure 4A) is that it is densely connected and does not contain a single v-structure, which means that the PC* algorithm will not be able to determine the directionality of any link. In contrast, the one major modification by Evans and Wilkins (2000), which makes the link SMELL → TASTE monodirectional, leads to two v-structures which we might find recoverable. This means that we should be able to apply the algorithm and expect to receive at least some directed links. Still, this example illustrates the issue of a lack of identifiability in more densely connected maps, leading to fewer opportunities to detect v-structures. The expected diachronic map (with the change) has exactly two v-structures: TOUCH → TASTE ← SMELL and SEE → TASTE ← SMELL. After adding the three arrows, the lack of adjacent unshielded triples means that directionality inference could not be propagated any further, i.e., the maximum we can hope for is to infer the three directed links TOUCH → TASTE, SEE → TASTE, and SMELL → TASTE.

Figure 4

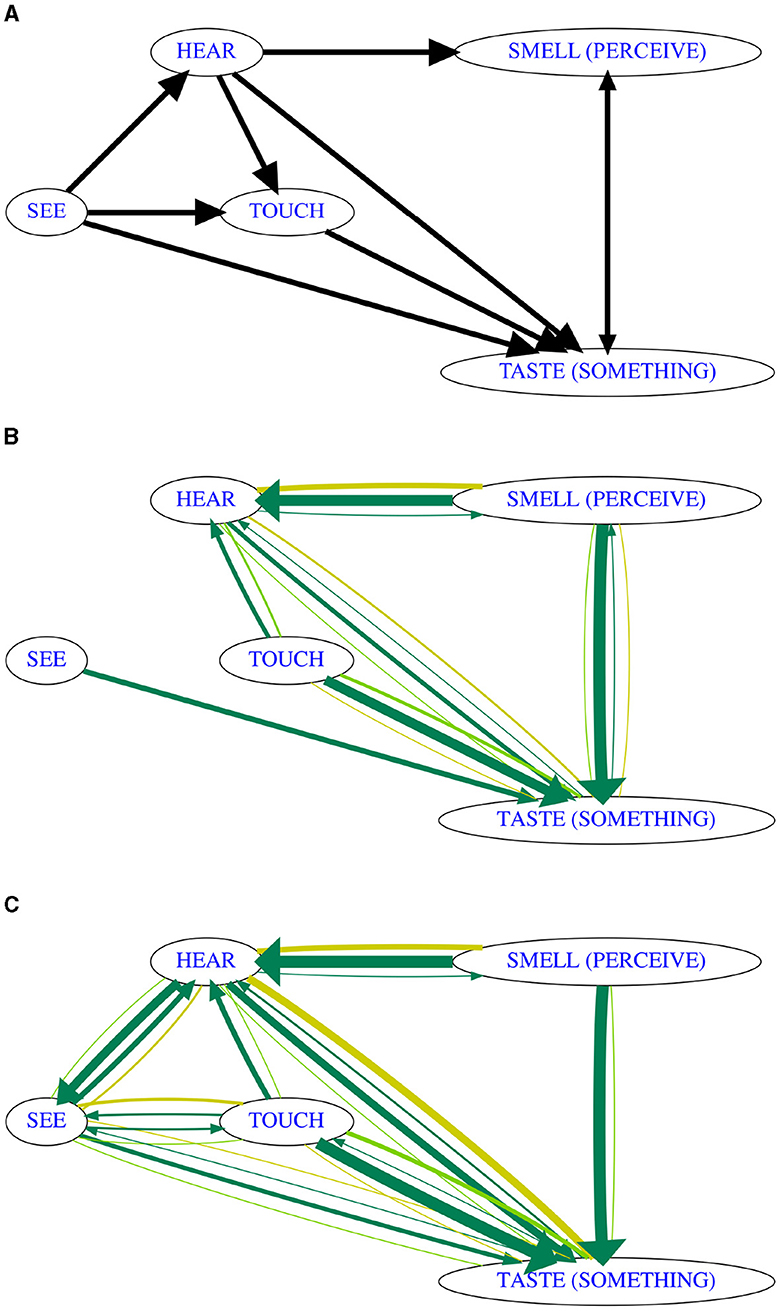
Figure 4. Results of diachronic map inference (bootstrap with random link processing order) on CLICS³ data about verbs of perception. (A) CLICS approximation of map by Viberg (1983). (B) Based on 293 languages where data for all meanings was available. (C) Based on 1,071 languages where data for at most two of the meanings were missing.

To maximize the amount of CLICS³ data which we can use for the inference, we limit the analysis to the five CLICS meanings which were classified by Wilkins as belonging to the dynamic system of experience: SEE, HEAR, TOUCH, SMELL (PERCEIVE), and TASTE (SOMETHING). Not all languages in CLICS³ have data for these five meanings, and the uneven coverage can be expected to cause problems for map inference. However, unlike during inference over larger sets of meanings (as in Example 1), where larger numbers of gaps are unavoidable, on this smaller set of meanings, the gap threshold θ_g can be applied successfully, because there will be more than enough languages with (near-)complete data for these five meanings. The fact that data sparsity forces us to limit the analysis in this way is problematic from the perspective of the underlying assumption of causal sufficiency, because there is some evidence (Vanhove, 2008) that the colexifications between SEE and the other perception meanings are mediated by cognition, which implies that on a better dataset, meanings such as THINK or UNDERSTAND should have been included in addition to better approximate causal sufficiency.

Figures 4B, C show the consensus maps for different choices of θ_g. It turns out that for the less frequent colexifications to become visible in the consensus map, we need to include all languages where data is available only for three out the five meanings (Figure 4C). At this gap threshold, the causal skeleton is exactly the one inferred by Viberg (1983), again demonstrating the good performance of the algorithm in inferring synchronic semantic maps, and that even less common colexifications are attested sufficiently in the CLICS³ database.

As expected, directionality inference is a challenge. The three links for which we could have expected a directional signal are all oriented correctly in the vast majority of samples, and we get some of the expected unidirectional evidence for the arrow HEAR → TASTE (SOMETHING) in addition, but there are wrongly directed arrows TOUCH → HEAR and SMELL (PERCEIVE) → HEAR in a majority of samples, and evidence for the remaining two links is inconclusive. In order to understand why this happens, we inspect a run on a single sample, the result of which is visualized in Figure 5. It turns out that the problems in directionality inference are ultimately due to the fact that the three meanings HEAR, TOUCH, SMELL (PERCEIVE) are never jointly part of any isolectic set in the entire CLICS³ database, which causes a spurious v-structure TOUCH → HEAR ← SMELL (PERCEIVE) to be inferred. This is one of the false positives in v-structure detection which we were expecting due to the low frequency of large isolectic sets in the database. In this case, the assumption that all v-structures were detected leads to a further propagation of the spurious wrong directionalities: Because TOUCH — SEE — HEAR was found not to be a v-structure (there are colexifications!), the directional evidence TOUCH → HEAR propagates into HEAR → SEE on those samples where the TOUCH — HEAR link exists. With adequate amounts of cross-linguistic data, this type of problem should occur much less frequently.

Figure 5

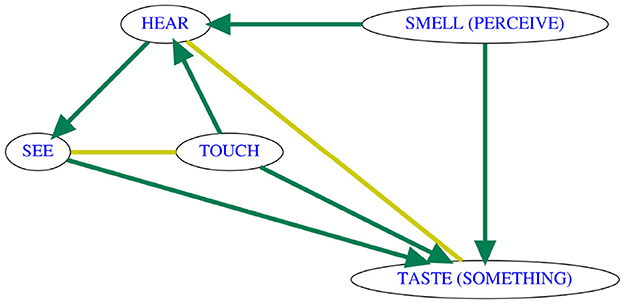
Figure 5. Typical output of PC* on a sample underlying the consensus map in Figure 4C, illustrating that the errors are the consequence of a spurious v-structure which leads to arrow propagation.

4 Discussion

This article has demonstrated that the PC* algorithm for the discovery of causal graphs from observational data can be used to infer synchronic semantic maps from input data in the shape of isolectic sets that encode cross-linguistic polysemies. To ensure that the connected component criterion holds, we can use a flow-based conditional independence test, which was originally developed for the causal inference of phylogenetic networks. The PC* algorithm can use this criterion to motivate link deletion decisions, thinning out an initially fully connected graph until no further links can be removed, implementing the minimality property of a semantic map.

Unlike previous algorithms for semantic map inference, the algorithm comes with a systematic way of inferring the directionality of links, which can be used to automatically infer a diachronic signal even from purely synchronic input data. The method can thus be seen as a computational approach to leveraging the diachronic signal that has always been assumed to be hidden in polysemy data, as many synchronic polysemies will in fact represent intermediate stages of semantic change. Directionality inference ultimately relies on the assumption that whenever two meanings are connected only via links to a third meaning, we would expect to see some polysemies involving the three meanings, unless the third meaning is the target of two separate pathways of semantic extension from either direction.

It is important to be aware of the fact that due to its reliance on these unshielded triples, the PC* algorithm can only determine a directional signal in sparse structures, and that it works best on input data which contains many isolectic sets covering at least three meanings. We have seen that the spurious v-structures resulting from a lack of such sets can have a large impact on the results, and such a lack is typical of the unbalanced onomasiological datasets that research on large-scale inference of semantic maps has had to work with so far. Whenever a massively cross-linguistic, but semasiologically oriented dataset is available for some domain, the algorithm can be expected to be much more resilient against spurious v-structures resulting from a lack of larger isolectic sets. The same positive effect of larger isolectic sets could be expected from datasets which take loose colexification into account.

Dellert (2019) developed and evaluated some alternative ways of determining arrow directionality which are designed to relax the sparseness and set size requirements substantially, but additional experimentation suggests that while these methods (Unique Flow Ratio and Triangle Score Sum) work reasonably well on large amounts of cognacy data, they do not provide any advantage over the much more theoretically well-founded PC* algorithm with flow separation for semantic map inference, at least not given the amount and quality of data that can be extracted from the CLICS³ database or similar resources.

The second major concern addressed by this article is the question of how much of the assumed underlying semantic map is actually identifiable based on the small amounts of hand-curated data which are typically the basis of published semantic maps. For this purpose, my flexible implementation of the PC* algorithm supports both bootstrapping of observations and randomization of link processing order, resulting in a large number of semantic maps which can be summarized into a consensus map. This consensus map shows the links which would be likely to appear on other language samples of the same size, and which will appear in most semantic maps derived from such varying input data. In our analysis of the seminal work by François (2008), we found that only a very small core of the semantic map can actually be considered safely established based on the data compiled for that study. Uncertainty estimation has the potential to serve as a more objective criterion of whether the amount of data was actually sufficient to draw any given conclusion about a universal of lexification.

Beyond simple uncertainty estimation, several promising directions could be explored by expanding on the methodology introduced by this article. For instance, if we know that our dictionary data are more complete and reliable for certain languages than for others, the resampling could be adjusted to take such differences into account, e.g., by resampling not on the language level, but within batches of isolectic sets of similar size, reliability, or gappiness.

This could also be a first step toward answering a major open question for the field. In the cases where applying θ_g will leave us with insufficient data, how severe are the consequences of the gaps in lexical coverage which are unavoidable in large-scale lexical databases? It is very likely that, as in the case of phylogenetic lexical flow inference, the information measures will have to be normalized in order to compensate for unequal amounts of data for different meanings, though this will make it more difficult to maintain clearly interpretable threshold values for successful conditional independence tests. Beyond normalization, it could be worthwhile to explore whether imputation of missing meaning-form mappings could be feasible. There are clear cases where such a strategy does not seem too risky (as when a verb means SEE and SMELL, but we lack the data for HEAR), but how frequently do such simple cases occur, and can we use sophisticated imputation techniques to fill in many blanks in our unavoidably gappy lexical datasets?

Systematic exploration of the estimated uncertainties in the outputs on datasets of different size and shape could yield more objective answers to many more general questions of relevance to lexical typologists: How many languages do we really need to sample in order to infer a reliable semantic map? How many spurious colexification patterns must we expect to pollute our map when we work with a language sample of a given size? Which data sources and data collection methods can help increase the reliability of the inferred universals of lexification?

Data availability statement

The datasets and the software presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: https://github.com/jdellert/causal-semantic-maps and https://zenodo.org/records/10152577.

Author contributions

JD: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work has been supported by the European Research Council (ERC) under the Horizon 2020 research and innovation programme (CrossLingference, grant agreement no. 834050, awarded to Gerhard Jäger).

Acknowledgments

The author would like to thank Terry Regier for sharing the original code described in Regier et al. (2013), and giving his permission to publish an adapted version together with this publication. Further thanks go to Gerhard Jäger and the colleagues from the CrossLingference project (especially Christian Bentz and Tim Wientzek) for their valuable feedback and interested questions after a presentation of preliminary results, to the editors for their patience in waiting for this contribution to finally materialize, and to the two reviewers for their helpful suggestions about which parts of the originally submitted version needed further refinement.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anderson, L. B. (1982). “The “Perfect” as a universal and as a language-specific category,” in Tense-Aspect: Between Semantics and Pragmatics, Volume 1 of Typological Studies in Language, ed. P. J. Hopper (Amsterdam: John Benjamins), 227–264. doi: 10.1075/tsl.1.16and

Crossref Full Text | Google Scholar

Colombo, D., and Maathuis, M. H. (2012). A modification of the PC algorithm yielding order-independent skeletons. CoRR abs/1211.3295. doi: 10.48550/arXiv.1211.3295

Crossref Full Text | Google Scholar

Croft, W. (2002). Typology and Universals, 2nd ed. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511840579

Crossref Full Text | Google Scholar

Dellert, J. (2016). “Using causal inference to detect directional tendencies in semantic evolution,” in The Evolution of Language: Proceedings of the 11th International Conference (EVOLANGX11) Bristol: Evolang Scientific Committee.

Google Scholar

Dellert, J. (2019). Information-Theoretic Causal Inference of Lexical Flow. Berlin: Language Science Press.

Google Scholar

Evans, N., and Wilkins, D. (2000). In the mind's ear: the semantic extensions of perception verbs in Australian languages. Language 76, 546–592. doi: 10.2307/417135

Crossref Full Text | Google Scholar

François, A. (2008). “Semantic maps and the typology of colexification: Intertwining polysemous networks across languages,” in From Polysemy to Semantic Change: Towards a Typology of Lexical Semantic Associations. Number 106 in Studies in Language Companion Series, ed. M. Vanhove (Amsterdam: Benjamins), 163–215. doi: 10.1075/slcs.106.09fra

Crossref Full Text | Google Scholar

François, A. (2022). Lexical tectonics: mapping structural change in patterns of lexification. Z. Sprachwiss. 41, 89–123. doi: 10.1515/zfs-2021-2041

Crossref Full Text | Google Scholar

Georgakopoulos, T., and Polis, S. (2018). The semantic map model: state of the art and future avenues for linguistic research. Linguistics Lang. Compass. 12, e12270. doi: 10.1111/lnc3.12270

Crossref Full Text | Google Scholar

Georgakopoulos, T., and Polis, S. (2021). Lexical diachronic semantic maps. the diachrony of time-related lexemes. J. Hist. Linguist. 11, 367–420. doi: 10.1075/jhl.19018.geo

Crossref Full Text | Google Scholar

Georgakopoulos, T., and Polis, S. (2022). New avenues and challenges in semantic map research (with a case study in the semantic field of emotions). Z. Sprachwiss. 41, 1–30. doi: 10.1515/zfs-2021-2039

Crossref Full Text | Google Scholar

Glymour, C., Zhang, K., and Spirtes, P. (2019). Review of causal discovery methods based on graphical models. Front. Genet. 10, 524. doi: 10.3389/fgene.2019.00524

PubMed Abstract | Crossref Full Text | Google Scholar

Haspelmath, M. (2003). “The geometry of grammatical meaning: semantic maps and cross-linguistic comparison,” in The New Psychology of Language, Vol. 2, ed. M. Tomasello (Mahwah, NJ: Lawrence Erlbaum), 211–242.

Google Scholar

Pearl, J. (2009). Causality. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511803161

Crossref Full Text | Google Scholar

Ramsey, J., Spirtes, P., and Zhang, J. (2006). “Adjacency-faithfulness and conservative causal inference,” in Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence, UAI'06 (Arlington, VA: AUAI Press), 401–408.

Google Scholar

Regier, T., Khetarpal, N., and Majid, A. (2013). Inferring semantic maps. Linguist. Typol. 17, 89–105. doi: 10.1515/lity-2013-0003

Crossref Full Text | Google Scholar

Rzymski, C., Tresoldi, T., Greenhill, S., Wu, M.-S., Schweikhard, N. E., Koptjevskaja-Tamm, M., et al. (2020). The database of cross-linguistic colexifications, reproducible analysis of cross- linguistic polysemies. Sci. Data 7, 1–12. doi: 10.1038/s41597-019-0341-x

PubMed Abstract | Crossref Full Text | Google Scholar

Spirtes, P., and Glymour, C. (1991). An algorithm for fast recovery of sparse causal graphs. Soc. Sci. Comput. Rev. 9, 62–72. doi: 10.1177/089443939100900106

Crossref Full Text | Google Scholar

Spirtes, P., Glymour, C., and Scheines, R. (2000). Causation, Prediction, and Search, 2nd ed. Cambridge, MA: MIT Press. doi: 10.7551/mitpress/1754.001.0001

Crossref Full Text | Google Scholar

Steudel, B., Janzing, D., and Schölkopf, B. (2010). “Causal Markov condition for submodular information measures,” in Proceedings of the 23rd Annual Conference on Learning Theory, eds A. T. Kalai, and M. Mohri (Madison, WI: OmniPress), 464–476.

Google Scholar

Vanhove, M. (2008). “Semantic associations between sensory modalities, prehension and mental perceptions,” in From Polysemy to Semantic Change: Towards a Typology of Lexical Semantic Associations. Number 106 in Studies in Language Companion Series, ed. M. Vanhove (Amsterdam: Benjamins), 341–370. doi: 10.1075/slcs.106.17van

Crossref Full Text | Google Scholar

Viberg, Å. (1983). The verbs of perception: a typological study. Linguistics 21, 123–162. doi: 10.1515/ling.1983.21.1.123

Crossref Full Text | Google Scholar

Wilkins, D. (1996). “Natural tendencies of semantic change and the search for cognates,” in The Comparative Method Reviewed: Regularity and Irregularity in Language Change, eds M. Durie, and M. Ross (Oxford: Oxford University Press), 264–304. doi: 10.1093/oso/9780195066074.003.0010

Crossref Full Text | Google Scholar