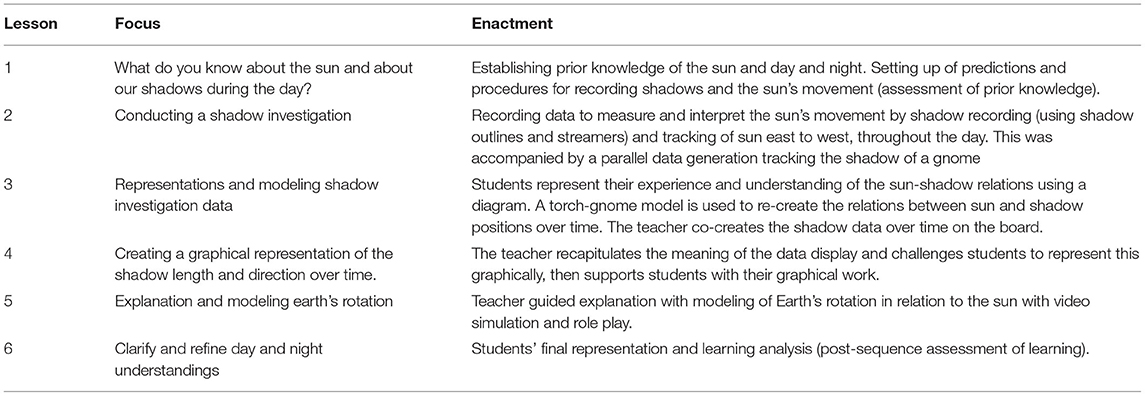
- School of Education, Deakin University, Geelong, VIC, Australia
The multimodal nature of knowledge development and learning in science is now increasingly recognized. While researchers have focused on identifying how different representational modes afford meaning-making, the question of how students are guided to link, confirm and expand similar and different meanings across modes, called ‘transduction', has been less explored. This transduction process is fundamental to students realizing, aligning, generating and coordinating meanings across representations to learn concepts and processes in science. In this paper we focus on a learning sequence in primary school astronomy designed around representational work to explore the teacher's key role in supporting student transduction. In the Interdisciplinary Mathematics and Science (IMS) project we developed a pedagogy with stages of orienting, posing representational challenges, evaluating and building consensus, and applying and extending conceptual understanding. We use micro-ethnographic analysis of the teacher's strategic framing and interactions with students and their artifacts to: (1) identify what enables student transduction of meanings as they engage with material and representational work, and (2) the role of the teacher in anticipating and addressing challenges for students in integrating meanings across multiple, multimodal representations of astronomy phenomena.
Multimodal Reasoning in Learning Science
There is now broad recognition that scientific knowledge claims necessarily need to be represented through multiple modes because different modes do complementary work (Lemke, 1990, 1998; Latour, 1999; Gooding, 2004). By implication, science students, in being inducted into these disciplinary literacy practices (Tytler et al., 2018), need to learn how to identify, link and integrate and abstract meanings within and across linguistic, visual, actional and mathematical modes to understand and communicate scientific knowledge (Lemke, 1998). Kress and Van Leeuwen (2006, p. 39) labeled this multimodal process “transduction.” They claimed that different sign systems or modes enable students to construct divergent, expanded and duplicated meanings that comprise the entailments of scientific processes and concepts. Therefore, transduction is understood as a complex dual process of recognizing both complementarity and consistency of meanings in representations across modes. However, this initial account left open the questions of (a) how exactly students achieve this cohesion in meaning-making, and (b) how teachers support this crucial aspect of science learning.
In this paper we review the growing literature on these two issues to propose a pragmatist account of student transductive meaning-making. We draw mainly on Peirce's (1955, 1998) semiotic theory of sign functions for reasoning applied to the disciplinary and epistemological affordances of different sign systems. Transduction is therefore understood as students' reasoning as they engage with semiotic resources (Prain, 2019; Prain and Tytler, 2021). We then focus on a learning sequence in primary school astronomy designed around representational work to demonstrate the teacher's key role in supporting student transduction. The astronomy topic is part of the Interdisciplinary Mathematics and Science (IMS) project, with a four-stage pedagogy where the teacher orients students, poses representational challenges, evaluates and builds consensus about key concepts, and applies and extends conceptual understanding (Tytler et al., 2021a). We use micro-ethnographic analysis of the teacher's strategic framing and interactions with students and their artifacts to: (1) identify how a Peircean analysis can characterize what enables transductive meaning-making; and (2) show how the teacher anticipates and addresses transductive challenges for students in integrating meanings across multiple, multimodal representations of astronomy phenomena.
Theorizing Meaning-Making in Science
From a socio-semiotic perspective, Kress and Van Leeuwen (2006) and Lemke (1998, 2003), leading theorists on multimodal learning, have focused on showing how sign systems function to enable individuals to make and share meanings. Agreeing that sign-makers need to see links between features in signs and their referents to make these meanings, these researchers have offered complementary perspectives in explaining what mainly enables this process. For Kress and Van Leeuwen (2006) signs are governed by grammatical structures that “point to particular interpretations of experience and forms of social interaction” (p. 2). They claimed that grammars in different modes provide conventions for how to order and analyse data, but also offer scope for transformations that align with these conventions. For example, the evolution over centuries of what and how graphs signify supports this view. These researchers defined signs as agent-motivated conjunctions between “signifiers (forms) and signifieds (meaning)” (p. 8). They acknowledged the necessary cognitive dimension to meaning-making but sought to emphasize the importance of sign grammars.
Kress and Van Leeuwen (2006) borrowed the term “transduction” (p. 39) to name how meanings in one mode are remade in another, entailing “translation and transcoding” (p. 39). They broadly claimed that verbal and visual means of communication “can be used to realize the “same” fundamental systems of meaning that constitute our cultures, but that each does so by means of its own specific forms, does so differently, and independently” (p. 19). They noted that “not everything that can be realized in language can also be realized by the means of images, and vice versa” (Kress and Van Leeuwen, 2006, p. 17), and “even when we can express what seem to be the same meanings in either image-form or writing or speech, they will be realized differently” (p. 2). However, once a non-verbal mode has been expressed and “available as externalized objective expression,” it can be made “differently available for verbal expression” (p. 39). However, this account does not explain what enables transduction. While a knowledge of grammatical conventions contributes to within-mode meaning-making in transduction, these conventions struggle to explain the diversity of reasoning processes needed to establish cohesion of meanings across modes.
To address this issue, Lemke (2003, 2015), drawing on Peirce (1955, 1998), claimed that signs mediate all human reasoning and problem-solving. For Peirce (1998) signs are the fundamental tools of logic in that they mediate between referents and meanings, by standing in for referents or for other signs. Referents cover many categories including made and found objects, features of objects, actions, experiences, practices, and contexts in the world. In reasoning in science, referents can also become signs or abstractions that provide a shorthand for further reasoning, where the sign is understood as standing in for a given science reality, such as “electricity.” Signs in science not only name referents but also interpret them within frameworks of explanatory models. Signs thus enable chains of reasoning through prompting inferential insights and also through analysis of their adequacy as stand-ins as well as their internal adequacy or coherence in representing model-based reasoning. In this way, both referents and signs can also prompt new or revised meanings, and subsequent new signs, altering how referents are then understood. Depending on the situation and custom, any referent can function as a sign with potential for stable or changing meanings. For example, Sutton (1992, p. 50) noted major changes to the scientific meaning of “cell” from its use over 300 years ago to describe the honeycomb-like structure of cork. For young students, the meaning of the apparent daily movement of the sun can be altered by an inquiry into why shadow lengths and directions change in relation to that movement.
In analyzing how signs enable and enact reasoning, Peirce (1955) proposed a theory of sign functions that shape what can be reasoned about and with. In his initial triadic system, there are three types of signs, consisting of icons, indexes and symbols. Icons are signs in which the sign/meaning relationship is based on likeness. This can include physical resemblance between the sign and referent such as a simplified drawing of the sun, or signs that show conceptual similarity such as the use of arrows on a page to depict the direction of earth rotation. Indexes are signs that point to other referents beyond the sign, such as smoke indicating fire. More complex indexical signs are evident in the meanings enabled by interpreting, for example, data from scientific instruments, graphs, or indexes in books that point to their thematic content. Signs can also function as abstract symbols that depend on agreed cultural conventions between sign, meaning, and referent, such as “enzymes,” “conduction,” and “thermal capacity.” In other words, signs enable reasoning through relations of likeness, causality and/or flagging of further signs/meanings, and as agreed more abstract symbols for referents. Peirce (1998) subsequently recognized that all three sign functions often interlock and influence any meaning-making process.
Lemke (2003) claimed that this triadic sign system clarifies reasoning processes in general and in science, where the integration of this system is needed to understand and communicate the multimodal hybrid nature of scientific concepts. We consider that Peirce's sign functions also provide an insightful framework for interpreting how students achieve transduction and how teachers support this process. By making these sign functions explicit in the focus of inquiry, teachers can encourage students to notice, interpret, and make meanings and inferences between signs/meaning relationships in different modes, based on resemblances in features of signs, causal inferences and implications, and guided abstraction from concrete to more conceptual understandings. What students reason about and with will inevitably vary, case by case, depending on students' prior understandings, the nature of the topic, their take-up of the reasoning functions of signs used in different modes, and sign structure affordances, and the forms and degree of entailed abstraction, evident in Peirce's triadic system. Organizing data into a graph, interpreting subsequent patterns, and inferring new meanings in this more abstract sign system is an example of how iconic, indexical and symbolic functions provide affordances for reasoning. In summary, learners need to reason using complementary sign system functions and affordances to realize, justify and apply scientific concepts and models.
Following this perspective, we developed a model of representation construction affordances (RCA) to explain what broadly enables students to understand and use different modes of representation to learn in science (Prain and Tytler, 2012). By “representation” we mean an intended sign in the Peircean sense, and in this paper we use these terms interchangeably. Following Peirce (1998) we recognize the semiotic potential of all referents to function as signs depending on context and participant purposes. However, beyond this generic semiotic potential, there are epistemic or disciplinary sign practices with particular affordances. For example, diagrams can enact iconic spatial and structural meanings that words can re-represent but not resemble in their form of expression, and while diagrams have affordances, they also have limitations in the amount and kinds of meanings they can represent (Lemon and Pratt, 1997). Disciplinary sign practices not only include the use of technical terminology and multimodal sign systems such as graphs and diagrams, but also entail signs for guiding learning and claim-making. For example, when a science teacher points at what she wants students to notice particularly about a specimen, this gesture is part of a recognizable assembly of disciplinary meaning-making signs associated with guided inquiry and the value of precise observation. We further claim that all representational modes have particular affordances (Gibson, 1979) that act as productive constraints on reasoning, to address two requirements in persuasive scientific claim-making and modeling (Tytler et al., 2020; Prain and Tytler, 2021). These requirements are that a representation should (a) show a correspondence between explanatory features and key features of the phenomena, and (b) demonstrate internal coherence or self-consistency as an explanatory account. We recognize that Gibson (1979) understood affordances as non-representational, but claim that reasoning about these two requirements in scientific claim-making as representations points to the key epistemological affordances of signs in science learning. Applying these reasoning requirements to signs is fundamental to student transduction.
In seeking to clarify further how transduction works for learners, or fails to work, other researchers have tended to draw on Kress and Van Leeuwen's (2006) lead. Stein (2008) and Svensson and Eriksson (2020, p. 1) claimed that learners follow grammar-like chains or “links” in semiosis to achieve transmodal meanings. Newfield (2014, p. 6) proposed that transduction must include “the transmodal moment,” where an idea is realized in a different mode in a chain of semiosis. She claimed that this moment can alter “meaning, orientation, disposition, subjectivity, identity and affect,” and show how modes “call up the semiotic practices of different communities at different historical periods” (p. 14). However, this account leaves open the question of what exactly enables transmodal ideation. Transduction failure tends to be interpreted as gaps in learners' relevant conceptual knowledge leading to an inability to interpret sign variation. Patron et al. (2021) claimed that students attempting transduction from one visual mode to another promoted deeper chemistry learning by uncovering new dimensions, but these researchers also noted that left unassisted, students struggled with this relatively constrained form of transmodal ideation. Minor surface changes to 3D representations were also found to confuse primary students about underlying concepts (Prain and Waldrip, 2006), indicating their critical role in meaning-making. Volkwyn et al. (2019, 2020) claimed that older learners build semiotic links to develop a coherent sense of concepts across modes through disciplinary sign affordances, where some signs (in this case an arrow in physics) can function as a “placeholder” (p. 16) for new and expanded disciplinary meanings within and across different modes. They claimed that science teachers should “encourage and confirm correct transductions “(p. 26). Volkwyn (2020); Volkwyn et al. (2020) draws on variation theory (see for example Marton and Pang, 2006) to frame transduction as a key source of variation in learning situations. He claims that because different modes have different affordances, transductions always require additions and subtractions of meaning. In transductions, then, students notice new aspects of a given concept, while attempting to produce a coherent account of the concept across multiple modes.
We consider that Peirce's rudimentary triadic model of sign functions provides leads on how students can reason across modes. In the following astronomy case study, we interpret one teachers' intentions and practices using this triadic model. We seek to show the multiple ways he orients and supports learners through an inquiry process to seek and understand new abstract disciplinary scientific meanings through guided use of everyday, purpose-built, improvised, and conventional sign systems in relation to material and symbolic referents.
Context of Study: The IMS Project
The Interdisciplinary Mathematics and Science (IMS: https://imslearning.org/) project aims to explore the potential alignments and learning advantages of linking mathematics and science across a range of year levels. We have developed learning sequences across the primary year levels 1–6 in a range of topics using a design-based research approach, exploring principles of productive alignment of disciplines such that learning in each is mutually reinforcing (Tytler et al., 2021a). In these sequences, often the topic is science-based, with learning in mathematics enriched by being authentically driven by science contexts and questions. Mathematics concepts represented in the sequence are diverse, often including measurement and variation, number concepts, data modeling, and spatial thinking. The pedagogy underpinning the approach draws strongly on the pragmatist semiotic principles, and particularly on the interdisciplinary, model-based approach of Lehrer and Schauble (Lehrer and Schauble, 2006, 2012; Lehrer et al., 2006; Lehrer, 2009, 2021; Manz et al., 2020). We regard robust foundational learning as occurring through the guided construction, evaluation, revision/refinement and coordination of representations/signs and sign systems (Prain and Tytler, 2012; Tytler et al., 2013). The pedagogy we have developed (Tytler et al., in press) in IMS charts a path through representation challenges which elicit varied student responses, which the teacher strategically draws on to reach consensus about productive representational systems. A key aspect of the pedagogy is the progressive linking of students' prior everyday meanings for referents and their sign systems to the more abstracted sign systems that open up scientific perspectives, often entailing mathematical modeling of phenomena. Support of transduction across these sign/meaning/referent systems is thus fundamental to the pedagogy.
IMS has involved working with primary school teachers and students over 3 years, tracking the same cohort of students and engaging with a fresh set of teachers each year who we work with to develop and refine learning sequences. Over the 3 years the project has involved 35 teachers and six cohorts of up to 70 students over three classes.
Research Methodology/Design
The project has used a design-based methodology (Cobb et al., 2003) based on a cycle of cooperative planning and review with teachers (Severance et al., 2016), trialing, data generation and cooperative evaluation, and revision refinement. Each year we held full day workshops with participating teachers to introduce them to the principles underpinning the approach, and the pedagogy, utilizing examples from previous learning sequences. Sequences were planned to be consistent with the state curriculum, and to involve a back-and-forth between representational work in science and mathematics that arose naturally from the inquiry questions driving the sequence and were mutually reinforcing. Prior to the implementation of the sequence we held planning meetings with the participating teachers who commented on details of the approach, viability of the activities, and raised questions about the types of support that might be appropriate for the often challenging tasks we designed. The research team was present at the school for each lesson, helping with equipment and videotaping the lessons of a case study teacher using two cameras—one focused on the teacher and another on one or more student groups as they worked. Students' artifacts from each class were collected, photographed and returned. During these visits we held informal discussions with teachers to discuss progress and ascertain student engagement with learning, and at times discussed possible modifications to the sequence. As we will see from the interview data with Colin, our focus teacher for this particular study, the groups of teachers would regularly and independently compare notes and discuss approaches to draw off each other's experience to enhance student learning. Thus, while the sequence of inquiry questions and activities were designed by the team, teachers felt free to adapt these to the needs of their own students and their own practices. In the analysis in this paper, therefore, we are describing in broad terms the sequence of activities we ourselves designed, but the details of teacher-student interactions represent the insights and pedagogical approach of our case study teacher, Colin, who creatively adapted the activities to the contextual needs of his students. The astronomy sequence occurred for the Grade 1 students (age 6) in the final term of the first year of the project. We were fortunate in selecting Colin as our case study teacher, in that his teaching approach proved to be naturally aligned with our expectations of guided inquiry based on a sensitive assessment of students' learning needs. This was the third sequence from that first year, following a short sequence on describing motion, and a schoolground ecology sequence involving students investigating and documenting living things across sample plots, leading to a substantial focus on graphical work in modeling the distribution of living things across habitats (Tytler et al., in press).
This paper focuses on teacher support of student transduction for four lessons of the astronomy learning sequence where students learnt about the apparent movement of the sun across the sky through linking this with the shadow variation on four occasions during one day. Data sources for the analysis include student work samples for each lesson, video records of Colin interacting with the whole class or small groups of students, and a post sequence interview to probe Colin's perspectives on his approach. The video transcripts of the four lessons were examined to identify episodes that involve transductive demands on students in developing new sign systems through which they pursue their inquiry, for instance creating a chalk-line representation linking the sun's position to shadow length and direction. This approach, of purposefully selecting key “examples” (MacLure, 2010) that generate fresh insights into a phenomenon, is described in some detail in Ferguson et al. (2019). We describe the approach as micro-ethnographic (Baker et al., 2008) in that it involves the construction of an account of classroom practices using detailed analysis and interpretation of classroom discursive patterns in an iterative process of video review, researcher discussion, theory review and construction, analysis of artifacts, and interviews.
In this sequence students are introduced to the scientific and mathematical sign conventions through which astronomical/shadow relations are understood in the discipline. We focus in the paper on Colin's pedagogical moves in response to his judgments of students' learning needs and challenges (i.e., the transduction demands implicit in multimodal reasoning about relevant data and its representation) in representing sun-shadow relations. In the episodes we use Peirce's categories of signs to make sense of how Colin seeks to support student transductive reasoning across modes. Students' learning challenges and outcomes are not focused on directly but are to varying degrees explicit or implicit in the teacher-student interactions and in Colin's framing and negotiation of the tasks and of students' productions.
Teaching and Learning Astronomy
Astronomy is taught across a wide range of levels, with primary school sequences often focusing on night and day and features of the solar system. In upper primary school or more commonly lower secondary school, the focus is on more complex spatial phenomena of moon phases, stars and star movement, and cosmology in the later secondary school (Salimpour et al., 2020). Research has consistently demonstrated a range of misconceptions across a variety of astronomical phenomena, including earth-sun relations (Vosniadou and Brewer, 1992), seasons, moon phases and eclipses etc., despite repeated exposure to teaching (Danaia and McKinnon, 2008; Lelliott and Rollnick, 2010). A major challenge for learning about astronomical phenomena is the need for visualization and spatial reasoning, entailing coordination of earth-based and space-based representational systems (Hegarty and Waller, 2004; Padalker and Ramadas, 2008; Plummer, 2014; Hubber and Tytler, 2017; Tytler et al., 2021b).
Visualization is increasingly acknowledged as central to learning in a range of science disciplines (Gilbert, 2005), involving the coordination of systems of representation through which we coordinate visuo-spatial relations such as diagrams, 3D models and simulations. These are fundamental to astronomy learning, entailing diagrams of earth's orbit, rotation and tilt in relation to the sun to explain the year, day and seasons, and models and diagrams of these and movement of celestial objects. In our previous research involving cross-national studies of learning about day-night relations and moon phases in primary schools, we (Tytler et al., 2017) identified commonalities in the ways teachers in the three countries introduced and coordinated, using strategic talk and gesture, a series of representations including diagrams, video simulations, models and role plays, to build meaning across these representational modes and systems. More recently, we have examined the way that students reason to establish meaning across modes through establishing correspondence and coherence of meanings across 2D diagrams and 3D models (Prain and Tytler, 2021). In the current study we explore in more detail the way that a teacher supports the transduction of meaning across modes for younger students exploring the link between the sun's apparent movement and shadow changes over a day.
The learning sequence, described in Table 1, began with an exploration of students' prior knowledge about the sun's movement and shadows, and the posing of the major inquiry question which occupied the first four lessons: What is the pattern of shadows over the day and how does that relate to the sun? The core data generation lesson involved tracking the changing length of shadows by a variety of means, including in Colin's class streamers (decided by consensus) whose lengths were measured using an informal block system. Lessons 3 and 4 involved the creation of a set of increasingly abstract representations of the shadow variation in relation to the sun. In the fourth lesson a space perspective was explored using video animations and a torch and model globe to establish the reason for night and day. This was linked back to the shadow results. In the current paper we focus on the teacher, Colin's support of transduction processes in lessons 2–4, in which he and the students creatively negotiated a series of linked signs through which meaning was established across multiple modes to enable students to transform their perceptions of shadows and sun from everyday meanings and signs to the abstracted sign systems by which science understands and represents these phenomena.
Results
In this section we describe Colin's actions at key points in the sequence to illustrate how he supports students to link meanings across different modes and multiple sign systems through a reiterative focus on the iconic, indexical and more abstract symbolic functions of signs in this meaning-making.
Episode 1: Supporting Construction of Signs for Shadow and Sun Position
From the beginning of the first shadow marking in the schoolground, Colin worked to explicitly link the position of the sun with the shadow direction (a transductive link recognizing the shadow as a marker of the sun's movement), because students, in tracing their shadows, were not inclined to notice this relationship. For this purpose he created a sequence of signs through which the link could be made explicit. First, he asked students to identify the position of the sun by pointing, modeling this himself. This is an indexical sign which acts as a marker, positioning the sun more precisely in relation to students' bodies by productively constraining their perception of its whereabouts. Second, he arranged for one of the group to stand in the direction of the sun, in order to bring out the relationship of the shadow direction to the sun's position (effectively transforming the sun's 3D position in the sky to a 2D direction along the schoolground surface). Figure 1 shows him working with one group to establish these two signs and their meanings.
Colin: Where do you think the sun is now? … Do you think Cerise is in a good spot?

Figure 1. Colin creating sign systems to mark the sun's position in the sky and on the 2D schoolground surface.
Following this, he encouraged groups to mark the spot where the student (Cerise) is standing with a chalked sun symbol, thus creating a sign representing the sun's direction that could be directly linked to the shadow tracing at that point in time.
We note, in this episode, Colin's responsiveness to students' learning needs (the challenge of linking sun and shadow directions) through creating a series of linked signs (pointing, then positioning the student, then the 2D chalked representation now available for re-representation for further analysis). These signs serve to sharpen the students' everyday perceptions of the sun's position, inviting a more focused set of meanings for the sun's movement in relation to shadow changes. In this process, students engage with transduction from embodied indication of the sun's position (pointing- an indexical sign) to material alignment of Cerise with the direction (again indexical but now with an iconic function in terms of its structural relations of position resembling that of the sun in space), and finally to a diagrammatic (chalk) inscription which we interpret as having indexical and iconic functions but now also a symbolic function in acting as a positioned symbol of the sun's direction in 2D space. The power of this symbolic representation lies in the possibility it opens up for further reasoning through manipulation of relative sun-shadow directional relations over time. The chalked shadow tracings are iconic signs of the shadows themselves (having structural similarity) but fixed spatially to represent the temporal changes in shadow position and size. Colin has thus engineered for the students a sequence of signs through which the conceptual linking of shadow to sun position can be flexibly inspected and discussed. Some of these links were deliberately planned, embedded in the logic of the sequence, but others (fixing the sun's position) were flexibly created to address students' learning needs. The signs in this sequence have specific modal affordances in the way that they productively constrain attention (Prain and Tytler, 2012) on aspects of the phenomena important for building disciplinary understandings. The affordance of the embodied pointing lies in constraining attention on the whereabouts of the sun. Positioning of Cerise further constrains attention on direction, as does the chalking of the sun symbol fixing it in 2D space, now available for reasoning about angular directions.
In the next stage of working toward the symbolic systems representing disciplinary understandings of sun-shadow relations, Episode 2 involves applying systematic measurement on the shadow diagrammatic representations, a further requirement that students transduce meanings across different representations of this measurement process.
Episode 2: Representing the Shadow Lengths With Streamers
In the second episode we discuss, Colin is working with the whole class gathered around one group's shadow tracing to construct a measure, using streamers as the class had previously decided, of the shadow length at each of the time points. He first described the process, and invited students to indicate which points on the shadow they should measure between. One student pointed at the middle of the shadow, but Colin affirmed a second suggestion to measure to the tip of the shadow as a better representation of the shadow length. A modeling process is implicit in the streamer measure, whereby the streamer becomes a simplified, indexical/iconic model with a structural relation to the shadow itself; its affordance being to simultaneously constrain and shape attention on the important feature of the shadow—it's length—that will be used to track changes over the day. Again, this is a transductive remaking of meaning (shadow outline to streamer length) that Colin carefully interprets for students. We can see, in the students' misinterpreting where the streamer should be placed, the transductive challenge of aligning the meaning of the streamer with the relevant feature of the shadow it is meant, from a scientific perspective, to represent.
Figures 2A–C show the subsequent stages through which Colin works with the students on the process of marking out the streamers. He assigns a student to pin one end of the streamer to the middle of the point the student was standing, and another student to “check” they were measuring correctly. In Figure 2A he models the identification of the streamer point corresponding to the shadow tip. In Figure 2B his gesture takes in the entire length of the streamer and he emphasizes the length as the distance between the ends of the shadow. In Figure 2C he now emphasizes that they have a representation of the shadow length that can be taken away as an abstracted version of the shadow itself that can be communicated to “M” (from the research team). Following this, he prompts and discusses the need to annotate the streamer with the time the shadow was recorded, to provide a full communication to “M,” pre-figuring the function of the streamers as a temporal record of shadow length changes. The streamer, as with any scientific measurement instrument, has an indexical function in pointing to, or standing in for a feature of the phenomenon, and is now available for inferential reasoning about material relations, in this case changing over time.

Figure 2. (A) Are you happy with that Moira? (Moira was checking the process). (B) One person's marked the start and one person's marked the end. (C) Now I can take it away and M will know “that's the length of our shadow” … we know how long it is.
In this episode, Colin has clarified several aspects of the transductive moves underpinning this modeling process: the choice of the shadow feature that is to be modeled; the process of carefully constructing the streamer as a valid measure; and the transportable nature of the streamer as a communicable, abstracted sign. These are all moves that invite students to shift meaning from the shadow traces to the streamer sign. In Peircean terms, we see the relation between these signs to be iconic in nature, in terms of correspondence in length, and indexical in terms of the streamer “standing in” for the more complex phenomenon of shadow shape. Note that the resemblance of the streamer to the shadow is more than simply physical in that it represents an abstraction of the shadow outline to one measure. We can see that measurement inevitably involves a transductive move, where students need to link across from the referent being measured, the measuring instrument, and the final abstracted number that results.
Again, we see Colin making the modeling process tangible and explicit to guide students' meaning-making across modes.
Episode 3: Working With the Gnome as Part of a Sign System
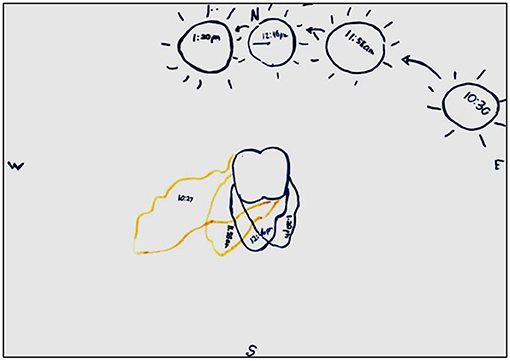
In each foray into the schoolground for groups to track their shadows, Colin gathers the class to model the process and its interpretation using a gnome placed on a sheet of paper. Over the day he continues to come back to the gnome to trace a further shadow, modeling the placing of the sun's position (opposite to the shadow, as described in Episode 1) and drawing attention to (a) the changes in shadow length and direction and (b) how this relates to the position of the sun.
In the third gnome shadow recording with the gnome, at 12 pm. Colin questions the group about what has happened to the shadow (Student: “it is getting smaller and moving round”). He elicits general agreement that this is because of the movement of the sun. Colin then explicitly links the two, indicating the movement of the shadow (Figure 3A), and then the corresponding movement of the sun (Figure 3B), using his finger to trace the direction of movement in an arc. In Figure 3C he links back to the position of the sun in the sky by orchestrating the class to point, then to predict where it will be for their next measure (Figure 3C).

Figure 3. (A) The shadow's moving toward the south—it looks like its coming around this way. What's happening to the sun? (B) The sun started here and moved over at 12 o'clock toward. (C) Where do you think the sun is? Where's it going to be?
The gnome exploration enabled Colin to illustrate to the class the process of constructing the shadow and sun position in multimodal sign systems, and to discuss the relation between them using talk and gesture, to establish correspondence and coherence features of these sign systems. In the diagram he also added the indexical/iconic signs of the compass directions. He takes students' suggestions of the general movement of the sun and makes the relations more explicit through gesture. As he points out features and questions students about patterns of relations, and asks for predictions, he draws attention to patterns in the gnome tracings over time in terms of length and direction, signaling a further abstracted sign of directional movement with his finger, which we will see transformed into (symbolic) arrows in subsequent lessons. He frequently links back to the position of the sun in the sky, now given new and enriched positional meaning by the sign systems of the gnome diagram. Figure 4 shows the diagram constructed over the four sessions outside, showing patterns of movement of the shadows and sun that enables inferences to be made about the relationships between these. Note that the establishment of meaning for each of these signs has been carefully constructed through prior inquiry processes involving transduction across different embodied and material signs. At this point in the sequence we can see how student understanding of the shadow-sun relations has been sharpened and enriched through teacher and student creation of and transduction between successive multimodal signs, each of which contains correspondences that Colin models through talk and gesture, and coherence in the linked meanings across modes. In having the sun image in the diagram stand in for a likeness to its referent, students are then invited to make sense of the pattern of relationships between the sun and the direction and length of the depicted gnome shadows.
Episode 4 (Lesson 3a): Constructing Diagrammatic Representations
In the lesson after the schoolground construction of shadow data, Colin poses a representational challenge for students to show what they learnt about the relationship between the sun and shadow movement using a diagram. During this task, Colin circulates and supports and challenges students to represent the relation between the shadow changes and the sun's movement. He focuses on the creation of representations that link to their observations and experience of the sun and shadows.
Colin: So what happened to your shadow during the day? What about at the start? Was it longer or shorter at the start?
Colin encourages Noel to specify the position of the sun in the diagram and affirms his gesture of sun movement across the page (Figure 5). Noel subsequently uses arrows to represent this movement, initially performed by his hand (Figure 6).
Colin subsequently held up Noel's drawing as an exemplar (Figure 7), encouraging the use of arrows and directional specificity. This was a frequent strategy he used to suggest and to establish shared agreement about aspects of sign grammar, in this case the use of arrows and compass directions. In these interventions he consistently links the representations to students' sign-making experience in the schoolground, pointing out in this case an inconsistency in Noel's account.
Colin: Look at Noel—He's written N E S W, which is very clear because he's thought about which way the sun goes, maybe you can think more about the arrow—which way the arrow's going—but you can see that the sun is moving through the sky. That's very clever. Have a think about the arrows—was it going from West to East or East to West? Which way did the sun go?
Episode 5 (Lesson 3a)—Gnome Modeling
Following students' construction of diagrams, Colin sets up a model of students' shadow experience with the gnome and now a torch to represent the sun casting a shadow (Figure 8). He flexibly changes the elevation and orientation of the torch (sun) to explore its effect on shadow direction and length. Through a question and answer sequence, he reinforces students' conceptions of the sun's movement, its elevation change during the day and how this is related to the shadow length, and the relation between the sun's direction and shadow direction. In this episode, we see how the torch-gnome model allows Colin to highlight spatial and temporal relations to enable students to re-organize their perceptions of the experience in the schoolground. His manipulation acts as a proto-model that allows a simplification of the sun-shadow relations. Having established links between the sun and shadow sign systems we argue that Colin can now engage the students in a more focused discussion of the spatial relations involved. In this episode we also see an example of the redundancy of meaning Colin regularly builds into his activities and talk, providing students with multiple entry points.
Episode 6—Ordering the Ribbons From One Group
In this part of Lesson 3a Colin uses one group's ribbons to develop an array on the board that represents the temporal changes to shadow length. He selects them in random order.
Colin: With one example (of a particular group) we're going to order them … So I'm going to hold them up (Figure 9A)
This one I have is 12 o'clock, the middle of the day. I am going to put it up. I want you to notice the length of the streamer, because that was the length of our shadow.
Colin: (Pulling out the 10:20 am image- Figure 9B) 10 o'clock—should I start it here? (holding to the left of 12:00- Figure 10C)
Students: Yes.
Colin: Ok, ‘cause I want to order them.
Colin: Now I have 12:50 (Looking at the array) 10:20, 12:00, 12:50. So it will be here? (placing to the right). Notice what is happening to the length.
Students: It's getting shorter
Colin: 1:20 (places the final streamer to the right of the 12:50 measure

Figure 10. (A) “As the sun started to track to the west the … shadow got longer again.”(B) “Because, as the sun gets lower in the sky to make our shadow get long again.”
In this sequence Colin constructs from the streamers an array that represents the temporal sequence spatially. As he does this, he continually checks with students the appropriate positioning and reminds them of their experience of the shadows and construction of the streamers as signs representing shadow length. We see, through a Peircean lens, the symbolic nature of the streamers as a form of proto-graph, with their meaning for students invested in a chain of transductive moves back through a series of sign systems.
Colin goes on to stimulate students' thinking about representing this in their books, a further transduction challenge.
Colin: How could we represent this in our books? How could we show the data clearly?
Student: We could use a graph, a column graph
Colin reinforces this as a good idea and gives students time to explore representing the data in their books.
Episode 7: Recapitulation of Sun's Movement and Streamer Display (Lesson 4)
In the following lesson Colin questions the class on their experience of the movement of the sun over the day, using gesture to sweep the agreed path from east to west, and asking students to join him in this action. He emphasizes, through questioning, that the sun at noon is high in the sky, in the north. He then recounts the series of sign construction experiences underpinning the board display with streamers that was constructed in Lesson 3.
Colin: We looked at our shadows at different times of the day. (Pointing to streamer/recording 1). We said that at 10:20 in the morning, we measured in blocks remember—we said that (student) had a shadow fourteen blocks long. At 12:00 the sun was higher in the sky and the … shadow was 8 blocks long, it got shorter. Then … (Figure 10A).
Colin continually links what happened to the sun, and shadow over the day in a recount of events that emphasizes the meaning underpinning this new sign system that effectively displays time unfolding across the board. He does this using language and gesture, sweeping his hand down the streamers to represent length, and in Figure 10B reproduces the simultaneous lowering of the sun and the lengthening of the shadow along the ground.
The streamers aligned across the board operate as one of a series of bridging representations (Pham and Tytler, 2021), pointing toward a more abstracted and formalized graphical representation, and back to a series of transductive moves that establish the streamers as signs for the shadow length over time, linked to the sun's movement across the sky.
Episode 8: Constructing a Graphical Sign System
Following the construction and establishment of what the streamer display means, Colin reminds students of the challenge to represent the data in graphical form. Students' graphs are not constrained by rules he has established, but again he attends to the establishment of sign grammatical conventions through the use of exemplary student work (see Anthony's graph, Figure 11), following which he circulates amongst the class helping them construct graphs, focusing attention on the conventions that render the graphs interpretable through appeal to their meaning as linked back through the chain of sign-making from their schoolground inquiry.
Colin: I asked everyone last week, how can we represent our data … How could we show all of this so that it was really clear?.. I would love to show you Anthony's graph (invites Anthony to explain his graph) ….
Anthony: (Explaining his graph and pointing) I used the measurement of the 14 blocks
Colin: … Then what did you do? What time is that?
Anthony: 10:20
Colin: So you've started your column graph at 10:20. What did you do here though (pointing to vertical axis) On this side of the bar—what have you got?
Anthony: Numbers (teacher repeats)
Colin: Look at the numbers, very clear and it's even too …. it's very clear and goes up to 20…. Is this very clear boys and girls?
…
Colin: What else have you added down here (pointing to horizontal axis).
Anthony: I've shown where it goes
Colin: Yes, you've put the direction into it to make it even clearer… What does this mean E N N W though? Is the direction of the shadows or the sun? I think it is the sun.
Colin emphasizes to students that they can come up with their own ideas (“I think some people had different ideas which is fine”). He then circulates around the class, helping them lay out and annotate axes to accommodate the data and guide them in constructing columns. In this way he attends to explicating and attending to students' competence with graphical conventions, but in doing so he continually refers back to the meaning of the streamer data on the board—recapitulating the transduction process. Figure 12 shows three examples of students' graphical work showing the variation.
Colin's Pedagogical Moves
From this sequence we can identify the following key features of Colin's practice in supporting students' meaning-making associated with new sign introduction/ invention and the multiple transductions that are involved:
1. The logic of the sequence plan which involved the progressive generation of signs of increasing specificity and symbolic abstraction, and Colin's flexible invention of informal bridging signs in response to students' transduction needs
2. The constant attention to and support of students' thinking about the meaning of the transductive link to new signs, through talk and gesture
3. The constant grounding of students' understanding of representations in their experience of sign construction
4. The constant moving back and forth in the discussion, including prompting and questioning, to ground each new sign with reference to students' joint experience, or to other signs
5. The redundancy built into the chain of representations, often involving recapping but using different and related models such as the torch and gnome, or recounting events that gave rise to particular signs
6. Challenging students to construct representations at different points in the sequence, as a means of probing ideas and using the variety of responses to build a shared view
7. The attention to sign conventions for the more formal representations (graphs, diagrams) through a process of construction, comparison/evaluation and subsequent refinement, building from students' interests and capabilities rather than imposing a formal system.
These strategies indicate general ways in which teachers can support student transduction. These include an explicit teacher focus on resemblances of structure and meaning between modes, inviting and confirming student transductions across modes, pointing out iconic and indexical functions of signs, and building redundancy through multiple demonstrations of how meanings are sought and established across modes.
Colin's Explication of His Intentions
In analyzing the sequence, we have described how Colin framed his and students' sign-making and transduction across signs in anticipation or response to their learning needs, resulting in a mix of planned sign-sequences involving transductive reasoning, and on-the-spot creation or re-casting of signs when students were challenged to notice the transductive meanings he was intending. Here we present excerpts from an interview with Colin as corroborative support for our interpretation of his intentions and practices. The interview took place at the end of his first year in the IMS project (which involved a short motion sequence, a schoolground ecology sequence which involved generating and representing data concerning living things in a range of sample plots, and finally the astronomy sequence). While he does not use a formal language of transduction, his focus on tapping into students' prior knowledge and allowing them to generate representations and refine them, rather than explicitly model the representational systems of science, is consistent with our interpretation of his careful support of students' meaning-making through questioning and open modeling. He also speaks to the increased student facility with diagrammatic representation and graphing through grounding these in students' experience of authentic data and building this capacity over time.
As we saw in analysis of the sequence, Colin supports students' sign-based reasoning processes by explicitly encouraging their own ideas and representational invention in relation to their experience of inquiry. A key aspect of Colin's pedagogy is to explore students' ideas through open questioning and building strategically on the variety of responses.
What I have liked about the units too is we do not set up anything too early, it's let them explore what they currently know and then we kind of build on it and then we show some examples, we do model but, of course, it's getting to step back– I think it's very easy for teachers to just go, “I'm gonna model everything straight away and make it really explicit,” but then they are kind of set in what they then can produce. But I think having it really open-ended, particularly from the start, you get a range of more responses as well, which has been really good.
Colin argued that exposure to graphical work through creating authentic data and linking that experience of collecting the data with the graphical forms had led, over two sequences, to students gaining surprising facility with graphing. This focus on transduction across signs that framed and created data through to the abstracted graphical conventions was a key feature of his practice, as we have shown.
… what is quite interesting too is when we went through the ecology unit and we were looking at the data and looking at the living things that they found and then transferring the graphing, would say that about 50% or 60% of them could do it accurately.
Then when we went back and did it again through astronomy and had the data presented then had to transfer it to the graph, I think it was about 80% plus who could do it accurately onto a graph. So, there was a big improvement in that area too by actually looking at the data and then transferring it to a graph and making sure that it linked. A lot of them, for example, just added numbers or the increments were wrong but this time it was a lot more accurate. So, I think the more that they did it, the more they used the data accurately as well and realizing the importance of the data too.
Colin talked about the advantages for both engagement and learning of stimulating students' prior ideas and generating representations based on direct experience of material inquiry. Through the project, he claimed to have learnt to trust and use students' prior knowledge to support further learning.
But astronomy, definitely, we found that even in the depth of discussion the children, you know, we had been saying that the sun tracks from the east to the west, like, it was just their language, their knowledge of north, south, east, west, for example, that was something that we would not expect year ones to know but now they are able to do it and just their explanation of how– Well, the relationship between the Earth and the sun, which is so much clearer, and they were really keen to know more, they wanted to learn more. So, I found that that unit in particular we found that their scientific knowledge really improved in that area.
Colin talked explicitly about the revisiting of a range of different representational systems and models to support meaning linkages. With regard to the linking of the shadow length with the sun's movement in the sky, he nominated revisiting representations and linking to new models as a chance to make meaningful connections across these. As we have argued, flexibility in creating and working across representational systems, and building in redundancy in sign/meaning/referent relationships to support all students' learning, is a key feature of his practice.
Interviewer: Do you think they were able to make the connection between time of day in terms of measurement, different times in the day and the length of the shadow?
Colin: Yes, they started to, they did.
Interviewer: Or did some make the connection and others–?
Colin: Some did and some did not at the start and then when we went back and we modeled it again in class with the globe and we looked at the shadows and the sun with a torch, when we did that activity we kind of then found that the children were kind of going, “Oh, the shadow's getting a bit longer here,” so, then we went back to our data, we had a look at the length of the shadows, what time of the day was it, we went back and had a look and then we said, “Can we see a pattern?” and they kind of were able to then identify at the end that the morning and afternoon the shadows were longer and in the middle of the day it was shorter, “But why?” because the sun was higher in the sky. So, they started to then have that, they did really start to get it. But what has been so fantastic is because– and you really need to, you need to have that repeated message in a way in the sequences, but it was not repeated in a way that it was presented the same way to them. So, it was prepared in a way that it was presented in a variety of different ways with the modeling, with the investigation so they were able to then really grasp that concept, yes.
Discussion
From a Peircean semiotic perspective, student transduction in this case study entailed students being supported to reason from everyday sign meanings and their referents to science's specialized multimodal sign systems to investigate and explain phenomena. Our starting point for the IMS project was that learning in schools involves induction into these disciplinary sign-making and interpreting practices and that classroom practice should mirror this process in important ways. We see in the sequence, and in Colin's interpretation of it, students are guided to create and appreciate chains of meaning that move systematically toward the more abstracted and symbolic sign systems through which scientific reasoning and meaning-making can proceed. This entails the graphical depiction of changing length of shadows over time, and the diagrammatic representation of the temporal progression of the sun from east to west through the northern part of the sky. Figure 13 is a representation of the chain of sign/meaning relationships that Colin and the students engaged with, each of which is linked to the next in a process of transduction through which the meaning extensions are understood. In this paper we have focused on: (1) a Peircean interpretation that we argue can flexibly capture how students' transductive meaning-making draws on indexical, iconic and/or symbolic sign functions, and across modes that have specific affordances that guide what is noticed and what can be more abstractly represented to support reasoning; and (2) how the teacher strategically and responsively guides this process.
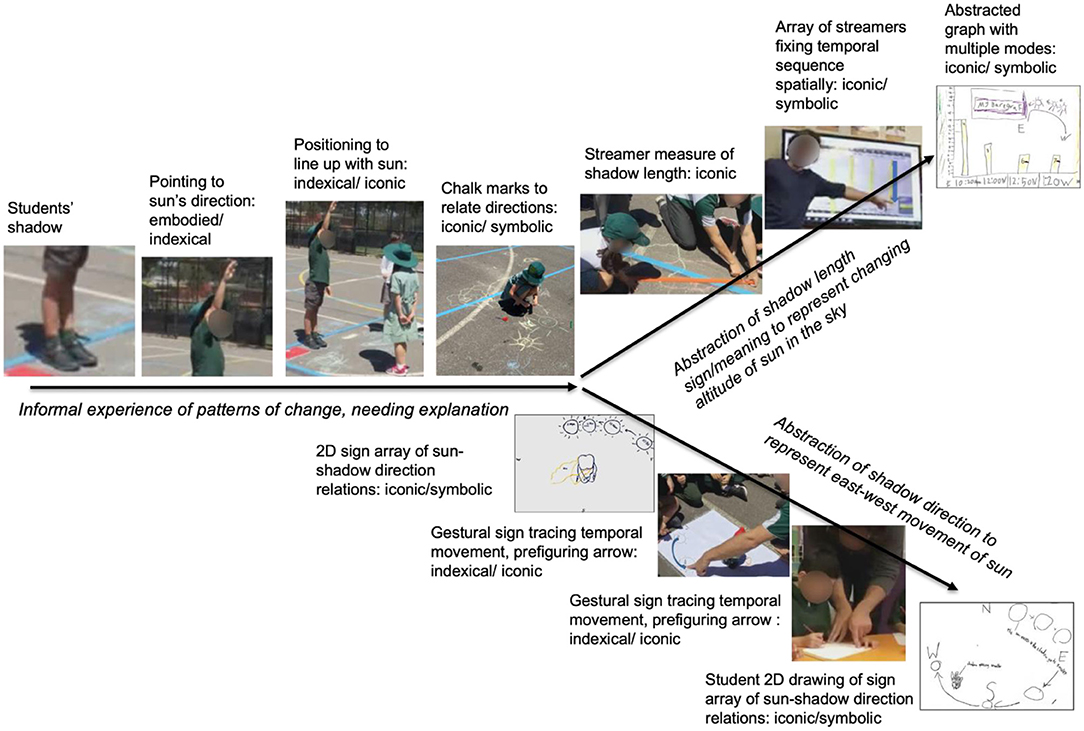
Figure 13. Sequence of teacher and student sign-making to support students' successive transductions of shadow-sun relations.
In tracing this semiotic process we have identified three separate sequences. The first four representations, two of which Colin inserted in response to student learning needs, were designed to progressively refine students' informal sense of changes to the shadow in relation to the sun's position. What follows are two distinct learning trajectories through different representational sequences. The top sequence involves guided inquiry into the measure of shadow length that is progressively refined through streamers laid along the shadow traces, then placed in temporal order on the board as a proto-model of graphical conventions, and finally to a graph itself which was progressively refined through discussion of conventions that enable clear grounding of the graph in this representational chain.
The other sequence entails representations on shadow direction progressively abstracting the angular change to shadow orientation related to the sun's east-west movement, introducing a diagrammatic representation of the temporal sequence through sweeping hand gestures which transform into curved arrows (prefiguring symbolic representation of angle size) and symbolic arrangement of compass directions. Characterizing signs as symbolic in this diagram, following Peirce, is based on recognition of the resolved sign/meaning/referent relationship of these signs in science discourse.
This case study represents an account of how relative beginners are taught through a highly focused sequence of sign-making about how scientists make and share claims about phenomena, and on what bases. While our analyses of student transduction challenges and support might seem for some readers over-complicated, our explication of this case confirms the complexities of multimodal reasoning required of students with and across signs in different modes in early primary school. While Peirce's triadic functions for signs can be readily applied to what students reason about and with, even this application to a relatively simple lesson sequence reveals the complexities entailed in the simultaneity of meanings made with and across actional, visual, spatial, temporal and linguistic signs that are new for the students. This case study indicates just one sequence of transductive demands where the teacher aimed to guide young students to understand part of the evidence for the earth's rotation. Other topics at other year levels clearly will entail different student transductive challenges, depending on how the scientific claims of the topic are represented. Therefore how teachers can guide student transduction is context-dependent.
Our study indicates that the teacher can model grammatical conventions for sign systems productively for student take-up, but these conventions set up but do not cover the cross-modal reasoning required of students to abstract meanings across material and symbolic signs. Following Peirce, we claim that to make transductions, students also need to recognize resemblances across sign/meaning relationships, make inferences and reduce or abstract material experiences into spatial, visual, temporal and mathematical signs within and across modes in ways that create new scientific signs and sign/meaning/referent relationships.
We do not consider that Peirce's epistemological and disciplinary account of sign functions should be understood as a transmodal grammar. In contrast with the particular conventions for using sign grammars to reason within modes, such as the conventions around organizing and interpreting data in a graph, Pierce's sign system is far less prescriptive and more flexible in how these sign functions can be reasoned about and with. For example, in our case study, we note that iconicity as a sign function can prompt and confirm many different reasoning processes and outcomes depending on teacher and learner focus. Iconic signs in this case study are variously created and interpreted as the bases for analogical reasoning, pattern spotting, noting structural and functional likenesses, and enacting proto-modeling. Colin variously points out iconic resemblances to invite the students to represent and reason across visual, spatial, temporal, actional, and mathematical meanings entailed in this science topic.
We also note theoretical implications for the role of teacher creativity in supporting student learning of transduction. Teaching science is traditionally conceptualized as highly constrained by disciplinary requirements. Everyday referent, sign, meaning relationships must be replaced by scientific ones. Ontological gaps in these everyday understandings must be filled by scientific realities. Explanatory models and their underpinning fixed sign systems are also to be understood and learnt as resolved models of forms of reasoning. However, what is evident in this case study is Colin's creative departure from, and engagement with, this set of constraints. At one point in the sequence in the sign system created by the class, time is represented spatially in cartoon-like sequential shapes, but this is a meaning-filled sign for the students. In groups, and around the gnome, we note Colin's flexibility in inventing and improvising signs and using talk and gesture to support these transductive moves dealing with spatial and temporal patterns, through which students' experiences are given new signs and meanings. Colin, in his many interactions, invites creative linking between their experience and this new way of thinking about it. He works to extend their sign systems to aid how they organize their recognition of patterns in and across multiple data collection events. Data are reduced to a manageable form and the students are invited to think about connections visually and spatially, fundamental requirements in transduction. The theoretical point is the value and even necessity of creative teacher engagement with disciplinary constraints for effective student learning, particularly in relation to transduction. As Colin noted in his interview, explicit teacher modeling of what needs to be learnt may seem efficient, but there were strong learning and motivational gains in supporting, inviting, and reviewing student invention in engaging with science's disciplinary meanings.
Data Availability Statement
The datasets presented in this article are not readily available because the original data sets are only available to the research team. Requests to access the datasets should be directed to cnVzc2VsbC50eXRsZXJAZGVha2luLmVkdS5hdQ==.
Ethics Statement
The studies involving human participants were reviewed and approved by Deakin University Human Ethics Advisory Group. Written informed consent to participate in this study was provided by the participants' legal guardian/next of kin.
Author Contributions
RT was involved in the sequence design and video analysis. VP led with the theoretical framework for analysis and discussion of theoretical implications. Both authors were involved in the preparation of the manuscript.
Funding
This research was conducted through a grant from the Australian Research Council, Award DP180102333.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Baker, W. D., Green, J. L., and Skukauskaite, A. (2008). “Video-enabled ethnographic research: A microethnographic perspective,” in How to do Educational Ethnography, ed G. Walford, 76–114. London: Tufnell Press.
Cobb, P., Confrey, J., Di Sessa, A., Lehrer, R., and Schauble, L. (2003). Design experiments in educational research. Educ. Res. 32, 9–13.
Danaia, L., and McKinnon, D. (2008). Common alternative astronomical conceptions encountered in junior secondary science classes: why is this so? Astron. Educ. Rev. 2, 32–53. doi: 10.3847/AER2007017
Ferguson, J., Aranda, G., Tytler, R., and Gorur, R. (2019). “Video research—Purposeful selection from rich data sets,” in Video-based research in education—Cross-disciplinary perspectives, eds Xu, L., Aranda, G., and Clarke, D. (Oxon, UK: Routledge), p. 124–139.
Gooding, D.. (2004). “Visualization, inference and explanation in the sciences,” in Studies in Multidisciplinarity, ed G. Malcolm (London: Elsevier), p. 1–25.
Hegarty, M., and Waller, D. (2004). A dissociation between mental rotation and perspective-taking spatial abilities. Intelligence 32, 175–191. doi: 10.1016/j.intell.2003.12.001
Hubber, P., and Tytler, R. (2017). “Enacting a representation construction approach to teaching and learning astronomy,” in Multiple Representations in Physics Education, eds D. Treagust, R. Duit, and H. Fischer (London: Springer), pp. 139–161.
Kress, G., and Van Leeuwen, T. (2006). Reading Images: The grammar of Visual Design. London, New York: Routledge.
Latour, B.. (1999). Pandora's Hope: Essays on the Reality of Science Studies. Cambridge, MA, Harvard University Press.
Lehrer, R.. (2009). Designing to develop disciplinary dispositions: Modeling natural systems. Am. Psychol. 64, 759–771. doi: 10.1037/0003-066X.64.8.759
Lehrer, R.. (2021). “Promoting transdisciplinary epistemic dialogue,” in The Learning Sciences in Conversation: Theories, Methodologies, and Boundary Spaces, eds M-C. Shanahan, B. Kim, K. Koh, P. Preciado-Babb, and M.A. Takeuchi (London: Routledge).
Lehrer, R., Konold, C., and Kim, M. J. (2006). Constructing data, modeling chance in the middle school. Paper presented at the annual meeting of the American Educational Research Association, San Francisco, CA.
Lehrer, R., and Schauble, L. (2006). “Cultivating model-based reasoning in science education,” in Cambridge Handbook of the Learning Sciences, ed K. Sawyer (Cambridge: Cambridge University Press), pp. 371–388.
Lehrer, R., and Schauble, L. (2012). Seeding evolutionary thinking by engaging children in modeling its foundations. Sci. Educ. 96, 701–724. doi: 10.1002/sce.20475
Lelliott, A., and Rollnick, M. (2010). Big ideas: a review of astronomy education research 1974–2008. Int. J. Sci. Educ. 32, 1771–1799. doi: 10.1080/09500690903214546
Lemke, J.. (1998). “Multiplying meaning: visual and verbal semiotics in scientific text,” in Reading Science, eds J. R. Martin and R. Veel (London: Routledge), pp. 87–113.
Lemke, J.. (2003). “Mathematics in the middle: Measure, picture, gesture, sign, and word,” in Educational Perspective on Mathematics as Semiosis: From Thinking to Interpreting to Knowing, eds M. Anderson, A. Saenz-Ludlow, S. Zellweger, and V. V. Cifarelli (Ottawa, Ontario, Canada: Legas), pp. 215–234.
Lemke, J.. (2015). “Feeling and meaning: a unitary bio-semiotic account,” in International Handbook of Semiotics, ed P. Trifonas (Dordrecht: Springer), pp. 589–616.
Lemon O. Pratt I. (1997) Spatial logic the complexity of diagrammatic reasoning. Mach. Graph. Visi. 6, 89–108.
MacLure, M.. (2010). The offence of theory. J. Educ. Policy 25, 277–286. doi: 10.1080/02680930903462316
Manz, E., Lehrer, R., and Schauble, L. (2020). Rethinking the classroom science investigation. J. Res. Sci. Teach. 57, 1–27. doi: 10.1002/tea.21625
Marton F. Pang M.-F. (2006) On some necessary conditions of learning. J. Learn. Sci. 15, 193–220. doi: 10.1207/s15327809jls1502_2
Newfield, D.. (2014). “Transformation, transduction and the transmodal moment,” in The Routledge Handbook of Multimodal Analysis, ed C. Jewitt (London: Routledge), p. 100–113.
Padalker, S., and Ramadas, J. (2008). Modelling the round earth through diagrams. Astronom. Educ. Rev. 2, 54–7. doi: 10.3847/AER2007018
Patron, E., Linder, C., and Wikman, S. (2021). Qualitatively different ways of unpacking visual representations when teaching intermolecular forces in upper secondary school. Sci. Educ. 105, 1173–2101. doi: 10.1002/sce.21662
Peirce, C. S.. (1955). “Logic as semiotic: the theory of signs,” in Philosophical Writings of Peirce, ed J. Buchler (New York, NY: Dover).
Peirce, C. S.. (1998). The essential Peirce: Selected philosophical writings. Bloomington: Indiana University Press.
Pham, L., and Tytler, R. (2021). The semiotic function of a bridging representation to support students' meaning-making in solution chemistry. Res. Sci. Educ. 21, 122. doi: 10.1007/s11165-021-10022-w
Plummer, J. D.. (2014). Spatial thinking as the dimension of progress in an astronomy learning progression. Stud. Sci. Educ. 50, 1–45. doi: 10.1080/03057267.2013.869039
Prain, V.. (2019). “Future research in learning, with, through and from scientific representations,” in Theorizing the Future of Science Education Research, eds V. Prain and B. Hand (New York, NY: Springer), pp. 151–168.
Prain, V., and Tytler, R. (2012). Learning through constructing representations in science: a framework of representational construction affordances. Int. J. Sci. Educ. 34, 2751–2773. doi: 10.1080/09500693.2011.626462
Prain, V., and Tytler, R. (2021). Theorizing learning in science through integrating multimodal representations. Res. Sci. Educ. 21, 7. doi: 10.1007/s11165-021-10025-7
Prain, V., and Waldrip, B. G. (2006). An exploratory study of teachers' and students' use of multi-modal representations of concepts in primary science. Int. J. Sci. Educ. 28, 1843–1866. doi: 10.1080/09500690600718294
Salimpour, S., Bartlett, S., Fitzgerald, M. T., McKinnon, D. H., Cutts, K. R., James, C. R., et al. (2020). The gateway science: a review of astronomy in the OECD school curricula, including China and South Africa. Res. Sci. Educ. 20, 2022. doi: 10.1007/s11165-020-09922-0
Severance, S., Penuel, W. R., Sumner, T., and Leary, H. (2016). Organizing for teacher agency in curricular co-design. J. Learn. Sci. 25, 531–564.
Stein, P.. (2008). Multimodal Pedagogies in Diverse Classroom: Representation, Rights and Resources. London: Routledge.
Svensson K. Eriksson U. (2020) Concept of a transductive link. Physic. Rev. Physic. Educ. Res. 16, 026101 doi: 10.1103/PhysRevPhysEducRes.16.026101
Tytler, R., Mulligan, J., Prain, V., White, P., Xu, L., Kirk, M., et al. (2021a). An interdisciplinary approach to primary school mathematics and science learning. Int. J. Sci. Educ. 43, 1926–1949. doi: 10.1080/09500693.2021.1946727
Tytler, R., Murcia, K., Hsiung, C.-T., and Ramseger, J. (2017). “Reasoning through representations,” in Quality Teaching in Primary Science Education: Cross-cultural Perspectives, eds M. Hackling, J. Ramseger, and H-L S. Chen (Dordrecht, the Netherlands: Springer), pp. 149–179.
Tytler, R., Prain, V., Aranda, G., Ferguson, J., and Gorur, R. (2020). Drawing to reason and learn in science. J. Res. Sci. Teach. 57, 209–231. doi: 10.1002/tea.21590
Tytler, R., Prain, V., and Hubber, P. (2018). “Representation construction as a core disciplinary literacy.” in Global Developments in Literacy Research for Science Education, eds K-S. Tang and K. Danielsson (Singapore: Springer), pp. 301–317.
Tytler, R., Prain, V., Hubber, P., and Waldrip, B. (2013). Constructing Representations to Learn in Science. Rotterdam, the Netherlands: Sense Publishers.
Tytler R. Prain V. Kirk M. Mulligan J. Nielsen C. Speldewinde C. (in press). Characterising a representation construction pedagogy for integrating science mathematics in the primary school. Int. J. Sci. Math. Educ. doi: 10.1007/s10763-022-10284-4.
Tytler, R., White, P., and Mulligan, J. (2021b). “Visualisation and spatial thinking in primary students' understandings of Astronomy,” in Engaging With Contemporary Challenges Through Science Education Research: Selected Papers From the ESERA 2019 Conference, eds O. Levrini, G. Tasquier, T. Amin, L. Branchetti, and M. Levin (New York, NY: Springer), pp. 291–304.
Volkwyn, T. S. (2020) Learning Physics Through Transduction: A Social Semiotic Approach. Uppsala: Acta Universitatis Upsaliensis. Available online at: http://uu.diva-portal.org/smash/record.jsf?pid=diva2%3A1475470&dswid=9809 (accessed May 2022)..
Volkwyn, T. S., Airey, J., Gregorči,č, B., and Heijkenskjöld, F. (2019). Transduction and science learning: multimodality in the physics laboratory. Designs Learn. 11, 16–29. doi: 10.16993/dfl.118
Volkwyn, T. S., Airey, J., Gregorči,č, B., and Linder, C. (2020). Learning to use coordinate systems in physics. Euro. J. Physics. 41, 045701. doi: 10.1088/1361-6404/ab8b54
Keywords: transduction, science teaching and learning, reasoning in science, multimodality, representations and reasoning, semiotics and education
Citation: Tytler R and Prain V (2022) Supporting Student Transduction of Meanings Across Modes in Primary School Astronomy. Front. Commun. 7:863591. doi: 10.3389/fcomm.2022.863591
Received: 27 January 2022; Accepted: 02 May 2022;
Published: 03 June 2022.
Edited by:
John A. Bateman, University of Bremen, GermanyReviewed by:
Fei Victor Lim, Nanyang Technological University, SingaporeAnna Shvarts, Utrecht University, Netherlands
Paul John Thibault, University of Agder, Norway
Copyright © 2022 Tytler and Prain. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Russell Tytler, cnVzc2VsbC50eXRsZXJAZGVha2luLmVkdS5hdQ==
 Russell Tytler
Russell Tytler Vaughan Prain
Vaughan Prain