Modeling Morphological Priming in German With Naive Discriminative Learning

Both localist and connectionist models, based on experimental results obtained for English and French, assume that the degree of semantic compositionality of a morphologically complex word is reflected in how it is processed. Since priming experiments using English and French morphologically related prime-target pairs reveal stronger priming when complex words are semantically transparent (e.g., refill–fill) compared to semantically more opaque pairs (e.g., restrain–strain), localist models set up connections between complex words and their stems only for semantically transparent pairs. Connectionist models have argued that the effect of transparency should arise as an epiphenomenon in PDP networks. However, for German, a series of studies has revealed equivalent priming for both transparent and opaque prime-target pairs, which suggests mediation of lexical access by the stem, independent of degrees of semantic compositionality. This study reports a priming experiment that replicates equivalent priming for transparent and opaque pairs. We show that these behavioral results can be straightforwardly modeled by a computational implementation of Word and Paradigm Morphology (WPM), Naive Discriminative Learning (NDL). Just as WPM, NDL eschews the theoretical construct of the morpheme. NDL succeeds in modeling the German priming data by inspecting the extent to which a discrimination network pre-activates the target lexome from the orthographic properties of the prime. Measures derived from an NDL network, complemented with a semantic similarity measure derived from distributional semantics, predict lexical decision latencies with somewhat improved precision compared to classical measures, such as word frequency, prime type, and human association ratings. We discuss both the methodological implications of our results, as well as their implications for models of the mental lexicon.

1. Introduction

Current mainstream models of lexical processing assume that complex words such as unmanagability comprise several morphemic constituents, un-, manage, -able, and -ity, that recur in the language in many other words. Since early research in the seventies (e.g., Taft and Forster, 1975), it has been argued that the recognition of morphologically complex words is mediated by such morphemic units (for a review of models of morphological processing, see Milin et al., 2017b).

One of the issues under investigation in this line of research is whether visual input is automatically decomposed into morphemes before semantics is accessed. Several studies have argued in favor of early morpho-orthographic decomposition (Longtin et al., 2003; Rastle et al., 2004; Rastle and Davis, 2008), but others argue that semantics is involved from the start (Feldman et al., 2009), that the effect is task dependent and is limited to the lexical decision task (Norris and Kinoshita, 2008; Dunabeitia et al., 2011; Marelli et al., 2013), or fail to replicate experimental results central to decompositional accounts (Milin et al., 2017a).

Another issue that is still unresolved is whether complex words are potentially accessed through two routes operating in parallel, one involving decomposition and the other whole-form based retrieval (Frauenfelder and Schreuder, 1992; Marslen-Wilson et al., 1994b; Baayen et al., 1997, 2003). Recent investigations that make use of survival analysis actually suggest that whole-word based effects precede in time constituent-based effects (Schmidtke et al., 2017).

A third issue concerns the role of semantic transparency. Priming studies conducted on English and French prefixed derivations that are semantically transparent, such as distrust, have reported facilitation of the recognition of their stems ( trust), as well as other prefixed or suffixed derivations, such as entrust or trustful. The same holds for suffixed derivations that are semantically transparent like production and productivité in French or confession and confessor in English, which prime each other and their stem (confess). The critical condition in this discussion, however, concerns semantically opaque (i.e., non-compositional) derivations, such as successor, which appear not to facilitate the recognition of stems like success. This latter finding was replicated under auditory prime presentations or visual priming at long exposure durations at 230 or 250 ms (e.g., Rastle et al., 2000; Feldman and Prostko, 2001; Pastizzo and Feldman, 2002; Feldman et al., 2004; Meunier and Longtin, 2007; Lavric et al., 2011). Localist accounts take these findings to indicate that only semantically transparent complex words are processed decompositionally, via their stem, while semantically opaque words are processed as whole word units. Although on different grounds, also distributed connectionist approaches assume that the facilitation between complex words and their stem depends on their meaning relation. In a series of cross-modal priming experiments, Gonnerman et al. (2007) showed for English that morphological effects vary according to the gradual overlap of form and meaning between word pairs. Indeed, word pairs with a strong phonological and semantic relation like preheat–heat induced stronger priming than words with a moderate phonological and semantic relation like midstream–stream, and words holding a low semantic relation like rehearse–hearse induced no priming at all. According to connectionist accounts of lexical processing, this result arises as the consequence of the extent to which orthographic, phonological, and semantic codes converge.

However, these findings for English and French contrast with results repeatedly obtained for German, where morphological priming appears to be unaffected by semantic transparency (Smolka et al., 2009, 2014, 2015, 2019). Under auditory or overt visual prime presentations, morphologically related complex verbs facilitated the recognition of their stem regardless of whether they were semantically transparent (aufstehen–stehen, “stand up”–“stand”) or opaque (verstehen–stehen, “understand”–“stand”). Smolka et al. interpreted these findings to indicate that a German native speaker processes a complex verb like verstehen by accessing the stem stehen irrespective of the whole-word meaning, and argued that morphological structure overrides meaning in the lexical processing of German complex words. To account for such stem effects without effects of semantic transparency, they hypothesized a model in which the frequency of the stem is the critical factor, such that stems of complex words are accessed and activated, independent of the meaning composition of the complex word.

These findings for German receive support from experiments on Dutch—a closely related language with a highly similar system of verbal prefixes, separable particles, and non-separable particles. Work by Schreuder et al. (1990), using an intramodal visual short SOA partial priming technique to study Dutch particle verbs, revealed morphological effects without modulation by semantic transparency. Experiments addressing speech production in Dutch (Roelofs, 1997a,b; Roelofs et al., 2002) likewise observed, using the implicit priming task, that priming effects were equivalent for transparent and opaque prime-target pairs. Morphological priming without effects of semantic transparency have recently been replicated in Dutch under overt prime presentations (Creemers et al., 2019; De Grauwe et al., 2019). Unprimed and primed visual lexical decision experiments on Dutch low-frequency suffixed words with high-frequency base words revealed that the semantics of opaque complex words were equally quickly available as the semantics of transparent complex words (Schreuder et al., 2003), contradicting the original prediction of this study that transparent words would show a processing advantage compared to their opaque counterparts.

Importantly, there are some studies in English, e.g., Gonnerman et al. (2007, Exp. 4) and Marslen-Wilson et al. (1994a, Exp. 5), that applied a similar cross-modal priming paradigm with auditory primes and visual targets, and with similar prefixed stimuli as in the abovementioned studies by Smolka and collaborators, but found no priming for semantically opaque pairs like rehearse–hearse (for similar ERP-results in English see Kielar and Joanisse, 2011). Thus, results for German and results for English appear at present to be genuinely irreconcilable¹.

In what follows, we first present an overt visual priming experiment that provides further evidence for the equivalent facilitation effects seen for German transparent and opaque prime-target pairs. The behavioral results are consistent with localist models in which connections between stems and derived words are hand-wired into a network, as argued by, e.g., Smolka et al. (2007, 2009, 2014, 2015) and Smolka and Eulitz (2018). However, this localist model is a post-hoc description of the experimental findings, and a computational implementation for this high-level theory is not available.

In this study, we proceed to show that the observed stem priming effects can be straightforwardly modeled by naive discriminative learning (NDL, Baayen et al., 2011, 2016a,b; Arnold et al., 2017; Divjak et al., 2017; Sering et al., 2018b; Tomaschek et al., 2019) without reference to stems or other morphological units, and without requiring hand-crafting of connections between such units. In fact, measures derived from an NDL network, complemented with a semantic similarity measure derived from distributional semantics, turn out to predict lexical decision latencies with greater precision compared to classical measures, such as word frequency, prime type, and semantic association ratings. Importantly, the NDL model predicts the effects of stem priming without a concomitant effect of semantic compositionality. According to the NDL model, the crucial predictor is the extent to which the target is pre-activated by the sublexical form features of the prime. In the final section, we discuss both the methodological implications of our results, as well as their implications for models of the mental lexicon.

2. The Priming Experiment

2.1. Previous Results for German Complex Verbs

German complex verbs present a very useful means to study the effects of morphological structure with or without meaning relatedness to the same base verb. German complex verbs are very productive and frequently used in standard German. The linguistic literature (Fleischer and Barz, 1992; Eisenberg, 2004) distinguishes two word formations: prefix verbs and particle verbs. Both consist of a verbal root and either a verbal prefix or a particle.

In spite of some prosodic and morphosyntactic differences (see Smolka et al., 2019), prefix and particle verbs share many similar semantic properties. Both may differ in the degree of semantic transparency with respect to the meaning of their base. For example, the particle an (“at”) only slightly alters the meaning of the base führen (“guide”) in the derivation anführen (“lead”), but radically does so with respect to the base schicken (“send”) in the opaque derivation anschicken (“get ready”). Similarly, the prefix ver- produces the transparent derivation verschicken (“mail”) as well as the opaque derivation verführen (“seduce”). Prefix and particle verbs are thus a particularly useful means by which the effects of meaning relatedness to the same base verb can be studied. For instance, derivations of the base tragen (“carry”), such as hintragen (“carry to”), forttragen (“carry away”), zurücktragen (“carry back”), abtragen (“carry off”), auftragen (“apply”), vertragen (“get along”), ertragen (“suffer”), alter the meaning relatedness from fully transparent to fully opaque with respect to the base. It is important to note that, in general, complex verbs in German are true etymological derivations of their base, regardless of the degree of semantic transparency they share with it. Because morphological effects of prefix and particle verbs are alike in German (see Smolka and Eulitz, 2018; Smolka et al., 2019) and Dutch (Schriefers et al., 1991), henceforth, we refer to them as “complex verbs” or “derived verbs.”

Previous findings on complex verbs in German have shown that these verbs strongly facilitate the recognition of their stem, without any effect of semantic transparency (Smolka et al., 2009, 2014, 2015, 2019; Smolka and Eulitz, 2018). That is, semantically opaque verbs, such as verstehen (“understand”) primed their base stehen (“stand”) to the same extent as did transparent verbs, such as aufstehen (“stand up”). Further, the priming by both types of morphological primes was stronger than that by either purely semantically related primes like aufspringen (“jump up”) or purely form-related primes like bestehlen (“steal”). The morphological effects remained unaffected by semantic transparency under conditions that were sensitive to detecting semantic and form similarity, that is, when semantic controls like verlangen–fordern (“require”–“demand”) and Biene–Honig (“bee”–“honey”) induced semantic facilitation or when form-controls with embedded stems, as in bekleiden–leiden (“dress”–“suffer”) and Bordell–Bord (“brothel”–“board”) induced form inhibition (see Exp. 3 in Smolka et al., 2014). This offered assurance that the lack of a semantic transparency effect between semantically transparent and opaque complex verbs was not a null effect but rather indicated that morphological relatedness overrides both semantic and form relatedness.

Further studies explored the circumstances of stem facilitation in more detail. For example, in spite of several differences in the phonological and morpho-syntactic properties of prefix and particle verbs, prefix verbs showed processing patterns that were substantially the same as those for particle verbs and, crucially, were uninfluenced by semantic transparency (Smolka et al., 2019). Furthermore, stem access occurs regardless of the directionality of prime and target entwerfen–werfen vs. werfen–entwerfen vs. entwerfen–bewerfen (Smolka and Eulitz, 2011).

Stem access is modality independent, as it occurs under both intra-modal (visual-visual) and cross-modal (auditory-visual) priming conditions (Smolka et al., 2014, 2019). Finally, event-related brain potentials revealed wide-spread N400 brain potentials in response to semantically transparent and opaque verbs without effects of semantic transparency—N400 brain potentials that are generally taken to be characteristic to indicate expectancy and (semantic) meaning integration. Most importantly, these brain potentials revealed that stem facilitation in German occurs without an overt behavioral response and is stronger than the activation by purely semantically related verbs or form-related verbs (Smolka et al., 2015).

The present experiment was closely modeled after previous experiments addressing priming effects for German verb pairs (e.g., Smolka et al., 2009, 2014).

2.2. Design

We compared the differential effects of semantic, form, or morphological relatedness between complex verbs and a base verb in four priming conditions: (a) semantic condition, where the complex verb was a synonym of the target verb, (b) morphological transparent condition, where the complex verb was a semantically transparent derivation of the target verb, (c) morphological opaque condition, where the complex verb was a semantically opaque derivation of the target verb, and (d) form condition, where the base of the complex verb was form-related with the base of the target. We measured lexical decision latencies to the target verbs and calculated priming relative to an unrelated control condition. In addition to the (unrelated minus related) priming effects, the influence of the stem should surface in the comparison of the conditions (a) and (b), where both types of primes are synonyms of the base verb—the former holding a different stem as the target, the latter holding the same stem as the target; the influence of the degree of semantic transparency should surface in the comparison between conditions (b) and (c), where both types of primes are true morphological derivations of the base target. The influence of form similarity should surface in the comparison between conditions (c) and (d), where both types of primes have stems that are form-similar with the target.

As in our previous experiments, we were interested in tapping into lexical processing, when participants are aware of the prime and integrate its meaning, and thus applied overt visual priming at a long SOA (see Milin et al., 2017b, for a comparison between masked and overt priming paradigms). We used only verbs as materials to avoid word category effects, and inserted a large number of fillers to prevent expectancy or strategic effects. Different from our previous experiments, though, we applied a between-subject and between-target design.

In summary, the primes in all conditions were complex verbs with the same morphological structure and were thus (a) of the same word category, and (b) closely matched on distributional variables like lemma frequency, number of syllables and letters. They differed only with respect to the morphological, semantic, or form-relatedness with the target. Prime conditions are exemplified in Table 1; all critical items are listed in Appendix A. Our prediction is that both semantically transparent and opaque complex verbs will induce the same amount of priming to their base, and that this priming will be stronger than the priming by either semantically related or form-related verbs.

TABLE 1

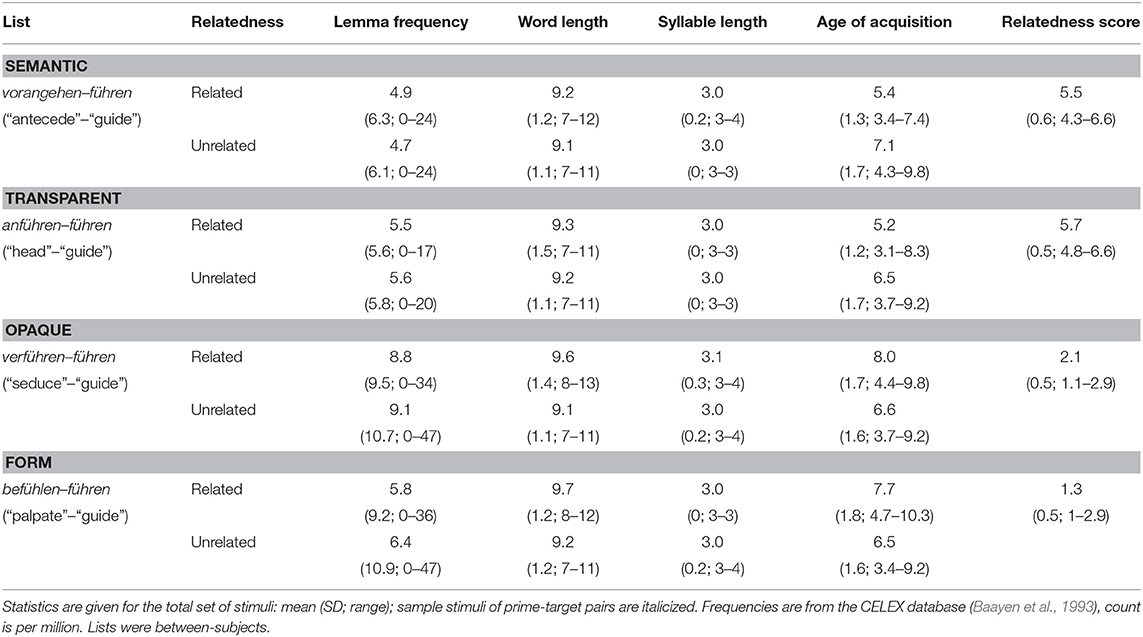
Table 1. Stimulus characteristics of related primes and their matched unrelated controls in the semantic synonym list, semantically transparent list, semantically opaque list, and form control list.

2.3. Method

2.3.1. Participants

Fifty students of the University of Konstanz participated in the experiment (14 males; mean age = 22.69, range 19–32). All were native speakers of German, were not dyslexic, and had normal or corrected-to-normal vision. They were paid for their participation.

2.3.2. Materials

As critical stimuli, 88 prime-target pairs with complex verbs as primes and base verbs as targets were selected from the CELEX German lexical database (Baayen et al., 1993), 22 pairs in each of four conditions (see also Table 1): (a) morphologically unrelated synonyms of the base (e.g., vorangehen–führen, “antecede”–“guide”), (b) morphologically related synonyms of the base, these were semantically transparent derivations of the base, (e.g., anführen–führen, “head”–“guide”), (c) semantically opaque derivations of the base (e.g., verführen–führen, “seduce”–“guide”), and (d) semantically and morphologically unrelated form controls that changed a letter in the stem (by retaining the stem's onset and changing a letter in the rime, e.g., befühlen–führen, “palpate”–“guide”). Complex verbs in conditions (a) and (b) were synonyms of the target base and were selected by means of the online synonym dictionaries http://www.canoo.net/ and https://synonyme.woxikon.de/.

For each of the 88 related primes, we selected an unrelated control that served as baseline and (a) was morphologically, semantically, and orthographically unrelated to the target and (b) matched the related prime in word class, morphological complexity (i.e., it was a complex verb), number of letters and syllables. In addition, control primes were pair-wise matched to the related primes on lemma frequency according to CELEX. Furthermore, primes across conditions were matched on lemma frequency according to CELEX.

The critical set of 88 prime-target pairs was selected from a pool of verb pairs that had been subjected to semantic association tests, in which participants rated the meaning relatedness between the verbs of each prime-target pair on a 7-point scale from completely unrelated (1) to highly related (7) (for a detailed description of the database see Smolka and Eulitz (2018). The following criteria determined whether a verb pair was included in the critical set: The mean ratings for a semantically-related pair (in the synonym and semantically transparent conditions) had to be higher than 4, and those for a semantically unrelated pair (in the semantically opaque and form-related conditions) lower than 3. The set of words that were included in the experiment had mean ratings of 5.5 (range 4.3–6.7) for synonyms, 5.7 (range 4.78–6.56) for semantically transparent derivations, 2.13 (range 1.5–2.88) for semantically opaque derivations, and 1.7 (range 1.0–2.89) for form-related pairs. Table 1 provides the prime characteristics (lemma frequency, number of letters and syllables, meaning relatedness); the Appendix lists all stimuli.

In order to prevent strategical processes, a total of 140 prime-target pairs was added as fillers. All had complex verbs as primes, 48 had verbs and 92 had pseudoverbs as targets. With respect to the former, 18 of the 48 prime-verb fillers comprised related prime-target pairs of the other lists. These types were included to assure that participants would not detect a certain type of prime-target relatedness in a list. For example, list A held six items of list B, six of list C, and six of list D as fillers. The other 30 prime-target pairs were semantically, morphologically, and orthographically unrelated.

Regarding the prime-pseudoverb fillers, 44 of the pseudoverb targets were closely matched to the critical verb targets by keeping the onset of the verbs' first syllable (e.g., binden–binken). To further ensure that participants did not respond with “word” decisions for any trial where prime and target were orthographically similar, eleven pseudoverbs were preceded by a form-related prime (e.g., umwerben–wersen) to mimick the form condition. All pseudoverbs were constructed by exchanging one or two letters in real verbs, while preserving the phonotactic constraints of German.

The between-subject design had the following list composition: Each list comprised 184 prime-target pairs, half of these holding verbs, the other half pseudoverbs as targets. Of the 92 prime-verb pairs, 22 were related prime-target pairs of either condition (a), (b), (c), or (d), 22 were matched unrelated prime-target pairs, and 48 were filler pairs (30 unrelated and 18 of other related conditions). The 92 prime-pseudoverb-target pairs included 44 form-matched and 48 unrelated pairs.

Overall, the large amount of fillers in the present study reduced the proportion of (a) critical prime-target pairs to 24% per list or 48% of prime-verb pairs, and (b) related prime-target pairs (including critical and filler pairs) to 22% per list or 43% of verb pairs. Napps and Fowler (1987) showed that a reduction in the proportion of related items from 75% to 25% reduced both facilitatory and inhibitory effects. A significant reduction of related items in the present study should thus discourage participants from expecting a particular related verb target and thus prevent both expectancy and failed expectancy effects. All filler items differed from the critical items. Throughout the experiment, all primes and targets were presented in the infinitive (stem/-en), which is also the citation form in German.

2.3.3. Apparatus

Stimuli were presented on a 18.1″ monitor, connected to an IBM-compatible AMD Atlon 1.4 GHz personal computer. Stimulus presentation and data collection were controlled by the Presentation software developed by Neurobehavioral Systems (https://www.neurobs.com). Response latencies were recorded from the left and right buttons of a push-button box.

2.3.4. Procedure

Each participant saw only one list. Each list was divided into four blocks, each block containing the same amount of stimuli per condition. The critical prime-target pairs were rotated over the four blocks according to a Latin Square design in such a way that the related and unrelated primes of the same target were separated by a block. The related fillers (form-related prime-pseudoverb pairs, related prime-verb pairs) and unrelated filler pairs were evenly allocated to the blocks.

In total, an experimental session comprised 184 prime-target pairs, with 66 pairs per block. Within blocks, prime-target pairs were randomized separately for each participant. Twenty additional prime-target pairs were used as practice trials. Participants were tested individually in a dimly lit room, seated at a viewing distance of about 60 cm from the screen. Stimuli were presented in Sans-Serif letters on a black background. To ensure that primes and targets were perceived as physically distinct stimuli, primes were presented in uppercase letters, point 32, in light blue (RGB: 0-255-255), 20 points above the center of the screen. Targets were presented centrally in lowercase letters, point 36, in yellow (RGB: 255-255-35).

Each trial started with a fixation cross in the center of the screen for 300 ms. This was followed by the presentation of the prime for 400 ms, followed by an offset (i.e., a blank screen) for 100 ms, resulting in a stimulus onset asynchrony (SOA) of 500 ms. After the offset, the target immediately followed and remained on the screen until a participant's response. The intertrial interval was 1,500 ms. Participants were instructed to make lexical decisions to the targets, as fast and as accurately as possible. “Word” responses were given with the index finger of the dominant hand, “pseudoword” responses with the subordinate hand. Feedback was given on both correct (“richtig”) and incorrect (“falsch”) responses during the practice session, and on incorrect responses during the experimental session. The experiment lasted for about 12 min, during which participants self-administered the breaks between blocks.

2.4. Results

A generalized additive mixed model (Wood, 2017) was fitted to the inverse-transformed reaction times with predictors Prime Type (using treatment coding, with the unrelated condition as reference level) and log target frequency². Random intercepts were included for target and prime, and a factor smooth for the interaction of subject by trial number (see Baayen et al., 2017, for detailed discussion of this non-linear counterpart to what in a linear mixed model would be obtained with by-subject random intercepts and by-subject random slopes for trial). Table 2 presents the model summary. Prime-target pairs in the semantic condition were responded to slightly more quickly than prime-target pairs in the unrelated condition. Prime-target pairs in the transparent and opaque conditions showed substantially larger facilitation of equal magnitude. Prime-target pairs in the form condition elicited reaction times that did not differ from those seen in the control condition.

TABLE 2

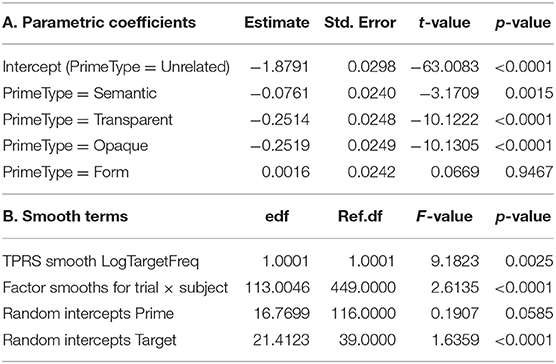
Table 2. Generalized additive mixed model fitted to inverse-transformed primed lexical decision latencies.

To obtain further insight into the effects of the predictors not only for the median, but across the distribution of reaction times, we fitted quantile GAMs to the deciles 0.1, 0.2, …, 0.9, using the qgam package (Fasiolo et al., 2017)³. For the median, the quantile GAM also complements the Gaussian GAMM reported in Table 2. The Gaussian GAMM could have been expanded with further random effects for the interaction of subject by priming effect, but such models run the risk of overspecification (Bates et al., 2015). More importantly, the distribution of the residuals showed clear deviation from normality that resisted correction. As quantile GAMS are distribution free, simple main effects can be studied without having to bring complex random effects into the model as a safeguard against anti-conservative p-values.

Figure 1 presents, from top left to bottom right, the effects of Prime Type for the deciles 0.1, 0.2, …, 0.9. The p-values above the bars concern the contrasts with the unrelated condition (the reference level). Across the distribution, the form condition was never significantly different from the unrelated condition. The small effect of the semantic condition hardly varied in magnitude across deciles, but was no longer significant at the last decile. The magnitude of the effects for the transparent and opaque conditions was significantly different from that for the unrelated condition across all deciles, and increased in especially the last three deciles. Across the deciles, the transparent condition showed a growing increase in facilitation compared to the opaque condition, but as indicated by the p-values in red, the difference between these two conditions was never significant.

FIGURE 1

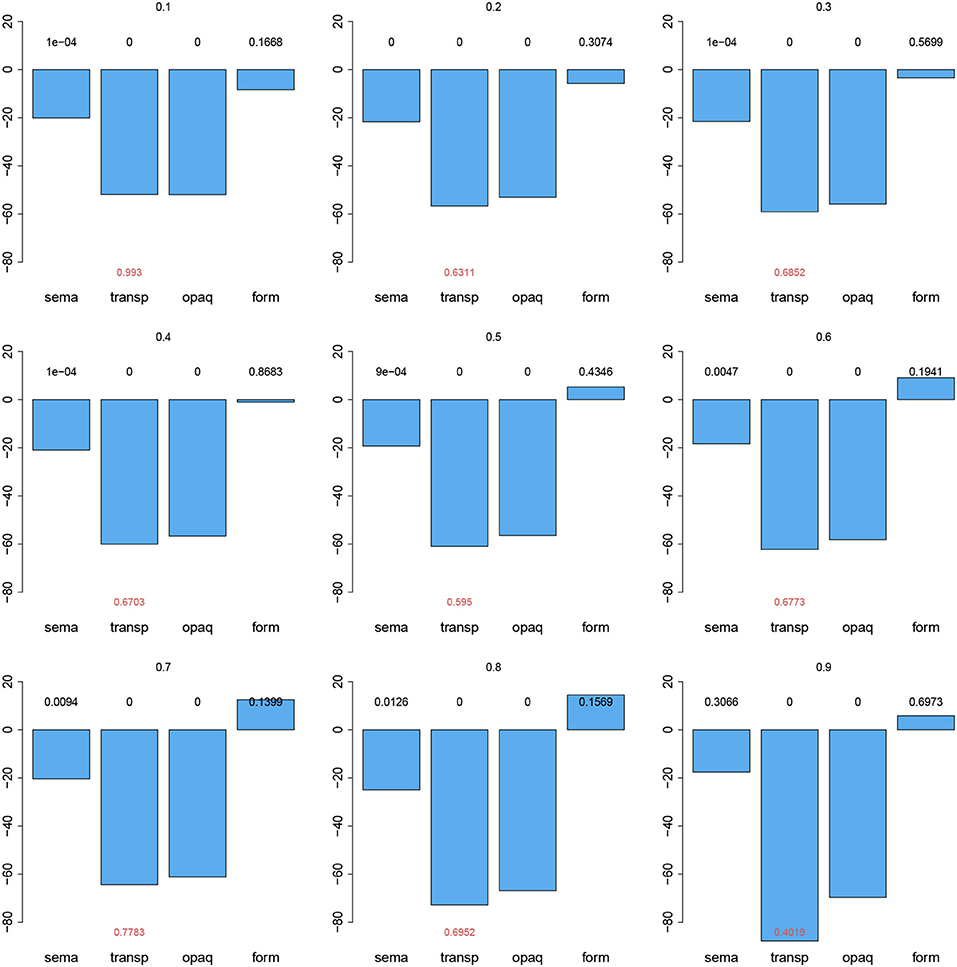
Figure 1. Effects of Prime Type (with unrelated as reference level) in a Quantile GAM fitted to primed lexical decision latencies, for deciles 0.1, 0.2, …, 0.9.

Figure 2 visualizes the effect of target frequency. From the second decile onwards, target frequency was significant, with greater frequencies affording shorter reaction times, as expected. The magnitude of the frequency effect, as well as its confidence interval, increased across deciles.

FIGURE 2

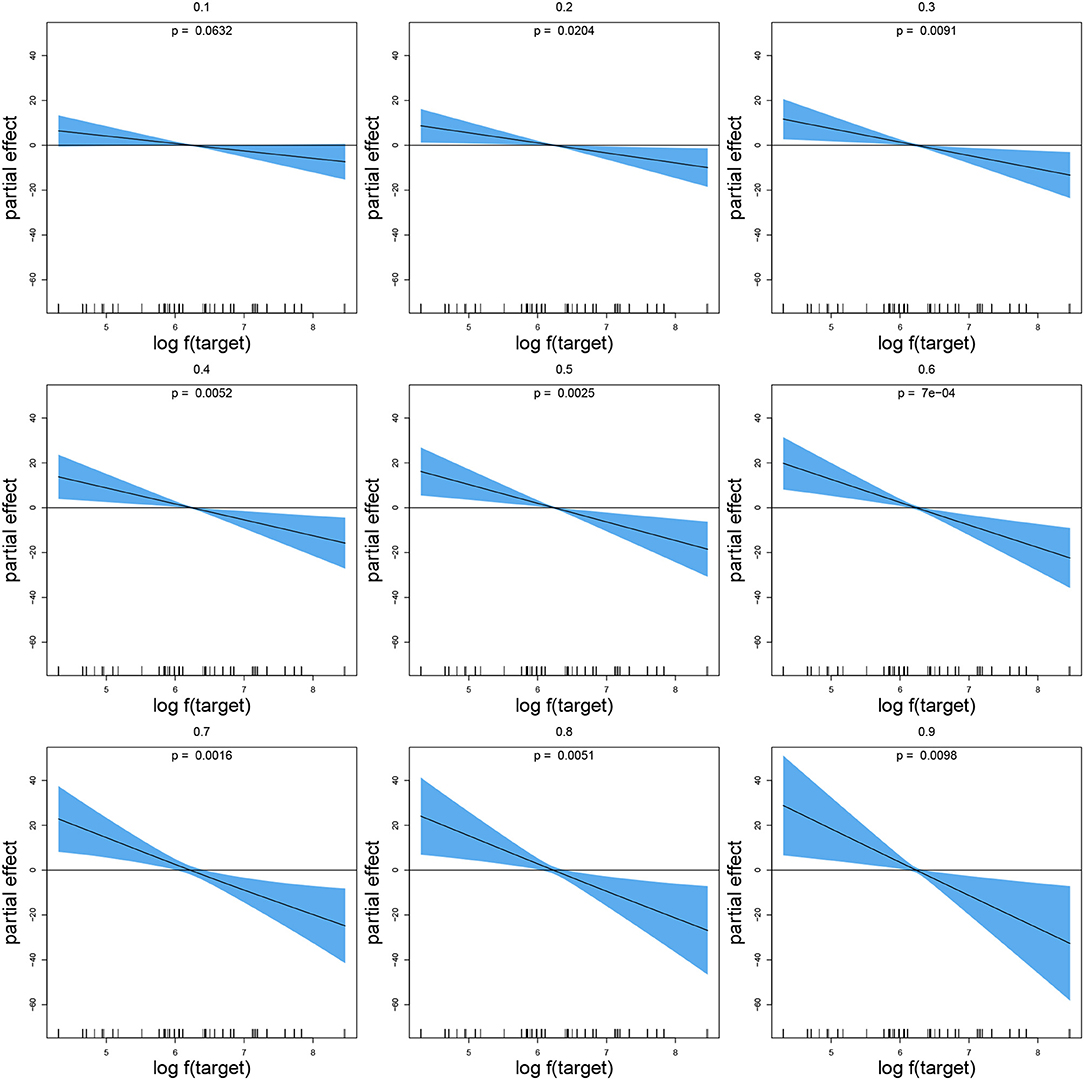
Figure 2. Partial effect of log target frequency in a Quantile GAM fitted to primed lexical decision latencies, for deciles 0.1, 0.2, …, 0.9.

In summary, replicating earlier studies, morphologically related primes elicited a substantial priming effect that did not vary with semantic transparency. The priming effect tended to be somewhat stronger at larger deciles, for which the effect of target frequency was also somewhat larger.

When the transparent and opaque priming conditions are considered in isolation, it might be argued that participants are superficially scanning primes and targets for shared stems, providing a word response when a match is found, and a non-word response otherwise. Such a task strategy can be ruled out, however, due to the high proportion of unrelated fillers, and once the other two priming conditions are taken into consideration. If subjects would indeed have been scanning for stems shared by prime and target, then the Unrelated and Semantic conditions should have elicited the same mean reaction times, contrary to fact. Clearly, participants processed the word stimuli more deeply than a form-based scan suggests. Furthermore, since form-based evaluation of pairs in the Form condition is more difficult given the substantial similarity of the stems, longer reaction times are predicted for the Form condition compared to the Unrelated condition. Also this prediction is falsified by the data: The means for the Form and Unrelated condition do not differ significantly.

At first sight, it might be argued that the present between-participants design has strengthened the opaque priming effects. However, given that all our previously conducted experiments used within-participants designs (e.g., three visual priming experiments in Smolka et al., 2009; one cross-modal and two visual priming experiments in Smolka et al., 2014; two cross-modal priming experiments in Smolka et al., 2019; and one visual EEG priming experiment in Smolka et al., 2015) and yielded equivalent priming by opaque and transparent prime-target pairs, we are confident that our present findings are not due to a design limitation.

We therefore conclude that the behavioral results of “pure morphological priming” without semantic transparency effects in German, as well as the older results obtained for speech production in Dutch, appear to indicate a fundamental role in lexical processing for morphemic units, such as the stem. However, perhaps surprisingly, developments in current linguistic morphology indicate that the theoretical construct of the morpheme is in many ways problematic. In what follows, we show that the present results can be explained within the framework of naive discriminative learning, even though this theory eschews morphemic units altogether.

3. Computational Modeling With Naive Discriminative Learning

Before introducing naive discriminative learning (NDL), we first provide a brief overview of developments in theoretical morphology over the last decades that motivated the development of NDL.

3.1. Developments in Theoretical Morphology

The concept of the morpheme, as the minimal linguistic sign combining form and meaning, traces its history to the American structuralists that sought to further systematize the work of Leonard Bloomfield (see Blevins, 2016, for detailed discussion). The morpheme as minimal sign has made it into many introductory textbooks (e.g., Plag, 2003; Butz and Kutter, 2016). The hypothesis that semantically transparent complex words are processed compositionally, whereas semantically opaque words are processed as units, is itself motivated by the belief that morphemes are linguistic signs. For semantically opaque words, the link between form and meaning is broken, the morpheme is no longer a true sign, and hence the rules operating over true signs in comprehension and production are no longer relevant.

The theoretical construct of the morpheme as smallest sign of the language system has met with substantial criticism (see e.g., Matthews, 1974; Beard, 1977; Aronoff, 1994; Stump, 2001; Blevins, 2016). Whereas the morpheme-as-sign appears a reasonably useful construct for agglutinating languages, such as Turkish, as well as for morphologically simple languages, such as English (but see Blevins, 2003), it fails to provide much insight for typologically very dissimilar languages, such as Latin, Estonian, or Navajo (see e.g., Baayen et al., 2018, 2019; Chuang et al., 2019, for detailed discussion). One important insight from theoretical morphology is that systematicities in form are not coupled in a straightforward one-to-one way with systematicities in meaning. Realizational theories of morphology (e.g., Stump, 2001) therefore focus on how sets of semantic features are expressed in phonological form, without seeking to find atomic form features that line up with atomic semantic features. Interestingly, as pointed out by Beard (1977), form and meaning are subject to their own laws of historical change or resistance to change.

Within realizational theories, two main approaches have been developed, Realizational Morphology and Word and Paradigm Morphology. Realizational Morphology formalizes how bundles of semantic (typically inflectional) features are realized in phonological form by making use of units for stems, stem variants, and the morphs (now named exponents) that realize (or express) sets of inflectional or derivational features (see e.g., Stump, 2001). Realizational Morphology is to some extent compatible with localist models in psychology, in that the stems and exponents of realizational morphology can be seen as corresponding to the “morphemes” (now understood strictly as form-only units, henceforth “morphs”) in localist networks. The compatibility is only partial, however, as current localist models typically remain underspecified as to how, in comprehension, the pertinent semantic feature bundles are activated once the proper exponents have been identified. For instance, in the localist interactive activation model of Veríssimo (2018)⁴, the exponent -er that is activated by the form teacher has a connection to a lemma node for ER as deverbal nominalization, but no link is given from the -er exponent to an inflectional function that in English is also realized with -er, namely, the comparative. Furthermore, even the node for deverbal -ER is semantically underspecified, as -ER realizes a range of semantic functions, including AGENT, INSTRUMENT, CAUSER, and PATIENT (Booij, 1986; Bauer et al., 2015).

A further, empirical, problem for decompositional theories that take the first step in lexical processing to be driven by units for morphs are experiments indicating that quantitative measures tied to properties of whole words, rather than their component morphs, are predictive much earlier in time than expected. For eye-tracking studies on Dutch and Finnish, see Kuperman et al. (2008, 2009, 2010) and for reaction times analyzed with survival analysis, see Schmidtke et al. (2017). These authors consistently find that measures linked to whole words are predictive for shorter response times, and that measures linked to morphs are predictive for longer response times. This strongly suggests that properties of whole words determine early processing and properties of morphs arise later in processing.

There is a more general problem specifically with models that make use of localist networks and the mechanism of interactive activation to implement lexical access. First of all, interactive activation is a very expensive mechanism, as inhibitory connections between morpheme nodes grow quadratically with the number of nodes, and access times increase polynomially or even exponentially. Furthermore, interactive activation as a method for candidate selection in a what amounts to a straightforward classification task is unattractive as it would have to be implemented separately for each classification task that the brain has to carry out. Redgrave et al. (1999) and Gurney et al. (2001) therefore propose a central single mechanism, supposed to be carried out by the basal ganglia, that receives a probability distribution of alternatives as input from any system requiring response selection, and returns the best-supported candidate (see Stewart et al., 2012, for an implementation of their algorithm with spiking neurons).

The second main approach within morpheme-free theories, Word and Paradigm Morphology, rejects the psychological reality of stems and exponents, and calls upon proportional analogies between words to explain how words are produced and comprehended (Matthews, 1974; Blevins, 2003, 2006, 2016). Although attractive at a high level of abstraction, without computational implementation, supposed proportional analogies within paradigms do not generate quantitative predictions that can be tested experimentally. As discussed in detail by Baayen et al. (2019), discrimination learning provides a computational formalization of Word and Paradigm Morphology that does generate testable and falsifiable predictions.

In what follows, we will use NDL to estimate a distribution of activations (which, if so desired, could be transformed into probabilities using softmax) over the set of possible word meanings given the visual input. Specifically, we investigate whether we can predict how prior presentation of a prime word affects the activation of the target meaning.

3.2. Morphological Processing Without Morphemes

Naive discriminative learning is not the first cognitive computational model that seeks to move away from morphemes. The explanatory adequacy of the morpheme for understanding lexical processing has also been questioned within psychology by the parallel distributed processing programme (McClelland and Rumelhart, 1986; Rumelhart and McClelland, 1986). As mentioned previously, the triangle model (Harm and Seidenberg, 2004) has been argued to explain the effects of semantic transparency observed for English derived words as reflecting the convergence of phonological and semantic codes (Plaut and Gonnerman, 2000; Gonnerman and Anderson, 2001; Gonnerman et al., 2007). It is noteworthy, however, that to our knowledge, actual simulation studies demonstrating this have not been forthcoming. Importantly, if indeed the triangle model makes correct predictions for English, then one would expect its predictions for German to be wrong, because it would predict semantic transparency effects and no priming for semantically opaque word pairs.

Like the PDP programme, the twin theories of Naive Discriminative Learning (NDL Baayen et al., 2011, 2016b; Sering et al., 2018b) and Linear Discriminative Learning (Baayen et al., 2018, 2019), eschew the construct of the morpheme. But instead of using backpropagation multi-layer networks, NDL and LDL build on simple networks with input units that are fully connected to all output units.

An NDL network is defined by its weight matrix W. By way of example, consider the following weight matrix,

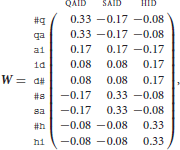
which is visualized in Figure 3. The output nodes are on the inner circle in red, and the input nodes in the outer circle in blue. A star layout was chosen in order to guarantee readability of the connection weights. The network corresponding to this weight matrix comprises nine sublexical input units, shown in the left margin of the matrix. We refer to these units, here the letter bigrams of the words qaid, said, and hid, as cues; the # symbol (a + in Figure 3 represents the space character). There are three output units, the outcomes, shown in the upper margin of the matrix. The entries in the matrix present the connection strengths of the digraphs to the lexical outcomes. The digraph qa provides strong support (0.33) for QAID (“tribal chieftain”), and sa provides strong support (0.33) for SAID. Conversely, ai, which is a valid cue for two words, QAID and SAID, has connection strengths to these lexomes of only 0.17. The weights from hi and sa to QAID are negative, −0.08 and −0.17, respectively. For QAID, the cue that best discriminates this word from the other two words is qa. Conversely, sa is a (somewhat less strong) discriminative cue arguing against QAID. Informally, we can say that the model concludes the outcome must be QAID given qa, and that the outcome cannot be QAID given sa.

FIGURE 3

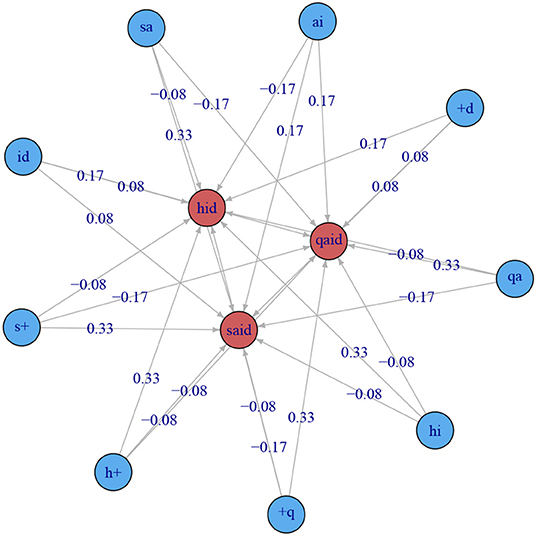
Figure 3. The two-layer network corresponding to W. The outer vertices in blue represent the input nodes, the inner vertices in red represent the output nodes. All input nodes are connected to each of the three output nodes. Each edge in the graph is associated with a weight which specifies the support that an input node provides for an output node.

In the present example, form cues are letter pairs, but other features have been found to be effective as well. Depending on the language and its writing conventions, larger letter or phone n-grams (typically with 1 < n ≤ 4) may outperform letter bigrams. For auditory comprehension, low-level acoustic features have been developed for modeling auditory comprehension (Arnold et al., 2017; Shafaei Bajestan and Baayen, 2018; Baayen et al., 2019). For visual word recognition, low-level visual “histograms of gradient orientation” features have been applied successfully in (Linke et al., 2017).

The total support a_j for an outcome j given the set of cues ${C}$ in the visual input to the model, henceforth its activation, is obtained by summing the weights on the connections from these cues to that outcome:

$\begin{array}{l}{a}_j={\displaystyle \sum _{i\in {C}}}{w}_{ij}.\end{array}$

For QAID (j = 1), the total evidence a₁ given the cues #q, qa, ai, id, and d# is 0.33 + 0.33 + 0.17 + 0.08 + 0.08 = 1.

The values of the weights are straightforward to estimate. We represent the digraph cues of the words by a matrix C, with a 1 representing the presence of a cue in the word, and a 0 its absence:

We also represent the outcomes using a matrix, again using binary coding:

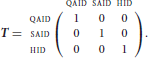
The vectors representing the outcomes in an NDL network are orthogonal: each pair of row vectors of T is uncorrelated. The weight matrix W follows by solving⁵

$\begin{array}{l}CW=T.\end{array}$

In other words, W projects words' forms, represented by vectors in a form space {C}, onto words' meanings, represented by vectors in a semantic space {T}⁶.

The outcomes of an NDL network represent lexical meanings that are discriminated in a language. Milin et al. (2017a) refer to these outcomes as lexomes, which they interpret as pointers to (or identifiers of) locations (or vectors) in some high-dimensional space as familiar from distributional semantics (see e.g., Landauer and Dumais, 1997; Mikolov et al., 2013). However, as illustrated above with the T matrix, NDL's lexomes can themselves be represented as high-dimensional vectors, the length k of which is equal to the total number of lexomes. The vector for a given lexome has one bit on and all other bits off (cf. Sering et al., 2018b). Thus, the lexomes jointly define a k-dimensional orthonormal space.

However, the orthonormality of the outcome space does not do justice to the fact that some lexomes are more similar to each other than others. Within the general framework of NDL, such similarities can be taken into account, but to do so, measures gauging semantic similarity have to be calculated from a separate semantic space that constructs lexomes' semantic vectors (known as word embeddings in computational linguistics) from a corpus. A technical complication is that, because many words share semantic similarities, the dimensionality of NDL's semantic space, k, is much higher than it need be. As a consequence, the classification accuracy of the model is lower than it could be (see Baayen et al., 2019, for detailed discussion).

The twin model of NDL, LDL, therefore replaces the one-hot encoded semantic vectors as exemplified by T by real-valued vectors. For the present example, this amounts to replacing T by a matrix, such as S:

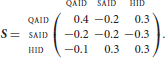
Actual corpus-based semantic vectors are much longer than this simple example suggests, with hundreds or even thousands of elements. The method implemented in Baayen et al. (2019) produces vectors the values of which represent a given lexome's collocational strengths with all the other lexomes in the corpus.

Model accuracy is evaluated by examining how close a predicted semantic vector $\widehat{s}$ is to the targeted semantic vector s, a row vector of S. In the case of NDL, this evaluation is straightforward: The lexome that is best supported by the form features in the input, and that thus receives the highest activation, is selected. In the case of LDL, that word ω is selected as recognized for which the predicted semantic vector $\widehat{s}$ is most strongly correlated with the targeted semantic vector s_ω.

As the dimensionality of the row vectors of S, T, and C can be large, with thousands or tens of thousands of values, we refer to the network W as a “wide learning” network, as opposed to “deep learning” networks which have multiple layers but usually much smaller numbers of units on these layers.

Of specific relevance to the present study is how NDL and LDL deal with morphologically complex words. With respect to the forms of complex words, exactly the same encoding scheme is used as for simple words, with either n-grams or low-level modality-specific features used as descriptor sets. No attempt is made to find morpheme boundaries, stems, affixes, or allomorphs.

At the semantic level, both NDL and LDL are analytical. NDL couples inflected words, such as walked and swam with the lexomes WALK and PAST, and SWIM and PAST, respectively. In the example worked out in Table 3, the word form walk has LX6 as identifier; the lexome for past is indexed by LX4. The form walked is linked with both LX6 and LX4. For clarity of exposition, instead of using indices, we refer to lexomes using small caps: WALK and PAST. An NDL network is thus trained to predict, for morphologically complex words, on the basis of the form features in the input, the simultaneous presence of two (or more) lexomes. Mathematically, as illustrated in the top half of Table 3, this amounts to predicting the sum of the one-hot encoded vectors for the stem (WALK) and the inflectional function (PAST). Thus, NDL treats the recognition of complex words as a multi-label classification problem (Sering et al., 2018b).

TABLE 3

Table 3. Semantic vector representations for inflected words in NDL (top) and LDL (bottom).

LDL proceeds in exactly the same way, as illustrated in the bottom half of Table 3. Again, the semantic vector of the content lexome and the semantic vector of the inflection are added. The columns now label semantic dimensions. In the model of Baayen et al. (2019), these dimensions quantify collocational strengths with—in the present example—10 well-discriminated lexomes. Regular past tense forms, such as walked and irregular past tense forms, such as swam are treated identically at the semantic level. It is left to the mapping W (the network taking form vectors as input and producing semantic vectors as output) to ensure that the different forms of regular and irregular verbs are properly mapped on the pertinent semantic vectors.

The NDL model as laid out by Baayen et al. (2011) treats transparent derived words in the same way as inflections, but assigns opaque derived words their own lexomes. For opaque words in which the semantics of the affix are present, even though there is no clear contribution from the semantics of the base word, a lexome for the affix is also included (e.g., employer: EMPLOY + ER; cryptic: CRYPTIC + IC).

The LDL model, by contrast, takes the idea seriously that derivation serves word formation, in the onomasiological sense. Notably, derived words are almost always characterized by semantic idiosyncracies, the exception being inflection-like derivation, such as adverbial -ly in English⁷. For instance, the English word worker denotes not just “someone who works,” but “one that works especially at manual or industrial labor or with a particular material,” a “factory worker,” “a member of the working class,” or “any of the sexually underdeveloped and usually sterile members of a colony of social ants, bees, wasps, or termites that perform most of the labor and protective duties of the colony” (https://www.merriam-webster.com/dictionary/worker, s.v.). Given these semantic idiosyncracies, when constructing semantic vectors from a corpus, LDL assigns each derived word its own lexome. However, in order to allow the model to assign an approximate interpretation to unseen derived words, each occurrence of a derived word is also coupled with a lexome for the semantic function of the affix. For instance, worker (in the sense of the bee) is associated with the lexomes WORKER and AGENT, and amplifier with the lexomes AMPLIFIER and INSTRUMENT. In this way, semantic vectors are created for derivational functions, along with semantic vectors for the derived words themselves (see Baayen et al., 2019, for detailed discussion and computational and empirical evaluation)⁸.

To put LDL and NDL in perspective, consider the substantial advances made in recent years in machine learning and its applications in natural language engineering. Computational linguistics initially worked with deterministic systems applying symbolic units and formal grammars defined over these units. It then became apparent that considerable improvement in performance could be obtained by making these systems probabilistic. The revolution in machine learning that has unfolded over the last decade has made clear that yet another substantial step forward can be made by moving away from hand-crafted systems building on rules and representations, and to make use instead of deep learning networks, such as autoencoders, LSTM networks for sequence to sequence modeling, and deep convolutional networks, outperforming almost all classical symbolic algorithms on tasks as diverse as playing Go (AlphaGo, Silver et al., 2016) and speech recognition (deep speech, Hannun et al., 2014). How far current natural language processing technology has moved away from concepts in classical (psycho)linguistics theory is exemplified by Hannun et al. (2014), announcing in their abstract that they “…do not need a phoneme dictionary, nor even the concept of a ‘phoneme”' (p. 1).

The downside of the algorithmic revolution in machine learning is that what exactly the new networks are doing often remains a black box. What is clear, however, is that these networks are sensitive to what in regression models would be higher-order non-linear interactions between predictors (Cheng et al., 2018). Crucially, such complex interactions are impossible to reason through analytically. As a consequence, models for lexical processing that are constructed analytically by hand-crafting lexical representations for stems and exponents, and hand-crafting inhibitory or excitatory connections between these representations, as in standard interactive activation models, are unable to generate sufficiently accurate estimates for predicting with precision aspects of human lexical processing.

We note here that NDL and LDL provide high-level functional formalizations of lexical processing. They should not be taken as models for actual neural processing: biological neural networks involve cells that fire stochastically, with connections that are stochastic (Kappel et al., 2015, 2017) as well. Furthermore, most neural computations involve ensembles of spiking neurons (Eliasmith et al., 2012).

NDL and LDL are developed to provide a linguistically fully interpretable model using mathematically well-understood networks that, even though very simple, are powerful enough to capture important aspects of the interactional complexities in language, and to generate predictions that are sufficiently precise to be pitted against experimental data. Although NDL and LDL make use of the simplest possible networks, these networks can, in combination with carefully chosen input features, be surprisingly effective. For instance, for auditory word recognition, an NDL model trained on the audio of individual words extracted from 20 hours of German free conversation correctly recognized around 20% of the words, an accuracy that was subsequently found to be within the range of human recognition accuracy (Arnold et al., 2017). Furthermore, Shafaei Bajestan and Baayen (2018) observed that NDL outperforms deep speech networks by a factor 2 on isolated word recognition. With respect to visual word recognition, Linke et al. (2017) showed, using low-level visual features, that NDL outperforms deep convolutional networks (Hannagan et al., 2014) on the task of predicting word learning in baboons (Grainger et al., 2012). For a systematic comparison of NDL/LDL with interactive activation and parallel distributed processing approaches, the reader is referred to Appendix B.

3.3. Computational Modeling With Naive Discriminative Learning

In the present study, we model our experiment with NDL, rather than LDL, for two reasons. First, it turns out that NDL, the simpler model, is adequate. Second, work is in progress to derive corpus-based semantic vectors for German along the lines of Baayen et al. (2019), which will include semantic vectors for inflectional and derivational semantic functions, but these vectors are not yet available to us.

The steps in modeling with NDL are the following. First, the data on which the network is to be trained have to be prepared. Next, the weights on the connections from the form features to the lexomes are estimated. Once the network has been trained, it can be used to generate predictions for the magnitude of the priming effect. In the present study, we generate these predictions by inspecting the extent to which the form features of the prime support the lexome of the target.

3.3.1. Data Preparation

The data on which we trained our NDL network comprised 18,411 lemmas taken from the CELEX database, under the restrictions that (i) they contained no more than two morphemes according to the CELEX parses, (ii) that the word was not a compound, and (iii) that it either had a non-zero CELEX frequency or occurred as a stimulus in the experiment. One stimulus word, betraten, was not listed in CELEX, and hence this form was not included in the simulation study. For each lemma, its phonological representation and its frequency were retrieved from CELEX. As form cues, we used triphones (for the importance of the phonological route in reading, see Baayen et al., 2019, and references cited there).

Each lemma was assigned its own lexome (but homophones were collapsed). The decision to assign each lemma its own lexome follows Baayen et al. (2019) and departs from Baayen et al. (2011). This similar treatment of transparent and opaque verbs is motivated by several theoretical considerations. First, there is no binary distinction between transparent and opaque. The meanings of particle verbs lie on a continuum between relatively semantically compositional and relatively semantically opaque. Second, even the compositional interpretation of a supposedly transparent verb, such as aufstehen (“stand up”) is not straightforward in the absence of situational experience—the particle auf (roughly meaning on or onto) may express a wide range of meanings, depending on cotext and context. In what follows, we therefore assume that even transparent complex words possess somewhat idiosyncratic meanings, and hence should receive their own lexomes in the NDL network.

The resulting input to the model was a file with 4,492,525 rows and two columns, one column spelling out a word's triphones, and the other column listing its lexome. Each word appeared in the file with a number of tokens equal to its frequency in CELEX. The order of the words in the file was randomized.

3.3.2. Training the Network

An NDL network with 10,180 input nodes (triphones) and 18,404 output nodes (lexomes) was trained on the input list, with incremental updating of the weights on the connections from features in the input to the lexomes, using the learning rule of Rescorla and Wagner (1972) (λ = 1, α = 0.001, β = 1; i.e., with a learning rate of 0.001). As there were 4,492,525 learning events in the input file, the total number of times that weights were updated was 4,492,525⁹.

3.4. Modeling Priming

To model the effect of priming, we presented the triphones of the prime to the network, and summed the weights on the connections from these triphones to the pertinent target to obtain a measure of the extent to which the prime pre-activates its target (henceforth PrimeToTargetPreActivation). Figure 4, upper left panel, presents a boxplot for PrimeToTargetPreActivation as a function of PrimeType. Interestingly, the opaque and transparent prime types comprise prime-target pairs for which the prime provides substantial and roughly the same amount of pre-activation for the target. For the other prime types, pre-activation is close to zero. Form-related prime-target pairs show some pre-activation, but this pre-activation is much reduced compared to the prime-target pairs in the opaque and transparent conditions.

FIGURE 4

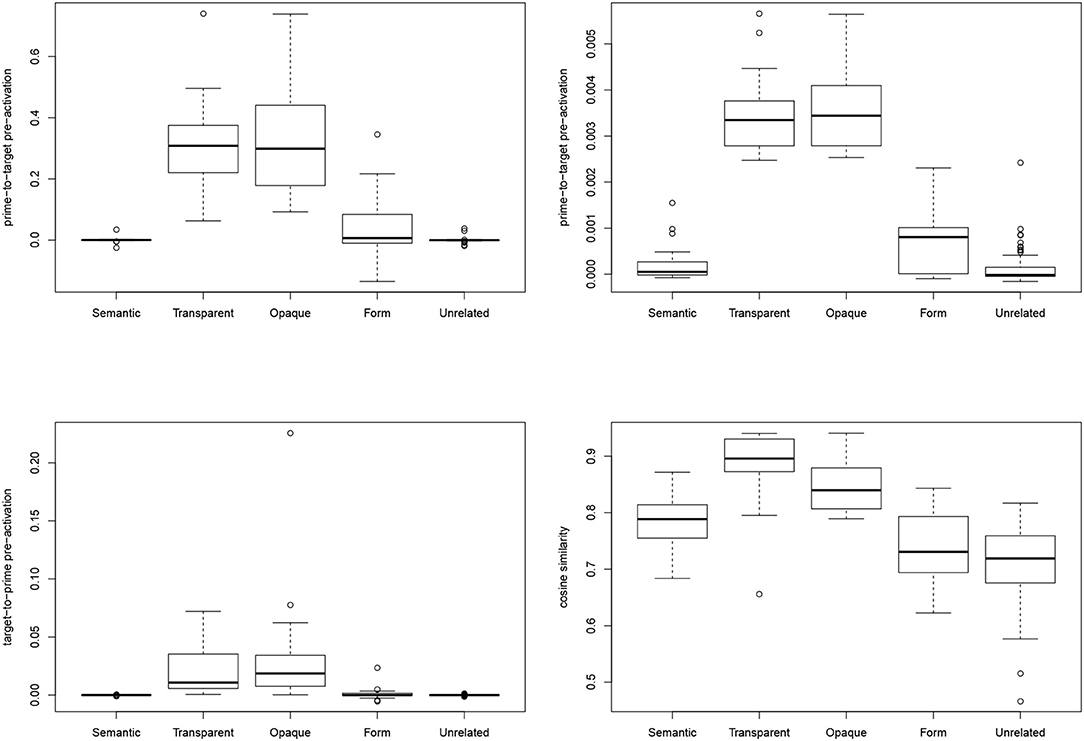
Figure 4. Predicted NDL Prime-to-Target Pre-Activation using empirical word frequencies (upper left panel), Predicted NDL Prime-to-Target Pre-Activation using uniformly distributed frequencies (upper right panel), Target-to-Prime Pre-Activation using empirical frequencies (lower left panel), and Prime-target Cosine Similarity (lower right panel), broken down by prime type.

The upper right panel of Figure 4 presents the results obtained when the empirical frequencies with which words were presented to the NDL network are replaced by uniformly distributed frequencies. This type-based simulation generates predictions that are very similar to those of the token-based simulation. This result shows that imprecisions in the frequency counts underlying the token-based analysis are not responsible for the model's predictions.

Above, we called attention to the finding of Smolka and Eulitz (2011) that very similar priming effects are seen when the order of prime and target is reversed. We therefore also ran a simulation in which we reversed the order of prime and target, and investigated the extent to which the current targets (now primes) co-activate the current primes (now targets). The distributions of the predicted pre-activations are presented in the lower left panel of Figure 4 (target-to-prime pre-activation). Apart from one extreme outlier for the opaque condition, the pattern of results is qualitatively the same as for the Prime-to-Target Pre-Activation presented in the upper panel. For both simulations, there is no significant difference in the mean for the opaque and transparent conditions, whereas these two conditions have means that are significantly larger than those of the other three condition (Wilcoxon-tests with Bonferroni correction). In summary, our NDL model generates the correct prediction that the priming effect does not depend on the order of prime and target.

Reaction times are expected to be inversely proportional to PrimeToTargetPreActivation. We therefore ran a linear model on the stimuli, and used the reciprocal of PrimeToTargetPreActivation as response variable, based on the simulation in which the model was presented with the empirical word frequencies. As the resulting distribution is highly skewed, the response variable was transformed to log(1/(PrimeToTargetPreActivation + 0.14)¹⁰. The opaque and transparent priming conditions were supported as having significantly shorter simulated reaction times compared to the unrelated condition (both p ≪ 0.0001), in contrast to the other two conditions (both p > 0.5).

Recall that the outcome vectors of NDL are orthogonal, and that hence the present NDL models all make predictions that are driven purely by form similarity. The model is blind to potential semantic similarities between primes and targets, not only for the primes and targets in the transparent and opaque conditions, but also to semantic similarities present for the other prime types. To understand to what extent semantic similarities might be at issue in addition to form similarities, we therefore inspected prime and target's semantic similarity using distributional semantics.

3.5. Semantic Vectors From Tweets

As LDL-based semantic vectors for German are currently under construction, we fell back on the word embeddings (semantic vectors) provided at http://www.spinningbytes.com/resources/wordembeddings/ (Cieliebak et al., 2017; Deriu et al., 2017). These embeddings (obtained with word2vec, Mikolov et al., 2013) are 300-dimensional vectors derived from a 50 million word corpus of German tweets. Tweets are relatively short text messages that reflect spontaneous and rather emotional conversation. Tweets from facebook have been shown to outperform frequencies from standard text corpora in predicting lexical decision latencies (Herdağdelen and Marelli, 2017).

Cieliebak et al. (2017) and Deriu et al. (2017) provide separate semantic vectors for words' inflected variants. For instance, the particle verb vorwerfen (“accuse”) occurs in their database in the forms vorwerfen (infinitive and 1st or 3rd person plural present), vorwerfe (1st person singular present), vorwirfst (2nd person singular present), vorwirft (3rd person singular present), vorwerft (2nd person plural present), vorgeworfen (past participle), and vorzuwerfen (infinitive construction with zu). As we can expect for tweets, not all inflected forms, in particular the more formal ones, appear in the database. Importantly, the semantic vectors are probably obtained without taking into account that the particle of a particle verb can appear separated from its verb, sometimes at a considerable distance (see Schreuder, 1990, for discussion of the cognitive consequences of this separation), as in the sentence “Sie wirft ihm seinen Leichtsinn vor,” “She accuses him of his thoughtlessness.” Given the computational complexity of identifying particle-verb combinations when the particle appears at a distance, it is highly likely that for split particle verbs, the base verb of the verb-particle combination is processed as if it were a simple verb (e.g., werfe, wirfst, wirft, werfen, and werft, 1st, 2nd, and 3rd person singular and plural present, respectively). As a consequence, the semantic similarity of simple verbs and particle verbs computed from the word embeddings provided by Cieliebak et al. (2017) and Deriu et al. (2017) is in all likelihood larger than it should be.

Not all words in the experiment are in this database; but for six words, we were able to replace the infinitive by a related form (einpassen → reinpassen, verqualmen → verqualmt, fortlaufen → fortlaufend, bestürzen → bestürzend, verfinstern → verfinstert, beschneien → beschneites).

For each prime-target pair for which we had data, we calculated the cosine similarity of the semantic vectors of prime and target, henceforth Prime-to-Target Cosine Similarity. Figure 4, lower right panel, shows that the transparent pairs have the greatest semantic similarity, followed by the opaque pairs, then the semantic pairs and the form pairs, and the least semantic similarity by the unrelated pairs.

Surprisingly, the semantic controls have a rather low semantic similarity, substantially less than that of the opaque pairs. A linear model with the semantic primes as reference level clarifies that the semantic pairs are on a par with the form controls, more similar than the unrelated pairs, but less similar than both the opaque and transparent pairs (Table 4).

TABLE 4

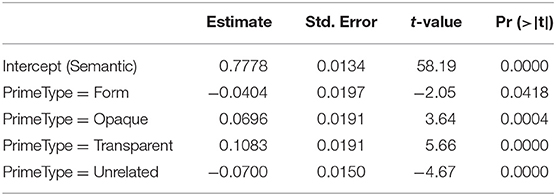
Table 4. Effect of PrimeType in a linear model predicting cosine similarity, using treatment coding with the semantic condition as reference level.

There is a striking discrepancy between the assessment of semantic similarity across prime types based on the cosine similarity of the semantic vectors on the one hand, and an assessment based on the ratings for semantic relatedness between word pairs, as documented in Table 1. In the former, semantic pairs pattern with form controls and differ from transparent ones, while in the latter, semantic pairs pattern with transparent pairs (5.5 and 5.7, respectively), and opaque pairs with form-related ones (2.1 and 1.7, respectively).

Most important to our study is that the opaque pairs show significantly less semantic similarity than the transparent ones (p < 0.0047, Wilcoxon test): The analysis of word embeddings confirms that there is a true difference in semantic transparency between the transparent and opaque prime-target pairs. And yet, this difference is not reflected in our reaction times.

Given the strong track record of semantic vectors in both psychology and computational linguistics, the question arises of whether the prime-target cosine similarities are predictive for reaction times, and how the magnitude of their predictivity compares to that of the NDL Prime-to-Target Pre-Activation.

3.6. Putting It All Together: Predicting Reaction Times

To address these questions, we fitted a new GAMM to the inverse-transformed reaction times of our experiment, replacing the factorial predictor PrimeType with the model-based predictor Prime-to-Target Pre-Activation. We also replaced target frequency by the activation that the target word receives from its own triphones (henceforth TargetActivation, see Baayen et al. (2011) for detailed analyses using this measure). Target activation is proportional to frequency, and hence larger values of target activation are expected to indicate shorter response times¹¹.

Of the experimental dataset, about 7% of the observations was lost due to 7 words not being available in CELEX or in the dataset of word embeddings. To set a baseline for model comparison, we refitted the GAMM discussed above to the 1999 datapoints of the reduced dataset. The fREML score for this model was 360.76. A main effects model replacing Target Frequency by Target Activation, PrimeType by Prime-to-Target Pre-Activation, and as additional predictor the Prime-to-Target Cosine Similarity had a slightly higher fREML score, 370.97. An improved model was obtained by allowing the three new covariates to interact, using a tensor product smooth. The fREML score of this model, summarized in Table 5, was 354.16. A chi-squared test for model comparison (implemented in the compareML function of the itsadug package van Rij et al., 2017) suggests that the investment of 4 additional effective degrees of freedom is significant (p = 0.010). As the models are not nested and the increase in goodness of fit is moderate (6.6 fREML units), we conclude that—to obtain a model that is at least equally good—it is possible to replace the classical predictors, such as Frequency and PrimeType by model-based predictors without loss of prediction accuracy¹².

TABLE 5

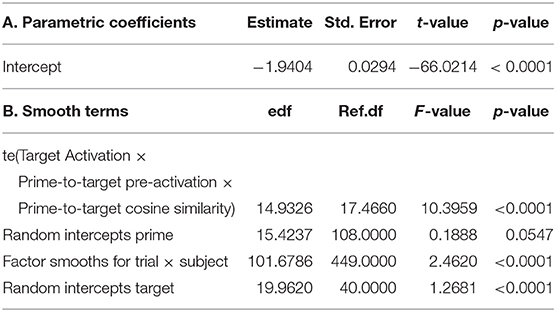
Table 5. GAMM fitted to inverse transformed reaction times using model-based predictors; te(): tensor product smooth.

The three-way interaction involving Target Frequency, Prime-To-Target Pre-Activation, and Prime-to-TargetCosine Similarity is visualized in Figure 5. The five panels show the joint effect of the first two predictors for selected quantiles of Prime-to-TargetCosine Similarity: From top left, to bottom right, Prime-to-Target Cosine Similarity is set to its 0.1, 0.3, 0.5, 0.7, and 0.9 deciles. Darker shades of blue indicate shorter reaction times, and darker shades of yellow longer RTs.

FIGURE 5

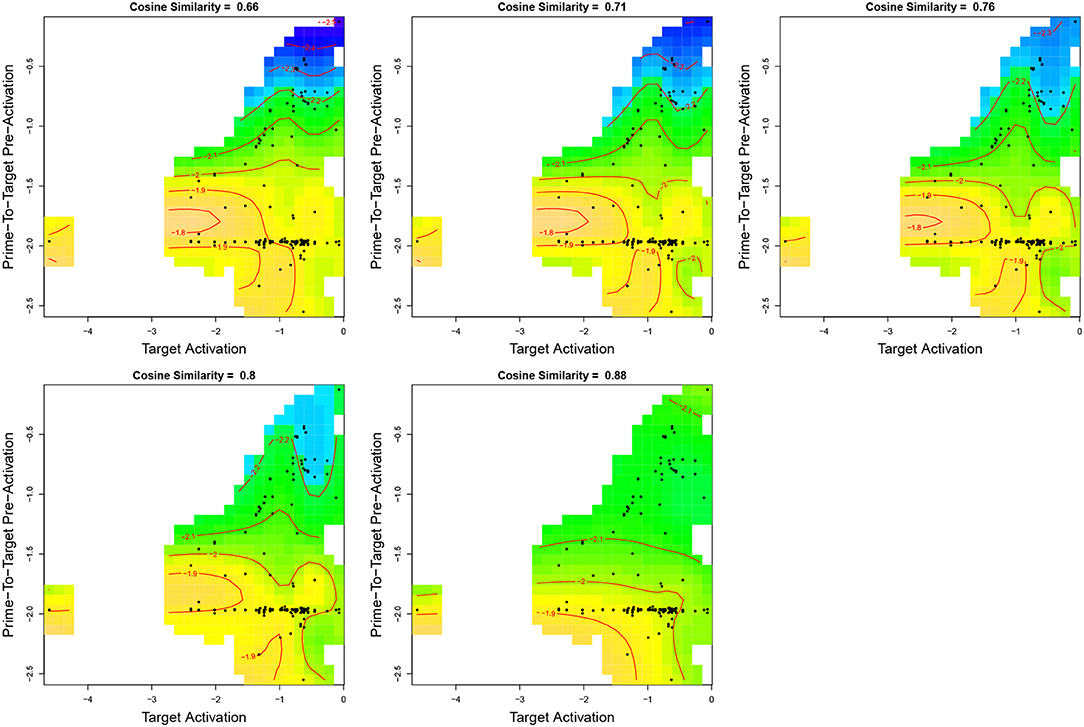
Figure 5. Interaction of Target Activation by Prime-to-Target Pre-Activation by Prime-to-Target Cosine Similarity in a GAMM fitted to the inverse-transformed reaction times. Darker shades of blue indicate shorter reaction times, and darker shades of yellow longer RTs. For visualization, one extreme outlier value for Prime-to-Target Pre-Activation was removed (13 datapoints). Contour lines are 0.1 inverse RT units apart.

As can be seen in the upper left panel (for the first decile of Cosine Similarity), reaction times decrease slightly as Target Activation is increased, but only when there is little Prime-To-Target Pre-Activation. A clear effect of Prime-to-TargetPre-Activation is present for the larger values of Target Activation.

Recall that, as shown in Figure 4, transparent and opaque prime-target pairs have the same mean pre-activation, whereas the mean cosine similarity is greater for transparent prime-target pairs compared to opaque pairs. If both pre-activation and cosine similarity would have independent effects, one would expect a difference in the mean reaction times for these two prime types, contrary to fact. The interaction of pre-activation by target activation by cosine similarity resolves this issue by decreasing the effect of pre-activation as cosine similarity increases. When prime and target are more similar semantically, the effect of pre-activation is reduced, and reaction times are longer than would otherwise have been the case. This increase in RTs may reflect the cognitive system slowing down to deal with two signals for very similar meanings being presented in quick succession in a way that is extremely rare in natural language.

We checked whether the association ratings that were used for stimulus preparation were predictive for the reaction times. This turned out not to be the case, not for the model with classical predictors, nor when the association ratings were added to the model with discrimination-based predictors.

Finally, Table 6 presents the fREML scores for the full model, and the three models obtained when one covariate is removed at a time. Since smaller fREML scores indicate a better fit, Table 6 clarifies that Prime-to-Target Pre-Activation is the most important covariate, as its exclusion results in the worst model fit (386.11). The variable importances of Prime-to-TargetCosine Similarity is also substantial (383.49) whereas removing Target Activation from the model specification reduces model fit only slightly (361.62). The model that best predicts (AIC 354.16) pure morphological priming includes all three factors: Prime-to-Target Pre-Activation (capturing Prime Type), Prime-to-Target Cosine Similarity (capturing minor semantic effects), and Target Activation (capturing the frequency effect).

TABLE 6

Table 6. fREML scores for four models: the full model, a model without Prime-to-Target Cosine Similarity, a model without Prime-to-Target Pre-Activation, and a model without Target Activation.

4. Discussion

We presented an overt primed visual lexical decision experiment that replicated earlier results for German complex verbs: Priming effects were large and equivalent for semantically transparent and semantically opaque prime-target pairs.

These findings add to the cumulative evidence of “pure morphological priming” patterns that suggest stem access independent of semantic compositionality in German, in contrast to English and French, where semantic compositionality has been reported to co-determine word processing.

One could argue that the fact that we used verbs might account for these cross-language differences, in particular because the majority of the verbs in German hold prefixes or particles. Indeed, there are only few studies in English that applied prefixed stimuli that can be interpreted as verbs, such as preheat–heat (e.g., Exp. 5 in Marslen-Wilson et al., 1994b; Exp. 4 in Gonnerman et al., 2007; EEG-experiment in Kielar and Joanisse, 2011). In these experiments, though, opaque prime-target pairs like rehearse–hearse did not induce priming, which contrasts with our findings in German. Furthermore, in a previous study (Exp. 3 in Smolka et al., 2014), we applied both verbs and nouns or adjectives in the same experiment to make sure that the opaque priming effects are not due to the fact that participants see verbs only. It might indeed be the case that, in German, morphological constituents assume a more prominent role than prefixes and suffixes in nouns and adjectives in languages as English and French, and that the complexity and structure of the language affects its (lexical) processing (Günther et al., 2019).

Most importantly, because neither localist nor connectionist models of lexical processing are able to account for the German findings, Smolka et al. (2009, 2014, 2019) proposed a stem-based frequency account, according to which stems constitute the crucial morphological units regulating lexical access in German, irrespective of semantic transparency.

In the present study, we took the next step and modeled the German stem priming patterns using naive discriminative learning (NDL). This morpheme-free computational model clarifies that the observed priming effects across all prime types may follow straightforwardly from basic principles of discrimination learning. The extent to which sublexical features of the prime (letter triphones) pre-activate the lexome of the target is the strongest predictor for the reaction times. A substantially smaller effect emerged for the activation of the target (comparable to a frequency effect). The semantic similarity of prime and target as gauged by the cosine similarity measure also had a solid effect.

The semantic vectors (word embeddings) used for calculating the cosine similarity between primes and their targets were taken from a database of German tweets. It is noteworthy that the cosine similarity measure provided good support for the transparent prime-target pairs being on average more semantically similar than the opaque prime-target pairs. However, this difference between the two prime types was not reflected in the corresponding mean reaction times.

A three-way interaction between prime-to-target pre-activation, target activation, and prime-target cosine similarity detected by a generalized additive mixed model fitted to the reaction times clarified that as the semantic similarity of primes and targets increases, the facilitatory effect of pre-activation decreases. Apparently, when primes and targets are more similar, pre-activation by the prime forces the cognitive system to slow down in order to resolve the near simultaneous activation of two very similar, but conflicting, meanings.

Interestingly, even though across prime types stimuli were matched for association ratings, these ratings were not predictive for reaction times. Stimuli were not matched across prime types for the cosines of the angles between primes' and targets' tweet-based semantic vectors, yet, surprisingly, these were predictive for reaction times. This finding is particularly surprising for the present data on German, as in previous work semantic similarity measures (not only human but also vector-based measures like LSA (Landauer and Dumais, 1997) and HAL (Lund and Burgess, 1996)) were observed not to be predictive of reaction times. It is conceivable that the present semantic measure is superior to LSA and HAL, due to it being calculated from a large volume of tweets—Herdağdelen and Marelli (2017) point out that measures based on distributional semantics calculated from corpora of social media provide excellent predictivity for lexical processing.

A caveat is in order, though, with respect to the cosine similarity measure, as in all likelihood particle verbs and their simple counterparts are estimated to be somewhat more similar than they should be. Particles can be separated by several words from their stems, and these stems will therefore be treated as simple verbs by the algorithm constructing semantic vectors (especially when the particle falls outside word2vec's 5-word moving window). This, however, implies that the cosine similarity measure must be less sensitive than it could have been: The vector for the simple verb is artifactually shifted in the direction of the vector of its particle verb, with the extent of this shift depending on the frequency of the simple verb, and the frequencies of the separated and non-separated derived particle verbs. As simple verbs typically occur with several particles, the semantic vectors for these simple verbs are likely to have shifted somewhat in the direction of the centroid of the vectors of its particle verbs.

Nevertheless, the present tweet-based semantic vectors contribute to the prediction of reaction times. Importantly, there is no a-priori reason for assuming that the rate at which particles occur separated from their stem would differ across prime types. As a consequence, the partial confounding of particle verbs and simple verbs by the distributional semantics algorithm generating the semantic vectors cannot be the main cause of the different distributions of cosine similarities across the different prime types (in this context, it is worth noting that any skewing in frequency counts of complex and simple verbs does not affect the qualitative pattern of results for the predictor with the greatest effect size, the prime-to-target activation measure, as shown by the simulation in which all words are presented to the network with exactly the same frequency. We leave answering the question of why this particular frequency measure appears to be effective as predictor for the present reaction times to further research).

An important result is that a generalized additive mixed model fitted to the reaction times provides a fit that is at least as good, if not slightly better, when the activation, pre-activation, and cosine similarity measures are used, compared to when prime type and frequency of occurrence are used as predictors (reduction in fREML score: 6.6, which, for 4 degrees of freedom is significant (p = 0.010) according to the chi-squared test implemented in the compareML function of the itsadug package)¹³.

The theoretical contribution of this study is that it challenges the general localist interactive activation framework that dominates the current discourse on morphological processing. Stems and morphemes are assumed to be psychologically real (see e.g., Zwitserlood, 2018), and to excite or inhibit each other. Furthermore, these high-level concepts are apparently understood to be sufficient for explaining the effects of experimental manipulations. NDL, by contrast, provides a framework within which quantitative measures can be derived that can be pitted against experimental response variables. NDL (and LDL) make use of the simplest possible network, the mathematics of which are well understood—in essence, NDL is nothing more (or less) than incremental multivariate multiple (logistic) regression. An NDL model is essentially parameter-free¹⁴, and driven completely by the distributional properties of the words in the corpus it is trained on. NDL, just as the interactive activation framework, requires the analyst to make decisions on input and output nodes, but unlike the interactive activation framework, no hand-crafting of connections is required, and no search is required for finding a set of parameters that make the model behave in the way desired. As a consequence, the measures derived from an NDL network can be used simply as a statistical tool for assessing how well a word's meaning can be “classified” or “discriminated” given its form features. As expected, reaction times become shorter when target meanings are better discriminated, i.e., when target activation is higher and the probability of the target being correctly classified is greater. Furthermore, when a morphologically related prime is presented to the network, a distribution of activations over the lexomes ensues in which the activation of the target is greater compared to trials with primes that are not morphologically related. This pre-activation of the target by reading the prime apparently carries over to the reading of the target¹⁵.

Although NDL-based measures can be used in the same way as measures such as word frequency and neighborhood density, the linguistic theory underlying NDL holds that morphemes (in the sense of minimal signs) as well as sublexical form units, such as stems and exponents are not necessary. At the same time, this theory is analytical at the semantic level. What Baayen et al. (2019) and Baayen et al. (2018) have shown for LDL is that accurate mappings between form vectors and distributional semantic vectors can be set up with linear transformations, i.e., with simple two-layer networks (and no hidden layers). The more comprehensive model of the mental lexicon developed in Baayen et al. (2019) and Chuang et al. (2019) makes use of multiple such networks to generate quantitative predictions for auditory comprehension (with audio as input), visual comprehension, and speech production. A proof of concept that inflected forms of rich paradigms can be predicted from their corresponding semantic vectors without requiring sublexical form units, such as stems and exponents is provided by Baayen et al. (2018). It is within this wider context that the present computational modeling of overt primed visual lexical decision comes into its own.

It is important to note that the design decision to assign complex verbs their own lexome, irrespective of semantic transparency, following Baayen et al. (2019), is crucial for enabling NDL to simulate the German behavioral priming data. This design decision is well-motivated, as it is widely recognized that in word formation, in contrast to inflection, complex forms almost always have their idiosyncratic shades of meaning, even when classified as “transparent.”

We have shown that the effect of morphological priming can be modeled precisely with a simple network that eschews morphemes and sublexical units, such as stems, affixes, and exponents, a result that is consistent with Word and Paradigm Morphology (Blevins, 2016) and the model of the mental lexicon proposed in Baayen et al. (2019). Do these findings imply that morphemes or morphs do not have any psychological or cognitive reality? Answering this question is not straightforward.

First, it is logically possible that morphemes are actually cognitively real and crucially involved in the lexical processing of German verbs. In this case, NDL is no more than a machine learning algorithm that generates correct predictions, but for the wrong reasons. To give substance to this argumentation, it will be essential for alternative explicit computational models to be put forward to champion the cause of units representing morphemes.

Second, the sublexical cues (triphones) that are shared by prime and target drive the prime-to-target pre-activation. For the prime-target pair ANSTOSSEN, STOSSEN, the set of shared trigrams is Sto, tos, os@, s@n, s@n, @n#, and the set of trigrams unique to only one of the two words is #an, anS, nSt, and #St. Figure 6 presents the connection strengths of these cues to the lexome STOSSEN (upper panel) and ANSTOSSEN (lower panel). The cues that occur in both lexomes (the blue dots with inner red dots) support STOSSEN (upper panel), or ANSTOSSEN (lower panel) to exactly the same extent—as expected, as the cues are sublexical features that by definition must provide the same support for STOSSEN irrespective of whether they are embedded in the word form Stos@n or anStos@n.

FIGURE 6

Figure 6. Connection weights from triphones to the lexome STOSSEN (upper panel), and to the lexome ANSTOSSEN (lower panel). As the primes are of much lower frequency of occurrence than the targets, the magnitude of weights in the lower panel is substantially reduced compared to the upper panel. In the lower panel, the blue and red disks are presented on the same scale as the upper panel. The disks in gray and black represent the same datapoints, but now on an enlarged scale, depicted at the right-hand side of the plot.

Figure 6 brings to the fore two important points. First, the two central triphones of the stem that are shared by both the simple and the complex verb, Sto and tos, provide substantial contributions to the (pre-)activation of both STOSSEN and ANSTOSSEN, as expected. This observation fits well with the stem-frequency hypothesis, according to which the stem is the crucial unit mediating lexical access. Second, however, triphones at the boundary of the stem can have even greater strengths than these central triphones. For STOSSEN, this is the case for os@, and for ANSTOSSEN, this happens for both nSt and os@. The boundary triphone s@n also makes a non-negligible, albeit much smaller, contribution to the activation of these lexomes. Crucially, it is exactly here that NDL moves beyond the stem-frequency hypothesis. Triphones at the boundary of the stem often carry substantial discriminatory potential. The boundary triphone os@ is important for discriminating (AN)STOSSEN from nominal lexomes, such as TROSS, STOSS, SCHLOSS and adjectival lexomes, such as GROSS, and the boundary triphone nSt is important for discriminating ANSTOSSEN from STOSSEN (note its high positive value as cue for ANSTOSSEN and its slightly negative value as cue for STOSSEN).

In other words, the present NDL model can be viewed as a refinement of the stem-frequency model that, by taking into account not only central sublexical features of the stem, but also the discriminatory potential of features at the stem boundary, achieves superior predictivity¹⁶.

Third, NDL (and LDL) target implicit learning, the continuous recalibration of the lexicon that goes on without conscious thought and attention, similar to the way that object recognition is continually recalibrated (Marsolek, 2008). The finding of Smolka et al. (2015) that morphological priming effects are visible in evoked response potentials even in the absence of behavioral correlates is consistent with NDL capturing subliminal lexical processing. However, we also reflect on language, we enjoy word play, we have poetry, we teach grammar in schools, and in second language teaching we instruct learners how to put words together from their parts. Patients suffering from a stroke may benefit from explicit instruction about how inflected words can be put together (Nault, 2010). This knowledge about language is cognitively real, and it may also affect lexicality decisions in meta-linguistic tasks, such as primed lexicality decision making. NDL and LDL, however, are blind to this higher-order knowledge.

Fourth, in LDL, we can ask the question of how the triphone or trigram units used for its form vectors might be organized in two-dimensional space. The ordering of such units in the model's form vectors is not cognitively meaningful, but their organization in a 2-D plane, used as approximation of the cortical surface, might reveal interesting clustering. Depending on language and inflectional or derivational function, clusters in 2D space are indeed sometimes visible in triphone graphs when projected onto a plane, subject to constraints of stress minimization under self-organization (see Baayen et al., 2018, for detailed discussion). Topographic patterning under self-organization is also observed by Chersi et al. (2014); Marzi et al. (2018), who use temporal self-organizing maps (TSOMs). In their theory, trajectories in these maps capture, albeit fluidly, stems, and affixes. Since in this theory these trajectories subserve production, they can be viewed as morpheme-like units that are algorithmically functional for speech production. By contrast, the clusters of triphones that emerge under self-organization in NDL/LDL have no such algorithmically functional role. They typically do not form consecutive sequences of phones as found for stems and affixes in TSOMs. They emerge purely as a consequence of self-organizational constraints on spatial clustering of triphones given their overlap. If such clusters could be shown to correctly describe neuronal organization at more detailed levels of neurobiological modeling, then if such clusters were to be detected by brain imaging techniques, they should not be mistaken for evidence supporting algorithmically functional morphemes. In short, morpheme-like clusters can arise in NDL/LDL, without having any of the algorithmic functionalities commonly attributed to morphemes. Thus, these clusters of units are fundamentally different from neuronal clusters that might be hypothesized to underly localist morpheme units in interactive activation models.

Fifth, NDL and LDL are based on wide learning networks, simple two-layer networks with large numbers of units that can be trained very quickly, the mathematics of which are well-understood, and that can perform with surprising accuracy given well-chosen input and output representations (see e.g., Linke et al., 2017; Shafaei Bajestan and Baayen, 2018). Deep learning networks offer architectures in which units on hidden layers have the potential to become sensitive to, and in some sense “represent,” morpheme-like units. Such networks are powerful statistical classifiers, but require decisions about the number of hidden layers, the number of units on these layers, and where to position convolutional and/or recurrent layers. Unfortunately, deep learning networks are widely recognized to have a “black box” nature, although progress is being made toward understanding why they work (see e.g., Cheng et al., 2018; Daniel and Yeung, 2019). NDL and LDL are specifically designed to provide both interpretational transparency and accurate and falsifiable predictions.

Importantly, what sets both wide learning and deep learning apart from the interactive activation framework is, first, that the former models are dynamically learning classifiers whereas the latter approach builds on the idea of a static classifier with a large number of parameters that have to be set manually, and second, that the former are end-to-end models whereas the latter solves only a partial task. The interactive activation framework is set up to select one word form and suppress all others, given visual input, but it remains silent about the semantics to which this form is supposed to provide access. This approach is still chained to the metaphor of the paper dictionary, in which form entries have to be located that, once found, provide access to meaning (see also Elman, 2009, for detailed criticism of the dictionary metaphor). By contrast, wide learning, following many practical applications in computational linguistics that make use of deep learning, is set up to predict the ultimate true goal of comprehension: the semantics targeted by the input signal. The results obtained with NDL and LDL obtained thus far suggest that this goal can be reached without mediation by form units, such as stems, affixes, or exponents. It is likely that future versions of the general LDL model of Baayen et al. (2019) will incorporate deep learning for some of its components, sacrificing interpretational transparency for increased accuracy. If morph-like units arise in such versions of the model, these units will not be part of a classical morphological calculus with symbolic representations and rules operating on these representations, such as proposed by Chomsky and Halle (1968) and Pinker (1999). Their function would be to statistically integrate high-dimensional evidence for semantics in interaction with large numbers of other such units.

In the light of these considerations, it is clear that the present study cannot provide a full answer to the question of whether morphemes are, or are not, cognitively real. Clearly, the behavioral findings that have been interpreted as evidence for stem-driven lexical access are real. What the present study adds to this is that there actually is another possible interpretation for the observed priming effects, namely, prime-to-target pre-activation in a discriminative lexicon. The discriminative lexicon provides detailed quantitative predictions within a larger conceptual framework that is informed by recent developments in linguistic morphology, using a computational algorithm that is completely driven by the distributional properties of the lexicon, and that does not require (nor allow) tuning of free parameters to bring the model's performance in line with the observed data. The present modeling results thus challenge proponents of morpheme-driven, decompositional, lexicons to demonstrate that their high-level conceptual theories can actually be made to work algorithmically. This in turn will make it possible to pit against each other the detailed quantitative predictions of morpheme-based and morpheme-free models.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Ethics Statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author Contributions

ES ran the experiment. RB did the modeling. Both the authors contributed to the writing of the manuscript.

Funding

This study was supported by the VolkswagenStiftung, Grant FP 561/11, awarded to ES, and by ERC advanced grant 742545-WIDE to RB.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge support from the Open Access Publishing Fund of University of Tübingen.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomm.2020.00017/full#supplementary-material

Footnotes

1. ^See Smolka et al. (2014) and Günther et al. (2019) for possible explanations.

2. ^Frequency was added as a covariate to the model for three reasons. First, frequency varied within priming conditions, and since frequency is a strong predictor of response latencies in the visual lexical decision task, the presence of a frequency effect certifies that participants were engaging with the task, rather than performing on the basis of some high-level task-specific strategies, such as searching for similar letter substrings. Second, we wanted to make sure that any differences in frequency between priming conditions, related not to mean frequencies, but to imbalances in the distributions of frequencies within the separate priming conditions, cannot be held responsible for the observed priming effects. Third, we were interested in exploring to what extent the magnitude of the frequency effect might change across the distribution of reaction times.

3. ^Quantile regression is a statistical method for predicting the quantiles of a response variable. Standard regression methods consider only the mean of the response, which, if the response is Gaussian, is equal to the median, which in turn is the 5th decile. However, a researcher's interest may be not in predicting the mean, but a specific quantile. For instance, an electricity company may be interested in balancing atomic power and water power. Energy from water power is scarce, but the (limited) amount of power generated can be varied quickly in time as demand changes. Energy from atomic plants is available in large quantities, but the amount of energy generated can be varied only very slowly over time. To balance atomic power and water power, it can be of interest to generate 98% of the energy demand using atomic power, and supplement the remaining energy demand from water power. In this case, quantile regression can be used to predict the 98 percentile of energy demand as a function of time (Fasiolo et al., 2017). For the analysis of reaction times, quantile regression can be used to clarify where in the distribution of reaction times effects are present, and to investigate whether effects change in magnitude across the distribution (see e.g., Tomaschek et al., 2018, for an application in phonetics).

4. ^To our knowledge, this poster presentation is the only computational study addressing morphological processing that makes use of the interactive activation framework.

5. ^In R: W = ginv(C) %*% T, see Baayen et al. (2018) and Baayen et al. (2019) for further details on linear transformations from form to meaning (and from meaning to form).

6. ^The weight matrix W is identical to the weight matrix obtained by applying the equilibrium equations of Danks (2003) for the Rescorla-Wagner learning rule (Rescorla and Wagner, 1972) that was used by Baayen et al. (2011), see Sering et al. (2018b) for detailed discussion. W is also identical to the matrix of beta weights of a multivariate multiple regression model regressing the semantic vectors on the form vectors.

7. ^The reason that adverbial -ly is generally treated as derivational is that the word category of words with -ly is not identical to the word category of its base word.

8. ^For a compositional approach to the semantics of complex words using distributional semantics, see Lazaridou et al. (2013) and Marelli and Baroni (2015).

9. ^Optimized software, e.g., Sering et al. (2017), makes it possible to harness multiple cores in parallel. Using 6 cores, training the network takes <10 min. Incremental learning is much faster than weight estimation by means of the Danks equilibrium equations, which were used by Baayen et al. (2011).

10. ^The shift 0.14 is slightly larger than the absolute value of the most negative pre-activation. This shift thus ensures that all pre-activation values are positive, so that a log-transform becomes possible.

11. ^Both activation measures were log-transformed after adding a small number, 0.14 for Prime-to-Target Pre-Activation and 0.01 for Target Activation, to ensure that all pertinent numbers were positive before taking logarithms.

12. ^Including an interaction of PrimeType by Target Frequency in the GAMM with classical predictors led to an increase in the fREML score, indicating overfitting and increased model complexity without increased prediction accuracy.

13. ^When the analysis is restricted to the prime-target pairs in the Opaque and Transparent conditions, the model with NDL predictors again outperforms the model with classical predictors, now by 24.4 fREML units (for 8 edf, p < 0.0001). This provides further support against the present result being due to subjects using a task strategy using stem identity as response criterion.

14. ^The learning rule of Rescorla and Wagner has several parameters that were introduced specifically to model differences in the salience of input features and the importance to the animal of different outcomes. In our implementation, we always set λ (representing the maximum amount of learning) to 1, and use a fixed learning rate (the product of the α and β parameters). In Baayen et al. (2011), the learning rate was 0.01, but subsequent work showed optimal performance when the learning rate is set to 0.001. For the simulation reported here, these values were used, and no simulations were run with different values.

15. ^The NDL framework currently does not provide mechanisms that account for how the cognitive system reaches a response on the basis of lexome activations. Analyses with the generalized additive model indicate non-linear interactions for these mechanisms. At present, all we can do is bring these non-linearities to light with GAMs, in the hope that across experiments consistent patterns will emerge that then can be the subject of further computational modeling.

16. ^For detailed discussion of the importance of sublexical features at the boundary of morphemic units from a discrimination learning perspective, see Baayen et al. (2016b). For frailty at stem boundaries in speech production, see Baayen et al. (2019).

References

Arnold, D., Tomaschek, F., Lopez, F., Sering, T., and Baayen, R. H. (2017). Words from spontaneous conversational speech can be recognized with human-like accuracy by an error-driven learning algorithm that discriminates between meanings straight from smart acoustic features, bypassing the phoneme as recognition unit. PLoS ONE 12:e0174623. doi: 10.1371/journal.pone.0174623

PubMed Abstract | CrossRef Full Text | Google Scholar

Aronoff, M. (1994). Morphology by Itself: Stems and Inflectional Classes. Cambridge, MA: The MIT Press.

Google Scholar

Baayen, R. H., Chuang, Y., and Blevins, J. P. (2018). Inflectional morphology with linear mappings. Ment. Lexicon 13, 232–270. doi: 10.1075/ml.18010.baa

CrossRef Full Text | Google Scholar

Baayen, R. H., Chuang, Y.-Y., Shafaei-Bajestan, E., and Blevins, J. (2019). The discriminative lexicon: a unified computational model for the lexicon and lexical processing in comprehension and production grounded not in (de)composition but in linear discriminative learning. Complexity 2019:4895891. doi: 10.1155/2019/4895891

CrossRef Full Text | Google Scholar

Baayen, R. H., Dijkstra, T., and Schreuder, R. (1997). Singulars and plurals in Dutch: evidence for a parallel dual route model. J. Mem. Lang. 36, 94–117. doi: 10.1006/jmla.1997.2509

CrossRef Full Text | Google Scholar

Baayen, R. H., McQueen, J., Dijkstra, T., and Schreuder, R. (2003). “Frequency effects in regular inflectional morphology: revisiting Dutch plurals,” in Morphological Structure in Language Processing, eds R. H. Baayen and R. Schreuder (Berlin: Mouton de Gruyter), 355–390.

Google Scholar

Baayen, R. H., Milin, P., Filipović Durdević, D., Hendrix, P., and Marelli, M. (2011). An amorphous model for morphological processing in visual comprehension based on naive discriminative learning. Psychol. Rev. 118, 438–482. doi: 10.1037/a0023851

PubMed Abstract | CrossRef Full Text | Google Scholar

Baayen, R. H., Milin, P., and Ramscar, M. (2016a). Frequency in lexical processing. Aphasiology 30, 1174–1220. doi: 10.1080/02687038.2016.1147767

CrossRef Full Text | Google Scholar

Baayen, R. H., Piepenbrock, R., and van Rijn, H. (1993). The CELEX Lexical Database (CD-ROM). Linguistic Data Consortium, University of Pennsylvania, Philadelphia, PA.

Google Scholar

Baayen, R. H., Shaoul, C., Willits, J., and Ramscar, M. (2016b). Comprehension without segmentation: A proof of concept with naive discriminative learning. Lang. Cogn. Neurosci. 31, 106–128. doi: 10.1080/23273798.2015.1065336

CrossRef Full Text | Google Scholar

Baayen, R. H., Vasishth, S., Bates, D., and Kliegl, R. (2017). The cave of shadows. Addressing the human factor with generalized additive mixed models. J. Mem. Lang. 94, 206–234. doi: 10.1016/j.jml.2016.11.006

CrossRef Full Text | Google Scholar

Bates, D. M., Kliegl, R., Vasishth, S., and Baayen, R. H. (2015). Parsimonious mixed models. arxiv 1506.04967.

Google Scholar

Bauer, L., Lieber, R., and Plag, I. (2015). The Oxford Reference Guide to English Morphology. Oxford: Oxford University Press.

Google Scholar

Beard, R. (1977). On the extent and nature of irregularity in the lexicon. Lingua 42, 305–341. doi: 10.1016/0024-3841(77)90102-4

CrossRef Full Text | Google Scholar

Blevins, J. P. (2003). Stems and paradigms. Language 79, 737–767. doi: 10.1353/lan.2003.0206

CrossRef Full Text | Google Scholar

Blevins, J. P. (2006). Word-based morphology. J. Linguist. 42, 531–573. doi: 10.1017/S0022226706004191

CrossRef Full Text | Google Scholar

Blevins, J. P. (2016). Word and Paradigm Morphology. Oxford: Oxford University Press.

Google Scholar

Booij, G. E. (1986). Form and meaning in morphology: the case of Dutch ‘agent nouns’. Linguistics 24, 503–517. doi: 10.1515/ling.1986.24.3.503

CrossRef Full Text | Google Scholar

Butz, M. V., and Kutter, E. F. (2016). How the Mind Comes Into Being: Introducing Cognitive Science From a Functional and Computational Perspective. Oxford: Oxford University Press.

Google Scholar

Cheng, X., Khomtchouk, B., Matloff, N., and Mohanty, P. (2018). Polynomial regression as an alternative to neural nets. arXiv 1806.06850.

Google Scholar

Chersi, F., Ferro, M., Pezzulo, G., and Pirrelli, V. (2014). Topological self-organization and prediction learning support both action and lexical chains in the brain. Top. Cogn. Sci. 6, 476–491. doi: 10.1111/tops.12094

PubMed Abstract | CrossRef Full Text | Google Scholar

Chomsky, N., and Halle, M. (1968). The Sound Pattern of English. New York, NY: Harper and Row.

Google Scholar

Chuang, Y., Vollmer, M.-L., Shafaei-Bajestan, E., Gahl, S., Hendrix, P., and Baayen, R. H. (2019). The Processing of Nonword Form and Meaning in Production and Comprehension: A Computational Modeling Approach Using Linear Discriminative Learning. University of Tübingen.

Google Scholar

Cieliebak, M., Dertu, J., Uzdilli, F., and Egger, D. (2017). “A twitter corpus and benchmark resources for german sentiment analysis,” in Proceedings of the 4th International Workshop on Natural Language Processing for Social Media (SocialNLP 2017) (Valencia).

Google Scholar

Creemers, A., Goodwin Davies, A., Wilder, R. J., Tamminga, M., and Embick, D. (2019). Opacity, transparency, and morphological priming: a study of prefixed verbs in Dutch. J. Mem. Lang. 110:104055. doi: 10.1016/j.jml.2019.104055

CrossRef Full Text | Google Scholar

Daniel, W. B., and Yeung, E. (2019). A constructive approach for one-shot training of neural networks using hypercube-based topological coverings. arXiv 1901.02878.

Google Scholar

Danks, D. (2003). Equilibria of the Rescorla-Wagner model. J. Math. Psychol. 47, 109–121. doi: 10.1016/S0022-2496(02)00016-0

CrossRef Full Text | Google Scholar

De Grauwe, S., Lemhöfer, K., and Schriefers, H. (2019). Processing derived verbs: the role of motor-relatedness and type of morphological priming. Lang. Cogn. Neurosci. 34, 973–990. doi: 10.1080/23273798.2019.1599129

CrossRef Full Text | Google Scholar

Deriu, J., Lucchi, A., De Luca, V., Severyn, A., Müller, S., Cieliebak, M., et al. (2017). “Leveraging large amounts of weakly supervised data for multi-language sentiment classification,” in Proceedings of the 26th International World Wide Web Conference (WWW-2017) (Perth, WA). doi: 10.1145/3038912.3052611

CrossRef Full Text | Google Scholar

Divjak, D., Milin, P., and Baayen, R. H. (2017). A learning perspective on individual differences in skilled reading: exploring and exploiting orthographic and semantic discrimination cues. J. Exp. Psychol. Learn. Mem. Cogn. 43, 1730–1751. doi: 10.1037/xlm0000410

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunabeitia, J., Kinoshita, S., Carreiras, M., and Norris, D. (2011). Is morpho-orthographic decomposition purely orthographic? Evidence from masked priming in the same-different task. Lang. Cogn. Process. 26, 509–529. doi: 10.1080/01690965.2010.499215

CrossRef Full Text | Google Scholar

Eisenberg, P. (2004). Grundriss der deutschen Grammatik: Das Wort. 2nd Edn. Vol. 1. Stuttgart; Weimar: J. B. Metzler.

Eliasmith, C., Stewart, T. C., Choo, X., Bekolay, T., DeWolf, T., Tang, Y., et al. (2012). A large-scale model of the functioning brain. Science 338, 1202–1205. doi: 10.1126/science.1225266

PubMed Abstract | CrossRef Full Text | Google Scholar

Elman, J. L. (2009). On the meaning of words and dinosaur bones: lexical knowledge without a lexicon. Cogn. Sci. 33, 547–582. doi: 10.1111/j.1551-6709.2009.01023.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Fasiolo, M., Goude, Y., Nedellec, R., and Wood, S. (2017). Fast Calibrated Additive Quantile Regression. Available online at: https://github.com/mfasiolo/qgam

Feldman, L., and Prostko, B. (2001). Graded aspects of morphological processing: task and processing time. Brain Lang. 81, 1–16. doi: 10.1006/brln.2001.2503

PubMed Abstract | CrossRef Full Text | Google Scholar

Feldman, L. B., O'Connor, P. A., and Moscoso del Prado Martin, F. (2009). Early morphological processing is morpho-semantic and not simply morpho-orthographic: evidence from the masked priming paradigm. Psychon. Bull. Rev. 16, 684–691. doi: 10.3758/PBR.16.4.684

CrossRef Full Text | Google Scholar

Feldman, L. B., Soltano, E. G., Pastizzo, M. J., and Francis, S. E. (2004). What do graded effects of semantic transparency reveal about morphological processing? Brain Lang. 90, 17–30. doi: 10.1016/S0093-934X(03)00416-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Fleischer, W., and Barz, I. (1992). Wortbildung der deutschen gegenwartssprache. Tübingen: Max Niemeyer Verlag.

Google Scholar

Frauenfelder, U. H., and Schreuder, R. (1992). “Constraining psycholinguistic models of morphological processing and representation: the role of productivity,” in Yearbook of Morphology 1991, eds G. E. Booij and J. V. Marle (Dordrecht: Kluwer Academic Publishers), 165–183. doi: 10.1007/978-94-011-2516-1_10

CrossRef Full Text | Google Scholar

Gonnerman, L., and Anderson, E. (2001). “Graded semantic and phonological similarity effects in morphologically complex words,” in Morphology 2000: Selected Papers From the 9th Morphology Meeting, eds S. Bendjaballah, W. Dressler, O. E. Pfeiffer, and M. D. Voeikova (Amsterdam: John Benjamins), 137–148. doi: 10.1075/cilt.218.12gon

CrossRef Full Text | Google Scholar

Gonnerman, L. M., Seidenberg, M. S., and Andersen, E. S. (2007). Graded semantic and phonological similarity effects in priming: evidence for a distributed connectionist approach to morphology. J. Exp. Psychol. Gen. 136:323. doi: 10.1037/0096-3445.136.2.323

PubMed Abstract | CrossRef Full Text | Google Scholar

Grainger, J., Dufau, S., Montant, M., Ziegler, J. C., and Fagot, J. (2012). Orthographic processing in baboons (Papio papio). Science 336, 245–248. doi: 10.1126/science.1218152

PubMed Abstract | CrossRef Full Text | Google Scholar

Günther, F., Smolka, E., and Marelli, M. (2019). ‘Understanding’ differs between English and German: capturing systematic language differences of complex words. Cortex 116, 168–175. doi: 10.1016/j.cortex.2018.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Gurney, K., Prescott, T., and Redgrave, P. (2001). A computational model of action selection in the basal ganglia. Biol. Cybern. 84, 401–423. doi: 10.1007/PL00007984

CrossRef Full Text | Google Scholar

Hannagan, T., Ziegler, J. C., Dufau, S., Fagot, J., and Grainger, J. (2014). Deep learning of orthographic representations in baboons. PLoS ONE 9:e84843. doi: 10.1371/journal.pone.0084843

PubMed Abstract | CrossRef Full Text | Google Scholar

Hannun, A., Case, C., Casper, J., Catanzaro, B., Diamos, G., Elsen, E., et al. (2014). Deep speech: scaling up end-to-end speech recognition. arXiv 1412.5567.

Google Scholar

Harm, M. W., and Seidenberg, M. S. (2004). Computing the meanings of words in reading: cooperative division of labor between visual and phonological processes. Psychol. Rev. 111, 662–720. doi: 10.1037/0033-295X.111.3.662

PubMed Abstract | CrossRef Full Text | Google Scholar

Herdağdelen, A., and Marelli, M. (2017). Social media and language processing: how facebook and twitter provide the best frequency estimates for studying word recognition. Cogn. Sci. 41, 976–995. doi: 10.1111/cogs.12392

PubMed Abstract | CrossRef Full Text | Google Scholar

Kappel, D., Habenschuss, S., Legenstein, R., and Maass, W. (2015). Network plasticity as bayesian inference. PLoS Comput. Biol. 11:e1004485. doi: 10.1371/journal.pcbi.1004485

PubMed Abstract | CrossRef Full Text | Google Scholar

Kappel, D., Legenstein, R., Habenschuss, S., Hsieh, M., and Maass, W. (2017). Reward-based stochastic self-configuration of neural circuits. arXiv 1704.04238.

Google Scholar

Kielar, A., and Joanisse, M. F. (2011). The role of semantic and phonological factors in word recognition: an erp cross-modal priming study of derivational morphology. Neuropsychologia 49, 161–177. doi: 10.1016/j.neuropsychologia.2010.11.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuperman, V., Bertram, R., and Baayen, R. H. (2008). Morphological dynamics in compound processing. Lang. Cogn. Process. 23, 1089–1132. doi: 10.1080/01690960802193688

CrossRef Full Text | Google Scholar

Kuperman, V., Bertram, R., and Baayen, R. H. (2010). Processing trade-offs in the reading of Dutch derived words. J. Mem. Lang. 62, 83–97. doi: 10.1016/j.jml.2009.10.001

CrossRef Full Text | Google Scholar

Kuperman, V., Schreuder, R., Bertram, R., and Baayen, R. H. (2009). Reading of multimorphemic Dutch compounds: towards a multiple route model of lexical processing. J. Exp. Psychol. 35, 876–895. doi: 10.1037/a0013484

CrossRef Full Text | Google Scholar

Landauer, T., and Dumais, S. (1997). A solution to Plato's problem: the latent semantic analysis theory of acquisition, induction and representation of knowledge. Psychol. Rev. 104, 211–240. doi: 10.1037/0033-295X.104.2.211

CrossRef Full Text | Google Scholar

Lavric, A., Rastle, K., and Clapp, A. (2011). What do fully visible primes and brain potentials reveal about morphological decomposition? Psychophysiology 48, 676–686. doi: 10.1111/j.1469-8986.2010.01125.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lazaridou, A., Marelli, M., Zamparelli, R., and Baroni, M. (2013). “Compositionally derived representations of morphologically complex words in distributional semantics,” in Proceedings of the 51st Annual Meeting of the Association for Computational Linguistics - ACL (1) (Sofia: Association for Computational Linguistics), 1517–1526.

Google Scholar

Linke, M., Broeker, F., Ramscar, M., and Baayen, R. H. (2017). Are baboons learning “orthographic” representations? Probably not. PLoS ONE 12:e0183876. doi: 10.1371/journal.pone.0183876

PubMed Abstract | CrossRef Full Text | Google Scholar

Longtin, C., Segui, J., and Hallé, P. (2003). Morphological priming without morphological relationship. Lang. Cogn. Process. 18, 313–34. doi: 10.1080/01690960244000036

CrossRef Full Text | Google Scholar

Lund, K., and Burgess, C. (1996). Producing high-dimensional semantic spaces from lexical co-occurrence. Behav. Res. Methods Instr. Comput. 28, 203–208. doi: 10.3758/BF03204766

CrossRef Full Text | Google Scholar

Marelli, M., Amenta, S., Morone, E. A., and Crepaldi, D. (2013). Meaning is in the beholder's eye: morpho-semantic effects in masked priming. Psychon. Bull. Rev. 20, 534–541. doi: 10.3758/s13423-012-0363-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Marelli, M., and Baroni, M. (2015). Affixation in semantic space: modeling morpheme meanings with compositional distributional semantics. Psychol. Rev. 122:485. doi: 10.1037/a0039267

PubMed Abstract | CrossRef Full Text | Google Scholar

Marslen-Wilson, W., Older, L., Janssen, D., and Waksler, S. (1994a). “Stems and affixes: local and non-local attachment,” in Paper Presented to the Experimental Psychology Society (London).

Marslen-Wilson, W., Tyler, L. K., Waksler, R., and Older, L. (1994b). Morphology and meaning in the English mental lexicon. Psychol. Rev. 101, 3–33. doi: 10.1037/0033-295X.101.1.3

CrossRef Full Text | Google Scholar

Marsolek, C. J. (2008). What antipriming reveals about priming. Trends Cogn. Sci. 12, 176–181. doi: 10.1016/j.tics.2008.02.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Marzi, C., Ferro, M., and Pirrelli, V. (2018). “Is inflectional irregularity dysfunctional to human processing?” in Abstract Booklet, The Mental Lexicon 2018, ed V. Kuperman (Edmonton, AB: University of Alberta), 60.

Matthews, P. H. (1974). Morphology. An Introduction to the Theory of Word Structure. Cambridge: Cambridge University Press.

McClelland, J. L., and Rumelhart, D. E. (Eds.). (1986). Parallel Distributed Processing. Explorations in the Microstructure of Cognition. Vol. 2: Psychological and Biological Models. Cambridge, MA: MIT Press.

Google Scholar

Meunier, F., and Longtin, C. (2007). Morphological decomposition and semantic integration in word processing. J. Mem. Lang. 56, 457–471. doi: 10.1016/j.jml.2006.11.005

CrossRef Full Text | Google Scholar

Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and Dean, J. (2013). “Distributed representations of words and phrases and their compositionality,” in Advances in Neural Information Processing Systems, eds C. J. C. Burges, L. Bottou, M. Welling, Z. Ghahramani, and K. Q. Weinberger (Curran Associates, Inc), 26, 3111–3119. Available online at: http://papers.nips.cc/paper/5021-distributed-representations-of-words-and-phrases-and-their-compositionality.pdf

Google Scholar

Milin, P., Feldman, L. B., Ramscar, M., Hendrix, P., and Baayen, R. H. (2017a). Discrimination in lexical decision. PLoS ONE 12:e0171935. doi: 10.1371/journal.pone.0171935

PubMed Abstract | CrossRef Full Text | Google Scholar

Milin, P., Smolka, E., and Feldman, L. B. (2017b). “Models 11 of lexical access and morphological processing,” in The Handbook of Psycholinguistics, eds E. M. Fernández and H. S. Cairns (Malden: Wiley-Blackwell), 240–268. doi: 10.1002/9781118829516.ch11

CrossRef Full Text | Google Scholar

Nault, K. (2010). Morphological therapy protocol. (Ph. D. thesis), University of Alberta, Edmonton, AB.

Google Scholar

Napps, S. E., and Fowler, C. A. (1987). Formal relationships among words and the organization of the mental lexicon. J Psycholinguist Res. 16, 257–272.

PubMed Abstract | Google Scholar

Norris, D., and Kinoshita, S. (2008). Perception as evidence accumulation and bayesian inference: insights from masked priming. J. Exp. Psychol. 137, 434–455. doi: 10.1037/a0012799

PubMed Abstract | CrossRef Full Text | Google Scholar

Pastizzo, M. J., and Feldman, L. B. (2002). Does prime modality influence morphological processing? Brian Lang. 81, 28–41. doi: 10.1006/brln.2001.2504

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinker, S. (1999). Words and Rules: The Ingredients of Language. London: Weidenfeld and Nicolson.

Plag, I. (2003). Word-Formation in English. Cambridge: Cambridge University Press.

Google Scholar

Plaut, D. C., and Gonnerman, L. M. (2000). Are non-semantic morphological effects incompatible with a distributed connectionist approach to lexical processing? Lang. Cogn. Process. 15, 445–485. doi: 10.1080/01690960050119661

CrossRef Full Text | Google Scholar

Rastle, K., and Davis, M. (2008). Morphological decomposition based on the analysis of orthography. Lang. Cogn. Process. 23, 942–971. doi: 10.1080/01690960802069730

CrossRef Full Text | Google Scholar

Rastle, K., Davis, M. H., Marslen-Wilson, W., and Tyler, L. K. (2000). Morphological and semantic effects in visual word recognition: a time-course study. Lang. Cogn. Process. 15, 507–537. doi: 10.1080/01690960050119689

CrossRef Full Text | Google Scholar

Rastle, K., Davis, M. H., and New, B. (2004). The broth in my brother's brothel: morpho-orthographic segmentation in visual word recognition. Psychon. Bull. Rev. 11, 1090–1098. doi: 10.3758/BF03196742

PubMed Abstract | CrossRef Full Text | Google Scholar

Redgrave, P., Prescott, T., and Gurney, K. (1999). The basal ganglia: a vertebrate solution to the selection problem? Neuroscience 89, 1009–1023. doi: 10.1016/S0306-4522(98)00319-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Rescorla, R. A., and Wagner, A. R. (1972). “A theory of Pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement,” in Classical Conditioning II: Current Research and Theory, eds A. H. Black and W. F. Prokasy (New York, NY: Appleton Century Crofts), 64–99.

Google Scholar

Roelofs, A. (1997a). A case for nondecomposition in conceptually driven word retrieval. J. Psycholinguist. Res. 26, 33–67. doi: 10.1023/A:1025060104569

CrossRef Full Text | Google Scholar

Roelofs, A. (1997b). “Morpheme frequency in speech production: testing WEAVER,” in Yearbook of Morphology 1996, eds G. E. Booij and J. Van Marle (Dordrecht: Kluwer), 135–154.

Google Scholar

Roelofs, A., Baayen, R. H., and van den Brink, D. (2002). Morphology by itself in planning the production of spoken words. Psychon. Bull. Rev. 9, 132–138. doi: 10.3758/BF03196269

PubMed Abstract | CrossRef Full Text | Google Scholar

Rumelhart, D. E., and McClelland, J. L. (1986). “On learning the past tenses of English verbs,” in Parallel Distributed Processing. Explorations in the Microstructure of Cognition. Vol. 2: Psychological and Biological Models, eds J. L. McClelland and D. E. Rumelhart (Cambridge, MA: The MIT Press), 216–271.

Google Scholar

Schmidtke, D., Matsuki, K., and Kuperman, V. (2017). Surviving blind decomposition: a distributional analysis of the time-course of complex word recognition. J. Exp. Psychol. Learn. Mem. Cogn. 43:1793. doi: 10.1037/xlm0000411

PubMed Abstract | CrossRef Full Text | Google Scholar

Schreuder, R. (1990). Lexical processing of verbs with separable particles. Yearb. Morphol. 3, 65–79.

Schreuder, R., Burani, C., and Baayen, R. H. (2003). “Parsing and semantic opacity” in Reading Complex Words. Cross-Language Studies, eds E. Assink and D. Sandra (Dordrecht: Kluwer), 159–189. doi: 10.1007/978-1-4757-3720-2_8

CrossRef Full Text | Google Scholar

Schreuder, R., Grendel, M., Poulisse, N., Roelofs, A., and Van de Voort, M. (1990). “Lexical processing, morphological complexity and reading,” in Comprehension Processes in Reading, eds D. A. Balotta, G. B. Flores d'Arcais, and K. Rayner (Hillsdale, NJ: Erlbaum), 125–141.

Google Scholar

Schriefers, H., Zwitserlood, P., and Roelofs, A. (1991). The identification of morphological complex spoken words: continuous processing or decomposition? J. Mem. Lang. 30, 26–47. doi: 10.1016/0749-596X(91)90009-9

CrossRef Full Text | Google Scholar

Sering, K., Weitz, M., Kuenstle, D., and Schneider, L. (2017). Pyndl: Naive Discriminative Learning in Python. doi: 10.5281/zenodo.597964

CrossRef Full Text | Google Scholar

Sering, T., Milin, P., and Baayen, R. H. (2018b). Language comprehension as a multiple label classification problem. Stat. Neerland. 72, 339–353. doi: 10.1111/stan.12134

CrossRef Full Text | Google Scholar

Shafaei Bajestan, E., and Baayen, R. H. (2018). “Wide learning for auditory comprehension,” in Interspeech (Hyderabad). doi: 10.21437/Interspeech.2018-2420

CrossRef Full Text | Google Scholar

Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L., Van Den Driessche, G., et al. (2016). Mastering the game of go with deep neural networks and tree search. Nature 529:484. doi: 10.1038/nature16961

PubMed Abstract | CrossRef Full Text | Google Scholar

Smolka, E., and Eulitz, C. (2011). “Asymmetric meaning assembly for semantically transparent and opaque complex verbs in German,” in Paper Presented at the Seventh International Morphological Processing Conference (MOPROC) (San Sebastian).

Smolka, E., and Eulitz, C. (2018). Psycholinguistic measures for German verb pairs: semantic trans-parency, semantic relatedness, verb family size, and age of reading acquisition. Behav. Res. Methods 50, 1540–1562. doi: 10.3758/s13428-018-1052-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Smolka, E., Gondan, M., and Rösler, F. (2015). Take a stand on understanding: electrophysiological evidence for stem access in german complex verbs. Front. Hum. Neurosci. 9:62. doi: 10.3389/fnhum.2015.00062

PubMed Abstract | CrossRef Full Text | Google Scholar

Smolka, E., Komlosi, S., and Rösler, F. (2009). When semantics means less than morphology: the processing of German prefixed verbs. Lang. Cogn. Process. 24, 337–375. doi: 10.1080/01690960802075497

CrossRef Full Text | Google Scholar

Smolka, E., Libben, G., and Dressler, W. U. (2019). When morphological structure overrides meaning: evidence from German prefix and particle verbs. Lang. Cogn. Neurosci. 34, 599–614. doi: 10.1080/23273798.2018.1552006

CrossRef Full Text | Google Scholar

Smolka, E., Preller, K. H., and Eulitz, C. (2014). ‘verstehen’ (‘understand’) primes ‘stehen’ (‘stand’): morphological structure overrides semantic compositionality in the lexical representation of German complex verbs. J. Mem. Lang. 72, 16–36. doi: 10.1016/j.jml.2013.12.002

CrossRef Full Text | Google Scholar

Smolka, E., Zwitserlood, P., and Rösler, F. (2007). Stem access in regular and irregular inflection: evidence from German participles. J. Mem. Lang. 57, 325–347. doi: 10.1016/j.jml.2007.04.005

CrossRef Full Text | Google Scholar

Stewart, T. C., Bekolay, T., and Eliasmith, C. (2012). Learning to select actions with spiking neurons in the basal ganglia. Front. Neurosci. 6:2. doi: 10.3389/fnins.2012.00002

PubMed Abstract | CrossRef Full Text | Google Scholar

Stump, G. (2001). Inflectional Morphology: A Theory of Paradigm Structure. Cambridge: Cambridge University Press.

Google Scholar

Taft, M., and Forster, K. I. (1975). Lexical storage and retrieval of prefixed words. J. Verb. Learn. Verb. Behav. 14, 638–647. doi: 10.1016/S0022-5371(75)80051-X

CrossRef Full Text | Google Scholar

Tomaschek, F., Plag, I., Ernestus, M., and Baayen, R. H. (2019). Phonetic effects of morphology and context: Modeling the duration of word-final S in english with naive discriminative learning. J. Linguist. 1–39. doi: 10.31234/osf.io/4bmwg

CrossRef Full Text | Google Scholar

Tomaschek, F., Tucker, B. V., Fasiolo, M., and Baayen, R. H. (2018). Practice makes perfect: the consequences of lexical proficiency for articulation. Linguist. Vanguard Band 4: Heft s2:20170018. doi: 10.1515/lingvan-2017-0018

CrossRef Full Text | Google Scholar

van Rij, J., Wieling, M., Baayen, R. H., and van Rijn, H. (2017). itsadug: Interpreting Time Series and Autocorrelated Data Using GAMMs. R package version 2.3.

Veríssimo, J. (2018). “Taking it a level higher: the leia model of complex word recognition,” in Poster Presented at AMLaP 2018 (Berlin).

Wood, S. N. (2017). Generalized Additive Models. New York, NY: Chapman & Hall; CRC. doi: 10.1201/9781315370279

PubMed Abstract | CrossRef Full Text | Google Scholar

Zwitserlood, P. (2018). “Processing and representation of morphological complexity in native language comprehension and production,” in The Construction of Words. Studies in Morphology, ed G. E. Booij (Cham: Springer), 4, 583–602.

Google Scholar