An energy-efficient process of non-deterministic computation drives the emergence of predictive models and exploratory behavior

Cortical neural networks encode information about the environment, combining data across sensory modalities to form predictive models of the world, which in turn drive behavioral output. Cortical population coding is probabilistic, with synchronous firing across the neural network achieved in the context of noisy inputs. The system-wide computational process, which encodes the likely state of the local environment, is achieved at a cost of only 20 Watts, indicating a deep connection between neuronal information processing and energy-efficient computation. This report presents a new framework for modeling non-deterministic computation in cortical neural networks, in terms of thermodynamic laws. Initially, free energy is expended to produce von Neumann entropy, then predictive value is extracted from that thermodynamic quantity of information. The extraction of predictive value during a single computation yields a percept, or a predictive semantical statement about the local environment, and the integration of sequential neural network states yields a temporal sequence of percepts, or a predictive syntactical statement about the cause-effect relationship between perceived events. The amount of predictive value available for computation is limited by the total amount of energy entering the system, and will always be incomplete, due to thermodynamic constraints. This process of thermodynamic computation naturally produces a rival energetic cost function, which minimizes energy expenditure: the system can either explore its local environment to gain potential predictive value, or it can exploit previously-acquired predictive value by triggering a contextually-relevant and thermodynamically-favored sequence of neural network states. The system grows into a more ordered state over time, as it physically encodes the predictive value acquired by interacting with its environment.

1 Introduction

Animals collect data about the world through multiple sensory modalities, transducing physical events in the local environment into electrical signals, then passing these data to dedicated processing centers within the central nervous system (Hubel and Wiesel, 1959; Fettiplace, 2017). In the cerebral cortex, information is integrated across multiple sensory modalities and compared with contextually-relevant predictions or expectations (Schultz and Dickinson, 2000; Lochmann and Deneve, 2011). This computational process informs the selection of behavior (Arnal et al., 2011; Wimmer et al., 2015). However, the mechanisms underlying information integration and predictive modeling at the systems level are currently not well understood.

Cortical neural networks encode both the state of the local environment and the divergence from expectations set by a predictive model (Melloni et al., 2011; Kok et al., 2012). Critically, any information that is found to have useful predictive value (with reliable temporal contingency) is encoded into memory storage through synaptic remodeling, which favors those same patterns of neural activity to re-occur in a similar context (Hebb, 1949; Turrigiano et al., 1998). Thus, neurons coordinate memory storage and processing functions within a single computational unit. Yet this synaptic remodeling is primarily a feature of cortical neurons, not spinal neurons. Although some spike timing-dependent plasticity occurs upon repetitive paired stimulation (Nishimura et al., 2013; Urbin et al., 2017; Ting et al., 2020) and after injury (Tan et al., 2008; Bradley et al., 2019; Simonetti and Kuner, 2020) in spinal circuits, cortical neurons engage in spontaneous synaptic remodeling under standard physiological conditions (Kapur et al., 1997; Huang et al., 2005; Zarnadze et al., 2016). The emergence of a more ordered system state in cortical neural networks during learning and development correlates with the construction of predictive cognitive models (Kitano and Fukai, 2004; Gotts, 2016).

Uncovering the natural processes by which cortical neural networks form predictive models over time may drive advances in both the cognitive sciences and the field of computational intelligence. As information is processed in cortical neural networks, predictive value is extracted and stored, and output behavior is selected in the context of both incoming sensory data and relevant past experience. This massively parallel computing process, which accesses predictive models stored in local memory, is highly energy-efficient. Yet it is not currently well understood how the cerebral cortex achieves this exascale computing power and a generalized problem-solving ability at an energetic cost of only 20 Watts (Sokoloff, 1981; Magistretti and Pellerin, 1999). This energetic efficiency is particularly surprising, given that cortical neurons retain sensitivity to random electrical noise in gating signaling outcomes (Stern et al., 1997; Lee et al., 1998; Dorval and White, 2005; Averbeck et al., 2006), a property that should be expected to reduce energy efficiency.

But importantly, prediction minimizes energetic expenditure. In cortical neural networks, prediction errors provide an energy efficient method of encoding how much a percept diverges from the contextual expectation (Friston and Kiebel, 2009; Adams et al., 2013). The “minimization of surprise” was proposed by Karl Friston to be the guiding force driving the improvement of predictive models, with new information continually prompting the revision of erroneous priors (Friston et al., 2006; Feldman and Friston, 2010). This view— embodied by “the free energy principle”—asserts that biological systems gradually achieve a more ordered configuration over time by identifying a more compatible state with their environment, simply by reducing predictive errors (Bellec et al., 2020). It should be noted however that “free energy” is a statistical quantity, not a thermodynamic quantity, in this particular neuroscientific context. Likewise, the concept of “free energy” has been employed in the machine learning field to solve optimization problems through a process of gradient descent (Scellier and Bengio, 2017). For the past 40 years, researchers have striven to explain computation, in both biological and simulated neural networks, in terms of “selecting an optimal system state from a large probability distribution” (Hopfield, 1987; Beck et al., 2008; Maoz et al., 2020). Yet a direct connection between noisy coding and energy efficiency has remained elusive. A deeper explanation of cortical computation, in terms of thermodynamics, is needed.

In this report, a new theoretical model is presented, tying together the concepts of computational free energy and thermodynamic free energy. Here, the macrostate of the cortical neural network is modeled as the mixed sum of all component microstates—the physical quantity of information, or von Neumann entropy, held by the system. The extraction of predictive value, or consistency, then compresses this thermodynamic quantity of information, as an optimal system state is selected from a large probability distribution. This computational process not only maximizes free energy availability; it also yields a multi-sensory percept, or a predictive semantical statement about the present state of the local environment, which is encoded by the cortical neural network state. These multi-sensory percepts are then integrated over time to form predictive syntactical statements about the relationship between perceived events, encoded by a sequence of cortical neural network states. This energy-efficient computational process naturally leads to the construction of predictive cognitive models.

Since energy is always conserved, the compression of information entropy must be paired with the release of thermal free energy, local to any reduction in uncertainty, in accordance with the Landauer principle (Landauer, 1961; Berut et al., 2012; Jun et al., 2014; Yan et al., 2018). This free energy can then be used to do work within the system, physically encoding the predictive value that was extracted from some thermodynamic quantity of information. This computational process allows a non-dissipative thermodynamic system to grow into a more ordered state over time, as it encodes predictive value. The amount of predictive value available during a computation is limited by the total amount of energy entering the system over that period of time, and will always be incomplete, due to thermodynamic constraints. The system will therefore respect the second law of thermodynamics and maintain some amount of uncertainty during predictive processing.

This new approach offers a theoretical framework for achieving energy-efficient non-deterministic computation in cortical neural networks, in terms of thermodynamic laws. It is also consistent with the extraordinary energy efficiency of the human brain. In addition to this broad explanatory power, this new approach offers testable hypotheses relating probabilistic computational processes to network-level dynamics and behavior.

2 Preliminaries

2.1 Justification for the approach

This approach applies several established principles in computational physics to model the entropy generated by the cerebral cortex as both a thermodynamic and a computational quantity. A step-by-step logical justification for this approach follows.

1. Entropy is both a computational quantity and a thermodynamic quantity. It is both a quantitative measure of all possible arrangements for the components of a thermodynamic system, and the amount of free energy expended to generate that quantity of information.

2. The brain is both a thermodynamic system and a computational system. The amount of thermodynamic entropy generated may be considered equivalent to the amount of computational entropy generated, with both represented by the von Neumann entropy of the system.

3. Cortical neurons allow random electrical noise to gate signaling outcomes, with the inherently probabilistic movement of electrons contributing to the likelihood of the cell reaching action potential threshold (Stern et al., 1997; Lee et al., 1998; Dorval and White, 2005; Averbeck et al., 2006). The inter-spike interval cannot be predicted by upstream inputs alone; random electrical noise materially contributes to the membrane potential.

4. Since cortical neurons allow statistically random events to affect the neuronal membrane potential, each cell should be modeled as a statistical ensemble of component pure states (von Neumann entropy) rather than a binary on- or off-state (Shannon entropy). The state of each neuronal membrane potential in the system is then the mixed sum of all component electron states.

5. A statistically random ensemble of neurons across the cortex fires synchronously, encoding a multisensory percept (Beck et al., 2008; Maoz et al., 2020). Wakeful awareness is characterized by this periodic activity at gamma frequencies (Csibra et al., 2000; Engel et al., 2001; Herrmann and Knight, 2001; Buzsaki and Draguhn, 2004).

6. Since the ensembles of cortical neurons which fire synchronously at periodic intervals are statistically random, these cells should be modeled as a statistical ensemble of component microstates (von Neumann entropy) rather than a statistical ensemble of binary computational units (Shannon entropy). The state of the network is then the mixed sum of all component neuron states.

7. Cortical neurons must generate a lot of entropy, since empirical studies have shown they allow random electrical noise to affect the membrane potential (Stern et al., 1997; Lee et al., 1998; Dorval and White, 2005; Averbeck et al., 2006).

8. Cortical neurons must not generate a lot of entropy, since empirical studies have shown them to be highly energy-efficient (Sokoloff, 1981; Magistretti and Pellerin, 1999).

9. The only way that Steps 7 and 8 can both be true is if cortical neurons generate entropy through noisy coding, then compress that thermodynamic and computational quantity by identifying correlations in the data.

10. von Neumann entropy can be compressed, as the system interacts with its surrounding environment and finds a mutually compatible state with that surrounding environment (Glansdorff and Prigogine, 1971; Hillert and Agren, 2006; Martyushev et al., 2007).

11. This process of information compression is equivalent to the extraction of predictive value; predictive value is a thermodynamic quantity, which can be extracted from the total amount of information entropy generated by a far-from-equilibrium non-dissipative system (Still et al., 2012).

12. The quantity of information compression is equivalent to the quantity of predictive value extracted during the computation.

13. The quantity of non-predictive value is equivalent to the net quantity of entropy generated by the system during the computation.

14. The quantity of predictive value extracted during the computation is equivalent to the correlations extracted (by the encoding system) from the total quantity of information during the computation.

15. In accordance with the Landauer principle, the quantity of information compression during the computation is equivalent to the quantity of free energy that is recovered by the system during the computation (Landauer, 1961; Berut et al., 2012; Jun et al., 2014; Yan et al., 2018).

16. Any free energy recovered by the system during information compression can be used to do work. This work may involve encoding the predictive value acquired during the computational timeframe into the physical state of the encoding system.

Definitions: Information is a distribution of possible system states, given by the von Neumann entropy of the system, or the mixed sum of all component pure states. Predictive value is a measure of correlation between system states, and the “correlation” between the encoding system and its surrounding environment is equivalent to the predictive value the encoding system has extracted upon interacting with its surrounding environment. Internal system states which match external system states have high predictive value, while internal system states which do not match external system states have low predictive value. When an internal system state “matches” an external system state, the external system state is parameterized by the internal system state, such that the predicted external system state is effectively represented by the internal system state.

In summary, cortical information processing can be effectively described in terms of von Neumann entropy. Here, the system generates information as both a thermodynamic and a computational quantity, and the laws of thermodynamics apply to any exchange of free energy and entropy within the system (Figure 1). The limits imposed by these laws are explored in the results section of this report.

Figure 1

Figure 1. A summary of key principles of this theoretical framework. The cortical neural network (system A) interacts with its surrounding environment (system B). During this thermodynamic computation, system A encodes the most likely and consistent state of system B. Critically, the far-from-equilibrium system A traps energy from system B to do work and create heat. In doing so, the first law of thermodynamics is satisfied: energy is neither created nor destroyed, and this value remains the sum of all free energy and temperature-entropy. Yet the distribution of all potential and kinetic energy across the system, represented by the Hamiltonian operator, can be optimized during the computation. The trial Hamiltonian always maximizes thermodynamic free energy and minimizes entropy, compared with the reference Hamiltonian. Critically, some amount of entropy or uncertainty will always remain at the completion of a thermodynamic computation. For this reason, the second law of thermodynamics is always satisfied: the entropy of system A plus the entropy of system B will always increase over time. Yet the entropy of the combined system can be minimized, as correlations are identified between the two systems, leading to information compression in accordance with the subadditivity rule. In summary, thermodynamic quantities are always constrained by the first and second laws of thermodynamics, even as the two systems evolve into a more mutually compatible state over time.

2.2 Entropy is a description of the system macrostate

For a classical thermodynamic system, the macrostate of the system is a distribution of microstates, given by the Gibbs entropy formula. With this classical approach, each computational unit is in a binary 0 or 1 state, and the neural network is modeled as a function of these component microstates. Here, k_B is the Boltzmann constant, E_i is the energy of microstate i, p_i is the probability that microstate occurs, and the Gibbs entropy of the system is given by S. This relationship is provided in Equation 1:

$\begin{array}{ll}S=-k_B{\displaystyle \sum }{p}_i\text{ ln }{p}_i.& (1)\end{array}$

Yet in cortical neural networks, a statistically random ensemble of cells fires synchronously at periodic intervals (Beck et al., 2008; Maoz et al., 2020). Therefore, the macrostate of the system is better described as a statistical ensemble of all component pure states, given by the von Neumann entropy formula (Bengtsson and Zyczkowski, 2007). With this method, each computational unit has some probability of being in a 0 or 1 state, as a function of its fluctuating membrane potential. Indeed, the membrane potential of each cortical neuron is affected by coincident upstream signals and random electrical noise (Stern et al., 1997; Lee et al., 1998; Dorval and White, 2005; Averbeck et al., 2006). This uncertainty, or the information encoded by each computational unit, can also be modeled as a statistical ensemble of component pure states, given by the von Neumann entropy formula, which is provided in Equation 2:

$\begin{array}{ll}S(\rho )=-\text{Tr }(\rho \text{ ln }\rho ),\text{ where }\rho ={\displaystyle \sum }{p}_x|{\psi }_x\rangle \langle {\psi }_x|.& (2)\end{array}$

Here, entropy is a high-dimensional volume of possible system states, represented by the trace across a density matrix ρ. ρ is the sum of all mutually orthogonal pure states ρ_x, each occurring with some probability p_x. As the encoding Thermodynamic System “A” is perturbed, by interacting with its surrounding environment, Thermodynamic System “B,” the density matrix undergoes a time evolution, from ${\rho }_{AB}\to {\rho }_{AB}^{\prime }$. During this time evolution, consistencies can be identified between the two particle systems (Schumacher, 1995; Bennett and Shor, 1998; Jozsa et al., 1998; Sciara et al., 2017). This non-deterministic process leads to the selection of a mutually-compatible system state. Here, entropy is additive in uncorrelated systems, but it is subtractive in correlated systems, as mutual redundancies in system states are recognized and reduced. This leads to the subadditivity rule:

$\begin{array}{ll}\begin{array}{l}S({\rho }_{AB})=S({\rho }_A)+S({\rho }_B)\\ =S({\rho }_A^{\prime })+S({\rho }_B^{\prime })\ge S({\rho }_{AB}^{\prime }).\end{array}\hfill & (3)\end{array}$

A cortical neural network is a far-from equilibrium thermodynamic system that actively acquires energy to accomplish work. That work involves encoding the state of the surrounding environment into the physical state of the system itself. This theoretical approach models the encoding process as a thermodynamic computation. The macrostate that results from this thermodynamic computation is not a deterministic outcome; rather, an optimal system state is selected in the present context from a large probability distribution. The most thermodynamically favored and “optimal” system state is the one that is both most correlated with the surrounding environment and most compatible with existing anatomical and physiological constraints. The physical compression of entropy, during a computation, causes the system to attain a more ordered state, as it becomes less random and more compatible with its surrounding environment.

3 Methods

3.1 Thermodynamic constraints on irreversible work

Thermodynamic System “A”—a cortical neural network identifies an optimal state in the context of its surrounding environment, Thermodynamic System “B,” by selecting the most consistent arrangement of microstates to encode the state of its surrounding environment. This mechanistic process of thermodynamic computation can be modeled with a Hamiltonian 〈H〉_t, which is the sum of all potential and kinetic energies in a non-equilibrium system. The Hamiltonian operates on a vector space, with some spectrum of eigenvalues, or possible outcomes. This computational process resolves the amount of free energy available to the system G_t, which is the total amount of energy in the system Ĥ less the temperature-entropy generated by the system TS_t. This relationship is provided in Equation 4:

$\begin{array}{ll}{G}_t={Ĥ}_t-T{S}_t.& (4)\end{array}$

The quantity of energy represented by the Hamiltonian remains the same over the timecourse, but the way energy is distributed across the system may change. This relationship between the Hamiltonian and the density matrix (or distribution of possible system states) is given by Equation 5:

$\begin{array}{ll}{\rho }_{AB}^{\prime }=U{\rho }_{AB}{U}^{†},\text{ where }U=\text{ exp }(-iĤt).& (5)\end{array}$

If no time has passed, or no interactions take place, the Hamiltonian is merely the sum of all degrees of freedom for all probabilistic components of the system. If however some time has passed, or interactions have taken place, the Hamiltonian Ĥ represents the time-dependent state of the system. This description of the system state is provided in Equation 6:

$\begin{array}{ll}i\hslash \frac{d\psi }{dt}=Ĥ\psi =E\psi .& (6)\end{array}$

The computation results in energy being effectively redistributed across the system, with some trial Hamiltonian maximizing free energy availability. That trial Hamiltonian—which maximizes the correlations between internal and external states, and therefore minimizes entropy or uncertainty— will be thermodynamically favored. Yet the full account must always be balanced - with the total amount of energy in the system, represented by the Hamiltonian, being the sum of all free energy G_t and temperature-entropy TS_t. The free energy of the trial Hamiltonian ${\langle \tilde{H}\rangle }_t$ must be greater than or equal to the free energy of the reference Hamiltonian 〈H〉_t. This is known as the Bogoliubov inequality:

$\begin{array}{ll}{\tilde{G}}_t={\langle \tilde{H}\rangle }_t-T{S}_t\ge G_t={\langle H\rangle }_t-T{S}_t.& (7)\end{array}$

During the computation, entropy is minimized and the free energy is maximized, as correlations are extracted between the encoding system and its surrounding environment. However, there are thermodynamic limits to this computational process. The Jarzynski equality, relating the quantity of free energy and work in non-equilibrium systems, holds (Jarzynski, 1997a,b). There simply cannot be more work dissipated toward entropy generation than the amount of energy expenditure. This relationship provides an equivalency between the average work dissipated to create entropy (an ensemble of possible measurements, given by $\bar{W}$), and the change in Gibbs free energy (given by ΔG), after some time has passed, with β = 1/k_BT. This relationship between energy expenditure and entropy is given by Equation 8:

$\begin{array}{ll}\overline{\text{exp}(-\beta W)}=\text{ exp }(-\beta \Delta G).& (8)\end{array}$

The overline marking the W term in this equation indicates an average over all possible realizations of a process which takes the system from starting state A (generally an equilibrium state) to ending state B (generally a non-equilibrium state). This average over possible realizations is an average over different possible fluctuations which could occur during the process, e.g., due to Brownian motion. This is exactly what is being modeled here, since the Hamiltonian accounts for all fluctuations affecting the membrane potential of each computational unit within the system. As a result of this noisy coding, the neural network has some distribution of possible system states, with one realization providing the best match for the surrounding environment. Each realization yields a slightly different value for the amount of free energy expended to do work. Both the reference Hamiltonian (which represents all possible paths for the system) and the trial Hamiltonian (which represents the actual path taken by the system) provide the sum of all free energy and temperature-entropy, but the trial Hamiltonian maximizes available free energy of the system and minimizes net entropy generation. So, the average work dissipated (given by the reference Hamiltonian) may be greater than the quantity of free energy expenditure; however, the specific work dissipated (given by the trial Hamiltonian) will always be less than or equal to the quantity of free energy expenditure.

Another strict thermodynamic equality, the Crooks fluctuation theorem, holds here as well—as in any path-dependent system state (Crooks, 1998). This rule relates the probability of any particular time-dependent trajectory (a → b) to its time-reversal trajectory (b → a). The Crooks fluctuation theorem requires all irreversible work (ΔW_a→b) to be greater than or equal to the difference in free energy between events and time-reversed events (ΔG = ΔG_a→b − ΔG_b→a). This theorem stipulates that, if the free energy required to do work is greater for the reversed sequence of events, compared with the forward sequence of events, the probability of forward events will be more likely than time-reversed events. This theorem, relating thermodynamic energy requirements with the probability of an event occurring, is given by Equation 9:

$\begin{array}{ll}\frac{P_{a\to b}}{P_{b\to a}}=\text{ exp }\beta (\Delta W_{a\to b}-\Delta G).& (9)\end{array}$

Any physical structure engaging in physical work will dissipate some amount of free energy toward entropy. However, this energy is not irreversibly lost (Callen and Welton, 1951). Indeed, the energy expended to create entropy cannot disappear, since energy can never be created nor destroyed. And since energy is always conserved, any compression of information entropy must be paired with the release of free energy. This conservation law, embodied by the first law of thermodynamics and the Landauer principle, has been empirically validated in recent years (Landauer, 1961; Berut et al., 2012; Jun et al., 2014; Yan et al., 2018). Any compression of information entropy, or reduction of uncertainty, must be paired with the release of free energy. This free energy can then be used to do thermodynamic work within the system. This work may involve, for example, encoding the most likely state of the surrounding environment into the state of the neural network.

3.2 Thermodynamic foundations of predictive inference

Entropy is a natural by-product of thermodynamic systems: a measure of inefficiency in doing work. Entropy is also a description of the physical system state: a vector map of all possible states for all atoms in a thermodynamic system after some time evolution. These two definitions are tied together in a system whose “work” is computing the most optimal system state to encode its environment. It is worth noting again that information compression is a known physical process that generates a discrete quantity of free energy (Landauer, 1961; Berut et al., 2012; Jun et al., 2014; Yan et al., 2018). This conversion of physical quantities is given by the Landauer limit, which provides the amount of energy released by the erasure of a single digital bit. That thermodynamic quantity of information is given by Equation 10:

$\begin{array}{ll}\langle W\rangle =k_{B}T(\text{log}2).& (10)\end{array}$

This concept can be extrapolated to computational systems with any number of possible microstates that trap energy to do computational work. The recently-derived Still dissipation theorem demonstrates that the quantity of non-predictive information in a system is proportional to the energy lost when an external driving signal changes by an incremental amount within a non-equilibrium system (Still et al., 2012). Here, the amount of information without predictive value is equal to the amount of work dissipated to entropy as the signal changes over a time course from x_{t = 0} (the immediately previous system state) to x_t (the present state):

$\begin{array}{ll}\begin{array}{l}\langle W_{diss}\left[x_{t=0}\to x_t\right]\rangle =k_{B}T\left[I_{mem}(t)-I_{pred}(t)\right]\\ =k_{B}T\left[I_{non-pred}(t)\right]\\ =k_{B}T\left[\Delta I\right].\end{array}& (11)\end{array}$

This equation stipulates that the total amount of information generated over some time evolution, subtracted by the amount of information with predictive value, is the amount of non-predictive information remaining after predictive value has been extracted. This quantity is dissipated to entropy upon the completion of the system-wide computation, and is therefore unavailable as free energy to do work (Sonntag et al., 2003). I_mem is equivalent to the total amount of information generated, or the amount of uncertainty gained by the system, over the timecourse. I_pred is the quantity of predictive value extracted during the thermodynamic computation. The net quantity remaining, I_non−pred, is the amount of work that has been dissipated to entropy upon completion of a thermodynamic computing cycle. That net quantity of non-predictive information is equal to the quantity of uncorrelated states between Systems A and B, which will always be greater than or equal to zero:

$\begin{array}{ll}\begin{array}{l}\langle W_{diss}\left[x_{t=0}\to x_t\right]\rangle =k_{B}T\left[\Delta I\right]\ge 0\\ =k_{B}T\left[S({\rho }_{AB}^{\prime })\right].\end{array}& (12)\end{array}$

As uncertainty increases, entropy is produced, and less free energy is available within the system to do work. As uncertainty decreases, entropy is compressed, and more free energy is available within the system to complete tasks, such as remodeling synapses. A system that encodes its environment can therefore become more ordered by interacting with its local environment and identifying correlations. It is even thermodynamically favored for a system to take on a more ordered state over time, as it encodes predictive value gained by interacting with its surrounding environment (Glansdorff and Prigogine, 1971; Hillert and Agren, 2006; Martyushev et al., 2007); indeed, the pruning of neural pathways during learning and development would not spontaneously occur if this were not the case.

Here, the spontaneous emergence of a more ordered system state naturally emerges over time, from a process of thermodynamic computation—as some quantity of information entropy is generated and compressed, through the extraction of predictive value. However, the first and second laws of thermodynamics are always respected—energy is never created nor destroyed, and there is always some net dissipation of energy to entropy over time (Figure 2).

Figure 2

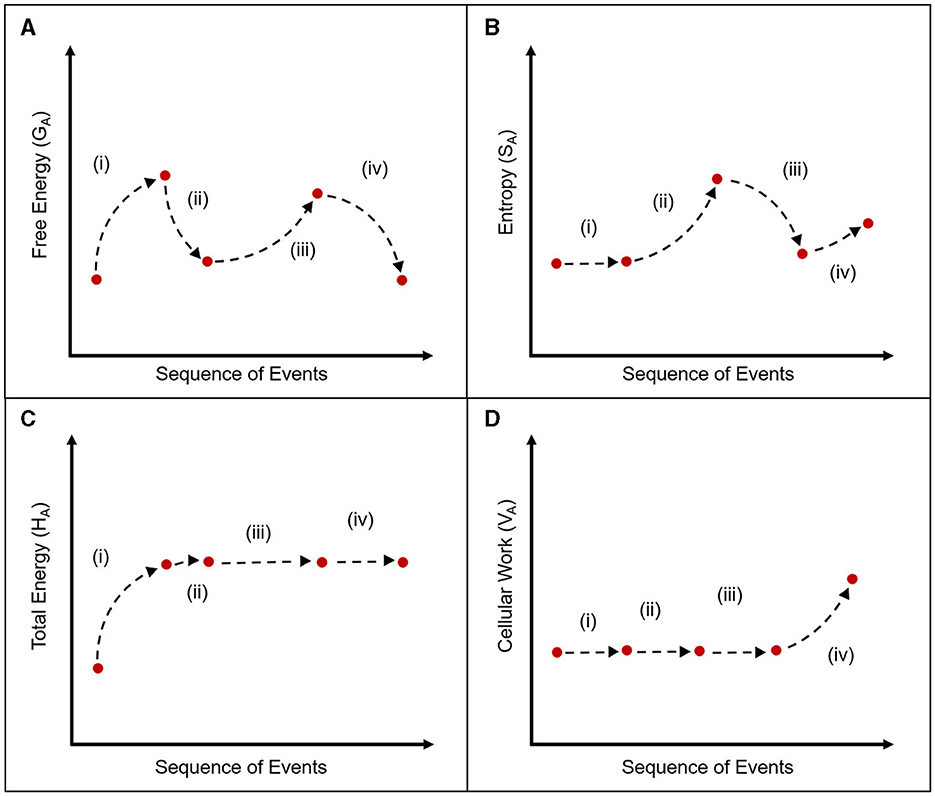
Figure 2. A graphical depiction of free energy and entropy. (A) A single thermodynamic computation cycle is comprised of four distinct phases, with regard to the free energy of system A (G_A): (i) System A traps energy from system B, and (ii) System A uses this energy to generate entropy [These two steps occur over the same time period, so that most free energy is distributed to entropy during noisy coding]. (iii) System A then compresses that quantity of entropy by the amount k_BT(I_pred), and partially recovers the original free energy expenditure through predictive processing. (iv) System A uses the newly available free energy to perform dissipative work, physically encoding the newly acquired predictive value into its anatomy and physiology. (B) The entropy of system A (S_A) can also be mapped during these four distinct phases: (i) The entropy of System A does not change as a direct result of trapping energy from system B. (ii) System A generates entropy as neurons engage in noisy coding [this value is S(ρ_A)]. (iii) System A then compresses that entropy by the amount k_BT(I_pred), releasing a proportional quantity of free energy during the predictive computation [this value is S(${\rho }_A^{\prime }$)]. (iv) The entropy of System A then increases as it uses the newly available free energy to perform dissipative work, to physically encode the predictive value acquired during the computation. (C) The value of the Hamiltonian operator is provided across all four stages of the computation. (D) The quantity of energy distributed toward cellular work is provided across all four stages of the computation.

4 Results

4.1 The first law limits the amount of predictive value in a quantity of information

In accordance with the second law of thermodynamics, entropy must always increase over time. However, far-from-equilibrium particle systems—which trap heat to do work—can either increase or decrease disorder locally. To prevent a violation of thermodynamic laws, free energy must be dissipated toward work whenever the system state becomes more ordered. Any reduction of uncertainty (k_BT[ΔI] = TΔS) must be balanced by an increase in free energy (ΔG), to balance the total energetic account. Any inefficiency in operations increases entropy, while a more ordered system state increases the amount of energetic currency available to do work.

The lower the value of TΔS, the greater the amount of free energy available to the system. The quantity of free energy can be maximized in two ways: (1) if the system does not generate much uncertainty or entropy (with the value of I_mem(t) approaching zero), or (2) if the entropy generated by the system over time t has a large amount of predictive value that can be extracted (with the value of I_mem(t)−I_pred(t) approaching zero). The reduction of possible system macrostates, or the compression of information entropy, is equivalent to the extraction of predictive value. This computational process is thermodynamically favored, because it provides the system with more available free energy.

If the quantity of information contains internal consistencies, that quantity is naturally reduced or compressed. Any redundant or compressible entropy (e.g., possible system states that are identical to previous system states) are highly predictable and are easily accepted. Conversely, information that is unreliable or anomalous (e.g., neural signals that are more likely to be errors than accurate reporting of stimuli) reduce the amount of predictive value available to the system, providing a measure of inefficiency or wasted energy.

It is useful for a thermodynamic computing system to direct attention toward a novel stimulus, in case that event provides useful predictions about subsequent events. If predictive value is successfully extracted from the information generated, there is little net energetic cost to the initial energetic expenditure. The free energy that is released by reducing uncertainty and maximizing predictive value is recovered and made available to do work within the system. In this model, a cortical neural network continually acquires information about the local environment through the sensory apparatus, encoding physical events into the probabilistic macrostate of an ensemble of computational units. Extracting predictive value from this “information” maximizes the free energy that is available to the system. This free energy can be used to implement structural change, leading to a more ordered system state that encodes the predictive value acquired during the computation.

Yet there is a limit to the amount of predictive value a system can have. Any system that gains a more ordered state has reduced the quantity of disorder or entropy; this may be true for a local, non-closed thermodynamic system, but it cannot be true for a closed system or the universe as a whole, because there must be some external energy source driving this computational work. The total information created by the system is limited by the amount of energy entering the system ΔE. Of the total information generated by the thermodynamic system, some amount will have predictive value, but the predictive value available will be limited by the total quantity of information held by the system. If the quantity of predictive value gained is greater than the amount of caloric energy expended to generate entropy, then the quantities in Equations 11, 12 would be negative, and energy would be created by the thermodynamic system through the act of information processing alone. Since the creation of energy is explicitly forbidden by the first law of thermodynamics, the amount of predictive value is limited by the amount of energy available to the system. As such, any thermodynamic system gaining a more ordered state by extracting predictive value must generate an incomplete predictive model.

If a thermodynamic computing system were ever to reach perfect predictability for all computable statements, with I_mem(t) = I_pred(t), all memory in the system would be erased, and there would be no information remaining to have predictive value. Therefore, no memory can continue to exist for any period of time with 100% predictive efficiency. If the value of I_mem(t)−I_pred(t) were to reach zero, all system memory would be erased.

This simple model demonstrates that extracting predictive value is both a thermodynamic process and a computational process. The first law of thermodynamics limits the amount of energy expended toward and recovered from entropy; this total quantity of energy turnover is constrained by the net quantity of energy entering the system. Since the physical process of compressing information is dependent on parsing predictive value, as provided in Still's equation, the quantity of disorder lost through computation must be equivalent to the amount of predictive value extracted by the system. Yet some disorder must always remain. If a system is perfectly ordered and perfectly predictive, it will cease to operate, because continued thermodynamic operation requires some uncertainty.

4.2 The predictive value in any set of computable statements will always be incomplete

In mathematical logic, any set of axioms which makes statements of truth is inherently limited and necessarily incomplete. It is useful to consider this rule on its own terms, before assessing whether it applies to physical systems performing logical operations. Gödel's first incompleteness theorem provides that there will always be statements within a set of axioms which are true but cannot be proven or disproven within the set of axioms itself. Gödel's second incompleteness theorem states that any set of axioms cannot contain any proof for the consistency of the set of axioms itself. As such, any logical system that evaluates both the internal consistency or “truth” of computable statements and the relationship of these statements to each other is necessarily incomplete (Gödel, 1931; Raatikainen, 2015).

These two incompleteness theorems assert that a set of axioms cannot be both completely true and completely known. Any number of statements can be held to be semantically true; the limit applies to full knowledge of their syntactical relationships. Equations 11, 12 show that this law of mathematical logic must be true for any thermodynamic computing system. Over time, any number of semantical statements may be decided by a system. If the system does not hold all semantical statements about the universe, then there will also be syntactical relationships that are not known, and its knowledge is incomplete. If the system does hold all semantical statements about the universe, then knowing all syntactical relationships between these axiomatic statements would complete the predictive value of the system. Once all knowledge is complete, the thermodynamic system becomes completely ordered. With no uncertainty, there would be no remaining entropy, all entropy would be converted to free energy, and the system would become disordered once again. Continued thermodynamic operation requires uncertainty, and thus, incompleteness.

This result is perhaps not surprising, as the relevance of incompleteness in relation to computing was formally addressed a century ago by the Entscheidungsproblem, or decision-problem, proposed by Hilbert and Ackermann, which posed the question of whether an algorithm or computer could decide the universal validity of any mathematical statement (Hilbert and Ackermann, 1928). Church and Turing quickly recognized there could be no computable function which determines whether two computational expressions are equivalent, thereby demonstrating the fundamental insolvability of the Entscheidungsproblem and the practicality of Gödel's incompleteness theorems in terms of computable statements (Church, 1936; Turing, 1936). Here, it is demonstrated that incompleteness is a fundamental limitation during the thermodynamic extraction of predictive value.

If no true-false decision can be made with regard to the relationship between computable statements, then the predictive value I_pred of the system is incomplete. As a result, some amount of work must be dissipated to ΔI, as unresolved information which simply cannot be reduced (yet) into a decisional outcome. Given the physical impossibility of computing the universal truth of all syntactical relationships between semantical statements, there will always be some value of I_non−pred and therefore a net positive amount of free energy dedicated to ΔI during a thermodynamic computation, in accordance with the second law of thermodynamics. Yet it is possible to minimize this quantity of ΔI, as predictive value is extracted: If a decision can be made, uncertainty is reduced and the system state encoding that predictive statement is selected from a distribution of possible system states.

4.3 A single thermodynamic computation yields a predictive semantical statement

In this model, a neural network selects an optimal system state, by extracting predictive value to make consistent statements about its surrounding environment. By parsing for predictive value, the encoding system takes on a more compatible state with its surrounding environment during the process of thermodynamic computation.

Although entropy is generated by the system, predictive value can be extracted, reducing the distribution of possible system states. During each computation, noise is filtered out and anomalies are detected; the most appropriate system state is selected, in the context of the surrounding environment. This computation is based on both incoming sensory data and the biophysical properties of each encoding unit.

During the computation, incoming sensory data is noisily encoded into the neural network and integrated into a system macrostate. That probability distribution (a physical quantity of information) is defined as the mixed sum of all component microstates, which evolve over time t. The system state is then resolved as consistencies are reduced and predictive value is extracted. During this computational process, information is compressed, free energy is released, an optimal system state is selected from a large probability distribution, and all other possible system states are discarded.

This computation effectively encodes a semantical statement about the local environment, or a “percept,” such as a simultaneous flash of light and a loud noise. Because this semantical statement is essentially a predictive model of the state of the world at the present moment, constructed from multiple sensory inputs, a reasonable decision in the context of any remaining uncertainty is to orient attention toward any novel or anomalous stimuli, in order to gather more information which might hold additional predictive value. Critically, any information gathered that is not consistent with previously-gathered information or concurrent information is likely to be discarded. This efficiency may lead to perceptual errors, particularly in the presence of unexpected events.

A multi-sensory percept is a “predictive semantical statement about the surrounding environment,” which corresponds to synchronous firing across the neural network (Figure 3A). A sequence of multi-sensory percepts, corresponding to a sequence of neural network states, can be integrated across the time domain. These longer computational cycles enable the construction of “predictive syntactical statements about reality” or predictive cognitive models of the likely cause-effect relationship between perceived events (Figure 3B).

Figure 3

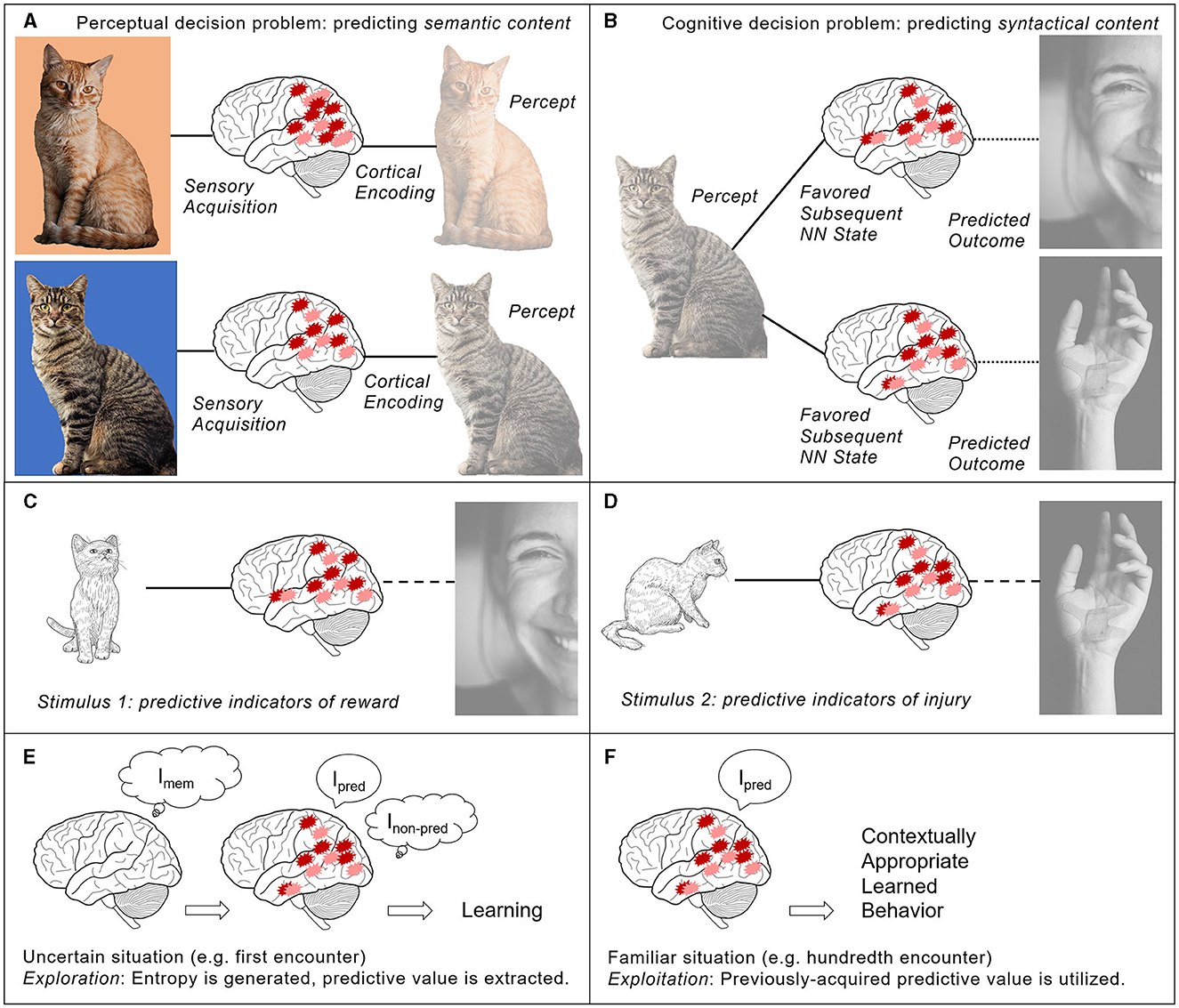
Figure 3. The proposed thermo-computational process naturally yields perceptual content, cognitive models, and an exploration/exploitation dynamic in behavior, as the neural network extracts predictive value from information. (A) A multi-sensory percept is a predictive semantical statement about the surrounding environment, e.g., “there is an orange striped cat” or “there is a black striped cat.” It is thermodynamically favored for any neural network that selects an optimal system state from some probability distribution, by interacting with its surrounding environment, to select the system state that is most correlated with its surrounding environment. However, inaccuracies may occur, given time constraints, energy constraints, or neuropathological deficits. (B) A cognitive model is a predictive syntactical statement about cause-effect relationships between perceived events, e.g., “Petting this cat may lead to a rewarding experience, resulting in a feeling of contentment and lower energy dissipation” or “Petting this cat may lead to a risk of injury, resulting in potential scratches and the dissipation of energy toward wound healing.” These predictive models of cause and effect allow the observer to hone stimulus-evoked behavior. However, inaccuracies may occur, particularly when predictors do not yield consistent outcomes. (C, D) Incoming sensory data may be highly uncertain, and so risk and reward cannot be accurately predicted in a given situation. Previous experience may provide relevant insight which can be applied to the present situation. (C) Petting a cat when it shows passive behavior, characterized by a relaxed posture and minimal eye contact, has previously resulted in reward for the observer, paired with the encoding of reward expectation in the nucleus accumbens. (D) Petting a cat when it shows aggressive behavior, characterized by a tense posture and direct eye contact, has previously resulted in injury to the observer, paired with the encoding of injury expectation in the amygdala. (E, F) An exploration/exploitation dynamic emerges from one simple rule: the minimization of energy dissipation. (E) Knowledge is gained through exploratory behavior (which requires energy expenditure) and extraction of reliable predictive indicators (which leads to partial energy recovery). Imem is the total amount of energy distributed toward information generation; Ipred is the amount of predictive value in that information (and the amount of energy recovered as information is compressed); Inon-pred is the net entropy created during the computational cycle. The free energy released during information compression is used to do the work of encoding predictive value through synaptic remodeling. (F) Knowledge, previously gained through lived experience, can be exploited in new circumstances (permitting the system to save energy). In the above example, the observer may reasonably predict a high risk of injury and a low risk of reward when approaching a cat making direct eye contact. This predictive indicator is stored in the neural network, thermodynamically favoring a sequence of neural activity and a contextually appropriate behavioral response upon stimulus presentation. The photo of a ginger striped cat, by Stéfano Girardelli, was provided under a creative commons license on Unsplash; the photo of a black striped cat, by Zane Lee, was provided under a creative commons license on Unsplash; the photo of a wounded hand, by Brian Patrick Tagalog, was provided under a creative commons license on Unsplash; the photo of a happy woman, by Kate Kozyrka, was provided under a creative commons license on Unsplash; the line drawing illustrations were provided by pch.vector on Freepik.

4.4 A sequence of thermodynamic computations yields a predictive syntactical statement

While entropy can decrease during the course of a computational cycle, through the extraction of predictive value, some amount of non-predictive value will always remain. In short, not all entropy can be compressed in a single computational cycle, because not all predictive value can be extracted. The relationship of that percept to subsequent events remains uncertain. This uncertainty can only be reduced by extracting additional predictive value. The system may integrate a temporal sequence of neural network states, encoding a temporal sequence of semantical statements, and extract a prediction regarding the likely cause-effect relationship between these perceived events. thereby creating a predictive model of the syntactical relationships between semantical statements.

During a single thermodynamic computation, the neural network encodes the most likely state of its surrounding environment. These computations can also be integrated over time, corresponding to a sequence of neural network states which encode a likely sequence of events occurring in the environment. Now, the amount of information held by the neural network is given by integrating the distribution of system macrostates over a longer timescale t, with this thermodynamic quantity equivalent to the net amount of free energy expended to produce entropy over multiple computational cycles. Any entropy that is not compressed or discarded during a single computational cycle remains available for further parsing.

Over the course of a single computational cycle, only semantical truth statements can be ascertained (e.g., there is a bright flash and a loud noise, with the coincident stimuli both emerging from the same approximate location). In that instant, there is no predictive value to assign syntactical relationships between these stimuli and any subsequent outcomes (e.g., these stimuli immediately precede some aversive or rewarding outcome for the observer). If these stimuli have been previously observed, with no adverse outcome, the stimuli may be tolerated (e.g., this combination of percepts is likely to be part of the annual fireworks display). Alternatively, if the stimuli have been previously observed, with an outcome that potentially affects survival, a decision can be taken to reduce the expected risk (e.g., this combination of percepts is likely to indicate gunfire nearby). If the stimuli are novel, they may be attended carefully. In the absence of contextually-relevant knowledge, gained from prior experience, the system must integrate information over multiple computational cycles and extract predictive value. Any new information gained by the system about its environment during a single computation has uncertain predictive value; this information cannot be fully reduced and therefore must be stored in working memory. However, the immediately subsequent moment may yield more information, permitting the system to assign some predictive syntactical relationship between the previously-acquired information and the incoming information (e.g., the neural network can decide whether this perceived stimulus combination is likely to indicate an innocuous or life-threatening event, and direct movement according to this cognitive model). If a stimulus has high predictive value, gained from prior experience, it may be thermodynamically favored for some particular sequence of neural network states to ensue, triggering stereotyped behavior in that context (Figures 3C–F).

Overlapping computational cycles may occur, with different timescales, as neural network states are temporally integrated. Short sequences of events may be fused together tightly, with the amount of predictive value determined in part by the salience and temporal contingency of sensory cues. Longer sequences of events may be tied together by common contextual cues or patterns of sensorimotor input-output behavior; these extended computations may include a multitude of shorter sequences. In each case, the extended computation includes semantical statements which are predicted to be syntactically related in some way. By integrating individual computations, each with some value of I_non−pred, into a sequence of computations, the system can extract additional predictive value.

A series of events with high predictive value will compress the quantity of entropy, thereby releasing free energy into the system to do work. Indeed, any time the system gains predictive value, it must balance the account by dissipating free energy toward work. Free energy is dissipated toward work, for example, as the system undertakes spontaneous structural remodeling to gain a more ordered system state, thereby encoding the predictive value acquired through lived experience. This synaptic remodeling process thermodynamically favors the re-occurrence of sequential neural network states and stereotyped behaviors in predictable contexts. This emergence of a more ordered state allows the organism to more easily navigate familiar environments, minimizing inefficiency and maximizing available free energy.

4.5 Thermodynamic computation yields a trade-off between exploration and exploitation

In this model of thermodynamic information processing, a single computation yields a “semantical” statement, while temporal sequences of neural network states encode “syntactical” statements. Over a lifetime, the neural network steadily acquires a more ordered state but cannot achieve full predictive value, due to the constraints discussed in Sections IVA and IVB.

Any information generated will be parsed for predictive value — and the more predictive value extracted from the information, the more free energy is released to do work. As the system performs work to remodel itself into a more organized state, disorder is reduced, less entropy or uncertainty is produced, and more free energy is available to the system—as long as the system continues to navigate familiar contexts.

This computational process is highly energy-efficient, because consistency minimizes uncertainty and maximizes free energy availability. In this model, a thermodynamic computing system will both expand its quantity of information, by engaging in exploratory behavior to acquire predictive value, and reduce its quantity of information, by exploiting previously-acquired predictive value and favoring previous patterns of neural activity. These two processes perform in opposition, with any decisional outcome relying on the minimization of energy dissipation. The rival energetic cost function leads a neural network to explore its environment, gaining predictive value, and to engage in habitual patterns of behavior, exploiting that predictive value in familiar contexts.

Each computation cycle culminates in a decision, with any output behavior dependent upon this rival energetic cost function. If the system predicts its own knowledge to be insufficient to navigate the present situation, the system will further explore its environment to gain information. If predictive value can be extracted, the information is compressed and there is little net energy expenditure to do that work, although there is an up-front expenditure. The system then remodels itself to encode that newly-acquired predictive value. If the system predicts its own knowledge to be sufficient to navigate the situation, the system will exploit any relevant previously-gained predictive value to select a contextually-appropriate action. If patterns of neural firing and behavior are readily activated by a familiar stimulus, with minimal uncertainty during the task, little net energy expenditure is needed to compute the decision.

4.6 Predictions

This theoretical approach to modeling non-deterministic computation in cortical neural networks makes some specific predictions with regard to the energy-efficiency of the brain (Stoll, 2024), the spontaneous release of thermal free energy upon information compression (Stoll, 2022a), and the contribution of these localized thermal fluctuations to cortical neuron signaling outcomes (Stoll, 2022b). This approach also makes specific predictions about the expected effects of electromagnetic stimulation and pharmacological interventions on perceptual content (Stoll, 2022c). Some further predictions of the theory, prompted by the present model, include.

4.6.1 Thermodynamic computation leads to maximal energy efficiency

In this model, cortical neurons engage in a physical form of computation, generating information through noisy coding, then compressing that thermodynamic and computational quantity by extracting predictive value. Here, each computational unit within the network is modeled as encoding von Neumann entropy (the mixed sum of all component pure states) rather than Shannon entropy (a simple binary 0 or 1 state). As such, much of the energy acquired by the system is dissipated to entropy during noisy coding; this places a limit on how much predictive value can be extracted and how much cellular work can be done.

The system can instantiate an internal system state which does not match previous internal states or current external states, but that would lead to greater net energy expenditure, or thermodynamic inefficiency (as provided in Equation 3). Therefore, it is thermodynamically favored for the encoding system to identify correlations with its surrounding environment, by extracting predictive value and reducing uncertainty. During the computation, the trial Hamiltonian will maximize free energy availability and minimize net entropy production (as provided in Equation 7). A key result of this model is that both thermodynamic and computational entropy will be minimized, while the amount of free energy dissipated toward physical work will be maximized. Over time, this should lead to near-perfect energy efficiency for the encoding system, with W_cellular approaches k_BT[I_pred(t)] approaches k_BT[I_mem(t)] approaches Ĥ. This leads to a falsifiable statement: W_cellular < Ĥ.

4.6.2 Thermodynamic computation drives synchronous firing of cells at a range of frequencies

In this model, a thermodynamic computation yields a predictive semantical statement regarding the most likely state of the surrounding environment, in a manner limited by the range and sensitivity of the sensory apparatus. As information is compressed, a single system state is realized and all other possible system states are discarded. Thus, the realization of a multi-modal “percept” corresponds to the synchronous firing of neurons across the network, at a periodic frequency tied to the length of the computation. Yet the syntactical relationship of that semantical statement to ensuing events remains uncertain. As a result, these individual computations, yielding “percepts,” may contribute to temporal sequences of neural network states, paired with information content, yielding a predictive cognitive model of causal relationships between perceived events. As predictive value is extracted, information is compressed over these longer timescales. Thus, these sequences of computations are predicted to result in synchronous firing at much slower frequencies. During wakeful awareness, both semantical and syntactical information is being parsed, so both fast and slow oscillations should be observed. This prediction of synchronous neural activity at nested frequencies is consistent with empirical observations in the cerebral cortex (Chrobak and Buzsaki, 1998; Engel and Singer, 2001; Harris and Gordon, 2015). During sleep, incoming sensory data is not being evaluated and so only syntactical relationships between previously-stored information is being parsed; as a result, sleep should be characterized by synchronous activity only at slower frequencies. This prediction is also consistent with empirical observation (Steriade et al., 2001; Mitra et al., 2015). These synchronous firing events are predicted to be disrupted by the absorption of thermal free energy release at relevant frequencies, or the random introduction of free energy.

4.6.3 Thermodynamic computation drives spontaneous remodeling of the encoding structure

The quantity of predictive value extracted during a computation is equivalent to the amount of information entropy compressed during that computation; this quantity must be exactly balanced by the amount of free energy released into the system and the amount of work then dissipated toward creating a more ordered system state. This work is expected to involve locally optimizing the system to encode the acquired predictive value (e.g., by remodeling the neural network structure to thermodynamically favor a certain pattern of neural activity in a familiar context). In short, the extraction of predictive value should be paired with the dissipation of work toward creating a more ordered system state which encodes that predictive value. Of course, cortical neurons are already known to spontaneously remodel their synaptic connections to encode learned information (Hebb, 1949). This structural remodeling is prompted by participation in network-wide synchronous activity (Zarnadze et al., 2016) and has been shown to affect each synapse in proportion to its initial contribution (Turrigiano et al., 1998). While the molecular mechanisms underlying synaptic plasticity are well-established, this theoretical model describes the relationship between free energy, entropy minimization, and spontaneous directed work, as uncertainty is resolved. Here, it is predicted that spontaneous self-remodeling is a natural output of a thermodynamic computation, in which predictive syntactical relationships are encoded in sequences of neural network states. Any unique sequence of neural activity is therefore expected to uniquely match representational information content. Alterations in information content should be paired with a conformational change in the encoding structure, to store the freshly-parsed information; conversely, any impairment to the encoding structure should be paired with a loss of stored information content. If instead the null hypothesis is true, and activity-dependent synaptic remodeling can be entirely explained by classical mechanisms, then this process should not be localized to synapses that have reduced uncertainty and should not be dependent on parsing predictive value to maximize free energy availability.

4.6.4 Thermodynamic computation yields an exploration/exploitation dynamic in behavior

In this model, the system identifies a compatible state with its surrounding environment, by maximizing predictive value or consistency. To gain predictive value, it is necessary to collect data from the environment, parse that dataset for predictive value, compress information, and subsequently encode that predictive value into the encoding structure, so this encoding system state is favored to repeat in a similar context. It is useful to attend to any incoming data that does not match existing predictive models, because this discrepancy signals a valuable opportunity to update the cognitive model with this new information. Therefore, a decision on how to act, given the incoming information, will rely on a rival energetic cost function: If knowledge is predicted to be sufficient to navigate the situation, the organism is unlikely to engage in exploration to gain additional predictive capacity. If knowledge is predicted to be insufficient to navigate the situation, the organism is likely to engage in exploration. Any change in the predicted risk of energy dissipation for exploration or non-exploration in a given context will shift the probability of exploration.

4.6.5 Thermodynamic computation carries the risk of predictive error

This model of thermodynamic computation is extraordinarily energy-efficient. However, two types of inefficiencies can occur. If existing knowledge is not exploited in familiar situations, time and energy may be wasted. If the consistency and predictive power of a new cognitive model is ignored in favor of holding onto a previous cognitive model, time and energy may also be wasted. While the former leads to unnecessary dissipation of energy toward exploration, the latter leads to potentially missing critical information. Some organisms may select the short-term savings gained by holding onto a previous cognitive model over the potential long-term energetic savings gained by deconstructing that cognitive model and constructing an improved model in its place.

To explore what might be true about the world, it is necessary to sacrifice time and energy resources for uncertain reward, with the prediction that this process will be worthwhile in the long term. In this theory, mental exploration takes thermodynamic work and some individuals may opt not to engage in the process, with the prediction there will be no payoff in doing so.

Exploration exposes the organism to uncertainty, thereby generating information with potential predictive value, while exploitation of knowledge that was previously gained through exploration makes good use of that predictive value. Ignoring incoming information may reduce energetic costs in the short term, but this strategy can impair prospects for survival in the longer term, so it is useful to accurately assess when knowledge is insufficient. The organism must compute the likely energetic cost of exploration against the potential cost of making a predictive error. For this reason, it is predicted that an individual capability for parsing information - and discarding inaccurate cognitive models in favor of more accurate cognitive models should provide a selective advantage, leading to measurable differences in survival outcomes, particularly when environmental conditions suddenly shift.

5 Discussion

The extraordinary energetic efficiency of the central nervous system has been noted, particularly amongst theorists who query whether this competence is intrinsically linked to the physical production of information entropy (Collell and Fauquet, 2015; Street, 2016) or the exascale computing capacity of the brain (Bellec et al., 2020; Keyes et al., 2020). In this model, energy is indeed being expended on entropy production—but rather than being irreversibly lost, this quantity is parsed during a periodic computational cycle of information generation and compression. Since unlikely or unfamiliar system states may hold predictive value, the quantity of entropy may be expanded to accommodate a new system state, even at an energetic cost, in order to reduce uncertainty in the longer term.

Interestingly, there are limits to the amount of predictive value in a quantity of information. These limits are given by the first law of thermodynamics. Indeed, any system that takes on a more ordered state has essentially reduced its entropy over the course of a computational cycle. But the amount of free energy that is dedicated toward ordering the system state cannot be greater than the amount of free energy that is gained through information compression. Some amount of work must also be dissipated to uncertainty, since having complete predictive value and continued operation is thermodynamically impossible. As such, there are intrinsic thermodynamic limits to the amount of work being done by the system and thermodynamic limits to the completeness of its predictive capacity.

A single computational cycle will both resolve the neural network state in the present moment and generate a semantic statement about the external environment, which is validated by orienting toward incoming sensory information. These semantical statements are held in working memory, and then integrated with subsequent neural network states to compute any syntactical relationships. Holding untrue semantic statements as true, and attempting to use these statements to form syntactical relationships with other semantical statements, is equivalent to energetic inefficiency. Yet information content which may have accurately reflected reality in some context could simply be inaccurate in a different context; the ability of the system to recognize the difference is largely determined by how effectively the neural network structure had been remodeled to encode that information. If the neural network remains adaptable, not completely ordered, more nuanced complexities can be noted and more predictive value can be gained, at some energetic expense.

This process of thermodynamic computation results in a rival energetic cost function, to maximize free energy. This rival energetic cost function drives a system to either maximize entropy production through exploration, to gain predictive value, or minimize entropy production through exploitation, to make effective use of previously-acquired predictive value. The system must first expend energy to generate information, then recover energy by compressing information. That free energy is then used to remodel the encoding structure itself, to store that predictive value, thus thermodynamically favoring the reoccurrence of sequential system states in a relevant or familiar context. The maximization of free energy is readily accomplished through cycles of information generation and compression, or by relying on the optimized system state that was already achieved by that process. The timescales of computations may overlap, with individual computations that encode multi-sensory percepts being integrated into short sequences of neural network states which encode possible relationships between perceived events. The overall temperature and energy flux of the system remain constant, permitting the non-equilibrium system to act as a net heat sink. In this view, neural networks—acting in accordance with the laws of thermodynamics—are expected to physically process information, undergoing non-deterministic computation.

Physically compressing information, by extracting predictive value, yields a single neural network state, encoding the likely present state of the local environment. The incompleteness of information compression in any single computational cycle leaves some entropy remaining, which can then be parsed for predictive value over longer timescales. By integrating information over longer timescales, the neural network may integrate temporal sequences of consistent system states to build predicted cause-effect relationships between perceived events. These mental models—which make predictions about the general structure and operation of the physical world; the likely behavior of other people, animals, and things in the environment; and the most effective way of acting in response to certain stimuli — are expected to be formed by thermodynamic computations occurring across the lifetime.

There is a long-standing ontological issue regarding the relationship between information and entropy. Both concepts describe the sum of all possible system states, so resolving this issue lies at the heart of thermodynamic computing. Biological neural networks are thermodynamic systems that produce entropy, like any other particle system. Yet unlike other entropy-producing thermodynamic systems—such as the steam engine—a biological neural network computes information, reducing disorder or randomness into a more optimal system state, with the system growing increasingly ordered over time as it interacts with its environment. In this model, neural networks both generate information and parse that information for predictive value. It is useful here to consider “information” as both the sum of all possible system states (its mathematical definition) and the meaning extracted from a messy dataset (its colloquial definition). In this theoretical model, these are two stages of the same computational process. As neural networks produce von Neumann entropy, they are physically producing disorder—a set of possible system states, or the mathematical definition of information. However that information is only useful if predictive value is extracted, a distribution of system states is compressed into a single outcome, free energy is released back into the system, and that free energy is used to remodel the encoding structure to store that predictive value. In other words, any thermodynamic system can create a distribution of possible system states, thereby producing entropy. But only a thermodynamic system capable of compressing that probability distribution into a single actualized system state will then parse consistency or predictive value from that information, store that predictive value for future use, and recall those predictions in relevant contexts.

Interestingly, this model of information generation and compression was first described in 1965 (Kirkaldy, 1965). The author, John Kirkaldy, states: “The evolution of the internal spontaneous process may be described as a path on the saddle surface of entropy production rate in the configuration space of the process variables. From any initial state of high entropy production the system evolves toward the saddle point by a series of regressions to temporary minima alternating with fluctuations which introduce new internal constraints and open new channels for regression... The state of consciousness is to be associated with the system undergoing regression.”

The present report places this process within the established groundwork of computational physics, with a thermodynamic information compression process described by Ben Schumacher and Peter Shor (Schumacher, 1995; Bennett and Shor, 1998). Yet the Kirkaldy paper and the present report may be considered equivalent. Kirkaldy focuses on the geometrical constraints of free energy as a boundary condition in neural systems, with a single saddle point serving as a global optimal result; meanwhile, the present study focuses on thermodynamic trade-offs between local minima at various timescales, with the system respecting the first and second law of thermodynamics at each local decision point. Kirkaldy models the system as opening new channels for search by the random nucleation of internal constraints; meanwhile, the present study models the intermediate states of higher entropy as an uncertain neuronal membrane potential, which is resolved as all local electron states are resolved. Both studies assume the brain is an inherently probabilistic system, and must be modeled accordingly; this assertion is supported by decades of neurophysiological research, demonstrating that individual neuron signaling outcomes and network-level dynamics are statistically random. Kirkaldy demonstrates that a process of non-equilibrium thermodynamic computation can cause the brain to spontaneously take on a more ordered state during learning, but the present report is able to explain perception, cognitive modeling, and decision-making behavior in terms of predictive processing. Yet it is worth noting: both of these reports only provide a systems-level description of the information generation and compression process, and so they require a stronger mechanistic basis at the cellular level, with these probabilistic computations formulated in terms of Hamiltonian operators (Stoll, 2022a), matrix mechanics (Stoll, 2022b), wave mechanics (Stoll, 2022c), or mean field theory (Stoll, 2024). In all, three major neuroscientific initiatives are needed: the development of deeper physiological models which incorporate probabilistic mechanics at the level of sodium ions at the neuronal membrane, physiological verification of these new theoretical approaches, and the integration of thermodynamic information processing into our understanding of cortical neural network dynamics.

Critically, in both the Kirkaldy paper and the present report, the outcomes of cortical neuron computations are non-deterministic, but not completely random; these cells will encode the “best match” between the system and its local environment. This approach fits well with other recent models emphasizing the role of contextual cues (Bruza et al., 2023) and cost calculations (Jara-Ettinger et al., 2020) in decision-making.

Usefully, this new model introduces a thermodynamic basis for optimal search strategies and predictive processing, with the extraction of predictive value during the search process minimizing the dissipation of free energy and maximizing the amount of free energy available to do work. As a result, any far-from-equilibrium thermodynamic system that traps heat to perform computational work will inevitably cycle between expanding the distribution of system states and pruning toward a more optimized system state. This computational process naturally yields an exploration/exploitation dynamic in behavior and the gradual emergence of a more ordered system state over time.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

ES designed, conducted, and wrote the study.

Funding

The author declares that this study received funding from the Western Institute for Advanced Study, with generous donations from Jason Palmer, Bala Parthasarathy, and Dave Parker. The funders were not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adams, R. A., Shipp, S., and Friston, K. J. (2013). Predictions not commands: active inference in the motor system. Brain Struct. Funct. 218, 611–643. doi: 10.1007/s00429-012-0475-5

PubMed Abstract | Crossref Full Text | Google Scholar

Arnal, L. H., Wyart, V., and Giraud, A. L. (2011). Transitions in neural oscillations reflect prediction errors generated in audiovisual speech. Nat. Neurosci. 14, 797–801. doi: 10.1038/nn.2810

PubMed Abstract | Crossref Full Text | Google Scholar

Averbeck, B. B., Latham, P. E., and Pouget, A. (2006). Neural correlations, population coding and computation. Nat. Rev. Neurosci. 7, 358–366. doi: 10.1038/nrn1888

PubMed Abstract | Crossref Full Text | Google Scholar

Beck, J. M., Ma, W. J., Kiani, R., Hanks, T., Churhcland, A. K., Roitman, J., et al. (2008). Probabilistic population codes for Bayesian decision making. Neuron 60, 1142–1152. doi: 10.1016/j.neuron.2008.09.021

PubMed Abstract | Crossref Full Text | Google Scholar

Bellec, G., Scherr, F., Subramoney, A., Hajek, E., Salaj, D., Legenstein, R., et al. (2020). A solution to the learning dilemma for recurrent networks of spiking neurons. Nat. Commun. 11:3625. doi: 10.1038/s41467-020-17236-y

PubMed Abstract | Crossref Full Text | Google Scholar

Bengtsson, I., and Zyczkowski, K. (2007). Geometry of Quantum States, 1st Edn, Chapter 12. Cambridge: Cambridge University Press.

Google Scholar

Bennett, C. H., and Shor, P. W. (1998). Quantum information theory. IEEE Trans. Inform. Theory 44, 2724–2742.

Google Scholar

Berut, A., Arakelyan, A., Petrosyan, A., Ciliberto, S., Dillenschneider, R., and Lutz, E. (2012). Experimental verification of Landauer's principle linking information and thermodynamics. Nature 483, 187–189.

PubMed Abstract | Google Scholar

Bradley, P. M., Denecke, C. K., Aljovic, A., Schmalz, A., Kerschensteiner, M., and Bareyre, F. M. (2019). Corticospinal circuit remodeling after central nervous system injury is dependent on neuronal activity. J. Exp. Med. 216, 2503–2514. doi: 10.1084/jem.20181406

PubMed Abstract | Crossref Full Text | Google Scholar

Bruza, P. D., Fell, L., Hoyte, P., Dehdashti, S., Obeid, A., Gibson, A., et al. (2023). Contextuality and context-sensitivity in probabilistic models of cognition. Cogn. Psychol. 140:101529. doi: 10.1016/j.cogpsych.2022.101529

PubMed Abstract | Crossref Full Text | Google Scholar

Buzsaki, G., and Draguhn, A. (2004). Neuronal oscillations in cortical neural networks. Science 304, 1926–1929. doi: 10.1126/science.1099745

Crossref Full Text | Google Scholar

Callen, H. B., and Welton, T. A. (1951). Irreversibility and generalized noise. Phys. Rev. 83:34.

Google Scholar

Chrobak, J. J., and Buzsaki, G. (1998). Gamma oscillations in the entorhinal cortex of the freely behaving rat. J. Neurosci. 18, 388–398.

PubMed Abstract | Google Scholar

Church, A. (1936). A Note on the Entscheidungsproblem. J. Symb. Logic 1, 40–41.

Google Scholar

Collell, G., and Fauquet, J. (2015). Brain activity and cognition: a connection from thermodynamics and information theory. Front. Psychol. 6:818. doi: 10.3389/fpsyg.2015.00818

PubMed Abstract | Crossref Full Text | Google Scholar

Crooks, G. E. (1998). Nonequilibrium measurements of free energy differences for microscopically reversible Markovian systems. J. Stat. Phys. 90:1481.

Google Scholar

Csibra, G., Davis, G., Spratling, M. W., and Johnson, M. H. (2000). Gamma oscillations and object processing in the infant brain. Science 290, 1582–1585. doi: 10.1126/science.290.5496.1582

PubMed Abstract | Crossref Full Text | Google Scholar

Dorval, A. D., and White, J. A. (2005). Channel noise is essential for perithreshold oscillations in entorhinal stellate neurons. J. Neurosci. 25 10025–10028. doi: 10.1523/JNEUROSCI.3557-05.2005

PubMed Abstract | Crossref Full Text | Google Scholar

Engel, A. K., Fries, P., and Singer, W. (2001). Dynamic predictions: oscillations and synchrony in top-down processing. Nat. Rev. Neurosci. 2, 704–716. doi: 10.1038/35094565

PubMed Abstract | Crossref Full Text | Google Scholar

Engel, A. K., and Singer, W. (2001). Temporal binding and the neural correlates of sensory awareness. Trends Cogn. Sci. 5, 16–25. doi: 10.1016/S1364-6613(00)01568-0

PubMed Abstract | Crossref Full Text | Google Scholar

Feldman, H., and Friston, K. (2010). Attention, uncertainty, and free-energy. Front. Hum. Neurosci. 4:215. doi: 10.3389/fnhum.2010.00215

PubMed Abstract | Crossref Full Text | Google Scholar

Fettiplace, R. (2017). Hair cell transduction, tuning and synaptic transmission in the mammalian cochlea. Compr. Physiol. 7, 1197–1227. doi: 10.1002/cphy.c160049

PubMed Abstract | Crossref Full Text | Google Scholar

Friston, K., and Kiebel, S. (2009). Predictive coding under the free-energy principle. Philos. Trans. R Soc. Lond. B 364, 1211–1221. doi: 10.1098/rstb.2008.0300

PubMed Abstract | Crossref Full Text | Google Scholar

Friston, K., Kilner, J., and Harrison, L. (2006). A free energy principle for the brain. J. Physiol. 100, 70–87. doi: 10.1016/j.jphysparis.2006.10.001

Crossref Full Text | Google Scholar

Glansdorff, P., and Prigogine, I. (1971). Thermodynamic Theory of Structure, Stability, and Fluctuations, Chapter 8. London: Wiley-Interscience.

Google Scholar

Gödel, K. (1931). Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I, Translated into English in 2000 by M. Hirzel. Monatshefte fr Mathematik Physik 38, 173–198.

Google Scholar

Gotts, S. J. (2016). Incremental learning of perceptual and conceptual representations and the puzzle of neural repetition suppression. Psychon. Bull. Rev. 23, 1055–1071. doi: 10.3758/s13423-015-0855-y

PubMed Abstract | Crossref Full Text | Google Scholar

Harris, A. Z., and Gordon, J. A. (2015). Long-range neural synchrony in behavior. Ann. Rev. Neurosci. 38, 171–194. doi: 10.1146/annurev-neuro-071714-034111

PubMed Abstract | Crossref Full Text | Google Scholar

Hebb, D. O. (1949). The Organization of Behavior, Chapter 6. New York, NY: Wiley and Sons.

Google Scholar

Herrmann, C. S., and Knight, R. T. (2001). Mechanisms of human attention: event-related potentials and oscillations. Neurosci. Biobehav. Rev. 25, 465–476. doi: 10.1016/S0149-7634(01)00027-6

PubMed Abstract | Crossref Full Text | Google Scholar

Hilbert, D., and Ackermann, W. (1928). Grundzge der theoretischen Logik, Translated into English in 1999 by L.M. Hammond, G.G. Leckie, and F. Steinhardt. Berlin: Springer-Verlag.

Google Scholar

Hillert, M., and Agren, J. (2006). Extremum principles for irreversible processes. Acta Mater. 54, 2063–2066. doi: 10.1016/j.actamat.2005.12.033

Crossref Full Text | Google Scholar

Hopfield, J. J. (1987). Learning algorithms and probability distributions in feed-forward and feed-back networks. Proc. Natl. Acad. Sci. U. S. A. 84, 8429–8433.

PubMed Abstract | Google Scholar

Huang, C. S., Shi, S. H., Ule, J., Ruggiu, M., Barker, L. A., Darnell, R. B., et al. (2005). Common molecular pathways mediate long-term potentiation of synaptic excitation and slow synaptic inhibition. Cell 123, 105–118. doi: 10.1016/j.cell.2005.07.033

PubMed Abstract | Crossref Full Text | Google Scholar

Hubel, D. H., and Wiesel, T. N. (1959). Receptive fields of single neurones in the cat's striate cortex. J. Physiol. 148, 574–591.

PubMed Abstract | Google Scholar

Jara-Ettinger, J., Schulz, L. E., and Tenenbaum, J. B. (2020). The Nave Utility Calculus as a unified, quantitative framework for action understanding. Cogn. Psychol. 123:101334. doi: 10.1016/j.cogpsych.2020.101334

PubMed Abstract | Crossref Full Text | Google Scholar

Jarzynski, C. (1997a). Equilibrium free-energy differences from nonequilibrium measurements: a master-equation approach. Phys. Rev. E 56:5018.

PubMed Abstract | Google Scholar

Jarzynski, C. (1997b). Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 78:2690.

Google Scholar

Jozsa, R., Horodecki, M., Horodecki, M., and Horodecki, R. (1998). Universal quantum information compression. Phys. Rev. Lett. 81:1714.

Google Scholar

Jun, Y., Gavrilov, M., and Beckhoefer, J. (2014). High-precision test of Landauers principle in a feedback trap. Phys. Rev. Lett. 113:190601. doi: 10.1103/PhysRevLett.113.190601

PubMed Abstract | Crossref Full Text | Google Scholar

Kapur, A., Pearce, R. A., Lytton, W. W., and Haberly, L. B. (1997). GABAA-mediated IPSCs in piriform cortex have fast and slow components with different properties and locations on pyramidal cells. J. Neurophysiol. 78, 2531–2545.

PubMed Abstract | Google Scholar

Keyes, D. E., Ltaief, H., and Turkiyyah, G. (2020). Hierarchical algorithms on hierarchical architectures. Philos. Trans. A Math. Phys. Eng. Sci. 378:20190055. doi: 10.1098/rsta.2019.0055

Crossref Full Text | Google Scholar

Kirkaldy, J. S. (1965). Thermodynamics of the human brain. Biophys. J. 5, 981–986.

Google Scholar

Kitano, K., and Fukai, T. (2004). Temporal characteristics of the predictive synchronous firing modeled by spike-timing-dependent plasticity. Learn. Mem. 11, 267–276. doi: 10.1101/lm.64904

PubMed Abstract | Crossref Full Text | Google Scholar

Kok, P., Jehee, J. F., and de Lange, F. P. (2012). Less is more: expectation sharpens representations in the primary visual cortex. Neuron 75, 265–270. doi: 10.1016/j.neuron.2012.04.034

PubMed Abstract | Crossref Full Text | Google Scholar

Landauer, R. (1961). Irreversibility and heat generation in the computing process. IBM J. Res. Devel. 5, 183–191.

Google Scholar

Lee, D., Port, N. L., Kruse, W., and Georgopoulos, A. P. (1998). Variability and correlated noise in the discharge of neurons in motor and parietal areas of the primate cortex. J. Neurosci. 18, 1161–1170.

PubMed Abstract | Google Scholar

Lochmann, T., and Deneve, S. (2011). Neural processing as causal inference. Curr. Opin. Neurobiol. 21, 774–781. doi: 10.1016/j.conb.2011.05.018

PubMed Abstract | Crossref Full Text | Google Scholar

Magistretti, P., and Pellerin, L. (1999). Cellular mechanisms of brain energy metabolism and their relevance to functional brain imaging. Philos. Trans. Roy Soc. Lond. B 354, 1155–1163.

PubMed Abstract | Google Scholar

Maoz, O., Tkacik, G., Esteki, M. S., Kiani, R., and Schneidman, E. (2020). Learning probabilistic neural representations with randomly connected circuits. Proc. Natl. Acad. Sci. U. S. A. 117, 25066–25073. doi: 10.1073/pnas.1912804117

PubMed Abstract | Crossref Full Text | Google Scholar

Martyushev, L. M., Nazarova, A. S., and Seleznev, V. D. (2007). On the problem of minimum entropy production in the nonequilibrium stationary state. J. Phys. A 40, 371–380. doi: 10.1088/1751-8113/40/3/002

Crossref Full Text | Google Scholar

Melloni, L., Schwiedrzik, C. M., Mller, N., Rodriguez, E., and Singer, W. (2011). Expectations change the signatures and timing of electrophysiological correlates of perceptual awareness. J. Neurosci. 31, 1386–1396. doi: 10.1523/JNEUROSCI.4570-10.2011

PubMed Abstract | Crossref Full Text | Google Scholar

Mitra, A., Snyder, A. Z., Tagliazucchi, E., Laufs, H., and Raichle, M. E. (2015). Propagated infra-slow intrinsic brain activity reorganizes across wake and slow wave sleep. ELife 4:10781. doi: 10.7554/eLife.10781

PubMed Abstract | Crossref Full Text | Google Scholar

Nishimura, Y., Perlmutter, S. I., Eaton, R. W., and Fetz, E. E. (2013). Spike-timing-dependent plasticity in primate corticospinal connections induced during free behavior. Neuron 80, 1301–1309. doi: 10.1016/j.neuron.2013.08.028

PubMed Abstract | Crossref Full Text | Google Scholar

Raatikainen, P. (2015). Gdel's Incompleteness Theorems. Stanford, CA: Stanford Encyclopedia of Philosophy.

Google Scholar

Scellier, B., and Bengio, Y. (2017). Equilibrium propagation: bridging the gap between energy-based models and backpropagation. Front. Comput. Neurosci. 11:24. doi: 10.3389/fncom.2017.00024

PubMed Abstract | Crossref Full Text | Google Scholar

Schultz, W., and Dickinson, A. (2000). Neuronal Coding of Prediction Errors. Ann. Rev. Neurosci. 23, 473–500. doi: 10.1146/annurev.neuro.23.1.473

PubMed Abstract | Crossref Full Text | Google Scholar

Schumacher, B. (1995). Quantum coding. Phys. Rev. A 51:2738.

Google Scholar

Sciara, S., Franco, R. L., and Compagno, G. (2017). Universality of Schmidt decomposition and particle identity. Sci. Rep. 7:44675. doi: 10.1038/srep44675

PubMed Abstract | Crossref Full Text | Google Scholar

Simonetti, M., and Kuner, R. (2020). Spinal Wnt5a plays a key role in spinal dendritic spine remodeling in neuropathic and inflammatory pain models and in the proalgesic effects of peripheral Wnt3a. J. Neurosci. 40, 6664–6677. doi: 10.1523/JNEUROSCI.2942-19.2020

PubMed Abstract | Crossref Full Text | Google Scholar

Sokoloff, L. (1981). Localization of functional activity in the central nervous system by measurement of glucose utilization with radioactive deoxyglucose. J. Cereb. Blood Flow Metab. 1, 7–36.

PubMed Abstract | Google Scholar

Sonntag, R. E., Borgnakke, C., and Van Wylen, G. J. (2003). Fundamentals of Thermodynamics, 6th Edn, Chapter 13. New York, NY: Wiley and Sons.

Google Scholar

Steriade, M., Timofeev, I., and Grenier, F. (2001). Natural waking and sleep states: a view from inside neocortical neurons. J. Neurophysiol. 85, 1969–1985. doi: 10.1152/jn.2001.85.5.1969

PubMed Abstract | Crossref Full Text | Google Scholar

Stern, E. A., Kincaid, A. E., and Wilson, C. J. (1997). Spontaneous subthreshold membrane potential fluctuations and action potential variability of rat corticostriatal and striatal neurons in vivo. J. Neurophysiol. 77, 1697–1715.

PubMed Abstract | Google Scholar

Still, S., Sivak, D. A., Bell, A. J., and Crooks, G. E. (2012). Thermodynamics of prediction. Phys. Rev. Lett. 109:120604. doi: 10.1103/PhysRevLett.109.120604

Crossref Full Text | Google Scholar

Stoll, E. A. (2022a). The mechanics underpinning non-deterministic computation in cortical neural networks. bioRxiv [Preprint]. doi: 10.1101/2022.12.03.518983

Crossref Full Text | Google Scholar

Stoll, E. A. (2022b). Random electrical noise drives non-deterministic computation in cortical neural networks. bioRxiv [Preprint]. doi: 10.1101/2022.12.03.518981

Crossref Full Text | Google Scholar

Stoll, E. A. (2022c). Modeling electron interference at the neuronal membrane yields a holographic projection of representative information content. bioRxiv [Preprint]. doi: 10.1101/2022.12.03.518989

Crossref Full Text | Google Scholar

Stoll, E. A. (2024). A thermodynamical model of non-deterministic computation in cortical neural networks. Phys. Biol. 21, 16003. doi: 10.1088/1478-3975/ad0f2d

PubMed Abstract | Crossref Full Text | Google Scholar

Street, S. (2016). Neurobiology as information physics. Front. Syst. Neurosci. 10:90. doi: 10.3389/fnsys.2016.00090

PubMed Abstract | Crossref Full Text | Google Scholar

Tan, A. M., Stamboulian, S., Chang, Y. W., Zhao, P., Hains, A. B., Waxman, S. G., et al. (2008). Neuropathic pain memory is maintained by Rac1-regulated dendritic spine remodeling after spinal cord injury. J. Neurosci. 28, 13173–13183. doi: 10.1523/JNEUROSCI.3142-08.2008

PubMed Abstract | Crossref Full Text | Google Scholar

Ting, W. K., Huot-Lavoie, M., and Ethier, C. (2020). Paired associative stimulation fails to induce plasticity in freely behaving intact rats. eNeuro 7:396. doi: 10.1523/ENEURO.0396-19.2020

PubMed Abstract | Crossref Full Text | Google Scholar

Turing, A. M. (1936). On computable numbers, with an application to the entscheidungsproblem. Proc. Lond. Math. Soc. 42, 230–265.

Google Scholar

Turrigiano, G. G., Leslie, K. R., Desai, N. H., Rutherford, L. C., and Nelson, S. B. (1998). Activity-dependent scaling of quantal amplitude in neocortical neurons. Nature 391, 892–896.

PubMed Abstract | Google Scholar

Urbin, M. A., Ozdemir, R. A., Tazoe, T., and Perez, M. A. (2017). Spike-timing-dependent plasticity in lower-limb motoneurons after human spinal cord injury. J. Neurophysiol. 118, 2171–2180. doi: 10.1152/jn.00111.2017

PubMed Abstract | Crossref Full Text | Google Scholar

Wimmer, K., Compte, A., Roxin, A., Peixoto, D., Renart, A., and Rocha, J. (2015). Sensory integration dynamics in a hierarchical network explains choice probabilities in cortical area MT. Nat. Commun. 6:177. doi: 10.1038/ncomms7177

PubMed Abstract | Crossref Full Text | Google Scholar

Yan, L. L., Xiong, T. P., Rehan, K., Zhou, F., Liang, D. F., Chen, L., et al. (2018). Single-atom demonstration of the quantum Landauer principle. Phys. Rev. Lett. 120:210601. doi: 10.1103/PhysRevLett.120.210601

PubMed Abstract | Crossref Full Text | Google Scholar

Zarnadze, S., Buerle, P., Santos-Torres, J., Bhm, C., Schmitz, D., Geiger, J. R. P., et al. (2016). Cell-specific synaptic plasticity induced by network oscillations. Elife 5:e14912. doi: 10.7554/eLife.14912

PubMed Abstract | Crossref Full Text | Google Scholar