On the elasticity, adhesion, and friction of PDMS at the nanometer scale

The interdependence of adhesion, friction, and elasticity of elastomers is relevant for various engineering applications. However, its investigation has been limited to smooth glass surfaces. We apply atomic force microscopy (AFM)-based methods to quantify PDMS’s elastic and tribological properties in single asperity contacts (quasi-static and sliding) with a nanometer-scale SiO_x asperity under dry conditions. The selected experimental approach allows us to model the contact initiation with PDMS and its degradation. Combining quasi-static and reciprocal sliding experiments, we identify several contributions to adhesion and friction: junction formation, elastic deformation, rupture, and adhesive material transfer. Furthermore, we find correlations between the elastic deformation of PDMS/SiO₂ junctions and their adhesion hysteresis on the one hand and the shear strength and the work of adhesion on the other.

Introduction

The phenomena of adhesion and friction, which have been the object of intensive research in the past century, are not just theoretical concepts. They are crucial in the design and operation of mechanical systems involving moving parts, such as in the fields of manufacturing and mobility, and more recently in the field of nano-/microelectromechanical systems (N/MEMS). Our research on the importance of interfacial phenomena becomes more crucial as the surface-to-volume ratio of such devices and systems increases, and it has practical implications for improving the performance and durability of these systems. Adhesion, friction, and the usually ensuing wear have been investigated in various environments, vacuum, vapors, and liquids, and across length scales for a wide range of contacting materials ranging from metals, ionically and covalently bounded solids, as well as polymers and elastomers (Bowden and Tabor, 1950; Rabinowicz, 1985; Israelachvili, 2011; Zeng and Zeng, 2013; Gnecco and Meyer, 2015).

The understanding of adhesion, friction, and wear of stiff materials has benefited from a larger body of knowledge of their structural, thermodynamic, and mechanical properties. For metals, for example, it is accepted that adhesion and friction phenomena arise from forming cold-welded junctions at their surface asperities and from their mechanical strength. During adhesion, a junction is loaded along the normal direction to its interface, while during sliding friction, a junction is loaded along the transversal direction to the same interface. In Ref. (McFarlane and Tabor, 1950), McFarlane and Tabor demonstrated a direct correlation between the friction coefficient and the adhesion coefficient for the case of steel on indium. The interrelation of adhesion and friction between metals can be schematically explained based on increased interatomic potential energy upon loading a junction since it results in the stretching of interatomic bonds (Landheer and de Gee, 1991). In the case of adhesion, the potential energy per unit area continues to increase until it is enough to overcome the formation of two new free surfaces. This critical amount of potential energy per unit area is equivalent to the work of adhesion, $W_{ad}={\gamma }_1+{\gamma }_2-{\gamma }_{1/2}$, where γ_1,2 are the surface energies of metals 1 and 2, and γ_1/2 is the interfacial energy between 1 and 2 and depends on the affinity between both materials. It is worth noting that the forces at play during the separation of a metallic junction are orders of magnitude larger than the attractive van der Waals forces experienced by two asperities while they are approaching one another. In the former case of separation, the interatomic forces correspond to metallic bonds, and the difference between the force versus relative distance curves between two asperities or surfaces upon approach and separation is referred to as an adhesion hysteresis (Briscoe and Tabor, 1972). The plastic deformation of metallic junctions upon separation may further enhance this difference. A similar picture can be drawn for the transversal loading of a metallic junction. In this case, though, the leading edge of an asperity forms a new junction while its trail forms new surface segments. The complete shearing of a junction thus corresponds to the balance of these two contributions, and the metallic interatomic energy mostly determines the shear strength of a metallic junction. It can also be enhanced by the work of plasticity of the same junction (Briscoe and Tabor, 1972).

Elastomers stand out from metals and other stiff materials due to their high compliance or low modulus of elasticity, large elastic strain, and stickiness. The molecular structure of an elastomer can be visualized as an amorphous arrangement of random macromolecular coils cross-linked by randomly distributed molecular segments. The characteristic mechanical behavior of elastomers arises from their cooperative structural reconfiguration upon application of stresses. This reorganization or motion of molecular segments requires a free volume into which segments can move and may require time. The time required for such a structural reorganization vanishes at temperatures well above the glass transition temperature. Then, upon applying stress, macromolecular coils reconfigure by cooperative pairs of bond rotations to align themselves along the stress direction. Thereby, translational motion is hindered by the cross-links. Owing to their large density of cross-links, the deformation of elastomers is reversible. However, their strain-stress curves exhibit a hysteretic behavior (Shanks et al., 2013). Polydimethylsiloxane (PDMS) is a widely used silicon-based organic elastomer. Owing to its ability to be molded and to replicate structures down to the nanometer scale, PDMS has found applications in the process of soft lithography as material for microfluidic or lab-on-chip devices, in the field of biomedicine and cosmetics, or as a protective coating material for electrodes, MEMS, electrical and optical parts (See Refs (Lee et al., 2008; Chen et al., 2013; Lee et al., 2007; Schneider et al., 2009; Penskiy et al., 2011; Camou et al., 2003; Hassler et al., 2011; Wang et al., 2018)). PDMS has also been used for sealants and packaging or to manufacture dry adhesive hierarchical structures, such as brushes or gecko-inspired structures (Landherr et al., 2011; Yu et al., 2012; Klittich et al., 2017; Lee et al., 2018; Xue et al., 2017); for several of these applications, elasticity, adhesion, and friction of PDMS are crucial.

Unlike metallic surfaces, the interfacial forces with polymer surfaces are of van der Waals’ nature, and their character does not depend on whether two polymer surfaces are approached toward each other or whether the formed interface is being pulled out. Their surface energy and adhesion force can be deduced from the separation-dependent magnitude of the attractive van der Waals force (Briscoe and Tabor, 1972). The adhesion force at play is often large enough to induce material transfer from one polymer surface to another.

The adhesion and friction of smooth rubber surfaces in contact with glass or steel counter bodies have been investigated for various loading scenarios in Ref. (Roberts and Thomas, 1975). Emphasis was paid to adhesion hysteresis, how it is affected by the time of contact, and its contribution to friction. By monitoring the time evolution of the contact radius between a rubber hemisphere and a glass coverslip with negligible weight, the authors determined the time evolution of the apparent surface energy by applying the JKR model for the case of zero applied load on the contact (Briscoe and Tabor, 1972). Thereby, the authors distinguished two scenarios: in one case, overloading, the coverslip had been pressed under the action of a weight several orders of magnitudes larger than itself onto a rubber hemisphere. The contact area decreased with time, and correspondingly, the apparent surface energy decreased towards its equilibrium value. In the opposite case of underloading, the glass and rubber surfaces were brought together until they just touched each other; the contact radius and corresponding surface energy were then observed to increase toward an equilibrium value. This difference between the contact areas under overloading and underloading conditions thus gives rise to an adhesion hysteresis. This hysteretic behavior is reflected in the velocity dependence of the friction of rubber, where leading and trail edges form out-of-equilibrium interfaces that correspond to the underloading and overloading conditions, respectively.

The tribological properties of PDMS have been investigated under different lubricated conditions. The friction coefficient of a PDMS/PDMS sliding contact strongly depends on the sliding velocity and the lubricant viscosity (Bongaerts et al., 2007). In Ref. (He et al., 2008), the dry macroscale friction coefficient of PDMS vs steel was found to be significantly affected by micro-texturing the surface of PDMS. In contrast, micro-friction measurements indicated a vanishing effect when the counter-sliding body becomes smaller than the length scale of the surface texture. The texture effect was thus attributed to the reduced contact area for textured surfaces. Generally, the dry friction of PDMS has been reported to follow the Johnson-Kendall-Roberts adhesive contact mechanical model for elastic solids (See Refs (Johnson et al., 1971)). This highlights the intertwined character of adhesion and friction of PDMS. Also, in line with this, the friction and adhesion of PDMS surfaces have been altered by surface modifications, highlighting the role of surface and interfacial energies (Chaudhury and Owen, 1993). Moreover, the elastic deformation of PDMS plays a non-negligible role in the rupture of adhesive PDMS junctions. The relative sliding of macroscopic interfaces with elastomers has been observed to proceed by waves of detachment across the contact area, referred to as Schallamach waves. The nucleation of such waves and their propagation across the interface between PDMS and a glass surface has been experimentally investigated in Refs. (Viswanathan et al., 2015; Zhibo et al., 2021). The authors identified elastic instabilities, e.g., wrinkles, immediately after an initial detachment event that corresponds to the nucleation of a single detachment wave, the critical force associated with it being dependent on the work of adhesion. Upon further sliding, the surfaces adhere anew ahead of the glass counter body, initiating the propagation of a Schallamach wave across the contact area. It is worth noting that the wavelength and amplitude of the wrinkles increase with the tangential force. Thereby, the initial wavelength of the wrinkle pattern can be determined from the elastic properties of PDMS. Furthermore, their relative angle to the sliding direction and the generation frequency of Schallamach waves increases with the sliding velocity. The wavelength of a Schallamach wave is typically in the order of magnitude of several hundreds of micrometers, and its propagation velocity is about 100 mm/s, regardless of the sliding velocity. There is, however, a critical sliding velocity for the generation of Schallamach waves that, under their experimental conditions, was reported by the authors in Ref (Viswanathan et al., 2015). to be $v_c\approx 150$ μm/s.

Thus, elastomer adhesion, friction, and elasticity are interdependent. The observations referred to above were limited to optically smooth surfaces. However, engineering surfaces have some roughness due to their manufacturing process, and their contact is initiated at asperities with typical dimensions in the nanometer range. Recently, the authors investigated the reciprocal sliding contact of a single asperity of SiOx with a PDMS surface by atomic force microscopy (AFM) (Caron, 2023). There, we distinguished between two frictional regimes concerning the applied normal force. We observed that friction increases linearly with the normal force in the range of attractive forces. In contrast, in the range of repulsive forces, friction follows a $F_n^{2/3}$-dependence that agrees with the load dependence of the contact area according to the JKR model (Johnson et al., 1971) and the shearing model of sliding friction. We attributed the linear friction dependence on the attractive normal force to the elastic deformation of a PDMS/SiO₂ junction upon sliding. Notably, a stick-slip motion of the SiO2 nano-asperity was observed in the same regime, which we explained based on the restoring force acting by supporting the cantilever spring.

In this work, we use atomic force microscopy (AFM)-based methods to extend our observations to the measurements of PDMS’ elastic and adhesive performances in single asperity contacts with a nanometer-scale SiO_x asperity under dry conditions. The selected experimental approach allows us to model the contact initiation and degradation between PDMS and an oxidized silicon surface. Such a modeled system is particularly relevant for MEMS applications relying on both materials investigated in this work. Combining quasi-static and reciprocal sliding experiments, we identify several correlations between the elasticity of PDMS, its apparent adhesion, and friction with a nanoscopic single asperity of SiO₂.

Materials preparation and characterization

We prepared a PDMS sample with a two-part liquid component kit (Sylgard 184 silicone elastomer manufactured and distributed by Dow Corning, United States). We ensured a precise ratio of 10:1 for the pre-polymer base and cross-linking curing agent. The mixture was then poured into a flask dish and cured for 30 min at 120°C. The results presented in this work were all obtained by AFM measurements of the airside of the PDMS sample. Before atomic force spectroscopy and friction force microscopy measurements, we conducted a thorough characterization of the surface morphology of the as-prepared sample by tapping mode (TM)-AFM using a stiff single-crystalline Si-cantilever (type NCHR, manufactured by NanoSensors, Switzerland).

Figure 1 showcases TM-AFM topography images of the PDMS sample recorded on scan areas of 2.5 μm × 2.5 μm and 1 μm × 1 μm and a typical height line profile indicating the position of topography peaks. The topography data in Figure 1 were summarized in one-dimensional height and peak-to-peak distance distributions (see Figure 2). We determined the roughness parameter R_q by fitting the height distribution with a Gaussian function and using the identity of the standard deviation with R_q. We found R_q ≈ 1 nm. Similarly, the distribution of lateral distances was fitted with a log-normal distribution to determine the mean lateral distance value, $\overline{D}$ ≈ 60 nm.

Figure 1

Figure 1. TM-AFM topography images of PDMS recorded on scan areas of (A) 2.5 μm × 2.5 μm and (B) 1 μm × 1 μm and (C) a typical height line profile.

Figure 2

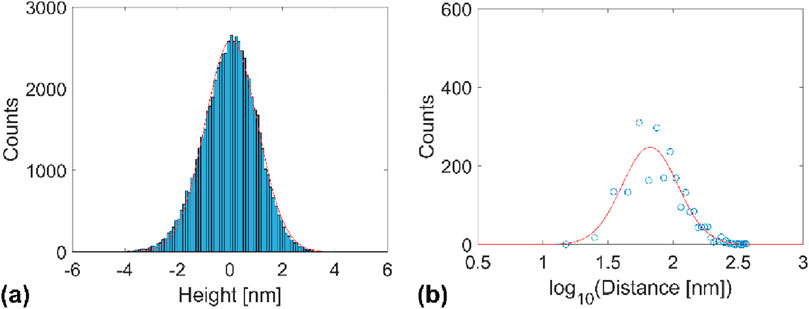
Figure 2. (A) One-dimensional height distribution and its Gaussian fit. (B) One-dimensional peak-to-peak distance distribution and its log-normal fit.

Experimental method

We conducted atomic force spectroscopy (AFS) and friction force microscopy (FFM) measurements in ambient conditions (T = 293 K, RH = 50%) with a Core AFM, using a soft single-crystalline silicon cantilever (type CONTR, manufactured by NanoSensors, Switzerland). Before AFS and FFM measurements, we analyzed the thermal noise of the cantilever to determine its bending stiffness C_n and the sensitivity of the position-sensitive photodiode (PSPD) of the AFM. Specifically, the bending stiffness was determined by Sader’s method (Sader et al., 1999), while we determined the PSPD sensitivity S using the equipartition theorem (Butt and Jaschke, 1995). The torsion stiffness of the cantilever was calculated according to $C_l=\frac{Gw{t}^3}{3h^{2}L}$, where w is the width, t is the thickness, L is the length of the cantilever, h is the tip height, and G is the shear modulus of silicon. We determined C_n = 0.369 N/m and C_l = 204.62 N/m for the cantilever used in this work. We calculated the normal and lateral forces from the vertical and lateral PSPD voltages V_n and V_l by $F_n=C_{n}S{V}_n$ and $F_l=\frac{3}{2}{C}_l\frac{h}{L}S{V}_l$ (Nonnenmacher et al., 1991).

We characterized PDMS’s elastic and adhesive behavior by AFS measurements. AFS measurements consisted of recording the normal force upon approach and retraction of the cantilever toward the sample surface for eight different approach and retraction velocities between 0.2 μm/s and 40 μm/s. For each velocity, measurements were repeated 15 times at the same location. Figure 3 shows a typical AFM force-distance (F_n-Z) curve recorded on PDMS with a single crystalline silicon tip. To determine the contact’s reduced elastic modulus, the approach part of the displayed F_n-Z curve was converted into a δ-F_n curve by considering that once contact has been established, the z-piezo extension corresponds to the sum of the cantilever deflection and the tip penetration into the sample, i.e., $Z=\delta +\frac{F_n}{C_n}$.

Figure 3

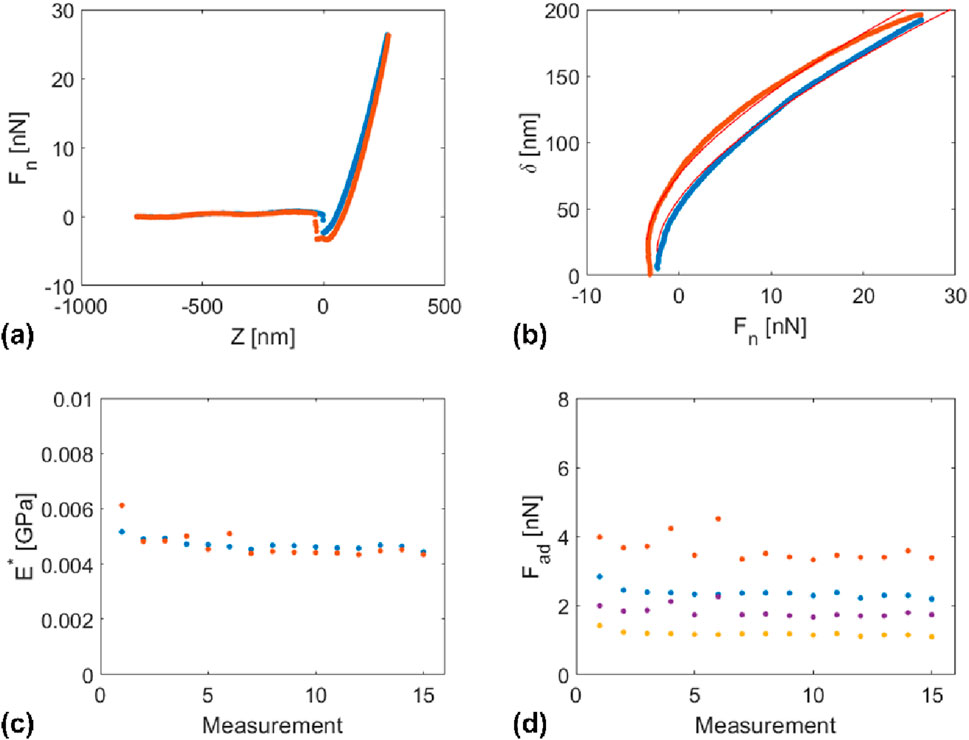
Figure 3. (A) Typical AFM force-distance (F_n-Z) curve recorded on PDMS, showing the approach part in blue (•) and the retraction part in orange (•). (B) Penetration-force (δ-F_n)-curves calculated from the approach and retraction parts of the experimental results in (A)) and fitting curve corresponding to the JKR model (red solid line). (C) Reduced elasticity modulus determined by fitting 15 δ-F_n (•) approach and (•) retraction curves with the JKR model, and (D) adhesion force evaluated from (•) the minimum force values of 15 F_n-Z approach curves (snap-in force), (•) the minimum force values of 15 F_n-Z retraction curves (snap-in force), (•) by fitting 15 approach δ-F_n curves with the JKR model, (•) by fitting 15 retraction δ-F_n curves with the JKR model.

Hertz’s theory of contact expresses the penetration depth in the case of an elastic sphere and contacting a half-infinite elastic solid by $\delta =\frac{a^2}{R}$, where a is the contact radius, and R is the sphere’s radius (in our case, the curvature radius of the tip) (Johnson, 1985). The same contact theory relates the contact radius to the normal force by $a=\sqrt[3]{\frac{3}{4}\frac{R{F}_n}{E^{*}}}$. In situations where adhesion cannot be neglected, the Johnson-Kendall-Roberts (JKR) model can describe the contact radius. In that case, $a=\sqrt[3]{\frac{3}{4}\frac{R}{E^{*}}\left[\left(F_n+F_{ad}\right)+2F_{ad}+\sqrt{4F_{ad}\left(F_n+F_{ad}\right)+{\left(2F_{ad}\right)}^2}\right]}$ and $F_{ad}=\frac{3}{2}\pi w_{a}R$, where $w_a$ is the work of adhesion. Figure 3 also shows results for the reduced elasticity modulus E^* and the adhesion force F_ad, evaluated by determining the minimum F_n values in the recorded F_n-Z curves or fitting their corresponding δ-F_n curves with the JKR model. Notably, E^* values determined from the approach and retraction part of the δ-F_n curves are in very good agreement. In contrast, our adhesion force results appear to differ depending on which part of the curves was selected, i.e., approach or retraction, and on the evaluation method, i.e., by selecting the minimum value in F_n-Z curves or fitting of δ-F_n curves. We discuss these differences in the section Results and discussion.

Furthermore, we analyzed the friction behavior of PDMS during reciprocal sliding contact by FFM. Thereby, an AFM-tip was scanned on PDMS perpendicular to the length axis of the cantilever over a scanning area A_s = 10 × 10 μm²; the sliding velocity along the fast scanning distance was v_s = 80 μm/s. Friction measurements were recorded over the same scanning area under increasing normal force values from F_n = $-35$ nN to F_n = 35 nN. By convention, negative F_n-values correspond to attractive contact forces, and positive values correspond to repulsive contact forces. Figures 4, 5 show height maps recorded in the forward (left to right) and backward (right to left) scanning directions and simultaneously recorded normal force and lateral force maps. Both figures also show representative line profiles corresponding to each signal.

Figure 4

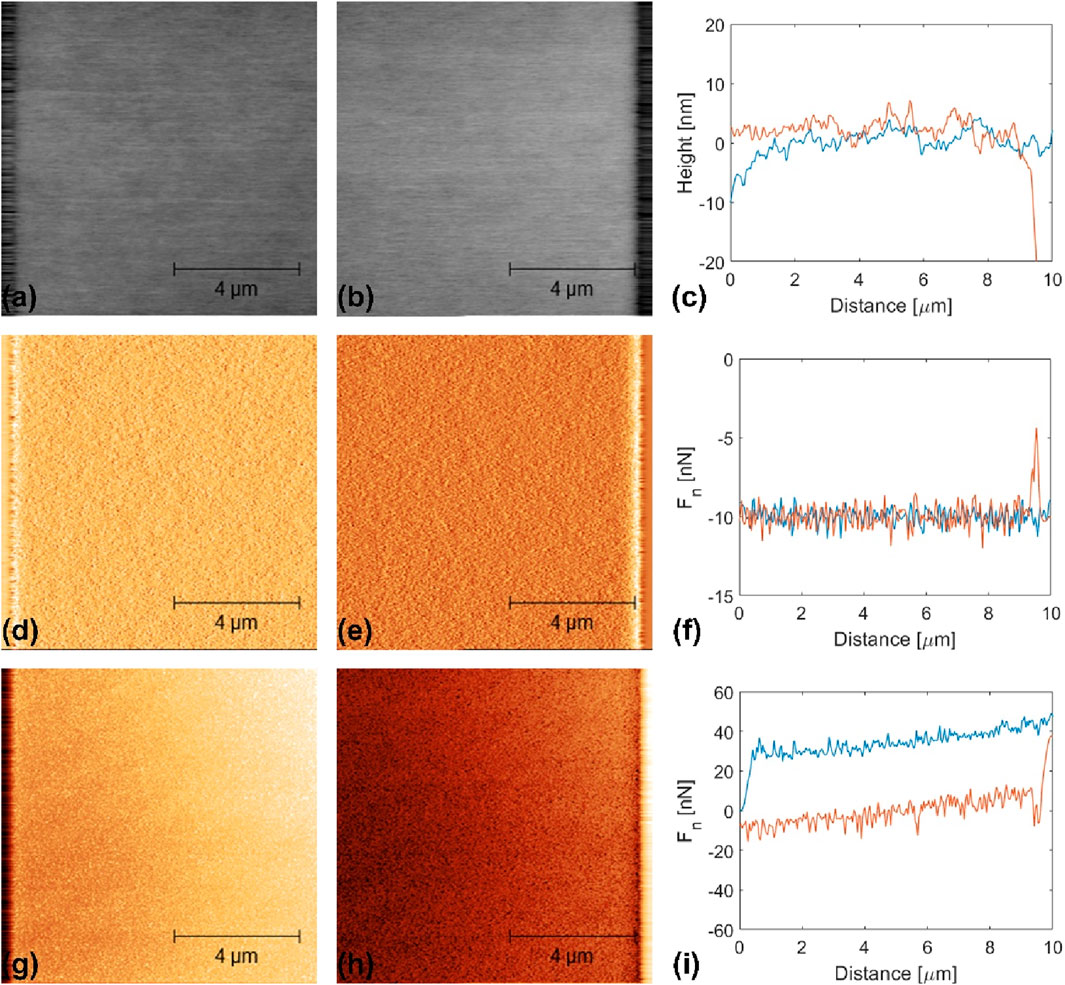
Figure 4. FFM results recorded on PDSM with F_n = −10 nN. (A–C) Height images recorded in (A) the forward and (B) backward scanning direction and (C) corresponding line profiles; (D–F) normal force recorded in (D) the forward and (E) backward scanning direction and (F) corresponding line profiles; (G–I) lateral force recorded in (G) the forward and (H) backward scanning direction and (I) corresponding line profiles. In (C–I), the line signals recorded in the forward scanning direction are plotted in blue, while those recorded in the backward scanning direction are plotted in orange.

Figure 5

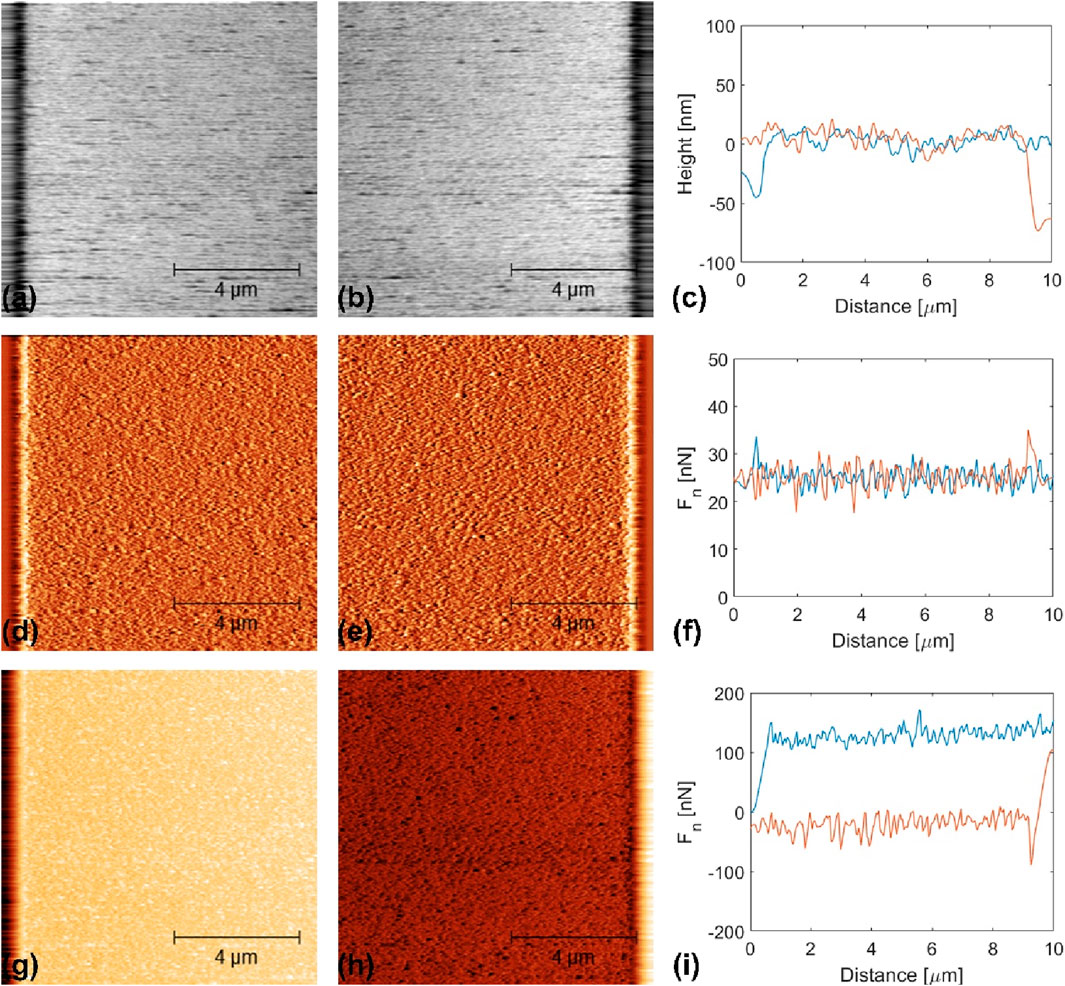
Figure 5. FFM results recorded on PDSM with F_n = 25 nN. (A–C) Height images recorded in (A) the forward and (B) backward scanning direction and (C) corresponding line profiles; (D–F) normal force recorded in (D) the forward and (E) backward scanning direction and (F) corresponding line profiles; (G–I) lateral force recorded in (G) the forward and (H) backward scanning direction and (I) corresponding line profiles. In (C–I), the line signals recorded in the forward scanning direction are plotted in blue, while those recorded in the backward scanning direction are plotted in orange.

We analyzed our experimental friction results, as showcased in Figures 4, 5, to determine the evolution of the interface roughness parameter R_q, the standard deviation of the normal force around its mean value ${\sigma }_{F_n}$, and the mean friction force and its standard deviation. For R_q and ${\sigma }_{F_n}$, we arbitrarily selected the signals recorded in the forward scanning direction. Further, we calculated the friction force maps according to $F_f=\frac{F_{l,fwd}-F_{l,bwd}}{2}$, where F_l,fwd and F_l,bwd are the lateral force images recorded in the forward and backward scanning directions, respectively.

The topography images shown in Figure 1 significantly differ from those in Figures 4, 5. The images in Figure 1 were recorded by TM-AFM with a large set point amplitude value to minimize the kinetic energy of the tip in the vicinity of the PDMS surface and, hence, their mechanical interactions. The topography images in Figure 1 are representative of the free PDMS surface. In contrast, the images in Figures 4, 5 were recorded in contact with a SiO_x tip and represent their interfacial interactions.

The images in Figures 4, 5 also differ from each other. The images shown in Figure 4 were recorded in the adhesive regime (F_n = $-$ 10 nN), while those in Figure 5 were measured in the regime of repulsive contact forces (F_n = 25 nN). In Ref. (Caron, 2023), we distinguished two distinct friction mechanisms for PDMS. In the adhesive regime, we found that deformation is mediated by the elongation of an adhesive junction and its subsequent slippage as enough potential energy is stored in the cantilever. In contrast, friction in the repulsive contact force regime is governed by the rupture of junctions and is associated with a stick-slip motion of the tip. There, the slippage of the tip is analogous to the propagation of a mode II crack.

Results and discussion

Figure 6 displays the dependence of the snap-in and pull-off forces between a SiO_x nano-asperity and PDMS on the approach and retraction velocity. In neither case do we observe a clear trend on the velocity of approach or retraction. However, the pull-out force values are slightly larger than the snap-in force values.

Figure 6

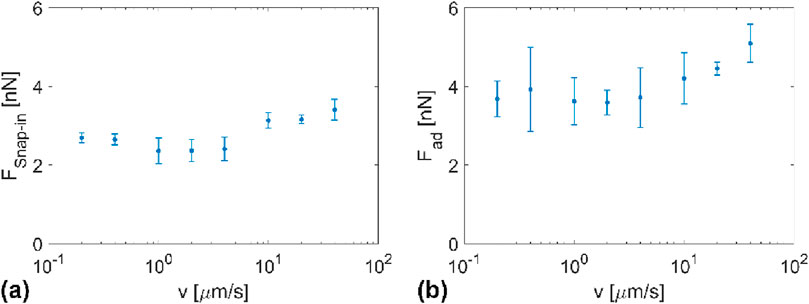
Figure 6. (A) Snap-in force and (B) pull-off force between a nanometer scale SiOx asperity and PDMS as a function of the approach or retraction velocity.

The pull-off force has been widely used to determine the interfacial energy between two contacting bodies (Dos Santos Ferreira et al., 2010). In the case of the JKR model for adhesive contact between elastic solids, the adhesion force or pull-off force, i.e., the force necessary to separate the two contacting bodies, relates to the work of adhesion $w_a$ by $F_{{ad}_{JKR}}=\frac{3}{2}\pi w_{a}R$, where R is the radius of the asperity. Alternatively, the Derjaguin-Muller-Toporov (DMT)-model relates the adhesion force to $w_a$ by $F_{{ad}_{DMT}}=2\pi w_{a}R$ (Derjaguin et al., 1975). Both models are complementary since they apply to different limiting cases. The suitability of these two models has been discussed based on the Tabor constant, $\mu =\frac{R{w_a}^2}{E^{{*}^2}{z}_0^3}$ and z₀ is the equilibrium separation of the surfaces (usually taken as an interatomic distance ∼0.5 nm): JKR model for μ > 5 and DMT model for μ < 0.1 (Greenwood, 1997). Using our experimental values for the pull-off force, E^* = 4 MPa (see discussion below) and R = 7–10 nm in agreement with the manufacturer’s data, we calculate μ $\gg$ 5.

In principle, the snap-in and pull-off forces are equivalent. In practice, the snap-in event might be too fast to measure accurately. Also, the contact time (aging effects), the preloading force, or deformation effects can affect the pull-off force. In Ref. (Toikka et al., 2000), retracting a glass sphere from a PDMS surface was accompanied by pulling a PDMS neck until rupture. To avoid overestimating the work of adhesion under overloading conditions, we first estimate w_a from the average snap-in force value and find, according to the JKR model, w_a = 90 mJ/m².

Furthermore, we suggest that the difference between snap-in and pull-off forces corresponds to the deformation of the neck. The difference between our experimental values for the pull-off and the snap-in forces is almost constant over the approach/retraction velocity domain used in this work: ΔF_ad = F_pull-off–F_snap-in ≈ 1 nN. Applying Hooke’s law, ΔF_ad = kΔδ, where k is the stiffness of the junction and Δδ is the elongation of the neck, and assuming $k=\frac{\pi a_0^2{E}^{*}}{\Delta \delta }$ for a cylindrical neck of length Δδ and radius a₀, and elasticity modulus E^* = 4 MPa, we obtain $\Delta F_{ad}=\pi a_0^2{E}^{*}$. Here, a₀ is taken to be equivalent to the tip radius a₀ = 10 nm, and we calculate $\Delta F_{ad}$ = 1.25 nN, which agrees well with our experimental value. In Ref. (Liu and Xia, 2013), the authors proposed a unified analysis framework for the adhesion of different elastic systems. The authors introduced different characteristic lengths to summarize the competition between elastic and interfacial energies and highlighted the importance of treating elastic deformation and adhesion together.

In this work, we also evaluated the adhesion force and the elasticity modulus E^* by fitting our experimental δ-F_n curves with a function from the JKR theory. We used both the approach and retraction parts of the curves (See section Experimental method and Figure 2). Figure 7 shows the velocity dependence of F_ad and E^* determined by fitting the approach and retraction parts of our penetration curves with the JKR model. As for the snap-in and pull-off forces, no clear dependence of the adhesion force on the velocity is observed in Figure 7. The adhesion force values determined from the approach parts of δ-F_n curves ($F_{{ad}_{JKR,in}}\approx$ 1.75 nN) are slightly lower than for the corresponding retraction parts ($F_{{ad}_{JKR,out}}\approx$ 2 nN); overall the $F_{{ad}_{JKR,in}}$ and $F_{{ad}_{JKR,out}}$ values are slightly lower than the F_snap-in and F_pull-off values, respectively. These results yield the work of adhesion between PDMS and SiO_x w_a = 53 or 60 mJ/m², depending on the selected direction of the tip motion, i.e., approach (in) or retraction (out).

Figure 7

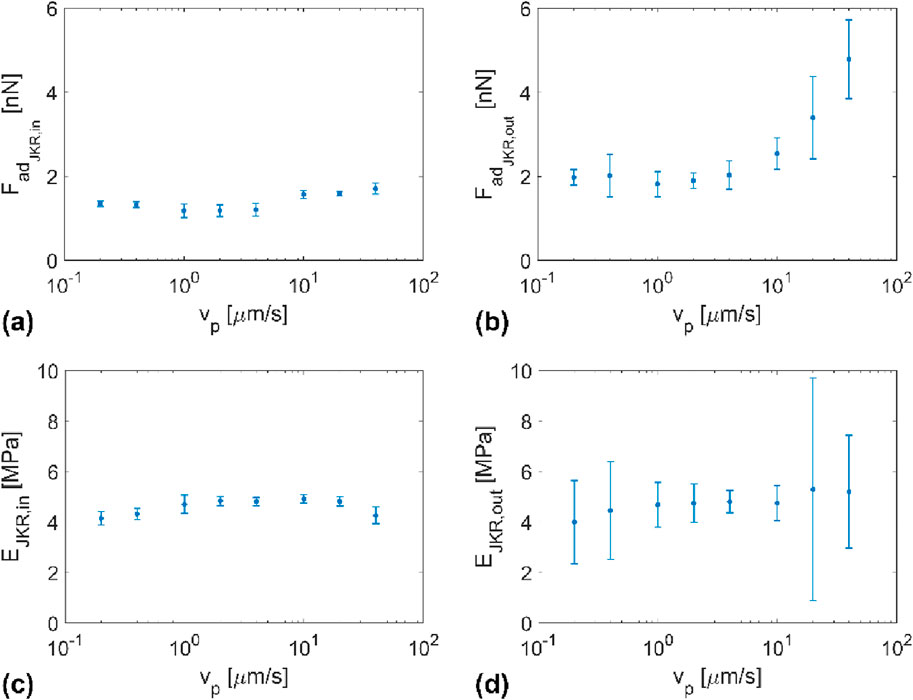
Figure 7. Velocity dependence of (A,B) the adhesion force and (C,D) the elasticity modulus of PDMS as determined by fitting the JKR model equation on experimental (δ-Fn) curves upon (A,C) approach and (B,D) retraction of the AFM tip.

The work of adhesion can be decomposed into the surface energies of both contacting materials and their interfacial energy, i.e., $w_{ad}={\gamma }_{PDMS}+{\gamma }_{{SiO}_x}-{\gamma }_{PDMS/{SiO}_x}$. In Ref. (Kim et al., 2019), the authors reported γ_PDMS = 10 mJ/m², while γ_SiO2 = 65 mJ/m² was reported in Ref. (Kim et al., 2019). Comparing the values determined for w_a in this work with these literature values for SiO₂ and PDMS implies that the interfacial energy between PDMS and SiO₂ is small (${\gamma }_{PDMS/{SiO}_2}$ < 22 mJ/m²). The E^*-values in Figure 7 are not affected by the direction of the penetration curves, i.e., approach or retraction. Also, the E^*-values do not show any trend in velocity, and we find that E^* = 4 MPa.

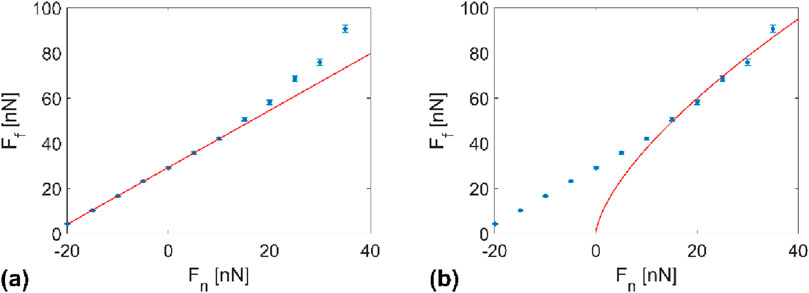
Figure 8 shows the normal force dependence of the friction force between PDMS and a nanometer scale SiO₂ asperity. As in Ref. (Caron, 2023), one observes that in the domain of negative normal force values, the friction force increases linearly with the applied force, while in the domain of repulsive contact force values, the F_f-F_n plot is best fitted by a function of the form $F_f=\tau A_c\left(F_n\right)$, where τ is the shear strength, and A_c is the contact area that depends on the normal force. The contact area is expressed by $A_c=\pi a^2$, where a is the contact radius.

Figure 8

Figure 8. Ff-Fn plots and their fitting with (A) a linear function and (B) a function of the form $F_f=\tau A_c\left(F_n\right)$.

It is important to note that the contact between the tip and sample surface was maintained for negative normal forces as low as $-$ 20 nN during reciprocal sliding. Extrapolating the linear fit function in Figure 7A indicates that the contact would rupture at a normal force value of $-$ 29.25 nN. This value is much larger than the force necessary to rupture the contact between a SiO₂ nanometer scale asperity and PDMS during force spectroscopy measurement. To explain this large difference, we suggest that, during sliding, the elongation of a PDMS neck is enhanced compared to its normal stretching. During reciprocal sliding, a PDMS neck is expected to experience loading components along its length axis and perpendicular to it. Hence, it should undergo both elongation and flexure. Assuming a deformation of λ ≈ 100 nm, equal to the stick-slip length determined in Ref. (Xue et al., 2017), the effective neck stiffness corresponding to the necessary force to rupture a PDMS neck should be k_eff ≈ 0.3 N/m. In Ref. (Xue et al., 2017), we determined a lateral contact stiffness of 0.2 N/m close to neck rupture.

At a normal value of ∼10 nN, we observe a transition from a F_n-to a $F_n^{3/2}$-dependence of the friction force. The latter dependence is attributed to shearing friction, in which case $F_f=\tau A_c\left(F_n\right)$. We determined the shear strength τ by fitting our experimental results with the above equation for shearing; we obtained τ = 25 MPa. This value is slightly larger than previously reported in Ref. (Caron, 2023), where we evaluated τ = 10 MPa, assuming an elasticity modulus E^* = 1.5 MPa. In this work, E^* = 4 MPa was determined experimentally, and the difference between in τ-values can be explained by the different E^* values injected in our fit model.

Similar to the suggestion in Ref. (Yoshizawa et al., 1993), we equate the energy dissipated during the sliding of a SiO₂ asperity on PDMS needs with the energy required to peel off the same asperity from PDMS: $\tau A_{c}x=w_a{A}_c$, or $\tau =\frac{w_a}{x}$, where x is a sliding distance, which we set as the contact radius a ≈R. We thus calculate τ ≈ 5–9 MPa, depending on the determined value of w_a. This calculation differs from the one in Ref. (Yoshizawa et al., 1993), where the authors used the difference between the w_a values determined upon retraction and approach of two surfaces. Both calculated and experimentally derived τ−values are in agreement. The value calculated based on w_a is, however, slightly lower than that determined by fitting our experimental friction data with the shearing model. A better calculation should include the hysteretic deformation of PDMS owing to its nonlinear elastic behavior.

After friction experiments, we imaged the tested area (see Figure 9). As in Ref. (Caron, 2023), we observe material removal. It is worth noting that no pileup was observed around the scanned area. This indicates that wear occurred by adhesive transfer. In this work, though, we did not image the tip after the completion of our measurements. The depth of wear is δ_w = 16.8 nm, corresponding to a wear coefficient $k_w=\frac{A_s{\delta }_w}{l_s\sum F_n}$ ≈ 4 × 10⁻⁴ mm³/Nm, where the sum over the normal force was taken from F_n = 10 nN to F_n = 35 nN. This value agrees with microtribological tests performed with a steel ball on PDMS (see Ref (Lee et al., 2021)).

Figure 9

Figure 9. postmortem topography images of the PDMS surface area subjected to tribological tests.

Conclusion

PDMS’s friction and adhesion mechanisms are intertwined and are affected by the elastic deformation of PDMS junctions. In this work, we show that the difference between the pull-off force and snap-in force of a nanometer-scale asperity corresponds to elastic deformation. Stretching along the PDMS junction axis is rather limited. Under sliding conditions, contact is maintained far beyond the adhesion force, implying further stretching of the junction. In this regime of tensile loading, friction increases linearly with the normal force. In contrast, friction follows a shearing model in the regime of repulsive force and is accompanied by adhesive wear. In this case, calculating the shear strength from the work of adhesion results in a slight underestimation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

WL: Formal Analysis, Investigation, Validation, Visualization, Writing–original draft, Writing–review and editing. JH: Data curation, Formal Analysis, Validation, Visualization, Writing–original draft, Writing–review and editing. JK: Formal Analysis, Investigation, Validation, Writing–original draft, Writing–review and editing. AC: Conceptualization, Methodology, Supervision, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors used the Grammarly software (www.grammarly.com) to verify the quality of the manuscript language.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anupama, S., Parameshwara, S., Prashanth, G. R., Renukappa, N. M., and Sundara Rajan, J. (2019). Study of surface energy of SiO2 and TiO2 on charge carrier mobility of rubrene organic field effect transistor. Proc. 3^rd Intern. Conf. Theo. Appl. Nanosci. Nanotechnol. doi:10.11159/tann19.135

CrossRef Full Text | Google Scholar

Bongaerts, J. H. H., Foutouni, K., and Stokes, J. R. (2007). Soft-tribology: lubrication in a compliant PDMS-PDMS contact. Tribo. Inter. 40, 1531–1542. doi:10.1016/j.triboint.2007.01.007

CrossRef Full Text | Google Scholar

Bowden, F. P., and Tabor, D. (1950). The friction and lubrication of solids. Oxford, U.K: Clarendon Press.

Google Scholar

Briscoe, B. J., and Tabor, D. (1972). Friction and adhesion. Surface forces in friction and adhesion. Faraday Spec. Discuss. Chem. Soc. 2 (7), 17. doi:10.1039/s19720200007

CrossRef Full Text | Google Scholar

Butt, H. J., and Jaschke, M. (1995). Calculation of thermal noise in atomic force microscopy. Nanotechnology 6, 1–7. doi:10.1088/0957-4484/6/1/001

CrossRef Full Text | Google Scholar

Camou, S., Fujita, H., and Fuji, T. (2003). PDSM 2D optical lens integrated microfluidic channels: principle and characterization. Lab. Chip 3, 40–45. doi:10.1039/B211280A

PubMed Abstract | CrossRef Full Text | Google Scholar

Caron, A. (2023). Deformation- and rupture-controlled friction between PDMS and a nanometer-scale SiOx single-asperity. Friction 11, 1755–1770. doi:10.1007/s40544-023-0742-1

CrossRef Full Text | Google Scholar

Chaudhury, M. K., and Owen, M. J. (1993). Adhesion hysteresis and friction. Langmuir 9, 29–31. doi:10.1021/la00025a009

CrossRef Full Text | Google Scholar

Chen, C. Y., Chang, C. L., Chien, T. F., and Luo, C. H. (2013). Flexible PDMS electrode for one-point wearable wireless bio-potential acquisition. Sensors Actuators A Phys. 203, 20–28. doi:10.1016/j.sna.2013.08.010

CrossRef Full Text | Google Scholar

Derjaguin, B. V., Muller, V. M., and Toporov, Y. P. (1975). Effect of contact deformations on the adhesion of particles. J. Colloid Interface Sci. 53, 314–326. doi:10.1016/0021-9797(75)90018-1

CrossRef Full Text | Google Scholar

Dos Santos Ferreira, O., Gelinck, E., de Graaf, D., and Fischer, H. (2010). Adhesion experiments using an AFM – parameters of influence. Appl. Surf. Sci. 257, 48–55. doi:10.1016/j.apsusc.2010.06.031

CrossRef Full Text | Google Scholar

E. Gnecco, and E. Meyer (2015). Fundamentals of friction and wear on the nanoscale. second edition (Springer).

Google Scholar

Greenwood, J. A. (1997). Adhesion of elastic spheres. Proc. R. Soc. Lond. A 453, 1277–1297. doi:10.1098/rspa.1997.0070

CrossRef Full Text | Google Scholar

Hassler, C., Boretius, T., and Stieglitz, T. (2011). Polymers for neural implants. J. Polym. Sci. Part B Polym. Phys. 49, 18–33. doi:10.1002/polb.22169

CrossRef Full Text | Google Scholar

He, G., Chen, W., and Wang, Q. J. (2008). Surface texture effect on friction of a microtextured poly(dimethylsiloxane) (PDMS). Tribo Lett. 31, 187–197. doi:10.1007/s11249-008-9351-0

CrossRef Full Text | Google Scholar

Israelachvili, J. N. (2011). Intermolecular and surface forces. third edition. Burlington, Massachusetts, U.S.A.: Academic Press.

Google Scholar

Johnson, K. L. (1985). Contact mechanics. Cambridge, UK: Cambridge University Press.

Google Scholar

Johnson, K. L., Kendall, K., and Roberts, A. D. (1971). Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A 324, 301–313. doi:10.1098/rspa.1971.0141

CrossRef Full Text | Google Scholar

Kim, Y. G., Lim, N., Kim, J., Kim, C., Lee, J., and Kwon, K.-H. (2019). Study on the surface energy characteristics of polydimethylsiloxane (PDMS) films modified by C4F8/O2/Ar plasma treatment. Appl. Surf. Sci. 477, 198–203. doi:10.1016/j.apsusc.2017.11.009

CrossRef Full Text | Google Scholar

Klittich, M. R., Wilson, M. C., Bernard, C., Rodrigo, R. M., Keith, A. J., Niewiarowski, P. H., et al. (2017). Influence of substrate modulus on gecko adhesion. Sci. Rep. 7, 43647. doi:10.1038/srep43647

PubMed Abstract | CrossRef Full Text | Google Scholar

Landheer, D., and de Gee, A. W. J. (1991). Adhesion, friction, and wear. MRS Bull. 16, 36–40. doi:10.1557/s0883769400055810

CrossRef Full Text | Google Scholar

Landherr, L. J. T., Cohen, C., Agarwal, P., and Archer, L. A. (2011). Interfacial friction and adhesion of polymer brushes. Langmuir 27, 9387–9395. doi:10.1021/la201396m

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J., Park, S., Choi, K., and Kim, G. (2008). Nano-scale patterning using the roll-type UV-nanoimprint lithography tool. Microelectron. Eng. 85 (861), 865. doi:10.1016/j.mee.2007.12.059

CrossRef Full Text | Google Scholar

Lee, J. H., Lee, H. S., Lee, B. K., Choi, W. S., Choi, H. Y., and Yoon, J. B. (2007). Simple liquid crystal display backlight unit comprising only a single-sheet micropatterned polydimethylsiloxane (PDMS) light-guide plate. Opt. Lett. 32, 2665–2667. doi:10.1364/ol.32.002665

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, S. H., Kim, S. W., Kang, B. S., Chang, P.-S., and Kwak, M. K. (2018). Scalable and continuous fabrication of bio-inspired dry adhesives with a thermosetting polymer. Soft Matter 14, 2586–2593. doi:10.1039/c7sm02354e

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, S.-J., Kim, G.-M., and Kim, C.-L. (2021). Effect of glass bubbles on friction and wear characteristics of PDMS-based composites. Coatings 11, 603. doi:10.3390/coatings11050603

CrossRef Full Text | Google Scholar

Liu, J.-L., and Xia, R. (2013). A unified analysis of a micro-beam, droplet and CNT ring adhered on a substrate: calculation of variation with movable boundaries. Acta Mech. Sin. 29, 62–72. doi:10.1007/s10409-012-0202-8

CrossRef Full Text | Google Scholar

McFarlane, J. S., and Tabor, D. (1950). Relation between friction and adhesion. Proc. R. Soc. Lond. A 202, 244–253. doi:10.1098/rspa.1950.0097

CrossRef Full Text | Google Scholar

Nonnenmacher, M., Greschner, J., Wolter, O., and Kassing, R. (1991). Scanning force microscopy with micromachined silicon sensors. J. Vac. Sci. and Technol. B Microelectron. Nanom. Struct. Process. Meas. Phenom. 9, 1358–1362. doi:10.1116/1.585196

CrossRef Full Text | Google Scholar

Penskiy, I., Gerratt, A., and Bergbreiter, S. (2011). Friction, adhesion and wear properties of PDMS films on silicon sidewalls. J. Micromech. Microeng. 21, 105013. doi:10.1088/0960-1317/21/10/105013

CrossRef Full Text | Google Scholar

Rabinowicz, E. (1985). Friction and wear of materials. Hoboken, New Jersey, U.S.A.: John Wiley and Sons.

Google Scholar

Roberts, A. D., and Thomas, A. G. (1975). The adhesion and friction of smooth rubber surfaces. Wear 33, 45–64. doi:10.1016/0043-1648(75)90223-9

CrossRef Full Text | Google Scholar

Sader, J. E., Chon, J. W. M., and Mulvaney, P. (1999). Calibration of rectangular atomic force microscope cantilevers. Rev. Sci. Instrum. 70, 3967–3969. doi:10.1063/1.1150021

CrossRef Full Text | Google Scholar

Schneider, F., Draheim, J., Kamberger, R., and Wallrabe, U. (2009). Process and material properties of polydimethylsiloxane (PDMS) for Optical MEMS. Sensors Actuators A Phys. 151, 95–99. doi:10.1016/j.sna.2009.01.026

CrossRef Full Text | Google Scholar

Shanks, R. A., and Kongs, I. (2013). “General purpose elastomers: structure, chemistry, physics and performance,” in Advances in elastomers I, Advanced structured materials 11. Editor P. M. Visakh, (Berlin Heidelberg, Germany: Springer), 11–45.

CrossRef Full Text | Google Scholar

Toikka, G., Spinks, G. M., and Brown, H. R. (2000). Interactions between micron-sized glass particles and poly(dimethylsiloxane) in the absence and presence of applied load. J. Adhesion 74, 317–340. doi:10.1080/00218460008034534

CrossRef Full Text | Google Scholar

Viswanathan, K., Mahato, A., and Chandrasekar, S. (2015). Nucleation and propagation of solitary Schallamach waves. Phys. Rev. E 91, 012408–012410. doi:10.1103/physreve.91.012408

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Huang, Q., Zhu, W., Yang, M., and Lewis, E. (2018). Novel optical fiber SPR temperature sensor based on MMF-PCF-MMF structure and gold-PDMS film. Opt. Express 26, 1910–1917. doi:10.1364/oe.26.001910

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue, L., Sanz, B., Luo, A., Turner, K. T., Wang, X., Tan, D., et al. (2017). Hybrid surface patterns mimicking the design of the adhesive toe pad of tree frog. ACS Nano 11, 9711–9719. doi:10.1021/acsnano.7b04994

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoshizawa, H., Chen, Y. L., and Israelachvili, J. (1993). Fundamental mechanisms of interfacial friction. 1. Relation between adhesion and friction. J. Phys. Chem. 97, 4128–4140. doi:10.1021/j100118a033

CrossRef Full Text | Google Scholar

Yu, J., Chary, S., Das, S., Tamelier, J., Turner, K. L., and Israelachvili, J. N. (2012). Friction and adhesion of gecko-inspired PDMS flaps on rough surfaces. Langmuir 28, 11527–11534. doi:10.1021/la301783q

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeng, H. (2013). “Adhesion and friction mechanisms of polymer surfaces and thin films,” in Polymer adhesion, friction, and lubrication. Editor H. Zeng (Hoboken, New Jersey, U.S.A.: John Wiley and Sons), 391–442.

CrossRef Full Text | Google Scholar

Zhibo, C., Zhaoqian, S., Dandan, H., Genzong, L., Jian, W., Benlong, S., et al. (2021). From small wrinkles to Schallamach waves during rubber friction: in situ experiment and 3D simulation. Polym. Test. 96, 107084. doi:10.1016/j.polymertesting.2021.107084

CrossRef Full Text | Google Scholar