- 1School of Geography, Earth and Atmospheric Sciences, University of Melbourne, Melbourne, VIC, Australia
- 2ARC Centre of Excellence for Climate Extremes, Melbourne, VIC, Australia
- 3Melbourne Energy Institute, University of Melbourne, Melbourne, VIC, Australia
This study examines several methods and new ideas for climate analysis, including expanded ensembles, that combine model projections from different greenhouse gas emissions pathways and different time periods. These methods are tested on Australian projections data previously made available based on outputs from the Energy Sector for Climate Information (ESCI) project that included all available dynamical downscaling approaches with bias correction designed with attention to detail on extremes. The expanded ensemble method provides larger sample sizes to help enhance confidence, with results showing that the projected changes per degree of global warming have relatively small differences when calculated using two different emission pathways and different time periods, with smaller differences than variations between individual models in the ensemble. Results include maps of mean values and extremes for temperature and rainfall metrics, as well as for compound events associated with dangerous bushfire weather conditions, providing new insights on climate change in Australia. The results also show that extremely dangerous fire conditions such as those of the Black Summer 2019/2020 and of Black Saturday in February 2009 are currently still very rare, but that climate change has already increased the chance of their occurrence, as well as larger increases projected in the future for higher amounts of greenhouse gas emissions. New analysis is also presented for changes in rainfall-based metrics associated with agriculture and biogeography such as Goyder’s Line, discussed in relation to the use of climate analogues for adaptation decision making.
1 Introduction
Understanding how the climate might change in the future is important for effective decision making and adaptation and there are growing needs for climate services in many sectors of society (e.g., environmental management, emergency services, health, finance, agriculture, water availability and energy) (Kirono et al., 2020; Burrell et al., 2020; Ukkola et al., 2020; IPCC, 2021; Wasko et al., 2024). These needs often require climate analysis for specific time periods, locations or emission pathways, including for extremes as well as mean values, noting that many of the largest impacts from human-caused climate change are being experienced through changes in extremes (Perkins-Kirkpatrick et al., 2016; Guerreiro et al., 2018; Rauniyar and Power, 2020; van Oldenborgh et al., 2021).
Global climate models (GCMs) are a useful tool to aid in understanding fundamental processes in the climate system including potential future climate changes, while noting a wide range of uncertainties around this as detailed in reports such as those of the (IPCC, 2021; Iturbide et al., 2021). This includes uncertainties associated with the range of future pathways that might be followed for anthropogenic greenhouse gas emissions (Taylor et al., 2012). Furthermore, GCMs can simulate many key aspects of the Earth’s climate, particularly for large-scale features, but have a limited ability to simulate some aspects (e.g., fine-scale physical processes in particular). For example, the resolution of GCMs is currently not fine enough to directly simulate convective processes such as those that cause thunderstorms and associated rainfall in convective updrafts, with the simulation of these processes requiring much finer-scale (high resolution) modelling (Huang et al., 1987; Dowdy et al., 2019; Gutowski et al., 2020). Fine-scale dynamical downscaling that uses regional climate models (RCMs) applied to GCM output data can help reduce some limitations of GCMs. However, RCM approaches are also not perfect at simulating some processes and many uncertainties still exist, including biases associated with the GCM providing boundary conditions, as well as model resolutions typically not fine enough for accurately simulating some processes such as fine-scale turbulence and entrainment (Droegemeier and Wilhelmson, 1987; Hoogewind et al., 2017; Huang et al., 1987; Dowdy et al., 2021; Nishant et al., 2021; Su et al., 2021; Thatcher, 2021). As such, analysis methods and interpretation of data for climate projections should be considered appropriately, with a focus on minimizing uncertainties in results where feasible.
There are many sets of climate projections data available through Australia, including existing data sets produced previously by various State and Federal Government groups. These include projections based on the CMIP5 set of GCM simulations (Taylor et al., 2012) with RCM downscaling approaches applied for the Australian region: referred to as NARCliM (Evans et al., 2014; Nishant et al., 2021), CCAM (McGregor, 2005; Thatcher, 2021) and BARPA (Su et al., 2021; Thatcher, 2021). The Energy Sector Climate Information (ESCI) project (Dowdy et al., 2021; Thatcher, 2021) was the first to bring together climate projections across Australia including based on those three downscaling approaches (NARCliM, CCAM, and BARPA), leading to the collation of a 16-member model ensemble of bias corrected projections (as detailed in Section 2.2). This ensemble of projections was selected for use here to test the main aims of this study: i.e., to examine several methods and new ideas for climate analysis of mean values and extremes through Australia. These methods include the use of expanded ensembles for increased sample size, based on combining different emissions pathways and time periods for the projected changes per degree of global warming, with further details in the following paragraphs. It is also noted that there are steps currently underway in Australian State and Territory as well as Federal groups for producing new sets of climate projections for the Australian region based on applying RCMs to CMIP6 GCMs (Grose et al., 2020; Howard et al., 2023; Stassen et al., 2023; Di Virgilio et al., 2024), including some initial steps to apply bias correction (Zhang et al., 2024), providing scope for future studies to extend the analyses presented here to bias corrected RCM downscaling of CMIP6 projections for Australia (which are currently not available).
This study tests some climate analysis methods including using expanded ensembles to help increase sample sizes, noting that larger sample sizes can help reduce uncertainties, particularly for extremes (Gumbel, 1958; Koutsoyiannis, 2004; Dowdy, 2023). Results are presented here for mean values and for extremes throughout Australia, including for metrics based on temperature, rainfall and fire weather conditions. This analysis is intended to be complementary to other existing climate information (e.g., Iturbide et al. (2021)), noting that consideration of a broad range of data, methods and other information sources is often beneficial for assessing climate risk.
A particular focus of this study is on examining projected changes calculated per degree of global warming [e.g., King et al. (2017, 2021)]. Projections calculated in this way could potentially be combined with similar estimates from other modelling ensembles (e.g., based on a wide range of emission pathways used in other modelling experiments). Another aspect explored here is on how model ensembles can be utilized to represent changes in extremes, such as for weather conditions associated with some of the extremely severe wildfire events that have occurred in recent years with disastrous impacts. In addition to impacts of climate change on human and built environments, many ecological impacts are also occurring such as through changing habitats for threatened species. One example is considered here using a rainfall-based biogeographical indicator, mapping changes in where desert ecoregions may be likely to occur as compared to more heavily vegetated regions.
2 Materials and methods
2.1 Weather metrics
The analysis presented here uses several weather metrics that are often considered for climate risk and adaptation purposes in Australia, including near-surface daily maximum temperature (tasmax; with units of °C) and minimum temperature (tasmin; with units of °C), as well as daily precipitation (pr; with units of mm). The Forest Fire Danger Index (FFDI: unitless; McArthur, 1967) is also used, interpreted here as a useful way to combine several weather conditions known to influence fire behavior, noting various similar fire weather indices are also available and used in other regions of the world. The FFDI is calculated as shown in Equation 1 using inputs of daily maximum temperature, mid-afternoon (i.e., 0600 Universal Time from the 6-hourly model data used here corresponds to mid-afternoon local time for Australia) values of relative humidity and wind speed, as well as a Drought Factor based here on the Keetch Byram Drought Index (KBDI) (Keetch and Byram, 1968) that estimates accumulated moisture deficit based on rainfall and temperature. Further details on FFDI are also available in previous studies including for FFDI data sets based on observations and model projections (Dowdy, 2020).
where T = Temperature (°C), RH = relative humidity (%), V = horizontal wind speed averaged over a 10-min period at a height of 10 m above the surface (km.hr.−1) and DF = Drought Factor (unitless).
The results presented in this study include analysis of mean values as well as of extremes based on exceeding various thresholds. There are many ways to analyze extremes, such as defining individual thresholds for each location defined by a particular occurrence frequency. For example, metrics of the order of 90th to 99th percentile for the magnitude of a value are used for representing extremes in some studies (Dowdy, 2020; Peter et al., 2024), representing extremes that occur several times a year on average based on daily values. However, what is considered extreme is somewhat arbitrary and could depend on the intended application, noting that for design standards extremes are typically defined using multi-year return periods, e.g., very rare events that may be expected to occur on average only once in several years (Gumbel, 1958; Wasko et al., 2024). Extremes can also be defined based on fixed magnitude thresholds applied through a broad region. For example, the number of days with maximum temperature above 45°C (or similarly for 46°C, or 47°C, etc.) could be examined at all locations throughout Australia. This means that some places will exceed a given threshold more frequently than other places, such that results should be interpreted accordingly. This study includes analysis for extremes defined using percentile-based thresholds, showing results based on exceeding a threshold corresponding to the value that is exceeded once a year on average (equal to the 99.7th percentile) during a historical period from 1980 to 2005. Some results are also shown using a fixed magnitude threshold, based on daily minimum temperature being lower than 0°C, noting relevance for freezing of water at that temperature.
2.2 Dataset selection
Many different sources of climate projections data are available for Australia. Some examples include State and Territory activities for individual regions within Australia (e.g., Corney et al. (2010); Evans et al. (2014); Fita et al. (2016); Clarke et al. (2019)) as well as other examples with national coverage such as collated by previous projects including Climate Change in Australia (CSIRO and Bureau of Meteorology, 2015), the ESCI project (Dowdy et al., 2021; Thatcher, 2021) and the National Hydrological Projections (NHP) project (Srikanthan et al., 2022; Vogel et al., 2023; Peter et al., 2024).
The projection data selected for use here were based on an ensemble collated by the ESCI project that included outputs from the CMIP5 set of GCM projections (Taylor et al., 2012) with three different RCM approaches applied: NARCliM (New South Wales and Australian Regional Climate Modelling: Evans et al., 2014; Nishant et al., 2021), CCAM (Conformal Cubic Atmospheric Model) (McGregor, 2005; Thatcher, 2021) and BARPA (Bureau of Meteorology Atmospheric Regional Projections for Australia) (Su et al., 2021; Thatcher, 2021). These data have been used in various previous applications and studies have documented aspects such as model assessment, representativeness and projected future changes for many different quantities relating to those data (CSIRO and Bureau of Meteorology, 2015; Dowdy et al., 2021; Thatcher, 2021). The ensemble consists of 16 members from a range of model approaches as follows:
- Dynamical downscaling using the NARCliM modelling approach (NSW and ACT Regional Climate Model) applied for the Australian region to three GCMs (ACCESS1-0, ACCESS1-3 and CanESM2) with two configurations of each, providing six ensemble members.
- Dynamical downscaling using the CCAM modelling approach (conformal cubic atmospheric model) applied for the Australian region to five GCMs (ACCESS1-0, CanESM2, GFDL-ESM2M, MIROC5 and NorESM1-M), providing five ensemble members.
- Dynamical downscaling using the BARPA modelling approach (Bureau of Meteorology Atmospheric Regional Projections for Australia), initially for eastern Australian then also similarly for western Australia to cover the entire Australian region, applied to one GCM (ACCESS1-0 GCM) providing one ensemble member.
- Four GCMs without downscaling applied (ACCESS1-0, CNRMCM5, GFDL-ESM2M and MIROC5 GCMs), providing four ensemble members.
The 16-member model ensemble covers a historical baseline period from 1980 to 2005 as well as the period from 2006 to 2099 using two different emissions pathways: a low-moderate emissions pathway (RCP4.5) and a high emissions pathway (RCP8.5) (Taylor et al., 2012). Global average temperature data for each GCM (obtained from https://github.com/traupach/warming_levels) were used for the analysis of projected changes per degree of global warming, with a boxcar moving average of ±10 years applied to those temperature data to help represent the average climate around a given time period.
The ESCI project also applied bias correction to the projections data using the QME (Quantile Matching for Extremes) (Dowdy et al., 2021; Dowdy, 2023; Peter et al., 2024). The QME bias correction in the ESCI project was applied to the projections data at 0.05×0.05-degree grid cells in latitude and longitude through Australia, with quantile-quantile matching to the observations-based dataset known as AWAP (Jones et al., 2009). Previous studies have found the AWAP data to be suitable for use in climate analysis (King et al., 2013) while noting limitations such as the observations network being relatively sparse in parts of the central and western desert regions where additional care should be taken when interpreting results.
The climate analysis presented here using the ESCI projections dataset as described above is intended to provide examples of plausible climate change, including based on ensemble-based metrics, while noting that values above or below those given could also be possible and acknowledging a broad range of factors that contribute to confidence and uncertainties. The range of model spread is also considered here, providing additional estimates of plausible changes above and below the ensemble mean. Additionally, a smoothing of 0.25-degrees is applied to figures in this study, as a moving average in latitude and longitude, to help the interpretation of regional features. For results throughout this study, projected changes are shown only if they are statistically significant at the 90% confidence level (using bootstrapping with 500 iterations).
2.3 Expanded ensemble approach
An expanded ensemble of model data is used in this study with an aim of increasing sample size for enhanced confidence in results. This is based on calculating the projected change per degree of global warming for several combinations of different emission pathways with different time periods, then using all of those projected changes together to increase the number of members in the ensemble. The available emission pathways in the dataset used here included relatively low (RCP4.5) and high (RCP8.5) pathways. Emissions in recent decades have been following the high emissions pathway RCP8.5 more closely than other emissions pathways (Schwalm et al., 2020), while noting that reductions in global emissions in coming decades are likely such that RCP8.5 could be considered a high pathway when considering this likelihood for later this century (Taylor et al., 2012; IPCC, 2021). The steps used are as follows:
1. The projected changes per degree of global warming are calculated for a relatively low emission pathway (RCP4.5) corresponding to a climate period of ±10 years centered on when each model reaches 1°C of global warming above the mean for the historical period 1980 to 2005 (as listed in Table 1). As an example of how this is done for one of the 16 ensemble members, the BARPA downscaling is based on the GCM called ACCESS1-0 which reaches 1°C of global warming above that historical period around the year 2031 as shown in Table 1 (i.e., 1°C above the historical mean global temperature for the period 1980 to 2005). As such, the projected change for that ensemble member is calculated as the average change in annual rainfall from the historical period (i.e., 1980 to 2005) to the period 2021 to 2041 (i.e., ±10 years centered on 2031). This approach is repeated individually for each of the 16 ensemble members, for the years listed in Table 1 corresponding to the GCMs the projections are based on (with details on the 16 ensemble members as listed in Section 2.2). The ensemble average of the projected change at each grid cell is then calculated.
2. A similar method is used to the above step 1 for the projections from the low emissions pathway, but using a later time period for each model, based on when they reach 1.5°C global warming above the historical period 1980 to 2005 (as listed in Table 1). The projected changes are then divided by 1.5, so that they represent the change per degree of global warming.
3. The methods used for steps 1 and 2 are repeated for the high emission pathway (RCP8.5). This includes using the time periods listed in Table 1 for the high emissions pathway.
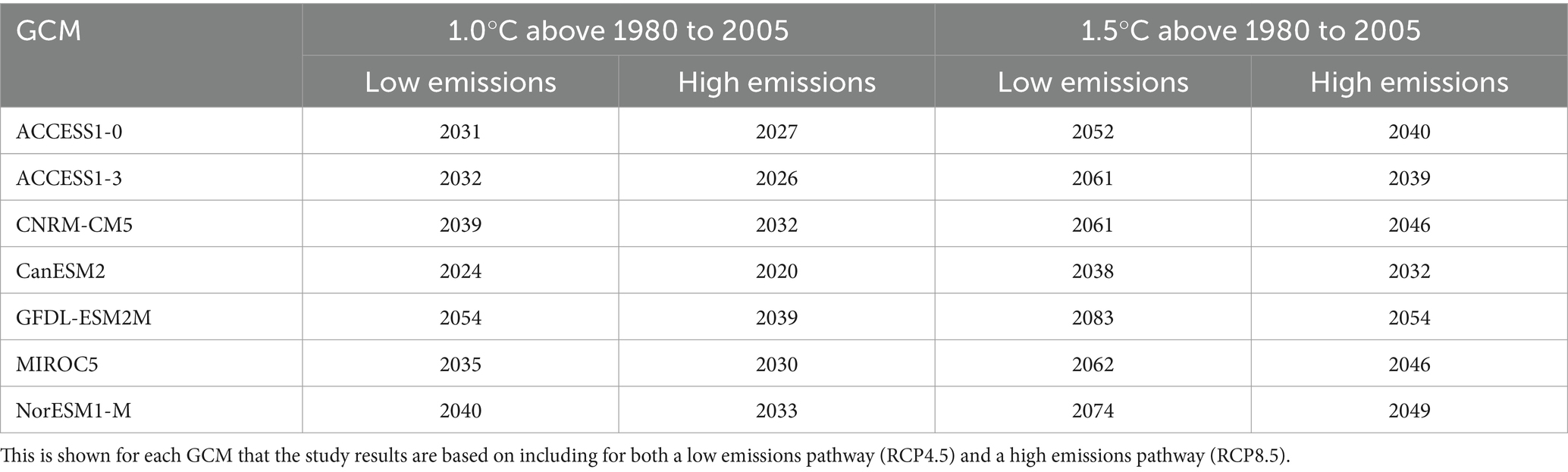
Table 1. The timing (year) for when each GCM shows either 1.0°C or 1.5°C warming of the global average surface air temperature, with the warming calculated above the mean for the historical period 1980 to 2005.
The above steps are one example of how this could be done, noting a range of other variations based on this that might be considered in future potential research and applications. For example, instead of 1°C and 1.5°C global warming, it could similarly be done for other warming levels (e.g., 2°C or more perhaps), such as depending on the emissions pathway or time periods considered for a given application.
An important point to note is that the changes calculated here per degree of global warming are intended to be interpreted considering that about 1.1°C of global warming has already occurred due to anthropogenic causes since industrialization (IPCC, 2021). As such, the change per degree of global warming can be interpreted as an estimate of the change that has already occurred due to human-caused climate change (or a slight underestimation given global warming in now slightly higher than 1°C). Additionally, further anthropogenic global warming is expected in coming decades added on top of these changes that have already occurred, with potential to soon exceed global warming above the 1.5°C level recommended to try to limit the worst impacts of climate change (King et al., 2017; IPCC, 2021).
3 Results
3.1 Rainfall analyses
Rainfall is highly variable in Australia, including on seasonal to interannual time scales, due to the influence of modes of natural climate variability such as ENSO (Nicholls et al., 1997; King et al., 2015a; McKay et al., 2023). As such, it can be beneficial to have large sample sizes when examining the climatology of Australian rainfall. Methods are tested here for expanding the sample size based on combining model data from different time periods and emissions pathways.
Figure 1A shows the mean annual rainfall based on the 16-member model ensemble for a historical period from 1980 to 2005 based on the available data from the ESCI projections dataset. There are higher totals in northern and eastern Australia and lower values in inland regions consistent with observations noting uncertainties for rain data in regions of sparse observations such as some of those shown here with low values of mean rainfall (e.g., King (2023)). Projected changes in annual rainfall are also shown in Figure 1, calculated using a range of different methods that are described here as follows. Figure 1B shows the projected change for a low emission pathway (RCP4.5) corresponding to a climate period of ±10 years centered on when each model reaches 1 degree of global warming above the mean for the historical period (as listed in Table 1), following the method detailed in Section 2.3. Those projections indicate decreased mean rainfall through many regions of Australia, with the main exceptions of northwest and adjacent inland regions, along the east coast in a narrow region, as well as for the island of Tasmania to the south of the Australian continent for which increased rainfall is shown.
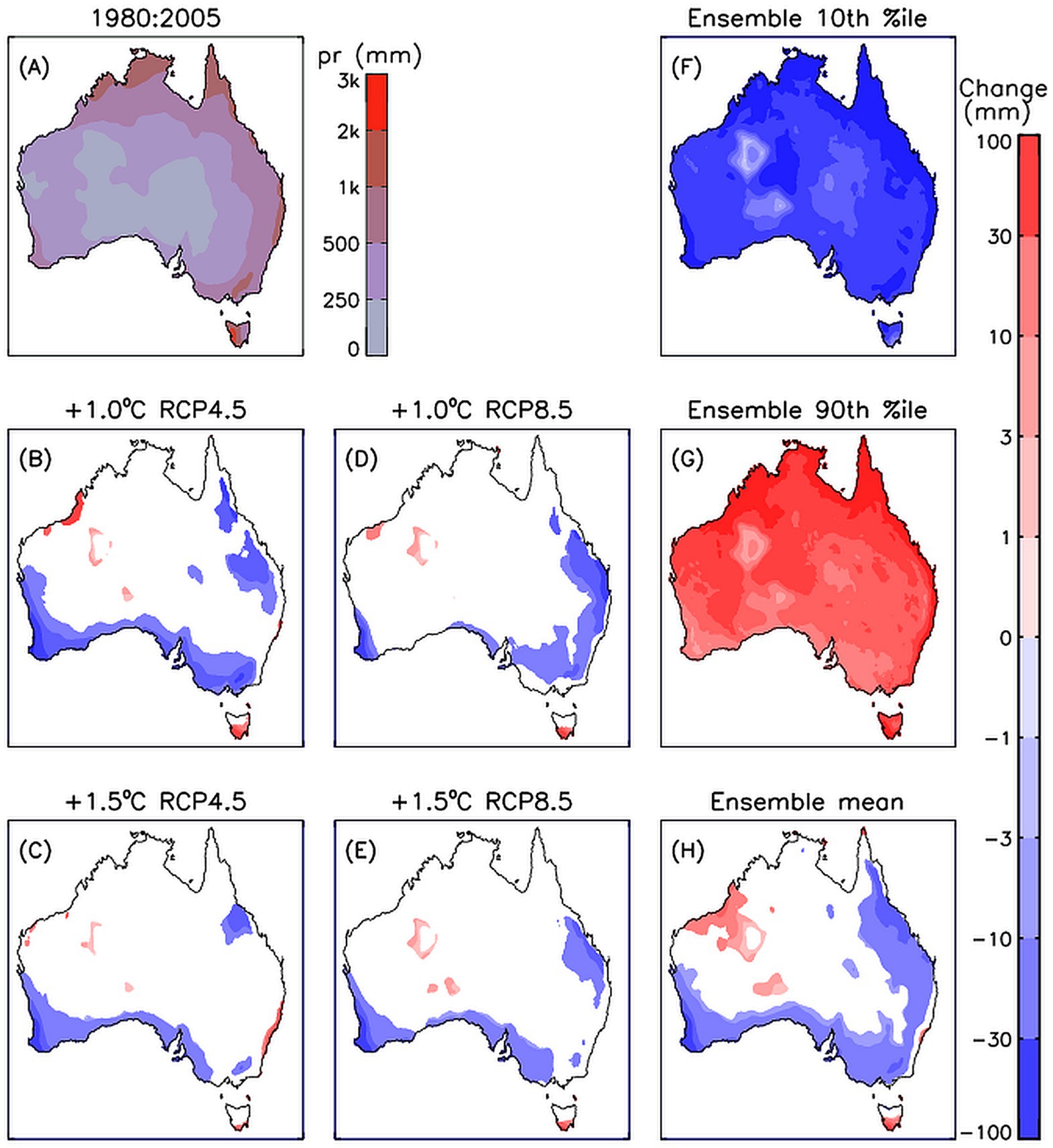
Figure 1. Mean annual precipitation shown for a historical period 1980:2005 (A) based on the 16-member model ensemble. The change per degree of global warming is also shown for four different climate periods corresponding to an additional 1°C (B) and 1.5°C (C) warming following a low emissions pathway (RCP4.5) and 1°C (D) and 1.5°C (E) warming following a high emissions pathway (RCP8.5). To provide an indication of the range within the model ensemble members used to calculate the change per degree of warming, the 10th (F) and 90th (G) percentiles of the modelled changes are shown together with the mean (H). Results are shown for changes only if statistically significant above 90% confidence level.
A similar method is used for the results shown in Figure 1C, but using a later time period for each model, based on when they reach 1.5 degrees of global warming for the low emissions pathway (as listed in Table 1). The projected changes are then divided by 1.5, so that they represent the change per degree of global warming. This results in similar magnitudes for the projected changes in Figure 1C to what was seen previously in Figure 1B, as they both now represent the change per degree of global warming, even though Figure 1C is based on data from later time periods than used for Figure 1B. The methods used for Figures 1D,E are the same as used for Figures 1B,C, respectively, apart from being based on a high emission pathway for the projections and their corresponding time periods (as listed in Table 1).
The four different versions of the projected changes per degree of global warming (Figures 1B–E) show some similar spatial features such as reduced rainfall projected in many locations with increases around the northwest. Some small-scale localized variations are also indicated, such as narrow region of increased rainfall not apparent along the east coast in Figure 1D to the extent seen in Figure 1B. However, some of these fine-scale details might relate to natural variability, including from weather processes and randomness noting the inherent chaotic nature of the atmosphere (Lorenz, 1965), and potentially could look somewhat different if a larger sample size was available.
The general similarities between the changes calculated per degree warming in those four different ways (as shown in Figures 1B–E) suggests potential for considering those data all together in combination with each other. This expanded ensemble, based on using 2 emissions pathways and 2 different time periods for each model in the 16-member ensemble, effectively provides 64 estimates of the projected change per degree of warming (i.e., 2 × 2 × 16 = 64 members). The mean change based on that 64-member expanded ensemble is shown in Figure 1H. Additionally, to provide an indication of the variation between models, the 10th and 90th percentiles of the projected change is shown in Figures 1F,G, respectively. Those percentiles are calculated individually for each grid cell location. For example, the 10th percentile value at a given location is the projected change for the model ensemble member that has the 6th smallest projected change from the 64-member ensemble. Similarly, the 90th percentile value at a given location is the projected change for the model ensemble member that has the 6th largest projected change from the 64-member ensemble.
The variation between models in the ensemble is considerable, as demonstrated by the 10th and 90th percentile changes being opposite in sign at all locations throughout Australia (Figures 1F,G). This variation is much larger than the degree of variation between the four methods shown in Figures 1B–E. Another notable feature of these results is that significant changes (at a 90% statistical confidence level) are identified for a much larger area for the expanded ensemble (Figure 1H) than for its constituents (Figures 1B–E).
Annual rainfall projections are considered further in Figure 2, presenting results based on the 250 mm contour line for a region of southern Australia. Metrics such as this can be associated with drought and vegetation–weather relationships relevant for ecology, fire management or agricultural sectors. One example is Goyder’s Line, such as approximated by 250 mm annual rainfall, noting a range of other measures can also be used for that agricultural indicator (Meinig, 1961; Nidumolu et al., 2012; Tozer et al., 2014). This 250 mm contour line is shown for the historical period 1980 to 2005, as well as changes in that line corresponding to different global warming levels (using the results shown in Figure 1H), such as +1°C and + 2°C above that historical period. The results shown in Figure 2 are an example of considering how the future climate in a particular location might become similar to the climate from other locations based on what they had in the past (e.g., based on their historical climate). This relates to the concept of a ‘climate analogue’ between different locations and time periods, such as examined in King (2023) for some Australian locations.
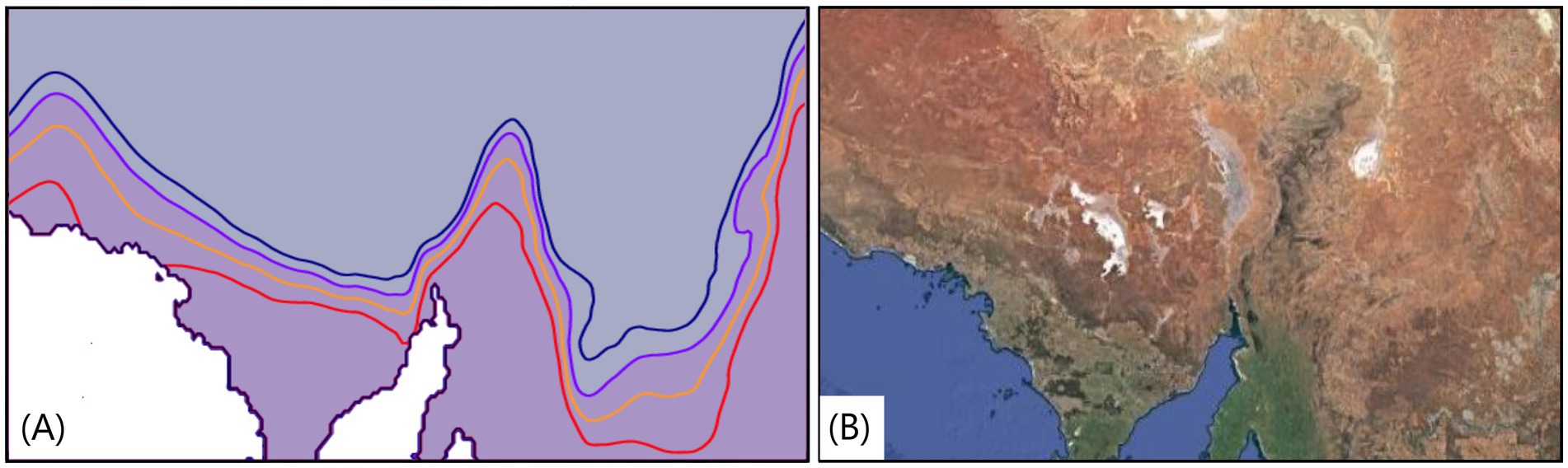
Figure 2. Changes in the 250 mm contour line of annual average rainfall in a region of the central southern coast of the Australian continent (A). This contour line is shown for the period 1980:2005 (light purple line), as well as for changes in that line corresponding to different global warming levels of +1°C (orange line), +2°C (red line) and −1°C (dark blue line). The changes per degree of global warming is using the expanded ensemble results from Figure 1. This contour line relates to guidance metrics sometimes considered for agricultural decision making, such as Goyder’s Line in this region. The satellite image (B) obtained from Google Maps August 2024 also indicates that this rainfall contour line is broadly similar to where ecosystems change from the light brown desert regions in the north to the darker brown and green vegetated regions towards the south in general.
The results show that the 250 mm contour line moves further south for higher global warming amounts (Figure 2). The historical period used here already has some global warming above the preindustrial period, noting that about 1°C global warming has already occurred (IPCC, 2021), such that a contour line is also shown in Figure 1 corresponding to −1°C below that historical period of 1980 to 2005, which results in the 250 mm contour line shifting further to the north. A satellite image is also shown in Figure 2 for qualitative illustrative purposes, with somewhat similar spatial patterns (i.e., variations between vegetation and desert regions) to what is indicated based on the 250 mm rainfall contour. For example, this provides some indication of where ecosystems currently change from the light brown desert regions in northern regions to the darker brown and green vegetated regions towards the more southern regions in general, while noting potential for many other metrics and climate analogue approaches that could also potentially be considered.
Results such as presented in Figure 2, or similar analyses for other metrics, might be useful for different types of climate adaptation. For example, one kind of adaptation (‘Type 1’) might involve moving away from a current location, to be a location that has a similar future projected climate to what the current location had in the past. A second type of adaptation (‘Type 2’) might involve not moving away from a current location, but instead changing the situation at that location such as to be more similar to other locations with similar past climates to what is projected in the future for the current location (to the extent that may be possible). Maps similar to Figure 2 that show a range of suitable locations for these different types of climate analogues might be useful for various ecological decision making, including in relation to threatened species management in our changing climate.
3.2 Temperature analyses
Results are presented for daily maximum temperature (tasmax) in Figure 3, using the same set of methods as used for rainfall in Figure 1. Mean values are shown for the historical period, similar to observations-based data such as King (2023), with projected changes also shown based on multiple methods that are detailed here as follows. The temperature projections show little variation depending on the emissions pathway and degree of global warming (i.e., comparing the panels for Figures 3B–E).
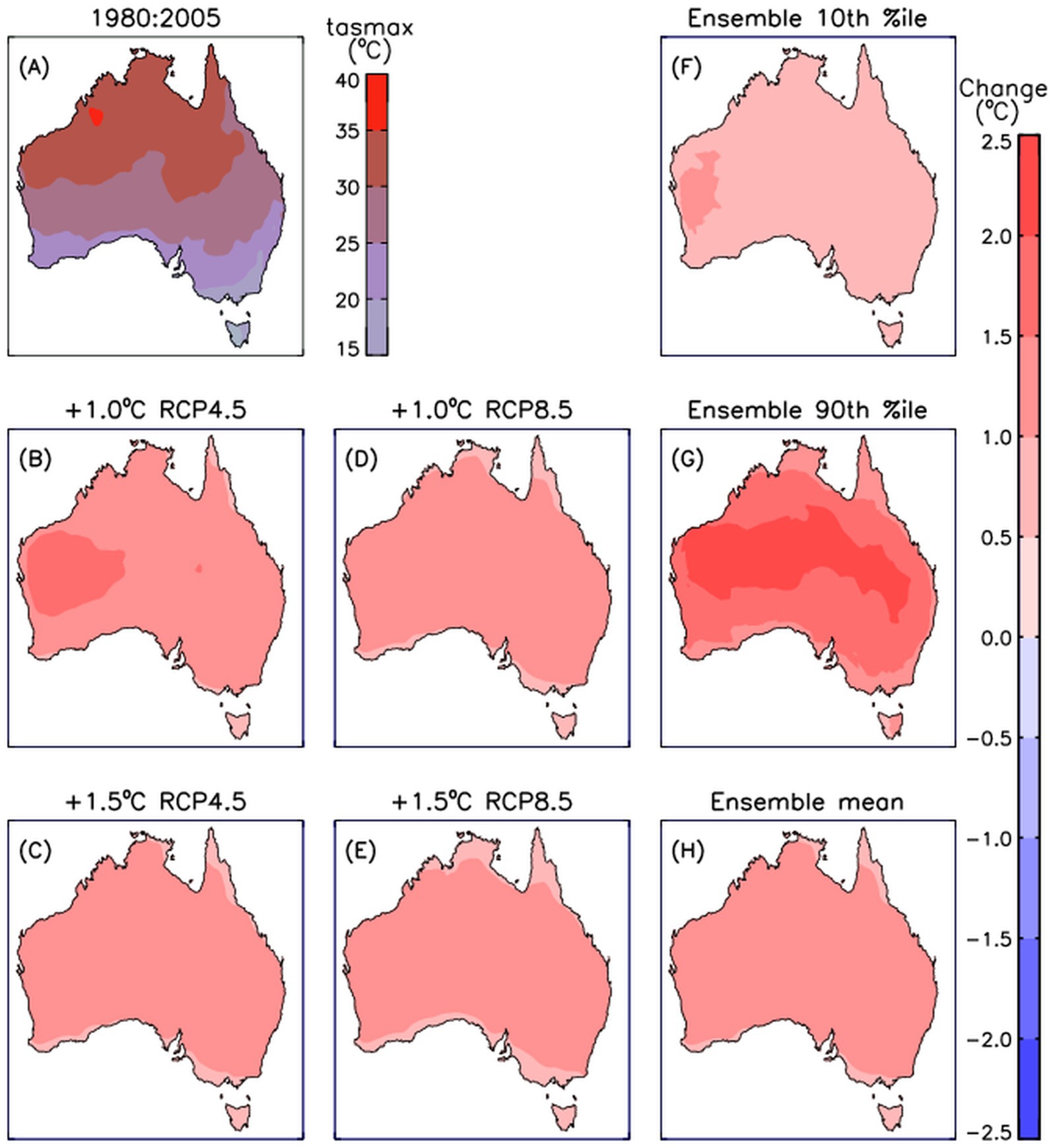
Figure 3. Mean daily maximum temperature at the surface shown for a historical period 1980:2005 (A) based on the 16-member model ensemble. The change per degree of global warming is also shown for four different climate periods corresponding to an additional 1°C (B) and 1.5°C (C) warming following a low emissions pathway (RCP4.5) and 1°C (D) and 1.5°C (E) warming following a high emissions pathway (RCP8.5). To provide an indication of the range within the model ensemble members used to calculate the change per degree of warming, the 10th (F) and 90th (G) percentiles of the modelled changes are shown together with the mean (H). Results are shown for changes only if statistically significant above 90% confidence level.
It is useful to confirm this strong consistency in projections calculated per degree of warming using these four different methods, given that there is some potential for variations in this. For example, the global mean surface temperature is largely associated with ocean regions, with ocean temperatures warming more slowly than land regions (IPCC, 2021). If the land-ocean temperature difference changes over time, then land regions potentially could have different changes per degree global warming for different time periods. However, the land-sea temperature difference scales approximately linearly with global warming for different emission pathways such as RCP4.5 and RCP8.5 (IPCC, 2021). The linearity in the relationship can be accounted for, such as demonstrated here by dividing the projected changes for 1.5°C global warming by 1.5 to convert to changes per degree global warming. Consequently, the results presented in Figures 3B–E are useful in showing similar magnitude changes per degree of global warming when calculated using these four different approaches representing different time periods and different emissions pathways.
Figure 3 also shows results based on combining the projected changes per degree of warming from those 4 different methods for use as an expanded ensemble. The mean change based on that expanded ensemble is shown (Figure 3H), together with the 10th percentiles (Figure 3F) and 90th percentiles (Figure 3G) of the model values from the ensemble. Those metrics are calculated individually for each grid cell location. A feature of these projections is somewhat larger increases for inland regions, particularly towards the west of the continent, as compared to near-coastal regions in general. As seen for the rainfall projections (Figure 1), the ensemble range as represented by the 10th and 90th percentiles (Figures 3F,G) is broader than the differences in results between the four methods used to calculate the per degree warming projected changes (i.e., differences between results shown in Figures 3B–E). However, the values are all positive in sign throughout Australia, including for both the 10th and 90th percentiles of the ensemble range, in contrast to the larger degree of variation seen for the rainfall range (Figures 1F,G) which had opposite signs of change between the 10th and 90th percentiles at all locations.
3.3 Fire weather analyses
Results are presented for daily values of the Forest Fire Danger Index (FFDI) in Figure 4. This uses the same methods as used for rainfall and temperature in Figures 1, 2, respectively. The average daily FFDI values are shown in Figure 4A, showing higher values for inland regions than for regions closer to the coast in general, consistent with previous studies such as Dowdy (2020). The four methods used for the projected changes, based on the two different emission pathways and two different magnitudes of global warming (i.e., Figures 4B–E), all show increases throughout Australia. This is broadly similar to previous studies that have also shown future increases in FFDI based on gridded model projections throughout Australia (Dowdy et al., 2019).
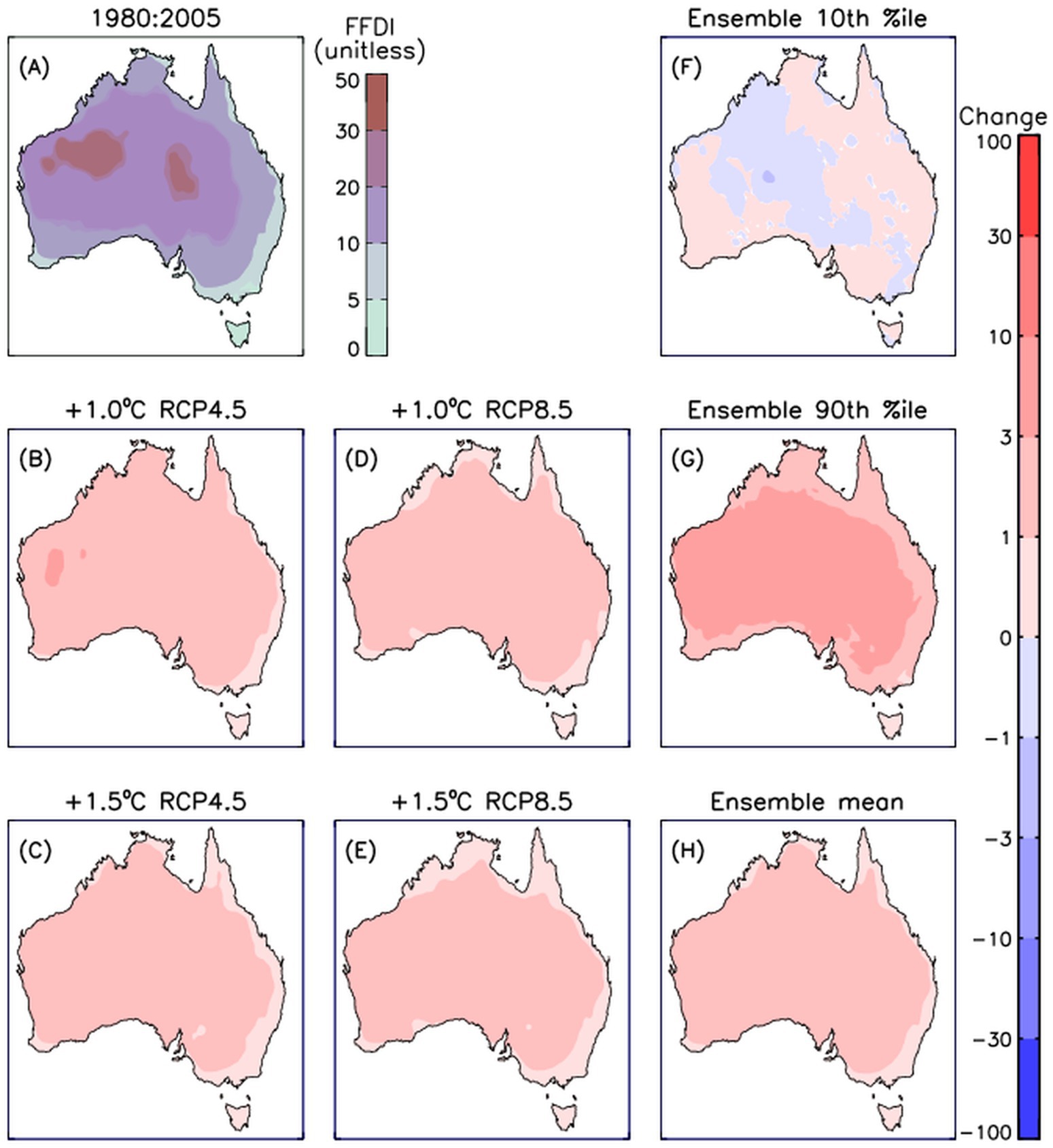
Figure 4. Mean daily Forest Fire Danger Index (FFDI) shown for a historical period 1980:2005 (A) based on the 16-member model ensemble. The change per degree of global warming is also shown for four different climate periods corresponding to an additional 1°C (B) and 1.5°C (C) warming following a low emissions pathway (RCP4.5) and 1°C (D) and 1.5°C (E) warming following a high emissions pathway (RCP8.5). To provide an indication of the range within the model ensemble members used to calculate the change per degree of warming, the 10th (F) and 90th (G) percentiles of the modelled changes are shown together with the mean (H). Results are shown for changes only if statistically significant above 90% confidence level.
Relatively little variation in results between these four methods is apparent (Figures 4B–E). It is useful to have confirmed this is the case, given potential for some variations as discussed above in relation to the temperature results.
Figure 4 also shows results based on combining the projected changes per degree of warming from those 4 different methods (as shown in Figures 4B–E) for use as an expanded ensemble. The mean change based on that expanded ensemble is shown (Figure 4H), together with the 10th percentiles (Figure 4F) and 90th percentiles (Figure 4G) of that ensemble. The mean values of the expanded ensemble show increases projected through all regions of Australia (Figure 4H). There are some locations where reductions are indicated based on the 10th percentile of the ensemble range (Figure 4F), including for regions in the northwest and nearby inland locations, noting that those locations also showed potential for increased rainfall (e.g., from Figure 1H). However, the magnitudes of those FFDI reductions for the 10th percentile range projections are relatively small, including as compared to the ensemble mean increases (Figure 4H) and the much larger magnitude increases for the 90th percentile of the model ensemble (Figure 4G).
3.4 Extremes analyses
Extremes are examined in this section based on the value that is exceeded on average once per year during the historical period 1980 to 2005 (referred to here as the 1-year return period). These historical threshold values are shown for precipitation (Figure 5A), daily maximum temperature (Figure 6A) and FFDI (Figure 7A). Projected changes are also shown in Figures 5–7, based on how the occurrence frequency of exceeding the 1-yr return period changes per degree of global warming. Similar to the figures in the previous sections, the projected changes are presented individually for the four different methods of calculating the changes per degree of global warming: i.e., two different emission pathways for each of the two different magnitudes of global warming. Expanded ensemble results are also shown similar to the approach used in previous sections, based on combining the ensemble results from those four different methods, including for the expanded ensemble average values, as well as the 10th and 90th percentiles of the expanded ensemble.
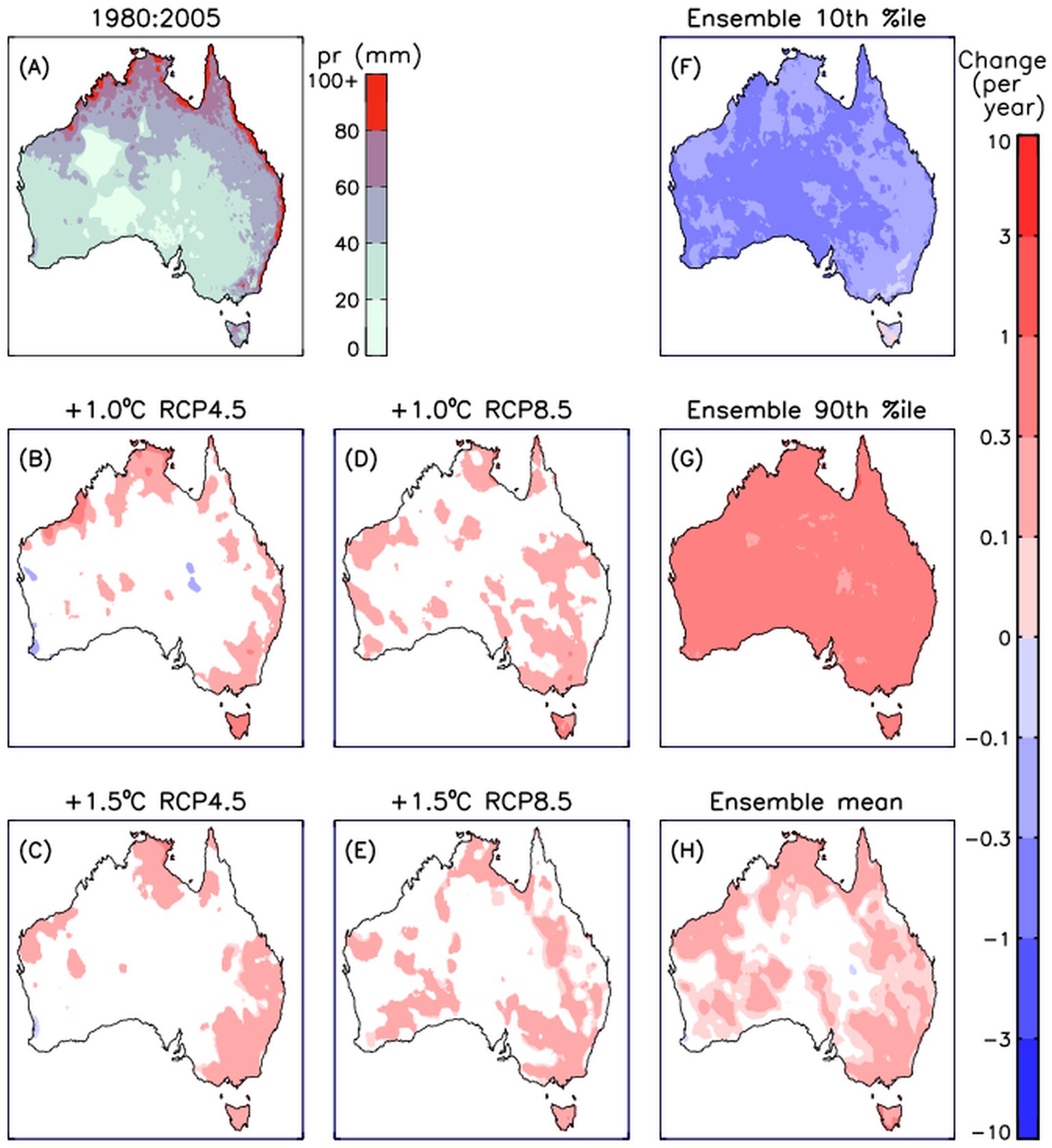
Figure 5. Extreme values of daily rainfall are shown for the value exceeded on average once per year at each location during the historical period 1980 to 2005 (A) based on the 16-member model ensemble. Changes in the annual average occurrence frequency of exceeding that threshold at each location are also shown. The changes are calculated per degree of global warming for four different climate periods corresponding to an additional 1°C (B) and 1.5°C (C) warming following a low emissions pathway (RCP4.5) and 1°C (D) and 1.5°C (E) warming following a high emissions pathway (RCP8.5). To provide an indication of the range within the model ensemble members used to calculate the change per degree of warming, the 10th (F) and 90th (G) percentiles of the modelled changes are shown together with the mean (H). Results are shown for changes only if statistically significant above 90% confidence level.
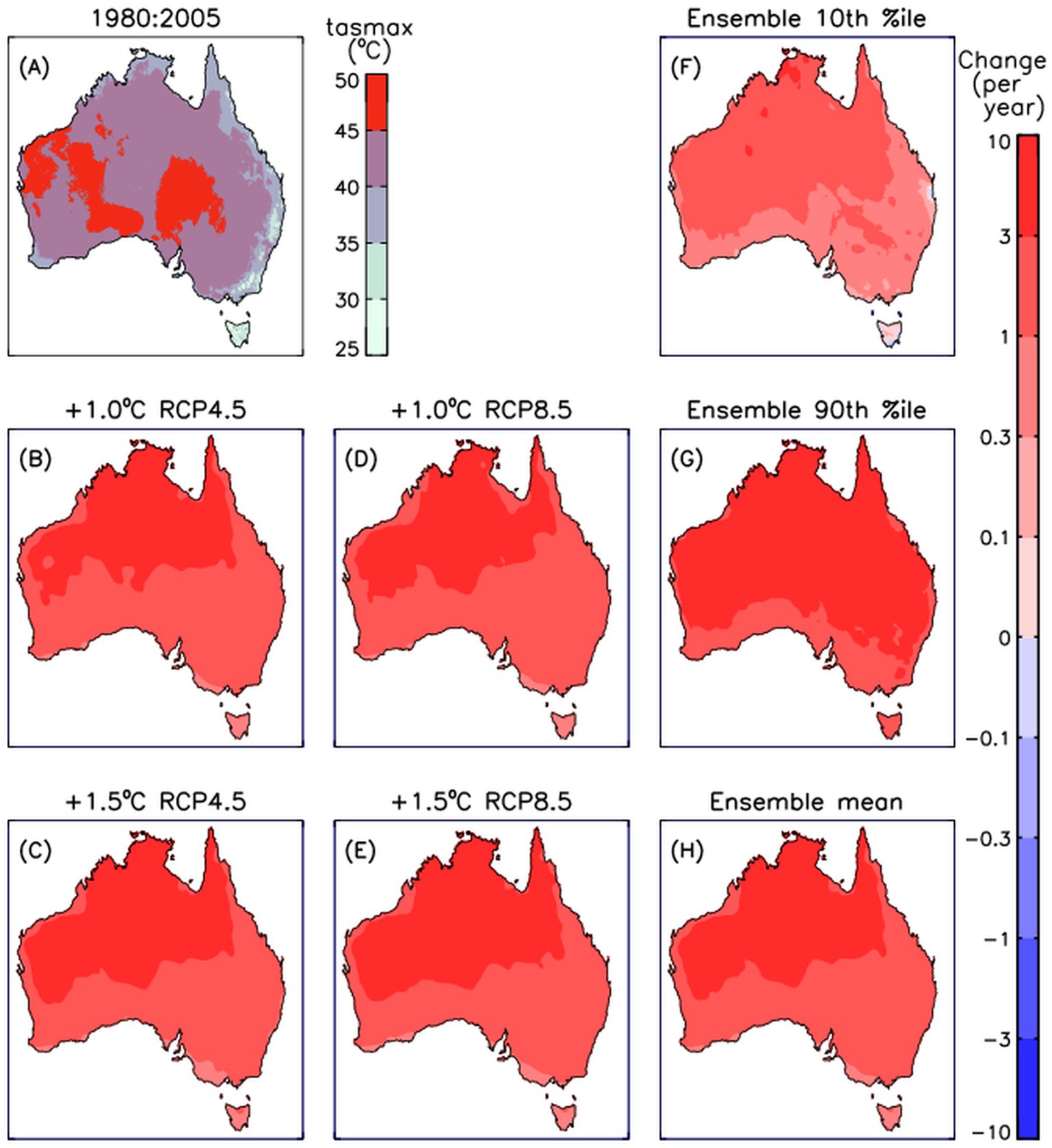
Figure 6. Extreme values of daily maximum temperature at the surface are shown for the value exceeded on average once per year at each location during the historical period 1980 to 2005 (A) based on the 16-member model ensemble. Changes in the annual average occurrence frequency of exceeding that threshold at each location are also shown. The changes are calculated per degree of global warming for four different climate periods corresponding to an additional 1°C (B) and 1.5°C (C) warming following a low emissions pathway (RCP4.5) and 1°C (D) and 1.5°C (E) warming following a high emissions pathway (RCP8.5). To provide an indication of the range within the model ensemble members used to calculate the change per degree of warming, the 10th (F) and 90th (G) percentiles of the modelled changes are shown together with the mean (H). Results are shown for changes only if statistically significant above 90% confidence level.
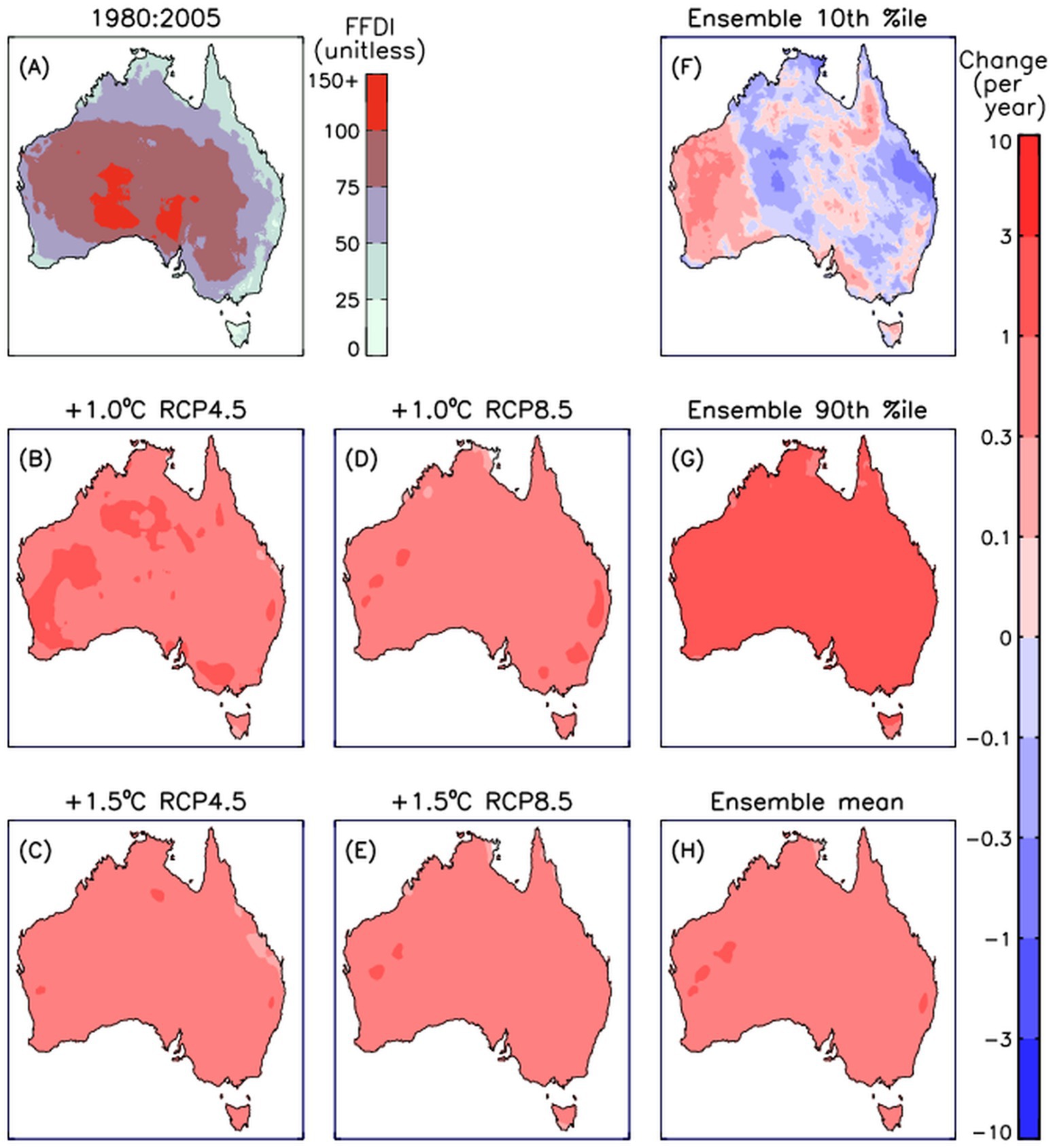
Figure 7. Extreme values of daily FFDI are shown for the value exceeded on average once per year at each location during the historical period 1980 to 2005 (A) based on the 16-member model ensemble. Changes in the annual average occurrence frequency of exceeding that threshold at each location are also shown. The changes are calculated per degree of global warming for four different climate periods corresponding to an additional 1°C (B) and 1.5°C (C) warming following a low emissions pathway (RCP4.5) and 1°C (D) and 1.5°C (E) warming following a high emissions pathway (RCP8.5). To provide an indication of the range within the model ensemble members used to calculate the change per degree of warming, the 10th (F) and 90th (G) percentiles of the modelled changes are shown together with the mean (H). Results are shown for changes only if statistically significant above 90% confidence level.
The projections for rainfall extremes clearly show increases in general throughout Australia (Figures 5B–E). This is very different to the projections for mean rainfall that showed decreases through most of Australia (e.g., from Figure 1H), noting some similarities to previous future projections that have also indicated extreme rain increases in Australia in general including in some locations where mean rainfall decreases (CSIRO and Bureau of Meteorology, 2015). The projected changes are positive in most locations, but with some small-scale variations. Those variations include some projected decreases shown interspersed closely with regions of projected increase, while noting that the locations of projected decreases are not very consistent between the different methods shown (Figures 5B–E), suggesting relatively low confidence in those regions due to potential influences of natural variability to some degree (e.g., from weather and chaotic processes (Lorenz, 1965)). The expanded ensemble results have less of that small-scale spatial variation, as well as with a larger area shown statistically significant results. This highlights the point that climate analysis of rainfall extremes could benefit from using sample sizes as large as possible, given large variability in rainfall (as was also discussed in Section 3.1).
The projected increases in occurrence frequency for these classes of extremes such as shown in Figure 5 is a commonly reported finding of many other climate change studies. This includes many examples of studies that provide physical process understanding behind what is causing the changes in extremes for Australia (CSIRO and Bureau of Meteorology, 2015; Perkins-Kirkpatrick et al., 2016, 2022; Dowdy, 2018; Guerreiro et al., 2018; Clarke and Evans, 2019; Dowdy et al., 2019; Dey et al., 2019; Gross et al., 2019; Harris and Lucas, 2019; Rauniyar and Power, 2020; NESP, 2020; van Oldenborgh et al., 2021). A recent example of this is Wasko et al. (2024), presenting a systematic review of studies examining the influence of climate change on extreme rainfall and flooding in Australia, finding a central estimate of 8% increase per degree global warming in the intensity of extreme daily rainfall in general throughout Australia.
The projected changes in extremes of daily maximum temperature (Figure 6) and FFDI (Figure 7) are positive in sign throughout Australia. This is the case for each of the four different approaches used to calculate the change per degree of global warming (i.e., two different emission pathways for each of the two different magnitudes of global warming) as well as for the expanded ensemble results. The 10th percentiles of the expanded ensemble are also positive in sign for daily maximum temperature (Figure 6F), whereas some locations are negative in sign for FFDI (Figure 7F) indicating a somewhat larger degree of uncertainty.
In addition to the methods described above for analysis of extremes, there are also many other useful ways for climate analysis to be presented and communicated, such as when considering the detection and attribution of changes. Examples include examining time series, such as annual values of a metric representing extremes, for analysis of the timing of emergence for human-caused climate change influences on extremes (e.g., King et al. (2015b)). Other methods can consider the differences between two time periods or changes per degree warming such as shown in Figure 5, including based on metrics such as the fraction of attributable risk (FAR: e.g., Allen (2003) and Perkins-Kirkpatrick et al. (2022)). FAR is equal to 1 – the inverse of the Probability Ratio (PR, also sometimes known as the Risk Ratio), where PR may be calculated as Pfact/Pcfact with Pfact the probability of an event occurring in a state with more global warming than an earlier reference state and Pcfact the probability of an event occurring in that reference state (Lewis and Karoly, 2013; Perkins-Kirkpatrick et al., 2022). For example, Pfact could represent a current climate period or a future projected climate period and Pcfact could represent a historical climate period.
As an example of time series analysis for extremes, Figure 8 presents annual values of FFDI averaged throughout Australia for December. This is shown individually for each of the 16 members of the model ensemble from 2006 to 2,100, for the low emissions path (RCP4.5) and the high emissions path (RCP8.5), as well as for the observations-based FFDI data that covers the period back to 1950 (Dowdy, 2020). The Black Summer of 2019/2020 had the most severe fire weather on record for Australia, including particularly high values (daily FFDI >40) on average for Australia in December 2019 as shown in Figure 8. The ESCI projections dataset is used here to examine how the occurrence of conditions similar to those observed in December 2019 is influence by climate change. The results show that values of around that magnitude rarely occur in the model-based FFDI data for the current climate period, with a much greater occurrence frequency for higher amounts of global warming that occur towards the later part of the century for these emissions pathways. This is particularly apparent for the high emissions path, but also seen to some degree for the low emissions path.
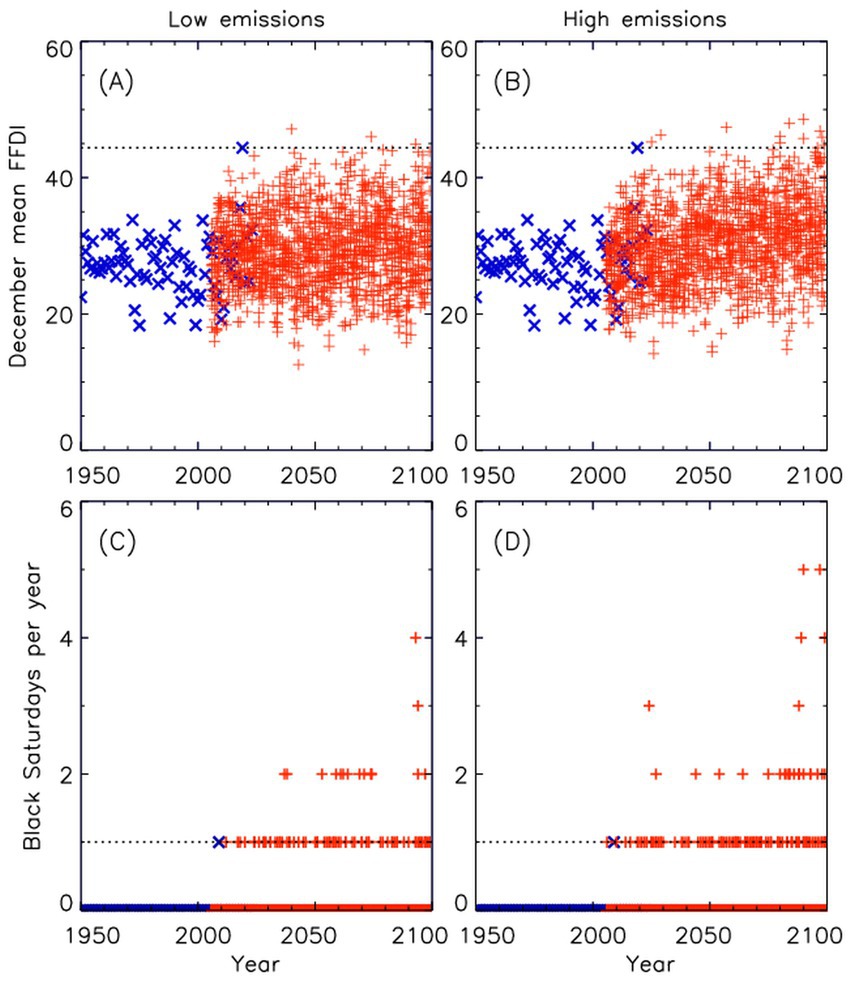
Figure 8. Changes in extremes of the daily Forest Fire Danger Index (FFDI). This is shown for the 16-member model ensemble from 2006 to 2099 (red “+” symbols) for a low emissions pathway (RCP4.5: left panels) and a high emissions pathway (RCP8.5: right panels), as well as for data based on observations from 1950 to 2023 (blue “x” symbols). Results are shown for the national mean value of FFDI for December in each year (upper panels) with the dotted line showing the observations-based value for December 2019 during the “Black Summer.” Results are also shown for how many days per year have FFDI ≥136 for Melbourne (based on the grid location for 144.9°E and 37.8°S) as occurred on “Black Saturday” 7 February 2009 for the observations-based data.
In contrast to average values for the whole of Australia as discussed above, Figure 8 also considers more localized extreme fire weather events. Analysis is presented based on Black Saturday 7 February 2009 where the observations-based FFDI value was 136 for Melbourne (corresponding to the grid location for 144.9°E and 37.8°S: Dowdy (2020) and Pepler et al. (2018)), noting that 173 people tragically lost their lives from the fires on that day (BS Royal Commission report to be referenced). The results show how often the model data have FFDI ≥136 calculated individually for each of the 16 members of the model ensemble from 2006 to 2,100. This is presented individually for the low and the high emissions paths available for the ESCI projections dataset. The model data show that values exceeding this threshold are relatively rare around the time of Black Saturday but become more frequent in time through this century. A faster rate of increase is apparent for the high emissions path, with a more moderate rate of increase for the low emissions pathway, further demonstrating the influence of greenhouse gas emissions on causing more dangerous weather conditions for fires.
This analysis also helps indicate the value of increased sample size for enhanced confidence in projections. For example, if considering the model data used here from when the period of projections starts until now (i.e., the 19-yr period from 2006 to 2024), rare events such as those fire weather extremes examined in Figure 6 do not occur in several of the individual model ensemble members. However, when using the 16-member ensemble as shown in each panel of Figure 8, the sample size is now effectively 16 times larger for that 19-yr period. These results also show that consideration of model data based on both emission pathways here can increase the sample size further (i.e., doubling the sample size) to help represent rare extremes such as Black Saturday and the Black Summer. This is similar in concept to the UNprecedented Simulated Extreme Ensemble (UNSEEN) approach, using larger sample sizes from models to consider potential for rare events that might have been unlikely to have occurred within a limited period of available observations (Thompson et al., 2019; Kelder et al., 2020).
A final example of analysis for extremes is presented here in Figure 9. This uses the same methods used for Figures 1, 3, 4, but presented for the occurrence frequency of days per year with temperature less than 0°C (based on daily minimum temperature: tasmin). The results show that this occurs very rarely through many midlatitude parts of Australia, including not at all in some locations particularly for northern Australia. The projected changes based on the 16-member ensemble average are broadly similar between the four different methods shown in Figures 9B–E: i.e., for the low or high emissions pathways based on the timing of 1°C or 1.5°C warming above the historical period 1980 to 2005.
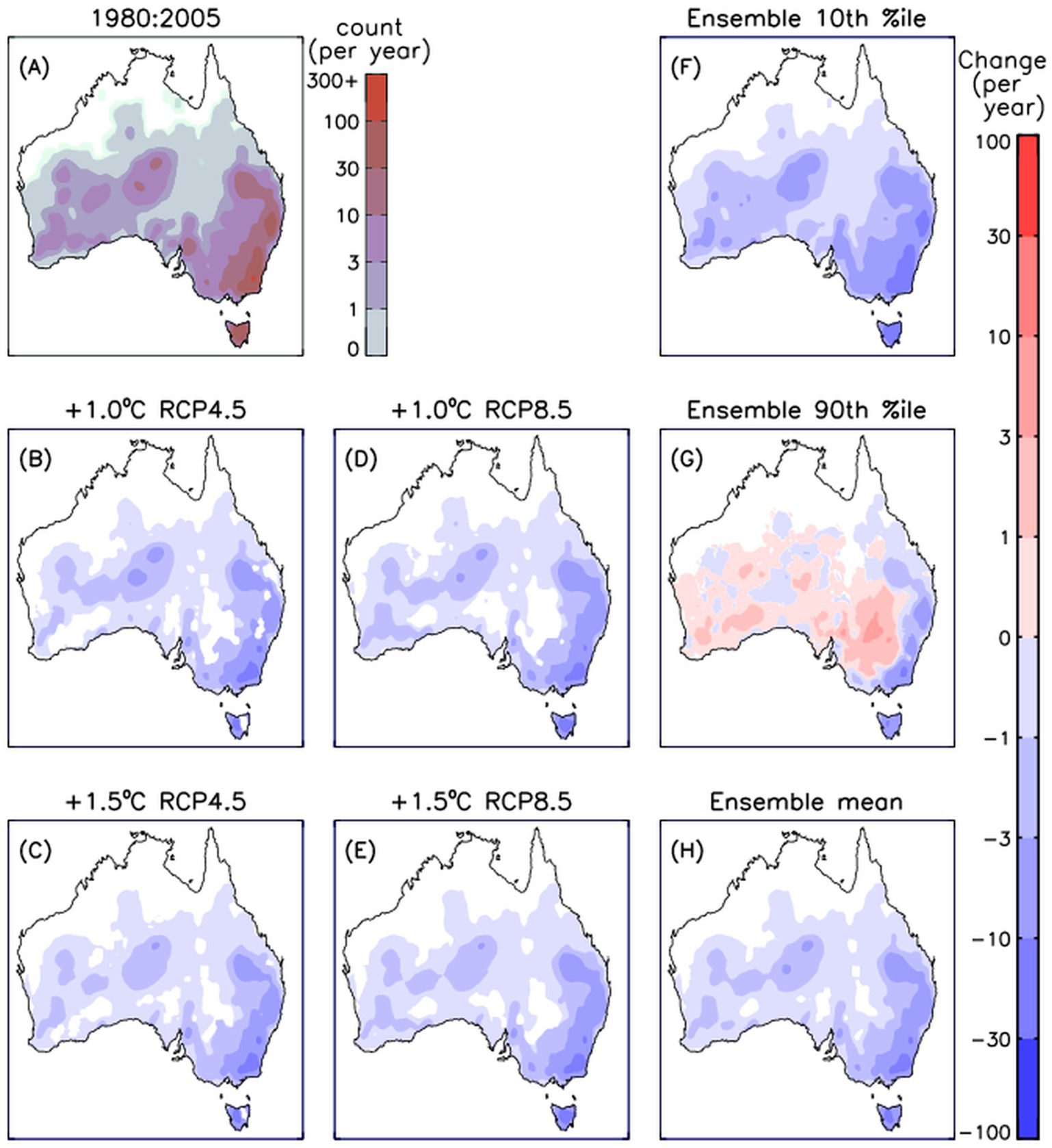
Figure 9. Average annual number of days with daily minimum temperature at the surface less than 0°C, shown for a historical period 1980:2005 (A) based on the 16-member model ensemble. The change per degree of global warming is also shown for four different climate periods corresponding to an additional 1°C (B) and 1.5°C (C) warming following a low emissions pathway (RCP4.5) and 1°C (D) and 1.5°C (E) warming following a high emissions pathway (RCP8.5). To provide an indication of the range within the model ensemble members used to calculate the change per degree of warming, the 10th (F) and 90th (G) percentiles of the modelled changes are shown together with the mean (H). Results are shown for changes only if statistically significant above 90% confidence level.
Combining the projected changes per degree of global warming from those four methods into an expanded ensemble of 64 members is used to show the ensemble mean and the ensemble range. The changes are all negative in sign for the mean, with larger magnitude negative changes for the 90th percentiles. There are some positive values for the 10th percentiles in central and western regions, with negative values in the east. The potential for global warming to cause an increased frequency of extremely cold days in parts of Australia could potentially relate to decreased cloudiness leading to colder nights in some cases. For example, a strengthening of the subtropical ridge over southern and central parts of Australia due to climate change (Dittus et al., 2014; CSIRO and Bureau of Meteorology, 2015; Pepler et al., 2018) could potentially lead to decreased cloudiness. However, further research might be beneficial to explore reasons for the differences between eastern Australia with negative values compared to central and western regions with positive values in Figure 9H, such as potential orographic influences on nocturnal cloudiness in the more mountainous region of the Great Dividing Range along eastern Australia.
4 Discussion
Climate analysis was presented here through Australia, with a focus on examining new methods and ideas to help provide insight on climate change. A key aim of this analysis was to present a broad range of different types of information, including based on some novel approaches such as expanded ensembles (comprising multiple emissions pathways and/or time periods), as well as examining extremes in several different ways using an ensemble including bias-corrected RCM data. The influence of human-caused climate change was examined for mean values as well as for extremes for bushfire weather conditions, temperatures and rainfall, noting that similar results could also be provided using variations on these methods (such as different time periods or different metrics for defining extremes). Climate analogues were also discussed, based on how conditions are changing over time in different regions through Australia, noting potential relevance for some climate adaptation applications such as based on biogeographical analyses.
The methods and results presented here are intended to be complementary to those of previous studies. This includes studies based on observations, modelling and physical process understanding that have showed human-caused climate changes in Australia, such as for increased temperatures and heat extremes (CSIRO and Bureau of Meteorology, 2015; Perkins-Kirkpatrick et al., 2016; Gross et al., 2019), more dangerous fire weather conditions (Dowdy, 2018; Clarke and Evans, 2019; Di Virgilio et al., 2022; Dowdy et al., 2019; Harris and Lucas, 2019; van Oldenborgh et al., 2021), as well as changes in rainfall including drying in some regions for mean rainfall and increased intensity for extreme rainfall (CSIRO and Bureau of Meteorology, 2015; Guerreiro et al., 2018; Dey et al., 2019; Rauniyar and Power, 2020) noting relevance of this for flooding (Power and Callaghan, 2016; Wasko et al., 2024).
Climate analysis such as presented here could potentially also add additional variables, time periods, emissions paths, metrics (e.g., frequency-based metrics for extremes), as well as regional guidance on other hazard-related phenomena of relevance to user groups, depending on what is feasible to provide based on user needs (e.g., climate information needs for effective decision making). Decisions often need to be made regardless of whether or not the required climate analysis is available, such as analysis for a specific location or extreme value, noting that this information is not always readily available. Climate analysis for a wide range of locations including for various measures of extremes could therefore be beneficial to make available where feasible, with guidance details and other documentation typically being important to provide as part of the climate information to help communicate uncertainties and intended applications.
Various regional features in the projections for mean values were documented for temperature, rainfall and fire weather. Substantial changes in occurrence frequency for extremes were also detailed, including for temperature, rainfall and fire weather metrics. This includes changes that are indicated to have already occurred due to human-caused climate change over recent decades, including for extremes, noting relevance to climate event attribution. These trends in mean and extreme values are projected to continue into the future, as shown based on various methods presented here. With the magnitude of change being dependent on the rate of anthropogenic greenhouse gas emissions. Expanded ensembles of projections calculated per degree of global warming, based on combining data for multiple emissions pathways and time periods, were found to be a useful way to increase sample size. This could be beneficial for some analysis in cases where there is a considerable amount of natural variability, such as is the case for rainfall in Australia.
It was noted that land-sea temperature differences scale approximately linearly with global warming for different emission pathways such as RCP4.5 and RCP8.5 (IPCC, 2021). It was shown here that this linearity can be accounted for, such as shown in Figures 1, 3–7, 9 by dividing the projected changes for 1.5°C global warming by 1.5 to convert to changes per degree global warming. Those results showed that the projected changes per degree of global warming have relatively small differences when calculated using two different emission pathways and different time periods, with smaller differences than variations between individual models in the ensemble. Using an expanded ensemble such as this approach, based on combining data from different emissions pathways and time periods, can therefore provide a useful increase in sample size (e.g., four times larger sample size in the examples presented here).
Projected changes were also mapped throughout Australia showing how some locations may become more like other locations in the future, such as presented in Figure 2 for annual rainfall thresholds. This was discussed in relation to the concept of ‘climate analogues’ as a means of communicating changes, such as described in King (2023). This sort of information could be used for various applications, including for different types of adaptation activities as follows. For example, one type of adaptation could consider how the climate at a given location becomes similar to other locations based on their historical climate (Type 1); another type of adaptation could consider how other locations become similar to a given location based on its historical climate (Type 2). Type 1 analogues could potentially be useful for climate change adaptation without changing location (e.g., considering changes in practices or infrastructure without moving locations), while Type 2 analogues could potentially be useful for climate change adaptation involving relocation.
Extremes of fire weather were examined using time series analysis, including in relation to broad-scale extremes of Black Summer in December 2019 for Australia, as well as more localized short-duration extremes of Black Saturday 7 February 2009 for Melbourne in southeast Australia. The model data showed extremes similar in magnitude to those events occurring in this current climate period, then becoming more frequent depending on the degree of global warming over this century. These findings suggest that extremes such as those events are not completely unexpected for the current climate, but that we should expect these types of events to occur more often as our climate continues to warm in coming decades. The projections show examples where the fire weather conditions are more extreme than those past events such as Black Summer and Black Saturday, while noting that such cases are relatively rare even later in this century (e.g., from Figure 8). This indicates that these types of extreme conditions are not likely to be the ‘new normal’ anytime soon (e.g., in coming decades for the first half of this century), but that climate change is ‘loading the dice’ toward an increased chance of their occurrence, with larger increases for higher amounts of greenhouse gas emissions.
This climate analysis aims to contribute towards an enhanced understanding of how climate change can influence weather conditions and extremes, with a focus here on using a broad range of methods applied for many localized regions and spatial maps throughout Australia. These methods and analyses are intended to be useful as part of broader knowledge and capabilities relevant to climate risk assessment and adaptation. Given the apparent scalability of local projections over Australia with per degree global warming, there is an opportunity to make better use of available data by combining regional ensembles. Such an approach may well work in other regions of the world where non-greenhouse gas forcing changes in 21st century scenarios are limited, i.e., outside of the South and East Asia regions. We would encourage further regional investigations to maximize the utility of existing data across scenarios for better sampling of extremes.
Data availability statement
Publicly available datasets were analyzed in this study. This data can be found here: the data generated and used for this study can be found in Zenodo (doi: 10.5281/zenodo.14299141), as well as available on request from the lead author, following CC-BY 4.0 license as detailed here: https://creativecommons.org/licenses/by/4.0/. The data used here is based on the ESCI dataset produced in previous projects, as described in Section 2 of this study, and accessed on the Australian National Computational Infrastructure (NCI) facilities.
Author contributions
AD: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. AK: Formal analysis, Investigation, Validation, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Funding for this research was provided through the University of Melbourne including with support from the Centre of Excellence for Climate Extremes (CLEX), the Melbourne Energy Institute (MEI) and the Zee Lab in collaboration with the Victorian Government.
Acknowledgments
The projections model data are all based on the CMIP5 set of simulations, with acknowledgment to the various modelling groups for the GCM as described in Section 2. The NARCliM/WRF data were produced through the NSW State Government and ACT Government in collaboration with UNSW with acknowledgement to the NARCliM v1.5 modelling team (Nishant et al., 2021). The CCAM data were produced within the CSIRO including by Marcus Thatcher and others. The BARPA data used here were produced within the Bureau of Meteorology BARPA team including Chun-Hsu Su, Christian Stassen, Harvey Ye, Andrew Dowdy, Peter Steinle and Greg Roff. An early step of applying bilinear interpolation for some model data to match the observations data grid prior to QME calibration was previously provided by Marcus Thatcher and Harvey Ye through the ESCI project.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Burrell, A. L., Evans, J. P., and De Kauwe, M. G. (2020). Anthropogenic climate change has driven over 5 million km2 of drylands towards desertification. Nat. Commun. 11, 1–11. doi: 10.1038/s41467-020-17710-7
Clarke, H., and Evans, J. P. (2019). Exploring the future change space for fire weather in Southeast Australia. Theor. Appl. Climatol. 136, 513–527. doi: 10.1007/s00704-018-2507-4
Clarke, J. M., Grose, M., Thatcher, M., Hernaman, V., Heady, C., Round, V., et al. (2019). Victorian climate projections 2019 technical report. Melbourne: Victorian State Government.
Corney, S. P., Katzfey, J., McGregor, J. L., Grose, M. R., Bennett, J., White, C. J., et al. (2010). Climate Futures for Tasmania: climate modelling technical report. ACE CRC, Hobart, Tasmania.
CSIRO and Bureau of Meteorology (2015). Climate change in Australia information for Australia’s natural resource management regions: Technical report. Australia: CSIRO and Bureau of Meteorology.
Dey, R., Lewis, S. C., Arblaster, J. M., and Abram, N. J. (2019). A review of past and projected changes in Australia’s rainfall. Wiley Interdiscip. Rev. Clim. Chang. 10:e577. doi: 10.1002/wcc.577
Di Virgilio, G., Evans, J., Ji, F., Tam, E., Kala, J., Andrys, J., et al. (2024). Design, evaluation and future projections of the NARCliM2. 0 CORDEX-CMIP6 Australasia regional climate ensemble. Geosci. Model Dev. Discuss. [Preprint]. 1–48. doi: 10.5194/gmd-2024-87
Di Virgilio, G., Ji, F., Tam, E., Nishant, N., Evans, J., Thomas, C., et al. (2022). Selecting CMIP6 GCMs for CORDEX dynamical downscaling: model performance, Independence, and climate change signals. Earth’s Future 10:625. doi: 10.1029/2021EF002625
Dittus, A. J., Karoly, D. J., Lewis, S. C., and Alexander, L. V. (2014). An investigation of some unexpected frost day increases in southern Australia. Austr. Meteorol. Oceanogr. J. 64, 261–271. doi: 10.22499/2.6404.002
Dowdy, A. J. (2018). Climatological variability of fire weather in Australia. J. Appl. Meteorol. Climatol. 57, 221–234. doi: 10.1175/JAMC-D-17-0167.1
Dowdy, A. J. (2020). Seamless climate change projections and seasonal predictions for bushfires in Australia. J. Southern Hemisphere Earth Syst. Sci. 70, 120–138. doi: 10.1071/ES20001
Dowdy, A. J. (2023). A bias correction method designed for weather and climate extremes Bureau Research Report BRR087. Docklands: Bureau of Meteorology.
Dowdy, A. J., Brown, A., Pepler, P., Thatcher, M., Rafter, T., Evans, J., et al. (2021). Extreme temperature, wind and bushfire weather projections using a standardised method Bureau Research Report BRR055. Docklands: Bureau of Meteorology.
Dowdy, A. J., Ye, H., Pepler, A., Thatcher, M., Osbrough, S. L., Evans, J. P., et al. (2019). Future changes in extreme weather and pyroconvection risk factors for Australian wildfires. Sci. Rep. 9, 10073–10011. doi: 10.1038/s41598-019-46362-x
Droegemeier, K., and Wilhelmson, R. (1987). Numerical simulation of thunderstorm outflow dynamics. Part I: outflow sensitivity experiments and turbulence dynamics. J. Atmos. Sci. 44, 1180–1210. doi: 10.1175/1520-0469(1987)044<1180:NSOTOD>2.0.CO;2
Evans, J. P., Ji, F., Lee, C., Smith, P., Argüeso, D., and Fita, L. (2014). Design of a regional climate modelling projection ensemble experiment–NARCliM. Geosci. Model Dev. 7, 621–629. doi: 10.5194/gmd-7-621-2014
Fita, L., Evans, J. P., Argüeso, D., King, A., and Liu, Y. (2016). Evaluation of the regional climate response in Australia to large-scale climate modes in the historical NARCliM simulations. Clim. Dyn. 49, 2815–2829. doi: 10.1007/s00382-016-3484-x
Grose, M. R., Narsey, S., Delage, F. P., Dowdy, A. J., Bador, M., Boschat, G., et al. (2020). Insights from CMIP6 for Australia’s future climate. Earth’s. Future 8:1469. doi: 10.1029/2019EF001469
Gross, M. H., Donat, M. G., and Alexander, L. V. (2019). Changes in daily temperature extremes relative to the mean in CMIP5 models and observations. Int. J. Climatol. 39, 5273–5291. doi: 10.1002/joc.6138
Guerreiro, S. B., Fowler, H. J., Barbero, R., Westra, S., Lenderink, G., Blenkinsop, S., et al. (2018). Detection of continental-scale intensification of hourly rainfall extremes. Nat. Clim. Chang. 8, 803–807. doi: 10.1038/s41558-018-0245-3
Gutowski, W. J., Ullrich, P. A., Hall, A., Leung, L. R., O’Brien, T. A., Patricola, C. M., et al. (2020). The ongoing need for high-resolution regional climate models: process understanding and stakeholder information. Bull. Am. Meteorol. Soc. 101, E664–E683. doi: 10.1175/BAMS-D-19-0113.1
Harris, S., and Lucas, C. (2019). Understanding the variability of Australian fire weather between 1973 and 2017. PLoS One 14:e0222328. doi: 10.1371/journal.pone.0222328
Hoogewind, K., Baldwin, M., and Trapp, R. (2017). The impact of climate change on hazardous convective weather in the United States: insight from high-resolution dynamical downscaling. J. Clim. 30, 10081–10100. doi: 10.1175/JCLI-D-16-0885.1
Howard, E., Su, C. H., Stassen, C., Naha, R., Ye, H., Pepler, A., et al. (2023). Performance and process-based evaluation of the BARPA-R Australasian regional climate model version 1. Geosci. Model Dev. Discuss. 17, 1–34. doi: 10.5194/gmd-17-731-2024
Huang, D., Yan, P., Zhu, J., Zhang, Y., Kuang, X., and Cheng, J. (1987). Uncertainty of global summer precipitation in the CMIP5 models: a comparison between high-resolution and low-resolution models. Theor. Appl. Climatol. 132, 55–69. doi: 10.1007/s00704-017-2078-9
IPCC (2021). “Summary for policymakers” in Climate change 2021: The physical science basis. Contribution of working group I to the sixth assessment report of the intergovernmental panel on climate change. eds. A. Zhai, S. L. Pirani, C. Connors, S. Péan, and N. Berger.
Iturbide, M., Fernández, J., Gutiérrez, J. M., Bedia, J., Cimadevilla, E., Díez-Sierra, J., et al. (2021). Repository supporting the implementation of FAIR principles in the IPCC-WG1 atlas. Zenodo. 9:629. doi: 10.5281/zenodo.3691645
Jones, D. A., Wang, W., and Fawcett, R. (2009). High-quality spatial climate data-sets for Australia. Austr. Meteorol. Oceanogr. J. 58, 233–248. doi: 10.22499/2.5804.003
Keetch, J. J., and Byram, G. M. (1968). A drought index for forest fire control. USDA Forest Service, Research Paper SE-38.
Kelder, T., Müller, M., Slater, L. J., Marjoribanks, T. I., Wilby, R. L., Prudhomme, C., et al. (2020). Using UNSEEN trends to detect decadal changes in 100-year precipitation extremes. Climate Atmosph. Sci. 3:47. doi: 10.1038/s41612-020-00149-4
King, A. D. (2023). Identifying historical climate changes in Australia through spatial analogs. Environ. Res. Lett. 18:044018. doi: 10.1088/1748-9326/acc2d4
King, A. D., Alexander, L. V., and Donat, M. G. (2013). The efficacy of using gridded data to examine extreme rainfall characteristics: a case study for Australia. Int. J. Climatol. 33, 2376–2387. doi: 10.1002/joc.3588
King, A. D., Borowiak, A. R., Brown, J. R., Frame, D. J., Harrington, L. J., Min, S. K., et al. (2021). Transient and quasi-equilibrium climate states at 1.5 C and 2 C global warming. Earth’s. Future 9:274.
King, A. D., Donat, M. G., Alexander, L. V., and Karoly, D. J. (2015a). The ENSO-Australian rainfall teleconnection in reanalysis and CMIP5. Clim. Dyn. 44, 2623–2635. doi: 10.1007/s00382-014-2159-8
King, A. D., Donat, M. G., Fischer, E. M., Hawkins, E., Alexander, L. V., Karoly, D. J., et al. (2015b). The timing of anthropogenic emergence in simulated climate extremes. Environ. Res. Lett. 10:094015. doi: 10.1088/1748-9326/10/9/094015
King, A., Karoly, D., and Henley, B. (2017). Australian climate extremes at 1.5 °C and 2 °C of global warming. Nat. Clim Change 7, 412–416. doi: 10.1038/nclimate3296
Kirono, D. G., Round, V., Heady, C., Chiew, F. H., and Osbrough, S. (2020). Drought projections for Australia: updated results and analysis of model simulations. Weather Climate Extremes 30:100280. doi: 10.1016/j.wace.2020.100280
Koutsoyiannis, D. (2004). Statistics of extremes and estimation of extreme rainfall: I theoretical investigation. Hydrol. Sci. J. 49:430. doi: 10.1623/hysj.49.4.575.54430
Lewis, S. C., and Karoly, D. J. (2013). Anthropogenic contributions to Australia’s record summer temperatures of 2013. Geophys. Res. Lett. 40, 3705–3709. doi: 10.1002/grl.50673
Lorenz, E. N. (1965). A study of the predictability of a 28-variable atmospheric model. Tellus A 17, 321–333. doi: 10.1111/j.2153-3490.1965.tb01424.x
McArthur, A. G. (1967). Fire behaviour in eucalypt forests: Forestry and timber bureau, Report no 107. Canberra.
McGregor, J. L. (2005). C-CAM: geometric aspects and dynamical formulation. Aspendale, VIC: CSIRO Marine and Atmospheric Research Tech.
McKay, R., Boschat, G., Rudeva, I., Pepler, A., Purich, A., Dowdy, A., et al. (2023). Can southern Australian rainfall decline be explained? A review of possible drivers. Wiley Interdiscip. Rev. Clim. Chang. 14:e820. doi: 10.1002/wcc.820
Meinig, D. W. (1961). Goyder’s line of rainfall: the role of a geographic concept in south Australian land policy and agricultural settlement. Agric. Hist. 35, 207–214.
NESP (2020). CMSI science report from ESCC hub of NESP. Earth systems and climate change hub of the National Environmental Science Program (NESP). ISBN of the publication.
Nicholls, N., Drosdowsky, W., and Lavery, B. (1997). Australian rainfall variability and change. Weather 52, 66–72. doi: 10.1002/j.1477-8696.1997.tb06274.x
Nidumolu, U., Hayman, P., Howden, S., and Alexander, B. (2012). Re-evaluating the margin of the south Australian grain belt in a changing climate. Clim. Res. 51, 249–260. doi: 10.3354/CR01075
Nishant, N., Evans, J. P., Di Virgilio, G., Downes, S. M., Ji, F., Cheung, K. K., et al. (2021). Introducing NARCliM1. 5: evaluating the performance of regional climate projections for Southeast Australia for 1950–2100. Earth’s. Future 9:e2020EF001833. doi: 10.1029/2020EF001833
Pepler, A., Ashcroft, L., and Trewin, B. (2018). The relationship between the subtropical ridge and Australian temperatures. J. Southern Hemisph. Earth Syst. Sci. 68, 201–214. doi: 10.1071/ES18011
Perkins-Kirkpatrick, S. E., Stone, D. A., Mitchell, D. M., Rosier, S., King, A. D., Lo, Y. T. E., et al. (2022). On the attribution of the impacts of extreme weather events to anthropogenic climate change. Environ. Res. Lett. 17:024009. doi: 10.1088/1748-9326/ac44c8
Perkins-Kirkpatrick, S. E., White, C. J., Alexander, L. V., Argüeso, D., Boschat, G., Cowan, T., et al. (2016). Natural hazards in Australia: heatwaves. Clim. Chang. 139, 101–114. doi: 10.1007/s10584-016-1650-0
Peter, J., Vogel, E., Sharples, W., Bende-Michl, U., Wilson, L., Hope, P., et al. (2024). Continental-scale bias-corrected climate and hydrological projections for Australia. Geosci. Model Dev. 17, 2755–2781. doi: 10.5194/gmd-17-2755-2024
Power, S. B., and Callaghan, J. (2016). Variability in severe coastal flooding, associated storms, and death tolls in southeastern Australia since the mid-nineteenth century. J. Appl. Meteorol. Climatol. 55, 1139–1149. doi: 10.1175/JAMC-D-15-0146.1
Rauniyar, S. P., and Power, S. B. (2020). The impact of anthropogenic forcing and natural processes on past, present, and future rainfall over Victoria, Australia. J. Climate 33, 8087–8106. doi: 10.1175/JCLI-D-19-0759.1
Schwalm, C. R., Glendon, S., and Duffy, P. B. (2020). RCP8. 5 tracks cumulative CO2 emissions. Proc. Natl. Acad. Sci. 117, 19656–19657. doi: 10.1073/pnas.2007117117
Srikanthan, S., Bende-Michl, U., and Wilson, L. (2022). National Hydrological Projections – design and methodology. Bureau of Meteorology, Melbourne, Australia
Stassen, C., Su, C. H., Dowdy, A., Franklin, C., Howard, E., and Steinle, P. (2023). Development and assessment of regional atmospheric nudging in ACCESS. Melbourne: Bureau of Meteorology.
Su, C. H., Ye, H., Dowdy, A. J., Pepler, A., Stassen, C., and Brown, A. (2021). Towards ACCESS-based regional climate projections for Australia. Docklands: Bureau of Meteorology.
Taylor, K. E., Stouffer, R. J., and Meehl, G. A. (2012). An overview of CMIP5 and the experiment design. Bull. Amer. Met. Soc. 93, 485–498. doi: 10.1175/BAMS-D-11-00094.1
Thatcher, M. (2021). ESCI technical report on downscaling and evaluating data sets CSIRO and BoM. Melbourne, Australia: CSIRO.
Thompson, V., Dunstone, N. J., Scaife, A. A., Smith, D. M., Hardiman, S. C., Ren, H. L., et al. (2019). Risk and dynamics of unprecedented hot months in south East China. Clim. Dyn. 52, 2585–2596. doi: 10.1007/s00382-018-4281-5
Tozer, C., Verdon-Kidd, D., and Kiem, A. (2014). Temporal and spatial variability of the cropping limit in South Australia. Clim. Res. 60, 25–34. doi: 10.3354/CR01218
Ukkola, A. M., De Kauwe, M. G., Roderick, M. L., Abramowitz, G., and Pitman, A. J. (2020). Robust future changes in meteorological drought in CMIP6 projections despite uncertainty in precipitation. Geophys. Res. Lett. 47:p.e2020GL087820. doi: 10.1029/2020GL087820
van Oldenborgh, G. J., Krikken, F., Lewis, S., Leach, N. J., Lehner, F., Saunders, K. R., et al. (2021). Attribution of the Australian bushfire risk to anthropogenic climate change. Nat. Hazards Earth Syst. Sci. 21, 941–960. doi: 10.5194/nhess-21-941-2021
Vogel, E., Johnson, F., Marshall, L., Bende-Michl, U., Wilson, L., Peter, J. R., et al. (2023). An evaluation framework for downscaling and bias correction in climate change impact studies. J. Hydrol. 622:129693. doi: 10.1016/j.jhydrol.2023.129693
Wasko, C., Westra, S., Nathan, R., Pepler, A., Raupach, T. H., Dowdy, A., et al. (2024). A systematic review of climate change science relevant to Australian design flood estimation. Hydrol. Earth Syst. Sci. 28, 1251–1285. doi: 10.5194/hess-28-1251-2024
Keywords: climate change, extremes, hazards, fire, adaptation, bias correction, downscaling
Citation: Dowdy A and King A (2025) Novel climate analysis methods applied to the Australian ESCI projections data. Front. Clim. 6:1492228. doi: 10.3389/fclim.2024.1492228
Edited by:
Mark Williamson, University of Exeter, United KingdomReviewed by:
Asmerom F. Beraki, University of Pretoria, South AfricaAngshuman Modak, Indian Institute of Technology Bombay, India
Copyright © 2025 Dowdy and King. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrew Dowdy, YW5kcmV3LmRvd2R5QHVuaW1lbGIuZWR1LmF1
 Andrew Dowdy
Andrew Dowdy Andrew King
Andrew King